Current Electricity - Result Question 37
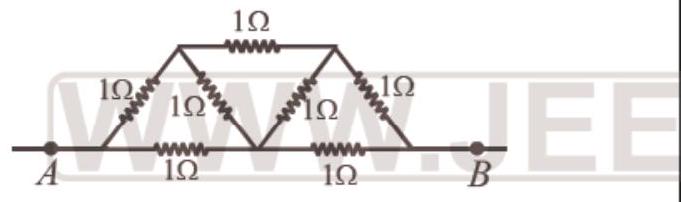
39. In the network shown in the Fig, each resistance is $1 \Omega$. The effective resistance between $A$ and $B$ is
(a) $\frac{4}{3} \Omega$
(b) $\frac{3}{2} \Omega$
(c) $7 \Omega$
(d) $\frac{8}{7} \Omega$
Show Answer
Answer:
Correct Answer: 39. (d)
Solution:
- (d) At $A$ current is distributed and at $B$ currents are collected. Between $A$ and $B$, the distribution is symmetrical. It has been shown in the figure. It appears that current in $A O$ and $O B$ remains same. At $O$, current $i_4$ returns back without any change. If we detach $O$ from $A B$ there will not be any change in distribution.
Now, $C O & O D$ will be in series hence its total resistance $=2 \Omega$
It is in parallel with $C D$, so, equivalent resistance
$=\frac{2 \times 1}{2+1}=\frac{2}{3} \Omega$
This equivalent resistance is in series with $A C$ $& D B$, so, total resistance
$=\frac{2}{3}+1+1=\frac{8}{3} \Omega$
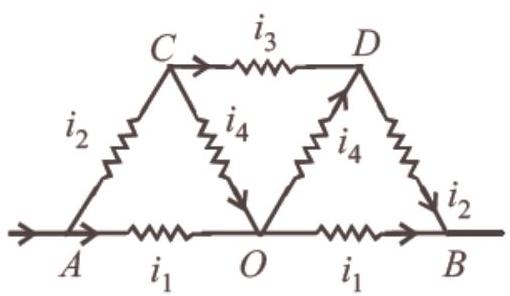
Now $\frac{8}{3} \Omega$ is parallel to $A B$, that is, $2 \Omega$, so total resistance
$=\frac{8 / 3 \times 2}{8 / 3+2}=\frac{16 / 3}{14 / 3}=\frac{16}{14}=\frac{8}{7} \Omega$
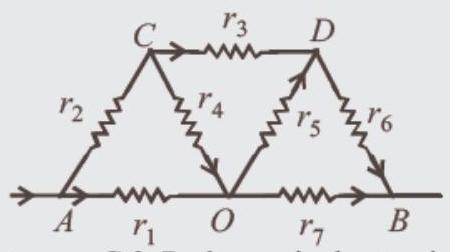
Between $C & D$, the equivalent resistance is given by
$ 1 / r=\frac{1}{r_3}+\frac{1}{(r_4+r_5)}=1+\frac{1}{2}=\frac{3}{2} $
Equivalent resistance along
$ A C D B=1+\frac{2}{3}+1=\frac{8}{3} $
$\therefore$ Effective resistance between $A$ and $B$ is
$ .\frac{1}{R}=\frac{3}{8}+\frac{1}{2}=\frac{7}{8} \text{ or } R=\frac{8}{7} \Omega] $
