Thermodynamics and Thermochemistry 1 Question 42
45. For an ideal gas, consider only
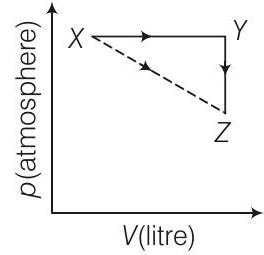
[Take
(a)
(b)
(c)
(d)
Show Answer
Solution:
- (a) Entropy is a state function, change in entropy in a cyclic process is zero.
Analysis of options (b) and (c)
Work is a non-stable function, it does depends on the path followed. 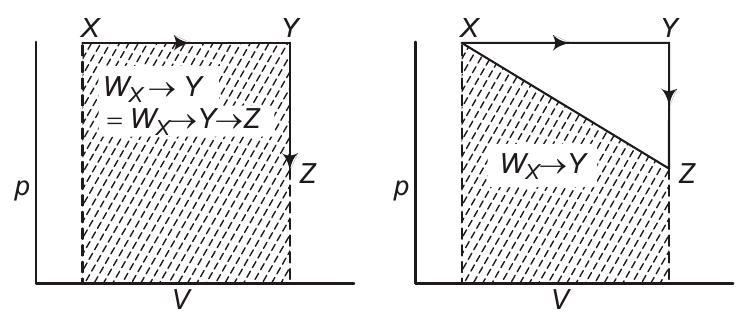
As shown above






