Equilibrium - Result Question 10
####11. The dissociation equilibrium of a gas $A B_2$ can be represented as :
[2008]
$2 A B_2(g) \rightarrow 2 A B(g)+B_2(g)$
The degree of dissociation is ’ $x$ ’ and is small compared to 1 . The expression relating the degree of dissociation $(x)$ with equilibrium constant $K_p$ and total pressure $P$ is :
(a) $(2 K_p / P)$
(b) $(2 K_p / P)^{1 / 3}$
(c) $(2 K_p / P)^{1 / 2}$
(d) $(K_p / P)$
Show Answer
Solution:
- (b) For the reaction
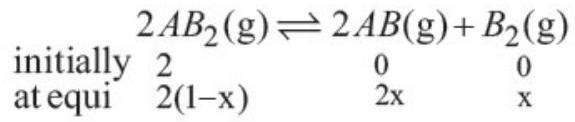
The partial pressure at equilibrium are calculated on the basis of total number of moles at equilibrium.
Total number of moles
$=2(1-x)+2 x+x=(2+x)$
$\therefore \quad P _{A B_2}=\frac{2(1-x)}{(2+x)} \times P$ where $P$ is the total pressure.
$P _{A B}=\frac{2 x}{(2+x)} \times P, P _{B_2}=\frac{x}{(2+x)} \times P$
Since $x$ is very small so can be neglected in denominator
Thus, we get
$ P _{A B_2}=(1-x) \times P \quad P _{A B}=x \times P $ $P _{B_2}=\frac{x}{2} \times P$
Now, $K_P=\frac{(P _{A B})^{2}(P _{B_2})}{(P _{A B_2})^{2}}=\frac{(x)^{2} \times P^{2} \cdot P \times \frac{x}{2}}{(1-x)^{2} \times P^{2}}$
$=\frac{x^{3} \cdot P^{3}}{2 \times 1 \times P^{2}}$
$[\because 1-x \simeq 1]$
$=\frac{x^{3} . P}{2}$ or $x^{3}=\frac{2 . K_p}{P}$ or $x=(\frac{2 K_p}{P})^{\frac{1}{3}}$






