Chapter 8

GRAVITATION

MCQ I

8.1 The earth is an approximate sphere. If the interior contained matter which is not of the same density everywhere, then on the surface of the earth, the acceleration due to gravity

(a) will be directed towards the centre but not the same everywhere.

(b) will have the same value everywhere but not directed towards the centre.

(c) will be same everywhere in magnitude directed towards the centre.

(d) cannot be zero at any point.

8.2 As observed from earth, the sun appears to move in an approximate circular orbit. For the motion of another planet like mercury as observed from earth, this would

(a) be similarly true.

(b) not be true because the force between earth and mercury is not inverse square law.

(c) not be true because the major gravitational force on mercury is due to sun.

(d) not be true because mercury is influenced by forces other than gravitational forces.

8.3 Different points in earth are at slightly different distances from the sun and hence experience different forces due to gravitation. For a rigid body, we know that if various forces act at various points in it, the resultant motion is as if a net force acts on the c.m. (centre of mass) causing translation and a net torque at the c.m. causing rotation around an axis through the c.m. For the earth-sun system (approximating the earth as a uniform density sphere)

(a) the torque is zero.

(b) the torque causes the earth to spin.

(c) the rigid body result is not applicable since the earth is not even approximately a rigid body.

(d) the torque causes the earth to move around the sun.

8.4 Satellites orbiting the earth have finite life and sometimes debris of satellites fall to the earth. This is because,

(a) the solar cells and batteries in satellites run out.

(b) the laws of gravitation predict a trajectory spiralling inwards.

(c) of viscous forces causing the speed of satellite and hence height to gradually decrease.

(d) of collisions with other satellites.

8.5 Both earth and moon are subject to the gravitational force of the sun. As observed from the sun, the orbit of the moon

(a) will be elliptical.

(b) will not be strictly elliptical because the total gravitational force on it is not central.

(c) is not elliptical but will necessarily be a closed curve.

(d) deviates considerably from being elliptical due to influence of planets other than earth.

8.6 In our solar system, the inter-planetary region has chunks of matter (much smaller in size compared to planets) called asteroids. They

(a) will not move around the sun since they have very small masses compared to sun.

(b) will move in an irregular way because of their small masses and will drift away into outer space.

(c) will move around the sun in closed orbits but not obey Kepler’s laws.

(d) will move in orbits like planets and obey Kepler’s laws.

8.7 Choose the wrong option.

(a) Inertial mass is a measure of difficulty of accelerating a body by an external force whereas the gravitational mass is relevant in determining the gravitational force on it by an external mass.

(b) That the gravitational mass and inertial mass are equal is an experimental result.

(c) That the acceleration due to gravity on earth is the same for all bodies is due to the equality of gravitational mass and inertial mass.

(d) Gravitational mass of a particle like proton can depend on the presence of neighouring heavy objects but the inertial mass cannot.

8.8 Particles of masses $2 M, m$ and $M$ are respectively at points A, B and $\mathrm{C}$ with $\mathrm{AB}=1 / 2(\mathrm{BC})$. $m$ is much-much smaller than $M$ and at time $t=0$, they are all at rest (Fig. 8.1).

At subsequent times before any collision takes place:

Fig. 8.1

(a) $m$ will remain at rest.

(b) $m$ will move towards $M$.

(c) $m$ will move towards $2 M$.

(d) $m$ will have oscillatory motion.

MCQ II

8.9 Which of the following options are correct?

(a) Acceleration due to gravity decreases with increasing altitude.

(b) Acceleration due to gravity increases with increasing depth (assume the earth to be a sphere of uniform density).

(c) Acceleration due to gravity increases with increasing latitude.

(d) Acceleration due to gravity is independent of the mass of the earth.

8.10 If the law of gravitation, instead of being inverse-square law, becomes an inverse-cube law-

(a) planets will not have elliptic orbits.

(b) circular orbits of planets is not possible.

(c) projectile motion of a stone thrown by hand on the surface of the earth will be approximately parabolic.

(d) there will be no gravitational force inside a spherical shell of uniform density.

8.11 If the mass of sun were ten times smaller and gravitational constant $G$ were ten times larger in magnitudes-

(a) walking on ground would became more difficult.

(b) the acceleration due to gravity on earth will not change.

(c) raindrops will fall much faster.

(d) airplanes will have to travel much faster.

8.12 If the sun and the planets carried huge amounts of opposite charges,

(a) all three of Kepler’s laws would still be valid.

(b) only the third law will be valid.

(c) the second law will not change.

(d) the first law will still be valid.

8.13 There have been suggestions that the value of the gravitational constant $G$ becomes smaller when considered over very large time period (in billions of years) in the future. If that happens, for our earth,

(a) nothing will change.

(b) we will become hotter after billions of years.

(c) we will be going around but not strictly in closed orbits.

(d) after sufficiently long time we will leave the solar system.

8.14 Supposing Newton’s law of gravitation for gravitation forces $\mathbf{F_1}$ and $\mathbf{F_2}$ between two masses $m_{1}$ and $m_{2}$ at positions $\mathbf{r_1}$ and $\mathbf{r_2}$ read $F_1$ $=-F_2=-\frac{r_{12}}{r_{12}^{3}} G M_{O}^{2}\left(\frac{m_{1} m_{2}}{M_{0}^{2}}\right)^{n}$ where $M_{0}$ is a constant of dimension of mass, $r_{12}=\mathbf{r_1}-\mathbf{r_2}$ and $\mathrm{n}$ is a number. In such a case,

(a) the acceleration due to gravity on earth will be different for different objects.

(b) none of the three laws of Kepler will be valid.

(c) only the third law will become invalid.

(d) for $n$ negative, an object lighter than water will sink in water.

8.15 Which of the following are true?

(a) A polar satellite goes around the earth’s pole in northsouth direction.

(b) A geostationary satellite goes around the earth in east-west direction.

(c) A geostationary satellite goes around the earth in west-east direction.

(d) A polar satellite goes around the earth in east-west direction.

8.16 The centre of mass of an extended body on the surface of the earth and its centre of gravity

(a) are always at the same point for any size of the body.

(b) are always at the same point only for spherical bodies.

(c) can never be at the same point.

(d) is close to each other for objects, say of sizes less than $100 \mathrm{~m}$.

(e) both can change if the object is taken deep inside the earth.

VSA

8.17 Molecules in air in the atmosphere are attracted by gravitational force of the earth. Explain why all of them do not fall into the earth just like an apple falling from a tree.

8.18 Give one example each of central force and non-central force.

8.19 Draw areal velocity versus time graph for mars.

8.20 What is the direction of areal velocity of the earth around the sun?

8.21 How is the gravitational force between two point masses affected when they are dipped in water keeping the separation between them the same?

8.22 Is it possibe for a body to have inertia but no weight?

8.23 We can shield a charge from electric fields by putting it inside a hollow conductor. Can we shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?

8.24 An astronaut inside a small spaceship orbiting around the earth cannot detect gravity. If the space station orbiting around the earth has a large size, can he hope to detect gravity?

8.25 The gravitational force between a hollow spherical shell (of radius $\mathrm{R}$ and uniform density) and a point mass is $F$. Show the nature of $F$ vs $r$ graph where $r$ is the distance of the point from the centre of the hollow spherical shell of uniform density.

8.26 Out of aphelion and perihelion, where is the speed of the earth more and why?

8.27 What is the angle between the equatorial plane and the orbital plane of

(a) Polar satellite?

(b) Geostationary satellite?

SA

8.28 Mean solar day is the time interval between two successive noon when sun passes through zenith point (meridian).

Sidereal day is the time interval between two successive transit of a distant star through the zenith point (meridian).

By drawing appropriate diagram showing earth’s spin and orbital motion, show that mean solar day is four minutes longer than the sidereal day. In other words, distant stars would rise 4 minutes early every successive day.

(Hint: you may assume circular orbit for the earth).

8.29 Two identical heavy spheres are separated by a distance 10 times their radius. Will an object placed at the mid point of the line joining their centres be in stable equilibrium or unstable equilibrium? Give reason for your answer.

8.30 Show the nature of the following graph for a satellite orbiting the earth.

(a) KE vs orbital radius $R$

(b) PE vs orbital radius $R$

(c) TE $v$ s orbital radius $R$.

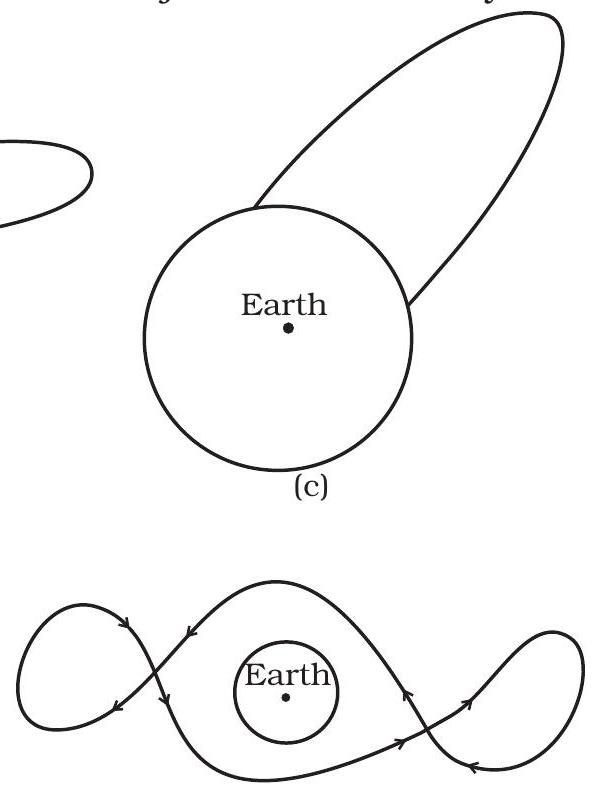
8.31 Shown are several curves (Fig. 8.2). Explain with reason, which ones amongst them can be possible trajectories traced by a projectile (neglect air friction).

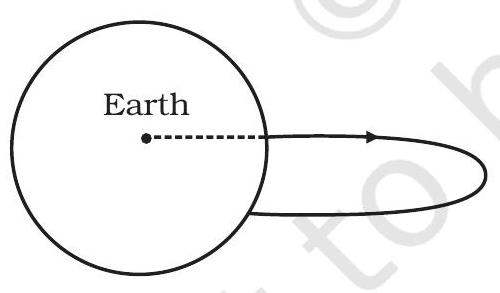
(a)

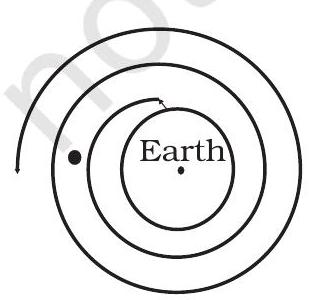
(d)

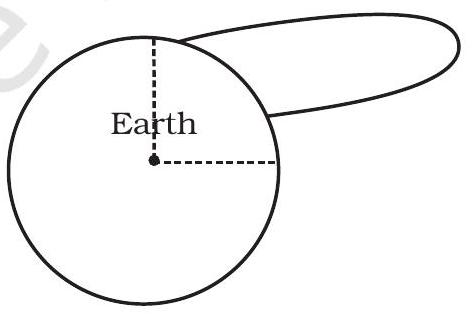
(b)

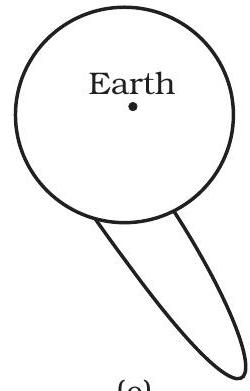
(e)

(f)

Fig. 8.2

8.32 An object of mass $m$ is raised from the surface of the earth to a height equal to the radius of the earth, that is, taken from a distance $R$ to $2 R$ from the centre of the earth. What is the gain in its potential energy?

8.33 A mass $m$ is placed at $\mathrm{P}$ a distance $h$ along the normal through the centre $O$ of a thin circular ring of mass $M$ and radius $r$ (Fig. 8.3).

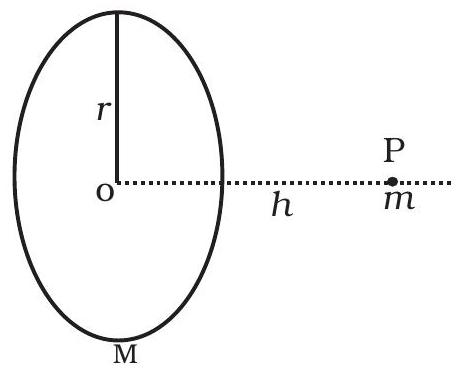
Fig. 8.3

If the mass is removed further away such that OP becomes $2 h$, by what factor the force of gravitation will decrease, if $h=r$ ?

LA

8.34 A star like the sun has several bodies moving around it at different distances. Consider that all of them are moving in circular orbits. Let $r$ be the distance of the body from the centre of the star and let its linear velocity be $v$, angular velocity $\omega$, kinetic energy $K$, gravitational potential energy $U$, total energy $E$ and angular momentum $l$. As the radius $r$ of the orbit increases, determine which of the above quantities increase and which ones decrease.

8.35 Six point masses of mass $m$ each are at the vertices of a regular hexagon of side $l$. Calculate the force on any of the masses.

8.36 A satellite is to be placed in equatorial geostationary orbit around earth for communication.

(a) Calculate height of such a satellite.

(b) Find out the minimum number of satellites that are needed to cover entire earth so that at least one satellites is visible from any point on the equator.

$\left[M=6 \times 10^{24} \mathrm{~kg}, R=6400 \mathrm{~km}, T=24 \mathrm{~h}, \mathrm{G}=6.67 \times 10^{-11}\right.$ SI units $]$

8.37 Earth’s orbit is an ellipse with eccentricity 0.0167. Thus, earth’s distance from the sun and speed as it moves around the sun varies from day to day. This means that the length of the solar day is not constant through the year. Assume that earth’s spin axis is normal to its orbital plane and find out the length of the shortest and the longest day. A day should be taken from noon to noon. Does this explain variation of length of the day during the year?

8.38 A satellite is in an elliptic orbit around the earth with aphelion of $6 R$ and perihelion of $2 R$ where $R=6400 \mathrm{~km}$ is the radius of the earth. Find eccentricity of the orbit. Find the velocity of the satellite at apogee and perigee. What should be done if this satellite has to be transferred to a circular orbit of radius $6 R$ ?

$\left[\mathrm{G}=6.67 \times 10^{-11}\right.$ SI units and $\left.M=6 \times 10^{24} \mathrm{~kg}\right]$

Solutions 8

8.1 (d)

8.2 (c)

8.3 (a)

8.4 (c)

8.5 (b)

8.6 (d)

8.7 (d)

8.8 (c)

8.9 (a), (c)

8.10 (a), (c)

8.11 (a), (c), (d)

8.12 (c), (d)

8.13 (c), (d)

8.14 (a), (c), (d)

8.15 (a), (c)

8.16 (d)

8.17 Molecules experience the vertically downward force due to gravity just like an apple falling from a tree. Due to thermal motion, which is random, their velocity is not in the vertical direction. The downward force of gravity causes the density of air in the atmosphere close to earth higher than the density as we go up.

8.18 Central force; gravitational force of a point mass, electrostatic force due to a point charge.

Non-central force: spin-dependent nuclear forces, magnetic force between two current carrying loops.

8.19

8.20 It is normal to the plane containing the earth and the sun as areal velocity

$\frac{\Delta \mathbf{A}}{\Delta t}=\frac{1}{2} \mathbf{r} \times \mathbf{v} \Delta t$.

8.21 It remains same as the gravitational force is independent of the medium separating the masses.

8.22 Yes, a body will always have mass but the gravitational force on it can be zero; for example, when it is kept at the centre of the earth.

8.23 No.

8.24 Yes, if the size of the spaceship is large enough for him to detect the variation in $g$.

8.25

8.26 At perihelion because the earth has to cover greater linear distance to keep the areal velocity constant.

8.27 $\begin{array}{ll}\text { (a) } 90^{\circ} & \text { (b) } 0^{\circ}\end{array}$

8.28 Every day the earth advances in the orbit by approximately $1^{\circ}$. Then, it will have to rotate by $361^{\circ}$ (which we define as 1 day) to have sun at zenith point again. Since $361^{\circ}$ corresponds to 24 hours; extra $1^{\circ}$ corresponds to approximately 4 minute [3 $\mathrm{min} 59$ seconds].

8.29 Consider moving the mass at the middle by a small amount $h$ to the right. Then the forces on it are: $\frac{\mathrm{GMm}}{(R-h)^{2}}$ to the right and $\frac{G M m}{(R+h)^{2}}$ to the left. The first is larger than the

second. Hence the net force will also be towards the right. Hence the equilibrium is unstable.

8.30

8.31 The trajectory of a particle under gravitational force of the earth will be a conic section (for motion outside the earth) with the centre of the earth as a focus. Only (c) meets this requirement.

Exemplar Problems-Physics

8.32 $\mathrm{mgR} / 2$.

8.33 Only the horizontal component (i.e. along the line joining $m$ and O) will survive. The horizontal component of the force on any point on the ring changes by a factor:

$\left[\frac{2 r}{\left(4 r^{2}+r^{2}\right)^{3 / 2}}\right]\left[\frac{\mu}{\left(r^{2}+r^{2}\right)^{3 / 2}}\right]$

$=\frac{4 \sqrt{2}}{5 \sqrt{5}}$.

8.34 As $r$ increases:

$U\left(=-\frac{G M m}{r}\right)$ increases.

$v_{c}\left(=\sqrt{\frac{G M}{r}}\right)$ decreases.

$\omega\left(=\frac{v_{c}}{r} \times \frac{1}{r^{3 / 2}}\right)$ decreases.

$K$ decreases because $v$ increases.

$E$ increase because $|U|=2 \mathrm{~K}$ and $U<\mathrm{O}$

$l$ increases because $m v r \propto \sqrt{r}$.

8.35 $\mathrm{AB}=\mathrm{C}$

$(\mathrm{AC})=2 \mathrm{AG}=2 \cdot l \cdot \frac{\sqrt{3}}{2}=\sqrt{3} l$

$\mathrm{AD}=\mathrm{AH}+\mathrm{HJ}+\mathrm{JD}$

$=\frac{l}{2}+l+\frac{l}{2}$

$=21$.

$A E=A C=\sqrt{3} l, \mathrm{AF}=l$

Force along $\mathrm{AD}$ due to $m$ at $\mathrm{F}$ and $\mathrm{B}$

$=G m^{2}\left[\frac{1}{l^{2}}\right] \frac{1}{2}+G m^{2}\left[\frac{1}{l^{2}}\right] \frac{1}{2}=\frac{G m^{2}}{l^{2}}$

Force along $\mathrm{AD}$ due to masses at $\mathrm{E}$ and $\mathrm{C}$

$=G m^{2} \frac{1}{3 l^{2}} \cos (30)+\frac{G m^{2}}{3 l^{2}} \cos \left(30^{\circ}\right)$ $=\frac{G m^{2}}{3 l^{2}} \sqrt{3}=\frac{G m^{2}}{\sqrt{3} l^{2}}$.

Force due to mass $M$ at $\mathrm{D}$

$=\frac{G m^{2}}{4 l^{2}}$.

$\therefore$ Total Force $=\frac{G m^{2}}{l^{2}}\left[1+\frac{1}{\sqrt{3}}+\frac{1}{4}\right]$.

8.36 (a) $r=\left(\frac{G M T^{2}}{4 \pi^{2}}\right)^{1 / 3}$

$$ \begin{aligned} \therefore h & =\frac{G M T^{2}}{4 \pi^{2}}{ }^{1 / 3}-R \ & =4.23 \times 10^{7}-6.4 \times 10^{6} \ & =3.59 \times 10^{7} \mathrm{~m} . \end{aligned} $$

(b) $\theta=\cos ^{-1} \frac{R}{R+h}$

$$ \begin{aligned} & =\cos ^{-1} \frac{1}{1+h / r} \ & =\cos ^{-1} \frac{1}{1+5.61} \end{aligned} $$

$$ =81^{\circ} 18^{\prime} $$

$\therefore 2 \theta=162^{\circ} 36^{\prime}$

$\frac{360^{\circ}}{2 \theta} \approx 2.21 ;$ Hence minimum number $=3$.

8.37 Angular momentem and areal velocity are constant as earth orbits the sun.

At perigee $r_{p}^{2} \omega_{p}=r_{a}^{2} \omega_{a}$ at apogee.

If ’ $a$ ’ is the semi-major axis of earth’s orbit, then $r_{p}=a(1-e)$ and $r_{a}=a(1+e)$.

$\therefore \frac{\omega_{p}}{\omega_{\mathrm{a}}}=\left(\frac{1+e}{1-e}\right)^{2}, e=0.0167$

$\therefore \frac{\omega_{\mathrm{p}}}{\omega_{\mathrm{a}}}=1.0691$

Let $\omega$ be angular speed which is geometric mean of $\omega_{\mathrm{p}}$ and $\omega_{\mathrm{a}}$ and corresponds to mean solar day,

$\therefore\left(\frac{\omega_{\mathrm{p}}}{\omega}\right)\left(\frac{\omega}{\omega_{\mathrm{a}}}\right)=1.0691$

$\therefore \frac{\omega_{\mathrm{p}}}{\omega}=\frac{\omega}{\omega_{\mathrm{a}}}=1.034$.

If $\omega$ corresponds to $1^{\circ}$ per day

(mean angular speed), then

$\omega_{\mathrm{p}}=1.034$ per day and $\omega_{\mathrm{a}}=0.967$ per day. Since $361^{\circ}=14 \mathrm{hrs}$ : mean solar day, we get 361.034 which corresponds to $24 \mathrm{hrs} 8.14$ " (8.1" longer) and $360.967^{\circ}$ corresponds to $23 \mathrm{hrs} 59 \mathrm{~min} 52^{\prime \prime}$ (7.9" smaller).

This does not explain the actual variation of the length of the day during the year.

8.38 $\quad r_{a}=a(1+e)=6 R$

$r_{p}=a(1-e)=2 R \quad \Rightarrow e=\frac{1}{2}$

Conservation of angular momentum:

angular momentum at perigee $=$ angular momentum at apogee

$\therefore m v_{p} r_{p}=m v_{a} r_{a}$

$\therefore \frac{v_{a}}{v_{p}}=\frac{1}{3}$.

Conservation of Energy:

Energy at perigee $=$ Energy at apogee

$\frac{1}{2} m v_{p}^{2}-\frac{G M m}{r_{p}}=\frac{1}{2} m v_{a}^{2}-\frac{G M m}{r_{a}}$

$\therefore v_{p}^{2}\left(1-\frac{1}{9}\right)=-2 G M\left[\frac{1}{r_{a}}-\frac{1}{r_{p}}\right]=2 G M\left[\frac{1}{r_{a}}-\frac{1}{r_{p}}\right]$

$v_{p}=\frac{2 G M\left[\frac{1}{r_{p}}-\frac{1}{r_{a}}\right]^{1 / 2}}{\left[1-\left(v_{a} / v_{p}\right)\right]^{2}}=\left[\frac{\frac{2 G M}{R}\left[\frac{1}{2}-\frac{1}{6}\right]}{\left(1-\frac{1}{9}\right)}\right]^{1 / 2}$

$$ =\left(\frac{2 / 3}{8 / 9} \frac{G M}{R}\right)^{1 / 2}=\sqrt{\frac{3}{4} \frac{G M}{R}}=6.85 \mathrm{~km} / \mathrm{s} $$

$v_{p}=6.85 \mathrm{~km} / \mathrm{s} \quad, v_{a}=2.28 \mathrm{~km} / \mathrm{s}$.

For $r=6 R, v_{c}=\sqrt{\frac{G M}{6 R}}=3.23 \mathrm{~km} / \mathrm{s}$.

Hence to transfer to a circular orbit at apogee, we have to boost the velocity by $\Delta=(3.23-2.28)=0.95 \mathrm{~km} / \mathrm{s}$. This can be done by suitably firing rockets from the satellite.