Chapter Six

WORK, ENERGY

AND POWER

MCQ I

6.1 An electron and a proton are moving under the influence of mutual forces. In calculating the change in the kinetic energy of the system during motion, one ignores the magnetic force of one on another. This is because,

(a) the two magnetic forces are equal and opposite, so they produce no net effect.

(b) the magnetic forces do no work on each particle.

(c) the magnetic forces do equal and opposite (but non-zero) work on each particle.

(d) the magenetic forces are necessarily negligible.

6.2 A proton is kept at rest. A positively charged particle is released from rest at a distance $d$ in its field. Consider two experiments; one in which the charged particle is also a proton and in another, a positron. In the same time $t$, the work done on the two moving charged particles is

(a) same as the same force law is involved in the two experiments.

(b) less for the case of a positron, as the positron moves away more rapidly and the force on it weakens.

(c) more for the case of a positron, as the positron moves away a larger distance.

(d) same as the work done by charged particle on the stationary proton.

6.3 A man squatting on the ground gets straight up and stand. The force of reaction of ground on the man during the process is

(a) constant and equal to $\mathrm{mg}$ in magnitude.

(b) constant and greater than $\mathrm{mg}$ in magnitude.

(c) variable but always greater than $\mathrm{mg}$.

(d) at first greater than $\mathrm{mg}$, and later becomes equal to $\mathrm{mg}$.

6.4 A bicyclist comes to a skidding stop in $10 \mathrm{~m}$. During this process, the force on the bicycle due to the road is $200 \mathrm{~N}$ and is directly opposed to the motion. The work done by the cycle on the road is

(a) $+2000 J$

(b) $-200 \mathrm{~J}$

(c) zero

(d) $-20,000 J$

6.5 A body is falling freely under the action of gravity alone in vacuum. Which of the following quantities remain constant during the fall?

(a) Kinetic energy.

(b) Potential energy.

(c) Total mechanical energy.

(d) Total linear momentum.

6.6 During inelastic collision between two bodies, which of the following quantities always remain conserved?

(a) Total kinetic energy.

(b) Total mechanical energy.

(c) Total linear momentum.

(d) Speed of each body.

6.7 Two inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track as shown in Fig. 6.1.

Fig. 6.1

Which of the following statement is correct?

(a) Both the stones reach the bottom at the same time but not with the same speed.

(b) Both the stones reach the bottom with the same speed and stone I reaches the bottom earlier than stone II.

(c) Both the stones reach the bottom with the same speed and stone II reaches the bottom earlier than stone I.

(d) Both the stones reach the bottom at different times and with different speeds.

6.8 The potential energy function for a particle executing linear SHM is given by $V(x)=\frac{1}{2} k x^{2}$ where $k$ is the force constant of the oscillator (Fig. 6.2). For $k=0.5 \mathrm{~N} / \mathrm{m}$, the graph of $V(x)$ versus $x$ is shown in the figure. A particle of total energy $E$ turns back when it reaches $x= \pm x_{m}$. If $V$ and $K$ indicate the P.E. and K.E., respectively of the particle at $x=+x_{m}$, then which of the following is correct?

Fig. 6.2

(a) $\quad V=\mathrm{O}, \quad K=E$

(b) $\quad V=E, \quad K=O$

(c) $V<E, \quad K=\mathrm{O}$

(d) $\quad V=\mathrm{O}, \quad \mathrm{K}<\mathrm{E}$.

6.9 Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed $V$ as shown in Fig. 6.3.

$\vec{V}$ Fig. 6.3

If the collision is elastic, which of the following (Fig. 6.4) is a possible result after collision?

$\mathrm{V}=0$

$\mathrm{V} / 2$

(a)

(b) (c)

(d)

Fig. 6.4

6.10 A body of mass $0.5 \mathrm{~kg}$ travels in a straight line with velocity $v=a$ $x^{3 / 2}$ where $a=5 \mathrm{~m}^{-1 / 2} \mathrm{~s}^{-1}$. The work done by the net force during its displacement from $x=0$ to $x=2 \mathrm{~m}$ is

(a) $1.5 \mathrm{~J}$

(b) $50 \mathrm{~J}$

(c) $10 \mathrm{~J}$

(d) $100 \mathrm{~J}$

6.11 A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in Fig. 6.5 correctly shows the displacement-time curve for its motion?

(a)

(b)

(c)

(d)

Fig. 6.5

6.12 Which of the diagrams shown in Fig. 6.6 most closely shows the variation in kinetic energy of the earth as it moves once around the sun in its elliptical orbit?

(a)

(b)

(c)

(d)

Fig. 6.6

6.13 Which of the diagrams shown in Fig. 6.7 represents variation of total mechanical energy of a pendulum oscillating in air as function of time?

(a)

(c)

(d)

Fig. 6.7

6.14 A mass of $5 \mathrm{~kg}$ is moving along a circular path of radius $1 \mathrm{~m}$. If the mass moves with 300 revolutions per minute, its kinetic energy would be

(a) $250 \pi^{2}$

(b) $100 \pi^{2}$

(c) $5 \pi^{2}$

(d) 0

6.15 A raindrop falling from a height $h$ above ground, attains a near terminal velocity when it has fallen through a height (3/4)h. Which of the diagrams shown in Fig. 6.8 correctly shows the change in kinetic and potential energy of the drop during its fall up to the ground?

(a)

(b)

(c)

(d)

Fig. 6.8

6.16 In a shotput event an athlete throws the shotput of mass $10 \mathrm{~kg}$ with an initial speed of $1 \mathrm{~m} \mathrm{~s}^{-1}$ at $45^{\circ}$ from a height $1.5 \mathrm{~m}$ above ground. Assuming air resistance to be negligible and acceleration due to gravity to be $10 \mathrm{~m} \mathrm{~s}^{-2}$, the kinetic energy of the shotput when it just reaches the ground will be

(a) $2.5 \mathrm{~J}$

(b) $5.0 \mathrm{~J}$

(c) $52.5 \mathrm{~J}$

(d) $155.0 \mathrm{~J}$

6.17 Which of the diagrams in Fig. 6.9 correctly shows the change in kinetic energy of an iron sphere falling freely in a lake having sufficient depth to impart it a terminal velocity?

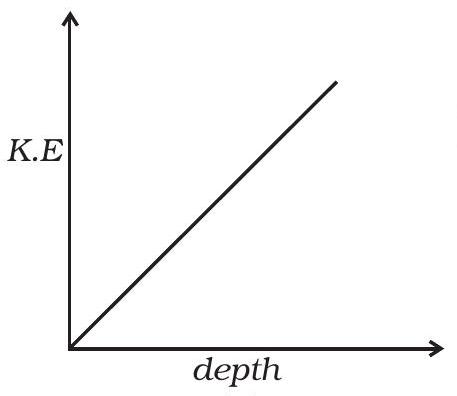
(a)

(b)

(c)

(d)

Fig. 6.9

6.18 A cricket ball of mass $150 \mathrm{~g}$ moving with a speed of $126 \mathrm{~km} / \mathrm{h}$ hits at the middle of the bat, held firmly at its position by the batsman. The ball moves straight back to the bowler after hitting the bat. Assuming that collision between ball and bat is completely elastic and the two remain in contact for $0.001 \mathrm{~s}$, the force that the batsman had to apply to hold the bat firmly at its place would be

(a) $10.5 \mathrm{~N}$

(b) $21 \mathrm{~N}$

(c) $1.05 \times 10^{4} \mathrm{~N}$

(d) $2.1 \times 10^{4} \mathrm{~N}$

MCQ II

6.19 A man, of mass $m$, standing at the bottom of the staircase, of height $L$ climbs it and stands at its top.

(a) Work done by all forces on man is equal to the rise in potential energy $\mathrm{mgL}$.

(b) Work done by all forces on man is zero.

(c) Work done by the gravitational force on man is $m g L$.

(d) The reaction force from a step does not do work because the point of application of the force does not move while the force exists.

6.20 A bullet of mass $m$ fired at $30^{\circ}$ to the horizontal leaves the barrel of the gun with a velocity $v$. The bullet hits a soft target at a height $h$ above the ground while it is moving downward and emerges out with half the kinetic energy it had before hitting the target.

Which of the following statements are correct in respect of bullet after it emerges out of the target?

(a) The velocity of the bullet will be reduced to half its initial value.

(b) The velocity of the bullet will be more than half of its earlier velocity.

(c) The bullet will continue to move along the same parabolic path.

(d) The bullet will move in a different parabolic path.

(e) The bullet will fall vertically downward after hitting the target.

(f) The internal energy of the particles of the target will increase.

6.21 Two blocks $M_{1}$ and $M_{2}$ having equal mass are free to move on a horizontal frictionless surface. $M_{2}$ is attached to a massless spring as shown in Fig. 6.10. Iniially $M_{2}$ is at rest and $M_{1}$ is moving toward $M_{2}$ with speed $v$ and collides head-on with $M_{2}$.

(a) While spring is fully compressed all the KE of $M_{1}$ is stored as $\mathrm{PE}$ of spring.

(b) While spring is fully compressed the system momentum is not conserved, though final momentum is equal to initial momentum.

(c) If spring is massless, the final state of the $M_{1}$ is state of rest.

(d) If the surface on which blocks are moving has friction, then collision cannot be elastic.

Fig. 6.10

VSA

6.22 A rough inclined plane is placed on a cart moving with a constant velocity $u$ on horizontal ground. A block of mass $M$ rests on the incline. Is any work done by force of friction between the block and incline? Is there then a dissipation of energy?

6.23 Why is electrical power required at all when the elevator is descending? Why should there be a limit on the number of passengers in this case?

6.24 A body is being raised to a height $h$ from the surface of earth. What is the sign of work done by

(a) applied force

(b) gravitational force?

6.25 Calculate the work done by a car against gravity in moving along a straight horizontal road. The mass of the car is $400 \mathrm{~kg}$ and the distance moved is $2 \mathrm{~m}$.

6.26 A body falls towards earth in air. Will its total mechanical energy be conserved during the fall? Justify.

6.27 A body is moved along a closed loop. Is the work done in moving the body necessarily zero? If not, state the condition under which work done over a closed path is always zero.

6.28 In an elastic collision of two billiard balls, which of the following quantities remain conserved during the short time of collision of the balls (i.e., when they are in contact).

(a) Kinetic energy.

(b) Total linear momentum?

Give reason for your answer in each case.

6.29 Calculate the power of a crane in watts, which lifts a mass of $100 \mathrm{~kg}$ to a height of $10 \mathrm{~m}$ in $20 \mathrm{~s}$.

6.30 The average work done by a human heart while it beats once is 0.5 $\mathrm{J}$. Calculate the power used by heart if it beats 72 times in a minute.

6.31 Give example of a situation in which an applied force does not result in a change in kinetic energy.

6.32 Two bodies of unequal mass are moving in the same direction with equal kinetic energy. The two bodies are brought to rest by applying retarding force of same magnitude. How would the distance moved by them before coming to rest compare?

6.33 A bob of mass m suspended by a light string of length $L$ is whirled into a vertical circle as shown in Fig. 6.11. What will be the trajectory of the particle if the string is cut at

Fig. 6.11

(a) Point B?

(b) Point C?

(c) Point X?

SA

6.34 A graph of potential energy $V(x)$ verses $x$ is shown in Fig. 6.12. A particle of energy $E_{0}$ is executing motion in it. Draw graph of velocity and kinetic energy versus $x$ for one complete cycle AFA.

Fig. 6.12

6.35 A ball of mass $m$, moving with a speed $2 v_{0}$, collides inelastically $\left(e>0\right)$ with an identical ball at rest. Show that

(a) For head-on collision, both the balls move forward.

(b) For a general collision, the angle between the two velocities of scattered balls is less than $90^{\circ}$.

6.36 Consider a one-dimensional motion of a particle with total energy $\mathrm{E}$. There are four regions $\mathrm{A}, \mathrm{B}, \mathrm{C}$ and $\mathrm{D}$ in which the relation between potential energy $V$, kinetic energy $(\mathrm{K})$ and total energy $E$ is as given below:

Region A : $V>E$

Region B : $V<E$

Region $\mathrm{C}: K>E$

Region $\mathrm{D}: V>K$

State with reason in each case whether a particle can be found in the given region or not.

6.37 The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in Fig. 6.13.

If the length of the pendulum is $1 \mathrm{~m}$, calculate

(a) the height to which bob A will rise after collision.

(b) the speed with which bob B starts moving. Neglect the size of the bobs and assume the collision to be elastic.

Fig. 6.13

6.38 A raindrop of mass $1.00 \mathrm{~g}$ falling from a height of $1 \mathrm{~km}$ hits the ground with a speed of $50 \mathrm{~m} \mathrm{~s}^{-1}$. Calculate

(a) the loss of P.E. of the drop.

(b) the gain in K.E. of the drop.

(c) Is the gain in K.E. equal to loss of P.E.? If not why.

Take $g=10 \mathrm{~m} \mathrm{~s}^{-2}$

6.39 Two pendulums with identical bobs and lengths are suspended from a common support such that in rest position the two bobs are in contact (Fig. 6.14). One of the bobs is released after being displaced by $10^{\circ}$ so that it collides elastically head-on with the other bob.

(a) Describe the motion of two bobs.

(b) Draw a graph showing variation in energy of either pendulum with time, for $0 \leq t \leq 2 T$, where $T$ is the period of each pendulum.

Fig. 6.14

6.40 Suppose the average mass of raindrops is $3.0 \times 10^{-5} \mathrm{~kg}$ and their average terminal velocity $9 \mathrm{~m} \mathrm{~s}^{-1}$. Calculate the energy transferred by rain to each square metre of the surface at a place which receives $100 \mathrm{~cm}$ of rain in a year.

6.41 An engine is attached to a wagon through a shock absorber of length $1.5 \mathrm{~m}$. The system with a total mass of $50,000 \mathrm{~kg}$ is moving with a speed of $36 \mathrm{~km} \mathrm{~h}^{-1}$ when the brakes are applied to bring it to rest. In the process of the system being brought to rest, the spring of the shock absorber gets compressed by $1.0 \mathrm{~m}$. If $90 %$ of energy of the wagon is lost due to friction, calculate the spring constant.

6.42 An adult weighing $600 \mathrm{~N}$ raises the centre of gravity of his body by $0.25 \mathrm{~m}$ while taking each step of $1 \mathrm{~m}$ length in jogging. If he jogs for $6 \mathrm{~km}$, calculate the energy utilised by him in jogging assuming that there is no energy loss due to friction of ground and air. Assuming that the body of the adult is capable of converting 10% of energy intake in the form of food, calculate the energy equivalents of food that would be required to compensate energy utilised for jogging.

6.43 On complete combustion a litre of petrol gives off heat equivalent to $3 \times 10^{7} \mathrm{~J}$. In a test drive a car weighing $1200 \mathrm{~kg}$. including the mass of driver, runs $15 \mathrm{~km}$ per litre while moving with a uniform speed on a straight track. Assuming that friction offered by the road surface and air to be uniform, calculate the force of friction acting on the car during the test drive, if the efficiency of the car engine were 0.5.

LA

6.44 A block of mass $1 \mathrm{~kg}$ is pushed up a surface inclined to horizontal at an angle of $30^{\circ}$ by a force of $10 \mathrm{~N}$ parallel to the inclined surface (Fig. 6.15). The coefficient of friction between block and the incline is 0.1 . If the block is pushed up by $10 \mathrm{~m}$ along the incline, calulate

Fig. 6.15

(a) work done against gravity

(b) work done against force of friction

(c) increase in potential energy

(d) increase in kinetic energy

(e) work done by applied force.

6.45 A curved surface is shown in Fig. 6.16. The portion BCD is free of friction. There are three spherical balls of identical radii and masses. Balls are released from rest one by one from A which is at a slightly greater height than $\mathrm{C}$. With the surface $A B$, ball 1 has large enough friction to cause rolling down without slipping; ball 2 has a small friction and ball 3 has a negligible friction.

Fig. 6.16

(a) For which balls is total mechanical energy conserved?

(b) Which ball (s) can reach D?

(c) For balls which do not reach D, which of the balls can reach back A?

6.46 A rocket accelerates straight up by ejecting gas downwards. In a small time interval $\Delta t$, it ejects a gas of mass $\Delta m$ at a relative speed $u$. Calculate $\mathrm{KE}$ of the entire system at $t+\Delta t$ and $t$ and show that the device that ejects gas does work $=(1 / 2) \Delta m u^{2}$ in this time interval (neglect gravity).

6.47 Two identical steel cubes (masses $50 \mathrm{~g}$, side $1 \mathrm{~cm}$ ) collide head-on face to face with a speed of $10 \mathrm{~cm} / \mathrm{s}$ each. Find the maximum compression of each. Young’s modulus for steel $=Y=2 \times 10^{11} \mathrm{~N} / \mathrm{m}^{2}$.

6.48 A baloon filled with helium rises against gravity increasing its potential energy. The speed of the baloon also increases as it rises. How do you reconcile this with the law of conservation of mechanical energy? You can neglect viscous drag of air and assume that density of air is constant.

Solutions 6

6.1 (b)

6.2 (c)

6.3 (d)

6.4 (c)

6.5 $\quad(\mathrm{c})$

6.6 (c)

6.7 (c)

6.8 (b)

6.9 (b)

6.10 (b)

6.11 (b) as displacement $\alpha t^{3 / 2}$

6.12 (d)

6.13 (d)

6.14 (a)

6.15 (b)

6.16 (d)

6.17 (b)

6.18 (c)

6.19 (b), (d)

6.20 (b), (d), (f)

6.21 (c)

6.22 Yes, No.

6.23 To prevent elevator from falling freely under gravity.

6.24 (a) Positive, (b) Negative

6.25 Work done against gravity in moving along horizontal road is zero .

6.26 No, because resistive force of air also acts on the body which is a non-conservative force. So the gain in $\mathrm{KE}$ would be smaller than the loss in PE.

6.27 No, work done over each closed path is necessarily zero only if all the forces acting on the system are conservative.

6.28 (b) Total linear momentum.

While balls are in contact, there may be deformation which means elastic potential energy which came from part of KE. Momentum is always conserved.

6.29 Power $=\frac{m g h}{T}=\frac{100 \times 9.8 \times 10}{20} \mathrm{~W}=490 \mathrm{~W}$

6.30 $P=\frac{\Delta E}{\Delta t}=\frac{0.5 \times 72}{60}=0.6$ watts

6.31 A charged particle moving in an uniform magnetic field.

6.32 Work done $=$ change in $\mathrm{KE}$

Both bodies had same $\mathrm{KE}$ and hence same amount of work is needed to be done. Since force aplied is same, they would come to rest within the same distance.

6.33 (a) Straight line: vertical, downward

(b) Parabolic path with vertex at C.

(c) Parabolic path with vertex higher than $\mathrm{C}$.

6.34

6.35 (a) For head on collission:

Conservation of momentum $\Rightarrow 2 m v_{0}=m v_{1}+m v_{2}$

Or $2 v_{0}=v_{1}+v_{2}$

and $e=\frac{v_{2}-v_{1}}{2 v_{0}} \Rightarrow v_{2}=v_{1}+2 v_{0} e$

$\therefore 2 v_{1}=2 v_{0}-2 e v_{0}$

$\therefore \quad v_{1}=v_{0}(1-e)$

Since $e<1 \Rightarrow v_{1}$ has the same sign as $v_{0}$, therefore the ball moves on after collission.

(b) Conservation of momentum $\Rightarrow \mathbf{p}=\mathbf{p_1}+\mathbf{p_2}$

But $\mathrm{KE}$ is lost $\Rightarrow \frac{p^{2}}{2 m}>\frac{p_{2}{ }^{2}}{2 m}+\frac{p_{2}{ }^{2}}{2 m}$

$\therefore p^{2}>p_{1}{ }^{2}+p_{2}^{2}$

Thus $\mathbf{p}, \mathbf{p_1}$ and $\mathbf{p_2}$ are related as shown in the figure.

$\theta$ is acute (less than $\left.90^{\circ}\right)\left(p^{2}=p_{1}{ }^{2}+p_{2}{ }^{2}\right.$ would give $\left.\theta=90^{\circ}\right)$

6.36 Region A : No, as KE will become negative.

Region B : Yes, total energy can be greater than PE for non zero K.E.

Region C: Yes, KE can be greater than total energy if its PE is negative.

Region D : Yes, as PE can be greater than KE.

6.37 (a) Ball A transfers its entire momentum to the ball on the table and does not rise at all.

(b) $v=\sqrt{2 g h}=4.42 \mathrm{~m} / \mathrm{s}$

6.38 (a) Loss of PE $=m g h=1 \times 10^{-3} \times 10 \times 10^{-3}=10 \mathrm{~J}$

(b) Gain in $\mathrm{KE}=\frac{1}{2} m v^{2}=\frac{1}{2} \times 10^{-3} \times 2500=1.25 \mathrm{~J}$

(c) No, because a part of $\mathrm{PE}$ is used up in doing work against the viscous drag of air.

6.39 (b)

6.40 $m=3.0 \times 10^{-5} \mathrm{~kg} \quad \rho=10^{-3} \mathrm{~kg} / \mathrm{m}^{2} \quad v=9 \mathrm{~m} / \mathrm{s}$

$A=1 \mathrm{~m}^{2} \quad \mathrm{~h}=100 \mathrm{~cm} \Rightarrow n=1 \mathrm{~m}^{3}$

$M=\rho v=10^{-3} \mathrm{~kg}, E=\frac{1}{2} M v^{2}=\frac{1}{2} \times 10^{3} \times(9)^{2}=4.05 \times 10^{4} \mathrm{~J}$.

6.41 $\mathrm{KE}=\frac{1}{2} m v^{2} \cong \frac{1}{2} \times 5 \times 10^{4} \times 10^{2}$

$$ =2.5 \times 10^{5} \mathrm{~J} \text {. } $$

$10 %$ of this is stored in the spring.

$$ \begin{array}{r} \frac{1}{2} k x^{2}=2.5 \times 10^{4} \ x=1 \mathrm{~m} \end{array} $$

$k=5 \times 10^{4} \mathrm{~N} / \mathrm{m}$.

6.42 In $6 \mathrm{~km}$ there are 6000 steps.

$\therefore E=6000(\mathrm{mg}) \mathrm{h}$

$$ =6000 \times 600 \times 0.25 $$

$$ =9 \times 10^{5} \mathrm{~J} \text {. } $$

This is $10 %$ of intake.

$\therefore \quad$ Intake energy $=10 \mathrm{E}=9 \times 10^{6} \mathrm{~J}$.

6.43 With 0.5 efficiency, 1 litre generates $1.5 \times 10^{7} \mathrm{~J}$, which is used for 15 $\mathrm{km}$ drive.

$\therefore F d=1.5 \times 10^{7} \mathrm{~J}$. with $d=15000 \mathrm{~m}$

$\therefore F=1000 \mathrm{~N}$ : force of friction.

6.44 (a) $W_{\mathrm{g}}=m g \sin \theta d=1 \times 10 \times 0.5 \times 10=50 \mathrm{~J}$.

(b) $W_{\mathrm{f}}=\mu m g \cos \theta \quad d=0.1 \times 10 \times 0.866 \times 10=8.66 \mathrm{~J}$.

(c) $\Delta \mathrm{U}=m g h=1 \times 10 \times 5=50 \mathrm{~J}$

(d) $a={F-(m g \sin \theta+\mu m g \cos \theta)}=[10-5.87]$

$$ =4.13 \mathrm{~m} / \mathrm{s}^{2} $$

$$ \begin{aligned} & v=u+a t \text { or } v^{2}=u^{2}+2 a d \ & \Delta K=\frac{1}{2} m v^{2}-\frac{1}{2} m u^{2}=\operatorname{mad}=41.3 \mathrm{~J} \end{aligned} $$

(e) $W=F d=100 \mathrm{~J}$

6.45 (a) Energy is conserved for balls 1 and 3.

(b) Ball 1 acquires rotational energy, ball 2 loses energy by friction.

They cannot cross at C. Ball 3 can cross over.

(c) Ball 1, 2 turn back before reaching C. Because of loss of energy, ball 2 cannot reach back to $A$. Ball 1 has a rotational motion in “wrong” sense when it reaches B. It cannot roll back to A, because of kinetic friction.

6.46 $(K E)_{t+\Delta t}=\frac{1}{2}(M-\Delta m)(v+\Delta v)^{2}+\frac{1}{2} \Delta m(v-u)^{2}$

rocket gas

$(K E)_{t}=\frac{1}{2} M v^{2}$

$=\frac{1}{2} M v^{2}+M v \Delta v-\Delta m v u+\frac{1}{2} \Delta m u^{2} = W$

$KE_{t+\Delta t}-(KE)_{t}=(M \Delta v-\Delta mu) v\frac{1}{2} \Delta mu^2=\frac{1}{2} \Delta mu^2=W$

(By Work - Energy theorem)

Since $\left(\frac{Mdv}{dt}=\left(\frac{dm}{dt}\right)(|u|)\right) \Rightarrow(M \Delta v-\Delta mu)=0$

6.47 Hooke’s law : $\frac{F}{A}=\mathrm{Y} \frac{\Delta L}{L}$

where $\mathrm{A}$ is the surface area and $L$ is length of the side of the cube. If $k$ is spring or compression constant, then $F=k \Delta L$

$\therefore k=Y \frac{A}{L}=Y L$

Initial $\mathrm{KE}=2 \times \frac{1}{2} m v^{2}=5 \times 10^{-4} \mathrm{~J}$

Final $\mathrm{PE}=2 \times \frac{1}{2} k(\Delta L)^{2}$

$\therefore \Delta L=\sqrt{\frac{K E}{k}}=\sqrt{\frac{K E}{\mathrm{Y} L}}=\sqrt{\frac{5 \times 10^{-4}}{2 \times 10^{11} \times 0.1}}=1.58 \times 10^{-7} \mathrm{~m}$

6.48 Let $m, V, \rho_{H e}$ denote respectively the mass, volume and density of helium baloon and $\rho_{\text {air }}$ be density of air

Volume $V$ of baloon displaces volume $V$ of air.

$$ \begin{equation*} \text { So, } \mathrm{V}\left(\rho_{\text {air }}-\rho_{H e}\right) g=m a \tag{1} \end{equation*} $$

Integrating with respect to $t$,

$$ \begin{align*} & V\left(\rho_{\text {air }}-\rho_{H e}\right) g t=m v \ & \Rightarrow \frac{1}{2} m v^{2}=\frac{1}{2} m \frac{V^{2}}{m^{2}}\left(\rho_{\text {air }}-\rho_{H e}\right)^{2} g^{2} t^{2}=\frac{1}{2 m} V^{2}\left(\rho_{\text {air }}-\rho_{H e}\right)^{2} g^{2} t^{2} \tag{2} \end{align*} $$

If the baloon rises to a height $h$, from $s=u t+\frac{1}{2} a t^{2}$,

we get $h=\frac{1}{2} a t^{2}=\frac{1}{2} \frac{V\left(\rho_{\text {air }}-\rho_{\text {he }}\right)}{m} g t^{2}$

From Eqs. (3) and (2),

$$ \begin{gathered} \frac{1}{2} m v^{2}=\left[V\left(\rho_{a}-\rho_{H e}\right) g\right]\left[\frac{1}{2 m} V\left(\rho_{a}-\rho_{H e}\right) g t^{2}\right] \ =V\left(\rho_{a}-\rho_{H e}\right) g h \end{gathered} $$

Rearranging the terms,

$\Rightarrow \frac{1}{2} m v^{2}+V \rho_{\text {He }} g h=V \rho_{\text {air }} h g$

$K E_{\text {baloon }} P E_{\text {baloon }}$ change in $P E$ of air.

So, as the baloon goes up, an equal volume of air comes down, increase in $\mathrm{PE}$ and $\mathrm{KE}$ of the baloon is at the cost of $\mathrm{PE}$ of air [which comes down].