Thermodynamics
Unit 6
Thermodynamics
I. Multiple Choice Questions (Type-I)
1. Thermodynamics is not concerned about ———.
(i) energy changes involved in a chemical reaction.
(ii) the extent to which a chemical reaction proceeds.
(iii) the rate at which a reaction proceeds.
(iv) the feasibility of a chemical reaction.
2. Which of the following statements is correct?
(i) The presence of reacting species in a covered beaker is an example of open system.
(ii) There is an exchange of energy as well as matter between the system and the surroundings in a closed system.
(iii) The presence of reactants in a closed vessel made up of copper is an example of a closed system.
(iv) The presence of reactants in a thermos flask or any other closed insulated vessel is an example of a closed system.
3. The state of a gas can be described by quoting the relationship between ——.
(i) pressure, volume, temperature
(ii) temperature, amount, pressure
(iii) amount, volume, temperature
(iv) pressure, volume, temperature, amount
4. The volume of gas is reduced to half from its original volume. The specific heat will be ——–.
(i) reduce to half
(ii) be doubled (iii)
remain constant
(iv) increase four times
5. During complete combustion of one mole of butane, $2658 kJ$ of heat is released. The thermochemical reaction for above change is
(i) $2 C_4 H _{10}(g)+13 O_2(g) \longrightarrow 8 CO_2(g)+10 H_2 O(l) \Delta_c H=-2658.0 kJ mol^{-1}$
(ii) $C_4 H _{10}(g)+\frac{13}{2} O_2(g) \longrightarrow 4 CO_2(g)+5 H_2 O(g) \Delta_c H=-1329.0 kJ mol^{-1}$
(iii) $\quad C_4 H _{10}(g)+\frac{13}{2} O_2(g) \longrightarrow 4 CO_2(g)+5 H_2 O(l) \Delta_c H=-2658.0 kJ mol^{-1}$
(iv) $C_4 H _{10}(g)+\frac{13}{2} O_2(g) \longrightarrow 4 CO_2(g)+5 H_2 O(l) \Delta_c H=+2658.0 kJ mol^{-1}$
6. $\Delta_f U^{\ominus}$ of formation of $CH_4(g)$ at certain temperature is $-393 kJ mol{ }^{-1}$. The value of $\Delta_f H^{\ominus}$ is
(i) zero
(ii) $<\Delta_f U^{\ominus}$
(iii) $>\Delta_f U^{\ominus}$
(iv) equal to $\Delta_f U^{\ominus}$
7. In an adiabatic process, no transfer of heat takes place between system and surroundings. Choose the correct option for free expansion of an ideal gas under adiabatic condition from the following.
(i) $\quad q=0, \Delta T \neq 0, w=0$
(ii) $\quad q \neq 0, \Delta T=0, w=0$
(iii) $q=0, \Delta T=0, w=0$
(iv) $q=0, \Delta T<0, w \neq 0$
8. The pressure-volume work for an ideal gas can be calculated by using the expression $w=-\int _{V_i}^{V_f} p _{\text{ex }} d V$. The work can also be calculated from the $p V$ - plot by using the area under the curve within the specified limits. When an ideal gas is compressed (a) reversibly or (b) irreversibly from volume $V_i$ to $V_f$. choose the correct option.
(i) $w$ (reversible) $=w$ (irreversible)
(ii) $w$ (reversible) $<w$ (irreversible)
(iii) $w$ (reversible) $>w$ (irreversible)
(iv) $w$ (reversible) $w$ (irreversible) $+p _{ex} . \Delta V$
9. The entropy change can be calculated by using the expression $\Delta S=\frac{q _{\text{rev }}}{T}$. When water freezes in a glass beaker, choose the correct statement amongst the following :
(i) $\quad \Delta S$ (system) decreases but $\Delta S$ (surroundings) remains the same.
(ii) $\Delta S$ (system) increases but $\Delta S$ (surroundings) decreases.
(iii) $\quad \Delta S$ (system) decreases but $\Delta S$ (surroundings) increases.
(iv) $\Delta S$ (system) decreases and $\Delta S$ (surroundings) also decreases.
10. On the basis of thermochemical equations (a), (b) and (c), find out which of the algebric relationships given in options (i) to (iv) is correct.
(a) $C$ (graphite) $+O_2$ (g) $\longrightarrow CO_2(g) ; \Delta_r H=x kJ mol^{-1}$
(b) $\quad C$ (graphite) $+\frac{1}{2} O_2(g) \longrightarrow CO(g) ; \Delta_r H=y kJ mol^{-1}$
(c) $CO(g)+\frac{1}{2} O_2(g) \longrightarrow CO_2(g) ; \Delta_r H=z kJ mol^{-1}$
(i) $z=x+y$
(ii) $x=y-z$
(iii) $x=y+z$
(iv) $y=2 z-x$
11. Consider the reactions given below. On the basis of these reactions find out which of the algebric relations given in options (i) to (iv) is correct?
(a) $C(g)+4 H(g) \longrightarrow CH_4(g) ; \Delta_r H=x kJ mol^{-1}$
(b) $C$ (graphite,s) $+2 H_2(g) \longrightarrow CH_4(g) ; \Delta_r H=y kJ mol^{-1}$
(i) $x=y$
(ii) $x=2 y$
(iii) $x>y$
(iv) $x<y$
12. The enthalpies of elements in their standard states are taken as zero. The enthalpy of formation of a compound
(i) is always negative
(ii) is always positive
(iii) may be positive or negative
(iv) is never negative
13. Enthalpy of sublimation of a substance is equal to
(i) enthalpy of fusion + enthalpy of vapourisation
(ii) enthalpy of fusion
(iii) enthalpy of vapourisation
(iv) twice the enthalpy of vapourisation
14. Which of the following is not correct?
(i) $\quad \Delta G$ is zero for a reversible reaction
(ii) $\Delta G$ is positive for a spontaneous reaction
(iii) $\Delta G$ is negative for a spontaneous reaction
(iv) $\Delta G$ is positive for a non-spontaneous reaction
II. Multiple Choice Questions (Type-II)
In the following questions two or more options may be correct.
15. Thermodynamics mainly deals with
(i) interrelation of various forms of energy and their transformation from one form to another.
(ii) energy changes in the processes which depend only on initial and final states of the microscopic systems containing a few molecules.
(iii) how and at what rate these energy transformations are carried out.
(iv) the system in equilibrium state or moving from one equilibrium state to another equilibrium state.
16. In an exothermic reaction, heat is evolved, and system loses heat to the surrounding. For such system
(i) $q_p$ will be negative
(ii) $\Delta_r H$ will be negative
(iii) $q_p$ will be positive
(iv) $\Delta_r H$ will be positive
17. The spontaneity means, having the potential to proceed without the assistance of external agency. The processes which occur spontaneously are
(i) flow of heat from colder to warmer body.
(ii) gas in a container contracting into one corner.
(iii) gas expanding to fill the available volume.
(iv) burning carbon in oxygen to give carbon dioxide.
18. For an ideal gas, the work of reversible expansion under isothermal condition can be calculated by using the expression $w=-n R T \ln \frac{V_f}{V_i}$
71 Thermodynamics
A sample containing $1.0 mol$ of an ideal gas is expanded isothermally and reversibly to ten times of its original volume, in two separate experiments. The expansion is carried out at $300 K$ and at $600 K$ respectively. Choose the correct option.
(i) Work done at $600 K$ is 20 times the work done at $300 K$.
(ii) Work done at $300 K$ is twice the work done at $600 K$.
(iii) Work done at $600 K$ is twice the work done at $300 K$.
(iv) $\Delta U=0$ in both cases.
19. Consider the following reaction between zinc and oxygen and choose the correct options out of the options given below :
$2 Zn(s)+O_2(g) \longrightarrow 2 ZnO(s) ; \quad \Delta H=-693.8 kJ mol^{-1}$
(i) The enthalpy of two moles of $ZnO$ is less than the total enthalpy of two moles of $Zn$ and one mole of oxygen by $693.8 kJ$.
(ii) The enthalpy of two moles of $ZnO$ is more than the total enthalpy of two moles of $Zn$ and one mole of oxygen by $693.8 kJ$.
(iii) $693.8 kJ mol^{-1}$ energy is evolved in the reaction.
(iv) $693.8 kJ mol^{-1}$ energy is absorbed in the reaction.
III. Short Answer Type
20. $18.0 g$ of water completely vapourises at $100^{\circ} C$ and 1 bar pressure and the enthalpy change in the process is $40.79 kJ mol^{-1}$. What will be the enthalpy change for vapourising two moles of water under the same conditions? What is the standard enthalphy of vapourisation for water?
21. One mole of acetone requires less heat to vapourise than $1 mol$ of water. Which of the two liquids has higher enthalpy of vapourisation?
22. Standard molar enthalpy of formation, $\Delta_f H^{\ominus}$ is just a special case of enthalpy of reaction, $\Delta_r H^{\ominus}$. Is the $\Delta_r H^{\ominus}$ for the following reaction same as $\Delta_f H^{\ominus}$ ? Give reason for your answer.
$CaO(s)+CO_2(g) \to CaCO_3(s) ; \quad \Delta_f H^{\ominus}=-178.3 kJ mol^{-1}$
23. The value of $\Delta_f H^{\ominus}$ for $NH_3$ is $-91.8 kJ mol^{-1}$. Calculate enthalpy change for the following reaction :
$2 NH_3(g) \to N_2(g)+3 H_2(g)$
24. Enthalpy is an extensive property. In general, if enthalpy of an overall reaction $A \to B$ along one route is $\Delta_r H$ and $\Delta_r H_1, \Delta_r H_2, \Delta_r H_3 \ldots$. represent enthalpies of intermediate reactions leading to product $B$. What will be the relation between $\Delta_r H$ for overall reaction and $\Delta_r H_1, \Delta_r H_2 \ldots$. etc. for intermediate reactions.
25. The enthalpy of atomisation for the reaction $CH_4(g) \to C(g)+4 H(g)$ is $1665 kJ mol^{-1}$. What is the bond energy of $C-H$ bond?
26. Use the following data to calculate $\Delta _{\text{lattice }} H^{\ominus}$ for $NaBr$.
$\Delta _{\text{sub }} H^{\ominus}$ for sodium metal $=108.4 kJ mol^{-1}$
Ionization enthalpy of sodium $=496 kJ mol^{-1}$
Electron gain enthalpy of bromine $=-325 kJ mol^{-1}$
Bond dissociation enthalpy of bromine $=192 kJ mol^{-1}$
$\Delta_f H^{\ominus}$ for $NaBr(s)=-360.1 kJ mol^{-1}$
27. Given that $\Delta H=0$ for mixing of two gases. Explain whether the diffusion of these gases into each other in a closed container is a spontaneous process or not?
28. Heat has randomising influence on a system and temperature is the measure of average chaotic motion of particles in the system. Write the mathematical relation which relates these three parameters.
29. Increase in enthalpy of the surroundings is equal to decrease in enthalpy of the system. Will the temperature of system and surroundings be the same when they are in thermal equilibrium?
30. At $298 K$. $K_p$ for the reaction $N_2 O_4(g) \rightarrow 2 NO_2(g)$ is 0.98 . Predict whether the reaction is spontaneous or not.
31. A sample of $1.0 mol$ of a monoatomic ideal gas is taken through a cyclic process of expansion and compression as shown in Fig. 6.1. What will be the value of $\Delta H$ for the cycle as a whole?

Fig. : 6.1
32. The standard molar entropy of $H_2 O(l)$ is $70 J K^{-1} mol^{-1}$. Will the standard molar entropy of $H_2 O(s)$ be more, or less than $70 J K^{-1} mol^{-1}$ ?
33. Identify the state functions and path functions out of the following : enthalpy, entropy, heat, temperature, work, free energy.
34. The molar enthalpy of vapourisation of acetone is less than that of water. Why?
35. Which quantity out of $\Delta_r G$ and $\Delta_r G^{\ominus}$ will be zero at equilibrium?
36. Predict the change in internal energy for an isolated system at constant volume
37. Although heat is a path function but heat absorbed by the system under certain specific conditions is independent of path. What are those conditions? Explain.
38. Expansion of a gas in vacuum is called free expansion. Calculate the work done and the change in internal energy when 1 litre of ideal gas expands isothermally into vacuum until its total volume is 5 litre?
39. Heat capacity $(C_p)$ is an extensive property but specific heat (c) is an intensive property. What will be the relation between $C_p$ and $c$ for $1 mol$ of water?
40. The difference between $C_P$ and $C_V$ can be derived using the empirical relation $H=U+p V$. Calculate the difference between $C_P$ and $C_V$ for 10 moles of an ideal gas.
41. If the combustion of $1 g$ of graphite produces $20.7 kJ$ of heat, what will be molar enthalpy change? Give the significance of sign also.
42. The net enthalpy change of a reaction is the amount of energy required to break all the bonds in reactant molecules minus amount of energy required to form all the bonds in the product molecules. What will be the enthalpy change for the following reaction.
$H_2(g)+Br_2(g) \to 2 HBr(g)$
Given that Bond energy of $H_2, Br_2$ and $HBr$ is $435 kJ mol^{-1}, 192 kJ mol^{-1}$ and $368 kJ mol^{-1}$ respectively.
43. The enthalpy of vapourisation of $CCl_4$ is $30.5 kJ mol^{-1}$. Calculate the heat required for the vapourisation of $284 g$ of $CCl_4$ at constant pressure. (Molar mass of $CCl_4=154 g mol^{-1}$ ).
44. The enthalpy of reaction for the reaction :
$2 H_2(g)+O_2(g) \to 2 H_2 O(l)$ is $\Delta_r H^{\ominus}=-572 kJ mol^{-1}$.
What will be standard enthalpy of formation of $H_2 O(l)$ ?
45. What will be the work done on an ideal gas enclosed in a cylinder, when it is compressed by a constant external pressure, $p _{\text{ext }}$ in a single step as shown in Fig. 6.2. Explain graphically.
46. How will you calculate work done on an ideal gas in a compression, when change in pressure is carried out in infinite steps?
47. Represent the potential energy/enthalpy change in
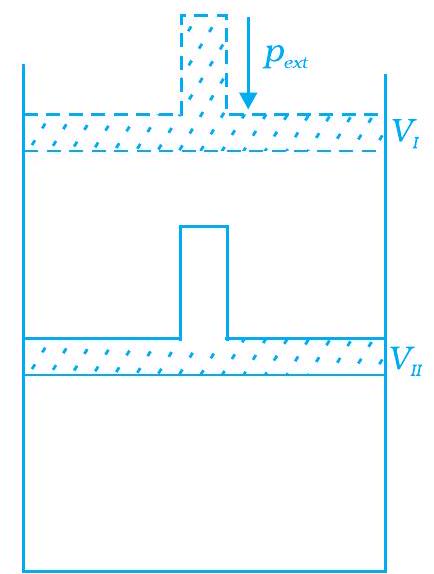
Fig. : 6.2 the following processes graphically.
(a) Throwing a stone from the ground to roof.
(b) $\frac{1}{2} H_2(g)+\frac{1}{2} Cl_2(g) \rightarrow HCl(g) \quad \Delta_r H^{\ominus}=-92.32 kJ mol^{-1}$
In which of the processes potential energy/enthalpy change is contributing factor to the spontaneity?
48. Enthalpy diagram for a particular reaction is given in Fig. 6.3. Is it possible to decide spontaneity of a reaction from given diagram. Explain.
49. $1.0 mol$ of a monoatomic ideal gas is expanded from state (1) to state (2) as shown in Fig. 6.4. Calculate the work done for the expansion of gas from state (1) to state (2) at $298 K$.

50. An ideal gas is allowed to expand against a constant pressure of 2 bar from $10 L$ to $50 L$ in one step. Calculate the amount of work done by the gas. If the same expansion were carried out reversibly, will the work done be higher or lower than the earlier case?
(Given that $1 L$ bar $=100 J$ )
Fig. : 6.3

Fig. : 6.4
IV Matching type
In the following questions more than one correlation is possible between options of both columns.
51. Match the following :
| A | B |
|---|---|
| (i) Adiabatic process | (a) Heat |
| (ii) Isolated system | (b) At constant volume |
| (iii) Isothermal change | (c) First law of thermodynamics |
| (iv) Path function | (d) No exchange of energy and matter |
| (v) State function | (e) No transfer of heat |
| (vi) $\Delta U=q$ | (f) Constant temperature |
| (vii) Law of conservation of energy | (g) Internal energy |
| (viii) Reversible process | (h) $p _{\text{ext }}=0$ |
| (ix) Free expansion | (i) At constant pressure |
| (x) $\Delta H=q$ | (j) Infinitely slow process which proceeds through |
| a series of equilibrium states. | |
| (xi) Intensive property | (k) Entropy |
| (xii) Extensive property | (l) Pressure |
| (m) Specific heat |
52. Match the following processes with entropy change:
| Reaction | Entropy change |
|---|---|
| (i) A liquid vapourises | (a) $\Delta S=0$ |
| (ii) Reaction is non-spontaneous at all | |
| temperatures and $\Delta H$ is positive | (b) $\Delta S=$ positive |
| (iii) Reversible expansion of an ideal gas | (c) $\Delta S=$ negative |
53. Match the following parameters with description for spontaneity :
| — | $\Delta$ (Parameters) | — | — | Description |
|---|---|---|---|---|
| — | $\Delta_r H^{\ominus}$ | $\Delta_r \mathbf{S}^{\ominus}$ | $\Delta_r G^{\ominus}$ | — |
| (i) | + | - | + | (a) Non-spontaneous at high temperature. |
| (ii) | - | - | + at high T | (b) Spontaneous at all temperatures |
| (iii) | - | + | - | (c) Non-spontaneous at all temperatures |
54. Match the following:
| (i) Entropy of vapourisation | (a) decreases |
|---|---|
| (ii) $K$ for spontaneous process | (b) is always positive |
| (iii) Crystalline solid state | (c) lowest entropy |
| (iv) $\Delta U$ in adiabatic expansion of ideal gas | (d) $\frac{\Delta H_{\text{vap }}}{T_b}$ |
V. Assertion and Reason Type
In the following questions a statement of Assertion (A) followed by a statement of Reason (R) is given. Choose the correct option out of the choices given below each question.
55. Assertion (A): Combustion of all organic compounds is an exothermic reaction.
Reason (R) : The enthalpies of all elements in their standard state are zero.
(i) Both $A$ and $R$ are true and $R$ is the correct explanation of $A$.
(ii) Both $A$ and $R$ are true but $R$ is not the correct explanation of $A$.
(iii) $A$ is true but $R$ is false.
(iv) $A$ is false but $R$ is true.
56. Assertion (A) : Spontaneous process is an irreversible process and may be reversed by some external agency.
Reason (R): Decrease in enthalpy is a contributory factor for spontaneity.
(i) Both $A$ and $R$ are true and $R$ is the correct explanation of $A$.
(ii) Both $A$ and $R$ are true but $R$ is not the correct explanation of $A$.
(iii) $A$ is true but $R$ is false.
(iv) $A$ is false but $R$ is true.
57. Assertion (A) : A liquid crystallises into a solid and is accompanied by decrease in entropy.
Reason (R) : In crystals, molecules organise in an ordered manner.
(i) Both $A$ and $R$ are true and $R$ is the correct explanation of $A$.
(ii) Both $A$ and $R$ are true but $R$ is not the correct explanation of $A$.
(iii) $A$ is true but $R$ is false.
(iv) $A$ is false but $R$ is true.
VI. Long Answer Type
58. Derive the relationship between $\Delta H$ and $\Delta U$ for an ideal gas. Explain each term involved in the equation.
59. Extensive properties depend on the quantity of matter but intensive properties do not. Explain whether the following properties are extensive or intensive.
Mass, internal energy, pressure, heat capacity, molar heat capacity, density, mole fraction, specific heat, temperature and molarity.
60. The lattice enthalpy of an ionic compound is the enthalpy when one mole of an ionic compound present in its gaseous state, dissociates into its ions. It is impossible to determine it directly by experiment. Suggest and explain an indirect method to measure lattice enthalpy of $NaCl(s)$.
61. $\Delta G$ is net energy available to do useful work and is thus a measure of “free energy”. Show mathematically that $\Delta G$ is a measure of free energy. Find the unit of $\Delta G$. If a reaction has positive enthalpy change and positive entropy change, under what condition will the reaction be spontaneous?
62. Graphically show the total work done in an expansion when the state of an ideal gas is changed reversibly and isothermally from $(p_i, V_i)$ to $(p_f, V_f)$. With the help of a $p V$ plot compare the work done in the above case with that carried out against a constant external pressure $p_f$.
ANSWERS
I. Multiple Choice Questions (Type-I)
1. (iii)
2. (iii)
3. (iv)
4. (iii)
5. (iii)
6. (ii)
7. (iii)
Justification : free expansion $\quad w=0$
adiabatic process $q=0$
$\Delta U=q+w=0$, this means that internal energy remains constant. Therefore, $\Delta T=0$.
In ideal gas there is no intermolecular attraction. Hence when such a gas expands under adiabatic conditions into a vaccum no heat is absorbed or evolved since no external work is done to separate the molecules.
8. (ii) $w$ (reversible) $<w$ (irreversible)
Justification: Area under the curve is always more in irreversible compression as can be seen from Fig. 6.5 (a) and (b).

(a) Reversible compression

(b) Irreversible compression
Fig. : 6.5
9. (iii)
Justification : Freezing is exothermic process. The heat released increases the entropy of surrounding.
10. (iii)
11. (iii)
Justification: Same bonds are formed in reaction (a) and (b) but bonds between reactant molecules are broken only in reaction (b).
12. (iii)
13. (i)
14. (ii)
II. Multiple Choice Questions (Type-II)
15. (i), (iv)
16. (i), (ii)
17. (iii), (iv)
18. (iii), (iv)
Justification: $\frac{w _{600 K}}{w _{\text{зоок }}}=\frac{1 \times R \times 600 K \ln \frac{10}{1}}{1 \times R \times 300 K \ln \frac{10}{1}}=\frac{600}{300}=2$
For isothermal expansion of ideal gases, $\Delta U=0$
since temperature is constant this means there is no change in internal energy.
Therefore, $\Delta U=0$
19. (i), (iii)
III. Short Answer Type
20. $\quad+81.58 kJ, \Delta _{\text{vap }} H^{\ominus}=+40.79 kJ mol^{-1}$
21. Water
22. No, since $CaCO_3$ has been formed from other compounds and not from its constituent elements.
23. $\Delta_r H^{\ominus}=+91.8 kJ mol^{-1}$
24. $\Delta_r H=\Delta_r H_1+\Delta_r H_2+\Delta_r H_3 \ldots$.
25. $\frac{1665}{4} kJ mol^{-1}=416.2 kJ mol^{-1}$
26. $\quad+735.5 kJ mol^{-1}$
27. It is spontaneous process. Although enthalpy change is zero but randomness or disorder (i.e., $\Delta S$ ) increases. Therefore, in equation $\Delta G=\Delta H-T \Delta S$, the term $T \Delta S$ will be negative. Hence, $\Delta G$ will be negative.
28. $\Delta S=\frac{q _{\text{rev }}}{T}$
29. Yes
30. The reaction is spontaneous
$\Delta_r G^{\ominus}=-R T \ln K_p$
31. $\Delta H($ cycle $)=0$
32. Less, because ice is more ordered than $H_2 O(l)$.
33. State Functions : Enthalpy, Entropy, Temperature, Free energy Path Functions : Heat, Work
34. Because of strong hydrogen bonding in water, its enthalpy of vapourisation is more.
35. $\Delta_r G$ will always be zero.
$\Delta_r G^{\ominus}$ is zero for $K=1$ because $\Delta G^{\ominus}=-RT \ln K, \Delta G^{\ominus}$ will be non zero for other values of $K$.
36. For isolated system, there is no transfer of energy as heat or as work i.e., $w=0$ and $q=0$. According to the first law of thermodynamics.
$ \begin{aligned} \Delta U & =q+w \\ & =0+0=0 \\ \therefore \quad \Delta U & =0 \end{aligned} $
37. At constant volume
By first law of thermodynamics:
$ \begin{aligned} q & =\Delta U+(-w) \\ (-w) & =p \Delta V \\ \therefore \quad q & =\Delta U+p \Delta V \\ \Delta V & =0, \text{ since volume is constant. } \\ \therefore \quad q_V & =\Delta U+0 \\ \Rightarrow \quad q_V & =\Delta U=\text{ change in internal energy } \end{aligned} $
At constant pressure
$ q_p=\Delta U+p \Delta V $
But, $\Delta U+p \Delta V=\Delta H$
$ \therefore \quad q_p=\Delta H=\text{ change in enthalpy. } $
So, at a constant volume and at constant pressure heat change is a state function because it is equal to change in internal energy and change in enthalpy respectively which are state functions.
38. $(-w)=p _{\text{ext }}(V_2-V_1)=0 \times(5-1)=0$
For isothermal expansion $q=0$
By first law of thermodynamics
$ \begin{aligned} q & =\Delta U+(-w) \\ \Rightarrow \quad 0 & =\Delta U+0 \text{ so } \Delta U=0 \end{aligned} $
39. For water, heat capacity $=18 \times$ specific heat
or
$ C_p=18 \times c $
Specific heat $=c=4.18 Jg^{-1} K^{-1}$
Heat capacity $=C_p=18 \times 4.18 JK^{-1}=75.3 J K^{-1}$
40. $C_P-C_V=n R$
$ =10 \times 4.184 J $
41. Molar enthalpy change of graphite
$ \begin{aligned} & =-20.7 kJ g^{-1} \times 12 g mol^{-1} \\ \therefore \Delta H & =-2.48 \times 10^{2} kJ mol^{-1} \end{aligned} $
Negative value of $\Delta H \Rightarrow$ exothermic reaction.
42. $\Delta_r H^{\ominus}=$ Bond energy of $H_2+$ Bond energy of $Br_2-2 \times$ Bond energy of $HBr$
$ =435+192-(2 \times 368) kJ mol^{-1} $
$\Rightarrow \Delta_r H^{\ominus}=-109 kJ mol^{-1}$
43. $q_p=\Delta H=30.5 kJ mol^{-1}$
$\therefore$ Heat required for vapourisation of $284 g of CCl_4=\frac{284 g}{154 g mol^{-1}} \times 30.5 kJ mol^{-1}$
$ =56.2 kJ $
44. According to the definition of standard enthalpy of formation, the enthalpy change for the following reaction will be standard enthalpy of formation of $H_2 O(l)$
$H_2(g)+\frac{1}{2} O_2(g) \to H_2 O(l)$.
or the standard enthalpy of formation of $H_2 O(l)$ will be half of the enthalpy of the given equation i.e., $\Delta_r H^{\ominus}$ is also halved.
$\Delta_f H _{H_2 O}^{\ominus}(l)=\frac{1}{2} 凶_r H^{\ominus}=\frac{-572 kJ mol^{-1}}{2}=-286 kJ / mol$.
45. Work done on an ideal gas can be calculated from $p-V$ graph shown in Fig. 6.6. Work done is equal to the shaded area $A B V_I V _{\text{II }}$.
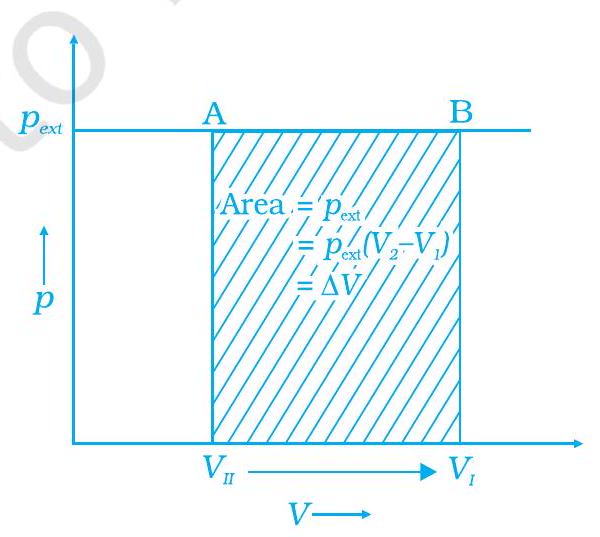
Fig. : 6.6
46. The work done can be calculated with the help of $p-V$ plot. A $p-V$ plot of the work of compression which is carried out by change in pressure in infinite steps, is given in Fig. 6.7. Shaded area represents the work done on the gas.

Fig. : 6.7
47.

(a)

(b)
Fig. : 6.8 Enthalpy change in processes (a) and (b)
48. No.
Enthalpy is one of the contributory factors in deciding spontaneity but it is not the only factor. One must look for contribution of another factor i.e., entropy also, for getting the correct result.
49. It is clear from the figure that the process has been carried out in infinite steps, hence it is isothermal reversible expansion.
$w=-2.303 n R T \log \frac{V_2}{V_1}$
But, $p_1 V_1=p_2 V_2 \Rightarrow \frac{V_2}{V_1}=\frac{p_1}{p_2}=\frac{2}{1}=2$
$ \begin{aligned} \therefore \quad w & =-2.303 nRT \log \frac{p_1}{p_2} \\ & =-2.303 \times 1 mol \times 8.314 J mol^{-1} K^{-1} \times 298 K^{-1} \times \log 2 \\ & =-2.303 \times 8.314 \times 298 \times 0.3010 J=-1717.46 J \end{aligned} $
50. $w=-p _{ex}(V_f-V_i)=-2 \times 40=-80 L$ bar $=-8 kJ$
The negative sign shows that work is done by the system on the surrounding. Work done will be more in the reversible expansion because internal pressure and exernal pressure are almost same at every step.
IV. Matching Type
51. (i) $\to$ (e) $\quad$ (ii) $\to$ (d) $\quad$ (iii) $\to$ (f) $\quad$ (iv) $\to$ (a)
(v)$\to$(g),(k),(l) $\quad$ (vi) $\to$ (b) $\quad$ (vii) $\to$ (c) $\quad$ (viii) $\to$(j)
(ix) $\to$ (h) $\quad$ (x)$\to$(i) $\quad$ (xi) $\to$(a),(1),(m) $\quad$ (xii)$\to$(g),(k)
52. (i) $\to$ (b) $\quad$ (ii) $\to$ (c) $\quad$ (iii) $\to$ (a)
53. (i) $\to$ (c) $\quad$ (ii) $\to$ (a) $\quad$ (iii) $\to$ (b)
54. (i) $\to$ (b), (d) $\quad$ (ii) $\r\to$ (b) $\quad$ (iii) $\to$ (c) $\quad$ (iv) $\to$ (a)
V. Assertion and Reason Type
55. (ii)
56. (ii)
57. (i)
V. Long Answer Type
59. Hint : Ratio of two extensive properties is always intensive $\frac{\text{ Extensive }}{\text{ Extensive }}=$ Intensive .
e.g., Mole fraction $=\frac{\text{ Moles }}{\text{ Total number of moles }}=\frac{(\text{ Extensive })}{(\text{ Extensive })}$
60. $-Na(s)+\frac{1}{2} Cl_2(g) \to Na^{+}(g)+Cl^{-}(g) ; \quad \Delta _{\text{lattice }} H^{\ominus}$
- Bonn - Haber Cycle
- Steps to measure lattice enthalpy from Bonn - Haber cycle
- Sublimation of sodium metal
(1) $Na$ (s) $arrow Na$ (g); $\quad \Delta _{\text{sub }} H^{\ominus}$
(2) Ionisation of sodium atoms
$ Na(g) \to Na^{+}(g)+e^{-}(g) ; \quad \Delta_t H^{\ominus} \text{ i.e., ionisation enthalpy } $
(3) Dissociation of chlorine molecule
$ \begin{gathered} \frac{1}{2} Cl_2(g) \to Cl(g) ; \quad \frac{1}{2} \Delta _{\text{bond }} H^{\ominus} \quad \text{ i.e., } \\ \text{ enthe-half of bond dissociation } \end{gathered} $
(4) $Cl(g)+e^{-}(g) \to Cl^{-}(g) ; \quad \Delta _{eg} H^{\ominus} \quad$ i.e., electron gain enthalpy.

61. $\Delta S _{\text{Total }}=\Delta S _{\text{sus }}+\Delta S _{\text{surr }}$
$ \begin{aligned} \Delta S _{\text{Total }} & =\Delta S _{\text{sys }}+\frac{-\Delta H _{\text{sys }}}{T} \\ T \Delta S _{\text{Total }} & =T \Delta S _{\text{sys }}-\Delta H _{\text{sys }} \end{aligned} $
For spontaneous change, $\Delta S _{\text{total }}>0$
$ \begin{matrix} \therefore & T \Delta S _{s y s}-\Delta H _{s y s}>0 \\ \Rightarrow & -(\Delta H _{s y s}-T \Delta S _{s y s})>0 \end{matrix} $
But, $\Delta H _{\text{sys }}-T \Delta S _{\text{sys }}=\Delta G _{\text{sys }}$
$\therefore \quad-\Delta G _{\text{sys }}>0$
$\Rightarrow \Delta G _{\text{sys }}=\Delta H _{\text{sys }}-T \Delta S _{\text{sys }}<0$
$\Delta H _{\text{sys }}=$ Enthalpy change of a reaction.
$T \Delta S _{\text{sys }}=$ Energy which is not available to do useful work .
$\Delta G _{\text{sys }}=$ Energy available for doing useful work.
- Unit of $\Delta G$ is Joule
- The reaction will be spontaneous at high temperature.
62.

Fig. : 6.9
(i) Reversible Work is represented by the combined areas and prin.
(ii) Work against constant pressure, $p_f$ is represented by the area Work (i) $>$ Work (ii)






