9.1 INTRODUCTION

Nature has endowed the human eye (retina) with the sensitivity to detect electromagnetic waves within a small range of the electromagnetic spectrum. Electromagnetic radiation belonging to this region of the spectrum (wavelength of about $400 \mathrm{~nm}$ to $750 \mathrm{~nm}$ ) is called light. It is mainly through light and the sense of vision that we know and interpret the world around us.

There are two things that we can intuitively mention about light from common experience. First, that it travels with enormous speed and second, that it travels in a straight line. It took some time for people to realise that the speed of light is finite and measurable. Its presently accepted value in vacuum is $c=2.99792458 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}$. For many purposes, it suffices to take $c=3 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}$. The speed of light in vacuum is the highest speed attainable in nature.

The intuitive notion that light travels in a straight line seems to contradict what we have learnt in Chapter 8, that light is an electromagnetic wave of wavelength belonging to the visible part of the spectrum. How to reconcile the two facts? The answer is that the wavelength of light is very small compared to the size of ordinary objects that we encounter commonly (generally of the order of a few $\mathrm{cm}$ or larger). In this situation, as you will learn in Chapter 10, a light wave can be considered to travel from one point to another, along a straight line joining them. The path is called a ray of light, and a bundle of such rays constitutes a beam of light.

In this chapter, we consider the phenomena of reflection, refraction and dispersion of light, using the ray picture of light. Using the basic laws of reflection and refraction, we shall study the image formation by plane and spherical reflecting and refracting surfaces. We then go on to describe the construction and working of some important optical instruments, including the human eye.

9.2 Reflection of Light by Spherical Mirrors

FIGURE 9.1 The incident ray, reflected ray and the normal to the reflecting surface lie in the same plane.

We are familiar with the laws of reflection. The angle of reflection (i.e., the angle between reflected ray and the normal to the reflecting surface or the mirror) equals the angle of incidence (angle between incident ray and the normal). Also that the incident ray, reflected ray and the normal to the reflecting surface at the point of incidence lie in the same plane (Fig. 9.1). These laws are valid at each point on any reflecting surface whether plane or curved. However, we shall restrict our discussion to the special case of curved surfaces, that is, spherical surfaces. The normal in this case is to be taken as normal to the tangent to surface at the point of incidence. That is, the normal is along the radius, the line joining the centre of curvature of the mirror to the point of incidence.

We have already studied that the geometric centre of a spherical mirror is called its pole while that of a spherical lens is called its optical centre. The line joining the pole and the centre of curvature of the spherical mirror is known as the principal axis. In the case of spherical lenses, the principal axis is the line joining the optical centre with its principal focus as you will see later.

FIGURE 9.2 The Cartesian Sign Convention.

9.2.1 Sign convention

To derive the relevant formulae for reflection by spherical mirrors and refraction by spherical lenses, we must first adopt a sign convention for measuring distances. In this book, we shall follow the Cartesian sign convention. According to this convention, all distances are measured from the pole of the mirror or the optical centre of the lens. The distances measured in the same direction as the incident light are taken as positive and those measured in the direction opposite to the direction of incident light are taken as negative (Fig. 9.2).

principal axis ( $x$-axis) of the mirror/lens are taken as positive (Fig. 9.2).

The heights measured downwards are taken as negative.

With a common accepted convention, it turns out that a single formula for spherical mirrors and a single formula for spherical lenses can handle all different cases.

9.2.2 Focal length of spherical mirrors

Figure 9.3 shows what happens when a parallel beam of light is incident on (a) a concave mirror, and (b) a convex mirror. We assume that the rays are paraxial, i.e., they are incident at points close to the pole $\mathrm{P}$ of the mirror and make small angles with the principal axis. The reflected rays converge at a point $\mathrm{F}$ on the principal axis of a concave mirror [Fig. 9.3(a)]. For a convex mirror, the reflected rays appear to diverge from a point $\mathrm{F}$ on its principal axis [Fig. 9.3(b)]. The point $\mathrm{F}$ is called the principal focus of the mirror. If the parallel paraxial beam of light were incident, making some angle with the principal axis, the reflected rays would converge (or appear to diverge) from a point in a plane through $\mathrm{F}$ normal to the principal axis. This is called the focal plane of the mirror [Fig. 9.3(c)].

(c)

FIGURE 9.3 Focus of a concave and convex mirror.

The distance between the focus $\mathrm{F}$ and the pole $\mathrm{P}$ of the mirror is called the focal length of the mirror, denoted by $f$. We now show that $f=R / 2$, where $R$ is the radius of curvature of the mirror. The geometry of reflection of an incident ray is shown in Fig. 9.4.

Let $\mathrm{C}$ be the centre of curvature of the mirror. Consider a ray parallel to the principal axis striking the mirror at $\mathrm{M}$. Then $\mathrm{CM}$ will be perpendicular to the mirror at M. Let $\theta$ be the angle of incidence, and MD

FIGURE 9.4 Geometry of reflection of an incident ray on (a) concave spherical mirror, and (b) convex spherical mirror.

FIGURE 9.5 Ray diagram for image formation by a concave mirror.

Now, be the perpendicular from $\mathrm{M}$ on the principal axis. Then,

$$ \angle \mathrm{MCP}=\theta \text { and } \angle \mathrm{MFP}=2 \theta $$

$$ \begin{equation*} \tan \theta=\frac{\mathrm{MD}}{\mathrm{CD}} \text { and } \tan 2 \theta=\frac{\mathrm{MD}}{\mathrm{FD}} \tag{9.1} \end{equation*} $$

For small $\theta$, which is true for paraxial rays, $\tan \theta \approx \theta$, $\tan 2 \theta \approx 2 \theta$. Therefore, Eq. (9.1) gives

$$ \begin{equation*} \frac{\mathrm{MD}}{\mathrm{FD}}=2 \frac{\mathrm{MD}}{\mathrm{CD}} \tag{9.2} \end{equation*} $$

or, $\mathrm{FD}=\frac{\mathrm{CD}}{2}$

Now, for small $\theta$, the point $D$ is very close to the point $P$. Therefore, $\mathrm{FD}=f$ and $\mathrm{CD}=R$. Equation (9.2) then gives $f=R / 2$

9.2.3 The mirror equation

If rays emanating from a point actually meet at another point after reflection and/or refraction, that point is called the image of the first point. The image is real if the rays actually converge to the point; it is virtual if the rays do not actually meet but appear to diverge from the point when produced backwards. An image is thus a point-to-point correspondence with the object established through reflection and/or refraction.

In principle, we can take any two rays emanating from a point on an object, trace their paths, find their point of intersection and thus, obtain the image of the point due to reflection at a spherical mirror. In practice, however, it is convenient to choose any two of the following rays:

(i) The ray from the point which is parallel to the principal axis. The reflected ray goes through the focus of the mirror.

(ii) The ray passing through the centre of curvature of a concave mirror or appearing to pass through it for a convex mirror. The reflected ray simply retraces the path.

(iii) The ray passing through (or directed towards) the focus of the concave mirror or appearing to pass through (or directed towards) the focus of a convex mirror. The reflected ray is parallel to the principal axis.

(iv) The ray incident at any angle at the pole. The reflected ray follows laws of reflection.

Figure 9.5 shows the ray diagram considering three rays. It shows the image $\mathrm{A}^{\prime} \mathrm{B}^{\prime}$ (in this case, real) of an object $\mathrm{AB}$ formed by a concave mirror. It does not mean that only three rays emanate from the point A. An infinite number of rays emanate from any source, in all directions. Thus, point $\mathrm{A}^{\prime}$ is image point of $\mathrm{A}$ if every ray originating at point $\mathrm{A}$ and falling on the concave mirror after reflection passes through the point $\mathrm{A}^{\prime}$.

We now derive the mirror equation or the relation between the object distance $(u)$, image distance $(v)$ and the focal length $(f)$.

From Fig. 9.5, the two right-angled triangles $\mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{F}$ and MPF are similar. (For paraxial rays, MP can be considered to be a straight line perpendicular to CP.) Therefore,

$$ \begin{align*} & \frac{\mathrm{B}^{\prime} \mathrm{A}^{\prime}}{\mathrm{PM}}=\frac{\mathrm{B}^{\prime} \mathrm{F}}{\mathrm{FP}} \\ & \text { or } \frac{\mathrm{B}^{\prime} \mathrm{A}^{\prime}}{\mathrm{BA}}=\frac{\mathrm{B}^{\prime} \mathrm{F}}{\mathrm{FP}}(\because \mathrm{PM}=\mathrm{AB}) \tag{9.4} \end{align*} $$

Since $\angle \mathrm{APB}=\angle \mathrm{A}^{\prime} \mathrm{PB}^{\prime}$, the right angled triangles $\mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{P}$ and $\mathrm{ABP}$ are also similar. Therefore,

$$ \begin{equation*} \frac{\mathrm{B}^{\prime} \mathrm{A}^{\prime}}{\mathrm{B} \mathrm{A}}=\frac{\mathrm{B}^{\prime} \mathrm{P}}{\mathrm{BP}} \tag{9.5} \end{equation*} $$

Comparing Eqs. (9.4) and (9.5), we get

$$ \begin{equation*} \frac{B^{\prime} F}{F P}=\frac{B^{\prime} P-F P}{F P}=\frac{B^{\prime} P}{B P} \tag{9.6} \end{equation*} $$

Equation (9.6) is a relation involving magnitude of distances. We now apply the sign convention. We note that light travels from the object to the mirror MPN. Hence this is taken as the positive direction. To reach the object $A B$, image $\mathrm{A}^{\prime} \mathrm{B}^{\prime}$ as well as the focus $\mathrm{F}$ from the pole $\mathrm{P}$, we have to travel opposite to the direction of incident light. Hence, all the three will have negative signs. Thus,

$$ \mathrm{B}^{\prime} \mathrm{P}=-v, \mathrm{FP}=-f, \mathrm{BP}=-u $$

Using these in Eq. (9.6), we get

$$ \frac{-v+f}{-f}=\frac{-v}{-u} $$

or $\frac{v-f}{f}=\frac{v}{u}$

$$ \frac{v}{f}=1+\frac{v}{u} $$

Dividing it by $v$, we get

$$ \begin{equation*} \frac{1}{v}+\frac{1}{u}=\frac{1}{f} \tag{9.7} \end{equation*} $$

This relation is known as the mirror equation.

The size of the image relative to the size of the object is another important quantity to consider. We define linear magnification $(m)$ as the ratio of the height of the image $\left(h^{\prime}\right)$ to the height of the object $(h)$ :

$$ \begin{equation*} m=\frac{h^{\prime}}{h} \tag{9.8} \end{equation*} $$

$h$ and $h^{\prime}$ will be taken positive or negative in accordance with the accepted sign convention. In triangles $\mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{P}$ and $\mathrm{ABP}$, we have,

$$ \frac{\mathrm{B}^{\prime} \mathrm{A}^{\prime}}{\mathrm{BA}}=\frac{\mathrm{B}^{\prime} \mathrm{P}}{\mathrm{BP}} $$

With the sign convention, this becomes

$$ \frac{-h^{\prime}}{h}=\frac{-v}{-u} $$

so that

$$ \begin{equation*} m=\frac{h^{\prime}}{h}=-\frac{v}{u} \tag{9.9} \end{equation*} $$

We have derived here the mirror equation, Eq. (9.7), and the magnification formula, Eq. (9.9), for the case of real, inverted image formed by a concave mirror. With the proper use of sign convention, these are, in fact, valid for all the cases of reflection by a spherical mirror (concave or convex) whether the image formed is real or virtual. Figure 9.6 shows the ray diagrams for virtual image formed by a concave and convex mirror. You should verify that Eqs. (9.7) and (9.9) are valid for these cases as well.

FIGURE 9.6 Image formation by (a) a concave mirror with object between $\mathrm{P}$ and $\mathrm{F}$, and (b) a convex mirror.

Example 9.1 Suppose that the lower half of the concave mirror’s reflecting surface in Fig. 9.6 is covered with an opaque (non-reflective) material. What effect will this have on the image of an object placed in front of the mirror?

Solution You may think that the image will now show only half of the object, but taking the laws of reflection to be true for all points of the remaining part of the mirror, the image will be that of the whole object. However, as the area of the reflecting surface has been reduced, the intensity of the image will be low (in this case, half).

Example 9.2 A mobile phone lies along the principal axis of a concave mirror, as shown in Fig. 9.7. Show by suitable diagram, the formation of its image. Explain why the magnification is not uniform. Will the distortion of image depend on the location of the phone with respect to the mirror?

FIGURE 9.7

Solution

The ray diagram for the formation of the image of the phone is shown in Fig. 9.7. The image of the part which is on the plane perpendicular to principal axis will be on the same plane. It will be of the same size, i.e., $B^{\prime} C=B C$. You can yourself realise why the image is distorted.

Example 9.3 An object is placed at (i) $10 \mathrm{~cm}$, (ii) $5 \mathrm{~cm}$ in front of a concave mirror of radius of curvature $15 \mathrm{~cm}$. Find the position, nature, and magnification of the image in each case.

Solution

The focal length $f=-15 / 2 \mathrm{~cm}=-7.5 \mathrm{~cm}$

(i) The object distance $u=-10 \mathrm{~cm}$. Then Eq. (9.7) gives

$$ \begin{aligned} & \frac{1}{v}+\frac{1}{-10}=\frac{1}{-7.5} \\ & \text { or } \quad v=\frac{10 \times 7.5}{-2.5}=-30 \mathrm{~cm} \end{aligned} $$

The image is $30 \mathrm{~cm}$ from the mirror on the same side as the object.

Also, magnification $m=-\frac{v}{u}=-\frac{(-30)}{(-10)}=-3$

The image is magnified, real and inverted.

(ii) The object distance $u=-5 \mathrm{~cm}$. Then from Eq. (9.7),

$$ \begin{aligned} & \frac{1}{v}+\frac{1}{-5}=\frac{1}{-7.5} \\ & \text { or } v=\frac{5 \times 7.5}{(7.5-5)}=15 \mathrm{~cm} \end{aligned} $$

This image is formed at $15 \mathrm{~cm}$ behind the mirror. It is a virtual image.

$$ \text { Magnification } m=-\frac{v}{u}=-\frac{15}{(-5)}=3 $$

The image is magnified, virtual and erect.

Example 9.4 Suppose while sitting in a parked car, you notice a jogger approaching towards you in the side view mirror of $R=2 \mathrm{~m}$. If the jogger is running at a speed of $5 \mathrm{~m} \mathrm{~s}^{-1}$, how fast the image of the jogger appear to move when the jogger is (a) $39 \mathrm{~m}$, (b) $29 \mathrm{~m}$, (c) $19 \mathrm{~m}$, and (d) 9 m away.

Solution

From the mirror equation, Eq. (9.7), we get $v=\frac{f u}{u-f}$

For convex mirror, since $R=2 \mathrm{~m}, f=1 \mathrm{~m}$. Then

for $u=-39 \mathrm{~m}, v=\frac{(-39) \times 1}{-39-1}=\frac{39}{40} \mathrm{~m}$

Since the jogger moves at a constant speed of $5 \mathrm{~m} \mathrm{~s}^{-1}$, after $1 \mathrm{~s}$ the position of the image $v$ (for $u=-39+5=-34$ ) is $(34 / 35) \mathrm{m}$.

The shift in the position of image in $1 \mathrm{~s}$ is

$$ \frac{39}{40}-\frac{34}{35}=\frac{1365-1360}{1400}=\frac{5}{1400}=\frac{1}{280} \mathrm{~m} $$

Therefore, the average speed of the image when the jogger is between $39 \mathrm{~m}$ and $34 \mathrm{~m}$ from the mirror, is $(1 / 280) \mathrm{m} \mathrm{s}^{-1}$

Similarly, it can be seen that for $u=-29 \mathrm{~m},-19 \mathrm{~m}$ and $-9 \mathrm{~m}$, the speed with which the image appears to move is

$$ \frac{1}{150} \mathrm{~m} \mathrm{~s}^{-1}, \frac{1}{60} \mathrm{~m} \mathrm{~s}^{-1} \text { and } \frac{1}{10} \mathrm{~m} \mathrm{~s}^{-1} \text {, respectively. } $$

Although the jogger has been moving with a constant speed, the speed of his/her image appears to increase substantially as he/she moves closer to the mirror. This phenomenon can be noticed by any person sitting in a stationary car or a bus. In case of moving vehicles, a similar phenomenon could be observed if the vehicle in the rear is moving closer with a constant speed.

9.3 Refraction

When a beam of light encounters another transparent medium, a part of light gets reflected back into the first medium while the rest enters the other. A ray of light represents a beam. The direction of propagation of an obliquely incident $\left(0^{\circ}<i<90^{\circ}\right)$ ray of light that enters the other medium, changes at the interface of the two media. This phenomenon is called refraction of light. Snell experimentally obtained the following laws of refraction:

(1)

FIGURE 9.8 Refraction and reflection of light. (i) The incident ray, the refracted ray and the normal to the interface at the point of incidence, all lie in the same plane.

(ii) The ratio of the sine of the angle of incidence to the sine of angle of refraction is constant. Remember that the angles of incidence $(i)$ and refraction $(r)$ are the angles that the incident and its refracted ray make with the normal, respectively. We have

$$ \begin{equation*} \frac{\sin i}{\sin r}=n_{21} \tag{9.10} \end{equation*} $$

where $n_{21}$ is a constant, called the refractive index of the second medium with respect to the first medium. Equation (9.10) is the well-known Snell’s law of refraction. We note that $n_{21}$ is a characteristic of the pair of media (and also depends on the wavelength of light), but is independent of the angle of incidence.

From Eq. (9.10), if $n_{21}>1, r<i$, i.e., the refracted ray bends towards the normal. In such a case medium 2 is said to be optically denser (or denser, in short) than medium 1 . On the other hand, if $n_{21}<1, r>i$, the refracted ray bends away from the normal. This is the case when incident ray in a denser medium refracts into a rarer medium.

Note: Optical density should not be confused with mass density, which is mass per unit volume. It is possible that mass density of an optically denser medium may be less than that of an optically rarer medium (optical density is the ratio of the speed of light in two media). For example, turpentine and water. Mass density of turpentine is less than that of water but its optical density is higher.

If $n_{21}$ is the refractive index of medium 2 with respect to medium 1 and $n_{12}$ the refractive index of medium 1 with respect to medium 2 , then it should be clear that

$$ \begin{equation*} n_{12}=\frac{1}{n_{21}} \tag{9.11} \end{equation*} $$

It also follows that if $n_{32}$ is the refractive index of medium 3 with respect to medium 2 then $n_{32}=$ $n_{31} \times n_{12}$, where $n_{31}$ is the refractive index of medium 3 with respect to medium 1.

Some elementary results based on the laws of refraction follow immediately. For a rectangular slab, refraction takes place at two interfaces (airglass and glass-air). It is easily seen from Fig. 9.9 that $r_{2}=i_{1}$, i.e., the emergent ray is parallel to the incident ray-there is no deviation, but it does suffer lateral displacement/shift with respect to the incident ray. Another familiar observation is that the bottom of a tank filled with water appears to be raised (Fig. 9.10). For viewing near the normal direction, it can be shown that the apparent depth $\left(h_{1}\right)$ is real depth $\left(h_{2}\right)$ divided by the refractive index of the medium (water).

9.4 Total Internal Reflection

When light travels from an optically denser medium to a rarer medium at the interface, it is partly reflected back into the same medium and partly refracted to the second medium. This reflection is called the internal reflection.

When a ray of light enters from a denser medium to a rarer medium, it bends away from the normal, for example, the ray $\mathrm{AO_1} \mathrm{~B}$ in Fig. 9.11. The incident ray $\mathrm{AO_1}$ is partially reflected $\left(\mathrm{O_1} \mathrm{C}\right)$ and partially transmitted $\left(\mathrm{O_1} \mathrm{~B}\right)$ or refracted, the angle of refraction $(r)$ being larger than the angle of incidence (i). As the angle of incidence increases, so does the angle of

FIGURE 9.11 Refraction and internal reflection of rays from a point $\mathrm{A}$ in the denser medium (water) incident at different angles at the interface with a rarer medium (air). refraction, till for the ray $\mathrm{AO_3}$, the angle of refraction is $\pi / 2$. The refracted ray is bent so much away from the normal that it grazes the surface at the interface between the two media. This is shown by the ray $\mathrm{AO_3} \mathrm{D}$ in Fig. 9.11. If the angle of incidence is increased still further (e.g., the ray $\mathrm{AO_4}$ ), refraction is not possible, and the incident ray is totally reflected. This is called total internal reflection. When light gets reflected by a surface, normally some fraction of it gets transmitted. The reflected ray, therefore, is always less intense than the incident ray, howsoever smooth the reflecting surface may be. In total internal reflection, on the other hand,

no transmission of light takes place.

The angle of incidence corresponding to an angle of refraction $90^{\circ}$, say $\angle \mathrm{AO_3} \mathrm{~N}$, is called the critical angle $\left(i_{c}\right)$ for the given pair of media. We see from Snell’s law [Eq. (9.10)] that if the relative refractive index of the refracting medium is less than one then, since the maximum value of sin $r$ is unity, there is an upper limit to the value of $\sin i$ for which the law can be satisfied, that is, $i=i_{c}$ such that

$$ \begin{equation*} \sin i_{c}=n_{21} \tag{9.12} \end{equation*} $$

For values of $i$ larger than $i_{c}$, Snell’s law of refraction cannot be satisfied, and hence no refraction is possible.

The refractive index of denser medium 1 with respect to rarer medium 2 will be $n_{12}=1 / \sin i_{c}$. Some typical critical angles are listed in Table 9.1.

Table 9.1 Critical angle of some transparent media with Respect to air

Substance medium	Refractive index	Critical angle
Water	1.33	48.75
Crown glass	1.52	41.14
Dense flint glass	1.62	37.31
Diamond	2.42	24.41

A demonstration for total internal reflection

All optical phenomena can be demonstrated very easily with the use of a laser torch or pointer, which is easily available nowadays. Take a glass beaker with clear water in it. Add a few drops of milk or any other suspension to water and stir so that water becomes a little turbid. Take a laser pointer and shine its beam through the turbid water. You will find that the path of the beam inside the water shines brightly.

Shine the beam from below the beaker such that it strikes at the upper water surface at the other end. Do you find that it undergoes partial reflection (which is seen as a spot on the table below) and partial refraction [which comes out in the air and is seen as a spot on the roof; Fig. 9.12(a)]? Now direct the laser beam from one side of the beaker such that it strikes the upper surface of water more obliquely [Fig. 9.12(b)]. Adjust the direction of laser beam until you find the angle for which the refraction above the water surface is totally absent and the beam is totally reflected back to water. This is total internal reflection at its simplest.

Pour this water in a long test tube and shine the laser light from top, as shown in Fig. 9.12(c). Adjust the direction of the laser beam such that it is totally internally reflected every time it strikes the walls of the tube. This is similar to what happens in optical fibres.

Take care not to look into the laser beam directly and not to point it at anybody’s face.

9.4.1 Total internal reflection in nature and its technelogical applications

(i) Prism: Prisms designed to bend light by $90^{\circ}$ or by $180^{\circ}$ make use of total internal reflection [Fig. 9.13(a) and (b)]. Such a prism is also used to invert images without chxanging their size [Fig. 9.13(c)].

In the first two cases, the critical angle $i_{c}$ for the material of the prism must be less than $45^{\circ}$. We see from Table 9.1 that this is true for both crown glass and dense flint glass.

(ii) Optical fibres: Nowadays optical fibres are extensively used for transmitting audio and video signals through long distances. Optical fibres too make use of the phenomenon of total internal reflection. Optical fibres are fabricated with high quality composite glass/quartz fibres. Each fibre consists of a core and cladding. The refractive index of the material of the core is higher than that of the cladding.

When a signal in the form of light is directed at one end of the fibre at a suitable angle, it undergoes repeated total internal reflections along the length of the fibre and finally comes out at the other end (Fig. 9.14). Since light undergoes total internal reflection at each stage, there is no appreciable loss in the intensity of the light signal. Optical fibres are fabricated such that light reflected at one side of inner surface strikes the other at an angle larger than the critical angle. Even if the fibre is bent, light can easily travel along its length. Thus, an optical fibre can be used to act as an optical pipe.

A bundle of optical fibres can be put to several uses. Optical fibres are extensively used for transmitting and receiving

FIGURE 9.12

Observing total internal reflection in water with a laser beam (refraction due to glass of beaker neglected being very thin).

FIGURE 9.13 Prisms designed to bend rays by $90^{\circ}$ and $180^{\circ}$ or to invert image without changing its size make use of total internal reflection.

231

FIGURE 9.14 Light undergoes successive total internal reflections as it moves through an optical fibre. electrical signals which are converted to light by suitable transducers. Obviously, optical fibres can also be used for transmission of optical signals. For example, these are used as a ’light pipe’ to facilitate visual examination of internal organs like esophagus, stomach and intestines. You might have seen a commonly available decorative lamp with fine plastic fibres with their free ends forming a fountain like structure. The other end of the fibres is fixed over an electric lamp. When the

lamp is switched on, the light travels from the bottom of each fibre and appears at the tip of its free end as a dot of light. The fibres in such decorative lamps are optical fibres.

The main requirement in fabricating optical fibres is that there should be very little absorption of light as it travels for long distances inside them. This has been achieved by purification and special preparation of materials such as quartz. In silica glass fibres, it is possible to transmit more than $95 %$ of the light over a fibre length of $1 \mathrm{~km}$. (Compare with what you expect for a block of ordinary window glass $1 \mathrm{~km}$ thick.)

9.5 Refraction at Spherical Surfaces And By Lenses

We have so far considered refraction at a plane interface. We shall now consider refraction at a spherical interface between two transparent media. An infinitesimal part of a spherical surface can be regarded as planar and the same laws of refraction can be applied at every point on the surface. Just as for reflection by a spherical mirror, the normal at the point of incidence is perpendicular to the tangent plane to the spherical surface at that point and, therefore, passes through its centre of curvature. We first consider refraction by a single spherical surface and follow it by thin lenses. A thin lens is a transparent optical medium bounded by two surfaces; at least one of which should be spherical. Applying the formula for image formation by a single spherical surface successively at the two surfaces of a lens, we shall obtain the lens maker’s formula and then the lens formula.

9.5.1 Refraction at a spherical surface

Figure 9.15 shows the geometry of formation of image $I$ of an object $O$ on the principal axis of a spherical surface with centre of curvature $\mathrm{C}$, and radius of curvature $R$. The rays are incident from a medium of refractive index $n_{1}$, to another of refractive index $n_{2}$. As before, we take the aperture (or the lateral size) of the surface to be small compared to other distances involved, so that small angle approximation can be made. In particular, NM will be taken to be nearly equal to the length of the perpendicular from the point $\mathrm{N}$ on the principal axis. We have, for small angles,

$$ \tan \angle \mathrm{NOM}=\frac{\mathrm{MN}}{\mathrm{OM}} $$

$$ \begin{aligned} & \tan \angle \mathrm{NCM}=\frac{\mathrm{MN}}{\mathrm{MC}} \\ & \tan \angle \mathrm{NIM}=\frac{\mathrm{MN}}{\mathrm{MI}} \end{aligned} $$

Now, for $\triangle \mathrm{NOC}, i$ is the exterior angle. Therefore, $i$ $=\angle \mathrm{NOM}+\angle \mathrm{NCM}$

$$ \begin{equation*} i=\frac{\mathrm{MN}}{\mathrm{OM}}+\frac{\mathrm{MN}}{\mathrm{MC}} \tag{9.13} \end{equation*} $$

Similarly,

$$ r=\angle \mathrm{NCM}-\angle \mathrm{NIM} $$

i.e., $r=\frac{\mathrm{MN}}{\mathrm{MC}}-\frac{\mathrm{MN}}{\mathrm{MI}}$

Now, by Snell’s law

$$ n_{1} \sin i=n_{2} \sin r $$

or for small angles

$$ n_{1} i=n_{2} r $$

Substituting $i$ and $r$ from Eqs. (9.13) and (9.14), we get

$$ \frac{n_{1}}{\mathrm{OM}}+\frac{n_{2}}{\mathrm{MI}}=\frac{n_{2}-n_{1}}{\mathrm{MC}} $$

FIGURE 9.15 Refraction at a spherical surface separating two media.

Here, OM, MI and MC represent magnitudes of distances. Applying the Cartesian sign convention,

$$ \mathrm{OM}=-u, \mathrm{MI}=+v, \mathrm{MC}=+R $$

Substituting these in Eq. (9.15), we get

$$ \begin{equation*} \frac{n_{2}}{v}-\frac{n_{1}}{u}=\frac{n_{2}-n_{1}}{R} \tag{9.16} \end{equation*} $$

Equation (9.16) gives us a relation between object and image distance in terms of refractive index of the medium and the radius of curvature of the curved spherical surface. It holds for any curved spherical surface.

Example 9.5 Light from a point source in air falls on a spherical glass surface ( $n=1.5$ and radius of curvature $=20 \mathrm{~cm}$ ). The distance of the light source from the glass surface is $100 \mathrm{~cm}$. At what position the image is formed?

Solution

We use the relation given by Eq. (9.16). Here $u=-100 \mathrm{~cm}, v=?, R=+20 \mathrm{~cm}, n_{1}=1$, and $n_{2}=1.5$.

We then have

$\frac{1.5}{v}+\frac{1}{100}=\frac{0.5}{20}$

or $v=+100 \mathrm{~cm}$

The image is formed at a distance of $100 \mathrm{~cm}$ from the glass surface, in the direction of incident light.

9.5.2 Refraction by a lens

Figure 9.16(a) shows the geometry of image formation by a double convex lens. The image formation can be seen in terms of two steps: (i) The first refracting surface forms the image $I_{1}$ of the object $O$ [Fig. 9.16(b)]. The image $I_{1}$ acts as a virtual object for the second surface that forms the image at I [Fig. 9.16(c)]. Applying Eq. (9.15) to the first interface $A B C$, we get

$$ \begin{equation*} \frac{n_{1}}{\mathrm{OB}}+\frac{n_{2}}{\mathrm{BI_1}}=\frac{n_{2}-n_{1}}{\mathrm{BC_1}} \tag{9.17} \end{equation*} $$

FIGURE 9.16 (a) The position of object, and the image formed by a double convex lens,

(b) Refraction at the first spherical surface and

(c) Refraction at the second spherical surface. A similar procedure applied to the second interface* $\mathrm{ADC}$ gives,

$$ \begin{equation*} -\frac{n_{2}}{\mathrm{DI_1}}+\frac{n_{1}}{\mathrm{DI}}=\frac{n_{2}-n_{1}}{\mathrm{DC_2}} \tag{9.18} \end{equation*} $$

For a thin lens, $\mathrm{BI_1}=\mathrm{DI_1}$. Adding Eqs. (9.17) and (9.18), we get

$$ \begin{equation*} \frac{n_{1}}{\mathrm{OB}}+\frac{n_{1}}{\mathrm{DI}}=\left(n_{2}-n_{1}\right) \frac{1}{\mathrm{BC_1}}+\frac{1}{\mathrm{DC_2}} \tag{9.19} \end{equation*} $$

Suppose the object is at infinity, i.e., $\mathrm{OB} \rightarrow \infty$ and $\mathrm{DI}=f$, Eq. (9.19) gives

$\frac{n_{1}}{f}=\left(n_{2}-n_{1}\right) \quad \frac{1}{\mathrm{BC_1}}+\frac{1}{\mathrm{DC_2}}$

The point where image of an object placed at infinity is formed is called the focus $\mathrm{F}$, of the lens and the distance $f$ gives its focal length. A lens has two foci, $\mathrm{F}$ and $\mathrm{F}^{\prime}$, on either side of it (Fig. 9.16). By the sign convention,

$$ \begin{aligned} & \mathrm{BC_1}=+R_{1}, \\ & \mathrm{DC_2}=-R_{2} \end{aligned} $$

So Eq. (9.20) can be written as

$\frac{1}{f}=\left(n_{21}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right) \quad\left(\because n_{21}=\frac{n_{2}}{n_{1}}\right)$

Equation (9.21) is known as the lens maker’s formula. It is useful to design lenses of desired focal length using surfaces of suitable radii of curvature. Note that the formula is true for a concave lens also. In that case $R_{1}$ is negative, $R_{2}$ positive and therefore, $f$ is negative.

• Note that now the refractive index of the medium on the right side of ADC is $n_{1}$ while on its left it is $n_{2}$. Further $\mathrm{DI_1}$ is negative as the distance is measured against the direction of incident light.

From Eqs. (9.19) and (9.20), we get

$$ \begin{equation*} \frac{n_{1}}{\mathrm{OB}}+\frac{n_{1}}{\mathrm{DI}}=\frac{n_{1}}{f} \tag{9.22} \end{equation*} $$

Again, in the thin lens approximation, B and D are both close to the optical centre of the lens. Applying the sign convention,

$\mathrm{BO}=-u, \mathrm{DI}=+v$, we get

$\frac{1}{v}-\frac{1}{u}=\frac{1}{f}$

Equation (9.23) is the familiar thin lens formula. Though we derived it for a real image formed by a convex lens, the formula is valid for both convex as well as concave lenses and for both real and virtual images.

It is worth mentioning that the two foci, $\mathrm{F}$ and $\mathrm{F}^{\prime}$, of a double convex or concave lens are equidistant from the optical centre. The focus on the side of the (original) source of light is called the first focal point, whereas the other is called the second focal point.

To find the image of an object by a lens, we can, in principle, take any two rays emanating from a point on an object; trace their paths using the laws of refraction and find the point where the refracted rays meet (or appear to meet). In practice, however, it is convenient to choose any two of the following rays:

(i) A ray emanating from the object parallel to the principal axis of the lens after refraction passes through the second principal focus $\mathrm{F}^{\prime}$ (in a convex lens) or appears to diverge (in a concave lens) from the first principal focus $\mathrm{F}$.

(ii) A ray of light, passing through the optical centre of the lens, emerges without any deviation after refraction.

(iii) (a) A ray of light passing through the first principal focus of a convex lens [Fig. 9.17(a)] emerges parallel to the principal axis after refraction.

(b) A ray of light incident on a concave lens appearing to meet the principal axis at second focus point emerges parallel to the principal axis after refraction [Fig. 9.17(b)].

Figures 9.17(a) and (b) illustrate these rules for a convex and a concave lens, respectively. You should practice drawing similar ray diagrams for different positions of the object with respect to the lens and also verify that the lens formula, Eq. (9.23), holds good for all cases.

Here again it must be remembered that each point on an object gives out infinite number of rays. All these rays will pass through the same image point after refraction at the lens.

Magnification $(m)$ produced by a lens is defined, like that for a mirror, as the ratio of the

FIGURE 9.17 Tracing rays through (a) convex lens (b) concave lens. in the same way as for spherical mirrors, it is easily seen that for a lens

$$ \begin{equation*} \mathrm{m}=\frac{h^{\prime}}{h}=\frac{v}{u} \tag{9.24} \end{equation*} $$

When we apply the sign convention, we see that, for erect (and virtual) image formed by a convex or concave lens, $m$ is positive, while for an inverted (and real) image, $m$ is negative.

Example 9.6 A magician during a show makes a glass lens with $n=1.47$ disappear in a trough of liquid. What is the refractive index of the liquid? Could the liquid be water?

Solution

The refractive index of the liquid must be equal to 1.47 in order to make the lens disappear. This means $n_{1}=n_{2}$. This gives $1 / f=0$ or $f \rightarrow \infty$. The lens in the liquid will act like a plane sheet of glass. No, the liquid is not water. It could be glycerine.

FIGURE 9.18 Power of a lens.

9.5.3 Power of a lens

Power of a lens is a measure of the convergence or divergence, which a lens introduces in the light falling on it. Clearly, a lens of shorter focal length bends the incident light more, while converging it in case of a convex lens and diverging it in case of a concave lens. The power $P$ of a lens is defined as the tangent of the angle by which it converges or diverges a beam of light parallel to the principal axis falling at unit distance from the optical centre (Fig. 9.18).

$$ \tan \delta=\frac{h}{f} ; \text { if } h=1, \quad \tan \delta=\frac{1}{f} \quad \text { or } \delta=\frac{1}{f} \quad \text { for small } $$

value of $\delta$. Thus,

$$ \begin{equation*} P=\frac{1}{f} \tag{9.25} \end{equation*} $$

The SI unit for power of a lens is dioptre (D): $1 \mathrm{D}=1 \mathrm{~m}^{-1}$. The power of a lens of focal length of 1 metre is one dioptre. Power of a lens is positive for a converging lens and negative for a diverging lens. Thus, when an optician prescribes a corrective lens of power +2.5 D, the required lens is a convex lens of focal length $+40 \mathrm{~cm}$. A lens of power of $-4.0 \mathrm{D}$ means a concave lens of focal length $-25 \mathrm{~cm}$.

Example 9.7 (i) If $f=0.5 \mathrm{~m}$ for a glass lens, what is the power of the lens? (ii) The radii of curvature of the faces of a double convex lens are $10 \mathrm{~cm}$ and $15 \mathrm{~cm}$. Its focal length is $12 \mathrm{~cm}$. What is the refractive index of glass? (iii) A convex lens has $20 \mathrm{~cm}$ focal length in air. What is focal length in water? (Refractive index of air-water $=1.33$, refractive index for air-glass $=1.5$.)

Solution

(i) Power $=+2$ dioptre.

(ii) Here, we have $f=+12 \mathrm{~cm}, R_{1}=+10 \mathrm{~cm}, R_{2}=-15 \mathrm{~cm}$.

Refractive index of air is taken as unity.

We use the lens formula of Eq. (9.22). The sign convention has to be applied for $f, R_{1}$ and $R_{2}$.

Substituting the values, we have

$\frac{1}{12}=(n-1) \quad \frac{1}{10}-\frac{1}{-15}$

This gives $n=1.5$.

(iii) For a glass lens in air, $n_{2}=1.5, n_{1}=1, f=+20 \mathrm{~cm}$. Hence, the lens formula gives

$\frac{1}{20}=0.5 \frac{1}{R_{1}}-\frac{1}{R_{2}}$

For the same glass lens in water, $n_{2}=1.5, n_{1}=1.33$. Therefore,

$$ \begin{equation*} \frac{1.33}{f}=(1.5-1.33) \frac{1}{R_{1}}-\frac{1}{R_{2}} \tag{9.26} \end{equation*} $$

Combining these two equations, we find $f=+78.2 \mathrm{~cm}$.

9.5.4 Combination of thin lenses in contact

Consider two lenses $\mathrm{A}$ and $\mathrm{B}$ of focal length $f_{1}$ and $f_{2}$ placed in contact with each other. Let the object be placed at a point $\mathrm{O}$ beyond the focus of the first lens A (Fig. 9.19). The first lens produces an image at $I_{1}$. Since image $I_{1}$ is real, it serves as a virtual object for the second lens B, producing the final image at I. It must, however, be borne in mind that formation of image by the first lens is presumed only to facilitate determination of the position of the final image. In fact, the direction of rays emerging from the first lens gets modified in accordance with

FIGURE 9.19 Image formation by a combination of two thin lenses in contact. the angle at which they strike the second lens. Since the lenses are thin, we assume the optical centres of the lenses to be coincident. Let this central point be denoted by $P$.

For the image formed by the first lens $\mathrm{A}$, we get

$$ \begin{equation*} \frac{1}{v_{1}}-\frac{1}{u}=\frac{1}{f_{1}} \tag{9.27} \end{equation*} $$

For the image formed by the second lens B, we get

$$ \begin{equation*} \frac{1}{v}-\frac{1}{v_{1}}=\frac{1}{f_{2}} \tag{9.28} \end{equation*} $$

Adding Eqs. (9.27) and (9.28), we get

$$ \begin{equation*} \frac{1}{v}-\frac{1}{u}=\frac{1}{f_{1}}+\frac{1}{f_{2}} \tag{9.29} \end{equation*} $$

If the two lens-system is regarded as equivalent to a single lens of focal length $f$, we have

$$ \frac{1}{v}-\frac{1}{u}=\frac{1}{f} $$

so that we get

$$ \begin{equation*} \frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}} \tag{9.30} \end{equation*} $$

The derivation is valid for any number of thin lenses in contact. If several thin lenses of focal length $f_{1}, f_{2}, f_{3}, \ldots$ are in contact, the effective focal length of their combination is given by

$$ \begin{equation*} \frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}+\frac{1}{f_{3}}+\ldots \tag{9.31} \end{equation*} $$

In terms of power, Eq. (9.31) can be written as

$$ \begin{equation*} P=P_{1}+P_{2}+P_{3}+\ldots \tag{9.32} \end{equation*} $$

where $P$ is the net power of the lens combination. Note that the sum in Eq. (9.32) is an algebraic sum of individual powers, so some of the terms on the right side may be positive (for convex lenses) and some negative (for concave lenses). Combination of lenses helps to obtain diverging or converging lenses of desired magnification. It also enhances sharpness of the image. Since the image formed by the first lens becomes the object for the second, Eq. (9.25) implies that the total magnification $m$ of the combination is a product of magnification $\left(m_{1}, m_{2}, m_{3}, \ldots\right)$ of individual lenses

$$ \begin{equation*} m=m_{1} m_{2} m_{3} \ldots \tag{9.33} \end{equation*} $$

Such a system of combination of lenses is commonly used in designing lenses for cameras, microscopes, telescopes and other optical instruments.

Example 9.8 Find the position of the image formed by the lens combination given in the Fig. 9.20.

FIGURE 9.20

Solution Image formed by the first lens

$$ \frac{1}{v_{1}}-\frac{1}{u_{1}}=\frac{1}{f_{1}} $$

$\frac{1}{v_{1}}-\frac{1}{-30}=\frac{1}{10}$

or $v_{1}=15 \mathrm{~cm}$

$$ \text { or } \quad v_{1}=15 \mathrm{~cm} $$

The image formed by the first lens serves as the object for the second. This is at a distance of $(15-5) \mathrm{cm}=10 \mathrm{~cm}$ to the right of the second lens. Though the image is real, it serves as a virtual object for the second lens, which means that the rays appear to come from it for the second lens.

$\frac{1}{v_{2}}-\frac{1}{10}=\frac{1}{-10}$

or $v_{2}=\infty$

The virtual image is formed at an infinite distance to the left of the second lens. This acts as an object for the third lens.

$\frac{1}{v_{3}}-\frac{1}{u_{3}}=\frac{1}{f_{3}}$

or $\frac{1}{v_{3}}=\frac{1}{\infty}+\frac{1}{30}$

or $v_{3}=30 \mathrm{~cm}$

The final image is formed $30 \mathrm{~cm}$ to the right of the third lens.

9.6 Refraction through a Prism

Figure 9.21 shows the passage of light through a triangular prism $\mathrm{ABC}$. The angles of incidence and refraction at the first face $\mathrm{AB}$ are $i$ and $r_{1}$, while the angle of incidence (from glass to air) at the second face $\mathrm{AC}$ is $r_{2}$ and the angle of refraction or emergence $e$. The angle between the emergent ray $\mathrm{RS}$ and the direction of the incident ray $\mathrm{PQ}$ is called the angle of deviation, $\delta$.

In the quadrilateral AQNR, two of the angles (at the vertices $\mathrm{Q}$ and $\mathrm{R}$ ) are right angles. Therefore, the sum of the other angles of the quadrilateral is $180^{\circ}$.

$\angle A+\angle \mathrm{QNR}=180^{\circ}$

FIGURE 9.21 A ray of light passing through a triangular glass prism.

From the triangle $\mathrm{QNR}$,

$$ r_{1}+r_{2}+\angle \mathrm{QNR}=180^{\circ} $$

Comparing these two equations, we get

$$ \begin{equation*} r_{1}+r_{2}=A \tag{9.34} \end{equation*} $$

The total deviation $\delta$ is the sum of deviations at the two faces,

$$ \delta=\left(i-r_{1}\right)+\left(e-r_{2}\right) $$

that is,

$$ \begin{equation*} \delta=i+e-A \tag{9.35} \end{equation*} $$

Thus, the angle of deviation depends on the angle of incidence. A plot between the angle of deviation and angle of incidence is shown in Fig. 9.22. You can see that, in general, any given value of $\delta$, except for $i=e$, corresponds to two values $i$ and hence of $e$. This, in fact, is expected from the symmetry of $i$ and $e$ in Eq. (9.35), i.e., $\delta$ remains the same if $i$

FIGURE 9.22 Plot of angle of deviation ( $\delta$ ) versus angle of incidence $(i)$ for a triangular prism. and $e$ are interchanged. Physically, this is related to the fact that the path of ray in Fig. 9.21 can be traced back, resulting in the same angle of deviation. At the minimum deviation $D_{m}$, the refracted ray inside the prism becomes parallel to its base. We have

$$ \delta=D_{m}, i=e \text { which implies } r_{1}=r_{2} $$

Equation (9.34) gives

$$ \begin{equation*} 2 r=A \text { or } r=\frac{A}{2} \tag{9.36} \end{equation*} $$

In the same way, Eq. (9.35) gives

$$ \begin{equation*} D_{\mathrm{m}}=2 i-A, \text { or } i=\left(A+D_{\mathrm{m}}\right) / 2 \tag{9.37} \end{equation*} $$

The refractive index of the prism is

$$ \begin{equation*} n_{21}=\frac{n_{2}}{n_{1}}=\frac{\sin \left[\left(A+D_{m}\right) / 2\right]}{\sin [A / 2]} \tag{9.38} \end{equation*} $$

The angles $A$ and $D_{m}$ can be measured experimentally. Equation (9.38) thus provides a method of determining refractive index of the material of the prism.

For a small angle prism, i.e., a thin prism, $D_{m}$ is also very small, and we get

$$ \begin{aligned} & n_{21}=\frac{\sin \left[\left(A+D_{m}\right) / 2\right]}{\sin [A / 2]} \simeq \frac{\left(A+D_{m}\right) / 2}{A / 2} \\ & D_{m}=\left(n_{21}-1\right) A \end{aligned} $$

It implies that, thin prisms do not deviate light much.

9.7 OPTICAL INSTRUMENTS

A number of optical devices and instruments have been designed utilising reflecting and refracting properties of mirrors, lenses and prisms. Periscope, kaleidoscope, binoculars, telescopes, microscopes are some examples of optical devices and instruments that are in common use. Our eye is, of course, one of the most important optical device the nature has endowed us with. We have already studied about the human eye in Class X. We now go on to describe the principles of working of the microscope and the telescope.

9.7.1 The microscope

A simple magnifier or microscope is a converging lens of small focal length (Fig. 9.23). In order to use such a lens as a microscope, the lens is held near the object, one focal length away or less, and the eye is positioned close to the lens on the other side. The idea is to get an erect, magnified and virtual image of the object at a distance so that it can be viewed comfortably, i.e., at $25 \mathrm{~cm}$ or more. If the object is at a distance $f$, the

Eye focussed at infinity

FIGURE 9.23 A simple microscope; (a) the magnifying lens is located such that the image is at the near point, (b) the angle subtanded by the object, is the same as that at the near point, and (c) the object near the focal point of the lens; the image is far off but closer than infinity.

than the focal length of the lens, the image is virtual and closer than infinity. Although the closest comfortable distance for viewing the image is when it is at the near point (distance $D \cong 25 \mathrm{~cm}$ ), it causes some strain on the eye. Therefore, the image formed at infinity is often considered most suitable for viewing by the relaxed eye. We show both cases, the first in Fig. 9.23(a), and the second in Fig. 9.23(b) and (c).

The linear magnification $m$, for the image formed at the near point $D$, by a simple microscope can be obtained by using the relation

$$ m=\frac{v}{u}=v \frac{1}{v}-\frac{1}{f}=1-\frac{v}{f} $$

Now according to our sign convention, $v$ is negative, and is equal in magnitude to $D$. Thus, the magnification is

$$ \begin{equation*} m=1+\frac{D}{f} \tag{9.39} \end{equation*} $$

Since $D$ is about $25 \mathrm{~cm}$, to have a magnification of six, one needs a convex lens of focal length, $f=5 \mathrm{~cm}$.

Note that $m=h^{\prime} / h$ where $h$ is the size of the object and $h^{\prime}$ the size of the image. This is also the ratio of the angle subtended by the image to that subtended by the object, if placed at $D$ for comfortable viewing. (Note that this is not the angle actually subtended by the object at the eye, which is $h / u$.) What a single-lens simple magnifier achieves is that it allows the object to be brought closer to the eye than $D$.

We will now find the magnification when the image is at infinity. In this case we will have to obtained the angular magnification. Suppose the object has a height $h$. The maximum angle it can subtend, and be clearly visible (without a lens), is when it is at the near point, i.e., a distance $D$. The angle subtended is then given by

$$ \begin{equation*} \tan \theta_{o}=\frac{h}{D} \approx \theta_{o} \tag{9.40} \end{equation*} $$

We now find the angle subtended at the eye by the image when the object is at $u$. From the relations

$$ \frac{h^{\prime}}{h}=m=\frac{v}{u} $$

we have the angle subtended by the image

$\tan \theta_{i}=\frac{h^{\prime}}{-v}=\frac{h}{-v} \cdot \frac{v}{u}=\frac{h}{-u} \approx \theta$. The angle subtended by the object, when it is at $u=-f$.

$$ \begin{equation*} \theta_{i}=\frac{h}{f} \tag{9.41} \end{equation*} $$

as is clear from Fig. 9.23(c). The angular magnification is, therefore

$$ \begin{equation*} m=\frac{\theta_{i}}{\theta_{o}}=\frac{D}{f} \tag{9.42} \end{equation*} $$

This is one less than the magnification when the image is at the near point, Eq. (9.39), but the viewing is more comfortable and the difference in magnification is usually small. In subsequent discussions of optical instruments (microscope and telescope) we shall assume the image to be at infinity.

FIGURE 9.24 Ray diagram for the formation of image by a compound microscope.

A simple microscope has a limited maximum magnification $(\leq)$ for realistic focal lengths. For much larger magnifications, one uses two lenses, one compounding the effect of the other. This is known as a compound microscope. A schematic diagram of a compound microscope is shown in Fig. 9.24. The lens nearest the object, called the objective, forms a real, inverted, magnified image of the object. This serves as the object for the second lens, the eyepiece, which functions essentially like a simple microscope or magnifier, produces the final image, which is enlarged and virtual. The first inverted image is thus near (at or within) the focal plane of the eyepiece, at a distance appropriate for final image formation at infinity, or a little closer for image formation at the near point. Clearly, the final image is inverted with respect to the original object.

We now obtain the magnification due to a compound microscope. The ray diagram of Fig. 9.24 shows that the (linear) magnification due to the objective, namely $h^{\prime} / h$, equals

$$ \begin{equation*} m_{O}=\frac{h^{\prime}}{h}=\frac{L}{f_{o}} \tag{9.43} \end{equation*} $$

where we have used the result

$$ \tan \beta=\frac{h}{f_{o}}=\frac{h^{\prime}}{L} $$

Here $h^{\prime}$ is the size of the first image, the object size being $h$ and $f_{o}$ being the focal length of the objective. The first image is formed near the focal point of the eyepiece. The distance $L$, i.e., the distance between the second focal point of the objective and the first focal point of the eyepiece (focal length $f_{e}$ ) is called the tube length of the compound microscope.

As the first inverted image is near the focal point of the eyepiece, we use the result from the discussion above for the simple microscope to obtain the (angular) magnification $m_{e}$ due to it [Eq. (9.39)], when the final image is formed at the near point, is

$$ \begin{equation*} m_{e}=1+\frac{D}{f_{e}} \tag{a} \end{equation*} $$

When the final image is formed at infinity, the angular magnification due to the eyepiece [Eq. (9.42)] is

$$ \begin{equation*} m_{e}=\left(D / f_{e}\right) \tag{b} \end{equation*} $$

Thus, the total magnification [according to Eq. (9.33)], when the image is formed at infinity, is

$$ \begin{equation*} m=m_{o} m_{e}=\frac{L}{f_{o}} \quad \frac{D}{f_{e}} \tag{9.45} \end{equation*} $$

Clearly, to achieve a large magnification of a small object (hence the name microscope), the objective and eyepiece should have small focal lengths. In practice, it is difficult to make the focal length much smaller than $1 \mathrm{~cm}$. Also large lenses are required to make L large.

For example, with an objective with $f_{o}=1.0 \mathrm{~cm}$, and an eyepiece with focal length $f_{e}=2.0 \mathrm{~cm}$, and a tube length of $20 \mathrm{~cm}$, the magnification is

$$ \begin{aligned} m=m_{o} m_{e}= & \frac{L}{f_{o}} \quad \frac{D}{f_{e}} \\ & =\frac{20}{1} \times \frac{25}{2}=250 \end{aligned} $$

Various other factors such as illumination of the object, contribute to the quality and visibility of the image. In modern microscopes, multicomponent lenses are used for both the objective and the eyepiece to improve image quality by minimising various optical aberrations (defects) in lenses.

9.7.2 Telescope

The telescope is used to provide angular magnification of distant objects (Fig. 9.25). It also has an objective and an eyepiece. But here, the objective has a large focal length and a much larger aperture than the eyepiece. Light from a distant object enters the objective and a real image is formed in the tube at its second focal point. The eyepiece magnifies this image producing a final inverted image. The magnifying power $m$ is the ratio of the angle $\beta$ subtended at the eye by the final image to the angle $\alpha$ which the object subtends at the lens or the eye. Hence

$$ \begin{equation*} m \approx \frac{\beta}{\alpha} \approx \frac{h}{f_{e}} \cdot \frac{f_{o}}{h}=\frac{f_{o}}{f_{e}} \tag{9.46} \end{equation*} $$

In this case, the length of the telescope tube is $f_{o}+f_{e}$.

Terrestrial telescopes have, in addition, a pair of inverting lenses to make the final image erect. Refracting telescopes can be used both for terrestrial and astronomical observations. For example, consider a telescope whose objective has a focal length of $100 \mathrm{~cm}$ and the eyepiece a focal length of $1 \mathrm{~cm}$. The magnifying power of this telescope is $\mathrm{m}=100 / 1=100$.

Let us consider a pair of stars of actual separation 1’ (one minute of arc). The stars appear as though they are separated by an angle of $100 \times$ $1^{\prime}=100^{\prime}=1.67^{\circ}$.

FIGURE 9.25 A refracting telescope.

The main considerations with an astronomical telescope are its light gathering power and its resolution or resolving power. The former clearly depends on the area of the objective. With larger diameters, fainter objects can be observed. The resolving power, or the ability to observe two objects distinctly, which are in very nearly the same direction, also depends on the diameter of the objective. So, the desirable aim in optical telescopes is to make them with objective of large diameter. The largest lens objective in use has a diameter of $40 \mathrm{inch}(\sim 1.02 \mathrm{~m})$. It is at the Yerkes Observatory in Wisconsin, USA. Such big lenses tend to be very heavy and therefore, difficult to make and support by their edges. Further, it is rather difficult and expensive to make such large sized lenses which form images that are free from any kind of chromatic aberration and distortions.

For these reasons, modern telescopes use a concave mirror rather than a lens for the objective. Telescopes with mirror objectives are called reflecting telescopes. There is no chromatic aberration in a mirror. Mechanical support is much less of a problem since a mirror weighs much less than a lens of equivalent optical quality, and can be supported over its entire back surface, not just over its rim. One obvious problem with a reflecting telescope is that the objective mirror focusses light inside

FIGURE 9.26 Schematic diagram of a reflecting telescope (Cassegrain).

the telescope tube. One must have an eyepiece and the observer right there, obstructing some light (depending on the size of the observer cage). This is what is done in the very large 200 inch ( 5.08 m) diameters, Mt. Palomar telescope, California. The viewer sits near the focal point of the mirror, in a small cage. Another solution to the problem is to deflect the light being focussed by another mirror. One such arrangement using a convex secondary mirror to focus the incident light, which now passes through a hole in the objective primary mirror, is shown in Fig. 9.26. This is known as a Cassegrain telescope, after its inventor. It has the advantages of a large focal length in a short telescope. The largest telescope in India is in Kavalur, Tamil Nadu. It is a $2.34 \mathrm{~m}$ diameter reflecting telescope (Cassegrain). It was ground, polished, set up, and is being used by the Indian Institute of Astrophysics, Bangalore. The largest reflecting telescopes in the world are the pair of Keck telescopes in Hawaii, USA, with a reflector of 10 metre in diameter.

SUMMARY

1. Reflection is governed by the equation $\angle i=\angle r^{\prime}$ and refraction by the Snell’s law, $\sin i / \sin r=n$, where the incident ray, reflected ray, refracted ray and normal lie in the same plane. Angles of incidence, reflection and refraction are $i, r^{\prime}$ and $r$, respectively.

2. The critical angle of incidence $i_{c}$ for a ray incident from a denser to rarer medium, is that angle for which the angle of refraction is $90^{\circ}$. For $i>i_{c}$, total internal reflection occurs. Multiple internal reflections in diamond $\left(i_{c} \cong 24.4^{\circ}\right)$, totally reflecting prisms and mirage, are some examples of total internal reflection. Optical fibres consist of glass fibres coated with a thin layer of material of lower refractive index. Light incident at an angle at one end comes out at the other, after multiple internal reflections, even if the fibre is bent.

3. Cartesian sign convention: Distances measured in the same direction as the incident light are positive; those measured in the opposite direction are negative. All distances are measured from the pole/optic centre of the mirror/lens on the principal axis. The heights measured upwards above $x$-axis and normal to the principal axis of the mirror/ lens are taken as positive. The heights measured downwards are taken as negative.

4. Mirror equation:

$\frac{1}{v}+\frac{1}{u}=\frac{1}{f}$

where $u$ and $v$ are object and image distances, respectively and $f$ is the focal length of the mirror. $f$ is (approximately) half the radius of curvature R. $f$ is negative for concave mirror; $f$ is positive for a convex mirror.

5. For a prism of the angle $A$, of refractive index $n_{2}$ placed in a medium of refractive index $n_{1}$,

$n_{21}=\frac{n_{2}}{n_{1}}=\frac{\sin \left(A+D_{m}\right) / 2}{\sin (A / 2)}$

where $D_{m}$ is the angle of minimum deviation.

6. For refraction through a spherical interface (from medium 1 to 2 of refractive index $n_{1}$ and $n_{2}$, respectively)

$\frac{n_{2}}{v}-\frac{n_{1}}{u}=\frac{n_{2}-n_{1}}{R}$

Thin lens formula

$\frac{1}{v}-\frac{1}{u}=\frac{1}{f}$

Lens maker’s formula

$\frac{1}{f}=\frac{\left(n_{2}-n_{1}\right)}{n_{1}} \frac{1}{R_{1}}-\frac{1}{R_{2}}$

$R_{1}$ and $R_{2}$ are the radii of curvature of the lens surfaces. $f$ is positive for a converging lens; $f$ is negative for a diverging lens. The power of a lens $P=1 / f$.

The SI unit for power of a lens is dioptre (D): $1 \mathrm{D}=1 \mathrm{~m}^{-1}$.

If several thin lenses of focal length $f_{1}, f_{2}, f_{3}, \ldots$ are in contact, the effective focal length of their combination, is given by

$\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}+\frac{1}{f_{3}}+\ldots$

The total power of a combination of several lenses is $P=P_{1}+P_{2}+P_{3}+\ldots$

7. Dispersion is the splitting of light into its constituent colour.

8. Magnifying power $m$ of a simple microscope is given by $m=1+(D / f)$, where $D=25 \mathrm{~cm}$ is the least distance of distinct vision and $f$ is the focal length of the convex lens. If the image is at infinity, $m=D / f$. For a compound microscope, the magnifying power is given by $m=m_{e} \times m_{0}$ where $m_{e}=1+\left(D / f_{e}\right)$, is the magnification due to the eyepiece and $m_{o}$ is the magnification produced by the objective. Approximately,

$m=\frac{L}{f_{o}} \times \frac{D}{f_{e}}$

where $f_{\mathrm{o}}$ and $f_{e}$ are the focal lengths of the objective and eyepiece, respectively, and $L$ is the distance between their focal points.

9. Magnifying power $m$ of a telescope is the ratio of the angle $\beta$ subtended at the eye by the image to the angle $\alpha$ subtended at the eye by the object.

$$ m=\frac{\beta}{\alpha}=\frac{f_{o}}{f_{e}} $$

where $f_{0}$ and $f_{e}$ are the focal lengths of the objective and eyepiece, respectively.

POINTS TO PONDER

1. The laws of reflection and refraction are true for all surfaces and pairs of media at the point of the incidence.

2. The real image of an object placed between $f$ and $2 f$ from a convex lens can be seen on a screen placed at the image location. If the screen is removed, is the image still there? This question puzzles many, because it is difficult to reconcile ourselves with an image suspended in air without a screen. But the image does exist. Rays from a given point on the object are converging to an image point in space and diverging away. The screen simply diffuses these rays, some of which reach our eye and we see the image. This can be seen by the images formed in air during a laser show.

3. Image formation needs regular reflection/refraction. In principle, all rays from a given point should reach the same image point. This is why you do not see your image by an irregular reflecting object, say the page of a book.

4. Thick lenses give coloured images due to dispersion. The variety in colour of objects we see around us is due to the constituent colours of the light incident on them. A monochromatic light may produce an entirely different perception about the colours on an object as seen in white light.

5. For a simple microscope, the angular size of the object equals the angular size of the image. Yet it offers magnification because we can keep the small object much closer to the eye than $25 \mathrm{~cm}$ and hence have it subtend a large angle. The image is at $25 \mathrm{~cm}$ which we can see. Without the microscope, you would need to keep the small object at $25 \mathrm{~cm}$ which would subtend a very small angle.

EXERCISES

9.1 A small candle, $2.5 \mathrm{~cm}$ in size is placed at $27 \mathrm{~cm}$ in front of a concave mirror of radius of curvature $36 \mathrm{~cm}$. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?

Show Answer

Answer

Size of the candle, $h=2.5 \mathrm{~cm}$

Image size $=h$,

Object distance, $u=-27 \mathrm{~cm}$

Radius of curvature of the concave mirror, $R=-36 \mathrm{~cm}$

Focal length of the concave mirror, $f=\frac{R}{2}=-18 \mathrm{~cm}$

Image distance $=v$

The image distance can be obtained using the mirror formula:

$\frac{1}{u}+\frac{1}{v}=\frac{1}{f}$

$\frac{1}{v}=\frac{1}{f}-\frac{1}{u}$

$$ =\frac{1}{-18}-\frac{1}{-27}=\frac{-3+2}{54}=-\frac{1}{54} $$

$\therefore v=-54 \mathrm{~cm}$

Therefore, the screen should be placed $54 \mathrm{~cm}$ away from the mirror to obtain a sharp image.

The magnification of the image is given as:

$$ \begin{aligned} & m=\frac{h^{\prime}}{h}=-\frac{v}{u} \\ & \therefore h^{\prime}=-\frac{v}{u} \times h \\ & \quad=-\left(\frac{-54}{-27}\right) \times 2.5=-5 \mathrm{~cm} \end{aligned} $$

The height of the candle’s image is $5 \mathrm{~cm}$. The negative sign indicates that the image is inverted and virtual.

If the candle is moved closer to the mirror, then the screen will have to be moved away from the mirror in order to obtain the image.

9.2 A $4.5 \mathrm{~cm}$ needle is placed $12 \mathrm{~cm}$ away from a convex mirror of focal length $15 \mathrm{~cm}$. Give the location of the image and the magnification. Describe what happens as the needle is moved farther from the mirror.

Show Answer

Answer

Height of the needle, $h_{1}=4.5 \mathrm{~cm}$

Object distance, $u=-12 \mathrm{~cm}$

Focal length of the convex mirror, $f=15 \mathrm{~cm}$

Image distance $=v$

The value of $v$ can be obtained using the mirror formula:

$$ \begin{aligned} & \frac{1}{u}+\frac{1}{v}=\frac{1}{f} \\ & \frac{1}{v}=\frac{1}{f}-\frac{1}{u} \\ & \quad=\frac{1}{15}+\frac{1}{12}=\frac{4+5}{60}=\frac{9}{60} \\ & \therefore v=\frac{60}{9}=6.7 \mathrm{~cm} \end{aligned} $$

Hence, the image of the needle is $6.7 \mathrm{~cm}$ away from the mirror. Also, it is on the other side of the mirror.

The image size is given by the magnification formula:

$$ \begin{aligned} m= & \frac{h_{2}}{h_{1}}=-\frac{v}{u} \\ \therefore h_{2} & =-\frac{v}{u} \times h_{1} \\ & =\frac{-6.7}{-12} \times 4.5=+2.5 \mathrm{~cm} \end{aligned} $$

Hence, magnification of the image, $m=\frac{h_{2}}{h_{1}}=\frac{2.5}{4.5}=0.56$

The height of the image is $2.5 \mathrm{~cm}$. The positive sign indicates that the image is erect, virtual, and diminished.

If the needle is moved farther from the mirror, the image will also move away from the mirror, and the size of the image will reduce gradually.

9.3 A tank is filled with water to a height of $12.5 \mathrm{~cm}$. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be $9.4 \mathrm{~cm}$. What is the refractive index of water? If water is replaced by a liquid of refractive index 1.63 up to the same height, by what distance would the microscope have to be moved to focus on the needle again?

Show Answer

Answer

Actual depth of the needle in water, $h_{1}=12.5 \mathrm{~cm}$

Apparent depth of the needle in water, $h_{2}=9.4 \mathrm{~cm}$

Refractive index of water $=\mu$

The value of $\mu$ can be obtained as follows:

$$ \begin{aligned} \mu & =\frac{h_{1}}{h_{2}} \\ & =\frac{12.5}{9.4} \approx 1.33 \end{aligned} $$

Hence, the refractive index of water is about 1.33.

Water is replaced by a liquid of refractive index, $\mu^{\prime}=1.63$

The actual depth of the needle remains the same, but its apparent depth changes. Let $y$ be the new apparent depth of the needle. Hence, we can write the relation:

$$ \begin{aligned} \mu^{\prime} & =\frac{h_{1}}{y} \\ \therefore y & =\frac{h_{1}}{\mu^{\prime}} \\ & =\frac{12.5}{1.63}=7.67 \mathrm{~cm} \end{aligned} $$

Hence, the new apparent depth of the needle is $7.67 \mathrm{~cm}$. It is less than $h_{2}$. Therefore, to focus the needle again, the microscope should be moved up.

$\therefore$ Distance by which the microscope should be moved up $=9.4-7.67$

$=1.73 \mathrm{~cm}$

9.4 Figures 9.27(a) and (b) show refraction of a ray in air incident at $60^{\circ}$ with the normal to a glass-air and water-air interface, respectively. Predict the angle of refraction in glass when the angle of incidence in water is $45^{\circ}$ with the normal to a water-glass interface [Fig. 9.27(c)].

FIGURE 9.27

Show Answer

Answer

As per the given figure, for the glass - air interface:

Angle of incidence, $i=60^{\circ}$

Angle of refraction, $r=35^{\circ}$

The relative refractive index of glass with respect to air is given by Snell’s law as:

$$ \begin{align*} \mu_{\mathrm{g}}^{\mathrm{a}} & =\frac{\sin i}{\sin r} \\ & =\frac{\sin 60^{\circ}}{\sin 35^{\circ}}=\frac{0.8660}{0.5736}=1.51 \tag{1} \end{align*} $$

As per the given figure, for the air - water interface:

Angle of incidence, $i=60^{\circ}$

Angle of refraction, $r=47^{\circ}$

The relative refractive index of water with respect to air is given by Snell’s law as:

$$ \begin{align*} \mu_{\mathrm{w}}^{\mathrm{a}} & =\frac{\sin i}{\sin r} \\ & =\frac{\sin 60}{\sin 47}=\frac{0.8660}{0.7314}=1.184 \tag{2} \end{align*} $$

Using (1) and (2), the relative refractive index of glass with respect to water can be obtained as:

$$ \begin{aligned} \mu_{\mathrm{g}}^{\mathrm{w}} & =\frac{\mu_{\mathrm{g}}^{\mathrm{a}}}{\mu_{\mathrm{w}}^{\mathrm{a}}} \\ & =\frac{1.51}{1.184}=1.275 \end{aligned} $$

The following figure shows the situation involving the glass - water interface.

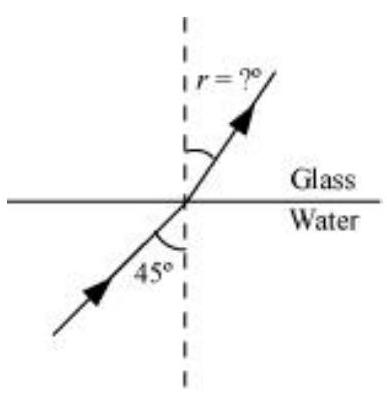
Angle of incidence, $i=45^{\circ}$

Angle of refraction $=r$

From Snell’s law, $r$ can be calculated as:

$$ \begin{aligned} & \frac{\sin i}{\sin r}=\mu_{\mathrm{g}}^{\mathrm{w}} \\ & \frac{\sin 45^{\circ}}{\sin r}=1.275 \\ & \sin r=\frac{\frac{1}{\sqrt{2}}}{1.275}=0.5546 \\ & \therefore r=\sin ^{-1}(0.5546)=38.68^{\circ} \end{aligned} $$

Hence, the angle of refraction at the water - glass interface is $38.68^{\circ}$.

9.5 A small bulb is placed at the bottom of a tank containing water to a depth of $80 \mathrm{~cm}$. What is the area of the surface of water through which light from the bulb can emerge out? Refractive index of water is 1.33. (Consider the bulb to be a point source.)

Show Answer

Answer

Actual depth of the bulb in water, $d_{1}=80 \mathrm{~cm}=0.8 \mathrm{~m}$

Refractive index of water, $\mu=1.33$

The given situation is shown in the following figure:

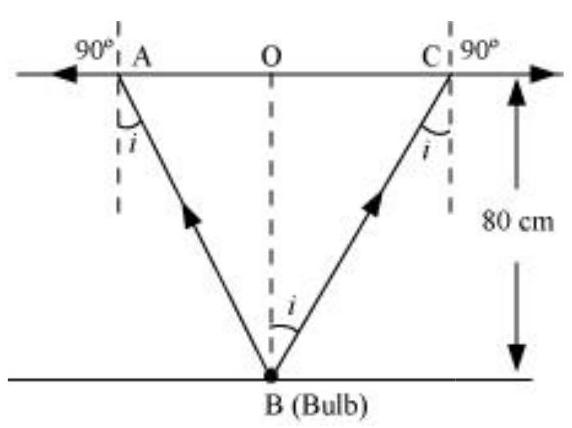
Where,

$i=$ Angle of incidence

$r=$ Angle of refraction $=90^{\circ}$

Since the bulb is a point source, the emergent light can be considered as a circle of radius, $R=\frac{A C}{2}=A O=O B$

Using Snell’ law, we can write the relation for the refractive index of water as:

$$ \begin{aligned} & \mu=\frac{\sin r}{\sin i} \\ & 1.33=\frac{\sin 90^{\circ}}{\sin i} \\ & \therefore i=\sin ^{-1}\left(\frac{1}{1.33}\right)=48.75^{\circ} \end{aligned} $$

Using the given figure, we have the relation:

$\tan i=\frac{O C}{O B}=\frac{R}{d_{1}}$

$\therefore R=\tan 48.75^{\circ} \times 0.8=0.91 \mathrm{~m}$

$\therefore$ Area of the surface of water $=\pi R^{2}=\pi(0.91)^{2}=2.61 \mathrm{~m}^{2}$

Hence, the area of the surface of water through which the light from the bulb can emerge is approximately $2.61 \mathrm{~m}^{2}$.

9.6 A prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. The angle of minimum deviation is measured to be $40^{\circ}$. What is the refractive index of the material of the prism? The refracting angle of the prism is $60^{\circ}$. If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light.

Show Answer

Answer

Angle of minimum deviation, $\delta_{\mathrm{m}}=40^{\circ}$

Angle of the prism, $A=60^{\circ}$

Refractive index of water, $\mu=1.33$

Refractive index of the material of the prism $=\mu^{\prime}$

The angle of deviation is related to refractive index $\left(\mu^{\prime}\right)$ as:

$$ \begin{aligned} \mu^{\prime} & =\frac{\sin \frac{\left(A+\delta_{m}\right)}{2}}{\sin \frac{A}{2}} \\ & =\frac{\sin \frac{\left(60^{\circ}+40^{\circ}\right)}{2}}{\sin \frac{60^{\circ}}{2}}=\frac{\sin 50^{\circ}}{\sin 30^{\circ}}=1.532 \end{aligned} $$

Hence, the refractive index of the material of the prism is 1.532 .

Since the prism is placed in water, let $\delta_{\mathrm{m}}{ }^{\prime}$ be the new angle of minimum deviation for the same prism.

The refractive index of glass with respect to water is given by the relation:

$$ \begin{aligned} & \mu_{\mathrm{g}}^{\mathrm{w}}=\frac{\mu^{\prime}}{\mu}=\frac{\sin \frac{\left(A+\delta_{\mathrm{m}}{ }^{\prime}\right)}{2}}{\sin \frac{A}{2}} \\ & \sin \frac{\left(A+\delta_{\mathrm{m}}{ }^{\prime}\right)}{2}=\frac{\mu^{\prime}}{\mu} \sin \frac{A}{2} \\ & \sin \frac{\left(A+\delta_{\mathrm{m}}{ }^{\prime}\right)}{2}=\frac{1.532}{1.33} \times \sin \frac{60^{\circ}}{2}=0.5759 \\ & \frac{\left(A+\delta_{\mathrm{m}}{ }^{\prime}\right)}{2}=\sin ^{-1} 0.5759=35.16^{\circ} \\ & 60^{\circ}+\delta_{\mathrm{m}}{ }^{\prime}=70.32^{\circ} \\ & \therefore \delta_{\mathrm{m}}{ }^{\circ}=70.32^{\circ}-60^{\circ}=10.32^{\circ} \end{aligned} $$

Hence, the new minimum angle of deviation is $10.32^{\circ}$.

9.7 Double-convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of the same radius of curvature. What is the radius of curvature required if the focal length is to be $20 \mathrm{~cm}$ ?

Show Answer

Answer

Refractive index of glass, $\mu=1.55$

Focal length of the double-convex lens, $f=20 \mathrm{~cm}$

Radius of curvature of one face of the lens $=R_{1}$

Radius of curvature of the other face of the lens $=R_{2}$

Radius of curvature of the double-convex lens $=R$

$\therefore R_{1}=R$ and $R_{2}=-R$

The value of $R$ can be calculated as:

$$ \begin{aligned} & \frac{1}{f}=(\mu-1)\left[\frac{1}{R_{1}}-\frac{1}{R_{2}}\right] \\ & \frac{1}{20}=(1.55-1)\left[\frac{1}{R}+\frac{1}{R}\right] \\ & \frac{1}{20}=0.55 \times \frac{2}{R} \\ & \therefore R=0.55 \times 2 \times 20=22 \mathrm{~cm} \end{aligned} $$

Hence, the radius of curvature of the double-convex lens is $22 \mathrm{~cm}$.

9.8 A beam of light converges at a point P. Now a lens is placed in the path of the convergent beam $12 \mathrm{~cm}$ from $\mathrm{P}$. At what point does the beam converge if the lens is (a) a convex lens of focal length $20 \mathrm{~cm}$, and (b) a concave lens of focal length $16 \mathrm{~cm}$ ?

Show Answer

Answer

In the given situation, the object is virtual and the image formed is real.

Object distance, $u=+12 \mathrm{~cm}$

Focal length of the convex lens, $f=20 \mathrm{~cm}$

Image distance $=v$

According to the lens formula, we have the relation:

$$ \begin{aligned} & \frac{1}{v}-\frac{1}{u}=\frac{1}{f} \\ & \frac{1}{v}-\frac{1}{12}=\frac{1}{20} \\ & \frac{1}{v}=\frac{1}{20}+\frac{1}{12}=\frac{3+5}{60}=\frac{8}{60} \\ & \therefore v=\frac{60}{8}=7.5 \mathrm{~cm} \end{aligned} $$

Hence, the image is formed $7.5 \mathrm{~cm}$ away from the lens, toward its right.

Focal length of the concave lens, $f=-16 \mathrm{~cm}$

Image distance $=v$

According to the lens formula, we have the relation:

$$ \begin{aligned} & \frac{1}{v}-\frac{1}{u}=\frac{1}{f} \\ & \frac{1}{v}=-\frac{1}{16}+\frac{1}{12}=\frac{-3+4}{48}=\frac{1}{48} \\ & \therefore v=48 \mathrm{~cm} \end{aligned} $$

Hence, the image is formed $48 \mathrm{~cm}$ away from the lens, toward its right.

9.9 An object of size $3.0 \mathrm{~cm}$ is placed $14 \mathrm{~cm}$ in front of a concave lens of focal length $21 \mathrm{~cm}$. Describe the image produced by the lens. What happens if the object is moved further away from the lens?

Show Answer

Answer

Size of the object, $h_{1}=3 \mathrm{~cm}$

Object distance, $u=-14 \mathrm{~cm}$

Focal length of the concave lens, $f=-21 \mathrm{~cm}$

Image distance $=v$

According to the lens formula, we have the relation:

$$ \begin{aligned} & \frac{1}{v}-\frac{1}{u}=\frac{1}{f} \\ & \frac{1}{v}=-\frac{1}{21}-\frac{1}{14}=\frac{-2-3}{42}=\frac{-5}{42} \\ & \therefore v=-\frac{42}{5}=-8.4 \mathrm{~cm} \end{aligned} $$

Hence, the image is formed on the other side of the lens, $8.4 \mathrm{~cm}$ away from it. The negative sign shows that the image is erect and virtual.

The magnification of the image is given as:

$$ \begin{aligned} & m=\frac{\text { Image height }\left(h_{2}\right)}{\text { Object height }\left(h_{1}\right)}=\frac{v}{u} \\ & \therefore h_{2}=\frac{-8.4}{-14} \times 3=0.6 \times 3=1.8 \mathrm{~cm} \end{aligned} $$

Hence, the height of the image is $1.8 \mathrm{~cm}$.

If the object is moved further away from the lens, then the virtual image will move toward the focus of the lens, but not beyond it. The size of the image will decrease with the increase in the object distance.

9.10 What is the focal length of a convex lens of focal length $30 \mathrm{~cm}$ in contact with a concave lens of focal length $20 \mathrm{~cm}$ ? Is the system a converging or a diverging lens? Ignore thickness of the lenses.

Show Answer

Answer

Focal length of the convex lens, $f_{1}=30 \mathrm{~cm}$

Focal length of the concave lens, $f_{2}=-20 \mathrm{~cm}$

Focal length of the system of lenses $=f$

The equivalent focal length of a system of two lenses in contact is given as:

$\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}$

$\frac{1}{f}=\frac{1}{30}-\frac{1}{20}=\frac{2-3}{60}=-\frac{1}{60}$

$\therefore f=-60 \mathrm{~cm}$

Hence, the focal length of the combination of lenses is $60 \mathrm{~cm}$. The negative sign indicates that the system of lenses acts as a diverging lens.

9.11 A compound microscope consists of an objective lens of focal length $2.0 \mathrm{~cm}$ and an eyepiece of focal length $6.25 \mathrm{~cm}$ separated by a distance of $15 \mathrm{~cm}$. How far from the objective should an object be placed in order to obtain the final image at (a) the least distance of distinct vision $(25 \mathrm{~cm})$, and (b) at infinity? What is the magnifying power of the microscope in each case?

Show Answer

Answer

Focal length of the objective lens, $f_{1}=2.0 \mathrm{~cm}$

Focal length of the eyepiece, $f_{2}=6.25 \mathrm{~cm}$

Distance between the objective lens and the eyepiece, $d=15 \mathrm{~cm}$

Least distance of distinct vision, $d^{\prime}=25 \mathrm{~cm}$

$\therefore$ Image distance for the eyepiece, $v_{2}=-25 \mathrm{~cm}$

Object distance for the eyepiece $=u_{2}$

According to the lens formula, we have the relation:

$$ \begin{aligned} & \frac{1}{v_{2}}-\frac{1}{u_{2}}=\frac{1}{f_{2}} \\ & \frac{1}{u_{2}}=\frac{1}{v_{2}}-\frac{1}{f_{2}} \\ & \quad=\frac{1}{-25}-\frac{1}{6.25}=\frac{-1-4}{25}=\frac{-5}{25} \\ & \therefore u_{2}=-5 \mathrm{~cm} \end{aligned} $$

Image distance for the objective lens, $v_{1}=d+u_{2}=15-5=10 \mathrm{~cm}$

Object distance for the objective lens $=u_{1}$

According to the lens formula, we have the relation:

$$ \begin{aligned} & \frac{1}{v_{1}}-\frac{1}{u_{1}}=\frac{1}{f_{1}} \\ & \frac{1}{u_{1}}=\frac{1}{v_{1}}-\frac{1}{f_{1}} \\ & \quad=\frac{1}{10}-\frac{1}{2}=\frac{1-5}{10}=\frac{-4}{10} \\ & \therefore u_{1}=-2.5 \mathrm{~cm} \end{aligned} $$

Magnitude of the object distance, $\left|u_{1}\right|=2.5 \mathrm{~cm}$

The magnifying power of a compound microscope is given by the relation:

$$ \begin{aligned} m & =\frac{v_{1}}{\left|u_{1}\right|}\left(1+\frac{d^{\prime}}{f_{2}}\right) \\ & =\frac{10}{2.5}\left(1+\frac{25}{6.25}\right)=4(1+4)=20 \end{aligned} $$

Hence, the magnifying power of the microscope is 20 .

The final image is formed at infinity.

$\therefore$ Image distance for the eyepiece, ${ }^{v_{2}}=\infty$

Object distance for the eyepiece $=u_{2}$

According to the lens formula, we have the relation:

$$ \begin{aligned} & \frac{1}{v_{2}}-\frac{1}{u_{2}}=\frac{1}{f_{2}} \\ & \frac{1}{\infty}-\frac{1}{u_{2}}=\frac{1}{6.25} \\ & \therefore u_{2}=-6.25 \mathrm{~cm} \end{aligned} $$

Image distance for the objective lens, $v_{1}=d+u_{2}=15-6.25=8.75 \mathrm{~cm}$

Object distance for the objective lens $=u_{1}$

According to the lens formula, we have the relation:

$$ \begin{aligned} & \frac{1}{v_{1}}-\frac{1}{u_{1}}=\frac{1}{f_{1}} \\ & \frac{1}{u_{1}}=\frac{1}{v_{1}}-\frac{1}{f_{1}} \\ & \quad=\frac{1}{8.75}-\frac{1}{2.0}=\frac{2-8.75}{17.5} \\ & \therefore u_{1}=-\frac{17.5}{6.75}=-2.59 \mathrm{~cm} \end{aligned} $$

Magnitude of the object distance, $\left|u_{1}\right|=2.59 \mathrm{~cm}$

The magnifying power of a compound microscope is given by the relation:

$$ \begin{aligned} m & =\frac{v_{1}}{\left|u_{1}\right|}\left(\frac{d^{\prime}}{\left|u_{2}\right|}\right) \\ & =\frac{8.75}{2.59} \times \frac{25}{6.25}=13.51 \end{aligned} $$

Hence, the magnifying power of the microscope is 13.51 .

9.12 A person with a normal near point $(25 \mathrm{~cm})$ using a compound microscope with objective of focal length $8.0 \mathrm{~mm}$ and an eyepiece of focal length $2.5 \mathrm{~cm}$ can bring an object placed at $9.0 \mathrm{~mm}$ from the objective in sharp focus. What is the separation between the two lenses? Calculate the magnifying power of the microscope,

Show Answer

Answer

Focal length of the objective lens, $f_{0}=8 \mathrm{~mm}=0.8 \mathrm{~cm}$

Focal length of the eyepiece, $f_{\mathrm{e}}=2.5 \mathrm{~cm}$

Object distance for the objective lens, $u_{0}=-9.0 \mathrm{~mm}=-0.9 \mathrm{~cm}$

Least distance of distant vision, $d=25 \mathrm{~cm}$

Image distance for the eyepiece, $v_{\mathrm{e}}=-d=-25 \mathrm{~cm}$

Object distance for the eyepiece $=u_{\mathrm{e}}$

Using the lens formula, we can obtain the value of $u_{\mathrm{e}}$ as:

$$ \begin{aligned} & \frac{1}{v_{\mathrm{e}}}-\frac{1}{u_{\mathrm{e}}}=\frac{1}{f_{\mathrm{e}}} \\ & \frac{1}{u_{\mathrm{e}}}=\frac{1}{v_{\mathrm{e}}}-\frac{1}{f_{\mathrm{e}}} \\ & =\frac{1}{-25}-\frac{1}{2.5}=\frac{-1-10}{25}=\frac{-11}{25} \\ & \therefore u_{\mathrm{e}}=-\frac{25}{11}=-2.27 \mathrm{~cm} \end{aligned} $$

We can also obtain the value of the image distance for the objective lens $\left(v_{o}\right)$ using the lens formula.

$$ \begin{aligned} & \frac{1}{v_{0}}-\frac{1}{u_{0}}=\frac{1}{f_{0}} \\ & \frac{1}{v_{0}}=\frac{1}{f_{0}}+\frac{1}{u_{0}} \\ & =\frac{1}{0.8}-\frac{1}{0.9}=\frac{0.9-0.8}{0.72}=\frac{0.1}{0.72} \\ & \therefore v_{0}=7.2 \mathrm{~cm} \end{aligned} $$

The distance between the objective lens and the eyepiece $=\left|u_{\mathrm{e}}\right|+v_{\mathrm{o}}$

$=2.27+7.2$

$=9.47 \mathrm{~cm}$

The magnifying power of the microscope is calculated as:

$$ \begin{aligned} & \frac{v_{\mathrm{o}}}{\left|u_{\mathrm{o}}\right|}\left(1+\frac{d}{f_{\mathrm{e}}}\right) \\ & =\frac{7.2}{0.9}\left(1+\frac{25}{2.5}\right)=8(1+10)=88 \end{aligned} $$

Hence, the magnifying power of the microscope is 88 .

9.13 A small telescope has an objective lens of focal length $144 \mathrm{~cm}$ and an eyepiece of focal length $6.0 \mathrm{~cm}$. What is the magnifying power of the telescope? What is the separation between the objective and the eyepiece?

Show Answer

Answer

Focal length of the objective lens, $f_{\mathrm{o}}=144 \mathrm{~cm}$

Focal length of the eyepiece, $f_{\mathrm{e}}=6.0 \mathrm{~cm}$

The magnifying power of the telescope is given as:

$$ \begin{aligned} m & =\frac{f_{\mathrm{o}}}{f_{\mathrm{e}}} \\ & =\frac{144}{6}=24 \end{aligned} $$

The separation between the objective lens and the eyepiece is calculated as:

$$ \begin{aligned} & f_{\mathrm{o}}+f_{\mathrm{e}} \\ & =144+6=150 \mathrm{~cm} \end{aligned} $$

Hence, the magnifying power of the telescope is 24 and the separation between the objective lens and the eyepiece is $150 \mathrm{~cm}$.

9.14 (a) A giant refracting telescope at an observatory has an objective lens of focal length $15 \mathrm{~m}$. If an eyepiece of focal length $1.0 \mathrm{~cm}$ is used, what is the angular magnification of the telescope?

(b) If this telescope is used to view the moon, what is the diameter of the image of the moon formed by the objective lens? The diameter of the moon is $3.48 \times 10^{6} \mathrm{~m}$, and the radius of lunar orbit is $3.8 \times 10^{8} \mathrm{~m}$.

Show Answer

Answer

Focal length of the objective lens, $f_{\mathrm{o}}=15 \mathrm{~m}=15 \times 10^{2} \mathrm{~cm}$

Focal length of the eyepiece, $f_{\mathrm{e}}=1.0 \mathrm{~cm}$

The angular magnification of a telescope is given as:

$$ \begin{aligned} \alpha & =\frac{f_{\mathrm{o}}}{f_{\mathrm{e}}} \\ & =\frac{15 \times 10^{2}}{1.0}=1500 \end{aligned} $$

Hence, the angular magnification of the given refracting telescope is 1500 .

Diameter of the moon, $d=3.48 \times 10^{6} \mathrm{~m}$

Radius of the lunar orbit, $r_{0}=3.8 \times 10^{8} \mathrm{~m}$

Let $d^{\prime}$ be the diameter of the image of the moon formed by the objective lens.

The angle subtended by the diameter of the moon is equal to the angle subtended by the image.

$$ \begin{aligned} & \frac{d}{r_{0}}=\frac{d^{\prime}}{f_{0}} \\ & \frac{3.48 \times 10^{6}}{3.8 \times 10^{8}}=\frac{d^{\prime}}{15} \\ & \therefore d^{\prime}=\frac{3.48}{3.8} \times 10^{-2} \times 15 \\ & \quad=13.74 \times 10^{-2} \mathrm{~m}=13.74 \mathrm{~cm} \end{aligned} $$

Hence, the diameter of the moon’s image formed by the objective lens is $13.74 \mathrm{~cm}$

9.15 Use the mirror equation to deduce that:

(a) an object placed between $f$ and $2 f$ of a concave mirror produces a real image beyond $2 f$.

(b) a convex mirror always produces a virtual image independent of the location of the object.

(c) the virtual image produced by a convex mirror is always diminished in size and is located between the focus and the pole.

(d) an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.

[Note: This exercise helps you deduce algebraically properties of images that one obtains from explicit ray diagrams.]

Show Answer

Answer

For a concave mirror, the focal length $(f)$ is negative.

$\therefore f<0$

When the object is placed on the left side of the mirror, the object distance $(u)$ is negative.

$\therefore u<0$

For image distance $v$, we can write the lens formula as:

$\frac{1}{v}-\frac{1}{u}=\frac{1}{f}$

$\frac{1}{v}=\frac{1}{f}-\frac{1}{u}$

The object lies between $f$ and $2 f$.

$$ \begin{align*} & \therefore 2 f<u<f \quad(\because u \text { and } f \text { are negative }) \\ & \frac{1}{2 f}>\frac{1}{u}>\frac{1}{f} \\ & -\frac{1}{2 f}<-\frac{1}{u}<-\frac{1}{f} \\ & \frac{1}{f}-\frac{1}{2 f}<\frac{1}{f}-\frac{1}{u}<0 \tag{2} \end{align*} $$

Using equation (1), we get:

$\frac{1}{2 f}<\frac{1}{v}<0$

$$ \begin{aligned} & \therefore \frac{1}{v} \text { is negative, i.e., } v \text { is negative. } \\ & \frac{1}{2 f}<\frac{1}{v} \\ & 2 f>v \\ & -v>-2 f \end{aligned} $$

Therefore, the image lies beyond $2 f$.

For a convex mirror, the focal length $(f)$ is positive.

$\therefore f>0$

When the object is placed on the left side of the mirror, the object distance $(u)$ is negative.

$\therefore u<0$

For image distance $v$, we have the mirror formula:

$\frac{1}{v}+\frac{1}{u}=\frac{1}{f}$

$\frac{1}{v}=\frac{1}{f}-\frac{1}{u}$

Using equation (2), we can conclude that:

$\frac{1}{v}<0$

$v>0$

Thus, the image is formed on the back side of the mirror.

Hence, a convex mirror always produces a virtual image, regardless of the object distance.

For a convex mirror, the focal length $(f)$ is positive.

$\therefore f>0$

When the object is placed on the left side of the mirror, the object distance $(u)$ is negative, $\therefore u<0$

For image distance $v$, we have the mirror formula: $\frac{1}{v}+\frac{1}{u}=\frac{1}{f}$ $\frac{1}{v}=\frac{1}{f}-\frac{1}{u}$

But we have $u<0$

$\therefore \frac{1}{v}>\frac{1}{f}$

$v<f$

Hence, the image formed is diminished and is located between the focus $(f)$ and the pole.

For a concave mirror, the focal length $(f)$ is negative.

$\therefore f<0$

When the object is placed on the left side of the mirror, the object distance $(u)$ is negative.

$\therefore u<0$

It is placed between the focus $(f)$ and the pole.

$\therefore f>u>0$

$\frac{1}{f}<\frac{1}{u}<0$

$\frac{1}{f}-\frac{1}{u}<0$

For image distance $v$, we have the mirror formula:

$\frac{1}{v}+\frac{1}{u}=\frac{1}{f}$

$\frac{1}{v}=\frac{1}{f}-\frac{1}{u}$

$\therefore \frac{1}{v}<0$

$v>0$

The image is formed on the right side of the mirror. Hence, it is a virtual image.

For $u<0$ and $v>0$, we can write:

$\frac{1}{u}>\frac{1}{v}$

$v>u$

Magnification, $m=\frac{v}{u}$

Hence, the formed image is enlarged.

9.16 A small pin fixed on a table top is viewed from above from a distance of $50 \mathrm{~cm}$. By what distance would the pin appear to be raised if it is viewed from the same point through a $15 \mathrm{~cm}$ thick glass slab held parallel to the table? Refractive index of glass $=1.5$. Does the answer depend on the location of the slab?

Show Answer

Answer

Actual depth of the pin, $d=15 \mathrm{~cm}$

Apparent dept of the pin $=d^{\prime}$

Refractive index of glass, $\mu=1.5$

Ratio of actual depth to the apparent depth is equal to the refractive index of glass, i.e.

$$ \begin{aligned} & \mu=\frac{d}{d^{\prime}} \\ & \therefore d^{\prime}=\frac{d}{\mu} \\ & \quad=\frac{15}{1.5}=10 \mathrm{~cm} \end{aligned} $$

The distance at which the pin appears to be raised $=d^{\prime}-d$

$$ =15-10=5 \mathrm{~cm} $$

For a small angle of incidence, this distance does not depend upon the location of the slab.

9.17 (a) Figure 9.28 shows a cross-section of a ’light pipe’ made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure.

FIGURE 9.28 (b) What is the answer if there is no outer covering of the pipe?

Show Answer

Answer

Refractive index of the glass fibre, $\mu_{1}=1.68$

Refractive index of the outer covering of the pipe, ${ }_{2}=1.44$

Angle of incidence $=i$

Angle of refraction $=r$

Angle of incidence at the interface $=i$

The refractive index $(\mu)$ of the inner core - outer core interface is given as:

$$ \begin{aligned} & \mu=\frac{\mu_{2}}{\mu_{1}}=\frac{1}{\sin i^{\prime}} \\ & \sin i^{\prime}=\frac{\mu_{1}}{\mu_{2}} \\ & \quad=\frac{1.44}{1.68}=0.8571 \\ & \therefore i^{\prime}=59^{\circ} \end{aligned} $$

For the critical angle, total internal reflection (TIR) takes place only when $i>i^{\prime}$, i.e., $i>$ $59^{\circ}$

Maximum angle of reflection, ${ }^{r_{\max }}=90^{\circ}-i^{\prime}=90^{\circ}-59^{\circ}=31^{\circ}$

Let, ${ }_{\max }$ be the maximum angle of incidence.

The refractive index at the air - glass interface, $\mu_{1}=1.68$

We have the relation for the maximum angles of incidence and reflection as:

$$ \begin{aligned} & \mu_{1}=\frac{\sin i_{\max }}{\sin r_{\max }} \\ & \sin i_{\max }=\mu_{1} \sin r_{\max } \\ & =1.68 \sin 31^{\circ} \\ & =1.68 \times 0.5150 \\ & =0.8652 \\ & \therefore i_{\max }=\sin ^{-1} 0.8652 \approx 60^{\circ} \end{aligned} $$

Thus, all the rays incident at angles lying in the range $0<i<60^{\circ}$ will suffer total internal reflection.

If the outer covering of the pipe is not present, then:

Refractive index of the outer pipe, $\mu_{1}=$ Refractive index of air $=1$

For the angle of incidence $i=90^{\circ}$, we can write Snell’s law at the air - pipe interface as:

$$ \begin{aligned} & \frac{\sin i}{\sin r}=\mu_{2}=1.68 \\ & \sin r=\frac{\sin 90^{\circ}}{1.68}=\frac{1}{1.68} \\ & r=\sin ^{-1}(0.5952) \\ & \quad=36.5^{\circ} \\ & \therefore i^{\prime}=90^{\circ}-36.5^{\circ}=53.5^{\circ} \end{aligned} $$

Since $i^{\prime}>r$, all incident rays will suffer total internal reflection.

9.18 The image of a small electric bulb fixed on the wall of a room is to be obtained on the opposite wall $3 \mathrm{~m}$ away by means of a large convex lens. What is the maximum possible focal length of the lens required for the purpose?

Show Answer

Answer

Distance between the object and the image, $d=3 \mathrm{~m}$

Maximum focal length of the convex lens $=f_{\max }$

For real images, the maximum focal length is given as:

$$ \begin{aligned} f_{\max } & =\frac{d}{4} \\ & =\frac{3}{4}=0.75 \mathrm{~m} \end{aligned} $$

Hence, for the required purpose, the maximum possible focal length of the convex lens is $0.75 \mathrm{~m}$.

9.19 A screen is placed $90 \mathrm{~cm}$ from an object. The image of the object on the screen is formed by a convex lens at two different locations separated by $20 \mathrm{~cm}$. Determine the focal length of the lens.

Show Answer

Answer

Distance between the image (screen) and the object, $D=90 \mathrm{~cm}$

Distance between two locations of the convex lens, $d=20 \mathrm{~cm}$

Focal length of the lens $=f$

Focal length is related to $d$ and $D$ as:

$$ \begin{aligned} f & =\frac{D^{2}-d^{2}}{4 D} \\ & =\frac{(90)^{2}-(20)^{2}}{4 \times 90}=\frac{770}{36}=21.39 \mathrm{~cm} \end{aligned} $$

Therefore, the focal length of the convex lens is $21.39 \mathrm{~cm}$.

9.20 (a) Determine the ’effective focal length’ of the combination of the two lenses in Exercise 9.10, if they are placed $8.0 \mathrm{~cm}$ apart with their principal axes coincident. Does the answer depend on which side of the combination a beam of parallel light is incident? Is the notion of effective focal length of this system useful at all?

(b) An object $1.5 \mathrm{~cm}$ in size is placed on the side of the convex lens in the arrangement (a) above. The distance between the object and the convex lens is $40 \mathrm{~cm}$. Determine the magnification produced by the two-lens system, and the size of the image.

Show Answer

Answer

Focal length of the convex lens, $f_{1}=30 \mathrm{~cm}$

Focal length of the concave lens, $f_{2}=-20 \mathrm{~cm}$

Distance between the two lenses, $d=8.0 \mathrm{~cm}$

When the parallel beam of light is incident on the convex lens first:

According to the lens formula, we have:

$\frac{1}{v_{1}}-\frac{1}{u_{1}}=\frac{1}{f_{1}}$

Where,

$u_{1}=$ Object distance $=\infty$

$v_{1}=$ Image distance

$\frac{1}{v_{1}}=\frac{1}{30}-\frac{1}{\infty}=\frac{1}{30}$

$\therefore v_{1}=30 \mathrm{~cm}$

The image will act as a virtual object for the concave lens.

Applying lens formula to the concave lens, we have:

$\frac{1}{v_{2}}-\frac{1}{u_{2}}=\frac{1}{f_{2}}$

Where,

$u_{2}=$ Object distance

$=(30-d)=30-8=22 \mathrm{~cm}$

$v_{2}=$ Image distance

$\frac{1}{v_{2}}=\frac{1}{22}-\frac{1}{20}=\frac{10-11}{220}=\frac{-1}{220}$

$\therefore v_{2}=-220 \mathrm{~cm}$

The parallel incident beam appears to diverge from a point that is $\left(220-\frac{d}{2}=220-4\right) 216 \mathrm{~cm}$

from the centre of the combination of the two lenses.

(ii) When the parallel beam of light is incident, from the left, on the concave lens first:

According to the lens formula, we have:

$\frac{1}{v_{2}}-\frac{1}{u_{2}}=\frac{1}{f_{2}}$ $\frac{1}{v_{2}}=\frac{1}{f_{2}}+\frac{1}{u_{2}}$

Where,

$u_{2}=$ Object distance $=-\infty$

$v_{2}=$ Image distance

$\frac{1}{v_{2}}=\frac{1}{-20}+\frac{1}{-\infty}=-\frac{1}{20}$

$\therefore v_{2}=-20 \mathrm{~cm}$

The image will act as a real object for the convex lens.

Applying lens formula to the convex lens, we have:

$\frac{1}{v_{1}}-\frac{1}{u_{1}}=\frac{1}{f_{1}}$

Where,

$u_{1}=$ Object distance

$=-(20+d)=-(20+8)=-28 \mathrm{~cm}$

$v_{1}=$ Image distance

$\frac{1}{v_{1}}=\frac{1}{30}+\frac{1}{-28}=\frac{14-15}{420}=\frac{-1}{420}$

$\therefore v_{2}=-420 \mathrm{~cm}$

Hence, the parallel incident beam appear to diverge from a point that is $(420-4) 416 \mathrm{~cm}$ from the left of the centre of the combination of the two lenses.

The answer does depend on the side of the combination at which the parallel beam of light is incident. The notion of effective focal length does not seem to be useful for this combination.

Height of the image, $h_{1}=1.5 \mathrm{~cm}$

Object distance from the side of the convex lens, $u_{1}=-40 \mathrm{~cm}$

$\left|u_{1}\right|=40 \mathrm{~cm}$

According to the lens formula: $\frac{1}{v_{1}}-\frac{1}{u_{1}}=\frac{1}{f_{1}}$

Where,

$v_{1}=$ Image distance

$\frac{1}{v_{1}}=\frac{1}{30}+\frac{1}{-40}=\frac{4-3}{120}=\frac{1}{120}$

$\therefore v_{1}=120 \mathrm{~cm}$

Magnification, $\quad m=\frac{v_{1}}{\left|u_{1}\right|}$

$=\frac{120}{40}=3$

Hence, the magnification due to the convex lens is 3 .

The image formed by the convex lens acts as an object for the concave lens.

According to the lens formula:

$\frac{1}{v_{2}}-\frac{1}{u_{2}}=\frac{1}{f_{2}}$

Where,

$u_{2}=$ Object distance

$=+(120-8)=112 \mathrm{~cm}$.

$v_{2}=$ Image distance

$\frac{1}{v_{2}}=\frac{1}{-20}+\frac{1}{112}=\frac{-112+20}{2240}=\frac{-92}{2240}$

$\therefore v_{2}=\frac{-2240}{92} \mathrm{~cm}$

Magnification, $\quad m^{\prime}=\left|\frac{v_{2}}{u_{2}}\right|$

$=\frac{2240}{92} \times \frac{1}{112}=\frac{20}{92}$

Hence, the magnification due to the concave lens is $\frac{20}{92}$.

The magnification produced by the combination of the two lenses is calculated as:

$m \times m^{\prime}$

$=3 \times \frac{20}{92}=\frac{60}{92}=0.652$

The magnification of the combination is given as:

$\frac{h_{2}}{h_{1}}=0.652$ $h_{2}=0.652 \times h_{1}$

Where,

$h_{1}=$ Object size $=1.5 \mathrm{~cm}$

$h_{2}=$ Size of the image

$\therefore h_{2}=0.652 \times 1.5=0.98 \mathrm{~cm}$

Hence, the height of the image is $0.98 \mathrm{~cm}$.

9.21 At what angle should a ray of light be incident on the face of a prism of refracting angle $60^{\circ}$ so that it just suffers total internal reflection at the other face? The refractive index of the material of the prism is 1.524 .

Show Answer

Answer

The incident, refracted, and emergent rays associated with a glass prism $\mathrm{ABC}$ are shown in the given figure.

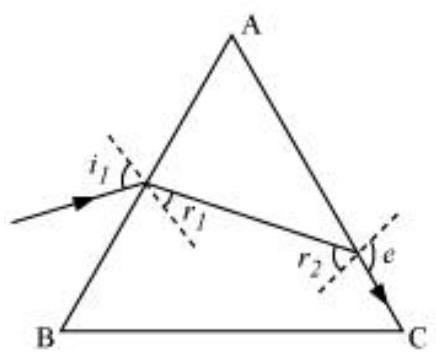
Angle of prism, $\angle A=60^{\circ}$

Refractive index of the prism, $\mu=1.524$

$i_{1}=$ Incident angle

$r_{1}=$ Refracted angle

$r_{2}=$ Angle of incidence at the face AC

$e=$ Emergent angle $=90^{\circ}$

According to Snell’s law, for face AC, we can have:

$$ \begin{aligned} \frac{\sin e}{\sin r_{2}} & =\mu \\ \sin r_{2} & =\frac{1}{\mu} \times \sin 90^{\circ} \\ & =\frac{1}{1.524}=0.6562 \\ \therefore r_{2} & =\sin ^{-1} 0.6562 \approx 41^{\circ} \end{aligned} $$

It is clear from the figure that angle $A=r_{1}+r_{2}$

$\therefore r_{1}=A-r_{2}=60-41=19^{\circ}$

According to Snell’s law, we have the relation:

$$ \begin{aligned} & \mu=\frac{\sin i_{1}}{\sin r_{1}} \\ & \begin{aligned} \sin i_{1} & =\mu \sin r_{1} \\ & =1.524 \times \sin 19^{\circ}=0.496 \\ \therefore i_{1}= & 29.75^{\circ} \end{aligned} \end{aligned} $$

Hence, the angle of incidence is $29.75^{\circ}$.

9.22 A card sheet divided into squares each of size $1 \mathrm{~mm}^{2}$ is being viewed at a distance of $9 \mathrm{~cm}$ through a magnifying glass (a converging lens of focal length $9 \mathrm{~cm}$ ) held close to the eye.

(a) What is the magnification produced by the lens? How much is the area of each square in the virtual image?

(b) What is the angular magnification (magnifying power) of the lens?

(c) Is the magnification in (a) equal to the magnifying power in (b)? Explain.

Show Answer

Answer

Area of each square, $A=1 \mathrm{~mm}^{2}$

Object distance, $u=-9 \mathrm{~cm}$

Focal length of a converging lens, $f=10 \mathrm{~cm}$

For image distance $v$, the lens formula can be written as:

$$ \begin{aligned} & \frac{1}{f}=\frac{1}{v}-\frac{1}{u} \\ & \frac{1}{10}=\frac{1}{v}+\frac{1}{9} \\ & \frac{1}{v}=-\frac{1}{90} \\ & \therefore v=-90 \mathrm{~cm} \end{aligned} $$

Magnification, $\quad m=\frac{v}{u}$

$$ =\frac{-90}{-9}=10 $$

$\therefore$ Area of each square in the virtual image $=(10)^{2} A$

$=10^{2} \times 1=100 \mathrm{~mm}^{2}$

$=1 \mathrm{~cm}^{2}$

Magnifying power of the lens

$$ =\frac{d}{|u|}=\frac{25}{9}=2.8 $$

The magnification in (a) is not the same as the magnifying power in (b).

The magnification magnitude is $\left(\left|\frac{v}{u}\right|\right)$ and the magnifying power is $\left(\frac{d}{|u|}\right)$.

The two quantities will be equal when the image is formed at the near point $(25 \mathrm{~cm})$.

9.23 (a) At what distance should the lens be held from the card sheet in Exercise 9.22 in order to view the squares distinctly with the maximum possible magnifying power?

(b) What is the magnification in this case?

(c) Is the magnification equal to the magnifying power in this case? Explain.

Show Answer

Answer

The maximum possible magnification is obtained when the image is formed at the near point $(d=25 \mathrm{~cm})$.

Image distance, $v=-d=-25 \mathrm{~cm}$

Focal length, $f=10 \mathrm{~cm}$

Object distance $=u$

According to the lens formula, we have:

$$ \begin{aligned} \frac{1}{f} & =\frac{1}{v}-\frac{1}{u} \\ \frac{1}{u} & =\frac{1}{v}-\frac{1}{f} \\ & =\frac{1}{-25}-\frac{1}{10}=\frac{-2-5}{50}=-\frac{7}{50} \\ \therefore u & =-\frac{50}{7}=-7.14 \mathrm{~cm} \end{aligned} $$

Hence, to view the squares distinctly, the lens should be kept $7.14 \mathrm{~cm}$ away from them.

Magnification $=$

$$ \left|\frac{v}{u}\right|=\frac{25}{50}=3.5 $$

Magnifying power $=$

$$ \frac{d}{u}=\frac{25}{50}=3.5 $$

Since the image is formed at the near point $(25 \mathrm{~cm})$, the magnifying power is equal to the magnitude of magnification.

9.24 What should be the distance between the object in Exercise 9.23 and the magnifying glass if the virtual image of each square in the figure is to have an area of $6.25 \mathrm{~mm}^{2}$. Would you be able to see the squares distinctly with your eyes very close to the magnifier?

[Note: Exercises 9.22 to 9.24 will help you clearly understand the difference between magnification in absolute size and the angular magnification (or magnifying power) of an instrument.]

Show Answer

Answer

Area of the virtual image of each square, $A=6.25 \mathrm{~mm}^{2}$

Area of each square, $A_{0}=1 \mathrm{~mm}^{2}$

Hence, the linear magnification of the object can be calculated as:

$$ \begin{aligned} m & =\sqrt{\frac{A}{A_{0}}} \\ & =\sqrt{\frac{6.25}{1}}=2.5 \end{aligned} $$

But $m=\frac{\text { Image distance }(v)}{\text { Object distance }(u)}$

$$ \begin{align*} \therefore v & =m u \\ & =2.5 u \tag{1} \end{align*} $$

Focal length of the magnifying glass, $f=10 \mathrm{~cm}$

According to the lens formula, we have the relation:

$$ \begin{aligned} & \frac{1}{f}=\frac{1}{v}-\frac{1}{u} \\ & \frac{1}{10}=\frac{1}{2.5 u}-\frac{1}{u}=\frac{1}{u}\left(\frac{1}{2.5}-\frac{1}{1}\right)=\frac{1}{u}\left(\frac{1-2.5}{2.5}\right) \\ & \therefore u=-\frac{1.5 \times 10}{2.5}=-6 \mathrm{~cm} \end{aligned} $$

And $v=2.5 u$

$$ =2.5 \times 6=-15 \mathrm{~cm} $$

The virtual image is formed at a distance of $15 \mathrm{~cm}$, which is less than the near point (i.e., $25 \mathrm{~cm}$ ) of a normal eye. Hence, it cannot be seen by the eyes distinctly.

9.25 Answer the following questions:

(a) The angle subtended at the eye by an object is equal to the angle subtended at the eye by the virtual image produced by a magnifying glass. In what sense then does a magnifying glass provide angular magnification?

(b) In viewing through a magnifying glass, one usually positions one’s eyes very close to the lens. Does angular magnification change if the eye is moved back?

(c) Magnifying power of a simple microscope is inversely proportional to the focal length of the lens. What then stops us from using a convex lens of smaller and smaller focal length and achieving greater and greater magnifying power?

(d) Why must both the objective and the eyepiece of a compound microscope have short focal lengths?

(e) When viewing through a compound microscope, our eyes should be positioned not on the eyepiece but a short distance away from it for best viewing. Why? How much should be that short distance between the eye and eyepiece?

Show Answer

Answer

(a)Though the image size is bigger than the object, the angular size of the image is equal to the angular size of the object. A magnifying glass helps one see the objects placed closer than the least distance of distinct vision (i.e., $25 \mathrm{~cm}$ ). A closer object causes a larger angular size. A magnifying glass provides angular magnification. Without magnification, the object cannot be placed closer to the eye. With magnification, the object can be placed much closer to the eye.

Yes, the angular magnification changes. When the distance between the eye and a magnifying glass is increased, the angular magnification decreases a little. This is because the angle subtended at the eye is slightly less than the angle subtended at the lens. Image distance does not have any effect on angular magnification.

The focal length of a convex lens cannot be decreased by a greater amount. This is because making lenses having very small focal lengths is not easy. Spherical and chromatic aberrations are produced by a convex lens having a very small focal length.

The angular magnification produced by the eyepiece of a compound microscope is $\left[\left(\frac{25}{f_{\mathrm{e}}}\right)+1\right]$

Where,

$f_{\mathrm{e}}=$ Focal length of the eyepiece

It can be inferred that if $f_{\mathrm{e}}$ is small, then angular magnification of the eyepiece will be large.

The angular magnification of the objective lens of a compound microscope is given as

$$ \frac{1}{\left(\left|u_{\mathrm{o}}\right| f_{\mathrm{o}}\right)} $$

Where,

$u_{\mathrm{o}}=$ Object distance for the objective lens

$f_{\mathrm{o}}=$ Focal length of the objective

The magnification is large when $u_{\mathrm{o}}>f_{\mathrm{o}}$. In the case of a microscope, the object is kept close to the objective lens. Hence, the object distance is very little. Since ${ }^{u_{\mathrm{o}}}$ is small, $f_{\mathrm{o}}$ will be even smaller. Therefore, $f_{\mathrm{e}}$ and $f_{\mathrm{o}}$ are both small in the given condition.

(e)When we place our eyes too close to the eyepiece of a compound microscope, we are unable to collect much refracted light. As a result, the field of view decreases substantially. Hence, the clarity of the image gets blurred.

The best position of the eye for viewing through a compound microscope is at the eyering attached to the eyepiece. The precise location of the eye depends on the separation between the objective lens and the eyepiece.

9.26 An angular magnification (magnifying power) of $30 \mathrm{X}$ is desired using an objective of focal length $1.25 \mathrm{~cm}$ and an eyepiece of focal length $5 \mathrm{~cm}$. How will you set up the compound microscope?

Show Answer

Answer

Focal length of the objective lens, $f_{\mathrm{o}}=1.25 \mathrm{~cm}$

Focal length of the eyepiece, $f_{\mathrm{e}}=5 \mathrm{~cm}$

Least distance of distinct vision, $d=25 \mathrm{~cm}$

Angular magnification of the compound microscope $=30 \mathrm{X}$

Total magnifying power of the compound microscope, $m=30$

The angular magnification of the eyepiece is given by the relation:

$$ \begin{aligned} m_{\mathrm{e}} & =\left(1+\frac{d}{f_{\mathrm{e}}}\right) \\ & =\left(1+\frac{25}{5}\right)=6 \end{aligned} $$

The angular magnification of the objective lens $\left(m_{\mathrm{o}}\right)$ is related to $m_{\mathrm{e}}$ as:

$$ \begin{aligned} & m_{\mathrm{o}} m_{\mathrm{e}}=m \\ & m_{\mathrm{o}}=\frac{m}{m_{\mathrm{e}}} \\ &= \frac{30}{6}=5 \end{aligned} $$

We also have the relation:

$m_{\mathrm{o}}=\frac{\text { Image distance for the objective lens }\left(v_{\mathrm{o}}\right)}{\text { Object distance for the objective lens }\left(-u_{\mathrm{o}}\right)}$

$5=\frac{v_{\mathrm{o}}}{-u_{\mathrm{o}}}$

$\therefore v_{\mathrm{o}}=-5 u_{\mathrm{o}}$

Applying the lens formula for the objective lens:

$$ \begin{aligned} & \frac{1}{f_{0}}=\frac{1}{v_{0}}-\frac{1}{u_{0}} \\ & \frac{1}{1.25}=\frac{1}{-5 u_{0}}-\frac{1}{u_{0}}=\frac{-6}{5 u_{\mathrm{o}}} \\ & \begin{aligned} \therefore u_{\mathrm{o}} & =\frac{-6}{5} \times 1.25=-1.5 \mathrm{~cm} \\ \text { And } v_{\mathrm{o}} & =-5 u_{\mathrm{o}} \\ & =-5 \times(-1.5)=7.5 \mathrm{~cm} \end{aligned} \end{aligned} $$

The object should be placed $1.5 \mathrm{~cm}$ away from the objective lens to obtain the desired magnification.

Applying the lens formula for the eyepiece:

$\frac{1}{v_{\mathrm{e}}}-\frac{1}{u_{\mathrm{e}}}=\frac{1}{f_{\mathrm{e}}}$

Where,

$v_{\mathrm{e}}=$ Image distance for the eyepiece $=-d=-25 \mathrm{~cm}$

$u_{\mathrm{e}}=$ Object distance for the eyepiece

$$ \begin{aligned} & \frac{1}{u_{\mathrm{e}}}=\frac{1}{v_{\mathrm{e}}}-\frac{1}{f_{\mathrm{e}}} \\ & =\frac{-1}{25}-\frac{1}{5}=-\frac{6}{25} \\ & \therefore u_{\mathrm{e}}=-4.17 \mathrm{~cm} \end{aligned} $$

Separation between the objective lens and the eyepiece $=\left|u_{\mathrm{e}}\right|+\left|v_{\mathrm{o}}\right|$

$$ \begin{aligned} & =4.17+7.5 \\ & =11.67 \mathrm{~cm} \end{aligned} $$

Therefore, the separation between the objective lens and the eyepiece should be $11.67 \mathrm{~cm}$.

9.27 A small telescope has an objective lens of focal length $140 \mathrm{~cm}$ and an eyepiece of focal length $5.0 \mathrm{~cm}$. What is the magnifying power of the telescope for viewing distant objects when

(a) the telescope is in normal adjustment (i.e., when the final image is at infinity)?

(b) the final image is formed at the least distance of distinct vision $(25 \mathrm{~cm})$ ?

9.28 (a) For the telescope described in Exercise 9.27 (a), what is the separation between the objective lens and the eyepiece?

(b) If this telescope is used to view a $100 \mathrm{~m}$ tall tower $3 \mathrm{~km}$ away, what is the height of the image of the tower formed by the objective lens?

(c) What is the height of the final image of the tower if it is formed at $25 \mathrm{~cm}$ ?

9.29 A Cassegrain telescope uses two mirrors as shown in Fig. 9.26. Such a telescope is built with the mirrors $20 \mathrm{~mm}$ apart. If the radius of curvature of the large mirror is $220 \mathrm{~mm}$ and the small mirror is $140 \mathrm{~mm}$, where will the final image of an object at infinity be?

Show Answer

Answer

Focal length of the objective lens, $f_{\mathrm{o}}=140 \mathrm{~cm}$

Focal length of the eyepiece, $f_{\mathrm{e}}=5 \mathrm{~cm}$

In normal adjustment, the separation between the objective lens and the eyepiece $=f_{\mathrm{o}}+f_{\mathrm{e}}=140+5=145 \mathrm{~cm}$

Height of the tower, $h_{1}=100 \mathrm{~m}$

Distance of the tower (object) from the telescope, $u=3 \mathrm{~km}=3000 \mathrm{~m}$

The angle subtended by the tower at the telescope is given as:

$$ \begin{aligned} \theta & =\frac{h_{1}}{u} \\ & =\frac{100}{3000}=\frac{1}{30} \mathrm{rad} \end{aligned} $$

The angle subtended by the image produced by the objective lens is given as:

$$ \theta=\frac{h_{2}}{f_{0}}=\frac{h_{2}}{140} \mathrm{rad} $$

Where,

$h_{2}=$ Height of the image of the tower formed by the objective lens

$$ \begin{aligned} & \frac{1}{30}=\frac{h_{2}}{140} \\ & \therefore h_{2}=\frac{140}{30}=4.7 \mathrm{~cm} \end{aligned} $$

Therefore, the objective lens forms a $4.7 \mathrm{~cm}$ tall image of the tower.

Image is formed at a distance, $d=25 \mathrm{~cm}$

The magnification of the eyepiece is given by the relation:

$$ \begin{aligned} m & =1+\frac{d}{f_{\mathrm{e}}} \\ & =1+\frac{25}{5}=1+5=6 \end{aligned} $$

Height of the final image $=m h_{2}=6 \times 4.7=28.2 \mathrm{~cm}$

Hence, the height of the final image of the tower is $28.2 \mathrm{~cm}$.

9.30 Light incident normally on a plane mirror attached to a galvanometer coil retraces backwards as shown in Fig. 9.29. A current in the coil produces a deflection of $3.5^{\circ}$ of the mirror. What is the displacement of the reflected spot of light on a screen placed $1.5 \mathrm{~m}$ away?

FIGURE 9.29

Show Answer

Answer

Angle of deflection, $\theta=3.5^{\circ}$

Distance of the screen from the mirror, $D=1.5 \mathrm{~m}$

The reflected rays get deflected by an amount twice the angle of deflection i.e., $2 \theta=7.0^{\circ}$

The displacement $(d)$ of the reflected spot of light on the screen is given as:

$\tan 2 \theta=\frac{d}{1.5}$

$\therefore d=1.5 \times \tan 7^{\circ}=0.184 \mathrm{~m}=18.4 \mathrm{~cm}$

Hence, the displacement of the reflected spot of light is $18.4 \mathrm{~cm}$.

9.31 Figure 9.30 shows an equiconvex lens (of refractive index 1.50) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be $45.0 \mathrm{~cm}$. The liquid is removed and the experiment is repeated. The new distance is measured to be $30.0 \mathrm{~cm}$. What is the refractive index of the liquid?

FIGURE 9.30

Show Answer

Answer

Focal length of the convex lens, $f_{1}=30 \mathrm{~cm}$

The liquid acts as a mirror. Focal length of the liquid $=f_{2}$

Focal length of the system (convex lens + liquid), $f=45 \mathrm{~cm}$

For a pair of optical systems placed in contact, the equivalent focal length is given as:

$$ \begin{aligned} & \frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}} \\ & \begin{aligned} \frac{1}{f_{2}} & =\frac{1}{f}-\frac{1}{f_{1}} \\ & =\frac{1}{45}-\frac{1}{30}=-\frac{1}{90} \\ \therefore f_{2} & =-90 \mathrm{~cm} \end{aligned} \end{aligned} $$

Let the refractive index of the lens be ${ }^{\mu_{1}}$ and the radius of curvature of one surface be $R$. Hence, the radius of curvature of the other surface is $-R$.

$R$ can be obtained using the relation:

$$ \begin{aligned} & \frac{1}{f_{1}}=\left(\mu_{1}-1\right)\left(\frac{1}{R}+\frac{1}{-R}\right) \\ & \frac{1}{30}=(1.5-1)\left(\frac{2}{R}\right) \\ & \therefore R=\frac{30}{0.5 \times 2}=30 \mathrm{~cm} \end{aligned} $$

Let ${ }^{\mu_{2}}$ be the refractive index of the liquid.

Radius of curvature of the liquid on the side of the plane mirror $=\infty$

Radius of curvature of the liquid on the side of the lens, $R=-30 \mathrm{~cm}$

The value of ${ }^{\mu_{2}}$ can be calculated using the relation:

$\frac{1}{f_{2}}=\left(\mu_{2}-1\right)\left[\frac{1}{-R}-\frac{1}{\infty}\right]$

$\frac{-1}{90}=\left(\mu_{2}-1\right)\left[\frac{1}{+30}-0\right]$

$\mu_{2}-1=\frac{1}{3}$

$\therefore \mu_{2}=\frac{4}{3}=1.33$

Hence, the refractive index of the liquid is 1.33 .