UNIT 7

EQUILIBRIUM

Chemical equilibria are important in numerous biological and environmental processes. For example, equilibria involving $\mathrm{O_2}$ molecules and the protein hemoglobin play a crucial role in the transport and delivery of $\mathrm{O_2}$ from our lungs to our muscles. Similar equilibria involving $\mathrm{CO}$ molecules and hemoglobin account for the toxicity of $\mathrm{CO}$.

When a liquid evaporates in a closed container, molecules with relatively higher kinetic energy escape the liquid surface into the vapour phase and number of liquid molecules from the vapour phase strike the liquid surface and are retained in the liquid phase. It gives rise to a constant vapour pressure because of an equilibrium in which the number of molecules leaving the liquid equals the number returning to liquid from the vapour. We say that the system has reached equilibrium state at this stage. However, this is not static equilibrium and there is a lot of activity at the boundary between the liquid and the vapour. Thus, at equilibrium, the rate of evaporation is equal to the rate of condensation. It may be represented by

$$ \mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H_2} \mathrm{O}(\text { vap) } $$

The double half arrows indicate that the processes in both the directions are going on simultaneously. The mixture of reactants and products in the equilibrium state is called an equilibrium mixture.

Equilibrium can be established for both physical processes and chemical reactions. The reaction may be fast or slow depending on the experimental conditions and the nature of the reactants. When the reactants in a closed vessel at a particular temperature react to give products, the concentrations of the reactants keep on decreasing, while those of products keep on increasing for some time after which there is no change in the concentrations of either of the reactants or products. This stage of the system is the dynamic equilibrium and the rates of the forward and reverse reactions become equal. It is due to this dynamic equilibrium stage that there is no change in the concentrations of various species in the reaction mixture. Based on the extent to which the reactions proceed to reach the state of chemical equilibrium, these may be classified in three groups.

(i) The reactions that proceed nearly to completion and only negligible concentrations of the reactants are left. In some cases, it may not be even possible to detect these experimentally.

(ii) The reactions in which only small amounts of products are formed and most of the reactants remain unchanged at equilibrium stage.

(iii) The reactions in which the concentrations of the reactants and products are comparable, when the system is in equilibrium.

The extent of a reaction in equilibrium varies with the experimental conditions such as concentrations of reactants, temperature, etc. Optimisation of the operational conditions is very important in industry and laboratory so that equilibrium is favorable in the direction of the desired product. Some important aspects of equilibrium involving physical and chemical processes are dealt in this unit along with the equilibrium involving ions in aqueous solutions which is called as ionic equilibrium.

7.1 EQUILIBRIUM IN PHYSICAL PROCESSES

The characteristics of system at equilibrium are better understood if we examine some physical processes. The most familiar examples are phase transformation processes, e.g.,

$$ \begin{aligned} \text { solid } & \rightleftharpoons \text { liquid } \\ \text { liquid } & \rightleftharpoons \text { gas } \\ \text { solid } & \rightleftharpoons \text { gas } \end{aligned} $$

7.1.1 Solid-Liquid Equilibrium

Ice and water kept in a perfectly insulated thermos flask (no exchange of heat between its contents and the surroundings) at $273 \mathrm{~K}$ and the atmospheric pressure are in equilibrium state and the system shows interesting characteristic features. We observe that the mass of ice and water do not change with time and the temperature remains constant. However, the equilibrium is not static. The intense activity can be noticed at the boundary between ice and water. Molecules from the liquid water collide against ice and adhere to it and some molecules of ice escape into liquid phase. There is no change of mass of ice and water, as the rates of transfer of molecules from ice into water and of reverse transfer from water into ice are equal at atmospheric pressure and $273 \mathrm{~K}$.

It is obvious that ice and water are in equilibrium only at particular temperature and pressure. For any pure substance at atmospheric pressure, the temperature at which the solid and liquid phases are at equilibrium is called the normal melting point or normal freezing point of the substance. The system here is in dynamic equilibrium and we can infer the following:

(i) Both the opposing processes occur simultaneously.

(ii) Both the processes occur at the same rate so that the amount of ice and water remains constant.

7.1.2 Liquid-Vapour Equilibrium

This equilibrium can be better understood if we consider the example of a transparent box carrying a U-tube with mercury (manometer). Drying agent like anhydrous calcium chloride (or phosphorus penta-oxide) is placed for a few hours in the box. After removing the drying agent by tilting the box on one side, a watch glass (or petri dish) containing water is quickly placed inside the box. It will be observed that the mercury level in the right limb of the manometer slowly increases and finally attains a constant value, that is, the pressure inside the box increases and reaches a constant value. Also the volume of water in the watch glass decreases (Fig. 6.1). Initially there was no water vapour (or very less) inside the box. As water evaporated the pressure in the box increased due to addition of water molecules into the gaseous phase inside the box. The rate of evaporation is constant.

However, the rate of increase in pressure decreases with time due to condensation of vapour into water. Finally it leads to an equilibrium condition when there is no net evaporation. This implies that the number of water molecules from the gaseous state into the liquid state also increases till the equilibrium is attained i.e.,

rate of evaporation= rate of condensation

$$ \mathrm{H_2} \mathrm{O}(1) \rightleftharpoons \mathrm{H_2} \mathrm{O}(\text { vap) } $$

At equilibrium the pressure exerted by the water molecules at a given temperature remains constant and is called the equilibrium vapour pressure of water (or just vapour pressure of water); vapour pressure of water increases with temperature. If the above experiment is repeated with methyl alcohol, acetone and ether, it is observed that different liquids have different equilibrium vapour pressures at the same temperature, and the liquid which has a higher vapour pressure is more volatile and has a lower boiling point.

If we expose three watch glasses containing separately $1 \mathrm{~mL}$ each of acetone, ethyl alcohol, and water to atmosphere and repeat the experiment with different volumes of the liquids in a warmer room, it is observed that in all such cases the liquid eventually disappears and the time taken for complete evaporation depends on (i) the nature of the liquid, (ii) the amount of the liquid and (iii) the temperature. When the watch glass is open to the atmosphere, the rate of evaporation remains constant but the molecules are dispersed into large volume of the room. As a consequence the rate of condensation from vapour to liquid state is much less than the rate of evaporation. These are open systems and it is not possible to reach equilibrium in an open system.

Water and water vapour are in equilibrium position at atmospheric pressure (1.013 bar) and at $100^{\circ} \mathrm{C}$ in a closed vessel. The boiling point of water is $100^{\circ} \mathrm{C}$ at 1.013 bar pressure. For any pure liquid at one atmospheric pressure (1.013 bar), the temperature at which the liquid and vapours are at equilibrium is called normal boiling point of the liquid. Boiling point of the liquid depends on the atmospheric pressure. It depends on the altitude of the place; at high altitude the boiling point decreases.

7.1.3 Solid - Vapour Equilibrium

Let us now consider the systems where solids sublime to vapour phase. If we place solid iodine in a closed vessel, after sometime the vessel gets filled up with violet vapour and the intensity of colour increases with time. After certain time the intensity of colour becomes constant and at this stage equilibrium is attained. Hence solid iodine sublimes to give iodine vapour and the iodine vapour condenses to give solid iodine. The equilibrium can be represented as,

$\mathrm{I_2}$ (solid) $\rightleftharpoons \mathrm{I_2}$ (vapour)

Other examples showing this kind of equilibrium are,

Camphor (solid) $\rightleftharpoons$ Camphor (vapour)

$\mathrm{NH_4} \mathrm{Cl}$ (solid) $\rightleftharpoons \mathrm{NH_4} \mathrm{Cl}$ (vapour)

7.1.4 Equilibrium Involving Dissolution of Solid or Gases in Liquids

Solids in liquids

We know from our experience that we can dissolve only a limited amount of salt or sugar in a given amount of water at room temperature. If we make a thick sugar syrup solution by dissolving sugar at a higher temperature, sugar crystals separate out if we cool the syrup to the room temperature. We call it a saturated solution when no more of solute can be dissolved in it at a given temperature. The concentration of the solute in a saturated solution depends upon the temperature. In a saturated solution, a dynamic equilibrium exits between the solute molecules in the solid state and in the solution:

Sugar (solution) $\rightleftharpoons$ Sugar (solid), and

the rate of dissolution of sugar $=$ rate of crystallisation of sugar.

Equality of the two rates and dynamic nature of equilibrium has been confirmed with the help of radioactive sugar. If we drop some radioactive sugar into saturated solution of non-radioactive sugar, then after some time radioactivity is observed both in the solution and in the solid sugar. Initially there were no radioactive sugar molecules in the solution but due to dynamic nature of equilibrium, there is exchange between the radioactive and non-radioactive sugar molecules between the two phases. The ratio of the radioactive to non-radioactive molecules in the solution increases till it attains a constant value.

Gases in liquids

When a soda water bottle is opened, some of the carbon dioxide gas dissolved in it fizzes out rapidly. The phenomenon arises due to difference in solubility of carbon dioxide at different pressures. There is equilibrium between the molecules in the gaseous state and the molecules dissolved in the liquid under pressure i.e.,

$$ \mathrm{CO_2} \text { (gas) } \rightleftharpoons \mathrm{CO_2} \text { (in solution) } $$

This equilibrium is governed by Henry’s law, which states that the mass of a gas dissolved in a given mass of a solvent at any temperature is proportional to the pressure of the gas above the solvent. This amount decreases with increase of temperature. The soda water bottle is sealed under pressure of gas when its solubility in water is high. As soon as the bottle is opened, some of the dissolved carbon dioxide gas escapes to reach a new equilibrium condition required for the lower pressure, namely its partial pressure in the atmosphere. This is how the soda water in bottle when left open to the air for some time, turns ‘flat’. It can be generalised that:

(i) For solid $\rightleftharpoons$ liquid equilibrium, there is only one temperature (melting point) at 1 atm (1.013 bar) at which the two phases can coexist. If there is no exchange of heat with the surroundings, the mass of the two phases remains constant.

(ii) For liquid $\rightleftharpoons$ vapour equilibrium, the vapour pressure is constant at a given temperature.

(iii) For dissolution of solids in liquids, the solubility is constant at a given temperature.

(iv) For dissolution of gases in liquids, the concentration of a gas in liquid is proportional to the pressure (concentration) of the gas over the liquid. These observations are summarised in Table 6.1

Table 6.1 Some Features of Physical Equilibria

Process	Conclusion
Liquid $\rightleftharpoons$ Vapour $\mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H_2} \mathrm{O}(\mathrm{g})$	$p_{\mathrm{H_2} \mathrm{O}}$ constant at given temperature
Solid $\rightleftharpoons$ Liquid $\mathrm{H_2} \mathrm{O}(\mathrm{s}) \rightleftharpoons \mathrm{H_2} \mathrm{O}(1)$	Melting point is fixed at constant pressure
Solute $(\mathrm{s}) \rightleftharpoons$ Solute (solution) Sugar $(\mathrm{s}) \rightleftharpoons$ Sugar ( solution)	Concentration of solute in solution is constant at a given temperature
$\operatorname{Gas}(\mathrm{g}) \rightleftharpoons \mathrm{Gas}(\mathrm{aq})$ $\mathrm{CO_2}(\mathrm{~g}) \rightleftharpoons \mathrm{CO_2}(\mathrm{aq})$	[gas $(\mathrm{g})]$ is constant at a given temperature $\left[\mathrm{CO_2}(\mathrm{aq})\right] /\left[\mathrm{CO_2}(\mathrm{~g})\right]$ is constant at a given temperature

6.1.5 General Characteristics of Equilibria Involving Physical Processes

For the physical processes discussed above, following characteristics are common to the system at equilibrium:

(i) Equilibrium is possible only in a closed system at a given temperature.

(ii) Both the opposing processes occur at the same rate and there is a dynamic but stable condition.

(iii) All measurable properties of the system remain constant.

(iv) When equilibrium is attained for a physical process, it is characterised by constant value of one of its parameters at a given temperature. Table 6.1 lists such quantities.

(v) The magnitude of such quantities at any stage indicates the extent to which the physical process has proceeded before reaching equilibrium.

7.2 EQUILIBRIUM IN CHEMICAL PROCESSES - DYNAMIC EQUILIBRIUM

Analogous to the physical systems chemical reactions also attain a state of equilibrium. These reactions can occur both in forward and backward directions. When the rates of the forward and reverse reactions become equal, the concentrations of the reactants and the products remain constant. This is the stage of chemical equilibrium. This equilibrium is dynamic in nature as it consists of a forward reaction in which the reactants give product(s) and reverse reaction in which product(s) gives the original reactants.

For a better comprehension, let us consider a general case of a reversible reaction,

$$ \mathrm{A}+\mathrm{B} \rightleftharpoons \mathrm{C}+\mathrm{D} $$

With passage of time, there is accumulation of the products $\mathrm{C}$ and $\mathrm{D}$ and depletion of the reactants A and B (Fig. 6.2). This leads to a decrease in the rate of forward reaction and an increase in the rate of the reverse reaction,

Eventually, the two reactions occur at the same rate and the system reaches a state of equilibrium.

Similarly, the reaction can reach the state of equilibrium even if we start with only $\mathrm{C}$ and $\mathrm{D}$; that is, no A and B being present initially, as the equilibrium can be reached from either direction.

The dynamic nature of chemical equilibrium can be demonstrated in the synthesis of ammonia by Haber’s process. In a series of experiments, Haber started with known amounts of dinitrogen and dihydrogen maintained at high temperature and pressure and at regular intervals determined the amount of ammonia present. He was successful in determining also the concentration of unreacted dihydrogen and dinitrogen. Fig. 6.4 (page 174) shows that after a certain time the composition of the mixture remains the same even though some of the reactants are still present. This constancy in composition indicates that the reaction has reached equilibrium. In order to understand the dynamic nature of the reaction, synthesis of ammonia is carried out with exactly the same starting conditions (of partial pressure and temperature) but using $\mathrm{D_2}$ (deuterium) in place of $\mathrm{H_2}$. The reaction mixtures starting either with $\mathrm{H_2}$ or $\mathrm{D_2}$ reach equilibrium with the same composition, except that $\mathrm{D_2}$ and $\mathrm{ND_3}$ are present instead of $\mathrm{H_2}$ and $\mathrm{NH_3}$. After

$$ \mathrm{N_2}(\mathrm{~g})+3 \mathrm{H_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH_3}(\mathrm{~g}) $$

equilibrium is attained, these two mixtures $\left(\mathrm{H_2}, \mathrm{~N_2}, \mathrm{NH_3}\right.$ and $\left.\mathrm{D_2}, \mathrm{~N_2}, \mathrm{ND_3}\right)$ are mixed together and left for a while. Later, when this mixture is analysed, it is found that the concentration of ammonia is just the same as before. However, when this mixture is analysed by a mass spectrometer, it is found that ammonia and all deuterium containing forms of ammonia $\left(\mathrm{NH_3}, \mathrm{NH_2} \mathrm{D}, \mathrm{NHD_2}\right.$ and $\mathrm{ND_3}$ ) and dihydrogen and its deutrated forms $\left(\mathrm{H_2}, \mathrm{HD}\right.$ and $\left.\mathrm{D_2}\right)$ are present. Thus one can conclude that scrambling of $\mathrm{H}$ and $\mathrm{D}$ atoms in the molecules must result from a continuation of the forward and reverse reactions in the mixture. If the reaction had simply stopped when they reached equilibrium, then there would have been no mixing of isotopes in this way.

Use of isotope (deuterium) in the formation of ammonia clearly indicates that chemical reactions reach a state of dynamic equilibrium in which the rates of forward and reverse reactions are equal and there is no net change in composition.

Equilibrium can be attained from both sides, whether we start reaction by taking, $\mathrm{H_2}(\mathrm{~g})$ and $\mathrm{N_2}(\mathrm{~g})$ and get $\mathrm{NH_3}(\mathrm{~g})$ or by taking $\mathrm{NH_3}(\mathrm{~g})$ and decomposing it into $\mathrm{N_2}(\mathrm{~g})$ and $\mathrm{H_2}(\mathrm{~g})$.

$$ \mathrm{N_2}(\mathrm{~g})+3 \mathrm{H_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH_3}(\mathrm{~g}) $$

$$ 2 \mathrm{NH_3}(\mathrm{~g}) \rightleftharpoons \mathrm{N_2}(\mathrm{~g})+3 \mathrm{H_2}(\mathrm{~g}) $$

Similarly let us consider the reaction, $\mathrm{H_2}(\mathrm{~g})+\mathrm{I_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})$. If we start with equal initial concentration of $\mathrm{H_2}$ and $\mathrm{I_2}$, the reaction proceeds in the forward direction and the concentration of $\mathrm{H_2}$ and $\mathrm{I_2}$ decreases while that of $\mathrm{HI}$ increases, until all of these become constant at equilibrium (Fig. 6.5). We can also start with $\mathrm{HI}$ alone and make the reaction to proceed in the reverse direction; the concentration of HI will decrease and concentration of $\mathrm{H_2}$ and $\mathrm{I_2}$ will increase until they all become constant when equilibrium is reached (Fig. 6.5). If total number of $\mathrm{H}$ and I atoms are same in a given volume, the same equilibrium mixture is obtained whether we start it from pure reactants or pure product.

Dynamic Equilibrium - A Student’s Activity

Equilibrium whether in a physical or in a chemical system, is always of dynamic nature. This can be demonstrated by the use of radioactive isotopes. This is not feasible in a school laboratory. However this concept can be easily comprehended by performing the following activity. The activity can be performed in a group of 5 or 6 students.

Take two $100 \mathrm{~mL}$ measuring cylinders (marked as 1 and 2 ) and two glass tubes each of $30 \mathrm{~cm}$ length. Diameter of the tubes may be same or different in the range of $3-5 \mathrm{~mm}$. Fill nearly half of the measuring cylinder-1 with coloured water (for this purpose add a crystal of potassium permanganate to water) and keep second cylinder (number 2) empty.

Put one tube in cylinder 1 and second in cylinder 2. Immerse one tube in cylinder 1 , close its upper tip with a finger and transfer the coloured water contained in its lower portion to cylinder 2. Using second tube, kept in $2^{\text {nd }}$ cylinder, transfer the coloured water in a similar manner from cylinder 2 to cylinder 1 . In this way keep on transferring coloured water using the two glass tubes from cylinder 1 to 2 and from 2 to 1 till you notice that the level of coloured water in both the cylinders becomes constant.

If you continue intertransferring coloured solution between the cylinders, there will not be any further change in the levels of coloured water in two cylinders. If we take analogy of ’level’ of coloured water with ‘concentration’ of reactants and products in the two cylinders, we can say the process of transfer, which continues even after the constancy of level, is indicative of dynamic nature of the process. If we repeat the experiment taking two tubes of different diameters we find that at equilibrium the level of coloured water in two cylinders is different. How far diameters are responsible for change in levels in two cylinders? Empty cylinder (2) is an indicator of no product in it at the beginning.

7.3 LAW OF CHEMICAL EQUILIBRIUM AND EQUILIBRIUM CONSTANT

A mixture of reactants and products in the equilibrium state is called an equilibrium mixture. In this section we shall address a number of important questions about the composition of equilibrium mixtures: What is the relationship between the concentrations of reactants and products in an equilibrium mixture? How can we determine equilibrium concentrations from initial concentrations? What factors can be exploited to alter the composition of an equilibrium mixture? The last question in particular is important when choosing conditions for synthesis of industrial chemicals such as $\mathrm{H_2}, \mathrm{NH_3}, \mathrm{CaO}$ etc.

To answer these questions, let us consider a general reversible reaction:

$$ \mathrm{A}+\mathrm{B} \rightleftharpoons \mathrm{C}+\mathrm{D} $$

where $\mathrm{A}$ and $\mathrm{B}$ are the reactants, $\mathrm{C}$ and $\mathrm{D}$ are the products in the balanced chemical equation. On the basis of experimental studies of many reversible reactions, the Norwegian chemists Cato Maximillian Guldberg and Peter Waage proposed in 1864 that the concentrations in an equilibrium mixture are related by the following equilibrium equation,

$$ \begin{equation*} K_{c}=\frac{[\mathrm{C}][\mathrm{D}]}{[\mathrm{A}][\mathrm{B}]} \tag{7.1} \end{equation*} $$

(6.1) where $K_{c}$ is the equilibrium constant and the expression on the right side is called the equilibrium constant expression.

The equilibrium equation is also known as the law of mass action because in the early days of chemistry, concentration was called “active mass”. In order to appreciate their work better, let us consider reaction between gaseous $\mathrm{H_2}$ and $\mathrm{I_2}$ carried out in a sealed vessel at $731 \mathrm{~K}$.

$$ \begin{aligned} & \mathrm{H_2}(\mathrm{~g})+\mathrm{I_2}(\mathrm{~g}) \rightleftharpoons\\ & 1 \mathrm{~mol} \quad 1 \mathrm{~mol} \end{aligned} \begin{aligned} & 2 \mathrm{HI}(\mathrm{g}) \\ & 2 \mathrm{~mol} \end{aligned} $$

Six sets of experiments with varying initial conditions were performed, starting with only gaseous $\mathrm{H_2}$ and $\mathrm{I_2}$ in a sealed reaction vessel in first four experiments $(1,2,3$ and 4$)$ and only $\mathrm{HI}$ in other two experiments (5 and 6). Experiment 1, 2, 3 and 4 were performed taking different concentrations of $\mathrm{H_2}$ and / or $\mathrm{I_2}$, and with time it was observed that intensity of the purple colour remained constant and equilibrium was attained. Similarly, for experiments 5 and 6 , the equilibrium was attained from the opposite direction.

Data obtained from all six sets of experiments are given in Table 6.2.

It is evident from the experiments 1,2 , 3 and 4 that number of moles of dihydrogen reacted $=$ number of moles of iodine reacted $=1 / 2$ (number of moles of HI formed). Also, experiments 5 and 6 indicate that,

$[H_2(~g)]{eq} = [I_2(g)]{eq}$

Knowing the above facts, in order to establish a relationship between concentrations of the reactants and products, several combinations can be tried. Let us consider the simple expression,

$$ [\mathrm{HI}(\mathrm{g})]{\mathrm{eq}} /\left[\mathrm{H_2}(\mathrm{~g})\right]{\mathrm{eq}}\left[\mathrm{I_2}(\mathrm{~g})\right]_{\mathrm{eq}} $$

It can be seen from Table 6.3 that if we put the equilibrium concentrations of the reactants and products, the above expression

is far from constant. However, if we consider the expression,

$$ [\mathrm{HI}(\mathrm{g})]{\mathrm{eq}}^{2} /\left[\mathrm{H_2}(\mathrm{~g})\right]{\mathrm{eq}}\left[\mathrm{I_2}(\mathrm{~g})\right]_{\mathrm{eq}} $$

we find that this expression gives constant value (as shown in Table 6.3) in all the six cases. It can be seen that in this expression the power of the concentration for reactants and products are actually the stoichiometric coefficients in the equation for the chemical reaction. Thus, for the reaction $\mathrm{H_2}(\mathrm{~g})+\mathrm{I_2}(\mathrm{~g}) \rightleftharpoons$ $2 \mathrm{HI}(\mathrm{g})$, following equation 6.1 , the equilibrium constant $K_{c}$ is written as,

$$ \begin{equation*} K_{c}=[\mathrm{HI}(\mathrm{g})]{\mathrm{eq}}^{2} /\left[\mathrm{H_2}(\mathrm{~g})\right]{\mathrm{eq}}\left[\mathrm{I_2}(\mathrm{~g})\right]_{\mathrm{eq}} \tag{7.2} \end{equation*} $$

Generally the subscript ’eq’ (used for equilibrium) is omitted from the concentration terms. It is taken for granted that the concentrations in the expression for $K_{c}$ are equilibrium values. We, therefore, write,

$$ \begin{equation*} K_{c}=[\mathrm{HI}(\mathrm{g})]^{2} /\left[\mathrm{H_2}(\mathrm{~g})\right]\left[\mathrm{I_2}(\mathrm{~g})\right] \tag{7.3} \end{equation*} $$

The subscript ’ $c$ ’ indicates that $K_{c}$ is expressed in concentrations of $\mathrm{mol} \mathrm{L}^{-1}$.

At a given temperature, the product of concentrations of the reaction products raised to the respective stoichiometric coefficient in the balanced chemical equation divided by the product of concentrations of the reactants raised to their individual stoichiometric coefficients has a constant value. This is known as the Equilibrium Law or Law of Chemical Equilibrium. The equilibrium constant for a general reaction,

$\mathrm{aA}+\mathrm{bB} \rightleftharpoons \mathrm{cC}+\mathrm{d} \mathrm{D}$

is expressed as,

$K_{c}=[\mathrm{C}]^{c}[\mathrm{D}]^{\mathrm{d}} /[\mathrm{A}]^{\mathrm{a}}[\mathrm{B}]^{\mathrm{b}}$

where $[A],[B],[C]$ and $[D]$ are the equilibrium concentrations of the reactants and products.

Equilibrium constant for the reaction, $4 \mathrm{NH_3}(\mathrm{~g})+5 \mathrm{O_2}(\mathrm{~g}) \rightleftharpoons 4 \mathrm{NO}(\mathrm{g})+6 \mathrm{H_2} \mathrm{O}(\mathrm{g})$ is written as

$$ K_{c}=[\mathrm{NO}]^{4}\left[\mathrm{H_2} \mathrm{O}\right]^{6} /\left[\mathrm{NH_3}\right]^{4}\left[\mathrm{O_2}\right]^{5} $$

Molar concentration of different species is indicated by enclosing these in square bracket and, as mentioned above, it is implied that these are equilibrium concentrations. While writing expression for equilibrium constant, symbol for phases ( $\mathrm{s}, 1, \mathrm{~g})$ are generally ignored.

Let us write equilibrium constant for the reaction, $$\mathrm{H_2}(\mathrm{~g})+\mathrm{I_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})\tag{7.5}$$

$$ \begin{equation*} \text { as, } K_{c}=[\mathrm{HI}]^{2} /\left[\mathrm{H_2}\right]\left[\mathrm{I_2}\right]=\mathrm{x} \tag{7.6} \end{equation*} $$

The equilibrium constant for the reverse reaction, $2 \mathrm{HI}(\mathrm{g}) \rightleftharpoons \mathrm{H_2}(\mathrm{~g})+\mathrm{I_2}(\mathrm{~g})$, at the same temperature is,

$$K_{c}=\left[\mathrm{H_2}\right]\left[\mathrm{I_2}\right] /[\mathrm{HI}]^{2}=1 / \mathrm{x}=1 / K_{c} \tag{7.7}$$

$$\text{Thus,} \quad \quad K_{c}=1 / K_{c} \tag{7.8}$$

Equilibrium constant for the reverse reaction is the inverse of the equilibrium constant for the reaction in the forward direction.If we change the stoichiometric coefficients in a chemical equation by multiplying throughout by a factor then we must make sure that the expression for equilibrium constant also reflects that change. For example, if the reaction (6.5) is written as,

$$ \begin{equation*} 1 / 2 \mathrm{H_2}(\mathrm{~g})+1 / 2 \mathrm{I_2}(\mathrm{~g}) \rightleftharpoons \mathrm{HI}(\mathrm{g}) \tag{7.9} \end{equation*} $$

the equilibrium constant for the above reaction is given by

$$ \begin{aligned} K_{c}^{\prime \prime}=[\mathrm{HI}] /\left[\mathrm{H_2}\right]^{1 / 2}\left[\mathrm{I_2}\right]^{1 / 2} & =\left{[\mathrm{HI}]^{2} /\left[\mathrm{H_2}\right]\left[\mathrm{I_2}\right]\right}^{1 / 2} \\ = & \mathrm{x}^{1 / 2}=K_{c}^{1 / 2}(6.10) \end{aligned} $$

On multiplying the equation (7.5) by $\mathrm{n}$, we get $\mathrm{nH_2}(\mathrm{~g})+\mathrm{nI_2}(\mathrm{~g}) \mathrm{D} \rightleftharpoons 2 \mathrm{nHI}(\mathrm{g})$

Therefore, equilibrium constant for the reaction is equal to $K_{c}{ }^{n}$. These findings are summarised in Table 6.4. It should be noted that because the equilibrium constants $K_{c}$ and $K_{c}$ have different numerical values, it is important to specify the form of the balanced chemical equation when quoting the value of an equilibrium constant.

Table 6.4 Relations between Equilibrium Constants for a General Reaction and its Multiples.

Chemical equation	Equilibrium constant
$\mathrm{a} \mathrm{A}+\mathrm{b} \mathrm{B} \rightleftharpoons \mathrm{c} \mathrm{C}+\mathrm{dD}$	$K_{c}$
$\mathrm{c} \mathrm{C}+\mathrm{d} \mathrm{D} \rightleftharpoons \mathrm{a} \mathrm{A}+\mathrm{b} \mathrm{B}$	$K_{c}^{\prime}=\left(1 / K_{c}\right)$
$\mathrm{na} \mathrm{A}+\mathrm{nb} \mathrm{B} \rightleftharpoons \mathrm{ncC}+\mathrm{ndD}$	$K_{c}^{\prime \prime}=\left(K_{c}^{n}\right)$

Problem 7.1

The following concentrations were obtained for the formation of $\mathrm{NH_3}$ from $\mathrm{N_2}$ and $\mathrm{H_2}$ at equilibrium at $500 \mathrm{~K}$. $\left[\mathrm{N_2}\right]=1.5 \times 10^{-2} \mathrm{M} .\left[\mathrm{H_2}\right]=3.0 \times 10^{-2} \mathrm{M}$ and $\left[\mathrm{NH_3}\right]=1.2 \times 10^{-2} \mathrm{M}$. Calculate equilibrium constant.

Solution

The equilibrium constant for the reaction, $\mathrm{N_2}(\mathrm{~g})+3 \mathrm{H_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH_3}(\mathrm{~g})$ can be written as,

$$ \begin{aligned} K_{c} & =\frac{\left[\mathrm{NH_3}(\mathrm{~g})\right]^{2}}{\left[\mathrm{~N_2}(\mathrm{~g})\right]\left[\mathrm{H_2}(\mathrm{~g})\right]^{3}} \\ & =\frac{\left(1.2 \times 10^{-2}\right)^{2}}{\left(1.5 \times 10^{-2}\right)\left(3.0 \times 10^{-2}\right)^{3}} \\ & =0.106 \times 10^{4}=1.06 \times 10^{3} \end{aligned} $$

Problem 7.2

At equilibrium, the concentrations of $\mathrm{N_2}=3.0 \times 10^{-3} \mathrm{M}, \mathrm{O_2}=4.2 \times 10^{-3} \mathrm{M}$ and $\mathrm{NO}=2.8 \times 10^{-3} \mathrm{M}$ in a sealed vessel at $800 \mathrm{~K}$. What will be $K_{c}$ for the reaction

$$ \mathrm{N_2}(\mathrm{~g})+\mathrm{O_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g}) $$

Solution

For the reaction equilibrium constant, $K_{c}$ can be written as,

$$ \begin{aligned} K_{c} & =\frac{[\mathrm{NO}]^{2}}{\left[\mathrm{~N_2}\right]\left[\mathrm{O_2}\right]} \\ & =\frac{\left(2.8 \times 10^{-3} \mathrm{M}\right)^{2}}{\left(3.0 \times 10^{-3} \mathrm{M}\right)\left(4.2 \times 10^{-3} \mathrm{M}\right)} \\ = & 0.622 \end{aligned} $$

7.4 HOMOGENEOUS EQUILIBRIA

In a homogeneous system, all the reactants and products are in the same phase. For example, in the gaseous reaction, $\mathrm{N_2}(\mathrm{~g})+3 \mathrm{H_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH_3}(\mathrm{~g})$, reactants and products are in the homogeneous phase. Similarly, for the reactions,

$\mathrm{CH_3} \mathrm{COOC_2} \mathrm{H_5}(\mathrm{aq})+\mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{CH_3} \mathrm{COOH}(\mathrm{aq})$ $+\mathrm{C_2} \mathrm{H_5} \mathrm{OH}(\mathrm{aq})$

and, $\mathrm{Fe}^{3+}(\mathrm{aq})+\mathrm{SCN}^{-}(\mathrm{aq}) \rightleftharpoons \mathrm{Fe}(\mathrm{SCN})^{2+}(\mathrm{aq})$

all the reactants and products are in homogeneous solution phase. We shall now consider equilibrium constant for some homogeneous reactions.

7.4.1 Equilibrium Constant in Gaseous Systems

So far we have expressed equilibrium constant of the reactions in terms of molar concentration of the reactants and products, and used symbol, $K_{c}$ for it. For reactions involving gases, however, it is usually more convenient to express the equilibrium constant in terms of partial pressure.

The ideal gas equation is written as, $p V=n \mathrm{R} T$

$\Rightarrow p=\frac{n}{V} \mathrm{R} T$

Here, $p$ is the pressure in $\mathrm{Pa}, n$ is the number of moles of the gas, $V$ is the volume in $m^{3}$ and $T$ is the temperature in Kelvin

Therefore,

$n / V$ is concentration expressed in $\mathrm{mol} / \mathrm{m}^{3}$

If concentration $\mathrm{c}$, is in $\mathrm{mol} / \mathrm{L}$ or $\mathrm{mol} / \mathrm{dm}^{3}$, and $p$ is in bar then

$p=c \mathrm{R} T$,

We can also write $p=$ [gas] R $T$.

Here, $\mathrm{R}=0.0831$ bar litre/ $\mathrm{mol} \mathrm{K}$

At constant temperature, the pressure of the gas is proportional to its concentration i.e., $p \propto$ [gas]

For reaction in equilibrium

$\mathrm{H_2}(\mathrm{~g})+\mathrm{I_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})$

We can write either

$K_{\mathrm{c}}=\frac{[\mathrm{HI}(\mathrm{g})]^{2}}{\left[\mathrm{H_2}(\mathrm{~g})\right]\left[\mathrm{I_2}(\mathrm{~g})\right]}$

or $$K_{c}=\frac{\left(p_{H I}\right)^{2}}{\left(p_{\mathrm{H_2}}\right)\left(p_{I_{2}}\right)} \tag{7.12}$$

Further, since $p_{\mathrm{HI}}=[\mathrm{HI}(\mathrm{g})] \mathrm{R} T$

$$ \begin{aligned} p_{\mathrm{I_2}} & =\left[\mathrm{I_2}(\mathrm{~g})\right] \mathrm{R} T \\ p_{\mathrm{H_2}} & =\left[\mathrm{H_2}(\mathrm{~g})\right] \mathrm{R} T \end{aligned} $$

Therefore,

$$ \begin{gather*} K_{p}=\frac{\left(p_{\mathrm{HI}}\right)^{2}}{\left(p_{\mathrm{H_2}}\right)\left(p_{\mathrm{I_2}}\right)}=\frac{[\mathrm{HI}(\mathrm{g})]^{2}[\mathrm{R} T]^{2}}{\left[\mathrm{H_2}(\mathrm{~g})\right] \mathrm{R} T \cdot\left[\mathrm{I_2}(\mathrm{~g})\right] \mathrm{R} T} \\ =\frac{[\mathrm{HI}(\mathrm{g})]^{2}}{\left[\mathrm{H_2}(\mathrm{~g})\right]\left[\mathrm{I_2}(\mathrm{~g})\right]}=K_{c} \tag{7.13} \end{gather*} $$

In this example, $K_{p}=K_{c}$ i.e., both equilibrium constants are equal. However, this is not always the case. For example in reaction

$$ \mathrm{N_2}(\mathrm{~g})+3 \mathrm{H_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH_3}(\mathrm{~g}) $$

$$ \begin{aligned} K_{p} & =\frac{\left(p_{\mathrm{NH_3}}\right)^{2}}{\left(p_{N_{2}}\right)\left(p_{\mathrm{H_2}}\right)^{3}} \\ & =\frac{\left[\mathrm{NH_3}(\mathrm{~g})\right]^{2}[\mathrm{R} T]^{2}}{\left[\mathrm{~N_2}(\mathrm{~g})\right] \mathrm{R} T \cdot\left[H_{2}(\mathrm{~g})\right]^{3}(\mathrm{R} T)^{3}} \end{aligned} $$

$$ \begin{equation*} =\frac{\left[\mathrm{NH_3}(\mathrm{~g})\right]^{2}[\mathrm{R} T]^{-2}}{\left[\mathrm{~N_2}(\mathrm{~g})\right]\left[H_{2}(\mathrm{~g})\right]^{3}}=K_{c}(\mathrm{R} T)^{-2} \tag{7.14} \end{equation*} $$

or $K_{p}=K_{c}(\mathrm{R} T)^{-2}$

Similarly, for a general reaction

$$ \mathrm{aA}+\mathrm{bB} \rightleftharpoons \mathrm{cC}+\mathrm{dD} $$

$$ \begin{align*} K_{p}= & \frac{\left(p_{C}^{c}\right)\left(p_{D}^{d}\right)}{\left(p_{\mathrm{A}}^{a}\right)\left(p_{B}^{b}\right)}=\frac{[\mathrm{C}]^{c}[\mathrm{D}]^{d}(\mathrm{R} T)^{(c+d)}}{[\mathrm{A}]^{a}[\mathrm{~B}]^{b}(\mathrm{R} T)^{(a+b)}} \\ & =\frac{[\mathrm{C}]^{c}[\mathrm{D}]^{d}}{[\mathrm{~A}]^{a}[\mathrm{~B}]^{b}}(\mathrm{R} T)^{(c+d)-(a+b)} \\ & =\frac{[\mathrm{C}]^{c}[\mathrm{D}]^{d}}{[\mathrm{~A}]^{a}[\mathrm{~B}]^{b}}(\mathrm{R} T)^{\Delta n}=K_{c}(\mathrm{R} T)^{\Delta n} \tag{7.15} \end{align*} $$

where $\Delta n=$ (number of moles of gaseous products) - (number of moles of gaseous reactants) in the balanced chemical equation. It is necessary that while calculating the value of $K_{p}$, pressure should be expressed in bar because standard state for pressure is 1 bar. We know from Unit 1 that:

1 pascal, $\mathrm{Pa}=1 \mathrm{Nm}^{-2}$, and $1 \mathrm{bar}=10^{5} \mathrm{~Pa}$

$K_{p}$ values for a few selected reactions at different temperatures are given in Table 6.5

Table 6.5 Equilibrium Constants, $\mathrm{Kp}$ for a Few Selected Reactions

Reaction	Temperature $/ \mathbf{K}$	$\mathbf{K_p}$
$\mathrm{N_2}(\mathrm{~g})+3 \mathrm{H_2}(\mathrm{~g}) \leftrightharpoons 2 \mathrm{NH_3}$	298	$6.8 \times 10^{5}$
	400	41
	500	$3.6 \times 10^{-2}$
$2 \mathrm{SO_2}(\mathrm{~g})+\mathrm{O_2}(\mathrm{~g}) \leftrightharpoons 2 \mathrm{SO_3}(\mathrm{~g})$	298	$4.0 \times 10^{24}$
	500	$2.5 \times 10^{10}$
	700	$3.0 \times 10^{4}$
$\mathrm{~N_2} \mathrm{O_4}(\mathrm{~g}) \leftrightharpoons 2 \mathrm{NO_2}(\mathrm{~g})$	298	0.98
	400	47.9
	500	1700

Problem 7.3

$\mathrm{PCl_5}, \mathrm{PCl_3}$ and $\mathrm{Cl_2}$ are at equilibrium at 500 $\mathrm{K}$ and having concentration $1.59 \mathrm{M} \mathrm{PCl_3}$, $1.59 \mathrm{M} \mathrm{Cl_2}$ and $1.41 \mathrm{M} \mathrm{PCl_5}$.

Calculate $K_{c}$ for the reaction,

Solution

$$ \mathrm{PCl_5} \rightleftharpoons \mathrm{PCl_3}+\mathrm{Cl_2} $$

The equilibrium constant $K_{c}$ for the above reaction can be written as,

$$ K_{\mathrm{c}}=\frac{\left[\mathrm{PCl_3}\right]\left[\mathrm{Cl_2}\right]}{\left[\mathrm{PCl_5}\right]}=\frac{(1.59)^{2}}{(1.41)}=1.79 $$

Problem 7.4

The value of $K_{c}=4.24$ at $800 \mathrm{~K}$ for the reaction,

$\mathrm{CO}(\mathrm{g})+\mathrm{H_2} \mathrm{O}(\mathrm{g}) \rightleftharpoons \mathrm{CO_2}(\mathrm{~g})+\mathrm{H_2}(\mathrm{~g})$

Calculate equilibrium concentrations of $\mathrm{CO_2}$, $\mathrm{H_2}, \mathrm{CO}$ and $\mathrm{H_2} \mathrm{O}$ at $800 \mathrm{~K}$, if only $\mathrm{CO}$ and $\mathrm{H_2} \mathrm{O}$ are present initially at concentrations of $0.10 \mathrm{M}$ each.

Solution

For the reaction,

$$ \mathrm{CO}(\mathrm{g})+\mathrm{H_2} \mathrm{O}(\mathrm{g}) \rightleftharpoons \mathrm{CO_2}(\mathrm{~g})+\mathrm{H_2}(\mathrm{~g}) $$

Initial concentration:

$$ \begin{array}{llll} 0.1 \mathrm{M} & 0.1 \mathrm{M} & 0 & 0 \end{array} $$

Let $\mathrm{x}$ mole per litre of each of the product be formed.

At equilibrium:

$$ \begin{array}{llll} (0.1-x) M & (0.1-x) M & x M & x M \end{array} $$

where $x$ is the amount of $\mathrm{CO_2}$ and $\mathrm{H_2}$ at equilibrium.

Hence, equilibrium constant can be written as,

$K_{c}=\mathrm{x}^{2} /(0.1-\mathrm{x})^{2}=4.24$

$\mathrm{x}^{2}=4.24\left(0.01+\mathrm{x}^{2}-0.2 \mathrm{x}\right)$

$\mathrm{x}^{2}=0.0424+4.24 \mathrm{x}^{2}-0.848 \mathrm{x}$

$3.24 \mathrm{x}^{2}-0.848 \mathrm{x}+0.0424=0$

$\mathrm{a}=3.24, \mathrm{~b}=-0.848, \mathrm{c}=0.0424$

(for quadratic equation $a x^{2}+b x+c=0$,

$$ x=\frac{\left(-b \pm \sqrt{b^{2}-4 a c}\right)}{2 a} $$

$x=0.848 \pm \sqrt{ }(0.848)^{2}-4(3.24)(0.0424) / (3.24 \times 2)$

$x=(0.848 \pm 0.4118) / 6.48$

$x_{1}=(0.848-0.4118) / 6.48=0.067$

$\mathrm{x_2}=(0.848+0.4118) / 6.48=0.194$

the value 0.194 should be neglected because it will give concentration of the reactant which is more than initial concentration.

Hence the equilibrium concentrations are,

$$ \begin{aligned} & {\left[\mathrm{CO_2}\right]=\left[\mathrm{H_2}\right]=\mathrm{x}=0.067 \mathrm{M}} \\ & {[\mathrm{CO}]=\left[\mathrm{H_2} \mathrm{O}\right]=0.1-0.067=0.033 \mathrm{M}} \end{aligned} $$

Problem 7.5

For the equilibrium,

$2 \mathrm{NOCl}(\mathrm{g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g})+\mathrm{Cl_2}(\mathrm{~g})$

the value of the equilibrium constant, $K_{c}$ is $3.75 \times 10^{-6}$ at $1069 \mathrm{~K}$. Calculate the $K_{p}$ for the reaction at this temperature?

Solution

We know that,

$K_{p}=K_{c}(\mathrm{R} T)^{\Delta n}$

For the above reaction,

$\Delta n=(2+1)-2=1$

$K_{p}=3.75 \times 10^{-6}(0.0831 \times 1069)$

$K_{p}=0.033$

7.5 HETEROGENEOUS EQUILIBRIA

Equilibrium in a system having more than one phase is called heterogeneous equilibrium. The equilibrium between water vapour and liquid water in a closed container is an example of heterogeneous equilibrium.

$$ \mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H_2} \mathrm{O}(\mathrm{g}) $$

In this example, there is a gas phase and a liquid phase. In the same way, equilibrium between a solid and its saturated solution,

$\mathrm{Ca}(\mathrm{OH})_{2}(\mathrm{~s})+(\mathrm{aq}) \rightleftharpoons \mathrm{Ca}^{2+}(\mathrm{aq})+2 \mathrm{OH}^{-}(\mathrm{aq})$

is a heterogeneous equilibrium.

Heterogeneous equilibria often involve pure solids or liquids. We can simplify equilibrium expressions for the heterogeneous equilibria involving a pure liquid or a pure solid, as the molar concentration of a pure solid or liquid is constant (i.e., independent of the amount present). In other words if a substance ’ $\mathrm{X}$ ’ is involved, then $[\mathrm{X}(\mathrm{s})]$ and $[\mathrm{X}(1)]$ are constant, whatever the amount of ’ $\mathrm{X}$ ’ is taken. Contrary to this, $[\mathrm{X}(\mathrm{g})]$ and $[\mathrm{X}(\mathrm{aq})]$ will vary as the amount of $\mathrm{X}$ in a given volume varies. Let us take thermal dissociation of calcium carbonate which is an interesting and important example of heterogeneous chemical equilibrium.

$\mathrm{CaCO_3}(\mathrm{~s}) \stackrel{\Delta}{\rightleftharpoons} \mathrm{CaO}(\mathrm{s})+\mathrm{CO_2}(\mathrm{~g})$

On the basis of the stoichiometric equation, we can write,

$$ K_{c}=\frac{[\mathrm{CaO}(\mathrm{s})]\left[\mathrm{CO_2}(\mathrm{~g})\right]}{\left[\mathrm{CaCO_3}(\mathrm{~s})\right]} $$

Since $\left[\mathrm{CaCO_3}(\mathrm{~s})\right]$ and $[\mathrm{CaO}(\mathrm{s})]$ are both constant, therefore modified equilibrium constant for the thermal decomposition of calcium carbonate will be

$$ \begin{align*} & K_{c}^{\prime}=\left[\mathrm{CO_2}(\mathrm{~g})\right] \tag{7.17}\\ & \text { or } K_{p}=p_{\mathrm{CO_2}} \tag{7.18} \end{align*} $$

This shows that at a particular temperature, there is a constant concentration or pressure of $\mathrm{CO_2}$ in equilibrium with $\mathrm{CaO}$ (s) and $\mathrm{CaCO_3}(\mathrm{~s})$. Experimentally it has been found that at $1100 \mathrm{~K}$, the pressure of $\mathrm{CO_2}$ in equilibrium with $\mathrm{CaCO_3}(\mathrm{~s})$ and $\mathrm{CaO}(\mathrm{s})$, is $2.0 \times 10^{5} \mathrm{~Pa}$. Therefore, equilibrium constant at $1100 \mathrm{~K}$ for the above reaction is:

$$ K_{p}=P_{\mathrm{CO_2}}=2 \times 10^{5} \mathrm{~Pa} / 10^{5} \mathrm{~Pa}=2.00 $$

Similarly, in the equilibrium between nickel, carbon monoxide and nickel carbonyl (used in the purification of nickel),

$$ \mathrm{Ni}(\mathrm{s})+4 \mathrm{CO}(\mathrm{g}) \rightleftharpoons \mathrm{Ni}(\mathrm{CO})_{4}(\mathrm{~g}) $$

the equilibrium constant is written as

$$ K_{c}=\frac{\left[\mathrm{Ni}(\mathrm{CO})_{4}\right]}{[\mathrm{CO}]^{4}} $$

It must be remembered that for the existence of heterogeneous equilibrium pure solids or liquids must also be present (however small the amount may be) at equilibrium, but their concentrations or partial pressures do not appear in the expression of the equilibrium constant. In the reaction,

$$ \begin{gathered} \mathrm{Ag_2} \mathrm{O}(\mathrm{s})+2 \mathrm{HNO_3}(\mathrm{aq}) \rightleftharpoons 2 \mathrm{AgNO_3}(\mathrm{aq})+\mathrm{H_2} \mathrm{O}(\mathrm{l}) \\ \mathrm{K_c}=\frac{\left[\mathrm{AgNO_3}\right]^{2}}{\left[\mathrm{HNO_3}\right]^{2}} \end{gathered} $$

Units of Equilibrium Constant

The value of equilibrium constant $K_{\mathrm{c}}$ can be calculated by substituting the concentration terms in $\mathrm{mol} / \mathrm{L}$ and for $K_{p}$ partial pressure is substituted in $\mathrm{Pa}, \mathrm{kPa}$, bar or atm. This results in units of equilibrium constant based on molarity or pressure, unless the exponents of both the numerator and denominator are same.

For the reactions, unit.

$\mathrm{H_2}(\mathrm{~g})+\mathrm{I_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}, K_{\mathrm{c}}$ and $K_{p}$ have no

$\mathrm{N_2} \mathrm{O_4}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO_2}(\mathrm{~g}), K_{\mathrm{c}}$ has unit $\mathrm{mol} / \mathrm{L}$ and $K_{p}$ has unit bar

Equilibrium constants can also be expressed as dimensionless quantities if the standard state of reactants and products are specified. For a pure gas, the standard state is 1 bar. Therefore a pressure of 4 bar in standard state can be expressed as 4 bar $/ 1$ bar $=4$, which is a dimensionless number. Standard state $\left(c_{0}\right)$ for a solute is 1 molar solution and all concentrations can be measured with respect to it. The numerical value of equilibrium constant depends on the standard state chosen. Thus, in this system both $K_{p}$ and $K_{c}$ are dimensionless quantities but have different numerical values due to different standard states.

Problem 7.6

The value of $K_{p}$ for the reaction,

$\mathrm{CO_2}(\mathrm{~g})+\mathrm{C}(\mathrm{s}) \rightleftharpoons 2 \mathrm{CO}(\mathrm{g})$ is 3.0 at $1000 \mathrm{~K}$. If initially $P_{\mathrm{CO_2}}=0.48$ bar and $P_{C O}=0$ bar and pure graphite is present, calculate the equilibrium partial pressures of $\mathrm{CO}$ and $\mathrm{CO_2}$.

Solution

For the reaction, let ’ $x$ ’ be the decrease in pressure of $\mathrm{CO_2}$, then

Initial

$$ \mathrm{CO_2}(\mathrm{~g})+\mathrm{C}(\mathrm{s}) \rightleftharpoons 2 \mathrm{CO}(\mathrm{g}) $$

pressure: 0.48 bar 0

At equilibrium:

$$ (0.48-x) \text { bar } \quad 2 x \text { bar } $$

$$ \begin{aligned} & K_{p}=\frac{p_{C O}^{2}}{p_{\mathrm{CO_2}}} \\ & K_{p}=(2 \mathrm{x})^{2} /(0.48-\mathrm{x})=3 \\ & 4 \mathrm{x}^{2}=3(0.48-\mathrm{x}) \\ & 4 \mathrm{x}^{2}=1.44-\mathrm{x} \\ & 4 \mathrm{x}^{2}+3 \mathrm{x}-1.44=0 \\ & \mathrm{a}=4, \mathrm{~b}=3, \mathrm{c}=-1.44 \end{aligned} $$

$\mathrm{x}=\frac{\left(-\mathrm{b} \pm \sqrt{\mathrm{b}^{2}-4 \mathrm{ac}}\right)}{2 \mathrm{a}}$

$=\left[-3 \pm \sqrt{ }(3)^{2}-4(4)(-1.44)\right] / 2 \times 4$

$=(-3 \pm 5.66) / 8$

$=(-3+5.66) / 8$ (as value of $x$ cannot be negative hence we neglect that value)

$\mathrm{x}=2.66 / 8=0.33$

The equilibrium partial pressures are,

$p_{\mathrm{CO_2}}=2 \mathrm{x}=2 \times 0.33=0.66$ bar

$p_{\mathrm{CO_2}}=0.48-\mathrm{x}=0.48-0.33=0.15$ bar

7.6 APPLICATIONS OF EQUILIBRIUM CONSTANTS

Before considering the applications of equilibrium constants, let us summarise the important features of equilibrium constants as follows:

1. Expression for equilibrium constant is applicable only when concentrations of the reactants and products have attained constant value at equilibrium state.
2. The value of equilibrium constant is independent of initial concentrations of the reactants and products.
3. Equilibrium constant is temperature dependent having one unique value for a particular reaction represented by a balanced equation at a given temperature.
4. The equilibrium constant for the reverse reaction is equal to the inverse of the equilibrium constant for the forward reaction.
5. The equilibrium constant $K$ for a reaction is related to the equilibrium constant of the corresponding reaction, whose equation is obtained by multiplying or dividing the equation for the original reaction by a small integer.

Let us consider applications of equilibrium constant to:

• predict the extent of a reaction on the basis of its magnitude,

• predict the direction of the reaction, and

• calculate equilibrium concentrations.

7.6.1 Predicting the Extent of a Reaction

The numerical value of the equilibrium constant for a reaction indicates the extent of the reaction. But it is important to note that an equilibrium constant does not give any information about the rate at which the equilibrium is reached. The magnitude of $K_{c}$ or $K_{p}$ is directly proportional to the concentrations of products (as these appear in the numerator of equilibrium constant expression) and inversely proportional to the concentrations of the reactants (these appear in the denominator). This implies that a high value of $K$ is suggestive of a high concentration of products and vice-versa.

We can make the following generalisations concerning the composition of equilibrium mixtures:

• If $K_{\mathrm{c}}>10^{3}$, products predominate over reactants, i.e., if $K_{c}$ is very large, the reaction proceeds nearly to completion. Consider the following examples:

$\quad \quad$ (a) The reaction of $\mathrm{H_2}$ with $\mathrm{O_2}$ at $500 \mathrm{~K}$ has a very large equilibrium constant, $K_{\mathrm{c}}=2.4 \times 10^{47}$.

$\quad \quad$ (b) $\mathrm{H_2}$ (g) $+\mathrm{Cl_2}$ (g) $\rightleftharpoons 2 \mathrm{HCl}(\mathrm{g})$ at $300 \mathrm{~K}$ has $K_{\mathrm{c}}=4.0 \times 10^{31}$.

$\quad \quad$ (c) $\mathrm{H_2}(\mathrm{~g})+\mathrm{Br_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HBr}$ (g) at $300 \mathrm{~K}$, $K_{c}=5.4 \times 10^{18}$

• If $K_{c}<10^{-3}$, reactants predominate over products, i.e., if $K_{c}$ is very small, the reaction proceeds rarely. Consider the following examples: $\quad \quad$ (a) The decomposition of $\mathrm{H_2} \mathrm{O}$ into $\mathrm{H_2}$ and $\mathrm{O_2}$ at $500 \mathrm{~K}$ has a very small equilibrium constant, $K_{c}=4.1 \times 10^{-48}$

$\quad \quad$ (b) $\mathrm{N_2}(\mathrm{~g})+\mathrm{O_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g})$, at $298 \mathrm{~K}$ has $K_{c}=4.8 \times 10^{-31}$.

• If $K_{c}$ is in the range of $10^{-3}$ to $10^{3}$, appreciable concentrations of both reactants and products are present. Consider the following examples:

$\quad \quad$ (a) For reaction of $\mathrm{H_2}$ with $\mathrm{I_2}$ to give $\mathrm{HI}$, $K_{c}=57.0$ at $700 \mathrm{~K}$.

$\quad \quad$ (b) Also, gas phase decomposition of $\mathrm{N_2} \mathrm{O_4}$ to $\mathrm{NO_2}$ is another reaction with a value of $K_{c}=4.64 \times 10^{-3}$ at $25^{\circ} \mathrm{C}$ which is neither too small nor too large. Hence, equilibrium mixtures contain appreciable concentrations of both $\mathrm{N_2} \mathrm{O_4}$ and $\mathrm{NO_2}$.

These generarlisations are illustrated in Fig. 6.6

6.6.2 Predicting the Direction of the Reaction

The equilibrium constant helps in predicting the direction in which a given reaction will proceed at any stage. For this purpose, we calculate the reaction quotient $Q$. The reaction quotient, $Q\left(Q_{c}\right.$ with molar concentrations and $Q_{P}$ with partial pressures) is defined in the same way as the equilibrium constant $K_{c}$ except that the concentrations in $Q_{c}$ are not necessarily equilibrium values. For a general reaction:

$$\mathrm{a} \mathrm{A}+\mathrm{bB} \rightleftharpoons \mathrm{c} \mathrm{C}+\mathrm{d} \mathrm{D} \tag{6.19}$$

$$Q_{c}=[\mathrm{C}]^{\mathrm{c}}[\mathrm{D}]^{\mathrm{d}} /[\mathrm{A}]^{\mathrm{a}}[\mathrm{B}]^{\mathrm{b}}\tag{6.20}$$

Then,

If $Q_{c}>K_{c}$, the reaction will proceed in the direction of reactants (reverse reaction).

If $Q_{c}<K_{c}$, the reaction will proceed in the direction of the products (forward reaction). If $Q_{c}=K_{c}$, the reaction mixture is already at equilibrium.

Consider the gaseous reaction of $\mathrm{H_2}$ with $\mathrm{I_2}$,

$\mathrm{H_2}(\mathrm{~g})+\mathrm{I_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g}) ; K_{c}=57.0$ at $700 \mathrm{~K}$.

Suppose we have molar concentrations $\left[\mathrm{H_2}\right]_t=0.10 \mathrm{M},\left[\mathrm{I_2}\right]_t=0.20 \mathrm{M}$ and $[\mathrm{HI}]_t=0.40 \mathrm{M}$. (the subscript $t$ on the concentration symbols means that the concentrations were measured at some arbitrary time $t$, not necessarily at equilibrium).

Thus, the reaction quotient, $Q_{c}$ at this stage of the reaction is given by, $Q_{c}=[\mathrm{HI}]_t^{2} /\left[\mathrm{H_2}\right]_t\left[\mathrm{I_2}\right]_t=(0.40)^{2} /(0.10) \times(0.20)$

$$ =8.0 $$

Now, in this case, $Q_{c}$ (8.0) does not equal $K_{c}(57.0)$, so the mixture of $\mathrm{H_2}(\mathrm{~g}), \mathrm{I_2}(\mathrm{~g})$ and $\mathrm{HI}(\mathrm{g})$ is not at equilibrium; that is, more $\mathrm{H_2}(\mathrm{~g})$ and $\mathrm{I_2}(\mathrm{~g})$ will react to form more $\mathrm{HI}(\mathrm{g})$ and their concentrations will decrease till $Q_{c}=K_{c}$.

The reaction quotient, $Q_{c}$ is useful in predicting the direction of reaction by comparing the values of $Q_{c}$ and $K_{c}$.

Thus, we can make the following generalisations concerning the direction of the reaction (Fig. 6.7) :

• If $Q_{c}<K_{c}$, net reaction goes from left to right
• If $Q_{c}>K_{c}$, net reaction goes from right to left.
• If $Q_{c}=K_{c}$, no net reaction occurs.

Problem 7.7

The value of $K_{c}$ for the reaction $2 \mathrm{~A} \rightleftharpoons \mathrm{B}+\mathrm{C}$ is $2 \times 10^{-3}$. At a given time, the composition of reaction mixture is $[A]=[B]=[C]=3 \times 10^{-4} \mathrm{M}$. In which direction the reaction will proceed?

Solution

For the reaction the reaction quotient $Q_{c}$ is given by,

$Q_{c}=[\mathrm{B}][\mathrm{C}] /[\mathrm{A}]^{2}$

as $[\mathrm{A}]=[\mathrm{B}]=[\mathrm{C}]=3 \times 10^{-4} \mathrm{M}$

$Q_{c}=\left(3 \times 10^{-4}\right)\left(3 \times 10^{-4}\right) /\left(3 \times 10^{-4}\right)^{2}=1$

as $Q_{c}>K_{c}$ so the reaction will proceed in the reverse direction.

7.6.3 Calculating Equilibrium Concentrations

In case of a problem in which we know the initial concentrations but do not know any of the equilibrium concentrations, the following three steps shall be followed:

Step 1. Write the balanced equation for the reaction.

Step 2. Under the balanced equation, make a table that lists for each substance involved in the reaction:

(a) the initial concentration,

(b) the change in concentration on going to equilibrium, and

(c) the equilibrium concentration.

In constructing the table, define $\mathrm{x}$ as the concentration ( $\mathrm{mol} / \mathrm{L})$ of one of the substances that reacts on going to equilibrium, then use the stoichiometry of the reaction to determine the concentrations of the other substances in terms of $\mathrm{x}$.

Step 3. Substitute the equilibrium concentrations into the equilibrium equation for the reaction and solve for $\mathrm{x}$. If you are to solve a quadratic equation choose the mathematical solution that makes chemical sense.

Step 4. Calculate the equilibrium concentrations from the calculated value of $\mathrm{x}$.

Step 5. Check your results by substituting them into the equilibrium equation.

Problem 7.8

$13.8 \mathrm{~g}$ of $\mathrm{N_2} \mathrm{O_4}$ was placed in a $1 \mathrm{~L}$ reaction vessel at $400 \mathrm{~K}$ and allowed to attain equilibrium

$\mathrm{N_2} \mathrm{O_4}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO_2}(\mathrm{~g})$ The total pressure at equilbrium was found to be 9.15 bar. Calculate $K_{c}, K_{p}$ and partial pressure at equilibrium.

Solution

We know $p V=n R T$

Total volume $(V)=1 \mathrm{~L}$

Molecular mass of $\mathrm{N_2} \mathrm{O_4}=92 \mathrm{~g}$

Number of moles $=13.8 \mathrm{~g} / 92 \mathrm{~g}=0.15$

of the gas ( $n$ )

Gas constant $(\mathrm{R})=0.083$ bar $\mathrm{L} \mathrm{mol}^{-1} \mathrm{~K}^{-1}$

Temperature $(T)=400 \mathrm{~K}$

$p V=n \mathrm{R} T$

$p \times 1 \mathrm{~L}=0.15 \mathrm{~mol} \times 0.083$ bar $\mathrm{L} \mathrm{mol}^{-1} \mathrm{~K}^{-1}$

$\times 400 \mathrm{~K}$

$p=4.98$ bar

$$ \begin{equation*} \mathrm{N_2} \mathrm{O_4} \rightleftharpoons 2 \mathrm{NO_2} \end{equation*} $$

Initial pressure: $4.98 \mathrm{bar} \quad \quad \quad 0 $

At equilibrium: $(4.98-\mathrm{x})$ bar $2 \mathrm{x}$ bar Hence,

$p_{\text {total }}$ at equilibrium $=p_{\mathrm{N_2} \mathrm{O_4}}+p_{\mathrm{NO_2}}$

$9.15=(4.98-\mathrm{x})+2 \mathrm{x}$

$9.15=4.98+x$

$x=9.15-4.98=4.17$ bar

Partial pressures at equilibrium are,

$p_{\mathrm{N_2} \mathrm{O_4}}=4.98-4.17=0.81$ bar

$p_{\mathrm{NO_2}}=2 \mathrm{x}=2 \times 4.17=8.34 \mathrm{bar}$

$K_{p}=\left(p_{\mathrm{NO_2}}\right)^{2} / p_{\mathrm{N_2} \mathrm{O_4}}$

$=(8.34)^{2} / 0.81=85.87$

$K_{p}=K_{\mathrm{c}}(\mathrm{R} T)^{\Delta n}$

$85.87=K_{c}(0.083 \times 400)^{1}$

$K_{c}=2.586=2.6$

Problem 7.9

$3.00 \mathrm{~mol}$ of $\mathrm{PCl_5}$ kept in $1 \mathrm{~L}$ closed reaction vessel was allowed to attain equilibrium at $380 \mathrm{~K}$. Calculate composition of the mixture at equilibrium. $K_{c}=1.80$

Solution

Initial

$$ \mathrm{PCl_5} \rightleftharpoons \mathrm{PCl_3}+\mathrm{Cl_2} $$

$ \quad \text{concentration:} 3.0 \quad\quad\quad 0 \quad\quad\quad 0$

Let $\mathrm{x} \mathrm{mol}$ per litre of $\mathrm{PCl_5}$ be dissociated, At equilibrium:

$$ (3-x) \quad\quad\quad \mathrm{x} \quad\quad\quad \mathrm{x} $$

$K_{c}=\left[\mathrm{PCl_3}\right]\left[\mathrm{Cl_2}\right] /\left[\mathrm{PCl_5}\right]$

$1.8=\mathrm{x}^{2} /(3-\mathrm{x})$

$\mathrm{x}^{2}+1.8 \mathrm{x}-5.4=0$

$x=\left[-1.8 \pm \sqrt{ }(1.8)^{2}-4(-5.4)\right] / 2$

$x=[-1.8 \pm \sqrt{ } 3.24+21.6] / 2$

$\mathrm{x}=[-1.8 \pm 4.98] / 2$

$\mathrm{x}=[-1.8+4.98] / 2=1.59$

$\left[\mathrm{PCl_5}\right]=3.0-\mathrm{x}=3-1.59=1.41 \mathrm{M}$

$\left[\mathrm{PCl_3}\right]=\left[\mathrm{Cl_2}\right]=\mathrm{x}=1.59 \mathrm{M}$

7.7 RELATIONSHIP BETWEEN EQUILIBRIUM CONSTANT $K$, REACTION QUOTIENT $Q$ AND GIBBS ENERGY $G$

The value of $K_{c}$ for a reaction does not depend on the rate of the reaction. However, as you have studied in Unit 5, it is directly related to the thermodynamics of the reaction and in particular, to the change in Gibbs energy, $\Delta G$. If,

• $\Delta G$ is negative, then the reaction is spontaneous and proceeds in the forward direction.
• $\Delta G$ is positive, then reaction is considered non-spontaneous. Instead, as reverse reaction would have a negative $\Delta G$, the products of the forward reaction shall be converted to the reactants.
• $\Delta G$ is 0 , reaction has achieved equilibrium; at this point, there is no longer any free energy left to drive the reaction.

A mathematical expression of this thermodynamic view of equilibrium can be described by the following equation:

$$\Delta G=\Delta G^{\ominus}+\mathrm{RT} \ln Q \tag{7.21}$$

where, $G^{\ominus}$ is standard Gibbs energy.

At equilibrium, when $\Delta G=0$ and $Q=K_{c}$, the 7.21) becomes,

$\Delta G=\Delta G^{\ominus}+\mathrm{R} T \ln K=0$

$$\Delta G^{\ominus}=-\mathrm{R} T \ln K\tag{7.22}$$

$\ln K=-\Delta G^{\ominus} / \mathrm{R} T$ Taking antilog of both sides, we get,

$$ \begin{equation*} K=\mathrm{e}^{-\Delta G \ominus / R T} \tag{7.23} \end{equation*} $$

Hence, using the equation (7.23), the reaction spontaneity can be interpreted in terms of the value of $\Delta G^{\ominus}$.

• If $\Delta G^{\ominus}<0$, then $-\Delta G^{\ominus} / \mathrm{R} T$ is positive, and $e^{-\Delta DG^\circ }< / RT > 1$, making $K > 1 $, which implies a spontaneous reaction or the reaction which proceeds in the forward direction to such an extent that the products are present predominantly.

• If $\Delta G^{\ominus}>0$, then $-\Delta G^{\ominus} / \mathrm{R} T$ is negative, and $\mathrm{e}^{-\Delta G^{\ominus}</ \mathrm{RT}} 1$, that is , $K<1$, which implies a non-spontaneous reaction or a reaction which proceeds in the forward direction to such a small degree that only a very minute quantity of product is formed.

Problem 7.10

The value of $\Delta G^{\ominus}$ for the phosphorylation of glucose in glycolysis is $13.8 \mathrm{~kJ} / \mathrm{mol}$. Find the value of $K_{c}$ at $298 \mathrm{~K}$.

Solution

$\Delta G^{\ominus}=13.8 \mathrm{~kJ} / \mathrm{mol}=13.8 \times 10^{3} \mathrm{~J} / \mathrm{mol}$

Also, $\Delta G^{\ominus}=-\mathrm{RT} \ln K_{c}$

Hence, $\ln K_{c}=-13.8 \times 10^{3} \mathrm{~J} / \mathrm{mol}$

(8.314 $\left.\mathrm{J} \mathrm{mol}^{-1} \mathrm{~K}^{-1} \times 298 \mathrm{~K}\right)$

$\ln K_{\mathrm{c}}=-5.569$

$K_{\text {c }}=\mathrm{e}^{-5.569}$

$K_{\mathrm{c}}=3.81 \times 10^{-3}$

Problem 7.11

Hydrolysis of sucrose gives,

Sucrose $+\mathrm{H_2} \mathrm{O} \rightleftharpoons$ Glucose + Fructose

Equilibrium constant $K_{c}$ for the reaction is $2 \times 10^{13}$ at $300 \mathrm{~K}$. Calculate $\Delta G^{\ominus}$ at $300 \mathrm{~K}$.

Solution

$$ \begin{aligned} & \Delta G^{\ominus}=-\mathrm{R} T \ln K_{c} \\ & \Delta G^{\ominus}=-8.314 \mathrm{~J}^{-1} \mathrm{~mol}^{-1} \mathrm{~K}^{-1 \times} \\ & \quad 300 \mathrm{~K} \times \ln \left(2 \times 10^{13}\right) \\ & \Delta G^{\ominus}=-7.64 \times 10^{4} \mathrm{~J} \mathrm{~mol}^{-1} \end{aligned} $$

7.8 FACTORS AFFECTING EQUILIBRIA

One of the principal goals of chemical synthesis is to maximise the conversion of the reactants to products while minimising the expenditure of energy. This implies maximum yield of products at mild temperature and pressure conditions. If it does not happen, then the experimental conditions need to be adjusted. For example, in the Haber process for the synthesis of ammonia from $\mathrm{N_2}$ and $\mathrm{H_2}$, the choice of experimental conditions is of real economic importance. Annual world production of ammonia is about hundred million tones, primarily for use as fertilisers.

Equilibrium constant, $K_{c}$ is independent of initial concentrations. But if a system at equilibrium is subjected to a change in the concentration of one or more of the reacting substances, then the system is no longer at equilibrium; and net reaction takes place in some direction until the system returns to equilibrium once again. Similarly, a change in temperature or pressure of the system may also alter the equilibrium. In order to decide what course the reaction adopts and make a qualitative prediction about the effect of a change in conditions on equilibrium we use Le Chatelier’s principle. It states that a change in any of the factors that determine the equilibrium conditions of a system will cause the system to change in such a manner so as to reduce or to counteract the effect of the change. This is applicable to all physical and chemical equilibria.

We shall now be discussing factors which can influence the equilibrium.

7.8.1 Effect of Concentration Change

In general, when equilibrium is disturbed by the addition/removal of any reactant/ products, Le Chatelier’s principle predicts that:

• The concentration stress of an added reactant/product is relieved by net reaction in the direction that consumes the added substance.
• The concentration stress of a removed reactant/product is relieved by net reaction in the direction that replenishes the removed substance. or in other words, “When the concentration of any of the reactants or products in a reaction at equilibrium is changed, the composition of the equilibrium mixture changes so as to minimize the effect of concentration changes”.

Let us take the reaction,

$$ \mathrm{H_2}(\mathrm{~g})+\mathrm{I_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g}) $$

If $\mathrm{H_2}$ is added to the reaction mixture at equilibrium, then the equilibrium of the reaction is disturbed. In order to restore it, the reaction proceeds in a direction wherein $\mathrm{H_2}$ is consumed, i.e., more of $\mathrm{H_2}$ and $\mathrm{I_2}$ react to form $\mathrm{HI}$ and finally the equilibrium shifts in right (forward) direction (Fig.6.8). This is in accordance with the Le Chatelier’s principle which implies that in case of addition of a reactant/product, a new equilibrium will be set up in which the concentration of the reactant/product should be less than what it was after the addition but more than what it was in the original mixture.

The same point can be explained in terms of the reaction quotient, $Q_{c}$,

$$ Q_{c}=[\mathrm{HI}]^{2} /\left[\mathrm{H_2}\right]\left[\mathrm{I_2}\right] $$

Addition of hydrogen at equilibrium results in value of $Q_{c}$ being less than $K_{c}$. Thus, in order to attain equilibrium again reaction moves in the forward direction. Similarly, we can say that removal of a product also boosts the forward reaction and increases the concentration of the products and this has great commercial application in cases of reactions, where the product is a gas or a volatile substance. In case of manufacture of ammonia, ammonia is liquified and removed from the reaction mixture so that reaction keeps moving in forward direction. Similarly, in the large scale production of $\mathrm{CaO}$ (used as important building material) from $\mathrm{CaCO_3}$, constant removal of $\mathrm{CO_2}$ from the kiln drives the reaction to completion. It should be remembered that continuous removal of a product maintains $Q_{c}$ at a value less than $K_{c}$ and reaction continues to move in the forward direction.

Effect of Concentration - An experiment

This can be demonstrated by the following reaction:

$$\underset{\text{yellow}}{\mathrm{Fe}^{3+}(\mathrm{aq})}+\underset{\text{colourless}}{\mathrm{SCN}^{-}(\mathrm{aq})} \rightleftharpoons\underset{\text{deep red}}{[\mathrm{Fe}(\mathrm{SCN})]^{2+}(\mathrm{aq})} \tag{7.24}$$

yellow deep red

$$K_{c}=\frac{\left[\mathrm{Fe}(\mathrm{SCN})^{2+}(\mathrm{aq})\right]}{\left[\mathrm{Fe}^{3+}(\mathrm{aq})\right]\left[\mathrm{SCN}^{-}(\mathrm{aq})\right]} \tag{7.25}$$

A reddish colour appears on adding two drops of $0.002 \mathrm{M}$ potassium thiocynate solution to $1 \mathrm{~mL}$ of $0.2 \mathrm{M}$ iron(III) nitrate solution due to the formation of $[\mathrm{Fe}(\mathrm{SCN})]^{2+}$. The intensity of the red colour becomes constant on attaining equilibrium. This equilibrium can be shifted in either forward or reverse directions depending on our choice of adding a reactant or a product. The equilibrium can be shifted in the opposite direction by adding reagents that remove $\mathrm{Fe}^{3+}$ or $\mathrm{SCN}^{-}$ions. For example, oxalic acid $\left(\mathrm{H_2} \mathrm{C_2} \mathrm{O_4}\right)$, reacts with $\mathrm{Fe}^{3+}$ ions to form the stable complex ion $\left[\mathrm{Fe}\left(\mathrm{C_2} \mathrm{O_4}\right)_{3}\right]^{3-}$, thus decreasing the concentration of free $\mathrm{Fe}^{3+}(\mathrm{aq})$. In accordance with the Le Chatelier’s principle, the concentration stress of removed $\mathrm{Fe}^{3+}$ is relieved by dissociation of $[\mathrm{Fe}(\mathrm{SCN})]^{2+}$ to replenish the $\mathrm{Fe}^{3+}$ ions. Because the concentration of $[\mathrm{Fe}(\mathrm{SCN})]^{2+}$ decreases, the intensity of red colour decreases.

Addition of aq. $\mathrm{HgCl_2}$ also decreases red colour because $\mathrm{Hg}^{2+}$ reacts with $\mathrm{SCN}^{-}$ions to form stable complex ion $\left[\mathrm{Hg}(\mathrm{SCN})_{4}\right]^{2-}$. Removal of free $\mathrm{SCN}^{-}$(aq) shifts the equilibrium in equation (6.24) from right to left to replenish $\mathrm{SCN}^{-}$ions. Addition of potassium thiocyanate on the other hand increases the colour intensity of the solution as it shift the equilibrium to right.

7.8.2 Effect of Pressure Change

A pressure change obtained by changing the volume can affect the yield of products in case of a gaseous reaction where the total number of moles of gaseous reactants and total number of moles of gaseous products are different. In applying Le Chatelier’s principle to a heterogeneous equilibrium the effect of pressure changes on solids and liquids can be ignored because the volume (and concentration) of a solution/liquid is nearly independent of pressure.

Consider the reaction,

$$ \mathrm{CO}(\mathrm{g})+3 \mathrm{H_2}(\mathrm{~g}) \rightleftharpoons \mathrm{CH_4}(\mathrm{~g})+\mathrm{H_2} \mathrm{O}(\mathrm{g}) $$

Here, $4 \mathrm{~mol}$ of gaseous reactants $\left(\mathrm{CO}+3 \mathrm{H_2}\right)$ become $2 \mathrm{~mol}$ of gaseous products $\left(\mathrm{CH_4}{ }^{+}\right.$ $\mathrm{H_2} \mathrm{O}$ ). Suppose equilibrium mixture (for above reaction) kept in a cylinder fitted with a piston at constant temperature is compressed to one half of its original volume. Then, total pressure will be doubled (according to $p V=$ constant). The partial pressure and therefore, concentration of reactants and products have changed and the mixture is no longer at equilibrium. The direction in which the reaction goes to re-establish equilibrium can be predicted by applying the Le Chatelier’s principle. Since pressure has doubled, the equilibrium now shifts in the forward direction, a direction in which the number of moles of the gas or pressure decreases (we know pressure is proportional to moles of the gas). This can also be understood by using reaction quotient, $Q_{c}$. Let $[\mathrm{CO}],\left[\mathrm{H_2}\right],\left[\mathrm{CH_4}\right]$ and $\left[\mathrm{H_2} \mathrm{O}\right]$ be the molar concentrations at equilibrium for methanation reaction. When volume of the reaction mixture is halved, the partial pressure and the concentration are doubled. We obtain the reaction quotient by replacing each equilibrium concentration by double its value.

$$ Q_{c}=\frac{\left[\mathrm{CH_4}(\mathrm{~g})\right]\left[\mathrm{H_2} \mathrm{O}(\mathrm{g})\right]}{[\mathrm{CO}(\mathrm{g})]\left[\mathrm{H_2}(\mathrm{~g})\right]^{3}} $$

As $Q_{c}<K_{c}$, the reaction proceeds in the forward direction.

In reaction $\mathrm{C}(\mathrm{s})+\mathrm{CO_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{CO}(\mathrm{g})$, when pressure is increased, the reaction goes in the reverse direction because the number of moles of gas increases in the forward direction.

7.8.3 Effect of Inert Gas Addition

If the volume is kept constant and an inert gas such as argon is added which does not take part in the reaction, the equilibrium remains undisturbed. It is because the addition of an inert gas at constant volume does not change the partial pressures or the molar reaction. The reaction quotient changes only if the added gas is a reactant or product involved in the reaction.

7.8.4 Effect of Temperature Change

Whenever an equilibrium is disturbed by a change in the concentration, pressure or volume, the composition of the equilibrium mixture changes because the reaction quotient, $Q_{c}$ no longer equals the equilibrium constant, $K_{\mathrm{c}}$. However, when a change in temperature occurs, the value of equilibrium constant, $K_{c}$ is changed.

In general, the temperature dependence of the equilibrium constant depends on the sign of $\Delta H$ for the reaction.

• The equilibrium constant for an exothermic reaction (negative $\Delta H$ ) decreases as the temperature increases.
• The equilibrium constant for an endothermic reaction (positive $\Delta H$ ) increases as the temperature increases.

Temperature changes affect the equilibrium constant and rates of reactions. Production of ammonia according to the reaction,

$$ \begin{aligned} & \mathrm{N_2}(\mathrm{~g})+3 \mathrm{H_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH_3}(\mathrm{~g}) ; \\ & \Delta H=-92.38 \mathrm{~kJ} \mathrm{~mol}^{-1} \end{aligned} $$

is an exothermic process. According to Le Chatelier’s principle, raising the temperature shifts the equilibrium to left and decreases the equilibrium concentration of ammonia. In other words, low temperature is favourable for high yield of ammonia, but practically very low temperatures slow down the reaction and thus a catalyst is used.

Effect of Temperature - An experiment

Effect of temperature on equilibrium can be demonstrated by taking $\mathrm{NO_2}$ gas (brown in colour) which dimerises into $\mathrm{N_2} \mathrm{O_4}$ gas (colourless).

$$ 2 \mathrm{NO_2}(\mathrm{~g}) \rightleftharpoons \mathrm{N_2} \mathrm{O_4}(\mathrm{~g}) ; \Delta H=-57.2 \mathrm{~kJ} \mathrm{~mol}^{-1} $$

$\mathrm{NO_2}$ gas prepared by addition of $\mathrm{Cu}$ turnings to conc. $\mathrm{HNO_3}$ is collected in two $5 \mathrm{~mL}$ test tubes (ensuring same intensity of colour of gas in each tube) and stopper sealed with araldite. Three $250 \mathrm{~mL}$ beakers 1,2 and 3 containing freesing mixture, water at room temperature and hot water (363K), respectively, are taken (Fig. 6.9). Both the test tubes are placed in beaker 2 for 8-10 minutes. After this one is placed in beaker 1 and the other in beaker 3. The effect of temperature on direction of reaction is depicted very well in this experiment. At low temperatures in beaker 1, the forward reaction of formation of $\mathrm{N_2} \mathrm{O_4}$ is preferred, as reaction is exothermic, and thus, intensity of brown colour due to $\mathrm{NO_2}$ decreases. While in beaker 3, high temperature favours the reverse reaction of

formation of $\mathrm{NO_2}$ and thus, the brown colour intensifies.

Effect of temperature can also be seen in an endothermic reaction,

$$ \begin{aligned} & {\underset{\text{pink}}{\left[\mathrm{Co}\left(\mathrm{H_2} \mathrm{O}\right)_{6}\right]^{3+}(\mathrm{aq})} + \underset{\text{colourless}}{4 \mathrm{Cl}^{-}(\mathrm{aq})} \rightleftharpoons \underset{\text{blue}}{\left[\mathrm{CoCl_4}\right]^{2-}(\mathrm{aq})} + } 6 \mathrm{H_2} \mathrm{O}(1) \\ \end{aligned} $$

At room temperature, the equilibrium mixture is blue due to $\left[\mathrm{CoCl_4}\right]^{2-}$. When cooled in a freesing mixture, the colour of the mixture turns pink due to $\left[\mathrm{Co}\left(\mathrm{H_2} \mathrm{O}\right)_{6}\right]^{3+}$.

7.8.5 Effect of a Catalyst

A catalyst increases the rate of the chemical reaction by making available a new low energy pathway for the conversion of reactants to products. It increases the rate of forward and reverse reactions that pass through the same transition state and does not affect equilibrium. Catalyst lowers the activation energy for the forward and reverse reactions by exactly the same amount. Catalyst does not affect the equilibrium composition of a reaction mixture. It does not appear in the balanced chemical equation or in the equilibrium constant expression.

Let us consider the formation of $\mathrm{NH_3}$ from dinitrogen and dihydrogen which is highly exothermic reaction and proceeds with decrease in total number of moles formed as compared to the reactants. Equilibrium constant decreases with increase in temperature. At low temperature rate decreases and it takes long time to reach at equilibrium, whereas high temperatures give satisfactory rates but poor yields.

German chemist, Fritz Haber discovered that a catalyst consisting of iron catalyse the reaction to occur at a satisfactory rate at temperatures, where the equilibrium concentration of $\mathrm{NH_3}$ is reasonably favourable. Since the number of moles formed in the reaction is less than those of reactants, the yield of $\mathrm{NH_3}$ can be improved by increasing the pressure.

Optimum conditions of temperature and pressure for the synthesis of $\mathrm{NH_3}$ using catalyst are around $500^{\circ} \mathrm{C}$ and $200 \mathrm{~atm}$. Similarly, in manufacture of sulphuric acid by contact process,

$2 \mathrm{SO_2}(\mathrm{~g})+\mathrm{O_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{SO_3}(\mathrm{~g}) ; K_{c}=1.7 \times 10^{26}$

though the value of $K$ is suggestive of reaction going to completion, but practically the oxidation of $\mathrm{SO_2}$ to $\mathrm{SO_3}$ is very slow. Thus, platinum or divanadium penta-oxide $\left(\mathrm{V_2} \mathrm{O_5}\right)$ is used as catalyst to increase the rate of the reaction.

Note: If a reaction has an exceedingly small $K$, a catalyst would be of little help.

7.9 IONIC EQUILIBRIUM IN SOLUTION

Under the effect of change of concentration on the direction of equilibrium, you have incidently come across with the following equilibrium which involves ions:

$\mathrm{Fe}^{3+}(\mathrm{aq})+\mathrm{SCN}^{-}(\mathrm{aq}) \rightleftharpoons[\mathrm{Fe}(\mathrm{SCN})]^{2+}(\mathrm{aq})$

There are numerous equilibria that involve ions only. In the following sections we will study the equilibria involving ions. It is well known that the aqueous solution of sugar does not conduct electricity. However, when common salt (sodium chloride) is added to water it conducts electricity. Also, the conductance of electricity increases with an increase in concentration of common salt. Michael Faraday classified the substances into two categories based on their ability to conduct electricity. One category of substances conduct electricity in their aqueous solutions and are called electrolytes while the other do not and are thus, referred to as non-electrolytes. Faraday further classified electrolytes into strong and weak electrolytes. Strong electrolytes on dissolution in water are ionized almost completely, while the weak electrolytes are only partially dissociated. For example, an aqueous solution of sodium chloride is comprised entirely of sodium ions and chloride ions, while that of acetic acid mainly contains unionized acetic acid molecules and only some acetate ions and hydronium ions. This is because there is almost $100 %$ ionization in case of sodium chloride as compared to less than $5 %$ ionization of acetic acid which is a weak electrolyte. It should be noted that in weak electrolytes, equilibrium is established between ions and the unionized molecules. This type of equilibrium involving ions in aqueous solution is called ionic equilibrium. Acids, bases and salts come under the category of electrolytes and may act as either strong or weak electrolytes.

7.10 ACIDS, BASES AND SALTS

Acids, bases and salts find widespread occurrence in nature. Hydrochloric acid present in the gastric juice is secreted by the lining of our stomach in a significant amount of 1.2-1.5 L/day and is essential for digestive processes. Acetic acid is known to be the main constituent of vinegar. Lemon and orange juices contain citric and ascorbic acids, and tartaric acid is found in tamarind paste. As most of the acids taste sour, the word “acid” has been derived from a latin word “acidus” meaning sour. Acids are known to turn blue litmus paper into red and liberate dihydrogen on reacting with some metals. Similarly, bases are known to turn red litmus paper blue, taste bitter and feel soapy. A common example of a base is washing soda used for washing purposes. When acids and bases are mixed in the right proportion they react with each other to give salts. Some commonly known examples of salts are sodium chloride, barium sulphate, sodium nitrate. Sodium chloride (common salt) is an important component of our diet and is formed by reaction between hydrochloric acid and sodium hydroxide. It exists in solid state as a cluster of positively charged sodium ions and negatively charged chloride ions which are held together due to electrostatic interactions between oppositely charged species (Fig.6.10). The electrostatic forces between two charges are inversely proportional to dielectric constant of the medium. Water, a universal solvent, possesses a very high dielectric constant of 80 . Thus, when sodium chloride is dissolved in water, the electrostatic interactions are reduced by a factor of 80 and this facilitates the ions to move freely in the solution. Also, they are well-separated due to hydration with water molecules.

Comparing, the ionization of hydrochloric acid with that of acetic acid in water we find that though both of them are polar covalent

molecules, former is completely ionized into its constituent ions, while the latter is only partially ionized $(<5 %)$. The extent to which ionization occurs depends upon the strength of the bond and the extent of solvation of ions produced. The terms dissociation and ionization have earlier been used with different meaning. Dissociation refers to the process of separation of ions in water already existing as such in the solid state of the solute, as in sodium chloride. On the other hand, ionization corresponds to a process in which a neutral molecule splits into charged ions in the solution. Here, we shall not distinguish between the two and use the two terms interchangeably.

Faraday was born near London into a family of very limited means. At the age of 14 he was an apprentice to a kind bookbinder who allowed Faraday to read the books he was binding. Through a fortunate chance he became laboratory assistant to Davy, and during 1813-4, Faraday accompanied him to the Continent. During this trip he gained much from the experience of coming into contact with many of the leading scientists of the time. In 1825, he succeeded Davy as Director of the Royal Institution laboratories, and in 1833 he also became the first Fullerian Professor of Chemistry. Faraday’s first important work was on analytical chemistry. After 1821 much of his work was on electricity and magnetism and different electromagnetic phenomena. His ideas have led to the establishment of modern field theory. He discovered his two laws of electrolysis in 1834. Faraday was a very modest and kind hearted person. He declined all honours and avoided scientific controversies. He preferred to work alone and never had any assistant. He disseminated science in a variety of ways including his Friday evening discourses, which he founded at the Royal Institution. He has been very famous for his Christmas lecture on the ‘Chemical History of a Candle’. He published nearly 450 scientific papers.

7.10.1 Arrhenius Concept of Acids and Bases

According to Arrhenius theory, acids are substances that dissociates in water to give hydrogen ions $H^{+}(a q)$ and bases are substances that produce hydroxyl ions $\mathrm{OH}^{-}(\mathrm{aq})$. The ionization of an acid HX (aq) can be represented by the following equations:

$$ \begin{gathered} \mathrm{HX}(\mathrm{aq}) \rightarrow \mathrm{H}^{+}(\mathrm{aq})+\mathrm{X}^{-}(\mathrm{aq}) \\ \text { or } \\ \mathrm{HX}(\mathrm{aq})+\mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{H_3} \mathrm{O}^{+}(\mathrm{aq})+\mathrm{X}^{-}(\mathrm{aq}) \end{gathered} $$

A bare proton, $\mathrm{H}^{+}$ is very reactive and cannot exist freely in aqueous solutions.

Thus, it bonds to the oxygen atom of a solvent water molecule to give trigonal pyramidal hydronium ion, $\mathrm{H_3} \mathrm{O}^{+}\{\left[\mathrm{H}\left(\mathrm{H_2} \mathrm{O}\right)\right]^{+}\}$ (see box). In this chapter we shall use $\mathrm{H}^{+}(\mathrm{aq})$ and $\mathrm{H_3} \mathrm{O}^{+}(\mathrm{aq})$ interchangeably to mean the same i.e., a hydrated proton.

Similarly, a base molecule like $\mathrm{MOH}$ ionizes in aqueous solution according to the equation:

$$ \mathrm{MOH}(\mathrm{aq}) \rightarrow \mathrm{M}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq}) $$

The hydroxyl ion also exists in the hydrated form in the aqueous solution. Arrhenius concept of acid and base, however, suffers from the limitation of being applicable only to aqueous solutions and also, does not account for the basicity of substances like, ammonia which do not possess a hydroxyl group.

Hydronium and Hydroxyl Ions

Hydrogen ion by itself is a bare proton with very small size ( $\sim 10^{-15} \mathrm{~m}$ radius) and intense electric field, binds itself with the water molecule at one of the two available lone pairs on it giving $\mathrm{H_3} \mathrm{O}^{+}$. This species has been detected in many compounds (e.g., $\mathrm{H_3} \mathrm{O}^{+} \mathrm{Cl}^{-}$) in the solid state. In aqueous solution the hydronium ion is further hydrated to give species like $\mathrm{H_5} \mathrm{O_2}^{+}, \mathrm{H_7} \mathrm{O_3}{ }^{+}$and $\mathrm{H_9} \mathrm{O_4}^{+}$. Similarly the hydroxyl ion is hydrated to give several ionic species like $\mathrm{H_3} \mathrm{O_2}^{-}, \mathrm{H_5} \mathrm{O_3}^{-}$ and $\mathrm{H_7} \mathrm{O_4}^{-}$etc.

7.10.2 The Brönsted-Lowry Acids and Bases

The Danish chemist, Johannes Brönsted and the English chemist, Thomas M. Lowry gave a more general definition of acids and bases. According to Brönsted-Lowry theory, acid is a substance that is capable of donating a hydrogen ion $H^{+}$and bases are substances capable of accepting a hydrogen ion, $H^{+}$. In short, acids are proton donors and bases are proton acceptors.

Consider the example of dissolution of $\mathrm{NH_3}$ in $\mathrm{H_2} \mathrm{O}$ represented by the following equation:

The basic solution is formed due to the presence of hydroxyl ions. In this reaction, water molecule acts as proton donor and ammonia molecule acts as proton acceptor and are thus, called Lowry-Brönsted acid and base, respectively. In the reverse reaction, $\mathrm{H}^{+}$is transferred from $\mathrm{NH_4}^{+}$to $\mathrm{OH}^{-}$. In this case, $\mathrm{NH_4}^{+}$acts as a Bronsted acid while $\mathrm{OH}^{-}$acted as a Brönsted base. The acid-base pair that differs only by one proton is called a conjugate acid-base pair. Therefore, $\mathrm{OH}^{-}$ is called the conjugate base of an acid $\mathrm{H_2} \mathrm{O}$ and $\mathrm{NH_4}^{+}$is called conjugate acid of the base $\mathrm{NH_3}$. If Brönsted acid is a strong acid then its conjugate base is a weak base and viceversa. It may be noted that conjugate acid has one extra proton and each conjugate base has one less proton.

Consider the example of ionization of hydrochloric acid in water. $\mathrm{HCl}(\mathrm{aq})$ acts as an acid by donating a proton to $\mathrm{H_2} \mathrm{O}$ molecule which acts as a base.

It can be seen in the above equation, that water acts as a base because it accepts the proton. The species $\mathrm{H_3} \mathrm{O}^{+}$is produced when water accepts a proton from $\mathrm{HCl}$. Therefore, $\mathrm{Cl}^{-}$is a conjugate base of $\mathrm{HCl}$ and $\mathrm{HCl}$ is the conjugate acid of base $\mathrm{Cl}^{-}$. Similarly, $\mathrm{H_2} \mathrm{O}$ is a conjugate base of an acid $\mathrm{H_3} \mathrm{O}^{+}$and $\mathrm{H_3} \mathrm{O}^{+}$is a conjugate acid of base $\mathrm{H_2} \mathrm{O}$.

It is interesting to observe the dual role of water as an acid and a base. In case of reaction with $\mathrm{HCl}$ water acts as a base while in case of ammonia it acts as an acid by donating a proton.

Arrhenius was born near Uppsala, Sweden. He presented his thesis, on the conductivities of electrolyte solutions, to the University of Uppsala in 1884. For the next five years he travelled extensively and visited a number of research centers in Europe. In 1895 he was appointed professor of physics at the newly formed University of Stockholm, serving its rector from 1897 to 1902. From 1905 until his death he was Director of physical chemistry at the Nobel Institute in Stockholm. He continued to work for many years on electrolytic solutions. In 1899 he discussed the temperature dependence of reaction rates on the basis of an equation, now usually known as Arrhenius equation.

He worked in a variety of fields, and made important contributions to immunochemistry, cosmology, the origin of life, and the causes of ice age. He was Nobel Prize in Chemistry in 1903 for his theory of electrolytic dissociation and its use in the development of chemistry.

Problem 7.12

What will be the conjugate bases for the following Brönsted acids: $\mathrm{HF}, \mathrm{H_2} \mathrm{SO_4}$ and $\mathrm{HCO_3}^{-}$?

Solution

The conjugate bases should have one proton less in each case and therefore the corresponding conjugate bases are: $\mathrm{F}^{-}$, $\mathrm{HSO_4}^{-}$and $\mathrm{CO_3}^{2-}$ respectively.

Problem 7.13

Write the conjugate acids for the following Brönsted bases: $\mathrm{NH_2}^{-}, \mathrm{NH_3}$ and $\mathrm{HCOO}^{-}$.

Solution

The conjugate acid should have one extra proton in each case and therefore the corresponding conjugate acids are: $\mathrm{NH_3}$, $\mathrm{NH_4}^{+}$and $\mathrm{HCOOH}$ respectively.

Problem 7.14

The species: $\mathrm{H_2} \mathrm{O}, \mathrm{HCO_3}^{-}, \mathrm{HSO_4}^{-}$and $\mathrm{NH_3}$ can act both as Bronsted acids and bases. For each case give the corresponding conjugate acid and conjugate base.

Solution

The answer is given in the following Table:

Species	Conjugate acid	Conjugate base
$\mathrm{H_2} \mathrm{O}$	$\mathrm{H_3} \mathrm{O}^{+}$	$\mathrm{OH}^{-}$
$\mathrm{HCO_3}^{-}$	$\mathrm{H_2} \mathrm{CO_3}$	$\mathrm{CO_3}^{2-}$
$\mathrm{HSO_4}^{-}$	$\mathrm{H_2} \mathrm{SO_4}$	$\mathrm{SO_4}^{2-}$
$\mathrm{NH_3}$	$\mathrm{NH_4}^{+}$	$\mathrm{NH_2}^{-}$

7.10.3 Lewis Acids and Bases

G.N. Lewis in 1923 defined an acid as a species which accepts electron pair and base which donates an electron pair. As far as bases are concerned, there is not much difference between Brönsted-Lowry and Lewis concepts, as the base provides a lone pair in both the cases. However, in Lewis concept many acids do not have proton. A typical example is reaction of electron deficient species $\mathrm{BF_3}$ with $\mathrm{NH_3}$.

$\mathrm{BF_3}$ does not have a proton but still acts as an acid and reacts with $\mathrm{NH_3}$ by accepting its lone pair of electrons. The reaction can be represented by,

$$ \mathrm{BF_3}+: \mathrm{NH_3} \rightarrow \mathrm{BF_3}: \mathrm{NH_3} $$

Electron deficient species like $\mathrm{AlCl_3}, \mathrm{Co}^{3+}$, $\mathrm{Mg}^{2+}$, etc. can act as Lewis acids while species like $\mathrm{H_2} \mathrm{O}, \mathrm{NH_3}, \mathrm{OH}^{-}$etc. which can donate a pair of electrons, can act as Lewis bases.

Problem 7.15

Classify the following species into Lewis acids and Lewis bases and show how these act as such: (a) $\mathrm{HO}^{-}$ (b) $\mathrm{F}^{-}$ (c) $\mathrm{H}^{+}$ (d) $\mathrm{BCl_3}$

Solution

(a) Hydroxyl ion is a Lewis base as it can donate an electron lone pair (: $\left.\mathrm{OH}^{-}\right)$.

(b) Flouride ion acts as a Lewis base as it can donate any one of its four electron lone pairs.

(c) A proton is a Lewis acid as it can accept a lone pair of electrons from bases like hydroxyl ion and fluoride ion.

(d) $\mathrm{BCl_3}$ acts as a Lewis acid as it can accept a lone pair of electrons from species like ammonia or amine molecules.

7.11 IONIZATION OF ACIDS AND BASES

Arrhenius concept of acids and bases becomes useful in case of ionization of acids and bases as mostly ionizations in chemical and biological systems occur in aqueous medium. Strong acids like perchloric acid $\left(\mathrm{HClO_4}\right)$, hydrochloric acid $(\mathrm{HCl})$, hydrobromic acid $(\mathrm{HBr})$, hyrdoiodic acid (HI), nitric acid $\left(\mathrm{HNO_3}\right)$ and sulphuric acid $\left(\mathrm{H_2} \mathrm{SO_4}\right)$ are termed strong because they are almost completely dissociated into their constituent ions in an aqueous medium, thereby acting as proton $\left(\mathrm{H}^{+}\right)$donors. Similarly, strong bases like lithium hydroxide $(\mathrm{LiOH})$, sodium hydroxide $(\mathrm{NaOH})$, potassium hydroxide $(\mathrm{KOH})$, caesium hydroxide $(\mathrm{CsOH})$ and barium hydroxide $\mathrm{Ba}(\mathrm{OH})_{2}$ are almost completely dissociated into ions in an aqueous medium giving hydroxyl ions, $\mathrm{OH}^{-}$. According to Arrhenius concept they are strong acids and bases as they are able to completely dissociate and produce $\mathrm{H_3} \mathrm{O}^{+}$and $\mathrm{OH}^{-}$ions respectively in the medium. Alternatively, the strength of an acid or base may also be gauged in terms of Brönsted-Lowry concept of acids and bases, wherein a strong acid means a good proton donor and a strong base implies a good proton acceptor. Consider, the acid-base dissociation equilibrium of a weak acid $\mathrm{HA}$,

$$ \begin{aligned} & \underset{\text{acid}}{\mathrm{HA}(\mathrm{aq})} + \underset{\text{base}}{\mathrm{H_2} \mathrm{O}(\mathrm{l})} \rightleftharpoons \underset{\text{conjugate acid}}{\mathrm{H_3} \mathrm{O}^{+}(\mathrm{aq})} + \underset{\text{conjugate base}}{\mathrm{A}^{-}(\mathrm{aq})} \\ \end{aligned} $$

In section 7.10 .2 we saw that acid (or base) dissociation equilibrium is dynamic involving a transfer of proton in forward and reverse directions. Now, the question arises that if the equilibrium is dynamic then with passage of time which direction is favoured? What is the driving force behind it? In order to answer these questions we shall deal into the issue of comparing the strengths of the two acids (or bases) involved in the dissociation equilibrium. Consider the two acids $\mathrm{HA}$ and $\mathrm{H_3} \mathrm{O}^{+}$ present in the above mentioned acid-dissociation equilibrium. We have to see which amongst them is a stronger proton donor. Whichever exceeds in its tendency of donating a proton over the other shall be termed as the stronger acid and the equilibrium will shift in the direction of weaker acid. Say, if HA is a stronger acid than $\mathrm{H_3} \mathrm{O}^{+}$, then $\mathrm{HA}$ will donate protons and not $\mathrm{H_3} \mathrm{O}^{+}$, and the solution will mainly contain $\mathrm{A}^{-}$ and $\mathrm{H_3} \mathrm{O}^{+}$ ions. The equilibrium moves in the direction of formation of weaker acid and weaker base because the stronger acid donates a proton to the stronger base.

It follows that as a strong acid dissociates completely in water, the resulting base formed would be very weak i.e., strong acids have very weak conjugate bases. Strong acids like perchloric acid $\left(\mathrm{HClO_4}\right)$, hydrochloric acid $(\mathrm{HCl})$, hydrobromic acid $(\mathrm{HBr})$, hydroiodic acid (HI), nitric acid $\left(\mathrm{HNO_3}\right)$ and sulphuric acid $\left(\mathrm{H_2} \mathrm{SO_4}\right)$ will give conjugate base ions $\mathrm{ClO_4}^{-}, \mathrm{Cl}$, $\mathrm{Br}^{-}, \mathrm{I}^{-}, \mathrm{NO_3}^{-}$ and $\mathrm{HSO_4}^{-}$, which are much weaker bases than $\mathrm{H_2} \mathrm{O}$. Similarly a very strong base would give a very weak conjugate acid. On the other hand, a weak acid say HA is only partially dissociated in aqueous medium and thus, the solution mainly contains undissociated HA molecules. Typical weak acids are nitrous acid $\left(\mathrm{HNO_2}\right)$, hydrofluoric acid ( $\mathrm{HF}$ ) and acetic acid $\left(\mathrm{CH_3} \mathrm{COOH}\right)$. It should be noted that the weak acids have very strong conjugate bases. For example, $\mathrm{NH_2}^{-}, \mathrm{O}^{2-}$ and $\mathrm{H}^{-}$are very good proton acceptors and thus, much stronger bases than $\mathrm{H_2} \mathrm{O}$.

Certain water soluble organic compounds like phenolphthalein and bromothymol blue behave as weak acids and exhibit different colours in their acid (HIn) and conjugate base (In ${ }^{-}$ forms.

$\underset{\substack{\text{acid indicator} \\ \text{colour A}}}{Hln(aq)} + H_2 O (l) \rightleftharpoons \underset{\text{conjugate acid}}{H_3O^+ \text{(aq)}} + \underset{\substack{\text{conjugate} \\ \text{colour B}}}{ln^- \text{(aq)}}$

Such compounds are useful as indicators in acid-base titrations, and finding out $\mathrm{H}^{+}$ion concentration.

7.11.1 The Ionization Constant of Water and its Ionic Product

Some substances like water are unique in their ability of acting both as an acid and a base. We have seen this in case of water in section 6.10.2. In presence of an acid, HA it accepts a proton and acts as the base while in the presence of a base, $\mathrm{B}^{-}$it acts as an acid by donating a proton. In pure water, one $\mathrm{H_2} \mathrm{O}$ molecule donates proton and acts as an acid and another water molecules accepts a proton and acts as a base at the same time. The following equilibrium exists:

$\underset{\text { acid }}{\mathrm{H_2} \mathrm{O}(\mathrm{l})}+ \underset{\text { base }}{\mathrm{H_2} \mathrm{O}(\mathrm{l})} \rightleftharpoons \underset{\text{conjugate base}}{\mathrm{H_3} \mathrm{O}^{+}(\mathrm{aq})} + \underset{\text{conjugated acid}}{\mathrm{OH}^{-}(\mathrm{aq})}$

The dissociation constant is represented by,

$$ \begin{equation*} K=\left[\mathrm{H_3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right] /\left[\mathrm{H_2} \mathrm{O}\right] \tag{7.26} \end{equation*} $$

The concentration of water is omitted from the denominator as water is a pure liquid and its concentration remains constant. $\left[\mathrm{H_2} \mathrm{O}\right]$ is incorporated within the equilibrium constant to give a new constant, $K_{\mathrm{w}}$, which is called the ionic product of water.

$$ \begin{equation*} K_{\mathrm{w}}=\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right] \tag{7.27} \end{equation*} $$

The concentration of $\mathrm{H}^{+}$has been found out experimentally as $1.0 \times 10^{-7} \mathrm{M}$ at $298 \mathrm{~K}$. And, as dissociation of water produces equal number of $\mathrm{H}^{+}$and $\mathrm{OH}^{-}$ions, the concentration of hydroxyl ions, $\left[\mathrm{OH}^{-}\right]=\left[\mathrm{H}^{+}\right]=1.0 \times 10^{-7} \mathrm{M}$. Thus, the value of $K_{\mathrm{w}}$ at $298 \mathrm{~K}$,

$$K_{\mathrm{w}}=\left[\mathrm{H_3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=\left(1 \times 10^{-7}\right)^{2}=1 \times 10^{-14} \mathrm{M}^{2} \tag{7.28}$$

The value of $K_{w}$ is temperature dependent as it is an equilibrium constant.

The density of pure water is $1000 \mathrm{~g} / \mathrm{L}$ and its molar mass is $18.0 \mathrm{~g} / \mathrm{mol}$. From this the molarity of pure water can be given as,

$\left[\mathrm{H_2} \mathrm{O}\right]=(1000 \mathrm{~g} / \mathrm{L})(1 \mathrm{~mol} / 18.0 \mathrm{~g})=55.55 \mathrm{M}$. Therefore, the ratio of dissociated water to that of undissociated water can be given as: $10^{-7} /(55.55)=1.8 \times 10^{-9}$ or $\sim 2$ in $10^{-9}$ (thus, equilibrium lies mainly towards undissociated water)

We can distinguish acidic, neutral and basic aqueous solutions by the relative values of the $\mathrm{H_3} \mathrm{O}^{+}$and $\mathrm{OH}^{-}$concentrations:

$$ \begin{aligned} & \text { Acidic: }\left[\mathrm{H_3} \mathrm{O}^{+}\right]>\left[\mathrm{OH}^{-}\right] \\ & \text {Neutral: }\left[\mathrm{H_3} \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right] \\ & \text {Basic : }\left[\mathrm{H_3} \mathrm{O}^{+}\right]<\left[\mathrm{OH}^{-}\right] \end{aligned} $$

7.11.2 The pH Scale

Hydronium ion concentration in molarity is more conveniently expressed on a logarithmic scale known as the $\mathbf{p H}$ scale. The $\mathrm{pH}$ of a solution is defined as the negative logarithm to base 10 of the activity $\left(a_{\mathrm{H}^{+}}\right)$of hydrogen ion. In dilute solutions $(<0.01 \mathrm{M})$, activity of hydrogen ion $\left(\mathrm{H}^{+}\right)$is equal in magnitude to molarity represented by $\left[\mathrm{H}^{+}\right]$. It should be noted that activity has no units and is defined as:

$$ \mathrm{a_\mathrm{H}^{+}}=\left[\mathrm{H}^{+}\right] / \mathrm{mol} \mathrm{L}^{-1} $$

From the definition of $\mathrm{pH}$, the following can be written,

$$ \mathrm{pH}=-\log \mathrm{a_\mathrm{H}^{+}}=-\log \{\left[\mathrm{H}^{+}\right] / \mathrm{mol} \mathrm{L}^{-1}\} $$

Thus, an acidic solution of $\mathrm{HCl}\left(10^{-2} \mathrm{M}\right)$ will have a $\mathrm{pH}=2$. Similarly, a basic solution of $\mathrm{NaOH}$ having $\left[\mathrm{OH}^{-}\right]=10^{-4} \mathrm{M}$ and $\left[\mathrm{H_3} \mathrm{O}^{+}\right]=$ $10^{-10} \mathrm{M}$ will have a $\mathrm{pH}=10$. At $25^{\circ} \mathrm{C}$, pure water has a concentration of hydrogen ions, $\left[\mathrm{H}^{+}\right]=10^{-7} \mathrm{M}$. Hence, the $\mathrm{pH}$ of pure water is given as:

$$ \mathrm{pH}=-\log \left(10^{-7}\right)=7 $$

Acidic solutions possess a concentration of hydrogen ions, $\left[\mathrm{H}^{+}\right]>10^{-7} \mathrm{M}$, while basic solutions possess a concentration of hydrogen ions, $\left[\mathrm{H}^{+}\right]<10^{-7} \mathrm{M}$. thus, we can summarise that

Acidic solution has $\mathrm{pH}<7$

Basic solution has $\mathrm{pH}>7$

Neutral solution has $\mathrm{pH}=7$

Now again, consider the equation (7.28) at $298 \mathrm{~K}$

$$ K_{\mathrm{w}}=\left[\mathrm{H_3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=10^{-14} $$

Taking negative logarithm on both sides of equation, we obtain

$$ \begin{align*} -\log K_{\mathrm{w}} & =-\log \{\left[\mathrm{H_3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]\} \\ & =-\log \left[\mathrm{H_3} \mathrm{O}^{+}\right]-\log \left[\mathrm{OH}^{-}\right] \\ & =-\log 10^{-14} \\ \mathrm{p} K_{\mathrm{w}}= & \mathrm{pH}+\mathrm{pOH}=14 \tag{7.29} \end{align*} $$

Note that although $K_{\mathrm{w}}$ may change with temperature the variations in $\mathrm{pH}$ with temperature are so small that we often ignore it.

$\mathrm{p} K_{\mathrm{w}}$ is a very important quantity for aqueous solutions and controls the relative concentrations of hydrogen and hydroxyl ions as their product is a constant. It should be noted that as the $\mathrm{pH}$ scale is logarithmic, a change in $\mathrm{pH}$ by just one unit also means change in $\left[\mathrm{H}^{+}\right]$by a factor of 10. Similarly, when the hydrogen ion concentration, $\left[\mathrm{H}^{+}\right]$ changes by a factor of 100 , the value of $\mathrm{pH}$ changes by 2 units. Now you can realise why the change in $\mathrm{pH}$ with temperature is often ignored.

Measurement of $\mathrm{pH}$ of a solution is very essential as its value should be known when dealing with biological and cosmetic applications. The $\mathrm{pH}$ of a solution can be found roughly with the help of $\mathrm{pH}$ paper that has different colour in solutions of different $\mathrm{pH}$. Now-a-days $\mathrm{pH}$ paper is available with four strips on it. The different strips have different colours (Fig. 6.11) at the same pH. The $\mathrm{pH}$ in the range of 1-14 can be determined with an accuracy of $\sim 0.5$ using $\mathrm{pH}$ paper.

For greater accuracy pH meters are used. pH meter is a device that measures the pH-dependent electrical potential of the test solution within 0.001 precision. pH meters of the size of a writing pen are now available in the market. The pH of some very common substances are given in Table 7.5 (page 212).

Problem 7.16

The concentration of hydrogen ion in a sample of soft drink is $3.8 \times 10^{-3} \mathrm{M}$. what is its $\mathrm{pH}$ ?

Solution

$\mathrm{pH}=-\log \left[3.8 \times 10^{-3}\right]$

$=-\{\log [3.8]+\log \left[10^{-3}\right]\}$

$=-{(0.58)+(-3.0)}=-{-2.42}=2.42$

Therefore, the $\mathrm{pH}$ of the soft drink is 2.42 and it can be inferred that it is acidic.

Table 6.5 The pH of Some Common Substances

Name of the Fluid	pH	Name of the Fluid	pH
Saturated solution of NaOH	$\sim 15$	Black Coffee	5.0
O.1 M NaOH solution	13	Tomato juice	$\sim 4.2$
Lime water	10.5	Soft drinks and vinegar	$\sim 3.0$
Milk of magnesia	10	Lemon juice	$\sim 2.2$
Egg white, sea water	7.8	Gastric juice	$\sim 1.2$
Human blood	7.4	1 M HCl solution	$\sim 0$
Milk	6.8	Concentrated HCl	$\sim-1.0$
Human Saliva	6.4

Problem 7.17

Calculate $\mathrm{pH}$ of a $1.0 \times 10^{-8} \mathrm{M}$ solution of $\mathrm{HCl}$.

Solution

$$ \begin{aligned} & 2 \mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H_3} \mathrm{O}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq}) \\ & K_{\mathrm{w}}=\left[\mathrm{OH}^{-}\right]\left[\mathrm{H_3} \mathrm{O}^{+}\right] \\ & \quad=10^{-14} \end{aligned} $$

Let, $x=\left[\mathrm{OH}^{-}\right]=\left[\mathrm{H_3} \mathrm{O}^{+}\right]$from $\mathrm{H_2} \mathrm{O}$. The $\mathrm{H_3} \mathrm{O}^{+}$concentration is generated (i) from the ionization of $\mathrm{HCl}$ dissolved i.e.,

$\mathrm{HCl}(\mathrm{aq})+\mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H_3} \mathrm{O}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})$ and (ii) from ionization of $\mathrm{H_2} \mathrm{O}$. In these very dilute solutions, both sources of $\mathrm{H_3} \mathrm{O}^{+}$must be considered:

$\left[\mathrm{H_3} \mathrm{O}^{+}\right]=10^{-8}+\mathrm{x}$

$K_{\mathrm{w}}=\left(10^{-8}+\mathrm{x}\right)(\mathrm{x})=10^{-14}$

or $\mathrm{x}^{2}+10^{-8} \mathrm{x}-10^{-14}=0$

$\left[\mathrm{OH}^{-}\right]=\mathrm{x}=9.5 \times 10^{-8}$

So, $\mathrm{pOH}=7.02$ and $\mathrm{pH}=6.98$

7.11.3 Ionization Constants of Weak Acids

Consider a weak acid HX that is partially ionized in the aqueous solution. The equilibrium can be expressed by:

$ \begin{aligned} & \underset{\text { Initial }}{\mathrm{HX}(\mathrm{aq})} +\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{X}^{-}(\mathrm{aq}) \end{aligned} $

$ \begin{aligned} & \text { concentration (M) } \quad \quad \quad 0 \quad \quad \quad 0 \end{aligned} $

Let $\alpha$ be the extent of ionization

Change (M)

$\begin{array}{lll}-\mathrm{c} \alpha & +\mathrm{c} \alpha & +\mathrm{c} \alpha\end{array}$

Equilibrium concentration (M)

$\begin{array}{ccc}\mathrm{c}-\mathrm{c} \alpha & \mathrm{c} \alpha \quad \mathrm{c} \alpha \end{array}$

Here, $\mathrm{c}=$ initial concentration of the undissociated acid, $\mathrm{HX}$ at time, $\mathrm{t}=0 . \alpha=$ extent up to which HX is ionized into ions. Using these notations, we can derive the equilibrium constant for the above discussed acid-dissociation equilibrium:

$$ K_{\mathrm{a}}=\mathrm{c}^{2} \alpha^{2} / \mathrm{c}(1-\alpha)=\mathrm{c} \alpha^{2} / 1-\alpha $$

$K_{\mathrm{a}}$ is called the dissociation or ionization constant of acid HX. It can be represented alternatively in terms of molar concentration as follows,

$$ \begin{equation*} K_{\mathrm{a}}=\left[\mathrm{H}^{+}\right]\left[\mathrm{X}^{-}\right] /[\mathrm{HX}] \tag{7.30} \end{equation*} $$

At a given temperature $T, K_{\mathrm{a}}$ is a measure of the strength of the acid $\mathrm{HX}$ i.e., larger the value of $K_{a}$, the stronger is the acid. $K_{\mathrm{a}}$ is a dimensionless quantity with the understanding that the standard state concentration of all species is $1 \mathrm{M}$.

The values of the ionization constants of some selected weak acids are given in Table 6.6.

Table 6.6 The Ionization Constants of Some Selected Weak Acids (at 298K)

Acid	Ionization Constant, $\boldsymbol{K_\mathrm{a}}$
Hydrofluoric Acid $(\mathrm{HF})$	$3.5 \times 10^{-4}$
Nitrous Acid $\left(\mathrm{HNO_2}\right)$	$4.5 \times 10^{-4}$
Formic Acid $(\mathrm{HCOOH})$	$1.8 \times 10^{-4}$
Niacin $\left(\mathrm{C_5} \mathrm{H_4} \mathrm{NCOOH}\right)$	$1.5 \times 10^{-5}$
Acetic Acid $\left(\mathrm{CH_3} \mathrm{COOH}\right)$	$1.74 \times 10^{-5}$
Benzoic Acid $\left(\mathrm{C_6} \mathrm{H_5} \mathrm{COOH}\right)$	$6.5 \times 10^{-5}$
Hypochlorous Acid $(\mathrm{HCIO})$	$3.0 \times 10^{-8}$
Hydrocyanic Acid $(\mathrm{HCN})$	$4.9 \times 10^{-10}$
Phenol $\left(\mathrm{C_6} \mathrm{H_5} \mathrm{OH}\right)$	$1.3 \times 10^{-10}$

The $\mathrm{pH}$ scale for the hydrogen ion concentration has been so useful that besides $\mathrm{p} K_{\mathrm{w}}$, it has been extended to other species and quantities. Thus, we have:

$$ \begin{equation*} \mathrm{p} K_{\mathrm{a}}=-\log \left(K_{\mathrm{a}}\right) \tag{7.31} \end{equation*} $$

Knowing the ionization constant, $K_{\mathrm{a}}$ of an acid and its initial concentration, c, it is possible to calculate the equilibrium concentration of all species and also the degree of ionization of the acid and the $\mathrm{pH}$ of the solution.

A general step-wise approach can be adopted to evaluate the $\mathrm{pH}$ of the weak electrolyte as follows:

Step 1. The species present before dissociation are identified as Brönsted-Lowry acids/bases.

Step 2. Balanced equations for all possible reactions i.e., with a species acting both as acid as well as base are written.

Step 3. The reaction with the higher $K_{\mathrm{a}}$ is identified as the primary reaction whilst the other is a subsidiary reaction.

Step 4. Enlist in a tabular form the following values for each of the species in the primary reaction

(a) Initial concentration, c.

(b) Change in concentration on proceeding to equilibrium in terms of $\alpha$, degree of ionization.

(c) Equilibrium concentration.

Step 5. Substitute equilibrium concentrations into equilibrium constant equation for principal reaction and solve for $\alpha$.

Step 6. Calculate the concentration of species in principal reaction.

Step 7. Calculate $\mathrm{pH}=-\log \left[\mathrm{H_3} \mathrm{O}^{+}\right]$

The above mentioned methodology has been elucidated in the following examples.

Problem 7.18

The ionization constant of $\mathrm{HF}$ is $3.2 \times 10^{-4}$. Calculate the degree of dissociation of $\mathrm{HF}$ in its $0.02 \mathrm{M}$ solution. Calculate the concentration of all species present $\left(\mathrm{H_3} \mathrm{O}^{+}, \mathrm{F}^{-}\right.$and $\left.\mathrm{HF}\right)$ in the solution and its $\mathrm{pH}$.

Solution

The following proton transfer reactions are possible:

1. $\mathrm{HF}+\mathrm{H_2} \mathrm{O} \rightleftharpoons \mathrm{H_3} \mathrm{O}^{+}+\mathrm{F}^{-}$

$$ K_{\mathrm{a}}=3.2 \times 10^{-4} $$

2. $\mathrm{H_2} \mathrm{O}+\mathrm{H_2} \mathrm{O} \rightleftharpoons \mathrm{H_3} \mathrm{O}^{+}+\mathrm{OH}^{-}$

$$ K_{\mathrm{w}}=1.0 \times 10^{-14} $$

As $K_{\mathrm{a}}$ » $K_{\mathrm{w}}$, [1] is the principle reaction.

$$ \mathrm{HF}+\mathrm{H_2} \mathrm{O} \rightleftharpoons \mathrm{H_3} \mathrm{O}^{+}+\mathrm{F}^{-} $$

Initial

concentration (M)

$ \quad \quad \quad $ $ \quad \quad \quad $ 0.02 $ \quad \quad \quad $ 0 $ \quad \quad \quad $ 0

Change (M)

$$ -0.02 \alpha \quad+0.02 \alpha+0.02 \alpha $$

Equilibrium

concentration (M)

$$ 0.02-0.02 \alpha \quad 0.02 \alpha \quad 0.02 \alpha $$

Substituting equilibrium concentrations in the equilibrium reaction for principal reaction gives:

$K_{\mathrm{a}}=(0.02 \alpha)^{2} /(0.02-0.02 \alpha)$

$=0.02 \alpha^{2} /(1-\alpha)=3.2 \times 10^{-4}$

We obtain the following quadratic equation: $\alpha^{2}+1.6 \times 10^{-2} \alpha-1.6 \times 10^{-2}=0$

The quadratic equation in $\alpha$ can be solved and the two values of the roots are:

$\alpha=+0.12$ and -0.12

The negative root is not acceptable and hence,

$\alpha=0.12$

This means that the degree of ionization, $\alpha=0.12$, then equilibrium concentrations of other species viz., $\mathrm{HF}, \mathrm{F}^{-}$and $\mathrm{H_3} \mathrm{O}^{+}$are given by:

$$ \begin{aligned} {\left[\mathrm{H_3} \mathrm{O}^{+}\right]=\left[\mathrm{F}^{-}\right]=\mathrm{c} \alpha } & =0.02 \times 0.12 \\ & =2.4 \times 10^{-3} \mathrm{M} \end{aligned} $$

$[\mathrm{HF}]=\mathrm{c}(1-\alpha)=0.02(1-0.12)$

$=17.6 \times 10^{-3} \mathrm{M}$

$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]=-\log \left(2.4 \times 10^{-3}\right)=2.62$

Problem 7.19

The $\mathrm{pH}$ of $0.1 \mathrm{M}$ monobasic acid is 4.50 . Calculate the concentration of species $\mathrm{H}^{+}, \mathrm{A}^{-}$ and HA at equilibrium. Also, determine the value of $K_{a}$ and $\mathrm{p} K_{a}$ of the monobasic acid.

Solution

$$ \mathrm{pH}=-\log \left[\mathrm{H}^{+}\right] $$

Therefore, $\left[\mathrm{H}^{+}\right]=10^{-\mathrm{pH}}=10^{-4.50}$

$$ =3.16 \times 10^{-5} $$

$\left[\mathrm{H}^{+}\right]=\left[\mathrm{A}^{-}\right]=3.16 \times 10^{-5}$

Thus, $\quad K_{\mathrm{a}}=\left[\mathrm{H}^{+}\right]\left[\mathrm{A}^{-}\right] /[\mathrm{HA}]$

$[\mathrm{HA}]_{\text {eqlbm }}=0.1-\left(3.16 \times 10^{-5}\right) \simeq 0.1$

$K_{\mathrm{a}}=\left(3.16 \times 10^{-5}\right)^{2} / 0.1=1.0 \times 10^{-8}$

$\mathrm{p} K_{\mathrm{a}}=-\log \left(10^{-8}\right)=8$

Alternatively, “Percent dissociation” is another useful method for measure of strength of a weak acid and is given as:

Percent dissociation

$$=[\mathrm{HA}]\text {dissociated } / [\mathrm{HA}]\text {initial } \times 100 \% \tag{7.32}$$

Problem 7.20

Calculate the $\mathrm{pH}$ of $0.08 \mathrm{M}$ solution of hypochlorous acid, $\mathrm{HOCl}$. The ionization constant of the acid is $2.5 \times 10^{-5}$. Determine the percent dissociation of $\mathrm{HOCl}$.

Solution

$\mathrm{HOCl}(\mathrm{aq})+\mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H_3} \mathrm{O}^{+}(\mathrm{aq})+\mathrm{ClO}^{-}(\mathrm{aq})$

Initial concentration (M)

$ \quad \quad \quad $ 0.08 $ \quad \quad \quad $ 0 $ \quad \quad \quad $ 0

Change to reach equilibrium concentration (M)

$$ -\mathrm{x} \quad \quad \quad +\mathrm{x} \quad \quad \quad +\mathrm{x} $$

equilibrium concentartion (M)

$\begin{array}{lll}0.08-\mathrm{x} \quad \quad \quad & \mathrm{x} \quad \quad \quad & \mathrm{x}\end{array}$

$K_{\mathrm{a}}=\{\left[\mathrm{H_3} \mathrm{O}^{+}\right]\left[\mathrm{ClO}^{-}\right] /[\mathrm{HOCl}]\}$

$=x^{2} /(0.08-x)$

As $\mathrm{x} < < 0.08$, therefore $0.08-\mathrm{x} \simeq 0.08$

$\mathrm{x}^{2} / 0.08=2.5 \times 10^{-5}$

$\mathrm{x}^{2}=2.0 \times 10^{-6}$, thus, $\mathrm{x}=1.41 \times 10^{-3}$

$\left[\mathrm{H}^{+}\right]=1.41 \times 10^{-3} \mathrm{M}$.

Therefore,

Percent dissociation

$$ \begin{aligned} & =\{[\mathrm{HOCl}]{dissociated } /[\mathrm{HOCl}]{initial }\} \times 100 \\ \end{aligned} $$

$=\{[\mathrm{HOCl}]{dissociated } /[\mathrm{HOCl}]{initial }\} \times 100$

$$ \begin{aligned} & =1.41 \times 10^{-3} \times 10^{2} / 0.08=1.76 \% \\ & \mathrm{pH}=-\log \left(1.41 \times 10^{-3}\right)=2.85 \end{aligned} $$

7.11.4 Ionization of Weak Bases

The ionization of base $\mathrm{MOH}$ can be represented by equation:

$$ \mathrm{MOH}(\mathrm{aq}) \rightleftharpoons \mathrm{M}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq}) $$

In a weak base there is partial ionization of $\mathrm{MOH}$ into $\mathrm{M}^{+}$and $\mathrm{OH}^{-}$, the case is similar to that of acid-dissociation equilibrium. The equilibrium constant for base ionization is called base ionization constant and is represented by $K_{\mathrm{b}}$. It can be expressed in terms of concentration in molarity of various species in equilibrium by the following equation:

$$K_{\mathrm{b}}=\left[\mathrm{M}^{+}\right]\left[\mathrm{OH}^{-}\right] /[\mathrm{MOH}] \tag{7.33}$$

Alternatively, if $\mathrm{c}=$ initial concentration of base and $\alpha=$ degree of ionization of base i.e. the extent to which the base ionizes. When equilibrium is reached, the equilibrium constant can be written as:

$K_{b}=(\mathrm{c} \alpha)^{2} / \mathrm{c}(1-\alpha)=\mathrm{c} \alpha^{2} /(1-\alpha)$

The values of the ionization constants of some selected weak bases, $K_{b}$ are given in Table 6.7.

Table 6.7 The Values of the Ionization Constant of Some Weak Bases at $298 \mathrm{~K}$

Base	$\boldsymbol{K_\mathbf{b}}$
Dimethylamine, $\left(\mathrm{CH_3}\right)_{2} \mathrm{NH}$	$5.4 \times 10^{-4}$
Triethylamine, $\left(\mathrm{C_2} \mathrm{H_5}\right)_{3} \mathrm{~N}$	$6.45 \times 10^{-5}$
Ammonia, $\mathrm{NH_3}$ or $\mathrm{NH_4} \mathrm{OH}$	$1.77 \times 10^{-5}$
Quinine, $(\mathrm{A}$ plant product)	$1.10 \times 10^{-6}$
Pyridine, $\mathrm{C_5} \mathrm{H_5} \mathrm{~N}$	$1.77 \times 10^{-9}$
Aniline, $\mathrm{C_6} \mathrm{H_5} \mathrm{NH_2}$	$4.27 \times 10^{-10}$
Urea, $\mathrm{CO}\left(\mathrm{NH_2}\right)_{2}$	$1.3 \times 10^{-14}$

Many organic compounds like amines are weak bases. Amines are derivatives of ammonia in which one or more hydrogen atoms are replaced by another group. For example, methylamine, codeine, quinine and nicotine all behave as very weak bases due to their very small $K_{\mathrm{b}}$. Ammonia produces $\mathrm{OH}^{-}$in aqueous solution:

$$ \mathrm{NH_3}(\mathrm{aq})+\mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{NH_4}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq}) $$

The $\mathrm{pH}$ scale for the hydrogen ion concentration has been extended to get:

$$\mathrm{p} K_{b}=-\log \left(K_{b}\right) \tag{7.34}$$

Problem 7.21

The $\mathrm{pH}$ of $0.004 \mathrm{M}$ hydrazine solution is 9.7. Calculate its ionization constant $K_{\mathrm{b}}$ and $\mathrm{p} K_{\mathrm{b}}$.

Solution

$\mathrm{NH_2} \mathrm{NH_2}+\mathrm{H_2} \mathrm{O} \rightleftharpoons \mathrm{NH_2} \mathrm{NH_3}{ }^{+}+\mathrm{OH}^{-}$

From the $\mathrm{pH}$ we can calculate the hydrogen ion concentration. Knowing hydrogen ion concentration and the ionic product of water we can calculate the concentration of hydroxyl ions. Thus we have:

$\left[\mathrm{H}^{+}\right]=\operatorname{antilog}(-\mathrm{pH})$

$=\operatorname{antilog}(-9.7)=1.67 \times 10^{-10}$

$\left[\mathrm{OH}^{-}\right]=K_{\mathrm{w}} /\left[\mathrm{H}^{+}\right]=1 \times 10^{-14} / 1.67 \times 10^{-10}$

$$ =5.98 \times 10^{-5} $$

The concentration of the corresponding hydrazinium ion is also the same as that of hydroxyl ion. The concentration of both these ions is very small so the concentration of the undissociated base can be taken equal to $0.004 \mathrm{M}$.

Thus,

$K_{\mathrm{b}}=\left[\mathrm{NH_2} \mathrm{NH_3}^{+}\right]\left[\mathrm{OH}^{-}\right] /\left[\mathrm{NH_2} \mathrm{NH_2}\right]$

$=\left(5.98 \times 10^{-5}\right)^{2} / 0.004=8.96 \times 10^{-7}$

$\mathrm{p} K_{\mathrm{b}}=-\log K_{\mathrm{b}}=-\log \left(8.96 \times 10^{-7}\right)=6.04$.

Problem 7.22

Calculate the $\mathrm{pH}$ of the solution in which $0.2 \mathrm{M} \mathrm{NH_4} \mathrm{Cl}$ and $0.1 \mathrm{M} \mathrm{NH_3}$ are present. The $\mathrm{pK_\mathrm{b}}$ of ammonia solution is 4.75.

Solution

$\mathrm{NH_3}+\mathrm{H_2} \mathrm{O} \rightleftharpoons \mathrm{NH_4}^{+}+\mathrm{OH}^{-}$

The ionization constant of $\mathrm{NH_3}$,

$K_{\mathrm{b}}=\operatorname{antilog}\left(-\mathrm{p} K_{\mathrm{b}}\right)$ i.e.

$$ \begin{aligned} & K_{\mathrm{b}}=10^{-4.75}=1.77 \times 10^{-5} \mathrm{M} \\ & \mathrm{NH_3}+\mathrm{H_2} \mathrm{O} \rightleftharpoons \mathrm{NH_4}^{+}+\mathrm{OH}^{-} \end{aligned} $$

Initial concentration (M)

$$ \begin{equation*} 0.10 \quad \quad \quad \quad 0.20 \quad \quad \quad \quad 0 \end{equation*} $$

Change to reach

equilibrium $(\mathrm{M})$

$$ \begin{equation*} -x \quad \quad \quad \quad +x \quad \quad \quad \quad +x \end{equation*} $$

At equilibrium (M)

$$ \begin{equation*} 0.10-x \quad \quad \quad \quad 0.20+x \quad \quad \quad \quad +x \end{equation*} $$

$K_{\mathrm{b}}=\left[\mathrm{NH_4}^{+}\right]\left[\mathrm{OH}^{-}\right] /\left[\mathrm{NH_3}\right]$

$=(0.20+\mathrm{x})(\mathrm{x}) /(0.1-\mathrm{x})=1.77 \times 10^{-5}$

As $K_{\mathrm{b}}$ is small, we can neglect $\mathrm{x}$ in comparison to $0.1 \mathrm{M}$ and $0.2 \mathrm{M}$. Thus,

$\left[\mathrm{OH}^{-}\right]=\mathrm{x}=0.88 \times 10^{-5}$

Therefore, $\left[\mathrm{H}^{+}\right]=1.12 \times 10^{-9}$

$\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]=8.95$.

7.11.5 Relation between $K_{\mathrm{a}}$ and $K_{\mathrm{b}}$

As seen earlier in this chapter, $K_{\mathrm{a}}$ and $K_{\mathrm{b}}$ represent the strength of an acid and a base, respectively. In case of a conjugate acid-base pair, they are related in a simple manner so that if one is known, the other can be deduced. Considering the example of $\mathrm{NH_4}^{+}$and $\mathrm{NH_3}$ we see,

$$ \begin{aligned} & \mathrm{NH_4}^{+}(\mathrm{aq})+\mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H_3} \mathrm{O}^{+}(\mathrm{aq})+\mathrm{NH_3}(\mathrm{aq}) \\ & \quad K_{\mathrm{a}}=\left[\mathrm{H_3} \mathrm{O}^{+}\right]\left[\mathrm{NH_3}\right] /\left[\mathrm{NH_4}^{+}\right]=5.6 \times 10^{-10} \\ & \mathrm{NH_3}(\mathrm{aq})+\mathrm{H_2} \mathrm{O}(1) \rightleftharpoons \mathrm{NH_4}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq}) \\ & K_{\mathrm{b}}=\left[\mathrm{NH_4}^{+}\right]\left[\mathrm{OH}^{-}\right] / \mathrm{NH_3}=1.8 \times 10^{-5} \\ & \text { Net: } 2 \mathrm{H_2} \mathrm{O}(1) \rightleftharpoons \mathrm{H_3} \mathrm{O}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq}) \\ & K_{\mathrm{w}}=\left[\mathrm{H_3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=1.0 \times 10^{-14} \mathrm{M} \end{aligned} $$

Where, $K_{\mathrm{a}}$ represents the strength of $\mathrm{NH_4}^{+}$ as an acid and $K_{\mathrm{b}}$ represents the strength of $\mathrm{NH_3}$ as a base.

It can be seen from the net reaction that the equilibrium constant is equal to the product of equilibrium constants $K_{\mathrm{a}}$ and $K_{\mathrm{b}}$ for the reactions added. Thus,

$$ \begin{aligned} K_{\mathrm{a}} \times & K_{\mathrm{b}}=\{\left[\mathrm{H_3} \mathrm{O}^{+}\right]\left[\mathrm{NH_3}\right] /\left[\mathrm{NH_4}^{+}\right]\} \times\{\left[\mathrm{NH_4}^{+}\right] \left[\mathrm{OH}^{-}\right] /\left[\mathrm{NH_3}\right]\} \\ \end{aligned} $$

$$ \begin{aligned} = & {\left[\mathrm{H_3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=K_{\mathrm{w}} } \\ & =\left(5.6 \times 10^{-10}\right) \times\left(1.8 \times 10^{-5}\right)=1.0 \times 10^{-14} \mathrm{M} \end{aligned} $$

This can be extended to make a generalisation. The equilibrium constant for a net reaction obtained after adding two (or more) reactions equals the product of the equilibrium constants for individual reactions:

$$ \begin{equation*} K_{\mathrm{NET}}=K_{1} \times K_{2} \times \ldots \ldots \tag{7.35} \end{equation*} $$

Similarly, in case of a conjugate acid-base pair,

$$ \begin{equation*} K_{\mathrm{a}} \times K_{\mathrm{b}}=K_{\mathrm{w}} \tag{7.36} \end{equation*} $$

Knowing one, the other can be obtained. It should be noted that a strong acid will have a weak conjugate base and vice-versa.

Alternatively, the above expression $K_{\mathrm{w}}=K_{\mathrm{a}} \times K_{\mathrm{b}}$, can also be obtained by considering the base-dissociation equilibrium reaction:

$$ \begin{aligned} & \mathrm{B}(\mathrm{aq})+\mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{BH}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq}) \\ & K_{\mathrm{b}}=\left[\mathrm{BH}^{+}\right]\left[\mathrm{OH}^{-}\right] /[\mathrm{B}] \end{aligned} $$

As the concentration of water remains constant it has been omitted from the denominator and incorporated within the dissociation constant. Then multiplying and dividing the above expression by $\left[\mathrm{H}^{+}\right]$, we get:

$$ \begin{aligned} K_{\mathrm{b}} & = \left[\mathrm{BH}^{+}\right] \left[\mathrm{OH}^{-}\right] \left[\mathrm{H}^{+}\right] / [\mathrm{B}] \left[\mathrm{H}^{+} \right] \\ \end{aligned} $$

$$ \begin{aligned} & =\{ \left[\mathrm{OH}^{-}\right] \left[\mathrm{H}^{+} \right]\}\{ \left[\mathrm{BH}^{+} \right] /[\mathrm{B}] \left[\mathrm{H}^{+} \right]\} \\ & =K_{\mathrm{w}} / K_{\mathrm{a}} \\ \text { or } & K_{\mathrm{a}} \times K_{\mathrm{b}}=K_{\mathrm{w}} \end{aligned} $$

It may be noted that if we take negative logarithm of both sides of the equation, then $\mathrm{p} K$ values of the conjugate acid and base are related to each other by the equation:

$$ \mathrm{p} K_{\mathrm{a}}+\mathrm{p} K_{\mathrm{b}}=\mathrm{p} K_{\mathrm{w}}=14(\text { at } 298 \mathrm{~K}) $$

Problem 7.23

Determine the degree of ionization and $\mathrm{pH}$ of a $0.05 \mathrm{M}$ of ammonia solution. The ionization constant of ammonia can be taken from Table 6.7. Also, calculate the ionization constant of the conjugate acid of ammonia.

Solution

The ionization of $\mathrm{NH_3}$ in water is represented by equation: $\mathrm{NH_3}+\mathrm{H_2} \mathrm{O} \rightleftharpoons \mathrm{NH_4}^{+}+\mathrm{OH}^{-}$ We use equation (6.33) to calculate hydroxyl ion concentration,

$\left[\mathrm{OH}^{-}\right]=\mathrm{c} \alpha=0.05 \alpha$

$K_{\mathrm{b}}=0.05 \alpha^{2} /(1-\alpha)$

The value of $\alpha$ is small, therefore the quadratic equation can be simplified by neglecting $\alpha$ in comparison to 1 in the denominator on right hand side of the equation,

Thus,

$$ \begin{aligned} K_{\mathrm{b}}=\mathrm{c} \alpha^{2} \text { or } \alpha & =\sqrt{ }\left(1.77 \times 10^{-5} / 0.05\right) \\ & =0.018 . \end{aligned} $$

$\left[\mathrm{OH}^{-}\right]=\mathrm{c} \alpha=0.05 \times 0.018=9.4 \times 10^{-4} \mathrm{M}$.

$\left[\mathrm{H}^{+}\right]=K_{\mathrm{w}} /\left[\mathrm{OH}^{-}\right]=10^{-14} /\left(9.4 \times 10^{-4}\right)$

$$ =1.06 \times 10^{-11} $$

$\mathrm{pH}=-\log \left(1.06 \times 10^{-11}\right)=10.97$.

Now, using the relation for conjugate acid-base pair,

$K_{\mathrm{a}} \times K_{\mathrm{b}}=K_{\mathrm{w}}$

using the value of $K_{b}$ of $\mathrm{NH_3}$ from Table 7.7.

We can determine the concentration of conjugate acid $\mathrm{NH_4}^{+}$

$$ \begin{aligned} K_{\mathrm{a}}=K_{\mathrm{w}} / K_{\mathrm{b}} & =10^{-14} / 1.77 \times 10^{-5} \\ & =5.64 \times 10^{-10} . \end{aligned} $$

7.11.6 Di- and Polybasic Acids and Di- and Polyacidic Bases

Some of the acids like oxalic acid, sulphuric acid and phosphoric acids have more than one ionizable proton per molecule of the acid. Such acids are known as polybasic or polyprotic acids.

The ionization reactions for example for a dibasic acid $\mathrm{H_2} \mathrm{X}$ are represented by the equations:

$$ \begin{aligned} & \mathrm{H_2} \mathrm{X}(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{HX}^{-}(\mathrm{aq}) \\ & \mathrm{HX}^{-}(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{X}^{2-}(\mathrm{aq}) \end{aligned} $$

And the corresponding equilibrium constants are given below:

$$ K_{a_{1}}=\{\left[\mathrm{H}^{+}\right]\left[\mathrm{HX}^{-}\right]\} /\left[\mathrm{H_2} \mathrm{X}\right] \text { and } $$

$$ K_{\mathrm{a_2}}=\{\left[\mathrm{H}^{+}\right]\left[\mathrm{X}^{2-}\right]\} / \left[\mathrm{HX}^{-}\right] $$

Here, $K_{\mathrm{a_1}}$ and $K_{\mathrm{a_2}}$ are called the first and second ionization constants respectively of the acid $\mathrm{H_2}$ X. Similarly, for tribasic acids like $\mathrm{H_3} \mathrm{PO_4}$ we have three ionization constants. The values of the ionization constants for some common polyprotic acids are given in Table 6.8.

Table 6.8 The Ionization Constants of Some Common Polyprotic Acids (298K)

Acid	$\boldsymbol{K_\mathrm{a_\mathbf{1}}}$	$\boldsymbol{K_\mathrm{a_\mathbf{2}}}$	$\boldsymbol{K_\mathrm{a_\mathbf{3}}}$
Oxalic Acid	$5.9 \times 10^{-2}$	$6.4 \times 10^{-5}$
Ascorbic Acid	$7.4 \times 10^{-4}$	$1.6 \times 10^{-12}$
Sulphurous Acid	$1.7 \times 10^{-2}$	$6.4 \times 10^{-8}$
Sulphuric Acid	Very large	$1.2 \times 10^{-2}$
Carbonic Acid	$4.3 \times 10^{-7}$	$5.6 \times 10^{-11}$
Citric Acid	$7.4 \times 10^{-4}$	$1.7 \times 10^{-5}$	$4.0 \times 10^{-7}$
Phosphoric Acid	$7.5 \times 10^{-3}$	$6.2 \times 10^{-8}$	$4.2 \times 10^{-13}$

It can be seen that higher order ionization constants $\left(K_{\mathrm{a_2}}, K_{\mathrm{a_3}}\right)$ are smaller than the lower order ionization constant $\left(K_{a_{1}}\right)$ of a polyprotic acid. The reason for this is that it is more difficult to remove a positively charged proton from a negative ion due to electrostatic forces. This can be seen in the case of removing a proton from the uncharged $\mathrm{H_2} \mathrm{CO_3}$ as compared from a negatively charged $\mathrm{HCO_3}^{-}$. Similarly, it is more difficult to remove a proton from a doubly charged $\mathrm{HPO_4}^{2-}$ anion as compared to $\mathrm{H_2} \mathrm{PO_4}^{-}$.

Polyprotic acid solutions contain a mixture of acids like $\mathrm{H_2} \mathrm{~A}, \mathrm{HA}^{-}$and $\mathrm{A}^{2-}$ in case of a diprotic acid. $\mathrm{H_2} \mathrm{~A}$ being a strong acid, the primary reaction involves the dissociation of $\mathrm{H_2} \mathrm{~A}$, and $\mathrm{H_3} \mathrm{O}^{+}$in the solution comes mainly from the first dissociation step.

7.11.7 Factors Affecting Acid Strength

Having discussed quantitatively the strengths of acids and bases, we come to a stage where we can calculate the $\mathrm{pH}$ of a given acid solution. But, the curiosity rises about why should some acids be stronger than others? What factors are responsible for making them stronger? The answer lies in its being a complex phenomenon. But, broadly speaking we can say that the extent of dissociation of an acid depends on the strength and polarity of the $\mathrm{H}-\mathrm{A}$ bond. In general, when strength of $\mathrm{H}-\mathrm{A}$ bond decreases, that is, the energy required to break the bond decreases, HA becomes a stronger acid. Also, when the H-A bond becomes more polar i.e., the electronegativity difference between the atoms $\mathrm{H}$ and $\mathrm{A}$ increases and there is marked charge separation, cleavage of the bond becomes easier thereby increasing the acidity.

But it should be noted that while comparing elements in the same group of the periodic table, $\mathrm{H}-\mathrm{A}$ bond strength is a more important factor in determining acidity than its polar nature. As the size of A increases down the group, H-A bond strength decreases and so the acid strength increases. For example,

Similarly, $\mathrm{H_2} \mathrm{~S}$ is stronger acid than $\mathrm{H_2} \mathrm{O}$.

But, when we discuss elements in the same row of the periodic table, H-A bond polarity becomes the deciding factor for determining the acid strength. As the electronegativity of A increases, the strength of the acid also increases. For example,

7.11.8 Common Ion Effect in the Ionization of Acids and Bases

Consider an example of acetic acid dissociation equilibrium represented as:

$\mathrm{CH_3} \mathrm{COOH}(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{CH_3} \mathrm{COO}^{-}(\mathrm{aq})$

or $\mathrm{HAc}(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{Ac}^{-}(\mathrm{aq})$

$K_{\mathrm{a}}=\left[\mathrm{H}^{+}\right]\left[\mathrm{Ac}^{-}\right] /[\mathrm{HAc}]$

Addition of acetate ions to an acetic acid solution results in decreasing the concentration of hydrogen ions, $\left[\mathrm{H}^{+}\right]$. Also, if $\mathrm{H}^{+}$ions are added from an external source then the equilibrium moves in the direction of undissociated acetic acid i.e., in a direction of reducing the concentration of hydrogen ions, $\left[\mathrm{H}^{+}\right]$. This phenomenon is an example of common ion effect. It can be defined as a shift in equilibrium on adding a substance that provides more of an ionic species already present in the dissociation equilibrium. Thus, we can say that common ion effect is a phenomenon based on the Le Chatelier’s principle discussed in section 7.8.

In order to evaluate the $\mathrm{pH}$ of the solution resulting on addition of $0.05 \mathrm{M}$ acetate ion to $0.05 \mathrm{M}$ acetic acid solution, we shall consider the acetic acid dissociation equilibrium once again,

$$ \mathrm{HAc}(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{Ac}^{-}(\mathrm{aq}) $$

Initial concentration $(\mathrm{M})$

$$ 0.05 \quad \quad\quad 0 \quad \quad\quad 0.05 $$

Let $\mathrm{x}$ be the extent of ionization of acetic acid.

Change in concentration (M)

$-\mathrm{x} \quad\quad\quad +\mathrm{x}\quad\quad\quad +\mathrm{x}$

Equilibrium concentration (M)

$$ 0.05-x \quad \quad\quad x \quad\quad\quad 0.05+x $$

Therefore,

$K_{\mathrm{a}}=\left[\mathrm{H}^{+}\right]\left[\mathrm{Ac}^{-}\right] /[\mathrm{H} \mathrm{Ac}]={(0.05+\mathrm{x})(\mathrm{x})} /(0.05-\mathrm{x})$

As $K_{\mathrm{a}}$ is small for a very weak acid, $\mathrm{x}«0.05$.

Hence, $(0.05+\mathrm{x}) \approx(0.05-\mathrm{x}) \approx 0.05$

Thus,

$1.8 \times 10^{-5}=(\mathrm{x})(0.05+\mathrm{x}) /(0.05-\mathrm{x})$

$=\mathrm{x}(0.05) /(0.05)=\mathrm{x}=\left[\mathrm{H}^{+}\right]=1.8 \times 10^{-5} \mathrm{M}$

$\mathrm{pH}=-\log \left(1.8 \times 10^{-5}\right)=4.74$

Problem 7.24

Calculate the $\mathrm{pH}$ of a $0.10 \mathrm{M}$ ammonia solution. Calculate the $\mathrm{pH}$ after $50.0 \mathrm{~mL}$ of this solution is treated with $25.0 \mathrm{~mL}$ of $0.10 \mathrm{M} \mathrm{HCl}$. The dissociation constant of ammonia, $K_{\mathrm{b}}=1.77 \times 10^{-5}$

Solution

$$ \mathrm{NH_3} + \mathrm{H_2} \mathrm{O} \rightarrow \mathrm{NH_4}^{+} + \mathrm{OH}^{-} $$

$$ K_{\mathrm{b}}=\left[\mathrm{NH_4}^{+}\right]\left[\mathrm{OH}^{-}\right] /\left[\mathrm{NH_3}\right]=1.77 \times 10^{-5} $$

Before neutralization,

$\left[\mathrm{NH_4}^{+}\right]=\left[\mathrm{OH}^{-}\right]=\mathrm{x}$

$\left[\mathrm{NH_3}\right]=0.10-\mathrm{x} \simeq 0.10$

$\mathrm{x}^{2} / 0.10=1.77 \times 10^{-5}$ Thus, $\mathrm{x}=1.33 \times 10^{-3}=\left[\mathrm{OH}^{-}\right]$

Therefore, $\left[\mathrm{H}^{+}\right]=K_{\mathrm{w}} /\left[\mathrm{OH}^{-}\right]=10^{-14} /$

$$ \left(1.33 \times 10^{-3}\right)=7.51 \times 10^{-12} $$

$\mathrm{pH}=-\log \left(7.5 \times 10^{-12}\right)=11.12$

On addition of $25 \mathrm{~mL}$ of $0.1 \mathrm{M} \mathrm{HCl}$ solution (i.e., $2.5 \mathrm{mmol}$ of $\mathrm{HCl}$ ) to 50 $\mathrm{mL}$ of $0.1 \mathrm{M}$ ammonia solution (i.e., 5 $\mathrm{mmol}$ of $\mathrm{NH_3}$ ), $2.5 \mathrm{mmol}$ of ammonia molecules are neutralized. The resulting $75 \mathrm{~mL}$ solution contains the remaining unneutralized $2.5 \mathrm{mmol}$ of $\mathrm{NH_3}$ molecules and $2.5 \mathrm{mmol}$ of $\mathrm{NH_4}^{+}$.

$\underset{2.5}{\mathrm{NH_3}} + \underset{2.5}{\mathrm{HCl}} \rightarrow \underset{0}{\mathrm{NH_4}^{+}} + \underset{0}{\mathrm{Cl}^{-}} $

At equilibrium 0 $\quad \quad \quad $ 0 $\quad \quad \quad $ 2.5 $\quad \quad \quad $ 2.5

The resulting $75 \mathrm{~mL}$ of solution contains $2.5 \mathrm{mmol}$ of $\mathrm{NH_4}^{+}$ions (i.e., $0.033 \mathrm{M}$ ) and $2.5 \mathrm{mmol}$ (i.e., $0.033 \mathrm{M}$ ) of uneutralised $\mathrm{NH_3}$ molecules. This $\mathrm{NH_3}$ exists in the following equilibrium:

$\underset{0.033M-y}{\mathrm{NH_4OH}} \rightleftharpoons \underset{y}{\mathrm{NH_4}^{+}} + \underset{y}{\mathrm{OH}^{-}} $

where, $\mathrm{y}=\left[\mathrm{OH}^{-}\right]=$ $\left[\mathrm{NH_4}^{+}\right]$

The final $75 \mathrm{~mL}$ solution after neutralisation already contains $2.5 \mathrm{~m} \mathrm{~mol} \mathrm{NH_4}^{+}$ions (i.e. $0.033 \mathrm{M}$ ), thus total concentration of $\mathrm{NH_4}^{+}$ions is given as:

$\left[\mathrm{NH_4}^{+}\right]=0.033+\mathrm{y}$

As $\mathrm{y}$ is small, $\left[\mathrm{NH_4} \mathrm{OH}\right] \simeq 0.033 \mathrm{M}$ and $\left[\mathrm{NH_4}^{+}\right] \simeq 0.033 \mathrm{M}$.

We know,

$$ \begin{aligned} K_{\mathrm{b}} & =\left[\mathrm{NH_4}^{+}\right]\left[\mathrm{OH}^{-}\right] /\left[\mathrm{NH_4} \mathrm{OH}\right] \ & =\mathrm{y}(0.033) /(0.033)=1.77 \times 10^{-5} \mathrm{M} \end{aligned} $$

Thus, $\mathrm{y}=1.77 \times 10^{-5}=\left[\mathrm{OH}^{-}\right]$

$\left[\mathrm{H}^{+}\right]=10^{-14} / 1.77 \times 10^{-5}=0.56 \times 10^{-9}$

Hence, $\mathrm{pH}=9.24$

7.11.9 Hydrolysis of Salts and the pH of their Solutions

Salts formed by the reactions between acids and bases in definite proportions, undergo ionization in water. The cations/anions formed on ionization of salts either exist as hydrated ions in aqueous solutions or interact with water to reform corresponding acids/ bases depending upon the nature of salts. The later process of interaction between water and cations/anions or both of salts is called hydrolysis. The $\mathrm{pH}$ of the solution gets affected by this interaction. The cations (e.g., $\mathrm{Na}^{+}, \mathrm{K}^{+}, \mathrm{Ca}^{2+}, \mathrm{Ba}^{2+}$, etc.) of strong bases and anions (e.g., $\mathrm{Cl}^{-}, \mathrm{Br}^{-}, \mathrm{NO_3}^{-}, \mathrm{ClO_4}^{-}$etc.) of strong acids simply get hydrated but do not hydrolyse, and therefore the solutions of salts formed from strong acids and bases are neutral i.e., their pH is 7 . However, the other category of salts do undergo hydrolysis.

We now consider the hydrolysis of the salts of the following types :

(i) salts of weak acid and strong base e.g., $\mathrm{CH_3} \mathrm{COONa}$.

(ii) salts of strong acid and weak base e.g., $\mathrm{NH_4} \mathrm{Cl}$, and

(iii) salts of weak acid and weak base, e.g., $\mathrm{CH_3} \mathrm{COONH_4}$.

In the first case, $\mathrm{CH_3} \mathrm{COONa}$ being a salt of weak acid, $\mathrm{CH_3} \mathrm{COOH}$ and strong base, $\mathrm{NaOH}$ gets completely ionised in aqueous solution. $\mathrm{CH_3} \mathrm{COONa}(\mathrm{aq}) \rightarrow \mathrm{CH_3} \mathrm{COO}^{-}(\mathrm{aq})+\mathrm{Na}^{+}(\mathrm{aq})$

Acetate ion thus formed undergoes hydrolysis in water to give acetic acid and $\mathrm{OH}^{-}$ions

$\mathrm{CH_3} \mathrm{COO}^{-}(\mathrm{aq})+\mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{CH_3} \mathrm{COOH}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})$

Acetic acid being a weak acid $\left(K_{\mathrm{a}}=1.8 \times 10^{-5}\right)$ remains mainly unionised in solution. This results in increase of $\mathrm{OH}^{-}$ion concentration in solution making it alkaline. The $\mathrm{pH}$ of such a solution is more than 7 .

Similarly, $\mathrm{NH_4} \mathrm{Cl}$ formed from weak base, $\mathrm{NH_4} \mathrm{OH}$ and strong acid, $\mathrm{HCl}$, in water dissociates completely.

$\mathrm{NH_4} \mathrm{Cl}(\mathrm{aq}) \rightarrow \mathrm{NH_4}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})$

Ammonium ions undergo hydrolysis with water to form $\mathrm{NH_4} \mathrm{OH}$ and $\mathrm{H}^{+}$ions

$\mathrm{NH_4}^{+}(\mathrm{aq})+\mathrm{H_2} \mathrm{O}(1) \rightleftharpoons \mathrm{NH_4} \mathrm{OH}(\mathrm{aq})+\mathrm{H}^{+}(\mathrm{aq})$

Ammonium hydroxide is a weak base $\left(K_{\mathrm{b}}=1.77 \times 10^{-5}\right)$ and therefore remains almost unionised in solution. This results in increased of $\mathrm{H}^{+}$ion concentration in solution making the solution acidic. Thus, the $\mathrm{pH}$ of $\mathrm{NH_4} \mathrm{Cl}$ solution in water is less than 7 .

Consider the hydrolysis of $\mathrm{CH_3} \mathrm{COONH_4}$ salt formed from weak acid and weak base. The ions formed undergo hydrolysis as follow:

$\mathrm{CH_3} \mathrm{COO}^{-}+\mathrm{NH_4}^{+}+\mathrm{H_2} \mathrm{O} \rightleftharpoons \mathrm{CH_3} \mathrm{COOH}+$ $\mathrm{NH_4} \mathrm{OH}$

$\mathrm{CH_3} \mathrm{COOH}$ and $\mathrm{NH_4} \mathrm{OH}$, also remain into partially dissociated form:

$$ \begin{aligned} & \mathrm{CH_3} \mathrm{COOH} \rightleftharpoons \mathrm{CH_3} \mathrm{COO}^{-}+\mathrm{H}^{+} \\ & \mathrm{NH_4} \mathrm{OH} \rightleftharpoons \quad \mathrm{NH_4}^{+}+\mathrm{OH}^{-} \\ & \mathrm{H_2} \mathrm{O} \rightleftharpoons \mathrm{H}^{+}+\mathrm{OH}^{-} \end{aligned} $$

Without going into detailed calculation, it can be said that degree of hydrolysis is independent of concentration of solution, and $\mathrm{pH}$ of such solutions is determined by their $\mathrm{p} K$ values:

$$ \begin{equation*} \mathrm{pH}=7+1 / 2\left(\mathrm{p} K_{\mathrm{a}}-\mathrm{p} K_{\mathrm{b}}\right) \tag{7.38} \end{equation*} $$

The $\mathrm{pH}$ of solution can be greater than 7 , if the difference is positive and it will be less than 7 , if the difference is negative.

Problem 7.25

The $\mathrm{p} K_{\mathrm{a}}$ of acetic acid and $\mathrm{p} K_{b}$ of ammonium hydroxide are 4.76 and 4.75 respectively. Calculate the $\mathrm{pH}$ of ammonium acetate solution.

Solution

$$ \begin{aligned} \mathrm{pH} & =7+1 / 2\left[\mathrm{p} K_{\mathrm{a}}-\mathrm{p} K_{\mathrm{b}}\right] \\ & =7+1 / 2[4.76-4.75] \\ & =7+1 / 2[0.01]=7+0.005=7.005 \end{aligned} $$

7.12 BUFFER SOLUTIONS

Many body fluids e.g., blood or urine have definite $\mathrm{pH}$ and any deviation in their $\mathrm{pH}$ indicates malfunctioning of the body. The control of $\mathrm{pH}$ is also very important in many chemical and biochemical processes. Many medical and cosmetic formulations require that these be kept and administered at a particular $\mathrm{pH}$. The solutions which resist change in $\mathrm{pH}$ on dilution or with the addition of small amounts of acid or alkali are called Buffer Solutions. Buffer solutions of known $\mathrm{pH}$ can be prepared from the knowledge of $\mathrm{p} K_{\mathrm{a}}$ of the acid or $\mathrm{p} K_{\mathrm{b}}$ of base and by controlling the ratio of the salt and acid or salt and base. A mixture of acetic acid and sodium acetate acts as buffer solution around pH 4.75 and a mixture of ammonium chloride and ammonium hydroxide acts as a buffer around $\mathrm{pH}$ 9.25. You will learn more about buffer solutions in higher classes.

7.12.1 Designing Buffer Solution

Knowledge of $\mathrm{p} K_{a}, \mathrm{p} K_{b}$ and equilibrium constant help us to prepare the buffer solution of known $\mathrm{pH}$. Let us see how we can do this.

Preparation of Acidic Buffer

To prepare a buffer of acidic $\mathrm{pH}$ we use weak acid and its salt formed with strong base. We develop the equation relating the $\mathrm{pH}$, the equilibrium constant, $K_{a}$ of weak acid and ratio of concentration of weak acid and its conjugate base. For the general case where the weak acid HA ionises in water,

$$ \mathrm{HA}+\mathrm{H_2} \mathrm{O} \leftrightharpoons \mathrm{H_3} \mathrm{O}^{+}+\mathrm{A}^{-} $$

For which we can write the expression

$$ K_{a}=\frac{\left[\mathrm{H_3} \mathrm{O}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]} $$

Rearranging the expression we have,

$$ \left[\mathrm{H_3} \mathrm{O}^{+}\right]=K_{a} \frac{[\mathrm{HA}]}{\left[\mathrm{A}^{-}\right]} $$

Taking logarithm on both the sides and rearranging the terms we get -

$$ \begin{gather*} \mathrm{pK_a}=\mathrm{pH}-\log \frac{\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]} \\ \text { Or } \\ \mathrm{pH}=\mathrm{pK_a}+\log \frac{\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]} \tag{7.39} \end{gather*} $$

$$\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{\left[\text { Conjugate base, } \mathrm{A}^{-}\right]}{[\text {Acid, } \mathrm{HA}]} \tag{7.40}$$

The expression (7.40) is known as Henderson-Hasselbalch equation. The quantity $\frac{\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}$ is the ratio of concentration of conjugate base (anion) of the acid and the acid present in the mixture. Since acid is a weak acid, it ionises to a very little extent and concentration of [HA] is negligibly different from concentration of acid taken to form buffer. Also, most of the conjugate base, $\left[\mathrm{A}^{-}\right]$, comes from the ionisation of salt of the acid. Therefore, the concentration of conjugate base will be negligibly different from the concentration of salt. Thus, equation (6.40) takes the form:

$$ p \mathrm{H}=p K_{a}+\log \frac{[\text { Salt }]}{[\text { Acid }]} $$

In the equation (6.39), if the concentration of $\left[\mathrm{A}^{-}\right]$is equal to the concentration of $[\mathrm{HA}]$, then $\mathrm{pH}=\mathrm{p} K_{a}$ because value of $\log 1$ is zero. Thus if we take molar concentration of acid and salt (conjugate base) same, the $\mathrm{pH}$ of the buffer solution will be equal to the $\mathrm{p} K_{a}$ of the acid. So for preparing the buffer solution of the required $\mathrm{pH}$ we select that acid whose $\mathrm{p} K_{a}$ is close to the required $\mathrm{pH}$. For acetic acid $\mathrm{p} K_{\mathrm{a}}$ value is 4.76, therefore $\mathrm{pH}$ of the buffer solution formed by acetic acid and sodium acetate taken in equal molar concentration will be around 4.76.

A similar analysis of a buffer made with a weak base and its conjugate acid leads to the result,

$$ \begin{equation*} \mathrm{pOH}=\mathrm{p} K_{\mathrm{b}}+\log \frac{\left[\text { Conjugate acid, } \mathrm{BH}^{+}\right]}{[\text {Base, } \mathrm{B}]} \tag{7.41} \end{equation*} $$

$\mathrm{pH}$ of the buffer solution can be calculated by using the equation $\mathrm{pH}+\mathrm{pOH}=14$.

We know that $\mathrm{pH}+\mathrm{pOH}=\mathrm{p} K_{\mathrm{w}}$ and $\mathrm{p} K_{\mathrm{a}}+\mathrm{p} K_{\mathrm{b}}=\mathrm{p} K_{\mathrm{w}}$. On putting these values in equation (6.41) it takes the form as follows:

$$ \mathrm{p} K_{\mathrm{w}}-\mathrm{pH}=\mathrm{p} K_{\mathrm{w}}-\mathrm{p} K_{a}+\log \frac{\left[\text { Conjugate acid, } \mathrm{BH}^{+}\right]}{[\text {Base, } \mathrm{B}]} $$

or

$$ \begin{equation*} \mathrm{pH}=\mathrm{p} K_{a}+\log \frac{\left[\text { Conjugate acid, } \mathrm{BH}^{+}\right]}{[\text {Base }, \mathrm{B}]} \tag{7.42} \end{equation*} $$

If molar concentration of base and its conjugate acid (cation) is same then $\mathrm{pH}$ of the buffer solution will be same as $\mathrm{p} K_{a}$ for the base. $\mathrm{p} K_{a}$ value for ammonia is $\mathrm{s} 9.25$; therefore a buffer of pH close to 9.25 can be obtained by taking ammonia solution and ammonium chloride solution of same molar concentration. For a buffer solution formed by ammonium chloride and ammonium hydroxide, equation (6.42) becomes:

$$ \mathrm{pH}=9.25+\log \frac{\left[\text { Conjugate acid, } \mathrm{BH}^{+}\right]}{[\text {Base }, \mathrm{B}]} $$

$\mathrm{pH}$ of the buffer solution is not affected by dilution because ratio under the logarithmic term remains unchanged.

7.13 SOLUBILITY EQUILIBRIA OF SPARINGLY SOLUBLE SALTS

We have already known that the solubility of ionic solids in water varies a great deal. Some of these (like calcium chloride) are so soluble that they are hygroscopic in nature and even absorb water vapour from atmosphere. Others (such as lithium fluoride) have so little solubility that they are commonly termed as insoluble. The solubility depends on a number of factors important amongst which are the lattice enthalpy of the salt and the solvation enthalpy of the ions in a solution. For a salt to dissolve in a solvent the strong forces of attraction between its ions (lattice enthalpy) must be overcome by the ion-solvent interactions. The solvation enthalpy of ions is referred to in terms of solvation which is always negative i.e. energy is released in the process of solvation. The amount of solvation enthalpy depends on the nature of the solvent. In case of a nonpolar (covalent) solvent, solvation enthalpy is small and hence, not sufficient to overcome lattice enthalpy of the salt. Consequently, the salt does not dissolve in non-polar solvent. As a general rule, for a salt to be able to dissolve in a particular solvent its solvation enthalpy must be greater than its lattice enthalpy so that the latter may be overcome by former. Each salt has its characteristic solubility which depends on temperature. We classify salts on the basis of their solubility in the following three categories.

Category I	Soluble	Solubility $>0.1 \mathrm{M}$
Category II	Slightly Soluble	$0.01 \mathrm{M}<$ Solubility $<0.1 \mathrm{M}$
Category III	Sparingly Soluble	Solubility $<0.01 \mathrm{M}$

We shall now consider the equilibrium between the sparingly soluble ionic salt and its saturated aqueous solution.

7.13.1 Solubility Product Constant

Let us now have a solid like barium sulphate in contact with its saturated aqueous solution. The equilibrium between the undisolved solid and the ions in a saturated solution can be represented by the equation:

$\mathrm{BaSO_4}(\mathrm{~s}) \xrightleftharpoons[{\text{in water}}]{\text{Saturated solution}} \mathrm{Ba}^{2+}(\mathrm{aq})+\mathrm{SO_4}^{2-}(\mathrm{aq})$,

The equilibrium constant is given by the equation:

$$ K=\{\left[\mathrm{Ba}^{2+}\right]\left[\mathrm{SO_4}^{2-}\right]\} /\left[\mathrm{BaSO_4}\right] $$

For a pure solid substance the concentration remains constant and we can write

$$ \begin{equation*} K_{\mathrm{sp}}=\mathrm{K}\left[\mathrm{BaSO_4}\right]=\left[\mathrm{Ba}^{2+}\right]\left[\mathrm{SO_4}^{2-}\right] \tag{7.43} \end{equation*} $$

We call $K_{\mathrm{sp}}$ the solubility product constant or simply solubility product. The experimental value of $K_{\mathrm{sp}}$ in above equation at $298 \mathrm{~K}$ is $1.1 \times 10^{-10}$. This means that for solid barium sulphate in equilibrium with its saturated solution, the product of the concentrations of barium and sulphate ions is equal to its solubility product constant. The concentrations of the two ions will be equal to the molar solubility of the barium sulphate. If molar solubility is $\mathrm{S}$, then

$$ \begin{aligned} & 1.1 \times 10^{-10}=(\mathrm{S})(\mathrm{S})=\mathrm{S}^{2} \\ & \text { or } \quad \mathrm{S}=1.05 \times 10^{-5} \end{aligned} $$

Thus, molar solubility of barium sulphate will be equal to $1.05 \times 10^{-5} \mathrm{~mol} \mathrm{~L}^{-1}$.

A salt may give on dissociation two or more than two anions and cations carrying different charges. For example, consider a salt like zirconium phosphate of molecular formula $\left(\mathrm{Zr}^{4+}\right)_3\left(\mathrm{PO_4}{ }^{3-}\right)_4$. It dissociates into 3 zirconium cations of charge +4 and 4 phosphate anions of charge -3 . If the molar solubility of zirconium phosphate is $\mathrm{S}$, then it can be seen from the stoichiometry of the compound that

$$ \begin{aligned} & [\mathrm{Zr}^{4+}]=3 \mathrm{~S} \text { and }[\mathrm{PO_4}^{3-}]=4 \mathrm{S} \\ \end{aligned} $$

$$ \begin{aligned} & \text { and } K_{\mathrm{sp}}=(3 \mathrm{~S})^{3}(4 \mathrm{~S})^{4}=6912(\mathrm{~S})^{7} \\ & \text { or } \mathrm{S}= \{K_{\mathrm{sp}} / \left(3^{3} \times 4^{4}\right)\}^{1 / 7}= \left(K_{\mathrm{sp}} / 6912 \right)^{1 / 7} \end{aligned} $$

A solid salt of the general formula $\mathrm{M_\mathrm{x}}^{\mathrm{p+}} \mathrm{X_\mathrm{y}}^{\mathrm{q}}$ with molar solubility $\mathrm{S}$ in equilibrium with its saturated solution may be represented by the equation:

$$ \begin{aligned} & \mathrm{M_\mathrm{x}} \mathrm{X_\mathrm{y}}(\mathrm{s}) \rightleftharpoons \mathrm{xM}^{\mathrm{p}+}(\mathrm{aq})+\mathrm{yX}^{\mathrm{q}^{-}}(\mathrm{aq}) \\ & \left(\text { where } \mathrm{x} \times \mathrm{p}^{+}=\mathrm{y} \times \mathrm{q}^{-}\right) \end{aligned} $$

And its solubility product constant is given by:

$$ \begin{aligned} & K_{\mathrm{sp}}=\left[\mathrm{M}^{\mathrm{p}+}\right]^{\mathrm{x}}\left[\mathrm{X}^{\mathrm{q}-}\right]^{\mathrm{y}}=(\mathrm{xS})^{\mathrm{x}}(\mathrm{yS})^{\mathrm{y}} \tag{7.44} \\ \end{aligned} $$

$$ \begin{aligned} & =x^{x} \cdot y^{y} \cdot S^{(x+y)} \\ & \mathrm{S}^{(\mathrm{x}+\mathrm{y})}=K_{\mathrm{sp}} / \mathrm{x}^{\mathrm{x}} \cdot \mathrm{y}^{\mathrm{y}} \\ \end{aligned} $$

$$ \begin{aligned} & \mathrm{S}=\left(K_{\mathrm{sp}} / \mathrm{x}^{\mathrm{x}} \cdot \mathrm{y}^{\mathrm{y}}\right)^{1 / \mathrm{x}+\mathrm{y}} \tag{7.45} \end{aligned} $$

The term $K_{\mathrm{sp}}$ in equation is given by $Q_{\mathrm{sp}}$ (section 6.6.2) when the concentration of one or more species is not the concentration under equilibrium. Obviously under equilibrium conditions $K_{\mathrm{sp}}=Q_{\mathrm{sp}}$ but otherwise it gives the direction of the processes of precipitation or dissolution. The solubility product constants of a number of common salts at $298 \mathrm{~K}$ are given in Table 7.9.

Problem 7.26

Calculate the solubility of $\mathrm{A_2} \mathrm{X_3}$ in pure water, assuming that neither kind of ion reacts with water. The solubility product of $\mathrm{A_2} \mathrm{X_3}, K_{\mathrm{sp}}=1.1 \times 10^{-23}$.

Solution

$\mathrm{A_2} \mathrm{X_3} \rightarrow 2 \mathrm{~A}^{3+}+3 \mathrm{X}^{2-}$

$K_{\text {sp }}=\left[\mathrm{A}^{3+}\right]^{2}\left[\mathrm{X}^{2-}\right]^{3}=1.1 \times 10^{-23}$

If $\mathrm{S}=$ solubility of $\mathrm{A_2} \mathrm{X_3}$, then

$\left[\mathrm{A}^{3+}\right]=2 \mathrm{~S} ;\left[\mathrm{X}^{2-}\right]=3 \mathrm{~S}$

therefore, $K_{\mathrm{sp}}=(2 \mathrm{~S})^{2}(3 \mathrm{~S})^{3}=108 \mathrm{~S}^{5}$

$$ =1.1 \times 10^{-23} $$

thus, $\mathrm{S}^{5}=1 \times 10^{-25}$

$\mathrm{S}=1.0 \times 10^{-5} \mathrm{~mol} / \mathrm{L}$.

Name of the Salt	Formula	$\boldsymbol{K_\text {sp }}$
Silver Bromide	$\mathrm{AgBr}$	$5.0 \times 10^{-13}$
Silver Carbonate	$\mathrm{Ag_2} \mathrm{CO_3}$	$8.1 \times 10^{-12}$
Silver Chromate	$\mathrm{Ag_2} \mathrm{CrO_4}$	$1.1 \times 10^{-12}$
Silver Chloride	$\mathrm{AgCl}$	$1.8 \times 10^{-10}$
Silver Iodide	AgI	$8.3 \times 10^{-17}$
Silver Sulphate	$\mathrm{Ag_2} \mathrm{SO_4}$	$1.4 \times 10^{-5}$
Aluminium Hydroxide	$\mathrm{Al}(\mathrm{OH})_{3}$	$1.3 \times 10^{-33}$
Barium Chromate	$\mathrm{BaCrO_4}$	$1.2 \times 10^{-10}$
Barium Fluoride	$\mathrm{BaF_2}$	$1.0 \times 10^{-6}$
Barium Sulphate	$\mathrm{BaSO_4}$	$1.1 \times 10^{-10}$
Calcium Carbonate	$\mathrm{CaCO_3}$	$2.8 \times 10^{-9}$
Calcium Fluoride	$\mathrm{CaF_2}$	$5.3 \times 10^{-9}$
Calcium Hydroxide	$\mathrm{Ca}(\mathrm{OH})_{2}$	$5.5 \times 10^{-6}$
Calcium Oxalate	$\mathrm{CaC_2} \mathrm{O_4}$	$4.0 \times 10^{-9}$
Calcium Sulphate	$\mathrm{CaSO_4}$	$9.1 \times 10^{-6}$
Cadmium Hydroxide	$\mathrm{Cd}(\mathrm{OH})_{2}$	$2.5 \times 10^{-14}$
Cadmium Sulphide	$\mathrm{CdS}$	$8.0 \times 10^{-27}$
Chromic Hydroxide	$\mathrm{Cr}(\mathrm{OH})_{3}$	$6.3 \times 10^{-31}$
Cuprous Bromide	$\mathrm{CuBr}$	$5.3 \times 10^{-9}$
Cupric Carbonate	$\mathrm{CuCO_3}$	$1.4 \times 10^{-10}$
Cuprous Chloride	$\mathrm{CuCl}$	$1.7 \times 10^{-6}$
Cupric Hydroxide	$\mathrm{Cu}(\mathrm{OH})_{2}$	$2.2 \times 10^{-20}$
Cuprous Iodide	CuI	$1.1 \times 10^{-12}$
Cupric Sulphide	CuS	$6.3 \times 10^{-36}-1$
Ferrous Carbonate	$\mathrm{FeCO_3}$	$3.2 \times 10^{-11}$
Ferrous Hydroxide	$\mathrm{Fe}(\mathrm{OH})_{2}$	$8.0 \times 10^{-16}$
Ferric Hydroxide	$\mathrm{Fe}(\mathrm{OH})_{3}$	$1.0 \times 10^{-38}$
Ferrous Sulphide	$\mathrm{FeS}$	$6.3 \times 10^{-18}$
Mercurous Bromide	$\mathrm{Hg_2} \mathrm{Br_2}$	$5.6 \times 10^{-23}$
Mercurous Chloride	$\mathrm{Hg_2} \mathrm{Cl_2}$	$1.3 \times 10^{-18}$
Mercurous Iodide	$\mathrm{Hg_2} \mathrm{I_2}$	$4.5 \times 10^{-29}$
Mercurous Sulphate	$\mathrm{Hg_2} \mathrm{SO_4}$	$7.4 \times 10^{-7}$
Mercuric Sulphide	HgS	$4.0 \times 10^{-53}$
Magnesium Carbonate	$\mathrm{MgCO_3}$	$3.5 \times 10^{-8}$
Magnesium Fluoride	$\mathrm{MgF_2}$	$6.5 \times 10^{-9}$
Magnesium Hydroxide	$\mathrm{Mg}(\mathrm{OH})_{2}$	$1.8 \times 10^{-11}$
Magnesium Oxalate	$\mathrm{MgC_2} \mathrm{O_4}$	$7.0 \times 10^{-7}$
Manganese Carbonate	$\mathrm{MnCO_3}$	$1.8 \times 10^{-11}$
Manganese Sulphide	$\mathrm{MnS}$	$2.5 \times 10^{-13}$
Nickel Hydroxide	$\mathrm{Ni}(\mathrm{OH})_{2}$	$2.0 \times 10-15$
Nickel Sulphide	NiS	$4.7 \times 10^{-5}$
Lead Bromide	$\mathrm{PbBr_2}$	$4.0 \times 10^{-5}$
Lead Carbonate	$\mathrm{PbCO_3}$	$7.4 \times 10^{-14}$
Lead Chloride	$\mathrm{PbCl_2}$	$1.6 \times 10^{-5}$
Lead Fluoride	$\mathrm{PbF_2}$	$7.7 \times 10^{-8}$
Lead Hydroxide	$\mathrm{Pb}(\mathrm{OH})_{2}$	$1.2 \times 10^{-15}$
Lead Iodide	$\mathrm{PbI_2}$	$7.1 \times 10^{-9}$
Lead Sulphate	$\mathrm{PbSO_4}$	$1.6 \times 10^{-8}$
Lead Sulphide	$\mathrm{PbS}$	$8.0 \times 10^{-28}$
Stannous Hydroxide	$\mathrm{Sn}(\mathrm{OH})_{2}$	$1.4 \times 10^{-28}$
Stannous Sulphide	$\mathrm{SnS}$	$1.0 \times 10^{-25}$
Strontium Carbonate	$\mathrm{SrCO_3}$	$1.1 \times 10^{-10}$
Strontium Fluoride	$\mathrm{SrF_2}$	$2.5 \times 10^{-9}$
Strontium Sulphate	$\mathrm{SrSO_4}$	$3.2 \times 10^{-7}$
Thallous Bromide	$\mathrm{TlBr}$	$3.4 \times 10^{-6}$
Thallous Chloride	$\mathrm{TlCl}$	$1.7 \times 10^{-4}$
Thallous Iodide	TII	$6.5 \times 10^{-8}$
Zinc Carbonate	$\mathrm{ZnCO_3}$	$1.4 \times 10^{-11}$
Zinc Hydroxide	$\mathrm{Zn}(\mathrm{OH})_{2}$	$1.0 \times 10^{-15}$
Zinc Sulphide	$\mathrm{ZnS}$	$1.6 \times 10^{-24}$

Problem 7.27

The values of $K_{\mathrm{sp}}$ of two sparingly soluble salts $\mathrm{Ni}(\mathrm{OH})_{2}$ and $\mathrm{AgCN}$ are $2.0 \times 10^{-15}$ and $6 \times 0^{-17}$ respectively. Which salt is more soluble? Explain.

Solution

$$ \mathrm{AgCN} \rightleftharpoons \mathrm{Ag}^{+}+\mathrm{CN}^{-} $$

Table 6.9 The Solubility Product Constants, $K_{\mathrm{sp}}$ of Some Common Ionic Salts at 298K.

$$ \begin{aligned} & K_{\mathrm{sp}}= \left[\mathrm{Ag}^{+}\right] \left[\mathrm{CN}^{-} \right]=6 \times 10^{-17} \\ & \mathrm{Ni}(\mathrm{OH})_{2} \rightleftharpoons \mathrm{Ni}^{2+}+2 \mathrm{OH}^{-} \\ \end{aligned} $$

$$ \begin{aligned} & K_{\mathrm{sp}}= \left[\mathrm{Ni}^{2+} \right] \left[\mathrm{OH}^{-} \right]^{2}=2 \times 10^{-15} \\ & \text { Let } \left[\mathrm{Ag}^{+} \right]=\mathrm{S_1} \text {, then } \left[\mathrm{CN}^{-} \right]=\mathrm{S_1} \\ & \text { Let } \left[\mathrm{Ni}^{2+} \right]=\mathrm{S_2}, \text { then } \left[\mathrm{OH}^{-} \right]=2 \mathrm{~S_2} \\ & \mathrm{~S_1}^{2}=6 \times 10^{-17}, \mathrm{~S_1}=7.8 \times 10^{-9} \\ & \left(\mathrm{~S_2} \right) \left(2 \mathrm{~S_2} \right)^{2}=2 \times 10^{-15}, \mathrm{~S_2}=0.58 \times 10^{-4} \\ & \mathrm{Ni}(\mathrm{OH})_{2} \text { is more soluble than AgCN. } \end{aligned} $$

7.13.2 Common Ion Effect on Solubility of Ionic Salts

It is expected from Le Chatelier’s principle that if we increase the concentration of any one of the ions, it should combine with the ion of its opposite charge and some of the salt will be precipitated till once again $K_{\mathrm{sp}}=$ $Q_{\mathrm{sp}}$. Similarly, if the concentration of one of the ions is decreased, more salt will dissolve to increase the concentration of both the ions till once again $K_{\mathrm{sp}}=Q_{\mathrm{sp}}$. This is applicable even to soluble salts like sodium chloride except that due to higher concentrations of the ions, we use their activities instead of their molarities in the expression for $Q_{\mathrm{sp}}$. Thus if we take a saturated solution of sodium chloride and pass $\mathrm{HCl}$ gas through it, then sodium chloride is precipitated due to increased concentration (activity) of chloride ion available from the dissociation of $\mathrm{HCl}$. Sodium chloride thus obtained is of very high purity and we can get rid of impurities like sodium and magnesium sulphates. The common ion effect is also used for almost complete precipitation of a particular ion as its sparingly soluble salt, with very low value of solubility product for gravimetric estimation. Thus we can precipitate silver ion as silver chloride, ferric ion as its hydroxide (or hydrated ferric oxide) and barium ion as its sulphate for quantitative estimations.

Problem 7.28

Calculate the molar solubility of $\mathrm{Ni}(\mathrm{OH})_2$ in $0.10 \mathrm{M} \mathrm{NaOH}$. The ionic product of $\mathrm{Ni}(\mathrm{OH})_2$ is $2.0 \times 10^{-15}$.

Solution

Let the solubility of $\mathrm{Ni}(\mathrm{OH})_{2}$ be equal to $\mathrm{S}$.

Dissolution of $\mathrm{S} \mathrm{mol} / \mathrm{L}$ of $\mathrm{Ni}(\mathrm{OH})_{2}$ provides $\mathrm{S} \mathrm{mol} / \mathrm{L}$ of $\mathrm{Ni}^{2+}$ and $2 \mathrm{~S} \mathrm{~mol} / \mathrm{L}$ of $\mathrm{OH}^{-}$, but the total concentration of $\mathrm{OH}^{-}=(0.10+2 \mathrm{~S})$ $\mathrm{mol} / \mathrm{L}$ because the solution already contains $0.10 \mathrm{~mol} / \mathrm{L}$ of $\mathrm{OH}^{-}$from $\mathrm{NaOH}$.

$$ \begin{aligned} K_{\mathrm{sp}}=2.0 \times 10^{-15} & =\left[\mathrm{Ni}^{2+}\right]\left[\mathrm{OH}^{-}\right]^{2} \\ & =(\mathrm{S})(0.10+2 \mathrm{~S})^{2} \end{aligned} $$

As $K_{\mathrm{sp}}$ is small, $2 \mathrm{~S}«0.10$, thus, $(0.10+2 \mathrm{~S}) \approx 0.10$

Hence,

$$ \begin{aligned} & 2.0 \times 10^{-15}=\mathrm{S}(0.10)^{2} \\ & \mathrm{~S}=2.0 \times 10^{-13} \mathrm{M}=\left[\mathrm{Ni}^{2+}\right] \end{aligned} $$

The solubility of salts of weak acids like phosphates increases at lower $\mathrm{pH}$. This is because at lower $\mathrm{pH}$ the concentration of the anion decreases due to its protonation. This in turn increase the solubility of the salt so that $K_{\mathrm{sp}}=Q_{\mathrm{sp}}$. We have to satisfy two equilibria simultaneously i.e.,

$$ \begin{aligned} & K_{\mathrm{sp}}=\left[\mathrm{M}^{+}\right]\left[\mathrm{X}^{-}\right], \\ & \mathrm{HX}(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{X}^{-}(\mathrm{aq}) ; \\ & K_{\mathrm{a}}=\frac{\left[\mathrm{H}^{+}(\mathrm{aq})\right]\left[\mathrm{X}^{-}(\mathrm{aq})\right]}{[\mathrm{HX}(\mathrm{aq})]} \\ & {\left[\mathrm{X}^{-}\right] /[\mathrm{HX}]=K_{\mathrm{a}} /\left[\mathrm{H}^{+}\right]} \end{aligned} $$

Taking inverse of both side and adding 1 we get

$$ \begin{aligned} & \frac{[\mathrm{HX}]}{\left[\mathrm{X}^{-}\right]}+1=\frac{\left[\mathrm{H}^{+}\right]}{K_{\mathrm{a}}}+1 \\ \\ & \frac{[\mathrm{HX}]+\left[\mathrm{H}^{-}\right]}{\left[\mathrm{X}^{-}\right]}=\frac{\left[\mathrm{H}^{+}\right]+K_{\mathrm{a}}}{K_{\mathrm{a}}} \end{aligned} $$

Now, again taking inverse, we get

$ [\mathrm{X}^{-} ] / \{ [\mathrm{X}^{-} ]+[\mathrm{HX}] \}=\mathrm{f}=K_{\mathrm{a}} / (K_{\mathrm{a}}+ [\mathrm{H}^{+} ] )$ and it can be seen that ’ $\mathrm{f}$ ’ decreases as pH decreases. If $S$ is the solubility of the salt at a given $\mathrm{pH}$ then

$$ \begin{align*} & K_{\mathrm{sp}}=[\mathrm{S}][\mathrm{f} \mathrm{~S}]=\mathrm{S}^{2} \{K_a / (K_a+ [\mathrm{H}^{+} ] ) \} \text {and } \\ \end{align*} $$

$$ \begin{align*} & \mathrm{S}= \{K_{\mathrm{sp}} ( [\mathrm{H}^{+} ]+K_{\mathrm{a}} ) / K_{\mathrm{a}} \}^{1 / 2} \tag{7.46} \end{align*} $$

Thus solubility $\mathrm{S}$ increases with increase in $\left[\mathrm{H}^{+}\right]$or decrease in $\mathrm{pH}$.

SUMMARY

When the number of molecules leaving the liquid to vapour equals the number of molecules returning to the liquid from vapour, equilibrium is said to be attained and is dynamic in nature. Equilibrium can be established for both physical and chemical processes and at this stage rate of forward and reverse reactions are equal. Equilibrium constant, $\boldsymbol{K_c}$ is expressed as the concentration of products divided by reactants, each term raised to the stoichiometric coefficient.

$$ \begin{gathered} \text { For reaction, } \mathrm{a} \mathrm{A}+\mathrm{b} \mathrm{B} \rightleftharpoons \mathrm{c} \mathrm{C}+\mathrm{d} \mathrm{D} \\ K_{\mathrm{c}}=[\mathrm{C}]^{\mathrm{c}}[\mathrm{D}]^{\mathrm{d}} /[\mathrm{A}]^{\mathrm{a}}[\mathrm{B}]^{\mathrm{b}} \end{gathered} $$

Equilibrium constant has constant value at a fixed temperature and at this stage all the macroscopic properties such as concentration, pressure, etc. become constant. For a gaseous reaction equilibrium constant is expressed as $K_{p}$ and is written by replacing concentration terms by partial pressures in $K_{c}$ expression. The direction of reaction can be predicted by reaction quotient $Q_{c}$ which is equal to $K_{c}$ at equilibrium. Le Chatelier’s principle states that the change in any factor such as temperature, pressure, concentration, etc. will cause the equilibrium to shift in such a direction so as to reduce or counteract the effect of the change. It can be used to study the effect of various factors such as temperature, concentration, pressure, catalyst and inert gases on the direction of equilibrium and to control the yield of products by controlling these factors. Catalyst does not effect the equilibrium composition of a reaction mixture but increases the rate of chemical reaction by making available a new lower energy pathway for conversion of reactants to products and vice-versa.

All substances that conduct electricity in aqueous solutions are called electrolytes. Acids, bases and salts are electrolytes and the conduction of electricity by their aqueous solutions is due to anions and cations produced by the dissociation or ionization of electrolytes in aqueous solution. The strong electrolytes are completely dissociated. In weak electrolytes there is equilibrium between the ions and the unionized electrolyte molecules. According to Arrhenius, acids give hydrogen ions while bases produce hydroxyl ions in their aqueous solutions. Brönsted-Lowry on the other hand, defined an acid as a proton donor and a base as a proton acceptor. When a Brönsted-Lowry acid reacts with a base, it produces its conjugate base and a conjugate acid corresponding to the base with which it reacts. Thus a conjugate pair of acid-base differs only by one proton. Lewis further generalised the definition of an acid as an electron pair acceptor and a base as an electron pair donor. The expressions for ionization (equilibrium) constants of weak acids $\left(K_{\mathrm{a}}\right)$ and weak bases $\left(K_{\mathrm{b}}\right)$ are developed using Arrhenius definition. The degree of ionization and its dependence on concentration and common ion are discussed. The $\mathbf{p H}$ scale $\left(\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]\right)$for the hydrogen ion concentration (activity) has been introduced and extended to other quantities ( $\left.\mathrm{pOH}=-\log \left[\mathrm{OH}^{-}\right]\right) ; \mathrm{p} K_{\mathrm{a}}=-\log \left[\mathrm{K_\mathrm{a}}\right]$; $\mathrm{p} K_{\mathrm{b}}=-\log \left[K_{\mathrm{b}}\right]$; and $\mathrm{p} K_{\mathrm{w}}=-\log \left[K_{\mathrm{w}}\right]$ etc.). The ionization of water has been considered and we note that the equation: $\mathrm{pH}+\mathrm{pOH}=\mathrm{pK_\mathrm{w}}$ is always satisfied. The salts of strong acid and weak base, weak acid and strong base, and weak acid and weak base undergo hydrolysis in aqueous solution. The definition of buffer solutions, and their importance are discussed briefly. The solubility equilibrium of sparingly soluble salts is discussed and the equilibrium constant is introduced as solubility product constant $\left(K_{\mathrm{sp}}\right)$. Its relationship with solubility of the salt is established. The conditions of precipitation of the salt from their solutions or their dissolution in water are worked out. The role of common ion and the solubility of sparingly soluble salts is also discussed.

SUGGESTED ACTIVITIES FOR STUDENTS REGARDING THIS UNIT

(a) The student may use $\mathrm{pH}$ paper in determining the $\mathrm{pH}$ of fresh juices of various vegetables and fruits, soft drinks, body fluids and also that of water samples available.

(b) The $\mathrm{pH}$ paper may also be used to determine the $\mathrm{pH}$ of different salt solutions and from that he/she may determine if these are formed from strong/weak acids and bases.

(c) They may prepare some buffer solutions by mixing the solutions of sodium acetate and acetic acid and determine their $\mathrm{pH}$ using $\mathrm{pH}$ paper.

(d) They may be provided with different indicators to observe their colours in solutions of varying $\mathrm{pH}$.

(e) They may perform some acid-base titrations using indicators.

(f) They may observe common ion effect on the solubility of sparingly soluble salts.

(g) If $\mathrm{pH}$ meter is available in their school, they may measure the $\mathrm{pH}$ with it and compare the results obtained with that of the $\mathrm{pH}$ paper.

EXERCISES

7.1 A liquid is in equilibrium with its vapour in a sealed container at a fixed temperature. The volume of the container is suddenly increased.

a) What is the initial effect of the change on vapour pressure?

b) How do rates of evaporation and condensation change initially?

c) What happens when equilibrium is restored finally and what will be the final vapour pressure?

Show Answer

Answer

(a) If the volume of the container is suddenly increased, then the vapour pressure would decrease initially. This is because the amount of vapour remains the same, but the volume increases suddenly. As a result, the same amount of vapour is distributed in a larger volume.

(b) Since the temperature is constant, the rate of evaporation also remains constant. When the volume of the container is increased, the density of the vapour phase decreases. As a result, the rate of collisions of the vapour particles also decreases. Hence, the rate of condensation decreases initially.

(c) When equilibrium is restored finally, the rate of evaporation becomes equal to the rate of condensation. In this case, only the volume changes while the temperature remains constant. The vapour pressure depends on temperature and not on volume. Hence, the final vapour pressure will be equal to the original vapour pressure of the system.

7.2 What is $K_{\mathrm{c}}$ for the following equilibrium when the equilibrium concentration of each substance is: $\left[\mathrm{SO_2}\right]=0.60 \mathrm{M},\left[\mathrm{O_2}\right]=0.82 \mathrm{M}$ and $\left[\mathrm{SO_3}\right]=1.90 \mathrm{M}$ ?

$$ 2 \mathrm{SO_2}(\mathrm{~g})+\mathrm{O_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{SO_3}(\mathrm{~g}) $$

Answer :

The equilibrium constant $(K_c)$ for the give reaction is:

$ \begin{aligned} K_c & =\frac{[SO_3]^{2}}{[SO_2]^{2}[O_2]} \\ & =\frac{(1.90)^{2} M^{2}}{(0.60)^{2}(0.821) M^{3}} \\ & =12.239 M^{-1} \text{ (approximately) } \end{aligned} $

Hence, $K_c$ for the equilibrium is $12.239 M^{-1}$.

7.3 At a certain temperature and total pressure of $10^{5} \mathrm{~Pa}$, iodine vapour contains $40 %$ by volume of I atoms

$$ \mathrm{I_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{I}(\mathrm{g}) $$

Calculate $K_{p}$ for the equilibrium.

Show Answer

Answer

Partial pressure of I atoms,

$p_1=\frac{40}{100} \times p _{\text{total }}$

$=\frac{40}{100} \times 10^{5}$

$=4 \times 10^{4} Pa$

Partial pressure of $I_2$ molecules,

$ \begin{aligned} & p _{I_2}=\frac{60}{100} \times p _{\text{total }} \\ & =\frac{60}{100} \times 10^{5} \\ & =6 \times 10^{4} Pa \end{aligned} $

Now, for the given reaction,

$ \begin{aligned} K_p & =\frac{(p I)^{2}}{p _{I_2}} \\ & =\frac{(4 \times 10^{4})^{2} Pa^{2}}{6 \times 10^{4} Pa} \\ & =2.67 \times 10^{4} Pa \end{aligned} $

7.4 Write the expression for the equilibrium constant, $K_{c}$ for each of the following reactions:

(i) $2 \mathrm{NOCl}(\mathrm{g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g})+\mathrm{Cl_2}(\mathrm{~g})$

(ii) $2 \mathrm{Cu}\left(\mathrm{NO_3}\right)_{2}(\mathrm{~s}) \rightleftharpoons 2 \mathrm{CuO}(\mathrm{s})+4 \mathrm{NO_2}(\mathrm{~g})+\mathrm{O_2}(\mathrm{~g})$

(iii) $\mathrm{CH_3} \mathrm{COOC_2} \mathrm{H_5}(\mathrm{aq})+\mathrm{H_2} \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{CH_3} \mathrm{COOH}(\mathrm{aq})+\mathrm{C_2} \mathrm{H_5} \mathrm{OH}(\mathrm{aq})$

(iv) $\mathrm{Fe}^{3+}(\mathrm{aq})+3 \mathrm{OH}^{-}(\mathrm{aq}) \rightleftharpoons \mathrm{Fe}(\mathrm{OH})_{3}(\mathrm{~s})$

(v) $\mathrm{I_2}(\mathrm{~s})+5 \mathrm{~F_2} \rightleftharpoons 2 \mathrm{IF_5}$

Show Answer

Answer

(i) $\quad K_c=\frac{[NO _{(g)}]^{2}[Cl _{2(g)}]}{[NOCl _{(g)}]^{2}}$

(ii) $\quad K_c=\frac{[CuO _{(s)}]^{2}[NO _{2(g)}]^{4}[O _{2(g)}]}{[Cu(NO_3) _{2(s)}]^{2}}$

$ =[NO _{2(g)}]^{4}[O _{2(g)}] $

(iii) $K_c=\frac{[CH_3 COOH _{(a q)}][C_2 H_5 OH _{(a q)}]}{[CH_3 COOC_2 H _{5(a q)}][H_2 O _{(l)}]}=\frac{[CH_3 COOH _{(a q)}][C_2 H_5 OH _{(a q)}]}{[CH_3 COOC_2 H _{5(a q)}]}$

(iv) $K_c=\frac{[Fe(OH) _{3(s)}]}{[Fe _{(a q)}^{3+}][OH _{(a q)}^{-}]^{3}}$

$ =\frac{1}{[Fe _{(a q)}^{3+}][OH _{(a q)}^{-}]^{3}} $

(v) $\quad K_c=\frac{[IF_5]^{2}}{[I _{2(s)}][F_2]^{5}}$

$=\frac{[IF_5]^{2}}{[F_2]^{5}}$

7.5 Find out the value of $K_{c}$ for each of the following equilibria from the value of $K_{p}$ :

(i) $2 \mathrm{NOCl}(\mathrm{g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g})+\mathrm{Cl_2}(\mathrm{~g}) ; K_{p}=1.8 \times 10^{-2}$ at $500 \mathrm{~K}$

(ii) $\mathrm{CaCO_3}$ (s) $\rightleftharpoons \mathrm{CaO}$ (s) $+\mathrm{CO_2}(\mathrm{~g}) ; K_{p}=167$ at $1073 \mathrm{~K}$

Show Answer

Answer

The relation between $K_p$ and $K_c$ is given as:

$K_p=K_c(RT)^{\Delta n}$

(a) Here,

$\Delta n=3-2=1$

$R=0.0831$ barLmol $^{-1} K^{-1}$

$T=500 K$

$K_p=1.8 \times 10^{-2}$

Now,

$K_p=K_c(R T)^{\Delta n}$

$\Rightarrow 1.8 \times 10^{-2}=K_c(0.0831 \times 500)^{1}$

$\Rightarrow K_c=\frac{1.8 \times 10^{-2}}{0.0831 \times 500}$

$ =4.33 \times 10^{-4} \text{ (approximately) } $

(b) Here,

$\Delta n=2$ - $1=1$

$R=0.0831$ barLmol $^{-1} K^{-1}$

$T=1073 K$

$K_p=167$

Now,

$K_p=K_c(R T)^{\Delta n}$

$\Rightarrow 167=K_c(0.0831 \times 1073)^{\Delta n}$

$\Rightarrow K_c=\frac{167}{0.0831 \times 1073}$

$=1.87$ (approximately)

7.6 For the following equilibrium, $K_{c}=6.3 \times 10^{14}$ at $1000 \mathrm{~K}$

$\mathrm{NO}(\mathrm{g})+\mathrm{O_3}(\mathrm{~g}) \rightleftharpoons \mathrm{NO_2}(\mathrm{~g})+\mathrm{O_2}(\mathrm{~g})$

Both the forward and reverse reactions in the equilibrium are elementary bimolecular reactions. What is $K_{c}$, for the reverse reaction?

Show Answer

Answer

It is given that $K_C$ for the forward reaction is $6.3 \times 10^{14}$.

Then, $K_C$ for the reverse reaction will be,

$ \begin{aligned} K_C^{\prime} & =\frac{1}{K_C} \\ & =\frac{1}{6.3 \times 10^{14}} \\ & =1.59 \times 10^{-15} \end{aligned} $

7.7 Explain why pure liquids and solids can be ignored while writing the equilibrium constant expression?

Show Answer

Answer

For a pure substance (both solids and liquids),

$ \begin{aligned} {[\text{ Pure substance }] } & =\frac{\text{ Number of moles }}{\text{ Volume }} \\ & =\frac{\text{ Mass } / \text{ molecular mass }}{\text{ Volume }} \\ & =\frac{\text{ Mass }}{\text{ Volume } \times \text{ Molecular mass }} \\ & =\frac{\text{ Density }}{\text{ Molecular mass }} \end{aligned} $

Now, the molecular mass and density (at a particular temperature) of a pure substance is always fixed and is accounted for in the equilibrium constant. Therefore, the values of pure substances are not mentioned in the equilibrium constant expression.

7.8 Reaction between $\mathrm{N_2}$ and $\mathrm{O_2-}$ takes place as follows:

$$ 2 \mathrm{~N_2}(\mathrm{~g})+\mathrm{O_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{~N_2} \mathrm{O}(\mathrm{g}) $$

If a mixture of $0.482 \mathrm{~mol} \mathrm{~N_2}$ and $0.933 \mathrm{~mol}$ of $\mathrm{O_2}$ is placed in a $10 \mathrm{~L}$ reaction vessel and allowed to form $\mathrm{N_2} \mathrm{O}$ at a temperature for which $K_{c}=2.0 \times 10^{-37}$, determine the composition of equilibrium mixture.

Show Answer

Answer

Let the concentration of $N_2 O$ at equilibrium be $x$.

The given reaction is:

	$2 N _{2(g)}+$	$O _{2(g)}$	$\longleftrightarrow$
Initial conc. $\quad 0.482 mol$	$0.933 mol$	0
At equilibrium $(0.482-x) mol$	$(1.933-x) mol$	$x$ mol

Therefore, at equilibrium, in the $10 L$ vessel:

$[N_2]=\frac{0.482-x}{10},[O_2]=\frac{0.933-x / 2}{10},[N_2 O]=\frac{x}{10}$

The value of equilibrium constant i.e., $K_C=2.0 \times 10^{9 a+37}$ is very small. Therefore, the amount of $N_2$ and $O_2$ reacted is also very small. Thus, $x$ can be neglected from the expressions of molar concentrations of $N_2$ and $O_2$.

Then,

$[N_2]=\frac{0.482}{10}=0.0482 mol L^{-1}$ and $[O_2]=\frac{0.933}{10}=0.0933 mol L^{-1}$

Now,

$ \begin{aligned} & K_C=\frac{[N_2 O _{(g)}]^{2}}{[N _{2(g)}]^{2}[O _{2(g)}]} \\ & \Rightarrow 2.0 \times 10^{-37}=\frac{(\frac{x}{10})^{2}}{(0.0482)^{2}(0.0933)} \\ & \Rightarrow \frac{x^{2}}{100}=2.0 \times 10^{-37} \times(0.0482)^{2} \times(0.0933) \\ & \Rightarrow x^{2}=43.35 \times 10^{-40} \\ & \Rightarrow x=6.6 \times 10^{-20} \\ & {[N_2 O]=\frac{x}{10}=\frac{6.6 \times 10^{-20}}{10}} \\ & =6.6 \times 10^{-21} \end{aligned} $

7.9 Nitric oxide reacts with $\mathrm{Br_2}$ and gives nitrosyl bromide as per reaction given below:

$$ 2 \mathrm{NO}(\mathrm{g})+\mathrm{Br_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NOBr}(\mathrm{g}) $$

When $0.087 \mathrm{~mol}$ of $\mathrm{NO}$ and $0.0437 \mathrm{~mol}$ of $\mathrm{Br_2}$ are mixed in a closed container at constant temperature, $0.0518 \mathrm{~mol}$ of $\mathrm{NOBr}$ is obtained at equilibrium. Calculate equilibrium amount of $\mathrm{NO}$ and $\mathrm{Br_2}$.

Show Answer

Answer

The given reaction is:

$ 2 NO _{(g)}+Br _{2(g)} \longleftrightarrow 2 NOBr _{(g)} $

$2 mol \quad 1 mol \quad 2 mol$

Now, 2 mol of $NOBr$ are formed from $2 mol$ of $NO$. Therefore, $0.0518 mol$ of $NOBr$ are formed from $0.0518 mol$ of $NO$.

Again, 2 mol of $NOBr$ are formed from $1 mol$ of $Br$.

Therefore, $0.0518 mol$ of $NOBr$ are formed from $\frac{0.0518}{2} mol$ of $Br$, or $0.0259 mol$ of NO.

The amount of $NO$ and $Br$ present initially is as follows:

$[NO]=0.087 mol[Br_2]=0.0437 mol$

Therefore, the amount of NO present at equilibrium is:

$[N O]=0.087$ – 0.0518

$=0.0352 mol$

And, the amount of $Br$ present at equilibrium is:

$[Br_2]=0.0437$ â€" 0.0259

$=0.0178 mol$

7.10 At $450 \mathrm{~K}, K_{p}=2.0 \times 10^{10} /$ bar for the given reaction at equilibrium.

What is $K_{c}$ at this temperature ?

$$ 2 \mathrm{SO_2}(\mathrm{~g})+\mathrm{O_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{SO_3}(\mathrm{~g}) $$

Show Answer

Answer

For the given reaction,

$\Delta n=2$ â€" 3 = â€" 1

$T=450 K$

$R=0.0831$ bar $L$ bar $K^{\hat{a} \epsilon^{-1}} mol^{\hat{a} \epsilon^{* 1} 1}$ $K_p=2.0 \times 10^{10} bar^{Ae{ }^{e} 1}$

We know that,

$ \begin{aligned} & K_P=K_C(R T) \Delta n \\ & \begin{aligned} & \Rightarrow 2.0 \times 10^{10} bar^{-1}=K_C(0.0831 L bar K^{-1} mol^{-1} \times 450 K)^{-1} \\ & \Rightarrow K_C=\frac{2.0 \times 10^{10} bar^{-1}}{(0.0831 L bar K^{-1} mol^{-1} \times 450 K)^{-1}} \\ &=(2.0 \times 10^{10} bar^{-1})(0.0831 Lbar K^{-1} mol^{-1} \times 450 K) \\ &=74.79 \times 10^{10} L mol^{-1} \\ &=7.48 \times 10^{11} L mol^{-1} \\ &=7.48 \times 10^{11} M^{-1} \end{aligned} \end{aligned} $

7.11 A sample of $\mathrm{HI}(\mathrm{g})$ is placed in flask at a pressure of $0.2 \mathrm{~atm}$. At equilibrium the partial pressure of $\mathrm{HI}(\mathrm{g})$ is $0.04 \mathrm{~atm}$. What is $K_{p}$ for the given equilibrium ?

$$ 2 \mathrm{HI}(\mathrm{g}) \rightleftharpoons \mathrm{H_2}(\mathrm{~g})+\mathrm{I_2}(\mathrm{~g}) $$

Show Answer

Answer

The initial concentration of $HI$ is $0.2 atm$. At equilibrium, it has a partial pressure of $0.04 atm$. Therefore, a decrease in the pressure of $HI$ is $0.2 \hat{a} E^{\prime \prime} 0.04=0.16$. The given reaction is:

$ 2 HI _{(g)} \longleftrightarrow H _{2(g)}+I _{2(g)} $

Initial conc. $\quad 0.2 atm$

$0 \quad 0$

At equilibrium $\quad 0.04 atm$

$ \begin{aligned} & \frac{0.16}{2} \quad \frac{2.15}{2} \\ & =0.08 atm=0.08 atm \end{aligned} $

Therefore,

$ \begin{aligned} K_p & =\frac{p _{H_2} \times p _{I_2}}{p_HI^{2}} \\ & =\frac{0.08 \times 0.08}{(0.04)^{2}} \\ & =\frac{0.0064}{0.0016} \\ & =4.0 \end{aligned} $

Hence, the value of $K_p$ for the given equilibrium is 4.0 .

7.12 A mixture of $1.57 \mathrm{~mol}$ of $\mathrm{N_2}, 1.92 \mathrm{~mol}$ of $\mathrm{H_2}$ and $8.13 \mathrm{~mol}$ of $\mathrm{NH_3}$ is introduced into a $20 \mathrm{~L}$ reaction vessel at $500 \mathrm{~K}$. At this temperature, the equilibrium constant, $K_{\mathrm{c}}$ for the reaction $\mathrm{N_2}(\mathrm{~g})+3 \mathrm{H_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH_3}(\mathrm{~g})$ is $1.7 \times 10^{2}$. Is the reaction mixture at equilibrium? If not, what is the direction of the net reaction?

Show Answer

Answer

The given reaction is:

$N _{2(g)}+3 H _{2(g)} \longleftrightarrow 2 NH _{3(g)}$

The given concentration of various species is

$[N_2]=\frac{1.57}{20} mol L^{-1} \quad[H_2]=\frac{1.92}{20} mol L^{-1}$

$[NH_3]=\frac{8.13}{20} mol L^{-1}$

Now, reaction quotient $Q_c$ is:

$ \begin{aligned} Q_C & =\frac{[NH_3]^{2}}{[N_2][H_2]^{3}} \\ & =\frac{(\frac{(8.13)}{20})^{2}}{(\frac{1.57}{20})(\frac{1.92}{20})^{3}} \\ & =2.4 \times 10^{3} \end{aligned} $

Since $Q_C \neq K_C$, the reaction mixture is not at equilibrium.

Again, $Q_C>K_C$. Hence, the reaction will proceed in the reverse direction.

7.13 The equilibrium constant expression for a gas reaction is,

$$ K_{c}=\frac{\left[\mathrm{NH_3}\right]^{4}\left[\mathrm{O_2}\right]^{5}}{[\mathrm{NO}]^{4}\left[\mathrm{H_2} \mathrm{O}\right]^{6}} $$

Write the balanced chemical equation corresponding to this expression.

Show Answer

Answer

The balanced chemical equation corresponding to the given expression can be written as:

$4 NO _{(g)}+6 H_2 O _{(g)} \longleftrightarrow 4 NH _{3(g)}+5 O _{2(g)}$

7.14 One mole of $\mathrm{H_2} \mathrm{O}$ and one mole of $\mathrm{CO}$ are taken in $10 \mathrm{~L}$ vessel and heated to $725 \mathrm{~K}$. At equilibrium $40 %$ of water (by mass) reacts with $\mathrm{CO}$ according to the equation,

$$ \mathrm{H_2} \mathrm{O}(\mathrm{g})+\mathrm{CO}(\mathrm{g}) \rightleftharpoons \mathrm{H_2}(\mathrm{~g})+\mathrm{CO_2}(\mathrm{~g}) $$

Calculate the equilibrium constant for the reaction.

Show Answer

Answer

The given reaction is:

$ \begin{aligned} & H_2 O _{(g)}+CO _{(g)} \longleftrightarrow H _{2(g)}+CO _{2(g)} \\ & \begin{matrix} \text{ Initial conc. } & \frac{1}{10} M & \frac{1}{10} M & 0 & 0 \end{matrix} \\ & \text{ At equilibrium } \quad \frac{1-0.4}{10} M \quad \frac{1-0.4}{10} M \quad \frac{0.4}{10} M \quad \frac{0.4}{10} M \\ & =0.06 M \quad=0.06 M \quad=0.04 M \quad=0.04 M \end{aligned} $

Therefore, the equilibrium constant for the reaction,

$ \begin{aligned} K_C & =\frac{[H_2][CO_2]}{[H_2 O][CO]} \\ & =\frac{0.04 \times 0.04}{0.06 \times 0.06} \\ & =0.444 \text{ (approximately) } \end{aligned} $

7.15 At $700 \mathrm{~K}$, equilibrium constant for the reaction:

$$ \mathrm{H_2}(\mathrm{~g})+\mathrm{I_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g}) $$

is 54.8. If $0.5 \mathrm{~mol} \mathrm{~L}^{-1}$ of $\mathrm{HI}(\mathrm{g})$ is present at equilibrium at $700 \mathrm{~K}$, what are the concentration of $\mathrm{H_2}(\mathrm{~g})$ and $\mathrm{I_2}(\mathrm{~g})$ assuming that we initially started with $\mathrm{HI}(\mathrm{g})$ and allowed it to reach equilibrium at $700 \mathrm{~K}$ ?

Show Answer

Answer

It is given that equilibrium constant $K_C$ for the reaction

$H _{2(g)}+I _{2(g)} \longleftrightarrow 2 HI _{(g)}$ is 54.8.

Therefore, at equilibrium, the equilibrium constant $K_C^{\prime}$ for the reaction

$2 HI _{(g)} \longleftrightarrow H _{2(g)}+I _{2(g)}$ will be $\frac{1}{54.8}$.

$[HI]=0.5 molL^{-1}$

Let the concentrations of hydrogen and iodine at equilibrium be $x molL^{\text{af }}{ }^{-1}$

$[H_2]=[I_2]=x mol L^{-1}$

Therefore, $\frac{[H_2][I_2]}{[HI]^{2}}=K_C^{\prime}$

$\Rightarrow \frac{x \times x}{(0.5)^{2}}=\frac{1}{54.8}$

$\Rightarrow x^{2}=\frac{0.25}{54.8}$

$\Rightarrow x=0.06754$

$x=0.068 molL^{-1}$ (approximately)

Hence, at equilibrium, $[H_2]=[I_2]=0.068 mol L^{-1}$.

7.16 What is the equilibrium concentration of each of the substances in the equilibrium when the initial concentration of $\mathrm{ICl}$ was $0.78 \mathrm{M}$ ?

$2 \mathrm{ICl}(\mathrm{g}) \rightleftharpoons \mathrm{I_2}(\mathrm{~g})+\mathrm{Cl_2}(\mathrm{~g}) ; \quad K_{c}=0.14$

Show Answer

Answer

The given reaction is:

	$2 ICl(g)$	Ã $\phi a ̂ € _{¡} \AA^{\prime}$	$I_2(g)+$
Initial conc.	$0.78 M$	0	0
At equilibrium	$(0.78-2 x) N$	$x M$	$x N$

Now, we can write, $\frac{[I_2][Cl_2]}{[ICl]^{2}}=K_C$

$\Rightarrow \frac{x \times x}{(0.78-2 x)^{2}}=0.14$

$\Rightarrow \frac{x^{2}}{(0.78-2 x)^{2}}=0.14$

$\Rightarrow \frac{x}{0.78-2 x}=0.374$

$\Rightarrow x=0.292-0.748 x$

$\Rightarrow 1.748 x=0.292$

$\Rightarrow x=0.167$

Hence, at equilibrium,

$[ICl]=[I 2]=$

7.17 $K_{p}=0.04 \mathrm{~atm}$ at $899 \mathrm{~K}$ for the equilibrium shown below. What is the equilibrium concentration of $\mathrm{C_2} \mathrm{H_6}$ when it is placed in a flask at $4.0 \mathrm{~atm}$ pressure and allowed to come to equilibrium?

$$ \mathrm{C_2} \mathrm{H_6}(\mathrm{~g}) \rightleftharpoons \mathrm{C_2} \mathrm{H_4}(\mathrm{~g})+\mathrm{H_2}(\mathrm{~g}) $$

Show Answer

Answer

Let $p$ be the pressure exerted by ethene and hydrogen gas (each) at equilibrium.

Now, according to the reaction,

Initial conc.

$ C_2 H _{6(g)} \longleftrightarrow C_2 H _{4(g)}+H _{2(g)} $

At equilibrium 4.0atm 0 0

We can write,

$ \begin{aligned} & \frac{p _{C_2 H_4} \times p _{H_2}}{p _{C_2 H_6}}=K_p \\ & \Rightarrow \frac{p \times p}{4.0-p}=0.04 \\ & \Rightarrow p^{2}+0.16-0.04 p \\ & \Rightarrow p^{2}+0.04 p-0.16=0 \\ & \text{ Now }, p=\frac{-0.04 \pm \sqrt{(0.04)^{2}-4 \times 1 \times(-0.16)}}{2 \times 1} \\ & \quad=\frac{-0.04 \pm 0.80}{2} \\ & \quad=\frac{0.76}{2} \quad(\text{ Taking positive value}) \\ & \quad=0.38 \end{aligned} $

Hence, at equilibrium,

$ \begin{aligned} {[C_2 H_6]-4-p } & =4-0.38 \\ & =3.62 atm \end{aligned} $

7.18 Ethyl acetate is formed by the reaction between ethanol and acetic acid and the equilibrium is represented as:

$$ \mathrm{CH_3} \mathrm{COOH}(1)+\mathrm{C_2} \mathrm{H_5} \mathrm{OH}(1) \rightleftharpoons \mathrm{CH_3} \mathrm{COOC_2} \mathrm{H_5}(1)+\mathrm{H_2} \mathrm{O}(1) $$

(i) Write the concentration ratio (reaction quotient), $Q_{\mathrm{c}}$, for this reaction (note: water is not in excess and is not a solvent in this reaction)

(ii) At $293 \mathrm{~K}$, if one starts with $1.00 \mathrm{~mol}$ of acetic acid and $0.18 \mathrm{~mol}$ of ethanol, there is $0.171 \mathrm{~mol}$ of ethyl acetate in the final equilibrium mixture. Calculate the equilibrium constant.

(iii) Starting with $0.5 \mathrm{~mol}$ of ethanol and $1.0 \mathrm{~mol}$ of acetic acid and maintaining it at $293 \mathrm{~K}, 0.214 \mathrm{~mol}$ of ethyl acetate is found after sometime. Has equilibrium been reached?

Show Answer

Answer

(i) Reaction quotient,

$ Q_C=\frac{[CH_3 COOC_2 H_5][H_2 O]}{[CH_3 COOH][C_2 H_5 OH]} $

(ii) Let the volume of the reaction mixture be $V$. Also, here we will consider that water is a solvent and is present in excess.

The given reaction is:

$ \begin{matrix} \text{ At equilibrium } & \frac{1-0.171}{V} & \frac{0.18-0.171}{V} & \frac{0.171}{V} M & \frac{0.171}{V} M \\ = & \frac{0.829}{V} M & =\frac{0.009}{V} M & \end{matrix} $

Therefore, equilibrium constant for the given reaction is:

$ \begin{aligned} K_C & =\frac{[CH_3 COOC_2 H_5][H_2 O]}{[CH_3 COOH][C_2 H_5 OH]} \\ & =\frac{\frac{0.171}{V} \times \frac{0.171}{V}}{\frac{0.829}{V} \times \frac{0.009}{V}}=3.919 \\ = & 3.92(\text{ approximately }) \end{aligned} $

(iii) Let the volume of the reaction mixture be $V$.

$ \begin{matrix} \text{ After some time } & \frac{10-0.214}{V} & \frac{0.5-0.214}{V} & \frac{0.214}{V} M & \frac{0.214}{V} M \\ & =\frac{0.786}{V} M & =\frac{0.286}{V} M & \end{matrix} $

Therefore, the reaction quotient is,

$ \begin{aligned} Q_C & =\frac{[CH_3 COOC_2 H_5][H_2 O]}{[CH_3 COOH][C_2 H_5 OH]} \\ & =\frac{\frac{0.214}{V} \times \frac{0.214}{V}}{\frac{0.786}{V} \times \frac{0.286}{V}} \\ & =0.2037 \\ & =0204 \text{ (approximately) } \end{aligned} $

Since $Q_C<K_C$, equilibrium has not been reached.

7.19 A sample of pure $\mathrm{PCl_5}$ was introduced into an evacuated vessel at 473 K. After equilibrium was attained, concentration of $\mathrm{PCl_5}$ was found to be $0.5 \times 10^{-1} \mathrm{~mol} \mathrm{~L}^{-1}$. If value of $K_{\mathrm{c}}$ is $8.3 \times 10^{-3}$, what are the concentrations of $\mathrm{PCl_3}$ and $\mathrm{Cl_2}$ at equilibrium?

$$ \mathrm{PCl_5}(\mathrm{~g}) \rightleftharpoons \mathrm{PCl_3}(\mathrm{~g})+\mathrm{Cl_2}(\mathrm{~g}) $$

Show Answer

Answer

Let the concentrations of both $PCl_3$ and $Cl_2$ at equilibrium be $x$ molL ${ }^{\hat{e} e^{-1}}$. The given reaction is:

At equilibrium $0.5 \times 10^{-1} mol L^{-1} \quad x mol L^{-1} \quad x mol L^{-1}$

It is given that the value of equilibrium constant, $K_C$ is $8.3 \times 10^{-3}$.

Now we can write the expression for equilibrium as:

$ \begin{aligned} & \frac{[PCl_2][Cl_2]}{[PCl_5]}=K_C \\ & \Rightarrow \frac{x \times x}{0.5 \times 10^{-1}}=8.3 \times 10^{-3} \\ & \Rightarrow x^{2}=4.15 \times 10^{-4} \\ & \Rightarrow x=2.04 \times 10^{-2} \\ & \quad=0.0204 \\ & \quad=0.02 \text{ (approximately) } \end{aligned} $

Therefore, at equilibrium,

$[PCl_3]=[Cl_2]=0.02 mol L{ }^{-1}$.

7.20 One of the reaction that takes place in producing steel from iron ore is the reduction of iron(II) oxide by carbon monoxide to give iron metal and $\mathrm{CO_2}$.

$\mathrm{FeO}(\mathrm{s})+\mathrm{CO}(\mathrm{g}) \rightleftharpoons \mathrm{Fe}(\mathrm{s})+\mathrm{CO_2}(\mathrm{~g}) ; K_{p}=0.265 \mathrm{~atm}$ at $1050 \mathrm{~K}$

What are the equilibrium partial pressures of $\mathrm{CO}$ and $\mathrm{CO_2}$ at $1050 \mathrm{~K}$ if the initial partial pressures are: $p_{\mathrm{CO}}=1.4 \mathrm{~atm}$ and $p_{\mathrm{CO_2}}=0.80 \mathrm{~atm}$ ?

Show Answer

Answer

For the given reaction,

Initialy, $\quad 1.4 atm \quad 0.80 atm$

$ \begin{aligned} Q_p & =\frac{p _{CO_2}}{p _{CO}} \\ & =\frac{0.80}{1.4} \\ & =0.571 \end{aligned} $

It is given that $K_p=0.265$.

Since $Q_P>K_P$, the reaction will proceed in the backward direction.

Therefore, we can say that the pressure of $CO$ will increase while the pressure of $CO_2$ will decrease.

Now, let the increase in pressure of $CO=$ decrease in pressure of $CO_2$ be $p$.

Then, we can write,

$ \begin{aligned} & K_P=\frac{p _{CO_2}}{p _{CO}} \\ & \Rightarrow 0.265=\frac{0.80-p}{1.4+p} \\ & \Rightarrow 0.371+0.265 p=0.80-p \\ & \Rightarrow 1.265 p=0.429 \\ & \Rightarrow p=0.339 atm \end{aligned} $

Therefore, equilibrium partial of $CO_2, p _{CO_2}=0.80-0.339=0.461 atm$.

And, equilibrium partial pressure of $CO, p _{CO}=1.4+0.339=1.739 atm$.

7.21 Equilibrium constant, $K_{c}$ for the reaction

$$ \mathrm{N_2}(\mathrm{~g})+3 \mathrm{H_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH_3}(\mathrm{~g}) \text { at } 500 \mathrm{~K} \text { is } 0.061 $$

At a particular time, the analysis shows that composition of the reaction mixture is $3.0 \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~N_2}, 2.0 \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{H_2}$ and $0.5 \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{NH_3}$. Is the reaction at equilibrium? If not in which direction does the reaction tend to proceed to reach equilibrium?

Show Answer

Answer

The given reaction is:

$ N _{2(g)}+3 H _{2(g)} \longleftrightarrow \quad 2 NH _{3(g)} $

At a particular time: $3.0 mol L^{-1} \quad 2.0 mol L^{-1} \quad 0.5 mol L^{-1}$

Now, we know that,

$ \begin{aligned} Q_C & =\frac{[NH_3]^{2}}{[N_2][H_2]^{3}} \\ & =\frac{(0.5)^{2}}{(3.0)(2.0)^{3}} \\ & =0.0104 \end{aligned} $

It is given that $K_C=0.061$.

Since $Q_C \neq K_C$, the reaction is not at equilibrium.

Since $Q_C<K_C$, the reaction will proceed in the forward direction to reach equilibrium.

7.22 Bromine monochloride, $\mathrm{BrCl}$ decomposes into bromine and chlorine and reaches the equilibrium:

$$ 2 \mathrm{BrCl}(\mathrm{g}) \rightleftharpoons \mathrm{Br_2}(\mathrm{~g})+\mathrm{Cl_2}(\mathrm{~g}) $$

for which $K_{\mathrm{c}}=32$ at $500 \mathrm{~K}$. If initially pure $\mathrm{BrCl}$ is present at a concentration of $3.3 \times 10^{-3} \mathrm{~mol} \mathrm{~L}^{-1}$, what is its molar concentration in the mixture at equilibrium?

Show Answer

Answer

Let the amount of bromine and chlorine formed at equilibrium be $x$. The given reaction is:

Now, we can write,

$ \begin{aligned} & \frac{[Br_2][Cl_2]}{[BrCl^{2}.}=K_C \\ \Rightarrow & \frac{x \times x}{(3.3 \times 10^{-3}-2 x)^{2}}=32 \\ \Rightarrow & \frac{x}{3.3 \times 10^{-3}-2 x}=5.66 \\ \Rightarrow & x=18.678 \times 10^{-3}-11.32 x \\ \Rightarrow & 12.32 x=18.678 \times 10^{-3} \\ \Rightarrow & x=1.5 \times 10^{-3} \end{aligned} $

Therefore, at equilibrium,

$ \begin{aligned} {[BrCl] } & =3.3 \times 10^{-3}-(2 \times 1.5 \times 10^{-3}) \\ & =3.3 \times 10^{-3}-3.0 \times 10^{-3} \\ & =0.3 \times 10^{-3} \\ & =3.0 \times 10^{-4} molL^{-1} \end{aligned} $

7.23 At $1127 \mathrm{~K}$ and $1 \mathrm{~atm}$ pressure, a gaseous mixture of $\mathrm{CO}$ and $\mathrm{CO_2}$ in equilibrium with soild carbon has $90.55 %$ CO by mass

$$ \mathrm{C}(\mathrm{s})+\mathrm{CO_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{CO}(\mathrm{g}) $$

Calculate $K_{\mathrm{c}}$ for this reaction at the above temperature.

Show Answer

Answer

Let the total mass of the gaseous mixture be $100 g$.

Mass of $CO=90.55 g$

And, mass of $CO_2=(100 a \in " 90.55)=9.45 g$

Now, number of moles of $CO$,

$ n _{CO}=\frac{90.55}{28}=3.234 mol $

Number of moles of $CO_2$

$ n _{CO_2}=\frac{9.45}{44}=0.215 mol $

Partial pressure of $CO$,

$ \begin{aligned} p _{CO} & =\frac{n _{CO}}{n _{CO}+n _{CO_2}} \times p _{\text{total }} \\ & =\frac{3.234}{3.234+0.215} \times 1 \\ & =0.938 atm \end{aligned} $

Partial pressure of $CO_2$,

$ \begin{aligned} p _{CO_2} & =\frac{n _{CO_2}}{n _{CO}+n _{CO_2}} \times p _{\text{total }} \\ & =\frac{0.215}{3.234+0.215} \times 1 \\ & =0.062 atm \end{aligned} $

Therefore, $K_P=\frac{[CO]^{2}}{[CO_2]}$

$ \begin{aligned} & =\frac{(0.938)^{2}}{0.062} \\ & =14.19 \end{aligned} $

For the given reaction,

$\Delta n=2 \hat{a} \mathfrake^{\prime \prime} 1=1$

We know that,

$K_p=K_C(R T)^{\Delta r}$

$\Rightarrow 14.19=K_C(0.082 \times 1127)^{\prime}$

$\Rightarrow K_C=\frac{14.19}{0.082 \times 1127}$

$=0.154$ (approximately)

7.24 Calculate a) $\Delta G^{\ominus}$ and b) the equilibrium constant for the formation of $\mathrm{NO_2}$ from $\mathrm{NO}$ and $\mathrm{O_2}$ at $298 \mathrm{~K}$

$$ \mathrm{NO}(\mathrm{g})+1 / 2 \mathrm{O_2}(\mathrm{~g}) \rightleftharpoons \mathrm{NO_2}(\mathrm{~g}) $$

where

$\Delta_{\mathrm{f}} G^{\ominus}\left(\mathrm{NO_2}\right)=52.0 \mathrm{~kJ} / \mathrm{mol}$

$\Delta_{\mathrm{f}} G^{\ominus}(\mathrm{NO})=87.0 \mathrm{~kJ} / \mathrm{mol}$

$\Delta_{\mathrm{f}} G^{\ominus}\left(\mathrm{O_2}\right)=0 \mathrm{~kJ} / \mathrm{mol}$

Show Answer

Answer

(a) For the given reaction,

$\Delta G^{\circ}=\Delta G^{\circ}$ ( Products) â $\epsilon^{\prime \prime} \Delta G^{\circ}$ ( Reactants)

$\Delta G^{\circ}=52.0$ â€" ${87.0+0}$

= âe" $.35.0 kJ mol|^{\hat{\epsilon} e^{\prime \prime}}$

(b) We know that,

$\Delta G^{\circ}=RT \log K_c$

$\Delta G^{\circ}=2.303 RT \log K_c$

$K_c=\frac{-35.0 \times 10^{-3}}{-2.303 \times 8.314 \times 298}$

$=6.134$

$\therefore K_c=$ antilog (6.134)

$=1.36 \times 10^{6}$

Hence, the equilibrium constant for the given reaction $K_c$ is $1.36 \times 10^{6}$

7.25 Does the number of moles of reaction products increase, decrease or remain same when each of the following equilibria is subjected to a decrease in pressure by increasing the volume?

(a) $\mathrm{PCl} 5(\mathrm{~g}) \rightleftharpoons \mathrm{PCl} 3(\mathrm{~g})+\mathrm{Cl} 2(\mathrm{~g})$

(b) $\mathrm{CaO}(\mathrm{s})+\mathrm{CO} 2(\mathrm{~g}) \rightleftharpoons \mathrm{CaCO} 3(\mathrm{~s})$

(c) $3 \mathrm{Fe}(\mathrm{s})+4 \mathrm{H_2} \mathrm{O}(\mathrm{g}) \rightleftharpoons \mathrm{Fe_3} \mathrm{O_4}(\mathrm{~s})+4 \mathrm{H_2}(\mathrm{~g})$

Show Answer

Answer

(a) The number of moles of reaction products will increase. According to Le Chatelier’s principle, if pressure is decreased, then the equilibrium shifts in the direction in which the number of moles of gases is more. In the given reaction, the number of moles of gaseous products is more than that of gaseous reactants. Thus, the reaction will proceed in the forward direction. As a result, the number of moles of reaction products will increase.

(b) The number of moles of reaction products will decrease.

(c) The number of moles of reaction products remains the same.

7.26 Which of the following reactions will get affected by increasing the pressure? Also, mention whether change will cause the reaction to go into forward or backward direction.

(i) $\mathrm{COCl_2}(\mathrm{~g}) \rightleftharpoons \mathrm{CO}(\mathrm{g})+\mathrm{Cl_2}(\mathrm{~g})$

(ii) $\mathrm{CH} 4(\mathrm{~g})+2 \mathrm{~S} 2(\mathrm{~g}) \rightleftharpoons \mathrm{CS} 2(\mathrm{~g})+2 \mathrm{H} 2 \mathrm{~S}(\mathrm{~g})$

(iii) $\mathrm{CO} 2(\mathrm{~g})+\mathrm{C}(\mathrm{s}) \rightleftharpoons 2 \mathrm{CO}(\mathrm{g})$

(iv) $2 \mathrm{H} 2(\mathrm{~g})+\mathrm{CO}(\mathrm{g}) \rightleftharpoons \mathrm{CH} 3 \mathrm{OH}(\mathrm{g})$

(v) $\mathrm{CaCO} 3(\mathrm{~s}) \rightleftharpoons \mathrm{CaO}(\mathrm{s})+\mathrm{CO} 2(\mathrm{~g})$

(vi) $4 \mathrm{NH_3}(\mathrm{~g})+5 \mathrm{O_2}(\mathrm{~g}) \rightleftharpoons 4 \mathrm{NO}(\mathrm{g})+6 \mathrm{H_2} \mathrm{O}(\mathrm{g})$

Show Answer

Answer

The reactions given in (i), (iii), (iv), (v), and (vi) will get affected by increasing the pressure.

The reaction given in (iv) will proceed in the forward direction because the number of moles of gaseous reactants is more than that of gaseous products.

The reactions given in (i), (iii), (v), and (vi) will shift in the backward direction because the number of moles of gaseous reactants is less than that of gaseous products.

7.27 The equilibrium constant for the following reaction is $1.6 \times 10^{5}$ at $1024 \mathrm{~K}$ $\mathrm{H_2}(\mathrm{~g})+\mathrm{Br_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HBr}(\mathrm{g})$

Find the equilibrium pressure of all gases if 10.0 bar of $\mathrm{HBr}$ is introduced into a sealed container at $1024 \mathrm{~K}$.

Show Answer

Answer

Given,

$K _{\text{P for the reaction i.e., }} H _{2(g)}+Br _{2(g)} \longleftrightarrow 2 HBr _{(g)}$ is $1.6 \times 10^{5}$.

Therefore, for the reaction $2 HBr _{(g)} \longleftrightarrow H _{2(g)}+Br _{2(g)}$, the equilibrium constant will be,

$ \begin{aligned} K_P^{\prime} & =\frac{1}{K_P} \\ & =\frac{1}{1.6 \times 10^{5}} \\ & =6.25 \times 10^{-6} \end{aligned} $

Now, let $p$ be the pressure of both $H_2$ and $Br_2$ at equilibrium.

	$2 HBr _{(g)}$	$\longleftrightarrow$	$H _{2(g)}+Br _{2(g)}$
Initial conc.	10		0	0
At equilibrium	$10-2 p$		$p$	$p$

Now, we can write,

$ \begin{aligned} & \frac{p _{HBr} \times p_2}{p_HBr^{2}}=K_P^{\prime} \\ & \frac{p \times p}{(10-2 p)^{2}}=6.25 \times 10^{-6} \end{aligned} $

$\frac{p}{10-2 p}=2.5 \times 10^{-3}$

$p=2.5 \times 10^{-2}-(5.0 \times 10^{-3}) p$

$p+(5.0 \times 10^{-3}) p=2.5 \times 10^{-2}$

$(1005 \times 10^{-3}) p=2.5 \times 10^{-2}$

$p=2.49 \times 10^{-2}$ bar $=2.5 \times 10^{-2}$ bar (approximately)

Therefore, at equilibrium,

$[H_2]=[Br_2]=2.49 \times 10^{-2}$ bar

$[HBr]=10-2 \times(2.49 \times 10^{-2})$ bar

$=9.95 bar=10 bar$ (approximately)

7.28 Dihydrogen gas is obtained from natural gas by partial oxidation with steam as per following endothermic reaction:

$\mathrm{CH_4}(\mathrm{~g})+\mathrm{H_2} \mathrm{O}(\mathrm{g}) \rightleftharpoons \mathrm{CO}(\mathrm{g})+3 \mathrm{H_2}(\mathrm{~g})$

(a) Write as expression for $\mathrm{Kp}$ for the above reaction.

(b) How will the values of $\mathrm{Kp}$ and composition of equilibrium mixture be affected by

(i) increasing the pressure

(ii) increasing the temperature

(iii) using a catalyst?

Show Answer

Answer

(a) For the given reaction, $K_P = \frac{p_{CO} \times p^3_{H_2}}{p_{CH_4} \times p_{H_2 O}}$

(b) (i) According to Le Chatelier’s principle, the equilibrium will shift in the backward direction.

(ii) According to Le Chatelier’s principle, as the reaction is endothermic, the equilibrium will shift in the forward direction.

(iii) The equilibrium of the reaction is not affected by the presence of a catalyst. A catalyst only increases the rate of a reaction. Thus, equilibrium will be attained quickly.

7.29 Describe the effect of:

a) addition of $\mathrm{H} 2$

b) addition of $\mathrm{CH} 3 \mathrm{OH}$

c) removal of $\mathrm{CO}$

d) removal of $\mathrm{CH_3} \mathrm{OH}$

on the equilibrium of the reaction:

$$ 2 \mathrm{H_2}(\mathrm{~g})+\mathrm{CO}(\mathrm{g}) \rightleftharpoons \mathrm{CH_3} \mathrm{OH}(\mathrm{g}) $$

Show Answer

Answer

(a) According to Le Chatelier’s principle, on addition of $H_2$, the equilibrium of the given reaction will shift in the forward direction.

(b) On addition of $CH_3 OH$, the equilibrium will shift in the backward direction.

(c) On removing $CO$, the equilibrium will shift in the backward direction.

(d) On removing $CH_3 OH$, the equilibrium will shift in the forward direction.

7.30 At $473 \mathrm{~K}$, equilibrium constant $K_{c}$ for decomposition of phosphorus pentachloride, $\mathrm{PCl_5}$ is $8.3 \times 10^{-3}$. If decomposition is depicted as, $\mathrm{PCl_5}(\mathrm{~g}) \rightleftharpoons \mathrm{PCl_3}(\mathrm{~g})+\mathrm{Cl_2}(\mathrm{~g}) \quad \Delta_{\mathrm{r}} H^{\ominus}=124.0 \mathrm{~kJ} \mathrm{~mol}{ }^{-1}$

a) write an expression for $\mathrm{Kc}$ for the reaction.

b) what is the value of $\mathrm{Kc}$ for the reverse reaction at the same temperature?

c) what would be the effect on $K_{c}$ if (i) more $\mathrm{PCl_5}$ is added (ii) pressure is increased (iii) the temperature is increased?

Show Answer

Answer (a)

(b) Value of $K_c$ for the reverse reaction at the same temperature is:

$ \begin{aligned} K_c^{\prime} & =\frac{1}{K_c} \\ & =\frac{1}{8.3 \times 10^{-3}}=1.2048 \times 10^{2} \\ & =120-48 \end{aligned} $

(c) (i) $K_c$ would remain the same because in this case, the temperature remains the same.

(ii) $K_c$ is constant at constant temperature. Thus, in this case, $K_c$ would not change.

(iii) In an endothermic reaction, the value of $K_c$ increases with an increase in temperature. Since the given reaction in an endothermic reaction, the value of $K_c$ will increase if the temperature is increased.

7.31 Dihydrogen gas used in Haber’s process is produced by reacting methane from natural gas with high temperature steam. The first stage of two stage reaction involves the formation of $\mathrm{CO}$ and $\mathrm{H_2}$. In second stage, $\mathrm{CO}$ formed in first stage is reacted with more steam in water gas shift reaction,

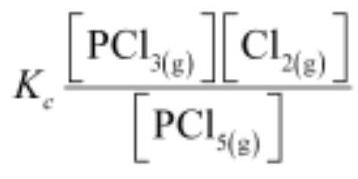
$\mathrm{CO}(\mathrm{g})+\mathrm{H_2} \mathrm{O}(\mathrm{g}) \rightleftharpoons \mathrm{CO_2}(\mathrm{~g})+\mathrm{H_2}(\mathrm{~g})$

If a reaction vessel at $400^{\circ} \mathrm{C}$ is charged with an equimolar mixture of $\mathrm{CO}$ and steam such that $p_{\text {co }}=p_{\mathrm{H_2} \mathrm{O}}=4.0$ bar, what will be the partial pressure of $\mathrm{H_2}$ at equilibrium? $K_{p}=10.1$ at $400^{\circ} \mathrm{C}$

Show Answer

Answer

Let the partial pressure of both carbon dioxide and hydrogen gas be $p$. The given reaction is:

$ CO _{(g)}+H_2 O _{(g)} \longleftrightarrow CO _{2(g)}+H _{2(g)} $

$\begin{matrix} \text{ Initial conc. } & 4.0 bar & 4.0 bar & 0\end{matrix} $

$\begin{matrix} \text{ At equilibrium } & 4.0-p & 4.0-p & p\end{matrix} $

It is given that $K_p=10.1$.

Now,

$ \begin{aligned} & \frac{p _{CO_2} \times p _{H_2}}{p _{COH} \times p_2}=K_P \\ & \Rightarrow \frac{p \times p}{(4.0-p)(4.0-p)}=10.1 \\ & \Rightarrow \frac{p}{4.0-p}=3.178 \\ & \Rightarrow p=12.712-3.178 p \\ & \Rightarrow 4.178 p=12.712 \\ & \Rightarrow p=3.04 \end{aligned} $

Hence, at equilibrium, the partial pressure of $H_2$ will be 3.04 bar.

7.32 Predict which of the following reaction will have appreciable concentration of reactants and products:

a) $\mathrm{Cl} 2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{Cl}(\mathrm{g}) \mathrm{Kc}=5 \times 10-39$

b) $\mathrm{Cl} 2(\mathrm{~g})+2 \mathrm{NO}(\mathrm{g}) \rightleftharpoons 2 \mathrm{NOCl}(\mathrm{g}) \quad \mathrm{Kc}=3.7 \times 108$

c) $\mathrm{Cl} 2(\mathrm{~g})+2 \mathrm{NO_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO_2} \mathrm{Cl}(\mathrm{g}) K_{c}=1.8$

Show Answer

Answer

If the value of $K_c$ lies between $10^{-3}$ and $10^{3}$, a reaction has appreciable concentration of reactants and products. Thus, the reaction given in (c) will have appreciable concentration of reactants and products.

7.33 The value of $K_{c}$ for the reaction $3 \mathrm{O_2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{O_3}(\mathrm{~g})$ is $2.0 \times 10^{-50}$ at $25^{\circ} \mathrm{C}$. If the equilibrium concentration of $\mathrm{O_2}$ in air at $25^{\circ} \mathrm{C}$ is $1.6 \times 10^{-2}$, what is the concentration of $\mathrm{O_3}$ ?

Show Answer

Answer

The given reaction is: $3 O _{2(g)} \longleftrightarrow 2 O _{3(g)}$

Then, $K_C=\frac{[O _{3(g)}]^{2}}{[O _{2(g)}]^{3}}$

It is given that $K_C=2.0 \times 10^{-50}$ and $[O _{2(g)}]=1.6 \times 10^{-2}$.

Then, we have,

$2.0 \times 10^{-50}=\frac{[O _{3(g)}]^{2}}{[1.6 \times 10^{-2}]^{3}}$

$\Rightarrow[O _{3(g)}]^{2}=2.0 \times 10^{-50} \times(1.6 \times 10^{-2})^{3}$

$\Rightarrow[O _{3(g)}]^{2}=8.192 \times 10^{-56}$

$\Rightarrow[O _{3(g)}]=2.86 \times 10^{-28} M$

Hence, the concentration of $O_3$ is $2.86 \times 10^{-28} M$.

7.34 The reaction, $\mathrm{CO}(\mathrm{g})+3 \mathrm{H_2}(\mathrm{~g}) \rightleftharpoons \mathrm{CH_4}(\mathrm{~g})+\mathrm{H_2} \mathrm{O}(\mathrm{g})$

is at equilibrium at $1300 \mathrm{~K}$ in a $1 \mathrm{~L}$ flask. It also contain $0.30 \mathrm{~mol}$ of $\mathrm{CO}, 0.10 \mathrm{~mol}$ of $\mathrm{H_2}$ and $0.02 \mathrm{~mol}$ of $\mathrm{H_2} \mathrm{O}$ and an unknown amount of $\mathrm{CH_4}$ in the flask. Determine the concentration of $\mathrm{CH_4}$ in the mixture. The equilibrium constant, $K_{c}$ for the reaction at the given temperature is 3.90 .

Show Answer

Answer

Let the concentration of methane at equilibrium be $x$.

$ CO _{(g)}+3 H _{2(g)} \longleftrightarrow CH _{4(g)}+H_2 O _{(g)} $

At equilibrium $\frac{0.3}{1}=0.3 M \quad \frac{0.1}{1}=0.1 M \quad x \quad \frac{0.02}{1}=0.02 M$

It is given that $K_c=3.90$.

Therefore,

$ \begin{gathered} \frac{[CH _{4(g)}][H_2 O _{(g)}]}{[CO _{(g)}][H _{2(g)}]^{3}}=K_c \\ \Rightarrow \frac{x \times 0.02}{0.3 \times(0.1)^{3}}=3.90 \\ \Rightarrow x=\frac{3.90 \times 0.3 \times(0.1)^{3}}{0.02} \\ \quad=\frac{0.00117}{0.02} \\ =0.0585 M \\ =5.85 \times 10^{-2} M \end{gathered} $

Hence, the concentration of $CH_4$ at equilibrium is $5.85 \times 10^{\hat{\epsilon} \epsilon^{2} 2} M$.

7.35 What is meant by the conjugate acid-base pair? Find the conjugate acid/base for the following species:

$\mathrm{HNO_2}, \mathrm{CN}^{-}, \mathrm{HClO_4} \mathrm{~F}^{-}, \mathrm{OH}^{-}, \mathrm{CO_3}^{2-}$, and $\mathrm{S}^{2-}$

Show Answer

Answer

A conjugate acid-base pair is a pair that differs only by one proton.

The conjugate acid-base for the given species is mentioned in the table below.

7.36 Which of the followings are Lewis acids? $\mathrm{H_2} \mathrm{O}, \mathrm{BF_3}, \mathrm{H}^{+}$, and $\mathrm{NH_4}^{+}$

Show Answer

Answer

Lewis acids are those acids which can accept a pair of electrons. For example, $BF_3, H^{+}$, and $NH_4^{+}$are Lewis acids.

7.37 What will be the conjugate bases for the Brönsted acids: $\mathrm{HF}, \mathrm{H_2} \mathrm{SO_4}$ and $\mathrm{HCO_3}^{-}$?

Show Answer

Answer

The table below lists the conjugate bases for the given Bronsted acids.

Bronsted acid

HF

$H_2 SO_4$

$HCO_3^{-}$

Conjugate base

Fî́"

$HSO_4^{-}$

$CO_3^{2-}$

7.38 Write the conjugate acids for the following Brönsted bases: $\mathrm{NH_2}^{-}, \mathrm{NH_3}$ and $\mathrm{HCOO}^{-}$.

Show Answer

Answer

The table below lists the conjugate acids for the given Bronsted bases.

Bronsted base

$NH_2^{-}$

$NH_3$

$HCOO^{\text{ве" }}$ Conjugate acid

$NH_3$

$NH_4^{+}$

$HCOOH$

7.39 The species: $\mathrm{H_2} \mathrm{O}, \mathrm{HCO_3}^{-}, \mathrm{HSO_4}^{-}$and $\mathrm{NH_3}$ can act both as Brönsted acids and bases. For each case give the corresponding conjugate acid and base.

Show Answer

Answer

The table below lists the conjugate acids and conjugate bases for the given species.

Species

$H_2 O$

$HCO_3^{-}$

$HSO_4^{-}$

$NH_3$

Conjugate acid

$H_3 O^{+}$

$H_2 CO_3$

$H_2 SO_4$

$NH_4^{+}$

Conjugate base

$OH^{\text{їe" }}$

$CO_3^{2-}$

$SO_4^{2-}$

$NH_2^{-}$

7.40 Classify the following species into Lewis acids and Lewis bases and show how these act as Lewis acid/base: (a) $\mathrm{OH}^{-}$(b) $\mathrm{F}^{-}$(c) $\mathrm{H}^{+}$(d) $\mathrm{BCl_3}$.

Show Answer

Answer

(a) $OH^{-}$is a Lewis base since it can donate its lone pair of electrons.

(b) $F^{-}$is a Lewis base since it can donate a pair of electrons.

(c) $H^{+}$is a Lewis acid since it can accept a pair of electrons.

(d) $BCl_3$ is a Lewis acid since it can accept a pair of electrons.

7.41 The concentration of hydrogen ion in a sample of soft drink is $3.8 \times 10^{-3} \mathrm{M}$. What is its $\mathrm{pH}$ ?

Show Answer

Answer

Given,

$[H^{+}]=3.8 \times 10^{-3} M$

$\therefore pH$ value of soft drink

$=-\log [H^{+}]$

$ \begin{aligned} & =-\log (3.8 \times 10^{-3}) \\ & =-\log 3.8-\log 10^{-3} \\ & =-\log 3.8+3 \\ & =-0.58+3 \\ & =2.42 \end{aligned} $

7.42 The $\mathrm{pH}$ of a sample of vinegar is 3.76. Calculate the concentration of hydrogen ion in it.

Show Answer

Answer

Given,

$pH=3.76$

It is known that,

$ \begin{aligned} & pH=-\log [H^{+}] \\ & \Rightarrow \log [H^{+}]=-pH \\ & \Rightarrow[H^{+}]=antilog(-pH) \\ & =\text{ antil og }(-3.76) \\ & =1.74 \times 10^{-4} M \end{aligned} $

Hence, the concentration of hydrogen ion in the given sample of vinegar is $1.74 \times 10^{\hat{\epsilon} \mathbf{E}^{4}} M$.

7.43 The ionization constant of $\mathrm{HF}, \mathrm{HCOOH}$ and $\mathrm{HCN}$ at $298 \mathrm{~K}$ are $6.8 \times 10^{-4}$, $1.8 \times 10^{-4}$ and $4.8 \times 10^{-9}$ respectively. Calculate the ionization constants of the corresponding conjugate base.

Show Answer

Answer

It is known that,

$K_b=\frac{K_w}{K_a}$

Given,

$K_a$ of $HF=6.8 \times 10^{\hat{E}} E^{44}$

Hence, $K_b$ of its conjugate base $F^{\hat{a} \epsilon} \epsilon^{n}$ $=\frac{K_w}{K_a}$

$=\frac{10^{-14}}{6.8 \times 10^{-4}}$

$=1.5 \times 10^{-11}$

Given,

$K_a$ of $HCOOH=1.8 \times 10^{\text{afe-4 }}$

Hence, $K_b$ of its conjugate base $HCOO^{\hat{A} \epsilon}$

$=\frac{K_w}{K_a}$

$=\frac{10^{-14}}{1.8 \times 10^{-4}}$

$=5.6 \times 10^{-11}$

Given,

$K _{\text{a }}$ of $HCN=4.8 \times 10^{\text{вес9 }}$

Hence, $K_b$ of its conjugate base $CN^{\text{ate- }}$

$=\frac{K_w}{K_a}$

$=\frac{10^{-14}}{4.8 \times 10^{-9}}$

$=2.08 \times 10^{-6}$

7.44 The ionization constant of phenol is $1.0 \times 10^{-10}$. What is the concentration of phenolate ion in $0.05 \mathrm{M}$ solution of phenol? What will be its degree of ionization if the solution is also $0.01 \mathrm{M}$ in sodium phenolate?

Show Answer

Answer

Ionization of phenol:

As the value of the ionization constant is very less, $x$ will be very small. Thus, we can ignore $x$ in the denominator.

$ \begin{aligned} \therefore x & =\sqrt{1 \times 10^{-10} \times 0.05} \\ & =\sqrt{5 \times 10^{-12}} \\ & =2.2 \times 10^{-6} M=[H_3 O^{+}] \end{aligned} $

Since $[H_3 O^{+}]=[C_6 H_5 O^{-}]$,

$[C_6 H_5 O^{-}]=2.2 \times 10^{-6} M$.

Now, let $\tilde{A} \phi \ddot{E}+\hat{A}$ be the degree of ionization of phenol in the presence of $0.01 M C_6 H_5 ONa$.

$ C_6 H_5 ONa \longrightarrow C_6 H_5 O^{-}+Na^{+} $

Conc.

$ 0.01 $

Also,

$ \begin{aligned} & \quad C_6 H_5 OH+H_2 O \longleftrightarrow C_6 H_5 O^{-}+H_3 O^{+} \\ & \text{Conc. } 0.05-0.05 \alpha \\ & {[C_6 H_5 OH]=0.05-0.05 \alpha ; 0.05 M} \end{aligned} $

$ \begin{aligned} & {[C_6 H_5 O^{-}]=0.01+0.05 \alpha ; 0.01 M} \\ & {[H_3 O^{+}]=0.05 \alpha} \\ & K_a=\frac{[C_6 H_5 O^{-}][H_3 O^{+}]}{[C_6 H_5 OH]} \\ & K_a=\frac{(0.01)(0.05 \alpha)}{0.05} \\ & 1.0 \times 10^{-10}=.01 \alpha \\ & \alpha=1 \times 10^{-8} \end{aligned} $

7.45 The first ionization constant of $\mathrm{H_2} \mathrm{~S}$ is $9.1 \times 10^{-8}$. Calculate the concentration of $\mathrm{HS}^{-}$ion in its $0.1 \mathrm{M}$ solution. How will this concentration be affected if the solution is $0.1 \mathrm{M}$ in $\mathrm{HCl}$ also? If the second dissociation constant of $\mathrm{H_2} \mathrm{~S}$ is $1.2 \times 10^{-13}$, calculate the concentration of $\mathrm{S}^{2-}$ under both conditions.

Show Answer

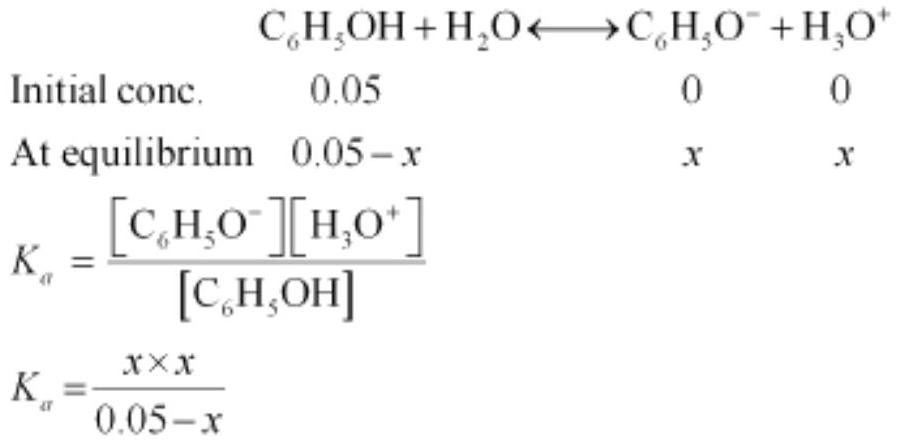
Answer

(i) To calculate the concentration of $HS^{\hat{a} \epsilon}$ " ion:

Case I (in the absence of $HCl$ ):

Let the concentration of $HS^{\hat{a} et^{\prime \prime}}$ be $x M$.

$ \begin{aligned} & H_2 S \longleftrightarrow H^{+}+HS^{-} \\ & \begin{matrix} C_i & 0.1 & 0 & 0 \end{matrix} \\ & \begin{matrix} C_f & 0.1-x & x & x \end{matrix} \\ & \text{ Then, } K _{a_1}=\frac{[H^{+}][HS^{-}]}{[H_2 S]} \\ & 9.1 \times 10^{-8}=\frac{(x)(x)}{0.1-x} \\ & (9.1 \times 10^{-8})(0.1-x)=x^{2} \end{aligned} $

Taking $0.1-x M ; 0.1 M$, we have $(9.1 \times 10^{-8})(0.1)=x^{2}$.

$ \begin{aligned} & 9.1 \times 10^{-9}=x^{2} \\ & x=\sqrt{9.1 \times 10^{-9}} \\ & \quad=9.54 \times 10^{-5} M \\ & \Rightarrow[HS^{-}]=9.54 \times 10^{-5} M \end{aligned} $

Case II (in the presence of $HCl$ ):

In the presence of $0.1 M$ of $HCl$, let $[HS^{-}]$be $y M$.

Then, $\quad H_2 S \longleftrightarrow HS^{-}+H^{+}$

$\begin{matrix} C_i & 0.1 & 0 & 0\end{matrix} $

$C_f \quad 0.1-y \quad y \quad y$

Also, $\quad HCl \longleftrightarrow H^{+}+Cl^{-}$

$0.1 \quad 0.1$

Now, $K _{a_1}=\frac{[HS^{-}][H^{+}]}{[H_2 S]}$

$K_{a_1}=\frac{[y] (0.1+y)}{(0.1-y)}$

$9.1 \times 10^{-8}=\frac{y \times 0.1}{0.1} \quad(\because 0.1-y ; 0.1 M)$ (and $0.1+y ; 0.1 M$ )

$9.1 \times 10^{-8}=y$

$\Rightarrow[HS^{-}]=9.1 \times 10^{-8}$

(ii) To calculate the concentration of $[S^{2-}]$ :

Case I (in the absence of $0.1 M HCl$ ):

$HS^{-} \longleftrightarrow H^{+}+S^{2-}$

$[HS^{-}]=9.54 \times 10^{-5} M$ (From first ionization, case I)

Let $[S^{2-}]$ be $X$.

Also, $[H^{+}]=9.54 \times 10^{-5} M$ (From first ionization, case I)

$K _{a_2}=\frac{[H^{+}][S^{2-}]}{[HS^{-}]}$

$K _{a_2}=\frac{(9.54 \times 10^{-5})(X)}{9.54 \times 10^{-5}}$

$1.2 \times 10^{-13}=X=[S^{2-}]$

Case II (in the presence of $0.1 M HCl$ ):

Again, let the concentration of $HS^{\hat{a} \epsilon^{\prime \prime}}$ be $X^{\prime} M$.

$ \begin{aligned} & {[HS^{-}]=9.1 \times 10^{-8} M \text{ (From first ionization, case II) }} \\ & {[H^{+}]=0.1 M _{(\text{From } HCl, \text{ case II) }}} \end{aligned} $

$ \begin{aligned} & {[S^{2-}]=X^{\prime}} \\ & \text{ Then, } K _{a_2}=\frac{[H^{+}][S^{2-}]}{[HS^{-}]} \\ & 1.2 \times 10^{-13}=\frac{(0.1)(X^{\prime})}{9.1 \times 10^{-8}} \\ & 10.92 \times 10^{-21}=0.1 X^{\prime} \\ & \frac{10.92 \times 10^{-21}}{0.1}=X^{\prime} \\ & X^{\prime}=\frac{1.092 \times 10^{-20}}{0.1} \\ & =1.092 \times 10^{-19} M \\ & \Rightarrow K _{a_1}=1.74 \times 10^{-5} \end{aligned} $

7.46 The ionization constant of acetic acid is $1.74 \times 10^{-5}$. Calculate the degree of dissociation of acetic acid in its $0.05 \mathrm{M}$ solution. Calculate the concentration of acetate ion in the solution and its $\mathrm{pH}$.

Show Answer

Answer

Method 1

1. $\quad CH_3 COOH \longleftrightarrow CH_3 COO^{-}+H^{+} \quad K_a=1.74 \times 10^{-5}$
2. $H_2 O+H_2 O \longleftrightarrow H_3 O^{+}+OH^{-} \quad K_w=1.0 \times 10^{-14}$

Since $K a \gg K_w$ :

$ \begin{matrix} CH_3 COOH+H_2 O \longleftrightarrow CH_3 COO^{-}+H_3 O^{+} \\ 0.05 & 0 & 0 \\ 0.05-.05 \alpha & 0.05 \alpha & 0.05 \alpha \\ K_a & =\frac{(.05 \alpha)(.05 \alpha)}{(.05-0.05 \alpha)} \\ & =\frac{(.05 \alpha)(0.05 \alpha)}{.05(1-\alpha)} \\ & =\frac{.05 \alpha^{2}}{1-\alpha} \end{matrix} $

$ \begin{aligned} & 1.74 \times 10^{-5}=\frac{0.05 \alpha^{2}}{1-\alpha} \\ & 1.74 \times 10^{-5}-1.74 \times 10^{-5} \alpha=0.05 \alpha^{2} \\ & 0.05 \alpha^{2}+1.74 \times 10^{-5} \alpha-1.74 \times 10^{-5} \\ & D=b^{2}-4 a c \\ & =(1.74 \times 10^{-5})^{2}-4(.05)(1.74 \times 10^{-5}) \\ & =3.02 \times 10^{-25}+.348 \times 10^{-5} \\ & \alpha=\sqrt{\frac{K_a}{c}} \\ & \alpha=\sqrt{\frac{1.74 \times 10^{-5}}{.05}} \\ & =\sqrt{\frac{34.8 \times 10^{-5} \times 10}{10}} \\ & =\sqrt{3.48 \times 10^{-6}} \\ & =CH_3 COOH \longleftrightarrow CH_3 COO^{-}+H^{+} \end{aligned} $

$\alpha \underline{1.86 \times 10^{-3}}$

$ \begin{aligned} {[CH_3 COO^{-}] } & =0.05 \times 1.86 \times 10^{-3} \\ & =\frac{0.93 \times 10^{-3}}{1000} \\ & =.000093 \end{aligned} $

Method 2

Degree of dissociation,

$\alpha=\sqrt{\frac{K_a}{c}}$

$c=0.05 M$

$K_a=1.74 \times 10^{a^{\mathrm{a \epsilon}} e^{5}}$

Then, $\alpha=\sqrt{\frac{1.74 \times 10^{-5}}{.05}}$

$ \begin{aligned} & \alpha=\sqrt{34.8 \times 10^{-5}} \\ & \alpha=\sqrt{3.48} \times 10^{-4} \\ & \alpha=1.8610^{-2} \end{aligned} $

$CH_3 COOH \longleftrightarrow CH_3 COO^{-}+H^{+}$

Thus, concentration of $CH_3 COOâ \epsilon^{\prime \prime}=$ c.a

$ \begin{aligned} & =.05 \times 1.86 \times 10^{-2} \\ & =.093 \times 10^{-2} \\ & =.00093 M \\ & \text{ Since }[oAc^{-}]=[H^{+}] \\ & {[H^{+}]=.00093=.093 \times 10^{-2} .} \\ & pH=-\log [H^{+}] \\ & =-\log (.093 \times 10^{-2}) \\ & \therefore pH=3.03 \end{aligned} $

Hence, the concentration of acetate ion in the solution is $0.00093 M$ and its $Ph$ is 3.03 .

7.47 It has been found that the $\mathrm{pH}$ of a $0.01 \mathrm{M}$ solution of an organic acid is 4.15. Calculate the concentration of the anion, the ionization constant of the acid and its $\mathrm{p} K_{\mathrm{a}}$.

Show Answer

Answer

Let the organic acid be HA.

$\Rightarrow HA \longleftrightarrow H^{+}+A^{-}$

Concentration of $HA=0.01 M$

$pH=4.15$

$-\log [H^{+}]=4.15$

$[H^{+}]=7.08 \times 10^{-5}$

$K_a=\frac{[H^{+}][A^{-}]}{[HA]}$

$[H^{+}]=[A^{-}]=7.08 \times 10^{-5}$

$[HA]=0.01$

Then,

$ \begin{aligned} K_a & =\frac{(7.08 \times 10^{-5})(7.08 \times 10^{-5})}{0.01} \\ K_a & =5.01 \times 10^{-7} \\ p K_a & =-\log K_a \\ & =-\log (5.01 \times 10^{-7}) \\ p K_a & =6.3001 \end{aligned} $

7.48 Assuming complete dissociation, calculate the $\mathrm{pH}$ of the following solutions: (a) $0.003 \mathrm{M} \mathrm{HCl}$

(b) $0.005 \mathrm{M} \mathrm{NaOH}$

(c) $0.002 \mathrm{M} \mathrm{HBr}$

(d) $0.002 \mathrm{M} \mathrm{KOH}$

Show Answer

Answer

(i) $0.003 MHCl$ :

$H_2 O+HCl \longleftrightarrow H_3 O^{+}+Cl^{-}$

Since $HCl$ is completely ionized,

$ \begin{aligned} & {[H_3 O^{+}]=[HCl] .} \\ & \Rightarrow[H_3 O^{+}]=0.003 \end{aligned} $

Now,

$ \begin{aligned} pH & =-\log [H_3 O^{+}]=-\log (.003) \\ & =2.52 \end{aligned} $

Hence, the $pH$ of the solution is 2.52 .

(ii) $0.005 MNaOH$ :

$ \begin{aligned} & NaOH _{(a q)} \longleftrightarrow Na _{(a q)}^{+}+HO _{(a q)}^{-} \\ & {[HO^{-}]=[NaOH]} \\ & \Rightarrow[HO^{-}]=.005 \\ & pOH=-\log [HO^{-}]=-\log (.005) \\ & pOH=2.30 \\ & \therefore pH=14-2.30 \\ & \quad=11.70 \end{aligned} $

Hence, the $pH$ of the solution is 11.70 .

(iii) $0.002 HBr$ :

$ \begin{aligned} & HBr+H_2 O \longleftrightarrow H_3 O^{+}+Br^{-} \\ & {[H_3 O^{+}]=[HBr]} \\ & \Rightarrow[H_3 O^{+}]=.002 \\ & \therefore pH=-\log [H_3 O^{+}] \\ & \quad=-\log (0.002) \\ & \quad=2.69 \end{aligned} $

Hence, the $pH$ of the solution is 2.69 .

(iv) $0.002 M KOH$ :

$ \begin{aligned} & KOH _{(a q)} \longleftrightarrow K _{(a q)}^{+}+OH _{(a q)}^{-} \\ & {[OH^{-}]=[KOH]} \\ & \Rightarrow[OH^{-}]=.002 \\ & \text{ Now, pOH }=-\log [OH^{-}] \\ & \quad=2.69 \\ & \begin{matrix} \therefore pH=14-2.69 \\ =11.31 \end{matrix} \end{aligned} $

Hence, the $pH$ of the solution is 11.31 .

7.49 Calculate the $\mathrm{pH}$ of the following solutions: a) $2 \mathrm{~g}$ of $\mathrm{T1OH}$ dissolved in water to give 2 litre of solution.

b) $0.3 \mathrm{~g}$ of $\mathrm{Ca}(\mathrm{OH})_{2}$ dissolved in water to give $500 \mathrm{~mL}$ of solution.

c) $0.3 \mathrm{~g}$ of $\mathrm{NaOH}$ dissolved in water to give $200 \mathrm{~mL}$ of solution.

d) $1 \mathrm{~mL}$ of $13.6 \mathrm{M} \mathrm{HCl}$ is diluted with water to give 1 litre of solution.

Show Answer

Answer

(a) For $2 g$ of $TIOH$ dissolved in water to give $2 L$ of solution:

$ \begin{aligned} {[TlOH _{(a q)}] } & =\frac{2}{2} g / L \\ & =\frac{2}{2} \times \frac{1}{221} M \\ & =\frac{1}{221} M \end{aligned} $

$TlOH _{(a q)} \longrightarrow Tl _{(a q)}^{+}+OH _{(a q)}^{-}$

$[OH _{(a q)}^{-}]=[TlOH _{(o q)}]=\frac{1}{221} M$

$K_w=[H^{+}][OH^{-}]$

$10^{-14}=H^{+}$

$221 \times 10^{-14}=[H^{+}]$

$ \begin{aligned} \Rightarrow pH=-\log [H^{+}] & =-\log (221 \times 10^{-14}) \\ & =-\log (2.21 \times 10^{-12}) \\ & =11.65 \end{aligned} $

(b) For $0.3 g$ of $Ca(OH)_2$ dissolved in water to give $500 mL$ of solution:

$ \begin{aligned} & Ca(OH)_2 \longrightarrow Ca^{2+}+2 OH^{-} \\ & {[Ca(OH)_2]=0.3 \times \frac{1000}{500}=0.6 M} \\ & {[OH^{-} _{a q}]=2 \times[Ca(OH) _{2 a q}]=2 \times 0.6} \\ & =1.2 M \\ & {[H^{+}]=\frac{K_w}{[OH _{a q}^{-}]}} \\ & =\frac{10-14}{1.2} M \\ & =0.833 \times 10^{-14} \\ & pH=-\log (0.833 \times 10^{-14}) \\ & =-\log (8.33 \times 10^{-13}) \\ & =(-0.902+13) \\ & =12.098 \end{aligned} $

(c) For $0.3 g$ of $NaOH$ dissolved in water to give $200 mL$ of solution: $NaOH \longrightarrow Na _{(a q)}^{+}+OH _{(a q)}^{-}$

$[NaOH]=0.3 \times \frac{1000}{200}=1.5 M$

$[OH^{-} _{a q}]=1.5 M$

Then, $[H^{+}]=\frac{10^{-14}}{1.5}$

$ =6.66 \times 10^{-13} $

$pH=-\log (6.66 \times 10^{-13})$

$ =12.18 $

(d) For $1 mL$ of $13.6 M HCl$ diluted with water to give $1 L$ of solution:

$13.6 \times 1 mL=M_2 \times 1000 mL$

(Before dilution) (After dilution)

$13.6 \times 10^{\hat{\mathrm{\epsilon}}{ }^{43}}=M_2 \times 1 L$

$M_2=1.36 \times 10^{\hat{\mathrm{\epsilon}}} en^{2}$

$[H^{+}]=1.36 \times 10^{\text{âE"2 }}$

$pH=\hat{a} €^{\prime \prime} \log (1.36 \times 10^{\hat{a} \epsilon^{* 2}})$

$=(\hat{a} €$ “" $0.1335+2)$

$=1.866 \tilde{A} \phi \ddot{E} \dagger \hat{A} 1 / 41.87$

7.50 The degree of ionization of a $0.1 \mathrm{M}$ bromoacetic acid solution is 0.132 . Calculate the $\mathrm{pH}$ of the solution and the $p K_{\mathrm{a}}$ of bromoacetic acid.

Show Answer

Answer

Degree of ionization, $\alpha=0.132$

Concentration, $c=0.1 M$

Thus, the concentration of $H_3 O^{+}=c . \alpha$

$=0.1 \times 0.132$

$=0.0132$

$ \begin{aligned} pH & =-\log [H^{+}] \\ & =-\log (0.0132) \\ & =1.879: 1.88 \end{aligned} $

Now,

$ \begin{aligned} K_a & =C \alpha^{2} \\ & =0.1 \times(0.132)^{2} \\ K_a & =.0017 \\ p K_a & =2.75 \end{aligned} $

7.51 The $\mathrm{pH}$ of $0.005 \mathrm{M}$ codeine $\left(\mathrm{C_18} \mathrm{H_21} \mathrm{NO_3}\right)$ solution is 9.95. Calculate its ionization constant and $\mathrm{p} K_{\mathrm{b}}$.

Show Answer

Answer

$c=0.005$

$pH=9.95$

$pOH=4.05$

$pH=\hat{a} €^{\prime \prime} \log (4.105)$

$4.05=-\log [OH^{-}]$

$[OH^{-}]=8.91 \times 10^{-5}$

$c \alpha=8.91 \times 10^{-5}$

$\alpha=\frac{8.91 \times 10^{-5}}{5 \times 10^{-3}}=1.782 \times 10^{-2}$

Thus, $K_b=c \alpha^{2}$

$ \begin{aligned} & =0.005 \times(1.782)^{2} \times 10^{-4} \\ & =0.005 \times 3.1755 \times 10^{-4} \\ & =0.0158 \times 10^{-4} \end{aligned} $

$K_b=1.58 \times 10^{-6}$

$P k_b=-\log K_b$

$=-\log (1.58 \times 10^{-6})$

$=5.80$

7.52 What is the $\mathrm{pH}$ of $0.001 \mathrm{M}$ aniline solution? The ionization constant of aniline can be taken from Table 6.7. Calculate the degree of ionization of aniline in the solution. Also calculate the ionization constant of the conjugate acid of aniline.

Show Answer

Answer

$K_b=4.27 \times 10^{\text{âย" } 10}$

$c=0.001 M$

$pH=$ ?

$\alpha=$ ?

$k_b=c \alpha^{2}$

$4.27 \times 10^{-10}=0.001 \times \alpha^{2}$

$4270 \times 10^{-10}=\alpha^{2}$

$65.34 \times 10^{-5}=\alpha=6.53 \times 10^{-4}$

Then, $[$ anion $]=c \alpha=.001 \times 65.34 \times 10^{-5}$

$ =.065 \times 10^{-5} $

$pOH=-\log (.065 \times 10^{-5})$

$ =6.187 $

$pH=7.813$

Now,

$K_a \times K_b=K_w$

$\therefore 4.27 \times 10^{-10} \times K_a=K_w$

$K_a=\frac{10^{-14}}{4.27 \times 10^{-10}}$

$ =2.34 \times 10^{-5} $

Thus, the ionization constant of the conjugate acid of aniline is $2.34 \times 10^{\frac{1}{\epsilon} \cdot 5}$.

7.53 Calculate the degree of ionization of $0.05 \mathrm{M}$ acetic acid if its $\mathrm{p} K_{\mathrm{a}}$ value is 4.74. How is the degree of dissociation affected when its solution also contains (a) $0.01 \mathrm{M}$ (b) $0.1 \mathrm{M}$ in $\mathrm{HCl}$ ?

Show Answer

Answer

$ \begin{aligned} & c=0.05 M \\ & p K_a=4.74 \\ & p K_a=-\log (K_a) \\ & K_a=1.82 \times 10^{-5} \\ & K_a=c \alpha^{2} \quad \alpha=\sqrt{\frac{K_a}{c}} \\ & \alpha=\sqrt{\frac{1.82 \times 10^{-5}}{5 \times 10^{-2}}}=1.908 \times 10^{-2} \end{aligned} $

When $HCl$ is added to the solution, the concentration of $H^{+}$ions will increase. Therefore, the equilibrium will shift in the backward direction i.e., dissociation of acetic acid will decrease.

Case I: When $0.01 M HCl$ is taken.

Let $x$ be the amount of acetic acid dissociated after the addition of $HCl$.

	$CH_3 COOH$	$\longleftrightarrow$	$H^{+}$	+
Initial conc.	$0.05 M$		0	0
After dissociation	$0.05-x$		$0.01+x$	$x$

As the dissociation of a very small amount of acetic acid will take place, the values i.e., 0.05 â€" $x$ and $0.01+x$ can be taken as 0.05 and 0.01 respectively.

$ \begin{aligned} K_a & =\frac{[CH_3 COO^{-}][H^{+}]}{[CH_3 COOH]} \\ \therefore K_a & =\frac{(0.01) x}{0.05} \\ x & =\frac{1.82 \times 10^{-5} \times 0.05}{0.01} \\ x & =1.82 \times 10^{-3} \times 0.05 M \end{aligned} $

Now,

$ \begin{aligned} & =\frac{1.82 \times 10^{-3} \times 0.05}{0.05} \\ & =1.82 \times 10^{-3} \end{aligned} $

$ \alpha=\frac{\text{ Amount of acid dissociated }}{\text{ Amount of acid taken }} $

Case II: When $0.1 M HCl$ is taken.

Let the amount of acetic acid dissociated in this case be $X$. As we have done in the first case, the concentrations of various species involved in the reaction are:

$ \begin{aligned} & {[CH_3 COOH]=0.05-X ; 0.05 M} \\ & {[CH_3 COO^{-}]=X} \\ & {[H^{+}]=0.1+X ; 0.1 M} \\ & K_a=\frac{[CH_3 COO^{-}][H^{+}]}{[CH_3 COOH^{-}]} \\ & \therefore K_a=\frac{(0.1) X}{0.05} \\ & x=\frac{1.82 \times 10^{-5} \times 0.05}{0.1} \\ & x=1.82 \times 10^{-4} \times 0.05 M \end{aligned} $

Now,

$ \begin{aligned} \alpha & =\frac{\text{ Amount of acid dissociated }}{\text{ Amount of acid taken }} \\ & =\frac{1.82 \times 10^{-4} \times 0.05}{0.05} \\ & =1.82 \times 10^{-4} \end{aligned} $

7.54 The ionization constant of dimethylamine is $5.4 \times 10^{-4}$. Calculate its degree of ionization in its $0.02 \mathrm{M}$ solution. What percentage of dimethylamine is ionized if the solution is also $0.1 \mathrm{M}$ in $\mathrm{NaOH}$ ?

Show Answer

Answer

$K_b=5.4 \times 10^{-4}$

$c=0.02 M$

Then, $\alpha=\sqrt{\frac{K_b}{c}}$

$ \begin{aligned} & =\sqrt{\frac{5.4 \times 10^{-4}}{0.02}} \\ & =0.1643 \end{aligned} $

Now, if $0.1 M$ of $NaOH$ is added to the solution, then $NaOH$ (being a strong base) undergoes complete ionization.

$ \begin{aligned} & NaOH _{(a q)} \longleftrightarrow Na _{(a q)}^{+}+OH _{(a q)}^{-} \\ & 0.1 M \quad 0.1 M \end{aligned} $

And, $(CH_3)_2 NH$ $H_2 O$ $\longleftrightarrow$ $(0.02-x)$ $; 0.02 M$ $(CH_3)_2 NH_2^{+}+\overline{O} H$ $x$ $x$ $; 0.1 M$

Then, $[(CH_3)_2 NH_2^{+}]=x$

$[OH^{-}]=x+0.1 ; 0.1$

$\Rightarrow K_b=\frac{[(CH_3)_2 NH_2^{+}][OH^{-}]}{[(CH_3)_2 NH]}$

$5.4 \times 10^{-4}=\frac{x \times 0.1}{0.02}$

$x=0.0054$

It means that in the presence of $0.1 M NaOH, 0.54 %$ of dimethylamine will get dissociated.

7.55 Calculate the hydrogen ion concentration in the following biological fluids whose $\mathrm{pH}$ are given below:

(a) Human muscle-fluid, 6.83

(b) Human stomach fluid, 1.2

(c) Human blood, 7.38

(d) Human saliva, 6.4.

Show Answer

Answer

(a) Human muscle fluid 6.83:

$pH=6.83$

$pH=-\log [H^{+}]$

$\therefore 6.83=-\log [H^{+}]$

$[H^{+}]=1.48 \times 10^{-7} M$

(b) Human stomach fluid, 1.2:

$pH=1.2$

$1.2=-\log [H^{+}]$

$\therefore[H^{+}]=0.063$

(c) Human blood, 7.38:

$pH=7.38=-\log [H^{+}]$ $\therefore[H^{+}]=4.17 \times 10^{-8} M$

(d) Human saliva, 6.4:

$pH=6.4$

$6.4=-\log [H^{+}]$

$[H^{+}]=3.98 \times 10^{-7}$

7.56 The pH of milk, black coffee, tomato juice, lemon juice and egg white are 6.8, 5.0, 4.2, 2.2 and 7.8 respectively. Calculate corresponding hydrogen ion concentration in each.

Show Answer

Answer

The hydrogen ion concentration in the given substances can be calculated by using the given relation:

$pH=\hat{a} \epsilon^{\prime \prime} \log [H^{+}]$

(i) $pH$ of milk $=6.8$

Since, $pH=a \ell^{\prime \prime} \log [H^{+}]$

$6.8=\hat{a} €^{\prime \prime} \log [H^{+}]$

$\log [H^{+}]=$â€" 6.8

$[H^{+}]=anitlog(\hat{a}.$ éc $.^{\prime 6} .8)$

$=1.5 \times 10^{-7} M$

(ii) $pH$ of black coffee $=5.0$

Since, $pH=a \ell^{\prime \prime} \log [H^{+}]$

$5.0=\hat{a} \ell^{\prime \prime} \log [H^{+}]$

$\log [H^{+}]=$â€" 5.0

$[H^{+}]=anitlog(\hat{a}.$ e“ $.^{\prime} 5.0)$

$=10^{-5} M$

(iii) $pH$ of tomato juice $=4.2$

Since, $pH=a \in \in^{\prime \prime} \log [H^{+}]$

$4.2=\hat{a} \ell^{\prime \prime} \log [H^{+}]$

$\log [H^{+}]=\hat{a}$ e" $^{4.2}$

$[H^{+}]=anitlog(\widehat{a}.$ Є“ $.^{\prime 4.2})$

$=6.31 \times 10^{-5} M$

(iv) $pH$ of lemon juice $=2.2$

Since, $pH=a \in \in^{\prime \prime} \log [H^{+}]$ $2.2=\hat{a} €^{\prime \prime} \log [H^{+}]$

$\log [H^{+}]=\hat{a} e^{*} 2.2$

$[H^{+}]=anitlog(\hat{a} €^{\prime \prime 2} 2)$

$=6.31 \times 10^{-3} M$

(v) $pH$ of egg white $=7.8$

Since, $pH=\hat{a} \epsilon^{\prime \prime} \log [H^{+}]$

$7.8=\hat{a} €^{\prime \prime} \log [H^{+}]$

$\log [H^{+}]=\hat{a} e^{“} 7.8$

$[H^{+}]=anitlog(\hat{a} \in^{\prime \prime} 7.8)$

$=1.58 \times 10^{-8} M$

7.57 If $0.561 \mathrm{~g}$ of $\mathrm{KOH}$ is dissolved in water to give $200 \mathrm{~mL}$ of solution at $298 \mathrm{~K}$. Calculate the concentrations of potassium, hydrogen and hydroxyl ions. What is its $\mathrm{pH}$ ?

Show Answer

Answer

$[KOH _{a q}]=\frac{0.561}{\frac{1}{5}} g / L$

$=2.805 g / L$

$=2.805 \times \frac{1}{56.11} M$

$=.05 M$

$KOH _{(a q)} \to K _{(a q)}^{+}+OH^{-} _{(a q)}$

$[OH^{-}]=.05 M=[K^{+}]$

$[H^{+}][H^{-}]=K_w$

$[H^{+}] \frac{K_w}{[OH^{-}]}$

$=\frac{10^{-14}}{0.05}=2 \times 10^{-13} M$

$\therefore pH=12.70$

7.58 The solubility of $\mathrm{Sr}(\mathrm{OH})_{2}$ at $298 \mathrm{~K}$ is $19.23 \mathrm{~g} / \mathrm{L}$ of solution. Calculate the concentrations of strontium and hydroxyl ions and the $\mathrm{pH}$ of the solution.

Show Answer

Answer

Solubility of $Sr(OH)_2=19.23 g / L$

Then, concentration of $Sr(OH)_2$

$=\frac{19.23}{121.63} M$

$=0.1581 M$

$Sr(OH) _{2(a q)} \longrightarrow Sr^{2+} _{(a q)}+2(OH^{-}) _{(a q)}$

$\therefore[Sr^{2+}]=0.1581 M$

$[OH^{-}]=2 \times 0.1581 M=0.3126 M$

Now,

$K_w=[OH^{-}][H^{+}]$

$\frac{10^{-14}}{0.3126}=[H^{+}]$

$\Rightarrow[H^{+}]=3.2 \times 10^{-14}$

$\therefore pH=13.495 ; 13.50$

7.59 The ionization constant of propanoic acid is $1.32 \times 10^{-5}$. Calculate the degree of ionization of the acid in its $0.05 \mathrm{M}$ solution and also its $\mathrm{pH}$. What will be its degree of ionization if the solution is $0.01 \mathrm{M}$ in $\mathrm{HCl}$ also?

Show Answer

Answer

Let the degree of ionization of propanoic acid be $\alpha$.

Then, representing propionic acid as HA, we have:

$ \begin{aligned} & HA+H_2 O \longleftrightarrow H_3 O^{+}+A^{-} \\ & (.05-0.0 \alpha) \approx .05 \end{aligned} $

$ \begin{gathered} .05 \alpha \\ K_a=\frac{[H_3 O^{+}][A^{-}]}{[HA]} \\ \quad=\frac{(.05 \alpha)(.05 \alpha)}{0.05}=.05 \alpha^{2} \\ \alpha=\sqrt{\frac{K_a}{.05}}=1.63 \times 10^{-2} \\ \text{ Then, }[H_3 O^{+}]=.05 \alpha=.05 \times 1.63 \times 10^{-2}=K_b .15 \times 10^{-4} M \\ \therefore pH=3.09 \end{gathered} $

In the presence of $0.1 M$ of $HCl$, let $\alpha^{\prime}$ be the degree of ionization.

$ \begin{aligned} & \text{ Then, }[H_3 O^{+}]=0.01 \\ & {[A^{-}]=005 \alpha^{\prime}} \\ & {[HA]=.05} \\ & K_a=\frac{0.01 \times .05 \alpha^{\prime}}{.05} \\ & 1.32 \times 10^{-5}=.01 \times \alpha^{\prime} \\ & \alpha^{\prime}=1.32 \times 10^{-3} \end{aligned} $

7.60 The $\mathrm{pH}$ of $0.1 \mathrm{M}$ solution of cyanic acid (HCNO) is 2.34. Calculate the ionization constant of the acid and its degree of ionization in the solution.

Show Answer

Answer

$c=0.1 M$

$pH=2.34$ $-\log [H^{+}]=pH$

$-\log [H^{+}]=2.34$

$[H^{+}]=4.5 \times 10^{-3}$

Also,

$[H^{+}]=c \alpha$

$4.5 \times 10^{-3}=0.1 \times \alpha$

$\frac{4.5 \times 10^{-3}}{0.1}=\alpha$

$\alpha=45 \times 10^{-3}=.045$

Then,

$K_a=c \alpha^{2}$

$=0.1 \times(45 \times 10^{-3})^{2}$

$=202.5 \times 10^{-6}$

$=2.02 \times 10^{-4}$

7.61 The ionization constant of nitrous acid is $4.5 \times 10^{-4}$. Calculate the $\mathrm{pH}$ of $0.04 \mathrm{M}$ sodium nitrite solution and also its degree of hydrolysis.

Show Answer

Answer

$NaNO_2$ is the salt of a strong base $(NaOH)$ and a weak acid $(HNO_2)$.

$NO_2^{-}+H_2 O \longleftrightarrow HNO_2+OH^{-}$

$K_h=\frac{[HNO_2][OH^{-}]}{[NO_2^{-}]}$

$\Rightarrow \frac{K_w}{K_a}=\frac{10^{-14}}{4.5 \times 10^{-4}}=.22 \times 10^{-10}$

Now, If $x$ moles of the salt undergo hydrolysis, then the concentration of various species present in the solution will be: $[NO_2^{-}]=.04-x ; 0.04$

$[HNO_2]=x$

$[OH^{-}]=x$

$K_h=\frac{x^{2}}{0.04}=0.22 \times 10^{-10}$

$x^{2}=.0088 \times 10^{-10}$

$x=.093 \times 10^{-5}$

$\therefore[OH^{-}]=0.093 \times 10^{-5} M$

$[H_3 O^{+}]=\frac{10^{-14}}{.093 \times 10^{-5}}=10.75 \times 10^{-9} M$

$\Rightarrow pH=-\log (10.75 \times 10^{-9})$

$=7.96$

Therefore, degree of hydrolysis

$=\frac{x}{0.04}=\frac{.093 \times 10^{-5}}{.04}=2.325 \times 10^{0^{2 \epsilon \cdot 5}}$

7.62 A $0.02 \mathrm{M}$ solution of pyridinium hydrochloride has $\mathrm{pH}=3.44$. Calculate the ionization constant of pyridine.

Show Answer

Answer

$pH=3.44$

We know that,

$pH=a €^{\prime \prime} \log [H^{+}]$

$\therefore[H^{+}]=3.63 \times 10^{-4}$

Then, $K_h=\frac{(3.63 \times 10^{-4})^{2}}{0.02} \quad(\because$ concentration $=0.02 M)$

$\Rightarrow K_h=6.6 \times 10^{-6}$

Now, $K_h=\frac{K_w}{K_a}$

$\Rightarrow K_a=\frac{K_w}{K_h}=\frac{10^{-14}}{6.6 \times 10^{-6}}$

$=1.51 \times 10^{-9}$

7.63 Predict if the solutions of the following salts are neutral, acidic or basic:

$\mathrm{NaCl}, \mathrm{KBr}, \mathrm{NaCN}, \mathrm{NH_4} \mathrm{NO_3}, \mathrm{NaNO_2}$ and $\mathrm{KF}$

Show Answer

Answer

(i) $NaCl$ :

$ NaCl+H_2 O \longleftrightarrow \underset{\text{ Strong base }}{NaOH}+\underset{\text{ Strong acid }}{HCl} $

Therefore, it is a neutral solution.

(ii) $KBr$ :

Therefore, it is a neutral solution.

(iii) $NaCN$ :

$ \begin{aligned} & NaCN+H_2 O \longleftrightarrow HCN+NaOH \\ & \text{ Weak acid Strong base } \end{aligned} $

Therefore, it is a basic solution.

(iv) $NH_4 NO_3$

$ NH_4 NO_3+H_2 O \longleftrightarrow \underset{\text{ Weak base }}{NH_4 OH+\underset{\text{ Strong acid }}{HNO_3}} $

Therefore, it is an acidic solution.

(v) $NaNO_2$

$ NaNO_2+H_2 O \longleftrightarrow \underset{\text{ Strong base }}{NaOH}+\underset{\text{ Weak acid }}{HNO_2} $

Therefore, it is a basic solution.

(vi) $KF$

$ \begin{aligned} & KF+H_2 O \longleftrightarrow KOH+HF \\ & \text{ Strong base Weak acid } \end{aligned} $

Therefore, it is a basic solution.

7.64 The ionization constant of chloroacetic acid is $1.35 \times 10^{-3}$. What will be the pH of $0.1 \mathrm{M}$ acid and its $0.1 \mathrm{M}$ sodium salt solution?

Show Answer

Answer

It is given that $K_a$ for $ClCH_2 COOH$ is $1.35 \times 10^{2 \epsilon^{*} 33}$.

$ \begin{aligned} & \Rightarrow K_a=c \alpha^{2} \\ & \therefore \alpha=\sqrt{\frac{K_a}{c}} \\ & \quad=\sqrt{\frac{1.35 \times 10^{-3}}{0.1}} \quad(\therefore \text{ concentration of acid }=0.1 m) \\ & \begin{aligned} \alpha & =\sqrt{1.35 \times 10^{-2}} \\ & =0.116 \\ \therefore[H^{+}] & =c \alpha=0.1 \times 0.116 \\ \quad & =.0116 \\ \Rightarrow pH & =-\log [H^{+}]=1.94 \end{aligned} \end{aligned} $

$ClCH_2 COONa$ is the salt of a weak acid i.e., $ClCH_2 COOH$ and a strong base i.e., $NaOH$.

$ \begin{aligned} & ClCH_2 COO^{-}+H_2 O \longleftrightarrow ClCH_2 COOH+OH^{-} \\ & K_h=\frac{[ClCH_2 COOH][OH^{-}]}{[ClCH_2 COO^{-}]} \\ & K_h=\frac{K_w}{K_a} \\ & K_h=\frac{10^{-14}}{1.35 \times 10^{-3}} \\ & =0.740 \times 10^{-11} \\ & \text{ Also, } .K_h=\frac{x^{2}}{0.1} \quad (\text{ where } x \text{ is the concentration of } OH^{-} \text{and } ClCH_2 COOH) \\ & 0.740 \times 10^{-11}=\frac{x^{2}}{0.1} \\ & 0.074 \times 10^{-11}=x^{2} \\ & \Rightarrow x^{2}=0.74 \times 10^{-12} \\ & \begin{matrix} x=0.86 \times 10^{-6} \\ {[OH^{-}]=0.86 \times 10^{-6}} \\ \therefore[H^{+}]=\frac{K_w}{0.86 \times 10^{-6}} \\ \quad=\frac{10^{-14}}{0.86 \times 10^{-6}} \\ {[H^{+}]=1.162 \times 10^{-8}} \\ pH=-\log [H^{+}] \\ =7.94 \end{matrix} \end{aligned} $

7.65 Ionic product of water at $310 \mathrm{~K}$ is $2.7 \times 10^{-14}$. What is the $\mathrm{pH}$ of neutral water at this temperature?

Show Answer

Answer

Ionic product, $K_w=[H^{+}][OH^{-}]$

Let $[H^{+}]=x$.

Since $[H^{+}]=[OH^{-}], K_w=x^{2}$.

$\Rightarrow K_w$ at $310 K$ is $2.7 \times 10^{-14}$.

$\therefore 2.7 \times 10^{-14}=x^{2}$

$\Rightarrow x=1.64 \times 10^{-7}$

$\Rightarrow[H^{+}]=1.64 \times 10^{-7}$

$\Rightarrow pH=-\log [H^{+}]$

$=-\log [1.64 \times 10^{-7}]$

$=6.78$

Hence, the $pH$ of neutral water is 6.78 .

7.66 Calculate the $\mathrm{pH}$ of the resultant mixtures:

a) $10 \mathrm{~mL}$ of $0.2 \mathrm{M} \mathrm{Ca}(\mathrm{OH})_{2}+25 \mathrm{~mL}$ of $0.1 \mathrm{M} \mathrm{HCl}$

b) $10 \mathrm{~mL}$ of $0.01 \mathrm{M} \mathrm{H_2} \mathrm{SO_4}+10 \mathrm{~mL}$ of $0.01 \mathrm{M} \mathrm{Ca}(\mathrm{OH})_{2}$

c) $10 \mathrm{~mL}$ of $0.1 \mathrm{M} \mathrm{H_2} \mathrm{SO_4}+10 \mathrm{~mL}$ of $0.1 \mathrm{M} \mathrm{KOH}$

Show Answer

Answer

(a)

Moles of $H_3 O^{+}=\frac{25 \times 0.1}{1000}=.0025 mol$

Moles of $OH^{-}=\frac{10 \times 0.2 \times 2}{1000}=.0040 mol$

Thus, excess of $OH^{-}=.0015 mol$

$ \begin{aligned} & {[OH^{-}]=\frac{.0015}{35 \times 10^{-3}} mol / L=.0428} \\ & \begin{aligned} pOH & =-\log [OH] \\ & =1.36 \\ pH & =14-1.36 \\ & =12.63 \quad \text{ (not matched) } \end{aligned} \end{aligned} $

Moles of $H_3 O^{+}=\frac{2 \times 10 \times 0.01}{1000}=.0002 mol$

Moles of $OH^{-}=\frac{2 \times 10 \times .01}{1000}=.0002 mol$

Since there is neither an excess of $H_3 O^{+}$or $OH^{-}$, the solution is neutral. Hence, $pH=7$.

(c)

Moles of $OH^{-}=\frac{10 \times 0.1}{1000}=0.001 mol$

Excess of $H_3 O^{+}=.001 mol$

Thus, $[H_3 O^{+}]=\frac{.001}{20 \times 10^{-3}}=\frac{10^{-3}}{20 \times 10^{-3}}=.05$

$\therefore pH=-\log (0.05)$

$=1.30$

7.67 Determine the solubilities of silver chromate, barium chromate, ferric hydroxide, lead chloride and mercurous iodide at $298 \mathrm{~K}$ from their solubility product constants given in Table 6.9. Determine also the molarities of individual ions.

Show Answer

Answer

(1) Silver chromate:

$ Ag_2 CrO_4 \longrightarrow 2 Ag^{+}+CrO_4{ }^{2-} $

Then,

$K _{s p}=[Ag^{+}]^{2}[CrO_4{ }^{2-}]$

Let the solubility of $Ag_2 CrO_4$ be s.

$\Rightarrow[Ag^{+}] 2 s$ and $[CrO_4{ }^{2-}]=s$

Then,

$K _{s p}=(2 s)^{2} . s=4 s^{3}$

$\Rightarrow 1.1 \times 10^{-12}=4 s^{3}$

$.275 \times 10^{-12}=s^{3}$

$s=0.65 \times 10^{-4} M$

Molarity of $Ag^{+}=2 s=2 \times 0.65 \times 10^{e^{-4}}=1.30 \times 10^{a \epsilon^{-4}} M$

Molarity of $CrO_4{ }^{2-}=s=0.65 \times 10^{ae \cdot 4} M$

(2) Barium chromate:

$BaCrO_4 \longrightarrow Ba^{2+}+CrO_4{ }^{2-}$

Then, $K _{s p}=[Ba^{2+}][CrO_4{ }^{2-}]$

Let $s$ be the solubility of $BaCrO_4$.

Thus, $[Ba^{2+}]=s$ and $[CrO_4^{2-}]=s$

$\Rightarrow K _{S P}=s^{2}$

$\Rightarrow 1.2 \times 10^{-10}=s^{2}$

$\Rightarrow s=1.09 \times 10^{-5} M$

Molarity of $Ba^{2+}=$ Molarity of $CrO_4{ }^{2-}=s=1.09 \times 10^{-5} M$

(3) Ferric hydroxide:

$Fe(OH)_3 \longrightarrow Fe^{2+}+3 OH^{-}$

$K _{s p}=[Fe^{2+}][OH^{-}]^{3}$

Let $s$ be the solubility of $Fe(OH)_3$.

Thus, $[Fe^{3+}]=s$ and $[OH^{-}]=3 s$

$\Rightarrow K _{s p}=s .(3 s)^{3}$

$ =s .27 s^{3} $

$K _{s p}=27 s^{4}$

$1.0 \times 10^{-38}=27 s^{4}$

$.037 \times 10^{-38}=s^{4}$

$.00037 \times 10^{-36}=s^{4} \quad \Rightarrow 1.39 \times 10^{-10} M=S$

Molarity of $Fe^{3+}=s=1.39 \times 10^{-10} M$

Molarity of $OH^{-}=3 s=4.17 \times 10^{-10} M$

(4) Lead chloride:

$PbCl_2 \longrightarrow Pb^{2+}+2 Cl^{-}$

$K _{S P}=[Pb^{2+}][Cl^{-}]^{2}$

Let $K _{S P}$ be the solubility of $PbCl_2$. $[PB^{2+}]=s$ and $[Cl^{-}]=2 s$

Thus, $K _{s p}=s .(2 s)^{2}$

$=4 s^{3}$

$\Rightarrow 1.6 \times 10^{-5}=4 s^{3}$

$\Rightarrow 0.4 \times 10^{-5}=s^{3}$

$4 \times 10^{-6}=s^{3} \Rightarrow 1.58 \times 10^{-2} M=S .1$

Molarity of $PB^{2+}=s=1.58 \times 10^{-2} M$

Molarity of chloride $=2 s=3.16 \times 10^{-2} M$

(5) Mercurous iodid

6.68 The solubility product constant of $\mathrm{Ag_2} \mathrm{CrO_4}$ and $\mathrm{AgBr}$ are $1.1 \times 10^{-12}$ and $5.0 \times 10^{-13}$ respectively. Calculate the ratio of the molarities of their saturated solutions

Show Answer

Answer

Let $s$ be the solubility of $Ag_2 CrO_4$.

Then, $Ag_2 CrO_4 \longleftrightarrow Ag^{2+}+2 CrO_4^{-}$

$K _{s p}=(2 s)^{2} . s=4 s^{3}$

$1.1 \times 10^{-12}=4 s^{3}$

$s=6.5 \times 10^{-5} M$

Let $s^{\prime}$ be the solubility of AgBr.

$AgBr _{(s)} \longleftrightarrow Ag^{+}+Br^{-}$

$K _{s p}=s^{\prime 2}=5.0 \times 10^{-13}$

$\therefore s^{\prime}=7.07 \times 10^{-7} M$

Therefore, the ratio of the molarities of their saturated solution is $\frac{s}{s^{\prime}}=\frac{6.5 \times 10^{-5} M}{7.07 \times 10^{-7} M}=91.9$.

7.69 Equal volumes of $0.002 \mathrm{M}$ solutions of sodium iodate and cupric chlorate are mixed together. Will it lead to precipitation of copper iodate? (For cupric iodate $\left.K_{\text {sp }}=7.4 \times 10^{-8}\right)$.

Show Answer

Answer

When equal volumes of sodium iodate and cupric chlorate solutions are mixed together, then the molar concentrations of both solutions are reduced to half i.e., $0.001 M$.

Then,

$ \begin{aligned} & NalO_3 \to Na^{+}+10_3^{-} \\ & 0.001 M \quad 0.001 M \\ & Cu(ClO_3)_2 \to Cu^{2+}+2 ClO_3^{-} \\ & 0.001 M \quad 0.001 M \end{aligned} $

Now, the solubility equilibrium for copper iodate can be written as:

$ Cu(10_3)_2 \to Cu^{2+} _{(aq)}+210 _{3(aq)}^{-} $

Ionic product of copper iodate:

$ \begin{aligned} & =[Cu^{2+}][10_3^{-}]^{2} \\ & =(0.001)(0.001)^{2} \\ & =1 \times 10^{-9} \end{aligned} $

Since the ionic product $(1 \times 10^{\hat{\epsilon} \epsilon^{-9}})$ is less than $K _{s p}(7.4 \times 10^{\hat{a} \epsilon^{" 8}})$, precipitation will not occur.

7.70 The ionization constant of benzoic acid is $6.46 \times 10^{-5}$ and $K_{\mathrm{sp}}$ for silver benzoate is $2.5 \times 10^{-13}$. How many times is silver benzoate more soluble in a buffer of $\mathrm{pH} 3.19$ compared to its solubility in pure water?

Show Answer

Answer

Since $pH=3.19$,

$ [H_3 O^{+}]=6.46 \times 10^{-4} M $

$C_6 H_5 COOH+H_2 O \longleftrightarrow C_6 H_5 COO^{-}+H_3 O$

$K_a \frac{[C_6 H_5 COO^{-}][H_3 O^{+}]}{[C_6 H_5 COOH]}$

$ \frac{[C_6 H_5 COOH]}{[C_6 H_5 COO^{-}]}=\frac{[H_3 O^{+}]}{K_a}=\frac{6.46 \times 10^{-4}}{6.46 \times 10^{-5}}=10 $

Let the solubility of $C_6 H_5 COOAg$ be $x mol / L$.

Then,

$ \begin{aligned} & {[Ag^{+}]=x} \\ & {[C_6 H_5 COOH]+[C_6 H_5 COO^{-}]=x} \\ & 10[C_6 H_5 COO^{-}]+[C_6 H_5 COO^{-}]=x \\ & {[C_6 H_5 COO^{-}]=\frac{x}{11}} \\ & K _{s p}[Ag^{+}][C_6 H_5 COO^{-}] \\ & 2.5 \times 10^{-13}=x(\frac{x}{11}) \\ & x=1.66 \times 10^{-6} mol / L \end{aligned} $

Now, let the solubility of $C_6 H_5 COOAg$ be $x^{\prime} mol / L$.

Then, $[Ag^{+}]=x^{\prime} M$ and $[CH_3 COO^{-}]=x^{\prime} M$.

$K _{s p}=[Ag^{+}][CH_3 COO^{-}]$

$K _{s p}=(x^{\prime})^{2}$

$x^{\prime}=\sqrt{K _{s p}}=\sqrt{2.5 \times 10^{-13}}=5 \times 10^{-7} mol / L$

$\therefore \frac{x}{x^{\prime}}=\frac{1.66 \times 10^{-6}}{5 \times 10^{-7}}=3.32$

Hence, $C_6 H_5 COOAg$ is approximately 3.317 times more soluble in a low $pH$ solution.

7.71 What is the maximum concentration of equimolar solutions of ferrous sulphate and sodium sulphide so that when mixed in equal volumes, there is no precipitation of iron sulphide? (For iron sulphide, $K_{\mathrm{sp}}=6.3 \times 10^{-18}$ ).

Show Answer

Answer

Let the maximum concentration of each solution be $x mol / L$. After mixing, the volume of the concentrations of each solution will be reduced to half i.e., $\frac{x}{2}$.

$ \therefore[FeSO_4]=[Na_2 S]=\frac{x}{2} M $

Then, $[Fe^{2+}]=[FeSO_4]=\frac{x}{2} M$

Also, $[S^{2-}]=[Na_2 S]=\frac{x}{2} M$

$FeS _{(s)} \longleftrightarrow Fe^{2+} _{(a q)}+S^{2-} _{(a q)}$

$K _{s p}=[Fe^{2+}][S^{2-}]$

$6.3 \times 10^{-18}=(\frac{x}{2})(\frac{x}{2})$

$\frac{x^{2}}{4}=6.3 \times 10^{-18}$

$\Rightarrow x=5.02 \times 10^{-9}$

If the concentrations of both solutions are equal to or less than $5.02 \times 10^{ae 9} M$, then there will be no precipitation of iron sulphide.

7.72 What is the minimum volume of water required to dissolve $1 \mathrm{~g}$ of calcium sulphate at $298 \mathrm{~K}$ ? (For calcium sulphate, $K_{\mathrm{sp}}$ is $9.1 \times 10^{-6}$ ).

Show Answer

Answer

$CaSO _{4(s)} \longleftrightarrow Ca^{2+} _{(a q)}+SO_4^{2-} _{(a q)}$

$K _{s p}=[Ca^{2+}][SO_4^{2-}]$

Let the solubility of $CaSO_4$ be $s$.

Then, $K _{s p}=s^{2}$

$9.1 \times 10^{-6}=s^{2}$

$s=3.02 \times 10^{-3} mol / L$

Molecular mass of $CaSO_4=136 g / mol$

Solubility of $CaSO_4$ in gram $/ L=3.02 \times 10^{ae e} \times 136$

$=0.41 g / L$

This means that we need $1 L$ of water to dissolve $0.41 g$ of $CaSO_4$

Therefore, to dissolve $1 g$ of $CaSO_4$ we require $=\frac{1}{0.41} L=2.44 L$ of water.

7.73 The concentration of sulphide ion in $0.1 \mathrm{M} \mathrm{HCl}$ solution saturated with hydrogen sulphide is $1.0 \times 10^{-19} \mathrm{M}$. If $10 \mathrm{~mL}$ of this is added to $5 \mathrm{~mL}$ of $0.04 \mathrm{M}$ solution of the following: $\mathrm{FeSO_4}, \mathrm{MnCl_2}, \mathrm{ZnCl_2}$ and $\mathrm{CdCl_2}$. in which of these solutions precipitation will take place?

Show Answer

Answer

For precipitation to take place, it is required that the calculated ionic product exceeds the $K _{s p}$ value.

Before mixing:

$ [S^{2-}]=1.0 \times 10^{-19} M[M^{2+}]=0.04 M $

volume $=10 mL \quad$ volume $=5 mL$

After mixing:

$ [S^{2-}]=? \quad[M^{2+}]=? $

volume $=(10+5)=15 mL \quad$ volume $=15 mL$

$ \begin{aligned} & {[S^{2-}]=\frac{1.0 \times 10^{-19} \times 10}{15}=6.67 \times 10^{-20} M} \\ & {[M^{2+}]=\frac{0.04 \times 5}{15}=1.33 \times 10^{-2} M} \end{aligned} $

$ \begin{aligned} \text{ Ionic product } & =[M^{2+}][S^{2-}] \\ & =(1.33 \times 10^{-2})(6.67 \times 10^{-20}) \\ & =8.87 \times 10^{-22} \end{aligned} $

This ionic product exceeds the $K _{s p}$ of $Zns$ and $CdS$. Therefore, precipitation will occur in $CdCl_2$ and $ZnCl_2$ solutions.