Learning Objectives

After going through this unit, you will be able to understand, appreciate and apply the following concepts:

• Concept of communication system.

• Propagation of em-waves.

• Different modes of (wireless) propagation of em-waves-ground wave, sky wave and space wave propagation.

• Basic idea of modulation.

• Need for modulation.

• Different types of modulation-AM, FM and PM.

• Advantages and disadvantages of FM over AM.

CONCEPT MAP

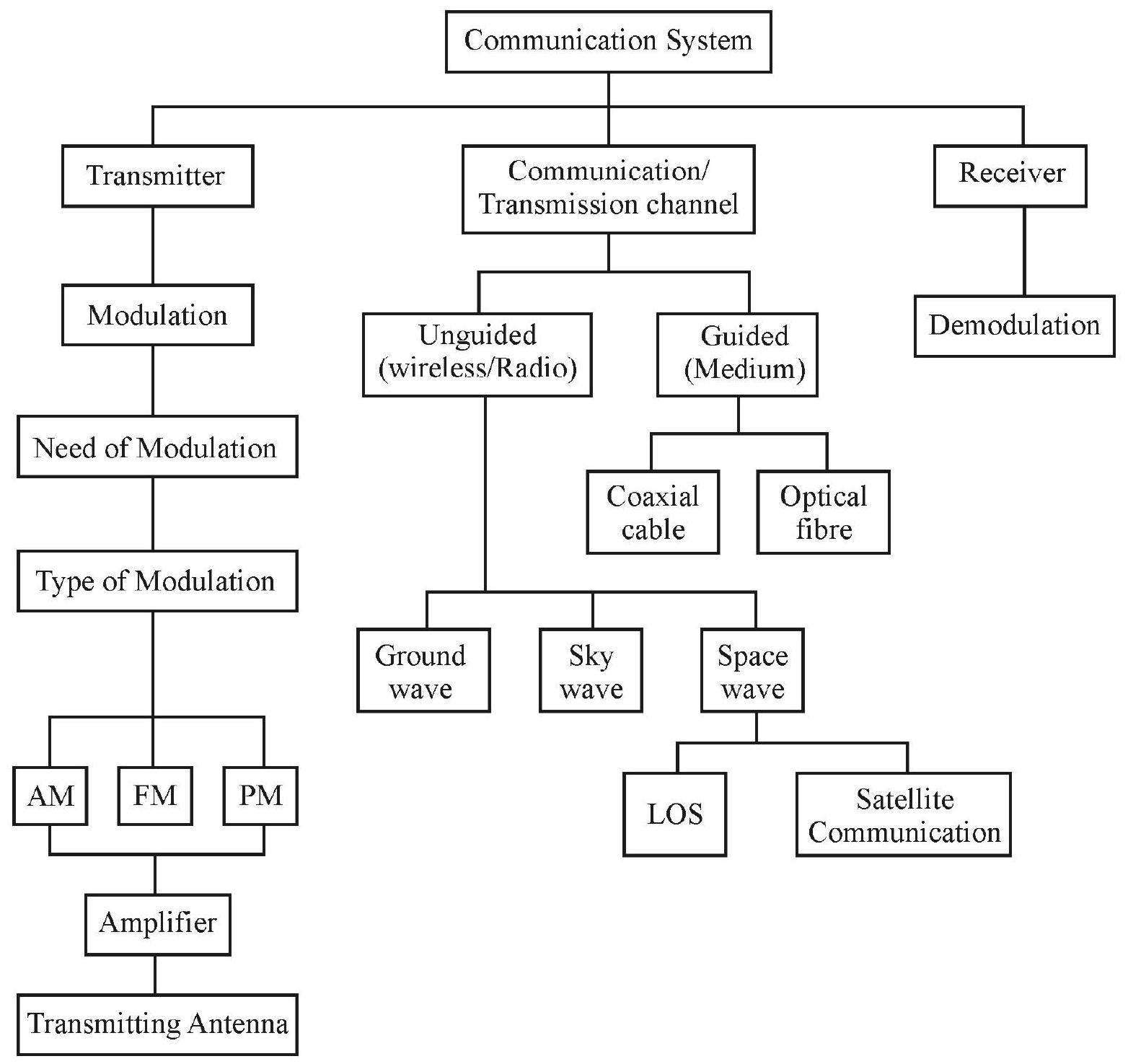
Communication System

Communication is the process of transmission of information from one point and it reception at another point. The set up used to achieve this goal, is termed as ‘communication system’. The purpose of a communication system, therefore, is to transmit information from a source, located at one place, to a receiver, located at another place.

Elements of a Communication System

A communication system consists of three basic parts (i) transmitter (ii) communication channel and (iii) reciever. The block diagram given below depicts the general form of a communication system.

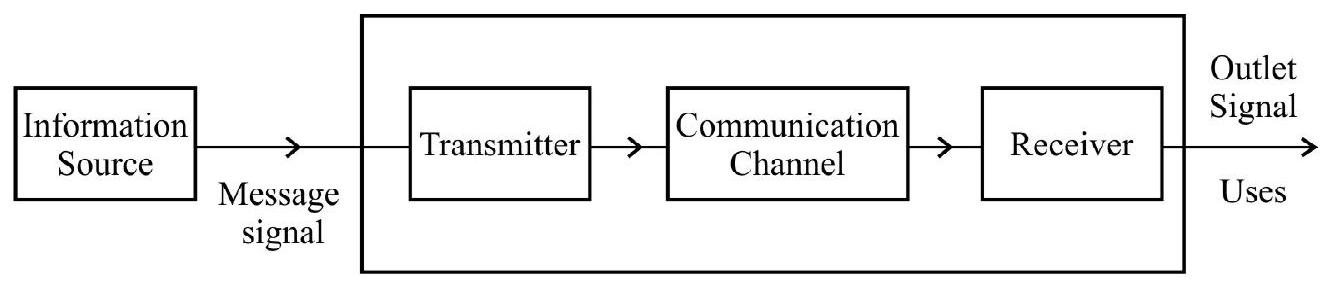
Fig. 1: Communication System

In a communication system, the transmitter transmits the message signal. The purpose of the transmitter is to convert the message signal, produced by the source of information, into a form suitable for transmission through the relevant communication channel. This modification is often achieved by means of a process known as ‘modulation’.

The communication channel carriers the modulated wave, form, from the transmitter to the receiver. This ‘channel’ can be a transmission line (as in telephony), an optical fibre (as in optical communication) or merely ‘free space’ in which the signal is radiated as an electromagnetic wave (wireless communication).

The main purpose of a receiver is to reconstruct the original message from the ‘signal received by it, after propagation through the channel. This is accomplished by using a process known as ‘demodulation’; this process is the reverse of the ‘modulation’ process, used in the transmitter.

Modes of Communication

There are two basic modes of communication: ‘point to point and ‘broadcast mode.

In the ‘point to point’ communication mode, communication takes place over a link between a single transmitter and a receive. ‘Telephony’ is the most familiar example of this mode of communication. In contrast, in the broadcast mode, there are a large number of receivers, corresponding to a single transmitter. Radio and television are two of the well known examples of this mode of communication.

Basic Terminology used in Communication System

We now familiarize ourselves with the basic terms used in communication systems.

1. Transducer: This is any device which converts one form of energy into another form. An electrical transducer may be defined as a device that converts the variations in some physical variable (pressure, displacement, force, temperature) into corresponding variations in an electrical signal given out at its output. For example microphone and loudspeakers act as transducers. They convert sound signals into electrical signal and vice-versa.

2. Message Signal: It is a time varying electrical signal, generated from some original signal, using an appropriate transducer. These signals can be analogue or digital in nature.

3. Attenuation: The loss of strength (or energy) of a signal, while propagating through a medium, is known as attenuation.

4. Range: It is the largest distance between source and a distination, upto which the transmitted signal can be received with sufficient strength.

5. Bandwidth: Bandwidth refers to the frequency range over which the equipment, of a channel, operates. It may also be viewed as (i) the position of the (e.m.) spectrum occupied by the signal, or (ii) as the difference of the highest frequency to the lowest frequency, within which transmission is taking place.

6. Repeater: A ‘repeater’ is the combination of a receiver and a transmitter. A repeater picks up the signal from the transmitter, amplifies it and retransmits it to the receiver. Repeaters are used to extend the range of a communication system. A communication satellite is essentially a repeater station in a space.

Bandwidth of a Signal

In a communication system, the message signal can be voice, music, picture or computer data. All of these ‘signals’, have ‘different ranges of frequencies’. For example speech signals require a bandwidth of 2800 $\mathrm{Hz}$, for commercial telephonic communication. To transmit music, an approximate bandwidth of $20\mathrm{KHz}$ is required video signals, for transmisstion of pictures, require $4.2\mathrm{MHz}$ of bandwidth. A T.V. signal (having both video and audio parts) usually has $6\mathrm{MHz}$ of bandwidth for transmission.

Some Important Wireless Communication

Nature of Service/Broadcast	Frequency Band
FM Radio	$88-108\mathrm{MHz}$
VHF TV	$54-88\mathrm{MHz}$
UHF TV	$420-890\mathrm{MHz}$
Cellular Mobile Phone	$896-901\mathrm{MHz}$ (Mobile to Base Station)
	$840-935\mathrm{MHz}$ (Base Station to Mobile)

Bandwidth of Transmission Medium

The commonly used transmission medium (communication channel) are wireless (radio communication) free space, coaxial cables and fibre optic cables. Coaxial cables are widely used ‘wire based medium’, which offers a bandwidth of approximately $750\mathrm{MHz}$. Communication through free space, using radio waves, takes place over a very wide range of frequencies, from few $\mathrm{KHz}$ to a few $\mathrm{GHz}$. Optical communication, using optical fibres, is performed over the frequency range of $1\mathrm{THz}$ to $1000\mathrm{THz}$. An optical fibre can offer a transmission bandwidth in excess of $100\mathrm{GHz}$.

Propagation of Electromagnetic Waves

In communication using radio waves, an antenna, at the transmitter end, radiates, the em-waves, which propagate through free space and reach the receiving antenna at the other end. An electromagnetic wave (em-wave), may be divided into various parts. The part, which propagates along the surface of earth is called surface wave (ground wave propagation). The remainder part moves towards the ionosphere and gets reflected by this ionosphere. Such type of propagation is called sky wave. Sky wave propagation can takes place for frequency up to about $30\mathrm{MHz}$. Above this frequency, electromagnetic waves essentially propagate as space waves. Space waves are used for line of sight communication and satellite communication.

Ground Wave

This mode of propagation is also called surface wave propagation as the wave glides over the surface of the earth. A wave induces current in the ground over which it passes; it is attenuated as a result of absorption of energy by the earth. The attenuation of surface wave increases very rapidly with increases in frequency. Hence this mode of propagation is limited to freqeuncy as up to few MHz.

Sky Wave

In the frequency range, from few $\mathrm{MHz}$ to $30\mathrm{MHz}$, long distance communication can be achieved by ionospheric reflection of radiowaves back towards earth. The ionospheric layer acts as a reflector over the range of frequencies ranging from about $3\mathrm{MHz}$ to about $30\mathrm{MHz}$. The critical frequency, for reflection is given by ${\mathrm{f}}_{\mathrm{C}}=9{\left({\mathrm{N}}_{max}\right)}^{1/2}$, where ${\mathrm{N}}_{max}$ is the maximum electron density in the concerned layer of ionosphere. As different layers of the ionosphere act as gets reflectors, any wave directed at a certain angle, gets reflected and returns to the earth. There may exist a distance, from the transmitter, measured along the surface of earth, to the point where the wave return to earth after reflection from ionosphere; this distance is known as ‘skip distance’; this is shown in the figure (2) below.

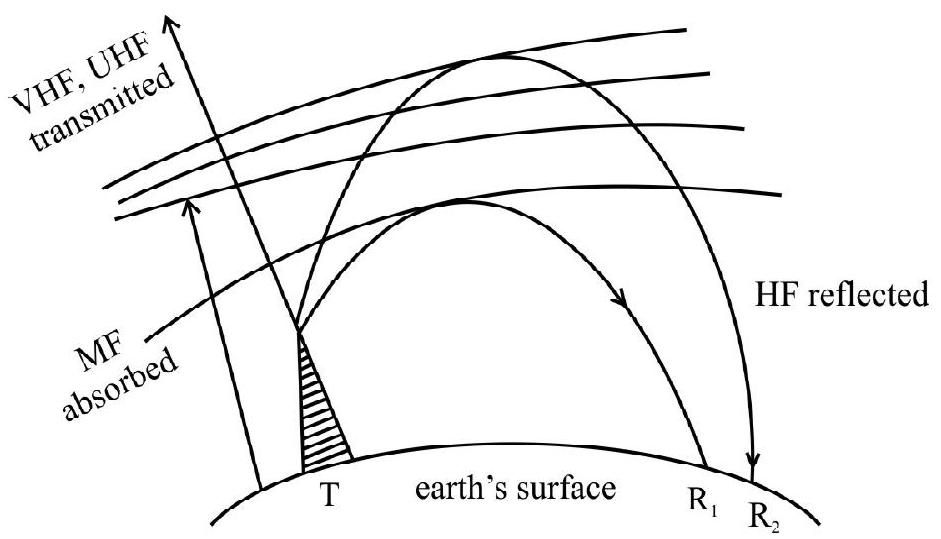
Fig. 2

Using multiple loops, in which the wave is reflected between the ionosphere and earth’s surface several times the propagation range can be increased.

Space Wave

A space wave propagates along a straight line; from the transmitting antenna to the receiving antenna. Space waves are used for line of sight (LOS) communication as well as satellite communication. At frequencies above $40\mathrm{MHz}$, communication is essentially limited to LOS. Because of their ’line of sight’ nature of propagation, direct waves get blocked at some point by the curvature of earth, this is shown in the figure (3).

The distance, $\mathrm{d}$, is known as the radio horizon of the transmitting antenna. The value ofd is (approximately) proportional to the square root of its height of the transmitting antenna. This can be seen as follows

We have,

$\begin{array}{rl}& (\mathrm{OQ}{)}^2=(\mathrm{OR}{)}^2+(\mathrm{QR}{)}^2\\ & \Rightarrow (\mathrm{R}+\mathrm{h}{)}^2={\mathrm{R}}^2+{\mathrm{d}}^2\\ & \therefore \mathrm{d}\simeq \sqrt{2\mathrm{Rh}}(\text{ as }\mathrm{R}»\mathrm{h})\end{array}$

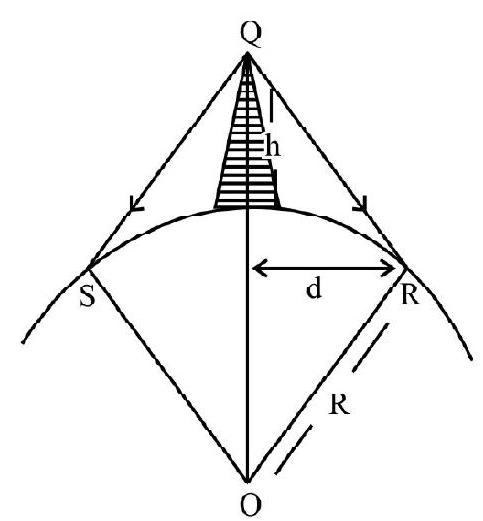
Fig. 3

Here $\mathrm{h}$ is the height of the transmitting antenna and ’ $\mathrm{d}$ ’ is the radio horizon.

If the signal is to be received beyond the horizon then the receiving anteena must be high enough to intercept the ’line of sight’ waves.

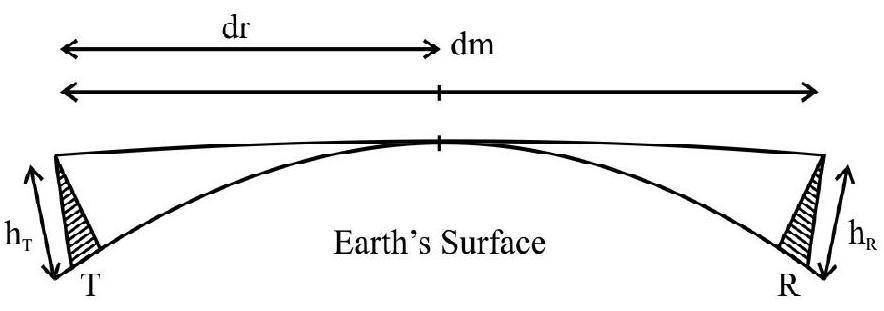
Fig. 4

The maximum ’line of sight’ distance, $d_m$, between the two antenna, having heights $h_T$ and $h_R$ above earth’s surface, is given by

${\mathrm{d}}_{\mathrm{m}}=\sqrt{2{\mathrm{Rh}}_{\mathrm{T}}+2{\mathrm{Rh}}_{\mathrm{R}}}$

An Interesting Feature of ‘Space Wave Propagation’

The propagation of e.m. waves, from the transmitter to the receiver, via space wave propagation, can take place in two ways:

(i) direct ’line of sight’ propagation from the transmitter to the receiver.

(ii) transmission from the transmitter towards the earth’s surface; reflection from the earth’s surface and receiving of the reflected waves by the receiver.

The two waves, at the reveiver, will in general, arrive with a certain phase difference between them. We can easily calculate this phase difference and see its affect on the ‘resultant field strength’ received at the receiver, under the assumption that the reflecting point, on the earth, is mid-way between the transmitter and receiver. Let a transmitter, of height ${\mathrm{H}}_{\mathrm{T}}$ and a receiver, of height ${\mathrm{H}}_{\mathrm{R}}$, be located a distance $\mathrm{d}$ apart from each other.

We than have

Direct path $=\mathrm{AB}$

$\begin{array}{rl}& ={[{\mathrm{d}}^2+({\mathrm{H}}_{\mathrm{T}}\sim {\mathrm{H}}_{\mathrm{R}})]}^{1/2}\\ & =\mathrm{d}{[1+\left({\displaystyle \frac{{\mathrm{H}}_{\mathrm{T}}\sim {\mathrm{H}}_{\mathrm{R}}}{\mathrm{d}}}\right)]}^{1/2}\\ & \approx \mathrm{d}[1+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{{\mathrm{H}}_{\mathrm{T}}\sim {\mathrm{H}}_{\mathrm{R}}}{\mathrm{d}}}\right)}^2]\end{array}$

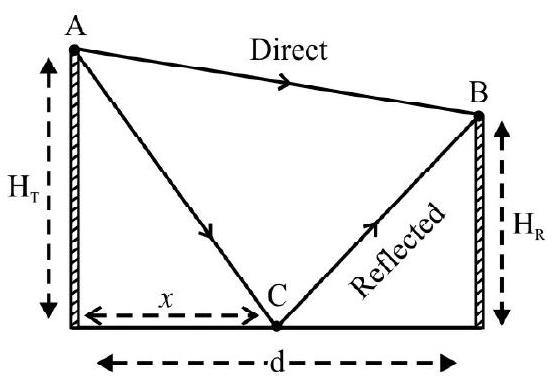
Fig. 5

(If ${\mathrm{H}}_{\mathrm{T}}$ and ${\mathrm{H}}_{\mathrm{R}}$ are both small compared to d)

The reflected wave’s path $=(\mathrm{AC}+\mathrm{CB})$

$\begin{array}{rl}& ={[(x{)}^2+{\mathrm{H}}_{\mathrm{T}}]}^{1/2}+{[(\mathrm{d}-x{)}^2+{\mathrm{H}}_{\mathrm{R}}^2]}^{1/2}\\ & =x{[1+\left({\displaystyle \frac{{\mathrm{H}}_{\mathrm{T}}^2}{x}}\right)]}^{1/2}+{[(\mathrm{d}-x){\left({\displaystyle \frac{{\mathrm{H}}_{\mathrm{R}}}{\mathrm{d}-x}}\right)}^2]}^{1/2}\end{array}$

$\begin{array}{rl}& \simeq x[1+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{{\mathrm{H}}_{\mathrm{T}}}{x}}\right)}^2]+(\mathrm{d}-x)[1+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{{\mathrm{H}}_{\mathrm{R}}}{\mathrm{d}-x}}\right)}^2]\\ & =\mathrm{d}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\mathrm{H}}_{\mathrm{T}}^2}{x}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\mathrm{H}}_{\mathrm{R}}^2}{(\mathrm{d}-x)}}\\ & =\mathrm{d}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\mathrm{H}}_{\mathrm{T}}^2(\mathrm{d}-x)+{\mathrm{H}}_{\mathrm{R}}^2(x)}{[x(\mathrm{d}-x)]}}\end{array}$

For simplification, we may take $x={\displaystyle \frac{\mathrm{d}}{2}}$

We than have,

Reflected wave’s path $\simeq \mathrm{d}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{({\mathrm{H}}_{\mathrm{T}}{}^2+{\mathrm{H}}_{\mathrm{R}}{}^2)}{\mathbf{d}/2}}$

$=\mathrm{d}+{\displaystyle \frac{({\mathrm{H}}_{\mathrm{T}}^2+{\mathrm{H}}_{\mathrm{R}}^2)}{\mathrm{d}}}$

$\therefore$ Path difference between the two waves arriving, at the receiver

$\begin{array}{rl}& ={\displaystyle \frac{({\mathrm{H}}_{\mathrm{T}}^2+{\mathrm{H}}_{\mathrm{R}}^2)-({\mathrm{H}}_{\mathrm{T}}^2+{\mathrm{H}}_{\mathrm{R}}^2-2{\mathrm{H}}_{\mathrm{T}}{\mathrm{H}}_{\mathrm{R}})}{\mathrm{d}}}\\ & =\left({\displaystyle \frac{2{\mathrm{H}}_{\mathrm{T}}{\mathrm{H}}_{\mathrm{R}}}{\mathrm{d}}}\right)\end{array}$

$\therefore$ Corresponding phase difference $={\displaystyle \frac{2\pi }{\lambda }}\left(2{\displaystyle \frac{{\mathrm{H}}_{\mathrm{T}}{\mathrm{H}}_{\mathrm{R}}}{\mathrm{d}}}\right)={\displaystyle \frac{4\pi }{\lambda }}\left({\displaystyle \frac{{\mathrm{H}}_{\mathrm{T}}{\mathrm{H}}_{\mathrm{R}}}{\mathrm{d}}}\right)$

The total phase difference, however, will have an additional contribution of $\pi$, caused by the reflection of the wave from ground (rarer to denser media reflection). Hence the total phase difference, between the two waves, arriving at the receiver, is

$\varphi =[\pi +{\displaystyle \frac{4\pi }{\lambda }}{\displaystyle \frac{{\mathrm{H}}_{\mathrm{T}}{\mathrm{H}}_{\mathrm{R}}}{\mathrm{d}}}]$

The resultant field strength, at the receiver, can now be estimated. For simplification, we can take the individual field strengths, of the two waves arriving at the receiver, to be identical (say E’ each). We then have, in this special case,

Resultant field strength $={[E^2+E^2+2E\cdot E\cos \varphi ]}^{1/2}$

$\begin{array}{rl}& =\sqrt{2}\mathrm{E}(1+\cos \varphi {)}^{1/2}\\ & =\sqrt{2}\mathrm{E}{[1+\cos (\pi +{\displaystyle \frac{4\pi }{\lambda }}{\displaystyle \frac{{\mathrm{H}}_{\mathrm{T}}{\mathrm{H}}_{\mathrm{R}}}{\mathrm{d}}})]}^{1/2}\\ & =\sqrt{2}\mathrm{E}{[1-\cos (\pi +{\displaystyle \frac{4\pi }{\lambda }}{\displaystyle \frac{{\mathrm{H}}_{\mathrm{T}}{\mathrm{H}}_{\mathrm{R}}}{\mathrm{d}}})]}^{1/2}\\ & =\sqrt{2}\mathrm{E}{[2{\sin }^2\left({\displaystyle \frac{2\pi }{\lambda }}{\displaystyle \frac{{\mathrm{H}}_{\mathrm{T}}{\mathrm{H}}_{\mathrm{R}}}{\mathrm{d}}}\right)]}^{1/2}\\ & =2\mathrm{E}\sin \left({\displaystyle \frac{2\pi }{\lambda }}{\displaystyle \frac{{\mathrm{H}}_{\mathrm{T}}{\mathrm{H}}_{\mathrm{R}}}{\mathrm{d}}}\right)\end{array}$

Example-1:

A TV tower has a height of $150\mathrm{m}$. How much population the TV broadcast covers if the average population density around the tower is $1000/{\mathrm{km}}^2$ (radius of earth is $6.4\times {10}^6\mathrm{m}$ )

Show Answer

Solution:

The radius of the region, covered by TV broadcast, in given by

$\mathrm{r}=\sqrt{2\mathrm{Rh}}$

The area of region covered will be

$\begin{array}{rl}& \mathrm{A}=\pi {\mathrm{r}}^2\\ & =2\pi \mathrm{hR}\\ & =\pi \times 2\times 64\times {10}^6\times 150{\mathrm{m}}^2\\ & 12.8\pi \times 150{\mathrm{m}}^2\end{array}$

$\therefore$ Population covered $=12.8\pi \times 150\times 1000$

$\simeq 6.03$ millions.

Example-2:

Which of the following frequencies, will be suitable for ‘beyond the horizon’ communication using sky wves?

(1) $10\mathrm{KHz}$

(2) $10\mathrm{MHz}$

(3) $1\mathrm{GHz}$

(4) $1000\mathrm{GHz}$

Show Answer

Solution:

$10\mathrm{KHz}$ can not be used for long distance communication and $1\mathrm{GHz}$ and $1000\mathrm{GHz}$ will penetrate through the ionosphere. It is only $10\mathrm{MHz}$ that can get reflected back from the ionosphere.

Example-3:

Which means of propagation is used for frequencies in the UHF (Ultra High Frequencies) range?

Show Answer

Solution:

Space wave propagation; either line of sight communication or satellite communication.

Modulation

For reasons listed below, the original low frequency message/information signal cannot be directly transmitted (as e.m. waves) over long distances. Therefore, at the transmitter end, such a low frequency message signal is superimposed on a high frequency wave, which acts as a ‘carrier’ of the information. This process is knowns as modulation.

Necessity of Modulation

Modulation is necessary because of the following reasons:

1. Size of Antenna or Areial: The antenna should have a size compaable to the wavelength of signal (at least $\lambda /4$ ) so that it may properly ‘sense’ the time variations of the signal. Hence, we can obtain transmissions (of e.m. waves) with resonable antenna lengths, only if the transmisstion frequency is high.

2. Effective Power Radiated by an Antenna: The power, radiated by an antenna of effective length ’ $\ell$ ’ is proportional to $(1/\lambda {)}^2$. This implies that with same length ’ $\ell$ ‘, the radiated power increases with decreasing wavelength i.e., increasing freqeuncy.

3. The use of high frequency (carrier) waves, ‘used’ during modulation, also helps to avoid mixing up of signals from different transmitters. This aim is achieved by alooting a (distance, non over-lapping) band of frequencies to each message signal during its transmissions.

From, the above discussion we conclude that there is a need for ’translating’ the original low frequency message signals into high frequency signals, before transmisstion. This transformation must be done in a way such that the ’translated’ signal still possesses the information contrained in the original signal. The high frequency wave, we use for this purpose, is known as the carrier wave.

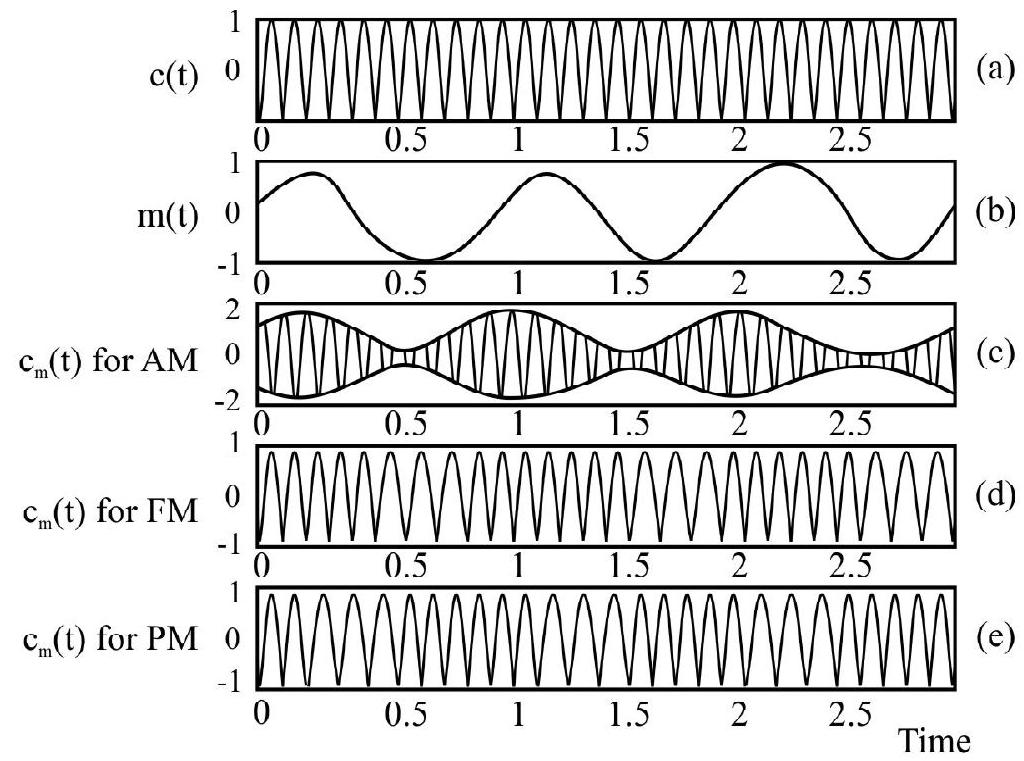
Fig. 6: Modulation of carrier wave

(a) a (b) a modulating signal

(c) amplitude modulation (d) modulation and

(e) phase modulation

During the process of modulation, any of the three parameters: ‘amplitude’, ‘frequency’ or ‘phase’, of the carrier wave, is controlled by the amplitude of the original message or information signal. This results in three types of modulation.

(i) Amplitude modulation (AM)

(ii) Frequency modulation (FM)

(iii) Phase modulation (PM)

These three types of modulation have been shown in the figure (6) given above.

Amplitude Modulation (AM)

In amplitude modulation the amplitude of the carrier $\mathrm{c}(\mathrm{t})$ is varied in accordance with the amplitude of information signal or modulating signal $(\mathrm{m}(\mathrm{t}))$

Let $\mathrm{c}(\mathrm{t})(={\mathrm{A}}_{\mathrm{c}}\sin {\omega }_{\mathrm{c}}\mathrm{t})$, be the carrier wave and $m(t)(=A_m\sin {\omega }_{m}t)$ be the modulating signal or information signal.

Then amplitude modulated signal is given by

$\begin{array}{rl}& c_m(t)=(A_c+A_m\sin {\omega }_{m}t)\sin {\omega }_{c}t\\ & =A_c\sin {\omega }_{c}t+{\displaystyle \frac{\mu A_c}{2}}\cos ({\omega }_c-{\omega }_m)t\\ & =-{\displaystyle \frac{\mu A_c}{2}}\cos ({\omega }_c-{\omega }_m)t\end{array}$

Here $\mu ={\mathrm{A}}_{\mathrm{m}}/{\mathrm{A}}_{\mathrm{c}}$ it is known as the modulation index.

$\mu$ is kept $<1$ to avoid distortion.

The difference $({\omega }_{\mathrm{c}}-{\omega }_{\mathrm{m}})$, and the sum $({\omega }_{\mathrm{c}}+{\omega }_{\mathrm{m}})$, are, respectively called the ’lower side’ and ‘upper side’ frequencies.

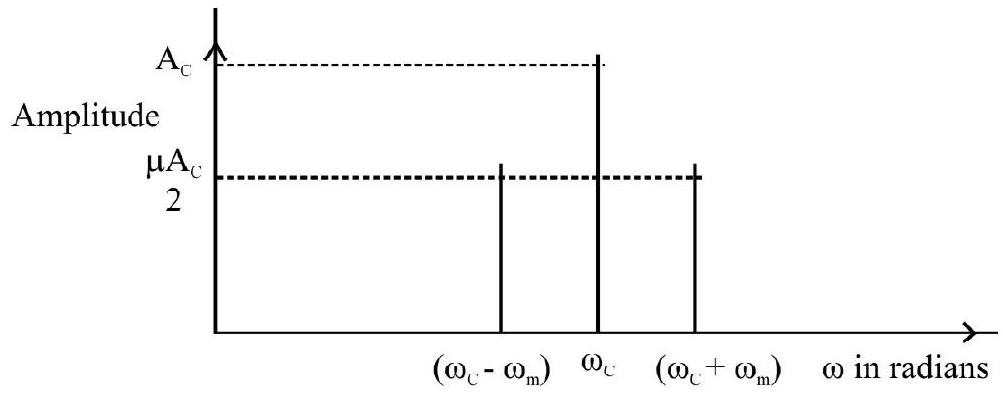
Fig. 7: A plot of amplitude versus $\omega$ for an amplitude modulated signal

It is important to ensure that the broadcast frequencies (carrier waves) are sufficiently spaced out so that sidebands do not overlap. Different stations can then operate without interfering with each other.

Power Distribution between the (Original) ‘Carrier Wave’ and the ‘Side Bands’ in an Amplitude Modulated (Carrier) Wave

When a carrier wave

$c(t)=A_c\sin \left({\omega }_{c}t\right)$

is amplitude modulated by a message signal

$\mathrm{m}(\mathrm{t})={\mathrm{A}}_{\mathrm{m}}\sin \left({\omega }_{\mathrm{m}}\mathrm{t}\right)$

the resulting AM carrier wave

$C_{mt}=[A_c+A_m\sin \left({\omega }_{m}t\right)]\sin \left({\omega }_{c}t\right)$

can be rewritten as

$\begin{array}{rl}& C_{mt}=A_c\sin {\omega }_{m}t+{\displaystyle \frac{\mu A_c}{2}}\cos \left[({\omega }_c-{\omega }_m)t\right]\\ & -\mu {\displaystyle \frac{A_c}{2}}\cos \left[({\omega }_c+{\omega }_m)t\right]\end{array}$

where $=\mu ={\displaystyle \frac{{\mathrm{A}}_{\mathrm{m}}}{{\mathrm{A}}_{\mathrm{c}}}}=$ modulation index.

The AM carrier wave, therefore, has its power distributed between the original carrier wave and the two side bands accompyaning it. Their relative ‘shares’ depend on the value of $\mu$, the modulation index. Let us see there ‘relative shares’ of power.

We have

Power of the original carrier wave $={\left[{\displaystyle \frac{{\mathbf{A}}_{\mathrm{C}}/\sqrt{2}}{\mathrm{R}}}\right]}^2$

$=\left[{\displaystyle \frac{{\mathrm{A}}_{\mathrm{c}}^2}{2\mathrm{R}}}\right]$

and power of each of the sideband waves

$\begin{array}{rl}& ={\left[{\displaystyle \frac{\left({\mu }^{A_c}/2\sqrt{2}\right)}{R}}\right]}^2\\ & =\left({\mu }^2{\displaystyle \frac{A_c^2}{4R}}\right)\end{array}$

Here $\mathrm{R}$ is the effective rsistance of the ‘modulator circuit’.

$\therefore {\displaystyle \frac{\text{ Power is the two sidebands }}{\text{ Power is the original carrier }}}={\displaystyle \frac{{\mu }^2{A}_c{}^2/4R}{A_C{}^2/2R}}={\left({\displaystyle \frac{\mu }{2}}\right)}^2$

And total power $={\displaystyle \frac{A_c{}^2}{2R}}[1+2\times {\displaystyle \frac{{\mu }^2}{2}}]={\displaystyle \frac{A_c{}^2}{2R}}(1+{\mu }^2)$

Example-4:

A message signale of frequency $5\mathrm{kHz}$ and peak voltage of 7.5 volts is used to modulate a carrier of frequencies $2\mathrm{MHz}$ and peak voltage of 15 volts. Determine (a) modulation index, (b) the side bands produced.

Show Answer

Solution:

(a) Modulation index $=7.5/15=0.5$

(b) THe side bands are at $(2000+8\mathrm{kHz})=2008\mathrm{kHz}$ and $(2000-8\mathrm{KHz})=1992\mathrm{kHz}$.

Frequency Modulation (FM)

In this type of modulcation, the frequency of the carrier wave is varied in accordance with the amplitude of the modulating / information signal, this is shown in Figure 6(b).

Advantage of FM over AM

1. The FM signals has a larger bandwidth. Therefore, to accomodate more FM signals, on a particular frequency spectrum, without adjacent channel interference, higher carrier frequencies are used.

2. In FM signals, the intelligence is in the form of frequency variations. Hence the noise generated by atmospheric or man made electric discharge, does not affect the intelligence. Hence FM leads to less noisy transmission and reception.

3. Reproduction of the signal, at the receiver end, is of much better quality. FM is therefore, better for transmisstion of music.

Phase Modulation (PM)

The modulated wave follows the phase of the modulating / information signals as shown in Fig. 6 (c)

Production of Amplitude Modulated Wave

Amplitude modulation can be produced by a variety of methods. A simple method is shown in the block diagram of Fig. 8.

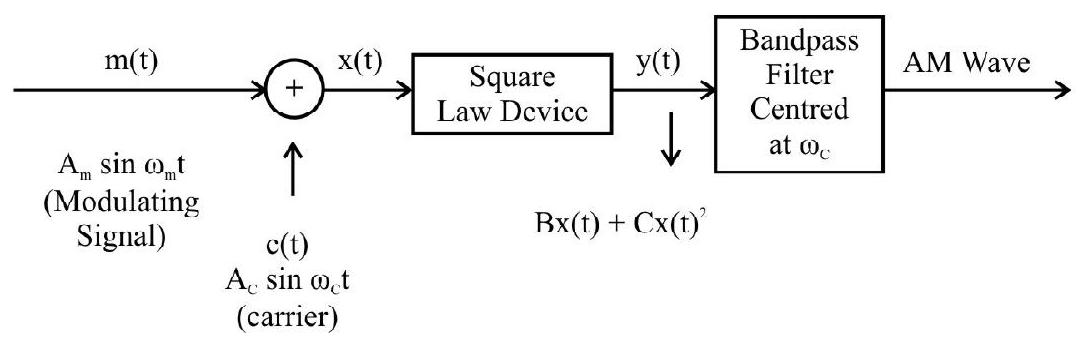
Fig. 8: Block diagram of a simple modulator for obtaining an AM signal

It is usual to have a ‘power amplifier’ for providing the necessary power to the output of an ‘amplitude modulator’. The output of the power amplifier, is fed into the ’transmitting antenna’ whose size is appropriate for good transmission.

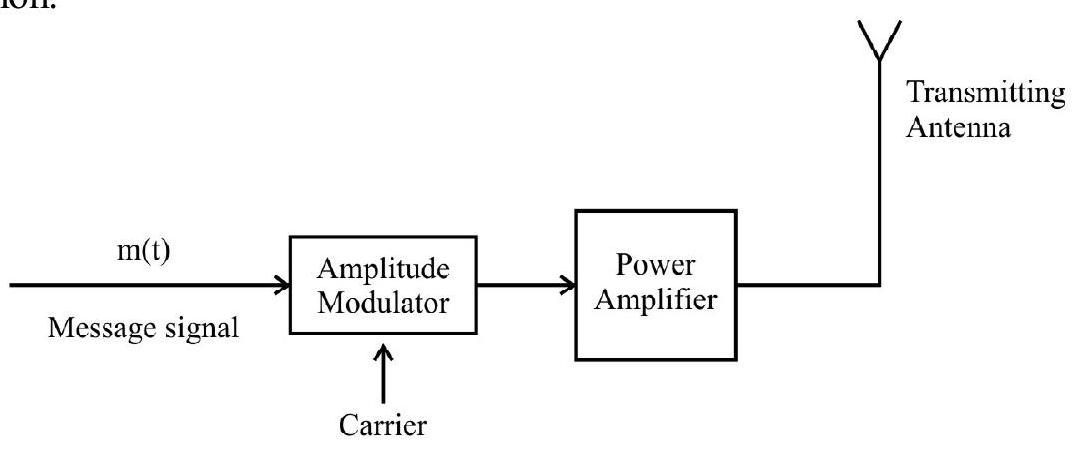
Fig. 9: Block diagram of a transmitler

Detection of Amplitude Modulated Wave

The amplitude modulated signal, when received by the receiving antenna, is made to go throgh the different stages, shown is the block diagram given below.

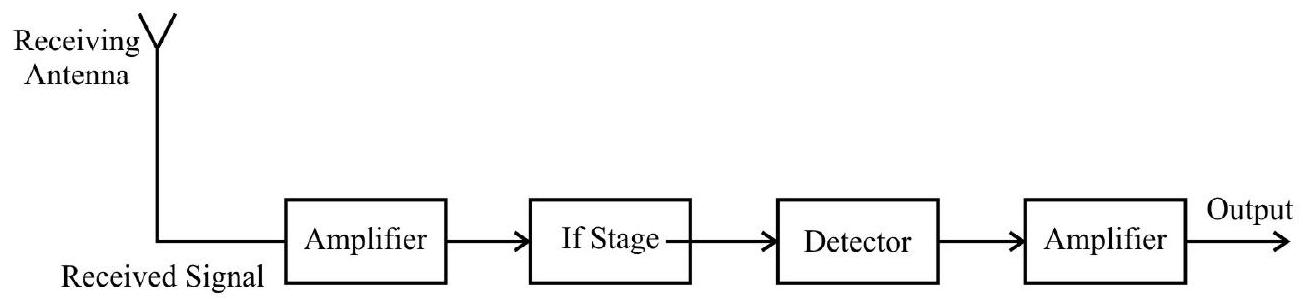
Fig. 10: Block diagram of a receiver

The signal received, is first amplified by using an appropriate amplifier. This is necessary to compensate for the energy lost during transmission. The IF (intermediate frequency) stage changes the (high) carrier frequency to a lower frequency. This helps in further processing of the signal. The detector receives the output of the IF stage and ‘separates out’ the ‘message signal’ from it. Another amplifier then amplifies this ‘message signal’ (received from the detector) before it is received as the output.

Detection

The (amplifier) modulated carrier wave has frequencies $({\omega }_{\mathrm{c}}\pm {\omega }_{\mathrm{m}})$ in addition to its own frequency ${\omega }_{\mathrm{c}}$. The detector helps is recovering the message signal, of frequency ${\omega }_{\mathrm{m}}$, from this Am wave. The block diagram given below, shows a simple method of achieving this aim.

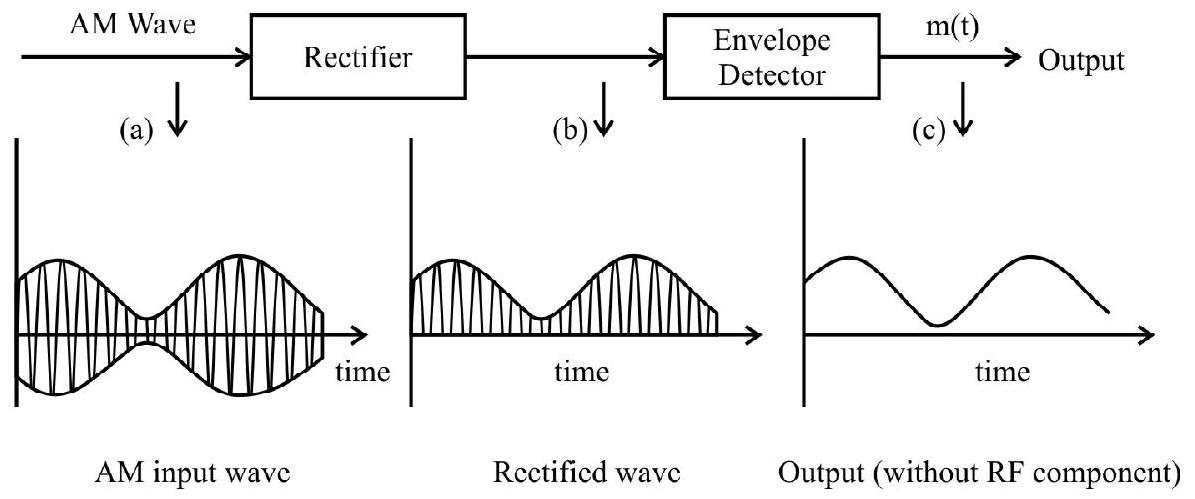
Fig. 11: Block diagram of a detector for AM signal

As shown here, the rectitier converts the Alvi wave into the torm shown. I he ’envelope detector’ then ’extracts’ the ’envelope’ of the rectified signal; this is the original message signal. [We use suitable circuits (like to RC circuit) to work as ’envelope detector’].

PROBLEMS FOR PRACTICE

1. What is the coverage range of television transmitting station if the height of transmitting atenna is $200\mathrm{m}$ ? Radius of earth $=6.4\times {10}^6\mathrm{m}$. If the population density of area is $4000{\mathrm{per}}^2{\mathrm{km}}^2$, then how much population is covered?

Show Answer

[Answer: $51\mathrm{km},3.2\times {10}^7$]

2. A transmitting antenna of height $\mathrm{h}$ and the receiving antenna of height $45\mathrm{m}$ are separated by a distance of $48\mathrm{km}$ for satisfactory communication $\stackrel{0}{m}$ line of sight mode of communication. Find the value of h

Show Answer

[Answer: $45\mathrm{m}$ ]

3. For an amplitude modulated wave, the maximum amplitude is found to be $10\mathrm{V}$, while the minimum amplitude is found to be $2\mathrm{V}$. Find the modulation index.

Show Answer

[Answer: $4/3$ ]

4. A TV tower has a height of $100\mathrm{m}$. If the average population density around the tower is $1500{\mathrm{km}}^2$, then the population covered by T.V broadcast is $n\times {10}^6$. What is the value of $n$ ? Radius of earth is $6.37\times {10}^6\mathrm{m}$.

Show Answer

[Answer: 6]

5. When the modulating frequency in frequency modulating system is $400\mathrm{Hz}$ and the modulating voltage is $2\mathrm{V}$; the modulation index is 40 . If the modulating signal is ${\mathrm{V}}_{\mathrm{m}}=4\sin 400\pi \mathrm{t}$ volt, then find the modulation index?

Show Answer

[Answer: 160]

6. What should be the length of dipole antenna for a carrier wave of frequency $6\times {10}^8\mathrm{Hz}$.

Show Answer

[Answer: $0.125\mathrm{m}$ ]

7. An AM wave is represented by ${\mathrm{c}}_{\mathrm{m}}(\mathrm{t})=6(1+0.5\cos 12560\mathrm{t})\cos 22\times {10}^5\mathrm{t}$. Calcualte:

(i) amplitude and frequency of carrier.

(ii) frequency of the modulating signal.

(iii) modulation index.

(iv) maximum and minimum amplitude of the AM wave.

Show Answer

[Answer: (i) ${\mathrm{A}}_{\mathrm{c}}6\mathrm{V},{\omega }_{\mathrm{c}}=22\times {10}^5\mathrm{rad}/\mathrm{s},{\omega }_{\mathrm{m}}=12560\mathrm{rad}/\mathrm{s},\mu =0.05,{\mathrm{A}}_{max}=9\mathrm{V},{\mathrm{A}}_{min}=3\mathrm{V}]$

8. An audio signal of amplitude one half the carrier amplitude is employed in amplitude modulation. What is the modulation index?

Show Answer

[Answer: $0.5$]

9. If the whole earth is to be connected by LOS communication using space waves (no restriction to antenna size or tower height), what is the minimum number of antennas required? Calculate the tower height of these anteenas in terms of earth’s surface?

Show Answer

[Answer: 6 antennas of height equal to radius of earth]

10. Calculate the percentage increase in the signal reception, if the height of TV tower is increased by $44\mathrm{\%}$.

Show Answer

[Answer: $20\mathrm{\%}$]

11. An AM wave is modulated by $25\mathrm{\%}$. What is the percentage saving in power if the carrier as well as one of the sidebands are suppressed?

Show Answer

[Answer: $98.4\mathrm{\%}$]

12. A sinusoidal carrier voltage of frequency $1.5\mathrm{MHz}$ and amplitude 50 volt is amplitude modulated by sinusoidal voltage of frequency $10\mathrm{KHz}$ producing $50$ modulation. Calculate the frequency of upper and lower sidebands.

Show Answer

[Answer: $1510\mathrm{Hz},1490\mathrm{Hz}$ ]

13. For skywave propagation of a $10\mathrm{MHz}$ signal, what should be the minimum electron density in ionosphere?

Show Answer

[Answer: $1.2\times {10}^3{\mathrm{m}}^{-3}$ ]

14. For an amplitude modulated wave, the maximum amplitude is found to be $10\mathrm{V}$ while the minimum amplitude is found to be $2\mathrm{V}$. Determine the modulation index.

Show Answer

[Answer: $2/3$ ]

15. In short wave communication waves, which frequency will be reflected back by the ionospheric layer having electron density ${10}^{11}\mathrm{per}{\mathrm{m}}^{-3}$.

Show Answer

[Answer: $2\mathrm{MHz}$]

Question Bank

Key Learning Points

1. Electronic communication is the act of transmission of information. Every communication system has three essential features, transmitter, medium / channel and receiver.

2. There are two basic modes of communication point to point and broadcast.

3. Information converted in electrical form and suitable for transmission is called a signal. Two important forms of communication system are Analog and digital. The information to be transmitted is generally in continuous waveform for Analog while for the digital it has only discrete or quantised levels.

4. Every message signal occupies a range of frequencies. The bandwidth refers to the frequency range over the spectrum occupied by the signal.

5. Most of the signals are in audio form, which cannot be transmitted over a long distance becuase:

(i) the antenna or aerial should have a size comparable to the wavelength of signal.

(ii) power radiated $\propto {\displaystyle \frac{1}{{\lambda }^2}}$. For good transmission, we need high powers and hence smaller wavelengths or higher frequencies.

(iii) low frequency signals transmitted as such will get mixed up and there is no way to distinguish between them.

Hence to transmit audio frequency signals, we use a high frequency signal called the carrier wave.

6. At transmitter, information contained in the low frequency message signal is superimposed on high frequency wave, which act as a carrier of the information. This process is known as modulation.

7. In modulation, some characterstics of the carrier signal like amplitude frequency or phase varies in accordance with the modulation or message signal. Correspondingly, they are called Amplitude Modulated (AM), Freqeuncy Modulated (FM) or Phase Modulated (PM) waves.

8. For transmisstion over long distances, signals are radiated into sapce using devices called antennas. The radiated signals propagate as electromagnetic waves and the mode of propagation is influenced by the presence of the earth and its atmosphere.

9. The radio waves which travel through atmosphere following the surface of earth are known as ground waves or surface waves. The ground wave propagation becomes weaker with increase in frequency. Hence ground wave propagation is suitable for low and medium frequency i.e. upto 20 MHz only.

10. In the frequency range from $2\mathrm{MHz}$ to $30\mathrm{MHz}$, long distance communication can be achieved by ionospheric reflection of radio waves back towards the earth. This mode of propagation is called sky wave propagation. If the frequency of radiowave is more than critical frequency it will not be reflected by ionosphere. The critical frequency of a sky wave for reflection from a layer of atmosphere is given by

${\mathrm{f}}_{\mathrm{c}}=9{\left({\mathrm{N}}_{max}\right)}^{1/2}\text{, where }\mathrm{N}\text{ is the number density of electron }/{\mathrm{m}}^3\text{ of a particular layer. }$

11. Space waves are radiowaves of very high frequency (between $30\mathrm{MHz}$ to $300\mathrm{MHz}$ or more). These waves are used for line of sight communication (LOS) and satellite communication.

12. The range of communication of space wave propagation can be increased by increasing the heights of transmitting and receiving antenna.

13. If ${\mathrm{h}}_{\mathrm{T}}$ is the height of transmiting antenna and $\mathrm{d}$ is the distance of receiving antenna from transmitting antenna then:

$\mathrm{d}=\sqrt{2{\mathrm{h}}_{\mathrm{T}}\mathrm{R}}$, where $\mathrm{R}$ is the radius of the earth.

For T.V. signal, area covered $=\pi {\mathrm{d}}^2=\pi 2\mathrm{Rh}$

Population covered $=$ population density $\times$ area covered.

If receiving antenna is at a height $h$, then maximum line of sight distance $d_{\mathrm{m}}$ between two antennas will be

${\mathrm{d}}_{\mathrm{m}}=\sqrt{2{\mathrm{h}}_{\mathrm{T}}\mathrm{R}}+\sqrt{2{\mathrm{h}}_{\mathrm{r}}\mathrm{R}}$

14. The satellite communication is a mode of communication of signal between transmitter and receiver through satellite. A communication satellite is a space craft, provided with microwave receiver and transmitter. It is placed in a geostationary orbit. The height $\mathrm{H}$ above the surface of the earth, for a geostationary satellite is

$\mathrm{H}={\left({\displaystyle \frac{\mathrm{GmT}}{4{\pi }^2}}\right)}^{1/3}-\mathrm{R}$

where $\mathrm{m}$ is the mass of earth, $\mathrm{R}$ the radius of earth and $\mathrm{T}$ time taken by the satellite to complete one orbit.

15. The AM carrier wave has, in addition to its own frequency ${\omega }_c$, two side bands of frequencies $({\omega }_{\mathrm{c}}+{\omega }_{\mathrm{m}})$ and $({\omega }_{\mathrm{c}}-{\omega }_{\mathrm{m}})$. Hence the bandwidth of the AM carrier wave is $2{\omega }_{\mathrm{m}}$.

16. If $\mathrm{c}(\mathrm{t})={\mathrm{A}}_{\mathrm{c}}\sin {\omega }_{\mathrm{c}}\mathrm{t}$ represents carrier wave and $\mathrm{m}(\mathrm{t})={\mathrm{A}}_{\mathrm{m}}\sin {\omega }_{\mathrm{m}}\mathrm{t}$ represent the message signal, then amplitude modulated signal is given by:

$c_m(t)=A_c\sin {\omega }_{c}t+\mu A_c\sin {\omega }_{m}t+\sin {\omega }_{c}t$

where $\mu ={\displaystyle \frac{A_m}{A_c}}$ is the modulation index. In practice $\mu$ is kept $<1$ to avoid distortion.

17. Amplitude modulated wave ${\mathrm{c}}_{\mathrm{m}}(\mathrm{t})$ can be produced by application of the message signal and the carrier wave to a non-linear device followed by a band pass filter.

18. AM signal cannot be transmitted as such. The modulator is to be followed by a power amplifier which provides the necessary power and then the modulated signal is fed to an antenna of appropriate size for radiation.

19. AM detection, which is the process of recovering the modulating signal from an AM waveform; is carried out using a rectifier and envelope detector.

20. For detection of amplitude modulated wave, the essential condition is ${\displaystyle \frac{1}{{\mathrm{f}}_{\mathrm{c}}}}«\mathrm{RC}$

where $f_c$ the frequency of carrier wave and $\mathrm{RC}$ time constant of envelope detector (simple RC circuit).

Average

Message signal

1. An audio message signal is a piece of information, which at a particular time,

(1) has only single value

(2) can have two values

(3) can hve a single value, or two values, depending on the time instant

(4) must have multiple values

Show Answer

Correct answer: (1)

Solution:

Audio signal, at a particular time, have only a single value, as their variation with time, is (usually) basically of the form shown here.

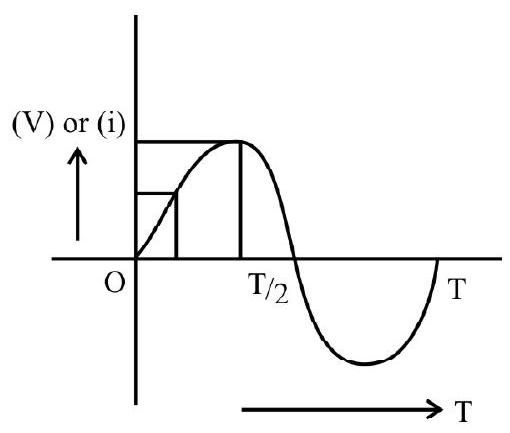
Average

Basic Elements of a Communication System

2. The ‘information source’, whose ‘message signal’ needs to be transmitted is (i) a picture (ii) a (audio) musical composition and (iii) a ‘pressure variation’. The transducers, likely to be used in the three cases, would be (respectively):

(1) based on photoelectric effect, based on piezoelectric effect and a microphone.

(2) based on piezoelectric effect, microphone and based on photoelectric effect.

(3) based on photoelectric effect; a microphone and based on piezoelectric effect.

(4) based on magneto-restriction effect; a microphone and based on photoelectric effect.

Show Answer

Correct answer: (3)

Solution:

A transducer is (usually) a device / setup that converts variations in a givn physical variable into their corresponding electrical variations. It thus ‘readies’ the message signal for transmission over large distances. For ‘picture’ (variations in light intensity) the relevant transducer is based on the ‘photoelectric effect’. For audio musical compositions (variations in sound intensity) the relevant transducer is the microphone. For pressure variation relevant transducer is based on the phenomenon of ‘piezo electric effect’.

Easy

Devices used in Communication System

3. The role of the satellites, in ’line of sight’ communication mode, can be regarded as similar to the role of a

(1) Transducer

(2) Transmitter

(3) Receiver

(4) Repeater

Show Answer

Correct answer: (4)

Solution:

The satellites, used for communication purposes, receive signals (from a transmitting station on the earth), amplify it and retransmit it (generally at a different carrier frequency) back towards the receiving stations on the earth. The role is, therefore, similar to that of a repeater. The repeater also picks up the signal from the transmitter, and retransmits it to the receiver, after amplifying it and (sometimes) changing its carrier frequency.

Easy

Space and Sky Wave Propagation

4. In the trosophere,

(1) Density of air molecules increases with increase in the altitude; and temperature decreases with increase in the altitude.

(2) Density of air molecules decreases with increases in the altitude; and temperature increases with increase in the altitutde.

(3) Density of air molecules and temperature, both increase with increase in the altitude.

(4) Density of air molecules and temperature, both decreases with increase in the altitude.

Show Answer

Correct answer: (4)

Solution:

The density of air molecules, as well as temperature of the air, have lower values at higher altitudes.

Easy

Space and Sky Wave Propagation

5. The atmospheric region which acts as ‘radio mirror’ is

(1) Troposphere

(2) Stratosphere

(3) Ionosphere

(4) Both troposphere and stratosphere

Show Answer

Correct answer: (3)

Solution:

Ionosphere (having a lot of air molecules ionised) reflects the radio waves back to the earth’s surface).

Easy

Space and Sky Wave Propagation

6. Thickest layer of the ionosphere is

(1) D layer

(2) E layer

(3) F1 layer

(4) F2 layer

Show Answer

Correct answer: (4)

Solution:

The approximate height of the four layers is as follows.

D layer $-65-75\mathrm{km}$

E layer $-100\mathrm{km}$

F1 layer - $170-190\mathrm{km}$

F2 layer $-300\mathrm{km}$ (at night) and $250-400\mathrm{km}$ (during day)

Easy

Space and Sky Wave Propagation

7. Locus of points at which direct rays from the antenna are tangential to the earth surface is called as,

(1) Critical circle

(2) Radio horizon

(3) Skip distance

(4) Verticalheight

Show Answer

Correct answer: (2)

Solution:

The radio horizon is a measure of the distance between the transmitter and the receiver, when the receiver is receving the ’line of sight’ rays from the transmitter.

Easy

Space and Sky Wave Propagation

8. The atmospheric layer which reflects low frequency waves and absorbs medium frequency waves is,

(1) Troposphere

(2) D layer of the ionosphere

(3) E layer of the ionosphere

(4) F1 layer of the ionosphere

Show Answer

Correct answer: (2)

Solution:

It is the D layer, of the ionosphere which reflects low frequency waves and absorbs medium frequency waves.

Average

Propagation of EM Waves

9. The (usual) modes of propagation of EM waves, having a frequency.

(i) less than a few $\mathrm{MHz}$

(ii) from a few MHz to (30-40) $\mathrm{MHz}$

(iii) above $40\mathrm{MHz}$

are respectively,

(1) Ground waves, space waves, sky waves

(2) Ground waves, sky waves, space waves

(3) Sky waves, space waves, ground waves

(4) Space waves, ground waves, sky waves

Show Answer

Correct answer: (2)

Solution:

In the ground wave mode of propagation the wave glides over the surface of the earth. This mode can be used only for frequencies less than a few MHz.

The sky wave uses the ionospheric reflection of radio waves; the ionospere does not reflect back waves of frequencies more than $(30-40)\mathrm{MHz}$.

The space wave mode of propagation is used for line sight communication and satellite communication is done primarily through this mode only.

Average

Propagation of EM Waves

10. With increase in frequency of the EM waves, to be transmitted via ground wave propagation, there is

(1) an increase in attenuation, but no change in the range of coverage

(2) a decrease in attenuation, but no change in the range of coverage

(3) an increase in attenuation, there is also a change in range of coverage

(4) a decrease in attenuation, there is also a change in the range of coverage

Show Answer

Correct answer: (3)

Solution:

In ground wave propagation, the attenuation of surface waves increases (very rapidly) with increase in frequency. The range of coverage also depends on the frequency of the transmitted EM Wave.

Average

Propagation of EM Waves

11. Four students made the following statements about the propagation of EM waves via the ground wave mode:

(A) The waves glide over the surface of the earth and lose energy because of the currents, induced by them, in the ground.

(B) This mode is useful for transmission of EM waves of frequencies more than $40\mathrm{MHz}$, the range of coverage gets limited due to the curvature of the earth.

(C) The waves propagate throgh air, this mode is useful only for EM waves of frequencies less than a few MHz.

(D) The wves glide over the surface of the earth; they lose energy primarily because of the energy absorbed by the intervening air.

The correct statement is that of student.

(1) $\mathrm{A}$

(2) $\mathrm{B}$

(3) $\mathrm{C}$

(4) $\mathrm{D}$

Show Answer

Correct answer: (1)

Solution:

In the ground wave mode of propagation, the wave glides over the surface of the earth. It induces currents in the ground over which it passes and this results in its loss of energy. This mode is practicable only for frequencies less than a few MHz.

Easy

Propagation of EM Waves

12. The peak of ionisation density, within the ionosphere, occurs neither at very low nor at very great heights; it occurs at some intermediate height. This is because at these intermediate heights, the

(1) Intensity of solar radiation, as well as the molecular concentration (of air molecule) attain their peak values.

(2) Intensity of solar radiation is at its peak, the molecular concentration (of air molecules) is also reasonably high.

(3) Intensity of solar radiation is resonably high; the molecular concentration (of air molecules) is at its peak value.

(4) Intensity of solar radiation, as well as the molecular concentration (of air molecules) are both reasonably high.

Show Answer

Correct answer: (4)

Solution:

The solar radiation is intense at great heights; the molecular concentration (of air molecules) is very high near the surface of the earth. At intermediate heights, both these terms are reasonably high; this results in a peak of ionisation density only at intermediate heights.

Average

Propagation of EM Waves

13. The process of ‘ionospheric reflection’ of radio waves is basically a process of

(1) Absorption and re-radiation; it results in a change of direction of propagation without any change in frequency

(2) Absorption and re-radiation; it results in a change of direction of propagation accompanied with a change in frequency.

(3) Reflection, akin to reflection from a plane mirror; it results in a change of direction of propagation accompanied with a change in frequency

(4) Reflection, akin to reflection from a concave mirror; it results in a change of direction of propagation without any change in frequency

Show Answer

Correct answer: (1)

Solution:

The ions absorb the incoming EM waves and start oscillating at its frequency. As per the EM theory, they then act as a source of EM aves whose frequency equals the frequency of oscillation of the ions.

Ionispheric reflection is, therefore, basically a process of absorption and ’re-radiation’; there is a change in the direction of propagation out no change a frequency.

Easy

Propagation of EM Waves

14. The phenomenon in optics, that is similar to the phenomenon of ionospheric reflection of radio waves, (by the ionosphere) is the phenomenon of

(1) Redfraction of light rays

(2) Diffused, irregular reflection, of light rays

(3) Regular, intense, reflection, of light rays

(4) Total internal reflection, of light rays

Show Answer

Correct answer: (4)

Solution:

Ionospheric reflection, of radio waves, may be regarded as similar to the phenomenon of ’total internal reflection’ in optics.

Easy

Space Wave Propagation

15. The height of a T.V. tower is 180 m. The distance up to which the transmission can be made from this tower is (nearly)

(1) 18 Km

(2) 48 Km

(3) 64 Km

(4) 90 Km

Show Answer

Correct answer: (2)

Solution:

The transmission range

$$\begin{array}{c}d=\sqrt{2\mathrm{Rh}}\\ \therefore d=\sqrt{2\times 6.4\times {10}^6\times 180}\end{array}$$

$$\begin{array}{rl}& =\sqrt{128\times 18}\times {10}^3\mathrm{m}\\ & =\sqrt{64\times 36}\times {10}^3\mathrm{m}\\ & =48\times {10}^3\mathrm{m}\\ & =48\mathrm{km}\end{array}$$

Average

Space Wave Propagation

16. The percentage, by which the transmission range of a T.V. tower, would be affected, when the height of the tower is increased by $21$ is (nearly).

(1) $10\mathrm{\%}$

(2) $11.5\mathrm{\%}$

(3) $21\mathrm{\%}$

(4) $42\mathrm{\%}$

Show Answer

Correct answer: (1)

Solution:

Original transmission range,

$$\begin{array}{}\text{(1)}& \mathrm{d}=\sqrt{2\mathrm{hR}}\end{array}$$

New height $h^{\prime }=(h+{\displaystyle \frac{21h}{100}})=1.21h$

$\therefore$ New transmission range,

$$\begin{array}{}\text{(3)}& {\mathrm{d}}^{\prime }=\sqrt{2{\mathrm{h}}^{\prime }\mathrm{R}}=\sqrt{2\times 1.21\mathrm{hR}}=1.1\mathrm{d}\text{ (using equation) }\end{array}$$

$\therefore$ Percentage increase in range

$$\begin{array}{rl}& =\left({\displaystyle \frac{d^{\prime }-d}{d}}\right)\times 100\\ & =\left({\displaystyle \frac{1.1\mathrm{d}-\mathrm{d}}{\mathrm{d}}}\right)\times 100=10\mathrm{\%}\end{array}$$

Average

Propagation of EM Waves

17. Let the radius of earth be devoted by $R$. The graph’s, representing, the co-relation between the height $(\mathrm{H})$ of a transmitting antenna and its radio horizon $\left({\mathrm{d}}_{\mathrm{m}}\right)$, is/are the graph/s labelled as graphs.

(1) (A) and (B)

(2) (B) and (C)

(3) (C) and (A)

(4) (C) and (D)

Show Answer

Correct answer: (3)

Solution:

The radio horizon, ${\mathrm{d}}_{\mathrm{m}}$, of a transmitting antenna, in related to its height $(\mathrm{H})$, through the relation.

$${\mathrm{d}}_{\mathrm{m}}=\sqrt{2\mathrm{RH}}(\mathrm{R}=\text{ Radius of the earth })$$

$\therefore {\mathrm{d}}_{\mathrm{m}}{}^2=2\mathrm{RH}$

Hence a graph, between ${\mathrm{d}}_{\mathrm{m}}$ and $\sqrt{\mathrm{H}}$, as well as that between ${\mathrm{d}}_{\mathrm{m}}{}^2$ and $\mathrm{H}$, would be a straight line, passing through the origin and having a slope 2R. It is graphs (A) and (C), that meet all these requirements.

Difficult

Propagation of EM Waves

18. In the diagram shown here, EM Waves, sent from a transmitting antenna, are being received back on the earth via ionosheric reflection. One can say that the

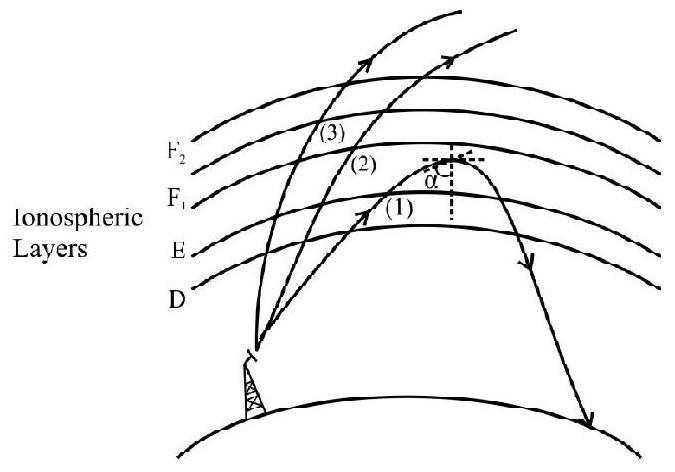
(1) (Relative) redfractive index, of the ionospheric layer, between the $\mathrm{E}$ and $\mathrm{F}$ layers in less than $\left({\displaystyle \frac{1}{\sin \alpha }}\right)$.

(2) (Relative) redfractive index, of the ionospheric layer, between the $\mathrm{E}$ and $\mathrm{F}$ layers, is, of the order of, or more than $\left({\displaystyle \frac{1}{\sin \alpha }}\right)$.

(3) Rays (2) and (3) are incident at angles greater than the critical angles for the layers ${\mathrm{F}}_1$ and ${\mathrm{F}}_2$.

(4) There are no ions at all, in the ionospheric layers above the layer ${\mathrm{F}}_1$, that can cause ionospheric reflection.

Show Answer

Correct answer: (2)

Solution:

The bending of EM waves, via ionospheric reflection, is similar to the phenomenon of total internal refelection. For TIR, we have,

$$\mu ={\displaystyle \frac{1}{\sin {\theta }_C}}$$

where ${\theta }_C$ is the critical angle for the given pair of media.

For $\mu$ less than $\left({\displaystyle \frac{1}{\sin {\theta }_{\mathrm{C}}}}\right)$ these can be no TIR when the angle of incidence is ${\theta }_{\mathrm{C}}$ or less.

Hence statements (1) and (3) are incorrect. Statement (4) is also incorrect as the layers mentioned have a relatively low ion………….

Difficult

Propagation of EM Waves

19. Suppose a given TV transmission system (using space wave mode of propagation), were set up in which the sum total $(\mathrm{H})$ of the height of the transmitting antenna $\left({\mathrm{H}}_{\mathrm{T}}\right)$ and the receiving antenna $\left({\mathrm{H}}_{\mathrm{R}}\right)$ remains constant. The ratio $\left({\mathrm{H}}_{\mathrm{T}}/{\mathrm{H}}_{\mathrm{R}}\right)$ to achieve maximum ’line of sight’ distance, between the two antennas, should be

(1) $2:3$

(2) $3:2$

(3) $1:1$

(4) $2:1$

Show Answer

Correct answer: (3)

Solution:

The line of sight distance, between the two antennas in given by

$${\mathrm{d}}_{\mathrm{m}}={\left(2{\mathrm{RH}}_{\mathrm{T}}\right)}^{1/2}+{\left(2{\mathrm{RH}}_{\mathrm{R}}\right)}^{1/2}$$

( $\mathrm{R}=$ radius of the earth)

$$={\left(2\mathrm{R}(\mathrm{H}-{\mathrm{H}}_{\mathrm{R}})\right)}^{1/2}+{\left(2{\mathrm{RH}}_{\mathrm{R}}\right)}^{1/2}$$

For maximum value of $d_m$, we should have

$$\begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\left({\mathrm{d}}_{\mathrm{m}}\right)}{{\mathrm{dH}}_{\mathrm{R}}}}=0\\ \therefore & {\displaystyle \frac{1}{2}}(-2\mathrm{R})+{\left(2\mathrm{R}(\mathrm{H}-{\mathrm{H}}_{\mathrm{R}})\right)}^{-1/2}+{\displaystyle \frac{1}{2}}{\left(2{\mathrm{RH}}_{\mathrm{R}}\right)}^{-1/2}(2\mathrm{R})=0\\ \text{ or }& {\displaystyle \frac{-1}{{\left[2\mathrm{R}(\mathrm{H}-{\mathrm{H}}_{\mathrm{R}})\right]}^{1/2}}}+{\displaystyle \frac{1}{{\left(2{\mathrm{RH}}_{\mathrm{R}}\right)}^{1/2}}}=0\\ \therefore & {\displaystyle \frac{-{\left(2{\mathrm{RH}}_{\mathrm{R}}\right)}^{1/2}+{\left(2\mathrm{R}(\mathrm{H}-{\mathrm{H}}_{\mathrm{R}})\right)}^{1/2}}{{\text{ Matter Not Clear }}^{1/2}}}=0\end{array}$$

or ${\left[2\mathrm{R}(\mathrm{H}-{\mathrm{H}}_{\mathrm{R}})\right]}^{1/2}={\left(2{\mathrm{RH}}_{\mathrm{R}}\right)}^{1/2}$

or $\mathrm{H}-{\mathrm{H}}_{\mathrm{R}}={\mathrm{H}}_{\mathrm{R}}$

$\therefore {\mathrm{H}}_{\mathrm{R}}={\displaystyle \frac{\mathrm{H}}{2}}$

$\therefore {\mathrm{H}}_{\mathrm{T}}=\mathrm{H}-{\mathrm{H}}_{\mathrm{R}}={\displaystyle \frac{\mathrm{H}}{2}}$

$\therefore {\displaystyle \frac{{\mathrm{H}}_{\mathrm{T}}}{{\mathrm{H}}_{\mathrm{R}}}}=(1:1)$

Average

Propagation of EM Waves

20. The height of a transmitting antenna, and its ‘redio horizon’, are denoted by $\mathbf{H}$ and $\mathbf{d}$ respectively. The radius of the earth is denoted by $R$. One can then say that a graph between.

(1) ${\mathrm{d}}_{\mathrm{m}}{}^2$ and $\mathrm{H}$ would be similar to the (time) ${}^2$ displacement graph of a particle, starting from rest and having a uniform acceleration a.

(2) ${\mathrm{d}}_{\mathrm{m}}$ and $\mathrm{H}$ would be similar to the graph between pressure and volume of an ideal gas under isothermal conditions.

(3) ${\mathrm{d}}_{\mathrm{m}}$ and $\sqrt{\mathrm{H}}$ would be similar to the displacement time graph of a particle having an initial velocity $u$ and a uniform acceleration a.

(4) ${\mathrm{d}}_{\mathrm{m}}$ and ${\mathrm{H}}^2$ would be similar to the graph between volume and temperature of an ideal gas under isobasic conditions.

Show Answer

Correct answer: (1)

Solution:

We known that ${\mathrm{d}}_{\mathrm{m}}=\sqrt{2\mathrm{RH}}$

$$\therefore {\mathrm{d}}_{\mathrm{m}}^2=(2\mathrm{R})\mathrm{H}$$

We also know that, for a particle starting from rest and having a uniformacceleration a,

$$\mathrm{s}={\displaystyle \frac{1}{2}}{\mathrm{at}}^2\text{ or }{\mathrm{t}}^2=\left({\displaystyle \frac{2}{\mathrm{a}}}\right)\mathrm{s}$$

$\therefore$ A graph between ${\mathrm{d}}_{\mathrm{m}}{}^2$ and $\mathrm{H}$ would be similar to the (time) ${}^2$ - displacement graph, of a particle starting from rest and having a uniform acceleration a.

The other listed (graphs - pairs) do not match.

Difficult

Propagation EM Waves

21. Let $\mathrm{R}$ and $\mathrm{M}$ denote the radius and mass of the earth and let $\mathrm{H}$ be the height of a geostationary satellite above the surface of the earth. Let $T_E$ denote the time taken by the earth to complete one rotation about its own axis.

The minimum time delay between the transmission of a signal, and its ‘receiving back’ on earth, after ‘reflection’ from a geostationary satellite, would be

(1) ${\displaystyle \frac{1}{\mathrm{c}}}[{\left({\displaystyle \frac{{\mathrm{GMT}}_{\mathrm{E}}}{2\pi }}\right)}^{1/3}-\mathrm{R}]$

(2) ${\displaystyle \frac{2}{\mathrm{c}}}[{\left({\displaystyle \frac{{\mathrm{GMT}}_{\mathrm{E}}^2}{4{\pi }^2}}\right)}^{1/3}-\mathrm{R}]$

(3) ${\displaystyle \frac{2}{\mathrm{c}}}[{\left({\displaystyle \frac{{\mathrm{GMT}}_{\mathrm{E}}}{4{\pi }^2}}\right)}^{1/3}+\mathrm{R}]$

(4) ${\displaystyle \frac{1}{\mathrm{c}}}[{\left({\displaystyle \frac{{\mathrm{GMT}}_{\mathrm{E}}}{2\pi }}\right)}^{1/3}+\mathrm{R}]$

Show Answer

Correct answer: (2)

Solution:

For a geostationary satellite, at a height $\mathrm{H}$ above the surface of the earth, we have

$${\displaystyle \frac{{\mathrm{mv}}^2}{(\mathrm{R}+\mathrm{H})}}={\displaystyle \frac{\mathrm{GmM}}{(\mathrm{R}+\mathrm{H}{)}^2}}$$

or $v=\sqrt{{\displaystyle \frac{GM}{(\mathrm{R}+\mathrm{H})}}}$

$\therefore$ Time taken by the satellite to complete one orbit.

$$\begin{array}{rl}& =\mathrm{T}={\displaystyle \frac{2\pi (\mathrm{R}+\mathrm{H})}{\mathrm{v}}}={\displaystyle \frac{2\pi (\mathrm{R}+\mathrm{H})\sqrt{(\mathrm{R}+\mathrm{H})}}{\sqrt{\mathrm{GM}}}}\\ & ={\displaystyle \frac{2\pi (\mathrm{R}+\mathrm{H}{)}^{3/2}}{\sqrt{\mathrm{GM}}}}\end{array}$$

This must equal, ${\mathrm{T}}_{\mathrm{E}}$, the time taken by the earth to complete one rotation on its axis. Hence

$${\mathrm{T}}_{\mathrm{E}}={\displaystyle \frac{2\pi (\mathrm{R}+\mathrm{H}{)}^{3/2}}{\sqrt{\mathrm{GM}}}}$$

or ${\displaystyle \frac{{\mathrm{T}}_{\mathrm{E}}^2\mathrm{GM}}{4{\pi }^2}}=(\mathrm{R}+\mathrm{H}{)}^3$

$\therefore (\mathrm{R}+\mathrm{H})={\left[{\displaystyle \frac{{\mathrm{T}}_{\mathrm{E}}^2}{4{\pi }^2}}\mathrm{GM}\right]}^{1/3}$

$\therefore \mathrm{H}=[{\left({\displaystyle \frac{{\mathrm{GMT}}_{\mathrm{E}}^2}{4{\pi }^2}}\right)}^{1/3}-\mathrm{R}]$

The minimum distance the signal has to travel equals $(\mathrm{H}+\mathrm{H})$, i.e. $2\mathrm{H}$.

Hence,

Minimum time dalay $={\displaystyle \frac{2\mathrm{H}}{\mathrm{C}}}$

$$={\displaystyle \frac{2}{\mathrm{C}}}[{\left({\displaystyle \frac{{\mathrm{GMT}}_{\mathrm{E}}^2}{4{\pi }^2}}\right)}^{1/3}-\mathrm{R}]$$

Average

Propagation of EM Waves

22. The ‘space wave’ mode of propagation of EM waves is used for LOS communication as well as for ‘satellite communication’. During satellite communication.

(1) The frequencies used are generally in the radio wave and microwave part of the e.m. spectrum; the satellite usually retransmits the signal at a carrier freqeuncy different from the carrier freqeuncy of its incoming signal.

(2) The frequencies used are generally in the infrared and microwave part of the e.m. spectrum; the satellite always retransmits the signal at the same carrier frequency as that of the incoming signal.

(3) The frequencies used are generally in the radio and microwave part of the e.m. spectrum; the satellite always transmits the signal at the same carrier frequency as that of the incoming signal.

(4) The frequencies used are generally in the infrared part of the e.m. spectrum; the satellite usually retransmits the signal at a carrier freqeuncy different from the carrier frequency of the incoming signal.

Show Answer

Correct answer: (1)

Solution:

The frequencies, used in satellite communication, are generally in the radio and microwave parts of the e.m. spectrum.

The satellite receives the signal, amplified and usually refransmitts it at a carrier frequency different from the carrier frequency of the incoming signal. It does so to avoid intermixing of the outgoing signal.

Average

‘Line of Sight’ Propagation E.M. Waves

23. For the ‘combination’ of a transmitting antenna, of height ${\mathrm{H}}_{\mathrm{T}}$ and a receiving antenna, of height $H_R$, their ‘radio horizon’ equals $x$ when $H_R=H_T$. Without changing the height of the receivng antenna, the height of the transmitting antenna is increased to 4 times its earlier value. The new value of their ‘radio horizon’ would be.

(1) $1.5x$

(2) $2x$

(3) $3x$

(4) $4x$

Show Answer

Correct answer: (1)

Solution:

The radio horizon is given by

$$\mathrm{d}=\sqrt{2{\mathrm{HR}}_{\mathrm{T}}}+\sqrt{2{\mathrm{RH}}_{\mathrm{R}}}$$

In the first case, then

$$x=\sqrt{2{\mathrm{RH}}_{\mathrm{T}}}+\sqrt{2{\mathrm{RH}}_{\mathrm{R}}}=2\sqrt{2{\mathrm{RH}}_{\mathrm{T}}}$$

In the second case, if $x^{\prime }$ is the radio horizon,

We have,

$$\begin{array}{rl}& x^{\prime }=\sqrt{2\mathrm{R}\cdot 4{\mathrm{H}}_{\mathrm{T}}}+\sqrt{2{\mathrm{RH}}_{\mathrm{T}}}\\ & =3\sqrt{2{\mathrm{RH}}_{\mathrm{T}}}={\displaystyle \frac{3x}{2}}\end{array}$$

$\therefore$ Now value of ‘radio horizon’ $={\displaystyle \frac{3x}{2}}$

$$=1.5x$$

Easy

Bandwidth of Transmission Media

24. The bandwidth of three different transmission media, say, A, B, C, are $(750\mathrm{MHz})$, (from a few $\mathrm{kHz}$ to a few $\mathrm{GHz}$ ) and (up to $100\mathrm{GHz}$ ). The media A, B and C, are (respectively), likely to be

(1) (wire/a co-axial cable), optical fibres and air (or space)

(2) air (or sapce), (wire / a co-axial cable) and optical fibres

(3) a (wire co-axial cable); air (or space) and optical fibres

(4) air (or space); (wire / a co-axial cable) and optical fibres

Show Answer

Correct answer: (3)

Solution:

(Wires / Co-axial cables) have relatively small bandwidths _ of the order of $750\mathrm{MHz}$.

Air (or space) has bandwidth ranging from a few $\mathrm{kHz}$ to a few $\mathrm{GHz}$. Optical fibres _ a real revolution in communication technology have bandwidth that can go up to about $100\mathrm{GHz}$.

Easy

Modulation

25. It is known that the height of a transmission antenna should preferably be of the order. The length of antenna at a place is $0.75\mathrm{m}$. Its optimum transmission frequency would be (nearly)

(1) $25\mathrm{MHz}$

(2) $50\mathrm{MHz}$

(3) $75\mathrm{MHz}$

(4) $100\mathrm{MHz}$

Show Answer

Correct answer: (4)

Solution:

Length of antenna required $={\displaystyle \frac{\lambda }{4}}$

$$\begin{array}{rl}\lambda & =4\ell \\ & =(4\times 0.75)\mathrm{m}=3\mathrm{m}\\ \therefore \gamma & ={\displaystyle \frac{\mathrm{C}}{\lambda }}={\displaystyle \frac{3\times {10}^8}{3\mathrm{m}}}\mathrm{m}/\mathrm{s}\\ & ={\displaystyle \frac{{10}^8}{5}}={10}^2\mathrm{MHz}\\ & =100\mathrm{MHz}\end{array}$$

Easy

‘Need for Modulation’

26. If an audio signal were to be transmitted directly over a long distance, the minimum size of transmitting antenna would be of the order of

(1) $(500)\mathrm{m}$

(2) $1\mathrm{km}$

(3) $2\mathrm{km}$

(4) $4\mathrm{km}$

Show Answer

Correct answer: (4)

Solution:

Considering the upper limit of the audio frequency range (i.e. $20\mathrm{kHz}$ ), the wavelength, of the corresponding e.m. wave (of this frequency), would be

$$\begin{array}{rl}& \lambda ={\displaystyle \frac{\mathrm{C}}{\gamma }}={\displaystyle \frac{3\times {10}^8}{2\times {10}^4}}\mathrm{m}=1.5\times {10}^4\mathrm{m}\\ & =15\times {10}^3\mathrm{m}\simeq 15\mathrm{km}\end{array}$$

The optimum size of the antenna being, of the order of ${\displaystyle \frac{\lambda }{4}}$, we need to have an antenna size of the order of $3.75\mathrm{km}(\simeq 4\mathrm{km})$.

Easy

Amplitude Modulation

27. A carrier wave $\mathbf{c}(t)$, shown below, is amplitude modulated by the message signal $m(t)$ shown above. The shape, of the resultant amplitude modulated wave, would than be s per the figure labelled as figure.

(1) A

(2) B

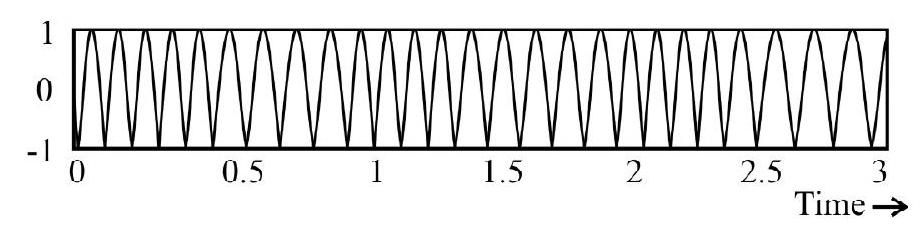
(3) C

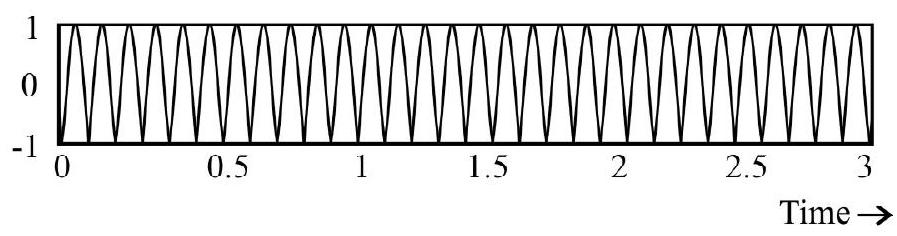
(4) D

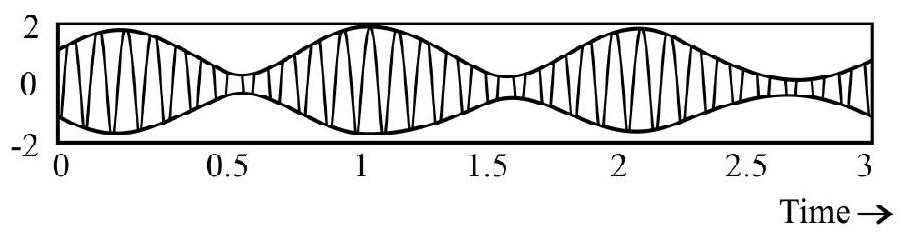
Show Answer

Correct answer: (4)

Solution:

There is no change in the frequency of the carrier wave when it is aplitude modulated by a message signal. However, the peak value of its amplitude (on the positive as well as the negative side) does not remain constant; it varies as per the variations of the message signal. It is only diagram (D) that shows (correctly) the variations in the amplitude (as per the message signal) of the carrier wave.

Average

Amplitude Modulation

28. A carrier wave

$$\mathbf{c}(\mathbf{t})={\mathbf{A}}_{\mathrm{c}}\sin \left({\omega }_{\mathrm{c}}\mathbf{t}\right)$$

is amplitude modulated by a message signal

$$m(t)=A_m\sin \left({\omega }_{c}t\right)\text{ where }{A}_m=10\mathrm{V}$$

The AM wave has a modulation index of 0.5 and side bands of frequencies $1010\mathrm{kHz}$ and $990\mathrm{kHz}$. The value of $A_c$ and the frequencies of the carrier wave, and the message signal, are, respectively.

(1) $5\mathrm{V};1\mathrm{MHz}$ and $20\mathrm{kHz}$

(2) $5\mathrm{V};2\mathrm{MHz}$ and $10\mathrm{kHz}$

(3) $20\mathrm{V};1\mathrm{MHz}$ and $10\mathrm{kHz}$

(4) $20\mathrm{V};2\mathrm{MHz}$ and $20\mathrm{kHz}$

Show Answer

Correct answer: (3)

Solution:

We know that

Modulation index $=\mu ={\displaystyle \frac{A_m}{A_c}}={\displaystyle \frac{10\mathrm{V}}{A_c}}$

$\therefore {\mathrm{A}}_{\mathrm{c}}={\displaystyle \frac{10}{0.5}}\mathrm{V}=20\mathrm{V}$

Also ‘side bands’ have frequencies

$$({\gamma }_c-{\gamma }_m)\text{ and }({\gamma }_c+{\gamma }_m)$$

$\therefore {\gamma }_{\mathrm{c}}+{\gamma }_{\mathrm{m}}=1010\mathrm{kHz}$

and ${\gamma }_{\mathrm{c}}-{\gamma }_{\mathrm{m}}=900\mathrm{kHz}$

These give

$${\gamma }_{\mathrm{c}}=1000\mathrm{kHz}=1\mathrm{MHz}$$

and

$${\gamma }_{\mathrm{m}}=10\mathrm{kHz}$$

Difficult

Amplitude Modulation

29. A carrier wave

$$\mathbf{c}(\mathbf{t})={\mathbf{A}}_{\mathrm{c}}\sin \left({\omega }_{\mathrm{c}}\mathbf{t}\right)$$

is amplitude modulated by a message signal

$$\mathbf{m}(\mathbf{t})={\mathbf{A}}_{\mathrm{m}}\sin \left({\omega }_{\mathrm{m}}\mathbf{t}\right)$$

The equation, for the (amplitude) modulated wave, and the rms value of its amplitude (over the time interval 0 to ${\displaystyle \frac{2\pi }{{\omega }_{\mathrm{m}}}}$ ) would then be, respectively.

(1) $[A_c\sin \left({\omega }_{m}t\right)+A_n\sin \left({\omega }_{m}t\right)]$ and $\left({\displaystyle \frac{A_c+A_m}{\sqrt{2}}}\right)$

(2) $[A_c+A_m\sin \left({\omega }_{m}t\right)]\sin \left({\omega }_{m}t\right)$ and ${(A_m^2+{\displaystyle \frac{A_m^2}{2}})}^{1/2}$

(3) $[A_c+A_c\sin \left({\omega }_{c}t\right)]\sin \left({\omega }_{m}t\right)$ and ${(A_m^2+{\displaystyle \frac{A_m^2}{2}})}^{1/2}$

(4) $[{\mathrm{A}}_{\mathrm{c}}\sin \left({\omega }_{\mathrm{c}}\mathrm{t}\right)\sim {\mathrm{A}}_{\mathrm{n}}\sin \left({\omega }_{\mathrm{m}}\mathrm{t}\right)]$ and $\left({\displaystyle \frac{{\mathrm{A}}_{\mathrm{c}}\sim {\mathrm{A}}_{\mathrm{m}}}{\sqrt{2}}}\right)$

Show Answer

Correct answer: (2)

Solution:

When a carrier wave is amplitude modulated, by message signal, it is the amplitude, of the carrier wave, that is made to vary in accordance with the message signal. Hence the equation for the amplitude modulated wave is

$$[A_c+A_m\sin \left({\omega }_{m}t\right)]\sin {\omega }_{c}t$$

The rms valus of its amplitude is the rms value of the term $[A_c+A_m\sin \left({\omega }_{m}t\right)]$. The rms value is the square root of the average of

$$[A_c+A_m\sin \left({\omega }_{m}t\right)]$$

i.e. square root of the average of

$$[A_c^2+A_m^2{\sin }^2\left({\omega }_{m}t\right)+2A_c{A}_m{\sin }^2\left({\omega }_{m}t\right)]$$

Difficult

Amplitude Modulation

30. A carrier wave

$$\mathbf{c}(\mathbf{t})={\mathbf{A}}_{\mathrm{c}}\sin \left({\omega }_{\mathrm{c}}\mathbf{t}\right)$$

is amplitude modulated by a message signal

$$\mathbf{m}(\mathbf{t})={\mathbf{A}}_{\mathrm{m}}\sin \left({\omega }_{\mathrm{m}}\mathbf{t}\right)$$

The amplitude modulated wave can be regarded as made up of the

(1) original carrier wave of frequency ${\omega }_c$ and amplitude $A_c$ and two sinusoidal waves, each of amplitude $\left({\mathrm{A}}_{\mathrm{m}}/2\right)$ and frequencies $({\omega }_{\mathrm{c}}\pm {\omega }_{\mathrm{m}})$.

(2) original carrier wave of frequency ${\omega }_c$ and amplitude $({\mathrm{A}}_{\mathrm{c}}+{\mathrm{A}}_{\mathrm{m}})$ and two sinusoidal waves, of amplitude ${\mathrm{A}}_{\mathrm{m}}$ each and frequencies $({\omega }_{\mathrm{c}}\pm {\omega }_{\mathrm{m}})$.

(3) modified carrier wave of frequency $({\omega }_c+{\omega }_m)$ and amplitude ${\mathrm{A}}_{\mathrm{c}}$ and two sinusoidal waves, of amplitude $\left({\mathrm{A}}_{\mathrm{m}}/2\right)$ each and frequencies $({\omega }_{\mathrm{c}}\pm {\omega }_{\mathrm{m}})$.

(4) modified carrier wave of frequency $({\omega }_c-{\omega }_m)$ and amplitude $A_c$ and two sinusoidal waves, of amplitude ${\mathrm{A}}_{\mathrm{m}}$ each and frequencies $({\omega }_{\mathrm{c}}\pm {\omega }_{\mathrm{m}})$.

Show Answer

Correct answer: (1)

Solution:

The equation of the amplitude modulated carrier wave is

$$\begin{array}{rl}& [A_c+A_m\sin \left({\omega }_{m}t\right)]\sin \left({\omega }_{c}t\right)\\ & =A_c\sin \left({\omega }_{c}t\right)+{\displaystyle \frac{A_m}{2}}[2\sin \left({\omega }_{m}t\right)\sin \left({\omega }_{c}t\right)]\\ & =A_c\sin \left({\omega }_{c}t\right)+{\displaystyle \frac{A_m}{2}}[\cos ({\omega }_c-{\omega }_m)t-\cos ({\omega }_c+{\omega }_m)t]\end{array}$$

Hence the amplitude modulated carrier wave can be regarded as made up of the

(i) original carrier wave of amplitude ${\mathrm{A}}_{\mathrm{c}}$ and frequency ${\omega }_c$ and

(ii) two sinusoidal waves, each of amplitude $\left({\displaystyle \frac{A_m}{2}}\right)$ and frequencies $({\omega }_c\pm {\omega }_m)$.

Difficult

Amplitude Modulation

31. In the process of amplitude modulation, the modulating (message) signal $\mathbf{m}(t)[={\mathbf{A}}_{\mathrm{m}}\sin \left({\omega }_{\mathrm{m}}t\right)]$ is added to the carrier wave $c(t)[={\mathbf{A}}_{\mathrm{c}}\sin \left({\omega }_{\mathrm{c}}t\right)]$, to produce the output signal $x(t)[=A_m\sin \left({\omega }_{c}t\right)+A_c\sin \left({\omega }_{c}t\right)]$. The devices, through which this signal is made to pass, before being fed into the transmitting antenna (as an AM wave), are sequence wise, the

(1) power amplifier, square law device and band pass filter.

(2) band pass filter, power amplifier and square law device.

(3) square law device, band pass filter and power amplifier.

(4) power amplifier, band pass filter and square law device.

Show Answer

Correct answer: (3)

Solution:

The sequence of (amplitude) modulation, of the carrier wave by the message signal is as per the block diagram shown here.

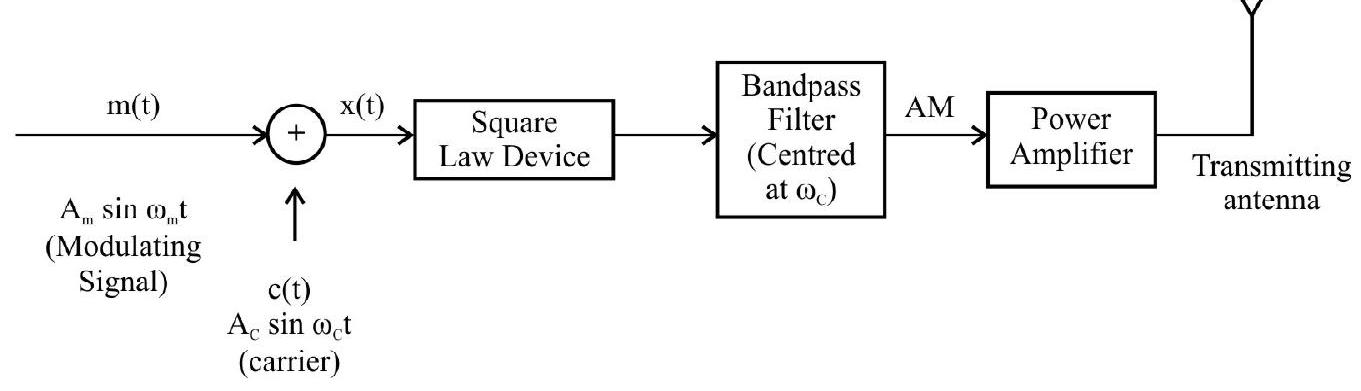
After adding the message signal $\mathrm{m}(\mathrm{t})$ to the carrier wave $\mathrm{c}(\mathrm{t})$, the signal $x(\mathrm{t})$ is produced. This is passed into a square law device whose output contains a d.c. term and sinusoidal of frequencies ${\omega }_{\mathrm{m}},2{\omega }_{\mathrm{m}},{\omega }_{\mathrm{c}}$, $2{\omega }_{\mathrm{c}},({\omega }_{\mathrm{c}}-{\omega }_{\mathrm{m}})$ and $({\omega }_{\mathrm{c}}+{\omega }_{\mathrm{m}})$. The band pass filter than rejects the d.c. term and sinusoids of frequencies ${\omega }_{\mathrm{c}},({\omega }_{\mathrm{c}}-{\omega }_{\mathrm{m}})$ and $({\omega }_{\mathrm{c}}+{\omega }_{\mathrm{m}})$. This output is the AM wave which has its central frequency ${\omega }_{\mathrm{c}}$ an its side band frequencies $({\omega }_{\mathrm{c}}-{\omega }_{\mathrm{m}})$ and $({\omega }_{\mathrm{c}}+{\omega }_{\mathrm{m}})$.

The output of the band pass filter is followed by a power amplifier. This provides it the necessary power. This power argumental signal is than fed into an appropriate sized transmitting antenna which than radiates it out into space.

Easy

Modulation

32. The two well known types of modulation are the amplitude modulation (AM) and frequency modulation (FM). In each of these, one of the characterstics (amplitude $={\mathbf{A}}_c$, frequency $=$ $f_c$, of the carrier wave, may be made to vary as per the variations of the (varying) ‘amplitude’ $(=A_m)$ or the frequency $(=f_m)$ of the message signal. The relevant correlation is:

(1) During $AM$, it is $A_c$ that varies as per $f_m$ and during $FM$, it is $f_c$ that varies as per $A_m$.

(2) During AM, it is ${\mathrm{A}}_{\mathrm{c}}$ that varies as ${\mathrm{A}}_{\mathrm{m}}$ and during $\mathrm{FM}$, it is ${\mathrm{f}}_{\mathrm{c}}$ that varies as per ${\mathrm{f}}_{\mathrm{m}}$

(3) During AM, it is ${\mathrm{A}}_{\mathrm{c}}$; and during FM, it is ${\mathrm{f}}_{\mathrm{c}}$ that both vary as per ${\mathrm{f}}_{\mathrm{m}}$

(4) During AM, it is ${\mathrm{A}}_{\mathrm{c}}$; and during FM, it is ${\mathrm{f}}_{\mathrm{c}}$ that both vary as per ${\mathrm{A}}_{\mathrm{m}}$

Show Answer

Correct answer: (2)

Solution:

During amplitude modulation, it is the amplitude, of the carrier wave, that varies in accordance with the variation of the ‘amplitude’ of the message signal.

During frequency modulation it is the frequency, of the carrier wave, that varies is accordance with the variations of the ‘amplitude’ of the message signal.

Average

AM and FM

33. The following are some statements about amplitude modulation (AM) and frequency modulation (FM):

(A) The SNR (Signal to noise ratio) is better for AM as compared to FM.

(B) During FM, linear amplifiers are not required because FM signals have a constant amplitude.

(C) The operating range of AM as well as FM are nearly of the same order.

(D) The fidelity of reception, for FM, is much better than for AM.

The correct statement/s, from the above, is / are the statement / s.

(1) (B) only

(2) (B) and (D) only

(3) (A) and (C) only

(4) (C) only

Show Answer

Correct answer: (2)

Solution:

Statement (A) is incorrect; it is the other way round.

Statement (C) is incorrect; the operating range of FM is higher than that of AM.

Statement (B) and (D) are both correct statements.

Average

AM and FM

34. The following are some statement about AM (amplitude modulation) and FM (frequency modulation):

(A) The circuitary for AM is more complex than that for FM.

(B) The bandwidth of the signals, during AM, is twice the freqeuncy of the message signal.

(C) The bandwidth of the signals, during FM, is much more than twice the frequency of the message signals.

(D) During frequency modulation, the frequency of the carrier wave varies in accordance with the frequency of the message signals.

The correct statement’s, from the above, is / are the statement / s.

(1) (A) and (C)

(2) (B) only

(3) (D) only

(4) (B) and (C)

Show Answer

Correct answer: (4)

Solution:

Statement (A) is incorrect; it is the other way round.

Statement (D) is incorrect; during FM, the frequency of the carrier wave varies in accordance with the ‘amplitude’ of the message signal.

Statement (B) and (C) are both correct. During AM, the sideband frequency being $({\omega }_{\mathrm{c}}-{\omega }_{\mathrm{m}})$ and $({\omega }_{\mathrm{c}}+{\omega }_{\mathrm{m}})$, the bandwidth of the signal is $2{\omega }_{\mathrm{m}}$.

During FM, the bandwith of the signal is much higher than $2\omega$.

Average

Bandwidth

35. A carrier wave of frequency $2\mathrm{MHz}$, is amplitude modulated by a given message signal. The ‘message signal’ contains a mix-up of audio signals of frequencies $750\mathrm{Hz},1200\mathrm{Hz}$ and $5000\mathrm{Hz}$.

The bandwidth of the resultant AM carrier wave can be

(1) $4.250\mathrm{kHz}$

(2) $10\mathrm{kHz}$

(3) $1995.750\mathrm{kHz}$

(4) $2004.250\mathrm{kHz}$

Show Answer

Correct answer: (2)

Solution:

The Am carrier wave has, in addition to its own carrier frequency, two sidebands of frequencies $({\omega }_{\mathrm{c}}-{\omega }_{\mathrm{m}})$ and $({\omega }_{\mathrm{c}}+{\omega }_{\mathrm{m}})$. The ‘bandwidth’, of a signal, equals the difference between its highest frequency and its lowest frequency. Hence the bandwidth, of the AM carrier wave, is

$$({\omega }_{\mathrm{c}}+{\omega }_{\mathrm{m}})-({\omega }_{\mathrm{c}}-{\omega }_{\mathrm{m}})=2{\omega }_{\mathrm{m}}$$

Its bandwidth is, therefore, twice the frequency of the modulating (message) signal. In the given case, the message signal contains $5000\mathrm{Hz}$ as its highest frequency. Hence the bandwidth can be taken as $10\mathrm{kHz}$.

Difficult

Bandwidth

36. The carrier waves $c_1(t)$ and $c_2(t)$, of frequencies $75\mathrm{kHz}$, and $2.25\mathrm{MHz}$, are both ‘amplitude modulated’. The bandwidths, of the two resultant (AM) carrier waves, are $5\mathrm{kHz}$ each. The ‘amount of information’, carried by the two AM carrier waves $[c_{1\mathrm{m}}(t)$ and $c_{2\mathrm{m}}(t)]$ would then be

(1) More for the wave ${\mathrm{c}}_{2\mathrm{m}}(\mathrm{t})$ than for the wave ${\mathrm{c}}_{1\mathrm{m}}(\mathrm{t})$

(2) Similar for both the waves

(3) In the ratio $1:3$, for the waves ${\mathrm{c}}_{1\mathrm{m}}(\mathrm{t})$ and ${\mathrm{c}}_{2\mathrm{m}}(\mathrm{t})$

(4) In the ratio 3:1, for the waves $c_{1\mathrm{m}}(t)$ and $c_{2\mathrm{m}}(t)$

Show Answer

Correct answer: (2)

Solution:

We know that the bandwidth, of an AM carrier wave, is twice the frequency of its modulating (or message) signal. It does not depend on the frequency of the carrier wave itself.

Here the bandwidth, in the two cases, is given to be identical. This implies taht the ‘message signals’, in the two cases, are similar. We can, therefore, take the ‘amount of information’, carried by the two carrier waves (of different frequencies) to be similar.

Difficult

Amplitude Modulation / Bandwidth

37. A carrier wave, $\mathbf{c}(\mathbf{t})$, given by

$$c(t)=[12\sin (4\pi \times {10}^{6}t)]$$

is amplitude modulated by a given sinusoidal volts message signal. The resultant (AM) carrier wave has a modulation index of $75$ and a bandwidth that is $2$ of the carrier wave frequency. The equations for this message signal is

(1) on $(t)=[16\sin (4\pi \times {10}^4)]$ volt

(2) on $(t)=[9\sin (4\pi \times {10}^{4}t)]$ volt

(3) on $(t)=[9\sin (8\pi \times {10}^{4}t)]$ volt

(4) $\mathrm{on}(\mathrm{t})=[16\sin (8\pi \times {10}^4\mathrm{t})]$ volt

Show Answer

Correct answer: (2)

Solution:

We know that

Modulation index, $\mu ={\displaystyle \frac{A_m}{A_c}}$

$$\begin{array}{rl}& \therefore {\displaystyle \frac{75}{100}}={\displaystyle \frac{A_m}{12}}\\ & \therefore A_m=9\text{ volt }\end{array}$$

Further, for an (AM) carrier wave,

Bandwidth $=2\times$ frequency of the message signal.

$$\begin{array}{rl}& \therefore {\displaystyle \frac{2}{100}}\times [2\times {10}^6]=2\times v_{\mathrm{m}}\\ & \therefore v_{\mathrm{m}}=2\times {10}^4\mathrm{Hz}\end{array}$$

$\therefore$ The equation for the message signal is

$$\mathrm{m}(\mathrm{t})=[9\sin (2\pi \times (2\times {10}^4)\mathrm{t})]\text{ volt }$$

Easy

Amplitude Modulation

38. The amplitude modulated wave, shown here, is processed (at the receiver end), successively, into the forms (a) and (b), shown alongside.

The devices, used for getting the AM input wave into the forms (a) and (bv), are known, respectively, as

(1) rectifier and transducer

(2) rectifier and envelope detector

(3) transducer and evelope detector

(4) transducer and rectifier

Show Answer

Correct answer: (2)

Solution:

At the receiving end, the AM intant wave is first rectified by using a rectifier. The rectified output is then processed by an envelope detector which removes its RF component and gives its envelope (the original message signal) as its output.

Difficult

Amplitude Modulation and Frequency Modulation

39. A carrier wave

$$\mathbf{c}(\mathbf{t})={\mathbf{A}}_{\mathbf{c}}\sin \left({\omega }_{\mathrm{c}}\mathbf{t}\right)$$

is to be (i) amplitude modulated (ii) frequency modulated by a message signal

$$\mathbf{m}(\mathbf{t})={\mathbf{A}}_{\mathrm{m}}\sin \left({\omega }_{\mathrm{m}}\mathbf{t}\right)$$

The equations (i) $c_{\text{ma }}(t)$, for the amplitude modulated and (ii) $c_{mf}(t)$, for the frequency modulated, carrier wave, may then be expressed as

(1) $$\begin{array}{rl}& c_{ma}(t)=[A_c+A_m\sin \left({\omega }_{m}t\right)]\sin \left({\omega }_{c}t\right)\\ & \text{ and }{c}_{mf}(t)=\left[A_c[\sin ({\omega }_c+k{A}_m\sin {\omega }_{m}t)]t\right]\end{array}$$

(2) $${\mathrm{c}}_{\text{ma }}(t)=[{\mathrm{A}}_{\mathrm{c}}\sin \left({\omega }_{\mathrm{m}}\mathrm{t}\right)]\sin \left({\omega }_{\mathrm{c}}\mathrm{t}\right)$$

$$\begin{array}{}\text{(Incorrect)}& \text{ and }{c}_{mf}(t)=\left[A_c[\sin ({\omega }_c+k{A}_m\sin {\omega }_{m}t)]t\right]\end{array}$$

(3) $$\begin{array}{}\text{(3)}& c_{ma}(t)=[A_c\sin \left({\omega }_{m}t\right)]\sin \left({\omega }_{c}t\right)\end{array}$$

$$\begin{array}{}\text{(Incorrect)}& \text{ and }{c}_{mf}(t)=[A_c\sin ({\omega }_c+\sin \left({\omega }_{m}t\right))t]\end{array}$$

(4) $$\begin{array}{}\text{(4)}& {\mathrm{c}}_{\mathrm{ma}}(\mathrm{t})=[{\mathrm{A}}_{\mathrm{c}}+{\mathrm{A}}_{\mathrm{m}}\sin \left({\omega }_{\mathrm{m}}\mathrm{t}\right)]\sin \left({\omega }_{\mathrm{c}}\mathrm{t}\right)\end{array}$$

$$\begin{array}{}\text{(Incorrect)}& \text{ and }{c}_{mf}(t)=[A_c\sin ({\omega }_c+\sin \left({\omega }_{m}t\right))t]\end{array}$$

Show Answer

Correct answer: (1)

Solution:

In amplitude modulation, the amplitude, of the carrier, wave gets modified, in accordance with the ‘instantaneous amplitude’ of the message signal. Hence the instantaneous amplitude, of the carrier wave, has the form

$$A_c^{\prime }=A_c+A_m\sin \left({\omega }_{m}t\right)$$

Here there is no change in the frequency of the carrier wave. Hence the equation, for the amplitude modulated carrier wave, has the form

$$c_{ma}(t)=[A_c+A_m\sin \left({\omega }_{m}t\right)]\sin \left({\omega }_{c}t\right)$$

In frequency modulation, it is the frequency of the carrier wave that varies in accordance with the ‘instantaneous amplitude’ of the message signal. Hence the instantaneous frequency has the form

$${\omega }_c^{\prime }={\omega }_c+k(A_m\sin {\omega }_{m}t)$$

The factor $\mathrm{k}$ here would have the dimensions of (hertz / volt)].

Here there is no change in the amplitude of the carrier wave. Hence the equation for the frequency modulated carrier wave would have the form

$$\begin{array}{rl}& c_{mf}(t)=A_c\sin \left({\omega }_c^{\prime }t\right)\\ & =[A_c\sin ({\omega }_c+k{A}_m\sin {\omega }_{m}t)t]\end{array}$$

Difficult

Space and Sky Wave Propagation

40. In space wave propagation, radio waves (having wavelength $\lambda$ ) are transmitted from transmitter (having height $T$ ) and reaches the receiver (having height $R$ ) located at a distance, $d$, by two methods ($d»T,d»R$). The first is the direct transmisstion from transmitter to the antenna. The second is the transmisstion from transmitter to the earth surface, followed by reflection from the earth surface.

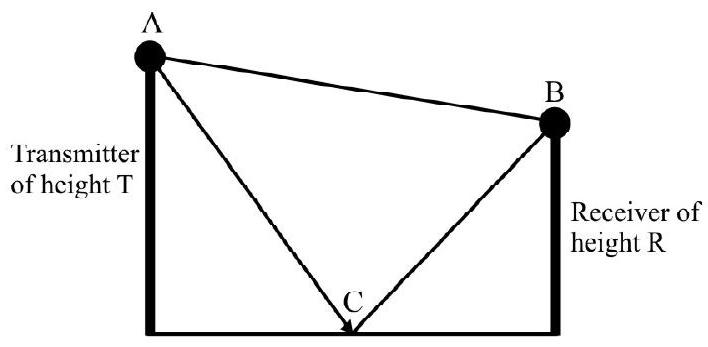
Distance between transmitter and receiver $-\mathrm{d}$

Assuming that the reflection, from the earth’s surface, takes place from a point midway between the transmitter and the receiver, the total phase difference between the two waves at the receiver will be:

(1) $\pi$

(2) ${\displaystyle \frac{4\pi \mathrm{TR}}{\lambda \mathrm{d}}}$

(3) ${\displaystyle \frac{4\pi \mathrm{TR}}{\lambda \mathrm{d}}}+\pi$

(4) ${\displaystyle \frac{4\pi \mathrm{TR}}{\lambda \mathrm{d}}}-\pi$

Show Answer

Correct answer: (3)

Solution:

The direct distance $(\mathrm{AB})$ traversed by the wave between the transmitter and the receiver can be calculated as,

$$\begin{array}{rl}& (AB{)}^2=d^2+(T-R{)}^2\\ & \Rightarrow AB=d{[1-{\displaystyle \frac{T-R^2}{d^2}}]}^{{\displaystyle \frac{1}{2}}}=d+{\displaystyle \frac{1}{2}}{\displaystyle \frac{(T-R{)}^2}{d}}\end{array}$$

Similarly, the distance (AC plus CB) traversed by the wave between the transmitter and the receiver will be given by,

$$\mathrm{AC}+\mathrm{CB}=\mathrm{d}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{(\mathrm{T}+\mathrm{R}{)}^2}{\mathrm{d}}}$$

Path difference $(\mathrm{\Delta })$ between the two wave at the receiver $=(\mathrm{AC}+\mathrm{CB})-(\mathrm{AB})$

$$\mathrm{\Delta }=\{\mathrm{d}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{(\mathrm{T}+\mathrm{R}{)}^2}{{\mathrm{d}}^2}}\}-\{\mathrm{d}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{(\mathrm{T}-\mathrm{R}{)}^2}{{\mathrm{d}}^2}}\}={\displaystyle \frac{2\mathrm{TR}}{\mathrm{d}}}$$

Phase difference $=\delta ={\displaystyle \frac{2\pi }{\lambda }}\mathrm{\Delta }={\displaystyle \frac{4\pi \mathrm{TR}}{\lambda \mathrm{d}}}$

Since the second wave gets reflected from the earth surface, which a denser medium, therefore, an additional phase difference is of $\pi$ will be introduced.

Total phase difference $=\pi +{\displaystyle \frac{4\pi \mathrm{TR}}{\lambda \mathrm{d}}}$

Difficult

Space and Sky Wave Propagation

41. In space wave propagation, radio waves (having wavelength $\lambda$ ) are transmitted from transmitter (having height $T$ ) and reaches the receiver (having height $R$ ) located at a distance, $d$, by two methods $(d«T,d«R)$. The first is the direct transmisstion from transmitter to the antenna. The second is the transmisstion from transmitter to the earth surface, followed by reflection from the earth surface.

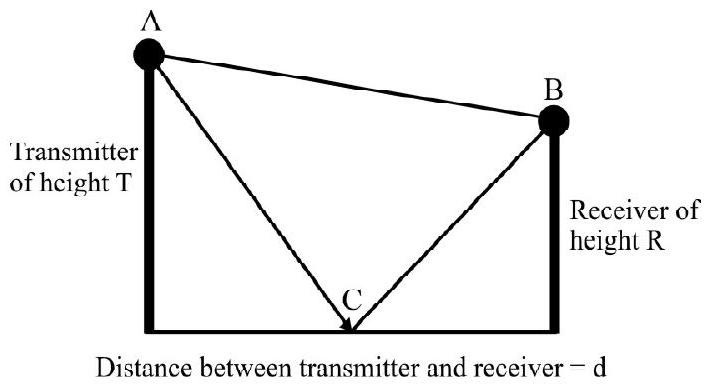
It may be assumed that the reflection, from the earth’s surface takes place from a point midway between the transmitter and the receiver. Considering that the amplitude of both the waves is $\mathrm{E}$, then the resultant field strength amplitude $\left({\mathrm{E}}_{\mathrm{R}}\right)$ will be equal to,

(1) $12\mathrm{E}\sin \left({\displaystyle \frac{4\pi \mathrm{TR}}{\lambda \mathrm{d}}}\right)$

(2) $12\mathrm{E}\sin \left({\displaystyle \frac{2\pi \mathrm{TR}}{\lambda \mathrm{d}}}\right)$

(3) $12\mathrm{E}\cos \left({\displaystyle \frac{4\pi \mathrm{TR}}{\lambda \mathrm{d}}}\right)$

(4) $12\mathrm{E}\cos \left({\displaystyle \frac{2\pi \mathrm{TR}}{\lambda \mathrm{d}}}\right)$

Show Answer

Correct answer: (2)

Solution:

The resultant field strength amplitude can be calculated as follows.

$$\begin{array}{rl}& (\mathrm{ER}{)}^2={\mathrm{E}}^2+{\mathrm{E}}^2+2\mathrm{E}\cdot \mathrm{E}\cos (\pi +{\displaystyle \frac{4\pi \mathrm{TR}}{\lambda \mathrm{d}}})\\ & =(\mathrm{ER}{)}^2=2{\mathrm{E}}^2[1+\cos (\pi +{\displaystyle \frac{4\pi \mathrm{TR}}{\lambda \mathrm{d}}})]\\ & =(\mathrm{ER}{)}^2=2{\mathrm{E}}^2[2{\cos }^2\left({\displaystyle \frac{\pi +{\displaystyle \frac{4\pi \mathrm{TR}}{\lambda \mathrm{d}}}}{2}}\right)]\\ & ={\mathrm{E}}_{\mathrm{R}}=2\mathrm{E}\cos ({\displaystyle \frac{\pi }{2}}+{\displaystyle \frac{2\pi \mathrm{TR}}{\lambda \mathrm{d}}})\\ & ={\mathrm{E}}_{\mathrm{R}}=2\mathrm{E}\sin \left({\displaystyle \frac{2\pi \mathrm{TR}}{\lambda \mathrm{d}}}\right)\\ & =2{\mathrm{E}}^2[+2{(-\sin (\pi +{\displaystyle \frac{4\pi \mathrm{TR}}{\lambda \mathrm{d}}}))}^2]\\ & =4{\mathrm{E}}^2{\sin }^2\left({\displaystyle \frac{2\pi \mathrm{TR}}{\lambda \mathrm{d}}}\right)\end{array}$$

$$\therefore {\mathrm{E}}_{\mathrm{R}}=2\mathrm{E}\sin \left(\frac{2\pi \mathrm{TR}}{\mathrm{d}}\right)$$

Average

Amplitude Modulation

42. At $100\mathrm{\%}$ modulation, let the total power in the sidebands be $x\mathrm{\%}$ of the total power of the amplitude modulated wave. Here, ${}^{\prime }x$ ’ is equal to,

(1) 25

(2) 33.3

(3) 75

(4) 100

Show Answer

Correct answer: (2)

Solution:

fraction of total power carried by the sidebands $={\displaystyle \frac{{\mathrm{m}}^2}{2+{\mathrm{m}}^2}}$

Therefore, at $100\mathrm{\%}$ modulation, sidebands carry only $1/3$ rd of the total power.

Difficult

Space and Sky Wave Propagation

43. In space wave propagation, radio waves (having wavelength $\lambda$ ) are transmitted from transmitter (having height $T$ ) and reaches the receiver (having height $R$ ) located at a distance, $d$, by two methods ( $d«T,d«R)$. The first is the direct transmisstion from transmitter to the antenna. The second is the transmisstion from transmitter to the earth surface, followed by reflection from the earth surface.

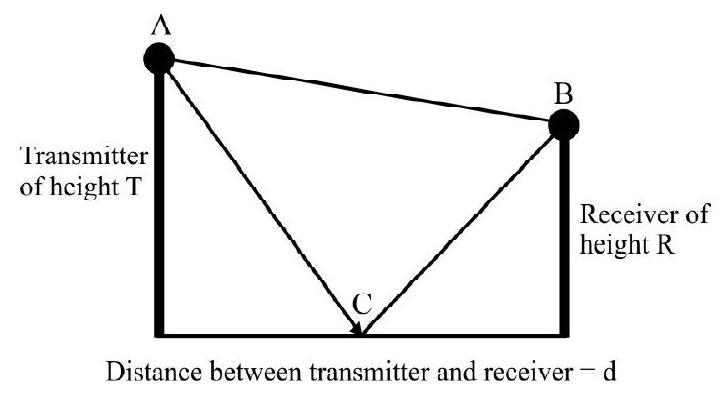
It may be assumed that the reflection, from the earth’s surface takes place from a point midway between the transmitter and the receiver. If the height of the transmitting antenna is doubled, then, the total field strength at the receiver will:

(1) Remain same

(2) Get doubled

(3) Get halved

(4) Increase by $\sqrt{2}$ times

Show Answer

Correct answer: (2)

Solution:

Consider that the amplitude of both the waves is $\mathrm{E}$, then the resultant field strength amplitude $\left({\mathrm{E}}_{\mathrm{R}}\right)$ will be equal to,

$${\mathrm{E}}_{\mathrm{R}}=+2\mathrm{E}\sin \left({\displaystyle \frac{2\pi \mathrm{TR}}{\lambda \mathrm{d}}}\right)$$

But since, $\mathrm{d}»\mathrm{T},\mathrm{d}»\mathrm{R}$, therefore,

$${\mathrm{E}}_{\mathrm{R}}+2\mathrm{E}\left({\displaystyle \frac{2\pi \mathrm{TR}}{\lambda \mathrm{d}}}\right)=-{\displaystyle \frac{4\mathrm{E}\pi \mathrm{TR}}{\lambda \mathrm{d}}}$$

$\Rightarrow {\mathrm{E}}_{\mathrm{R}}\propto \mathrm{T}$

Difficult

Amplitude Modulation

44. The modulation index of an amplitude modulated wave is 0.4 . The fraction of total power carried by the central carrier wave will be equal to,

(1) $40\mathrm{\%}$

(2) $80\mathrm{\%}$

(3) $92.6\mathrm{\%}$

(4) $100\mathrm{\%}$

Show Answer

Correct answer: (3)

Solution:

Power of the central carrier wave $=P_C={\displaystyle \frac{V_C^2}{R}}$

Total power $=\mathrm{P}={\displaystyle \frac{{\mathrm{V}}_{\mathrm{C}}^2}{\mathrm{R}}}\left[{\displaystyle \frac{2+{\mathrm{m}}^2}{2}}\right]$

$$={\displaystyle \frac{{\mathrm{P}}_{\mathrm{C}}}{\mathrm{P}}}={\displaystyle \frac{2}{2+{\mathrm{m}}^2}}={\displaystyle \frac{2}{2+0.16}}=92.6\mathrm{\%}$$

Average

Amplitude Modulation

45. As the value of the modulation index increases,

(1) Amplitude of the central band increases

(2) Amplitude of the central band decreases

(3) Total power carried by the sidebands increases

(4) Total power carried by the sidebands decreases

Show Answer

Correct answer: (3)

Solution:

Amplitude of the central band is independent of the modulation index.

fraction of total power carried by the central carrier wave $={\displaystyle \frac{2}{2+{\mathrm{m}}^2}}$

fraction of total power cariied by the sidebands $={\displaystyle \frac{{\mathrm{m}}^2}{2+{\mathrm{m}}^2}}$

Therefore, as the modulation index increases, the useful power carried by the central band decreases, but the carried by the sidebands increases.

Difficult

Amplitude Modulation

46. In the modulation index is $80\mathrm{\%}$, then, power in each sideband is $x\mathrm{\%}$ of that in the central carrier band. Here, ’ $x$ ’ is equal to,

(1) 0

(2) 16

(3) 20

(4) 32

Show Answer

Correct answer: (2)

Solution:

Power carried by the central carrier wave $={\mathrm{P}}_{\mathrm{C}}={\displaystyle \frac{{\mathrm{V}}_{\mathrm{C}}^2}{2\mathrm{R}}}$

Power carried by each sidebands $={\mathrm{P}}_{\mathrm{S}}={\displaystyle \frac{{\mathrm{m}}^2{\mathrm{V}}_{\mathrm{C}}^2}{8\mathrm{R}}}$

Therefore, at $80$ modulation.

$${\displaystyle \frac{{\mathrm{P}}_{\mathrm{S}}}{{\mathrm{P}}_{\mathrm{C}}}}={\displaystyle \frac{{\mathrm{m}}^2}{4}}=16\mathrm{\%}$$

Difficult

Amplitude Modulation

47. Instantaneous voltage of the amplitude modulated wave is given by

$$v_{\mathrm{AM}}={\mathrm{V}}_{\mathrm{C}}(1+\mathrm{m}\sin {\omega }_{\mathrm{m}}\mathrm{t})\sin {\omega }_{\mathrm{c}}\mathrm{t}$$

Assuming that the effective resistance of the modulator circuit is R, the total power of the amplitude modulated wave will be equal to,

(1) ${\displaystyle \frac{{\mathrm{V}}_{\mathrm{C}}^2}{2\mathrm{R}}}$

(2) ${\displaystyle \frac{m^2{V}_C^2}{8R}}$

(3) ${\displaystyle \frac{m^2{V}_C^2}{4R}}$

(4) ${\displaystyle \frac{{\mathrm{V}}_{\mathrm{C}}^2}{2\mathrm{R}}}\left[{\displaystyle \frac{1+{\mathrm{m}}^2}{2}}\right]$

Show Answer

Correct answer: (4)

Solution:

The instantaneous voltage of the amplitude modulated wave can be written as,

$$v_A=V_C\sin 2\pi f_{c}t+{\displaystyle \frac{m{V}_C}{2}}\cos (2\pi f_c-2\pi f_m)t-{\displaystyle \frac{m{V}_C}{2}}\cos (2\pi f_c+2\pi f_m)t$$

Power of the central carrier wave $=P_C={\displaystyle \frac{{\left({\mathrm{v}}_{\mathrm{C}}/\sqrt{2}\right)}^2}{\mathrm{R}}}{\displaystyle \frac{{\mathrm{V}}_{\mathrm{C}}^2}{2\mathrm{R}}}$

Power of the two sidebands $=P_S={\displaystyle \frac{{\left({\mathrm{mv}}_{\mathrm{C}}/2\sqrt{2}\right)}^2}{R}}+{\displaystyle \frac{{\left({\mathrm{mv}}_{\mathrm{C}}/2\sqrt{2}\right)}^2}{\mathrm{R}}}={\displaystyle \frac{{\mathrm{m}}^2{\mathrm{V}}_{\mathrm{C}}^2}{2\mathrm{R}}}$

Total power $=\mathrm{P}={\mathrm{P}}_{\mathrm{C}}+{\mathrm{P}}_{\mathrm{S}}={\displaystyle \frac{{\mathrm{V}}_{\mathrm{C}}^2}{2\mathrm{R}}}+{\displaystyle \frac{{\mathrm{m}}^2{\mathrm{V}}_{\mathrm{C}}^2}{4\mathrm{R}}}={\displaystyle \frac{{\mathrm{V}}_{\mathrm{C}}^2}{2\mathrm{R}}}[1+{\mathrm{m}}^2]$

Easy

Amplitude Modulation

48. In a communication system, the process of modulation is done at the

(1) Transmitter

(2) Receiver

(3) Channel between the transmitter and receiver

(4) Both transmitter and receiver

Show Answer

Correct answer: (1)

Solution:

It is necessary to modulate the (usual) low frequency message signals before they can be transmitted for communication over large distances.

Easy

Amplitude Modulation

49. Im aplitude modulation,

(1) Amplitude of the low frequency carrier signal is varied in accordance with the high frequency message signal

(2) Amplitude of the high frequency carrier signal is varied in accordance with the low frequency message signal

(3) Amplitude of the low frequency carrier signal is varied in accordance with the high frequency carrier signal

(4) Amplitude of the high frequency carrier signal is varied in accordance with the low frequency carrier signal

Show Answer

Correct answer: (2)

Solution:

We need a high frequency carrier wave for effective transmisstion of low frequency message signals in amplitude modulation, it is the amplitude of the high frequency carriers wave that is varied in accordance with the low frequency message signal.

Average

Amplitude Modulation

50. Suppose the carrier wave is modulated in accordance with the amplitude of a message signal.

The modulation index is $\mathrm{m}$. The Instantaneous carrier voltage is represented by, $v_{\mathrm{c}}={\mathrm{V}}_{\mathrm{C}}\sin {\omega }_{\mathrm{c}}\mathrm{t}$. The instantaneous modulating voltage is presented by, $v_{\mathrm{m}}={\mathrm{V}}_{\mathrm{m}}\sin {\omega }_{\mathrm{m}}\mathrm{t}$. Amplitude of the amplitude modulated wave will be represented by,

(1) ${\mathrm{V}}_{\mathrm{c}}\sin {\omega }_{\mathrm{c}}\mathrm{t}$

(2) $V_m\sin {\omega }_{m}t$

(3) ${\mathrm{V}}_{\mathrm{c}}(1+\sin {\omega }_{\mathrm{m}}\mathrm{t})$

(4) $V_c(1+\sin {\omega }_{m}t)\sin {\omega }_{c}t$

Show Answer

Correct answer: (3)

Solution:

Modulation index $=\mathrm{m}={\displaystyle \frac{{\mathrm{V}}_{\mathrm{m}}}{{\mathrm{V}}_{\mathrm{c}}}}$

Amplitude of the amplitue modulated wave will be given by,

$$V_{AM}=V_c+v_m=V_c+v_m\sin {\omega }_{m}t=v_c+\sin v_c{\omega }_{m}t=v_c(1+m\sin {\omega }_{m}t)$$

Average

Amplitude Modulation

51. Suppose the carrier wave is modulated in accordance with the amplitude of a message signal.

The modulation index is $\mathrm{m}$. The Instantaneous carrier voltage is represented by, $v_{\mathrm{c}}={\mathrm{V}}_{\mathrm{C}}\sin {\omega }_{\mathrm{c}}\mathrm{t}$. The instantaneous modulating voltage is presented by, $v_{\mathrm{m}}={\mathrm{V}}_{\mathrm{m}}\sin {\omega }_{\mathrm{m}}\mathrm{t}$. The time variation of the instantaneous voltage, of the amplitude modulated wave, will be represented by,

(1) $V_c\sin {\omega }_{\mathrm{c}}\mathrm{t}$

(2) ${\mathrm{V}}_{\mathrm{m}}\sin {\omega }_{\mathrm{m}}\mathrm{t}$

(3) ${\mathrm{V}}_{\mathrm{c}}(1+\sin {\omega }_{\mathrm{m}}\mathrm{t})$

(4) $V_c(1+\sin {\omega }_{m}t)\sin {\omega }_{c}t$

Show Answer

Correct answer: (4)

Solution:

Modulation index $=\mathrm{m}={\displaystyle \frac{{\mathrm{V}}_{\mathrm{m}}}{{\mathrm{V}}_{\mathrm{c}}}}$

Amplitude of the amplitue modulated wave will be given by,

$${\mathrm{V}}_{\mathrm{AM}}={\mathrm{V}}_{\mathrm{c}}+{\mathrm{V}}_{\mathrm{m}}={\mathrm{V}}_{\mathrm{c}}+{\mathrm{v}}_{\mathrm{m}}\sin {\omega }_{\mathrm{m}}\mathrm{t}={\mathrm{v}}_{\mathrm{c}}+\sin {\mathrm{v}}_{\mathrm{c}}{\omega }_{\mathrm{m}}\mathrm{t}={\mathrm{v}}_{\mathrm{c}}(1+\mathrm{m}\sin {\omega }_{\mathrm{m}}\mathrm{t})$$

Instantaneous voltage of the amplitude modulated wave will be equal to,

$$v_{\mathrm{AM}}={\mathrm{V}}_{\mathrm{c}}(1+\mathrm{m}\sin {\omega }_{\mathrm{m}}\mathrm{t})\sin {\omega }_{\mathrm{c}}\mathrm{t}$$

Average

Amplitude Modulation

52. Suppose the carrier wave is modulated in accordance with the amplitude of a message signal.

The modulation index is $\mathrm{m}$. The Instantaneous carrier voltage is represented by, $v_{\mathrm{c}}={\mathrm{V}}_{\mathrm{c}}\sin 2\pi {\mathrm{f}}_{\mathrm{c}}\mathrm{t}$. The instantaneous modulating voltage is presented by, $v_{\mathrm{m}}={\mathrm{V}}_{\mathrm{m}}\sin 2\pi {\mathrm{f}}_{\mathrm{m}}\mathrm{t}$.

The bandwidth of the amplitude modulated wave is equal to,

(1) $2f_m$

(2) $2f_c$

(3) $f_c-f_m$

(4) $f_c+f_m$

Show Answer

Correct answer: (1)

Solution:

Instantaneous voltage of the amplitude modulated wave is represented by,

$$\begin{array}{rl}& v_{Am}=V_c\sin 2\pi f_{c}t+m{V}_c\sin 2\pi f_{m}t\sin 2\pi f_{c}t\\ & =V_c\sin 2\pi f_{c}t+{\displaystyle \frac{m{V}_c}{2}}\cos (2\pi f_c-2\pi f_m)t-{\displaystyle \frac{m{V}_c}{2}}\cos (2\pi f_c+2\pi f_m)t\end{array}$$

This implies that in addition to the original central frequency, there exist side bands in an amplitude modulated wave. The frequency of upper sideband is equal to, $f_c+f_m$. The frequency of lower sideband is equal to $f_c$ $-f_m$. The bandwidth is the difference in frequency of the side bands, which is given by,

Bandwidth $=({\mathrm{f}}_{\mathrm{c}}+{\mathrm{f}}_{\mathrm{m}}-{\mathrm{f}}_{\mathrm{c}}+{\mathrm{f}}_{\mathrm{m}})=2{\mathrm{f}}_{\mathrm{m}}$

Difficult

Amplitude Modulation

53. An amplitude modulated wave is represented by,

$$v_{\mathrm{AM}}=4(1+0.2\sin 314\mathrm{t})\sin (314\times {10}^{2}t)$$

For this wave, one can say that

(1) Frequency of the upper sideband is $5000\mathrm{Hz}$; and frequency of the lower sideband is $50\mathrm{Hz}$

(2) Frequency of the upper sideband is $100\mathrm{Hz}$; and frequency of the lower sideband is $50\mathrm{Hz}$

(3) Frequency of the upper sideband is $5050\mathrm{Hz}$; and frequency of the lower sideband is $4950\mathrm{Hz}$

(4) Frequency of the upper sideband is $314\times {10}^2\mathrm{Hz}$; and frequency of the lower sideband is $314\mathrm{Hz}$

Show Answer

Correct answer: (3)

Solution:

According to the expression,

Frequency of the modulating wave $={\mathrm{f}}_{\mathrm{m}}={\displaystyle \frac{1}{2\pi }}314=50\mathrm{Hz}$

Frequency of the carrier wave $=f_m={\displaystyle \frac{1}{2\pi }}(314={10}^2)=5000\mathrm{Hz}$

Therefore,

Frequency of the upper sideband $={\mathrm{f}}_{\mathrm{c}}-{\mathrm{f}}_{\mathrm{m}}=5050\mathrm{Hz}$

Frequency of the lower sideband $=f_c-f_m=4950\mathrm{Hz}$

Average

Amplitude Modulation

54. An amplitude modulated wave is represented by,

$$v_{\mathrm{AM}}=4(1+0.2\sin 314\mathrm{t})\sin (314\times {10}^{2}t)$$

The bandwidth of the amplitude modulated wave is equal to,

(1) $50\mathrm{Hz}$

(2) $1000\mathrm{Hz}$

(3) $314\mathrm{Hz}$

(4) $314\times {10}^2$

Show Answer

Correct answer: (2)

Solution:

According to the expression,

Frequency of the modulating wave $={\mathrm{f}}_{\mathrm{m}}={\displaystyle \frac{1}{2\pi }}314=50\mathrm{Hz}$

Frequency of the carrier wave $={\mathrm{f}}_{\mathrm{c}}={\displaystyle \frac{1}{2\pi }}314\times {10}^2=50\times {10}^2\mathrm{Hz}$

Therefore, bandwidth $2{\mathrm{f}}_{\mathrm{m}}=100\mathrm{Hz}$

Average

Amplitude Modulation

55. An amplitude modulated wave is represented by,

$$v_{\mathrm{AM}}=4(1+0.2\sin 314\mathrm{t})\sin (314\times {10}^{2}t)$$

The minimum and the maximum amplitude of the amplitude modulated wave will be respectively equal to,

(1) 0,1 units

(2) 0,4 units

(3) 3.2 units and 4.8 units

(4) 1.6 units and 8 units

Show Answer

Correct answer: (2)

Solution:

$${\mathrm{V}}_{\mathrm{c}}=4$$

Modulated Index $=\mathrm{m}=0.2$

Minimum amplitude $=4(1-0.2)=3.2\mathrm{V}$

Maximum amplitude $=4(1+0.2)=4.8\mathrm{V}$

Easy

Amplitude Modulation

56. The amplitude of a carrier wave, having a peak amplitude of $50\mathrm{V}$, is made to vary between $75\mathrm{V}$ and $25\mathrm{V}$ after its amplitude modouls modulation index will be equal to,

(1) 0

(2) 0.25

(3) 0.5

(4) 0.75

Show Answer

Correct answer: (3)

Solution:

Modulation index $=\mathrm{m}={\displaystyle \frac{{\mathrm{V}}_{\text{max }}-{\mathrm{V}}_{\text{min }}}{{\mathrm{V}}_{\text{max }}+{\mathrm{V}}_{\text{min }}}}{\displaystyle \frac{75-25}{75+25}}=0.5$

Easy

Amplitude Modulation

57. An amplitude modulated wave is represented by,

$$v_{\mathrm{AM}}=4(1+0.2\sin 314t)\sin (314\times {10}^{2}t)$$

Amplitude of the sidebands will be equal to,

(1) $0.4\mathrm{V}$

(2) $0.8\mathrm{V}$

(3) $1.2\mathrm{V}$

(4) $4\mathrm{V}$

Show Answer

Correct answer: (1)

Solution:

Instantaneous voltage of the amplitue modulated wave is represented by,

$$v_{AM}=V_C\sin 2\pi f_{c}t+{\displaystyle \frac{m{V}_C}{2}}\cos (2\pi f_c-2\pi f_m)t-{\displaystyle \frac{m{V}_C}{2}}\cos (2\pi f_c+2\pi f_m)t$$

Here,

$$V_c=4$$

Modulation $\mathrm{Index}=\mathrm{m}=0.2$

Therefore, amplitude of the sidebands $={\displaystyle \frac{{\mathrm{mV}}_{\mathrm{C}}}{2}}=0.4\mathrm{V}$