Learning Objectives

After going through this unit, you will be able to understand, appreciate and apply the following concepts:

• Distinguish between conductors, semi-conductors and insulators.

• Discuss the intrinsic semi-conductor, its conductivity and factors affecting its conductivity.

• Appreciate the fact of delibrate addition of impurity in a pure semi-conductor to enhance its conductivity, that is ‘doping process’.

• Distinguish between p-type and n-type semi-conductor on the basis of nature of dopant (impurity) atom.

• Discuss the formation of a p-n junction and semi-conductor diode.

• Discribe the working of a p-n finction diode in forward bias and reverse bias.

• Discribe the characterstics of an ideal p-n junction diode and sketch its current-voltage relation.

• Outline the use of several forms of special purpose diodes, including zener diode, LED, photodiode and solar cell.

• Design a circuit which explains the action of p-n junction diode as rectifier.

• Explain the basic theory and operation of junction transition (npn configuration as well as pnp configuration).

• Describe the characterstics of a junction transistor - input characterstics, output characterstics and transfer characterstics.

• Calculate the input resistance, output resistance and current gains in $\mathrm{CE}$ and $\mathrm{CB}$ configurations by solving Kirchaff’s loop equations for input and output circuits.

• Describe the switching action of npn transistor in CE configuration by making reference to its voltage (input / output) transfer / mutual characterstics.

• Describe the amplification or amplifier action of transistor in CE configuration by making reference to output characterstics (a small change in base current leading to comparitvely large change in collector current).

• Derive the voltage gain, ac current gain and power gain of an amplifier.

• Describe the action of transistor as an oscillator by making reference to feadback process and tank / oscillatoryLC circuit.

• Distinguish between analogue and digital circuits.

• Define and describe the basic logic gates OR, AND, NOT, NAND and NOR.

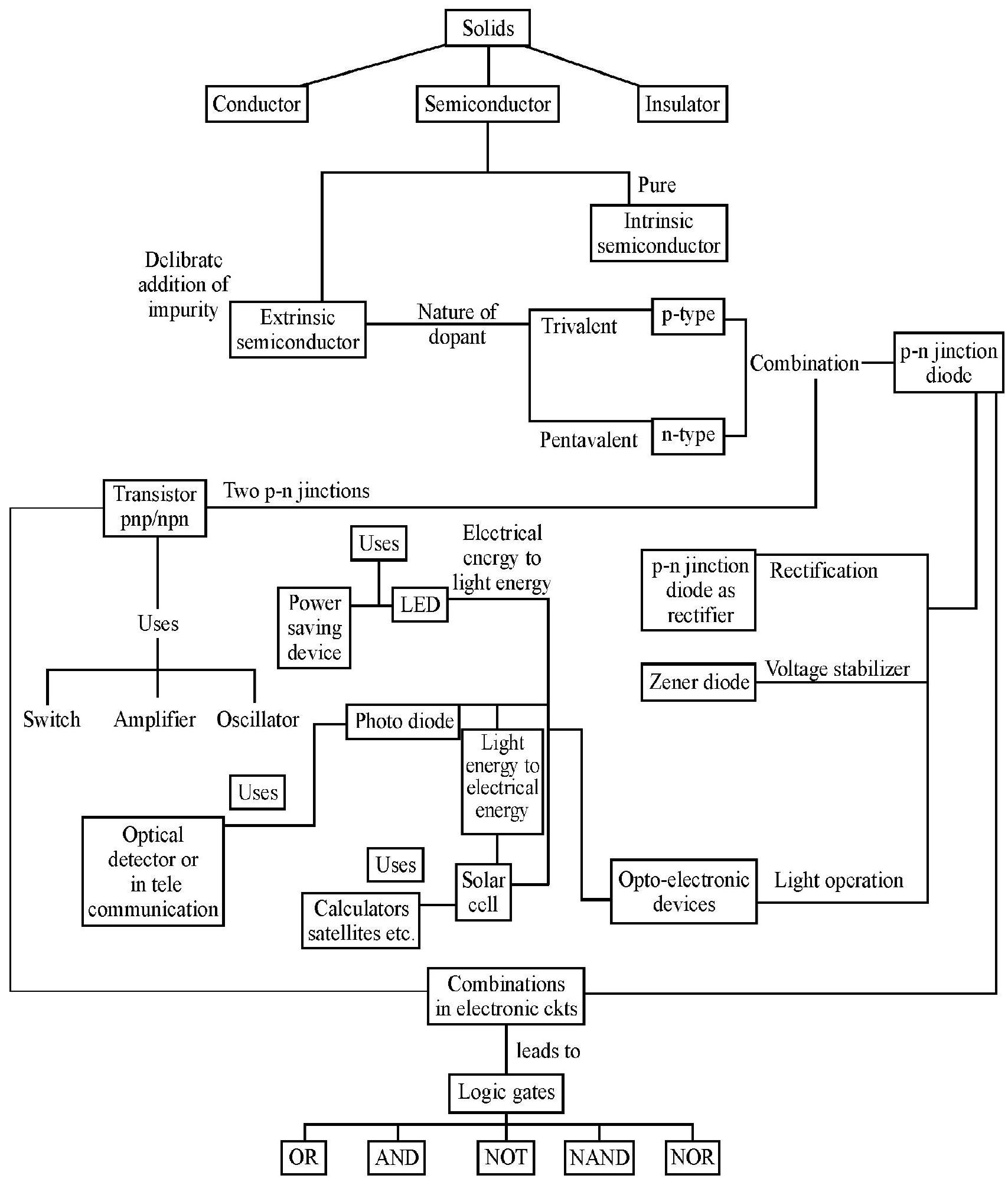
Semiconductor and Electronic Devices

Semiconductors: The semiconductors and solids whose electrical conductivity lies between very high conductivity of metals and very low conductivity of insulators. The pure seminconductors are insulators at very low temperature. Their resistance decreases as their temperature increases, which is a behaviour opposite to that of a metal. The most common semiconductors are elemental semiconductors, example silicon $(\mathrm{Si})$ and germanium $(\mathrm{Ge})$ and compound semiconductors example inorganic $\mathrm{CdS}, \mathrm{GaAs}, \mathrm{CdSe}$, InP etc.

Classifiction of solids inot conductors, insulators and semiconductors on the basis of energy band diagram

Energy Band

According to Bohr’s theory in an isolated atom; the allowed energy state of an electron depends on the principle quantum number (n).For a particular value of $n$ there is only one allowed energy state. The allowed energy states are seprated from one another by a forbidden region or energy gap. Fig. shows energy state for $\mathrm{n}=1$ (ground state) and $\mathrm{n}=2$ (the first excited state). We say energy state of an isolated atom are singlets i.e. there is one value of allowed energy for a particular value of $n$.

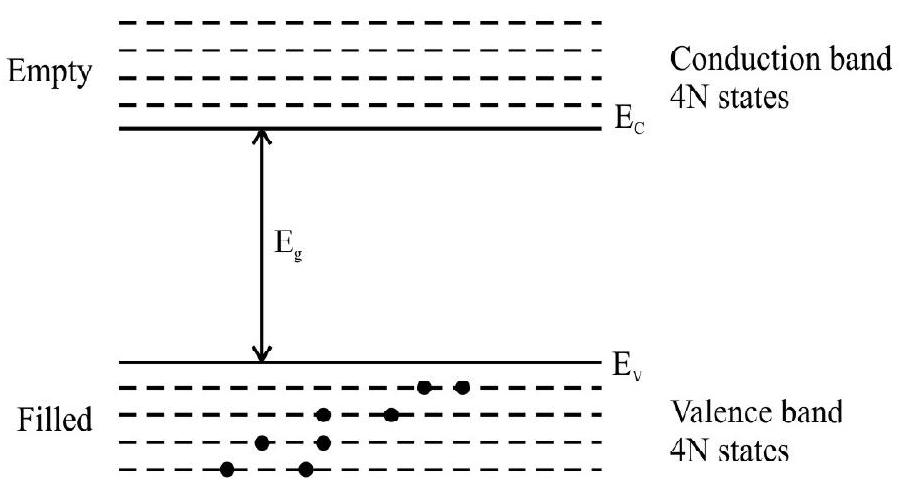
Fig. 1: Energy band positions in a semiconductor at $\mathrm{OK}$

In a solid we have a large number of atoms/molecules very closely packed. The electron in one atom experience a force due to neighbouring atoms/molecules also. We say we have intracting atoms. To consider the effect of interaction we confine our attention on electrons in the outermost orbit around the atoms (i.e. valency electrons). For “two interacting atoms” we find that for one value of $n$ there are two nearly allowed energy states i.e. energy states become doublets. The allowed energy states are triplets (i.e. three nearby energy states for one value of $n$ ) for three interacting atoms. Generallising the result; in a solid number of interacting atoms is very large $\left(\sim 10^{20}\right)$. For one value of $n$ we have about $10^{20}$ allowed energy states in a small energy range. The energy is continuous variable within this small rnge. This is known as an energy band. The energy band corresponding to valence electrons is known as valence band. The energy band for next value of $\mathrm{n}$ is known as the conduction band. In general there is a forbidden region (where here is no allowed energy state) between the valency and the conduction band. This is known as the energy gap (Eg) as shown in Fig 1. This is known as band theory of solids.

With no external energy available the valency electrons reside in valence band i.e. energy states in valency band are filled. There are no electrons in conduction band i.e. the conduction band is empty as shown in Fig. 1.

The energy gap Eg may be zero, small or large. This leads to classification of materials as conductors; semiconductor or insulators.

Case-I : Conductors

When the conductioin band is partically filled and valence band is partially empty or when the conduction band and valence band overlap each other $(\mathrm{Eg}=0)$. The electron can easily more from valence to conduction band i.e. are mobile. This makes large number of free electrons available for electrical conduction. Thereore, the resistance of such materials is very low and conductivity very high. These materials are referred as metals.

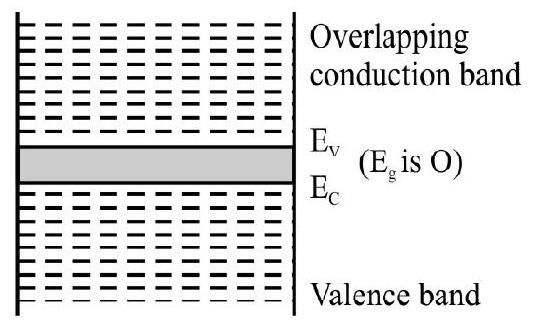
Fig. 2: Mctals or Conductors

Case-II : Insulators

In this case a large energy gap ( $\mathrm{Eg}$ ) exists $[\mathrm{Eg}>3 \mathrm{eV}]$. There are no free electrons in the conduction band. As the energy gap is so large that electrons cannot be excited from the valence band to the conduction band by thermal excitation. This is the case of insulators.

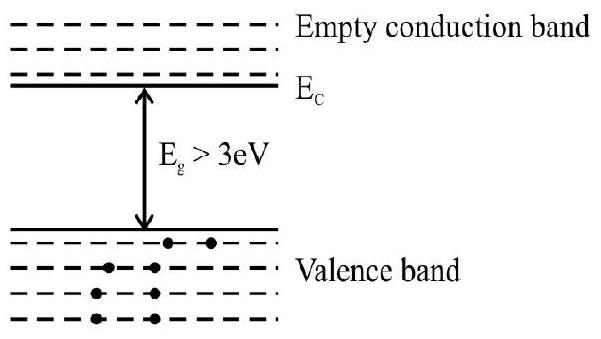
Fig. 3: Insulators

Case-III : Semi-conductors

In this case, there is a finite and a small energy gap $[\mathrm{Eg}>3 \mathrm{eV}]$ exists. Because of this small $\mathrm{Eg}$, at room temperature some electrons cross the energy gap and enter the conductor band. The electrons that jump to cnoduction band are mobile. The valency created in valence band is also mobile in valence band. They behave as positive changes and are also responsible for conduction in a semi-conductor. Hence its resistance is not as high as that of insulators. There conductivity can be increased with rise in the temperature, as due to thermal excitation, more and more electrons can cross the energy gap (Eg). These materials are referred as semiconductors.

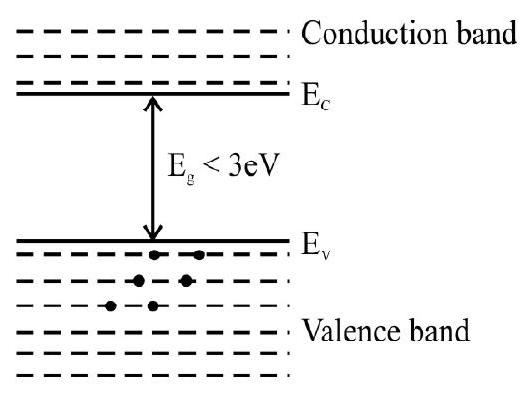
Fig. 4: Semiconductors

Intrinsic Semiconductor

A pure semiconductor, free from any inpurity is called ‘intrinsic’ semiconductor. Its electrical conductivity, which arises by thermal excitation of electrons from the valence band to the conduction band is known as intrinsic conductivity. Most commonly known intrinsic semiconductors are cryslats of Ge and Si. We know that an atom of Si or Ge has four valence electrons. In its crystalline structure, energy Si or Ge atom tends to share one of its four valence electrons with each of its four nearest neighbour atoms and also to take share of one electron from each such neighbour. These shared electron pairs are referred to as forming a covalent bond or valence bond.

At very low temperature, all the valence electrons are tightly bound (all bonds are intact). As the temperature increases, due to thermal excitation, some of there electrons may break-away and cross over to the conduction bond (becomes free electron and available for conduction). This creates a vacancy in the bond. The neighbourhood from which the free electrons $(-q)$ has come out leaves a vacancy with an effective change $(+q)$. This vacancy with effective change $+q$ is called a ‘hole’.

In intrinsic semiconductors, the number of free electrons $n _{e}$ is equal to the number of holes $n _{h}$. That is $\mathrm{n} _{\mathrm{e}}=\mathrm{n} _{\mathrm{h}}=\mathrm{n} _{\mathrm{i}}$, where $\mathrm{n} _{\mathrm{i}}$ is called intrinsic charge carrier concentration.

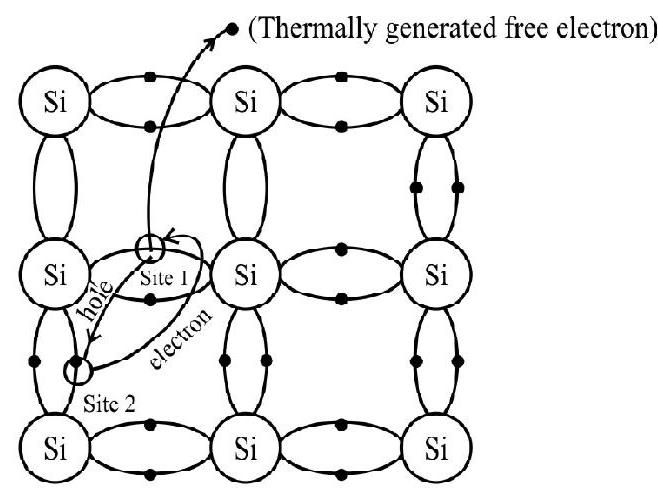
Fig. 4: Schematic model of generation of electron hole pair in silicon crystal

When an electric field is applied to the pure semiconductor, the free elctrons in the conduction band move in a direction opposite to the field, and the holes in the valence band move in the direction of field both giving rise to electric current. (The motion of holes is however, the motion of bounded electrons from one vacancy to the next within the valence band in a direction opposite to the applied field).

Hence, under the action of an electric field, the holes move towards negative potential giving rise to hole current $\mathrm{I} _{\mathrm{h}}$ and free electrons move towards positive polential giving rise to conduction curret $\mathrm{I} _{\mathrm{e}}$. The total current, $\mathrm{I}$ is this the sum of conduction (electron) current $\mathrm{I} _{\mathrm{e}}$ and the hole current $\mathrm{I} _{\mathrm{h}}$

$$ \mathrm{I}=\mathrm{I} _{\mathrm{e}}+\mathrm{I} _{\mathrm{h}} $$

Fig. (5) shows free electrons in conduction band and holes in valence band in the energy-band diagram.

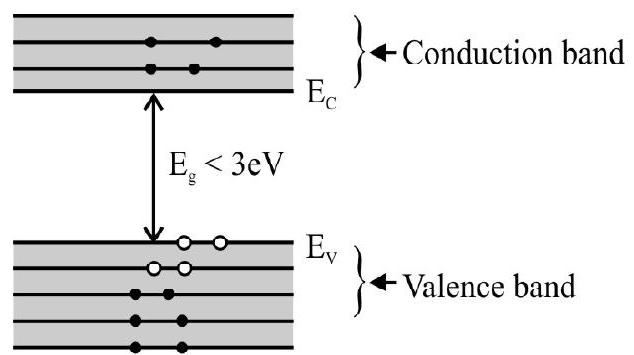
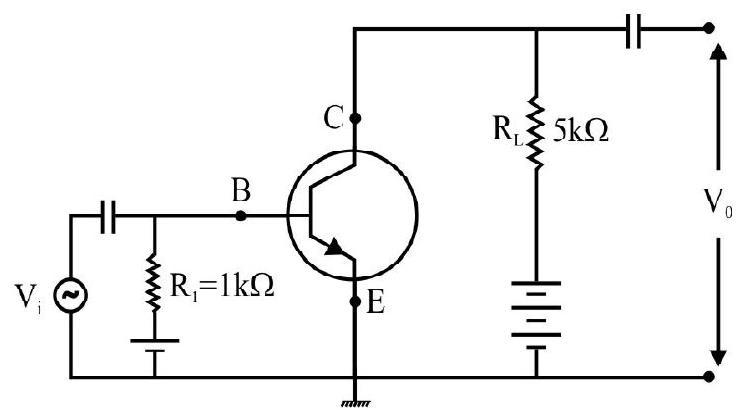
Fig. 5: At $\mathrm{T}>\mathrm{OK}$, thermally generated four electron hole pairs in intrinsic semiconductor

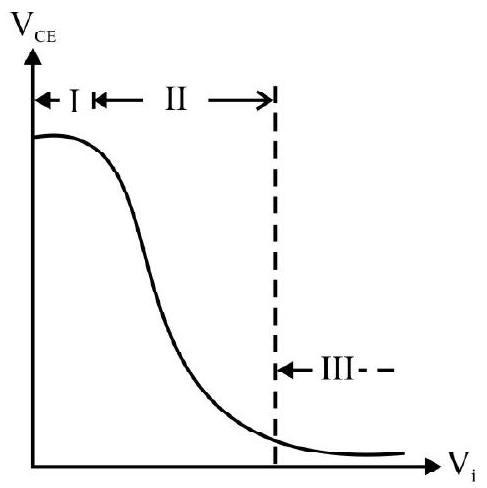
It may be noted that, at equilibrium, the rate of generation of electron-hole pair is equal to the rate of recombination of electron-hole pair.

Extrinic Semiconductor

The conductivity of intrinsic semiconductor depends on its temperature, and very small at room temperature. If, however a small amount of suitable impurity is deliberately added to the pure semiconductor, then the conductivity is significantaly increased. Such materials are known as ’extrinsic’ or ‘doped’ semiconductors. The deliberate addition of a desirable impurity is called doping and the impurity atoms are called dopants.

The dopant has to be such taht it does not distort the original physical and chemical properties of pure crystal.Forthis a small amout say, a few parts per million (impurity atoms per $10^{8}$ pure atoms) of approximately same size of original atom is added.

There are two types of dopants used in doping the letravalent Si or Ge.

(i) Pentavalent - Like Assenic (As), Antimony (Sb), Phosphorous (P) etc.

(ii) Trivalent - Like Indium(In), Boron (B), Aluminium (Al) etc.

n-type Semiconductor

When a pentavalent impurity (Valency 5) atom is added pure Si or Ge, four of the five valence electrons of the impurity atom form covalent bonds with one each valence electrons of four Ge or Si atoms surrounding it; while the fifth remains very weakly bound to the parent atom. As a result inonisation energy required to set this electron free is very small and even at room temperature it will be free to move about in the crystal. [For example, the energy required is $0.01 \mathrm{eV}$ for $\mathrm{Ge}$ and $0.05 \mathrm{eV}$ for $\mathrm{Si}$ ]. Thus, the pentravalent dopant is donating one extra electron for conduction and hence is konwn as donor impurity.

In a doped semiconductor the total number of conduction electrons $n _{e}$ is due to electrons contributed by donors and those generated intrinsically, while the total number of holes $\mathrm{n} _{\mathrm{h}}$, is only due to the holes intrinscially. Hence electrons become the majority charge carriers and holes the minority carriers. These semiconductros are therefore known as n-type semiconductors. For n-type semiconductor, we have

$$ n _{e}»n _{h} $$

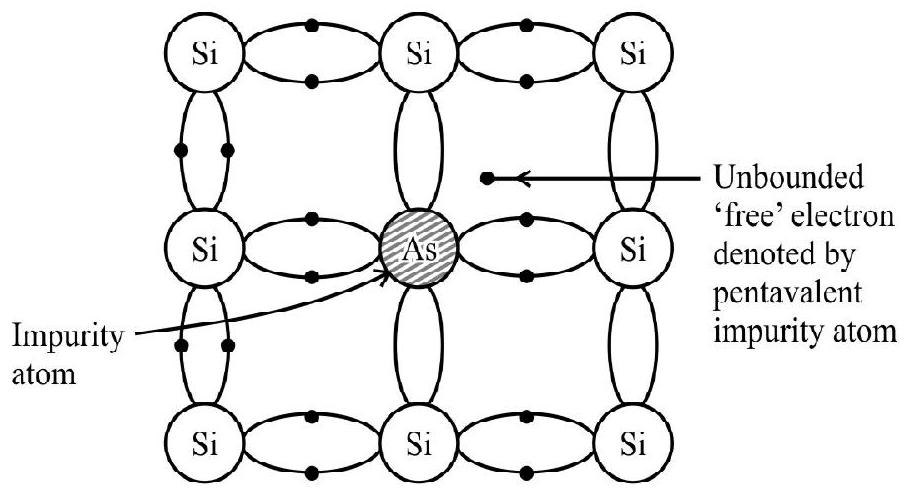
Fig. 6: n-type Semiconductor

p-type Semiconductor

When a trivalent inpurity (valency 3) atom is added to pure $\mathrm{Si}$ or $\mathrm{Ge}$, as the dopant has one valence electron less than $\mathrm{Si}$ or $\mathrm{Ge}$, therefore thin impurity atoms can form covalent bonds with neighbouring three origincal atoms but does not have any fourth electron to offer to original fourth atom. So the bond between fourth atom and trivalent impurity atom has a valency or hole. When an external electric field is applied, an electron bound to neighbouring Ge or Si atom may jump to fill this vacancy, leaving a vacancy or hole at its own stie.

This phenomenon continuous, these holes are in addition to the intrinsically generated hole, while the source of conduction (free) electrons is only intrinsic generation. Thus, for such a material, the holes are the majority carriers and electrons are minority carriers. Therefore, extrinsic semiconductor doped with privalent impurity is called $\mathrm{p}-$ type semiconductor. For p-type semiconductor we have,

$$ \mathrm{n} _{\mathrm{h}}>\mathrm{n} _{\mathrm{e}} $$

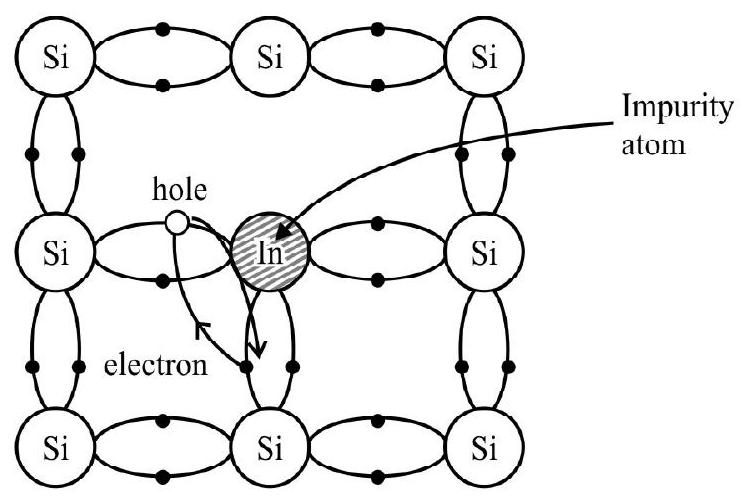
Fig. 7: p-type Semiconductor

Important Conclusion

(i) Extrinsic semiconductor (n-type or p-type) maintains an overall charge neutrality as the charge of additional charge carriers is just equal and opposite to that of ionised cores in the lattice (Crystal).

(ii) The electron hole concentration in an extrinsic semiconductor in thermal equilibrium is given by

$$ \mathrm{n} _{\mathrm{e}} \mathrm{n} _{\mathrm{h}}=\mathrm{n} _{\mathrm{i}}^{2} $$

(iii) The semiconductors energy band structure is affected by doping. In case of exterinsic semiconductors additional energy states due to donor impurities and acceptor impurities also exist. In the energy band diagram of n-type semiconductor, the donor energy level $\mathrm{E} _{\mathrm{D}}$ is slightly below the bottom of conduction band and electrons from this level move to conduction band with a very small supply of energy as shown in figure 8(a). Similarly, for $\mathrm{p}$-type semiconductor the acceptor energy level $\mathrm{E} _{\mathrm{A}}$ is slightly above the top of the valence band as shown with a very small suplly of energy an electron from the valence band can jump to the level of $\mathrm{E} _{\mathrm{A}}$ as shown in figure 8(b).

(iv) Distinction between intrinsic and Extrinsic Semiconductors

	Intrinsic Semiconductor		Extrinsic Semiconductor
1.	It is a pure, natural semiconductor, such as pure $\mathrm{Ge}$ and pure $\mathrm{Si}$.		It is prepared by adding a small quantity of impurity to a pure semiconductor, such as $\mathrm{n}-$ and $\mathrm{p}$ - type semiconductors.
2.	In it the concentrations of electrons and and holes are equal.		In it the two concentrations are unequal. There is an excess of electrons in $n$-type semiconductor and an excess of holes in p-type semiconductors.
3.	Its electrical conductivity is very low.		Its electrical conductivity is significantly high.
4.	Its conductivity cannot be controlled.		Its conductivity can be controlled by adjusting the quantity of the impurity added.
5.	Its conductivity increases exponentially with temperature.		Its conductivity also increases with temperature, but not exponentially.

(v) Distinction between $\mathbf{n}$-type and p-type Semiconductors

	n-type Semiconductor		p-type Semiconductor
1.	It is an extrinsic semiconductor obtained by adding a pentavelent impurity to a pure intrinsic semiconductor.		It is also an extrinsic semiconductor obtained by adding a trivalent impurity to a pure intrinsic semiconductor.
2.	The impurity atoms added provide extra free electrons to the crystal lattice and are called donor atoms.		The impurity atoms added create holes in the crystal lattice and are impurity to a pure intrinsic semiconductor.
3.	The electrons are majority carriers and the holes minority carriers.		The holes are majority carriers and theelectron are minority carreris.
4.	The electrons concentration is much more than the hole concentration $\left(\mathrm{n} _{\mathrm{e}}»\mathrm{n} _{\mathrm{h}}\right)$.		The hole concentration is much more than the electron concentration $\left(\mathrm{n} _{\mathrm{h}}»\mathrm{n} _{\mathrm{e}}\right)$.

Example-1:

The number of silicon atoms per $\mathrm{m}^{3}$ is $5 \times 10^{28}$. This is doped simultaneously with $5 \times 10^{22}$ atoms per $\mathrm{m}^{3}$ of Assenic and $5 \times 10^{20} \mathrm{per} \mathrm{m}^{3}$ atoms of Indium. Calculate the number of electrons and holes. Given that $\mathrm{n} _{\mathrm{i}}=$ $1.5 \times 10^{16} \mathrm{~m}^{-3}$. Is the material n-type or p-type?

Show Answer

Solution:

Given $\mathrm{n} _{\mathrm{i}}=1.5 \times 10^{16} \mathrm{~m}^{-3}$

$ \mathrm{N} _{\mathrm{D}}=5 \times 10^{22} \text { atoms } \mathrm{m}^{3}$

$ \mathrm{~N} _{\mathrm{A}}=5 \times 10^{20} \text { atoms } \mathrm{m}^{3}$

as $\quad n _{e} n _{h}=n _{i}^{2}$ $\hspace{3 cm}$…….(1)

For charge neutrality

$\mathrm{N} _{\mathrm{D}}-\mathrm{N} _{\mathrm{A}}=\mathrm{n} _{\mathrm{e}}-\mathrm{n} _{\mathrm{h}}$ $\hspace{3 cm}$…….(2)

From (1) & (2), we get

$\begin{aligned} & n _{e}=\dfrac{1}{2}\left(N _{D}-N _{A}\right)+\sqrt{\left(N _{D}-N _{A}\right)^{2}+4 n _{i}^{2}}\\ & =\dfrac{1}{2} \times\left(5 \times 10^{22}-5 \times 10^{20}\right)+\sqrt{\left(5 \times 10^{22}-5 \times 10^{20}\right)^{2}+4 \times\left(1.5 \times 10^{16}\right)^{2}}\\ & =4.95 \times 10^{22} \text { atoms per } \mathrm{m}^{3} \end{aligned}$

$\Rightarrow \mathrm{n} _{\mathrm{h}}=\dfrac{\mathrm{n} _{\mathrm{i}}^{2}}{\mathrm{n} _{\mathrm{e}}}=\dfrac{\left(1.5 \times 10^{16}\right)^{2}}{4.95 \times 10^{22}} \simeq 4.75 \times 10^{9} \text { atoms per } \mathrm{m}^{3}$

as $\quad \quad n _{e}»n _{h}$

Semiconductor material is n-type.

Example-2:

Why does the electrical conductivity of a pure semiconductor increases on heating?

Show Answer

Solution:

As the temperature increases, more and more of the electrons in the valence band gain energy to cross the energy gap and enter the conduction band. This results in an increase in the number of charge carriers. Hence conductivity increases.

Example-3:

Are the mobilities of electron and hole equal in semiconductor.

Show Answer

Solution:

No, the electron mobility is higher than hole mobility because hole mobility is due to bounded electron movement in valence band.

Electrical Conductivity of a Semiconductor Crystal

We now know that when an external electric field is applied, the free electrons move opposite to the field and the holes in the direction of the field, thus constituting current in same direction.

Let us consider a cylinderical semiconductor of length $\ell$, area of cross-section ceoncentration $\mathrm{n} _{\mathrm{h}}$. When an electric field $\mathrm{E}$ is applied across the ends of a semiconductor then $\mathrm{E}=\dfrac{\mathrm{V}}{\ell}$, a potential gradient is set up across the length of semiconductor.

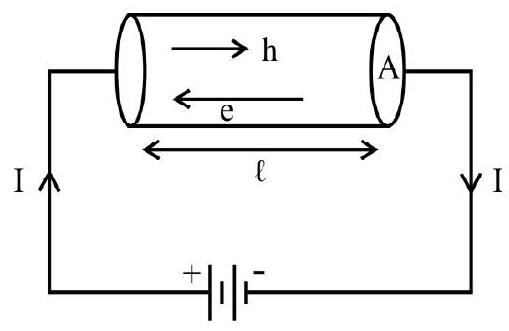
Also total current in the circuit, I will be

$\quad \quad I=I _{e}+I _{n}$

$\quad =\left(n _{e} e A V _{e}+n _{h} e A V _{h}\right)$

or $\quad \dfrac{\mathrm{I}}{\mathrm{A}}=\mathrm{e}\left(\mathrm{n} _{\mathrm{e}} \mathrm{V} _{\mathrm{e}}+\mathrm{n} _{\mathrm{h}} \mathrm{V} _{\mathrm{h}}\right)$

or $\quad \dfrac{V}{R A}=e\left(n _{e} V _{e}+n _{h} V _{h}\right)$

or $\quad \dfrac{\mathrm{V} A}{\rho \ell A}=\mathrm{e}\left(\mathrm{n} _{\mathrm{e}} \mathrm{V} _{\mathrm{e}}+\mathrm{n} _{\mathrm{h}} \mathrm{V} _{\mathrm{h}}\right)$

$\begin{aligned} &\quad \Rightarrow \sigma=\dfrac{1}{\rho}=\mathrm{e}\left(\mathrm{n} _{\mathrm{e}} \dfrac{\mathrm{V} _{\mathrm{e}}}{\mathrm{E}}+\mathrm{n} _{\mathrm{h}} \dfrac{\mathrm{V} _{\mathrm{h}}}{\mathrm{E}}\right)\\ &\quad \Rightarrow \sigma=\mathrm{e}\left(\mathrm{n} _{\mathrm{e}} \mathrm{u} _{\mathrm{e}}+\mathrm{n} _{\mathrm{h}} \mathrm{u} _{\mathrm{h}}\right) \end{aligned}$

$\mu _{\mathrm{e}}$ and $\mu _{\mathrm{h}}$ denote mobility of electron and hole respectively.

With rise in temperature charge carrier concentration increases exponentially whereas mobility ( $\mu _{\mathrm{e}}$ and $\mu _{h}$ ) decreases slightly. Hence, the conductivity of a semiconductor increases with rise in temperature.

p-n Junction

A $p-n$ junction is a boundary or interface between two types of semiconductor material, $p-$ type and $n-$ type, inside a single crystal of semiconductor. It is the basic building block of many semiconductor devices like diodes, transistor etc.

Formation of $\mathbf{p}-\mathbf{n}$ junction - consider a thin slice (wafer) of p-type semiconductor. By adding a small quantity of pentavalent impurity, a part of $p$-type wafer can be converted into $n$-type. The wafer now contains $\mathrm{p}$-region and $\mathrm{n}$-region and a interface or boundary between $\mathrm{p}$ and $\mathrm{n}$-region as shown figure (9).

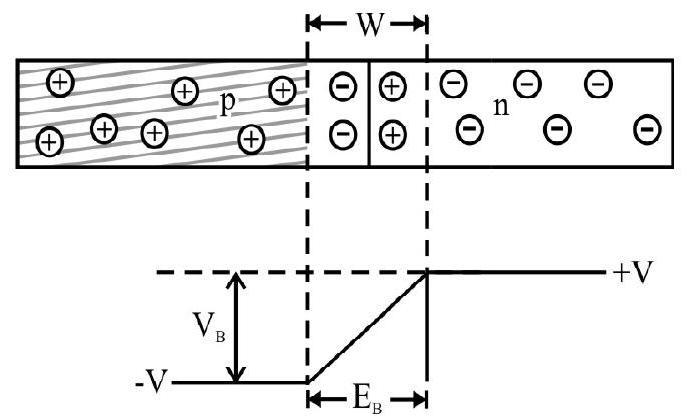
Fig. 9

As soon as junction is formed two important processes occur: diffusion and drift. As we already know that in n-type semiconductors concentration of electrons (free) is more than holes and in p-type concentration of holes is more than electrons. Hence due to the concentration gradient across $\mathrm{p}$ and $\mathrm{n}$ sides, holes diffuse from $\mathrm{p}$-side to $\mathrm{n}$-side and electrons diffuse from $\mathrm{n}$-side to $\mathrm{p}$-side.

This motion of charge carriers give rise to diffusion current across the junction. The diffused chargecarriers combine with their counterparts in the vicinity of the junction and neutralise each other. Thus, in the vicinity of the junction, positive charge (in the form of fixed donor ions) is built on the n-side and negative charge (in the form of fixed accepter ions) on the $\mathrm{p}$-side. Due to this accumulation of charge near the junction, an internal electric field directed from positive charge towards negative charge develops. Due to this field, an electron on $\mathrm{p}$-side of the junction moves to $\mathrm{n}$-side and a hole on $\mathrm{n}$-side of junction moves to $\mathrm{p}$-side. The motion of charge carriers to this field in called drift. Thus a drift current, which is opposite to the direction of diffusion current starts. As the accumulation of charge near junction increases, drift current increases. The process continues till the diffusion current equals drift current. Thus a $p-n$ junction is formed. In a p-n junction under equilibrium these is no current. But a net potential difference across the junction with $n$-side at higher potential. Since this junction potential tends to prevent the movement of electron from $\mathrm{n}$-side into $\mathrm{p}$-side, it is often called a barrier potential ’ $\mathrm{V} _{\mathrm{B}}$ ’ as shown in figure (10).

The region on either side of the junction which becomes depleted of the mobile charge carriers in called the ‘deplation layer’ or depletion ‘region’. The width of deplation layer is of the order of $10^{-6} \mathrm{~m}$. The barrier potential developed across the junction ’ $\mathrm{V} _{\mathrm{B}}$ ’ is about $0.3 \mathrm{~V}$ for Ge and about 0.7 for Si. The width of depletion layer decreases with rise in doping concentration as well as with rise in temperature.

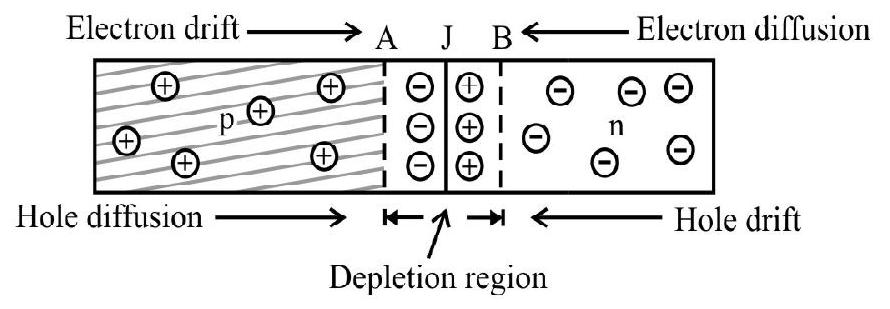
Fig. 10

Semiconductor Diode

A semiconductor diode is basically a $p$-n junction metallic contacts provided at the ends for the application of an external voltage. It is a two terminal device as shown in figure 11(a) and 11(b).

The equilibrium barrier potential ’ $\mathrm{V} _{\mathrm{B}}$ ’ can be altered by applying an external voltage ’ $\mathrm{V}$ ’ across the diode in two ways:

(i) By applying external field in the direction opposite to the barrier field (Forward bias).

(ii) By applying external fied in the direction of the barrier field (Reverse bias).

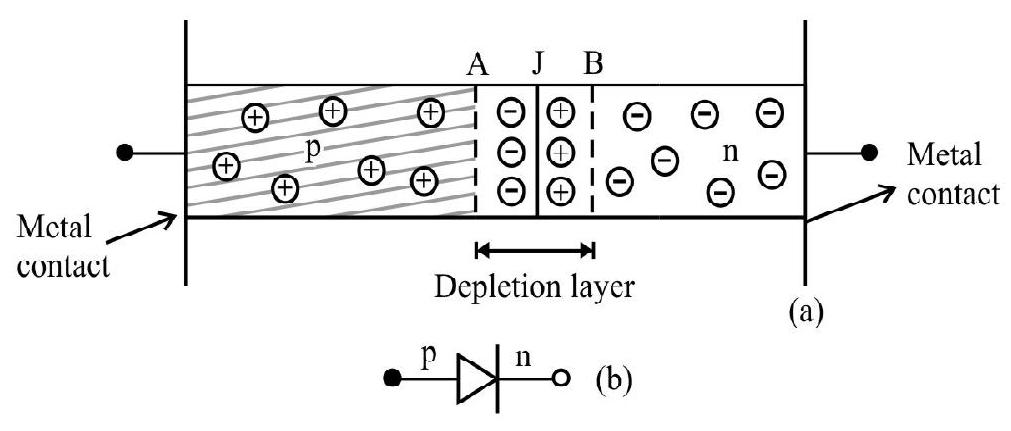
Fig. 11 (a): pn jinction diode (b) symbol

p-n Junction under Forward Bias

When an external voltage is applied across the diode opposite the inbuilt barrier potential $\mathrm{V} _{\mathrm{B}}$, it is said to be forward biased. That is forward bias means $\mathrm{p}$-side of the diode at higher potential with respect to the $n$-side of the diode as shown in Fig. 12(a). To apply forward bias we connect pside to the positive terminal of the battery and $\mathrm{n}$-side to the negative terminal. As a result, the depletion layer width decreases and the barrier height is reduced as shown in the figure 12(b). The effective barrier width under forward bias is $\left(\mathrm{V} _{0}-\mathrm{V}\right)$.

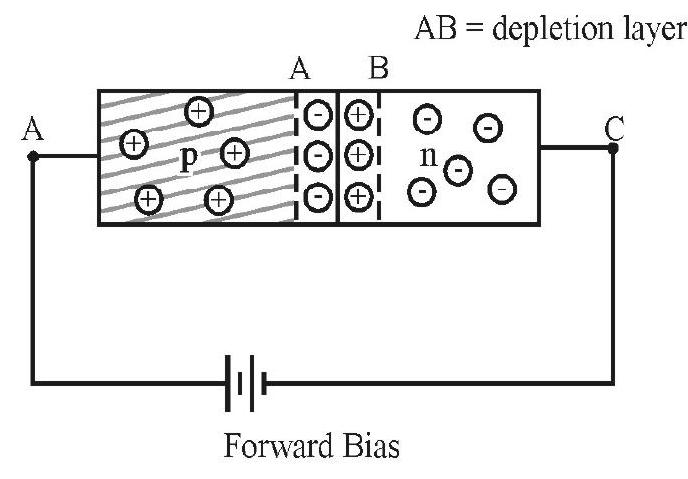
Fig. 12 (a)

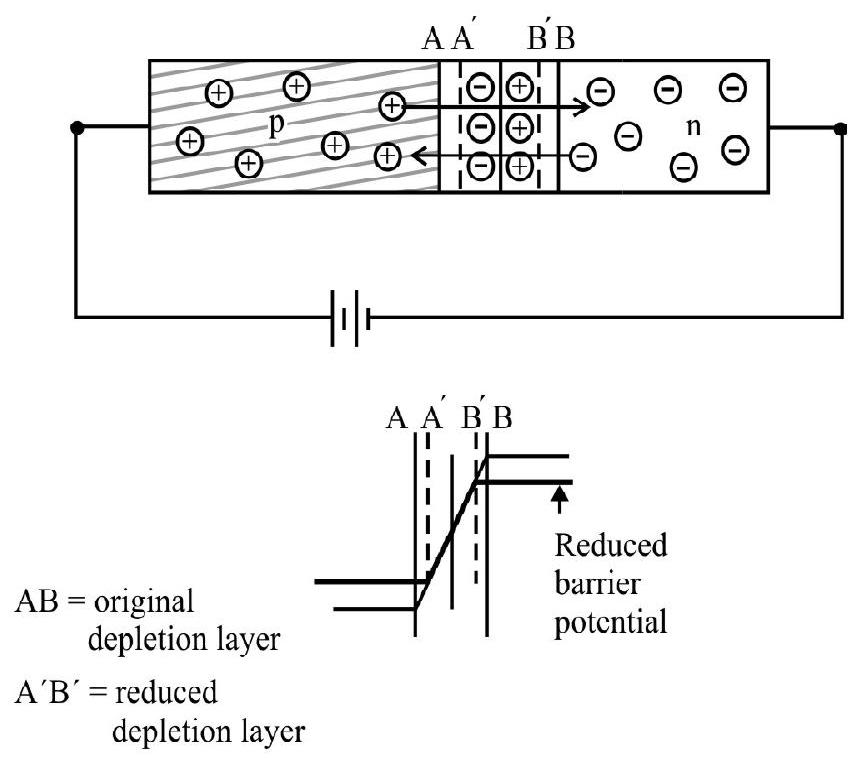
Fig. 12 (b)

If the applied voltage is small, the barrier potential will be reduced only slightly below the equilibrium $\left(V _{B}\right)$ value, so the current will be small. If we increase the applied voltage significantally, the barrier is ultimately eliminated and current increases exponentially. It is due to this reason that junction resistance is very low for the forward bias. For an ideal diode it should be zero forward bias resistance.

Hence in forward based junction, the applied electric field $\mathrm{E}$ dominates the barrier field $\mathrm{E} _{\mathrm{B}} \cdot$ As a result, the majority charge carriers (holes in $\mathrm{p}$-side and electrons in $\mathrm{n}$-side) are pulled towards the junction. This motion of charge carriers on either side give rise to the current. The total forward current is sum of hole diffusion current and current due to free electron diffusion. The magnitude of this current is usually in $\mathrm{mA}$.

Example-4:

A p-n junction diode is forward biased, what is the effect on the width of the depletion layer if the forward voltage is further increased?

Show Answer

Solution:

As the forward voltage ’ $\mathrm{V}$ ’ increases, the barrier $\left(\mathrm{V} _{\mathrm{B}}-\mathrm{V}\right)$ further decreases. Hence depletion width decreases further. When $\mathrm{V} _{\mathrm{B}}=\mathrm{V}$ then barrier is completely eliminated. The deplection layer width tends to zero.

pn Junction diode under Reverse Bias

When a external voltage is applied across the diode in the direction of the inbuilt barrier potential $\mathrm{V} _{\mathrm{B}}$, it is said to be reverse biased. That is reverse biased means $\mathrm{p}$-side of the diode at lower potential with respect to the $n$-side of the diode. To apply reverse bias, we connect negative terminal of the battery to the $\mathrm{p}$-side and positive terminal of the battery to the $\mathrm{n}$-side of the diode as shown in Fig. 13(a). As the direction of applied voltage in same as the directions of barrier potential, the barrier height increases and depletion layer width willdens as shown in Fig. 13(b) effective barrier height under reverse bias becomes $\left(V _{B}+V\right)$. This supresses the diffiustion current i.e. flow of electrons from $\mathrm{n}$-side to $\mathrm{p}$-side and holes from $\mathrm{p}$-side to $\mathrm{n}$-side. Thus, there is almost no current due to majority carriers. Hence resistance at junction in reverse bias in very hight. For an ideal diode, reverse bias resistance is considered to be infinite.

However, when the junction is reverse biased, a very small reverse current (uA) flows across the junction. This current is carried by few thermally generated minority carriers (electrons in $\mathrm{p}$-side and holes in $\mathrm{n-}$ side) which move across the junction under applied field $\mathrm{E}$. This diode reverse current is not much dependent on the applied voltage but depends upon the temperature.

The current under reverse bias is essentially voltage independent upto a critical reverse bias voltage, known as breakdown voltage $\left(\mathrm{V} _{\mathrm{br}}\right)$. When $\mathrm{V}=\mathrm{V} _{\mathrm{br}}$, the diode reverse current increases sharply. If the reverse/forward current exceeds the specified rated value (by the manufacturer), the diode gets destroyed due to overheating.

Example-5:

Indicate which of the following $\mathrm{p}-\mathrm{n}$ junction diodes are forward biased and which are reverse biased?

Show Answer

Solution:

a) R.B as p-side at lower potential

b) R.B as p-side at lower potential

c) F.B as p-side at higher potential

d) F.B as $p$-side at higher potential

V-I Characterstatics of a Diode

The current voltage characterstic curve of a $\mathrm{p}-\mathrm{n}$ junction diode is a graph showing the variation of current as a junction of applied voltage as shown in the figure 14(a) and (b).

The battery is connected to the diode through rehostat so that the applied voltage to the diode can be changed. For different values of V, the value of I is noted. Note that in forward bias measurement, we use milliammeter while we use microammeter in reverse bias, as current in reverse bias is significantly very small (due to drift of majority charge carriers).

As one can see in the graph above, the forward bias current increases very slowly, till the voltage across the diode crosses a certain value ’ $\mathrm{V} _{\text {th }}$ ‘. After this characteristic voltage ’ $\mathrm{V} _{\text {th }}$ ‘, the current increases exponentailly, even for a small increase in the forward bias voltage. This voltage is called threshold voltage or cut in voltage or Knee voltage (is $0.3 \mathrm{~V}$ for Ge diode and in $0.7 \mathrm{~V}$ for Si diode). The threshold voltage is numerically equal to barrier potential $\mathrm{V} _{\mathrm{B}}$, as at this point effect of barrier is completely elimination and junction resistance tends to zero.

For diode in reverse bias, the current is very small $(\sim \mu \mathrm{A})$ and almost remains constant with change in bias. It is called as reverse saturation current. However, for special cases, at very high reverse voltage (break down), the current suddenly increases.

Dynamic Resistance of a Junction Diode

The current voltage curve of a p-n junction diode shows that current does not vary linearly with voltage, that is ohm’s law is not obeyed. It is a non-linear device. In this case, we define, a quantity known as ‘dynamic resistance’ (or a.c. resistance) of $\mathrm{p}-\mathrm{n}$ junction diode. Dynamic resistance of a diode is defined as the ratio of small change in voltage $\Delta \mathrm{V}$ to a small change in current $\Delta \mathrm{I}$.

$$ \mathrm{r} _{\mathrm{d}}=\dfrac{\Delta \mathrm{V}}{\Delta \mathrm{I}} $$

The dynamic resistance is not constant. It depends on the operating voltage.

Important Conclusion

The above discussion shows that $\mathrm{p}-\mathrm{n}$ junction diode offers a very low resistance for the current to flow, when forward biased, but a very high resistances when reverse biased. We can say that an ideal $p-n$ junction diode has zero forward biased resistance and infinite reverse biased resistance. It thus passes current only in one direction (i.e. when forward bias). Hence an ideal $p-n$ junction diode has a unidirectional property. This property is used for rectification of a.c voltages.

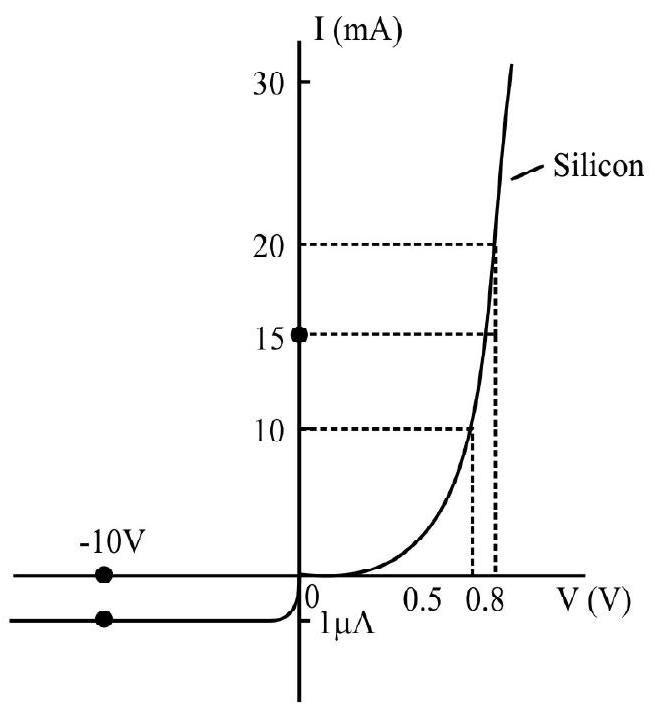
Example-6:

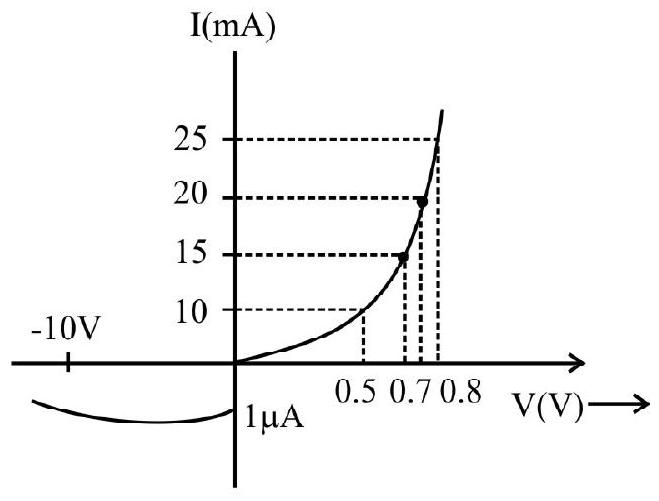
The V-I characteristic of a silicon diode is shown the fig. 14.17. Calculate the resistance of the diode at (a) $\mathrm{I} _{\mathrm{D}}=15$ and (b) $\mathrm{V} _{\mathrm{D}}=-10 \mathrm{~V}$.

Show Answer

Solution:

Considering the diode characteristics as a straight line between $\mathrm{I}=10 \mathrm{~mA}$ to $\mathrm{I}=20 \mathrm{~mA}$ passing through the origin, we can calculate the resistance using Ohm’s law.

(a) From the cure, at $\mathrm{I}=20 \mathrm{~mA}, \mathrm{~V}=0.8 \mathrm{~V}, \mathrm{I}=10 \mathrm{~mA}, \mathrm{~V}=0.7 \mathrm{~V}$

$$ \mathrm{r} _{\mathrm{fb}}=\Delta \mathrm{V} / \Delta \mathrm{I}=0 . \mathrm{IV} / 10 \mathrm{~mA}=10 \Omega $$

(b) From the curve at $\mathrm{V}=-10 \mathrm{~V}, \mathrm{I}=-1 \mu \mathrm{A}$,

Therefore,

$$ \mathrm{r} _{\mathrm{rb}}=10 \mathrm{~V} / 1 \mu \mathrm{A}=1.0 \times 10^{7} \Omega $$

Example-7:

When the voltage drop across a $\mathrm{p}-\mathrm{n}$ junction diode increased from $0.65 \mathrm{~V}$ to $0.7 \mathrm{~V}$, the change in the diode current is $5 \mathrm{~mA}$. Find the value of dynamic resistance of diode.

Show Answer

Solution:

$$ \begin{aligned} \mathrm{r} _{\mathrm{d}}=\dfrac{\Delta \mathrm{V}}{\Delta \mathrm{I}} & =\dfrac{(0.7-0.65) \mathrm{V}}{5 \times 10^{-3} \mathrm{~A}}\\ & =10 \Omega \end{aligned} $$

p-n Junction Diode as a Rectifier

Case-I: Half Wave Rectifier

From the V-I characterstic of a junction diode we known that is allows current to pass only when it is forward biased. So if an alternating voltage is applied across a diode the current flows only in that part of the cycle when the diode is forward biased. This property is used to rectify alternating voltages and the circuit used for this purpose is called a rectifier.

If an alternating voltage is applied across a diode in series with a load, a pulsating voltage will appear across the load only during the half cycles of the ac input during which the diode is forward biased. Such rectifier circuit, as shown in Fig. 17(a) is called a half-wave rectifier. The secondary of a transformer supplies the desired ac voltage across terminals $\mathrm{A}$ and $\mathrm{B}$. When the voltage at $\mathrm{A}$ is positive, the diode is forward biased and it conducts. When a is negative, the diode is reverse-biased and it does not conduct. The reverse saturation current of a diode is negligible and can be considered equal to zero for practical purposes. (The reverse breakdown voltage of the diode must be sufficiently higher than the peak ac voltage at the secondary of the transformer to protect the diode from reverse breakdown).

Therefore, in the positive half-cycle of ac there is a current through the load resistor $\mathrm{R} _{\mathrm{L}}$ and we get an ouput voltage, as shown in Fig. 17(b) whereas there is no current in the negative half-cycle. In the next positive half-cycle, again we get the output voltage. Thus, the output voltage, though still varying, is restricted to only one direction and is said to the rectified. Since the rectified output of this circuit is only for half of the input ac wave it is called as half-wave rectifier.

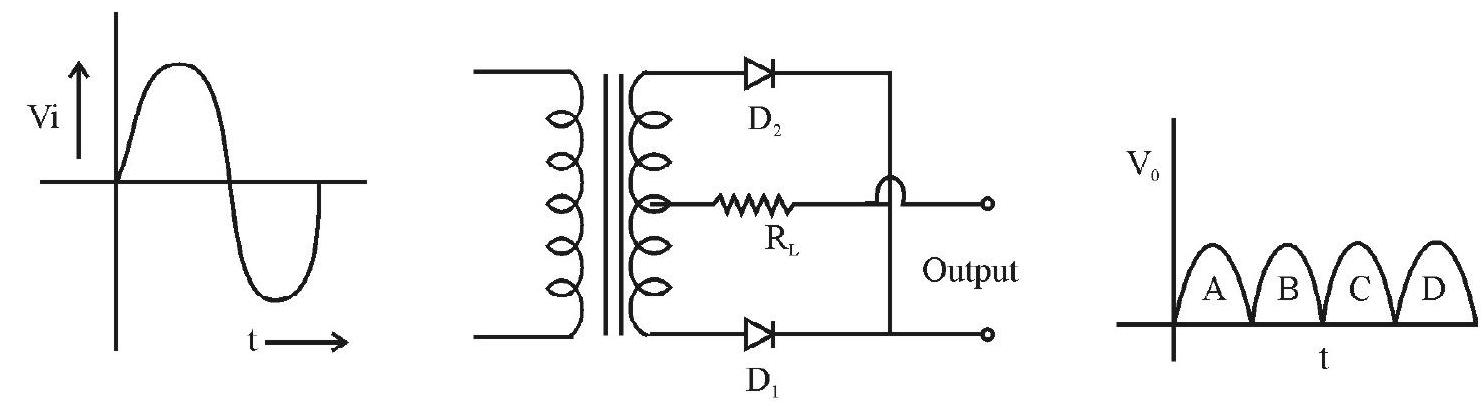
Case-II: Full-Wave Rectifier

The circuit using two diodes, shown in Fig. 18(a) gives output rectified voltage corresponding to both the positive as well as negative half of the ac cycle. Hence, it is known as full-wave rectifier. Here the p-side of the two diodes are connected to the ends of the secondary of the transformer. The n-side of the diodes are connected together and the output is taken between this common point of diodes and the midpoint of the secondary of the transformer. So for a full-wave rectifier the secondary of the transformer is provided with a centre tapping and so it is called centre-tap transformer. As can be seen from Fig. 18(b) the voltage rectified by each diode is only half the total secondary voltage. Each diode rectifies only for half the cycle, but the two diodes do so for alternate cycles. Thus, the output between their common terminals and the centre-tap of the transformer becomes a full-wave rectifier output.

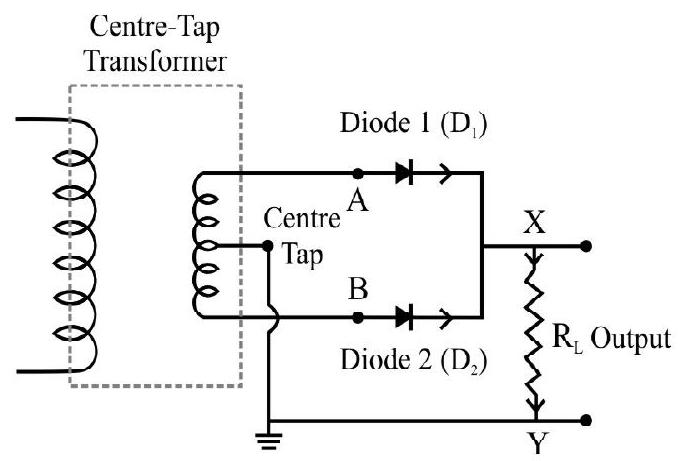
Fig. 18 (a): A full-wave rectifier circuit

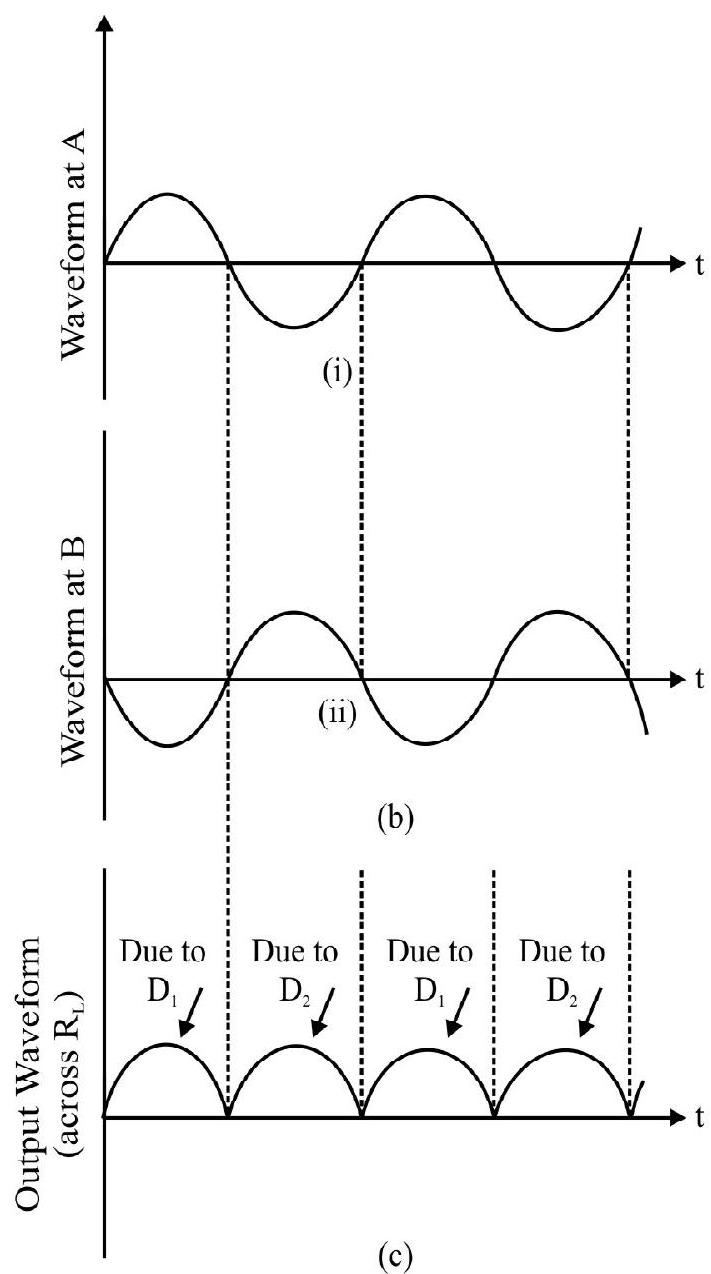
Fig. 18 (b): Input wave forms given to the diode $D _{1}$ at $A$ and to the diode $D _{2}$ at $B$ (c) Output waveform across the load RL connected in the full-wave rectifier circuit

Example-8:

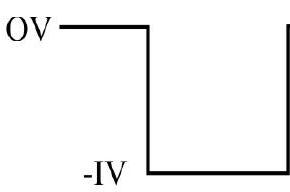
A square wave is applied to a $\mathrm{p}-\mathrm{n}$ junction diode, as shown. Draw the ouput wave form across the diode which is assumed to be ideal.

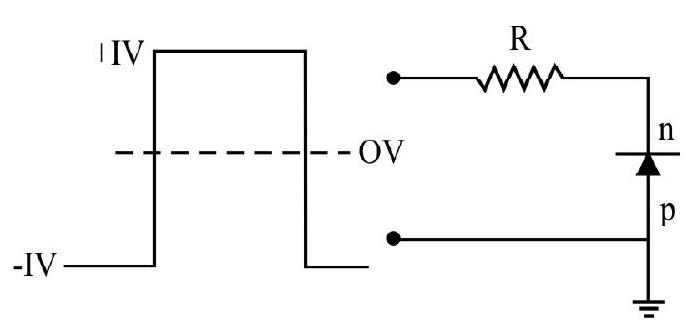
Show Answer

Solution:

The p-side of the diode is at zero potential (grounded). Therefore diode conducts only when negative half appears across the terminals (F.B) and does not conduct during positive half (R.B). Hence the output will be either $0 \mathrm{~V}$ or $-1 \mathrm{~V}$ as shown.

Special Purpose p-n Junction Diodes

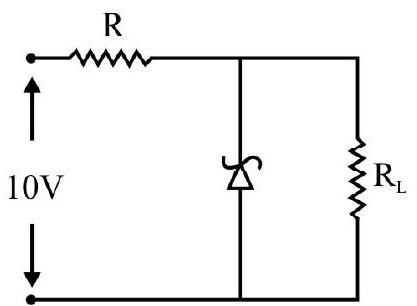
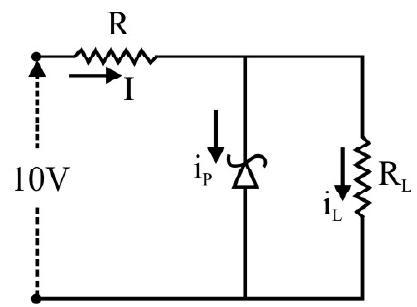
(i) Zener Diode

It is a voltage-regulating device based upon the phenomenon of avalanche breakdown in reverse biased $\mathrm{p}-\mathrm{n}$ junction diode.

When the reverse bias voltage is increased, there is an abrupt rise in reverse saturation current. When the reverse bias voltage reaches a certain value, known as ‘breakdown’ or ‘zerner’ voltage. Thus, in this region of the curve, the voltage across the diode remains constant for very large range of currents. We can use this region for the purpose of voltage stablizer or regulator at a pre-determined value, (used this manner, it is known as ‘zener diode’).

In the above circuit zener diode is selected with a zener voltage $V _{Z}$ equal the voltage desired across the load as shown in the above figure (19). Any change in the input d.c voltage is conducted by zener diode, maintaining the current through the load constant and hence output voltage remains constant. Thus the zener diode acts as a voltage regulator. Note that we have to select the zener diode according to the required ouput voltage and accordingly the series resistance $\mathrm{R} _{\mathrm{s}}$.

(ii) Photodiode

A photodiode is a special purpose $\mathrm{p}-\mathrm{n}$ junction diode fabricated with a transparent window to allow light to fall on the diode. It is operated under reverse bias. The circuit is shown in the figure 20(a). When no light is falling on the junction, reverse saturation current $(\mu \mathrm{A})$ flows. When light of appropriate frequency (i.e. energy of photon $(\mathrm{h} v$ ) greater than the energy gap ( $\mathrm{Eg}$ ) is made incident on the junction, additional electron-hole pairs are generated near the junction. These light generated charge carriers cross the junction and contribute to reverse saturation current.

The magnitude of the photoelectric current depends on the intensity of the incident light (number of photons of light incident per second).

The $\mathrm{p}-\mathrm{n}$ junction photodiodes can operate at frequencies of order of $1 \mathrm{MHz}$. hence they are used as photodectors to detect optical signals, light operated switched, computer punched cards and electronic counters etc.

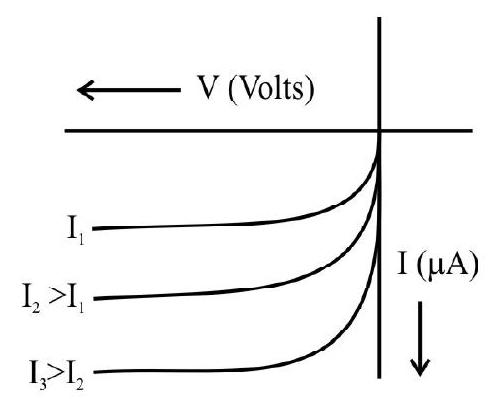
Fig. 20 (c)

I-V characterstic curves of a photodiode for different illumination intensities in reverse bias Fig. 20(c).

(iii) Light Emitting Diode

It is a heavily doped $p-n$ junction which under forward bias emits spontanteous radiation.

When a $\mathrm{p}-\mathrm{n}$ junction is forward biased, both the electrons and holes move towards junction. As they cross the junction, electron-hole pair recombination takes place. On recombination, the energy is released in the form of photons with energy equal to or slightly less than the band gap energy are emitted. In case of Ge or Si diodes, the energy released is infra-red radiation. If however special diodes are used for example gallium arsenide or indium phosphide, then energy released is visible light. The diode is then called light emitting diode.

The semiconductors used for fabrication of visible LED’s must have a band gap of $1.8 \mathrm{eV}$ (as spectral range of visible light is from $3 \mathrm{eV}$ to $1.8 \mathrm{eV}$ ). These LED’s are commonly used in remote controls, burgular alarm systems, optical communication etc.

I-V characterstic curve of a LED (similar to Si diode).

LED’s have following advantages over conventional in candescent lamps:

(a) low operational voltage and less power

(b) fast action and no warm up time required

(c) nearly monochromatic light

(d) fast on-off switching capability

(v) Solar Cell

A solar cell is a $\mathrm{p}-\mathrm{n}$ junction diode that converts solar energy directly into electrical energy. It is bascially a $p-n$ junction diode which generates emf when solar radiation falls on the $p-n$ junction. It works on the same principle as that of photodiode, except that no external bias voltage is applied and junction area is kept much larger for proper absorption of incident solar radiation.

A p-Si wafer of about 300 um of $n-\mathrm{Si}$ is over on which a thin layer of $0.3 \mathrm{um}$ of $\mathrm{n}-\mathrm{Si}$ is grown over on side by diffusion process. The other side of $\mathrm{p}-\mathrm{Si}$ in coated with a metal (back contact). On the top of n-Si layer a metal finger electrode (grid) is deposited. This acts as front contact.

The generation of emf by a solar cell, when light falls on, it is due to the following three processes:

(a) Generation of electron-hole pair due to light (with photon energy $\mathrm{h} v>\mathrm{E} _{\mathrm{g}}$ ) near junction.

(b) Separation of electron and hole due to barrier field at the junction.

(c) Electron reaching the n-side collected by front contact and hole reaching the $\mathrm{p}$-side collected by back contact.

Thus $\mathrm{p}$-side becomes positive and $\mathrm{n}$-side becomes negative giving rise to photo voltage (emf). When an external resistance ’ $R$ ’ is connected, a photoelectric current I flows through it.

Semiconductors with band gap close to $1.5 \mathrm{eV}$ are ideal materials for solar cell fabrication. The importantt criteria for solar cell fabrication are (i) band gap between $1 \mathrm{eV}$ to $1.8 \mathrm{eV}$ (ii) high optical absorption (iii) electrical conductivity (iv) availability of the raw material and (v) cost.

The solar cells are used to power electronic devices in satellites and space vehicles and also as power supply to some calculators.

The I-V characterstic curve of solar cell is drawn in the fourth quadrant of the co-ordinate exes. This is because a solar cell does not draw current but supplies the same to load as shown in Fig. 22(c).

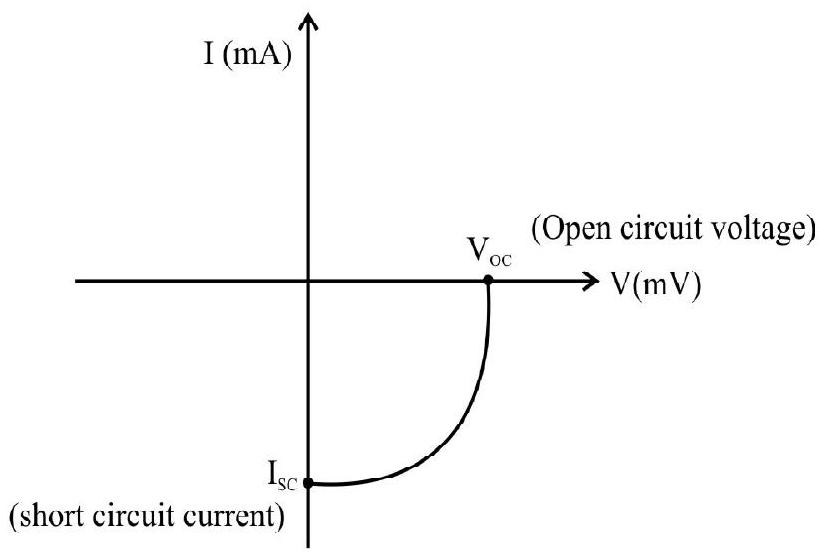
I-V characteristics of a solar cell

Fig. 22 (c)

Example-9:

In half wave rectification, what is the output frequency if the input frequency is $60 \mathrm{~Hz}$. What is the output frequency of a full wave rectifier for the same input frequency?

Show Answer

Solution:

(i) $60 \mathrm{~Hz}$ for half wave and

(ii) $120 \mathrm{~Hz}$ for full wave, as each half of cycle in full wave rectifier is conducted twice, one by each diode.

Example-10:

Ap-n photodiode is fabricated froma semiconductor with a band gap of $2.8 \mathrm{eV}$. Can it detect a wavelength of $6000 \mathrm{~nm}$ ?

Show Answer

Solution:

Energy of photon $\mathrm{E}=\mathrm{hv}=\dfrac{\mathrm{hc}}{\lambda}$

$$ \begin{aligned} & =\dfrac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{6000} \mathrm{~J}\\ & =\dfrac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{6000 \times 1.6 \times 10^{-19}} \mathrm{eV} \end{aligned} $$

No, it can not detect a wavelength of $6000 \mathrm{~nm}$. Because $\mathrm{E}=\mathrm{h} \nu$ has to be grater than $\mathrm{E} _{\mathrm{g}}$

Example-11:

In case of $\mathrm{p}-\mathrm{n}$ junction diode at high reverse bias, the current rises sharply. The value of reverse bias voltage in known as

(a) Cut of voltage

(b) Knee voltage

(c) Critical voltage

(d) Zener voltage

Show Answer

Solution:

(d) Zener voltage

Example-12:

For detecting light intensity, we use

(a) Photodiode in reverse bias

(b) Zener diode in reverse bias

(c) LED in forward bias

(d) Solar cell

Show Answer

Solution:

(a) Photodiode in reverse bias

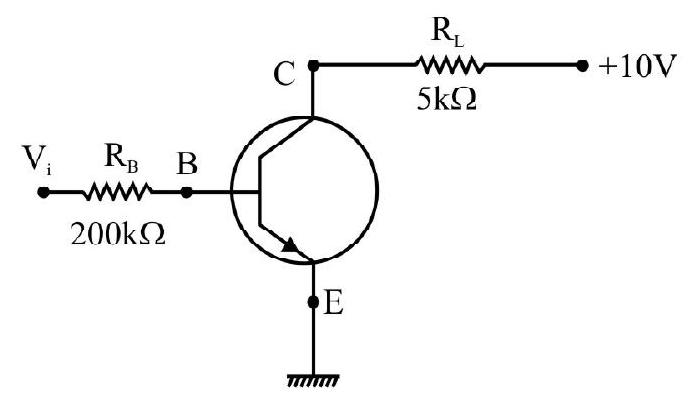
Junction Transistor

A transistor has three doped regions forming two $\mathrm{p}-\mathrm{n}$ junctions between them. Accordingly, there are two types of junction transistors:

(i) $\mathbf{n}-\mathbf{p}-\mathbf{n}$ transistor: Here two segments of $\mathbf{n}-$ type semiconductor (termed as emitter and collector) are separated by a segment of p-type semiconductor (base).

(ii) p-n-p Transsistor: Here two segments ofp-type semiconductor (turned as emitter and collector) are separated by a segment on $\mathrm{n}-$ type semiconductor (base).

All the three segments in $\mathrm{n}-\mathrm{p}-\mathrm{n} / \mathrm{p}-\mathrm{n}-\mathrm{p}$ transistor have different thickness and different doping levels as discussed below.

Emitter: This segment of transistor is of moderate size and heavily doped. It supplies large number of majority charge carriers for the current flow through transistor.

Base: This is the central segment. It is very thin and lightly doped, as it controls the passage of charge carriers from emitter to collector. So that not more than $5 %$ recombination takes place at base and majority of charge carriers move towards collector region.

Collector: This segment collects a major position of the majority charge carriers supplied by the emitter. For this purpose, collector side is moderately doped and larger in size compared to emitter.

Transistor can be used two ways:

(i) Transistor as an amplifier and

(ii) As a switch

Depending upon its usage, biasing of transistor is done.

First we consider transistor ability to amplify the input signal (Amplification means strengthening the weak input a.c signal). For amplification, emitter base junction is forward biased and the base collector junction reverse biased.

Action of a Transistor

Under the forward bias, the majority charge carriers (electron in npn/holes in pnp) in emitters enter the base region in large numbers. The base in thin and lightly doped, most of majority charge carriers entering it pass on to the collector as it is reversed biased. A few of them recombine with minority at base as shown in the figure 23 (a) and (b).

It is intersting to note taht due to forward bias, a large current enters the emitter base junction, but most of it is diverted to adjacent reverse biased base-collector junction and the current coming out of the base becomes a very small fraction of the current that entered the junction.

The current entering into the emitter from outside in equal to the emitter current $\mathrm{I} _{\mathrm{E}}$ similarly the current emerging from the base terminal is $\mathrm{I} _{\mathrm{B}}$ and that from collector terminal $\mathrm{I} _{C}$. According to Kirchoff’s law.

$\quad \quad \mathrm{I} _{\mathrm{E}}=\mathrm{I} _{\mathrm{C}}+\mathrm{I} _{\mathrm{B}}$

where $\mathrm{I} _{\mathrm{C}} \simeq \mathrm{I} _{\mathrm{E}}$

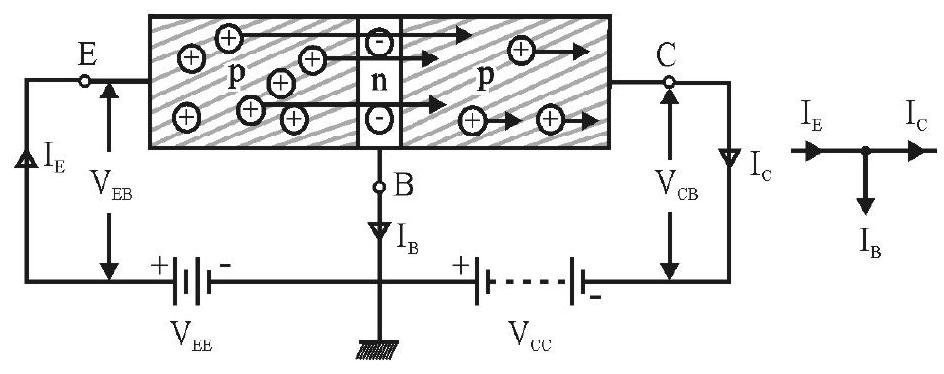
Fig. 23 (a): p-n-p transistor

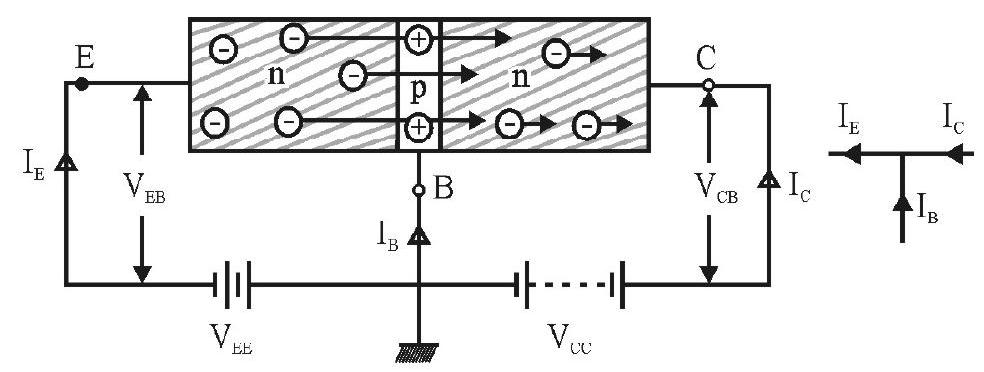
Fig. 23 (b): n-p-n transistor

Fig. 23: Transistor in “common-base configuration”

When the transistor is biased this way, emitter base junction forward biased and base-collector junction reverse biased it is said to be in active state.

The current gain $\alpha$; in common-base configuration is

$$ \alpha=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{E}}} $$

Since $\Delta \mathrm{I} _{\mathrm{E}}>\Delta \mathrm{I} _{\mathrm{C}} ; \alpha$ is less than one. This means there is no current gain in common-base configuration. This is one important factor for limited use of transistor in common base configuration.

The input resistance, $\mathrm{r} _{\mathrm{i}}$ is

$$ \mathrm{r} _{\mathrm{i}}=\left(\dfrac{\Delta \mathrm{V} _{\mathrm{EB}}}{\Delta \mathrm{I} _{\mathrm{E}}}\right) _{\mathrm{V} _{\mathrm{CB}}=\text { constant }} $$

The output resistance $r _{0}$ is

$$ \mathrm{r} _{0}=\left(\dfrac{\Delta \mathrm{V} _{\mathrm{CB}}}{\Delta \mathrm{I} _{\mathrm{C}}}\right) _{\mathrm{I} _{\mathrm{E}}=\text { constant }} $$

The input resistance $r _{i}$ is low whereas output resistance $r _{0}$ is high.

Transistor in Common-Emitter Configuration

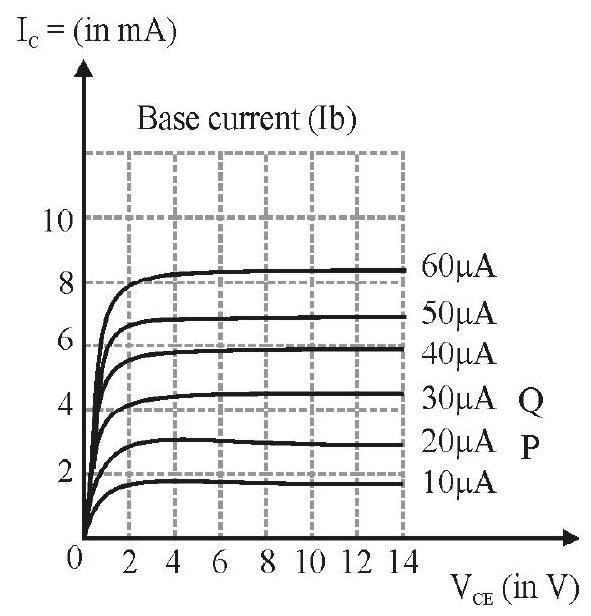
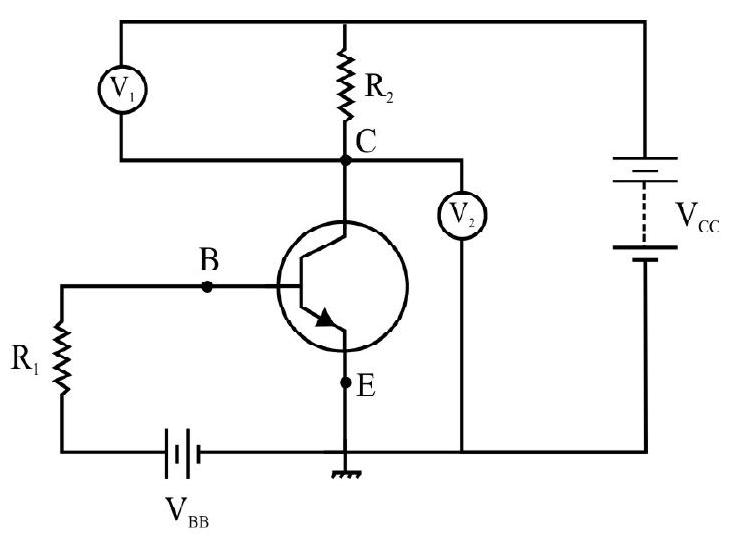
The graph showing the variation of current with voltage in a transistor is called transistor characterstics. The most widely used transistor is in common emitter configuration (CE).

When transistor is used in CE, congifuration, the input is between the base and emitter and output is between the collector and emitter. The circuit used to obtain the characterstics curves in shown in Fig. 24.

(i) Input Characterstics

A curve is plotted between the base current $I _{B}$ against base emitter voltage $V _{B E}$ keeping collectoremitter voltage $\mathrm{V} _{\mathrm{CE}}$ fixed. The $\mathrm{V} _{\mathrm{CE}}$ is kept large enough to make the base collector junction reverse biased. Therefore, for Si transistor input characterstics may be obtained for $\mathrm{V} _{\mathrm{CE}}$ somewhere in range of $3 \mathrm{~V}$ to $20 \mathrm{~V}$. Since increase in $\mathrm{V} _{\mathrm{CE}}$ appears as increase in $\mathrm{V} _{\mathrm{CB}}$, its effect on $\mathrm{I} _{\mathrm{B}}$ is negligible. As a consequences for different values of $\mathrm{V} _{\mathrm{CE}}$, we get identical curves. The input characterstics of a transistor are shown in the Fig. 25(a).

We define a term called input resistance ’ $r$ ‘.

Fig. 24: Circuit arrangement for studying the input and output characteristics of npn transistor in CE configuration

Input resistance $r _{i}$ - This is defined as the ratio of change in base emitter voltage $V _{B E}$ to the resulting change in base current $\mathrm{I} _{\mathrm{B}}$ at constant collector - emiter voltage $\mathrm{V} _{\mathrm{CE}}$.

$$ \mathrm{r} _{\mathrm{i}}=\left(\dfrac{\Delta \mathrm{V} _{\mathrm{BE}}}{\Delta \mathrm{I} _{\mathrm{B}}}\right) _{\mathrm{V} _{\mathrm{CE}}} $$

(ii) Ouput Characterstics

A curve is plotted between collector current $\mathrm{I} _{\mathrm{C}}$ and collector-emitter voltage $\mathrm{V} _{\mathrm{CE}}$ keeping base current $I _{B}$ constant. As $I _{B}$ increases, $I _{C}$ will increase proportionality. Hence plot of $I _{C}$ versus $V _{C E}$ will be different output curves correspoinding to different values of $\mathrm{I} _{\mathrm{B}}$ as shown in the Fig. 25(b)

Output resistance - This is defined as the ratio of change in collector emitter voltage $\left(\mathrm{V} _{\mathrm{CE}}\right)$ to the change in collector current $\left(\Delta \mathrm{I} _{\mathrm{C}}\right)$ at a constant base current $\left(\mathrm{I} _{\mathrm{B}}\right)$

$$ \mathrm{r} _{0}=\left(\dfrac{\Delta \mathrm{V} _{\mathrm{CE}}}{\Delta \mathrm{I} _{\mathrm{C}}}\right) _{\mathrm{I} _{\mathrm{B}}} $$

The linear segment of output characterstics can be used to calculate this parameter.

(iii) Mutual or Transfer Characterstics Curve

If base voltage $V _{B E}$ is increased by a small amount, both $I _{B}$ and $I _{C}$ will increase. Hence we defined a term called amplification factor $(\beta)$. This is defined as the ratio of change in collector curernt to the change in base current at a constant collector emitter voltage.

$$ \beta _{\mathrm{ac}}=\left(\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{B}}}\right) _{\mathrm{V} _{\mathrm{CE}}} $$

$\beta$ is a large positive number. i.e. there is a large current gain. This is one of the reasons why commonemitter configuration is used more frequently.

The transconductance $\mathrm{g} _{\mathrm{m}}$ is the ratio of change in output current $\left(\Delta \mathrm{I} _{C}\right)$ to the change in input voltage $\left(\Delta \mathrm{V} _{\mathrm{BE}}\right)$. Expressed mathematically

$$ \mathrm{g} _{\mathrm{m}}=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{VB} _{\mathrm{E}}} $$

Relation Between Transistor Parameters

By definition

$$ \mathrm{r} _{\mathrm{i}}=\dfrac{\Delta \mathrm{V} _{\mathrm{BE}}}{\Delta \mathrm{I} _{\mathrm{B}}} ; \quad \beta=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{B}}} $$

and $\quad \mathrm{g} _{\mathrm{m}}=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{VB} _{\mathrm{E}}}$

$\therefore \quad \dfrac{\beta}{r _{i}}=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{B}}} \times \dfrac{\Delta \mathrm{I} _{\mathrm{B}}}{\Delta \mathrm{V} _{\mathrm{BE}}}=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{B}}}=\mathrm{g} _{\mathrm{m}}$

Also $\quad \alpha=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{B}}}$ and $\Delta \mathrm{I} _{\mathrm{E}}=\Delta \mathrm{I} _{\mathrm{C}}+\Delta \mathrm{I} _{\mathrm{B}}$

$\therefore \quad \alpha=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{C}}+\Delta \mathrm{I} _{\mathrm{B}}}=\dfrac{\Delta \mathbf{I} _{\mathrm{C}} / \Delta \mathbf{I} _{\mathrm{B}}}{\Delta \mathbf{I} _{\mathrm{C}} / \Delta \mathbf{I} _{\mathrm{B}}+1}$

or $\quad \alpha=\dfrac{\beta}{\beta+1}$

Rearranging we get

$$ \beta=\dfrac{\alpha}{1-\alpha} $$

Fig. 25 (c) : Mutual or Transfer characteristics

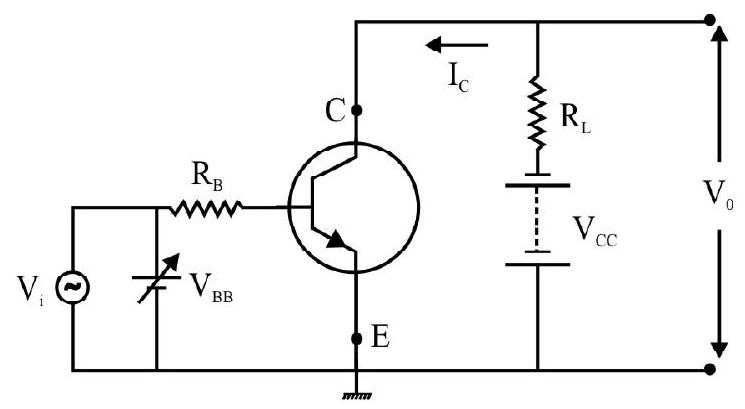
Transistor as an Amplifier

For using the transistor as an amplifier, we use active region of the transistor as shown in Fig. 25(c). As amplifier is used to amplify small and weak alternating signals $\left(\mathrm{V} _{\mathrm{i}}\right)$. Now let us superimpose an a.c signal $\mathrm{V} _{\mathrm{i}}$ (to be amplified) on the bias voltage $V _{B B}$ (d.c) as shown in the circuit diagram Fig. 26. The output signal is taken across collector and grounded emitter as shown in the Fig. 26.

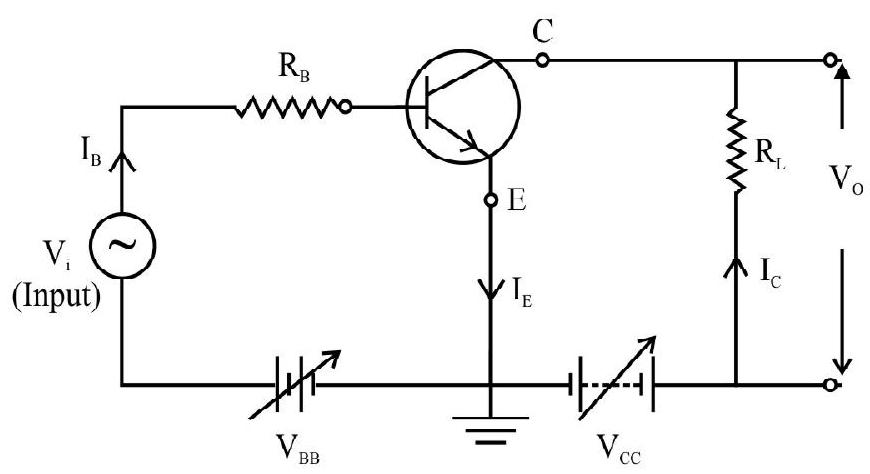
Fig. 26: Circuit arrangement for transistor as amplifier

First consider input a.c signal $\mathrm{V} _{\mathrm{i}}=0$; then

$\quad \quad \mathrm{V} _{\mathrm{CC}}+\mathrm{V} _{\mathrm{CE}}+\mathrm{I} _{\mathrm{C}} \mathrm{R} _{\mathrm{L}}$ $\hspace{3 cm}$ …….(1)

and $\quad \mathrm{V} _{\mathrm{BB}}=\mathrm{V} _{\mathrm{BE}}+\mathrm{I} _{\mathrm{B}} \mathrm{R} _{\mathrm{B}}$ $\hspace{3 cm}$ …….(2)

As $V _{C C}$ is fixed d.c source, this implies from equation (1)

$$ \Delta \mathrm{V} _{\mathrm{CC}}=0=\Delta \mathrm{V} _{\mathrm{CE}}+\Delta \mathrm{I} _{\mathrm{C}} \mathrm{R} _{\mathrm{L}} $$

That is change in $\mathrm{I} _{\mathrm{C}}$ due to change in $\mathrm{I} _{\mathrm{B}}$ causes a change in $\mathrm{V} _{\mathrm{CE}}$.

$$ \Delta \mathrm{V} _{\mathrm{CE}}=-\Delta \mathrm{I} _{\mathrm{C}} \mathrm{R} _{\mathrm{L}} $$

The change in $\mathrm{V} _{\mathrm{CE}}$ is the output a.c voltage $\mathrm{V} _{0}$.

$$ \Rightarrow \quad \mathrm{V} _{0}=\Delta \mathrm{V} _{\mathrm{CE}}=-\beta _{\mathrm{a} . \mathrm{c}} \Delta \mathrm{I} _{\mathrm{B}} \mathrm{R} _{\mathrm{L}} \quad\left(\because \beta _{\mathrm{a} . \mathrm{c}}=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{B}}}\right) $$

Hence voltage gain of the amplifier is

$$ \begin{aligned} & \mathrm{A} _{\mathrm{V}}=\dfrac{\mathrm{V} _{0}}{\mathrm{~V} _{\mathrm{i}}}=\dfrac{\Delta \mathrm{V} _{\mathrm{CE}}}{\mathrm{r} \Delta \mathrm{I} _{\mathrm{B}}}\\ & =-\dfrac{\beta _{\mathrm{a} . \mathrm{c}} \mathrm{R} _{\mathrm{L}}}{\mathrm{r}} \end{aligned} $$

The negative sign represents that output voltage is opposite with phase with the imput voltage.

The power gain / amplification of a transistor is given as $A _{P}=A _{V} \times \beta _{a . c}$

It must be noted that transistor is not a power generating device. The energy for the higher a.c power at the output is supplied by the input battery $\mathrm{V} _{\mathrm{BB}}$.

Transistor as an Oscillator

In the above discussion, we realize that an input a.c given to transistor appears as amplified output a.c signal. This means that an external input is necessary to sustain a.c signal in the ouput for an amplifier.

In an oscillator, we get an a.c output without any external input signal. In other words, an oscillator is a device that generates electric oscillations of constant amplitude and of a desired frequency, without any external inputs, the oscillations are self sustained.

To attain this, an amplifier is taken. A portion of the output power is returned back (feedback) to the input in same phase (positive feedback) with the starting power as shown in the Fig. 27 (a). The feedback can be achieved by inductive coupling (through mutual inductance) or LC or RC networks. Different types of oscillators essentially use different methods of coupling the output to input (feedback network). In the circuit given below Fig. 27(b) feedback is accomplished by inductive coupling from one coil ( $\left.\mathrm{T} _{1}\right)$ to another $\operatorname{coil}\left(\mathrm{T} _{2}\right)$. The resonant frequency $v$ of this tuned or tank (LC) circuit determines the frequency at which the oscillator oscillates.

$$ v=\dfrac{1}{2 \pi \sqrt{\mathrm{LC}}} $$

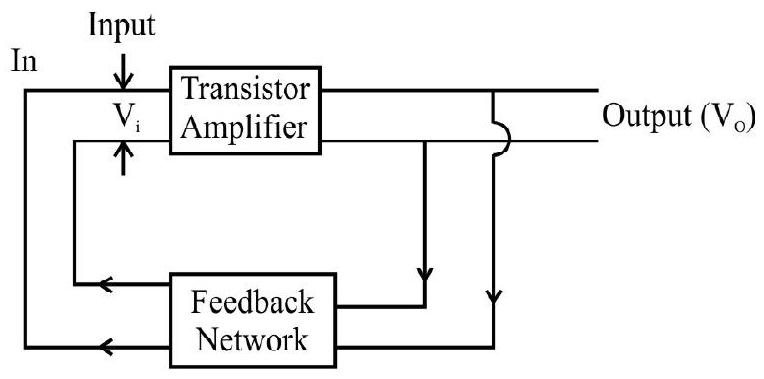
Fig. 27 (a) Principle of Oscillator

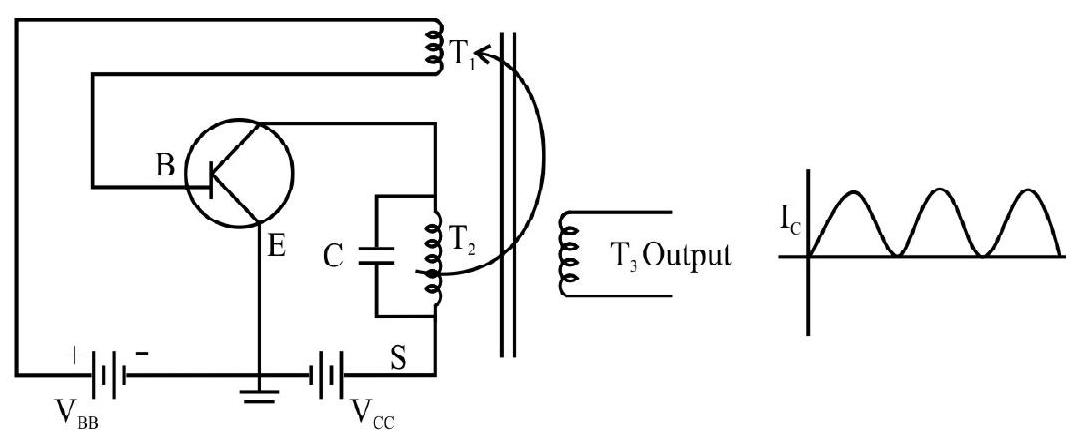
Fig. 27 (b) Circuit diagram of tuned collector oscillator

Transistor as a Switch

When the transistor is used in the cut off or saturation state it act as a swith as shown in the Fig. 25(c).

Let us try to analyse the behaviour of Si transistor as switch using $\mathrm{CE}$ configuration. For input $\mathrm{V} _{\mathrm{i}}$ less than $0.6 \mathrm{~V}$, the transistor will be in cut off state and current $\mathrm{I} _{\mathrm{C}}$ will be zero.

$$ \mathrm{I} _{\mathrm{B}}=\mathrm{I} _{\mathrm{C}}=0 $$

Hence $\mathrm{V} _{0}=\mathrm{V} _{\mathrm{CC}}$

(Using Kirchoff’s law in output circuit, $\mathrm{V} _{0}=\mathrm{V} _{\mathrm{CC}}=\mathrm{V} _{\mathrm{CE}}+\mathrm{I} _{\mathrm{C}} \mathrm{R} _{\mathrm{L}}$ )

When $V _{i}$ becomes greater than $0.6 \mathrm{~V}$ the transistor is in active state. With increase in $V _{i}$, As $\mathrm{I} _{\mathrm{C}} \mathrm{R} _{\mathrm{L}}$ term increases $\mathrm{V} _{0}$ decreases, and tends towards zero. Transistor in this state goes into saturation.

We can conclude that as long as $\mathrm{V} _{\mathrm{i}}$ is law and unable to forward bias the transistor, $\mathrm{V} _{0}$ is high $\left(=\mathrm{V} _{\mathrm{CC}}\right)$. If $\mathrm{V} _{\mathrm{i}}$ is high enough to derive the transistor into saturation, then $\mathrm{V} _{0}$ is low (near to zero). When the transistor is not conducting it is said to be switched off and when it is driven into saturation it is said to be switched on.

Alternatively, we can say that a low input to transistor gives a high output and a high input gives a low output. The switching circuits are designed in a way that transistor does not remain in active state.

Example-13:

In a silicon transistor, a change of $7.89 \mathrm{~mA}$ in the emitter current produces a change of $7.8 \mathrm{~mA}$ in the collector current. Find the required change in the base current to produce an equivalent change in the collector current?

Show Answer

Solution:

Given $\alpha=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{E}}}=\dfrac{7.8}{7.89}=0.98$

As $\quad \beta=\dfrac{\alpha}{1-\alpha}=\dfrac{0.98}{1-0.98}=86.7$

$\quad \quad \beta _{\mathrm{a} . \mathrm{c}}=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{B}}}$

$\Rightarrow \Delta \mathrm{I} _{\mathrm{B}}=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\beta _{\mathrm{a} . \mathrm{c}}}=\dfrac{7.8}{86.9} \simeq 90 \mu \mathrm{A}$

Example-14:

The input resistance of transistor is $665 \Omega$. Its base current when changed by $15 \mu \mathrm{A}$, results in a change of $2 \mathrm{~mA}$ in the collector current. The transistor is used as $\mathrm{CE}$ amplifier with load of $5 \mathrm{k} \Omega$. Find the voltage gain of the amplified.

Show Answer

Solution:

Voltage gain $A _{V}=\beta _{a . c} \dfrac{R _{L}}{r _{i}}$

$$ =\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{B}}} \dfrac{\mathrm{R} _{\mathrm{L}}}{\mathrm{r} _{\mathrm{i}}}=\dfrac{2 \times 10^{-3} \times 5000}{15 \times 10^{-6} \times 665}=1000 $$

Analogue Circuits and Digital Circuits

There are two types of electronic circuits analogue circuits and digital circuits.

In analogue circuits, the voltage orcurrent varries continuously with time. Such a signal is called ‘analogue signal’. This is in the form of typical sinusoidal walleform.

In digital electronics we use only two levels are called digital signals. This signal is represented by pulse waveform or square waveform. In digital circuits only two values (represented by 0 and 1 ) of the input and output voltage are permissible.

Logic Gates

A gate is a digitcal circuit which follows certain logical relationship between input and output voltage. Therefore, they are generally known as ’logic gate’, gates because they central the flow of information. Logic gates are used in calculators, digital watches, computers, robots, industrial control system and telecommunication etc.

The five common logic gates used are OR, AND, NOT, NAND and NOR.

(i) OR Gate

An OR gate has two inputs related by one output. The truth table and logic symbol (circuit symbol) are shown below. The output $\mathrm{Y}$ is 1 when either input $\mathrm{A}$ or $\mathrm{B}$ or both are 1 . That is if any of the input voltage is high input is high.

The Booliean representation of OR gate is

$\mathrm{Y}=\mathrm{A}+\mathrm{B}$

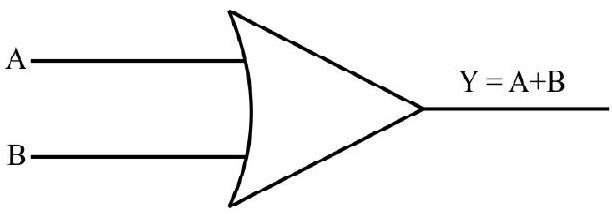
Logic Symbol

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{Y}=\mathrm{A}+\mathrm{B}$
0	0	0
0	1	1
1	0	1
1	1	1

Truth table

Fig. 29: The Boleean representation of OR gate is $\mathrm{Y}=\mathrm{A}+\mathrm{B}$

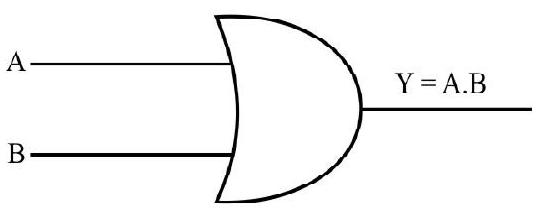
(ii) AND Gate

An AND gate has two inputs related by one output. The output $Y$ is 1 only when both inputs $A$ and $B$ are 1. That is if both the input voltages are high, then only output voltage is high. The logic symbol and truth table are given as below.

The Booliean representation of AND gate is

$$ Y=A \cdot B \text { or } Y=A \times B $$

Logic Symbol

$A$	$B$	$Y=A . B$
0	0	0
1	0	0
0	1	0
1	1	1

Truth table

Fig. 30: The Boleean representation of AND gate is $\mathrm{Y}-\mathrm{A} . \mathrm{B}$ or $\mathrm{Y}-\mathrm{A} \otimes \mathrm{B}$

(iii) NOT Gate

This is the most basic gate with one input related to one output. It gives inverted version of input voltage as output voltage. This is the reason it is also known as inverter. The logic symbol and truth table are given as below:

The Booliean representation of NOT gate is

$$ \mathrm{Y}=\overline{\mathrm{A}} $$

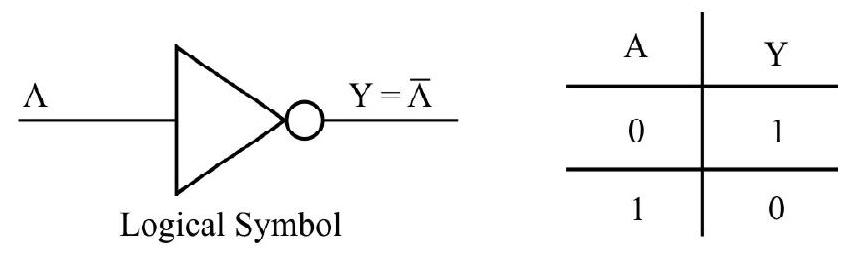
Truth table

Fig. 31 : The Boleean representation of NOT gate is $\mathrm{Y}=\overline{\mathrm{A}}$

(iv) NAND Gate

This is an AND gate followed by a NOTgate as shown in Fig. 32. If the inputs $A$ and $B$ are both1 the output $Y$ is not 1 .

NAND gates are also called universal gates since by using these gates we can realize other basic gates like OR, AND and NOT. The logic symbol and truth table are given below:

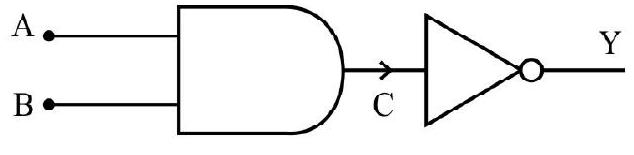
Fig. 32

The Booliean representation of NAND gate is

$$ \mathrm{Y}=\mathrm{A} \cdot \mathrm{B} $$

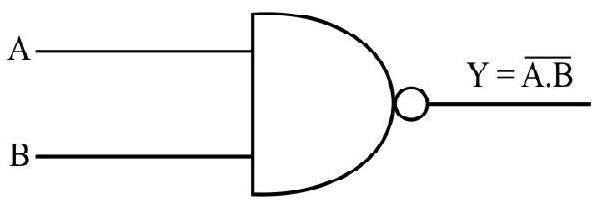
Logic Symbol

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{Y}$
0	0	1
0	1	1
1	0	1
1	1	0

Truth table

Fig. 33: The Boleean representation of NAND gate is $Y=\overline{A . B}$

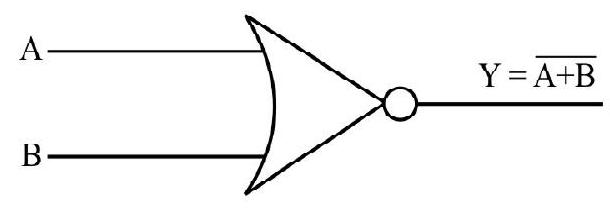
(v) NOR Gate

This is an OR gate followed by a NOT gate as shown in Fig. 34. Its output $Y$ is only 1 , when both inputs one 0 .

Thelogic symbol and truth table are given below:

The Booliean representation of NOR gate is

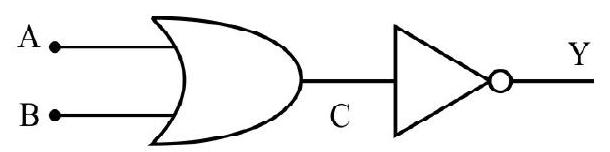
Fig. 34

$$ \mathrm{Y}=\mathrm{A}+\mathrm{B} $$

Logic Symbol

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{Y}$
0	0	1
0	1	0
1	0	0
1	1	0

Truth table

Fig. 35: The Boleean representation of NOR gate is $\mathrm{Y}=\overline{\mathrm{A}+\mathrm{B}}$

Example-15:

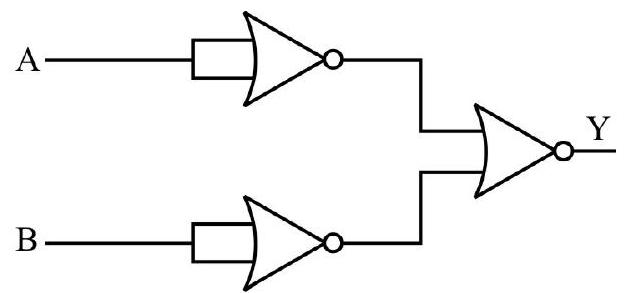
Write the truth table for a NAND gate connected as given in figure.

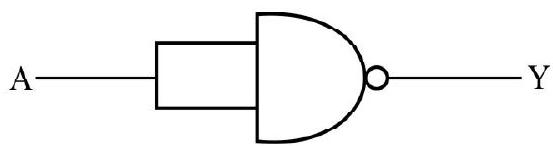
Show Answer

Solution:

The above operation represent one input connected to one output through NOT gate.

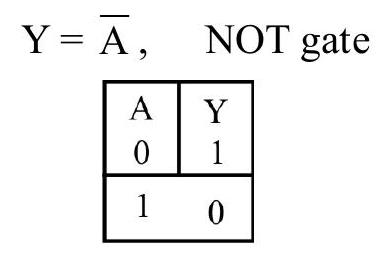
Example-16:

The output of an OR gate is connected to both the inputs of a NAND gate. Draw the logic circuit of this combination and the truth table.

Show Answer

Solution:

When two inputs of NAND are joined together, it works as NOT gates. The OR gate connected to NOT gate results in NOR gate.

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{C}=\mathrm{A}+\mathrm{B}$	$\mathrm{Y}=\overline{\mathrm{C}}$
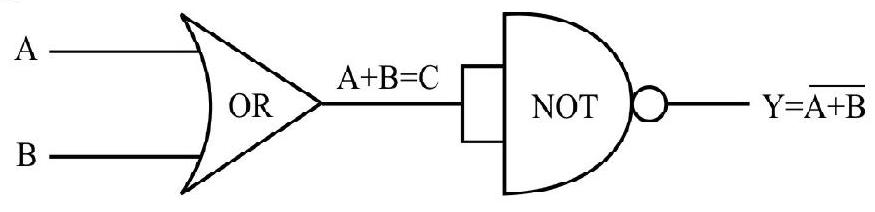
0	0	0	1
1	0	1	0
0	1	1	0
1	1	1	0

Example-17:

Write the truth table for the following combination of gates.

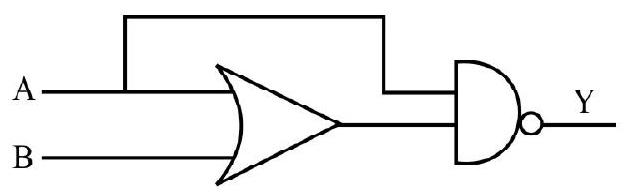
Show Answer

Solution:

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{C}=\mathrm{A} \mid \mathrm{B}$	$\mathrm{Y}=\overline{\mathrm{A} . \mathrm{C}}$
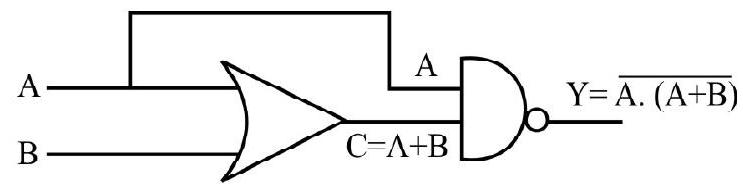
0	0	0	1
1	0	1	0
0	1	1	1
1	1	1	0

Example-18:

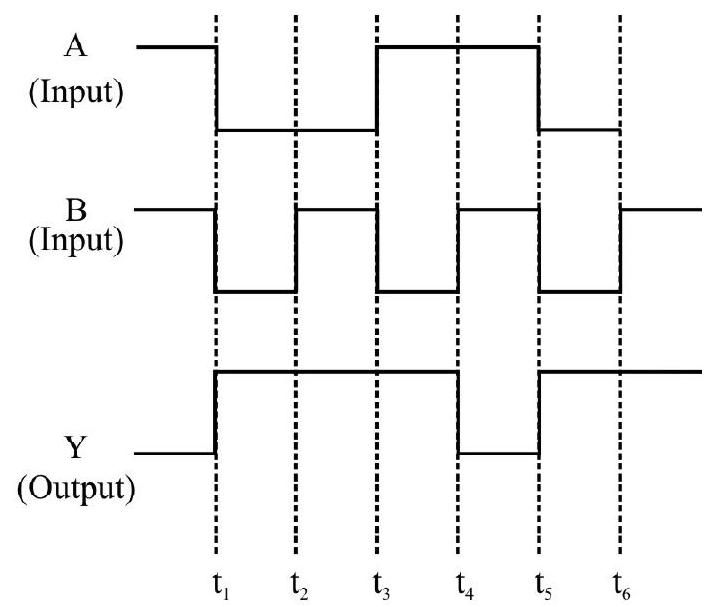
Justify the output waveform $(\mathrm{Y})$ of the OR gate for the following inputs A and $\mathrm{B}$ given in figure below

Show Answer

Solution:

Note the following:

At $\mathrm{t}<\mathrm{t} _{1} ; \quad \mathrm{A}=0, \mathrm{~B}=0 ; \quad$ Hence $\mathrm{Y}=0$

For $\mathrm{t} _{1}<\mathrm{t} _{2} ; \quad \mathrm{A}=1, \mathrm{~B}=0 ; \quad$ Hence $\mathrm{Y}=1$

For $\mathrm{t} _{2}<\mathrm{t} _{3} ; \quad \mathrm{A}=1, \mathrm{~B}=1 ; \quad$ Hence $\mathrm{Y}=1$

For $\mathrm{t} _{3}<\mathrm{t} _{4} ; \quad \mathrm{A}=0, \mathrm{~B}=1 ; \quad$ Hence $\mathrm{Y}=1$

For $\mathrm{t} _{4}<\mathrm{t} _{5} ; \quad \mathrm{A}=0, \mathrm{~B}=0 ; \quad$ Hence $\mathrm{Y}=0$

For $\mathrm{t} _{5}<\mathrm{t} _{6} ; \quad \mathrm{A}=1, \mathrm{~B}=0 ; \quad$ Hence $\mathrm{Y}=1$

For $\mathrm{t}<\mathrm{t} _{6} ; \quad \mathrm{A}=0, \mathrm{~B}=1 ; \quad$ Hence $\mathrm{Y}=1$

Therefore the waveform $Y$ will be as shown in the figure.

Example-19:

Sketch the output wavelength $Y$ for NAND gate having inputs $A$ and $B$ as shown below:

Show Answer

Solution:

Example-20:

Why are NAND and NOR gates called digital building blocks?

Show Answer

Solution:

The repeated use of NAND or NOR gate can produce all the three basic gates (OR AND and NOT) whose different combinations provide us large number of digital circuits. Hence NAND and NOR are called digital building blocks.

PROBLEMS FOR PRACTICE

1. A sample of pure Ge has a hole density of $10^{13} \mathrm{~cm}^{-3}$ at room temperature. When doped with antimony, the hole density falls to $10^{11} \mathrm{~cm}^{-3}$. Calculate the electron density of the doped Ge.

Show Answer

[Answer: $10^{15} \mathrm{~cm}^{-3}$ ]

2. The electrical conductivity of a semiconductor increases when radiation of wavelength shorter than $2480 \mathrm{~nm}$ is incident on it. Find the band gap of the semiconductor.

Show Answer

[Answer: $0.5 \mathrm{~eV}$ ]

3. When the voltage drop across a $\mathrm{p}-\mathrm{n}$ junction diode is increased from $0.65 \mathrm{~V}$ to $0.7 \mathrm{~V}$, the change in the diode current is $5 \mathrm{~mA}$. What is the dynamic resistance of the diode?

Show Answer

[Answer: $10 \Omega$ ]

4. A square wave as shown below is applied to a $\mathrm{p}-\mathrm{n}$ junction diode. Draw the output wave form across the diode assuming it to be ideal. 5. In a p-n junction diode, the current I can be expressed as:

$$ \mathrm{I}=\mathrm{I} _{0} \exp \left(\dfrac{\mathrm{eV}}{2 \mathrm{k} _{\mathrm{BT}}}-1\right) $$

where $\mathrm{I} _{0}$ is reverse saturation current, $\mathrm{V}$ is applied voltage for forward bias positive and reverse bias negative. I is the current through diode.

$\mathrm{k} _{\mathrm{B}}$ is the Boltzmann constant $\left(8.6 \times 10^{5} \mathrm{eV} / \mathrm{k}\right)$ and $\mathrm{T}$ is the absolute temperature. If for a given diode $\mathrm{I} _{0}=5 \times 10^{-12} \mathrm{~A}$ and $\mathrm{T}=300 \mathrm{k}$, then

(i) Find the forward current at forward voltage $0.6 \mathrm{~V}$.

(ii) What will be the increase in current if voltage across the diode is increased to $0.7 \mathrm{~V}$.

(iii) What is the dynamic resistance?

Show Answer

[Answer: (i) $0.629 \mathrm{~A}$, (ii) $2.97 \mathrm{~A}$, (iii) $0.336 \Omega$ ]

6. The circuit given below shows two diodes each with a forward bias resistance of $50 \mathrm{ohm}$ and with infinite backward resistance. If the battery voltage is $6 \mathrm{~V}$. Find the current through $100 \mathrm{ohm}$ resistance.

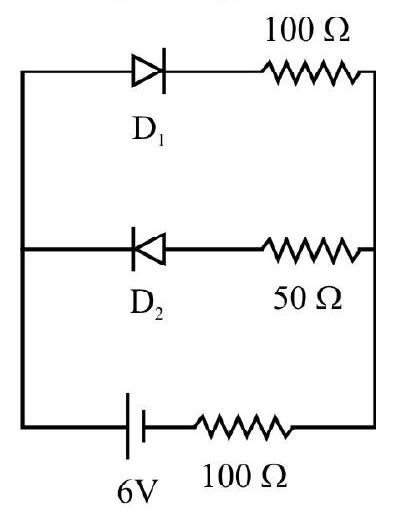
Show Answer

[Answer: $0.02 \mathrm{~A}$ ]

7. The V-I characterstics of silicon diode are shown above. Calculate the diode resistance at $\mathrm{I}=20$ $\mathrm{mA}$ and $\mathrm{V}=-10 \mathrm{~V}$.

Show Answer

[Answer: $10 \Omega, 10^{7} \Omega$ ]

8. In a common emitter amlifier an increase of $50 \mu \mathrm{A}$ in the base current causes an increase of $1 \mathrm{~mA}$ in the collector current. Calculate the current gain $\beta$. What will be the change in the emitter current? Calculate $\alpha$ from the obtained value of $\beta$.

Show Answer

[Answer: $20,1050 \mu \mathrm{A}, 0.95$ ]

9. In a npn transistor $10^{10}$ electrons enter the emitter in $10^{-6} \mathrm{~S} .2 \%$ of the electrons are lost in the base. Calculate the current amplification factor.

Show Answer

[Answer: 49]

10. An npn transistor is connected in common emitter configuration in which collector supply is $8 \mathrm{~V}$ and the voltage drop across the load resistance of $800 \Omega$ connected in the collector circuit is $0.8 \mathrm{~V}$. If the current amplification factor is 25 ; determine the collector emitter voltage $\mathrm{V} _{\mathrm{CE}}$ and base current $\mathrm{I} _{\mathrm{B}}$. It the input resistance of transition is $200 \Omega$. Calculate the voltage gain $\mathrm{A} _{\mathrm{V}}$ and power gain $\mathrm{A} _{\mathrm{p}}$.

Show Answer

[Answer: $\mathrm{V} _{\mathrm{CE}}=7.2 \mathrm{~V}, \mathrm{I} _{\mathrm{B}}=40 \mu \mathrm{A}, \mathrm{A} _{\mathrm{V}}=100, \mathrm{~A} _{\mathrm{P}}=2500$ ]

11. In the given circuit below, $\beta=100, \mathrm{~V} _{\mathrm{CC}}=24 \mathrm{~V}, \mathrm{R} _{\mathrm{C}}=4.7 \mathrm{k} \Omega, \mathrm{R} _{\mathrm{B}}=220 \mathrm{k} \Omega$.

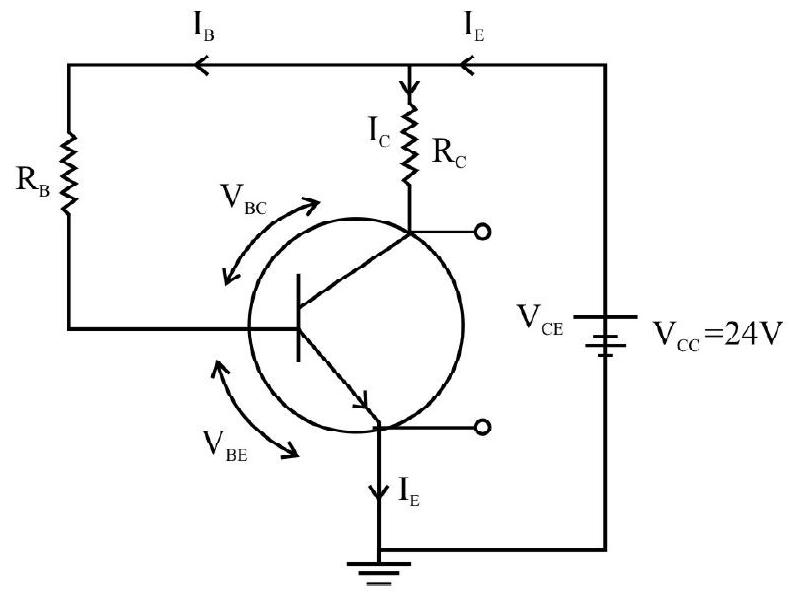
Find $\mathrm{V} _{\mathrm{CE}}, \mathrm{V} _{\mathrm{BE}}$ and $\mathrm{V} _{\mathrm{BE}}$, when $\mathrm{I} _{\mathrm{C}}=1.5 \mathrm{~mA}$.

Show Answer

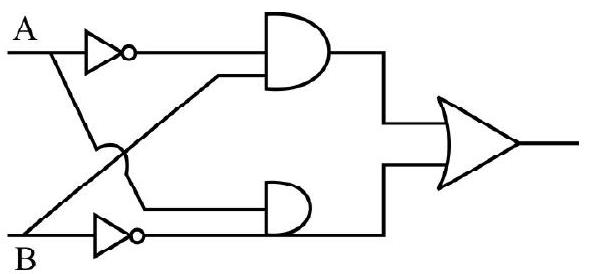
[Answer: $\mathrm{V} _{\mathrm{CE}}=16.95 \mathrm{~V}, \mathrm{~V} _{\mathrm{BE}}=20.7 \mathrm{~V}, \mathrm{~V} _{\mathrm{BC}}=3.75 \mathrm{~V}$]

12. Write the truth table for the following combination of gates.

[Answer: ]

13. Write the truth table for the following circuit. Identify the logic operation performed.

[Answer: ]

14. Two amplifiers are connected one after other in series. The first amplifier has a voltage gain of 10 and second has voltage gain of 20 . If the input signal is $0.01 \mathrm{~V}$, then calculate theinput a.c signal.

Show Answer

[Answer: 2V]

15. Out of the following combinations of gates given, identify the circuit, which performs the logic operation ‘AND’.

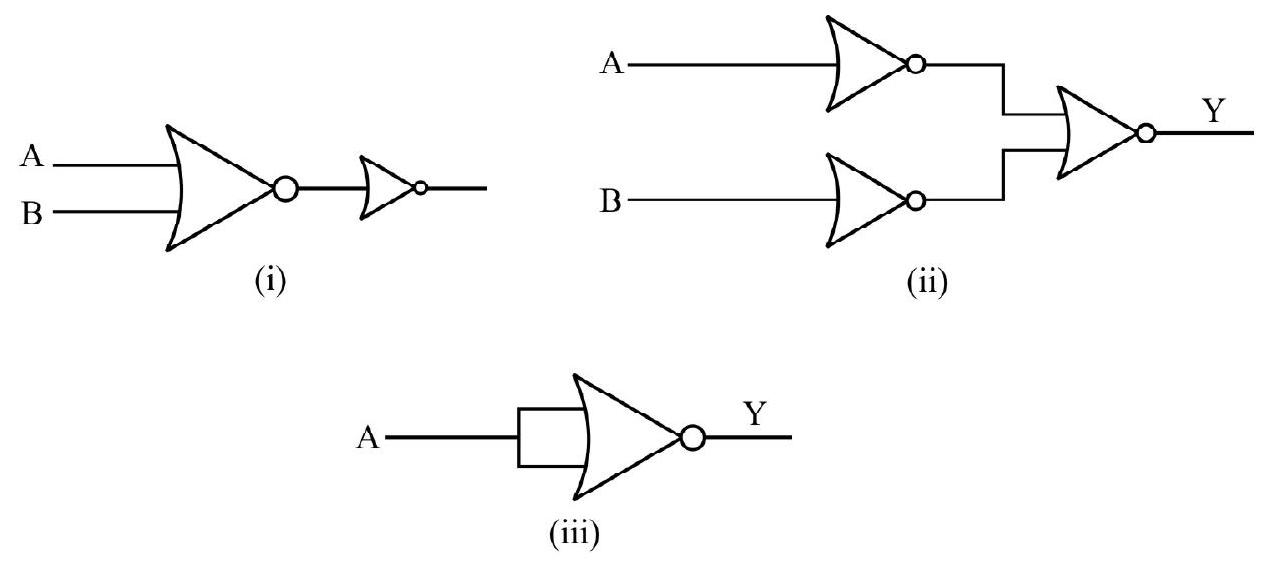
Show Answer

[Answer: (ii)]

Question Bank

Key Learning Points

1. The large number of energy levels confined in a small region of energy range of a given solid, consitute, a band known as ‘Energy Band’.

2. The upper energy levels are called conduction band and lower energy levels are called valence band.

3. In some solids, there is an energy gap in between conduction band and valence band; known as forbiddengap.

4. In metals, the conduction band and valence band partly overlap each other and there is no forbidden gap.

5. In isulators, forbidden gap is quite large $(\simeq 3 \mathrm{eV})$. Probability of electron moving to conduction band at room temeprature is negligible, even if electric field is applied. Hence there is no conductivity of the insulators.

6. In semiconductor, the forbidden gap is small ( 1 to $2 \mathrm{eV})$. These are perfect insulators at $\mathrm{OK}$. With the rise in temperature, their conductivity increases, because some of the electrons accquire thermal energy and cross over to the conduction band from valence band and act as free electrons, available for conductor.

7. A pure semiconductor which is free from every impurity is called intrinsic semiconductor. In intrinsic semiconductor $n _{e}=n _{h}=n _{i}$. Where $n _{e}$ and $n _{h}$ are number density of holes in valence band, $n _{i}$ the number density of intrinsic carriers and $n _{\mathrm{e}}$ the number density of electrons in the conduction band.

8. The process of delibrate addition of a desirable impurity to a pure semiconductor to modify its conductivity in a controlled manner; is called dopoing. The semiconductor so obtained is called extrinsic semiconductor. The impurity atoms added are called dopants.

9. When a pure semiconductor of Ge or $\mathrm{Si}$ is doped with a controlled amount of pentavelent impurity atom like assenic, antimony or bismuth etc. we obtain a n-type semiconductor with electrons as majority change carriers $\left(\mathrm{n} _{\mathrm{e}}»\mathrm{n} _{\mathrm{h}}\right)$ and impurity is called donor.

10. When a pure semiconductor of $\mathrm{Ge}$ or $\mathrm{Si}$ is doped with a controlled amount of trivalent impurity like induium, boron or aluminium etc. We obtain a p-type semiconductor with holes as majority change carriers $\left(\mathrm{n} _{\mathrm{h}}»\mathrm{n} _{\mathrm{e}}\right)$ and in this case impurity is called acceptor.

11. Energy band diagram for extrinsic semiconductor is modified. In n-type, there is additional donor level just below conductor band and in p-type there is additional acceptor level just above valence band.

12. The electrical conductivity of a semiconductor crystal is given by

$$ \sigma=\dfrac{1}{\rho}=\mathrm{e}\left(\mathrm{n} _{\mathrm{e}} \mu _{\mathrm{e}}+\mathrm{n} _{\mathrm{h}} \mu _{\mathrm{h}}\right) $$

13. When a semiconductor is heated, its resistance decreases, specific resistance decreases and electrical conductivity increases.

14. A thin layer formed on both sides of the $\mathrm{p}-\mathrm{n}$ junction, caused by the diffusion of charge carriers, which is devoid of the free charge carriers but has immobile ions is called depletion layer. The thickness of depletion layer is of the order of $\mu \mathrm{m}$.

15. The potential barrier or electric field set up across the junction depends upon the amount of doping of the semiconductor crystal and temperature.

16. During forward bias ( $\mathrm{p}-$ side at higher potential than $\mathrm{n}$-side), the width of depletion layer becomes thin and diode offers very low resistance. An ideal p-n junction diode in forward bias has zero resistance.

17. During reverse bias ( $n$-side at higher potential than $\mathrm{p}$-side), the width of depletion layer widens and diode offers very high resistance. An ideal $\mathrm{p}-\mathrm{n}$ junction diode in reverse bias has infinite resistance.

18. Voltage drop across the $\mathrm{p}-\mathrm{n}$ junction diode in forward bias is zero, whereas in reverse bias it is equal to the voltage applied.

19. The potential barrier at $\mathrm{p}-\mathrm{n}$ junction opposes the forward current. The kinetic energy required by the majority charge carriers to diffuse decreases $\left[\mathrm{q} _{\mathrm{B}}-\mathrm{V}\right]$; whereas it aids the reverse current. The kinetic energy required by the majority charge carriers to drift increases $\left[q\left(V _{B}+V\right)\right]$.

20. An ideal p-n junction diode has unidirectional property. It conducts only in one direction, when forward biased.

21. The ratio of change in applied (junction) voltage $(\Delta \mathrm{V})$ to change in forward current $(\Delta \mathrm{I})$ is called a dynamic resistance $r _{d}=\dfrac{\Delta V}{\Delta I}$.

22. The unidirectional property of an ideal $\mathrm{p}-\mathrm{n}$ junction diode is used in a device called rectifier.

23. In $p-n$ junction as a half wave rectifier, the frequency of the output signal is equal to the frequency of a.c to be rectified.

24. In $\mathrm{p}-\mathrm{n}$ junction as a full wave rectifier, the frequency of the output signal is equal to twice the frequency of a.c to be rectified.

25. There are special purpose $\mathrm{p}-\mathrm{n}$ junction diodes like zener diode, solar cell, photodiode and LED.

26. Zener diode is just like an ordinary $p$-n junction diode except that is is heavily doped in order to have a sharp reverse bias break down voltage. It is always connected in reverse bias and is used as voltage regulating device.

27. Photodiodes are the special type of diodes working in a reverse bias. These diodes work on the principle that change in the intensity of radiation results in change in reverse saturation current. For

this to happen, energy of incident photon must be greater than or equal to the barrier energy of the semiconductor. The photodiodes can be used as a photodector to detect optical signal.

28. Solar cell is a device in which light energy is converted into electrical energy. Semiconductors with band gap close to $1.5 \mathrm{eV}$ are ideal materials for solar cell fabrication. Solar cells are used to power electronic devices in sateliltes and space vehicle, calculators etc.

29. Light emitting diode, commonly known as ‘LED’ is a heavily doped $p-n$ junction which under forward bias emits spantaneous radiation. The semiconductor used for fabrication of visible LED’s must at least have a band gap of $1.8 \mathrm{eV}$ (as range of visible light is $3 \mathrm{eV}$ to $1.8 \mathrm{eV}$ ). The LED’s find extensive use in remote controls, buglar alarm systems and optical communication etc.

30. A junction transistor is a semiconductor device which obtained by growing a thinlayer of one type of semiconductor in between the two thick layers of other type of semiconductor. The most common configuration are pnp and npn transistor.

31. The junction transistor has three segments-emitter, base and collector. The function of emitter is to emit the majority charge carriers. Function of collector is to collect the majority charge carriers and base provides the proper bias for the collection of charge carriers.

32. The base region is very thin and lightly doped. The emitter is heavily doped.

33. During the action/working of a transistor.

$$ \mathrm{I} _{\mathrm{E}}=\mathrm{I} _{\mathrm{C}}+\mathrm{I} _{\mathrm{B}} $$

where $\mathrm{I} _{\mathrm{E}}$ is the emitter current, $\mathrm{I} _{\mathrm{C}}$ is the collector current and $\mathrm{I} _{\mathrm{B}}$ is the base current.

34. The transistor can be used as an amplifier in CE configuration. During amplification, input and output signal are $180^{\circ}$ out of phase. There is amplification of current, voltage and power of the given signal.

35. Current gain in CE configuration is given by $\beta=\dfrac{I _{C}}{I _{B}}$ and is greater than one.

36. Current gain in common base configuration is $\alpha=\dfrac{\mathrm{I} _{\mathrm{C}}}{\mathrm{I} _{\mathrm{E}}}$ and is slightly less than one.

37. A.C voltage gain in CE amplifier is given by $A _{v}=-\beta _{a . c} \dfrac{R _{o}}{R _{i}}$ where $R _{o}$ is output resistance of the transistor, $R _{i}$ is the input resistance of the transistor. $\beta _{a . c}$ is known as a.c current gain given by $\beta _{\mathrm{a} . \mathrm{c}}=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{B}}}$. Negative sign indicates the phase of $180^{\circ}$ between output and input signal.

38. A.C power gain in $\mathrm{CE}$ amplifier is given by

$$ \begin{aligned} & \mathrm{A} _{\mathrm{P}}=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{B}}} \times \dfrac{\Delta \mathrm{V} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{i}}}\\ \\ & =\beta _{\mathrm{a} . \mathrm{c}} \mathrm{A} _{\mathrm{V}}\\ \\ & =-\beta _{\mathrm{a} . \mathrm{c}}^{2} \dfrac{\mathrm{R} _{\mathrm{o}}}{\mathrm{R} _{\mathrm{i}}} \end{aligned} $$

39. In the transistor as an oscillator, a positive feedback is provided from on output tank circuit (LC) to the input circuit (transistor as amplifier) to obtain the sustain oscillations with constant amplitude. Hence oscillator is an amplifier with positive feedback.

40. Transistor is used as an amplifier only in active state. That is emitter base junction forward bias and base emitter junction reverse bias.

41. Transistor can be used as a switch in the cutoff or saturation state.

42. There are some special circuits which handle the digital data consisting of 0 and 1 levels. This forms digital circuits.

43. The digital circuit having logic relationship between input and output signal are called ’logic gates’.

44. The important basic logic gates are OR, AND, NOT, NAND and NOR gates.

45. NAND and NOR gates are considered as universal gates as these gates are building blocks of OR, AND and NOT gates.

Average

Semiconductors

1. Semiconductors are fourth group elements in periodic table. Silicon (Si), Carbon (C) and Germanium (Ge) att are fourth group elements in periodic talbe. Which of the following statement is correct?

(1) All are semiconductors

(2) Only Si and Ge are semiconductors

(3) Only carbon is semiconductor

(4) Carbon (C) and Germanium are semiconductors

Show Answer

Correct answer: (2)

Solution:

Only Si and Ge are semiconductors carbon is an insulator. The energy gap for Si and Ge is nearly $1.1 \mathrm{eV}$ and $0.7 \mathrm{eV}$ respectively. However energy gap in carbon is nearly $5.5 \mathrm{eV}$. This difference arises because electrons (valency) in carbon are present in second orbit. The attractive force on them due to nucleus is quite strong. The valenay electrons in $\mathrm{Si}$ and Ge are present is thered and forth orbit. Their binding to nucleus is therefore less stong as compared to carbon. This reflects itself in a law value of energy gap as compared to carbon.

Difficult

Semiconductors

2. Most of currently available semiconductor are elemental semiconductors $\mathrm{Si}$ or $\mathrm{Ge}$ and compound inorganic semiconductors. From 1990 onwards devices using organic semiconductors and semiconducting polymers have been developed. These are futuristic technology in gradients. The (a) in organic (b) organic and (c) organic polymer semiconductors are:

(1) (a) GaAs (b) CdSe (c) anthracene

(2) (a) GaAs (b) anthracene (c) polyanline

(3) (a) anthracene (b) GaAs (c) polyanline

(4) (a) CdSe (b) polyanline (a) anthracene

Show Answer

Correct answer: (2)

Solution:

Factual knowledge.

Easy

Semiconductors

3. A “Hole” in a semiconductor is produced when an electron breaks away from a covalent bond in a semiconductors. Which of the following statements regarding a hole is incorrect?

(1) A hole has same magnitude of charge as on an electron

(2) In an external eletric field a hole moves in a direction opposite to that of free electron

(3) The energy of a hole is less as compared to that of an electron

(4) In same external applied electric field the drift speed accquired by a hole is less than the drift speed accquired by a free electron

Show Answer

Correct answer: (3)

Solution:

The energy of hole is less than the energy of an electron.

Easy

Semiconductors

4. An intrinsic semiconductor is at a temperature of $27^{\circ} \mathrm{C}$. The probability of an electron jumping from valence band to conduction band

(1) does not vary as temeperature rises to $40^{\circ} \mathrm{C}$

(2) decreases linearly with rise in temperature

(3) increases exponentially as the energy gap increases

(4) decreases exponentially as the energy gap increases

Show Answer

Correct answer: (4)

Solution:

As energy gap increases the probability of electron jump from conduction to valency band decreases exponentially.

Easy

Semiconductors

5. An electric field of $40 \mathrm{~V} \mathrm{~cm}^{-1}$ is applied to a semiconductor crystal. A small amount of minority carriers are also injected into the crystal at one point. Due to the electric field, minority carriers move a through a disance of $2 \mathrm{~cm}$ in $40 \mu \mathrm{s}$. The mobility of the carriers will be,

(1) $500 \mathrm{~cm}^{2} \mathrm{~V}^{-1} \mathrm{sec}^{-1}$

(2) $1000 \mathrm{~cm}^{2} \mathrm{~V}^{-1} \mathrm{sec}^{-1}$

(3) $1250 \mathrm{~cm}^{2} \mathrm{~V}^{-1} \mathrm{sec}^{-1}$

(4) $2500 \mathrm{~cm}^{2} \mathrm{~V}^{-1} \mathrm{sec}^{-1}$

Show Answer

Correct answer: (3)

Solution:

Velocity of the carriers $=\nu=\dfrac{\text { distance travelled }}{\text { time taken }}=\dfrac{2}{40 \times 10^{-6}}=50000 \mathrm{~cm} \mathrm{~s}^{-1}$

Velocity is also given by, $\nu=\mu \mathrm{E}$

Mobility $=\mu=\dfrac{\nu}{\mathrm{E}}=\dfrac{50000}{40}=1250 \mathrm{~cm}^{2} \mathrm{~V}^{-1} \mathrm{sec}^{-1}$

Average

Conductivity of Semiconductors

6. Mobilities of electrons and holes in a sample of intransic germanium at room temperature are $0.36 \mathrm{~m}^{2} / \mathrm{Vs}$ and $0.17 \mathrm{~m}^{2} / \mathrm{Vs}$. The electron and hole densities are each equal to $2.5 \times 10^{19}$ $\mathbf{m}^{-3}$. The electrical conductivity of germanium is

(1) $0.47 \mathrm{~S} / \mathrm{m}$

(2) $1.09 \mathrm{~S} / \mathrm{m}$

(3) $2.12 \mathrm{~S} / \mathrm{m}$

(4) $5.18 \mathrm{~S} / \mathrm{m}$

Show Answer

Correct answer: (3)

Solution:

The conductivity of a semiconductive in terms of number density and mobility is

$$ \sigma=\dfrac{1}{\rho}=\mathrm{e}\left(\mu _{\mathrm{e}} \mathrm{n} _{\mathrm{e}}+\mu _{\mathrm{n}} \mathrm{h} _{\mathrm{h}}\right) $$

where $\mu _{\mathrm{e}}$ and $\mu _{\mathrm{n}}$ denote mobility of electron and hole, $\mathrm{n} _{\mathrm{e}}$ and $\mathrm{n} _{\mathrm{h}}$ is the number density of electron and hole respectively. Substituting given values, we have

$$ \sigma=1.6 \times 10^{-19}(0.36+0.17)\left(2.5 \times 10^{19}\right) $$

$$=2.12 \mathrm{~S} / \mathrm{m}$$

Easy

Extrinsic Semiconductors

7. The impurity atoms with which pure silicon should be doped to make a n-type semiconductor are those

(1) Boron

(2) Indium

(3) Antomony

(4) Aluminium

Show Answer

Correct answer: (3)

Solution:

As n-type semiconductor is obtained by adding pentavalent impurity atom. Hence impurity should be of antomony out of all the four choices given.

Average

Semiconductors

8. For the same dopant concentration, the n–type silicon semiconductor has _____________ as compared to a p-type silicon semiconductor.

(1) Higher conductivity

(2) Higher resistivity

(3) Lower mobility

(4) Lower net charge

Show Answer

Correct answer: (1)

Solution:

For the silicon semiconductor,

Mobility of electrons $=\mu _{\mathrm{e}}=1350 \mathrm{~cm}^{2} \mathrm{~V}^{-1} \mathrm{sec}^{-1}$

Mobility of holes $=\mu _{\mathrm{n}}=480 \mathrm{~cm}^{2} \mathrm{~V}^{-1} \mathrm{sec}^{-1}$

Conductivity of electrons $=\sigma=\mathrm{n} \times \mathrm{q} \times \mu _{\mathrm{e}}$

Conductivity of holes $=\sigma=p \times q \times \mu _{n}$

Now, since dopant concentration is same,

Concentration of electrons $(\mathrm{n})=$ concentration of holes $(\mathrm{p})$

Conductivity of n-type sample is more than $\mathrm{p}$-type sample.

Average

Semiconductors

9. At thermal equilibrium, the concentration of majority carriers in an n-type extrinsic semiconductor, is

(1) Inversely proportional to the intrinsic carrier concentration

(2) Directly proportional to the intrinsic carrier concentration

(3) Inversely proportional to the majority carrier concentration

(4) Directly proportional to the majority carrier concentration

Show Answer

Correct answer: (3)

Solution:

If $\mathrm{n} _{\mathrm{h}}$ is the concentration of holes (miniority carriers), $\mathrm{n} _{\mathrm{e}}$ is concentration of electrons (majority carriers) and $\mathrm{n} _{\mathrm{t}}$ is the intrinsic carrier concentration, then at thermal equilibrium, we have the relation,

$\quad\mathrm{n} _{\mathrm{h}} \times \mathrm{n} _{\mathrm{e}}=\mathrm{n} _{1}^{2}$

$\quad=\mathrm{n} _{\mathrm{h}}=\dfrac{\mathrm{n} _{\mathrm{i}}^{2}}{\mathrm{n} _{\mathrm{e}}}$

or $\quad\mathrm{n} _{\mathrm{h}} \propto \dfrac{1}{\mathrm{n} _{\mathrm{e}}}$

Average

Semiconductors

10. In a p-type semiconductor, the concentration ofholes is $2 \times 10^{15} \mathbf{~ c m}^{-3}$. The intrinsic carrier concentration is $2 \times 10^{10} \mathrm{~cm}^{-3}$. The concentration of electrons will be.

(1) $1 \times 10^{5} \mathrm{~cm}^{-3}$

(2) $2 \times 10^{5} \mathrm{~cm}^{-3}$

(3) $2 \times 10^{15} \mathrm{~cm}^{-3}$

(4) $2 \times 10^{20} \mathrm{~cm}^{-3}$

Show Answer

Correct answer: (2)

Solution:

If $n _{h}$ is the concentration of holes, $n _{e}$ is concentration of electrons and $n _{i}$ is the intrinsic carrier concentration, then we have the relation,

$$ \begin{aligned} & \mathrm{n} _{\mathrm{h}} \times \mathrm{n} _{\mathrm{e}}=\mathrm{n} _{\mathrm{i}}^{2}\\ & =\mathrm{n} _{\mathrm{e}}=\dfrac{\mathrm{n} _{\mathrm{i}}^{2}}{\mathrm{n} _{\mathrm{h}}}=2 \times 10^{5} \mathrm{~cm}^{-3} \end{aligned} $$

Average

Semiconductors

11. A silicon sample is uniformly doped with $2 \times 10^{15} \mathrm{Phosporous} \dfrac{\text { atoms }}{\mathrm{cm}^{3}}$ and $10^{15}$ Indium $\dfrac{\text { atoms }}{\mathrm{cm}^{3}}$. Assuming that the dopants are fully ionized, the sample will be

(1) n-type with carrier concentration of $10^{15} \mathrm{~cm}^{-3}$

(2) p-type with carrier concentration of $10^{15} \mathrm{~cm}^{-3}$

(3) n-type with carrier concentration of $2 \times 10^{15} \mathrm{~cm}^{-3}$

(4) p-type with carrier concentration of $2 \times 10^{15} \mathrm{~cm}^{-3}$

Show Answer

Correct answer: (1)

Solution:

Phosphorous is pentavalent impurity and will make the silicon sample n-type. Since the donor atoms are fully ionized.

Number of electrons $=\mathrm{N} _{\mathrm{D}}=2 \times 10^{15} \mathrm{~cm}^{-3}$

Indium is trivalent impurity and will make the silicon sample p-type. Since the acceptor atoms are fully ionized.

Number of holes $=\mathrm{N} _{\mathrm{A}}=10^{15} \mathrm{~cm}^{-3}$

Therefore, the sample will be n-type and the net carrier concentration will be $10^{15} \mathrm{~cm}^{-3}$

Average

Semiconductors

12. In an intrinsic semiconductors number density of electrons and holes is same and is $n$. The relaxation time of electrons and holes is $\tau _{\mathrm{e}}$ and $\tau _{\mathrm{h}}$ respectively. As temperature of semiconductor rises its conductivity increases. Which of the following statements is correct?

(1) Increase in conductivity is due to increase in n only

(2) Increase in conductivity is due to increase in relaxation time $\tau _{\mathrm{e}}$ and $\tau _{\mathrm{h}}$ only

(3) The increase in $n$ and decrease in relaxation time are equal contributes for increase in conductivity

(4) $\mathrm{n}$ increases, $\tau _{\mathrm{e}}$ and $\tau _{\mathrm{h}}$ decrease. Effect of increase in $\mathrm{n}$ is much more than the effect of decrease in $\tau _{\mathrm{e}}$ and $\tau _{\mathrm{h}}$.

Show Answer

Correct answer: (4)

Solution:

Facturial knowledge about semiconductors.

Easy

Semiconductors

13. Pure Si and $500 \mathrm{~K}$ has an equal number of electron and holes of concentration $1.5 \times 10^{16}$. Doping by indium increases hole concentration $\left(n _{h}\right)$ to $4.5 \times 10^{22} \mathrm{~m}^{-3}$. The doped semiconductor is

(1) n-type; with electron concentration of $5 \times 10^{22} \mathrm{~m}^{-3}$

(2) p-type; with electron concentration of $2.5 \times 10^{10} \mathrm{~m}^{-3}$

(3) n-type; with electron concentration of $2.5 \times 10^{23} \mathrm{~m}^{-3}$

(4) p-type; with electron concentration of $5 \times 10^{9} \mathrm{~m}^{-3}$

Show Answer

Correct answer: (4)

Solution:

Given ne $=1.5 \times 10^{16} \mathrm{~m}^{-3}, \mathrm{n} _{\mathrm{h}}=4.5 \times 10^{22} \mathrm{~m}^{-3}$

Let $\mathrm{n} _{\mathrm{e}}$ be the concentration of electrons we know

$$ \begin{aligned} & n _{e} n _{h}=n _{e}^{2}\\ \therefore \quad & n _{e}=\dfrac{n _{e}^{2}}{n _{h}}=\dfrac{\left(1.5 \times 10^{16}\right)^{2}}{4.5 \times 10^{22}}=0.5 \times 10^{10} \mathrm{~m}^{-3} \end{aligned} $$

Since $\mathrm{n} _{\mathrm{h}}>\mathrm{n} _{\mathrm{e}}$; the material as a p-type semiconductor. The electron concentration $=\mathrm{n} _{\mathrm{e}}=5 \times 10^{9} \mathrm{~m}^{-3}$.

Average

Semiconductors

14. A pure siliconn sample has $\mathrm{n} _{\mathrm{e}}=\mathbf{1 . 3} \times \mathbf{1 0}^{16} \mathrm{~m}^{-3}$. The material is doped with

(a) $10^{19}$ atoms $\mathrm{m}^{-3}$ of phosporous

(b) $\mathbf{2} \times 10^{19}$ atoms $\mathbf{m}^{-3}$ of boron

one by one. What is ratio of resistivity of doped sample in (a) and (b) due to majority charge carriers? Given:

Mobility of electrons $=0.125 \mathrm{~m}^{2} \mathrm{~V}^{-1} \mathrm{~s}^{-1}$, Mobility of holes $=0.0426 \mathrm{~m}^{2} \mathrm{~V}^{-1} \mathrm{~s}^{-1}$.

(1) 1

(2) 2

(3) $1 / 2$

(4) $2 / 3$

Show Answer

Correct answer: (4)

Solution:

(a) The majority charge carriers are electrons. $\mathrm{n} _{\mathrm{e}}=$ Number of free electrons $=10^{9} \mathrm{~m}^{-3} ; \mu _{\mathrm{e}}=$ $0.125 \mathrm{~m}^{2} \mathrm{~V}^{-1} \mathrm{~s}^{-1}, \rho _{\mathrm{e}}=$ Resistivity of material $=\dfrac{1}{\mathrm{n} _{\mathrm{e}} \mathrm{e} \mu _{\mathrm{e}}}$

$$ =\dfrac{1}{10^{19} \times 1.6 \times 10^{-19} \times 0.125}=5 \Omega \mathrm{m} $$

(b) The majority charge carriers are holes $\mathrm{n} _{\mathrm{h}}=$ Number of holes $=2 \times 10^{19} \mathrm{~m}^{-3}, \mu _{\mathrm{n}}=0.426 \mathrm{~m}^{2} \mathrm{~V}^{-1} \mathrm{~s}^{-1}$

$$ \begin{aligned} \rho _{\mathrm{R}}= & \text { Resistivity of material }=\dfrac{1}{\mathrm{n} _{\mathrm{h}} \mathrm{e} \mu _{\mathrm{h}}}\\ & =\dfrac{1}{2.10^{19} \times 1.6 \times 10^{-19} \times 0.0416}=7.5 \Omega \mathrm{m}\\ \therefore \quad & \dfrac{\rho _{\mathrm{e}}}{\rho _{\mathrm{h}}}=\dfrac{5}{7.5}=\dfrac{2}{3} \end{aligned} $$

Difficult

Semiconductors

15. A pure silicon semiconductor has a size of $10 \mathrm{~mm} \times 10 \mathrm{~mm} \times 1 \mathrm{~mm}$. There are $5 \times 10^{28}$ atoms per cubic metere in silicon. It is doped simultaneously with 1 part in one million of arsenic and one part per hundred million of Indium. The number density of intrinsic carriers in pure silicon is $1.5 \times 10^{16} \mathrm{~m}^{3}$. The number of electrons, $n _{e}$; and number of hole $n _{h}$ in semiconductor is

(1) $\mathrm{n} _{\mathrm{e}}=5 \times 10^{15} ; \mathrm{n} _{\mathrm{h}}=5 \times 10^{4}$

(2) $\mathrm{n} _{\mathrm{e}}=5 \times 10^{2} ; \mathrm{n} _{\mathrm{h}}=5 \times 10^{13}$

(3) $\mathrm{n} _{\mathrm{e}}=5.5 \times 10^{15} ; \mathrm{n} _{\mathrm{h}}=4.54 \times 10^{4}$

(4) $\mathrm{n} _{\mathrm{e}}=4.95 \times 10^{15} ; \mathrm{n} _{\mathrm{h}}=4.54 \times 10^{2}$

Show Answer

Correct answer: (4)

Solution:

Volume of given sample $=100 \times 10^{-9} \mathrm{~m}^{3}=10^{-7} \mathrm{~m}^{3}$

The extent of doping of assenic is more than that of indium.

The net extent of doping $=\left(10^{-6}-10^{-8}\right)=0.99 \times 10^{-6}$

$$ =5 \times 10^{23} \times 0.99 \times 10^{-6}=4.95 \times 10^{22} \mathrm{~m}^{-3} $$

$\mathrm{n} _{\mathrm{h}}=$ Number of holes $=\dfrac{\left(\mathrm{n} _{\mathrm{i}}\right)^{2}}{\mathrm{n} _{\mathrm{e}}}=\dfrac{\left(1.5 \times 10^{16}\right)^{2}}{4.95 \times 10^{22}}$

$$ =4.54 \times 10^{9} \mathrm{~m}^{-3} $$

The number of electrons in given sample $=4.95 \times 10^{22} \times 10^{-7}=4.95 \times 10^{15}$

The numbe of holes in given sample $=4.54 \times 10^{9} \times 10^{-7}=4.54 \times 10^{2}$

Average

Semiconductors

16. A pure germanium rod has a radius of $1 \mathrm{~cm}$ and length $4 \mathrm{~cm}$. A p.d of $4 \mathrm{~V}$ is applied across the ends of rod. The concentration of holes in the rod is $2.5 \times 10^{19} \mathrm{~m}^{-3}$. The mobility of electrons and holes is $0.36 \mathrm{~m}^{2} \mathrm{~V}^{-1} \mathrm{~s}^{-1}$ and $0.18 \mathrm{~m}^{2} \mathrm{~V}^{-1} \mathrm{~s}^{-1}$ respectively. The current in rod is

(1) $45.2 \mathrm{~mA}$

(2) $22.6 \mathrm{~mA}$

(3) $67.8 \mathrm{~mA}$

(4) $56.3 \mathrm{~mA}$

Show Answer

Correct answer: (3)

Solution:

The electric field in $\operatorname{rod}=\dfrac{\mathrm{V}}{\mathrm{L}}=\dfrac{4 \mathrm{~V}}{4 \times 10^{-2} \mathrm{~m}}=10^{2} \mathrm{Vm}^{-1}$

Let $\mathrm{v} _{\mathrm{e}}$ and $\mathrm{v} _{\mathrm{h}}$ be the average drift speed accquired by electron and holes respectively under the applied electric field. Let $\mu _{\mathrm{e}}$ and $\mu _{\mathrm{n}}$ be mobility of electron and hole. Then

$$ \mathrm{v} _{\mathrm{e}}=\mu _{\mathrm{e}} \mathrm{E} \text { and } \mathrm{v} _{\mathrm{n}}=\mu _{\mathrm{h}} \mathrm{E} $$

The current, $\mathrm{I} _{\mathrm{e}}$; due to motion of electrons is

$$ I _{e}=n _{e} \operatorname{aev} _{e} $$

Given $\mathrm{n} _{\mathrm{e}}=2.5 \times 10^{19} \mathrm{~m}^{-3} ; \mathrm{e}=1.6 \times 10^{-19} \mathrm{C} ; \mathrm{a}=3.14 \times 10^{-4} \mathrm{~m}^{2}$

$$ \begin{aligned} & \mu _{\mathrm{e}}=0.36 \mathrm{~m}^{2} \mathrm{~V}^{-1} \mathrm{~s}^{-1} ; \mathrm{E}=10^{2} \mathrm{Vm}^{-1}\\ & \therefore \quad I _{e}=2.5 \times 10^{19} \times 3.14 \times 10^{-4} \times 1.6 \times 10^{-19} \times 0.36 \times 10^{2} \mathrm{~A}\\ & =4.52 \times 10^{-2} \mathrm{~A}=45.2 \mathrm{~mA} \end{aligned} $$

Similarly the current $\mathrm{I} _{\mathrm{h}}$ due to holes is

$$ \begin{aligned} & \mathrm{I} _{\mathrm{h}}=\mathrm{n} _{\mathrm{h}} \mathrm{eav _{h }}=\mathrm{n} _{\mathrm{h}} \mathrm{ea} \mu _{\mathrm{h}} \mathrm{E}\\ & \simeq 22.6 \mathrm{~mA} \end{aligned} $$

The total current $I=I _{e}+I _{h}=67.8 \mathrm{~mA}$

Easy

Semiconductors

17. In a semiconductor doped with phospohrous the Fermi-level is $0.3 \mathrm{eV}$ below condition band $27^{\circ} \mathrm{C}$. The temperature is raised by $30^{\circ} \mathrm{C}$. The new Fermi-level is

(1) $0.14 \mathrm{eV}$ below conduction band

(2) $0.27 \mathrm{eV}$ below conduction band

(3) $0.63 \mathrm{eV}$ below conduction band

(4) $0.3 \mathrm{eV}$ below conduction band

Show Answer

Correct answer: (2)

Solution:

The doped semiconductive is a n-type semiconductor. The position of Fermi-level below conduction band is inversly proportional to the temperature of material on Kelvin scale. Given

$$ \begin{array}{ll} \mathrm{E} _{1}=0.3 \mathrm{eV}, \mathrm{T} _{1}=273+27=300 \mathrm{~K}\\ \mathrm{E} _{2}=? \quad \mathrm{~T} _{2}=273+57=330 \mathrm{~K} \end{array} $$

Now,

$$ \begin{aligned} & \dfrac{\mathrm{E} _{1}}{\mathrm{E} _{2}}=\dfrac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}\\ \therefore \quad & \dfrac{0.3}{\mathrm{E} _{2}}=\dfrac{330}{300} \quad \text { or } \quad \mathrm{E} _{2}=\dfrac{0.3 \times 300}{320} \mathrm{eV} \simeq 0.27 \mathrm{eV} \end{aligned} $$

Average

Junction Diode

18. The barrier potential of a $\mathbf{p}-\mathbf{n}$ junction depends on

(a) type of semiconductor

(b) amount of doping

(c) temperature.

Which one of the followings is correct?

(1) (a) and (b) only

(2) (b) only

(3) (b) and (c) only

(4) (a), (b) and (c)

Show Answer

Correct answer: (4)

Solution:

Factual knowledge about junction diode.

Easy

$p-n$ Junction

19. The width of depletion region in a p-n junction diode is $500 \mathrm{~nm}$ and an internse electric field of $6 \times 10^{5} \mathrm{~V} / \mathrm{m}$ is also found to exist. The height of potential barrier is

(1) $0.30 \mathrm{~V}$

(2) $0.40 \mathrm{~V}$

(3) $3 \mathrm{~V}$

(4) $4 \mathrm{~V}$

Show Answer

Correct answer: (1)

Solution:

Let $\mathrm{V}$ be potential barrier across depletion layer of width $\mathrm{d}$. $\mathrm{E}$ the electric field in the $|\mathrm{E}|=\mathrm{V} / \mathrm{d}$ or $\mathrm{V}=|\mathrm{E}| \cdot \mathrm{d}$

$$ \begin{array}{ll} \therefore \quad & \mathrm{V}=6 \times 10^{5} \times 500 \times 10^{-9}\\ & =0.30 \mathrm{~V} \end{array} $$

Difficult

$p-n$ Junction

20. A potential barrier of $0.5 \mathrm{~V}$ exists across a $\mathrm{p}-\mathrm{n}$ junction and width of the depletion layer is $0.3 \mu \mathrm{m}$. An electron with a speed $5 \times 10^{5} \mathrm{~m} / \mathrm{s}$ enters $p-$ side from $n-$ side. The velocity of electron in $\mathrm{p}$-side will be $\left(\mathrm{m} _{\mathrm{e}}=\mathbf{9 . 1} \times 10^{-31} \mathrm{Kg}, \mathrm{e}=1.6 \times 10^{-19} \mathrm{C}\right)$

(1) $2.5 \times 10^{5} \mathrm{~m} / \mathrm{s}$

(2) $2.7 \times 10^{5} \mathrm{~m} / \mathrm{s}$

(3) $3.7 \times 10^{5} \mathrm{~m} / \mathrm{s}$

(4) $5 \times 10^{5} \mathrm{~m} / \mathrm{s}$

Show Answer

Correct answer: (2)

Solution:

In a junction diode; due to depeltion layer p-region is at a lower potential than n-region. The electron enters depletion layer from $n$-region and emerges and from $p$-region. The electrode is retarded. Let $V _{1}$ and $V _{2}$ the speed of electron as it enters $n-$ region and emerges out of $p$-region. Then

$$ \dfrac{1}{2} \mathrm{~m} V _{2}^{2}=\dfrac{1}{2} \mathrm{~m} V _{1}^{2}-|\mathrm{e}| \mathrm{V} $$

where $\mathrm{V}$ is barier potential. Substituting given values.

$$ =\dfrac{1}{2} \times 9.1 \times 10^{-31} \mathrm{~V} _{2}^{2}=\dfrac{1}{2} 9.1 \times 10^{-31}\left(5 \times 10^{2}\right)^{2}-1.6 \times 10^{-19} \times 0.5 $$

On solving we get

$$ \Rightarrow \mathrm{V} _{2}=2.7 \times 10^{5} \mathrm{~m} / \mathrm{s} $$

Difficult

$p-n$ Junction

21. In a p-n junction a potential barrier of $300 \mathrm{meV}$ exists across the junction. A hole with a kinetic energy of $400 \mathrm{meV}$ approaches the junction. The $\mathrm{K}$.E of the hole when it crosses the junction (i) from $\mathrm{p}$ to $\mathrm{n}$-side and (ii) from $\mathrm{n}$ to $\mathrm{p}$-side will be

(1) $100 \mathrm{eV}, 700 \mathrm{eV}$

(2) $100 \mathrm{eV}, 100 \mathrm{eV}$

(3) $700 \mathrm{eV}, 700 \mathrm{eV}$

(4) $700 \mathrm{eV}, 100 \mathrm{eV}$

Show Answer

Correct answer: (1)

Solution:

The p-region is at a lower potential than $\mathrm{n}$-region in depletion layer when hole crosses depletion layer from $\mathrm{n}$ - to $\mathrm{p}$-side; it (hole) is accelelrated. Therefore

$\mathrm{K}=$ Kinetic energy of hole

$=\mathrm{Ki}+|\mathrm{e}| \mathrm{V}$

$=(400+300) \mathrm{meV}=700 \mathrm{meV}$

When hole crosses depletion layer from $\mathrm{p}-$ to $\mathrm{n}$-side, it is retarded. Therefore

$$ \begin{aligned} \mathrm{K}^{\prime}= & \mathrm{Ke}-|\mathrm{e}| \mathrm{V}\\ & =(400-300) \mathrm{meV}=100 \mathrm{meV} \end{aligned} $$

The correction choice is (1)

Difficult

$p-n$ Junction Diode

22. In a p-n junction there exists a barrier potential. Fig. (a) shows the three barrier potential of a p-n junction marked as I, II and III.

Fig. (b) shows a junction diode biased as.

The correct commbination of biasing and barrier potential is

(1) I and IV; II and V; III and VI

(2) II and IV; III and V; I and VI

(3) I and V; II and VI; III and IV

(4) I and VI; II and V; III and IV

Show Answer

Correct answer: (2)

Solution:

I and II and III show barrier potential of an unbiased; forward biased and reverse biased junction diode respectively. In Fig. (b); IV is a forward biased; V is a reverse biased and VI is forward biased; V is a reverse biased and $\mathrm{Vi}$ is unbiased junction diode. The correct commbination of biasing and junction potential is $(2)$.

Average

Diode

23. In a junction diode the current is zero if applied forward bias voltage is $0<\mathrm{V}<\mathbf{0 . 7} \mathrm{V}$. An electron experiences a force of $0.112 \mathrm{pN}$ inside the depletion layer. The thickness of depletion layer is

(1) $0.5 \mu \mathrm{m}$

(2) $0.7 \mu \mathrm{m}$

(3) $1 \mu \mathrm{m}$

(4) $1.5 \mu \mathrm{m}$

Show Answer

Correct answer: (3)

Solution:

Let $\mathrm{E}$ be electric field inside depletion layer due to junction potential, $\mathrm{V}$, across it. $x$ is thickness of depletion layer. Given

$\mathrm{F}=$ Force experienced by electron inside depletion layer

$$ =0.112 \times 10^{-12} \mathrm{~N}=|\mathrm{e}| \mathrm{E} $$

$\therefore \quad \mathrm{E}=\dfrac{1.12 \times 10^{-13}}{1.6 \times 10^{-19}} \mathrm{Vm}^{-1} \simeq 7 \times 10^{5} \mathrm{Vm}^{-1}$

Also $\mathrm{E}=\dfrac{\mathrm{V}}{x}$. Given junction potential $=\mathrm{V}=0.7 \mathrm{~V}$

The current in junction diode; in forward bias is zero is applied p.d is less than or equal to junction potential.

$\therefore \quad x=\dfrac{\mathrm{V}}{\mathrm{E}}=\dfrac{0.7}{7 \times 10^{5}}=10^{-6} \mathrm{~m}=1 \mu \mathrm{m}$

Difficult

Diode

24. In a junction diode $I$ is current when applied forward bias voltage is $V$ at a temperature $T$ on Kelvin scale. Then

(1) $\mathrm{I}=\mathrm{I} _{0} \dfrac{\mathrm{V}}{\mathrm{T}}$

(2) $I=I _{0} \dfrac{V^{1 / 2}}{T}$

(3) $\mathrm{I}=\mathrm{I} _{0} \exp \left[\dfrac{\mathrm{eV}}{\mathrm{kT}}\right]$

(4) $I=I _{0} \exp \left[-\dfrac{\mathrm{eV}}{\mathrm{kT}}\right]$

Show Answer

Correct answer: (3)

Solution:

The current I; in general; in a junction diode is

$$ \mathrm{I}=\mathrm{I} _{0}\left[\exp \left(\dfrac{\mathrm{eV}}{\mathrm{kT}}\right)-1\right] $$

Under forward bias conditions $\mathrm{V}$ is low and a positive number; $\exp \left[\dfrac{\mathrm{eV}}{\mathrm{kT}}\right]»1$; therefore

$$ \mathrm{I} \simeq \mathrm{I} _{0} \exp \left[\dfrac{\mathrm{eV}}{\mathrm{kT}}\right] $$

Under reverse bias conditions for high value of V; $\exp \left[\dfrac{\mathrm{eV}}{\mathrm{kT}}\right]»1 ;$ because $\mathrm{V}$ is high and a negative number. Therefore

$$ \mathrm{I} \simeq-\mathrm{I} _{0} $$

$\mathrm{I} _{0}$ is magnitude of reverse saturation current.

Average

$p-n$ Junction Diode

25. For a p-n junction diode which of the following statement is correct

(1) In forward biasing there is a diffusion and in reverse bias there is drifting of charge carriers across the junction.

(2) In forward bias there is drifting and in reverse bias there is diffusion of charge carriers across the junction.

(3) In both forward and reverse biasing the current is due to diffusion of charge carriers across the junction.

(4) In both forward and reverse bias there is current due to drifting of charge carriers across the junction.

Show Answer

Correct answer: (1)

Solution:

Factual knowledge about moment of charge carriers in a p-n junction diode.

Average

p–n Junction Diode

26. The current through an ideal $p-n$ junction shown in the circuit diagram will be

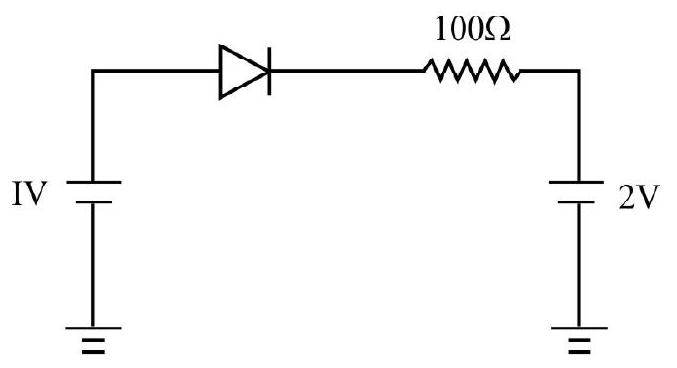
(1) zero

(2) $1 \mathrm{~mA}$

(3) $10 \mathrm{~mA}$

(4) $30 \mathrm{~mA}$

Show Answer

Correct answer: (1)

Solution:

As $p$ is at lower potential with respect to $n$-side. Hence diode is in reverse bias. In reverse bias diode does not conduct. i.e. current through diode is zero.

Average

p–n Junction Diode

27. In the circuit diagram shown below; the potential difference between the pionts $A$ and $B$ will be (assume diode is ideal)

(1) $0 \mathrm{~V}$

(2) $0.6 \mathrm{~V}$

(3) $3 \mathrm{~V}$

(4) $6 \mathrm{~V}$

Show Answer

Correct answer: (4)

Solution:

As the diode is in reversebias, ( $\mathrm{p}$-side at lower potential). The reverse biased resistance of an ideal diode is infinite. There is no current in circuit. There is no p.d across resistance $R=2 \Omega$. Hence p.d between points $\mathrm{A}$ and $\mathrm{B}$ is $6 \mathrm{~V}$.

Difficult

Diode

28. In Fig. (a) the forward bias ideal diode is D. The applied voltage at anode varies with time as shwon in FIg. (b). The variation of current in circuit as a function of time is (knee voltage of diode $=\mathbf{0 . 5} \mathrm{V}$ )

(a)

(b)

(1)

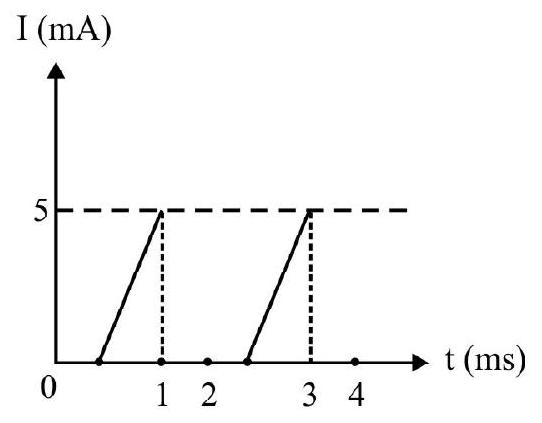
(2)

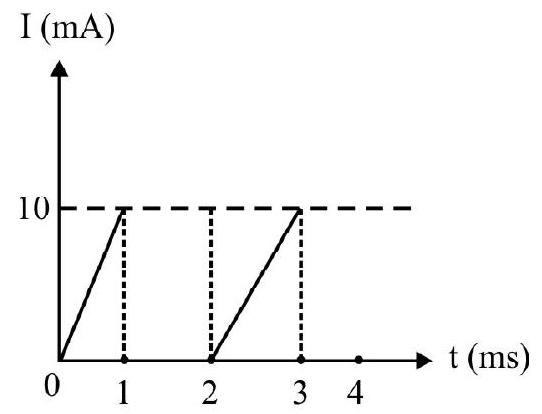
(3)

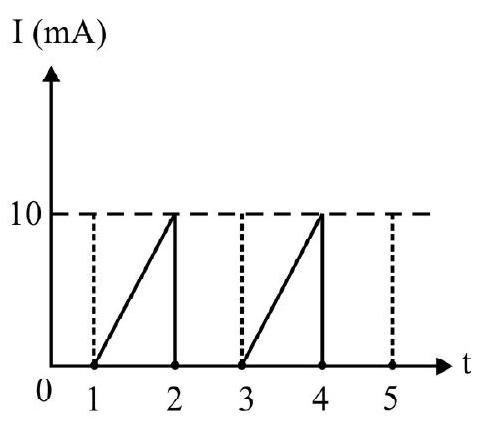
(4)

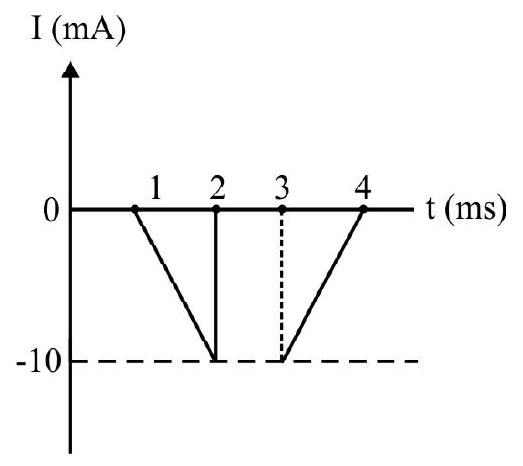
Show Answer

Correct answer: (1)

Solution:

From 0 to $1 \mathrm{~ms}$ anode $\mathrm{A}$ is at a higher potential than $\mathrm{C}$ as time increase. Diode is forward biased. Since knee voltage of diode is 0.5 when applied p.d is less than or equal to $0.05 \mathrm{~V}$ there is no current in circuit. The applied p.d is $0.5 \mathrm{~V}$ at $\mathrm{t}=0.5 \mathrm{~ms}$. Therefore current $\mathrm{I}$ in circuit is zero in time interval $0<\mathrm{to}<0.5 \mathrm{~ms}$. From $0.5 \mathrm{~ms}$ to $1 \mathrm{~ms}$ p.d of point increases from 0.5 to $1 \mathrm{~V}$. There is a current in circuit. $\mathrm{I} _{\max }$ at $\mathrm{t}=1 \mathrm{~ms}$ is

$$ \mathrm{I} _{\max }=\dfrac{1-05}{100} \mathrm{~A}=5 \mathrm{~mA} $$

In time interval $1<\mathrm{t}<2 \mathrm{~ms}$ anode $\mathrm{A}$ is at a lower potential than cathode $\mathrm{C}$. Diode is reverse biased. There is no current in circuit. This pattern repeats itself. The described variation of I with time are shown in (1).

Average

Diode

29. Fig. shows forward bias characterstics of a junction diode. The knee voltage and resistance of dide are:

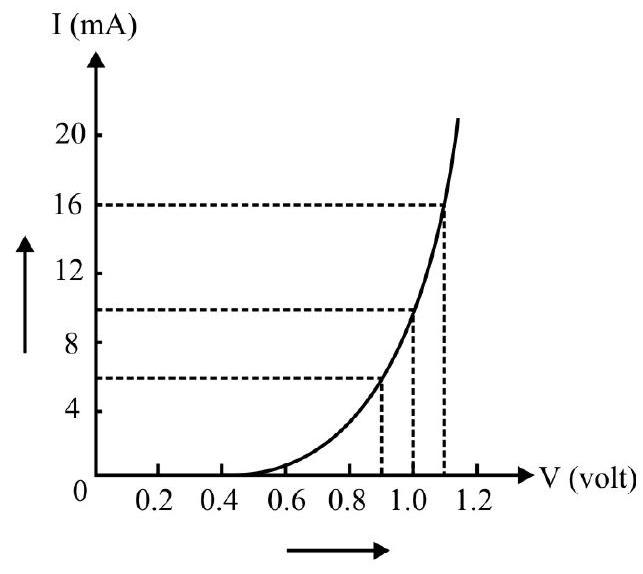
(1) $0.5 \mathrm{~V} ; 2 \Omega$

(2) $0.5 \mathrm{~V} ; 20 \Omega$

(3) $0 \mathrm{~V} ; 2 \Omega$

(4) $0.5 \mathrm{~V} ; 5 \Omega$

Show Answer

Correct answer: (2)

Solution:

The knee voltage of diode $=0.5 \mathrm{~V}$

Consider points $\mathrm{P}$ and $\mathrm{Q}$ on characterstics curve from graph;

$$ \Delta \mathrm{V}=1.1-0.9=0.2 \mathrm{~V} $$

$$ \Delta \mathrm{I}=16-6=10 \mathrm{~mA} $$

The resistance of diode $=r _{i}=\dfrac{\Delta V}{\Delta I}$

$$ =\dfrac{0.2}{10 \times 10^{-3}} \Omega=20 \Omega $$

Average

p–n Junction Diode

30. In the circuit given below, the value of the current is

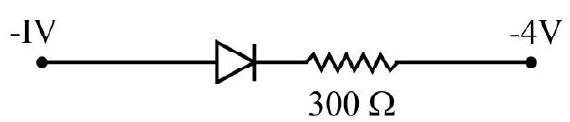
(1) Zero

(2) $10^{-2} \mathrm{~A}$

(3) $10^{-3} \mathrm{~A}$

(4) $10^{2} \mathrm{~A}$

Show Answer

Correct answer: (2)

Solution:

As $\mathrm{p}$-side is at higher potential than $\mathrm{n}$-side, the diode is forward biased. Hence

The forward current $=\mathrm{i} _{\mathrm{f}}=\dfrac{\Delta \mathrm{V}}{\mathrm{R}}$

$$ =\dfrac{[-1-(-4)]}{300}=10^{-2} \mathrm{~A} $$

Average

Semiconductor Diode

31. A silicon $\mathrm{PN}$ diode has a reverse saturation current of $20 \mu \mathrm{A}$ at a temperature of $20^{\circ} \mathrm{C}$. The reverse saturation current of the same diode at a temperature of $40^{\circ} \mathrm{C}$ will be,

(1) $10 \mu \mathrm{A}$

(2) $20 \mu \mathrm{A}$

(3) $40 \mu \mathrm{A}$

(4) $80 \mu \mathrm{A}$

Show Answer

Correct answer: (4)

Solution:

For a silicon pn junction, for every $10^{\circ} \mathrm{C}$ rise in temperature, the reverse saturation current gets doubled.

Average

p–n Junction Diode

32. In the given circuit, the junction diodes are ideal. The current through battery is

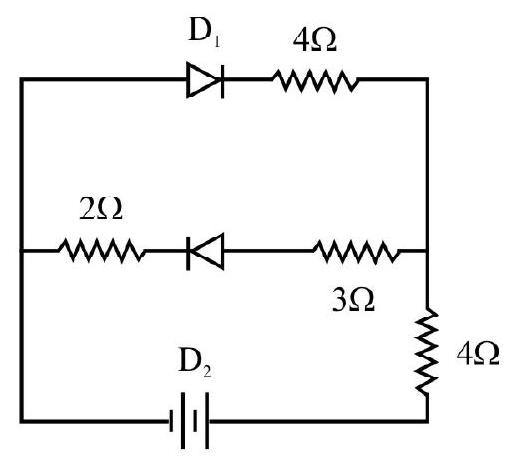
(1) $1 \mathrm{~A}$

(2) $2 \mathrm{~A}$

(3) $2.5 \mathrm{~A}$

(4) $3 \mathrm{~A}$

Show Answer

Correct answer: (2)

Solution:

In circuit, $D _{2}$ is forward biased and $D _{1}$ is reverse biased. The current through $D _{1}$ is zero. As diode $D _{2}$ is ideal, its resistance is zero. The equivalent circuit of the given arrangment is shown in Fig.

The current drawn from battery

$$ \begin{aligned} & =\mathrm{i}=\dfrac{\mathrm{E}}{\mathrm{R}+\mathrm{r}}=\dfrac{20 \mathrm{~V}}{(2+3+4+10) \Omega}\\ & =\dfrac{20}{10}=2 \mathrm{~A} \end{aligned} $$

Difficult

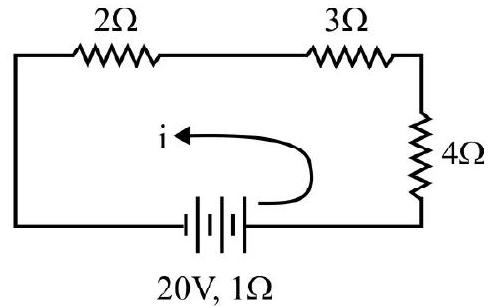
p–n Junction Diode

33. In the circuit given below, the junction diode $D$ is ideal. The p.d across $4 \Omega$ and $D$ respectively is:

(1) $0 \mathrm{~V}, 6 \mathrm{~V}$

(2) $2 \mathrm{~V}, 4 \mathrm{~V}$

(3) $4 \mathrm{~V}, 2 \mathrm{~V}$

(4) $6 \mathrm{~V}, 0 \mathrm{~V}$

Show Answer

Correct answer: (1)

Solution:

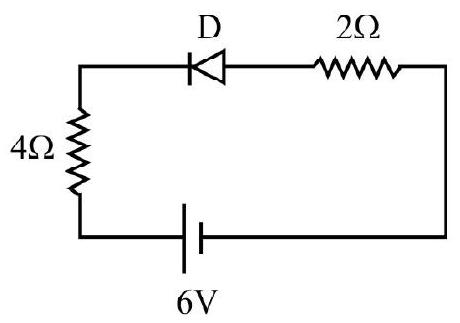
As junction diode is reverse biased, it offers infinite resistance in the circuit. Due to it, the current in the circuit is zero. Therefore p.d across $4 \Omega$ is zero. As a junction diode acts like open circuits, hence p.d across $\mathrm{D}=$ voltage of battery $=6 \mathrm{~V}$.

Difficult

Diode

34.

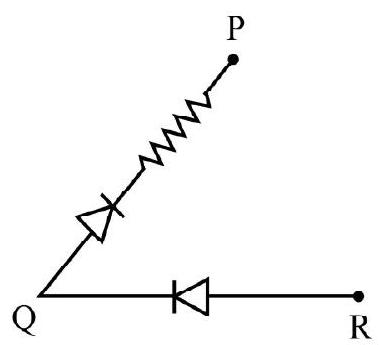
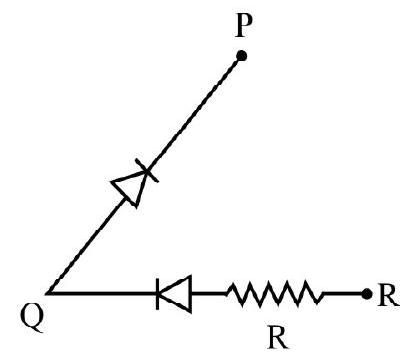
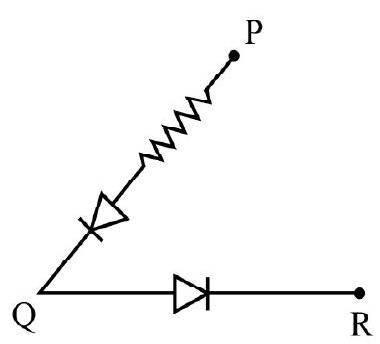
Fig. (a) shows a “black-box” with three connecting terminals P, Q and R. Three components two diodes and one resistance is connected across the three terminals in same unknown arrangement. Fig. (b) shows black-box connected as shown in circuit. In I vs V graph obtained when $P$ is negative and $Q$ is positive are shown in Fig. (c). The arrangment of components between $P, Q$ and $R$ is

(1)

(2)

(3)

(4)

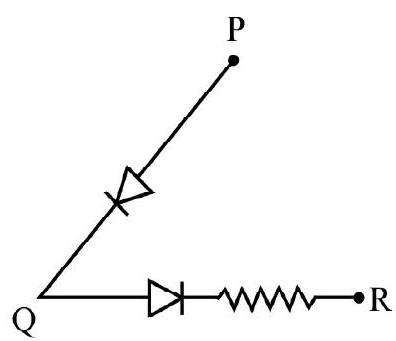
Show Answer

Correct answer: (1)

Solution:

The characterstics curve shown in Fig. (c) is forward bias characterstic of a diode with a knee voltage of $0.7 \mathrm{~V}$. Since $\mathrm{P}$ is connected to negative terminal and $\mathrm{Q}$ to positive terminal diode $\mathrm{D} _{1}$ is forward biased and has a series resistance R. Due to series resistance R, I vs V graph is a straight line. The forward bias resistance of diode is very small. This is shown in (1). In (2) diode between $P$ and $Q$ is forward biased but there is no series resistance. I vs $\mathrm{V}$ graph would be a almost vertical straight line. In (3) diode between $\mathrm{P}$ and $\mathrm{Q}$ is reverse biased therefore $\mathrm{I}=0$. Same is true for (4).

Hence correct answer is (1).

Average

Zener Diode

35. For a zener diode; which of the following statements is correct?

(1) n region is heavily doped only

(2) p region is heavily doped only

(3) Both n- and p-region is heavily doped

(4) A zener diode in a working circuit is always forward biased

Show Answer

Correct answer: (3)

Solution:

In a zener diode both $\mathrm{n}-$ and $\mathrm{p}$-regions are heavily doped.

For proper working in any circuit zener diode is always reverse biased.

Difficult

Zener Diode

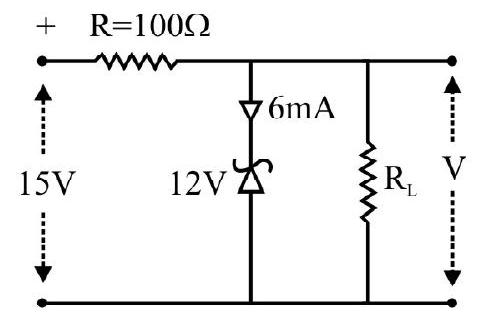
36. From the zener diode circuit shown in the figure given below, the current through zener is

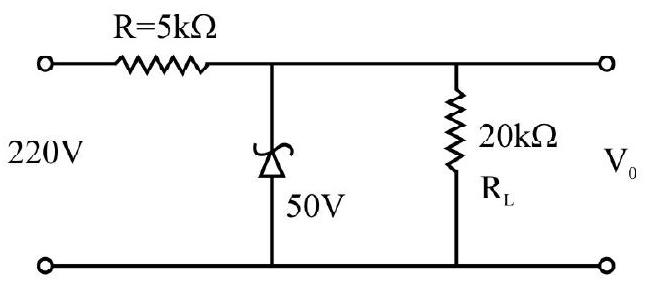
(1) $2.5 \mathrm{~mA}$

(2) $30 \mathrm{~mA}$

(3) $31.5 \mathrm{~mA}$

(4) $36.5 \mathrm{~mA}$

Show Answer

Correct answer: (3)

Solution:

Given, $\mathrm{R} _{\mathrm{L}}=20 \times 10^{3} \Omega$

$\mathrm{V} _{\mathrm{R}}=220 \mathrm{~V}$

$\mathrm{R}=5 \times 10^{3} \Omega$

$\mathrm{V} _{\mathrm{Z}}=50 \mathrm{~V}=$ Voltage drop across load $\mathrm{R} _{\mathrm{L}}$

$\therefore \quad \mathrm{I} _{\mathrm{L}}=$ The load current $=\dfrac{\mathrm{V} _{\mathrm{Z}}}{\mathrm{R} _{\mathrm{L}}}=\dfrac{50}{20 \times 10^{3}}$

$=2.5 \times 10^{-3} \mathrm{~A}$

$I=$ The current through $R=\dfrac{220-50}{5 \times 10^{3}}$

$$ =34 \times 20^{-3} \mathrm{~A} $$

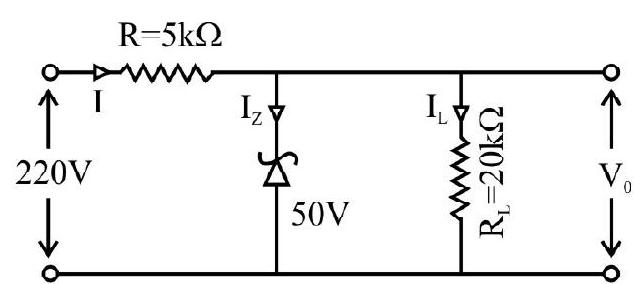
From Kirchoff’s current law,

$$ \begin{aligned} & \mathrm{I}=\mathrm{I} _{\mathrm{Z}}+\mathrm{I} _{\mathrm{L}}\\ & \Rightarrow \mathrm{I} _{\mathrm{Z}}=\mathrm{I}-\mathrm{I} _{\mathrm{L}}=(34-2.5) \times 10^{-3} \mathrm{~A}\\ & =31.5 \mathrm{~mA} \end{aligned} $$

Average

p–n Junction DIode

37. Silicon diode has a barrier potential of $0.7 \mathrm{~V}$. In the circuit given below, the value of voltage $V _{0}$ and current $I$ are:

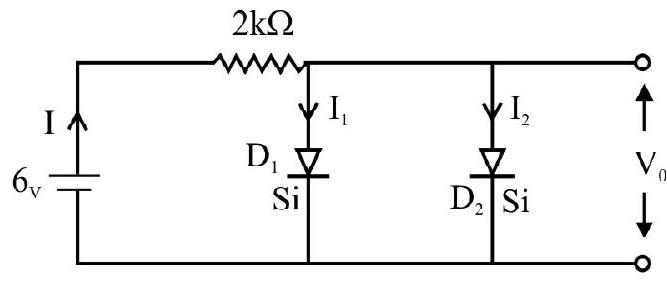
(1) $0.7 \mathrm{~V}, 2.65 \mathrm{~mA}$

(2) $0.7 \mathrm{~V}, 1.325 \mathrm{~mA}$

(3) $0 \mathrm{~V}, 2.30 \mathrm{~mA}$

(4) $0 \mathrm{~V}, 1.325 \mathrm{~mA}$

Show Answer

Correct answer: (1)

Solution:

Both the Si diodes are in F.B and are in parallel.

Hence $V _{0}=$ p.d across either $D _{1}$ or $D _{2}$ in F.B

$$ =0.7 \mathrm{~V}(\text { Barrier potential }) $$

Current $\mathrm{I}$ in the circuit $=\dfrac{\mathrm{V}-\mathrm{V} _{0}}{\mathrm{R}}$

$$ \begin{aligned} & =\dfrac{6-0.7}{2 \times 10^{3}}\\ & =2.65 \mathrm{~mA} \end{aligned} $$

Average

LED

38. For a Light-Emitting-Diode (LED) which of following statements is wrong?

(1) It is a heavily doped $\mathrm{p}-\mathrm{n}$ junction emitting spontaneous radiations when forward biased

(2) When forward biased the concentration of minority charge carriers increases rapidly on the sides of the junction boundary

(3) The energy released due to recommbination of electrons and holes is mostly transferred into the thermal energy of lattice vibrations

(4) LED emits light when it is reverse biased

Show Answer

Correct answer: (4)

Solution:

LED emitts light when it is forward biased. As forward current increases intensity of light emitted by LED also increases. When LED is reverse biased it emits no light. The LED is damaged when it is reverse biased.

Difficult

Diode

39.

Fig. (a) shows a half-wave rectifier. Fib. (b) is the $V$ is $I$ graph of diode used in half wave rectifier. The output of transformer is an A.C of amplitude $4 \mathrm{~V}, 50 \mathrm{~Hz}$. The output $V _{0}$ is

(1)

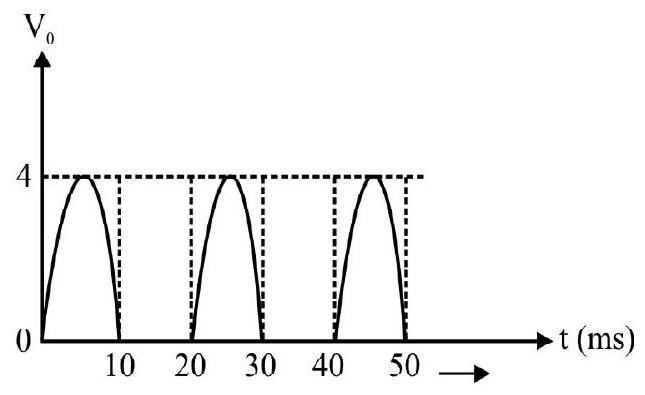
(2)

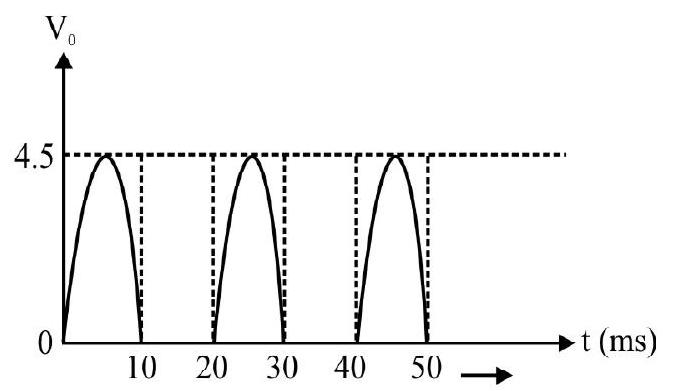
(3)

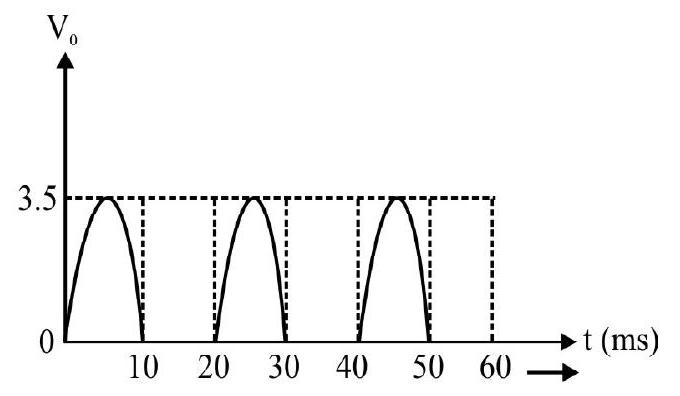
(4)

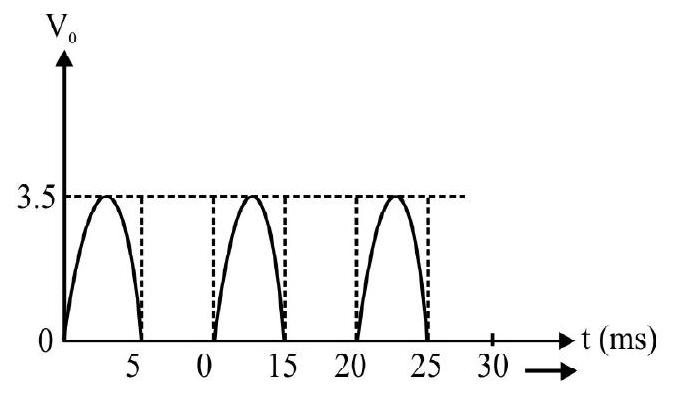
Show Answer

Correct answer: (3)

Solution:

The knee voltage of given diode, from Fig. (b) is $0.5 \mathrm{~V}$. When input voltage varies from 0 to $4 \mathrm{~V}$; diode conducts in voltage range $0.5<\mathrm{V}<35 \mathrm{~V}$. The amplitude of output voltage is $3.5 \mathrm{~V}$ and not $4 \mathrm{~V}$. The frequency of output is same as input i.e. $50 \mathrm{~Hz}$. For output shown in (4) amplitude of oscillations is correct but frequency is $100 \mathrm{~Hz}$. Hence (4) is not correct.

The correct output is given in (3).

Average

$p-n$ Junction Diode as Rectifier

40. A full wave rectifier circuit alongwith the output is shown in the figure. The contribution from diode ’ 1 ’ is

(1) C, D

(2) A, C

(3) B, D

(4) A, D

Show Answer

Correct answer: (3)

Solution:

At $\mathrm{t}=0$, positive half appears across ’ 2 ’ and negative half appears across ’ 1 ‘. Diode ’ 1 ’ conducts and ’ 2 ’ is in reverse bias, does not conduct at $t=T / 2$ same positive half appears across ’ 1 ‘. Diode ’ 1 ’ conducts this half again as it is in forward bias. Hence each positive half is conducted time first by diode ’ 2 ’ and then by diode ’ 1 ‘.

Average

Diode

41. An a.c voltage of peak value $10 \mathrm{~V}$ is connected in series with a silicon diode a load resistance of $100 \Omega$. The forward resistance of the diode to $20 \Omega$. The peak output voltage across the load resistance will be:

(1) $5 \mathrm{~V}$

(2) $7.75 \mathrm{~V}$

(3) $9.3 \mathrm{~V}$

(4) $10 \mathrm{~V}$

Show Answer

Correct answer: (2)

Solution:

Barrier potential of silicon diode $=0.7 \mathrm{~V}$

Peak current through the diode in the circuit $=\dfrac{10-0.7}{100+20}$

$$ =77.5 \mathrm{~mA} $$

Peak output voltage $=77.5 \mathrm{~mA} \times 100 \Omega$

$=7.75 \mathrm{~V}$

Difficult

Zener Diode

42. In the circuit shown inFig. the breakdown voltage and current of zener diode is $6.0 \mathrm{~V}$ and 35 $\mathrm{mA}$ respectively. The load current is $5 \mathrm{~mA}$. What is $R$ and $R _{L}$ ?

(1) $\mathrm{R}=100 \Omega, \mathrm{R} _{\mathrm{L}}=3 \mathrm{k} \Omega$

(2) $\mathrm{R}=25 \Omega, \mathrm{R} _{\mathrm{L}}=3 \mathrm{k} \Omega$

(3) $\mathrm{R}=100 \Omega, \mathrm{R} _{\mathrm{L}}=2 \mathrm{k} \Omega$

(4) $\mathrm{R}=25 \Omega, \mathrm{R} _{\mathrm{L}}=2 \mathrm{k} \Omega$

Show Answer

Correct answer: (1)

Solution:

In Fig. $\mathrm{I} _{\mathrm{D}}$ and $\mathrm{I} _{\mathrm{L}}$ are zener breakdown current and load current respectively. Given

$\mathrm{I} _{\mathrm{D}}=35 \mathrm{~mA} ; \mathrm{I} _{\mathrm{L}}=5 \mathrm{~mA}$

$\therefore \quad \mathrm{I}=\mathrm{I} _{\mathrm{D}}+\mathrm{I} _{\mathrm{L}}$

$$ =35+5=40 \mathrm{~mA} $$

The zener voltage drop $=\mathrm{V} _{\mathrm{D}}=6.0 \mathrm{~V}$.

Therefore $V _{R}=$ P.D across resistance $\mathrm{R}=10-6.0=4.0 \mathrm{~V}$

Obviously, $\mathrm{I}=\dfrac{\mathrm{V}}{\mathrm{R}} \quad$ or $\quad 40 \times 10^{-3}=\dfrac{4}{\mathrm{R}}$

$\therefore \mathrm{R}=100 \Omega$

Also, $\mathrm{R} _{\mathrm{L}}=\dfrac{\mathrm{V} _{\mathrm{L}}}{\mathrm{I} _{\mathrm{L}}}=\dfrac{6.0}{5 \times 10^{-3}} \Omega=3 \mathrm{k} \Omega$

Difficult

Zener Diode

43. In the circuit shown in Fig. the zener diode draws a current of $6 \mathrm{~mA}$ at breakdown voltage of $12 \mathrm{~V}$. The zener diode is rated an $12 \mathrm{~V}, 0.36 \mathrm{~W}$. The load resistance $R _{L}$ has a range of

(1) $2 \mathrm{~K} \Omega<\mathrm{R} _{\mathrm{L}} \leq \infty$

(2) $1 \mathrm{~K} \Omega \leq \mathrm{R} _{\mathrm{L}}<100 \mathrm{~K} \Omega$

(3) $0.5 \mathrm{~K} \Omega \leq \mathrm{R} _{\mathrm{L}} \leq \infty$

(4) $1.5 \mathrm{~K} \Omega \leq \mathrm{R} _{\mathrm{L}} \leq \infty$

Show Answer

Correct answer: (3)

Solution:

In loop ABEF; p.d across zener diode $=12 \mathrm{~V}$. Therefore p.d across resistance $\mathrm{R}=15-12=3 \mathrm{~V}$.

The current, I; as shown in Fig.; is

$$ I=\dfrac{3}{100} A=30 \mathrm{~mA} $$

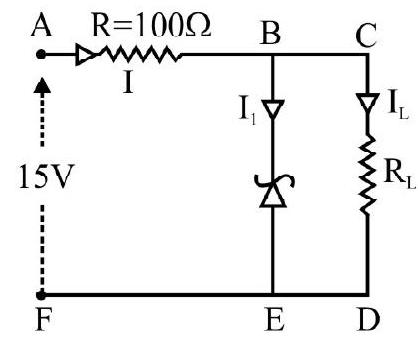
At branch point B; current I divides, $\mathrm{I} _{1}=$ current in zener diode $=6 \mathrm{~mA}$ (given); therefore

$$ \mathrm{I} _{\mathrm{L}}=\text { current in load } \mathrm{R} _{\mathrm{L}}=30-6=24 \mathrm{~mA} $$

$\therefore \quad \mathrm{R} _{\mathrm{L}}=\dfrac{12}{\mathrm{I} _{\mathrm{L}}}=\dfrac{12}{24 \times 10^{-3}} \Omega=0.5 \mathrm{k} \Omega$

Since zener diode is rated as $12 \mathrm{~V}, 0.36 \mathrm{~W}$, the maximum current it can with stand $=\dfrac{0.36}{12} \mathrm{~A}=30 \mathrm{~mA}$ when $R _{\mathrm{L}}$ increases, $\mathrm{I} _{\mathrm{L}}$ decreases and $\mathrm{I}$, increases. At $\mathrm{R} _{\mathrm{L}}=\infty$; the zener diode gap burnt because across it is $15 \mathrm{~V}$ which is more than its rated value.

Average

Diode

44. In Fig. shown $D _{1}$ and $D _{2}$ are ideal diodes. A battery of p.d $4 \mathrm{~V}$ is connected between points $X$ and $Y$. Current drawn from battery is $I _{1}$ and $I _{2}$ when point $X$ is connected to positive and negative terminal of battery; respectively. $I _{1} / I _{2}$ is

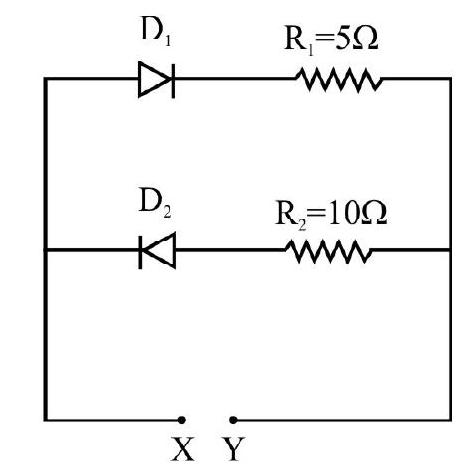
(1) 1

(2) 2

(3) $1 / 2$

(4) $2 / 3$

Show Answer

Correct answer: (2)

Solution:

When $X$ is connected to positive terminal of battery; diode $\mathrm{D} _{1}$ is forward biased and $\mathrm{D} _{2}$ is reverse biased. There is no current in $\mathrm{R} _{2}$ and $\mathrm{D} _{2}$. The current drawn; $\mathrm{I} _{1}$, from battery flows via diode $\mathrm{D} _{1}$ and $\mathrm{R} _{1}$. Since diode is ideal its forward biased resistance is zero. Therefore

$$ \mathrm{I} _{1}=\dfrac{4}{5}=0.8 \mathrm{~A} $$

When $\mathrm{X}$ is connected to negative terminal of battery; diode $\mathrm{D} _{1}$ is reversed biased and $\mathrm{D} _{2}$ is forward biased. Now current drawn from battery, $\mathrm{I} _{2}$ flows via diode $\mathrm{D} _{2}$ and resistance $\mathrm{R} _{2}$. Obviously

$$ \begin{gathered} \mathrm{I} _{2}=\dfrac{4}{10}=0.4 \mathrm{~A}\\ \therefore \quad \dfrac{\mathrm{I} _{1}}{\mathrm{I} _{2}}=\dfrac{0.8}{0.4}=2 \end{gathered} $$

Difficult

Diode

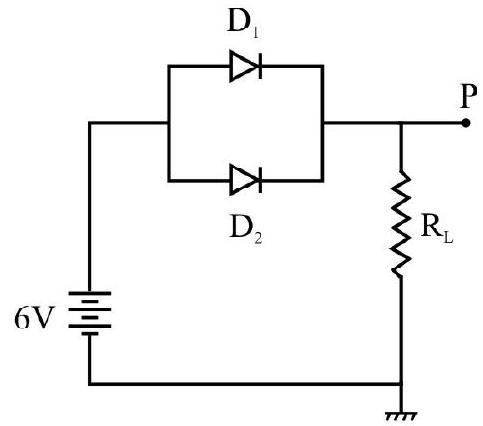
45. In Fig. shown $D _{1}$ is germanium and $D _{2}$ is a silicon diode. Knee voltage of $D _{1}$ and $D _{2}$ is $0.3 \mathrm{~V}$ and $0.7 \mathrm{~V}$ respectively. $R _{L}=5 \mathrm{~K} \Omega$. A current flows in circuit. The potential of point $P$ is

(1) $6 \mathrm{~V}$

(2) $5.7 \mathrm{~V}$

(3) $5.3 \mathrm{~V}$

(4) $5 \mathrm{~V}$

Show Answer

Correct answer: (2)

Solution:

Diode $\mathrm{D} _{1}$ and $\mathrm{D} _{2}$ are connected in parallel hence p.d across the two is same. The knee voltage of $\mathrm{D} _{1}$ is $0.3 \mathrm{~V}$. $\mathrm{D} _{1}$ starts conducting when $\mathrm{p} . \mathrm{d}$ across it is $0.3 \mathrm{~V}$ under this condition diode $\mathrm{D} _{2}$ does not conduct. Due to conduction of $\mathrm{D} _{1}$ there is a current in circuit. The p.d across load $\mathrm{R} _{\mathrm{L}}=6-0.3=5.7 \mathrm{~V}$. This end of $R _{L}$ is connected to point $P$, hence p.d at $P=5.7 \mathrm{~V}$.

Average

LED

46. The semiconductor used for fabrication of visible LEDs must atleast have a band gap of

(1) $1.1 \mathrm{eV}$

(2) $1.8 \mathrm{eV}$

(3) $2.1 \mathrm{eV}$

(4) $3.0 \mathrm{eV}$

Show Answer

Correct answer: (2)

Solution:

Spectral range of visible light is from $0.4 \mu \mathrm{m}$ to $0.7 \mu \mathrm{m}$. i.e. from about $3 \mathrm{eV}$ to $1.8 \mathrm{eV}$. Hence semiconductor used for fabrication of visible LEDs must have at least a gap of $1.8 \mathrm{eV}$.

Average

Photodiode

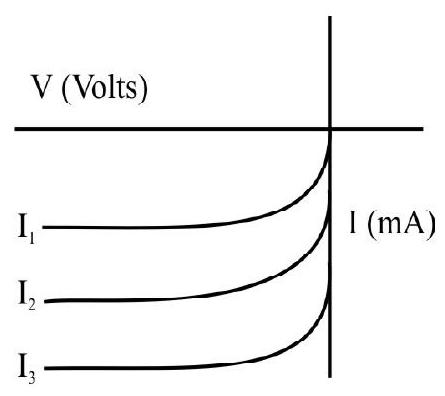
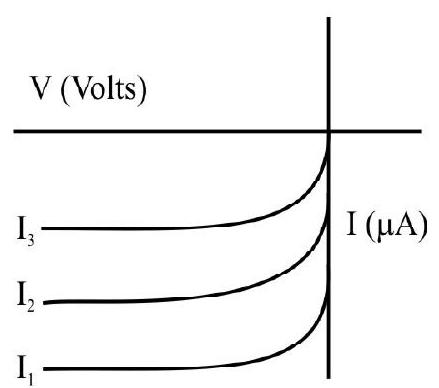
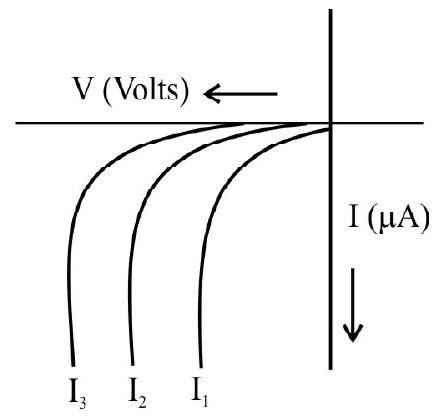
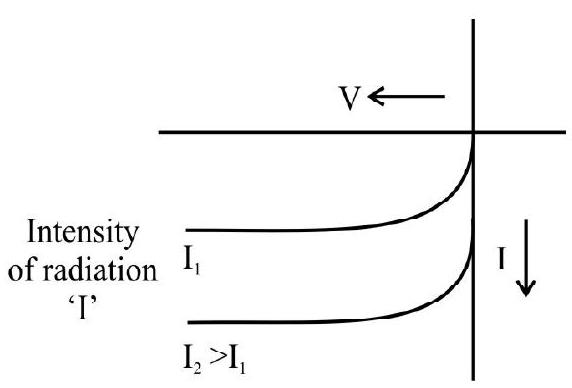
47. I-V characterstics of a photodiode for different illumination intensity $I _{3}>I _{2}>I _{1}$ is represented by the sketch.

(1)

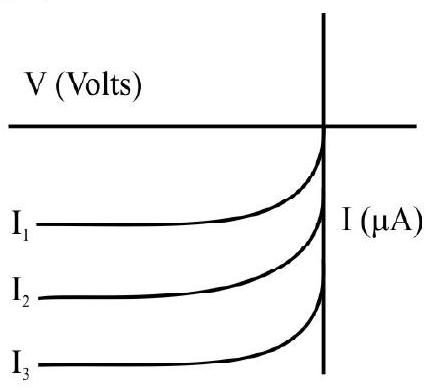
(2)

(3)

(4)

Show Answer

Correct answer: (1)

Solution:

In photodiode, change in the current is directly proportional to the change in the light intensity. It is operated in reverse bias.

Average

Solar Cell

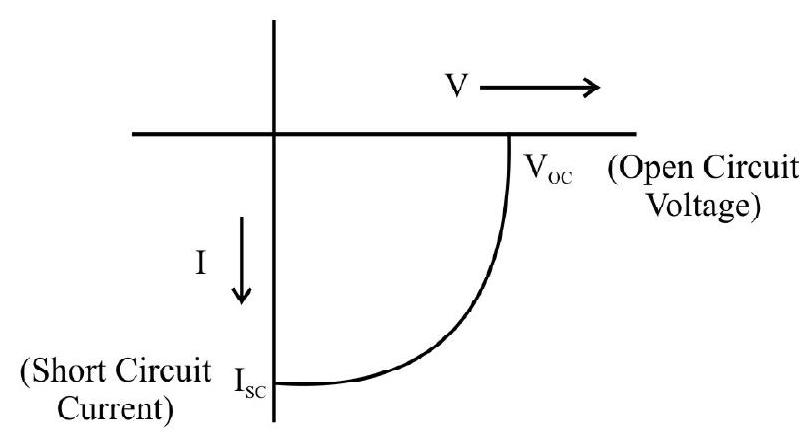
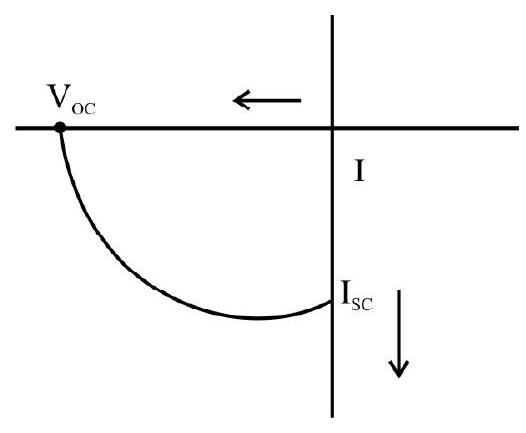
48. The $\mathbf{I}-\mathbf{V}$ characterstics of a solar cell is best represented by

(1)

(2)

(3)

(4)

Show Answer

Correct answer: (2)

Solution:

I-V characterstics of a solar cell is drawn in the fourth quadrant of the coordinate axes. This is shown in Fig. (2).

Average

LED

49. Intensity of light emitted by LED depends on

(1) Forward bias voltage

(2) Forward current

(3) Forward resistance

(4) Nature of semiconductor crystal

Show Answer

Correct answer: (2)

Solution:

Intensity of light emitted by LED depended on the forward current flowing in LED, with increase in forward current, intensity of light emitted increases.

Average

LED

50. Colour of the light emitted by LED depends on

(1) Forward bias voltage

(2) Reverse bias voltage

(3) Nature of semiconductor crystal

(4) Forward resistance

Show Answer

Correct answer: (3)

Solution:

Colour of the light emitted by LED depends on the energy gap of the semiconductor crystal. Hence the nature of the semiconductor crystal.

Easy

Semiconductors

51. Fig. shows V-I characterstic for a semiconductor device. Which of the following statements is correct?

(1) It is V-I characterstics of a solar cell, where point A represents open circuit voltage and point B short circuit current

(2) It is a solar cell and points A and B represent open circuit voltage and current respectively

(3) It is a photodiode and points A and B represent open circuit voltage and current respectively

(4) It is a LED and points A and B represent open circuit voltage and short circuit current respectively

Show Answer

Correct answer: (1)

Solution:

The given graph is $\mathrm{V}-\mathrm{I}$ characterstic of a solar cell. For open circuit $\mathrm{I}=0$; potential $\mathrm{V}$ equals applied e.m.f. This corresponds to point $A$ on characterstics curve. For short circuit $I=-I$ and potential $V=V=0$. This is point $B$ on given characterstic.

Easy

Transistor

52. If $x, y$ and $z$ are lengths of the emitter, base and collector of a transistor then:

(1) $\mathrm{z}>x>\mathrm{y}$

(2) $\mathrm{z}<x<\mathrm{y}$

(3) $\mathrm{z}<\mathrm{y}<x$

(4) $x=\mathrm{y}=\mathrm{z}$

Show Answer

Correct answer: (1)

Solution:

In a transistor area of collector $>$ area of emitter $>$ area of base for proper collection of majority charge carriers.

Easy

Transistor

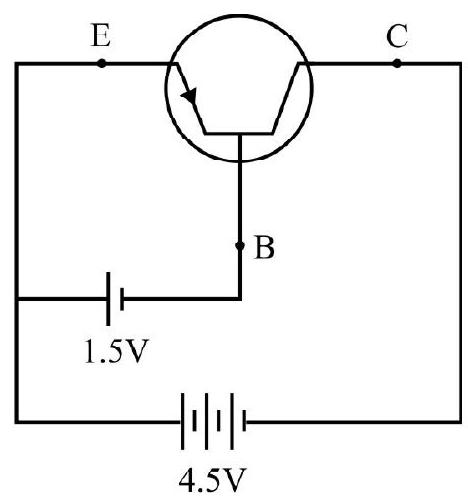
53. In Fig. shown what is nature of biasing of emitter and collector. What is $V _{\mathrm{EB}}$ and $V _{C B}$ ?

(1) E-forward biased, C-reverse biased, $\mathrm{V} _{\mathrm{EB}}=1.5 \mathrm{~V} ; \mathrm{V} _{\mathrm{CB}}=3.0 \mathrm{~V}$

(2) E-forward biased, C-forward biased, $\mathrm{V} _{\mathrm{EB}}=1.5 \mathrm{~V} ; \mathrm{V} _{\mathrm{CB}}=4.5 \mathrm{~V}$

(3) E-reverse biased, C-reverse biased, $\mathrm{V} _{\mathrm{EB}}=4.5 \mathrm{~V} ; \mathrm{V} _{\mathrm{CB}}=3.0 \mathrm{~V}$

(4) E-forward biased, C-forward biased, $\mathrm{V} _{\mathrm{EB}}=1.5 \mathrm{~V} ; \mathrm{V} _{\mathrm{CB}}=3.0 \mathrm{~V}$

Show Answer

Correct answer: (1)

Solution:

In the emitter base loop there is battery of p.d $1.5 \mathrm{~V}$. E is connected to positive terminal and B to -ve terminal. Since it is a $\mathrm{p}-\mathrm{n}-\mathrm{p}$ transistor, emitter is forward biased and $\mathrm{V} _{\mathrm{EB}}=1.5 \mathrm{~V}$. In the collector base loop.

$$ \mathrm{V} _{\mathrm{CB}}=1.5+4.5=3.0 \mathrm{~V} $$

The collector $\mathrm{C}$ is at a lower potential than base $\mathrm{B}$. The collector is reverse biased.

Average

Junction Transistor

54. In a junction transistor, the current gain in $\mathrm{CB}$ configuration is 0.99 . If input resistance is $2 \mathrm{k} \Omega$ and load connected to collector is $10 \mathrm{k} \Omega$, then voltage gain in $\mathrm{CE}$ configuration will be:

(1) 99

(2) 198

(3) 495

(4) 594

Show Answer

Correct answer: (3)

Solution:

Av, voltage gain in CE configuration $=\beta \dfrac{R _{L}}{r _{i}}$

$$ A v=\left(\dfrac{\alpha}{1-\alpha}\right) \dfrac{R _{L}}{r _{i}} $$

As given $\alpha=0.99$

$$ \begin{aligned} & r _{i}=2 \times 10^{3}\\ & \mathrm{R} _{\mathrm{L}}=10 \times 10^{3}\\ & \therefore \mathrm{Av}=\left(\dfrac{0.99}{1-0.99}\right) \times \dfrac{10 \times 10^{3}}{2 \times 10^{3}}\\ & =495 \end{aligned} $$

Average

Electronic Devices

55. In a $n-\mathbf{p}-\mathbf{n}$ transistor circuit, the collector current is $10 \mathrm{~mA}$. If $90 \%$ of the electrons emitted reach the collector then:

(1) Emitter current will be $9 \mathrm{~mA}$ and base current will be $1 \mathrm{~mA}$

(2) Emitter current will be $11 \mathrm{~mA}$ and base current will be $1 \mathrm{~mA}$

(3) Emitter current will be $11 \mathrm{~mA}$ and base current will be $-1 \mathrm{~mA}$

(4) Emitter current will be $9 \mathrm{~mA}$ and base current $1 \mathrm{~mA}$

Show Answer

Correct answer: (2)

Solution:

$$ \begin{aligned} & \text { As } \mathrm{I} _{\mathrm{E}}=\mathrm{I} _{\mathrm{B}}+\mathrm{I} _{\mathrm{C}}\\ & \qquad \mathrm{I} _{\mathrm{C}}=\dfrac{90}{100} \mathrm{I} _{\mathrm{E}} \text { (given) }\\ & \text { As } \mathrm{I} _{\mathrm{C}}=10 \mathrm{~mA} \Rightarrow \mathrm{I} _{\mathrm{E}}=11.1 \mathrm{~mA}\\ & \Rightarrow \quad \mathrm{I} _{\mathrm{E}} \simeq 11 \mathrm{~mA}\\ & \text { and } \mathrm{I} _{\mathrm{B}}=\mathrm{I} _{\mathrm{E}}-\mathrm{I} _{\mathrm{C}}\\ & =(11-10)=1 \mathrm{~mA} \end{aligned} $$

Easy

Junction Transistor

56. In a transistor the current amplification ’ $\alpha$ ’ is 0.9 . The change in collector current when base current changes by $4 \mathrm{~mA}$ is

(1) $4 \mathrm{~mA}$

(2) $12 \mathrm{~mA}$

(3) $24 \mathrm{~mA}$

(4) $36 \mathrm{~mA}$

Show Answer

Correct answer: (4)

Solution:

By definition, current gain $\alpha$ is

$$ \alpha=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{E}}}=0.9 $$

Also, $\mathrm{I} _{\mathrm{E}}=\mathrm{I} _{\mathrm{C}}+\mathrm{I} _{\mathrm{B}}$ or $\Delta \mathrm{I} _{\mathrm{E}}=\Delta \mathrm{I} _{\mathrm{C}}+\Delta \mathrm{I} _{\mathrm{B}}$.

Therefore $\Delta \mathrm{I} _{\mathrm{C}}+\Delta \mathrm{I} _{\mathrm{B}}=0.9$

$\Rightarrow \Delta \mathrm{I} _{\mathrm{C}}=0.9 \Delta \mathrm{I} _{\mathrm{C}}+0.9 \Delta \mathrm{I} _{\mathrm{B}}$

$\Rightarrow 0.1 \Delta \mathrm{I} _{\mathrm{C}}=0.9 \times 4 \mathrm{~mA}$

$=0.1 \Delta \mathrm{I} _{\mathrm{C}}=36 . \mathrm{mA}$

$=\Delta \mathrm{I} _{\mathrm{C}}=36 \mathrm{~mA}$

Average

Transistor

57. Is an $n-p-n$ transistor $10^{12}$ electrons enter emitter in $80 \mu \mathrm{s}$. The current gain $\alpha$ of transistor is 0.95 . The number of electrons flowing in the base expressed as a percentage of electrons entering emitter is

(1) 2

(2) 3

(3) 4

(4) 5

Show Answer

Correct answer: (4)

Solution:

$\mathrm{I} _{\mathrm{E}}=$ The emitter current $=$ Charge flowing per unit time in emitter

$$ =\dfrac{10^{12} \times 1.6 \times 10^{-19}}{80 \times 10^{-6}} \mathrm{c} / \mathrm{s}=3 \times 10^{-3} \mathrm{~A} $$

$I _{C}=$ The collector current $=\dfrac{I _{E}}{\alpha} \times \alpha$

$$ =2 \times 10^{-3} \times 0.95=1.9 \times 10^{-3} \mathrm{~A} $$

$\mathrm{I} _{\mathrm{B}}=$ The base current $=\mathrm{I} _{\mathrm{E}}-\mathrm{I} _{\mathrm{C}}=1.1 \times 10^{-3} \mathrm{~A}$

$\therefore \quad$ The percentage of emitter electrons flowing the base $=\dfrac{\mathrm{I} _{\mathrm{B}}}{\mathrm{I} _{\mathrm{E}}} \times 100 \%$

$=\dfrac{0.1 \times 10^{-3}}{2 \times 10^{-3}} \times 100 \%=5 \%$

Average

Transistor

58. Fig. shows common-emitter characterstic curve of a transistor. For $V _{C E}=10 V ; I _{B}=30$ $\mu \mathrm{A}$; the current gain $\beta _{\mathrm{AC}}$ and $\alpha$ is

(1) $150 ; 1$

(2) $100 ; 0.99$

(3) $150 ; 0.993$

(4) $150 ; 1.01$

Show Answer

Correct answer: (3)

Solution:

The current gain; $\beta _{\mathrm{AC}}$ in common emitter configuration is

$$ \beta _{\mathrm{AC}}=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{B}}} $$

For $\mathrm{V} _{\mathrm{CE}}=10 \mathrm{~V}, \mathrm{I} _{\mathrm{B}}=30 \mu \mathrm{A}$; the point on characterstics curve is $\mathrm{P}$. Consider two points $\mathrm{P}$ and $\mathrm{Q}$ as shown in Fig. For $\mathrm{V} _{\mathrm{CE}}=10 \mathrm{~V}$;

$\Delta \mathrm{I} _{\mathrm{C}}=(4.5-3) \mathrm{mA}=1.5 \mathrm{~mA}$

$\Delta \mathrm{I} _{\mathrm{B}}=(30-20) \mu \mathrm{A}=1.5 \mu \mathrm{A}$

$\therefore \quad \beta _{\mathrm{AC}}=\dfrac{1.5 \times 10^{-3}}{10 \times 10^{-6}}=150$

We know $\beta=\dfrac{\alpha}{1-\alpha}$; therefore

$$ 150=\dfrac{\alpha}{1-\alpha} \quad \text { or } \quad \alpha \simeq 0.993 $$

Average

Junction Transistor

59. The transfer ratio $\beta$ of a transistor is 50 . The input resistance of the transistor when used in the common emitter configuration is $1 \mathrm{k} \Omega$. The value of collector current for a peak value of input a.c voltage of 0.01 is

(1) $0.01 \mu \mathrm{A}$

(2) $0.25 \mu \mathrm{A}$

(3) $100 \mu \mathrm{A}$

(4) $500 \mu \mathrm{A}$

Show Answer

Correct answer: (4)

Solution:

Given $\beta=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{I} _{\mathrm{B}}}=50$ $\hspace{3 cm}$…………(1)

$\mathrm{R} _{\mathrm{i}}=1 \mathrm{k} \Omega=10^{3} \Omega$

as $\Delta \mathrm{I} _{\mathrm{B}}-\dfrac{\Delta \mathrm{V} _{\mathrm{i}}}{\mathrm{R} _{\mathrm{i}}}=\dfrac{0.01}{10^{3}}$

$=10^{-5} \mathrm{~A}$ $\hspace{5 cm}$…………(2)

From Eqns. (1) and (2) we have

$\begin{aligned} & \Delta \mathrm{I} _{\mathrm{C}}=50 \times 10^{-5} \mathrm{~A}\\ & =500 \mu \mathrm{A} \end{aligned}$

Average

Electronic Devices

60. A signal of $30 \mathrm{mV}$ is applied to a common emitter transistor amplifier circuit. Due tothis the change in base current and the change in the collector current are $20 \mu \mathrm{A}$ and $2 \mathrm{~mA}$ respectively. The load resistance is $15 \mathrm{k} \Omega$. The transconductance of the transistor is

(1) $0.032 \mathrm{~mho}$

(2) $0.067 \mathrm{~mho}$

(3) $0.15 \mathrm{~mho}$

(4) $15 \mathrm{~mho}$

Show Answer

Correct answer: (2)

Solution:

Transconductance $=g _{m}=\dfrac{\Delta \mathrm{I} _{\mathrm{C}}}{\Delta \mathrm{V} _{\mathrm{C}}}$

$=\dfrac{2 \times 10^{-3}}{30 \times 10^{-3}}=0.067 \mathrm{mho}$

Average

Transistor

61. A $\mathbf{n}-\mathbf{p}-\mathbf{n}$ transistor is used as an amplifier in (a) common-base (b) common-emitter configuration. The voltage gain in two cases is $A _{1}$ and $A _{2}$ respectively. The phase difference between input and output in the two cases is $\delta _{1}$ and $\delta _{2}$ respectively which of the following is correct?

(1) $\delta _{1}=\delta _{2}=-\pi ; \mathrm{A} _{1}=\mathrm{A} _{2}$

(2) $\delta _{1}=0 ; \delta _{2}=-\pi ; \mathrm{A} _{1}<\mathrm{A} _{2}$

(3) $\delta _{1}=-\pi ; \delta _{2}=0 ; \mathrm{A} _{1}>\mathrm{A} _{2}$

(4) $\delta _{1}=0 ; \delta _{2}=+\pi ; \mathrm{A} _{1}=\mathrm{A} _{2}$

Show Answer

Correct answer: (2)

Solution:

The common base configuration in an amplifier, the output and input are in phase i.e. $\delta _{1}=0$. However in common-emitter amplifier output is out of phase with input and output lags behind input i.e. $\delta _{2}=-\pi$. The voltage gain in common-emitter configuration is more than in common-base configuration i.e. $\mathrm{A} _{1}>\mathrm{A} _{2}$.

Difficult

Transistor

62. In the circuit shown in Fig. $V _{i}=5 V \cdot V _{B E}=0$ and $V _{C E}=0$. What is $I _{B}$ and $I _{C}$ ?

(1) $\mathrm{I} _{\mathrm{B}}=25 \mu \mathrm{A} ; \mathrm{I} _{\mathrm{C}}=2 \mathrm{~mA}$

(2) $\mathrm{I} _{\mathrm{B}}=2.5 \mu \mathrm{A} ; \mathrm{I} _{\mathrm{C}}=20 \mathrm{~mA}$

(3) $\mathrm{I} _{\mathrm{B}}=0 ; \mathrm{I} _{\mathrm{C}}=2 \mathrm{~mA}$

(4) $\mathrm{I} _{\mathrm{B}}=25 \mu \mathrm{A} ; \mathrm{I} _{\mathrm{C}}=20 \mathrm{~mA}$

Show Answer

Correct answer: (1)

Solution:

For base-emitter loop; using Kirchoff’s law

$$ \mathrm{I} _{\mathrm{B}} \mathrm{R} _{\mathrm{B}}+\mathrm{V} _{\mathrm{BE}}=\mathrm{V} _{\mathrm{i}} $$

where $I _{B}$ is base current. Given $V _{B E}=0 ; R _{B}=2 \times 10^{5} \Omega$

$\therefore \quad \mathrm{I} _{\mathrm{B}} \times 2 \times 10^{5}=5$

or $\quad \mathrm{I} _{\mathrm{B}}=2.5 \times 10^{-5} \mathrm{~A}=25 \mu \mathrm{A}$

For the collector-emitter loop; using Kirchoff’s law

$$ \mathrm{I} _{\mathrm{C}} \mathrm{R} _{\mathrm{L}}+\mathrm{V} _{\mathrm{CE}}=10 $$

Given $\mathrm{V} _{\mathrm{CE}}=0$ and $\mathrm{R} _{\mathrm{L}}=5 \mathrm{k} \Omega$; therefore

$$ \mathrm{I} _{\mathrm{C}}=\dfrac{10}{5 \times 10^{3}}=2 \mathrm{~mA} $$

Difficult

Transistor

63. Fig. shows a common-emitter amplifier circuit. $R _{\mathrm{L}}=2 \mathrm{k} \Omega ; R B=150 \mathrm{k} \Omega ; \beta=200 \mathrm{~V} _{\mathrm{CE}}=$ 0 and $V _{B B}=1 V$. Under saturation condition $I _{C}$ and $I _{B}$ are:

(1) $3 \mathrm{~mA} ; 15 \mu \mathrm{A}$

(2) $2 \mathrm{~mA} ; 15 \mu \mathrm{A}$

(3) $3 \mathrm{~mA} ; 10 \mu \mathrm{A}$

(4) $2 \mathrm{~mA} ; 10 \mu \mathrm{A}$

Show Answer

Correct answer: (1)

Solution:

Let $I _{C}$ be saturation collector current. Applying Kirchoff’s law to collector emitter loop; we have

$$ \mathrm{I} _{\mathrm{C}} \mathrm{R} _{\mathrm{L}}+\mathrm{V} _{\mathrm{CE}}=\mathrm{V} _{\mathrm{CC}} $$

Under saturation condition $\mathrm{V} _{\mathrm{CE}}=0$ (Given); therefore

$$ I _{C}=\dfrac{V _{C C}}{R _{L}}=\dfrac{6}{2 \times 10^{3}} A=3 \mathrm{~mA} $$

Let $I _{B}$ be the base current under saturation conditions. By definition

$$ \begin{aligned} \beta & =\dfrac{I _{C}}{I _{B}}\\ \therefore \quad I _{B} & =\dfrac{I _{C}}{\beta}=\dfrac{3}{200} \mathrm{~mA}=1.5 \times 10^{-5} \mathrm{~A}\\ & =15 \mu \mathrm{A} \end{aligned} $$

Difficult

Transistor

64. In the circuit shown; resistance $R _{1}$ is decreased; the reading of voltmeter $V _{1}$ and $V _{2}$.

(1) Remains same

(2) $V _{1}$ increases $V _{2}$ decreases

(3) $V _{1}$ and $V _{2}$ both increases

(4) $V _{1}$ decreases and $V _{2}$ increases

Show Answer

Correct answer: (2)

Solution:

When $R _{1}$ decreases; the base current $I _{B}$ increases. Due to increase in $I _{B}$; the collector current $I _{C}$ also increases. Reading of voltmeter $V _{1}$ measures $p$.d across resistance $R _{2}$ which is $I _{C} \cdot R _{2}$. Since $I _{C}$ increases reading of $V _{1}$ increases. Voltmeter $V _{2}$ measures $V _{C E}$. In collector emitter loop; using Kirchoffs law

$$ \mathrm{V} _{1}+\mathrm{V} _{\mathrm{CE}}=\mathrm{V} _{\mathrm{CC}} $$

or $\mathrm{V} _{\mathrm{CE}}=\mathrm{V} _{\mathrm{CC}}-\mathrm{V} _{1}$

As $V _{1}$ increases $V _{C E}$ decreases. Therefore reading of voltmeter $V _{2}$ decreases.

Average

Transistor as Amplifier

65. Fig. shows a common-emitter amplifier. The current gain $\alpha$ of transistor is 100/101. For an input signal voltage $V _{i}=2 \mathrm{mV}$; the output voltage $V _{0}$ is

(1) $50 \mathrm{mV}$

(2) $50 \mathrm{mV}$

(3) $1 \mathrm{~V}$

(4) $5 \mathrm{~V}$

Show Answer

Correct answer: (3)

Solution:

The voltage gain $=\left(\dfrac{\beta}{R _{i}}\right) R _{L}$

where $\beta$ is current gain in common emitter configuration.

$$ \beta=\dfrac{\alpha}{1-\alpha}=\dfrac{100 / \mathbf{1 0 1}}{1-\dfrac{100}{101}}=100 $$

In given circuit,

$$ \mathrm{R} _{\mathrm{L}}=5 \mathrm{k} \Omega, \mathrm{R} _{\mathrm{i}}=1 \mathrm{k} \Omega $$

$\therefore$ Voltage gain $=100 \times \dfrac{5}{1}=500$

Also voltage gain $=\dfrac{\mathrm{V} _{0}}{\mathrm{~V} _{\mathrm{i}}}$; therefore

$$ \mathrm{V} _{0}=500 \mathrm{~V} _{\mathrm{i}}=500 \times 2 \times 10^{-3} \mathrm{~V}=1 \mathrm{~V} $$

Average

Transistor

66. Fig. shows $V _{C E}$ v s $V _{i}$ characterstics of a transistor, known as transfer characterstics. The curve is divided into three regions as shown in Fig. The transistor is to be used as

(a) an amplifier (b) a switch. The part of transfer-characterstics used is

(1) (a) and (c) any of I, II or II

(2) (a) - region I, (b) - region II

(3) (a) - region II; (b) region I and III

(4) (b) region I and II (b) region II

Show Answer

Correct answer: (3)

Solution:

In a transistor if $\mathrm{V} _{\mathrm{i}}$ is low so that temitter-base junction is NOT FORWARD biased $\mathrm{V} _{0}$ is high. If $\mathrm{V} _{\mathrm{i}}$ is high the transistor is driven into saturation region and $\mathrm{V} _{0}$ is low. One of these two positions can be used as “off” and other as “on” state of transistor. The transistor works as a switch.

Region II is the “active region” of a transistor. In this region transistor is used as an amplifier. A small variation in $\mathrm{V} _{\mathrm{i}}$ produces a small change in input current $\mathrm{I} _{\mathrm{B}}$. This produces a large change in output current $\mathrm{I} _{\mathrm{C}}$ and therefore a large change in output voltage $\mathrm{V} _{0}$. This is amplification.

Average

Logic Gates

67. The combination of the gates as shown in the figure represents:

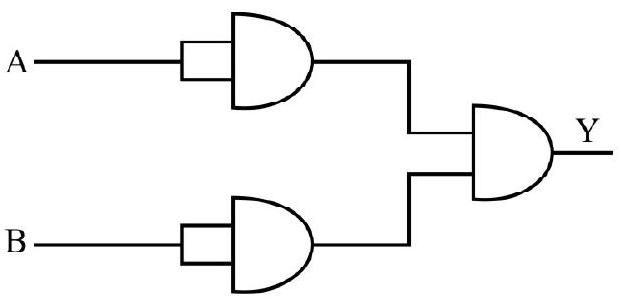
(1) NOR

(2) OR

(3) AND

(4) XOR

Show Answer

Correct answer: (2)

Solution:

The boolean expression of given combination of gates is written as:

$$ \mathrm{Y}=\overline{\overline{\mathrm{A}} \cdot \overline{\mathrm{B}}}=\overline{\overline{\mathrm{A}}}+\overline{\overline{\mathrm{B}}}=\mathrm{A}+\mathrm{B} $$

So, given combination represents OR gate.

Average

Logic Gates

68. The booliean expression for the circuit given in figure is:

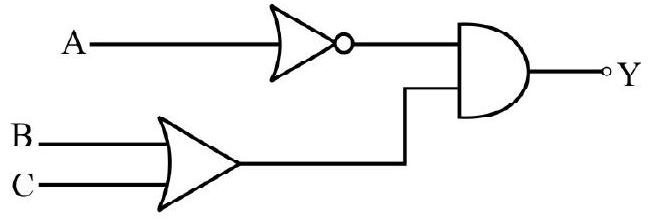
(1) $\mathrm{Y}=\overline{\mathrm{A}} \cdot \mathrm{B}+\mathrm{C}$

(2) $\mathrm{Y}=\overline{\mathrm{A}} \cdot(\overline{\mathrm{B}}+\overline{\mathrm{C}})$

(3) $\mathrm{Y}=\overline{\mathrm{A}} \cdot(\mathrm{B}+\overline{\mathrm{C}})$

(4) $\mathrm{Y}=\overline{\mathrm{A}} \cdot(\mathrm{B}+\mathrm{C})$

Show Answer

Correct answer: (4)

Solution:

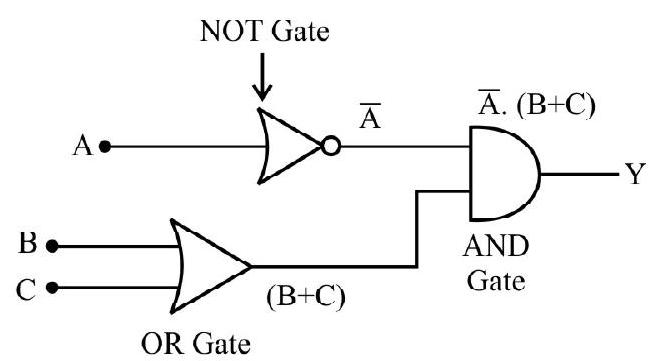
Difficult

Logic Gates

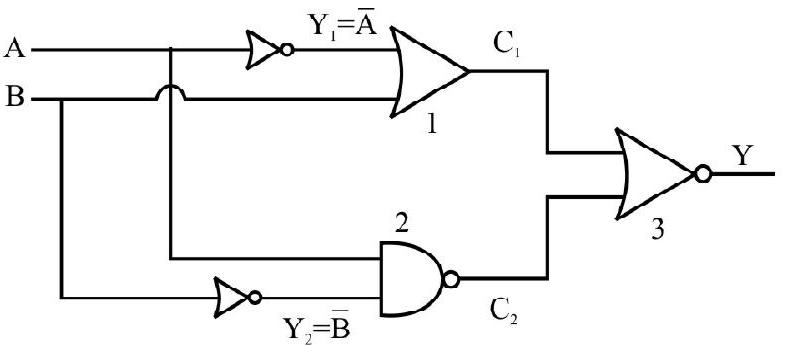
69. Figure shows combination of gates. For $\mathrm{Y}=1$ which of the following options is correct.

(1) $\mathrm{A}=0, \mathrm{~B}=1$

(2) $\mathrm{A}=1, \mathrm{~B}=1$

(3) $\mathrm{A}=1, \mathrm{~B}=0$

(4) $\mathrm{A}=0, \mathrm{~B}=0$

Show Answer

Correct answer: (3)

Solution:

For $\mathrm{A}=1, \mathrm{~B}=0$; the output of gate 1 (i.e. OR gate) $\mathrm{C} _{1}=0$. The output of gate $\mathrm{C} _{2}$ (i.e. NAND gate) $\mathrm{C} _{2}$ $=0 . C _{1}=0$ and $C _{2}=0$ are input of gate 3 which is NOR gate, hence outout $Y=1$.

Difficult

Binary Numbers

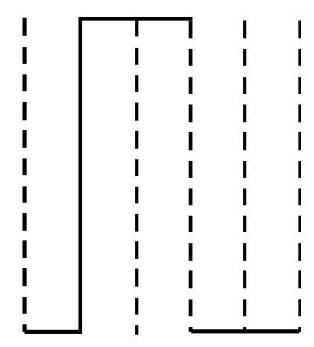
70. In binary system the decimal numbers are represented in terms of 0 and 1 . We use a low voltage pluse to represent binary 0 and a high voltage pluse to represent binary 1. Fig. (a) and (b) give the pluse representation of decimal number $X$ and $Y$ respectively. The pluse representation decimal number $(X+Y)$ is:

(1)

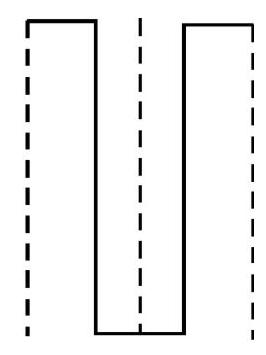
(2)

(3)

(4)

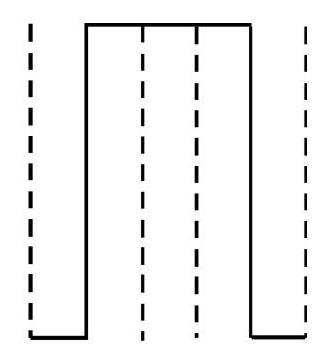
Show Answer

Correct answer: (3)

Solution:

The binary representation of $\mathrm{X}$ is 1001 . The decimal number $X=1(2)^{3}+0(2)^{1}+1(2)^{0}=9$

The binary representation of $\mathrm{Y}$ is 10101

The decimal number $\mathrm{Y}=1(2)^{4}+0(2)^{3}+1(2)^{2}+0(2)^{1}+1(2)^{0}=21$

The decimal number $\mathrm{X}+\mathrm{Y}=9+21=30$. The binary representation of $(\mathrm{X}+\mathrm{Y})$ is 11110 . The pluse representation of this number is as shown in (3).

Average

Logic Gates

71. To get the output $Y=1$ from the circuit given below, the input must be:

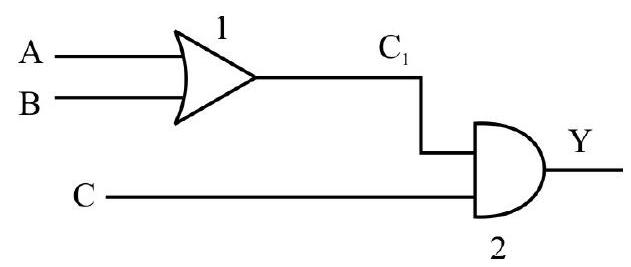
	A	B	C
(1)	0	1	0
(2)	1	0	0
(3)	1	0	1
(4)	1	1	1

Show Answer

Correct answer: (3)

Solution:

Gate 1 is OR gate. For $\mathrm{A}=1, \mathrm{~B}=0$ the output $\mathrm{C} _{1}=1 . \mathrm{C} _{1}=1$ and $\mathrm{C}=1$ are input of gate 2 which is an AND gate. The output $\mathrm{Y}=1$.

Average

Logic Gates

72. The logic circuit shown in the circuit below yeilds the truth table as given below. The gate ’ $p$ ’ in the circuit is:

(1) OR gate

(2) AND gate

(3) NAND gate

(4) NOR gate

Show Answer

Correct answer: (2)

Solution:

From the above circuit $\mathrm{Y}=\mathrm{A}+\mathrm{B}$.

i.e. it is for OR gate:

$\Rightarrow \mathrm{A}+\mathrm{P}=\mathrm{A}+\mathrm{B}$

or $\mathrm{A}+\mathrm{P}=\mathrm{A}+\mathrm{B} \cdot(\mathrm{A}+\overline{\mathrm{A}})$

$=\mathrm{A}+\mathrm{B} \cdot \mathrm{A}+\mathrm{B} \cdot \mathrm{A}$

$=\mathrm{A}+\overline{\mathrm{A}} \cdot \mathrm{B}$

$\mathrm{A}$	$\overline{\mathrm{A}}$	$\mathrm{B}$	$\mathrm{C} _{2}$	$\mathrm{Y}$
0	1	0	0	0
0	1	1	0 or 1	1
1	0	0	0 or 1	1
1	0	1	0 or 1	1

$\Rightarrow \quad \mathrm{P}=\overline{\mathrm{A}} . \mathrm{B}$ which is AND gate or

Let $\bar{A}$ and $B$ be input of unknown gate Pand $C _{2}$ output of $\mathrm{P} _{2} \mathrm{C} _{2}$ and $\mathrm{A}$ are input of on OR gate. Therefore

$\mathrm{A}$	$\overline{\mathrm{A}}$	$\mathrm{B}$	$\mathrm{C} _{2}$	$\mathrm{Y}$
0	1	0	0	0
0	1	1	1	1
1	0	0	0 or 1	1
1	0	1	0 or 1	1

For gate $\mathrm{P}$

$\overline{\mathrm{A}}$	$\mathrm{B}$	$\mathrm{C} _{2}$
0	0	0
0	1	0
1	0	0
1	1	1

This is truth table of AND gate. Therefore $\mathrm{P}$ is AND gate.

Average

Logic Gate

73. For the circutal arrangement shown the TRUTH table is

(1)

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{C}$
0	0	1
1	0	1
0	1	1
1	1	1

(2)

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{C}$
0	0	0
1	0	0
0	1	1
1	1	1

(3)

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{C}$
0	0	1
1	0	1
0	1	0
1	1	0

(4)

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{C}$
0	0	1
1	0	1
0	1	1
1	1	0

Show Answer

Correct answer: (4)

Solution:

Gate I and II are NOR gates with the two inputs joined together. Each gate acts as a NOT gate. The inputs of gate III are $\overline{\mathrm{A}}$ and $\overline{\mathrm{B}}$ gate III is a OR gate. The truth table is as shown below:

$\mathrm{A}$	$\mathrm{B}$	$\overline{\mathrm{A}}$	$\overline{\mathrm{B}}$	$\mathrm{C}$
0	0	1	1	1
0	1	1	0	1
1	0	0	1	1
1	1	0	0	0

Average

Logic Gates

74. The signals A and B shown in Fig. (a) are the used as inputs in circuit shown in FIg. (b). The output signal $C$ is

(1)

(2)

(3)

(4)

Show Answer

Correct answer: (1)

Solution:

Gate $\mathrm{I}$ is a NOR gate with the two input terminals shorted. It acts as a NOT gate. Gate II is NAND gate with input $\bar{A}$ and $B$. The binary representation of inputs $A, B$ and $C$ are:

$\Lambda$	$\mathrm{B}$	$\overline{\mathrm{A}}$	$\mathrm{C}$
1	0	0	1
0	1	1	0
0	1	1	0
1	0	0	1
1	1	0	1
0	1	1	0

The pluse representation of $\mathrm{C}$ is

Difficult

Logic Gates

75. The Booliean representation of a logic cate circuit using two inputs $A$ and $B$ having output $\mathrm{C}$ is

$$ \mathbf{C}=\overline{(\mathbf{A} \cdot \overline{\mathbf{B}}) \cdot(\overline{\mathbf{A}}+\mathbf{B})} $$

The correct circuit is:

(1)

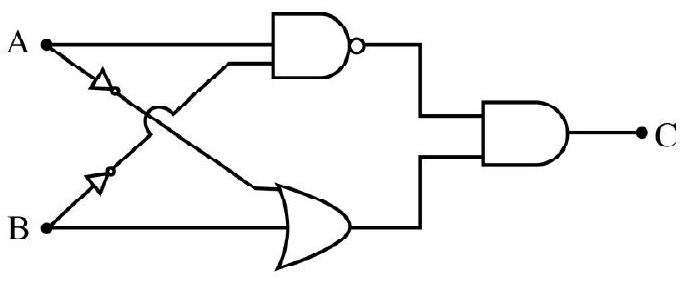
(2)

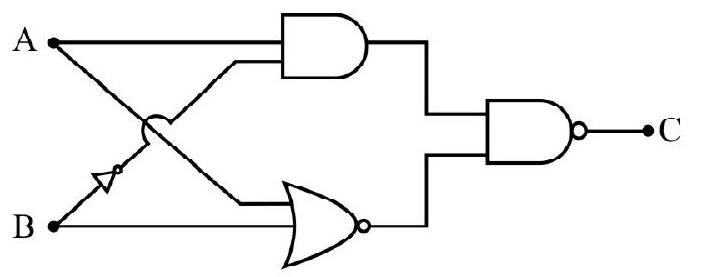
(3)

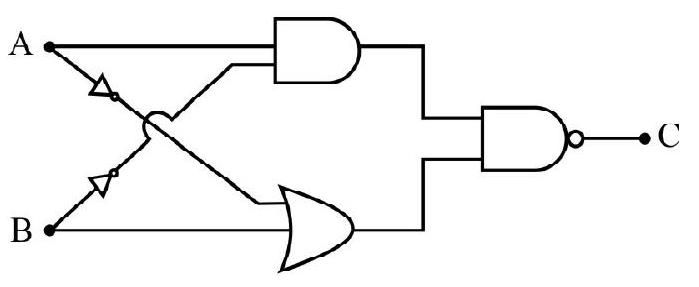
(4)

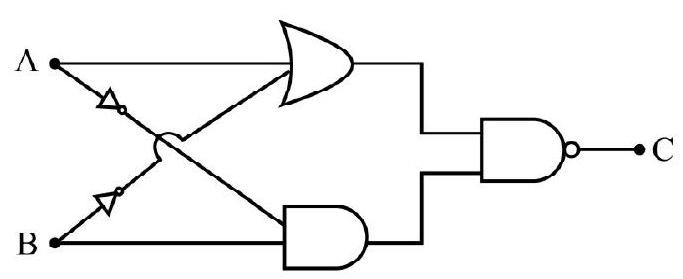
Show Answer

Correct answer: (3)

Solution:

Let $C _{1}=A \cdot \bar{B}$ and $C _{2}=\bar{A}+B$. $C _{1}$ is output of a AND gate using $A$ and $\bar{B}$ as inputs. $C _{2}$ is output of a OR gate using $\bar{A}$ and $B$ as input. $C _{1}$ and $C _{2}$ are inputs of a NAND gate. This is shown correctly in (3).

Difficult

Logic Gates

76. Four NAND gates are connected as shown in Fig. The arrangment is equivalent to

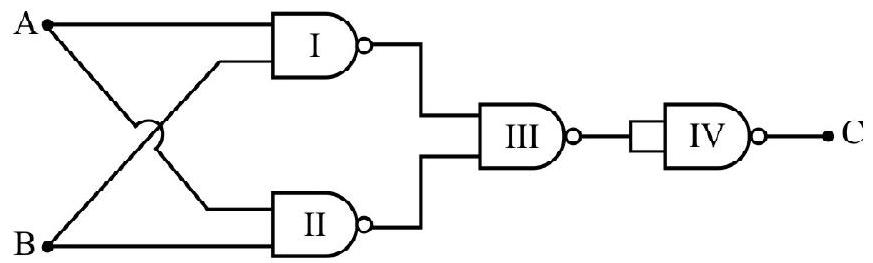
(1) One NAND gate

(2) One OR gate

(3) One NOR gate

(4) One NOT gate

Show Answer

Correct answer: (1)

Solution:

Gate I and II are used as NAND gates. Let their output be $\mathrm{C} _{1}$ and $\mathrm{C} _{2}$ respectively. $\mathrm{C} _{1}$ and $\mathrm{C} _{2}$ are inputs of gate III used as a NAND gate. Its output is $\mathrm{C} _{3} \cdot \mathrm{C} _{3}$ is input of gate IV used as a NOT gate. The final output C. The truth-table of the arrangement is

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{C} _{1}$	$\mathrm{C} _{2}$	$\mathrm{C} _{3}$	$\mathrm{C}$
0	0	1	1	0	1
0	1	1	1	0	1
1	0	1	1	0	1
1	1	0	0	1	0

From the truth-table we can make truth-table showing A, B and C only. This is truth-table of a NAND gate. The arrangment therefore is equivalent to a single NAND gate.

Average

Logic Gates

77. In the circuit shown in Fig. the output $Y$ is zero for inputs

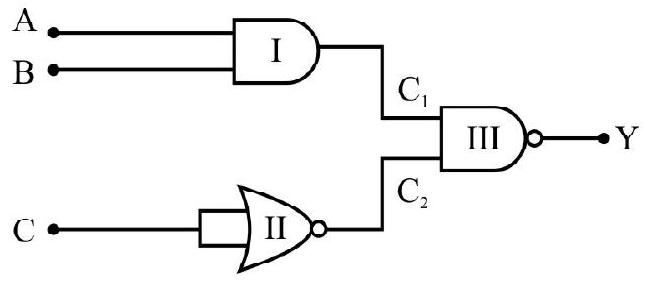
(1) $\mathrm{A}=1 ; \mathrm{B}=0 ; \mathrm{C}=0$

(2) $\mathrm{A}=0 ; \mathrm{B}=0 ; \mathrm{C}=0$

(3) $\mathrm{A}=0 ; \mathrm{B}=1 ; \mathrm{C}=0$

(4) $\mathrm{A}=1 ; \mathrm{B}=1 ; \mathrm{C}=0$

Show Answer

Correct answer: (4)

Solution:

Gate I is AND gate; gate II is NOR gate used as a NOT gate and gate III is NAND gate.

1. $\mathrm{A}=1 ; \mathrm{B}=1 ; \mathrm{C} _{1}=0 ; \mathrm{C} _{2}=1 ; \mathrm{Y}=1 ; \mathrm{C}=0$
2. $\mathrm{A}=0 ; \mathrm{B}=0 ; \mathrm{C} _{1}=0 ; \mathrm{C} _{2}=1 ; \mathrm{Y}=1 ; \mathrm{C}=0$
3. $\mathrm{A}=0 ; \mathrm{B}=1 ; \mathrm{C} _{1}=0 ; \mathrm{C} _{2}=0 ; \mathrm{Y}=1 ; \mathrm{C}=0$
4. $\mathrm{A}=1 ; \mathrm{B}=1 ; \mathrm{C} _{1}=1 ; \mathrm{C} _{2}=1 ; \mathrm{Y}=1 ; \mathrm{C}=0$

The correct choice is (4).

Difficult

Logic Gates

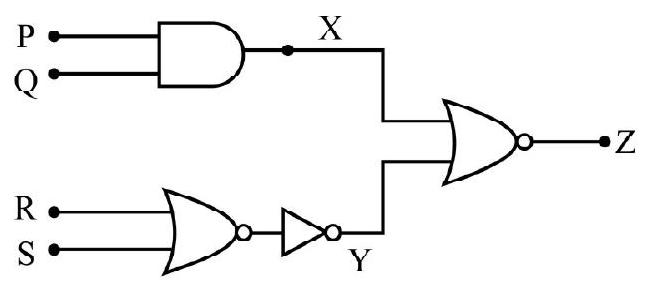
78. Fig. shows a logic commbination with $P, Q, R, S$ are inputs. When $P, Q, R$ and $S$ all are 1 ; the outputs $X, Y$ and $Z$ are 1,1 and 0 respectively. When input $P$ and $R$ are changed to state 0 with inputs $Q$ and $S$ still in state 1 ; the output $X, Y, Z$ change to:

(1) $\mathrm{X}=1 ; \mathrm{Y}=0 ; \mathrm{Z}=0$

(2) $\mathrm{X}=1 ; \mathrm{Y}=1 ; \mathrm{Z}=1$

(3) $\mathrm{X}=0 ; \mathrm{Y}=1 ; \mathrm{Z}=0$

(4) $\mathrm{X}=0 ; \mathrm{Y}=0 ; \mathrm{Z}=1$

Show Answer

Correct answer: (3)

Solution:

$\mathrm{P}$ and $\mathrm{Q}$ are inputs of aND gate. When $\mathrm{P}=0 ; \mathrm{Q}=1 ; \mathrm{X}=0$. $\mathrm{R}$ and $\mathrm{S}$ are inputs of a NOR gate and its output is input of a NOT gate. Obvisouly with $\mathrm{R}=0$ and $\mathrm{S}=1$; the output of NOR gate is 0 . This is input of NOT gate. Therefore $Y=1$. Now $X=0$ and $Y=1$ are inputs of a NOR gate; the output $Z=0$. This is correctly representation in (3).

Difficult

Logic Gates

79. Four NAND gates are joined together as shown in Fig; then the correct Truth-table of the arrangement is

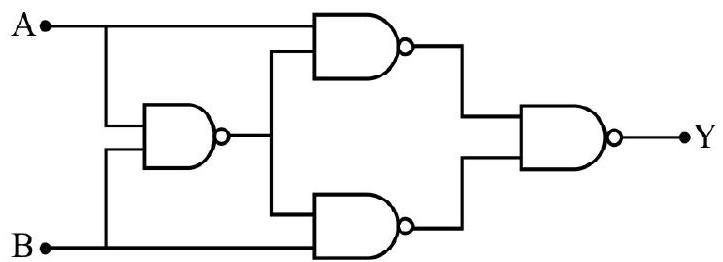
(1)

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{Y}$
0	0	0
0	1	1
1	0	1
1	1	0

(2)

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{Y}$
0	0	0
0	1	0
1	0	1
1	1	1

(3)

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{Y}$
0	0	1
0	1	1
1	0	0
1	1	0

(4)

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{Y}$
0	0	1
0	1	0
1	0	0
1	1	1

Show Answer

Correct answer: (1)

Solution:

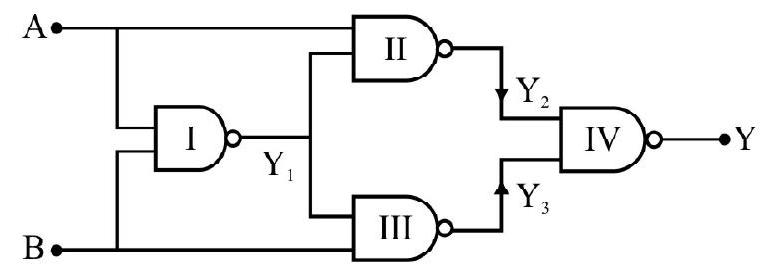
Difficult

Logic Gate

80. For the arrangment of logic gates shown in Fig. the Truth-table is

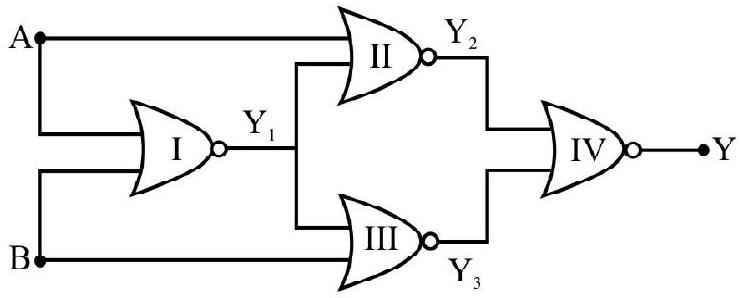
(1)

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{Y}$
0	0	0
0	1	1
1	0	1
1	1	1

(2)

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{Y}$
0	0	1
0	1	0
1	0	0
1	1	1

(3)

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{Y}$
0	0	1
0	1	1
1	0	0
1	1	0

(4)

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{Y}$
0	0	1
0	1	1
1	0	1
1	1	1

Show Answer

Correct answer: (4)

Solution:

Gate I, II and III are NOR gates and gate IV is NAND gate. Using the truth tables of gate involved we have

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{Y} _{1}$	$\mathrm{Y} _{2}$	$\mathrm{Y} _{3}$	$\mathrm{Y}$
0	0	1	0	0	1
0	1	0	1	0	1
1	0	0	0	1	1
1	1	0	0	0	1

In Fig. the gates have been numbered as I, II, III and IV. Their outputs are labled as $\mathrm{Y} _{1}, \mathrm{Y} _{2}, \mathrm{Y} _{3}$ and $\mathrm{Y}$ respetively. Using the Truth-table of NAND gate we have

$\mathrm{A}$	$\mathrm{B}$	$\mathrm{Y} _{1}$	$\mathrm{Y} _{2}$	$\mathrm{Y} _{3}$	$\mathrm{Y}$
0	0	1	1	1	0
0	1	1	1	0	1
1	0	1	0	1	1
1	1	0	1	1	0

In terms A, B and Y the correct Truth-table is given in (1).