Unit-18 Atoms & Nuclei
Learning Objectives
After going through thin unit, you will be able to understand, appreciate and apply the following concepts:
-
The significance and basic details of the alpha particle scattering experiment.
-
Rutherford’s model of the atom.
-
Bohr’s model; its basic postulates.
-
‘Energy Levels’ and their significance.
-
Hydrogen spectrum; its basic details.
-
The atomic nucleus.
-
Composition and size of the nucleus.
-
Atomic masses.
-
Isotopes, isobars and isotones.
-
The phenomenon of radioactivity.
-
The nature and basic properties of alpha, beta and gamma rays.
-
Radioactive decay law.
-
Mass energy relation.
-
Mass defect.
-
Binding energy per nucleon and its variation with mass number.
-
Nuclear fission.
-
Nuclear Fusion.
The Models of the Atom
Introduction: The discovery of the electron and the fact that electron is a common constituent of all matter established the fact that atom has a structure. To assign a model to the atom we have to picture the relative arrangement of positive and negative charges in the atom. In addition a viable model of atom must also explain the neutrality and stability of the atom. Further developments in this field established that under proper conditions, every atom emits a characterstic spectrum. Hence a successful model of the atom should also be able to explain this basic property of the atom.
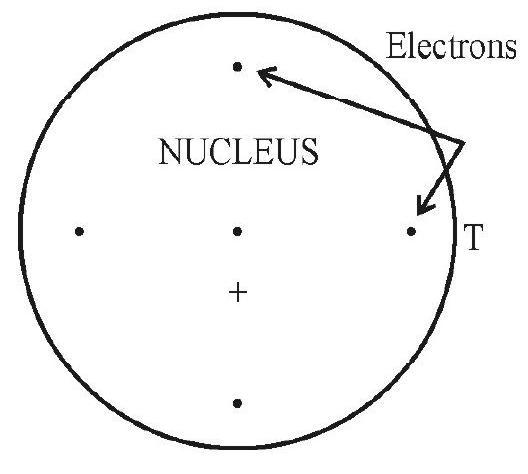
The Thomson Model
Thomson proposed a first viable model of the atom in 1904. In this model he visualized the positive charge of the atom to be distributed uniformly over the entire atom. The negative electrons were imagined as embedded in this continuous charge. This arrangment is somewhat similar to the arrangement of seeds in a watermelon. Figure shows the arrangement of electrons in atoms with atomic number

Rutherford’s
To experimentally test the viability of Thomson’s hypothesis, Rutherford proposed a historic experiment; the scattering of
Rutherford argued that if positive charge is uniformal distributed in atom, then
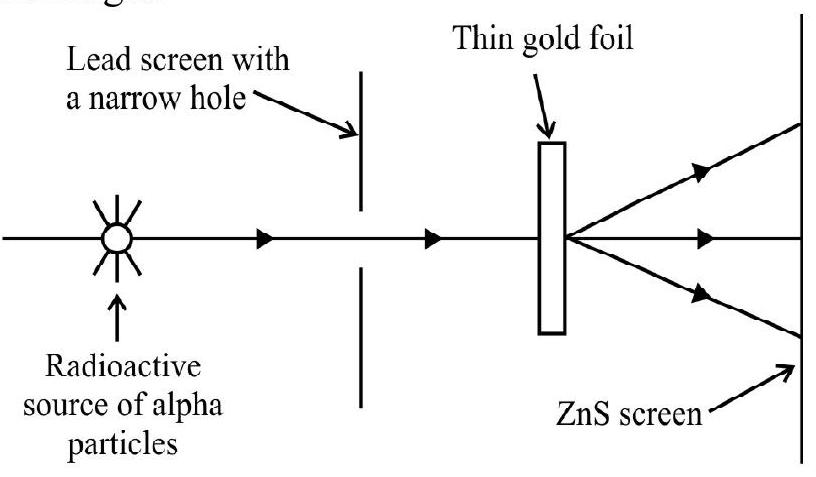
Geiger and Marsden discovered that most of a particles passed through gold foil with small deviation. But there were fews
(1) The atom has a small positively charged nucleus. The entire mass and positive charge of the atom is concentrated in the nucleus.
(2) The electrons move around the nucleus.
(3) Since the entire mass of the atom is concentrated in small nucleus most of the atom is empty.
(4) The fact that a very small number of
Rutherford Scattering Formula
(1) The distance of closet approach
where
(2) Impact Parameter
Impact parameter is defined as the perpendicular distance of the initial velocity vector of the
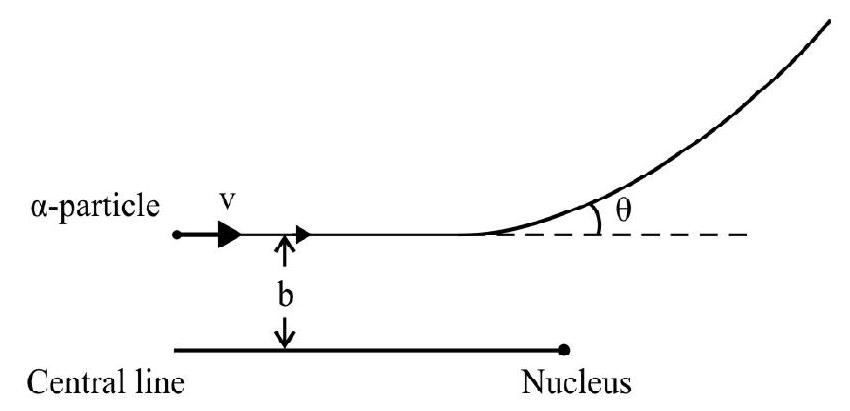
Fig. (b) shows thr
for particle 1 . The angle of scattering of 1 is more than that of 2 and 3 . This is because particle 1 is coming more close to nucleus
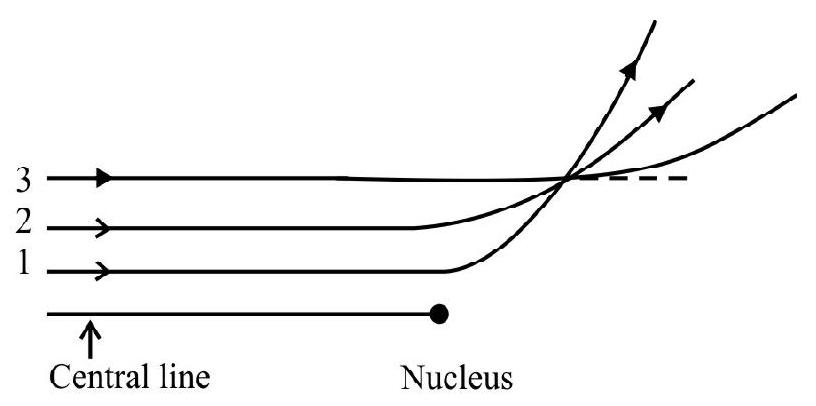
It can be shown that the number or
(1) directly proportional to thickness (
(2) directly proportional to atomic number (z) of scattering nuclei.
(3) inversly proportional to kinetic energy (K) of incident
(4) inversly proportional to
Rutherford Atomic Model
According to Rutherford the electrons are revolving around the nucleus in circular orbits (now we postulate eliptical orbits). This is very similar to the planetary model of the universe where planets are revolving round the sun in circular orbits. The attraction between the positively changed nucleus and negative electron provide the centripetal force acting on the electron moving in circular orbit.
For an electron of mass
In the Rutherford model all value of
Also
Obviously,
Since
Limitations of the Rutherford Model
(1) Rutherford model faced some serious problems when subjected to the demands of electromagnetic theory. According to classical electromagnetic theory an accelerated charge particle must emit electromagnetic radiation. Now an electron moving in a circular orbit around the nucleus must experience centripetal acceleration and hence in accordance with the demands of electromagnetic radiation will lose energy in the form of electromagnetic radiation. This energy loss will come from the atomic system itself. As a consequence the electron will be continuously pulled towards the nucleus. Hence an electron can not remain in an orbit of radius
As the electron goes nearer the nucleus, its speed increases continuously, the centripetal acceleration it experience also becomes more and it must emit more radiations. The net result of all this is that the electron crashes into nucleus after following a spiral path (in about
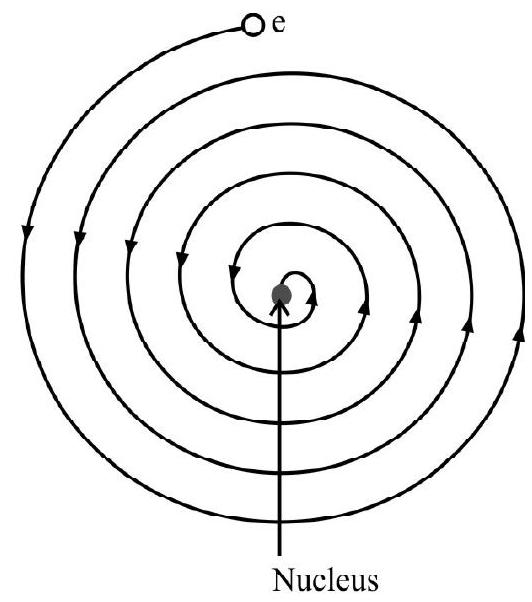
(2) Since electron in orbit losses energy continuously the spectrum of the atom should be a continuous spectrum. However atoms exhibit a characterstic line spectrum. This fact is also ’not in tune’ with the Rutherford model.
However the idea of a planetary atom was hard to discard. Efforts were made to overcome this difficulty which was ultimately successfully explained by Neil Bohr in 1913. However before Bohr’s published his theory a lot of experimental work was already available in the field of spectroscopy. It was established that emission of electromagnetic radiations in the form of spectral lines was the fundamental characterstics of the atoms. With the development in the experimental techniques, the wavelength of emitted spectral lines could be determined very accurately.
Spectrum of Hydrogen Atom
Carefull analysis of the experimental observatinos of the line spectrum emitted by hydrogen showed that it can be described in terms of empirical formulae. The hydrogen spectrum consists of the following series each named after it discoverer.
(1) The Lymann Series
The wave number
(2) For the Balmer Series
The Balmer series lies in the visible part of spectrum. The line for transition from
(3) For the Paschen Series
The Paschen series lies in the infrared region.
(4) For the Brackett Series
(5) For the Pfund series we have
The Brackett and the Pfund series lie in far infrared region.
The Bohr Atom
The postulate of Bohr’s theory are as follows:
(1) Bohr’s First Postulate: An electron revolving around the nucleus is not permitted to move in every possible orbit. It can move only in some “special orbits”. These orbits are known as stationary orbits. An electrons in a stationary orbit cannot lose energy according to the demands of classical electromagnetic theory.
To define these special orbits Bohr further postulated that the angular momentum of an electron in a stationary orbit is always an integral multiple of
where
(2) Bohr’s second postulate is designed to explain the emission of radiations by atoms. This postulate state that whenever an electron jumps from one stationary orbit to another the energy difference between the two is either emitted or absorbed as a quantum of radiation. Expressed mathematically
where
Bohr Formule
Let the charge of atomic nucleus be
Multiplyaing both sides of this equation by
We have
Squarring Bohr’s condition of Ist postutate we have
Comparing above two equations we have
Also we have
or
To calculate the energy of the electron in
Now P.E
and
Hence the energy of the electron in the
Using Bohr’s second postulate we can write
where
Putting the value of constants we get the value of
The experimental determined value of
Energy Level Diagrams
Energy level diagrams are a very useful and convenient way of representing various series of hydrogen spectra.
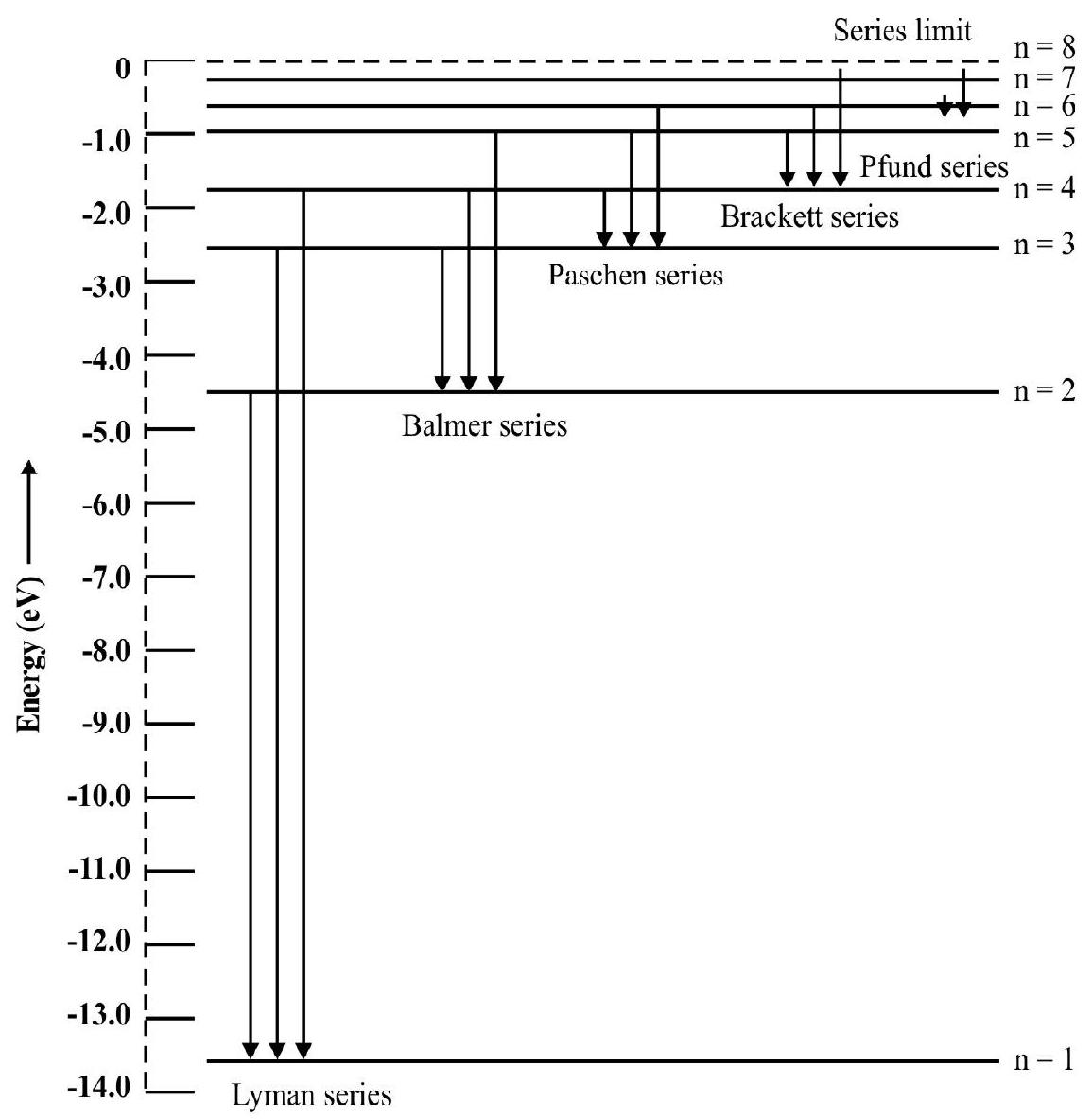
The energy expression of the electron in
For hydrogen
Limitations of Bohr atom
Bohr model can also be used for the studies of spectra of hydrogen like elements. Inspite of its tremendous success the Bohr model could not explain the observed fine structure of spectral lines in the hydrogen spectrum.
Example-1:
Which state of a triply ionized beryllium atom has the same orbital radius as that of the ground state of hydrogen.
Show Answer
Solution:
The expression for the radius of hydrogen and hydrogen like atoms is given by
Thus second orbit of triply ionized beryllium atom has the same radius as the ground state of hydrogen atom.
Example-2:
Find the first excitation potential of
Show Answer
Solution:
The energy of a hydrogen atom in the nth excited state is given by
Hence the energy of a ionised helium atom would be given by
for first excited state, the transition is from
Now for
and for
Hence the excitation energy of the
If
Then,
or
Example-3:
The Rydberg constant for hydrogen is
Show Answer
Solution:
For Lyman series we have
For short wavelength limit we must have
Hence
and for long wavelength limit we must have
or
Example-4:
Show that
Show Answer
Solution:
The Possible states when transition occur from
Further the atoms reaching the
Hence the possible number of transitions
Radioactivity
Radioactivity is the phenomenon in which we have spontaneous disintegration of the nucleus of one or more atoms with the emission of highly pentrating radiations. The phenomenon of radioactivity is confined entirely to heavier elements in the periodic table having atomic number ranging from 83 to 102 .
The phenomenon of radioactivity was accidently discovered by Becquerel. The phenomenon is independent of the external agents like temperature, pressure, electric or magnetic field and the ‘physical’ or chemical state of the specimen. It was M. Curie who gave the name raioactive to all substances capable of emitting these rays. A simple experiment by Rutherford established that the radioactive radiations consists of three components known as
Alpha Particles
1.
2.
3.
4. They are easily absorbed by matter.
5. They are scattered while passing through metal sheets.
6. They can produce artificial disintegration of an atom.
7.
The range represents the distance
Beta Particle
1.
2.
3. They have less ionizing power as compared to
4. They originate from the nucleus of disintegrating atom.
5. They do not show any definite range.
6. Their penetrating power is greater than that of
7.
8. Nucleus showing
and
Gamma Rays
1. Gamma rays are electromagnetic waves of very short wavelength. Speed of
2. Gamma rays are often emitted in conjunction with
3. They produced flourescene and affect photographic plates.
4. They are reflected from the surface of a crystal. This property of
5. They ionize gases very slightly.
6.
According to the development in the field of nuclear models it is now known that there are energy levels in the nucleus just like atoms (of the order of
Most radioactive nucleus after an alpha or beta emission leave the resultant nucleus in an excited state. This nucleus known as daughter nucleus reaches the ground state by a single or sometimes successive transition by emitting one or more gamma rays.
Laws of Radioactive Disintegration
The laws of radioactivity are brodally divided into two parts
(1) the qualitative law
and (2) the quantitative law
1. The Rutherford-Soddy’s Law
is the qualitative law. It tells the nature of daughter nucleus obtained in a ratioactive transformation.
(a) A particular radioactive nuecleus can emit either an
(b) When a radioactive nucleus
When a radioactive nucleus emits a
2. The Exponential Law
This is quantative law. It relates the number of radioactive atoms initially with the number of atoms present at
Hence it becomes obvions that radioactive disintegration are governed by the laws of probability. The phenomenon can only be described statistically.
Let
Hence
Integrating we have
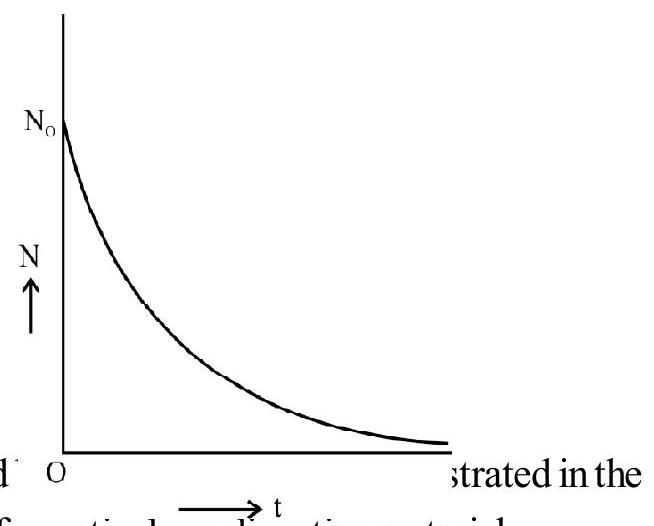
which means that radioactive disintegrations are governed figure.
The Half Life and the Mean Life
It is clear that a radioactive element will lose its activity after a infinite time and all radioactive element are identical in this respect. To distinguish one radioactive element from other as far as its activity is concerned we use the concept of half life. Half life
We define the concept of mean life to represent the above mentioned facts from a statistical point of view. We have already seen that it it only after an infinite time that the radioactivity of an element disappear completely. Hence out of disintergrating atoms some will disintegrate almost immediately and some other will disintegrate after an infinite time.
Thus actual life of a disintagrating atom can vary from 0 to
on inegrating above expression we have
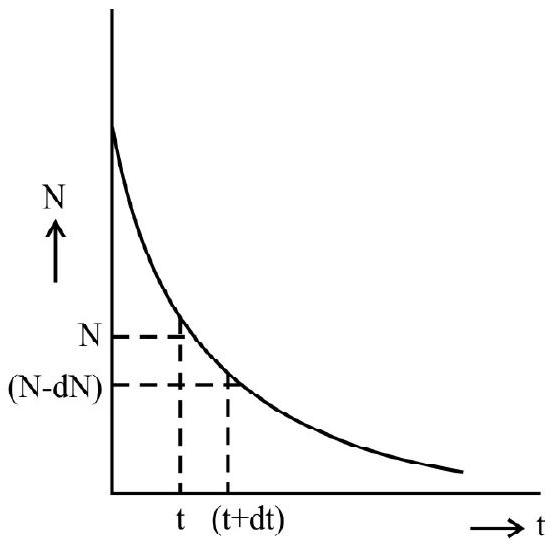
We thus have
The curie is the unit of radioactive disintegration. We have
1 curie
Example-5:
A radioactive sample has
Show Answer
Solution:
By the definction of half life we know that it represents the time after which the number of original atoms is reduced to half. Hence after one half life the number remaining is
Example-6:
The half life of is
Show Answer
Solution:
The number of atoms in
Since half life of
Now we know that
Hence activity of
Example-7:
One gram of radon has an activity of one curie. What activity of radon will accumulate from one milligram of pure radon in
Show Answer
Solution:
No. of atoms in
Half life of radon
Activity of
Example-8:
The activity of a radioactive sample is
Show Answer
Solution:
Activity of the sample in the begining
Activity of the samle after 5 minutes
or
Example-9:
Calculate the weight of one curie of RaB from its half life of 26.8 minute.
Show Answer
Solution:
Activity of
Half life of
Let
We know that
Weight of RaB having an activity of 1 curie
Example-10:
When the nucleus of copper
Show Answer
Solution:
Mean life
Atomic Nucleus
We know nucleus of an atom has the entire mass and positive charge of atom. The size of nucleus is about
The Proton-electron Model
According to Prout a nucleus
The hypothesis had to be rejected because the theoretical and experimental values of (1) nuclear spin and (2) nuclear magnetic moment are not in accord with theoretical calculated values and experimental values. Also uncertaintity principle is violated if electrons exist inside nucleus.
Nuclear Reactions
With the development of high energy particle accelerators, proton and
This is known as a nuclear-reaction. This is also known as transmutation of elements. We can now represent a general nuclear reaction as:
In any nuclear reaction mass number and atomic number are conserved i.e.
and
If however
Atomic Mass Unit
One atomic mass unit;
In accordance with Eintesin’s mass-energy equivalence relation
Energy equivalent to 1 a.m.u of mass
The Discovery of Neutron
Bathe and Becker carried out a nuclear reaction by bombarding Brylium
Applying the “mass-energy” conservation principle the theoretical energy of emitted
The Proton-Neutron Hypothesis
Immediately after the existence of neutron was experimentally confirmed physicst proposed the protonmeutron hypothesis of atomic nucleus. Protons and neutrons taken together are referred to as nucleons. According to this hypothesis a nucleus
The theoretical and experimental values of(1) nuclear spin and (2) nuclear magnetic moment are in agreement with theortical calculated and experimental values. Also the uncertaintity principle is not violated. The hypothesis also easily explains existance of isotopes; isobars etc. It is the presently accepted model of atomic nucleus.
Size of the Nucleus
We have already discussed the “parameter” the distance of closeset approach in Rutherford scattering formula. The value of
We assume nucleus to be spherical in shape and its size increases with the increase of number of nucleons. Thus the volume of a nucleus increases with its mass number A. Being a sphere of radius A, the volume of the nucleus viz.
where
Example-11:
Find the maximum energy that a
Acomic mass of
Show Answer
Solution:
Mass defect
Kinetic energy available in the given reaction is
This energy available is to be shared between emitted
Example-12:
A nucleus with
Show Answer
Solution:
We know that
Let
Example-13:
There is a stream of neutrons with a kinetic energy of
(mass of neutron
Show Answer
Solution:
Let
Then
The time dt taken by neutrons to travel a distance of
Since dt is very small as compared to half life of neutrons
Mass Defect and Binding Energy
Very accurate measurements of mass of atomic nuclei showed that the experimental mass
An important question that arises is : what happens to mass
Binding energy
We can also say an energy equivalent to the binding energy will have to be given to break a nucleus into its constituent nucleous lying very far off from one another.
Binding Energy of A Deutron
Mass of a proton
Mass of a neutron
Mass of a proton + Mass of a neutron
Experimental mass of a deutron nucleus
Binding Energy
The above result has been verified from a direct experiment. On bombarding a hydrogen nucleus with neutron, a neutron is captured in accordance with the reaction.
The energy of emitted
The energy released has to be
Stability of Nucleus and Binding Energy
A great deal of information about nuclei and their stability can be obtained from the studies of binding energy. However the calculation are in general, made for atoms rather than atomic nuclei. Calculation for binding energy per nucleon has been worked out for the various atoms in the periodic table. Figure shows the plot of binding energy per nuleon against the mass number. From the graph the following sailent features are observed.
(1) As a first approximation binding energy per nucleon starts with a low value of deutron and than increases rapidly.
(2) Some nuclei like
(3) After the rapid increase the binding energy per nucleon is found to decrease slowly as the number of nucleons increases beyond 60 .
(4) The nuclei in the region of the low to middle of peridic table are most tigetly bound. For example iron cobalt, nickel belong to this catagery.
(5) The analysis of curve shows that higher is the binding energy per nucleon, the more stable is the atom and vice versa.
The graph also gives us a very vital information. The shape of this average binding energy curve indicate that there are two general processes which can release energy fromnuclei.
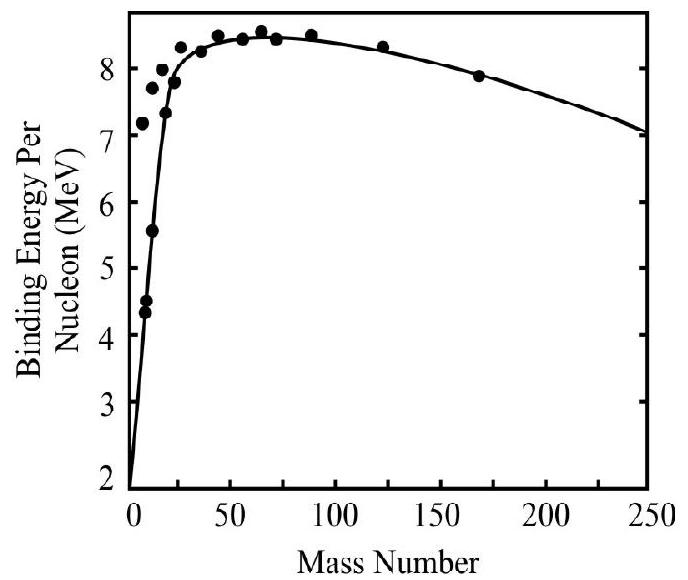
(a) Combining light nuclei into a more massive nucleus.
(b) Spilting up heavy nuclei of into nuclei medium mass.
This is because in both cases, the total binding energy of the products exceeds that of reactants. These two cases corresponds to phenomenon of nuclear fission and nuclear fusion.
Example-14:
Calculate the energy liberated when a single helium nucleus is formed by the fusion of two deuterium nuclei. Given
Mass of
Mass of
Show Answer
Solution:
The reaction can be written as
Mass defect
Hence energy released is
Nuclear Fission
When a uranium nucleus was bombared by neutrons, it was found that the products of the reaction were having a number of different half lives. It was assumed that in these reactions, we are producing trans uranium elements. If we attribute these different half lives to the successive disintegration of the same atom, one can explain the possibility of a single nucleus emitting several
O. Hahn and F. Strassmann then tried to identify the products of the reaction when uranium was barbarded will neutrons chemically and found to surprise of every one that these products were a number of different elements nearly all of which are in the centre of periodic table. They thus concluded that the uranium nucleus after the capture of a neutron seemed to be spilting apart into two nearly equal fragments as illustrated in the figure. These results were supported by Miss Lise Meitner and S. Frisch. They suggested that the neutron initiated a decomposition of the uranium nucleus into two nuclei of roughly equal size. The phenomenon was termed as nuclear fission.
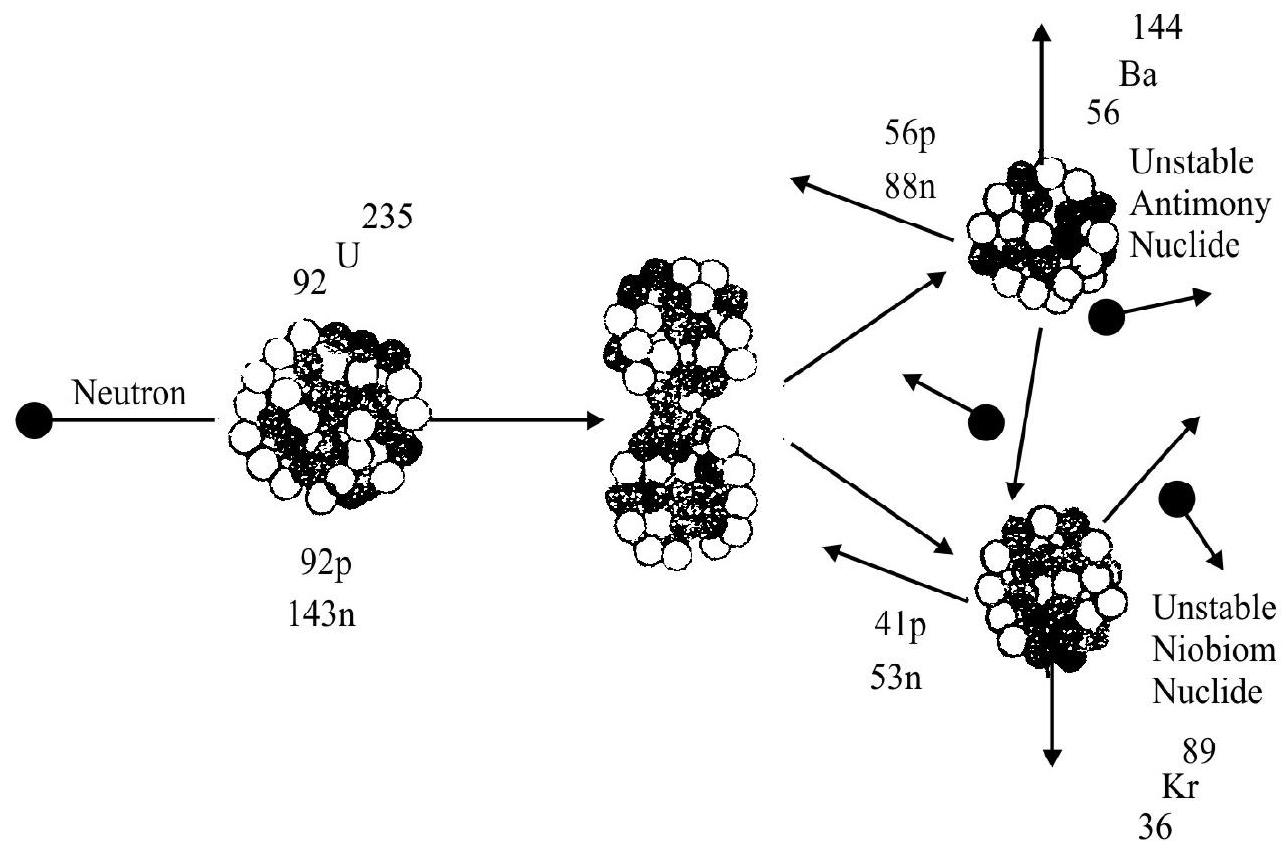
Fission
In general, fission fragments are not stable but contain an excess number of neutrons. Hence they either ejects neutrons or convert them into protons by ejecting
2.

Further experiment showed that uranium after neutron capture divides itself into many possible fragments each corresponding to elements near the centre of periodic table. We list below some of the possible fragment pairs.
1.
2.
3.
4.
5.
6.
This is the underlying principal of a fission bomb. We illustrate a chain reaction in the following diagram.
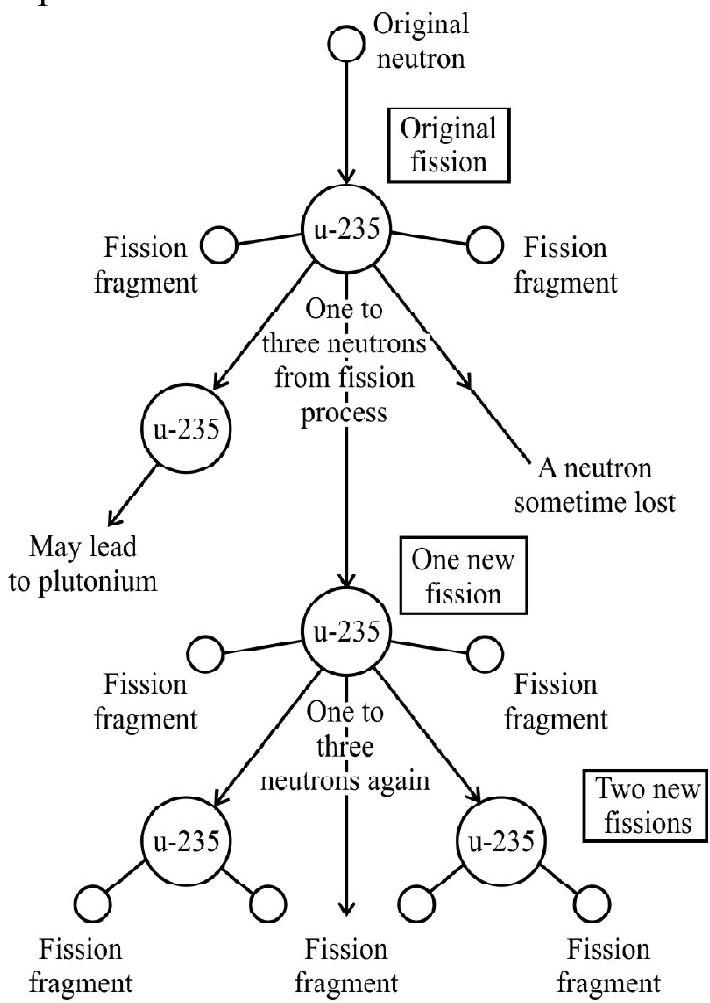
The explosive release of nuclear energy by fission is used in the design of bombs. In a bomb, the material is chosen and arranged in such a way that each neutron has the greatest possible probability of producing another fission. The arrangment ensures that on the average one fission leads to more than one subsequent fission, a rapidly increasing number of fissions occur each acompained by the release of about
Nuclear Reactor
We design a nuclear reactor on the basis of a controlled fission reaction by the arrangement of reactor material. A steady reaction is maintained, in which each fission produces on an average of one new fission. We try to achieve a critical balance for the production of controlled nuclear energy.
The fission of uranium by neutrons is self sustaining chain reaction in which 2.5 neutrons per fission are produced on the average. The reaction can therefore proceed in a sustained and controlled way if one of these neutrons is able to cause further fission and remaining 1.5 neutron are allowed to escape. To meet these requireements the nuclear reactor is made sufficiently large to increase the (surface / volume) to the desired optimum level. Further if need be the fuel is also surrounded by a neutron reflecting material. This helps to decrease the ’neutron loss’ if it is sufficiently fast. The essential parts of a nuclear reactor are shown in the figure.
1. Fissionable fuel (like enriched uranium) taken usually in the form of rods.
2. Control rods are made of some suitable neutron absorbing material like cadium. They are pushed in and out to control the rate of neutron absorption and hence the rate of further fission.
3. Moderator (like graphile, heavy water) that helps to slow down the fast neutrons and thus increasing the probability of their capture by uranium. It shares the energy of the fast moving nuetrons without actually absorbing them. The moderator is prefeably a material whose atomic mass is comparable to that of a neutron and which therefore causes a large energy exchange on each collision. The moderator is suitably mixed with the uranium fuel.
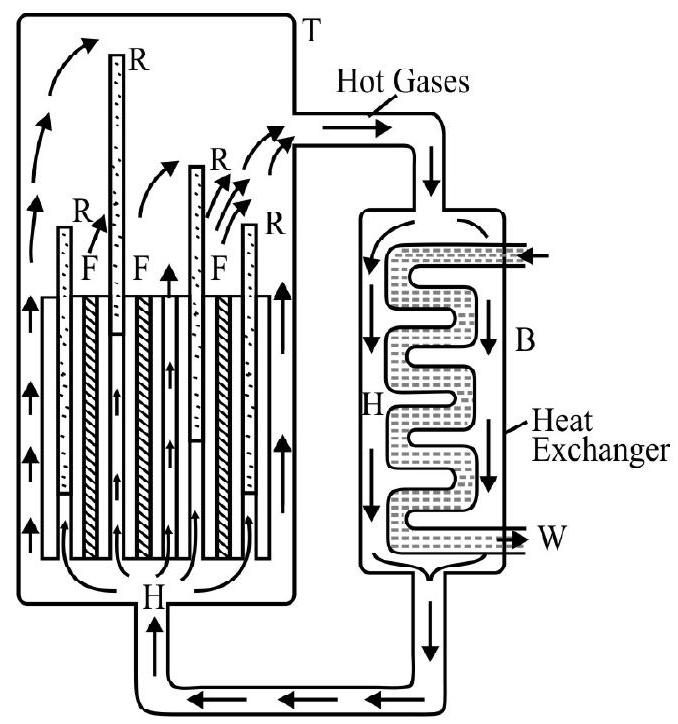
The nuclear reactor goes into operation when some stray neutrons initiate fission in the enriched uranium fuel. The moderator and control rods are then suitably adjused to sustain the chain reaction at a controlled rate. The energy released is used to produce steam in a steam generator. The steam then drives the turbines connected to the electric generator and thus help to produce electricity.
Nuclear Fusion
Nuclear energy can also possibly be obtained by the fusion process of light nuclei. The basic underlying principle to obtain fusion nuclear energy is to fuse two or more light nuclei of combined mass ’
Some typical fusion reactions had been produced in the labortary by bombarding (of appropriate targets) particles, accelerated to very high energies with suitable particle accerlators. Some typical fusion reactions are listed below:
One main reason the fusion energy release is becoming significantly important is the fact that theoretically there is a large scale possibility of obtaining energies from the fusion of deuterium and deuterium can be obtain in abudence at a significantlly low cost from the sea water. However there are numerous practical difficulties which are to be overcome before using fusion reactions as a source of nuclear energy.
The first and forcemost difficulty in bringing about fusion is that the nuclei to be fused are usually positive charged and so they tend to push apart because of very strong electrostatic repulsive forces. The only way out to overcome this difficulty is that nuclei must be raised to excessively high temperatures (estimated to be about 100 million degree). At such high temperature the random internal motion of particles would bring them within the range of nuclear forces for fusion to occur. This has been achieved in an uncontrolled way in so called fusion bomb.
However a fusion reactor is a distant future possiblity. First we have to develop techniques to achieve fantastic temperatures of 100 million degrees. Then we have to keep fusing nuclei in that region long enough to produce enough energy from the reaction to make it self sustained. The most serious difficulty is however to find suitable containers to confine the material while it is reacting at such high temperatures. Developments in Plasma Physcis has developed so called Magnetic Bottles. At temperature of 100 million degrees the nuclei of fusing nuclei are in an ionized state and behave like a swirring mass of electric charges. One can therefore hope that the under influence of specially designed configuration magnetic fields or electric fields, the reacting material in the form of “Plasma” can be confined within the field bounderies. Magnetic bottles can force the plasma to stay in the region bounded only by magnetic lines of force.
Fusion reactors, (when fully developed) will have the following distinct advantages viz. the nuclear fuel is usually obtained from water which would always be available. More over the products are free from radioactive waste and quite harmless.
Nuclear Forces
The three basic characterstics of nuclear forces are as follows:
1. Nuclear forces are very strong attractive forces.
2. Nuclear forces are short range forces.
3. Heavy nuclei for their stability must also have a repulsive component such that the nuclear forces are on the whole attractive.
We now proceed to discuss these points one by one.
Our studies of nuclear reactions shows that the energies involved in unclear reactions are tremendously large as compared to the corresponding energy changes involved in chemical reaction. This shows that the force which are responsible for holding of its nucleons must be very strong. Another clue about the fact that the nuclear forces are very strong is obtained from the enormously large value of nuclear densities. The fact that atomic nuclei are stable and contain protons within nuclear volumes provide another support to the strong nature of nuclear forces. The presence of protons within nucleus must involve enormously large electrostatic repulsive force. The only way one can explain the stability of the nucleus, is to assume the existance of very strong attractive forces between nucleons. These strong (and short range) nuclear forces must overcome the electrostatic repulsive forces. We have seen that the binding energy per nucleon (exception light nuclei) has the same value
would be
A clear deduction is that every nucleon in the nucleus does not interact with every other nucleon. Hence a nucleon is only intteracting with its immediate nearest neighbour. Thus nuclear forces must have a short range. Nuclear forces falls of very rapidly with the distance between two nucleons, the decrease has to be much more rapid than
Experimental studies show that if the nuclear forces holding the nucleons were entirely attractive, heavy nuclei would collapse. This is so because in heavy nuclei, the nucleon’s are so closed logether so that each one is within the range of attractive forces of every other nulceon. This would ultimately mean that within the same nuclear dimensions the attractive energy acting on each particle would grow with the total number of nucleons. This contradicts the facts observed in reality. Thus we all are led to unescaple conclusion that nuclear force must also have a repulsive component that saves the nuclei from collapsing. Thus nuclear forces only on the balance are attractive.
Example-15:
Calculate the force between two fission fragments of equal masses and sizes that are produced by the fission of
Show Answer
Solution:
Total mass number of
Mass number of each fragment
Charge on each fragment
Radius of nucleus so formed
Distance between the centres of two fragments
Example-16:
A nuclear explosion is required to deliver
Show Answer
Solution:
Energy required by nuclear explosion
Energy released by fission
No. of fission required per second
Number of fission required per year by
Hence amount of uranium fuel needed is
Example-17:
Calculate the mass of
Show Answer
Solution:
Now energy released per fusion is
Mass of
Hence required mass
Example-18:
The volume of water in the Great Lakes is
Show Answer
Solution:
The volume of water in the Great Lakes
The mass of water
Since molecular weight of water is 18 , the total number of molecules in water having a mass of
Since the abudance of deutorium is
Now the fusion of 6 deutorium atoms gives an energy of
Hence the total release of energy of
PROBLEMS FOR PRACTICE
1. With what energy an
Show Answer
[Answer:2. The number of alpha particle scattered at
Show Answer
[Answer: 25]3. If the first member of the Lyman’s series is
Show Answer
[Answer:4. The wave number of a spectral series are 4857, 19932, 25215, 27663 and 27997 show that the limit of this seires is approximately 32033 .
5. A
Show Answer
[Answer:6. Which level of the doubly ionized litium has the same energy as the ground state energy of the hydrogen atom.
Show Answer
[Answer:7. The energy needed to detach the electron of a hydrogen like ion in ground state is equal to
Show Answer
[Answer:8. A positive ion having just one electron ejects it when a photon of wavelength
Show Answer
[Answer:9. What is the energy of a hydrogen atom in the first exicted state if the potential energy is taken to zero in the ground state.
Show Answer
[Answer:10. Calculate the weight of
Show Answer
[Answer:11. Calculate the time required for
Show Answer
[Answer:12. 10 milligram of a radioactive material of half life period of two years are kept in a store for four years. How much of the matter remain unchanged.
Show Answer
[Answer:13. One milligram of thorium emits
Show Answer
[Answer:14. The half life of radium is 1500 year. In how many year will
Show Answer
[Answer: 1.995 year;15. The activity, of a radioactive sample falls from
Show Answer
[Answer: 40 minute]16. For every
Show Answer
[Answer:17. A certain radioaction substance has a half life of 5 years. What will be the probability of decay of this substance in 10 years.
Show Answer
[Answer: 75 %]18. Plutonium decays by the following reaction with a half life of 2400 years
If Plutonium is stored for 7200 years what fraction of it remains?
Show Answer
[Answer:19. An isolated rock was found to contain
Show Answer
[Answer:20. Obtain approximately the ratio of the nuclear radii of the gold isotope
Show Answer
[Answer: 1.23, of the order of one]21. The total binding energy of
Show Answer
[Answer:22. Find the mass of
The atomic mass of
Show Answer
[Answer: 14.003323]23. Calculate the energy required to remove an al pha particle from
Show Answer
[Answer:24. Calculate the energy released when a thermal neutron enters the nucleus of
Show Answer
[Answer:25. Find the binding energy per nucleon of
Show Answer
[Answer:26. The masses of
Show Answer
[Answer:27. How much energy will be produced on complete fission of one gram of uranum taking that only
Show Answer
[Answer:28. Calculate the power output of
Show Answer
[Answer:29. The fission of
Show Answer
[Answer: 8.78 day]30. In the fission of a single nucleus of
Show Answer
[Answer:31. When a atom of
Show Answer
[Answer:32. Calculate the energy released in the fusion reaction
Given the mass of an
Show Answer
[Answer: 25]33. Calculate the amount of energy released when two deuterium nuclei fuse into an
Mass of deuterium
Show Answer
[Answer:34. It is proposed to use nuclear fusion reaction
in a nuclear reactor of
Show Answer
[Answer: 121.39]35. Calculate the energy that can be obtained from
It is given that of natural water is heavy water (by number of molecules) and all the deuterium is used for fusion.
Show Answer
[Answer:: 3200 MJ]36. The count rate from a radioactive sample falls from
Show Answer
[Answer:37. The decay constant of
Show Answer
[Answer: 4]Question Bank
Key Learning Points
1. The discovery of the electron and the fact that electron is a common constituent of all matter established the fact that atom has a structure.
2. Any model of the atomic structure must explain the stability and the spectra of atoms.
3. According to Thomson’s model, the atoms consist of positively charged entities distributed uniformly over the entire body of the atom with negative electrons embeded in this continuous positive charge.
4. Geriger and Mardsen in their classic experiments on scattering of
5. Rutherford concluded from the results of Gerger and Madsen experiment that atoms contain a tiny nucleus in which positive charge and nearly all of its mass is concentrated.
6. The electrons in Rutherford model are assumed to be moving around the nucleus in circular orbits.
7. Rutherford atomic model could not explain the stability of the atoms when subjected to the demand of classical electromagnetic theory that any accelerated charged particle must emit energy in the form of electromagnetic radiation.
8. Bohr modified Rutherrod atomic model by introducing quantisation of angular momentum of electron orbits in which electron can revolve around the nucleus.
9. According to first postulate of Bohr’s theory the electron can move only in certain privileged orbits which are not sujbected to the demand of electromagnetic theory. These privileged orbits known as stationary orbits are the ones in which the angular momentum of the electron is an integral multiple of
10. According to Bohr’s theory any emission or absorption of radiation correspond to a transition between two stationary orbits.
If an electron transition take place from an allowed orbit with energy
The energy of an electron with quantum number
11. Bohr’s theory could successfully explain the spectra of various series in the hydrogen and hydrogen like atoms. However Bohr’s theory could not explain the fine structure of spectral lines.
12. The phenomenon of radioactivity is defined as the spontaneous disintegration of nuclei (with atomic number greater than that of lead) of one or more atoms with the emission of highy penetrating radiations.
13. The radioactive radiation consist of three distinct parts known as
14. According to Rutherford and Soddy theory whenever a radio disintegration occurs, it does so with the emission of a
15. In radioactive transformations, it is observed that the daughter from a given parent is also usually radioactive. The daughter nucleus changes to a new nucleus by an
16. Radioactive series occuring in nature are the uranium series, the actinum series, the thorium series and the neptunium series.
17. Radioactive disintegrations are governed by the laws of probabilily.
18. The mathematical relation representing the radioactive disintegration is expressed by the relation
where
19. Radioactivity in a radioactive element completely disappear only in an infinite time and all radioactive elements are identical in this respect.
20. To distinguish the activity of one radioactive element from another we introduce the concept of half and mean life.
21. The half life of a radioactive element is defined as the time in which the number of radioactive atoms is reduced to half of its initial value. The half life
22. The mean life is defined as the ratio of combined age of all the atoms and the number of atoms in the concerned sample. Mean life is given by the relation.
23. A curie is equal to
24. Radio isotopes can be used in tracer technique in agriculture, in industry and in radio carbon dating.
25. According to Rutherford atom has a small positively charged nucleus. Practically the whole mass of the atoms is concentrated in the nucleus.
The nucleus consists of protons and neutrons. Neutron were discovered by Chadwick.
26. It is found that radius of a nucleus varies as cube root of its mass number. It is found that very approximately
where
27. The energy changes encountered in nuclear reactions are due to conversion of mass into energy in accordance with Einstein relation
28. A detailed survey of all atoms reveal that atomic mass is always less than the sum of the masses of the constituent particles in free state. Thus the formation of an atom from its constituent particles always results in the appearance of mass defect.
29. The energy needed to break a nucleus into its constituent particles is known as binding energy.
30. The anlysis of the studies of binding energy shows that higher is the binding energy per nucleon the more stable is the atom and vice versa.
31. When uranium was bombarded with neutrons Fermi found that a compound nucleus is formed due to capture of neutron along with the emission of
32. Hahn and Strassman after a series of careful chemical analysis of the products formed when uranium was bombarded with neutrons established that uramum nucleus after the capture of neutron seemed to be spliting apart into two nearly equal fragments.
33. Lise Meitner and R. Frisch suggested that neutrons iniated a decomposition of the uranium nucleus into two nuclei of roughly equal size. The phenomenon was termed as nuclear fission.
34. Due to fission a uranium nucleus split up into a large number of pairs of fission fragments with an average number of 2.5 nuetrons as the products of the reaction. The reaction is accomplished with a release of large amount of energy.
35. The average energy released per fission of uranium nucleus is of the order of
36. The neutron released in the fission process promotes further fission and set up a self sustained chain reaction.
37. The uncontrolled self sustained reaction can result in explosive release of energy. This is the underlying principle of fission bomb.
38. Nuclear reactor is designed to achieve a controlled release of energy. By the arrangment of the reactor material a study chain reaction is maintained in which each fission produces an average of one new fission.
39. Nuclear fusion is the phenonmenon in which two light nuclei are fused together to form a single new nucleus. These reactions are accompanied by the release of nuclear energy.
40. It is now believed that fusion process is primarly responsible for the release of energy by the sun and stars.
41. The forces that are responsible for holding of the nucleon together in a nucleus are very strong nuclear forces.
42. Nuclear forces are very stong short range attractive forces.
43. Studies of nuclei with higher values of atomic number reveal that in addition to very strong attractive interactions nuclear forces also have a repulsive component that saves the nuclei from collapsing.
Average
Bohr’s Model of the Atom
1. An electron makes a transition from an excited state to the ground state of a hydrogen like atom / ion. During this transition of the electron, its
(1) kinetic energy; potential energy and total energy all decrease
(2) kinetic energy decreases, potential energy increases and total energy remains same (Incorrect)
(3) kinetic energy and total energy decrease but potential energy increases
(4) kinetic energy increases, but potential energy and total energy both decrease
Show Answer
Correct answer: (4)
Solution:
In the given transition, principal quantum number (n) decreases. Now the speed of the electron in the
Total energy
and Potential energy
Due to -ve sign, in the expression for T.E and P.E; both these energies decrease when
Hence option (4) is correct.
Average
Bohr’s Model of the Atom
2. Hydrogen
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
For a hydrogen like atom, of atomic number
Here
Hence option(3) is correct.
Difficult
Bohr’s Model of the Atom
3. A photon colloides with a stationary hydrogen atom, in its ground state, inelastically. Energy of the colloiding photon is
(1) 2 photons of energy
(2) 2 photons of energy
(3) 1 photons of energy
(4) 1 photons of energy
Show Answer
Correct answer: (3)
Solution:
The hydrogen atom, in its ground state, absorbs the incident photon of energy
The atom remains in the excited state for a time of the order of
Hence option (3) is correct.
Difficult
Bohr’s Model of the Atom
4. In a hypothetical hydrogen like atom; the electric potential between a proton and an electron, distant
where
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
The force, F, provides the centeripetal force for the electron, orbiting in its
From Bohr’s postulate, we also have
From Eqn. (1) and (2), we get,
Hence option (1) is correct.
Difficult
Bohr’s Model of the Atom
5. A hydrogen atom, and a doubly ionised lithium
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
For the hydrogen atom
For the doubly ionised lithium atom, we have
According to Bohr’s first postulate, the angular momentum of electron, in an orbit, is directly proportional to
The K.E of the electron, is an orbit, equals the |T.E.
We thus have
Hence option (3) is correct.
Average
Bohr’s Model of the Atom
6. A hydrogen atom emits a photon of wavelength
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
For hydrogen atom, the given transition, corresponds to an electron moving from
For the given ion; the electron jumps from
From equations (1) and (2), we have
Hence option (3) is correct.
Average
Bohr’s Model of the Atom
7. A diatomic molecules has a moment of inertia I. By Bohr’s quantisation condition, its rotational energy in the
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
Let
The rotational energy of the molecule
Hence option (4) is correct.
Difficult
Using Bohr’s Postulates
8. A molecule of,
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
Let
The rotational, K.E., (K), equals
We, therefore, have
Hence option (1) is correct
Difficult
Bohr’s Model of the Atom
9. A hydrogen atom, at rest, emits the
(1)
(2)
(3)
(4)
Correct answer: (2)
Solution:
The
The linear momentum of the emitted photon
The hydrogen atom is initially at rest. To conserve linear momentum, the recoil momentum of the hydrogen atom, is also p, directed in a direction opposite to the direction of motion of the photon. Hence the recoil
energy of the hydrogen atom
Hence option (2) is correct.
Difficult
Bohr’s Model of the Atom
10. A hydrogen like atom has the energy
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
We have
From Bohr’s theory,
From Eqn. (1) and (2) we have,
Hence option (4) is correct.
Difficult
Bohr’s Model of the Atom
11. A particle is restricted to move along the
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
Figure shows the alternate nodes and antinodes in the region between
Let

For a given value of m;
Also
Hence option(1) is correct.
Difficult
Bohr’s Model of the Atom
12. The radius of an orbit of the electron, in a hydrogen like atom, is
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
Since we are given that angular momentum
The radius,
The wavelength,
The three different ways, the atom can de-excute itself(from the state with
(i)
The corresponding wavelengths are
It follows that, out of the given values
Hence option (2) is correct.
Difficult
Bohr’s Model of the Atom
13. A hydrogen like atom, of atomic number
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
Let
When electron jumps, from
From Eqns. (1) and (2), we have
Substituting this value of
But
Hence option(1) is correct.
Difficult
Bohr’s Model of the Atom
14. A mixture, of hydrogen
(1) 2
(2) 3
(3) 4
(4) 5
Show Answer
Correct answer: (3)
Solution:
For hydrogen atom;
Hence
Excitation energy gained by the
For
The energy
Let
Hence option (3) is correct.
Average
Bohr’s Model of the Atom
15. A single electron revolves around a stationary nucleus of charge ze; (
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
The energy,
When this atom goes, from its first excited to its second excited state;
For the ground state of atom,
and
Hence option(2) is correct.
Difficult
Bohr’s Model of the Atom
16. In a hypothetical atom, the potential energy
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
Given
For an electron, in its circular orbit of radius
From Bohr’s first postulate
From Eqn. (2) and (3), we get
i.e.
The total energy,
Hence option(1) is correct.
Average
Radioactivity
17. The (radio) activities, of two materials
(1) 6 months
(2) 3 months
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
Let
Let
Given
Hence option(4) is correct.
Average
Radioactivity
18. Two radioactive materials
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
We assume that the given condition gets satisfied at
Let
Hence option (4) is correct
Average
Radioactivity
19. A radioactive material, having a mean life of
(1) One
(2) Half
(3) Two
(4) One and a half
Show Answer
Correct answer: (1)
Solution:
Let
Activity
Since
Substituting given values, we get
Hence option (1) is correct.
Average
Radioactivity
20. A radioactive nucleus has a half-life of one day. Starting with
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
Given,
At
The number of atom,
Hence option (2) is correct.
Difficult
Radioactivity
21. A radioactive element decays by
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
The total number of counts at any time is the number of nuclei that have disintegrated in that time. Therefore, if
and
Percentage change in counts in the time interval
Hence option (2) is correct.
Average
Radioactivity
22.
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
Let
The disintegration constant
At
Hence option(3) is correct.
Average
Radioactivity
23. A radioactive nucleus
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
The emission of an
The emission of a positive
Hence option (2) is correct.
Difficult
Radioactivity
24. A radioactive nucleus (of mass number
(
(1) -3.05
(2) +1.91
(3) -0.38
(4) +7.25
Show Answer
Correct answer: (1)
Solution:
The mass number of given nucleus
The atomic number of the nucleus
We know that mass number decreases by 4 , and atomic number by 2 , when one
Percentage change in
Hence option(1) is correct.
Difficult
Radioactivity
25. A radioactive nucleus,
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
When one atom of
Hence option(3) is correct.
Easy
Nucleus
26. A star can convert all its helium (He) nuclei completely into oxygen nuclei. The energy released, per oxygen nuclei formation, is (Mass of nucleus
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
The nuclear reaction is
Hence option (3) is correct.
Average
Nucleus
27. The only correct statement is:
(1) The nucleus
(2) The nucleus of
(3) Deutron and alpha particle can undergo complete fusion
(4) The nuclei
[Given; mass of
Show Answer
Correct answer: (3)
Solution:
Two light nuclei, of mass
A heavy nucleus, of mass
(1)
Mass of
Sum of masses of
Since
(2)
Sum of masses of
Since
(3)
Sum of mass of
Mass of
Since
(4)
Sum of mass of
Mass of
Since
Hence option (3) is correct.
Average
Nucleus
28. Figure shows a hypotetical binding energy per nucleon (B.E/A); versus (mass number) A curve. Which of the following statements is correct?
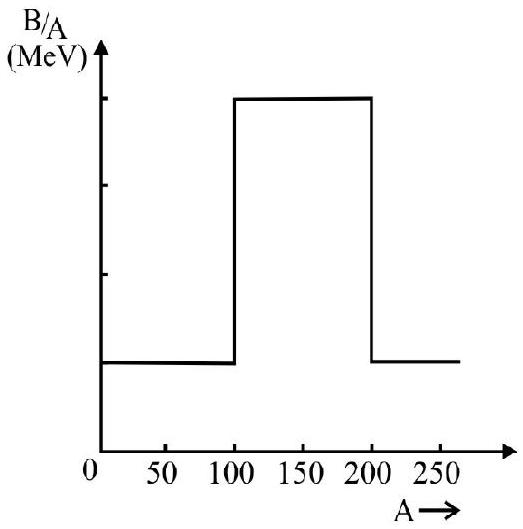
(1) Fusion of nuclei, having mass number in the range
(2) Fission of nuclei, having mass number in the range
(3) Fusion of nuclei, having mass number in the range
(4) Fission of nuclei, having mass number in the range
Show Answer
Correct answer: (3)
Solution:
Energy is released in a nuclear (fission or fusion) reaction, if the binding energy per nucleon of the products, is more than that for reactants. This is so only far statement (3). In all the other statements, B.E/nucleon, of products, is less than that of the reactants. In such a process energy, has to be absorbed.
Hence option(3) is correct.
Average
Nuclear Energy
29. In a process known as “pair-production” a
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
The process of “pair production” is
The total mass energy of electron position pair
For “pair production”, this must be the minimum energy of the
Hence option(3) is correct.
Difficult
Nuclear Energy
30. In a nuclear power generating station,
(1) 142
(2) 178
(3) 221
(4) 276
Show Answer
Correct answer: (2)
Solution:
Energy produced due to fission of one atom of
The number of atoms, in
The efficiency,
Time taken
Hence option (2) is correct.
Average
Rutherford Scattering
31. In a Rutherfod scattering experiment when a projectile of charge
(1) directly proportional to
(2) directly proportional to
(3) directly proportional to
(4) inversely proportional to
Correct answer: (3)
Solution:
When an particle is very far off it has only K.E (K). As it approaches the target its K.E decreases and electrostate P.E increases. At distance of closet approach
Hence option(3) is correct.
Average
Rutherford Scattering
32. An alpha nucleus of energy
(1) (1 / z e)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
We know that the kinetic energy of alpha nucleus is equal to potential energy of alpha nucleus and target nucleus at the distance of closeset approach
Hence
Hence option (3) is correct.
Average
33. The binding energy of a hydrogen like atom in ground state is
(1) 4
(2) 8
(3) 16
(4) 32
Show Answer
Correct answer: (1)
Solution:
The energy in ground state of a hydrogen like atom (atomic number
Hence
or
Hence
Hence option (1) is correct
Difficult
Bohr’s Theory
34. In an atom two electrons move around the nucleus in circular orbits of radii
(1)
(2)
(3)
(4) 8
Show Answer
Correct answer: (2)
Solution:
If the electron is moving with a velocity
Now from Bohr’s theory we have
Hence
Hence we write
Hence option (2) is correct
Average
Bohr’s Theory
35. According to Bohr’s theory, the minimum energy required to remove an electron from the ground state of doubly ionized
(1) 1.51
(2) 13.6
(3) 40.8
(4) 122.4
Show Answer
Correct answer: (4)
Solution:
According to Bohr’s theory for hydrogen and hydrogen like atoms, the energy in electron volts is given by the relation.
For doublly ionised
Hence option (4) is correct.
Difficult
Bohr’s Theory
36. The wavelength of the first spectral line in the Balmer series of hydrogen atom is
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
We know that Balmer series terminates at
or
The second line of Balmer series of ionzied helium atom corresponds to transition from
Hence
Hence option(1) is correct.
Difficult
Bohr’s Theory
37. Imagine an atom made up of a proton and a hypotheticle particle of double the mass of electron but having the same charge as that of the electron. Apply the Bohr atom model and consider all possible transition of the hypothetical particle to the first excited level.
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
The energy expression corresponding to
where
Hence
Also the energy expression can be written as
Energy of the hypothetical particle will be
The longest wavelength
which gives
Hence option(3) is correct.
Average
Bohr’s Theory
38. A muonic hydrogen atom is a bound state of a negatively charged muon of mass
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
We known that the ground state energy of the hydrogen atom is gien by
Since the mass of muonic hydrogen atom is 207 times the mass of the electron, the ground state energy of this mounic atom would be given by
Hence option (2) is correct.
Average
Bohr’s Thoery
39. The first excitation potential of hydrogen is
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
The first excitation potential of hydrogen atom is the potential for transition from Ist Bohr’s orbit to the second Bohr orbit.
Hence
Hence option(2) is correct.
Difficult
Bohr’s Thoery
40. The transition from the state
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
Energy of infrared radiation is less than the energy of ultraviolet radiation. As shown below the energy released will be less in option (4) while the energy released will be more in option (1), (2) and (3). Hence option (4) is correct.
For transition
For transition
For transition
For transition
For transition
From this data we find that option (4) is the correct option.
Average
Bohr’s Theory
41. An excited hydrogen atom emits a photon of wavelength
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
According to Bohr’s theory we have
or
Hence option(1) is correct.
Difficult
Bohr’s Theory
42. Hydrogen atom is excited from ground state to a state corresponding to principal quantum number 4. The number of spectral lines obtained in the emission spectra is given by
(1) 2
(2) 3
(3) 5
(4) 6
Show Answer
Correct answer: (4)
Solution:
The number of lines emitted in an emission spectra of Hydrogen corresponding to a transition from a state of quantum number
Hence option(4) is correct.
Average
Bohr’s Theory
43. In a hydrogen like atom, electron makes transition from an energy level with quantum number
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
According to Bohr’s theory of hydrogen atom, frequency of radiation emitted is given by relation
where
Since
or
Hence option(4) is correct.
Difficult
Bohr’s Theory
44. Electrons in hydrogen atom first jump from third excited state to second excited state and then from second excited state to the first excited state. The ratio of
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
For transition
For transitionto
From above two equations we have
Hence option (4) is correct.
Difficult
Bohr’s Theory
45. The binding energy of a hydrogen like atom in ground state is
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
The electron undergoes an elastic collision with the concerned atom. Since
Hence option(3) is correct.
Difficult
Bohr’s Theory
46. The different lines in Lyman’s series have their wavelength lying between
(1) 0 to
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
For Lyman series, the wavelength of lines is obtained from the relation
We will get a line with shortest wavelength corresponding to transition from
Hence
For longest wavelength we will have
Hence
Hence option (2) is correct.
Difficult
Bohr’s Theory
47. The ratio of wavelength
(1) 10
(2) 0.1
(3) 1.5
(4) 100
Show Answer
Correct answer: (3)
Solution:
The Pachen’s series is generated when transition from higher energy levels terminates at
or
Similarly
Hence option (3) is correct.
Difficult
Bohr’s Theory
48. The ratio of minimum to maximum wavelength in Balmer series is
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
Since the series involved is Balmer series, the transition terminates at
It is clear that
For minimum value of
Hence option(4) is correct.
Difficult
Bohr’s Theory
49. The ratio of the longest wavelengths corresponding to Lyman and Balmer series in hydrogen spectrum is
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
According to the relation
and for Balmer series
Hence option(2) is correct.
Difficult
Bohr’s Theory
50. An electron of a stationary hydrogen atom passes from the fifth energy level to the ground level. The velocity that the electron acquired as a result of photon emission will be
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
The wavelength of the emitted radiation when the transition take place from
Linear momentum of photon emitted is
Now
Hence option (2) is correct.
Difficult
Bohr’s Theory
51. A diatomic molecule is made up of two masses
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
Bohr’s condition for quantization of angular momentum is
where
If
The rotational energy of the given diatomic molecule is given by
Hence option (4) is correct.
Difficult
Bohr’s Theory
52. The electron in the hydrogen atom jumps from excited state
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
When a transition take place from state
Let
or
Hence option (3) is correct.
Difficult
Bohr’s Theory
53. A doubly ionized lithium atom can be considered as a hydrogen like atom with atomic number 3. An electron is to be excited from the first to third Bohr’s orbit (ionizon energy of hydrogen atom is
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
Th energy of the electron in
Energy
Energy
The wavelength
Hence option(2) is correct.
Difficult
Bohr’s Theory
54. The ionisation energy of the hydrogen atom is
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
We know the energy of an electron in th
for
Energy of photon
Hence option(1) is correct.
Difficult
Bohr’s Theory
55. A gas of identical hydrogen like atoms has some atoms in the lowest ground energy level
(1) 3
(2) 4
(3) 1
(4) 2
Show Answer
Correct answer: (1)
Solution:
Let
Also
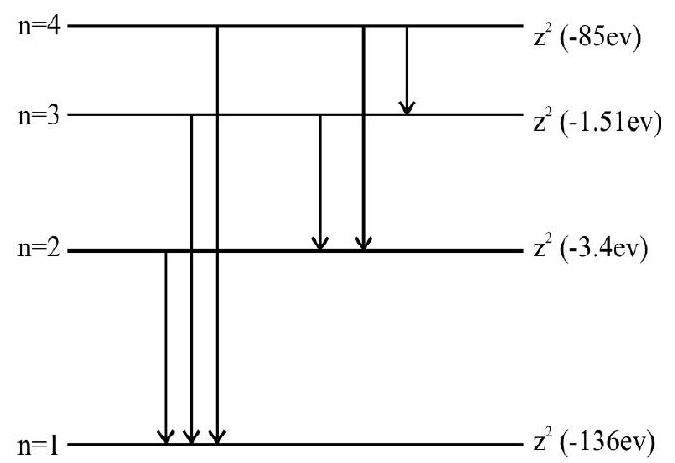
If the
It is possible that
Hence the quantum number of intially excited state
Hence option(1) is correct.
Average
Critical Potential
56. A critical potential for hydrogen is
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
Let
Then we have
Hence option (4) is correct.
57. Beta rays emitted by a radioactive material are
(1) electromagnetic radiations
(2) the electrons orbiting around the nucleus
(3) charged particles emitted by the nucleus
(4) neutral particle
Show Answer
Correct answer: (3)
Solution:
From the basic studies of the phenomenon of radioactivity, it is known that
Hence option(3) is correct.
Average
Radioactivity
58. Which of the follwing processes represent a
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
During
Hence option (3) is correct.
Average
Radioactivity
59. Half life of a radioactive substance
(1)
(2)
(3)
(4) 1
Show Answer
Correct answer: (2)
Solution:
After two half lives
Hence option(2) is correct.
Difficult
Radioactivity
60. A radioactive nucleus can decay by two difficient modes. The half life for the first mode is
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
Denoting by
The probability that an active nucleus decay by first mode in a small time dt is
Hence we must have
or
or
Hence option (2) is correct.
Difficult
Radioactivity
61. To determine the half life of radioactive element, a graph is plotted between
(1) 2
(2) 4
(3) 6
(4) 8
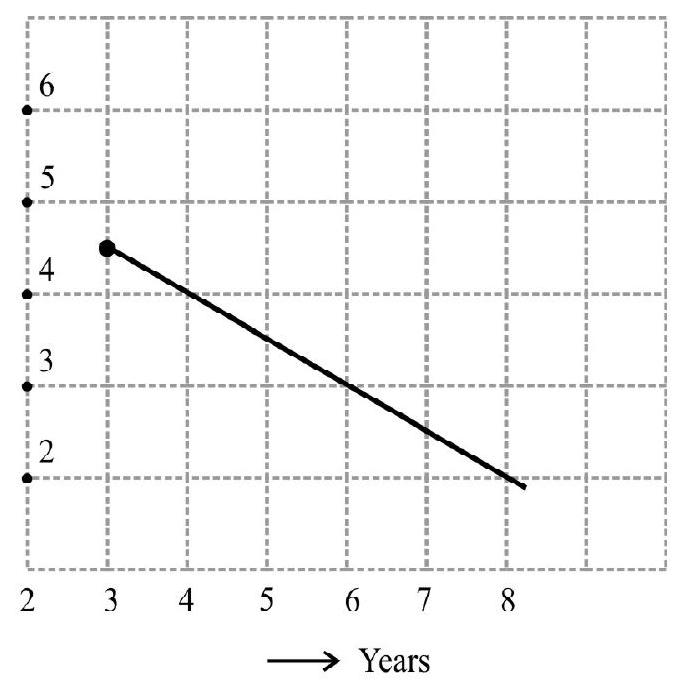
Show Answer
Correct answer: (4)
Solution:
which is of the form of a straight line
or
Half life
Now
Hence option (4) is correct.
Easy
Radioactivity
62. 10 milligrams of a radioactive material of half life two years are kept in a store for four years. Then the amount of the material remaining unchanged is
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
Half life of the given material
The time interval
The amount of mass remaining
Hence option (2) is correct.
Average
Radioactivity
63. For a given sample, the counting rate is
(1) 11 minute
(2) 5.99 minute
(3) 0.59 minute
(4) 0.11 minute
Show Answer
Correct answer: (2)
Solution:
Initial counting rate
Final counting rate after 5 minutes
or
Half life of sample
Hence option (2) is correct.
Difficult
Radioactivity
64. One milligram of thorium emits
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
Number of
No. of atoms in 1 milligram of thorium
Decay rate per second
Hence option (4) is correct.
Difficult
Radioactivity
65. A does of
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
Dose per
Number of disintegration
After one hour we can assume no decay.
Disintegration counted
Hence option(1) is correct.
Average
Radioactivity
66. Masses of two isobars
(1) Both isobars are stable (Incorrect)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
In
Hence option (4) is correct.
Difficult
Radioactivity
67. A radioactive sample consist of two distinct spices having equal number of atoms intially. The mean life one spices is
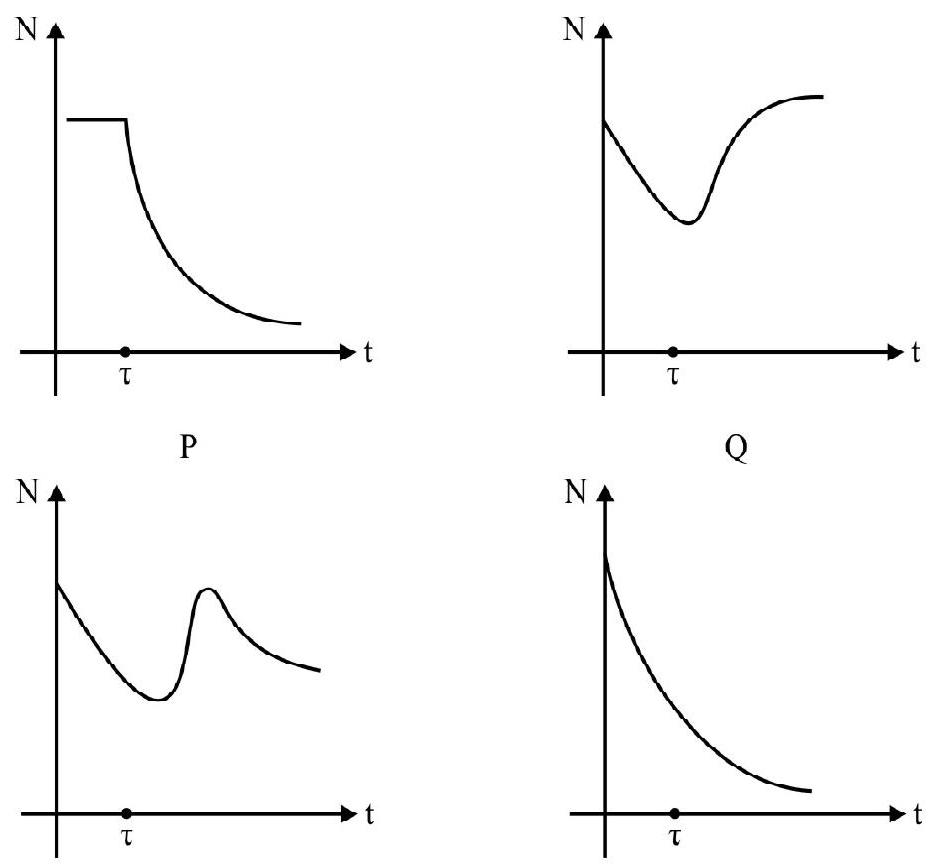
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
Since it is the process of radioactivity decay the total number of atoms cannot remains constant (as in option 1). Also the total number of atoms cannot ever increase (as in option 2 and 3). The total number of atoms can only decrease with time. Hence option (4) is the best plot.
Difficult
Radioactivity
68. An accident occurs in a laboratory in which a large amount of radioactive material with a known half life of 30 day becomes embedded on the floor walls etc. Tests show that the level of radiation is 32 times the permissible level of normal occupancy of the room. Assuming that the last statement is corerct, after how many days the laboratory can be safety occupied after.
(1) 32 days
(2) 100 days
(3) 20 days
(4) Lab can safety be reoccupied after an infinite time
Show Answer
Correct answer: (2)
Solution:
Since the initial value of radiation is 32 times the permissible level we have to find
Since the half life is 20 days, the lab will be safe for use after 5 half-lives i.e.,
Hence option (2) is correct.
Difficult
Radioactivity
69.
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
Since the amount of carbon-14 in atomsphere remain constant and a living matter acquires carbon from atmosphere, the count from a living matter represent the amount of carbon-14 present in atmosphere. The ancient wood which has now 50 counts per minute from
Representing by
Hence option (3) is coorect.
Easy
Nucleus
70. The total kinetic energy, of the electron antineutrinos pair, in the
(1) zero
(2) Much less than
(3) Nearly
(4) Much larger than
Show Answer
Correct answer: (2)
Solution:
The following reaction represents
In this decay process the kinetic energy of the pair of electron and antineutrons is constant. When K.E of electron is maximum, K.E. of
Maximum K.E of antineutron will be nearly
Hence option (3) is correct.
Difficult
Bohr’s Theory
71. Out of the following which one is not a possible energy for a photon to be emitted by a hydrogen atom.
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
According to Bohr’s theory the energy of a photon emitted when it makes a transition from a quantum state
Also the value of
From above we get
It is clear that
Hence option (2) is correct.
Easy
Nucleus
72. During a negative beta decay
(1) an atomic electron is ejected
(2) an electron which is already present within the nucleus is ejected
(3) A neutron in the nucleus decays emitting an electron
(4) A part of the binding energy of the nucleus is converted into an electron
Show Answer
Correct answer: (3)
Solution:
During a negative beta decay, the reaction which takes place is
Here
Hence option(3) is correct.
Difficult
Binding Energy
73. In the photo disintegration equation for the deutron the reaction energy is
From the mass spectrometer the mass differences between the doublet
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
The mass of neutron is given by
Errors:
(i) Energy
(ii) Doublet error
(iii) Hydrogen atom
Total maximum error is
Hence the mass of neutron is
Hence option(3) is correct.
Difficult
Binding Energy
74. The binding energy per nucleon for deuteron and helium are
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
Binding energy per nucleon for deutron
Total binding energy of deutron
Binding energy per nucleon for helium
Total binding of helium
Energy released
Hence option (1) is correct.
Difficult
Binding Energy
75. The curve in the figure shows the binding energy per nucleon versus mass number for four nuclei
(1)
(2)
(3)
(4)

Show Answer
Correct answer: (3)
Solution:
We know that energy is released when the total binding energy of products is more than the rectants.
In option (3) we find that.
Binding energy of reactants
Binding energy of products
Thus
In option 1
B. . of reactants
B.E of products
Not possible
Similar is the case for process (2) and (4).
Hence option(3) is correct.
Average
Nuclear Nuclear Reactions
76.
(1) nitrogen
(2) carbon
(3) boron
(4) oxygen
Show Answer
Correct answer: (2)
Solution:
In a nuclear reaction, the mass number and atomic number of reactants and products are conserved.
Hence
Obvisouly
Hence option (2) is correct.
Average
Nuclear Reactions
77. The nucleus of
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
The reaction
Represents the decay process of
Here
This energy would have to shared by
Hence option (4) is correct.
Difficult
Atoms and Nuclei
78. In the options given below, let E denotes the rest mass energy of a nucleus and n represent a neutron. The correct option is
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
Rest mass of parent nucleus should be greater than the rest mass of daughter nuclei. Hence option (1) is correct.
79. The fusion reaction
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
The reaction is represented by
Mass defect
Energy released
Since efficiency of the process is
Actual output per deutron atom is
Output required
No. of deutron atomsrequired to produce this output
Hence option (4) is correct.
Average
Nuclear Fusion
80. A certain mass of hydrogen is changed to helium by the process of fusion. The mass defect in fusion reaction is
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
Total mass defect
Total energy released
Since 4 nuclei of hydrogen fuse to form a helium nucleus.
Hence option (4) is correct.
Difficult
Nuclear Fusion
81. A star initially has
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
The given reactions are
Mass defect
Energy released
This is the energy produced by the consumption of 3 deutron atoms.
The energy released by
The average power radiated is
Hence option (3) is correct.










