Learning Objectives

After going through this unit, you will be able to understand, appreciate and apply the following concepts:

• Discovery of the phenomenon of photoelectricity.

• The importance of the experiments of Hallwache, Elster, Gaitel and Leonard.

• The failure of the classical e.m. theory in explaining the experimental results of photoelectricity.

• The introduction of the ‘photon theory’ of light, by Einstein.

• The mechanism of interaction of light, with the free electrons of the metal, in terms of the photon theory of light.

• Einstein’s photoelectric equation and its success in explaining the experimental results on photoelectricity.

• The concept of the threshold frequency / wavelength, for a given photosensitive surface.

• The “dual nature of light”.

• The extension of the concept of “dual nature” to matter.

• The concept of “matter waves”, or “deBroglie waves”.

• The basic expression for the wavelength (the deBroglie wavelength) associated with a particle.

• The dependence, of the deBroglie wavelength, for a charged particle (like the electron), on the ‘potential’ used to accelerate it.

• The Davisson and Germer experiment and its role in providing the required (experimental) support to the concept of matter waves.

The Photoelectric Effect

The phenomenon of photoelectricity was accidently discovered by Hertz. He was performing an experiment to test Maxwell’s electromagnetic theory. He by means of a spark dischange, was investigating production of electromagnetic waves. Hertz observed that high voltage spark across the detector loop were enhanced when the emitter plate was illuminated by ultraviolet light. It was prabably due to emission of charged particles from the plate due to incidence of ultraviolet radiction. Leonard then determined the e/m value of these particles and showed that they were electrons. Hallwachs, Elster and Giatel then experimentally established that photoemission depend upon.

(i) the nature of the emitter

(ii) the quality of the light used.

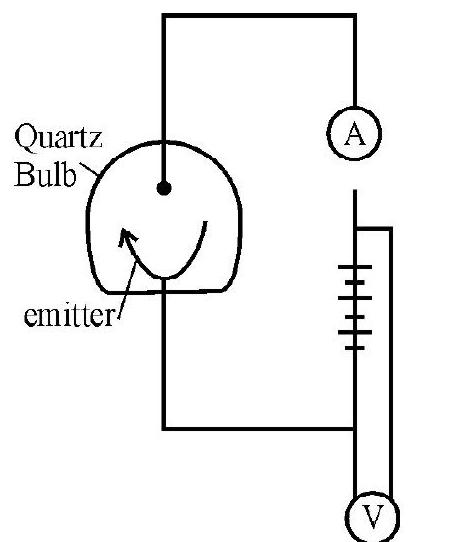
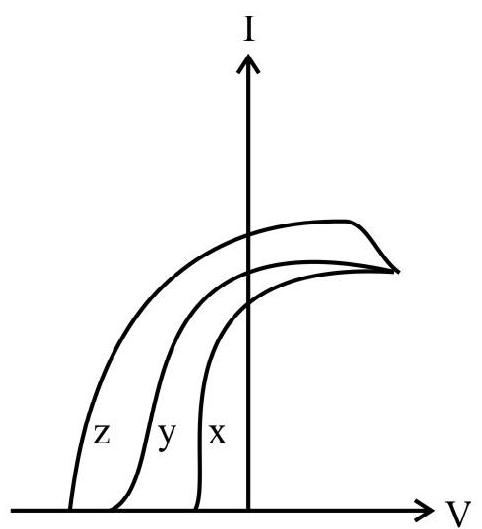
By a simple experimental arrangement shown in the figure the following sailent features of the phenomenon of photoelectric emission was established.

Sailent Features of Phenomenon of Photoelectricity

1. Photoelectric emission is an instanteous phenomenon.

$~$

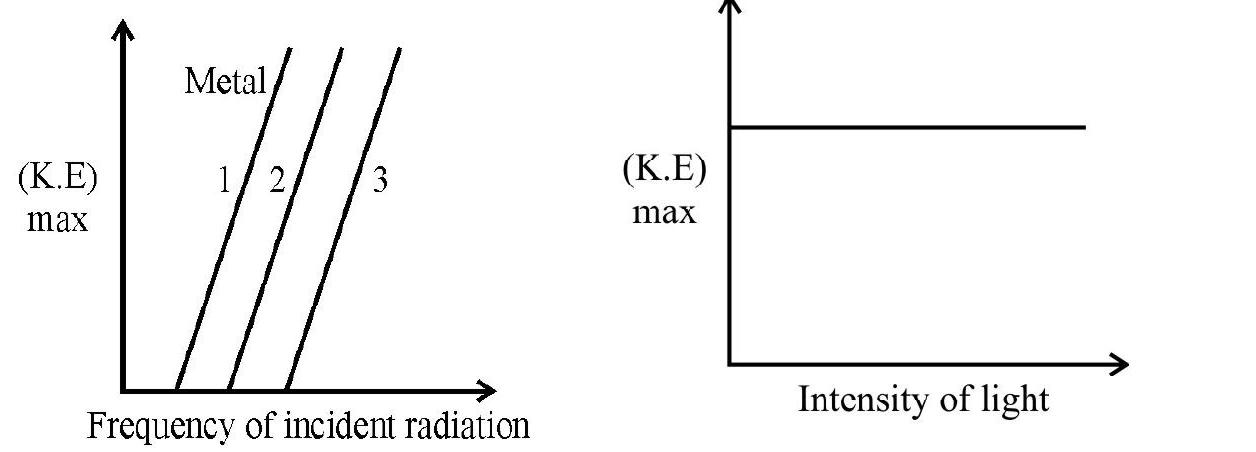
2. A photoemitter shows the photoelectric effect only if the incident radiation has a frequency above a certain value called the threshold frequency. This frequency is a characterstics of the photoemitter. Below threshold frequency no emission is possible whatever may be the intensity of light or whatever be the time span for which the light is incident on the photoemitter.

3. For a given frequency (above threshold) the number of photo electrons emitted is directly proportional to the intensity of light.

$~$

4. The maximum energy of the emitted photoelectrons is directly proportional to the frequency of incident light and has nothing to do with the intensity of light.

$~$

The maximum kinetic energy of the emitted photoelectrons from a photoemitter is measured by determining the stopping or retarding potential.

$~$

Variation of photoelectric current with collector plate potential for different frequencies of incident radictions (for same intensity)

5. There exists a energy distribution among the emitted photoelectrons from a photoemitter.

Failure of Electromagnetic Theory of Light

The above mentioned features of the phenonmenon of photoelectriciy were attempted to be explained by electromagnetic theory. However except fot the fact that electric and magnetic field associated with an electromagnetic wave can cause the emission of photoelectrons, the electromagnetic theory could not explain even a single fact concerning the observed features of the phenomenon.

It is natural to expect that the energy transmitted by light should smoothly and evenly distritube itself in the space. If it is so than each electron would intercept only an significant small amount of energy and would require a long time (may be days or years) to accumulate enough energy to escaope from the metal. Experimentally however it is observed that the photoemission is instantaneous.

Again on the basis of electromagnetic theory there should not be any thing like threshold frequency existing. There seemed to be no reason why sufficiently intense beam of low frequency liget would not be able to produce photoelectricity if low intensity radiation of higher frequency can produce it.

On classical theory we expect that light of high intensity, consisting of strong electric and magnetic fields, would give higher kinetic energy to the liberated electrons. This however does not happen. Also the electron’s energy should not depend particularly on the light frequency but it does.

Thus classical electromagnetic theory is not able to explain all the sailent features of the phenonmenon of photoelectricity.

Einstein’s Theory

The challange passed by photoelectricity was met by Einstein. Einstein’s took his clue from Planck’s explanation of black body spectrum. Einstein’s assumed that light consists of quantum packets of energy, the energy of a packet is $\mathrm{h} v$ where $\mathrm{h}$ is the Planck’s constant and $v$ is the frequency of light. These quantums of energy are called photons and travel with the velocity of light. According to Einstein when a photon of energy is incident on a metal surface the energy of the photon is absorbed by a free electron in the metal. A part of this energy of quantum $\mathrm{h} v$ is used by the free electron to overcome the binding influence of the nucleous (represented by the work function of emitter) and the remaining part of the energy is given to the emitted electron as its kinetic energy. Hence we can write

$$ \mathrm{h} v=\omega _{0}+\dfrac{1}{2} \mathrm{mv}^{2} \quad \text { or } \quad \dfrac{1}{2} \mathrm{mv}^{2}=\mathrm{h} v-\omega _{0} $$

The above equation is known as Einstein’s equation and is fundamental in explaining the facts of the phenomenon of photoelectricity.

1. According to Einstein’s theory the emission of electrons from a photoemitter is concieved as a collision process between a photon and electron and hence is a instantaneous phenomenon.

2. According to Einstein’s theory a more intense beam incident on a metal surface implies that more photons are being incident on the metal surface per unit area per unit time. Each photon involves itself a collision with an electron and consequently is emitted. The more is the number of incident photons the more will the number of collisions occuring and more is the number of photoelectrons emitted. Hence at a given appropriate frequency the photoelectric current is directly proportional to the intensity of light.

3. There exists a threshold frequency. We know that the quantum of energy of a photon is equal to $h v$. Increasing or decreasing $v$ accordingly will increase or decreases this value of quanta of energy. If we decrease $v$, then consquently the energy of the emitted electron will decreases because $\omega _{0}$ is a fixed parameter for a given emitter. Ultimately a stage will be reached when $\mathrm{h} v _{0}$ is just equal to $\omega _{0}$ ( $\mathrm{v} _{0}$ is the frequency when this happens). If we decreases this frequency further $h v _{0}$ will becomes less than $\omega _{0}$. Hence for frequencies less than $v _{0}$, the energy of the incident photon will not be able to liberate electron from its binding Influence. Hence there cannot be any emission for a frequency less than $v _{0}$. Since $\omega _{0}$ is a characterstics of a given emitter threshold frequency is also a characterstics of the emitter.

4. According to Einstein’s equation $\dfrac{1}{2} \mathrm{mv} _{\max }^{2}=\mathrm{h} v-\omega _{0}$

it is obvious that the maximum kinetic energy of the emitted photoelectron with depend linealy on the frequency of incidence light and has nothing to do with the intensity of light.

In terms of concept of stopping potential. we can also write $\dfrac{1}{2} \mathrm{mv} _{\max }^{2}=\mathrm{eV}$

5. The existance of energy distribution among the emitted electrons is explained as follows. In writing the relation $\dfrac{1}{2} \mathrm{mv}^{2}=\mathrm{h} v-\omega _{0}$

we assume that the emission take place at the surface of the emitter. However if a photon electron collision take place inside a emitter, the emitted electron will lose some energy due to collisions with the atoms in the lattice of the emitter and hence in this case Einstein’s equation will become

$$ \dfrac{1}{2} \mathrm{m} v^{2}=\mathrm{h} v-\omega _{0}-\omega _{\mathrm{c}} $$

where $\omega _{\mathrm{c}}$ represent the energy loss due to collisions. Since $\omega _{\mathrm{c}}$ can vary from zero to $\dfrac{1}{2} \mathrm{mv}^{2}$, there would exist a energy distribution among the emitted electrons.

Dual Nature of Light

The classical electromagnetic theory of light is very successful in explaining the phenomenon of interference. diffraction, polarisation etc. In fact these phenomenon can only be explained by this theory. However the electromagnetic theory was a complete failure in explaining the experimental facts of photoelectricity. Later on it was found that electromagnetic theory cannot explain the phenomenon of “Compton scattering” and “specific heat of solids”. One has to introduce the concept of photons (particles) to explain the above mentioned phenomenon. Naturally the questions arieses What is Light? Is it a wave entity or Is it a particle. The answer to this question is either or neither. We now regard light to have a dual nature. It mainfest itself as a wave in phenomenon like interference, diffraction, polarisation etc. while it shows photon (particle) behaviour in the phenomenon of photoelectricity and Compton scattering. However light can never exhibit both wave and particle behaviour simulataneously. These facts are further developed with astonishing results in the studies of Quantum Mechanics.

Example-1

Ultraviolet light of wavelength $280 \mathrm{~nm}$ is used in a experiment on photoelectric effect with lithium (work function $2.5 \mathrm{eV}$ ) cathode. Find

(i) the maximum kinetic energy of the photoelectrons

(ii) the stopping potential

Show Answer

Solution:

(i) Maximum kinetic energy is given by

$$ (\mathrm{K} . \mathrm{E}) _{\max }=\dfrac{\mathrm{hc}}{\lambda}-\omega _{0}=\dfrac{1242 \mathrm{eV}}{280 \mathrm{~nm}}-2.5 \mathrm{eV}=4.4-2.5=1.9 \mathrm{eV} $$

(ii) Stopping potential $\mathrm{V}$ is given by $\mathrm{eV}=(\mathrm{K} . \mathrm{E}) _{\max }$

$$ \mathrm{V}=\dfrac{(\mathrm{K} . \mathrm{E}) _{\max }}{\mathrm{e}}=\dfrac{1.9 \mathrm{eV}}{\mathrm{e}}=1.9 \mathrm{~V} $$

Example-2

Monochromatic radiation of wave length $640.2 \mathrm{~nm}$ from a neon lamp irridate a photosensitive material made of tungsten. The stopping voltage is found to be 0.541 . The source is replaced by an iron source and its $427.2 \mathrm{~nm}$ lines irridate the same photocell. What is the stopping potential now? (Work function for iron is $2.236 \mathrm{eV}$ )

Show Answer

Solution:

We have $\mathrm{eV} _{\mathrm{S}}=\dfrac{\mathrm{hc}}{\lambda}-\omega _{0}$ therefore $\omega _{0}=\dfrac{\mathrm{hc}}{\lambda}-\mathrm{eV} _{\mathrm{S}}$

For neon; $\omega _{0}=\dfrac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{640.2 \times 10^{-9}}-1.6 \times 10^{-19} \times 0.54=1.4 \mathrm{eV}$

Again using the relation $\mathrm{eV} _{\mathrm{S}}=\dfrac{\mathrm{hc}}{\lambda}-\omega _{0}$ for iron we have

$\mathrm{eV} _{\mathrm{S}}=\dfrac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{427.2 \times 10^{-9}}-2.236 \times 1.6 \times 10^{-19}=2.413 \times 10^{-19} \mathrm{~J}$

$\mathrm{V} _{\mathrm{S}}=\dfrac{2.413 \times 10^{-19}}{\mathrm{e}}=\dfrac{2.413 \times 10^{-19}}{1.6 \times 10^{-19}}=1.55 \mathrm{~V}$

Example-3

The work function for different metals given, below is

$$ \begin{aligned} & \mathrm{Na}=2.75 \mathrm{eV} \\ & \mathrm{K}=2.30 \mathrm{eV} \\ & \mathrm{Mo}=4.17 \mathrm{eV} \\ & \mathrm{Ni}=5.15 \mathrm{eV} \end{aligned} $$

Which of these metals will not give photoelectric emission for a radiation of $3300 \AA$ from a laser beam placed at $1 \mathrm{~m}$ away from the photocell. What would happen if laser is brought nearer and nearer.

Show Answer

Solution:

Energy of incident radiation $\mathrm{E}$ in electron volt is

$$ \mathrm{E}=\dfrac{\mathrm{hc}}{\lambda}=\dfrac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{3300 \times 10^{-10} \times 1.6 \times 10^{-19}}=3.75 \mathrm{eV} $$

From the values given in question it is obvious that photoemission will take place from $\mathrm{Na}$ and $\mathrm{K}$ but no emission can take place from $\mathrm{Mo}$ and $\mathrm{N} _{\mathrm{i}}$.

Bringing laser beam nearer and nearer will only increases the intensity of incident radiation. So the photoelectric current from $\mathrm{Na}$ and $\mathrm{K}$ will increase but no emission will take place from $\mathrm{Mo}$ and $\mathrm{N} _{\mathrm{i}}$.

Example-4

The work function of caesium is $2.14 \mathrm{eV}$. Find (a) the threshold frequency for caesium and (b) the wavelength of incident light if the photocurrent is brought to zero by a stopping potential of $0.60 \mathrm{~V}$.

Show Answer

Solution:

(a) Let $v _{0}$ be the threshold frequency. Then $\mathrm{h} v _{0}=\omega _{0}$

$$ \text { or } \quad v _{0}=\dfrac{\omega _{0}}{\mathrm{~h}}=\dfrac{2.14 \mathrm{eV}}{6.63 \times 10^{-34}}=5.16 \times 10^{14} \mathrm{~Hz} $$

(b) $\mathrm{eV} _{\mathrm{S}}=\mathrm{h} v-\omega _{0}=\dfrac{\mathrm{hc}}{\lambda}-\omega _{0}$

$$ \text { or } \quad \lambda=\dfrac{\mathrm{hc}}{\mathrm{eV} _{\mathrm{S}}+\omega _{0}} $$

$$ \begin{aligned} & \lambda=\dfrac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{(0.60 \mathrm{eV}+2.14 \mathrm{eV})}=\dfrac{19.89 \times 10^{-26}}{2.74 \times 1.6 \times 10^{-19}} \\ \\ & =454 \mathrm{~nm} \end{aligned} $$

Example-5

$\lambda$	$\rightarrow$	$2536 \AA$	$3132 \AA$	$3550 \AA$
$v$	$\rightarrow$	$1.18 \times 10^{15} \mathrm{~Hz}$	$0.958 \times 10^{15} \mathrm{~Hz}$	$0.822 \times 10^{15} \mathrm{~Hz}$
$\mathrm{~V} _{\mathrm{s}}$	$\rightarrow$	$1.95 \mathrm{~V}$	$0.98 \mathrm{~V}$	$0.50 \mathrm{~V}$

The above table gives the values of stopping potential which were obtained in a photoelectric experiment which was performed using calcium as emitter.

From this data, obtain the value of the Plank’s constant.

Show Answer

Solution:

The plot of $v$ against $\mathrm{V} _{\mathrm{s}}$ is a straight line and the slope of this straight line graph is equal to $\mathrm{h} / \mathrm{e}$

$\therefore \mathrm{h}=\mathrm{e} \times$ (slope of the graph)

Slope of the graph is $\dfrac{(1.95-0.50)}{(1.18-0.822)} \times 10^{15}$

$$ \begin{aligned} \therefore \mathrm{h}= & \dfrac{1.45}{0.358 \times 10^{15}} \times 1.6 \times 10^{-19} \\ & =6.48 \times 10^{-34} \mathrm{~J} . \mathrm{S} \end{aligned} $$

Matter Waves

The phenomenon of black body radiations could not be explained satisfactarly on the basis of classical theories of radiations till Max Planck’s introduced the radically, new concept of Quantisation. Later on the study of the phenomenon of photoelectricity and the failure of the classical electromagnetic theory in explanning the various features once again forced the scientists to take resort to the newly introduced Photon theory of light. Close to the heels of these phenomeon came a number of other discoveries which also required one to adopt the photon theory of radiations (X-ray scottering is a prominentexample). However the well established phenomeon of interference diffraction, polarisation etc. required one to adopt a wave picture of light. Ultimately light was given a sort of Dual Nature which sometimes manifest itself as waves and sometimes as particles i.e. photons.

Following the dual nature of light deBroglie suggested to think in terms of the same dual nature for Matter or particles. Arguing that nature would prefer symmatery, he made the bold assertion that just as radiation can sometime behave like particle, the matter should also sometimes behave as waves. Thus the idea of matter waves was born.

The deBroglie Formula

The deBroglie formula for calculating the wavelength to be associated with any material particle is analogous to the one for radiations. A photon of light frequency $v$ has an energy $h$. But if we consider it as a particle of mass moving with a velocity c its energy is $\mathrm{mc}^{2}$ and the momentum ( $\mathrm{p}$ ) is $\mathrm{mc}$. Equating the formulae for the energy we have

$$ \begin{aligned} \mathrm{mc}^{2} & =\mathrm{h} v \\ \mathrm{mc} & =\dfrac{\mathrm{h} v}{\mathrm{c}}=\dfrac{\mathrm{h}}{(\mathrm{c} / \mathrm{v})}=\dfrac{\mathrm{h}}{\lambda}\\ \text{Hence} \mathrm{P} & =\dfrac{\mathrm{h}}{\lambda} \quad \text{or} \quad \lambda=\dfrac{\mathrm{h}}{\mathrm{p}} \end{aligned} $$

deBroglie asserted that the same formula holds for matter also. Thus the wave length that must be associated with a material particle of momentum $p$ is given by

$$ \lambda=\dfrac{\mathrm{h}}{\mathrm{p}} $$

It is obvions that since the value of $h$ is very small, the wave properties of matter are likely to manifest themselves in the domain of the elementary particles.

Some important considerations regarding beBrogeli waves:

1. If we take into consideration relevestic variation of mass with velocity $\mathrm{v}$

$$ \mathrm{m}=\dfrac{\mathrm{m} _{0}}{\sqrt{1-\mathrm{v}^{2} / \mathrm{c}^{2}}} $$

The modified deBroglie formula for $\lambda$ becomes

$$ \lambda=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{~m} _{0} \mathrm{eV}}}\left(1-\dfrac{2 \mathrm{Ve}}{\mathrm{m} _{0} \mathrm{c}^{2}}\right) $$

2. Concept of Group Velocity

In our discussion so far we associated a single well defined wavelength (monochromatic) with a given particle. However we know that a monochromatic wave is infinite in extent and hence cannot be localized in a well defined region of space. This is contradictory to the observed behaviour of particles which are always well localized. To overcome this diffculty we introduce the idea of a wave packet. This wave packed is formed by superposition of a number of waves situated on and around the central wavelength given by the deBroglie relation. We assume that such a wave packet should have a resultant amplitude which is appreciable different from zero only in a small region of space having the dimensions of particle. The velocity of the component monochromatic waves making up the wave packet is known as Phase velocity (can be $>$ c) whereas the speed which with a wave packet of deBroglie wave travel is known as Goup velocity Experimentally it is the group velocity that is always measured.

3. Probability Interpretation to Matter Waves

Max Born suggested a probability interpretatation of the matter waves amplitudes. According to this interpretation the intensity (square of amplitude) of the matter wave at a point is determined by the probability density of the particle at that point (probability per unit volume).

4. Davission and Germer Experiment

Davission and Germer experiment was originally desinged to be a study of the scattering of electrons by a nickel crystal.Bascially the experiment consisted in directing a well defined beam of electrons on a nickel crystal and obeserving the scattered electron intensity as a function of the angle with the direction of incidence. As was to be expected they found the intensity to decrease continuously as the angle of scattering increased. However in the course of their experiment, the vaccum system broke drown and the nickel crystal acquired a coat of the oxide. To remove the oxide, the nickel crystal was reduced slowly in a hot oven. The whole system was reset and the experiment repeated. To the utter surprise of everyone, it was found that the scattered electron intensity now went through Maxima and Minima i.e. the electron were being diffracted.

The experimental arrangment used by Davission and Germer is shown in the figure. It consist of an electron gun. The electron gun is a tungsten filament coated with barium oxide. This is heated by a low voltage power supply. The accelerated emitted electrons fall upon a nickel target which is capable of rotation about an axis perpendicular to the plane of page. The scattered electrons are recieved by a moveable Faraday cylinder which had a sat in front of it. One could therefore measure the scattered electron intensity as a function of angle between the incident and scattered beam. From the developments in the field of X-ray diffraction one would expect that corresponding to a set of crystal plane the scattered electron intensity reach a maximum at a particular accelerating potential and at a particular angle of scattering. The polar graphs shown below, confirmed this observation.

$~$

The electron diffractions by (111) face of the nickel crystal. These graph show a clear and sharpen defined ‘HUMP’ at an accelerations potential of 54 volt at an angle of $50^{\circ}$.

The deBroglie wavelength $\lambda$ associated with electron for 54 volt is given

$$ \lambda=\dfrac{\mathrm{h}}{\mathrm{p}}=\dfrac{1.227}{\sqrt{\mathrm{v}}} \mathrm{nm}=0.167 \mathrm{~nm} $$

We can also calculate $\lambda$ by using Bragg’s technique ( $2 \mathrm{~d} \sin \theta=\lambda$ ) and the result obtained is in very good agreement with the experimental value.

Example-6

X-rays of wavelength $0.82 \AA$ fall on a metal plate. Find the wavelength associated with the photoelectron emitted (neglact the work function of the metal).

Show Answer

Solution:

Wave length of X-ray used to eject photoelectrons $=0.82 \AA$

Frequency $v=\dfrac{\mathrm{c}}{\lambda}=\dfrac{3 \times 10^{10}}{0.82 \times 10^{-8}}=3.544 \times 10^{12}$

Energy of emitted photoelectron $=\mathrm{h} \nu=6.6 \times 10^{-34} \times 0.354 \times 10^{12} \mathrm{~J}$

$\therefore \dfrac{1}{2} \mathrm{mv}^{2}=6.6 \times 3.54 \times 10^{-16}$

$ \mathrm{m}^{2} \mathrm{v}^{2}=2 \times 6.6 \times 3.54 \times 10^{-16} \times 9.1 \times 10^{-31} $

$\mathrm{mv}=\sqrt{2 \times 6.6 \times 3.54 \times 10^{-16} \times 9.1 \times 10^{-31}}=\sqrt{66 \times 7.08 \times 9.1 \times 10^{-24}}$

$\lambda=\dfrac{\mathrm{h}}{\mathrm{mv}}=\dfrac{6.6}{\sqrt{6.6 \times 7.08 \times 9.1}} \times \dfrac{10^{-34}}{10^{-24}}$

$ =0.1012 \AA $

Example-7

The first order Bragg maximum of electron diffraction in a nickel crystal $(\mathrm{d}=\mathbf{0 . 9 0 8 6} \AA)$; occured at a glancing angle of $65^{\circ}$. Calculate the deBroglie wavelength of the electrons and their velocity.

Show Answer

Solution:

From Bragg’s law we have $2 \mathrm{~d} \sin \theta=\mathrm{n} \lambda$

$2 \times 0.9086 \times \sin 65^{\circ}=\lambda$

$\lambda=1.8172 \times 0.9063=1.65 \AA$

Now, $v=\dfrac{h}{\mathrm{~m} \lambda}=\dfrac{6.6 \times 10^{-34}}{9.1 \times 10^{-31} \times 1.65 \times 10^{-10}}$

$=4.3 \times 10^{6} \mathrm{~m} / \mathrm{s}$

PROBLEMS FOR PRACTICE

1. A photo sensitive material emits electrons whose maximum velocity is $3 \times 10^{7} \mathrm{~ms}$. Calculate the stopping potential.

Show Answer

Answer: 2.559 volt

2. The work function for an emitter is $4.2 \mathrm{eV}$. How much potential difference will be required to stop photoemission of maximum energy electrons emitted by light of wavelength $2000 \AA$. For what wavelength of incident light, the stopping potential would be zero.

Show Answer

Answer: 2 volt; $2955 \AA$

3. If the photocurrent of a photocell is cut off by a retarding potential of 0.92 volt for monochromatic radiations of $2500 \AA$, what is the work function of the material?

Show Answer

Answer: $4.03 \mathrm{eV}$

4. The stopping potential for the fastest electrons from a tantalum surface is $1.59 \mathrm{eV}$. If the photoelectric work function is $4.12 \mathrm{eV}$, estimate the threshold frequency for tantalum and the frequency and wavelength of the radiation which caused the emission of above electrons.

Show Answer

Answer: $0.994 \times 10^{15} \mathrm{~s}^{-1}, 1.38 \times 10^{15} \mathrm{~s}^{-1}, 2.18 \times 10^{-7} \mathrm{~m}$

5. When potasium is radiated with light of wavelength $5.89 \times 10^{-7} \mathrm{~m}$ the stopping potential is $0.36 \mathrm{~V}$; when the wavelength of the incident radiation is $0.254 \times 10^{-6} \mathrm{~m}$ the stopping potential is $3.13 \mathrm{~V}$ Use this data to calculate the value of the Planck’s constant.

Show Answer

Answer: $6.60 \times 10^{-34} \mathrm{~J}-\mathrm{s}$

6. The ionisation energy of hydrogen atom is $13.6 \mathrm{eV}$. A photon of wavelength of $600 \times 10^{-10} \mathrm{~m}$ is absorbed by the hydrogen atom. Calculate the kinetic energy of the ejected electron.

Show Answer

Answer: $11.36 \times 10^{-19} \mathrm{~J}$

7. The most energetic electrons emitted from a surface by $3500 \AA$ photons are found to be bent in a $0.18 \mathrm{~m}$ circle by a magnetic field of $1.5 \times 10^{-5} \mathrm{wb} / \mathrm{m}^{2}$. Calculate the wave function of the material.

Show Answer

Answer: $2.90 \mathrm{eV}$

8. Photoelectrons of charge e and constant mass $m$ are liberated in vaccum with negligible velocities from the plate of a parallel place capacitor. A magnetic field is applied parallel to the plates. The seperation between the plates is $x$. Show that a potential difference

$$ \mathrm{V}=\dfrac{1}{2} x^{2}\left(\dfrac{-\mathrm{e}}{\mathrm{m}}\right) \beta^{2} $$

when applied across the capacitor will enable the electrons to just reach the positive plate.

9. Find the maximum magnitude of the linear momentum of a photoelectron emitted when a light of wavelength $400 \mathrm{~nm}$ falls on a metal having awork function $2.5 \mathrm{eV}$.

Show Answer

Answer: $4.2 \times 10^{-25} \mathrm{Kg} \mathrm{ms}^{-1}$

10. Figure show the plot of the stopping potential versus the frequency of light used in an experiment on photo electric effect. Find (i) the ratio $\mathrm{h} / \mathrm{e}$ and (ii) the work function

$~$

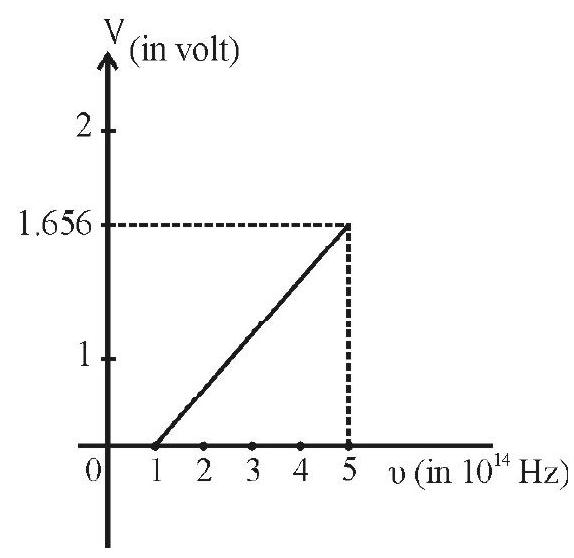
Show Answer

Answer: (i) $4.14 \times 10^{-15} \mathrm{eV} _{\mathrm{s}}$; (ii) $0.414 \mathrm{eV}$

11. Calculate the deBroglie wavelength associated with an $\alpha$ particle accelerated by a p.d of 25000 volt.

Show Answer

Answer: $6.390 \times 10^{-14} \mathrm{~m}$

12. Calcualte the deBroglie wavelength associated with an electron moving with $\dfrac{1}{10 \mathrm{th}}$ velocity of light.

Show Answer

Answer: $0.24 \times 10^{-10} \mathrm{~m}$

13. The equivalent wavelength of a moving electron is $0.24 \times 10^{-10} \mathrm{~m}$. What voltage applied between two grids will bring it to rest.

Show Answer

Answer: 2597 volt

14. When 400 volt electrons are diffracted by a crystal the angular diffraction pattern is identical with that produced by X-rays of wavelength $0.61 \AA$. Calculate the Planck’s constant.

Show Answer

Answer: $6.59 \times 10^{-34} \mathrm{~J}-\mathrm{s}$

15. The wavelength of a $1 \mathrm{KeV}$ photon is $1.24 \times 10^{-9} \mathrm{~m}$. What is the frequency of $1 \mathrm{MeV}$ photon.

Show Answer

Answer: $2.4 \times 10^{20} \mathrm{~Hz}$

16. Calculate the deBroglie wavelength associated with a sphere of mass $1 \mathrm{~kg}$ travelling with a speed of $1 \mathrm{~ms}^{-1}$.

Show Answer

Answer: $6.62 \times 10^{-34} \mathrm{~m}$

17. Show that the deBroglie wavlength of an electron.

(i) of energy $E$ is given by $\lambda=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{mE}}}$

and (ii) accelerated through a potential of $\mathrm{V}$ is given by $\lambda=\dfrac{12.27}{\sqrt{\mathrm{V}}} \AA$

Question Bank

Key Learning Points

1. The phenomenon of photoelectricity was discovered during Hertz’s experiment designed to demonstrate the existance electromagnetic waves.

2. On the basis of experimental studies photoelectricity has the following sailent features.

• Photoelectric emission is an instantneous phenomenon.

• There exists a threshold frequency below which no emission is possible no matter what may be intensity of illumination.

• The number of photoelectrons emitted per unit area, per unit time from a emitter is directly proportional to intencity of light.

• The maximum energy with which electrons are emitted from a emitter is directly proportional to the frequency of incident light but is independent of the intencity of light used.

• There exists a energy distribution among emitted electrons.

3. The classical electromagnetic theory failed to explain all the above mentioned features of photoelectricity.

4. However one cannot discard electromagnetic theory because then there is noway by which one could explain the phenomenon of interference, diffraction, polarisation dispersion etc.

5. Einstein’s introduced the idea of photons according to which light consists of photons of energy hv. Photons are endavoured as particles moving with velocity of light and having a rest mass of zero.

6. According to Einstein when a photon of energy $h v$ is incident on a metal surface the energy of the photon is absorbed by a free electron in the metal. A part of this energy of quantum $\mathrm{h} v$ is used by the free electron to overcome the binding influence of the nucleus and remaining part of this energy is given to the emitted electron as its kinetic energy. Hence

$$ \begin{gathered} \mathrm{h} v=\omega _{0}+\dfrac{1}{2} \mathrm{mv}^{2} \\ \text { or } \quad \dfrac{1}{2} m v^{2}=\mathrm{hv}-\omega _{0} \end{gathered} $$

This equation is known as Einstein’s photoelectric equation and this successfully explain the sailent features of photoelectricity.

7. In terms of the concept of stopping potential Einstein’s photoequation can be written as

$$ \mathrm{eV} _{\mathrm{s}}=\mathrm{h} v-\omega _{0} $$

8. Light is assigned a dual character.

9. Since it is a well known fact that nature love symmetery deBroglie argued that if light has to has a duel character, matter particles should also exhibit wave characterstics. He also assigned a wavelength $\lambda$ to a moving particle given by the relation

$$ \lambda=\dfrac{\mathrm{h}}{\mathrm{mv}}=\dfrac{\mathrm{h}}{\mathrm{p}} $$

and predicted that wave characterstics should be found with elementary particles.

10. Davision and Germer accidently obtained a diffraction pattern for accelerated electrons in an experiment designed to study the scattering of electrons by a Nickel crystal in vacuum.

Average

Photons

1. A $1000 \mathrm{~W}$ source of light is emitting light of wavelength $6000 \AA$. The number of photons emitted per second by the source is

(1) $6 \times 10^{20}$ photons $/ \mathrm{s}$

(2) $3 \times 10^{10}$ photons $/ \mathrm{s}$

(3) $10^{20} \mathrm{photons} / \mathrm{s}$

(4) $3 \times 10^{20}$ photons/s

Show Answer

Correct answer: (4)

Solution:

The number of photons emitted by per second by the source is given by $n=\dfrac{E \lambda}{h c}$

or $\mathrm{n}=\dfrac{100 \times 6 \times 10^{-7}}{6.62 \times 10^{-34} \times 3 \times 10^{8}}=3 \times 10^{20}$

Hence option (4) is correct.

Difficult

Photons

2. A photon of $3 \times 10^{-7}$ wavelength will

(1) have a energy $4.14 \mathrm{eV}$ and will lie near the ultra violet region

(2) have a energy of $4.14 \times 10^{-19} \mathrm{~J}$ and would lie in the deep red region

(3) have a energy of $4.414 \mathrm{eV}$ and would lie in the deep yellow region

(4) will have a energy of $4.14 \mathrm{eV}$ and would lie in the infra red region

Show Answer

Correct answer: (3)

Solution:

Wave length of the photon is $3 \times 10^{-7} \mathrm{~m}=3000 \AA$

The electromagnetic wave is near the ultra violet region

Energy of the photon $=\mathrm{h} v$

$$ =6.63 \times 10^{-34} \times \dfrac{3 \times 10^{8}}{3 \times 10^{-7}}=6.63 \times 10^{-19} \mathrm{~J}=\dfrac{6.63 \times 10^{-19}}{1.6 \times 10^{-19}} \mathrm{eV}=4.144 \mathrm{eV} $$

Hence option (1) is correct.

Average

Photoelectricity

3. Which one of the follownig graphs represent the variation of maximum kinetic energy of photo electrons emitted from a photoemitter with frequency?

(1) $\mathbf{A}$

(2) $\mathbf{B}$

(3) $\mathrm{C}$

(4) D

$~$

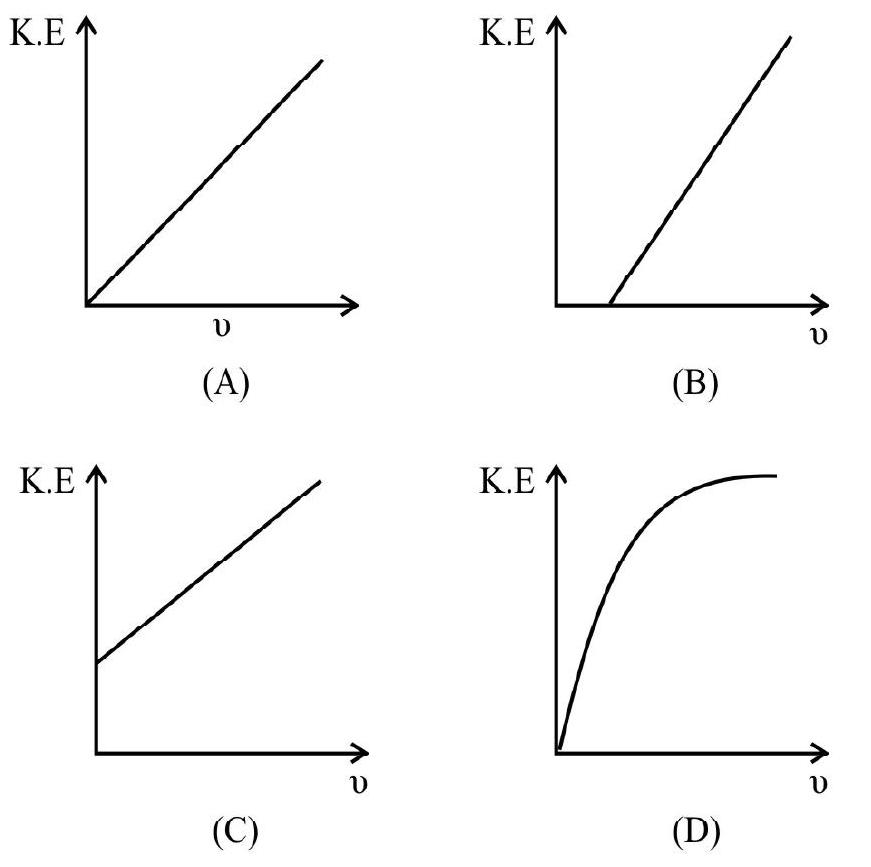
Show Answer

Correct answer: (2)

Solution:

Einstein’s photoelectric equation is $\dfrac{1}{2} \mathrm{mv} _{\max }^{2}=\mathrm{h} v-\omega _{0}$

This is of the form $y=m x$, the equation of a straight line with a negative $y$ intercept $t$ and slope $h$. To come out from a photo emitter a electron needs energy equal to the work function of the emitter and gets this energy from the energy h $v$ of the photons incident on the emitter. When the frequency of the incident photons is decreased the energy of the incident photons also decreases as $\omega _{0}$ is a constant.

Hence option (4) is correct.

Average

Photoelectricity

4. Which one of the following graphs represent correctly variation of photoelectric current

with the applied voltage?

(1) $\mathbf{A}$

(2) $\mathbf{B}$

(3) $\mathrm{C}$

(4) $\mathrm{D}$

$~$

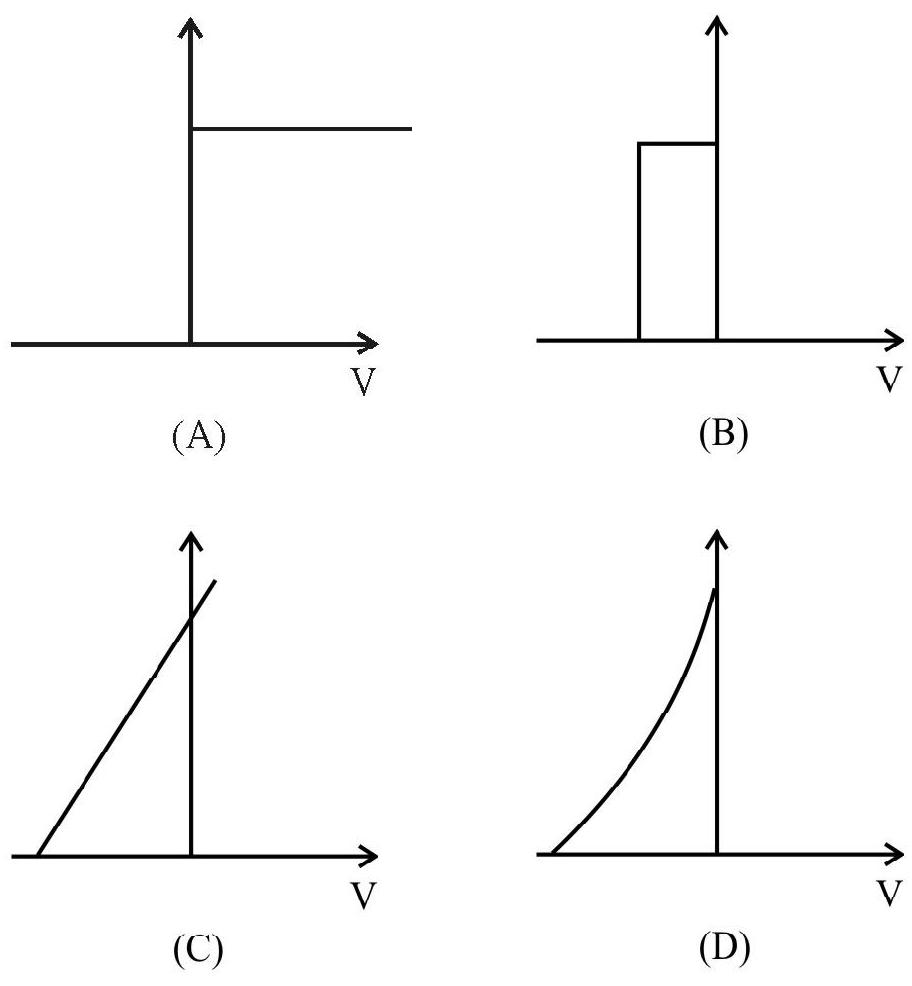
Show Answer

Correct answer: (4)

Solution:

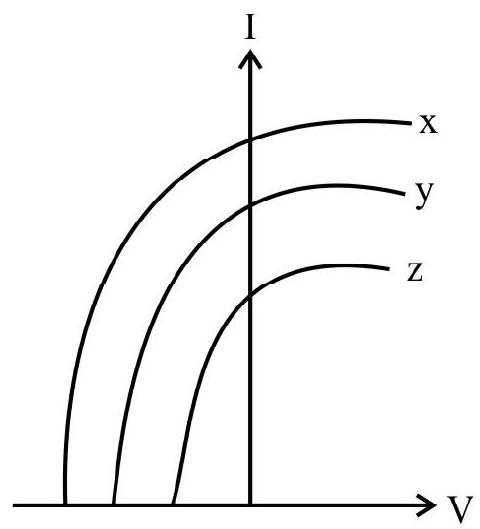
The circuit diagram to study the variation of the photoelectric current with voltage is shown. When the applied potential difference is large all the photo electron emitted by the emitter are collected on the collector. As we decrease the potential difference to zero and then negative values the number of emitted electrons collected by the collector starts decreasing and corresponding to limiting value, called stopping potential the collector is not able to collect anyone of the emitted electrons and photoelectric current tends to become zero. Graph (4) represents this variation.

$~$

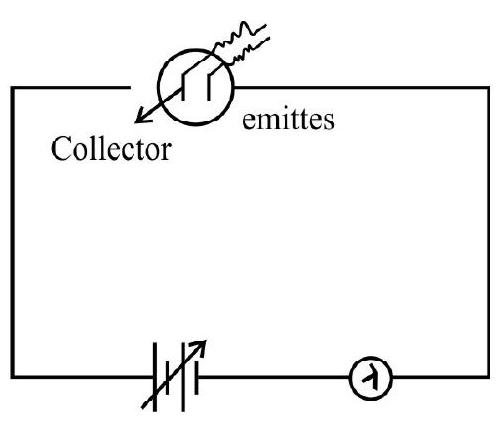
Hence option (4) is correct.

Average

Photoelectricity

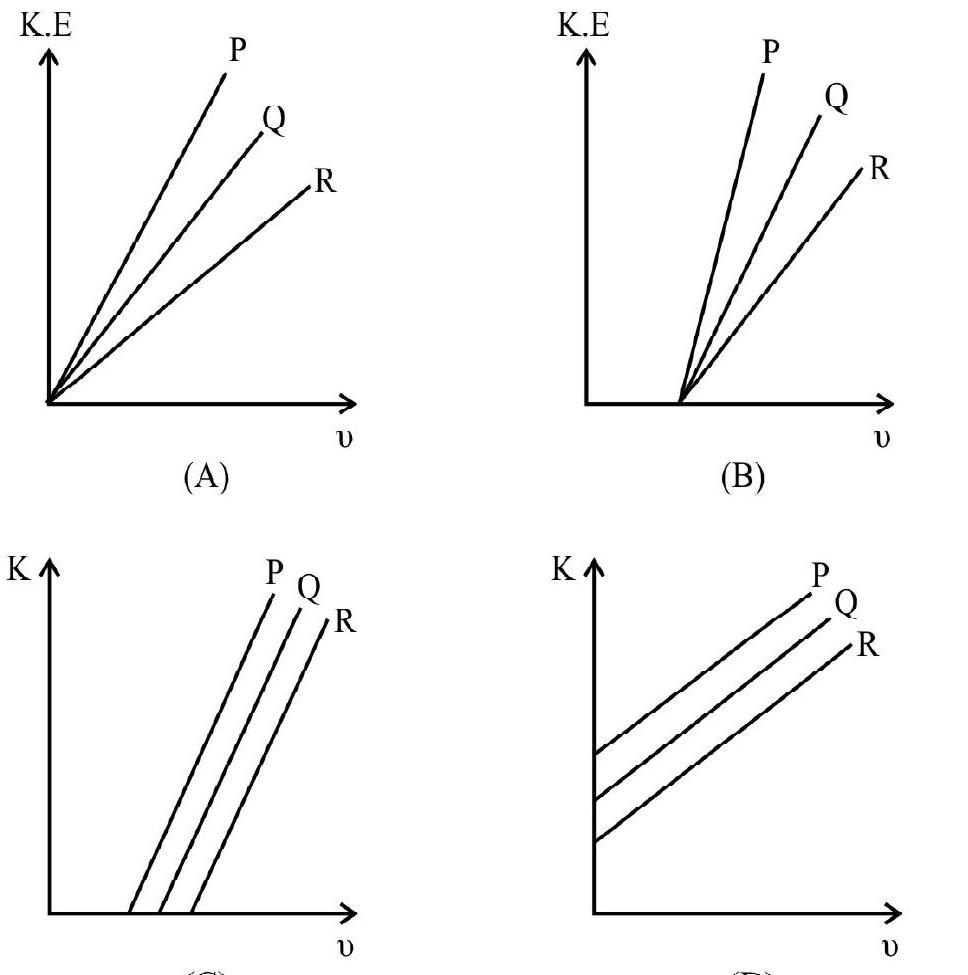
5. For three differenct metal $P, Q$ and $R$ photoemission is observed one by one; $\left(\dfrac{1}{2}\right) \operatorname{mv} v _{\max }^{2}$ (K.E) versus $v$ is plotted. Which one of the following represent the curves correctly?

(1) $\mathbf{A}$

(2) $\mathbf{B}$

(3) $\mathrm{C}$

(4) D

$~$

Show Answer

Correct answer: (3)

Solution:

As explained in previous question the metal $\mathrm{P}, \mathrm{Q}$ and $\mathrm{R}$ will have their own threshold frequncies. This fact is correctly represented by graph in option (3).

Average

Photoelectricity

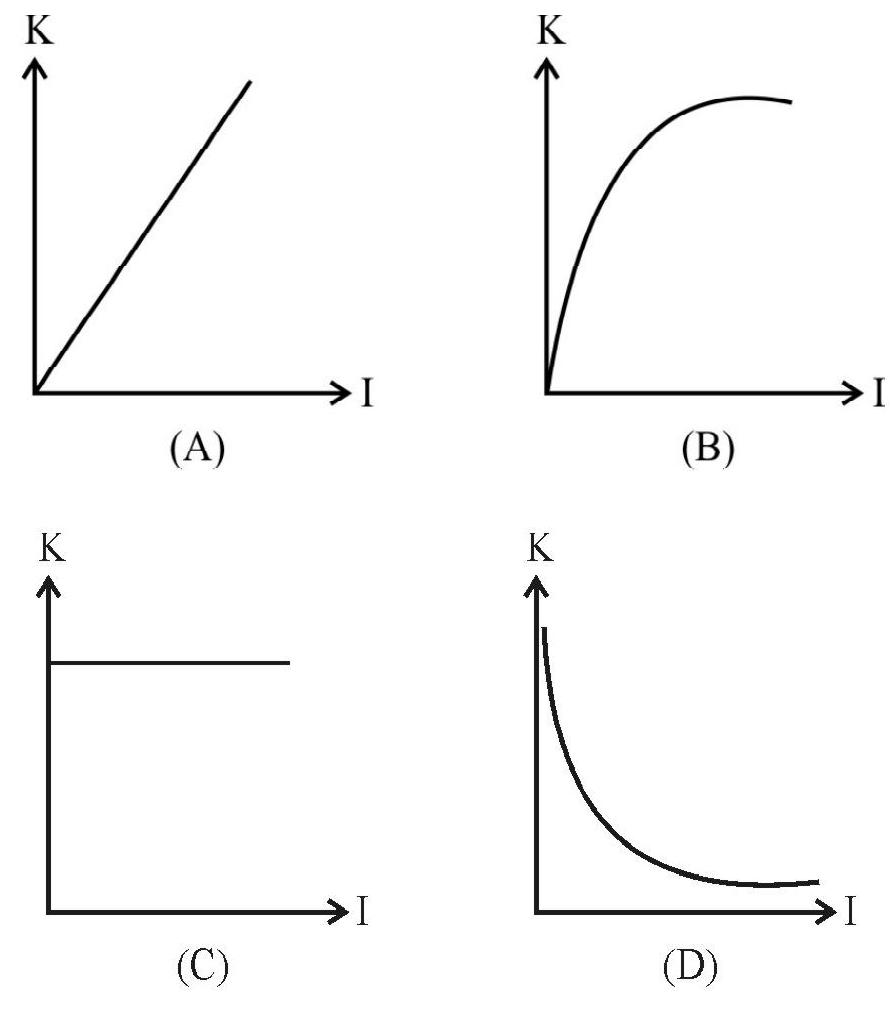
6. Which one of the following graphs represent correctly the variation of $\dfrac{1}{2} \mathrm{mv} _{\max }^{2}(\mathrm{k})$ with the intensity of incident radiations (I)

(1) $\mathbf{A}$

(2) $\mathrm{B}$

(3) $\mathrm{C}$

(4) $\mathrm{D}$

Show Answer

Correct answer: (3)

Solution:

It is an experimental observed fact that the maximum energy with which photoelectrons are emitted does not depend on the intensity of light but depends only on the frequency of the incident light.

Hence option (3) is correct.

Average

Photoelectricity

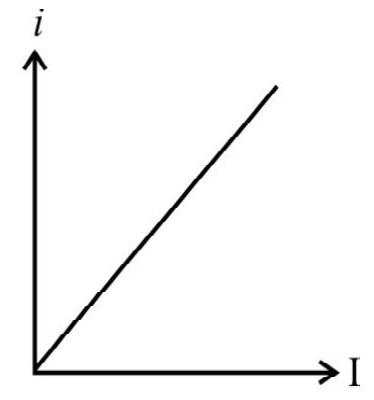
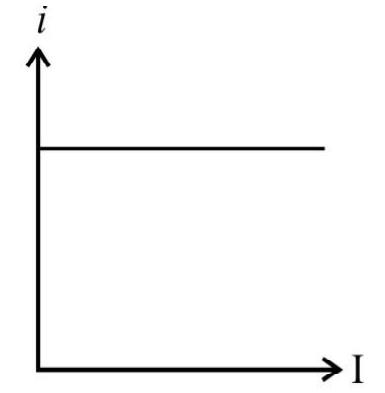
7. Which one of the following graphs represent correctly the variation of photoelectric current (i) with the intensity (I) of incident radiations?

(1) $\mathbf{A}$

(2) $\mathbf{B}$

(3) $\mathrm{C}$

(4) $\mathbf{D}$

(A)

$~$

(B)

$~$

(C)

$~$

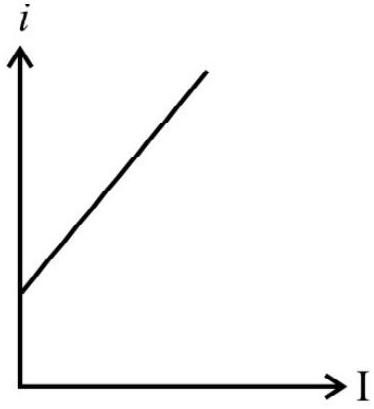
(D)

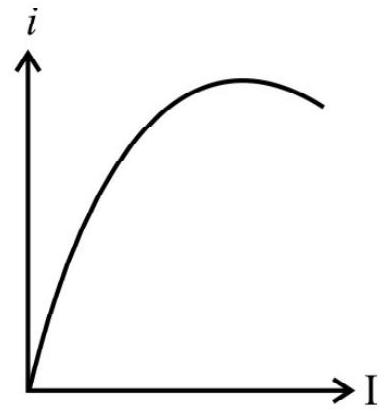
Show Answer

Correct answer: (2)

Solution:

With the increase of intensity of incident light, the number of photons striking the emitter surface per unit area per unit time increases. As each photon colliding and emitting one electron, the number of emitted electrons increases with increase in the increase of intensity of light. The graph in option (2) is representing this fact and therefore is the correct answer.

Hence option (2) is correct.

Average

Photoelectricity

8. Incident radiation, of a given frequency, (but variable intenstiy) is incident on a given photosensitive surface. The graph, that represents the variation of the photoelectric current, with the potential (applied across the photoelectric tube), is the graph numbered as graph.

(1) $\mathbf{A}$

(2) $\mathbf{B}$

(3) $\mathbf{C}$

(4) $\mathrm{D}$

$~$

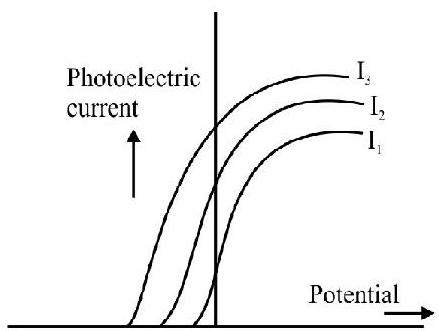
(A)

$~$

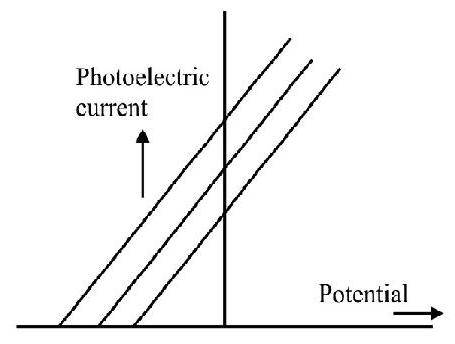
(C)

$~$

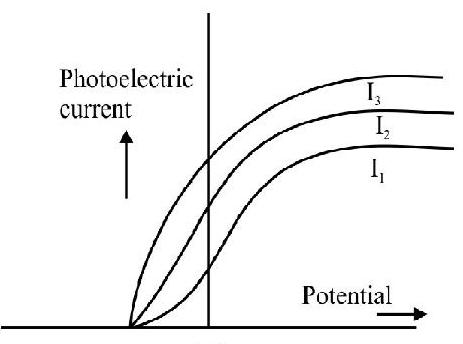
(B)

$~$

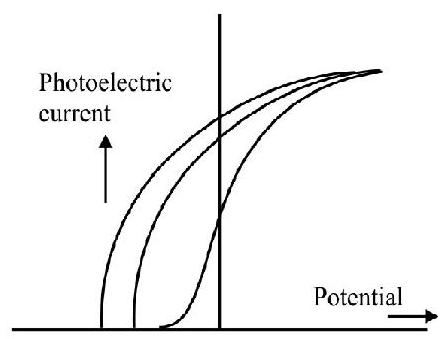
(D)

Show Answer

Correct answer: (2)

Solution:

Option (2) is correct graph. We know that stopping potential is inpendent of intensity of the incident radiation.

Difficult

Photoelectricity

9. Photoelectric effect experiment are performed using three different metal plates $(x, y, z)$ having work function equal to $2.0 \mathrm{eV}, 2.5 \mathrm{eV}$ and $3.0 \mathrm{eV}$, respectively. A light beam, containing wave length of $550 \mathrm{~nm}, 450 \mathrm{~nm}$ and $350 \mathrm{~nm}$, having equal intensity of illumination, is incident on each of the three plates. The correct I-V graph, of the three cases, is the graph numbered as graph.

(1) $\mathbf{A}$

(2) $\mathrm{B}$

(3) $\mathrm{C}$

(4) $\mathrm{D}$

$~$

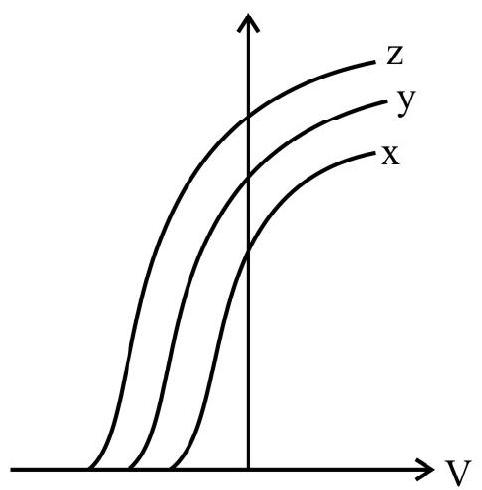
(A)

$~$

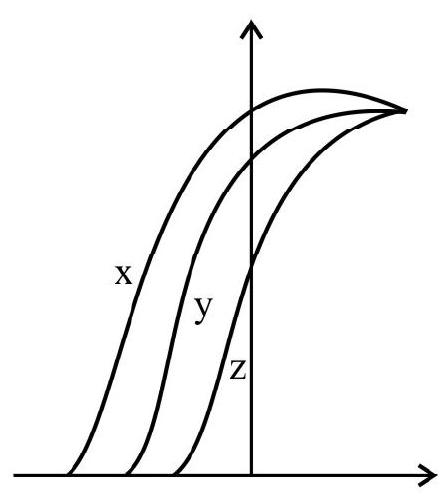
(C)

$~$

(B)

$~$

(D)

Show Answer

Correct answer: (4)

Solution:

$$ \begin{aligned} & \text { We have: Energy of a photon (in eV) }=\left[\dfrac{1240}{\text { wavelength (in } \mathrm{nm})}\right] \\ & \therefore \quad \mathrm{E} _{1} \cong \dfrac{1240}{500} \mathrm{eV}=2.25 \mathrm{eV} \\ & \mathrm{E} _{2} \cong \dfrac{1240}{450} \mathrm{eV}=2.75 \mathrm{eV} \\ & \mathrm{E} _{3} \cong \dfrac{1240}{350} \mathrm{eV}=3.54 \mathrm{eV} \end{aligned} $$

Thus it is clear $\mathrm{E} _{1}$ cannot emit photoelectrons from $\mathrm{y}$ and $\mathrm{z}$ plates $\mathrm{E} _{2}$ cannot emit photoelectrons from $\mathrm{z}$ plate.

Also work function of $x$ is least and it can emit photoelectrons for all the three wavelengths. Hence magnitude of the stopping potential, and saturation current both, will be maximum, for metal plate $x$.

Hence option (4) is correct.

Average

Photoelectricity

10. Which one of the following statement is not a part of the quantum theory of light?

(1) There is a minimum frequency of light below which no photoelectrons are emitted

(2) The maximum kinetic energy of photoelectron depends only on the frequency of light and not on the intensity

(3) Photoemission occurs when light of appropriate frequency but minimum intensity is incident

(4) The charge of photoelectrons is quantized

Show Answer

Correct answer: (4)

Solution:

Option (1),(2) and (3) are experimentally observed facts of the phenomenon of photoelectricity and are explained by Einstein’s theory of the photoelectricity. Option (4) refers to quantization of charge in general and is not a part of Einstein’s theory of photoelectric emission.

Hence option (4) is correct.

Difficult

Photoelectricity

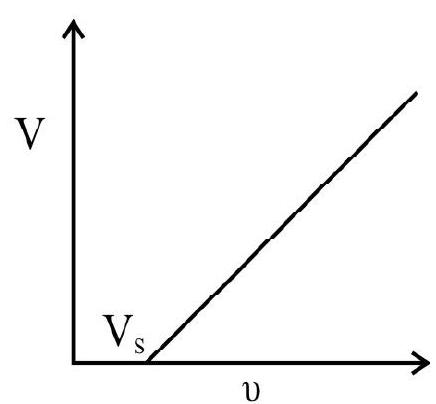
11. The graph between stopping potential versus frequency for a photoemitter is shwon in figure. Then

$~$

(1) The slope of the graph enable us to determine the work function of the emitter

(2) The slope of the graph is equal to Planck constant $h$

(3) The product of the slope of the graph and electronic change is equal to Planck’s constant ’ $h$ '

(4) The slope of the graph enables us to determine threshold wavelength of the emitter

Show Answer

Correct answer: (3)

Solution:

According to Einstein’s photoelectric equation we have $\dfrac{1}{2} \mathrm{~m} _{\max }^{\mathrm{v}^{2}}=h v-h v _{0}$

If $V _{S}$ is the stopping potential, then $\dfrac{1}{2} \mathrm{~m} _{\max }^{v^{2}}=e V _{S}$

$$ \therefore \mathrm{eV} _{\mathrm{s}}=\mathrm{h} \nu-\mathrm{h} \nu _{0} $$

Differenciating we get e $\Delta \mathrm{V} _{\mathrm{s}}=\mathrm{h} \Delta \nu$

or $\mathrm{h}=\mathrm{e} \times \dfrac{\Delta \mathrm{V} _{\mathrm{S}}}{\Delta \nu}$

But $\dfrac{\Delta \mathrm{V} _{\mathrm{S}}}{\Delta \nu}$ represents the slope of the graph

Hence $\mathrm{h}=\mathrm{eV}$ slope of $\mathrm{v}$ versus $\mathrm{V}$ graph.

Hence option (2) is correct.

Average

Photoelectricity

12. Light of two different frequencies whose photons have energies $1 \mathrm{eV}$ and $2.5 \mathrm{eV}$ respectively; successively illumminate a metal whose work function is $0.5 \mathrm{eV}$. The ratio of the maximum speed of the emitted electrons will be

(1) $1: 1$

(2) $1: 2$

(3) $2: 1$

(4) $1: 4$

Show Answer

Correct answer: (2)

Solution:

We have $\dfrac{1}{2} \mathrm{mv}^{2}=\mathrm{h} \nu-\omega _{0}$ or $\mathrm{E}=\mathrm{h} v-\mathrm{w} _{0} \quad\left(\because 1 / 2 \mathrm{mV}^{2}=\mathrm{E}\right)$

Thus $\mathrm{E} _{1}=(1-0.5)=0.5 \mathrm{eV} \quad \mathrm{E} _{2}=(2.5-0.5)=2 \mathrm{eV}$

$\dfrac{\mathrm{E} _{1}}{\mathrm{E} _{2}}=\dfrac{\dfrac{1}{2} \mathrm{mv} _{1}^{2}}{\dfrac{1}{2} \mathrm{mv} _{2}^{2}}=\dfrac{0.5}{2}$

or $\dfrac{\mathrm{v} _{1}^{2}}{\mathrm{v} _{2}^{2}}=\dfrac{1}{4} \quad \therefore \dfrac{\mathrm{v} _{1}}{\mathrm{v} _{2}}=\dfrac{1}{2}$

This option (2) is correct anser.

Average

Photoelectricity

13. The work function for sodium is 2.0 volt. Then the longest wavelength of light that will eject photoelectrons from the surface is

(1) $6000 \AA$

(2) $7000 \AA$

(3) $5900 \AA$

(4) $6100 \AA$

Show Answer

Correct answer: (1)

Solution:

The work function $\omega _{0}=\dfrac{h c}{\lambda _{0}}$ where $\lambda _{0}$ is the wavelength that can cause emission

Hence $\lambda _{0}=\dfrac{\mathrm{hc}}{\omega _{0}}=\dfrac{6.6 \times 10^{-34} \times 3 \times 10^{8}}{2 \times 1.6 \times 10^{-9}} \mathrm{~m}$

or $\quad \lambda _{0}=6000 \AA$

Hence option (1) is correct.

Average

Photoelectricity

14. A photo electric cell using caesium as the sensitive element is illuminated with light of wavelength of $4.2 \times 10^{-7} \mathrm{~m}$. The work function of caesium is $1.90 \mathrm{~V}$. The reverse potential which will supress the electron emission is

(1) $1.5 \mathrm{~V}$

(2) $1.9 \mathrm{~V}$

(3) $1.05 \mathrm{~V}$

(4) $1 \mathrm{~V}$

Show Answer

Correct answer: (3)

Solution:

From Einstein’s photoelectric equation we have $\mathrm{eV} _{\mathrm{s}}=\mathrm{h} \nu-\omega _{0}$

or $\mathrm{V} _{\mathrm{S}}=\dfrac{\mathrm{h} \nu}{\mathrm{e}}-\dfrac{\omega _{0}}{\mathrm{e}}=\dfrac{\mathrm{hc}}{\mathrm{e} \lambda}-\dfrac{\omega _{0}}{\mathrm{e}}$

$$ \begin{aligned} \mathrm{V} _{\mathrm{S}}= & \dfrac{6.6 \times 10^{-34} \times 3 \times 10^{8}}{1.6 \times 10^{-19} \times 4.2 \times 10^{-7}}-1.9 \\ & =(2.95-1.9) \mathrm{V}=1.05 \mathrm{~V} \end{aligned} $$

Alternately;

$$ \lambda=4.2 \times 10^{-7} \mathrm{~m}=420 \mathrm{~nm} $$

The energy of the photon in $\mathrm{eV}$ is $\mathrm{E}=\dfrac{1240}{420} \mathrm{eV}=2.5 \mathrm{eV}$

$$ \begin{aligned} & \mathrm{eV} \\ &= \mathrm{h} \nu-\omega _{0}=\mathrm{E}-\omega _{0} \\ &=2.95 \mathrm{eV}-1.90 \mathrm{eV}=1.05 \mathrm{eV} \\ & \therefore \quad \mathrm{V} _{\mathrm{S}}=\dfrac{1.05 \mathrm{eV}}{\mathrm{e}}=1.05 \mathrm{~V} \end{aligned} $$

Hence option (3) is correct.

Average

Photoelectricity

15. The maximum kinetic energy of photoelectron emitted from a surface when photons of energy $6 \mathrm{eV}$ fall on it is $4 \mathrm{eV}$. The stopping potential is

(1) $2 \mathbf{eV}$

(2) $4 \mathrm{eV}$

(3) $6 \mathrm{eV}$

(4) $0.4 \mathrm{eV}$

Show Answer

Correct answer: (2)

Solution:

Stopping potential is defined as the negative potential applied to a photoemitting surface as the negative potential which will stop the emission of the electrons from the surface even with maximum kinetic energy. Therefore stopping potential will be $4 \mathrm{eV}$.

Hence option (2) is correct.

Difficult

Photoelectricity

16. The energy of photoelectrons emitted from a metal surface is $\mathbf{1 . 6} \mathrm{eV}$. If the threshoold wavelength is $3000 \AA$, then the wavelength of incident light is

(1) $2164 \AA$

(2) $216.4 \AA$

(3) $21.64 \times 10^{-12} \mathrm{~m}$

(4) $0.2164 \AA$

Show Answer

Correct answer: (1)

Solution:

We are given the energy of emitted photoelectrons $1.6 \mathrm{eV}=1.6 \times 1.6 \times 10^{-19}=2.56 \times 10^{-19} \mathrm{~J}$

Hence $\dfrac{1}{2} \mathrm{mv}^{2}=2.56 \times 10^{-19} \mathrm{~J}$

Also $\dfrac{1}{2} \mathrm{mv}^{2}=\mathrm{hc}\left(\dfrac{1}{\lambda}-\dfrac{1}{\lambda _{0}}\right)$

or $\quad \dfrac{1}{\lambda}-\dfrac{1}{\lambda _{0}}=\dfrac{\dfrac{1}{2} \mathrm{mv}^{2}}{\mathrm{hc}}=\dfrac{2.56 \times 10^{-19}}{6.62 \times 10^{-34} \times 3 \times 10^{8}}=128.9 \times 10^{10}$

$$ \dfrac{1}{\lambda}=128.9 \times 10^{10}+\dfrac{1}{3 \times 10^{-7}} \quad\left[\because \lambda _{0}=3000 \AA\right] $$

Solving we get

$$ \lambda=2164 \AA $$

Hence option (1) is correct

Difficult

Photoelectricity

17. The minimum light intensity that can be percieved by the eye is about $10^{-10} \mathrm{Wm}^{-2}$. The area of the pupil of eye is $10^{-4} \mathrm{~m}^{2}$. Photons of wavelength $5.84 \times 10^{-7}$ enter the eye. Their number for the vision is

(1) $3 \times 10^{4}$

(2) $3 \times 10^{2}$

(3) $3 \times 10^{6}$

(4) $3 \times 10^{3}$

Show Answer

Correct answer: (1)

Solution:

Let $\mathrm{n}$ be the number of required photons. Then their energy is $\mathrm{n} h \nu=\dfrac{\mathrm{nhc}}{\lambda}$ and this must be equal to intensity of light $\times$ area of the pupil of eye and is given by $10^{-10} \times 10^{-4}$ $\dfrac{\mathrm{nhc}}{\lambda}=10^{-10} \times 10^{-4}$

or $\quad \mathrm{n}=\dfrac{10^{-4} \times 10^{-10} \times 5.84 \times 10^{-7}}{\left(6.6 \times 10^{-34}\right) \times 3 \times 10^{8}}=3 \times 10^{4}$

Hence option (1) is correct.

Difficult

Photoelectricity

18. When a piece of metal is illuminated by monochoromatic light of wavelength $\lambda$, then the stopping potential for photoelectric current is $2.5 \mathrm{eV}$. When the same surface is illuminated by light of wavelength $1.5 \lambda$, then the stopping potential is observed to have a value $V _{s}$. From this data the threshold wavelength of photoelectric emission is

(1) $2.5 \lambda$

(2) $2.25 \lambda$

(3) $2.75 \lambda$

(4) $2.00 \lambda$

Show Answer

Correct answer: (2)

Solution:

From Einstein’s photoelectric equation we have $\mathrm{eV} _{\mathrm{S}}=\mathrm{h} \nu-\omega _{0}=\dfrac{\mathrm{hc}}{\lambda}-\omega _{0}$ so that we can write from the data given in the question

$$ \begin{aligned} & \mathrm{eV} _{\mathrm{S}}(2.5)=\dfrac{\mathrm{hc}}{\lambda}-\omega _{0} \quad \text { or } \quad \mathrm{eV} _{\mathrm{S}}=\dfrac{\mathrm{hc}}{2.5 \lambda}-\dfrac{\omega _{0}}{2.5} \\ & \mathrm{eV} _{\mathrm{S}}=\dfrac{\mathrm{hc}}{1.5 \lambda}-\omega _{0} \end{aligned} $$

From above equations

$$ \begin{aligned} & \dfrac{\mathrm{hc}}{1.5 \lambda}-\omega _{0}=\dfrac{\mathrm{hc}}{2.5 \lambda}-\dfrac{\omega _{0}}{2.5} \\ & \dfrac{\mathrm{hc}}{\lambda}\left[\dfrac{1}{1.5}-\dfrac{1}{2.5}\right]=\omega _{0}\left(1-\dfrac{1}{2.5}\right)=\dfrac{3}{5} \omega _{0} \end{aligned} $$

$$ \dfrac{3}{5} \dfrac{\mathrm{hc}}{\lambda _{0}}=\dfrac{\mathrm{hc}}{\lambda}\left[\dfrac{1}{1.5}-\dfrac{1}{2.5}\right]=\dfrac{4}{15} \dfrac{\mathrm{hc}}{\lambda} $$

Hence $\lambda _{0}=\dfrac{9}{4} \lambda=2.25 \lambda$

Hence option (1) is correct.

Difficult

Photoelectricity

19. The retarding potential for a given photoelectric emitter is $3.0 \mathrm{~V}$. The photoelectric effect of this emitter begins at a frequency of $6 \times 10^{14} \mathrm{~Hz}$. Which frequency will eject electrons from this emitter?

(1) $6 \times 10^{14} \mathrm{~Hz}$

(2) $1.32 \times 10^{15} \mathrm{~Hz}$

(3) $132 \times 10^{20} \mathrm{~Hz}$

(4) $13.2 \times 10^{18} \mathrm{~Hz}$

Show Answer

Correct answer: (2)

Solution:

From Einstein’s photoelectric equation we

$$ \begin{aligned} & \quad \mathrm{eV} _{\mathrm{S}}=\mathrm{h} \nu-\mathrm{h} \nu _{0} \text { where } \mathrm{V} _{\mathrm{S}} \text { is the stopping potential } \\ & \therefore \mathrm{h} \nu=\mathrm{eV} _{\mathrm{S}}+\mathrm{h} \nu _{0} \text { or } \nu=\dfrac{\mathrm{eV} _{\mathrm{S}}}{\mathrm{h}}+\nu _{0} \\ & \nu=\dfrac{1.6 \times 10^{-19} \times 3}{6.62 \times 10^{-34}}+6 \times 10^{14} \\ & \quad=7.2 \times 10^{14}+6 \times 10^{14}=13.2 \times 10^{14}=1.32 \times 10^{15} \mathrm{~Hz} \end{aligned} $$

Hence option (2) is correct.

Difficult

Photoelectricity

20. The threshold wavelength of metallic silver is $3800 \AA$. Ultroviolet light of wavelength $2600 \AA$ is allowed to fall on silver. The maximum velocity of the emitted photoelectrons is

(1) $\sim 0.73 \times 10^6 \mathrm{~m} / \mathrm{s}$

(2) $\sim 0.73 \times 10^8 \mathrm{~m} / \mathrm{s}$

(3) $\sim 0.73 \times 10^5 \mathrm{~m} / \mathrm{s}$

(4) $\sim 0.73 \times 10^7 \mathrm{~m} / \mathrm{s}$

Show Answer

Solution:

$\omega _{0}=\dfrac{\mathrm{hc}}{\lambda}=\dfrac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{3800 \times 10^{-10}}=5.23 \times 10^{-19} \mathrm{~J}$

Now $\dfrac{1}{2} \mathrm{mv} _{\max }^{2}=\mathrm{h} \nu-\omega _{0}$

$\therefore \quad \mathrm{h} \nu=\dfrac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{2600 \times 10^{-10}}=7.65 \times 10^{-19} \mathrm{~J}$

$\therefore \quad \dfrac{1}{2} \mathrm{mv} _{\max }^{2} \approx(7.65-5.23) \times 10^{-19}=2.42 \times 10^{-19} \mathrm{~J}$

$$ \mathrm{v} _{\max }=\sqrt{\dfrac{2 \times 2.42 \times 10^{-19}}{9.11 \times 10^{-31}}} \approx 0.73 \times 10^{6} \mathrm{~m} / \mathrm{s} $$

Hence option (1) is correct.

Very Difficult

Photoelectricity

21. A beam of light has three wavelenghs $4144 \AA, 4972 \AA$ and $6216 \AA$ wth a total intensity of $3.6 \times 10^{-3} \mathrm{~W}$ equally distributed among the three wavelengths. This beam is incident on a area of $1 \mathrm{~cm}^{2}$ on a clean metal surface of work function $2.3 \mathrm{eV}$. It is given that each capable photon ejects one electron. The number of phoelectrons liberacted in (Assume there is no loss of light due to reflection).

(1) $5.5 \times 10^{11}$

(2) $11 \times 10^{11}$

(3) $11 \times 10^{12}$

(4) $11 \times 10^{10}$

Show Answer

Solution:

The threshold wavelength will be given by

$\lambda=\dfrac{\mathrm{hc}}{\omega _{0}}=\dfrac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{2.3 \times 1.6 \times 10^{-19}}=5.396 \times 10^{-7} \mathrm{~m}=5396 \AA$

Hence light of wavelength $6216 \AA$ will not emit photoelectrons from the metal surface. Since the total intensity of light is equally distributed among the wavelengths, the intensity which each wavelength will have

is $\dfrac{3.6 \times 10^{-3}}{3}=1.2 \times 10^{-3} \mathrm{Wm}^{-2}$

Power incident on the surface due to each wavelength is

$$ 1.2 \times 10^{-3} \times 10^{-4} \mathrm{~J} / \mathrm{s} \quad\left(\mathrm{A}=10^{-4}\right) $$

Energy of one photon of $\lambda _{1}=4144 \AA$ is $\dfrac{\mathrm{hC}}{\lambda _{1}}=\dfrac{6.62 \times 10^{-34} \times 3 \times 10^{8} \mathrm{~J}}{4144 \times 10^{-10}}$

Power incident on $1 \mathrm{~cm}^{2}=\mathrm{P} _{1}=1.2 \times 10^{-3} \times 10^{-4}=1.2 \times 10^{-7} \mathrm{~J} / \mathrm{s}$

$\therefore$ The number of electrons emitted by $\lambda _{1}=$ number of photon incident

or $\quad \mathrm{n} _{1}=\dfrac{\mathrm{P} _{1}}{\mathrm{E} _{1}}=\dfrac{1.2 \times 10^{-7}}{6.62 \times 3} \times 4144 \times 10^{16}=2.50393 \times 10^{11}$

Energy of one photon of $\lambda _{2}=4972 \AA$ is

$\mathrm{E} _{2}=\dfrac{\mathrm{hc}}{\lambda _{2}}=\dfrac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{4972 \times 10^{-10}} \mathrm{~J}$

Power incident of $1 \mathrm{~cm}^{2}=\mathrm{P} _{2}=1.2 \times 10^{-7} \mathrm{~J} / \mathrm{s}$

The number electrons emitted by $\lambda _{2}=$ number of photons of $\lambda _{2}$

or $\mathrm{n} _{2}=\dfrac{\mathrm{P} _{2}}{\mathrm{E} _{2}}=\dfrac{1.2 \times 10^{-7}}{6.62 \times 3} \times 4972 \times 10^{16}=3.00423 \times 10^{11}$

Hence total number of $\mathrm{e}^{-}$emitted $=\mathrm{n} _{1}+\mathrm{n} _{2}$

$$ =(2.50393+3.00423) \times 10^{11} \mathrm{~s}^{-1}=5.5 \times 10^{11} $$

Hence option (1) is correct.

Difficult

Photoelectricity

22. The electric field associated with a light wave is given by $E=E _{0} \sin \left[1.57 \times 10^{7} \mathrm{~m}^{-1}(\mathrm{ct}-\boldsymbol{x})\right]$. This light is used to emit photoelectron from a surface having a work function of $2.1 \mathrm{eV}$. The stopping potential is

(1) 0.1 volt

(2) 1 volt

(3) 11 volt

(4) 1.1 volt

Show Answer

Correct answer: (2)

Solution:

The equation of a harmonic wave is given by $\mathrm{E}=\mathrm{E} _{0} \sin \dfrac{2 \pi}{\lambda}(\mathrm{vt}-x)$

The electric field associated with incident light is given by $\mathrm{E} _{0} \sin 1.57 \times 10^{7} \mathrm{~ms}^{-1}(\mathrm{ct}-x)$ has the same form as of a harmonic wave.

Comparing the two we get $\dfrac{2 \pi}{\lambda}=1.57 \times 10^{7}$ or $\lambda=\dfrac{2 \pi}{1.57 \times 10^{7}} \mathrm{~m}$

Further $\mathrm{eV} _{\mathrm{S}}=\mathrm{hv}-\omega _{0}=\dfrac{\mathrm{hc}}{\lambda}-\omega _{0}$

or $\mathrm{V} _{\mathrm{S}}=\dfrac{\mathrm{hc}}{\mathrm{e} \lambda}-\dfrac{\omega _{0}}{\mathrm{e}}$

$\mathrm{V} _{\mathrm{S}}=\dfrac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{1.6 \times 10^{-9} \times 2 \times 3.142}-2.1=1.0 \mathrm{volt}$

Hence option(2) is correct

Difficult

Photoelectricity

23. The work function of potassium is $2.24 \mathrm{eV}$. The region of the elctro spectrum which liberates the electron from potassium is

(1) $5.5 \times 10^{-7}$ to $8 \times 10^{-7} \mathrm{~m}$

(2) $6 \times 10^{-7}$ to $7 \times 10^{-7} \mathrm{~m}$

(3) wavelengths longer than $5.52 \times 10^{-7} \mathrm{~m}$

(4) wavelengths shorter than $5.52 \times 10^{-7} \mathrm{~m}$

Show Answer

Correct answer: (4)

Solution:

The Einstein’s photoelectric equation is given by $\mathrm{h} \nu=\dfrac{1}{2} \mathrm{mv}^{2}+\omega _{0}$

When the electrons are just liberated $\mathrm{v}=0$ and the corresponding frequency is

$$ \nu=\dfrac{\omega}{\mathrm{h}}=\dfrac{2.24 \times 1.6 \times 10^{-19}}{6.6 \times 10^{-34}} \mathrm{~Hz}=5.43 \times 10^{14} \mathrm{~Hz} $$

Also $\lambda=\dfrac{\mathrm{c}}{\nu}=\dfrac{3 \times 10^{8}}{5.43 \times 10^{14}}=5.52 \times 10^{-7} \mathrm{~m}$

Hence wavelengths shorter than $5.52 \times 10^{-7} \mathrm{~m}$ can cause the emission of photoelectrons from potassium. Hence option(1) is correct

Difficult

Photoelectricity

24. A 100 watt light bulb giving monochromatic light of wavelength $6000 \AA$ is placed at the centre of a spherical chamber of radius $0.20 \mathrm{~m}$. It is given that only $50 \%$ energy supplied to the bulb is converted into energy. Assuming that the surface of the chamber is perfectly absorbing, the number of photons per second (average) arriving at the surface of spherical chamber is

(1) $1.51 \times 10^{20}$

(2) $0.15 \times 10^{20}$

(3) $15 \times 10^{23}$

(4) $15 \times 10^{18}$

Show Answer

Correct answer: (1)

Solution:

Energy of each photon $=\dfrac{\mathrm{hc}}{\lambda}=\dfrac{6.6 \times 10^{-34} \times 3 \times 10^{8}}{6 \times 10^{-7}}=3.3 \times 10^{-19} \mathrm{~J}$

Energy of light emitted by the bulb per second $\mathrm{E}$ is $=\dfrac{100 \times 50}{100}=50$ watt

Number of photons reaching the surface per second

$$ =\dfrac{\text { light energy incident per second }}{\text { energy of each photon }}=\dfrac{50 \mathrm{Js}^{-1}}{3.3 \times 10^{-19} \mathrm{~J}}=1.51 \times 10^{20} \mathrm{~s}^{-1} $$

Hence option(1) is correct

Difficult

Photoelectricity

25. An image of the sun is formed on the metal surface of a photocell and it produces a photoelectric current $I$. The lens forming the image is then replaced by another of the same diameter but only half the focal length. The photoelectric current in this case will be

(1) $\dfrac{\mathrm{I}}{2}$

(2) $\mathrm{I} / 12$

(3) $2 \mathrm{I}$

(4) $\mathrm{I}$

Show Answer

Correct answer: (4)

Solution:

The number of photoelectrons emitted from a metal surface is directly proportional to the intensity of light. When we replace the original lens with a lens of half the focal length but diameter of the lens remaining unchnaged, the intensity of light incident on metal surface remain unchanged and hence the value of the current will remain unchanged.

Hence option (4) is the correct answer.

Difficult

Photoelectricity

26. A caesium cell with a steady potential difference of 90 volt across it, is illuminated by a small light placed one meter away. When the same light is placed to two meter away, the electrons crossing the photo cell, will

(1) each carry one quarter of their previous energy

(2) each carry one quarter of their previous momentum

(3) are half as numerous

(4) one quarter as numerous

Show Answer

Correct answer: (4)

Solution:

Since the intensity of light varies inversely as the square of the distance; increasing the distance twice of the previous value the intensity of light incident on photocell will be reduced by a factor of 4 . Now the number of electrons emitted from a photo surface is directly proportional to the intensity of light, the number of photo electrons emitted will decrease by a factor of 4 . Hence they will be one quarter as numerous.

Hence option (4) is the correct answer.

Difficult

Photoelectricity

27. A monochromatic light of wavelength $\lambda$ is incident on an isolated metallic sphere of radius a. The threshold wavelength is $\lambda _{0}$ which is larger than $\lambda$. Before the emission of photoelectrons stops the number of photoelectrons emitted are ( $\mathrm{V}$ is the stoping potential)

(1) $\dfrac{\text { ahc }}{4 \pi \varepsilon _{0} \mathrm{e}^{2}}\left(\dfrac{1}{\lambda}-\dfrac{1}{\lambda _{0}}\right)$

(2) $\dfrac{4 \pi \varepsilon _{0} \mathrm{aV}}{\mathrm{e}^{2}}\left(\dfrac{1}{\lambda}-\dfrac{1}{\lambda _{0}}\right)$

(3) $\dfrac{4 \pi \varepsilon _{0} \mathrm{ahc}}{\mathrm{e}^{2}}\left(\dfrac{1}{\lambda}-\dfrac{1}{\lambda _{0}}\right)$

(4) $\dfrac{\mathrm{e}^{2} \mathrm{ahc}}{4 \pi \varepsilon _{0}}\left(\dfrac{1}{\lambda}-\dfrac{1}{\lambda _{0}}\right)$

Show Answer

Correct answer: (3)

Solution:

The metallic sphere becomes positive charged as the electron are emitted from it (sphere is isolated). Hence the electrons are subjected to an extra force. If the potential of sphere is raised to $V$, the energy the electrons should possess (minimum) so that photoemission is possible is $\mathrm{eV}+\omega _{0}$. The emission of photoeelctron will stop when

$$ \dfrac{\mathrm{hc}}{\lambda}=\mathrm{eV}+\omega _{0}=\dfrac{\mathrm{hc}}{\lambda _{0}}+\mathrm{eV} $$

$$ \mathrm{V}=\dfrac{\mathrm{hc}}{\mathrm{e}}\left(\dfrac{1}{\lambda}-\dfrac{1}{\lambda _{0}}\right) $$

The charge on the sphere which will raise the sphere potential to $\mathrm{V}$ is $\mathrm{Q}=\left(4 \pi \varepsilon _{0} \mathrm{a}\right) \mathrm{V}$

Hence the number of electrons emitted will be $\mathrm{n}=\dfrac{\mathrm{Q}}{\mathrm{e}}=\dfrac{4 \pi \varepsilon _{0} \mathrm{aV}}{\mathrm{e}}$

or $\mathrm{n}=\dfrac{4 \pi \varepsilon _{0} \mathrm{ahc}}{\mathrm{e}^{2}}\left(\dfrac{1}{\lambda}-\dfrac{1}{\lambda _{0}}\right)$

Hence option (3) is the correct answer.

Average

deBroglie Waves

28. An electron accelerated by a p.d of $\mathrm{V}$ possess a deBroglie wavelength $\lambda$. If the accelerating potential is increased by a factor 4 . The deBroglie wavelength of the electron will

(1) remain unchanged

(2) becomes 4 times

(3) become double

(4) become halved

Show Answer

Correct answer: (4)

Solution:

When an electron is accelerated through a potential $\mathrm{V}$ its energy becomes $\mathrm{eV}$ and hence $\dfrac{1}{2} \mathrm{mv}^{2}=\mathrm{eV}$

$$ \begin{gathered} \mathrm{v}=\sqrt{\dfrac{2 \mathrm{eV}}{\mathrm{m}}} \\ \lambda=\dfrac{\mathrm{h}}{\mathrm{p}}=\dfrac{\mathrm{h}}{\mathrm{mv}}=\dfrac{\mathrm{h}}{\mathrm{m} \sqrt{\dfrac{2 \mathrm{eV}}{\mathrm{m}}}}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{meV}}} \end{gathered} $$

Thus $\lambda \propto \dfrac{1}{\sqrt{\mathrm{V}}}$

Hence whenever $\mathrm{V}$ is increased by a factor of $4 \lambda$ will get halved.

Hence option (4) is the correct answer.

Average

deBroglie Waves

29. Relative to the original photon the photon that emerges after a collision with an electron has

(1) more energy

(2) more momentum

(3) higher frequency

(4) longer wavelength

Show Answer

Correct answer: (4)

Solution:

When the photon collides with an electron it share the energy with electron according to laws of conservation of energy and momentum. Hence its energy and verocity consequently will decrease and therefore in accordance with relation $\lambda=\dfrac{\mathrm{h}}{\mathrm{mv}}$ it will have a longer wavelength.

Hence option (4) is correct.

Average

deBroglie Waves

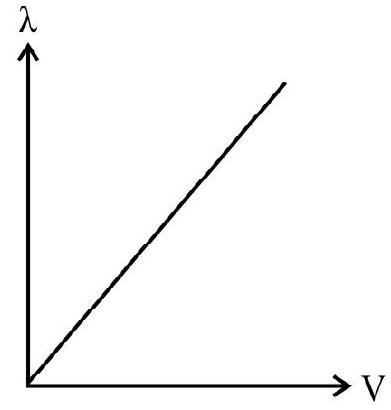
30. Which of the following graphs, represents the correct variation of the deBroglie wavelength with potential through which the electron is accelerated from rest?

(1) $\mathbf{A}$

(2) $\mathbf{B}$

(3) $\mathrm{C}$

(4) $\mathrm{D}$

$~$

(A)

$~$

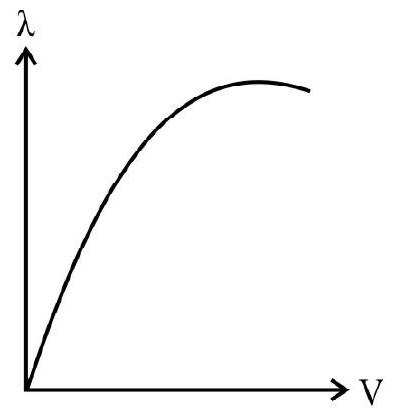
(B)

$~$

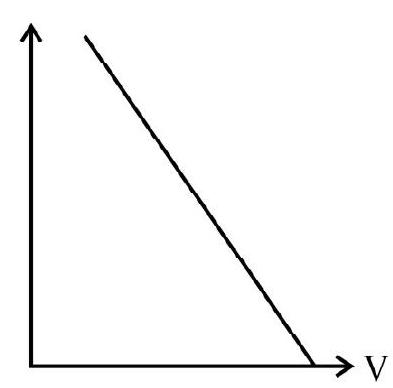
(C)

$~$

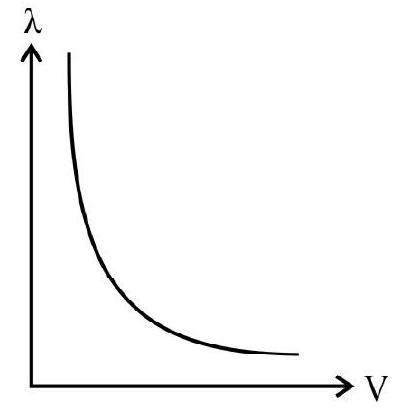
(D)

Show Answer

Correct answer: (4)

Solution:

We know that $\lambda=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{meV}}}$ or we can say that $\lambda \propto \dfrac{1}{\sqrt{\mathrm{V}}}$

Thus variation of $\lambda$ and $V$ will be a curve shown in option (4).

Hence option (4) is correct.

Average

deBroglie Waves

31. An electron, proton and an alpha particle all have the same kinetic energy. The deBroglie wavelength is

(1) shortest for the electron

(2) shortest for the proton

(3) shortest for the alpha particle

(4) are in the ratio of masses of electron proton and alpha particle

Show Answer

Correct answer: (3)

Solution:

The kinetic energy of a particle is $E _{K}=\dfrac{1}{2} m v^{2}=\dfrac{1}{2} \dfrac{(\mathrm{mv})^{2}}{m}=\dfrac{1}{2} \dfrac{p^{2}}{m}$

where $\mathrm{p}=\mathrm{mv}$, the momentum of the particle and is given by $\mathrm{p}=\sqrt{2 \mathrm{mE}}$

deBroglie wavelength $\lambda=\dfrac{\mathrm{h}}{\mathrm{p}}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{mE}}}$

So that we can conclude that $\lambda \propto \dfrac{1}{\sqrt{\mathrm{m}}}$

From the electron, proton and alpha particle, the alpha particle is the heaviest. Hence it will have the shortest deBroglie wavelength.

Hence option (3) is correct.

Average

deBroglie Waves

32. A particle is moving three time as fast as an electron. The ratio of the deBroglie wavelength of the particle to that of the electron is $1.813 \times 10^{-4}$. Indentify the particle

(1) decutron

(2) a particle

(3) a protonor a neutron

(4) particle cannot be identified from the given data

Show Answer

Correct answer: (3)

Solution:

Let $\lambda _{\mathrm{p}}$ and $\lambda _{\mathrm{e}}$ denote the deBroglie wavelength of the particle and electron

$$ \begin{aligned} & \lambda _{\mathrm{p}}=\dfrac{\mathrm{h}}{\mathrm{m} _{\mathrm{p}} \mathrm{v} _{\mathrm{p}}} \text { and } \lambda _{\mathrm{e}}=\dfrac{\mathrm{h}}{\mathrm{m} _{\mathrm{e}} \mathrm{v} _{\mathrm{e}}} \\ & \dfrac{\lambda _{\mathrm{p}}}{\lambda _{\mathrm{e}}}=\dfrac{\mathrm{m} _{\mathrm{e}} \mathrm{v} _{\mathrm{e}}}{\mathrm{m} _{\mathrm{p}} \mathrm{v} _{\mathrm{p}}}=\dfrac{\mathrm{m} _{\mathrm{e}}}{\mathrm{m} _{\mathrm{p}}} \times \dfrac{1}{3} \quad\left[\because \dfrac{\mathrm{v} _{\mathrm{e}}}{\mathrm{v} _{\mathrm{p}}}=\dfrac{1}{3} \text { (given) }\right] \\ & \mathrm{m} _{\mathrm{p}}=\dfrac{\mathrm{m} _{\mathrm{e}}}{3\left(\lambda _{\mathrm{p}} / \lambda _{\mathrm{e}}\right)}=\dfrac{9.11 \times 10^{-31}}{3 \times 1.813 \times^{-4}}=1.675 \times 10^{-27} \mathrm{Kg} \end{aligned} $$

This could be the mass of a proton or a neutron.

Hence option (3) is correct.

Difficult

deBroglie Waves

33. The energy of a proton is equal to the kinetic energy of a photon. The energy of the photon is E. Let $\lambda _{1}$ be deBroglie wavelength of proton and $\lambda _{2}$ the wavelength of photon. Then we have

(1) $\dfrac{\lambda _{1}}{\lambda _{2}}=\mathbf{E}^{0}$

(2) $\dfrac{\lambda _{1}}{\lambda _{2}}=\mathbf{E}^{-2}$

(3) $\dfrac{\lambda _{1}}{\lambda _{2}}=\mathbf{E}^{-1}$

(4) $\dfrac{\lambda _{1}}{\lambda _{2}}=\mathbf{E}^{1 / 2}$

Show Answer

Correct answer: (4)

Solution:

We will have $\lambda _{1}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{mE}}}$ and $\lambda _{2}=\dfrac{\mathrm{hc}}{\mathrm{E}}$

$\therefore \dfrac{\lambda _{1}}{\lambda _{2}}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{mE}}} / \dfrac{\mathrm{hc}}{\mathrm{E}}$

or $\dfrac{\lambda _{1}}{\lambda _{2}}=\mathrm{E}^{1 / 2}$

Hence option (4) is correct.

Difficult

deBroglie Waves

34. An electron of mass $m$ and charge $e$ initially at rest gets accelerated by a constant field $E$. The rate of change of a deBroglie wavelength of the electron with time is given by (relativistic variation of mass with time is to be ignored).

(1) $\dfrac{\text { cht }}{\mathrm{m}}$

(2) $\dfrac{\mathrm{h}}{\mathrm{eE}^{2}}$

(3) $\dfrac{\mathrm{h}}{\mathrm{eEt}}$

(4) $\dfrac{-\mathbf{m h}}{\mathbf{e E t}^{2}}$

Show Answer

Correct answer: (4)

Solution:

When an electrons is accelerated through a electric field we have $\mathbf{F}=\mathrm{eE}$

and the acceleration of the electron is given by $\mathrm{a}=\dfrac{\mathrm{e} \overline{\mathrm{E}}}{\mathrm{m}}$

Hence the velocity of the electron after it has remained in the field for a time $t$ is given $\mathrm{v}=\dfrac{\mathrm{eEt}}{\mathrm{m}}$

The wavelength of the deBroglie wave associated with this electron is $\lambda=\dfrac{\mathrm{h}}{\mathrm{mv}}=\dfrac{\mathrm{h}}{\mathrm{eEt}}$

$\therefore \dfrac{\mathrm{d} \lambda}{\mathrm{dt}}=\dfrac{-\mathrm{mh}}{\mathrm{eEt}^{2}}$

Hence option (4) is correct.

Difficult

deBroglie Waves

35. Which of the following statements is correct? (you are given the value of Boltzman’s constant)

(1) The deBroglie wavelength of thermal neutrons $\left(a^{\circ}{ }^{\circ} \mathrm{C}\right)$ is of the order of the distance between the atoms in a crystal

(2) The deBroglie wavelength of thermal neutrons is much larger than the distance between the atoms in a crystal

(3) The deBroglie wavelength of thermal neutrons is much smaller than the distance between the atoms in a crystal

(4) A beam of thermal neutrons cannot be used for investigating lattice structure by diffraction techniques

Show Answer

Correct answer: (1)

Solution:

The wavelength of neutrons of mass $m$ and moving with a velocity $v$ is $\lambda=\dfrac{\mathrm{h}}{\mathrm{mv}}$

Also $\mathrm{mv}=\sqrt{2 \mathrm{mE}}$ where $\mathrm{E}=\dfrac{1}{2} \mathrm{mv}^{2}$ is the kinetic energy of neutrons

Also $\mathrm{E}=\mathrm{kT}$ where $\mathrm{k}$ is the Boltzman’s constant and $\mathrm{T}$ is the absolute temperature

$\therefore \lambda=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{mE}}}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{mkT}}}$

Now $\mathrm{k} _{\mathrm{B}}=1.38 \times 10^{-23} \mathrm{JK}^{-1}$ and $\mathrm{T}=51^{0}$

Putting the values of the constants and solving we get $\lambda=1.7 \AA$

Thus the wavelength of thermal neutrons is of the order of few angstron units which is same as the order of distance beween the atoms in a crystal.

Hence option (1) is correct.

Difficult

deBroglie Waves

36. The deBroglie wavelength of electron in ground state of hydrogen atom is (given that the radius ofthe first orbit of hydrogen atom’s $0.53 \AA$ )

(1) $0.53 \AA$

(2) $3.33 \AA$

(3) $1.67 \AA$

(4) $3.33 \times 10^{-6} \mathrm{~m}$

Show Answer

Correct answer: (2)

Solution:

Since the electron is in ground state which implies that electron is in the first orbit of hydrogen atom with radius $0.53 \AA$. For first orbit the circumference of the orbit $2 \pi r$ is the deBroglie wavelength. Hence

$$ \lambda=2 \pi \mathrm{r}=2 \times 0.53 \times \pi=3.33 \AA $$

Hence option (2) is correct.

Average

Photoelectricity

37. The kinetic energy of electron is $E$ when the incident light has wavelength $\lambda$. To increase the kinetic energy to $2 \mathrm{E}$, the incident light must have wavelength

(1) $\dfrac{\mathrm{E} \lambda-\mathrm{hc}}{\mathrm{E} \lambda+\mathrm{hc}}$

(2) $\dfrac{h c \lambda}{E \lambda+h c}$

(3) $\dfrac{\mathrm{hc}}{\mathrm{E} \lambda+\mathrm{hc}}$

(4) $\dfrac{\mathrm{hc} \lambda}{\mathrm{E} \lambda-\mathrm{hc}}$

Show Answer

Correct answer: (2)

Solution:

We have $\mathrm{E}=\dfrac{\mathrm{hc}}{\lambda}-\omega _{0} \quad$ and $\quad 2 \mathrm{E}=\dfrac{\mathrm{hc}}{\lambda^{\prime}}-\omega _{0}$

$2 \mathrm{E}-\mathrm{E}=\dfrac{\mathrm{hc}}{\lambda^{\prime}}-\dfrac{\mathrm{hc}}{\lambda}$

or

$\mathrm{E}+\dfrac{\mathrm{hc}}{\lambda}=\dfrac{\mathrm{hc}}{\lambda^{\prime}}$

or $\quad \lambda^{\prime}=\dfrac{h c \lambda}{E \lambda+h c}$

Hence option (2) is correct.

Difficult

deBroglie Waves

38. An electron is moving will an initial velocity $V=V _{0} i$ and is in a magnetic field $B=B _{0} j$. Then its deBroglie wavelength

(1) remains constant

(2) increases as the electron moves round a circular path

(3) decreases as the electron moves round a circular path

(4) increases and decreases periodically

Show Answer

Correct answer: (1)

Solution:

When a particle moving in a direction perpendicular to the direction of the applied field the force acting on the electron is perpendicular to both the direction of moving particle and the field direction $[\mathbf{F}=-\operatorname{ce}(\mathbf{V} \times \mathbf{B})]$. Hence the magnitude of the velocity of the moving particle will not change and so its momentum remains constant. As $\lambda=\dfrac{\mathrm{h}}{\mathrm{p}}$, therefore $\lambda$ will remain constant.

Hence option (1) is correct.

Difficult

deBroglie Waves

39. A particle moves in a closed orbit across the origin due to a force which is directed towards the origin. The deBroglie wavelengh of the particle varies cyclically between two values $\lambda _{1}$ and $\lambda _{2}$ with $\lambda _{1}>\lambda _{2}$. Which of the following statement is correct?

(1) The particle could be moving in a circular path with origin as centre

(2) The particle could be moving in an elliptical orbit with origin as it focus

(3) When the particle is having deBroglie wavelength to $\lambda _{1}$ the particle is nearer the origin than when it value has $\lambda _{2}$ of its deBroglie wavelength

(4) The particle is at the same distance from the origin whether having deBroglie length $\lambda _{1} \text { or } \lambda _{2}$

Show Answer

Correct answer: (2)

Solution:

Since it is given that $\lambda _{1}$ and $\lambda _{2}$ are varying cyclically the particle would be moving in a elliptically orbit with origin as its one focus as shown

$$ \lambda _{1}=\dfrac{\mathrm{h}}{\mathrm{mv} _{1}} \text { and } \lambda _{2}=\dfrac{\mathrm{h}}{\mathrm{mv} _{2}} $$

Since $\lambda _{1}>\lambda _{2}$ therefore $\mathrm{v} _{2}>\mathrm{v} _{1}$

It can also be seen from the figure that $\mathrm{O}$ is close to $\mathrm{P}$ than $\mathrm{A}$.

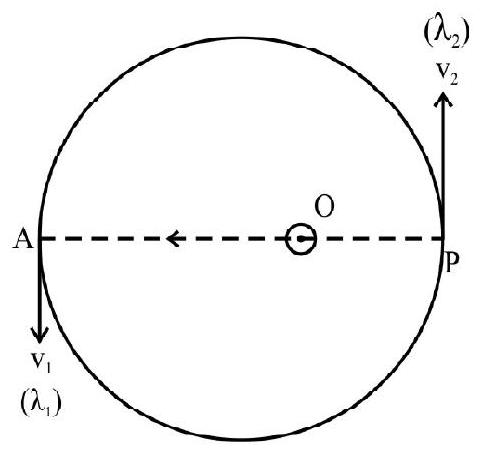
Hence option (2) is correct.

Difficult

deBroglie Waves

40. Which of the following statement is correct?

(1) The wave properties of matter can mainfest themselves with a moving particle of any size and mass

(2) The matter waves hypothesis contradicts the theory of relativily

(3) We associate a single well defined wavelength with a moving particle localized in a well defined region of space

(4) It is deBroglie wave group associated with a moving particle travelling with the same velocity as the moving particle

Show Answer

Correct answer: (4)

Solution:

The deBroglie wave associated with a moving particle cannot be a monochromatic wave as a wave train is infinite in extent and cannot be locarized in a well defined region of space. However a particle is well localized in space. According to detailed analysis, we associate a wave packet formed by the superposition of a number of waves situated on and around the central wavelength. The velocity of the component monochromatic waves making up the wave packet is known as PHASE velocity whereas the speed with which a wave packet of deBroglie waves travel is known as group velocity. It can be shown that it is the group velocity of wave packet with which a moving particle travel.

Hence option (4) is correct.

Average

Photoelectricity

41. The work function for aluminium surface is $4.2 \mathrm{eV}$. The cut off wavelength for photoelectric effect is

(1) $2955 \AA$

(2) $4200 \AA$

(3) $2000 \AA$

(4) $1000 \AA$

Show Answer

Correct answer: (1)

Solution:

The cut off wavelength is given by $\mathrm{h} \nu _{0}=\omega _{0}$

or $\dfrac{\mathrm{hc}}{\lambda _{0}}=\omega _{0}$

$\lambda _{0}=\dfrac{\mathrm{hc}}{\omega _{0}}=\dfrac{6.6 \times 10^{-34} \times 3 \times 10^{8}}{4.2 \times 1.6 \times 10^{-19}}=2955 \AA$

Hence option (1) is correct.

Average

Photoelectricity

42. A metal surface ejects electrons when green light is incident on it but no emission take place when yellow light is incident onit. The electrons will be emitted when the surface has

(1) Red light

(2) Blue light

(3) Heat rays

(4) Infrared light

Show Answer

Correct answer: (2)

Solution:

Green light ejects electrons but yellow does not. The only option out of given four only blue light can cause emission (VIGB YOUR).

Hence option (2) is correct.

Average

Photoelectricity

43. X-rays of frequency $v$ are used to iridate sodium and aluminium surfaces in two seperate experiments and the stopping potential determined

(1) The value of stopping potential is same for both sodium and aluminium surfaces

(2) The value of stopping potential is more for aluminium than for sodium

(3) The stopping potential is more for sodium than for aluminium

(4) The stopping potential also depends on the intensity of light used which is not specified in the question so, one cannot say which of the two metals will have a greater value for stopping potential

Show Answer

Correct answer: (3)

Solution:

From the relation $\mathrm{eV} _{\mathrm{S}}=\mathrm{h} \nu-\omega _{0}$

it is clear that the value of stopping potential for a given metal depend upon $\omega _{0}$ when a light of frequency $v$ is incident on a metal surface.

Now $\omega _{0}$ for sodium is 2.0 and $\omega _{0}$ for aluminum is 4.2

The metal surface having lower value of work function will have a larger value of stopping potential.

Hence option (3) is correct.

Average

Photoelectricity

44. The photoelectrons emitted from a metal surface are such that

(1) They all have same energy

(2) Their energies varies from zero to infinity

(3) Their energies vary from zero to a finite maximum

(4) Their energies vary randomly

Show Answer

Correct answer: (3)

Solution:

When incident photon liberates a electron not from the surface but inside the emitter the photoelectric equation becomes $\dfrac{1}{2} \mathrm{mv} _{\max }^{2}=\mathrm{hv}-\omega _{0}-\omega _{\mathrm{C}}$

where $\omega _{\mathrm{C}}$ is energy lost by the emitted electron in collision with lattice ions. When $\mathrm{w} _{\mathrm{C}}=0$ the emitted electron has the maximum energy and when $\mathrm{h} v$ is just equal to $\left(\omega _{0}+\omega _{\mathrm{C}}\right)$, the electron is emitted with zero energy.

Hence the option (3) is correct.

Average

deBroglie Waves

45. deBroglie wavelength of a photon is $2 \AA$. To have this wavelength associated with a proton, it must have a kinetic energy

(1) $2 \mathrm{eV}$

(2) $0.2 \mathrm{eV}$

(3) $0.02 \mathrm{eV}$

(4) 2 Joules

Show Answer

Correct answer: (3)

Solution:

From deBroglie relation we have $\lambda=\dfrac{\mathrm{h}}{\mathrm{m v}}$ or $\quad \mathrm{v}=\dfrac{\mathrm{h}}{\mathrm{m \lambda}}$

Now K.E $=\dfrac{1}{2} \mathrm{mv}^{2}=\dfrac{1}{2} \mathrm{~m}\left(\dfrac{\mathrm{h}}{\mathrm{m} \lambda}\right)^{2}$

Thus K.E $=\dfrac{1}{2}\left(\dfrac{\mathrm{hm}^{2}}{\mathrm{~m} \lambda}\right)^{2}=\dfrac{1}{2}\left(\dfrac{\mathrm{hm}}{\lambda}\right)^{2}$

Subsituting the values of $h$ and $\lambda$ we have

K. $\mathrm{E}=0.02 \mathrm{eV}$

Hence option (3) is correct.

Difficult

deBroglie Waves

46. X rays of wavelength $0.82 \AA$ are incident of a metal plate. The photoelectrons emitted from the metal surface will have a wavelength (neglect the work function of the metal)

(1) $0.01 \AA$

(2) $0.01 \times 10^{7} \mathrm{~m} / \mathrm{s}$

(3) $0.1012 \AA$

(4) $0.82 \AA$

Show Answer

Correct answer: (3)

Solution:

Frequency of incident $\mathrm{X}$ rays $v=\dfrac{\mathrm{c}}{\lambda} \quad \therefore \nu=\dfrac{3 \times 10^{10}}{0.82 \times 10^{-8}}$

Energy of emitted electron $=\mathrm{h} \nu=6.6 \times 10^{-34} \times \dfrac{3 \times 10^{10}}{0.82 \times 10^{-8}}$

Now $\dfrac{1}{2} \mathrm{mv}^{2}=\mathrm{E}$ or $\mathrm{mv}^{2}=2 \mathrm{E}$ or $\mathrm{m}^{2} \mathrm{v}^{2}=2 \mathrm{mE}$

$\mathrm{mv}=\sqrt{2 \mathrm{mE}}=\sqrt{2 \times 9.1 \times 10^{-31} \times \dfrac{6.6 \times 10^{-34} \times 3 \times 10^{10}}{0.82 \times 10^{-8}}}$

$\mathrm{mv}=\sqrt{6.6 \times 7.08 \times 9.1 \times 10^{-34}}$

$\lambda=\dfrac{\mathrm{h}}{\mathrm{mv}}=\dfrac{6.6 \times 10^{-34}}{\sqrt{6.6 \times 7.08 \times 9.1}} \times 10^{-34}$

$=0.1012 \AA$

Hence option(3) is correct

Difficult

deBroglie Waves

47. The deBroglie wavelength at which the relevastic correction becomes important for an electron is

(1) $10^{-6} \mathrm{~m}$

(2) $10^{-8} \mathrm{~m}$

(3) $10^{-10} \mathrm{~m}$

(4) $10^{-13} \mathrm{~m}$

Show Answer

Correct answer: (4)

Solution:

Since $\lambda=\dfrac{\mathrm{h}}{\mathrm{mv}} \quad \therefore \quad \mathrm{v}=\dfrac{\mathrm{h}}{\mathrm{m} \lambda}$

when $\lambda=10^{-6} \mathrm{~m}$ then $\mathrm{v}=\dfrac{6.6 \times 10^{-34}}{9.1 \times 10^{-31} \times 10^{-6}}=10^{3} \mathrm{~m} / \mathrm{s}$

when $\lambda=10^{-8} \mathrm{~m}$ then $\mathrm{v}=\dfrac{6.6 \times 10^{-34}}{9.1 \times 10^{-31} \times 10^{-8}}=10^{5} \mathrm{~m} / \mathrm{s}$

when $\lambda=10^{-10} \mathrm{~m}$ then $\mathrm{v}=\dfrac{6.6 \times 10^{-34}}{9.1 \times 10^{-31} \times 10^{-10}}=10^{7} \mathrm{~m} / \mathrm{s}$

when $\lambda=10^{-13} \mathrm{~m}$ then $\mathrm{v}=\dfrac{6.6 \times 10^{-34}}{9.1 \times 10^{-31} \times 10^{-13}}=10^{10} \mathrm{~m} / \mathrm{s}$

As in option (4), we find that when a electron has a wavelength of $10^{-13} \mathrm{~m}$ then the velocity with which electron has to move is $10^{10} \mathrm{~m} / \mathrm{s}$ which is greater than velocity of light. Hence relevestic correction is required in option (4).

Hence option(4) is correct

Average

Davisson and Germer Experiment

48. If a strong diffraction peak is observed when electrons are incident at an angle $\theta$ from the normal to a crystal, with a lattice distance $d$ between its the planes, the deBroglie length of electron is obtained from the relation

(1) $2 \mathrm{d} \sin \theta=\mathrm{n} \lambda$

(2) $\mathbf{d} \sin \theta=\mathrm{n} \lambda$

(3) $2 \mathrm{d} \cos \theta=\mathrm{n} \lambda$

(4) $2 \mathrm{d} \sin \theta=(\mathrm{n}+1) \lambda$

Show Answer

Correct answer: (1)

Solution:

The option (1) is based on Bragg’s law of diffraction from a crystal planes on the basis which $\lambda$ is calculated from Davisson’s and Germer’s experiment.

Hence option (1) is correct

Difficult

Davisson and Germer Experiment

49. The first order Bragg maximum of electron diffraction in a nickel crystal $(d=0.9086 \AA)$ occured at a glancing agnle of $65^{\circ}$. The velocity of the electrons undergoing diffraction is

(1) $4.3 \times 10^{6} \mathrm{~m} / \mathrm{s}$

(2) $2.15 \times 10^{6} \mathrm{~m} / \mathrm{s}$

(3) $4.3 \times 10^{3} \mathrm{~m} / \mathrm{s}$

(4) $2.15 \times 10^{7} \mathrm{~m} / \mathrm{s}$

Show Answer

Correct answer: (1)

Solution:

From Bragg’s law we have $2 \mathrm{~d} \sin \theta=\mathrm{n} \lambda$

or $2 \times 0.9086 \times \sin 65^{\circ}=\lambda$

or $\quad \lambda=1.8171 \times 0.9063=1.65 \AA$

Also from deBroglie’s relation $\mathrm{v}=\dfrac{\mathrm{h}}{\mathrm{m} \lambda}$

$$ \mathrm{v}=\dfrac{6.6 \times 10^{-34}}{9.1 \times 10^{-31} \times 1.65 \times 10^{-10}}=4.3 \times 10^{6} \mathrm{~m} / \mathrm{s} $$

Hence option (1) is correct

Difficult

Davisson and Germer Experiment

50. In a Davisson and Germer experiment it was observed that when a beam of $54 \mathrm{~eV}$ electron was diffracted by the $(1,1,1)$ planes of nickel crystal, (having $d=0.91 \AA$ ) a sharp maximum occured at an angle of incidence and scattering (relative to this family of Bragg planes) of $65^{\circ}$. The deBroglie wavelength $\lambda$ obtained from these observations and calculated by relation $\lambda=\dfrac{\mathbf{h}}{\mathbf{p}}$ are given by

(1) $1.65 \AA$ and $1.65 \AA$

(2) $1.65 \AA$ and $1.66 \AA$

(3) $1.67 \AA$ and $1.65 \AA$

(4) $1.65 \AA$ and $1.67 \AA$

Show Answer

Correct answer: (2)

Solution:

From Bragg’s relation $2 \mathrm{~d} \sin \theta=\lambda$

$$ \lambda=2 \times 0.91 \sin 65^{\circ}=1.65 \AA $$

From deBroglie relation

$$ \lambda=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{mE}}}=\dfrac{6.627 \times 10^{-34}}{\left[2 \times 9.1 \times 10^{-34} \times 54 \times 1.6 \times 10^{-19}\right]^{1 / 2}}=1.66 \AA $$

Hence option (2) is correct.

Difficult

Threshoold Frequency

51. For a constant frequency of the incident light, the graph between frequency $(v)$ of the incident light, and the magnitude $\left(V _{s}\right)$, of the stopping potential, for metal $A$, is as shown. Light of frequency ( $n v)(n>1)$, is now made to fall, one by one, on metal $A$ and another metal $B$. The magnitude of stopping potential, for this frequency for metal $B$, equal $V _{0}$. The (corresponding) magnitude of the stopping potential, for metal $A$, and the threshold frequency, for metal B, are equal, respectively, to

(1) $\left[(\mathrm{n}-1) \dfrac{\mathrm{h v _{0}}}{\mathrm{e}}\right] \text { and }\left[(\mathrm{n}-1) \mathrm{v} _{0}-\dfrac{\mathrm{e V} _{0}}{\mathrm{h}}\right]$

(2) $\left[(\mathrm{n}-1) \dfrac{\mathrm{h v _{0}}}{\mathrm{e}}\right] \text { and }\left[\mathrm{nv}_0-\dfrac{\mathrm{e V}_0}{\mathrm{h}}\right]$

(3) $\left[\mathrm{n} \dfrac{\mathrm{hv}}{\mathrm{e}}\right]$ and $\left[\mathrm{nv} \mathbf{v} _{0}-\dfrac{\mathrm{eV}}{\mathbf{h}}\right]$

(4) $\left[\mathrm{n} \dfrac{\mathrm{h} \mathbf{v} _{0}}{\mathrm{e}}\right]$ and $\left[(\mathrm{n}-1) \mathrm{v} _{0}-\dfrac{\mathrm{eV}}{\mathrm{h}}\right]$

Show Answer

Correct answer: (2)

Solution:

From the graph for metal $\mathrm{A}$, we see that its threhold frequency equals $v _{0}$. Hence when light of frequency $\mathrm{n} \mathrm{v} _{0}$ falls on it, the maximumenergy, of the emitted electrons, would equal $\left(\mathrm{h}(\mathrm{n}-1) \mathrm{v} _{0}\right)$. The corresponding magnitude, of the stopping potential would be $\left[\dfrac{(\mathrm{n}-1) \mathrm{h} \mathrm{v} _{0}}{\mathrm{e}}\right]$.

For metal $B$, the stopping potential being $\mathrm{V} _{0}$, the work function of this metal would equal $\left(\mathrm{n.h} \mathrm{v} _{0}-\mathrm{e V} _{0}\right)$. This implies that the threshold frequency, for this metal would be $\dfrac{\left(\mathrm{nh} \mathrm{v} _{0}-\mathrm{eV} _{0}\right)}{\mathrm{h}}=\left(\mathrm{n} \mathrm{v} _{0}-\dfrac{\mathrm{eV}}{\mathrm{h}}\right)$.

Hence option(2) is correct

Average

Einstein’s Photoelectric Equation

52. Lights, of frequencies $v _{1 \mathrm{i}}$ and $v _{2 \mathrm{i}}(i=1,2,3, \ldots . . n)$ are made to fall, one by one, on a given photosensitive surface. The corresponding magnitudes, of the stopping potential in the two cases, $\operatorname{are} \mathrm{V} _{1 \mathrm{i}}$ and $\mathrm{V} _{2 \mathrm{i}}(\mathrm{i}=1,2,3, \ldots . . \mathrm{n})$ respectively. Keeping the difference $\left(v _{2 \mathrm{i}}-v _{1 \mathrm{i}}\right)$ as constant $(=\Delta v)$, a graph is plotted between $V _{2 \mathrm{i}}$ (on the $y$-axis) and $V _{1 \mathrm{i}}$ (on the $x$-axis). The slope of this graph, and its intercept, on the $y$-axis, would then equal, respectively

(1) 1 and $\dfrac{\mathrm{h}(\Delta v)}{\mathrm{e}}$

(2) 1 and $\dfrac{\mathrm{e}(\Delta v)}{\mathrm{h}}$

(3) $\dfrac{\mathrm{h}}{\mathrm{e}}$ and $\dfrac{\mathbf{h}(\Delta \mathbf{v})}{\mathrm{e}}$

(4) $\dfrac{\mathrm{h}}{\mathrm{e}}$ and $\dfrac{\mathrm{e}(\Delta \boldsymbol{v})}{\mathrm{h}}$

Show Answer

Correct answer: (1)

Solution:

Let $\mathrm{W}$ be the work function of the given photosensitive surface. We than have, fromEinstein’s photoelectric equation,

$$ \begin{aligned} & \quad \mathrm{e} V _{1 \mathrm{i}}=\mathrm{h} \nu _{1 \mathrm{i}}-\mathrm{W} \text { and } e \mathrm{~V} _{2 \mathrm{i}}=\mathrm{h} \nu _{2 \mathrm{i}}-\mathrm{W} \\ \therefore & \mathrm{eV} _{2 \mathrm{i}}-\mathrm{eV} _{\mathrm{i} 2}=\mathrm{h}\left(\mathrm{\nu} _{2 \mathrm{i}}-\nu _{1 \mathrm{i}}\right) \\ \therefore & \mathrm{V} _{2 \mathrm{i}}=\mathrm{V} _{1 \mathrm{i}}+\dfrac{\mathrm{h}}{\mathrm{e}} \Delta \nu \end{aligned} $$

Comparing this with the standard equation, $\mathrm{y}=\mathrm{m} x+\mathrm{c}$,

we find that the slope, and intercept, of the given graph, are

1 and $\left(\dfrac{\mathrm{h}}{\mathrm{e}}\right) \Delta \nu$, respectively

Hence option(1) is correct

Difficult

Combination of Concepts of Particle Nature of Radiation and Wave Nature of Particles

53. The photons, of light of wavelength $\lambda$, have the same momentum as that of electrons (mass $=9.31 \times 10^{-31} \mathrm{~kg}$ ) moving with a speed of $1.6 \times 10^{3} \mathrm{~m} / \mathrm{s}$. If this light (of wavelength $\lambda$ ) is made to fall on a photosensitive surface of work function $1.793 \mathrm{eV}$, the ‘stopping potential’, needed to make the ‘photo current’ zero, is

(1) $2.5 \mathrm{~V}$

(2) $2.0 \mathrm{~V}$

(3) $1.5 \mathrm{~V}$

(4) $1.0 \mathrm{~V}$

Show Answer

Correct answer: (4)

Solution:

Momentum of photon $=\mathrm{h} / \lambda=$ momentum of electron $=\mathrm{mv}$

$\therefore \quad \lambda=\dfrac{\mathrm{h}}{\mathrm{mv}}$

$\therefore$ Energy of the photon $=\dfrac{\mathrm{hc}}{\lambda}=\dfrac{\mathrm{hc} . \mathrm{mv}}{\mathrm{h}}=\mathrm{c} . \mathrm{mv}=\dfrac{3 \times 10^{8} \times 9.31 \times 10^{-31} \times 1.6 \times 10^{3}}{1.6 \times 10^{-19}} \mathrm{eV}$

$$ =27.93 \times 10^{-1} \mathrm{eV}=2.793 \mathrm{eV} $$

Work function $=1.793 \mathrm{eV}$

$\therefore$ Energy of the most energatic emitted photoelectric $=(2.793-1.793) \mathrm{eV}=1 \mathrm{eV}$

$\therefore$ Stopping potential $=1 \mathrm{~V}$

Hence option (4) is correct

Average

Using de-Broglie Reltion for Photons

54. A beam of photons of light of wavelength, $\lambda$ strike a surface at an anle of incidence $\theta$ Assuming all the incident photons ( $N$ photons per second) to get reflected back in a perfect elastic way, the force exerted, by the incident light beam, on the surface, is

(1) $\left(2 \dfrac{\mathrm{Nh}}{\lambda} \cos \theta\right)$; directed normally downwords

(2) $\left(2 \dfrac{\mathrm{Nh}}{\lambda} \sin \theta\right)$; directed normally downwords

(3) $\left(2 \dfrac{\mathrm{Nh}}{\lambda} \sin \theta\right)$; directed normally upwords

(4) $\left(2 \dfrac{\mathrm{Nh}}{\lambda} \cos \theta\right)$; directed normally upwords

Show Answer

Correct answer: (3)

Solution:

The momentum of each photon, $\mathrm{p}=\mathrm{p}=\dfrac{\mathrm{h}}{\lambda}$

Its change in momentum, after getting reflected back, is

$$ \begin{aligned} & \Delta \mathbf{p}=(p \cos \theta \hat{\mathrm{i}}+\mathrm{p} \sin \theta \hat{\mathrm{j}})-(\mathrm{p} \cos \theta \hat{\mathrm{i}}-\mathrm{p} \sin \theta \hat{\mathrm{j}}) \\ & =2 \mathrm{p} \sin \theta \hat{\mathrm{j}}=\dfrac{2 \mathrm{~h}}{\lambda} \sin \theta \hat{\mathrm{j}} \end{aligned} $$

Rate of change of momentum $=$ Total change in momentum of all photons, incident on the surface, in one second $=\mathrm{N} \Delta \mathbf{p}=\dfrac{2 \mathrm{Nh}}{\lambda} \sin \theta \hat{\mathrm{j}}$

$\therefore$ Force exerted $=$ Rate of change of momentum $=\dfrac{2 \mathrm{Nh}}{\lambda} \sin \theta \hat{\mathrm{j}}$

$~$ $=\left(\dfrac{2 \mathrm{Nh}}{\lambda} \sin \theta\right)$, directed normally upwards

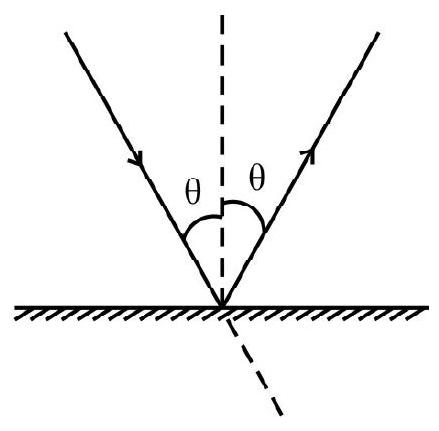
Hence option (3) is correct

Average

Einstein’s Photoelectric Equation

55. When light, of wave length $\lambda _{1}$, in incident on a given photosensitive surface, the ‘stopping potential’, for the emitted photoelectrons, equals $V _{1}$. On changing the wave length of incident light to $\lambda _{2}$, the new stopping potential, $V _{2}$, equals $2 V _{1}$. We would then have

(1) $\dfrac{\lambda _{2}}{\lambda _{1}}=\dfrac{1}{2}$

(2) $\dfrac{\lambda _{2}}{\lambda _{1}}=\dfrac{\left(\mathrm{hc}-\mathrm{e} \lambda _{1} \mathrm{~V} _{1}\right)}{\mathrm{hc}}$

(3) $\dfrac{\lambda _{2}}{\lambda _{1}}=\dfrac{\mathrm{hc}}{\left(\mathrm{hc}+\mathrm{e} \lambda _{1} \mathrm{~V} _{1}\right)}$

(4) $\dfrac{\lambda _{2}}{\lambda _{1}}=\dfrac{\left(h c-e \lambda _{1} V _{1}\right)}{\left(h c+e \lambda _{1} V _{1}\right)}$

Show Answer

Correct answer: (3)

Solution:

We have, as per Einstein’s photoelectric equation: $\dfrac{\mathrm{hc}}{\lambda _{1}}=\mathrm{K} _{1}+\mathrm{W}$

$\therefore \quad \mathrm{K} _{1}\left(=\mathrm{eV} _{1}\right)=\dfrac{\mathrm{hc}}{\lambda _{1}}-\mathrm{W}$

$\therefore \mathrm{W}\left(\dfrac{\mathrm{hc}}{\lambda _{1}}\right)-\mathrm{K} _{1} \quad$ or $\quad \mathrm{W}=\left(\dfrac{\mathrm{hc}}{\lambda _{1}}-\mathrm{eV} _{1}\right)$

Also $\dfrac{\mathrm{hc}}{\lambda _{2}}=\mathrm{K} _{2}+\mathrm{W}=\mathrm{K} _{2}+\left(\dfrac{\mathrm{hc}}{\lambda _{1}}-\mathrm{K} _{1}\right)=\left(\mathrm{K} _{2}-\mathrm{K} _{1}\right)+\dfrac{\mathrm{hc}}{\lambda _{1}}=\mathrm{e}\left(\mathrm{V} _{2}-\mathrm{V} _{1}\right)+\dfrac{\mathrm{hc}}{\lambda _{1}}$

$\therefore\left(\mathrm{V} _{2}-\mathrm{V} _{1}\right)=\dfrac{\mathrm{hc}}{\mathrm{e}}\left(\dfrac{1}{\lambda _{2}}-\dfrac{1}{\lambda _{1}}\right)$

Since $\mathrm{V} _{2}=2 \mathrm{~V} _{1}$, we have

$\mathrm{V} _{1} \times \dfrac{\mathrm{e}}{\mathrm{hc}}+\dfrac{1}{\lambda _{1}}=\dfrac{1}{\lambda _{2}}$

$\therefore \quad \lambda _{2}=\dfrac{\mathrm{hc} \lambda _{1}}{\left(\mathrm{e} \lambda _{1} \mathrm{~V} _{1}+\mathrm{hc}\right)}$

$\therefore \dfrac{\lambda _{2}}{\lambda _{1}}=\dfrac{\mathrm{hc}}{\mathrm{hc}+\mathrm{e} \lambda _{1} \mathrm{~V} _{1}}$

Hence option (3) is correct

Average

Einestein’s Photoelectric Equation

56. When light, of frequency $v _{1}$, is incident on a given photosensitive surface, the ‘stopping potential’ needed, equals $V _{1}$. On changing the frequency of incident light to $3 v _{1}$, the new value, of the stopping potential needed, equals $V _{2}$. We would then have

(1) $\mathbf{V} _{2}=3 \mathrm{~V} _{1}$

(2) $V _{2}=\left(V _{1}+\dfrac{2 \mathrm{h}}{e} \mathrm{v} _{1}\right)$

(3) $\mathbf{V} _{2}=\left(\mathbf{V} _{1}+\dfrac{3 \mathbf{h}}{\mathrm{e}} \mathbf{v} _{1}\right)$

(4) $\mathbf{V} _{2}=\mathrm{V} _{1}+\dfrac{4 \mathrm{~h}}{\mathrm{e}} \mathbf{v} _{1}$

Show Answer

Correct answer: (2)

Solution:

We have, as per Einstein’s photoelectric equation,

$$ \begin{array}{ll} & \mathrm{h} v _{1}=\mathrm{eV} _{1}+\mathrm{W} \text { and } \mathrm{h} v _{2}=\mathrm{eV} _{2}+\mathrm{W} \\ \therefore \quad & \mathrm{e}\left(\mathrm{V} _{2}-\mathrm{V} _{1}\right)=\mathrm{h}\left(\mathrm{v} _{2}-\mathrm{v} _{1}\right)=\mathrm{h} \cdot\left(2 \mathrm{v} _{1}\right) \\ \therefore & \mathrm{V} _{2}-\mathrm{V} _{1}=\dfrac{2 \mathrm{~h}}{\mathrm{e}} \mathrm{v} _{1} \\ \text { or } & \mathrm{V} _{2}=\left(\mathrm{V} _{1}+\dfrac{2 \mathrm{~h}}{\mathrm{e}} \mathrm{v} _{1}\right) \end{array} $$

Hence option(2) is correct

Average

Graph between ‘v’ and ‘V’

57. The intercepts, on the ’ $\nu$ ’ and ’ $V$ ’ axes, of the graph [between ‘frequency of incident radiation’ and ‘corresponding stopping potential’, (for a given photosensitive sufface)], equal, respectively,

(1) (The threshold frequency) and $\left(\dfrac{-1}{e}\right)$ times the work function), of the given photosensitive surface

(2) (The threshold frequency) and (’ $e$ ‘) times the work function), of the given photosensitive surface (Incorrect)

(3) (h times the threshold frequency) and (e) times the work function), of the given photosensitive surface

(4) $\left(\dfrac{1}{h}\right)$ times the threshold frequency) and $\left(\dfrac{-1}{e}\right)$ times the work function), of the given photosensitive surface

Show Answer

Correct answer: (1)

Solution:

We have, from Einstein’s photoelectric equation, $\mathrm{h} \nu=\mathrm{eV}+\mathrm{W}$

Intercept $\left(v _{0}\right)$ on the $v$ axis, (For $\mathrm{V}=0$ ), is given by $\mathrm{h} v _{0}=0+\mathrm{W}$

The corresponding frequency, therefore, equals $v _{0}$, the threshold frequency.

Intercept $\left(\mathrm{V} _{0}\right)$ on the $\mathrm{V}$-axis (for $v=0$ ), is given by $0=\mathrm{eV} _{0}+\mathrm{W}$

$\therefore \mathrm{V} _{0}=\left(-\dfrac{1}{\mathrm{e}} \mathrm{W}\right)$

Hence option(1) is correct

Difficult

‘Stopping Potential’

58. The path of an electron beam, moving in a uniform (and normal) magnetic field of $10^{-4} \mathrm{~T}$, gets bent into a circle of radius $18.2 \mathrm{~cm}$. A beam of light, having photons of energy $(1 / 10)^{\text {th }}$ of the kinetic energy of the above beam of electrons, is incident on a photosensitive surface of work function $1.912 \mathrm{eV}$. The ‘stopping potential’, needed to stop the emission of photoelectrons, would then equal

(1) $0.5 \mathrm{~V}$

(2) $1.0 \mathrm{~V}$

(3) $1.5 \mathrm{~V}$

(4) $2.0 \mathrm{~V}$

Show Answer

Correct answer: (2)

Solution:

For the electron beam, moving in a normal magnetic field, we have $\dfrac{\mathrm{mv}^{2}}{\mathrm{r}}=\mathrm{evB}$

$\therefore \mathrm{r}=\dfrac{\mathrm{mv}}{\mathrm{eB}}$

$\therefore$ K.E. of the electron beam $=\dfrac{1}{2} \mathrm{mv}^{2}=\dfrac{(\mathrm{mv})^{2}}{2 \mathrm{~m}}=\dfrac{(\mathrm{reB})^{2}}{2 \mathrm{~m}}$

$\therefore$ Energy of the incident photons $=\dfrac{1}{10} \dfrac{(\mathrm{reB})^{2}}{2 \mathrm{~m}}$

$$ =\dfrac{1}{20} \times \dfrac{18.2 \times 18.2 \times 10^{-4} \times\left(1.6 \times 10^{-19}\right)^{2} \times 10^{-8}}{9.1 \times 10^{-31}} \mathrm{~J}=29.12 \times 10^{-1} \mathrm{eV}=2.912 \mathrm{eV} $$

Work function $=1.912 \mathrm{eV}$

$\therefore$ Max. kinetic energy of emitted photoelectron $=1 \mathrm{eV}$

$\therefore$ ‘stopping’ potential $=1 \mathrm{~V}$

Hence option(2) is correct

Difficult

deBroglie Reltion + ‘Stopping Potential’

59. The wave length, of a monochromatic beam of light, is $n$ times the deBroglie wave length of a beam of electrons, accelerated through a p.d of $\mathrm{V}$ volts. When this light beam is incident on a photosensitive surface, (whose work function is 0.75 times the energy of a photon of the incident light), the ‘stopping potential’, for the emitted photoelectrons, equals $V _{s}$.

The slope of the graph, between $V _{s}$ (on the $y$-axis and $\sqrt{V}$, (on the $x$-axis), would equal

(1) $\left(\dfrac{\mathbf{m ~ c}^{2}}{8 \mathbf{n}^{2}}\right)^{1 / 2}$

(2) $\left(\dfrac{8 \mathrm{n}^2 \mathrm{e}^2}{\mathrm{m c}^2}\right)^{1 / 2}$

(3) $\left(\dfrac{16 \mathrm{mc}^{2}}{\mathrm{e}^{2} \mathrm{n}}\right)^{1 / 2}$

(4) $\left(\dfrac{\mathbf{n e}^{2}}{16 \mathrm{mc}^{2}}\right)^{1 / 2}$

Show Answer

Correct answer: (1)

Solution:

The deBroglie wavelength, $\lambda _{\mathrm{B}}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{meV}}}$

$\therefore$ Wavelength of light beam $=\lambda=\mathrm{n} \lambda _{\mathrm{B}}=\dfrac{\mathrm{nh}}{\sqrt{2 \mathrm{meV}}}$

$\therefore$ Energy of a photon $=\dfrac{\mathrm{hc}}{\lambda}=\dfrac{\mathrm{hc}}{\mathrm{nh}} \sqrt{2 \mathrm{meV}}=\dfrac{\mathrm{c} \sqrt{2 \mathrm{meV}}}{\mathrm{n}}$

$\therefore$ Work function $=0.75 \mathrm{c} \dfrac{\sqrt{2 \mathrm{meV}}}{\mathrm{n}}$

$\therefore$ Max. energy of the emitted photoelectrons $=0.25 \mathrm{c} \dfrac{\sqrt{2 \mathrm{meV}}}{\mathrm{n}}$

$\therefore$ Stopping potential, $\mathrm{V} _{\mathrm{S}}=0.25 \mathrm{c} \dfrac{\sqrt{2 \mathrm{meV}}}{\mathrm{n} \cdot \mathrm{e}}=\left(\sqrt{\dfrac{\mathrm{mc}^{2}}{8 \mathrm{n}^{2} \mathrm{e}}}\right) \cdot \sqrt{\mathrm{V}}$

$\therefore$ Slope of the required graph $=\left(\dfrac{\mathrm{mc}^{2}}{8 \mathrm{n}^{2} \mathrm{e}}\right)^{1 / 2}$

Hence option(1) is correct

Average

deBrogli Wavelength

60. The short wavelength limit of the $\mathbf{X}$-rays produced, through the ‘complete coversion’ of the energy of a beam of electrons, accelerated through a potential, $V$, is $0.4125 \AA$. Taking $\mathrm{h}=6.6 \times 10^{-34} \mathrm{~J}-\mathrm{s}$. The value of $\mathrm{V}$, and the deBroglie wavelength, associated with a beam of electrons, accelerated through a potential of $V$ volts, are (nearly) equal, respectively, to

(1) $30 \mathrm{kV}$ and $0.7 \AA$

(2) $30 \mathrm{kV}$ and $0.07 \AA$

(3) $3 \mathrm{kV}$ and $0.007 \mathrm{~nm}$

(4) $3 \mathrm{kV}$ and $0.7 \mathrm{~nm}$

Show Answer

Correct answer: (2)

Solution:

The energy of the accelerated beam of electrons $=\mathrm{eV}$. When this energy is completely converted into $\mathrm{X}$-rays of wavelength $0.4125 \AA$, we have

$$ \begin{aligned} & \mathrm{eV}=\dfrac{\mathrm{hc}}{0.4125 \times 10^{-10}} \\ \therefore \mathrm{V} & =\dfrac{6.6 \times 10^{-34} \times 3 \times 10^{8}}{0.4125 \times 10^{-10} \times 1.6 \times 10^{-19}}=30 \mathrm{keV} \end{aligned} $$

The corresponding deBroglie wavelength is $\lambda _{\mathrm{B}}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{meV}}}$

$$ =\dfrac{6.6 \times 10^{-34}}{\left(2 \times 9.1 \times 10^{-31} \times 1.6 \times 10^{-19} \times 30 \times 10^{3}\right)^{1 / 2}}=0.07 \AA $$

Hence option(2) is correct

Difficult

Photoelectric Emission and deBroglie Wavelength

61. A monochromatic beam of light, of wavelength $\lambda$, is incident on a photosensitive surface. The work function of the surface is $1 / n$ (where $n>1$ ) times the energy of a photon of the incident light. Let $\lambda _{\mathrm{B}}$ be the deBroglie wavelength, associated with the most energatic of the emitted photoelectrons. The slope of the graph, between $\lambda _{B}$ (on the y-axis) and $\sqrt{\lambda}$ (on the $x$-axis), would equal

(1) $\left(\dfrac{n h}{2(n-1) m c}\right)$

(2) $\left(\dfrac{n h}{2(n-1) m c}\right)^{1 / 2}$

(3) $\left(\dfrac{2(n-1) m^{2}}{n h}\right)$

(4) $\left(\dfrac{n h}{2(n-1) m c^{2}}\right)^{1 / 2}$

Show Answer

Correct answer: (2)

Solution:

Energy of a photon of the incident radiation $=\dfrac{\mathrm{hc}}{\lambda}$

Work function $=\dfrac{1}{\mathrm{n}} \dfrac{\mathrm{hc}}{\lambda}$

$\therefore$ Max. K.E. of the emitted photoelectrons $=\mathrm{K} _{\max }=\left(\dfrac{\mathrm{hc}}{\lambda}-\dfrac{1}{\mathrm{n}} \dfrac{\mathrm{hc}}{\lambda}\right)=\dfrac{\mathrm{hc}(\mathrm{n}-1)}{\mathrm{n} \lambda}$

Let $\lambda _{B}$ be the corresponding deBroglie wavelength

$\therefore \quad \lambda _{B}=\dfrac{h}{\sqrt{2 \mathrm{mK} _{\max }}}=\dfrac{\mathrm{h}(\mathrm{n} \lambda)^{1 / 2}}{[2 \mathrm{~m} \cdot \mathrm{hc}(\mathrm{n}-1)]^{1 / 2}}=\left[\dfrac{\mathrm{nh} \lambda}{2(\mathrm{n}-1) \mathrm{mc}}\right]^{1 / 2}=\left[\dfrac{\mathrm{nh}}{2(\mathrm{n}-1) \mathrm{mc}}\right]^{1 / 2}=\lambda^{1 / 2}$

$\therefore$ Slope of the required graph $=\left[\dfrac{\mathrm{nh}}{2(\mathrm{n}-1) \mathrm{mc}}\right]^{1 / 2}$

Hence option(2) is correct

Difficult

deBroglie Wavelength; Photon Energy

62. The resolving power, of an electron microscope (using on electron beam acelerated through a potential $\mathbf{V}$ ) is $\mathbf{n}$ times that of a given optical microscope. Given that the resolving power of (any) microscople is inversely proportional to the wavelength, (used by it) the energy of a photon, of the e.m. radiation, used in the given optical microscope, is

(1) $\left(\dfrac{\mathrm{n} \sqrt{\mathrm{eV}}}{2 \mathrm{mc}^{2}}\right)$

(2) $\left(\dfrac{\mathbf{m c}^{2} \mathrm{eV}}{2 \mathrm{n}}\right)^{1 / 2}$

(3) $\left(\dfrac{2 \mathrm{mc}^{2}}{\mathrm{n} \sqrt{\mathrm{eV}}}\right)$

(4) $\left(\dfrac{2 \mathbf{m c}^{2} \mathrm{eV}}{\mathbf{n}^{2}}\right)^{1 / 2}$

Show Answer

Correct answer: (4)

Solution:

The (deBrogli) wavelength, associated with the electron beam, in the electron microscope, is $\lambda _{\mathrm{B}}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{meV}}}$ The resolving power of the $\left(\propto\left(\dfrac{1}{\text { wavelength }}\right)\right)$ of the electron microscope being $n$ times that of the em waves (used in the optical microscope) the wavelength, $\lambda$, used in the optical microscope, is $\lambda=\mathrm{n} \lambda _{\mathrm{B}}$

$\therefore$ Energy of a photon $=\dfrac{\mathrm{hc}}{\lambda}=\dfrac{\mathrm{hc}}{\mathrm{n} \lambda _{\mathrm{B}}}$

$$ =\dfrac{\mathrm{hc}}{\mathrm{m}} \cdot \sqrt{\dfrac{2 \mathrm{meV}}{\mathrm{h}}}=\left(\dfrac{2 \mathrm{mc}^{2} \mathrm{eV}}{\mathrm{n}^{2}}\right)^{1 / 2} $$

Hence option(4) is correct

Difficult

deBroglie Wavelength and Energy of a Photon

63. The K.E. (K), of the electrons, having an associated deBroglie wavelength, $\lambda _{\mathrm{B}}$, is $1 / 2(n>1)$ times the energy of a photon of an e.m. radiation, of wavelength $\lambda$. The graph, that correctly depicts the relation between (appropriate functions), of $\lambda _{\mathrm{B}}$ and $\lambda$, is graph labelled as graph

(1) $\mathbf{A}$

(2) $\mathrm{B}$

(3) $\mathrm{C}$

(4) $\mathbf{D}$

Show Answer

Correct answer: (4)

Solution:

The deBroglie wavelength $\left(\lambda _{B}\right)$ is related to the kinetic energy $(\mathrm{K})$, of the electron beam, through the relation: $\lambda _{B}=\dfrac{h}{p}=\dfrac{h}{\sqrt{2 m K}}$

$\therefore \mathrm{K}=\left(\dfrac{\mathrm{h}^{2}}{\lambda _{\mathrm{B}}^{2}(2 \mathrm{~m})}\right)$

Energy (E) of the a photon of e.m. radiation, of wavelength, is given by $E=\dfrac{h c}{\lambda}$

Since $K=\dfrac{1}{n} E$ (given), we have $\dfrac{h^{2}}{\lambda _{B}^{2}(2 m)}=\dfrac{h c}{n \lambda}$

$\therefore \quad \lambda _{\mathrm{B}}^{2}=\left(\dfrac{\mathrm{nh}}{2 \mathrm{mc}}\right) \lambda$

The graph (D), is the only graph that correctly shows this relation between $\lambda _{B}^{2}$ and $\lambda$.

Hence option(4) is correct

Average

Threshold Wavelength, deBroglie Relation

64. The threshold wavelength of a given photosensitive suface is $\lambda _{0}$. When light of wavelength $\lambda\left(=\lambda _{0} / 2\right)$ is incident on this photosensitive surface, the ‘stopping potential’, needed to ‘stop’ the most energatic emitted photoelectrons, is $\mathbf{V}$.

If $\lambda _{B}$ denotes the deBroglie wavelength, associated with an electron, accelerated through a potential $V$, the ratio $\left(\dfrac{\lambda _{B}}{\sqrt{\lambda _{0}}}\right)$ equals

(1) $\left(\dfrac{2 \mathrm{eh}}{\mathrm{mc}}\right)^{1 / 2}$

(2) $\left(\dfrac{2 \mathrm{mc}}{\text { eh }}\right)^{1 / 2}$

(3) $\left(\dfrac{\mathbf{e h}}{2 \mathrm{mc}}\right)^{1 / 2}$

(4) $\left(\dfrac{\mathrm{mc}}{\mathbf{2 e h}}\right)^{1 / 2}$

Show Answer

Correct answer: (3)

Solution:

Energy of a photon of the incident light $=\dfrac{\mathrm{hc}}{\lambda}$

Work function $=$ Energy of a photon of light, of wavelength equal to the threshold wavelength $\left(\lambda _{0}\right)=\dfrac{\mathrm{hc}}{\lambda _{0}}$

$\therefore$ If V be the stopping potential, we have $\mathrm{eV}=\mathrm{hc}\left(\dfrac{1}{\lambda}-\dfrac{1}{\lambda _{0}}\right)=\dfrac{\mathrm{hc}\left(\lambda _{0}-\lambda\right)}{\lambda \lambda _{0}}$

$\therefore \mathrm{V}=\left(\dfrac{\mathrm{hc}}{\mathrm{e}} \dfrac{1}{\lambda _{0}}\right) \quad\left(\because \lambda=\dfrac{\lambda _{0}}{2}\right)$

The deBroglie wavelength, associated with an electron, accelerated through a potential $\mathrm{V}=\lambda _{\mathrm{B}}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{meV}}}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{me}}} \cdot\left(\dfrac{\mathrm{e} \lambda _{0}}{\mathrm{hc}}\right)^{1 / 2}=\left(\dfrac{\mathrm{he}}{2 \mathrm{mc}}\right)^{1 / 2} \lambda _{0}^{1 / 2}$

$\therefore \dfrac{\lambda _{\mathrm{B}}}{\sqrt{\lambda _{0}}}=\left(\dfrac{\mathrm{he}}{2 \mathrm{mc}}\right)^{1 / 2}$

Hence option (3) is correct

Average

deBroglie Relation + Photon Energy Relation

65. The deBroglie wavelength, associated with an electron, and the wavelength, associated with a $\gamma$-ray photon, are both equal to $1 \mathrm{pm}$. The ratio, of the energy of the $\gamma$-ray photon, to the kinetic energy, of the electron, is then euqal (nealry) to

(1) 0.82

(2) 1.64

(3) 8.2

(4) 16.4

Show Answer

Correct answer: (1)

Solution:

For the electron, $\lambda _{B}=\dfrac{h}{p}=\dfrac{h}{(2 m K)^{1 / 2}}$

$\therefore \mathrm{K}=\dfrac{\mathrm{h}^{2}}{2 \mathrm{~m} \lambda _{\mathrm{B}}^{2}}$

For the $\gamma$-ray photon, energy $=E=\dfrac{h c}{\lambda}$

$\therefore \dfrac{\mathrm{E}}{\mathrm{K}}=\dfrac{\mathrm{hc}}{\lambda} \times \dfrac{2 \mathrm{~m} \lambda _{\mathrm{B}}^{2}}{\mathrm{~h}^{2}}=\dfrac{2 \mathrm{mc} \lambda}{\mathrm{h}} \quad\left(\because \lambda _{\mathrm{B}}=\lambda\right)$

$$ =\dfrac{2 \times 9.1 \times 10^{-31} \times 3 \times 10^{8} \times 10^{-12}}{6.63 \times 10^{-34}}=0.82 \quad\left(\because \lambda=1 \mathrm{pm}=10^{-12} \mathrm{~m}\right) $$

Hence option(3) is correct

Average

deBroglie Relation + Photon Energy Relation

66. It is known that the average kinetic energy of a free electron, in a metal, is $3 / 2 \mathrm{kT}$. The (average) deBroglie wavelength, associtaed with the free electrons in a metal, maintained at a temperature $T$, is equal to the wavelength of a photon of energy $E$. The graph that correctly depicts the relation, between $T$ and $E$, is the graph labelled as graph

(1) $\mathbf{A}$

(2) $\mathrm{B}$

(3) $\mathrm{C}$

(4) $\mathrm{D}$

Show Answer

Correct answer: (3)

Solution:

The (average) deBroglie wavelength, associated with the free electrons, in a metal, at a temperature $\mathrm{T}$, is given by: $\lambda _{\mathrm{B}}=\dfrac{\mathrm{h}}{\left(2 \mathrm{~m} \dfrac{3}{2} \mathrm{kT}\right)^{1 / 2}}=\dfrac{\mathrm{h}}{(3 \mathrm{mkT})^{1 / 2}}$

The wavelength, $\lambda$, associated with a photon of energy $\mathrm{E}$, is given by $\mathrm{E}=\dfrac{\mathrm{hc}}{\lambda}$

$\therefore \lambda=\dfrac{\mathrm{hc}}{\mathrm{E}}$

Since $\lambda _{\mathrm{B}}=\lambda$ (given), we have $\dfrac{\mathrm{h}}{\sqrt{3 \mathrm{mkT}}}=\dfrac{\mathrm{hc}}{\mathrm{E}}$

This gives $\sqrt{\mathrm{T}}=\dfrac{\mathrm{E}}{\sqrt{3 \mathrm{mkc}^{2}}}$

or $\mathrm{T}=\left(\dfrac{1}{3 \mathrm{mkc}^{2}}\right) \mathrm{E}^{2}$

It is graph $\mathrm{C}$ that corresponds to this relation.

Hence option (3) is correct

Difficult

Photon Energy and Power of the Source

67. A monochromatic point source, of power $P$, radiates e.m. waves of wavelength $\lambda$. The number of photons, of this e.m. wave, that get transmitted, per second, through an aperture of radius $r$, located at a distance, ’ $d$ ‘, from the point source, is

(1) $\dfrac{\mathrm{P} \lambda}{4 \pi \mathrm{hc}}\left(\dfrac{\mathrm{d}}{\mathrm{r}}\right)^{2}$

(2) $\dfrac{\mathrm{P} \lambda}{4 \mathrm{hc}}\left(\dfrac{\mathrm{r}}{\mathrm{d}}\right)^{2}$

(3) $\dfrac{4 \pi \mathrm{hc}}{\mathrm{P} \lambda}\left(\dfrac{\mathrm{r}}{\mathrm{d}}\right)^{2}$

(4) $\dfrac{4 \mathrm{hc}}{\mathrm{P} \lambda}\left(\dfrac{\mathrm{d}}{\mathrm{r}}\right)^{2}$

Show Answer

Correct answer: (2)

Solution:

The energy of each photon $=\dfrac{\mathrm{hc}}{\lambda}$ and the power of the source $=\mathrm{P}=$ No. of photons emitted by the source, in one second,

$$ =\mathrm{N}=\mathrm{P} \div\left(\dfrac{\mathrm{hc}}{\lambda}\right)=\dfrac{\mathrm{P} \lambda}{\mathrm{hc}} $$

The aperture is at a distance $d$ from the point source. Hence the number of photons reaching a unit area, in one second, at the position of the aperture, is $\dfrac{\mathrm{N}}{4 \pi \mathrm{d}^{2}}=\dfrac{\mathrm{P} \lambda}{4 \pi \mathrm{hcd}^{2}}$

The aperture area is $\pi \mathrm{r}^{2}$. Hence the number of photons transmitted, per second, through the aperture, is

$$ \mathrm{n}=\left(\dfrac{\mathrm{P} \lambda}{4 \pi \mathrm{hcd^{2 }}}\right) \times\left(\pi \mathrm{r}^{2}\right)=\dfrac{\mathrm{P} \lambda}{4 \mathrm{hc}}\left(\dfrac{\mathrm{r}}{\mathrm{d}}\right)^{2} $$

Hence option(2) is correct

Average Einstein’s Photoelectrons Equation

68. When monochromatic light radiations, of wavelength $\lambda _{1}$ and $\lambda _{2}$, fall (one by one), on a given photosensitive surface ( of work function $W$ ), the ‘stopping potential’, needed inthe two cases, are $V _{1}$ and $V _{2}$, respectively. The value of Planck’s constant, can, then, be determined from the formula:

(1) $\mathrm{h}=\dfrac{\mathrm{e}\left(\mathrm{V} _{1}-\mathrm{V} _{2}\right) \cdot \lambda _{1} \lambda _{2}}{\mathrm{c}\left(\lambda _{2}-\lambda _{1}\right)}$

(2) $\mathrm{h}=\dfrac{\mathrm{e}\left(\mathrm{V} _{2}-\mathrm{V} _{1}\right) \cdot \lambda _{1} \lambda _{2}}{\mathrm{c}\left(\lambda _{2}+\lambda _{1}\right)}$

(3) $\mathrm{h}=\dfrac{\mathrm{c}\left(\lambda _{2}-\lambda _{1}\right)}{\mathrm{e}\left(\mathrm{V} _{2}-\mathrm{V} _{1}\right) \cdot \lambda _{1} \lambda _{2}}$

(4) $\mathbf{h}=\dfrac{\mathrm{c}\left(\lambda _{2}-\lambda _{1}\right)}{\mathrm{e}\left(\mathbf{V} _{1}-\mathbf{V} _{2}\right) \cdot \lambda _{1} \lambda _{2}}$

Show Answer

Correct answer: (1)

Solution:

From Einstein’s photoelectric equation, we have

$$ \begin{aligned} & \mathrm{eV} _{1}=\dfrac{\mathrm{hc}}{\lambda _{1}}-\mathrm{W} \text { and } \quad \mathrm{eV} _{2}=\dfrac{\mathrm{hc}}{\lambda _{2}}-\mathrm{W} \\ \therefore & \mathrm{e}\left(\mathrm{V} _{1}-\mathrm{V} _{2}\right)=\mathrm{hc}\left(\dfrac{1}{\lambda _{1}}-\dfrac{1}{\lambda _{2}}\right)=\mathrm{hc}\left(\dfrac{\lambda _{2}-\lambda _{1}}{\lambda _{1} \lambda _{2}}\right) \\ \therefore & \mathrm{h}=\left[\dfrac{\mathrm{e}\left(\mathrm{V} _{1}-\mathrm{V} _{2}\right) \lambda _{1} \lambda _{2}}{\mathrm{c}\left(\lambda _{2}-\lambda _{1}\right)}\right] \end{aligned} $$

Hence option(1) is correct

Average

Einstein’s Photoelectric Euqation

69. A uniform (normal) magnetic field, B, bends the path of the most energatic photoelectrons, (emitted from a given photosensitive surface due to the action of monochromatic radiations of wave length $\lambda$ ) into a circle of radius $r$. The work function, $W$, for the given photosensitive surface, equals

(1) $\left[\dfrac{\mathrm{hc}}{\lambda}+\dfrac{\mathrm{eBr}}{2 \mathrm{~m}}\right]$

(2) $\left[\dfrac{\mathrm{hc}}{\lambda}-\dfrac{\mathrm{eBr}}{2 \mathrm{~m}}\right]$

(3) $\left[\dfrac{h \mathbf{c}}{\lambda}-\dfrac{\mathrm{e}^{2} \mathbf{B}^{2} \mathbf{r}^{2}}{2 \mathrm{~m}}\right]$

(4) $\left[\dfrac{\mathbf{h c}}{\lambda}+\dfrac{\mathbf{e}^{2} \mathbf{B}^{2} \mathbf{r}^{2}}{2 \mathbf{m}}\right]$

Show Answer

Correct answer: (3)

Solution:

Let $\mathrm{W}$ be the work function of the given photosensitive surface. The K.E. (K), of the most energatic emitted photoelectrons, is then given by $\mathrm{K}=\left(\dfrac{\mathrm{hc}}{\lambda}-\mathrm{W}\right)$

Now $\mathrm{K}=\dfrac{1}{2} \mathrm{mv}^{2}$. The radius, $\mathrm{r}$, of the path into which these electrons get bent by a uniform (normal) magnetic field, is given by $\dfrac{\mathrm{mv}^{2}}{\mathrm{r}}=\mathrm{evB}$

$\therefore \quad \mathrm{r}=\dfrac{\mathrm{mv}}{\mathrm{eB}}=\dfrac{\sqrt{2 \mathrm{mK}}}{\mathrm{eB}}$

$\therefore \mathrm{K}=\dfrac{\mathrm{e}^{2} \mathrm{~B}^{2} \mathrm{r}^{2}}{2 \mathrm{~m}}$

$\therefore\left(\dfrac{\mathrm{hc}}{\lambda}-\mathrm{W}\right)=\dfrac{\mathrm{e}^{2} \mathrm{~B}^{2} \mathrm{r}^{2}}{2 \mathrm{~m}}$

or $\quad W=\left[\dfrac{h c}{\lambda}-\dfrac{\mathrm{e}^{2} \mathrm{~B}^{2} \mathrm{r}^{2}}{2 \mathrm{~m}}\right]$

Hence option(3) is correct

Difficult

No. of Photons Emitted by a Source of a Given Power

70. A light source, of power $P$, gives $x^{0} \%$ of its emitted energy, in the form of a monochromatic radiation of wavelength $\lambda$. This wavelength is less than the threshold wavelength $\left(\lambda _{0}\right)$ of a given photosensitive material.

A circular lamina, of radius $r$, (made from this given photosensitive material) is kept at a distance $d$ from the given light source. Assuming each incident photon (of radiation of wavelengh $\lambda$ ), to cause the emission of one photoelectron, the total charge $Q$, carried by all the photoelectrons, emitted in $t$ seconds, is

(1) $\mathbf{Q}=\left[\dfrac{2.5 \times 10^{-3} x \operatorname{te\lambda } \mathrm{P}(\mathrm{r} / \mathrm{d})^{2}}{\mathrm{hc}}\right]$

(2) $\mathbf{Q}=\left[\dfrac{10^{-2} x \text { te } \lambda \mathbf{P}(\mathrm{d} / \mathrm{r})^{2}}{\mathrm{hc}}\right]$

(3) $\mathbf{Q}=\left[\dfrac{10^{-2} x \operatorname{te} \lambda P(\mathrm{r} / \mathrm{d})^{2}}{\mathrm{hc}}\right]$

(4) $\mathbf{Q}=\left[\dfrac{2.5 \times 10^{-3} x \operatorname{te\lambda } \mathbf{P}(\mathrm{d} / \mathrm{r})^{2}}{\mathrm{hc}}\right]$

Show Answer

Correct answer: (1)

Solution:

The power, associtaed with the radiation of wavelength $\lambda$, equals $\dfrac{\mathrm{P} \times x}{100}=\dfrac{x \mathrm{P}}{100}=0.01 x \mathrm{P}$

Energy of one photon $=\dfrac{\mathrm{hc}}{\lambda}$

$\therefore$ Number of photons emitted per second $=\mathrm{N}=0.01 \times \mathrm{P} \div \dfrac{\mathrm{hc}}{\lambda}=\dfrac{0.01 \times \mathrm{P} \lambda}{\mathrm{hc}}$

At a distance d, the number of these photons, per unit area, is $\left(\dfrac{\mathrm{N}}{4 \pi \mathrm{d}^{2}}\right)$. Hence the number of photons, striking the circular lamina, in one second, is

$$ \mathrm{n}=\dfrac{\mathrm{N}}{4 \pi \mathrm{d}^{2}} \times \pi \mathrm{r}^{2}=\dfrac{\mathrm{N}}{4}\left(\dfrac{\mathrm{r}}{\mathrm{d}}\right)^{2} $$

In a time of t seconds, the number of emitted photoelectrons would be nt. The charges carried by them, equals nte. Hence

$$ \mathrm{Q}=\text { nte }=\dfrac{\mathrm{N}}{4} \dfrac{\mathrm{r}^{2}}{\mathrm{~d}^{2}} \cdot \text { te }=\dfrac{0.01 x \mathrm{P} \lambda}{4 \mathrm{hc}} \dfrac{\mathrm{r}^{2}}{\mathrm{~d}^{2}} \cdot \text { te }=\dfrac{0.0025 x \mathrm{P} \lambda \operatorname{ter}^{2}}{\left(\mathrm{hcd}^{2}\right)}=2.5 \times 10^{-3} \dfrac{x \mathrm{teP} \lambda}{\mathrm{hc}}\left(\dfrac{\mathrm{r}}{\mathrm{d}}\right)^{2} $$

Hence option(1) is correct

Average

Threhold Frequency

71. The ‘stopping potential’, needed to reduce the ‘photocurrent’ to zero, in a given set up, is 1.99 V. The given ‘set-up’, has a photosensitive surface being irradiated by a monochromatic radiation of wavelength $5000 \AA$. The treshhoold frequency, for the given photosensitive surface, is (nearly)

(1) $2.4 \times 10^{15} \mathrm{~Hz}$

(2) $1.2 \times 10^{15} \mathrm{~Hz}$

(3) $6 \times 10^{14} \mathrm{~Hz}$

(4) $3 \times 10^{14} \mathrm{~Hz}$

Show Answer

Correct answer: (2)

Solution:

Energy of a photon, of the incident radiation, $=\dfrac{\mathrm{hc}}{\lambda}=\dfrac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{5000 \times 10^{-10} \times 1.6 \times 10^{-19}} \mathrm{eV} \simeq 2.49 \mathrm{eV}$

Let $\mathrm{W}$ be the work function of the given photosensitive surface. We then have $\mathrm{W}=2.49 \mathrm{eV}-1.99$ $\mathrm{eV}=0.5 \mathrm{eV}$

$\therefore$ If $\nu _{0}$ is the threshold frequency, we have $\mathrm{h} \nu _{0}=\mathrm{W}=0.5 \times 1.6 \times 10^{-19} \mathrm{~J}$

$\therefore \quad \nu=\dfrac{8 \times 10^{-19}}{6.63 \times 10^{-34}} \mathrm{~Hz} \approx 1.2 \times 10^{15} \mathrm{~Hz}$

Hence option(2) is correct

Difficult

Threshold Wavelength; deBroglie Relation

72. A given photosensitive surface is being irradiated by a monochromatic radiation of wavelength $\lambda$. The stopping potential, needed in this set up, is $\mathbf{V} _{\mathrm{s}}$.

The deBroglie wavelength, associated with a beam of electrons, accelerated through a potential $\mathrm{V}$, equals the threshold wavelength for the above given photosensitive surface. The relation, between $\mathrm{V} _{\mathrm{s}}$ and $\mathrm{V}$, is then

(1) $\mathbf{V}=\dfrac{\mathbf{c}}{\mathbf{e}}\left[\mathbf{h}+\left(2 \mathbf{m e V} _{\mathrm{s}}\right)^{1 / 2}\right]$

(2) $\mathbf{V} _{\mathrm{s}}=\dfrac{\mathrm{c}}{\mathrm{e}}\left[\mathbf{h}+\lambda(2 \mathrm{meV})^{1 / 2}\right]$

(3) $\mathrm{V}=\dfrac{\mathrm{c}}{\mathrm{e}}\left[\mathrm{h}-\lambda\left(2 \mathrm{meV} _{\mathrm{s}}\right)^{1 / 2}\right]$

(4) $\mathbf{V} _{\mathrm{s}}=\dfrac{\mathfrak{c}}{\mathrm{e}}\left[\mathbf{h}-\lambda(2 \mathrm{meV})^{1 / 2}\right]$

Show Answer

Correct answer: (4)

Solution:

Let $\mathrm{W}$ be the work function for the given photosensitive surface. We then have $\dfrac{\mathrm{hc}}{\lambda}=\mathrm{eV} _{\mathrm{s}}+\mathrm{W}$

$\therefore \mathrm{W}=\left(\dfrac{\mathrm{hc}}{\lambda}-\mathrm{eV} _{\mathrm{s}}\right)$

If $\lambda _{0}$ be the threshold wavelength, for the given photosensitive surface, we have $\dfrac{\mathrm{hc}}{\lambda _{0}}=\mathrm{W}=\left(\dfrac{\mathrm{hc}}{\lambda}-\mathrm{eV} _{\mathrm{s}}\right)$

$\therefore \dfrac{1}{\lambda _{0}}=\dfrac{1}{\lambda}-\dfrac{\mathrm{eV}}{\mathrm{hc}}=\left(\dfrac{\mathrm{hc}-\mathrm{eV} _{\mathrm{s}} \lambda}{\mathrm{hc} \lambda}\right)$

$\therefore \quad \lambda _{0}=\left[\dfrac{\mathrm{hc}}{\left(\mathrm{hc}-\mathrm{eV} _{\mathrm{s}}\right)}\right] \lambda$

Also, the deBroglie wavelength, $\lambda _{\mathrm{B}}$, associated with the electron beam, is given by $\lambda _{\mathrm{B}}=\dfrac{\mathrm{h}}{(2 \mathrm{meV})^{1 / 2}}$

Since $\lambda _{\mathrm{B}}=\lambda _{0}$, we have

$\dfrac{\mathrm{h}}{(2 \mathrm{meV})^{1 / 2}}=\dfrac{\mathrm{hc} \lambda}{\left(\mathrm{hc}-\mathrm{eV} _{\mathrm{S}}\right)}$

or $\quad \mathrm{hc}-\mathrm{eV} _{\mathrm{S}}=(2 \mathrm{meV})^{1 / 2} \cdot \lambda \mathrm{c}$

or $\quad \mathrm{eV} _{\mathrm{S}}=\mathrm{hc}-(2 \mathrm{meV})^{1 / 2} \lambda \mathrm{c}=\mathrm{c}\left[\mathrm{h}-(2 \mathrm{meV})^{1 / 2} \lambda\right]$

$\therefore \mathrm{V} _{\mathrm{S}}=\dfrac{\mathrm{c}}{\mathrm{e}}\left[\mathrm{h}-\lambda(2 \mathrm{meV})^{1 / 2}\right]$

Hence option(4) is correct

Average

Einstein’s Photoelectric Equation

73. When monochromatic radiations, of frequencies $v _{1}$ and $v _{2}$, are made to fall (one by one) on a given photosensitive surface, the maximum kinetic energies, of the emitted photoelectrons, are $K _{1}$ and $K _{2}$, respectively. The value of Planck’s constant (h) and the threshold frequency $\left(\nu _{0}\right)$, (of the given photosensitive surface) are then given by

(1) $\mathbf{h}=\left(\dfrac{K _{1}+K _{2}}{v _{1}-v _{2}}\right)$ and $v _{0}=\dfrac{K _{1} v _{2}-K _{2} v _{1}}{\left(K _{1}-K _{2}\right)}$

(2) $\mathbf{h}=\left(\dfrac{\mathbf{K} _{1}+\mathbf{K} _{2}}{v _{1}+v _{2}}\right)$ and $v _{0}=\dfrac{K _{1} v _{2}+K _{2} v _{1}}{\left(\mathbf{K} _{1}+K _{2}\right)}$

(3) $\mathbf{h}=\left(\dfrac{\mathbf{K} _{1}+\mathbf{K} _{2}}{v _{1}+v _{2}}\right) \text { and } v _{0}=\dfrac{\mathbf{K} _{1} v _{2}-\mathbf{K} _{2} v _{1}}{\left(\mathbf{K} _{1}-\mathbf{K} _{2}\right)}$

(4) $\mathbf{h}=\left(\dfrac{K _{1}-K _{2}}{v _{1}-v _{2}}\right)$ and $v _{0}=\dfrac{K _{1} v _{2}+K _{2} v _{1}}{\left(K _{1}+K _{2}\right)}$

Show Answer

Correct answer: (1)

Solution:

From Einstein’s photoelectric equation, we get

$\mathrm{h} \nu _{1}=\mathrm{K} _{1}+\mathrm{W} \quad \text { and } \quad \mathrm{h} \nu _{2}=\mathrm{K} _{2}+\mathrm{W}$

where $\mathrm{W}$ is the work function of the given photosensitive surface.

We then have $\mathrm{h}\left(\nu _{1}-\nu _{2}\right)=\left(\mathrm{K} _{1}-\mathrm{K} _{2}\right)$

$\therefore \mathrm{h}=\dfrac{\left(\mathrm{K} _{1}-\mathrm{K} _{2}\right)}{\left(\nu _{1}-\nu _{2}\right)}$

This gives $\mathrm{W}=\mathrm{h} \nu _{1}-\mathrm{K} _{1}=\dfrac{\left(\mathrm{K} _{1}-\mathrm{K} _{2}\right)}{\left(\nu _{1}-\nu _{2}\right)} \nu _{1}-\mathrm{K} _{1}$

$=-\dfrac{\mathrm{K} _{2} \nu _{1}++\mathrm{K} _{1}\nu _{2}}{\left(\nu _{1}-\nu _{2}\right)}=\dfrac{\mathrm{K} _{1} \nu _{2}++\mathrm{K} _{2} \nu _{1}}{\left(\nu _{1}-\nu _{2}\right)}$

$\therefore$ Threshold frequency $\mathrm{v} _{0}=\dfrac{\mathrm{W}}{\mathrm{h}}=\dfrac{\mathrm{K} _{1} \nu _{2}-\mathrm{K} _{2} \nu _{1}}{\left(\mathrm{~K} _{1}-\mathrm{K} _{2}\right)}$

Hence option(1) is correct

Average

deBroglie Relation

74. The (average) kinetic energy of the free electrons ( mass $=m, \mid$ charged $\mid=e)$, in a metal, at a temperature $T$ in kelvin, equals ( $k=$ Boltzmann’s constant). If a graph were to be plotted between the (average) deBroglie wavelength $\left(\lambda _{B}\right)$, associated with these free electrons, and $\dfrac{1}{\sqrt{T}}$, the slope (s) of the graph, can be used to calculate the Boltzmann constant, $k$, through the relation

(1) $\mathbf{k}=\left(\dfrac{\mathbf{h}}{3 \mathrm{~ms}^{2}}\right)$

(2) $\mathbf{k}=\left(\dfrac{\mathbf{h}^{2}}{3 \mathrm{~ms}}\right)$

(3) $\mathbf{k}=\left(\dfrac{\mathbf{h}^{2}}{3 \mathbf{m s}^{2}}\right)$

(4) $\mathbf{k}=\left(\dfrac{\mathbf{h}^{2}}{2 \mathbf{m s}^{2}}\right)$

Show Answer

Correct answer: (3)

Solution:

The deBroglie wavelength, $\lambda$, is give by

$$ \lambda _{\mathrm{B}}=\dfrac{\mathrm{h}}{\mathrm{p}}=\dfrac{\mathrm{h}}{(2 \mathrm{mK})^{1 / 2}}(\mathrm{~K}=\text { Kinetic energy of free of electrons }) $$

$\therefore$ (Average) $\lambda _{\mathrm{B}}=\dfrac{\mathrm{h}}{\left(2 \mathrm{~m} \cdot \dfrac{3}{2} \mathrm{kT}\right)^{1 / 2}}=\dfrac{\mathrm{h}}{\sqrt{3 \mathrm{mkT}}}=\dfrac{\mathrm{h}}{\sqrt{3 \mathrm{mk}}} \cdot \dfrac{1}{\sqrt{\mathrm{T}}}$

$\therefore$ Slope (s) of the graph $=\dfrac{\mathrm{h}}{\sqrt{3 \mathrm{mk}}}$

$\therefore \mathrm{k}=\dfrac{\mathrm{h}^{2}}{3 \mathrm{~ms}^{2}}$

Hence option(3) is correct

Difficult

deBroglie Relation; Einstein’s Photoelectric Equation

75. The deBroglie wavelength, associated with electrons, accelerated through a potential $V$, equals $\lambda _{B}$. The threshold wavelength, for a given photosensitive surface is $n \lambda _{B}(n>1)$. If this photosensitive surface is irradiated with monochromatic radiation of wavelength $\left(\lambda _{\mathrm{B}} / \mathrm{n}\right)$, the stopping potential needed is $\mathbf{V} _{\mathrm{s}}$.

The relation, between $\mathrm{V} _{\mathrm{s}}$ and $\mathrm{V}$, can be expressed as

(1) $V _{s}=\left[\dfrac{\left(n^{2}-1\right) c}{n} \sqrt{\dfrac{2 m}{e}}\right] \sqrt{V}$

(2) $V=\left[\dfrac{n c}{\left(n^{2}-1\right)} \sqrt{\dfrac{2 m}{\mathrm{e}}}\right] \sqrt{V _{s}}$

(3) $\mathbf{V} _{\mathrm{s}}=\left[\dfrac{\mathrm{nc}}{\left(\mathrm{n}^{2}-1\right)} \sqrt{\dfrac{2 \mathrm{~m}}{\mathrm{e}}}\right] \sqrt{\mathrm{V}}$

(4) $V=\left[\dfrac{\left(n^{2}-1\right) c}{n} \sqrt{\dfrac{2 m}{e}}\right] \sqrt{V _{s}}$

Show Answer

Correct answer: (1)

Solution:

We can write $\lambda _{\mathrm{B}}$ as $\lambda _{\mathrm{B}}=\dfrac{\mathrm{h}}{\mathrm{p}}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{meV}}}$

The work function, of the photosensitive surface = energy of a photon of its ’threshold wavelength’ radiation $=\dfrac{\mathrm{hc}}{\mathrm{n} \lambda _{\mathrm{B}}}$

Energy of a photon of the incident radiation $=\dfrac{h c}{\left(\lambda _{B} / n\right)}=\dfrac{n h c}{\lambda _{B}}$

$\therefore$ As per Einstein’s photoelectric equation, we have $\mathrm{eV} _{\mathrm{S}}=\dfrac{\mathrm{nhc}}{\lambda _{\mathrm{B}}}-\dfrac{\mathrm{hc}}{\mathrm{n} \lambda _{\mathrm{B}}}=\dfrac{\left(\mathrm{n}^{2}-1\right) \mathrm{hc}}{\mathrm{n} \lambda _{\mathrm{B}}}$

$\therefore \quad \mathrm{V} _{\mathrm{S}}=\dfrac{\left(\mathrm{n}^{2}-1\right) \mathrm{hc}}{\mathrm{ne}} \dfrac{1}{\lambda _{\mathrm{B}}}=\dfrac{\left(\mathrm{n}^{2}-1\right) \mathrm{hc}}{\mathrm{ne}} \cdot \dfrac{\sqrt{2 \mathrm{meV}}}{\mathrm{h}}=\left[\dfrac{\left(\mathrm{n}^{2}-1\right) \mathrm{c}}{\mathrm{n}} \cdot \sqrt{\dfrac{2 \mathrm{~m}}{\mathrm{e}}}\right] \sqrt{\mathrm{V}}$

This is the required relation between $\mathrm{V} _{\mathrm{S}}$ and $\mathrm{V}$.

Hence option(1) is correct

Average

deBroglie Wavelength

76. It may be assumed that the average kinetic energy, of a free particle, at a temperature $T$, equals $3 / 2 \mathrm{kT}(\mathrm{k}=$ Boltzmann constant). The (average) deBroglie wavelength, associated with a free electron ( mass $=m$ ) at a temperature $T _{1}$, equals the (average) deBroglie wavelength, associated with a free $\alpha$-particle (mass $=M$ ) at a temperature $T$. Similarly, the deBroglie wavelength, associated with an electron, accelerated through a potential $\mathrm{V} _{1}$, equals the deBroglie wavelength, associated with an $\alpha$-particle, accelerated through a potential $V _{2}$. The temperatures, $\left(T _{1}\right.$ and $\left.T _{2}\right)$ and the potentials, $\left(V _{1}\right.$ and $\left.V _{2}\right)$, would then be related as

(1) $\mathrm{T} _{2} \mathrm{~V} _{1}=2 \mathrm{~T} _{1} \mathrm{~V} _{2}$

(2) $2 \mathrm{~T} _{2} \mathrm{~V} _{1}=\mathrm{T} _{1} \mathrm{~V} _{2}$

(3) $2 \mathrm{~T} _{2} \mathrm{~V} _{2}=\mathrm{T} _{1} \mathrm{~V} _{1}$

(4) $\mathrm{T} _{2} \mathrm{~V} _{2}=2 \mathrm{~T} _{1} \mathrm{~V} _{1}$

Show Answer

Correct answer: (1)

Solution:

For the electron, we have $\lambda _{\mathrm{e}}=\dfrac{\mathrm{h}}{\mathrm{p}}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{mK}}}=\dfrac{\mathrm{h}}{\left(3 \mathrm{mkT} _{1}\right)^{1 / 2}}$

For the $\alpha$-particle, we similarly, have $\lambda _{\alpha}=\dfrac{\mathrm{h}}{\left(3 \mathrm{Mk} \mathrm{T} _{2}\right)^{1 / 2}}$

Since $\lambda _{\alpha}=\lambda _{\mathrm{e}}$, we have $\mathrm{MT} _{2}=\mathrm{mT} _{1}$

or $\dfrac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=\dfrac{\mathrm{M}}{\mathrm{m}}$

Again, we have, for the electron $\lambda _{\mathrm{e}}^{\prime}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{meV} _{1}}}$

and for the $\alpha$ particle, we have $\lambda _{\alpha}^{\prime}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{M}(2 \mathrm{e}) \mathrm{V} _{2}}}$

Since $\lambda _{\alpha}^{\prime}=\lambda _{\mathrm{e}}^{\prime}$, we have

$$ 4 \mathrm{MV} _{2}=2 \mathrm{mV} _{1} $$

or $\dfrac{\mathrm{V} _{1}}{\mathrm{~V} _{2}}=\dfrac{4 \mathrm{M}}{2 \mathrm{~m}}=\dfrac{2 \mathrm{M}}{\mathrm{m}}$

Comparing the two ratios, we get $\dfrac{V _{1}}{V _{2}}=\dfrac{2 T _{1}}{T _{2}}$

or $\mathrm{T} _{2} \mathrm{~V} _{1}=2 \mathrm{~T} _{1} \mathrm{~V} _{2}$

Hence option(1) is correct

Average

Graphs Related to Photoelectric Effect

77. For a constant intensity of the incident radiation, the graphs between the frequency $(\nu)$ of the incident, and the magnitude $\left(V _{s}\right)$ of the corresponding stopping pontential, for different photosensitive surfaces, have the form shown here.

Let the intercepts, of these graphs, on the ‘potential’ and the ‘frequency’ axes, be denoted by $y _{i}$ and $x _{i}(i=1,2,3, \ldots . . n)$ for different photosensitive surfaces. The graph, between $y _{i}$ and $x _{i}$, would then have the form of the graph, labelled as graph

(1) $\mathrm{A}$

(2) $\mathrm{B}$

(3) $\mathrm{C}$

(4) $\mathrm{D}$

Show Answer

Correct answer: (2)

Solution:

As per Einstein’s photoelectric equation, we have

$$ \dfrac{1}{2} \mathrm{mv} _{\max }^{2}=\mathrm{e}\left|\mathrm{V} _{\mathrm{s}}\right|=\mathrm{h} \nu-\mathrm{W} \quad(\mathrm{e}=\text { magnitude of electronic charge }) $$

$\therefore$ Intercept on the $v$-axis $\left(=\nu _{0}\right)$ is given by (taking $\left.\mathrm{V} _{\mathrm{S}}=0\right) 0=\mathrm{h} \nu _{0}-\mathrm{W}$

$\therefore \nu _{0}=\dfrac{\mathrm{W}}{\mathrm{h}}$

Similarly, the intercept on the $\mathrm{V} _{\mathrm{S}}$ axis $\left(=\mathrm{V} _{\mathrm{SO}}\right.$, say) is given by (taking $v=0$ )

$$ \mathrm{eV} _{\mathrm{so}}=0-\mathrm{W} $$

or $\mathrm{V} _{\mathrm{so}}=-\mathrm{W} / \mathrm{e}$

$\therefore$ The relation between $\left(\mathrm{y} _{\mathrm{i}}\right)$ and $\left(x _{\mathrm{i}}\right)$ is $-\mathrm{e} \mathrm{y} _{\mathrm{i}}=\mathrm{h} x _{\mathrm{i}}(=\mathrm{W}$, each $)$

or $\quad \mathrm{y} _{\mathrm{i}}=\left(-\dfrac{\mathrm{h}}{\mathrm{e}} x _{\mathrm{i}}\right)$

The required graph is therefore, a straight line passing through the origin and having a negative slope (slope $=(-\mathrm{h} / \mathrm{e})$.

These requirement are met only by the graph labelled as graph B.

Hence option(2) is correct

Difficult

deBroglie Wavelength

78. An $\alpha$-particle (mass $=M$ ), having an initial kinetic energy K, approaches ‘head-on’, towards a (for-off) stationary nucleus, having an atomic number $z$. It comes up to a distance, $a _{0}$, of the nucleus before (momentarily) coming to rest, and then turning back.

The deBroglie wavelengths, associated with this $\alpha$-particle, in its initial position (when its kinetic energy is $\mathrm{K}$ ) equals $\lambda _{0}$. The relation, between $\lambda _{0}$ and $\mathrm{a} _{0}$, is

(1) $\lambda _{0}=\left(\dfrac{\mathrm{Mze}^{2}}{\pi \varepsilon _{0} \mathbf{h}^{2}}\right) \mathrm{a} _{0}^{2}$

(2) $\mathbf{a} _{0}=\left(\dfrac{\mathrm{Mze}^{2}}{\pi \varepsilon _{0} \mathbf{h}^{2}}\right) \lambda _{0}^{2}$

(3) $\mathbf{a} _{0}=\left(\dfrac{\pi \varepsilon _{0} \mathbf{h}^{2}}{\mathrm{Mze}^{2}}\right) \lambda _{0}^{2}$

(4) $\lambda _{0}=\left(\dfrac{\pi \varepsilon _{0} \mathbf{h}^{2}}{\mathrm{Mze}^{2}}\right) \mathbf{a} _{0}^{2}$

Show Answer

Correct answer: (2)

Solution:

As the [positively charged, $\alpha$-particle having a charge (+2e)] approaches the stationary (positively charged) nucleus (having a charge + ze), its kinetic energy keeps on decreasing and becomes (momentarily) zero when it is at a distance $a _{0}$ from the nucleus. At this position, $K$ equals the potential energy of the ’nucleus alpha particle’ system. We, therefore, have

$$ \begin{aligned} \mathrm{K} & =\dfrac{1}{4 \pi \varepsilon _{0}} \cdot \dfrac{(\mathrm{ze})(2 \mathrm{e})}{\mathrm{a} _{0}} \\ \therefore \quad \mathrm{a} _{0} & =\dfrac{1}{4 \pi \varepsilon _{0}} \dfrac{2 \mathrm{ze}^{2}}{\mathrm{~K}} \end{aligned} $$

The deBroglie wavelength, associated with the $\alpha$-particle, when its kinetic energy is $\mathrm{K}$, is given by

$$ \begin{aligned} & \lambda _{0}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{MK}}}(\mathrm{M}=\text { mass of } \alpha \text {-particle }) \\ & \therefore \mathrm{K}=\dfrac{\mathrm{h}^{2}}{2 \mathrm{M} \lambda _{0}^{2}} \end{aligned} $$

We thus have $\mathrm{K}=\dfrac{\mathrm{h}^{2}}{2 \mathrm{M} \lambda _{0}^{2}}=\dfrac{1}{4 \pi \varepsilon _{0}} \dfrac{2 \mathrm{ze}^{2}}{\mathrm{a} _{0}}$

$\therefore \quad \mathrm{a} _{0}=\dfrac{1}{4 \pi \varepsilon _{0}} \dfrac{2 \mathrm{ze}^{2} 2 \mathrm{M}}{\mathrm{h}^{2}} \lambda _{0}^{2}=\left(\dfrac{\mathrm{Mze}^{2}}{\pi \varepsilon _{0} \mathrm{~h}^{2}}\right) \lambda _{0}^{2}$

This is the required relation.

Hence option (2) is correct.

Average

deBroglie Relation; Photon Energy Relation

79. The kinetic energy, of an electron, having an associated deBroglie wavelength $\lambda _{B}$, equals $K$. The energy of a photon, of a radiation of wavelength $\lambda _{P}$, equals $\mathrm{nK}$. The graph that is in accord with the relation between $\lambda _{B}$ and $\lambda _{P}$, is the graph labelled as graph.

(1) $\mathrm{A}$

(2) $\mathrm{B}$

(3) $\mathrm{C}$

(4) $\mathrm{D}$

Show Answer

Correct answer: (3)

Solution:

For the electron, having a kinetic energy K, we have, as per deBroglie relation, $\lambda _{\mathrm{B}}=\dfrac{\mathrm{h}}{\mathrm{p}}=\dfrac{\mathrm{h}}{(2 \mathrm{mK})^{1 / 2}}$

$\therefore \mathrm{K}=\dfrac{\mathrm{h}^{2}}{2 \mathrm{~m} \lambda _{\mathrm{B}}^{2}}$

Also, photon energy $=\dfrac{\mathrm{hc}}{\lambda _{\mathrm{P}}}$

$\therefore \mathrm{nK}=\dfrac{\mathrm{hc}}{\lambda _{\mathrm{P}}}$ or $\mathrm{K}=\dfrac{\mathrm{hc}}{\mathrm{n} \lambda _{\mathrm{P}}}$

We this have $\dfrac{\mathrm{hc}}{\mathrm{n} \lambda _{\mathrm{P}}}=\dfrac{\mathrm{h}^{2}}{2 \mathrm{~m} \lambda _{\mathrm{B}}^{2}}$

$\therefore 2 \mathrm{~m} \lambda _{\mathrm{B}}^{2}=\dfrac{\mathrm{nh}}{\mathrm{c}} \lambda _{\mathrm{P}} \quad$ or $\quad \lambda _{\mathrm{B}}^{2}=\left(\dfrac{\mathrm{nh}}{2 \mathrm{mc}}\right) \lambda _{\mathrm{P}}$

The graph, between $\lambda _{B}^{2}$ and $\lambda _{P}$, would, therefore, a straight line, passing through the origin. It is only graph $\mathrm{C}$ that is in accord with these requirements.

Hence option (3) is correct.

Average

Relating deBroglie Wavelength with Photon Wavelengths

80. Three charged particles, having charges $\left(q _{1}, q _{2}, q _{3}\right)$ and masses $\left(m _{1}, m _{2}, m _{3}\right)$, are accelerated (from rest) through potential $\mathrm{V} _{1}, \mathrm{~V} _{2}$ and $\mathrm{V} _{3}$, respectively. Their associated deBroglie wavelengths are equal, respectively, to the wavelengths of photons, having energies $E _{1}, E _{2}$ and $\mathrm{E} _{3}$. We would then have:

(1) $\mathbf{E}_1: \mathbf{E}_2: \mathbf{E}_3=\mathbf{q}_1 \mathbf{m}_1 \mathbf{V}_1: \mathbf{q}_2 \mathbf{m}_2 \mathbf{V}_2: \mathbf{q}_3 \mathbf{m}_3 V_3$

(2) $\mathbf{E}_1: \mathbf{E}_2: \mathbf{E}_3=\mathbf{q}_3 \mathbf{m}_3 \mathbf{V}_3: \mathbf{q}_2 \mathbf{m}_2 \mathbf{V}_2: \mathbf{q}_1 \mathbf{m}_1 \mathbf{V}_1$

(3) $\mathbf{E} _{1}: \mathbf{E} _{2}: \mathbf{E} _{3}=\sqrt{\mathbf{m} _{1} \mathbf{V} _{1} \mathbf{q} _{1}}: \sqrt {\mathbf{m} _{2} \mathbf{V} _{2} \mathbf{q} _{2}}: \sqrt{\mathbf{m} _{3} \mathbf{V} _{3} \mathbf{q} _{3}}$

(4) $\mathbf{E} _{1}: \mathbf{E} _{2}: \mathbf{E} _{3}=\sqrt{\mathbf{m} _{3} \mathbf{V} _{3} \mathbf{q} _{3}}: \sqrt{\mathbf{m} _{2} \mathbf{V} _{2} \mathbf{q} _{2}}: \sqrt{\mathbf{m} _{1} \mathbf{V} _{1} \mathbf{q} _{1}}$

Show Answer

Correct answer: (3)

Solution:

The kinetic energy, acquired by a particle of charge q, when accelerated (from rest), through a potential V, is $\mathrm{K}=\mathrm{qV}$

Also deBroglie wavelength, $\lambda=\dfrac{\mathrm{h}}{\mathrm{p}}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{mK}}}=\dfrac{\mathrm{h}}{\sqrt{2 \mathrm{mqV}}}$

The wavelength $\left(\lambda^{\prime}\right)$, associated with a photon of energy E, is given by $h v^{\prime}=\dfrac{h c}{\lambda^{\prime}}=E$

$\therefore \quad \lambda^{\prime}=\dfrac{\mathrm{hc}}{\mathrm{E}}$

As per the statement given, we have

$$ \begin{aligned} & \quad \dfrac{h}{\sqrt{2 \mathrm{~m} _{1} \mathrm{q} _{1} \mathrm{~V} _{1}}}=\dfrac{h c}{\mathrm{E} _{1}} \quad \dfrac{h}{\sqrt{2 \mathrm{~m} _{2} \mathrm{q} _{2} \mathrm{~V} _{2}}}=\dfrac{h c}{\mathrm{E} _{2}} \quad \dfrac{h}{\sqrt{2 \mathrm{~m} _{3} \mathrm{q} _{3} \mathrm{~V} _{3}}}=\dfrac{h c}{\mathrm{E} _{3}} \\ & \therefore \quad \dfrac{\mathrm{c}}{\mathrm{E} _{1}}=\dfrac{1}{\sqrt{2 \mathrm{~m} _{1} \mathrm{q} _{1} \mathrm{~V} _{1}}} \quad \text { or } \quad \mathrm{E} _{1}=c \sqrt{2 \mathrm{~m} _{1} \mathrm{q} _{1} \mathrm{~V} _{1}} \end{aligned} $$

Similarly $E _{2}=c \sqrt{2 m _{2} q _{2} V _{2}}$ and $E _{3}=c \sqrt{2 m _{3} q _{3} V _{3}}$

$\therefore \mathrm{E} _{1}: \mathrm{E} _{2}: \mathrm{E} _{3}=\sqrt{\mathrm{m} _{1} \mathrm{q} _{1} \mathrm{~V} _{1}}: \sqrt{\mathrm{m} _{2} \mathrm{q} _{2} \mathrm{~V} _{2}}: \sqrt{\mathrm{m} _{3} \mathrm{q} _{3} \mathrm{~V} _{3}}$

Hence option (3) is correct.