UNIT 15 ELECTROMAGNETIC WAVES
Learning Objectives
To enable the learners to understand the following concepts / topics, analyse and appreciate them incorporating the previous knowledge, enhance their application skills in various concepts, develop values and life skills required in furthering their overall personality.
- Maxwell’s equations and production of electromagnetic waves.
- Concept of displacement current.
- Source / origin of electromagnetic waves.
- Nature of EM waves and their expressions.
- Properties of EM waves.
- Intensity, radiation pressure and momentum of EM-waves.
- Poynting vector
- Various types of waves is EM- spectrum, their names, frequencies and uses.
- Applications of EM waves.
Introduction
James Clark Maxwell, in taking stock of our knowledge of electricity and magnetism, summarised basic results in terms of four equations known as Maxwells equations. He also showed that one of these equations known as Ampere’s circuital law needed some modification. This was achieved by introducing the concept of displacement current. Maxwell also shared that the electric and magnetic fields satisfy equation of wave motion and co-exist with one another. He postulated the existence of what is now known as electromagnetic waves. In this unit we will discuss these ideas in a very simple, elementary way.
Maxwells Equations
The four Maxwell’s equations are:
(1) Gauss Law of Electrostatics
According to Gauss law the electric flux
(2) Gauss Law of Magnetostatics
The net magnetic flux
This is basically a restatement of the fact that magnetic monopoles donot exist.
(3) Ampere is Circuital Law
The law states that the line integral of magetic field over any closed surface equals
(4) Faraday’s Law of Electromagnetic Induction
The induced emf is numerically equal to the time rate of change of magnetic flux.
The Displacement Current
Maxwell pointed a fundamental inadequecy of the above four equations. Maxwell argued that if a varying magnetic flux produces an induced electric field and therefore an induced emf, a varying electric flux should also produce an induced magnetic field due to an induced current. In other words Maxwell demanded “Parity” between electric and magnetic fields.
Maxwell also shared that the Ampere’s circuital law as expressed in Eqn (3); in general; is not valid. As expressed in Eqn (3); the law is valid for direct currents (d.c). But is is not applicable to alternating currents.
We know that a direct current cannot flow through a capacitor. However an a.c current can flow through a capacitor, though an insulator is present between plates of the capacitor. Obviously conduction electrons ,that move in wires conneting a.c source to capacitor, cannot flow from one plate of the capacitor to the other. How circuit is completed when a.c current flows?
To overcome these difficulties Maxwell proposed that a new current, now known as displacement current
The modified Ampere’s circuital law is
where
Though displacement current is not due to movement of free electrons; it has same effects as conduction current. We say displacement current can produce a magnetic field in the same manner as a conduction current.
Existence of Displacement Currnet
We discuss briefly, by using idea of displacement current, how do we get a continuity of current through a capacitor connected across an a.c. Let a capacitor (parallel-plate) of capacity
The capacity
The conduction current
According to Maxwell, in between plates of capacitor there is a varying electric flux which produces displacement current
The displacement current,
From eqns (8) and (9) we have
Let
Electromagnetic Waves
Maxwell, using modified Ampere’s law and the other three equations showed that the electric field (E) and the magnetic field (B) satisfy the equation.
These two equatinos are standard equations of wave motion. The speed of waves
For free space
and
Origin of Electromagnetic Wave
Maxwell explained theoretically, the production of EM waves with the help of the two equations, namely:
and
In order to produce a magnetic field, we require a time varying electric field in space and a time-varying electric field can only be produced by an accelerating or oscillating electric change. Hence an oscillating electric change acts as the source of EM waves. As long as the charge continues to oscillate, EM waves are produced from those oscillations.
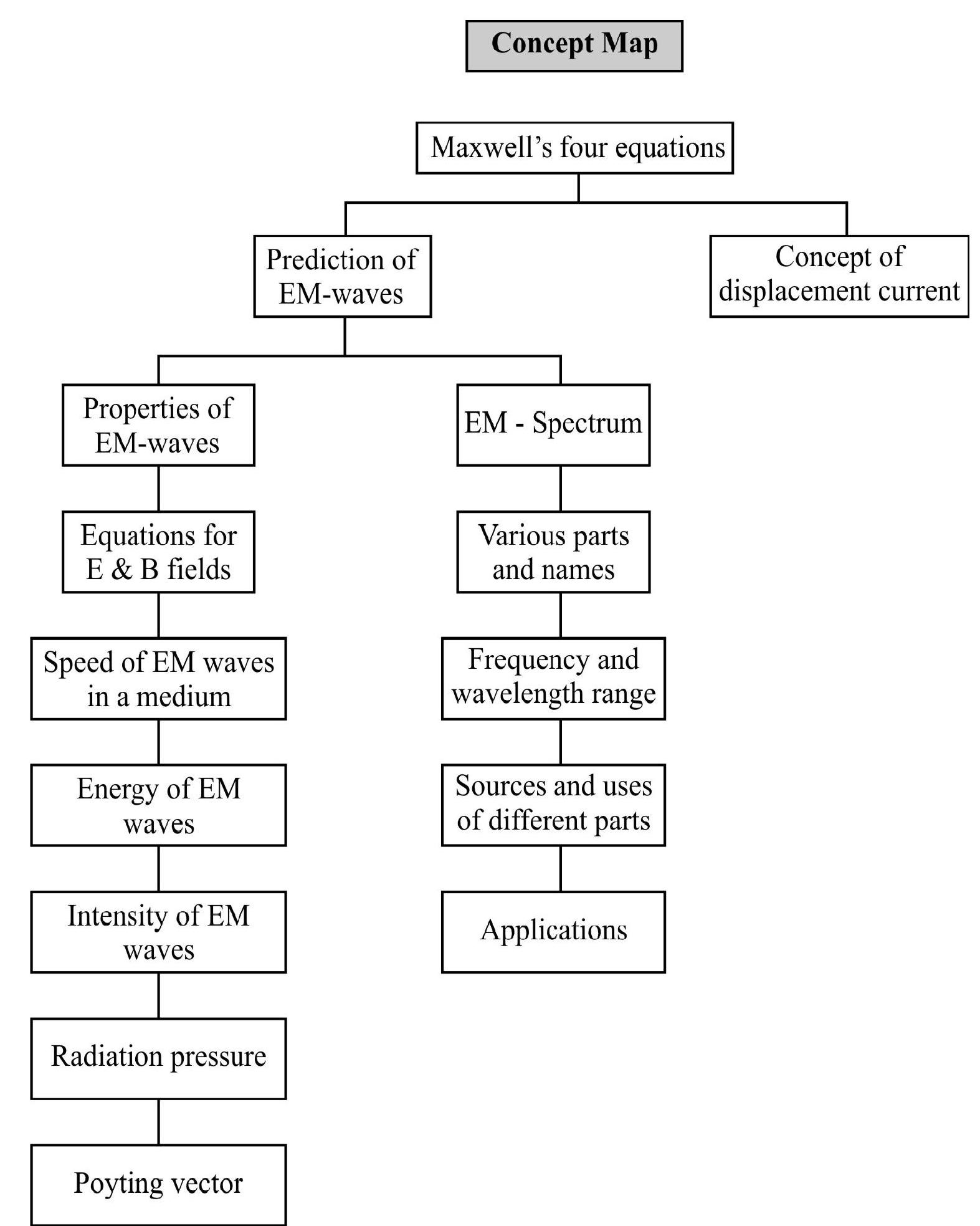
Nature of Electromagnetic Waves
An electromagnetic wave produced by oscillating charge (and transmitted with the help of a dipole antenna) consists of time-varying E and B fields, the variation in one sustaining the production of the other. As we know, the varition in E-field is the source of displacement current
Electromagnetic waves propagate, in space with the speed equal to that of light (c). If the electric field
Since
or
or
and
or
or
Here,
and
Using Maxwell’s equations it can be proved that:
or
It can also be proved, from Maxwell’s equations, that the electric field amplitude
As we know, both E and B fields in EM wave vary is same phase, equation (15.21) can also be written as:
[Here
It is well known to all that light, an electromagnetic wave, does propagate through glass and water. We have also seen, in earlier uits, that electric and magnetic field can be established in material medium and that the total electric field inside a medium is described in terms of permittivity
Thus the speed of electromegnetic waves, and therefore light, can be written in terms of
Here
Here
Heinrich RudolfHertz not only proved that accelerating / oscillating charges produced electromagnetic waves, but also demonstrated these waves, which had wavelength ten million times that of the light waves, could be diffracted, refracted and polarised. Further Hertz produced stationary electromagnetic waves and determined their wavelength, by measuring the distance between two successive nodes. As the frequency of the wave (equal to the frequency of the oscillator) is known, he then calculated the speed of these waves using the equation
The electric and the magnetic fields of an electromagnetic wave are plane polarised. This nature of EM waves can be easily understood in the response of a portable AM radio to a broadcasting station. If the radio has a telescopic antenna it responds to the electric field of the signal. When this antenna is kept horizontal the signal strength will be greatly diminished.
Electromagnetic waves do carry energy and momentum, like other waves. To establish this, consider a plane perpendicular to the direction of propagation of the electromagnetic wave. If there are electric charges (like the free electrons in a conductor) in this plane, they will be set and sustained in motion by the electric and magnetic fields of the EM wave. The charges thus acquire energy and momentum from these waves. We have seen in earlier units, that, in a region of free space, with electric field
Since electromagnetic waves contain both electric and magnetic fields, there is non-zero energy density associated with the electromagnetic waves and therefore, they carry energy.
The great technological importance of EM waves stems from the fact that they carry energy from one place to another. The radio, TV and mobile signals carry energy. Light carry energy from the sun to the earth, thus making things visible to human eye, helping leaves to photo-synthesis and enabling solar panels to produce electricity.
Since electromagnetic waves carry momentum, they can also exert pressure, called radiation pressure. If the total energy transferred to a surface, in time
This radiation pressure, exerted by sunlight, is found to be of the order of
Suppose EM waves are incident normally on the surface of a perfectly black block of surface area A and thickness
Characterstics and Properties of EM Waves
1. Electromagnetic waves are produced by accelerating or oscillating electric charges.
2. They are self-sustaining oscillations of electric and magnetic fields, which are coupled to each other.
3. The time-varying electric and magnetic fields are mutually perpendicular and are perpendicular to the direction of propagation of the wave.
Hence electromagnetic waves are transverse is nature.
4. The coupled sinusoidal electric and magnetic field variations are occuring in same phase, so that they attain their maximum or peak values at the same time.
5. Electromagnetic waves do not require any material medium for propagation.
6. They propagate in free space with a speed equal to
7. When electromagnetic wave propagate through a material medium, the speed becomes
(v for any material medium is lesser than
8. The speed of electromagnetic waves is also obtained as ratio of the magnitude of electric field to that of the magnetic field at any instant
9. EM waves do not carry any charge and so they are not deflected by external static electric or magnetic fields.
10. All the electromagnetic waves, irrespective of their frequency (low or high), travel with the speed equal to
11. The speed of EM waves follows the general expression for wave-speed,
12. Experiments by Hertz demonstrated that elecromagnetic waves of any frequency (or wavelength) undergo refraction, diffraction, polarisation and can form standing waves.
13. Electromagnetic waves carry energy which is shared equally by the electric field
In a region of space where
Here
where
Therefore,
and
The total average energy density possed by the electromagnetic waves is therefore,
Therefore, total energy density
or
or
14. Electromagnetic waves carry energy and linear momentum(
(In case the waves are totally reflected from the surface, backwards, than the momentum transferred to the surface will be zero)
15. Since electromagnetic waves possess momentum, they can exert radiation pressure.
16. The intensity of electromagnetic radiation (I), during the propagation of the EM wave, at a point, is defined as the amount of energy passing through unit normal area around that point in unit time.
That is:
or
If
Since
17. If
It may be noted that a vector called poynting vector (S) gives the magnitude and direction of energy transported by the EM waves per second per unit normal area, and
Now, by definition,
or
or
or
or
18. The total energy transferred to a black surface, over a cycle, by normally incident EM waves is equal to :
Example-1:
A plane electromagnetic wave of frequency
Show Answer
Solution :
Given :
As we know that
Now,
Example-2:
The magnetic field in a plane electromagnetic wave is given as:
(a) What is the wave length and frequency of the wave?
(b) What is the expression for the electric field?
Show Answer
Solution :
Given
(i)
(ii)
(iii)
(iv)
When we compare the above given equation with:
(a)
Also,
(b)
Since the wave velocity (v) is along
or
Example-3:
Light with an energy flux of
Show Answer
Solution :
Given : Energy flux
Therefore, energy falling on
Hence, total momentum delivered (for complete absorption) on to
Therefore the average force exerted on the surface is:
Example-4:
Calculate the amplitude of electric and magnetic fields produced by the radiation coming from a 100 watt bulb, at a distance of
Show Answer
Solution :
The bulb, as a point source,radiates light in all directions unformly. At a distance of
Therefore, the intensity of light at
Half of this intensity is provided by the electric field and half is provided by the magnetic field of the radiation.
Now, we have,
or
Hence,
(Note that, even though the magnetic field amplitude is extremely small, as compared to electric field magnitude, the energy associated with both of then are equal. Further
Example-5:
Suppose that the electric field amplitude of an electromagnetic wave is
(a) Determine the values of
(b) Obtain the expression for
Show Answer
Solution :
Given :
(a)
(b) Suppose the wave propagate in the positive
Expression for
Example-6:
Suppose that the electric field part of an electromagnetic wave in vacuum is :
Obtain the:
(i) direction of propagation
(ii) wavelength
(iii) frequency
(iv) amplitude of the mangetic field part
(v) expression for the magnetic field part of the wave
Show Answer
Solution :
Given:
The standard equation for
Comparing the two we get:
(i) The direction of wave propagation is
(ii)
(iii)
(iv)
(v)
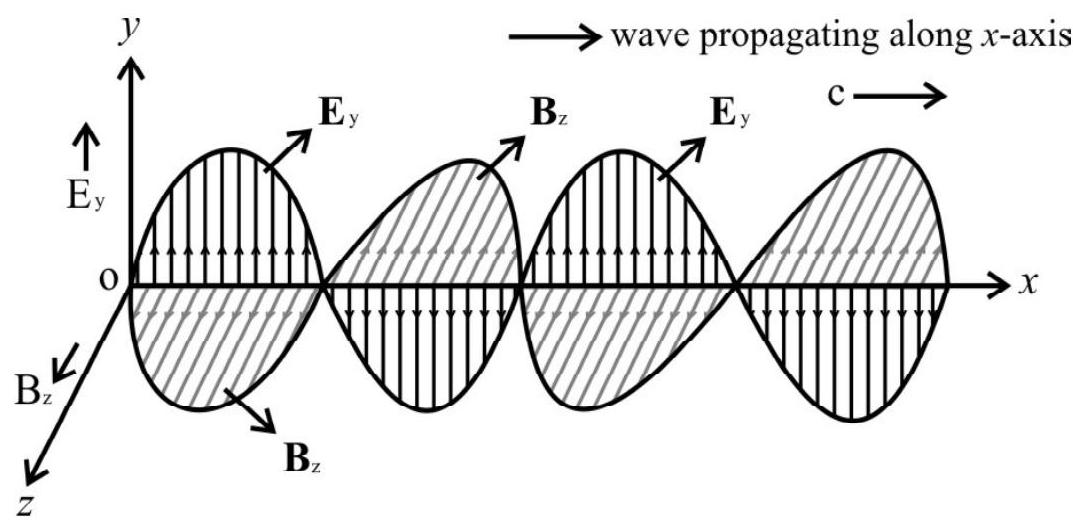
Electromagnetic Spectrum
After Hertz’s experimental demonstration regarding electromagnetic waves, establihing Maxwell’s theory, several types of electromagnetic waves were discovered, in addition to the familiar and well known visible
light wave. Now we are all aware that EM waves include visible light, ultra violet radiation, infrared waves,
The orderly distribution and classification of electromagnetic waves, according to their frequency or wavelength is known as the electromagnetic spectrum.
The electromagnetic spectrum has a wide range of wavelength, varying from about
The following figure, and the table below it, give the details of the various regions of the electromagnetic spectrum with their range of frequency and wavelength, their production as well as the means of their detection. It may be noticed that there is no sharp division between the different regions.
The Electromagnetic Spectrum
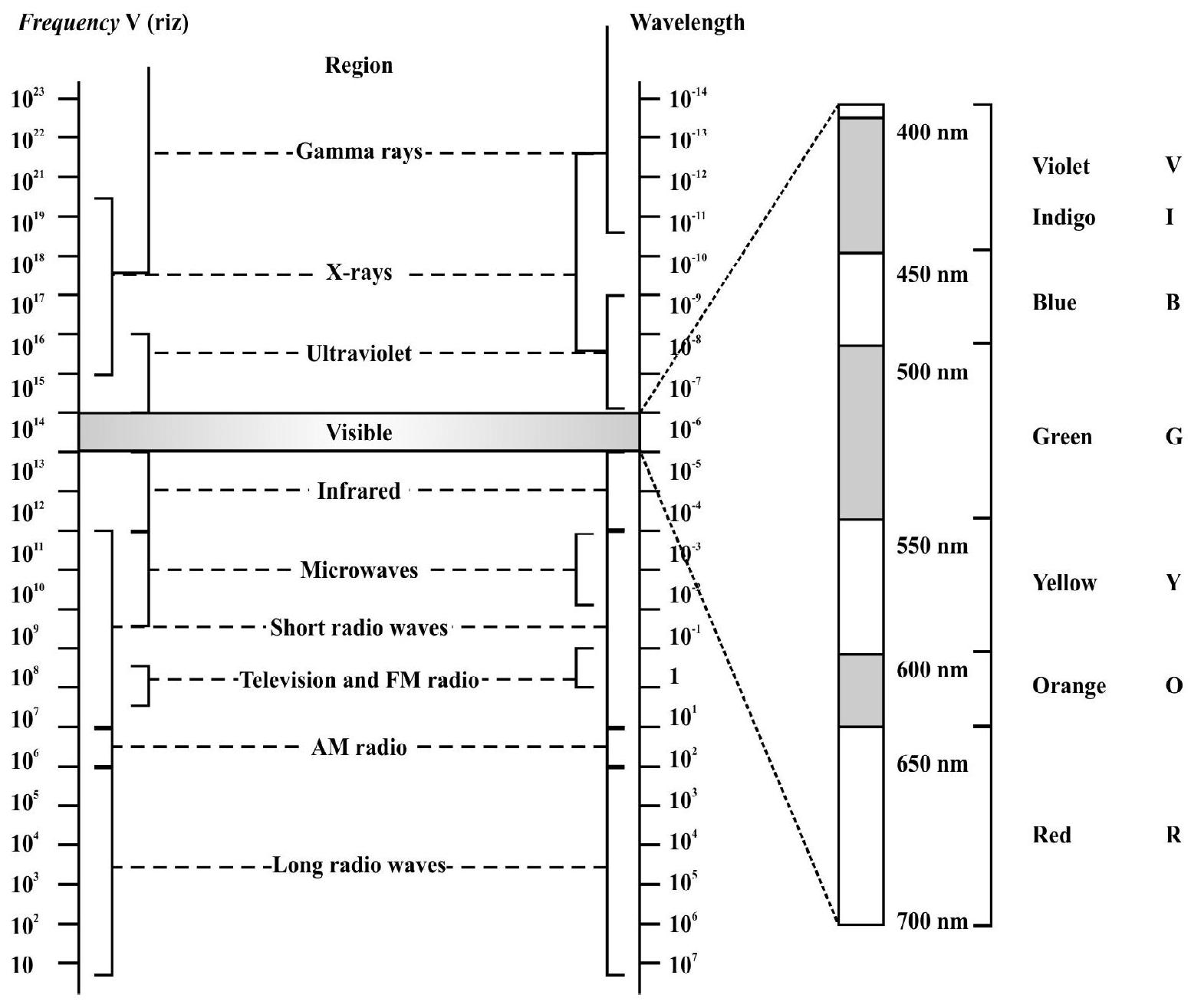
Different types of EM waves and their brief discription
| S. No. | Type | Wavelength range |
Frequency range, (Hz) |
Production | Detection |
|---|---|---|---|---|---|
| 1. | Radio waves |
Oscillating circuit or rapid acceleration and decelerations of electrons in aerials |
Receiver’s aerials | ||
| 2. | Microwaves | Khystron valve or magnetron valve |
Point contact diodes |
||
| 3. | Infrared waves |
Vibration of atoms and molecules |
Thermopiles, Bolometer, Infrared photographic films |
||
| 4. | Visible light waves |
Excitation of valency electrons in atoms, electrons in atoms emit light when they move from one energy level to a lower energy level |
The human eye, Photocells, Photog- raphic film/plate |
||
| 5. | Ultravoilet waves |
Excitation of atoms, spark and arc lamps, inner shell electrons in atoms moving from one energy level to a lower level |
Photocells, photographic film |
||
| 6. | of inner shell electrons |
Photographic film, Gaiger tubes, Ionisation chamber |
|||
| 7. | Gamma rays | Radioactive decay of the nucleus, Nuclear origin |
Photographic film, Ionisation chamber |
The Electromagnetic Spectrum
Main Regions of EM Spectrum and uses and Applications of these Region
The entire electromagnetic spectrum is broadly classified in the following regions, in the order of the decreasing wave length (or increasing frequency). We now describe each region, briefly, including some elementary facts about the use of various electromagnetic waves.
(i) Radio Waves
They are produced by the oscillating charges at the ends of a dipole antenna connected to an oscillating voltage source. These radio waves have a frequency range from about
In early radio-communication, amplitude modulated (AM) waves were used. AM radio were used for this purpose. There are two bands of AM waves (a) Medium wave band (MW bnad), with frequency ranging from
TV waves employ EM waves in the frequency range from
The ultra High frequency (UHF) band extends from
(ii) Microwaves
They are short-wave length radio waves, having frequency range from
By virture of their short wave length, microwaves can be transmitted through large distances, without much spreading, like a narrow beam. Thus they are very effectively used in RADAR systems, aircraft navigation and satellite communication.
Microwaves are used in speed guns to measure the speed of fast moving objects and detecting the service speeds of tennis and squash balls, cricket balls, automobile vehicles etc.
Microwaves are also used in Microwave oven for cooking purposes. (Microwave oven works on the principle of resonance between the elcgric field vibrations of the microwaves and electric field variations around the highly polarised water molecules (or dipoles) due to the vibrational and rotational motions of the water molecules. They both have the same or almost same frequencies, producing resonance. It may be noted that at resonance maximum absorption of energy takes place. Hence water moelculas absorbes energy from microwaves due to resonance. In the microwave oven, the energy absored by water molecules heats up these molecules and they then conduct (transfer) the heat to the other food particles, heating the entire food).
(iii) Infrared Waves
These waves have frequency range from
They are produced or emitted by all hot objects and molecules. These waves are easily absorbed by objects in the surroundings, there by cansing heating effect in them. Because of this, infrared (IR) radiations are some times referred to as ‘heat waves’.
Infrared waves (or radiations) are used for a variaty of applications like:
- Physical therapy for treating muscular strain (infrared lamps are used for this).
- Solar water heater, solar cooker, solar cells, remote sensing satellites.
- Drying purposes (fruits and vegetables).
- Night vision goggles
- Imprared LEDs, used in remote controles to operate electronic systems in TV sets, video recorders, hi-fi system, ACs, set-top boxes etc.
- Green houses to keep plants warm.
(Infrared waves trapped by green house gases like
(iv) Visible Light
This is the most familiar form of electromagnetic waves. Even though this region forms a significant part of solar spectrum, it is in fact only a very small part of the whole electromagnetic spectrum. Human eye is sensitive only to this part of the EM spectrum.
The visible light waves have a frequency range from
The visible light waves are produced by de-excitation of valance electrons from higher energy to lower energy levels.
(v) Ultra Violet Waves (UV Rays)
This region has a range of frequencies from
Sun is the most aboudant source of U-V rays. They are also produced by special U-V lamps, very hot objects, mercury arcs and welding iron arcs.
Over-exposure to
adversely affecting the absorption of
Ultravoilet radiations have wide range of uses like:
- in preserving food stuff, by killing germs and bacteria using U-V rays.
- in burglar alarms.
- In the detection of forged documents.
- in finger print analysis.
- in checking and testing mineral samples (through flourescence caused by
- U-V lamps used in water purifiers.
- In LASIK
(It may be noted that UV rays are easily absorbed by ordinary glass and therefore special glass goggles or face masks with glass windows help welders protect their eyes from the UV rays produced by welding arcs).
(vi)
This part of the EM waves has the range of frequencies from about
- They are used as treatment tool for certain forms of cancer.
- These rays are used for detection of bone fractures, unauthourised presence of hidden objects like precious metals and stones, bullets etc. inside human body as well as explosive and drugs hidden in the body.
- These rays are used for scientific research in crystal structure etc.
- They are used in engineering, to detect and test any faults, cracks and flows in structures built with metals and concrete.
- They are also used to test the uniformity of insulating materials and to detect leakage of oils in underground pipes.
(It may be noted that over-exposure to
(vii) Gamma Rays (
These rays have a frequency range from about
They are used in medical field to destroy cancer cells (radio-therapy).
Soft
Example-7:
Use Wien’s formula :
Show Answer
Solution :
Given:
Example-8:
Given below are some famous numbers associated with electromagnetic radiation in different contexts in physics. State the part of electromagnetic spectrum to which each belongs to:
(i)
(ii)
(iii)
(iv)
(v)
Show Answer
Solution :
(i) Given wave length corresponds to short wavelength radio-waves.
(ii) High frequency end of radio waves (short radio waves).
(iii)
(iv)
(v) Given
Which lies high frequency
Example-9:
Electromagnetic waves with wavelenth
(i)
(i)
(iii)
(iv)
(a) Identify and name the part of EM spectrum to which these radiation belong.
(b) Arrange them in the ascending order of their wavelength magnitude.
(c) Write one more application for each of them.
Show Answer
Solution :
(a)
(b)
(c)
EXERCISE
1. The magnetic field of a beam emerging from a filter facing a flood light is given as:
What is the average intensity of the bean?
Show Answer
Answer:
Solution:
Given
Therefore,
Now,
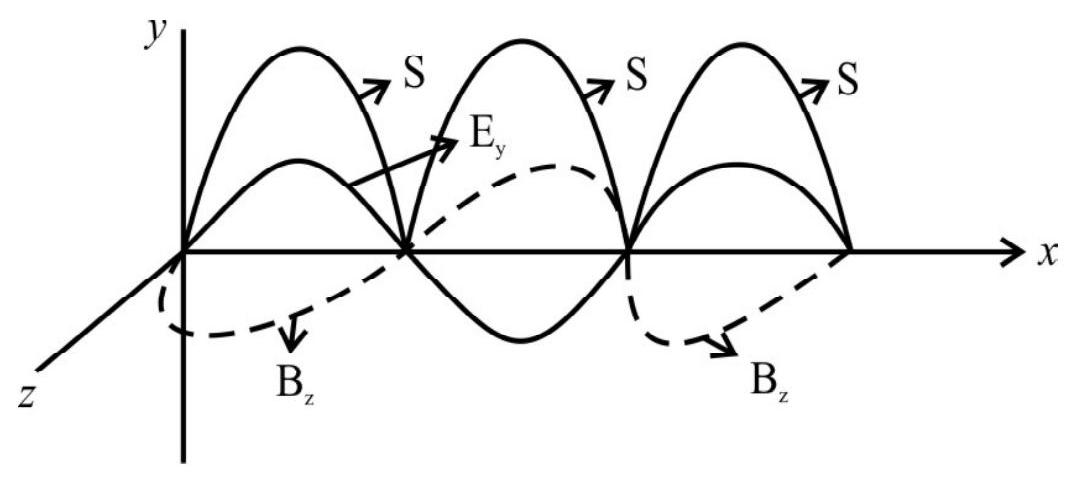
2. Poyting vector
Show graphically the variation of
Show Answer
Solution:
For an EM-wave propagating along
Now,
and
Hence, the graph of
3. Show that the radiation pressure exerted by an EM-wave of intensity I on a surface, kept in vaccum, for complete absorption is
Show Answer
Solution:
Force
or
or
or
or
But
Hence,
4. For frequency
Show Answer
Answer:
Solution:
Let
Therefore, the field
Hence, the conduction current density is
or
Now, the displacement current density is
where
Hence,
Answer:
5. If
Show Answer
Answer:
Solution:
Defractive index
Now,
Question Bank
Key Learning Points
1. Maxwell’s equation for displacement current
2. The above equation along with Faraday’s equation for emf induced in space
together, as Maxwell’s first two equation in electromagnetic wave theory predicted the production EM waves, which travel with the speed of light.
3. Along with the above two equations, the equations for Gauss’s theorem in electrostatics and magnetism (namely
4. Hertz experiments to produce and detect EM waves demonstrated the validity of Maxwell’s theory.
5. The main properties of Em waves are:
(i) They are made up of coupled time varying electric and magnetic fields (simusoidally varying).
(ii) The variation is E-field produces the B-field and vice-versa.
(iii)
(iv)
(v) The equation for the sinusoidal
where,
Also,
(vi)
(vii) For any material medium,
(viii) The wave velocity is also equal to the ratio of E-field to B-field at any instant of time.
i.e.
(ix) EM-waves carry energy. Where these waves are absorbed, the enery gets transferred to the material which absorbs the waves.
(x) The average energy density carried by the
or
(xi)
(xii) The total energy density of an EM-wave is
or
or
(xiii) The intensity (I) of EM-waves is defined as the total energy flowing through unit normal area in one second.
(xiv) Since EM-waves carry energy and momentum these waves can exert pressure (called radiation pressure) on the incident surface for total absorption,
(xv) Pointing vector
Also,
(xiv) To produce a continuous train ofEM waves, we need an oscillating / accelerating charge. This is done with the help of dipole antenna connected to oscillating voltage source. The frequency of EM waves is exactly equal to the frequency of the oscillating charge or oscillating voltage source.
6. The electromagnetic spectrum consists of different regions; namely. Radio waves, micro waves, infrared radiations, visible light, ultraviolet rays,
Easy
Source of Electromagnetic Waves
1. Electromagnetic waves are produced by
(1) charges at rest, having the same linear charge density along two mutually perpendicular directions.
(2) equal charges, moving with equal uniform velocities, along two mutually perpendicular directinos.
(3) planer rectangular coils having a steady current flowing through them.
(4) charges that move with a continuously changing velocity
Show Answer
Correct answer: (4)
Solution:
Maxwell’s theory, of EM waves, tells us that charges, when accelerated, radiate EM waves. It is only charges, moving with a changing velocity, that can be regarded as accelerated charges. Therefore, it is only such charges that can be a source of EM waves.
Average
Equations for EM Waves
2. An electromagnetic wave, propagating along the
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
For an EM wave, propagating along the
Average
Features of EM Waves
3. From the following, the only incorrect statement, about EM waves, is the statement:
(1) “EM waves can correspond only to self-sustaining oscillations of electric and magnetic fields in vaccum”.
(2) ‘We do not need the hypothesis of the (hypothetical) medium ’the ether’, to understand the production, and propagation, of EM waves”.
(3) “EM waves can propagate through material media”.
(4) “The standard, of length, the metre, is defined in terms of the (strictly) constant value of the velocity of EM waves in vaccum”.
Show Answer
Correct answer: (1)
Solution:
Statement (1) is incorrect, because of the presence of the word ‘only’ in it. EM waves can correspond to self sustaining oscillations of electric and magnetic fields, in vaccum, as well as in material media.
Statement (2), (3) and (4) are all (now) well known correct statements about EM waves.
Average
Relating E and B Vector
4. The electric field, in a plane
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
The magnitude of the magnetic field, in an EM wave, is related to the corresponding magnitude of electric field, through the relation
Hence the magnitude of the magnetic field (at the same point and at the same time), equals
Further, the direction of propagation (i.e., the direction
Here
This gives
Hence
Difficult
Relating Directions of E and B
5. The magnetic field, (at a particular point
The electric field, for this EM wave again at the point
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
A close look, at the equation for
The direction of
Average
Wavelength Estimation
6. The electric field (in
The wavelength,
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
Comparing the given equation with its standard form, namely,
Also, the amplitude,
Average
Frequency Estimation
7. The magnetic field, (in tesla) in a plane EM wave, propagating along the
The frequency of the EM wave, and the part of the EM spectrum, to which this wave could belong, are given, respectively, by
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
Comparing the given equation with its standard form, namely,
This frequency corresponds to the (short radio wave / microwave) part of the EM spectrum. (The infrared waves have frequencies of the order of
Average
Estimating the Velocity of EM Waves
8. The electric field (in SI Units), in a plane EM wave, propagating along the
The speed of propagation of this wave (as per this data), and the part of the EM spectrum, to which this wave corresponds, are given respectively, by
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
Comparing the given equation, with its standard form, namely
This corresponds to the green colour in the visible part of EM spectrum.
Also speed of propagation
Average
Writing the Equation for Electric Field of an EM-Wave
9. An EM wave has a wavelength
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
We have
and
We, therefore, use these values of
Difficult
Writing the Equation for the Magnetic Field of an EM-Wave
10. An EM-wave has a wavelength of
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
The direction of transmission of energy (given to be along the
and
The direction of propagation, being the
Average
Electromagnetic Spectrum
11. The oscillating electric field (
and
The parts of the EM spectrum, to which waves (1) and (2), are likely to belong, are
(1) UV rays and microwaves, respectively
(2)
(3)
(4) UV rays and microwaves, respectively
Show Answer
Correct answer: (2)
Solution:
For wave (1),
This wavelength value corresponds to
For wave (2),
This wavelength value corresponds to infrared rays.
Hence waves (1) and (2) are likely to be
Average
EM Spectrum
12. The equation
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
For option (1),
For option (2),
For option (3),
For option (4),
(In each case, the value of
Hence only option (3) could correspond to the representatin of microwaves.
Average
Related Values of
13. A student writes the following expression for the oscillations of the magnetic field of an em wave:
Assuming that his choice of the value, of the coefficient of
(1) less than the correct value by (nearly)
(2) more than the correct value by
(3) less than the correct value by (nearly)
(4) more than the correct value by
Show Answer
Correct answer: (1)
Solution:
As per the stand form of representation, namely
the values of the coefficient of
Since
The given value is
Average
Related Values of
14. A student writes the following expression, for the oscillation of the electric field of an em wave:
Assuming that she has correctly written the value of the coefficient of
(1) less than its correct value by (nearly)
(2) more than its correct value by (nearly)
(3) less than its correct value by (nearly)
(4) more than its correct value by (nearly)
Show Answer
Correct answer: (2)
Solution:
As per the standard representation, namely
The given value is
This is more than the correct value by
Average
Identifying the Part of the EM Spectrum
15. The oscillation, of the magnetic field, of an EM wave, propagating along the
This EM wave could be visible light if the values of
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
We have
For option(1)
For option(2)
For option(3)
For option (4)
(In each case, the value of
Hence only option (3) could correspond to visible light.
Average
Characterstics of EM Waves
16. In the figure drawn here, the points A, B, C, D, E, F and G, on the
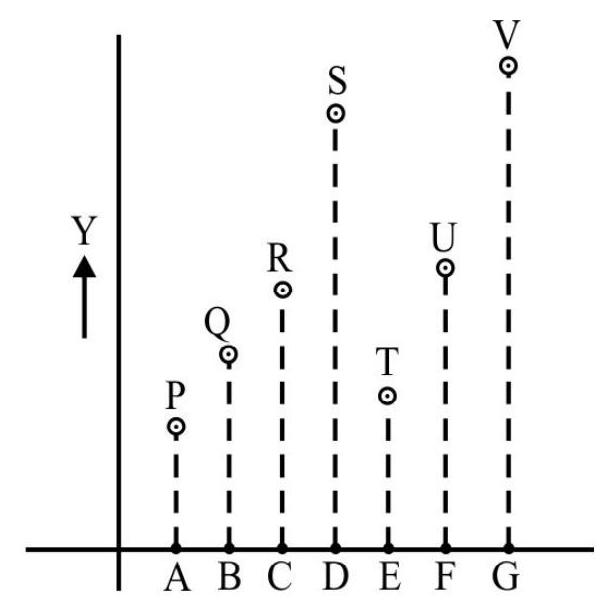
(1) wavelength
(2) frequency (
(3) angular frequency
(4) velocity (v), in vaccum, or the wave number (
Show Answer
Correct answer: (2)
Solution:
For the given order of points A, B, C, D, E, F, G; the frequency increases for the first four waves; then decreases (to a value between the first two radius); then increases but to a value between the third and fourth values and finally increases to a value higher than all the other values. The wave number
Hence option(2) is the only correct option.
Average
Characterstics of EM Waves
17. An em wave is propagating along the positive
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
The wave is propagating along the (+ ve)
Further, the cross product
Hence option (1), consistent with both these requirements, is the correct option.
Easy
Electromagnetic Spectrum
18. The angular frequencies, for three em waves
(1)
(2)
(3) visible light, infrared rays, radiowaves
(4) uv - rays, radiowaves, visible light
Show Answer
Correct answer: (4)
Solution:
We are given that
The three em waves must, therefore, have their frequencies as per this requirement. In all the options given,
Average
Electromagnetic Spectrum
19. The wave number (
(1) infrared rays, uv rays, visible light
(2) visible light, uv rays,
(3) radiowaves, visible light, uv rays
(4) microwaves, visible light,
Show Answer
Correct answer: (1)
Solution:
We have
Also we must have
This ordering of wavelenghts is valid only in option (1). In all the other three options,
Hence option (1) is the correct choice.
Difficult
Electromagnetic Spectrum
20. The velocity (v), in a given material medium, has values
(1)
(2) uv rays, visible light, microwaves
(3) infrared rays, uv rays, radiowaves
(4)
Show Answer
Correct answer: (3)
Solution:
We know that the refractive index of a medium decreases with increase in wavelength
Further, since
‘Higher wavelength implies a higher speed of light in the medium.’
We are given that
Hence option (3) is the correct choice.
Difficult
Electromagnetic Spectrum
21. An em wave is propagating along the
(1)
(2)
(3)
(4) y-axis and z-axis, respectively
Show Answer
Correct answer: (1)
Solution:
When the wave propagates along the
The charge, initially at rest, experiences a force due to the
Easy
Transfer of Energy by EM Waves
22. EM waves can transport energy;
(1) however, it is only the
(2) however, it is only the
(3) both the
(4) both the
Show Answer
Correct answer: (4)
Solution:
EM waves, (having energy associated with their electric and magnetic fields) can transport energy from one place to another.
Both the electric and mangetic fields contribute, in this transfer of energy. Further, the energy of an EM wave, is shared equally between its electric and magnetic fields. Hence the ratio of their contributions, in the transfer of energy, equals
Easy
Transfer of Energy and Momentum by EM Waves
23.
(1) EM waves can transport energy (through their
(2) EM waves can transport energy (through their
(3) EM waves can transport energy as well as momentum (through their
(4) EM waves can transport energy as well as momentum (through their
Show Answer
Correct answer: (4)
Solution:
EM waves (having energy, associated with their electric and magnetic fields) can transport energy from one place to another.
It has been shown that they can trasnfer momentum also.
The electric, and the magnetic fields, of an em wave, contribute equally in this transfer of energy and momentum.
Easy
Energy Density of the E and B Fields
24. The (instantaneous) energy density (energy per unit volume) of the electric and magnetic fields, of an em wave, are equal, respectively, to
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
The (instantaneous) energy density (energy per unit volume), of the electric and magnetic fields, of an em wave, is given by;
(Volume) energy density of electric field
and (volume) energy density of magnetic field
Here
The energy, of an em wave, in shared equally between its electric and magnetic fields. We, therefore, also have
Easy
Transfer of Energy, Momentum and ‘Pressure’by EM Waves
25. It has been experimentally demonstrated that
(1) EM waves can transport energy but not momentum
(2) EM waves can transport energy but not momentum; however, they do exert a ‘radiation pressure’
(3) EM waves can transport both energy and momentum; however, they do not exert any ‘radiation pressure’
(4) EM waves can transport both energy and momentum; they also exert a ‘radiation pressure’
Show Answer
Correct answer: (4)
Solution:
EM waves (having energy associated with their electric and magnetic fields) can transfer energy from one place to another.
It has been shown that they can transfer momentum also (Total momentum delivered in time
The average rate of transfer of momentum
This force, per unit area of the surface, would then equal the ‘radiation pressure’.
Average
Energy Transfer by EM Waves
26. The total energy transfered to a (perfectly black) surface of area
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
We know that
(Volume) energy density of electric field
(Volume) energy density of magnetic field
The energy, of the em wave, is shared equally between its electric and magnetic fields.
Over one complete cycle, we need to use
[We cannot use
The volume absorbing this energy
Hence total energy transferred over one complete cycle
Difficult
Force due to EM Wave
27. An electromagnetic wave (of frequency
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
We know that
(Volume) energy density of electric field
(Volume) energy density of magnetic field
The energy, of the em wave, is shared equally between its electric and magnetic fields.
Over one complete cycle, we need to use
Time taken
Difficult
Energy of an EM Wave
28. The oscillatory electric field, of an em wave, propagating along the
This em wave is incident on a perfectly black circular disc, of diameter
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
We know that
(Volume) energy density of electric field
(Volume) energy density of magnetic field
The energy of the EM wave is shared equally between the electric and the magnetic fields.
Over one complete cycle, we need to use
Also
We also have
The volume of the circuluar disc
Difficult
Energy Transfer by an EM Wave
29. The oscillatory magnetic field, of an em wave, propagating along the (-)
This em wave is incident on a perfectly black circular disc (or radius
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
We know that
(Volume) energy density of the electric field
(Volume) energy density of the magnetic field
The energy, of the em wave, is shared equally between the electric + magnetic fields. Over one complete cycle, we need to use
Also
Difficult
Pressure due to EM Wavess
30. The oscillatory electric field, of an em wave propagating along the
This em wave is incident on a perfectly black surface (of area
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
We know that
(Volume) energy density of electric field
(Volume) energy density of magnetic field
The energy of the em wave is shared equally between its electric and magnetic fields.
Over, one complete cycle, we need to use
Also
Average radiation pressure
Average f Intensity of an EM Wave
31. The intensity (I) of an em wave (having
magnetic fields), can be expressed in the form:(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
The intensity (at a given point), of an em wave, equals the energy received there per unit area per unit time.
Consider an em wave, propagating along the
The volume of this cyilnder is
The em wave (covering a distance
Through the cross section (= unity) of this cylinder in one second.
Hence energy transferred per unit area per unit time.
Average
Peak Value of Electric Field in an EM Wave
32. The peak value of the electric field, in the light radiated by a given (point) source of power
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
The intensity, I, of the light radiated by a (point) source of power
The intensity also equals
This gives
Average
Peak Value of the Magnetic Field in an EM Wave
33. Agiven (point) source, of power
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
The intensity, I, of the light from a (point) source of power
The intensity I also equals
Thus
This dependance of
Average
Comparison of Peak Value, of Electric Fields of Two EM Waves
34. The peak value of the electric field, in the light radiated by a point source of power
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
The peak value, of the electric field (
Average
Comparison of Peak Value, of Electric Fields of Two EM Waves
35. The ratio, of the rms values of the magnetic fields in the em waves, radiated by two point sources, at points distance
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
The rms value of the magnetic field (
For the given data, we then have
where
Easy
Momentum Transfer due to EM Waves
36. An em wave, originating from a source, is radiating out
(1) zero
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
The surface, being a perfectly reflecting surface, does not absorbe the incident em at all. Hence the energy absorbed, and, therefore, the momentum delivered to the surface, are zero each. The average force (= rate of change of momentum) is, therefore, zero.
Average
Relating between rms Value of Electric Field in an EM Wave + its Intensity
37. The rms value, of the electric field, in the em waves, produced a point source, at a distance of
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
Let
Average
Relation between the Peak Value of the Magnetic Field of an EM Wave and its Intensity
38. The peak value of the magnetic field, at a certain point, for an em wave is
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
Average
Intensity of EM Wave + Force Exerted on a Surface
39. EM Waves having a uniform and constant, intensity I, are incident normally on a (perfectly black) surface of area
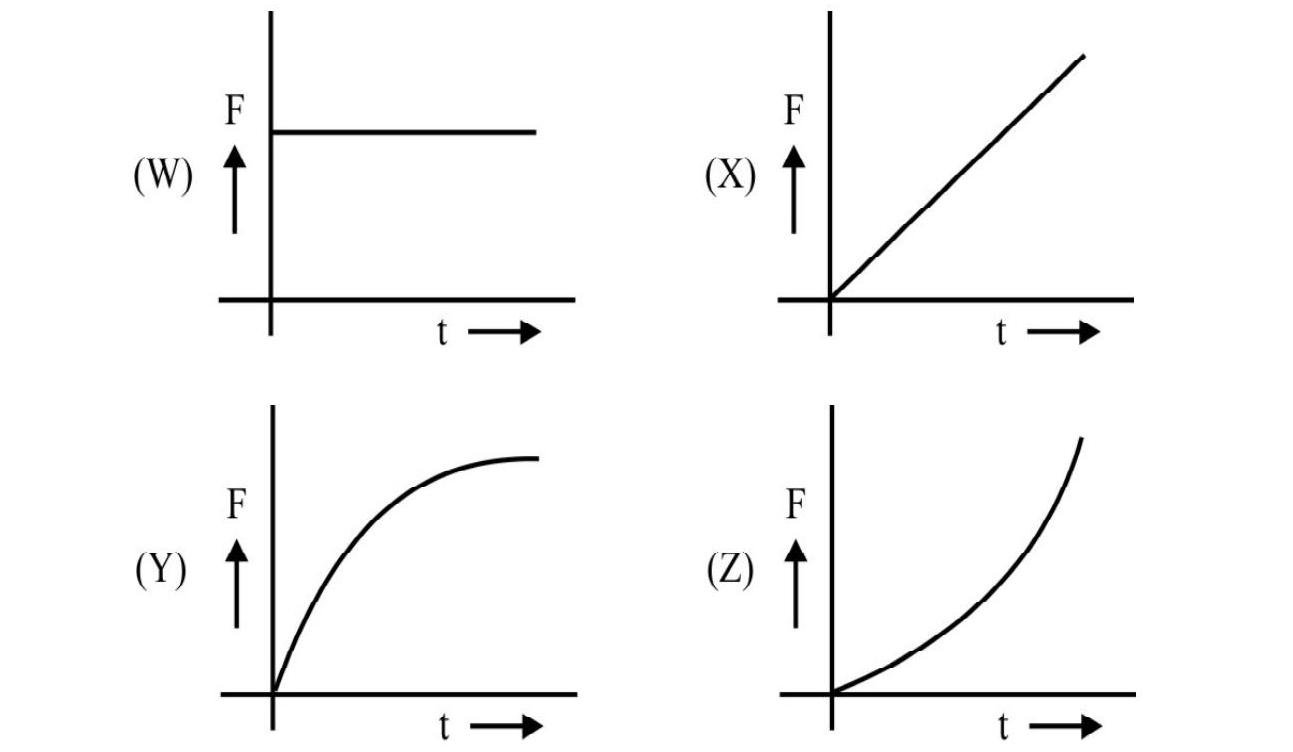
(1)
(2)
(3)
(4) Z
Show Answer
Correct answer: (1)
Solution:
When EM Waves, of intensity I, are incident normally, on a surface of area A for a time t, the total energy absorbed by the (black) surface is
Therefore, the total momentum, delivered to the surface, is
The average force thus does not depend on the time,
Aveage
Radiation Pressure due to an EM Wave
40. EM waves, of a uniform intensity
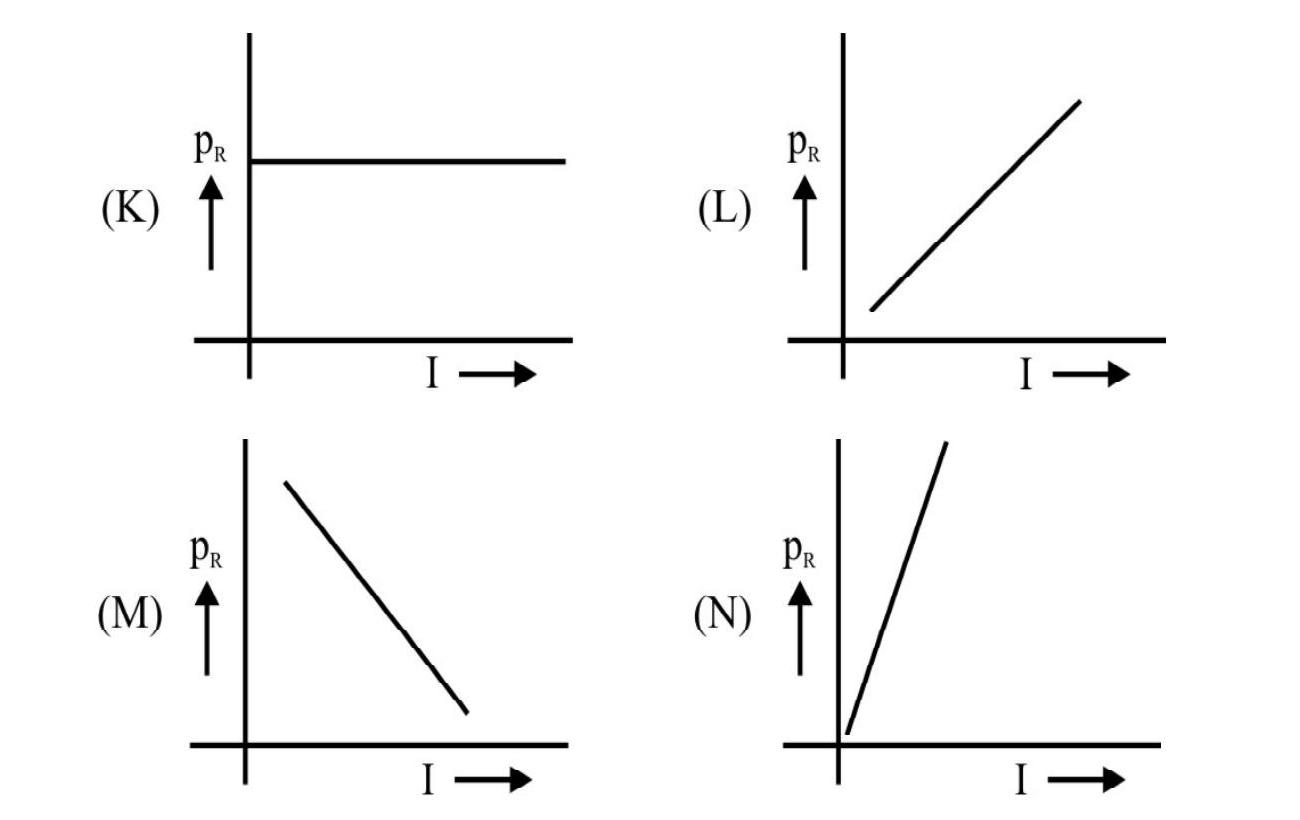
(1)
(2) L; and its slope would be (nearly)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
When em waves, of intensity I, are incident normally, on a surface of area A, for a time t, the total energy, absorbed by the black surface, is
The take momentum, delivered to the surface, is
The graph between
Difficult
Radiation Pressure
41. Electromagnetic waves of intensity I, are incident normally on a material surface. If the reflected, transmitted and absorbed parts of these waves (by the material) are in the same ratio, then the radiation pressure
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (2)
Solution:
Let
Therefore, intensity, I = Energy recieved per unit normal area in one second.
Now, momentum imparted for computer absorption (i.e. if the surface is a perfectly block-body surface), is :
Pressure (p) exerted on the surface will then be:
or
or
Now, for complete / total reflection, where the EM waves get bounced back with speed c, the change in momentum is, zero
For complete transmission,
Now, here,
Hence, the total pressure on the surface, here, will be;
Pressure
Correct answer is :
Difficult
Poynting Vector
42. An infinitely long thin wire has a uniform charge density of
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
The figure given aside represents the situation. Due to the uniform
The electric field at
The magnetic field at
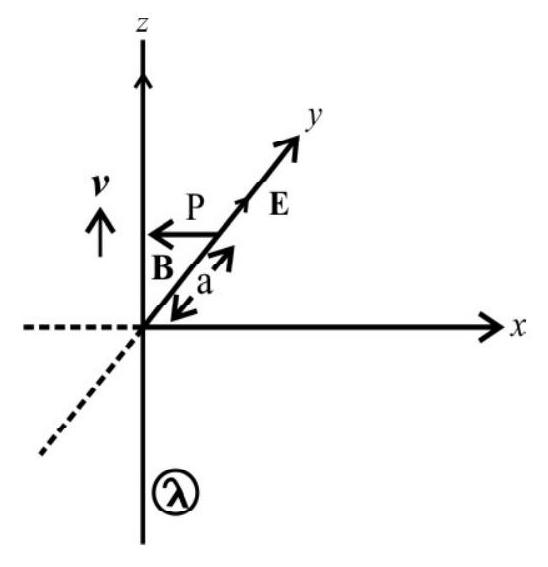
or
Correct answer: (3)
Average
Intensity of EM Wave / Poynting Vector
43. The SI unit of the poynting vector (S) defined by the formula:
(1) volt-tesla
(2) volt - metre - ampere
(3) joule - metre
(4) watt - metre
Show Answer
Correct answer: (4)
Solution:
The magnitude of
Answer (4) is correct.
Difficult
Speed EM Waves
44. An electromagnetic wave of frequency
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
Given,
Now,
Speed of EM wave in the medium will be
where
Here
i.e. refractive index,
But
Average
EM Spectrum
45. A monochromatic source of power
(1)
(2) uv-radiation
(3) visible light
(4) infrarred waves
Show Answer
Correct answer: (2)
Solution:
Given
Since efficiency is
Now,
Average
Intensity of EM Waves
46. A point source of electromagnetic radiation has an average power output of
(1)
(2) 30
(3)
(4) 300
Show Answer
Correct answer: (2)
Solution:
Intensity at a distance of
Now,
or
or
Easy
EM Spectrum
47. The range of wavelengths allotted for commercial
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (3)
Solution:
The range of frequencies alloted for FM radio is:
Now this frequency range corresponds to a wavelength range of
or
Correct answer: (3)
Average
Properties of EM Waves
48. The electric field vector
and
where
(1) zero
(2)
(3)
(4)
Show Answer
Correct answer: (4)
Solution:
The vectors
Therefore,
Correct answer: (4)
Average
EM Spectrum
49. Monochromatic source, of power
(1) gamma rays
(2)
(3) microwaves
(4) infrared waves
Show Answer
Correct answer: (2)
Solution:
Power
or
This is in the range of frequencies for
Correct option is (2)
Difficult
Intensity EM Radiations
50. The maximum value of electric field, of the total radiant energy per unit ara (normal to the direction of incidence), recieved at a distance
(1)
(2)
(3)
(4)
Show Answer
Correct answer: (1)
Solution:
Energy radiated by the surface of the star per second
Energy recieved per unit normal area per second at a distance
But
or










