Unit 11 Electrostatics
Learning Objectives
After going through this, unit you will be able to understand, appreciate and apply the following concept:
- Identify different type of charges.
- Determine the electric force between two point charges using Coulomb’s Law.
- Apply Coulambl’s law to a system of point charges to determine the net force on a charge.
- Calculate the electric field due to a point charge or system of point charges.
- Determine the electric flux through a surface.
- Use Guass law to find electric field of various charge distribution.
- Determine the torque experienced by an electric dipole in a uniform electric field.
- Distinguish between electric potential and electric potential energy.
- Calculate the electric potential of a configuration of point charges.
- Determine how electric field strength is related to electric potential and electrostatic potential energy.
- Calculate the capacitance of a given electric network, energy stored in a parallel plate capacitor with and without dielectric.
Concept Map of Electrostatics
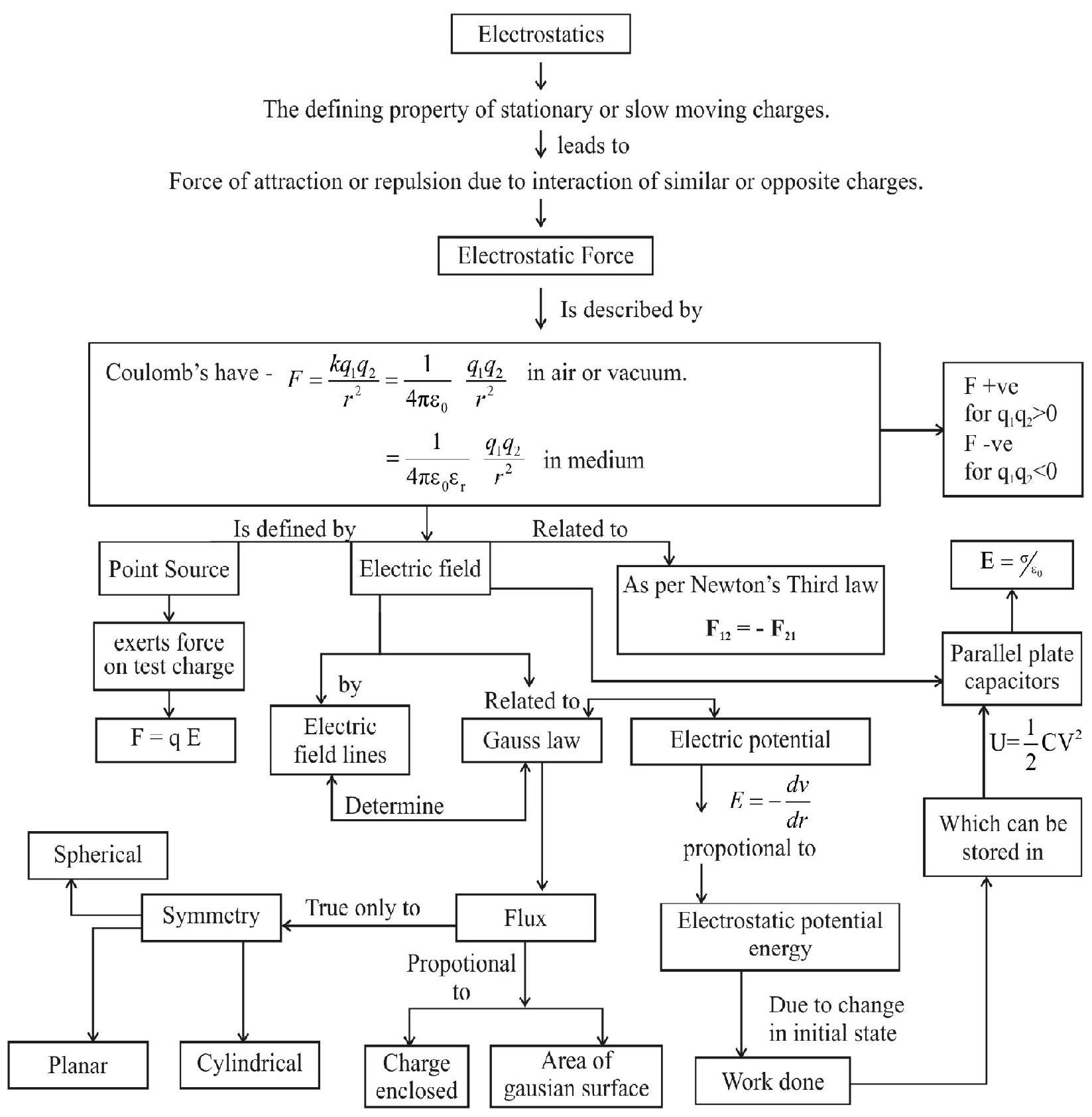
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties associated with charges at rest.
Electric Charge
Electric charge is an intrinsic characterstics of the fundamental particles of matter giving rise to all electric and magnetic forces and interactions.
From simple experiments on frictional electricity, it has been known that some materials, such as amber or ebonite, on being rubbed with, wool get ’electrically charged’. Similarly, when a glass rod is rubbed with silk cloth, the glass rod gets ’ electrically charged’. However, the charges of these two rods are of different types. One can infer that there are two types, of charges in nature: ‘glass rod type’ and ’ebonite rod type’. The first type has been called as ‘positive charge’ while the second type has been called the ’negative charge’. The changes were named as ‘positive’ and ’negative’ by the American scientist, Benjamin Fraklin, in 1750. When the ‘positive’ and ’negative’ charges on an object, are not in equal amounts, there is a net charge on the object, that can interact with other objects. We regard such an object as an ’electrified’ or " ‘charged’ object. When an object has no net charge, it is said to be electrically neutral.
It has been observed that: “Like charges repel each other and unlike charges attract each other.”
Basic Properties of Electric Charge
1. Charge is quantised : Electric charge can have only discrete values. The smallest discrete value that can exist in nature is the charge on the electron, ’
2. Charge is conserved : For an isolated system, its total charge remains constant. “charge is neither created nor distroyed”, it can only be tansferred from one object to the other.
3. Charge is additive: If a system contains ’
Charges thus add up like ‘real numbers’, they are scalars like mass.
4. Charge is invariant : The numerical value of the charge on an isolated object is independent of its state of rest or motion.
The S.I. Unit of charge is the ‘Coulomb’. It is defined in terms of ’electric current’. ‘One Coulomb’ equals the charge, transferred in one second, across the cross section of a wire carrying a current of one ampere.
Coulomb’s Law
We have noted that two like charges repel each other while two unlike charges attract each other. This force of interaction, between two charges is known as ’electric force’ or ‘coulomb force’. On the basis of experiments, coulomb gave a law for finding the magnitude of the force acting between two point charges.
According to Coulomb’s law; two stationary point charges,
or
The constant
For mediums other than vacuum (or air) the force between the charges is given by:
Here
Here
The above expression can, therefore, be written as
Important Points Regarding Coulomb’s Law
1. The Coulomb force, acts along the straight line, connecting the ponits of location of the two ‘point’ charges.
2. The law can be used to define the SI unit of charge the ‘Coulomb’.
3. For a point charge, the coulomb force due to it is ‘central’ and has a spherical symmetry.
4. For materials media the value of ’
Coulomb’s Law in Vector Form
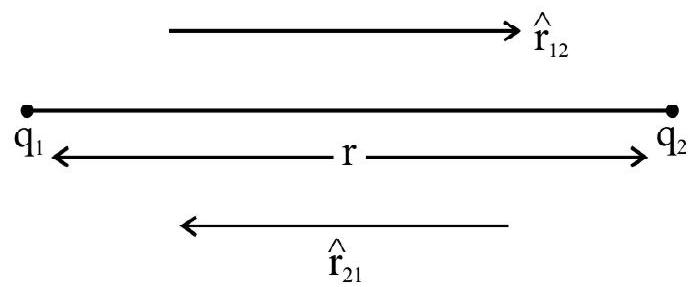
It
Where
The force, on
Here
In general, one can write:
Here
How to Solve Problems using Coulomb’s Law
1. Find the magnitude of force, using Coulomb’s law, ignoring the signs of charges. Signs only indicate the direction of force.
2. Decide whether the force, due to a given charge, is attractive or repulsive, express it by drawing vectors.
Principle of Superposition of Charges
When more than two charges are present in space, Coulomb’s law holds for every pair of charges. Thus, the net force on any charge is the ‘vector’ sum of the forces exerted on it by all other charges, taking one charge at a time.
This is known as the principle of super position for charges.
Thus if there are
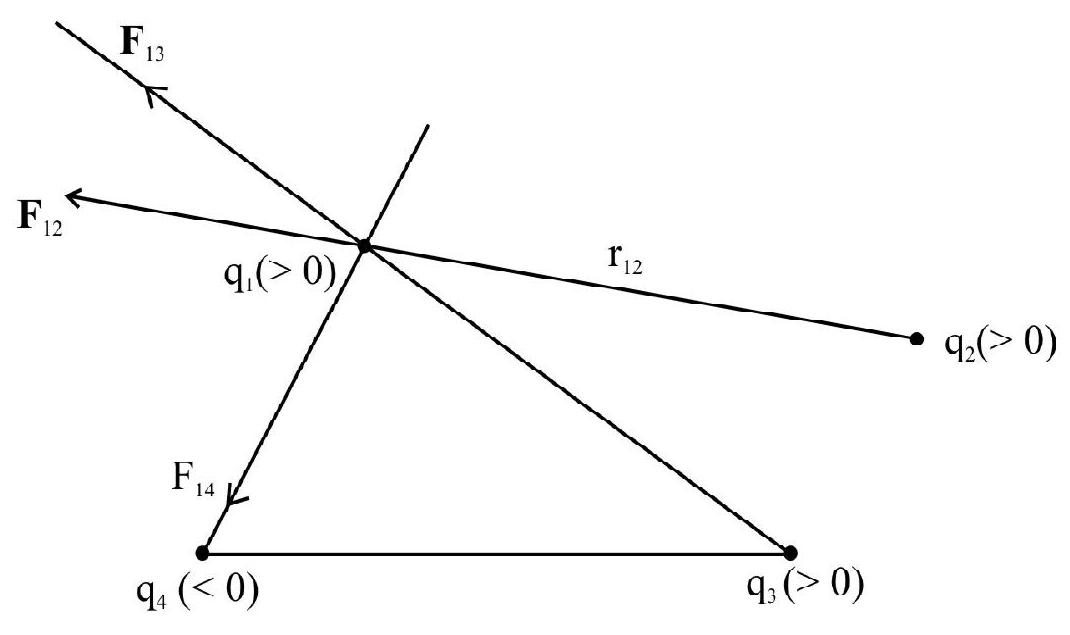
Here the ‘individual forces’ are unaffected due to the presence of other charges.
or
Here
Example-(1):
A given charge
Show Answer
Solution:
Let charge on one object be ’
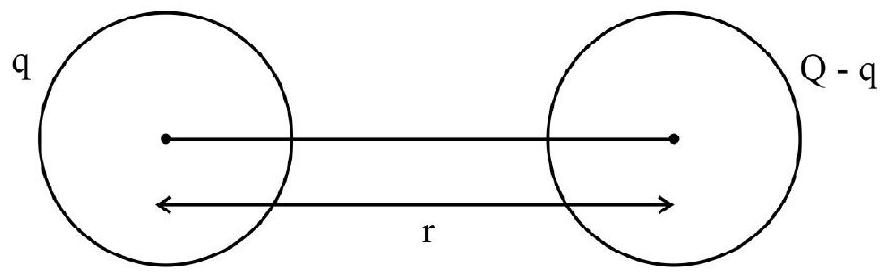
For
Thus, the charge should equally divided between the two objects.
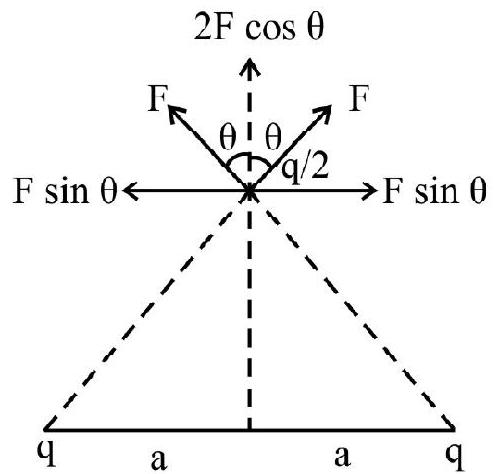
Example-(2):
Two ‘free’ point charges,
Show Answer
Solution:
Let charges be placed as shown in the figure.
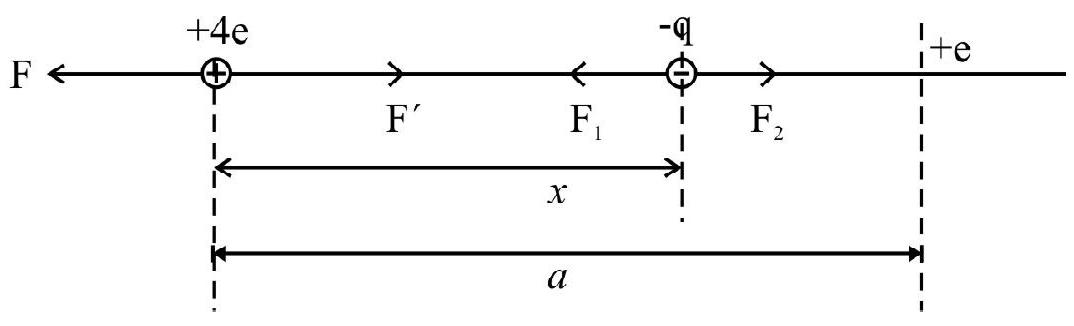
The charge
For equilibrium of charge ( ‘-q )
This charge has to be kept at a distance
It is easy to see that the equilibrium of the system is an unstable equilibrium.
Example-(3):
Two identical spheres, having unequal opposite charges, are placed at a distance
Show Answer
Solution:
Since the spheres are identical after touching them they will acquire similar and equal charges. Suppose the charge on each is ’
Concept of Electric Field
Let us consider an electric change
To measure the strength or intensity of an electric field of any point, we may place a small positive charge
That, if
The test charge must be negligibly small so that the source charge,
The electric field, due to a single point charge, kept in vacuum (or air) is given by
Important Points Regarding the Electric Field
- Once the field strenght
A positive charge would experience a force in the direction of the electric field while a negative charge would do so in a direction opposite to that of field.
- Electric field, due to a system of charges, at a point, is the vector sum of the electric fields at that point due to the individual charges.
-
Electric field, due to a point charge, points away from the charge if it is a positive charge and towards it if it is negative charge.
-
Electric field, of a point charge, has a spherical summetry.
Example-(4):
The figure shows system of two equal (in magnitude) point charges. Charge
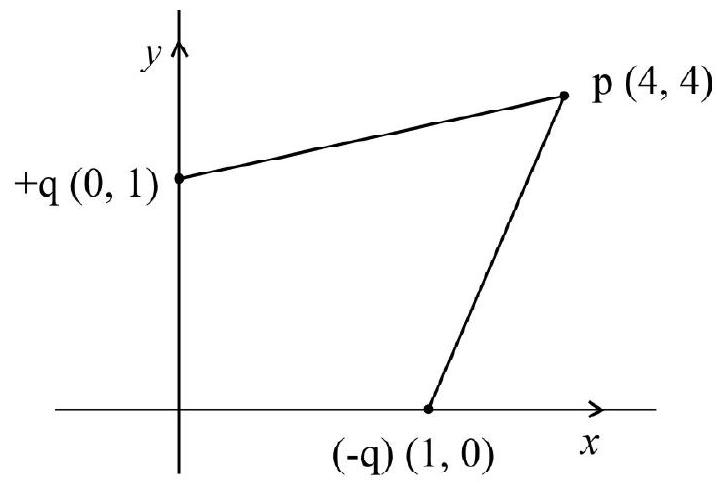
Show Answer
Solution:
We have,
Continuous Charge Distributions
A system of closely spaced charges may be thought of as forming a continuous charge distribution. There are three kinds of continuous charge distributions- linear charge distribution, surface charge distribution and volume charge distribution. The electric field due to a continuous charge distribution, can be obtained in the same way as for a system of discrete charges using Coulomb’s law and the principle of super position. We first find the electric field due to small element ’
Example-(5):
Axial electric field due to a circular loop of charge : (charged ring)
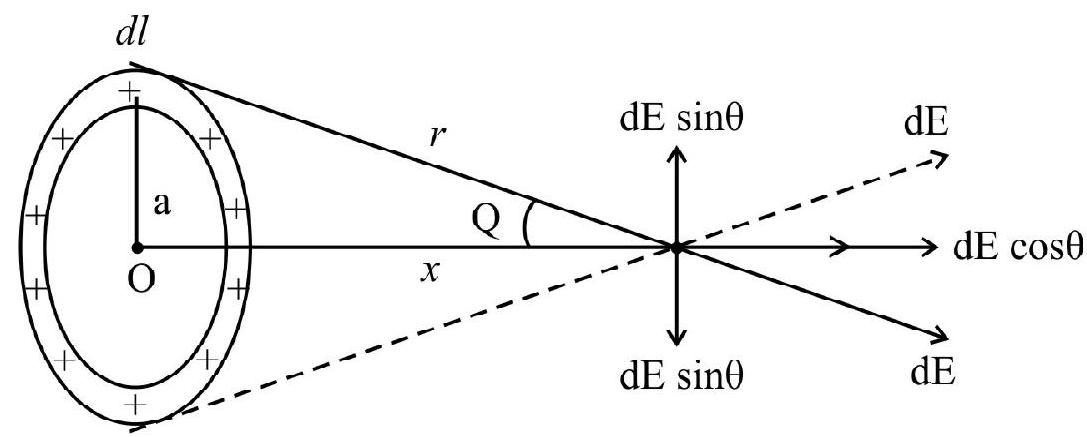
Let us consider a uniformly charged ring of radius ’
Show Answer
Solution:
Consider a small (line) element ’
The magnitude of,
Now consider another element
This
If ’
If
Thus, for points on the axis, at distances much larger than the radius of the ring, the ring bahaves like a point charge.
Some Important Results for
- Super position of electric field - electric field at a point due to a system of charges is the vector sum of the electric fields at that point due to individual charges.
- The electric field due to continuous charge distribution can be obtained in much the same way as for a system of discrete charges using Coulomb’s law and the super position principle. First we find the electric field due to small element dq and then integrate the expression for whole body.
Electric field due to various (discrete / continous) charge distribution
We write below some important results for the electric field due to some charge configurations.
(i) Electric field strength due to a point charge at any point ’

(ii) Electric field strength due to a finite line charge with charge density ’
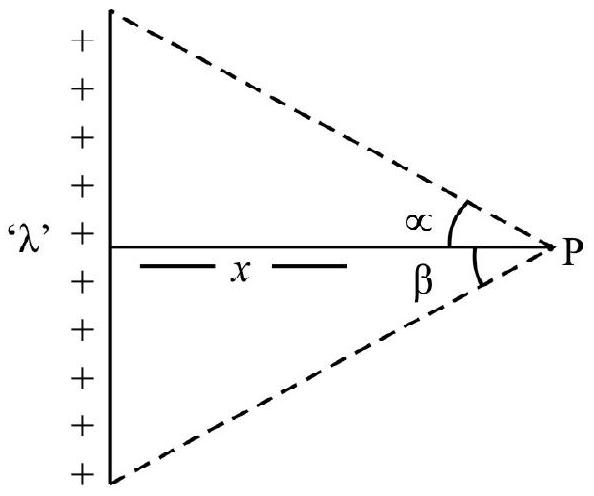
where
(iii) Electric field strength due to a infinite charge with charge density ’
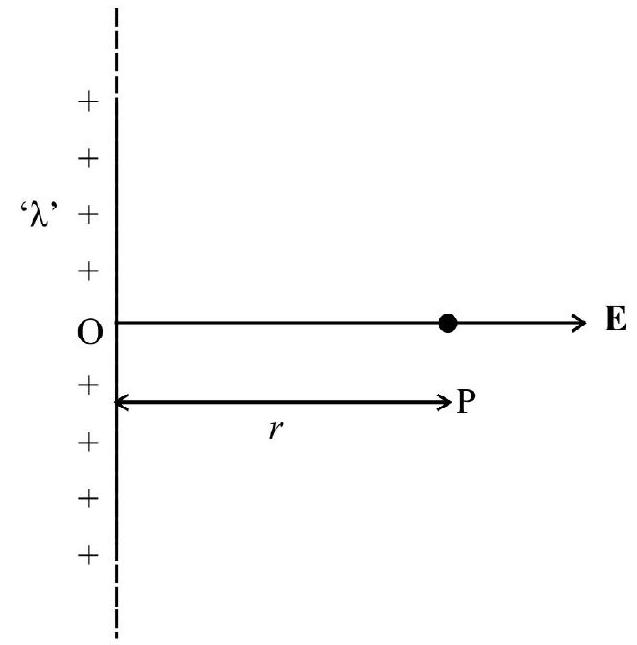
(iv) Electric field strength due to a circular ring of radius ’
If
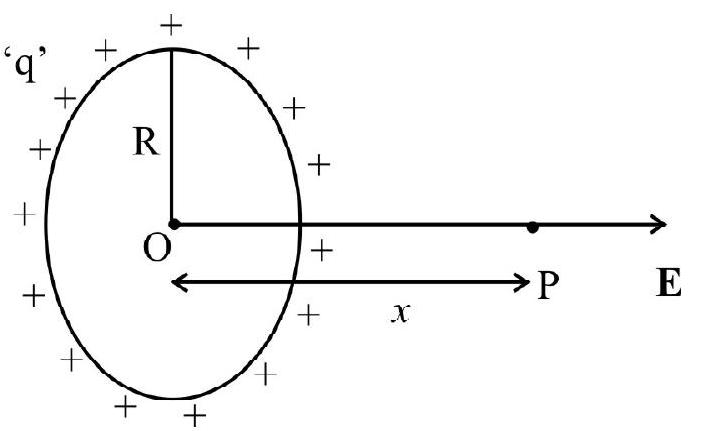
Behaves like point charge.
(v) Electric field strength due to a uniformly surface charged, disc of radius ’
If
Disc behaves like point charge.
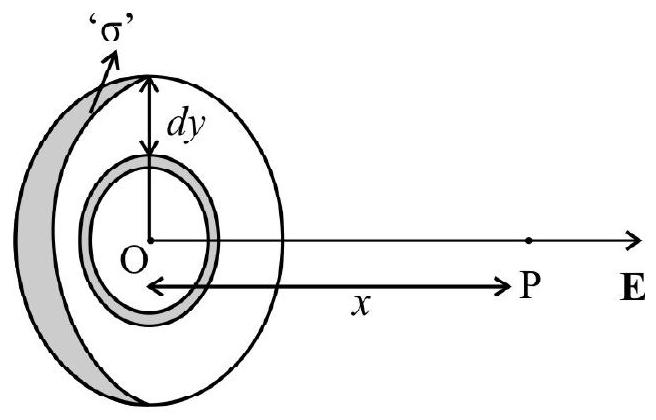
If
Disc behaves like then plane sheet.
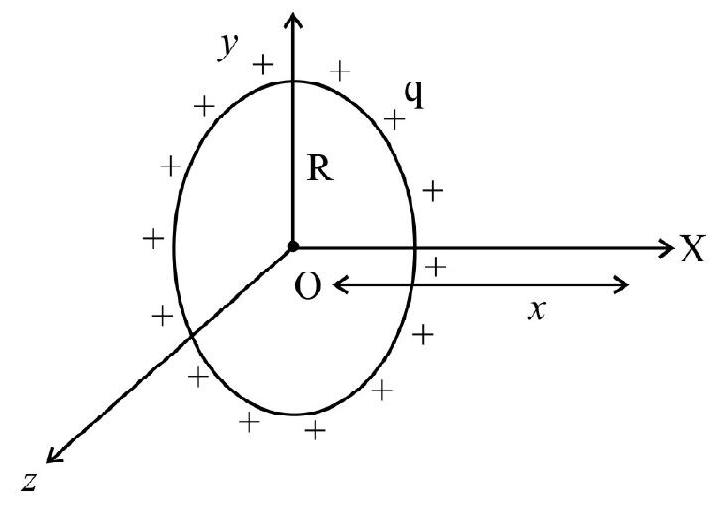
Example-(6):
A ring of radius
Show Answer
Solution:
We have,
For maximum field intensity
The plot is an shown.
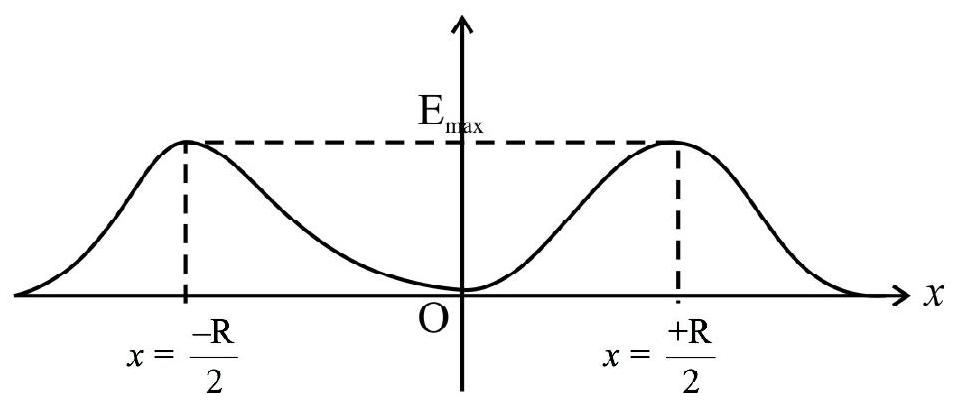
Example-7:
A pair of charges,
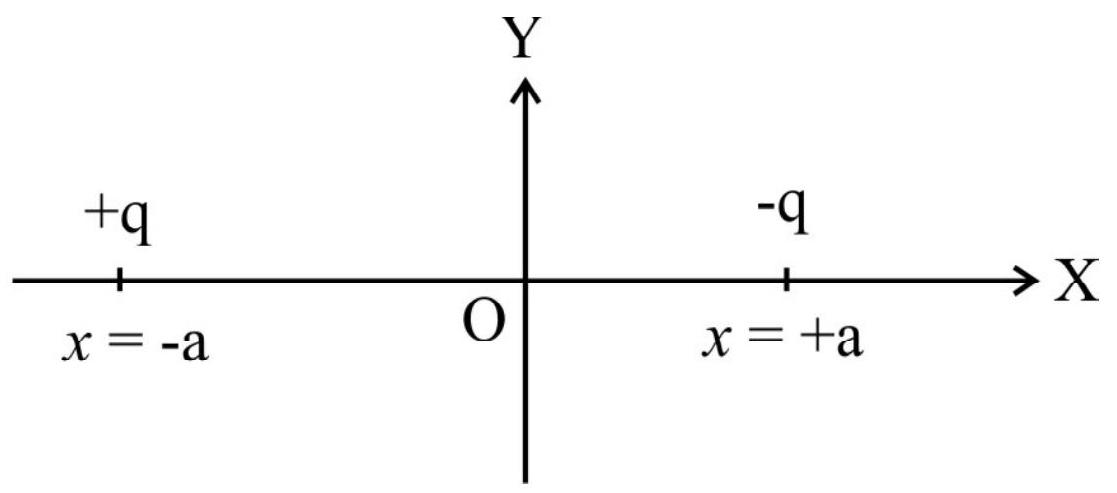
Show Answer
Solution:
The variation is as shown.
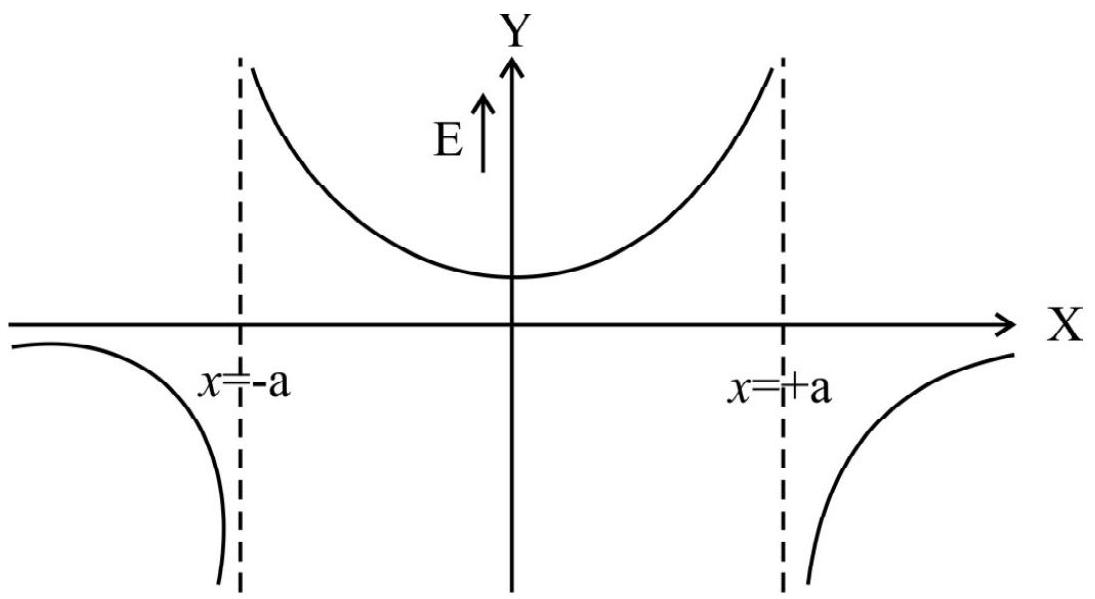
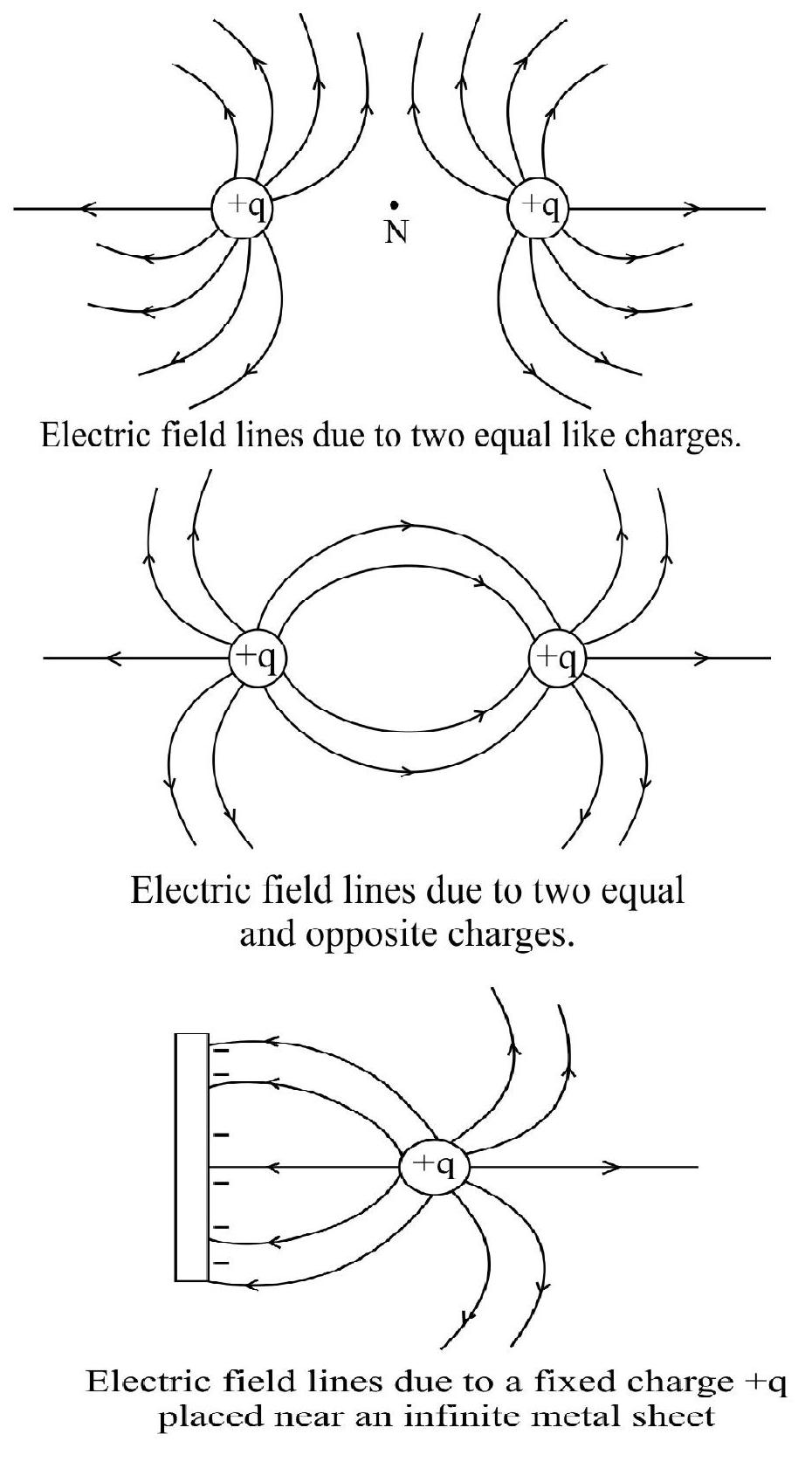
Electric Field Lines
An electric field line is a curve drawn in three dimensions in such a way that the tangent at each ponit on the curve gives the direction of electric field at that point.
The idea of electric lines of force, or the electric field lines, introduced by Micheal Faraday, is a way to visualize electrislatic field geometrically.
The properties of electric field Inies are:
(i) Electric field lines are continuous curves in an electric field; starting from a positive charge and ending on a negative charge.
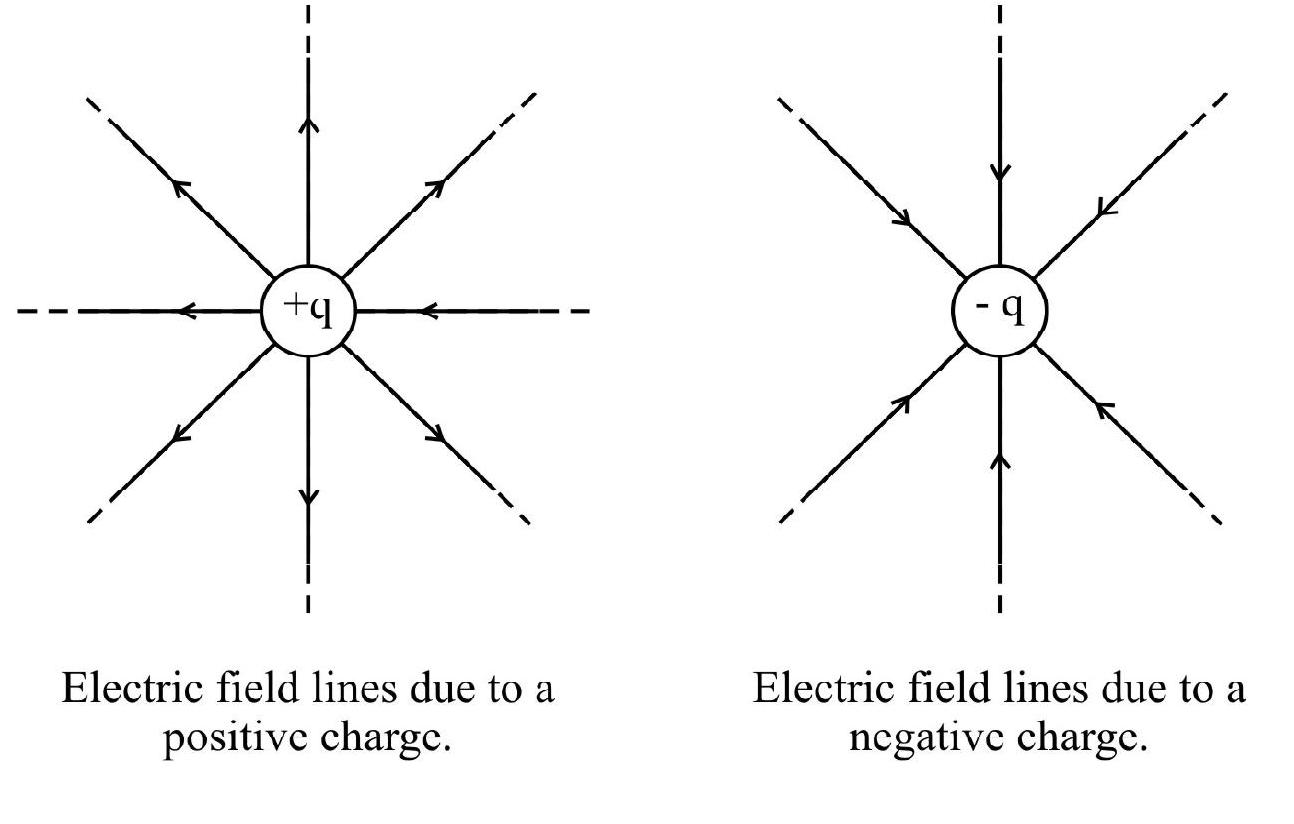
(ii) Two electric field lines never intersect.
(iii) Electric field lines do not pass through, they leave, or end, on a charged conductor normally.
(iv) The relative closeness of field lines indicates the relative strength of electric field at different points; crowded lines represent strong field regions while distant field lines correspond to a weak field. Further, if the field lines are uniformly spaced parallel straight lines, the field is uniform.
(v) It is not necessary that a small test charge released at a point in an electric field will move along the field line passing through that ponit. The field lines give the direction of acceleration they do not essentialy give the direction of motion of charge.
Electric Dipole
An electric dipole is a pair of equal and opposite charges
The basic characterstics of a dipole is its electric dipole moment
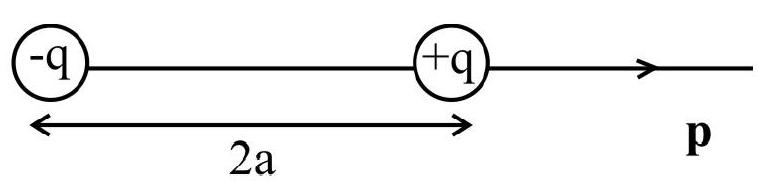
Dipole moment is thus a vector quantity; its direction is the direction of the dipole axis, from
Electric field Intensity due to an Electric Dipole
(i) Axial position : The field, on the axis, at a distance ’
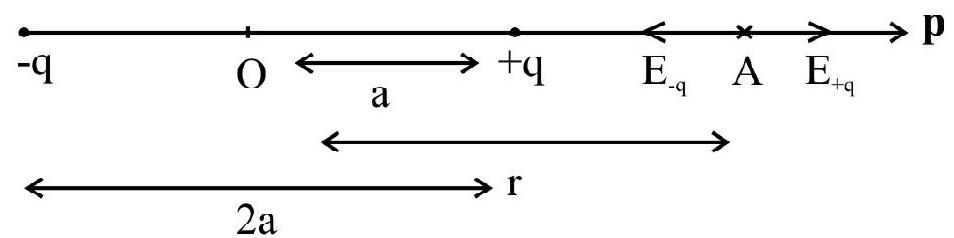
The electric field on axial position ’
For an ideal electric dipole
Thus, Electric field is along the direction of
(ii) Equitorial position : The field on the equitorial plane (i.e. plane perperndicular to the axis and passing through its centre) at a distance ’
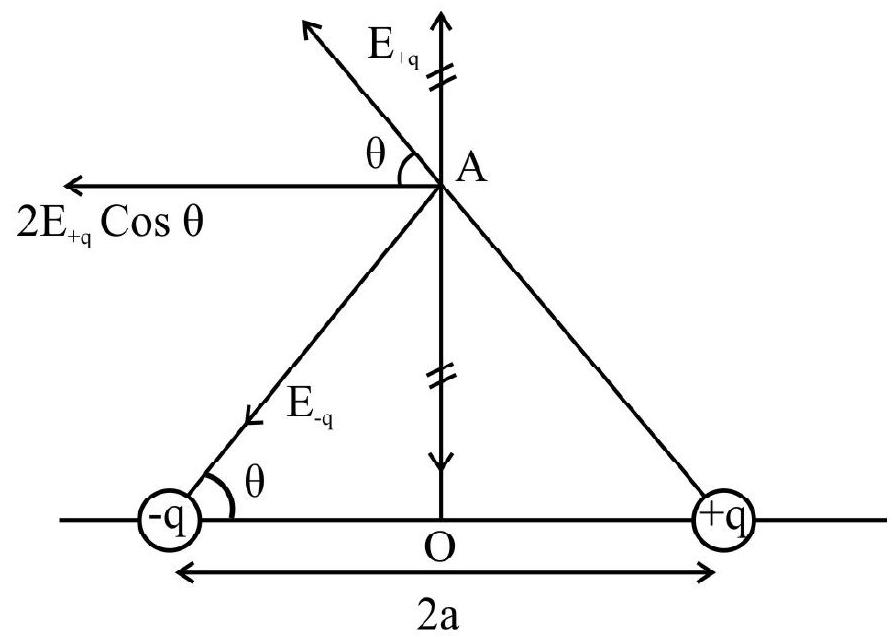
As seen in the diagram above, electric field on equitorial position is only due to the horizontal components of electric fields due to
For an ideal dipole :
Thus, electric field is in the direction opposite to
For the same value of the distance ’
(iii) Field at any general ponit ’
Let ’
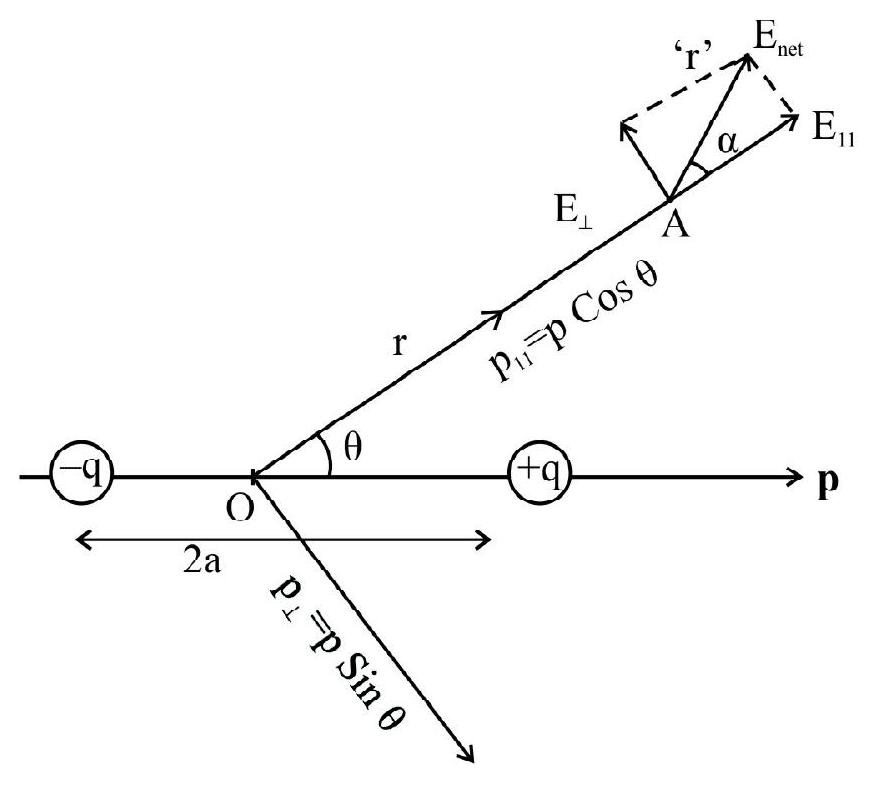
Hence,
and
This (general) electric field, at any point ’
Example-(8):
The electric field, due to a short dipole, at a distance
Show Answer
Solution:
We are given that
Electric dipole placed in a uniform external field
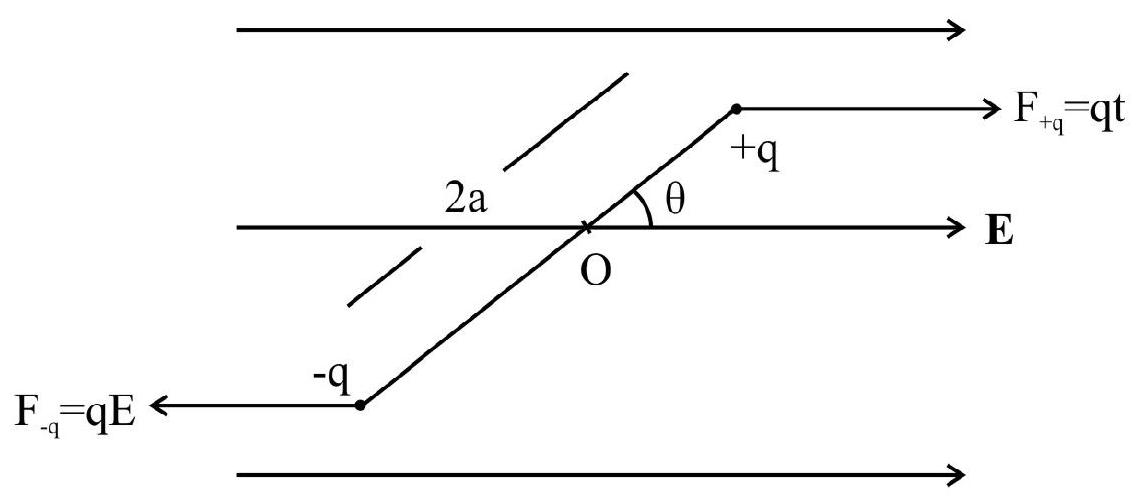
When a dipole is placed in uniform external field, the net translation motion is zero as:
However, the forces
where
The direction of
Hence, due to this torque, the dipole tries to allign itself parallel to the direction of electric field. This is its position of stable equilibrium.
Special Case : When the dipole is placed in a non-uniform external electric field, the charges of dipole experience unequal forces; therefore, net force on the dipole is not zero. Now dipole has both translation as well as rotational motion.
Example-(9):
In a certain region of space, electric field is along the
The dipole moment, for a segment of length

The net force, on this elementaldipole, is
This force is directed along the direction of the dipole moment, i.e., the (-ve) direction of
Work done in Rotation of a Dipole
Suppose the dipole is initially kept in a uniform electric field at an angle
Now to turn it to a position at an anode
work done by the field is
This work done is stored in the form of electrostatic potential energy. Thus, potential energy of a dipole in uniform electric field will be
For conservative forces,
We take

and
The dipole is in stable equilibrium.
At
and
Here dipole is in unstable equilibrium.
Special Case:
If a dipole is given a small angular displacement ’
Where I is the moment of inertia of the dipole about an axis passing through its centre. This is because the torque will act like a restoring torque:
Electric Flux
The electric flux
The vector area element
For an area element of a closed surface,
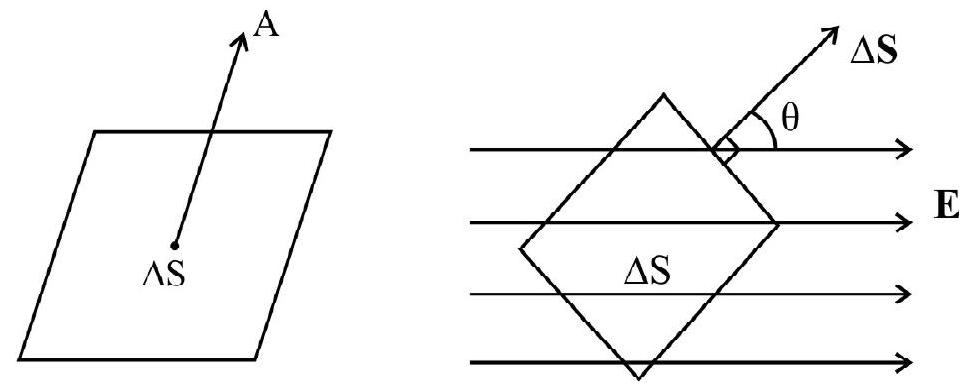
The total flux, ’
The SI unit of electric flux, is
Gauss Law
The electric flux, through any closed surface ’
The integral
-
The term q on the right side of Gauss’s law includes the sum of the charges enclosed by the surface. The charges my be located anywhere inside the surface.
-
The surface that we choose for application of Gauss’s law is called as the Gaussian surface.
-
On the left side of gauss law, for calculation of
-
Gauss law is based on the inverse square dependence on distance contained in the Coulomb’s law. Any violation of Gauss’s law will indicate departure from the inverse square law.
-
Gauss law is expecially useful in determining electric field
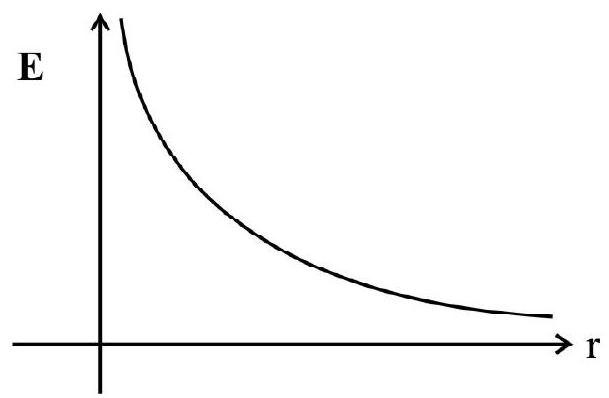
(a) Thin infinitely long straight wire of uniform linear charge density ’
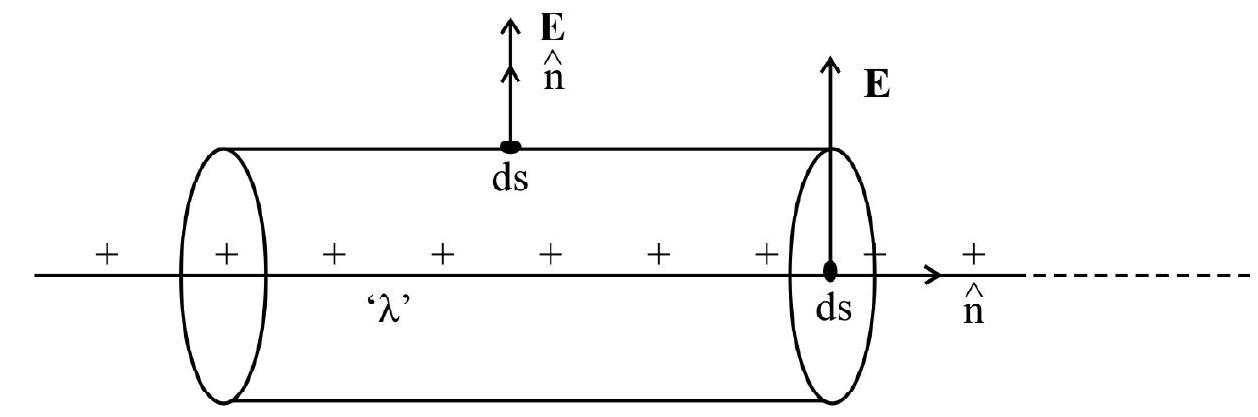
where ’
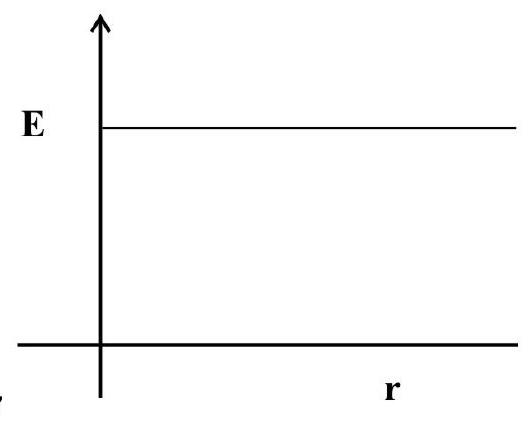
(b) Infinite thin non-conducting plane sheet, of uniform surface charge density ’
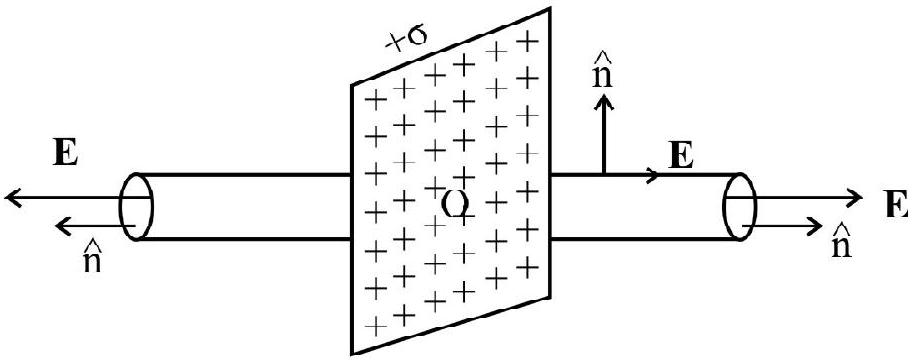
where
side. For conducting sheet
(c) Thin shperical shell of uniform surface charge density ’
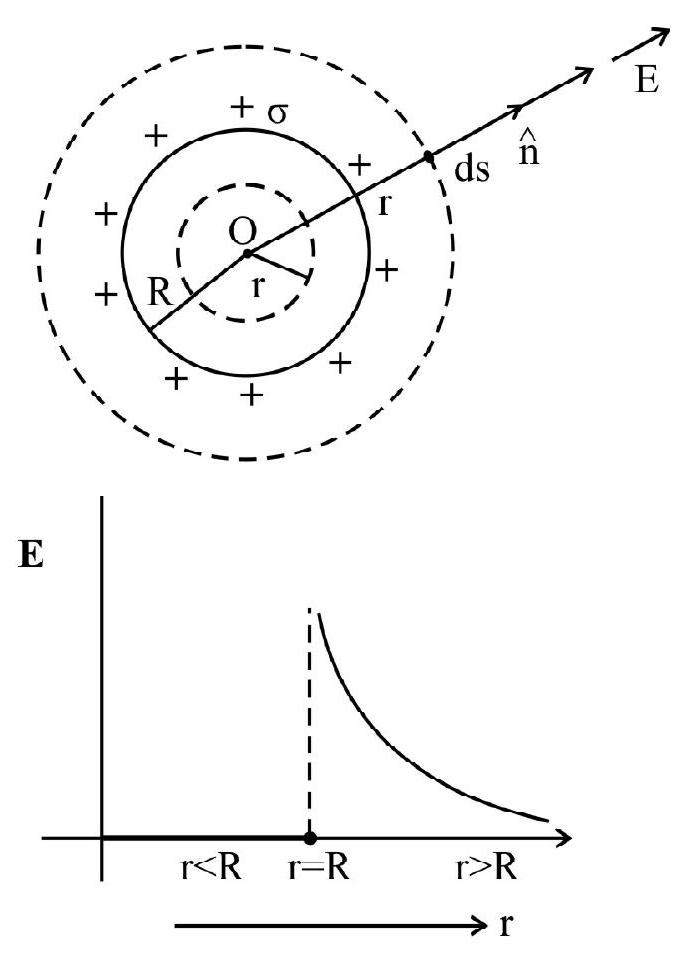
where
The electric field inside the shell iszero and outside it behaves as that of a point charge.
(d) Long (Non-conducting) uniformly charged rod/cylinder having uniform volume charged density ’
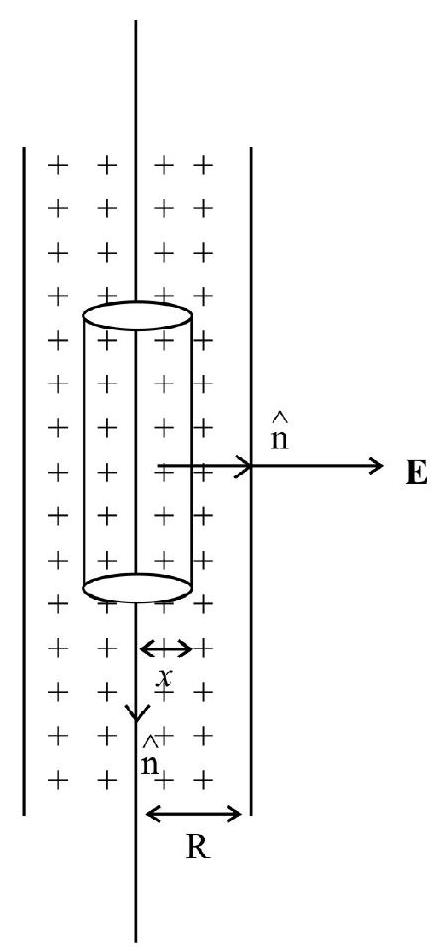
Where
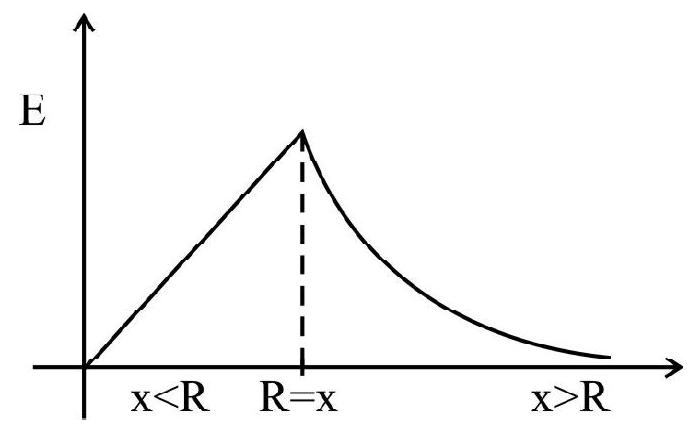
(e) Solid (Non-conducting) sphere of total charge ’
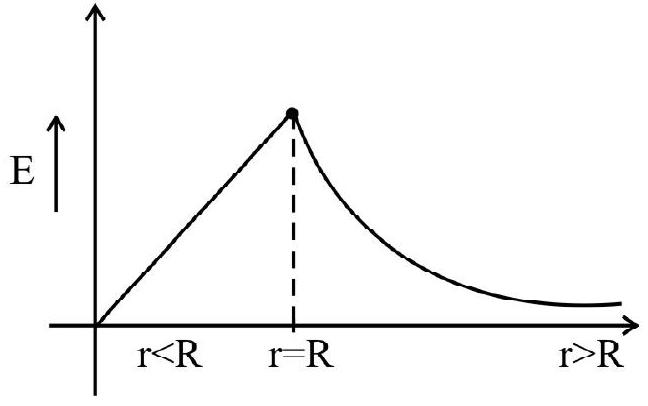
For a solid conductor
Hence, A conducting solid sphere acts like a spherical shell.
(f) Long uniformaly charged conducting cylinder / rod.
For a conductor, electric field strength at interior points is zero.

(g) Two infinite thin plates having uniform surface charge density held parallel to each other.
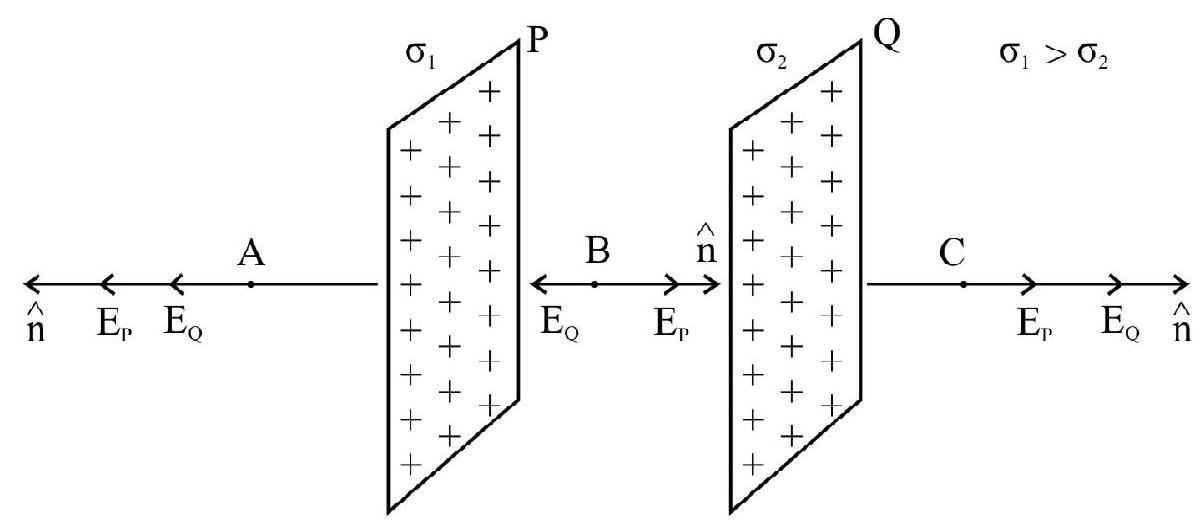
Special Case : For two plane sheets with equal and opposite charge densities.
Example-(10):
A point charge
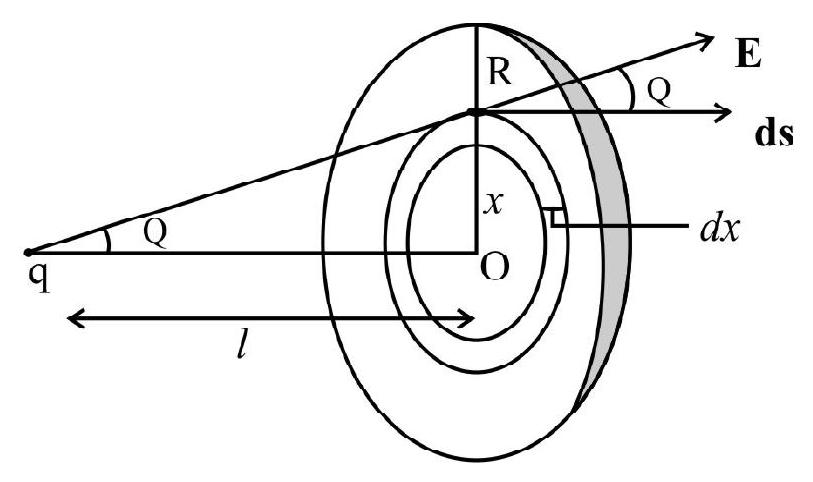
Show Answer
Solution:
Consider an elemental ring on the disc surface; of radius
Area of this strip
Electric field ’
If
Total flux through the disc surface,
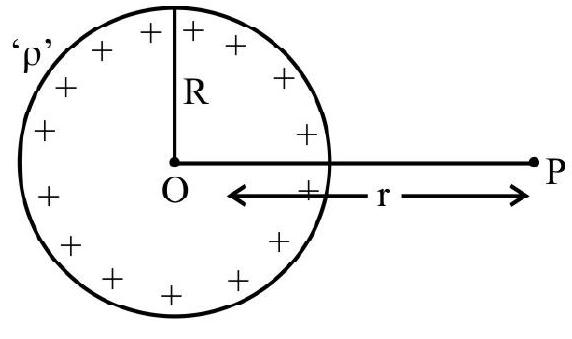
Example-(11):
Consider a ring of radius ’
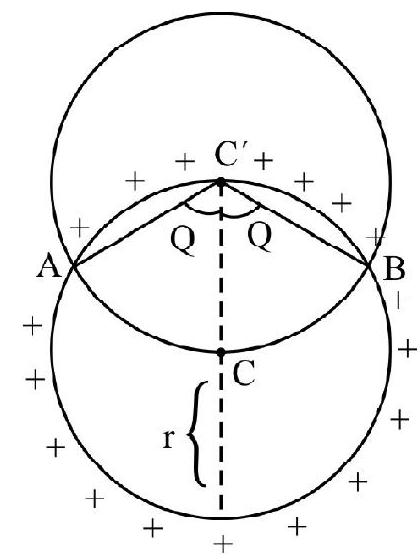
Show Answer
Solution:
It is clear from the geometry of the figure that
hence, enclosed charge is
Using Gauss law, electric flux passing through the surface of sphere.
Example-(12):
A spherical conducting shell of inner radius
(a) What is the surface charge density on the (i) inner surface (ii) outer surface of the shell?
(b) Write the expression for the electric field at a point
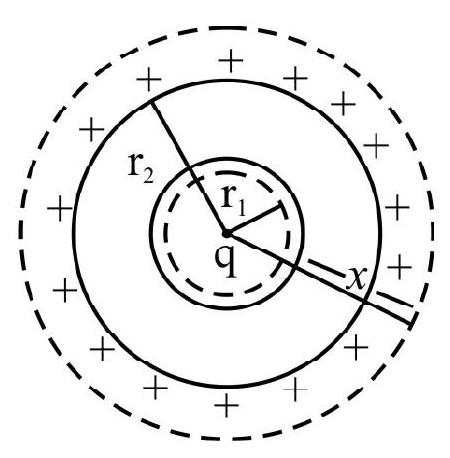
Show Answer
Solution:
(a) (i) Surface charge density on the inner surface of the shell.
(ii) Surface charge density on the outer surface of the shell.
(b) Using Gauss’s law
The Conservation Nature of the Electrostatic Field
It is an important property of electrostatic fields that the line integral of electric field,
depends only on the initial and final position and is independent of the path taken in going from Ato B.
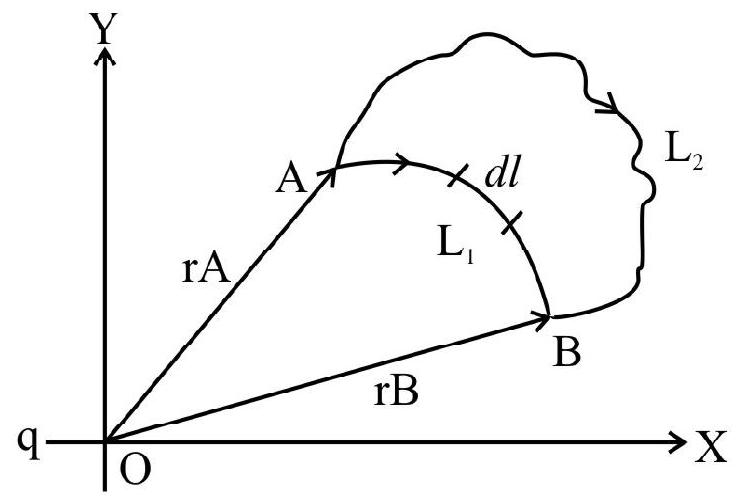
Consider two points A and B in the electrostatic field of a charge ’
We then get:
The line integral is, therefore, seem to be independent of path connecting A and B. We can conclude that line integral of electrostatic field (does not depends upon the curve
For a closed curve the initial and final positions are the same. Hence
The line integral of electrostatic field over a closed path is zero; the electrostatic field is conservative in nature.
Consider the work done in displacing a unit positive charge through a distance ’
Total work done, in moving a unit positive charge from
Thus line intergral of electric field represents the amount of work done is moving a unit positive charge, between two given points, in an electrostatic field.
This work done by the elctrostatic force, is path independent, as electrostatic force is conservative in nature. The concept of potential energy exists only in the case of conservative forces. When electrostatic force exists, between two or more point charges within system, we can assign a potential energy
Electrostatic Potential Energy
Consider an electrostatic field ’
Thus, work done by external force in moving a charge q from
This work done is against electrostatic repulsive force
Thus, potential energy difference -
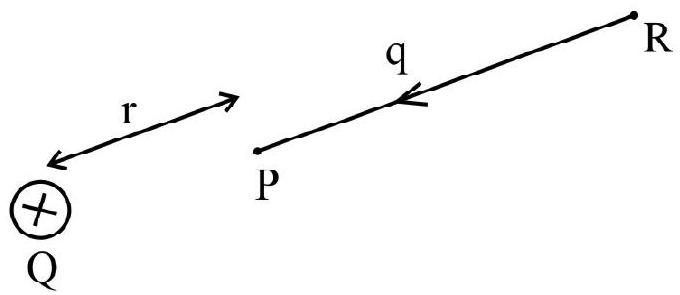
Therefore we can define electric potential energy difference between two points as the work required to be done by an external force in moving (without acceleration) charge q from one point to another for electric field of any arbitary charge configuration.
A convenient choice is to have electrostatic potential energy zero at infinity with his choice if we take point ’
Thus, potential energy of a charge
Electric Potential at a Point
Electric / electrostatic potential ’
Thus,
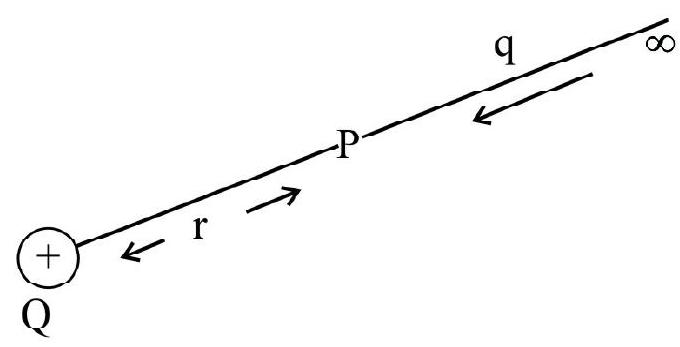
Hence potential
Important Points
- Electric potential at a point is also equal to the negative of the work done by the field in taking the unit positive charge from infinity to that point i.e.
The above result is valid only for electric potential of a point charge. If we wish to find the electric potential due to a continuous charge distribution (charged extended body), we first find the potential due to an element charge ’
Electric Potential due to Various Charge Distribution
(i) Electric potential due to an isolated point charge at a point ’

for
(ii) Electric potential due to a system of ’
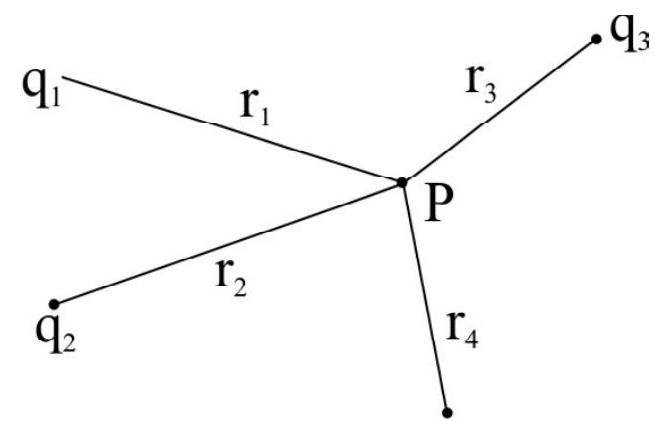
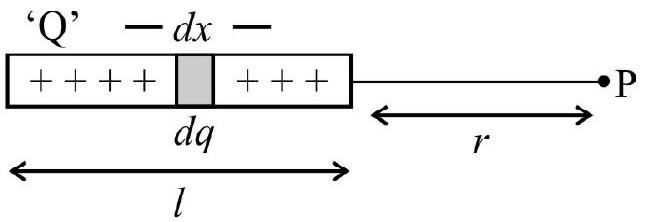
(iii) Electrical potential due to a charged rod of length ’
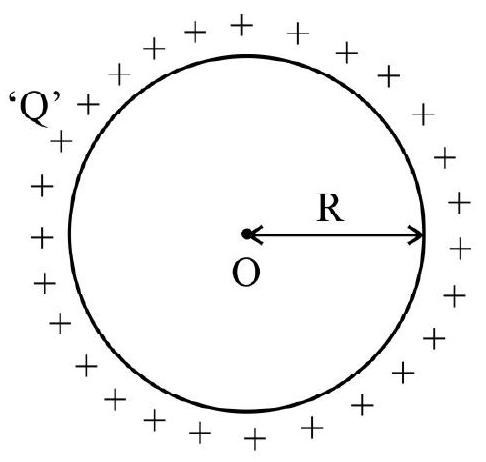
(iv) Electric potential due to a charged ring having uniform charge ’
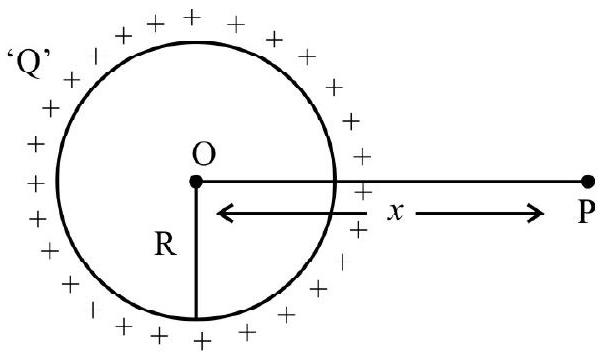
(v) Electric potential due to a uniformally charged sing on the axis of the ring at a point ’
(vi) Electric field due to a circular disc of radius
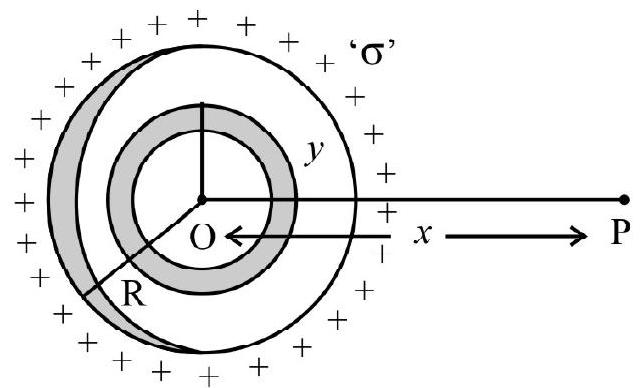
(vii) Electric field due to a solid spere of radius ’
Example-(13):
A metal sphere
Show Answer
Solution:
(a)
(b)
(c) Potential at the centre of sphere is same as on the surface.
Example-(14):
Eight changed water droplets, each with a radius
Show Answer
Solution:
Let
As charge is conserved total charge
Potential of bigger drop
Relation between Electric Field Strength and Electric Potential
Consider two surfaces
Let a unit positive charge is moved from
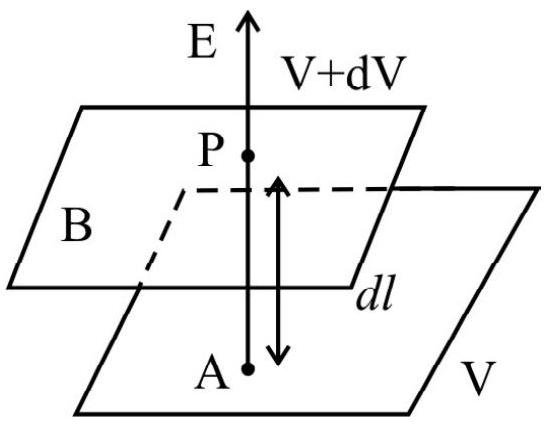
Thus,
or
or
Important Conclusion
- Electric field always pionts in the direction in which the potenital decreases steepest.
- Magnitude of the component of electric field (in any direction) is given by the change in the manitude of potential per unit displacement. In otehr words magnitude of component of electric field is numerically equal to the potential gradient.
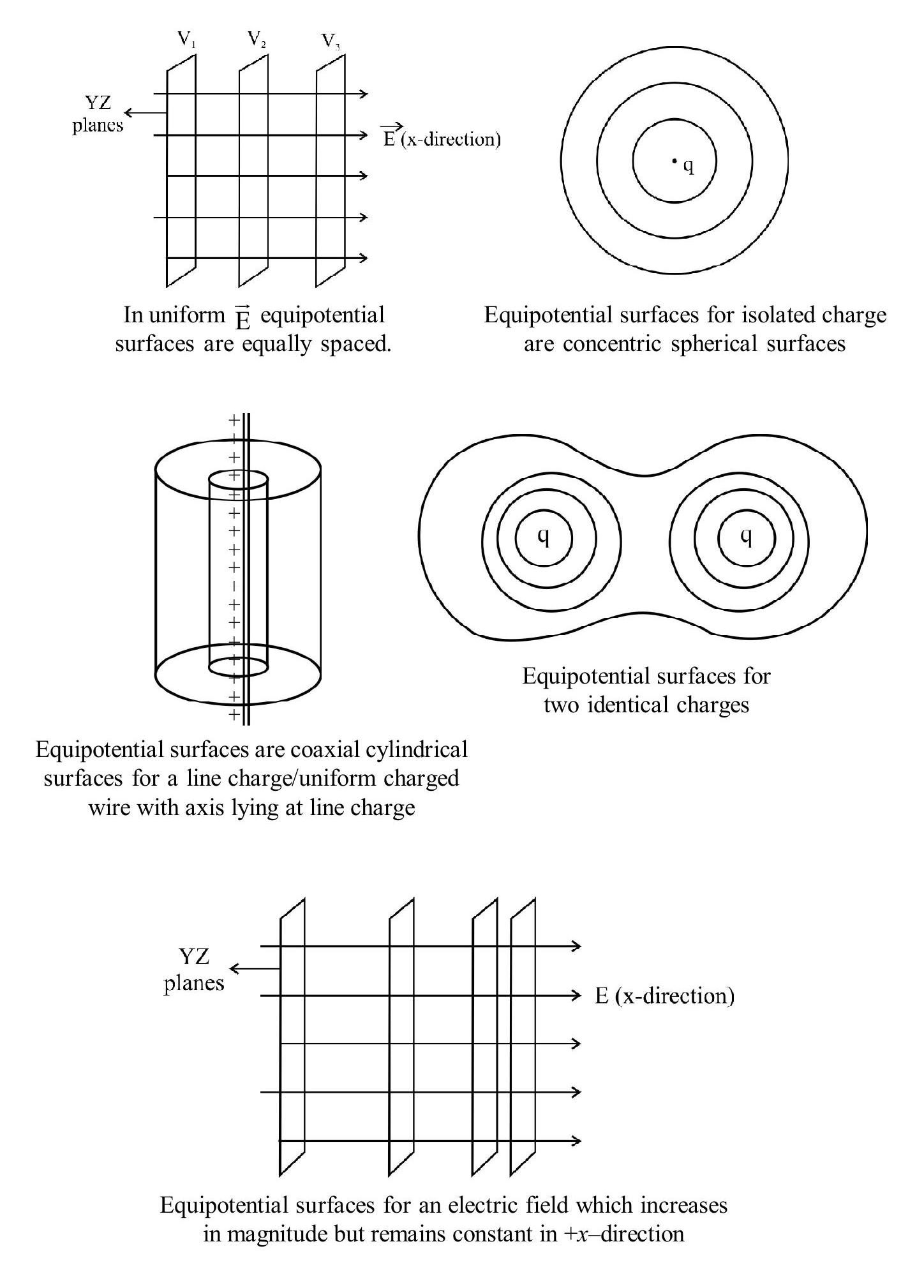
Equipotential Surface
Equipotential surface is a surface over which potential has a constant value.
Hence, no work is required to move a test charge on the equipotential surface. Thus, electric field, at every point, is normal to the equipotential surafce passing through that point.
Qualitatively, we can determine the magnitude and direction of electric field by understanding the following points about equipotential surfaces:
(i) The density of equipotential surfaces gives an idea about the magnitude of electric field. Higher the density, larger the field strength.
(ii) The direction of electric field is normal to equipotential at every point and points in the direction of decreasing potential.
Example-(15):
The potential of an electrostatic field is given by
Show Answer
Solution:
We known that
Also
Hence
Example-(16):
The figure shows field lines and equipotentials (dashed lines)
(i) Find the external work done to move a
(ii) Also, determine the work done by the electric field.
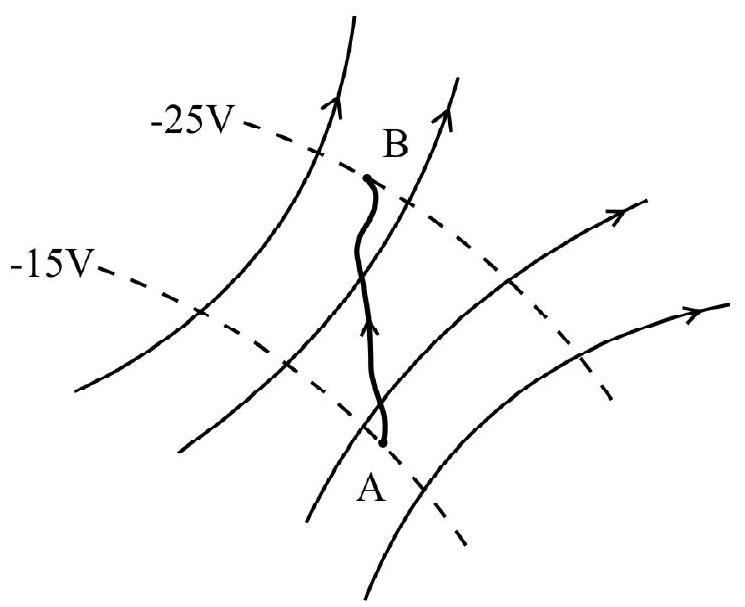
Show Answer
Solution:
Since electric field is conservative, therefore, work done by electric force is independent of path.
Using work-energy theorem, we have
The there is no change in speed,
Electric Potential due to an Electric Dipole
Consider an electric dipole consisting of two charges
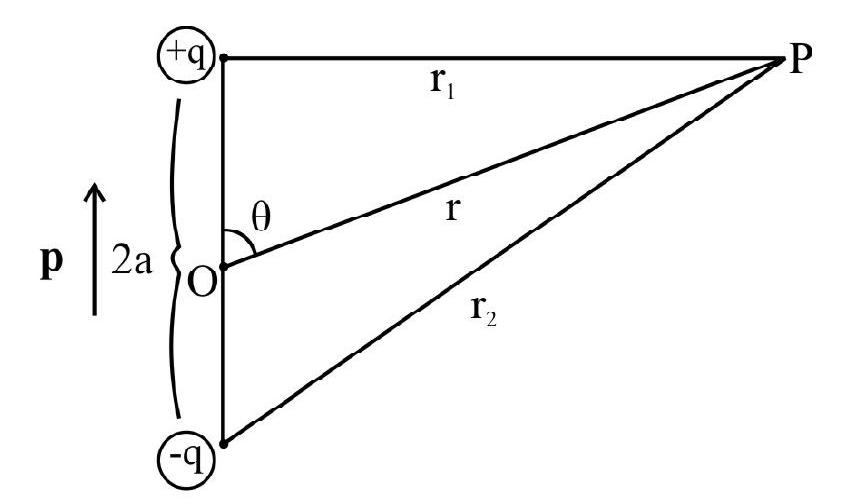
Where ’
as
if
If
Important Conclusion
The potential due to a dipole, depends not just on distance r, but also an the angle ’
Electric Potential Energy of a System of ’
The electric potential energy of a system of ’
If
Potential Energy in an External Field
- Potential energy of a single point charge in external field at ’
- Potential energy of a system of two charges in an external field,
- Potential energy of an electric dipole havnig dipole moment ’
Example-(17):
Two charges
Show Answer
Solution:
Mutual interaction energy of two charges will be
The additional energy of interaction in external field will be
Electrostatics of Conductors
In conductors, electric charges (elections) are free move throughout the volume of such bodies. When there is not net motion of free charges within the conductor, the conductor is in electrostatic equilibrium. The following are the properties of a conductor in electrostatic equilibrium.
(i) Electrostatic field is zero everywhere inside the conductor.
(ii) Net volume charge density inside a conductor is zero. Any excess charge must reside at the surface.
(iii) At the surface of a charged conductor an electrostatic field must be normal to the surface at every point.
(iv) Electrostatic potential is constant throughout the volume of conductor and has the same value (inside) as an its surafce.
(v) Electric field at the surface of a charged conductor is:
Where
Electrostatic Shielding
If there is a cavity inside the conductor or it is hollow, the field strength inside the cavity equals zero, whatever is the field outside the conductor.
Hence whatever be the charge and field configuration outside, any cavity in a conductor remains sheilded from outside electric infulence. This is known as electrostatic sheilding.
Important Points
- If a charge ’
- If a charge ’
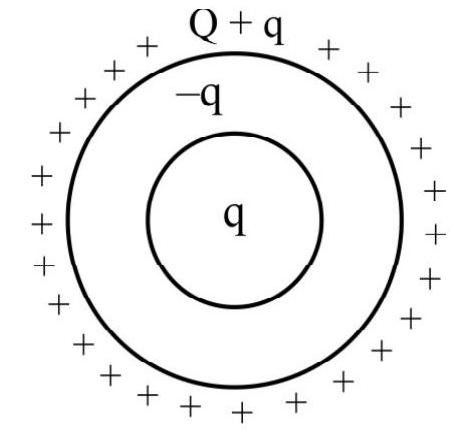
Example-(18):
A small sphere, of radius
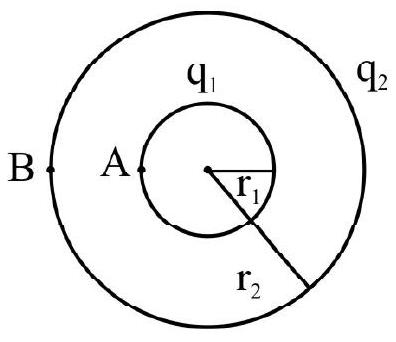
Show Answer
Solution:
Electric potential at the point ’
Electric potential at the piont ’
The p.d
Hence inner small sphere is always at higher potential and if connected by a wire, charge will immediately flow from the sphere to the shell.
Dielectrics
Dielectrics are (generally) non-conducting substances. Glass, plastic, mica, oil etc. are examples of dielectrics. The molecules of a dielectric, substance may be ‘polar’ or ’non-polar’ in nature.
When a dielectric material is placed in an external field, the elctric porperties get modified. In case of nonpolar molecules (zero permanent dipole moment of molecules) the positive and negative charges of the molecules experience electrostatic forces in opposite direction. Therefore, the centre of two charges get separated from each other. The molecules thus acquire an induced electric dipole moment in the direction of the field.
Let us now consider a dielectric whose molecules are polar (i.e. having a permanent electric dipole moments). In the absence of any external electric field, the individual dipoles (molecules) are oriented at random; hence the net dipole moment of the dielectric is zero. When such a dielectric is placed in electric field, the molecules tend to allign themselves parallel to the field due to the torque experienced by them in the field. Thus, a net dipole moment, is produced in the field.
We can thus conclude that, an electric field, induced in a dielectric, (polar or non-polar) a net dipole moment along the direction of the field. This phenomenon is known as dielectric polarisation or polarisation of matter.
Behaviour of dielectric slab is an electric field
Suppose a slab of dielectric material is placed in a uniform electric field
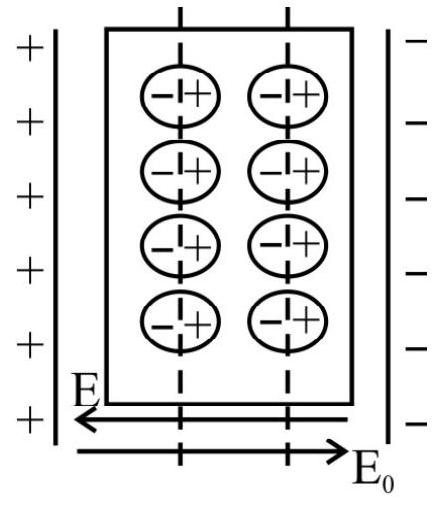
The induced dipole moment, per unit volume, is denoted by the vector
Where
Capacitors
A capacitor is a system of two conductors separated by an insulator usually, in practice, the two conductors have charges
The conductors may be charged by connecting them to the two terminals of a battery.
Relation between
The electric field in the region between the conductors is proportional to the charge
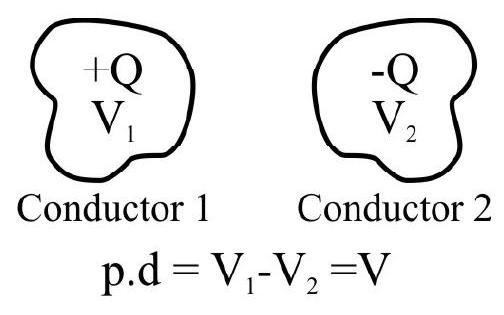
Consequently,
Mathematically
i.e.
The capacitance
The SI unit of capacitance is 1 farad
The equation shows that for large
The proportionality, between
Capacitors are mainly used to store charge and electrical energy. A capacitor with fixed capacitance is symbollically shown as

, while the one with variable capacitance is shown as
 .
.
Depending upon their geometry, capacitors are categorised as:
(i) Parallel plate capacitors
(ii) Cylindrical capacitors
(iii) Spherical capacitors
Capacitance of a Parallel Plate Capacitor
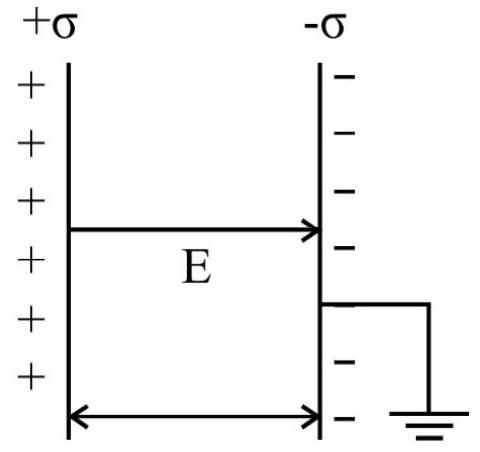
A parallel plate capacitor consists of two conducting long plates parallel to each other and separated by a small distance which is small compared to linear dimensions of plates.
The electric field between the plates is given by
Where
If
As potential difference between the plates in given by
Capacitance of parallel plate is given by
If the space between the plates is filled by a medium, of dielectric constant
Energy Stored in a Capacitor
The energy of a charged capacitor is measured by the total work done in charging the capacitor to a given potential.
This work done is stored as electrostatic potential energy in the field of capactor and is given by.
Energy density is the energy stored per unit volume. For the parallel place capacitor, we have
Combination of Capacitors
When there is a combination of capacitors in a circuit, we can replace the combination with an equivalent capacitor.
An equivalent capacitor is a single capacitor that has the same value of capacitance as that of actual combination.
(i)
- In series combination the equivalent capacitance is always less than the least value of the capacitances, given in the electrical network.
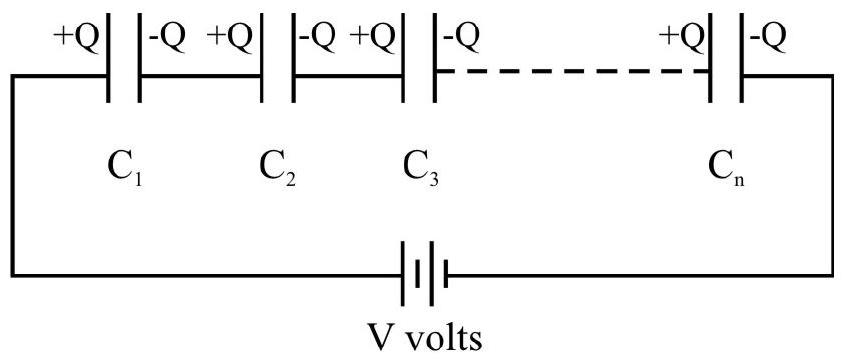
-
As charge in constant,
-
Energy stored in series combination is given by
(ii)
Thus for ’
- In parallel combination equivalent capacitance is always greater than the largest value of capacitance given in combination.
- As
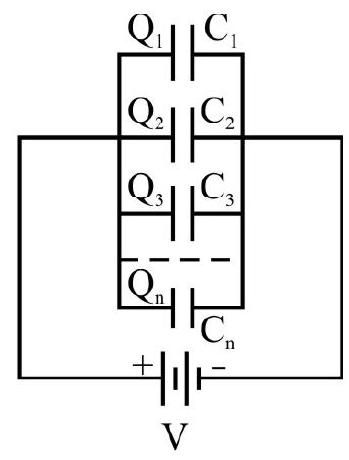
- Energy stored in parallel combination is given by:
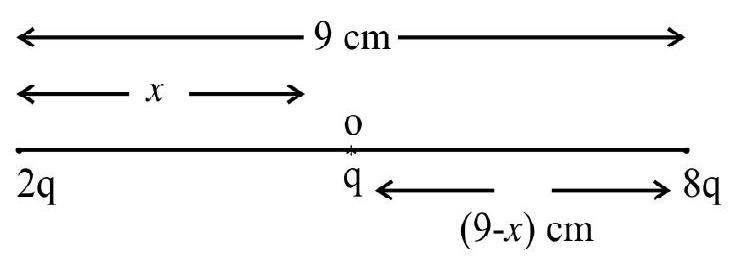
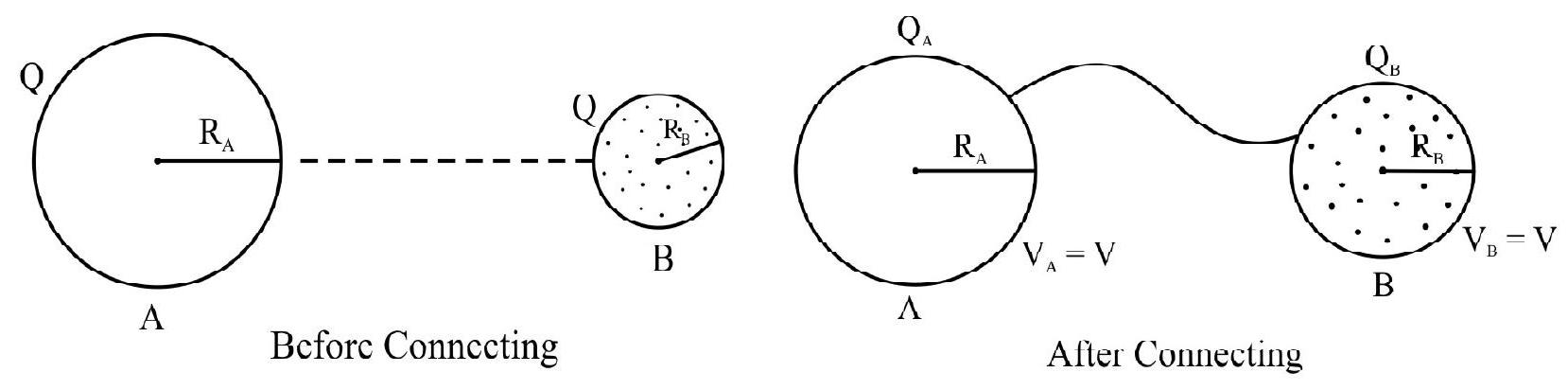
Redistribution of Charges
Consider two insulated capacitors A and B of capacitance
common potential. Thus charges are redistributed but total charge
Before connection:
After connection:
Hence there is a loss in electrostatic energy in the form of heat.
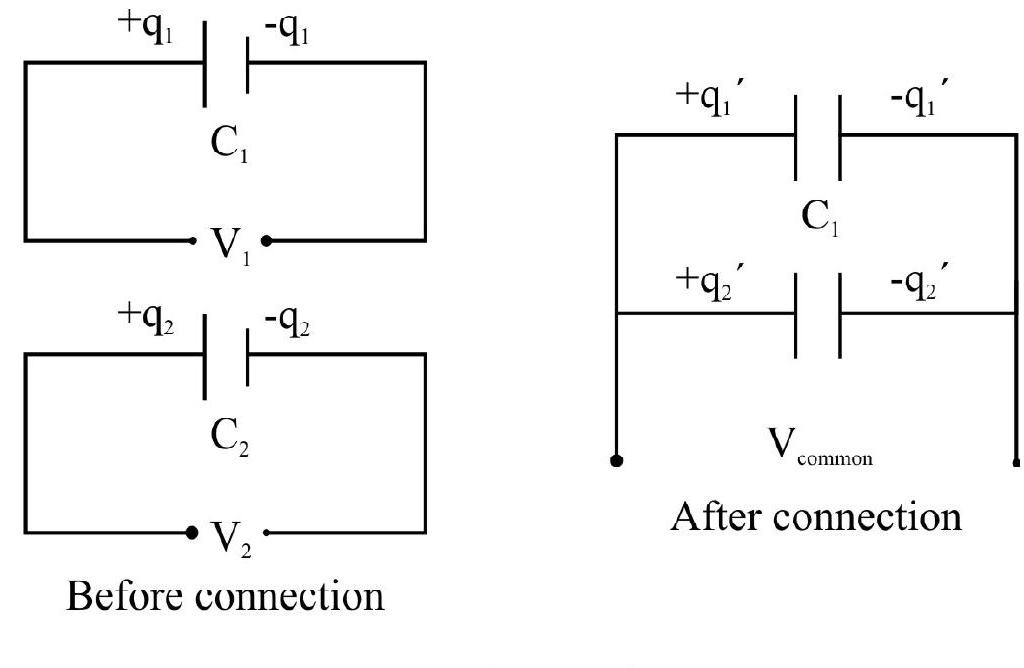
Before connection
Change on
Change on
‘Dielectric’ in a Parallel Plate Capacitor
Consider a parallel plate capacitor, having two large plates, each of area A, separated by a distance ’
Situation-1: A dielectric, of constant
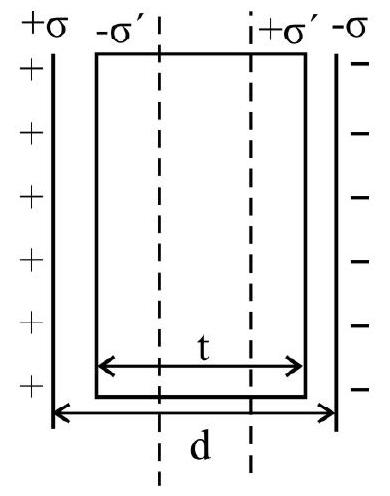
Let the thickness of dielectric slab be
As capacitor is fully changed and battery disconnected, charge on each plate,
The potential between the plates decreases from its value
out,
The energy stored in the field of capacitor decreases from its original value
We have,
and
and
Situation-2: A dielectric slab of constant
Energy stored from its original value
Example-(19):
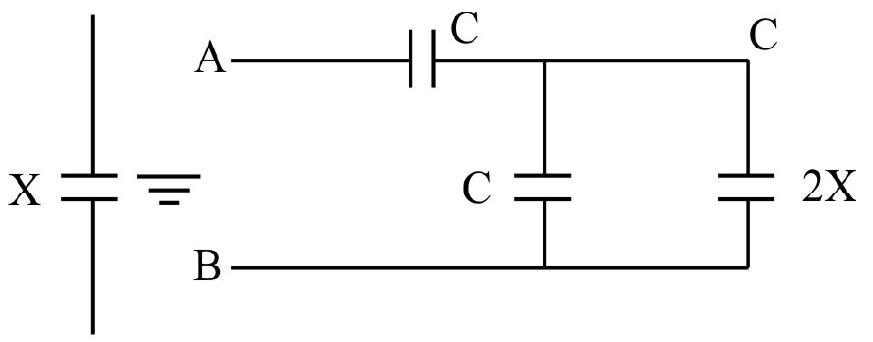
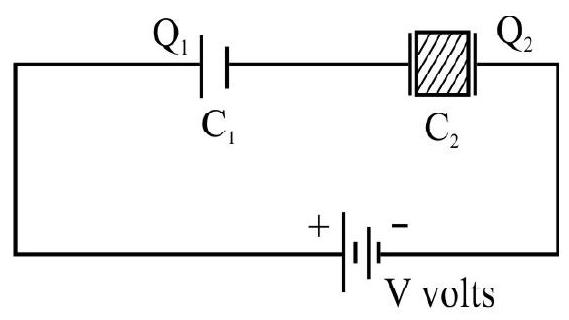
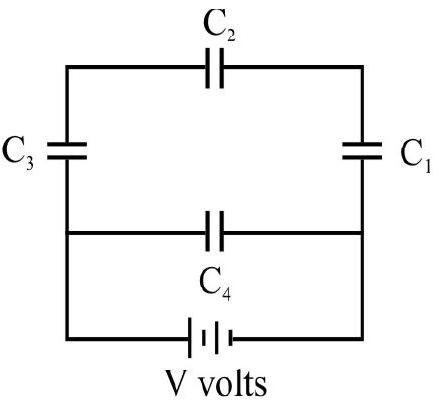
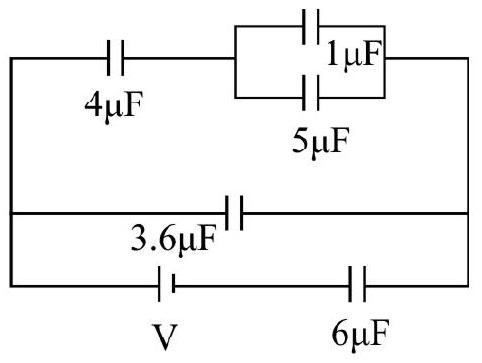
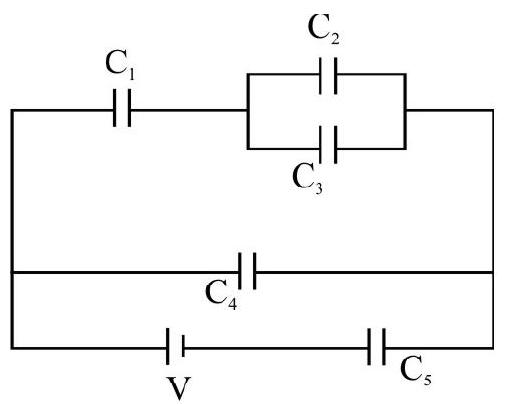
Find the equivalent capacitance between points
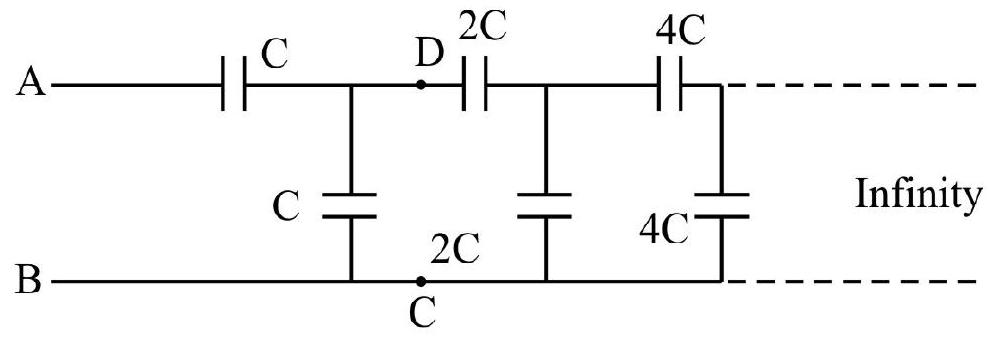
Show Answer
Solution:
Let the equivalent capacitance is
Example-(20):
In a parallel plate capacitor of capacitance
Show Answer
Solution:
It is important to note that if the capacitance of the parallel plate capacitor is ’
Thus, the potential of plate A will be,
and that of
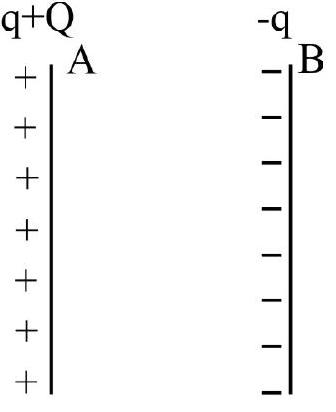
The p.d. between the plates, now will be:
Therefore
Example-(21):
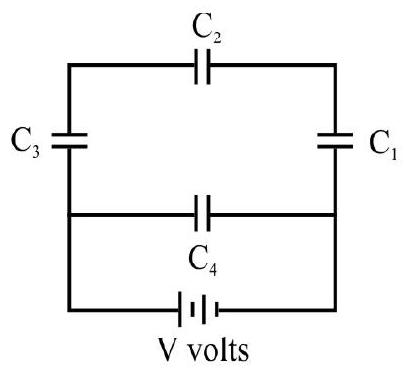
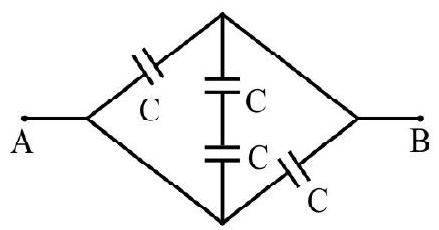
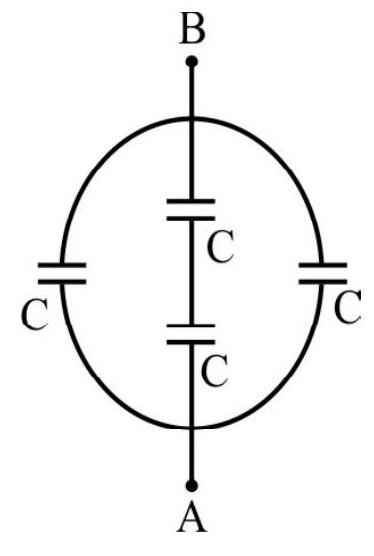
Find out capacitance between
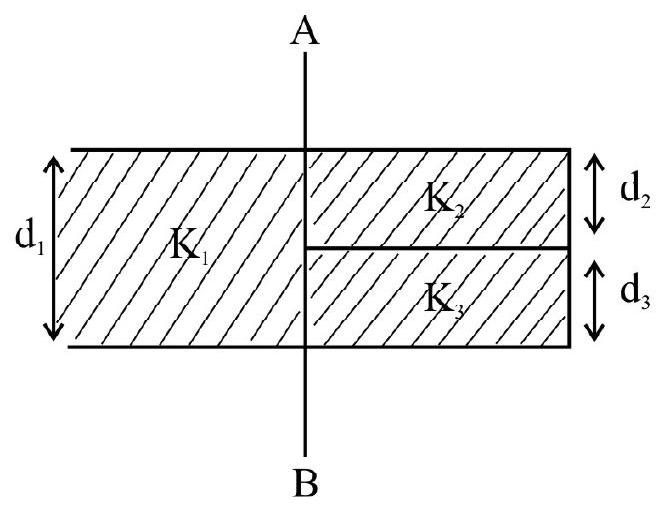
Show Answer
Solution:
The capacitor behaves like three individual capacitors
Thus,
ADDITIONAL EXAMPLES
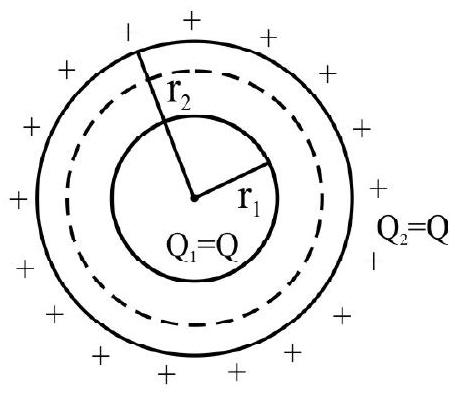
1. The region between two concentric spheres of radii ’
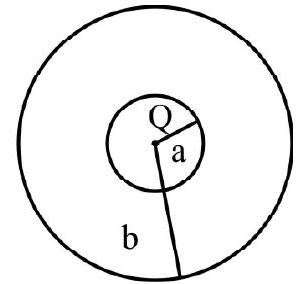
(1)
(2)
(3)
(4)
Correct option (4)
Show Answer
Solution:
Let
This has to be independent of r. We, therefore, have
2. A long cylinderal shell carries positive surface charge
(Figures are schematic and not drawn to scale)
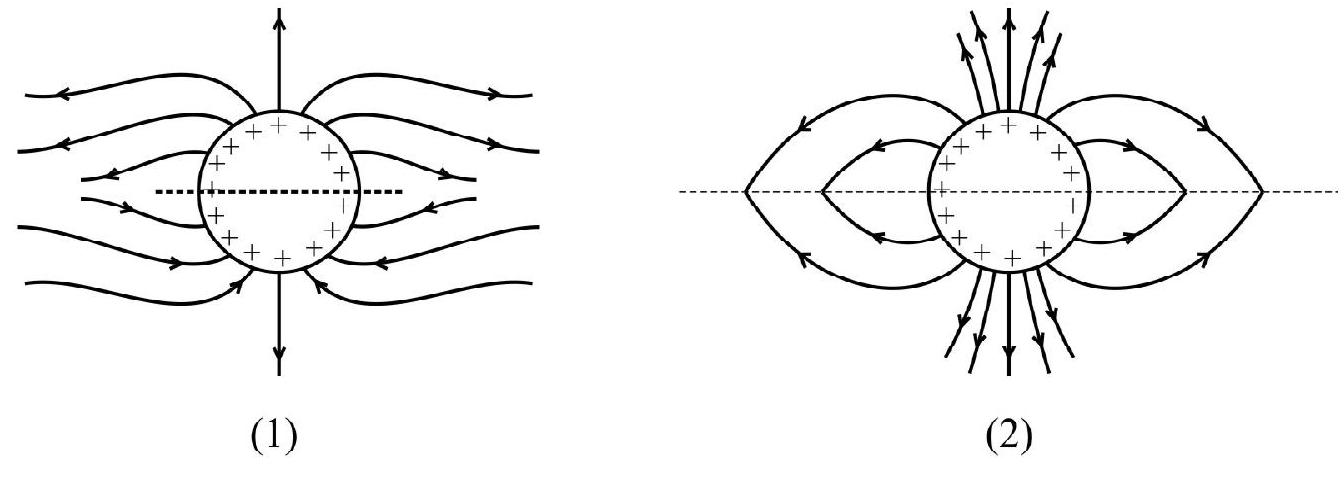
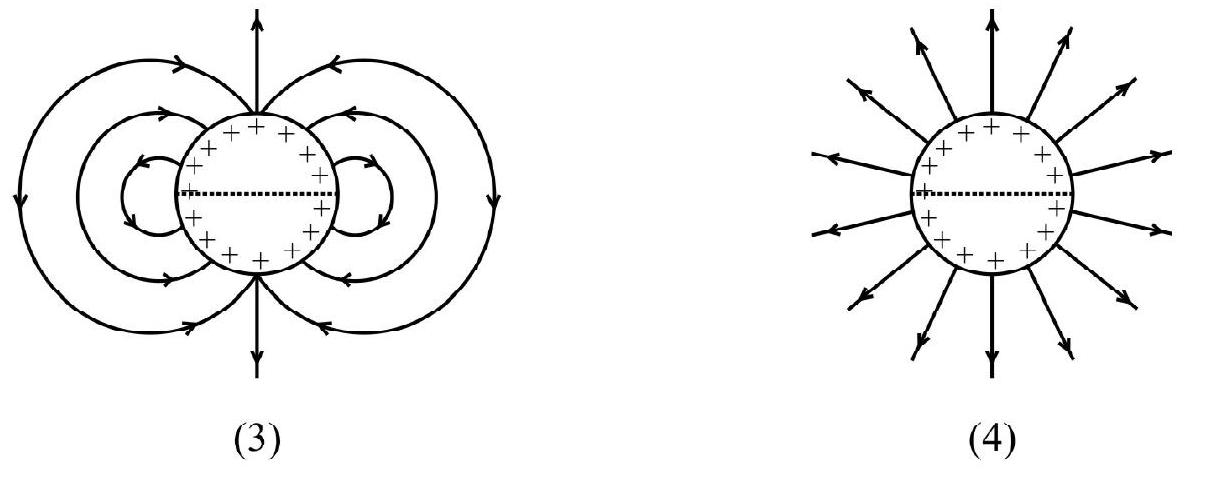
Correct option (3)
(IIT 2015)
Show Answer
Solution:
The correct figure is figure 3 . This is because electric field lines start from positive charges and terminate on negative charges.
3. Assume that an electric field
Correct option (1)
(IIT 2014)
Show Answer
Solution:
We have,
4. A uniformly charged solid sphere of radius
(1)
(2)
(3)
Correct option (1)
Show Answer
Solution:
Let the sphere have a charge
(i) On the surface
(ii) inside
(At the cenre
Therefore, radius of equi-potential at the centre of sphere is zero.
Let
Let
Let
and
5. A combination of capacitor is set up as shown in the figure. The magnitude of the electric field, due to a point charge
(1)
(2)
(3)
(4)
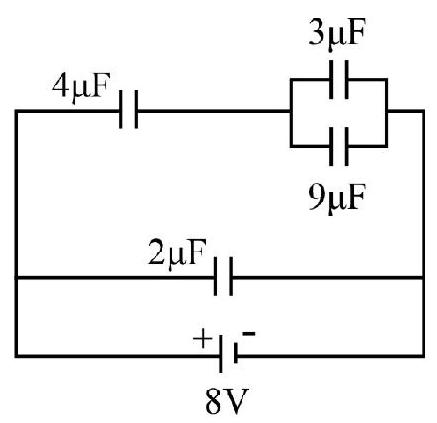
Correct option (2)
(IIT 2015)
Show Answer
Solution:
The equivalent capacitance of the top row is
This charge, on the
Hence
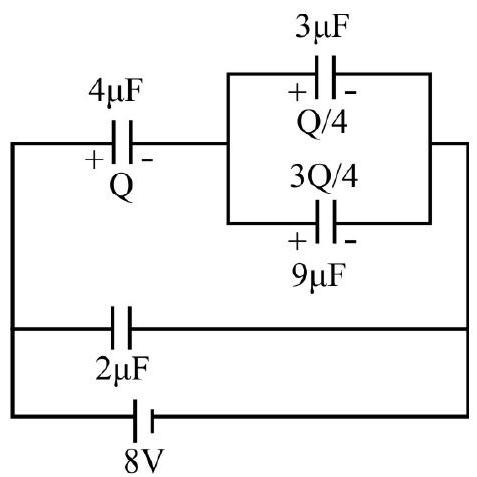
Hence,
6. In the given circuit, charge
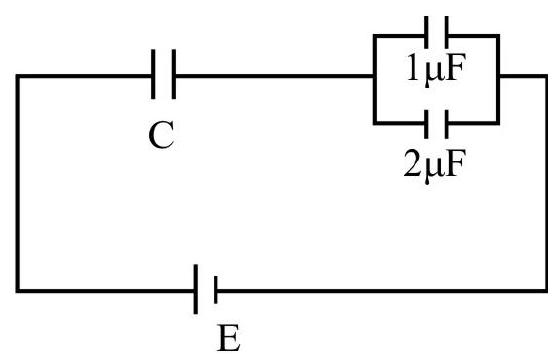
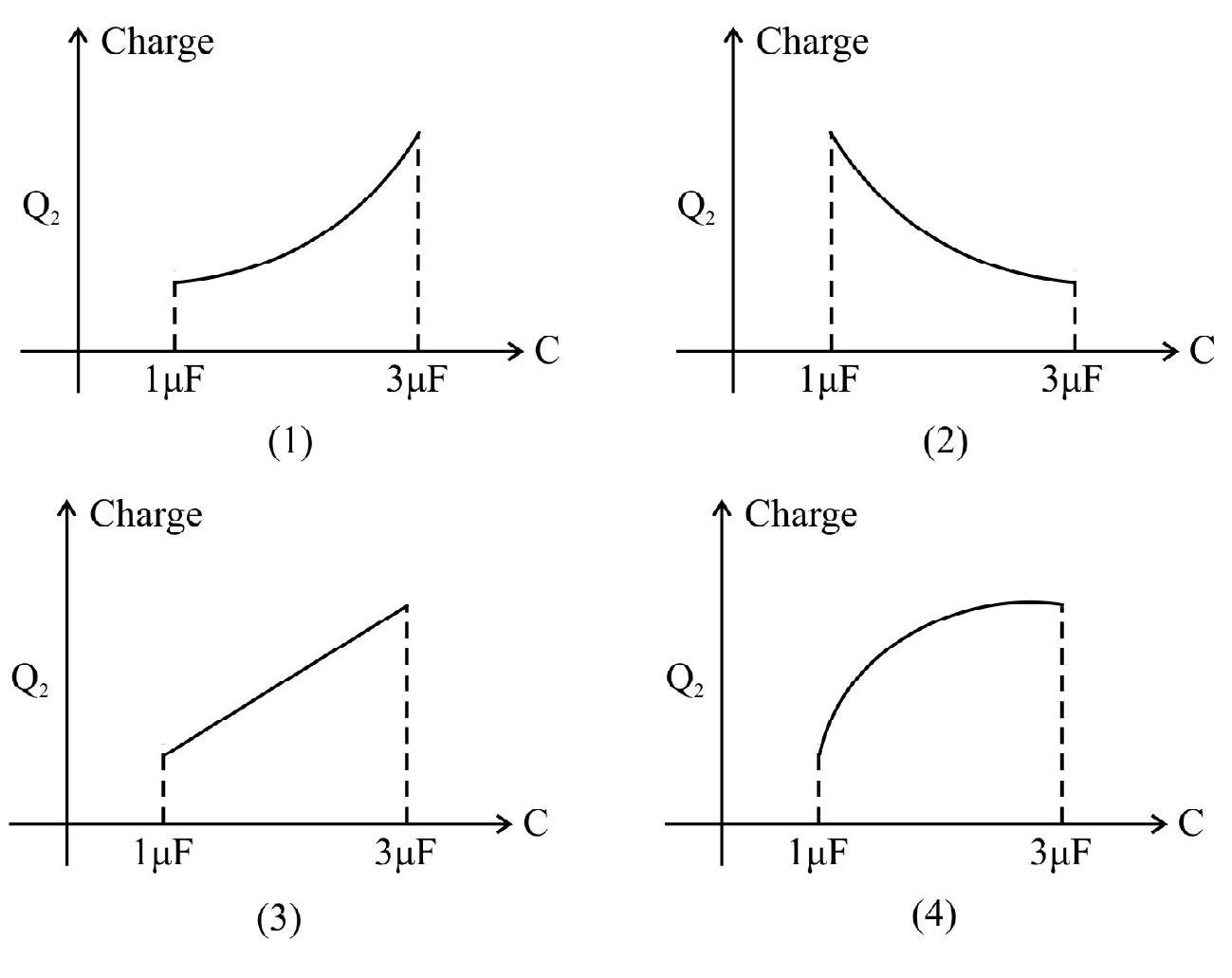
Correct option (1)
(IIT 2015)
Show Answer
Solution:
For
For
For
Also change in
7. A parallel plate capacitor is made of two circular plates separated by a distance of
(1)
(2)
(3)
(4)
Correct option (3)
(IIT 2014)
Show Answer
Solution:
Electric field (between the plates of the parallel plate capacitor)
8. A charge

(1)
(2)
(3)
(4)
Correct option (3)
(IIT 2013)
Show Answer
Solution:
Potential at
9. Two capacitors
(1)
(2)
(3)
(4)
Correct option (1)
(IIT 2013)
Show Answer
Solution:
We need to have the charges on the two, to be equal in magnitude.
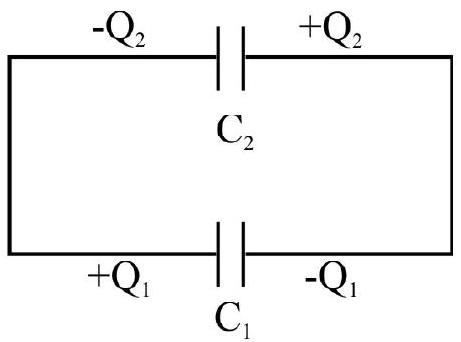
10. Two charges, each equal to
Correct option (4)
(IIT 2013)
Show Answer
Solution:
We see from the figure, that
For
PROBLEMS FOR PRACTICE
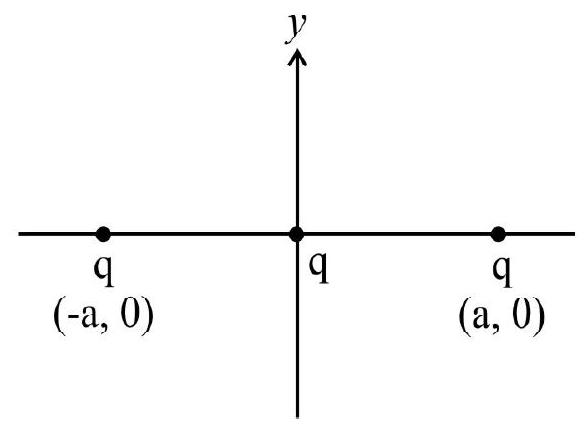
1. Two equal point charges
Show Answer
Answer:2. Two identical charged spheres are suspended in air by strings of equal lengths and make an angle of
Show Answer
Answer:3.
Show Answer
Answer:4. There is a uniform electric field
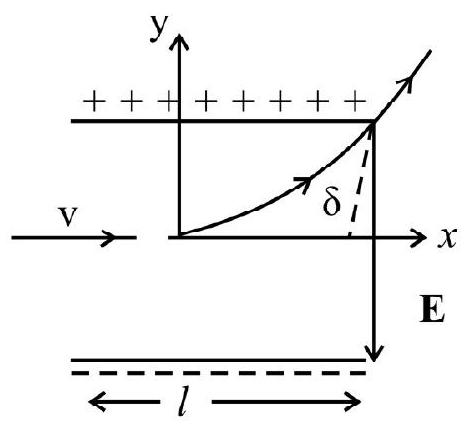
Show Answer
Answer:5. Two point charges of
Show Answer
Answer:6. Three point charges
[Hint: For minimum potential energy the charges of maximum magnitude should be farthest apart. Such that

7. Three point charges of
Show Answer
Answer:[Hint: Work required is stored as the additional potential energy of the system.]
8. A change
Show Answer
Answer:9. Two electric dipoles of moments
10. Two charges
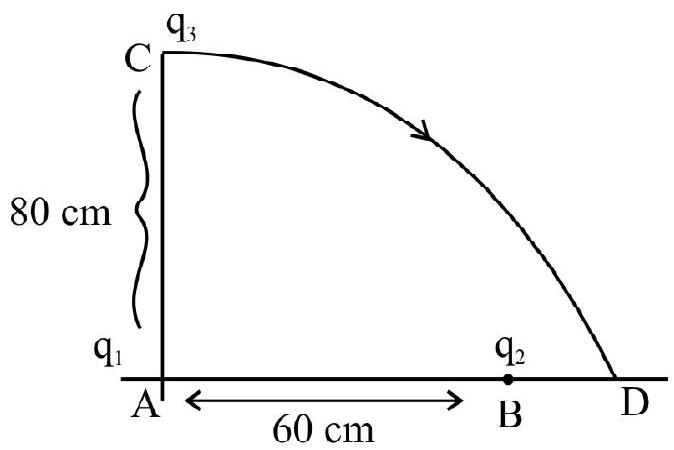
Show Answer
Answer:11. In the figure given, the electric field
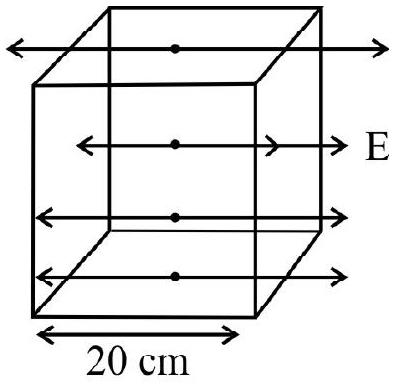
Show Answer
Answer:12. In a region of space, the electric field is given by
Show Answer
Answer: 300 Units13. Electric field in the given figure is directed along
(i) The electric flux through the cube.
(ii) Net charge enlosed within the cube.
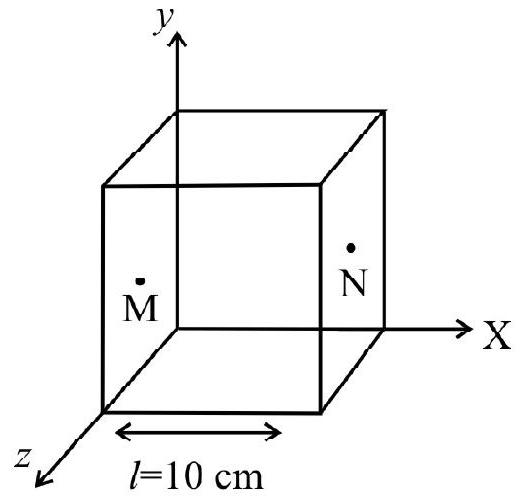
Given
Show Answer
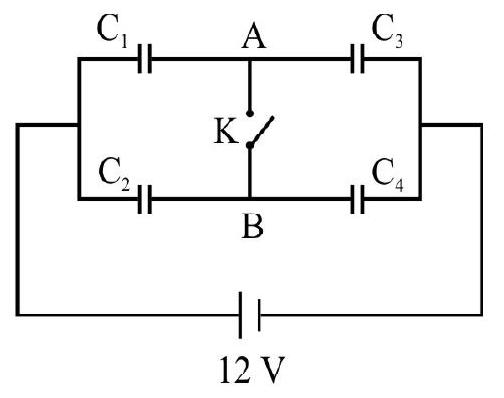
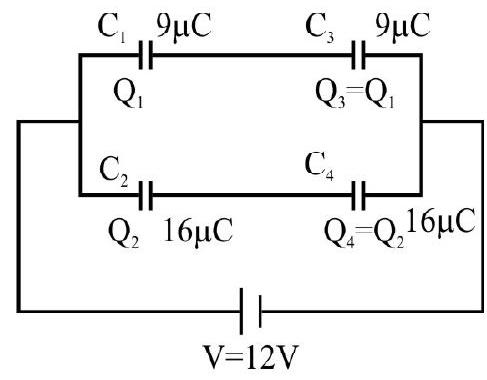
Answer:14. In the given circuit, if the ponit
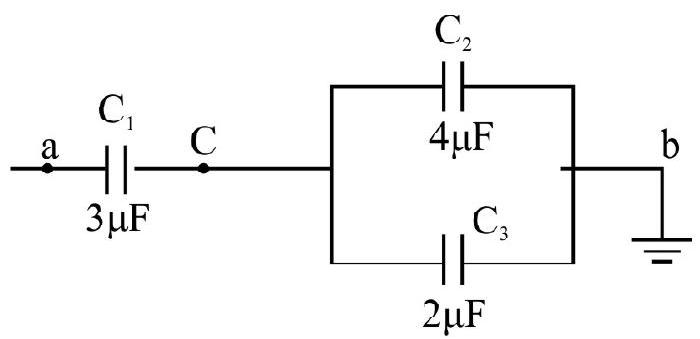
Show Answer
Answer: Charge on
Charge on
Charge on
15. In the given network of capacitor, find the effective capacitance betwen the points P and Q. Given,
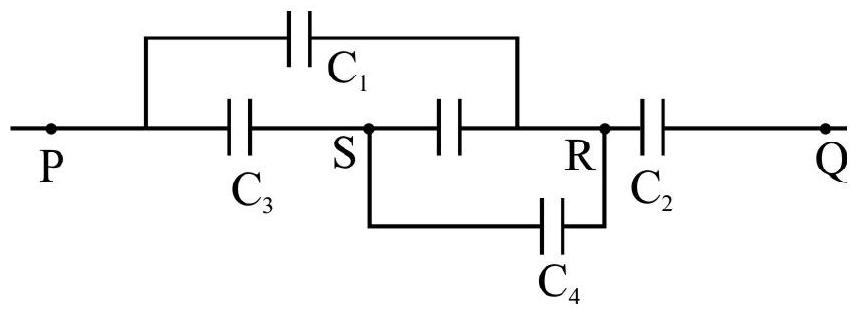
Hint: This is a wheatsone bridge arrangement. The bridge formed by capacitors is balanced
16. A20
Show Answer
Answer:17. Two capacitors
Show Answer
Answer: p.d. across each18. A parallel plate capacitor contains one mica sheet of thickness
Show Answer
Answer:19. A
Show Answer
Answer: (i)
(ii)
20. Find the equivalent capacitance between the given combination.
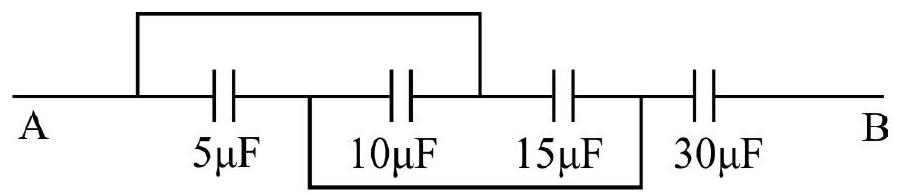
Show Answer
Answer:Question Bank
Key Learning Points
1. There are two types of charges in nature, like charges repel and unlike charges attract.
2. Electric charges has three basic properties; quantisation, additivity and conservation.
3. Coulomb’s Law: The mutual electrostatic force between two point charges (stationary) is directly propotional to the product
In vector form, coulamb’s law is written as
4. Electrostatic forces in medium decreases by a factor of dielectric constant of medium (k)
5. We can use superposition principle for computing the net force on any charge due to any configuration of charges.
6. Electric field strength
It is radially outwards from
7. From the knowledge of electric field strength
8. An electrostatic field line is a curve drawn in such a way that tanget at every point on the curve gives the direction of field at that point.
9. Electric field intensity at a point is equal to the number of field lines crossing normally a unit area around that point or the magnitude of field is represented by the density of field lines around that point.
10. Electric field strength of an electric dipole
(i) On axial line of electric dipole at a distance ’
(ii) On equitorial plane at a distance ’
Thus, the electric field due to a dipole falls off at large distances, at a much faster rate
11. Electric field due to a single point charge has a spherically symmetry whereas that due to an electric dipole has cylindrical symmetry.
12. In a uniform electric field
13. Amount of work done in rotating the dipole through a small angle is given by
14. The flux
Where
15. Gauss Law: The flux of electric field through any closed surface
It is used for symmetric charge configuration and is independent of size and shape of gaussian surface.
16. In the situation, when gaussain surface is so chosen that there are some charges inside and some outside, the electric field (whose flux is calculated) is due to all the charges, both inside and outside the closed surface. However for electric flux, only inside charges contribute.
17. In case of a shpere (solid / hollow), electric field intensity at an external point varies as
18. Electrostatic force is a conservative force work done in bringing a test charge
which is the difference of potential energy of test charge
19. Electric potential at a point is numerically equal to the total amount of work done in bringing a unit positive charge from
For a point charge ’
20. For a charge configuration, the potential at a point
Where
21. Potential energy stored in a system of charges is the work done (by an external agency) in assembling the charges at their locations.
22. Electric potential at a point due to an electric dipole with position vector ’
On the dipole axis
On the equitorial plane
23. Magnitude of electric field is given by change in the magnitude of potential per unit displacement (potential gradient) and its direction is always towards decreasing potential.
24. Electrostatic field ’
Charges in a conductor can reside over the surface. Potential is constant within and on the surface of conductors. In a cavity, within a conductor, the electric field is zero. Any charge placed in the cavity, will appear over the surface of conductor.
25. For a parallel plate capacitor (with vacuum or air between the plates) its capacitance
26. For capacitors in the series combination, the total capacitance is given by
where ’
where p.d. across the plates of each capacitors remains same.
27. The energy ’
The energy density (energy per unit volume) in a region of
Average
1. In figure, two positive charges
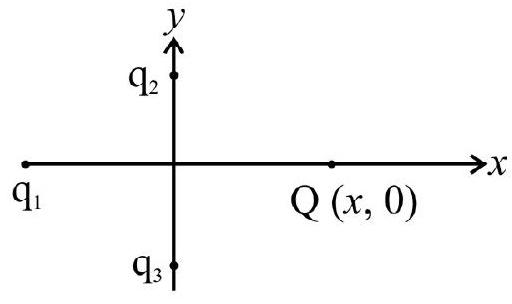
(1) shall increase along the positive
(2) shall decrease along the positive
(3) shall point along negative
(4) shall increas but direction charnges because of the intersection of
Show Answer
Correct Answer: (1)
Solution:
As
When a positive charge ’
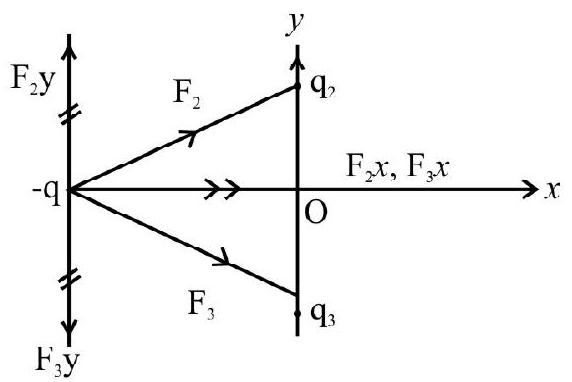
Correct answer: (1)
Easy
2. A small object with change
(1) positive with magnitude
(2) positive with magnitude
(3) negative with magnitude
(4) positive with magnitude
Show Answer
Correct Answer: (2)
Solution:
For equilibrium
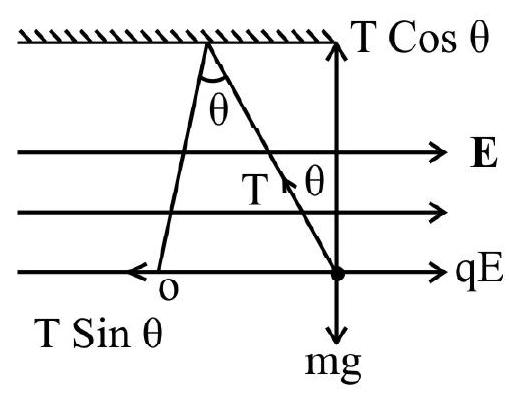
Correct answer: (2)
Average
3. A tiny spherical oil drop carrying a net charge
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (4)
Solution:
When drop is balanced in still air under the effect of electric field then
When electric field in switched off, drop falls with terminal velocity.
From (1) and (2)
or
or
Correct answer: (4)
Difficult
4. Two identical charged sheres suspended from a common point by two massless strings of length
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (4)
Solution:
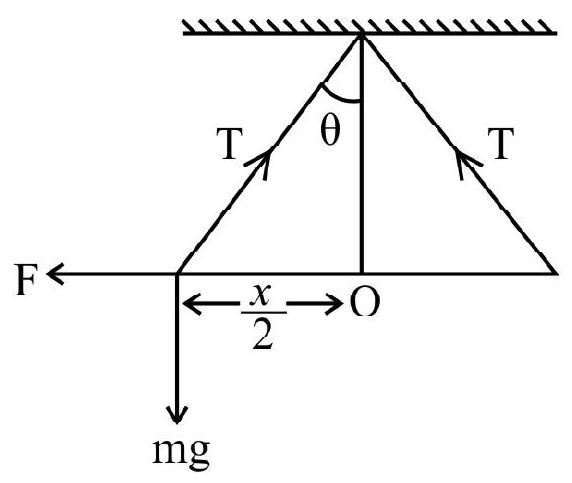
if
or
or
Correct answer: (4)
Average
5. Three charges
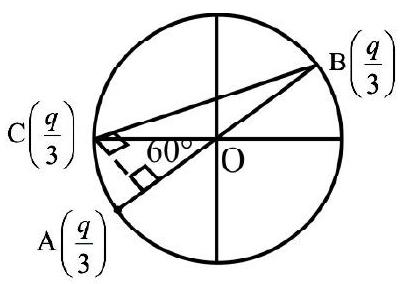
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
as
Correct answer: (3)
Easy
6. Two point charges
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (1)
Solution:
Let ’
Electric field due to
From (1) & (2)
Correct answer: (1)
Difficult
7. Let there be a spherical symmetric charge distribution with charge density varying as
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (4)
Solution:
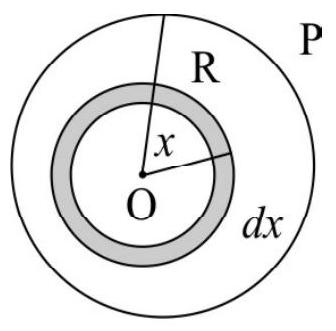
Electric field intensity at a point on this sheprical surface is
Correct answer: (4)
Difficult
8. A positively charged metal ring a radius
(1) periodic provided
(2) simple harmonic for all the values of
(3) approximately simple harmonic provided
(4) such that it crosses centre of ring ’
Show Answer
Correct Answer: (3)
Solution:
The elctric field at the point ’
Away from the centre of the ring.
Now force on ’
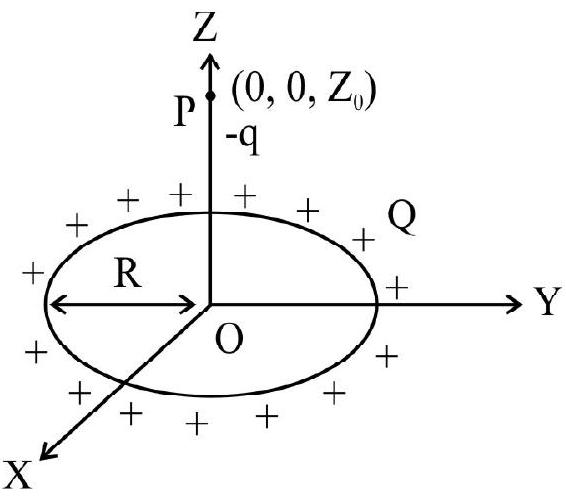
[Acts towards centre ’
For
Where
The above equation represents S.H.M. as
Correct answer: (3)
Average
9. Three infinitely charged sheets are kept parallel to 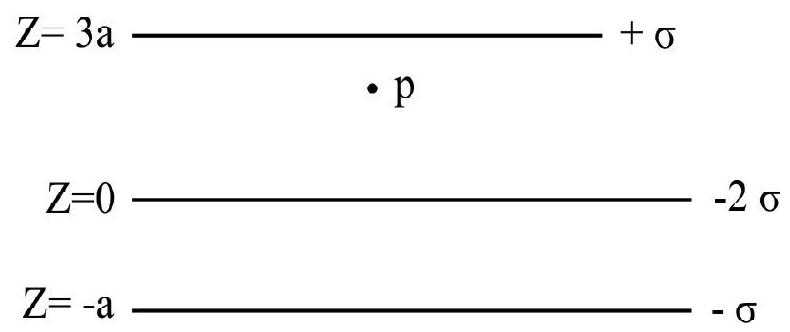
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
For infinite long sheet, electric field is given by
Electric field due to charge density
Electric field due to change density
Hence total electric field at point ’
or
or
Correct answer: (3)
Average
10. A thin semi-circular ring of radius
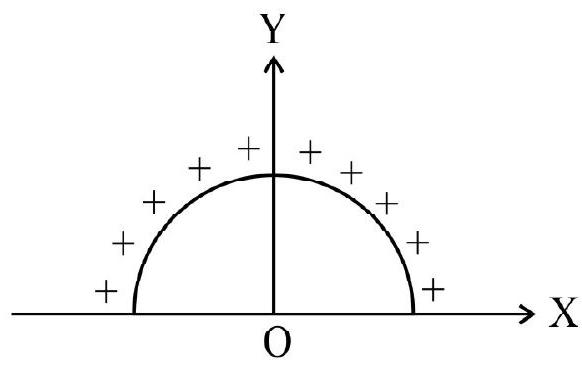
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
Charge on element ’
Electric field due to this element is
As shown in the figure, one can realise that components along
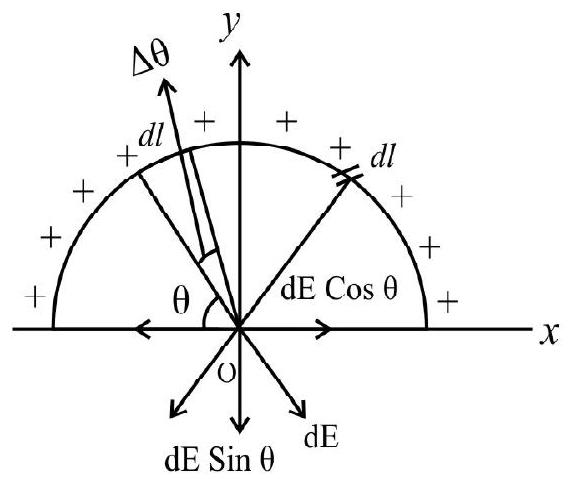
or
Correct answer: (3)
Average
11. In the figure given below, equipotential lines are drawn at
The work done in moving a change of
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (4)
Solution:
Work done is independent of path taken. Hence
Correct answer: (4)
Average
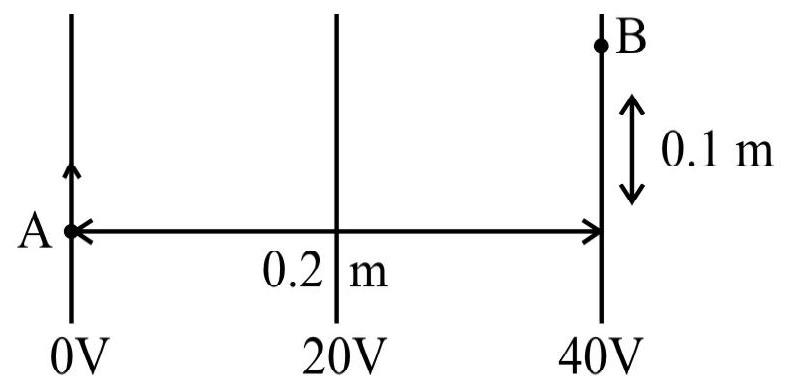
12. The infinite long wire having linear change density ’
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
Electric field due to infinite long wire is equal to
as
So potentialat A,
and potential at
Work done in moving
Correct answer is (2)
Difficult
13. A solid conducting sphere having a charge
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
Initially,
When outer shell is given a charge of ’
or
Correct answer: (2)
Average
14. A conducting spherical bubble of radius
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
As volume remains constant
Where
Correct answer is (3)
Difficult
15. Two point charges each of charge
(1) maximum force and minimum potential energy
(2) minimum force and maximum potential energy
(3) maximum force and maximum potential energy
(4) minimum force and minimum potential energy
Show Answer
Correct Answer: (4)
Solution:
Net force on
Let the charge
as
For
Hence charge at origin will have minimum minimum potential energy.
Correct answer: (4)
Average
16. A proton and an
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
According to conservation of energy-
According to conservation of momentum.
From(1) and (3)
(K.E)
Correct answer: (2)
Average
17. The electric field strength in a region is given as
(1) zero
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
At a point
Correct answer: (2)
Average
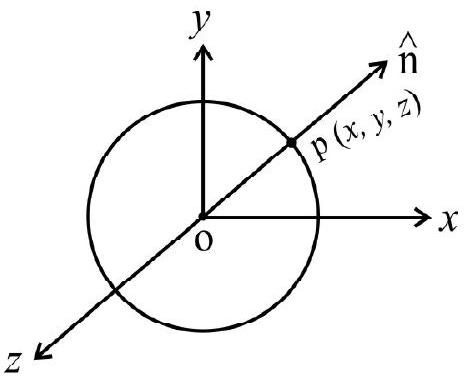
18. Consider an electric field,
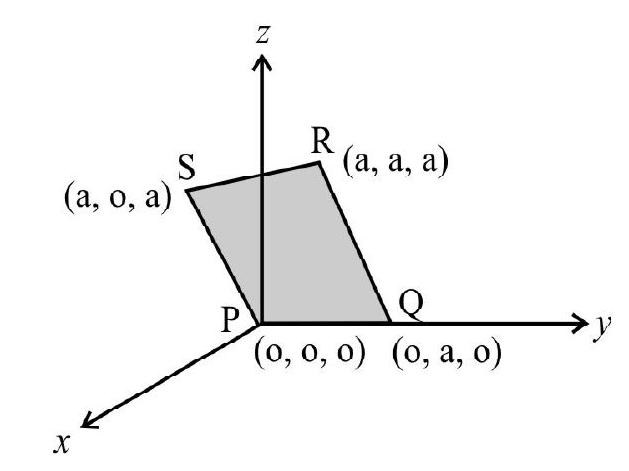
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
The shaded area
Electric flux
Correct answer: (3)
Average
19. Three charges
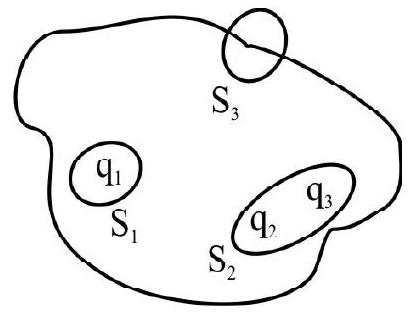
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
As the flux is due to all the charges present inside the gaussian surface. hence flux through
or
or
or
Correct answer: (2)
Difficult
20. The volume charge density as a function of distance
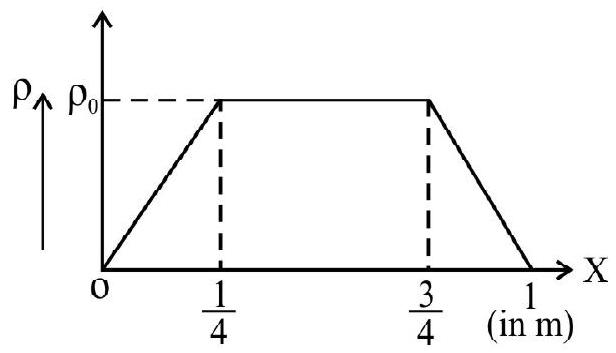
(1)
(2)
(3)
(4) 1 SI Units
Show Answer
Correct Answer: (3)
Solution:
Let ’
As flux passing throught the cube will be given by
Correct answer: (3)
Average
21. A cavity is created in the conducting shell having uniform charge distribution of +8 units as shown in the figure. Now if a charge of +4 units in placed at the centre of cavity. Which set of equations correctly describe the magnitude of electric field.
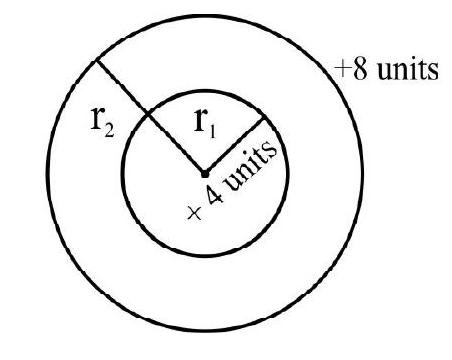
| (1) | |||
| (2) | |||
| (3) | |||
| (4) |
Show Answer
Correct Answer: (2)
Solution:
In electrostatic equilibrium, field inside conductor is zero (for
As charge placed at cavity, will appear over the surface of conductor, hance
Thus,
Correct answer: (2)
Average
22. A spherical shell with an inner surface of radius ’
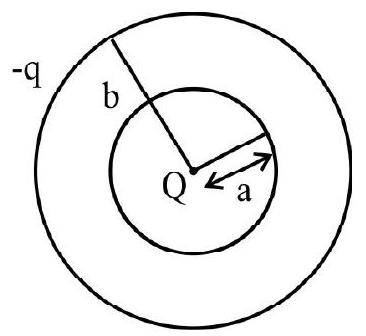
Assuming that the electrostatic potential is zero at infinite distance. The elctrostatic potential at a distance ’
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (4)
Solution:
The charge ’
Correct answer: (4)
Average
23. A parallel plate capacitor with air as the dielectric and having the same thickness as the separation between the plates is introduced so as to fill one fourth of the capacitor as shown in the figure.
| air | |
|---|---|
The new capacitance will be-
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (1)
Solution:
The capacitance
Let
The combination acts like parallel combination such that:
Correct answer: (1)
Average
24. Two identical capacitors 1 and 2 are connected in series to a battary of ’
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
Let ’
Before dielectric is removed.
[Charge in series remains same]
When slab from
As
From (1) & (2)
Correct answer: (3)
Easy
25. A capacitor of
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (4)
Solution:
or
or
or
Correct answer: (4)
Easy
26. Two conducting sphere
Both are positively charged and isolated from surroundings. They had been connected by a connecting wire but the wire is removed after some time.
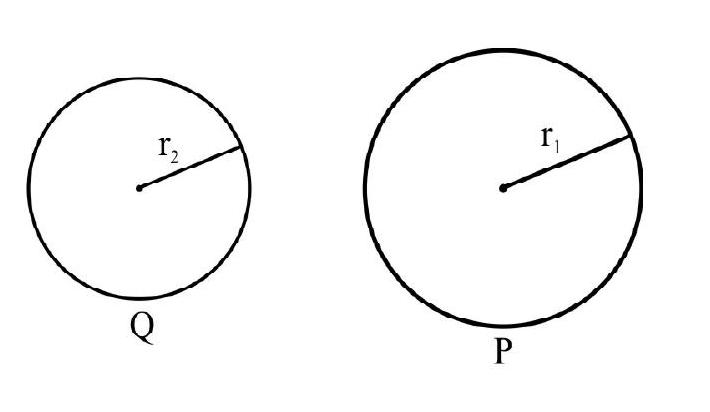
Which of the following statements are true;
(a) Sphere
(b) Both spheres are at same potential
(c) Magnitude of charge on
(d) Both the shperes will be having same charge after removal of wire
(1) (a) and (d)
(2) (b) and (d)
(3) (b) and (c)
(4) (c) and (a)
Show Answer
Correct Answer: (3)
Solution:
When both conducting spheres are connected by a wire, there will be redistribution of charge till they accquire the same potential (statement (b) is correct).
As
Correct answer: (3)
Difficult
Redistribution of Charges
27. Two capacitor
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
When terminals of opposite sign one connected together, the magnitude of net charges finally is equal to the difference of charges before the connection.
Initial charge on
Initial charge on
The energy of system
or
or
Correct answer: (2)
Average
Capacitor (Parallel-Plate)
28. The force exerted by each plate on the other plate of a parallel plate capacitor of capacitance ’
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
Force exerted by each plate on the other plate of a parallel plate capacitor is given by
where
Also
Correct answer: (2)
Difficult
Combination of Capacitors
29. Five similar capacitor plates, each of area A, are placed at a equal distance ’
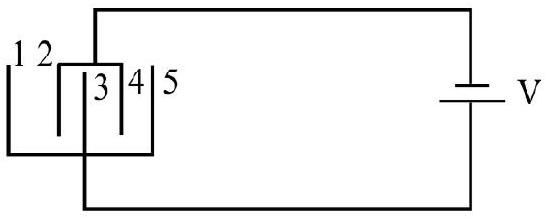
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
From equivalent circuit diagram, charge on first plate is
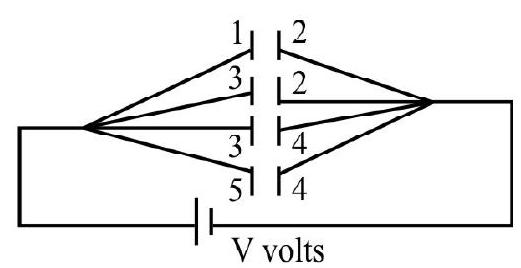
Charge on fourth plate
As plate 4 is repeated twice, hence charge on 4 will be
i.e.
Hence correct answer will be (2)
Average
Capacitor
30. A network of four capacitor of capacitance equal to
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
As in the given network
This combination
In parallel combination ’
or
As Q’ is the charge on
Hence,
Correct answer: (2)
Average
Electric Flux
31. Consider an electric field
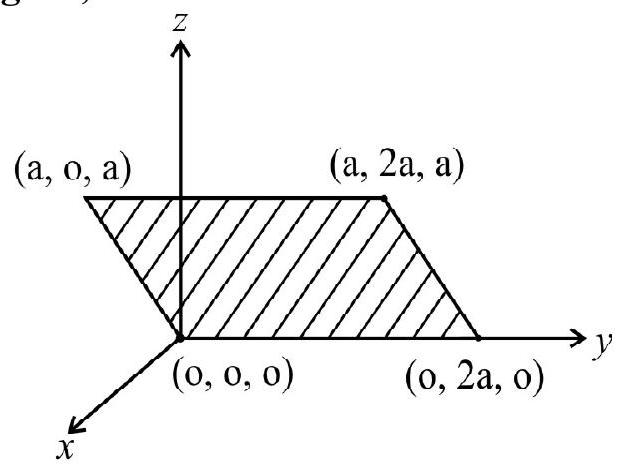
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
Flux,
Correct answer is
Difficult
Electric Fied
32. Two oppositely charged non-conducting solid spheres, of radii
(1) -4
(2)
(3)
(4) 2
Show Answer
Correct Answer: (2)
Solution:
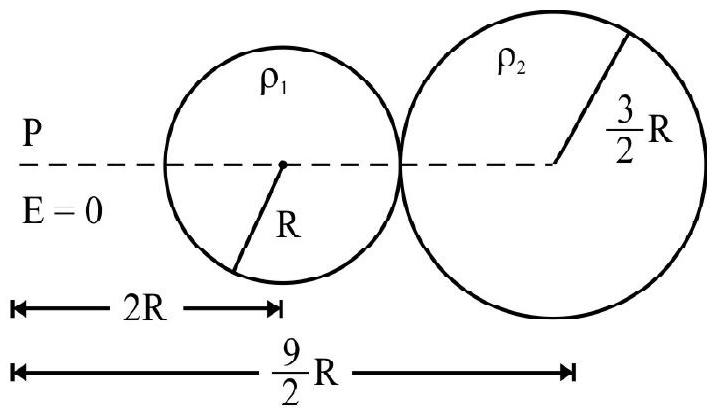
Since the spheres are oppositely charged, the point
Let
Now,
or
or
As one of the charge is negative,
Correct answer is
Difficult
Electric Potential Energy
33. Three piont charges
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
For minimum potential energy, the charges of maximum energy should be at farthest position. Therefore the charges of
Here,
The potential energy of this system is:
or
But, for
Hence,
or
or
or
or
The correct answer is:
Correct answer: (2)
Average
Electric Potential
34. When the intensity of electric field becomes
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (4)
Solution:
For the maximum values,
But,
Therefore, the maximum potential it can have is
Correct answer: (4)
Difficult
Electric Potential
35. A spherical metal shell
(i)
(ii)
(iii)
(iv)
(1) (i), (ii) and (iii)
(2) (i), (iii) and (iv)
(3) (ii) and (iv)
(4) (i), (ii), (iii) and (iv)
Show Answer
Correct Answer: (2)
Solution:
For metal sphere or shell, charges reside only on the surface. As there is no charge inside, by using Gauss’s theorem, we can show that
So statement (i) is correct.
Let the charges on
The final potential of
Therefore
So,
or
Since
So, optino (3) gives a correct statement.
Now,
or
So, option (1) is an incorrect statement.
Electric field
But,
Hence, option (4) is a correct statement.
Difficult
Electric Force
36. A tiny spherical oil drop carrying a net charge
(1) 2
(2) 3
(3) 4
(4) 5
Show Answer
Correct Answer: (4)
Solution:
Since the drop is balanced is a vertically upward electric field, the change q on it should be positive and so few electrons will be missing from it.
We find qusing the following equations.
When the drop is balanced,
or
When it falls with terminal velocity
Since field is switched off, we have,
or
From (1) and (2), we have
or
But
Correct answer: (4)
Difficult
Capacitor with Dielectric
37. The capacitance of parallel plate capacitor is
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
With air as dielectric, the capacitance of a parallel plate capacitor is;
Now, with a dielectric slab of thickness
When
After charging the battery is removed. Hence the change Q will remain unchanged, there after. How, suppose the capacitance changes to
Here,
Since
Now, energy loss, when the slab is placed
This energy loss will appear as surplus heat produced in the slab. So heat produced in the slab
Difficult
Combination of Capacitor
38. In the given network,
(1) 2.4
(2) 1.8
(3) 0.8
(4) 0.2
Show Answer
Correct Answer: (1)
Solution:
When
Now, When
Here,
Here, the effective capactitance
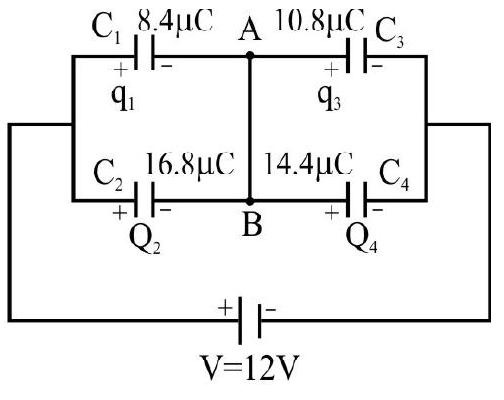
So, chnage on
Hence, potential difference across
Similary,
Now,
Initial change on the
Final change on the
Change flowing down through
Now, initial change on
Final change on + ve plate of
Hence, total change flowing down through
Correct answer: (1)
Difficult
Combination of Capacitor
39. A, B, C, and
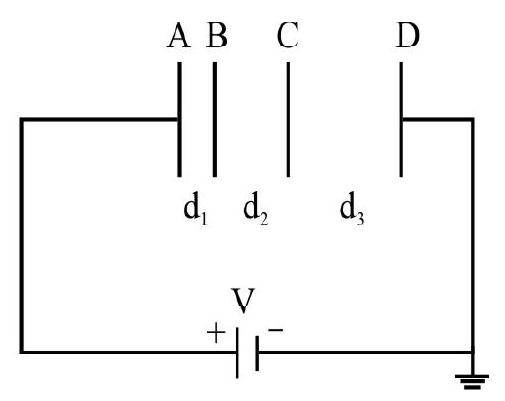
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
The arrangement is equivalent to three capacitors of
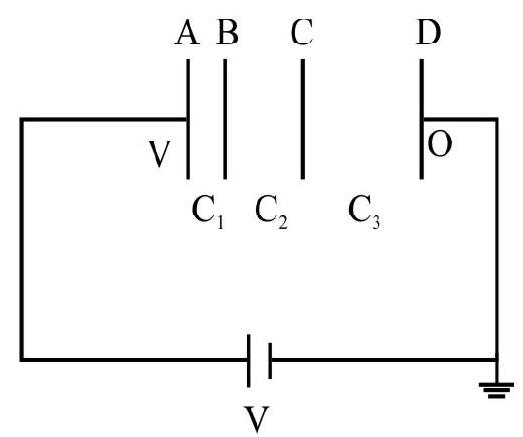
If
or
or
or
The charge stored in system is:
q is same for all.
Potential difference for
Potential difference for
Now, from the figure given:
Now,
or
Correct answer: (3)
Average
Electric field due to Spherical Body
40. Consider a sphere of radius
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
Let
Now, the total charge of the sphere of radius
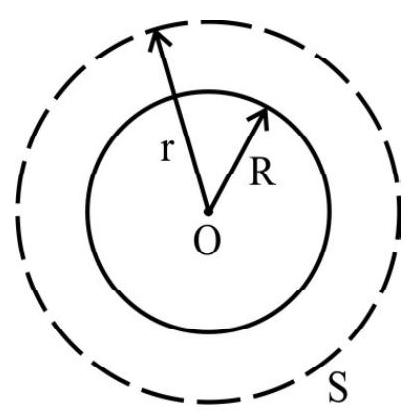
or
or
By Gauss’s theorem,
From(1), (2) and (3), we have:
Correct answer: (2)
Average
Electric Field due to a Charged Shell
41. Two concentric conducting thin spherical shells
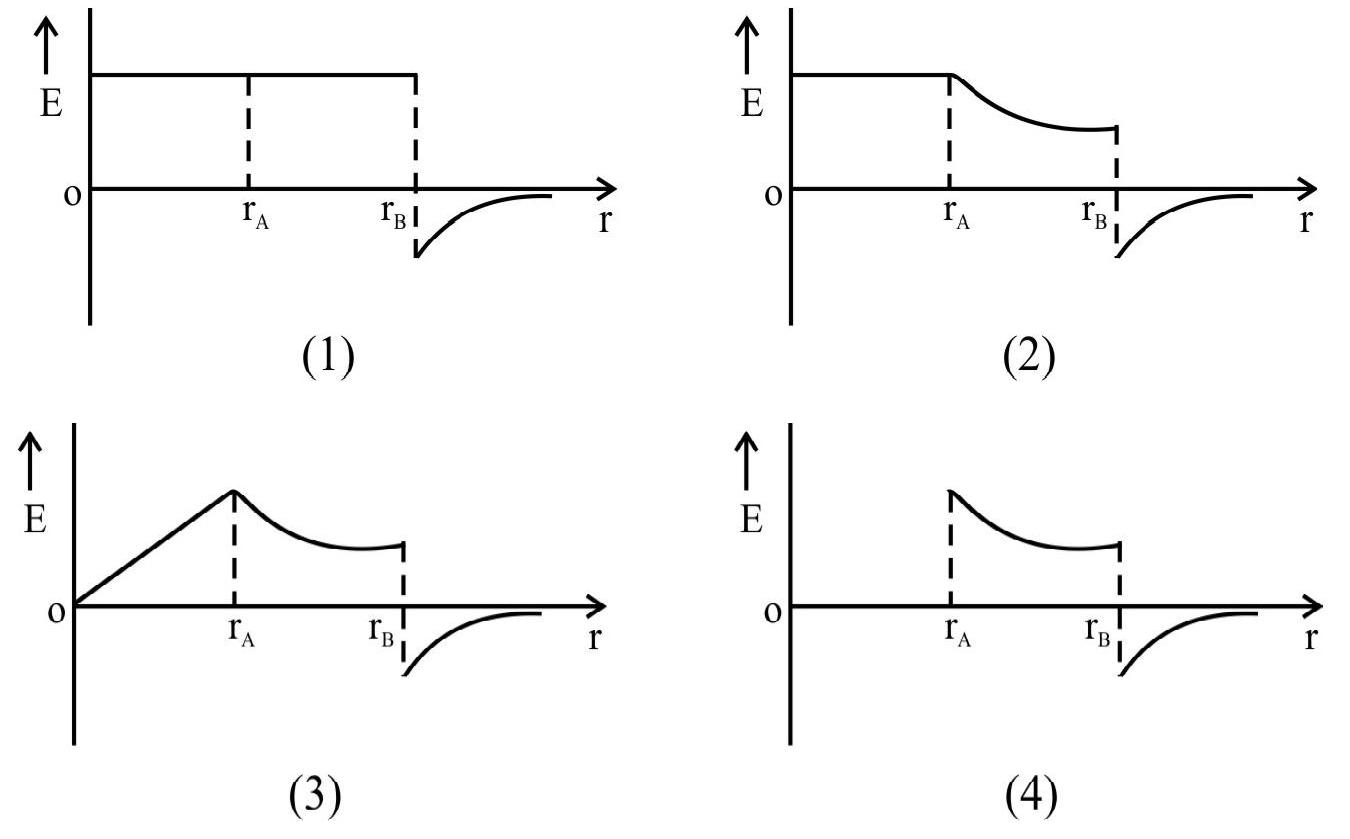
Show Answer
Correct Answer: (4)
Solution:
As the shells are made of conductors, charges reside only on their surfaces. Therefore electric field inside the shell, due to the charge on its surface will be zero.
Therefor, inside shell A, there no field due to charge on A or charge on B. In the space between A and B, the field is due to charge on A only. Since charge on in
Now, outside shell B, the charges on A and B behave like point charges at the common centre.
For
or
Therefore,
For
Therefore,
Correct graph is (4).
Easy
Potential
42. The potential of the electr ic field at any point
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
Correct answer: (3)
Easy
Electric Flux
43. In the figure given,
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
The flux crossing spherical surface
or
or
or
Similarly,
But,
or
Correct answer: (3)
Easy
Electric Flux
44. Point chargers of magnitude
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
The situation is shown is the figure. Clearly,
$$
Correct answer: (3)
Average
Electric Field due to Charged Sphere
45. At a point which is
(1)
(2)
(3)
(4) zero
Show Answer
Correct Answer: (3)
Solution:
Let
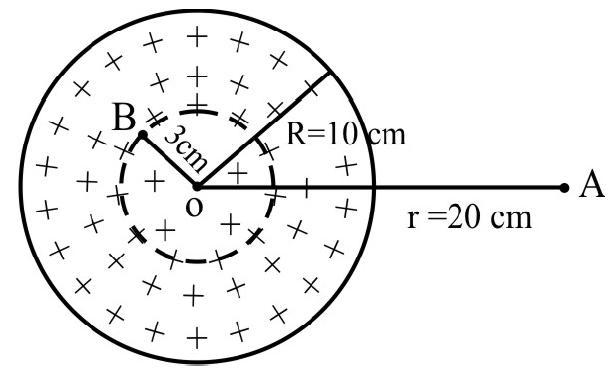
Now, at
or
At
The field at
Correct answer: (3)
Easy
Capacitance of conductor
46. Taking earth to be a spherical conductor of diameter
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (1)
Solution:
The capacitance of a spherical conductor is
Correct answer: (1)
Average
Electric Force
47. Four charges, equal to
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
For equilibrium, the net force should be zero. Taking
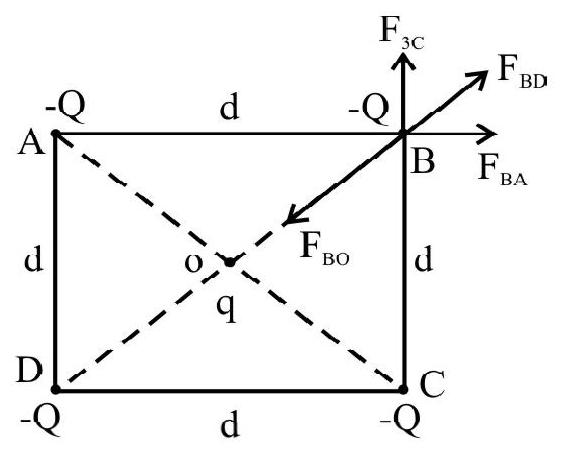
Now,
For equilibrium,
or
or
Correct answer: (2)
Easy
Electric Potential
48. A metal sphere
(1) zero
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
Let the charge on A be ’
Then,
or
When
Now, potential on the surface or at any point inside a charged conductor remains the same.
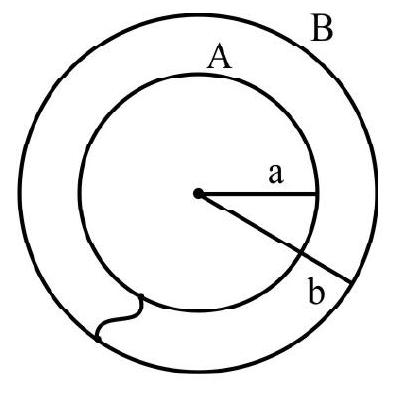
or
Correct answer: (3)
Difficult
Electric Potential
49. A thin disc of radius
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (1)
Solution:
Let
Assuming that the disc be divided large number of elementary rings, each ring will produced a potential of
The charge on one such elementary ring, as shown in the figure is:
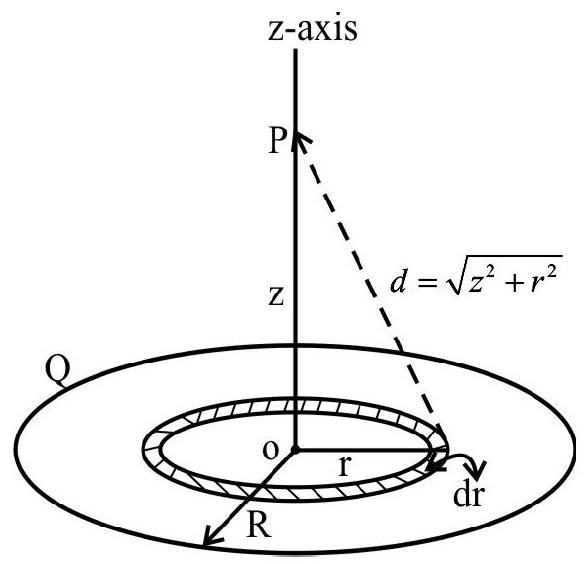
So,
Now, at
Correct answer: (1)
Difficult
Electric Field
50. A simple pendulum, of length ’
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (1)
Solution:
There are two forces on the bob, as shown in the figure. (i)
So the resultant force on the bob is
In equilibrium position of the bob, this for
Now, suppose the pendulum is disturbed through a small angle
The restoring force developed on the bob will be:
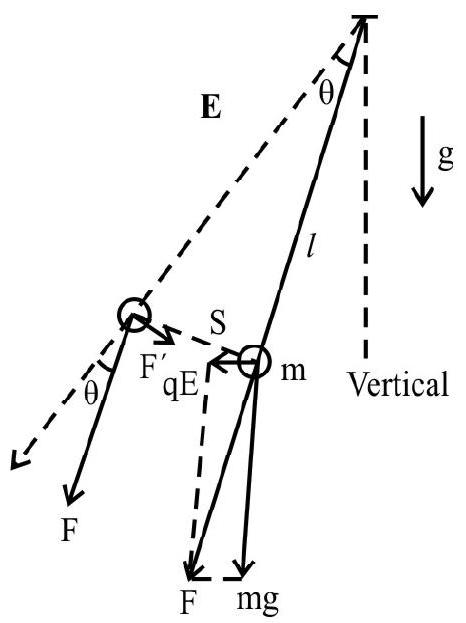
or
or
or
This is of the form,
Now,
or
Correct answer: (1)
Average
Motion in Electric Field
51. A small copper ball, of density
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
The ball will remain suspended in oil when the force due to electric field balances the apparent weight of the ball in the oil.
or
or
Here, Density of copper
Density of oil
Correct answer: (2)
Average
Principle of Superposition of Charges
52. Point charges of value
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
For equilibrium, there should be two equal and opposite forces on each charge. This condition is statified, here, only if the third charge ’

And the third charge should be negative.
For charge
For charge
Correct answer: (3)
Average
Motion of charge in uniform Electric Field
53. A particle of mass ’
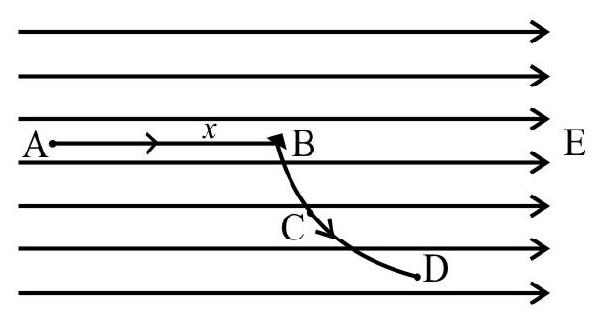
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
The electric field will produce a constant acceleration of
The velocity attained by
or
After collision, this
acceleration remains the same in magnitude and direction (along
Hence, its velocity, will again increases to
Therefore, at
Correct answer: (3)
Difficult
Electric field
54. Two co-axial circular rings of radius
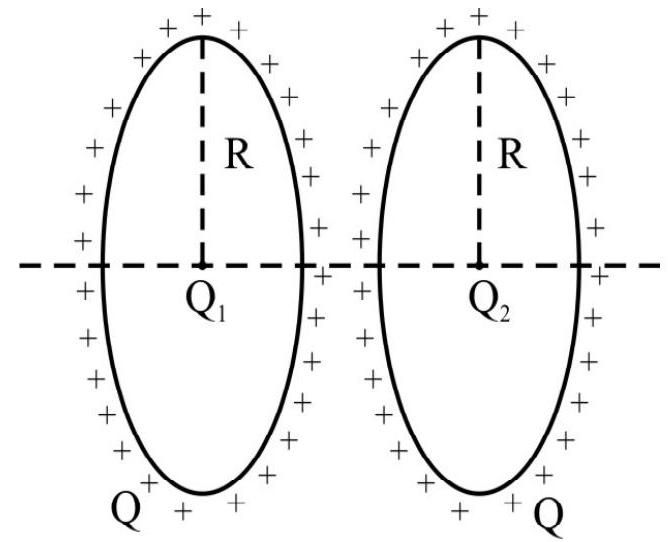
(1)
(2)
(3)
(4) zero
Show Answer
Correct Answer: (1)
Solution:
When the field is maximum, the distance
The field due to the charge on the ring at its own centre is always zero.
Correct answer: (1)
Easy
Continuous Charge Distribution
55. A conducting sphere
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (4)
Solution:
When the spheres are brought to contact, they share the total charge in such a way that the potential of both are same.
i.e.
If
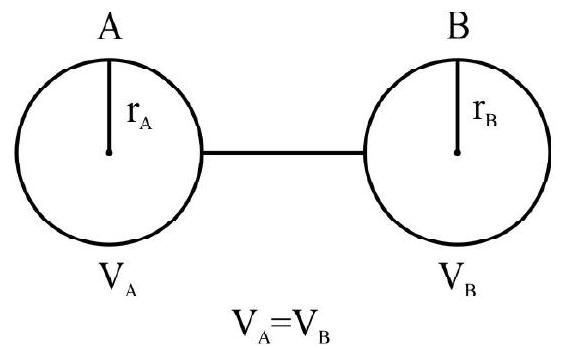
Since
or
Correct answer: (4)
Easy
Electric Dipole
56. A dipole consisting of two point charges of
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (4)
Solution:
Let the dipole moment be
Now,
Correct answer: (4)
Average
Principle of superposition of Charges
57. An infinite number of point charges, each of magnitude
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
Correct answer: (3)
Average
Electric Field Lines
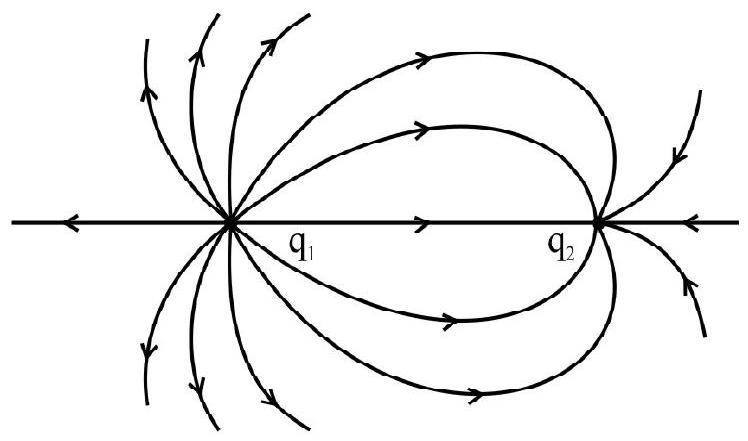
58. The figure shows a few electric field lines for a system of two charges
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (1)
Solution:
Here,
Now, for
Hence field is zero at some distance to the right of
Easy
Surface Charge Density
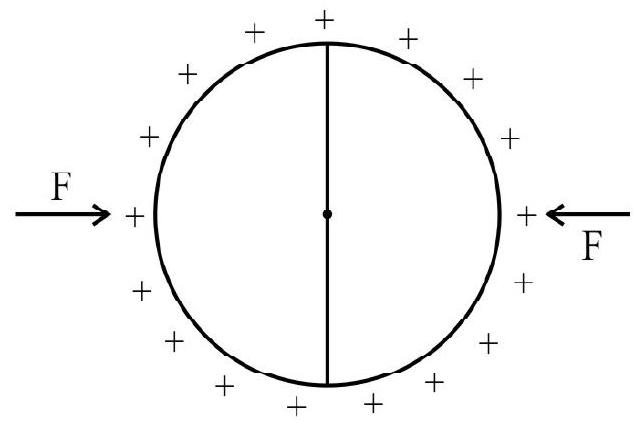
59. A uniformly charged thin spherical shell, made of a co-conducting material, of radius
(1)
(2)
(3)
(4)
Show Answer
Solution:
According to the principles of homofensity of dimensions, the correct option is the one which has dimensions same as that of force i.e.
Now,
Correct answer: (1)
Difficult
Electric Field
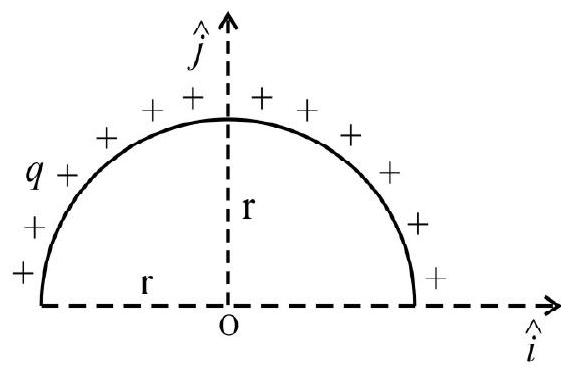
60. A thin semicircular ring of radius ’
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (4)
Solution:
Consider an element of length
The charge on this element on this element is
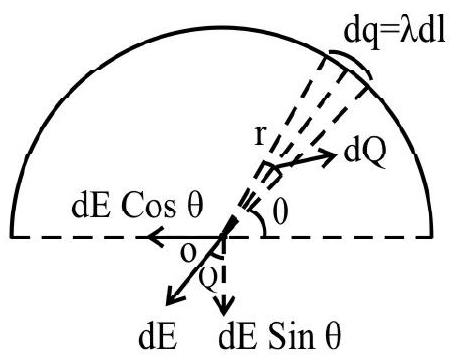
Now the field
Resolving
Correct answer: (4)
Difficult
Continuous Charge Distribution
61. A spherically symmetric charge distribution is set-up with the charge density varying according to the expression:
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
Consider a thin elementary of radius

Now,
Correct answer: (3)
Easy
Electric Field and Potential
62. Three point charges of
(1) The field is non-zero and the potential is zero.
(2) The field is zero and the potential is non-zero.
(3) Both field and potential are non-zero.
(4) Both field and potential are zero.
Show Answer
Correct Answer: (1)
Solution:
As shown in the figure, the resultant of fields
But the potential is:
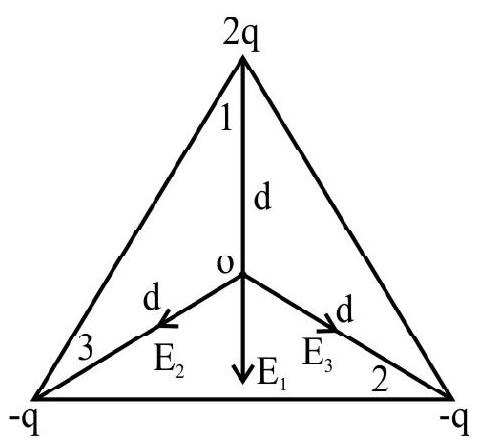
Correct answer: (1)
Easy
Electrostatic Potential Energy
63. Three point charges of
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
The intial and final arrangements are as shown in the diagram.
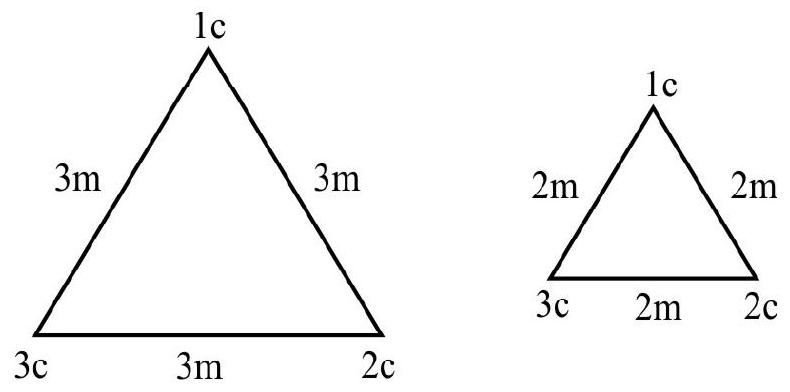
Correct answer: (2)
Average
Electric Potential
64. For the rectangle
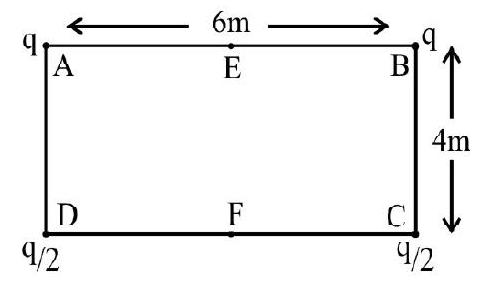
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
The potential at point
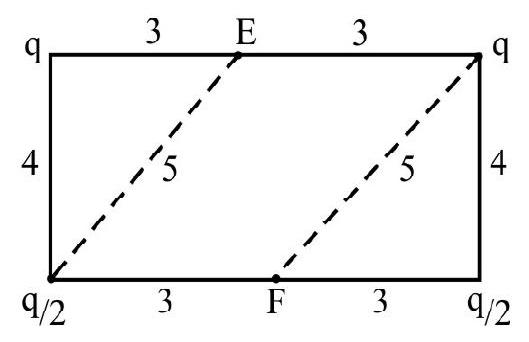
Correct answer is (2)
Difficult
Electric Potential
65. A long straight conducting wire is uniformly charged with density of
Kinetic energy of this charge, when it has moved through a distance of
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (1)
Solution:
The kinetic energy of the particle at
Where

Now,
Correct answer: (1)
Difficult
Principle of Superposition of Charges
66. Ten positively charged paritcles are kept fixed on the
(1)
(2) 495 Kilo newton
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
Correct answer: (2)
Easy
Electric Field
67. A charge of

(1) Q
(2)
(3)
(4) zero
Show Answer
Correct Answer: (4)
Solution:
As the spherical surface
Hence flux crossing
Therefore totalcharge enclosed by it also in zero.
Correct answer: (4)
Easy
Capacitor
68. A network of six identical capacitors, each of value
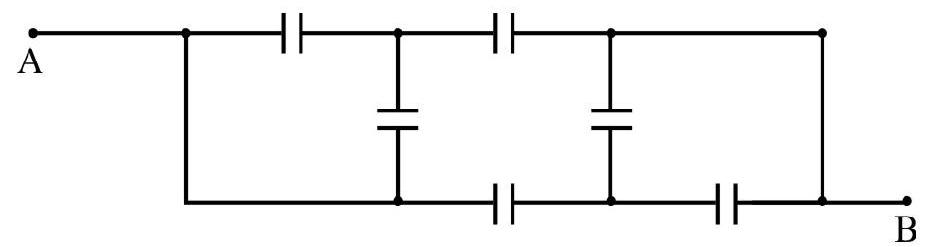
The equivalent capacitance between
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (4)
Solution:
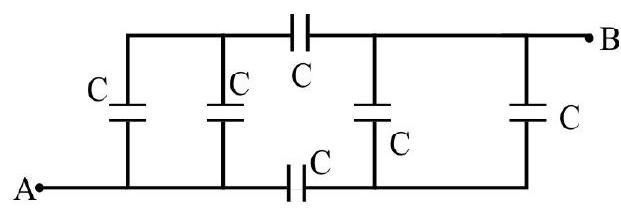
The given network can be re-drawn as below.
or
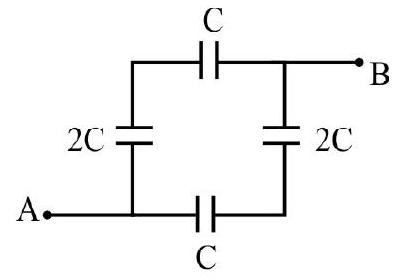
Or
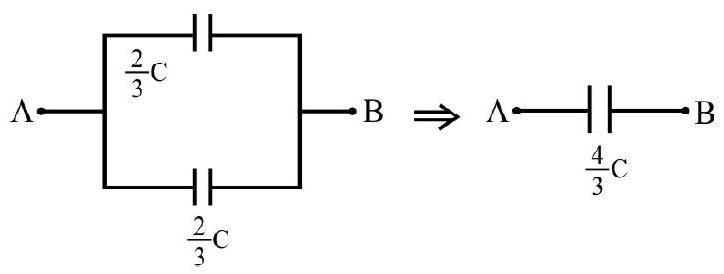
Correct answer: (4)
Average
Capacitor
69. In the figure below, the charge on the
The potential difference
(1) 10 Volt
(2) 20 Volt
(3) 23.3 Volt
(4) 46.6 Volt
Show Answer
Correct Answer: (2)
Solution:
Since
Charge on this
Therefore potential difference across the
Now,
With a potential difference of
Now
Correct answer: (2)
Average
Capacitor
70. Four identical capacitors are connected together as shown in the figure. A battery of
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (1)
Solution:
Now, the above combination can be re-drawn as shown.
But
or
Correct answer: (1)
Easy
Capacitor
71. A
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
Common potential
Energy loss
Correct answer: (2)
Average
Capacitor
72. All the capacitors in the figure have the same capacitance of
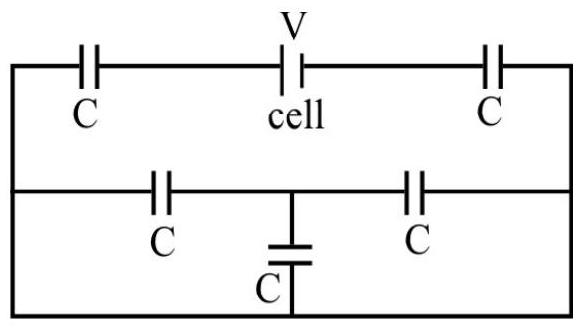
The total charge stored in the combination is:
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
The combination can be re-drawn as shown. Since the three capacitors in the middle have no potential difference across, than,
The other two are is series with
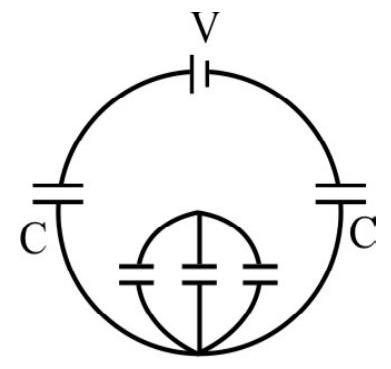
and
Correct answer: (3)
Average
Capacitor
73. Keeping other relevant parameters constant, which of the follwing plots is / are incorrectly drawn, in case of a capacitor. (Notation have usual meaning).

(1) (c) and (e)
(2) (b), (c) and (d)
(3) (d) and (e)
(4) (b) and (e)
Show Answer
Correct Answer: (1)
Solution:
(a)
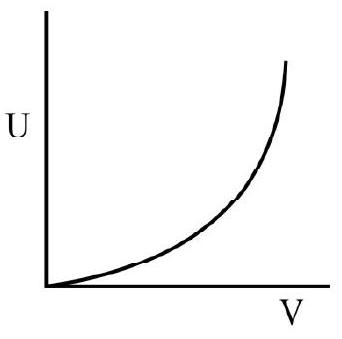
Graph of U vs V is parabola (Correct) .
(b)
Graph is correct
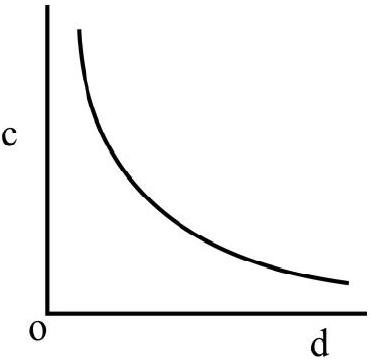
(c)
So,

Graph is incorrect.
(d)
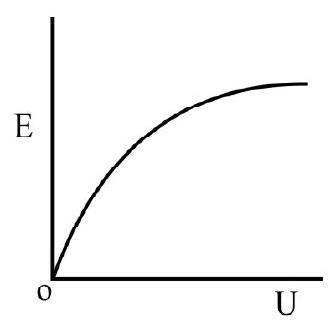
Graph is correct.
(e)
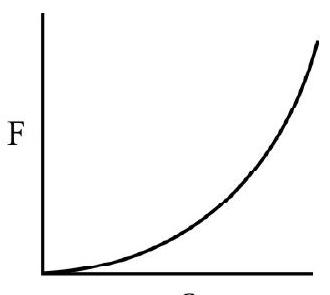
So graph has parabolic bending towards
Correct answer: (1)
Average
Dielectric
74.
(1)
(2) 5C, V, 5Q, 5U and E
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
Both the cases are represented in the diagram.
(i) Capacitance increases to
(ii)
(iii) Charge
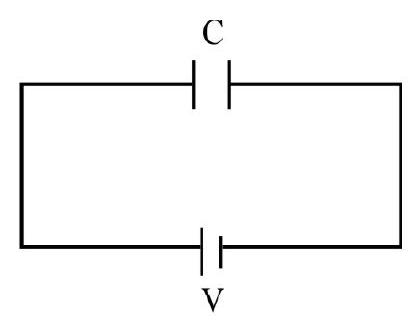
New charge is
(iv)
New

(v) If
Now,
Correct answer: (2)
Easy
Electrostatic Force
75. Two positive ions, each carrying a charge ’
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (4)
Solution:
or
Correct answer: (4)
Easy
Electric Dipole
76. The dipole moment, of a deuteron and an electron, separated by a distance of 1.6 femtometre is:
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (4)
Solution:

Here
Correct answer: (4)
Average
Capacitors
77. A series combination of
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (1)
Solution:
For series,
and
For parallel,
and
But,
or
Correct answer: (1)
Average
Electrostatic Potential Energy
78. Three identical charges, each of
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (4)
Solution:
Given,
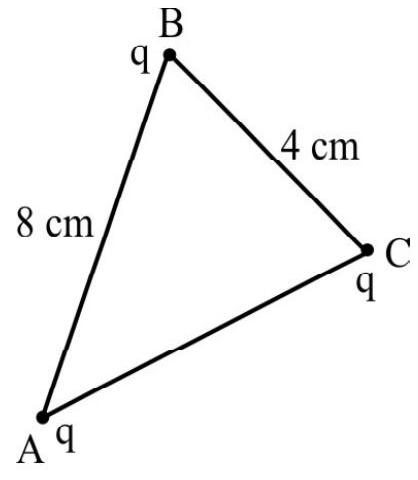
Now,
Hence
The potential
Now,
Correct answer: (4)
Easy
Electrostatic Charge
79. Two bodies A and B carry charges of
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
A has higher negative charge and so electrons should be transferred from A to B.
Let
or 2 ne
Correct answer: (2)
Average
Electrostaic Force
80. Two identical helium filled balloons
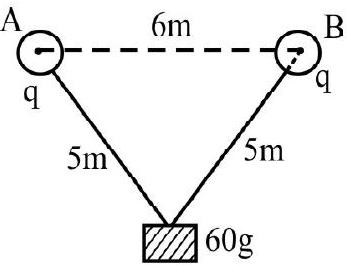
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (1)
Solution:
At equilibrium
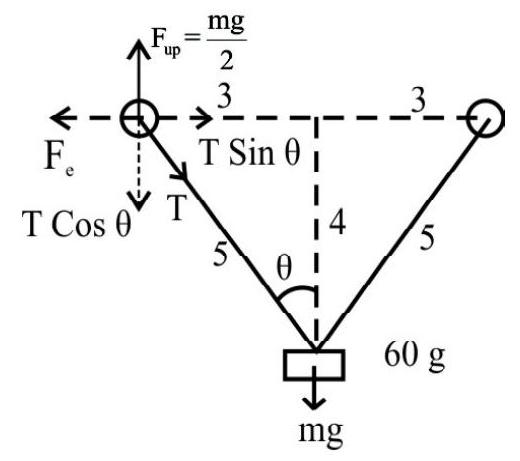
Correct answer: (1)
Average
Electric Dipole
81. A dipole of very small length and dipole moment
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (3)
Solution:
Difficult
Electrostatic Potential Energy
82. The electrostatic energy of a nucleous can be considered as the work done against electrostatic forces in assemblying the
Therefore the electrostatic energy assocaited with a nucleus is given by:
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
The uniform density of charge in a nucelus is given by:
We regard the nucleus as a sphere having a uniform charge distribution.
The work done to increase in radius of sphere
Putting
or
Correct answer: (2)
Difficult
Electrostatic Potential Energy
83. A conducting sphere of radius
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (1)
Solution:
Let us consider a point
The clectric field at
Let the energy density at this point
The energy lying in a spherical slab formed between two concentric spheres of radii
Correct answer: (1)
Easy
Dielectric
84. A polar dielectric is placed in a external field
(1) The external field
(2) The external field will allign all the atoms and molecules of the given dielectric in its own direction.
(3) The dielectric will be have as if it is equivlent to a large number of tiny dipoles situated in vaccum.
(4) The dielectric will behave as if it is equivalent to a large number of tiny dipoles situated in the material of dielectric.
Show Answer
Correct Answer: (3)
Solution:
A polar dielectric has a built in dipole moment. In the absence of an external field these dipoles are orineted complete by at randomly. The net dipole moment associated with any macroscoping small volume element is zero. When an electric field is applied there is is a small induced dipole moment and also a torque is exerted on all permanent dipole and the field tends to allign the dipoles in its own direction. Thermal motion tends to oppose this alignment so that at given temperature some alignment in the direction of the field is produced in equilibrium condition. Due to this aligment there is now some net dipole moment associated with each macroscoping small element of the dielectric. Hence a dielectric placed in an external field can be considered as equivalent to a large number of tiny dipole stituated in vacuum.
Correct answer: (3)
Easy
Dielectric
85. In the reaction
For a linear dielectric, while of the following statement is correct
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (4)
Solution:
The statement (4) is established by experiment.
Average
Dielectric
86. If
(1)
(2)
(3)
(4)
Show Answer
Correct Answer: (2)
Solution:
We have,
or
Now,
From equations 1, 2 and 3 we obtain.
Correct answer: (2)










