Introduction

We are all familiar with the meaning of the term ‘periodic motion’. The motion, of a particle, or an object, is said to be ‘periodic’ if the particle / object has the same ‘state of motion’ (same position co-ordinates, same velocity and same acceleration) after the same (regular) interval of time. This (regular) interval of time, after which the ‘motion’ gets repeated (again and again) is called the ’time period’, or just the ‘period’ of the given ‘periodic motion’.

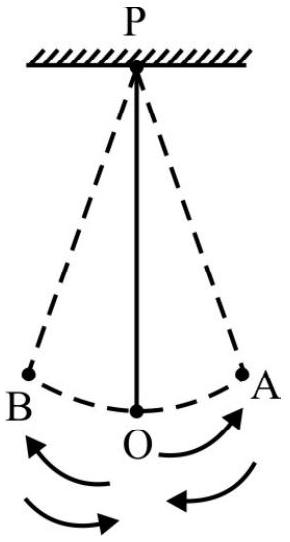
A simple, and familiar, example of ‘periodic motion’ is the motion ofa ‘simple pendulum’. The ‘simple pendulum’, shown here, (when set in oscillations, by giving a push, say), starts from its mean position ’ $\mathrm{O}$ ‘, goes up to some point $\mathrm{A}$, comes back to $\mathrm{O}$, goes to a (almost) symmetrically located point $\mathrm{B}$, on the other side; comes back to $\mathrm{A}$; and then repeats this cycle again and again. Here it is important to note that the ’time period’ of the pendulum is the time taken by it to complete the four sub steps cycle: $(\mathrm{O}$ to $\mathrm{A})$, $\mathrm{A}$ to $\mathrm{O}) ;(\mathrm{O}$ to $\mathrm{B}$ ) and ( $\mathrm{B}$ to $\mathrm{O}$ ). It is only when the pendulum comes back to $\mathrm{O}$, after going to point $\mathrm{B}$ (on the other side), that it is in the same ‘state of motion’ (same position, same velocity and same acceleration). Note that when it comes back to $\mathrm{O}$ after just going up to point A, it is not in the same state of motion as at ‘start’; its velocity, at this stage is directed opposite to its velocity at the ‘start’.

Periodic motions can be of different kinds. The motion of a particle / object, repeatedly moving along a circular / elliptical path (with a constant speed), the motion of a simple pendulum (described above) and the ’to-and-fro’ motion, of the free end of a rod (whose other end has been clamped to a table, say) are all examples of ‘periodic motions’. However, for the second and the third example, given above, we usually use the terms ‘oscillatory motion’ and ‘vibration motion’, respectively. We may say that:

“All oscillatory and all vibratory motions are necessarily ‘periodic motions’; however, all ‘periodic motions’ would not necessarily be referred to as oscillatory / vibratory motion”.

Oscillatory and Vibrating Motions

A periodic motion is referred to as an ‘oscillatory motion’ if it is a periodic ’to and fro’ motion, about some central or mean position. The path followed by an oscillating particle is not a ‘closed path’ unlike the path followed by a particle, executing a ‘periodic motion’, along a circular or elliptical path.

The term ‘oscillatory motion, or ‘oscillations’, has now been given a general meaning; it is used for situations where no mechanical / physical particle or object, is ’executing oscillations’. We now speak of oscillating electric / magnetic fields (electromagnetic waves) even though there is no mechanical/ physical particle executing these ‘oscillations’.

The term ‘vibratory motion’ is generally restricted to ‘mechanical oscillations’. We generally speak of ‘vibrations’ only when a mechanical/ physical particle (object) is oscillating. We can have vibrating rods, vibrating atoms / molecules, or vibrations in a metal plate, or vibrations in the earth’s crust.

Periodic Functions

We know that if a quantity ’ $y$ ’ depends on another quantity, $x$, it is said that ’ $y$ ’ is a function of ’ $x$ ‘. This is expressed through the expression:

$$ \mathrm{y}=\mathrm{f}(x) $$

This mathematical concept of ‘functions’, can be used for description of ‘motion’. A particle is said to be in motion if its position co-ordinates (in terms of an appropriate frame of reference) keep on changing with time. In terms of the concept of functions, we would say that the position co-ordinates, of a moving particle, are (varying) functions of time.

What kind of a function would be needed for describing a periodic / oscillatory motion? It is clear that we would now need a ‘function (of time)’ that acquires the same value (again and again) when time changes by an amount that is equal to, or is an integral multiple of, the ’time period’ of the periodic / oscillatory motion under consideration. All such functions, that repeat their values after regular intervals of time, are known as ‘periodic functions’ (of time). We thus need ‘periodic functions’ to have a mathematical description of periodic / oscillatory motions.

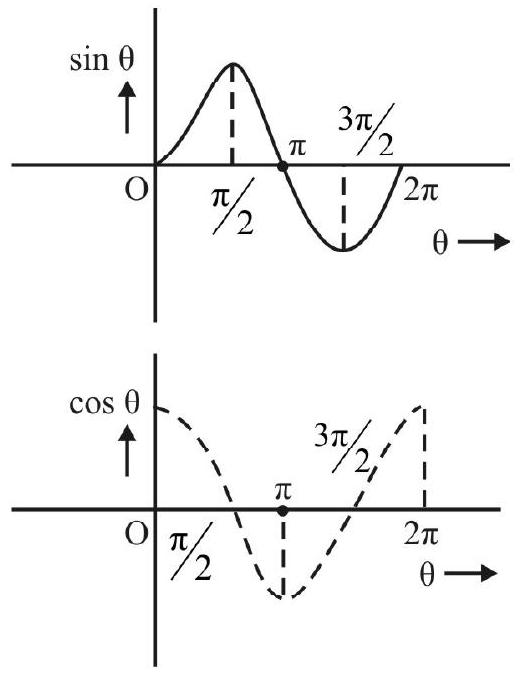
All trigonometric functions, and, in particular, the ‘SINE’ and the ‘COSINE’ functions, are periodic functions of time. The graphs of $\sin \theta$ and $\cos \theta$, against $\theta$, shown here, illustrate their periodic nature. It is clear, therefore, that the ‘sine’ and ‘cosine’ functions play a vital role in describing ‘periodic / oscillatory’ motions.

Period and Frequency of a Periodic Motion

The (constant) time, taken by a particle to complete a cycle of its motion (i.e., to comeback to the same ‘state of motion’), is known as the ’time period’ (or just the ‘period’) of that periodic motion. It is usually denoted by the symbol $\mathrm{T}$.

The number of complete cycles of its motion, completed by a particle executing a periodic motion, in a unit time, is known as the frequency of its periodic motion. It is usually denoted by the symbol n, or by the greek alphabet, $v$.

The unit of frequency would clearly by s ${ }^{-1}$. This unit has been given a name: hertz (Hz); in honour of Heinrich Hertz.

It is easy to surmise that the frequency $(\mathrm{n})$ and the time period $(\mathrm{T})$, of a given periodic motion, are related to each other as

$$ \mathrm{n}=\left(\frac{1}{\mathrm{~T}}\right) \quad \text { or } \quad \mathrm{T}=\left(\frac{1}{\mathrm{n}}\right) $$

Another useful term, often used for periodic / oscillatory motions, is the ‘angular frequency’. It is denoted by the greek alphabet, $\omega$, and is related to the frequency $(v)$, through the relation:

$$ \omega=2 \pi \nu \quad \text { or } \quad v=\left(\frac{\omega}{2 \pi}\right) $$

In terms of $\omega$, we would then have

$$ \mathrm{T}=\left(\frac{2 \pi}{\omega}\right) $$

We use the unit $\left(\mathrm{s}^{-1}\right)$ for angular frequency. The use of its equivalent unit $[\mathrm{hertz}(\mathrm{Hz})]$ is usually restricted only to ‘frequency’. For angular frequency, the unit used is $\mathrm{s}^{-1}$, or its extended form, $(\mathrm{rad} / \mathrm{s})$.

‘Displacement-Time’ Relation for a ‘Periodic Motion’

As per its definition, the displacement, of a particle, executive a periodic motion, must repeat its value, again and again, after the same regular interval of time. This may be expressed mathematically as:

$$ y(t+T)=y(t) $$

It implies that the value of the displacement, say $y$, at time instants ’ $t$ ’ and $(t+T)$, is the same. The displacement thus repeats its value after a regular time interval, $\mathrm{T}$, the ’time period’ of that ‘periodic motion’.

The above mathematical relation can correspond to very many forms of the ‘displacement-time’ graph for a periodic motion. The graphs, shown below, are some of the possible forms of the ‘displacement-time’ graphs for a periodic motion.

For all these graphs, we have

$$ \mathrm{y}\left(\mathrm{t}^{\prime}\right)=\mathrm{y}(\mathrm{t}+\mathrm{T})=\mathrm{y}(\mathrm{t}) $$

An Interesting Result

A close look, at the ‘displacement-time’ graphs, shown above, reveals that while the first two of them correspond to the ‘sine’ and ‘cosine’ functions, respectively, the other two do not correspond to any simple trigonometric function. All these graphs, however, correspond to ‘periodic motions’, because, for all of them,

$$ y(t+T)=y(t) $$

A mathematician, by the name Fourier, gave us a very useful and interesting result, known as the ‘Fourier Theorem’. In simple terms, this theorem tells us that any periodic variation (irrespective of the shape of its graph) can be ’equated’ to the superposition of a sufficient number of ‘sinusoidal (sine or cosine) variations’. Thus all periodic functions can be ‘regarded’ as the ‘sum’ of a ‘sufficient, and suitable, number’ of ‘appropriate sinusoidal functions’.

It follows then that, in principle, we can understand the ‘details’ of any ‘periodic motion’ simply through our understanding of the details of the sinusoidal ‘periodic motions’. We can, therefore, think of ‘sinusoidal periodic motions’ as the ‘basis’ of all ‘periodic motions’. A clear understanding and analysis, of the ‘details and features’, of sinusoidal periodic motions, may be ‘viewed’ as (quite) sufficient for ‘understanding’ any general periodic motion.

Restoring Force

Suppose a particle, initially present at its mean, or central position (say O), is to execute oscillatory motion. It may be displaced to the right, say, by giving it a ‘push’. It would, in terms of the ’law of inertia’ (Newton’s first law of motion) then go on moving to the right, unless compelled, by some external force, to change its ‘state of motion’. It follows that if it has to execute ‘oscillatory motion’, it needs to be ‘brought back’ towards O. For this an external force, directed to the left (i.e., opposite to the direction along which it was displaced), must act on it. This ’external force’ is known as a ‘restoring force’ as it is ’trying’ to ‘restore’ the particle back to its initial equilibrium position.

We must also note that after the particle starts moving left (under the action of the restoring force), it would not, straightaway, stop at $\mathrm{O}$, because of inertia. It would ‘overshoot’ point $\mathrm{O}$ and move farther to the left. The ‘restoring force’, must now change its direction and start acting to the ‘right. This implies that the particle can execute oscillations only if the external (restoring) force, acting on it, at any instant, is directed opposite to its ‘instantaneous displacement’.

We can note another feature of the external (restoring) force. The magnitude of this external (restoring) force, acting on an oscillating particle, has to be a function of the instantaneous displacement (from the equilibrium position, $(\mathrm{O})$ of the oscillating particle. Thus, at any instant,

$$ \mathrm{F} _{x}=-\mathrm{f}(x) $$

Hence $\mathrm{F} _{x}$ is the (restoring) force, acting on the oscillating particle, when its displacement is $x$. The term $\mathrm{f}(x)$ represents a (general) function of $x$. The negative sign is there because the directions, of the instantaneous (restoring) force, and displacement, are opposite to each other.

The simplest form, of the function $\mathrm{f}(x)$, is that of ‘direct proportionality’. Thus, in its simplest form,

$$ \mathrm{f}(x)=\mathrm{k} x $$

The (restoring) force, corresponding to this form of the function $\mathrm{f}(x)$, is

$$ \mathrm{F} _{x}=-\mathrm{k} x $$

It follows that we can think of a particle as executing the ‘simplest form of oscillatory motion’ if the (restoring) force, acting on it, at any instant is directly proportional to its instantaneous displacement (from its mean, or equilibrium, position). This simplest form, of oscillatory motion, has been given the name ‘simple harmonic motion’ (SHM).

Simple Harmonic Motion

Simple harmonic motion (SHM) is the simplest form of oscillatory motion. A particle is said to execute a SHM when it oscillates under the action of a (restoring) force that is always directed opposite to its instantaneous displacement (from its mean position) and whose instantaneous magnitude varies in direct proportion to the magnitude of its instantaneous displacement.

In mathematical terms, it implies that

$$ \mathrm{F} _{x}=-\mathrm{k} x $$

Now, $\mathrm{F} _{x}=\mathrm{Ma} _{x}$, where $\mathrm{M}$ is the mass of the oscillating particle and $\mathrm{a} _{x}$ is the magnitude of its instantaneous acceleration when its displacement is $x$.

$\therefore$ For a particle executing SHM, we have

$\therefore \mathrm{Ma} _{x}=-\mathrm{k} x$

or $\quad \mathrm{a} _{x}=-\frac{\mathrm{k}}{\mathrm{M}} x=-\omega^{2} x$

$$ \left(\omega^{2}=\frac{k}{M}\right) $$

We may, therefore, also say;

“An oscillating particle is said to execute a S.H.M if its acceleration is always directed towards its mean (or central) position and the instantaneous magnitude, of this acceleration, varies in direct proportion to the magnitude of the instantaneous displacement of the particle (from its mean (or central) position).

We know that

$$ \mathrm{a} _{x}=\frac{\mathrm{dv} _{x}}{\mathrm{dt}}=\frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}} $$

$\therefore$ For a particle in SHM, we have

$$ \begin{gathered} \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-\omega^{2} x \\ \text { or } \quad \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}+\omega^{2} x=0 \end{gathered} $$

We speak of this equation as the ‘differential equation’ for a simple harmonic motion.

Example-1:

Two simple harmonic motions are represented by $x=\mathrm{a} \sin \left(\omega \mathrm{t}+\frac{\pi}{4}\right)$ and $x=\mathrm{b} \sin \left(\omega \mathrm{t}+\frac{\pi}{3}\right)$, respectively. Their corresponding differential equations will be

(1) $\frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}+\left(\omega+\frac{\pi}{4}\right)^{2} x=0$ and $\frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}+\left(\omega+\frac{\pi}{3}\right)^{2} x=0$

(2) $\frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}-\left(\omega+\frac{\pi}{4}\right)^{2} x=0$ and $\frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}+\left(\omega+\frac{\pi}{3}\right)^{2} x=0$

(3) $\frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}+\left(\omega+\frac{\pi}{4}\right)^{2} x=0$ and $\frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}-\left(\omega+\frac{\pi}{3}\right)^{2} x=0$

(4) $\frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}+\omega^{2} x=0$ and $\frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}+\omega^{2} x=0$

Show Answer

Solution:

For the first equation, we have

$$ \frac{\mathrm{d} x}{\mathrm{dt}}=\mathrm{a} \omega \cos \left(\omega \mathrm{t}+\frac{\pi}{4}\right) $$

and $\quad \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-\mathrm{a} \omega^{2} \sin \left(\omega \mathrm{t}+\frac{\pi}{4}\right)=-\omega^{2} x$

$$ \therefore \quad \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}+\omega^{2} x=0 $$

For the second equation, we have

$$ \frac{\mathrm{d} x}{\mathrm{dt}}=-\mathrm{b} \omega \sin \left(\omega \mathrm{t}+\frac{\pi}{3}\right) $$

and $\quad \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-\mathrm{b} \omega^{2} \cos \left(\omega \mathrm{t}+\frac{\pi}{3}\right)=\omega^{2} x$

$\therefore \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}+\omega^{2} x=0$

Thus the differential equation, for both the SHM’s, is the same, namely

$$ \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}+\omega^{2} x=0 $$

Solution of the (Differential) Equation for a SHM

We may solve the above differential equation for the SHM of a particle. Let us assume that the particle, executing SHM is oscillating, (about its mean position, $O$ ) between the points A and B; then $|\mathrm{OA}|=|\mathrm{OB}|$ $=\mathrm{a}$, is known as the ‘amplitude’ of the SHM.

The differential equation, for a SHM, can be written as

$$ \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-\omega^{2} x $$

or $\quad\left(\frac{d v}{d t}\right)=-\omega^{2} x$

where $\mathrm{v}=\frac{\mathrm{d} x}{\mathrm{dt}}$, is the instantaneous velocity of the particle.

Now, $\frac{\mathrm{dv}}{\mathrm{dt}}=\frac{\mathrm{dv}}{\mathrm{d} x} \cdot \frac{\mathrm{d} x}{\mathrm{dt}}=\mathrm{v} \frac{\mathrm{dv}}{\mathrm{d} x}$

$\therefore \quad \mathrm{v} \frac{\mathrm{dv}}{\mathrm{dx}}=-\omega^{2} x$

or $\quad \int \mathrm{v} d \mathrm{v}=-\int \omega^{2} x \mathrm{~d} x$

or $\quad \frac{\mathrm{v}^{2}}{2}=-\omega^{2} \frac{x^{2}}{2}+$ constant

The value of the constant can be found by remembering that the instantaneous velocity, of the particle, becomes zero when it is at either of its extreme positions (A or B). Thus

$$ \mathrm{v}=0 \text { when } x=+\mathrm{a} $$

We, therefore, get

$0=-\frac{\omega^{2} \mathrm{a}^{2}}{2}+$ constant

$\therefore$ constant $=-\frac{\omega^{2} \mathrm{a}^{2}}{2}$

We this have

$\frac{\mathrm{v}^{2}}{2}=\frac{\omega^{2}}{2}\left(\mathrm{a}^{2}-x^{2}\right)$

$\therefore \quad \mathrm{v}=\left(\frac{\mathrm{d} x}{\mathrm{dt}}\right)=\omega \sqrt{\mathrm{a}^{2}-x^{2}}$

$\therefore \int \frac{\mathrm{d} x}{\sqrt{\mathrm{a}^{2}-x^{2}}}=\omega \int \mathrm{dt}$

or

$$ \sin ^{-1} \frac{x}{a}=\omega t+\phi $$

where $\phi$ is a constant of integration.

$\therefore \quad x=\mathrm{a} \sin (\omega \mathrm{t}+\phi)$

The instantaneous displacement, of a particle, executing a SHM, is thus a sinusoidal function of time.

The form of this sinusoidal function depends on the choice of the ‘zero’ of time. If, at $t=0$ (i.e., at the start), the particle is at its mean position, we have $x=0$ at $\mathrm{t}=0$.

$\therefore$ In this case,

$$ 0=a \sin (0+\phi)=a \sin \phi $$

This implies that $\phi=0$. Thus if the ‘zero’ of time is chosen to be the (time) instant at which the particle is in its mean position, the instantaneous displacement, $x$, of the particle, is a SINE function of time:

$$ x=\mathrm{a} \sin \omega \mathrm{t} $$

If, however, the ‘zero’ of the time is taken to be the instant at which the particle is at its extreme position (i.e. $x= \pm \mathrm{a}$ at $\mathrm{t}=0$ ), we have

$$ \pm \mathrm{a}=\mathrm{a} \sin \phi $$

$\therefore \sin \phi= \pm 1 \quad$ or $\quad \phi= \pm \frac{\pi}{2}$

Thus, in this case,

$$ \begin{array}{r} x=\mathrm{a} \sin \left(\omega \mathrm{t} \pm \frac{\pi}{2}\right) \\ = \pm \mathrm{a} \cos \omega \mathrm{t} \end{array} $$

Thus, if the ‘zero’ of time is taken to be instant at which the particle is at either of the extreme positions, its instantaneous displacement is a COSINE function of time.

When the ‘zero’ of time is taken as the instant at which the particle is somewhere in between its mean and (either) extreme position, the instantaneous displacement will be described by the sinusoidal function.

$$ x=\mathrm{a} \sin (\omega \mathrm{t}+\phi) $$

The value of $\phi$ will be determined by the value of $x(0<|x|<a)$ at $t=0$.

Relation between Circular Motion and ‘Simple Harmonic Motion’

Consider a particle moving along a circular path with a uniform angular speed $\omega$. Let the particle be at the position, say $\mathrm{P}$, at $\mathrm{t}=0$. Let $<\mathrm{POP}^{\prime}$, (where $\mathrm{P} _{0}^{\prime} \mathrm{OP} _{0}$ is a horizontal diameter of the circle) be $\phi$. If the particle moves to a position $\mathrm{P}^{\prime}$, at a time $\mathrm{t},\left\langle\mathrm{P}^{\prime} \mathrm{OP}=\theta=\omega \mathrm{t}\right.$.

Drop a perpendicular from $\mathrm{P}^{\prime}$, on to the vertical diameter, $\mathrm{CD}$, of the circle. The foot of this perpendicular, is at a (vertical) distance $O Q$ from the centre of the circle. We then have, (from the right angled triangle $O P ’ Q$ ).

$$ \frac{\mathrm{OQ}}{\mathrm{QP}^{\prime}}=\cos \left(\frac{\pi}{2}-(\theta+\phi)\right) $$

$$ =\sin (\theta+\phi)=\sin (\omega t+\phi) $$

$\therefore \mathrm{OQ}=\mathrm{OP}^{\prime} \sin (\omega \mathrm{t}+\phi)=\mathrm{a} \sin (\omega \mathrm{t}+\phi)$

where $\mathrm{a}=\mathrm{OP}^{\prime}=$ radius of the circle.

The distance OQ is thus seen to be a sinusoidal function of time. This, as we have seen above, is also the nature of variation (with time) of a particle executing a simple harmonic motion. It follows that we can think of the point $\mathrm{Q}$ (the foot of the perpendicular, on to the (vertical) diameter DC of the circle) as executing a SHM about the centre, $O$, of the circle.

We can, therefore, say that:

“A simple harmonic motion can be regarded as the ‘projection’ of a uniform circular motion on to a diameter of the circle”.

It is seen, from above, that

(i) If te particle $\mathrm{P}$ were at the position $\mathrm{P} _{0}$ at $\mathrm{t}=0$, we would have $\phi=0$ and

$$ \mathrm{OQ}=\mathrm{a} \sin \omega \mathrm{t} $$

(ii) If the particle were at the position $\mathrm{C}(/ \mathrm{D})$ at $\mathrm{t}=0$, we would have $\phi=\frac{\pi}{2}\left(/\left(-\frac{\pi}{2}\right)\right)$

$$ \begin{gathered} \text { and } \mathrm{OQ}=\mathrm{a} \sin \left(\omega \mathrm{t} \pm \frac{\pi}{2}\right) \\ = \pm \mathrm{a} \cos \omega \mathrm{t} \end{gathered} $$

These results are in agreement with the (similar) results obtained above through the solution of the differential equation for a simple harmonic motion. We thus have the very useful result:

“A simple harmonic motion (oscillation), can be regarded as the’projection’, of a uniform circular motion on to a diameter of the circle”.

This ’equivalence’, between a SHM and a circular motion, helps us to ‘arrive at’ and ‘understand’, many results for SHM through our understanding, of the corresponding results, for a uniform circular motion. The circular path, associated with a given SHM, is known as its ‘circle of reference’. We can say that

(i) The centre, $\mathrm{O}$, of the circle, corresponds to the mean (or central) position of the particle executing SHM.

(ii) The radius, a, of the circle, equals the ‘amplitude’ of the particle executing SHM. (iii) For a given SHM, the circle (associated with it) is known as its ‘reference circle’.

(iv) The particle $(\mathrm{P})$, moving along the circle, is often referred to as the ‘generating point’.

The (above mentioned) equivalence, between a SHM and a circular motion, is valid irrespective of the diameter chosen for ‘receiving’ the ‘projected’ point.

“A SHM is thus nothing but the projection of a uniform circular motion on to a diameter of the circle”.

‘Phase’ of a Particle Executing a SHM

The displacement (from the mean / central position) of a particle, executing a SHM, is expressed as:

$$ x=\mathrm{a} \sin (\omega \mathrm{t}+\phi) $$

The instantaneous displacement, of the particle, also helps us to find its instantaneous velocity and its instantaneous acceleration. It is worth noting here that it is the instantaneous value of the quantity $(\omega \mathrm{t}+\phi)$, (the argument of the sine function in the expression for displacement), that enables us to find all these quantities, related to the instantaneous ‘state of motion’ of the particle. We call the term $(\omega t+\phi)$ as the (instantaneous) phase of the particle executing SHM.

Thus the ‘phase’, of the oscillating particle, at any instant (any position), is a ’term’ / ‘quantity’ that determines the parameters (displacement, velocity, acceleration) that define / determine the instantaneous ‘state of motion’ of the particle.

Thus, for a particle, executing a SHM,

Phase, at an instant, $\mathrm{t},=\delta=(\omega \mathrm{t}+\phi)$

It follows that the ‘phase difference’, for two time instants, $t$, and $(t+\Delta t)$, is

$$ \begin{gathered} \Delta \delta=[\omega(\mathrm{t}+\Delta \mathrm{t})+\phi]-[\omega \mathrm{t}+\phi] \\ =\omega \Delta \mathrm{t} \\ =\frac{2 \pi}{\mathrm{T}}(\Delta \mathrm{t}) \end{gathered} $$

where $\mathrm{T}$ is the ’time period’ of the oscillating particle. It follows that if $\Delta \mathrm{t}=\mathrm{nT}$, we would have

$$ \Delta \delta=\mathrm{n} .2 \pi $$

The value of $\sin (2 n \pi+\theta)$ (as well as other trigonometric functions) being the same as that of $\sin \theta$, it follows that the particle would be back in the same ‘state of motion’, after time intervals that are an integral

multiple of its ’time period’. In terms of ‘phase’, we express this by saying that at time intervals, that are nT apart, the partile is in the ‘same phase’. Thus a phase difference

$$ \Delta \delta=2 \pi \mathrm{n} \quad(\mathrm{n}=0,1,2,3, \ldots \ldots \ldots) $$

implies the same, or identical, ‘phase states’ of the particles.

Again, since

$$ [\sin (2 \mathrm{n}+1) \pi+\theta]=-\sin \theta \quad(\mathrm{n}=0,1,2,3, \ldots \ldots \ldots) $$

The particle would be having ’equal in magnitude but opposite in direction’ displacement at time intervals that are half integral multiples of its time period. We express this by saying that at time intervals, that are $\frac{(2 n+1) \mathrm{T}}{2}$ apart, the particle is in ‘opposite in phase’ states of its motion.

Thus a phase difference

$$ \Delta \delta=(2 \mathrm{n}+1) \pi \quad(\mathrm{n}=0,1,2,3, \ldots \ldots \ldots) $$

implies the ‘opposite in phase’ states of motion of the particle.

‘Epoch’

Another simple point, about the ‘phase term’ is worth noting. The phase term

$$ \delta=(\omega \mathrm{t}+\phi) $$

has the value $\delta _{0}=\phi$, at $\mathrm{t}=0$. The term, $\phi$, thus represents the value of the phase at the start of the motion of the oscillating particle. We call this initial value of the phase (i.e. phase at $t=0$ ) as the ’epoch’ of the oscillating particle.

It is conventional, and convenient, to (usually) take $\phi=0$ for an oscillating particle. However, when the oscillations of two, or more, oscillating particles are to be described by taking a common instant as $t=0$, (for all of them), the value of the epoch may be ‘zero’ for one of them but may, or may not, be zero for the others.

Example-2:

A simple harmonic motion is described by the equation

$$ x=\mathrm{a} \sin \left(\omega \mathrm{t}+\frac{\pi}{4}\right) $$

The phase difference, between two positions of the particle, at $x=\frac{\mathrm{a}}{3}$ and $x=\frac{\mathrm{a}}{2}$ is

(1) $\left[\frac{\pi}{6}-\sin ^{-1} \frac{1}{3}\right]$

(2) $\left[\frac{5 \pi}{12}-\sin ^{-1} \frac{1}{3}\right]$

(3) $\left[\frac{\pi}{6}+\sin ^{-1} \frac{1}{3}\right]$

(4) $\left[\frac{5 \pi}{12}+\sin ^{-1} \frac{1}{3}\right]$

Show Answer

Solution:

The phase equals $\left(\omega \mathrm{t}+\frac{\pi}{4}\right)$

For $x=\frac{\mathrm{a}}{3}$, we have

$$ \begin{gathered} \frac{\mathrm{a}}{3}=\mathrm{a} \sin \left(\omega \mathrm{t} _{1}+\frac{\pi}{4}\right) \\ \therefore \quad\left(\omega \mathrm{t} _{1}+\frac{\pi}{4}\right)=\phi _{1}-\sin ^{-1}\left(\frac{1}{3}\right) \end{gathered} $$

For $x=\frac{\mathrm{a}}{2}$, we have

$$ \begin{gathered} \frac{\mathrm{a}}{2}=\mathrm{a} \sin \left(\omega \mathrm{t} _{2}+\frac{\pi}{4}\right) \\ \therefore \quad \sin \left(\omega \mathrm{t} _{2}+\frac{\pi}{4}\right)=\frac{1}{2}=\sin \frac{\pi}{6} \\ \therefore \quad\left(\omega \mathrm{t} _{2}+\frac{\pi}{4}\right)=\phi _{2}=\left(\frac{\pi}{6}\right) \end{gathered} $$

$\therefore$ Phase difference $=\phi _{2}-\phi _{1}$

$$ =\left[\frac{\pi}{6}-\sin ^{-1} \frac{1}{3}\right] $$

Example-3:

A particle is executing a SHM described by

$$ x-a \sin \left(\omega t+\frac{\pi}{6}\right) $$

The phase difference, between two positions of the particle, at $t=\frac{T}{3}$ and $t=\frac{T}{2}(T=$ time period of the SHM), is

(1) $\frac{2 \pi}{3}$

(2) $\frac{\pi}{3}$

(3) $\frac{\pi}{6}$

(4) $\frac{\pi}{2}$

Show Answer

Solution:

The phase of the particle equals $\left(\omega t+\frac{\pi}{6}\right)$

At $\mathrm{t}=\frac{\mathrm{T}}{3}$, phase $=\phi _{1}=\omega \frac{\mathrm{T}}{3}+\frac{\pi}{6}$

$$ =\left(\frac{2 \pi}{T} \cdot \frac{T}{3}+\frac{\pi}{6}\right)=\frac{5 \pi}{6} $$

At $\mathrm{t}=\frac{\mathrm{T}}{2}$, phase $=\phi _{2}=\left(\omega \frac{\mathrm{T}}{2}+\frac{\pi}{6}\right)$

$$ =\left(\frac{(2 \pi)}{\mathrm{T}} \cdot \frac{\mathrm{T}}{3}+\frac{\pi}{6}\right)=\frac{7 \pi}{6} $$

$\therefore$ Phase difference $=\phi _{2}-\phi _{1}=\left(\frac{7 \pi}{6}-\frac{5 \pi}{6}\right)=\frac{2 \pi}{6}=\frac{\pi}{3}$

‘Velocity’ and ‘Acceleration’ for a Particle Executing SHM

We have already learnt that the instantaneous displacement, $x$, of a particle, executing a SHM, is given by

$$ x=\mathrm{a} \sin (\omega \mathrm{t}+\phi) $$

The displacement is thus described by sinusoidal function whose maximum value (i.e., displacement amplitude) equals a and whose phase term, $\delta _{x}$, has a value $(\omega \mathrm{t}+\phi)$.

The instantaneous velocity, v, equals $\frac{\mathrm{d} x}{\mathrm{dt}}$.

Hence, $v=\frac{d}{d t}[a \sin (\omega t+\phi)]$

$$ \begin{aligned} & =\mathrm{a} \omega \cos (\omega \mathrm{t}+\phi) \\ & =\mathrm{a} \omega \sin \left(\omega \mathrm{t}+\phi+\frac{\pi}{2}\right) \quad\left[\because \sin \left(\frac{\pi}{2}+\theta\right)=\cos \theta\right] \end{aligned} $$

We notice that the velocity has a maximum value (which may be referred to as “velocity amplitude”) equal to a $\omega$. Also the argument of the sine term, which may be called the phase term, $\delta _{v}$, for velocity, has a value $\left[(\omega t+\phi)+\frac{\pi}{2}\right]$. Thus

$$ \delta _{\mathrm{v}}=\left[(\omega \mathrm{t}+\phi)+\frac{\pi}{2}\right] $$

The ‘phase difference’, between the phase terms for velocity and displacement, i.e.

$$ \delta _{v x}=\delta _{\mathrm{v}}-\delta _{x}=\left(\omega \mathrm{t}+\phi+\frac{\pi}{2}\right)-(\omega \mathrm{t}+\phi)=\frac{\pi}{2} $$

The velocity is thus seen to ’lead’ the displacement in phase value, by $\left(\frac{\pi}{2}\right)$.

Again the instantaneous acceleration, say, $f$, equals $\frac{\mathrm{dv}}{\mathrm{dt}}$. Hence

$$ \begin{aligned} \mathrm{f}=\frac{\mathrm{dv}}{\mathrm{dt}} & =\frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=\frac{\mathrm{d}}{\mathrm{dt}}(\mathrm{a} \omega \cos (\omega \mathrm{t}+\phi)) \\ & =\mathrm{a} \omega(-\omega \sin (\omega \mathrm{t}+\phi)) \\ & =-\mathrm{a} \omega^{2} \sin (\omega \mathrm{t}+\phi) \\ & =\mathrm{a} \omega^{2} \sin [(\omega \mathrm{t}+\phi)+\pi] \end{aligned} $$

The instantaneous acceleration, for the particle, leads its instantaneous displacement, in phase value, by $\pi$.

These ‘relations’ lead us to result the particle has its maximum velocity $(=a \omega)$ at the instant when its displacement is zero, i.e., at the ‘mean position’. Also the velocity has its minimum magnitude (= zero) when its displacement has its maximum magnitude ( $=\mathrm{a}=$ displacement amplitude), i.e., at the two extreme positions.

The acceleration, however, (being directly proportional to displacement magnitude) has its maximum and minimum magnitudes at the same instant at which the displacement has such magnitudes; its direction, however, is always opposite to that of the displacement.

These features of the instantaneous displacement, velocity and acceleration, for a particle, executing a SHM, are shown through the graphs (i), (ii) and (iii) showing the dependence of these quantities on time. It is important to note here that these graphs have been drawn for a particle for which the ’epoch’ (i.e., the phase value, at the start, i.e., at $\mathrm{t}=0$ ) equals ‘zero’.

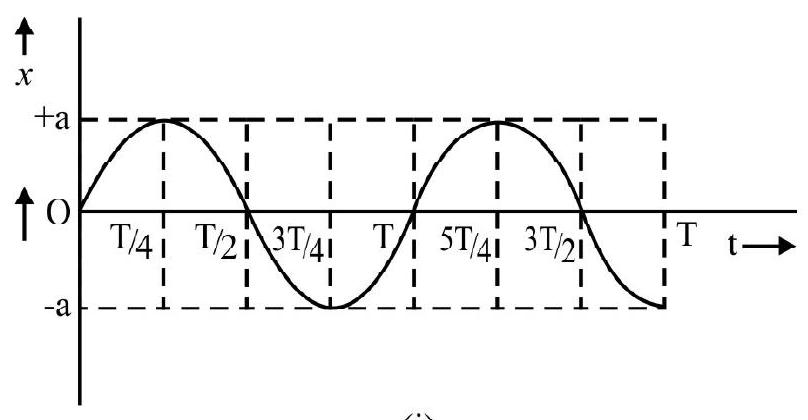
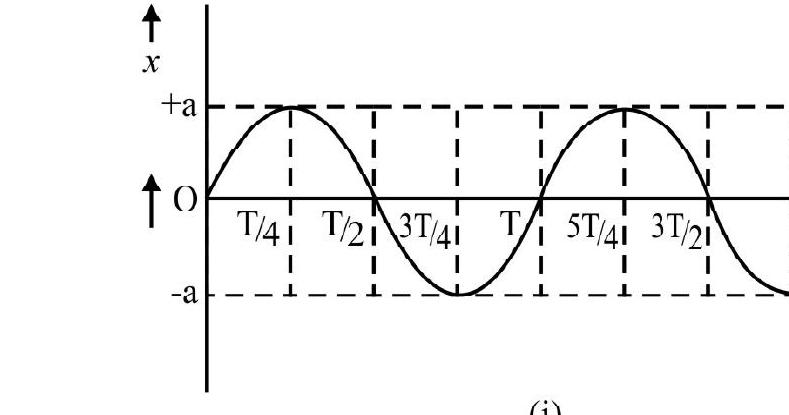
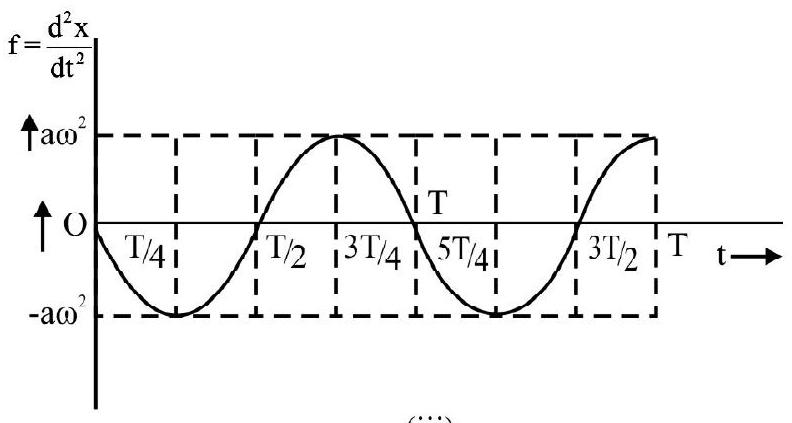(i)

(ii)

(iii)

Velocity and Acceleration, as a Function of Displacement (for a particle, Executing a SHM):

The instantaneous displacement, for a particle, executing a SHM, is given by

$$ x=\mathrm{a} \sin (\omega \mathrm{t}+\phi) $$

Its instantaneous velocity, v, given by

$$ \mathrm{v}=\frac{\mathrm{d} x}{\mathrm{dt}}=\mathrm{a} \omega \cos (\omega \mathrm{t}+\phi) $$

can also be rewritten as

$$ \mathrm{v}=\mathrm{a} \omega\left[1-\sin ^{2}(\omega \mathrm{t}+\phi)\right]^{1 / 2}=\mathrm{a} \omega\left[1-\left(\frac{x}{\mathrm{a}}\right)^{2}\right]^{1 / 2}=\omega \sqrt{\mathrm{a}^{2}-x^{2}} $$

We thus get an expression showing, explicit, the dependence of ‘velocity’ on ‘displacement’ (for a particle executing a SHM). This expression again shows that the velocity of the particle has its maximum value $(=\mathrm{a} \omega)$ at $x=0$ (i.e., at the mean position) and its minimum value $(=0)$ at $x= \pm \mathrm{a}$ (i.e., at either of the two extreme positions).

Again, the acceleration

$$ \begin{aligned} \mathrm{f}\left(=\frac{\mathrm{dv}}{\mathrm{dt}}\right. & \left.=\frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}\right)=-\mathrm{a} \omega^{2} \sin (\omega \mathrm{t}+\phi) \\ & =\mathrm{a} \omega^{2} \cdot \frac{x}{\mathrm{a}}=-\omega^{2} x \end{aligned} $$

The acceleration is thus seen to be a ‘direct proportionality’ function of displacement. The negative sign, in the above expression, is as per the basic ‘definition’ of SHM; (the instantaneous direction of the ‘acceleration’ is opposite to that of the instantaneous ‘displacement’).

The Kinetic, Potential and ‘Total’, Energy of a Particle, in SHM

We have seen above that, for a particle, in SHM, its instantaneous velocity, is given by

$$ v=\mathrm{a} \omega \cos (\omega \mathrm{t}+\phi) \quad \text { or } \quad v=\omega \sqrt{\mathrm{a}^{2}-x^{2}} $$

The instantaneous kinetic energy ( $=\mathrm{K})$, of the particle, is, therefore, given by

$$ \mathrm{K}=\frac{1}{2} \mathrm{mv}^{2}=\frac{1}{2} \mathrm{ma}^{2} \omega^{2} \cos ^{2}(\omega \mathrm{t}+\phi) $$

or $\quad \mathrm{K}=\frac{1}{2} \mathrm{mv}^{2}=\frac{1}{2} \mathrm{~m} \omega^{2}\left(\mathrm{a}^{2}-x^{2}\right)$

To find the expression for the instantaneous potential energy $(=\mathrm{U})$, we notice that the instantaneous restoring force, $\mathrm{F} _{x}$, has a magnitude, given by

$$ \mathrm{F} _{x}=\mathrm{m}\left|\mathrm{f} _{x}\right|=\mathrm{m} \omega^{2} x $$

The infinitesimal work done, in changing the displacement from $x$ to $(x+\mathrm{d} x)$, is given by

$$ \mathrm{dW}=\left(\mathrm{F} _{x}\right) \mathrm{d} x=\mathrm{m} \omega^{2} x \mathrm{~d} x $$

The total work done, in displacing the particle, from $x=0$ to $x=x$, is

$$ \mathrm{W}=\int _{0}^{x} \mathrm{dW}=\frac{1}{2} \mathrm{~m} \omega^{2} x^{2} $$

It is this work that equals the instantaneous potential energy of the particle. Thus

$$ \begin{aligned} & \mathrm{U}=\frac{1}{2} \mathrm{~m} \omega^{2} x^{2} \\ & =\frac{1}{2} \mathrm{~m} \omega^{2}(\mathrm{a} \sin (\omega \mathrm{t}+\phi))^{2} \\ & =\frac{1}{2} \mathrm{ma}^{2} \omega^{2} \sin ^{2}(\omega \mathrm{t}+\phi) \end{aligned} $$

The total energy, E, of the particle, at any instant, is

$$ \mathrm{E}=\mathrm{K}+\mathrm{U} $$

We thus see that

$$ \begin{aligned} & E=\frac{1}{2} m \omega^{2} a^{2} \cos ^{2}(\omega t+\phi)+\frac{1}{2} m \omega^{2} a^{2} \sin ^{2}(\omega t+\phi) \\ & =\frac{1}{2} m \omega^{2} a^{2} \end{aligned} $$

Alternatively;

$$ \begin{aligned} & \mathrm{E}=\frac{1}{2} \mathrm{~m} \omega^{2}\left(\mathrm{a}^{2}-x^{2}\right)+\frac{1}{2} \mathrm{~m} \omega^{2} x^{2} \\ & =\frac{1}{2} \mathrm{~m} \omega^{2} \mathrm{a}^{2} \end{aligned} $$

The total energy, of the particle, is thus seen to have a constant value $\left(=\frac{1}{2} \mathrm{~m} \omega^{2} \mathrm{a}^{2}\right)$, at all instants. It is proportional to the

(i) square of the displacement amplitude (=a), of the oscillating particle.

(ii) square of the constant, $\omega$, for the oscillating particle.

Since $\omega=\frac{2 \pi}{T}=2 \pi \nu$ we can also say that the total energy, of a particle, executing a SHM, is directly proportional to the square of its frequency, or inversely proportional to the square of the time period of its oscillations.

The graphs, showing the dependence of $\mathrm{K}, \mathrm{U}$ and $\mathrm{E}$, on time, $\mathrm{t}$, (when $\phi=$ epoch = zero) have the forms shown below.

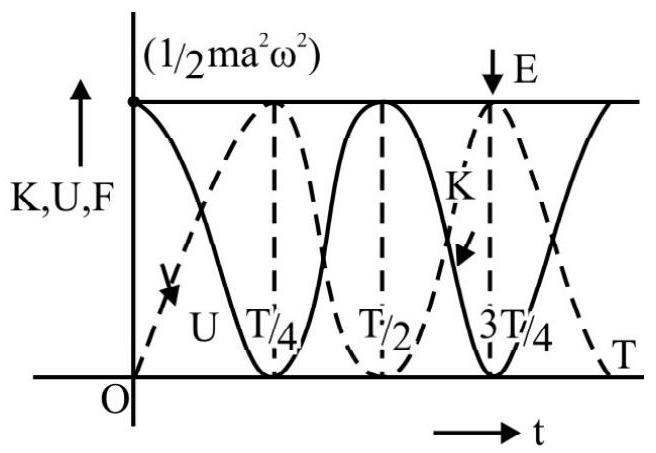
Another simple fact (about the energy of the particle executing a SHM) is worth noting. The average kinetic energy $(\overline{\mathrm{K}})$ and the average potential energy $(\overline{\mathrm{U}})$, of the particle, (over one complete oscillation) are each equal to $\frac{1}{2}\left(\frac{1}{2} \mathrm{ma}^{2} \omega^{2}\right)=\frac{1}{4} \mathrm{ma}^{2} \omega^{2}$.

(This is because the average values, of both $\sin ^{2}(\omega t+\phi)$, as well as $\cos ^{2}(\omega t+\phi)$, over one complete cycle, are equal to $\frac{1}{2}$ each).

The total energy, of the particle, executing a SHM, is thus, on the average, half kinetic and half potential, in form.

Example-4:

A particle, of mass $\mathrm{m}$, is executing a SHM of amplitude A and angular frequency, $\omega$. The ratio of the kinetic energy values and the potential energy values, of the particle, at (i) $x=\frac{\mathrm{A}}{\sqrt{2}}$ and (ii) $x=\frac{\mathrm{A}}{\sqrt{3}}$ equal, respectively,

(1) (i) $(1: 1)$; (ii) $(2: 1)$

(2) (i) $(2: 1)$; (ii) $(1: 1)$

(3) (i) $(2: 1)$; (ii) $(3: 1)$

(4) (i) $(3: 1) ;$ (ii) $2: 1$

Show Answer

Solution:

The K.E and P.E values are given by

$\mathrm{K} . \mathrm{E}=\frac{1}{2} \mathrm{~m} \omega^{2}\left(\mathrm{~A}^{2}-x^{2}\right)$

P.E $=\frac{1}{2} \mathrm{~m} \omega^{2} x^{2}$

(i) Hence at $x=\frac{\mathrm{A}}{\sqrt{2}}$, we have

$$ \begin{aligned} & \mathrm{K} . \mathrm{E}=\frac{1}{2} \mathrm{~m} \omega^{2}\left(\mathrm{~A}^{2}-\frac{\mathrm{A}^{2}}{2}\right)=\frac{1}{2} \mathrm{~m} \omega^{2} \cdot \frac{1}{2} \mathrm{~A}^{2} \\ & \text { P.E }=\frac{1}{2} \mathrm{~m} \omega^{2} \frac{\mathrm{A}^{2}}{2} \end{aligned} $$

Ratio of $\frac{\text { K.E }}{\text { P.E }}=1: 1$ (ii) At $x=\mathrm{A} / \sqrt{3}$, we have

$$ \begin{aligned} & \text { K.E }=\frac{1}{2} m \omega^{2}\left(\mathrm{~A}^{2}-\frac{\mathrm{A}^{2}}{3}\right)=\frac{1}{2} \mathrm{~m} \omega^{2} \cdot \frac{2}{3} \mathrm{~A}^{2} \\ & \text { P.E }=\frac{1}{2} \mathrm{~m} \omega^{2} \frac{\mathrm{A}^{2}}{3}=\frac{1}{2} \mathrm{~m} \omega^{2} \cdot \frac{1}{3} \mathrm{~A}^{2} \\ & \therefore \text { Ratio of } \frac{\mathrm{K} \cdot \mathrm{E}}{\text { P.E }}=2: 1 \end{aligned} $$

Example-5:

An object, of mass $200 \mathrm{~g}$, executes simple harmonic oscillations, along the $x$-axis, with a frequency of $\left(\frac{25}{\pi}\right) \mathrm{Hz}$. At the position $x=4 \mathrm{~cm}$, the object has kinetic energy of $0.5 \mathrm{~J}$ and potential energy of $0.4 \mathrm{~J}$. The amplitude of oscillations, and the velocity, of the object, at the mean position, are, respectively

(1) $6 \mathrm{~cm}$ and $30 \mathrm{~ms}^{-1}$

(2) $4 \mathrm{~cm}$ and $20 \mathrm{~ms}^{-1}$

(3) $6 \mathrm{~cm}$ and $20 \mathrm{~ms}^{-1}$

(4) $4 \mathrm{~cm}$ and $30 \mathrm{~ms}^{-1}$

Show Answer

Solution:

The total energy of the particle, at $x=4 \mathrm{~cm}$, is

$$ (0.5+0.4) \mathrm{J}=0.9 \mathrm{~J} $$

This remains constant at all positions. The value of this total energy equals $\frac{1}{2} \mathrm{ma}^{2} \omega^{2}$ where $\mathrm{a}=$ amplitude of oscillations.

We are given that $\mathrm{m}=200 \mathrm{~g}=0.2 \mathrm{~kg}$. Also $\omega=2 \pi v$

$\therefore \omega=2 \pi\left(\frac{25}{\pi}\right) \mathrm{rads}^{-1}$

$=50 \mathrm{rad} \mathrm{s}^{-1}$

$$ \begin{aligned} & \therefore \quad 0.9=\frac{1}{2} \times 0.2 \times a^{2} \times(50)^{2} \\ & \text { or } \quad a^{2} \times 250=0.9 \\ & \therefore \quad a=\left(\frac{0.9}{250}\right)^{1 / 2}=\frac{3}{50} \mathrm{~m}=6 \mathrm{~cm} \end{aligned} $$

Velocity at the mean position = Maximum value of velocity

$$ =\mathrm{a} \omega=0.6 \times 50 \mathrm{~ms}^{-1}=30 \mathrm{~ms}^{-1} $$

‘Force Constant’ of a Spring

Let there be a uniform spring made from a given material and having a given (normal) length and diameter. It turns out that one needs a definite force, say $\Delta \mathrm{F}$, to change (extend / compress) the length, of such a given spring, by an amount, say $\Delta \ell$. The force needed $(\Delta \mathrm{F})$ is found to be directly proportional to the change in length $(\Delta \ell)$, associated with it. The ratio

$$ \frac{\Delta \mathrm{F}}{\Delta \ell}=\mathrm{k}, \text { say } $$

is, therefore, a ‘constant’ for a spring, made from a given material and having a given length and diameter. We call ’ $\mathrm{k}$ ’ as the ‘force constant’ or the ‘spring factor’, for the given spring. It may be thought of as the ‘force needed to change (extend / compress) the length of the given spring bya ‘unit amount’. ’ $\mathrm{k}$ ‘, thus, has units of $\left(\frac{N}{m}\right)$, in SI units.

The ‘force constant’ of a spring, depends on the

(i) nature of the material of the spring.

(ii) original (or, unstretched), length $(\ell)$ of the spring.

For springs, made of the same material and having the same area of cross-section, the more the length of the spring, the less is the ‘force constant’ and vice-versa.

(iii) (original) diameter (d), or the area of ‘cross section’, of the spring.

For springs made of the same material, and having the same length, the ‘force-constant’ increases with an increase in the area of the cross-section and ‘vice-versa’.

These results, in a way, are similar to the corresponding results for the longitudinal extension of a wire. We know that, for a wire undergoing a longitudinal extension;

$$ \mathrm{Y}=\frac{\mathrm{F} / \mathrm{A}}{\Delta d / \ell} $$

Here $\mathrm{Y}$ is the Young’s modulus for the material of the wire. We can rewrite this result as

$$ \mathrm{F}=\mathrm{Y} \cdot\left(\frac{\Delta \ell}{\ell}\right) \cdot \mathrm{A} $$

The applied force, $\mathrm{F}$, can be ’thought of’ as the ‘force constant’ for the wire if $\Delta \ell=1$ unit. Thus, for a wire,

Force constant $=\mathrm{k}=\left(\mathrm{Y} \cdot \frac{\mathrm{A}}{\ell}\right)$

It follows that the force constant

(i) depends on the material of the wire

(ii) decreases with an increase in the length of the wire

(iii) increases with an increase in the area of cross section (or diameter), of the wire.

These conclusions, for a wire, are similar to the ‘results’, for a spring, quoted above.

Oscillations of a Spring

We first consider a system, in which a light spring, having a mass $M$ attached at its one end, is kept horizontally on a smooth table. The other end, of the spring, is fixed to a rigid support.

Let the mass $M$ be stretched by a small amount, say $x$, towards the right. The spring then develops a restoring force $(=\mathrm{k} x)$; this ‘restoring force’ then tries to bring the spring, and, therefore, the mass M, back to its original (unstretched)

position. For the mass M, we may then write

$$ \begin{gathered} \mathrm{M} \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-\mathrm{k} x \\ \text { or } \quad \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-\frac{\mathrm{k}}{\mathrm{M}} x=-\omega^{2} x \quad\left(\omega^{2}=\frac{\mathrm{k}}{\mathrm{M}}\right) \end{gathered} $$

This being the equation of a simple harmonic motion, we may say that the mass, as well as the spring attached to it, will, therefore, start executing simple harmonic oscillations. The time period of these oscillations, is

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k}}} $$

Example-6:

A mass M, attached to a spring, oscillates with a period of $2 \mathrm{~s}$. On increasing the mass by $2 \mathrm{~kg}$, the period increases by $1 \mathrm{~s}$. The value of $\mathrm{M}$ is

(1) $1.6 \mathrm{~kg}$

(2) $2.0 \mathrm{~kg}$

(3) $2.4 \mathrm{~kg}$

(4) $2.8 \mathrm{~kg}$

Show Answer

Solution:

Let $\mathrm{k}$ be the spring constant. We then have, as per the given data,

$$ 2=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k}}} $$

and $\quad 2+1=2 \pi \sqrt{\frac{\mathrm{M}+2}{\mathrm{k}}}$

$\therefore \frac{3}{2}=\sqrt{\frac{M+2}{M}}$

or $\quad \frac{M+2}{M}=\frac{9}{4}$

$\therefore \frac{2}{\mathrm{M}}=\frac{9}{4}-1=\frac{5}{4}$

$\therefore \quad \mathrm{M}=\frac{8}{5} \mathrm{~kg}=1.6 \mathrm{~kg}$

We next consider the case of a mass $\mathrm{M}$, suspended from the ‘free end’ of a vertically hanging light spring of normal length $\mathrm{L}$. The other end, of the spring, is held in its position, by a rigid support. The equilibrium length of the spring is now the length (say, $\mathrm{L}+\ell$ ) which it has under the action of the force exerted on it by the weight $(=\mathrm{Mg}$ ), of the mass M. For equilibrium, we now have

$$ \mathrm{k} \ell=\mathrm{Mg} $$

where $\mathrm{k}$ is the ‘force constant’ of the spring. Hence

$$ \mathrm{k}=\frac{\mathrm{Mg}}{\ell} $$

Let the mass $\mathrm{M}$, be now pulled down vertically, by a (small) amount, say, $\mathrm{y}$, and then ’let-go’. As soon as the mass is ’let-go’, the total restoring force $(=\mathrm{k}(\ell+\mathrm{y}))$, now comes into play. The net downward force, on the mass M, now is

$$ \begin{gathered} \mathrm{F}=\mathrm{Mg}-\mathrm{k}(\ell+\mathrm{y})=\mathrm{Mg}-\left(\frac{\mathrm{Mg}}{\ell}(\ell+\mathrm{y})\right) \\ =-\frac{\mathrm{Mg}}{\ell} \mathrm{y}=-\mathrm{ky} \end{gathered} $$

The equation of motion, of the mass $\mathrm{M}$, is

$$ \mathrm{M} \frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dt}^{2}}=-\mathrm{ky} $$

or

$$ \frac{d^{2} y}{d t^{2}}=-\left(\frac{k}{M}\right) y=-\omega^{2} y $$

This equation has the form of the equation of a SHM. The ‘pulled-down’ (and then ’let-go’) mass, therefore, starts oscillating harmonically, about the ‘central position’, corresponding to the equilibrium length $(L+\ell)$, of the spring. The ’time-period’, of the oscillations, is

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k}}} $$

‘Combinations’ of Two Springs

We may have a mass attached to a combination of two (light) springs. This may be done in two ways:

(i) The ‘series’ combination and

(ii) The parallel combination

These two ways of ‘combination’ are shown in the figure below. It can be shown (as explained in the examples given) that the ’equivalent spring constants’, of these two ‘combinations’ are given by

$$ \mathrm{k} _{\text {equivalent }}(\text { series combination })=\frac{\mathrm{k} _{1} \mathrm{k} _{2}}{\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)} $$

and $\quad \mathrm{k} _{\text {equivalent }}($ parallel combination $)=\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)$

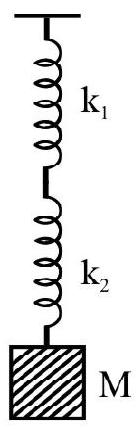(a) Series Combination

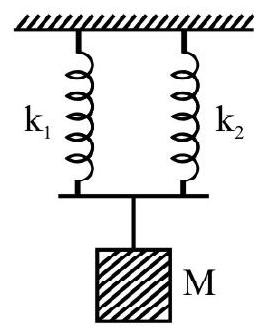
(b) Parallel Combination

Two ways of attaching a mass to a combination of two springs.

Example-7:

A system of two springs, of spring constants $\mathrm{k} _{1}$ and $\mathrm{k} _{2}$, arranged as shown, has a mass $\mathrm{M}$ attached at its free end. When the mass in pulled down a little, and ’let-go’, it would execute oscillations that are

(1) Simple harmonic and have a time period $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{M}\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}{\mathrm{k} _{1} \mathrm{k} _{2}}}$

(2) Simple harmonic and have a time period $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{M}}{\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}}$

(3) Periodic, but not simple harmonic; and have a time period $T=2 \pi \sqrt{\frac{M}{\left(k _{1}+k _{2}\right)}}$

(4) Periodic, but not simple harmonic; and have a time period $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{M}\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}{\mathrm{k} _{1} \mathrm{k} _{2}}}$

Show Answer

Solution:

When the mass is pulled down a little (say $\Delta \mathrm{L}$ ), the (restoring) force, set up in the spring, is proportional to $\Delta \mathrm{L}$ and tends to bring the mass back to its original position. Hence the oscillations, of the mass $\mathrm{M}$, are simple harmonic.

The same force $\mathrm{Mg}$ acts on both the springs. Hence their extensions, say $\ell _{1}$ and $\ell _{2}$, are given by

$$ \ell _{1}=\frac{\mathrm{Mg}}{\mathrm{k} _{1}} \text { and } \ell _{2}=\frac{\mathrm{Mg}}{\mathrm{k} _{2}} $$

Total extension of both the spring is $\left(\ell _{1}+\ell _{2}\right)(=\ell$, say $)$.

$\therefore$ If ’ $\mathrm{k}$ ’ is the equivalent spring constant of the combination, we have $\ell=\frac{\mathrm{Mg}}{\mathrm{k}}$

Using $\ell=\ell _{1}+\ell _{2}$, we get $\frac{\mathrm{Mg}}{\mathrm{k}}=\frac{\mathrm{Mg}}{\mathrm{k} _{1}}+\frac{\mathrm{Mg}}{\mathrm{k} _{2}}$

This gives $\mathrm{k}=\frac{\mathrm{k} _{1} \mathrm{k} _{2}}{\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}$

Hence the time period of oscillations

$\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k}}}=2 \pi \sqrt{\frac{\mathrm{M}\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}{\mathrm{k} _{1} \mathrm{k} _{2}}}$

Example-8:

Two springs, of spring constants $\mathrm{k} _{1}$ and $\mathrm{k} _{2}$, having equal lengths, are arranged in a ‘parallel combination’, as shown. A mass M, attached to their common free end, is pulled down a little and ’let-go’. The resulting oscillations, of the mass $\mathrm{M}$, would be simple harmonic oscillations, having a time period $\mathrm{T}$, where $\mathrm{T}$ equals:

(1) $2 \pi \sqrt{\frac{\mathrm{M}\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}{\mathrm{k} _{1} \mathrm{k} _{2}}}$

(2) $2 \pi \sqrt{\frac{\mathrm{M}\left(\mathrm{k} _{1} / \mathrm{k} _{2}\right)}{\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}}$

(3) $2 \pi \sqrt{\frac{\mathrm{M}\left(\mathrm{k} _{2} / \mathrm{k} _{1}\right)}{\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}}$

(4) $2 \pi \sqrt{\frac{M}{k _{1}+k _{2}}}$

Show Answer

Solution:

Here both the springs get extended by equal amounts, say $\ell$. We, therefore have $\frac{\mathrm{F} _{1}}{\ell}=\mathrm{k} _{1}$ and $\frac{\mathrm{F} _{2}}{\ell}=\mathrm{k} _{2}$, where $\mathrm{F} _{1}+\mathrm{F} _{2}=\mathrm{Mg}$

Also if $k$ is the equivalent spring constant, we have

$\frac{\mathrm{Mg}}{\mathrm{k}}=\ell \quad($ or $\mathrm{Mg}=\mathrm{k} \ell)$

But $\mathrm{Mg}=\mathrm{F} _{1}+\mathrm{F} _{2}=\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right) \ell$

$\therefore \mathrm{k} \ell=\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right) \ell$

or $\quad \mathrm{k}=\mathrm{k} _{1}+\mathrm{k} _{2}$

The equivalent spring constant, in the parallel combination is, therefore, just the sum of the individual spring constants. The time period of oscillations, of the mass M, is

$$ \begin{aligned} & \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k}}} \\ & =2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k} _{1}+\mathrm{k} _{2}}} \end{aligned} $$

Example-9:

A spring, of spring constant $\mathrm{k}$, is cut into n equal parts. When a block of mass $\mathrm{M}$ is attached to a

(i) series combination of these $n$ parts, its time period equals $\mathrm{T} _{1}$.

(ii) parallel combination of these $\mathrm{n}$ parts, its time period equals $\mathrm{T} _{2}$.

The ratio $\left(\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}\right)$ equals

(1) $\frac{1}{\mathrm{n}}$

(2) $\frac{1}{\mathrm{n}^{2}}$

(3) $\mathrm{n}$

(4) $\mathrm{n}^{2}$

Show Answer

Solution:

The spring constant, of each part, becomes $n$ times the value of the spring constant of the original whole spring. (i) For the series combination, the equivalent spring constant $\left(\mathrm{K} _{\mathrm{S}}\right)$ of n springs, each of spring constant $\mathrm{nk}$, is given by

$$ \begin{aligned} & \frac{1}{\mathrm{k} _{\mathrm{s}}}=\frac{1}{\mathrm{nk}}+\frac{1}{\mathrm{nk}}+\ldots \ldots=\frac{\mathrm{n}}{\mathrm{nk}}=\frac{1}{\mathrm{k}} \\ \therefore & \mathrm{k} _{\mathrm{s}}=\mathrm{k} \\ \therefore & \mathrm{T} _{1}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k}}} \end{aligned} $$

(ii) For the parallel combination, the equivalent spring constant $\left(\mathrm{k} _{\mathrm{p}}\right)$, ofn springs, each of spring constant $\mathrm{nk}$, is given by

$$ \begin{aligned} & \mathrm{k} _{\mathrm{p}}=\mathrm{nk}+\mathrm{nk}+\mathrm{nk}+\ldots \ldots . .=\mathrm{n} \cdot \mathrm{nk}=\mathrm{n}^{2} \mathrm{k} \\ \therefore & \mathrm{T} _{2}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{n}^{2} \mathrm{k}}}=\frac{1}{\mathrm{n}}\left(2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k}}}\right)=\frac{\mathrm{T} _{1}}{\mathrm{n}} \\ \therefore & \frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=\mathrm{n} \end{aligned} $$

Example-10:

The free mass $\mathrm{m}$, on the left, moving with a velocity $\mathrm{v}$, hits the mass $\mathrm{m}$, attached to the spring (spring constant $=\mathrm{k}$ ), and gets stuck to it. The amplitude of the resulting SHM oscillations, of the combined mass, (assuming the horizontal surface to be smooth), equals

(1) $\sqrt{\frac{\mathrm{v}^{2}}{2 \mathrm{k}}}$

(2) $\sqrt{\frac{\mathrm{mv}^{2}}{\mathrm{k}}}$

(3) $\sqrt{\frac{2 m v^{2}}{k}}$

(4) $\sqrt{\frac{ m v^{2}}{4k}}$

Show Answer

Solution:

The mass (2m), ‘formed’ after the inelastic collision, will move with a velocity $\frac{\mathrm{v}}{2}$, as per the law of conservation of momentum.

Hence its kinetic energy $=\frac{1}{2}(2 \mathrm{~m})\left(\frac{\mathrm{v}}{2}\right)^{2}=\frac{\mathrm{mv}^{2}}{4}$

The total energy, of the resulting SHM, is therefore, $\frac{\mathrm{mv}^{2}}{4}$.

This must equal $\frac{1}{2} \mathrm{kA}^{2}$ where $\mathrm{A}$ is the amplitude of this SHM. Hence

$$ \frac{1}{2} \mathrm{kA}^{2}=\frac{1}{4} \mathrm{mv}^{2} $$

or $\mathrm{A}=\sqrt{\frac{\mathrm{mv}^{2}}{2 \mathrm{k}}}$

Example-11:

A system of three identical light springs, each of force constant, $k$, is arranged as shown. A particle of mass $\mathrm{m}$, kept at the joint point, $\mathrm{O}$, of the three springs, is pushed slightly downwards vertically along the direction OQ. When released, the time period, of its oscillations will be

(1) $\mathrm{T}=2 \pi\left(\frac{\mathrm{m}}{\sqrt{2} \mathrm{k}}\right)^{1 / 2}$

(2) $\mathrm{T}=2 \pi\left(\frac{\mathrm{m}}{2 \mathrm{k}}\right)^{1 / 2}$

(3) $\mathrm{T}=2 \pi\left(\frac{\mathrm{m}}{2 \sqrt{2} \mathrm{k}}\right)^{1 / 2}$

(4) $\mathrm{T}=2 \pi\left(\frac{\mathrm{m}}{4 \mathrm{k}}\right)^{1 / 2}$

Show Answer

Solution:

When the mass, $\mathrm{M}$, is pushed vertically downwards, along $\mathrm{OQ}$, through distance $\mathrm{r} _{\mathrm{s}}$ the springs $\mathrm{PO}$ and RO will get extended by amounts $\mathrm{r} _{\mathrm{s}} \cos 45^{\circ}$ each.

The restoring force, on mass $\mathrm{m}$, due to the spring $\mathrm{OQ}$, is $\mathrm{k} _{\mathrm{s}}$ (directed along QO). The springs PO and OR, develop restoring forces of $\mathrm{k}\left(\mathrm{r} _{\mathrm{s}} \cos 45^{\circ}\right)$ each, directed along OP and OR, respectively. Their resultant $\left(2 \mathrm{k} _{\mathrm{s}} \cos 45^{\circ}\right) \cos 45^{\circ}$, is directed along QO. Hence the total restoring force, on mass $\mathrm{m}$, is $\left[\mathrm{kr} _{\mathrm{s}}+\left(2 \mathrm{k} _{\mathrm{s}} \cos 45^{\circ}\right) \cos 45^{\circ}\right]$, directed along QO.

This equals $\left(2 \mathrm{k} \mathrm{r} _{\mathrm{s}}\right.$ ). Hence the effective spring constant, of the combination is $2 \mathrm{k}$.

$\therefore$ Time period of oscillations of mass $m$

$$ =\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{2 \mathrm{k}}} $$

Example-12:

A mass $m$ is attached to a combination of three identical springs, each of spring constant $k$, in the manner shown. The mass $m$ is pulled down a little and ’let-go’. The time period, of its oscillations, would be

(1) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}+2 \mathrm{k} \cos ^{2} \theta}} $

(2) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}\left(\mathrm{k}+2 \cos ^{2} \theta\right)}{2 \mathrm{k} \cos ^{2} \theta}} $

(3) $T=2 \pi \sqrt{\frac{\mathrm{m}\left(1+2 \cos ^{2} \theta\right)}{2 \mathrm{k} \cos ^{2} \theta}}$

(4) $T=2 \pi \sqrt{\frac{m\left(2 k \cos ^{2} \theta\right)}{\left(1+2 \cos ^{2} \theta\right)}}$

Show Answer

Solution:

Let the mass $m$ extend the spring $\mathrm{OB}$ by an amount $\mathrm{y}$. This extends, in turn, each of the springs $\mathrm{OA}$ and $\mathrm{OC}$ by an amount $y \cos \theta$.

The restoring forces $(\mathrm{k} y \cos \theta)$ each, developed in the springs $\mathrm{OA}$ and $\mathrm{OC}$, give a resultant restoring force of $2(k y \cos \theta) .(\cos \theta)$ along BC. Coupled with the restoring force $(k y)$, developed in the spring

$\mathrm{OB}$, the total restoring force is that due to the restoring forces $(\mathrm{ky})$ and $2\left(\mathrm{k}^{2} \cos ^{2} \theta\right) \mathrm{y}$, developed in the springs $\mathrm{OB}$, and the equivalent of springs $\mathrm{OA}$ and $\mathrm{OC}$, connected in series.

The equivalent spring constant, of the series combination of a spring of spring constant $k$, with another of spring constant $\left(2 \mathrm{k} \cos ^{2} \theta\right)$, is

$$ \mathrm{k} _{\mathrm{eq}}=\left(\frac{\mathrm{k} 2 \mathrm{k} \cos ^{2} \theta}{\mathrm{k}+2 \mathrm{k} \cos ^{2} \theta}\right)=\left(\frac{2 \mathrm{k} \cos ^{2} \theta}{1+2 \cos ^{2} \theta}\right) $$

The time period is

$$ \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k} _{\mathrm{eq}}}}=2 \pi \sqrt{\frac{\mathrm{m}\left(1+2 \cos ^{2} \theta\right)}{2 \mathrm{k} \cos ^{2} \theta}} $$

Example-13:

Two masses $m _{1}$ and $m _{2}$ are joined to each other through a light spring of spring constant $k$. The system is kept on a smooth horizontal surface and the two masses are pulled slightly in opposite directions, and ’let-go’. The time period, of their resulting oscillations, would be

(1) $2 \pi \sqrt{\frac{m _{1} m _{2}}{2\left(m _{1}+m _{2}\right)}}$

(2) $2 \pi \sqrt{\frac{\left(\mathrm{m} _{1}+\mathrm{m} _{2}\right)}{\mathrm{k}}} $

(3) $2 \pi \sqrt{\frac{\left(\mathrm{m} _{1} \sim \mathrm{m} _{2}\right)}{\mathrm{k}}}$

(4) $2 \pi \sqrt{\frac{2\left(\mathrm{~m} _{1}+\mathrm{m} _{2}\right)}{\mathrm{k}}}$

Show Answer

Solution:

Let mass $m _{1}$ be displaced through a distance $x _{1}$ to left and let mass $m _{2}$ be displaced through a distance $x _{2}$ to the right. The total stretching of the spring, say $x$, then given by

$$ x=x _{1}+x _{2} $$

Hence $\frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=\frac{\mathrm{d}^{2} x _{1}}{\mathrm{dt}^{2}}+\frac{\mathrm{d}^{2} x _{2}}{\mathrm{dt}^{2}}$

The restoring force, on either mass, is $k x$. However, for masses $m _{1}$ and $m _{2}$, their force equations would be

$\left(\mathrm{m} _{1} \frac{\mathrm{d}^{2} x _{1}}{\mathrm{dt}^{2}}=-\mathrm{k} x\right)$ and $\left(\mathrm{m} _{2} \frac{\mathrm{d}^{2} x _{2}}{\mathrm{dt}^{2}}=-\mathrm{k} x\right)$

$\therefore \quad \frac{\mathrm{d}^{2} x _{1}}{\mathrm{dt}^{2}}=-\frac{\mathrm{k}}{\mathrm{m} _{1}} x \quad$ and $\quad \frac{\mathrm{d}^{2} x _{2}}{\mathrm{dt}^{2}}=-\frac{\mathrm{k}}{\mathrm{m} _{2}} x$

$\therefore \quad \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-\left(\frac{\mathrm{k}}{\mathrm{m} _{1}}+\frac{\mathrm{k}}{\mathrm{m} _{2}}\right) x=-\omega^{2} x$

where $\omega^{2}=\mathrm{k}\left(\frac{\mathrm{m} _{1}+\mathrm{m} _{2}}{\mathrm{~m} _{1} \mathrm{~m} _{2}}\right)$

The time period of oscillations, of the system, is, therefore,

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\left(\frac{\mathrm{m} _{1} \mathrm{~m} _{2}}{\mathrm{k}\left(\mathrm{m} _{1}+\mathrm{m} _{2}\right)}\right)} $$

[Note: This result implies that such a system behaves like an equivalent mass $m\left(=\left(\frac{m _{1} m _{2}}{m _{1}+m _{2}}\right)\right)$ attached to a spring. We refer to $m$ as the reduced mass of the given combination of masses $m _{1}$ and $m _{2}$ ].

Example-14:

A system, made up of a mass m, a smooth pulley, a light string and a light spring (of spring constant $\mathrm{k}$ ) is set up as shown. On displacing the mass $\mathrm{m}$ slightly, from its equilibrium position, and ’letting it go’, its period of oscillation would be

(1) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$

(2) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{2 \mathrm{k}}}$

(3) $\mathrm{T}=2 \pi \sqrt{\frac{2 \mathrm{~m}}{\mathrm{k}}}$

(4) $\mathrm{T}=2 \pi \sqrt{\frac{4 \mathrm{~m}}{\mathrm{k}}}$

Show Answer

Solution:

Let the mass $m$ be displaced through a distance $x$. The spring would then stretch by a distance $\frac{x}{2}$ only. Hence the restoring force, set up in it, equals $\frac{\mathrm{k} x}{2}$.

If $\mathrm{T}$ is the tension in the string, we would then have

$$ \mathrm{T}+\mathrm{T}=\frac{\mathrm{k} x}{2} $$

or $\mathrm{T}=\frac{\mathrm{k} x}{4}$

The tension, in the string, is in the direction of the restoring force set up in the spring. If, therefore, tends to restore the mass $m$ back to its equilibrium position. We, therefore, have

$$ \mathrm{m} \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-\frac{\mathrm{k} x}{4} $$

or $\quad \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=\omega^{2} x \quad$ where $\quad \omega^{2}=\frac{\mathrm{k}}{4 \mathrm{~m}}$

The mass, therefore, executes SHM of time period

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{4 \mathrm{~m}}{\mathrm{k}}} $$

Example-15:

A long uniform rod, of length $\mathrm{L}$ and mass $\mathrm{M}$, is free to rotate in a vertical plane about a horizontal axis through one end. The rod’s other end is joined to a vertical spring (spring constant $=k$ ) whose other end is joined to the ground. The rod is horizontal in its equilibrium position.

The time period of (small) oscillations, of the rod, when it is tilted slightly and ’let-go’, is

(1) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k}}}$

(2) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{M}}{2 \mathrm{k}}}$

(3) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{M}}{3 \mathrm{k}}}$

(4) $T=2 \pi \sqrt{\frac{M}{4 k}}$

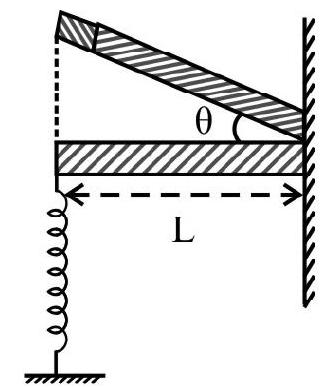
Show Answer

Solution:

The (small) stretching, of the spring, due to the tilting of the rod through an angle $\theta$, is (nearly) L $\theta$.

The restoring force $(\simeq k(L \theta))$, produces a restoring torque of magnitude $(k L \theta) \times L=k L^{2} \theta$

The moment of inertia, of the rod, about its one end, is $\left(\frac{1}{3} \mathrm{ML}^{2}\right)$

Using the equation $\mathrm{I} \frac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}=-\tau$ we find that $\omega^{2}=\frac{\mathrm{kL}^{2}}{\mathrm{I}}=\frac{\mathrm{kL}^{2} \cdot 3}{\mathrm{ML}^{2}}=\frac{3 \mathrm{k}}{\mathrm{M}}$

$\therefore$ Time period, $\mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{M}}{3 \mathrm{k}}}$

‘Simple Pendulum’

A simple pendulum executes simple harmonic oscillations only when the amplitude of these oscillations is (very) small. This can be seen as follows.

Let the bob of a simple pendulum, of mass $\mathrm{m}$, be displaced, from its mean position $(\mathrm{O})$, to a point $\mathrm{A}$, and ’let-go’. The weight $(\mathrm{W})$ of the bob, and tension (T) in the string, then act along the directions shown. The tension, $\mathrm{T}$, balances the component $\mathrm{mg} \cos \theta$ of the weight. The unbalanced component, $\mathrm{mg} \sin \theta$, acts as a ‘restoring force’, as it tends to bring the bob back to its equilibrium position (O).

For small values of $\theta$, we have

$$ \sin \theta \simeq \theta $$

$\therefore$ Restoring force $\simeq \mathrm{mg} \theta$

$$ =\operatorname{mg} \frac{x}{\ell} \quad \text { where } \quad x=\mathrm{OA} $$

$\therefore$ The equation of motion, of the bob, is

$$ \mathrm{m} \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-\mathrm{mg} \frac{x}{\ell} $$

or $\quad \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=\left(\frac{-\mathrm{g}}{\ell}\right) x=-\omega^{2} x \quad\left(\right.$ where $\left.\omega^{2}=\frac{\mathrm{g}}{\ell}\right)$

This, now, is the equation of a simple harmonic motion. Hence the simple pendulum executes simple harmonic oscillations when the amplitude of these oscillations is (very) small. The time period, $\mathrm{T}$, of these oscillations, is

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\ell}{\mathrm{g}}} $$

It is interesting here to note that the time period of oscillations of a simple pendulum is independent of the mass of the bob.

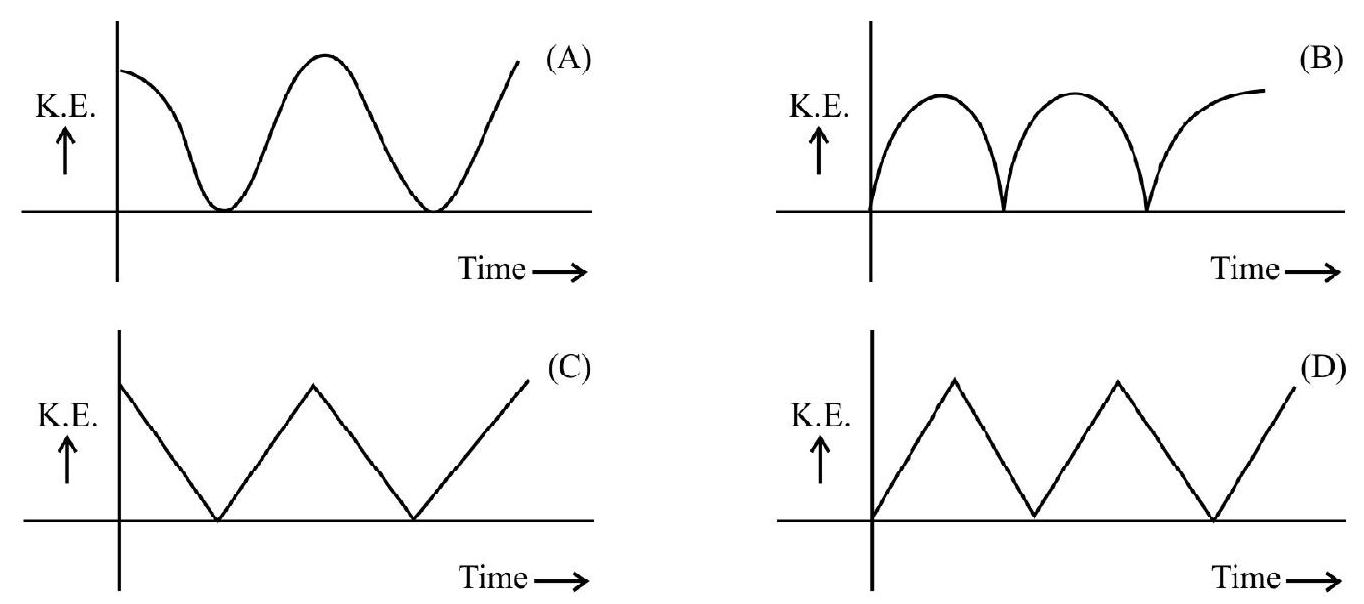
Example-16:

The time variation, of the acceleration of a particle, executing SHM, is as shown below.

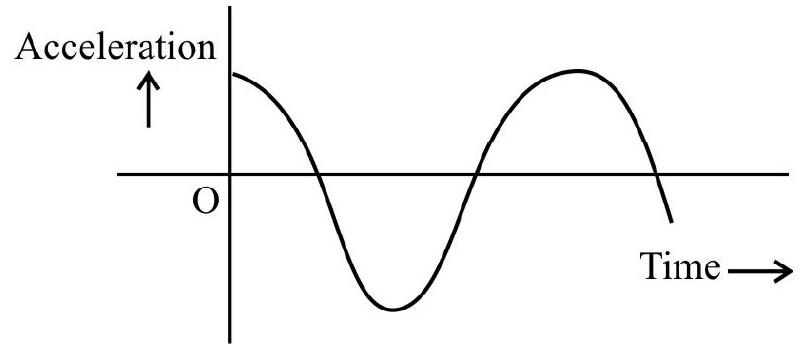
The time variation, of the kinetic energy of this particle, would then correspond to the graph labelled as graph

(1) $\mathrm{A}$

(2) $\mathrm{B}$

(3) $\mathrm{C}$

(4) $\mathrm{D}$

Show Answer

Solution:

The given graph, showing the variation of acceleration with time, shows that the acceleration is varying with time as a cosine function.

Hence the velocity (integral of a cosine function) would vary with time as a sine function. The K.E would,therefore, vary as the square of $\sin \theta$. It is only graph $B$ that corresponds to the variation, with time, of $\sin ^{2} \omega t$.

Example-17:

A simple pendulum, of length $\mathrm{L}$, has a spring (of spring constant $\mathrm{k}$ ) attached to it at a distance $\mathrm{h}$ below its point of suspension. The time period, of (very) small amplitude oscillations of this pendulum, would be

(1) $2 \pi \sqrt{\left(\frac{\mathrm{mL}^{2}}{\mathrm{mgL}+\mathrm{kh}^{2}}\right)}$

(2) $2 \pi \sqrt{\left(\frac{\mathrm{m}\left(\mathrm{L}^{2}+\mathrm{h}^{2}\right)}{\mathrm{mgL}+\mathrm{kh}^{2}}\right)}$

(3) $2 \pi \sqrt{\frac{\mathrm{mL}}{\mathrm{mgL}-\mathrm{kh}^{2}}}$

(4) $2 \pi \sqrt{\left(\frac{\mathrm{m}\left(\mathrm{L}^{2}+\mathrm{h}^{2}\right)}{\mathrm{mgL}-\mathrm{kh}^{2}}\right)}$

Show Answer

Solution:

Let the bob be turned through a small angle, $\theta$, to the left of its equilibrium position. This stretches the spring by an amount $\Delta x$. where $\Delta x \simeq \mathrm{h} \theta$.

The restoring forces, acting on the bob, are now

(i) the component $\mathrm{mg}(\sin \theta),(\approx \operatorname{mg} \theta)$, of its weight

(ii) the force $\mathrm{k}(\mathrm{h} \theta)$, due to the stretching of the spring.

The total restoring torque is, therefore,

$$ \tau=(\operatorname{mg} \theta) \mathrm{L}+(\operatorname{kh} \theta) \mathrm{h} $$

The equation of motion of the bob is

$$ \begin{aligned} & \mathrm{I}\left(\frac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}\right)=-\tau \\ & \text { or } \quad \mathrm{mL}^{2}\left(\frac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}\right)=-\left(\mathrm{mgL}+\mathrm{kh}^{2}\right) \theta \\ & \therefore \quad \frac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}=\frac{\left(\mathrm{mgL}+\mathrm{kh}^{2}\right) \theta}{\mathrm{mL}^{2}} \\ & \quad=-\omega^{2} \theta \end{aligned} $$

where $\omega^{2}=\frac{\left(\mathrm{mg} \mathrm{L}+\mathrm{kh}^{2}\right)}{\left(\mathrm{mL}^{2}\right)}$

The bob, therefore, executes (angular) SHM of period,

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{mL}^{2}}{\left(\mathrm{mgL}+\mathrm{kh}^{2}\right)}} $$

Example-18:

A ring of radius $r$, is suspended from a point on its circumference. The angular frequency, of its small oscillations, would be

(1) $\frac{1}{2 \pi} \sqrt{\frac{\mathrm{g}}{\mathrm{r}}}$

(2) $\frac{1}{2 \pi} \sqrt{\frac{\mathrm{g}}{2 \mathrm{r}}}$

(3) $\sqrt{\frac{\mathrm{g}}{\mathrm{r}}}$

(4) $\sqrt{\frac{g}{2 r}}$

Show Answer

Solution:

Let the ring be displaced slightly from its equilibrium position. The restoring torque, $($ due to its weight $=\mathrm{mg})$, is

$$ \tau \simeq \operatorname{mg}(\mathrm{r} \theta) $$

The moment of inertia, I, of the ring, about its point of suspension, is

$$ \mathrm{I}=\left(\mathrm{mr}^{2}\right)+\left(\mathrm{mr}^{2}\right)=2 \mathrm{mr}^{2} $$

Its equation of motion is

$$ \begin{aligned} & \mathrm{I} \frac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}=-\tau=-\operatorname{mgr} \theta \\ & \therefore \quad \frac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}=-\left(\frac{\mathrm{mgr}}{2 \mathrm{mr}^{2}}\right) \theta=-\omega^{2} \theta \end{aligned} $$

where $\omega^{2}=\frac{g}{2 \mathrm{r}}$

$\therefore$ Angular frequency $=\omega=\sqrt{\frac{g}{2 \mathrm{r}}}$

Example-19:

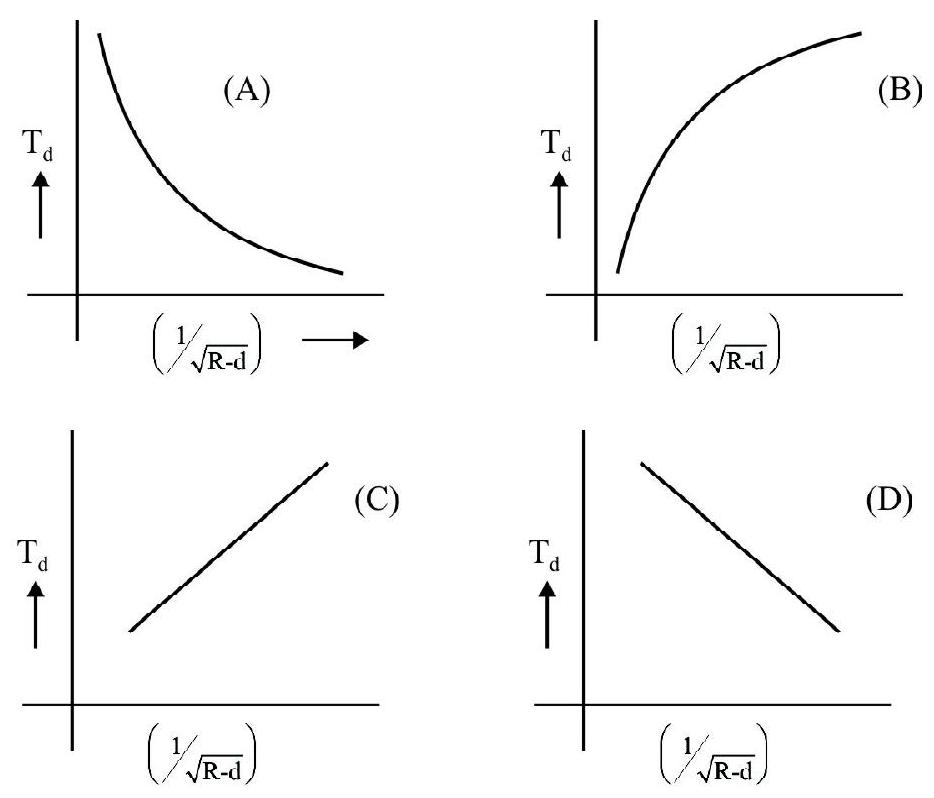
Let a simple pendulum, of a given length, be taken to a depth $\mathrm{d}$ below the earth’s (radius $=\mathrm{R}$ ) surface. If the time period $\mathrm{T} _{\mathrm{d}}$, of the pendulum, were to be plotted as a function of $\left(\frac{1}{\sqrt{(\mathrm{R}-\mathrm{d})}}\right)$ the variation would

be represented by the graph labelled as graph.

(1) A

(2) $\mathrm{B}$

(3) $\mathrm{C}$

(4) $\mathrm{D}$

Show Answer

Solution:

Let $g$ and $g _{d}$ be the values of the acceleration due to gravity on the earth’s surface, and at a point at a depth d, below the earth’s surface. We can then write, for the weight of a particle mass $m$,

$\mathrm{w} _{\text {surface }}=\mathrm{mg}=\frac{\mathrm{GMm}}{\mathrm{R}^{2}}=\frac{\mathrm{G}\left(\frac{4 \pi}{3} \mathrm{R}^{3} \rho\right) \mathrm{m}}{\mathrm{R}^{2}}=\frac{4 \pi}{3} \mathrm{~m} \rho \mathrm{GR}$

$\mathrm{w} _{\mathrm{d}}=\mathrm{mg} _{\mathrm{d}}=\frac{\mathrm{GM}^{\prime} \mathrm{m}}{(\mathrm{R}-\mathrm{d})^{2}}=\frac{\mathrm{G}\left(\frac{4 \pi}{3}(\mathrm{R}-\mathrm{d})^{3} \rho\right) \mathrm{m}}{(\mathrm{R}-\mathrm{d})^{2}}=\frac{4 \pi}{3} \mathrm{~m} \rho \mathrm{G}(\mathrm{R}-\mathrm{d})$

$\therefore \frac{\mathrm{g}}{\mathrm{g} _{\mathrm{d}}}=\frac{\mathrm{R}}{\mathrm{R}-\mathrm{d}}$

Now $\mathrm{T} _{\mathrm{d}}=2 \pi \sqrt{\frac{\ell}{\mathrm{g} _{\mathrm{d}}}}=2 \pi \sqrt{\frac{\ell}{\left(\frac{4 \pi}{3} \rho \mathrm{G}\right)(\mathrm{R}-\mathrm{d})}}$

For a pendulum of given length $=2 \pi\left(\frac{3 \ell}{4 \pi \rho G}\right)^{1 / 2}=$ Constant

$$ \mathrm{T} _{\mathrm{d}} \alpha \frac{1}{\sqrt{(\mathrm{R}-\mathrm{d})}} $$

Hence a graph of $\mathrm{T} _{\mathrm{d}}$ against $\frac{1}{\sqrt{\mathrm{R}-\mathrm{d}}}$ would be a straight line, with a positive slope.

Example-20:

The bob of a simple pendulum is so constrained that it oscillates (i) for a length $\ell$ for one half of its oscillations and (ii) for a length $\frac{\ell}{4}$ of for the other half of its oscillation.

Find the length of a simple pendulum whose time period is six times that of the ‘constrained pendulum’.

Show Answer

Solution:

The time period of the constrained pendulum is

$\mathrm{t}=\frac{1}{2}\left[2 \pi \sqrt{\frac{\ell}{\mathrm{g}}}\right]+\frac{1}{2}\left[2 \pi \sqrt{\frac{\frac {\ell}{4}}{\mathrm{g}}}\right]$

$$ \begin{aligned} & =\pi\left[\sqrt{\frac{\ell}{\mathrm{g}}}+\frac{1}{2} \sqrt{\frac{\ell}{\mathrm{g}}}\right] \\ & =\frac{3}{2} \pi\left[\sqrt{\frac{\ell}{\mathrm{g}}}\right] \end{aligned} $$

$\therefore$ The time period of the required pendulum is

$$ \begin{aligned} \mathrm{t}^{\prime}=6 \mathrm{t} & =9 \pi \sqrt{\frac{\ell}{\mathrm{g}}} \\ & =\pi \sqrt{\frac{81 \ell}{\mathrm{g}}}=2 \pi \sqrt{\frac{81 \ell}{4 \mathrm{~g}}} \\ & =2 \pi \sqrt{\frac{\ell^{\prime}}{\mathrm{g}}} \quad \text { where } \quad \ell^{\prime}=\frac{81}{4} \ell \end{aligned} $$

Thus the length of the required pendulum is $\frac{81}{4} \ell$ or $(20.25 \ell)$

Example-21:

A solid rectangular block of wood (density $=\sigma$ ), of dimensions L, B and $\mathrm{H}$, is floating in water $($ density $=\rho$ ) with its ’ $H$ ’ side vertical. The block is depressed slightly, (through a vertical distance $z$ ) and ’let-go’. The nature of the resulting oscillations of the block, and the time period, $\mathrm{T}$, of these oscillations, are, respectively,

(1) Periodic but not SHM; $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{H \sigma}}{\rho \mathrm{g}}}$

(2) Periodic but not SHM; $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{H} \rho}{\sigma g}}$

(3) $\mathrm{SHM} ; \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{H} \rho}{\sigma g}}$

(4) $\mathrm{SHM} ; \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{H} \sigma}{\rho \mathrm{g}}}$

Show Answer

Solution:

The block, would initially, be floating vertically, with a height $h$ under water, such that

$$ \begin{aligned} & (\mathrm{LBh} \rho) \mathrm{g}=(\mathrm{LBH} \sigma) \mathrm{g} \\ & \therefore \mathrm{h}=\mathrm{H} \frac{\sigma}{\rho} \end{aligned} $$

When the block is depressed through a vertical distance $\mathrm{z}$; its ’new height’, under water, becomes $(\mathrm{h}+\mathrm{z})$. The upthrust (due to the displaced water) now becomes $[\mathrm{LB}(\mathrm{h}+\mathrm{z}) \rho] \mathrm{g}$ while the weight of the block continues to be $[\mathrm{LBH} \sigma] \mathrm{g}$. The net upward (or restoring) force, $\mathrm{F}$, acting on the block, is

$$ \begin{aligned} \mathrm{F}=\mathrm{LB} & (\mathrm{h}+\mathrm{z}) \rho \mathrm{g}-\mathrm{LBH} \sigma \mathrm{g} \\ & =(\mathrm{LB} \rho) \mathrm{gz} \quad(\because \mathrm{LBh} \rho \mathrm{g}=\mathrm{LBH} \sigma \mathrm{g}) \end{aligned} $$

Thus $\mathrm{F} \alpha \mathrm{z}$ and $\mathrm{F}$ is directed opposite to $\mathrm{z}$. Hence the oscillations of the block are simple harmonic in nature.

The equation of motion of the block is

$$ (\mathrm{LBH} \sigma) \frac{\mathrm{d}^{2} \mathrm{z}}{\mathrm{dt}^{2}}=-(\mathrm{LB} \rho \mathrm{g}) \mathrm{gZ} \quad(\because \mathrm{LBH} \sigma=\mathrm{M}=\text { mass of block }) $$

or $\quad \frac{\mathrm{d}^{2} \mathrm{z}}{\mathrm{dt}^{2}}=-\left(\frac{\rho}{\sigma \mathrm{H}} \mathrm{g}\right) \mathrm{z}=-\omega^{2} g$

where $\omega^{2}=\left(\frac{\rho}{\sigma \mathrm{H}} \mathrm{g}\right)$

The time period, $\mathrm{T}$, of the oscillations of the block, is

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\sigma \mathrm{H}}{\rho \mathrm{g}}} $$

Now $\frac{\sigma H}{\rho}=h=$ The initial (equilibrium) ‘height’ of the block under water.

$$ \therefore \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{h}}{\mathrm{g}}} $$

[Note: The time period of oscillations of the block is identical with that of a simple pendulum of length $h$. We can, therefore say; “A block, floating in a liquid, and made to ‘oscillate’, as described, can be considered ’equivalent’ to a simple pendulum whose length equals the initial (equilibrium) ‘height’ of the block dipping inside the liquid’].

Example-22:

A large vessel, of a base volume $\mathrm{V}$, has a long narrow neck (having an area of cross section $=\mathrm{a}$ and a height $\mathrm{h}$, so that $\mathrm{ah}=\mathrm{v}$, the volume of the neck) of volume $\mathrm{v},(\mathrm{v}«$ V). The neck is closed by a stopper of mass $m$ and the vessel contains an ideal gas at a pressure $\mathrm{P}(\mathrm{P}=$ atmospheric pressure $)$. The stopper, initially at the top of the neck, is depressed slightly through a distance $\mathrm{z}$ and ’let-go’. The nature of the resulting oscillations of the stopper, and the time period, $\mathrm{T}$, of these oscillations, are, respectively

(1) Periodic but not SHM; $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{mV}}{\mathrm{Pa}^{2}}}$

(2) Periodic but not SHM; $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{Pa}^{2}}{\mathrm{mV}}}$

(3) $\mathrm{SHM} ; \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{mV}}{\mathrm{Pa}^{2}}}$

(4) SHM; $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{Pa}^{2}}{\mathrm{mV}}}$

Show Answer

Solution:

The initial pressure, and volume, of the ideal gas, contained in the vessel, are $\mathrm{P}$ and $(\mathrm{V}+\mathrm{v})$, respectively. When the stopper is depressed through a distance $z$, the volume of the gas becomes $[V+a(h-z)]$. Hence its pressure increases to $(\mathrm{P}+\Delta \mathrm{P})$ such that

$$ \begin{aligned} & {[\mathrm{P}+\Delta \mathrm{P}][\mathrm{V}+\mathrm{a}(\mathrm{h}-\mathrm{z})]=\mathrm{P}(\mathrm{V}+\mathrm{v})} \\ & \quad=\mathrm{P}[\mathrm{V}+\mathrm{ah}] \end{aligned} $$

[Note that we are assuming here that Boyle’s law remains valid, i.e., the slight depression of the stopper causes changes in the volume, and pressure, of the gas under isothermal conditions. This is a reasonable assumption as the slight depression of the stopper, in the narrow neck, is not likely to cause any noticeable change in the temperature of the gas].

Hence,

$$ -\mathrm{Paz}+\Delta \mathrm{P}[\mathrm{V}+\mathrm{a}(\mathrm{h}-\mathrm{z})]=0 $$

or

$$ \Delta \mathrm{P}=\frac{+\mathrm{Paz}}{[\mathrm{V}+\mathrm{a}(\mathrm{h}-\mathrm{z})]} \approx+\left(\frac{\mathrm{Pa}}{\mathrm{V}}\right) \mathrm{z} $$

$(\because \mathrm{V}»\mathrm{v}$ and $\mathrm{v}(=\mathrm{ah})>\mathrm{a}(\mathrm{h}-\mathrm{z}))$

The (slight) increase in pressure, of the gas inside the vessel, would exert an upward force, $\mathrm{F}$, on the stopper where $\mathrm{F}=(\Delta \mathrm{P}) \mathrm{a}$. The force, being upward, is a restoring force as it is trying to ‘restore’ the stopper back to its initial position. Also $F\left(\simeq \frac{\mathrm{P}}{\mathrm{V}} \mathrm{a}^{2} \mathrm{z}\right)$ is directly proportional to $\mathrm{z}$. Hence the oscillations, of the stopper, are simple harmonic in nature. The equation of motion, of the stopper, is

$\mathrm{m} \frac{\mathrm{d}^{2} \mathrm{z}}{\mathrm{dt}^{2}}=-\mathrm{F} \simeq-\left(\frac{\mathrm{P}}{\mathrm{V}} \mathrm{a}^{2}\right) \mathrm{z}$

$\therefore \frac{\mathrm{d}^{2} \mathrm{z}}{\mathrm{dt}^{2}}=-\left(\frac{\mathrm{Pa}^{2}}{\mathrm{mV}}\right) \mathrm{z}=-\omega^{2} \mathrm{z}$

where $\omega^{2}=\left(\frac{\mathrm{Pa}^{2}}{\mathrm{mV}}\right)$

The time period, T, of the (S.H.) oscillations of the stopper, is

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{mV}}{\mathrm{Pa}^{2}}} $$

[Note: We may also say that, Bulk modulus, B, is given by

$$ \mathrm{B}=\frac{-\Delta \mathrm{P}}{(\Delta \mathrm{V} / \mathrm{v})} $$

$\therefore \quad \Delta \mathrm{P}=-\mathrm{B} \frac{\Delta \mathrm{V}}{\mathrm{V}}=\frac{-\mathrm{Baz}}{\mathrm{V}}$

$\therefore \quad \mathrm{F}=\Delta \mathrm{Pa}=\frac{-\mathrm{Ba}^{2}}{\mathrm{~V}} \mathrm{z}=-\mathrm{kz}$

$\omega^{2}=\frac{\mathrm{Ba}^{2}}{\mathrm{mV}} \quad$ or $\quad \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{mV}}{\mathrm{Ba}^{2}}}$

Since $\mathrm{B}=\mathrm{P}$, for an ideal gas, under isothermal conditions, we get the same result as before].

Example-23:

A ‘U-tube’ of uniform area of cross-section A, is filled with an ideal a liquid of density $\rho$, such that the liquid level, is both the limbs, is at an equilibrium height, $\mathrm{H}$, above the base. Using a plastic spatula, the liquid, in one of the limbs, is depressed slightly, through a distance, $z$, and ’let-go’. The time period, $\mathrm{T}$, of the resulting oscillations, of the liquid in the U-tube, would than be

(1) directly proportional to A but inversely proportional to $\rho$.

(2) directly proportional to A but would be independent of $\rho$.

(3) inversely proportional to $\rho$ but would be independent of A.

(4) independent of both $\rho$ and A.

Show Answer

Solution:

When the liquid level is pushed down, by an amount $\mathrm{z}$ in one limb, it has to go up, by an amount $z$, in the other limb. [Ideal liquids are

(b) incompressible]. The weight, of the extra volume v (=A.2 z), of the liquid in one limb, provides the restoring force that tends to ‘push up’ the liquid that was pushed down by the spatula. This weight, therefore, provides a restoring force, $\mathrm{F}$, whose magnitude, is

$$ F=(v \rho) g=(2 A \rho g) z $$

The mass , M , of the liquid , set into oscillations , is the total mass (= A.d2H.ρ) of the qid in the U - tube Hence the equation of the motion, of the oscillating liquid, is

$$ \begin{aligned} & (2 \mathrm{AH} \rho) \frac{\mathrm{d}^{2} \mathrm{z}}{\mathrm{dt}^{2}}=-(2 \mathrm{~A} \rho \mathrm{g}) \mathrm{z} \\ & \text { or } \quad \frac{\mathrm{d}^{2} \mathrm{z}}{\mathrm{dt}^{2}}=\frac{-(2 \mathrm{~A} \rho \mathrm{g}) \mathrm{z}}{2 \mathrm{AH} \rho} \\ & =\frac{\mathrm{g}}{\mathrm{H}} \mathrm{z}=-\omega^{2} \mathrm{z} \end{aligned} $$

where $\omega^{2}=\frac{g}{H}$

The oscillations, of the liquid, are, therefore, simple harmonic in nature and have a time period, $\mathrm{T}$, given by

$$ \begin{aligned} & \mathrm{T}=\frac{2 \pi}{\omega} \\ & =2 \pi \sqrt{\frac{\mathrm{H}}{\mathrm{g}}} \end{aligned} $$

The time period thus depends on the initial height, $\mathrm{H}$, of the liquid level an either limb but in independent of both the area of cross section (A) of the tube and the density $(\rho)$ of the liquid poured in it.

Free Vibrations

When a ‘system’, capable of oscillating is displaced from its normal (equilibrium) position and ’let-go’, it starts oscillating. These oscillations are due to the ‘restoring forces’, set up within the system, because of its displacement from its equilibrium position. We call such oscillations, of a ‘system’, as its ‘free’, or, ’natural’, oscillations.

The basic feature, of the free, or natural, oscillations (of a given system), is that these oscillations take place without any ’external force’ acting on the system. These oscillations are due, purely to the (internal) ‘restoring forces’ developed within the system. The time period and frequency of oscillations, of the ‘free oscillations’ of a system, are a characteristics of the system and depend only on its characteristics features.

It is important to note that the concept of free oscillations is, strictly speaking, an idealized concept. The total absence of external forces, on a system executing free oscillations, is a ‘requirement’ that is seldom met in actual situations. Thus a simple pendulum, displaced and ’let-go’, is said to execute ‘free’ oscillations. However ’external forces’, like the damping due to air / surrounding media, are necessarily acting on the system. These ‘damping forces’ cause a progressive reduction in the ‘amplitude’ of oscillations and also, to a small extent), affect the time period and frequency of the oscillations. However, for systems like a simple pendulum oscillating in air, the ‘damping effects’ are very small and can be neglected. Oscillations, of a system, under such conditions, are a ‘close approximation’ to the ideal ‘free oscillations’.

The only force, acting on a freely oscillating system, is the (net) restoring force (an internal force) acting on it. The equation of motion, of a freely oscillating system, therefore, has the form

$$ \mathrm{m} \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-\mathrm{F}(x) $$

The simplest functional form, of the restoring force, is $\mathrm{F}(x)=\mathrm{k} x$. The equation of motion, in this case, has the form

$$ \begin{aligned} & \mathrm{m} \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-\mathrm{k} x \\ & \text { or } \quad \mathrm{m} \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}+\omega^{2} x=0 \quad\left(\omega^{2}=\frac{\mathrm{k}}{\mathrm{m}}\right) \end{aligned} $$

This, as we now know, is the equation of motion of a simple harmonic motion, having a time period

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}}} $$

and a frequency

$$ v=\frac{\omega}{2 \pi}=\frac{1}{2 \pi} \sqrt{\frac{k}{m}} $$

The constant, $\mathrm{k}$, in these expressions, is numerically equal to the restoring force per unit displacement. It is referred to as the ‘force constant’/ spring constant / stiffness for the oscillating system, under consideration. The constant $\mathrm{m}$, the mass of the oscillating sytem, is sometimes also referred to as the ‘inertia factor’.

Damped Oscillations

We have seen above that the concept of ‘free oscillations’, strictly speaking, is an idealized concept. The oscillating system is generally oscillating in a medium (usually air) and, therefore, experiences some external force, due to the viscosity, etc., of the surrounding medium. Because of these sampling / dissipative forces, the energy, associated with oscillations, keeps on decreasing; this effect is usually observed through a progressive decrease in the ‘amplitude’ of oscillations. This rate of decrease of the amplitude may be small / large, depending on whether the damping / dissipative forces are small or large.

Damping forces cause, not only a decrease in the amplitude of oscillations, but also an increase in the time period of oscillations. The frequency of oscillations, consequently, decreases.

The exact form of the expression, for the damping forces, is usually difficult to write. One would need to know the exact nature of the ‘damping force’ and the ‘force law’ governing it (‘information’, that is usually not available). Quite often, however, the damping effects are due to the ‘viscosity’ of the surrounding medium. The instantaneous damping force, due to viscosity, is usually taken to be proportional to the

instantaneous velocity (i.e., the instantaneous value of $\frac{\mathrm{d} x}{\mathrm{dt}}$ ). We may, therefore, say that the equation of motion of a particle,executing a damped simple harmonic motion, may be written as

$$ \mathrm{m} \frac{\mathrm{d}^{2} x}{\mathrm{dt}}=-\alpha \frac{\mathrm{d} x}{\mathrm{dt}}+(-\mathrm{k} x) $$

where $\alpha$ is the ‘damping constant’ (dependent, usually, on the coefficient of viscosity) of the medium and $\mathrm{k}$ is the ‘force constant’, characteristics of the oscillating system.

We, therefore, have

$$ \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}+\frac{\alpha}{\mathrm{m}} \frac{\mathrm{d} x}{\mathrm{dt}}+\frac{\mathrm{k}}{\mathrm{m}} x=0 $$

or $\quad \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}+2 \mathrm{~b} \frac{\mathrm{d} x}{\mathrm{dt}}+\omega^{2} x=0$

(Here $2 b=\frac{\alpha}{m}$ and $\omega^{2}=\frac{k}{m}$ )

The ‘solution’, of this equation, for the ‘damped simple harmonic motion’, has the form:

$$ x=\mathrm{ae}^{-\alpha \mathrm{t}} \sin \left[\sqrt{\omega^{2}-\mathrm{b}^{2}} \mathrm{t}+\phi\right] $$

We notice two important features of this ‘solution’.

(1) The amplitude, A, of oscillations, now equals $\mathrm{ae}^{-\alpha t}$. It is, therefore, an exponentially decreasing function of time. The magnitude, of the rate of decrease of A with time, i.e. $\frac{\mathrm{dA}}{\mathrm{dt}}\left(=\mathrm{a} \alpha \mathrm{e}^{-\alpha t}\right)$, therefore, depends on $\alpha$, the ‘damping constant’ of the medium.

(2) The time period, $T$, of oscillations, is now governed by the equality.

$$ \begin{aligned} & \left(\sqrt{\omega^{2}-b^{2}}\right)(t+T)-\left(\sqrt{\omega^{2}-b^{2}}\right) t=2 \pi \\ & \therefore \quad T=\frac{2 \pi}{\sqrt{\omega^{2}-b^{2}}} \end{aligned} $$

The time period is thus seen to depend on $\mathrm{b}(\alpha / 2 \mathrm{~m})$, a term dependent on the ‘damping constant’ of the medium. Damping is seen to increase the time period to a value more than the “free time period value’ $\left(=\frac{2 \pi}{\omega}\right)$; the frequency of oscillations, consequently, decreases.

The ‘displacement-time’ graph, for a damped harmonic motion, has the form shown. The dotted (curved) lines, (which correspond to the curve joining the successive amplitude values of the oscillations) are nothing but the decaying / decreasing exponential curves.

Forced Oscillations

A system is said to execute ‘forced oscillations’ if there is an external force, acting on it, while it is executing its oscillations. This external force may be:

(1) A periodic force that is applied to just ‘offset’ the effects of damping forces acting on an otherwise ‘freely oscillating system’. This external force may keep on supplying as much energy to the system as it loses due to the damping / dissipative forces acting on it. The system would then keep on oscillating with a ‘constant amplitude’ as long as the external periodic force keeps on acting on it.

(2) Aperiodic force that keeps on acting continuously on the system and, thereby, makes it oscillate with its own time period / frequency. The oscillation characteristics (amplitude, time period / frequency), of the system are then controlled / governed by the strength and time period / frequency of the applied periodic force.

It is the second type of oscillations, executed and controlled, through the externally applied periodic force, that are usually referred to as the ‘forced oscillations’ of a given system. As we have already noted, the amplitude, of such forced oscillations, will depend on the strength of the externally applied periodic force; the time period / frequency, of such forced oscillations will depend on the time period / frequency of the externally applied periodic force.

The externally applied periodic force, may, in general, be any periodic function of time. In its simplest form, it may be a sine or cosine function of time. Assuming such a sinusoidal form for the externally applied periodic force, the general equation of motion, of an oscillating system of mass M, may be written as

$\mathrm{m} \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=\mathrm{f} _{0}^{\prime} \sin \left(\omega _{0} \mathrm{t}\right)-\alpha \frac{\mathrm{d} x}{\mathrm{dt}}-\mathrm{k} x$

or $\quad \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}+2 \mathrm{~b} \frac{\mathrm{d} x}{\mathrm{dt}}+\omega^{2} x=\mathrm{f} _{0} \sin \omega _{0} \mathrm{t}$

(where $2 b=\frac{\alpha}{m}, \omega^{2}=\frac{k}{m}$, and $f _{0}=\frac{f _{0}^{\prime}}{m}$ )

This general equation may be solved by using the appropriate techniques for solving differential equations of this form. The appropriate interpretation of the ‘solution’, enables us to understand the characteristics and features of ‘forced oscillations’.

There is one important type of forced oscillations, that we talk about, (in some detail), now. The ‘forced oscillations’, of a give system, can become its ‘resonant oscillations’, if the frequency of the externally applied periodic force, matches its natural frequency of oscillations. Such resonant oscillations play an important role in very many practical situations.

Resonance

The phenomenon of ‘resonance’ is a special case of ‘forced oscillations’. We have already noted that a ‘system’, capable of executing an oscillating motion,

(1) oscillates with its characteristic natural frequency ( say $v _{0}$ ) if it is ’let-go’ after being displaced from its normal equilibrium position. This natural frequency, generally, depends on the stiffness (or force constant) and the ‘inertia factor’ (or mass) of the oscillating system.

(2) oscillates with the frequency (say $v$ ) of the external periodic force if this (periodic) force acts continuously on the oscillating system.

We can have a special situation in which the frequency $(v)$ of the external periodic force matches the natural frequency $\left(v _{0}\right)$ of the oscillating system. In such a case, the amplitude of oscillations, of the system, becomes quite large. We call this special type of forced oscillations as ‘resonant oscillations’.

An important point here is worth noting. We have already seen that free, or natural, oscillations are an idealization; any oscillating system is, almost invariably, oscillating under the action of some (external) damping force. This ‘damping force’ increases the time period and decreases the frequency in comparison to their ideal (zero damping) values. The external periodic force will cause, such a ‘practical’ oscillating system, to execute resonant oscillations, when its frequency, matches the modified (because of damping) ’natural’ frequency of the oscillating system.

The phenomenon of ‘resonance’ is observed, and put to use, in a wide variety of practical situations.

Examples and Uses of Resonance

A familiar example of ‘resonance’ is in the ’tuning’ of a radio. When the ’tuning circuit’, in a radio receiver, is adjusted to match the frequency of the desired transmitter, the ‘output’ of the receiver is (almost) exclusively that of this particular transmitter.

Resonance can cause dangerous rolling of ships and boats and dangerous vibrations of bridges. Steps are taken to ensure that there is very little chance of such objects executing resonant oscillations.

Musical instruments, particularly the stringed ones and tuning forks, are often made to use the phenomenon of resonance to give stronger and / or more melodious ‘outputs’.

Children often use the phenomenon of ‘resonance’ to make the ‘swing’ have a large and sustained amplitude of its vibrations.

Microwave ovens also use ‘microwaves’ of appropriate frequency so as to make the water molecules, present in almost all food items, execute (large amplitude) resonant oscillations. This, is turn, helps in heating the food items.

Wave Motion

We all know that if one end of a metal rod is kept in contact with a source of heat, the other end too becomes hot after sometime. We say that this is because of the ‘flow’ of ‘heat energy’ through the rod. The ‘particles’ of the rod, in contact with the heat source, ’take in’ heat energy from it, and pass this to their immediate neighboring particles. These particles, in turn, pass the heat energy to their ‘immediate neighbors’, and so on, till the heat energy reaches the other end of the rod.

There is ‘something special’ about this ‘flow’ of heat energy. The heat energy flows from ‘particle to particle without any of the particles leaving their respective mean positions. The constituent particles, of the metal rod,just oscillate about their ‘mean positions’ but keep on passing the heat energy from one point to the next. We thus get a transfer of (heat) energy, from one end of the rod to its other end, without any material movement of the particles of the rod.

Is it possible to transfer mechanical energy, too, from one point in a medium to another, without any material movement of the particles of the medium? The answer is ‘yes’. It is often observed that disturbance, ‘created’ at one point in the medium, moves ‘on and on’ and affects the ‘other points’ in the medium. A simple practical example of this is the movement of the ‘disturbance’, created at one point, on the water surface (in a lake / pond etc.), by the impact of a stone. The mechanical energy, associated with the (created) disturbance, passes on all over the water surface without any actual movement of the particles of water on the surface. We call this method of transfer of energy, from one point to another, in a medium, as ‘wave motion’.

The important thing to note about ‘wave motion’ is this ‘waves’ help to transfer energy, from one place to another, without the movement, or transfer, of any ‘physical entity - ’the particles’ - of the medium. ‘Wave-motion’ thus provides an alternative natural method of ’transfer of energy’. [The other method (involving the movement of material particles) is to impart kinetic energy to the particles at one point, and let these particles move over, and carry, their kinetic energy to ‘another point’].

Sustained Wave Motion

We all know that the ‘waves’, or ‘ripples’, created on the surface of water by the throwing a stone on it, last but for a ‘short while’. A momentary disturbance creates ‘waves’ that ‘fade away’ quite soon. It is clear then that it is only a sustained disturbance that can cause a sustained wave-motion. If the sustained disturbance is a periodic disturbance, we would have a (sustained) periodic wave motion in the medium.

The simplest periodic oscillation, as we now know, are simple harmonic oscillations. The waves, having a ‘simple harmonic disturbance’ as their ‘source’ (cause), are known as ‘simple harmonic waves’. These waves are the simplest type of periodic waves. We, therefore, study the basic details, and ideas, of wave motion through a detailed understanding of the characteristics of ‘simple harmonic waves’.

Simple Harmonic Waves

When the periodic disturbance, ‘creating’ waves in a given medium, is a simple harmonic motion, the resulting wave is referred to as a ‘simple harmonic wave’.

We can easily get the equation for a ‘one dimensional’ simple harmonic wave. Let the periodic disturbance, creating a wave, be a simple harmonic oscillation having the origin as its mean, or equilibrium, position. If the speed of propagation, of the disturbance, in the given medium be $\mathrm{v}$, we can make the following two statements:

(1) The disturbance, created at the origin at the time $t=0$, will reach a point, at a distance $x$ from the origin, at a time $\mathrm{t}$ where $\mathrm{t}=\frac{\mathrm{x}}{\mathrm{v}}$.

(2) The disturbance, at the point $x$, at time $\mathrm{t}$, was the disturbance, at the origin, at a time $\mathrm{t}^{\prime}$ where $\mathrm{t}^{\prime}=\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)$

The second statement is, in a way, the ‘reverse’ of the first statement. It enables us to obtain the equation of the $(\mathrm{SH})$ wave.

We notice that disturbance at $(x=x)$, at $(t \Rightarrow t)=$ disturbance at the origin $(x=0)$, at $\left(t=\Rightarrow t^{\prime}\right)$ where $\mathrm{t}^{\prime}=\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)$

The disturbance, at the origin, (being a S.H motion) has the form

$$ \xi=\mathrm{A} \sin \omega \mathrm{t} $$

Hence the value of this disturbance, at $(x=0)$ and at time instant $\mathrm{t}^{\prime}\left(\mathrm{t}^{\prime}=\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)\right)$, is

$$ \xi=\mathrm{A} \sin \omega \mathrm{t}^{\prime}=\mathrm{A} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right) $$

This equation now gives the disturbance, at any point $(x=x)$ at any time $(t=t)$. It is, therefore, regarded as the equation of a simple harmonic wave. Thus the equation, of a (one-dimensions) simple harmonic wave, is

$$ \xi=\mathrm{A} \sin \left[\omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)\right] $$

It is important to remember that this equation corresponds to a simple harmonic wave propagating along the positive direction of $x$-axis.

[Note: It is desirable to remember that when there is a negative sign (between the ’ $t$ ’ and ’ $x$ ’ terms (in the equation of a (simple harmonic wave) we have a wave propagating along the positive $x$-axis. A positive sign, (between the $t$ and $x$ terms) would, therefore, represent a wave propagating along the negative $x$ axis].

Differential Equation for Wave-Motion

We start with the equation for a simple harmonic wave. This equation (for a wave propagating along the positive $x$-axis) has the form:

$$ \xi=\left[\mathrm{A} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)\right] $$

$\xi$ is thus a function of time, $\mathrm{t}$, as well as the position co-ordinate, $x$. We, therefore, have

$$ \frac{\partial \xi}{\partial x}=\frac{-\mathrm{A} \omega}{\mathrm{v}} \cos \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right) $$

Also,

$$ \begin{aligned} & \quad \frac{\partial \xi}{\partial \mathrm{t}}=+\mathrm{A} \omega \cos \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right) \\ & \therefore \quad \frac{\partial^{2} \xi}{\partial x^{2}}=-\mathrm{A} \frac{\omega^{2}}{\mathrm{v}^{2}} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right) \\ & \text { and } \frac{\partial^{2} \xi}{\partial \mathrm{t}^{2}}=-\mathrm{A} \omega^{2} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right) \end{aligned} $$

We thus find that

$$ \frac{\partial^{2} \xi}{\partial x^{2}}=\frac{1}{\mathrm{v}^{2}} \frac{\partial^{2} \xi}{\partial \mathrm{t}^{2}} $$

We call this equation as the differential equation for (one-dimensional) wave motion. It turns out that the differential form of the wave equation, namely

$$ \frac{\partial^{2} \xi}{\partial x^{2}}=\frac{1}{\mathrm{v}^{2}} \frac{\partial^{2} \xi}{\partial \mathrm{t}^{2}} $$

is also valid for waves that may not be simple harmonic waves. We, therefore, regard the above differential equation as the ‘general equation’ for (one-dimensional) wave motion. The equation of the simple harmonic wave, namely,

$$ \xi=\mathrm{A} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right) $$

is just one of the many possible ‘solutions’ of this differential equation.

Definitions of Some Terms Connected with Wave Motion

We now get familiar with some terms, often used, in wave motion.

Amplitude (A): This equals the ‘maximum disturbance’ (or maximum displacement), of any particle of the medium, from its normal or equilibrium position. It equals the maximum displacement (from the mean position) of the particle executing the (simple harmonic) oscillations that initiate the wave motion.

Wave Length $(\lambda)$ : This equals the (regular and minimum) separation between any two particles of the medium, that are in identical ‘phase’ of their respective oscillations.

Time Period (T) : The time period ( $\mathrm{T}$ ), of a wave, may be thought of as the time taken by the wave propagating with a speed $v$, (the wave speed) to cover a distance equal to the wave length of the wave. We thus notice that

$$ \mathrm{T}=\lambda / \mathrm{v} $$

Frequency $(v)$ : This equals the number of ‘complete oscillations’, executed by the wave, in one second. It follows that

$$ v=\frac{1}{\mathrm{~T}} \quad \text { or } \quad \mathrm{T}=\frac{1}{v} $$

We thus find (from $\mathrm{T}=\frac{\lambda}{\mathrm{v}}$ ) that $\mathbf{v}=\mathbf{n} \boldsymbol{\lambda}$

Angular Frequency ( $\omega$ ): This equals $2 \pi$ times the frequency of the wave motion. Thus

$$ \omega=2 \pi v $$

Wave Number (k) : This equals $2 \pi$ times the reciprocal of the wave length. Thus

$$ \mathrm{k}=2 \pi \frac{1}{\lambda}=\frac{2 \pi}{\lambda} $$

Phase : For the S.H. wave, we have the equation

$$ \xi=\mathrm{A} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right) $$

The argument of the sine term, namely

$$ \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right) $$

represents the ‘phase’ of the wave.

The ‘phase difference’, for a wave, can be defined in two ways:

(i) The phase difference (at a given location) depends on the time difference. Thus

$$ \phi _{1}=\omega\left(\mathrm{t} _{1}-\frac{x}{\mathrm{v}}\right) $$

and $\phi _{2}=\omega \frac{\left(\mathrm{t} _{2}-x\right)}{\mathrm{v}}$

$\therefore\left(\phi _{1}-\phi _{2}\right)=\omega\left(\mathrm{t} _{1}-\mathrm{t} _{2}\right)$

We have,

If $\left(\mathrm{t} _{1}-\mathrm{t} _{2}\right)=\mathrm{nT},(\mathrm{n}=0,1,2,3, \ldots \ldots$.

$$ \left(\phi _{1}-\phi _{2}\right)=\omega \cdot \mathrm{nT}=\mathrm{n} \cdot 2 \pi \quad\left(\because \mathrm{T}=\frac{2 \pi}{\omega}\right) $$

The particle, at a given location, is, therefore, in the ‘same phase’ at time instants that are separated by an integral multiple of the time period of the wave.

(ii) The phase difference (at a given time instant) depends on the locations of the two points. Thus

$$ \phi _{1}=\omega\left(\mathrm{t}-\frac{x _{1}}{\mathrm{v}}\right) $$

and $\quad \phi _{2}=\omega\left(\mathrm{t}-\frac{x _{2}}{\mathrm{v}}\right)$

$\therefore \quad\left(\phi _{1}-\phi _{2}\right)=\frac{\omega}{\mathrm{v}}\left(x _{2}-x _{1}\right)$

Now $\frac{\omega}{\mathrm{v}}=\frac{2 \pi v}{v \lambda}=\frac{2 \pi}{\lambda}$

(We have seen above that $v=v \lambda$, i.e., speed of wave equals the product of its frequency and its wave length)

$\therefore\left(\phi _{1}-\phi _{2}\right)=\frac{2 \pi}{\lambda}\left(x _{2}-x _{1}\right)$

If $\left(x _{2}-x _{1}\right)=\mathrm{n} \lambda,(\mathrm{n}=0,1,2,3, \ldots \ldots$.$) , we have$

$\left(\phi _{1}-\phi _{2}\right)=\frac{2 \pi}{\lambda}(\mathrm{n} \lambda)=2 \pi \mathrm{n}$

It follows that, at a given time instant, two particles, that are separated by a distance equal to an integral multiple of the wavelength, would be in the ‘same phase’. This result, incidentally is, in tune with the definition of ‘wavelength’.

Inter Relations between the Above Terms

We rewrite the different relations between the various terms defined above. We have

(i) $\quad \mathrm{T}=\frac{1}{v} \quad$ and $\quad v=\frac{1}{\mathrm{~T}}$

(ii) $\omega=2 \pi v ; v=\frac{\omega}{2 \pi}$ and $\mathrm{T}=\frac{2 \pi}{\omega}$

(iii) $\mathrm{k}=\frac{2 \pi}{\lambda}$ and $\lambda=\frac{2 \pi}{\mathrm{k}}$

(iv) $v=\frac{\lambda}{\mathrm{T}}=v \lambda$

(v) $\frac{\omega}{\mathrm{k}}=\frac{2 \pi \nu}{(2 \pi / \lambda)}=v \lambda=\mathrm{v}$

(vi) Phase of a given point (at a given location, (say $x)$ ) at a given time instant, (say $\mathrm{t})=\omega\left(\mathrm{t}-\frac{\mathrm{x}}{\mathrm{v}}\right)$

$$ \begin{aligned} & =2 \pi v\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right) \\ & =2 \pi\left(v \mathrm{t}-\frac{v x}{\mathrm{v}}\right) \\ & =2 \pi\left(\frac{\mathrm{t}}{\mathrm{T}}-\frac{x}{\mathrm{v}}\right) \\ & =(\omega \mathrm{t}-\mathrm{k} x) \end{aligned} $$

Different forms of the Equation of a (one-dimensional) Simple Harmonic Wave

The equation, of a simple harmonic wave, has been obtained as

$$ \xi=\mathrm{A} \sin \left(\mathrm{t}-\frac{x}{\mathrm{v}}\right) $$

The term $\omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)(=\phi$, say $)$, represents the ‘phase’ of the wave. This, as noted above, can be written in a variety of ways. Hence the equation, for a simple harmonic wave, can be rewritten in many different forms. We have:

$$ \begin{aligned} & \xi=A \sin \left[\omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)\right] \\ & =\mathrm{A} \sin \left[2 \pi v\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)\right] \\ & =\mathrm{A} \sin \left[2 \pi\left(v \mathrm{t}-v \frac{x}{\mathrm{v}}\right)\right] \\ & =\mathrm{A} \sin \left[2 \pi\left(\frac{\mathrm{t}}{\mathrm{T}}-\frac{x}{\lambda}\right)\right] \\ & =\mathrm{A} \sin [(\omega \mathrm{t}-\mathrm{k} x)] \end{aligned} $$

We may use any of these forms; the form used depends on the nature of the problem.

Longitudinal and Transverse Waves

A wave is said to be a longitudinal wave if the direction, of ‘displacement’, of the ‘particles of the medium’, is the same as the direction along which the wave is propagating.

Sound waves are a well known example of longitudinal waves.

A wave is said to be a transverse wave if the direction, of ‘displacement’, of the ‘particles of the medium’, and the direction of propagation of the wave, are along mutually perpendicular directions.

Light waves are known to be transverse waves.

[Note: The phenomenon, or ‘property’, that can help us polarization he longitudinal, or transverse, nature of a wave, is the phenomenon of ‘polarization’. It is only, transverse waves that can be polarized; longitudinal waves do not exhibit the phenomenon of polarization.

It follows that if a wave exhibits the phenomenon of ‘polarization’, it has to be a transverse wave].

Speed of a Wave

The speed with which the ‘disturbance’, associated with a wave motion, propagates through a medium, is known as the speed of the wave. It depends upon the nature, and properties, of the medium. It turns out that, $v$, the speed of propagation of a (mechanical) wave, in a medium, is given by

$$ v=\sqrt{\frac{E}{\rho}} $$

Here $\mathrm{E}$ is the (relevant) modulus of elasticity of the medium and $\rho$ is its density.

For solids, E can correspond to any of its three moduli of elasticity: the Young’s modulus (Y), the Bulk modulus $(\mathrm{K}$ ) or the Shear modulus $(\eta)$. Solids, therefore permit the propagation of longitudinal, as well as transverse, waves through them.

For gases, the only (relevant) modulus of elasticity is the bulk modulus; gases, therefore, permit the propagation of longitudinal waves only. Sound waves, that normally propagate through air, are longitudinal waves only.

It is interesting to note here that the speed of propagation of electromagnetic waves (that do not require a medium for their propagation) also depends on the medium through which they are propagating. The relevant formula, for their speed of propagation, is

$$ \mathrm{v}=\frac{1}{\sqrt{\mu \varepsilon}} $$

Here $\mu$ is the magnetic permeability of the medium and $\varepsilon$ is the (electric) permittivity of the medium. For vacuum, the corresponding formula is

$$ \mathrm{v}(=\mathrm{c})=\frac{1}{\sqrt{\mu _{0} \varepsilon _{0}}} $$

The speed, c, the speed of propagation of all types of e.m. waves, in vacuum, is a universal constant. It also represents the maximum speed with which any signal, information or phenomenon can propagate in nature. Einstein postulated that the speed of propagation of light (or any other e.m. wave) in vacuum, is same for ‘ALL’ observers, irrespective of whether they are at rest or in motion.

The ratio, of the speed of light in vacuum $(=\mathrm{c})$ to its speed in a given medium, equals the absolute refractive index $(=n)$ of that medium. We can write

$$ \begin{aligned} & \mathrm{n}=\frac{\mathrm{c}}{\mathrm{v}}=\frac{1}{\sqrt{\mu _{0} \varepsilon _{0}}} \cdot \sqrt{\mu \varepsilon} \\ & =\left(\frac{\mu}{\mu _{0}}\right)^{1 / 2}\left(\frac{\mathrm{e}}{\varepsilon _{0}}\right)^{1 / 2}=\sqrt{\mu _{\mathrm{r}} \varepsilon _{\mathrm{r}}} \end{aligned} $$

Here $\mu _{\mathrm{r}}\left(=\frac{\mu}{\mu _{0}}\right)$ and $\varepsilon _{\mathrm{r}}\left(=\frac{\varepsilon}{\varepsilon _{0}}\right)$, are known as the relative magnetic permeability and relative (electric) permittivity of the given medium.

Speed of Sound in Gases

The speed of sound, in gases, is given by

$$ \mathrm{v}=\sqrt{\frac{\mathrm{K}}{\rho}} $$

where $\mathrm{K}=$ bulk modulus and $\rho=$ density of gas

Using the Boyle’s law equation, (valid under isothermal conditions), $\mathrm{PV}=$ constant, along with the definition of bulk modulus $\left(\mathrm{K}=\frac{\Delta \mathrm{P}}{(-\Delta \mathrm{V} / \mathrm{V})}\right)$, we get

$\mathrm{K}=\mathrm{P}$ (under isothermal conditions)

$$ \therefore \quad v=\sqrt{\frac{P}{\rho}} $$

This formula, for the speed of sound in gases, was first given by Newton and is known as Newton’s formula for the speed of sound in air (and other gases)

Using the appropriate values for $\mathrm{P}$ and $\rho$, this formula gives the speed of sound, in air, under normal conditions, as close to $280 \mathrm{~m} / \mathrm{s}$. This value, however, is far too small compared to the experimentally determined value of $\mathrm{v}$, which is close to $330 \mathrm{~m} / \mathrm{s}$.

It was Laplace who suggested that one needs to assume that the propagation of sound, through air, takes place under adiabatic (and not isothermal, (as assumed by Newton)) conditions. The appropriate equation is, therefore $\mathrm{PV}^{\gamma}=$ constant (and not $\mathrm{PV}=$ constant). From this equation, we get $\mathrm{K}\left(=\frac{\Delta \mathrm{P}}{(-\Delta \mathrm{V} / \mathrm{V})}\right)$ as $\gamma \mathrm{P}$. Hence the formula, for the speed of sound, takes the form

$$ \mathrm{v}=\sqrt{\frac{\gamma \mathrm{P}}{\rho}} $$

This formula gave a value of a v close to its experimentally measured value. It is, therefore, now taken as the accepted formula for the speed of sound in gases.

Conclusions Based on Laplace’s Formula

Laplace’s formula, for the speed of sound in air (and other gases) is

$$ \mathrm{v}=\sqrt{\frac{\gamma \mathrm{P}}{\rho}} $$

From this formula, and the known formulae for gases, we can conclude that

(i) Speed of sound, in a given gas, does not change with ‘change in pressures’ (This is because a change of pressure causes a proportionate change in density; the ratio $\frac{\mathrm{P}}{\rho}$, therefore, remains constant).

(ii) The speed of sound, in a given gas, depends on its temperature (on the kelvin scale) as per the relation

$$ \frac{\mathrm{v} _{\mathrm{T}}}{\mathrm{v} _{0}}=\sqrt{\frac{\mathrm{T}}{\mathrm{T} _{0}}} $$

i.e., the speed of sound, in a given gas, is directly proportional to the square root of its absolute (or kelvin) temperature.

One can also conclude that the presence of humidity (i.e., water vapour), in air, leads to an increase in the speed of sound.

Speed of Waves in a Stretched String

When a string, having a linear mass density $m$ (i.e. $m=$ mass per unit length of the string), is stretched by a tension $T$, the speed of propagation of waves, through it, is given by

$$ v=\sqrt{\mathrm{T} / \mathrm{m}} $$

Remembering that the relevant modulus of elasticity, for a string, is the Young’s modulus of its material, it is easy to see that this formula is consistent with the formula

$$ v=\sqrt{\frac{Y}{\rho}} $$

This is so because

$$ \mathrm{m}=\left(\pi \mathrm{r}^{2} \times 1\right) \rho $$

and $\quad \mathrm{Y}=\frac{\mathrm{T}}{\pi \mathrm{r}^{2}} \times \frac{1}{\Delta \ell}$

Taking $\Delta \ell=1$, we get

$\mathrm{T}=\pi \mathrm{r}^{2} \mathrm{Y} \times 1$

$\therefore \frac{T}{m}=\frac{\pi r^{2} Y}{\left(\pi r^{2} \times 1\right) \rho}=\frac{Y}{\rho}$

$\therefore \quad v=\sqrt{\frac{Y}{\rho}}=\sqrt{\frac{T}{m}}$

Reflection of Waves

Whenever waves propagating in a given medium, reach its boundary, or interface, with another medium, they can get reflected (as well as refracted). The reflection of waves takes place as per the usual law of reflection. The angle of reflection equals the angle of incidence.

The reflected wave would, obviously, be propagating in a direction reverse of that of the incident wave. There is, however, another interesting fact, about reflection of waves, that needs to be carefully understood and noted. This is as follows:

(i) The reflection of waves may take place when a wave, propagating in a rarer medium, encounters an interface which has a denser medium on the other side. The reflected waves then not only reverse their direction of propagation; they also undergo a ‘reversal of their phase’, i.e., the ‘phase’, of the reflected wave, differs from that of the incident wave, by $\pi$. Hence if the equation of the incident (S.H) wave is

$$ \xi _{\mathrm{i}}=\mathrm{A} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right) $$

The equation of the reflected wave (reflected at a ‘rarer to denser’ boundary), would be

$$ \xi _{\mathrm{R}}=\mathrm{A} \sin \left[\omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)+\pi\right] $$

(The change of sign, of the $x$-term, is because of a reversal in the direction of the propagation)

We may also write

$$ \xi _{\mathrm{R}}=-\mathrm{A} \sin \omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right) $$

For this case, if the incident wave were a wave propagating along the negative $x$-axis, its representation, as well as that of its reflected wave (reflected from a rarer to a denser interface) would be represented by the equations:

$$ \xi _{\mathrm{i}}=\mathrm{A} \sin \omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right) $$

and $\quad \xi _{\mathrm{R}}=\mathrm{A} \sin \left[\omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)+\pi\right]$

$$ =-\mathrm{A} \sin \left[\omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)\right] $$

(ii) When the reflection of waves takes place at ‘a denser to a rarer’ interface, the reflected wave just reverses its direction of propagation without any reversal, or change, of phase. In this case, if the incident wave were represented by

$$ \xi _{\mathrm{i}}=\mathrm{A} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right) $$

The reflected wave would be

$$ \xi _{\mathrm{R}}=\mathrm{A} \sin \omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right) $$

Similarly, for an incident wave propagating along the negative $x$-axis, the equations, of the incident and reflected waves would be

$$ \xi _{\mathrm{i}}=\mathrm{A} \sin \omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right) $$

and $\xi _{\mathrm{R}}=\mathrm{A} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)$

These results can be summarized, in a tabular form, as follows:

Nature of Reflection	Whether there is any ‘reversal’ of		Equation of
	Direction of Propagation	Phase	Incident Wave	Reflected Wave
From Denser to Rarer Interface	(i) Yes	No	$\xi _{\mathrm{i}}=\mathrm{A} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)$	$\xi _{\mathrm{R}}=\mathrm{A} \sin \omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)$
	(ii) Yes	No	$\xi _{\mathrm{i}}=\mathrm{A} \sin \omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)$	$\xi _{\mathrm{R}}=\mathrm{A} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)$
	(i) Yes	Yes (Phase changes by $\pi$ )	$\xi _{\mathrm{i}}=\mathrm{A} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)$	$\xi _{\mathrm{R}}=\mathrm{A} \sin \left[\omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)+\pi\right]$ $\left.=-\mathrm{A} \sin \omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)+\pi\right]$
	(ii) Yes	Yes (Phase changes by $\pi)$	$\xi _{\mathrm{i}}=\mathrm{A} \sin \omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)$	$\xi _{\mathrm{R}}=\mathrm{A} \sin \left[\omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)\right.$
				$\left.=-\mathrm{A} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)+\pi\right]$

Principle of Superposition of Waves

According to the principle of superposition of waves:

“When two, or more, waves are simultaneously propagating in a given medium, the resultant displacement, at any point of the medium, is the vector sum of the displacements, at that point, due to each of the waves”.

The principle of superposition has a essential corollary:

“The effect, of any given wave, at any point, in a medium, remains unaffected even if other wave/s, are

simultaneously producing their own disturbance/s at that point”.

A practical illustration of this feature is provided by the fact that we are easily able to recognize the voice of our friend / known acquaintance, in a room, even if other persons are simultaneously speaking in that room.

Phenomenon Resulting from ‘Superposition of Waves’

When two, or more waves, are simultaneously present in a medium, their ‘superposition’ can lead to many interesting phenomenon. We will talk, in some detail, about two of the phenomenon - ‘standing waves’ and ‘beats’ - that arise from the superposition of two waves. It is the nature, and the interrelation, between the characteristics features of the two (superposing) waves, that decides the nature of the resulting phenomenon.

Standing Waves / Stationary Waves

‘Standing (stationary) waves’ are produced as a result of the superposition of two identical waves, propagating along opposite directions. In practice, it is (usually) the superposition of a ‘direct’ wave and its ‘reflected’ wave (with, or without, change of phase) that results in the formation of ‘standing waves’.

Beats

When two waves, of (preferably) equal amplitude, propagating along the same direction, and having (slightly) different frequencies, are superposed on each other, the resulting phenomenon is known as the phenomenon of ‘beats’. The phenomenon of ‘beats’ may be viewed as a special case of the general phenomenon of ‘interference’.

We now discuss these two phenomenon in some detail.

The basic features of standing / stationary waves can be easily understood through the relevant mathematical analysis. These waves are the result of the superposition of a ‘direct’ wave and its ‘reflected’ wave. Let us just assume that the ‘reflection’ takes place without any ‘phase reversal(i.e., the reflection is from a ‘denser’ to a ‘rarer’ interface). We have, in this case,

For the direct wave $\xi _{\mathrm{i}}=\mathrm{a} \sin \omega\left(\mathrm{t}-\frac{\mathrm{x}}{\mathrm{v}}\right)$,

The corresponding reflected wave is: $\xi _{\mathrm{R}}=\mathrm{a} \sin \omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)$

The resultant displacement, say $\xi$, due to the superposition of these two waves, is

$$ \xi=\xi _{\mathrm{i}}+\xi _{\mathrm{R}}=\mathrm{a}\left[\sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)+\sin \omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)\right] $$

$$ =\left[2 \mathrm{a} \cos \left(\frac{\omega x}{\mathrm{v}}\right)\right] \sin \omega \mathrm{t}=\mathrm{A} \sin \omega \mathrm{t} $$

where $\mathrm{A}=2 \mathrm{a} \cos \frac{\omega x}{\mathrm{v}}=2 \mathrm{a} \cos \left(\frac{2 \pi x}{\lambda}\right)$

$$ \left(\because \frac{\omega}{\mathrm{v}}=\frac{2 \pi v}{v \lambda}=\frac{2 \pi}{\lambda}\right) $$

The ‘amplitude’, A, of the resultant wave, (at a given time), therefore, varies with the location of the point. We have

$\mathrm{A}= \pm 2 \mathrm{a}$ wherever $\frac{2 \pi x}{\lambda}=\mathrm{n} \lambda ;\left(\right.$ i.e. $\left.x=\frac{\mathrm{n} \lambda}{2}\right)$

Also $\mathrm{A}=0$ wherever $\frac{2 \pi x}{\lambda}=(2 \mathrm{n}+1) \frac{\lambda}{2} ;\left(\right.$ i.e. $\left.x=(2 \mathrm{n}+1) \frac{\lambda}{4}\right)$

The set of points (corresponding to $\mathrm{A}= \pm 2 \mathrm{a}$ ), are the points $x=0, \frac{\lambda}{2}, 2 \frac{\lambda}{2}, 3 \frac{\lambda}{2}, \ldots \ldots .$. These are known as the antinodal points, or just ‘ANTINODES’ of thre resultant wave.

It is important to note that any two successive antinodes are a distance $\lambda / 2$ apart from each other.

Similarly, the set of points, corresponding to $\mathrm{A}=0$, are the points

$$ x=\frac{\lambda}{4}, 3 \frac{\lambda}{4}, 5 \frac{\lambda}{2}, 7 \frac{\lambda}{2} $$

These are known as the ’nodal points’, or just the NODES, of the resultant wave.

If is important to note that the successive nodal points are also a distance $\lambda / 2$ apart from each other. From the ’locations’ of the ‘antinodal’, and the nodal points,we also observe that

(i) there is always a nodal point in between two successive antinodal points, and vice-versa.

(ii) a nodal point is separated, from its immediate (neighbouring) antinodal point, by a distance $\frac{\lambda}{4}$, and vice-versa.

Another important point is worth noting,. The displacement, of the resultant wave, is given by

$$ \xi=A \sin \omega \mathrm{t}\left(\mathrm{A}=2 \mathrm{a} \cos \frac{\omega x}{\mathrm{v}}\right) $$

At the nodes, $\mathrm{A}=0$. Hence, at these points, $\xi=0$; irrespective of the value of $\mathrm{t}$. The NODES are, therefore, points of ‘permanent rest’. The resultant disturbance, at these points is zero; irrespective of the time instant considered.

Again, at the antinodes, $\mathrm{A}= \pm 2 \mathrm{a}$ and

$$ \xi= \pm 2 \mathrm{a} \sin \omega \mathrm{t} $$

The resultant displacement, as the antinodes, therefore, varies with time in a sinusoidal way. It is equal to $\pm 2 \mathrm{a}$ when $\sin \omega \mathrm{t}= \pm 1$, i.e. when $\omega \mathrm{t}=\frac{(2 \mathrm{n}+1) \pi}{2}$.

Thus the resultant displacement, at the antinodes, equals $\pm 2 \mathrm{a}$ at those time instant, $\mathrm{t}$, for which

$$ \mathrm{t}=(2 \mathrm{n}+1) \frac{\pi}{2 \omega}=(2 \mathrm{n}+1) \frac{\mathrm{T}}{4} $$

Thus $\xi= \pm 2 \mathrm{a}$ at $\mathrm{t}=\frac{\mathrm{T}}{4}, \frac{3 \mathrm{~T}}{4}, \frac{5 \mathrm{~T}}{4}, \ldots \ldots \ldots \ldots$

The two successive time instants, at which the resultant displacement, at the antinodes, has a magnitude of 2a, are thus seen to be $\frac{T}{2}$ apart from each other. Further, the two successive time instants, at which the resultant displacement, at the antinodes, is either $+2 \mathrm{a}$ each, or $-2 \mathrm{a}$ each, are seen to be $\mathrm{T}$ apart from each other.

The resultant displacement, at the antinodes, therefore, varies in a simple harmonic way with a time period equal to $\mathrm{T}\left(=\frac{2 \pi}{\omega}\right)$, which, incidently, is also the time period of the two waves (direct and reflected) getting superposed.

Again, from

$$ \xi=\mathrm{A} \sin \omega \mathrm{t} $$

we notice that at time instants, $t$, given by

$$ \begin{aligned} & \omega \mathrm{t}=\mathrm{n} \pi \\ & \text { or } \quad \mathrm{t}=\frac{\mathrm{n} \pi}{\omega}=\mathrm{n} \cdot \frac{\mathrm{T}}{2} \\ & \text { i.e., at } \mathrm{t}=0, \frac{\mathrm{T}}{2}, \mathrm{~T}, \frac{3 \mathrm{~T}}{2}, \ldots \ldots \ldots \ldots \ldots \end{aligned} $$

$\xi=0$, at all points, irrespective of the value of A, i.e., irrespective of the location of the points. This includes the ‘antinodal points’ too.

Thus at time instants

$$ \mathrm{t}=0, \frac{\mathrm{T}}{2}, \mathrm{~T}, \frac{3 \mathrm{~T}}{2} $$

(which are separated from each other, again by an amount $\frac{\mathrm{T}}{2}$ ), the resultant displacement at the antinodal points, is zero.

These time instant are, therefore, instants at, which the whole of the medium is ‘momentarily at rest’.

Basic Difference Between ‘Standing Waves’ and ‘Ordinary (or Progressive) Waves’

We know that in an ordinary (or progressive), wave, the disturbance (having its characteristics ‘phase’) at one point, keeps on progressing throughout the medium. The phase condition (or disturbance) at one point, reaches another point at a distance $\lambda$ (= wave length) from it, in a time $\mathrm{T}=($ time period of the wave). The ‘phase’, therefore, keeps on ‘progressing’, in (an ordinary) wave motion, with a speed $\mathrm{v}\left[=\frac{\lambda}{\mathrm{T}}=v \lambda(v=\right.$ frequency of wave $\left.)\right]$.

For the standing waves, we have seen above that the nodal points, or ’nodes’, are points that ‘remain at rest’ throughout, i.e., at all time instants. The resultant displacement, at the antinodal points varies from $[(+2 \mathrm{a})$ to $(0)]$ to $[(-2 \mathrm{a})$ to $(0)]$ to $[(+2 \mathrm{a})]$, over a total time interval $\mathrm{T}$, in a simple harmonic way. Two successive nodal points, as well as two successive antinodal points, have a separation $\frac{\lambda}{2}$ each.

There is, therefore, no continuous, or progressive, transfer of ‘phase’ (of one point) to the other successive points. The wave does not ‘appear to move’ throughout the medium. Rather, the medium appears to get broken into ‘segments’, where each ‘segment’, contained between the successive ’nodal points’, appears to be executing a vibrating motion with a time period, $\mathrm{T}$. The appearance, of a string, (in which standing waves have been produced through the superposition of a direct wave with its corresponding reflected wave) is of the form shown below.

The name, standing / stationary waves, for this type of the resultant ‘wave’, can now be understood. The apparent, standing (or ‘stationary’) appearance of the medium (broken into ‘segments’, executing vibratory motion, with the ‘segments’, ‘staying’ where they are) justifies the use of the adjective ‘standing’ or ‘stationary’. The noun ‘waves’ is still used because (i) this pattern results from the superposition of two waves and (ii) the ‘phase conditions’, at the nodal, and antinodal points (as well as their intermediate points) are ‘getting repeated’ (over points separated by distance of $\frac{\lambda}{2}$ each).

The phase (= argument of the sine term), for a standing wave, just equals $(\omega t)$. Hence the ‘phase’ at a given time, has the same value for all points of the medium. This implies that all points of the medium, reach their respective maximum / minimum/intermediate displacements (ranging from 0 to $\pm 2 \mathrm{a}$ ) together.

There being no continuous transfer of phase (from one point to another), there is no net transfer of energy in a standing / stationary wave.

Standing / Stationary waves, formed by the superposition of a direct and its corresponding reflected wave, when the reflected wave undergoes a ‘phase reversal’ also.

Let us now consider the case where the reflection takes place at a ‘rarer to denser medium’ interface. We have already noted that, in such a reflection, there is not only a reversal of the direction of propagation, but also a reversal of phase. The equations, of the ‘direct’ and the ‘reflected’ waves, in this case, are, respectively,

$$ \xi _{\mathrm{i}}=\mathrm{a} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right) $$

and $\quad \xi _{\mathrm{R}}=\mathrm{a} \sin \left[\omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)+\pi\right]$

$\therefore$ The displacement, $\xi$, of the resultant wave, is

$$ \begin{aligned} \xi=\mathrm{a} \sin & {\left[\omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)\right]-\mathrm{a} \sin \left[\omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)\right] } \\ & =2 \mathrm{a} \cos \omega \mathrm{t} \sin \left(\frac{\omega \mathrm{t}}{\mathrm{v}}\right) \\ & =\left(2 \mathrm{a} \sin \frac{\omega x}{\mathrm{v}}\right) \cos \omega \mathrm{t}=\mathrm{a} \cos \omega \mathrm{t} \end{aligned} $$

where $\mathrm{A}=2 \mathrm{a} \sin \frac{\omega x}{\mathrm{v}}=2 \mathrm{a} \sin \left(\frac{2 \pi x}{\lambda}\right)$

The amplitude, $\mathrm{A}$, of the resultant wave, is now given by

$$ A=2 a \sin \left(\frac{2 \pi x}{\lambda}\right) $$

$\therefore$ A has its maximum magnitude $(=2 a)$ at points for which

$$ \frac{2 \pi x}{\lambda}=(2 n+1) \frac{\pi}{2} \quad \text { or } \quad x=(2 n+1) \frac{\lambda}{4} $$

The antinodal points, or antinodes, are now located at points for which

$$ x=\frac{\lambda}{4}, \frac{3 \lambda}{4}, \frac{5 \lambda}{4}, \ldots \ldots \ldots \ldots $$

Similarly $A=0$, at points, for which

$$ \frac{2 \pi x}{\lambda}=\mathrm{n} \pi \quad \text { or } \quad x=\frac{\mathrm{n} \lambda}{2} $$

The nodal points, or nodes, are now located at points for which

$$ x=0, \frac{\lambda}{2}, \lambda, \frac{3 \lambda}{2}, \ldots \ldots \ldots \ldots $$

The locations, of the nodal and antinodal points, are now seen to have got ‘interchanged’, with respect to their locations in the case of ‘reflection without phase reversal’.

Further

$$ \xi=2 \mathrm{a} \cos \omega \mathrm{t} $$

$\therefore \quad \xi=0$ at time instants $t$ for which

$$ \omega \mathrm{t}=\frac{(2 \mathrm{n}+1) \pi}{2} $$

or $\quad t=\frac{(2 n+1) \pi}{2 \omega}=(2 n+1) \frac{T}{4}$

Thus, at the time instants,

$$ \frac{T}{4}, \frac{3 \mathrm{~T}}{4}, \frac{5 \mathrm{~T}}{4}, \ldots \ldots \ldots \ldots $$

the resultant displacement is zero at all points of the medium.

Again

$\xi= \pm 2 \mathrm{a}$, at the antinodal points, at time instants, $\mathrm{t}$, for which

$$ \omega \mathrm{t}=\mathrm{n} \pi \quad \text { or } \quad \mathrm{t}=\frac{\mathrm{nT}}{2} $$

Thus at the instants,

$$ \mathrm{t}=0, \frac{\mathrm{T}}{2}, \mathrm{~T}, \frac{3 \mathrm{~T}}{2}, \ldots \ldots \ldots \ldots $$

the antinodal points (as well as all other points of the medium) have the maximum magnitude for their respective displacements.

The timings, of the time instants, at which their is maximum magnitude of its displacement for (all points) and the time instants, at which the whole of the medium is ‘momentarily at rest’, are also seen to have got ‘interchanged’ (with respect to their values in case of reflection ‘without phase reversal’).

Apart from this interchange of ’ $x$ and t’ values, all the other results and conclusions, for the standing / stationary waves, formed in the case, are exactly the same as in the earlier case of standing / stationary waves (i.e. the case where reflection takes place without any phase reversal).

Standing Waves in Strings

Consider a string of length $\mathrm{L}$, fixed at its two ends, and stretched by a tension $\mathrm{T}$. If $\mathrm{m}$ be the mass per unit length of this string, the waves, if any, propagating in this string, would do so with a speed $v$ where

$$ v=\sqrt{\frac{T}{m}} $$

Let the string be given a slight transverse displacement (at, say, its mid-point) and ’let-go’. The resulting transverse waves, produced in the string, get reflected from each of its fixed ends. The superposition, of the direct and the reflected waves, then produces standing / stationary waves in the string.

We now need to remember that the string, has been fixed at its two ends. Hence these ends cannot vibrate; they have to be ’nodal points’, or nodes, of any stationary wave pattern, formed in the string. We also know that there has to be an ‘antinode’, between two nodes and vice-versa. The permissible pattern; of the stationary waves, that can get formed in the string, can, therefore, be as shown below.

$\lambda=\ell=\frac{2 \ell}{2}$

The simplest, of these permissible modes, is clearly the first ‘mode’, for which the wavelength equals twice the length of the string. The frequency, corresponding to this ‘mode’ of vibration, is

$$ \mathrm{n} _{1}=\frac{\mathrm{v}}{\lambda}=\frac{1}{2 \ell} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}} $$

Similarly, the frequencies, corresponding to the second and third ‘modes’ of vibration, are

$$ \mathrm{n} _{2}=\frac{2 \mathrm{v}}{2 \ell}=\frac{2}{2 \ell} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}} $$

and $\quad \mathrm{n} _{3}=\frac{3 \mathrm{v}}{2 \ell}=\frac{3}{2 \ell} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}}$

and so on.

We notice that $\mathrm{n} _{2}=2 \mathrm{n} _{1}, \mathrm{n} _{3}=3 \mathrm{n} _{1} \ldots \ldots \ldots \ldots$

Hence, in general, the permissible frequencies, of the different modes of vibrations, of a string fixed at both ends, are

$$ \mathrm{n} _{\mathrm{p}}=\frac{\mathrm{p}}{2 \ell} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}} \quad(\mathrm{p}=1,2,3, \ldots \ldots \ldots . .) $$

The basic frequency $\left(\mathrm{n} _{1}\right)$ is known as the frequency of vibration of the ‘fundamental mode’, or the ‘first harmonic’ (for a string fixed at both ends and subjected to tension). The other permissible frequencies of vibration, of such a string, are all integral multiples of this basic or fundamental frequency. The frequency $n _{p}$ ( $p$ times $\left.n _{1}\right)$ is known as the frequency of the $p^{\text {th }}(p=1,2,3, \ldots \ldots \ldots . . . .$.$) harmonic.$

Stationary Waves in Organ Pipes (or Air Columns)

Here we consider two types of organ pipes (or air columns) : (i) organ pipes that are OPEN at both ends, called ‘open pipes’ and (ii) organ pipes, that are CLOSED at one end, called ‘closed pipes’.

When stationary waves are formed in any one of these pipes (through a superposition of the ‘direct’ and the ‘reflected’ wave), we have to remember the following:

(1) The open end $/ \mathrm{s}$ has/have to be antinodal point $/ \mathrm{s}$.

(2) The closed end has to be a ’nodal’ point.

(3) There would always be a ’node’ between two ‘antinodes’ and an ‘antinode’ between two ’nodes’.

(4) The separation, between two successive nodes / two successive antinodes, equals $\frac{\lambda}{2}$.

(5) The separation between a ’node’ and its immediate ‘antinode’ (or between an ‘antinode’ and its immediate ’node’) equals $\frac{\lambda}{4}$.

The simplest mode of vibration, of a given organ pipe (consistent with the above requirements), is known as its ‘fundamental’ mode of vibration. The other such permissible modes of vibration, are known as ‘harmonics’.

The diagrams, given below, indicate the first three permissible modes of vibration of an ‘open organ pipe’ as well as a ‘closed organ pipe’.

The fundamental mode of vibration, of an open organ pipe, has a frequency

$$ \mathrm{n} _{1}=\frac{\mathrm{v}}{\lambda _{1}}=\frac{\mathrm{v}}{2 \ell} $$

The frequencies, of the next two modes, are

$$ \mathrm{n} _{2}=\frac{\mathrm{v}}{\ell}=2 \mathrm{n} _{1} $$

and

$$ \mathrm{n} _{3}=3 \frac{\mathrm{v}}{2 \ell}=3 \mathrm{n} _{1} \ldots \ldots \ldots \ldots . . \text { and so on. } $$

We thus notice that in an open organ pipe, the permissible frequencies of vibration, are ‘all’ integral multiples of the fundamental frequency. We often express this by saying that, in an open pipe,

“All harmonics (all integral multiples of the fundamental frequency) are permissbile, or available”.

The frequency, $\mathrm{n} _{2}$, is called the ‘first overtone’, or the ‘second harmonic’. Similarly the frequency, $\mathrm{n} _{3}$, is the ‘second overtone’, or the third harmonic, and so on.

We next notice that fundamental mode of vibration, of a closed pipe, has a frequency

$$ \mathrm{n} _{1}=\frac{\mathrm{v}}{\lambda _{1}}=\frac{\mathrm{v}}{4 \ell} $$

The frequencies, of the next two modes, are

$$ \mathrm{n} _{2}=\frac{\mathrm{v}}{\lambda _{2}}=\frac{3 \mathrm{v}}{4 \ell}=3 \mathrm{n} _{1} $$

and $\quad \mathrm{n} _{3}=\frac{\mathrm{v}}{\lambda _{3}}=\frac{5 \mathrm{v}}{4 \ell}=5 \mathrm{n} _{1}$

and so on.

We thus note that, in a closed pipe, the permissible frequencies of vibration are only the ODD INTERGRAL multiples of the fundamental frequency. We often express this by saying that in a “closed pipe”:

“Only the ODD harmonics (only ODD integral multiples of the fundamental frequency) are permissible, or available.

The frequency, $n _{2},\left(=3 n _{1}\right)$ permissible in a closed pipe, is known as the third harmonic; similarly the frequency $n _{3}=\left(5 n _{1}\right)$, is known as the fifth harmonic; and so on.

It is interesting to note that under identical atmospheric / surrounding conditions (so that $\mathrm{v}$, the velocity of waves has the same value), the fundamental frequency of an open organ pipe, is twice the fundamental frequency of a ‘closed pipe’, of equal length.

Example-24:

The equation, of a moving pulse, is $\mathrm{y}(x, \mathrm{t})=\frac{\mathrm{a}}{\mathrm{b}+(x+\mathrm{vt})^{2}}$

For this pulse, one can say that it is a pulse moving along the

(1) positive side of $x$-axis, and it is not symmetric at the start.

(2) negative side of $x$-axis, and it is not symmetric at the start.

(3) negative side of $x$-axis, and it is symmetric at the start.

(4) positive side of $x$-axis, and it is symmetric at the start.

Show Answer

Solution:

Since there is a +ve sign between the $x$ and $t$ terms, the given equation represents a pulse propagating along the negative side of $x$-axis.

The pulse would be symmetric, at the start, if, at $\mathrm{t}=0$,

$$ \mathrm{y}\left(\text { at } x=+x _{0}, \text { say }\right)=\mathrm{y}\left(\text { at } x=-x _{0}\right) $$

Now at $\mathrm{t}=0$

$$ \mathrm{y}\left(\text { at } x=+x _{0}\right)=\frac{\mathrm{a}}{\mathrm{b}+x _{0}^{2}} $$

and $\quad \mathrm{y}\left(\mathrm{at} x=-x _{0}\right)=\frac{\mathrm{a}}{\mathrm{b}+\left(-x _{0}\right)^{2}}=\frac{\mathrm{a}}{\mathrm{b}+x _{0}^{2}}$

$\therefore \mathrm{y}\left(\right.$ at $\left.x=+x _{0}\right)=\mathrm{y}\left(\right.$ at $\left.x=-x _{0}\right)$

Hence the given equation represents a symmetric pulse moving along the negative side of $\mathrm{x}$-axis.

Example-25:

The general equation, of a pulse moving along positive $x$-axis, has the form

$$ \mathrm{y}=\frac{\mathrm{a}}{\mathrm{b}+(x-\mathrm{vt})^{2}} $$

where $v$ is the speed of propagation of the wave.

The amplitude of a moving pulse, propagating along positive $x$-axis, is given by

$$ \mathrm{y}=\frac{\mathrm{a}}{\mathrm{b}+\mathrm{x}^{2}} \text { at } \mathrm{t}=0 \quad \text { and } \quad \mathrm{y}=\frac{\mathrm{a}}{\mathrm{b}+(x-\mathrm{c})^{2}} \text { at } \mathrm{t}=\mathrm{n} $$

The speed of propagation, of the pulse, equals

(1) $\frac{\mathrm{c}}{\mathrm{n}}$

(2) $\frac{(b+c)}{n}$

(3) nc

(4) $\mathrm{n}(\mathrm{b}+\mathrm{c})$

Show Answer

Solution:

The general equation, of a pulse moving along positive $x$-axis, has the form

$$ \mathrm{y}=\frac{\mathrm{a}}{\mathrm{b}+(x-\mathrm{vt})^{2}} $$

where $v$ is the speed of propagation of the wave. We thus have:

At $\mathrm{t}=0, \mathrm{y}=\frac{\mathrm{a}}{\mathrm{b}+\mathrm{x}^{2}}$

and at $\mathrm{t}=\mathrm{n}, \mathrm{y}=\frac{\mathrm{a}}{\mathrm{b}+(x-\mathrm{nv})^{2}}$

We are also given that at $\mathrm{t}=\mathrm{n}$

$$ \mathrm{y}=\frac{\mathrm{a}}{\mathrm{b}+(x-\mathrm{c})^{2}} $$

We thus notice that

$$ \begin{array}{r} n \mathrm{v}=\mathrm{c} \\ \therefore \quad \mathrm{v}=\left(\frac{\mathrm{c}}{\mathrm{n}}\right) \end{array} $$

Example-26:

A light string, stretched under a tension $T$, has a sinusoidal transverse wave propagating along it. The mass per unit length of the string is $m$ and the amplitude of this propagating wave is $A$.

If the maximum speed, of any point on the string, is $\frac{1}{\mathrm{n}}$ times the speed of propagation of the wave through it, the frequency $(v)$ and the wavelength $(\lambda)$, of the wave, can be expressed as

(1) $\quad v=\frac{1}{2 \pi \mathrm{nA}} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}} ; \quad \lambda=\left(\frac{\mathrm{nA}}{2 \pi}\right)$

(2) $\quad v=\frac{2 \pi}{\mathrm{nA}} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}} ; \quad \lambda=2 \pi \mathrm{nA}$

(3) $\quad v=\frac{1}{2 \pi \mathrm{nA}} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}} ; \lambda=2 \pi \mathrm{nA}$

(4) $\quad v=\frac{2 \pi}{\mathrm{nA}} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}} ; \lambda=\frac{\mathrm{nA}}{2 \pi}$

Show Answer

Solution:

The speed of propagation, of the wave, through the string, is given by

$$ v=\sqrt{\frac{T}{m}} $$

The maximum speed (i.e., the velocity amplitude), for a point, on the string, is given by

$$ \mathrm{v} _{\max }=\mathrm{A} \omega \quad(\omega=\text { angular frequency }) $$

$\therefore \quad \mathrm{A} \omega=\frac{1}{\mathrm{n}} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}}$

$\therefore \omega(=2 \pi v)=\frac{1}{\mathrm{nA}} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}}$

$\therefore \quad v=\frac{1}{2 \pi \mathrm{nA}} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}}$

Also $\lambda=\frac{v}{v}=\sqrt{\frac{T}{m}} \times 2 \pi \mathrm{nA} \times \sqrt{\frac{m}{T}}$

$$ =2 \pi \mathrm{nA} $$

Example-27:

The temperature, $T$, between two points A and B, separated by a distance, $\mathrm{L}$, (in air) varies as

$$ \mathrm{T}(x)=\mathrm{T} _{0}+\alpha x $$

The velocity of sound, in air, varies with temperature, as

$$ \mathrm{v}(\mathrm{T})=\mathrm{k} \sqrt{\mathrm{T}} $$

The time, $t$, taken by sound, to propagate from point $A$ to point $B$, equals

(1) $\frac{2 \mathrm{~kL}}{\left[\left(\mathrm{~T} _{\mathrm{B}}\right)^{1 / 2}-\left(\mathrm{T} _{0}\right)^{1 / 2}\right]}$

(2) $\frac{2 \mathrm{~L}}{\mathrm{k}\left(\mathrm{T} _{\mathrm{B}}^{1 / 2}+\mathrm{T} _{0}^{1 / 2}\right)}$

(3) $\frac{2 L k}{\left(T _{B}\right)^{1 / 2}+\left(T _{0}\right)^{1 / 2}}$

(4) $\frac{2 \mathrm{~L}}{\mathrm{k}\left(\left(\mathrm{T} _{\mathrm{B}}\right)^{1 / 2}+\left(\mathrm{T} _{0}\right)^{1 / 2}\right)}$

Show Answer

Solution:

The temperature, at a segment of length $\mathrm{d} x$, located at a distance $x$ from point $\mathrm{A}$, is

$$ \mathrm{T}(x)=\mathrm{T} _{0}+\alpha x $$

$\therefore$ Velocity of sound, over this segment, is

$$ \mathrm{v}(x)=\mathrm{k} \sqrt{\mathrm{T}(x)}=\mathrm{k} \sqrt{\left(\mathrm{T} _{0}+\alpha x\right)} $$

The time, dt, taken to cover this distance, is

$$ \mathrm{dt}=\frac{\mathrm{d} x}{\mathrm{v}(x)}=\frac{\mathrm{d} x}{\mathrm{k}}\left(\mathrm{T} _{0}+\alpha x\right)^{-1 / 2} $$

$\therefore$ Time taken, to move from $\mathrm{A}$ to $\mathrm{B}$, is

$$ \begin{aligned} & \mathrm{t}=\int _{x=0}^{x=\mathrm{L}} \frac{1}{\mathrm{k}}\left(\mathrm{T} _{0}+\alpha x\right)^{-1 / 2} \mathrm{~d} x \\ & =\left|\frac{1}{\mathrm{k} \alpha} \frac{\left(\mathrm{T} _{0}+\alpha x\right)^{1 / 2}}{(1 / 2)}\right| _{x=0}^{x=\mathrm{L}}=\frac{2}{\mathrm{k} \alpha}\left[\left(\mathrm{T} _{0}+\alpha \mathrm{L}\right)^{1 / 2}-\left(\mathrm{T} _{0}\right)^{1 / 2}\right] \\ & =\frac{2}{\mathrm{k} \alpha}\left[\left(\mathrm{T} _{\mathrm{B}}\right)^{1 / 2}-\left(\mathrm{T} _{0}\right)^{1 / 2}\right] \end{aligned} $$

But $\alpha=\left(\frac{\mathrm{T} _{\mathrm{B}}-\mathrm{T} _{0}}{\mathrm{~L}}\right)$

$$ \therefore \mathrm{t}=\frac{2 \mathrm{~L}}{\mathrm{k}\left(\left(\mathrm{T} _{\mathrm{B}}\right)^{1 / 2}+\left(\mathrm{T} _{0}\right)^{1 / 2}\right)} $$

Example-28:

The displacement, $\mathrm{y}$, of a particle executing periodic motion, is given by

$$ y=4 \cos ^{2}\left(\frac{t}{2}\right) \sin (1000 t) $$

The number of harmonic motions, that when superposed, can result in this periodic motion, is

(1) two

(2) three

(3) four

(4) five

Show Answer

Solution:

We have $\mathrm{y}=4 \cos ^{2}\left(\frac{\mathrm{t}}{2}\right) \sin (1000 \mathrm{t})$

$$ \begin{aligned} & =4\left(\frac{1+\cos t}{2}\right) \sin 1000 t \\ & =2 \sin 1000 t+2 \cos \sin 1000 t \\ & =2 \sin 1000 t+\sin (1001 t)+\sin (999) t \end{aligned} $$

Each of the three terms represents a harmonic motion. Hence the given expression, for periodic motion, can result through the superposition of three harmonic motions.

Beats

The phenomenon of beats, is another important phenomenon associated with the ‘superposition’ of waves. “Beats” are observed when two waves of different frequencies, and, in general, different amplitudes, are superposed on each other. In case of sound waves, “Beats” are distinctly, and clearly, observed when the frequencies of the two waves differ only by a small amount and when their amplitudes are (nearly) equal to each other.

Let the two waves be represented by

$$ \xi _{\mathrm{i}}=\mathrm{a} _{1} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)=\mathrm{a} _{1} \sin (\omega \mathrm{t}-\mathrm{k} x) $$

and

$$ \xi _{2}=\mathrm{a} _{2} \sin \left(\omega^{\prime} \mathrm{t}-\mathrm{k}^{\prime} x+\phi\right) $$

Let $\omega^{\prime}=\omega+\Delta \omega \quad\left(\mathrm{k}=\omega=\frac{2 \pi}{\lambda}=\right.$ wave number $)$

Then, we have $\mathrm{k}^{\prime}=\frac{\omega^{\prime}}{\mathrm{v}}$

$$ =\frac{\omega+\Delta \omega}{\mathrm{v}}=\frac{\omega}{\mathrm{v}}+\frac{\Delta \omega}{\mathrm{v}} $$

$\approx \mathrm{k}$ if $\Delta \omega«\omega$

$$ \begin{aligned} \therefore \quad \xi _{2} & =\mathrm{a} _{2} \sin [(\omega+\Delta \omega) \mathrm{t}-\mathrm{k} x+\phi] \\ & =\mathrm{a} _{2} \sin [(\omega \mathrm{t}-\mathrm{k} x)+(\phi+(\Delta \omega))] \\ & =\mathrm{a} _{2} \sin [(\omega \mathrm{t}-\mathrm{k} x)+\theta] \end{aligned} $$

where $\theta(=\phi+(\Delta \omega) \mathrm{t})$ is a function of time.

Let us put $(\omega \mathrm{t}-\mathrm{k} x)=\alpha$. We then have

$$ \xi _{\mathrm{i}}=\mathrm{a} _{1} \sin \alpha $$

and

$$ \begin{aligned} & \xi _{2}=a _{2} \sin (\alpha+\theta) \\ & =a _{2}[\sin \alpha \cos \theta+\cos \alpha \sin \theta] \end{aligned} $$

The resultant wave, formed by the superposition of these two waves, is represented by

$$ \begin{aligned} & \xi=\xi _{1}+\xi _{2} \\ & =a _{1} \sin \alpha+a _{2} \sin \alpha \cos \theta+a _{2} \cos \alpha \sin \theta \\ & =\left(a _{1}+a _{2} \cos \theta\right) \sin \alpha+\left(a _{2} \sin \theta\right) \cos \alpha \end{aligned} $$

We now put

$$ a _{1}+a _{2} \cos \theta=R \cos \beta $$

and

$$ \mathrm{a} _{2} \sin \theta=\mathrm{R} \sin \beta $$

We then have

$$ \begin{aligned} & \xi=R \sin \alpha \cos \beta+\mathrm{R} \cos \alpha \sin \beta \\ & =\mathrm{R} \sin (\alpha+\beta) \\ & =\mathrm{R} \sin [(\omega \mathrm{t}-\mathrm{k} x)+\beta] \end{aligned} $$

The resultant wave thus has an amplitude $\mathrm{R}$ and a phase $(\omega \mathrm{t}-\mathrm{k} x+\beta)$.

$\mathrm{R}$ and $\beta$ are given by

$$ \begin{aligned} & \mathrm{R}^{2}=\mathrm{a} _{1}^{2}+\mathrm{a} _{2}^{2} \cos ^{2} \theta+2 \mathrm{a} _{1} \mathrm{a} _{2} \cos \theta+\mathrm{a} _{2}^{2} \sin ^{2} \theta \\ & =\mathrm{a} _{1}^{2}+\mathrm{a} _{2}^{2}+2 \mathrm{a} _{1} \mathrm{a} _{2} \cos \theta \end{aligned} $$

and $\tan \beta=\left[\frac{a _{2} \sin \theta}{a _{1}+a _{2} \cos \theta}\right]$

Now $\quad \theta=\phi+(\Delta \omega) \mathrm{t}$

Hence both $\mathrm{R}$ and $\beta$ change with time. The resultant amplitude, $\mathrm{R}$, is maximum $\left(=\mathrm{a} _{1}+\mathrm{a} _{2}\right)$, when

$$ \theta=\mathrm{n} .2 \pi $$

Let $\phi+(\Delta \omega) \mathrm{t} _{1}=\mathrm{n} .2 \pi$

and $\phi+(\Delta \omega) \mathrm{t} _{2}=(\mathrm{n}+1) .2 \pi$

This given $(\Delta \omega)\left[\mathrm{t} _{2}-\mathrm{t} _{1}\right]=2 \pi$

or

$$ \left(\mathrm{t} _{2}-\mathrm{t} _{1}\right)=\frac{2 \pi}{\Delta \omega} $$

The resultant amplitude is thus maximum when

$$ \left(\mathrm{t} _{2}-\mathrm{t} _{1}\right)=\frac{2 \pi}{\Delta \omega}, \frac{4 \pi}{\Delta \omega}, \frac{6 \pi}{\Delta \omega}, \ldots \ldots \ldots $$

The time interval, between two successive maxima, of the resultant amplitude, is $\frac{2 \pi}{\Delta \omega}$.

Similarly $R$ is minimum $\left(=a _{1} \sim a _{2}\right)$, when

$$ \theta=(2 n+1) \pi $$

This again gives the time instants, corresponding to ‘minima’ as

$$ \frac{\pi}{\Delta \omega}, \frac{3 \pi}{\Delta \omega}, \frac{5 \pi}{\Delta \omega}, \ldots \ldots \ldots \ldots \ldots \ldots $$

We call the cycle of maxima, followed by a minima, and then again followed by another maxima, as making up one ‘BEAT’. The time period, of the beats, is therefore, $\frac{2 \pi}{\Delta \omega}$. This gives the frequency of beats as $\frac{\Delta \omega}{2 \pi}=\frac{[2 \pi(v+\Delta v)-2 \pi \nu]}{2 \pi}=\Delta v=$ difference in the frequency of two waves.

In case of sound waves, ‘maxima’ would be a large sound while the ‘minima’ would be a ‘weak’ sound. The frequency of a (maxima, minima, maxima) cycle is the difference of the two frequencies.

If the difference of two frequencies is more than ten, the two successive maxima would be separated by less than $\left(\frac{1}{10}\right)$ s. In such a case, because of the persistence of hearing, we would not be able to hear the cycle of maxima, minima, maxima and would just get an average (nearly) constant sound. Thus to hear beats clearly (in case of sound), the two superposing waves should differ ‘just a little’ in their frequencies.

Doppler Effect

“Doppler effect is the phenomenon of the observed change in the frequency (wavelength) of a wave, due to the presence of a relative motion between the observer and the source of waves”.

This effect, initially observed and analysed for sound waves, has now been found it be valid for all types of waves including electromagnetic waves. In fact, it is the observed “Red shift” (decrease in frequency or increase in wavelength), in the spectral lines of the ’light’ of stars, that provides a very significant ‘support’ to the big bang theory of the origin of universe.

Doppler Effect Formulae for Sound

A “relative motion” between an observer, and a source of sound, can exist when

(1) The observer is at rest but the source is moving (with a velocity, $\mathrm{v} _{\mathrm{s}}$, say).

(2) The observer is moving (with a velocity, $\mathrm{v} _{0}$, say), but the source is at rest.

(3) The ‘source’ and the ‘observer’ are both in motion.

The explanation, of the ‘basic cause’ of ‘Doppler change in frequency’, is different for cases (1) and (2) and the effects are not identical even for equal values of $\mathrm{v} _{\mathrm{s}}$ and $\mathrm{v} _{0}$. Case (3) can be regarded as a ‘combination’ of cases (1) and (2).

Let us now derive the formulae for ‘Doppler change in frequency’ for all these cases. We will assume that the velocity of sound, in still air, equals v. (In case of a wind blowing, the component of the velocity of wind; along the direction of propagation of sound, will need to be added to $v$ to get the relevant value for the ‘velocity of sound’).

Case-I : Source Moving; Observer at Rest

Let the source be moving, with a speed $v _{s}$, towards the observer. The source ’emits’ the waves with a frequency n. In this case the first wave ’emitted’, from point $O$, say, will reach a point $Q$, distant $\mathrm{v}$ ( = velocity of waves), from $\mathrm{O}$, after 1 second. Meanwhile the source would have reached the point $\mathrm{P}\left(\right.$ where $\mathrm{OP}=\mathrm{v} _{\varsigma}$ ) in 1 second and would have just ’emitted’ its $n$th wave at the point $P$. All the $n$ waves have, therefore,

now got 'contained' in a distance PQ $\left(=\left(\mathrm{v}-\mathrm{v} _{\mathrm{s}}\right)\right)$. Hence the apparent wavelength, of each wave, now, is $\lambda^{\prime}$, where $\lambda^{\prime}=\left(\frac{\mathrm{v}-\mathrm{v} _{\mathrm{s}}}{\mathrm{n}}\right)$. The apparent frequency is, therefore,

$$ \mathrm{n}^{\prime}=\frac{\mathrm{v}}{\lambda^{\prime}}=\left(\frac{\mathrm{v}}{\mathrm{v}-\mathrm{v} _{\mathrm{s}}}\right) \mathrm{n} $$

It is this formula that gives the apparent (increased) frequency of the source when it is moving towards a stationary observer.

If the source were moving away from the observer, the corresponding formula would be

$$ \begin{aligned} & \mathrm{n}^{\prime}=\frac{\mathrm{v}}{\mathrm{v}-\left(-\mathrm{v} _{\mathrm{s}}\right)} \mathrm{n} \\ & =\left(\frac{\mathrm{v}}{\mathrm{v}+\mathrm{v} _{\mathrm{s}}}\right) \mathrm{n} \end{aligned} $$

Case-II : Source at Rest; Observer Moving

Let us imagine that the observer is moving with a speed $\mathrm{v} _{0}$ towards a stationary source. The waves, emitted by the source, (which would have moved towards a stationary observer with a speed v), would now appear to be approaching the observer with a speed $\left(v+v _{0}\right)$. The number of waves, reaching the observer in one second ( $=$ observed frequency of the source) would, therefore, increase by a factor $\left(\frac{\mathrm{v}+\mathrm{v} _{0}}{\mathrm{v}}\right)$. Hence the apparent frequency, in this case, is

$$ \mathrm{n}^{\prime}=\left[\left(\frac{\mathrm{v}+\mathrm{v} _{0}}{\mathrm{v}}\right)\right] \mathrm{n} $$

If the observer were moving away from the source, the apparent frequency would be given by

$$ \mathrm{n}^{\prime}=\left[\frac{\mathrm{v}+\left(-\mathrm{v} _{0}\right)}{\mathrm{v}}\right] \mathrm{n}=\left[\frac{\mathrm{v}-\mathrm{v} _{0}}{\mathrm{v}}\right] \mathrm{n} $$

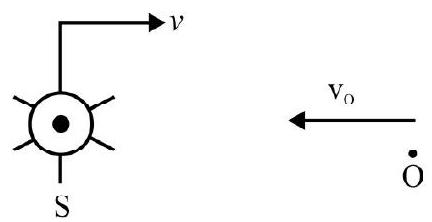
Case-III : Source and Observer Both Moving

Let the source be moving towards the observer with a speed $\mathrm{v} _{\mathrm{s}}$. Let the observer also be moving towards the source with a speed $\mathrm{v} _{0}$.

The apparent change in frequency can now be thought of as being brought about, in two steps, by two different processes:

(i) The movement of the source, towards the observer, may be thought of as causing an apparent decrease in the wavelength of the waves. This causes the true frequency, $n$, of the waves, to have an apparent value $\mathrm{n}$ “, where

$$ \mathrm{n}^{\prime \prime}=\left(\frac{\mathrm{v}}{\mathrm{v}-\mathrm{v} _{\mathrm{s}}}\right) \mathrm{n} $$

(ii) The movement of the observer, towards the source, may be thought of as causing an apparent increase in the velocity of the emitted waves. This apparent increase in velocity may be thought of causing an apparent increase in the frequency $\mathrm{n}$ " (the frequency of the source, as modified by the motion of the source towards the observer). The new modified apparent frequency would be

$$ \begin{aligned} & \mathrm{n}^{\prime}=\left(\frac{\mathrm{v}+\mathrm{v} _{0}}{\mathrm{v}}\right) \mathrm{n}^{\prime \prime} \\ & =\left(\frac{\mathrm{v}+\mathrm{v} _{0}}{\mathrm{v}}\right) \cdot\left(\frac{\mathrm{v}}{\mathrm{v}-\mathrm{v} _{\mathrm{s}}}\right) \mathrm{n} \\ \therefore \quad \mathrm{n}^{\prime} & =\left(\frac{\mathrm{v}+\mathrm{v} _{0}}{\mathrm{v}-\mathrm{v} _{\mathrm{s}}}\right) \mathrm{n} \end{aligned} $$

General Formula for Doppler Effect

We may take the formula

$$ \mathrm{n}^{\prime}=\left(\frac{\mathrm{v}+\mathrm{v} _{0}}{\mathrm{v}-\mathrm{v} _{\mathrm{s}}}\right) \mathrm{n} $$

as the general formula for finding the apparent (Doppler) frequency, $\mathrm{n}^{\prime}$, (corresponding to the true frequency n), of a given source of sound. We have to here remember:

(i) In this formula, it has been assumed that both the source, and the observer, are moving towards each other.

(ii) In case the source / observer is moving away from the observer / source, the velocity $\mathrm{v} _{\mathrm{s}} / \mathrm{v} _{\mathrm{o}}$ is be assigned a negative sign. The modified forms of this formula (which are all really ‘contained’ in this formula), for the other three possibilities, have been given below. The corresponding diagrams have also been shown along side.

Keeping the suggsomu sign wun unum in mind, we need, however, to remember only the formula given at the top.

Example-29:

Two trains run at the same speed $(\mathrm{v}=90 \mathrm{~km} / \mathrm{h})$ along a straight track, one after the other, with a separation $\ell=2 \mathrm{~km}$. At the instant when they are located symmetrically relative to the point Aat a distance $b(=1 \mathrm{~km})$ from the track, both emit a brief signal of frequency $n=500 \mathrm{~Hz}$. If the speed of sound is $\mathrm{V}=350 \mathrm{~m} / \mathrm{s}$, the frequency of beats, at $\mathrm{A}$, would be,

(1) $30 \mathrm{~Hz}$

(2) $40 \mathrm{~Hz}$

(3) $50 \mathrm{~Hz}$

(4) $60 \mathrm{~Hz}$

Show Answer

Solution:

To find the frequency of the wave arriving at A we have to consider the component of velocity of the trains along CA for the first train and along DA for the second train.

$\therefore \quad \mathrm{n} _{1}=\frac{\mathrm{v}-0}{\mathrm{v}-\mathrm{v} \cos \theta} \times \mathrm{n}=\frac{\mathrm{nv}}{\mathrm{v}-\mathrm{v} \cos \theta}$ where $\cos \theta=\frac{\mathrm{AO}}{\mathrm{CO}}$

and

$$ \mathrm{n} _{2}=\frac{\mathrm{nv}}{\mathrm{v}+\mathrm{v} \cos \theta} $$

$\therefore \quad \Delta \mathrm{n}=\mathrm{n} _{1}-\mathrm{n} _{2}=\frac{2 \mathrm{nv} v \cos \theta}{\mathrm{v}^{2}-v \cos ^{2} \theta}$

Here $\cos \theta=\frac{\ell / 2}{\sqrt{\mathrm{b}^{2}+\ell^{2} / 4}}=\frac{\ell}{\sqrt{4 \mathrm{~b}^{2}+\ell^{2}}}=\frac{2}{\sqrt{4+4}}=\frac{\ell}{\sqrt{2}}$

$\therefore \Delta \mathrm{n}=\frac{2 \times 500 \times 350 \times 25 \times 0.707}{350^{2}-25^{2} \times \frac{1}{2}} \mathrm{~Hz}=50 \mathrm{~Hz}$

Thus the beat frequency, at A, would be $50 \mathrm{~Hz}$.

PROBLEMS FOR PRACTICE

1. A simple pendulum (of length $\mathrm{L}$ ) is suspended from the ceiling of a car. If the car were to accelerate, with a uniform acceleration a $(\mathrm{a}<\mathrm{g})$ on a horizontal road, the time period, of the pendulum, within the car, would be

(1) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{L}}{(\mathrm{a}+\mathrm{g})}}$

(2) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{L}}{\left(\mathrm{a}^{2}+\mathrm{g}^{2}\right)}}$

(3) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{L}}{\left(\mathrm{g}^{2}-\mathrm{a}^{2}\right)}}$

(4) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{L}}{(\mathrm{g}-\mathrm{a})}}$

2. A rod, of mass $M$ and length $L$, is pivoted about its one end. It is displaced slightly from its equilibrium position an ’let-go’. The period, of its SH oscillations, is given by

(1) $\mathrm{T}=2 \pi \sqrt{\frac{3 \mathrm{~L}}{2 \mathrm{~g}}}$

(2) $\mathrm{T}=2 \pi \sqrt{\frac{2 \mathrm{~L}}{3 \mathrm{~g}}}$

(3) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{L}}{2 \mathrm{~g}}}$

(4) $\mathrm{T}=2 \pi \sqrt{\frac{3 \mathrm{~L}}{\mathrm{~g}}}$

3. A uniform meter rod, of mass $100 \mathrm{~g}$, is suspended through its mid-point. If it is displaced slightly from its equilibrium position and ’let-go’, the time period, of its oscillations, would be (nearly)

(1) $1.4 \mathrm{~s}$

(2) $1.6 \mathrm{~s}$

(3) $1.8 \mathrm{~s}$

(4) $2.0 \mathrm{~s}$

4. A block is resting on a piston, which is executing a SHM of period $1.0 \mathrm{~s}$ along the vertical direction. The block gets separated from the piston when its amplitude of motion becomes A. At this amplitude of its motion, the maximum velocity of the piston equals $\mathrm{V}$.

The values, of $\mathrm{A}$ and $\mathrm{V}$, are respectively

(1) $0.248 \mathrm{M}$ and $1.56 \mathrm{~m} / \mathrm{s}$

(2) $0.288 \mathrm{M}$ and $2.06 \mathrm{~m} / \mathrm{s}$

(3) $0.348 \mathrm{M}$ and $2.56 \mathrm{~m} / \mathrm{s}$

(4) $0.448 \mathrm{M}$ and $3.06 \mathrm{~m} / \mathrm{s}$

5. A block, of mass $\mathrm{M}$, is attached to a spring of spring constant $2.45 \mathrm{~N} / \mathrm{m}$. When the block is displaced through a distance of $16 \mathrm{~cm}$ from its equilibrium position, and let-go, it has a velocity of $56 \mathrm{~m} / \mathrm{s}$ at its mean position. The mass $\mathrm{M}$ is

(1) $0.1 \mathrm{~kg}$

(2) $0.2 \mathrm{~kg}$

(3) $0.3 \mathrm{~kg}$

(4) $0.4 \mathrm{~kg}$

6. A block, of density $\rho _{\mathrm{B}}$, has a horizontal cross-sectional area $\mathrm{A}$ and a vertical height $\mathrm{h}$. It floats in a fluid of density $\rho _{\mathrm{f}}$. The block is pushed down and released. It then executes SHM of angular frequency

(1) $\omega=\sqrt{\frac{\rho _{\mathrm{f}} \mathrm{g}}{\rho _{\mathrm{B}} \mathrm{h}}}$

(2) $\omega=\sqrt{\frac{\rho _{\mathrm{B}} \mathrm{g}}{\rho _{\mathrm{f}} \mathrm{h}}}$

(3) $\omega=\sqrt{\frac{\rho _{\mathrm{B}} \mathrm{h}}{\rho _{\mathrm{f}} \mathrm{g}}}$

(4) $\omega=\sqrt{\frac{2 \rho _{\mathrm{B}} \mathrm{g}}{\rho _{\mathrm{f}} \mathrm{h}}}$

7. A solid sphere, of radius R, is floating in a liquid of density $\rho$ with half of its volume submerged. If the sphere is slightly pushed and released, it starts performing simple harmonic motion. The frequency of these oscillations equals

(1) $\mathrm{f}=\frac{1}{2 \pi} \sqrt{\frac{2 \mathrm{~g}}{3 \mathrm{R}}}$

(2) $\mathrm{f}=\frac{1}{2 \pi} \sqrt{\frac{3 \mathrm{~g}}{2 \mathrm{R}}}$

(3) $\mathrm{f}=\frac{1}{2 \pi} \sqrt{\frac{\mathrm{g}}{2 \mathrm{R}}}$

(4) $\mathrm{f}=\frac{1}{2 \pi} \sqrt{\frac{3 \mathrm{~g}}{\mathrm{R}}}$

8. A particle of mass $M$ is resting, at the mean position, on a spherical smooth surface of radius $R$. If it is displaced (very) slightly from its mean position and ’let-go’, it would execute SHM of period

(1) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{R}}{2 \mathrm{~g}}}$

(2) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{R}}{\mathrm{g}}}$

(3) $\mathrm{T}=2 \pi \sqrt{\frac{3}{2} \frac{\mathrm{R}}{\mathrm{g}}}$

(4) $\mathrm{T}=2 \pi \sqrt{\frac{2 \mathrm{R}}{\mathrm{g}}}$

9. Two light springs, a smooth pulley, a light string and a mass $m$ are set up as shown. On displacing the mass slightly from its equilibrium position and ’letting it go’, its period of oscillation would be

(1) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}\left(\mathrm{k} _{1}+4 \mathrm{k} _{2}\right)}{\mathrm{k} _{1} \mathrm{k} _{2}}}$

(2) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}\left(4 \mathrm{k} _{1}+\mathrm{k} _{2}\right)}{\mathrm{k} _{1} \mathrm{k} _{2}}}$

(3) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}{\mathrm{k} _{1} \mathrm{k} _{2}}}$

(4) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}{4 \mathrm{k} _{1} \mathrm{k} _{2}}}$

10. The maximum speed of a particle executing SHM is $1 \mathrm{~m} / \mathrm{s}$ and maximum acceleration is $1.57 \mathrm{~m} / \mathrm{s}^{2}$. Its time period is

(1) $1 \mathrm{~s}$

(2) $4 \mathrm{~s}$

(3) $2 \mathrm{~s}$

(4) $3 \mathrm{~s}$

11. The KE and PE of a particle, executing SHM with amplitude A, are K and U, respectively. The displacement from the mean position, where the potential energy of the body is one-fourth of its total energy; is

(1) $\mathrm{A} \sqrt{2}$

(2) $\frac{\mathrm{A}}{2}$

(3) $\frac{\mathrm{A}}{4}$

(4) $\mathrm{A}$

12. In an oscillating block-spring system the spring constant is $2.45 \mathrm{~N} / \mathrm{m}$, the amplitude is $10 \mathrm{~cm}$ and the maximum speed is $56 \mathrm{~cm} / \mathrm{s}$. The mass of the block equals

(1) $0.1 \mathrm{~kg}$

(2) $0.3 \mathrm{~kg}$

(3) $0.2 \mathrm{~kg}$

(4) $0.4 \mathrm{~kg}$

13. A block of mass $m=1 \mathrm{~kg}$ is placed on top of another block of mass $M=5 \mathrm{~kg}$ that is attached to a horizontal spring $(\mathrm{k}=20 \mathrm{~N} / \mathrm{m})$, as shown in the figure. The coefficient of static friction between the blocks is $\mu$. The lower block slides on a frictionless horizontal surface with an amplitude of oscillation $A=0.4 \mathrm{~m}$. The minimum value of $\mu$, for which the upper block would not slip, relative to the lower block, is

(1) 0.126

(2) 0.136

(3) 0.146

(4) 0.156

14. A horizontal spring block system of (force constant $\mathrm{k}$ ) and mass M executes SHM of frequency $\mathrm{F}$ with amplitude A. When the block is passing through its equilibrium position, an object of mass $m$ is put on it and the two move together. The new amplitude and frequency of oscillations would be

(1) $f \sqrt{\frac{M}{m+m}}$ and $\left(\frac{m+M}{M}\right) A$

(2) $f \sqrt{\frac{M}{m+m}}$ and $\left(\frac{M}{m+M}\right) A$

(3) $f \sqrt{\frac{m+m}{M}}$ and $\left(\frac{m+M}{M}\right) A$

(4) $f \sqrt{\frac{m+m}{M}}$ and $\left(\frac{M}{m+M}\right) A$

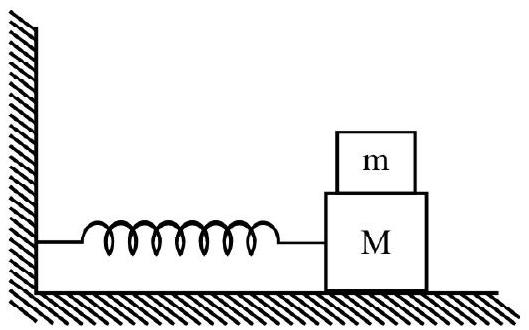
15. A weightless spring, which has a force constant $k$, oscillates with frequency $f$ when a mass $m$ is suspended from it. The The spring is cut into two halves and a mass $2 \mathrm{~m}$ is suspended from one of the halves. The frequency of oscillation will now be:

(1) $\mathrm{f}$

(2) $2 \mathrm{f}$

(3) $\frac{f}{2}^{1 / 2}$

(4) $\mathrm{f} \times 2^{1 / 2}$

16. A uniform cylinder of length $L$ and mass $M$, having cross-sectional area $A$, is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density $\rho$ at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with a small amplitude. If the force constant of the spring is $k$, the frequency of oscillation of the cylinder is

(1) $\frac{1}{2 \pi}\left(\frac{\mathrm{k}-\mathrm{A} \rho \mathrm{g}}{\mathrm{M}}\right)^{1 / 2}$

(2) $\frac{1}{2 \pi}\left(\frac{\mathrm{k}+\mathrm{A} \rho \mathrm{g}}{\mathrm{M}}\right)^{1 / 2}$

(3) $\frac{1}{2 \pi}\left(\frac{\mathrm{k}+\rho g \mathrm{L}^{2}}{\mathrm{M}}\right)^{1 / 2}$

(4) $\frac{1}{2 \pi}\left(\frac{\mathrm{k}+\mathrm{A} \rho g}{\mathrm{~A} \rho g}\right)^{1 / 2}$

17. A mass $m$ is suspended from two identical springs in the manner shown. The time period of its vertical oscillations is

(1) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{2 \mathrm{k} \cos \theta}}$

(2) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m} 2 \cos \theta}{\mathrm{k}}}$

(3) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{2 \mathrm{k} \cos 2 \theta}}$

(4) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m} 2 \cos ^{2} \theta}{\mathrm{k}}}$

18. A mass $m$ is suspended from three indetical springs in the manner shown. The time period, of its vertical oscillations, is

(1) $T=2 \pi \sqrt{\frac{m}{k\left(1+2 \cos ^{2} \theta\right)}}$

(2) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{2 \mathrm{k}}}$

(3) $\mathrm{T}=2 \pi \sqrt{\frac{2 \mathrm{~m}}{\mathrm{k}}}$

(4) $T=2 \pi \sqrt{\frac{2 m\left(\cos ^{2} \theta\right)}{\mathrm{k}\left(1+2 \cos ^{2} \theta\right)}}$

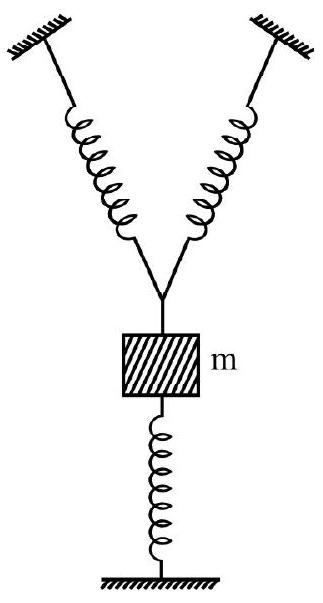
19. A spring, of stiffness constant $\mathrm{k}$ and natural length $\ell$, is cut into two parts in the ratio 3:1. A mass $\mathrm{m}$ is attached to the two parts in the manner shown.

The time period, of oscillations of the mass, when slightly displaced and ’let-go’, would be

(1) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{7 \mathrm{k}}}$

(2) $\mathrm{T}=2 \pi \sqrt{\frac{3 \mathrm{~m}}{\mathrm{k}}}$

(3) $\mathrm{T}=2 \pi \sqrt{\frac{3 \mathrm{~m}}{16 \mathrm{k}}}$

(4) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{16 \mathrm{k}}}$

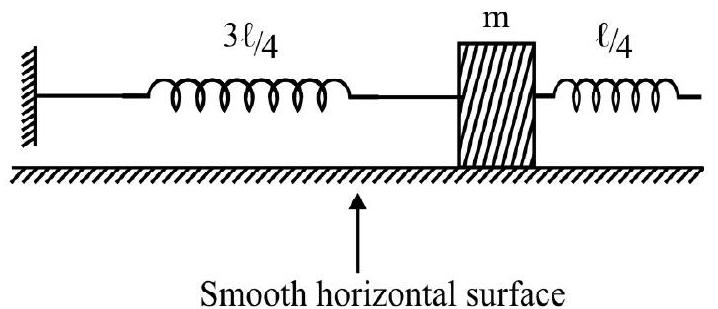
20. Imagine a tunnel to be dug through the earth (radius $=\mathrm{R}$ ) from its north pole to its south pole. If a mass $m$ were to be dropped into this tunnel, say from its north pole side, the motion of this mass would be

(1) A translatory motion with an acceleration that for increases during the first half of its motion and decreases during the second half ofits motion.

(2) A translatory motion with an acceleration that decreases during the first half of its motion and increases during the second half of its motion.

(3) A non simple harmonic but periodic motion with a time period $T=2 \pi \sqrt{\frac{R}{2 g _{s}}}$ $\left(g _{s}=\right.$ acceleration due to gravity on the surface of the earth).

(4) A simple harmonic motion with a time period $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{R}}{\mathrm{g} _{\mathrm{s}}}}$ ( $\mathrm{g} _{\mathrm{s}}=$ acceleration due to gravity on the surface of the earth).

21. On a smooth inclined plane, a body of mass $\mathrm{M}$ is attached between two light springs. The other ends of the springs are fixed to firm supports. If each spring has force constant $k$, the period of oscillation of the body is

(1) $2 \pi\left(\frac{\mathrm{M}}{2 \mathrm{k}}\right)^{1 / 2}$

(2) $2 \pi\left(\frac{2 \mathrm{M}}{\mathrm{k}}\right)^{1 / 2}$

(3) $2 \pi\left(\frac{\mathrm{Mg} \sin \theta}{2 \mathrm{k}}\right)^{1/ 2}$

(4) $2 \pi\left[\frac{2 \mathrm{Mg}}{\mathrm{k}}\right]^{1 / 2}$

22. In the figure shown, a spring mass system is placed on a horizontal smooth surface in between two vertical rigid walls $\mathrm{W} _{1}$ and $\mathrm{W} _{2}$. One end of the spring (spring constant $=\mathrm{k}$ ) is fixed with wall $\mathrm{W} _{1}$ and other end is attached with mass $m$ which is free to move. Initially, spring is tension free and having natural length $\ell _{0}$. Mass $\mathrm{m}$ is compressed through distance a and released. Taking the collision between wall $\mathrm{W} _{2}$ and mass $\mathrm{m}$ as elastic, the average force, exerted by mass $\mathrm{m}$ on wall $\mathrm{W} _{2}$, is

(1) $\frac{2 \mathrm{aK}}{\pi}$

(2) $\frac{\mathrm{aK}}{\mathrm{m}}$

(3) $\frac{\mathrm{aK}}{\pi}$

(4) $\frac{2 \mathrm{aK}}{\mathrm{m}}$

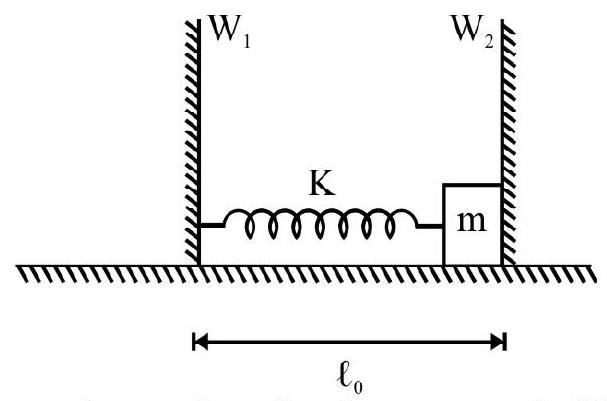
23. Two masses, $m _{1}$ and $m _{2}$ are suspended together by a massless spring of spring constant $k$. When the masses are in equilibrium, $\mathrm{m} _{1}$ is removed without disturbing the system. The angular frequency, and amplitude of oscillation, of $\mathrm{m} _{2}$, would equal (respectively)

(1) $\sqrt{\frac{\mathrm{k}}{\mathrm{m} _{2}}}$ and $\left(\frac{\mathrm{m} _{1} \mathrm{~g}}{\mathrm{k}}\right)$

(2) $\sqrt{\frac{\mathrm{k}}{\mathrm{m} _{1}}}$ and $\left(\frac{\mathrm{m} _{2} \mathrm{~g}}{\mathrm{k}}\right)$

(3) $\sqrt{\frac{\mathrm{k}}{\mathrm{m} _{1}}}$ and $\left(\frac{\mathrm{m} _{2} \mathrm{~g}}{\mathrm{k}}\right)$

(4) $\sqrt{\frac{\mathrm{k}}{\mathrm{m} _{2}}}$ and $\left(\frac{\mathrm{m} _{2} \mathrm{~g}}{\mathrm{k}}\right)$

24. A block, of mass $0.5 \mathrm{~kg}$, moving on a horizontal frictionless surface at $2.0 \mathrm{~m} / \mathrm{s}$, collides with, and sticks, to a massless pan at the end of a horizontal spring whose stiffness constant is $32 \mathrm{~N} / \mathrm{m}$ (as shown in the figure). The expression, for $x(\mathrm{t})$, the displacement from the equilibrium position, as a function of time, would be

(1) $0.25 \sin (8) \mathrm{t}$

(2) $0.5 \sin (8) \mathrm{t}$

(3) $0.3 \sin (8) \mathrm{t}$

(4) $0.4 \sin (8) \mathrm{t}$

25. A wave is represented by the equation:

$$ \mathrm{y}=\mathrm{A} \sin \left[10 \pi x+18 \pi \mathrm{t}+\left(\frac{\pi}{3}\right)\right] $$

where $x$ is in $\mathrm{m}$ and $\mathrm{t}$ in $\mathrm{s}$. The expression represents:

(1) a wave propagating in positive $x$-direction with velocity $1.5 \mathrm{~m} / \mathrm{s}$

(2) a wave propagating in negative $x$-direction with velocity $2.0 \mathrm{~m} / \mathrm{s}$

(3) a wave propagating in negative $x$-direction with wavelength $2.0 \mathrm{~m}$

(4) a wave propagating in positive $x$-direction with wavelength $2.0 \mathrm{~m}$

26. Equation of a wave, propagating in a medium, is $y=a \sin (b t-c x)$. Which of the following statements, about this wave is incorrect?

(1) Ratio of the displacement amplitude, with which the particles of medium oscillate, to the wavelength, is equal to $\frac{\mathrm{ac}}{2 \pi}$.

(2) Ratio of the velocity oscillation amplitude of medium particles, to the wave propagation velocity, is equal to ac.

(3) Oscillation amplitude of relative deformation of the medium is directly proportional to velocity oscillation amplitude of medium particles.

(4) The wave is propagating along the negative $x$-axis.

27. A wave disturbance in a medium is described by $\mathrm{y}(x, \mathrm{t})=0.02 \cos \left(50 \pi \mathrm{t}+\frac{\pi}{2}\right) \cos (10 \pi x)$ where $x$ and $y$ are in meters and $t$ in seconds. For this wave:

(1) A node occurs at $x=0.3 \mathrm{~m}$

(2) An antinode occurs at $x=0.15 \mathrm{~m}$

(3) The speed of the wave is $5.0 \mathrm{~m} / \mathrm{s}$

(4) The wavelength is $0.4 \mathrm{~m}$

28. The equation of a wave is $\mathrm{y}=\frac{5}{2} \sin \left(\mathrm{t}-\frac{x}{2}\right)$, where displacement is in $\mathrm{cm}$ and time is in second. At a given time the phase angle, between two particle that are $12 \mathrm{~cm}$ apart, is

(1) $6^{0}$

(2) 6 radian

(3) $3^{0}$

(4) 3 radian

29. A plane sound wave is propagating in a medium. In reference to a frame A, its equation is y $y=a \cos (\omega t-k x)$. With reference to another frame B, moving with a constant velocity $v$ in the direction of propagation of the wave, the equation of the wave would be:

(1) $\mathrm{y}=\mathrm{a} \cos [(\omega+\mathrm{kv}) \mathrm{t}-\mathrm{kx}]$

(2) $\mathrm{y}=-\mathrm{a} \cos [(\omega-\mathrm{kv}) \mathrm{t}-\mathrm{k} x]$

(3) $\mathrm{y}=\mathrm{a} \cos [(\omega-\mathrm{kv}) \mathrm{t}-\mathrm{k} x]$

(4) $\mathrm{y}=\mathrm{a} \cos [(\omega+\mathrm{kv}) \mathrm{t}+\mathrm{kx}]$

30. A transverse wave is represent by the equation $\mathrm{y}=\mathrm{y} _{0} \sin \frac{2 \pi}{\lambda}(\mathrm{vt}-x)$. The maximum particle velocity would be two times the wave velocity, if $\lambda$ equals

(1) $\lambda=\frac{\pi y _{0}}{2}$

(2) $\lambda=\pi y _{0}$

(3) $\lambda=2 \pi y _{0}$

(4) $\lambda=\frac{2 \pi \mathrm{y} _{0}}{2}$

31. The equation of a plane progressive wave is $\mathrm{y}=\frac{\mathrm{a}}{\pi} \sin \frac{2 \pi}{3}\left(\mathrm{t}-\frac{x}{\mathrm{~b}}\right)$. If maximum velocity of medium particles, and the velocity of wave, are equal to each other, the ratio $\frac{\mathrm{a}}{\mathrm{b}}$ would equal

(1) $\frac{2}{3}$

(2) $\frac{3}{2}$

(3) $\frac{1}{2}$

(4) $\frac{2}{1}$

32. In melde’s experiment (on stationary waves) a string, passing over a smooth pulley, carries a stone at one end, while its other end is attached to a vibrating tunning fork. The string shows 8 loops. When the stone is immersed in water 10 loops are formed. The relative density, of the stone, is

(1) $\frac{25}{9}$

(2) $\frac{16}{9}$

(3) $\frac{25}{11}$

(4) $\frac{16}{11}$

33. The equations of four waves are given below:

(i) $\mathrm{y} _{1}=\mathrm{a} \sin \omega\left(\mathrm{t}-\frac{\mathrm{x}}{\mathrm{v}}\right)$

(ii) $\mathrm{y} _{2}=\mathrm{a} \sin \omega\left(\mathrm{t}+\frac{\mathrm{x}}{\mathrm{v}}\right)$

(iii) $\mathrm{z} _{1}=\mathrm{a} \sin \omega\left(\mathrm{t}-\frac{\mathrm{x}}{\mathrm{v}}\right)$

(iv) $\mathrm{z} _{2}=\mathrm{a} \sin \omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)$

For these waves, the only correct statement is

(1) On superposition of waves (i) and (iii), a stationary wave, having amplitude $2 \mathrm{a}$, will be formed.

(2) Superposition of waves (ii) and (iii) will result in a wave propagating along $x$-axis.

(3) On superposition of waves (ii) and (iv), a stationary wave, having amplitude $a \sqrt{2}$, will be formed.

(4) On superposition of waves (iii) and (iv), a transverse stationary wave will be formed.

34. Which of the following statements is correct for stationary waves?

(1) Nodes and anti nodes are formed in case of transverse stationary waves only.

(2) Nodes and anti nodes are formed in case of longitudinal stationary waves only.

(3) Nodes and anti nodes are formed in case of all the stationary waves.

(4) Phase is transferred from one point to another point, along the wave, in case of all stationary waves.

35. The shortest length of a resonance tube, which resonates with a tuning fork of $256 \mathrm{~Hz}$, is $32 \mathrm{~cm}$. The corresponding length for a fork of frequency $384 \mathrm{~Hz}$, is $20.8 \mathrm{~cm}$. The end-correction, and velocity of sound in air, are equal, respectively, to

(1) $1.6 \mathrm{~cm}$ and $344 \mathrm{~ms}^{-1}$

(2) $0.8 \mathrm{~cm}$ and $344 \mathrm{~ms}^{-1}$

(3) $0.8 \mathrm{~cm}$ and $322 \mathrm{~ms}^{-1}$

(4) $1.6 \mathrm{~cm}$ and $322 \mathrm{~ms}^{-1}$

36. A tuning fork gives 15 beats per second when sounded with a sonometer wire of length $200 \mathrm{~cm}$; it gives 20 beats per second with that of a sonometer wire of length $250 \mathrm{~cm}$.

(Tension and mass per unit length are $1.25 \mathrm{kgwt}$ and $0.025 \times 10^{-3} \mathrm{~kg}$, respectively and $\mathrm{g}=9.8 \mathrm{~ms}^{-2}$. The frequency of the fork is

(1) $190 \mathrm{~Hz}$

(2) $160 \mathrm{~Hz}$

(3) $180 \mathrm{~Hz}$

(4) $140 \mathrm{hz}$

37. An observer A is moving directly towards a stationary sound source; another observer $\mathrm{B}$ is moving away from that very source with the same velocity.

Which of the following statements is correct?

(1) Frequency recorded by $\mathrm{A}$ is greater than that recorded by $\mathrm{B}$.

(2) Average of frequencies recorded by $A$ and $B$ is (nearly) equal to the natural frequency of the source.

(3) Both A and B will record the natural frequency of the source.

(4) Frequency recorded by $\mathrm{A}$ is equal to that recorded by $\mathrm{B}$.

38. A source and an observer are located at the same point. The source starts moving away from the observer at $t=0$, with a constant acceleration a. If natural frequency of the source is $n _{0}$ and speed of sound in air is $u$, the apparent frequency, observed by the observer at time $t$, will be

(1) equal to $\left(\frac{n _{0} v}{v+a t}\right)$

(2) equal to $\left(\frac{\mathrm{n} _{0} \mathrm{v}}{\mathrm{v}-\mathrm{at}}\right)$

(3) greater than $\left(\frac{n _{0} v}{v+a t}\right)$

(4) less than $\left(\frac{\mathrm{n} _{0} \mathrm{v}}{\mathrm{v}-\mathrm{at}}\right)$

				Answer key
1.	$(1)$	2.	$(2)$	3.	$(2)$	4.	$(1)$	5.	$(2)$
6.	$(1)$	7.	$(2)$	8.	$(2)$	9.	$(2)$	10.	$(2)$
11.	$(2)$	12.	$(3)$	13.	$(2)$	14.	$(2)$	15.	$(1)$
16.	$(2)$	17.	$(3)$	18.	$(1)$	19.	$(3)$	20.	$(4)$
21.	$(1)$	22.	$(1)$	23.	$(1)$	24.	$(1)$	25.	$(3)$
26.	$(4)$	27.	$(3)$	28.	$(2)$	29.	$(3)$	30.	$(2)$
31.	$(2)$	32.	$(1)$	33.	$(4)$	34.	$(3)$	35.	$(1)$
36.	$(2)$	37.	$(2)$	38.	$(3)$

Question Bank

Key Learning Points

Oscillations

1. A motion is said to be ‘periodic’ if the particle / object has the same ‘state of motion’ (same position co-ordinates, same velocity, same acceleration) after the same (regular) interval of time.

2. All oscillatory and all vibratory motions are necessarily periodic; however all ‘periodic motions’ would not necessarily be oscillatory / vibratory in nature.

3. An oscillatory motion is a ’to and fro’ periodic motion about some central or mean position.

4. We need a periodic function $(\mathrm{f}(\mathrm{t}+\mathrm{T})=\mathrm{f}(\mathrm{t}))$ to have a mathematical description of a periodic or oscillatory motion.

5. The terms : time period (T), frequency (n) and angular frequency $(\omega)$, for a periodic motion, are related to each other as

$$ \mathrm{T}=\frac{1}{\mathrm{n}}=\frac{2 \pi}{\omega} $$

6. A particle executes an oscillatory motion under the action of a ‘restoring force’.

7. The simplest oscillatory motions are the ones that get represented through simple linear sinusoidal function of time.

8. Fourier’s theorem enables us to analyse any general periodic motion through sinusoidal functions.

9. A particle executes the simplest form of oscillatory motion if the instantaneous ‘restoring force’, acting on it, is directly proportional to its instantaneous displacement from its mean (or central) position.

10. The simplest form of oscillatory motion is the ‘simple harmonic motion’ (SHM).

11. A particle is said to execute a SHM if it oscillates under the action of a (restoring) force that is always directed opposite to its instantaneous displacement (from its mean position) and whose instantaneous magnitude varies in direct proportion to the magnitude of its instantaneous displacement.

12. In mathematical terms, a SHM is expressed through the equation

$$ \mathrm{F} _{x}=-\mathrm{k} x $$

or $\mathrm{ma} _{x}=-\mathrm{k} x$

or $\quad \mathrm{a} _{x}=-\omega^{2} x \quad\left(\right.$ where $\left.\omega^{2}=\frac{\mathrm{k}}{\mathrm{m}}\right)$

Since $\mathrm{a} _{x}=\frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}$ we get the equation

$$ \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}+\omega^{2} x=0 $$

as the ‘differential equation’ for a simple harmonic motion.

13. The simplest functions, that are ‘solutions’ of the above equation, are

$$ x=a \sin \omega t \quad ; \quad x=a \cos \omega t $$

14. A SHM can also be regarded as the ‘projection’ of a uniform circular motion on to a diameter of the circle. The circular path, associated with a given SHM, is known as its ‘circle of reference’.

15. The “phase”, of an oscillating particle, at any instant / any position, is a term / quantity that determines the parameters (displacement/ velocity / acceleration) that determine / define the instantaneous state of motion of the particle.

16. For a particle, executing a SHM, the argument of the sine / cosine function, expressing it, determined its ‘instantaneous phase’.

17. The general expression, for ‘phase’, is $\delta=(\omega t+\phi)$

The value of phase, at $t=0$, (the ‘initial phase’) of the oscillating particle, is known as its ’epoch’. Thus epoch $(=$ Value of $\delta$ at $t=0)=\phi$.

18. For a SHM,described by the equation,

$$ y=a \sin (\omega t+\phi) $$

The velocity, $v=a \omega \cos (\omega t+\phi)=\omega \sqrt{a^{2}-y^{2}}$

and the acceleration, $\mathrm{f}=\mathrm{a} \omega^{2} \sin (\omega \mathrm{t}+\phi)=-\omega^{2} \mathrm{y}$

19. The kinetic energy $(\mathrm{K})$, potential energy $(\mathrm{U})$ and total energy $(\mathrm{E})$, of a particle, executing SHM, are given by

$$ \begin{aligned} & \mathrm{K}=\frac{1}{2} \mathrm{ma}^{2} \omega^{2} \cos ^{2}(\omega \mathrm{t}+\phi)=\frac{1}{2} \mathrm{~m} \omega^{2}\left(\mathrm{a}^{2}-x^{2}\right) \\ & \mathrm{U}=\frac{1}{2} \mathrm{ma}^{2} \omega^{2} \sin ^{2}(\omega \mathrm{t}+\phi)=\frac{1}{2} \mathrm{~m} \omega^{2} x^{2} \\ & \mathrm{E}=\frac{1}{2} \mathrm{ma}^{2} \omega^{2} \end{aligned} $$

20. The total energy, of a particle executing SHM, is, on the average, half kinetic and half potential in form.

21. The force (or spring) constant ( $\mathrm{k}$ ), of a given spring, may be thought of as the force needed to change (extend /compress) the length of a given spring, by a unit amount. ’ $k$ ’ thus has units of $\mathrm{N} / \mathrm{m}$.

22. Using the formula for Young’s modulus (Y)

$$ \mathrm{Y}=\frac{\mathrm{F} \cdot(\Delta \mathrm{L})}{\mathrm{A} \cdot \mathrm{L}} $$

One can say that the force constant (k), of a spring, may be expressed as

$$ \mathrm{k}(\text { Value of } \mathrm{F} \text { for } \Delta \mathrm{L}=1 \text { unit })=\frac{\mathrm{YA}}{\mathrm{L}} $$

23. For the (SH) oscillations of a mass $\mathrm{M}$, attached to a (light) spring of spring constant, $\mathrm{k}$, the time period, $\mathrm{T}$, is given by

$$ \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k}}} $$

24. The ’equivalent spring constants’, of a series and a parallel combination, of two (light) springs, of spring constants $\mathrm{k} _{1}$ and $\mathrm{k} _{2}$, are given by

$$ \mathrm{k} _{\text {series }}=\frac{\mathrm{k} _{1} \mathrm{k} _{2}}{\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)} $$

and $\mathrm{k} _{\text {parallel }}=\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)$

25. The oscillations of a simple pendulum are (strictly speaking) simple harmonic only if the amplitude of its oscillations is (very) small.

26. The time period, $\mathrm{T}$, of the $\mathrm{SH}$ oscillations, of a simple pendulum of length $\mathrm{L}$, is given by

$$ \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{L}}{\mathrm{g}}} $$

27. We can have simple harmonic oscillations when

(i) A block, floating in a liquid, is pushed / pulled a little and ’let-go’.

(ii) A cork, kept in the narrow neck of a large vessel, is pushed / pulled slightly and ’let-go’.

(iii) The liquid, in one limb, of a U-tube, is pushed / pulled slightly and ’let-go’.

28. These can be many more similar examples. The important point to note is that, to decide whether a given object, is executing simple harmonic oscillations or not, we should calculate the net force acting on it, when it is displaced (slightly) from its equilibrium (mean / central) position. If this net force turns out to have

(i) a direction opposite to that of the displacement,

(ii) a magnitude proportional to the magnitude of its displacement, the particle is executing simple harmonic oscillations. If both these requirements are not simultaneously satisfied, the motion, of the particle would not be a SHM.

29. When a particle / system oscillates, only under the action of the restoring force set up, because of its being displaced from its equilibrium position, it is said to be executing its free, or natural, oscillations / vibrations.

30. The concept of ‘free’ oscillations is an idealized concept. A practical oscillating system (almost) always has one or more external forces acting on it.

31. When a particle is oscillating in a medium (usually air), it experience (energy consuming) dissipative forces due to viscosity / friction etc. As a result, the amplitude of oscillations keeps on decreasing and (depending upon the nature and magnitude of such dissipative forces), after some time, the oscillations ‘die down’ or stop.

32. We call such oscillations (oscillations in the presence of dissipative (energy consuming) forces) as ‘damped oscillations’.

33. We can also have a particle / system oscillating under the action of an external periodic force. Such oscillations (oscillations due to some external periodic force) are known as ‘forced oscillations’.

34. For ‘forced oscillations’, we can have a special phenomenon, known as the phenomenon of ‘resonance’.

35. ‘Resonant oscillations’ are a special case of ‘forced oscillations’ in which the frequency of the external periodic force matches the natural (or free oscillation) frequency of the oscillating particle / system.

36. The tuning of a radius, microwave ovens, musical instruments, the swing used by children, the dangerous oscillations, of hanging bridges or boats / ships, etc., are some of the examples of situations / ‘setups’ in which ‘resonance’ plays an important part.

Waves

37. (Mechanical) wave motion is one of the two natural methods of transferring energy from one point to another in a (material) medium. In this type of motion, a ‘disturbance’, created at one point in a medium, propagates through the medium, without any material movement of the particles of the medium.

38. It is only a ‘sustained disturbance’ that can cause a sustained wave motion.

39. A sustained periodic disturbance can result in a sustained periodic wave motion.

40. The simplest type of wave motion is ‘simple harmonic waves’. These are caused by a sustained simple harmonic disturbance created at one point in a medium.

41. The equation of the simple harmonic waves, associated with a simple harmonic disturbance

$$ \mathrm{y}=\mathrm{A} \sin \omega \mathrm{t}, \quad \text { is } $$

$$ \xi=\mathrm{A} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right) $$

42. The equation, for a simple harmonic wave, can be put in several alternative forms, like

$$ \begin{aligned} \xi= & \mathrm{A} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)=\mathrm{A} \sin 2 \pi\left(\mathrm{vt}-\frac{\mathrm{x}}{\lambda}\right)=\mathrm{A} \sin 2 \pi\left(\frac{\mathrm{t}}{\mathrm{T}}-\frac{x}{\lambda}\right) \\ & =\mathrm{A} \sin (\omega \mathrm{t}-\mathrm{k} x) \end{aligned} $$

43. The differential equation of ‘wave-motion’ is

$$ \frac{\delta^{2} \xi}{\delta x^{2}}=\frac{1}{v^{2}} \frac{\delta^{2} \xi}{\delta \mathrm{t}^{2}} $$

44. The ‘solution’, of the differential equation, for wave motion can have the general form

$$ \xi=\operatorname{Af}(\omega \mathrm{t}-\mathrm{kx}) $$

The SH wave solution, namely,

$$ \xi=\mathrm{A} \sin (\omega \mathrm{t}-\mathrm{k} x) $$

is one of the many possible forms of the solutions of the differential equation for wave motion.

45. We define a number of terms : ‘amplitude’, ‘wave-length’, ’time period’, frequency, angular frequency, wave-number, phase and ‘phase difference’, for a wave-motion.

46. We have a simple relation

$$ \mathrm{v}=\mathrm{n} \lambda $$

between the velocity (v), frequency (n) and wavelength $(\lambda)$, of a wave.

47. The wave length $(\lambda)$, of a wave, equals the separation between any two points of the medium, that have the same phase at any given instant.

48. The ‘phase’ $(\phi)$, of a $(\mathrm{SH})$ wave, equals the general form of the argument of the sine function in its equation:

$$ \phi=\left[\omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)+\theta\right] $$

49. For a SH wave;

(i) The ‘difference’, between the ‘phases’ of a given particle, at two time instants separated by a time interval $(\Delta \mathrm{T})$, is given by

$$ \Delta \phi=\frac{2 \pi}{\mathrm{T}} \Delta \mathrm{T}=\omega(\Delta \mathrm{T}) $$

(ii) The ‘difference’, between the ‘phases’, at a given instant of time, between two particles of the medium, having a separation $\Delta x$, is

$$ \Delta \phi=\frac{2 \pi}{\lambda}(\Delta x)=\mathrm{k}(\Delta x) $$

50. Waves can be of two types: ’longitudinal’ waves and ’transverse’ waves. The phenomenon of polarization helps us to decide the nature of a given wave.

51. The speed of propagation, of a mechanical wave, in a given medium, is given by

$$ v=\sqrt{\frac{E}{\rho}} $$

( $E=$ the (relevant) modulus of elasticity of the medium; $\rho=$ density of the medium)

52. Electromagnetic waves are not mechanical waves. They can propagate even in vacuum. Their speed of propagation, in a medium, is given by

$$ \mathrm{v}=\frac{1}{\sqrt{\mu \varepsilon}} $$

where $\mu=$ magnetic permeability of the medium and $\varepsilon=$ (electric) permittivity of the medium.

53. The speed of sound, in gases, is given by

$$ \mathrm{v}=\sqrt{\frac{\mathrm{K}}{\rho}} $$

54. Newton assumed that the propagation of sound, in gases, takes place under isothermal conditions. $\mathrm{He}$, therefore, used the (isothermal) value of its Bulk modulus ( $\mathrm{K}$ ) to give the formula

$$ \mathrm{v}=\sqrt{\frac{\mathrm{P}}{\rho}} \quad(\mathrm{P}=\text { pressure }) $$

for the speed of sound in a gas.

55. Newton’s formula did not agree with experimental results. Laplace, therefore, modified it by assuming that the propagation of sound, in a gas, takes place under adiabatic conditions.

56. Laplace’s modified formula, for the speed of sound, in a gas, is

$$ \mathrm{v}=\sqrt{\frac{\gamma \mathrm{P}}{\rho}} $$

Here $\gamma\left(=\mathrm{C} _{\mathrm{p}} / \mathrm{C} _{\mathrm{v}}\right)$ is the ratio of the two specific heat capacities of the gas.

57. Laplace’s formula leads to the results,

(i) $\quad \mathrm{v} \propto \sqrt{\mathrm{T}}(\mathrm{T}=$ absolute temperature $)$

(ii) $\quad v$ is independent of changes in pressure

58. The speed of propagation of waves, in a stretched string, is given by

$$ v=\sqrt{\frac{T}{m}} $$

( $\mathrm{T}=\mathrm{Tension}$ in the string; $\mathrm{m}=$ mass per unit length of the string)

59. The reflection of waves, in a medium, takes place as per the usual laws of reflection.

60. The reflection of a wave, may take place at a ‘from rarer to denser medium interface’. This type of reflection not only reverses the ‘direction of propagation’ but also reverses the ‘phase’ of the wave. Thus, in such a reflection, an incident wave, represented by

$$ \xi _{\mathrm{i}}=\mathrm{A} \sin \omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right) $$

gets reflected as a wave, represented by

$$ \xi _{\mathrm{R}}=\mathrm{A} \sin \left[\omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)+\pi\right] $$

61. For reflection of a ‘from denser to rarer medium’ interface, an incident wave gets reflected without any phase reversal. Hence, in such a case, an incident wave, represented by

$$ \xi _{\mathrm{i}}=\mathrm{A} \sin \left[\omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)\right] $$

gets reflected as a wave represented by

$$ \xi _{\mathrm{R}}=\mathrm{A} \sin \left[\omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)\right] $$

62. The resultant disturbance, at any point in a medium, in which two, or more, waves are simultaneously present, is determined through a principle, known as the principle of superposition.

63. The “principle of superposition” may be expressed mathematically through the equation:

$$ \mathrm{y}=\mathrm{y} _{1}+\mathrm{y} _{2}+\mathrm{y} _{3}+ $$

Here $y$ is the resultant disturbance, at any point, where the disturbances, due to the individual waves, are $y _{1}, y _{2}, y _{3} \ldots \ldots \ldots . . .$. . The addition, mentioned here, is a ‘vector’ addition of the terms on the right.

64. Depending on the nature, and the relevant features of the two (or more) waves being superposed, their ‘resultant’ can be associated with a number of phenomenon.

65. The superposition of two waves, of (preferably, but not necessarily) equal amplitude, equal frequency and having a constant (in time) phase difference, results in the phenomenon of interference.

66. The superposition of two identical waves, propagating in opposite directions, and having a phase difference of 0 or $\pi$, results in the phenomenon of stationary, or standing, waves.

67. The superposition of two waves, of (preferably equal amplitude) and (very) slightly different frequencies, results in the phenomenon of ‘beats’.

68. Standing waves are usually produced through the superposition of a ‘direct wave’ with its ‘reflected wave’.

69. When standing waves are produced through the superposition of a direct wave

$$ \mathrm{y} _{1}=\mathrm{a} \sin \left[\omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)\right] $$

with its reflected wave

$$ \mathrm{y} _{2}=\mathrm{a} \sin \left[\omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)\right] $$

(reflected without any change of phase), the resultant displacement is given by

$$ \mathrm{y}=\mathrm{y} _{1}+\mathrm{y} _{2}=\left[2 \mathrm{a} \cos \frac{\omega x}{\mathrm{v}}\right] \sin (\omega \mathrm{t}) $$

70. In this case, the amplitude $\mathrm{A}\left(=2 \mathrm{a} \cos \left(\frac{\omega x}{\mathrm{v}}\right)\right)$, of the resultant wave,

(i) $\text { equals zero, wherever } \frac{2 \pi}{\lambda} x=(2 n+1) \frac{\pi}{2} $

i.e. $x=(2 n+1) \frac{\pi}{4}$

These points, of zero disturbance, are called NODAL points or nodes. The resultant disturbance, at the nodes, is zero at all times.

(ii) can equal $\pm 2 \mathrm{a}$ wherever $\frac{2 \pi}{\lambda} x=\mathrm{n} \lambda$

i.e. $x=\frac{\mathrm{n} \lambda}{2}$

These points of maximum disturbance, at any given instant of time, are called ANTINODAL points or Antinodes. However, unlike the nodes, the resultant disturbance, at the antinodes, varies between $(+2 a), 0,(-2 a)$, depending on the value of $(\sin \omega t)$. The resultant disturbance, even at the antinodes, become zero at all these time instants at which $\sin \omega t=0$. These time instants correspond to $\omega \mathrm{t}=\mathrm{n} \pi$. At these time instants, the whole of the medium, momentarily, has zero disturbance.

71. Successive nodes, as well as successive antinodes, are $\frac{\lambda}{2}$ apart from each other.

72. The distance between a node, and its adjacent antinode, equals $\frac{\lambda}{4}$.

73. There is always a ’node’ between two successive ‘antinodes’ and vice-versa.

74. When standing waves are produced through the superposition of a direct wave

$$ \mathrm{y} _{1}=\mathrm{a} \sin \left[\omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)\right] $$

with its reflected wave

$$ \mathrm{y} _{2}=\mathrm{a} \sin \left[\omega\left(\mathrm{t}-\frac{x}{\mathrm{v}}\right)+\pi\right]=-\mathrm{a} \sin \left[\omega\left(\mathrm{t}+\frac{x}{\mathrm{v}}\right)\right] $$

(reflected with a reversal of its phase), the resultant wave is given by

$$ y=y _{1}+y _{2}=\left(2 a \sin \frac{\omega x}{v}\right)(\cos \omega t)=A \cos \omega t $$

75. The nodal points, in this case, are located at points for which

$$ \frac{2 \pi x}{\lambda}=\mathrm{n} \pi \quad \text { or } \quad x=\frac{\mathrm{n} \lambda}{2} $$

76. The antinodal points, in this case, are located at points for which

$$ \frac{2 \pi x}{\lambda}=(2 n+1) \frac{\pi}{2} \quad \text { or } \quad x=(2 n+1) \frac{\lambda}{4} $$

77. The time instants, at which the whole of the medium is momentarily having zero disturbance, in this case, are given by

$$ \omega \mathrm{t}=(2 \mathrm{n}+1) \frac{\pi}{2} $$

78. All other features, of the ’nodal’ and ‘antinodal’ points, are the same for this case as they are for the case discussed before.

79. Standing waves can be produced in a stretched string, of length $\ell$, linear mass density (mass per unit length) $\mathrm{m}$, stretched under a tension $\mathrm{T}$. Its permissible modes of vibration have frequencies given by

$$ v _{\mathrm{n}}=\frac{\mathrm{n}}{2 \ell} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}} \quad(\mathrm{n}=1,2,3 \ldots \ldots \ldots . .) $$

These permissible modes have wave lengths given by

$$ \lambda _{\mathrm{n}}=\frac{2 \ell}{\mathrm{n}} \quad\left(\because \text { The velocity of the waves equals } \sqrt{\frac{\mathrm{T}}{\mathrm{m}}}\right) $$

80. The simplest, mode of vibration, is known as the ‘fundamental mode’ or ‘first harmonic’. The other permissible modes are known as the ‘second harmonic’, ’third harmonic’, and so on.

81. Standing waves can also be produced in air columns, present in a pipe open at both ends (open pipe) or a pipe closed at one end (closed pipe).

82. For an open pipe (of length $\ell$ ), the fundamental mode, or first harmonic, has a frequency $\left(\frac{\mathrm{v}}{2 \ell}\right)$ and a wave length $(2 \ell)$. Here $v$ stands for the velocity of sound in air.

83. The other permissible modes (for an open pipe) have frequencies that are all integral multiples of the frequency of the fundamental mode. The corresponding wavelengths are $\frac{2 \ell}{\mathrm{n}}(\mathrm{n}=1,2,3, \ldots \ldots \ldots$.$) .$

84. For a closed pipe, (of length $\ell$ ), the fundamental mode, or first harmonic, has a frequency $\left(\frac{\mathrm{v}}{4 \ell}\right)$ and a wavelength $(4 \ell)$.

85. The other permissible nodes (for a closed pipe), have frequencies that are odd integral multiples of the fundamental frequency. The permissible frequencies, here, are thus $(2 n+1) \frac{\mathrm{v}}{4 \ell}(\mathrm{n}=0,1,2$, $3, \ldots \ldots.$) . The corresponding wavelengths are $\left(\frac{4 \ell}{2 \mathrm{n}+1}\right)$.

86. In an open pipe, the first, second, third,……., i.e. all harmonics are permissible. In a closed pipe,only the first, third, fifth,…….., i.e. only the odd harmonics are permissible.

87. The superposition of two waves of (slightly) different frequencies, and equal, or unequal, amplitudes, results in a phenomenon known as the phenomenon of beats.

88. In the case of sound waves, beats are associated with a ‘rise’, followed by a ‘fall’, and again a ‘rise’, in the intensity of the resultant sound. This is also referred to as ‘waxing, waning and waxing’ of the resultant sound. One such cycle makes up one ‘beat’.

89. The beat frequency equals the difference in the frequencies of the two waves being superposed.

90. Because of ‘persistence of hearing effect in the human ear’, we can hear beats clearly only if the difference in frequencies, of the two waves, is less than 10.

91. ‘Doppler effect’ is the phenomenon in which the ‘apparent frequency’ of a source, as observed by an observer, depends on the magnitude, and direction, of the ‘relative velocity’ between then.

92. If $v$ is the magnitude of the velocity of sound in (still) air, $v _{0}$ the magnitude of the velocity of the observer and $\mathrm{v} _{\mathrm{s}}$ the magnitude of the velocity of the source, the apparent frequency (n’) of a source, having a true frequency $\mathrm{n}$, is given by the general Doppler effect formula:

$$ \mathrm{n}^{\prime}=\left[\frac{\mathrm{v}+\mathrm{v} _{0}}{\mathrm{v}-\mathrm{v} _{\mathrm{s}}}\right] \mathrm{n} $$

Here ’true frequency’, implies the frequency of the source as observed by an observer that is at rest relative to the source.

93. The important points, to be kept in mind, while using the above formula, are:

(i) The velocity of sound, in the presence of a wind, would be $(v+w)$, where $w$ is the component of the velocity of wind in the direction of propagation of sound.

(ii) The terms $\mathrm{v} _{0}$ and $\mathrm{v} _{\mathrm{s}}$ are to be treated as algebraic quantities that have to be assigned a $(+)$ or $(-)$ sign as per the following convention:

(a) “A (+) sign will be attached to $\mathrm{v} _{0}$ if the observer is moving towards (or approaching) the source. For an observer moving away (or receding) from the source, the term $\mathrm{v} _{0}$ would be attached a $(-)$ sign”.

(b) “A (+ve) sign will be attached to $\mathrm{v} _{\mathrm{s}}$ if the source is moving towards (or approaching) the observer. For a source moving away (or receding) from the observer, the term $\mathrm{v} _{\mathrm{s}}$ would be attached a $(-)$ sign”.

1. A simple harmonic motion is represented by the equation

$$ y=b \cos \omega t $$

The graph, representing the phase relation, between its displacement, velocity and acceleration, is the graph labelled as graph.

(1) $\mathrm{A}$

(2) $\mathrm{B}$

(3) $\mathrm{C}$

(4) $\mathrm{D}$

Show Answer

Correct answer: (4)

Solution:

We have

$$ y=b \cos \omega t $$

$\therefore \quad \mathrm{v}=\frac{\mathrm{dy}}{\mathrm{dt}}=-\mathrm{b} \omega \sin \omega \mathrm{t}$

and $\mathrm{a}=\frac{\mathrm{dv}}{\mathrm{dt}}=-\mathrm{b} \omega^{2} \cos \omega \mathrm{t}$

$\therefore A t \mathrm{t}=0$

$y=b ; v=0, a=-b \omega^{2}$

and at $\mathrm{t}=\frac{\pi}{2 \omega}$

$\mathrm{y}=0, \mathrm{v}=-\mathrm{b} \omega, \mathrm{a}=0$

These features correspond to graph (D) only.

2. The differential equation, corresponding to sinusoidal waves, represented by

$$ y=a \sin (\omega t-k x) $$

has the form $\frac{\partial^{2} \mathbf{y}}{\partial x^{2}}=\frac{1}{\mathbf{v}^{2}} \frac{\partial^{2} \mathbf{y}}{\partial \mathbf{t}^{2}}\left(\mathbf{v}=\frac{\omega}{\mathbf{k}}\right)$

The general functional equation, for a periodic wave

$$ y=\mathbf{a f}(\omega \mathbf{t}-\mathbf{k} x) $$

(1) can represent a sinusoidal wave but its differential equation form would be different from above

(2) cannot represent a sinusoidal wave but its differential equation form would be same as above

(3) cannot represent a sinusoidal wave; its differential equation form would also be different from above

(4) can represent a sinusoidal wave; its differential equation form would also be the same as above

Show Answer

Correct answer: (4)

Solution:

The general functional form, for a periodic wave, can represent a sinusoidal $(\mathrm{SH})$ wave if

$$ \text { af }(\omega \mathrm{t}-\mathrm{k} x) $$

corresponds to $\quad \mathrm{a} \sin (\omega \mathrm{t}-\mathrm{k} x)$ or $\quad \mathrm{a} \cos (\omega \mathrm{t}-\mathrm{k} x)$

Its differential form is same as above. This is because

$$ \begin{aligned} & \frac{\partial \mathrm{y}}{\partial \mathrm{t}}=\mathrm{a} \omega \mathrm{f}^{\prime}(\omega \mathrm{t}-\mathrm{k} x) \\ & \frac{\partial^{2} \mathrm{y}}{\partial \mathrm{t}^{2}}=\mathrm{a} \omega^{2} \mathrm{f}^{\prime \prime}(\omega \mathrm{t}-\mathrm{kx}) \end{aligned} $$

Also,

$$ \begin{aligned} \frac{\partial \mathrm{y}}{\partial x} & =\mathrm{a}(-\mathrm{k}) \mathrm{f}^{\prime}(\omega \mathrm{t}-\mathrm{k} x) \\ \frac{\partial^{2} \mathrm{y}}{\partial x^{2}} & =\mathrm{ak}^{2} \mathrm{f}^{\prime \prime}(\omega \mathrm{t}-\mathrm{k} x) \\ \therefore \quad \frac{\partial^{2} \mathrm{y}}{\partial x^{2}} & =\frac{\mathrm{k}^{2}}{\omega^{2}} \frac{\partial^{2} \mathrm{y}}{\partial \mathrm{t}^{2}}=\frac{1}{\mathrm{v}^{2}} \frac{\partial^{2} \mathrm{y}}{\partial \mathrm{t}^{2}} \quad\left(\because \quad \mathrm{v}=\frac{\omega}{\mathrm{k}}\right) \end{aligned} $$

3. A particle, executing SHM of amplitude a and time period T, has its maximum (positive) displacement at $t=0$. The graph representing the variation of its velocity, with time, is the graph labelled as graph

(1) $\mathrm{A}$

(2) $\mathrm{B}$

(3) $\mathrm{C}$

(4) $\mathrm{D}$

Show Answer

Correct answer: (3)

Solution:

The particle has its maximum (positive) displacement at $t=0$. Hence its SHM would be represented by

$$ \begin{aligned} y & =a \cos \omega t \\ \therefore \quad v & =-a \omega \sin \omega t \\ & =-\left(a \cdot \frac{2 \pi}{T}\right) \sin \left(\frac{2 \pi t}{T}\right) \\ & =-\left(\frac{2 \pi a}{T}\right) \sin \left(\frac{2 \pi t}{T}\right) \end{aligned} $$

It is graph (c) that correctly represents the variation of velocity, with time, as per this equation.

4. The kinetic energy, of a particle, describing SHM (of amplitude a), becomes $\frac{1}{3}$ of its kinetic energy at its mean position, when it is at a distance $x$ from the mean position. The distance $x$, and the (magnitude of the) fraction, corresponding to its acceleration at this position divided by its maximum acceleration, are, respectively

(1) $\left( \pm \sqrt{\frac{2}{3}} \mathrm{a}\right)$ and $\sqrt{\frac{2}{3}}$

(2) $\left( \pm \frac{1}{3} \mathrm{a}\right)$ and $\frac{1}{3}$

(3) $\left( \pm \frac{2}{3} \mathrm{a}\right)$ and $\frac{2}{3}$

(4) $\left( \pm \sqrt{\frac{1}{3} \mathrm{a}}\right)$ and $\sqrt{\frac{1}{3}}$

Show Answer

Correct answer: (1)

Solution:

The K.E (K) of a particle, describing SHM, (of amplitude a and angular frequency $\omega$ ), is given by

$$ \mathrm{K}=\frac{1}{2} \mathrm{~m} \omega^{2}\left(\mathrm{a}^{2}-x^{2}\right) $$

(Here $x=$ distance from mean position)

$\therefore \mathrm{K} _{0}=$ Kinetic energy at the mean position $(x=0)$,

$$ =\frac{1}{2} \mathrm{~m} \omega^{2} \mathrm{a}^{2} $$

$\therefore\left(\frac{1}{2} \mathrm{~m} \omega^{2} \mathrm{a}^{2}\right) \times \frac{1}{3}=\frac{1}{2} \mathrm{~m} \omega^{2}\left(\mathrm{a}^{2}-x^{2}\right)$

or $\frac{\mathrm{a}^{2}}{3}=\mathrm{a}^{2}-x^{2}$

or $\quad x^{2}=\frac{2}{3} \mathrm{a}^{2}$

$\therefore \quad x=\left( \pm \sqrt{\frac{2}{3}}\right) \mathrm{a}$

$\mid$ MaximumAcceleration $|=| \mathrm{a} \omega^{2} \mid$

$\mid$ Acceleration at a distance $x$ from the mean position $|=| \omega^{2} x \mid$

$\therefore$ Required fraction $=\left|\frac{x}{\mathrm{a}}\right|=\sqrt{\frac{2}{3}}$

5. A particle is executing a SHM of amplitude $A$ and angular frequency, $\omega$. Two students describe the details of the SHM by taking $t=0$ when the particle is ( $i$ ) in its mean position, and moving to the right; (ii) at its extreme right position.

The magnitude of the phase difference, between the (a) velocity and displacement and (b) acceleration and velocity, as described by students (i) and (ii), would be, respectively

(1) $\left(\frac{\pi}{2}, \frac{\pi}{2}\right)$ and $\left(\frac{\pi}{2}, \pi\right)$

(2) $\left(\frac{\pi}{2}, \pi\right)$ and $\left(\frac{\pi}{2}, \pi\right)$

(3) $\left(\frac{\pi}{2}, \frac{\pi}{2}\right)$ and $\left(\frac{\pi}{2}, \frac{\pi}{2}\right)$

(4) $(\pi, \pi)$ and $(\pi, \pi)$

Show Answer

Correct answer: (3)

Solution:

The displacement equation, for student (i), is

$$ \begin{gathered} y=A \sin \omega t \\ \therefore \quad v=\frac{d y}{d t}=A \omega \cos \omega t=A \omega \sin \left(\omega t+\frac{\pi}{2}\right) \\ \quad a=\frac{d v}{d t}=-A \omega^{2} \sin \omega t=A \omega^{2} \sin (\omega t+\pi) \end{gathered} $$

Hence magnitude of phase difference between

velocity and displacement $=\frac{\pi}{2}$

and Acceleration and velocity $=(\omega \mathrm{t}+\pi)-\left(\omega \mathrm{t}+\frac{\pi}{2}\right)=\frac{\pi}{2}$

For student (ii), we would have

$$ \mathrm{y}=\mathrm{A} \cos \omega \mathrm{t} ; \mathrm{v}=\frac{\mathrm{dy}}{\mathrm{dt}}=-\mathrm{A} \omega \sin \omega \mathrm{t}=\mathrm{A} \omega \cos \left(\omega \mathrm{t}+\frac{\pi}{2}\right) $$

and $\quad \mathrm{a}=\frac{\mathrm{dv}}{\mathrm{dt}}=-\mathrm{A} \omega^{2} \cos \omega \mathrm{t}=\mathrm{A} \omega^{2} \cos (\omega \mathrm{t}+\pi)$

$\therefore$ Magnitude of phase difference between velocity and displacement $=\frac{\pi}{2}$ and between acceleration and velocity $=(\omega \mathrm{t}+\pi)-\left(\omega \mathrm{t}+\frac{\pi}{2}\right)$ $=\frac{\pi}{2}$

$\therefore$ In both cases we have $\left(\frac{\pi}{2}, \frac{\pi}{2}\right)$ and $\left(\frac{\pi}{2}, \frac{\pi}{2}\right)$ as the correct choice.

6. A particle is executing a simple harmonic motion of amplitude a and frequency $n$. At $t=0$, this particle is at its mean position and is moving along the positive direction of its displacement. Its SHM can be viewed as the projection, on a vertical diameter (say), of the circular motion, of a particle, moving

(1) anticlockwise, with an angular speed $\mathrm{n}$, is a circle of diameter a

(2) clockwise, with an angular speed $n$, in a circle of diameter $2 a$

(3) anticlockwise, with an angular speed ( $2 \pi n)$, in a circle of diameter $2 a$

(4) clockwise, with an angular speed ( $2 \pi n)$, in a circle of diameter a

Show Answer

Correct answer: (3)

Solution:

The particle $(\mathrm{P})$ in the circle, must move anticlockwise, so that its projection, $(\mathrm{N})$, on a vertical diameter, moves along the positive direction, at $\mathrm{t}=0$.

Let the angular speed of the particle be $\omega$. At, $t=t$, we then have

$$ \mathrm{ON}=\mathrm{r} \sin \theta=\mathrm{r} \sin \omega \mathrm{t} $$

The amplitude, of the motion of the projection point $\mathrm{N}$, equals $\mathrm{r}$. The motion of the projection point, $\mathrm{N}$, as

per the above equation, is simple harmonic. Its frequency is $\frac{\omega}{2 \pi}$. It would equal $\mathrm{n}$ if $\omega=2 \pi \mathrm{n}$

We thus see that the given SHM can be viewed as the projection, on a vertical diameter, of the circular motion of a particle moving anticlockwise with an angular speed $(2 \pi n)$, in a circle of radius a, i.e. diameter 2a.

7. Two particle, (1) and (2), execute SHM’s of equal amplitude and frequency along (near to each other) parallel straight line. They are observed to cross points $\mathrm{C}$ and $\mathrm{C}^{\prime}$, in their respective paths,

together, but in opposite directions. Here $O C=O^{\prime} C^{\prime}=\frac{1}{2} a \cdot(a=$ common amplitude). The ’epoch’ difference, for these particles, equals

(1) $30^{\circ}$

(2) $60^{\circ}$

(3) $90^{\circ}$

(4) $120^{\circ}$

Show Answer

Correct answer: (4)

Solution:

Let $\theta$ be the epoch difference between the two particles. We then have

$$ \frac{\mathrm{a}}{2}=\mathrm{y} _{1}=\mathrm{a} \sin \omega \mathrm{t} _{1} \quad \text { and } \quad \frac{\mathrm{a}}{2}=\mathrm{y} _{2}=\mathrm{a} \sin \left(\omega \mathrm{t} _{1}+\theta\right) $$

$\therefore \sin \omega \mathrm{t} _{1}=\frac{1}{2}$ and hence $\cos \omega \mathrm{t} _{1}=\sqrt{1-\frac{1}{4}}$

$$ =\frac{\sqrt{3}}{2} $$

$\therefore \quad \frac{1}{2}=\sin \omega \mathrm{t} _{1} \cos \theta+\cos \omega \mathrm{t} _{1} \sin \theta$

$$ \begin{aligned} & =\frac{1}{2} \cos \theta+\frac{\sqrt{3}}{2} \sin \theta \\ \therefore & 1-\cos \theta=\sqrt{3} \sin \theta \\ \therefore & 1+\cos ^{2} \theta-2 \cos \theta=3 \sin ^{2} \theta=3\left(1-\cos ^{2} \theta\right) \\ \therefore & 4 \cos ^{2} \theta-2 \cos \theta-2=0 \quad \text { or } \quad 2 \cos ^{2} \theta-\cos \theta-1=0 \\ \therefore & \cos \theta=\frac{1 \pm \sqrt{1+8}}{4}=\frac{1+3}{4}=-\frac{1}{2} \text { or } 1 \\ \therefore & \theta=\frac{2 \pi}{3} \text { or } 0^{\circ} \end{aligned} $$

The second value $\left(\theta=0^{0}\right)$ would require the two particles to ‘stay in phase’ throughout. That is not true for the given set of particles. Hence

$$ \theta=\frac{2 \pi}{3}=120^{\circ} $$

8. A simple pendulum is executing small amplitude $\mathrm{SH}$ oscillations between two points that are $\ell \mathrm{cm}$ apart from each other. The time period of its oscillations is $T$ seconds and the pendulum bob is at the mean position at $t=0$. The time, $t$, at which it would be at a distance $\frac{\ell}{4}$ (to the right) from its mean position, and its velocity at that time, would, respectively, be

(1) $\frac{\mathrm{T}}{6} ; \frac{\pi \ell}{2 \mathrm{~T}}$

(2) $\frac{\mathrm{T}}{12} ; \frac{\sqrt{3} \pi \ell}{2 \mathrm{~T}}$

(3) $\frac{\mathrm{T}}{12} ; \frac{\pi \ell}{2 \mathrm{~T}}$

(4) $\frac{\mathrm{T}}{6} ; \frac{\sqrt{3} \pi \ell}{2 \mathrm{~T}}$

Show Answer

Correct answer: (2)

Solution:

Let the SH motion of the pendulum be represented by

$$ x=\frac{\ell}{2} \sin (\omega \mathrm{t}+\phi) $$

At $\mathrm{t}=0, x=0$. This gives $\phi=0$

Now $\frac{\ell}{4}=\frac{\ell}{2} \sin \omega \mathrm{t}$

$\therefore \sin \omega \mathrm{t}=\frac{1}{2}$

or $\quad \frac{2 \pi}{\mathrm{T}} \cdot \mathrm{t}=\frac{\pi}{6}$

$\therefore \mathrm{t}=\frac{\mathrm{T}}{12}$

The velocity, $v$, is given by

$\mathrm{v}=\frac{\mathrm{d} x}{\mathrm{dt}}=\frac{\ell}{2} \omega \cos (\omega \mathrm{t})$

$\therefore$ At $\mathrm{t}=\frac{\mathrm{T}}{12}$, we have

$\mathrm{v}=\frac{\ell}{2} \cdot \frac{2 \pi}{\mathrm{T}} \cos \left(\frac{2 \pi}{\mathrm{T}} \cdot \frac{\mathrm{T}}{12}\right)$

$$ =\frac{\ell \pi}{\mathrm{T}} \cdot \frac{\sqrt{3}}{2}=\left(\frac{\sqrt{3} \pi \ell}{2 \mathrm{~T}}\right) $$

9. A particle is executing SHM of amplitude A and time period T. Its displacement, at $\mathbf{t}=\mathbf{0}$, equals $\frac{A}{2}$ to the right of the mean position. Its epoch, and its phase, when its displacement is $\frac{A}{2}$ to the left of the mean position, are equal, respectively, to

(1) $\frac{\pi}{6} ; \frac{7 \pi}{6}$

(2) $\frac{2 \pi}{3} ; \frac{2 \pi}{3}$

(3) $\frac{2 \pi}{3} ; \frac{7 \pi}{6}$

(4) $\frac{7 \pi}{6} ; \frac{9 \pi}{16}$

Show Answer

Correct answer: (1)

Solution:

The general expression, for describing a given SHM, is

$$ y=A \sin (\omega t+\epsilon) $$

We are given that, at $\mathrm{t}=0, \mathrm{y}=+\frac{\mathrm{A}}{2}$

$\therefore \quad \frac{\mathrm{A}}{2}=\mathrm{A} \sin (\omega \times 0+\varepsilon)$

$\therefore \quad \varepsilon$ is equal to $30^{\circ}$ or $\frac{\pi}{6}$

Thus the phase, at $\mathrm{t}=0,=$ epoch $=\frac{\pi}{6}$

When $\mathrm{y}=-\mathrm{A} / 2$, we have

$$ -\frac{\mathrm{A}}{2}=\mathrm{A} \sin \left(\omega \mathrm{t}+\frac{\pi}{6}\right) $$

or $\quad-\frac{1}{2}=\sin \left(\omega \mathrm{t}+\frac{\pi}{6}\right)$

$\therefore\left(\omega t+\frac{\pi}{6}\right)=210^{0}=\frac{7 \pi}{6}$

$\therefore$ Phase at this instant $=\frac{7 \pi}{6}$

10. A particle is executing a SHM, of time period $T$ second, about the origin and along the $z _{-}$ axis. At $\mathbf{t}=0$, its displacement equals $+\mathrm{A}$ while its velocity is zero. Its velocity and acceleration when its displacement, from the origin, is $z=+\frac{\sqrt{3} A}{2}$, would be, respectively

(1) $-\frac{\sqrt{3} \pi \mathrm{A}}{2 \mathrm{~T}}$ and $-\frac{2 \pi^{2} \mathrm{~A} \sqrt{3}}{\mathrm{~T}^{2}}$

(2) $-\frac{\pi \mathrm{A}}{\mathrm{T}}$ and $-\frac{2 \pi^{2} \mathrm{~A}}{\mathrm{~T}^{2}}$

(3) $-\frac{\sqrt{3} \pi \mathrm{A}}{2 \mathrm{~T}}$ and $-\frac{2 \pi^{2} \mathrm{~A}}{\mathrm{~T}^{2}}$

(4) $-\frac{-\pi \mathrm{A}}{2 \mathrm{~T}}$ and $-\frac{2 \pi^{2} \mathrm{~A} \sqrt{3}}{\mathrm{~T}^{2}}$

Show Answer

Correct answer: (4)

Solution:

At $\mathrm{t}=0$, the displacement $=+\mathrm{A}$ and velocity $=$ zero.

The amplitude, of its oscillations, is, therefore, A and the SHM would be represented by

$$ \mathrm{z}=\mathrm{A} \cos \omega \mathrm{t} $$

$\therefore \quad \mathrm{v}=\frac{\mathrm{dz}}{\mathrm{dt}}=-\mathrm{A} \omega \sin \omega \mathrm{t}$

and $\quad \mathrm{a}=\frac{\mathrm{dv}}{\mathrm{dt}}=-\mathrm{A} \omega^{2} \cos \omega \mathrm{t}$

When the displacement equals $\frac{\sqrt{3} \mathrm{a}}{2}$, we have

$$ \frac{\mathrm{A} \sqrt{3}}{2}=\mathrm{A} \cos \omega \mathrm{t} \quad \text { or } \quad \cos \frac{2 \pi \mathrm{t}}{\mathrm{T}}=\frac{\sqrt{3}}{2} $$

$\therefore \quad \frac{2 \pi \mathrm{t}}{\mathrm{T}}=\frac{\pi}{6} \quad$ or $\quad \mathrm{t}=\frac{\mathrm{T}}{12}$

$\therefore \quad \mathrm{v}=-\mathrm{A} \cdot \frac{2 \pi}{\mathrm{T}} \sin \left(\frac{2 \pi}{\mathrm{T}} \cdot \frac{\mathrm{T}}{12}\right)$

$=-\frac{2 \pi \mathrm{A}}{\mathrm{T}} \frac{1}{2}=-\frac{\pi \mathrm{A}}{2 \mathrm{~T}}$

$\therefore$ Acceleration $=\mathrm{a}=-\mathrm{A} \omega^{2} \cdot \cos \frac{\pi}{6}=-\mathrm{A} \frac{4 \pi^{2}}{\mathrm{~T}^{2}} \cdot \frac{\sqrt{3}}{2}$

$$ =-\frac{2 \pi^{2} \mathrm{~A} \sqrt{3}}{\mathrm{~T}^{2}} $$

11. The motion, of a particle, in described by the equation

$$ y=c \sin \omega t+\left(2 c d+d^{2}\right)^{1 / 2} \cos \omega t $$

The nature of this motion, and its amplitude and initial phase, are, respectively,

(1) simple harmonic motion; amplitude $=(c+d)$; initial phase $=\tan ^{-1} \frac{c}{\left(2 c d+d^{2}\right)^{1 / 2}}$

(2) simple harmonic motion; amplitude $=(\mathrm{c}+\mathrm{d})$; initial phase $=\tan ^{-1} \frac{\left(2 \mathrm{~cd}+\mathrm{d}^{2}\right)^{1 / 2}}{\mathrm{c}}$

(3) simple harmonic motion; amplitude $=(\mathrm{c}+\mathrm{d})$; initial phase $=\tan ^{-1} \frac{\left(2 \mathrm{~cd}+\mathrm{d}^{2}\right)^{1 / 2}}{\mathrm{c}^{2}} \quad$

(4) simple harmonic motion; amplitude $=(c+d)$; initial phase $=\tan ^{-1} \frac{c^{2}}{\left(2 c d+d^{2}\right)^{1 / 2}}$

Show Answer

Correct answer: (2)

Solution:

We are given that $\mathrm{y}=\mathrm{c} \sin \omega \mathrm{t}+\left(2 \mathrm{~cd}+\mathrm{d}^{2}\right)^{1 / 2} \cos \omega \mathrm{t}$

Let us put $\mathrm{y}=\mathrm{R} \sin (\omega \mathrm{t}+\phi)$

$\therefore \mathrm{R} \sin \omega \mathrm{t} \cos \phi+\mathrm{R} \cos \omega \mathrm{t} \sin \phi=\mathrm{c} \sin \omega \mathrm{t}+\left(2 \mathrm{~cd}+\mathrm{d}^{2}\right)^{1 / 2} \times \cos \omega \mathrm{t}$

For this equality to be valid, we need to have

$$ \mathrm{R} \cos \phi=\mathrm{c} \quad \text { and } \quad \mathrm{R} \sin \phi=\left(2 \mathrm{~cd}+\mathrm{d}^{2}\right)^{1 / 2} $$

This implies that $\mathrm{R}^{2}\left(\cos ^{2} \phi+\sin ^{2} \phi\right)=(\mathrm{c})^{2}+\left(2 \mathrm{~cd}+\mathrm{d}^{2}\right)$

or $\mathrm{R}^{2}=\mathrm{c}^{2}+\mathrm{d}^{2}+2 \mathrm{~cd}=(\mathrm{c}+\mathrm{d})^{2}$

$\therefore \quad \mathrm{R}=(\mathrm{c}+\mathrm{d})$

and $\tan \phi=\frac{\left(2 \mathrm{~cd}+\mathrm{d}^{2}\right)^{1 / 2}}{\mathrm{c}}$

We can, therefore, put the given equation, namely

$$ y=c \sin \omega t+\left(2 c d+d^{2}\right)^{1 / 2} \cos \omega t $$

in the form $\mathrm{y}=\mathrm{R} \sin (\omega \mathrm{t}+\phi)$

This is the equation of a SHM whose

amplitude $=\mathrm{R}=(\mathrm{c}+\mathrm{d})$

and initial phase angle $=\phi=\tan ^{-1}\left[\frac{\left(2 \mathrm{~cd}+\mathrm{d}^{2}\right)^{1 / 2}}{\mathrm{c}}\right]$

12. The time periods, of a given simple pendulum, as measured in an elevator at rest; moving upwards with an acceleration $\frac{g}{9}$; and moving downwards with an acceleration $\frac{g}{16}$; are found to be, $T _{0}, T _{u}$ and $T _{d}$ respectively. The ratios $\left(\frac{T _{u}}{T _{0}}\right)$ and $\left(\frac{T _{d}}{T _{u}}\right)$, would respectively, equal (nearly)

(1) 1.3 and 0.8

(2) 0.8 and 1.3

(3) 0.9 and 1.1

(4) 1.1 and 0.9

Show Answer

Correct answer: (3)

Solution:

Let the length of the simple pendulum be $\ell$.

We then have

$$ \begin{aligned} & \mathrm{T} _{0}=2 \pi \sqrt{\frac{\ell}{\mathrm{g}}} \\ & \mathrm{T} _{\mathrm{u}}=2 \pi \sqrt{\frac{\ell}{\mathrm{g} _{\mathrm{u}}}} \text { where } \mathrm{g} _{\mathrm{u}}=\mathrm{g}+\frac{\mathrm{g}}{9}=\frac{10}{9} \mathrm{~g} \end{aligned} $$

and $T _{d}=2 \pi \sqrt{\frac{\ell}{g _{d}}}$ where $g _{d}=g-\frac{g}{16}=\frac{15}{16} g$

$$ \therefore \frac{\mathrm{T} _{\mathrm{u}}}{\mathrm{T} _{0}}=\sqrt{\frac{\mathrm{g}}{\mathrm{g} _{\mathrm{u}}}}=\sqrt{\frac{9}{10}}=\frac{3}{\sqrt{10}} \approx 0.9 $$

and $\frac{\mathrm{T} _{\mathrm{d}}}{\mathrm{T} _{\mathrm{u}}}=\sqrt{\frac{\mathrm{g} _{\mathrm{u}}}{\mathrm{g} _{\mathrm{d}}}}=\sqrt{\frac{10}{9} \times \frac{16}{15}}=\frac{4}{3} \sqrt{\frac{2}{3}}$

$$ =\left(\frac{4 \sqrt{2}}{3 \sqrt{3}}\right) \approx 1.1 $$

13. The oscillations of a given mass, attached to a given spring, are executed in two ways, as shown in figure (a) and (b). Assuming that the spring is light and the horizontal table surface is smooth, the ratio of the time periods of oscillations in the two cases, will be

(1) $\frac{T _{1}}{T _{2}}=1: 1$

(2) $\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=1: 2$

(3) $\frac{T _{1}}{T _{2}}=1: 4$

(4) $\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=2: 1$

Show Answer

Correct answer: (1)

Solution:

Let the mass $\mathrm{m}$ be stretched by a small amount $\mathrm{y}$. The restoring force, acting on it, is then $\mathrm{ky}$ ( $\mathrm{k}=$ spring constant). The equation of motion is

$$ \begin{aligned} & \mathrm{m} \frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dt}^{2}}=-\mathrm{ky} \\ \therefore & \frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dt}^{2}}=\frac{-\mathrm{k}}{\mathrm{m}} \mathrm{y}=-\omega^{2} \mathrm{y} \quad\left(\omega^{2}=\frac{\mathrm{k}}{\mathrm{m}}\right) \\ \therefore & \mathrm{T} _{1}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}}} \end{aligned} $$

In the second case also, when the spring is stretched by a small amount $x$, the restoring force, is $\mathrm{k} x$. The equation of motion, is

$$ \mathrm{m} \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-\mathrm{k} x $$

$\therefore \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=\frac{-\mathrm{k}}{\mathrm{m}} x=-\omega^{2} x \quad\left(\omega^{2}=\frac{\mathrm{k}}{\mathrm{m}}\right)$

$\therefore \quad \mathrm{T} _{2}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$

$\therefore \frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=(1: 1)$

14. An experiment, on finding the time period of vertical oscillations of a mass $M$ attached to a light spring, is done under three conditions, as shown. If both ’ $k$ ’ and ’ $M$ ’ are large compared to ’ $a$ ‘, the product $\left(T _{2} T _{3}\right.$ ) would be, approximately, equal to

(1) $\mathrm{T}_1^2\left(1+\frac{\mathrm{a}}{2}\left(\frac{1}{\mathrm{M}}-\frac{1}{\mathrm{k}}\right)\right)$

(2) $\mathrm{T}_1^2\left(1+\mathrm{a}\left(\frac{1}{\mathrm{k}}-\frac{1}{\mathrm{M}}\right)\right)$

(3) $\mathrm{T}_1^2\left(1+\mathrm{a}\left(\frac{\mathrm{l}}{\mathrm{M}}-\frac{1}{\mathrm{k}}\right)\right)$

(4) $\mathrm{T}_1^2\left(1+\frac{\mathrm{a}}{2}\left(\frac{1}{\mathrm{k}}-\frac{1}{\mathrm{M}}\right)\right)$

Show Answer

Correct answer: (1)

Solution:

We have $\mathrm{T} _{1}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k}}}$

$$ \mathrm{T} _{2}=2 \pi \sqrt{\frac{\mathrm{M}+\mathrm{a}}{\mathrm{k}}} $$

and $\quad T _{3}=2 \pi \sqrt{\frac{M}{k+a}}$

$\therefore \mathrm{T} _{2} \mathrm{~T} _{3}=4 \pi^{2} \sqrt{\frac{\mathrm{M}(\mathrm{M}+\mathrm{a})}{\mathrm{k}(\mathrm{k}+\mathrm{a})}}$

Now $\frac{M(M+a)}{k(k+a)}=\frac{M^{2}\left(1+\frac{a}{M}\right)}{k^{2}\left(1+\frac{a}{k}\right)}=\frac{M^{2}}{k^{2}}\left(1+\frac{a}{M}\right)\left(1+\frac{a}{k}\right)^{-1}$

$\therefore \sqrt{\frac{M(M+a)}{k(k+a)}} \simeq \frac{M}{k}\left(1+\frac{a}{M}\right)^{-1 / 2}\left(1+\frac{a}{k}\right)^{-1 / 2}$

$\approx \frac{\mathrm{M}}{\mathrm{k}}\left(1+\frac{1}{2} \frac{\mathrm{a}}{\mathrm{M}}\right)\left(1-\frac{1}{2} \frac{\mathrm{a}}{\mathrm{k}}\right)$

$\therefore \quad \mathrm{T} _{2} \mathrm{~T} _{3} \simeq \mathrm{T} _{1}^{2}\left(1+\frac{\mathrm{a}}{2}\left(\frac{1}{\mathrm{M}}-\frac{1}{\mathrm{k}}\right)\right)$

15. A rectangular block of copper (density $=\rho$ ), of mass $M$, when suspended from a light spring (spring constant $=k$ ), can execute (vertical) SH oscillation of period T. If this block, still attached to the spring, were to be completely immersed in water (density $=\rho _{0}$ ), and made to execute vertical oscillations by slightly stretching (and releasing) the spring, the new time period of its oscillations would be

(1) $\mathrm{T}$

(2) $\left(1-\frac{\rho _{0}}{\rho}\right)^{1 / 2} \mathrm{~T}$

(3) $\sqrt{\frac{\rho _{0}}{\rho}} \mathrm{T}$

(4) $\quad\left(1-\frac{\rho _{0}}{\rho}\right) \mathrm{T}$

Show Answer

Correct answer: (1)

Solution:

When a mass $\mathrm{M}$ is attached to the lower and of a (vertical) light spring, and made to execute oscillations, its resulting SH oscillations have a time period $\mathrm{T}$ where

$$ \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k}}} \quad(\mathrm{k}=\text { spring constant }) $$

When the copper block (of volume $\mathrm{V}=\frac{\mathrm{M}}{\rho}$ ) is completely immersed in water, it experiences an upward buoyant force of magnitude $v \rho _{0} g$. Its apparent weight, therefore, is $\left(v \rho g-v \rho _{0} g\right)=\operatorname{vg}\left(\rho-\rho _{0}\right)$

$$ =\operatorname{vgg}\left(1-\frac{\rho _{0}}{\rho}\right)=\operatorname{Mg}\left(1-\frac{\rho _{0}}{\rho}\right) $$

However, there is no change in its mass. The time period, of oscillations, depends only on the mass of the suspended object and on the spring constant of the spring. Neither of these changes when the copper block gets submerged in water. Hence the time period will remain the same, as before.

16. A given light spring, of length $L$ and spring constant $k$, is cut into two parts whose lengths are in the ratio p:q. The two parts are fixed vertically to two separate ‘supports’ and masses qM and $\mathrm{pM}$ are attached to then. The time periods of the (vertical) SH oscillations, of the two masses, are $T _{1}$ and $T _{2}$. The ratio $\left(T _{1} / T _{2}\right)$ equals

Time period $=\mathrm{T} _{1} \quad$ Time period $=\mathrm{T} _{2}$

(1) 1

(2) $\frac{p q}{(p+q)}$

(3) $\sqrt{\frac{p q}{(p+q)}}$

(4) $\sqrt{\frac{p+q}{(p q)}}$

Show Answer

Correct answer: (1)

Solution:

The lengths, of the two parts of the spring, are

$$ \ell _{1}=\frac{p}{p+q} L \text { and } \ell _{2}=\frac{q}{p+q} L $$

The spring constant, of a spring, being inversely proportional to length, we can say that the spring constants of the two parts will be

$\mathrm{k} _{1}=\frac{\mathrm{L}}{\ell _{1}} \mathrm{k}=\frac{(\mathrm{p}+\mathrm{q})}{\mathrm{p}} \mathrm{k}$ and $\mathrm{k} _{2}=\frac{\mathrm{L}}{\ell _{2}} \mathrm{k}=\frac{(\mathrm{p}+\mathrm{q})}{\mathrm{q}} \mathrm{k}$

$\left(\because \mathrm{k}=\operatorname{constant} \times \frac{1}{\mathrm{~L}} ; \mathrm{k} _{1}=\operatorname{constant} \times \frac{1}{\ell _{1}} ; \mathrm{k} _{2}=\operatorname{constant} \times \frac{1}{\ell _{2}}\right)$

Now $\mathrm{T} _{1}=2 \pi \sqrt{\frac{\mathrm{M} _{1}}{\mathrm{k} _{1}}}=2 \pi \sqrt{\frac{\mathrm{qM} \cdot \mathrm{p}}{(\mathrm{p}+\mathrm{q}) \mathrm{k}}}$ and $\quad \mathrm{T} _{2}=2 \pi \sqrt{\frac{\mathrm{M} _{2}}{\mathrm{k} _{2}}}=2 \pi \sqrt{\frac{\mathrm{pM} \cdot \mathrm{q}}{(\mathrm{p}+\mathrm{q}) \mathrm{k}}}$

$\therefore \frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=1$

17. A light spring, suspended vertically from the top of an elevator, has a mass $M$ attached to it. The time periods, of the (vertical) SH oscillations of mass M, when the elevator is

(i) stationary, equals $\mathbf{T} _{0}$

(ii) moving up with an acceleration $(\mathrm{g} / 9)$, equals $\mathrm{T} _{1}$.

(iii) moving down its an acceleration $(\mathrm{g} / 16)$, equals $\mathrm{T} _{2}$.

The ratios $\left(\frac{T _{0}}{T _{1}}\right)$ and $\left(\frac{T _{1}}{T _{2}}\right)$ would equal, respectively

(1) $\left(\frac{\sqrt{10}}{3}\right)$ and $\left(\frac{\sqrt{15}}{4}\right)$

(2) $\left(\frac{3}{\sqrt{10}}\right)$ and $\left(\frac{4}{\sqrt{15}}\right)$

(3) (3) and $\left(\frac{4}{3}\right)$

(4) 1 and 1

Show Answer

Correct answer: (4)

Solution:

The time period, of the vertical oscillations, of a mass, attached to a light spring, is given by

$$ \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k}}} \quad(\mathrm{k}=\text { spring constant }) $$

For the three cases given the effective values, of the acceleration due to gravity, are

(i) g (ii) $\left(g+\frac{g}{9}\right)=\frac{10 g}{9}$ and (iii) $\left(\mathrm{g}-\frac{\mathrm{g}}{16}\right)=\frac{15}{16} \mathrm{~g}$

However, the mass (M) of the object, as well as the spring constant (k), of the spring, do not depend on the value of the acceleration due to gravity. The time period will, therefore, have the same value in all the three cases. Hence

$$ \left(\frac{\mathrm{T} _{0}}{\mathrm{~T}}=1\right) \text { and }\left(\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}\right)=1 $$

18. A light spring, arranged (horizontally) above a smooth horizontal table, has a small spherical ball of mass $M$ connected to its free end. The ball is given a charge $+Q$ and another small spherical ball, carrying a charge $-n Q$ is brought near it, momentarily, and then removed for away. The centres of the two balls were brought a distance $R$ apart. The spring got extended by an amount $r _{s}$ and, as a result, the ball attached to it, started oscillating. The time period, of

these oscillations of the ball, equals

(1) $\frac{\mathrm{Q}}{4 \pi \mathrm{R}}\left(\frac{\mathrm{n}}{\pi \mathrm{M} \varepsilon _{0} \mathrm{r} _{\mathrm{s}}}\right)^{1 / 2}$

(2) $\frac{4 \pi^{3 / 2} \mathrm{R}}{\mathrm{Q}}\left(\frac{\mathrm{M} \varepsilon _{0} \mathrm{r} _{\mathrm{s}}}{\mathrm{n}}\right)^{1 / 2}$

(3) $\frac{\mathrm{Q}}{4 \pi \mathrm{R}}\left(\frac{4 \pi \varepsilon _{0} \mathrm{Mr} _{\mathrm{s}}}{\mathrm{n}}\right)^{1 / 2}$

(4) $\frac{\mathrm{Q}}{4 \pi^{3 / 2} \mathrm{R}}\left(\frac{\mathrm{n}}{\mathrm{M} \in _{0} \mathrm{r} _{\mathrm{s}}}\right)^{1 / 2}$

Show Answer

Correct answer: (2)

Solution:

The (momentary) force, exerted on the spring, equals

$$ \mathrm{F}=\frac{1}{4 \pi \varepsilon _{0}} \frac{\mathrm{Q}(\mathrm{nQ})}{\mathrm{R}^{2}}=\frac{\mathrm{nQ}^{2}}{4 \pi \varepsilon _{0} \mathrm{R}^{2}} $$

This force extends the spring by an amount $r _{s}$. Hence the force constant, $k$, of the spring, is

$$ \mathrm{k}=\frac{\mathrm{F}}{\mathrm{r} _{\mathrm{s}}}=\frac{\mathrm{nQ}^{2}}{4 \pi \varepsilon _{0} \mathrm{R}^{2} \mathrm{r} _{\mathrm{s}}} $$

The time period, $\mathrm{T}$ is, therefore, given by

$$ \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k}}}=\frac{4 \pi^{3 / 2} \mathrm{R}}{\mathrm{Q}}\left(\frac{\mathrm{M} \in _{0} \mathrm{r} _{\mathrm{s}}}{\mathrm{n}}\right)^{1 / 2} $$

19. A particle of mass $M$, is executing simple harmonic oscillations of amplitude $A$. The maximum energy, of this oscillating particle, is $\mathrm{E} _{0}$.

The time period, $T$, of this oscillating particle, and its velocity $\mathbf{v} _{x}$, when it is displaced a distance $x\left(=\frac{A \sqrt{3}}{2}\right)$ from its mean position, can be expressed, in terms of $E _{0}$, as

(1) $\mathrm{T}=\left(\frac{2 \pi^{2} \mathrm{MA}^{2}}{\mathrm{E} _{0}}\right)^{1 / 2} ; \quad \mathrm{v} _{x}=\left(\frac{\mathrm{E} _{0}}{2 \mathrm{M}}\right)^{1 / 2}$

(2) $\mathrm{T}=\left(\frac{\pi^{2} \mathrm{MA}^{2}}{2 \mathrm{E} _{0}}\right)^{1 / 2} ; \quad \mathrm{v} _{x}=\left(\frac{2 \mathrm{E} _{0}}{\mathrm{M}}\right)^{1 / 2}$

(3) $\mathrm{T}=\left(\frac{2 \pi^{2} \mathrm{MA}^{2}}{\mathrm{E} _{0}}\right)^{1 / 2} ; \mathrm{v} _{x}=\left(\frac{2 \mathrm{E} _{0}}{\mathrm{M}}\right)^{1 / 2}$

(4) $\mathrm{T}=\left(\frac{\pi^{2} \mathrm{MA}^{2}}{2 \mathrm{E} _{0}}\right)^{1 / 2} ; \mathrm{v} _{x}=\left(\frac{\mathrm{E} _{0}}{2 \mathrm{M}}\right)^{1 / 2}$

Show Answer

Correct answer: (1)

Solution:

The maximum energy of a particle, executing SHM, is given by

$$ \mathrm{E} _{0}=\frac{1}{2} \mathrm{M} \omega^{2} \mathrm{~A}^{2} $$

$\therefore \omega^{2}=\frac{2 \mathrm{E} _{0}}{\mathrm{MA}^{2}}$

$\therefore \omega=\frac{1}{\mathrm{~A}} \sqrt{\frac{2 \mathrm{E} _{0}}{\mathrm{M}}}$

$\therefore$ Time period, $\mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \mathrm{A} \sqrt{\frac{\mathrm{M}}{2 \mathrm{E} _{0}}}=\sqrt{\frac{2 \pi^{2} \mathrm{MA}^{2}}{\mathrm{E} _{0}}}$

Also $\mathrm{v} _{x}=\omega\left(\mathrm{A}^{2}-x^{2}\right)^{1 / 2}$

$\therefore$ For $x=\frac{\mathrm{A} \sqrt{3}}{2}$, we have

$\mathrm{v} _{x}=\omega\left(\mathrm{A}^{2}-\frac{3}{4} \mathrm{~A}^{2}\right)^{1 / 2}$

$=\frac{1}{2} \omega \mathrm{A}$

$=\frac{1}{2} \mathrm{~A} \cdot \frac{1}{\mathrm{~A}} \sqrt{\frac{2 \mathrm{E} _{0}}{\mathrm{M}}}$

$=\sqrt{\frac{\mathrm{E} _{0}}{2 \mathrm{M}}}$

20. Two long straight parallel wires, carrying (like) currents $I _{1}$ and $I _{2}$, and kept a distance $d$ apart in vacuum, attract each other with a force $F _{0}$.

A light spring, carrying a mass $M$ at its free end, is suspended vertically. This spring gets extended by an amount $z _{0}$ when a force $F _{0}$ is applied at its free end. The time period of the (vertical) SH oscillations, of the mass M, attached to the spring, equals

(1) $(2 \pi)\left(\frac{\left(\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}\right)}{\left(\mathrm{Mz} _{0} \mathrm{~d}\right)}\right)^{1 / 2}$

(2) $\frac{1}{2 \pi}\left(\frac{\left(\mathrm{Mz} _{0} \mathrm{~d}\right)}{\left(\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}\right)}\right)^{1 / 2}$

(3) $(2 \pi)^{3 / 2}\left(\frac{\left(\mathrm{Mz} _{0} \mathrm{~d}\right)}{\left(\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}\right)}\right)^{1 / 2}$

(4) $(2 \pi)\left(\frac{\left(\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}\right)}{\left(\mathrm{Mz} _{0} \mathrm{~d}\right)}\right)^{1 / 2}$

Show Answer

Correct answer: (3)

Solution:

The force, $\mathrm{F} _{0}$, is known to be given by

$$ \mathrm{F} _{0}=\frac{\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}}{2 \pi \mathrm{d}} $$

Hence the force constant, of the spring, is

$$ \mathrm{k}=\frac{\mathrm{F} _{0}}{\mathrm{z} _{0}}=\frac{\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}}{2 \pi \mathrm{z} _{0} \mathrm{~d}} $$

The time period, of the (SH) oscillations of the mass $\mathrm{M}$, is

$$ \begin{aligned} \mathrm{T} & =2 \pi \sqrt{\frac{\mathrm{M}}{k}} \\ \therefore \quad \mathrm{T} & =2 \pi \sqrt{\frac{\mathrm{M} \times 2 \pi \mathrm{z} _{0} \mathrm{~d}}{\left(\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}\right)}} \\ & =(2 \pi)^{3 / 2} \sqrt{\left(\frac{\mathrm{M} \mathrm{z} _{0} \mathrm{~d}}{\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}}\right)} \end{aligned} $$

21. Two simple harmonic motions are represented by

$$ \begin{aligned} & y _{1}=10 \sin \left(4 \pi t+\frac{\pi}{4}\right) \\ & y _{2}=5(\sin 3 \pi t+\sqrt{3} \cos 3 \pi t) \end{aligned} $$

The ratio of their amplitudes, and the magnitude of the phase difference between them, are, respectively,

(1) 1 and $\pi \mathrm{t}$

(2) 2 and $\pi\left(\mathrm{t}-\frac{1}{12}\right)$

(3) 1 and $\pi\left(t-\frac{1}{12}\right)$

(4) 2 and $\pi(t)$

Show Answer

Correct answer: (3)

Solution:

We first rewrite the equation for $\mathrm{y} _{2}$ in the ‘standard form’.

Let us put

$$ \mathrm{R} \cos \theta=5 \text { and } \mathrm{R} \sin \theta=5 \sqrt{3} $$

$\therefore \mathrm{R}^{2}=25+75=100$ or $\mathrm{R}=10$

Also $\tan \theta=\sqrt{3} \quad$ or $\quad \theta=\frac{\pi}{3}$

We now rewrite $y _{2}$ as

$$ \begin{aligned} & y _{2}=R(\cos \theta \sin 3 \pi t+\sin \theta \cos 3 \pi t) \\ & =R \sin (3 \pi t+\theta)=10 \sin \left(3 \pi t+\frac{\pi}{3}\right) \end{aligned} $$

$\therefore$ Ratio of amplitudes $=\frac{10}{10}=1$

Also,

Phase difference $=\left(3 \pi \mathrm{t}+\frac{\pi}{3}\right)-\left(4 \pi \mathrm{t}+\frac{\pi}{4}\right)$

$$ =-\pi \mathrm{t}+\frac{\pi}{12}=-\pi\left[(\mathrm{t})-\frac{1}{12}\right] $$

$\therefore \mid$ Phase difference $\left\lvert,=\pi\left(t-\frac{1}{12}\right)\right.$

22. One end of a long metallic wire, of length $L$, is tied to the ceiling. The other end is tied to a massless spring of spring constant $\mathrm{K}$. A mass $\mathrm{m}$ hangs freely from the free and of the spring. The area of cross section of the wire, and the Young’s modulus of its material, are A and $Y$, respectively. If the mass is slightly pulled down, it will oscillate with a time period $T$ equal to

(1) $2 \pi\left(\frac{\mathrm{m}}{\mathrm{K}}\right)^{1 / 2}$

(2) $2 \pi\left(\frac{\mathrm{m}(\mathrm{YA}+\mathrm{KL})}{\mathrm{YAK}}\right)^{1 / 2}$

(3) $2 \pi\left(\frac{\mathrm{mYA}}{\mathrm{KL}}\right)^{1 / 2}$

(4) $2 \pi\left(\frac{\mathrm{mL}}{\mathrm{YA}}\right)^{1 / 2}$

Show Answer

Correct answer: (2)

Solution:

For the wire, if $\Delta \ell$ is the increase in length, we have

$$ \mathrm{Y}=\frac{\mathrm{F} / \mathrm{A}}{\Delta t / \mathrm{L}} $$

$\therefore \quad \mathrm{F}=\mathrm{Y} \cdot \frac{\Delta \mathrm{L}}{\mathrm{L}} \cdot \mathrm{A}=\left(\frac{\mathrm{YA}}{\mathrm{L}}\right) \cdot \Delta \mathrm{L}$

$\therefore$ The wire can be thought of as a ‘spring’, of spring constant $\mathrm{K}$ ‘, where

$$ \mathrm{K}^{\prime}=\left(\frac{\mathrm{YA}}{\mathrm{L}}\right) $$

The wire, and the spring, are connected in ‘series’. Hence the equivalent spring constant, of their combination ,is

$$ \begin{aligned} K _{e q}= & \frac{k k^{\prime}}{k+k^{\prime}}=\frac{k^{Y A} / L}{k+k^{\prime}}=\frac{k^{Y A} / L}{(k+Y A / L)} \\ = & \frac{k Y A}{(k L+Y A)} \end{aligned} $$

Hence the time period, $T$, of the mass $m$, is given by

$$ \begin{aligned} \mathrm{T}=2 & \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k} _{\mathrm{eq}}}} \\ & =2 \pi \sqrt{\frac{\mathrm{m}(\mathrm{YA}+\mathrm{KL})}{(\mathrm{YAK})}} \\ & =2 \pi\left(\frac{\mathrm{m}(\mathrm{YA}+\mathrm{KL})}{\mathrm{YAK}}\right)^{1 / 2} \end{aligned} $$

23. A system of two identical springs (having a spring constant $K$ ) is used to hold a rod $\mathrm{PQ}$ (of mass $m$ and length $\ell$ ) in a horizontal position, as shown. If the rod were tilted through a (small) angle $\beta$ and ’let-go’, it executes SH oscillations, of time period T, where $T$ equals

(1) $2 \pi \sqrt{\frac{\mathrm{m}}{3 \mathrm{~K}}}$

(2) $2 \pi \sqrt{\frac{\mathrm{m}}{6 \mathrm{~K}}}$

(3) $2 \pi \sqrt{\frac{2 \mathrm{~m}}{3 \mathrm{~K}}}$

(4) $2 \pi \sqrt{\frac{5 \mathrm{~m}}{6 \mathrm{~K}}}$

Show Answer

Correct answer: (2)

Solution:

The tilting of the rod, to the position $\mathrm{P}^{\prime} \mathrm{Q}$ ‘, would result in compressing the springs by an amount

$$ \mathrm{QQ}^{\prime}\left(=\mathrm{PP}^{\prime}\right) \text { which equals } \frac{\ell}{2} \sin \beta \approx \frac{\ell}{2} \beta \text { (if } \beta \text { is small) } $$

The (restoring) force, developed in each spring is ky where $\mathrm{y}=Q Q^{\prime}=P P^{\prime}$. The two equal forces are directed opposite to each other and have different lines of action. Hence they constitute a (restoring) couple whose magnitude equals $(\mathrm{ky}) \cdot \ell$. The equation of (angular) motion, of the rod, is

$$ \mathrm{I} \frac{\mathrm{d}^{2} \beta}{\mathrm{dt}^{2}}=-\mathrm{k} \ell \mathrm{y}=-\mathrm{k} \ell \cdot \frac{\ell}{2} \beta=-\frac{\mathrm{k} \ell^{2}}{2} \beta $$

Here $\mathrm{I}=$ moment of inertia of the rod about the axis through its centre $=\frac{\mathrm{m} \ell^{2}}{12}$

$\therefore \frac{\mathrm{d}^{2} \beta}{\mathrm{dt}^{2}}=\frac{-\mathrm{k} \ell^{2}}{2} \times \frac{12}{\mathrm{~m} \ell^{2}} \cdot \beta=-\frac{6 \mathrm{k}}{\mathrm{m}} \beta=-\omega^{2} \beta$

where $\omega^{2}=\frac{6 \mathrm{~A}}{\mathrm{~m}}$

The rod, therefore, executes angular SH oscillations of time period, $\mathrm{T}$, where

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{m}}{6 \mathrm{k}}} $$

24. A small ball, of mass $m$, in lying at the centre of a smooth concave surface of radius of curvature $R$. The ball is displaced to one side and ’let-go’. The resulting oscillations of the ball would be simple harmonic

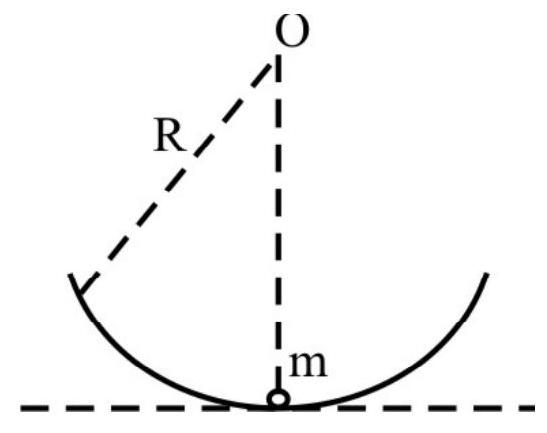
(1) only if the displacement in small; their time period, T, equals $2 \pi \sqrt{\frac{\mathrm{R}}{\mathrm{g}}}$

(2) for all displacements of the ball; their time period, T equals $2 \pi \sqrt{\frac{\mathrm{R}}{\mathrm{g}}}$

(3) for all displacements of the ball; their time period, T, equals $2 \pi \sqrt{\frac{2 R}{g}}$

(4) only if the displacement is small; their time period, $T$, equals $2 \pi \sqrt{\frac{2 R}{g}}$

Show Answer

Correct answer: (1)

Solution:

When the ball is displaced from its equilibrium position, the line joining it to the centre of the surface will get inclined at an angle $\theta$ to the vertical. Its free body diagram, now, is an shown.

The component $\mathrm{mg} \cos \theta$ gets balanced by the normal reaction, $\mathrm{N}$, of the surface, on the ball. The component $\mathrm{mg} \sin \theta$ acts as the restoring force.

For small values of $\theta, \operatorname{mg} \sin \theta \approx \operatorname{mg} \theta=\frac{\operatorname{mg} x}{\mathrm{R}}$

$\therefore$ The (restoring) force is proportional to the displacement $(x)$ only if the displacement in small. It is only under this condition that the ball will execute SH oscillations. The time period of the oscillations is

$$ \mathrm{T}=\frac{2 \pi}{\omega} \quad \text { where }=\omega^{2}=\frac{\mathrm{g}}{\mathrm{R}} $$

$\therefore \quad \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{R}}{\mathrm{g}}}$

25. Rectangular blocks, of the same base area (A) but different heights $(\mathrm{H})$, made from different (lighter than water) materials of different densities ( $\rho$ ), are made to float, one by one, in a tall container of water (density $=\sigma$ ). When slightly pushed down and ’let-go’, they are observed to execute SH oscillations of the same time period as that of a second’s pendulum. The relation that would hold, in such a case, is

(1) $\mathrm{H}=\left(\frac{\mathrm{g} \sigma}{\pi^{2} \rho}\right)$

(2) $\mathrm{H}=\left(\frac{\pi^{2} \rho}{\mathrm{g} \sigma}\right)$

(3) $\mathrm{H}=\left(\frac{2 \mathrm{~g} \sigma}{\pi^{2} \rho}\right)$

(4) $\mathrm{H}=\left(\frac{2 \pi^{2} \rho}{\mathrm{g} \sigma}\right)$

Show Answer

Correct answer: (1)

Solution:

The time period, of a block floating in a liquid, equals the time period of a simple pendulum whose length $(\ell)$ equals the ‘height’ (h) of the block that gets submerged in the liquid.

For a block of density $\rho$, floating in a liquid of density $\sigma$, the height submerged (h) is related to its total height $(\mathrm{H})$, as per the relation:

$$ h=H\left(\frac{\rho}{\sigma}\right) $$

As per the statement of the question, $h$ should equal the length $\left(\ell _{s}\right)$ of a second’s pendulum. For a second’s pendulum, we have

$$ \begin{aligned} & \mathrm{T}(=2 \mathrm{~s})=2 \pi \sqrt{\frac{\ell _{\mathrm{s}}}{\mathrm{g}}} \\ & \therefore \quad \ell _{\mathrm{s}}=\frac{4 \mathrm{~g}}{4 \pi^{2}}=\frac{\mathrm{g}}{\pi^{2}} \end{aligned} $$

We, therefore, have

$$ \mathrm{h}=\frac{\mathrm{H} \rho}{\sigma}=\frac{\mathrm{g}}{\pi^{2}} $$

or $\quad H=\left(\frac{g \sigma}{\pi^{2} \rho}\right)$

26. Four students were asked to label the variables ( $Y$ and $X$ ), for the graph dream here. Their suggestions were as follows:

(A) graph between $P$ and $T(Y=P, X=T)$, for a given mass of an ideal gas, under isochoric conditions

(B) Graph between $H$ and $\rho(Y=H, X=\rho)$ where $H=$ height of a rectangular block and $\rho=$ density of its material. The graph is drawn for different floating block, floating in a given liquid,

when their SH oscillations (caused by pushing the block a little downwards) have the same time period.

(C) Graph between $\mathrm{V}$ and $\mathrm{I}(\mathrm{Y}=\mathrm{V}, \mathrm{X}=\mathrm{I})$, for an ohmic resistor.

(D) Graph between $P$ and $V(Y=P, X=V)$, for a given mass of a gas, under isothermal conditions.

The suggestions are correct for students

(1) A and B

(2) B and $\mathrm{C}$

(3) C and D

(4) D and B

Show Answer

Correct answer: (4)

Solution:

(i) Suggestion (A) is incorrect because the suggested graph would be a straight line.

(ii) Suggestion (B) is correct. The equivalent simple pendulum length, for a floating block, is given by

$$ \mathrm{h}=\mathrm{H} \cdot \frac{\rho}{\sigma} $$

( $\sigma=$ density of liquid)

For the same value of time period, $h$ should remain constant. Hence

$$ \mathrm{H} \rho=\text { constant } \text { or } \mathrm{H} \alpha \frac{1}{\rho} $$

The graph shown also corresponds to an inverse proportionality between $\mathrm{Y}$ and $\mathrm{X}$.

(iii) Suggestion (C) is incorrect, the suggested graph would be a straight line.

(iv) Suggestion (D) is correct as for a given mass of a gas (under isothermal conditions), $\mathrm{PV}=$ constant, or $\mathrm{P} \alpha \frac{1}{\mathrm{~V}}$.

Thus suggestions (B) and (D) are correct.

27. A particle $P$, of mass $M$, is rotating in a circular path of radius $R$. It starts from the position $P _{0}$, at $t=0$, and completes $n$ rotations in one minute.

The ‘projections’, of this particle, are taken on a (i) vertical (ii) horizontal diameter of its circular path. The motion, of these two projection points, will be simple harmonic motions that can be described, respectively, by the equations:

(1) $[\mathrm{y}=\mathrm{R} \sin \mathrm{nt}]$ and $[x=\mathrm{R} \cos \mathrm{nt}]$

(2) $[\mathrm{y}=\mathrm{R} \cos \mathrm{nt}]$ and $[x=\mathrm{R} \sin \mathrm{nt}]$

(3) $\left[\mathrm{y}=\mathrm{R} \cos \left(\frac{\pi \mathrm{n}}{30}\right) \mathrm{t}\right]$ and $\left[x=\mathrm{R} \sin \left(\frac{\pi \mathrm{n}}{30}\right) \mathrm{t}\right]$

(4) $\left[\mathrm{y}=\mathrm{R} \sin \left(\frac{\pi \mathrm{n}}{30}\right) \mathrm{t}\right]$ and $\left[x=\mathrm{R} \cos \left(\frac{\pi \mathrm{n}}{30}\right) \mathrm{t}\right]$

Show Answer

Correct answer: (4)

Solution:

Let the particle be at the position $P _{t}$, at $t=t$, in its circular path. Its ‘projections’, on the vertical and horizontal diameters, are the points $\mathrm{K}$ and $\mathrm{L}$, respectively.

Now $\omega=\frac{2 \pi \mathrm{n}}{60} \mathrm{rad} / \mathrm{s}=\frac{\pi \mathrm{n}}{30} \mathrm{rad} \mathrm{s}^{-1}$

and $\theta=\omega \mathrm{t}$

$\therefore\left[\mathrm{OK}=\mathrm{y}=\mathrm{R} \sin \theta=\mathrm{R} \sin \omega \mathrm{t}=\mathrm{R} \sin \left(\frac{\pi \mathrm{n}}{30}\right) \mathrm{t}\right]$

and $\left[\mathrm{OL}=x=\mathrm{R} \cos \theta=\mathrm{R} \cos \omega \mathrm{t}=\mathrm{R} \cos \left(\frac{\pi \mathrm{n}}{30}\right)\right]$

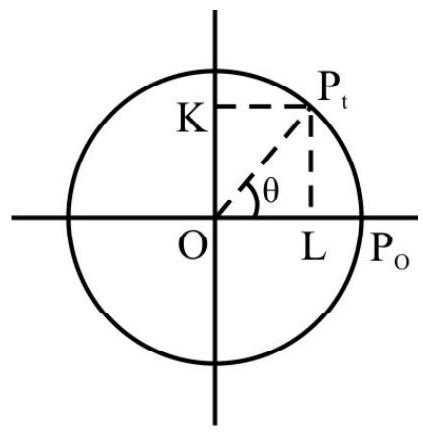
The two projection points, therefore, execute simple harmonic motions, described, respectively, by the equations

$$ \mathrm{y}=\mathrm{R} \sin \left(\frac{\pi \mathrm{n}}{30}\right) \mathrm{t} \text { and } x=\mathrm{R} \cos \left(\frac{\pi \mathrm{n}}{30}\right) \mathrm{t} $$

28. A particle, of mass $M$, is executing simple harmonic oscillations of amplitude $A$ and angular frequency $\omega$. The ratio of its P.E., to its total energy, when its displacement from the mean position is $\boldsymbol{x} _{\mathbf{1}}$, equals $\mathrm{R}$. The ratio of its K.E., to its total energy, when its displacement from the mean position is $x _{2}$, again equals $R$.

It a triangle were to be formed, using $x _{1}, x _{2}$ and $A$ as its three sides, this triangle would be

(1) a ‘straight line triangle’, with $x _{1}+x _{2}=\mathrm{A}$

(2) an acute angled triangle

(3) a right angled triangle

(4) an obtuse angled triangle

Show Answer

Correct answer: (3)

Solution:

We are given that

$$ \frac{\frac{1}{2} M \omega^{2} x _{1}^{2}}{\frac{1}{2} M \omega^{2} A^{2}}=R=\frac{\frac{1}{2} M \omega^{2}\left(A^{2}-x _{2}^{2}\right)}{\frac{1}{2} M \omega^{2} A^{2}} $$

$\therefore \quad x _{1}^{2}=\mathrm{A}^{2}-x _{2}^{2}$

or $\quad x _{1}^{2}+x _{2}^{2}=\mathrm{A}^{2}$

The triangle, formed by using $x _{1}, x _{2}$ and $A$ as its three sides, would, therefore, be a right angled triangle.

29. A combination of two springs, of spring constant $k _{1}$ and $k _{2}$, are arranged as shown. The mass $M$, present in between, lies on a smooth floor. When it is given a slight push / pull to one side and ’let-go’, it starts oscillating. The time period, $T$, of these oscillations, is given by

(1) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{M}}{\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}}$

(2) $T=2 \pi \sqrt{\frac{M}{\left(k _{1} \sim k _{2}\right)}}$

(3) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{k} _{1} \mathrm{k} _{2}}{\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}}$

(4) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{k} _{1} \mathrm{k} _{2}}{\left(\mathrm{k} _{1} \sim \mathrm{k} _{2}\right)}}$

Show Answer

Correct answer: (1)

Solution:

Let the mass $\mathrm{M}$ be moved a little (say $\Delta \ell$ ) to the right. The spring (1) then get elongated by an amount $\Delta \ell$ and exerts a restoring force $\mathrm{k} _{1} \Delta \ell$, directed to the left. The spring (2), simultaneously, gets compressed by an amount $\Delta \ell$. It too, therefore, exerts a restoring force, $\mathrm{k} _{2} \ell$, directed to the left. The total restoring force, acting on the mass $\mathrm{M}$, is, therefore, $\left[\mathrm{k} _{1} \Delta \ell+\mathrm{k} _{2} \Delta \ell\right]=\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right) \Delta \ell$, directed to the left. This is equivalent to the restoring force of a single (equivalent) spring, of spring constant $ \mathrm{k} _{1}+\mathrm{k} _{2}$. Hence equivalent spring constant (of the given set up) is $\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)$

$\therefore$ Time period $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{M}}{\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}}$

30. A large container, of volume $V$, has a long narrow neck, closed by a cork of mass $m$. The container contains an ideal gas (at a pressure $P$ ) maintained at a constant temperature $T$. The area of cross section of the neck is $A$ and the density of the gas is $\rho$. The cork, in the neck, is pushed down a small distance $y$ and ’let-go’. The resulting oscillations of the cork would be simple harmonic with a time period

(1) $\mathrm{T}=2 \pi \mathrm{V} \sqrt{\frac{\rho}{\mathrm{PA}}}$

(2) $\mathrm{T}=\frac{2 \pi}{\mathrm{A}}\left(\frac{\mathrm{mV}}{\mathrm{P}}\right)^{1 / 2}$

(3) $\mathrm{T}=2 \pi \mathrm{A}\left(\frac{\mathrm{P}}{\mathrm{mV}}\right)^{1 / 2}$

(4) $\mathrm{T}=2 \pi\left(\frac{\mathrm{AP}}{\mathrm{mV}}\right)^{1 / 2}$

Show Answer

Correct answer: (2)

Solution:

Let the cork be pushed down through a small distance $\Delta \mathrm{y}$. The volume of the gas decreases by a small amount $\Delta \mathrm{V}$ where $\Delta \mathrm{V}=\mathrm{A} \Delta \mathrm{y}$. The pressure of the gas would, therefore, increase by a small amount $\Delta \mathrm{P}$ such that

$$ (\mathrm{P}+\Delta \mathrm{P})(\mathrm{V}-\Delta \mathrm{V})=\mathrm{PV} \quad \text { (Change is isothermal) } $$

$\therefore \quad-\mathrm{P} \Delta \mathrm{V}+\mathrm{V} \Delta \mathrm{P}=0$ [neglecting $(\Delta \mathrm{P} \Delta \mathrm{V})$ term $]$

or $\quad \Delta \mathrm{P}=\mathrm{P} \frac{\Delta \mathrm{V}}{\mathrm{V}}$

$\therefore$ Restoring force on the cork $=\mathrm{A} \Delta \mathrm{P}$

$$ \begin{aligned} & =A P \frac{\Delta V}{V}=\frac{A P}{V}(A \Delta y) \\ & =\frac{A^{2} P}{V} \Delta y \end{aligned} $$

$\therefore$ Equation of motion of the cork is

$\mathrm{m} \frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dt}^{2}}=-\frac{\mathrm{A}^{2} \mathrm{P}}{\mathrm{V}} \Delta \mathrm{y}$

or $\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dt}^{2}}=-\frac{\mathrm{A}^{2} \mathrm{P}}{\mathrm{mV}} \Delta \mathrm{y}=-\omega^{2} \mathrm{y}$

where $\omega^{2}=\frac{A^{2} P}{m V}$

The oscillations, of the cork, are, therefore, simple harmonic with a time period, $\mathrm{T}$, where

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi\left(\frac{\mathrm{mV}}{\mathrm{A}^{2} \mathrm{P}}\right)^{1 / 2} $$

31. A spring, of spring constant $k$, has two masses $m _{1}$ and $m _{2}$, attached at its lower end. When the system is in equilibrium, the mass $m _{1}$ is gently removed. The amplitude, and time period, of the resulting oscillations of $m _{2}$, would be, respectively

(1) $\left(\frac{\mathrm{m} _{1} \mathrm{~g}}{\mathrm{k}}\right)$ and $2 \pi \sqrt{\frac{\mathrm{m} _{1}}{\mathrm{k}}}$

(2) $\left(\frac{\mathrm{m} _{2} \mathrm{~g}}{\mathrm{k}}\right)$ and $2 \pi \sqrt{\frac{\mathrm{m} _{2}}{\mathrm{k}}}$

(3) $\left(\frac{\mathrm{m} _{1} g}{\mathrm{k}}\right)$ and $2 \pi \sqrt{\frac{\mathrm{m} _{2}}{\mathrm{k}}}$

(4) $\left(\frac{\mathrm{m} _{2} \mathrm{~g}}{\mathrm{k}}\right)$ and $2 \pi \sqrt{\frac{\mathrm{m} _{1}}{\mathrm{k}}}$

Show Answer

Correct answer: (3)

Solution:

The equilibrium extension, say $y$, of the spring, when both the masses $m _{1}$ and $m _{2}$ are suspended from it, equals $\left(\mathrm{m} _{1}+\mathrm{m} _{2}\right) \frac{\mathrm{g}}{\mathrm{k}}$.

On removing the mass $m _{1}$, the equilibrium extension would be only $\left(\frac{m _{2} g}{k}\right)$. Hence when the mass $m _{1}$ is gently removed, the mass $m _{2}$ would have an unbalanced extension $\left(\frac{m _{1} g}{k}\right)$. This would, therefore, be the amplitude of its oscillations. Hence $A=\left(\frac{m _{1} g}{k}\right)$

The restoring force, on mass $\mathrm{m} _{2}$ is equal to $\mathrm{ky} _{1}\left(=\mathrm{M} _{1} \mathrm{~g}\right)$ where $\mathrm{y} _{1}$ would have been the extension of the spring under the mass $m _{1}$ alone. Hence its equation of motion is

$$ \mathrm{m} _{2} \frac{\mathrm{d}^{2} \mathrm{y} _{1}}{\mathrm{dt}^{2}}=-\mathrm{k} \mathrm{y} _{1} $$

$\therefore$ The oscillations of $\mathrm{m} _{2}$ are simple harmonic with $\omega^{2}=\frac{\mathrm{k}}{\mathrm{m} _{2}}$.

Hence $\omega=\sqrt{\frac{\mathrm{k}}{\mathrm{m} _{2}}}$

$\therefore \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m} _{2}}{\mathrm{k}}}$

32. A light wire, of length $L$ and area of cross-section $A$, is made from a material whose Young’s modulus of elasticity is $Y$. When this wire is suspended vertically and a mass $M$ is attached to its lower end, it gets extended by an amount $\ell$.

On further pushing down the mass by an amount $\Delta \ell$, and then letting it go, the mass starts oscillating. Assuming idealized conditions, the time period, of these SH oscillations of the mass $M$, would be

(1) $2 \pi\left(\frac{\mathrm{M}^{2} \mathrm{~L}}{\mathrm{AY}}\right)^{1 / 2}$

(2) $2 \pi\left(\frac{\mathrm{L}^{2} \mathrm{M}}{\mathrm{AY}}\right)^{1 / 2}$

(3) $2 \pi \sqrt{\frac{\mathrm{ML}}{\mathrm{AY}}}$

(4) $2 \pi \sqrt{\frac{\mathrm{AY}}{\mathrm{ML}}}$

Show Answer

Correct answer: (3)

Solution:

The relation, giving the extension $\ell$, due to the weight of the mass $\mathrm{M}$, is

$$ \mathrm{Y}=\frac{\mathrm{Mg} / \mathrm{A}}{\ell / \mathrm{L}}=\frac{\mathrm{MgL}}{\ell \mathrm{A}} $$

$\therefore \quad \ell=\left(\frac{\mathrm{L}}{\mathrm{AY}}\right)(\mathrm{Mg})$

Hence, the force, $\mathrm{f}$, developed as a restoring (elastic) force due to the additions pulling down, of the mass $\mathrm{M}$, by an amount $\Delta \ell$, would be given by

$$ \Delta \ell=\frac{\mathrm{L}}{\mathrm{AY}} \mathrm{f} $$

or $\quad \mathrm{f}=\mathrm{AY} \frac{\Delta \ell}{\mathrm{L}}=\left(\frac{\mathrm{AY}}{\mathrm{L}}\right) \Delta \ell$

$\therefore$ The restoring force (acting opposite to the displacement) on the mass $\mathrm{M}$ is proportional to its displacement. The mass M can, therefore, be thought of as executing SH oscillations. For these oscillations,

$$ \omega^{2}=\frac{A Y}{L} \cdot \frac{1}{M} $$

$\therefore$ Time period, of these oscillations, is

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{ML}}{\mathrm{AY}}} $$

[Note: Here it is being assumed that the wire, in a way, acts like a ‘spring’ and gets ’extended and compressed’ repeatedly. This in practice, will last for but a few oscillations].

33. A combination of two blocks, of masses $M _{1}$ and $M _{2}$, is attached to a spring (spring constant $=k$ ) with the lower mass $M _{1}$ (to which the spring is attached) resting on a smooth horizontal surface. The coefficient of friction between the two blocks is $\mu$. The ‘combination’ is stretched to extend the spring by an amount $A$ and ’let-go’.

The minimum value of $\mu$, for which the ‘combination’ would stay intact, is

(1) $\frac{A k}{\left(M_1+M_2\right) g}$

(2) $\frac{\mathrm{Ak}}{\left(\mathrm{M}_2 \mathrm{~g}\right)}$

(3) $\frac{\mathrm{M}_1 \mathrm{~g}}{(\mathrm{Ak})}$

(4) $\frac{\left(M_1+M_2\right) g}{(A k)}$

Show Answer

Correct answer: (1)

Solution:

The restoring force, developed in the spring, when it is extended by an amount A, equals kA. The resulting (restoring) acceleration, of the ‘combination’ is $\frac{k}{\left(M _{1}+M _{2}\right)} A$.

Hence, for the SH oscillations, of the ‘combination’ we have

$$ \omega^{2}=\frac{\mathrm{k}}{\left(\mathrm{M} _{1}+\mathrm{M} _{2}\right)} $$

The maximum value of the acceleration of the combination, as we know, is $\mathrm{A} \omega^{2}(\mathrm{~A}=$ amplitude of oscillation).

Also the maximum force of friction, between $\mathrm{M} _{2}$ and $\mathrm{M} _{1}$, is $\mu \mathrm{M} _{2} \mathrm{~g}$. This can give mass $\mathrm{M} _{2}$ a maximum acceleration of $\mu \mathrm{g}$.

The ‘combination’ can stay intact only if

$$ \mu g=A \omega^{2}=\frac{A k}{\left(M _{1}+M _{2}\right)} $$

or if $\mu=\frac{A k}{\left(M _{1}+M _{2}\right) g}$

This is then the minimum value that $\mu$ must have.

34. The two limbs, of a $U$-tube, have unequal cross sections, say $a _{1}$ and $a _{2}$. A given liquid, ( $d$ ensity $=\rho$ ) is poured into the $U$-tube and allowed to attain its equilibrium position.

The liquid, in the narrower limb, say, is now pushed down through a small distance, say $y _{1}$, and ’let-go’. The resulting (SH) oscillations, of the whole mass of liquid in the U-tube, would have a time period, $T$, given by

(1) $\mathrm{T}=2 \pi \sqrt{\frac{\left(\frac{\mathrm{a} _{1}}{\mathrm{a} _{2}}+1\right) \mathrm{g}}{\mathrm{g}}}$

(2) $\mathrm{T}=2 \pi \sqrt{\frac{\left(\frac{\mathrm{a} _{2}}{\mathrm{a} _{1}}+1\right) \mathrm{h}}{\mathrm{g}}}$

(3) $\mathrm{T}=2 \pi \sqrt{\frac{\left(\frac{\mathrm{a} _{1}}{\mathrm{a} _{2}}\right) \mathrm{h}}{\mathrm{g}}}$

(4) $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{h}}{\mathrm{g}}}$

Show Answer

Correct answer: (4)

Solution:

The mass, $\mathrm{M}$, of the liquid, in the U-tube, is

$$ M=\left(a _{1} h _{1}+a _{2} h _{2}\right) \rho $$

Also, in the initial equilibrium position, we have, for equality of pressure,

$$ \begin{gathered} \quad \mathrm{h} _{1} \rho \mathrm{g}=\mathrm{h} _{2} \rho \mathrm{g} \\ \therefore \quad \mathrm{h} _{1}=\mathrm{h} _{2}=\mathrm{h}(\text { say }) \\ \therefore \quad \mathrm{M}=\left(\mathrm{a} _{1}+\mathrm{a} _{2}\right) \mathrm{h} \rho \end{gathered} $$

When the liquid is pushed down a distance $y$ in the narrow limb, it would rise a distance $y^{\prime}$ in the wide limb, such that

$$ a _{1} y=a _{2} y^{\prime} \quad \text { or } \quad y^{\prime}=\left(\frac{a _{1}}{a _{2}}\right) y $$

The pressure difference, in the two limbs, now is

$$ \begin{aligned} \Delta \mathrm{P}= & \left(\mathrm{h}+\mathrm{y}^{\prime}\right) \rho g-(\mathrm{h}-\mathrm{y}) \rho \mathrm{g} \\ & =\left(\mathrm{y}^{\prime}+\mathrm{y}\right) \rho \mathrm{g} \end{aligned} $$

$$ =\left(\frac{\mathrm{a} _{1}}{\mathrm{a} _{2}}+1\right) \rho g \mathrm{y} $$

The force, pushing the liquid downwards, in the wider limb is

$$ \begin{aligned} \mathrm{a} _{2} \Delta \mathrm{P} & =\mathrm{a} _{2}\left(\frac{\mathrm{a} _{1}}{\mathrm{a} _{2}}+1\right) \rho g \mathrm{y} \\ & =\left[\left(\mathrm{a} _{1}+\mathrm{a} _{2}\right) \rho \mathrm{g}\right] \mathrm{y} \end{aligned} $$

The restoring force is, therefore, proportional to the displacement and directed opposite to it. The oscillatinos are, therefore, SH oscillations for which

$$ \begin{aligned} \omega^{2}= & \frac{\left[\left(a _{1}+a _{2}\right) \rho g\right]}{M} \\ & =\frac{\left(a _{1}+a _{2}\right) \rho g}{\left(a _{1}+a _{2}\right) h \rho}=\frac{g}{h} \end{aligned} $$

The time period, $\mathrm{T}$, of the oscillations, is therefore,

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{h}}{\mathrm{g}}} $$

35. Two immiscible liquids, of densities $\rho _{1}$ and $\rho _{2}\left(\rho _{1}>\rho _{2}\right)$, are poured into the two limbs of a uniform $U$-tube of cross section a. Their equilibrium heights, above the base, are $h _{1}$ and $h _{2}$, respectively. The heavier liquid is pushed down a little and ’let-go’. The resulting SH oscillations, of the whole mass of the liquid, will have a time period $T$, where

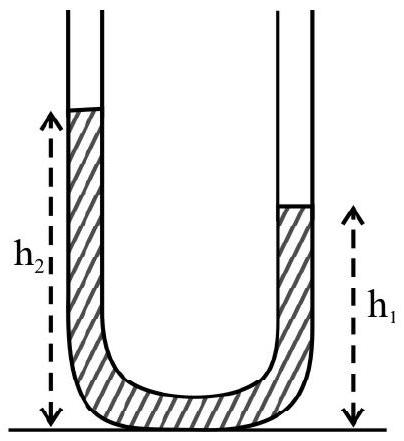
(1) $\mathrm{T}=2 \pi \sqrt{\frac{\left(\rho _{1}+\rho _{2}\right) \mathrm{h} _{1}}{2 \rho _{1} g}}$

(2) $\mathrm{T}=2 \pi \sqrt{\frac{2 \rho _{2} \mathrm{~h} _{1}}{\left(\rho _{1}+\rho _{2}\right) g}}$

(3) $T=2 \pi \sqrt{\frac{2 \rho _{1} h _{1}}{\left(\rho _{1}+\rho _{2}\right) g}}$

(4) $\mathrm{T}=2 \pi \sqrt{\frac{2 \rho _{1} \mathrm{~h} _{2}}{\left(\rho _{1}+\rho _{2}\right) g}}$

Show Answer

Correct answer: (3)

Solution:

The mass $\mathrm{M}$, of the (whole) liquid in the U-tube, is

$$ M=a h _{1} \rho _{1}+a h _{2} \rho _{2}=a\left(h _{1} \rho _{2}+h _{2} \rho _{2}\right) $$

Also, in the initial equilibrium position, we have

$$ h _{1} \rho _{1} g=h _{2} \rho _{2} g \quad \text { or } \quad h _{1} \rho _{1}=h _{2} \rho _{2} $$

$\therefore M=2 \mathrm{ah} _{1} \rho _{1}\left(=2 \mathrm{ah} _{2} \rho _{2}\right)$

When the (heavier) liquid is pushed down a distance y, the lighter liquid will rise a distance $y$. The pressure difference, in the two limbs, is now

$$ \begin{aligned} \Delta P= & g\left(h _{2}+y\right) \rho _{2}-g\left(h _{1}-y\right) \rho _{1} \\ & =g\left[h _{2} \rho _{2}+y \rho _{2}-h _{1} \rho _{1}+y \rho _{1}\right] \\ & =g y\left(\rho _{2}+\rho _{1}\right) \quad\left(\therefore h _{2} \rho _{2}=h _{1} \rho _{1}\right) \end{aligned} $$

The force, pushing the heavier liquid up is

$$ \mathrm{a} \Delta \mathrm{P}=\operatorname{ag}\left(\rho _{1}+\rho _{2}\right) \mathrm{y} $$

The (restoring) force is, therefore, proportional to the displacement and directed opposite to it. The oscillations are, therefore, SH oscillations for which

$$ \omega^{2}=\frac{\operatorname{ag}\left(\rho _{1}+\rho _{2}\right)}{2 a h _{1} \rho _{1}}=\frac{g\left(\rho _{1}+\rho _{2}\right)}{2 h _{1} \rho _{1}} $$

The time period, $\mathrm{T}$, of the oscillations, is, therefore, given by

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{2 \rho _{1}}{\left(\rho _{1}+\rho _{2}\right)} \frac{\mathrm{h} _{1}}{\mathrm{~g}}} $$

[Note: We could also write

$$ \omega^{2}=\frac{\operatorname{ag}\left(\rho _{1}+\rho _{2}\right)}{2 \mathrm{a} \mathrm{h} _{2} \rho _{2}}=\frac{\mathrm{g}\left(\rho _{1}+\rho _{2}\right)}{2 \rho _{2} \mathrm{~h} _{2}} $$

$\therefore$ We would also have

$$ \mathrm{T}=2 \pi \sqrt{\frac{2 \rho _{2} \mathrm{~h} _{2}}{\left(\rho _{1}+\rho _{2}\right) g}} $$

(we could get this result by noting that $\rho _{1} h _{1}=\rho _{2} h _{2}$ )]

36. A uniformly charged ring, of radius $R$, has a total positive charge $Q$ (uniformly) distributed over it. A particle, of mass $M$, and having a negative charge $(-q)$ is placed, on the axis of the ring, at a distance $x$ from its centre. If $x«R$, the negative charge can execute SH oscillations of time period $T$, where $T$ equals

(1) $2 \pi \sqrt{\frac{\mathrm{mR}^{3}}{4 \pi \varepsilon _{0} \mathrm{qQ}}}$

(2) $2 \pi \sqrt{\frac{4 \pi \varepsilon _{0} \mathrm{mR}^{3}}{\mathrm{qQ}}}$

(3) $2 \pi \sqrt{\frac{4 \pi \varepsilon _{0} \mathrm{qQ}}{\mathrm{mR}^{3}}}$

(4) $2 \pi \sqrt{\frac{\mathrm{qQ}}{4 \pi \varepsilon _{0} \mathrm{mR}^{3}}}$

Show Answer

Correct answer: (2)

Solution:

The electric field, due to the uniformly charged ring (carrying a positive charge $\mathrm{Q}$ ), at an axial point is

$$ \mathbf{E}=\frac{1}{4 \pi \varepsilon _{0}} \frac{\mathrm{Q} x}{\left(\mathrm{R}^{2}+x^{2}\right)^{3 / 2}} \hat{\mathrm{i}} $$

The force, on the negative charge, is

$$ \mathbf{F}=\frac{1}{4 \pi \varepsilon _{0}} \frac{\mathrm{qQ} x}{\left(\mathrm{R} _{1}^{2}+x^{2}\right)^{3 / 2}}(-\hat{\mathrm{i}}) $$

$\therefore$ For the particle, we can write

$$ \mathrm{m} \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=\frac{1}{4 \pi \varepsilon _{0}} \frac{\mathrm{qQ}}{\left(\mathrm{R}^{2}+x^{2}\right)^{3 / 2}}(-x) $$

For $x«\mathrm{R}$, we can write

$$ \begin{aligned} & \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}} \simeq \frac{-1}{4 \pi \varepsilon _{0}} \frac{1}{\mathrm{~m}} \frac{\mathrm{qQ}}{\mathrm{R}^{3}} x \\ & =-\omega^{2} x \quad\left(\text { where } \omega^{2}=\frac{1}{4 \pi \varepsilon _{0}} \frac{\mathrm{qQ}}{\mathrm{mR}^{3}}\right) \end{aligned} $$

The motion of the particle can, therefore, be simple harmonic when $x«\mathrm{R}$. The time period, of these $\mathrm{SH}$ oscillations, is

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{4 \pi \varepsilon _{0} \mathrm{MR}^{3}}{\mathrm{qQ}}} $$

37. A system of two identical (oppositely rolling) cylinders, having their centres on same horizontal line, along the $x$-axis, support a rectangular lamina (of mass $M$ and length $L$ ) when it is placed symmetrically on these two cylinders, kept under its two edges.

The coefficient of friction, between the lamina and the cylinder surfaces, is $\mu$. The lamina is given a slight push, say by an amount $\Delta x$, to the right. Assuming that the lamina continues to remain horizontal and in contact with the cylinders (without rotating), it will execute $\mathrm{SH}$ oscillations of time period, $T$, where $T$ equals

(1) $2 \pi \sqrt{\frac{2 \mu \mathrm{g}}{\ell}}$

(2) $2 \pi \sqrt{\frac{\ell}{\mu g}}$

(3) $2 \pi \sqrt{\frac{2 \ell}{\mu g}}$

(4) $2 \pi \sqrt{\frac{\ell}{2 \mu g}}$

Show Answer

Correct answer: (4)

Solution:

In the initial (symmetrical) equilibrium position, if $\mathrm{N} _{1}$ and $\mathrm{N} _{2}$ are the normal reactions due to the two cylinders, we have $\left(\mathrm{N} _{1}+\mathrm{N} _{2}=\mathrm{Mg}\right.$ ) and $\mathrm{N} _{1} \cdot \frac{\ell}{2}=\mathrm{N} _{2} \cdot \frac{\ell}{2}$ (there is no rotation of the lamina). Hence $\mathrm{N} _{1}=\mathrm{N} _{2}$ $=\frac{\mathrm{Mg}}{2}$

When the lamina, is pushed a distance $\Delta x$ to the right, it still remains horizontal and, also, does not rotate at all. If $\mathrm{N} _{1}^{\prime}$ and $\mathrm{N} _{2}^{\prime}$ are the normal reactions, due to the cylinders, on the left and right respectively, we have

$$ \mathrm{N} _{1}^{\prime}+\mathrm{N} _{2}^{\prime}=\mathrm{Mg} \quad \text { and } \quad \mathrm{N} _{1}^{\prime}\left(\frac{\ell}{2}-\Delta x\right)=\mathrm{N} _{2}^{\prime}\left(\ell _{2}+\Delta x\right) $$

These give

$$ \mathrm{N} _{1}^{\prime}=\frac{\mathrm{Mg}}{\ell}\left(\frac{\ell}{2}+\Delta x\right) $$

and $\quad \mathrm{N} _{2}^{\prime}=\frac{\mathrm{Mg}}{\ell}\left(\frac{\ell}{2}-\Delta x\right)$

The forces of friction, due to the two cylinders, are

$$ \begin{aligned} \mathrm{f} _{1} & =\mu \mathrm{N} _{1}^{\prime} \quad \text { and } \quad \mathrm{f} _{2}=\mu \mathrm{N} _{2}^{\prime} \\ \therefore \quad \mathrm{f} _{1} & =\frac{\mu \mathrm{Mg}}{\ell}\left(\frac{\ell}{2}+\Delta x\right) \\ \mathrm{f} _{2} & =\frac{\mu \mathrm{Mg}}{\ell}\left(\frac{\ell}{2}-\Delta x\right) \end{aligned} $$

The net force of friction, acting as a restoring force, is

$$ \left(\mathrm{f} _{1}-\mathrm{f} _{2}\right)=\frac{\mu \mathrm{Mg}}{\ell} \cdot 2 \Delta x $$

The equation of motion, of the lamina, is

$$ \mathrm{M} \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=\frac{-2 \mu \mathrm{Mg}}{\ell} \Delta x $$

The lamina, therefore, executes SHM for which

$$ \omega^{2}=\frac{2 \mu g}{\ell} $$

$\therefore$ The time period of these oscillations is

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\ell}{2 \mu \mathrm{g}}} $$

38. A given mass, $M$, is attached, one by one, to two springs (of spring constants $k _{1}$ and $k _{2}$ ) and to their ‘series’ and ‘parallel’ combinations. The time periods, of the vertical (SH) oscillations, of the mass, in the four cases, are $T _{1}, T _{2}, T _{3}$ and $T _{4}$, respectively. The ratios $\left(\frac{T _{1}}{T _{3}}\right)$ and $\left(\frac{T _{2}}{T _{4}}\right)$ are equal, respectively, to

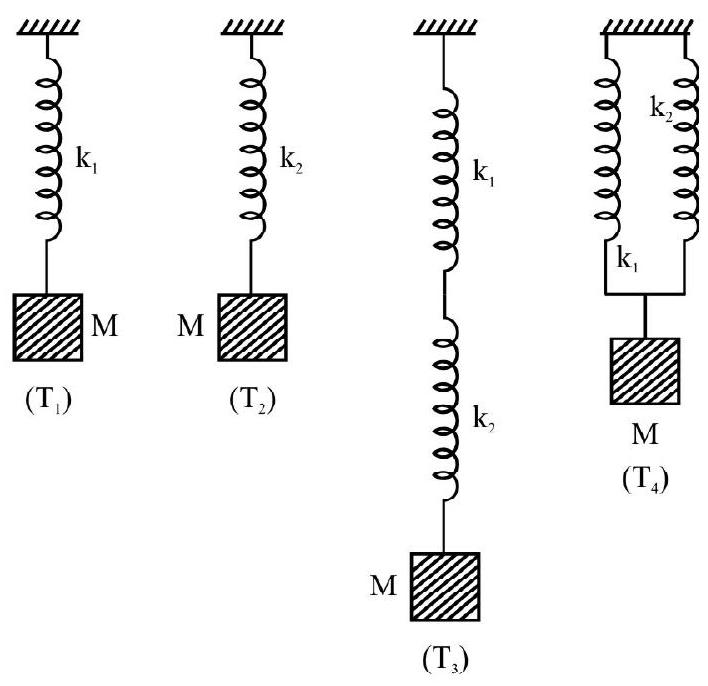
(1) $\frac{\mathrm{T} _{1}}{\mathrm{~T} _{3}}=\left(\frac{\mathrm{k} _{1}+\mathrm{k} _{2}}{\mathrm{k} _{1}}\right)^{1 / 2} ; \frac{\mathrm{T} _{2}}{\mathrm{~T} _{4}}=\left(\frac{\mathrm{k} _{2}}{\mathrm{k} _{1}+\mathrm{k} _{2}}\right)^{1 / 2}$

(2) $\frac{\mathrm{T} _{1}}{\mathrm{~T} _{3}}=\left(\frac{\mathrm{k} _{1}}{\mathrm{k} _{1}+\mathrm{k} _{2}}\right)^{1 / 2} ; \frac{\mathrm{T} _{2}}{\mathrm{~T} _{4}}=\left(\frac{\mathrm{k} _{1}+\mathrm{k} _{2}}{\mathrm{k} _{2}}\right)^{1 / 2}$

(3) $\frac{\mathrm{T} _{1}}{\mathrm{~T} _{3}}=\left(\frac{\mathrm{k} _{2}}{\mathrm{k} _{1}+\mathrm{k} _{2}}\right)^{1 / 2} ; \frac{\mathrm{T} _{2}}{\mathrm{~T} _{4}}=\left(\frac{\mathrm{k} _{1}+\mathrm{k} _{2}}{\mathrm{k} _{2}}\right)^{1 / 2}$

(4) $\frac{\mathrm{T} _{1}}{\mathrm{~T} _{3}}=\left(\frac{\mathrm{k} _{2}}{\mathrm{k} _{1}+\mathrm{k} _{2}}\right)^{1 / 2} ; \frac{\mathrm{T} _{2}}{\mathrm{~T} _{4}}=\left(\frac{\mathrm{k} _{2}}{\mathrm{k} _{1}+\mathrm{k} _{2}}\right)^{1 / 2}$

Show Answer

Correct answer: (3)

Solution:

We have $T _{1}=2 \pi \sqrt{\frac{M}{k _{1}}} ; \quad T _{2}=2 \pi \sqrt{\frac{M}{k _{2}}}$

Also, for the ‘series’ combination, equivalent spring constant $=\mathrm{k} _{\mathrm{S}}=\frac{\mathrm{k} _{1} \mathrm{k} _{2}}{\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}$ and, for the ‘parallel’ combination, equivalent spring constant, $\mathrm{k} _{\mathrm{P}}=\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)$

$\therefore \mathrm{T} _{3}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k} _{\mathrm{S}}}}=2 \pi \sqrt{\frac{\mathrm{M}\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}{\mathrm{k} _{1} \mathrm{k} _{2}}}$

and $\quad \mathrm{T} _{4}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k} _{\mathrm{P}}}}=2 \pi \sqrt{\frac{\mathrm{M}}{\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}}$

$\therefore \frac{\mathrm{T} _{1}}{\mathrm{~T} _{3}}=\left[\frac{\mathrm{k} _{2}}{\left(\mathrm{k} _{1}+\mathrm{k} _{2}\right)}\right]^{1 / 2}$ and $\frac{\mathrm{T} _{2}}{\mathrm{~T} _{4}}=\left(\frac{\mathrm{k} _{1}+\mathrm{k} _{2}}{\mathrm{k} _{2}}\right)^{1 / 2}$

39. A system of three charges is set up in the XY plane, as shown. The negative charges are kept fixed in their respective positions while the positive charge in free to move. This positive charge will then

(1) execute simple harmonic motion, about the origin, on the $x$-axis

(2) move to the origin and stay at rest there (Incorrect)

(3) get displaced to a far-off position

(4) execute an oscillatory motion that is not simple harmonic in nature

Show Answer

Correct answer: (4)

Solution:

The net force, on the charge $+Q$, due to the two negative charges, in the position shown, is

$$ \mathrm{F} _{\mathrm{net}}=\frac{1}{4 \pi \varepsilon _{0}} \frac{2 \mathrm{q}^{2}}{5 \mathrm{a}^{2}} 2 \cos \theta $$

directed to the left, along the $x$-axis.

$$ \therefore \quad \mathrm{F} _{\text {net }}=\frac{1}{4 \pi \varepsilon _{0}} \frac{8 \mathrm{q}^{2}}{5 \sqrt{5} \mathrm{a}^{2}} \quad\left(\because \cos \theta=\frac{2}{\sqrt{5}}\right) $$

Let the charge $2 \mathrm{q}$ be moved a distance $\Delta \mathrm{a}$, to the right, along the $x$-axis. The net force, on it, now, would be

$$ \mathrm{F} _{\text {net }}^{\prime}=\frac{1}{4 \pi \varepsilon _{0}} \frac{2 \mathrm{q}^{2}}{\left[\mathrm{a}^{2}+(2 \mathrm{a}+\Delta \mathrm{a})^{2}\right]} \frac{(2 \mathrm{a}+\Delta \mathrm{a})}{\left[\mathrm{a}^{2}+(2 \mathrm{a}+\Delta \mathrm{a})^{2}\right]^{1 / 2}} $$

It is again directed to the left. The force, therefore, acts as a restoring force. Hence the charge $2 q$ can execute an oscillatory motion.

However, the expression for $\mathrm{F} _{\text {net }}^{\prime}$ reveals that it is not quite proportional to $\Delta \mathrm{a}$. Hence the oscillations are not simple harmonic in nature.

40. A horizontal platform, of mass $M$, has a black of mass $M$ kept on its edge. The combination is attached to a (light) vertical spring of spring constant $k$, and held, with the spring in its ’normal length’ position.

On letting the combination ’ $g 0$ ‘, it starts executing oscillations. The block will just leave the platform, when it has risen a distance $y$ above its ’lowest position’, if

(1) $\mathrm{y}>\left(\frac{\mathrm{Mg}}{\mathrm{k}}\right)$

(2) $\mathrm{y}>\left(\frac{2 \mathrm{Mg}}{\mathrm{k}}\right)$

(3) $\mathrm{y}>\left(\frac{3 \mathrm{Mg}}{\mathrm{k}}\right)$

(4) $\mathrm{y}>\left(\frac{4 \mathrm{Mg}}{\mathrm{k}}\right)$

Show Answer

Correct answer: (4)

Solution:

The oscillations, of the combination, when ’let-go’, will be simple harmonic oscillations for which

$$ \omega^{2}=\frac{k}{(M+M)}=\frac{k}{2 M} $$

The amplitude of oscillations will equal the extension, say $\ell$, of the spring.

We would have

$$ \ell=\left(\frac{2 \mathrm{Mg}}{\mathrm{k}}\right) $$

When the combination rises above its mean position, it experiences a downward acceleration. If this downward (oscillation based) acceleration exceeds the acceleration due to gravity, the mass $M$ will no longer remain attached to the platform.

Magnitude of acceleration at a distance, $\mathrm{s}$, above its mean position $=\omega^{2} \mathrm{~s}$

This distance is a distance $(\ell+\mathrm{s})$ above the lowest position of the platform. Calling $\mathrm{y}=(\ell+\mathrm{s})$, the block will leave the platform (when it is at a distance y above its lowest position) if

$$ \begin{gathered} \omega^{2} s>g \\ \text { or } \quad s>\left(\frac{g}{\omega^{2}}\right) \end{gathered} $$

or if $(\ell+\mathrm{s})>\left(\ell+\frac{\mathrm{g}}{\omega^{2}}\right)$

or if $\mathrm{y}>\left(\ell+\frac{\mathrm{g}}{\omega^{2}}\right)\left[=\left(\ell+\frac{\mathrm{g} .2 \mathrm{M}}{\mathrm{k}}\right)\right]$

Thus the required condition is

$$ \mathrm{y}>\left(\ell+\frac{2 \mathrm{Mg}}{\mathrm{k}}\right) $$

or $\quad \mathrm{y}>\left(\frac{4 \mathrm{Mg}}{\mathrm{k}}\right) \quad\left(\because \ell=\frac{2 \mathrm{Mg}}{\mathrm{k}}\right)$

41. A rigid cubical block, $A$, of small mass $M$ and side $L$, is fixed rigidly to another cubical block B, of the same dimensions, so that the lower face of it completely covers the upper face of $B$. The lower face of $B$ is rigidly held on a horizontal surface. The modulus of rigidity $(\boldsymbol{\eta})$, of the material of $A$, has a low value.

A small force, $F$, is applied perpendicular to one of the side faces of $A$ and then withdrawn. The time period, of the small (resulting) oscillations of $A$, is given by

(1) $2 \pi \sqrt{\mathrm{M \eta L}}$

(2) $2 \pi \sqrt{\frac{\mathrm{M}}{\eta \mathrm{L}}}$

(3) $2 \pi \sqrt{\frac{\mathrm{ML}}{\eta}}$

(4) $2 \pi \sqrt{\frac{\mathrm{M} \eta}{\mathrm{L}}}$

Show Answer

Correct answer: (2)

Solution:

The lower face of $A$ has been rigidly fixed to the upper face of $B$. Hence when a force $F$ is applied perpendicular to one of the side faces of A, it would get ‘sheared’. If the shear strain equals $\theta$, we have

$$ \theta \simeq \frac{\Delta \mathrm{L}}{\mathrm{L}} $$

Because of elasticity, the block A will tend to return to its normal (shear free) position, after the withdrawal of force $F$.

Hence it would execute oscillations. We have

$$ \begin{aligned} & \eta=\frac{F / A}{\theta} \\ & =\frac{(F / A) \cdot L}{\Delta L} \end{aligned} $$

$\therefore \quad \mathrm{F}=\eta \cdot \frac{\Delta \mathrm{L}}{\mathrm{L}} \mathrm{A}=\eta \cdot \frac{\Delta \mathrm{L}}{\mathrm{L}} \cdot \mathrm{L}^{2} \quad\left(\because \mathrm{A}=\mathrm{L}^{2}\right)$

$\therefore \quad \mathrm{F}=(\eta \mathrm{L}) \Delta \mathrm{L}$

The restoring force is thus proportional to displacement. Hence block A will execute harmonic oscillations.

For these oscillations,

$$ \omega^{2}=\frac{\eta L}{M} $$

$\therefore$ The time period, of these oscillations, is

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{M}}{\eta \ell}} $$

42. Two non-viscous, incompressible and immiscible liquids of densities $\rho$ and $1.5 \rho$ are poured into the two limbs of a circular tube of radius $R$, and small cross section, kept fixed in a vertical plane. Each liquid occupies one fourth the circumference of the tube.

The whole liquid is given a small displacement from its equilibrium position. Its resulting SH oscillations would have a time period, T, where $T$ equals

(1) $\left(\frac{2 \pi^{3} \mathrm{R}}{\mathrm{g} \cos \theta}\right)^{1 / 2}$

(2) $\left(\frac{2 \pi^{3} R \cos \theta}{g}\right)^{1 / 2}$

(3) $2 \pi\left(\frac{\mathrm{R} \cos \theta}{\mathrm{g}}\right)^{1 / 2}$

(4) $2 \pi\left(\frac{\mathrm{R}}{\mathrm{g} \cos \theta}\right)^{1 / 2}$

Show Answer

Correct answer: (1)

Solution:

Let $\mathrm{S}$ be the cross sectional area of the tube. The sum of the mass of the two liquids is then

$$ \begin{aligned} M= & {\left[S\left(\frac{2 \pi R}{4}\right) \rho _{1}+S\left(\frac{2 \pi R}{4}\right) \rho _{2}\right]=S \frac{2 \pi R}{4}(\rho+1.5 \rho) } \\ & =\frac{5 \pi R S}{4} \rho \end{aligned} $$

Its moment of inertia, $\mathrm{I}$, about the vertical line through, $\mathrm{O}$ is $\mathrm{I}=\mathrm{MR}^{2}=\frac{5 \pi \mathrm{R} \rho \mathrm{R}^{3}}{4}$

Let the liquids be pushed (slightly) at $\mathrm{A}$, in the anticlockwise sense so that point A moves to a lower position $\mathrm{A}^{\prime}$ and point $\mathrm{B}$ moves to a higher position $\mathrm{B}^{\prime}$. If the angles $\mathrm{A}^{\prime} \mathrm{OA}$ and $\mathrm{B}^{\prime} \mathrm{OB}$ are denoted by $\alpha$ each, we would have $\mathrm{BB}^{\prime}=\mathrm{AA}^{\prime}=\mathrm{R} \alpha$. The ‘weights’ of the extra masses of the liquids, in these two segments, would provide torque (in the same sense) that would tend to restore the displaced liquid back into its original position. The weights equal

$$ \left((\mathrm{S})\left(\mathrm{BB}^{\prime}\right) \cdot \rho \mathrm{g}\right) \text { and }\left(\mathrm{S}\left(\mathrm{AA}^{\prime}\right)(1.5 \rho) \mathrm{g}\right) \text { respectively. } $$

The distance, of the lines of action, of these ‘weights’, from the vertical line, are $\mathrm{R} \cos \theta$ each. Hence the total restoring torque is

$$ \begin{aligned} \tau & =[\mathrm{S}(\mathrm{R} \alpha) \rho \mathrm{g}+\mathrm{S}(\mathrm{R} \alpha)(1.5 \rho \mathrm{g})] \cdot \mathrm{R} \cos \theta \\ \therefore & \tau=\left[\mathrm{SR}^{2}(2.5 \rho \mathrm{g}) \cos \theta\right] \alpha \end{aligned} $$

The equation of motion of the oscillating liquid is

$$ \begin{gathered} \mathrm{I} \frac{\mathrm{d}^{2} \alpha}{\mathrm{dt}^{2}}=-\tau \\ \therefore \quad \frac{\mathrm{d}^{2} \alpha}{\mathrm{dt}^{2}}=-\frac{\tau}{\mathrm{I}}=\left[-\frac{4 \mathrm{SR}^{2}(2.5) \rho \mathrm{g} \cos \theta}{5 \pi \mathrm{R}^{3} \mathrm{~S} \rho}\right] \alpha \\ \quad=-\left[\frac{2}{\pi \mathrm{R}} \mathrm{g} \cos \theta\right] \alpha \end{gathered} $$

The oscillations are, therefore, simple harmonic oscillations for which

$$ \omega^{2}=\frac{2 g \cos \theta}{\pi \mathrm{R}} $$

$\therefore$ Time period, $\mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\pi \mathrm{R}}{2 \mathrm{~g} \cos \theta}}$

$$ \therefore T=\sqrt{\frac{4 \pi^{3} R}{2 g \cos \theta}}=\sqrt{\frac{2 \pi^{3} R}{g \cos \theta}} $$

43. A light spring (spring constant $=k$ ) a cylinder (length $=L$, Area of cross section $=\mathbf{A}$, mass $=M$ ) and a liquid (density $=\rho$ ) container are set-up as shown. The cylinder is half submerged in the liquid at equilibrium. It is given a small downward push, and released, so that it starts oscillating vertically. The frequency, of these oscillations, is given by

(1) $\frac{1}{2 \pi}\left(\frac{\mathrm{k}-\mathrm{A} \rho \mathrm{g}}{\mathrm{M}}\right)^{1 / 2}$

(2) $\frac{1}{2 \pi}\left(\frac{\mathrm{k}+\mathrm{A} \rho \mathrm{g}}{\mathrm{M}}\right)^{1 / 2}$

(3) $\frac{1}{2 \pi}\left(\frac{\mathrm{k}+\rho \mathrm{gL}^{2}}{\mathrm{M}}\right)^{1 / 2}$

(4) $\frac{1}{2 \pi}\left(\frac{\mathrm{k}+\mathrm{A} \rho \mathrm{g}}{\mathrm{A} \rho \mathrm{g}}\right)^{1 / 2}$

Show Answer

Correct answer: (2)

Solution:

The effective restoring force, acting on the cylinder, when it is given a small downward push, is the sum of the

(i) restoring force, due to the spring getting extended. It equals ky where $\mathrm{y}=$ (small) downward displacement of the cylinder.

(ii) Buoyant force, due to the weight of the extra volume ( $=$ Ay) of liquid displaced by the cylinder. This equal $(\mathrm{Ay})(\rho \mathrm{g})$.

Hence the equation of motion of the cylinder is

$$ M \frac{d^{2} y}{d t^{2}}=-(k y+A \rho g y)=-(k+A \rho g) y $$

For this SH Motion,

$$ \omega^{2}=\left(\frac{\mathrm{k}+\mathrm{A} \rho \mathrm{g}}{\mathrm{M}}\right) $$

Hence the frequency of oscillations is

$$ v=\frac{\omega}{2 \pi}=\frac{1}{2 \pi} \sqrt{\left(\frac{\mathrm{k}+\mathrm{A} \rho \mathrm{g}}{\mathrm{M}}\right)} $$

44. A point particle of mass $M$ is attached to one end of a massless rigid non conducting rod of length L. Another point particle of the same mass is attached to the other end of the rod. The two particles carry charges $+q$ and $-q$, respectively.

This arrangement is held in a region of the uniform electric field such that the rod makes a small angle $\theta\left(\sim 5^{0}\right)$ with the field direction. If the rod is set free (so that it can rotate about its centre) the time period of its oscillations, and the minimum time, which it would take to become parallel to the field direction, are given, respectively, by

(1) $2 \pi\left(\frac{2 \mathrm{ML}}{\mathrm{qE}}\right)^{1 / 2}$ and $\frac{\pi}{2}\left(\frac{2 \mathrm{ML}}{\mathrm{qE}}\right)^{1 / 2}$

(2) $2 \pi\left(\frac{M L}{2 q E}\right)^{1 / 2}$ and $\frac{\pi}{2}\left(\frac{M L}{2 q E}\right)^{1 / 2}$

(3) $2 \pi\left(\frac{\mathrm{ML}}{\mathrm{qE}}\right)^{1 / 2}$ and $\pi\left(\frac{\mathrm{ML}}{\mathrm{qE}}\right)^{1 / 2}$

(4) $2 \pi\left(\frac{2 \mathrm{ML}}{\mathrm{qE}}\right)^{1 / 2}$ and $\pi\left(\frac{2 \mathrm{ML}}{\mathrm{qE}}\right)^{1 / 2}$

Show Answer

Correct answer: (2)

Solution:

The rod can be viewed as a dipole of dipole moment $p=q . L$

The torque, experienced by it due to the electric field, is

$$ \tau=|\mathbf{p} \times \mathbf{E}|=\mathrm{qLE} \sin \theta \approx \mathrm{qLE} \theta $$

This torque, being a restoring torque, the equation of motion of the rod is

$$ \mathrm{I} \frac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}=-\tau=-(\mathrm{qLE}) \theta $$

For the dipole, $\mathrm{I}=\frac{\mathrm{ML}^{2}}{4}+\mathrm{M} \frac{\mathrm{L}^{2}}{4}=\frac{\mathrm{ML}^{2}}{2}$

$\therefore \frac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}=-\frac{2 \mathrm{qL}}{\mathrm{ML}^{2}} \mathrm{E} \theta=-\left(\frac{2 \mathrm{qE}}{\mathrm{ML}}\right) \theta$

The motion of the rod is, therefore, simple harmonic for which

$$ \omega^{2}=\left(\frac{2 \mathrm{qE}}{\mathrm{ML}}\right) $$

$\therefore$ Time period of oscillations

$$ \mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{ML}}{2 \mathrm{qE}}} $$

The rod will become parallel to the field (after it is set free) in a time $\frac{\mathrm{T}}{4}$. Hence this time is $\left(\frac{\pi}{2} \sqrt{\frac{\mathrm{ML}}{2 \mathrm{qE}}}\right)$.

45. Four springs, having lengths in the ratio $1: 2: 3: 4$, are made from a given roll of wire of a given material.

The time periods, of simple harmonic oscillations of a given mass $M$, when attached to a spring having a spring constant equivalent to the (i) series combination (ii) parallel combination, of these four springs, are $T _{1}$ and $T _{2}$, respectively. The ratio $\left(T _{1} / T _{2}\right)$ equals (nearly)

(1) 4.3

(2) 4.6

(3) 4.9

(4) 5.2

Show Answer

Correct answer: (2)

Solution:

The spring constant (for same material and same area of cross section) can be taken as inversely proportional to the length of the spring.

Hence the spring constants, of the four springs, may be taken as

$$ \frac{\mathrm{k}}{1}, \frac{\mathrm{k}}{2}, \frac{\mathrm{k}}{3}, \frac{\mathrm{k}}{4} $$

For the series combination, the equivalent spring constant, say $\mathrm{K} _{1}$, in given by

$$ \begin{aligned} & \frac{1}{\mathrm{~K} _{1}}=\frac{1}{\mathrm{k}}+\frac{2}{\mathrm{k}}+\frac{3}{\mathrm{k}}+\frac{4}{\mathrm{k}}=\frac{10}{\mathrm{k}} \\ & \therefore \mathrm{K} _{1}=\mathrm{k} / 10 \end{aligned} $$

For the parallel combination, the equivalent spring constant, say $\mathrm{K} _{2}$, is given by

$$ \mathrm{K} _{2}=\frac{\mathrm{k}}{1}+\frac{\mathrm{k}}{2}+\frac{\mathrm{k}}{3}+\frac{\mathrm{k}}{4}=\left(\frac{12+6+4+3}{12}\right) \mathrm{k}=\frac{25}{12} \mathrm{k} $$

Now $\mathrm{T} _{1}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{K} _{1}}}$ and $\mathrm{T} _{2}=2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{K} _{2}}}$

$$ \begin{aligned} & \therefore \quad \frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=\sqrt{\frac{\mathrm{K} _{2}}{\mathrm{~K} _{1}}}=\sqrt{\frac{25}{12} \mathrm{k} \times \frac{10}{\mathrm{k}}}=\sqrt{20.83} \\ & \simeq 4.56 \approx 4.6 \end{aligned} $$

46. Two bodies, of equal masses $M$ each, are suspended from two massless springs of spring constants $k _{1}$ and $k _{2}$, respectively. If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of vibrations of the first body, to that of the second body, is

(1) $\frac{\mathrm{k} _{1}}{\mathrm{k} _{2}}$

(2) $\sqrt{\frac{\mathrm{k} _{1}}{\mathrm{k} _{2}}}$

(3) $\frac{\mathrm{k} _{2}}{\mathrm{k} _{1}}$

(4) $\sqrt{\frac{\mathrm{k} _{2}}{\mathrm{k} _{1}}} $

Show Answer

Correct answer: (4)

Solution:

For the two springs, we have

$$ \omega _{1}^{2}=\frac{k _{1}}{M} $$

and $\quad \omega _{2}^{2}=\frac{\mathrm{k} _{2}}{\mathrm{M}}$

Let $\mathrm{A} _{1}$ and $\mathrm{A} _{2}$ be the amplitudes of their vibrations.

Now maximum velocity $=$ velocity amplitude $=A \omega$

We, therefore, have

$$ \begin{aligned} & A _{1} \sqrt{\frac{k _{1}}{M}}=A _{1} \sqrt{\frac{k _{2}}{M}} \\ & \therefore \frac{\mathrm{A} _{1}}{\mathrm{~A} _{2}}=\sqrt{\frac{\mathrm{k} _{2}}{\mathrm{k} _{1}}} \end{aligned} $$

47. A long horizontal wire, which is free to move in a vertical plane, carries a steady current of $20 \mathrm{~A}$. It is in equilibrium when it is as shown at a height a over another parallel long wire $C D$ which is fixed in a

horizontal plane and carries a (unlike) steady current of $30 \mathrm{~A}$.

When the wire AB is depressed very slightly and ’let-go’, it executes oscillations which are

(1) Simple harmonic, with a time period $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{a}}{\mathrm{g}}}$

(2) Simple harmonic, with a time period $\mathrm{T}=2 \pi \sqrt{\left(\frac{\mathrm{I} _{1}}{\mathrm{I} _{2}} \frac{\mathrm{a}}{\mathrm{g}}\right)}$

(3) Periodic but not simple harmonic, their time period equals $2 \pi \sqrt{\frac{\mathrm{a}}{\mathrm{g}}}$

(4) Periodic but not simple harmonic, their time period equals $2 \pi \sqrt{\left(\frac{\mathrm{I} _{1}}{\mathrm{I} _{2}} \frac{\mathrm{a}}{\mathrm{g}}\right)}$

Show Answer

Correct answer: (1)

Solution:

The force (per unit length) between the two wires, equals $\frac{\mu _{0} I _{1} I _{2}}{2 \pi \mathrm{a}}$. At equilibrium, it balances the weight per unit length of the wire $\mathrm{AB}$, as it is directed upwards.

$\therefore \frac{\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}}{2 \pi \mathrm{a}}=\lambda \mathrm{g} \quad(\lambda=$ linear mass density of wire $\mathrm{AB}) \hspace{40mm}………(1)$

Let the wire $A B$ be depressed a small distance $y$. The magnetic force (which is directed upwards) now equals

$$ \frac{\mu _{0} I _{1} I _{2}}{2 \pi(a-y)}=\frac{\mu _{0} I _{1} I _{2}}{2 \pi a}\left(1-\frac{y}{a}\right)^{-1} $$

$$ \begin{equation*} \simeq \frac{\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}}{2 \pi \mathrm{a}}\left(1+\frac{\mathrm{y}}{\mathrm{a}}\right)(\because \text { y is very small in comparison to } \mathrm{a}) \tag{2} \end{equation*} $$

The net upward force is

$$ \begin{aligned} & \frac{\mu _{0} I _{1} I _{2}}{2 \pi \mathrm{a}}\left(1+\frac{\mathrm{y}}{\mathrm{a}}\right)-\lambda \mathrm{g} \\ & =\frac{\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}}{2 \pi \mathrm{a}}+\frac{\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}}{2 \pi \mathrm{a}^{2}} \mathrm{y}-\left(\frac{\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}}{2 \pi \mathrm{a}}\right) \quad \text { [fromEqn. (1)] } \\ & =\left(\frac{\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}}{2 \pi \mathrm{a}^{2}}\right) \mathrm{y} \end{aligned} $$

The net (restoring) force is, therefore, directed opposite to the displacement and is proportional to the displacement. Hence the oscillations of wire AB will be simple harmonic.

For these oscillations, we have

$$ \begin{array}{ll} \omega^{2}=\frac{1}{\lambda}\left(\frac{\mu _{0} I _{1} I _{2}}{2 \pi \mathrm{a}^{2}}\right) & (\lambda=\text { mass of a unit length) } \\ =\left(\frac{2 \pi \mathrm{ag}}{\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}}\right) \frac{\mu _{0} \mathrm{I} _{1} \mathrm{I} _{2}}{2 \pi \mathrm{a}^{2}} & \text { [from Eqn. (1)] } \\ =\frac{\mathrm{g}}{\mathrm{a}} & \tag{1} \end{array} $$

$\therefore$ Time period of oscillations $=2 \pi \sqrt{\frac{\mathrm{g}}{\mathrm{a}}}$

48. Two identical balls, $A$ and $B$, each of mass $0.2 \mathrm{~kg}$, are attached to two identical massless springs. The spring mass system is constrained to move inside a rigid smooth pipe bent in the form of a circle. The pipe is fixed in a horizontal plane. The centres of the balls can move in a circle of radius $6 \mathrm{~cm}$. Each spring has a natural length of $(6 \pi) \mathrm{cm}$ and spring constant of $0.1 \mathrm{~N} / \mathrm{m}$. Initially, both the balls are displaced by an angle $\theta=\frac{\pi}{6}$ radians with respect to the diameter $P Q$ of the circle, and are released from rest. The frequency of oscillation of ball $B$ would be

(1) $\left(\frac{2}{\pi}\right) \mathrm{Hz}$

(2) $\left(\frac{1.5}{\pi}\right) \mathrm{Hz}$

(3) $\left(\frac{1}{\pi}\right) \mathrm{Hz}$

(4) $\left(\frac{0.5}{\pi}\right) \mathrm{Hz}$

Show Answer

Correct answer: (3)

Solution:

For $\theta=\frac{\pi}{6}$, the linear displacement $x(=\mathrm{AP}=\mathrm{BQ})$ of each ball is $\mathrm{R} \theta=\mathrm{R} \frac{\pi}{6}$. This compresses the spring

$\mathrm{S} _{\mathrm{i}}$, and elongates the spring $\mathrm{S} _{2}$, by $2 x$, i.e., R. $\frac{\pi}{3}=(0.06) \frac{\pi}{3} \mathrm{~m}=(0.02 \pi) \mathrm{m}$

This results in a total restoring force $\mathrm{F}=(2 \mathrm{k} x+2 \mathrm{k} x)=4 \mathrm{k} x$ on the ball $\mathrm{B}$. Hence its equation of motion is

$$ \mathrm{m} \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-4 \mathrm{k} x $$

or $\quad \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-\left(\frac{4 \mathrm{k}}{\mathrm{m}}\right) x=-\omega^{2} x$

The oscillations, of ball B, are, therefore, simple harmonic. The time period, $\mathrm{T}$, is $\mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{m}}{4 \mathrm{k}}}$

$$ \begin{aligned} & \quad=\pi \sqrt{\frac{\mathrm{m}}{\mathrm{R}}} \\ & \quad=\left[\pi \sqrt{\frac{0.1}{0.1}}\right] \mathrm{s}=(\pi) \text { seconds } \\ & \therefore \text { Frequency }=\left(\frac{1}{\pi}\right) \mathrm{Hz} \end{aligned} $$

49. Two light springs, of spring constants $k _{1}(=1.8 \mathrm{~N} / \mathrm{m})$ and $k _{2}(=3.2 \mathrm{~N} / \mathrm{m})$, and a block of mass $M(=0.2 \mathrm{~kg})$ are in one line $A B$ on a smooth horizontal table such that one end of each spring in fixed and the other end is free. The distance $\mathrm{CD}$, between the free ends, is $0.6 \mathrm{~m}$

If the block moves in the part $\mathrm{CD}$ or $\mathrm{DC}$ along $\mathrm{AB}$, with a constant velocity $1.2 \mathrm{~m} / \mathrm{s}$, (i.e. between the springs) it would execute oscillation of time period (nearly) equal to

(1) $4.8 \mathrm{~s}$

(2) $3.8 \mathrm{~s}$

(3) $2.8 \mathrm{~s}$

(4) $1.8 \mathrm{~s}$

Show Answer

Correct answer: (3)

Solution:

The block’s oscillations can be thought of as made up of three parts:

(i) The block moves from $\mathrm{C}$ to $\mathrm{D}$, and back from $\mathrm{D}$ to $\mathrm{C}$, without being in contact with either of the springs. It would take a total time

$$ \mathrm{t} _{1}=\frac{2 \times 0.6 \mathrm{~m}}{(1.2 \mathrm{~m} / \mathrm{s})}=1 \mathrm{~s} $$

to complete this part $[(\mathrm{C}$ to $\mathrm{D})$ and (D to C) $]$ of its motion.

(ii) While moving to the right, and reaching the free end of the spring there $\left(\mathrm{k} _{2}=3.2 \mathrm{~N} / \mathrm{m}\right)$, it would compress it. As a result, the spring would make it oscillate with a time period equal to $2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k} _{2}}}$. However, after compressing the spring (for $1 / 4^{\text {th }}$ of its time period), it would move back towards D and would reach $\mathrm{D}$ again in a time equal to $14^{\text {th }}$ of its time period. Hence the time taken by it to oscillate (to the right of $\mathrm{D}$ and back to $\mathrm{D}$ ) is $1 / 2$ of the time period. This time, $\mathrm{t} _{2}$, equals

$$ \mathrm{t} _{2}=\frac{1}{2} \cdot 2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k} _{2}}}=\pi \sqrt{\frac{0.2}{3.2}} \mathrm{~s}=\frac{\pi}{4} \mathrm{~s} $$

(iii) After coming back to $\mathrm{D}$, the block moves the distance $\mathrm{DC}$ with its constant velocity of $1.2 \mathrm{~m} / \mathrm{s}$. (The time taken for this has already been included in $\mathrm{t} _{1}$ ). When it reaches $\mathrm{C}$, it compresses the other spring, and again comes back to $\mathrm{C}$, in a time $\mathrm{t} _{3}$ where

$$ \mathrm{t} _{3}=\frac{1}{2} \cdot 2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{k} _{1}}}=\pi \sqrt{\frac{0.2}{1.8}} \mathrm{~s}=\frac{\pi}{3} \mathrm{~s} $$

The total time period of its complete oscillation is, therefore,

$$ \begin{aligned} & \mathrm{T}=\mathrm{t} _{1}+\mathrm{t} _{2}+\mathrm{t} _{3}=\left(1+\frac{\pi}{4}+\frac{\pi}{3}\right) \mathrm{s}=\left(1+\frac{7 \pi}{12}\right) \mathrm{s} \\ & \simeq\left(1+\frac{7}{12} \times \frac{22}{7}\right) \mathrm{s}=\left(1+\frac{11}{6}\right) \mathrm{s} \approx 2.8 \mathrm{~s} \end{aligned} $$

50. A spring, of spring constant $k$, is attached to a cylinder of mass $M$ and radius $R$. The cylinder rests on a smooth horizontal surface. When the spring is stretched from its equilibrium position and ’let-go’ the cylinder starts rolling on the horizontal surface without slipping. The time period, of the resulting motion of the cylinder, is

(1) $2 \pi \sqrt{\frac{\mathrm{M}}{2 \mathrm{k}}}$

(2) $\pi \sqrt{\frac{6 \mathrm{M}}{\mathrm{k}}}$

(3) $2 \pi \sqrt{\frac{3 \mathrm{M}}{\mathrm{k}}}$

(4) $\pi \sqrt{\frac{\mathrm{M}}{2 \mathrm{k}}}$

Show Answer

Correct answer: (2)

Solution:

Let I denote the moment of inertia of the cylinder about its own axis. We than have $\mathrm{I}=\frac{1}{2} \mathrm{MR}^{2}$.

At any instant when the spring has been stretched through a distance $x$ from the its equilibrium position, let E be the total energy of the ‘spring-cylinder’ system. We have

$\mathrm{E}=$ Potential energy of the stretched spring + Rotational K.E of the cylinder + translational K.E of the cylinder

$$ \begin{aligned} & =\frac{1}{2} \mathrm{k} x^{2}+\frac{1}{2} \mathrm{I} \omega^{2}+\frac{1}{2} \mathrm{Mv}^{2} \\ & =\frac{1}{2} \mathrm{k} x^{2}+\frac{1}{2}\left(\frac{1}{2} \mathrm{MR}^{2}\right) \times\left(\frac{\mathrm{v}}{\mathrm{R}}\right)^{2}+\frac{1}{2} \mathrm{mv}^{2} \\ & =\frac{1}{2} \mathrm{k} x^{2}+\frac{3}{4} \mathrm{Mv}^{2} \end{aligned} $$

or $\quad \mathrm{E}=\frac{1}{2} \mathrm{k} x^{2}+\frac{3}{4} \mathrm{M}\left(\frac{\mathrm{d} x}{\mathrm{dt}}\right)^{2}$

$\therefore \frac{\mathrm{dE}}{\mathrm{dt}}(=0)=\frac{1}{2} \mathrm{k} \cdot 2 x \frac{\mathrm{d} x}{\mathrm{dt}}+\frac{3}{2} \mathrm{M}\left(\frac{\mathrm{d} x}{\mathrm{dt}}\right)\left(\frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}\right)$

$=\frac{\mathrm{d} x}{\mathrm{dt}}\left[\mathrm{k} x+\frac{3}{2} \mathrm{M} \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}\right]$

Since $\frac{\mathrm{d} x}{\mathrm{dt}}$ is not equal to 0 , we have

$$ \frac{3}{2} \mathrm{M} \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-\mathrm{k} x $$

or $\quad \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=-\frac{2}{3}\left(\frac{\mathrm{k}}{\mathrm{M}}\right) x$

$=-\omega^{2} x$

where $\omega^{2}=\frac{2}{3} \frac{\mathrm{k}}{\mathrm{M}}$

The motion of the cylinder is, therefore, sample harmonic is nature. Its time period, T, is given by

$$ \begin{aligned} \mathrm{T}=\frac{2 \pi}{\omega} & =2 \pi \sqrt{\frac{3 \mathrm{M}}{2 \mathrm{k}}} \\ & =\pi\left(\frac{6 \mathrm{M}}{\mathrm{k}}\right)^{1 / 2} \end{aligned} $$

51. The displacement of the medium, in a sound wave, is given by the equation

$$ y=A \cos (a x+b t) $$

where $A, a$ and $b$ are all positive constant. The wave is reflected by an obstacle at $\boldsymbol{x}=\mathbf{0}$. The intensity of the reflected wave is 0.64 times that of the incident wave. The wavelength and frequency of the incident wave, and the amplitude of the reflected wave, are, respectively,

(1) $\frac{2 \pi}{\mathrm{a}}, \frac{\mathrm{b}}{2 \pi}$ and $0.8 \mathrm{~A}$

(2) $\frac{2 \pi}{\mathrm{a}}, \frac{\mathrm{b}}{2 \pi}$ and $0.64 \mathrm{~A}$

(3) $\frac{\mathrm{a}}{2 \pi}, \frac{2 \pi}{\mathrm{b}}$ and $0.8 \mathrm{~A}$

(4) $\frac{\mathrm{a}}{2 \pi}, \frac{2 \pi}{\mathrm{b}}$ and $0.64 \mathrm{~A}$

Show Answer

Correct answer: (1)

Solution:

The given equation represents a wave propagating along the negative $x$-axis.

Here the coefficient of $x=\mathrm{a}=\mathrm{k}=\frac{2 \pi}{\lambda}$

$$ \therefore \quad \lambda=\frac{2 \pi}{\mathrm{a}} $$

Also the coefficient of $\mathrm{t}=\mathrm{b}=\omega=\frac{2 \pi}{\mathrm{T}}=2 \pi \mathrm{v}$

$\therefore \quad v=\frac{b}{2 \pi}$

The intensity of reflected wave, being 0.64 times that of the incident wave, its amplitude must be $\sqrt{0.64}$ i.e., 0.8 times that of the incident wave.

Hence amplitude of reflected wave

$$ =0.8 \mathrm{~A} $$

52. A wave is represented by the equation

$$ y=A \sin \left(10 \pi x+15 \pi t+\frac{\pi}{3}\right) $$

We can say that the (i) direction of propagation, (ii) the wavelength (iii) the frequency and (iv) the velocity of this wave, are respectively:

(1) Positive $x$-axis; $0.4 \mathrm{~m} ; 7.5 \mathrm{~Hz}$ and $3.0 \mathrm{~ms}^{-1}$

(2) Negative $x$-axis; $0.2 \mathrm{~m} ; 7.5 \mathrm{~Hz}$ and $1.5 \mathrm{~ms}^{-1}$

(3) Negative $x$-axis; $0.4 \mathrm{~m} ; 7.5 \mathrm{~Hz}$ and $3.0 \mathrm{~ms}^{-1}$

(4) Positive $x$-axis; $0.2 \mathrm{~m} ; 7.5 \mathrm{~Hz}$ and $1.5 \mathrm{~ms}^{-1}$

Show Answer

Correct answer: (2)

Solution:

The wave equation has a positive sign between the $(x)$ and $(t)$ terms in the argument of the SINE function. Hence it is a wave propagating along the $(-\mathrm{ve}) x$-axis.

Further coefficient of $x=\mathrm{k}=\frac{2 \pi}{\lambda}=10 \pi$

$\therefore \quad \lambda=\frac{1}{5} \mathrm{~m}=0.2 \mathrm{~m}$

Also coefficient of $t=\omega=2 \pi \nu=15 \pi$

$\therefore \quad v=7.5 \mathrm{~Hz}$

Velocity $\mathrm{v}=$ frequency $\times$ wavelength $=7.5 \times \frac{1}{5} \mathrm{~ms}^{-1}$

$=1.5 \mathrm{~ms}^{-1}$

53. A transverse wave is described by the equation

$$ y=y _{0} \sin 2 \pi\left(f t-\frac{x}{\lambda}\right) $$

The maximum particle velocity, of this wave, equals 4 times the wave velocity. The wavelength of this wave, would be related to its displacement amplitude through the relation

(1) $\lambda=\pi \frac{y _{0}}{4}$

(2) $\lambda=\pi \frac{y _{0}}{2}$

(3) $\lambda=\pi y _{0}$

(4) $\lambda=2 \pi y _{0}$

Show Answer

Correct answer: (2)

Solution:

The given equation is

$$ \begin{gathered} \mathrm{y}=\mathrm{y} _{0} \sin 2 \pi\left(\mathrm{ft}-\frac{x}{\lambda}\right) \\ \therefore \frac{\mathrm{dy}}{\mathrm{dt}}=\left(2 \pi \mathrm{f} \mathrm{y} _{0}\right) \sin \left[2 \pi\left(\mathrm{ft}-\frac{x}{\lambda}\right)\right] \end{gathered} $$

$\therefore$ Particle velocity $\left(=\frac{\mathrm{dy}}{\mathrm{dt}}\right)$ has an ‘amplitude’ (or maximum value) equal to $\left(2 \pi \mathrm{fy} _{0}\right)$

The wave velocity is $\mathrm{v}=\mathrm{f} \lambda$

We are given that

$$ 2 \pi \mathrm{fy} _{0}=4 \mathrm{f} \lambda $$

$\therefore \lambda=\left(\frac{\pi \mathrm{y} _{0}}{2}\right)$

54. A uniform rope, of length $12 \mathrm{~m}$ and mass $6 \mathrm{~kg}$, hangs vertically from a rigid support. A block of mass $2 \mathrm{~kg}$, is attached to the free end of the rope. A transverse pulse, of wavelength $6 \mathrm{~cm}$, is produced at the lower and of the rope. The wavelength, of this pulse, when it reaches the top of the rope, would be

(1) $0.06 \mathrm{~m}$

(2) $0.12 \mathrm{~m}$

(3) $0.18 \mathrm{~m}$

(4) $0.24 \mathrm{~m}$

Show Answer

Correct answer: (2)

Solution:

The tensions, at the lower and at the upper ends of the rope, are $[2 \mathrm{~g}]$ and $[(2+6) \mathrm{g}]$ newton, respectively. (Here ’ $\mathrm{g}$ ’ is the acceleration due to gravity).

The velocity, $v$, of the wave, at any point of the rope, where the tension, equals $T$, is given by

$$ v=\sqrt{\frac{T}{m}}(m=\text { mass per unit length of the rope }) $$

At the lower end, the wavelength of the transverse wave, is given to be $6 \mathrm{~cm}$. The tension at

the lower end, being $(2 \mathrm{~g})$ newton, the frequency of this transverse pulse, at the lower end of the rope, is

$$ \mathrm{n}=\frac{\mathrm{v}}{\lambda}=\sqrt{\frac{2 \mathrm{~g}}{\mathrm{~m}}} \times\left(\frac{1}{6 \times 10^{-2}}\right) $$

The frequency remains the same when the pulse reaches the upper end of the rope. However, the velocity, at the upper end, would equal $\sqrt{\frac{8 g}{m}}$ and the wavelength would have a new value, say, $\lambda^{\prime}$. We would then have, at the upper end

$$ \begin{aligned} & \sqrt{\frac{8 \mathrm{~g}}{\mathrm{~m}}} \times \frac{1}{\lambda^{\prime}}=\mathrm{n}=\frac{1}{\left(6 \times 10^{-2}\right)} \times \sqrt{\frac{2 \mathrm{~g}}{\mathrm{~m}}} \\ & \therefore \quad \frac{2}{\lambda^{\prime}}=\frac{1}{\left(6 \times 10^{-2}\right)} \\ & \therefore \quad \lambda^{\prime}=\left(2 \times 6 \times 10^{-2}\right) \mathrm{m}=0.12 \mathrm{~m} \end{aligned} $$

55. A sound wave is propagating in a (ideal) gas for which the ratio of its two specific heat capacities $\left(\frac{\mathbf{C} _{\mathrm{P}}}{\mathbf{C} _{\mathrm{V}}}\right)$ equals $\gamma _{0}$. The equilibrium values, of the temperature, and pressure, of the gas equal $T$ and $P$, respectively.

The change in temperature $(\Delta T)$ and the change in pressure $(\Delta \mathrm{P})$ of the gas, due to the propagation of the sound wave, are related to each other as

(1) $\frac{\Delta \mathrm{T}}{\mathrm{T}}=\left(1-\frac{1}{\gamma}\right) \frac{\Delta \mathrm{P}}{\mathrm{P}}$

(2) $\frac{\Delta \mathrm{T}}{\mathrm{T}}=\left(1+\frac{1}{\gamma}\right) \frac{\Delta \mathrm{P}}{\mathrm{P}}$

(3) $\frac{\Delta \mathrm{T}}{\mathrm{T}}=\frac{1}{\gamma} \frac{\Delta \mathrm{P}}{\mathrm{P}}$

(4) $\frac{\Delta \mathrm{T}}{\mathrm{T}}=\gamma \frac{\Delta \mathrm{P}}{\mathrm{P}}$

Show Answer

Correct answer: (1)

Solution:

From the (ideal) gas equation, we have (for one mole of the gas)

$\mathrm{PV}=\mathrm{RT}$

$\mathrm{PdV}+\mathrm{VdP}=\mathrm{R} \Delta \mathrm{T}$

$\therefore \quad \frac{\mathrm{P} \Delta \mathrm{V}+\mathrm{V} \Delta \mathrm{P}}{\mathrm{PV}}=\frac{\mathrm{R} \Delta \mathrm{T}}{\mathrm{RT}}=\frac{\Delta \mathrm{T}}{\mathrm{T}}$

or $\quad \frac{\Delta \mathrm{V}}{\mathrm{V}}+\frac{\Delta \mathrm{P}}{\mathrm{P}}=\frac{\Delta \mathrm{T}}{\mathrm{T}} \hspace{40mm}. . . . . . (1)$

When sound waves propagate through a gas, they do so under adiabatic conditions. Hence

$$ \mathrm{PV}^{\gamma}=\text { constant } $$

$\therefore \mathrm{P}(\gamma) \mathrm{v}^{\gamma-1} \Delta \mathrm{V}+\mathrm{V}^{\gamma} \Delta \mathrm{P}=0$

or $\quad(\gamma \mathrm{P}) \Delta \mathrm{V}+\mathrm{V} \Delta \mathrm{P}=0$

$\therefore \frac{\Delta \mathrm{V}}{\mathrm{V}}=-\frac{\Delta \mathrm{P}}{\gamma \mathrm{P}}$

We thus get (using Eqn. (i))

$$ \begin{array}{r} -\frac{\Delta \mathrm{P}}{\gamma \mathrm{P}}+\frac{\Delta \mathrm{P}}{\mathrm{P}}=\frac{\Delta \mathrm{T}}{\mathrm{T}} \\ \text { or } \quad \frac{\Delta \mathrm{T}}{\mathrm{T}}=\left(1-\frac{1}{\gamma}\right) \frac{\Delta \mathrm{P}}{\mathrm{P}} \end{array} $$

56. A wave, represented by the equation

$$ y=A \cos (k x-\omega t) $$

, is superposed with another wave to form a stationary wave. If the point, $\boldsymbol{x}=\mathbf{0}$, is a node, the equation, for the other wave, is

(1) $\mathrm{A} \sin (\mathrm{k} x+\omega \mathrm{t})$

(2) $-\mathrm{A} \cos (\mathrm{k} x-\omega \mathrm{t})$

(3) $-\mathrm{A} \cos (\mathrm{k} x+\omega \mathrm{t})$

(4) $-\mathrm{A} \sin (\mathrm{k} x-\omega \mathrm{t})$

Show Answer

Correct answer: (3)

Solution:

For formation of stationary waves, the two waves must be identical and must propagate in opposite directions. From the given equations, it is equation (3) that meets these criterion (for forming stationary waves with the given wave, as well as the requirement that $x=0$ is a node). Hence the equation, for the other wave, is

$$ \mathrm{y} _{2}=-\mathrm{A} \cos (\mathrm{k} x+\omega \mathrm{t}) $$

[Note: The superposition of $y$ and $\mathrm{y} _{2}$, gives as its resultant

$\mathrm{y}=\mathrm{y} _{1}+\mathrm{y} _{2}=\mathrm{A}[\cos (\mathrm{k} x-\omega \mathrm{t})-\cos (\mathrm{k} x+\omega \mathrm{t})]$

$$ =2 \mathrm{~A}[\sin (\mathrm{k} x)][\sin \omega \mathrm{t}] $$

This has a node at $x=0\left(\right.$ and at $\left.\left.x=\frac{\mathrm{n} \pi}{\mathrm{k}}\right)\right]$

57. The waves, represented by

$$ z _{1}=A \cos (k x-\omega t) $$

and $z _{3}=A \cos (\mathbf{k y}-\omega \mathbf{t})$,

are super posed. The points, in the $(\boldsymbol{x}, \mathbf{y})$ plane, where the resultant intensity (i) will be zero at all times (ii) may equal $4 \mathrm{~A}^{2}$ at some time instant, are the points for which, (respectively),

(1) $(x-\mathrm{y})=\frac{2 \mathrm{n} \pi}{\mathrm{k}}$ and $(x-\mathrm{y})=(2 \mathrm{n}+1) \frac{\pi}{\mathrm{k}}$

(2) $(x-\mathrm{y})=(2 \mathrm{n}+1) \frac{\pi}{2 \mathrm{k}}$ and $(x-\mathrm{y})=\frac{\mathrm{n} \pi}{\mathrm{k}}$

(3) $(x-\mathrm{y})=\frac{\mathrm{n} \pi}{\mathrm{k}}$ and $(x-\mathrm{y})=(2 \mathrm{n}+1) \frac{\pi}{2 \mathrm{k}}$

(4) $(x-\mathrm{y})=(2 \mathrm{n}+1) \frac{\pi}{\mathrm{k}}$ and $(x-\mathrm{y})=\frac{2 \mathrm{n} \pi}{\mathrm{k}}$

Show Answer

Correct answer: (2)

Solution:

The wave, resulting from superposition of $z _{1}$ and $z _{3}$, is given by

$$ \begin{aligned} & \mathrm{z}=\mathrm{z} _{1}+\mathrm{z} _{3} \\ & =2 \mathrm{~A} \cos \left(\frac{\mathrm{k}(x+\mathrm{y})-2 \omega \mathrm{t}}{2}\right) \cos (\mathrm{k}(x-\mathrm{y})) \\ & =[2 \mathrm{~A} \cos \mathrm{k}(x-\mathrm{y})]\left[\cos \left\{\frac{\mathrm{k}(x+\mathrm{y})-2 \omega \mathrm{t}}{2}\right\}\right] \\ & =\mathrm{A}^{\prime} \cos \left[\frac{\mathrm{k}(x+\mathrm{y})}{2}-\omega \mathrm{t}\right] \end{aligned} $$

The amplitude of the resultant wave, is $\mathrm{A}^{\prime}$. Now

(i) $\quad \mathrm{A}^{\prime}=0$ if $\cos \mathrm{k}(x-\mathrm{y})=0$

$$ \begin{aligned} & \therefore \quad \mathrm{k}(x-\mathrm{y})=(2 \mathrm{n}+1) \frac{\pi}{2} \\ & \text { or } \quad(x-\mathrm{y})=(2 \mathrm{n}+1) \frac{\pi}{2 \mathrm{k}} \end{aligned} $$

(ii) Similarly $\mathrm{A}^{\prime}= \pm 2 \mathrm{~A}$ (so that intensity $=4 \mathrm{~A}^{2}$ )

$$ \begin{array}{ll} \text { If } & \cos \mathrm{k}(x-\mathrm{y})= \pm 1 \\ \text { or } & \mathrm{k}(x-\mathrm{y})=\mathrm{n} \pi \\ \text { or } & (x-\mathrm{y})=\left(\frac{\mathrm{n} \pi}{\mathrm{k}}\right) \end{array} $$

(This result for case (ii) will hold only at those times for which $\cos \left[\frac{\mathrm{k}(x+\mathrm{y})}{2}-\omega \mathrm{t}\right]= \pm 1$ )

58. Two waves, represented by

$$ z _{1}=A \cos (k x-\omega t) $$

and $z _{2}=A \cos (k x+\omega t)$

are superposed.The magnitude of the amplitude of the resultant wave, would equal $A$ and 0 , respectively, at points, for which $x$ equals

(1) $\frac{\pi}{2 \mathrm{k}}(4 \mathrm{n} \pm 1)$, and $\frac{\pi}{\mathrm{k}}(2 \mathrm{n} \pm 1)$

(2) $\frac{\pi}{3 \mathrm{k}}(6 \mathrm{n} \pm 1)$, and $\frac{\pi}{\mathrm{k}}(2 \mathrm{n} \pm 1)$

(3) $\frac{\pi}{\mathrm{k}}(2 \mathrm{n} \pm 1)$, and $\frac{\pi}{2 \mathrm{k}}(4 \mathrm{n} \pm 1)$

(4) $\frac{\pi}{3 \mathrm{k}}(6 \mathrm{n} \pm 1)$, and $\frac{\pi}{2 \mathrm{k}}(4 \mathrm{n} \pm 1)$

Show Answer

Correct answer: (4)

Solution:

The equation, for the superposed wave, is

$$ \begin{aligned} & \mathrm{z}=\mathrm{z} _{1}+\mathrm{z} _{2}=\mathrm{A}[\cos (\mathrm{kx}-\omega \mathrm{t})+\cos (\mathrm{k} x+\omega \mathrm{t})] \\ & =2 \mathrm{~A} \cos \mathrm{kx} \cos \omega \mathrm{t} \\ & =\mathrm{A}^{\prime} \cos \omega \mathrm{t} \quad\left(\mathrm{A}^{\prime}=2 \mathrm{~A} \cos \mathrm{k} x\right) \end{aligned} $$

The amplitude, of the resultant wave, is $\mathrm{A}^{\prime}$.

Now $\mathrm{A}^{\prime}=2 \mathrm{~A} \cos \mathrm{k} x$

$\therefore\left|\mathrm{A}^{\prime}\right|=\mathrm{A}$ if $\quad \cos \mathrm{k} x= \pm \frac{1}{2}$

or if $\mathrm{k} x=\left(2 \mathrm{n} \pi \pm \frac{\pi}{3}\right)$

or if $x=\frac{\pi}{3 \mathrm{k}}(6 \mathrm{n} \pm 1)$

Also $\mathrm{A}^{\prime}=0$ if $\cos \mathrm{k} x=0$

or if $\mathrm{k} x=(2 \mathrm{n} \pm 1) \frac{\pi}{2}$

or if $\quad x=\frac{\pi}{2 k}(4 n \pm 1)$

59. The following equations represent transverse waves:

$$ \begin{aligned} & z _{1}=A \cos (k x-\omega t) \\ & z _{2}=A \cos (k x+\omega t) \\ & z _{3}=A \cos (k y-\omega t) \end{aligned} $$

The superposition, of waves ( $z _{1}$ and $z _{2}$ ) and ( $z _{1}$ and $z _{3}$ ), would produce, respectively,

(1) (Standing waves) and (interference)

(2) (Standing waves) and (waves propagating in a direction making an angle of $45^{\circ}$ with both the positive $x$ and y axis)

(3) (Waves propagating in a direction making an angle of $45^{\circ}$ with the positive $x$ and $y$ axis) and (interference)

(4) (Waves propagating in a direction making an angle of $45^{\circ}$ with the positive $x$ and $y$ axis) and (standing waves)

Show Answer

Correct answer: (2)

Solution:

Waves, represented by $z _{1}$ and $z _{2}$, are waves with equal amplitude and frequency. They are propagating along the positive $x$ axis and negative $x$ axis, respectively. Hence their superposition would result in the production of standing waves.

The wave, represented by $z _{3}$, is a wave propagating along the positive y axis. Hence, its superposition with $z _{1}$, would result in a wave propagating in a direction making an angle of $45^{\circ}$ with the positive $x$ and positive y axis.

60. The diagram shows a cylinder, $\mathrm{AB}$, of length $1 \mathrm{~m}$, that has been fitted with (i) a thin flexible diaphragm $\mathrm{C}$ at the middle (ii) two other thin flexible diaphragm, $A$ and $B$, at its two ends.

The velocities of sound, in oxygen and hydrogen, are given to be $300 \mathrm{~ms}^{-1}$ and $1100 \mathrm{~ms}^{-1}$, respectively. If diaphragms, $A$ and $B$, are set into vibrations of the same frequency, the minimum

$1 \mathrm{~m}$ value of this frequency, for which diagram $\mathrm{C}$ is a node, equals.

(1) $4125 \mathrm{~Hz}$

(2) $3300 \mathrm{~Hz}$

(3) $2425 \mathrm{~Hz}$

(4) $1650 \mathrm{~Hz}$

Show Answer

Correct answer: (4)

Solution:

We are given that the diaphragm, at the middle, has to be a node. Hence we can consider the oxygen and hydrogen parts of the cylinder as two closed pipes of length $\ell\left(=\frac{1}{2} \mathrm{~m}\right)$ each. The possible wave lengths, of the stationary waves, produced in these columns are

$$ \lambda=4 \ell, \frac{4 \ell}{3}, \frac{4 \ell}{5}, \ldots \ldots $$

i.e. $\quad \lambda=\frac{4 \ell}{(2 \mathrm{n}+1)}(\mathrm{n}=0,1,2,3, \ldots \ldots)$

The general value, of the possible frequencies, are, therefore,

$$ v _{\mathrm{n}}=\frac{\mathrm{v}}{\lambda _{\mathrm{n}}}=\frac{\mathrm{v}}{4 \ell}(2 \mathrm{n}+1) $$

For hydrogen and oxygen, the velocities being different, we would have to use different values of so that the frequencies are equal. Let these values be $n _{1}$ and $n _{2}$. We than have

$$ \frac{1100}{4 \ell}\left(2 \mathrm{n} _{1}+1\right)=\frac{300}{4 \ell}\left(2 \mathrm{n} _{2}+1\right) $$

or $11\left(2 \mathrm{n} _{1}+1\right)=3\left(2 \mathrm{n} _{2}+1\right)$

The minimum values of $\mathrm{n} _{1}$ and $\mathrm{n} _{2}$, for which this equality can hold, are

$$ \mathrm{n} _{1}=1 \text { and } \mathrm{n} _{2}=5 $$

(for these, the values of LHS and RHS are $11 \times 3$ and $3 \times 11$, i.e. 33 each)

We, therefore, get the required minimum value of frequency, by using $n _{1}=1$ and $v=1100 \mathrm{~m} / \mathrm{s}$ (or $n=5$ and $\mathrm{v}=300 \mathrm{~m} / \mathrm{s}$ ). In either case, we get

$$ v _{\mathrm{n}}=\frac{1100}{\left(4 \times \frac{1}{2}\right)}(2 \times 1+1) \mathrm{Hz}=1650 \mathrm{~Hz} $$

$\left(\right.$ or $\left.v _{\mathrm{n}}=\frac{300}{\left(4 \times \frac{1}{2}\right)}(2 \times 5+1) \mathrm{Hz}=1650 \mathrm{~Hz}\right)$

61. The displacement of the medium, in a sound wave, in given by the equation

$$ y _{1}=A \cos (a x+b t) $$

where $A, a$ and $b$ are positive content. The wave in reflected (without phase change) by an obstacle situated at $x=0$ and the intensity, of the reflected wave is 0.64 times that of the incident wave. The resultant of the superposition of the original and the reflected waves, can be expressed as a

(1) traveling wave $\left(y _{3}=0.36 A \cos (a x+b t)\right)$ and a standing wave $\left(y _{4}=0.64 A \cos a x \cos b t\right)$

(2) traveling wave $\left(y _{3}=0.2 \mathrm{~A} \cos (\mathrm{a} x-\mathrm{bt})\right)$ and a standing wave $\left(\mathrm{y} _{4}=0.8 \mathrm{~A} \cos \mathrm{ax} \cos \mathrm{bt}\right)$

(3) traveling wave $\left(y _{3}=0.36 \mathrm{~A} \cos (a x-b t)\right)$ and a standing wave $\left(y _{4}=1.28 \mathrm{~A} \cos a x \cos b t\right)$

(4) traveling wave $\left(y _{3}=0.2 \mathrm{~A} \cos (a x+b t)\right)$ and a standing wave $\left(y _{4}=1.6 \mathrm{~A} \cos a x \cos b t\right)$

Show Answer

Correct answer: (4)

Solution:

The reflected wave would be a wave propagating along the positive $x$-axis. Its amplitude is $\sqrt{0.64}$ i.e. 0.8 times that of the incident wave. Hence the reflected wave would be represented by

$$ \mathrm{y} _{2}=0.8 \mathrm{~A} \cos (\mathrm{ax}-\mathrm{bt}) $$

The superposition, of the original and reflected waves, therefore, gives, as its resultant,

$$ \begin{aligned} & y=y _{1}+y _{2} \\ \therefore y & =A \cos (a x+b t)+0.8 A \cos (a x-b t) \\ & =0.2 A \cos (a x+b t)+0.8 A[\cos (a x+b t)+\cos (a x-b t] \\ & =0.2 A \cos (a x+b t)+0.8 A[2 \cos a x \cos b t] \\ & =0.2 A \cos (a x+b t)+(1.6 A \cos a x \cos b t) \end{aligned} $$

The first, of these two terms, represents a traveling wave, propagating along the negative $x$-axis, while the second term represents a standing wave.

62. The velocity of sound, in air, in $320 \mathrm{~m} / \mathrm{s}$. A string, $25 \mathrm{~cm}$ long, having a mass $2.5 \mathrm{~g}$ and kept under a tension $T$, has been set vibrating in its first overtone.

A pipe, closed at one end, is $40 \mathrm{~cm}$ long and the air column in it is vibrating with its fundamental frequency. The number of beats, between the two sources, is 8 beats/s. On decreasing the tension in the string to $(T-\Delta T)$, the beat frequency is observed to decrease. The (original) tension, $T$, equals (nearly)

(1) $7 \mathrm{~N}$

(2) $27 \mathrm{~N}$

(3) $54 \mathrm{~N}$

(4) $108 \mathrm{~N}$

Show Answer

Correct answer: (2)

Solution:

The mass per unit length, of the string, is

$$ \begin{aligned} & \mathrm{m}=\frac{2.5 \mathrm{~g}}{25 \mathrm{~cm}}=\frac{0.1 \mathrm{~g}}{\mathrm{~cm}}=\frac{10^{-1} \times 10^{-3} \mathrm{~kg}}{10^{-2} \mathrm{~m}} \\ & =10^{-2} \mathrm{~kg} / \mathrm{m} \end{aligned} $$

$\therefore$ The frequency of the first overtone is

$$ \mathrm{n} _{1}=2 \times \frac{1}{2 \ell} \sqrt{\frac{\mathrm{T}}{\mathrm{M}}}=\frac{1}{\ell} \sqrt{\frac{\mathrm{T}}{10^{-2}}}=\frac{10}{\ell} \sqrt{\mathrm{T}} $$

The fundamental frequency of the air column, in the closed pipe is

$$ \mathrm{n} _{\mathrm{f}}=\frac{\mathrm{v}}{4 \ell}=\frac{320}{4 \times 40 \times 10^{-2}} \mathrm{~Hz}=200 \mathrm{~Hz} $$

The frequency of beats being 8 , we can have

$$ \mathrm{n} _{1}=192 \mathrm{~Hz} \quad \text { or } \quad \mathrm{n} _{1}=208 \mathrm{~Hz} $$

When the tension $\mathrm{T}$ is decreased to $(\mathrm{T}-\Delta \mathrm{T})$, the frequency $\mathrm{n} _{1}$ would also decrease. We are given that the beat frequency now decreases. Hence the original value of $\mathrm{n} _{1}$ has to be $208 \mathrm{~Hz}$.

$\therefore 208=\frac{10}{\ell} \sqrt{\mathrm{T}}=\frac{10}{25 \times 10^{-2}} \sqrt{\mathrm{T}}=40 \sqrt{\mathrm{T}}$

$\therefore \frac{208 \times 208}{40 \times 40}=\mathrm{T}$ or $\mathrm{T} \simeq 27 \mathrm{~N}$

63. The velocity of sound, in air, equals $v$. An air-column, in a pipe, which is closed at one end is in resonance with a stretched wire, having a vibrating length $\ell$, a mass per unit length $\mathrm{m}$, and vibrating under a tension $T$. The length $L$, of air column in the closed pipe, equals

(1) $\left(\frac{4 \mathrm{mv}^{2}}{\ell^{2} \mathrm{mT}}\right)^{1 / 2}$

(2) $\left(\frac{\mathrm{v}^{2} \ell^{2}}{4 \mathrm{mT}}\right)^{1 / 2}$

(3) $\left(\frac{m v^{2} \ell^{2}}{4 T}\right)^{1 / 2}$

(4) $\left(\frac{m v^{2} \ell^{2}}{T}\right)^{1 / 2}$

Show Answer

Correct answer: (3)

Solution:

The (fundamental) frequency of vibration of the stretched wire, is given by

$$ v=\frac{1}{2 \ell} \sqrt{\frac{T}{M}} $$

For the air-column, in a pipe closed at one end, the length (L) of the air-column, corresponding to its fundamental mode of vibratino, equals $\frac{\lambda}{4}$. Hence $\lambda=4 \mathrm{~L}$. The corresponding frequency of vibration is

$$ v^{\prime}=\frac{v}{\lambda}=\frac{v}{4 L} $$

For resonance,

$$ \begin{aligned} v^{\prime} & =v \\ \therefore \quad \frac{v}{4 L} & =\frac{1}{2 \ell} \sqrt{\frac{T}{M}} \\ \text { or } \quad L & =\frac{v \ell}{2} \sqrt{\frac{M}{T}}=\sqrt{\frac{\ell^{2} v^{2} \mathrm{M}}{4 T}} \end{aligned} $$

64. The velocity of sound, in air, is equal to $320 \mathrm{~ms}^{-1}$. A tube of a certain diameter, and of length $0.48 \mathrm{~m}$, is open at both ends. If its fundamental frequency is found to be $320 \mathrm{~Hz}$, the diameter of the tube is (nearly) equal to

(1) $6.66 \mathrm{~cm}$

(2) $4.99 \mathrm{~cm}$

(3) $3.33 \mathrm{~cm}$

(4) $1.67 \mathrm{~cm}$

Show Answer

Correct answer: (3)

Solution:

The velocity of sound is $320 \mathrm{~m} / \mathrm{s}$

Fundamental frequency $=320 \mathrm{~Hz}$

$\therefore$ Wavelength, $\lambda,=\frac{320}{320} \mathrm{~m}=1 \mathrm{~m}$

For a pipe, open at both ends, the wavelength $(\lambda)$ of the fundamental mode, is related to the length, $\ell$, of the tube as

$$ \frac{\lambda}{2}=\ell \quad \text { or } \quad \lambda=2 \ell $$

$\therefore$ The effective length of the given open tube

$$ =\frac{1}{2} \mathrm{~m}=50 \mathrm{~cm} $$

The given value of length is $48 \mathrm{~cm}$. This the difference $(=2 \mathrm{~cm})$ must be the ’end-correction'.

Now (total) end-correction (at both ends of the open tube)

$=2 \times 0.3 \mathrm{D}(\mathrm{D}=$ diameter of the tube $)$

$\therefore 0.6 \mathrm{D}=2 \mathrm{~cm}$

or

$\mathrm{D}=\frac{2}{0.6} \mathrm{~cm}=3.33 \mathrm{~cm}$

65. The velocity of sound, in air is $328 \mathrm{~m} / \mathrm{s}$. A pipe, closed at one end, and having a length of $\mathbf{1 ~} \mathbf{~ m}$, and a diameter of $\mathbf{8} \mathbf{~ c m}$, can resonate for sounds of frequencies

(1) $2 \mathrm{~Hz}$ and $246 \mathrm{~Hz}$

(2) $80 \mathrm{~Hz}$ and $240 \mathrm{~Hz}$

(3) $82 \mathrm{~Hz}$ and $164 \mathrm{~Hz}$

(4) $2 \mathrm{~Hz}$ and $160 \mathrm{~Hz}$

Show Answer

Correct answer: (2)

Solution:

For the first (or fundamental) mode of vibration, we have

$$ \frac{1+0.3 \times 0.08}{4}=\frac{\lambda}{4} $$

$\therefore \quad \lambda=4(1.024)=4.096 \mathrm{~m}$

$\therefore \mathrm{n}=\frac{328}{4.096} \mathrm{~Hz} \simeq 80 \mathrm{~Hz}$

For the next permitted mode of vibration, we have

$$ (1+0.3 \times 0.08)=\frac{3 \lambda}{4} $$

$\therefore \lambda=\frac{4.096}{3} \mathrm{~m}$

$\therefore \quad n^{\prime}=\frac{328 \times 3}{4.096} \mathrm{~Hz} \simeq 240 \mathrm{~Hz}$

66. An organ pipe $P _{1}$, closed at one end and vibrating in its third harmonic mode, and another pipe $P _{2}$, open at both ends, and vibrating in its fourth harmonic mode, are both in resonance with a given tuning fork. The ratio, of the length of $P _{1}$, to that of $P _{2}$, is

(1) $\frac{8}{3}$

(2) $\frac{3}{8}$

(3) $\frac{1}{2}$

(4) $\frac{1}{3}$

Show Answer

Correct answer: (2)

Solution:

For the closed pipe, of length $\ell _{1}$, the frequency of the third harmonic is

$$ \mathrm{n} _{3}=3 \frac{\mathrm{v}}{4 \ell _{1}} $$

For the open pipe, of length $\ell _{2}$, the frequency of the fourth harmonic is

$$ \mathrm{n} _{4}=4 \frac{\mathrm{v}}{2 \ell _{1}}=\frac{2 \mathrm{v}}{\ell _{2}} $$

As per the given data

$$ \mathrm{n} _{3}=\mathrm{n} _{4} $$

$\therefore \frac{3 \mathrm{v}}{3 \ell _{1}}=\frac{2 \mathrm{v}}{\ell _{2}}$

$\therefore \frac{\ell _{1}}{\ell _{2}}=\frac{3}{8}$

67. The vibrating length ( $L$ ) of a sonometer wire, has an (unknown) mass M. A graph is plotted between the tension, $T$ in the wire (on the $x$-axis), and the square of its fundamental frequency $\left(n^{2}\right)$, of vibration (on the $y$-axis). The mass, $M$, would then be related to the slope (s) of the graph, through the relation:

(1) $\mathrm{M}=4 \frac{\mathrm{L}}{\mathrm{s}}$

(2) $\mathrm{M}=2 \frac{\mathrm{L}}{\mathrm{s}}$

(3) $\mathrm{M}=4 \frac{\mathrm{s}}{\mathrm{L}}$

(4) $\mathrm{M}=4 \mathrm{Ls}$

Show Answer

Correct answer: (4)

Solution:

We know that

$\mathrm{n}=\frac{1}{2 \mathrm{~L}} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}}$

$$ =\frac{1}{2 \mathrm{~L}} \sqrt{\frac{\mathrm{TL}}{\mathrm{M}}}=\frac{1}{2} \sqrt{\frac{\mathrm{T}}{\mathrm{LM}}} $$

$\therefore \quad \mathrm{n}^{2}=\frac{1}{4} \frac{\mathrm{T}}{\mathrm{LM}}$

or $\quad n^{2}=\left(\frac{1}{4 \mathrm{LM}}\right) \mathrm{T}$

$\therefore$ The slope of the graph, between $\mathrm{n}^{2}$ (on the $\mathrm{y}$-axis) and $\mathrm{T}$ (on the $x$-axis) equals $\frac{1}{4 \mathrm{LM}}$

$\therefore \mathrm{s}=\frac{1}{4 \mathrm{LM}}$

or $\quad \mathrm{M}=4 \mathrm{LS}$

68. A string, of mass $M$ and length $L$, is clamped at its two ends. Its transverse displacement is represented by

$$ y=A \sin (k x) \cos (\omega t) $$

The tension, in the string, is given by

(1) $\left(\frac{k}{\omega} \frac{M}{L}\right)$

(2) $\left(\frac{\omega^{2}}{\mathrm{k}^{2}} \frac{\mathrm{M}}{\mathrm{L}}\right)$

(3) $\left(\frac{\omega}{\mathrm{k}} \frac{\mathrm{L}}{\mathrm{M}}\right)$

(4) $\left(\frac{\mathrm{k}^{2}}{\omega^{2}} \frac{\mathrm{M}}{\mathrm{L}}\right)$

Show Answer

Correct answer: (2)

Solution:

The given equation can be written as

$$ \begin{aligned} & y=\frac{A}{2}[2 \sin k x \cos \omega t] \\ & =\frac{A}{2}[\sin (k x+\omega t)+\sin (k x-\omega t)] \end{aligned} $$

The wave number and the angular frequency, of the two constituent waves, making up the given ‘wave’, are $\mathrm{k}$ and $\omega$ respectively.

$\therefore$ Velocity of each wave $=\nu \lambda=\frac{\omega}{2 \pi} \frac{2 \pi}{\mathrm{k}}=\frac{\omega}{\mathrm{k}}$

But $\mathrm{v}=\sqrt{\frac{\mathrm{T}}{\mathrm{m}}} \quad\left(\right.$ where $\mathrm{m}=$ mass per unit $=\frac{\mathrm{m}}{\mathrm{L}}$ )

$\therefore \sqrt{\frac{\mathrm{TL}}{\mathrm{M}}}=\frac{\omega}{\mathrm{k}}$

or $\quad \mathrm{T}=\left(\frac{\omega^{2}}{\mathrm{k}^{2}} \frac{\mathrm{M}}{\mathrm{L}}\right)$

69. In a sonometer wire, the tension is maintained by suspending a $25 \mathrm{~kg}$ mass from the free end of the wire. The suspended mass has a volume of $0.009 \mathrm{~m}^{3}$. The fundamental frequency of vibration of the wire is $250 \mathrm{~Hz}$. If the suspended mass is completely immersed in water, the fundamental frequency would become

(1) $200 \mathrm{~Hz}$

(2) $180 \mathrm{~Hz}$

(3) $160 \mathrm{~Hz}$

(4) $125 \mathrm{~Hz}$

Show Answer

Correct answer: (1)

Solution:

The fundamental frequency is given by

$$ \mathrm{n}=\frac{1}{2 \ell} \sqrt{\frac{\mathrm{T}}{\mathrm{m}}}=\frac{1}{2 \ell} \sqrt{\frac{\mathrm{Mg}}{\mathrm{m}}}=\frac{1}{2 \ell} \sqrt{\frac{(25) \mathrm{g}}{\mathrm{m}}} $$

On suspending the mass in water, its weight will become

$$ \left[\left(25-0.009 \times 10^{3}\right) \mathrm{g}\right] \text { newton }=(16) \mathrm{g} \text { newton } $$

$\therefore$ The new fundamental frequency would be $\mathrm{n}^{\prime}=\frac{1}{2 \ell} \sqrt{\frac{(16) \mathrm{g}}{\mathrm{m}}}$

$\therefore \frac{\mathrm{n}^{\prime}}{\mathrm{n}}=\sqrt{\frac{16 \mathrm{~g}}{25 \mathrm{~g}}}=\frac{4}{5}$ $\therefore \quad n^{\prime}=\frac{4}{5} \times 250 \mathrm{~Hz}=200 \mathrm{~Hz}$

70. A steel wire (Young’s modulus $=2 \times 10^{11} \mathrm{~N} / \mathbf{m}^{2}$; coefficient of linear expansion $=1.21 \times 10^{-5} /{ }^{0} \mathrm{C}$ ) has a length of $1 \mathrm{~m}$, a uniform area of cross section of $10^{-6} \mathrm{~m}^{2}$, and a mass of $0.1 \mathrm{~kg}$. It is rigidly fixed at both ends. The temperature of this wire is lowered by $20^{\circ} \mathrm{C}$ and transverse waves are then set up in it by plucking it in the middle. The frequency, of the fundamental mode of vibration of the string, would equal (nearly)

(1) $11 \mathrm{~Hz}$

(2) $17 \mathrm{~Hz}$

(3) $22 \mathrm{~Hz}$

(4) $34 \mathrm{~Hz}$

Show Answer

Correct answer: (1)

Solution:

The frequency of the fundamental mode of vibration of a string, is given by

$$ \mathrm{n}=\frac{1}{2 \ell} \sqrt{\frac{\mathrm{T}}{\mathrm{M}}} $$

We are given that $\mathrm{m}=\frac{0.1 \mathrm{~kg}}{1 \mathrm{~m}}=0.1 \mathrm{~kg} / \mathrm{m}$ and $\ell=1 \mathrm{~m}$

When the temperature of the wire is lowered, it contracts and this contraction developes a tension is it, as it is rigidly fixed at its two ends. This tension, say, T, can be calculated by using the formula for Young’s modulus:

$$ \begin{aligned} & \mathrm{Y}=\frac{\text { Stress }}{\text { Strain }}=\frac{\left(\mathrm{T} / 10^{-6}\right)}{(\Delta \mathrm{L} / 1)} \\ & \begin{aligned} \therefore \quad \mathrm{T} & =\mathrm{Y}(\Delta \mathrm{L}) \times 10^{-6} \text { newton } \\ & =2 \times 10^{11}(\Delta \mathrm{L}) \times 10^{-6} \text { newton } \\ & =\left[2 \times 10^{5}(\Delta \mathrm{L})\right] \text { newton } \end{aligned} \end{aligned} $$

Now, $\Delta \mathrm{L}=\ell^{\prime}-\ell$

$$ \begin{aligned} & =[\ell(1-\alpha \Delta \mathrm{t})-\ell] \\ & =-\alpha \ell \Delta \mathrm{t} \\ \therefore \quad|\Delta \mathrm{L}| & =\left(1.21 \times 10^{-5} \times 1 \times 20\right) \mathrm{m}=2.42 \times 10^{-4} \mathrm{~m} \\ \therefore \quad \mathrm{T} & =2 \times 10^{5} \times 2.42 \times 10^{-4} \mathrm{~N} \\ & =4.84 \times 10 \mathrm{~N}=48.4 \mathrm{~N} \\ \therefore \quad \mathrm{n} & =\left[\frac{1}{2 \times 1} \sqrt{\frac{48.4}{0.1}}\right] \mathrm{Hz} \\ & =\left[\frac{1}{2} \sqrt{484}\right] \mathrm{Hz}=\frac{22}{2} \mathrm{~Hz} \\ & =11 \mathrm{~Hz} \end{aligned} $$

[Note: We have used the value $\ell=1 \mathrm{~m}$, even for the contracted wire, because the change in its length $\left(\Delta \mathrm{L}=2.42 \times 10^{-4} \mathrm{~m}\right.$ ) is very small in comparison to the original length $(=1 \mathrm{~m})$ of the wire].

71. The velocity of sound, in air, equals $330 \mathrm{~m} / \mathrm{s}$. A source that can emit sound of frequency 256 $\mathrm{Hz}$, is held by an observer. The source and the observer, both move towards a (reflecting) wall with a speed of $5 \mathrm{~m} / \mathrm{s}$. The number of beats, heard by the observer, per second would be close to

(1) 5

(2) 6

(3) 7

(4) 8

Show Answer

Correct answer: (4)

Solution:

There being no relative motion between the observer and (the (direct) sound from) the source, the frequency of the direct sound, as heard by the observer, would be $256 \mathrm{~Hz}$.

For the reflected sound, the apparent source of sound (the ‘image’ of the direct sound in the wall) is moving towards the observer with a velocity of $5 \mathrm{~m} / \mathrm{s}$. Also, the observer is moving towards, this (apparent) source (of reflected sound) with a velocity of $5 \mathrm{~m} / \mathrm{s}$. Hence the apparent frequency of the (reflected) sound would be

$$ \begin{aligned} n^{\prime}= & \frac{v}{\left(v-v _{s}\right)}\left(\frac{v+v _{0}}{v}\right) \times 256 \mathrm{~Hz} \\ & =\frac{330+5}{330-5} \times 256 \mathrm{~Hz}=\frac{335}{325} \times 256 \mathrm{~Hz} \\ & =263.88 \mathrm{~Hz} \simeq 264 \mathrm{~Hz} \end{aligned} $$

Hence, frequency of beats

$=(264-256) / \mathrm{s}=8$ per second

72. A source of sound, of (true) frequency $1122 \mathrm{~Hz}$ is moving with a velocity of $10 \mathrm{~m} / \mathrm{s}$ towards a wall. An observer, at rest, is positioned between the source and the wall. The velocity of sound, in air, is $340 \mathrm{~m} / \mathrm{s}$. The frequency of beats, heard by this (stationary) observer, would be

(1) Zero

(2) One

(3) Two

(4) Three

Show Answer

Correct answer: (1)

Solution:

The two sounds, reaching the stationary observer, are (i) the direct sound and (ii) the reflected (from the wall) sound. For both these sounds the ‘source’ (real or virtual (the reflected sound)) is moving towards the (stationary) observer with the same speed. Hence, the apparent frequencies of both the sounds, are equal to each other. Hence no beats would be heard (by the stationary observer).

73. The frequency of beats, corresponding to the simultaneous sounding of two turning forks (of frequencies $n _{1}$ and $n _{2}$ ), equals $n$.

The turning fork, of frequency $n _{1}$ is in resonance with a length $\ell$ of the air column in a given resonance tube. The other turning fork, of frequency $n _{2}$, shows resonance, with the air column in the same tube, when its length is increased to $(\ell+\Delta \ell)$. The frequencies, $n _{1}$ and $\mathbf{n} _{2}$, can then be expressed as

(1) $\mathrm{n} _{1}=\left(1+\frac{2 \Delta \ell}{\ell}\right) \mathrm{n} ; \quad \mathrm{n} _{2}=\left(\frac{\ell}{\Delta \ell}\right) \mathrm{n}$

(2) $\mathrm{n} _{1}=\left(\frac{\ell}{\Delta \ell}\right) ; \mathrm{n} _{2}=\left(1+\frac{2 \Delta \ell}{\ell}\right) \mathrm{n}$

(3) $\mathrm{n} _{1}=\left(1+\frac{\ell}{\Delta \ell}\right) \mathrm{n} ; \quad \mathrm{n} _{2}=\left(\frac{\ell}{\Delta \ell}\right) \mathrm{n}$

(4) $\mathrm{n} _{1}=\left(1-\frac{\ell}{\Delta \ell}\right) \mathrm{n} ; \quad \mathrm{n} _{2}=\left(1+\frac{\ell}{\Delta \ell}\right) \mathrm{n}$

Show Answer

Correct answer: (3)

Solution:

We have ( $\mathrm{v}=$ velocity of sound in air)

$$ \mathrm{n} _{1}=\frac{\mathrm{v}}{4 \ell} $$

and $\mathrm{n} _{2}=\frac{\mathrm{v}}{4(\ell+\Delta \ell)}$

$\therefore \frac{\mathrm{n} _{1}}{\mathrm{n} _{2}}=\frac{\ell+\Delta \ell}{\ell}=1+\left(\frac{\Delta \ell}{\ell}\right)$

Also $\mathrm{n} _{1}-\mathrm{n} _{2}=\mathrm{n}$ (given)

$\therefore \mathrm{n} _{2}\left[\left(1+\frac{\Delta \ell}{\ell}\right)-1\right]=\mathrm{n}$

or $\mathrm{n} _{2}=\frac{\mathrm{n} \cdot \ell}{\Delta \ell}$

and $\mathrm{n} _{1}=\mathrm{n} _{2}+\mathrm{n}=\mathrm{n}\left(1+\frac{\ell}{\Delta \ell}\right)$

74. The speed of sound, in air, may be assumed to be $300 \mathrm{~m} / \mathrm{s}$. A sonometer wire, under tension of $64 \mathrm{~N}$, vibrating in its fundamental mode, is in resonance with a vibrating tuning fork. The vibrating portion, of the sonometer wire, has a length of $10 \mathrm{~cm}$ which has a mass of $1 \mathrm{~g}$.

If the vibrating tuning fork is moved away from the vibrating wire, with a constant speed, $\mathbf{v} _{\mathrm{s}}$, an observer, standing near the sonometer wire, hears 1 beat per second. The speed, $\mathrm{v}$, equals (nearly)

(1) $0.20 \mathrm{~m} / \mathrm{s}$

(2) $0.25 \mathrm{~m} / \mathrm{s}$

(3) $0.40 \mathrm{~m} / \mathrm{s}$

(4) $0.75 \mathrm{~m} / \mathrm{s}$

Show Answer

Correct answer: (4)

Solution:

The fundamental frequency, of the vibrating sonometer wire, is

$$ \begin{aligned} & \mathrm{n}=\frac{1}{2 \ell} \sqrt{\frac{\mathrm{T}}{\mathrm{M}}}=\left[\frac{1}{2 \times 10 \times 10^{-2}} \sqrt{\frac{64}{\left(10^{-3} / 10^{-1}\right)}}\right] \mathrm{Hz} \\ & =5 \times 8 \times 10 \mathrm{~Hz}=400 \mathrm{~Hz} \end{aligned} $$

This is also the true frequency of the vibrating tuning fork. Its apparent frequency, to the observer, appears to be $(400-1) \mathrm{Hz}$

$$ =399 \mathrm{~Hz} $$

[Since the source is moving away from the observer, its apparent frequency would be less than its true frequency].

Hence,

$$ \begin{aligned} & 399 \times \frac{300}{300+\mathrm{v} _{\mathrm{s}}}=400 \\ & \text { or } \quad \frac{300+\mathrm{v} _{\mathrm{s}}}{300}=\frac{400}{399}=\frac{399+1}{399} \\ & \therefore \quad 1+\frac{\mathrm{v} _{\mathrm{s}}}{300}=1+\frac{1}{399} \end{aligned} $$

$\therefore \quad \mathrm{v} _{\mathrm{s}}=\frac{300}{399} \mathrm{~m} / \mathrm{s}$

$=0.75 \mathrm{~m} / \mathrm{s}$

75. Three (sinusoidal) sources, of frequencies ( $n-1), n$ and $(n+1)$ are sounded together. They produce sounds of equal intensity. The time instants, at which their resultant sound will be (i) maximum (ii) minimum and (iii) the frequency of beats, in the resultant sound, would be (respectively),

(1) $[(\mathrm{p})(\mathrm{p}=0,1,2,3, \ldots \ldots)] ;\left[\left(\mathrm{p}+\frac{1}{3}\right)(\mathrm{p}=0,1,2,3, \ldots \ldots)\right] ;(1) / \mathrm{s}$

(2) $\left[\left(\mathrm{p}+\frac{2}{3}\right)(\mathrm{p})(\mathrm{p}=0,1,2,3, \ldots \ldots)\right] ;[(\mathrm{p})(\mathrm{p}=0,1,2,3, \ldots \ldots)] ;(2) / \mathrm{s}$

(3) $\left[\left(\mathrm{p}+\frac{1}{3}\right)(\mathrm{p})(\mathrm{p}=0,1,2,3, \ldots \ldots)\right] ;[(\mathrm{p})(\mathrm{p}=0,1,2,3, \ldots \ldots)] ;(3) / \mathrm{s}$

(4) $[(\mathrm{p})(\mathrm{p}=0,1,2,3, \ldots \ldots)] ;\left[\left(\mathrm{p}+\frac{2}{3}\right)(\mathrm{p}=0,1,2,3, \ldots \ldots)\right] ;(4) / \mathrm{s}$

Show Answer

Correct answer: (1)

Solution:

The three sources produce sounds given by

$$ \mathrm{y} _{1}=\mathrm{a} \sin [2 \pi(\mathrm{n}-1) \mathrm{t}] ; \mathrm{y} _{2}=\mathrm{a} \sin (2 \pi \mathrm{nt}) \text { and } \mathrm{y} _{3}=\mathrm{a} \sin [2 \pi(\mathrm{n}+1) \mathrm{t}] $$

Their resultant is given by

$$ \begin{aligned} y=y _{1} & +y _{2}+y _{3}=\left(y _{1}+y _{3}\right)+y _{2} \\ & =[2 a \sin (2 \pi n t) \cos (2 \pi t)]+a \sin (2 \pi n t) \\ & =a \sin (2 \pi n t)[1+\cos (2 \pi t)] \\ & =A \sin (2 \pi n t) \text { where } A=(1+2 \cos 2 \pi t) \end{aligned} $$

The maxima of ‘A’, correspond to $\cos 2 \pi \mathrm{t}=+1$

There occur when $2 \pi t=(2 \pi p)(p=0,1,2,3)$

$\therefore$ Maxima occur at $\mathrm{t}=\mathrm{p}(\mathrm{p}=0,1,2,3, \ldots \ldots \ldots$.

Similarly, we have $\mathrm{A}=0$ (minima) when

$$ 1+2 \cos 2 \pi t=0 \quad \text { or } \quad \cos 2 \pi t=-\frac{1}{2}=\cos 2 \frac{\pi}{3} $$

These occur at times for which

$$ \begin{aligned} & 2 \pi t=(2 p \pi)+\left(\frac{2 \pi}{3}\right) \\ & \text { or } \quad t=\left(p+\frac{1}{3}\right) \quad(p=0,1,2,3, \ldots \ldots) \\ & \quad=\frac{1}{3}, \frac{4}{3}, \frac{7}{3}, \ldots \ldots \end{aligned} $$

Thus minima occur at

$$ \mathrm{t}=\left(\mathrm{p}+\frac{1}{3}\right)(\mathrm{p}=0,1,2,3, \ldots \ldots) $$

The time interval between two successive maxima or minima (a minima occuring between two successive maxima and vice-versa) is $1 \mathrm{~s}$. Hence time period of one beat $=1 \mathrm{~s}$.

$\therefore$ Frequency of beats $=(1)$ per second.

76. A turning fork, tied to a string of length $\ell$, is whirled around in a circle at the rate of (N) rpm. The velocity of sound is $k$ times the linear speed of the rotating tuning fork.

The turning fork is set into vibrations and its frequency is observed by a stationary observer located in its plane of rotation. The ratio, of the frequencies of the highest and the lowest notes, for this observer, would be

(1) $\mathrm{k}: 1$

(2) $(\mathrm{k}+1): \mathrm{k}$

(3) $\mathrm{k}:(\mathrm{k}-1)$

(4) $(\mathrm{k}+1):(\mathrm{k}-1)$

Show Answer

Correct answer: (4)

Solution:

The angular speed of the tuning fork,

$$ \omega=\frac{2 \pi \mathrm{N}}{60} / \text { second }=\left(\frac{\pi \mathrm{N}}{30}\right) \mathrm{s}^{-1} $$

The linear speed $=\mathrm{r} \omega=\ell \frac{\pi \mathrm{N}}{30} \mathrm{~ms}^{-1} \quad(\because \mathrm{r}=\ell)$

$\therefore$ Speed of sound $=\left(\mathrm{k} \ell \frac{\pi \mathrm{N}}{30}\right) \mathrm{ms}^{-1}$

For the stationary observer, frequency of highest note is

$$ \begin{aligned} & \mathrm{n} _{\mathrm{h}}=\frac{\mathrm{v}}{\mathrm{v}-\mathrm{v} _{\mathrm{s}}} \mathrm{n} \quad(\mathrm{n}=\text { true frequency }) \\ & =\frac{(\mathrm{k} \ell \pi \mathrm{N} / 30) \mathrm{n}}{\left(\mathrm{k} \ell \mathrm{N} / 30-\ell \frac{\pi \mathrm{N}}{30}\right)}=\frac{\mathrm{k}}{\mathrm{k}-1} \mathrm{n} \end{aligned} $$

Similarly, frequency of lowest note is

$$ \begin{array}{r} \mathrm{n} _{\ell}=\left(\frac{\mathrm{k}}{\mathrm{k}+1}\right) \mathrm{n} \\ \therefore \quad \frac{\mathrm{n} _{\mathrm{h}}}{\mathrm{n} _{\ell}}=\left(\frac{\mathrm{k}+1}{\mathrm{k}-1}\right) \end{array} $$

77. The velocity of sound in air equals $320 \mathrm{~ms}^{-1}$. A bus is moving towards a huge wall with a velocity of $5 \mathrm{~ms}^{-1}$. If the driver sounds a horn of frequency $200 \mathrm{~Hz}$, the frequency of the beats, heard by a passenger of the bus, will be (nearly)

(1) 2 per second

(2) 4 per second

(3) 6 per second

(4) 8 per second

Show Answer

Correct answer: (3)

Solution:

For the bus passenger, the frequency of the ‘direct’ sound is $200 \mathrm{~Hz}$.

The sound ‘reflected’ by the wall, can be thought of as coming from a source approaching the observer with a speed of $5 \mathrm{~ms}^{-1}$. At the same time, the observer is approaching the source with a speed of $5 \mathrm{~ms}^{-1}$. Hence the apparent frequency of the ‘reflected sound’ will be

$$ \begin{aligned} & n^{\prime}=\left(\frac{v+v _{0}}{v-v _{s}}\right) n \\ & =\left(\frac{320+5}{320-5}\right) \times 200 \mathrm{~Hz} \simeq 206 \mathrm{~Hz} \end{aligned} $$

$\therefore$ Frequency of beats $\simeq 6$ per second

78. Two tuning forks, with natural frequency of $340 \mathrm{~Hz}$ each, move relative to a stationary observer. While one fork moves away from the observer, the other moves towards him, with the same speed. The observer hears beats of frequency $3 \mathrm{~Hz}$. The common speed, of the two forks, expressed as a fraction of the speed of sound (v), is (nearly)

(1) $\frac{\mathrm{V}}{114}$

(2) $\frac{\mathrm{v}}{227}$

(3) $\frac{\mathrm{v}}{284}$

(4) $\frac{\mathrm{V}}{341}$

Show Answer

Correct answer: (2)

Solution:

Let the common speed of the two forks be $\left(\frac{\mathrm{v}}{\mathrm{x}}\right)$.

The apparent frequency, of the fork moving away, is

$$ \mathrm{n} _{1}^{\prime}=\frac{\mathrm{v}}{\mathrm{v}+\left(\frac{\mathrm{v}}{x}\right)} \mathrm{n}=\left(\frac{x}{x+1}\right) \mathrm{n} $$

The apparent frequency of the fork, moving towards, is

$$ \mathrm{n} _{2}^{\prime}=\frac{\mathrm{v}}{\left(\mathrm{v}-\frac{\mathrm{v}}{x}\right)}=\left(\frac{x}{x-1}\right) \mathrm{n} $$

$\therefore$ Frequency of beats $=\mathrm{n} _{2}^{\prime}-\mathrm{n} _{1}^{\prime}=x \mathrm{n}\left[\frac{1}{(x-1)}-\frac{1}{(x+1)}\right]$

$$ =\frac{2 x \mathrm{n}}{x^{2}-1} $$

We thus have

$$ \frac{2 x \times 340}{x^{2}-1}=3 $$

or $\quad 3 x^{2}-680 x-3=0$

$\therefore \quad x=\frac{680 \pm \sqrt{(680)^{2}+36}}{6} \simeq \frac{680 \pm 680}{6} \simeq 227$

$\therefore$ Speed of each tuning fork $\simeq \frac{\mathrm{V}}{227}$

79. The velocity of sound, in air, equals $1200 \mathrm{~km}$ / hour. A train, approaching a hill, at a speed of $40 \mathrm{~km} / \mathrm{hour}$, sounds a whistle at a frequency of $580 \mathrm{~Hz}$, when it is at a distance of $1 \mathrm{~km}$ from the hill. A wind, with a speed of $40 \mathrm{~km} / \mathrm{hour}$, is blowing in the direction of the train.

The frequency of the whistle, as heard by an observer on the hill, and the frequency of the echo, as heard by the driver, would (nearly) equal, respectively,

(1) $610 \mathrm{~Hz}$ and $621 \mathrm{~Hz}$

(2) $600 \mathrm{~Hz}$ and $631 \mathrm{~Hz}$

(3) $610 \mathrm{~Hz}$ and $631 \mathrm{~Hz}$

(4) $600 \mathrm{~Hz}$ and $621 \mathrm{~Hz}$

Show Answer

Correct answer: (4)

Solution:

(i) For the observer, on the hill, it is the source that is approaching it. Hence the apparent frequency, of the whistle, would be

$$ \begin{aligned} & n^{\prime}=\frac{v^{\prime}}{v^{\prime}-v _{s}} n=\frac{(1200+40)}{(1200+40)-40} \times 580 \mathrm{~Hz} \\ & =\frac{1240}{1200} \times 580 \mathrm{~Hz} \simeq 600 \mathrm{~Hz} \end{aligned} $$

(Here the (apparent) velocity of sound is $(1200+40) \mathrm{km} / \mathrm{hr}$ )

(ii) When the driver hears the echo, the source (reflected sound from the hill) as well as the observer are both approaching each other. Hence the apparent frequency, is

$$ \mathrm{n}^{\prime \prime}=\frac{\mathrm{v}^{\prime \prime}+\mathrm{v} _{0}}{\mathrm{v}^{\prime}-\mathrm{v} _{\mathrm{s}}} \mathrm{n} $$

Here the apparent velocity of sound, v" equals ( $1200-40) \mathrm{km} / \mathrm{hr}$

i.e., $1160 \mathrm{~km} / \mathrm{hour}$

Hence,

$$ \begin{aligned} & \mathrm{n} “=\frac{1160+40}{1160-40} \times 580 \mathrm{~Hz} \\ & =\frac{1200}{1120} \times 580 \mathrm{~Hz} \\ & \simeq 621 \mathrm{~Hz} \end{aligned} $$

80. A source of sound (velocity of sound $=330 \mathrm{~ms}^{-1}$ ) is moving along a circular orbit, of radius $3 \mathrm{~m}$, with an angular velocity of $10 \mathrm{rad} / \mathrm{s}$. A sound detector, located far away from the source, is executing linear simple harmonic motion, along the line BD,

with an amplitude $\mathrm{BC}=\mathrm{CD}=6 \mathrm{~m}$. The frequency, of oscillations, of the detector, is $\left(\frac{5}{\pi}\right)$ per second.

The source emits sound waves of frequency $340 \mathrm{~Hz}$. The maximum and minimum values, of the source frequency, as recorded by the detector, would equal (nearly)

(1) $453 \mathrm{~Hz}$ and $284 \mathrm{~Hz}$

(2) $453 \mathrm{~Hz}$ and $255 \mathrm{~Hz}$

(3) $442 \mathrm{~Hz}$ and $255 \mathrm{~Hz}$

(4) $442 \mathrm{~Hz}$ and $284 \mathrm{~Hz}$

Show Answer

Correct answer: (3)

Solution:

The linear velocity of the source, in its circular path is

$$ \mathrm{v}=\mathrm{r} \omega=3 \times 10 \mathrm{~m} / \mathrm{s}=30 \mathrm{~m} / \mathrm{s} $$

Its time period, of rotation is

$$ \mathrm{T}=\frac{2 \pi \mathrm{r}}{\mathrm{V}}=\frac{2 \pi \times 3}{30} \mathrm{~s}=\frac{\pi}{5} \mathrm{~s} $$

The detector (frequency being $\left(\frac{5}{\pi}\right) \mathrm{rad} / \mathrm{s}$ ), has a time period of $\left(\frac{\pi}{5}\right) \mathrm{s}$ i.e., the same as that of the source.

The detector (executing a SHM), has a continuously varying velocity. However, its velocity amplitude is

$$ \begin{aligned} & \mathrm{v} _{\max }=\mathrm{a} \omega=2 \pi \mathrm{a} \nu \\ & =2 \pi \times 6 \times \frac{5}{\pi} \mathrm{ms}^{-1}=60 \mathrm{~ms}^{-1} \end{aligned} $$

The source, and the detector, are having the same time period. We can, therefore, have situations where the source and detector are both

(i) approaching each other

(ii) moving away from each other.

In these two cases, (when the detector has its maximum velocity), the detector would record the maximum and the minimum (apparent) frequencies of the source. We have

$$ \begin{aligned} & \mathrm{n} _{\max }=\frac{\mathrm{v}+\mathrm{v} _{0}}{\mathrm{v}-\mathrm{v} _{\mathrm{s}}} \mathrm{n} \\ & =\left(\frac{330+60}{330-30}\right) \mathrm{n}=\frac{390}{300} \times 340 \mathrm{~Hz} \\ & =441 \mathrm{~Hz} \end{aligned} $$

and $\mathrm{n} _{\min }=\left(\frac{\mathrm{v}-\mathrm{v} _{0}}{\mathrm{v}+\mathrm{v} _{\mathrm{s}}}\right) \mathrm{n}$

$=\left(\frac{330-60}{300+30}\right) \mathrm{n}=\frac{270}{360} \times 340 \mathrm{~Hz}$

$=255 \mathrm{~Hz}$