Unit 09 Kinetic Theory of Gases
Introduction
The atoms / molecules of a gas at any finite temperature are in a state of random motion. This is because interatomic / molecular forces are weak. The atoms / molecules undergo collisions with one another and the walls of the container. Kinetic theory of gases explains the observed (experimental) gas laws in terms of the random motion of the atoms or molecules of gas.
Gas Laws
For a gas; there is an appreciable change in volume due to changes of pressure. To describe the state or condition of a gas its (1) volume (2) pressure and (3) temperature must be specified. These are known as the state parameters of a gas. A change in any one of them effects the others. The gas laws are the relation between any two of these parameters when the third is constant. The three important; experimental, gas laws are:
(1) BOYLE’S LAW
The law was discovered by Robert Boyle in 1662. According to Boyle’s law for a given mass of a gas; temperature $(\mathrm{T})$ remaining constant; the volume $(\mathrm{V})$ is inversely proportional to the pressure $(\mathrm{P})$.
Expressed mathematically,
$$ \mathrm{V} \alpha \frac{1}{\mathrm{P}} ; \quad \mathrm{T}=\mathrm{constant} $$
or $\quad \mathrm{PV}=$ constant
Fig. 1 (a) and (b) show the $\mathrm{P} v s \mathrm{~V}$ and $\mathrm{P} v s 1 / \mathrm{V}$ graph for a given mass of gas at a constant temperature.
(2) CHARLE’S LAW
Fig. 1
A.C Charles; in 1787; studied the variation in volume of gas with temperature; pressure remaining constant. According to Charle’s law. at constant pressure; the change in volume $(\Delta \mathrm{V})$ per unit volume at $0^{\circ} \mathrm{C}\left(\mathrm{V} _{0}\right)$ per degree change in temperature is a constant. Let $\mathrm{V} _{0}$ and $\mathrm{V}$ denote the volume of gas at $0^{\circ} \mathrm{C}$ and $\theta^{\circ} \mathrm{C}$ at constant pressure, then
$$ \begin{equation*} \frac{\mathrm{V}-\mathrm{V} _{0}}{\mathrm{~V} _{0} \theta}=\text { constant }=\gamma _{\mathrm{P}} \tag{1} \end{equation*} $$
$\gamma _{\mathrm{p}}$ is known as coefficient of volume expansion of gas at constant pressure. Experiments show $\gamma _{p}=1 / 273.15$. Eqn. (1) can be written as
$$ \begin{equation*} \mathrm{V}=\mathrm{V} _{0}\left(1+\gamma _{\mathrm{p}} \theta\right) \tag{2} \end{equation*} $$
This law is also referred as law of volume. Eqn (2) is rewritten as
$$ \frac{\mathrm{V}}{\mathrm{V} _{0}}=1+\frac{\theta}{273.15}=\frac{273.15+\theta}{273.15}=\frac{\mathrm{T}}{\mathrm{T} _{0}} $$
or $\quad \frac{\mathrm{V}}{\mathrm{T}}=$ constant
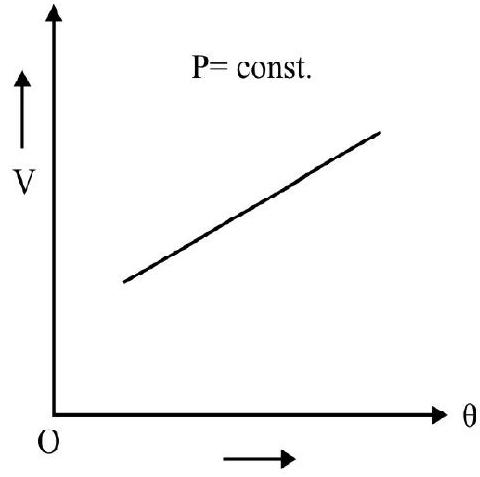
Fig. 2
$\mathrm{T} _{0}$ and $\mathrm{T}$ denote absolute temperature of gas at $0^{\circ} \mathrm{C}$ and $\theta^{\circ} \mathrm{C}$ respectively.
(3) GAY LUSSAC’S LAW
Gay Lussac studied variation of pressure of a gas with temperature at constant volume. It is also known as law of pressures. According to this law:
at constant volume; the change in pressure $(\Delta \mathrm{P})$ per unit pressure at $0^{\circ} \mathrm{C}\left(\mathrm{P} _{0}\right)$ per degree change in temperature is a constant. Let $\mathrm{P} _{0}$ and $\mathrm{P}$ denote pressure of gas at $0^{\circ} \mathrm{C}$ and $\theta^{\circ} \mathrm{C}$ at constant volume, then
$$ \begin{equation*} \frac{\Delta \mathrm{P}}{\mathrm{P} _{0} \times \theta}=\frac{\mathrm{P}-\mathrm{P} _{0}}{\mathrm{P} _{0} \theta}=\mathrm{constant}=\gamma _{\mathrm{V}} \tag{3} \end{equation*} $$
$\gamma _{\mathrm{v}}$ is known as the coefficient of pressure expansion at constant volume. Experiments show $\gamma _{\mathrm{V}}=1 / 273.15$. Eqn. (3) is rewritten as
$$ \begin{equation*} \mathrm{P}=\mathrm{P} _{0}\left(1+\gamma _{\mathrm{V}} \theta\right) \tag{4} \end{equation*} $$
Let $\mathrm{T} _{0}$ and $\mathrm{T}$ be the absolute temperature of gas at $0^{\circ} \mathrm{C}$ and $\theta^{\circ} \mathrm{C}$ respectively. Then $\mathrm{T} _{0}=273.15$, $\mathrm{T}=272.15+\theta$
Eqn. (4) can be written as
$$ \frac{\mathrm{P}}{\mathrm{P} _{0}}=1+\frac{\theta}{273.15}=\frac{273.15+\theta}{273.15}=\frac{\mathrm{T}}{\mathrm{T} _{0}} $$
or $\frac{\mathrm{P}}{\mathrm{T}}=$ constant $; \hspace{40mm}. . . . . . . (5)$
According to Eqn. (5) volume remaining constant the pressure of a given mass of gas is directly proportional to its absolute temperature. Fig. 3 (a) and (b) show $\mathrm{P}$ vs $\theta$; and $\mathrm{P}$ vs $\mathrm{T}$ graph of gas at constant volume.
A Perfect Gas
A perfect gas is one; in which the atoms / molecules don’t exert any force of attraction on one another. In practice no gas can be a $100 \%$ perfect gas. However for gases at high temperature and low pressure the above stated condition is nearly satisfied. We can say that any gas at low pressure and high temperature is nearly a perfect gas.
Perfect Gas Equation
This is an equation relating pressure $(\mathrm{P})$; volume $(\mathrm{V})$ and absolute temperature $(\mathrm{T})$ of a given state of an ideal (or perfect) gas. Combining Boyle’s and Charle’s law we get
$$ \begin{equation*} \mathrm{PV}=\mathrm{nRT} \tag{6} \end{equation*} $$
where $\mathrm{n}$ is the number of moles contained in the given mass of gas. Let $\mathrm{m}$ and $\mathrm{M}$ represent the mass of gas and the molar mass respectively. Then $n=\frac{m}{M}$. $R$ is a the universal molar gas constant. From Eqn. (6); we have
$$ \mathrm{R}=\frac{\mathrm{PV}}{\mathrm{nT}} $$
PV $=\frac{\text { Force }}{\text { Area }} \times$ volume $=$ Force $\times$ distance $=$ work
The universal gas constant equals work done by (or on) the gas per mole per degree Kelvin. Experiments show that $\mathrm{R}=8.31 \mathrm{~J} \mathrm{~mole}^{-1} \mathrm{~K}^{-1}$. Dimensions of $\mathrm{R}$ are
$$ [R]=\frac{M L^{-1} T^{-2} \times L^{3}}{K}=M L^{2} T^{-2} K^{-1} $$
Example-1:
A tube closed at both ends is divided into two equal parts by a mercury column $10 \mathrm{~cm}$ long. The tube is lying horizontally with the two parts containing air at atmospheric pressure. The tube is turned so that it is vertical. Calculate the displacement of mercury column. Atmospheric pressure $=76 \mathrm{~cm}$ of mercury column.
Show Answer
Solution:
Fig. 4
Fig. 4 (a) shows the tube in horizontal position. The two parts of tube are of equal length of $45 \mathrm{~cm}$ each. $\mathrm{P} _{1}=\mathrm{P} _{\mathrm{atm}}$ is pressure of air in each part of tube. $\mathrm{V} _{1}=$ volume of air in each part $=\mathrm{a} \times 0.45$ where $\mathrm{a}=$ area of cross-section of tube. Fig. 4 (b) shows tube in vertical position. Let $x \mathrm{~cm}$ be the displacement of mercury column. Let $\mathrm{P} _{1}^{\prime}$ and $\mathrm{P} _{2}^{\prime}$ be pressure of air in the two parts of tube. Clearly
$$ \begin{equation*} \mathrm{P} _{2}^{\prime}=\mathrm{P} _{1}^{\prime}+10 \mathrm{~cm} \text { of Hg column } \tag{1} \end{equation*} $$
Applying Boyle’s law to upper part of air column in Fig. 4 (b)
$0.76 \times 0.45=\mathrm{P} _{1}^{\prime} \times(0.45+x)$
or $\quad \mathrm{P} _{1}^{\prime}=\frac{0.76 \times 0.45}{(0.45+x)}. . . . . . . . . . . . (2)$
Similarly for the gas in lower part of tube
$$ 0.76 \times 0.45=\mathrm{P} _{2}^{\prime} \times(0.45-x) $$
or $\quad \mathrm{P} _{2}^{\prime}=\frac{0.76 \times 0.45}{(0.45-x)} \hspace{40mm} . . . . . . . . (3)$
From Eqns (1), (2) and (3) we get
$$ \frac{0.76 \times 0.45}{(0.45-x)}=\frac{0.76 \times 0.45}{(0.45+x)}+0.1 $$
On solving for $x$, we get
$$ x=0.029 \mathrm{~m}=2.9 \mathrm{~cm} $$
Example-2:
Show that for a gas obeying Boyle’s law; $\frac{P}{n _{1}}=$ constant; where $P$ is the pressure and $n _{1}$ is the number of molecules per unit volume of gas.
Show Answer
Solution:
For a given mass $\mathrm{m}$; of gas of molecular mass $\mathrm{M}$ at constant temperature $\mathrm{T}$ on absolute scale
$$ \mathrm{PV}=\left(\frac{\mathrm{m}}{\mathrm{M}}\right) \mathrm{RT} $$
or $\quad \frac{\mathrm{P}}{(\mathrm{m} / \mathrm{v})}=\frac{\mathrm{RT}}{\mathrm{M}}=$ constant. . . . . . . . . . . . . . . . (1)
Let $\mathrm{n} _{1}$ be number of atoms / molecules per unit volume. Then
$$ \begin{equation*} \mathrm{m}=\mathrm{n} _{1} \mathrm{~V} \times \mathrm{m} _{0} \tag{2} \end{equation*} $$
where $\mathrm{m} _{0}$ is mass of one atom / molecule of gas. From Eqns. (1) and (2) we have
$$ \frac{\mathrm{P}}{\mathrm{n} _{1} \times \mathrm{m} _{0}}=\mathrm{constant} $$
Since $\mathrm{m} _{0}$ is a constant $\frac{\mathrm{P}}{\mathrm{n} _{1}}$ is another constant.
Example-3:
A container contains $10^{5}$ c.c of air at 2 atmospheric pressure at $127^{\circ} \mathrm{C}$. What is the number of molecules of air in container? At N.T.P gas has $2.7 \times 10^{25}$ molecules per cubic meter.
Show Answer
Solution:
Given; for the container;
$\mathrm{V}=$ Volume of air $=10^{5} \mathrm{c} . \mathrm{c}=0.1 \mathrm{~m}^{3}$
$\mathrm{P}=$ Pressure of air $=2 \mathrm{~atm}=2 \times 1.01 \times 10^{5} \mathrm{Nm}^{-2}$
$\mathrm{T}=$ Temperature on Kelvin scale $=127+273=400 \mathrm{~K}$
Let $\mathrm{V} _{0}$ be the volume of air in container at N.T.P. From gas-equation
$$ \frac{\mathrm{PV}}{\mathrm{T}}=\frac{\mathrm{P} _{0} \mathrm{~V} _{0}}{\mathrm{~T} _{0}} \quad \text { or } \quad \mathrm{V} _{0}=\left(\frac{\mathrm{P}}{\mathrm{P} _{0}}\right)\left(\frac{\mathrm{T} _{0}}{\mathrm{~T}}\right) \mathrm{V} $$
or $\quad \mathrm{V} _{0}=\frac{2 \times 1.01 \times 10^{5} \times 273 \times 0.1}{1.01 \times 10^{5} \times 400} \mathrm{~m}^{3}=0.1365 \mathrm{~m}^{3}$
Number of air molecules in container $=0.1365 \times 2.7 \times 10^{25} \simeq 3.685 \times 10^{24}$
Example-4:
Volume of $1 \mathrm{~g}$ of oxygen at N.T.P conditions is 700 c.c. Molecular mass of oxygen $=32 \mathrm{~g}$. What is $\mathbf{R}$ ?
Show Answer
Solution:
Given; $\mathrm{V}=700 \mathrm{c.c}=7 \times 10^{-4} \mathrm{~m}^{3} ; \mathrm{P}=1 \mathrm{~atm}=1.01 \times 10^{5} \mathrm{~Pa}, \mathrm{~m}=$ mass of oxygen $=1 \mathrm{~g}, \mathrm{~T}=273 \mathrm{~K}$. $\mathrm{M}=$ Molar mass of oxygen $=32 \mathrm{~g}, \mathrm{n}=$ number of moles $=\frac{\mathrm{m}}{\mathrm{M}}=\frac{1}{32}$. From ideal gas equation
$$ \mathrm{PV}=\mathrm{nRT} \text { or } \mathrm{R}=\frac{\mathrm{PV}}{\mathrm{nT}} $$
Substituting given value of parameters we have
$$ \mathrm{R}=\frac{1.01 \times 10^{5} \times 7 \times 10^{-4}}{\left(\frac{1}{32}\right) \times 273} \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1} \simeq 8.31 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1} $$
Work done by/on a gas
Consider an ideal gas at a pressure P inside a cylinder-piston arrangement as shown in Fig. 5 (a). Let A be area of cross-section of piston. The gas pushes piston to position CD by an infinitesimally small amount $\mathrm{d} x$ as shown in Fig. 5(b). Let dW be work done by the gas. Obviously
$$ \mathrm{dW}=(\mathrm{P} . \mathrm{A} .) \cdot \mathrm{d} x=\mathrm{PdV} $$
where $\mathrm{A} \cdot \mathrm{d} x=\mathrm{dV}=$ infinitesimally small amount of change in volume of gas. For any finite change; the total work done is
$$ \mathrm{W}=\int \mathrm{PdV} $$
$\mathrm{W}$ depends on the manner in which change takes place from the initial to the final state. The work done is numerically equal to area under $\mathrm{P}-\mathrm{V}$ graph showing the change in the gas. The expression for work done in a few standard processes are:
(i) Isochoric process, i.e. volume $\mathrm{V}=$ constant
$\therefore \mathrm{dV}=0$ and $\int \mathrm{PdV}=0$. In words; no work is done on or by gas in an isochoric process.
(ii) Isobaric process, i.e. pressure $=\mathrm{P}=$ constant
$$ \therefore \quad \mathrm{W}=\mathrm{P} \int _{\mathrm{V} _{\mathrm{i}}}^{\mathrm{V} _{\mathrm{f}}} \mathrm{dV}=\mathrm{P}\left(\mathrm{V} _{\mathrm{f}}-\mathrm{V} _{\mathrm{i}}\right)=\mathrm{nR}\left[\mathrm{T} _{\mathrm{f}}-\mathrm{T} _{\mathrm{i}}\right] $$
(iii) Isothermal process, i.e. temperature $=\mathrm{T}=$ constant
$$ \mathrm{W}=\mathrm{P} \int _{\mathrm{V} _{\mathrm{i}}}^{\mathrm{V} _{\mathrm{f}}} \mathrm{PdV}=2.303 \mathrm{RT} \log \left(\frac{\mathrm{V} _{\mathrm{f}}}{\mathrm{V} _{\mathrm{i}}}\right) $$
(iv) Adiabatic process, i.e. heat content $=\mathrm{Q}=$ constant
$W=P \int_{V_i}^{V_f} P d V=\frac{1}{(\gamma-1)}\left[P_i V_i-P_f V_f\right]=\frac{n R}{(\gamma-1)}\left[T_i-T_f\right]$
Assumptions of Kinetic Theory of Gases
Clausius and Maxwell developed the kinetic theory of gases to explain the gas laws in terms of motion of atoms / molecules of gas. The followings are the simplifying assumptions of the theory.
(1) All gases are made of atoms / molecules. All atoms / molecules of a gives gas are identical. The atoms / molecules of different gases are different from one another.
(2) The atoms / molecules have a negligible size (diameter of the order of $2 \times 10^{-10} \mathrm{~m}$ ) as compared to distance between them. The total volume of atoms / molecules is negligible as compared to the volume of the container; the gas is confined to.
(3) The interatomic / molecular force between atoms / molecules of a gas is negligible. The atoms / molecules are considered to be in a state of free motion.
(4) The atoms / molecules of a gas are regarded as perfectly elastic spheres.
(5) The atoms / molecules are in a state of continuous, rapid, random motion. They move in all directions with different speeds ranging from zeroth infinity and obey Newton’s laws of motion.
(6) Due to their random motion the atoms / molecules collide with one another and the walls of the container. The collisions are perfectly elastic. The time taken in a collision is negligible.
(7) In between two collisions the atom/ molecules moves in a straight line path. Distance between two consecutive collisions is known as free path. Free path is not a constant. The average distance between two consecutive collisions is known as the mean free path and is a constant for a given state of gas.
(8) The average time between two collisions is known as the mean relaxation time.
Pressure Exerted by a Gas
The atoms / molecules of a gas at any finite temperature, continuously undergo collisions with the walls of the container. During each collision the atom $/$ molecule suffer a finite change in linear momentum. The rate of change of the linear momentum equals the force the container exerts on atoms / molecules. In accordance with Newton’s third law; the atoms / molecules exert an equal and opposite force on the walls of container. This force per unit area is the pressure the gas exerts on the walls of the container.
Expression for Pressure Due to an Ideal Gas
Consider an ideal gas inside a cube of side $(\ell)$ as shown in Fig. 6(a). Let the cube contain $\mathrm{n}$ atoms / molecules each of mass $m$. Let $\mathbf{v} _{i} ; j=1,2,3, \ldots . . N$ be the velocity different atoms / molecules. Resolve velocity vector (v) of every particle into its rectangular components $\mathrm{v} _{x}, \mathrm{v} _{\mathrm{y}}$ and $\mathrm{v} _{\mathrm{z}}$ as shown in Fig. 6(b). Then
$$ \begin{equation*} \mathrm{v}^{2}=\mathrm{v} _{x}^{2}+\mathrm{v} _{\mathrm{y}}^{2}+\mathrm{v} _{\mathrm{z}}^{2} \tag{1} \end{equation*} $$
Consider one atom / molecule moving along $x$-axis with speed $\mathrm{v} _{x}$ as shown in Fig. 6(a). The atom/ molecules undergoes a collision with face $A B C D$ of cube and rebound backs with speed $-\mathrm{v} _{x}$. The change in linear momentum $=-\mathrm{mv} _{x}-\mathrm{mv} _{x}$ $=-2 \mathrm{mv} _{x}$. This atom $/$ molecules goes to the opposite face OEFG; undergoes a collision and comes back to face $A B C D$. The time between two consecutive collision on
$\mathrm{ABCD}$ is $\frac{2 \ell}{\mathrm{v} _{x}}$. The number of
collision in one second $=\frac{\mathrm{v} _{x}}{2 \ell}$. Therefore the magnitude of rate of change of linear momentum is the force $\mathrm{f} _{x}$ this atom/ molecule exerts on face ABCD. Obviously
$$ \begin{equation*} \mathrm{f} _{x}=2 \mathrm{mv} _{x} \times \frac{\mathrm{v} _{x}}{2 \ell}=\frac{\mathrm{mv} _{x}^{2}}{\ell} \tag{2} \end{equation*} $$
Taking into account collisions due to all atoms / molecules of gas; the total force $\mathrm{F} _{x}$ onABCD is
$$ \begin{equation*} \mathrm{F} _{x}=\sum \mathrm{f} _{x}=\sum _{\mathrm{j}=1}^{\mathrm{N}}\left(\frac{\mathrm{mv} _{\mathrm{j} x}^{2}}{\ell}\right) \tag{3} \end{equation*} $$
The pressure $\mathrm{P} _{x}$; along $\mathrm{X}$-axis, is
$$ \begin{equation*} \mathrm{P} _{x}=\frac{\mathrm{F} _{x}}{\ell^{2}}=\frac{\mathrm{m}}{\ell^{3}} \sum _{\mathrm{j}=1}^{\mathrm{N}} \mathrm{v} _{\mathrm{j} x}^{2}=\frac{\mathrm{m}}{\mathrm{V}} \sum _{\mathrm{j}=1}^{\mathrm{N}} \mathrm{v} _{\mathrm{j} x}^{2} \tag{4} \end{equation*} $$
$\mathrm{V}=\ell^{3}=$ volume of cubical container. Similarly the pressure along $\mathrm{Y}$ and $\mathrm{Z}$ axis is
$$ \begin{gather*} P _{y}=\frac{m}{V} \sum _{j=1}^{N} v _{j y}^{2} ; P _{z}=\frac{m}{V} \sum _{j=1}^{N} v _{j z}^{2} \\ \therefore \quad P _{x}+P _{y}+P _{z}=\frac{m}{V}\left[\sum _{j=1}^{N}\left(v _{j x}^{2}+v _{j y}^{2}+v _{j z}^{2}\right)\right]=\frac{m}{V}\left[\sum _{j=1}^{N} v _{j}^{2}\right] \tag{5} \end{gather*} $$
The pressure exerted by gas is same in every direction i.e., $\mathrm{P} _{x}=\mathrm{P} _{\mathrm{y}}=\mathrm{P} _{\mathrm{z}}=\mathrm{P}$ (say). Obviously
$$ \begin{equation*} P=\frac{m}{3 V}\left[\sum _{j=1}^{N} v _{j}^{2}\right]=\frac{m N}{3 v}\left(v _{r m s}^{2}\right) \tag{6} \end{equation*} $$
where $\mathrm{v} _{\mathrm{rms}}^{2}=\frac{\Sigma\left(\mathrm{v} _{\mathrm{j}}^{2}\right)}{\mathrm{N}}=\frac{\mathrm{v} _{1}^{2}+\mathrm{v} _{2}^{2}+\ldots . .+\mathrm{v} _{\mathrm{N}}^{2}}{\mathrm{~N}}$
$\mathrm{v} _{\mathrm{rms}}$ is the root mean square velocity of gas atoms / molecules. Also $\mathrm{mN}=\mathrm{m} _{1}=$ Total mass of gas in cube and $\frac{\mathrm{m} _{1}}{\mathrm{~V}}=\rho=$ density of the gas. Eqn (7) can be rewritten as
$$ \begin{equation*} \mathrm{P}=\frac{1}{3} \rho \mathrm{v} _{\mathrm{rms}}^{2} \tag{8} \end{equation*} $$
THE (1) MEAN (OR AVERAGE) (2) THE ROOT-MEAN SQUARE AND (3) MOST PROBABLE; VELOCITY OF GAS ATOMS/MOLECULES
(1) Mean (average) velocity (v) is the average of the velocities of atoms / molecules of gas. By definition
$$ \mathbf{v}=\frac{\text { Sum total of speed of all atoms } / \text { molecules }}{\text { The total number of atoms } / \text { molecules }} $$
$$ \begin{equation*} =\frac{\mathrm{v} _{1}+\mathrm{v} _{2}+\ldots \ldots+\mathrm{v} _{\mathrm{N}}}{\mathrm{N}}=\frac{1}{\mathrm{~N}} \sum _{\mathrm{j}=1}^{\mathrm{N}} \mathrm{v} _{\mathrm{j}} \tag{1} \end{equation*} $$
Using Maxwell-Boltzmann statistics it can be shown that
$$ \begin{equation*} \mathbf{v}=\sqrt{\frac{8 \mathrm{kT}}{\pi \mathrm{m}}} \tag{2} \end{equation*} $$
$\mathrm{k}$ is the Boltzmann’s constant.
(2) Root-mean-square velocity $\left(v _{\mathrm{rms}}\right)$ is the square root of the mean of the square of the velocities of atoms / molecules. Obviously
$$ \mathrm{v} _{\mathrm{rms}}=\sqrt{\left(\frac{\mathrm{v} _{1}^{2}+\mathrm{v} _{2}^{2}+\ldots . .+\mathrm{v} _{\mathrm{N}}^{2}}{\mathrm{~N}}\right)} $$
In terms of the pressure $(\mathrm{P})$ and density of gas
$$ \mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{P}}{\rho}} \quad[\text { Eqn. }=\mathrm{n}(\text { viii })] $$
(3) Most probable velocity $\left(\mathrm{v} _{\mathrm{m}}\right)$
We know that velocity of an atom/ molecule can vary from zero to infinity. Let $\mathrm{dN}$ be the number of atom / molecules having velocity in internal $\mathrm{v}$ and $\mathrm{v}+\mathrm{dv} \cdot \frac{\mathrm{dN}}{\mathrm{N}}$ is the fraction of atoms or molecules having speed $\mathrm{v}$. The graph of $\left(\frac{\mathrm{dN}}{\mathrm{N}}\right) v s$ $\mathrm{v}$ is shown in Fig. $7 \mathrm{v} _{\mathrm{m}}$ is the speed for which $\left(\frac{\mathrm{dN}}{\mathrm{N}}\right)$ is
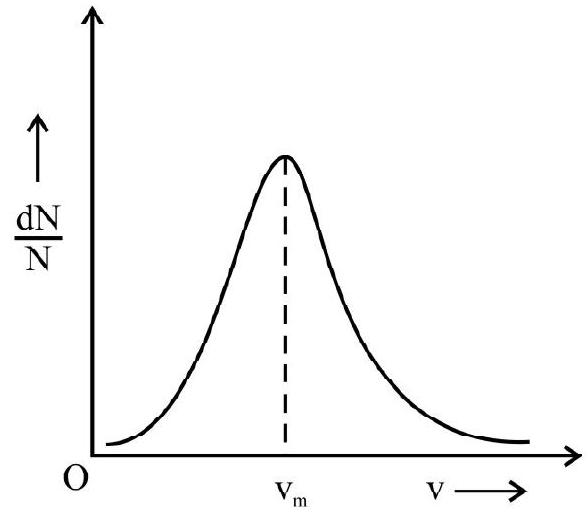
Fig. 7 maximum. $\mathrm{v} _{\mathrm{m}}$ is the most probable velocity of the atoms or molecules of gas. It can be shown that
$$ \mathrm{v} _{\mathrm{m}}=\sqrt{\frac{2 \mathrm{kT}}{\mathrm{m}}} $$
where $\mathrm{k}=$ Boltzmann’s constant; $\mathrm{m}=$ mass of each atom $/$ molecule, $\mathrm{T}=$ temperature of gas on Kelvin scale.
KINETIC INTERPRETATION OF TEMPERATURE
The expression for pressure, $\mathrm{P}$; exerted by a gas is
$$ \begin{equation*} \mathrm{P}=\frac{\mathrm{mN}}{3 \mathrm{~V}} \mathrm{v} _{\mathrm{rms}}^{2}=\frac{\mathrm{M} _{1} \mathrm{v} _{\mathrm{rms}}^{2}}{3 \mathrm{~V}} \tag{1} \end{equation*} $$
Let $E=\frac{1}{2} M _{1} v _{\text {rms }}^{2}=$ The total kinetic energy of atoms or molecules of the gas. In terms of energy, E, Eqn. (1) is rewritten as
$$ \begin{equation*} \mathrm{PV}=\frac{2}{3} \mathrm{E}=\frac{1}{3}\left[\mathrm{mNv} _{\mathrm{rms}}^{2}\right] \tag{2} \end{equation*} $$
According to the ideal gas equation
$$ \begin{equation*} \mathrm{PV}=\mathrm{nRT}=\left(\frac{\mathrm{mN}}{\mathrm{M}}\right) \mathrm{RT} \tag{3} \end{equation*} $$
where $\mathrm{M}$ is molar mass of gas. From Eqns. (2) and (3) we have
$$ \begin{equation*} \left(\frac{\mathrm{R}}{\mathrm{M}}\right) \mathrm{T}=\frac{1}{3} \mathrm{v} _{\mathrm{rms}}^{2} \tag{4} \end{equation*} $$
Let $\mathrm{N} _{\mathrm{AV}}$ be the Avogadro’s number. It is the number of atoms or molecules in one-mole of gas. Obviously $\mathrm{M}=\mathrm{mN} _{\mathrm{AV}}$. Using this we rewrite Eqn (4) as
$$ \begin{equation*} \left(\frac{\mathrm{R}}{\mathrm{N} _{\mathrm{AV}}}\right) \mathrm{T}=\frac{2}{3}\left(\frac{1}{2} \mathrm{mv} _{\mathrm{rms}}^{2}\right) \tag{5} \end{equation*} $$
$\frac{\mathrm{R}}{\mathrm{N} _{\mathrm{AV}}}=\mathrm{k}=$ Boltzmann’s constant. Therefore
$\frac{1}{2} \mathrm{mv} _{\mathrm{rms}}^{2}=$ Kinetic energy of one atom or molecules of gas $=\frac{3}{2} \mathrm{kT} \hspace{22mm}$ (6)
From Eqn (6) we conclude that temperature of gas (T) is a measure of the translational kinetic energy of the atoms / molecules of gas. This is the kinetic interpretation of temperature. From Eqn. (1);
$$ \mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{PV}}{\mathrm{M} _{1}}} $$
Also from ideal gas equation
$$ \begin{array}{r} \mathrm{PV}=\left(\frac{\mathrm{M} _{1}}{\mathrm{M}}\right) \mathrm{RT} \\ \therefore \quad \mathrm{V} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}} \tag{7} \end{array} $$
At $\mathrm{T}=0 \mathrm{~K} ; \mathrm{v} _{\mathrm{rms}}=0$. In other words absolute zero of temperature is that temperature at which there is no motion of atoms / molecules of gas.
GAS LAWS AND KINETIC THEORY
The various gas-laws can be easily obtained from the expression for pressure $(\mathrm{P})$ exerted by a gas.
(1) Boyle’s Law
We have
$$ \mathrm{P}=\frac{\mathrm{M} _{1}}{3 \mathrm{~V}} \mathrm{v} _{\mathrm{rms}}^{2} $$
or $\quad \mathrm{PV}=\frac{\mathrm{M} _{1} \mathrm{v} _{\mathrm{ms}}^{2}}{3}$
According to kinetic interpretation of temperature; $\mathrm{v} _{\mathrm{rms}}^{2}$ is directly proportional to $\mathrm{T}$. At constant temperature $\mathrm{v} _{\mathrm{rms}}$ is also constant. For a given mass $\mathrm{M} _{1}$ of gas
$$ \mathrm{PV}=\text { constant } $$
This is Boyle’s law.
(2) charles’s Law
We rewrite expression for pressure, $\mathrm{P}$; as
$$ \mathrm{V}=\frac{\mathrm{M} _{1}}{3 \mathrm{P}} \mathrm{v} _{\mathrm{rms}}^{2} $$
At constant pressure, i.e. $\mathrm{P}=$ constant; $\mathrm{V}$ is directly proportional to $\mathrm{v} _{\mathrm{rms}}^{2}$ or $\mathrm{T}$.
$$ \therefore \quad \frac{\mathrm{V}}{\mathrm{T}}=\text { constant } $$
This is charles’s law.
(3) Dalton’s Law of Partial Pressure
Consider a mixture of gases in an enclosure of volume V. Let $\mathrm{P} _{1}, \mathrm{P} _{2}, \mathrm{P} _{3} \ldots \ldots$. . be the pressure exerted by individual gases. Let $\mathrm{N} _{1}, \mathrm{~N} _{2}, \mathrm{~N} _{3} \ldots \ldots .$. be the number of atoms / molecules of each gas.
$v_{1_{m x}}, v_{2_{m a}}, v_3 \ldots \ldots . . . . \text { be the root mean square speed of atoms } / \text { molecules of each gas. Then }$
$v_{1_{\max }}, v_{2_{\max }}, v_{3_{\max }} \ldots \ldots \ldots .$ be the root mean square speed of atoms / molecules of each gas . Then
$P_1=\frac{m_1 N_1}{3 V} v_{1_{max}^2} ; P_2=\frac{m_2 N_2}{3 V} v_2^2 ; \ldots \ldots . .$
$m_1 , m_2. . . . . . . $ denote the mass of one atom / molecules of each gas . Therefore
$\mathrm{P}_1+\mathrm{P}_2+\mathrm{P}_3+\ldots \ldots \ldots \frac{1}{3 \mathrm{~V}}\left[\mathrm{~m}_1 \mathrm{v} _ {1 _ {\mathrm{rms}}}^2+\mathrm{m}_2 \mathrm{v} _ {2 _ {\mathrm{rms}}}^2+\ldots . .\right]$
All the gases in mixture are at same temperature. In other words kinetic energy of each individual atom/molecule of different gases is same, i.e.
$\frac{1}{2} \mathrm{~m} _ 1 \mathrm{v} _ {1 \mathrm{~rms}}^2=\frac{1}{2} \mathrm{~m} _ 2 \mathrm{v} _{1 _ {\mathrm{rms}}}^2=\ldots \ldots . .=\frac{1}{2} \mathrm{mv} _ {2 _ {\mathrm{rms}}}^2$
$$ \therefore \quad \mathrm{P} _{1}+\mathrm{P} _{2}+\mathrm{P} _{3}+\ldots \ldots \ldots=\frac{1}{3}\left(\frac{\mathrm{mN}}{\mathrm{V}}\right) \mathrm{v} _{\mathrm{rms}}^{2} $$
where $\mathrm{N}=\mathrm{N} _{1}+\mathrm{N} _{2}+\ldots \ldots$; Also $\frac{1}{3}\left(\frac{\mathrm{mN}}{\mathrm{V}}\right) \mathrm{v} _{\mathrm{ms}}^{2}=\mathrm{P}=$ The total pressure of the mixture; i.e.
$\mathrm{P} _{1}+\mathrm{P} _{2}+\mathrm{P} _{3}+\ldots \ldots \ldots \ldots \ldots .=\mathrm{P}$
This is Dalton’s law of partial pressure.
Example-5:
$v$ is the rms speed of atoms of gas at a temperature of $27^{\circ} \mathrm{C}$. What is change in temperature if the rms speed of the atoms increases by $50 \%$ ?
Show Answer
Solution:
$\mathrm{T}=$ The initial temperature of gas $=273+27=300 \mathrm{~K}$
Let $\mathrm{T} _{1}$ be the temperature of gas, so that the rms speed $=\mathrm{v} _{1}=\mathrm{v}+\frac{\mathrm{v}}{2}=\frac{3 \mathrm{v}}{2}$. We know $\mathrm{v} _{\mathrm{rms}} \alpha \sqrt{\mathrm{T}}$; therefore
$$ \frac{\mathrm{v}}{\left(\frac{3}{2} \mathrm{v}\right)}=\sqrt{\frac{273}{\mathrm{~T} _{1}}} $$
or
$$ \mathrm{T} _{1}=675 \mathrm{~K} $$
The change in temperature of gas $=675-300=375 \mathrm{~K}=375^{\circ} \mathrm{C}$
Example-6:
A nitrogen molecule on surface of earth has a speed equal to rms speed of nitrogen molecule at $0^{\circ} \mathrm{C}$. This molecule rises vertically upwards without any collision. What is the height to which it rises. Assume $\mathrm{g}$ is constant and equal $9.8 \mathrm{~ms}^{-2}$. Given
Mass of nitrogen molecule $=4.65 \times 10^{-26} \mathrm{~kg}$
Boltzmann’s constant $=\mathrm{k}=1.38 \times 10^{-23} \mathrm{JK}^{-1}$
Show Answer
Solution:
Let $\mathrm{v}=\mathrm{v} _{\mathrm{rms}}=\mathrm{r}$.m.s speed of nitrogen molecules
$$ =\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}}=\sqrt{\frac{3 \mathrm{RT}}{\mathrm{mN} _{\mathrm{AV}}}} $$
where $\mathrm{m}$ is mass of one atom of nitrogen and $\mathrm{N} _{\mathrm{AV}}$ is the Avogadro’s number. We know $\frac{\mathrm{R}}{\mathrm{N} _{\mathrm{AV}}}=\mathrm{k}=$ The Boltzmann’s constant. Therefore
$$ \mathrm{v}=\sqrt{\frac{3 \mathrm{kT}}{\mathrm{m}}}=\sqrt{\frac{3 \times 1.38 \times 10^{-23} \times 273}{4.65 \times 10^{-26}}} \mathrm{~ms}^{-1} \simeq 492.9 \mathrm{~ms}^{-1} $$
Let $\mathrm{H}$ be the vertical height to which the nitrogen molecules rises above earth’s surface. Then
$$ \begin{aligned} & 0-\mathrm{v}^{2}=2(-\mathrm{g}) \mathrm{H} \quad \text { or } \quad \mathrm{H}=\frac{\mathrm{v}^{2}}{2 \mathrm{~g}} \\ & \therefore \mathrm{H}=\frac{(492.9)^{2}}{2 \times 9.8} \mathrm{~m} \approx 12.4 \mathrm{~km} \end{aligned} $$
Example-7:
Calculate the number of molecules in $1 \mathrm{c} . \mathrm{c}$ of a perfect gas at $27^{\circ} \mathrm{C}$ at a pressure of $20 \mathrm{~mm}$ of Hg. Mean K.E of one molecule at $27^{0} \mathrm{C}=4 \times 10^{-21} \mathrm{~J}$. Density of $\mathrm{Hg}=13.6 \times 10^{3} \mathrm{kgm}^{-3}$; $\mathrm{k}=\mathbf{1 . 3 8} \times 10^{-23} \mathrm{JK}^{-1}$.
Show Answer
Solution:
The mean kinetic energy of one molecule $=\frac{3}{2} \mathrm{kT}$. Given
$$ \begin{equation*} \frac{3}{2} \mathrm{kT}=4 \times 10^{-21} \mathrm{~J} \tag{1} \end{equation*} $$
Let $m _{1}$ and $m$ denote mass of one atom and mass of 1 c.c of gas respectively. Let $N _{1}$ be number of molecules in $1 \mathrm{c} . \mathrm{c}$ of gas. Obviously $\mathrm{m}=\mathrm{m} _{1} \mathrm{~N}$. Let $\mathrm{M}$ be the molar mass of gas. Then $\mathrm{M}=\mathrm{m} _{1} \mathrm{~N} _{\mathrm{AV}}$. where $\mathrm{N} _{\mathrm{AV}}=$ Avogadro’s number. From ideal gas equation
$$ \begin{align*} \quad P V & =\left(\frac{m}{M}\right) R T=N\left(\frac{R}{N _{A V}}\right) \mathrm{T}=N k T \\ \therefore \quad N & =\frac{P V}{k T} \tag{2} \end{align*} $$
Given,
$\mathrm{P}=20 \mathrm{~mm}$ of $\mathrm{Hg}=20 \times 10^{-3} \times 13.6 \times 10^{3} \times 9.8 \mathrm{~Pa}$
$\mathrm{V}=1 \mathrm{c} . \mathrm{c}=10^{-6} \mathrm{~m}^{3} ; \mathrm{T}=273+27=300 \mathrm{~K}$, and $\mathrm{k}=1.38 \times 10^{-23} \mathrm{JK}^{-1}$
Substituting given values in Eqn. (2) we have
$$ \mathrm{N}=\frac{20 \times 13.6 \times 9.8 \times 10^{-6}}{1.38 \times 10^{-23} \times 300} \simeq 6.44 \times 10^{17} $$
DEGREES OF FREEDOM
The total number of independent co-ordinates required to describe completely the position and configuration of the system is known as its degrees of freedom.
Consider a single point mass having translational motion. Let the particle move along a straight line (say X axis). The position of particle is specified by one co-ordinates (say $x$ ). The particle has one degree of freedom. For the particle moving in a plane (say X-Y plane); two co-ordinates ( $x$ and $y$ ) are required to specify its position. The particle has two degrees of freedom. If the particle moves in space three coordinates (say $x, y$ and $\mathrm{z}$ ) are required to specify its position. The particle has three degrees of freedom.
Consider a system of $\mathrm{N}-$ particles having a specific configuration. $3 \mathrm{~N}$ is total number of co-ordinates required to specify position of every particle of system. Let $\mathrm{R}$ be the number of relations amongst position of particles. $R$ depends on configuration of the arrangement. The number of degrees of freedom (n) of the system is $(3 \mathrm{~N}-\mathrm{R})$; i.e.
$$ \mathrm{n}=3 \mathrm{~N}-\mathrm{R} $$
For monoatomic system; $\mathrm{N}=1, \mathrm{R}=0 ; \mathrm{n}=3$.
For a diatomic molecule $\mathrm{N}=2 ; \mathrm{R}=1$; therefore
$$ \mathrm{n}=3 \times 2-1=5 $$
For a triatomic molecule, $\mathrm{N}=3, \mathrm{R}=2$; therefore
$$ \mathrm{m}=3 \times 3-2=7 $$
In a similar manner we can find out degrees of freedom due to rotational motion. For a system having both translational and rotational motion, the total number of degrees of freedom is the sum of degrees of freedom for translational and rotational motion.
BOLTZMANN’S LAW OF EQUI-PARTITION OF ENERGY
According to the kinetic interpretation of temperature; we know that the total kinetic energy of one atom or
molecule of gas is $\frac{3}{2} \mathrm{kT} ; \mathrm{k}=$ Boltzmann’s constant; $\mathrm{T}=$ Temperature of gas on Kelvin scale of temperature.
One atom moving in space has three degree of freedom. Therefore
Energy per degree of freedom $=\frac{1}{2} \mathrm{kT}$
This is Boltzmann’s law of equipartition of energy.
SPECIFIC HEAT OF GASES
We know that the molar specific heat of a gas at constant volume; $\mathrm{C} _{\mathrm{v}}$, is the heat required to raise the temperature of one mole of gas by one degree; volume remaining constant. Let dQ be heat given to one mole of gas at constant volume so that its temperature rises by dT. By definition of specific heat
$$ \begin{equation*} \mathrm{dQ}=1 . \mathrm{C} _{\mathrm{v}} \cdot \mathrm{dT} \tag{1} \end{equation*} $$
From first law of thermodynamics
$$ \begin{equation*} \mathrm{dQ}=\mathrm{dU}+\mathrm{dW} \tag{2} \end{equation*} $$
For gas at constant volume, $\mathrm{dW}=0$. Therefore
$$ \mathrm{dQ}=\mathrm{dU}=\mathrm{C} _{\mathrm{v}} \mathrm{dT} \hspace{85mm}(3) $$
or $\quad C _{V}=\frac{d U}{d T}$
For the same gas; molar specific heat at constant pressure; $\mathrm{C} _{\mathrm{p}}$; is amount of heat required to raise temperature of one mole of gas by one degree, pressure remaining constant. $\mathrm{Let} _{\mathrm{dQ}}^{1}$ be heat given to one mole of gas to change its temperature by $\mathrm{dT}$ at constant pressure. By definition of specific heat
$$ \begin{equation*} \mathrm{dQ} _{1}=1 . \mathrm{C} _{\mathrm{P}} \mathrm{dT} \tag{4} \end{equation*} $$
From first law of thermodynamics
$$ \begin{equation*} \mathrm{dQ} _{1}=\mathrm{dU}+\mathrm{PdV} \tag{5} \end{equation*} $$
where $\mathrm{P}$ is constant pressure of gas and $\mathrm{dV}$ is change in volume. From ideal gas equation
$$ \mathrm{PV}=\mathrm{RT} \quad[\because \mathrm{n}=1] $$
Differentiate
$$ \mathrm{PdV}+\mathrm{VdP}=\mathrm{RdT} $$
At constant pressure, $\mathrm{dP}=0$, therefore
$$ \begin{equation*} \mathrm{PdV}=\mathrm{RdT} \tag{6} \end{equation*} $$
From Eqns. (4), (5) and (6) we have
$$ \begin{equation*} \mathrm{C} _{\mathrm{P}} \mathrm{dT}=\mathrm{C} _{\mathrm{v}} \mathrm{dT}+\mathrm{RdT} \end{equation*} $$
or $\quad \mathrm{C} _{\mathrm{P}}-\mathrm{C} _{\mathrm{v}}=\mathrm{R} \hspace{85mm} (7)$
The ratio of $\mathrm{C} _{\mathrm{P}}$ and $\mathrm{C} _{\mathrm{V}}$ is a constant for a gas and written as $\gamma$; i.e.
$$ \begin{equation*} \gamma=\frac{C _{\mathrm{P}}}{\mathrm{C} _{\mathrm{V}}} \tag{8} \end{equation*} $$
Since $\mathrm{C} _{\mathrm{p}}>\mathrm{C} _{\mathrm{v}}$ [Eqn. (8)]; $\gamma$ is more than one
SPECIFIC HEAT OF GASES AND DEGREES OF FREEDOM
Consider one mole of an ideal gas at temperature $T$ on Kelvin scale. Let $n$ be the total number of degrees of freedom for each atom/ molecule of gas. Using Boltzmann’s law of equipartition of energy; the internal energy; $U$ of gas
$$ \begin{align*} & U=n\left(\frac{1}{2} \mathrm{kT}\right) \times \mathrm{N} _{\mathrm{AV}} \\ & \therefore \quad \mathrm{C} _{\mathrm{V}}=\frac{\mathrm{dU}}{\mathrm{dT}}=\frac{\mathrm{nRT}}{2} \tag{1} \end{align*} $$
$$ \left[\because \quad \mathrm{N} _{\mathrm{AV}} \mathrm{k}=\mathrm{R}\right] $$
The specific heat of gas at constant pressure; $\mathrm{C} _{\mathrm{p}}$; is
$$ \begin{equation*} \mathrm{C} _{\mathrm{P}}=\mathrm{C} _{\mathrm{V}}+\mathrm{R}=\left(\frac{\mathrm{n}}{2}+1\right) \mathrm{RT} \tag{2} \end{equation*} $$
$\gamma$ for the gas is
$$ \begin{align*} & \gamma=\frac{\mathrm{C} _{\mathrm{P}}}{\mathrm{C} _{\mathrm{V}}}=\frac{\frac{\mathrm{n}}{2}}{\frac{\mathrm{n}}{2}+1} \\ & =1+\frac{2}{\mathrm{n}} \tag{3} \end{align*} $$
The following tables gives; $\mathrm{n} ; \mathrm{C} _{\mathrm{v}}, \mathrm{C} _{\mathrm{p}}$ and $\gamma$ for monoatomic; diatomic and triatomic gases.
| S.No. | Nature ofGas | Degrees ofFreedom (n) | $\mathrm{C} _{\mathrm{V}}=\frac{\mathrm{n}}{2} \mathrm{R}$ | $\mathrm{C} _{\mathrm{P}}=\left(\frac{\mathrm{n}}{2}+1\right) \mathrm{R}$ | $\gamma=\frac{\mathrm{C} _{\mathrm{P}}}{\mathrm{C} _{\mathrm{v}}}$ |
|---|---|---|---|---|---|
| 1. | Mono-atomic | 3 | $\frac{3}{2} \mathrm{R}$ | $\frac{5}{2} \mathrm{R}$ | $\frac{5}{3} \simeq 1.67$ |
| 2. | Dia-atomic | 5 | $\frac{5}{2} \mathrm{R}$ | $\frac{7}{2} \mathrm{R}$ | $\frac{7}{5}=1.4$ |
| 3. | Tri-atomic | 7 | $\frac{7}{2} \mathrm{R}$ | $\frac{9}{2} \mathrm{R}$ | $\frac{9}{7} \simeq 1.28$ |
We can rewrite $\mathrm{C} _{\mathrm{P}}$ and $\mathrm{C} _{\mathrm{V}}$ in terms of $\gamma$. From Eqns. (1) and (2)
$$ \begin{equation*} \mathrm{C} _{\mathrm{V}}=\frac{\mathrm{RT}}{\gamma-1} \quad \text { and } \quad \mathrm{C} _{\mathrm{P}}=\frac{\gamma \mathrm{RT}}{(\gamma-1)} \tag{4} \end{equation*} $$
$\gamma$ - FOR A MIXTURE OF GASES
Consider a mixture having $\mathrm{n} _{1}$ moles of gas 1 , having $\gamma=\gamma _{1} ; \mathrm{n} _{2}$ moles of gas 2 having $\gamma=\gamma _{2} \ldots \ldots .$. and so on. Let the mixture by at a temperature $T$ on Kelvin scale. Let $\gamma _{m}$ be $\frac{C _{P}}{C _{v}}$ for the mixture. The total internal energy of mixture is sum of internal energy of each constituent. Therefore
$$ \frac{\left[\mathrm{n} _{1}+\mathrm{n} _{2}+\ldots \ldots .\right] \mathrm{RT}}{\left(\gamma _{\mathrm{m}}-1\right)}=\frac{\mathrm{n} _{1} \mathrm{RT}}{\left(\gamma _{1}-1\right)}+\frac{\mathrm{n} _{2} \mathrm{RT}}{\left(\gamma _{2}-1\right)}+\ldots \ldots $$
or
$$ \frac{n _{1}+n _{2}+\ldots \ldots}{\left(\gamma _{m}-1\right)}=\frac{n _{1}}{\left(\gamma _{1}-1\right)}+\frac{n _{2}}{\left(\gamma _{2}-1\right)}+\ldots \ldots $$
Knowing $\left(\mathrm{n} _{1}, \gamma _{1}\right) ;\left(\mathrm{n} _{2}, \gamma _{2}\right) \ldots \ldots . \gamma _{\mathrm{m}}$ is easily calculated.
Example-8:
A gas mixture consists of 2 moles of oxygen and 4 moles of argon at temperature T. Neglecting all vibrational modes, the total internal energy of the system is
(a) 4 RT
(b) $15 \mathrm{RT}$
(c) 9 RT
(b) $11 \mathrm{RT}$
Show Answer
Solution:
The internal energy, $U$, of $n$ moles of an ideal gas at temperature $T$ is
$$ U=nC _{V} T $$
where $C_{v}$ is specific heat of gas at constant volume. Oxygen is a diatomic gas,
$C _v=\frac{5}{2} R ; \hspace{5 mm} n _{0 _2}=2$
$\mathrm{U} _{1}=$ Internal energy of oxygen in mixture
$$ =2 \times \frac{5}{2} \mathrm{RT}=5 \mathrm{RT} $$
Argon is a monoatomic gas, $\mathrm{C} _{\mathrm{v}}=\frac{3}{2} \mathrm{R}$ and $\mathrm{n}=4$, therefore
$\mathrm{U} _{2}=$ Internal energy of argon in mixture
$$ =4 \times\left(\frac{3 \mathrm{R}}{2}\right) \mathrm{T}=6 \mathrm{RT} $$
The total internal energy of mixture $=\mathrm{U} _{1}+\mathrm{U} _{2}$
$$ =5 \mathrm{RT}+6 \mathrm{RT}=11 \mathrm{RT} $$
Correct choice is (d)
Example-9:
Three closed vessels A, B and C at same temperature T contain gases which obey Maxwell distribution of velocities. Vessel $A$ contains only $\mathrm{O} _{2}$; B only $\mathrm{N} _{2}$ and $\mathrm{C}$ a mixture of equal quantities of $\mathrm{O} _{2}$ and $\mathrm{N} _{2}$. If average speed of the $\mathrm{O} _{2}$ molecules in vessel $A$ is $\mathbf{v} _{1}$; that of $\mathrm{N} _{2}$ molecules in vessel $B$ is $v _{2}$ the average speed of molecules in $C$ is
(a) $\frac{\mathrm{v} _{1}+\mathrm{v} _{2}}{2}$
(b) $\frac{2 \mathbf{v} _{1}^{2} \mathbf{v} _{2}^{2}}{\mathbf{v} _{1}^{2}+\mathbf{v} _{2}^{2}}$
(c) $\left(\mathbf{v} _{1} \mathbf{v} _{2}\right)^{1 / 2}$
(d) $\frac{2 v _{1} v _{2}}{v _{1}+v _{2}}$
Show Answer
Solution:
The average speed $v$ of molecules of an ideal gas is
$$ v=\sqrt{\frac{8 R T}{\pi M}} \quad \text { or } \quad v \alpha \sqrt{\frac{T}{M}} $$
$\therefore \mathrm{M} \propto \frac{\mathrm{I}}{\mathrm{v}^{2}} \hspace{40mm}. . . . . . . (1)$
For vessel A, B and C
$$ \begin{aligned} & \mathrm{M} _{0 _{2}} \propto \frac{\mathrm{T}}{\mathrm{v} _{1}^{2}} ; \mathrm{M} _{\mathrm{N} _{2}} \propto \frac{\mathrm{T}}{\mathrm{v} _{2}^{2}} \\ & \mathrm{M} \propto \frac{\mathrm{T}}{\mathrm{v}^{2}} \end{aligned} $$
Obviously $\mathrm{M}=\frac{\mathrm{M} _{0 _{2}}+\mathrm{M} _{\mathrm{N} _{2}}}{2}$
$\therefore \frac{1}{\mathrm{v}^{2}}=\frac{1}{2}\left[\frac{1}{\mathrm{v} _{1}^{2}}+\frac{1}{\mathrm{v} _{2}^{2}}\right]$ or $\mathrm{v}^{2}=\frac{2 \mathrm{v} _{1}^{2} \mathrm{v} _{2}^{2}}{\mathrm{v} _{1}^{2}+\mathrm{v} _{2}^{2}}$
The correct choice is (b)
Example-10:
$\mathbf{v} ; \mathbf{v} _{\mathrm{rms}}$ and $\mathrm{v} _{\mathrm{P}}$ respectively denote the mean speed; root mean square speed and the most probable speed of the molecules of an ideal gas at absolute temperature T. The mass of the molecules is m. Then
(a) no molecule can have a speed greater than $\sqrt{2} \mathbf{v} _{\text {rms }}$
(b) no molecules can have a speed less than $\frac{\mathrm{v} _{\mathrm{P}}}{\sqrt{2}}$
(c) $\mathbf{v} _{\mathbf{P}}<\mathbf{v}>\mathbf{v} _{\text {rms }}$
(b) the average kinetic energy of a molecule is $\frac{3}{4} \mathrm{mv} _{\mathrm{P}}^{2}$
Show Answer
Solution:
We know;
$$ \mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}} ; \mathrm{v}=\sqrt{\frac{8 \mathrm{RT}}{\pi \mathrm{M}}} \quad \text { and } \quad \mathrm{v} _{\mathrm{P}}=\sqrt{\frac{2 \mathrm{RT}}{\mathrm{M}}} $$
Obviously $\mathrm{v} _{\mathrm{P}}<\mathrm{v}<\mathrm{v} _{\mathrm{rms}}$
Also $\mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3}{2}} \mathrm{v} _{\mathrm{P}}$
The average kinetic energy of a gas molecule
$$ =\frac{1}{2} \mathrm{mv} _{\mathrm{rms}}^{2}=\frac{3}{4} \mathrm{mv} _{\mathrm{P}}^{2} $$
Therefore (c) and (d) both are correct.
Example-11:
The rms speed of oxygen molecule $\left(\mathrm{O} _{2}\right)$ at certain temperature is $T$ (degree Kelvin) is $v$. The temperature is doubled and oxygen gas dissociates into atomic oxygen. The rms speed is
(a) $\mathbf{v}$
(b) $\mathbf{v} / 2$
(c) $2 \mathrm{v}$
(b) $4 \mathrm{v}$
Show Answer
Solution:
We know
$$ \mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}} \quad \text { or } \quad \mathrm{v} _{\mathrm{rm}} \alpha \sqrt{\frac{\mathrm{T}}{\mathrm{M}}} $$
Given $v=\sqrt{\frac{3 R T}{M}}=$ r.m.s speed of oxygen at $T$
$v^{\prime}=$ r.m.s speed of dissociated oxygen
$$ =\sqrt{\frac{3 \mathrm{R}(2 \mathrm{~T})}{\mathrm{m}^{\prime}}} $$
$\mathrm{m}^{\prime}=$ Atomic mass of dissociated oxygen $=\frac{\mathrm{m}}{2}$. Therefore
$$ \mathrm{v}^{\prime}=2 \mathrm{v} $$
Correct choice is (c)
Example-12:
$C _{V}$ and $C _{P}$ denote molar specific heat of a gas at constant volume and constant pressure respectively. Then
(a) $\left(\mathrm{C} _{\mathrm{P}}-\mathrm{C} _{\mathrm{v}}\right)$ is larger for a diatomic ideal gas than for a monoatomic gas
(b) $\left(\mathrm{C} _{\mathrm{P}}+\mathrm{C} _{\mathrm{v}}\right)$ is larger for a diatomic gas than for a monoatomic gas
(c) $\frac{\mathrm{C} _{\mathrm{P}}}{\mathrm{C} _{\mathrm{V}}}$ is larger for a diatomic gas than for a monoatomic gas
(d) $\mathrm{C} _{\mathrm{p}} \cdot \mathrm{C} _{\mathrm{v}}$ is larger for a diatomic gas than for an ideal monoatomic gas
Show Answer
Solution:
We know for monoatomic gas
$$ \mathrm{C} _{\mathrm{V}}=\frac{3}{2} \mathrm{R} \quad \text { and } \quad \mathrm{C} _{\mathrm{P}}=\frac{5}{2} \mathrm{R} $$
$\therefore \quad \mathrm{C} _{\mathrm{P}}-\mathrm{C} _{\mathrm{V}}=\mathrm{R} ; \mathrm{C} _{\mathrm{P}}+\mathrm{C} _{\mathrm{V}}=4 \mathrm{R} ; \frac{\mathrm{C} _{\mathrm{P}}}{\mathrm{C} _{\mathrm{V}}}=\frac{5}{3}=1.67$
and
$$ \mathrm{C} _{\mathrm{P}} \cdot \mathrm{C} _{\mathrm{V}}=\frac{15}{4} \mathrm{R}^{2} $$
For diatomic gas;
$\mathrm{C} _{\mathrm{V}}=\frac{5}{2} \mathrm{R} ; \quad \mathrm{C} _{\mathrm{P}}=\frac{7}{2} \mathrm{R}$
$\therefore \quad \mathrm{C} _{\mathrm{P}}-\mathrm{C} _{\mathrm{V}}=\mathrm{R} ; \mathrm{C} _{\mathrm{P}}+\mathrm{C} _{\mathrm{V}}=6 \mathrm{R} ; \frac{\mathrm{C} _{\mathrm{P}}}{\mathrm{C} _{\mathrm{V}}}=\frac{7}{5}=1.4$
and $\quad \mathrm{C} _{\mathrm{P}} \times \mathrm{C} _{\mathrm{V}}=\frac{35}{4} \mathrm{R}$
Obviously (b) and (d) both are correct.
Example-13:
One mole of oxygen is heated from $0^{\circ} \mathrm{C}$; at constant pressure till its volume increase by $10 \%$. What is the quantity of heat required? The specific heat of oxygen at constant pressure is $0.22 \mathrm{cal} \mathrm{g}^{-1} \mathrm{~K}^{-1}$. If the same quantity of heat was supplied to gas at constant volume, what will be the final temperature?
Show Answer
Solution:
At constant pressure; from charles’s law $\frac{\mathrm{V}}{\mathrm{T}}=$ constant. Given
$\mathrm{V} _{1}=\mathrm{V}, \mathrm{T} _{1}=0^{\circ} \mathrm{C}=273 \mathrm{~K} ; \mathrm{V} _{2}=1.1 \mathrm{~V}, \mathrm{~T} _{2}=$ ?
$\therefore \frac{\mathrm{V}}{273}=\frac{1.1 \mathrm{~V}}{\mathrm{~T} _{2}}$
or $\quad \mathrm{T} _{2}=300.3 \mathrm{~K}$
$\mathrm{C} _{\mathrm{P}}=$ Molar specific heat of oxygen at constant pressure
$$ =\mathrm{MC} _{\mathrm{P}}=32 \times 0.22=7.04 \mathrm{Cal} \quad \mathrm{mole}^{-1} \mathrm{~K}^{-1} $$
$\mathrm{Q} _{1}=$ Heat required $=\mathrm{nC} _{\mathrm{P}}(\Delta \mathrm{T})=\mathrm{nC} _{\mathrm{P}}\left(\mathrm{T} _{2}-\mathrm{T} _{1}\right)$
$$ \begin{aligned} & =1 \times 7.04 \times(300.3-273)=7.04 \times 27.3 \mathrm{Cal} \\ & \simeq 192.2 \mathrm{Cal} .=192.2 \times 4.2 \mathrm{~J} \simeq 807.24 \mathrm{~J} \end{aligned} $$
Let $\mathrm{C} _{\mathrm{v}}$ be molar specific heat of oxygen at constant volume. We have
$\mathrm{C} _{\mathrm{V}}=\mathrm{C} _{\mathrm{P}}-\mathrm{R}=7.04-2=5.04 \mathrm{Cal}$.
$\left[\because \mathrm{R}=2 \mathrm{Cal} \quad \mathrm{mole}^{-1} \mathrm{~K}^{-1}\right]$
Let $\mathrm{T} _{3}$ be final temperature when 192.2 cal of heat is given to gas at constant volume. Then
$$ 192.2=1 \times 5.04\left[\mathrm{~T} _{3}-273\right] $$
$\mathrm{T} _{3} \simeq 38+273 \simeq 311 \mathrm{~K}$
Rise in temperature $=311-273 \simeq 38^{\circ} \mathrm{C}$
Example-14:
An ideal diatomic gas is heated at constant pressure ( $=1$ atmosphere). $210 \mathrm{~J}$ of heat is given to gas. What is
(1) change in internal energy of gas
(2) work done by the gas? $\left[\mathrm{R}=8.31 \mathrm{~J} \mathrm{~mole}^{-1} \mathrm{~K}^{-1}\right]$
Show Answer
Solution:
For a diatomic gas
$$ \mathrm{C} _{\mathrm{P}}=\frac{7}{2} \mathrm{R} \quad \text { and } \quad \mathrm{C} _{\mathrm{V}}=\frac{5}{2} \mathrm{R} $$
Let $T _{1}$ and $T _{2}$ be initial and final temperature of gas. Then heat supplied, $d Q$, is
$$ \mathrm{dQ}=\mathrm{nC} _{\mathrm{P}}\left(\mathrm{T} _{2}-\mathrm{T} _{1}\right) $$
The change in internal energy; $\mathrm{dU}$, is
$$ \begin{array}{r} \mathrm{dU}=\mathrm{nC} _{\mathrm{V}}\left(\mathrm{T} _{2}-\mathrm{T} _{1}\right) \\ \therefore \quad \frac{\mathrm{dQ}}{\mathrm{dU}}=\frac{\mathrm{C} _{\mathrm{P}}}{\mathrm{C} _{\mathrm{V}}}=\frac{7}{5}=1.4 \end{array} $$
or $\quad \mathrm{dU}=\frac{210}{1.4} \mathrm{~J}=150 \mathrm{~J}$
From first law of thermodynamics
$$ \mathrm{dQ}=\mathrm{dU}+\mathrm{dW} $$
$\therefore \mathrm{dW}=$ Work done by the gas $=\mathrm{dQ}-\mathrm{dU}$
$$ =210-150=60 \mathrm{~J} $$
PROBLEMS FOR PRACTICE
1. A $1 \mathrm{~m}$ long tube closed at one end placed horizontally traps $15 \mathrm{~cm}$ column of air using $76 \mathrm{~cm}$ long mercury thread. What is column of mercury flowing out of tube if kept vertically?
1 atmospheric pressure $=76 \mathrm{~cm}$ of $\mathrm{Hg}$.
Show Answer
Answer: $23.8 \mathrm{~cm}$ of Hg flows out2. A given mass of gas at $-73^{\circ} \mathrm{C}$ in a container exerts a pressure of $0.5 \mathrm{mof} \mathrm{Hg}$ column. The temperature of gas in container is raised to $27^{\circ} \mathrm{C}$. What is pressure exerted by the gas?
Show Answer
Answer: $0.75 \mathrm{~m}$ of Hg3. A cylinder of volume 30 litre contains oxygen at $27^{\circ} \mathrm{C}$ and 15 atmospheric pressure. Some gas is taken out of cylinder the pressure of gas drops to 11 atmosphere and final temperature is $17^{\circ} \mathrm{C}$. What is mass of oxygen taken out? $\left(\mathrm{R}=8.3 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}\right.$; molecular mass of oxygen $\left.=32\right)$
Show Answer
Answer: $0.141 \mathrm{~kg}$4. What is rms velocity of hydrogen at N.T.P? Also estimate kinetic energy of 1 gram of hydrogen. Density of hydrogen at N.T.P $=0.09 \mathrm{kgm}^{-3}$.
Show Answer
Answer: $\sim 1837 ms^{-1} ; \sim 3403 J$5. At what temperature rms speed of an atom of argon gas is same as that helium atom at $-20^{\circ} \mathrm{C}$. Atomic mass of argon $=39.9$, Atomic mass of helium $=4$
Show Answer
Answer: $2524 \mathrm{~K}$6. $20 \mathrm{~g}$ of nitrogen at room temperature has its temperature raised by $55^{\circ} \mathrm{C}$ at constant pressure. What is heat required? Given $\mathrm{R}=8.3 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$. Molecular mass of nitrogen $=28 \mathrm{~g}$.
Show Answer
Answer: $1141.25 \mathrm{~J}$7. Specific heat of argon at constant pressure is $0.125 \mathrm{cal} \mathrm{g}^{-1} \mathrm{~K}^{-1}$ and at constant volume is $0.075 \mathrm{cal} \mathrm{g}^{-1} \mathrm{~K}^{-1}$. What is density of argon at NTP.
Show Answer
Answer: $1.77 \mathrm{~kg} \mathrm{~m}^{-3}$8. Calculate the total number of degrees of freedom of 15 c.c of nitrogen at 1 atmospheric pressure; at $0^{\circ} \mathrm{C}$.
Show Answer
Answer: $2.015 \times 10^{21}$9. Half mole of a monoatomic gas, one mole of a diatomic gas and two moles of a triatomic gas are present in a mixture. What is $\gamma$ of mixture?
Show Answer
Answer: 1.33410. What is the ratio of internal energy of helium and hydrogen at a temperature of $327^{\circ} \mathrm{C}$ ?
Show Answer
Answer: $3 / 7$11. A vessel of volume $2 \times 10^{4}$ c.c contains a mixture of hydrogen and helium at $20^{\circ} \mathrm{C}$. The total mass of mixture $=5 \mathrm{~g}$. What is ratio of mass of hydrogen and mass of helium in mixture?
Show Answer
Answer: 0.512. A cylinder of volume 5000 c.c contains gaseous hydrogen at NTP. The temperature of gas is decreased by $55^{\circ} \mathrm{C}$.
(a) What is change in internal energy of hydrogen?
(b) What is amount of heat lost?
Show Answer
Answer: (a) $-0.249 \mathrm{~kJ}$, (b) $+0.249 \mathrm{~kJ}$13. At what temperature the rms speed of gas atoms equals escape velocity from the gravitational field of earth? Given $\mathrm{g}=9.8 \mathrm{~ms}^{-2}, \mathrm{R}=$ radius of earth $=6400 \mathrm{Km}$. Escape velocity from earth $=11.2 \mathrm{kms}^{-1}$.
Show Answer
Answer: $100 \mathrm{~K}$14. The surface temperature of Sun is about $6 \times 10^{3} \mathrm{~K}$. What is
(a) r.m.s speed and
(b) average kinetic energy of hydrogen molecule on Sun?
Show Answer
Answer: (a) $8.65 \mathrm{kms}^{-1}$, (b) $1.25 \times 10^{-19} \mathrm{~J}$15. Calculated the internal energy at $127^{\circ} \mathrm{C}$ of a mixture of 1 mole of a monoatomic; 1.5 mole of a diatomic and 0.5 mole of a triatomic gas. $\mathrm{R}=8.31 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$.
Show Answer
Answer: 23.27 KJQuestion Bank
Key Learning Points
1. According to kinetic theory of gases, the atoms or molecules of gases are in a state of random motion at any finite temperature.
2. Experimental studies give us the gas laws. These are:
(a) Boyle’s law: For a given mass of a gas at constant temperature $\mathrm{PV}=$ constant; $\mathrm{P}=$ pressure of gas, $\mathrm{V}=$ volume of gas.
(b) charles’s law: For a gas at constant pressure, $\mathrm{V} / \mathrm{T}=$ constant; $\mathrm{T}$ is temperature of gas on Kelvin scale.
(c) Gay Lussac’s law: For a gas at constant volume; $\mathrm{P} / \mathrm{T}=$ constant.
3. A perfect gas obey’s gas law under all conditions of pressure and temperature. No gas can be hundred percent perfect. However a gas at low pressure and high temperature behaves nearly like a perfect gas.
4. The perfect gas equation is
$$ \mathrm{PV}=\mathrm{nRT}=\left(\frac{\mathrm{m}}{\mathrm{M}}\right) \mathrm{RT} $$
$n=\frac{m}{M}=$ Number of moles of gas, $m=$ mass of gas, $M=$ Molar mass of gas.
5. A gas at pressure $\mathrm{P}$, volume $\mathrm{V}$ undergoes an infinitesimal change $\mathrm{dV}$ in volume. The work done on or by the gas $=\mathrm{dW}=\mathrm{PdV}$. For a finite change;
$$ \mathrm{W}=\text { Total work done }=\int \mathrm{PdV}=\text { Area under } \mathrm{P} v s \mathrm{~V} \text { graph. } $$
6. To simplify calculations in kinetic theory we assume
(a) Atoms or molecules are all identical, having negligible size i.e. are point masses.
(b) There is no interatomic or intermolecular force between gas atoms or molecules.
(c) The atom or molecules undergo perfectly elastic collision with the walls of container.
(d) The average distance between two consecutive collisions is known as mean free path and the average time between collisions is known as mean relaxation time.
7. The pressure exerted by gas is due to the change in the linear momentum of an atom or molecule due to a collision. The expression for pressure, $\mathrm{P}$, exerted by gas is
$$ \mathrm{P}=\frac{1}{3} \rho \mathrm{v} _{\mathrm{rms}}^{2} $$
where $\rho$ is density of gas and $\mathrm{v} _{\mathrm{ms}}$ is the root-mean square velocity of atoms or molecules of gas. Let $\mathrm{v} _{1}, \mathrm{v} _{2}, \ldots \ldots \ldots \ldots \mathrm{v} _{\mathrm{N}}$ be the velocity of $\mathrm{N}-$ atoms or molecules of gas under consideration. Then
$$ \mathrm{v} _{\mathrm{rms}}=\left[\frac{\mathrm{v} _{1}^{2}+\mathrm{v} _{2}^{2}+\ldots \ldots . . \mathrm{v} _{\mathrm{N}}^{2}}{\mathrm{~N}}\right]^{1 / 2} $$
8. The mean velocity $(\mathbf{v}) ;$ rms velocity $\left(\mathrm{v} _{\mathrm{rms}}\right)$ and most probable velocity $\mathrm{v} _{\mathrm{P}}$ are:
$$ \mathrm{v}=\sqrt{\frac{8 \mathrm{kT}}{\pi \mathrm{m}}} ; \mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{P}}{\rho}} ; \mathrm{v} _{\mathrm{P}}=\sqrt{\frac{2 \mathrm{kT}}{\mathrm{m}}} $$
$\mathrm{k}=$ Boltzmann’s constant; $\mathrm{m}=$ mass of one atom or molecules of gas.
9. The temperature ( $\mathrm{T}$ ) of a gas is a measure of average kinetic energy of each atom or molecule of gas. The kinetic energy of one atom or molecules of gas is
$$ \frac{1}{2} \mathrm{mv} _{\mathrm{rms}}^{2}=\frac{3}{2} \mathrm{kT} $$
10. In terms of temperature $(\mathrm{T})$ and molar mass $(\mathrm{M})$;
$$ \mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}} $$
11. The degrees of freedom are the number of independent co-ordinates required to completely describe position and configuration of a system. For one atom, having translational motion the degree of freedom are 1,2 and 3; if the atom has one dimensional, two dimensional or three dimensional motion.
12. For a system of $\mathrm{N}$-atoms, the degrees of freedom, $\mathrm{n}$, is
$$ \mathrm{n}=3 \mathrm{~N}-\mathrm{R} $$
where $\mathrm{R}$ is number of relations amongst position of atoms or molecules.
For monoatomic; diatomic and triatomic gas degrees of freedom of translational motion is 3,5 and 7 respectively.
13. According to Boltzmann’s law of equipartition of energy; energy per degree of freedom $=\frac{1}{2} \mathrm{k} \mathrm{T}$.
14. For a gas we define:
$\mathrm{C} _{\mathrm{v}}=$ Molar specific heat at constant volume $=$ Heat required to raise temperature of one mole of gas by one degree at constant volume.
$\mathrm{C} _{\mathrm{P}}=$ Molar specific heat at constant pressure $=$ Heat required to raise temperature of one mole of gas by one degree at constant pressure.
It can be show that
$$ \mathrm{C} _{\mathrm{P}}-\mathrm{C} _{\mathrm{V}}=\mathrm{R} $$
15. $\gamma=\frac{\mathrm{C} _{\mathrm{P}}}{\mathrm{C} _{\mathrm{V}}}=$ The ratio of the two specific heats of gas $\gamma$ is always more than one.
16. In terms of degrees of freedom, $n$;
$$ \mathrm{C} _{\mathrm{V}}=\frac{\mathrm{nR}}{2} ; \mathrm{C} _{\mathrm{P}}=\left(\frac{\mathrm{n}}{2}+1\right) \mathrm{R} ; \gamma=\frac{\mathrm{C} _{\mathrm{P}}}{\mathrm{C} _{\mathrm{V}}}=1+\frac{2}{\mathrm{n}} $$
17. For monoatomic gas;
$$ \mathrm{C} _{\mathrm{v}}=\frac{3}{2} \mathrm{R} ; \mathrm{C} _{\mathrm{P}}=\frac{5}{2} \mathrm{R} ; \gamma=\frac{5}{3}=1.67 $$
For diatomic gas;
$$ \mathrm{C} _{\mathrm{V}}=\frac{5}{2} \mathrm{R} ; \mathrm{C} _{\mathrm{P}}=\frac{7}{2} \mathrm{R} ; \gamma=\frac{7}{4}=1.4 $$
For triatomic gas;
$$ \mathrm{C} _{\mathrm{v}}=\frac{7}{2} \mathrm{R} ; \mathrm{C} _{\mathrm{P}}=\frac{9}{2} \mathrm{R} ; \gamma=\frac{9}{7} \simeq 1.28 $$
18. For a mixture of $n _{1}, n _{2}, \ldots \ldots .$. moles of gases having $\frac{C _{P}}{C _{v}}$ as $\gamma _{1}, \gamma _{2}, \ldots \ldots$ etc. $\gamma _{m}=\frac{C _{P}}{C _{V}}$ of the mixture is given by
$$ \frac{\mathrm{n} _{1}+\mathrm{n} _{2}+\ldots \ldots}{\left(\gamma _{\mathrm{m}}-1\right)}=\frac{\mathrm{n} _{1}}{\left(\gamma _{1}-1\right)}+\frac{\mathrm{n} _{2}}{\left(\gamma _{2}-1\right)}+\ldots $$
1. An air bubble starts rising from the bottom of lake. Its diameter is $3.6 \mathrm{~mm}$ at the bottom and $4 \mathrm{~mm}$ at the surface. The depth of the lake is $250 \mathrm{~cm}$ and temperature at the surface is $40^{\circ} \mathrm{C}$. The temperature at the bottom of the lake is (Given atmospheric pressure $=76 \mathrm{~cm}$ of $\mathrm{Hg}$ and $\mathrm{g}=9.80 \mathrm{~ms}^{-2}$, specific gravity of $\mathrm{Hg}=\mathbf{1 3 . 6}$ )
(1) $10.27^{\circ} \mathrm{C}$
(2) $9.4^{\circ} \mathrm{C}$
(3) $11.37^{\circ} \mathrm{C}$
(4) $12.4^{\circ} \mathrm{C}$
Show Answer
Correct answer: (2)
Solution:
At the bottom of lake
$\mathrm{V} _{1}=$ volume of bubble $=\frac{4}{3} \pi \mathrm{r} _{1}^{3}=\frac{4}{3} \pi(0.18)^{3} \times 10^{-6} \mathrm{~m}^{3}$
$\mathrm{P} _{1}=$ The total pressure at the bottom of lake
$=$ atmospheric pressure + pressure due to a column $250 \mathrm{~cm}$ of water
$$ =0.76 \times 13.6 \times 10^{3} \times 9.8+2.50 \times 10^{3} \times 9.8 $$
$=1257928 \mathrm{~Pa} \simeq 1.285 \times 10^{5} \mathrm{~Pa}$
$\mathrm{T} _{1}=$ Temperature at the bottom of lake $=$ ?
At the surface of lake
$\mathrm{P} _{2}=$ The total pressure $=$ The atmospheric pressure $=1.013 \times 10^{5} \mathrm{~Pa}$
Volume of bubble at surface of lake $=\mathrm{V} _{2}=\frac{4}{3} \pi(0.2)^{3} \times 10^{-6} \mathrm{~m}^{3}$
$\mathrm{T} _{2}=273+40^{\circ} \mathrm{C}=313 \mathrm{~K}$
Applying gas equation $\frac{\mathrm{P} _{1} \mathrm{~V} _{1}}{\mathrm{~T} _{1}}=\frac{\mathrm{P} _{2} \mathrm{~V} _{2}}{\mathrm{~T} _{2}}$ we have
$$ \mathrm{T} _{1}=\frac{\mathrm{P} _{1} \mathrm{~V} _{1} \mathrm{~T} _{2}}{\mathrm{P} _{2} \mathrm{~V} _{2}} $$
$$ \begin{gathered} =\frac{1.26 \times 10^{5} \times(0.18)^{3} \times 313}{1.013 \times 10^{5} \times(0.2)^{3}} \\ \simeq \frac{2.300}{0.00814}=282.56 \mathrm{~K} \\ \mathrm{~T} _{1}=282.56-273.16=9.4^{\circ} \mathrm{C} \end{gathered} $$
2. The average kinetic energy of translational motion of the molecule of an ideal gas at $0^{\circ} \mathrm{C}$ and $100^{\circ} \mathrm{C}$ respectively is
(Given Avogadro’s number $\mathrm{N}=6.02 \times 10^{23}$ and Boltzmann’s constant $\mathrm{k}=1.38 \times 10^{-23} \mathrm{~J} / \mathrm{K}$ ).
(1) $5.65 \times 10^{-21} \mathrm{~J} /$ molecule, and $7.72 \times 10^{-21} \mathrm{~J} /$ molecule
(2) $5.65 \times 10^{-21} \mathrm{~J} /$ molecule, and $5.65 \times 10^{-19} \mathrm{~J} /$ molecule
(3) $5.65 \times 10^{-21} \mathrm{~J} /$ molecule, and $5.67 \times 10^{-23} \mathrm{~J} /$ molecule
(4) $7.72 \times 10^{-21} \mathrm{~J} /$ molecule, and $7.72 \times 10^{-19} \mathrm{~J} /$ molecule
Show Answer
Correct answer: (1)
Solution:
Kinetic energy of translation at $0^{\circ} \mathrm{C}=\mathrm{K}=\frac{3}{2} \mathrm{kT}$
$$ \begin{aligned} & =\frac{3}{2} \times 1.38 \times 10^{-23} \times 273 \\ & =5.65 \times 10^{-21} \mathrm{~J} / \text { molecule } \end{aligned} $$
$\mathrm{KE}$ at $100^{\circ} \mathrm{C}=\frac{3}{2} \times 1.38 \times 10^{-23} \times 373$
$$ =7.72 \times 10^{-21} \mathrm{~J} / \mathrm{molecule} $$
The correct choice is (1)
3. The root mean square speed of hydrogen molecules at a temperature of $27^{\circ} \mathrm{C}$ is
(1) $1.93 \times 10^{3} \mathrm{~ms}^{-1}$
(2) $5.79 \times 10^{2} \mathrm{~ms}^{-1}$
(3) $2.37 \times 10^{2} \mathrm{~ms}^{-1}$
(4) $2.37 \times 10^{3} \mathrm{~ms}^{-1}$
Show Answer
Correct answer: (1)
Solution:
Root mean square speed $=\mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}}$
$\mathrm{M}=$ The molar mass of hydrogen gas $=2 \mathrm{~g}=2 \times 10^{-3} \mathrm{~kg}, \mathrm{~T}=273+27=300 \mathrm{~K}$
$$ \therefore \quad \mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \times 8.31 \times 300}{2 \times 10^{-3}}}=1.93 \times 10^{3} \mathrm{~ms}^{-1} $$
4. The temperature at which the oxygen molecules would have the same rms speed as of hydrogen molecule at $300 \mathrm{~K}$ is
(1) $2400 \mathrm{~K}$
(2) $1200 \mathrm{~K}$
(3) $4800 \mathrm{~K}$
(4) $300 \mathrm{~K}$
Show Answer
Correct answer: (3)
Solution:
Let $\mathrm{T} _{0}$ and $\mathrm{M} _{0}$ be the absolute temperature and molecular mass of oxygen. $\mathrm{T} _{\mathrm{H}}$ and $\mathrm{M} _{\mathrm{H}}$ denote the absolute temperature and molecular mass of hydrogen. Given $\left(\mathrm{V} _{\mathrm{rms}}\right) _{0}=\left(\mathrm{V} _{\mathrm{rms}}\right) _{\mathrm{H} _{2}}$
$$ \begin{aligned} & \therefore \sqrt{\frac{3 \mathrm{RT} _{0}}{\mathrm{M} _{0}}}=\sqrt{\frac{3 \mathrm{RT} _{\mathrm{H}}}{\mathrm{M} _{\mathrm{H}}}} \\ & \sqrt{\frac{3 \mathrm{RT} _{0}}{\mathrm{M} _{0}}}=\sqrt{\frac{3 \times \mathrm{R} \times 300}{\mathrm{M} _{\mathrm{H}}}} \\ & \text { or } \frac{\mathrm{T} _{0}}{300}=\frac{\mathrm{M} _{0}}{\mathrm{M} _{\mathrm{H}}}=16 \\ & {\left[\because \mathrm{M} _{0}=16 \mathrm{M} _{\mathrm{H}}\right]} \\ & \therefore \quad \mathrm{T} _{0}=4800 \mathrm{~K} \end{aligned} $$
5. The average translational energy and the root mean square speed of molecule in a sample of oxygen at $300 \mathrm{~K}$, are $6.21 \times 10^{-21} \mathrm{~J}$ and $484 \mathrm{~ms}^{-1}$, respectively. The corresponding values at $600 \mathrm{~K}$ would be
(1) $1.242 \times 10^{-20} \mathrm{~J}$ and $968 \mathrm{~ms}^{-1}$
(2) $3.06 \times 10^{-21} \mathrm{~J}$ and $484 \mathrm{~ms}^{-1}$
(3) $3.06 \times 10^{-21} \mathrm{~J}$ and $584 \mathrm{~ms}^{-1}$
(4) $1.242 \times 10^{-20} \mathrm{~J}$ and $684 \mathrm{~ms}^{-1}$
Show Answer
Correct answer: (4)
Solution:
We know
The kinetic energy $=\mathrm{K}=\frac{3}{2} \mathrm{kT}=\frac{1}{2} \mathrm{mv} _{\mathrm{rms}}^{2}$, therefore
$$ \begin{aligned} & \frac{\mathrm{K} _{2}}{\mathrm{~K} _{1}}=\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}=2 \\ & \mathrm{~K} _{2}=2 \mathrm{~K} _{1}=1.242 \times 10^{-20} \mathrm{~J} \end{aligned} $$
We know $v _{\text {rms }}=\sqrt{\frac{3 R T}{M}}$, therefore
$$ \begin{aligned} & \frac{\left(\mathrm{v} _{\mathrm{rms}}\right) _{1}}{\left(\mathrm{v} _{\mathrm{rms}}\right) _{2}}=\sqrt{\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}} \\ & \text { or }\left(\mathrm{v} _{\mathrm{rms}}\right) _{2}=\sqrt{\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}} \times\left(\mathrm{v} _{\mathrm{rms}}\right) _{1} \\ & \quad=\sqrt{2} \times 484=684 \mathrm{~ms}^{-1 /} \end{aligned} $$
6. One mole of an ideal monoatomic gas is at temperature of $300 \mathrm{~K} _{0}$. Its volume is doubled keeping its pressure constant. The change in internal energy is
(1) $3.735 \times 10^{3} \mathrm{~J}$
(2) $6.225 \times 10^{3} \mathrm{~J}$
(3) $8.715 \times 10^{3} \mathrm{~J}$
(4) $6.225 \times 10^{2} \mathrm{~J}$
Show Answer
Correct answer: (1)
Solution:
At constant pressure, volume is directly proportional to temperature. Therefore
$$ \frac{\mathrm{V} _{1}}{\mathrm{~V} _{2}}=\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}} $$
or $\mathrm{T} _{2}=\frac{\mathrm{V} _{2} \mathrm{~T} _{1}}{\mathrm{~V} _{1}}=\frac{2 \mathrm{~V} \times 300}{\mathrm{~V}}=600 \mathrm{~K}$
$\Delta \mathrm{U}=$ The change in internal energy $=\mathrm{nC} _{\mathrm{v}}(\Delta \mathrm{T})$
$=\frac{f}{2} n R\left(T _{2}-T _{1}\right)$, where $f=$ number of degrees of freedom and equals 3 for a monoatomic gas.
$\therefore \Delta \mathrm{U}=\frac{3}{2} \times 1 \times 8.3(600-300)=450 \times 8.3 \mathrm{~J}$
$=3.735 \times 10^{3} \mathrm{~J}$
7. The root mean square speed of molecules of gas whose density is $1.4 \mathrm{~kg} / \mathbf{m}^{3}$ at a pressure $76 \mathrm{~cm}$ of $\mathrm{Hg}$ (specific gravity of mercury $13.6 \mathrm{and} \mathrm{g}=9.81 \mathrm{~ms}^{-2}$ ) will be
(1) $4.66 \times 10^{2} \mathrm{~ms}^{-1}$
(2) $4.66 \times 10^{2} \mathrm{cms}^{-1}$
(3) $2.33 \times 10^{2} \mathrm{~ms}^{-1}$
(4) $2.33 \times 10^{2} \mathrm{cms}^{-1}$
Show Answer
Correct answer: (1)
Solution:
Pressure, $\mathrm{P}$, exerted by an ideal gas on the walls of the container is
$$ \begin{aligned} & \mathrm{P}=\frac{1}{3} \rho \mathrm{v} _{\mathrm{rms}}^{2} \\ & \therefore \mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{P}}{\rho}} \end{aligned} $$
Given $\mathrm{P}=0.76 \times 13.6 \times 10^{3} \times 9.81 \mathrm{~Pa}$, and $\rho=1.4 \mathrm{kgm}^{-3}$. Substituting values we have
$$ \mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \times 0.76 \times 13.6 \times 1000 \times 9.81}{1.4}}=4.66 \times 10^{2} \mathrm{~ms}^{-1} $$
8. The temperature at which the root mean square speed of molecules of a gas is double of its value at $0^{\circ} \mathrm{C}$, is
(1) $819^{\circ} \mathrm{C}$
(2) $1092^{\circ} \mathrm{C}$
(3) $273^{\circ} \mathrm{C}$
(4) $386^{\circ} \mathrm{C}$
Show Answer
Correct answer: (1)
Solution:
We know, the r.m.s speed of molecules of a gas is
$$ \begin{gathered} \mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}} \\ \therefore \frac{\left(\mathrm{v} _{\mathrm{rms}}\right) _{1}}{\left(\mathrm{v} _{\mathrm{rms}}\right) _{2}}=\sqrt{\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}} \\ \text { or } \frac{2 \mathrm{v}}{\mathrm{v}}=\sqrt{\frac{\mathrm{T} _{2}}{273}} \\ \mathrm{~T} _{2}=4 \times 273=1092 \mathrm{~K}=1092-273=819^{\circ} \mathrm{C} \end{gathered} $$
9. A certain mass of hydrogen has a volume of $100 \mathrm{~cm}^{3}$ at a pressure at $10^{5} \mathrm{~N} / \mathrm{m}^{2}$ at $27^{\circ} \mathrm{C}$. The mass of hydrogen is
(Given molecular weight of hydrogen is $2 \mathrm{~g}$ and $\mathrm{R}=8.31 \mathrm{~J} \mathrm{~mole}^{-1} \mathrm{~K}^{-1}$ )
(1) $2 \times 10^{-6} \mathrm{~kg}$
(2) $1.6 \times 10^{-5} \mathrm{~kg}$
(3) $4 \times 10^{-6} \mathrm{~kg}$
(4) $8 \times 10^{-6} \mathrm{~kg}$
Show Answer
Correct answer: (4)
Solution:
Let the number of moles of hydrogen be ’ $n$ ‘. From ideal gas equation
$$ \begin{gathered} \mathrm{PV}=\mathrm{nRT} \\ \mathrm{n}=\frac{\mathrm{PV}}{\mathrm{RT}}=\frac{10^{5} \times 100 \times 10^{-6}}{8.31 \times 300}=\frac{1}{83 \times 3} \end{gathered} $$
Since mass of one mole of hydrogen is $2 \mathrm{~g}$; the mass, $\mathrm{m}$, of hydrogen is
$\mathrm{m}=\frac{1}{83 \times 3} \times 2 \mathrm{~g}=0.008 \mathrm{~g}=8 \times 10^{-6} \mathrm{~kg}$
10. A vessel of volume $8.0 \times 10^{-3} \mathrm{~m}^{3}$ contains an ideal gas at $300 \mathrm{~K}$ at $200 \mathrm{kPa}$. The gas is allowed to leak till pressure falls to $125 \mathrm{kPa}$. The amount of gas (in moles) leaked will be (Assume temperature remains constant)
(1) 0.60 mole
(2) 0.12 mole
(3) 0.24 mole
(4) 0.48 mole
Show Answer
Correct answer: (3)
Solution:
The number of moles of the gas in the vessel is given by $n=\frac{P V}{R T}$.
Let the number of moles before and after leakage be $n _{1}$ and $n _{2}$.
$$ \mathrm{n} _{1}=\frac{\mathrm{P} _{1} \mathrm{~V}}{\mathrm{RT}}, \mathrm{n} _{2}=\frac{\mathrm{P} _{2} \mathrm{~V}}{\mathrm{RT}} $$
The amount of gas leaked in moles $=\mathrm{n} _{1}-\mathrm{n} _{2}=\frac{\left(\mathrm{P} _{1}-\mathrm{P} _{2}\right) \mathrm{V}}{\mathrm{RT}}$.
$$ =\frac{(200-125) \times 10^{3} \times 8 \times 10^{-3}}{8.31 \times 300}=0.24 \mathrm{~mole} $$
11. A mixture of hydrogen and oxygen has volume $2000 \mathrm{~cm}^{3}$, temperature $300 \mathrm{~K}$, pressure 100 $\mathrm{kPa}$ and mass 0.76 gram, the mass of hydrogen and oxygen in the mixture are:
(1) $0.12 \mathrm{~g}$ and $0.64 \mathrm{~g}$ respectively
(2) $0.06 \mathrm{~g}$ and $0.70 \mathrm{~g}$ respectively
(3) $0.64 \mathrm{~g}$ and $0.12 \mathrm{~g}$ respectively
(4) $0.24 \mathrm{~g}$ and $0.52 \mathrm{~g}$ respectively
Show Answer
Correct answer: (1)
Solution:
Let the number of moles of hydrogen and oxygen in the mixture be $n _{1}$ and $n _{2}$. The pressure of the mixture
$$ \mathrm{P}=\frac{\mathrm{n} _{1} \mathrm{RT}}{\mathrm{V}}+\frac{\mathrm{n} _{2} \mathrm{RT}}{\mathrm{V}}=\left(\mathrm{n} _{1}+\mathrm{n} _{2}\right) \frac{\mathrm{RT}}{\mathrm{V}} $$
Substituting given values we have
$100 \times 10^{3}=\left(\mathrm{n} _{1}+\mathrm{n} _{2}\right) \frac{8.31 \times 300}{2000 \times 10^{-6}}$
or $\mathrm{n} _{1}+\mathrm{n} _{2}=0.08$ mole $\hspace{50mm} . . . . . (1)$
The mass of the mixture $=0.76 \mathrm{~g}$. Obviously
$\mathrm{n} _{1} \times 2+\mathrm{n} _{2} \times 32=0.76$
$\mathrm{n} _{1}+16 \mathrm{n} _{2}=0.38 \hspace{60mm} . . . . . (2)$
Solving Eqns (1) and (2) we have
$$ \mathrm{n} _{1}=0.06, \mathrm{n} _{2}=0.02 $$
Hence mass of hydrogen $=\mathrm{n} _{1} \times 2=0.12 \mathrm{~g}$, mass of the oxygen $=0.02 \times 32=0.64 \mathrm{~g}$
12. Two closed vessels of equal volume contain air at $105 \mathrm{kPa}, 300 \mathrm{~K}$ and are connected through a narrow tube. One of the vessel is maintained at $300 \mathrm{~K}$ and other at $400 \mathrm{~K}$, then the equilibrium pressure in the vessels is
(1) $72.5 \mathrm{kPa}$
(2) $120 \mathrm{kPa}$
(3) $250 \mathrm{kPa}$
(4) $500 \mathrm{kPa}$
Show Answer
Correct answer: (2)
Solution:
Let the initial pressure, volume, and temperature in each vessel be $\mathrm{P} _{0}(=105 \mathrm{kPa}), \mathrm{V} _{0}$ and $\mathrm{T} _{0}(=300 \mathrm{~K})$, the number of moles in each vessel be $n$. When the first vessel be maintained at $300 \mathrm{~K}$ and second at $400 \mathrm{~K}$,
Let number of moles of air be $\mathrm{n} _{1}$ and $\mathrm{n} _{2}$ in each vessel and equilibrium pressure be comes $\mathrm{P}^{\prime}$.
$$ \begin{align*} & \mathrm{P} _{0} \mathrm{~V} _{0}=\mathrm{nRT} _{0} \tag{1} \\ & \mathrm{P}^{\prime} \mathrm{V} _{0}=\mathrm{n} _{1} \mathrm{RT} _{0} \tag{2} \\ & \mathrm{P}^{\prime} \mathrm{V} _{0}=\mathrm{n} _{2} \mathrm{RT}^{\prime} \tag{3} \end{align*} $$
and $\mathrm{n} _{1}+\mathrm{n} _{2}=2 \mathrm{n} \hspace{40mm}. . . . . . . . (4)$
FromEqns (1), (2), (3) and (4) we get
$$ \begin{aligned} & \frac{\mathrm{P}^{\prime} \mathrm{V} _{0}}{\mathrm{RT} _{0}}+\frac{\mathrm{P}^{\prime} \mathrm{V} _{0}}{\mathrm{RT}^{\prime}}=2 \frac{\mathrm{P} _{0} \mathrm{~V} _{0}}{\mathrm{RT} _{0}} \\ & \text { or } \mathrm{P}^{\prime}\left(\frac{\mathrm{T}^{\prime}+\mathrm{T} _{0}}{\mathrm{~T} _{0}+\mathrm{T}^{\prime}}\right)=\frac{2 \mathrm{P} _{0}}{\mathrm{~T} _{0}} \\ & \therefore \quad \mathrm{P}^{\prime}=\frac{2 \mathrm{P} _{0} \mathrm{~T}^{\prime}}{\mathrm{T}^{\prime}+\mathrm{T} _{0}}=\frac{2 \times 105 \times 10^{3} \times 400}{400+300} \\ & =120 \mathrm{kPa} \end{aligned} $$
13. A vessel of volume $\mathbf{V} _{0}$ contains an ideal gas at pressure $P _{0}$ and temperature T. Gas is continuously pumped out of the vessel at a constant volume rate $\frac{d V}{d t}=r$, keeping the temperature constant. The pressure of the gas taken out equals the pressure inside the vessel, the time taken before half the original gas is pumped out will be
(1) $t=\frac{2.303 \mathrm{~V} _{0} \log 2}{\mathrm{r}}$
(2) $\mathbf{t}=\frac{\mathbf{V} _{0}}{\mathbf{r}}$
(3) $t=\frac{2.303 \text { rlog2 }}{V _{0}}$
(4) $\mathbf{t}=\frac{\mathbf{r l o g} 2}{\mathbf{V} _{0}}$
Show Answer
Correct answer: (1)
Solution:
Given $\frac{\mathrm{dV}}{\mathrm{dt}}=\mathrm{r}$ or, $\mathrm{dV}=\mathrm{rdt}$
Let volume of the container be $\mathrm{V} _{0}$. Let $\mathrm{dP}$ and $\mathrm{dV}$ denote the change in pressure and volume due to gas taken out in time interval $t$ and $t+d t$. At constant temperature $\mathrm{PV}=$ constant; therefore
$$ \begin{aligned} & \mathrm{PdV}=-\mathrm{V} _{0} \mathrm{dP}, \text { or } \mathrm{Prdt}=-\mathrm{V} _{0} \mathrm{dP} \\ & \therefore \frac{\mathrm{dP}}{\mathrm{P}}=-\left(\frac{\mathrm{rdt}}{\mathrm{V} _{0}}\right) \end{aligned} $$
Integrate and rearranging we have
$$ \begin{equation*} \mathrm{P}=\mathrm{P} _{0} \mathrm{e}^{\left(-\frac{\mathrm{rt}}{\mathrm{V} _{0}}\right)} \tag{1} \end{equation*} $$
Let $\mathrm{P}=\frac{\mathrm{P} _{0}}{2}$ at $\mathrm{t}=\mathrm{t} _{0}$, From Eqn. (1) we have
$$ \frac{1}{2}=1 \times \mathrm{e}^{\left(-\frac{\mathrm{rt}}{\mathrm{V} _{0}}\right)} $$
$\therefore 2=\mathrm{e}^{\left(+\frac{\mathrm{rt}}{\mathrm{V} _{0}}\right)} \quad$ or $\quad \ell n 2=\frac{\mathrm{rt}}{\mathrm{V} _{0}}$
$\therefore \quad \mathrm{t}=\frac{\mathrm{V} _{0} \ln 2}{\mathrm{r}}=\frac{2.303 \mathrm{~V} _{0} \log 2}{\mathrm{r}}$
14. The average translational kinetic energy of air molecules is $0.040 \mathrm{eV}$. The temperature of the air is (Given Boltzmann’s constant $\mathrm{k}=1.38 \times 10^{-23} \mathrm{~J} / \mathrm{K}, 1 \mathrm{eV}=\mathbf{1 . 6}^{-6} \mathbf{1 0}^{-19} \mathrm{~J}$ )
(1) $310^{\circ} \mathrm{C}$
(2) $37^{\circ} \mathrm{C}$
(3) $37 \mathrm{~K}$
(4) $930 \mathrm{~K}$
Show Answer
Correct answer: (2)
Solution:
Average translational kinetic energy of one air molecule $=\frac{3}{2} \mathrm{kT}$. Given
$$ \begin{aligned} & \frac{3}{2} \mathrm{kT}=0.04 \times 1.6 \times 10^{-19} \mathrm{~J} \\ & \text { or } \frac{3}{2} \times 1.38 \times 10^{-23} \times \mathrm{T}=0.04 \times 1.6 \times 10^{-19} \\ \therefore \quad \mathrm{T} & =310 \mathrm{~K}=(310-273)^{0} \mathrm{C}=37^{\circ} \mathrm{C} \end{aligned} $$
15. The temperature at which the rms speed of hydrogen molecules becomes double the rms speed at $300 \mathrm{~K}$, is
(1) $300 \mathrm{~K}$
(2) $900 \mathrm{~K}$
(3) $1200 \mathrm{~K}$
(4) $600 \mathrm{~K}$
Show Answer
Correct answer: (2)
Solution:
We know $\mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}}$, therefore
$\frac{\left(\mathrm{v} _{\mathrm{rms}}\right) _{1}}{\left(\mathrm{v} _{\mathrm{rms}}\right) _{2}}=\sqrt{\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}}$
Given $\left(\mathrm{v} _{\mathrm{rms}}\right) _{2}=2\left(\mathrm{v} _{\mathrm{rms}}\right) _{1}$ and $T _{1}=300 \mathrm{~K}$. Substituting values we get
$\left(\frac{\mathrm{V}}{2 \mathrm{~V}}\right)^{2}=\frac{300}{\mathrm{~T} _{2}}$
$\mathrm{T} _{2}=1200 \mathrm{~K}$
16. The average time taken by the oxygen molecule to travel a distance equal to the diameter of the earth with a constant speed equal to the average speed of oxygen molecule at $300 \mathrm{~K}$ will be (Radius of Earth $=6400 \mathrm{~km}$ )
(1) 4 hour
(2) 8 hour
(3) 7.39 hour
(4) Nearly 15 hour
Show Answer
Correct answer: (2)
Solution:
We know the average speed $\mathrm{v} _{\mathrm{av}}$, is given by
$$ \begin{aligned} & \mathrm{v} _{\mathrm{av}}=\sqrt{\frac{8 \mathrm{RT}}{\pi \mathrm{M}}} \\ & =\sqrt{\frac{8 \times 8.31 \times 300}{3.14 \times .032}}=445.25 \mathrm{~ms}^{-1} \end{aligned} $$
The time taken $\mathrm{t}=\frac{\text { distance travelled }}{\text { speed }}$
$$ =\frac{2 \times 6400 \times 10^{3}}{445.25}=28.747 \times 10^{3} \mathrm{~s} \simeq 8 \mathrm{hr} $$
17. Average magnitude of linear momentum of a helium molecule in a sample of helium gas at $0^{\circ} \mathrm{C}$, will be (Mass of helium molecule $=6.64 \times 10^{-27} \mathrm{~kg}$, Boltzmann’s constant $\left.=\mathbf{k}=\mathbf{1 . 3 8} \times 10^{-23} \mathbf{J k g}^{-1}\right)$
(1) $8 \times 10^{-24} \mathrm{~kg} \mathrm{~ms}^{-1}$
(2) $8.0 \times 10^{-27} \mathrm{~kg} \mathrm{~ms}^{-1}$
(3) $8.66 \times 10^{-24} \mathrm{~kg} \mathrm{~ms}^{-1}$
(4) $8.66 \times 10^{-27} \mathrm{~kg} \mathrm{~ms}^{-1}$
Show Answer
Correct answer: (2)
Solution:
The average speed of a molecule is
$$ \begin{aligned} & \mathrm{v} _{\mathrm{av}}=\sqrt{\frac{8 \mathrm{RT}}{\pi \mathrm{M}}} \\ & =\sqrt{\frac{8 \times 8.31 \times 273}{3.14 \times 4 \times 10^{-3}}}=1.20 \times 10^{3} \mathrm{~ms}^{-1} \end{aligned} $$
Linear momentum of helium molecule $=$ Mass $\times$ velocity
$$ \begin{aligned} & =6.64 \times 10^{-27} \times 1.20 \times 10^{3} \mathrm{~kg} \mathrm{~ms}^{-1} \\ & \approx 8.0 \times 10^{-24} \mathrm{~kg} \mathrm{~ms}^{-1} \end{aligned} $$
18. The mean speed of the molecules of hydrogen equals the mean speed of molecules of the helium. The ratio of temperature of hydrogen and helium will be
(1) $1: 4$
(2) $2: 1$
(3) $1: 2$
(4) $4: 1$
Show Answer
Correct answer: (3)
Solution:
We know the average speed of an atom or molecule is
$$ \mathrm{v} _{\mathrm{av}}=\sqrt{\frac{8 \mathrm{RT}}{\pi \mathrm{M}}} $$
For hydrogen $\mathrm{M}=2 \mathrm{~g}$ and $\mathrm{M} _{\mathrm{He}}=4 \mathrm{~g}$. Given $\left(\mathrm{V} _{\mathrm{av}}\right) _{\mathrm{H}}=\left(\mathrm{V} _{\mathrm{av}}\right) _{\mathrm{He}}$ therefore
$$ \sqrt{\frac{8 \mathrm{RT} _{1}}{\pi \mathrm{M} _{\mathrm{H}}}}=\sqrt{\frac{8 \mathrm{RT} _{2}}{\pi \mathrm{M} _{\mathrm{He}}}} \text { or } \frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=\frac{\mathrm{M} _{1}}{\mathrm{M} _{2}}=\frac{1}{2} $$
19. The temperature at which the mean speed of the molecules of hydrogen gas equals the escape speed from the earth is
Given escape speed from the earth $=11.2 \mathrm{kms}^{-1}=11.2 \times 10^{3} \mathrm{~ms}^{-1}$.
(1) $11849 \mathrm{~K}$
(2) $1180 \mathrm{~K}$
(3) $1145 \mathrm{~K}$
(4) $849^{\circ} \mathrm{C}$
Show Answer
Correct answer: (1)
Solution:
The average speed, $\mathrm{v} _{\mathrm{av}}$ of hydrogen molecule is
$$ \mathrm{v} _{\mathrm{av}}=\sqrt{\frac{8 \mathrm{RT}}{\pi \mathrm{M}}} $$
Given $\mathrm{v} _{\mathrm{av}}=\mathrm{v} _{\mathrm{esp}} ;$; herefore
$$ \begin{gathered} 11.2 \times 10^{3}=\sqrt{\frac{8 \times 8.31 \times \mathrm{T}}{3.14 \times 2 \times 10^{-3}}} \\ \mathrm{~T}=\frac{11.2 \times 11.2 \times 10^{6} \times 3.14 \times 2 \times 10^{-3}}{8 \times 8.31} \simeq 11849 \mathrm{~K} \end{gathered} $$
20. One kilogram of a diatomic gas is at a pressure of $8 \times 10^{4} \mathrm{Nm}^{-2}$. The density of the gas is $4 \mathrm{~kg} \mathrm{~m}^{-3}$. The energy of the gas due to its thermal motion is
(1) $3 \times 10^{4} \mathrm{~J}$
(2) $5 \times 10^{4} \mathrm{~J}$
(3) $6 \times 10^{4} \mathrm{~J}$
(4) $7 \times 10^{4} \mathrm{~J}$
Show Answer
Correct answer: (2)
Solution:
For a diatomic gas having $\mathrm{n}$ moles, the internal energy is $\mathrm{U}=\frac{5}{2} \mathrm{nRT}$ $\left[\mathrm{Clf} \mathrm{Cv}=\frac{5}{2} \mathrm{R}\right]$
Using gas equation $\mathrm{PV}=\mathrm{nRT}$, we rewrite $\mathrm{v}$ as
$$ \mathrm{U}=\frac{5}{2} \mathrm{PV} $$
The volume of gas $=\mathrm{V}=\frac{\text { mass }}{\text { density }}=\frac{1 \mathrm{~kg}}{4 \mathrm{~kg} \mathrm{~m}^{-3}}$
$\therefore \mathrm{U}=\frac{5}{2} \times 8 \times 10^{4} \times \frac{1}{4}=5 \times 10^{4} \mathrm{~J}$
21. One mole of an ideal gas is contained in a cubical vessel ABCDEFGH at $300 \mathrm{~K}$, one face EFGH of the vessel is made up of material which totally absorbs any gas molecules incident on it. At any given time
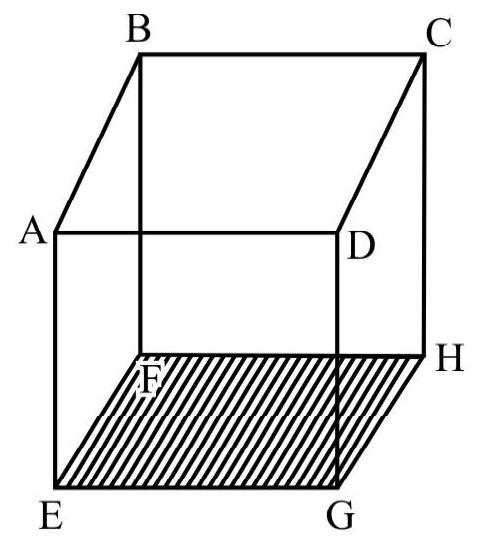
Fig. 1
(1) The pressure on EFGH would be zero
(2) The pressure on all the faces will be equal
(3) The pressure on EFGH would be double the pressure on $\mathrm{ABCD}$
(4) The pressure on EFGH would be half that on $\mathrm{ABCD}$
Show Answer
Correct answer: (4)
Solution:
Momentum transferred to the face $\mathrm{ABCD}$ due to collision of one atom $=2 \mathrm{mv}$
[The momentum of the gas molecule striking the face $\mathrm{ABCD}$ changes from mv to $-\mathrm{mv}$.]
As the face EFGH absorbs the gas molecule and it does not rebound therefore momentum transferred to this wall is mv only.
Since pressure is due to the total momentum of the gas molecules transferred to a face per second. Hence option (4) is correct answer.
22. A cylinder containing an ideal gas is in vertical position, and has a piston of mass $M$, that is able to move up or down without friction as shown in Fig. 2. If the temperature of gas inside cylinder is increased, then
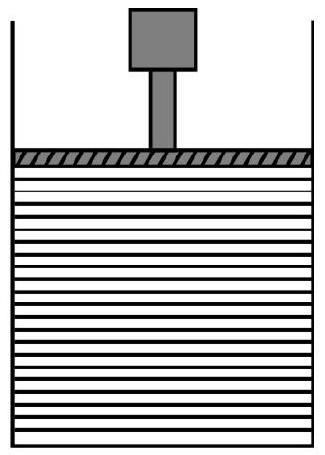
Fig. 2
(1) Both $P$ and $V$ of the gas will change (Incorrect)
(2) Only P will increase according to charles’s law
(3) $V$ will change but not $P$.
(4) P will change but not $\mathrm{V}$
Show Answer
Correct answer: (3)
Solution:
$\mathrm{P}=$ The total pressure on gas in cylinder
$=$ Atmospheric pressure + pressure due to mass of piston
$=\mathrm{P} _{\mathrm{at}}+\frac{\mathrm{Mg}}{\mathrm{A}}=\mathrm{constant}$
where $\mathrm{A}=$ area of cross-section of piston.
As the temperature is increased, only the volume increases in accordance with charles’s law as the piston moves up without friction.
23. Volume versus temperature graphs for a given mass of an ideal gas are shown in Fig. 3, at two different values of constant pressure. The correct relation between $P _{1}$ and $P _{2}$ is
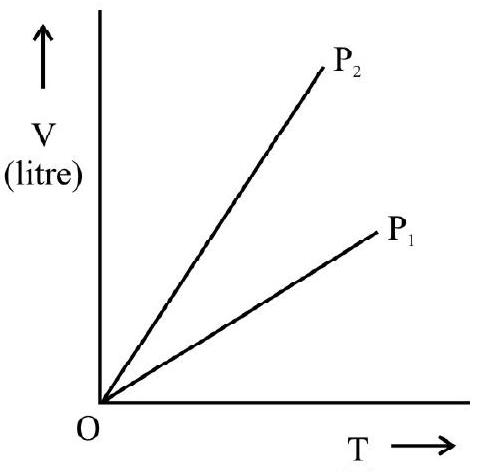
(K)
(1) $\mathbf{P} _{1}>\mathbf{P} _{2}$
(2) $\mathbf{P} _{1}=\mathrm{P} _{2}$
(3) $\mathbf{P} _{1}<\mathbf{P} _{2}$
(4) No conclusion can be drawn as we have insufficient information
Show Answer
Correct answer: (1)
Solution:
From the gas equation
$$ \begin{equation*} \mathrm{PV}=\mathrm{RT} \quad \text { or } \quad \mathrm{V}=\left(\frac{\mathrm{R}}{\mathrm{P}}\right) \mathrm{T} \tag{1} \end{equation*} $$
For $\mathrm{P}=$ constant, equation (1) is equation of a straight line. The slope of straight line is inversely proportion to pressure $\mathrm{P}$. Therefore
$$ \mathrm{P} _{1}>\mathrm{P} _{2} $$
24. The molecules of a given mass of a gas have root mean square speed of $100 \mathrm{~ms}^{-1}$ at $27^{\circ} \mathrm{C}$ and 1.00 atmospheric pressure. The root mean square speed of the molecules of the gas at $127^{\circ} \mathrm{C}$ and 2.0 atmospheric pressure will be
(1) $\frac{200}{\sqrt{3}} \mathrm{~ms}^{-1}$
(2) $100 \sqrt{2} \mathrm{~ms}^{-1}$
(3) $\frac{141.4}{\sqrt{2}} \mathrm{~ms}^{-1}$
(4) $\frac{200}{3} \mathrm{~ms}^{-1}$
Show Answer
Correct answer: (1)
Solution:
Given $\mathrm{T} _{1}=300 \mathrm{~K}, \mathrm{~T} _{2}=400 \mathrm{~K}, \mathrm{P} _{1}=1 \mathrm{~atm}, \mathrm{P} _{2}=2 \mathrm{~atm}$
From the ideal gas equation
$$ \frac{\mathrm{P} _{1} \mathrm{~V} _{1}}{\mathrm{~T} _{1}}=\frac{\mathrm{P} _{2} \mathrm{~V} _{2}}{\mathrm{~T} _{2}} $$
$\therefore \frac{\mathrm{V} _{1}}{\mathrm{~V} _{2}}=\frac{\mathrm{P} _{2} \mathrm{~T} _{1}}{\mathrm{P} _{1} \mathrm{~T} _{2}}=\frac{2 \times 300}{1 \times 400}=\frac{3}{2}$
We know $P _{1}=\frac{M}{3 V _{1}} v _{\text {rms }}^{2}$, and $P _{2}=\frac{M}{3 V _{2}} v _{\text {rms }}^{2}$
$\therefore \frac{\mathrm{P} _{1} \mathrm{~V} _{1}}{\mathrm{P} _{2} \mathrm{~V} _{2}}=\frac{\left(\mathrm{v} _{\mathrm{rms}}\right) _{1}^{2}}{\left(\mathrm{v} _{\mathrm{rms}}\right) _{2}^{2}}$
Substituting given values we get
$\frac{1}{2} \times \frac{3}{2}=\left(\frac{100}{\mathrm{v} _{\mathrm{rms}}}\right) _{2}^{2} ; \quad$ or $\quad \frac{\sqrt{3}}{2}=\frac{100}{\left(\mathrm{v} _{\mathrm{rms}}\right) _{2}}$
$\therefore\left(\mathrm{v} _{\mathrm{rms}}\right) _{2}=\frac{200}{\sqrt{3}} \mathrm{~ms}^{-1}$
25. Which of the following graph depicts behavior of an ideal gas?
Show Answer
Correct answer: (1)
Solution:
Graph (1) is correct as it represents $\mathrm{V} \alpha \mathrm{T}$ (at constant $\mathrm{P}$ ) which is Charle’s law.
Graph (2) is wrong as $\mathrm{P}$ and $\mathrm{V}$ graph at constant temperature will be rectangular hyperbola not a straight line.
Graph (3) is wrong as P is not inversely proportional to temperature at constant V. From charles’s law at constant volume $\mathrm{P}$ is directly proportional to $\mathrm{T}$, i.e. $\mathrm{P}$ vs $\mathrm{T}$ graph is a straight line.
Graph (4) is wrong as for a given mass of gas $\mathrm{PV}$ should increase on increasing temperature $\mathrm{T}$.
26. Two gases are under identical conditions of temperature, pressure and volume. The ratio of mean free paths of two molecules of gas having molecular diameter $1 \mathrm{~A}$ and $2 \mathrm{~A}$ is
(1) $2: 1$
(2) $4: 1$
(3) $8: 1$
(4) $1: 4$
Show Answer
Correct answer: (2)
Solution:
We know the mean free path
$$ \bar{\ell}=\frac{1}{\sqrt{2} \pi \mathrm{d}^{2} \mathrm{n} _{\mathrm{v}}} $$
where $\mathrm{d}=$ diameter of gaseous molecules, $\mathrm{n} _{\mathrm{v}}=$ number of molecules per unit volume. For a given gas $\bar{\ell}$ is inversely proportional to $\mathrm{d}^{2}$. Therefore
$\frac{\bar{\ell} _{1}}{\overline{\ell _{2}}}=\frac{\mathrm{d} _{2}^{2}}{\mathrm{~d} _{1}^{2}}=\left(\frac{2}{1}\right)^{2}=4: 1$
27. Nitrogen gas is contained in a container at a pressure $2.0 \mathrm{~atm}$ and temperature $17^{\circ} \mathrm{C}$, the radius of nitrogen molecules is roughly $1.0 \mathrm{~A}$. The ratio of collision time and the time for which molecules moves freely between two successive collision will be (Take molecular mass of nitrogen $=\mathbf{2 8 . 0 4}$ )
(1) $1: 550$
(2) $550: 1$
(3) $1: 1$
(4) $1: 2$
Show Answer
Correct answer: (1)
Solution:
Mean free path $\bar{\ell}=\frac{1}{\sqrt{2} \pi \mathrm{d}^{2} \mathrm{n} _{\mathrm{v}}}=\frac{\mathrm{k} _{\mathrm{B}} \mathrm{T}}{\sqrt{2} \pi \mathrm{d}^{2} \mathrm{P}} \hspace{50mm}. . . . . . . (1)$
Given $\mathrm{T}=273+17=290 \mathrm{~K} \hspace{30mm}$ [as $\left.\mathrm{P}=\mathrm{n} _{\mathrm{v}} \mathrm{k} _{\mathrm{B}} \mathrm{T}\right]$
$\mathrm{P}=2 \mathrm{~atm}=2 \times 1.013 \times 10^{5} \mathrm{~N} / \mathrm{m}^{2}$
$\mathrm{k} _{\mathrm{B}}=1.38 \times 10^{-23} \mathrm{~J} / \mathrm{K}, \mathrm{d}=2 \mathrm{~A}^{0}=2 \times 10^{-10} \mathrm{~m}$
Substituting values in Eqn(1) we have
$$ \begin{aligned} & \bar{\ell}=\frac{1.38 \times 10^{-23} \times 290}{\sqrt{2} \times 3.14 \times 4 \times 10^{-20} \times 2 \times 1.013 \times 10^{5}} \simeq 1.1 \times 10^{-7} \mathrm{~m} \\ & \mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{k} _{\mathrm{B}} \mathrm{T}}{\mathrm{m}}}=\sqrt{\frac{3 \times 1.38 \times 10^{-23} \times 290}{28 \times 1.66 \times 10^{-27}}} \quad\left(1 \mathrm{amu}=1.66 \times 10^{-27} \mathrm{~kg}\right) \\ & \quad \simeq 5.1 \times 10^{2} \mathrm{~ms}^{-1} \end{aligned} $$
Collision frequency $\mathrm{f}=\frac{\mathrm{v} _{\text {rms }}}{\ell}=\frac{5.1 \times 10^{2}}{1.1 \times 10^{-7}}=4.6 \times 10^{9} \mathrm{~s}^{-1}$
Time between two consecutive collisions $\mathrm{t}=\frac{\mathrm{d}}{\mathrm{v}}=\frac{2 \times 10^{-10}}{5.1 \times 10^{2}}=4 \times 10^{-13} \mathrm{~s}$
Time between two successive collision $=\mathrm{T}=\frac{1}{\mathrm{t}}=\frac{1}{4.6 \times 10^{9}}=2.2 \times 10^{-10} \mathrm{~s}$
$\therefore \frac{\mathrm{t}}{\mathrm{T}}=\frac{4 \times 10^{-13}}{2.2 \times 10^{-10}}=\frac{1}{550}$
28. A gaseous mixture consists of molecules of types $A, B$ and $C$ with masses $m _{A}>m _{B}>m _{C}$. The correct relation between their average kinetic energy is
(1) $\mathrm{K} _{\mathrm{A}}>\mathbf{K} _{\mathrm{B}}>\mathbf{K} _{\mathrm{C}}$
(2) $\mathbf{K} _{\mathrm{A}}<\mathrm{K} _{\mathrm{B}}<\mathrm{K} _{\mathrm{C}}$
(3) $\mathbf{K} _{\mathrm{A}}=\mathrm{K} _{\mathrm{B}}=\mathrm{K} _{\mathrm{C}}$
(4) $\mathbf{K} _{\mathrm{A}}=\mathbf{K} _{\mathrm{B}}<\mathbf{K} _{\mathrm{C}}$
Show Answer
Correct answer: (3)
Solution:
Average kinetic energy of translation per molecule
$$ \mathrm{K}=\frac{3}{2} \mathrm{k} _{\mathrm{B}} \mathrm{T} $$
where $\mathrm{k} _{\mathrm{B}}=$ Boltzmann’s constant, $\mathrm{T}=$ The absolute temperature of gas.
Obviously $\mathrm{K}$ is independent of mass of the molecule, i.e.
$$ \mathrm{K} _{\mathrm{A}}=\mathrm{K} _{\mathrm{B}}=\mathrm{K} _{\mathrm{C}} $$
29. Air is pumped into a cycle tyre. Which of the following statements is correct?
(1) Volume increases, pressure decreases and Boyle’s law is obeyed
(2) Volume decreases and pressure increases and Boyle’s law is obeyed
(3) Volume increases and pressure also increases, Boyle’s law not obeyed
(4) Volume increases, pressure increases but Boyle’s law is not obeyed
Show Answer
Correct answer: (3)
Solution:
Volume and pressure both increases, and Boyle’s law is not followed, because Boyle’s law is applicable only for the fixed mass of a gas, but in this case air molecules are pumped into the tyre, hence mass of air in the tyre increases.
30. A balloon has 5.0 gram mole of helium at $7^{\circ} \mathrm{C}$. The total internal energy of the system is
(1) $1.74 \times 10^{4} \mathrm{~J}$
(2) $3.84 \times 10^{3} \mathrm{~J}$
(3) $4.35 \times 10^{3} \mathrm{~J}$
(4) $5.80 \times 10^{3} \mathrm{~J}$
Show Answer
Correct answer: (1)
Solution:
$\mathrm{N}=$ Number of the atoms in 5.0 gram mole $=$ number of moles $\times$ Avogadro’s number $=5 \times 6.023 \times 10^{23}$ $\simeq 30 \times 10^{23}$ atoms
The total internal energy $=\mathrm{N} \times \frac{3}{2} \mathrm{k} _{\mathrm{B}} \mathrm{T}$
$$ =30 \times 10^{23} \times \frac{3}{2} \times 1.38 \times 10^{-23} \times 280=1.74 \times 10^{4} \mathrm{~J} $$
31. An insulated container containing monoatomic gas of molar mass $M$ is moving with velocity $\mathrm{v} _{0}$. The container is suddenly stopped, the change in its temperature is
(1) $\frac{\mathbf{M v} _{0}^{2}}{\mathrm{R}}$
(2) $\frac{M v _{0}^{2}}{5 \mathrm{R}}$
(3) $\frac{M v _{0}^{2}}{7 \mathrm{R}}$
(4) $\frac{\mathbf{M v} _{0}^{2}}{3 \mathrm{R}}$
Show Answer
Correct answer: (4)
Solution:
Let ’ $n$ ’ be the number of moles of the monoatomic gas in the container. Since molar mass of the gas is $M$ the total mass of the gas $=\mathrm{Mn}$
Change in kinetic energy of the gas, when container suddenly stops
$$ \Delta \mathrm{K}=\frac{1}{2}(\mathrm{Mn}) \mathrm{v} _{0}^{2}-0=\frac{1}{2}(\mathrm{Mn}) \mathrm{v} _{0}^{2} $$
Due to change $\Delta \mathrm{K}$ in internal energy of the gas let $\Delta \mathrm{T}$ be the change in temperature. Then
$$ \Delta \mathrm{U}=\mathrm{n} \times\left(\frac{3}{2} \mathrm{R}\right) \Delta \mathrm{T} \quad\left(\text { Clf } \Delta \mathrm{U}=\mathrm{nC} _{\mathrm{v}} \Delta \mathrm{T}, \mathrm{C} _{\mathrm{v}}=\frac{3}{2} \mathrm{R} \text { for monoatomic gas }\right) $$
Given $\Delta \mathrm{U}=\Delta \mathrm{K}$, hence
$$ \mathrm{n} \times \frac{3}{2} \mathrm{R} \Delta \mathrm{T}=\frac{1}{2} \mathrm{Mnv} _{0}^{2} $$
or $\Delta \mathrm{T}=\frac{\mathrm{Mv} _{0}^{2}}{3 \mathrm{R}}$
32. An ideal gas contains $10 \%$ of molecules with speed $200 \mathrm{~m} / \mathrm{s}, 20 \%$ molecules with speed $400 \mathrm{~m} / \mathrm{s}, 40 \%$ molecules have speed of $600 \mathrm{~m} / \mathrm{s}, 20 \%$ of molecules have speed $800 \mathrm{~m} / \mathrm{s}$ and remaining $10 \%$ moves with $1000 \mathrm{~m} / \mathrm{s}$ speed; the mass of the gas in $3 \times 10^{-26} \mathrm{~kg}$. The temperature of gas is
(1) $296 \mathrm{~K}$
(2) $888 \mathrm{~K}$
(3) $177 \mathrm{~K}$
(4) $127 \mathrm{~K}$
Show Answer
Correct answer: (1)
Solution:
The r.m.s speed, $\mathrm{v} _{\mathrm{rms}}$, of the gas molecules is
$$ \begin{aligned} \mathrm{v} _{\mathrm{rms}} & =\sqrt{\frac{10(200)^{2}+20(400)^{2}+40(600)^{2}+20(800)^{2}+10(1000)^{2}}{10}} \\ & =6.39 \times 10^{2} \mathrm{~ms}^{-1} \end{aligned} $$
From Boltzmann’s law of equipartition of energy
$$ \begin{aligned} & \frac{1}{2} \mathrm{mv} _{\mathrm{rms}}^{2}=\frac{3}{2} \mathrm{k} _{\mathrm{B}} \mathrm{T} \\ & \therefore \quad \mathrm{T}=\frac{\mathrm{mv} _{\mathrm{rms}}^{2}}{3 \mathrm{k} _{\mathrm{B}}}=\frac{3 \times 10^{-26} \times\left(6.39 \times 10^{2}\right)^{2}}{3 \times 1.38 \times 10^{-23}} \\ & \quad=29.6 \times 10=296 \mathrm{~K} \end{aligned} $$
33. One mole of an ideal gas (monoatomic) is mixed with one mole of diatomic gas, the ratio of specific heats at constant pressure and at constant volume, for the mixture is
(1) $\frac{3}{2}$
(2) $\frac{4}{3}$
(3) $\frac{35}{25}$
(4) $\frac{23}{15}$
Show Answer
Correct answer: (1)
Solution:
$\gamma$ for mixture is given by
$\frac{\mathrm{n} _{1}+\mathrm{n} _{2}}{\gamma-1}=\frac{\mathrm{n} _{1}}{\gamma _{1}-1}+\frac{\mathrm{n} _{2}}{\gamma _{2}-1}$
Given $\mathrm{n} _{1}=1, \mathrm{n} _{2}=1, \gamma _{1}=5 / 3$ (for monoatomic gas), and $\gamma _{2}=\frac{7}{5}$ (for monoatomic gas)
$\therefore \frac{1+1}{\gamma-1}=\frac{1}{\left(\frac{5}{3}-1\right)}+\frac{1}{\left(\frac{7}{5}-1\right)}$
or $\gamma=\frac{3}{2}$
34. The ratio of vapour densities of two gases at a given pressure in $9: 8$. The ratio of their $\mathrm{rms}$ speed is
(1) $3: 2 \sqrt{3}$
(2) $2 \sqrt{2}: 3$
(3) $9: 8$
(4) $8: 9$
Show Answer
Correct answer: (2)
Solution:
We know $\mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{P}}{\rho}}$
where $\mathrm{P}$ is pressure and $\rho$ density of gas. For same $\mathrm{P}$;
$$ \begin{aligned} \frac{\left(\mathrm{v} _{\mathrm{rms}}\right) _{1}}{\left(\mathrm{v} _{\mathrm{rms}}\right) _{2}} & =\sqrt{\frac{\rho _{2}}{\rho _{1}}} \\ & =\sqrt{\frac{8}{9}}=2 \sqrt{2}: 3 \end{aligned} $$
35. A thermally insulated vessel contains an ideal gas of molecular mass $M$ and ratio of specific heats $\gamma$. It is moving with speed $v$ and is suddenly brought to rest. Assuming no heat is lost to the surroundings, its temperature, on kelvin scale, increases by
(1) $\left[\frac{\gamma-1}{2 R}\right] \mathbf{M v}^{2}$
(2) $\left[\frac{\gamma-1}{2(\gamma+1) R}\right] M v^{2}$
(3) $\left[\frac{\gamma-1}{2 \gamma R}\right] M v^{2}$
(4) $\frac{\gamma \mathbf{M v}^{2}}{2}$
Show Answer
Correct answer: (1)
Solution:
As vessels comes to rest their is an increase in kinetic energy of atoms or molecules in it. Due to this the internal energy of gas changes. From law of conservation of energy
$$ \frac{1}{2} \mathrm{mv}^{2}=\mathrm{nC} _{\mathrm{v}} \mathrm{dT} $$
where $m$ is mass of gas and $n$ is number of moles of gas. We have
$\mathrm{n}=\frac{\mathrm{m}}{\mathrm{M}}, \mathrm{C} _{\mathrm{v}}=\frac{\mathrm{R}}{\gamma-1}$
$$ \therefore \quad \frac{1}{2} \mathrm{mv}^{2}=\frac{\mathrm{m}}{\mathrm{M}}\left(\frac{\mathrm{R}}{\gamma-1}\right) \mathrm{dT} $$
where $\mathrm{dT}$ is increase in temperature on Kelvin scale. Obviously
$$ \mathrm{dT}=\left[\frac{(\gamma-1)}{2 \mathrm{R}}\right] \mathrm{Mv}^{2} $$
36. Two non reactive monoatomic ideal gases have their atomic masses in the ratio $2: 3$. The ratio of their partial pressures, when enclosed in a vessel kept at constant temperature, is 4:3. The ratio of their densities is
(1) $1: 4$
(2) $1: 2$
(3) $6: 9$
(4) $8: 9$
Show Answer
Correct answer: (4)
Solution:
The pressure $\mathrm{P}$ exerted by a gas of molar mass $\mathrm{M}$ having mass $\mathrm{m}$ is
$\mathrm{P}=\left(\frac{\mathrm{m}}{\mathrm{M}}\right) \frac{\mathrm{RT}}{\mathrm{V}}=\frac{\rho \mathrm{RT}}{\mathrm{M}}$
At constant temperature, $\mathrm{T}$, obviously
$\frac{\mathrm{P} _{1}}{\mathrm{P} _{2}}=\frac{\rho _{1} / \mathrm{M} _{1}}{\rho _{2} / \mathrm{M} _{2}}=\frac{\rho _{1} \mathrm{M} _{2}}{\rho _{2} \mathrm{M} _{1}}$
or $\frac{\rho _{1}}{\rho _{2}}=\left(\frac{P _{1}}{P _{2}}\right)\left(\frac{M _{1}}{M _{2}}\right)=\left(\frac{4}{3}\right)\left(\frac{2}{3}\right)=8: 9$
37. The average translational energy and rms speed of molecules in a sample of oxygen gas at $300 \mathrm{~K}$ are $6.21 \times 10^{-21} \mathrm{~J}$ and $484 \mathrm{~ms}^{-1}$ respectively. The corresponding values at $600 \mathrm{~K}$ will be
(1) $12.42 \times 10^{-21} \mathrm{~J}, 968 \mathrm{~ms}^{-1}$
(2) $8.78 \times 10^{-21} \mathrm{~J}, 984 \mathrm{~ms}^{-1}$
(3) $6.21 \times 10^{-21} \mathrm{~J}, 968 \mathrm{~ms}^{-1}$
(4) $12.42 \times 10^{-21} \mathrm{~J}, 684 \mathrm{~ms}^{-1}$
Show Answer
Correct answer: (4)
Solution:
We know the average translational energy is directly proportional to the temperature therefore
Energy at $600 \mathrm{~K}=2 \times$ Energy at $300 \mathrm{~K}=12.42 \times 10^{-21} \mathrm{~J}$
The r.m.s speed $\mathrm{v} _{\mathrm{rms}}$ is directly to proportional to $\sqrt{\mathrm{T}}$; therefore
$\frac{\left(\mathrm{v} _{\mathrm{rms}}\right) _{1}}{\left(\mathrm{v} _{\mathrm{rms}}\right) _{2}}=\sqrt{\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}}=\sqrt{\frac{600}{300}}=\sqrt{\frac{1}{2}}$
$\left(\mathrm{v} _{\mathrm{rms}}\right) _{2}=\sqrt{2} \times 484=684 \mathrm{~ms}^{-1}$
38. An open glass tube is immersed in mercury in such a way that a length of $8 \mathrm{~cm}$ extends above the $\mathrm{Hg}$ level as shown in Fig. 4. The open end of the tube is then closed and sealed and the tube is raised vertically by an additional $46 \mathrm{~cm}$. The length of the air column above mercury in the tube now will be
(1) $38 \mathrm{~cm}$
(2) $6 \mathrm{~cm}$
(3) $16 \mathrm{~cm}$
(4) $22 \mathrm{~cm}$
Show Answer
Correct answer: (3)
Solution:
Let $A$ be the area of cross-section of the tube. $\mathrm{P} _{1}, \mathrm{~V} _{1}$ denote pressure and volume of air in tube initially. $\mathrm{P} _{2}$, $V _{2}$ are corresponding quantities when one end of tube has been scaled. Under isothermal conditions
$$ \mathrm{P} _{1} \mathrm{~V} _{1}=\mathrm{P} _{2} \mathrm{~V} _{2} $$
or $\quad \mathrm{P} _{0} 8 \times \mathrm{A}=\mathrm{P} _{2} \times(54-x) \mathrm{A}$
where $x$ is length of mercury inside tube as shown in Fig. 4
$\therefore 8 \mathrm{P} _{0}=\mathrm{P} _{2}(54-x) \hspace{40mm} . . . . . . . . (1)$
But $\mathrm{P} _{1}=\mathrm{P} _{2}+\rho g x$
or $\mathrm{P} _{2}=\mathrm{P} _{0}-\rho \mathrm{g} x \hspace{40mm} . . . . . . . . (2)$
From Eqns (i) and (ii) we have
$8 \mathrm{P} _{0}=\left(\mathrm{P} _{0}-\rho \mathrm{g} x\right)(54-x)$
Taking $\mathrm{P} _{0}=76 \mathrm{~cm}$ of $\mathrm{Hg}$ column we get
$8(76)=(76-x)(54-x)$
$\therefore x=38 \mathrm{~cm}$
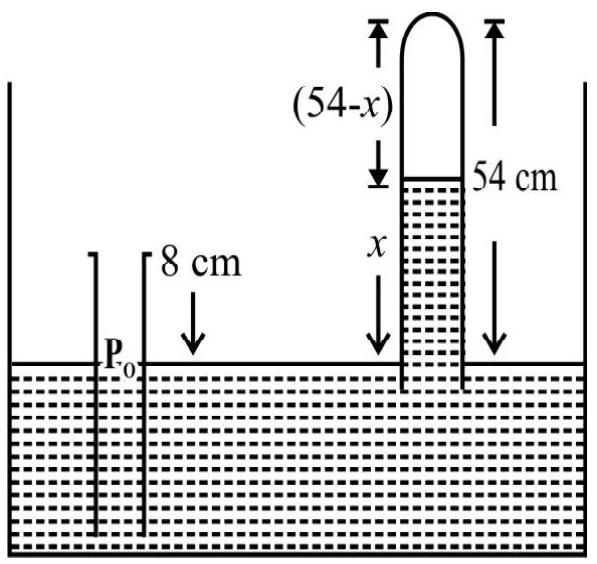
Fig. 4
The length of air column in closed tube $=54-38=16 \mathrm{~cm}$
39. Three perfect monoatomic gases at absolute temperatures $T _{1}, T _{2}$ and $T _{3}$ are mixed. The masses of the molecules are $m _{1}, m _{2}$ and $m _{3}$ and the number of moles are $n _{1}, n _{2}$ and $n _{3}$ respectively. Assuming no loss of energy the final temperature of the mixture is
(1) $\frac{n _{1}^{2} T _{1}^{2}+n _{2}^{2} T _{2}^{2}+n _{3}^{2} T _{3}^{2}}{n _{1} T _{1}+n _{2} T _{2}+n _{3} T _{3}}$
(2) $\frac{T _{1}+T _{2}+T _{3}}{3}$
(3) $\frac{n _{1} T _{1}+n _{2} T _{2}+n _{3} T _{3}}{n _{1}+n _{2}+n _{3}}$
(4) $\frac{n _{1} T _{1}^{2}+n _{2} T _{2}^{2}+n _{3} T _{3}^{2}}{n _{1}+n _{2}+n _{3}}$
Show Answer
Correct answer: (3)
Solution:
The total internal energy of mixture $=\mathrm{U}=\mathrm{U} _{1}+\mathrm{U} _{2}+\mathrm{U} _{3}$
$$ \begin{equation*} =\mathrm{n} _{1} \mathrm{C} _{\mathrm{v}} \mathrm{T} _{1}+\mathrm{n} _{2} \mathrm{C} _{\mathrm{v}} \mathrm{T} _{2}+\mathrm{n} _{3} \mathrm{C} _{\mathrm{v}} \mathrm{T} _{3} \tag{i} \end{equation*} $$
Let $\mathrm{T}$ be temperature of mixture, then
$$ \begin{equation*} \mathrm{U}=\left(\mathrm{n} _{1}+\mathrm{n} _{2}+\mathrm{n} _{3}\right) \mathrm{C} _{\mathrm{v}} \mathrm{T} \tag{ii} \end{equation*} $$
From Eqns (i) and (ii) we have
$$ \begin{aligned} & \left(\mathrm{n} _{1}+\mathrm{n} _{2}+\mathrm{n} _{3}\right) \mathrm{C} _{\mathrm{v}} \mathrm{T}=\left(\mathrm{n} _{1} \mathrm{~T} _{1}+\mathrm{n} _{2} \mathrm{~T} _{2}+\mathrm{n} _{3} \mathrm{~T} _{3}\right) \mathrm{C} _{\mathrm{v}} \\ & \therefore \mathrm{T}=\frac{\mathrm{n} _{1} \mathrm{~T} _{1}+\mathrm{n} _{3} \mathrm{~T} _{3}+\mathrm{n} _{3} \mathrm{~T} _{3}}{\mathrm{n} _{1}+\mathrm{n} _{2}+\mathrm{n} _{3}} \end{aligned} $$
40. $\mathbf{v} _{\text {avg }}, \mathbf{v} _{\mathrm{rms}}$ and $\mathbf{v} _{\mathrm{mps}}$ denote the mean speed, $\mathrm{rms}$ speed and most probable speed of molecules in an ideal monoatomic gas at absolute temperature $T$, the mass of the molecules is $m$, then
(1) No molecule can have speed greater than $\sqrt{2} v _{\mathrm{rms}}$
(2) No molecule can have speed less than $v _{\text {mps }} \sqrt{2}$
(3) $\mathbf{v} _{\text {mps }}<\mathbf{v} _{\text {avg }}<\mathbf{v} _{\text {rms }}$
(4) The average kinetic energy of a molecules is $\frac{3}{4} \mathrm{mv} _{\mathrm{mps}}^{2}$
Show Answer
Correct answer: (4)
Solution:
We know the relation between $\mathrm{v} _{\mathrm{rms}}$ and $\mathrm{v} _{\mathrm{mps}}$ is
$\mathrm{v} _{\mathrm{mps}}=\sqrt{\frac{2}{3}} \mathrm{v} _{\mathrm{rms}}$
$\therefore \mathrm{v} _{\mathrm{ms}}^{2}=\frac{3}{2} \mathrm{v} _{\mathrm{mps}}^{2}$
Thus average kinetic energy for molecule
$$ =\frac{1}{2} \mathrm{mv} _{\mathrm{rms}}^{2}=\frac{3}{4} \mathrm{mv} _{\mathrm{mps}}^{2} $$
41. Pressure versus temperature graph of an ideal gas at constant volume is a straight line ’ $A$ ’ as shown in Fig. 5. The mass of the gas is doubled and volume is halved. The corresponding pressure $v$ s temperature graph is given by
(1) $\mathbf{A}$
(2) $\mathbf{B}$
(3) $\mathbf{C}$
(4) None of the above
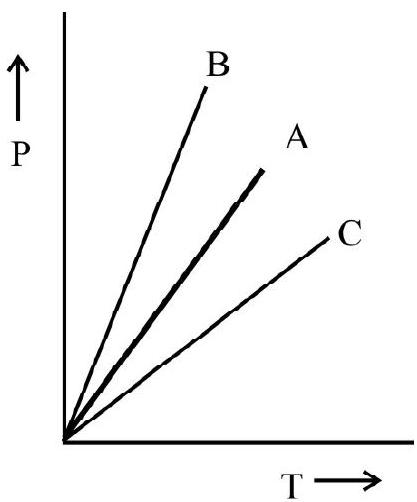Fig. 5
Show Answer
Correct answer: (2)
Solution:
For an ideal gas
$$ \mathrm{PV}=\mathrm{nRT} $$
where $\mathrm{n}=$ number of moles. For mass $\mathrm{m}$ of gas having molar mass $\mathrm{M} ; \mathrm{n}=\frac{\mathrm{m}}{\mathrm{M}}$. Therefore
$$ \mathrm{P}=\frac{\mathrm{nRT}}{\mathrm{V}}=\frac{\mathrm{mRT}}{\mathrm{MV}} $$
or $\quad \mathrm{P}=\left(\frac{\mathrm{mR}}{\mathrm{MV}}\right) \mathrm{T}$
Obviously at constant volume $\mathrm{P}-\mathrm{T}$ graph is a straight line having a slope $=\frac{\mathrm{mR}}{\mathrm{MV}}$. When $\mathrm{m}$ is doubled and volume is halved the slope of $\mathrm{P} v s \mathrm{~T}$ becomes 4 times its earlier value i.e. increases.
Hence graph B is correct.
42. Two gases occupy two containers $A$ and $B$. The gas in $A$ of volume $0.11 \mathrm{~m}^{3}$ exerts a pressure of $1.38 \mathrm{MPa}$. The gas in $B$ of volume $0.16 \mathrm{~m}^{3}$ exerts a pressure of $0.69 \mathrm{MPa}$. Two containers are connected to one another by a tube of negligible volume and the gases are allowed to intermix. The equilibrium pressure in the container if the temperature remains constant will be
(1) $2.81 \mathrm{MPa}$
(2) $0.485 \mathrm{MPa}$
(3) $1.84 \mathrm{MPa}$
(4) $0.97 \mathrm{MPa}$
Show Answer
Correct answer: (4)
Solution:
Let $n _{1}$ and $n _{2}$ be number of moles of gas in A and B. For mixture the number of moles, $n$, is
$$ \mathrm{n}=\mathrm{n} _{1}+\mathrm{n} _{2} $$
From ideal gas equation $\mathrm{n}=\frac{\mathrm{PV}}{\mathrm{RT}}$. At constant temperature
$$ \mathrm{P}\left(\mathrm{V} _{1}+\mathrm{V} _{2}\right)=\mathrm{P} _{1} \mathrm{~V} _{1}+\mathrm{P} _{2} \mathrm{~V} _{2} $$
where $\mathrm{P}$ is equilibrium pressure in both containers.
$$ \begin{aligned} \therefore \quad \mathrm{P} & =\frac{\mathrm{P} _{1} \mathrm{~V} _{1}+\mathrm{P} _{2} \mathrm{~V} _{2}}{\mathrm{~V} _{1}+\mathrm{V} _{2}} \\ & =\frac{1.38 \times 0.11+0.69 \times 0.16}{0.11+0.16} \mathrm{MPa} \\ & =0.97 \mathrm{MPa} \end{aligned} $$
43. A partially inflated balloon contains $500 \mathrm{~m}^{3}$ of helium at $27^{\circ} \mathrm{C}$ and $1 \mathrm{~atm}$ pressure. What is the volume of the helium at an attitude of $18000 \mathrm{ft}$, where the pressure is $0.5 \mathrm{~atm}$ and temperature is $-3^{0} \mathrm{C}$ ?
(1) $300 \mathrm{~m}^{3}$
(2) $900 \mathrm{~m}^{3}$
(3) $1800 \mathrm{~m}^{3}$
(4) $600 \mathrm{~m}^{3}$
Show Answer
Correct answer: (2)
Solution:
From the ideal gas equation $\mathrm{PV}=\mathrm{nRT}$; for same mass of gas (i.e. $\mathrm{n}=$ constant)
$\frac{\mathrm{P} _{1} \mathrm{~V} _{1}}{\mathrm{~T} _{1}}=\frac{\mathrm{P} _{2} \mathrm{~V} _{2}}{\mathrm{~T} _{2}} \quad$ or $\quad \mathrm{V} _{2}=\left(\frac{\mathrm{P} _{1} \mathrm{~V} _{1}}{\mathrm{P} _{2}}\right) \frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}$ $=\left(\frac{\mathrm{P} _{1}}{\mathrm{P} _{2}}\right)\left(\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}\right) \mathrm{V} _{1}$
Substituting given values we have
$\mathrm{V} _{2}=\frac{1}{0.5} \times \frac{270}{300} \times 500=900 \mathrm{~m}^{3}$
44. An ideal gas exerts a pressure of $1.52 \mathrm{MPa}$. When its temperature is $298.15 \mathrm{~K}$ and its volume is $10^{-2} \mathrm{~m}^{3}$. If the gas is (i) molecular hydrogen and (ii) oxygen the ratio of mass density is
(1) $1: 16$
(2) $1: 8$
(3) $1: 32$
(4) $16: 1$
Show Answer
Correct answer: (1)
Solution:
Number of moles of the gas; using ideal gas equation is $\mathrm{n}=\frac{\mathrm{PV}}{\mathrm{RT}}=\frac{1.52 \times 10^{6} \times 10^{-2}}{8.314 \times 298.15}=6.13$
The density of gas $=\rho=\frac{\text { mass }}{\text { volume }}=\frac{\mathrm{nM}}{\mathrm{V}}$. Therefore
$\rho _{\mathrm{H}}=\frac{\mathrm{nM} _{\mathrm{H}}}{\mathrm{V}}$, and $\rho _{0}=\frac{\mathrm{nM} _{0}}{\mathrm{~V}}$
Obviously
$$ \frac{\rho _{\mathrm{H}}}{\rho _{0}}=\frac{\mathrm{M} _{\mathrm{H}}}{\mathrm{M} _{0}}=\frac{1}{16} $$
45. One gram mole of oxygen at $27^{\circ} \mathrm{C}$ and one atmospheric pressure is enclosed in a vessel. Assuming the molecules are moving with rms speed, the number of collisions per second which the molecules make with one square meter area of the vessel is
(1) $1.965 \times 10^{27}$
(2) $3.93 \times 10^{27}$
(3) $0.9825 \times 10^{27}$
(4) $5.895 \times 10^{27}$
Show Answer
Correct answer: (1)
Solution:
Mass of one oxygen molecule $\mathrm{m}=\frac{\mathrm{M}}{\mathrm{N} _{\mathrm{Av}}}=\frac{32}{6.02 \times 10^{23}}=5.316 \times 10^{-23} \mathrm{~g}$
The r.m.s speed of oxygen
$\mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{kT}}{\mathrm{m}}}$
$$ =\sqrt{\frac{3 \times 1.38 \times 10^{-23} \times 300}{5.316 \times 10^{-26}}}=483.35 \mathrm{~ms}^{-1} $$
Change in linear momentum in one collision of molecule with the wall
$$ \begin{aligned} & \Delta \mathrm{P}=2 \mathrm{mv} _{\mathrm{rms}}=2 \times 5.316 \times 10^{-26} \times 483.35 \mathrm{~kg} \mathrm{~ms}^{-1} \\ & =5.14 \times 10^{-23} \mathrm{~kg} \mathrm{~ms}^{-1} \end{aligned} $$
Let ’ $n$ ’ be the number of collisions of the molecules with the wall per second. The force, F, exerted by the molecules on the wall is
$$ \mathrm{F}=\mathrm{n} \Delta \mathrm{P}=\mathrm{n} \times 5.14 \times 10^{-23} \mathrm{~N} $$
Since pressure $=\frac{\text { Force }}{\text { Area }}$, for unit area of the wall, the pressure equals force. Therefore
$\mathrm{n} \times 5.14 \times 10^{-23}=1$ atmospheric pressure $=1.01 \times 10^{5}$
or $\mathrm{n}=1.965 \times 10^{27}$
46. An ideal diatomic gas with $C _{V}=\frac{5}{2} R$ occupies a volume $V _{i}$ at constant pressure $P _{i}$. The gas undergoes a process in which pressure is directly proportional to volume. At the end of the process, the rms speed of the gas molecules has doubled from its initial value, the amount of the energy transferred to the gas in the form of heat is
(1) $9 \mathrm{P} _{\mathrm{i}} \mathbf{V} _{\mathrm{i}}$
(2) $6 \mathbf{P} _{\mathrm{i}} \mathbf{V} _{\mathrm{i}}$
(3) $15 \mathrm{P} _{\mathrm{i}} \mathrm{V} _{\mathrm{i}}$
(4) $21 \mathrm{P} _{\mathrm{i}} \mathrm{V} _{\mathrm{i}}$
Show Answer
Correct answer: (1)
Solution:
As per the questions $\mathrm{P}$ is directly proportional to $\mathrm{V}$ or $\mathrm{PV}^{-1}=$ constant. Molar heat capacity in the process $\mathrm{PV}^{x}=$ constant; $x=-1$; is
$\mathrm{C}=\frac{\mathrm{R}}{\gamma-1}+\frac{\mathrm{R}}{1-x}=\mathrm{C} _{\mathrm{v}}+\frac{\mathrm{R}}{1-x}$
$\therefore \quad \mathrm{C}=\mathrm{C} _{\mathrm{v}}+\frac{\mathrm{R}}{2}=\frac{5}{2} \mathrm{R}+\frac{\mathrm{R}}{2}=3 \mathrm{R} \hspace{50mm} . . . . . (1)$
At the end of the process the rms speed of gas molecules gets doubled. Therefore the temperature becomes fourfold. The heat $\Delta \mathrm{Q}$; received by the gas is
$$ \begin{aligned} \Delta \mathrm{Q}= & \mathrm{nC} \Delta \mathrm{T}=\mathrm{nC}\left(\mathrm{T} _{\mathrm{f}}-\mathrm{T} _{\mathrm{i}}\right) \\ & =\mathrm{nC}\left(4 \mathrm{~T} _{\mathrm{i}}-\mathrm{T} _{\mathrm{i}}\right)=\mathrm{n} \times 3 \mathrm{R} \times 3 \mathrm{~T} _{\mathrm{i}} \\ & =9\left(\mathrm{nRT} _{\mathrm{i}}\right)=9 \mathrm{P} _{\mathrm{i}} \mathrm{V} _{\mathrm{i}} \end{aligned} $$
47. A cubical box of side $1 \mathrm{~m}$ contains helium gas $(M=4)$ at a pressure of $100 \mathrm{Nm}^{-2}$. A molecule hits the wall of the container 500 times in one second without hitting other molecules and travels parallel to one edge with rms speed. The total mass of the helium gas in the box is $\left(\mathbf{R}=\mathbf{8 . 3 1 4} \mathrm{J \quad mole}^{-1} \mathrm{~K}^{-1}\right)$
(1) $6.0 \times 10^{-4} \mathrm{~kg}$
(2) $0.75 \times 10^{-4} \mathrm{~kg}$
(3) $3.0 \times 10^{-4} \mathrm{~kg}$
(4) $12 \times 10^{-4} \mathrm{~kg}$
Show Answer
Correct answer: (3)
Solution:
Time period of collision of molecule with the wall $=\frac{1}{500} \mathrm{~s}$.
Let $x$ be the side of the cube. The molecule travels a distance $2 x$ between two consecutive collisions with the same wall with a constant speed equal to $\mathrm{v} _{\mathrm{rms}}$. Obviously
$$ \begin{aligned} & \frac{2 x}{\mathrm{v} _{\mathrm{rms}}}=\frac{1}{500} \\ & \text { or } \mathrm{v} _{\mathrm{rms}}=1000 \mathrm{~ms}^{-1} \end{aligned} $$
The temperature, $T$, of gas, using kinetic interpretation of temperature and Boltzmann’s law of equipartition of energy is
$$ \frac{1}{2} \mathrm{Mv} _{\mathrm{rms}}^{2}=\left(\frac{3}{2} \mathrm{kT}\right) \mathrm{N} _{\mathrm{AV}}=\frac{3}{2} \mathrm{RT} $$
or $\mathrm{T}=\frac{\mathrm{Mv} _{\mathrm{rms}}}{3 \mathrm{R}}$
$$ =\frac{(1000)^{2} \times 4 \times 10^{-3}}{3 \times 8.314}=160 \mathrm{~K} $$
Also, $P V=n R T, V=\left(\frac{m}{M}\right)$ RT
where $m$ is mass of gas. Obviously
$$ \mathrm{m}=\frac{\mathrm{MPV}}{\mathrm{RT}}=\frac{4 \times 10^{-3} \times 100 \times 1}{8.31 \times 160}=3 \times 10^{-4} \mathrm{~kg} $$
48. A cubical box of side $1 \mathrm{~m}$ contains helium gas (atomic weight $4 \mathrm{~g}$ ) at a pressure of $100 \mathrm{Nm}^{-2}$. During an observation time of 1 second an atom traveling with the root mean square speed parallel to one of the edges of the cube, was found to make 500 collision with the particular wall without any collision with other atoms. The temperature of the gas is
$\left(\mathrm{R}=8.314 \mathrm{~J} / \mathrm{mol} \mathrm{K}, \mathrm{k}=\right.$ Boltzmann’s constant $\left.=1.38 \times 10^{-23} \mathrm{JK}^{-1}\right)$
(1) $80 \mathrm{~K}$
(2) $640 \mathrm{~K}$
(3) $160 \mathrm{~K}$
(4) $40 \mathrm{~K}$
Show Answer
Correct answer: (3)
Solution:
Time between two consecutive collisions with one wall $=\frac{1}{500}$ s. Let ’ $\ell$ ’ be the length of the cube. Time between two consecutive collisions on same walls is $\frac{2 \ell}{\mathrm{v} _{\mathrm{rms}}}$. $\therefore \quad \frac{1}{500}=\frac{2 \ell}{\mathrm{v} _{\mathrm{rms}}}$ or $\mathrm{v} _{\mathrm{rms}}=1000 \mathrm{~ms}^{-1}$
We know, $\mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}}$; therefore
$\mathrm{T}=\frac{\mathrm{Mv} _{\text {rms }}^{2}}{3 \mathrm{R}}=\frac{4 \times 10^{-3} \times(1000)^{2}}{3 \times 8.314}$
$=160 \mathrm{~K}$
49. For a diatomic gas molecules which rotate but does not vibrate, the heat capacity at constant pressure is greater than that at constant volume by $29.1 \mathrm{JK}^{-1}$, the values of heat capacities at constant volume and at constant pressure are
(1) $101.85 \mathrm{JK}^{-1}$ and $72.75 \mathrm{JK}^{-1}$
(2) $72.75 \mathrm{JK}^{-1}$ and $101.85 \mathrm{JK}^{-1}$
(3) $43.65 \mathrm{JK}^{-1}$ and $72.75 \mathrm{JK}^{-1}$
(4) $72.75 \mathrm{JK}^{-1}$ and $43.65 \mathrm{JK}^{-1}$
Show Answer
Correct answer: (2)
Solution:
Let $\mathrm{C} _{\mathrm{P}}$ and $\mathrm{C} _{\mathrm{V}}$ be the molar specific heat of gas at constant pressure and constant volume respectively. Let $\mathrm{n}$ be number of moles. Given
$\left(\mathrm{C} _{\mathrm{P}}-\mathrm{C} _{\mathrm{V}}\right)=\mathrm{nR}=29.1 \mathrm{JK}^{-1}$
$\therefore \mathrm{n}=\frac{29.1}{8.314}$ mole $=3.5 \mathrm{~mole}$
Let $C _{v}^{\prime}$ be the specific heat of $n$ moles of gas at constant volume. Obviously
$\mathrm{C} _{\mathrm{v}}^{\prime}=\mathrm{nC} _{\mathrm{v}}=3.5 \times \frac{5}{2} \mathrm{R}=3.5 \times \frac{5}{2} \times 8.314=72.75 \mathrm{JK}^{-1}$
Also, $\mathrm{C} _{\mathrm{P}}^{\prime}-\mathrm{C} _{\mathrm{V}}^{\prime}=\mathrm{nR}$; therefore
$$ \begin{aligned} & \mathrm{C} _{\mathrm{P}}^{\prime}=\mathrm{nR}+\mathrm{C} _{\mathrm{v}}^{\prime}=\mathrm{n} \times \frac{7}{2} \mathrm{R}=3.5 \times \frac{7}{2} \times 8.314 \\ & =101.85 \mathrm{JK}^{-1} \end{aligned} $$
50. At $0^{0} \mathrm{C}$ and $1 \mathrm{~atm}$ pressure, the densities of air, oxygen and nitrogen are $1.284 \mathrm{~kg} \mathrm{~m}^{-3}$, $1.429 \mathrm{~kg} \mathrm{~m}^{-3}$ and $1.251 \mathrm{~kg} \mathrm{~m}^{-3}$ respectively. The percentage in terms of mass of Nitrogen in air, from given data assuming only given gases are present in air is
(1) 76.4
(2) 23.6
(3) 13.7
(4) 86.3
Show Answer
Correct answer: (1)
Solution:
Let $n _{1}$ and $n _{2}$ be the fraction of oxygen and nitrogen in air. $\rho _{1}, \rho _{2}$ and $\rho$ denote density of oxygen, nitrogen and air respectively. Then
$\rho=\frac{n _{1} \rho _{1}+n _{2} \rho _{2}}{n _{1}+n _{2}}$. But $n _{1}+n _{2}=1 ;$ or $n _{1}=1-n _{2}$. Therefore
$\rho=\frac{\left(1-\mathrm{n} _{2}\right) \rho _{1}+\mathrm{n} _{2} \rho _{2}}{1}=\rho _{1}+\mathrm{n} _{2}\left(\rho _{2}-\rho _{1}\right)$
$\therefore \quad \mathrm{n} _{2}=\frac{\rho-\rho _{1}}{\rho _{2}-\rho _{1}}=\frac{1.293-1.429}{1.251-1.429}$
$=\frac{136}{178} \times 100=76.4 \%$
51. An ideal diatomic gas at 300 K has molecules of moment of inertia $8.28 \times 10^{-38}g cm^2$ . The root mean square angular velocity of the molecules in radian per second is
(1) $1 \times 10^{12}$
(2) $\frac{1}{\sqrt{2}} \times 10^{12}$
(3) $\sqrt{3} \times 10^{12}$
(4) $\sqrt{\frac{3}{2}} \times 10^{12}$
Show Answer
Correct answer: (1)
Solution:
Rotational kinetic energy $=\frac{1}{2} \mathrm{I} \omega^{2} \hspace{50mm} . . . . . . . . . .(1)$
where $\omega$ is root mean square angular speed. There are two degrees of freedom of rotational motion i.e. clockwise or anticlockwise. Using Boltzmann’s law of equipartition of energy
Rotational $\mathrm{K} . \mathrm{E}=2\left(\frac{1}{2} \mathrm{kT}\right) \hspace{40mm} . . . . . . .(2)$
From Eqns. (1) and (2) we have
$$ \begin{gathered} \omega=\sqrt{\frac{2 \mathrm{kT}}{\mathrm{I}}}=\sqrt{\frac{2 \times 1.38 \times 10^{-23} \times 300}{8.28 \times 10^{-38} \times 10^{-7}}} \\ =10^{12} \sqrt{\frac{6 \times 1.38}{828}}=10^{12} \end{gathered} $$
52. The mass of hydrogen molecules is $3.32 \times 10^{-27} \mathrm{~kg}$. If $10^{23}$ hydrogen molecules strikes per second at $2 \mathrm{~cm}^{2}$ area of a rigid wall at an angle $\theta=45^{\circ}$ with the normal as shown in Fig. 6 and rebound back with a speed of $1000 \mathrm{~ms}^{-1}$. Then the pressure exerted on the wall is
(1) $2.34 \times 10^{3} \mathrm{~Pa}$
(2) $0.23 \times 10^{3} \mathrm{~Pa}$
(3) $0.23 \times 10^{-5} \mathrm{~Pa}$
(4) $23.4 \times 10^{3} \mathrm{~Pa}$
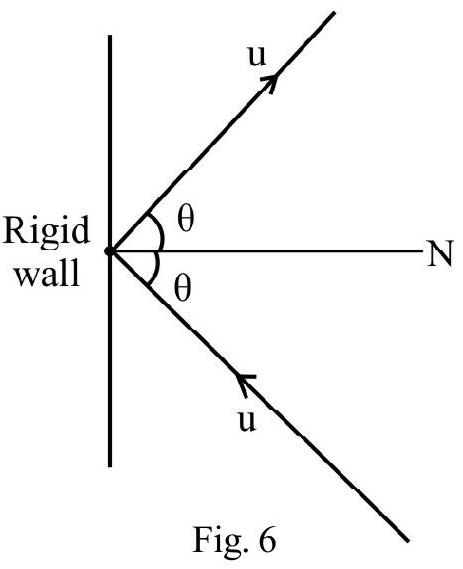Fig. 6
Show Answer
Correct answer: (1)
Solution:
Change in linear momentum of the hydrogen molecule due to one collision with the wall
$$ \begin{aligned} |\Delta \mathbf{P}| & =2 \mathrm{mu} \cos \theta=2 \times 3.32 \times 10^{-27} \times 1000 \times \cos 45^{0} \\ & =3.32 \sqrt{2} \times 10^{-24} \mathrm{kgm} \mathrm{s}^{-1} \end{aligned} $$
$\mathrm{F}=$ Force exerted on the wall by the molecules $=$ Total change in linear momentum of molecules in $1 \mathrm{~s}$.
$$ =10^{23} \times|\Delta \mathrm{P}|=3.32 \sqrt{2} \times 10^{-24} \times 10^{23} \mathrm{~N} $$
The pressure $\mathrm{P}$ exerted on the wall
$$ \mathrm{P}=\frac{\mathrm{F}}{\mathrm{A}}=\frac{3.32 \sqrt{2} \times 10^{-1}}{2 \times 10^{-4}}=2.34 \times 10^{3} \mathrm{~Pa} $$
53. The pressure ( $P$ ) and density ( $\rho$ ) of a given mass of a gas expressed by Boyle’s law $P=C \rho$ where $C$ is a constant. The statement is true
(1) for any gas under all conditions
(2) for some gases under some conditions
(3) only if the temperature in kept constant
(4) for monoatomic gases only
Show Answer
Correct answer: (3)
Solution:
Boyle’s law states that $\mathrm{P}$ is directly proportional to $\frac{1}{\mathrm{~V}}$ at constant temperature. Hence option(3) is correct.
54. Three closed vessels $A, B$ and $C$ are at same temperature $T$ and contain gases which obey Maxwell distribution law of velocity. Vessel $A$ contains $O _{2}$, with molecules having an average speed of $V _{1}$. Vessel B contains only $N _{2}$ with molecules having an average speed $V _{2}$. Vessel ’ $C$ ’ contains mixture of equal quantities of $\mathrm{O} _{2}$ and $\mathrm{N} _{2}$. The average speed of the $\mathrm{O} _{2}$ molecules in the mixture is
(1) $\left(\frac{V _{1}+V _{2}}{2}\right)$
(2) $\sqrt{\frac{V _{1}^{2}+V _{2}^{2}}{2}}$
(3) $\sqrt{\mathrm{V} _{1} \mathrm{~V} _{2}}$
(4) $\mathrm{V} _{1}$
Show Answer
Correct answer: (4)
Solution:
As the temperature of mixture is same as that of the vessel $\mathrm{A}$ and $\mathrm{B}$ hence average speed of $\mathrm{O} _{2}$ molecules in mixture will be same as in vessel $\mathrm{A}$ i.e. $\mathrm{V} _{1}$.
55. 28 gram of $\mathbf{N} _{2}$ gas is contained in a flask at pressure of $10 \mathrm{~atm}$ and a temperature of $57^{\circ} \mathrm{C}$. Due to leakage in the flask, the pressure is reduced to half and temperature to $27^{\circ} \mathrm{C}$. The quantity of $\mathbf{N} _{2}$ gas that leaked out is
(1) $\frac{11}{20} \mathrm{~g}$
(2) $\frac{20}{11} \mathrm{~g}$
(3) $\frac{5}{63} \mathrm{~g}$
(4) $\frac{63}{5} \mathrm{~g}$
Show Answer
Correct answer: (4)
Solution:
Let $n _{1}$ and $n _{2}$ be the number of moles of $\mathrm{N} _{2}$ present in flask initially and finally. Then from ideal gas equation
$\mathrm{n} _{1}=\frac{\mathrm{P} _{1} \mathrm{~V}}{\mathrm{RT} _{1}}$ and $\mathrm{n} _{2} \frac{\mathrm{P} _{2} \mathrm{~V}}{\mathrm{RT} _{2}}$. Therefore $\frac{\mathrm{n} _{1}}{\mathrm{n} _{2}}=\frac{\mathrm{P} _{1} \mathrm{~T} _{2}}{\mathrm{P} _{2} \mathrm{~T} _{1}}=\frac{10 \times 300}{5 \times 330}=\frac{600}{330}=\frac{20}{11}$ or $\mathrm{n} _{2}=\frac{11}{20} \mathrm{n} _{1}$
Let $\mathrm{M}$ be the molar mass of $\mathrm{N} _{2}$. Obviously the mass $\Delta \mathrm{m}$ of $\mathrm{N} _{2}$ that has leaked out is
$$ \begin{aligned} \Delta \mathrm{m}= & \left(\mathrm{n} _{1}-\mathrm{n} _{2}\right) \mathrm{M}=\frac{9}{20} \mathrm{M} \\ & =\frac{9}{20} \times 28=\frac{63}{5} \mathrm{~g} \end{aligned} $$
56. In a given process the pressure of gas remains constant. The temperature of the gas is doubled. The change in volume is
(1) $\mathbf{1 0 0 \%}$
(2) $\mathbf{2 0 0 \%}$
(3) $\mathbf{5 0 \%}$
(4) $25 \%$
Show Answer
Correct answer: (1)
Solution:
We know according to Charles law, at constant pressure $\mathrm{V}$ is directly proportional to $\mathrm{T}$. Therefore
$\frac{\mathrm{V} _{1}}{\mathrm{~V} _{2}}=\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=\frac{\mathrm{T}}{2 \mathrm{~T}}=\frac{1}{2}$
$\therefore \mathrm{V} _{2}=2 \mathrm{~V} _{1}$
The percentage change in volume of gas is
$\frac{\Delta \mathrm{V}}{\mathrm{V}} \times 100=\frac{2 \mathrm{~V} _{1}-\mathrm{V} _{1}}{\mathrm{~V} _{1}} \times 100=100 \%$
57. Fig. 7 shows the $P V$ diagram of an ideal gas. For the process ab the correct statement is
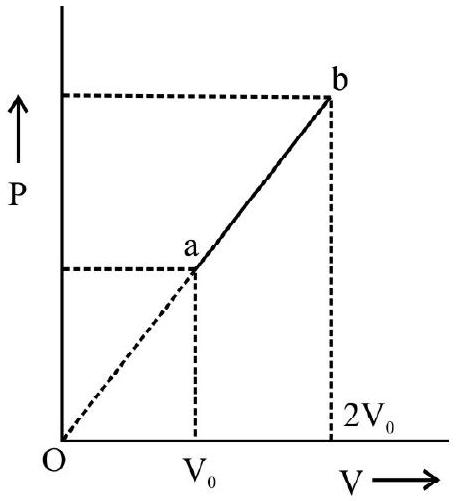
Fig. 7
(1) Density of the gas has doubled.
(2) Temperature of the gas has doubled.
(3) Internal energy of gas becomes four times.
(4) T-V graph is a hyperbola.
Show Answer
Correct answer: (3)
Solution:
$\mathrm{P}$ vs V graph is a straight line therefore its slope is constant. Considering points a and $b$ we have
$$ \frac{\mathrm{P} _{\mathrm{a}}}{\mathrm{V} _{0}}=\frac{\mathrm{P} _{\mathrm{b}}}{2 \mathrm{~V} _{0}} \quad \text { or } \quad \frac{\mathrm{P} _{\mathrm{a}}}{\mathrm{P} _{\mathrm{b}}}=\frac{1}{2} $$
Let $T _{a}$ and $T _{b}$ be temperature of the gas at point $a$ and $b$. From ideal gas equation.
$$ \frac{\mathrm{T} _{\mathrm{b}}}{\mathrm{T} _{\mathrm{a}}}=\frac{\mathrm{P} _{\mathrm{b}} \mathrm{V} _{\mathrm{b}}}{\mathrm{P} _{\mathrm{a}} \mathrm{V} _{\mathrm{a}}}=\frac{2 \mathrm{P} _{0} \times 2 \mathrm{~V} _{0}}{\mathrm{P} _{0} \mathrm{~V} _{0}}=4 $$
or $\quad \mathrm{T} _{\mathrm{b}}=4 \mathrm{~T} _{\mathrm{a}}$
As internal energy $U$ is directly proportional to temperature, the internal energy increases to four times.
Given $\mathrm{P} \alpha \mathrm{V}$, using ideal gas equation
$$ \frac{\mathrm{RT}}{\mathrm{V}} \alpha \mathrm{V} \quad \text { or } \quad \mathrm{T} \alpha \mathrm{V}^{2} $$
Hence $\mathrm{T}$ vs $\mathrm{V}$ graph will be parabola.
58. During an experiment, an ideal gas is found to obey the condition $\mathrm{VP}^{2}=$ constant. The gas is initially at temperature $T$, pressure $P$ and volume $V$. The gas expands to volume $4 \mathrm{~V}$. Which of the following statement is correct ?
(1) The pressure of the gas changes to $P / 2$
(2) The temperature of the gas changes to 4T
(3) The graph of $P$ vs $T$ is a parabola
(4) The graph of $T$ vs $V$ is a straight line
Show Answer
Correct answer: (1)
Solution:
For the given process
$$ \begin{equation*} \mathrm{P}^{2} \mathrm{~V}=\text { constant } \tag{1} \end{equation*} $$
From ideal gas equation we have
$$ \begin{equation*} \mathrm{V}=\frac{\mathrm{nRT}}{\mathrm{P}} \tag{2} \end{equation*} $$
Using Eqn (2) we rewrite Eqn(1) as
$$ \begin{equation*} \mathrm{PT}=\text { constant } \tag{3} \end{equation*} $$
Eqn (1) can also be rewritten as $\mathrm{T}^{2} \mathrm{~V}^{-1}=$ constant $\hspace{30mm} . . . . . . . . (4)$
Let $\mathrm{P} _{1}, \mathrm{~V} _{1}, \mathrm{~T} _{1}$ be initial parameters of gas. The final value of the parameters is $\mathrm{P} _{2}, \mathrm{~V} _{2}$ and $\mathrm{T} _{2}$. From Eqn (1)
$$ \frac{\mathrm{P} _{2}}{\mathrm{P} _{1}}=\sqrt{\frac{\mathrm{V} _{1}}{\mathrm{~V} _{2}}}=\sqrt{\frac{\mathrm{V}}{4 \mathrm{~V}}}=\frac{1}{2} $$
or $\quad \mathrm{P} _{2}=\frac{\mathrm{P} _{1}}{2}=\frac{\mathrm{P}}{2}$
This is option (1).
Using Eqn(3);
$$ \begin{aligned} & \frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}=\frac{\mathrm{P} _{1}}{\mathrm{P} _{2}}=2 \\ & \mathrm{~T} _{2}=2 \mathrm{~T} _{1}=2 \mathrm{~T} \end{aligned} $$
From Eqn. (3); $\mathrm{P}$ vs $\mathrm{T}$ graph will be a hyperbola. From Eqn (4) $\mathrm{T}^{2} \mathrm{vs} \mathrm{V}$ graph is a straight line.
Obviously option (1) is the only correct statement.
59. During an experiment, an ideal gas in found to obey a condition $\frac{P^{2}}{\rho}=$ constant (where $\rho=$ density of the gas). The gas is initially at temperature $T$, pressure $P$ and has density $\rho$. The gas expands such that the density changes to $\frac{\rho}{2}$. Which of the following statements is
correct?
(1) The pressure of the gas changes to $\sqrt{2} P$.
(2) The temperature of the gas changes to $\sqrt{2} T$.
(3) The $\mathrm{P}$ vs $\mathrm{T}$ graph is parabola.
(4) The P vs T graph is straight line.
Show Answer
Correct answer: (2)
Solution:
Given $\frac{\mathrm{P}^{2}}{\rho}=$ constant $=\mathrm{C} _{1}$ (say) $\hspace{30mm} . . . . . . . .(1)$
$\therefore \quad \mathrm{P}^{2} \mathrm{~V}=$ constant $\hspace{30mm} . . . . . . . .(2)$
$$ \left[\because \quad \rho=\frac{\mathrm{m}}{\mathrm{V}}\right] $$
From the gas equation $\mathrm{V}=\frac{\mathrm{nRT}}{\mathrm{P}}$. We can rewrite Eqn. (1) as $\mathrm{P}^{2}\left(\frac{\mathrm{nRT}}{\mathrm{P}}\right)=\mathrm{C} _{1}$
or $\mathrm{PT}=\mathrm{C} _{2}$ $\hspace{30mm} . . . . . . . .(3)$
where $\mathrm{C} _{2}=\frac{\mathrm{C} _{1}}{\mathrm{nR}}$ is another constant. $\mathrm{P}$ vs $\mathrm{T}$ graph is a hyperbola.
From Eqn(1)
$\frac{P _{1}}{P _{2}}=\sqrt{\frac{\rho _{2}}{\rho _{1}}}=\sqrt{\frac{\rho}{(\rho / 2)}}=\sqrt{2}$
$\therefore \mathrm{P} _{2}=\frac{\mathrm{P} _{1}}{\sqrt{2}}=\frac{\mathrm{P}}{\sqrt{2}}$
From Eqn (3) we have
$\mathrm{P} _{1} \mathrm{~T} _{1}=\mathrm{P} _{2} \mathrm{~T} _{2} \quad$ or $\quad \frac{\mathrm{P} _{1}}{\mathrm{P} _{2}}=\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}$
$\therefore \frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}=\sqrt{2} \quad$ or $\quad \mathrm{T} _{2}=\sqrt{2} \mathrm{~T}$
The only correct statement is option (2).
60. A nitrogen gas molecule moves vertically upwards with its root mean square speed at $0^{\circ} \mathrm{C}$ from the surface of earth. There are no collision of the molecule with other molecules. Then it will rise to an approximate height of $\left(\mathrm{g}=10 \mathrm{~ms}^{-2}\right)$
(1) $8 \mathrm{~km}$
(2) $12 \mathrm{~m}$
(3) $12 \mathrm{~km}$
(4) $8 \mathrm{~m}$
Show Answer
Correct answer: (3)
Solution:
Since there are no collisions the initial K.E of molecule is converted into gravitational P.E. Assuming that height $\mathrm{h}$ to which molecule rises is small as compared to radius of earth, $\mathrm{g}$ remain same. From law of conservation of energy.
$$ \frac{1}{2} \mathrm{mv} _{\mathrm{rms}}^{2}=\mathrm{mgh} \text { or } \mathrm{v} _{\mathrm{rms}}^{2}=2 \mathrm{gh} $$
The r.m.s speed, $\mathrm{v} _{\mathrm{rms}}$, at temperature $\mathrm{T}$ on Kelvin scale is $\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}}$. Therefore
$$ \left(\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}}\right)^{2}=2 \mathrm{gh} $$
or $\quad \frac{3 \mathrm{RT}}{2 \mathrm{Mg}}=\mathrm{h}$
Substituting given values; we have
$\mathrm{h}=\frac{3 \times 8.31 \times 273}{2 \times 10 \times 28 \times 10^{-3}} \mathrm{~m}$
$$ =\frac{6805.89}{560 \times 10^{-3}} \simeq 12 \mathrm{~km} $$
61. In Fig. 8 the expansion of an ideal gas of mass $(\mathrm{m})$ at a constant pressure $(\mathrm{P}$ ) is given by the straight line $B$. Then the expansion of the same ideal gas of mass $2 \mathrm{~m}$ at pressure $2 \mathrm{P}$ is given
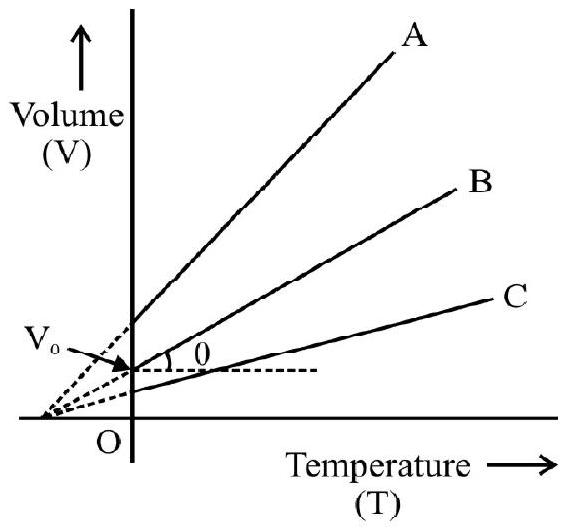
(1) $\mathrm{C}$
(2) $\mathbf{A}$
(3) $\mathbf{B}$
(4) Given information is insufficient.
Show Answer
Correct answer: (3)
Solution:
For the given straight line B; we have
$$ \begin{equation*} \mathrm{V}=\mathrm{V} _{0}+(\tan \theta) \mathrm{T} \tag{1} \end{equation*} $$
From the ideal gas equation
$$ \begin{equation*} \mathrm{PV}=\mathrm{nRT}=\left(\frac{\mathrm{m}}{\mathrm{M}}\right) \mathrm{RT} \tag{2} \end{equation*} $$
From Eqns. (1) and (2) we have
$$ \begin{array}{r} \mathrm{P}\left[\mathrm{V} _{0}+(\tan \theta) \times \mathrm{T}\right]=\left(\frac{\mathrm{m}}{\mathrm{M}}\right) \mathrm{RT} \\ (\mathrm{PT}) \tan \theta=\left(\frac{\mathrm{m}}{\mathrm{M}}\right) \mathrm{RT}-\mathrm{PV} _{0} \end{array} $$
$$ \begin{align*} & \tan \theta=\frac{1}{\mathrm{PT}}\left[\left(\frac{\mathrm{m}}{\mathrm{M}}\right) \mathrm{RT}-\mathrm{PV} _{0}\right] \\ & =\left(\frac{\mathrm{mR}}{\mathrm{PM}}\right)-\left(\frac{\mathrm{V} _{0}}{\mathrm{~T}}\right) \tag{3} \end{align*} $$
For $\mathrm{P}^{\prime}=2 \mathrm{P} ; \mathrm{m}^{\prime}=2 \mathrm{~m}$ there is no change in $\tan \theta$.
Hence graph B represents the given expansion.
62. The variation of internal energy $V$ of an ideal gas with increase in pressure $P$ is shown in Fig. 9. Which of the following pressure vs volume graph is equivalent to graph shown in Fig. 9?
Show Answer
Correct answer: (2)
Solution:
From the given graph pressure is directly proportional to internal energy (U). We know internal energy is directly proportional temperature (i.e. $\mathrm{U} \alpha \mathrm{T}$ ). Therefore
$$ P \propto T $$
From charles’s law $\mathrm{P} \alpha \mathrm{T}$ if volume remains constant. The given graph is equivalent to $\mathrm{V}=$ constant. This is shown in (2)
63. The temperature at the which the root mean square speed of hydrogen molecules equals to the escape speed from the surface of the moon, is
(Given radius of moon $=1750 \mathrm{~km}, \mathrm{~g} _{\mathrm{m}}=1.6 \mathrm{~m} / \mathrm{s}^{2}$ )
(1) $176^{\circ} \mathrm{C}$
(2) $449^{\circ} \mathrm{C}$
(3) $224.5^{\circ} \mathrm{C}$
(4) $-48.5^{\circ} \mathrm{C}$
Show Answer
Correct answer: (1)
Solution:
The root mean square speed of the molecules of hydrogen gas is
$$ \left(\mathrm{V} _{\mathrm{rms}}\right)=\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M} _{\mathrm{H} _{2}}}} $$
where $\mathrm{M} _{\mathrm{H} _{2}}$ is molar mass of hydrogen. The escape speed from moon
$$ \mathrm{V} _{\mathrm{esp}}=\sqrt{2 \mathrm{~g} _{\mathrm{m}} \mathrm{R} _{\mathrm{m}}} $$
Given $V _{\text {esp }}=V _{\text {rms }} ;$ therefore
$$ \begin{array}{r} \sqrt{2 g _{m} R _{m}}= \sqrt{\frac{3 R T}{M _ {H _{2}}}} \\ \text { or } \quad \frac{2 g _{m} R _{m} M _{H _{2}}}{3 R}=T \end{array} $$
Substituting given values, we have
$$ \mathrm{T}=\frac{2 \times 1.6 \times 1750 \times 10^{3} \times 2 \times 10^{-3}}{3 \times 8.314}=449 \mathrm{~K} $$
The surface temperature of moon on Celsius scale
$$ =(449-273)=176^{\circ} \mathrm{C} $$
64. Fig. 10 shows the variation of temperature $T$ as a function of volume $\mathbf{V}$ for one mole of an ideal gas. Which of the following curves best represents the variation of pressure as a function of volume?
Show Answer
Correct answer: (1)
Solution:
The equation of given straight line is
$$ \begin{equation*} \mathrm{T}=\mathrm{T} _{0}+\left(\tan 45^{\circ}\right) \mathrm{V}=\mathrm{T} _{0}+\mathrm{V} \tag{1} \end{equation*} $$
From the ideal gas equation
$$ \begin{align*} & \quad \mathrm{PV}=\mathrm{nRT}=\mathrm{nR}\left(\mathrm{T} _{0}+\mathrm{V}\right) \\ & =\mathrm{nRT} _{0}+\mathrm{nRV} \\ & \text { or } \quad \mathrm{P}=\mathrm{nR}+\frac{\mathrm{nRT} _{0}}{\mathrm{~V}} \\ & \text { or } \quad \mathrm{P}=\mathrm{a}+\frac{\mathrm{b}}{\mathrm{V}} \tag{2} \end{align*} $$
where $\mathrm{a}=\mathrm{nR}$ and $\mathrm{b}=\mathrm{nRT}{ } _{0}$; both are constant. $\mathrm{P} v s \mathrm{~V}$ graph is a rectangular hyperbola. The correct choice is (1).
65. The number of degrees of freedom of molecules in a gas whose molar heat capacity in $29 \mathrm{~J} /$ mole $\mathrm{K}$ in the process $\mathrm{PT}=$ constant will be
(1) 3
(2) 5
(3) 7
(4) 6
Show Answer
Correct answer: (1)
Solution:
Molar heat capacity $\mathrm{C}$ for a process $\mathrm{PV}^{\mathrm{a}}=$ const is given by
$$ \begin{equation*} \mathrm{C}=\mathrm{C} _{\mathrm{v}}+\frac{\mathrm{R}}{1-\mathrm{a}}, \text { and } \mathrm{C} _{\mathrm{v}}=\frac{\mathrm{f}}{2} \mathrm{R} \tag{1} \end{equation*} $$
where $f$ is the number of degree of freedom of molecules.
For the process $\mathrm{PT}=$ constant using the gas equation we have
$$ \mathrm{PV}=\mathrm{nRT} \quad \text { or } \mathrm{T}=\frac{\mathrm{PV}}{\mathrm{nR}} $$
Substituting this value of $\mathrm{T}$ in the given process (i.e. $\mathrm{PT}=$ constant); we have
$$ \mathrm{P} \times \frac{\mathrm{PV}}{\mathrm{nR}}=\text { constant } ; \text { or } \mathrm{P}^{2} \mathrm{~V}=\text { constant } $$
$\therefore \mathrm{PV}^{1 / 2}=$ constant
Since $\mathrm{PV}^{\mathrm{a}}=$ constant. For the given process $\mathrm{a}=\frac{1}{2}$. Substituting values of a in Eqn. (1) we have
$$ \begin{equation*} C=\frac{f}{2} R+\frac{R}{(1-1 / 2)}=\frac{f R}{2}+2 R=\left(\frac{f}{2}+2\right) R \tag{2} \end{equation*} $$
Substituting given value ofC in Eqn(2) we have
$$ 29=\left(\frac{\mathrm{f}}{2}+2\right) \mathrm{R} $$
or $\quad\left(\frac{f}{2}+2\right)=\frac{29}{8.314}=3.488$
$\therefore \quad \frac{\mathrm{f}}{2}=3.488-2=2.976 \approx 3$
66. An ideal gas $\left(\frac{\mathbf{C} _{\mathrm{P}}}{\mathbf{C} _{\mathrm{V}}}=\gamma\right)$ is taken through a process in which pressure and volume vary as $\mathbf{P}=\mathbf{a V}^{\mathrm{b}}$. What is value of $\mathrm{b}$ for which the specific heat capacity in the process is zero?
(1) $\gamma$
(2) $-\gamma$
(3) $\frac{1}{\gamma}$
(4) $-\frac{1}{\gamma}$
Show Answer
Correct answer: (2)
Solution:
$\mathrm{P}=\mathrm{aV}^{\mathrm{b}}$ or $\mathrm{PV}^{-\mathrm{b}}=$ constant $\hspace{40mm} . . . . . . . (1)$
Specific heat capacity $\mathrm{C}=\frac{\Delta \mathrm{Q}}{\mathrm{n} \Delta \mathrm{T}}$ will be zero when $\Delta \mathrm{Q}=0$ and $\Delta \mathrm{T} \neq 0$. The process is adiabatic. We know for adiabatic process
$\mathrm{PV}^{\gamma}=$ constant $\hspace{40mm} . . . . . . . (2)$
From Eqns. (1) and (2) we have
$$ \gamma=-b $$
67. In a certain gas $(2 / 5)$ of the total energy of molecules is associate with rotation of molecules and rest of it is associated with the motion of centre of mass. The energy supplied to one mole of the gas at constant volume to raise the temperature by $1^{0}$ is
(1) $ 29.09 \mathrm{~J}$
(2) $12.47 \mathrm{~J}$
(3) $ 20.8 \mathrm{~J}$
(4) $10.4 \mathrm{~J}$
Show Answer
Correct answer: (3)
Solution:
For a molecule having simultaneous translational and rotational motion, we are given
The kinetic energy ofc.m $=\frac{3}{5}$ of the total energy of translation, and the rotational kinetic energy $=\frac{2}{5}$ of the total energy. Therefore the gas is diatomic i.e. $\mathrm{C} _{\mathrm{v}}=\frac{5}{2} \mathrm{R}$.
$\Delta \mathrm{Q}=$ The energy required to change temperature by $\Delta \mathrm{T}$
$=\mathrm{nC} _{\mathrm{v}} \Delta \mathrm{T}=1 \times \frac{5}{2} \times 8.314 \times 1=20.8 \mathrm{~J}$
68. The temperature at which the r.m.s speed of gaseous hydrogen molecules (molecular weight 2) equals the r.m.s speed of oxygen molecules (molecular weight 32 ) at $47^{\circ} \mathrm{C}$ is
(1) $-\mathbf{2 7 0}^{\circ} \mathrm{C}$
(2) $294^{\circ} \mathrm{C}$
(3) $-253^{\circ} \mathrm{C}$
(4) $20^{\circ} \mathrm{C}$
Show Answer
Correct answer: (3)
Solution:
The r.m.s speed of the molecules in a gas is given by
$$ \mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}} $$
Given $\mathrm{v} _{\mathrm{rms}}$ of hydrogen at temperature $\mathrm{T} _{\mathrm{H}}$ is same as of oxygen at $\mathrm{T} _{0}$. Therefore
$$ \begin{aligned} & \sqrt{\frac{3 \mathrm{RT} _{\mathrm{H}}}{\mathrm{M} _{\mathrm{H}}}}=\sqrt{\frac{3 \mathrm{RT} _{0}}{\mathrm{M} _{0}}} \text { or } \frac{\mathrm{T} _{\mathrm{H}}}{\mathrm{M} _{\mathrm{H}}}=\frac{\mathrm{T} _{0}}{\mathrm{M} _{0}} \\ & \therefore \quad \mathrm{T} _{\mathrm{H}}=\frac{\mathrm{T} _{0}}{\mathrm{M} _{0}} \times \mathrm{M} _{\mathrm{H}}=\frac{(273+47)}{32} \times 2=\frac{640}{32}=20 \mathrm{~K} \end{aligned} $$
Temperature on celsius scale $=20-273=-253^{\circ} \mathrm{C}$
69. Air is pumped into an automobile tube up to a pressure of $200 \mathrm{kPa}$ in the morning when the air temperature is $22^{\circ} \mathrm{C}$. During the day time, temperature rises to $42^{\circ} \mathrm{C}$ and the tube expands by $2 \%$ the pressure of the air in the tube now is
(1) $212 \mathrm{kPa}$
(2) $209 \mathrm{kPa}$
(3) $206 \mathrm{kPa}$
(4) $200 \mathrm{kPa}$
Show Answer
Correct answer: (2)
Solution:
According to ideal gas equation $\mathrm{PV}=\mathrm{nRT}$
$$ \begin{equation*} \therefore \quad \frac{\mathrm{P} _{1} \mathrm{~V} _{1}}{\mathrm{~T} _{1}}=\frac{\mathrm{P} _{2} \mathrm{~V} _{2}}{\mathrm{~T} _{2}} \tag{1} \end{equation*} $$
Given
$\mathrm{P} _{1}=200 \mathrm{kPa}, \mathrm{V} _{1}=\mathrm{V}, \mathrm{T} _{1}=273+22=295 \mathrm{~K}$
$\mathrm{P} _{2}=?, \mathrm{~V} _{2}=\mathrm{V}+0.02 \mathrm{~V}=(1.02) \mathrm{V}, \mathrm{T} _{2}=273+42=315 \mathrm{~K}$
Substituting given values in Eqn (1) we have
$$ \begin{aligned} & \frac{200 \times \mathrm{V}}{295}=\frac{\mathrm{P} _{2} \times 1.02 \mathrm{~V}}{315} \\ & \therefore \mathrm{P} _{2}=209 \mathrm{kPa} \end{aligned} $$
70. Two different masses $m$ and $3 \mathrm{~m}$ of an ideal gas are heated separately in a vessel of constant volume. The graph of pressure $P$ versus the absolute temperature $T$ for two gases are shown in Fig. 11 as $A$ and B. The ratio of slopes of curve $B$ to curve $A$ is:
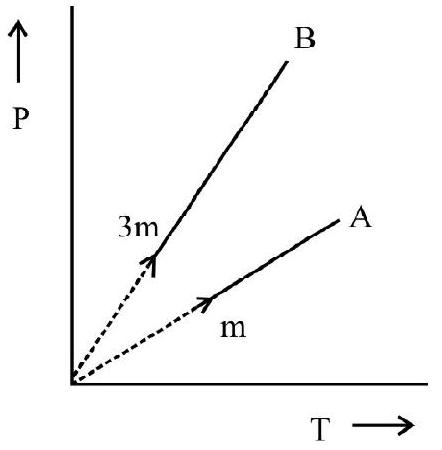
(1) $3: 1$
(2) $1: 3$
(3) $9: 1$
(4) $1: 9$
Show Answer
Correct answer: (1)
Solution:
For an ideal gas of molecular mass M having mass $\mathrm{m}$, we have
$$ \begin{aligned} \mathrm{PV} & =\mathrm{nRT}=\left(\frac{\mathrm{m}}{\mathrm{M}}\right) \mathrm{RT} \\ \text { or } \quad \mathrm{P} & =\left(\frac{\mathrm{mR}}{\mathrm{MV}}\right) \mathrm{T} \end{aligned} $$
At constant volume P $v s \mathrm{~T}$ graph is a straight line. The slope of graph is directly proportional to $\mathrm{m}$. Therefore
$$ \frac{(\text { Slope }) _{\mathrm{B}}}{(\text { Slope }) _{\mathrm{A}}}=\frac{3}{1}=3: 1 $$
71. For a gas, if the ratio of molar specific heats at constant pressure and volume is $\gamma$, the value of degree of freedom is
(1) $\frac{2}{\gamma-1}$
(2) $\frac{5}{2}(\gamma-1)$
(3) $\frac{3 \gamma-1}{2 \gamma-1}$
(4) $\frac{9}{2}(\gamma-1)$
Show Answer
Correct answer: (1)
Solution:
For the molar specific heat at constant pressure $\mathrm{C} _{\mathrm{P}}$ and at constant volume $\mathrm{C} _{\mathrm{V}}$;
$$ \begin{equation*} \mathrm{C} _{\mathrm{P}}-\mathrm{C} _{\mathrm{V}}=\mathrm{R} ; \text { and } \mathrm{C} _{\mathrm{V}}=\left(\frac{\mathrm{f}}{2}\right) \mathrm{R} \tag{1} \end{equation*} $$
where f is number of degrees of freedom. Obviously
$$ \begin{aligned} & C _{P}=R+C _{V} \\ \gamma & =\frac{R}{C _{V}}+1=\frac{2}{f}+1 \\ \therefore \quad & f=\frac{2}{(\gamma-1)} \end{aligned} $$
72. Air is filled at $60^{\circ} \mathrm{C}$ in a vessel of open mouth the vessel is heated to a temperature $\mathbf{T}$ so that $\frac{1}{4}^{\text {th }}$ part of air escapes. Assuming the volume of the vessel remaining constant, the value of ’ $T$ ’ is
(1) $333^{\circ} \mathrm{C}$
(2) $171^{\circ} \mathrm{C}$
(3) $444^{\circ} \mathrm{C}$
(4) $80^{\circ} \mathrm{C}$
Show Answer
Correct answer: (2)
Solution:
For open mouth vessel, pressure is constant volume is also given constant. Hence from gas equation $\mathrm{PV}=\mathrm{nRT}=\frac{\mathrm{m}}{\mathrm{M}} \mathrm{RT} _{\text {we have }}$
$$ \mathrm{T} \alpha \frac{1}{\mathrm{~m}} $$
$\therefore \frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=\frac{\mathrm{m} _{2}}{\mathrm{~m} _{1}} \hspace{40mm} . . . . . . . . (1)$
Given $\frac{1}{4}^{\text {th }}$ part of air escapes, so remaining mass in the vessel $m _{2}=\frac{3}{4} m _{1}$
From Eqns. (1) we have
$$ \begin{gathered} \frac{273+60}{\mathrm{~T} _{2}}=\frac{\frac{3}{4} \mathrm{~m} _{1}}{\mathrm{~m} _{1}} \\ \mathrm{~T} _{2}=\mathrm{T}=\frac{333 \times 4}{3}=444 \mathrm{~K}=171^{\circ} \mathrm{C} \end{gathered} $$
73. A gas is filled in a cylinder and its temperature is increased by $20 \%$ on Kelvin scale and volume is reduced by $10 \%$ keeping pressure constant. The percentage of the gas that will leak out is
(1) $15 \%$
(2) $25 \%$
(3) $\mathbf{4 0 \%}$
(4) $30 \%$
Show Answer
Correct answer: (2)
Solution:
Let $\mathrm{V}$ and $\mathrm{T}$ denote initial volume and temperature of gas. The corresponding quantities finally are $\mathrm{V} _{1}, \mathrm{~T} _{1}$.
From charles’s law $\mathrm{V} \alpha \mathrm{T}$ (P remaining constant) therefore.
$$ \frac{\mathrm{V}}{\mathrm{T}}=\frac{\mathrm{V} _{1}}{\mathrm{~T} _{1}} $$
or $\quad \frac{\mathrm{V}}{\mathrm{T}}=\frac{\mathrm{V} _{1}}{1.2 \mathrm{~T}}$ or $\mathrm{V}^{\prime}=1.2 \mathrm{~V}$
$V _{1}$ would have been the volume of gas if there was leakage in cylinder. However the final volume $\mathrm{V}^{\prime}=\mathrm{V}-0.1 \mathrm{~V}=0.9 \mathrm{~V}$.
$\therefore$ Percentage of volume leaked out $=\frac{(1.2-0.9) \mathrm{V}}{1.2 \mathrm{~V}} \times 100=25 \%$
74. What is the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at $2 \mathrm{~atm}$ pressure and temperature $17^{\circ} \mathrm{C}$ ? Take the radius of nitrogen molecule $1 \mathrm{~A}$, molecular mass $=28, \mathrm{k} _{\mathrm{B}}=1.38 \times 10^{-23} \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$ and $1 \mathrm{~atm}=1.013 \times 10^{5} \mathrm{Nm}^{-2}$
(1) $2.2 \times 10^{-7} \mathrm{~m}, 2.58 \times 10^{9}$
(2) $1.1 \times 10^{-7} \mathrm{~m}, 4.58 \times 10^{8}$
(3) $1.1 \times 10^{-7} \mathrm{~m}, 4.58 \times 10^{9}$
(4) $2.2 \times 10^{-7} \mathrm{~m}, 3.58 \times 10^{9}$
Show Answer
Correct answer: (3)
Solution:
Mean free path of a molecule of diameter $d$
$$ \begin{aligned} & \bar{\ell}=\frac{\mathrm{k} _{\mathrm{B}} \mathrm{T}}{\sqrt{2} \pi \rho \mathrm{d}^{2}}=\frac{\left(1.38 \times 10^{-23}\right)(290)}{\sqrt{2} \times 3.14 \times 2.026 \times 10^{5} \times\left(2.0 \times 10^{-10}\right)^{2}} \\ & =1.11 \times 10^{-7} \mathrm{~m} \\ & \mathrm{v} _{\mathrm{rms}}=\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}}=\sqrt{\frac{3 \times 8.314 \times 290}{28 \times 10^{-3}}}=508.24 \mathrm{~ms}^{-1} \end{aligned} $$
The collision frequency equals the number of collisions per second.
$$ =\frac{\mathrm{v} _{\mathrm{rms}}}{\bar{\ell}}=\frac{508.24}{1.11 \times 10^{-7}}=4.58 \times 10^{9} $$
75. A partition divides a container, having insulated walls, into two compartments I and II as shown in Fig. 12. The same gas is filled the compartments, the ratio of the number of molecules in compartments I and II is
| $\mathrm{P}, \mathrm{V}$, | $2 \mathrm{P}, 2 \mathrm{~V}$, |
|---|---|
| $\mathrm{T}$ | $\mathrm{T}$ |
| $\mathrm{I}$ | $\mathrm{II}$ |
(1) $6: 1$
(2) $1: 6$
(3) $4: 1$
(4) $1: 4$
Show Answer
Correct answer: (4)
Solution:
From ideal gas equation; for a gas of mass $m$ having molecular mass $M$
$$ \mathrm{PV}=\frac{\mathrm{m}}{\mathrm{M}} \mathrm{RT} $$
Let $\mathrm{m} _{1}$ be mass of one molecule of gas and $\mathrm{N}$ number of molecules having mass $\mathrm{m}$. Then
$$ \begin{aligned} & \mathrm{PV}=\frac{\mathrm{m} _{1} \mathrm{~N}}{\mathrm{M}} \mathrm{RT}=\frac{\mathrm{N}}{\mathrm{N} _{\mathrm{AV}}} \mathrm{RT} \quad\left[\because \mathrm{m} _{1} \mathrm{~N} _{\mathrm{AV}}=\mathrm{M}\right] \\ & =\mathrm{Nk} _{\mathrm{B}} \mathrm{T} \end{aligned} $$
where $\mathrm{k} _{\mathrm{B}}=\frac{\mathrm{R}}{\mathrm{N} _{\mathrm{AV}}}=$ Boltzmann’s constant. Let $\mathrm{N} _{1}$ and $\mathrm{N} _{2}$ be number of molecules in compartment I and II respectively. Obviously
$$ \frac{\mathrm{N} _{1}}{\mathrm{~N} _{2}}=\left(\frac{\mathrm{P} _{1}}{\mathrm{P} _{2}}\right)\left(\frac{\mathrm{V} _{1}}{\mathrm{~V} _{2}}\right)\left(\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}\right)=\left(\frac{\mathrm{P}}{2 \mathrm{P}}\right)=\left(\frac{\mathrm{V}}{2 \mathrm{~V}}\right)\left(\frac{\mathrm{T}}{\mathrm{T}}\right)=\frac{1}{4} $$
76. For an ideal gas $\mathrm{VP}^{3}=$ constant. Initial temperature and volume of the gas are $\mathbf{T}$ and $\mathbf{V}$ respectively. The gas expands to a volume $27 \mathrm{~V}$. The temperature of gas is
(4) $\mathrm{9T}$
(4) $\mathrm{27T}$
(3) $\frac{T}{9}$
(4) $\mathrm{T}$
Show Answer
Correct answer: (1)
Solution:
Given $\mathrm{VP}^{3}=$ constant $=\mathrm{K}$ Obviously
$$ \begin{equation*} P=\frac{K^{\prime}}{V^{1 / 3}} \tag{1} \end{equation*} $$
where $\mathrm{K}^{\prime}$ is another constant. From ideal gas equation we get $\mathrm{PV}=\mathrm{nRT}$
$$ \begin{align*} & \left(\frac{\mathrm{K}^{\prime}}{\mathrm{V}^{1 / 3}}\right) \mathrm{V}=\mathrm{nRT} \\ & \mathrm{K}^{\prime} \mathrm{V}^{2 / 3}=\mathrm{nRT} \tag{2} \end{align*} $$
Let $\mathrm{V} _{1}, \mathrm{~T} _{1}$ be the initial volume and temperature of gas. $\mathrm{V} _{2}$ and $\mathrm{T} _{2}$ are corresponding final values.
From Eqn. (2) we have
$$ \begin{aligned} & \left(\frac{\mathrm{V} _{1}}{\mathrm{~V} _{2}}\right)^{2 / 3}=\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}} \\ & \therefore \quad \frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=\left(\frac{\mathrm{V}}{27 \mathrm{~V}}\right)^{2 / 3} \\ & =\left[\left(\frac{1}{27}\right)^{1 / 3}\right]^{2}=\left(\frac{1}{3}\right)^{2} \\ & \therefore \frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=\frac{1}{9} \text { or } \mathrm{T} _{2}=9 \mathrm{~T} _{1} \end{aligned} $$
77. The molar specific heat at constant pressure of an ideal gas is $\frac{7}{2} R$. The ratio of specific heat at constant pressure to that at constant volume is
(1) $\frac{5}{7}$
(2) $\frac{8}{7}$
(3) $\frac{7}{5}$
(4) $\frac{9}{7}$
Show Answer
Correct answer: (3)
Solution:
Given molar specific heat at constant pressure $\mathrm{C} _{\mathrm{P}}=\frac{7}{2} \mathrm{R}$.
Since $\mathrm{C} _{\mathrm{P}}-\mathrm{C} _{\mathrm{V}}=\mathrm{R}$
$$ \begin{aligned} & \mathrm{C} _{\mathrm{V}}=\mathrm{C} _{\mathrm{P}}-\mathrm{R}=\frac{7}{2} \mathrm{R}-\mathrm{R}=\frac{5}{2} \mathrm{R} \\ \therefore \quad & \frac{\mathrm{C} _{\mathrm{P}}}{\mathrm{C} _{\mathrm{V}}}=\frac{\frac{7}{2} \mathrm{R}}{\frac{5}{2} \mathrm{R}}=\frac{7}{5} \end{aligned} $$
78. In a certain gas, the ratio of the speed of sound and root mean square speed is $\sqrt{\frac{5}{9}}$. The gas undergoes a process given by $\mathrm{PT}=$ constant. The molar specific heat for the process is:
(1) $\frac{R}{2}$
(2) $\frac{3 R}{2}$
(3) $\frac{5 R}{2}$
(4) $\frac{7 R}{2}$
Show Answer
Correct answer: (4)
Solution:
Given
$$ \frac{\text { speed of sound in gas }}{\text { root mean square speed of gas }}=\sqrt{\frac{5}{9}} $$
$$ \begin{aligned} & \therefore \sqrt{\frac{\gamma \mathrm{RT} / \mathrm{M}}{3 \mathrm{RT} / \mathrm{M}}}=\sqrt{\frac{5}{9}} \\ & \text { or } \frac{\gamma}{3}=\frac{5}{9} \therefore \gamma=\frac{5}{3} . \end{aligned} $$
The given gas is monoatomic. For the process gas undergoes PT = constant. Using ideal gas equation we rewrite the given relation as $\mathrm{PV}^{1 / 2}=$ constant .
Comparing with $\mathrm{PV}^{x}=$ constant we have $x=\frac{1}{2}$
Molar specific heat for the relation $\mathrm{PV}^{x}=$ constant is
$$ \begin{aligned} \mathrm{C}= & \mathrm{C} _{\mathrm{V}}+\frac{\mathrm{R}}{(1-x)} \\ & =\frac{3}{2} \mathrm{R}+\frac{\mathrm{R}}{\left(1-\frac{1}{2}\right)}=\frac{7}{2} \mathrm{R} \end{aligned} $$
79. If one mole of a monoatomic gas $\left(\gamma=\frac{5}{3}\right)$ is mixed with one mole of a diatomic gas $\left(\gamma=\frac{7}{5}\right)$, the value of $\gamma$ for the mixture is
(1) $\mathbf{1 . 4 0}$
(2) 1.50
(3) 1.53
(4) 3.07
Show Answer
Correct answer: (2)
Solution:
We know for monoatomic gas $\mathrm{C} _{\mathrm{V} _{1}}=\frac{3}{2} \mathrm{R}$ and for diatomic gas $\mathrm{C} _{\mathrm{V} _{2}}=\frac{5}{2} \mathrm{R}$. Therefore
$\left(\mathrm{C} _{\mathrm{v}}\right) _{\text {mix }}=\frac{\mathrm{n} _{1} \mathrm{C} _{\mathrm{v} _{1}}+\mathrm{n} _{2} \mathrm{C} _{\mathrm{v} _{2}}}{\mathrm{n} _{1}+\mathrm{n} _{2}}$
$$ =\frac{(1)\left(\frac{3}{2} \mathrm{R}\right)+(1)\left(\frac{5}{2}\right) \mathrm{R}}{1+1}=2 \mathrm{R} $$
$\left(C _{P}\right) _{\text {mix }}=C _{V}+R=3 R$. Therefore
$\gamma _{\text {mix }}=\frac{\left(\mathrm{C} _{\mathrm{p}}\right) _{\text {mix }}}{\left(\mathrm{C} _{\mathrm{v}}\right) _{\text {mix }}}=\frac{3 \mathrm{R}}{2 \mathrm{R}}=\frac{3}{2}=1.5$
80. For hydrogen $\mathrm{c} _{\mathrm{p}}-\mathrm{c} _{\mathrm{v}}=\mathrm{n} _{1}$ and for nitrogen $\mathrm{c} _{\mathrm{P}}-\mathrm{c} _{\mathrm{V}}=\mathrm{n} _{2}$ where $\mathrm{c} _{\mathrm{p}}$ and $\mathrm{c} _{\mathrm{V}}$ represents specific heat per unit mass respectively at constant pressure and constant volume respectively. The relation between $n _{1}$ and $n _{2}$ is:
(Molecular weight of hydrogen $=2$, and molecular weight of nitrogen $=14$ )
(1) $\mathbf{n} _{2}=14 \mathrm{n} _{1}$
(2) $\mathbf{n} _{2}=7 \mathbf{n} _{1}$
(3) $\mathbf{n} _{1}=7 \mathrm{n} _{2}$
(4) $\mathrm{n} _{1}=14 \mathrm{n} _{2}$
Show Answer
Correct answer: (3)
Solution:
Let $\mathrm{C} _{\mathrm{p}}$ and $\mathrm{C} _{\mathrm{v}}$ be the molar specific heat of gas. Then $\mathrm{c} _{\mathrm{p}}$ and $\mathrm{c} _{\mathrm{v}}$ are $\mathrm{C} _{\mathrm{p}} / \mathrm{M}$ and $\mathrm{C} _{\mathrm{v}} / \mathrm{M}$ respectively where $\mathrm{M}$ is molar mass of gas. Obviously
$$ \begin{aligned} & \mathrm{c} _{\mathrm{P}}-\mathrm{c} _{\mathrm{V}}=\frac{\mathrm{C} _{\mathrm{P}}-\mathrm{C} _{\mathrm{V}}}{\mathrm{M}}=\frac{\mathrm{R}}{\mathrm{M}} \\ & \therefore \frac{\left(\mathrm{C} _{\mathrm{P}}-\mathrm{C} _{\mathrm{V}}\right) _{\mathrm{H}}}{\left(\mathrm{C} _{\mathrm{P}}-\mathrm{C} _{\mathrm{V}}\right) _{\mathrm{N}}}=\frac{\mathrm{n} _{1}}{\mathrm{n} _{2}}=\frac{\mathrm{M} _{\mathrm{N}}}{\mathrm{M} _{\mathrm{H}}} \\ & \text { or } \frac{\mathrm{n} _{1}}{\mathrm{n} _{2}}=\frac{14}{2}=7 \end{aligned} $$
