Introduction

The subject of thermodynamics was initially developed to study the interrelation between heat energy and mechanical energy. As the subject developed its scope also got widened and a present it is a subject concerned with the inter-relation between heat energy and energy in other forms.

System and Surroundings

While studying thermodynamics we generally focus our attention on a particular region of spice or a finite portion of matter. This particular region of space or piece of matter, in which our attention is concentrated from the point of view of thermodynamics constitute a thermodynamic system. Everything around it which can effect its behavior and properties, there make up the surroundings.

Thermodynamic Variables

In the studies of thermodynamics we can concentrate our attention on the interior of the system. However we still describe the internal behaviour of the system in terms of some macroscopic quantities that control or effect its internal state. Experimentally it is observed that whenever a chemically defined homogenous system is in a state of equilibrium, its thermodynamic behaviour can generally be studied in terms of its two macroscopic properties - volume (v) and pressure (p). The quantities $\mathrm{p}$ and $\mathrm{v}$ are often referred to as the thermodynamic variables of state for the gives system.

Thermodynamic State

We use the variables pressure, volume and temperature to specify the thermodynamic state of a given system. Usually we have a relation between there three variables so that only two of their are really independent. Hence any two of these there variables are sufficient to specify a thermodynamic state.

Equation State

Thermodynamics state variable describe equilibrium states of systems. The mathematical relation between state variables the pressure the volume and the temperature is called the equation of state. The equation of state for an ideal gas having $n$ moles can be expressed as

$$ \mathrm{PV}=\mathrm{nRT} $$

Real gases may have more complicated equation of state

The above equation applies to isothermal change. For adiabatic change, the equation of state is represented by

$$ \mathrm{PV}^{\gamma}=\text { constant here } $$

where $\gamma$ is the ratio of two specific heat of the gas.

Concept of Temperature

Temperature

We first discuss the concept of temperature in simple terms and then we will discuss the concept more rigorously from the point of view of zeroth law of thermodynamics. The temperature of a given object has been assigned a meaning similar to the level of a liquid. When two differently heated bodies are put in contact, there is a flow of heat from one to other. We say that this “flow” is because of a difference in temperature between the two bodies. The flow (by itself) is always from a body at a higher temperature to one at a lower temperature (very similar to a flow of liquid). The heat ‘flow’ continues until the two bodies attain a common temperature. It was these types of considerations that led Maxwell to define temperature as the ultimate state of the body with reference to its ability to communicate heat to other bodies.

Thermodynamics Processes

We discuss below the definitions of the basic types of thermodynamic processes.

Quasi-static Process

A quasi-static process is an infinitely slow process such that system remains in thermal and chemical equilibrium with the surroundings. In a quasi static process, at every stage, the temperature and pressure of the surroundings differ only infinitesimally from those of the system.

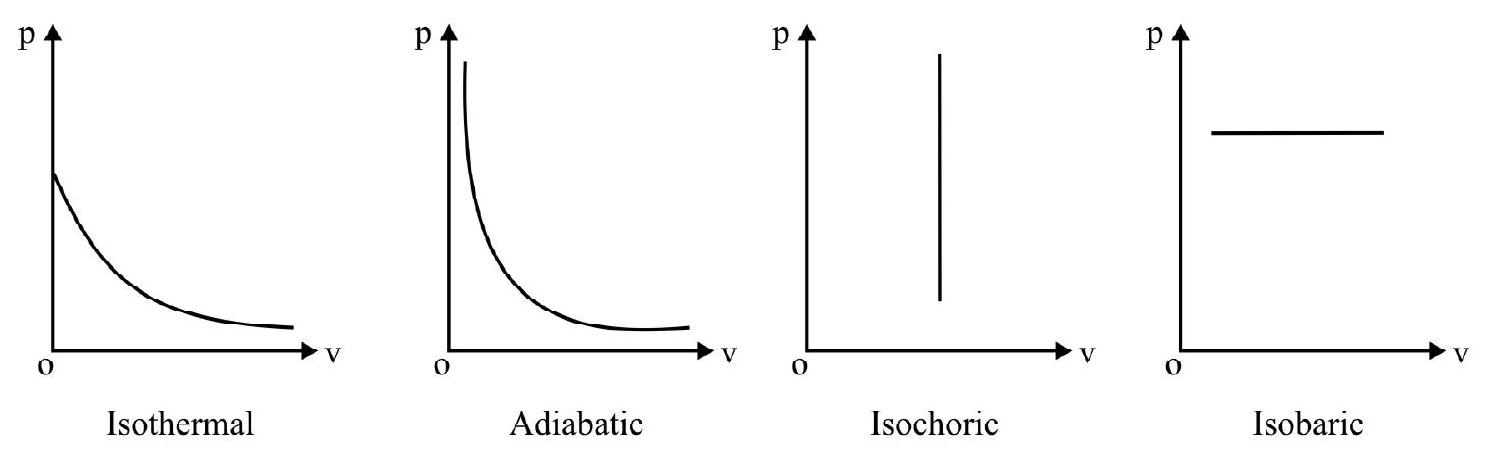
Isothermal Process

An isothermal process is a process in which temperature remains constant. If $\mathrm{T}$ is the temperature of a system on the absolute scale, then in an isothermal process $\Delta \mathrm{T}=0$.

Adiabctic Process

An adiabatic process is a process in which no heat enters or leaves the system. If $Q$ be in heat content of a system, than in an adiabatic process $\Delta \mathrm{Q}=0$

Isochoric Process

An isochoric process is one in which leave is no change in volume of the system. If $v$ is the volume of a system, then in an isochoric process $\Delta \mathrm{v}=0$.

Isobaric Process

An isobaric process is one in which there is no change in the pressure of the system. If $p$ is the pressure of a system than in isobaric process $\Delta \mathrm{p}=0$.

The following diagrams indicate the way the volume of ideal gas the changes with pressure for each of the above process.

Indicator Diagrams

In indicator diagram allows us to study how the volume of the system changes will changes in its pressure even if the process under consideration is not of the above mentioned processes. An indicator diagram tells us, in a graphical form the manner of variation of the pressure of a given system with changes in its volume. This type of diagram provides an indication of the way the state of the system has been allowed to change.

It can be shown that the shaded area of an indicator diagram tells us the work done by the system when its volume is allowed to change from an

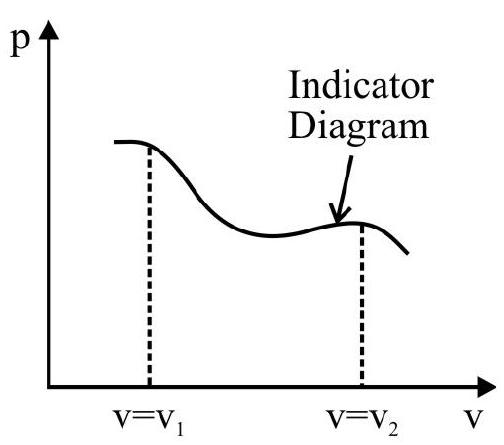initial value $v _{1}$ to a final value $v _{2}$.

Thermal Equilibrium

It is a matter of common experience that when two different system are brought in contact with each other, there is in general, a change in the thermodynamic variables characterizing them such as volume pressure etc. These changes are generally brought about by transfer of heat from one to other system. The change in the values of the thermodynamics variables of the two system continues for a while but ultimately a state is reached when these variable stop changing any further. When this happens we say that the two systems have attained a state of thermal equilibrium with each other.

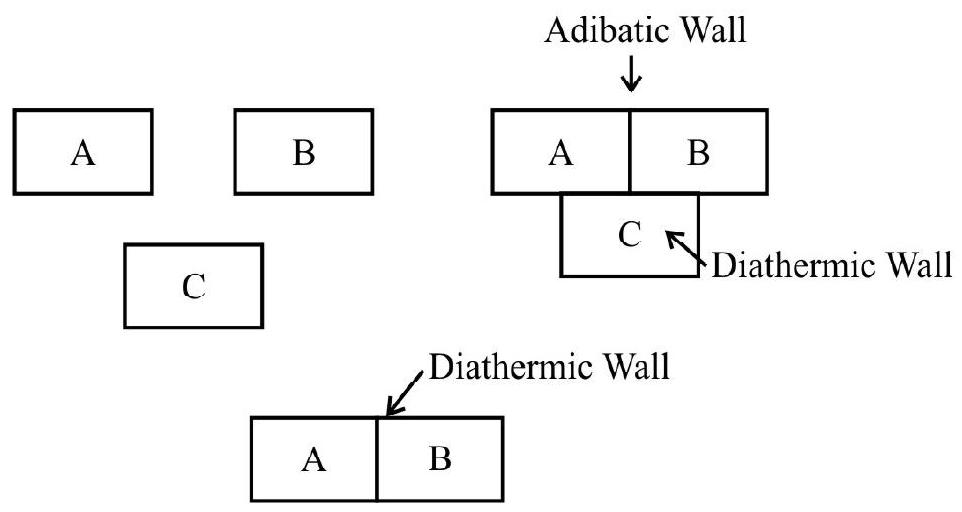
Let us consider three systems A, B and C. Imagine that we have separated A and B by materials which do not allow any heat transfer between them(i.e. by an adiabatic wall). At the same time let both $A$ and $B$ be in contact will system $\mathrm{C}$ with a wall which allows heat to pass freely (i.e. a diathermic wall). As a result both $A$ and $B$ will their attain thermal equilibrium with system $C$. After this has happened let us put a diathermic wall between $A$ and $B$ and adiabatic walls between $A$ and $C$ and $B$ and $C$. It is then found that the values of thermodynamics variables do not show any further change, that is A and $\mathrm{B}$ are also in thermal equilibrium with each other. These experimental facts are often stated in the form.

Two systems which are in thermal equilibrium with a third one, are also in thermal equilibrium with each other.

The above statement is now considered as one of the basic law of thermodynamics and referred to as the Zeroth Law of Thermodynamics.

The zeroth law of thermodynamics is now regarded as the basis of the existence of the concept of temperature. The zeroth law implies that various systems, in thermal equilibrium with one another have some property which is common among all of them. This property we designate as temperature. This temperature of a system is a property that keeps us to decide whether this system would or would not be in thermal equilibrium with another system. It is clear then that temperature can be measured by observing some property of a particular system which varies will the addition of heat.

Heat

It is well known that when two system at different temperature are brought in contact will each other, something flows from the one at a higher temperature to a lower temperature until both acquire a common temperature intermediate between their original values. This “something” is what we commonly call heat. We consider heat as a form of energy and define heat as the energy that as transferred between a system and its surrounding because of a temperature between the two.

The transfer must of course, be in accordance will the principle of conservation of energy. The unit of heat is Joule. In the early stages of development when heat was thought to be something special and distinct, it was measured in a particular unit called the calorie. It is now know that 1 calorie is 4.18 Joule.

From the studies of kinetic theory we know that heat energy is due to the random motion of the molecules.

Work

In our studies of mechanics we are familiar with the definition and concept of work. However in thermodynamics studies we have to carefully distinguish between external work and internal work. For a defined system, external work will constitute the work done by the system as a whole on its surroundings whereas internal work will be the work done by the different parts of the system on one another. The work done as used in thermodynamics refers only to external work, internal work has no place in thermodynamics. Thus we can say that work involves some interaction between a system and its surroundings is of relevance in thermodynamics. Internal like the work done by the forces acting between the molecules of a real gas undergoing an expansion does not constitute work in a thermodynamical sense.

One of the most commonly discussed system in thermodynamics consist of a gas contained in a cylinder with a leak proof movable piston as shown in figure. When the gas undergoes an expansion (or compression) the piston moves and can thus do useful external work. Let to calculate this work done. Let $\mathrm{p}$ be the pressure exerted by the system on the piston of cross sectional area $\mathrm{A}$. The total force exerted on the piston is then clearly pA. If this force moves the piston through a distance $\mathrm{d} x$, the work done in this infinitesimal expansion is

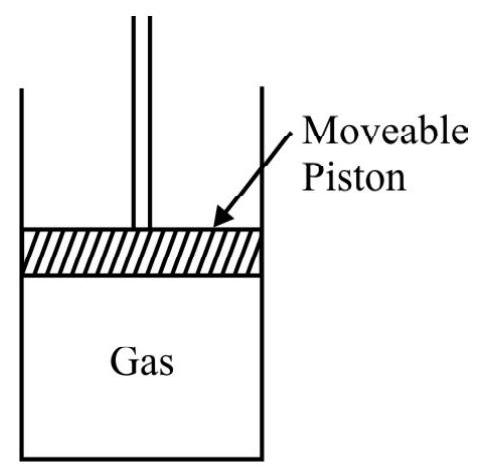
$$ \mathrm{dw}=(\mathrm{pA}) \times \mathrm{d} x=\mathrm{p}(\mathrm{Ad} x)=\mathrm{pdv} $$

The total works done in a finite expansion from an initial volume $v _{1}$ to a final volume $v _{2}$ is therefore given by

$$ \mathrm{dw}=\int _{\mathrm{v} _{1}}^{\mathrm{v} _{2}} \mathrm{pdv} $$

We will work out the work done in an isothermal process and an adiabatic process in later section of our discussions.

Work done during a Cyclic Process

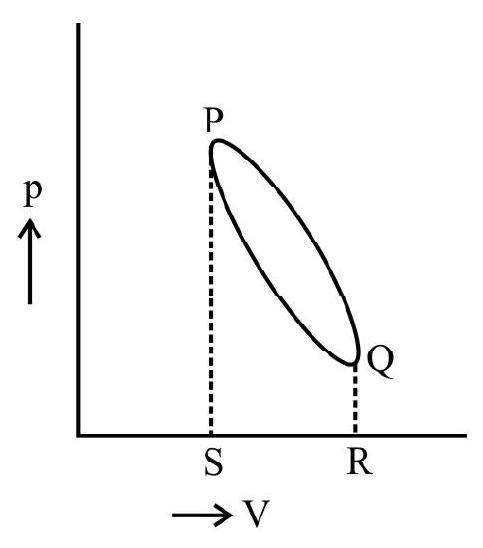
A cyclic process is of characterized by the fact that the system returns to its initial state after undergoing a series of changes. It can be proved that network done diving a cyclic process is numerically equal to the area of the loop representing the cycle.

For example, as shown in the figure the network done during the cycle PQ RS is equal to the area PQ RS.

One should note that heat and work are two distinct modes of energy transfer to a system that result in change in its internal energy (discussed in next article). Heat is energy transfer due to temperature difference between the system and the surroundings. Work is mode of energy transfer brought about, for example, by moving the piston of a cylinder containing the gas by raising or lowering the weight connected to the piston.

When we apply the heat to a gas, mode of energy transfer is random motion of the gas molecules. When a piston is compressed in gas, in a way it is regarded as the mode of energy transfer that produces organized motion of the gas molecules.

Example-1:

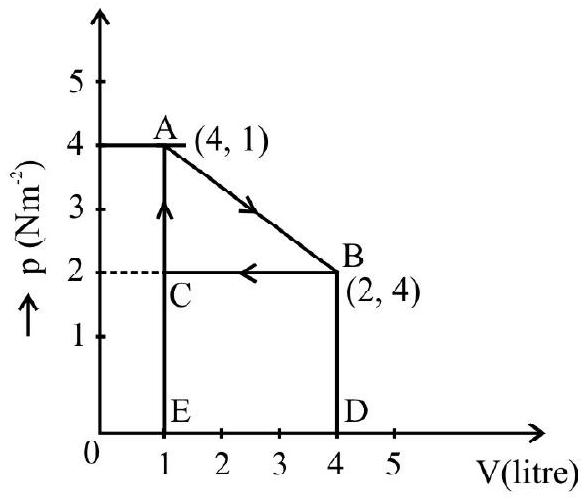
The $\mathrm{p}-\mathrm{v}$ diagram for a cyclic process is a triangle $\mathrm{ABC}$ drawn in order. The co-ordinates of $A, B, C$ are $(4,1),(2,4)$ and $(2$, 1). The co-ordinates are in the order $\mathrm{pv}$ ( $\mathrm{p}$ is in $\mathrm{Nm}^{-2}$ and volume in litre), calculate the work done in complete cycle.

Show Answer

Solution:

Work done during the process from $\mathrm{A}$ to $\mathrm{B}$ (expansion) is

$\mathrm{W} _{\mathrm{AB}}=$ Area of trapezium ABDEA

$\mathrm{A}=$ Area of triangle $\mathrm{ABC}+$ Area of rectangle $\mathrm{BDEC}$

$$ \begin{aligned} & =\frac{1}{2}(\mathrm{BC} \times \mathrm{AC})+(\mathrm{DE} \times \mathrm{CE}) \\ & =\frac{1}{2}(4-1) \times(4-2)+(4-1)(2-0)=9 \times 10^{-3} \mathrm{~J} \end{aligned} $$

This work done is positive

Work done during the process $\mathrm{B}$ to $\mathrm{C}$ (Compession) is

$$ \begin{aligned} \mathrm{W} _{\mathrm{BC}}= & -\mathrm{BCDE}-\mathrm{DE} \times \mathrm{CE} \\ & =-3 \times 10^{-3} \times 2=-6 \times 10^{-3} \mathrm{~J} \end{aligned} $$

This work done is negative

Work done during the process $\mathrm{CA}$ is zero because there is no change in going from $\mathrm{C}$ to $\mathrm{A}$.

Work done in complete cycle $\mathrm{W}=+$ Area $\mathrm{ABC}=\mathrm{W} _{\mathrm{AB}}+\mathrm{W} _{\mathrm{BC}}+\mathrm{W} _{\mathrm{CA}}$

$$ =3 \times 10^{-3} \mathrm{~J} $$

Internal Energy

The concept of internal energy is another useful concept used in thermodynamics. The internal energy is regarded as the energy that is intrinsically associated or stored in a system. Under proper conditions, this energy can enable the system to do work. Thus for example an explosive mixture, on explosion and a compressed gas on expansion, can do the useful mechanical work by virtue of the energy that is intrinsically stored in it.

According to our knowledge of structure of atom we regard the internal energy of a system as the kinetic and potential energy of the atoms molecules electrons and nuclear etc. of which the system is composed. A some what formal definition of the internal energy of a system is obtained as follows:

Consider a system that is thermally insulated from its surroundings and let some work (W) be done on it. The performance of this “adiabatic” work will cause a change in the internal energy of the system from an initial value $u _{i}$ to a find value $u _{\mathrm{f}}$ such that

$$ -W=u _{f}-u _{i} $$

The negative sign is attached to $\mathrm{W}$ because as per convention work done on the system is to be regarded as negative.

The above equation enables us to determine internal energy changes. It can also be used to define internal energy of a state provided the state " $\mathrm{i}$ " is a standard reference state.

Also the definition of internal energy as given above is useful because it turns out that the internal energy of a system in a particular state depends only upon that state and neither on the past history of the system nor upon the way the system has arrived at that particular state (unlike work which is a path dependent function whereas internal energy is a path independent point function). It is therefore a characteristics function of a given state. Formally one can say that the internal energy of a system in all cases is a single valued function of the variables of the state of the system. The fact that such a single valued energy function can be associated with each state of a given system is of fundamental importance of thermodynamics.

First Law of Thermodynamics

We have discussed above that when a work $\mathrm{W}$ is done on a thermally insulated system to change it from an initial state ’ $i$ ’ to a final sate ’ $f$ ’ then

$$ -\mathrm{W}=\mathrm{u} _{\mathrm{f}}-\mathrm{u} _{\mathrm{i}} $$

where $u _{i}$ and $u _{f}$ are the internal energies of the system in the initial and final states.

Suppose now that the system is not thermally insulated and is again made to change its internal energy from an initial value $u _{i}$ to a final value $u _{f}$ Since the system is now not thermally insulated some heat $Q$ can enter it in addition to the work done on it. By the principle of conservation of energy, we must have

$$ \mathrm{Q}+(-\mathrm{W})=\mathrm{u} _{\mathrm{f}}-\mathrm{u} _{\mathrm{i}} $$

Above equation represents the principle of conservation of energy as applied to a process involving heat transactions. It is often regarded as the mathematical formation of the First Law of Thermodynamics. Hence according to first law of thermodynamics.

The increase in internal energy of a system is equal to the sum of work done on the system and the heat added to it. We can rewrite the equation in the form:

$$ \mathrm{Q}=\left(\mathrm{U} _{\mathrm{f}}-\mathrm{U} _{\mathrm{i}}\right)+\mathrm{W} $$

In differential form above equation can be written as:

$$ \delta \mathrm{Q}=\delta \mathrm{u}+\delta \mathrm{W} $$

i.e. when heat is added to a system, the heat added equals the sum of the of the change in internal energy and the external work done by the system. This is as it should be once it is realized that (i) heat is a form of energy and (ii) the total energy of a given system is a conserved quantity.

Application of the First Law of Thermodynamics

Isothermal Process

In an isothermal process heat is transferred from a system to the surroundings with out any change in temperature i.e. $\Delta \mathrm{T}=0$.

For an ideal gas $\delta \mathrm{u}=0$ for an isothermal process. This is because the internal energy of such a gas is solely made up of the kinetic energy of constituent atoms and molecules and this does not change as long as temperature remains constant. Hence for an ideal gas from the first law of thermodynamics we have

$$ \delta \mathrm{Q}=\delta \mathrm{W} $$

Now we know that the work done by a gas diving are isothermal expansion is given by

$$ \delta \mathrm{W}=\mathrm{pdv} $$

For an ideal gas expanding from an initial volume $\mathrm{v} _{1}$ to a final value $\mathrm{v} _{2}$, the workdone equals

$$ \mathrm{W}=\int _{\mathrm{v} _{1}}^{\mathrm{v} _{2}} \mathrm{pdv}=\mathrm{nRT} \log _{\mathrm{e}}\left(\frac{\mathrm{v} _{2}}{\mathrm{v} _{1}}\right) $$

or

$$ \mathrm{W}=2.303 \mathrm{nRT} \log _{10}\left(\frac{\mathrm{v} _{2}}{\mathrm{v} _{1}}\right) $$

Adiabatic Process

In an adiabatic process the system is thermally insulated from its surroundings so that no heat enters or leave it. Thus $\Delta \mathrm{Q}=0$ for such a process so that from the first law of thermodynamics, we have

$$ \delta \mathrm{u}+\delta \mathrm{W}=0 $$

Considering a kilogram mole of an ideal gas this relation can be been shown to lead to the well known adiabatic process relation

$$ \mathrm{pv}^{\gamma}=\text { constant or } \mathrm{pv}^{\gamma}=\mathrm{k} $$

This relation can be used to calculate the work done during an adiabatic expansion.

As before

$$ \mathrm{W} _{\mathrm{adia}}=\int _{\mathrm{v} _{1}}^{\mathrm{v} _{2}} \mathrm{pdv} $$

Since $\mathrm{pv}^{\gamma}=\mathrm{k}$ we have

$$ \begin{gathered} \mathrm{p}=\mathrm{kv^{- \gamma }} \\ \therefore \quad \mathrm{W} _{\mathrm{adia}}=\int _{\mathrm{v} _{1}}^{\mathrm{v} _{2}} \mathrm{kv^{- \gamma } \mathrm { dv }} \\ \text { or } \quad \mathrm{W} _{\text {adia }}=\mathrm{k}\left|\frac{\mathrm{v}^{1-\gamma}}{1-\gamma}\right| _{\mathrm{v} _{1}}^{\mathrm{v} _{1}} \end{gathered} $$

Since $\mathrm{k}=\mathrm{p} _{1} \mathrm{v} _{1}^{\gamma}=\mathrm{p} _{2} \mathrm{v} _{2}^{\gamma}$

$$ \begin{aligned} \mathrm{W} _{\text {adia }}= & \frac{1}{\mathrm{r}-1}\left[\mathrm{p} _{1} \mathrm{v} _{1}^{\gamma} \mathrm{v} _{1}^{1-\gamma}-\mathrm{p} _{2} \mathrm{v} _{2}^{4} \mathrm{v} _{\mathrm{r}}^{1-\gamma}\right] \\ = & \frac{1}{\gamma-1}\left[\mathrm{p} _{1} \mathrm{v} _{1}-\mathrm{p} _{2} \mathrm{v} _{2}\right] \\ \text { or } \quad & =\frac{1}{1-\gamma}\left[\mathrm{p} _{2} \mathrm{v} _{2}-\mathrm{p} _{1} \mathrm{v} _{1}\right] \end{aligned} $$

Isochromatic Process

In an isochoric process $v$ is constant, so no work is done on or by the gas. From the first law of thermodynamics viz.

$$ \delta \mathrm{Q}=\delta \mathrm{u}+\delta \mathrm{W} $$

The heat abserbed by the gas goes entirely to change its internal energy and its temperature.

Isobaric Process

In an isobaric process, $\mathrm{P}$ is fixed. Work done by the gas is

$$ \mathrm{W}-\mathrm{p}\left(\mathrm{v} _{2}-\mathrm{v} _{1}\right)=\mathrm{nR}\left(\mathrm{T} _{2}-\mathrm{T} _{1}\right) $$

Since temperature changes so does internal energy. The heat absorbed goes partly to increase internal energy and partly to do work.

Cyclic Process

In a cyclic process the system returns to its initial state. Since internal energy is a state variable $\delta u=0$ for a given cyclic process. Hence from first law of thermodynamics viz

$$ \delta \mathrm{Q}=\delta \mathrm{u}+\delta \mathrm{W} $$

The total heat absorbed equals the work done by the system.

Example-2:

In changing the state of a gas adiabatically from an equilibrium state A to another equilibrium state $B$ an amount of work equal to $22.3 \mathrm{~J}$ is done on the system. If the gas as is taken from state A to state B via a process in which the net heat absorbed by the system is $9.35 \mathrm{cal}$, low much is the net work done by the system in latter case?

Given $1 \mathrm{Cal}=4.19 \mathrm{~J}$

Show Answer

Solution:

Since the work is done on the system is given to be negative, therefore heat absorbed by the system is positive.

For an adiabatic process $\mathrm{Q}=0$ and $\mathrm{W}=-22.3 \mathrm{~J}$

From $\mathrm{I}^{\mathrm{st}}$ law of thermodynamic

$$ \begin{aligned} & Q=\mathrm{du}+W \\ & 0=\mathrm{du}-22.3 \mathrm{~J} \\ & \therefore \mathrm{du}=22.3 \mathrm{~J} \end{aligned} $$

In the second process

$$ \begin{aligned} & Q=9.35 \mathrm{Cal}=9.35 \times 4.19 \mathrm{~J}=39.2 \mathrm{~J} \\ & \therefore \mathrm{W}=\mathrm{Q}-\mathrm{du}=39.2-22.3=16.9 \mathrm{~J} \end{aligned} $$

Example-3:

An ideal gas is taken through a cyclic thermodynamic process through four steps. The amount of heat in these steps are $Q _{1}=5960 \mathrm{~J}, Q _{2}=-5585 \mathrm{~J}, Q _{3}=-2980 \mathrm{~J}$ and $Q _{4}=3645 \mathrm{~J}$ respectively. The corresponding works involved are $W _{1}=2200 \mathrm{~J}, W _{2}=-825 \mathrm{~J}, W _{3}=-1100 \mathrm{~J}$ and $W _{4}$ respectively. Find $\mathbf{W} _{4}$ ?

Show Answer

Solution:

By the first law of thermodynamics

$$ \mathrm{dQ}=\mathrm{du}+\mathrm{dW} $$

However du is zero because the process is cyclic which implies that

$$ \mathrm{dQ}=\mathrm{dW} $$

which means that we can write

$$ \begin{aligned} & \mathrm{Q} _{1}+\mathrm{Q} _{2}+\mathrm{Q} _{3}+\mathrm{Q} _{4}=\mathrm{W} _{1}+\mathrm{W} _{2}+\mathrm{W} _{3}+\mathrm{W} _{4} \\ & \text { or } \quad 5960-5580-2980+3645=2200-825-1100+\mathrm{W} _{4} \\ & \mathrm{~W} _{4}=(5960+3645+825+1100)-(5585+2980+2200) \\ & =765 \mathrm{~J} \end{aligned} $$

Example-4:

In a given process on an ideal gas $\mathrm{dW}=0$ and $\mathrm{dQ}<0$. What happens to the temperature of the gas.

Show Answer

Solution:

We have

$$ \mathrm{dQ}=\mathrm{du}+\mathrm{dW} $$

We are give that $\mathrm{dW}=0$ and $\mathrm{dQ}<0$, so we can conclude that $\mathrm{dU}<0$

Further for an ideal gas $\mathrm{u} \propto \mathrm{T}$ so that $\mathrm{dT}<0$. Which implies that the temperature of the gas decreases.

Example-5:

1. 1.0 mole of an ideal monochromatic gas is carried around the cycle shown in the adjoining figure. Calculate the heat $\Delta \mathrm{Q}$ the change in internal energy $\Delta \mathrm{u}$ and the work done $\Delta \mathrm{w}$ for each of the three processes and cycle as a whole value at points 2 and 3.

Show Answer

Solution:

The process in going from A to $\mathrm{B}$ is isochoric (volume constant). Hence the work $\Delta \mathrm{w}$ done in the process

$$ \Delta \mathrm{w} _{1}=\mathrm{pdv}=0 $$

Let $\Delta \mathrm{Q}$ ben the heat energy absorbed in going from $\mathrm{A}$ to $\mathrm{B}$.

From the first law of thermodynamics

$$ \begin{aligned} & \Delta \mathrm{Q} _{1}=\Delta \mathrm{u} _{1}+\Delta \mathrm{w} _{1}=\Delta \mathrm{u} _{1}=\mathrm{Mc} _{\mathrm{v}} \Delta \mathrm{T} \\ & \Delta \mathrm{Q} _{1}=1 \times\left(\frac{3 \mathrm{R}}{2}\right)(600-300)=\left(\frac{3}{2}\right) \times 8.31 \times 300 \mathrm{~J}=3739.5 \mathrm{~J} \end{aligned} $$

Let $\Delta \mathrm{w} _{2}$ be the work done in going from $\mathrm{B}$ to $\mathrm{C}$.

From first law of thermodynamic

$$ \mathrm{O}=\Delta \mathrm{Q} _{2}=\Delta \mathrm{u} _{2}+\Delta \mathrm{w} _{2} $$

or

$$ \Delta \mathrm{w} _{2}=\Delta \mathrm{u} _{2}=1805.25 \mathrm{~J} $$

The process from $\mathrm{C}$ to $\mathrm{A}$ is isobaric (pressure constant)

Heat $\Delta \mathrm{Q} _{3}$ involved in the process is

$$ \begin{gathered} \Delta \mathrm{Q} _{3}=\mathrm{Mc} _{\mathrm{p}} \Delta \mathrm{T} \\ \Delta \mathrm{Q} _{3}=\left(1 \times \frac{5 \mathrm{R} \times \mathrm{R}}{2}\right)(300-455)=\frac{5 \times 8.31}{2} \times 155 \mathrm{~J}=3220.125^{-} \mathrm{J} \end{gathered} $$

The change in the internal energy $\Delta \mathrm{u} _{2}=\mathrm{Mc} _{\mathrm{v}} \Delta \mathrm{T}$

$$ =\left(1 \times \frac{3}{2} \mathrm{R}\right)(300-450)=\frac{3 \times 8.31}{2} \times 155 \mathrm{~J}=-1929.75 \mathrm{~J} $$

From the first law of thermodynamics

or $\quad \Delta \mathrm{w} _{3}=\Delta \mathrm{Q}-\Delta \mathrm{u} _{3}=-3220.125^{-}-(1929.75)$

$$ \Delta \mathrm{Q} _{3}=\Delta \mathrm{u} _{3}+\Delta \mathrm{w} _{3} $$

$$ =-1290.2375 \mathrm{~J} $$

For the complete process

$\Delta \mathrm{Q}=\Delta \mathrm{Q} _{1}+\Delta \mathrm{Q} _{2}+\Delta \mathrm{Q} _{3}=3739.5+\mathrm{O}-3220.12=519.375 \mathrm{~J}$

and

$$ \begin{aligned} & \Delta \mathrm{w}=\Delta \mathrm{w} _{1}+\Delta \mathrm{w} _{2}+\Delta \mathrm{w} _{3} \\ & =0+1805.25-1290.375=514.875 \mathrm{~J} \end{aligned} $$

Also $\Delta \mathrm{u}=\Delta \mathrm{u} _{1}+\Delta \mathrm{u} _{2}+\Delta \mathrm{u} _{3}$

$$ =3739.5-1805.25-1929.75=4.5 \mathrm{~J} $$

Limitation of the first Law of Thermodynamics

First law of thermodynamic can be regarded as essentially a statement of the principle of conservation of energy as applied to processes involving transfer of heat. A serious limitation of this law is that it does not specific any information regarding the direction of heat transfer. The law cannot answer the basic questions why heat always flows from a body at a higher temperature to one at lower temperature and the versa. It is significant to note that either was transfer of heat will not violate the energy conservation principle.

The first law of thermodynamics can not answer the question into work can heat be totally converted? (since mechanical work done in a process can be totally converted into heat).

Thus we find that first low of thermodynamics cannot answer these two basic questions. We will be discussing that answers to these questions can be provided by the second law thermodynamics.

Reversible and Irreversible Process

The concept of reversibility is one of the very important concept used in thermodynamics. From a thermodynamics point of view, a process is said to be reversible if an infinites small change in external condition will result in all changes taking place in the direct process being exactly. repeated in the inverse order and opposite sense. The idea can easily be extended to a cycle of operations. Thus a given set of cyclic operations will constitute a reversible cycle only if it is made up of a succession of reversible changes so that the cycle when traversed in the reverse reestablish the initial state of the working substance.

Reversibility is an idealized concept. Strictly speaking no natural process is a reversible phenomenon. A process can be reversible only if it is quasistatic and their are no dissipative effects. For example, a quasi static isothermal expansion of an ideal gas in a cylinder fitted with frictionless moveable piston is a reversible process.

Irreversible Process

Any process which cannot be retrace of in the reverse direction exactly is called an irreversible process. All naturally occurring processes are irreversible in the strict sense of the term. This is because dissipative effects such as viscosity, friction etc. are an inseparable ingredient of any normally occurring process. Still we tend the tract a number of actual physical processes as if they are reversible.

Conversion of Heat into Work - Heat Engines

Since energy in the form of heat is available all around us in utmost unlimited quantities, attempts were made to develop means by which heat can be converted into work. A heat engine, a device to convert heat into work must have the following essential constituents or parts.

(a) There must be a working substance which may serve as a vehicle or medium through which heat may pass through the engine. The functions of the engine is based on the thermal properties of its working substance.

(b) There must be a source or reservoir of heat which supplies the heat to the engine. This source must have a very large thermal capacity so that finite amount of heat drawn from it does not produce an change in its temperature.

(c) In addition to the source and the working substance, a heat engine also needs a cold body or heat sink maintained at a constant lower temperature. The heat sink must again be a body of very large thermal capacity so that the absorption of any finite amount of heat by it does not cause any appreciable rise in its temperature.

In order that the same working substance may continuously be used to convert the heat of the source into useful work it is necessary for it to go through a cycle of operations. This is possible if the working substance first absorbs a quantity $Q$ of heat from the source, does

some useful mechanical work $\mathrm{W}$ and finally repeat the “left over” extra heat $\mathrm{Q}$ ’ to the sink and return back to its original conditions to again go through same cycle of changes. The work done, is therefore equal to heat utilized i.e (Q-Q’). So that the efficiency $\eta$ of the engine is

$$ \eta=\frac{\mathrm{W}}{\mathrm{Q}}=\frac{\mathrm{Q}-\mathrm{Q}^{\prime}}{\mathrm{Q}}=\left(1-\frac{\mathrm{Q}^{\prime}}{\mathrm{Q}}\right) $$

It is clear that a engine will have $100 \%$ efficiency only if $Q^{\prime}=0$ i.e engine works without rejecting any heat to sink. Human experience forbid such a possibility because if it were possible. It would result in producing perpetual motion of second kind.

The Carnot Engine

The first hypothetical engine was constructed by Sadi Carnot in 1824. For working of such a engine, the engine has to extract a certain quantity of heat from the source convert a part of it to work and to reject the balance to a heat sink. To get useful work done heat must pass from the source to the sink through the working substance.

These considerations led him to think of the following ideal arrangement for his engine.

The working substance is contained in a cylinder closed by a perfectly fitting

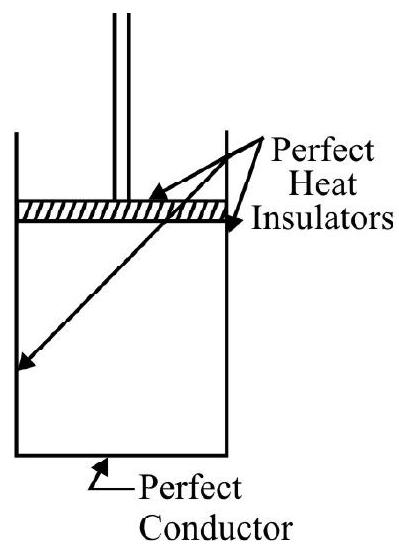but completely frictionless piston. The piston and the cylinder walls are assumed to be perfectly heat insulating materials; the base of the cylinder is however perfect conductor. The heat source $S _{1}$ is suppose to be capable of supplying any amount of heat without any change in its constant temperature $T$. Similarly the heat sink $S _{2}$ can take in any amount of heat without any change in 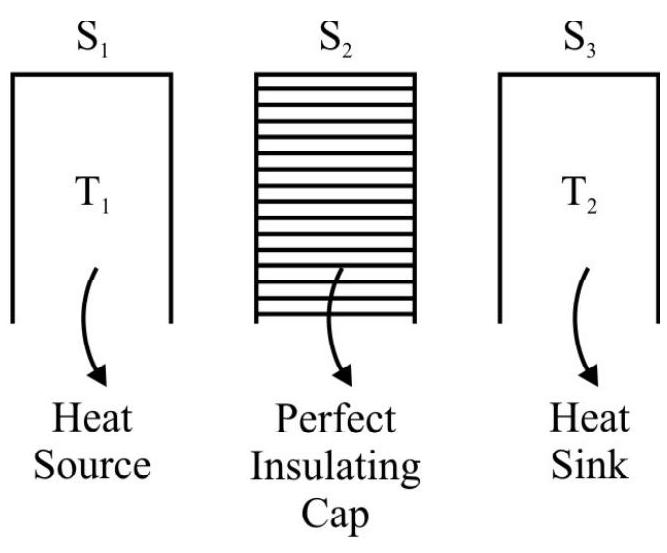constant temperature T. Both the source and the sink are supposed to have perfectly conducting tops. Further to seal the base of the cylinder as and when needed, we are also equipped with a perfectly insulating cap $\mathrm{S} _{2}$ which can exactly fit the base of the cylinder.

Let the cylinder be initially placed with it base in contact with the heat source so that the gas in it is at the temperature $T _{1}$. The condition of the working substance in it (a perfect gas) will then be represented by some point $\mathrm{A}$ on the indicator diagram. Now let the following steps of cyclic operations be performed.

(i) With the cylinder placed in contact will $\mathrm{S} _{1}$, let the pressure on the piston be decreased slightly so that the gas in it undergoes a slow expansion. The expansions assumed to take place so slowly that the heat absorbed by the gas from the source keeps pace with the work done by it and the temperature of the gas stays constant. The isothermal expansion of the gas is, therefore a reversible process. If the gas is assumed to expand up to a condition represented by a point $B$, it will do an amount of work equal to area $\mathrm{ABba}$ (see figure). This work is equal to the heat absorbed $\mathrm{Q}$ from the source during isothermal expansion.

(ii) The cylinder is now placed in contact with the insulating cap $\mathrm{S} _{2}$ and the piston

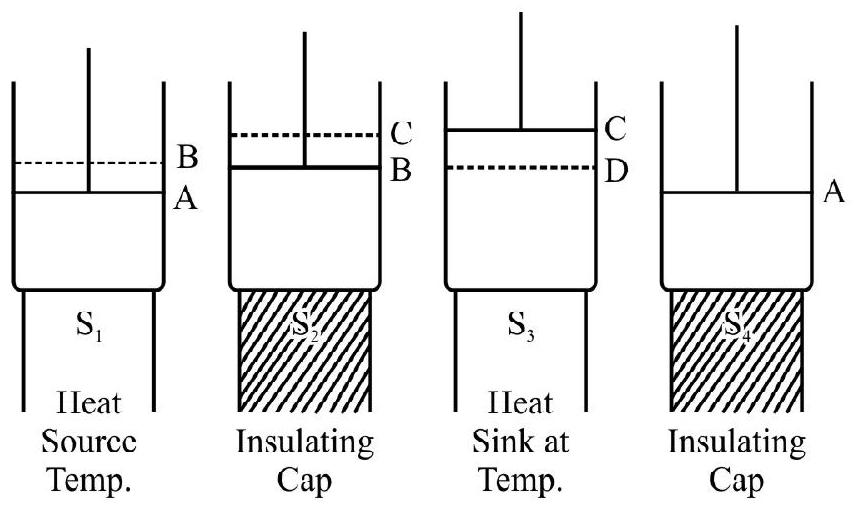is allowed to expand by inertia. This expansion now take place without any heat entering or leaving the system i.e under adiabatic conditions. The expansion is allowed to continue till the temperature of the gas falls to a value $\mathrm{T} _{2}$; the temperature of the sink. The final state of the gas is represented by a point $\mathrm{C}$ on the indicator diagram so that the gas does a work represented by the area BCcd during the adiabatic expansion.

(iii) The cylinder is next placed on the heat sink $\mathrm{S} _{2}$ and the pressure on the piston is increased very slowly. During the compression work is done on the gas and the heat developed is passed on to the sink. Again as in the first step, the work done and heat

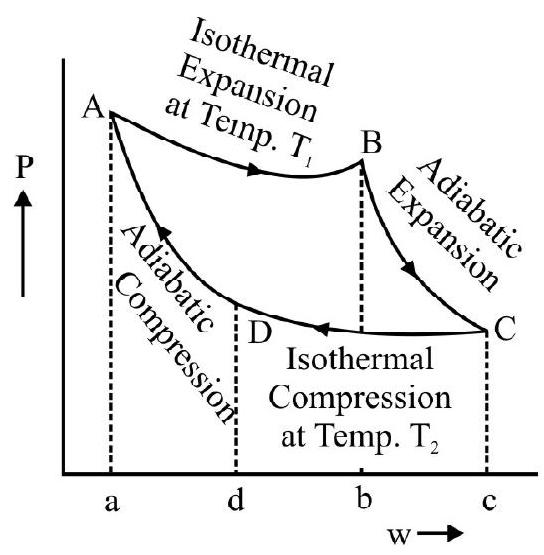developed are supposed to keep pace with each other so that the temperature of the gas stays constant at the value $\mathrm{T} _{2}$. The gas is thus made to undergo an isothermal compression in a reversible fashion and its final state at the end of this step is represented by a point $\mathrm{D}$ on the indicator diagram. The work done on the gas in this step is represented by the area $\mathrm{CcdD}$ and this is equal to the heat Q' rejected to the sink.

(iv) Finally the cylinder is again placed on the insulating stand $\mathrm{S} _{2}$ and the gas in it is slowly compressed till it is restored to its original condition represented by the point $\mathrm{A}$. The compression again takes without any transfer of heat either way i.e under adiabatic conditions. Its temperature will therefore rise and the compression is continued till the temperature again risen back to the value $\mathrm{T} _{2}$ the temperature of source. The compression is again assumed to be done very slowly i.e in a reversible fashion. The work done on the gas during the adiabatic compression is equal to the are a DdaA.

Thus we find that by the above mentioned steps, the working substance is exactly restored to its original condition and can, therefore, be made to undergo the same cycle again. During this cycle an amount of heat Q has been absorbed from the source and an amount Q’ rejected to the sink. The net work done by the gas during one cycle is the difference of work done on it and the work done by it. This is clearly see to be

$$ \mathrm{W}=\text { Area } \mathrm{ABba}+\text { Area } \mathrm{BCcb}-\text { Area } \mathrm{CcdD}-\text { Area DdaA }=\text { Area } \mathrm{ABCD} $$

This work done is equal to the difference heat absorbed Q and the heat rejected Q’ by the working substance during one cycle.

The efficiency $\eta$ of the engine is therefore

$$ \eta=\frac{\mathrm{w}}{\mathrm{Q}}=\frac{\mathrm{Q}-\mathrm{Q}^{\prime}}{\mathrm{Q}}=1-\frac{\mathrm{Q}^{\prime}}{\mathrm{Q}} $$

Assuming the gas to be perfect, it can be shown that the efficiency of cannot engine is

$$ \eta=1-\frac{Q^{\prime}}{Q}=\left(1-\frac{T _{2}}{T _{1}}\right) $$

The Refrigerator - The Carnot Cycle in Reverse

We have seen that the function of a heat engine is to absorb heat from a source at a high temperature, convert a part of it to work and reject the rest of it to a heat sin $\mathrm{k}$. Let us now image a cycle carried in reverse. Let there be a device that absorbs some heat a lower temperature, has some work done on it and rejects a large amount at a higher temperature.A device that performs a cyclic operations in this manner is called a refrigerator and the system undergoing a cycle a refrigerant.

Since the carnot cycle is performed through steps that are perfectly reversible. It can be traversed in the reverse order in the order $\mathrm{ABCBA}$. When the process is carried out in this way, we have what may be called a Carnot refrigerator. Here an amount of heat $\mathrm{Q}$ ’ is taken from the $\sin \mathrm{k}$ and on amount of heat $\mathrm{Q}$ given to the source.

In this case an amount of work equal to area $\mathrm{ABCD}$ will be done on the

working substance. The refrigerator is thus a device that is capable of pumping out heat from a cold body as a result of the work done on its working substance. The effectiveness of a refrigerator can, therefore be measured by the ratio of heat $Q^{\prime}$ pumped out from the cold body to the work $\left(\mathrm{Q}-\mathrm{Q}^{\prime}\right)$ done on the machine. This ratio is called the coefficient of performance. Hence the

Co-efficient of performance of a refrigeration $=\frac{Q^{\prime}}{Q-Q^{\prime}}=\frac{T _{2}}{T _{1}-T _{2}}$

Example-6:

A Carnot cycle is performed by air initially at $327^{\circ} \mathrm{C}$. Each stage represents a compression or expansion in the ratio 1:6. Calculate (i) the lowest temperature and efficiency of the cycle.

Given $\gamma=1.4$

Show Answer

Solution:

Here $\mathrm{T} _{1}=327+273=600 \mathrm{~K}$ and $\frac{\mathrm{v} _{1}}{\mathrm{v} _{2}}=\frac{1}{6}$

We know that $\mathrm{T} _{2} \mathrm{v} _{2}^{\gamma-1}=\mathrm{T} _{1} \mathrm{v} _{1}^{\gamma-1}$

$\therefore \quad \mathrm{T} _{2}=\left(\frac{\mathrm{v} _{1}}{\mathrm{v} _{2}}\right)^{\gamma-1} \times \mathrm{T} _{1}=\left(\frac{1}{6}\right)^{1.4-1} \times 600=293 \mathrm{~K}$ or $20^{\circ} \mathrm{C}$

(ii) Efficiency $\eta=1-\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}=1-\frac{293}{600}=0.512$

or $\eta=51.2 \%$

Example-7:

A Carnot engine has its source at $100^{\circ} \mathrm{C}$ and the sink is maintained at a constant temperature $0^{\circ} \mathrm{C}$ by means of ice. If the engine is working at the rate of $100 \mathrm{watt}$, how much ice will melt in one minute? Specific latent heat of ice is $333 \times 10^{3} \mathrm{~J} / \mathrm{Kg}$

Show Answer

Solution:

The efficiency of carnot engine is given by $\eta=1-\frac{T _{2}}{T _{1}}$

$\mathrm{T} 2=$ temperature of $\sin \mathrm{k}=0+273=273^{\circ} \mathrm{K}$

$\mathrm{T} _{1}=$ temperature of source $=100+273=370^{\circ} \mathrm{K}$

$\therefore \quad \eta=\frac{\mathrm{w}}{\mathrm{Q}}=\left(1-\frac{273}{373}\right)=\frac{100}{373}$

Now $\mathrm{W}=$ work done by the engine $=100 \mathrm{~J} / \mathrm{s}$

$\mathrm{Q}=$ heat absorbed from the source $=373 \mathrm{~J} / \mathrm{s}$

Let Q’ be the heat rejected to the $\sin \mathrm{k}$

Since $\frac{\mathrm{Q}}{\mathrm{Q}^{\prime}}=\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}$ we have

$\mathrm{Q}^{\prime}=\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}} \mathrm{Q}=\frac{273}{373} \times 373=273 \mathrm{~J} / \mathrm{s}$

Heat rejected to the sink in one minute. $273 \times 60=16380 \mathrm{~J}$

Hence mass of ice inserted in one minute $=\frac{16380}{333 \times 10^{3}} \mathrm{Kg}=0.049 \mathrm{Kg}$

Example-8:

A carnot engine having a perfect gas as the working substance is driven backward and is used for freezing water already at $0^{\circ} \mathrm{C}$. If the engine is driven by a 500 watt electric motor having an efficiency of $60 \%$ how long will it take to freeze $15 \mathrm{Kg}$ of water. Take $15^{\circ} \mathrm{C}$ and $0^{\circ} \mathrm{C}$ as the working temperatures of the engine and assume that there are no heat loses in the refrigerating system.

Specific latent heat of ice $=333 \times 10^{3} \mathrm{~J} / \mathrm{Kg}$

Show Answer

Solution:

The effective power of the motor used to drive the engine is $500 \times \frac{6}{100}$ watt $=300$ watt

Since the latent heat of ice is $333 \times 10^{3} \mathrm{~J} / \mathrm{Kg}$ the heat energy that must be extracted to freeze $15 \mathrm{Kg}$ of water at ${ }^{\circ} \mathrm{C}=15 \times 333 \times 10^{3}$

$$ =50.05 \times 10^{3} \mathrm{~J} $$

Now the co-efficient of performance of a Carnot engine working as a refrigerator

$$ =\frac{\text { Heat pumped out from the source }}{\text { Work done on the machine }}=\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}-\mathrm{T} _{2}}=\frac{273}{288-273}=\frac{273}{15} $$

The work done on the machine is $300 \mathrm{~J} / \mathrm{s}$. Hence the heat pumped out from the cold water per second

$$ =\frac{273}{15} \times 300 \mathrm{~J}-5460 \mathrm{~J} $$

The total heat that must be pumped out is $50.05 \times 10^{3} \mathrm{~J}$. Hence the time taken for the entire process is

$$ =\frac{50.05 \times 10^{5}}{5460}=15.28 \text { minute } $$

Example-9:

Two Carnot engines $A$ and $B$ are operated in series. The first one $A$ receives heat at $800 \mathrm{~K}$ and rejects to a reservoir at temperature $T$. The second engine $B$ receives the heat rejected by the first engine and in turn rejects to a heat reserved at 300 . Calculate $T$ when the outputs of two engines are equal.

Show Answer

Solution:

We have $T _{1}=800 \mathrm{~K}$ and $T _{2}=T \mathrm{~K}$ (Say) for the engine A.

Also $\eta _{A}=1-\frac{T _{2}}{T}=1-\frac{800}{T}$

Further $\frac{\mathrm{Q}^{\prime}}{\mathrm{Q}}=\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}=\frac{\mathrm{T}}{800}$

Workout by the engine $\mathrm{A}, \mathrm{w} _{\mathrm{A}}$ is

$$ \begin{array}{cl} \mathrm{w} _{\mathrm{A}}=\mathrm{Q} _{\mathrm{A}}-\mathrm{Q} _{\mathrm{A}}^{\prime}=\eta _{\mathrm{A}} \times \mathrm{Q} & {\left[\because \eta _{\mathrm{A}}=1-\frac{\mathrm{Q}^{\prime}}{\mathrm{Q}}\right]} \\ \mathrm{w} _{\mathrm{A}}=\left(1-\frac{\mathrm{T}}{800}\right) \mathrm{Q} \\ \eta _{\mathrm{B}}=1-\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}=1-\frac{300}{\mathrm{~T}} \end{array} $$

and $\quad \mathrm{w} _{\mathrm{B}}=\mathrm{Q}-\mathrm{Q}^{\prime}=\eta _{\mathrm{B}}$

$\mathrm{w} _{\mathrm{B}}=\mathrm{Q} _{\mathrm{B}}-\mathrm{Q} _{\mathrm{B}}^{\prime}=\eta _{\mathrm{B}} \times \mathrm{Q} _{\mathrm{B}}=\left(1-\frac{300}{\mathrm{~T}}\right) \mathrm{Q} _{\mathrm{B}}^{\prime}$

Since the engine $B$ absorbs the heat rejected by the engine $A$ so $Q _{B}^{\prime}=Q _{A}$

$\mathrm{w} _{\mathrm{B}}=\left(1-\frac{300}{\mathrm{~T}}\right) \mathrm{Q} _{\mathrm{B}}$

When the output of the two engines are equal we have $\mathrm{w} _{\mathrm{A}}=\mathrm{w} _{\mathrm{B}}$

$(1-\mathrm{T} / 800) \mathrm{Q}=\left(1-\frac{300}{\mathrm{~T}}\right) \frac{\mathrm{Q}^{\prime}}{\mathrm{Q}}=\left(1-\frac{300}{\mathrm{~T}}\right) \frac{\mathrm{T}}{800}$

Solving we get $\mathrm{T}=550 \mathrm{k}$

Example-10:

A reversible engine converts one sixth of heat which it absorbs from source into work. When the temperature of the sin $\mathrm{k}$ is reduced by $82^{\circ} \mathrm{C}$ its efficient is doubled. Compute the temperature of source and heat of sink.

Show Answer

Solution:

Let $\mathrm{T} _{1} \mathrm{~K}$ and $\mathrm{T} _{2} \mathrm{~K}$ be the temperature of source and sink respectively. If $\mathrm{Q} _{1}$ is heat absorbed and $\mathrm{Q} _{2}$ heat given back to sink, the efficiency $\eta$ of the engine is

$$ \begin{array}{ll} & \eta=1-\frac{T _{2}}{T _{1}} \\ \text { or } \quad \eta=\frac{1}{6}=\frac{T _{1}-T _{2}}{T _{1}} \\ \text { or } \quad T _{1}=6 T _{1}-6 T _{2} \quad \text { or } \quad 6 T _{2}=5 T \\ \therefore \quad T _{1}=\left(\frac{6}{5}\right) T _{2} …………… (1) \end{array} $$

When the temperature of sin $\mathrm{k}$ is lowered by $82^{\circ}$ i.e $355 \mathrm{~K}$, the efficiency is doubled.

$$ \text { v } \eta=2 \times \frac{1}{6}=\frac{1}{3} $$

Let $T _{2}^{\prime}$ be the new temperature of the sink obviously $T _{2}^{\prime}=T _{2}-355$

$$ \begin{equation*} \eta^{\prime}=1-\frac{\mathrm{T} _{2}^{\prime}}{\mathrm{T} _{1}} \quad \text { or } \quad \frac{1}{3}=1-\frac{\left(\mathrm{T} _{2}-355\right)}{\mathrm{T}} \end{equation*} $$

or $\quad 3 \mathrm{~T} _{2}=2 \mathrm{~T} _{1}+1065 ………………(2)$

From equation (1) and (2) we get

$$ \begin{aligned} & 3 \mathrm{~T} _{2}-2 \times\left(\frac{6}{5}\right) \mathrm{T} _{2}+1065 \text { or } \frac{3 \mathrm{~T} _{2}}{5}=1065 \\ & \mathrm{~T} _{2}=1065 \times \frac{5}{3}=1775 \mathrm{~K} \text { and } \mathrm{T} _{1}=\frac{6}{5} \times 1775=2130 \mathrm{~K} \end{aligned} $$

Example-11:

The ice in a cold storage melts at the rate of $2 \mathrm{Kg}$ per hour when the external temperature is $20^{\circ} \mathrm{C}$. Find the minimum power output of the motor used to drive the refrigerator which just prevents ice from melting. Latent heat of fusion of ice $=80 \mathrm{Cal} / \mathrm{g}$ and $\mathrm{J}=4.2 \mathrm{~J} / \mathrm{Cal}$.

Show Answer

Solution:

The co-efficient of performance of a refrigerator is given by

$$ \begin{array}{r} \omega=\frac{\mathrm{Q} _{2}}{\mathrm{~W}}=\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}-\mathrm{T} _{2}} \\ \therefore \quad \omega=\frac{273}{293-273}=\frac{273}{20} \tag{1} \end{array} $$

Also in the relation $\omega=\frac{\mathrm{Q} _{2}}{\mathrm{~W}}, \mathrm{Q} _{2}$ is the quantity of heat which should be taken out by the refrigerator to prevent the melting of $2 \mathrm{Kg}$ of the per hour at $0^{\circ} \mathrm{C}$.

$\therefore \mathrm{Q} _{2}=\frac{2 \times 1000 \times 80}{60 \times 60}$ cal per second

Hence we have

$$ \begin{gathered} \omega=\frac{273}{20}=\frac{2000 \times 80}{3600} \times \frac{1}{W} \\ \therefore \quad \omega=\frac{20 \times 2000 \times 80}{273 \times 3600}=13.60 \text { watt } \\ \text { or } \quad W=\frac{13.68}{746} \text { H.P }=0.18 \text { H.P } \end{gathered} $$

The Second Law of Thermodynamics

We have already seen in our discussions that whereas work may be totally converted into heat, the converse is not true. This fact has been referred to as one sided convertibility by Willard Gibbs.

These facts concerning of heat into work have now been embodied in the form of an important principle of nature. This principle is called the second law of thermodynamics and has been stated in a number of different forms all of which can be shown to be equivalent to one another.

Kelvin and Planck stated the second law of thermodynamics as follows:

It is impossible to construct an engine that operating in a cycle, will produce no effect other than extraction of heat from a reservoir and the performance of an equal amount of work.

Clausius stated the Law as follows:

It is impossible for a self acting machine un aided by any external agency to convey heat from one body to another at a higher temperature or heat cannot by itself pass from a colder to a warmer body. Ostwald stated the law thus: it is impossible to have perpetual motion of the second kind.

The great significance of the second law of thermodynamics that it provides us answers to question which the first law has left unanswered. The second law tell us the natural direction of heat flow from a hotter to a colder body. It also guides about the way heat can be converted into work and the limits of such a conversion. It is, in fact, tells us heat energy is unique in a way because unlike other forms of energy, it can be utilized under specific conditions and that too partly.

The second law of thermodynamics is purely based on observations and facts summarizing our experience in the process of converting heat into work. We, however have a very deep rooted fact in the validity of

his law for no machine has been devised which works in violation of this law. Indeed all the deductions and predications made on the basis of this law have stood the test of time and experiments. No wonder then that the second law of thermodynamics is now regarded as universal law of nature.

Cornot’s Theorem

The carnot’s theorem states:

It is not possible to have any heat engine more efficient than a reversible Carnot’s engine between two given temperatures.

To prove Carnot’s theorem let us consider two heat engines A and B working between temperatures $\mathrm{T} _{1}$ and $\mathrm{T} _{2}$. Let $\mathrm{A}$ be the reversible Carnot’s engine and $\mathrm{B}$ any other engine. If possible let $\mathrm{B}$ be more efficient than $\mathrm{A}$.

i.e. $\quad \eta _{B}>\eta _{A}$

But $\quad \eta _{\mathrm{B}}=\frac{\mathrm{w} _{\mathrm{B}}}{\mathrm{Q}}$ and $\eta _{\mathrm{A}}=\frac{\mathrm{w} _{\mathrm{A}}}{\mathrm{Q}}$

$\therefore \mathrm{W} _{\mathrm{B}}>\mathrm{W} _{\mathrm{A}}$

Let us now combine engine $A$ and $B$ as shown in figure. We use $B$ as a heat engine and $\mathrm{A}$ as a refrigerator. The engine $\mathrm{B}$ working as a heat engine extracts heat $\mathrm{Q}$ from source at temperature $\mathrm{T} _{1}$ does work and

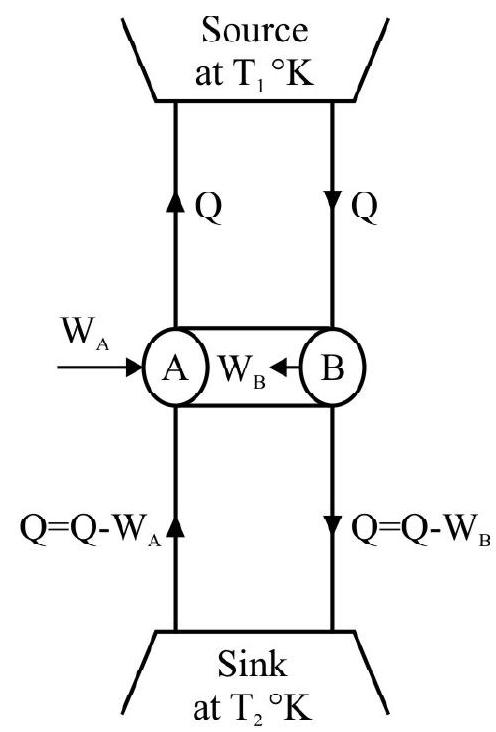
reject heat $\mathrm{Q}^{\prime}=\mathrm{Q}-\mathrm{W} _{\mathrm{B}}$ to $\sin \mathrm{k}$. From the work $\mathrm{W} _{\mathrm{B}}$ done on engine $\mathrm{A}$ and it use as a refrigerator. [Since $\eta _{B}>\eta _{A}$, therefore $W _{B}>W _{A}$ ]. Engine A working as refrigerator extracts heat $Q _{1}^{\prime}$ from sink at temperature $T _{2} K$ and gives heat $Q$ to source at temperature $T _{1} K$. The net effect of this combined machine is to extract heat.

$\mathrm{Q} _{1}^{\prime}-\mathrm{Q}^{\prime}=\left(\mathrm{Q}-\mathrm{W} _{\mathrm{A}}\right)-\left(\mathrm{Q}-\mathrm{W} _{\mathrm{B}}\right)=\mathrm{W} _{\mathrm{B}}-\mathrm{W} _{\mathrm{A}}$ from the sink. The net work done by the machine is $\mathrm{W} _{\mathrm{B}}-\mathrm{W} _{\mathrm{A}}$ from single body sink and converts the whole of it into work without producing any change in the source or surroundings. This is against the second law of thermodynamics. Hence our assumption $\eta _{B}>\eta _{A}$ must be wrong. In other words no heat Cornot engine can be more efficient than a reversible Carnot’s engine.

PROBLEMS FOR PRACTICES

1. Calculate the work done by the gas whose thermodynamical behavior is represented by right angled triangle $\mathrm{ABC}$ on $\mathrm{P}-\mathrm{V}$ diagram. The $\mathrm{P}-\mathrm{V}$ co-ordinates are $\mathrm{A}(20,0), \mathrm{B}(10,12)$ and $\mathrm{C}(10,6)$ when $\mathrm{P}$ is in $\mathrm{Nm}^{-2}$ and $\mathrm{V}$ is in $\mathrm{m}^{-3}$.

Show Answer

Answer.: $30 \mathrm{~J}$

2. One mole of an ideal gas undergoes a cyclic change $\mathrm{ABCD}$ where the $\mathrm{P}-\mathrm{V}$ co-ordinates are $\mathrm{A}(5,1), \mathrm{B}(5,3), \mathrm{C}(2,3)$ and $\mathrm{D}(2,1)$. $\mathrm{P}$ is in atmosphere and $\mathrm{V}$ is in litres. Calculate the work done along $\mathrm{AB}, \mathrm{BC}, \mathrm{CD}$ and $\mathrm{DA}$ and the net work done in the process. Given a atmosphere $=1.01 \times 10^{5}$ $\mathrm{Nm}^{-2}$.

Show Answer

Answer.: $10.0 \mathrm{~J}, 0,-404 \mathrm{~J}, 0$ and $606 \mathrm{~J}$

3. Calculate the change in internal energy of a block of copper of mass $200 \mathrm{~g}$ when it is heated from $25^{\circ} \mathrm{C}$ to $75^{\circ} \mathrm{C}$. Given specific heat of copper $=0.1 \mathrm{Cal} \mathrm{g}^{-1} \mathrm{C}^{-1}$. Change in volume can be considered to be reversible.

Show Answer

Answer.: $4200 \mathrm{~J}$

4. At $0^{\circ} \mathrm{C}$ and normal atmospheric pressure, the volume of $1 \mathrm{~g}$ of water increases from $1 \mathrm{~cm}^{3}$ to 1.091 $\mathrm{cm}^{3}$ on freezing. What will be change in its internal energy. Given

Latent heat of melting of ice $=80 \mathrm{Cal} \mathrm{g}^{-1}$ and normal atmospheric pressures is $1.013 \times 10^{5} \mathrm{Nm}^{-1}$.

Show Answer

Answer.: $-80 \mathrm{Cal}$

5. A volume of $10 \mathrm{~m}^{3}$ of a liquid is supplied with $100 \mathrm{~K}$ cal of heat and expands at constant pressure of 10 atmosphere to a final volume of $10.2 \mathrm{~m}^{3}$. Calculate the change in internal energy.

Show Answer

Answer.: $52 \mathrm{~K} \mathrm{cal}$

6. An electric heater supplies heat to a system at a rate of $100 \mathrm{~W}$. If system perform work at a rate of 75 joules per second, at what rate is the internal energy increasing?

Show Answer

Answer.: $25 \mathrm{~W}$

7. A Carnot engine is designed to operate between $600 \mathrm{~K}$ and $300 \mathrm{~K}$. The engine is observed to produce $1.96 \mathrm{KJ}$ of mechanical energy per kilo calorie of absorbed heat. Compare the actual and the practical efficiency of the engine.

Show Answer

Answer.: $50 \% ; 47 \%$

8. A reversible engine takes in heat from a reservoir of heat at $527^{\circ}$ and gives out heat to the sink at $127^{\circ} \mathrm{C}$. How much heat per second must it take from reservoir in order to produce useful work at the rate of 750 watt.

Show Answer

Answer.: $1500 \mathrm{~J}$

9. A reversible heat engine operates with as efficiency of $50 \%$. If during each cycle it rejects $150 \mathrm{Cal}$ to a reservoir of heat at $30^{\circ} \mathrm{C}$ then (i) what is the temperature of other reservoir and (ii) how much work does it caring out per cycle.

Show Answer

Answer.: (i) $333^{\circ} \mathrm{C}$ (ii) $630 \mathrm{~J}$

10. In a heat engine the temperature of the source and sink are $500 \mathrm{~K}$ and $375 \mathrm{~K}$. If the engine consumes $25 \times 10^{5} \mathrm{~J}$ per cycle find (i) the efficiency of the engine (ii) work done per cycle and (iii) heat related to the sink per cycle.

Show Answer

Answer.: $25 \%, 6.25 \times 10^{5} \mathrm{~J}, 18.75 \times 10^{5} \mathrm{~J}$

11. A Carnot cycle operating between $\mathrm{T} _{1}=500 \mathrm{~K}$ and $\mathrm{T} _{2}=300 \mathrm{~K}$ producing $1 \mathrm{KJ}$ of mechanical work. per cycle. Find the heat transferred to the engine by the reservoirs

Show Answer

Answer.: $\mathrm{Q} _{1}=2500, \mathrm{Q} _{2}=1500 \mathrm{~J}$

12. A Carnot engine has its source at $100^{\circ} \mathrm{C}$ and the sink is maintained at a constant temperature by means of ice. If the engine is working at the rate of 100 watt, how much ice will melt in one minute? Specific latent heat of the $333 \times 10^{3} \mathrm{~J} / \mathrm{Kg}$.

Show Answer

Answer.: $4.92 \times 10^{-2} \mathrm{Kg}$

13. A reversible engine converts one sixth of the heat input into work. When the temperature of the sink reduced by $62^{\circ} \mathrm{C}$, its efficiency is doubled. Find the temperature of the source and the sink.

Show Answer

Answer.: $1737^{\circ} \mathrm{C}, 1402^{\circ} \mathrm{C}$

14. A Carnot cycle is performed by 1 litre of air $(\gamma=1.4)$ initially at $327^{\circ} \mathrm{C}$ at a pressure of 12 atmosphere. Each state represents a compression or expansion ratio 1.6. Calculate the lowest temperature and efficiency of the cycle.

Show Answer

Answer.: $20^{\circ} \mathrm{C}, 51.1 \%$

15. In a refrigerator, the motor is $1 \mathrm{kw}$ power and heat is transferred from $-3^{\circ} \mathrm{C}$ to $27^{\circ}$. Find the heat taken out of the refrigerator per second assuming its efficiency is $50 \%$ of a perfect engine.

Show Answer

Answer.: $19 \mathrm{KJ}$

16. A freezer has a coefficient of performance 5 . When $3.6 \times 10^{6} \mathrm{~J}$ work is done on the freezer, what is the mass of water at $0^{\circ} \mathrm{C}$ converted into ice cubes at $0^{\circ} \mathrm{C}$ ? Latent heat of fusion of water $=80 \mathrm{~K} \mathrm{cal} / \mathrm{Kg}$.

Show Answer

Answer.: $53.5 \mathrm{Kg}$

17. In a refrigerator heat from inside at $277^{\circ} \mathrm{K}$ is transferred to a room at $300^{\circ} \mathrm{K}$. How many joules of heat shall be delivered to the room for each joule of electric energy consumed ideally?

Show Answer

Answer.: $13.04 \mathrm{~J}$

Question Bank

Key Learning Points

1. Heat and temperature may be considered as related to each other as ‘cause’ and ’effect’.

2. Maxwell has defined temperature as the thermal state of a body with reference to its ability to communicate heat to other bodies.

3. In thermodynamics we distinguish clearly between a system and its surroundings.

4. We generally take the pressure and volume and temperature of a system as the thermodynamic variables.

5. The concept of thermal equilibrium is used to define temperature.

6. According to the zeroth law of thermodynamics two systems which are individually in thermal equilibrium with a third one are also in equilibrium with each other.

7. The temperature of a system is a property which enables us to decide whether this system would or would not be in thermal equilibrium with another system.

8. In thermodynamics the term work refers only to external work, internal work has no place in thermodynamics.

9. The work done during an isothermal expansion of an ideal gas is given by $\mathrm{W}=2.303 \mathrm{nRT} \log _{e}\left(\mathrm{~V} _{2} / \mathrm{V} _{1}\right)$.

10. The work done during an adiabatic expansion of an ideal gas is given by

$$ \mathrm{W}=\frac{\mathrm{k}}{1-\gamma}\left(\mathrm{p} _{2} \mathrm{v} _{2}-\mathrm{p} _{1} \mathrm{v} _{1}\right) $$

11. In an isochoric process $v$ is constant so no work is done on it or by the gas.

12. In an isobaric process $p$ is constant and the work done by the gas to given by

$$ \mathrm{W}=\mathrm{p}\left(\mathrm{v} _{2}-\mathrm{v} _{1}\right)=\mathrm{nR}\left(\mathrm{T} _{2}-\mathrm{T} _{1}\right) $$

13. The equation of state for an ideal gas having $n$ mole can be expressed as

$$ \mathrm{Pv}=\mathrm{nRT} $$

For an adiabatic change is given by

$$ \mathrm{Pv}^{\gamma}=\text { constant } $$

14. The performance of an adiabatic work $\mathrm{W}$ cause the internal energy of a system to change from $\mathrm{u} _{\mathrm{i}}$ to a value $u _{\mathrm{f}}$ such that

$$ \mathrm{W}=\mathrm{u} _{\mathrm{f}}-\mathrm{u} _{\mathrm{i}} $$

15. The internal energy of a system is a characteristic function of the given state of the system.

16. According to the first law of thermodynamic the increase $(\delta u)$ in the internal energy of the system is equal to the sum of the work done on the system $(=-\delta \mathrm{w})$ and the heat $(\delta \mathrm{Q})$ added to it

$$ \begin{aligned} & \delta \mathrm{u}=\delta \mathrm{Q}+(-\delta \mathrm{w}) \\ & \delta \mathrm{Q}=\delta \mathrm{u}+\delta \mathrm{w} \end{aligned} $$

17. Thermodynamics processes can take place under isothermal $(\delta \mathrm{T}=0)$ adiabatic $(\delta \mathrm{Q}=0)$, isochoric $(\delta \mathrm{v}=0)$ and isobaric $(\delta \mathrm{P}=0)$ conditions.

18. A given set of cyclic changes constitutes a reversible process if it is made up a succession of reversible changes so that the cycle when traced in the reverse order re-establishes the initial state of working substance. Natural processor are generally irreversible.

19. The first law does not tell us anything about the direction of heat transfer. To overcome this limitation, the second law of the thermodynamics was formulated.

20. Heat engines are devices that convert heat into work. They are made up of three essential parts (i) a working substance (ii) a reservoir of heat and (iii) a heat sink.

The efficiency $\eta$ of a heat engine is defined as

$$ \eta=\frac{W}{Q}=1-\frac{Q^{\prime}}{Q} $$

where Q and Q’ are the heat taken in from the source and the heat rejected to the sink. W is the work done by the engine.

21. Sadi Carnot suggested (1824), the essential details of a hypothetical ideal heat engine its efficiency was shown to be given by

$$ \eta=1-\frac{Q^{\prime}}{Q}=1-\frac{T^{\prime}}{T} $$

where $\mathrm{T}$ and $\mathrm{T}^{\prime}$ are the (constant) temperatures ( $\mathrm{K}$ ) of heat source any heat sink respectively.

22. The refrigerator may be regarded as a heat engine in reverse. Its co-efficient of performance is defined by $=\frac{Q^{\prime}}{Q-Q^{\prime}}$.

where Q’ and Q are the heats pumped out from the cold body (sink) and given to the (hotter) surrounding (source) respectively.

For an ideal refrigerator co-efficient of performance $=\frac{\mathrm{T}^{\prime}}{\mathrm{T}-\mathrm{T}^{\prime}}$

23. According to second law of thermodynamics. It is impossible to construct an engine that operating in cycle will produce no effect other than extraction of heat from a reservoir and performance of equal amount of work.

$$ O R $$

It is impossible for a self acting machine unaided by an external agency to convey heat from one body to another at a higher temperature or heat cannot by itself, pass from a colder to a warmer body.

24. The two statements can be shown to equivalent to each other.

According to Carnot theorem: It is impossible to have any heat engine more efficient than a reversible Carnot’s engine, working between two given temperatures.

1. One mole of ideal gas in a cylinder is compressed reversibly by increasing the pressure from $1 \mathrm{~atm}$ to $10 \mathrm{~atm}$ at a constant temperature $500 \mathrm{~K}$. The work done on the gas during compression is

(given $\mathrm{R}=\mathbf{8 . 3 1 4 5} \mathrm{J} \mathrm{mol}^{-1} \mathrm{~K}^{-1}$ )

(1) $-4160 \mathrm{~J}$

(2) $+4160 \mathrm{~J}$

(3) $-9570 \mathrm{~J}$

(4) $+9570 \mathrm{~J}$

Show Answer

Correct answer: (4)

Solution:

As given the process is an isothermal process, work done by n moles of gas expands or contracts reversibly from $\mathrm{v} _{1}$ to $\mathrm{v} _{2}$ volume at constant temperature $\mathrm{T}$ is given by

$$ \begin{equation*} \mathrm{w}=\mathrm{nRT} \ell \ln \left(\frac{\mathrm{v} _{\mathrm{f}}}{\mathrm{v} _{\mathrm{i}}}\right) \tag{1} \end{equation*} $$

As $\mathrm{PV}=$ constant for isothermal process, we have $\mathrm{P} _{\mathrm{i}} \mathrm{v} _{\mathrm{i}}=\mathrm{P} _{\mathrm{f}} \mathrm{v} _{\mathrm{f}}$

$$ \begin{equation*} \therefore \frac{\mathrm{v} _{\mathrm{f}}}{\mathrm{v} _{\mathrm{i}}}=\frac{\mathrm{P} _{\mathrm{i}}}{\mathrm{P} _{\mathrm{f}}} \tag{2} \end{equation*} $$

From (1) & (2)

$$ \mathrm{W}=\mathrm{nRT} \ell \mathrm{n}\left(\frac{\mathrm{P} _{\mathrm{i}}}{\mathrm{P} _{\mathrm{f}}}\right) $$

$\mathrm{W}^{\prime}$, work done on the gas $=-\mathrm{W}$, work done by the gas

$$ \begin{aligned} \mathrm{W}^{\prime}= & -\mathrm{nRT} \ell \mathrm{n}\left(\frac{\mathrm{P} _{\mathrm{i}}}{\mathrm{P} _{\mathrm{f}}}\right) \\ & =-1 \times 8.3145 \times 500 \ln \left(\frac{1}{10}\right) \\ & =-1 \times 8.3145 \times 500(-\ln 10)=8.3145 \times 500 \times 2.303 \log _{\mathrm{e}} 10 \\ & =9570 \mathrm{~J} \end{aligned} $$

Work done on the system in positive; as system gains heat energy during compression.

Hence option (4) is correct.

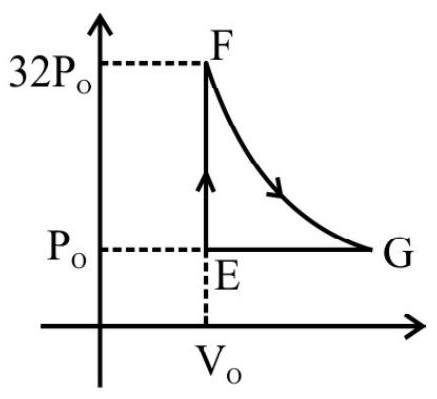
2. One mole of a monoatomic ideal gas in taken along a cyclic process $\mathbf{E} \rightarrow \mathbf{F} \rightarrow \mathbf{G} \rightarrow \mathbf{E}$. The processes involved are purely isochoric, isothermal and isobaric respectively. The amount of work done from $F \rightarrow G$ is

(1) $24 \mathrm{P} _{0} \mathrm{v} _{0}$

(2) $31 \mathrm{P} _{0} \mathrm{v} _{0}$

(3) $36 \mathrm{P} _{0} \mathrm{v} _{0}$

(4) $160 \mathrm{P} _{0} \mathrm{v} _{0} \ln ^{2}$

Show Answer

Correct answer: (4)

Solution:

As $\mathrm{F} \rightarrow \mathrm{G}$ is isothermal process, ’ $\mathrm{T}$ ’ is constant so, $\mathrm{P} \propto \frac{1}{\mathrm{~V}}$ and $\mathrm{Pv}=$ constant

$\mathrm{P} _{1} \mathrm{~V} _{1}=\mathrm{P} _{2} \mathrm{~V} _{2}=32 \mathrm{P} _{0} \mathrm{v} _{0}=\mathrm{P} _{0} \mathrm{v} _{0}$

$$ \therefore \mathrm{v} _{2}=32 \mathrm{v} _{0} $$

Work done by the gas in isothermal process is $\mathrm{W}=\mathrm{nRT} \ell \mathrm{n}\left(\frac{\mathrm{v} _{\mathrm{f}}}{\mathrm{v} _{\mathrm{i}}}\right)$

$$ \begin{aligned} & =1 \times 32 \mathrm{P} _{0} \mathrm{v} _{0} \ln \left(\frac{32 \mathrm{v} _{0}}{\mathrm{v} _{0}}\right) \quad \quad[\text { as } \mathrm{Pv}=\mathrm{nRT} & \mathrm{n}=1] \\ & =32 \mathrm{P} _{0} \mathrm{v} _{0} \ln 25=32 \times 5 \mathrm{P} _{0} \mathrm{v} _{0} \ln 2=160 \mathrm{P} _{0} \mathrm{v} _{0} \ln 2 \end{aligned} $$

Hence option (4) is correct.

3. An ideal gas expands isothermally from a volume $v _{1}$ to $v _{2}$ and then compressed to original volume $v _{1}$ adiabatically. Initial pressure is $P _{1}$ and final pressure is $P _{3}$. If $W$ is the total work done in the process, then we have

(1) $\mathrm{P} _{3}>\mathrm{P} _{1}, \mathrm{~W}>0$

(2) $\mathrm{P} _{3}<\mathrm{P} _{1}, \mathrm{~W}<0$

(3) $\mathrm{P} _{3}>\mathrm{P} _{1}, \mathrm{~W}<0$

(4) $\mathrm{P} _{3}=\mathrm{P} _{1}, \mathrm{~W}=0$

Show Answer

Correct answer: (3)

Solution:

For isothermal process we have $\mathrm{P} _{1} \mathrm{~V} _{1}=\mathrm{P} _{2} \mathrm{~V} _{2}$

or $\quad \mathrm{P} _{1}=\left(\frac{\mathrm{V} _{2}}{\mathrm{~V} _{1}}\right) \mathrm{P} _{2} ……………..(1)$

For adiabatic process

$$ \mathrm{P} _{3} \mathrm{~V} _{1}^{\gamma}=\mathrm{P} _{2} \mathrm{~V} _{2}^{\gamma} $$

or $\quad \mathrm{P} _{3}=\left(\frac{\mathrm{V} _{2}}{\mathrm{~V} _{1}}\right)^{\gamma} \mathrm{P} _{2} ……………..(2)$

as $\gamma>1$ from(1) & (2)

Hence $\mathrm{P} _{3}<\mathrm{P} _{1}$

As slope of adiabatic curve is greater than that of isothermal process curve as shown in the $\mathrm{P}-\mathrm{v}$ diagram.

$\Rightarrow$ Area under adiabatic curve $>$ Area under isothermal curve.

$\Rightarrow$ Negative work $>$ Positive work (as seen from $\mathrm{P}-\mathrm{v}$ diagram)

$\Rightarrow$ Total work done $\mathrm{W}>0$.

Hence $\mathrm{P} _{3}>\mathrm{P} _{2}, \mathrm{~W}<0$.

Hence option (3) is correct.

4. In a process $v \propto T^{2}$, temperature of 2 moles of a gas in increased by $200 \mathrm{~K}$. Work done by the gas in this process will be

(1) $600 \mathrm{R}$

(2) $800 \mathrm{R}$

(3) $1000 \mathrm{R}$

(4) $1200 \mathrm{R}$

Show Answer

Correct answer: (2)

Solution:

Given $\mathrm{v} \propto \mathrm{T}^{2}$

$\therefore \mathrm{v}=\mathrm{aT}^{2}$ (where $\mathrm{a}$ is constant of proportionality).

$\Rightarrow \mathrm{dv}=\mathrm{a} 2 \mathrm{TdT}…………………(1)$

As $\mathrm{P}=\frac{\mathrm{nRT}}{\mathrm{V}}=\frac{\mathrm{nRT}}{\mathrm{aT}^{2}}=\frac{\mathrm{nR}}{\mathrm{aT}} ……………..(2)$

From (1) & (2), we have

$$ \begin{aligned} & \mathrm{Pdv}=2 \mathrm{nRdT} \\ & \therefore \quad \mathrm{w}=\int \mathrm{Pdv}=\int _{\mathrm{T} _{1}}^{\mathrm{T} _{2}} 2 \mathrm{nRdT}=2 \mathrm{nR}\left(\mathrm{T} _{2}-\mathrm{T} _{1}\right)=2 \times 2 \times \mathrm{R} \times 200 \\ & =800 \mathrm{R} \end{aligned} $$

Hence option (2) is correct.

5. V-T graph of an ideal gas is shown in the figure. Work done by the gas in complete cyclic process ‘abcda’ is

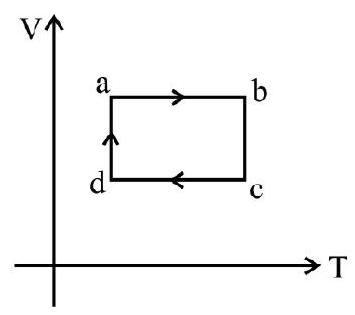
(1) zero

(2) negative

(3) positive

(4) $\mathrm{nRT} \ln \left(\frac{\mathrm{v} _{\mathrm{a}}}{\mathrm{v} _{\mathrm{d}}}\right)$

Show Answer

Correct answer: (2)

Solution:

$\begin{array}{ll}\mathrm{W} _{\mathrm{ab}}=\mathrm{W} _{\mathrm{cd}}=0 \text { as } \mathrm{v} \text { is constant } & \text { [isochoric process] }\end{array}$

$\mathrm{W} _{\mathrm{da}}=\mathrm{nRt} _{\mathrm{a}} \ln \left(\frac{\mathrm{V} _{\mathrm{a}}}{\mathrm{V} _{\mathrm{d}}}\right) \quad$ [isothermal process]

$\mathrm{W} _{\mathrm{bc}}=\mathrm{nRt} _{\mathrm{b}} \ell \mathrm{n}\left(\frac{\mathrm{V} _{\mathrm{c}}}{\mathrm{V} _{\mathrm{b}}}\right)=-\mathrm{nRT} _{\mathrm{b}}\left(\frac{\mathrm{V} _{\mathrm{a}}}{\mathrm{V} _{\mathrm{d}}}\right)$

Work done by complete cycle $=\mathrm{W} _{\mathrm{da}}+\mathrm{W} _{\mathrm{bc}}$

$\mathrm{n}=\mathrm{R}\left(\mathrm{T} _{\mathrm{a}}-\mathrm{T} _{\mathrm{b}}\right) \ln \left(\frac{\mathrm{V} _{\mathrm{a}}}{\mathrm{V} _{\mathrm{d}}}\right)$

As $\mathrm{T} _{\mathrm{b}}>\mathrm{T} _{\mathrm{a}}^{\prime}$ Work done is negative.

Hence option (2) is correct.

6. During which of the following process does heat rejection takes place in Carnot cycle:

(1) Isothermal expansion

(2) Adiabatic expansion

(3) Isothermal compression

(4) Adiabatic compression

Show Answer

Solution:

A carnot cycle is a combination of isothermal expansion and compression and adiabatic expansion and compression. The cycle is carried out in four stages:

First stage isothermal expansion

Second stage adiabatic expansion

Third stage isothermal compression

Fourth stage adiabatic compression

During third stage, the place the gas in contact with cold reservoir and do an isothermal compression. In compression of the gas, work in done on the gas. As temperature is constant, $d v=0$. Hence $d w=d \theta$, ‘dQ’ amount given out to the cold reservoir.

Hence option (3) is correct.

7. A carnot engine operating between temperatures $T _{1}$ and $T _{2}$ has efficiency $(1 / 6)$. When $T _{2}$ is lowered by $62 \mathrm{~K}$, its efficiency increases to $(1 / 3)$. Then $T _{1}$ and $T _{2}$ are, respectively

(1) $310 \mathrm{~K}, 248 \mathrm{~K}$

(2) $330 \mathrm{~K}, 268 \mathrm{~K}$

(3) $372 \mathrm{~K}, 310 \mathrm{~K}$

(4) $372 \mathrm{~K}, 330 \mathrm{~K}$

Show Answer

Correct answer: (3)

Solution:

Efficiency ’ $\eta$ ’ of carnot engine is given by $\eta=1-\frac{T _{2}}{T _{1}}$

$$ \begin{equation*} \frac{1}{6}=1-\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}………….(1) \end{equation*} $$

or $\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}=1-\frac{1}{6}=\frac{5}{6}………………(2)$

When $T _{2}$ is lowered by $62 \mathrm{~K}$ then

$$ \begin{align*} & \frac{1}{3}=1-\frac{\left(\mathrm{T} _{2}-62\right)}{\mathrm{T} _{1}} \\ & \frac{\mathrm{T} _{2}-62}{\mathrm{~T} _{1}}=1-\frac{1}{3}=\frac{2}{3} \tag{3} \end{align*} $$

From (2) & (3), we have $\frac{\mathrm{T} _{2}-62}{\frac{6}{5} \mathrm{~T} _{2}}=\frac{2}{3}$

$$ \frac{5\left(\mathrm{~T} _{2}-62\right)}{6 \mathrm{~T} _{2}}=\frac{2}{3} $$

$5 \mathrm{~T} _{2}-310=4 \mathrm{~T} _{2} \Rightarrow \mathrm{T} _{2}=310 \mathrm{~K}$

From equation (2) we have $\mathrm{T} _{1}=\frac{6 \times 310}{5}=372 \mathrm{~K}$

Hence option (3) is correct.

8. A carnot engine whose sink is at $300 \mathrm{~K}$ has an efficiency of $40 \%$. By how much should be temperature of source be increased so as to increase its efficiency by $50 \%$ of original efficiency?

(1) $380 \mathrm{~K}$

(2) $275 \mathrm{~K}$

(3) $325 \mathrm{~K}$

(4) $250 \mathrm{~K}$

Show Answer

Correct answer: (4)

Solution:

Efficiency of a carnot engine is given by

$$ \begin{aligned} \eta & =1-\frac{T _{2}}{T _{1}} \\ \text { or } \quad \frac{T _{2}}{T _{1}} & =1-\eta=1-\frac{40}{100}=\frac{3}{5} \end{aligned} $$

$\Rightarrow \mathrm{T} _{1}=\frac{5}{3} \times \mathrm{T} _{2}=\frac{5}{3} \times 300=500 \mathrm{~K}$

Increase in the efficiency $=50 \%$ of $40 \%=20 \%$

Now new effieiency $=40 \%+20 \%=60 \%$

Hence $\frac{600}{100}=1-\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}^{\prime}}$

(where $\mathrm{T} _{1}^{\prime}$ is new temperature of source)

or $\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}^{\prime}}=1-\frac{60}{100}=\frac{2}{5}$

$\Rightarrow \mathrm{T} _{1}^{\prime}=\frac{5}{2} \times \mathrm{T} _{2}=\frac{5}{2} \times 300=750 \mathrm{~K}$

Increase in the temperature of source is $\mathrm{T} _{1}^{\prime}-\mathrm{T} _{1}=750-500=250 \mathrm{~K}$

Hence option (4) is correct.

9. A carnot engine used first an ideal monoatomic gas ’ $x$ ’ and then another ideal monoatomic gas ’ $y$ ‘. If the source and sink temperatures are $401^{\circ} \mathrm{C}$ and $64^{\circ} \mathrm{C}$ respectively and the engine extracts $1000 \mathrm{~J}$ of heat in each cycle, then area enclosed by $\mathrm{P}-\mathrm{v}$ diagram is:

(1) $100 \mathrm{~J}$

(2) $300 \mathrm{~J}$

(3) $500 \mathrm{~J}$

(4) $700 \mathrm{~J}$

Show Answer

Correct answer: (3)

Solution:

Efficiency of carnot engine does not depend upon the nature of the gas; but only on the temperature of source and sink.

Let $\mathrm{T} _{1}$ be the source temperature and $\mathrm{T} _{2}$ the sink temperature

Then we have $\eta=1-\frac{T _{2}}{T _{1}}$ or $\quad \frac{\mathrm{W}}{\mathrm{Q} _{1}}=\frac{\mathrm{T} _{1}-\mathrm{T} _{2}}{\mathrm{~T} _{1}}$

Given $\mathrm{T} _{1}=401^{\circ} \mathrm{C}=674 \mathrm{~K} \mathrm{~T} _{2}=64^{\circ} \mathrm{C}=337 \mathrm{~K}$

$\Rightarrow \mathrm{W}=\mathrm{Q} _{1}\left(\frac{\mathrm{T} _{1}-\mathrm{T} _{2}}{\mathrm{~T} _{1}}\right)=1000\left(\frac{674-337}{674}\right)=1000 \times \frac{337}{674}=500 \mathrm{~J}$

Area enclosed by $\mathrm{P}-\mathrm{v}$ diagram $=$ Net work done $=500 \mathrm{~J}$

Hence option (3) is correct.

10. A refrigerator with coefficient of performance $\frac{1}{3}$ releases $200 \mathrm{~J}$ of heat to a hot reservoir, then the work done on the working substance is:

(1) $\frac{200}{3} \mathrm{~J}$

(2) $\frac{400}{3} \mathrm{~J}$

(3) $50 \mathrm{~J}$

(4) $150 \mathrm{~J}$

Show Answer

Correct answer: (4)

Solution:

The coefficient of performance of a refrigerator is given by:

$$ \beta=\frac{Q _{2}}{W}=\frac{Q _{2}}{Q _{1}-Q _{2}} $$

where $\mathrm{Q} _{1}=$ amount of heat released to the hot reservoir

$\mathrm{Q} _{2}=$ amount of heat extracted from the cold reservoir

$\mathrm{W}=$ work done on the working substance

Given $\beta=\frac{1}{3} Q _{1}=200 \mathrm{~J}$

$\beta=\frac{1}{3}=\frac{Q _{2}}{200-Q _{3}}$

$\Rightarrow \mathrm{Q} _{2}=50 \mathrm{~J}$

as

$$ \mathrm{W}=\mathrm{Q} _{1}-\mathrm{Q} _{2}=500-50=150 \mathrm{~J} $$

Hence option (4) is correct.

11. The temperature of inside and outside of a refrigerator are $270 \mathrm{~K}$ and $303 \mathrm{~K}$ respectively. Assuming that the refrigerator cycle is reversible, for every joule of work done the heat delivered to the surroundings will be nearly:

(1) $10 \mathrm{~J}$

(2) $20 \mathrm{~J}$

(3) $30 \mathrm{~J}$

(4) $50 \mathrm{~J}$

Show Answer

Correct answer: (1)

Solution:

As coefficient of performance $\beta=\frac{Q _{2}}{W}$

$\beta=\frac{T _{L}}{T _{H}-T _{L}}$

Given $T _{L}=270 \mathrm{~K}$

$\mathrm{T} _{\mathrm{H}}=373 \mathrm{~K}$

and $\mathrm{W}=1 \mathrm{~J}$

$\Rightarrow \frac{\mathrm{Q} _{2}}{1}=\frac{270}{303-273}=\frac{270}{30}=9 \mathrm{~J}$

Hence the heat delivered to the surroundings $\mathrm{Q} _{1}=\mathrm{Q} _{2}+\mathrm{W}=9+1=10 \mathrm{~J}$.

Hence option (1) is correct.

12. A graph of pressure versus volume (P-v diagram) for an ideal gas for different processes in as shown. In the graph curve $O B$ represents:

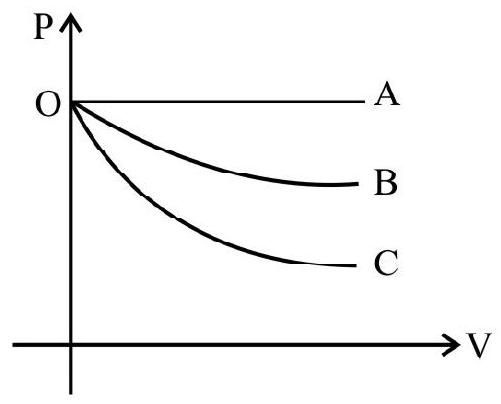
(1) isochoric process

(2) isothermal process

(3) isobaric process

(4) adiabatic process

Show Answer

Correct answer: (3)

Solution:

In the graph:

Curve OA represents isobaric process as pressure in constant.

As the slope of adiabatic process is more sleeper than isothermal. Hence curve OB represents isothermal process.

Hence option (3) is correct.

13. A motor car tyre has a pressure of 2 atmosphere at $27^{\circ} \mathrm{C}$. It suddenly bursts. If $\frac{C _{P}}{C _{v}}=1.4$for air, then the resulting temperature is:

(1) $27 \mathrm{~K}$

(2) $27^{\circ} \mathrm{C}$

(3) $-27^{\circ} \mathrm{C}$

(4) $246^{\circ} \mathrm{C}$

Show Answer

Correct answer: (3)

Solution:

As process is adiabatic

$$ \mathrm{T}^{\mathrm{r}} \mathrm{v}^{1-\gamma}=\text { constant } $$

or $\quad \mathrm{TP}^{(\mathrm{1-r} / \mathrm{y})}=$ constant

or $\quad \mathrm{T} _{1} \mathrm{P} _{1}^{\left(\frac{1-r}{y}\right)}=\mathrm{T} _{2} \mathrm{P} _{2}^{\left(\frac{1-r}{y}\right)}$

or $\quad \mathrm{T} _{2}=\mathrm{T} _{1}\left(\frac{\mathrm{P} _{2}}{\mathrm{P} _{1}}\right)^{(\frac{1-r}{y})}=300\left(\frac{1}{2}\right)^{0.4 / 1. 4}=\frac{300}{(2)^{2 / 7}}$

$=246 \mathrm{~K}=-27^{\circ} \mathrm{C}$

Hence option (3) is correct.

14. The relation between $U, P$ and $v$ for an ideal gas in adiabatic process is given by relation $\mathbf{U}=\mathbf{a}+\mathbf{b P v}$, symbols having usual meaning. The value of adiabatic exponent $(\gamma)$ of this gas is

(1) $\frac{\mathrm{b}+1}{\mathrm{~b}}$

(2) $\frac{\mathrm{b}+1}{\mathrm{a}}$

(3) $\frac{a+1}{b}$

(4) $\frac{a}{a+b}$

Show Answer

Correct answer: (1)

Solution:

As $\mathrm{U}=\mathrm{a}+\mathrm{Pv}$

we have $d V=b(P d v+v d P)$

In adiabatic process $\mathrm{dU}=-\mathrm{dW}=-\mathrm{Pdv}$

Substituting in above equation we get

$$ \begin{aligned} & (b+1) P d V+b(V d P)=0 \\ & \left(\frac{b+1}{b}\right) \frac{d V}{V}+\frac{d P}{P}=0 \end{aligned} $$

Integration we get $\mathrm{PV}{ }^{\left(\frac{b+1}{b}\right)}=$ constant

$\Rightarrow \gamma=\frac{\mathrm{b}+1}{\mathrm{~b}}$

Hence option (1) is correct.

15. For one mole of a monoatomic gas, the slope of $P-v$ diagram in adiabatic process is:

(1) $-\frac{\mathrm{RT}}{\mathrm{V}^{2}}$

(2) $-\frac{\mathrm{P}}{\mathrm{V}}$

(3) $-\frac{5}{3} \frac{\mathrm{RT}}{\mathrm{V}}$

(4) $-\frac{5}{3} \frac{\mathrm{RT}}{\mathrm{V}^{2}}$

Show Answer

Correct answer: (4)

Solution:

Slope of $\mathrm{P}-\mathrm{V}$ diagram in adiabatic process. $=-\frac{\gamma \mathrm{P}}{\mathrm{V}}=-\frac{5}{3} \frac{\mathrm{P}}{\mathrm{V}} \hspace{40mm}. . . . . . . (1)$

For one mole of ideal gas, we have $\mathrm{P}=\frac{\mathrm{RT}}{\mathrm{V}}$

$$ \begin{equation*} \Rightarrow \quad \mathrm{P}=\frac{\mathrm{RT}}{\mathrm{V}} \tag{2} \end{equation*} $$

From (1) & (2)

Slope of $\mathrm{P}-\mathrm{v}$ diagram in adiabatic process $=-\frac{5}{3} \frac{\mathrm{RT}}{\mathrm{v}^{2}}$

Hence option (4) is correct.

16. One mole of an ideal gas goes from an initial state $A$ to final state $B$ via two processes. It first undergo isothermal expansion from $v$ to $3 \mathrm{v}$ and then its volume is reduced from $3 \mathrm{v}$ to $\mathrm{v}$ at constant pressure. The correct $\mathrm{P}-\mathrm{v}$ diagram representing the two processes is given by graphs marked as $L, M, N, O$ respectively. The correct graph is given by

(1) L

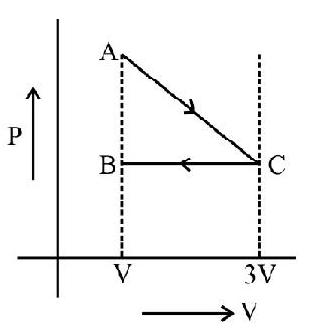
(2) $\mathrm{M}$

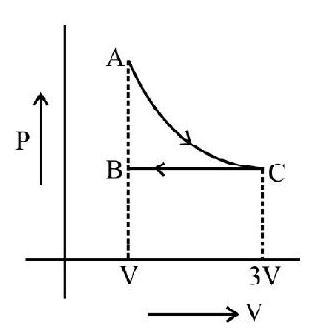
(3) $\mathrm{N}$

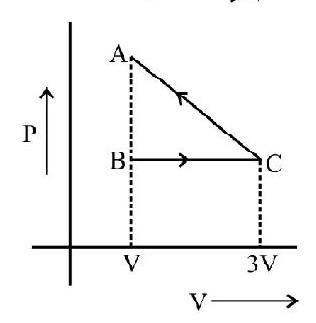
(4) $\mathrm{Q}$

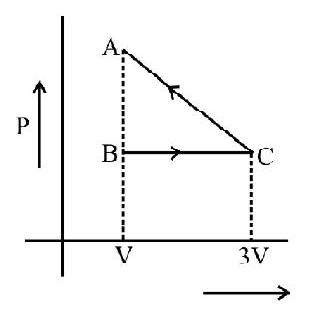
Show Answer

Correct answer: (2)

Solution:

First: As process is isothermal expansion $(\mathrm{A}-\mathrm{C}) \mathrm{T}$ constant

$$ \begin{aligned} & \Rightarrow \mathrm{PV}=\text { constant } \\ & \Rightarrow \mathrm{P} \propto \frac{1}{\mathrm{~V}} \quad \text { Boyle’s law } \\ & \text { or } \mathrm{P} _{1} \mathrm{v}=\mathrm{P} _{2}(3 \mathrm{~V}) \Rightarrow \mathrm{P} _{2}=\frac{\mathrm{P} _{1}}{3} \end{aligned} $$

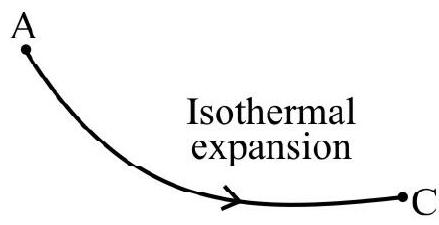
Second: $\mathrm{C}-\mathrm{B}$ is isobaric process $\mathrm{P}$ is constant

Hence graph is a straight line parallel to horizontal axis.

Hence, graph of option (2) is correct as shown here.

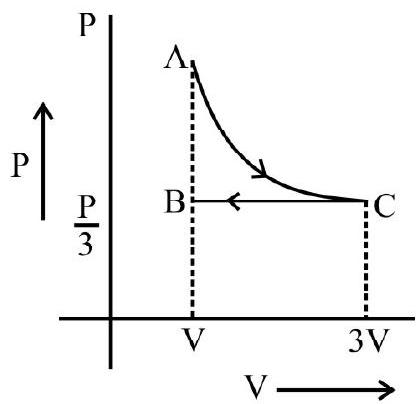
17. Figure illustrates a cycle conducted with $n$ moles of an ideal gas. In the states $a$ and $b$ the gas temperature are $T _{a}$ and $T _{b}$; respectively. Temperature of the gas in the state $C$ is:

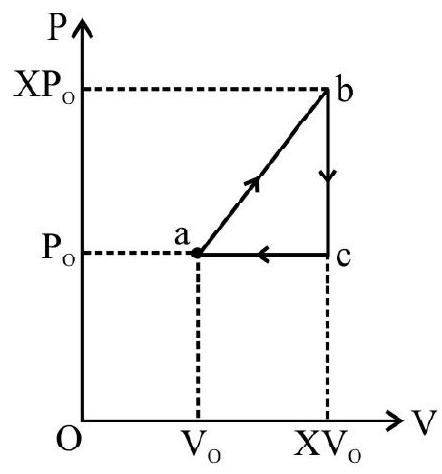
(1) $\sqrt{\mathrm{T} _{\mathrm{a}} \mathrm{T} _{\mathrm{b}}}$

(2) $T _{a}+T _{b}$

(3) $\frac{T _{a} T _{b}}{T _{a}+T _{b}}$

(4) $\frac{\left(\mathrm{T} _{\mathrm{a}}+\mathrm{T} _{\mathrm{b}}\right)}{2}$

Show Answer

Correct answer: (1)

Solution:

As $\mathrm{PV}=\mathrm{nRT}$, we have $\mathrm{T}=\frac{\mathrm{PV}}{\mathrm{nR}}$

$\Rightarrow \mathrm{T} _{\mathrm{a}}=\frac{\mathrm{P} _{0} \mathrm{~V} _{0}}{\mathrm{nR}}$ and $\mathrm{T} _{\mathrm{b}}=\frac{x^{2} \mathrm{P} _{0} \mathrm{~V} _{0}}{\mathrm{nR}}$

$\Rightarrow x=\sqrt{\frac{\mathrm{T} _{\mathrm{b}}}{\mathrm{T} _{\mathrm{a}}}}$

Now $\mathrm{T} _{\mathrm{c}}=\frac{x^{2} \mathrm{P} _{0} \mathrm{~V} _{0}}{\mathrm{nR}}=\left(\sqrt{\frac{\mathrm{T} _{\mathrm{b}}}{\mathrm{T} _{\mathrm{a}}}}\right) \mathrm{T} _{\mathrm{a}}=\sqrt{\mathrm{T} _{\mathrm{a}} \mathrm{T} _{\mathrm{b}}}$

Hence option (1) is correct.

18. The internal energy of a gas is given by $U=3 P V$. It expands from $V _{0}$ to $2 V _{0}$ against a constant pressure $\mathbf{P} _{0}$

The heat absorbed by the gas in the process is

(1) $\mathrm{P} _{0} \mathrm{v} _{0}$

(2) $2 \mathrm{P} _{0} \mathrm{v} _{0}$

(3) $3 \mathrm{P} _{0} \mathrm{v} _{0}$

(4) $4 \mathrm{P} _{0} \mathrm{v} _{0}$

Show Answer

Correct answer: (4)

Solution:

Work done $\mathrm{dw}=\mathrm{Pdv}=\mathrm{P}\left(\mathrm{V} _{\mathrm{f}}-\mathrm{V} _{\mathrm{i}}\right)=\mathrm{P}\left(2 \mathrm{~V} _{0}-\mathrm{V} _{0}\right)=\mathrm{P} _{0} \mathrm{~V} _{0} …………..(1)$

Change in internal energy $d U=U _{f}-u _{i}$

$$ \begin{equation*} \mathrm{dU}=3 \mathrm{P}\left(2 \mathrm{~V} _{0}\right)-3 \mathrm{PV} _{0}=3 \mathrm{P} _{0} \mathrm{~V} _{0} \tag{2} \end{equation*} $$

According to first law of thermodynamics

$$ \mathrm{dQ}=\mathrm{dU}+\mathrm{dw} $$

or $\quad \mathrm{dQ}=3 \mathrm{P} _{0} \mathrm{~V} _{0}+\mathrm{P} _{0} \mathrm{~V} _{0}$

From (1) & (2), we have dQ $=4 \mathrm{P} _{0} \mathrm{~V} _{0}$

Hence option (4) is correct.

19. When a system is taken through initial state $i$ to final state $f$ through ibf, 80 cal of heat in absorbed by the system and $60 \mathrm{cal}$ of work in done by it. If the system is taken through iaf, 30 cal of heat is absorbed, then the work done by the system is

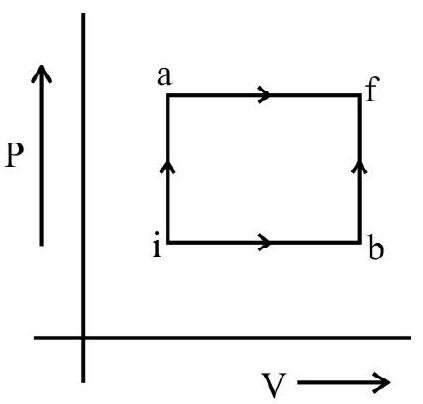
(1) $10 \mathrm{cal}$

(2) $20 \mathrm{cal}$

(3) $30 \mathrm{cal}$

(4) $40 \mathrm{cal}$

Show Answer

Correct answer: (1)

Solution:

According to first law of thermodynamics

$$ \mathrm{d} \theta=\mathrm{dU}+\mathrm{dW} $$

For the process ibf, we have $80=\mathrm{dU}+60$

or

$\mathrm{dU}=20 \mathrm{Cal}$.

Since dU is independent of path taken, the internal energy change is same for both the paths ibf and iaf.

Hence for iaf

$\mathrm{dW}=\mathrm{d} \theta-\mathrm{dU}=30-20=10 \mathrm{cal}$

Hence option (1) is correct.

20. An ideal gas with adiabatic exponent $\gamma$ is heated at constant pressure. It absorbed ’ $Q$ ’ amount of heat. The fractions of heat absorbed in raising the internal energy and performing the work is:

(1) $1-\frac{1}{\gamma}$

(2) $\frac{1}{\gamma}$

(3) $\frac{1}{\gamma}-1$

(4) $\gamma$

Show Answer

Correct answer: (1)

Solution:

At constant pressure heat absorbed by the system is:

$$ \mathrm{dQ}=\mathrm{nC} _{\mathrm{p}} \mathrm{dT} $$

and internal energy $\mathrm{dU}=\mathrm{nC} _{\mathrm{v}} \mathrm{dT}$

Therefore fraction $\frac{\mathrm{dU}}{\mathrm{dQ}}=\frac{\mathrm{nC} _{\mathrm{v}} \mathrm{dT}}{\mathrm{nC} _{\mathrm{P}} \mathrm{dT}}=\frac{\mathrm{C} _{\mathrm{v}}}{\mathrm{C} _{\mathrm{P}}}=\frac{1}{\gamma}$

From first law of thermodynamics

$$ \mathrm{dQ}=\mathrm{dU}+\mathrm{dW} $$

or $\frac{\mathrm{dW}}{\mathrm{dQ}}=\frac{\mathrm{dQ}-\mathrm{dW}}{\mathrm{dQ}}=1-\frac{\mathrm{dU}}{\mathrm{dQ}}=1-\frac{1}{\mathrm{r}}$

Hence option (1) is correct.

21. An ideal gas is taken from state $\mathbf{P}$ to state $\mathbf{Q}$ and then to state $\mathbf{R}$. If the process $\mathbf{P} \rightarrow \mathbf{Q}$ is adiabatic and $Q \rightarrow R$ is isothermal; then the true statement about the change in temperature $\Delta T$ and heat $Q$ transferred during $P \rightarrow Q$.

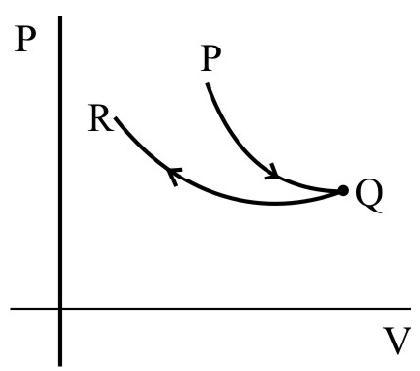
(1) $\Delta \mathrm{T}>0 \quad \mathrm{Q}>0$

(2) $\Delta \mathrm{T}<0 \quad \mathrm{Q}=0$

(3) $\Delta \mathrm{T}=0 \quad \mathrm{Q}=0$

(4) $\Delta \mathrm{T}=0 \quad \mathrm{Q}<0$

Show Answer

Correct answer: (2)

Solution:

As the process $\mathrm{P} \rightarrow \mathrm{Q}$ is adiabatic expansion $\mathrm{Q}=0$

As $\mathrm{dQ}=\mathrm{dU}+\mathrm{dW} \Rightarrow \mathrm{dW}=\mathrm{dU}$

Also in adiabatic process

$$ \mathrm{TV}^{\gamma-1}=\text { constant } $$

As volume increases, $\mathrm{T}$ decreases $\neq \Delta \mathrm{T}<0$

Hence option (2) is correct.

22. One mole of a monoatomic ideal gas undergoes the process $\mathbf{A} \rightarrow \mathbf{B}$ in the given diagram. The specific heat for this process is

(1) $\frac{3 R}{2}$

(2) $\frac{13 \mathrm{R}}{6}$

(3) $\frac{5 \mathrm{R}}{2}$

(4) $2 \mathrm{R}$

Show Answer

Correct answer: (2)

Solution:

As $\mathrm{dQ}=\mathrm{dU}+\mathrm{dW}$

or $1 \times \mathrm{CdT}=\mathrm{dU}+\mathrm{dW}$ where $\mathrm{C}$ is the specific heat of gas

$\Rightarrow \mathrm{C}=\frac{1}{\mathrm{dT}}(\mathrm{dU}+\mathrm{dW})$

$$ \begin{equation*} =\mathrm{C} _{\mathrm{V}}+\frac{\mathrm{C} _{\mathrm{V}}}{\mathrm{dt}} \quad\left[\text { as } \mathrm{dU}=\mathrm{C} _{\mathrm{v}} \mathrm{dT}\right] \tag{1} \end{equation*} $$

For the given process

Work done $=\mathrm{dW}=$ area under the $\mathrm{P}-\mathrm{V}$ diagram

$\Rightarrow \mathrm{w}=$ Area of trapezium $(\mathrm{ABCD})=\frac{1}{2} \times 4 \mathrm{~V} _{0} \times 9 \mathrm{P} _{0}$

$$ \begin{equation*} =18 \mathrm{P} _{0} \mathrm{~V} _{0} \tag{2} \end{equation*} $$

Also $\mathrm{dT}=\mathrm{T} _{2}-\mathrm{T} _{1}$

[For ideal gas $(\mathrm{n}=1), \mathrm{Pv}=\mathrm{nRT}$

$=\frac{\mathrm{P} _{2} \mathrm{~V} _{2}-\mathrm{P} _{1} \mathrm{~V} _{1}}{\mathrm{R}}$

$\left.\mathrm{PV}=1 \times \mathrm{RT} \Rightarrow \mathrm{T}=\frac{\mathrm{PV}}{\mathrm{R}}\right]$

$$ \begin{equation*} =\frac{\left(6 \mathrm{P} _{0}\right)\left(5 \mathrm{~V} _{0}\right)-\left(3 \mathrm{P} _{0} \mathrm{~V} _{0}\right)}{\mathrm{R}}=\frac{27 \mathrm{P} _{0} \mathrm{~V} _{0}}{\mathrm{R}} \tag{3} \end{equation*} $$

For ideal gas (monoatomic) $\mathrm{C} _{\mathrm{v}}=\frac{3}{2} \mathrm{R}$ . . . . . . . . . . . . . . . . . . . . . . . . .(4)

Substituting (2), (3) and (4) in Eqn. (1), we get

$\mathrm{C}=\frac{3}{2} \mathrm{R}+\frac{18 \mathrm{P} _{0} \mathrm{~V} _{0}}{27 \mathrm{P} _{0} \mathrm{~V} _{0}} \times \mathrm{R}=\frac{3}{2} \mathrm{R}+\frac{2 \mathrm{R}}{3}=\frac{13 \mathrm{R}}{6}$

Hence option (2) is correct.

23. For a monoatomic gas, the work done at constant pressure is $\mathrm{W}$. The heat supplied at constant volume for the same rise in temperature of the gas is:

(1) $\frac{\mathrm{W}}{2}$

(2) $\frac{3 \mathrm{~W}}{2}$

(3) $\frac{5 \mathrm{~W}}{2}$

(4) $\mathrm{W}$

Show Answer

Correct answer: (2)

Solution:

As dQ $=\mathrm{dU}+\mathrm{dW}$

For constant pressure $\mathrm{dQ}=\mathrm{C} _{\mathrm{p}} \mathrm{dT}+\mathrm{W}$

$\Rightarrow \mathrm{dT}=\frac{(\mathrm{dQ}-\mathrm{W})}{\mathrm{C} _{\mathrm{P}}} . . . . . . . . . . . . . . . . . . . . .(1)$

For constant volume $\mathrm{dQ}=\mathrm{C} _{\mathrm{v}} \mathrm{dT}$ as $\mathrm{dW}=0$

$$ =\frac{\mathrm{C} _{\mathrm{v}}(\mathrm{dQ}-\mathrm{W})}{\mathrm{C} _{\mathrm{P}}} \text { from (1) } $$

$\Rightarrow \frac{\mathrm{C} _{\mathrm{P}}}{\mathrm{C} _{\mathrm{v}}} \mathrm{dQ}=\mathrm{dQ}-\mathrm{W} \quad \gamma \mathrm{dQ}=\mathrm{dQ}-\mathrm{W}$

$\Rightarrow(\gamma-1) \mathrm{dQ}=-\mathrm{W}$ for monoatomic gas $\gamma=\frac{5}{3}$

$$ \left(\frac{5}{3}-1\right) \mathrm{dQ}=-\mathrm{W} \frac{2}{3} \mathrm{dQ}=-\mathrm{W} $$

or $\quad \mathrm{dQ}=-\frac{3 \mathrm{~W}}{2} \quad(-\mathrm{ve}$ sign indicates heat supplied to the system)

Hence option (2) is correct.

24. A sample of ideal gas taken through a closed cycle is presented by $\mathbf{P}-\mathbf{v}$ diagram. The process $1 \rightarrow \mathbf{2}$ is perfectly isothermal. Which of the following is true about the internal energy and work done by the gas during the process $3 \rightarrow 1$.

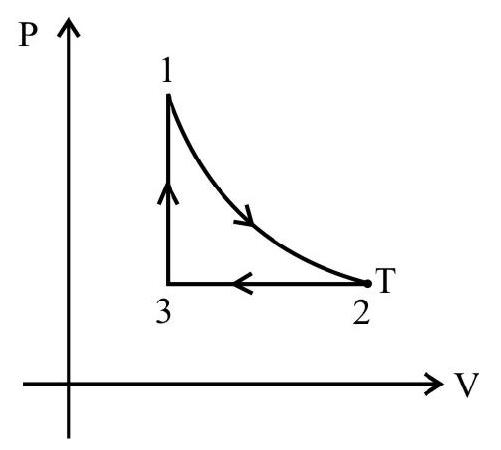
(1) $\Delta \mathrm{U}=0$, work done by the gas $>0$

(2) $\Delta \mathrm{U}>0$, work done by the gas $=0$

(3) $\Delta \mathrm{U}<0$, work done by the gas $<0$

(4) $\Delta \mathrm{U}=0$, work done by the gas $<0$

Show Answer

Correct answer: (2)

Solution:

As process $3 \rightarrow 1$ is isochoric process $\mathrm{v}$ constant

$\mathrm{dW}=\mathrm{PdV}=0$ and $\mathrm{V}$ by the gas $=0$

For ideal gas $\mathrm{PV}=\mathrm{nRT}$

As $\mathrm{V}$ constant $\mathrm{P} \propto \mathrm{T}$

Also $\Delta \mathrm{U}=\mathrm{nC} _{\mathrm{v}} \mathrm{dT} \quad$ [As $\mathrm{P}$ increases, $\mathrm{T}$ increases]

$\Rightarrow \Delta \mathrm{U}>0$

Hence option (2) is correct.

25. Internal energy of ’ $x$ ’ moles of hydrogen at temperature $T$ is equal to the internal energy of ’ $y$ ’ moles of helium at temperature $2 T$. Then the ratio $x / y$ is

(1) $(3 / 5)$

(2) $(2 / 3)$

(3) $(6 / 5)$

(4) $(3 / 7)$

Show Answer

Correct answer: (3)

Solution:

Internal energy of ’ $n$ ’ moles of an ideal gas at temperature $T$ is given by

$$ \mathrm{U}=\frac{\mathrm{f}}{2} \mathrm{nRT} \text { where } \mathrm{f} \text { is degree of freedom } $$

as $\mathrm{U} _{1}=\mathrm{U} _{2}$ given [where $\mathrm{U} _{1}$ is internal energy of hydrogen and $\mathrm{U} _{2}$ of helium]

$\Rightarrow \frac{\mathrm{f} _{1} x \mathrm{~T} _{1}}{2}=\frac{\mathrm{f} _{2} x \mathrm{~T} _{2}}{2}$

$\Rightarrow \frac{x}{\mathrm{y}}=\frac{\mathrm{f} _{2}}{\mathrm{f} _{1}} \times \frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}=\frac{3}{5} \times \frac{2}{1}=\frac{6}{5} \quad\left(\therefore \mathrm{f} _{2}=3\right.$ for helium and $\mathrm{f} _{1}=5$ for hydrogen $)$

Hence option (3) is correct.

26. P-v diagram of an ideal gas is an shown in figure. Work done by the gas in the process $\mathrm{ABCD}$ is

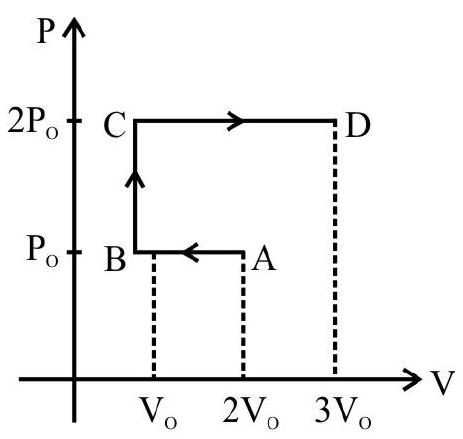
(1) $4 \mathrm{P} _{0} \mathrm{~V} _{0}$

(2) $2 \mathrm{P} _{0} \mathrm{~V} _{0}$

(3) $3 \mathrm{P} _{0} \mathrm{~V} _{0}$

(4) $\mathrm{P} _{0} \mathrm{~V} _{0}$

Show Answer

Correct answer: (3)

Solution:

$$ \begin{gathered} \mathrm{W} _{\mathrm{AB}}=\mathrm{P} \Delta \mathrm{V}=\mathrm{P}\left(\mathrm{v} _{0}-2 \mathrm{v} _{0}\right)=-\mathrm{P} _{0} \mathrm{~V} _{0} \\ \mathrm{~W} _{\mathrm{BC}}=\mathrm{P} \Delta \mathrm{V}=0 \text { as } \Delta \mathrm{V}=0 \\ \mathrm{~W} _{\mathrm{CD}}=\mathrm{P} \Delta \mathrm{V}=2 \mathrm{P} _{0}\left(3 \mathrm{~V} _{0}-\mathrm{V} _{0}\right)=4 \mathrm{P} _{0} \mathrm{~V} _{0} \\ \Rightarrow \mathrm{W} _{\mathrm{A}} \rightarrow \mathrm{B} \rightarrow \mathrm{C} \rightarrow \mathrm{D}=\mathrm{W} _{\mathrm{AB}}+\mathrm{W} _{\mathrm{BC}}+\mathrm{W} _{\mathrm{CD}} \\ =-\mathrm{P} _{0} \mathrm{~V} _{0}+0+4 \mathrm{P} _{0} \mathrm{~V} _{0}=3 \mathrm{P} _{0} \mathrm{~V} _{0} \end{gathered} $$

Hence option (3) is correct.

27. A fixed mass of gas is taken through a process $\mathbf{A} \rightarrow \mathbf{B} \rightarrow \mathbf{C} \rightarrow \mathbf{A}$, here $\mathbf{A} \rightarrow \mathbf{B}$ is isobaric process, $B \rightarrow C$ is adiabatic and $C \rightarrow A$ is isothermal process, the pressure and volume at C well be, (Take $\gamma=1.5)$

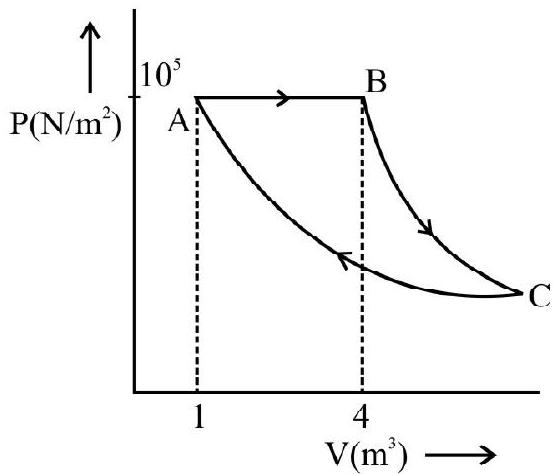
(1) $10^{5} \mathrm{~N} / \mathrm{m}^{2}$ and $8 \mathrm{~m}^{3}$ respectively

(2) $1.56 \times 10^{3} \mathrm{~N} / \mathrm{m}^{2}$ and $16 \mathrm{~m}^{3}$

(3) $1.56 \times 10^{3} \mathrm{~N} / \mathrm{m}^{2}$ and $64 \mathrm{~m}^{3}$

(4) $2.50 \times 10^{4} \mathrm{~N} / \mathrm{m}^{2}$ and $16 \mathrm{~m}^{3}$ respectively

Show Answer

Correct answer: (3)

Solution:

For adiabatic process $B C$, we have $P _{B} V _{B}^{\gamma}=P _{C} V _{C}^{\gamma}$

For isothermal process CA, we have $\mathrm{P} _{\mathrm{A}} \mathrm{V} _{\mathrm{A}}=\mathrm{P} _{\mathrm{C}} \mathrm{V} _{\mathrm{C}}$

From above two equations

$$ \begin{gathered} \mathrm{V} _{\mathrm{C}}=\left[\frac{\mathrm{V} _{\mathrm{B}}^{\gamma}}{\mathrm{V} _{\mathrm{A}}}\right]^{\frac{1}{\mathrm{r}-1}}=64 \mathrm{~m}^{3} \\ \mathrm{P} _{\mathrm{C}}=\frac{\mathrm{P} _{\mathrm{A}} \mathrm{V} _{\mathrm{A}}}{\mathrm{V} _{\mathrm{C}}}=\frac{10^{5}}{64}=1.56 \times 10^{3} \mathrm{~N} / \mathrm{m}^{2} \end{gathered} $$

Hence option (3) is correct.

28. A monoatomic ideal gas, initially at temperature ${ } _{1}$ is enclosed in a cylinder fitted with a frictionless piston, the gas is allowed to expand adiabatically to a temperature $T _{2}$, by releasing the piston suddenly. If $L _{1}$ and $L _{2}$ are the lengths of gas column before and after expansion respectively then $\frac{T _{1}}{T _{2}}$ is given by

(1) $\left(\frac{\mathrm{L} _{1}}{\mathrm{~L} _{2}}\right)^{\frac{2}{3}}$

(2) $\frac{\mathrm{L} _{1}}{\mathrm{~L} _{2}}$

(3) $\frac{\mathrm{L} _{2}}{\mathrm{~L} _{1}}$

(4) $\left(\frac{\mathrm{L} _{2}}{\mathrm{~L} _{1}}\right)^{\frac{2}{3}}$

Show Answer

Correct answer: (4)

Solution:

$\mathrm{TV}^{\gamma-1}=$ constant

$\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=\left(\frac{\mathrm{V} _{2}}{\mathrm{~V} _{1}}\right)^{\gamma-1}=\left(\frac{\mathrm{L} _{2}}{\mathrm{~L} _{1}}\right)^{\frac{5}{3}-1}=\left(\frac{\mathrm{L} _{2}}{\mathrm{~L} _{1}}\right)^{\frac{2}{3}}$

Hence option (4) is correct.

29. In an adiabatic change, the pressure $P$ and temperature $T$ of a diatomic gas are related by relation $\mathbf{P} \propto \mathbf{T}$. where $\alpha$ equals

(1) 1.67

(2) 0.4

(3) 0.6

(4) 3.5

Show Answer

Correct answer: (4)

Solution:

$\mathrm{P}^{1-\gamma} \mathrm{T}^{\gamma}=$ constant

$\mathrm{P}^{1-\gamma} \propto \mathrm{T}^{\gamma}$ or $\mathrm{P}^{\gamma-1} \propto \mathrm{T}^{\gamma}$ $P \propto T^{y / r-1}$

As $\frac{\gamma}{\gamma-1}=\frac{7 / 5}{\frac{7}{5}-1}=\frac{7}{2}=3.5$ for diatomic gas

$\therefore \alpha=3.5$

Hence option (4) is correct.

30. An ideal gas of adiabatic exponent ’ $\gamma$ ’ is expanded so that the amount of heat transferred to the gas is equal to the decrease its internal energy, then the equation of the process in terms of variables $T$ and $v$ is

(1) $\operatorname{TV}\left(\frac{\gamma-1}{2}\right)=$ constant

(2) $\operatorname{TV}\left(\frac{\gamma-2}{2}\right)=$ constant

(3) $\operatorname{TV}\left(\frac{\gamma-1}{4}\right)=$ constant

(4) $\operatorname{TV}\left(\frac{\gamma-2}{4}\right)=$ constant

Show Answer

Correct answer: (1)

Solution:

$\Delta \mathrm{Q}=\Delta \mathrm{U}+\Delta \mathrm{W}=-\Delta \mathrm{Q}+\Delta \mathrm{W}$

$\Rightarrow \Delta \mathrm{W}=2 \Delta \mathrm{Q}$

$\Delta \mathrm{U}=\mathrm{nC} _{\mathrm{v}} \Delta \mathrm{T}=\mathrm{n} \frac{\mathrm{f}}{2} \mathrm{R} \Delta \mathrm{T}=\frac{\mathrm{n}}{\mathrm{r}-1} \mathrm{R} \Delta \mathrm{T}=-\Delta \mathrm{Q}$

$\left[\right.$ As $\left.\gamma=\frac{\mathrm{f}+2}{\mathrm{f}}=1+\frac{2}{\mathrm{f}} \Rightarrow \mathrm{f}=\frac{2}{\gamma-1}\right]$

$\Delta \mathrm{W}=\int \mathrm{Pdv}=2 \Delta \mathrm{Q}=-\frac{2 \mathrm{n}}{\gamma-1} \mathrm{R} \Delta \mathrm{T}$

$$ =\frac{2 \mathrm{nR} \Delta \mathrm{T}}{1-\gamma}=\frac{\mathrm{nR} \Delta \mathrm{T}}{1-\mathrm{a}} $$

For polytrophic process with $\mathrm{PV}^{\mathrm{a}}=$ constant.

$$ \therefore \frac{2}{1-\gamma}=\frac{1}{1-\mathrm{a}} $$

$$ \Rightarrow \mathrm{a}=\frac{1+\gamma}{2} $$

$\Rightarrow \mathrm{PV}^{\mathrm{a}}=$ const $=\mathrm{PV}^{\frac{1+\gamma}{2}}=$ const

$$ \mathrm{PV}=\mathrm{nRT} \Rightarrow \mathrm{P}=\frac{\mathrm{nRT}}{\mathrm{V}} $$

$$ \Rightarrow \mathrm{TV} \frac{1+\gamma}{2}-1=\text { const. } \Rightarrow \mathrm{TV} \frac{\gamma-1}{2}=\text { const. } $$

Hence option (1) is correct.

31. Given figure shows the variation of the force applied by ideal gas on a piston undergoes a process during which piston position changes from $0.1 \mathrm{~m}$ to $0.4 \mathrm{~m}$. If the interval energy of the system at the end of the process is $2.5 \mathrm{~J}$ higher, then the heat absorbed during the process is

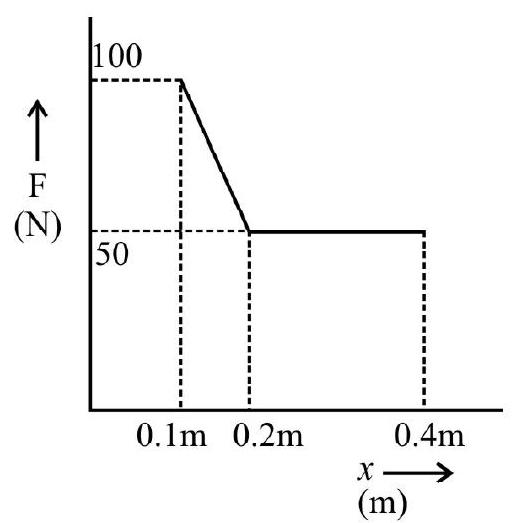
(1) $15 \mathrm{~J}$

(2) $17.5 \mathrm{~J}$

(3) $20 \mathrm{~J}$

(4) $22.5 \mathrm{~J}$

Show Answer

Correct answer: (3)

Solution:

Work done $=\frac{1}{2} \times 0.1 \times(100-50)+0.2 \mathrm{~m} \times 50=17.5 \mathrm{~J}$

$\Delta \mathrm{U}=2.5 \mathrm{~J}$

$\therefore \Delta \mathrm{Q}=\Delta \mathrm{U}+\Delta \mathrm{W}=2.5+17.5=20.0 \mathrm{~J}$

Hence option (3) is correct.

32. In the following $\mathbf{v}-\mathbf{T}$ diagram, what is relation between $\mathrm{P} _{1}$ and $\mathrm{P} _{2}$.

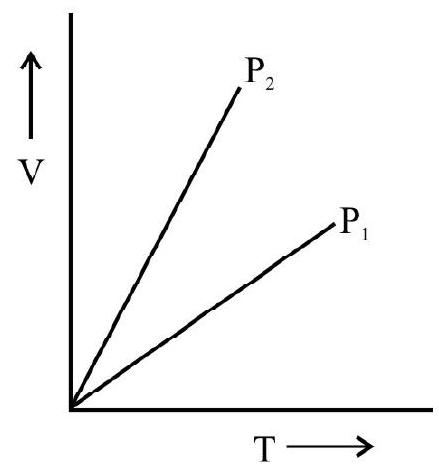
(1) $\mathrm{P} _{1}=\mathrm{P} _{2}$

(2) $\mathrm{P} _{2}>\mathrm{P} _{1}$

(3) $\mathrm{P} _{2}<\mathrm{P} _{1}$

(4) None of the above

Show Answer

Correct answer: (3)

Solution:

Since $P V=n R T$ it gives $\Rightarrow \frac{V}{n R T}=\frac{1}{P}$

$\Rightarrow \frac{\mathrm{V}}{\mathrm{T}}=$ slope $=\frac{1}{\mathrm{P}}$

$\therefore$ Slope of line $\mathrm{P} _{1}<$ slope of line $\mathrm{P} _{2}$

Hence $\mathrm{P} _{1}>\mathrm{P} _{2}$

Hence option(3) is correct.

33. Figure shows a cylindrical tube with adiabatic walls and fitted with an adiabatic separation, the separation can be slid into the tube by an external mechanism. Ideal gas is injected $(\gamma=1.5)$ in two sides at equal pressure and temperature, the separator remains in equilibrium at the middle. It is now slid to a position where it divides the tube in the ratio $1: 3$, the ratio of the temperatures in the two parts of the tube well be

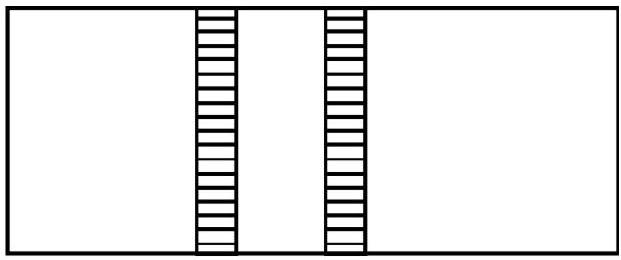
(1) $1: 1$

(2) $1: 2$

(3) $1: \sqrt{3}$

(4) $\sqrt{3}: 1$

Show Answer

Correct answer: (4)

Solution:

Given $\gamma=1.5$

For adiabatic process $\mathrm{Tv}^{\gamma-1}=$ constant

$\Rightarrow \mathrm{T} _{1} \mathrm{~V} _{1}^{\gamma-1}=\mathrm{T} _{2} \mathrm{~V} _{2}^{\gamma-1}$

Given $V _{1}=\frac{V}{4}, V _{2}=\frac{3 \mathrm{~V}}{4}$

Since all other conditions remain the same, we have

$$ \begin{gathered} \mathrm{T} _{2}\left(\frac{3 \mathrm{~V}}{4}\right)^{1.5-1}=\mathrm{T} _{1}\left(\frac{\mathrm{V}}{4}\right)^{1.5-1} \\ \frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}=\left(\frac{1}{3}\right)^{0.5}=1: \sqrt{3} \end{gathered} $$

$\Rightarrow \frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=\sqrt{3}: 1$

Hence option (4) is correct.

34. An amount $Q$ of heat is added to a monoatomic ideal gas in a process in which the gas performs the work $Q / 2$ on its surroundings. The molar heat capacity for the process will be

(1) $\mathrm{R}$

(2) $2 \mathrm{R}$

(3) $3 \mathrm{R}$

(4) $4 \mathrm{R}$

Show Answer

Correct answer: (3)

Solution:

Amount of heat given $=\mathrm{Q}$ and the Work done $=\frac{\mathrm{Q}}{2}$

$\Delta \mathrm{Q}=\Delta \mathrm{U}+\Delta \mathrm{W}$

$\Delta \mathrm{U}=\Delta \mathrm{Q}-\Delta \mathrm{W}=\frac{\mathrm{Q}}{2}$

$\mathrm{nC} _{\mathrm{P}} \Delta \mathrm{T}=\frac{\mathrm{Q}}{2}$

For monoatomic gas $\Delta \mathrm{U}=\frac{3}{2} \mathrm{nRT}$

$\frac{\mathrm{Q}}{2}=\frac{3}{2} \mathrm{nTR} \quad \mathrm{Q}=3 \mathrm{nRT}$

Also $\mathrm{Q}=\mathrm{nC} _{\mathrm{p}} \mathrm{dT}$

$\Rightarrow \mathrm{nC} _{\mathrm{P}} \mathrm{T}=3 \mathrm{RnT}=\mathrm{C} _{\mathrm{P}}=3 \mathrm{R}$

Hence option (3) is correct.

35. A gas is taken through a cyclic process ABCA as shown in figure. If 2.4 cal of heat is given in the process, then the value of joules heat equivalent ’ $\mathrm{J}$ ’ will be.

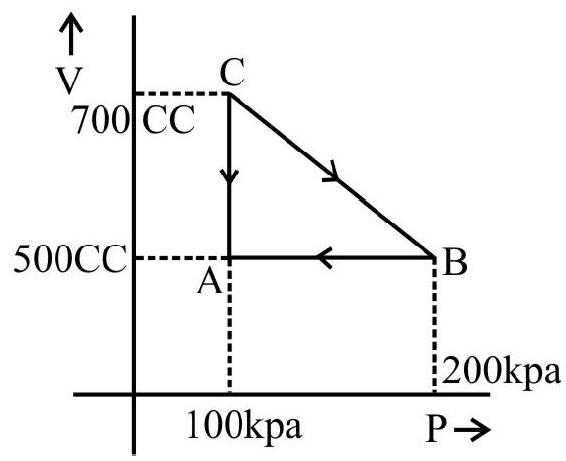
(1) $4.18 \mathrm{~J} / \mathrm{cal}$

(2) $2.18 \mathrm{~J} / \mathrm{cal}$

(3) $10 \mathrm{~J} / \mathrm{cal}$

(4) $2.4 \mathrm{~J} / \mathrm{cal}$

Show Answer

Correct answer: (1)

Solution:

$$ \Delta \mathrm{Q}=2.4 \mathrm{cal} $$

Work one during the process $\Delta \mathrm{W}=$ area under the curve

$$ =\frac{1}{2} \times(200-100) \times 10^{3} \times(700-500) \times 10^{-6}=10 \mathrm{~J} $$

$\Delta \mathrm{U}=0$ (Being cyclic process)

$\Delta \mathrm{W}=\Delta \mathrm{Q}+\Delta \mathrm{U}$

$\Delta \mathrm{Q}=\Delta \mathrm{W}$

$2.4 \mathrm{~J}=10$

$\mathrm{J}=4.18 \mathrm{~J} / \mathrm{cal}$

Hence option (1) is correct.

36. Figure shows a paddle wheel coupled to a mass of $12 \mathrm{Kg}$ through fixed frictionless pulleys, the paddle is immersed in a liquid of heat capacity $4200 \mathrm{JK}^{-1}$, kept in an adiabatic container. Consider a time internal in which the $12 \mathrm{Kg}$ block falls slowly through $70 \mathrm{~cm}$, the amount of work done on the liquid and the rise in its temperature in this time will be

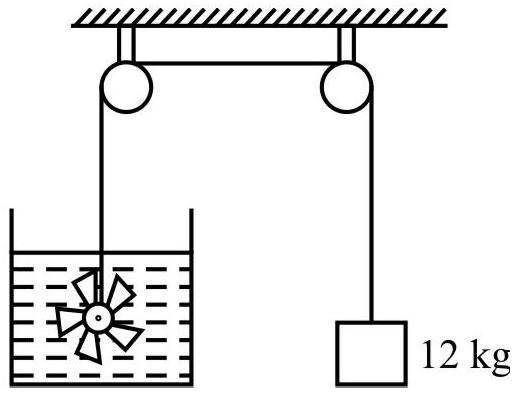
(1) $84 \mathrm{~J}$ and $0.02^{\circ} \mathrm{C}$

(2) zero and $0.02 \mathrm{~K}$

(3) $84 \mathrm{~J}$ and $0.0017 \mathrm{~K}$

(4) zero and $0.0017^{\circ} \mathrm{C}$

Show Answer

Correct answer: (1)

Solution:

Work done an the liquid $=$ potential energy lost by $12 \mathrm{Kg}$ mass $=\mathrm{mgh}$

$$ =12 \times 10 \times 0.70=84 \mathrm{~J} $$

Let rise in temperature be $\Delta \mathrm{T}$

$\mathrm{Q}=\mathrm{ms} \Delta \mathrm{T}$

$84=1 \times 4200 \Delta \mathrm{T} \quad($ for $\mathrm{m}=1 \mathrm{Kg})$

$\Rightarrow \Delta \mathrm{T}=\frac{84}{4200}=0.02 \mathrm{C}$

Hence option (1) is correct answer.

37. Certain amount of an ideal gas is contained in a closed vessel, which is moving with the velocity $\mathrm{v}$, the rise in temperature of the gas, when the vessel in suddenly stopped is (M is molecular mass, $\gamma=\frac{\mathbf{c} _{\mathrm{P}}}{\mathbf{c} _{\mathrm{v}}}$ )

(1) $\frac{\operatorname{Mv}^{2}(\gamma-1)}{2 \mathrm{R}}$

(2) $\frac{\mathrm{Mv}^{2}(\gamma+1)}{2 \mathrm{R}}$

(3) $\frac{M v^{2}}{2 R \gamma}$

(4) $\frac{\mathrm{Mv}^{2}}{2 \mathrm{R}(\gamma+1)}$

Show Answer

Correct answer: (1)

Solution:

Kinetic energy of vessel $=\frac{1}{2} \mathrm{Mv}^{2}$

Due to the stop of vessel, ordered motion of the molecules becomes disordered, increasing thereby internal energy.

$$ \begin{gathered} \Delta \mathrm{U}=\mathrm{nc} _{\mathrm{v}} \Delta \mathrm{T}=\frac{1}{2} \mathrm{mV}^{2}=\frac{1}{2}(\mathrm{nM}) \mathrm{v}^{2} \\ \Delta \mathrm{T}=\frac{\mathrm{Mv}^{2}}{2 \mathrm{c} _{\mathrm{v}}} \end{gathered} $$

As $\quad \mathrm{c} _{\mathrm{v}}=\frac{\mathrm{R}}{\gamma-1}$ we have

$$ \Delta \mathrm{T}=\frac{\mathrm{mv}^{2}}{2 \mathrm{R}}(\gamma-1) $$

Hence option(1) is correct

38. A gas expands with temperature ascending to relation $\mathrm{V}=\mathrm{KT}^{2 / 3}$, where $\mathrm{K}$ is any constant. The work done when the temperature changes by $60 \mathrm{~K}$.

(1) $10 \mathrm{R}$

(2) $30 \mathrm{R}$

(3) $40 \mathrm{R}$

(4) $20 \mathrm{R}$

Show Answer

Correct answer: (3)

Solution:

Given $\mathrm{V}=\mathrm{KT}^{2 / 3}$

$\frac{\mathrm{dV}}{\mathrm{dt}}=\mathrm{K} \frac{2}{3} \mathrm{~T}^{2 / 3-1}=\mathrm{K} 2 / 3 \mathrm{~T}^{-1 / 3}$

$\mathrm{dv}=\frac{2}{3} \mathrm{KT}^{-1 / \mathrm{dt}}$

$\therefore \frac{\mathrm{dV}}{\mathrm{v}}=\frac{\frac{2}{3} \mathrm{KT}^{-1 / 3} \mathrm{dt}}{\mathrm{KT}^{2 / 3}}=\frac{2}{3} \frac{\mathrm{dT}}{\mathrm{T}}$

Now work done $\mathrm{W}=\int _{\mathrm{T} _{1}}^{\mathrm{T} _{2}} \mathrm{PdV}=\int _{\mathrm{T} _{1}}^{\mathrm{T} _{2}} \frac{\mathrm{RT}}{\mathrm{V}} \cdot \mathrm{dv}=\int _{\mathrm{T} _{1}}^{\mathrm{T} _{2}} \mathrm{RT}\left(\frac{2}{3} \frac{\mathrm{dT}}{\mathrm{T}}\right)$

$$ =\frac{2}{3} \mathrm{R}\left(\mathrm{T} _{2}-\mathrm{T} _{1}\right)=\frac{2}{3} \mathrm{R} \times 60=40 \mathrm{R} $$

Hence option (3) is correct.

39. Consider the containers $A$ and $B$ containing identical gases at same pressure, volume and temperature, the gas in container $A$ is compressed to half of its original volume isothermally, while the gas in container $B$ is compressed to half of its original volume adiabatically, the ratio of final pressure of gas in $B$ to that of gas in $A$ is

(1) $2^{\gamma-1}$

(2) $\left(\frac{1}{2}\right)^{\gamma-1}$

(3) $\left(\frac{1}{1-\gamma}\right)^{2}$

(4) $\left(\frac{1}{1-\gamma}\right)$

Show Answer

Correct answer: (1)

Solution:

When the compression is isothermal for gas in A, we have $\mathrm{P} _{2} \mathrm{~V} _{2}=\mathrm{P} _{1} \mathrm{~V} _{1}$

$$ P _{2}=\frac{P _{1} V _{1}}{V _{2}}=2 P _{1} $$

For gas in $\mathrm{B}$, compression is adiabatic so we have $\mathrm{P} _{2}^{\prime} \mathrm{P} _{2}^{\prime \gamma}=\mathrm{P} _{1} \mathrm{v} _{1}^{\gamma}$

$\mathrm{P} _{2}^{\prime}=\mathrm{P} _{1}\left(\frac{\mathrm{V} _{1}}{\mathrm{~V} _{2}}\right)^{\gamma}=2^{\gamma} \mathrm{P} _{1}$

$\Rightarrow \frac{\mathrm{P} _{2}^{\prime}}{\mathrm{P} _{1}}=\frac{2^{\gamma}}{2}=2^{\gamma-1}$

Hence option (1) is correct.

40. The given P.v diagram represents the thermodynamic cycle of an engine, operating with an ideal monoatomic gas, the amount of heat, extracted from the source in a single cycle is

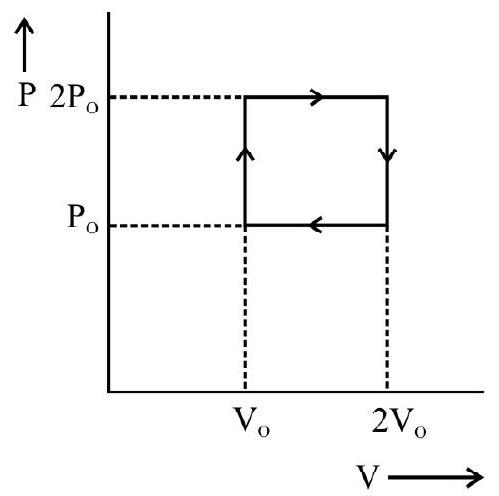
(1) $\mathrm{P} _{0} \mathrm{~V} _{0}$

(2) $\frac{13}{2} \mathrm{P} _{0} \mathrm{~V} _{0}$

(3) $\frac{11}{2} \mathrm{P} _{0} \mathrm{~V} _{0}$

(4) $4 \mathrm{P} _{0} \mathrm{~V} _{0}$

Show Answer

Correct answer: (2)

Solution:

The amount of heat, extracted from the source is given by $\mathrm{H}=\mathrm{nC} _{\mathrm{v}} \Delta \mathrm{T}+\mathrm{nC} _{\mathrm{p}} \Delta \mathrm{T}$

$$ \begin{aligned} & =\mathrm{n} \frac{3}{2} \mathrm{R}\left(2 \mathrm{~T} _{0}-\mathrm{T} _{0}\right)+\mathrm{n}\left(\frac{5}{2} \mathrm{R}\right)\left(4 \mathrm{~T} _{0}-2 \mathrm{~T} _{0}\right) \\ & =\frac{3 \mathrm{RnT} _{0}}{2}+5 \mathrm{nRT} _{0}=\frac{13}{2} \mathrm{RnT} _{0} \\ & =\frac{13}{2} \mathrm{P} _{0} \mathrm{~V} _{0} \end{aligned} $$

Hence option (2) is correct.

41. A carnot engine absorbs $6 \times 10^{5}$ cal at $227^{\circ} \mathrm{C}$, the work done per cycle by the engine, if its sink is maintained at $127^{\circ} \mathrm{C}$ is

(1) $15 \times 10^{8} \mathrm{~J}$

(2) $15 \times 10^{4} \mathrm{~J}$

(3) $5 \times 10^{5} \mathrm{~J}$

(4) $2 \times 10^{4} \mathrm{~J}$

Show Answer

Correct answer: (3)

Solution:

Given $\mathrm{Q} _{1}=6 \times 10^{5} \mathrm{Cal} \quad \mathrm{T} _{1}=500 \mathrm{~K} \quad \mathrm{~T} _{2}=400 \mathrm{~K}$

As $\frac{\mathrm{Q} _{2}}{\mathrm{Q} _{1}}=\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}$ $\mathrm{Q} _{2}=\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}} \times \mathrm{Q} _{1}=\frac{400}{500} \times 6 \times 10^{5}=4.8 \times 10^{5} \mathrm{Cal}$

Work done $\mathrm{W}=\mathrm{Q} _{1}-\mathrm{Q} _{2}$

$$ \begin{aligned} & =6 \times 10^{5}-4.8 \times 10^{5}=1.2 \times 10^{5} \mathrm{Cal} \\ & =1.2 \times 4.2 \times 10^{5} \mathrm{~J}=5.04 \times 10^{5} \mathrm{~J}=5.0 \times 10^{5} \mathrm{~J} \end{aligned} $$

Hence option (3) is correct

42. One gram of air initially at NTP is compressed adiabatically to half its volume, (density of air at $\mathrm{NTP}=1.29 \times 10^{-3} \mathrm{gram} / \mathrm{cm}^{3}$, and $\gamma=1.4$ ) the work done in the process will be

(1) $62.75 \mathrm{~J}$

(2) $-62.75 \mathrm{~J}$

(3) $82.75 \mathrm{~J}$

(4) $-82.75 \mathrm{~J}$

Show Answer

Correct answer: (2)

Solution:

As given air at NTP, we have $T _{1}=273 \mathrm{~K}$

$$ \begin{aligned} & \quad \mathrm{P} _{1}=1.013 \times 10^{6} \text { dyne } / \mathrm{cm}^{2}, \gamma=1.4, \mathrm{P}=1.29 \times 10^{-3} \\ & \therefore \quad \mathrm{V} _{1}=\frac{\text { Mass }}{\text { density }}=\frac{1}{1.29 \times 10^{-3}}=775.2 \mathrm{~cm}^{3} \\ & \mathrm{~V} _{2}=\frac{\mathrm{V} _{1}}{2}=387.6 \mathrm{~cm}^{3} \\ & \mathrm{P} _{1} \mathrm{~V} _{1}^{\mathrm{r}}=\mathrm{P} _{2} \mathrm{~V} _{2}^{\mathrm{r}} \quad \text { or } \quad \mathrm{P} _{2}=\mathrm{P} _{1}\left(\frac{\mathrm{V} _{1}}{\mathrm{~V} _{2}}\right)^{\mathrm{r}} \\ & \quad=1.013 \times 10^{6}\left(\frac{\mathrm{V} _{1}}{\mathrm{~V} _{1 / 2}}\right)^{1.4}=2.673 \times 10^{6} \text { dynes } / \mathrm{cm}^{2} \end{aligned} $$

Work done during adiabatic change $\mathrm{W}=\frac{\mathrm{P} _{1} \mathrm{~V} _{1}-\mathrm{P} _{2} \mathrm{~V} _{2}}{\gamma-1}$

$$ \begin{aligned} & =\frac{1.013 \times 10^{6} \times 775.2-2.673 \times 10^{6} \times 387.6}{1.4-1} \\ & =6.27 \times 10^{8} \mathrm{erg}=-62.75 \mathrm{~J} \end{aligned} $$

Hence option (2) is correct.

43. A closed system receives $200 \mathrm{KJ}$ of heat at constant volume. It then rejects $100 \mathrm{KJ}$ of heat, while it has $50 \mathrm{KJ}$ of work done on it at constant pressure. If an adiabatic process can be found which will restore the system to its initial state, the work done by the system during this process is:

(1) $100 \mathrm{KJ}$

(2) $150 \mathrm{KJ}$

(3) $-150 \mathrm{KJ}$

(4) $200 \mathrm{KJ}$

Show Answer

Correct answer: (3)

Solution:

Given $\Delta \mathrm{Q} _{\mathrm{AB}}=200 \mathrm{KJ}=\mathrm{nC} _{\mathrm{v}} \Delta \mathrm{T}$

$$ \begin{aligned} & \Delta \mathrm{U} _{\mathrm{BC}}=-100 \mathrm{KJ} \Delta \mathrm{w} _{\mathrm{BC}}=-50 \mathrm{KJ} \Delta \mathrm{w} _{\mathrm{AB}}=0 \\ \Rightarrow & \Delta \mathrm{U} _{\mathrm{AB}}=200 \mathrm{KJ} \Delta \mathrm{Q} _{\mathrm{CA}}=0 \\ \text { or } \quad & 200 \mathrm{KJ}-100 \mathrm{KJ}+\Delta \mathrm{U} _{\mathrm{CA}}=0 \\ & \Delta \mathrm{U} _{\mathrm{CA}}=-100 \mathrm{KJ} \\ & \Delta \mathrm{Q} _{\mathrm{AB}}+\Delta \mathrm{Q} _{\mathrm{BC}}+\Delta \mathrm{Q} _{\mathrm{CA}}=0 \\ & =200 \mathrm{KJ}+(-100 \mathrm{KJ}-50 \mathrm{KJ})+0=50 \mathrm{KJ} \\ \Rightarrow & \Delta \mathrm{W} _{\mathrm{AB}}+\Delta \mathrm{W} _{\mathrm{BC}}+\Delta \mathrm{W} _{\mathrm{CA}}=0+200 \mathrm{KJ}+\Delta \mathrm{W} _{\mathrm{CA}} \\ & =\Delta \mathrm{Q} _{\mathrm{ABC}}=50 \mathrm{KJ} \end{aligned} $$

$\Rightarrow \Delta \mathrm{W} _{\mathrm{CA}}=-150 \mathrm{KJ}$

Hence option (3) is correct.

44. If $\mathbf{W} _{\mathrm{ABC}}$ is the work done is process $\mathrm{A} \rightarrow \mathrm{B} \rightarrow \mathbf{C}$ and $\mathrm{W} _{\mathrm{DEF}}$ is the work done in process $\mathbf{D} \rightarrow \mathbf{E} \rightarrow \mathbf{F}$ as shown in figure, then

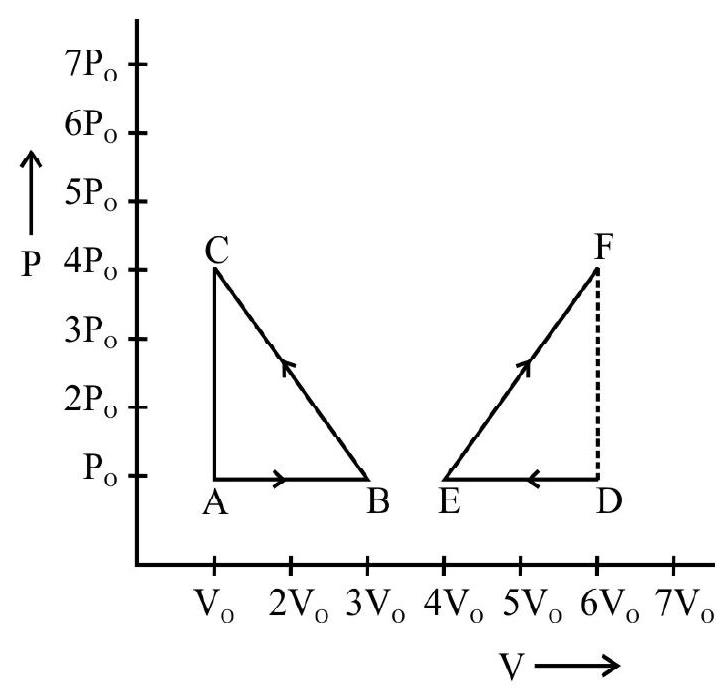
(1) $\left|\mathrm{W} _{\mathrm{DEF}}\right|>\left|\mathrm{W} _{\mathrm{ABC}}\right|$

(2) $\left|\mathrm{W} _{\mathrm{DEF}}\right|<\left|\mathrm{W} _{\mathrm{ABC}}\right|$

(3) $\mathrm{W} _{\mathrm{DEF}}=\mathrm{W} _{\mathrm{ABC}}$

(4) $\mathrm{W} _{\mathrm{DEF}}=-\mathrm{W} _{\mathrm{ABC}}$

Show Answer

Correct answer: (2)

Solution:

Work done for process $\mathrm{ABC}=$ Area within the curve $=\frac{1}{2} \mathrm{AB} \times \mathrm{AC}$

$$ =\frac{1}{2}\left(3 \mathrm{~V} _{0}-\mathrm{V} _{0}\right)\left(4 \mathrm{P} _{0}-\mathrm{P} _{0}\right)=3 \mathrm{P} _{0} \mathrm{~V} _{0} $$

Work done for process DEF $=\frac{1}{2} \mathrm{ED} \times \mathrm{DF}$

$$ =\frac{1}{2}\left(4 \mathrm{~V} _{0}-6 \mathrm{~V} _{0}\right)\left(4 \mathrm{P} _{0}-\mathrm{P} _{0}\right)=-3 \mathrm{P} _{0} \mathrm{~V} _{0} $$

Hence $\mathrm{W} _{\mathrm{DEC}}=-\mathrm{W} _{\mathrm{ABC}}$

Hence option (4) is correct.

45. An ideal monoatomic gas in carried around the cycle $A B C D A$ as shown in figure, the efficiency per cycle is

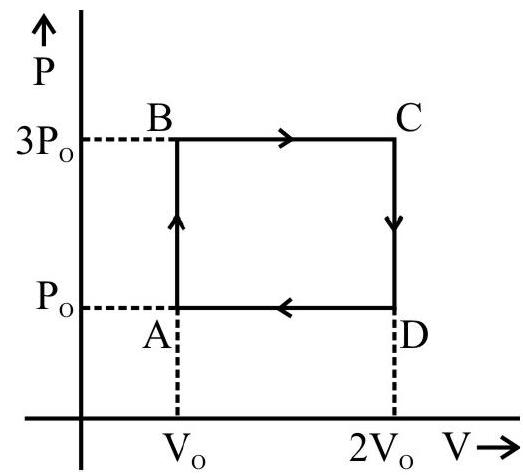
(1) $\frac{4}{21}$

(2) $\frac{2}{21}$

(3) $\frac{4}{31}$

(4) $\frac{2}{31}$

Show Answer

Correct answer: (1)

Solution:

Work done $\Delta \mathrm{W}=\left(3 \mathrm{P} _{0}-\mathrm{P} _{0}\right)\left(2 \mathrm{~V} _{0}-\mathrm{V} _{0}\right)=2 \mathrm{P} _{0} \mathrm{~V} _{0}$

$$ \begin{aligned} \Delta \mathrm{Q} _{\text {supplied }} & =\mathrm{n} \frac{3}{2} \mathrm{R}\left(\frac{3 \mathrm{P} _{0} \mathrm{~V} _{0}}{\mathrm{nR}}-\frac{\mathrm{P} _{0} \mathrm{~V} _{0}}{\mathrm{nR}}\right)+\mathrm{n} \frac{5}{2} \mathrm{R}\left(\frac{3 \mathrm{P} _{0} 2 \mathrm{~V} _{0}}{\mathrm{nR}}-\frac{3 \mathrm{P} _{0} \mathrm{~V} _{0}}{\mathrm{nR}}\right) \\ = & \frac{3}{2} \mathrm{nR} \frac{2 \mathrm{P} _{0} \mathrm{~V} _{0}}{\mathrm{nR}}+\frac{5}{2} \mathrm{nR} \frac{3 \mathrm{P} _{0} \mathrm{~V} _{0}}{\mathrm{nR}}=3 \mathrm{P} _{0} \mathrm{~V} _{0}+\frac{15}{2} \mathrm{P} _{0} \mathrm{~V}=\frac{21}{2} \mathrm{P} _{0} \mathrm{~V} _{0} \end{aligned} $$

Hence efficiency $\eta=\frac{\Delta \mathrm{W}}{\Delta \mathrm{Q}}=\frac{2 \mathrm{P} _{0} \mathrm{~V} _{0}}{\frac{21}{2} \mathrm{P} _{0} \mathrm{~V} _{0}}=\frac{4}{21}$

Hence option (1) is correct.

46. One mole of an ideal gas of temperature $T _{1}$ expands slowly according to the law $\frac{P}{V}=$ constant, its final temperature is $T _{2}$, the work done by the gas is

(1) $\mathrm{R}\left(\mathrm{T} _{2}-\mathrm{T} _{1}\right)$

(2) $2 \mathrm{R}\left(\mathrm{T} _{2}-\mathrm{T} _{1}\right)$

(3) $\frac{\mathrm{R}}{2}\left(\mathrm{~T} _{2}-\mathrm{T} _{1}\right)$

(4) $\frac{2 \mathrm{R}}{3}\left(\mathrm{~T} _{2}-\mathrm{T} _{1}\right)$

Show Answer

Correct answer: (3)

Solution:

Work done $\mathrm{W}=\int \mathrm{PdV}$

Given $\frac{\mathrm{P}}{\mathrm{V}}=$ constant (c), so we must have $\mathrm{P}=\mathrm{cV}$

$\therefore \mathrm{W}=\int \mathrm{cVdV}=\mathrm{c}\left(\frac{\mathrm{V}^{2}}{2}\right)=\frac{1}{2} \mathrm{cVV}=\frac{1}{2} \mathrm{PV}$

$$ =\frac{1}{2} \mathrm{nR}\left(\mathrm{T} _{2}-\mathrm{T} _{1}\right)=\frac{\mathrm{R}}{2} \times 1\left(\mathrm{~T} _{2}-\mathrm{T} _{1}\right)=\frac{\mathrm{R}}{2}\left(\mathrm{~T} _{2}-\mathrm{T} _{1}\right) $$

Hence option (3) is correct.

47. Two moles of helium gas undergo a cyclic process as shown in figure, assuming the gas to be an ideal, the net change in heat energy and total work done will be

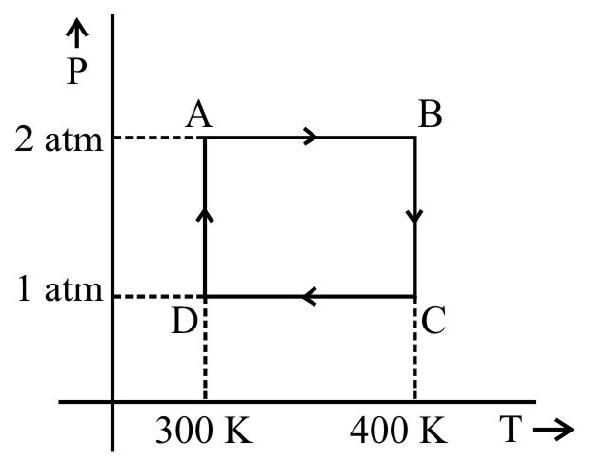
(1) $1153 \mathrm{~J}, 1153 \mathrm{~J}$

(2) $1153 \mathrm{~J}$, zero

(3) zero, $1153 \mathrm{~J}$

(4) $5761 \mathrm{~J}, 5761 \mathrm{~J}$

Show Answer

Correct answer: (1)

Solution:

Corresponding Pv diagram is shown in the figure

$\mathrm{v} _{\mathrm{A}}=\frac{\mathrm{nRT} _{\mathrm{A}}}{\mathrm{P} _{\mathrm{A}}}=\frac{2 \mathrm{R} \times 300}{2 \times 10^{5}}=3 \times 10^{-3} \mathrm{R}$

$\mathrm{v} _{\mathrm{B}}=\frac{2 \mathrm{R} \times 400}{2 \times 10^{5}}=4 \times 10^{-3} \mathrm{R}$

$\mathrm{v} _{\mathrm{C}}=\frac{2 \mathrm{R} \times 400}{10^{5}}=8 \times 10^{-3} \mathrm{R}$

$\mathrm{v} _{\mathrm{D}}=\frac{2 \mathrm{R} \times 300}{10^{5}}=6 \times 10^{-3} \mathrm{R}$

$\Delta \mathrm{W}=2 \times 10^{5} \times(4-3) \times 10^{-3} \mathrm{R}+2 \mathrm{R} \times 400 \ln \left(\frac{8}{4}\right)+1 \times 10^{5} \times(6-8) \times 10^{-3} \mathrm{R}+2 \mathrm{R} \times 300 \ln \left(\frac{3}{6}\right)$

$=200 \mathrm{R}+800 \mathrm{R} \ell \mathrm{n} 2-200 \mathrm{R}-600 \mathrm{R} \ell \mathrm{n} 2=200 \mathrm{R} \ell \mathrm{n} 2$

$=200 \times 8.31 \times 0.3010 \times 2.303=1153 \mathrm{~J}$

As $\Delta \mathrm{Q}=\Delta \mathrm{U}+\Delta \mathrm{W}$

But $\Delta \mathrm{U}=0$ for cyclic process

$\Rightarrow \Delta \mathrm{Q}=\Delta \mathrm{W}$

Hence option (1) is correct.

48. In the given figure, $1 \mathrm{~K}$ mole of a sample of helium gas is put through the cycle of operations, $B C$ is an isothermal process and $P _{A}=1.00 \mathrm{~atm}, v _{A}=22.4 \mathrm{~m}^{3}, P _{B}=\mathbf{2 . 0 0} \mathrm{atm}$, the value of $T _{A}, T _{B}$ and $v _{C}$ will be

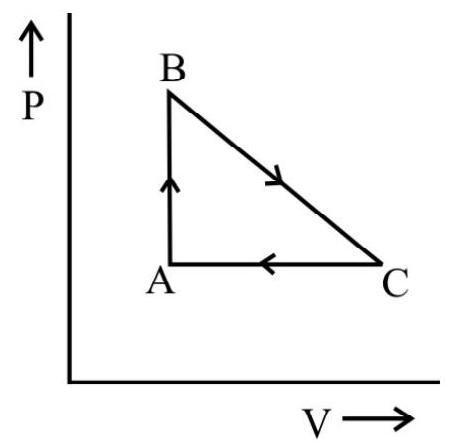
(1) $273 \mathrm{~K}, 546 \mathrm{~K}, 44.8 \mathrm{~m}^{3}$

(2) $546 \mathrm{~K}, 273 \mathrm{~K}, 22.4 \mathrm{~m}^{3}$

(3) $273 \mathrm{~K}, 546 \mathrm{~K}, 22.4 \mathrm{~m}^{3}$

(4) $546 \mathrm{~K}, 273 \mathrm{~K}, 44.8 \mathrm{~m}^{3}$

Show Answer

Correct answer: (1)

Solution:

$\mathrm{T} _{\mathrm{A}}=\frac{\mathrm{P} _{\mathrm{A}} \mathrm{V} _{\mathrm{A}}}{\mathrm{nR}}=\frac{1.01 \times 10^{5} \times 22.4}{10^{3} \times 8.314}=273 \mathrm{~K}$

$\mathrm{T} _{\mathrm{B}}=\frac{\mathrm{P} _{\mathrm{B}} \mathrm{V} _{\mathrm{B}}}{\mathrm{nR}}=\frac{2 \mathrm{P} _{\mathrm{A}} \mathrm{V} _{\mathrm{A}}}{\mathrm{nR}}=546 \mathrm{~K}$

$\mathrm{v} _{\mathrm{C}}=\frac{\mathrm{nRT} _{\mathrm{C}}}{\mathrm{P} _{\mathrm{C}}}=\frac{\mathrm{nRT} _{\mathrm{B}}}{\mathrm{P} _{\mathrm{A}}}=\frac{2 \mathrm{nRT} _{\mathrm{A}}}{\mathrm{P} _{\mathrm{A}}}=2 \mathrm{v} _{\mathrm{A}}=44.8 \mathrm{~m}^{3}$

Hence option (1) is correct.

49. A monoatomic gas in expanded adiabatically from volume $V _{0}$ to $2 V _{0}$, then is brought back to the initial state through an isothermal and isochoric process, the efficiency of the cycle well be:

(1) $20.0 \%$

(2) $78.67 \%$

(3) $21.33 \%$

(4) $100 \%$

Show Answer

Correct answer: (3)

Solution:

Work done $\Delta \mathrm{W} _{\mathrm{AB}}=\frac{\mathrm{P} _{\mathrm{B}} \mathrm{V} _{\mathrm{B}}-\mathrm{P} _{\mathrm{A}} \mathrm{V} _{\mathrm{A}}}{1-\gamma}$

$$ =\frac{3}{2}\left(\mathrm{P} _{\mathrm{A}} \mathrm{V} _{\mathrm{A}}-\mathrm{P} _{\mathrm{B}} \mathrm{V} _{\mathrm{B}}\right)=\frac{3}{2} \mathrm{nR}\left(\mathrm{T} _{\mathrm{A}}-\mathrm{T} _{\mathrm{B}}\right)=\frac{3}{2} \mathrm{nR}\left[\frac{\mathrm{T} _{\mathrm{A}}}{\mathrm{T} _{\mathrm{B}}}-1\right] \mathrm{T} _{\mathrm{B}} $$

But $\mathrm{Tv}^{\gamma-1}=$ constant

$$ \mathrm{T} _{1} \mathrm{~V} _{1}^{\gamma-1}=\mathrm{T} _{2} \mathrm{~V} _{2}^{\gamma-1} $$

$\Rightarrow \mathrm{T} _{\mathrm{A}} \mathrm{V} _{\mathrm{A}}^{\gamma-1}=\mathrm{T} _{\mathrm{B}} \mathrm{V} _{\mathrm{B}}^{\gamma-1}$

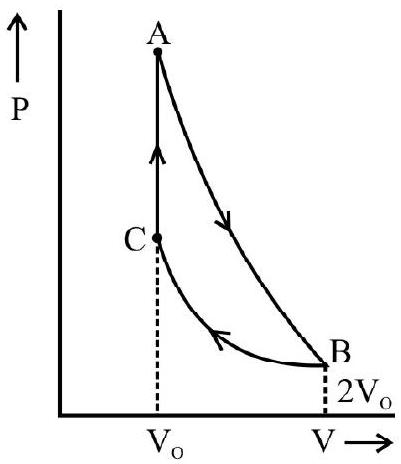
$\Rightarrow \frac{\mathrm{T} _{\mathrm{A}}}{\mathrm{T} _{\mathrm{B}}}=\left(\frac{\mathrm{V} _{\mathrm{B}}}{\mathrm{V} _{\mathrm{A}}}\right)^{\gamma-1}=(2)^{\frac{5}{3}-1}=2^{\frac{2}{3}}$

$\Rightarrow \Delta \mathrm{W} _{\mathrm{AB}}=\frac{3}{2} \mathrm{nR}\left[(2)^{\frac{2}{3}}-1\right] \mathrm{T} _{\mathrm{B}}$

$\Delta \mathrm{W} _{\mathrm{BC}}=\mathrm{nRT} _{\mathrm{B}} \ln \left(\frac{\mathrm{V} _{0}}{2 \mathrm{~V} _{0}}\right)=-\mathrm{nRT} _{\mathrm{B}} \ln (2), \Delta \mathrm{W} _{\mathrm{CA}}=0$

Heat supplied $\Delta \mathrm{Q} _{\mathrm{CA}}=\Delta \mathrm{U} _{\mathrm{CA}}=\frac{3}{2} \mathrm{nR}\left(\mathrm{T} _{\mathrm{A}}-\mathrm{T} _{\mathrm{C}}\right)=\frac{3}{2} \mathrm{nR}\left(\mathrm{T} _{\mathrm{A}}-\mathrm{T} _{\mathrm{B}}\right)$

$$ =\frac{3}{2} \mathrm{nRT} _{\mathrm{B}}\left(\frac{\mathrm{T} _{\mathrm{A}}}{\mathrm{T} _{\mathrm{B}}}-1\right)=\frac{3}{2} \mathrm{nRT} _{\mathrm{B}}\left((2)^{3 / 2}-1\right) $$

Hence efficiency $\eta=\frac{\Delta \mathrm{W}}{\Delta \mathrm{Q} _{\mathrm{CA}}}=\frac{3}{2} \mathrm{nRT} _{\mathrm{B}}\left(2^{2 / 3}-1\right)-\mathrm{nRT} _{\mathrm{B}} \ell \mathrm{n} 2+0=\frac{3}{2} \mathrm{nRT} _{\mathrm{B}}\left(2^{2 / 3}-1\right)$

$$ =1-\frac{2}{3} \frac{\ln 2}{\left(2^{2 / 3}-1\right)}=1-0.7867=0.213=21.33 \% $$

Hence option (3) is correct.

50. One mole of an ideal gas in taken through a cyclic process, the minimum temperature during the cycle is $300 \mathrm{~K}$, the net exchange of heat for complete cycle is

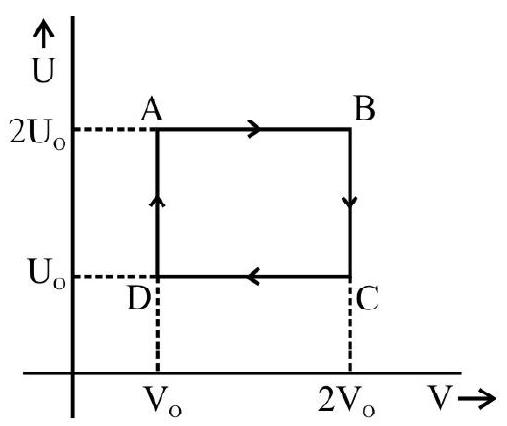
(1) $600 \mathrm{R} \ell \mathrm{n} 2$

(2) $300 \mathrm{R} \ell \mathrm{n} 2$

(3) $-300 \mathrm{R} \ln 2$

(4) $900 \mathrm{R} \ell \mathrm{n} 2$

Show Answer

Correct answer: (2)

Solution:

Temperature corresponding to points $\mathrm{D}=300 \mathrm{~K}$

As $\mathrm{U}=\mathrm{nc} _{\mathrm{V}} \mathrm{T}=1 \times \frac{3}{2} \mathrm{RT}=\frac{3}{2} \mathrm{RT}$, we have $\mathrm{T}=\frac{2 \mathrm{U}}{3 \mathrm{R}}$

$\mathrm{T} _{\mathrm{D}}=\frac{2 \mathrm{U} _{0}}{3 \mathrm{R}} \Rightarrow \mathrm{U} _{0}=450 \mathrm{R}$

$\mathrm{T} _{\mathrm{A}}=\frac{4 \mathrm{U} _{0}}{3 \mathrm{R}}=600 \mathrm{~K}$

$$ \begin{aligned} \Delta \mathrm{w} & =\Delta \mathrm{w} _{\mathrm{AB}}+\Delta \mathrm{w} _{\mathrm{BC}}+\Delta \mathrm{w} _{\mathrm{CD}}+\Delta \mathrm{w} _{\mathrm{DA}} \\ & =\mathrm{nRT} _{\mathrm{A}} \ell \mathrm{n}\left(\frac{2 \mathrm{~V} _{0}}{\mathrm{~V} _{0}}\right)+\mathrm{nRT} _{\mathrm{D}} \ln \left(\frac{\mathrm{V} _{0}}{2 \mathrm{~V} _{0}}\right) \\ & =\mathrm{nR}\left(\mathrm{T} _{\mathrm{A}}-\mathrm{T} _{\mathrm{D}}\right) \ln (2)=1 \times \mathrm{R} \times(600-300) \ln 2 \end{aligned} $$

$=300 \mathrm{R} \ln 2$

Since $\Delta \mathrm{U}=0$ we have $\Delta \mathrm{Q}=300 \mathrm{R} \ell \mathrm{n} 2$

Hence option (2) is correct.

51. Two moles of an ideal gas are undergo a cyclic process $1 \rightarrow \mathbf{2} \rightarrow \mathbf{3} \rightarrow \mathbf{1}$. If net exchange of heat in the process is $300 \mathrm{~J}$, the work done by the gas in the process $2 \rightarrow 3$ is

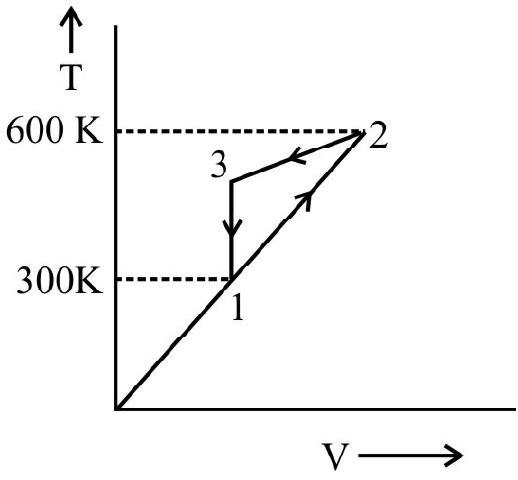
(1) $-500 \mathrm{~J}$

(2) $-5000 \mathrm{~J}$

(3) $-5288 \mathrm{~J}$

(4) zero J

Show Answer

Correct answer: (3)

Solution:

Total work done

$\Delta \mathrm{W}=\Delta \mathrm{W} _{1 \rightarrow 2}+\Delta \mathrm{W} _{2 \rightarrow 3}+\Delta \mathrm{W} _{3 \rightarrow 1}$

$\Delta \mathrm{W} _{1 \rightarrow 2}=\mathrm{P} \Delta \mathrm{V}=\mathrm{nR} \Delta \mathrm{T}=2 \times \mathrm{R}(600-300)=600 \mathrm{R}$

$\Delta \mathrm{W} _{3 \rightarrow 1}=0$

Also $\Delta \mathrm{Q}=\Delta \mathrm{W}+\Delta \mathrm{U}$

$\Rightarrow \Delta \mathrm{W}=\Delta \mathrm{Q} \quad($ as $\Delta \mathrm{U}=0)$

$$ -300 \mathrm{~J}=600 \mathrm{R}+\Delta \mathrm{W} _{2 \rightarrow 3}+0 $$

$$ \begin{aligned} \Rightarrow & \Delta \mathrm{W} _{2 \rightarrow 3}=-300-600 \mathrm{R} \\ & =300-600 \times 8.314 \\ & =-5288 \mathrm{~J} \end{aligned} $$

Hence option (3) is correct.

52. A gas follows a process $\mathbf{T V}^{\mathrm{n}-1}=$ constant, the bulk modulus of the gas in the process is given by

(1) (n-1) P

(2) $\frac{P}{(n-1)}$

(3) $\mathrm{nP}$

(4) $\frac{\mathrm{P}}{\mathrm{n}}$

Show Answer

Correct answer: (3)

Solution:

Rewriting the condition in terms of $\mathrm{P}$ and $\mathrm{V}$, we have $\mathrm{PV}=\mathrm{nRT}$

$\therefore \mathrm{T}=\frac{\mathrm{PV}}{\mathrm{nR}}$

Hence PV.V $\mathrm{V}^{\mathrm{n}-1}=$ constant or $\mathrm{PV}^{\mathrm{n}}=$ constant

P. $n v^{n-1}+v^{n} d P=0$

$\frac{\mathrm{dP}}{\mathrm{dv}}=\frac{\mathrm{PnV}^{\mathrm{n}-1}}{\mathrm{~V}^{\mathrm{n}}}=\mathrm{nPv}^{-1}=\frac{\mathrm{nP}}{\mathrm{V}}$

By definition $\mathrm{V} \frac{\mathrm{dP}}{\mathrm{dv}}=\mathrm{K}=$ Bulk modulus $=\mathrm{nP}$

Hence option (3) is correct.

53. A closed vessel 10 litre in volume contains a diatomic gas under a pressure of $10^{5} \mathrm{~N} / \mathbf{m}^{2}$. The amount of heat imparted to the gas to increase the pressure in the vessel five times, will be:

(1) $6 \times 10^{3} \mathrm{~J}$

(2) $10^{7} \mathrm{~J}$

(3) $10^{4} \mathrm{~J}$

(4) $10^{-6} \mathrm{~J}$

Show Answer

Correct answer: (3)

Solution:

Since change in volume $\Delta V=0$, we have

$\Delta \mathrm{W}=0$

But $\Delta \mathrm{Q}=\Delta \mathrm{U}+\Delta \mathrm{W}$

$$ \begin{aligned} \Delta \mathrm{Q}= & \Delta \mathrm{U}=\mathrm{nC} _{\mathrm{v}} \Delta \mathrm{T}=\mathrm{n} \times \frac{5}{2} \mathrm{R} \Delta \mathrm{T}=\frac{5}{2}\left(\mathrm{P} _{\mathrm{f}} \mathrm{V} _{\mathrm{f}}-\mathrm{P} _{\mathrm{i}} \mathrm{V} _{\mathrm{i}}\right) \\ & =\frac{5}{2}\left(\mathrm{P} _{\mathrm{f}}-\mathrm{P} _{\mathrm{i}}\right) \mathrm{v}=\frac{5}{2}(5 \mathrm{P}-\mathrm{P}) \mathrm{V} \\ & =\frac{5}{2} \times 4 \mathrm{Pv}=10 \mathrm{Pv}=10 \times 10^{+5} \times 10 \times 10^{-3} \\ \Delta \mathrm{Q} & =10^{4} \mathrm{~J} \end{aligned} $$

Hence option (3) is correct.

54. Two moles of a certain gas at temperature $T _{0}=300 \mathrm{~K}$ were cooled isochorically so that pressure of the gas got reduced 2 times. Then as a result of isochoric process the gas is allowed to expand till its temperature got back to its initial value. Total amount of heat absorbed in this process will be

(1) $4.98 \mathrm{KJ}$

(2) $2.49 \mathrm{KJ}$

(3) $2.49 \mathrm{~J}$

(4) $9.96 \mathrm{KJ}$

Show Answer

Correct answer: (2)

Solution:

For isochoric $\Delta \mathrm{W} _{\mathrm{AB}}=0$

$\Delta \mathrm{W} _{\mathrm{BC}}=\frac{\mathrm{P} _{0}}{2} \times \mathrm{V} _{0}=\frac{1}{2} \mathrm{P} _{0} \mathrm{~V} _{0}=\frac{1}{2} \mathrm{nRT} _{0}=300 \mathrm{R}$

$\Delta \mathrm{Q}=(\Delta \mathrm{U}+\Delta \mathrm{W}) _{\mathrm{AB}}+(\Delta \mathrm{U}+\Delta \mathrm{W}) _{\mathrm{BC}}$

$=(\Delta \mathrm{U}) _{\mathrm{AB}}+(\Delta \mathrm{U}) _{\mathrm{BC}}+(\Delta \mathrm{W}) _{\mathrm{BC}}$

Since $\mathrm{T} _{\mathrm{A}}=\mathrm{T} _{\mathrm{C}}$

$\therefore$ No change in the internal energy of the gas

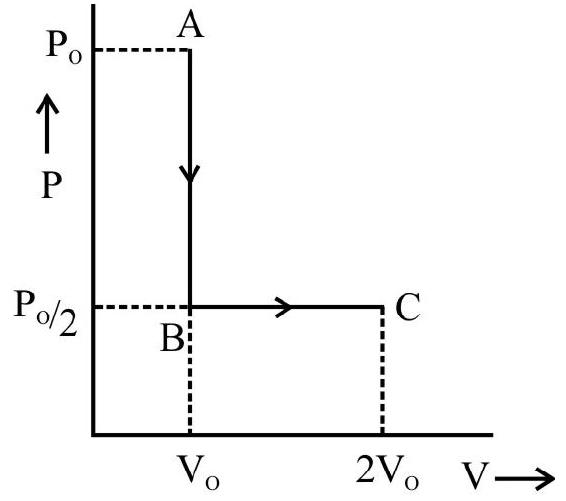
$$ \begin{gathered} \Delta \mathrm{U} _{\mathrm{AB}}+\Delta \mathrm{U} _{\mathrm{BC}}=0 \\ \therefore \Delta \mathrm{Q}=(\Delta \mathrm{W}) _{\mathrm{BC}}=300 \mathrm{R}=300 \times 8.31 \mathrm{~J} \\ =2493 \mathrm{~J}=2.49 \mathrm{~J} \end{gathered} $$

Hence option (2) is correct.

55. When 10 gram of water is heated from $0^{\circ} \mathrm{C}$ to $100^{\circ} \mathrm{C}$ and than converted into steam at $100 \mathrm{Kpa}$, the increase in internal energy of the water would be (given density of steam $=0.6 \mathrm{Kg} / \mathrm{m}^{3}$, specific heat capacity of water $=4200 \mathrm{~J} / \mathrm{Kg}$, and latent heat of vaporization of water $=2.5 \times 10^{6} \mathrm{~J} / \mathrm{Kg}$ )

(1) $2.92 \times 10^{4} \mathrm{~J}$

(2) $2.75 \times 10^{4} \mathrm{~J}$

(3) $2.50 \times 10^{4} \mathrm{~J}$

(4) $42 \times 10^{4} \mathrm{~J}$

Show Answer

Correct answer: (2)

Solution:

$$ \begin{aligned} & \Delta \mathrm{W}=\mathrm{P} \Delta \mathrm{v}=\mathrm{Pv} _{\mathrm{f}}=\mathrm{P} \frac{\mathrm{m}}{\mathrm{P}}=\frac{10^{5} \times 10 \times 10^{-3}}{0.6}=1666.67 \mathrm{~J} \\ & \begin{aligned} \Delta \mathrm{Q} & =\mathrm{ms} \Delta \mathrm{T}+\mathrm{mL} \\ & =10^{-2} \times 4200 \times 100+10^{-2} \times 25 \times 10^{5}=29200 \mathrm{~J} \\ \Delta \mathrm{U} & =\Delta \mathrm{Q}-\Delta \mathrm{W}=29200-1666.67 \\ & =2.75 \times 10^{4} \mathrm{~J} \end{aligned} \end{aligned} $$

Hence correction option is (2).

56. For an isobaric process, the ratio $\frac{\Delta Q}{\Delta \mathrm{W}}$ will be (given $\frac{\mathbf{c} _{\mathrm{P}}}{\mathbf{c} _{\mathrm{v}}}=\gamma$ )

(1) $\frac{(\gamma-1)}{\gamma}$

(2) $\frac{\gamma-1}{\gamma}$

(3) $\frac{\gamma}{\gamma-1}$

(4) $\frac{\gamma}{\gamma+1}$

Show Answer

Correct answer: (3)

Solution:

Since an isobaric process $\mathrm{P}=$ constant, we have $\mathrm{c}=\mathrm{c} _{\mathrm{P}}$

$$ \begin{aligned} & \Delta \mathrm{Q}=\mathrm{nc} _{\mathrm{P}} \Delta \mathrm{T} \\ & \Delta \mathrm{W}=\Delta \mathrm{Q}-\Delta \mathrm{U}=\mathrm{nc} _{\mathrm{P}} \Delta \mathrm{T}-\mathrm{nc} _{\mathrm{V}} \Delta \mathrm{T}=\mathrm{n}\left(\mathrm{c} _{\mathrm{P}}-\mathrm{c} _{\mathrm{V}}\right) \Delta \mathrm{T} \\ & \therefore \frac{\Delta \mathrm{Q}}{\Delta \mathrm{W}}=\frac{\mathrm{nc} _{\mathrm{P}} \Delta \mathrm{T}}{\mathrm{n}\left(\mathrm{c} _{\mathrm{P}}-\mathrm{c} _{\mathrm{V}}\right) \Delta \mathrm{T}} \end{aligned} $$

$$ =\frac{\mathrm{c} _{\mathrm{P}}}{\mathrm{c} _{\mathrm{P}}-\mathrm{c} _{\mathrm{V}}}=\frac{\mathrm{c} _{\mathrm{p}} / \mathrm{c} _{\mathrm{V}}}{\mathrm{c} _{\mathrm{p}} / \mathrm{c} _{\mathrm{V}}-1}=\frac{\gamma}{\gamma-1} $$

Hence option (3) is correct.

57. A well insulated box contains a partition dividing the box into two equal volumes as shown in figure, initially the left hand side contains an ideal monoatomic gas and other half is the vacuum, the partition is suddenly removed so that gas now is contained through out the box, the change in temperature of the gas and internal energy of the system would be respectively,

(1) Increase, Increase

(2) Increase, decrease

(3) Decrease, increase

(4) No change, no change

Show Answer

Correct answer: (4)

Solution:

Since the box in insulated, and gas against vacuum, i.e. zero pressure, that’s why no work has been done and there is no change in internal energy, thus temperature do not change. Hence correct option is no change in temperature and no change in internal energy.

Hence option (4) is correct.

58. An ideal gas is expanding such that $\mathbf{P T}^{2}=$ constant, the coefficient of volume expansion is

(1) $\frac{1}{\mathrm{~T}}$

(2) $\frac{2}{\mathrm{~T}}$

(3) $\frac{3}{\mathrm{~T}}$

(4) $\frac{4}{\mathrm{~T}}$

Show Answer

Correct answer: (3)

Solution:

$\mathrm{Pv}=\mathrm{nRT} \Rightarrow \mathrm{P}=\frac{\mathrm{nRT}}{\mathrm{V}}$

Since $\mathrm{PT}^{2}=$ constant therefore $\left(\frac{\mathrm{nRT}}{\mathrm{V}}\right) \mathrm{T}^{2}=$ constant

or $\quad \frac{\mathrm{T}^{3}}{\mathrm{~V}}=$ constant

$\Rightarrow \frac{1}{\mathrm{~V}}\left(3 \mathrm{~T}^{2}\right)+\frac{\mathrm{T}^{3}(-1)}{\mathrm{v}^{2}} \frac{\mathrm{dV}}{\mathrm{dT}}=0 \Rightarrow \frac{1}{\mathrm{~V}}\left(\frac{\mathrm{dV}}{\mathrm{dT}}\right)=\frac{3}{\mathrm{~T}}$

Also coefficient of volume expansion is given by $\gamma=\frac{\mathrm{dV}}{\mathrm{vdT}}$

$\therefore \gamma=\frac{3}{\mathrm{~T}}$

Hence option (3) is correct.

59. Consider an ideal gas confined in an isolated closed chamber, as the gas goes an adiabatic expansion. The average time of collision between molecules increases as $V^{q}$ where $V$ is the volume of the gas, the value of $q$ is

(1) $\frac{3 \gamma+5}{6}$

(2) $\frac{3 \gamma-5}{6}$

(3) $\frac{\gamma+1}{2}$

(4) $\frac{\gamma-1}{2}$

Show Answer

Correct answer: (3)

Solution:

Relaxation time $\tau=\frac{1}{\sqrt{2} \pi \mathrm{d}^{2} \mathrm{nv} _{\mathrm{rms}}}$

$$ \begin{aligned} & \mathrm{V} _{\mathrm{rms}} \propto \sqrt{\mathrm{T}}, \mathrm{n} \propto \frac{1}{\mathrm{~V}} \\ & \tau \propto \frac{\mathrm{V}}{\sqrt{\mathrm{T}}} \text { as } \mathrm{TV}^{\gamma-1}=\mathrm{k}(\text { constant }) \\ & \frac{1}{\mathrm{~T}}=\frac{\mathrm{V}^{\gamma-1}}{\mathrm{k}} \\ & \therefore \tau \quad \propto \mathrm{V} \sqrt{\mathrm{V}^{\mathrm{r}-1}} \text { or } \tau \propto \mathrm{V}^{1+\frac{\gamma-1}{2}} \\ & \text { or } \quad \tau \propto \mathrm{V}^{\frac{\gamma+1}{2}} \\ & \therefore \quad \mathrm{q}=\frac{\gamma+1}{2} \end{aligned} $$

Hence correct answer is option (3).

60. 5.6 litre of helium gas at STP is adiabatically compressed to 0.7 litre. Taking the initial temperature to be $T _{1}$, the work done in the process is

(1) $\frac{9}{8} \mathrm{RT} _{1}$

(2) $\frac{3}{2} \mathrm{RT} _{1}$

(3) $\frac{15}{8} \mathrm{RT} _{1}$

(4) $\frac{9}{2} \mathrm{RT} _{1}$

Show Answer

Correct answer: (1)

Solution:

For adiabatic process $\mathrm{Tv}^{\mathrm{r}-1}=\mathrm{K}$

$$ \mathrm{T} _{1}(5.6)^{2 / 3}=\mathrm{T} _{2}(0.7)^{2 / 3} $$

$\Rightarrow \mathrm{T} _{1}(8)^{2 / 3}=\mathrm{T} _{2}$

$\Rightarrow \mathrm{T} _{2}=4 \mathrm{~T} _{1}$

Work done $\mathrm{W}=\frac{\mathrm{nR} \Delta \mathrm{T}}{\mathrm{r}-1}=\frac{\frac{1}{4} \mathrm{R}\left(4 \mathrm{~T} _{1}-\mathrm{T} _{1}\right)}{\left(\frac{5}{3}-1\right)}=\frac{9}{8} \mathrm{RT} _{1}$

$\left(\right.$ where $\mathrm{n}=\frac{5.6 \text { litre }}{22.4 \text { litre } / \text { mole }}=\frac{1}{4}$ mole $)$

Hence option (1) is correct answer.

61. An ideal gas going through the cycle as shown in figure, the efficiency of the cyclic process will be

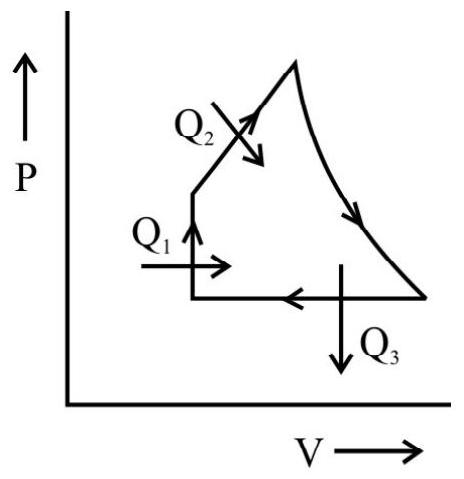
(1) $1-\frac{\mathrm{Q} _{3}}{\mathrm{Q} _{1}+\mathrm{Q} _{2}}$

(2) $1-\frac{\left(\mathrm{Q} _{1}+\mathrm{Q} _{2}\right)}{\mathrm{Q} _{3}}$

(3) $\frac{Q _{3}}{Q _{1}+Q _{2}}$

(4) $\frac{\mathrm{Q} _{1}+\mathrm{Q} _{2}}{\mathrm{Q} _{3}}$

Show Answer

Correct answer: (1)

Solution:

Efficiency $=\frac{\text { Work done }}{\text { Heat supplied }}$

Work done in this process $\left(\mathrm{Q} _{1}+\mathrm{Q} _{2}\right)-\mathrm{Q} _{3}$

Heat supplied $\left(Q _{1}+Q _{2}\right)$

Hence $\eta=\frac{\left(Q _{1}+Q _{2}\right)-Q _{3}}{Q _{1}+Q _{2}}=1-\frac{Q _{3}}{Q _{1}+Q _{2}}$

Hence option (1) is the correct answer.

62. Two identical containers $A$ and $B$ with frictionless pistons contains the same ideal gas at the same temperature and the same volume ’ $V$ ‘. The mass of gas contained in $A$ is $m _{A}$ and that in $B$ is $m _{B}$, the gas in each cylinder is now allowed to expand isothermally to the same final volume $2 \mathrm{v}$, the change in the pressure in $A$ and $B$ are found to be $\Delta \mathrm{P}$ and $1.5 \Delta \mathrm{P}$ respectively, then

(1) $4 \mathrm{~m} _{\mathrm{A}}=9 \mathrm{~m} _{\mathrm{B}}$

(2) $3 \mathrm{~m} _{\mathrm{A}}=2 \mathrm{~m} _{\mathrm{B}}$

(3) $2 \mathrm{~m} _{\mathrm{A}}=3 \mathrm{~m} _{\mathrm{B}}$

(4) $9 \mathrm{~m} _{\mathrm{A}}=4 \mathrm{~m} _{B}$

Show Answer

Correct answer: (2)

Solution:

For gas in $A, P _{1}=\left(\frac{m _{A}}{M}\right) \frac{R T}{V _{1}}$ and $P _{2}=\left(\frac{m A}{M}\right) \frac{R T}{V _{2}}$

$\therefore \Delta \mathrm{P}=\mathrm{P} _{2}-\mathrm{P} _{1}=\left(\frac{\mathrm{m} _{\mathrm{A}}}{\mathrm{m}}\right) \mathrm{RT}\left(\frac{1}{\mathrm{~V} _{1}}-\frac{1}{\mathrm{~V} _{2}}\right)$

Given $\mathrm{V} _{1}=\mathrm{V}, \mathrm{V} _{2}=2 \mathrm{~V}$

$\therefore \Delta \mathrm{P}=\left(\frac{\mathrm{RT}}{\mathrm{M}}\right) \frac{\mathrm{m} _{\mathrm{B}}}{2 \mathrm{~V}}$

Similarly for gas $\mathrm{m} _{\mathrm{B}}, 1.5 \Delta \mathrm{P}=\left(\frac{\mathrm{RT}}{\mathrm{M}}\right) \frac{\mathrm{m} _{\mathrm{B}}}{2 \mathrm{~V}}$

$\Rightarrow 2 \mathrm{~m} _{\mathrm{B}}=3 \mathrm{~m} _{\mathrm{A}}$

Hence option (2) is correct.

63. A gaseous mixture enclosed in a vessel consists of one gram mole of a gas A with $\gamma=(5 / 3)$ and same amount of gas B with $\gamma=(7 / 8)$ at temperature $T$, the gas A and B do not react with each other and are assumed to be ideal. The number of gram moles of gas B ( If $\gamma$ for the gaseous mixture is $\frac{19}{13}$ ) will be:

(1) 6 gram mole

(2) 4 gram mole

(3) 1 gram mole

(4) 2 gram mole

Show Answer

Correct answer: (4)

Solution:

For an ideal gas $\mathrm{C} _{\mathrm{P}}-\mathrm{C} _{\mathrm{v}}=\mathrm{R}$ and $\gamma=\frac{\mathrm{C} _{\mathrm{p}}}{\mathrm{C} _{\mathrm{v}}}$ which gives $\mathrm{C} _{\mathrm{v}}=\frac{\mathrm{R}}{\gamma-1}$

Hence $\left(\mathrm{C} _{\mathrm{v}}\right) _{1}=\frac{\mathrm{R}}{\frac{5}{3}-1}=\frac{3}{2} \mathrm{R},\left(\mathrm{C} _{\mathrm{v}}\right) _{2}=\frac{5}{2} \mathrm{R}$ and $\left(\mathrm{C} _{\mathrm{v}}\right) _{\text {mix }}=\frac{13}{6} \mathrm{R}$

From the principle of conservation of energy $\Delta \mathrm{U}=\Delta \mathrm{U} _{1}+\Delta \mathrm{U} _{2}$

$$ \left(\mathrm{U} _{1}+\mathrm{U} _{2}\right)\left(\mathrm{C} _{\mathrm{v}}\right) _{\text {mix }} \Delta \mathrm{T}=\mathrm{U} _{1}\left(\mathrm{C} _{\mathrm{V}}\right) _{1} \Delta \mathrm{T}+\mathrm{U} _{2}\left(\mathrm{C} _{\mathrm{v}}\right) _{2} \Delta \mathrm{T} $$

$\left(\mathrm{c} _{\mathrm{v}}\right) _{\text {mix }}=\frac{\mathrm{U} _{1}\left(\mathrm{c} _{\mathrm{v}}\right) _{1}+\mathrm{U} _{2}\left(\mathrm{c} _{\mathrm{v}}\right) _{2}}{\mathrm{U} _{1}+\mathrm{U} _{2}}$

$\frac{13}{6} \mathrm{R}=\frac{1 \times \frac{3}{2} \mathrm{R}+\mathrm{U} _{2} \times \frac{5}{2} \mathrm{R}}{1+\mathrm{U} _{2}}$

$\Rightarrow \mathrm{U} _{2}=2$ gram mole

Hence option (4) is correct.

64. Two rigid boxes containing ideal gases are placed on a table. Box a contains one mole of nitrogen at temperature $60 \mathrm{~K}$ to while box B contains one mole of helium at temperature $\left(\pi / 3 T _{0}\right)$, the box are then put into thermal contact with each other and heat flows between them until the gases reach a common final temperature (Ignore the heat capacities of the boxes). Then the final temperature $T _{F}$ in terms of $T _{0}$ is

(1) $\mathrm{T} _{\mathrm{f}}=\frac{5}{2} \mathrm{~T} _{0}$

(2) $\mathrm{T} _{\mathrm{f}}=\frac{3}{7} \mathrm{~T} _{0}$

(3) $\mathrm{T} _{\mathrm{f}}=\frac{7}{3} \mathrm{~T} _{0}$

(4) $\mathrm{T} _{\mathrm{f}}=\frac{3}{2} \mathrm{~T} _{0}$

Show Answer

Correct answer: (4)

Solution:

Change in internal energy $(\mathrm{dU})=\mathrm{C} _{\mathrm{v}} \mathrm{dT}$

$\mathrm{c} _{\mathrm{V}}$ for nitrogen $=\frac{5}{2} \mathrm{R}$ and for Helium $=\frac{3}{2} \mathrm{R}$

$\therefore \quad \mathrm{dU}=\frac{5}{2} \mathrm{R}\left(\mathrm{T} _{\mathrm{f}}-\mathrm{T} _{0}\right)+\frac{3}{2} \mathrm{R}\left(\mathrm{T} _{\mathrm{f}}-\mathrm{T} _{0}\right)$

But dU $=0$

$$ \begin{aligned} & 0=\frac{5}{2} \mathrm{R}\left(\mathrm{T} _{\mathrm{f}}-\mathrm{T} _{0}\right)+\frac{3}{2} \mathrm{R}\left(\mathrm{T} _{\mathrm{f}}-\mathrm{T} _{0}\right) \\ & \mathrm{T} _{\mathrm{f}}=3 / 2 \mathrm{~T} _{0} \end{aligned} $$

Hence option (4) is correct.

65. Consider a spherical shell of radius ’ $R$ ’ at temperature $T$, the black body inside it can be considered as an ideal gas of photons with internal energy per unit volume $u \propto T^{4}$ (where $u=\frac{U}{V}$ ) and pressure $P=\frac{1}{3}(U / v)$. If the shell now undergoes an adiabatic expansion, the relation between $T$ and $R$ is

(1) $\mathrm{T} \propto \mathrm{e}^{-\mathrm{R}}$

(2) $\mathrm{T} \propto \mathrm{e}^{-3 \mathrm{R}}$

(3) $\mathrm{T} \propto \frac{1}{\mathrm{R}}$

(4) $\mathrm{T} \propto \frac{1}{\mathrm{R}^{3}}$

Show Answer

Correct answer: (3)

Solution:

Given $\mathrm{P}=\frac{1}{3}\left(\frac{\mathrm{U}}{\mathrm{V}}\right)$

$\mathrm{PV}=\mathrm{nRT}$ we have $\mathrm{P}=\frac{\mathrm{nRT}}{\mathrm{V}}$

Since $\frac{\mathrm{U}}{\mathrm{V}} \propto \mathrm{T}^{4}$ we have $\mathrm{P} \alpha \mathrm{T}^{4}$

$\therefore \frac{\mathrm{nRT}}{\mathrm{V}} \propto \mathrm{T}^{4}$ or $\mathrm{VT}^{3}=$ constant

or $\left(\frac{4}{3} \pi \mathrm{R}^{3}\right) \mathrm{T}^{3}=$ constant $\Rightarrow \mathrm{R}^{3} \mathrm{~T}^{3}=$ constant $\quad \therefore \mathrm{RT}=$ constant

$\Rightarrow \mathrm{T} \propto \frac{1}{\mathrm{R}}$

Hence option (3) is correct.

66. When a gas expands along $A B$ it does $500 \mathrm{~J}$ of work and absorbs $250 \mathrm{~J}$ of heat, when the gas expands along $A C$ it does $700 \mathrm{~J}$ of work and absorbs $300 \mathrm{~J}$ of heat, when the gas makes a transition from $\mathrm{C}$ to $\mathrm{A}$ along $\mathrm{CDA}, 800 \mathrm{~J}$ of work is done on it from $\mathrm{C}$ to $\mathrm{D}$. Heat exchanged along CDA will be

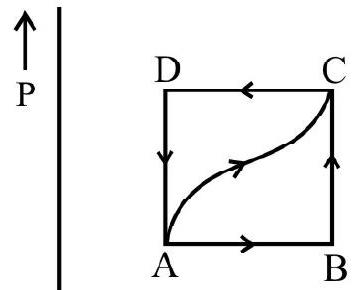
(1) $400 \mathrm{~J}$

(2) $-400 \mathrm{~J}$

(3) $-800 \mathrm{~J}$

(4) $800 \mathrm{~J}$

Show Answer

Correct answer: (2)

Solution:

Given $\Delta \mathrm{W} _{\mathrm{AB}}=+500 \mathrm{~J}$ and $\Delta \mathrm{Q} _{\mathrm{AB}}=+250 \mathrm{~J}$

According to first law of thermodynamics

$$ \begin{aligned} & \Delta \mathrm{Q} _{\mathrm{AB}}=\Delta \mathrm{U} _{\mathrm{AB}}+\Delta \mathrm{W} _{\mathrm{AB}} \\ & 250=\Delta \mathrm{U} _{\mathrm{AB}}+500 \\ & \Delta \mathrm{U} _{\mathrm{AB}}=-250 \mathrm{~J} ; \Delta \mathrm{W} _{\mathrm{AC}}=700 \mathrm{~J} ; \Delta \mathrm{Q} _{\mathrm{AC}}=300 \mathrm{~J} \end{aligned} $$

which gives $\Delta \mathrm{U} _{\mathrm{AC}}=-400 \mathrm{~J}$

$$ \Delta \mathrm{W} _{\mathrm{CDA}}=\Delta \mathrm{W} _{\mathrm{CD}}+\mathrm{W} _{\mathrm{DA}} $$

But $\Delta \mathrm{w} _{\mathrm{DA}}=0 \quad$ (Due to isochoric process)

$\therefore \Delta \mathrm{W} _{\mathrm{CDA}}=\Delta \mathrm{W} _{\mathrm{CD}}=-800 \mathrm{~J}$

$$ \Delta \mathrm{W} _{\mathrm{CDA}}+\Delta \mathrm{U} _{\mathrm{CDA}}=\Delta \mathrm{Q} _{\mathrm{CDA}} $$

Also $\Delta \mathrm{U} _{\mathrm{CDA}}=\Delta \mathrm{U} _{\mathrm{AC}}=-\Delta \mathrm{U} _{\mathrm{AC}}=400 \mathrm{~J}$

$\Rightarrow \Delta \mathrm{Q} _{\mathrm{CDA}}=-800+400 \mathrm{~J}=-400 \mathrm{~J}$

Hence option (2) is correct.

67. A bullet of mass 10 gram traveling horizontally at $200 \mathrm{~m} / \mathrm{s}$, strikes and embeds in a pendulum bob of mass $2.0 \mathrm{Kg}$, assuming that $c _{v}$ for the bob plus bullet is $3 R$, the increase in temperature of the system due to 40 collision will be (Take molecular mass of the system to be 200 gram/mole)

(1) $2.5^{\circ} \mathrm{C}$

(2) $199^{\circ} \mathrm{C}$

(3) $800^{\circ} \mathrm{C}$

(4) $0.8^{\circ} \mathrm{C}$

Show Answer

Correct answer: (4)

Solution:

The change in heat content $\Delta \mathrm{Q}=\mathrm{nC} _{\mathrm{v}} \Delta \mathrm{T}$ and $\mathrm{n}=\frac{\mathrm{m}}{\mathrm{M}}$

$\Delta \mathrm{T}=\frac{\Delta \mathrm{Q}}{\mathrm{nC} _{\mathrm{v}}}=\frac{\Delta \mathrm{Q}}{\frac{\mathrm{m}}{\mathrm{M}} \mathrm{C} _{\mathrm{v}}}=\frac{\mathrm{M} \Delta \mathrm{Q}}{\mathrm{mC} _{\mathrm{v}}}=\frac{\mathrm{m} \Delta \mathrm{Q}}{\mathrm{m} \times 3 \mathrm{R}}$

Heat $\Delta \mathrm{Q}=\Delta \mathrm{K}=\frac{\mathrm{P}^{2}}{2 \mathrm{~m} _{\mathrm{i}}}-\frac{\mathrm{P}^{2}}{2 \mathrm{~m} _{\mathrm{f}}}=\frac{\mathrm{P}^{2}}{2}\left(\frac{1}{\mathrm{~m} _{\mathrm{i}}}-\frac{1}{\mathrm{~m} _{\mathrm{f}}}\right)$

$$ =\frac{\left(10 \times 10^{-3} \times 200\right)^{2}}{2}\left(\frac{1}{10 \times 10^{-3}}-\frac{1}{2.01}\right)=199 \mathrm{~J} $$

$\therefore \quad \Delta \mathrm{T}=\frac{200 \times 199}{2010 \times 3 \times 8.314}=0.8^{\circ} \mathrm{C}$

Hence option (4) is correct.

68. An ideal gas is carried through a thermodynamic cycle consisting two isobaric and two isothermal process, as shown in figure the net work done in the entire cycle is given by

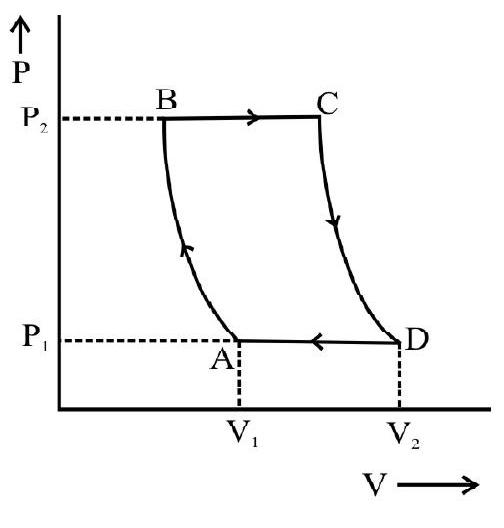
(1) $\mathrm{P} _{1}\left(\mathrm{~V} _{2}-\mathrm{V} _{1}\right) \ln \left(\frac{\mathrm{P} _{2}}{\mathrm{P} _{1}}\right)$

(2) $\mathrm{P} _{2}\left(\mathrm{~V} _{1}-\mathrm{V} _{2}\right) \ln \left(\frac{\mathrm{P} _{1}}{\mathrm{P} _{2}}\right)$

(3) $\mathrm{P} _{1}\left(\mathrm{~V} _{1}-\mathrm{V} _{2}\right) \ln \left(\frac{\mathrm{P} _{2}}{\mathrm{P} _{1}}\right)$

(4) $\mathrm{P} _{2}\left(\mathrm{~V} _{2}-\mathrm{V} _{1}\right) \ln \left(\frac{\mathrm{P} _{1}}{\mathrm{P} _{2}}\right)$

Show Answer

Correct answer: (1)

Solution:

Total work done $\Delta \mathrm{W}=\Delta \mathrm{W} _{\mathrm{AB}}+\Delta \mathrm{W} _{\mathrm{BC}}+\Delta \mathrm{W} _{\mathrm{CD}}+\Delta \mathrm{W} _{\mathrm{DA}}$

$$ \begin{aligned} & =\mathrm{nRT} _{1} \ln \left(\frac{\mathrm{P} _{1}}{\mathrm{P} _{2}}\right)+\mathrm{P} _{2}\left(\mathrm{~V} _{\mathrm{C}}-\mathrm{V} _{\mathrm{B}}\right)+\mathrm{nRT} _{2} \ln \left(\frac{\mathrm{P} _{2}}{\mathrm{P} _{1}}\right)+\mathrm{P} _{1}\left(\mathrm{~V} _{1}-\mathrm{V} _{2}\right) \\ & =\mathrm{nR}\left(\mathrm{T} _{2}-\mathrm{T} _{1}\right) \ln \left(\frac{\mathrm{P} _{2}}{\mathrm{P} _{1}}\right)+\mathrm{P} _{2} \mathrm{~V} _{\mathrm{C}}-\mathrm{P} _{2} \mathrm{~V} _{\mathrm{B}}+\mathrm{P} _{1} \mathrm{~V} _{1}-\mathrm{P} _{1} \mathrm{~V} _{2} \end{aligned} $$

Also for process $A B \quad P _{1} V _{1}=P _{2} V _{B}$

and for process $\mathrm{CD} \quad \mathrm{P} _{2} \mathrm{~V} _{\mathrm{C}}=\mathrm{P} _{2} \mathrm{~V} _{2}$

$\Rightarrow \Delta \mathrm{W}=\mathrm{nR}\left(\mathrm{T} _{2}-\mathrm{T} _{1}\right) \ln \left(\frac{\mathrm{P} _{2}}{\mathrm{P} _{1}}\right)=\left(\mathrm{P} _{2} \mathrm{~V} _{2}-\mathrm{P} _{1} \mathrm{~V} _{1}\right) \ln \left(\frac{\mathrm{P} _{2}}{\mathrm{P} _{1}}\right)$

Hence option (2) is correct.

69. The density versus pressure graph of one mole of an ideal monoatomic gas undergoing a cyclic process in shown in figure, the molecular mass of the gas is $M$, total work done in the process will be

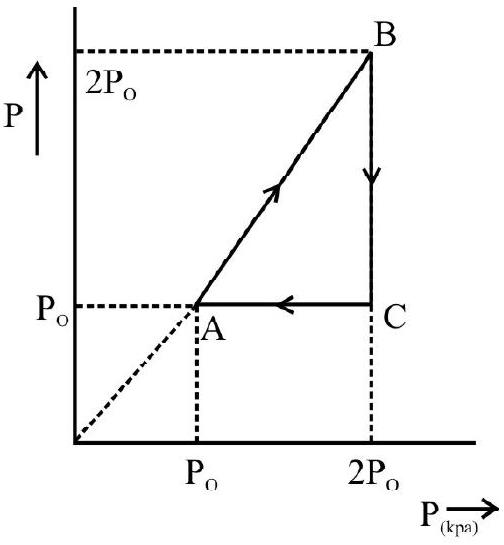
(1) $\frac{\mathrm{P} _{0} \mathrm{M}}{\mathrm{P} _{0}}(1-\ln 2)$

(2) $\frac{-\mathrm{P} _{0} \mathrm{M}}{\mathrm{P} _{0}} \ell \mathrm{n} 2$

(3) $\frac{\mathrm{P} _{0} \mathrm{M}}{\mathrm{P} _{0}}$

(4) zero

Show Answer

Correct answer: (1)

Solution:

Given $\mathrm{n}=1$ and $\mathrm{m}=\mathrm{M}$

Process $A B: \rho \propto \mathrm{P}$, as it is isothermal process $(\mathrm{T}=$ constant)

$$ \begin{gathered} \mathrm{P}=\frac{\mathrm{PM}}{\mathrm{RT}} \\ \mathrm{W} _{\mathrm{AB}}=\mathrm{RT} _{\mathrm{A}} \ln \frac{\mathrm{P} _{\mathrm{A}}}{\mathrm{P} _{\mathrm{B}}}=\mathrm{RT} _{\mathrm{A}} \ln \left(\frac{1}{2}\right)=\frac{-\mathrm{P} _{0} \mathrm{M}}{\mathrm{P} _{0}} \ln (2) \end{gathered} $$

Process $\mathrm{BC}$ is an isobaric process $(\mathrm{P}=$ constant $)$

$$ \mathrm{W} _{\mathrm{BC}}=\mathrm{P} _{\mathrm{B}}\left(\mathrm{v} _{\mathrm{C}}-\mathrm{v} _{\mathrm{B}}\right)=2 \mathrm{P} _{0}\left(\frac{\mathrm{M}}{\mathrm{P} _{\mathrm{C}}}-\frac{\mathrm{M}}{\mathrm{P} _{\mathrm{B}}}\right)=\frac{2 \mathrm{P} _{0} \mathrm{M}}{2 \mathrm{P} _{0}}=\frac{\mathrm{P} _{0} \mathrm{M}}{\mathrm{P} _{0}} $$

Process CA

$$ \begin{aligned} & \mathrm{W} _{\mathrm{CA}}: \text { As } \rho=\text { constant } \therefore \mathrm{V}=\text { constant } \\ & \therefore \mathrm{W} _{\mathrm{CA}}=0 \end{aligned} $$

Hence total work done $\mathrm{W}=\mathrm{W} _{\mathrm{AB}}+\mathrm{W} _{\mathrm{BC}}+\mathrm{W} _{\mathrm{CA}}$

$$ =-\frac{\mathrm{P} _{0} \mathrm{M}}{\mathrm{P}} \ell \operatorname{n} 2+\frac{\mathrm{P} _{0} \mathrm{M}}{\mathrm{P} _{0}}+0=\frac{\mathrm{P} _{0} \mathrm{M}}{\mathrm{P} _{0}}(1-\ell \mathrm{n} 2) $$

Hence option (1) is correct.

70. Two moles of a diatomic ideal gas is taken through a $P T=$ constant curve. Its temperature is increased from $\mathrm{T} _{0}$ to $2 \mathrm{~T} _{0}$, the work done by the system will be:

(1) $16 \mathrm{RT} _{0}$

(2) $2 \mathrm{RT} _{0}$

(3) $8 \mathrm{RT} _{0}$

(4) $\mathrm{RT} _{0}$

Show Answer

Correct answer: (3)

Solution:

Work done $\mathrm{W}=\int \mathrm{PdV}$

$\mathrm{PT}=\mathrm{P} _{1} \mathrm{~T} _{1}=\mathrm{P} _{2} \mathrm{~T} _{2}=$ constant (c)

$$ \mathrm{P}\left(\frac{\mathrm{PV}}{\mathrm{nR}}\right)=\mathrm{c} $$

$\mathrm{P}^{2} \mathrm{~V}=\mathrm{nRc}$ hence $\mathrm{P}=\sqrt{\frac{\mathrm{ncR}}{\mathrm{V}}}$

$\therefore \text { work done } W=\int P d V=\int_{v_1}^{v_2} \sqrt{\frac{n c R}{V}} d v=\sqrt{n c R} \int_{v_1}^{v_2} \frac{1}{\sqrt{V}} d V$

$$ \begin{aligned} & =\sqrt{\mathrm{ncR}}\left[2\left(\sqrt{\mathrm{V} _{2}}-\sqrt{\mathrm{V} _{1}}\right)\right]=2\left[\sqrt{\mathrm{nRP} _{2} \mathrm{~V} _{2} \mathrm{~T} _{2}}-\sqrt{\mathrm{nRP} _{1} \mathrm{~T} _{1} \mathrm{~V} _{1}}\right] \\ & =2 \mathrm{nR}\left(\mathrm{T} _{2}-\mathrm{T} _{1}\right)=8 \mathrm{RT} _{0} \end{aligned} $$

Hence option (3) is correct.

71. An ideal gas having initial pressure $P$, volume $v$ and temperature ’ $T$ ’ is allowed to expand adiabatically until its volume becomes $5.66 \mathrm{v}$, while its temperature falls to $\mathrm{T} / 2$, work done by the gas during expansion will be

[Given $(\mathbf{5 . 6 6})^{0.4}=\mathbf{2}$ ]

(1) $1.25 \mathrm{Pv}$

(2) $2 \mathrm{Pv}$

(3) $1.461 \mathrm{Pv}$

(4) 2.461

Show Answer

Correct answer: (1)

Solution:

Work done during adiabatic process for one mole gas is

$$ \begin{aligned} & \mathrm{W}=\frac{1}{1-\gamma}\left(\mathrm{P} _{2} \mathrm{~V} _{2}-\mathrm{P} _{1} \mathrm{~V} _{1}\right) \\ & \frac{\mathrm{P} _{1} \mathrm{~V} _{1}}{\mathrm{~T} _{1}}=\frac{\mathrm{P} _{2} \mathrm{~V} _{2}}{\mathrm{~T} _{2}} \\ & \mathrm{P} _{2}=\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}} \frac{\mathrm{P} _{1} \mathrm{~V} _{1}}{\mathrm{~V} _{2}}=\frac{1}{2} \frac{\mathrm{PV}}{5.66 \mathrm{v}}=\frac{\mathrm{P}}{11.32} \end{aligned} $$

$\therefore \quad \mathrm{W}=\frac{1}{1-1.4}\left[\frac{\mathrm{P}}{11.32} \times 5.66 \mathrm{~V}-\mathrm{PV}\right]=\frac{1}{-0.4} \times \frac{-\mathrm{Pv}}{2}$

Hence $\mathrm{W}=\frac{\mathrm{PV}}{0.8}=\frac{5}{4} \mathrm{Pv}=1.25 \mathrm{Pv}$

Hence correct option is (1)

72. The $\mathbf{P}-\mathbf{T}$ graph, for an ideal gas is shown in figure, corresponding $\mathbf{P}-\mathbf{V}$ graph for the given gas will be

Show Answer

Correct answer: (1)

Solution:

For process AB: It is an isothermal process with $T=$ constant and $\mathrm{P} _{\mathrm{B}}>\mathrm{P} _{\mathrm{A}}$

as $\mathrm{P} \propto \frac{1}{\mathrm{~V}} \Rightarrow \mathrm{PV}$ graph will be hyperbola with $\mathrm{P} _{\mathrm{B}}>\mathrm{P} _{\mathrm{A}}$

for Process BC: It is an isobaric process with $\mathrm{P}=$ constant

and $\mathrm{T} _{\mathrm{C}}>\mathrm{T} _{\mathrm{B}}$

as $\mathrm{P}$ constant $\therefore \mathrm{PV}$ graph will be a straight line parallel to $\mathrm{v}$ axis with $\mathrm{V} _{\mathrm{C}}>\mathrm{V} _{\mathrm{B}}$ (because $\mathrm{V} \propto \mathrm{T}$ is an isobaric process).

Hence graph (1) depicts correctly $\mathrm{P}-\mathrm{V}$ graph for the given gas

Hence option (1) is correct.

73. P-T graph of an ideal gas in shown in figure corresponding $\mathbf{V}-\mathrm{T}$ graph for the same gas will be

Show Answer

Correct answer: (2)

Solution:

For process $A B$ : As it is isothermal process with constant temperature $T$, and $\mathrm{P} _{B}>\mathrm{P} _{\mathrm{A}}$

$\therefore \mathrm{V}-\mathrm{T}$ graph will be a straight line parallel to $\mathrm{v}-$ axis with $\mathrm{V} _{\mathrm{B}}<\mathrm{V} _{\mathrm{A}}$.

For process $B C$ : As it is isobaric process with $\mathrm{P}=$ constant and $\mathrm{T} _{C}>\mathrm{T} _{\mathrm{B}}$

$\therefore \mathrm{V}-\mathrm{T}$ graph is a straight line passing through origin with $\mathrm{T} _{\mathrm{C}}>\mathrm{T} _{\mathrm{B}}$ and $\mathrm{V} _{\mathrm{B}}<\mathrm{V} _{\mathrm{A}}$.

Hence graph (2) depicts correct $\mathrm{V}-\mathrm{T}$ graph for the gas.

Hence optional (2) is correct.

74. $n$ moles of a monoatomic gas are taken around in a cyclic process consisting of four processes along ABCDA as shown. All lines on the Pv diagram have slope of magnitude $\left(P _{0} / V _{0}\right)$. The pressure at $a$ and $c$ is $P _{0}$ and the volumes at $A$ and $C$ are $\frac{V _{0}}{2}$ and $\frac{3 V _{0}}{2}$ respectively. The percentage efficiency of the cycle will be

(1) $18.18 \%$

(2) $40 \%$

(3) $45.45 \%$

(4) $20 \%$

Show Answer

Correct answer: (1)

Solution:

Total work done during the cycle

$\Delta \mathrm{W}=\left(\frac{3 \mathrm{~V} _{0}}{2}-\frac{\mathrm{V} _{0}}{2}\right)\left(\mathrm{P} _{\mathrm{B}}-\mathrm{P} _{0}\right)+\frac{1}{2}\left(\frac{3 \mathrm{~V} _{0}}{2}-\frac{\mathrm{V} _{0}}{2}\right)\left(\mathrm{P} _{0}-\mathrm{P} _{\mathrm{D}}\right)=\frac{1}{2} \mathrm{~V} _{0}\left(\mathrm{P} _{\mathrm{B}}-\mathrm{P} _{\mathrm{D}}\right)$

But $\mathrm{P} _{\mathrm{B}}=\mathrm{P} _{0}+\frac{\mathrm{P} _{0}}{\mathrm{~V} _{0}} \times \frac{\mathrm{V} _{0}}{2}=\frac{3 \mathrm{P} _{0}}{2}$

$$ \mathrm{P} _{\mathrm{D}}=\mathrm{P} _{0}-\frac{\mathrm{P} _{0}}{\mathrm{~V} _{0}} \times \frac{\mathrm{V} _{0}}{2}=\frac{\mathrm{P} _{0}}{2} $$

$\therefore \quad \Delta \mathrm{W}=\frac{1}{2} \mathrm{~V} _{0}\left(\frac{3 \mathrm{P} _{0}}{2}-\frac{\mathrm{P} _{0}}{2}\right)=\frac{1}{2} \mathrm{P} _{0} \mathrm{v} _{0}…………….(1)$

$\Delta \mathrm{W} _{\mathrm{ABC}}=\mathrm{P} _{0}\left(\frac{3 \mathrm{~V} _{0}}{2}-\frac{\mathrm{V} _{0}}{2}\right)+\frac{1}{2} \mathrm{~V} _{0}\left(\frac{3}{2} \mathrm{P} _{0}-\mathrm{P} _{0}\right)$

$=\mathrm{P} _{0} \mathrm{~V} _{0}+\frac{1}{4} \mathrm{P} _{0} \mathrm{~V} _{0}=\frac{5}{4} \mathrm{P} _{0} \mathrm{~V} _{0}$

$\Delta \mathrm{U} _{\mathrm{ABC}}=\mathrm{nC} _{\mathrm{V}}\left(\mathrm{T} _{\mathrm{C}}-\mathrm{T} _{\mathrm{A}}\right)=\mathrm{n} \times \frac{3}{2} \mathrm{R}\left[\frac{\mathrm{P} _{0} \frac{3 \mathrm{~V} _{0}}{2}}{\mathrm{nR}}-\frac{\mathrm{P} _{0} \frac{\mathrm{V} _{0}}{2}}{\mathrm{nR}}\right]=\frac{3}{2} \mathrm{P} _{0} \mathrm{~V} _{0}$

$\therefore \Delta \mathrm{Q} _{\text {supplied }}=\Delta \mathrm{w} _{\mathrm{ABC}}+\Delta \mathrm{U} _{\mathrm{ABC}}=\frac{5}{4} \mathrm{P} _{0} \mathrm{~V} _{0}+\frac{3}{2} \mathrm{P} _{0} \mathrm{~V} _{0}=\frac{11}{4} \mathrm{P} _{0} \mathrm{~V} _{0}$

$\therefore \quad \%$ efficiency $=\frac{\Delta \mathrm{W}}{\Delta \mathrm{Q} _{\text {supplied }}}=\frac{\frac{1}{2} \mathrm{P} _{0} \mathrm{~V} _{0}}{\frac{11}{4} \mathrm{P} _{0} \mathrm{~V} _{0}} \times 100=1818 \%$

Hence option (1) is correct.

75. A diatomic ideal gas is heated at constant volume until its pressure becomes three times, it is again heated at constant pressure until its volume is doubled. The molar heat capacity for the whole process will be

(1) $3.1 \mathrm{R}$

(2) $2.5 \mathrm{R}$

(3) $2.1 \mathrm{R}$

(4) $\mathrm{R}$

Show Answer

Correct answer: (1)

Solution:

Heat absorbed during heating at constant volume.

$\Delta \mathrm{Q} _{1}=\Delta \mathrm{U} _{1}=\mathrm{nC} _{\mathrm{v}} \Delta \mathrm{T}=\mathrm{n} \times \frac{5}{2} \mathrm{R}\left(3 \mathrm{~T} _{1}-\mathrm{T} _{1}\right)=5 \mathrm{nRT} _{1}$

Heat absorbed when gas is heated at constant pressure.

$\Delta \mathrm{Q} _{2}=\mathrm{nC} _{\mathrm{p}} \Delta \mathrm{T}=\mathrm{n} \times \frac{7}{2} \mathrm{R}\left(6 \mathrm{~T} _{1}-3 \mathrm{~T} _{1}\right)=\frac{21}{2} \mathrm{nRT} _{1}$

Hence total heat taken $\Delta \mathrm{Q}=\Delta \mathrm{Q} _{1}+\Delta \mathrm{Q} _{2}=5 \mathrm{nRT} _{1}+\frac{21}{2} \mathrm{nRT} _{1}=\frac{31}{2} \mathrm{nRT} _{1}$

$\therefore$ Molar heat capacity

$$ \mathrm{C}=\frac{\Delta \mathrm{Q}}{\mathrm{n} \Delta \mathrm{T}}=\frac{\frac{31}{2} \mathrm{nRT} _{1}}{\mathrm{n} \times\left(6 \mathrm{~T} _{1}-\mathrm{T} _{1}\right)}=3.1 \mathrm{R} $$

Hence option (1) is correct.

76. The freezer in a refrigerator is located on the top section so that

(1) The entire chamber of the refrigerator is cooled quickly due to convection

(2) The motor is not heated

(3) The heat gained from the environment is high

(4) The heat gained from the environments is low

Show Answer

Correct answer: (1)

Solution:

The upper cold denser air goes down while the lower warmer are goes up. The convection current so set up quickly cool the chamber or the refrigerator.

77. A diatomic gas is used in a carnot engine as the working substance. If during the adiabatic expansion part of the cycle the volume of the gas has increased from $v$ to $32 v$, the efficiency of the engine is

(1) 0.25

(2) 0.5

(3) 0.75

(4) 0.99

Show Answer

Correct answer: (3)

Solution:

For adiabatic expansion

$$ \begin{aligned} & \mathrm{T} _{1} \mathrm{~V} _{1}^{\gamma-1}=\mathrm{T} _{2} \mathrm{~V} _{2}^{\gamma-1} \\ \therefore & \frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=\left(\frac{\mathrm{V} _{2}}{\mathrm{~V} _{1}}\right)^{\mathrm{r}-1}=(32)^{\frac{7 / 3}{-1}},=(32)^{2 / 5}=4 \quad\left[\gamma \text { for a diatomic gas is } \frac{7}{5}\right] \end{aligned} $$

Efficiency of a carnot engine is given by

$\eta=\left(1-\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}\right)=\left(1-\frac{1}{4}\right)=0.75$

Hence option (3) is correct.

78. A sample of ideal gas has internal energy ’ $U$ ’ and is then compressed to one half of its original volume. While the temperature remains the same. The ratio of final internal energy $U$ ’ to initial internal energy $U$ is:

(1) $\frac{1}{4}$

(2) $\frac{1}{2}$

(3) 1

(4) 2

Show Answer

Correct answer: (3)

Solution:

For an ideal gas

$\mathrm{PV}=\mathrm{nRT}$

where $\mathrm{dU}=\mathrm{nC} _{\mathrm{v}} \mathrm{dT}$

as temperature remains constant in the process, $\mathrm{dT}=0$

Hence there is no change in internal energy $\mathrm{dU}=\mathrm{U}^{\prime}-\mathrm{U}^{-}=0$

Hence $\frac{\mathrm{U}^{\prime}}{\mathrm{U}}=1$

Hence option (3) is correct.

79. Volume versus temperature graph of two moles of helium gas is as shown in the figure. The ratio of heat absorbed and the work done by the gas in the process $A \rightarrow B$ is:

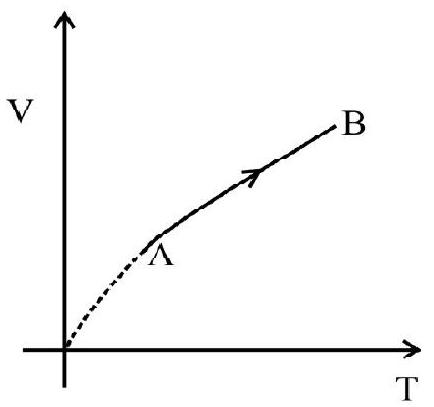
(1) 3

(2) $\frac{5}{2}$

(3) $\frac{5}{3}$

(4) $\frac{7}{2}$

Show Answer

Correct answer: (2)

Solution:

As $v-T$ graph is a straight line passing through origin:

Hence $\mathrm{V}$ or $\mathrm{P}=$ constant

$\therefore \quad \mathrm{dQ}=\mathrm{nC} _{\mathrm{P}} \mathrm{dT}$ and $\mathrm{dU}=\mathrm{nC} _{\mathrm{v}} \mathrm{dT}$

$\mathrm{dW}=\mathrm{dQ}-\mathrm{dU}=\mathrm{n}\left(\mathrm{C} _{\mathrm{p}}-\mathrm{C} _{\mathrm{v}}\right) \mathrm{dT}=\mathrm{nRdT}$

Hence $\frac{\mathrm{dQ}}{\mathrm{dW}}=\frac{\mathrm{C} _{\mathrm{P}}}{\mathrm{R}}=\frac{5}{2}$

80. The amount of heat given to a system is $40 \mathrm{~J}$ and the amount of work done on the system is $20 \mathrm{~J}$, then the change in internal energy of the system is:

(1) $-20 \mathrm{~J}$

(2) $+20 \mathrm{~J}$

(3) $-60 \mathrm{~J}$

(4) $+60 \mathrm{~J}$

Show Answer

Correct answer: (4)

Solution:

According to first law of thermodynamics

$\mathrm{dQ}=\mathrm{dU}+\mathrm{dW}$

Given $\mathrm{dQ}=40 \mathrm{~J}$

$\mathrm{dW}=-20 \mathrm{~J}$ (As work done on the system is negative by sign convention).

$\Rightarrow \mathrm{dU}=\mathrm{dQ}-\mathrm{dW}=40-(-20)$

$=60 \mathrm{~J}$