(A) ELASTICITY

An external applied force on a body can change its shape and / or size. Such forces are known as deforming forces. In general a body recovers its original shape and / or size when external deforming forces are removed. This is known as elasticity. In daily life we say a body is more elastic if we can easily change its shape or size. A layman says rubber is more elastic than steel because he can easily stretch a rubber band and not a steel wire. However in Physics; elasticity measures the opposition a body offers to changes in its shape and / or size. Therefore; in Physics, we say steel is more elastic than rubber.

Perfectly Elastic and Perfectly Plastic Body

A perfectly elastic body completely recovers its original dimensions when external deforming force is removed. This is an idealised concept. No body is perfectly elastic under all conditions. Quartz very nearly behaves like a perfectly elastic body.

A perfectly plastic body does not recover at all its original dimensions when external deforming force is removed. Putty; paraffin wax are nearly perfectly plastic bodies.

Stress

A body subjected to deforming forces is under stress. Due to interatomic / molecular forces, when distance between atoms / molecules changes from its equilibrium value, an internal restoring force comes into play. It is due to this internal force the body recovers its original dimensions when external deforming forces are removed. If there is no permanent change in the body; the internal restoring force is equal and opposite to the external applied force. Stress is internal restoring force per unit area. We can also say;

$$ \text { Stress }=\frac{\text { external deforming force }}{\text { area }} $$

The S.I unit of stress is $\frac{\mathrm{N}}{\mathrm{m}^{2}}(=\mathrm{Pa})$. [For a body in elastic limits] and its dimensions are $\mathrm{ML}^{-1} \mathrm{~T}^{-2}$. Commonly there are two types of stress.

(1) Normal Stress: The applied deforming force acts normally over the area of cross-section of body. It can be extensional (tensile) or compressional.

(2) Tangential Stress: The external applied force acts tangentially to the area of cross-section. Fig. 1 shows a cube having a rigidly fixed lower face $\mathrm{ABCD}$. $\mathrm{F}$ is tangential force applied to upper face EFGH. The shape of cube changes due to applied tangential stress.

Strain

Due to applied deforming force there is a change in dimensions of the body. Change in dimension per unit original dimension is known as strain, i.e.

$$ \text { Strain }=\frac{\text { change in dimension }}{\text { original dimension }} $$

Strain being a ratio of two similar dimensions is a pure number. It has no units or dimensions. There are three simple types of strain.

(1) Longitudinal Strain

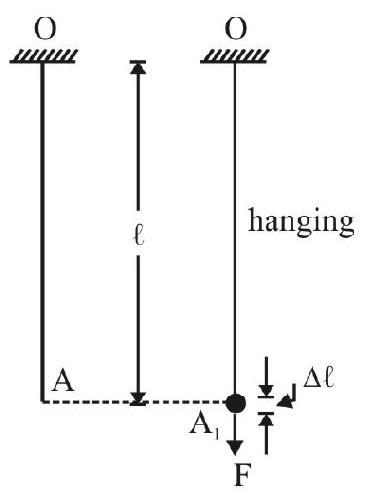
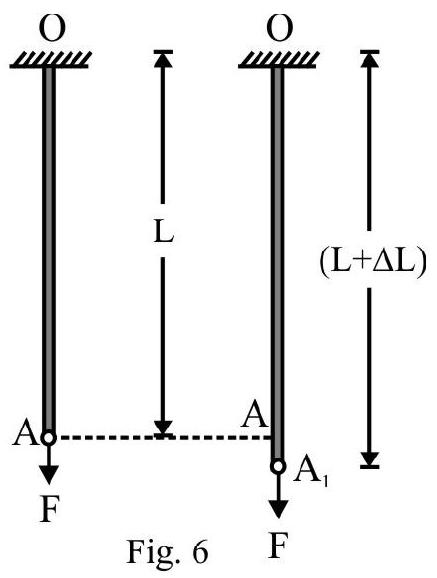
The external applied force produces a change in length. Fig. 2(a) shows a wire $\mathrm{OA}=\ell$ hanging vertically from a rigid support. In Fig. 2(b); the wire acquires length $\mathrm{OA} _{1}$, when external force $\mathrm{F}$ is applied.

$\mathrm{AA} _{1}=\Delta \ell=$ Change in length of wire. Then

The longitudinal strain $=\frac{\text { change in length }}{\text { original length }}=\frac{\Delta \ell}{\ell}$

(a)

Fig. 2

(2) Volumetric Strain

The external forces are applied in such a manner that here is a change in volume but no change in shape. Fig. 3 shows a cube ABCDEFGH of side $\mathrm{L}$ equal compressional force $\mathrm{F}$ is applied on all six faces as shown. The shape of cube remains same but its volume decreases. We have a volumetric strain.

Volumetric strain $=\frac{\text { change in volume }}{\text { original volume }}=\frac{\Delta \mathrm{v}}{\mathrm{v}}$

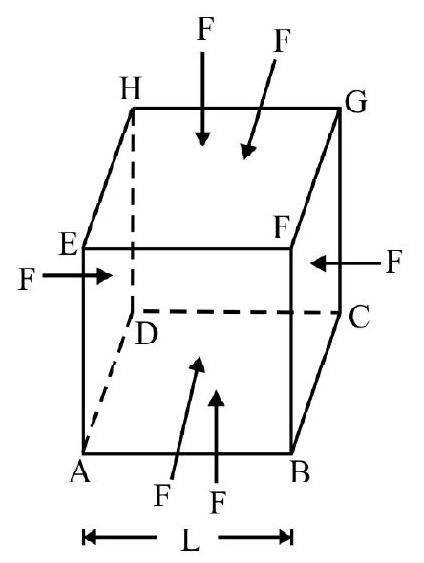
Fig. 3

(3) Shearing Strain

The external deforming forces are so applied that here is a change in shape but no change in volume. Obviously a tangential force has to be applied. Fig. 4 shows a cube ABCDEFGH of side L. The lower force $\mathrm{ABCD}$ is rigidly fixed. A tangential force $\mathrm{F}$ is applied along upper face EFGH. The shape of cube changes to a parallelepiped ( $A B C D E$ E’ $F^{\prime} G^{\prime} H^{\prime}$ ). The angle $\theta$ through which side $A E$ (which is originally perpendicular to the fixed face $\mathrm{ABCD}$ moves is known as angle of shear $(\theta)$. The shearing strain $=$ angle of shear

$$ \simeq \frac{\mathrm{EE}^{\prime}}{\mathrm{AE}}=\frac{\Delta \mathrm{L}}{\mathrm{L}} $$

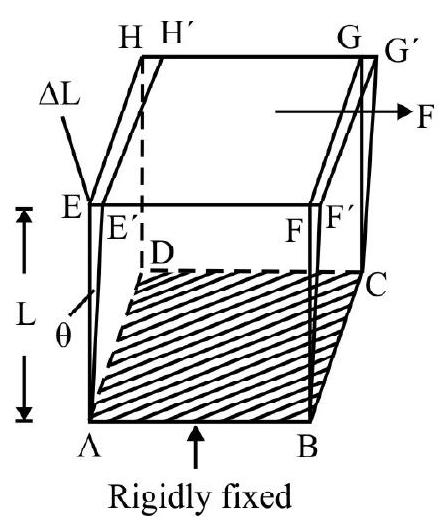
Fig. 4

Stress vs Strain

Stress and strain are like cause and effect. A relationship is expected between the two. For a wire suspended vertically from a rigid support; the stress is due to load attached to its free end and strain is measured in terms of increase in length. Experiments give stress vs strain graph as shown in Fig. 5. We note

(1) The part OP is linear, i.e. stress is directly proportional to strain. For any external applied load less than corresponding to point $\mathrm{P}$; on removal of load wire completely recovers its original length. The behaviour of wire is perfectly elastic.

(2) For loads more than corresponding to point $\mathrm{P}$ curve is not a straight line. For any load more than $\mathrm{P}$ say $\mathrm{P} _{1}$ in Fig. 5; on removing the load, the wire does not completely recover its original length. There is a permanent increase represented by $\mathrm{OO} _{1} \cdot \mathrm{OO} _{1}$ is a measure of permanent set. The load corresponding to point P measures the Elastic Limit. We can say that elastic limit is that maximum stress form which wire can completely recover its original length, when load is removed.

(3) Beyond point Q; we note that strain increases without increasing

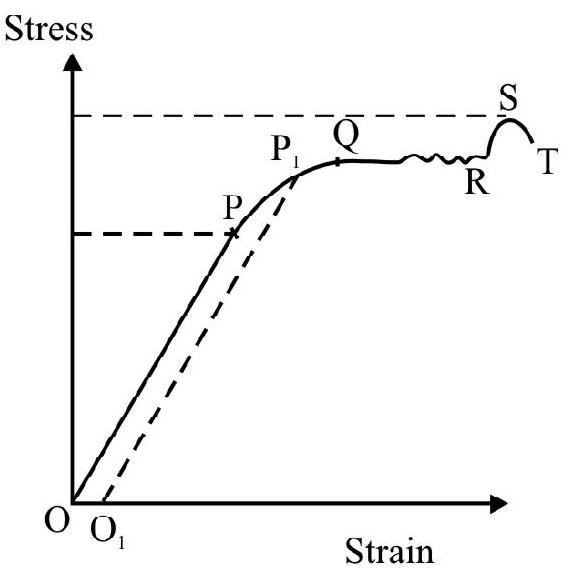
Fig. 5

stress (or load) we say wire has started flowing. Stress corresponding to point Q measures the yeilding point of the wire.

(4) Beyond point R the curve RST shows that if load is increased beyond its value for point R, thinning of wire starts producing weak spots and finally wire breaks from one of these weak spots. The stress corresponding to point $\mathrm{S}$ measures the breaking stress. Breaking stress has a definite value for a particular material. It does not depend on dimension of wire. However breaking force $=$ breaking stress $\times$ area of cross section, is not a constant for a given material. It depends on shape and size besides the nature of material.

Ductile and Brittle Materials

(1) A material showing a large plastic range beyond elastic limit is known as a ductile material. Copper, iron, aluminium, silver are ductile materials. They are used for making, wires, springs and sheet of material.

(2) A material having a small plastic region beyond elastic limit is known as a brittle material. Cast-iron; glass are brittle.

Hooke’s Law

Hooke on the basis of his early experiments found that within elastic limit; stress is directly proportional to strain; i.e. stress $\propto$ strain

or $\quad \frac{\text { Stress }}{\text { Strain }}=$ constant $=$ Modulus of elasticity

Types of Modulus of Elasticity

We know, there are three different types of strain. Corresponding to each type of strain there is one modulus of elasticity. The three moduli of elasticity are:

(1) Young’s Modulus (Y)

$\mathrm{Y}$ is defined in terms of longitudinal strain. By definition

$$ \text { Young’s Modulus }=Y=\frac{\text { normal stress }}{\text { longitudinal strain }} $$

Consider a wire of length $\mathrm{L}$, area of cross-section a. A force $\mathrm{F}$ is applied to its free end, perpendicular to its area of cross-section. Let $\Delta \mathrm{L}$ be change (increase) in length of wire.Then

$$ \text { Normal stress }=\frac{F}{a} $$

$$ \begin{aligned} & \text { Longitudinal strain }=\frac{\Delta \mathrm{L}}{\mathrm{L}} \\\ \therefore \quad \mathrm{Y} & =\frac{\mathrm{F} / \mathrm{a}}{\Delta \mathrm{L} / \mathrm{L}}=\frac{\mathrm{F} . \mathrm{L}}{\mathrm{a}(\Delta \mathrm{L})} \end{aligned} $$

$\mathrm{Y}$ is a constant for a material. $\mathrm{Y}$ does not depend on the dimensions of wire and external applied force. SI Unit of $\mathrm{Y}$ is $\mathrm{Nm}^{-2}=\mathrm{Pa}$ and its dimensions are $\mathrm{M}^{-1} \mathrm{LT}^{-2}$.

(2) The Bulk Modulus (K)

Bulk modulus involves volumetric change. It is the ratio of normal stress and the volumetric strain. Consider a body of volume V. Let $\mathrm{F}$ be external applied force over cross-sectional area ’ $\mathrm{a}$ ‘. $\Delta \mathrm{v}$ is the corresponding change in volume. By definition.

$$ \mathrm{K}=\text { The Bulk Modulus }=\frac{\text { Normal stress }}{\text { Volumetric strain }}=\frac{\mathrm{F} / \mathrm{a}}{\Delta \mathrm{V} / \mathrm{V}} $$

For a gas having a volume $\mathrm{V}$, let $\Delta \mathrm{P}$ be change in pressure (i.e. the normal stress) and $\Delta \mathrm{V}$ the corresponding change in volume. Then

$$ \mathrm{K}=\frac{\Delta \mathrm{P}}{-(\Delta \mathrm{V} / \mathrm{V})} $$

Note the negative sign in the above expression. If pressure on gas increases, $\Delta \mathrm{P}$ is positive number.

The volume of gas decrease, i.e. $\Delta \mathrm{v}$ is a negative number. $\mathrm{K}$ as defined is a positive number. For an ideal gas under isothermal conditions; $\mathrm{K} _{\mathrm{iso}}=\mathrm{P}=$ The pressure of gas. Under adiabatic conditions, $\mathrm{K} _{\mathrm{adi}}=\gamma \mathrm{P}$.

$$ \gamma=\frac{C _{P}}{C _{V}}=\text { The ratio of the two specific heat of gas. } $$

The reciprocal of bulk modulus $(\mathrm{K})$ is known as compressibility $(\chi)$. SI unit of compressibility is $\mathrm{N}^{-1} \mathrm{~m}^{2}$ or $(\mathrm{Pa})^{-1}$.

(3) Modulus of Rigidity $(\boldsymbol{\eta})$

It involves stearing strain. Refer to Fig. 4. A tangential stress F/a is applied on face EFGH of cube; the lower face $\mathrm{ABCD}$ is rigidly fixed. $\theta$ is the angle of shear and equals shearing strain. By definition

$$ \begin{aligned} \eta= & \text { The modulus of rigidity }=\frac{\text { Tangential stress }}{\text { Shearing strain }} \\ & =\frac{\mathrm{F} / \mathrm{a}}{\theta} \simeq \frac{\mathrm{F} / \mathrm{a}}{(\Delta \mathrm{L} / \ell)} \end{aligned} $$

The Poisson’s Ratio ( $\sigma$ )

Careful and accurate measurements show that when a wire of length $\mathrm{L}$ and diameter $\mathrm{D}$ experiences an extensional strain (i.e. length of wire increases); their is a decrease in its diameter. In general; we find that a strain in one direction is always accompanied by another strain in perpendicular direction. The latter strain is known as lateral strain. Within elastic limits; lateral strain is directly proportional to longitudinal strain. The ratio of the two strains is a constant, known as Poinsson’s ratio $(\sigma)$; i.e.

$\sigma=$ The Poisson’s ratio $=\frac{\text { Lateral strain }}{\text { Longitudinal strain }}$

For a wire of length $\mathrm{L}$ and diameter $\mathrm{D}$

$$ \sigma=\frac{-(\Delta \mathrm{D} / \mathrm{D})}{(\Delta \mathrm{L} / \mathrm{L})} $$

Value of $\sigma$ lies between -1 and 0.5 i.e. $-1<\sigma<0.5$

Elastic Potential Energy

Consider a wire of length $\mathrm{L}$; area of cross-section a. When wire is extended by $\Delta \mathrm{L}$ due to external applied force; work is done by the applied force to stretch the wire. This work done is stored in wire as its elastic potential energy. It can be shown that

Elastic potential energy per unit volume $=\frac{1}{2}$ stress $\times$ strain

$$ =\frac{1}{2}(\mathrm{Y}) \times(\text { strain })^{2} \quad[\because \text { stress }=\mathrm{Y} \times \text { strain }] $$

Applications of Elasticity

A few important; daily life; applications of elasticity are listed below:

(i) Metallic part of any machine is never subjected to a stress more than its elastic limit. This avoids permanent deformation in the machine.

(ii) Metallic ropes are used to lift heavy weights as in a crane. The diameter of rope required depends on the elastic limit of the material of rope. Normally an additional term the safety factor (generally 10) is used in design of the rope. The diameter is calculated by taking a load 10 times the desired load capacity.

(iii) In designing a beam or a pillar; in construction of roofs and bridges; the elastic properties of material and the load are the important factors. It can be shown that a beam of rectangular cross-section; will be able to bear more load if we increase its depth.

(iv) It can be shown that a hollow shaft is stronger than a solid shaft made of the same amount of material. In other words; torque required to twist a hollow cylinder is more than torque required to produce same twist in a solid cylinder of same mass and length. This is the reason electric poles have a hollow structure.

Example-1:

Two wires $A$ and $B$ of same material have lengths in ratio of $4: 3$ and radii in ratio of $1: 2$. The two are subjected to same external force $F$. What is ratio of (i) Young’s modulus (ii) stress (iii) strain and (iv) change in length of wires $A$ and $B$ ?

Show Answer

Solution:

Given, $\frac{\mathrm{L} _{\mathrm{A}}}{\mathrm{L} _{\mathrm{B}}}=\frac{4}{3} ; \frac{\mathrm{r} _{\mathrm{A}}}{\mathrm{r} _{\mathrm{B}}}=\frac{1}{2} ; \mathrm{F} _{\mathrm{A}}=\mathrm{F} _{\mathrm{B}}=\mathrm{F}$

(i) Since the material of wires A and B is same

$$ \frac{\mathrm{Y} _{\mathrm{A}}}{\mathrm{Y} _{\mathrm{B}}}=1 $$

(ii) $\frac{(\text { stress }) _{A}}{(\text { stress }) _{B}}=\frac{\mathrm{F} _{\mathrm{A}}}{\mathrm{F} _{\mathrm{B}}} \times \frac{\pi \mathrm{r} _{\mathrm{B}}^{2}}{\pi \mathrm{r} _{\mathrm{A}}^{2}}=\left(\frac{\mathrm{r} _{\mathrm{B}}}{\mathrm{r} _{\mathrm{A}}}\right)^{2} \quad\left[\because \mathrm{F} _{\mathrm{A}}=\mathrm{F} _{\mathrm{B}}\right]$

$$ =\left(\frac{2}{1}\right)^{2}=\frac{4}{1} $$

(iii) We know $\mathrm{Y}=\frac{\text { stress }}{\text { strain }}$ or strain $=\frac{\text { stress }}{\mathrm{Y}}$

$$ \begin{aligned} & \therefore \frac{(\text { strain }) _{\mathrm{A}}}{(\text { strain }) _{\mathrm{B}}}=\frac{(\text { stress }) _{\mathrm{A}}}{(\text { stress }) _{\mathrm{B}}} \times \frac{\mathrm{Y} _{\mathrm{B}}}{\mathrm{Y} _{\mathrm{A}}} \\ &=\frac{(\text { stress }) _{\mathrm{A}}}{(\text { stress }) _{\mathrm{B}}}=\frac{4}{1} \quad\left[\because \mathrm{Y} _{\mathrm{A}}=\mathrm{Y} _{\mathrm{B}}\right] \end{aligned} $$

(iv) Let $(\Delta \mathrm{L}) _{\mathrm{A}}$ and $(\Delta \mathrm{L}) _{\mathrm{B}}$ be the change in length of wires $\mathrm{A}$ and $\mathrm{B}$ respectively. Then

$$ \begin{aligned} & \frac{(\text { strain }) _{\mathrm{A}}}{(\operatorname{strain}) _{\mathrm{B}}}=\frac{(\Delta \mathrm{L}) _{\mathrm{A}}}{(\Delta \mathrm{L}) _{\mathrm{B}}} \times\left(\frac{\mathrm{L} _{\mathrm{B}}}{\mathrm{L} _{\mathrm{A}}}\right) \\ & \therefore \quad \frac{4}{1}=\frac{(\Delta \mathrm{L}) _{\mathrm{A}}}{(\Delta \mathrm{L}) _{\mathrm{B}}} \times \frac{3}{4} \\ & \text { or } \quad \frac{(\Delta \mathrm{L}) _{\mathrm{A}}}{(\Delta \mathrm{L}) _{\mathrm{B}}}=\frac{16}{3} \end{aligned} $$

Example-2:

Two wires A and B are made of materials having Young’s modulus in ratio of 16:15. The length of the two wires is in ratio of $4: 5$ and radii in ratio of $3: 2$. What is ratio of external applied force on A and $B$; so that change in length of the two wires is same?

Show Answer

Solution:

From definition of Young’s modulus $(Y)$, the change in length $(\Delta L)$ of a wire of original length $(\mathrm{L})$ radius $\mathrm{r}$ is

$$ (\Delta \mathrm{L})=\frac{\mathrm{F} \cdot \mathrm{L}}{\pi \mathrm{r}^{2} \mathrm{Y}} $$

Given $\frac{\mathrm{L} _{\mathrm{A}}}{\mathrm{L} _{\mathrm{B}}}=\frac{4}{5} ; \frac{\mathrm{r} _{\mathrm{A}}}{\mathrm{r} _{\mathrm{B}}}=\frac{3}{2}$ and $(\Delta \mathrm{L}) _{\mathrm{A}}=(\Delta \mathrm{L}) _{\mathrm{B}} ;$ therefore

$$ \frac{\mathrm{F} _{\mathrm{A}} \mathrm{L} _{\mathrm{A}}}{\pi \mathrm{r} _{\mathrm{A}}^{2} \mathrm{Y} _{\mathrm{A}}}=\frac{\mathrm{F} _{\mathrm{B}} \cdot \mathrm{L} _{\mathrm{B}}}{\pi \mathrm{r} _{\mathrm{B}}^{2} \mathrm{Y} _{\mathrm{B}}} $$

or $\quad \frac{F _{A}}{F _{B}}=\left(\frac{L _{B}}{L _{A}}\right)\left(\frac{r _{A}}{r _{B}}\right)^{2}\left(\frac{Y _{A}}{Y _{B}}\right)$

Substituting given values

$$ \frac{\mathrm{F} _{\mathrm{A}}}{\mathrm{F} _{\mathrm{B}}}=\left(\frac{5}{4}\right)\left(\frac{3}{2}\right)^{2}\left(\frac{16}{15}\right)=\frac{3}{1} $$

Example-3:

A wire of length $L$ is suspended in a vertical plane from a rigid support. A load $w$ is attached to its free end. The increase in length of wire is $\ell$. The same wire now passes over a fixed pulley and weight $w$ is attached to each free end of the wire. The total increase in length of wire is

(a) $\ell$

(b) $2 \ell$

(c) $\frac{\ell}{2}$

(d) $4 \ell$

Show Answer

Solution:

Let $\mathrm{Y}$ be the Young’s modulus of wire. Then

$$ \begin{equation*} \ell=\frac{\mathrm{w} \times \mathrm{L}}{\mathrm{aY}} \tag{1} \end{equation*} $$

When wire passes over pulley and load $w$ is attached to either end; the length of each part of wire is $\frac{L}{2}$.

Let $\ell^{\prime}$ be increase in length of one part due to applied load $\mathrm{w}$ at its free end. Then

$$ \ell^{\prime}=\frac{\mathrm{w}(\mathrm{L} / 2)}{\mathrm{aY}}=\frac{\mathrm{L}}{2} $$

$\therefore$ Total increase in length of wire $=2 \ell^{\prime}=\mathrm{L}$

Correct choice is (a).

Example-4:

Four identical hollow pillars each of length $1.5 \mathrm{~m}$ having inner and outer radii $20 \mathrm{~cm}$ and $40 \mathrm{~cm}$ respectively support a horizontal bridge. What is maximum load bridge can withstand if maximum permitted compression is $0.01 \%$ of original length of each column. Assume load is uniformly distributed over the four pillars. Given $1 \mathrm{kgf}=10 \mathrm{~N}$. Y=2×10 ${ }^{11} \mathrm{~Pa}$

Show Answer

Solution:

$\mathrm{a}=$ Area of cross-section of each pillar

$$ =3.14\left[(0.4)^{2}-(0.3)^{2}\right] \simeq 22 \times 10^{-2} \mathrm{~m}^{2} $$

$\mathrm{L}=1.5 \mathrm{~m}$ and $\frac{\Delta \mathrm{L}}{\mathrm{L}} \times 100=0.01$ or $\frac{\Delta \mathrm{L}}{\mathrm{L}}=10^{-4}$

Let $\mathrm{F}$ be the maximum force bridge can withstand. The force on each pillar $=\frac{\mathrm{F}}{4}$. Then

$$ 2 \times 10^{11}=\frac{(\mathrm{F} / 4)}{22 \times 10^{-2} \times 10^{-4}} $$

or

$$ \mathrm{F}=2 \times 10^{11} \times 4 \times 22 \times 10^{-6} \mathrm{~N}=176 \times 10^{5} \mathrm{~N} $$

$$ =176 \times 10^{4} \mathrm{~kg} \mathrm{wt} $$

Example-5:

A body has density $\rho$ on the surface of sea. The body is taken to the bottom of the sea. The percentage increase in density is $0.1 \%$ of $\rho$. What is depth of sea? Given

Compressibility of body $=10^{-11}(\mathrm{~Pa})^{-1} ; \mathrm{g}=10 \mathrm{~ms}^{-2}$; average density of sea water (assumed to be constant) $=10^{3} \mathrm{kgm}^{-3}$

Show Answer

Solution:

The density $(\rho)$ of a body of mass $m$ having volume $V$, is

$$ \rho=\frac{\mathrm{m}}{\mathrm{V}} $$

$\rho^{\prime}=$ The density of body at bottom of sea $=\frac{\mathrm{m}}{(\mathrm{V}+\Delta \mathrm{V})}$

Let $\Delta \mathrm{P}$ be additional pressure at bottom of sea due to a column of water of height $\mathrm{H}=$ depth of sea. Obvisouly $\Delta \mathrm{P}=\mathrm{H} \rho _{\mathrm{w}} \mathrm{g}$; where $\rho _{\mathrm{w}}=$ density of water.

$$ \therefore \frac{\rho^{\prime}}{\rho}=\frac{\mathrm{V}}{\mathrm{V}+\Delta \mathrm{V}}=\left(1+\frac{\Delta \mathrm{V}}{\mathrm{V}}\right)^{-1} \simeq 1-\frac{\Delta \mathrm{V}}{\mathrm{V}} $$

The fractinoal change in density of body $=\frac{\Delta \rho}{\rho}$

$$ \begin{equation*} \frac{\Delta \rho}{\rho}=\frac{\rho^{\prime}-\rho}{\rho}=-\left(\frac{\Delta V}{V}\right) \tag{1} \end{equation*} $$

By definition; the bulk modulus, $K$ of the material of the body is

$$ \begin{equation*} \mathrm{K}=\frac{\Delta \mathrm{P}}{-\Delta \mathrm{V} / \mathrm{V}} \quad \text { or } \quad-\left(\frac{\Delta \mathrm{V}}{\mathrm{V}}\right)=\frac{\Delta \mathrm{P}}{\mathrm{K}}=\chi(\Delta \mathrm{P}) \tag{2} \end{equation*} $$

where $\chi=\frac{1}{\mathrm{~K}}=$ The compressiblity of the body. From Eqns (1) and (2) we have

$$ \frac{\Delta \rho}{\rho}=\chi(\Delta \mathrm{P}) \text { or } \Delta \mathrm{P}=\frac{1}{\chi}\left(\frac{\Delta \rho}{\rho}\right) $$

Given $\frac{\Delta \rho}{\rho} \times 100=0.1$ or $\frac{\Delta \rho}{\rho}=10^{-3}$

$\therefore \quad \Delta \mathrm{P}=\frac{1}{10^{-11}} \times 10^{-3}=10^{8} \mathrm{~Pa} \hspace{40mm}. . . . . . . . . .(3)$

The depth of sea $=\mathrm{H}=\frac{\Delta \mathrm{P}}{\rho _{\mathrm{w}} \mathrm{g}}=\frac{10^{8}}{10^{3} \times 10}=10^{4} \mathrm{~m}=10 \mathrm{~km}$

Example-6:

A steel rope attached to a crane is designed to lift up a maximum load of 100 metric ton. What is minimum radius of rope? Given breaking stress of steel $=3.18 \times 10^{8} \mathrm{~Pa}$

Safety factor $=10, \mathrm{~g}=10 \mathrm{~ms}^{-2}$

Show Answer

Solution:

Maximum load $=100$ meteric ton $=10^{5} \mathrm{~kg}$

Safety factor of 10 means that even if load is ten times of the maximum premitted load the steel rope should not break. Therefore the maximum stress that the rope should be able to withstand $=\frac{10 \times 10^{5} \times 10}{\mathrm{a}} \mathrm{Nm}^{-2}$ where ’ $a$ ’ is area of cross-section of rope. This maximum stress is equal to the breaking stress;

i.e. $\frac{10^{7}}{3.14 \times(\mathrm{r})^{2}}=3.18 \times 10^{8}$

$$ \therefore \mathrm{r}^{2}=\frac{10^{7}}{3.14 \times 3.18 \times 10^{8}}=10^{-2} \mathrm{~m}^{2} $$

or

$$ \mathrm{r}=10^{-1} \mathrm{~m}=10 \mathrm{~cm} $$

Example-7:

The couple required to twist a cylinder by a unit of angle is known as “torsional rigidity” of cylinder. It is given by

$$ \tau=\frac{\pi r^{4} \eta}{2 \ell} $$

where $\eta$ is modulus of regidity of material of cylinder of radius $r$, length $\ell$. A solid cylinder of radius $r$ and an annular cylinder of inner radius $r _{1}$, outer radius $r _{2}$ have same length and mass. Show that torsinoal rigidity of annular cylinder is more.

Show Answer

Solution:

Let $\tau$ and $\tau^{\prime}$ be the torsional rigidity of the solid and annular cylinder. Then

$$ \begin{array}{r} \tau=\frac{\pi \eta \mathrm{r}^{4}}{2 \ell} \text { and } \tau^{\prime}=\frac{\pi \eta\left[\mathrm{r} _{2}^{4}-\mathrm{r} _{1}^{4}\right]}{2 \ell} \\ \therefore \quad \frac{\tau^{\prime}}{\tau}=\frac{\mathrm{r} _{2}^{4}-\mathrm{r} _{1}^{4}}{\mathrm{r}^{4}}=\frac{\left(\mathrm{r} _{2}^{2}+\mathrm{r} _{1}^{2}\right)\left(\mathrm{r} _{2}^{2}-\mathrm{r} _{1}^{2}\right)}{\mathrm{r}^{4}} \tag{1} \end{array} $$

The mass of the two cylinders is the same. Hence the two should also have equal volume of the material.

$$ \pi \mathrm{r}^{2} \ell=\pi\left(\mathrm{r} _{2}^{2}-\mathrm{r} _{1}^{2}\right) \cdot \ell $$

or $\quad \mathrm{r} _{2}^{2}-\mathrm{r} _{1}^{2}=\mathrm{r}^{2}$

From Eqns. (1) and (2) we have

$$ \begin{equation*} \frac{\tau^{\prime}}{\tau}=\frac{r _{2}^{2}+r _{1}^{2}}{r^{2}} \tag{3} \end{equation*} $$

Since $\mathrm{r}^{2}=\mathrm{r} _{2}^{2}-\mathrm{r} _{1}^{2} ; \mathrm{r} _{2}^{2}+\mathrm{r} _{1}^{2}$ is greater than $\mathrm{r}^{2}$.

From eqn. (3); $\frac{\tau^{\prime}}{\tau}>1$ or $\tau^{\prime}>\tau$

Example-8:

A rod of mass $M$; length $L$ is made of material of Young’s modulus $Y$. The rod rotates in a horizontal plane about an axis through its one end and perpendicular to length of rod with a constant angular speed $\omega$. The increase in length of rod is

( $\rho$ = density of material of the rod)

(a) $\frac{1}{2}\left(\frac{\rho \omega^{2}}{Y}\right) \mathbf{L}^{2}$

(b) $\frac{1}{3}\left(\frac{\rho \omega^{2}}{Y}\right) \mathbf{L}^{3}$

(c) $\frac{1}{2}\left(\frac{\rho \omega^{2}}{Y}\right) \mathbf{L}^{3}$

(d) $\frac{2}{3}\left(\frac{\rho \omega^{2}}{Y}\right) \mathbf{L}^{3}$

Show Answer

Solution:

Consider a small element of length $\mathrm{d} x$ of the rod at a distance $x$ from axis of rotation as shown in Fig. 7. Let $\mathrm{T}$ be tension at distance $x$ from axis of rotation.

Then $\mathrm{T}=$ Centerifugal force on the element considered $=(\mathrm{dm}) x \omega^{2}$

$\mathrm{dm}=$ mass of the element considered $=\mathrm{a}(\mathrm{d} x) \rho$

$\mathrm{a}=$ area of cross-section of rod; $\rho=$ density of rod.

$$ \therefore \quad \mathrm{T}=\mathrm{a} \rho \omega^{2} x \mathrm{~d} x $$

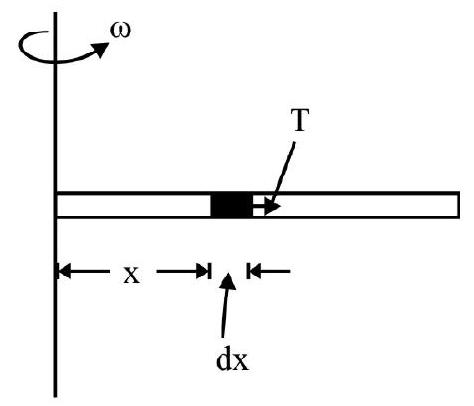
Fig. 7

The increase in length $(\mathrm{d} \ell$ ) of the element considered; in terms of Young’s modulus $(\mathrm{Y})$ is

$$ \begin{aligned} & \mathrm{d} \ell=\frac{\mathrm{T} x}{\mathrm{a} \mathrm{Y}} \\ & =\frac{\rho \omega^{2}}{\mathrm{Y}} x^{2} \mathrm{~d} x \end{aligned} $$

The total increase in length of rod $=\int _{x=0}^{x=\mathrm{L}} \mathrm{d} \ell$

$$ =\frac{\rho \omega^{2}}{\mathrm{Y}} \int _{0}^{\mathrm{L}} x^{2} \mathrm{~d} x=\frac{\rho \omega^{2} \mathrm{~L}^{3}}{3 \mathrm{Y}} $$

The correct choice is (b).

(B) HYDROSTATICS

Introduction

Any substance that starts to flow when an external force is applied is known as a fluid. Liquids and gases are fluids. They do not have any shape of their own; but take the shape of the container they are put in. Hydrostatics is the branch of physics in which we study fluids at rest.

Thrust and Pressure Due to a Liquid

A liquid at rest in a container exerts a force on the walls and bottom of the container. The force is exerted due to collisions of atoms / molecules of liquid with the walls of the container. In each collision, there in a change in linear momentum of atoms / molecules of the liquid. Conesquently, the wall exerts a force on atoms / molecules and vice-versa.

For a liquid at rest; the force exerted by the liquid is always normal to the area of surface in contact. If the force $\mathrm{F}$ is in any other direction than normal as shown in Fig. 1; we resolve it into rectangular components (1) $\mathrm{F} \cos \theta$ along surface and (2) $\mathrm{F} \sin \theta$ perpendicular to surface.

The component $\mathrm{F} \cos \theta$ will make liquid particles move along the surface, i.e. liquid is not at rest. For liquid to be at rest; $\mathrm{F} \cos \theta=0$ or $\theta=\frac{\pi}{2}$ The total force exerted by the liquid normal to the surface in contract is known as the thrust of liquid on the surface.

The normal thrust (or force) exerted per unit area of the surface in contract with liquid, is the pressure ( $\mathrm{P}$ )

exerted by the liquid on the suface i.e. $\mathrm{P}=\frac{\mathrm{F}}{\mathrm{A}}$. SI Unit of pressure is $\mathrm{Nm}^{-2}(\equiv \mathrm{Pa})$.

Force is a vector quantity but pressure is a scalar quantity. The direction of pressure at any point is always perpendicular to a small area around the point considered. Pressures add up algebraically. Also pressure is transmitted equally in all directions; therefore no direction can be associated with pressure.

Pressure Exerted by a Liquid Column

Fig. 2 shows a cylinder of cross sectional area ’ $a$ ‘. A liquid of density $\rho$ fills cylinder up to a height $h$. The pressure, $\mathrm{P}$, exerted by the liquid on the bottom of container is due to weight of liquid inside. The weight $\mathrm{W}=\mathrm{Mg} ; \mathrm{M}=$ Mass of liquid in container. $\mathrm{W}$ acts at right angles to the area of the base of cylinder. Also

$\mathrm{M}=$ volume of liquid $\times$ density of liquid

$$ =\mathrm{ah} \rho $$

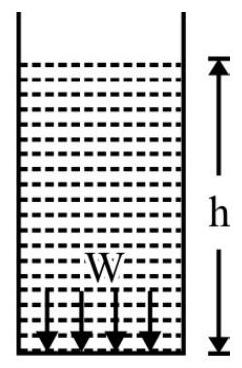Fig. 2

The pressure, $\mathrm{P}$; at bottom of container, by definition, is

$$ \begin{equation*} \mathrm{P}=\frac{\mathrm{W}}{\mathrm{a}}=\frac{(\mathrm{ah} \rho) \mathrm{g}}{\mathrm{a}}=\mathrm{h} \rho \mathrm{g} \tag{1} \end{equation*} $$

Note: $\mathrm{P}$ does not depend on the area of cross-section of cylinder considered. It is

(i) directly proportional to vertical height (h) of the liquid column.

(ii) directly proportional to density ( $\rho$ ) of the liquid.

(iii) directly proportional to acceleration due to gravity (g). Pressure given by Eqn. (1) is also known as hydrostatic pressure.

The Hydrostatic Paradox

Fig. 3 shows three containers of same base area but different shape. The three contain same liquid upto same vertical height. Obviously $\mathrm{w} _{2}>\mathrm{w} _{1}>\mathrm{w} _{3}$. Is $\mathrm{P} _{1}, \mathrm{P} _{2}, \mathrm{P} _{3}$ the pressure at bottom of the three vassels different? No; $\mathrm{P} _{1}=\mathrm{P} _{2}=\mathrm{P} _{3}$ in accordance with Eqn. (1). This is an apparent paradox. The paradox is resolved as follows. Consider a point $\mathrm{P}$ in contact with wall of container. In Fig. 3(a) force excerted by wall on liquid is normal to wall. The total force acting vertically downwards at bottom is $\mathrm{W} _{1}$ and $\mathrm{P} _{1}=\frac{\mathrm{W} _{1}}{\mathrm{~A}}$. In Fig. 3(b); the force of exerted by wall on liquid particle at $\mathrm{P}$ is normal to direction of wall. This force has a

(1) horizontal component $\mathrm{f} _{1}$ and (2) vertically upward component $\mathrm{f} _{2}$. It can be shown that $\sum \mathrm{f} _{2}=\left(\mathrm{W} _{2}-\mathrm{W} _{1}\right)$. The net vertically downward force on bottom in Fig. 3(b) is

$$ \mathrm{W} _{2}-\sum \mathrm{f} _{2}=\mathrm{W} _{2}-\left(\mathrm{W} _{2}-\mathrm{W} _{1}\right)=\mathrm{W} _{1} $$

Therefore pressure $\mathrm{P} _{2}=\frac{\mathrm{W} _{2}^{\prime}}{\mathrm{A}}=\frac{\mathrm{W} _{1}}{\mathrm{~A}}=\mathrm{P} _{1}$.

Similar consideration shows that $\mathrm{P} _{3}=\mathrm{P} _{2}=\mathrm{P} _{1}$

Pascal’s Law

According to Pascal’s law: neglecting the effect of gravity; pressure at every point in a liquid at rest is same.

We can also say that for a liquid at rest in an enclosed vessel a change of pressure at any point is transmitted equally in all directions. This is illustrated by the following two simple examples.

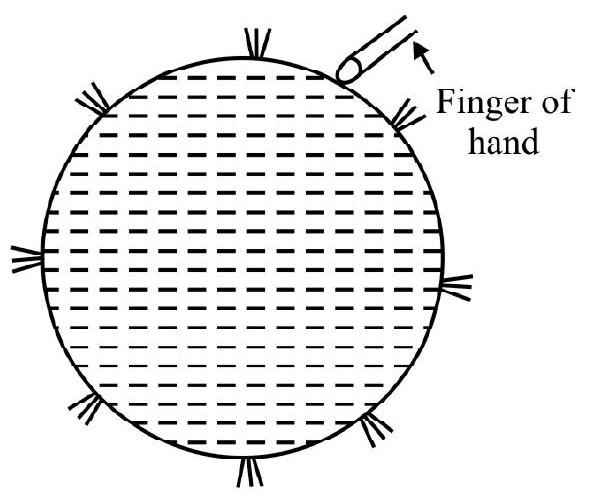Fig. 4

(1) Take a rubber ball having a number of fine pin-holes at different points on surface of the ball. Let us put water inside rubber ball through a large hole and then close the hole. Press the ball at any point with finger to increase pressure. Water emerges out of all pin-hole in the shape of fine streams as shown in Fig. 4.

(2) Fig. 5 shows three cylinder-pistons L, $\mathrm{M}$ and $\mathrm{N}$ of cross-sectional are $\mathrm{A} ; \mathrm{A} / 2$ and $2 \mathrm{~A}$ respectively. Piston $\mathrm{L}$ is pushed inwards with force $\mathrm{F}$. Force $\mathrm{F} / 2$ and $2 \mathrm{~F}$ have to be applied to $\mathrm{M}$ and $\mathrm{N}$ to keep them in equilibrium. Pressure at all three points is same.

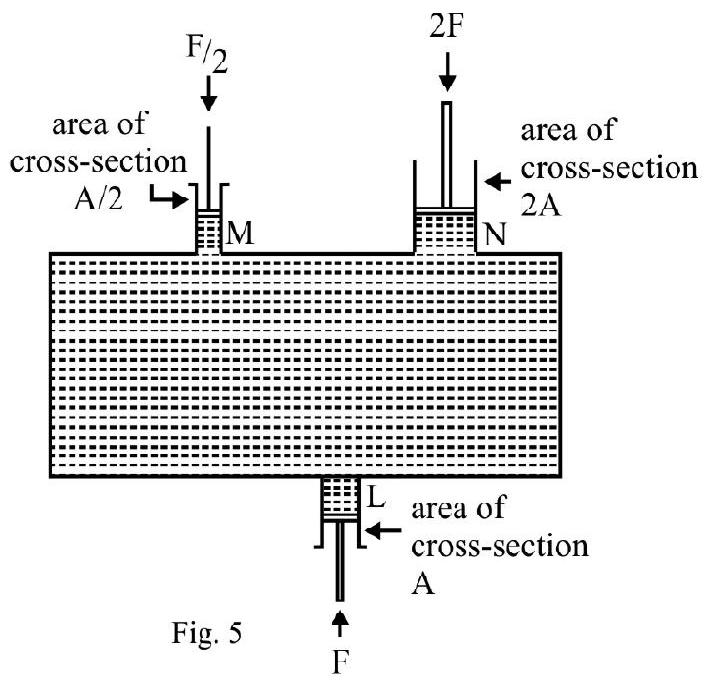
Applications of Pascal’s Law

(1) Hydraulic Lift:

It is an arrangement used to lift a heavy load like a car by applying a small force. Fig. 6 shows such an arrangement. $\mathrm{C}$ and $\mathrm{D}$ are two cylinders in contact with one another and filled with a fluid (say water). Area of cross-section; a, of part C is very small as compared to area of crosssection A of D. A small force $\mathrm{f}$ is applied to water column $\mathrm{C}$ as shown in Fig. 6. The pressure is $\mathrm{P}=\mathrm{f} / \mathrm{a}$. This pressure is transmitted to platform in

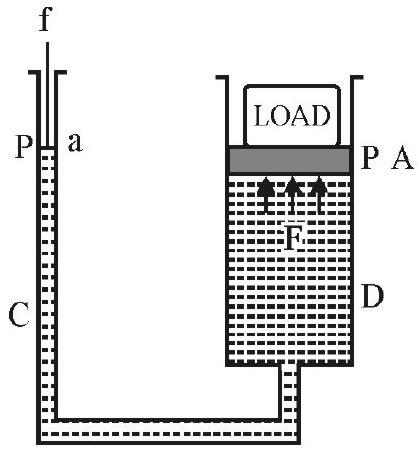
Fig. 6

D. The upward force on platform $=\mathrm{P} \times \mathrm{A}=\mathrm{f}(\mathrm{A} / \mathrm{a})$. Since $\mathrm{A} \gg>\mathrm{a} ; \mathrm{F}»\mathrm{f}$. This is used to lift platform $P$ having a load placed on it.

(2) Hydraulic Brakes:

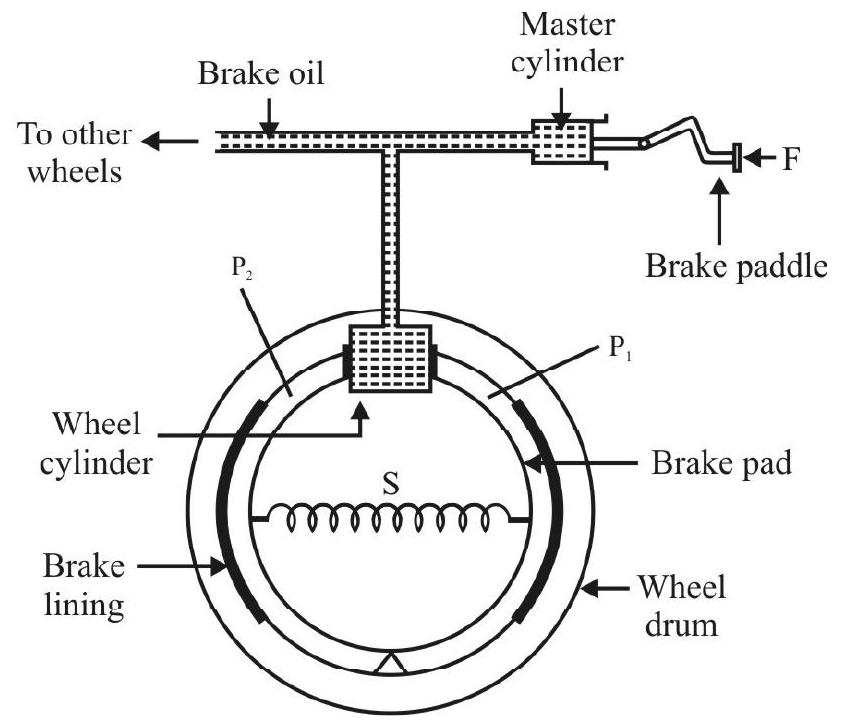
Fig. 7 shows a lablled; self explanatory diagram of brakes used in automobiles. A small force $\mathrm{F}$ applied on brake paddle produces sufficient pressure in brake oil via master cylinder. This pressure exerts sufficient force on pistons $\mathrm{P} _{1}$ and $\mathrm{P} _{2}$ attached to wheel cylinder of larger cross-section to push brake pads outward and bring in contact with moving wheel drum. Due to friction between the two braking effect is produced.

Atmospheric Pressure

Earth is surrounded by a gaseous envelope around it extending upto a few kilometers above surface of earth. This is earth’s atmosphere. The pressure exerted by these gases on earth is known as the atmospheric pressure. As in liquids, the pressure is due to weight of gases around earth’s atmosphere. These gases are not at rest; therefore earth’s atmosphere changes with time Torricelli showed experimentally (as shown in Fig. 8) that atmospheric pressure is equal to the pressure exerted by the mercury column in the tube above surface of mercury in beaker. At sea level; under STP conditions the height of mercury $\mathrm{h}=76 \mathrm{~cm}$ of Hg. Therefore;

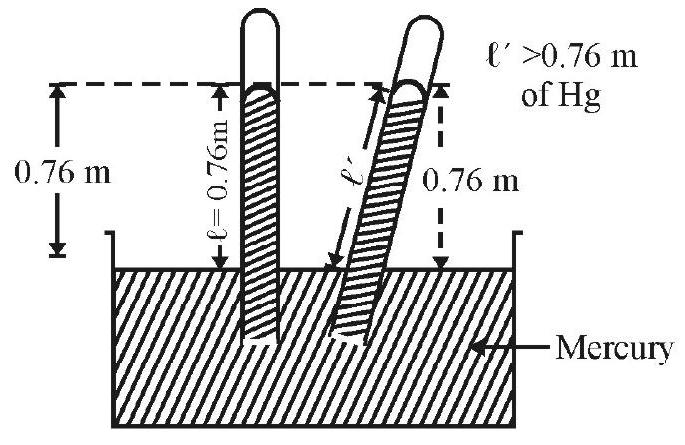
Fig. 8

$\mathrm{P}=$ The standard atmospheric pressure $=0.76 \mathrm{~m}$ of $\mathrm{Hg}$ column

$$ \begin{array}{ll} =0.76 \times 13.6 \times 10^{3} \times 9.8 \mathrm{Nm}^{-2} & \text { [i.e. } \mathrm{P}=\mathrm{h} \rho g] \\ =1.01 \times 10^{5} \mathrm{~Pa} & \end{array} $$

Example-9:

A liquid fills a cylinderical vessel of radius $R$ to a height $H=1.5 R$. What is ratio of total foce on bottom of cylinder and the total force on the vertical wall of cylinder?

(a) $\frac{3}{2}$

(b) $\frac{2}{3}$

(c) $\frac{3}{4}$

(d) $\frac{4}{3}$

Show Answer

Solution:

$F _{1}=$ The total force on bottom of cylinder $=$ Weight of liquid inside cylinder

$$ \begin{equation*} =\left(\pi \mathrm{R}^{2} \mathrm{H}\right) \rho \mathrm{g} \tag{1} \end{equation*} $$

$\rho=$ density of liquid, $g=$ acceleration due to gravity.

To calculate the total force on vertical wall of cylinder consider a layer of liquid defined by $y$ and $y+d y$ as shown in Fig. 9 . The pressure, $p$ at the layer considered;

$$ \mathrm{p}=\mathrm{y} \rho \mathrm{g} $$

The area of cross-section of liquid in the layer considered $=2 \pi \mathrm{R} . \mathrm{dy}$ $\mathrm{dF} _{2}=$ The force on the elementary part of vertical wall

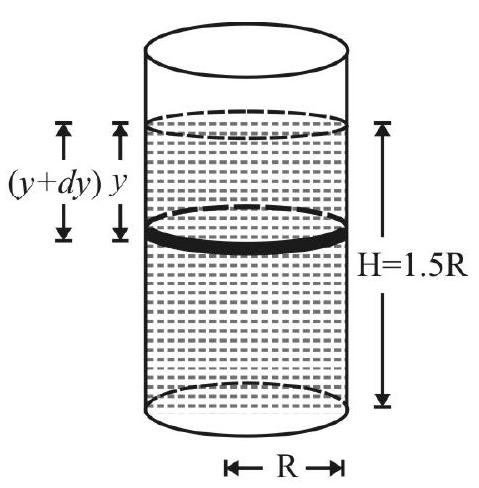
Fig. 9

$=\mathrm{p} \times 2 \pi \mathrm{Rdy}=2 \pi \mathrm{R} \rho \mathrm{gy} \mathrm{dy}$

$\therefore \quad \mathrm{F} _{2}=\int _{0}^{\mathrm{H}} \mathrm{dF} _{2}=2 \pi \mathrm{R} \rho \mathrm{g} \int _{0}^{\mathrm{H}} \mathrm{y} d \mathrm{y}=\pi \mathrm{H}^{2} \mathrm{R} \rho \mathrm{g} \hspace{20mm}. . . .. . .. (2)$

From Eqn. (1) and (2) we have

$$ \frac{\mathrm{F} _{1}}{\mathrm{~F} _{2}}=\frac{\left(\pi \mathrm{R}^{2} \mathrm{H}\right) \rho \mathrm{g}}{\left(\pi \mathrm{H}^{2} \mathrm{R}\right) \rho \mathrm{g}}=\frac{\mathrm{R}}{\mathrm{H}}=\frac{\mathrm{R}}{1.5 \mathrm{R}}=\frac{2}{3} $$

The correct choice is (b)

Example-10:

A tank of square cross-section is divided into two equal parts by a partition as shown in Fig. 10 The partition has a door, D; of cross-sectional area 40 $\mathrm{cm}^{2}$. The L.H.S of tank is filled with water and the R.H.S with a liquid of R.D $=1.7$ upto a height of $4 \mathrm{~m}$. What net force be applied on door to keep it closed? $\mathrm{g}=9.8 \mathrm{~ms}^{-2}$

Show Answer

Solution:

Regarding the size of the door as small in comparison to the height of water and liquid on the two sides; the pressure on door is nearly a constant.

Fig. 10

$\mathrm{P} _{1}=$ Pressure due to water column on door

$$ =\mathrm{H} \rho _{\mathrm{w}} \mathrm{g}=4 \times 10^{3} \times 9.8 \mathrm{~N} $$

$\mathrm{F} _{1}=$ The total force on door due to water

$$ \begin{aligned} & =\mathrm{A} \times \mathrm{P} _{1} ; \quad \mathrm{A}=\text { area of cross-section of door } \\ & =40 \times 10^{-4} \times 4 \times 10^{3} \times 9.8 \mathrm{~N}=156.9 \mathrm{~N} \end{aligned} $$

Similarly,

$\mathrm{P} _{2}=$ Pressure due liquid column on door.

$$ =\mathrm{H} \rho _{\mathrm{i}} \mathrm{g}=4 \times 1.7 \times 10^{3} \times 9.8 \mathrm{~N} $$

$\mathrm{F} _{2}=$ Total force on door to due to liquid

$$ =40 \times 10^{-4} \times 4 \times 1.7 \times 10^{3} \times 9.8=266.56 \mathrm{~N} $$

Since $\mathrm{F} _{2}>\mathrm{F} _{1}$, door on its own will open on the side of water. Therefore a force $\mathrm{F} _{2}-\mathrm{F} _{1}=109.76 \mathrm{~N}$ should be applied on door from the side of tank containing water.

Example-11:

A tube is filled with some volume of mercury. $10 \mathrm{~cm}$ column of water is pored above mercury in left hand limb and another liquid of $R . D=0.8$ is pored up to a height $h$ in the right hand limb. In equilibrium level of mercury in the two limbs is same. $h$ is

(a) $8.0 \mathrm{~cm}$

(b) $10.0 \mathrm{~cm}$

(c) $12.0 \mathrm{~cm}$

(d) $12.5 \mathrm{~cm}$

Show Answer

Solution:

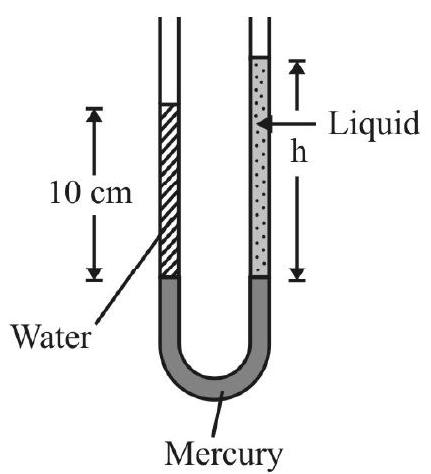
Fig. 11

Fig. 11 shows the arrangement in equilibrium. Since level of mercury is same in the two limbs; pressure due to water column of height $10 \mathrm{~cm}$ must be same as pressure due to liquid column of height $\mathrm{h} \mathrm{cm}$. Therefore

$$ 0.1 \times 10^{3} \times \mathrm{g}=\mathrm{h} \times 0.8 \times 10^{3} \times \mathrm{g} $$

or $\quad \mathrm{h}=\frac{0.1}{0.8} \mathrm{~m}$

$$ =0.125 \mathrm{~m}=12.5 \mathrm{~cm} $$

Correct choice is (4)

Example-12:

Fig. 12 shows a spherical container having a gas inside connected to a mercury manometer. In equilibrium the difference in level of $\mathbf{~ H g}$ in the two limbs is $24 \mathrm{~cm}$ as shown. Atmospheric pressure $=76 \mathrm{~cm}$ of Hg. What is pressure of gas inside the container? $\left(\mathrm{g}=10 \mathrm{~ms}^{-2}\right)$

Show Answer

Solution:

Let $\mathrm{P}$ be the pressure of gas in sheperical enclosure. $\mathrm{P} _{1}=$ Atmospheric pressure. Consider two points A and B at same level as shown in Fig. 12 Obvisouly $\mathrm{P} _{\mathrm{A}}=\mathrm{P} _{\mathrm{B}}$. Also $\mathrm{P} _{\mathrm{A}}=\mathrm{P}$ and $\mathrm{P} _{\mathrm{B}}=\mathrm{P} _{1}+$ Pressure due to $24 \mathrm{~cm}$ of Hg column.

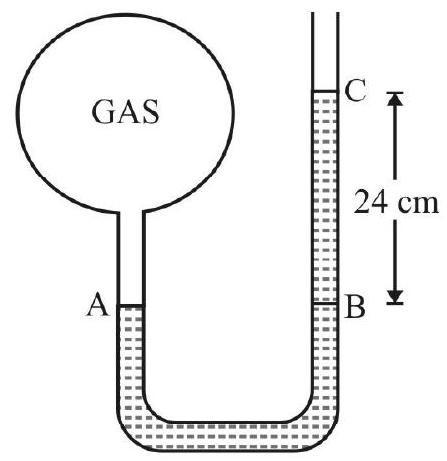Fig. 12

$\therefore \mathrm{P}=(0.76+0.24) \mathrm{m}$ of $\mathrm{Hg}$ column

$$ \begin{aligned} & =1 \times 13.6 \times 10^{3} \times 10 \mathrm{~Pa} \\ & =13.6 \times 10^{4} \mathrm{~Pa}=136 \mathrm{kPa} \end{aligned} $$

Example-13:

(a) A hydraulic lift has two limbs of radii in ratio of $1: 10$. A car of mass $500 \mathrm{~kg}$ is balanced by keeping a load of $\mathrm{m} \quad \mathrm{kg}$ on the other side. What is $\mathrm{m}$ ?

(b) The load (car) is lifted up by a distance of $0.1 \mathrm{~m}$. what is distance by which $\mathrm{m}$ moves? Efficiency of lift is $\mathbf{8 0 \%}$.

Show Answer

Solution:

(a) Let a and $\mathrm{A}$ be area of cross-section of piston having weight $\mathrm{m} \quad \mathrm{kg}$ and load of $500 \mathrm{~kg}$ on the other piston. Given

$$ \frac{\mathrm{a}}{\mathrm{A}}=\left(\frac{\mathrm{r}}{\mathrm{R}}\right)^{2}=\left(\frac{1}{10}\right)^{2}=\frac{1}{100} $$

From Pascal’s law

$$ \frac{500 \mathrm{kgf}}{\mathrm{A}}=\frac{\mathrm{m} \mathrm{kgf}}{\mathrm{a}} $$

or $\quad \mathrm{m}=500\left(\frac{\mathrm{a}}{\mathrm{A}}\right)=5 \mathrm{~kg}$

(b) The work done, w, in lifting car by $0.1 \mathrm{~m}$ is

$$ \mathrm{w}=500 \times 10 \times 0.1=500 \mathrm{~J} $$

This is output work done. Let w’ be the input workdone. Then

$$ \eta=\frac{w}{w^{\prime}} $$

or $\quad \mathrm{w}^{\prime}=\frac{\mathrm{w}}{\eta}=\frac{500}{0.8} \mathrm{~J}=625 \mathrm{~J}$

Let $\mathrm{s}$ be the distance moved by the piston having $\mathrm{m} \mathrm{kg}$ weight. Then

$$ \begin{gathered} \mathrm{w}^{\prime}=625=5 \times 10 \times \mathrm{s} \\ \text { or } \quad \mathrm{s}=\frac{625}{50} \mathrm{~m}=12.5 \mathrm{~m} \end{gathered} $$

SURFACE TENSION

Introduction

Careful observations show that the surface of a liquid at rest behaves like a stretched membrane. It tries to contract and have a minimum surface area. This property of the liquid surface is known as surface tension.

Illustrations of Surface Tension

(1) Small liquid drops are always spherical in shape. It can be shown that for a given volume; surface area of sphere is minimum. The spherical shape of drop indicates that liquid accquires a shape so that its surface area is minimum.

(2) A wire is bend into shape of a ring with a handle attached. Form a thin film of soap solution inside ring. A light thread is made into an irregular loop and gently placed over soap solution as show in Fig. 1 (a). With a sharp pin break soap film from inside loop by

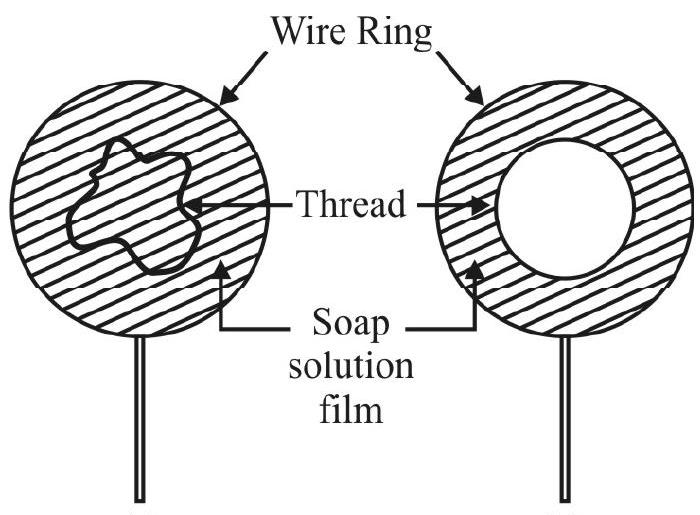
(a)

Fig. 1

(b) pricking it. The loop of thread immediately accquires shape of a perfect circle as shown in Fig. 1 (b). This is due to surface-tension effect. It can be shown that for a given periphery the area enclosed by a circle is maximum. When thread accquires shape of a circle the area of remaining soap film is minimum.

(3) A large mercury drop is broken into small droplets on the base of a clean dish. The small droplets formed have sherical shape. This is due to surface tension.

(4) Place a greased iron needle on a blotting paper and gently place it over surface of water in a beaker. Very soon blotting paper sinks inside water but iron needle remains floating on surface of water! Careful observations of surface of water with a microscope shows a small depression where of needle is. The water surface behaves like a streteched membrane. The weight of needle is balanced by the vertical component of forces of surface tension.

Molecular Theory of Surface Tension

In Fig. $2 \mathrm{XX}$ ’ is the surface of a liquid at rest. $\mathrm{X} _{1} \mathrm{X} _{1}^{\prime}$ is at a distance equal to the range of interatomic / molecular forces. Liquid between $\mathrm{XX}^{\prime}$ and $\mathrm{X} _{1} \mathrm{X} _{1}^{\prime}$ is known as surface film. For atom or molecule P; the “sphere of influence” (i.e. sphere of radius equal to range of interatomic / molecular force with $\mathrm{P}$ as center) is completely within liquid. Net interatomic / molecular force on $\mathrm{P}$ is zero. Same is true for atom $/$ molecule $\mathrm{Q}$ lying on lower face of surface film. No work is done by or against interatomic / molecular force when P moves up to Q. For atom/ molecular at $\mathrm{R}$; there is a net downward interatomic

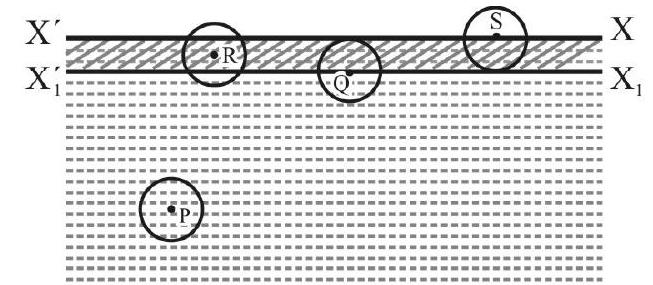
Fig. 2 / molecular force and it is maximum for atom / molecule at $\mathrm{S}$ (i.e. on surface film). When an atom or molecular moves from $\mathrm{Q}$ to $\mathrm{S}$, it has to do work against interatomic / molecular force. In other words potential energy due to interatomic / molecular forces of any atom/ molecule on surface $\mathrm{XX}^{\prime}$ is More than of an atom / molecular at $\mathrm{X} _{1} \mathrm{X} _{1}^{\prime}$ or below. This excess potential energy per unit area is known as free energy of liquid surface.

We know that equilbrium state of any system is one of minimum potential energy. For the liquid surface this will be so if liquid surface tries to accquire minimum surface area. This is the surface tension effect.

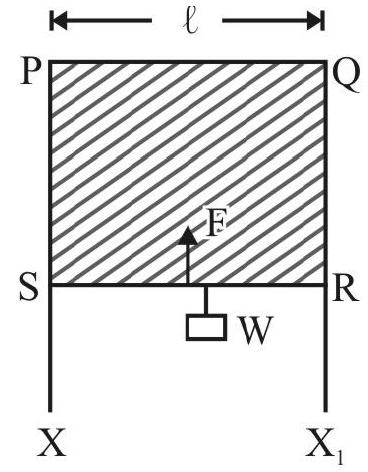
Surface Tension

(a)

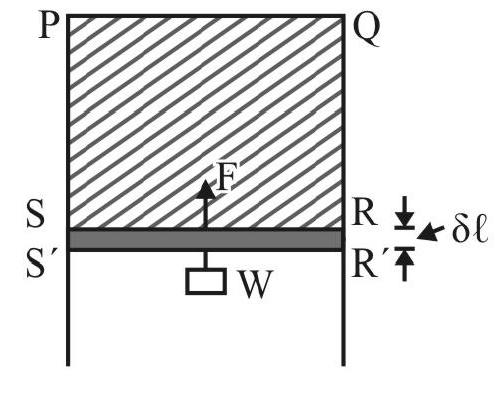
Fig. 3 (b)

Fig. 3 shows a frame $\mathrm{XPQX} X _{1}$ over which wire RS can slide without any friction. Form a liquid film of soap solution and place the arrangement in a vertical plane. Wire RS starts moving vertically upwards! This is due to surface tension. As wire RS move towards side PQ area of film decreases. This means there is a vertically upward force, $\mathrm{F}$, due to $\mathrm{S}$. T on RS. Suspend a small weight $\mathrm{w}$ from RS so that $\mathrm{RS}$ is in equilibrium. Obvisouly $\mathrm{F}=\mathrm{w}$. Experiments show $\mathrm{F}$ is directly proportional to $\mathrm{RS}=\ell$. We write, net force on RS due to surface tension as

$$ \mathrm{F}=2 \mathrm{~S} \ell $$

where $\mathrm{S}$ is a constant depending on nature of film. The factor of 2 in above equation is due to the presence of two free surfaces. Had three been only ONE free surface

$$ \mathrm{F}=\mathrm{S} \ell $$

$\mathrm{S}$ is known as surface tension of liqiud surface. It is numerically equal to force per length acting along the liquid surface (i.e. a tangential force) at right angles to any arbitrary line on the liquid surface. SI unit of S is $\mathrm{Nm}^{-1}$ and its dimensions are $\mathrm{MT}^{-2}$.

In Fig. 3 (b); wire RS is pulled down very slowly (so that surface film does not break) to position R’S’ by an infintesimally small distance $\delta \ell$. The work done, dw, against force of $\mathrm{S}$. T on $\mathrm{RS}=\mathrm{F} \times \delta \ell=2 \mathrm{~S} . \ell \times \delta x$. Let $\mathrm{E}$ be the free energy of liquid surface. The work done $\delta \mathrm{w}$ is used to increase the free energy of liquid surface.

Increase in free energy $=$ Additional area of film created $\times \mathrm{E}$

$$ \begin{aligned} & =2 \times \text { area } \mathrm{RR}^{\prime} \mathrm{SS}^{\prime} \times \mathrm{E} \\ & =2 \times \ell \times \delta \ell \times \mathrm{E} \end{aligned} $$

From law of conservation of energy

$$ 2 \mathrm{~S} \ell \times \delta \ell=2 \mathrm{E} . \ell \times \delta \ell $$

or $\quad \mathrm{S}=\mathrm{E}$

In words; temperature remaining constant; surface tension (S) equals the free energy (E) of the liquid surface.

Example-14:

A large sized spherical liquid drop of radius $R$ is broken into a large number ( $N$ ) of small droplets. What is work done? $S=$ surface tension of liquid.

Show Answer

Solution:

$A=$ The surface area of given big drop $=4 \pi R^{2}$

Let $r$ be radius of each droplet formed. Since there is no loss of mass, Volume of big drop $=$ Total volume of all droplets

$$ \frac{4 \pi}{3} R^{3}=N\left(\frac{4 \pi}{3} r^{3}\right) $$

$$ \text { or } \quad r=\frac{R}{(N)^{\frac{1}{3}}} $$

$A _{1}=$ The total surface of all droplets formed

$$ =\mathrm{N}\left(4 \pi \mathrm{r}^{2}\right)=\mathrm{N} \frac{\left(4 \pi \mathrm{R}^{2}\right)}{\mathrm{N}^{\frac{2}{3}}}=\mathrm{N}^{\frac{1}{3}}\left(4 \pi \mathrm{R}^{2}\right) $$

Since $\mathrm{N}$ is a large number, $\mathrm{N}^{\frac{1}{3}}>1$. i.e. $\mathrm{A} _{1}>\mathrm{A}$.

The increase in surface area is given by

$$ \Delta \mathrm{A}=\mathrm{A} _{1}-\mathrm{A}=\left(\mathrm{N}^{\frac{1}{3}}-1\right) 4 \pi \mathrm{R}^{2} $$

$\mathrm{W}=$ The work done $=$ Increase in free energy

$$ =(\Delta \mathrm{A}) \cdot \mathrm{E}=\left(\mathrm{N}^{\frac{1}{3}}-1\right) 4 \pi \mathrm{R}^{2} \mathrm{~S} \quad[\because \mathrm{S}=\mathrm{E}] $$

Example-15:

In Fig. 4 shown $P Q$ is wire of same size in all and the film is also of same liquid. In equilibrium

(1) $\mathbf{W} _{1}=\mathbf{W} _{2}=\mathbf{W} _{3}=\mathbf{W} _{4}$

(2) $\mathbf{W} _{1}>\mathbf{W} _{2}<\mathbf{W} _{3}=\mathbf{W} _{4}$

(3) $\mathbf{W} _{1}=\mathbf{W} _{2}<\mathbf{W} _{3}<\mathbf{W} _{4}$

(4) $\mathbf{W} _{1} \neq \mathbf{W} _{2} \neq \mathbf{W} _{3} \neq \mathbf{W} _{4}$

Show Answer

Solution:

Since the nature of film and length of slider $\mathrm{PQ}$ is same in all; the force of surface tension on $\mathrm{PQ}$ in all cases is same; therefore

$$ \mathrm{W} _{1}=\mathrm{W} _{2}=\mathrm{W} _{3}=\mathrm{W} _{4} $$

Choice (1) is correct.

Example-16:

A wire bent in the form of a ring of radius $5 \mathrm{~cm}$ rests on the surface of water in beaker. A force of 4.4 gwt is required to pull the ring free from surface of water. What is surface tension of water? ( $\left.\mathrm{g}=\mathbf{1 0} \mathrm{ms}^{-2}\right)$

Show Answer

Solution:

A thin film of water is formed in contact with ring. The force of S.T acts along the circumference of the ring. The liquid touches ring along both inner and outer circumference. The downward pull on ring due to $\mathrm{S} . \mathrm{T}=2[2 \pi \mathrm{rS}]$, where $\mathrm{S}$ is surface tension of water. This is equal to $4.4 \mathrm{~g}$ force. Therefore

$$ 4.4 \times 10^{-3} \times 10=2\left[2 \times 3.14 \times 5 \times 10^{-2}\right] \mathrm{S} $$

or

$$ \begin{aligned} & \mathrm{S}=\frac{4.4 \times 10^{-2}}{4 \times 3.14 \times 5 \times 10^{-2}} \mathrm{Nm}^{-1} \\ & =0.070 \mathrm{Nm}^{-1}=70 \times 10^{-3} \mathrm{Nm}^{-1} \end{aligned} $$

Excess Pressure Across a Curved Liquid Surface

In general, a liquid surface may be plane, concave or convex. Due to the shape of the liquid surface and force of surface tension, in general, the pressure across the two sides of the film is not same. The difference is known as the excess pressure across the liquid surface.

Fig. 5 (a) shows a molecule $\mathrm{O}$ on plane liquid surface. The force of surface tension $\mathrm{S}$, on $\mathrm{O}$ as shown in Fig. 5(a). The pressure across the two sides of the film is same; i.e. there is no pressure difference across the two sides of a plane surface.

Fig. 5 (b) shows a concave surface. The force of surface tension on molecule at $\mathrm{O}$ is shown in Fig. 5 (b) . Resolving $\mathrm{S}$ into horizontal and vertical components; there is a net outward force. Therefore pressure above liquid surface is more than pressure below it. The pressure on concave side is more.

Fig. 5 (c) shows a convex surface. There is net inward force on molecule O. In other words pressure on the lower surface is more than on its upper surface. There is a pressure difference across the surface.

We can conclude that a curved surface of a liquid will be in equilibrium if there is an excess pressure on the concave side of curved surface.

Excess pressure inside A (1) Liquid Drop and (2) Liquid Bubble

Small sized liquid drop or a bubble are shperical in shape due to surface tension. The liquid surface is curved; therefore as disscussed above there is an excess pressure; $\mathrm{p}$; inside the liquid drop or a bubble.

(1) Liquid Drop

Consider a liquid drop of radius $\mathrm{r}$, surface tension $\mathrm{S}$ as shown in Fig. 6. Let $\mathrm{p}$ be the excess pressure inside liquid drop. Very slowly we increase radius of drop to $(\mathrm{r}+\delta \mathrm{r})$. Work has to be done due to force because of excess pressure. Consider a small area $\delta \mathrm{A}$ on surface ofdrop. Force on area considered due to excess pressure $=$ p. $\delta \mathrm{A}$. Work done against surface tension to increase radius of drop by $\delta \mathrm{r}=(\mathrm{p} \cdot \delta \mathrm{A}) . \delta \mathrm{r}$. The total work done, $\delta \mathrm{W}$ is

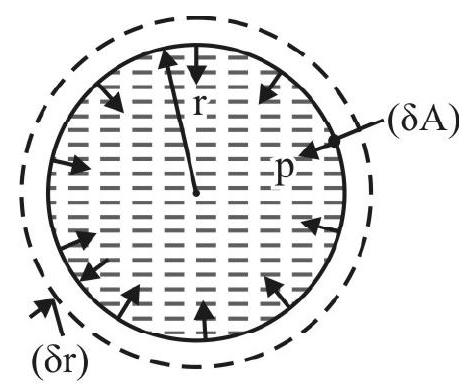
Fig. 6

$$ \begin{align*} \delta \mathrm{W} & =\sum(\mathrm{p} \cdot \delta \mathrm{A}) \cdot \delta \mathrm{r}=\mathrm{p}[\Sigma \delta \mathrm{A}] \cdot \delta \mathrm{r} \\ & =\mathrm{p} \cdot\left[4 \pi \mathrm{r}^{2}\right] \delta \mathrm{r} \tag{1} \end{align*} $$

$\left[\because \Sigma \delta \mathrm{A}=\right.$ Total surface area of liquid drop $\left.=4 \pi \mathrm{r}^{2}\right]$

The work done appears as increase in free energy $\delta \mathrm{E}$ of liquid drop. Obviously

$$ \begin{align*} \delta \mathrm{E} & =\text { Increase in surface area } \times \mathrm{S} \\ & =(4 \pi)\left[(\mathrm{r}+\delta \mathrm{r})^{2}-\mathrm{r}^{2}\right] \times \mathrm{S} \simeq 8 \pi \mathrm{rS} . \delta \mathrm{r} \tag{2} \end{align*} $$

From law of conservation of energy, $\delta \mathrm{W}=\delta \mathrm{E}$

$$ \begin{align*} & \therefore \quad p\left(4 \pi r^{2}\right) \delta r=(8 \pi r) S . \delta r \\ & \text { or } \quad p=\frac{2 S}{r} \tag{3} \end{align*} $$

(2) Liquid Bubble

A liquid bubble has two free surface. Therefore excess pressure $p=\frac{4 S}{r}$

Example-17:

A soap bubble of radius $r$ is formed in air. Excess pressure inside bubble is $p$. The bubble is now kept inside a soap solution. Assuming there is no change in its size; the excess pressure is

(a) $\mathbf{p}$

(b) $2 \mathbf{p}$

(c) $\frac{\mathbf{p}}{\mathbf{2}}$

(d) $\frac{3}{2} p$

Show Answer

Solution:

Soap bubble in air has two free surfaces. Excess pressure $=p=\frac{4 S}{r}$

Inside soap solution: the same bubble has only one free surface. The excess pressure $=\mathrm{p}^{\prime}=\frac{2 \mathrm{~S}}{\mathrm{r}}=\frac{\mathrm{p}}{2}$.

Choice (3) is correct.

Example-18:

Two soap bubbles $A$ and $B\left(r _{A}<r _{B}\right)$ isolated from one another are blown on the two ends of a $U$-tube as shown in Fig. 7. $V$ is a valve that isolates two bubbles from one another. On opening value $\mathbf{V}$

(1) There is no flow of air from A to $B$ or vice-versa

(2) Air flows from $B$ to $A$ till the size of the two become same.

(3) Air flows from A to B till either B brusts or A becomes extinct.

(4) Air alternatively flows from $A$ to $B$ and vice-versa.

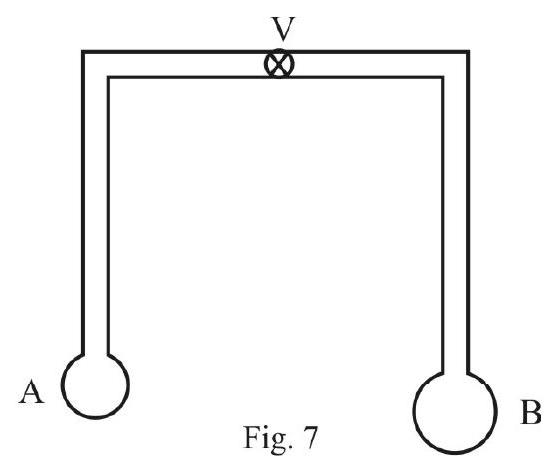
Show Answer

Solution:

Let $\mathrm{P}$ be the atmospheric pressure.

$\mathrm{P} _{\mathrm{A}}=$ Total pressure of air inside bubble $\mathrm{A}$

$=\mathrm{P}+\frac{4 \mathrm{~S}}{\mathrm{r} _{\mathrm{A}}}$

$\mathrm{P} _{\mathrm{B}}=$ Total pressure of air inside bubble $\mathrm{B}$.

$$ =P+\frac{4 S}{r _{B}} $$

Since $r _{A}<r _{B} ; P _{A}>P _{B}$. On opening value $V$; air flows from region of higher pressure to lower pressure i.e. air flows from $\mathrm{A}$ to $\mathrm{B}$, till either $\mathrm{B}$ brusts or $\mathrm{A}$ becomes extint.

Correct choice is (3).

Example-19:

A soap bubble of radius $0.2 \mathrm{~mm}$ is formed in air. What is ratio of excess pressure inside bubble and atmospheric pressure? Take atmospheric pressure $=10^{5} \mathrm{~Pa}$. Surface tension of soap solution $=2.5 \times 10^{-2} \mathrm{Nm}^{-1}$

Show Answer

Solution:

$\mathrm{p}=$ The excess pressure inside soap bubble

$$ =\frac{4 \mathrm{~S}}{\mathrm{r}}=\frac{4 \times 2.5 \times 10^{-2}}{2 \times 10^{-4}} \mathrm{~Pa}=5 \times 10^{2} \mathrm{~Pa} $$

$\mathrm{P}=$ The atmospheric pressure $=10^{5} \mathrm{~Pa}$

$\therefore \frac{\mathrm{p}}{\mathrm{P}}=\frac{5 \times 10^{2}}{10^{5}}=5 \times 10^{-3}$

Example-20:

Two soap bubbles of radii $a$ and $b$ in air coalesse together under isothermal conditions forming a bubble of radius $c$. $P$ is the atmospheric pressure, show that

$$ \frac{S}{P}=\frac{\left(a^{3}+b^{3}-c^{3}\right)}{4\left[c^{2}-a^{2}-b^{2}\right]} $$

$S$ is surface tension of soap solution.

Show Answer

Solution:

Let $\mathrm{P} _{1}, \mathrm{v} _{1}$ denote total pressure and volume of air in bubble of radius a. $\mathrm{P} _{2}, \mathrm{v} _{2}$

and $\mathrm{P} _{3}, \mathrm{v} _{3}$ are corresponding quantities for bubble of radius $b$ and $c$ respecitvely. Then

$$ \begin{array}{ll} P _{1}=\left(P+\frac{4 S}{a}\right) ; & v _{1}=\frac{4 \pi}{3} a^{3} \\ P _{2}=\left(P+\frac{4 S}{b}\right) ; & v _{2}=\frac{4 \pi}{3} b^{3} \end{array} $$

and

$$ P _{3}=\left(P+\frac{4 S}{c}\right) ; \quad v _{3}=\frac{4 \pi}{3} c^{3} $$

Under isothermal conditinos

$\begin{array}{ll} & \mathrm{P} _{1} \mathrm{v} _{1}+\mathrm{P} _{2} \mathrm{v} _{2}=\mathrm{P} _{3} \mathrm{v} _{3} \ \text { or } & {\left[\mathrm{P}+\frac{4 \mathrm{~S}}{\mathrm{a}}\right]\left[\frac{4 \pi}{3} \mathrm{a}^{3}\right]+\left[\mathrm{P}+\frac{4 \mathrm{~S}}{\mathrm{~b}}\right]\left[\frac{4 \pi}{3} \mathrm{~b}^{3}\right]=\left[\mathrm{P}+\frac{4 \mathrm{~S}}{\mathrm{c}}\right]\left[\frac{4 \pi}{3} \mathrm{c}^{3}\right]}\end{array}$

Rearranging term we have

$$ \begin{aligned} & \mathrm{P}\left[\left(\mathrm{a}^{3}+\mathrm{b}^{3}\right)-\mathrm{c}^{3}\right]=4 \mathrm{~S}\left[\mathrm{c}^{2}-\left(\mathrm{a}^{2}+\mathrm{b}^{2}\right)\right] \\ \therefore \quad & \frac{\mathrm{S}}{\mathrm{P}}=\frac{\mathrm{a}^{3}+\mathrm{b}^{3}-\mathrm{c}^{3}}{4\left(\mathrm{c}^{2}-\mathrm{a}^{2}-\mathrm{b}^{2}\right)} \end{aligned} $$

Forces of Adhesion and Cohesion

The interatomic / molecular force between atoms / molecules of same nature is known as force of cohesion. Interatomic / molecular force between (i) water molecules (ii) mercury atoms (iii) glass moleculus on one another is force of cohesion.

The interatomic / molecular force between atoms / molecule of different nature is known as force of adhesion. Force between water and air; mercury and walls of glass tube; glue and a piece of paper, is force of adhesion.

Water wets our hand or a glass container because force of adhesion is more than force of cohesion. Mercury does not wet hand or a glass container because force of cohesion is more than force of adhesion.

Shape of Liquid Meniscus

Consider two identical capillary tubes one filled with water and the other with mercury. The liquid meniscus is concave for water and convex for mercury. The shape of meniscus depends on the relative magnitude of force of adhesion and force of cohesion. It can be shown that the shape of meniscus is

(1) Concave if force of adhesion is more the force of cohesion, and

(2) Convex if force of cohesion is more than the force of adhesion.

A plane meniscus is also possible if force of adhesion equals the component of force of cohesion perpendicular to the wall.

The Angle of Contact

How much curved a meniscus will be, is expressed in terms of angle of contact. The angle of contact, $\theta$; between a liquid and a solid is the angle enclosed between the tangents to the liquid surface and the solid surface measured inside liquid.

Fig. 8 (a) shows a concave meniscus and Fig. 8 (b) convex meniscus. $P$ is a point of contact of liquid with the glass wall. PQ is tangent at $\mathrm{P}$ to meniscus. Angle RPQ is the angle $\theta$ of contact. Obvisouly $\theta$ is acute angle for a concave meniscus and is an obtuse angle for a convex meniscus. Value of $\theta$ depends on

(i) nature of liquid and solid in contact

(ii) nature of medium above free surface of liquid.

$\theta$ does not depend on the inclincation of solid to liquid surface. The angle of contact of mercury with glass is about $140^{\circ}$. Angle of contact for water and glass is about $8^{0}-10^{\circ}$.

Capillarity

A tube with a very fine bore is a capillary tube. A clean capillary tube open at both ends is dipped in a beaker containing (i) water (ii) mercury. Water rises up the capillary tube and mercury depresses (i.e. level falls) above the free surface in beaker. This rise or fall of liquid in a tube of very fine bore is known as capillarity.

Some common examples of capillarity are:

(i) Oil rises in the wick a lamp through small capillaries between the threads.

(ii) The tip of the “nib” of a pen is split. It uses capillary action for ink to flow.

(iii) Blotting paper absorbs water or ink. This is due to small pores in paper acting as a capillary.

(iv) Branches of a plant or tree get water from soil due to capillary action.

(v) Earthern vesseles used to cool water in summer use capillary action of small pores in the vessel. Water oozes out of vessel; gets evaporated by taking heat from the earthern vessel causing cooling.

Rise of Liquid in a Capillary Tube

An open capillary tube of radius $r$ is dipped inside a beaker containing water. In equilibrium water rises up to a height $h$ as shown in Fig. 9 (a). To understand capillary rise refer to Fig. 9 (b). When free surface of

water comes in contact with walls of capillary tube, the water meniscus inside capillary tube accquires a concave shape as shown in Fig. 9 (b); A is a point on upper side and B on lower side of meniscus. Clearly $\mathrm{P} _{\mathrm{A}}=\mathrm{P} _{\mathrm{at}} ; \mathrm{P} _{\mathrm{B}}=\mathrm{P} _{\mathrm{at}}-\frac{2 \mathrm{~S}}{\mathrm{r}}$; assuming radius of meniscus is same as that of capillary tube. Since $\mathrm{P} _{\mathrm{A}}>\mathrm{P} _{\mathrm{B}}$; there is net upward force that pulls water up. In Fig. 9 (c); equilibrium position is shown. For equilibrium.

Net upward force $=$ Weight of liquid inside capillary tube

Fig. 9 (d) shows enlarged view of capillary tube and meniscus. Assuming meniscus is hemispherical of same radius ( $\mathrm{r}$ ) as tube. $\mathrm{P}$ and $\mathrm{Q}$ are two diamaterially opposite water molecules in contact with wall of capillary tube. $\mathrm{S}$ is force of surface tension on wall due to water molecule. $\mathrm{R}$ is the reaction force, wall exerts on molecule, in accordance with Newton’s third law. Resolve $\mathrm{R}=\mathrm{S}$ into rectangular components (i) $\mathrm{S} \cos \theta$ and (ii) $\mathrm{S} \sin \theta$ as shown in Fig. 9 (d). The components $\mathrm{S} \sin \theta$ cancel one another. The net vertically upward force equals $S \cos \theta \cdot[2 \pi r]$. Neglecting the volume of liquid inside meniscus; the weight of liquid column $=\left(\pi r^{2} h\right) \rho g$; where $\rho$ is density of liquid.

At equilibrium $2 \pi \mathrm{r} S \cos \theta=\pi \mathrm{r}^{2} \mathrm{~h} \rho \mathrm{g}$

or $\mathrm{h}=\frac{2 \mathrm{~S} \cos \theta}{\mathrm{r} \rho \mathrm{g}}$

For glass and water, $\theta$ is an acute angle, $\mathrm{h}$ is a positive number, i.e. water rises inside capillary tube. For glass and mercury $\theta$ is an obtuse angle; $h$ is a negative number, i.e. mercury level falls inside capillary tube.

Rise of Liquid in a Tube of Insufficient Length

Consider a capillary tube of length $L$ and radius $r$. The height of liquid rise equals $h$. If $L$ and $r$ are such that $\mathrm{h}>\mathrm{L}$; we have a tube of insufficient length. Water does not shoot out of the upper end of the tube. It rises upto $\mathrm{h}=\mathrm{L}$ i.e. water fills tube completely and attains equilibrium. This is because the meniscus automatically readjusts its radius of convature so that equilibrium height equals L. Obvisouly radius of curvature of meniscus increases or it (meniscus) becomes less curved.

Variation of Surface Tension

(1) The presence of impurities dissolved in liquid or on its surface effects value of surface tension. For example if $\mathrm{NaCl}$ or $\mathrm{CuSO} _{4}$ is dissolved in water, surface tension of solution is different from that of water. Whether surface tension increases or decreases depends on the nature of impurity. S.T of sodium chloride solution is more than that of water. Solution of phenol dissolved in water has S.T less than that of water.

(2) The surface tension of liquid depends on temperature. S.T of a liquid decreases as temperature increases.

Example-21:

Two bubbles $A$ and $B$ of radius $r$ and $3 r$ are in equilibrium. What is radius of their common surface, shown by dotted line in Fig. 10.

Show Answer

Solution:

Excess pressure $\mathrm{p} _{\mathrm{A}}$ and $\mathrm{p} _{\mathrm{B}}$ inside the bubble $\mathrm{A}$ and $\mathrm{B}$ respectively is

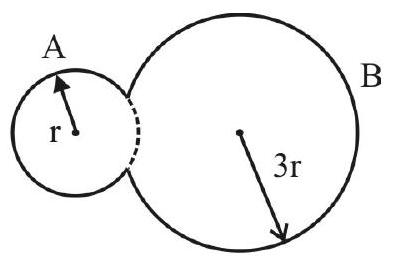
Fig. 10

$$ \mathrm{p} _{\mathrm{A}}=\frac{4 \mathrm{~S}}{\mathrm{r}} ; \quad \mathrm{p} _{\mathrm{B}}=\frac{4 \mathrm{~S}}{3 \mathrm{r}} $$

Let $\mathrm{R}$ be the radius of their common interface. In equilibrium

$$ \begin{gathered} \mathrm{p} _{\mathrm{A}}-\mathrm{p} _{\mathrm{B}}=\frac{4 \mathrm{~S}}{\mathrm{R}} \\ \text { or } \quad 4 \mathrm{~S}\left[\frac{1}{\mathrm{r}}-\frac{1}{3 \mathrm{r}}\right]=\frac{4 \mathrm{~S}}{\mathrm{R}} \quad \text { or } \mathrm{R}=\frac{3 \mathrm{r}}{2} \end{gathered} $$

Example-22:

A capillary tube of length $1 \mathrm{~m}$, radius $0.1 \mathrm{~m}$ is closed at one end. It is immersed in a beaker containing water as shown in Fig. 11. What is the height to which water rises?

Atmospheric pressure $=10^{5} \mathbf{P a}$

S.T of water $=\mathbf{7 0} \times 10^{-2} \mathbf{N m}^{-1} ; g=10 \mathrm{~ms}^{-2}$

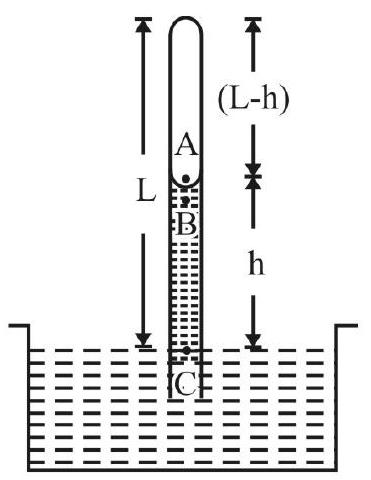
Fig. 11

Show Answer

Solution:

Let a be area of cross-section of capillary tube and $\mathrm{P} _{0}$ atmospheric pressure. $\mathrm{h}$ is height to which water rises. Let $\mathrm{P} _{\mathrm{A}}$ be pressure at A point in contact with concave surface just above it. Then from Boyle’s law

$$ \begin{align*} & \mathrm{P} _{0} \mathrm{a} \times \mathrm{L}=\mathrm{P} _{\mathrm{A}} \times \mathrm{a} \times(\mathrm{L}-\mathrm{h}) \quad[\mathrm{Clf} \quad \mathrm{Pv}=\text { constant for air in capillary tube }] \\ & \therefore \quad \mathrm{P} _{\mathrm{A}}=\frac{\mathrm{P} _{0} \mathrm{~L}}{(\mathrm{~L}-\mathrm{h})} \tag{1} \end{align*} $$

Let $P _{B}$ be pressure at point $B$ (point in contact with meniscus inside water). Assuming the radius of meniscus is same as of capillary tube.

$$ \begin{equation*} \mathrm{P} _{\mathrm{A}}-\mathrm{P} _{\mathrm{B}}=\frac{2 \mathrm{~S}}{\mathrm{r}} \tag{2} \end{equation*} $$

Also $\mathrm{P} _{\mathrm{C}}=\mathrm{P} _{0}=\mathrm{P} _{\mathrm{B}}+\mathrm{h} \rho \mathrm{g} \quad$ or $\quad \mathrm{P} _{\mathrm{B}}=\mathrm{P} _{0}-\mathrm{h} \rho \mathrm{g} \hspace{20mm}. . . . . . . . (3)$

From Eqns. (1), (2) and (3) we have

$$ \left[\frac{\mathrm{P} _{0} \mathrm{~L}}{(\mathrm{~L}-\mathrm{h})}\right]-\left(\mathrm{P} _{0}-\mathrm{h} \rho \mathrm{g}\right)=\frac{2 \mathrm{~S}}{\mathrm{r}} $$

or $\quad \frac{\mathrm{P} _{0} \mathrm{~h}}{\mathrm{~L}-\mathrm{h}}+\mathrm{h} \rho g=\frac{2 \mathrm{~S}}{\mathrm{r}} \hspace{20mm}. . . . . . . . (4) $

Given $\mathrm{P} _{0}=10^{4} \mathrm{~Pa} ; \mathrm{L}=1 \mathrm{~m} ; \mathrm{S}=70 \times 10^{-2} \mathrm{Nm}^{-1} ; \rho=10^{3} \mathrm{kgm}^{-3}$ and $\mathrm{g}=10 \mathrm{~ms}^{-2}$. Substituting values in Eqn (4) we have

$$ \begin{aligned} & \frac{10^{4} \mathrm{~h}}{(1-\mathrm{h})}+\mathrm{h} \times 10^{3} \times 10=\frac{2 \times 70 \times 10^{-2}}{10^{-4}} \\ & \frac{\mathrm{h}}{(1-\mathrm{h})}+\mathrm{h}=1.4 \\ & \mathrm{~h}+\mathrm{h}-\mathrm{h}^{2}=1.4-1.4 \mathrm{~h} \\ & \mathrm{~h}^{2}-3.4 \mathrm{~h}+1.4=0 \\ & \therefore \mathrm{h}=\frac{3.4 \pm \sqrt{(3.4)^{2}-5.6}}{2} \\ & =3.42 \mathrm{~m} \text { or } 0.48 \mathrm{~m} \end{aligned} $$

or

Since $\mathrm{L}=1 \mathrm{~m}, \mathrm{~h}=3.42 \mathrm{~m}$ is not possible. Therefore $\mathrm{h}=0.48 \mathrm{~m}=48 \mathrm{~cm}$

Example-23

Two capillary tube of radius $0.5 \mathrm{~mm}$ and $1.5 \mathrm{~mm}$ are joined together to form a U-tube as shown in Fig. 12. U-tube contains water. In equilibrium what is the difference of level of water in the two limbs. Given

S.T of water $=70 \times 10^{-2} \mathrm{Nm}^{-1} ;$ Density of water $=10^{3} \mathrm{kgm}^{-3} ; \mathrm{g}=10 \mathrm{~ms}^{-2}$.

Show Answer

Solution:

Consider points A, B and C, D on the two sides of meniscus in the two limbs of U-tube. $\mathrm{P} _{0}$ is atmospheric pressure. Then

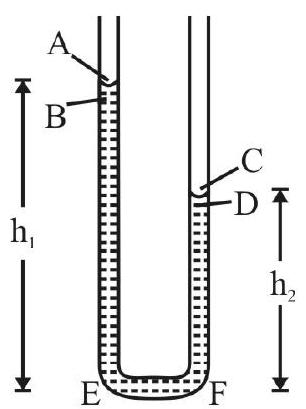
$$ \begin{gathered} \mathrm{P} _{\mathrm{A}}=\mathrm{P} _{\mathrm{C}}=\mathrm{P} _{0} \\ \mathrm{P} _{\mathrm{B}}=\mathrm{P} _{0}-\frac{2 \mathrm{~S}}{\mathrm{r} _{1}} ; \quad \mathrm{P} _{\mathrm{D}}=\mathrm{P} _{0}-\frac{2 \mathrm{~S}}{\mathrm{r} _{2}} \end{gathered} $$

$\mathrm{E}$ and $\mathrm{F}$ are two point at bottom of the two limbs of U-tube. In equilibrium $\mathrm{P} _{\mathrm{E}}=\mathrm{P} _{\mathrm{F}}$; i.e.

$$ \mathrm{P} _{\mathrm{B}}+\mathrm{h} _{1} \rho \mathrm{g}=\mathrm{P} _{\mathrm{D}}+\mathrm{h} _{2} \rho \mathrm{g} $$

or

$$ \mathrm{h} _{1}-\mathrm{h} _{2}=\frac{2 \mathrm{~S}}{\rho \mathrm{g}}\left[\frac{1}{\mathrm{r} _{1}}-\frac{1}{\mathrm{r} _{2}}\right] $$

Substituting given values of parameters;

$$ \begin{aligned} \mathrm{h} _{1}-\mathrm{h} _{2} & =\frac{2 \times 70 \times 10^{-2}}{10^{3} \times 10}\left[\left(\frac{1}{5 \times 10^{-4}}\right)-\left(\frac{1}{1.5 \times 10^{-3}}\right)\right] \\ & =\frac{2 \times 70 \times 10^{-2} \times 3.5}{5 \times 1.5} \mathrm{~m} \simeq 19.33 \mathrm{~cm} \end{aligned} $$

(C) HYDRODYNAMICS

Introduction

Hydrodynamics is a branch of physics involving study of fluids in motion. In general this is a very difficult branch of physics. We will consider in its most simple form. We will consider what we describe as streamlined flow.

Stream Lined and Turbulent Flow

(1) Stream lined flow of a liquid is a highly ordered flow of a liquid. The velocity of every liquid particle at one point is same as that of its predecessor. In general velocity of flow can be different at different points in space. This type of flow is similar to a column of millitary men marching on a

road. The liquid can be divided into different layers that slide over one another. Particles in one layer do not intermix with particles in an adjoining layer.

(2) Turblent flow is more common in liquids. Here velocity of a particle at one point in space is not same as of its predecessor. The liquid cannot be divided into non-interferring layers. A turbulent flow is similar to people moving in a very crowded bazzar. Generally flow of air at high speeds is turbulent. The flow of water in a sea having tidal waves or vortices is turbulent.

In our subsequent discussion we consider only stream-lined flow of liquids.

VISCOSITY

Consider a liquid having a stream-lined flow over a plane horizontal surface. To maintain this flow an external force has to be applied. If external force is removed; soon liquid comes to rest. Why? This is due to an internal force of friction between different liquid layers. This force destroys relative motion of liquid layers and liquid comes to rest. This property of liquid is known as viscosity.

We can say that the different liquid layers having a relative motion exert a tangential force (or a viscous drag) on one another; in such a manner so as to opposse the relative motion of layers under consideration. The viscous force opposses relative motion between liquid layers in a manner similar to friction between two solid surfaces in contact; this is the reason viscosity is considered as “internal friction” between liquid layers having relative motion.

The Coefficient of Viscosity $(\boldsymbol{\eta})$

Fig. 1 (a) shows streamlined flow of a liquid over a horizontal solid surface XX’ . Assuming that liquid layer in contact with $\mathrm{XX}^{\prime}$ is at rest, the speed of liquid particles increases as distance of layer from $\mathrm{XX}^{\prime}$ increases. This is indicated by a directed arrow at each layer. The length of arrow represents speed of particle in that layer. Fig. 1 (b) shows two liquid layers PQ and RS at distance $x$ and $x+\mathrm{d} x$ from XX’. The speed of particles in the two layer is $\mathrm{v}$ and $\mathrm{v}+\mathrm{dv}$ respectively. $\left(\frac{\mathrm{dv}}{\mathrm{d} x}\right)$ is known as velocity gradient. Let $\mathrm{F}$ be the viscous force between the two layers considered. Newton, from his experimental observations concluded that

(1) F is directly proportional to area of cross-section (A) of each liquid layer, i.e. F $\propto \mathrm{A}$.

(2) F is directly proportional to the velocity gradient between the layers considered, i.e. $\mathrm{F} \propto\left(\frac{\mathrm{dv}}{\mathrm{d} x}\right)$

According to Newton;

$$ \begin{equation*} \mathrm{F}=-\eta \mathrm{A}\left(\frac{\mathrm{dv}}{\mathrm{d} x}\right) \tag{1} \end{equation*} $$

where $\eta$ is a constant depending on nature of liquid. It is known as coefficient of viscosity.

The negative sign in Eqn. (1) indicates that direction of $\mathrm{F}$ is opposite to the direction of flow of liquid. Equation (1) is Newton’s law of viscous force.

Units and Dimensions of $\eta$

From Eqn. (1); if $\mathrm{A}=1$ unit, $\frac{\mathrm{dv}}{\mathrm{d} x}=1$ unit, $|\mathrm{F}|=\eta$. Expressed in words coefficient of viscosity is numerically equal to external applied force to maintain a unit difference or velocity between liquid layer a unit distance apart having unit area of cross-section. The SI unit of $\eta$ is $\frac{\mathrm{N}}{\mathrm{m}^{2}\left(\frac{\mathrm{ms}^{-1}}{\mathrm{~m}}\right)}=\mathrm{Ns}^{-1} \mathrm{~m}^{-2}$ The C.G.S unit of viscosity is poise. Obviously

1 poise $=1 \frac{\text { dyne }}{\mathrm{cm}^{2} \mathrm{~s}}=\frac{10^{-5} \mathrm{~N}}{\left(10^{-2}\right)^{2} \mathrm{~m}^{2} \mathrm{~s}}=10^{-1} \frac{\mathrm{N}}{\mathrm{m}^{2} \mathrm{~s}}$

$\therefore 10$ poise $=1$ SI unit of $\eta$. The SI unit in also called deca-poise.

The dimensions of $\eta$ are

$$ [\eta]=\frac{[\mathrm{F}]}{[\mathrm{A}]\left[\frac{\mathrm{dv}}{\mathrm{d} x}\right]}=\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}^{2}\left(\frac{\mathrm{LT}^{-1}}{\mathrm{~L}}\right)}=\mathrm{ML}^{-1} \mathrm{~T}^{-1} $$

Cause of Viscosity

Viscosity is due to intermolecular forces which come into play between different liquid layers in relative motion. Due to these forces, the faster moving layer tries to accelerate the adjoining slow moving layer. Similarly a slow moving layer tries to retard the adjoining fast moving layer of liquid. As a consequence, there is net backward dragging force. This is viscous force.

Viscosity Versus Solid Friction

The relative comparison of the two forces in a tabular form is given below.

S.No.	Solid Friction	Viscous Force
1.	Opposes relative motion between surfaces in contact	Opposses relative motion between adjoining liquid layers
2.	Is due to interatomic or intermolecular forces	Is due to intermolecular forces between molecules in adjoining layers
3.	$f _{i t}$ does not depend on	$\mathrm{F} _{\mathrm{vis}}$ depends on
	(i) area of surface in contact	(i) area of layers in contact
	(ii) the magnitude of relative velocity	(ii) velocity gradient between the layers

Stoke’s Law

Consider motion of a small sized; spherical body through a viscous medium at rest. The layer of medium in contact with the moving body accquires same speed as that of the body, i.e. there is no slipping between the body and the medium. However a layer of medium very far off from the body is at rest. In other words there is a relative motion between different layers of the medium. Due to viscosity of medium a backward dragging force acts on body and opposses motion of the body. Consider a spherical body of radius $r$; moving with speed $v$ in a medium of viscosity $\eta$. According to Stoke; the viscous force, F; on the body due to the medium is

$$ \begin{equation*} \mathrm{F}=6 \pi \eta \mathrm{rv} \tag{1} \end{equation*} $$

This is Stoke’s law. We can apply Stoke’s law to describe motion of rain drop from clouds towards earth through air.

Terminal Velocity

$$ \text { At } \mathbf{t}=0 $$

$$ \text { At } t=t $$

Consider a small sized spherical body at rest initially moving under gravity of earth through air (the viscous medium). Fig. 2 (a) shows forces acting on body at $\mathrm{t}=0 \mathrm{~W}=$ Weight of body. $\mathrm{B}=$ Bouyant force; $\mathrm{F} _{\mathrm{vis}}=$ Viscous force $=0$, because $\mathrm{v} _{0}=0$. The net downward acceleration.

$$ \begin{equation*} \mathrm{a} _{0}=\frac{\mathrm{W}-\mathrm{B}}{\mathrm{m}} \tag{2} \end{equation*} $$

Due to finite acceleration body accquires some speed. At $t=t$, instantaneous speed of body is $v$.

The instantaneous viscous force $=\mathrm{F} _{1}=6 \pi \eta \mathrm{rv} \neq 0$

The instantaneous acceleration $=\mathrm{a} _{1}=\frac{\mathrm{W}-\left(\mathrm{B}+\mathrm{F} _{1}\right)}{\mathrm{m}}<\mathrm{a} _{0}$

As $\mathrm{v}$ increases, $\mathrm{F} _{1}$ increases and instantaneous acceleration decreases. After sufficently long time, body has accquired a speed $\mathrm{v} _{\mathrm{T}}$ such that net force and therefore acceleration is zero. Hence onwards body moves with a constant speed, $\mathrm{v} _{\mathrm{T}}$; known as terminal velocity. From Fig. $2(\mathrm{c})$; when $\mathrm{v} _{\mathrm{v}} \mathrm{v} _{\mathrm{T}}$; we have

$$ \begin{equation*} \mathrm{B}+\mathrm{F} _{\mathrm{vis}}=\mathrm{W} \tag{3} \end{equation*} $$

Let $\rho$ be density of the body and $\sigma$ density of the medium. Then

$$ \mathrm{W}=\left(\frac{4 \pi}{3} \mathrm{r}^{3} \rho\right) \mathrm{g} ; \quad \mathrm{B}=\left(\frac{4 \pi}{3} \mathrm{r}^{3}\right) \sigma \mathrm{g} \quad \text { and } \mathrm{F} _{\mathrm{vis}}=6 \pi \eta \mathrm{rv} _{\mathrm{T}} $$

Therefore,

$$ \frac{4 \pi}{3} r^{3}(\rho-\sigma) g=6 \pi \eta \mathrm{rv} _{\mathrm{T}} $$

$$ \begin{equation*} \text { or } \quad \mathrm{v} _{\mathrm{T}}=\frac{2}{9}\left[\frac{\mathrm{r}^{2}(\rho-\sigma) \mathrm{g}}{\eta}\right] \tag{4} \end{equation*} $$

Eqn. (4) gives expression for the terminal velocity. If $\rho>\sigma, \mathrm{v} _{\mathrm{T}}$ is a positive number, the body moves vertically downwards. However if $\rho>\sigma, \mathrm{v} _{\mathrm{T}}$ is a negative number. This means body moves vertically upwards. Fig. 3 shows (i) $v$ vs $t$ and (ii) a vs $t$ graph for motion of body.

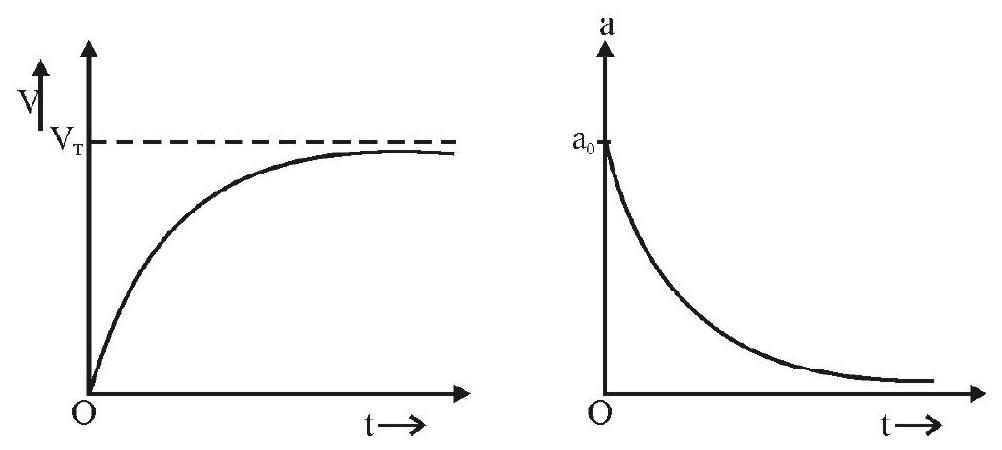
Fig. 3

Flow of a Viscous Liquid in a Horizontal Capillary Tube

A horizontal capillary tube $\mathrm{AB}$ of length $\ell$, radius $r$ has liquid pressure $\mathrm{P} _{1}$ and $\mathrm{P} _{2}\left(\mathrm{P} _{1}>\mathrm{P} _{2}\right)$ at its two ends $A$ and $B$ as shown in Fig. 4. A liquid of viscosity $\eta$ enters tube at end $A$ and emerges out at end $B=P _{1}-$ $\mathrm{P} _{2}=$ pressure difference across ends of tube. $\frac{\mathrm{P}}{\ell}=$ constant and is known as pressure gradient. Let $\mathrm{V}$ be volume of liquid flowing out from end $\mathrm{B}$ per second. $\mathrm{V}$ is known as rate of flow of liquid. Poiseullie showed that

$$ \mathrm{V}=\frac{\pi \mathrm{Pr}^{4}}{\delta \eta \ell} $$

This is known as Poiseullie’s equation

Variation of Viscosity with Temperature

(1) For liquids viscosity decreases as temperature increases. Let $\eta _{0}$ and $\eta _{t}$ be viscosity at $0^{\circ} \mathrm{C}$ and $t^{\circ} \mathrm{C}$ respectively. Then

$$ \eta _{t}=\frac{\eta _{0}}{\left(1+\alpha t+\beta t^{2}\right)} $$

$\alpha$ and $\beta$ are constants for a liquid.

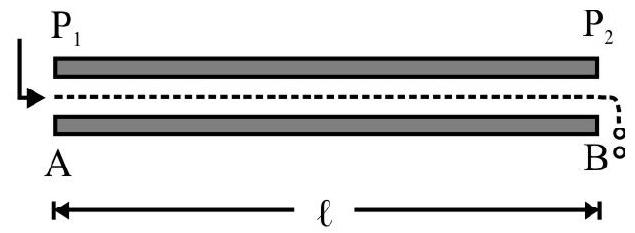
Fig. 4

(2) For gases; viscosity increases as temperature increases. Viscosity ( $\eta$ ) is directly proportional to square root of absolute temperature ( $\mathrm{T}$ ) of gas; i.e. $\eta \alpha \sqrt{\mathrm{T}}$.

Example-24:

$N$ identical drops each of radius $r$ accquire a terminal speed $v$ in a viscous medium. All drops coalese together to form a big drop. In the same medium the terminal velocity of big drop is $V$.

Then $\frac{\mathrm{V}}{\mathrm{V}}$ is

(a) $\mathrm{N}$

(b) $\mathrm{N}^{\frac{1}{3}}$

(c) $\mathrm{N}^{\frac{2}{3}}$

(d) $\mathrm{N}^{\frac{-2}{3}}$

Show Answer

Solution:

The terminal velocity is proportional to square of radius of drop. Let $\mathrm{R}$ be radius of big drop formed when all small drops coalese together. Then

$$ \begin{equation*} \frac{\mathrm{V}}{\mathrm{V}}=\left(\frac{\mathrm{R}}{\mathrm{r}}\right)^{2} \tag{1} \end{equation*} $$

Also, $\quad N\left(\frac{4 \pi}{3} r^{3}\right)=\frac{4 \pi}{3} R^{3} \quad$ or $\quad R=N^{\frac{1}{3}} r \hspace{20mm}. . . . . . . . (2)$

From Eqns. (1) and (2), we have

$$ \frac{\mathrm{V}}{\mathrm{V}}=\mathrm{N}^{\frac{2}{3}} $$

The correct choice is (c).

Example-25:

A small sized spherical body of radius $r$, density $\rho$ moves in a medium of density $\frac{\rho}{2}$, viscosity $\eta _{1}$. $V$ is the terminal velocity accquired by the body. The same body moves in another liquid of density $\frac{\rho}{4}$; viscosity $\eta _{2}$. The terminal velocity accquired is $1.5 \mathrm{~V}$. The ratio $\frac{\eta _{1}}{\eta _{2}}$ is

(a) $\frac{2}{3}$

(b) $\frac{3}{2}$

(c) $\frac{4}{9}$

(d) 1

Show Answer

Solution:

We know terminal velocity $\mathrm{v} _{\mathrm{T}}$ is

$$ \mathrm{v} _{\mathrm{T}}=\frac{2 \mathrm{r}^{2}(\rho-\sigma) \mathrm{g}}{\eta} $$

$\rho=$ density of body; $\sigma=$ density of medium and $\eta=$ visosity of medium.

For $1^{\text {st }}$ liquid; $\sigma _{1}=\frac{\rho}{2}$; therefore

$$ \begin{equation*} \mathrm{V}=\frac{2 \mathrm{r}^{2}\left(\rho-\frac{\rho}{2}\right) \mathrm{g}}{9 \eta _{1}}=\frac{\mathrm{r}^{2} \rho \mathrm{g}}{9 \eta _{1}} \tag{1} \end{equation*} $$

For $2^{\text {nd }}$ liquid; $\sigma _{2}=\frac{\rho}{4}$; therefore

$$ 1.5 \mathrm{~V}=\frac{2 \mathrm{r}^2\left(\rho-\frac{\rho}{4}\right) \mathrm{g}}{9 \eta_2}=\frac{3 \mathrm{r}^2 \rho \mathrm{g}}{18 \eta_2} \hspace{20mm}. . . . . . . . (2) $$

From Eqns. (1) and (2); we get $$ \begin{gathered} 1.5=\frac{3}{18 \eta_2} \times \frac{9 \eta_1}{1} \quad \text { or } \quad \frac{3}{2}=\frac{3}{2} \frac{\eta_1}{\eta_2} \ \therefore \frac{\eta_1}{\eta_2}=1 \end{gathered} $$

Correct choice is (d)

Example-26:

A small lead shot of radius $r$ density $\rho$ is dropped in a tank full of gylcerine. After some time the lead shot accquires a terminal speed $V . \sigma$ and $\eta$ denote density and viscosity of glycerine. The viscous force on lead shot when it has accquired terminal speed is

(a) $\mathrm{mg}$

(b) $\operatorname{mg}\left(1-\frac{\sigma}{\rho}\right)$

(c) $\operatorname{mg}\left(1-\frac{\rho}{\sigma}\right)$

(d) $\frac{\mathrm{mg}}{\left(1-\frac{\sigma}{\rho}\right)}$

Show Answer

Solution:

Let $\mathrm{W}, \mathrm{B}$ and $\mathrm{F}$ denote weight, bouyant and viscous force on lead shot respectively when it (lead shot) has accquired terminal speed. Under these conditions net force on lead shot is zero. This is so if

$$ \begin{array}{r} \mathrm{W}-\mathrm{B}=\mathrm{F} \\ \text { or } \quad \mathrm{mg}-\mathrm{B}=\mathrm{F} \tag{1} \end{array} $$

The bouyant force $\mathrm{B}$; according to Archimedes’, principle equals weight of liquid displaced.

$\therefore \mathrm{B}=$ Volume of lead shot $\times$ density of glycerine $\times \mathrm{g}$

$$ \begin{equation*} =\frac{\mathrm{m}}{\rho} \times \sigma \times \mathrm{g} \tag{2} \end{equation*} $$

From Eqns. (1) and (2) we have

$$ \begin{aligned} & F=m g-m g\left(\frac{\sigma}{\rho}\right) \\ & =m g\left[1-\frac{\sigma}{\rho}\right] \end{aligned} $$

The correct choice is (b)

Example-27:

Two capillary tubes $A$ and $B$ having same length and radii in ratio of 1: $\sqrt{2}$ are joined in series with one another. The pressure at the two ends is $11 P$ and P respectively. A liquid of viscosity $\eta$ flows through the arrangement. What is ratio of pressure gradients across tubes $A$ and $B$ ?

Show Answer

Solution:

Fig. 5 shows the two tubes A and $\mathrm{B}$ joined in series. Given $\mathrm{P} _{\mathrm{L}}=11 \mathrm{P}, \mathrm{P} _{\mathrm{N}}=\mathrm{P}$. Let pressure at common end $M$ be $x$. Given $\frac{r _{A}}{r _{B}}=\frac{1}{(2)^{\frac{1}{2}}}$. In series rate of flow of liquid in the two tubes is same; i.e. $V _{A}=V _{B}$ from Poiseullie’s equation.

$$ \frac{\pi(11 \mathrm{P}-x) \mathrm{r} _{\mathrm{A}}^{4}}{8 \eta \ell}=\frac{\pi(x-\mathrm{P}) \mathrm{r} _{\mathrm{B}}^{4}}{8 \eta \ell} $$

or $\quad \frac{11 \mathrm{P}-x}{x-\mathrm{P}}=\left(\frac{\mathrm{r} _{\mathrm{B}}}{\mathrm{r} _{\mathrm{A}}}\right)^{4}=[\sqrt{2}]^{4}$

Fig. 5

$\therefore \quad x=3 \mathrm{P}$

$\frac{\text { Pressure gradient across tube } \mathrm{A}}{\text { Pressure gradient across tube } \mathrm{B}}=\frac{(11 \mathrm{P}-3 \mathrm{P}) \mathrm{L}}{(3 \mathrm{P}-\mathrm{P}) }=\frac{4}{1}$

Example-28:

Three horizontal tubes of same radius $r$ having length $\mathrm{L}, 1.5 \mathrm{~L}$ and $2 \mathrm{~L}$ are connected at one end to a tank supplying water at a constant pressure head $h$. The length of a single tube of same radius having the same rate of flow as in the arrangement described; when connected to same constant pressure head tank is

(a) $4.5 \mathrm{~L}$

(b) $\frac{6 \mathrm{~L}}{13}$

(c) $\frac{6 \mathrm{~L}}{11}$

(d) $\frac{3 \mathrm{~L}}{5}$

Show Answer

Solution:

Let $V _{1}, V _{2}$ and $V _{3}$ be rate of flow of water in each tube. Then

$\mathrm{V} _{1}=\frac{\pi(\mathrm{h} \rho \mathrm{g}) \mathrm{r}^{4}}{8 \eta \mathrm{L}} ; \quad \mathrm{V} _{2}=\frac{\pi(\mathrm{h} \rho \mathrm{g}) \mathrm{r}^{4}}{8 \eta(1.5 \mathrm{~L})} ; \quad \mathrm{V} _{3}=\frac{\pi(\mathrm{h} \rho \mathrm{g}) \mathrm{r}^{4}}{8 \eta(2 \mathrm{~L})}$

$\mathrm{V}=$ The net of rate of flow in all three tubes

$$ \begin{equation*} =\mathrm{V} _{1}+\mathrm{V} _{2}+\mathrm{V} _{3}=\frac{\pi(\mathrm{h} \rho \mathrm{g}) \mathrm{r}^{4}}{8 \eta}\left[\frac{1}{\mathrm{~L}}+\frac{1}{1.5 \mathrm{~L}}+\frac{1}{2 \mathrm{~L}}\right] \tag{1} \end{equation*} $$

Let $\mathrm{L} _{\text {eq }}$ be the length of a single tube of radius $\mathrm{r}$ having rate of flow $\mathrm{V}$; for same pressure head as before. Then

$$ \begin{equation*} \mathrm{V}=\frac{\pi(\mathrm{h} \rho \mathrm{g}) \mathrm{r}^{4}}{8 \eta \mathrm{L} _{\mathrm{eq}}} \tag{2} \end{equation*} $$

From Eqns. (1) and (2) we have

$$ \frac{1}{\mathrm{~L} _{\mathrm{eq}}}=\frac{1}{\mathrm{~L}}+\frac{1}{1.5 \mathrm{~L}}+\frac{1}{2 \mathrm{~L}} $$

or $\quad \mathrm{L} _{\text {eq }}=\frac{6 \mathrm{~L}}{13}$

Streamlines and Tube of Flow

For a streamlined flow of a liquid; a stream line is the actual path followed by the liquid particles. In general stream line is a curve tangent to which at any point gives the direction of the velocity of the particle at that point. Two streamlines can never intersect one another. Streamlines are drawn in such a manner that their number crossing a unit area placed perpendicular to streamline equals speed of flow at that point. Obviously where stream-lines are crowded together, speed of flow is more and vice-versa.

A tube of flow is a collection of streamlines. The speed of flow of the liquid over any cross-section of a tube flow is same. Liquid entering a tube of flow at one end must emerge out from the other. No liquid can come out or enter in from the side walls of tube of flow.

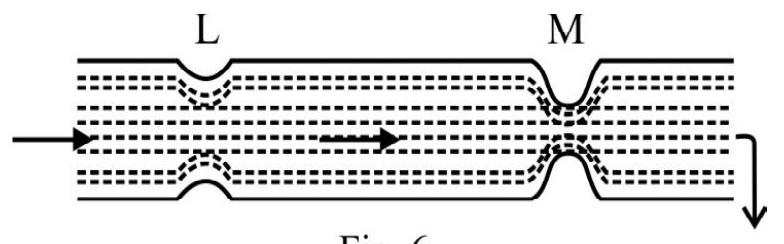
Fig. 6 shows a horizontal tube of flow of varying cross-section. $a _{1}, a _{2}$ is cross-section and $v _{1}, v _{2}$ is speed of flow of liquid at $\mathrm{L}$ and $\mathrm{M}$ respectively. Then

$$ \mathrm{a} _{1} \mathrm{v} _{1}=\mathrm{a} _{2} \mathrm{v} _{2} \quad \text { or } \quad \mathrm{av}=\mathrm{constant} $$

This is known as equation of continuity. If $\mathrm{a} _{1}>\mathrm{a} _{2}$; then $\mathrm{v} _{1}<\mathrm{v} _{2}$.

Critical Velocity

For a liquid flowing in a tube there is a velocity known as critical velocity (v). If speed of flow of liquid (v) is less than or equal to $v_c$ the flow is stream lined. However, it $v^{>} v_e$; the liquid flow is turbulent. The critical velocity (v) depends on:

(1) coefficient of viscosity of liquid $(\eta)$

(2) the density of the liquid ( $\rho$ ) and

(3) the radius of the tube $(\mathrm{r})$

It can be shown that

$$ \mathrm{v} _{\mathrm{c}}=\frac{\mathrm{K \eta}}{\rho \mathrm{r}} $$

$\mathrm{K}$ is a constant.

Reynold’s Number

Obsorne Reynold, in 1883, showed experimentally that the critical velocity ( $\mathrm{v} _{\mathrm{c}}$ ) of a liquid of viscosity $\eta$, flowing in a tube of diameter $\mathrm{D}$ is given by

$$ \mathrm{v} _{\mathrm{c}}=\frac{\mathrm{K \eta}}{\rho \mathrm{D}} $$

$\mathrm{R}$ is a pure number known as Reynold’s number

(1) For R lying between 0 and 2000 the flow is stream lined.

(2) For $\mathrm{R}>3000$; the flow is turbulent.

(3) For $2000<\mathrm{R}<3000$; the flow of liquid is unstable. It may change from streamlined to turbulent flow or vice-versa.

Physically, Reynold number is the ratio of the inertial force per unit area to the viscous force per unit area for a liquid in motion.

Energy of a Liquid in Motion

A liquid in motion possesses three types of energy. These are:

(1) Pressure energy, (2) Potential energy and (3) Kinetic energy.

(1) Pressure Energy: It is the energy of a liquid due to its pressure and is equal to the work done in pushing the liquid against pressure without imparting it any velocity. It can be shown that

$$ \text { Pressure energy per unit mass }=\frac{P}{\rho} $$

$P$ and $\rho$ denote liquid pressure and density respectively.

(2) Potential Energy: It is the energy possessed by the liquid due to its position (or height) above a conveniently chosen reference level. The potential energy per unit mass of a liquid at a height $\mathrm{h}$ $=\frac{\mathrm{mgh}}{\mathrm{m}}=\mathrm{gh}$

(3) Kinetic Energy: Is the energy possessed by a liquid due to its motion (or velocity). For a liquid moving with velocity $\mathrm{v}$,

The K.E per unit mass $=\frac{\frac{1}{2} \mathrm{mv}^{2}}{\mathrm{~m}}=\frac{1}{2} \mathrm{v}^{2}$

Bernoulli’s Theorem

Bernoulli’s theorem for a non-viscous, incompressible liquid is a restatement of law of conservation of energy.

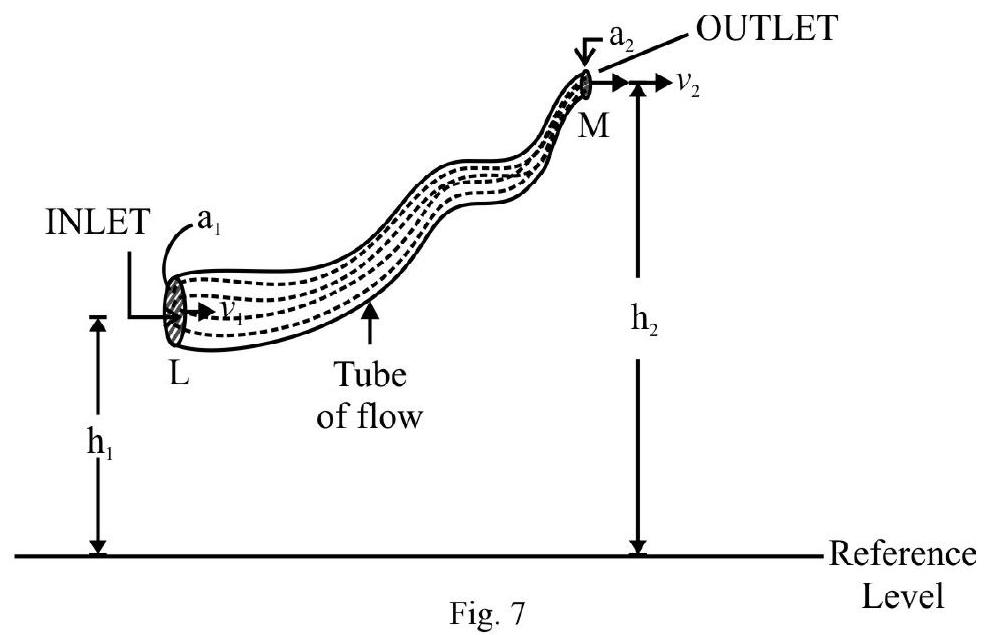
Fig. 7, shows a tube of flow of varying cross-section. Liquid flows from $L$ to M. Let $\mathrm{P} _{1}, \mathrm{v} _{1}$ and $\mathrm{a} _{1}$ denote liquid pressure, speed of flow and area of cross-section at inlet $\mathrm{L} . \mathrm{P} _{2}, \mathrm{v} _{2}$, and $\mathrm{a} _{2}$ are corresponding quantities for the outlet $\mathrm{M}$ of the tube of flow. Since liquid flows from $\mathrm{L}$ to $\mathrm{M}, \mathrm{P} _{1}>\mathrm{P} _{2}$. Applying law of conservation of energy it can be shown that

or

$$ \begin{aligned} & \frac{\mathrm{P} _{1}}{\rho}+\frac{1}{2} \mathrm{v} _{1}^{2}+\mathrm{gh} _{1}=\frac{\mathrm{P} _{2}}{\rho}+\frac{1}{2} \mathrm{v} _{2}^{2}+\mathrm{gh} _{2} \\ & \frac{\mathrm{P}}{\rho}+\frac{1}{2} \mathrm{v}^{2}+\mathrm{gh}=\text { constant } \end{aligned} $$

Expressed in words; the sum of the pressure energy; the kinetic energy and the potential energy per unit mass; in stream lined flow of an ideal liquid, is a constant. This is known as Bernoulli’s theorem.

Applications of Bernoulli’s Theorem

1. Velocity of Efflux

Fig. 8 shows a container having a liquid of density $\rho$ upto a height $\mathrm{H}$ above a narrow opening $\mathrm{O}$. Let $\mathrm{v}$ be the velocity of liquid coming out of $\mathrm{O} . \mathrm{P} _{0}$ is atmospheric pressure. According to Bernoulli’s theorem.

T.E per unit mass at $\mathrm{A}=$ T.E per unit mass at $\mathrm{O}$

$$ \begin{gathered} \frac{\mathrm{P} _{0}}{\rho}+0+\mathrm{gH}=\frac{\mathrm{P} _{0}}{\rho}+\frac{1}{2} \mathrm{v}^{2}+0 \\ \therefore \mathrm{v}=\sqrt{2 \mathrm{gH}} \end{gathered} $$

Let a be the area of cross-section of opening $\mathrm{O}$. The instantaneous rate of flow of liquid is

$$ =\mathrm{av}=\mathrm{a} \sqrt{2 \mathrm{gH}} $$

2. Venturimeter

It is an instrument used to measure rate of flow of a liquid. It is a horizontal tube having broad ends and a constriction, known as throat in the middle as shown in Fig. 9.

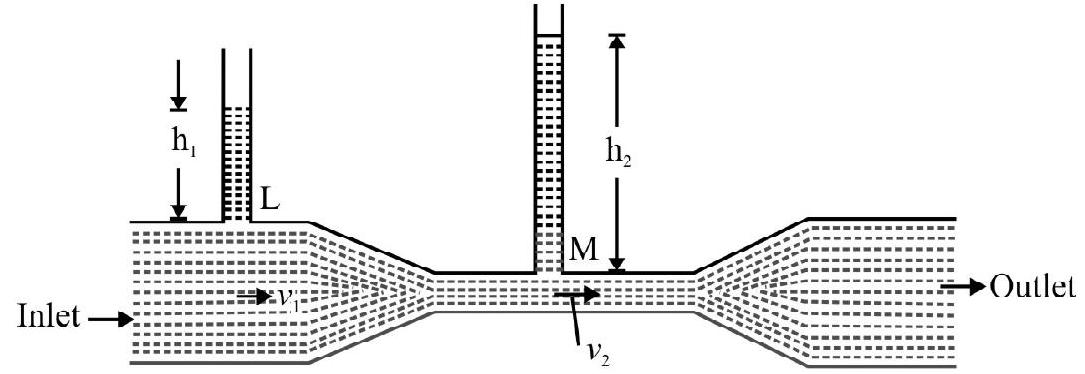
Fig. 9

Let $\mathrm{a} _{1}, \mathrm{P} _{1}, \mathrm{v} _{1}$, denote area of cross-section, pressure and speed of flow at $\mathrm{L}$. The corresponding quantities for point $M$ are $\mathrm{a} _{2}, \mathrm{P} _{2}, \mathrm{v} _{2}$. From equation of continuity $\mathrm{a} _{1} \mathrm{v} _{1}=\mathrm{a} _{2} \mathrm{v} _{2}$. Since $\mathrm{a} _{1}>\mathrm{a} _{2} ; \mathrm{v} _{1}<\mathrm{v} _{2}$. Also from Bernoulli’s theorem applied at point $\mathrm{L}$ and $\mathrm{M}$

$$ \begin{aligned} & \frac{\mathrm{P} _{1}}{\rho}+\frac{1}{2} \mathrm{v} _{1}^{2}+\mathrm{gH}=\frac{\mathrm{P} _{2}}{\rho}+\frac{1}{2} \mathrm{v} _{1}^{2}+\mathrm{gH} \\ & \text { or } \quad \frac{\mathrm{P} _{1}-\mathrm{P} _{2}}{\rho}=\frac{1}{2}\left(\mathrm{v} _{2}^{2}-\mathrm{v} _{1}^{2}\right) \end{aligned} $$

Since $\mathrm{v} _{2}>\mathrm{v} _{1} ; \mathrm{P} _{1}>\mathrm{P} _{2}$. In words in a horizontal stream lined flow where speed of flow increase pressure decreases. Using equation of continuity.

$$ \frac{\mathrm{P} _{1}-\mathrm{P} _{2}}{\rho}=\frac{1}{2}\left(\mathrm{v} _{2}^{2}-\frac{\mathrm{a} _{2}^{2}}{\mathrm{a} _{1}^{2}} \mathrm{v} _{2}^{2}\right) \quad \text { or } \quad \mathrm{v} _{2}=\mathrm{a} _{1} \sqrt{\frac{2\left(\mathrm{P} _{1}-\mathrm{P} _{2}\right)}{\left(\mathrm{a} _{1}^{2}-\mathrm{a} _{2}^{2}\right)}} $$

The rate of flow of liquid in tube $=\mathrm{a} _{2} \mathrm{v} _{2}$

$$ =\mathrm{a} _{1} \mathrm{a} _{2} \sqrt{\frac{2\left(\mathrm{P} _{1}-\mathrm{P} _{2}\right)}{\rho\left(\mathrm{a} _{1}^{2}-\mathrm{a} _{2}^{2}\right)}} $$

Some other applications of above fact that pressure decrease where speed of flow increase are:

(a) Two fast moving boats tend to collide if they come too close to one another. The speed of water in between boats is more than speed on other side of boat. Therefore pressure in between is less than pressure on sides. This produces a net force directed towards one another.

It is for the same reason that a person standing near edge of a railway platform is pulled towards a fast moving train passing by.

(b) In a storm; the roof (thached) of a a hut is blown off without any damage to walls. The speed of flow of air over the roof is very high whereas speed of flow inside hut is quite small. This results in a pressure difference across the roof with pressure being more inside. The net force on roof is sufficient to lift it up without any damage to walls.

(c) Lift of an aeroplane: The wing of an aeroplane (or aerofoil) is designed to be more curved at upper surface as compared to its lower surface as shown in Fig. 10. As aeroplane moves forward some stream lines over the two sides of the wing are shown in Fig. 10. Since upper surface is more curved speed of air flow above is more than the

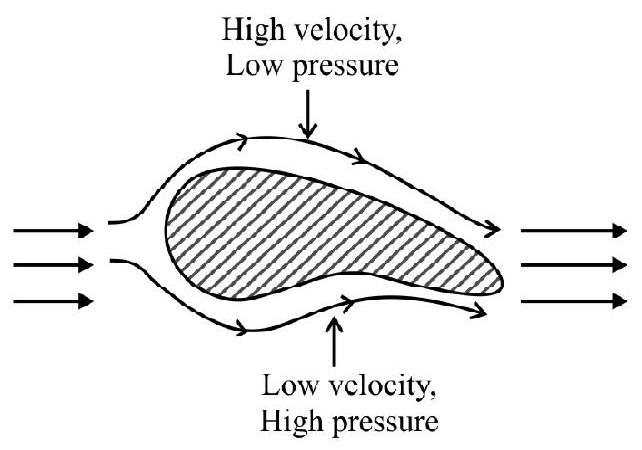
Fig. 10 less curved lower surface. Therefore pressure above wing is less than pressure below. This provides a part of uplift to the aeroplane.

(d) Atomiser or Sprayer: Fig. 11 shows a simple atomiser or sprayer. On pressing rubber bulb air rushes out of a very narrow opening $\mathrm{O}$ at high speed. Pressure at point $\mathrm{A}$ decreases as compared to pressure at $\mathrm{B}$. Liquid rises up the tube and emerges out at A. The blowing air (high speed) breaks up liquid drop into a large number of droplets. This is spraying action.

(3) Curved Path of a Spinning Ball

A spinning ball moving forward deviates from its original path. This is known as Magnus effect. To understand Magnus effect refer to Fig. 12

Fig. 11

Fig. 12 (a) shows stream lines in air if stationary ball only spins. Fig. 12 (b) shows stream lines if ball moves forward without any spin. Fig. 12 (c) shows resultant stream line when ball spins as well as moves forward. The stream lines are more curved below the ball. The speed of flow of air here is more. Therefore pressure at a point above is more than pressure below. There is a resultant force on ball directed downwards. This provides necessary centeripetal force to move the ball along a curved path.

Example-29:

A tank has a circular hole of radius $r$ at a depth $h$ and a square hole of side $\ell=\sqrt{3} r$ at a depth $3 \mathrm{~h}$. What is ratio of rate of flow of a liquid through the two holes?

Show Answer

Solution:

Let $\mathrm{v} _{1}$ and $\mathrm{v} _{2}$ be velocity of efflux from circular and square hole respectively. Then

$$ \mathrm{v} _{1}=\sqrt{2 \mathrm{gh}}, \quad \mathrm{v} _{2} \sqrt{2 \mathrm{~g}(3 \mathrm{~h})} $$

Let $V _{1}$ and $V _{2}$ be rate of flow of liquid through the two holes. Then

$$ \frac{\mathrm{V} _{1}}{\mathrm{~V} _{2}}=\frac{\pi \mathrm{r}^{2} \mathrm{v} _{1}}{\ell^{2} \mathrm{v} _{2}}=\frac{\pi \mathrm{r}^{2} \sqrt{2 \mathrm{gh}}}{3 \mathrm{r}^{2} \sqrt{2 \mathrm{~g}(3 \mathrm{~h})}}=\frac{\pi}{3 \sqrt{3}} $$

Example-30:

Water has a streamlined flow in a horizontal tube. The pressure is $2 \times 10^{4} \mathrm{~Pa}$ at a point where radius of tube is $1 \mathrm{~mm}$ and speed of flow is $2 \mathrm{~ms}^{-1}$. What is pressure at a point where radius of tube is $2 \mathbf{~ m m}$ ? Density of water $=10^{3} \mathbf{k g m}^{-3}$.

Show Answer

Solution:

Let $\mathrm{P} _{1}, \mathrm{~V} _{2}$ be pressure and speed of flow at point where $\mathrm{r}=1 \mathrm{~mm}$. The corresponding quantities for point where radius of tube is $2 \mathrm{~mm}$ are $\mathrm{P} _{2}$ and $\mathrm{v} _{2}$. From Bernoulli’s theorem.

$$ \begin{equation*} \frac{P _{1}}{\rho}+\frac{1}{2} v _{1}^{2}=\frac{P _{2}}{\rho}+\frac{1}{2} v _{2}^{2} \tag{1} \end{equation*} $$

From equation of continuity;

$$ \begin{align*} & 3.14 \times 10^{-6} \times 2=3.14 \times\left(2 \times 10^{-3}\right)^{2} \times \mathrm{v} _{2} \\ & \therefore \quad \mathrm{v} _{2}=\frac{2}{4} \mathrm{~ms}^{-1}=0.5 \mathrm{~ms}^{-1} \tag{2} \end{align*} $$

Given $\mathrm{P} _{1}=2 \times 10^{4} \mathrm{~Pa} ; \rho=10^{3} \mathrm{kgm}^{-3}$.

From Eqns. (1) and (2) we have

$$ \frac{2 \times 10^{4}}{10^{3}}+\frac{1}{2}(2)^{2}=\frac{\mathrm{P} _{2}}{10^{3}}+\frac{1}{2}(0.5)^{2} $$

or $\quad 20+2-0.125=\frac{\mathrm{P} _{2}}{10^{3}}$

$\therefore \mathrm{P} _{2}=2.1875 \times 10^{4} \mathrm{~Pa}$

Example-31:

A cylinder containing a liquid of density $\rho$ has a hole of cross-sectional area $A$ at A depth $h$. The cylinder is counter poised on a balance. The hole is opened what is initial reading of the balance?

Show Answer

Solution:

Let $y$ be height of liquid above hole at $t=t$. The instantaneous velocity of efflux $=\sqrt{2 g y}$. In time interval $\mathrm{t}, \mathrm{t}+\mathrm{dt}$; as liquid emerges out of hole the weight of liquid in cylinder decreases. The decrease in weight equals instantaneous rate of change of linear momentum of liquid emerging out. The instantaenous force, $\mathrm{F}$; is

$$ \begin{aligned} \mathrm{F}=\left(\frac{\mathrm{dm}}{\mathrm{dt}}\right) \mathrm{v} & =\mathrm{v} \frac{\mathrm{d}}{\mathrm{dt}}(\mathrm{V} \rho) \\ = & \rho \mathrm{v} \frac{\mathrm{dv}}{\mathrm{dt}} \end{aligned} $$

where $\frac{\mathrm{dV}}{\mathrm{dt}}$ is instantaneous rate of flow of liquid. Obvisouly

$$ \frac{\mathrm{dV}}{\mathrm{dt}}=\mathrm{Av} $$

$\therefore \mathrm{F}={\mathrm{A} \rho v^{2}}^{2} \mathrm{~A} \rho[2 \mathrm{gy}]$

At $\mathrm{t}=0 ; \mathrm{y}=\mathrm{h}$; therefore

$$ \mathrm{F} _{0}=2 \mathrm{~A} \rho \mathrm{gh} $$

Example-32:

A cylinder of radius $R$ has a hole of radius $r$ at a depth $H$ below the level of liquid in cylinder. At $\mathbf{t}=\mathbf{0}$, the hole is opened. What is time taken to reduce level of liquid to $\frac{\mathrm{H}}{2}$ ?

Show Answer

Solution:

As liquid emerges out of hole $\mathrm{O}$; the level of liquid above $\mathrm{O}$ in cylinder decreases. The velocity of efflux and rate of flow of liquid in cylinder decreases as time increases. Ley y be the instantaneous height of liquid above $\mathrm{O}$. The instantaneous rate of flow of liquid

$$ \frac{d V}{d t}=a \sqrt{2 g y}=\pi r^{2} \sqrt{2 g y} $$

Let $\mathrm{y}+\mathrm{dy}$ be level of liquid in cylinder at $\mathrm{t}=\mathrm{t}+\mathrm{dt}$.

Then $\mathrm{dV}=\pi \mathrm{R}^{2}(-\mathrm{dy})$. Therefore

$$ -\mathrm{R}^{2}\left(\frac{\mathrm{dy}}{\mathrm{dt}}\right)=\mathrm{r}^{2} \sqrt{2 \mathrm{gy}} $$

or $\quad \mathrm{dt}=-\left(\frac{\mathrm{R}^{2}}{\mathrm{r}^{2}}\right) \frac{\mathrm{dy}}{\sqrt{2 \mathrm{gy}}} \hspace{20mm}. . . . . . . . (1)$

Integrating Eqn. (1) within limits $y=H$ to $y=\frac{H}{2}$ gives the desired time t. Therefore

$$ \begin{aligned} & \int _{0}^{\mathrm{t}} \mathrm{dt}=-\left(\frac{\mathrm{R}^{2}}{\mathrm{r}^{2}}\right) _{\mathrm{H}}^{\mathrm{H} / 2} \frac{\mathrm{dy}}{\sqrt{2 \mathrm{gy}}} \\ & \mathrm{t}=-\left(\frac{\mathrm{R}^{2}}{\mathrm{r}^{2}}\right) \frac{1}{\sqrt{2 \mathrm{~g}}}\left|\frac{\mathrm{y}^{1 / 2}}{1 / 2}\right| _{\mathrm{H}}^{\frac{H}{2}} \\ & =\sqrt{\frac{2}{\mathrm{~g}}}\left(\frac{\mathrm{R}^{2}}{\mathrm{r}^{2}}\right)\left[\mathrm{H}^{1 / 2}-(\mathrm{H} /)^{1 / 2}\right] \end{aligned} $$

Example-33:

A non-viscous liquid of density $10^{3} \mathbf{k g m}^{-3}$ has a stream lined flow. $P Q$ is a tube of varying cross-section. The tube is kept in a vertical plane in gravity of earth. The area of cross section of tube at two points $P$ and $Q$ at height of $2 \mathrm{~m}$ and $5 \mathrm{~m}$; as shown in Fig. 14; is $4 \times 10^{-3} \mathrm{~m}^{2}$ and $8 \times 10^{-3} \mathrm{~m}^{2}$ respectively. The velocity of liquid at $P$ is $1 \mathbf{~ m s}^{-1}$. What is work done per unit volume by the pressure and the force of gravity as liquid flow from $P$ to $Q$ ? ( $\left.\mathrm{g}=9.8 \mathrm{~ms}^{-2}\right)$

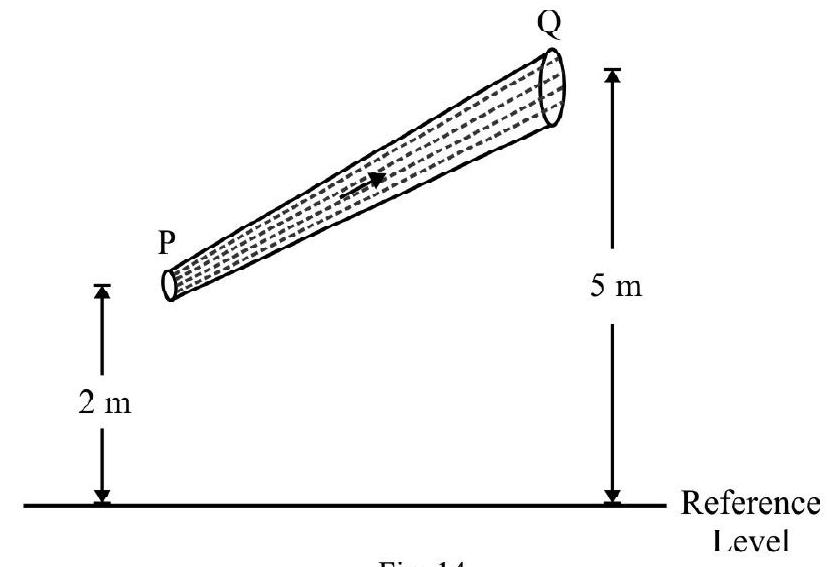
Гig. 14

Show Answer

Solution:

Let $\mathrm{P} _{1}, \mathrm{v} _{1}, \mathrm{~h} _{1}$ denote liquid pressure; speed of flow and height for end $\mathrm{P}$ of cross-sectional area $\mathrm{a} _{1}$. The corresponding quantities for end $\mathrm{Q}$ are $\mathrm{P} _{2}, \mathrm{v} _{2}, \mathrm{~h} _{2}$ and the area of cross-section is $\mathrm{a} _{2}$. From equation of continuity.

$$ \begin{array}{r} \mathrm{a} _{1} \mathrm{v} _{1}=\mathrm{a} _{2} \mathrm{v} _{2} \quad \text { or } \quad \mathrm{v} _{2}=\left(\frac{\mathrm{a} _{1}}{\mathrm{a} _{2}}\right) \mathrm{v} _{1} \\ \therefore \quad \mathrm{v} _{2}=\left(\frac{4 \times 10^{-3}}{8 \times 10^{-3}}\right) \times 1 \mathrm{~ms}^{-1}=0.5 \mathrm{~ms}^{-1} \end{array} $$

From Bernoulli’s theorem

$$ \frac{\mathrm{P} _{1}}{\rho}+\mathrm{gh} _{1}+\frac{1}{2} \mathrm{v} _{1}^{2}=\frac{\mathrm{P} _{2}}{\rho}+\mathrm{gh} _{2}+\frac{1}{2} \mathrm{v} _{2}^{2} $$

$\mathrm{W} _{1}=$ Work done per unit volume by force of pressure $=\mathrm{P} _{1}-\mathrm{P} _{2}$

$$ =\rho g\left(\mathrm{~h} _{2}-\mathrm{h} _{1}\right)+\frac{\rho}{2}\left(\mathrm{v} _{2}^{2}-\mathrm{v} _{1}^{2}\right) $$

Given $\mathrm{h} _{1}=2 \mathrm{~m}, \mathrm{~h} _{2}=5 \mathrm{~m}$; therefore

$$ \begin{aligned} \mathrm{W} _{1}=10^{3} & \times 9.8(5-2)+\frac{10^{3}}{2}\left[(0.5)^{2}-(1)^{2}\right] \\ & =10^{3}\left[9.8 \times 3-\frac{0.75}{2}\right] \\ & \simeq 29.025 \times 10^{3} \mathrm{Jm}^{-3} \end{aligned} $$

$\mathrm{W} _{2}=$ Work done by the force of gravity per unit volume

$$ =\rho \mathrm{g}\left(\mathrm{h} _{2}-\mathrm{h} _{1}\right)=10^{3} \times 9.8 \times(5-2)=29.4 \times 10^{3} \mathrm{Jm}^{-3} $$

(D) HEAT

Heat is a form of energy possessed by a body that produces psychological sensation of hot or cold. In terms of our present knowledge heat energy in due to motion of atoms / molecules of the body under consideration. In general the motion of atoms / molecules involves:

(i) translational motion

(ii) vibrational motion and

(iii) rotational motion

Heat possessed by a body is the sum of kinetic energy of the type (s) of motion involved.

Since heat is energy, SI unit of heat is joule. The CGS unit of heat is calorie. 1 cal. of heat is heat required to raise temperature of 1 gramme of water from $14.5^{\circ} \mathrm{C}$ to $15.5^{\circ} \mathrm{C}$.

Joule showed that heat energy can be converted into mechanical energy and vice-versa. Let $\mathrm{W}$ be work (mechnical) done and $\mathrm{H}$ heat produced. According to Joule;

$$ \frac{\mathrm{W}}{\mathrm{H}}=\text { constant }=\mathrm{J} $$

$\mathrm{J}$ is known as mechanical equivalent of heat. It is $4.18 \mathrm{~J} / \mathrm{cal}^{-1}$.

Temperature

Ordinarily we say temperature of a body is a measure of degree of hotness of coldness of body. A more precise definition is that the temperature of two bodies determines the direction of flow of heat between them when the two are in thermal contact with one another. Two bodies A and B are in thermal contact with one another, in thermal equilibrium with one another if there is no flow of heat between them. A precise definition of temperature using concept of thermal equilibrium is given by the zeroth law of thermodyanmics. According to this law if a body $\mathrm{A}$ is in thermal equilibrium with another body $\mathrm{C}$ and a body $\mathrm{B}$ is also in thermal equilibrium with $\mathrm{C}$; then $\mathrm{A}$ and $\mathrm{B}$ are necessarily in thermal equilibrium with one another. All three bodies $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ are at same temperature.

Measurement of Temperature

A device used to assign a quantitative measure to temperature is known as a thermometer. A thermometer makes use of the variation of some known property of a system that changes with temperature according to a known relation. Several type of thermometers like (i) ideal gas thermometer (ii) electric resistance thermometer (iii) thermoelectric thermometers (iv) mercury thermometer etc. are known.

Scale of Temperature

A scale of thermometer is a way of assigning numerical value to temperature. To define a scale of temperature we must define.

(1) zero of temperature and

(2) the size of one degree

Some common temperature scales that have been / are being used are:

(a) The Celsius Scale

The melting point of ice at S.T.P condition is taken as $0^{\circ} \mathrm{C}$ and boiling point of water at S.T.P as $100^{\circ} \mathrm{C}$. The interval is devided into hundred equal parts. Each part is $1^{\circ} \mathrm{C}$.

(b) The Fahrenheit Scale

The melting point of ice is chosen as $32^{\circ} \mathrm{F}$ and the boiling point as $212^{\circ} \mathrm{F}$. The interval is divided into 180 equal parts. Each part is $1^{\circ} \mathrm{F}$.

(c) The Roumer Scale

The melting point of ice is taken as $0^{\circ} \mathrm{R}$ and boiling point as $80^{\circ} \mathrm{R}$. The interval is divided into 80 equals parts. Each part is $1^{\circ} \mathrm{R}$.

(d) The Kelvin Scale or (The Absolute Scale)

The scale was designed by Lord Kelvin. In this scale the triple point of water is assigned a value of $273 \mathrm{~K}$ (more precisely 273.15). The boiling point of water under S.T.P is assigned a value of $373 \mathrm{~K}$ and the interval is divided into hundred equal parts and one part is $1 \mathrm{~K}$. Obvisouly size of degree in Kelvin scale and Celsius scale is same. However the zero of the two scales do not coincide.

Let C, F, R and K denote the temperature of a body on Celsius; Fahrenheit, Romer and Kelvin scale respectively. Then

$$ \frac{C}{5}=\frac{F-32}{9}=\frac{R}{4} $$

and $\mathrm{K}=273+\mathrm{C}$

Obviously $1^{\circ} \mathrm{C} \neq 1 \mathrm{~K}$, but a change of $1^{\circ} \mathrm{C}$ equals a change of $1 \mathrm{~K}$.

Thermal Expansion

1. SOLIDS

All solids expand on heating. This is known as thermal expansion. In terms of interatomic / molecular theory, at any given temperature there is a definite equilibrium distance between the atoms / molecules. When heat is given to the solid, the amplitude of oscillations of atoms / molecules increases; resulting in an increase in effective interatomic / molecular distance. This is thermal expansion. Let $\mathrm{U}$ be the potential energy of atoms / molecules a distance $\mathrm{r}$ apart. Fig. 1 shows U vs $r$ graph. $\mathrm{O}$ is the equilibrium position. Note graph is not symmetrical about $\mathrm{O}$.

Fig. 1

Thermal expansion of solids is of three type as described in what follows.

(a) Linear Expansion: When length of a body changes due to change in temperature we have linear expansion. $\mathrm{Let} \mathrm{~L} _{0}$ and $\mathrm{L} _{\mathrm{t}}$ denote length of a body at $0^{\circ} \mathrm{C}$ and $\mathrm{t}^{\circ} \mathrm{C}$ respectively. Experiemnts show that

$$ \mathrm{L} _{\mathrm{t}}=\mathrm{L} _{0}(1+\alpha \mathrm{t}) $$

$\alpha$ is a constant, depending on the nature of material. It is known as coefficient of linear expansion. Obviously.

$$ \alpha=\frac{\mathrm{L} _{\mathrm{t}}-\mathrm{L} _{0}}{\mathrm{~L} _{0} \mathrm{t}}=\frac{\Delta \mathrm{L}}{\mathrm{L} _{0} \mathrm{t}} $$

In words, coefficient of linear expansion is change in length per unit length per degree change in temperature. Its SI unit is $(\mathrm{K})^{-1}=\left({ }^{0} \mathrm{C}\right)^{-1}$.

(b) Superficial Expansion: When surface area of a body changes due to change of temperature we have superfacial expansion. Let $\mathrm{A} _{0}$ and $\mathrm{A} _{\mathrm{t}}$ denote surface area at $0^{\circ} \mathrm{C}$ and $t^{\circ} \mathrm{C}$ respectively. Experiments show that

$$ \mathrm{A} _{\mathrm{t}}=\mathrm{A} _{0}(1+\beta \mathrm{t}) $$

$\beta$ is a constant, depending on nature of material of the body. It is known as coefficient of superficial expansion. Obvisouly

$$ \beta=\frac{\mathrm{A} _{\mathrm{t}}-\mathrm{A} _{0}}{\mathrm{~A} _{0} \mathrm{t}}=\frac{\Delta \mathrm{A}}{\mathrm{A} _{0} \mathrm{t}} $$

(c) Cubical Expansion: The change in volume of a body due to change in temeprature is known as cubical expansion. Let $\mathrm{V} _{0}$ and $\mathrm{V} _{\mathrm{t}}$ denote volume of a body at $0^{\circ} \mathrm{C}$ and $t^{\circ} \mathrm{C}$ respectively. Experiments show that

$$ \mathrm{V} _{\mathrm{t}}=\mathrm{V} _{0}(1+\gamma \mathrm{t}) $$

$\gamma$ is a constant, depending on nature of body. It is known as coefficient of cubical expansion. Obvisouly

$$ \gamma=\frac{\mathrm{V} _{\mathrm{t}}-\mathrm{V} _{\mathrm{c}}}{\mathrm{V} _{0} \mathrm{t}}=\frac{\Delta \mathrm{V}}{\mathrm{V} _{0} \mathrm{t}} $$

For a homogeneous, isotropic solid, it can be shown that

$$ \begin{array}{r} \gamma \simeq 3 \alpha ; \quad \beta \simeq 2 \alpha \\ \text { or } \quad \alpha: \beta: \gamma:: 1: 2: 3 \end{array} $$

For an anisotropic material; let $\alpha _{x}, \alpha _{y}$ and $\alpha _{z}$ be coefficient of linear expansion along $x-, \mathrm{y}-$ and $\mathrm{z}$-axis respectively. Then

$$ \beta=\alpha _{x}+\alpha _{y} ; \quad \Upsilon=\alpha _{x}+\alpha _{y}+\alpha _{z} $$

Practical Applications of Thermal Expansion

(i) Railway lines are laid with a small gap between two iron rails.

(ii) There is an appropriate space between the iron girders used to support a bridge.

(iii) The iron rim around the wooden wheel of a cart is slightly smaller in diameter than the wheel.

(iv) To keep correct time during summer and winter; pendulum clocks are made of an alloy invar. This alloy has a negligible coefficient of linear expansion.

2. EXPANSION OF LIQUIDS

Since liquids do not have a definite shape or size we do not talk about the linear or superficial expansion of a liquid. We can only talk about cubical expansion. Since a liquid is put in a container and when liquid is heated and its volume increases the container also expands. If we do not take into account the expansion of the container, we have the apparent expansion of the liquid. However if we take into account the expansion of the container we observe the real expansion of the liquid.

(a) Coefficient of apparent expansion; $\gamma _{\mathrm{a}}$; is the apparent change in volume per unit volume per degree change in temperature, i.e. $\gamma _{\mathrm{a}}=\frac{(\Delta \mathrm{V}) _{\mathrm{a}}}{\mathrm{V} _{0} \mathrm{t}}$

(b) Coefficient of real expansion; $\gamma _{\mathrm{r}}$; is the real change in volume per unit volume per degree change in temperature; i.e. $\gamma _{\mathrm{r}}=\frac{(\Delta \mathrm{V}) _{\mathrm{r}}}{\mathrm{V} _{0} \mathrm{t}}$

Let $\gamma _{\mathrm{g}}$ be the coefficient of cubical expansion of the container. Obviously

$$ \gamma _{\mathrm{r}}=\gamma _{\mathrm{a}}+\gamma _{\mathrm{g}} $$

Water has a very peculiar behaviour when heated from $0^{\circ} \mathrm{C}$ onwards. From $0^{\circ} \mathrm{C}$ to $4^{\circ} \mathrm{C}$ volume of water decreases as temperature increases i.e. $\gamma$ is a negative number. However on heating water above $4^{0} \mathrm{C}$; its volume increases as temperature increases i.e. $\gamma$ is a positive number.

Example-34:

A brass wire $1.8 \mathrm{~m}$ long at $27^{\circ} \mathrm{C}$ is held taut with little tension between two rigid supports. If the wire is cooled to $-39^{\circ} \mathrm{C}$ what is tension developed in the wire of diameter is $2.0 \mathrm{~mm}$ ? Coefficient of linear expansion of brass $=2 \times 10^{-5}\left({ }^{0} \mathrm{C}\right)^{-1}$. Young’s modulus of brass $=0.9 \times 10^{11} \mathrm{~Pa}$.

Show Answer

Solution:

Let $\Delta \ell$ be the decrease in length of wire (if it were free) due to change in temperature.

$$ \begin{aligned} & \Delta \ell=\ell . \alpha(\Delta \theta) \\ & \text { or } \quad \frac{\Delta \ell}{\ell}=\alpha(\Delta \theta) \\ & =2 \times 10^{-5} \times 66=132 \times 10^{-5} \end{aligned} $$

This is elongational strain in wire due to tension in rigid support. Let $\mathrm{F}$ be force of tension on each support. By definition of Young’s modulus.

$$ \begin{aligned} \mathrm{Y} & =\frac{\mathrm{F} / a}{(\mathrm{~A} / t)} \ = 0.9 \times 10^{11} & =\frac{\mathrm{F}}{3.14 \times\left(10^{-3}\right)^2 \times 132 \times 10^{-5}} \end{aligned} $$

or $\quad \mathrm{F}=0.9 \times 10^{11} \times 3.14 \times 132 \times 10^{-11} \mathrm{~N}$

$\simeq 373 \mathrm{~N}$

Example-35:

Coefficient of cubical expansion of benzene and wood are $1.2 \times 10^{-3}\left({ }^{0} \mathrm{C}\right)^{-1}$ and $1.5 \times 10^{-4}\left({ }^{0} \mathrm{C}\right)^{-1}$. Density at $0^{0} \mathrm{C}$ of the two is $0.9 \times 10^{3} \mathrm{kgm}^{-3}$ and $0.88 \times 10^{3} \mathrm{kgm}^{-3}$. At what temperature wood will just sink is benzene?

Show Answer

Solution:

Let $\mathrm{V} _{0}$ and $\mathrm{V}$ be volume of a body of mass $\mathrm{M}$ at $0^{\circ} \mathrm{C}$ and $\mathrm{t}^{\circ} \mathrm{C}$ respectively. Then

$\rho _{0}=$ Density of body at $0^{\circ} \mathrm{C}=\frac{\mathrm{M}}{\mathrm{V} _{0}}$

$\rho _{t}=$ Density of body at $t^{\circ} \mathrm{C}=\frac{M}{V}$

Also $\mathrm{V}=\mathrm{V} _{0}(1+\gamma \mathrm{t})$; therefore

$$ \frac{\rho}{\rho _{0}}=\frac{V _{0}}{V}=(1+\gamma t)^{-1} \simeq(1-\gamma t) $$

or

$$ \rho=\rho _{0}(1-\gamma t) $$

Wood will just skin in benzene, if the density of wood equals that of benzene; i.e. $\rho _{w}=\rho _{B}$ at $t=t^{0} \mathrm{C}$. Therefore

$$ \begin{aligned} & 0.88 \times 10^{+3}\left[1-1.5 \times 10^{-4} \times \mathrm{t}\right]=0.9 \times 10^{3}\left[1-1.2 \times 10^{-3} \times \mathrm{t}\right] \\ & {\left[0.9 \times 1.02 \times 10^{-3}-0.88 \times 0.15 \times 10^{-3}\right] \mathrm{t}=0.9-0.88} \end{aligned} $$

or

$$ \mathrm{t}=\frac{0.02}{(1.08-0.132) \times 10^{-3}} \simeq 21.1^{\circ} \mathrm{C} $$

Example-36:

A capillary tube of area of cross-section a is filled with a mercury column of length $L$ as shown in Fig. 2. The increase in length of mercury column when temperature increases by $\Delta \theta$ is

( $\alpha=$ coefficient of linear expansion of capillary, $\gamma=$ coefficient of cubical expansion of mercury)

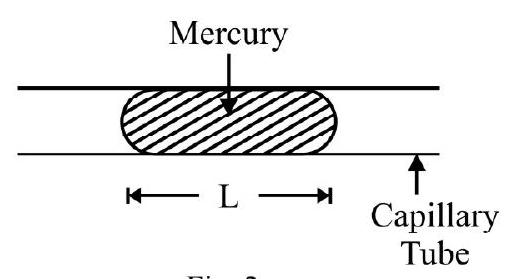
Fig. 2

(1) $\mathbf{L}(\gamma-\alpha) \Delta \theta$

(2) $\mathbf{L}(\gamma+\alpha) \Delta \theta$

(3) $\mathrm{L}(\gamma-2 \alpha) \Delta \theta$

(4) $\mathrm{L}(\gamma+2 \alpha) \Delta \theta$

Show Answer

Solution:

When temperature increases by $\Delta \theta$; let ’ $a$ ’ and ’ $L$ ’ be the area of cross-section of tube and length of mercury column.

$\mathrm{V}^{\prime}=$ volume of mercury column when temperature increases $=\mathrm{a}^{\prime} \mathrm{L}^{\prime}$

$\mathrm{V}=$ The initial volume of mercury column $=\mathrm{a} . \mathrm{L}$

We have

$$ \begin{gathered} \mathrm{V}^{\prime}=\mathrm{V}(1+\gamma \Delta \theta), \quad \text { and } \quad \mathrm{a}^{\prime}=\mathrm{a}(1+\alpha 2 \Delta \theta) \\ \therefore \quad \mathrm{L}^{\prime}=\frac{\mathrm{V}^{\prime}}{\mathrm{a}^{\prime}}=\frac{\mathrm{V}(1+\gamma \Delta \theta)}{\mathrm{a}(1+2 \alpha \Delta \theta)}=\mathrm{L}\left(\frac{1+\gamma \Delta \theta}{1+2 \alpha \Delta \theta}\right) \\ =\mathrm{L}(1+\gamma \Delta \theta)(1+2 \alpha \Delta \theta)^{-1} \end{gathered} $$

Using Binomial expansion and retaining first order terms, we have

$$ \begin{aligned} & \mathrm{L}^{\prime}=\mathrm{L}(1+\gamma \Delta \theta)(1-2 \alpha \Delta \theta) \\ & \simeq \mathrm{L}[1+(\gamma-2 \alpha) \Delta \theta] \end{aligned} $$

The increase in length of mercury column $=\mathrm{L}^{\prime}-\mathrm{L}$

$$ =\mathrm{L}(\gamma-2 \alpha) \Delta \theta $$

The correct choice is (3)

Example-37:

A bimetallic strip is formed out of two identical strips, one of copper and other of brass. The coefficients of linear expansion of the two are $\alpha _{1}$ and $\alpha _{2}\left(\alpha _{2}<\alpha _{1}\right)$ respectively. On heating the bimetallic strip through a temperature $\Delta \mathrm{T}$; the strip bends into an arc of a circle. What is radius of curvature of the strip?

Show Answer

Solution:

Let ’ $\ell$ ’ and ’ $t$ ’ be the initial length and thickness of two strips. Let $\ell$ and $\ell _{2}$ be the lengh of the two when temperature rises by $\Delta \mathrm{T}$. Since $\alpha _{2}>\alpha _{1}, \ell _{2}>\ell _{1}$. Due to this the bi-metallic strip bends into arc of a circle. Let $\mathrm{R}, \mathrm{R} _{1}$ and $\mathrm{R} _{2}$ be the mean radius; radius of copper and brass part as shown in Fig. 3. Obvisouly

$$ \begin{equation*} \mathrm{R} _{2}-\mathrm{R} _{1}=\mathrm{t} \tag{1} \end{equation*} $$

Let $\theta$ be the angle subtended at center $\mathrm{O}$ by the curved bi-metallic strip. Then

$$ \ell _{1}=\mathrm{R} _{1} \theta ; \ell _{2}=\mathrm{R} _{2} \theta $$

or $\quad \ell _{2}-\ell _{1}=\theta\left[\mathrm{R} _{2}-\mathrm{R} _{1}\right]=\theta \times \mathrm{t}$

$$ \begin{equation*} [\mathrm{Clf}=\mathrm{n}(1)] \tag{2} \end{equation*} $$

Also, $\quad \ell _{1}=\ell\left(1+\alpha _{1} \Delta \mathrm{T}\right) ; \ell _{2}=\ell\left(1+\alpha _{2} \Delta \mathrm{T}\right)$

or $\quad \ell _{2}-\ell _{1}=\ell\left(\alpha _{2}-\alpha _{1}\right) \Delta \mathrm{T} \hspace{20mm}. . . . . . . . (3)$

Also $\quad \ell=\mathrm{R} \theta$. From Eqns. (2) and (3) we have

$$ \theta=\frac{\ell}{R}=\frac{\left(\ell _{2}-\ell _{1}\right)}{\mathrm{t}} $$

or $\quad \frac{\ell}{\mathrm{R}}=\frac{\ell\left(\alpha _{2}-\alpha _{1}\right) \Delta \mathrm{T}}{\mathrm{t}}$

$\therefore \quad \mathrm{R}=\frac{\mathrm{t}}{\left(\alpha _{2}-\alpha _{1}\right) \Delta \mathrm{T}}$

Specific Heat Capacity

Consider of a body of mass m. Let $\Delta \mathrm{H}(\equiv \Delta \mathrm{Q})$ be the small amount of heat required to raise the temperature from $\theta^{0} \mathrm{C}$ to $(\theta+\Delta \theta)^{0} \mathrm{C}$. Experiments show that $\Delta \mathrm{Q}$ depends on

(1) mass of body (m) and

(2) nature of material of body

We write

$$ \begin{equation*} \Delta \mathrm{Q}=\mathrm{m}(\Delta \theta) . \mathrm{C} \tag{1} \end{equation*} $$

where $\mathrm{C}$ is a constant depending on nature of body $\mathrm{C}$ is known as specific heat capacity (or specific heat) of the body. Obviously.

$$ \begin{equation*} \mathrm{C}=\left(\frac{\Delta \mathrm{Q}}{\mathrm{m} \Delta \theta}\right) \tag{2} \end{equation*} $$

The specific heat capacity; $\mathrm{C}$; of a body is numerically equal to heat required to raise the temperature of unit mass by one degree. The CGS unit of $\mathrm{C}$ is $\mathrm{cal} / \mathrm{g}^{\circ} \mathrm{C}$ and the $\mathrm{SI}$ unit is $\mathrm{J} / \mathrm{kg} \quad \mathrm{K}$. Obvisouly

$$ \frac{1 \mathrm{cal}}{\mathrm{g}^{0} \mathrm{C}}=\frac{4.18 \mathrm{~J}}{\left(10^{-3} \mathrm{~kg}\right) \mathrm{K}}=4.18 \times 10^{3} \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1} $$

The specific heat of a material depends its state i.e. solid, liquid or gaseous. For example specific heat of ice. $=0.5 \mathrm{cal} \quad \mathrm{g}^{-1}\left({ }^{\circ} \mathrm{C}\right)^{-1}$. Specific heat of water $=1 \mathrm{cal} \quad \mathrm{g}^{-1}\left({ }^{\circ} \mathrm{C}\right)^{-1}$ and specific heat of steam $=0.47 \mathrm{cal} \quad \mathrm{g}^{-1}\left({ }^{0} \mathrm{C}\right)^{-1}$.

The molar specific heat of a material is heat required to raise the temperature of 1 gram-mole of material by one degree. Clearly

Molar specific heat $=$ Molar mass $\times$ specific heat capacity

Expressed mathematically

$$ \mathrm{C}=\text { Molar specific heat }=\frac{1}{\mathrm{n}}\left(\frac{\mathrm{dQ}}{\mathrm{d} \theta}\right) $$

$\mathrm{n}=$ number of moles of the material.

Variation of Specific Heat of Solids with Temperature

According to Dulong and Petit the specific heat per mole of a pure crystalline solid is nearly 6 cal mole ${ }^{-1} \mathrm{~K}^{-1}$. This is known as Dulong and Petit’s law and is nearly obeyed by a large number of substance near room temperature. However at low temperatures the specific heat decreases rapidly as show in Fig. 4. $\mathrm{C} _{\mathrm{v}}$ approaches zero as temeprature approaches absolute zero (i.e. OK).

Specific Heat of Water

Rowland experimentally determined accurately specific heat of water at different temperatures. Water has a very peculiar behaviour. Specific heat of water decreases as temperature rises from $0^{\circ} \mathrm{C}$ to $15^{\circ} \mathrm{C}$. For temperatures above $15^{\circ} \mathrm{C}$ specific heat increases as temperature increases. The variation is shown in Fig. 5. At $0^{\circ} \mathrm{C}$, $\mathrm{C}=1.008 \mathrm{cal} \quad \mathrm{g}^{-1}\left({ }^{\circ} \mathrm{C}\right)^{-1}$. It is almost $1.0 \mathrm{cal} \quad \mathrm{g}^{-1}\left({ }^{\circ} \mathrm{C}\right)$ at $15^{\circ} \mathrm{C}$. At $100^{\circ} \mathrm{C}$; it is $1.0057 \mathrm{cal} \quad \mathrm{g}^{-1}\left({ }^{\circ} \mathrm{C}\right)^{-1}$

Fig. 5

Thermal Capacity and Water Equivalent

The thermal capacity of a body is amount of heat required to raise its temperature by $1^{\circ} \mathrm{C}$ (or $1 \mathrm{~K}$ ). Obviously

Thermal capacity $=\mathrm{mc}$

where $m$ is mass of body and $c$ is the specific heat of body.

Water equivalent of a body is the mass of water which absorbs or evolves same amount of heat as is done by the body in changing its temperature by same amount. For a body of mass m; specific heat c; water equivalent $\omega$ is

$$ \begin{aligned} & \Delta \mathrm{Q}=\mathrm{m} \cdot \mathrm{c}(\Delta \theta)=\mathrm{w} \times 1 \times(\Delta \theta) \\ & \therefore \mathrm{w}=\mathrm{mc} \end{aligned} $$

Water equivalent of a body is numerically equal to its thermal capacity.

Latent Heat

When a change of state takes place, the heat absorbed or liberated does not produce any change in temperature. This is known as latent heat. Let $m$ be mass undergoing a change of state; the heat absorbed or liberated is

$$ \mathrm{H}(\equiv \mathrm{Q})=\mathrm{mL} $$

Latent heat is numerically equal to heat required to change state of unit mass without any change in temperature. For example ice at $0^{\circ} \mathrm{C}$ absorbs heat and gets converted into water at $0^{\circ} \mathrm{C}$ i.e.changes from solid to liquid state. This is known as latent heat of fusion. Latent heat of fusion of ice is $80 \mathrm{cal} \quad \mathrm{g}^{-1}$. When the change of state takes place from liquid to gaseous state at boiling point, we have latent heat of vaporisation. Water at $100^{\circ} \mathrm{C}$ is converted into steam at $100^{\circ} \mathrm{C}$. This involves latent heat of vaporisation. For water it is $540 \mathrm{cal} \quad \mathrm{g}^{-1}$.

Calorimetery

A calorimeter is a copper hollow cylindrical vassel provided with a stirrer; and an insulated lid. It is placed inside a heat insulated container like wood. A thermometer is inserted to note the temperature of calorimeter and contents.

Consider a calorimeter of mass $m$, made of material of specific heat $c _{1}$; containing, say, water of mass $M$ at a temperature $\theta _{1}^{0} \mathbf{C}$. A hot body of mass $\mathbf{M} _{1}$; at temperature $\theta _{2}^{0} \mathrm{C}\left(\theta _{2}>\theta _{1}\right)$ is put inside thermally insulated colorimeter. The equilibrium temperature of calorimeter and contents is $\theta^{\circ} \mathrm{C}$. According to principle of calorimetery.

Heat lost by hot body $=$ Heat gained by cold body.

Let $\mathrm{C}$ be specific heat of solid, then

$\mathrm{M} _{1} \mathrm{c}\left[\theta _{2}-\theta\right]=$ Heat lost by hot solid

$\left(M+\mathrm{mc} _{1}\right) \times 1 \times\left[\theta-\theta _{1}\right]=$ Heat gained by calorimeter and contents.

$\therefore \quad \mathrm{M} _{1} \mathrm{c}\left(\theta _{2}-\theta\right)=\left(\mathrm{M}+\mathrm{m} _{1} \mathrm{c} _{1}\right)\left(\theta-\theta _{1}\right)$

Knowing all parameters involved; $\mathrm{c}$ is easily calculated.

Example-38:

A calorimeter of water equivalent $25 \mathrm{~g}$ contains $75 \mathrm{~g}$ of water at $20^{\circ} \mathrm{C}$. A solid of mass $30 \mathrm{~g}$; specific heat $0.6 \mathrm{cal} \quad \mathrm{g}^{-1}\left({ }^{\circ} \mathrm{C}\right)^{-1}$ heated to $100^{\circ} \mathrm{C}$ is put inside a themally insulated calorimeter. What is equilibrium temperature of calorimeter and contents?

Show Answer

Solution:

Let $\theta$ be the equilibrium temperature of calorimeter and contents. Then

Heat gained by calorimeter and contents $=(75+25) \times 1 \times[\theta-20]$

$$ =100[\theta-20] \mathrm{cal} $$

Heat lost by the solid $=30 \times 0.6 \times[100-\theta]$ cal.

From principle of calorimetery

Heat gained $=$ Heat lost

or

$$ 100[\theta-20]=18[100-\theta] $$

or $\quad \theta=\frac{3800}{118} \simeq 32.2^{\circ} \mathrm{C}$

The equilibrium temperature of calorimeter and contents is $32.2^{\circ} \mathrm{C}$

Example-39:

A copper calorimeter of mass $50 \mathrm{~g}$ contains $105 \mathrm{~g}$ of water at $80^{\circ} \mathrm{C} .25 \mathrm{~g}$ of ice at $-10^{\circ} \mathrm{C}$ is added to thermally insultaed calorimeter. What is equilibrium temperature of calorimeter and contents? Given

Specific heat of $\mathrm{Cu}=0.4 \mathrm{cal} \quad \mathrm{g}^{-1}\left({ }^{\circ} \mathrm{C}\right)^{-1}$

Specific heat of ice $=0.5 \mathrm{cal} \quad \mathrm{g}^{-1}\left({ }^{\circ} \mathrm{C}\right)^{-1}$

Latent heat of fusion of ice $=80 \mathrm{cal} \quad \mathrm{g}^{-1}$

Show Answer

Solution:

Let $\theta$ be the equilibrium temperature of calorimeter and contents. Heat is lost by water and calorimeter. Obvisouly

Total heat lost $=$ Heat lost by calorimeter + Heat lost by water inside calorimeter

$$ \begin{align*} & =50 \times 0.4 \times(80-\theta)+105 \times 1 \times(80-\theta) \\ & =(20+105)(80-\theta)=125(80-\theta) \mathrm{cal} \tag{1} \end{align*} $$

Heat is gained by

(i) ice in raising its temperature from $-10^{\circ} \mathrm{C}$ to $0^{\circ} \mathrm{C}=25 \times 0.5 \times(10)=125 \mathrm{cal}$.

(ii) ice at $0^{\circ} \mathrm{C}$ to melt (i.e. latent heat) and get converted into water at $0^{\circ} \mathrm{C}=25 \times 80=2000 \mathrm{cal}$.

(iii) water obtained at $0^{\circ} \mathrm{C}$ to raise its temmperature from $0^{\circ} \mathrm{C}$ to $\theta^{\circ} \mathrm{C}=25 \times 1 \times \theta=25 \quad \theta$

$\therefore$ Total heat gained $=125+2000+25 \theta=[2125+25 \theta]$ cal.. . . . . . . . . . (2)

From principle of calorimetery;

$$ 125(80-\theta)=2125+25 \quad \theta $$

$\therefore \quad \theta=\frac{7875}{150} \simeq 52.5^{\circ} \mathrm{C}$

Example-40:

A calorimeter of water equivalent $20 \mathrm{~g}$ contains $60 \mathrm{~g}$ of water at $70^{\circ} \mathrm{C}$. $10 \mathrm{~g}$ of steam at $100^{\circ} \mathrm{C}$ is passed on to the thermally insulated calorimeter. What is equilibrium temperature of calorimeter and contents?

Latent heat of vaporisation of water $=540 \mathrm{k} \mathrm{cal}^{-1}$

Show Answer

Solution:

Let $\theta$ be the equilibrium temperature of calorimeter and contents.

Heat gained by calorimeter + water $=(20+60) \times 1 \times(\theta-70)$

$$ =80(\theta-70) \mathrm{cal} $$

Heat lost by steam $=$ Heat lost in condensing + Heat lost by water obtained at $100^{\circ} \mathrm{C}$ to $\theta^{\circ} \mathrm{C}$

$$ \begin{aligned} & =10 \times 540+10 \times 1 \times(100-\theta) \\ & =(6400-10 \quad \theta) \mathrm{cal} \end{aligned} $$

From principle of calorimetery

$$ 80(\theta-70)=6400-10 \quad \theta $$

or

$$ \theta=\frac{12000}{90}=133.3^{\circ} \mathrm{C} $$

This is not possible. If this happens temperature of steam at $100^{\circ} \mathrm{C}$ rises to $133.3^{\circ} \mathrm{C}$ and the calorimeter and contents also accquire temperature of $133.3^{\circ} \mathrm{C}$. This means there is only gain of heat! This is not possible. What is mistake in above calculation? We have assumed that the entire mass of steam condenses into water at $100^{\circ} \mathrm{C}$. This does not take place. Let $\mathrm{H} _{\text {max }}$ be maximum heat calorimeter and water can take to accquire a temperature of $100^{\circ} \mathrm{C}$. Obvisouly

$$ \begin{aligned} & \mathrm{H} _{\max }=(20+60) \times 1 \times(100-70) \mathrm{cal} \\ & =2400 \mathrm{cal} \end{aligned} $$

Once calorimeter and content accquire $100^{\circ} \mathrm{C}$; there is no flow of heat from steam to calorimeter and content. Therefore

$$ \text { Mass of steam condessed }=\frac{2400}{540} \mathrm{~g} \simeq 4.44 \mathrm{~g} $$

Only $4.44 \mathrm{~g}$ of steam condenses. Now calorimeter and steam are in thermal equilibrium i.e. at same temperature. The equilibrium temperature, therefore, is $100^{\circ} \mathrm{C}$.

TRANSFER OF HEAT

Introduction

Heat can be transferred from one place to another by three different ways. These are (i) conduction (ii) convection and (iii) radiation.

In a solid heat is transferred from one end to the other by conduction. In liquids and gases; the process is convection. Heat from a “hot body” (i.e. a body at high temperature) flows to distant places by thermal radiation. Earth is getting heat from Sun by radiation. We will discuss the three process one by one briefly.

CONDUCTION

In conduction a medium (i.e. solid material) is required. During the flow of heat the atoms / molecules of material do not move in the direction of heat flow. The atoms / molecules vibrate about their respective mean position. Heat is transferred from atoms / molecules in one layer to atoms / molecules in adjoining layer and the process repeats itself.

Thermal Conductivity

Consider a metal rod PQ of length $L$; area of cross section $\mathrm{A}$. The ends $\mathrm{P}$ and $\mathrm{Q}$ of rod are maintained at constant temperature $\theta _{1}^{0} \mathrm{C}$ and $\theta _{2}^{0} \mathrm{C}$ respectively $\left(\theta _{1}>\theta _{2}\right)$. Heat enters the hot end $P$; flows along rod and comes out from the other end Q. A number of thermometer are placed along the length of rod as shown in Fig. 6.

Initially we have a “Transient state”. In transient state heat recieved by any cross-section of rod is partially retained by the atoms / molecules at the cross-section and a part is passed on the atoms / molecules in next cross-section. The temperature of any cross-section starts rising and changes (increases) as time increases. The reading of different thermometers is different and varies with time. After sufficiently long time the metal rod acquires steady state. Now temperature of different parts of rod is different but does not change with time. During steady state the heat recieved by atoms / molecules in any cross-section is completely passed on to the atom/ molecules in adjoining layer. Whatever heat enters rod at hot end; emerges out at the cold end.

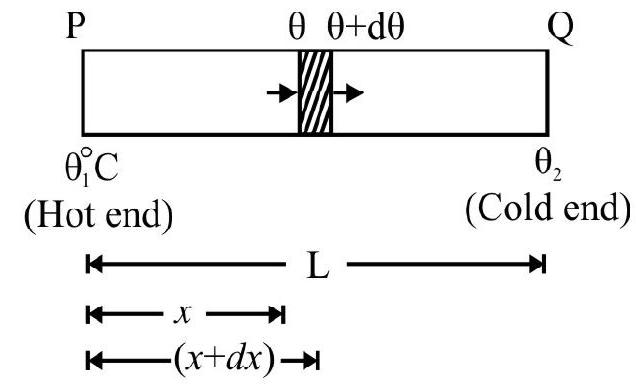
Fig. 7

Consider a small element of rod defined by $x$ and $(x+\mathrm{d} x)$ as shown in Fig. 7. The rate of flow of heat $\frac{\mathrm{dQ}}{\mathrm{dt}}$; under steady state is:

(i) directly proportional to $\frac{\mathrm{d} \theta}{\mathrm{d} x}$; known as temperature gradient.

(ii) directly proportional to area of cross-section (A). Combining the above factor, we say

$$ \begin{equation*} \frac{\mathrm{dQ}}{\mathrm{dt}}=-\mathrm{KA} \frac{\mathrm{d} \theta}{\mathrm{d} x} \tag{1} \end{equation*} $$

$\mathrm{K}$ is a constant depending on nature of material of rod. It is known as thermal cnoductivity. Note that in Eqn. (1) $; \frac{\mathrm{d} \theta}{\mathrm{d} x}$ is a negative number; therefore $\frac{\mathrm{dQ}}{\mathrm{dt}}$ is a positive quantity. For a rod having a constant temperature gradient; as shown in Fig. 7;

$$ \frac{\mathrm{d} \theta}{\mathrm{d} x}=\frac{\theta _{2}-\theta _{1}}{\mathrm{~L}}=-\left(\frac{\theta _{1}-\theta _{2}}{\mathrm{~L}}\right) $$

Eqn. (1) can be rewritten as

$\frac{\mathrm{dQ}}{\mathrm{dt}}=$ The rate of flow of heat $=\operatorname{KA}\left(\frac{\theta _{1}-\theta _{2}}{\mathrm{~L}}\right) \hspace{40mm} . . . . . . (2)$

From Eqn. (1); if $\mathrm{A}=1$ unit, $\frac{\mathrm{d} \theta}{\mathrm{d} x}=1$ unit, $\left|\frac{\mathrm{dQ}}{\mathrm{d} x}\right|=\mathrm{K}$

The coefficient of thermal conductivity is numerically equal to the rate of flow of heat across a rod of unit cross-section having a unit difference of temperature across unit length of rod. SI unit of $\mathrm{K}$ is

$\mathrm{Js}^{-1} / \mathrm{m}^{2}\left(\frac{\mathrm{K}}{\mathrm{m}}\right) \equiv \frac{\mathrm{W}}{\mathrm{mK}}=\mathrm{Wm}^{-1} \mathrm{~K}^{-1}$. The C.G.S unit $\mathrm{K}$ is $\left(\mathrm{cal} \quad \mathrm{s}^{-1}\right) \mathrm{cm}^{-1}\left({ }^{0} \mathrm{C}\right)^{-1}$

Dimensions of K are:

$$ \begin{aligned} & {[\mathrm{K}]=\frac{\left[\frac{\mathrm{dQ}}{\mathrm{dt}}\right]}{[\mathrm{A}]\left[\frac{\mathrm{d} \theta}{\mathrm{d} x}\right]}=\frac{\mathrm{ML}^{2} \mathrm{~T}^{-3}}{\mathrm{~L}^{2}\left(\frac{\theta}{\mathrm{L}}\right)}} \\ & =\mathrm{MLT}^{-3} \theta^{-1} \end{aligned} $$

$\mathrm{K}$ is a small number for bad conductors and is a large number for good conductors.

Equivalent Thermal Conductivity

Case 1. Rods in Series

Fig. 8 shows two rods of same cross-section, A; length $\mathrm{L} _{1}$ and $\mathrm{L} _{2}$ joined together. $\mathrm{K} _{1}$ and $\mathrm{K} _{2}$ is thermal conductivity of the two rods. Ends $\mathrm{L}$ and $N$ are maintained as constant temperature. $\theta _{1}$ and $\theta _{2}$ respectively. Let $\theta$ be the temperature of the common end M. In steady state rate of flow of heat $\frac{\mathrm{dQ}}{\mathrm{dt}}$ in the two rods is same; therefore

Fig. 8

$$ \begin{equation*} \frac{\mathrm{dQ}}{\mathrm{dt}}=\mathrm{K} _{1} \mathrm{~A}\left(\frac{\theta _{1}-\theta}{\mathrm{L} _{1}}\right)=\mathrm{K} _{2} \mathrm{~A}\left(\frac{\theta-\theta _{2}}{\mathrm{~L} _{2}}\right) \tag{1} \end{equation*} $$

Rearranging, we get

$$ \begin{equation*} \left(\theta _{1}-\theta\right)+\left(\theta-\theta _{2}\right)=\theta _{1}-\theta _{2}=\left(\frac{\mathrm{dQ}}{\mathrm{dt}}\right) \frac{1}{\mathrm{~A}}\left[\frac{\mathrm{L} _{1}}{\mathrm{~K} _{1}}+\frac{\mathrm{L} _{2}}{\mathrm{~K} _{2}}\right] \tag{2} \end{equation*} $$

Let $\mathrm{K} _{\mathrm{eq}}$ be the equivalent thermal conductivity of the arrangment. By definition

$$ \begin{array}{r} \frac{\mathrm{dQ}}{\mathrm{dt}}=\mathrm{K} _{\mathrm{eq}} \mathrm{A}\left(\frac{\theta _{1}-\theta _{2}}{\mathrm{~L} _{1}+\mathrm{L} _{2}}\right) \\ \therefore \quad \theta _{1}-\theta _{2}=\left(\frac{\mathrm{dQ}}{\mathrm{dt}}\right)\left(\frac{\mathrm{L} _{1}+\mathrm{L} _{2}}{\mathrm{~K} _{\mathrm{eq}} \mathrm{A}}\right) \tag{3} \end{array} $$

From Eqns. (1) and (3) we have

$$ \begin{equation*} \frac{\mathrm{L} _{1}}{\mathrm{~K} _{1}}+\frac{\mathrm{L} _{2}}{\mathrm{~K} _{2}}=\frac{\mathrm{L} _{1}+\mathrm{L} _{2}}{\mathrm{~K} _{\mathrm{eq}}} \tag{4} \end{equation*} $$

Case 2. Rods in Parallel

Fig. 9 shows two rods of same length $\mathrm{L}$; thermal conductivity $\mathrm{K} _{1}$ and $\mathrm{K} _{2}$ arranged co-axially as shown. The radius of rod of thermal conductivity $K _{1}$ and $K _{2}$ is $R _{1}$ and $R _{2}\left(>R _{1}\right)$ respectively. Let the ends be maintained at constant temperature $\theta _{1}$ and $\theta _{2}\left(\theta _{1}>\theta _{2}\right)$.

$\left(\frac{\mathrm{dQ}}{\mathrm{dt}}\right) _{1}=$ Rate of flow of heat in rod of conductivity $\mathrm{K} _{1}$

$$ \begin{equation*} =\mathrm{K} _{1}\left(\pi \mathrm{R} _{1}^{2}\right)\left(\frac{\theta _{1}-\theta _{2}}{\mathrm{~L}}\right) \tag{1} \end{equation*} $$

$\left(\frac{\mathrm{dQ}}{\mathrm{dt}}\right) _{2}=$ Rate of flow of heat in rod of conductivity $\mathrm{K} _{2}$

$$ \begin{equation*} =\mathrm{K} _{2}\left(\pi \mathrm{R} _{2}^{2}-\pi \mathrm{R} _{1}^{2}\right)\left(\frac{\theta _{1}-\theta _{2}}{\mathrm{~L}}\right) \tag{2} \end{equation*} $$

$\frac{\mathrm{dQ}}{\mathrm{dt}}=$ The net rate of flow of heat in the arrangement

$$ \begin{equation*} =\left(\frac{\mathrm{dQ}}{\mathrm{dt}}\right) _{1}+\left(\frac{\mathrm{dQ}}{\mathrm{dt}}\right) _{2}=\pi\left[\mathrm{K} _{1} \mathrm{R} _{1}^{2}+\mathrm{K} _{2}\left(\mathrm{R} _{2}^{2}-\mathrm{R} _{1}^{2}\right)\right]\left(\frac{\theta _{1}-\theta _{2}}{\mathrm{~L}}\right) \tag{3} \end{equation*} $$

Let $\mathrm{K} _{\mathrm{eq}}$ be the equivalent thermal conductivity of the arrangment. By definition

$$ \begin{equation*} \frac{\mathrm{dQ}}{\mathrm{dt}}=\mathrm{K} _{\mathrm{eq}} \pi \mathrm{R} _{2}^{2}\left(\frac{\theta _{1}-\theta _{2}}{\mathrm{~L}}\right) \tag{4} \end{equation*} $$

From Eqns. (3) and (4) we have

$$ \begin{aligned} & \mathrm{K} _{\mathrm{eq}}=\frac{\mathrm{K} _{1} \mathrm{R} _{1}^{2}+\mathrm{K} _{2}\left(\mathrm{R} _{2}^{2}-\mathrm{R} _{1}^{2}\right)}{\mathrm{R} _{2}^{2}} \\ & =\left(\mathrm{K} _{1}-\mathrm{K} _{2}\right) \frac{\mathrm{R} _{1}^{2}}{\mathrm{R} _{2}^{2}}+\mathrm{K} _{2} \end{aligned} $$

THERMAL RADIATION

Radiation is the process of transfer of heat from a hot body without any intervening medium; i.e. radiations can propagate in vacuum. The wave length range of thermal radiations is from $800 \quad \mathrm{~nm} \quad \mathrm{to} \quad 4 \times 10^{-4} \mathrm{~m}$. These radiations belong to the infra-red part of electromagnetic spectrum. Thermal radiations have same properties as light. The only difference is in their wave length. The wave length $(\lambda)$ of thermal radiation lies from $8 \times 10^{-7} \mathrm{~m}$ to $4 \times 10^{-7} \mathrm{~m}$ where as the wavelength range of light is $4 \times 10^{-7} \mathrm{~m}$ to $8 \times 10^{-7} \mathrm{~m}$. Energy associated with thermal radiations is less as compared to visible light.

Reflection; Transmission and Absorption Coefficients

Let $\mathrm{Q}$ be the energy of thermal radiations incident on a body. In a general; a part $\mathrm{Q} _{1}$ is reflected back; $\mathrm{Q} _{2}$ is transmitted and $Q _{3}$ is absorbed. From law of conservation of energy

$$ \begin{aligned} \mathrm{Q} & =\mathrm{Q} _{1}+\mathrm{Q} _{2}+\mathrm{Q} _{3} \\ \text { or } \quad & =\left(\frac{\mathrm{Q} _{1}}{\mathrm{Q}}\right)+\left(\frac{\mathrm{Q} _{2}}{\mathrm{Q}}\right)+\left(\frac{\mathrm{Q} _{3}}{\mathrm{Q}}\right) \\ & =\mathrm{r}+\mathrm{t}+\mathrm{a} \end{aligned} $$

where $r=\frac{Q _{1}}{Q}=$ The reflection coefficient or reflectance

$\mathrm{t}=\frac{\mathrm{Q} _{2}}{\mathrm{Q}}=$ The transmission coefficient or transmittance

and $\mathrm{a}=\frac{\mathrm{Q} _{3}}{\mathrm{Q}}=$ The absorption coefficient or absorptance of the body.

Perfectly Black Body

For a body, if $\mathrm{r}=\mathrm{t}=0$ and $\mathrm{a}=1$ the body is known as a perfectly black body. In words: a perfectly black body absorbs completely the radiations of all wavelengths incident on it. Practically no body can be $100 \%$ perfectly black. Lamp black is almost a perfectly black body.

According to Ferry, any hollow enclosure with a very narrow opening $\mathrm{O}$ behaves like a nearly perfectly black body. Fig. 10 shows Ferry’s black body.

Fig. 10

Important: Only the hole and not the entire sphere acts as a black body.

Kirchhoff’s Law

Everybody at a finite temperature emits thermal radiations of all wavelengths. Similarly a body absorbs radiations incident on it. The emissive power, $\mathrm{e} _{\lambda}$; of a body is the amount of energy emitted per unit area of a body in wave length range $\lambda$ and $\lambda+\mathrm{d} \lambda$. Similarly the absorptive power, $\mathrm{a} _{\lambda}$, is amount of energy absorbed per unit area in wave length range $\lambda$ and $\lambda+\mathrm{d} \lambda$.

According to Kirchhoff’s law, the ratio of emissive power and absorptive power of any body is a constant. The constant equals the emissive power $\left(\mathrm{E} _{\lambda}\right)$ of a perfectly black body.Expressed mathematically

$$ \frac{\mathrm{e} _{\lambda}}{\mathrm{a} _{\lambda}}=\text { constant }=\mathrm{E} _{\lambda} $$

We can also say that good emitters are good absorbers and vice-versa. Following examples are illustrations of Kirchhoff’s law.

(1) Take a piece of bone china having a black flower painted over a white back ground when viewed at room temperature. The black flower absorbs all incident radiation and the while part reflects all incident radiation. Heat this piece of bone china to a high temperature $\left(\sim 1000^{\circ} \mathrm{C}\right)$ and view inside a dark room. The flower appears white on a black background. This is in accordance with Kirchhoff’s law. The black flower is a good absorber and therefore a good emitter. The white background is a poor absorber and therefore a poor emitter.

(2) Sodium vapours, on heating emit two yellow lines known as $\mathrm{D} _{1}$ and $\mathrm{D} _{2}$ lines. If white light from an arc lamp (or sun) is made to pass through a chamber containing sodium vapours at low temperature; in the emergent light $\mathrm{D} _{1}$ and $\mathrm{D} _{2}$ lines are absent. Two dark lines are observed at the position of $\mathrm{D} _{1}$ and $\mathrm{D} _{2}$ lines. These are known as Fraunhofer’s dark lines. Hot sodium vapours are good emitter of $\mathrm{D} _{1}$ and $\mathrm{D} _{2}$ lines therefore cold sodium vapour is a good absorber of these two lines; in accordance with Kirchhoff’s law.

Stefan’s Law

According to Stefan’s law; the amount of energy radiated per unit area per unit time (E) by a perfectly black body is directly proportional to the fourth power of the absolute temperature ( $\mathrm{T}$ ) of the body. Expressed mathematically

$$ \mathrm{E}=\sigma \mathrm{T}^{4} $$

where $\sigma$ is a constant known as Stefan’s constant $\sigma=6.67 \times 10^{-8} \mathrm{Wm}^{-2} \mathrm{~K}^{-4}$. Dimension of $\sigma$ are:

$$ [\sigma]=\frac{[\mathrm{E}]}{[\mathrm{T}]^{4}}=\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2} / \mathrm{L}^{2} \mathrm{~T}}{\mathrm{~K}^{4}}=\mathrm{MT}^{-3} \mathrm{~K}^{-4} $$

For a body which is not perfectly black if $\varepsilon$ is the degree of blackness $(0<\varepsilon<1)$; the energy radiated per unit area per unit time is

$$ \mathrm{E}=\varepsilon \sigma \mathrm{T}^{4} $$

Consider a perfectly black body of surface area $\mathrm{A}$; at a temperature $\mathrm{T} _{1} \mathrm{~K}$ placed in a surrounding at a constant temperature $\mathrm{T} _{2} \mathrm{~K}\left(\mathrm{~T} _{2}<\mathrm{T} _{1}\right)$. The black body emits radiations to surroundings and absorbs radiation from surroudings. Since $\mathrm{T} _{1}>\mathrm{T} _{2}$; energy emitted to surroundings is more than energy recieved (asorbed) from surroundings. The instantaneous rate of loss of energy by hot body $=\mathrm{A} \sigma\left[\mathrm{T} _{1}^{4}-\mathrm{T} _{2}^{4}\right]$

Newton’s Law of Cooling from Stefan’s Law

According to Newton’s law of cooling; for small difference of temperature between a body and its surroundings; the rate of cooling of the body is directly proportional to the excess temperature of the body over the surroundings. Consider a body at a temperature $\mathrm{T}=\mathrm{T} _{0}+\Delta \mathrm{T}$ and the surroundings at a constant temperature $\mathrm{T} _{0}$.

The rate of cooling $=\mathrm{A} \sigma\left[\mathrm{T}^{4}-\mathrm{T} _{0}^{4}\right]$

$$ \begin{aligned} & =\mathrm{A} \sigma\left[\left(\mathrm{T} _{0}+\Delta \mathrm{T}\right)^{4}-\mathrm{T} _{0}^{4}\right] \\ & =\mathrm{A} \sigma \mathrm{T} _{0}^{4}\left[\left(1+\frac{\Delta \mathrm{T}}{\mathrm{T} _{0}}\right)^{4}-1\right] \end{aligned} $$

From Binomial theorem;

$$ \left(1+\frac{\Delta \mathrm{T}}{\mathrm{T} _{0}}\right)^{4} \simeq 1+4\left(\frac{\Delta \mathrm{T}}{\mathrm{T} _{0}}\right) $$

$\therefore$ The rate of cooling $\simeq \mathrm{A} _{\sigma} \mathrm{~T} _{0}^{4}\left[1+4\left(\frac{\Delta \mathrm{T}}{\mathrm{T} _{0}}\right)-1\right]$

$$ =\left(4 \mathrm{~A} \sigma \mathrm{T} _{0}^{3}\right) \Delta \mathrm{T} $$

Obviously rate of cooling is directly proportional to $\Delta \mathrm{T}$. This is Newton’s law of cooling.

Example-41:

Two rods $A$ and $B$ have lengths in ratio of $2: 3$ and thermal conductivity in ratio of 4:3. Temperature difference across ends of $B$ is double that across ends of $A$. The ratio of flow of heat; in steady state; in the two rods is same. $A _{1} / A _{2}$; the ratio of their area of cross-section is

(a) $1: 1$

(b) $16: 3$

(c) $16: 9$

(d) $9: 16$

Show Answer

Solution:

Let $\left(\theta _{1}-\theta _{2}\right) _{\mathrm{A}}$ be the difference across ends of rod $\mathrm{A}$. The temperature difference across ends of $\mathrm{B}$ is $\left(\theta _{1}-\theta _{2}\right) _{\mathrm{B}}=2\left(\theta _{1}-\theta _{2}\right) _{\mathrm{A}}$. Given

$\frac{\mathrm{L} _{1}}{\mathrm{~L} _{2}}=\frac{2}{3} ; \frac{\mathrm{K} _{1}}{\mathrm{~K} _{2}}=\frac{4}{3}$ and $\mathrm{Q} _{1}=\mathrm{Q} _{2}$

$\therefore \frac{\mathrm{K} _{1} \mathrm{~A} _{1}}{\mathrm{~L} _{1}}\left(\theta _{1}-\theta _{2}\right) _{\mathrm{A}}=\frac{\mathrm{K} _{2} \mathrm{~A} _{2}}{\mathrm{~L} _{2}}\left(\theta _{1}-\theta _{2}\right) _{\mathrm{B}}$

or $\quad \frac{\mathrm{A} _{1}}{\mathrm{~A} _{2}}=\left(\frac{\mathrm{K} _{2}}{\mathrm{~K} _{1}}\right) \frac{\mathrm{L} _{1}}{\mathrm{~L} _{2}} \cdot 2$

$$ =\left(\frac{3}{4}\right) \cdot 2 \times\left(\frac{2}{3}\right)=1 $$

Correct choice is (a)

Example-42:

A copper bar of length $75 \mathrm{~cm}$ and a bar of steel of length $125 \mathrm{~cm}$ are joined together at one end as shown in Fig. 11. Both have circular cross-section of diameter $2 \mathrm{~cm}$. The free ends of copper and steel bars are maintained at $100^{\circ} \mathrm{C}$ and $0^{\circ} \mathrm{C}$ respectively. What is steady state temperature of the common end of bars?

$\mathrm{K} _{\mathrm{cu}}=\mathbf{9 . 2} \times 10^{-2} \mathrm{kcal} . \mathrm{m}^{-1} \mathrm{~s}^{-1}\left({ }^{0} \mathrm{C}\right)^{-1}, \mathrm{~K} _{\text {steel }}=1.1 \times 10^{-2} \mathrm{kcal} . \mathrm{m}^{-1} \mathrm{~s}^{-1}\left({ }^{0} \mathrm{C}\right)^{-1}$.

Show Answer

Solution:

Fig. 11 shows the given arrangment. Let $\theta$ be the steady state temperature of common end. In steady state rate of flow of heat in the two bars is same. Therefore

$\mathrm{K} _{\text {cu }} \mathrm{A} \frac{[100-\theta]}{\mathrm{L} _{1}}=\mathrm{K} _{\text {steel }} \mathrm{A} \frac{[\theta-0]}{\mathrm{L} _{2}}$

$9.2 \times 10^{-2}\left[\frac{100-\theta}{0.75}\right]=1.1 \times 10^{-2}\left[\frac{\theta}{1.25}\right]$

$\frac{100-\theta}{\theta}=\frac{1.1 \times 75}{9.2 \times 125} \simeq 0.072$

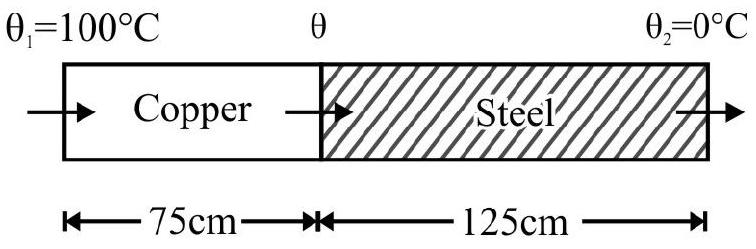Fig. 11

or $\quad \theta=\frac{100}{1.072} \simeq 93.3^{\circ} \mathrm{C}$

Example-43:

Fig. 12 shows two co-axial cylinder of same length radii $R$ and 2R. The thermal conductivity of inner and outer cylinder is $K$ and $K _{1}$ respectively. The equivalent thermal conductivity of the arrangment is $1.5 \mathrm{~K}$. Then $\mathrm{K} _{1}$ is

(a) $\frac{2 \mathrm{~K}}{3}$

(b) $\frac{3 \mathrm{~K}}{3}$

(c) $\frac{3 K}{5}$

(d) $\frac{5 \mathrm{~K}}{3}$

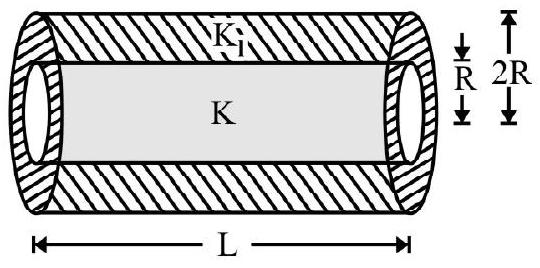
Fig. 12

Show Answer

Solution:

Let $\theta _{1}$ and $\theta _{2}$ be the temperature of the two ends of the arrangement. Then the rate of flow of heat is

$$ \pi(2 \mathrm{R})^{2} \mathrm{~K} _{\mathrm{eq}}\left(\frac{\theta _{1}-\theta _{2}}{\mathrm{~L}}\right)=\mathrm{K} \pi \mathrm{R}^{2} \frac{\left(\theta _{1}-\theta _{2}\right)}{\mathrm{L}}+\mathrm{K} _{1} \pi\left[(2 \mathrm{R})^{2}-(\mathrm{R})^{2}\right]\left(\frac{\theta _{1}-\theta _{2}}{\mathrm{~L}}\right) $$

or $\quad 4 \mathrm{~K} _{\mathrm{eq}}=\mathrm{K}+3 \mathrm{~K} _{1}$

or $\quad 4 \times 1.5 \mathrm{~K}=\mathrm{K}+3 \mathrm{~K} _{1}$

$$ \left[\because \mathrm{K} _{\mathrm{eq}}=1.5 \mathrm{~K}\right] $$

or $\quad \mathrm{K} _{1}=\left(\frac{5}{3}\right) \mathrm{K}$

The correct choice is (d)

Example-44:

Solar constant is the energy recieved by earth per unit area per minute from radiations emitted by Sun. It is $8.315 \times 10^{4} \mathrm{Jm}^{-2}(\mathrm{~min})^{-1}$. Estimate surface temperature of $\mathrm{Sun}$; assuming Sun behaves like a perfectly black body. Given radius of Sun $=7 \times 10^{5} \mathrm{~km}$; Distance between earth and sun $=\mathbf{1 . 5} \times 10^{8} \mathrm{~km}$.

$\left(\sigma=\mathbf{5 . 7 7} \times 10^{-8} \mathbf{W ~ m}^{-2} \mathbf{K}^{-4}\right)$

Show Answer

Solution:

Let $\mathrm{T}$ be surface temperature of Sun on Kelvin scale. The total energy, E, radiated per second by Sun; using Stefan’s law, is

$$ \mathrm{E}=\left(4 \pi \mathrm{R} _{\mathrm{S}}^{2}\right) \sigma \mathrm{T}^{4} $$

The energy is radiated uniformly in all directions. Consider a sphere of radius $\mathrm{R} _{\mathrm{ES}}$ center coincident with center of Sun. The energy, $\mathrm{E} _{1}$, crossing the surface of sphere per unit area per second is

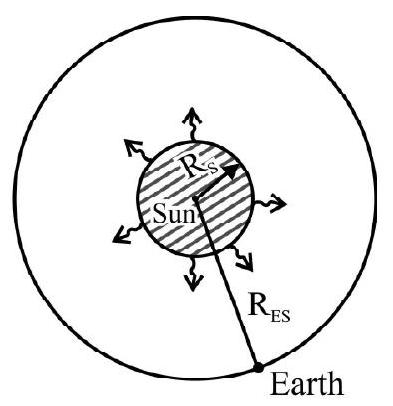
Fig. 13

$$ \mathrm{E} _{1}=\frac{\mathrm{E}}{4 \pi \mathrm{R} _{\mathrm{ES}}^{2}}=\left(\frac{\mathrm{R} _{\mathrm{S}}}{\mathrm{R} _{\mathrm{ES}}}\right)^{2} \sigma \mathrm{T}^{4} $$

$\mathrm{E} _{1}$ is energy recieved per unit area per second by earth due to solar radiation. From definition of solar constant

$\mathrm{s}=$ The solar constant $=\mathrm{E} _{1} \times 60=60\left(\frac{\mathrm{R} _{\mathrm{S}}}{\mathrm{R} _{\mathrm{ES}}}\right)^{2} \sigma \mathrm{T}^{4}$

Given; $\mathrm{s}=8.135 \times 10^{4} \mathrm{Jm}^{-2}(\mathrm{~mm})^{-1} ; \mathrm{R} _{\mathrm{S}}=7 \times 10^{8} \mathrm{~m}, \mathrm{R} _{\mathrm{ES}}=1.5 \times 10^{11} \mathrm{~m}$.

Substituting given values; $8.135 \times 10^{4}=60\left(\frac{7 \times 10^{8}}{1.5 \times 10^{11}}\right)^{2} \times 5.77 \times 10^{-8} \times \mathrm{T}^{4}$

$\therefore \quad \mathrm{T}=\left[\frac{8.135 \times\left(1.5 \times 10^{11}\right)^{2} \times 10^{4}}{60\left(7 \times 10^{8}\right)^{2} \times 5.77 \times 10^{-8}}\right]^{1 / 4}$

$\simeq 5732 \mathrm{~K}$

Example-45:

A body cools from $75^{\circ} \mathrm{C}$ to $70^{\circ} \mathrm{C}$ in 6 minute. In how much time will it cool from $55^{\circ} \mathrm{C}$ to $50^{\circ} \mathrm{C}$. The surrounding temperature is constant at $22.5^{\circ} \mathrm{C}$.

Show Answer

Solution:

According to Newton’s law of cooling

$$ \frac{\mathrm{dQ}}{\mathrm{dt}}=\mathrm{C} \times\left(\theta-\theta _{0}\right) $$

where $\mathrm{C}$ is a constant, $\theta-\theta _{0}=$ temperature difference between body and surroundings.

Case-1:

Average temperature of body $=\frac{75+70}{2}=72.5^{\circ} \mathrm{C}$

The average excess temperature of body over sourroundings $=(72.5-22.5)=50^{\circ} \mathrm{C}$

Let $\mathrm{Q}$ be total heat lost in time $\mathrm{t} _{1}=6$ minute. Then

$\mathrm{Q}=\mathrm{mc} \times(75-70)=\mathrm{k} \times 50 \times \mathrm{t} _{1} \hspace{40mm} . . .. . . . (1)$

where $\mathrm{k}$ is a constant of proportionality.

Case-2:

The average excess temperature of body over surroudings $=\left(\frac{55+50}{2}\right)-22.5=30^{\circ} \mathrm{C}$

Let $\mathrm{t} _{2}$ be time taken by the body to cool from $55^{\circ} \mathrm{C}$ to $50^{\circ} \mathrm{C}$. Then

$\mathrm{Q}=\operatorname{mc}(55-50)=\mathrm{k} \times 30 \times \mathrm{t} _{2} \hspace{40mm} . . .. . . . (2)$

From Eqns. (1) and (2) we have

$$ 50 \times \mathrm{t} _{1}=30 \times \mathrm{t} _{2} $$

or $\quad \mathrm{t} _{2}=\frac{5}{3} \mathrm{t} _{1}=\frac{5}{3} \times 6=10$ minute

Example-46:

Two spheres $A$ and $B$ of same material have radii $R$ and $2 R$ respectively. Both spheres are heated to same high temperature and allowed to cool in same surrounding at a constant temperature. The ratio of

(i) rate of loss of heat and

(ii) rate of cooling of the two speres is

(a) $2 ; 1$

(b) $1 ; 2$

(c) $1 / 4 ; 2$

(d) $2 ; 4$

Show Answer

Solution:

Let $\mathrm{T}$ and $\mathrm{T} _{0}$ denote the instantaneous temperature of a sphere and the surroundings respetively. The instantaneous rate of loss of heat.

$$ \begin{equation*} \frac{\mathrm{dQ}}{\mathrm{dt}}=\left(4 \pi \mathrm{R}^{2}\right) \varepsilon \sigma\left[\mathrm{T}^{4}-\mathrm{T} _{0}^{4}\right] \tag{1} \end{equation*} $$

where $\varepsilon$ is degree of blackness of either sphere. Therefore

$$ \frac{\left(\frac{\mathrm{dQ}}{\mathrm{dt}}\right) _{\mathrm{A}}}{\left(\frac{\mathrm{dQ}}{\mathrm{dt}}\right) _{\mathrm{B}}}=\left(\frac{\mathrm{R} _{\mathrm{A}}}{\mathrm{R} _{\mathrm{B}}}\right)^{2}=\left(\frac{1}{2}\right)^{2}=\frac{1}{4} $$

Let $\frac{\mathrm{dT}}{\mathrm{dt}}$ be the instantaneous rate of cooling.

Now, $\frac{\mathrm{dQ}}{\mathrm{dt}}=\mathrm{mc} \frac{\mathrm{dT}}{\mathrm{dt}}=\left(\frac{4 \pi}{3} \mathrm{R}^{3} \rho\right) \mathrm{c}\left(\frac{\mathrm{dT}}{\mathrm{dt}}\right)$

where $c$ is specific heat and $\rho$ density of material of sphere. Therefore

$$ \left(\frac{4 \pi}{3} \mathrm{R}^{3} \rho\right) \mathrm{c} \cdot \frac{\mathrm{dT}}{\mathrm{dt}}=\left(4 \pi \mathrm{R}^{2}\right) \varepsilon \sigma\left(\mathrm{T}^{4}-\mathrm{T} _{0}^{4}\right) $$

or $\quad \frac{\mathrm{dT}}{\mathrm{dt}}=\frac{3 \varepsilon \sigma\left(\mathrm{T}^{4}-\mathrm{T} _{0}^{4}\right)}{\mathrm{R} \sigma \mathrm{c}} \hspace{40mm}. . . .. . . . (2)$

From Eqn (2) it is obvious that

$\frac{\left(\frac{d T}{d t}\right) _{A}}{\left(\frac{d T}{d t}\right) _{B}}=\frac{R _{B}}{R _{A}}=2$

The correct choice is (c).

PROBLEMS FOR PRACTICE

[A] ELASTICITY

1. A steel wire $100 \mathrm{~cm}$ long has a radius of $1 \mathrm{~mm}$. It is suspended in a vertical plane from a rigid support. A load of $6 \mathrm{~kg}$ is attached to the free end. The length of wire increases by $0.088 \mathrm{~mm}$. What is Young’s modulus of steel? $\mathrm{g}=9.8 \mathrm{~ms}^{-2}$

Show Answer

Answer: $\simeq 2 \times 10^{11} \mathrm{~Pa}$

2. A steel wire of length $4.7 \mathrm{~m}$, cross-sectional area $30 \mathrm{~mm}^{2}$ stretches by same amount as a copper wire of length $3.5 \mathrm{~m}$, cross-section $40 \mathrm{~mm}^{2}$. What is ratio of $Y$ of steel and copper?

Show Answer

Answer: 1.79

3. A rod $2 \mathrm{~m}$ long is suspended horizontally in a vertical plane from a rigid support using two identical wires attached to its ends. One wire is of steel of area of cross-section $10 \mathrm{~mm}^{2}$ and the other is of brass of cross-sectional area $20 \mathrm{~mm}^{2}$. What is the position of a weight attached to the rod so that (i) stress (ii) strain, in the two wires is same?

Show Answer

Answer: (i) $1.33 \mathrm{~m}$ (ii) $1 \mathrm{~m}$

4. A wire of radius $\mathrm{r}$, length $\ell$; density $\rho$ is hung in a vertical plane from a rigid support. What is increase in length of wire due to its own weight? Y is Young’s modulus of wire.

Show Answer

Answer: $\frac{\ell^{2} \rho g}{\mathrm{Y}}$

5. A cable wire is made by twisting together 40 thin wires each of radius $1.26 \mathrm{~mm}$. The length of cable is $10 \mathrm{~m}$. It is used to lift a heavy body of mass $400 \mathrm{~kg}$. What is increase in length of cable?

$\left(\mathrm{Y}=2 \times 10^{11} \mathrm{~Pa} ; \mathrm{g}=10 \mathrm{~ms}^{-2}\right.$ )

Show Answer

Answer: $1 \mathrm{~mm}$

6. A rubber catapult is made of a rubber cord $420 \mathrm{~mm}$ long; having a radius of $3 \mathrm{~mm}$. The catapult is stretched by $20 \mathrm{~cm}$ and is used to launch a stone of mass $200 \mathrm{~g}$. The stone files away; with a speed of $2 \times 10^{3} \mathrm{mms}^{-1}$ on release. What is $Y$ for rubber?

Show Answer

Answer: $\simeq 3 \times 10^{6} \mathrm{~Pa}$

7. A steel wire is kept taut by suspending a load from its one end. It is used to measure the depth of sea. What is maximum depth that can be measured. Load suspended has mass negligible in comparision with the mass of steel wire.

Given, breaking stress of steel $=7.85 \times 10^{8} \mathrm{~Pa}$;

Relative density of steel $=7.7$;

Average density of sea water $=1 \mathrm{~g}(\mathrm{cc})^{-1}$ and $\mathrm{g}=9.8 \mathrm{~ms}^{-2}$

Show Answer

Answer: $11.96 \mathrm{~km}$

8. A metal has a relative density of 11 . It is subjected to a pressure of $20 \mathrm{kPa}$. What is change in R.D of metal? Compressibily of metal $=1.25 \times 10^{-10}(\mathrm{~Pa})^{-1}$

Show Answer

Answer: 0.28

9. A solid sphere of radius $1.5 \mathrm{~m}$ is submerged in a lake to depth of $10 \mathrm{~m}$. What is change in its volume. Bulk modulus of steel $=10^{12} \mathrm{~Pa}$

Show Answer

Answer: 1.39 c.c

10. Show that the ratio of the adiabatic and isothermal bulk modulus of a gas equals $\gamma=\frac{C _{P}}{C _{V}}$; where $C _{P}$ and $\mathrm{C} _{\mathrm{V}}$ denote molar specific heats of gas at constant pressure and constant volume respectively.

[B] HYDROSTATICS

11. A tank is filled with oil upto a height of $125 \mathrm{~cm}$. At its bottom there is a circular hole of radius $25 \mathrm{~mm}$. What force be applied to the other side of hole so that oil does not spill-over? R.D of oil $=0.5$; $\mathrm{g}=9.8 \mathrm{~ms}^{-2}$

Show Answer

Answer: $12 \mathrm{~N}$

12. A rectangular tank of cross-section $6 \times 10^{6} \mathrm{~cm}^{2}$ contains a oil layer $1 \mathrm{~m}$ high over water at the bottom up to a height of $60 \mathrm{~cm}$. What is (i) pressure (ii) thrust at bottom of tank? Atmospheric pressure $=1.013 \times 10^{2} \mathrm{kPa}$.

Show Answer

Answer: (i) 1.1306 $\times$ 102 kPa (ii) 678.4 kN

13. AU-tube contains some mercury in its two limbs. A column of gylecrine $100 \mathrm{~mm}$. Length is poured over mercury in left hand limb. Oil is poured over mercury in right hand limb till the upper layer of oil and glycerine in the two limbs is same. What is length of oil column? R.D of glycerine = 1.3; R.D of oil $=0.8 ;$ Density of mercury $=13.6 \mathrm{~g} /$ c.c.

Show Answer

Answer: $96 \mathrm{~mm}$

14. AU-tube is partially filled with water. An immisible liquid is poured in one limb of U-tube till it is at a height $x$ above the level of water in the other limb. Due to addition of liquid the level of water has risen by an amount y from its earlier value. What is R.D of liquid?

Show Answer

Answer: $\frac{2 y}{x+2 y}$

15. A ring of internal and external radius $85 \mathrm{~mm}$ and $87 \mathrm{~mm}$ is suspended from one pan of a balance which is counterpoised. The ring is made to touch surface of water in a beaker. An additional weight of $3.96 \mathrm{~g}$ has to be added to the other pan to counterpoise the balance. What is surface tension of water?

Show Answer

Answer: $72 \times 10^{-1} \mathrm{Nm}^{-1}$

16. A bubble of radius $10 \mathrm{~cm}$ is blown of soap solution of S.T $3 \times 10^{-2} \mathrm{Nm}^{-1}$. What is work done? What is additional work done so that the radius of bubble increases by $100 \%$ ?

Show Answer

Answer: $75.4 \mathrm{~mJ} ; 226.2 \mathrm{~mJ}$

17. AU-shaped hollow frame is placed in a vertical plane in gravity of earth. A slider of length $300 \mathrm{~mm}$ of negligible mass can slide freely over the frame. A soap film is formed in the arrangement. What mass be attached to slider to keep it in equilibrium? S.T of soap solution $=2.5 \times 10^{-2} \mathrm{Nm}^{-1}$.

Show Answer

Answer: $1.5 \mathrm{~g}$

18. 8 identical water drops each of mass $0.157 \mathrm{mg}$ combine together to form a bigger water drop. What is energy released? S.T of water $=72 \times 10^{-2} \mathrm{Nm}^{-1}$. Density of water $=10^{3} \mathrm{kgm}^{-3} ; \mathrm{g}=10 \mathrm{~ms}^{-2}$.

Show Answer

Answer: $0.905 \mu \mathrm{J}$

19. N identical droplets each of radius $r$ combine together under isothermal conditions forming a drop of radius R. S is surface tension of liquid of drop and $\rho$ its density. Show that temperature of big drop formed is $\frac{3 S}{\rho}\left[\left(\frac{1}{r}\right)-\left(\frac{1}{R}\right)\right]$ more than that of each droplet.

20. A spherical shell has a small hole of radius $\mathrm{r}$. It is immersed in a water tank upto a depth of $0.4 \mathrm{~m}$ before water starts entering in via the hole. What is $r$ ? Surface tension of water $=73 \times 10^{-1} \mathrm{Nm}^{-1}$; $\mathrm{g}=9.8 \mathrm{~ms}^{-2}$.

Show Answer

Answer: $3.7 \times 10^{-2} \mathrm{~mm}$

21. Two spherical bubbles of radii $r _{1}$ and $r _{2}$ coalese together to form a bubble under isothermal conditions. Show that

$$ 3 \mathrm{P}(\Delta \mathrm{V})+4 \mathrm{~S}(\Delta \mathrm{A})=0 $$

where $\mathrm{P}$ is atmospheric pressure and $\mathrm{S}$ is surface tension. $\Delta \mathrm{A}$ and $\Delta \mathrm{V}$ denote change in surface area and change in volume respectively due to coalesing together of bubbles.

22. Calculate excess pressure inside a soap bubble of radius $0.5 \mathrm{~cm}$. Surface tension of soap solution $=25 \times 10^{-1} \mathrm{Nm}^{-1}$. The bubble is taken inside a tank of soap solution to a depth of $0.4 \mathrm{~m}$. What is total pressure inside bubble? Assume there is no change in size of bubble. R.D of soap solution=1.2. Atmospheric pressure $=1.01 \times 10^{5} \mathrm{~Pa}$

Show Answer

Answer: $20 \mathrm{~Pa} ; 1.057 \times 10^{5} \mathrm{~Pa}$

23. Water rise upto a height of $80 \mathrm{~mm}$ in a capillary tube of radius $r$. Surface tension of water is $7 \times 10^{-2} \mathrm{Nm}^{-1}$. The capillary tube is cut to a length of $50 \mathrm{~cm}$. In equilibrium what is change in radius of curvature of meniscus?

Show Answer

Answer: Increases by $0.1015 \mathrm{~mm}$

24. In a capillary tube water rises by $100 \mathrm{~mm}$ whereas mercury depresses by $34.2 \mathrm{~mm}$. What is ratio of S.T of water and mercury? Angle of contact for water and mercury is $0^{\circ}$ and $135^{\circ}$ respectively. R.D of mercury $=13.6$

Show Answer

[Answer: 0.152]

25. A soap bubble of radius $r$ is blown at one end of a tube. The other end of tube is connected to a vassel of volume $\mathrm{V}$ filled with air at atmospheric pressure $\mathrm{P}$. Show that in equilibrium bubble accquires a radius $\mathrm{r} / 2$; if

$$ 2 \pi r^{2} S=\frac{4 S V}{r}-\frac{7 \pi r^{3} P}{2} $$

$S=$ Surface tension of soap solution.

Show Answer

Answer:

[C] HYDRO-DYNAMICS

26. A square plate of $10^{3}(\mathrm{~mm})^{2}$ lies on surface of an oil layer $2 \mathrm{~mm}$ thick. The plate moves with a constant speed of $30 \mathrm{~mm} \mathrm{~s}^{-1}$ when a tangential force of $23 \mathrm{~g}-\omega \mathrm{t}$ is applied to it. Assume there is no slipping. What is viscosity of oil? $\mathrm{g}=10 \mathrm{~ms}^{-2}$.

Show Answer

Answer: 1.55 SI unit

27. A human vein is considered as a capillary tube of radius $2 \mu \mathrm{m}$. Assuming a stream lined flow the speed of flow of blood at center of vein is $0.66 \mathrm{~ms}^{-1}$. What is pressure difference across ends of a vein $1 \mathrm{~mm}$ in length? The pressure at higher end of vein $=10^{4} \mathrm{~Pa}$. Viscosity of blood $=4 \times 10^{-3} \mathrm{Nsm}^{-2}$.

Show Answer

Answer: $19.5 \mathrm{~mm}$ of $\mathrm{Hg}$

28. In Millikan’s oil drop experiment a spherical drop of radius $2 \times 10^{-2} \mathrm{~mm}$ moves freely undergravity and acquires a terminal speed $\mathrm{v} _{\mathrm{T}}$. Neglecting bouyant force what is $\mathrm{v} _{\mathrm{T}}$ ?

R.D of oil $=1.2$; viscosity of air $=1.8 \times 10^{-1} \mathrm{mNsm}^{-2}$.

Show Answer

Answer: $\mathrm{Ans}: \sim 58.1 \mathrm{mms}^{-1}$

29. 8 identical drops each of radius $2 \mathrm{~mm}$ are falling in a viscous medium under gravity of earth. Each drop accuires a terminal speed of $0.5 \mathrm{cms}^{-1}$. The drops coalese together to form a bigger drop. What is terminal velocity of big drop formed?

Show Answer

Answer: $2 \mathrm{cms}^{-1}$

30. Water flows in a long horizontal capillary tube of diameter $20 \mathrm{~mm}$. What is the critical velocity of water? What is rate of flow (approximately) of water in the tube? Given

Viscosity of water $=10^{-3} \mathrm{Nsm}^{-2}$; Critical value of Reynold’s number $=3 \times 10^{3}$.

Show Answer

Answer: $15 \mathrm{cms}^{-1} ; 2.36 \times 10^{-5}(\mathrm{~m})^{3} \mathrm{~s}^{-1}$

31. Water flows through a capillary tube of radius $r$ length $\ell$ at a rate of $40 \mathrm{~mL}$ per second when connected to a pressure difference of $\mathrm{h} \quad \mathrm{cm}$ of water. Another tube of same length, radius $\mathrm{r} / 2$ is connected in series with the tube and the combination is connected across same pressure head. Calculate the pressure difference across each tube and rate of flow water through the combination.

Show Answer

Answer: $\mathrm{P}_1=\frac{\rho g h}{17} ; \mathrm{P}_2=\frac{16}{17} \rho \mathrm{gh} ; \mathrm{V}^{\prime}=2.353 \mathrm{mLs}^{-1} \text { ] }$

32. A cylinderical water tank has two small holes $\mathrm{A}$ and $\mathrm{B}$ in a vertical wall. Hole $\mathrm{A}$ is at a depth $\mathrm{y} _{1}$ from the surface of water in tank. Hole $B$ is at a height $y _{2}$ above bottom of tank. If $y _{1} / y _{2}=1$. What is the ratio of the horizontal distance on ground where water from the two holes hits ground?

Show Answer

Answer: 1

33. Two cylinders $\mathrm{L}$ and $\mathrm{M}$ have area of cross-section in ratio of 2:3. Both have a identical hole near the bottom. Cylinder L is filled water to a height of $20 \mathrm{~cm}$ and $M$ with mercury to a height of $15 \mathrm{~cm}$. What is ratio of velocity of efflux of water and mercury? R.D of mercury $=13.6 ; \mathrm{g}=10 \mathrm{~ms}^{-2}$

Show Answer

Answer: $\frac{2}{\sqrt{3}}$

34. In a test model experiment in a wind tunnel the speed of flow of air on the upper and lower wing of a plane is $100 \mathrm{~ms}^{-1}$ and $80 \mathrm{~ms}^{-1}$ respectively. The surface area of plane of wing is $2.5 \mathrm{~m}^{2}$. What is upthrust on the wing? Density of air $=1.3 \mathrm{~kg} \mathrm{~m}^{-3}$.

Show Answer

Answer: $6.552 \mathrm{kN}$

35. Water flows is a horizontal tube of varying cross-section. The pressure at a point $\mathrm{L}$ is $10 \mathrm{~mm}$ of $\mathrm{Hg}$ and speed of flow is $0.4 \mathrm{~ms}^{-1}$. What is pressure at a point $\mathrm{M}$ where speed of flow is $6.6 \mathrm{~ms}^{-1}$ ?

Show Answer

Answer: $6.26 \mathrm{~mm}$ of Hg

[D] HEAT

36. A rod of an alloy has a length of $62.406 \mathrm{~cm}$ at $21^{\circ} \mathrm{C}$. The temperature is raised by $10^{\circ} \mathrm{C}$. The increase in length of rod is $121.6 \mu \mathrm{m}$. What is

(i) length of rod at $0^{\circ} \mathrm{C}$ ?

(ii) coefficient of linear expansion of alloy?

Show Answer

Answer: (i) $ .62.380 \mathrm{~cm} \text { (ii) } 19.5 \times 10^{-6}\left({ }^{0} \mathrm{C}\right)^{-1}$

37. An iron ball of radius $30 \mathrm{~mm}$ is $10^{-2} \mathrm{~mm}$ too large than a hole is a brass plate when both at $30^{\circ} \mathrm{C}$. What is rise in temperature of the two so that the ball is just about to pass through the hole?

Coefficient of linear expansion of iron and brass is $1.9 \times 10^{-5}\left({ }^{0} \mathrm{C}\right)^{-1}$ and $1.2 \times 10^{-5}\left({ }^{\circ} \mathrm{C}\right)^{-1}$ respectively.

Show Answer

Answer: $.23.8^{\circ} \mathrm{C}$

38. A pendulum clock is a second’s clock at $15^{\circ} \mathrm{C}$. How much time does the clock gain or lose in a day when temperature increases by $20^{\circ} \mathrm{C}$.

Coefficient of linear expansion of material of pendulum $=2 \times 10^{-5}\left({ }^{0} \mathrm{C}\right)^{-1}$.

Show Answer

Answer: $17.28 \mathrm{~s}$, loss

39. A flask of volume $10^{3}$ c.c is partially filled with mercury in such a manner that the volume of air is flask is same at all temperatures. What is volume of mercury in flask?

$$ \gamma _{\text {glass }}=9 \times 10^{-6}(\mathrm{~K})^{-1} ; \gamma _{\mathrm{Hg}}=1.8 \times 10^{-4}\left({ }^{0} \mathrm{C}\right)^{-1} $$

Show Answer

Answer: 3.36 c.c

40. A sinker of true weight $\mathrm{w} _{0}$ has an apparent weight $\mathrm{w} _{1}$ when immersed completely in a liquid at $\theta _{1}^{0} \mathrm{C}$. The apparent weight is $\mathrm{w} _{2}$ when liquid is $\theta _{2}^{0} \mathrm{C}$. What is coefficient of cubical expansion of liquid? The coefficient of cubical expansion of sinker is $\gamma$.

Show Answer

Answer: $\frac{w_2-w_1}{(w_0-w_2)(\theta_2-\theta_1)}+\frac{\gamma(w_0-w_1)}{(w_0-w_2)}$

41. $5 \mathrm{~g}$ of water at $30^{\circ} \mathrm{C}$ and $5 \mathrm{~g}$ of ice at $-20^{\circ} \mathrm{C}$ are mixed together in a calorimeter. What is equlibrium temperature. Neglect water equivalent of calorimeter. Latent heat of fusion of ice $=80 \mathrm{cal} \quad \mathrm{g}^{-1}$. Specific heat of ice $=0.5 \mathrm{cal} \quad \mathrm{g}^{-1}\left({ }^{0} \mathrm{C}\right)^{-1}$.

Show Answer

Answer: $.0^{\circ} \mathrm{C}$

42. An aluminium container of mass $100 \mathrm{~g}$ contains $200 \mathrm{~g}$ of ice at $-20^{\circ} \mathrm{C}$. Heat is added to system at the rate of $100 \mathrm{cal} \mathrm{s}^{-1}$. What is temperature of system after 4 minute?

Specific heat of ice $=0.5 \mathrm{cal} \quad \mathrm{g}^{-1}\left({ }^{0} \mathrm{C}\right)^{-1}$; specific heat of aluminium $=0.2 \mathrm{cal} \quad \mathrm{g}^{-1}\left({ }^{0} \mathrm{C}\right)^{-1}$. Latent heat of fusion of ice $=80 \mathrm{cal} \quad \mathrm{g}^{-1}$.

Show Answer

Answer: $\sim 25.5^{\circ} \mathrm{C}$

43. A cubical ’thermocole’ box has a side of $0.3 \mathrm{~m}$ and a thickness of $50 \mathrm{~mm}$. $4 \mathrm{~kg}$ of ice is put inside box. What is mass of ice remaining in box after 6 hour?

Thermal conductivity of thermocole $=0.01 \mathrm{Wm}^{-1}\left({ }^{\circ} \mathrm{C}\right)^{-1}$. Outside temperature $=45^{\circ} \mathrm{C}$ (constant).

Show Answer

Answer: $2.95 \mathrm{~kg}$

44. Luminosity of Rigel star in Orion constellation is $17 \times 10^{3}$ times that of the Sun. Estimate temperature of the star. Surface temperature of Sun $=6 \times 10^{3} \mathrm{~K}$.

Show Answer

Answer: $68.52 \times 10^{3} \mathrm{~K}$

45. A $40 \mathrm{~W}$ tungestun lamp has a filament at a temperature of $2170^{\circ} \mathrm{C}$. The effective surface area of filament $=0.66 \mathrm{~cm}^{2}$. The degree of blackness of filament $=0.31$ What is Stefan’s constant?

Show Answer

Answer: $5.49 \times 10^{-8} \mathrm{Jm}^{-2} \mathrm{~s}^{-1}$

46. A body at $80^{\circ} \mathrm{C}$ cools to $64^{\circ} \mathrm{C}$ in 5 minute and to $52^{\circ} \mathrm{C}$ in 10 minute. What is temperature of body after 15 minute? What is temperature of surroundings?

Show Answer

Answer: $43^{\circ} \mathrm{C}, 16^{\circ} \mathrm{C}$

47. Earthen pots are used for cooling water in summer. A vessel contains M kg of water. The temperature of water decreases from $\theta _{1}^{0} \mathrm{C}$ to $\theta _{2}^{0} \mathrm{C}$ in $\tau$ second. Assume that a fraction f of heat of evaporation of mass $\sigma$ evaporating per second is taken from the vessel. Show that average rate of fall of temperature is $\frac{f \sigma L}{M C}$, where $L$ is latent heat of vaporation of water and $C$ is specific heat of water.

Question Bank

Key Learning Points

[A] ELASTICITY

1. Elasticity is the property of a body due to which body recovers its original dimensions when external deforming force is removed. A body that completely recovers its original dimensions is a perfectly elastic body. Abody that does not recover at all its original dimensions is a perfectly plastic body.

2. External applied force per unit area is known as stress. It can be either normal or tangential.

The change in dimension per unit original dimension is known as strain. Three simple types of strains are (i) longitudinal(ii) volumetric and (iii) shearing strain.

3. Stress versus strain graph is straight line (linear) upto some maximum value of external load. This maximum load gives elastic limit of the body. For external load more than elastic limit stress versus strain graph is non-linear. The yielding point is that external value ofload where the body (say a wire) starts flowing. Yielding is followed by breaking point.

4. Within elastic limit, stress is directly proportional to strain. Stress / strain is a constant known as modulus of elasticity. This is Hooke’s law.

5. Corresponding to three types of strain we have three different moduli of elasticity.

(a) Young’s modulus $(\mathrm{Y})$ is ratio of normal stress and longitudinal strain. For a wire of length $\mathrm{L}$ area of cross-section a; if $\Delta \mathrm{L}$ is change in length when an external normal force $\mathrm{F}$ is applied; then

$$ \mathrm{Y}=\text { Young’s modulus }=\frac{\text { normalstress }}{\text { long strain }}=\frac{\mathrm{F} / \mathrm{a}}{(\Delta \mathrm{L} / \mathrm{L})} $$

(b) Bulk modulus ( $\mathrm{K}$ ) is ratio of normal stress and volumetric strain. Let $\Delta \mathrm{P}$ be change in external stress applied to a body of volume $\mathrm{V} . \Delta \mathrm{V}$ is change in volume. Then

$$ \mathrm{K}=\text { Bulk modulus }=\frac{\text { normalstress }}{\text { volumeter strain }}=\frac{\Delta \mathrm{P}}{(\Delta \mathrm{v} / \mathrm{v})} $$

The reciprocal of $\mathrm{K}$ is known as compressibility $(\chi)$.

(c) Modulus of Rigidity $(\eta)$ is the ratio of tangential stress and angle of shear $(\phi)$;i.e.

$$ \eta=\frac{F / a}{\phi} $$

6. The work done by applied force in causing a strain is stored as elastic potential energy. Elastic potential energy per unit volume $=\frac{1}{2}$ stress $\times$ strain.

[B] HYDRO-STATICS

7. Hydrostatics is study of liquids at rest. A liquid at rest in a container exerts a pressure on the bottom and walls of container. Pressure $=P=\frac{F}{A}$ where $\mathrm{F}$ is force normal to the surface of cross-sectional area A. Pressure is a scalar quantity. SI unit of pressure is $\mathrm{Nm}^{-2}$.

8. A liquid column exerts a pressure at bottom of the container due to weight (w) of liquid in it. Let a container of cross-section A have a liquid of density $\rho$ upto a height (vertical) $h$. The pressure due to liquid column $=\mathrm{P}=\mathrm{h} \rho \mathrm{g}$.

9. According to Pascal’s law; pressure is transmitted equally in all directions by a liquid at rest. The hydraulic lift or hydraulic brakes are based on Pascal’s law.

10. The gaseous envelope around earth extending upto a few kilometers around earth is the atmosphere of earth. The pressure exerted by this gaseous envelope is known as atmosphere pressure. Under S.T.P condition it equals $76 \mathrm{~cm}$ of mercury column. It is nearly $1.01 \times 10^{5} \mathrm{~Pa}$.

11. Surface tension is the natural property of a liquid surface at rest. The liquid surface tries to contract and have a minimum surface area. Small liquid drops acquire spherical shape due to surface tension.

12. Surface tension is understood in terms of interatomic / molecular forces. The liquid between surface and a layer at a perpendicular distance equal to range of interatomic / molecular forces $\simeq 10^{-7} \mathrm{~m}$ is known as surface film. The potential energy of atoms / molecules on liquid surface is more than the potential energy of atom / molecules at the other end of surface film or deep below the surface. This excess potential energy per unit area is known as free-energy of liquid surface.

13. We know that state of equilibrium of any system is one of minimum potential energy. Applying this to liquid surface; the excess potential energy of atoms /molecules on surface of a liquid will be minimum if number of atoms / molecules making the surface is minimum. This will be so if liquid surface contracts and tries to decrease its surface area. This is surface tension.

14. Surface tension of a liquid (S) is the tangential force per unit length acting at right angles to any boundary line on the liquid surface. S.I unit of S.T is $\mathrm{Nm}^{-1}$. It can be shown that under isothermal conditions, surface tension $(S)$ is numerically equal to the free energy of the liquid surface.

15. In general a liquid surface is either concave or convex. Due to surface tension the pressure as concave side of the surface is more. This is known as excess pressure (p)

16. For a small sized liquid drop of radius $r$ the excess pressure $(p)$ inside drop is $\frac{2 S}{r}\left(\right.$ i.e. $\left.p=\frac{2 S}{r}\right)$. $S$ is surface tension of liquid.

17. Interatomic / molecular forces between atoms / molecules of same nature is known as force of cohesion. The same force between atoms / molecules of different nature is known as force of adhesion.

18. The liquid surface is concave if force of adhesion is more than force of cohesion. For example water in contact with glass. The liquid surface is convex if force of cohesion is more than force of adhesion. This is so for mercury in contact with glass. The meniscus of mercury in contact with glass is convex.

19. The angle of contact $(\theta)$ is the angle between the tangent to liquid surface and the glass wall (say) measured inside liquid. If $\theta$ is an acute angle; meniscus is concave. If $\theta$ is an obtuse angle, the meniscus is convex.

20. When a capillary tube; open at both ends is immersed in a beaker containing water; the level of water inside the capillary tube is more than in breaker. We say water rises inside capillary tube. This is known as capillarity.

21. The height h of a liquid inside a capillary tube of radius $r$, is

$$ \mathrm{h}=\frac{2 \mathrm{~S} \cos \theta}{2 \rho \mathrm{g}} $$

where $S$ is surface tension and $\theta$ angle of contact, $\rho$ is density of liquid. For a concave meniscus $0<\theta<\frac{\pi}{2} \mathrm{~h}$ is a positive number. This means liquid rises inside capillary tube. However it $\frac{\pi}{2}<\theta<\pi$, $\cos \theta$ and therefore $h$ is a negative number. This means liquid level falls inside the capillary tube.

22. Let the length ( $L$ ) of given capillary tube be less than the height $h$ to which liquid will rise in it. The liquid does not shoot out of the capillary tube. The tube is filled completely and equilibrium is attained. The radius of curvature of liquid meniscus automatically re adjusts itself to have equilibrium at $\mathrm{h}=\mathrm{L}$.

23. Surface tension of liquid decreases as temperature increases.

[C] HYDRO-DYNAMICS

24. Study of fluids in motion is hydro-dynamics. The flow of a liquid is divided into two catagories.

(a) Streamlined flow is a highly ordered flow of liquid. Velocity of every liquid particle at a given point in space is same. Liquid divides itself into different layers. Particles moving in one layer do not mix with liquid particles in adjoining layer.

(b) Turbulent flow is disordered flow of liquid particles. It is common in daily life. Velocity of one particle at a particular point in space is not same as of its predecessor.

25. In a stream lined flow of a liquid, the liquid particles in one layer exert a force on particles in an adjoining layer, in a direction so as to opposse their relative motion. In simple words there is a force oppossing the relative motion between the two liquid layers under consideration. This is known as viscosity. It is also considered as internal friction between the two liquid layers under consideration.

26. Consider two liquid layers at distance $x$ and $x+\mathrm{d} x$ from the liquid layer at rest as shown in Fig. The velocity of particles in the two layers is $\mathrm{v}$ and $\mathrm{v}+\mathrm{dv}, \frac{\mathrm{dv}}{\mathrm{d} x}$ is known as velocity gradient. The viscous force $\mathrm{F}$, between the two layers is

$$ \mathrm{F}=-\eta \mathrm{A} \frac{\mathrm{dv}}{\mathrm{d} x} $$

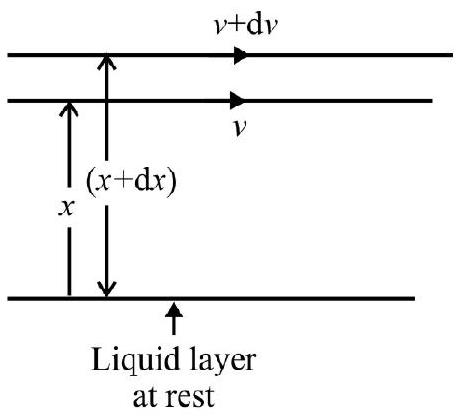
where $A$ is the area of cross-section of liquid layer. $\eta$ is a constant known as coefficient of viscosity. It depends on nature of liquid. The above law is Newton’s law of viscous force.

27. Coefficient of viscosity is numerically equal to the magnitude of external tangential force required to maintain a unit difference of velocity between layers unit distance apart having unit area of cross-section. SI unit of $\eta$ is $\mathrm{Nsm}^{-2}$. CGS unit of $\eta$ is poise. 1 poise $=0.1$ SI unit. Dimensions of $\eta$ are $\mathrm{ML}^{-1} \mathrm{~T}^{-1}$.

28. The viscous force, $\mathrm{F}$, on a small sized spherical body of radius $\mathrm{r}$; moving with a small speed $\mathrm{v}$, in a viscous medium of coefficient of viscosity $\eta$ is

$$ \mathrm{F}=6 \pi \eta \mathrm{rv} $$

This is known as Stoke’s law.

29. A small size sphere starting from rest moving under gravity of earth in a viscous medium experiences viscous force given by Stoke’s law. The sphere has a non-uniformly accelerated motion. The acceleration decreases as time increases. After sufficently long time the body accquires a constant velocity, known as “terminal velocity” $\left(\mathrm{v} _{\mathrm{T}}\right)$. The terminal velocity is

$$ \mathrm{v} _{\mathrm{T}}=\frac{2}{9}\left[\frac{\mathrm{r}^{2}(\rho-\sigma) \mathrm{g}}{\eta}\right] $$

where $\rho$ and $\sigma$ denote density of sphere and medium respectively. $\eta$ is coefficient of viscosity of medium.

30. A liquid of viscosity $\eta$; flows in a horizontal capillary tube of radius $\mathrm{r}$, length $\ell$. P is constant pressure difference across ends of the capillary tube. $\mathrm{V}$ is the volume of liquid flowing out per second. It is known as rate of flow of liquid.

$$ \mathrm{V}=\frac{\pi \mathrm{Pr}^{4}}{8 \eta \ell} $$

This is Poiseullie’s equation.

31. For liquids viscosity $\eta$ decreases as temperature increases. However for gases $\eta$ increases as temperature increases.

32. A stream line is the actual path followed by liquid particles having a stream lined flow. A collection of stream lines is a tube of flow. A liquid enters at one end where liquid pressure is high and emerges out of the other end of a tube of flow where the liquid pressure in lower.

33. Consider a liquid of viscosity $\eta$ moving in a capillary tube of radius $r$ with a velocity $v$. There is a velocity known as critical velocity $\left(v _{c}\right.$; such that if

$$ \begin{aligned} & 0<\mathrm{v} _{\mathrm{v}}<\text {; flow is stream lined, and } \\ & \mathrm{v} > \mathrm{v} _{\mathrm{c}} \text {; flow is turbulent } \end{aligned} $$

The critical velocity $\mathrm{v} _{\mathrm{c}}$ is

$$ \mathrm{v} _{\mathrm{c}}=\frac{\mathrm{K \eta}}{\rho \mathrm{r}} $$

$\mathrm{K}$ is a constant; $\rho$ is density of liquid in motion.

34. According to Osborne Reynold; for a liquid of density $\rho$; viscosity $\eta$, flowing in a tube of diameter, $D$; the critical velocity $\mathrm{v} _{\mathrm{c}}$ is

$$ \mathrm{v} _{\mathrm{c}}=\frac{\mathrm{R} \eta}{\rho \mathrm{D}} $$

$\mathrm{R}$ is a constant known as Reynold’s number. If $0<\mathrm{R}<2000$ flow is stream lined. For $2000<\mathrm{R}<3000$; the liquid flow is unstable and for $\mathrm{R}>3000$, the flow is turbulent.

35. In the stream lined flow of a liquid, the liquid possesses:

(i) pressure energy (ii) potential energy and (iii) kinetic energy.

36. According to Bernoulli’s theorem for stream lined flow of a liquid

$$ \frac{\mathrm{P}}{\rho}+\mathrm{gh}+\frac{\mathrm{v}^{2}}{2}=\mathrm{constant} $$

$\frac{\mathrm{P}}{\rho}$ is the pressure energy per unit mass; gh is the gravitational potential energy per unit mass and $\frac{\mathrm{v}^{2}}{2}$ is the kinetic energy per unit mass of the liquid in steady flow.

37. A tank contains a liquid at rest upto a height $h$ above a narrow opening $\mathrm{O}$. The velocity, $\mathrm{v}$, with which liquid emerges out of $\mathrm{O}$ is

$$ v=\sqrt{2 g h} $$

$v$ is known as velocity of efflux.

38. For a liquid flowing in a horizontal tube of varying cross-section; the velocity of flow (v) is more where area of cross-section is less and vice-versa. Where speed of flow increases liquids pressure decreases and vice-versa. Let $v _{1}$ and $v _{2}$ be velocity of flow at two points where area of crosssection of tube is $a _{1}$ and $a _{2}\left(a _{2}<a _{1}\right)$ respectively. Let $P _{1}$ and $P _{2}$ be liquids pressure at the two points.Then

$$ \frac{\mathrm{P} _{1}-\mathrm{P} _{2}}{\rho}=\frac{1}{2}\left(\mathrm{v} _{2}^{2}-\mathrm{v} _{1}^{2}\right) $$

Since $\mathrm{a} _{2}<\mathrm{a} _{1} ; \mathrm{v} _{2}>\mathrm{v} _{1}$; therefore $\mathrm{P} _{1}>\mathrm{P} _{2}$.

39. The above principle is used to explain:

(i) Two fast moving boats tend to collide when they come too close to one another.

(ii) A person can be sucked towards a high speed train if he (or she) is standing near the edge of plateform.

(iii) The thached roof of a hut is blown off during a storm in hills.

(iv) To provide a part of upthrust to an aeroplane due to design of wing of the plane.

(v) The curved path of a spinning ball moving forward.

[D] HEAT

40. Heat is a form of energy that produces a psychological sensation of hot or cold. Heat possessed by a body is due to motion of atoms / molecules involved. CGS unit of heat is calorie. 1 calorie $=4.2 \mathrm{~J}$

41. The temperature of a body is a parameter associated with it which determines the direction of flow of heat when the body is the thermal contact with another body. Two bodies are in in thermal equilibrium of their temperature is same.

42. C, F and R denote temperature of a body on Celsius; Fahrenheit and Römer scale respectively. Then

$$ \frac{C}{5}=\frac{F-32}{9}=\frac{R}{4} $$

On the kelvin scale (or absolute scale of temperature) the temperature $\mathrm{T}$ is

$$ \mathrm{T}=273+\mathrm{C} $$

43. In solids; there is an expansion on heating. This is known as thermal expansion. Solids have three simple types of expansion.

(a) Linear expansion takes into account change in length due to change in temperature. $\mathrm{L} _{0}$ and $\mathrm{L} _{\mathrm{t}}$ be length of a body at $0^{\circ} \mathrm{C}$ and $t^{\circ} \mathrm{C}$ respectively. Then

$$ \mathrm{L} _{\mathrm{t}}=\mathrm{L} _{0}(1+\alpha \mathrm{t}) $$

$\alpha$ is a constant known as coefficient of linear expansion.

(b) Superfacial expansion of a body takes into account change in surface area due to change of temperature.

$$ A _{t}=A _{0}(1+\beta t) $$

$\mathrm{A} _{0}$ and $\mathrm{A} _{\mathrm{t}}$ denote surface area at $0^{\circ} \mathrm{C}$ and $t^{\circ} \mathrm{C}$ respectively. $\beta$ is coefficient of superfacial expansion.

(c) Cubical expansion accounts for change in volume of a body due to change in temperature. Let $\mathrm{V} _{0}, \mathrm{~V} _{\mathrm{t}}$ be the volume of body at $0^{\circ} \mathrm{C}$ and $\mathrm{t}^{\circ} \mathrm{C}$ respectively. Then

$$ \mathrm{V} _{\mathrm{t}}=\mathrm{V} _{0}(1+\gamma \mathrm{t}) $$

$\gamma$ is coefficient of cubical expansion.

44. For a homogeneous, isotropic body.

$$ \gamma: \beta: \alpha:: 3: 2: 1 $$

45. For a liquid we only talk about cubical expansion. A liquid has to be present in a container. On heating the liquid and container both expand. If we donot take into account change in volume of container we have apparent expansion. On taking into account expansion of container we get the real expansion of liquid. Let $\gamma _{\mathrm{a}}, \gamma _{\mathrm{r}}$ be the coefficient of apparent and real cubical expansion. Then

$$ \gamma _{\mathrm{r}}=\gamma _{\mathrm{a}}+\gamma _{\mathrm{g}} $$

$\gamma _{\mathrm{g}}$ is coefficient of cubical expansion of container.

46. For a body of mass $\mathrm{m}$ the change in heat energy $\Delta \mathrm{H}(\equiv \Delta \mathrm{Q})$ for a change $\Delta \theta$ in temperature is

$$ \Delta \mathrm{H}(\equiv \Delta \mathrm{Q})=\operatorname{mc}(\Delta \theta) $$

$\mathrm{c}$ is a constant, known as specific heat capacity (or simply specific heat) of the body. $\mathrm{C}$ depends on nature of body. It is numerically equal to heat required to change temperature by one unit for body having unit mass. CGS unit of $\mathrm{C}$ is cal $\mathrm{g}^{-1}\left({ }^{0} \mathrm{C}\right)^{-1}$ and SI unit is $\mathrm{Jkg}^{-1}(\mathrm{~K})^{-1}$.

The molar specific heat $\mathrm{C}$ is heat required to change temperature by one degree of 1 gram-mole of material. Obviously $\mathrm{C}=\mathrm{Mc}$, where $\mathrm{M}=$ molar mass.

47. The thermal capacity of a body is numerically equal to heat required to raise the temperature of body by one degree. Obviously

Thermal capacity $=\mathrm{mc}$

48. Water equivalent of a calorimeter is mass of water that requires same amount of heat for same change of temperature as is required by the calorimeter. It is numerically equal to thermal capacity of calorimeter.

49. Latent heat is the heat required to change the state; i.e. from solid to liquid or from liquid to gaseous; without any change in temperature. Latent heat is numerically equal to heat required to change state of unit mass. Latent heat of fusion refers to change of state from solid to liquid, whereas latent heat of vaporisation involves change from liquid to gaseous state.

50. For a thermally isolated calorimeter; heat lost by hot body equals heat gained by body at lower temperature. This is a re statement of law of conservation of energy and is also known as principle of calorimetery.

51. Heat is transferred from one place to another in three different ways. These are

(i) conduction (ii) convection and (iii) radiation.

52. In thermal conduction a medium is required. The atoms $/$ molecules of medium do not move along with the heat flow. They only vibrate to and flow about their respective mean positions. Heat is passed on from atom or molecules in one layer to atoms / molecule in next layer and so on.

53. For a solid rod of length $\mathrm{L}$; area of cross-section $\mathrm{A}$; having its ends maintained at temperature $\theta _{1}^{0} \mathrm{C}$ and $\theta _{2}^{0} \mathrm{C}\left(\theta _{1}>\theta _{2}\right)$ respectively; in steady state.

$$ \frac{\mathrm{dQ}}{\mathrm{dt}}=\text { Rate of flow of heat }=\mathrm{KA}\left[\frac{\theta _{1}-\theta _{2}}{\mathrm{~L}}\right] $$

$\mathrm{K}$ is a constant for a particular material. It is known as thermal conductivity of the material.

54. Thermal conductivity $\mathrm{K}$ is numerically equal to rate of flow of heat in a rod of unit cross-section having a constant unit temperature gradient across it. SI unit of $\mathrm{K}$ is $\frac{\mathrm{W}}{\mathrm{m}^{2}} \mathrm{~K}$ and the CGS unit is cal $\mathrm{s}^{-1} \mathrm{~cm}^{2}\left({ }^{0} \mathrm{C}\right)^{-1}$. Dimensinos of $\mathrm{K}$ are $\mathrm{MLT}^{-3} \mathrm{~K}^{-1}$.

55. In radiations there is flow of energy without any intervening medium; i.e. radiations can propagate in vaccum. The wave length range of thermal radiation is $800 \mathrm{~nm}$ to $4 \times 10^{-4} \mathrm{~m}$.

56. When radiant energy $\mathrm{Q}$ is incident on a body a part $\mathrm{Q} _{1}$ is reflected back; $\mathrm{Q} _{2}$ is transmitted and $\mathrm{Q} _{3}$ is absorbed. Obviously

$$ \begin{gathered} \mathrm{Q}=\mathrm{Q} _{1}+\mathrm{Q} _{2}+\mathrm{Q} _{3} \\ \text { or } \quad 1=\left(\frac{\mathrm{Q} _{1}}{\mathrm{Q}}\right)+\left(\frac{\mathrm{Q} _{2}}{\mathrm{Q}}\right)+\left(\frac{\mathrm{Q} _{3}}{\mathrm{Q}}\right) \\ =\mathrm{r}+\mathrm{t}+\mathrm{a} \end{gathered} $$

where $r=\frac{Q _{1}}{Q}=$ The reflection coefficient; $t=\frac{Q _{2}}{Q}=$ The transmission coefficient and $\mathrm{a}=\frac{\mathrm{Q} _{3}}{\mathrm{Q}}=$ The absorption coefficient; the body.

57. A perfectly black body absorbs all radiations incident on it. For a perfectly black body

$$ \mathrm{r}=\mathrm{t}=0 \text { and } \mathrm{a}=1 $$

58. The emissive power, $\mathrm{e} _{\lambda}$; of a body is amount of energy emitted per unit area in wavelength range $\lambda$ and $\lambda+\mathrm{d} \lambda$.

The absorptive power, $\mathrm{a} _{\lambda}$; of a body is the amount of energy absorbed per unit area in wavelength range $\lambda, \lambda+\mathrm{d} \lambda$.

59. According to Kirchhoff’s law: for a perfectly black body, the ratio of emissive power $\left(\mathrm{e} _{\lambda}\right)$ and absorptive power $\left(\mathrm{a} _{\lambda}\right)$ of any body is a constant. The constant equals emissive power $\left(\mathrm{E} _{\lambda}\right)$ of a perfectly black body. Expressed mathematically

$$ \frac{\mathrm{e} _{\lambda}}{\mathrm{a} _{\lambda}}=\text { constant }=\mathrm{E} _{\lambda} $$

60. The energy emitted per unit area per unit time $\mathrm{E}$ by a perfectly black body is directly proportional to the “fourth power” of absolute temperature ( $\mathrm{T}$ ) of the body. Expressed mathematically

$$ \mathrm{E}=\sigma \mathrm{T}^{4} $$

This is known as Stefan’s law. $\sigma$ is a constant known as Stefan’s constant. $\sigma=5.67 \times 10^{-8} \mathrm{Wm}^{-2} \mathrm{~K}^{-4}$. Its dimensions are

$$ [\sigma]=\mathrm{MT}^{-3} \mathrm{~K}^{-4} $$

61. A body at a temperature $\mathrm{T}$ is placed in a surrounding at a constant temperature $\mathrm{T} _{0}\left(\mathrm{~T}>\mathrm{T} _{0}\right)$. For small difference of temperature; i.e. $\mathrm{T}=\mathrm{T} _{0}+\Delta \mathrm{T}$; the rate of loss of heat is directly proportional to the excess temperature $(\Delta \mathrm{T})$ of the body over its surroundings. This is known as Newton’s law of cooling.

1. The length of a metal wire is recorded to be $\ell _{1}$ under a tension $T _{1}$ and $\ell _{2}$ under a tension $T _{2}$. The natural length of the wire is

(1) $\frac{\ell _{1} \mathbf{T} _{1}^{2}+\ell _{2} \mathbf{T} _{2}^{2}}{\mathbf{T} _{1}^{2}+\mathbf{T} _{2}^{2}}$

(2) $\frac{\ell _{1} T _{2}^{2}+\ell _{2} T _{1}^{2}}{T _{2}^{2}+T _{1}^{2}}$

(3) $\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}\left(\ell _{1}+\ell _{2}\right)$

(4) $\frac{\ell _{1} \mathbf{T} _{2}-\ell _{2} \mathbf{T} _{1}}{\mathbf{T} _{2}-\mathrm{T} _{1}}$

Show Answer

Correct answer: (4)

Solution:

For a force $\mathrm{F}$ on a wire of length $\mathrm{L}$ elongated by $\Delta \mathrm{L}$; the Young’s modulus $\mathrm{Y}=\frac{\mathrm{FL}}{\mathrm{A} \Delta \mathrm{L}}$. As A(cross-sectional area) and $\mathrm{L}$ are constants; therefore

$\frac{\mathrm{F}}{\Delta \mathrm{L}}=\frac{\mathrm{YA}}{\mathrm{L}}=$ constant or $\Delta \mathrm{L} \alpha \mathrm{F}$. Therefore $\left(\ell _{1}-\mathrm{L}\right)$ and $\left(\ell _{2}-\mathrm{L}\right)$ are directly proportional to $\mathrm{T} _{1}$ and $\mathrm{T} _{2}$; i.e.

$$ \begin{aligned} & \frac{\ell _{1}-\mathrm{L}}{\ell _{2}-\mathrm{L}}=\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}} \\ & \text { or } \ell _{1} \mathrm{~T} _{2}-\mathrm{LT} _{2}=\ell _{2} \mathrm{~T} _{1}-\mathrm{LT} _{1} \\ & \mathrm{~L}\left(\mathrm{~T} _{2}-\mathrm{T} _{1}\right)=\ell _{1} \mathrm{~T} _{2}-\ell _{2} \mathrm{~T} _{1} \\ \therefore \quad & \mathrm{L}=\frac{\ell _{1} \mathrm{~T} _{2}-\ell _{2} \mathrm{~T} _{1}}{\mathrm{~T} _{2}-\mathrm{T} _{1}} \end{aligned} $$

2. The load versus extension graph for a one meter long wire suspended from a rigid support have the load on its free end is as shown in Fig.1. If the cross-sectional area of the wire is $1 \mathbf{~ m m}^{2}$, the value of Young’s modulus of the material of the wire is:

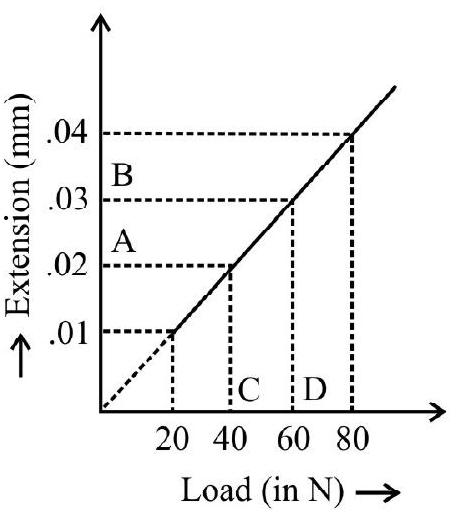
(1) $2 \times 10^{-12} \mathrm{Nm}^{-2}$

(2) $2 \times 10^{12} \mathrm{Nm}^{-2}$

(3) $0.5 \times 10^{-12} \mathrm{Nm}^{-2}$

(4) $2 \times 10^{11} \mathrm{Nm}^{-2}$

Show Answer

Correct answer: (2)

Solution:

We have, $\Delta \ell($ Extension $)=\frac{\mathrm{WL}}{\mathrm{AY}}$, whre $\mathrm{W}$ is applied load. Therefore $\Delta \ell=\left(\frac{\mathrm{L}}{\mathrm{AY}}\right) \mathrm{W}$

$\therefore$ From the given graph, slope $=\frac{\mathrm{L}}{\mathrm{AY}}$ or $\mathrm{Y}=\frac{\mathrm{L}}{\mathrm{A}(\text { slope })}$

Slope of the graph $=\frac{A B}{C D}=\frac{0.01 \mathrm{~mm}}{20 \mathrm{~N}}=\frac{10^{-5} \mathrm{~m}}{20}=\frac{1}{2} \times 10^{-6} \mathrm{mN}^{-1}$

Given $\mathrm{L}=1 \mathrm{~m}, \quad \mathrm{~A}=1 \mathrm{~mm}^{2}=\left(10^{-3} \mathrm{~m}\right)^{2}=10^{-6} \mathrm{~m}^{2}$

$$ \begin{aligned} \therefore \quad \mathrm{Y} & =\frac{\mathrm{L}}{\mathrm{A}} \cdot \frac{1}{\text { slope }} \\ & =\frac{1}{10^{-6}} \times \frac{2}{10^{-6}}=2 \times 10^{12} \mathrm{Nm}^{-2} \end{aligned} $$

3. In the Young’s modulus apparatus, a brick is suspended and it is found that the wire elongates by $2 \mathrm{~mm}$. The brick in now immersed in water (all other parameters of the set up remaining same) and the wire is found to contract by $0.6 \mathrm{~mm}$. The density of water is $1000 \mathrm{~kg} / \mathrm{m}^{-3}$. The density of the brick is

(1) $6666 \mathrm{~kg} \mathrm{~m}^{-3}$

(2) $3333 \mathrm{~kg} \mathrm{~m}^{-3}$

(3) $300 \mathrm{~kg} \mathrm{~m}^{-3}$

(4) $1200 \mathrm{~kg} \mathrm{~m}^{-3}$

Show Answer

Correct answer: (2)

Solution:

Let L, A and Y respectively denote the unstretached length, area of cross-section and Young’s modulus of the wire. $M$ is the mass of the brick. The increase in length of the wire with brick in air is given by

$$ \begin{align*} \Delta \mathrm{L} & =\frac{\mathrm{MgL}}{\mathrm{AY}}=2 \mathrm{~mm} \\ \text { or } \quad \frac{\mathrm{WL}}{\mathrm{AY}} & =2 \mathrm{~mm} \quad[\mathrm{~W}=\mathrm{Mg}=\text { Weight of brick in air }] \tag{1} \end{align*} $$

$\mathrm{W}^{\prime}$ denotes the weight of brick immersed in water, then

$$ \begin{equation*} \frac{\mathrm{W}^{\prime} \mathrm{L}}{\mathrm{AY}}=(2-0.6)=1.4 \mathrm{~mm} \tag{2} \end{equation*} $$

Loss of weight of brick immersed completely in water

$$ \begin{equation*} \mathrm{W}-\mathrm{W}^{\prime}=\frac{\mathrm{AY}}{\mathrm{L}}(2-1.4)=0.6\left(\frac{\mathrm{AY}}{\mathrm{L}}\right) \tag{3} \end{equation*} $$

from Eqns (1) and (3) we have

$\frac{\text { Weight of brick in air }}{\text { Loss of weight in water }}=\frac{\mathrm{W}}{\mathrm{W}-\mathrm{W}^{\prime}}=\frac{2}{0.6}$

$$ \begin{gathered} \frac{\mathrm{V} \rho \mathrm{g}}{\mathrm{V}(1000) \mathrm{g}}=\frac{2}{0.6} \\ \therefore \quad \\ \quad \rho=\frac{20000}{6}=3333 \mathrm{~kg} \mathrm{~m}^{-3} \end{gathered} $$

4. A steel wire elongates by $\ell \mathrm{mm}$ when a $5 \mathrm{~kg}$ load in hanged from it. The wire is now passed over a pulley and two loads of $4 \mathrm{~kg}$ and $2 \mathrm{~kg}$ are hung at the two ends. The enlongation in the wire will be

(1) $\frac{6}{5} \ell$

(2) $\frac{2}{5} \ell$

(3) $\frac{8}{15} \ell$

(4) $\frac{8}{5} \ell$

Show Answer

Correct answer: (3)

Solution:

Elongation of wire with $5 \mathrm{~kg}$ load $=\ell \quad \mathrm{mm}$

Tension in the wire when $2 \mathrm{~kg}$ and $4 \mathrm{~kg}$ loads are suspended from it is

$$ \mathrm{T}=\frac{2 \mathrm{mM}}{\mathrm{m}+\mathrm{M}}=\frac{2 \times 2 \times 4}{6}=\frac{8}{3} \mathrm{~kg} $$

$\therefore$ Elongation produced due to tension $\mathrm{T}$ in wire $=\frac{\ell}{5} \times \frac{8}{3}=\frac{8 \ell}{15} \mathrm{~mm}$

5. Fig. 2 shows the variation of potential energy $U$ between two molecules as a function of intermolecular separation $x$ between them. The values of $x$ at points $A, B$ and $C$ respectively are $0.58 \mathrm{~A} ; 1.3 \mathrm{~A}$ and $1.9 \mathrm{~A}$. The intermolecular forces at these points respectively are

(1) repulsive; zero; attractive

(2) zero; repulsive; attractive

(3) zero; repulsive; attractive

(4) attractive; zero; repulsive

Show Answer

Correct answer: (1)

Solution:

The force $F=-\left(\frac{d U}{d r}\right)$ therefore

At A; potential energy in positive. So the force is repulsive.

At $\mathrm{B} ; \mathrm{PE}$ is minimum, therefore $\mathrm{F}=-\frac{\mathrm{dU}}{\mathrm{dr}}=$ zero

At C; potential energy is negative. So the force is attractive.

The correct choice is (1).

6. A rubber rope of length $8 \mathrm{~m}$ is suspended from the ceiling of a room. Given

$\mathrm{Y}=5 \times 10^{6} \mathrm{Nm}^{-2}$ for rubber; $\rho _{\text {rubber }}=1.5 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3} ; \mathrm{g}=10 \mathrm{~ms}^{-2}$. The elongation in the rope due to its own weight is

(1) $96 \mathrm{~mm}$

(2) $24 \mathrm{~mm}$

(3) $48 \mathrm{~mm}$

(4) $344 \mathrm{~mm}$

Show Answer

Correct answer: (1)

Solution:

Mass of the rope $=$ Volume $\times$ Density

$$ \mathrm{M}=\mathrm{AL} \cdot \rho $$

The weight of the rope will act at its centre of gravity. So for the purpose of calculation of elongation; the original length of the rope is $\frac{\mathrm{L}}{2}$ Now

$\mathrm{Y}=\frac{\text { Stress }}{\text { Strain }}=\frac{\mathrm{Mg}}{\mathrm{A}}\left(\frac{\mathrm{L} / 2}{\Delta \mathrm{L}}\right)=\frac{(\mathrm{AL} \rho) \mathrm{gL}}{2 \mathrm{~A} \Delta \mathrm{L}}$

$\Delta \mathrm{L}=\frac{\rho \mathrm{gL}^{2}}{2 \mathrm{Y}}=\frac{1.5 \times 10^{3} \times 10 \times 8 \times 8}{2 \times 10 \times 10^{6}} \mathrm{~m} \simeq 69 \mathrm{~mm}$

7. A cube is made of a material of coefficient of linear expansion $\alpha$ and bulk modulus $\beta$. Pressure $P$ is applied on the cube from all the direction. The rise in temperature which the cube should be subjected in order to maintain original volume is

(1) $\frac{P}{3 \alpha \beta}$

(2) $\frac{3 \mathrm{P} \alpha}{\beta}$

(3) $\frac{3 \alpha \beta}{\mathrm{P}}$

(4) $\frac{P \beta}{3 \alpha}$

Show Answer

Correct answer: (1)

Solution:

The decrease in volume due to volumetric strain of pressure $\mathrm{P}$ should be equal to increase in volume due to thermal expansion. We have

$\beta=$ The Bulk modulus $=\frac{\mathrm{P}}{\text { Volumetric strain }}=\frac{\mathrm{P}}{\mathrm{v} / \mathrm{V}}=\frac{\mathrm{PV}}{\mathrm{V}}$

$\therefore \quad \mathrm{v}=\frac{\mathrm{PV}}{\beta} \hspace{40mm}. . . . . . . (1)$

$\mathrm{v}$ is decrease in volume

The volume $\mathrm{V}^{\prime}$ when temperature is raised to $\mathrm{t}^{\circ} \mathrm{C}=\mathrm{V}+\gamma \mathrm{Vt}=\mathrm{V}+3 \alpha \mathrm{Vt} \quad[\because \gamma=3 \alpha]$

Increase in volume $=\mathrm{v}=\mathrm{V}^{\prime}-\mathrm{V}=3 \alpha \mathrm{Vt} \hspace{40mm}. . . . . . . (2)$

From (1) and (2) we have

$$ \begin{gathered} \frac{\mathrm{PV}}{\beta}=3 \alpha \mathrm{Vt} \\ \text { or } \quad \mathrm{t}=\frac{\mathrm{P}}{3 \alpha \beta} \end{gathered} $$

8. The change in volume caused on stretching a rubber chord along its length is negligible. The Poission’s ratio for the material of the chord is

(1) 1

(2) $\frac{1}{2}$

(3) $\frac{1}{4}$

(4) 2

Show Answer

Correct answer: (2)

Solution:

Let ’ $r$ ’ be the radius of the rubber chord of length ’ $\ell$ ‘. Suppose the chord is stretched to increase its length

by $\Delta \ell$ resulting in a decrease $\Delta \mathrm{r}$ in its radius. We have Longitudinal strain $=\frac{\Delta \ell}{\ell}$, Lateral strain $=\frac{\Delta \mathrm{r}}{\mathrm{r}}$

As volume of the chord remains constant, we have

$$ \begin{array}{rlrl} \pi \mathrm{r}^{2} \ell & =\pi(\mathrm{r}-\Delta \mathrm{r})^{2}(\ell+\Delta \ell) & \\ & =\pi\left(\mathrm{r}^{2}-2 \mathrm{r} \Delta \mathrm{r}\right)(\ell+\Delta \ell) & & {\left[\text { Neglecting }(\Delta \mathrm{r})^{2}\right]} \\ \text { or } \quad \mathrm{r}^{2} \ell & =\mathrm{r}^{2} \ell-2 \mathrm{r} \ell \Delta \mathrm{r}+\mathrm{r}^{2} \Delta \ell & & \\ \therefore \quad 2 \mathrm{r} \ell \Delta \mathrm{r} & =\mathrm{r}^{2} \Delta \ell & & \\ 2 \ell \Delta \mathrm{r} & =\mathrm{r} \Delta \ell & & \\ \text { or } \quad \frac{\Delta \mathrm{r}}{\mathrm{r}} \cdot \frac{\ell}{\Delta \ell} & =\frac{1}{2} . \text { Therefore } & & \\ & \sigma & =\frac{\text { Lateral strain } \Delta \mathrm{r} \cdot \Delta \ell]}{\text { Longitudinal strain }}=\frac{\Delta \mathrm{r} / \mathrm{r}}{\Delta \ell / \ell}=\frac{1}{2} & \end{array} $$

9. A wire of length $\mathrm{L}$, radius r, Young’s modulus $Y$ shows an extension $x$ under a load $F$ suspended from its free and with other end fixed to ceiling. The extension produced in another wire of length $\frac{5}{4} \mathrm{~L} ;$ radius $2 \mathrm{r}$ and Young’s modulus $\frac{4}{5} \mathrm{Y}$ under a load $\frac{\mathrm{F}}{2}$ is

(1) $\frac{1}{8} x$

(2) $\frac{25}{8} x$

(3) $\frac{8}{25} x$

(4) $\frac{25}{128} x$

Show Answer

Correct answer: (4)

Solution:

For the given wire; extension $\Delta \ell$ is

$$ \Delta \ell=\frac{\mathrm{FL}}{\mathrm{AY}}=\frac{\mathrm{FL}}{\pi \mathrm{r}^{2} \mathrm{Y}} $$

For the new wire; given

$=\mathrm{F}^{\prime}=\frac{\mathrm{F}}{2} ; \mathrm{L}^{\prime}=\frac{5}{4} \mathrm{~L} ; \mathrm{r}^{\prime}=2 \mathrm{r}$ and $\mathrm{Y}^{\prime}=\frac{4}{5} \mathrm{Y}$

$\therefore$ Extension $=\Delta \ell=\frac{\left(\frac{\mathrm{F}}{2}\right)\left(\frac{5 \mathrm{~L}}{4}\right)}{\pi\left(2 \mathrm{r}^{2}\right)\left(\frac{4 \mathrm{Y}}{5}\right)}$

$$ =\frac{1}{2} \times \frac{5}{4} \times \frac{1}{4} \times \frac{5}{4} \cdot\left(\frac{\mathrm{FL}}{\pi \mathrm{r}^{2} \mathrm{Y}}\right)=\frac{25}{128} x $$

10. Two rods with identical dimension but different Young’s modulus of $4 \times 10^{11} \mathbf{N m}^{-2}$ and $6 \times 10^{11} \mathrm{Nm}^{-2}$ are joined end to end. An equivalent rod of identical dimensions is to be constructed. The Young’s modulus of the equivalent rod will be

(1) $5 \times 10^{11} \mathbf{N m}^{-2}$

(2) $2.4 \times 10^{11} \mathrm{Nm}^{-2}$

(3) $10 \times 10^{11} \mathrm{Nm}^{-2}$

(4) $12 \times 10^{11} \mathrm{Nm}^{-2}$

Show Answer

Correct answer: (2)

Solution:

Let $\mathrm{L}$ and $\mathrm{A}$ be the length and area of cross-section of each rod. Then

Extension in first rod $=(\Delta \ell) _{1}=\frac{\mathrm{FL}}{\mathrm{AY}} \hspace{40mm}. . . . . . . . (1)$

Extension in second rod $=(\Delta \ell) _{2}=\frac{\mathrm{FL}}{\mathrm{AY}} \hspace{40mm}. . . . . . . . (2)$

Total extension $=(\Delta \ell) _{1}+(\Delta \ell) _{2}$

Extension in the equivalent rod is also $(\Delta \ell) _{1}+(\Delta \ell) _{2}$. Let $\mathrm{Y}$ be Young’s modulus of the equivalent rod. Then

$$ \begin{equation*} (\Delta \ell) _{1}+(\Delta \ell) _{2}=\frac{\mathrm{FL}}{\mathrm{AY}} \tag{3} \end{equation*} $$

From Eqns (1), (2) and (3) we have

$$ \begin{aligned} & \frac{\mathrm{FL}}{\mathrm{AY}}=\frac{\mathrm{FL}}{\mathrm{AY_1}}+\frac{\mathrm{FL}}{\mathrm{AY_2}} \\ & \text { or } \quad \frac{1}{\mathrm{Y}}=\frac{1}{\mathrm{Y} _{1}}+\frac{1}{\mathrm{Y} _{2}} \quad \text { or } \quad \mathrm{Y}=\frac{\mathrm{Y} _{1} \mathrm{Y} _{2}}{\mathrm{Y} _{1}+\mathrm{Y} _{2}} \end{aligned} $$

Substituting give values of $\mathrm{Y} _{1}$ and $\mathrm{Y} _{2}$ we have

$$ Y=\frac{4 \times 6 \times 10^{22}}{(4+6) \times 10^{11}}=2.4 \times 10^{11} \mathrm{Nm}^{-2} $$

11. A light metal rod $A B$ of length ’ $L$ ’ is suspended from a rigid support and held horizontal by means of two vertical wires of equal length tied to its ends as shown in Fig. 3. The wires (1) and (2) have Young’s modulus $Y$ and $2 Y$ and radii ’ $a$ ’ and ’ $\frac{a}{3}$ ‘A weight ’ $W$ ’ is suspended from a point $C$ at a distance $x$ from end ’ $A$ ‘. In order to produce equal stress in the wires, the value of $x$ should be

(1) $\frac{\mathrm{L}}{3}$

(2) $\frac{L}{4}$

(3) $\frac{L}{9}$

(4) $\frac{\mathrm{L}}{\mathbf{1 0}}$

Show Answer

Correct answer: (4)

Solution:

Let $\mathrm{T}$ and $\mathrm{T}^{\prime}$ be tension in wires (1) and (2) respectively. Then given

Stress in wire (1) $=$ Stress in wire (2)

$$ \therefore \frac{\mathrm{T}}{\pi \mathrm{a}^{2}}=\frac{\mathrm{T}^{\prime}}{\pi(\mathrm{a} / 3)^{2}} $$

or $\mathrm{T}=9 \mathrm{~T}^{\prime}$

The rod $\mathrm{AB}$ remains horizontal if moments of $\mathrm{T}$ and $\mathrm{T}$ ’ about point $\mathrm{C}$ are equal and opposite, i.e.,

$$ \begin{aligned} & \quad \mathrm{T} \cdot x=\mathrm{T}^{\prime}(\mathrm{L}-x) \text { or } 9 \mathrm{~T}^{\prime} x=\mathrm{T}^{\prime}(\mathrm{L}-x) \\ & \therefore \quad x=\frac{\mathrm{L}}{10} \end{aligned} $$

12. A light metal rod $A B$ of length $L$ is suspended from a rigid support and held horizontal by two vertical wire of Young’s moduli $Y$ and $2 \mathrm{Y}$ and cross-sectional areas $\mathrm{A}$ and $2 \mathrm{~A}$ tied at the ends as shown in Fig. 4. A weight $W$ is suspended at a point $C$ at a distance $x$ from end A so that the rod still remain horizontal. Then $x$ is

(1) $\frac{1}{5} \mathrm{~L}$

(2) $\frac{4}{5} \mathrm{~L}$

(3) $\frac{8}{5} \mathrm{~L}$

(4) $\frac{16}{5} \mathrm{~L}$

Show Answer

Correct answer: (2)

Solution:

For the rod AB to remain horizontal with the load suspended; the increase in lengths of the two wire must be equal. Let $\mathrm{T} _{1}$ and $\mathrm{T} _{2}$ be tension in wires (1) and (2) respectively.

Increase in length of wire $(1)=\Delta \mathrm{L} _{1}=\frac{\mathrm{T} _{1} \mathrm{~L}}{\mathrm{AY}}$

Increase in length of wire $(2)=\Delta L _{2}=\frac{T _{2} L}{(2 A)(2 Y)}=\frac{T _{2} L}{4 A Y}$

Given $\Delta \mathrm{L} _{1}=\Delta \mathrm{L} _{2}$; therefore

$$ \mathrm{T} _{2}=4 \mathrm{~T} _{1} \text { and } \mathrm{T} _{2}+\mathrm{T} _{1}=\mathrm{W} $$

For the rod to remain horizontal, we have

$$ \begin{aligned} & \mathrm{T} _{1}(\mathrm{AC})=\mathrm{T} _{2}(\mathrm{CB}) \\ & \mathrm{T} _{1} x=4 \mathrm{~T} _{1}(\mathrm{~L}-x) \\ & x=\frac{4 \mathrm{~L}}{5} \end{aligned} $$

13. A massive pillar of height ’ $h$ ’ density $\rho$ and having uniform cross-section ’ $a$ ’ rests on a rigid base and supports a maximum vertical load $W$ newton at its upper end. The peak compressing strength of the pillar is $S$. Taking a safety factor of 10 ; the minimum area of cross-section of the pillar should be $\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)$

(1) $\frac{10 \mathrm{~W}}{\mathrm{~S}-100 \mathrm{~h} \rho}$

(2) $\frac{10 \mathrm{~W}}{\mathrm{~S}-10 \mathrm{~h} \rho}$

(3) $\frac{10 \mathrm{~W}}{\mathrm{~S}}$

(4) $\frac{10 \mathrm{S}}{\mathrm{W-10h\rho}}$

Show Answer

Correct answer: (1)

Solution:

The pillar supports the load $\mathrm{W}$ as well as its own weight at the bottom. Therefore

Total load $=$ Weight of the pillar $+\mathrm{W}$

$$ =(\text { ha } \rho) g+W $$

Stress on pillar $=\frac{(\text { ha } \rho) g+W}{a}$

This stress should not exceed $\frac{\mathrm{S}}{10}$ as safety factor desired is 10 . Therefore

$\frac{(\text { ha } \rho) g+W}{a}=\frac{S}{10}$

100 ha $\rho+10 \mathrm{~W}=$ a $\mathrm{S}$

$\left[\because \mathrm{g}=10 \mathrm{~ms}^{-2}\right]$

$\mathrm{a}(\mathrm{S}-100 \mathrm{~h} \rho)=10 \mathrm{~W}$

$\therefore \mathrm{a} _{\text {min }}=\frac{10 \mathrm{~W}}{\mathrm{~S}-100 \mathrm{~h} \rho}$

14. The following four wires $A, B, C$ and $D$ have their lengths, radii and Young’s modulus as tabulated below.

Wire	Length	Radius	Young’s Modulus
A	$\mathrm{L}$	$\mathrm{r}$	$3 \mathrm{Y}$
B	$2 \mathrm{~L}$	$2 \mathrm{r}$	$2 \mathrm{Y}$
C	$4 \mathrm{~L}$	$4 \mathrm{r}$	$\mathrm{Y} / 2$
D	$6 \mathrm{~L}$	$3 \mathrm{r}$	$\mathrm{Y} / 6$

When subjected to same load; the maximum extension will be observed in wire.

(1) $\mathbf{A}$

(2) $\mathbf{B}$

(3) $\mathrm{C}$

(4) $\mathrm{D}$

Show Answer

Correct answer: (4)

Solution:

We have extension $=\Delta \mathrm{L}=\frac{\mathrm{FL}}{\mathrm{AY}}=\frac{\mathrm{FL}}{\pi \mathrm{r}^{2} \mathrm{Y}}$

For the same load extension in proportional to $\frac{\mathrm{L}}{\mathrm{r}^{2} \mathrm{Y}}$. In other words the extension depends on the value of $\frac{\mathrm{L}}{\mathrm{r}^{2} \mathrm{Y}}$ of the wires. We have, the values of $\frac{\mathrm{L}}{\mathrm{r}^{2} \mathrm{Y}}$ in the following table.

$A$	$\frac{\mathrm{L}}{\mathrm{r}^{2} 3 \mathrm{Y}}=\frac{1}{3}\left(\frac{\mathrm{L}}{\mathrm{r}^{2} \mathrm{Y}}\right)$
$\mathrm{B}$	$\frac{2 \mathrm{~L}}{4 \mathrm{r}^{2} 2 \mathrm{Y}}=\frac{1}{4}\left(\frac{\mathrm{L}}{\mathrm{r}^{2} \mathrm{Y}}\right)$
$\mathrm{C}$	$\frac{4 \mathrm{~L} \times 2}{16 \mathrm{r}^{2} \mathrm{Y}}=\frac{1}{2}\left(\frac{\mathrm{L}}{\mathrm{r}^{2} \mathrm{Y}}\right)$
$\mathrm{D}$	$\frac{6 \mathrm{~L} \times 2}{9 \mathrm{r}^{2} \mathrm{Y}}=4\left(\frac{\mathrm{L}}{\mathrm{r}^{2} \mathrm{Y}}\right)$

As the value is maximum for $\mathrm{D}$; the extension will also be maximum in $\mathrm{D}$.

15. A solid sphere of radius $R$ when taken to a depth of $100 \mathrm{~m}$ in water gets compressed so that its radius decreases by $0.1 \%$. The value of bulk modulus of the material of the sphere is (density of water $=10^{3} \mathrm{~kg} \mathrm{~m}^{-3} ; \mathrm{g}=10 \mathrm{~ms}^{-2}$ )

(1) $10^{5} \mathrm{Nm}^{-2}$

(2) $\frac{1}{3} \times 10^{9} \mathrm{Nm}^{-2}$

(3) $10^{9} \mathrm{Nm}^{-2}$

(4) $\frac{4}{3} \times 10^{9} \mathrm{Nm}^{-2}$

Show Answer

Correct answer: (2)

Solution:

The pressure due to liquid column at $100 \mathrm{~m}$ depth $=\mathrm{h} \rho \mathrm{g}=10^{2} \times 10^{3} \times 10 \mathrm{Nm}^{-2}$

Let $\mathrm{V}$ be volume of sphere on surface of earth. Obviously

$$ \mathrm{V}=\frac{4}{3} \pi \mathrm{R}^{3} $$

Let $(\mathrm{V}-\Delta \mathrm{V})$ be the volume of sphere at a depth of $100 \mathrm{~m}$. Then

$$ \begin{aligned} \mathrm{V}- & \Delta \mathrm{V}=\frac{4}{3} \pi(\mathrm{R}-\Delta \mathrm{R})^{3} \\ = & \frac{4}{3} \pi \mathrm{R}^{3}\left[1-\frac{\Delta \mathrm{R}}{\mathrm{R}}\right]^{3} \simeq \frac{4 \pi}{3} \mathrm{R}^{3}\left(1-\frac{3 \Delta \mathrm{R}}{\mathrm{R}}\right) \end{aligned} $$

Given $\frac{\Delta \mathrm{R}}{\mathrm{R}} \times 100=0.1$.

$\therefore \mathrm{V}-\Delta \mathrm{V}=\mathrm{V}-\frac{3 \mathrm{~V}}{1000}$ or $\Delta \mathrm{V}=\frac{3 \mathrm{~V}}{1000}$

The volumetric strain $=\frac{\Delta \mathrm{V}}{\mathrm{V}}=\frac{3}{1000}$

Bulk Modulus $=\frac{\Delta \mathrm{P}}{\Delta \mathrm{V} / \mathrm{v}}=\frac{10^{6}}{3 / 1000}=\left(\frac{1}{3}\right) \times 10^{9} \mathrm{Nm}^{-2}$

16. Two steel plates are soldered on the two sides of a copper plate. All plates have equal cross-section A each. The coefficient of thermal expansion of copper and steel are $\alpha _{C}$ and $\alpha _{\mathrm{S}}$ and their Young’s moduli are $Y _{\mathrm{C}}$ and $Y _{\mathrm{s}}$. The temperature of the plates is raised by $t^{\circ} \mathrm{C}$ and plates retain their shape; the tension in the copper plate is

(1) $\frac{A Y _{C}+2 Y _{S}}{2 Y _{C} Y _{S}\left(\alpha _{C}-\alpha _{S}\right) t}$

(2) $\frac{2 A Y _{S} Y _{C}\left(\alpha _{C}-\alpha _{S}\right) t}{Y _{C}+2 Y _{S}}$

(3) $\frac{\mathbf{A} Y _{S} \mathbf{Y} _{\mathrm{C}}\left(\alpha _{C}-\alpha _{S}\right) t}{2 Y _{C}+Y _{S}}$

(4) $\frac{A Y _{S} Y _{C}\left(\alpha _{C}-\alpha _{S}\right) t}{2\left(Y _{C}+2 Y _{S}\right)}$

Show Answer

Correct answer: (2)

Solution:

Let $\mathrm{F} _{\mathrm{S}}$ be the tension in each of the steel plates and $\mathrm{F} _{\mathrm{C}}$ be tension in copper. Then from Fig. 5

$$ \begin{equation*} \mathrm{F} _{\mathrm{C}}=2 \mathrm{~F} _{\mathrm{S}} \tag{1} \end{equation*} $$

Also,

Thermal expansion in copper + Elastic compression in copper $=$ Thermal expansion in steel + Elastic elogation in steel.

$\therefore \quad \alpha _{C} \mathrm{Lt}-\left[\frac{2 \mathrm{~F} _{\mathrm{S}} \mathrm{L}}{\mathrm{AY} _{\mathrm{C}}}\right]=\alpha _{\mathrm{S}} \mathrm{Lt}+\left[\frac{\mathrm{F} _{\mathrm{s}} \mathrm{L}}{\mathrm{AY} _{\mathrm{S}}}\right]$

$\left(\alpha _{C}-\alpha _{S}\right) t=\frac{F _{S}}{A}\left[\frac{1}{Y _{S}}+\frac{2}{Y _{C}}\right]$

$=\frac{F _{S}}{A}\left[\frac{Y _{C}+2 Y _{S}}{Y _{C} Y _{S}}\right]$

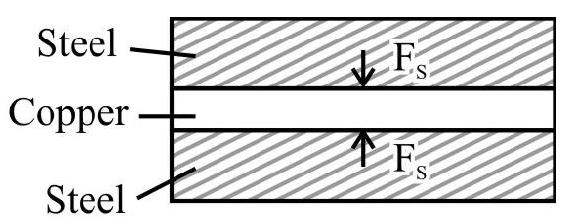
Fig. 5

$\therefore \quad F _{S}=\frac{A Y _{S} Y _{C}\left(\alpha _{C}-\alpha _{S}\right) t}{Y _{C}+2 Y _{S}}$

The tension $\mathrm{F} _{\mathrm{C}}$ in copper plate is

$$ \mathrm{F} _{\mathrm{C}}=2 \mathrm{~F} _{\mathrm{S}}=\frac{2 \mathrm{~A} \mathrm{Y} _{\mathrm{S}} \mathrm{Y} _{\mathrm{C}}\left(\alpha _{\mathrm{C}}-\alpha _{\mathrm{S}}\right) \mathrm{t}}{\mathrm{Y} _{\mathrm{C}}+2 \mathrm{Y} _{\mathrm{S}}} $$

17. A steel wire of length ’ $\ell$ ’ and radius of cross-section ’ $r$ ’ is stretched horizontally between two rigid supports attached at its ends. A load Mg suspended from its midpoint produces a depression of $x$ well within elastic limit of the material of the wire. The Young’s modulus of the material is

(1) $\frac{M g l^{2}}{8 \pi r^{2} x^{2}}$

(2) $\frac{8 \pi \mathbf{r}^{2} \mathrm{x}^{2}}{\mathbf{M g l ^ { 2 }}}$

(3) $\frac{M g l^{3}}{8 \pi r^{2} x^{3}}$

(4) $\frac{\mathrm{Mgl}}{8 \pi \mathrm{rx}^{2}}$

Show Answer

Correct answer: (3)

Solution:

In Fig. 6, $\mathrm{AB}$ is wire of length $\ell$. $\mathrm{M}$ is mass suspended from mid point $\mathrm{C}$. In equilibrium, point $\mathrm{C}$ moves to position $\mathrm{D}$ as shown in Fig. 6. Now

$\mathrm{AB}=\ell, \mathrm{BC}=\frac{\ell}{2}$ and $\mathrm{CD}=x$.

$\therefore \mathrm{DB}^{2}=x^{2}+\left(\frac{\ell}{2}\right)^{2}$

$\mathrm{DB}=\left[\left(\frac{\ell}{2}\right)^{2}+x^{2}\right]^{1 / 2}=\frac{\ell}{2}\left[1+\frac{x^{2}}{(\ell / 2)^{2}}\right]^{1 / 2}$

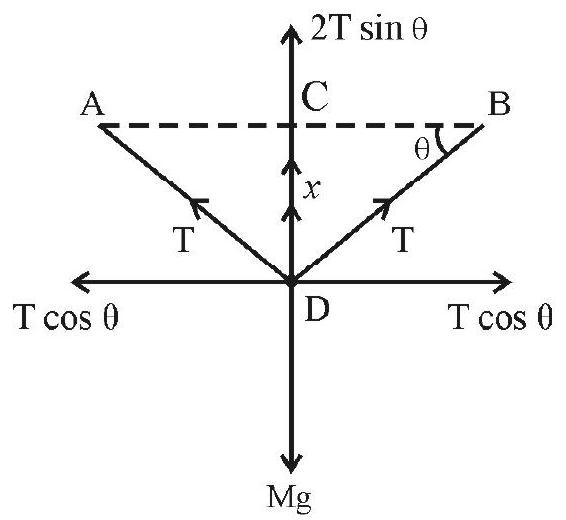
Fig. 6

$$ \simeq \frac{\ell}{2}\left[1+\frac{x^{2}}{2\left(\frac{\ell}{2}\right)^{2}}\right] $$

The Increased length of wire $=\mathrm{ADB}=2 \mathrm{DB}=\ell\left[1+\frac{2 x^{2}}{\ell^{2}}\right]=\ell+\frac{2 x^{2}}{\ell}$

$\therefore \quad$ Increase in length of wire $=\Delta \ell=\frac{2 x^{2}}{\ell}$

By definition

Strain $=\frac{\text { Increase in length }}{\text { Original length }}=\frac{2 x^{2}}{\ell^{2}}$, Stress $=\frac{\text { Tension } \mathrm{T}}{\text { Area }}=\frac{\mathrm{T}}{\pi \mathrm{r}^{2}}$

For equilibrium at point $\mathrm{D}$,

$2 \mathrm{~T} \sin \theta=\mathrm{Mg}$

$2 \mathrm{~T} \quad \theta=\mathrm{Mg} \quad[$ For small $\theta, \sin \theta \simeq \theta]$

$\therefore \mathrm{T}=\frac{\mathrm{Mg}}{2 \theta}=\frac{\mathrm{Mg}}{2\left(\frac{x}{\ell / 2}\right)}=\frac{\mathrm{Mg} \ell}{4 x}$

Substituting value of $T$, we have

Stress $=\frac{\mathrm{T}}{\pi \mathrm{r}^{2}}=\frac{\operatorname{Mg} \ell}{4 \pi \mathrm{r}^{2} x}$

Therefore

$\mathrm{Y}=\frac{\text { Stress }}{\text { Strain }}=\frac{\operatorname{Mg} \ell}{4 \pi \mathrm{r}^{2} x} \cdot \frac{\ell^{2}}{2 x^{2}}=\frac{\operatorname{Mg} \ell^{3}}{8 \pi \mathrm{r}^{2} \mathrm{x}^{3}}$

18. Two blocks of masses $m \mathrm{~kg}$ and $\mathrm{M} \mathrm{kg}$ are connected by a metal wire passing over a smooth pulley as shown in Fig.7. Given $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}$. The breaking stress in $\mathrm{Nm}^{-2}$, of the metal wire is $B$. The minimum radius ’ $r$ ’ of the wire to support the system without breaking is

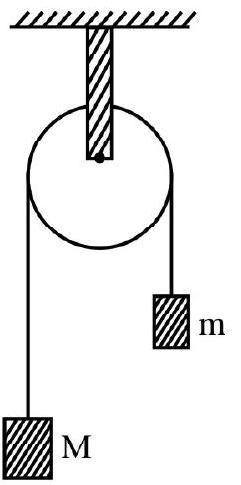
(1) $\sqrt{\frac{10(m+M)}{\pi B}}$

(2) $\sqrt{\frac{\pi(m+M) B}{20 m M}}$

(3) $\sqrt{\frac{10(M+m)}{\pi B}}$

(4) $\sqrt{\frac{20 m M}{\pi(m+M) B}}$

Show Answer

Correct answer: (4)

Solution:

The tension in the wire is given by

$$ T=\left(\frac{2 m M}{m+M}\right) g=\frac{20 m M}{m+M} $$

Stress developed $=\frac{T}{\pi r^{2}}=\frac{20 m M}{\pi(m+M) r^{2}}$

For the wire to support the system without breaking

$$ \frac{20 \mathrm{mM}}{\pi(\mathrm{m}+\mathrm{M}) \mathrm{r}^{2}}=\mathrm{B} $$

or $\quad \mathrm{r}^{2}=\frac{20 \mathrm{mM}}{\pi(\mathrm{m}+\mathrm{M}) \mathrm{B}}$

$\therefore r=\sqrt{\frac{20 m M}{\pi(m+M) B}}$

19. A metal wire of length ’ $L$ ’ is just streteched between two fixed points at a temperature $t _{1}^{0} C$. The tension in the wire of Young’s modulus $Y$ coefficient of linear expansion ’ $\alpha$ ’ when the temperature drops to $\mathbf{t} _{2}^{0} \mathrm{C}$ is

(1) $\frac{\alpha Y\left(t _{2}-t _{1}\right)}{\pi r^{2}}$

(2) $\pi \alpha r^{2} \mathbf{Y}\left(\mathbf{t} _{2}-\mathbf{t} _{1}\right)$

(3) $\frac{\alpha \pi r^{2} Y}{t _{2}-t _{1}}$

(4) $\frac{\alpha \pi \mathbf{r}^{2}\left(\mathbf{t} _{2}-\mathbf{t} _{1}\right)}{\mathrm{Y}}$

Show Answer

Correct answer: (2)

Solution:

The length $\mathrm{L}^{\prime}$ at temperature $\mathrm{t} _{2}^{0} \mathrm{C}$ is given by

$\mathrm{L}^{\prime}=\mathrm{L}\left[1+\alpha\left(\mathrm{t} _{2}-\mathrm{t} _{1}\right)\right]$

Change in length $=\mathrm{L}^{\prime}-\mathrm{L}=\alpha \mathrm{L}\left(\mathrm{t} _{2}-\mathrm{t} _{1}\right)$

Strain $=\frac{\text { Change in length }}{\text { Original length }}=\frac{\alpha \mathrm{L}\left(\mathrm{t} _{2}-\mathrm{t} _{1}\right)}{\mathrm{L}}=\alpha\left(\mathrm{t} _{2}-\mathrm{t} _{1}\right)$

Stress $=\mathrm{Y} \times$ strain $=\alpha \mathrm{Y}\left(\mathrm{t} _{2}-\mathrm{t} _{1}\right)$

$\frac{\text { Force }}{\text { Area }}=\frac{F}{\pi r^{2}}=\alpha Y\left(t _{2}-t _{1}\right)$

$\therefore$ Tension in wire $=\mathrm{F}=\pi \mathrm{r}^{2} \alpha \mathrm{Y}\left(\mathrm{t} _{2}-\mathrm{t} _{1}\right)$

20. A steel wire of area of cross-section $A$ is stretched within its elastic limit between two pillars $P _{1}$ and $P _{2}$ as shown in Fig. 8. A mass $M$ is suspended from the mid point of the wire. The strain produced in the wire is

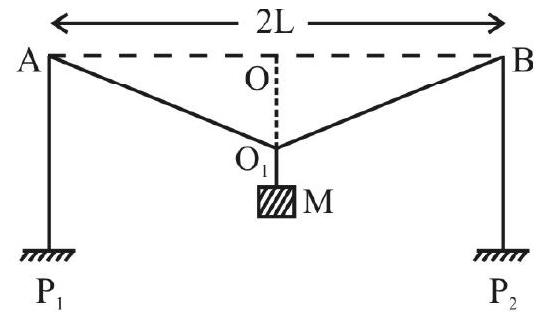
(1) $\frac{2 L}{x^{2}}$

(2) $\frac{x^{2}}{\mathbf{L}^{2}}$

(3) $\frac{x^{2}}{2 L^{2}}$

(4) $\frac{x^{2}}{4 L^{2}}$

Show Answer

Correct answer: (3)

Solution:

Fig. 9 shows wire in equilibrium under load M. $\mathrm{AO} _{1} \mathrm{~B}=2 \mathrm{~L}$ ’ is new length of wire. Obviously

$$ \mathrm{L}^{\prime}=\sqrt{x^{2}+\mathrm{L}^{2}} $$

or

$$ \mathrm{L}^{\prime}=\mathrm{L}\left(1+\frac{x^{2}}{\mathrm{~L}^{2}}\right)^{1 / 2} $$

$$ \simeq \mathrm{L}\left(1+\frac{x^{2}}{2 \mathrm{~L}^{2}}\right)=\mathrm{L}+\frac{x^{2}}{2 \mathrm{~L}} $$

Increase in length $=\Delta \mathrm{L}=2 \mathrm{~L}^{\prime}-2 \mathrm{~L}=2 \cdot \frac{x^{2}}{2 \mathrm{~L}}$

Strain $=\frac{\text { Increase in length }}{\text { Original length }}=\frac{2 \cdot x^{2}}{2 \mathrm{~L}} \cdot \frac{1}{2 \mathrm{~L}}=\frac{x^{2}}{2 \mathrm{~L}^{2}}$

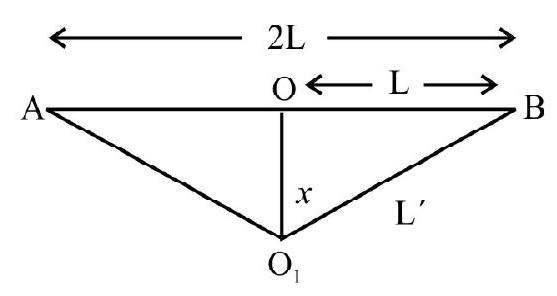
21. Two rods of different materials having coefficients of linear expansion $\alpha _{1} ; \alpha _{2}$ and Young’s moduli $Y _{1}$ and $Y _{1}$ respectively are fixed between two rigid massive walls. The rods are heated such that they undergo the same increase in temperature. There in no bending of the rods. If $\alpha _{1}: \alpha _{2}=2: 3$, the thermal stresses developed in the two rods are equal provided $Y _{1}: Y _{2}$ is equal to

(1) $2: 3$

(2) $1: 1$

(3) $3: 2$

(4) $4: 9$

Show Answer

Correct answer: (3)

Solution:

For an increase in temperature $\Delta \theta$; increase in length $\Delta \ell=\alpha \ell \Delta \theta$. Longitudinal strain due to rise in temperature $=\frac{\Delta \ell}{\ell}=\alpha \Delta \theta$. We know

$\frac{\text { Stress }}{\text { Strain }}=Y ;$ therefore

Thermal stress $=\mathrm{Y} \times$ strain $=\mathrm{Y} \alpha \Delta \theta$

Given thermal stress in the two wires is same.

$\therefore \mathrm{Y} _{1} \alpha _{1} \Delta \theta=\mathrm{Y} _{2} \alpha _{2} \Delta \theta$

$$ \therefore \quad \frac{Y _{1}}{Y _{2}}=\frac{\alpha _{2}}{\alpha _{1}}=\frac{3}{2} \quad\left[\text { Given } \frac{\alpha _{1}}{\alpha _{2}}=\frac{2}{3}\right] $$

22. A pendulum made of a uniform wire of cross-sectional area ’ $A$ ’ has time period $T$. When an additional mass $M$ in added to the bob, the time period changes to $T _{M}$. The Young’s modulus of the material of the wire is $Y$; then $\frac{1}{Y}$ is

(1) $\left[\left(\frac{T _{M}}{T}\right)^{2}-1\right] \frac{A}{M g}$

(2) $\left[\left(\frac{T _{M}}{T}\right)^{2}-1\right] \frac{M g}{A}$

(3) $\left[1-\left(\frac{T}{T _{M}}\right)^{2}\right] \frac{A}{M g}$

(4) $\left[1^{-}-\left(\frac{T _{M}}{T}\right)^{2}\right] \frac{A}{M g}$

( $\mathrm{g}=$ acceleration due to gravity)

Show Answer

Correct answer: (1)

Solution:

The time period $\mathrm{T}$ of a simple pendulum is

$$ \begin{equation*} \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{L}}{\mathrm{g}}} \tag{1} \end{equation*} $$

where $\mathrm{L}$ is the length of pendulum. An additional mass $\mathrm{M}$ increase the length by $\Delta \mathrm{L}$. Obviously $\Delta \mathrm{L}=\frac{\mathrm{MgL}}{\mathrm{AY}}$.

$\therefore$ Increased length of pendulum $=\mathrm{L}+\Delta \mathrm{L}=\mathrm{L}+\frac{\mathrm{MgL}}{\mathrm{AY}}$

$$ =\mathrm{L}\left[1+\frac{\mathrm{Mg}}{\mathrm{AY}}\right] $$

Due to increase in length, the time period $\mathrm{T} _{\mathrm{M}}$ is given by

$$ \mathrm{T} _{\mathrm{M}}=2 \pi \sqrt{\frac{\mathrm{L}\left(1+\frac{\mathrm{Mg}}{\mathrm{AY}}\right)}{\mathrm{g}}} $$

From Eqns (1) and (2) we have

$$ \begin{gathered} \left(\frac{\mathrm{T} _{\mathrm{M}}}{\mathrm{T}}\right)^{2}=1+\frac{\mathrm{Mg}}{\mathrm{AY}} \\ \therefore 1+\frac{\mathrm{Mg}}{\mathrm{AY}}=\left(\frac{\mathrm{T} _{\mathrm{M}}}{\mathrm{T}}\right)^{2} \\ \frac{\mathrm{Mg}}{\mathrm{AY}}=\left(\frac{\mathrm{T} _{\mathrm{M}}}{\mathrm{T}}\right)^{2}-1 \\ \text { or } \frac{1}{\mathrm{Y}}=\left[\left(\frac{\mathrm{T} _{\mathrm{M}}}{\mathrm{T}}\right)^{2}-1\right] \frac{\mathrm{A}}{\mathrm{Mg}} \end{gathered} $$

Correct option is (1)

23. Fig. 10 shows a tappered wire of length $L$ under an external force $F$. The radius at end $O$ and $A$ is $2 r$ and $r$ respectively. $Y$ is Young’s modulus of material of wire. A normal external force $F$ is applied at end $A$. The increase in length of wire is

Fig. 10

(1) $\frac{\mathrm{FL}}{\pi \mathbf{Y r^2}}$

(2) $\frac{\mathrm{FL}}{2 \pi \mathrm{Yr}^{2}}$

(3) $\frac{2 \mathrm{FL}}{3 \pi \mathrm{Yr}^{2}}$

(4) $\frac{3 \mathrm{FL}}{2 \pi \mathrm{Yr}^{2}}$

Show Answer

Correct answer: (2)

Solution:

The rate of change of radius along the length of wire

$$ \begin{equation*} =\frac{\mathrm{dr}}{\mathrm{dy}}=\alpha=\left(\frac{\mathrm{r}-2 \mathrm{r}}{\mathrm{L}}\right)=-\left(\frac{\mathrm{r}}{\mathrm{L}}\right) \tag{1} \end{equation*} $$

Consider a small element of wire define by y and $y+$ dy as shown in Fig. 11

$\mathrm{r} _{1}=$ The radius of the element considered $=[2 \mathrm{r}+\alpha \mathrm{y}]$

Let $d x$ by be the change in length of element of original length dy due to applied force F. Then

$$ \begin{gathered} \mathrm{Y}=\frac{\mathrm{F} / \pi \mathrm{r} _{1}^{2}}{\mathrm{dx} / \mathrm{dy}} \\ \text { or } \mathrm{d} x=\frac{\mathrm{F}}{\pi \mathrm{Y} \mathrm{r} _{1}^{2}} \mathrm{dy} \\ =\frac{\mathrm{F}}{\pi \mathrm{Y}[2 \mathrm{r}+\alpha \mathrm{y}]^{2}} \mathrm{dy} \end{gathered} $$

Integrate

$$ \int _{0}^{x} \mathrm{~d} x=\frac{\mathrm{F}}{\pi \mathrm{Y}} \int _{0}^{\mathrm{L}} \frac{\mathrm{dy}}{(2 \mathrm{r}-\alpha \mathrm{y})^{2}}=\frac{\mathrm{F}}{\pi \mathrm{Y}}\left|\frac{(2 \mathrm{r}+\alpha \mathrm{Y})^{-1}}{-\alpha}\right| _{0}^{\mathrm{L}} $$

$$ =\frac{\mathrm{F}}{\pi \mathrm{Y}\left(\frac{\mathrm{r}}{\mathrm{L}}\right)}\left[\left(\frac{1}{2 \mathrm{r}+\alpha \mathrm{L}}\right)-\left(\frac{1}{2 \mathrm{r}}\right)\right]=\frac{\mathrm{FL}}{\pi \mathrm{Yr}}\left[\left(\frac{1}{\mathrm{r}}\right)-\left(\frac{1}{2 \mathrm{r}}\right)\right]=\frac{\mathrm{FL}}{2 \pi \mathrm{Yr}^{2}} $$

24. In Fig. 12, the area of cross-section of wider tube is $800 \mathrm{~cm}^{2}$. A mass of $12 \mathrm{~kg}$ is placed on a massless; frictionless platform as shown. $h$ is the difference of height of water in the two limbs. $h$ is $\left(g=10 \mathrm{~ms}^{-2}\right)$

(1) $10 \mathrm{~cm}$

(2) $6 \mathrm{~cm}$

(3) $15 \mathrm{~cm}$

(4) $2 \mathrm{~cm}$

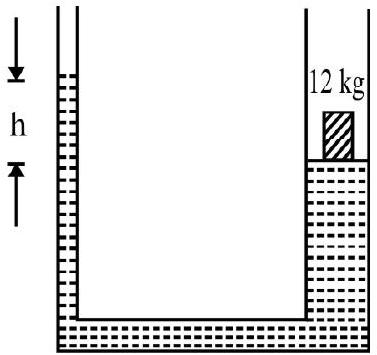Fig. 12

Show Answer

Correct answer: (3)

Solution:

$\mathrm{P}=$ The pressure on liquid due to weight placed

$$ \begin{equation*} =\frac{12 \times 10}{800 \times 10^{-4}} \mathrm{~Pa}=15 \times 10^{2} \mathrm{~Pa} \tag{1} \end{equation*} $$

From Pascal’s law pressure is transmitted equally in all directions in a liquid. Therefore

$$ \begin{equation*} \mathrm{P}=\mathrm{h} \rho \mathrm{g}=\mathrm{h} \times 10^{3} \times 10 \mathrm{~Pa} \tag{2} \end{equation*} $$

From Eqns. (1) and (2) we have

$$ \mathrm{h} \times 10^{4}=15 \times 10^{2} $$

or $\mathrm{h}=15 \times 10^{-2} \mathrm{~m}=15 \mathrm{~cm}$

25. Fig. 13 shows a closed tube $A B C D$ containing water at room teperature. End $A$ is heated and end $B$ is cooled. Which of the following statements is correct?

(1) Water does not circulate

(2) Water circulates in clockwise direction inside tube

(3) Water circulates in anticlockwise direction inside tube

(4) Water circulates clockwise along ADC and anticlockwise along ABC

Show Answer

Correct answer: (3)

Solution:

On heating end A; density of water at A decreases whereas on cooling end B; density of water at end B increases. Therefore liquid pressure $\mathrm{P} _{\mathrm{A}}$ and $\mathrm{P} _{\mathrm{B}}$ at ends $\mathrm{A}$ and $\mathrm{B}$ are such that $\mathrm{P} _{\mathrm{A}}<\mathrm{P} _{\mathrm{B}}$. The liquid (water) moves from region of higher pressure to lower pressure. Therefore water circulation is anticlockwise direction inside tube.

26. A closed enclosure contains an ideal gas. The pressure exerted by gas is same at all points inside enclosure. The enclosure is given an acceleration (uniform) in horizontal direction. The pressure in compartment now is

(1) same everywhere

(2) lower in front side

(3) lower in rear side

(4) lower on upper side

Show Answer

Correct answer: (2)

Solution:

Due to acceleration of compartment there is ficticous force an atoms / molecules of gas directed towards rear of enclosure. Therefore pressure of gas is more at rear of enclosure or equivalently we say pressure is lower in the front side of container.

27. A circular tube of radius $R$ is placed in a vertical plane. Two immisible liquids of density $\rho _{1}$ and $\rho _{2}$ are poured inside tube such that each liquid subtends an angle of $\frac{\pi}{2}$ at center $O$ as shown in Fig. $14 \rho _{1}: \rho _{2}: 3: 2$. The radius $O C$ makes an angle $\theta$ with the vertical. Then

(1) $\theta=\tan ^{-1}(3 / 2)$

(2) $\theta=\tan ^{-1}(2 / 3)$

(3) $\theta=\tan ^{-1}(2 / 5)$

(4) $\boldsymbol{\theta}=\tan ^{-1}(1 / 5)$

Fig. 14

Show Answer

Correct answer: (4)

Solution:

Let $h _{1}$ and $h _{2}$ be the vertical height above $C$ of the two liquids as shown in Fig. 15. Obviously $\mathrm{h} _{1}=\mathrm{OD}-\mathrm{OE}$

$$ =\mathrm{R}[\cos \theta-\sin \theta] $$

$\mathrm{h} _{2}=\mathrm{OD}+\mathrm{OB} _{1}$

$$ =\mathrm{R}[\cos \theta+\sin \theta] $$

In equilibrium

$$ \mathrm{h} _{1} \rho _{1} \mathrm{~g}=\mathrm{h} _{2} \rho _{2} \mathrm{~g} $$

Fig. 15 or $\mathrm{R}[\cos \theta-\sin \theta] \rho _{1}=\mathrm{R}[\cos \theta+\sin \theta] \rho _{2}$

$\therefore \frac{\rho _{1}}{\rho _{2}}=\frac{\cos \theta+\sin \theta}{\cos \theta-\sin \theta}=\frac{1+\tan \theta}{1-\tan \theta}$

Given $\frac{\rho _{1}}{\rho _{2}}=\frac{3}{2}$; therefore

$$ \begin{aligned} & \frac{3}{2}=\frac{1+\tan \theta}{1-\tan \theta} \text { or } \tan \theta=\frac{1}{5} \\ \therefore \quad & =\tan ^{-1}\left(\frac{1}{5}\right) \end{aligned} $$

28. A cylinder of radius $R$. Length $L=5 h$, has a hemispherical part of radius $R$ removed from its bottom. $M$ is mass of the remainnig part of cylinder of density $\rho _{1}$. It is suspended inside a liquid of density $\rho _{2}$ as shown in Fig.16. The upper face of cylinder is at a depth $h$ below the liquid level. The force on bottom of cylinder due to liquid is ( $P$ is atmospheric pressure)

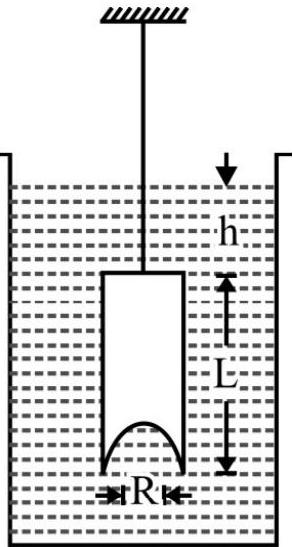
(1) $\pi R^{2}\left[\mathbf{P}+6 \rho _{2} g h\right]$

(2) $\pi R^{2}\left[\mathbf{P}+\rho _{2} g\left(6 h-\frac{2 R}{3}\right)\right]$

(3) $\pi R^{2}\left[P-\rho _{2} g\left(6 h-\frac{2 R}{3}\right)\right]$

(4) $\pi R^{2}\left[P+\rho _{2} g\left(5 h-\frac{2 R}{3}\right)\right]$

Show Answer

Correct answer: (2)

Solution:

In Fig. 17; $\mathrm{F} _{1}$ is force on upper face of cylinder. It is

$$ \begin{equation*} \mathrm{F} _{1}=\left(\mathrm{P}+\mathrm{h} \rho _{2} \mathrm{~g}\right) \pi \mathrm{R}^{2} \tag{1} \end{equation*} $$

$B$ is the bouyant force on cylinder. From Archemede’s principle

$\mathrm{B}=$ weight of liquid displaced

$$ =\mathrm{V} \times \rho _{2} \times \mathrm{g} $$

where $\mathrm{V}$ is volume of cylinder. Obviously

$$ \begin{aligned} \mathrm{V}= & \pi \mathrm{R}^{2} \mathrm{~L}-\frac{2 \pi}{3} \mathrm{R}^{3}=5 \pi \mathrm{R}^{2} \mathrm{~h}-\frac{2 \pi}{3} \mathrm{R}^{3} \\ & =\pi \mathrm{R}^{2}\left[5 \mathrm{~h}-\frac{2 \mathrm{R}}{3}\right] \end{aligned} $$

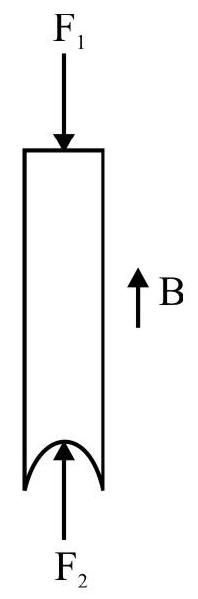Fig. 17

Let $\mathrm{F} _{2}$ be the upward force on bottom of cylinder. In equilibrium, $\mathrm{F} _{2}-\mathrm{F} _{1}=\mathrm{B}$;

$\therefore \mathrm{F} _{2}=\mathrm{F} _{1}+\mathrm{B}=\left(\mathrm{P}+\mathrm{h} \rho _{2} \mathrm{~g}\right) \pi \mathrm{R}^{2}+\pi \mathrm{R}^{2}\left[5 \mathrm{~h}-\frac{2 \mathrm{R}}{3}\right] \rho _{2} \mathrm{~g}$

$=\pi R^{2} \mathrm{P}+\pi \mathrm{R}^{2} \rho _{2} \mathrm{~g}\left[6 \mathrm{~h}-\frac{2 \mathrm{R}}{3}\right]$

$=\pi R^{2}\left[\mathrm{P}+\rho _{2} \mathrm{~g}\left(6 \mathrm{~h}-\frac{2 \mathrm{R}}{3}\right)\right]$

29. In Fig. 18, A is a cylinder of radius $2 r$; height $h$. The density of material of cylinder is $\rho$. The cylinder is inside a tank filled with a liquid of density $3 \rho$. The level of liquid in tank starts decreasing very slowly. When level of liquid is at a height $\mathrm{H}$ above the cylinder; it (the cylinder) is on brink of moving up. $\mathrm{H}$ is

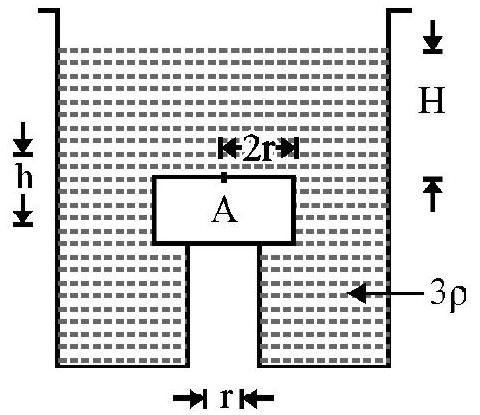
Fig. 18

(1) $\mathrm{h}$

(2) $\frac{4 \mathrm{~h}}{3}$

(3) $\frac{5 \mathrm{~h}}{3}$

(4) $\frac{5 \mathrm{~h}}{9}$

Show Answer

Correct answer: (3)

Solution:

$A _{1}=$ The area of cross-section of cylinder $=\pi(2 r)^{2}=4 \pi r^{2}$

$\mathrm{A} _{2}=$ The area of the base of cylinder in air $=\pi \mathrm{r}^{2}$

$A _{3}=$ The area of cylinder inside liquid $=A _{1}-A _{2}=3 \pi r^{2}$

Let $\mathrm{P} _{0}$ be the atmospheric pressure.

$\mathrm{F} _{1}=$ Force on upper face of cylinder $=\left(\mathrm{P} _{0}+3 \mathrm{H} \rho \mathrm{g}\right) 4 \pi \mathrm{r}^{2}$

$\mathrm{F} _{2}=$ Force on part of cylinder in air at its bottom $=\mathrm{P} _{0}\left(\pi \mathrm{r}^{2}\right)$

$\mathrm{F} _{3}=$ The force on bottom of cylinder inside liquid $=\left[\mathrm{P} _{0}+(\mathrm{H}+\mathrm{h}) \times 3 \rho \mathrm{g}\right] .3 \pi \mathrm{r}^{2}$

$\mathrm{W}=$ The weight of cylinder $=\left(4 \pi \mathrm{r}^{2} \mathrm{~h}\right) \rho \mathrm{g}$

The forces are shown in Fig. 19. When cylinder is on brink of rising up

$$ \begin{aligned} & \mathrm{F} _{1}+\mathrm{W}=\mathrm{F} _{2}+\mathrm{F} _{3} \\ & 4 \pi\left[\mathrm{P} _{0}+3 \mathrm{H} \rho \mathrm{g}\right] \mathrm{r}^{2}+4 \pi \mathrm{r}^{2} \mathrm{~h} \rho \mathrm{g}=\mathrm{P} _{0}\left(\pi \mathrm{r}^{2}\right)+\left[\mathrm{P} _{0}+(\mathrm{H}+\mathrm{h}) 3 \rho \mathrm{g}\right] \times 3 \pi \mathrm{r}^{2} \end{aligned} $$

or $\quad 4 \mathrm{P} _{0}+4(3 \mathrm{H}+\mathrm{h}) \rho g=\mathrm{P} _{0}+3 \mathrm{P} _{0}+9(\mathrm{H}+\mathrm{h}) \rho \mathrm{g}$

or $\quad 4(3 \mathrm{H}+\mathrm{h})=9(\mathrm{H}+\mathrm{h})$

or $3 \mathrm{H}=5 \mathrm{~h}$

$\therefore \quad \mathrm{H}=\frac{5}{3} \mathrm{~h}$

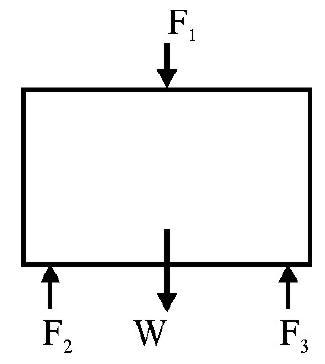Fig. 19

30. Fig. 20 shows a cylinder of length $L$ radius $R$ density $\frac{\rho}{3}$ placed inside a tank. The tank contains a liquid of density $\rho$. The level of liquid in tank is $\mathrm{H}$ above the bottom of cylinder. The cylinder is in equilibrium, $\mathrm{H}$ is

(1) $\frac{4 \mathrm{~L}}{9}$

(2) $\frac{5 \mathrm{~L}}{3}$

(3) $\frac{5 \mathrm{~L}}{9}$

(4) $\frac{2 \mathrm{~L}}{3}$

Fig. 20

Show Answer

Correct answer: (1)

Solution:

$\mathrm{A} _{1}=$ Area of cross-section of cylinder $=\pi \mathrm{R}^{2}$

$\mathrm{A} _{2}=$ Area of cylinder in air $=\left(\frac{\mathrm{R}}{2}\right)^{2}=\frac{\pi \mathrm{R}^{2}}{4}$

$\mathrm{A} _{3}=$ Area of bottom of cylinder inside liquid $=\mathrm{A} _{1}-\mathrm{A} _{2}=\frac{3}{4} \pi \mathrm{R}^{2}$

Fig. 21

Let $\mathrm{P} _{0}$ be the atmospheric pressure. The forces acting on cylinder as shown in Fig. 21. Obvisouly

$$ \begin{aligned} & \mathrm{F} _{1}=\mathrm{P} _{0} \pi \mathrm{R}^{2} ; \mathrm{F} _{2}=\mathrm{P} _{0}\left(\frac{\pi \mathrm{R}^{2}}{4}\right) \\ & \mathrm{F} _{3}=\left[\mathrm{P} _{0}+\mathrm{H} \rho \mathrm{g}\right] \frac{3 \pi \mathrm{R}^{2}}{4} ; \mathrm{W}=\pi \mathrm{R}^{2} \mathrm{~L} \frac{\rho}{3} \mathrm{~g} \end{aligned} $$

In equilibrium

$$ \begin{aligned} & \qquad \mathrm{F} _{1}+\mathrm{W}=\mathrm{F} _{2}+\mathrm{F} _{3} \\ & \mathrm{P} _{0} \pi \mathrm{R}^{2}+\frac{\pi \mathrm{R}^{2} \mathrm{~L} \rho \mathrm{g}}{3}=\frac{\pi \mathrm{P} _{0} \mathrm{R}^{2}}{4}+\left[3 \mathrm{P} _{0}+3 \mathrm{H} \rho \mathrm{g}\right] \frac{\pi \mathrm{R}^{2}}{4} \\ & \frac{\mathrm{L}}{3} \rho \mathrm{g}=\frac{3 \mathrm{H}}{4} \rho \mathrm{g} \\ & \text { or } \mathrm{H}=\frac{4 \mathrm{~L}}{9} \end{aligned} $$

31. A U-tube of uniform cross-section contains a liquid of density $\rho$ upto a height $h$ in each limb. The tube is rotated with a constant angular speed $\omega$ about one limb as axis as shown in Fig. 22. The difference in the level of the liquid in the two limbs of $U$-tube is

Fig. 22

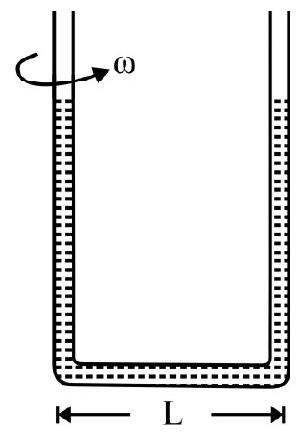
(1) $\frac{\omega^{2} L}{g}$

(2) $\frac{\omega^{2} L^{2}}{g}$

(3) $\frac{\omega^{2} L^{2}}{2 g}$

(4) $\frac{\omega L^{2}}{2 g^{2}}$

Show Answer

Correct answer: (3)

Solution:

Consider a small element LM of liquid defined by $x$ and $x+\mathrm{d} x$ as shown in Fig. 23 $\mathrm{dm}=$ The mass of element considered $=(\operatorname{Ad} x) \rho$

where $\mathrm{A}$ is area of cross-section of limb of U-tube. The element $\mathrm{LM}$ moves in a circular path of radius $x$. It experience centrifugal force $\mathrm{dF}$. Obviously

$$ \mathrm{dF}=(\mathrm{dm}) x \omega^{2}=\mathrm{A} \rho \omega^{2} x \mathrm{~d} x $$

Let $\mathrm{P} _{1}$ and $\mathrm{P} _{2}$ be liquid pressure at bottom of left and right hand limb. Then

$$ \left(\mathrm{P} _{2}-\mathrm{P} _{1}\right) \mathrm{A}=\int _{x=0}^{x=\mathrm{L}} \mathrm{dF}=\mathrm{A} \rho \omega^{2} \int _{0}^{\mathrm{L}} x \mathrm{~d} x $$

or $\mathrm{P} _{2}-\mathrm{P} _{1}=\frac{\rho \omega^{2} \mathrm{~L}^{2}}{2} \hspace{40mm}. . . . . . . . (i)$

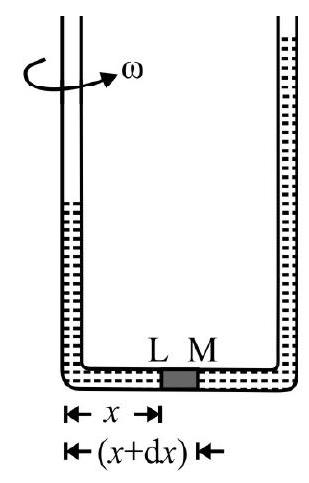
Fig. 23

Let $\mathrm{h}$ be the difference in level of liquid in the two limbs. Then

$$ \begin{equation*} \mathrm{P} _{2}-\mathrm{P} _{1}=\mathrm{h} \rho \mathrm{g} \tag{ii} \end{equation*} $$

From Eqns (i) and (ii) we have

$$ h=\frac{\omega^{2} L^{2}}{2 g} $$

32. A and $B$ are two solid spheres of radius $R$, density $\rho$ and $3 \rho$ respectively. The two spheres are connected to one another by a massless spring of spring constant $k$. The arrangement is immersed completely in a liquid of density $2 \rho$ as shown in Fig. 24. In equilibrium, the elongation of spring is

(1) $\frac{4 \pi R^{3} \rho g}{k}$

(2) $\frac{4 \pi R^{3} \rho g}{3 \mathrm{k}}$

(3) $\frac{8 \pi R^{3} \rho g}{3 \mathrm{k}}$

(4) $\frac{8 \pi R^{3} \rho g}{k}$

Fig. 24

Show Answer

Correct answer: (2)

Solution:

Let $\mathrm{x}$ be the extension of spring in equilibrium. The forces on sphere A and B are shown in Fig. 25 (a) and (b). We have

$$ W _{A}=\left(\frac{4 \pi}{3} R^{3} \rho\right) g ; \text { Buoyant force } B _{1}=2\left(\frac{4 \pi}{3} R^{3}\right) \rho g $$

For equilibrium of A

$$ \mathrm{B} _{1}=\mathrm{W} _{\mathrm{A}}+\mathrm{k} x $$

or $\quad \frac{8 \pi \mathrm{R}^{3} \rho \mathrm{g}}{3}=\frac{4 \pi \mathrm{R}^{3} \rho \mathrm{g}}{3}+\mathrm{k} x \hspace{40mm}. . . . . . . . (1)$

Similarly for sphere B;

$$ \mathrm{W} _{\mathrm{B}}=\left(\frac{4 \pi}{3} \mathrm{R}^{3}\right) 3 \rho \mathrm{g} ; \mathrm{B} _{2}=\left(\frac{4 \pi}{3} \mathrm{R}^{3}\right) 2 \rho \mathrm{g} $$

For equilibrium of $\mathrm{B} ; \mathrm{W} _{\mathrm{B}}=\mathrm{B} _{2}+\mathrm{kx} \hspace{40mm}. . . . . . . . (2)$.

$$ \therefore \frac{8 \pi \mathrm{R}^{3} \rho \mathrm{g}}{3}+\mathrm{k} x=\frac{12 \pi \mathrm{R}^{3} \rho \mathrm{g}}{3} $$

From Eqns. (1) and (2) we have

$$ x=\frac{4 \pi \mathrm{R}^{3} \rho g}{3 \mathrm{~K}} $$

33. Two solid spheres $A$ and $B$ of equal volume but different densities of $d _{A}$ and $d _{B}$ are connected by a string. They are fully immersed in a liquid of density $d _{F}$. They get arranged into an equilibrium state as shown in Fig. 26 with a tension in string. Which of the following is not correct?

(1) $d _{A}<d _{F}$

(2) $d _{B}>d _{F}$

(3) $d _{A}>d _{F}$

(4) $d _{A}+d _{B}=2 d _{P}$

Show Answer

Correct answer: (3)

Solution:

Let $\mathrm{V}$ be volume of sphere A or B. Fig. 27 (a) shows forces acting on sphere A. F = Bouyant force on A or $\mathrm{B}=\mathrm{Vd} _{\mathrm{F}g}$. For equilibrium of $\mathrm{A}$.

$$ \begin{align*} & \mathrm{F}=\mathrm{W} _{\mathrm{A}}+\mathrm{T} \\ & \mathrm{Vd} _{\mathrm{F}} \mathrm{g}=\mathrm{Vd} _{\mathrm{A}} \mathrm{g}+\mathrm{T} \tag{1} \end{align*} $$

Similarly Fig. 27 (b) shows forces acting on sphere B. For equilibrium

$$ \begin{equation*} \mathrm{T}+\mathrm{F}=\mathrm{W} _{\mathrm{B}} \end{equation*} $$

or $\quad \mathrm{T}+\mathrm{Vd} _{\mathrm{F}} \mathrm{g}=\mathrm{Vd} _{\mathrm{B}} \mathrm{g} \hspace{40mm}. . . . . . . . (2)$

Adding Eqns. (1) and (2) we have

$$ \begin{equation*} 2 \mathrm{~d} _{\mathrm{F}} \mathrm{Vg}=\left(\mathrm{d} _{\mathrm{A}}+\mathrm{d} _{\mathrm{B}}\right) \mathrm{Vg} \end{equation*} $$

or $\quad 2 d _{F}=d _{A}+d _{B} \hspace{40mm}. . . . . . . . (3)$

Eqn. (1) can be satisfied at $d _{F}>d _{A}$. This is option (1). From Eqn. (2); $d _{B}>d _{F}$. This is option (2). Eqn. (3) is option (4). The only option which is not correct is (3).

34. A cylinder of length $5 \mathrm{~h}$ is made of a material of density $\sigma$. The cylinder is in equilibrium as shown in Fig. 28, $\rho _{1}$ and $\rho _{2}$ respectively denote density of two immisible liquids 1 and 2. The cylinder is pushed vertically downwards so that its upper face just touches surface (upper) of liquid 1 and released. The initial acceleration of cylinder is

Fig. 28

(1) $\frac{\mathrm{g} \rho _{2}}{5 \sigma}$

(2) $\frac{g \rho _{1}}{5 \sigma}$

(3) $\mathbf{g}\left(\frac{\boldsymbol{\rho} _{1}}{\boldsymbol{\rho} _{2}}\right)$

(4) $\frac{\mathrm{g} \rho _{1}}{5 \rho _{2}}$

Show Answer

Correct answer: (1)

Solution:

Let A be the area of cross-section of cylinder. When cylinder is pushed down; its length inside liquid 2 increases by $h$. The extra bouyant force due to liquid 2 is net upward force, F; on cylinder. Therefore

$$ \mathrm{F}=(\mathrm{Ah}) \rho _{2} \mathrm{~g} $$

The total mass, $\mathrm{M}$, of cylinder is

$$ \mathrm{M}=\mathrm{A}(5 \mathrm{~h}) \sigma $$

The initial acceleration of cylinder when it is released $=\frac{F}{M}$

$$ =\frac{\mathrm{Ah} \rho _{2} \mathrm{~g}}{\mathrm{~A}(5 \mathrm{~h}) \sigma}=\frac{\mathrm{g} \rho _{2}}{5 \sigma} $$

35. The vertical limbs of $U$-tube are filled with a liqiuid of density $\rho$ upto a height $h$ on each side. The horizontal portion of the $U$-tube having length $2 \mathrm{~h}$ contains an immisible liquid of density $2 \rho$. The $U$-tube is moved horizontally with an acceleration of $g / 2$ parallel to the horizontal arm. In steady state the difference in the level of liquid in the vertical limbs is

(1) $\frac{2 h}{7}$

(2) $\frac{12 h}{5}$

(3) $\frac{4 \mathrm{~h}}{5}$

(4) $\frac{3 \mathrm{~h}}{5}$

Show Answer

Correct answer: (2)

Solution:

Fig. 29 (a) shows the given arrangement. Fig. 29 (b) shows the liquid levels when U-tube has a horizontal acceleration $\mathrm{a}^{*}=\mathrm{g} / 2$. Let the liquid level fall by an amount $x$ in limb M as shown in Fig. 29 (b).

$\mathrm{M}=$ Mass of liquid in horizontal part of $\mathrm{U}$-tube

$$ =[(2 \mathrm{~L}-x) \times 2 \rho+x \times \rho] \mathrm{a} $$

where $a$ is area of cross-section of the limb of U-tube. When U-tube has a horizontal acceleratio $a^{*}=\mathrm{g} / 2$ the liquid in horizontal part experiences a ficticous force $\mathrm{F} _{\text {fic }}$ directed towards limb L. Obvisouly

$\mathrm{F} _{\mathrm{fic}}=\mathrm{Ma}^{*}=[(2 \mathrm{~L}-x) \times 2 \rho+\rho x] \frac{\mathrm{ag}}{2} \hspace{40mm}. . . . . . . . (1) $

$\mathrm{F} _{\text {fic }}$ is equal to force $\mathrm{F}$ on bottom of limb $\mathrm{L} $ due to liquid pressure. Obviously

$$ \begin{equation*} \mathrm{F}=\mathrm{a}[\mathrm{h} \rho+x \times 2 \rho] \mathrm{g} \tag{2} \end{equation*} $$

From Eqns. (1) and (2) we have

$\mathrm{a}[2(2 \mathrm{~L}-x) \times \rho+\rho x] \frac{\mathrm{g}}{2}=\mathrm{a}[\mathrm{h} \rho+2 x \rho] \mathrm{g} \quad$ or $\quad x=\frac{6 \mathrm{~h}}{5}$

The difference in liquid level in the two limbs $=2 x=\frac{12 \mathrm{~h}}{5}$

36. A tank of width $4 \mathrm{~cm}$ is filled with a liquid. A thin wire of linear mass density $1 \mathrm{~g} \mathrm{~cm}^{-1}$ is gently placed over the liquid surface in the middle without breaking the surface film. The liquid surface is depressed by $10 / 7 \mathrm{~mm}$. The surface tension of liquid is $\left(\mathrm{g}=10 \mathrm{~ms}^{-2}\right)$

(1) $0.07 \mathrm{Nm}^{-1}$

(2) $0.7 \mathrm{Nm}^{-1}$

(3) $7 \mathrm{Nm}^{-1}$

(4) $70 \mathrm{Nm}^{-1}$

Show Answer

Correct answer: (4)

Solution:

Fig. 30 (a) shows wire W placed on surface of liquid. Fig. 30 (b) shows the depressed liquid surface. $\mathrm{S}$ is force of surface tension acting tangential along the surface. Resolving $\mathrm{S}$ into rectangular components; at equilibrium

$$ \begin{aligned} & 2 \mathrm{~S} \ell \sin \theta=\mathrm{mg} \ & \mathrm{m}=\text { mass of wire }=\lambda \ell \end{aligned} $$

where $\lambda$ is linear mass density of wire.

$$ \begin{equation*} \therefore \quad 2 \mathrm{~S} \ell \sin \theta=\lambda \ell \mathrm{g} \tag{1} \end{equation*} $$

Fig. 30

Also $\sin \theta \simeq \tan \theta=\frac{\mathrm{y}}{\omega / 2}=\frac{2 \mathrm{y}}{\omega} \hspace{40mm}. . . . . . . (2)$

From Eqns. (1) and (2) we have

$$ 2 \mathrm{~S} \times \frac{2 \mathrm{y}}{\omega}=\lambda \mathrm{g} $$

or $\quad S=\frac{\lambda \omega \mathrm{g}}{4 \mathrm{y}}$

Given $\lambda=\frac{1 \mathrm{~g}}{\mathrm{~cm}}=\frac{10^{-3} \mathrm{~kg}}{10^{-2} \mathrm{~m}}=10^{-1} \mathrm{~kg} \mathrm{~m}^{-1} ; \omega=4 \times 10^{-2} \mathrm{~m} ; y=\frac{10}{7} \times 10^{-3} \mathrm{~m}$

$$ \begin{gathered} \therefore \mathrm{S}=\frac{10^{-1} \times 4 \times 10^{-2} \times 10}{4 \times\left(\frac{10}{7} \times 10^{-3}\right)} \mathrm{Nm}^{-1} \\ =70 \mathrm{Nm}^{-1} \end{gathered} $$

37. Fig. 31 shows a three arm tube in which a liquid is filled up to height $\ell$. It is rotated with an angular speed $\omega$ about $\mathrm{YY}^{\prime}$ as axis passing through arm $\mathrm{B}$. The angular frequency $\omega$ at which level of liquid in arm $B$ becomes zero; is

(1) $\sqrt{\frac{2 g}{31}}$

(2) $\sqrt{\frac{g}{1}}$

(3) $\sqrt{\frac{3 g}{1}}$

(4) $\sqrt{\frac{3 g}{2 l}}$

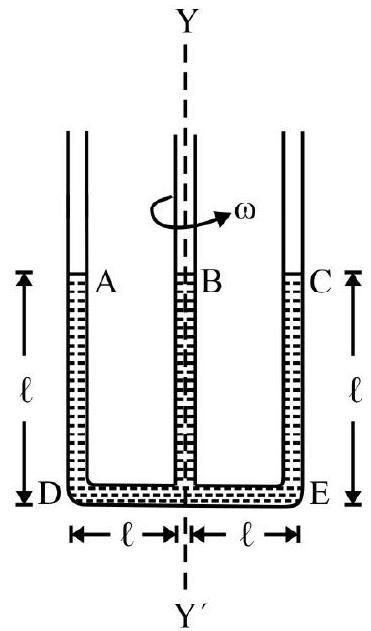Fig. 31

Show Answer

Correct answer: (2)

Solution:

Fig. 32 shows the arrangement when liquid level on tube $\mathrm{B}$ is zero. The liquid has risen in limb $\mathrm{A}$ and $\mathrm{C}$ by $\frac{\ell}{2}$. This is due to centerifugal force directed towards ends $\mathrm{D}$ or E experienced by liquid in the horizontal

part DF or FE. This force, $\mathrm{F}$, is

$$ \begin{equation*} \mathrm{F}=\mathrm{a} \rho\left[\frac{\omega^{2} \ell^{2}}{2}\right] \tag{1} \end{equation*} $$

where $\mathrm{a}$ is area of cross-section of each limb. In equilibrium $\mathrm{F}$ is equal to force at end $\mathrm{D}$ (or E) due to liquid column of height $\frac{3 \ell}{2}$. Therefore

$$ \mathrm{a} \rho\left[\frac{\omega^{2} \ell^{2}}{2}\right]=\mathrm{a}\left[\left(\frac{3 \ell}{2}\right) \rho \mathrm{g}\right] $$

Fig. 32

or $\quad \omega^{2}=\frac{3 \mathrm{~g}}{\ell}$

$\therefore \omega=\sqrt{\frac{3 \mathrm{~g}}{\ell}}$

38. Assume that a drop of liquid evaporates due to decrease in its surface energy so that its temperature remains unchanged. What should be the minimum radius of drop for this to be possible?

Surface tension $=T$; density of liquid $=\rho$, Latent heat of vaporation $=L$.

(IIT 2013, Main)

(1) $\frac{\rho L}{T}$

(2) $\sqrt{\frac{T}{\rho T}}$

(3) $\frac{T}{\rho L}$

(4) $\frac{2 T}{\rho \mathrm{L}}$

Show Answer

Correct answer: (4)

Solution:

The liquid drop evaporates if energy released due to decrease in surface area equals latent heat of vaporisation. Consider a drop of radius $r$. Let radius decreases by dr.

Surface energy released $=\mathrm{T}(\mathrm{ds})$

$$ \begin{equation*} =\operatorname{Td}\left[4 \pi \mathrm{r}^{2}\right]=8 \pi \mathrm{Trdr} \tag{1} \end{equation*} $$

The change in mass dm of drop due to change dr in radius

$$ =\left(4 \pi r^{2} d r\right) \rho $$

The latent heat of vaporisation $=(\mathrm{dm}) \mathrm{L}$

$$ \begin{equation*} =\left(4 \pi \rho r^{2} d r\right) \mathrm{L} \tag{2} \end{equation*} $$

From Eqns. (1) and (2) we have

$$ 8 \pi \mathrm{Trdr}=4 \pi \mathrm{L} \rho \mathrm{r}^{2} \mathrm{dr} $$

$$ \text { or } \quad r=\frac{2 T}{\rho L} $$

39. A bubble of a liquid of surface tension $S$ is blown to a radius $r$. The work done in blowing bubble is $\mathrm{W}$. The percentage change in work done in doubling the radius of the bubble is

(1) $100 \%$

(2) $\mathbf{2 0 0 \%}$

(3) $300 \%$

(4) $\mathbf{4 0 0 \%}$

Show Answer

Correct answer: (3)

Solution:

$\mathrm{W}=$ work done in blowing bubble of radius $\mathrm{r}$

$$ \begin{equation*} =2\left[4 \pi r^{2} S\right]=8 \pi r^{2} S \tag{1} \end{equation*} $$

$\mathrm{W}^{\prime}=$ work done in blowing a bubble of radius $2 \mathrm{r}$

$$ \begin{equation*} =2\left[4 \pi(2 r)^{2} S\right]=32 \pi r^{2} S \tag{2} \end{equation*} $$

$\%$ change in work done $=\frac{\mathrm{W}^{\prime}-\mathrm{W}}{\mathrm{W}} \times 100 \%$

$$ \begin{aligned} & =\left[\frac{24 \pi \mathrm{r}^{2} \mathrm{~S}}{8 \pi \mathrm{r}^{2} \mathrm{~S}}\right] \times 100 \\ & =300 \% \end{aligned} $$

40. A soap bubble is being blown at the end of a narrow tube of diameter 2r. Air moves with a speed $v$ inside tube and comes to rest inside bubble. Surface tension of soap solution is $S$ and $\rho$ is density of air. The bubble separates from tube when its radius is $R$. Which of the following statement is correct?

(1) $R$ is directly proportional to $r$

(2) $R$ is inversly proportional to $r$

(3) $R$ is independent of $r$

(4) $R$ is directly proportional to $r^{2}$

Show Answer

Correct answer: (3)

Solution:

Fig. 33 shows tube of radius $r$ and bubble blown at its end A of radius R. Air moves inside tube at a speed $\mathrm{v}$ and comes to rest inside bubble. The force exerted by air as it comes to rest at $\mathrm{B}$ inside bubble.

$$ \begin{equation*} \mathrm{F}=\rho A v^{2} \tag{1} \end{equation*} $$

$A=$ area of the bubble where air strikes it. The force on area at $B$ due to excess pressure.

$$ \begin{equation*} =\left(\frac{4 \mathrm{~S}}{\mathrm{R}}\right) \mathrm{A} \tag{2} \end{equation*} $$

The bubble is on brink of separating from tube if

$$ \mathrm{F}=\left(\frac{4 \mathrm{~S}}{\mathrm{R}}\right) \mathrm{A} $$

or $\rho A v^{2}=\left(\frac{4 S}{R}\right) A \hspace{40mm}. . . . . . . . (3)$

or $\quad \mathrm{R}=\frac{4 \mathrm{~S}}{\rho \mathrm{v}^{2}}$

From Eqn. (iii) we note, $\mathrm{R}$ does not depend on the radius $\mathrm{r}$ of the tube.

41. $A B$ is a glass tube of uniform cross-section. $V$ is a value which isolates ends $A$ and $B$ when closed. A bubble of radius $r$ and $2 r$ is blown at the two ends of the tube. The end $A$ is inside an enclosure having air at pressure $P$. The same for bubble at end $B$ is $2 P$ as shown in Fig. 34. On openning value $V$ air will flow from $B$ to $A$ if $(S=$ surface of tension).

(1) $\quad P=\frac{2 S}{r}$

(2) $P>\frac{2 S}{r}$

(3) $\mathbf{P}<\frac{2 \mathrm{~S}}{\mathrm{r}}$

(4) $\mathbf{P}=\frac{\mathrm{S}}{\mathrm{r}}$

Show Answer

Correct answer: (2)

Solution:

$\mathrm{P} _{\mathrm{A}}=$ Total pressure of air inside bubble $\mathrm{A}=\mathrm{P}+\frac{4 \mathrm{~S}}{\mathrm{r}}$

$\mathrm{P} _{\mathrm{B}}=$ The total pressure of air inside bubble $\mathrm{B}=2 \mathrm{P}+\frac{4 \mathrm{~S}}{2 \mathrm{r}}=2 \mathrm{P}+\frac{2 \mathrm{~S}}{\mathrm{r}}$

On opening value $\mathrm{V}$ air will flow from $\mathrm{B}$ to $\mathrm{A}$ if $\mathrm{P} _{\mathrm{B}}>\mathrm{P} _{\mathrm{A}}$

i.e. $2 P+\frac{2 S}{r}>P+\frac{4 S}{r}$

or $\mathrm{P}>\frac{2 \mathrm{~S}}{\mathrm{r}}$

42. A dropper is used to form a spherical drop. The radius of dropper is $r . R$ is radius of drop when it is on brink of getting detatched from dropper $(r«R)$. $S$ is the surface tension of liquid of drop. Then $\mathrm{R}$ is

(1) $\left[\frac{3 \mathrm{r}^{2} \mathrm{~S}}{2 \mathrm{pg}}\right]^{1 / 4}$

(2) $\left[\frac{3 r^{2} S}{2 \rho g}\right]^{1 / 3}$

(3) $\left[\frac{\mathbf{r}^{2} S}{2 \rho g}\right]^{1 / 4}$

(4) $\left[\frac{\mathbf{r}^{2} \mathbf{S}}{\boldsymbol{\rho g}}\right]^{1 / 3}$

Show Answer

Correct answer: (1)

Solution:

The liquid drop is on brink of detatching itself from dropper, when vertical force due to S.T is just equal to weight of drop formed.

In Fig. 35,

$\mathrm{AO} _{1}=\mathrm{r}=$ Radius of dropper

$\mathrm{AO}=\mathrm{R}=$ Radius of drop

The force of surface tension at A acts along tangent to spherical drop at $\mathrm{A}$. Resolve $\mathrm{S}$ in horizontal and vertical components. The horizontal components add to give zero resultant.

The net upward force due to $\mathrm{S} . \mathrm{T}=\mathrm{F}=\int \mathrm{S} \sin \theta . \mathrm{d} \ell$

$$ =2 \pi r \mathrm{~S} \sin \theta $$

Also from right angled $\triangle \mathrm{OAO} _{1}$

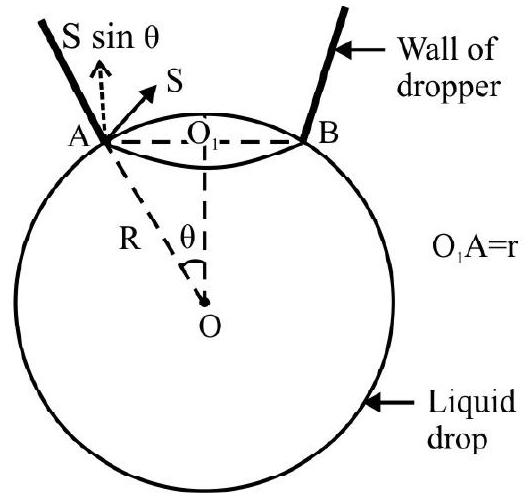Fig. 35

$$ \begin{aligned} & \sin \theta=\frac{A O _{1}}{A O}=\frac{r}{R} \\ & \therefore \quad \mathrm{F}=\frac{2 \pi \mathrm{r}^{2} \mathrm{~S}}{\mathrm{R}} \hspace{40mm}. . . . . . . . (1) \end{aligned} $$

The weight of drop $=\mathrm{W}=\frac{4 \pi}{3} \mathrm{R}^{3} \rho . \mathrm{g} \hspace{40mm}. . . . . . . . (2)$

From Eqns. (1) and (2) we have

$$ \frac{2 \pi r^{2} S}{R}=\frac{4 \pi}{3} R^{3} \rho g \quad \text { or } \quad R^{4}=\frac{3 r^{2} S}{2 \rho g} $$

43. Two bubbles $A$ and $B$ have radii in ratio of $1: 2$ and surface tension $S$. The bubbles are kept in a closed chamber where air is maintained at a constant pressure $P=\frac{4 S}{r _{A}}$. The ratio of number of moles of air in bubble $A$ and $B$ is (assume bubbles are at same temperature).

(1) 1

(2) $\frac{1}{8}$

(3) $\frac{1}{6}$

(4) $\frac{2}{3}$

Show Answer

Correct answer: (3)

Solution:

Fig. 36 shows bubbles A and B inside enclosed chamber. Given

$\mathrm{P}=$ Air pressure inside chamber $=\frac{4 \mathrm{~S}}{\mathrm{r}}$

$\mathrm{P} _{\mathrm{A}}=$ The pressure of air inside $\mathrm{A}=\mathrm{P}+\frac{4 \mathrm{~S}}{\mathrm{r}}=\frac{8 \mathrm{~S}}{\mathrm{r}}$

$\mathrm{V} _{\mathrm{A}}=$ Volume of air inside $\mathrm{A}=\frac{4 \pi}{3} \mathrm{r}^{3}$

Fig. 36

Similarly for bubble B

$\mathrm{P} _{\mathrm{B}}=$ The pressure of air inside $\mathrm{B}$

$$ =\mathrm{P}+\frac{4 \mathrm{~S}}{2 \mathrm{r}}=\frac{6 \mathrm{~S}}{\mathrm{r}} $$

$V _{B}=$ The volume of air inside B

$$ =\frac{4 \pi}{3}(2 r)^{3} $$

Let $n _{A}$ and $n _{B}$ be number of moles of air in bubble $A$ and $B$ respectively. Using ideal gas equation $P V=n R T$

$\frac{\mathrm{n} _{\mathrm{A}}}{\mathrm{n} _{\mathrm{B}}}=\frac{\mathrm{P} _{\mathrm{A}} \mathrm{V} _{\mathrm{A}}}{\mathrm{P} _{\mathrm{B}} \mathrm{V} _{\mathrm{B}}}=\frac{\left(\frac{8 \mathrm{~S}}{\mathrm{r}}\right)\left(\frac{4 \pi}{3} \mathrm{r}^{3}\right)}{\left(\frac{6 \mathrm{~S}}{\mathrm{r}}\right) 8\left(\frac{4 \pi}{3} \mathrm{r}^{3}\right)}=\frac{1}{6}$

44. A glass capillary tube is of the shape of a truncated cone with an apex angle $\alpha$, so that its two ends have cross-sections of different radii. When dipped in water vertically, water rises in it to a height $h$, where the radius of cross-section of tube is $b$. If surface tension of water is $S$; its density is $\rho$ and its angle of contact with glass is $\theta$; the value of $h$ will be ( $g$ is the acceleration due to gravity)

(1) $\frac{2 S}{b \rho g} \cos (\theta-\alpha)$

(2) $\frac{2 S}{b \rho g} \cos (\theta+\alpha)$

(3) $\frac{2 S}{b \rho g} \cos \left(\theta-\frac{\alpha}{2}\right)$

(4) $\frac{2 S}{b \rho g} \cos \left(\theta+\frac{\alpha}{2}\right)$

Fig. 37

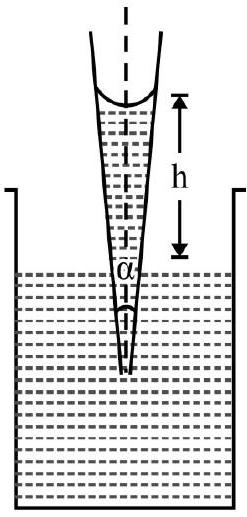
[IIT 2014 Adv.]

Show Answer

Correct answer: (4)

Solution:

In Fig. 37 (a); $A B$ is concave meniscus of water of radius of curvature $R$. In Fig. 37 (a) $\mathrm{AT}$ is tangent to meniscus at $\mathrm{A} . \mathrm{OB}=\mathrm{b}=$ radius of capillary tube at position of meniscus. $\angle \mathrm{A} _{1} \mathrm{AT}=\theta=$ angle of contact. Obviously $\angle \mathrm{Y}^{\prime} \mathrm{AT}=\angle \mathrm{Y}^{\prime} \mathrm{AA} _{1}+\angle \mathrm{A} _{1} \mathrm{AT}=\frac{\alpha}{2}+\theta$.

From right angled $\triangle \mathrm{AOC} ; \angle \mathrm{OAC}=\theta+\frac{\alpha}{2}$ and

$$ \begin{aligned} & \frac{\mathrm{OA}}{\mathrm{AC}}=\cos \left(\theta+\frac{\alpha}{2}\right) \text { or } \frac{\mathrm{b}}{\mathrm{R}}=\cos \left(\theta+\frac{\alpha}{2}\right) \\ & \therefore \quad \mathrm{R}=\frac{\mathrm{b}}{\cos \left(\theta+\frac{\alpha}{2}\right)} \end{aligned} $$

The height $\mathrm{h}=\frac{2 \mathrm{~S}}{\mathrm{R} \rho \mathrm{g}}=\frac{2 \mathrm{~S}}{\mathrm{~b} \rho \mathrm{g}} \cos \left(\theta+\frac{\alpha}{2}\right)$

45. On heating water, bubbles begin forming at the bottom of the vassel. The bubble detatches from the vassel and rises up. Take the bubble to be a sphere of radius $R$ and making a circular contact of radius $r$ with the bottom of the vassel. If $r«R$ and the surface tension of water is $T$, value of $r$ just before bubble detatches is (desnity of water is $\rho$ ).

Fig. 38

(1) $R^{2} \sqrt{\frac{2 \rho g}{3 T}}$

(2) $R^{2} \sqrt{\frac{\rho g}{6 T}}$

(3) $R^{2} \sqrt{\frac{\rho g}{T}}$

(4) $R^{2} \sqrt{\frac{3 \rho g}{T}}$

[IIT Main 2014, Main]

Show Answer

Correct answer: (1)

Solution:

Fig. 39 shows bubble in contact with bottom of vassel. AB is diameter of circle of contact with the vessel. $T$ is surface tension acting along tangent at the point of contact at $\mathrm{A}$. Resolve $\mathrm{T}$ into rectangular components. The horizontal components add up to zero and the net vertically downward force $\mathrm{F}$ is

$$ \begin{equation*} \mathrm{F}=\int(\mathrm{T} \sin \theta) \mathrm{d} \ell=2 \pi \mathrm{rT} \sin \theta \tag{1} \end{equation*} $$

The bubble detatches from the bottom if the bouyant force, $\mathrm{B}$ on it is such that $\mathrm{B} \geq \mathrm{F}$.

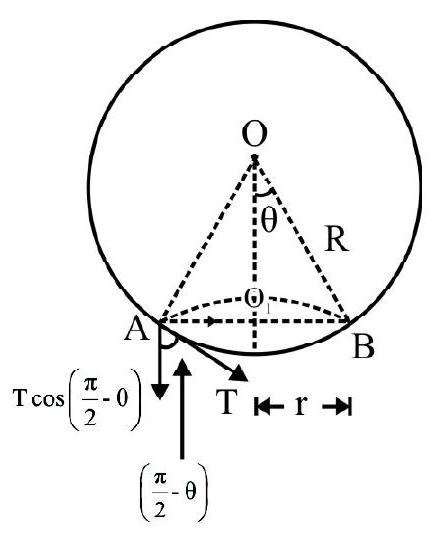
Fig. 39

Also $B=\frac{4 \pi}{3} R^{3} \rho g$

The bubble just detatches itself if $\mathrm{B}=\mathrm{F}$.

$$ \begin{equation*} \therefore \frac{4 \pi}{3} \mathrm{R}^{3} \rho \mathrm{g}=2 \pi \mathrm{r} \mathrm{T} \sin \theta \tag{2} \end{equation*} $$

From right angled $\Delta \mathrm{OO} _{1} \mathrm{~B}$

$$ \begin{equation*} \sin \theta=\frac{\mathrm{O} _{1} \mathrm{~B}}{\mathrm{OB}}=\frac{\mathrm{r}}{\mathrm{R}} \tag{3} \end{equation*} $$

From Eqns. (1), (2) and (3) we have

$$ \frac{4 \pi}{3} R^{3} \rho g=\frac{2 \pi r^{2}}{R} T $$

or $\quad r^{2}=\frac{2 R^{4} \rho g}{3 T}$

$\therefore \mathrm{r}^{2}=\mathrm{R}^{2} \sqrt{\frac{2 \rho \mathrm{g}}{3 \mathrm{~T}}}$

46. Water is poured vertically downwards inside a cylinder. Water is moving vertically downwards with a constant speed $v _{1}$ at the top of a cylinder as shown in Fig. 40. $O$ is an opening at a depth $h$ below the level of water in cylinder. A and a denote area of cross-section of cylinder and opening $O$ respectively. The rate of flow of water from $O$ is

Bernoulli’s Theorem

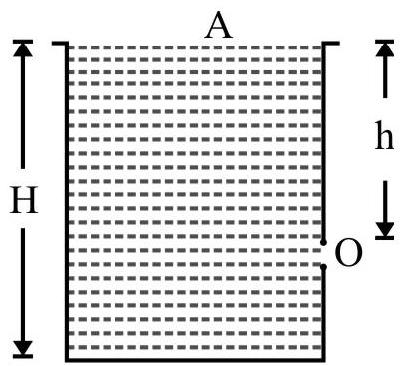
Fig. 40

(1) $a \sqrt{2 g h}$

(2) $a \sqrt{\frac{2 g h}{A^{2}-a^{2}}}$

(3) $\mathbf{A a} \sqrt{\frac{2 g h}{\left(\mathbf{A}^{2}-\mathbf{a}^{2}\right)}}$

(4) $\sqrt[A]{\frac{2 g h}{\left(\mathbf{A}^{2}-\mathbf{a}^{2}\right)}}$

Show Answer

Correct answer: (3)

Solution:

Let $\mathrm{P}$ be the atomospheric pressure and $\mathrm{v} _{2}$ speed of efflux of liquid from $\mathrm{O}$. Applying Bernoulli’s theorem at $\mathrm{A}$ and $\mathrm{O}$, we have

$$ \begin{equation*} \frac{\mathrm{P}}{\rho}+\mathrm{gH}+\frac{1}{2} \mathrm{v} _{1}^{2}=\frac{\mathrm{P}}{\rho}+\mathrm{g}(\mathrm{H}-\mathrm{h})+\frac{1}{2} \mathrm{v} _{2}^{2} \tag{1} \end{equation*} $$

We have taken base of cylinder as zero of gravitational potential energy. From equation of continuity.

$$ \begin{equation*} \mathrm{Av} _{1}=\mathrm{av} _{2} \tag{2} \end{equation*} $$

From Eqns. (1) and (2) we have

$$ \begin{array}{r} \quad \mathrm{gh}+\frac{1}{2} \mathrm{v} _{1}^{2}=\frac{1}{2} \mathrm{v} _{2}^{2} \\ 2 \mathrm{gh}=\mathrm{v} _{1}^{2}\left[1-\left(\frac{\mathrm{a}}{\mathrm{A}}\right)^{2}\right] \\ \therefore \quad \mathrm{v} _{2}=\mathrm{A} \sqrt{\frac{2 \mathrm{gh}}{\left(\mathrm{A}^{2}-\mathrm{a}^{2}\right)}} \tag{3} \end{array} $$

The rate of flow of liquid from $\mathrm{O}=\mathrm{av} _{2}$

$$ =\mathrm{Aa} \sqrt{\frac{2 \mathrm{gh}}{\left(\mathrm{A}^{2}-\mathrm{a}^{2}\right)}} $$

47. A tank is filled with a liquid of density $\rho$ upto a height $4 \mathrm{~h}$. There are two holes $\mathrm{O} _{1}$ and $\mathrm{O} _{2}$. $O _{1}$ is circular hole of radius $R$ and $O _{2}$ is a square hole of side $L . O _{1}$ is at a depth $h$ below the level of water in tank and $\mathrm{O} _{2}$ is at a height $h$ above the bottom of tank. The rate of flow of liquid from $\mathrm{O} _{2}$ is twice that from $\mathrm{O} _{1} . \mathrm{L} / \mathrm{R}$ is

(1) $\left[\frac{2 \pi}{3}\right]^{1 / 2}$

(2) $\left[\frac{\pi}{\sqrt{3}}\right]^{1 / 2}$

(3) $\left[\frac{2 \pi}{\sqrt{3}}\right]^{1 / 2}$

(4) $[\sqrt{2} \pi]^{1 / 2}$

Show Answer

Correct answer: (3)

Solution:

Let $v _{1}$ and $v _{2}$ be velocity of efflux of liquid from $\mathrm{O} _{1}$ and $\mathrm{O} _{2}$ respectively. From Torricelle’s theorem

$$ \mathrm{v} _{1}=\sqrt{2 \mathrm{gh}}, \quad \mathrm{v} _{2}=\sqrt{2 \mathrm{~g}(3 \mathrm{~h})} $$

Let $V _{1}$ and $V _{2}$ be rate of efflux of liquid from $\mathrm{O} _{1}$ and $\mathrm{O} _{2}$ respectively. Then

$$ \begin{aligned} & \mathrm{V} _{1}=\pi \mathrm{R}^{2} \mathrm{v} _{1}=\pi \mathrm{R}^{2} \sqrt{2 \mathrm{gh}} \\ & \mathrm{V} _{2}=\mathrm{L}^{2} \mathrm{v} _{2}=\mathrm{L}^{2} \sqrt{6 \mathrm{gh}} \end{aligned} $$

Given $\mathrm{V} _{2}=2 \mathrm{~V} _{1}$; therefore

$$ 2 \pi \mathrm{R}^{2} \sqrt{2 \mathrm{gh}}=\mathrm{L}^{2} \sqrt{6 \mathrm{gh}} $$

or $\frac{\mathrm{L}^{2}}{\mathrm{R}^{2}}=\frac{2 \pi}{\sqrt{3}}$

$\therefore \frac{\mathrm{L}}{\mathrm{R}}=\left[\frac{2 \pi}{\sqrt{3}}\right]^{1 / 2}$

48. A glass tumbler of length $L$ is open at both ends. The radius of upper and lower end is $2 R$ and $R$ as shown in Fig. Water is poured vertically at upper end with a constant speed $v$. The velocity of water as it emerges out of the lower end is

(1) $v_1+\sqrt{2gL}$

(2) $\sqrt{\frac{32 g L}{15}}$

(3) $\sqrt{\frac{8 g L}{3}}$

(4) $\sqrt{\frac{16 g L}{5}}$

Show Answer

Correct answer: (2)

Solution:

Let $\mathrm{P}$ be the atmospheric pressure and bottom of glass be the zero of gravitational potential energy. Let $\mathrm{v} _{1}$ and $v _{2}$ be speed of water at top and bottom of glass. From Bernoulli’s theorem

$$ \begin{equation*} \frac{\mathrm{P}}{\rho}+\frac{\mathrm{v} _{1}^{2}}{2}+\mathrm{gL}=\frac{\mathrm{P}}{\rho}+\frac{\mathrm{v} _{2}^{2}}{2}+0 \end{equation*} $$

or $\mathrm{v} _{2}^{2}=\mathrm{v} _{1}^{2}+2 \mathrm{gL} \hspace{40mm}. . . . . . . . (1)$

From equation of continuity

$$ \mathrm{v} _{1} \pi(2 \mathrm{R})^{2}=\mathrm{v} _{2} \pi(\mathrm{R})^{2} $$

or $\quad \mathrm{v} _{1}=\frac{\mathrm{v} _{2}}{4} \hspace{40mm}. . . . . . . . (2)$

From Eqns. (1) and (2) we have

$$ \mathrm{v} _{2}^{2}=\left(\frac{\mathrm{v} _{2}}{4}\right)^{2}+2 \mathrm{gL} $$

or $\quad \frac{15 \mathrm{v} _{2}^{2}}{16}=2 \mathrm{gL}$

$\therefore \quad \mathrm{v} _{2}=\sqrt{\frac{32 \mathrm{gL}}{15}}$

49. An open cylinderical container of negligible mass has cross-sectional area $A$. There is a small hole at the bottom having cross-sectional area $1 \%$ of the cylinder. The cylinder is placed on a smooth horizontal surface. The cylinder is filled with a liquid of density $\rho$. The mass of liquid in cylinder is M. At $t=0$ the hole is opened. The intial acceleration of cylinder is

(1) zero

(2) $\mathrm{g}$

(3) $\mathbf{g} \times 10^{-1}$

(4) $2 \mathrm{~g} \times 10^{-2}$

Show Answer

Correct answer: (4)

Solution:

Let $\mathrm{H}$ be the initial height of liquid in cylinder. Clearly

$$ \mathrm{AH} \rho=\mathrm{M} $$

$$ \begin{equation*} \therefore \quad H=\frac{M}{A \rho} \tag{1} \end{equation*} $$

Let $\mathrm{v} _{0}$ be the initial velocity of efflux of liquid through hole. From Bernoulli’s principle

$$ \mathrm{v} _{0}=\sqrt{2 \mathrm{gH}}=\sqrt{\frac{2 \mathrm{gM}}{\mathrm{A} \rho}} $$

Let $\mathrm{a}$ be area of cross-section of hole. Given $\mathrm{a}=\frac{\mathrm{A}}{100}$. Let $\mathrm{F} _{0}$ be the initial force on cylinder due to liquid flowing out from $\mathrm{O}$.

$$ \mathrm{F} _{0}=\mathrm{a\rho v_0^2}=\left(\frac{\mathrm{A}}{100}\right) \rho\left[\frac{2 \mathrm{gM}}{\mathrm{A} \rho}\right]=\frac{\mathrm{gM}}{50} $$

The initial acceleration of cylinder $=\mathrm{a} _{0}=\frac{\mathrm{F} _{0}}{\mathrm{M}}=\frac{\mathrm{g}}{50}$

$$ =2 \times 10^{-2} \times \mathrm{g} $$

50. An open cylinder is filled with two immisible liquids as shown in Fig. 43. $\rho _{1}$ and $\rho _{2}$ respectively denote density of liquids $\mathrm{I}$ and II. $O$ is a small hole in the middle of the lower part of cylinder. The velocity of efflux of liquid from $O$ is

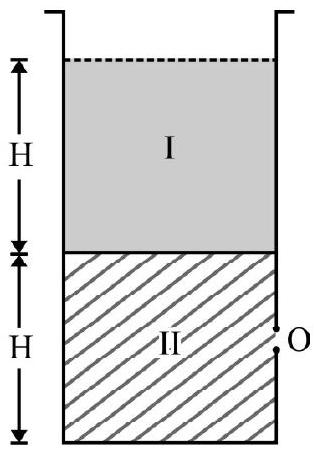Fig. 43

(1) $\sqrt{\text { 3gh }}$

(2) $\left[\left(1+\frac{\boldsymbol{\rho} _{1}}{\boldsymbol{\rho} _{2}}\right) \mathbf{g H}\right]^{1 / 2}$

(3) $\left[\left(1+\frac{2 \rho _{1}}{\rho _{2}}\right) \mathbf{g H}\right]^{1 / 2}$

(4) $\left[\left(1+\frac{\rho _{1}}{2 \rho _{2}}\right) \mathbf{g H}\right]^{1 / 2}$

Show Answer

Correct answer: (3)

Solution:

Let $\mathrm{P}$ be the atmospheric pressure. Taking the hole $\mathrm{O}$ as the zero of gravitational potential energy; from Bernoulli’s principle

$$ \begin{aligned} & \mathrm{P}+\rho _{1} \mathrm{gH}+\rho _{2} \mathrm{~g}\left(\frac{\mathrm{H}}{2}\right)=\mathrm{P}+\frac{1}{2} \rho _{2} \mathrm{v}^{2} \\ & \left(\rho _{1}+\frac{\rho _{2}}{2}\right) g H=\frac{1}{2} \rho _{2} \mathrm{v}^{2} \\ & \therefore \quad \mathrm{v}=\sqrt{\left[2\left(\frac{\rho _{1}}{\rho _{2}}\right)+1\right] \mathrm{gH}} \end{aligned} $$

51. The cylindrical tub of a spray gun has an area of cross-section $\mathbf{A}$. The other end has $\mathbf{N}$ holes each of cross-sectionl area a. The speed of liquid of the broader end is $v$. The speed of ejection of liquid from each hole of spray gun is

(1) $\mathbf{v} _{1}$

(2) $\mathbf{n v} _{1}$

(3) $\frac{\mathrm{Av}}{\mathrm{N}}$

(4) $\frac{\mathrm{Av}}{\mathrm{aN}}$

Show Answer

Correct answer: (4)

Solution:

$\mathrm{m} _{1}=$ The mass of liquid entering broad end of spray gun $=\mathrm{Av} \rho$

where $\rho$ is density of liquid. Let $v _{1}$ be speed of ejection of liquid from each hole of spray gun.

The mass of liquid emerging out of one hole $=\mathrm{m} _{2}^{\prime}=\mathrm{av} _{1} \rho$

The total mass of liquid emerging out of all holes

$$ =\mathrm{m} _{2}=\mathrm{Nm} _{2}^{\prime}=\mathrm{Nav} _{1} \rho $$

Since there is no loss of mass of liquid, $\mathrm{m} _{1}=\mathrm{m} _{2}$. Therefore

$$ \operatorname{Av} \rho=\mathrm{Nav} _{1} \rho $$

or $\quad \mathrm{v} _{1}=\left(\frac{\mathrm{A}}{\mathrm{a}}\right) \frac{\mathrm{v}}{\mathrm{N}}$

52. A man inside a lift holds a jar filled with a liquid of density $\rho$. The lower end of jar is at a height $H$ above floor of lift and has a small hole. With lift at rest the liquid emerging out hits floor of lift at a horizontal distance $D$ from a point below the hole on lift. The lift

(a) accelerates up with an acceleration $g / 10$

(b) accelerates downwards with an acceleration $g / 5$

The corresponding distance now is $D^{\prime}$. Then

(1) (a) $\mathbf{D}^{\prime}=\mathbf{D}$ (b) $\mathbf{D}^{\prime}=\mathbf{D}$

(2) (a) $D^{\prime}>D$ (b) $\mathbf{D}^{\prime}<\mathbf{D}$

(3) (a) $\mathrm{D}^{\prime}=\mathrm{D}$ (b) $\mathbf{D}^{\prime}>\mathbf{D}$

(4) (a) $\mathbf{D}^{\prime}=\mathrm{D}$ (b) $\mathbf{D}^{\prime}<\mathbf{D}$

Show Answer

Correct answer: (1)

Solution:

When lift is at rest

$\mathrm{v}=$ The speed of efflux of liquid from $\mathrm{O}=\sqrt{2 \mathrm{gH} _{1}}$

$\mathrm{D}=\mathrm{v} \times \sqrt{\frac{2 \mathrm{H}}{\mathrm{g}}}$

$$ \begin{align*} & =\sqrt{2 \mathrm{gH} _{1}} \times \sqrt{\frac{2 \mathrm{H}}{\mathrm{g}}} \\ & =2 \sqrt{\mathrm{H} _{1} \mathrm{H}} \tag{1} \end{align*} $$

When lift accelerates up or down effective value of $g$ changes.

In case (a) $g _{\text {eff }}>g$ and case (b) $g _{\text {eff }}<\mathrm{g}$.

From Eqn. (1); D does not depend on value of g. Therefore in both case (a) and (b); $D^{\prime}=D$.

Correct choice is (1)

53. A cylinderical tank of cross-sectional area $A$ has a hole $O$ of cross-section a as shown in Fig. 45. The tank is placed on a rigid horizontal plateform at a height $H$ above ground. Initially tank is filled with a liquid up to a height $h$. The time taken by tank to empty itself on opening $O$ is proportional to

(1) $\mathrm{Hh}$

(2) $\sqrt{\mathrm{Hh}}$

(3) $\sqrt{\mathrm{h}}$

(4) $\sqrt{\mathrm{h} / \mathrm{H}}$

Fig. 45

Show Answer

Correct answer: (3)

Solution:

$\mathrm{v}=$ The instantaneous velocity of efflux of liquid from $\mathrm{O}$

$$ =\sqrt{2 \mathrm{gy}} $$

where $y$ is the instantaneous height of liquid in tank above $\mathrm{O}$.

The instantaneous rate of flow of liquid from $\mathrm{O}=\mathrm{av}=-\mathrm{A} \frac{\mathrm{dy}}{\mathrm{dt}}$

where dy is change in level of liquid in tank in time interval $t$ and $t+d t$.

$$ \therefore \mathrm{dt}=-\left(\frac{\mathrm{A}}{\mathrm{a}}\right) \frac{\mathrm{dy}}{\sqrt{2 \mathrm{gy}}} $$

Integrating;

$$ \int _{0}^{T} d t=-\left[\frac{A}{a \sqrt{2 g}}\right] \int^{y=0} _ {y=h} y^{-1 / 2} d y=-\left[\frac{A}{a \sqrt{2 g}}\right]\left|\frac{y^{1 / 2}}{1 / 2}\right| _{h}^{0} $$

or $\quad T=\frac{A}{a} \sqrt{\frac{2 h}{g}}$

54. Water emerges out of a garden hose pipe. Assuming flow is stream-lined which of the following statement is correct.

(1) When hose pipe is held vertically up the stream spreads like a fountain but narrows down when hose pipe is held vertically down.

(2) When hose pipe is held vertically up the stream narrows down and spreads like a fountain when hose pipe is held vertically down.

(3) There is no spreading or narrowing down of stream when hose pipe is held vertically up or down.

(4) There is no spreading or narrowing down of stream when hose pipe is held vertically down.

Show Answer

Correct answer: (1)

Solution:

When hose pipe is held vertically up the speed of water particles decreases as they move up. The pressure inside water increases as compared to pressure outside stream. The stream therefore spreads out like a fountain.

When hose pipe is held vertically down speed of water particle increases. The pressure inside water stream is less than the pressure outside therefore water stream contracts.

55. Fig. 46 shows a “spray gun”. $N$ is the nozzle and $P$ is the piston. The radii of piston and nozzle are $20 \mathrm{~mm}$ and $1 \mathrm{~mm}$ respectively. When piston is pushed in; the air from gun rushes out of the nozzle. There is a liquid container attached to

gun as shown. As piston pushes out air the liquid from container rises into the nozzle end and is sprayed out. The piston is pushed in with a speed v. $\rho _{\mathrm{a}}$ and $\rho _{\ell}$ is density of air and liquid. The rate (volume per unit time) the liquid strayed is proportional to

(1) $\sqrt{\frac{\rho _{\mathrm{a}}}{\rho _{1}}}$

(2) $\sqrt{\boldsymbol{\rho} _{\mathrm{a}} \boldsymbol{\rho} _{\ell}}$

(3) $\sqrt{\frac{\rho _{1}}{\rho _{a}}}$

(4) $\boldsymbol{p} _{\ell}$

Show Answer

Correct answer: (1)

Solution:

Let $p _{1}$ be pressure of air in spray gun and liquid container. Let $v _{a}$ be speed at which air rushed out of nozzle and $p _{0}$ is atmospheric pressure. From Bernoulli’s theorem

$$ \begin{equation*} \mathrm{p} _{1}-\mathrm{p} _{0}=\frac{1}{2} \rho _{\mathrm{a}} \mathrm{v} _{\mathrm{a}}^{2} \tag{1} \end{equation*} $$

For the liquid in container; let $\mathrm{v} _{\ell}$ be speed at which liquid emerges out of nozzle. Then

$$ \begin{equation*} \mathrm{p} _{1}-\mathrm{p} _{0}=\frac{1}{2} \rho _{\ell} \mathrm{v} _{\ell}^{2} \tag{2} \end{equation*} $$

From Eqns. (1) and (2) we have

$$ \rho _{\mathrm{a}} \mathrm{v} _{\mathrm{a}}^{2}=\rho _{\ell} \mathrm{v} _{\ell}^{2} $$

$$ \text { or } \quad \mathrm{v} _{\ell}=\sqrt{\frac{\rho _{\mathrm{a}}}{\rho _{\ell}}} \mathrm{v} _{\mathrm{a}} $$

The rate of liquid strayed is directly proportional to $\mathrm{v} _{\ell}$ and therefore is directly proportional to $\sqrt{\frac{\rho _{\mathrm{a}}}{\rho _{\ell}}}$.

56. An air bubble $A$ of radius $r$ accquires a terminal speed $v$ in a water tank. A second bubble $B$ accquires a terminal speed $2 \mathrm{v}$ in same water tank. Bubbles $A$ and $B$ coalese to a form a bubble $C$. In same water tank terminal speed accquired by $C$ will be

(1) $3 \mathrm{v}$

(2) $(1+2 \sqrt{2})^{2} v$

(3) $(1+2 \sqrt{2})^{3 / 2} v$

(4) $[1+2 \sqrt{2}]^{\frac{2}{3}} v$

Show Answer

Correct answer: (4)

Solution:

We known terminal speed is directly proportional to square of radius of bubble. Let $r _{B}$ be radius of bubble B. Then

$$ \begin{equation*} \frac{2 \mathrm{v}}{\mathrm{v}}=\left(\frac{\mathrm{r} _{\mathrm{B}}}{\mathrm{r}}\right)^{2} \tag{1} \end{equation*} $$

or $\mathrm{r} _{\mathrm{B}}=\sqrt{2} \mathrm{r}$

Let $\mathrm{r} _{\mathrm{c}}$ be the radius of coalesd bubble $\mathrm{C}$ formed. Then

$$ \frac{4 \pi}{3}(r)^{3}+\frac{4 \pi}{3}(\sqrt{2} r)^{3}=\frac{4 \pi}{3} r _{c}^{3} $$

or $\quad\left[1+(2)^{3 / 2}\right] r^{3}=r _{c}^{3}$

or $\quad r _{c}=[1+2 \sqrt{2}]^{1 / 3} \mathrm{r}$

Let $\mathrm{V}$ be the terminal speed of bubble $\mathrm{C}$. Then

$$ \frac{\mathrm{V}}{\mathrm{v}}=\left(\frac{\mathrm{r} _{\mathrm{c}}}{\mathrm{r}}\right)^{2}=[1+2 \sqrt{2}]^{2 / 3} $$

or

$$ \mathrm{V}=[1+2 \sqrt{2}]^{2 / 3} \mathrm{v} $$

57. A small sphere of radius $r$ falls from rest in a viscous medium of coefficient of viscosity $\eta$. Heat is produced in sphere due to the viscous force of medium. The rate of heat produced in sphere when it has accquired terminal velocity is proportional to

(1) $\mathbf{r}^{3}$

(2) $\mathbf{r}^{4}$

(3) $\mathbf{r}^{5}$

(4) $\mathbf{r}^{6}$

Show Answer

Correct answer: (3)

Solution:

Let $v _{T}$ be the terminal velocity accquired by the sphere. We $k n o w v _{T} \alpha r^{2}$. The viscous force, $F$, on sphere when it has accquired terminal velocity is

$$ \mathrm{F}=6 \pi \eta \mathrm{rv} _{\mathrm{T}} \quad \alpha \quad \mathrm{r}^{3} \quad\left[\because \mathrm{v} _{\mathrm{T}} \alpha \mathrm{r}^{2}\right] $$

The rate of heat produced is rate of work done by sphere against viscous froce $=\mathrm{F} . \mathrm{v} _{\mathrm{T}}$. Since $\mathrm{F}$ is proportional to $\mathrm{r}^{3}$ and $\mathrm{v} _{\mathrm{T}}$ is proportional to $\mathrm{r}^{2}$ rate of heat produced is directly proportional to $\mathrm{r}^{5}$.

58. A spherical bubble is trapped inside a liquid of density $\rho _{1}$; coefficient of viscosity $\eta$. The bubble starts rising upwards. Besides the bouyant force; the following forces act on it.

(1) Only force of gravity

(2) The force due to gravity and the force due to pressure of liquid

(3) The force due to gravity; the force due to the pressure of the liquid and the force due to viscosity of liquid

(4) The force due to gravity and the force due to viscosity of the liquid

Show Answer

Correct answer: (4)

Solution:

As bubble moves up the bouyant force on it is due to the difference of liquid pressure at the liquid layer just in contact with the upper and lower of the bubble. The other forces on bubble are:

(1) force of gravity and

(2) the viscous force of the liquid

The correct option is (4)

59. A small sized spherical ball of radius $r$, mass $M$ is dropped in a viscous medium of coefficient of viscosity $\eta$. Neglect the bouyant force on ball. $v _{T}$ is the terminal velocity acquired by ball. $t _{1}$ is time taken by ball to acquire a speed $\frac{v _{T}}{4}$ from initial state. $t _{2}$ is time taken by ball to increase its speed from $\frac{v _{T}}{4}$ to $\frac{v _{T}}{2} \cdot \frac{t _{1}}{t _{2}}$ is

(1) $\ln \left(\frac{8}{9}\right)$

(2) $\frac{\ln \left(\frac{4}{3}\right)}{\ln \left(\frac{2}{3}\right)}$

(3) $\frac{\ln \left(\frac{3}{4}\right)}{\ln \left(\frac{3}{2}\right)}$

(4) $\ln \left(\frac{9}{8}\right)$

Show Answer

Correct answer: (2)

Solution:

When ball accquires terminal velocity $\mathrm{v} _{\mathrm{T}}$; net force on it (ball) is zero. In other words viscous force equals weight of ball, i.e.

$$ \begin{equation*} 6 \pi \eta \mathrm{rv} _{\mathrm{T}}=\mathrm{Mg} \tag{1} \end{equation*} $$

Let ’ $v$ ’ and ’ $a$ ’ denote instantaneous speed and acceleration of ball. The equation of motion of ball is

$$ \begin{aligned} & \mathrm{Ma}=\mathrm{M} \frac{\mathrm{dv}}{\mathrm{dt}}=(\mathrm{Mg}-6 \pi \eta \mathrm{rv}) \\ & \text { or } \quad \frac{\mathrm{dv}}{\mathrm{dt}}=\left(\mathrm{g}-\frac{6 \pi \eta \mathrm{rv}}{\mathrm{M}}\right) \\ & \therefore \quad \mathrm{dt}=\frac{\mathrm{dv}}{\left(\mathrm{g}-\frac{6 \pi \eta \mathrm{rv}}{\mathrm{M}}\right)} \\ & \therefore \quad \int _{0}^{\mathrm{t} _{1}} \mathrm{dt}=\mathrm{M} \int _{0}^{\mathrm{vT} / 4} \frac{\mathrm{dv}}{\mathrm{Mg}-6 \pi \eta \mathrm{rv})}=\mathrm{M}\left|\frac{\ell \mathrm{n}(\mathrm{Mg}-6 \pi \eta \mathrm{rv})}{-6 \pi \eta \mathrm{r}}\right| _{0}^{\mathrm{vT} / 4} \\ & \text { or } \quad \mathrm{t} _{1}=\frac{\mathrm{M}}{6 \pi \eta \mathrm{r}} \ln \left[\frac{\mathrm{Mg}}{\mathrm{Mg}-6 \pi \eta \mathrm{r}\left(\mathrm{v} _{\mathrm{T}} / 4\right)}\right]=\frac{\mathrm{M}}{6 \pi \eta \mathrm{r}} \ln \left[\frac{\mathrm{Mg}}{\mathrm{Mg}-\frac{\mathrm{Mg}}{4}}\right] \\ & \quad=\frac{\mathrm{M}}{6 \pi \eta \mathrm{r}} \ln \left[\frac{\mathrm{Mg}}{3 \frac{\mathrm{Mg}}{4}}\right] \end{aligned} $$

$$ \begin{equation*} =\frac{\mathrm{M}}{6 \pi \eta \mathrm{r}} \ln \left(\frac{4}{3}\right) \tag{2} \end{equation*} $$

Similarly

$$ \begin{align*} \int _{0}^{t _{2}} \mathrm{dt} & =\mathrm{M} \int _{\mathrm{tT} / 4}^{\mathrm{tT} / 2} \frac{\mathrm{dv}}{(\mathrm{Mg}-6 \pi \eta \mathrm{rv})} \\ & =\frac{\mathrm{M}}{6 \pi \eta \mathrm{r}} \ln \left[\frac{\frac{1}{2} \mathrm{Mg}}{\frac{3}{4} \mathrm{Mg}}\right] \\ & =\frac{\mathrm{M}}{6 \pi \eta \mathrm{r}} \ln \left(\frac{2}{3}\right) \tag{3} \end{align*} $$

From Eqns. (2) and (3) we have

$$ \frac{\mathrm{t} _{1}}{\mathrm{t} _{2}}=\frac{\ln (4 / 3)}{\ln (2 / 3)} $$

60. Two capillary tubes $\mathrm{AB}$ and $\mathrm{BC}$ have radii $\mathrm{r}$ and $\sqrt{2} \mathrm{r}$ lengths $3 \ell$ and $2 \ell$. The two are joined together as shown in Fig. 47. A viscous liquid of viscosity $\eta$ enters the arrangment at $A$ and flows out from $C . P _{C}=P _{0}$ and $P _{B}=2 P _{0}$ denote pressure at $C$ and $B$ in steady state. The ratio of pressure gradient along $A B$ and $\mathrm{BC}$ is

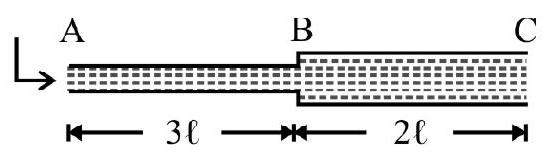
(1) $\frac{3}{2}$

(2) $3 \sqrt{2}$

(3) 3

(4) 4

Show Answer

Correct answer: (4)

Solution:

Let $P _{A}$ be pressure at end $A$. In steady state rate of flow of liquid in the two tubes is same. Therefore

$$ \frac{\pi\left[\mathrm{P} _{\mathrm{A}}-2 \mathrm{P} _{0}\right] \mathrm{r}^{4}}{8 \eta(3 \ell)}=\frac{\pi\left[2 \mathrm{P} _{0}-\mathrm{P} _{0}\right](\sqrt{2} \mathrm{r})^{4}}{8 \eta(2 \ell)} $$

or $\frac{\mathrm{P} _{\mathrm{A}}-2 \mathrm{P} _{0}}{3}=2 \mathrm{P} _{0} \quad \therefore \mathrm{P} _{\mathrm{A}}=8 \mathrm{P} _{0}$

$\frac{\text { Pressure gradient along } \mathrm{AB}}{\text { Pressure gradient along } \mathrm{BC}}=\frac{\left(8 \mathrm{P} _{0}-2 \mathrm{P} _{0}\right) / 3 \ell}{\left(2 \mathrm{P} _{0}-\mathrm{P} _{0}\right) / 2 \ell}=\frac{2\left(\mathrm{P} _{0} / \ell\right)}{\left(\frac{\left.\mathrm{P} _{0} / 2 \ell\right)}{}\right.}=4$

61. Fig. 48 shows an arrangment used to make water flow through a horizontal capillary tube LM using a water bottle. Which of the following statements is correct?

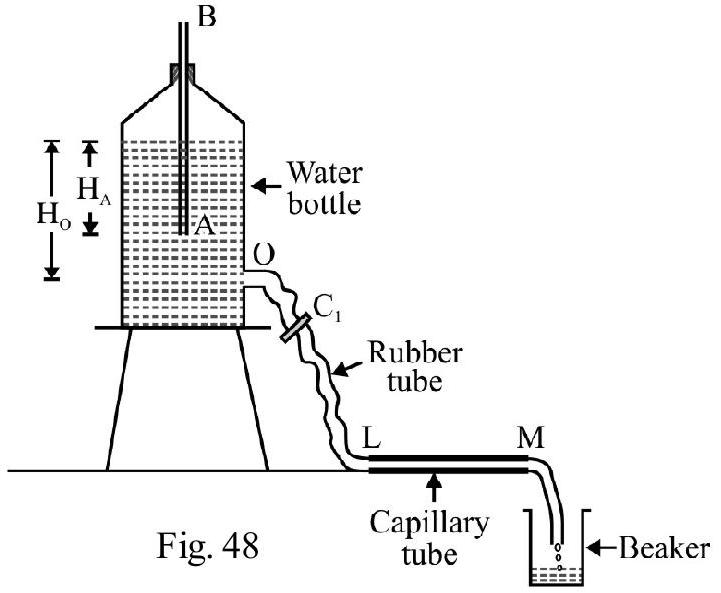
(1) Rate of flow of water is constant till level of water in water bottle falls upto point $O$

(2) Rate of flow of water decreases as level of water in water bottle decreases upto point O

(3) Rate of flow of water is constant till water level in bottle decreases upto point $A$ and then decreases as water level falls upto $O$

(4) Rate of flow of water decreaes till water level in bottle decreases upto point $A$ and then is constant till water level decreases upto $O$

Show Answer

Correct answer: (3)

Solution:

Let $\mathrm{h}$ be the instantaneous height of water above point $\mathrm{A}$. $\mathrm{P} _{0}$ is atmospheric pressure. $\mathrm{P} _{\mathrm{A}}=$ pressure of liquid in bottle at level $\mathrm{A}=\mathrm{P} _{0}$

$\mathrm{P}=$ Pressure of liquid at opening $\mathrm{O}$

$$ =\mathrm{P} _{\mathrm{A}}+\left(\mathrm{H} _{0}-\mathrm{h}\right) \rho \mathrm{g}=\mathrm{P} _{0}+\left(\mathrm{H}^{\prime}\right) \rho \mathrm{g} ; \text { where } \mathrm{H} _{0}-\mathrm{h}=\mathrm{H}^{\prime}=\mathrm{OA} $$

Pressure $\mathrm{P}$ is constant till water level in water bottle reaches point $\mathrm{A}$. Therefore rate of flow of water in capillary tube is constant. If level of water in bottle goes below point $\mathrm{A}$; pressure at $\mathrm{O}$ does not remain constant. It is equal to $\mathrm{P} _{0}+$ pressure due to water column above $\mathrm{O}$ but below $\mathrm{A}$. Since pressure at inlet of capillary tube varies (decreases) the rate of flow of water in capillary tube also decreaes.

62. A cylindrical tank of upper radius $R$, lower radius $r$ is filled with a liquid of density $\rho$. $A$ capillary tube LM is attached to of tank as shown in Fig. 49. When capillary tube is removed the liquid comes out of tank with speed $v _{2}$. An additional pressure $P$ is applied to upper end of liquid surface in tank. The rate of flow of a liquid of coefficient of viscosity $\eta$ through capillary tube is ( $\mathrm{P} _{0}=$ Atmospheric pressure $)$

Fig. 49

(1) $\pi v _{2}^{2}\left[1-\left(\frac{R}{r}\right)^{2}\right] \frac{a^{4}}{8 \eta l}$

(2) $\pi v _{2}^{2}\left[1-\left(\frac{r}{R}\right)^{2}\right] \frac{a^{4}}{8 \eta l}$

(3) $\pi v _{2}^{2}\left[1-\left(\frac{r}{R}\right)^{2}\right] \frac{a^{4}}{16 \eta l} $

(4) $\pi v _{2}^{2}\left[1-\left(\frac{R}{r}\right)^{2}\right] \frac{a^{4}}{16 \eta l}$

Show Answer

Correct answer: (3)

Solution:

Let $\mathrm{v} _{1}$ be speed of liquid on top of tank. $\mathrm{v} _{2}$ is speed of flow of liquid out of tank when capillary tube is detatched. Using Bernoulli’s theorem

$$ \mathrm{P}+\mathrm{P} _{0}+\frac{1}{2} \rho \mathrm{v} _{1}^{2}+\rho \mathrm{gH}=\mathrm{P} _{0}+\frac{1}{2} \mathrm{v} _{1}^{2} $$

or $\mathrm{P}+\rho \mathrm{gH}=\frac{1}{2}\left(\mathrm{v} _{2}^{2}-\mathrm{v} _{1}^{2}\right) \hspace{40mm}. . . . . . . . (1)$

From equation of continuity

$\mathrm{v} _{1}\left(\pi \mathrm{R}^{2}\right)=\mathrm{v} _{2}\left(\pi \mathrm{r}^{2}\right) \hspace{40mm}. . . . . . . . (2)$

$\therefore \quad \Delta \mathrm{P}=\mathrm{P}+\rho \mathrm{gh}=\frac{1}{2} \mathrm{v} _{2}^{2}\left[1-\left(\frac{\mathrm{r}}{\mathrm{R}}\right)^{2}\right]$

$\Delta \mathrm{P}$ is pressure difference across ends of capillary tube $\mathrm{LM}$. The rate of flow of liquid in capillary $\mathrm{V}$ is

$$ \mathrm{V}=\frac{\pi(\Delta \mathrm{P}) \mathrm{a}^{4}}{8 \eta \ell}=\frac{\pi \mathrm{v} _{2}^{2}\left[1-\left(\frac{\mathrm{r}}{\mathrm{R}}\right)^{2}\right] \mathrm{a}^{4}}{16 \eta \ell} $$

63. $x _{1}$ is thickness of ice layer on surface or a lake. The sorroundings temperature is constant $-\theta^{0} \mathrm{C} \cdot \mathrm{K}=$ Thermal conductivity of ice $L=$ Latent heat of fusion of ice. $\rho=$ density of water. The time in which the thickness of ice layer increases by $100 \%$ is

(1) $\frac{3 \rho \mathrm{L}}{\mathrm{K} \theta} \mathrm{x} _{1}^{2}$

(2) $\frac{4 \rho \mathrm{L}}{\mathrm{K} \theta} \mathrm{x} _{1}^{2}$

(3) $\frac{2 \rho L}{K \theta} x _{1}^{2}$

(4) $\frac{3 \rho \mathrm{L}}{2 \mathrm{~K} \theta} \mathrm{x} _{1}^{2}$

Show Answer

Correct answer: (4)

Solution:

Let A be area of cross-section of lake. $x$ is the thickness of layer of ice at $\mathrm{t}=\mathrm{t}$ and $x+\mathrm{d} x$ is thickness of ice layer at $\mathrm{t}=\mathrm{t}+\mathrm{dt}$. Obvisouly $\frac{\mathrm{dQ}}{\mathrm{dt}}=$ The rate of heat flow from water in lake to surroundings $=+K A \frac{[0-(-\theta)]}{x}$.

$$ \begin{equation*} =+\left[\frac{\mathrm{KA} \theta}{x}\right] \tag{1} \end{equation*} $$

Also, $\mathrm{dQ}=($ mass of ice formed in time interval $\mathrm{t}$ and $\mathrm{t}+\mathrm{dt}) \times$ latent heat of fusion of ice.

$$ \begin{equation*} =(\mathrm{A} \cdot \mathrm{dx}) \rho \times \mathrm{L}=(\mathrm{A} \rho \mathrm{L}) \mathrm{d} x \tag{2} \end{equation*} $$

From Eqns. (1) and (2) we have

$$ \mathrm{A} \rho \mathrm{L}\left(\frac{\mathrm{d} x}{\mathrm{dt}}\right)=+\frac{\mathrm{KA} \theta}{x} $$

or $\mathrm{dt}=\frac{\rho \mathrm{L}}{\mathrm{K} \theta} x \mathrm{~d} x$

$\therefore \int_0^{\mathrm{t}} \mathrm{dt}=\frac{\rho \mathrm{L}}{\mathrm{K} \theta} \int_{x_1}^{2 \mathrm{n}} x \mathrm{~d} x$

$\mathrm{t}=\frac{3 \rho \mathrm{L}}{2 \mathrm{~K} \theta} x _{1}^{2}$

64. Two spheres $A$ and $B$ of same material have radii $R$ and $4 R$. The temperature of $A$ and $B$ are 4T and 2T on absolute scale.The ratio of the energy radiated per second by the $A$ and $B$ is

(1) 1

(2) >1

(3) $<1$

(4) can lie any where between 0.5 and 1

Show Answer

Correct answer: (1)

Solution:

Let $\varepsilon$ be degree of blackness of the two spheres. From Stefan’s law.

$E _{1}=$ Energy radiated per second by sphere of radius $R$

$$ =\varepsilon \sigma\left[4 \pi \mathrm{R}^{2}\right](4 \mathrm{~T})^{4}=1024 \varepsilon \sigma \mathrm{T}^{4} $$

$\mathrm{E} _{2}=$ Energy radiated per second by sphere of radius $4 \mathrm{R}$

$$ =\varepsilon \sigma\left[4 \pi(4 \mathrm{R})^{2}\right](2 \mathrm{~T})^{4}=1024 \varepsilon \sigma \mathrm{T}^{4} $$

$\therefore \frac{\mathrm{E} _{1}}{\mathrm{E} _{2}}=1$

65. A perfectly black body $L$ of surface area $A$ is at $T _{1}$ kelvin. Another body $M$; having surface area $2 A$ is at a temperature $T _{2}$ kelvin. The degree of blackness of $M$ is $\varepsilon _{1}$. A third body $N$; having surface area $\frac{A}{2}$ is at a temperature $T _{3}=2 T _{2}$. The degree of blackness of $N$ is $\varepsilon _{2}$. The radiant power emitted by the three bodies is same. $\frac{\varepsilon _{1}}{\varepsilon _{2}}$ is:

(1) 2

(2) 4

(3) 8

(4) 1

Show Answer

Correct answer: (2)

Solution:

Let $\mathrm{W}$ be the radiant power (i.e. energy emitted per unit area per unit time) of the three bodies. From Stefan’s law;

1. For body $\mathrm{L}$

$$ \mathrm{W}=\sigma \mathrm{AT} _{1}^{4} $$

2. For body M;

$$ \mathrm{W}=\varepsilon _{1} \sigma(2 \mathrm{~A})\left(2 \mathrm{~T} _{2}\right)^{4}, \text { and } $$

3. For body N;

$$ \begin{aligned} & \quad \mathrm{W}=\varepsilon _{2} \sigma\left(\frac{\mathrm{A}}{2}\right)\left(2 \mathrm{~T} _{2}\right)^{4} \\ & \therefore \quad 2 \varepsilon _{1}=\frac{\varepsilon _{1}}{2}(2)^{4}=8 \varepsilon _{2} \\ & \text { or } \quad \frac{\varepsilon _{1}}{\varepsilon _{2}}=4 \end{aligned} $$

66. Two metallic spheres $S _{1}$ and $S _{2}$ are made of same material and have identical surface finish.The mass of $S _{1}$ is thrice that of $S _{2}$. Both the spheres are heated to the same high temperature and placed in same room having lower temperature but are thermally insulated from each other. The ratio of the initial rate of cooling of $S _{1}$ to that of $S _{2}$ is

(1) $\frac{1}{3}$

(2) $\frac{1}{\sqrt{3}}$

(3) $\frac{\sqrt{3}}{1}$

(4) $\left(\frac{1}{3}\right)^{1 / 3}$

Show Answer

Correct answer: (4)

Solution:

Let $\varepsilon$ be the degree of blackness of each sphere. The temperature of each sphere is TK. Let the room temperature be $\mathrm{T} _{0} \mathrm{~K}\left(\mathrm{~T} _{0}<\mathrm{T}\right)$. Let $\mathrm{M}$ and $\mathrm{R}$ denote mass and radius of sphere of density $\rho$. Then

$M=\frac{4 \pi}{3} R^{3} \rho$, and $A=$ The surface area of sphere $=4 \pi R^{2}$

$$ =4 \pi\left[\frac{3 \mathrm{M}}{4 \pi \rho}\right]^{2 / 3} $$

The rate of loss of heat $=\frac{\mathrm{dQ}}{\mathrm{dt}}=\varepsilon \sigma \mathrm{A}\left[\mathrm{T}^{4}-\mathrm{T} _{0}^{4}\right]$

Also $\mathrm{dQ}=\mathrm{M} \times \mathrm{s} \times \mathrm{dT}$; where $\mathrm{s}$ is specific heat of sphere.

$\therefore \frac{\mathrm{dT}}{\mathrm{dt}}=\frac{\varepsilon \sigma \mathrm{A}}{\mathrm{Ms}}\left[\mathrm{T}^{4}-\mathrm{T} _{0}^{\mathrm{r}}\right]=\frac{\varepsilon \sigma}{\mathrm{Ms}}\left[4 \pi\left\{\frac{3 \mathrm{M}}{4 \pi \rho}\right\}^{2 / 3}\right]\left[\mathrm{T}^{4}-\mathrm{T} _{0}^{4}\right]$

or $\quad \frac{\mathrm{dT}}{\mathrm{dt}} \propto \frac{1}{\mathrm{M}^{1 / 3}}$

$\therefore \frac{(\mathrm{dT} / \mathrm{dt}) _{1}}{(\mathrm{dT} / \mathrm{dt}) _{2}}=\left(\frac{\mathrm{M} _{2}}{\mathrm{M} _{1}}\right)^{1 / 3}=\left(\frac{1}{3}\right)^{1 / 3}$

67. A solid sphere of a material of density $\rho$; specific heat capacity $c$; having a radius $r$ is initially heated to a temperature $T _{1}$ kelvin. It is suspended inside a chamber whose walls are maintained at absolute zero of temperature. The degree of blackness of sphere is $\varepsilon$. The time taken for the temperature of sphere to reduces to $T _{2}\left(T _{2}<T _{1}\right)$ kelvin is

(1) $\frac{\mathbf{r \rho c}}{9 \varepsilon \sigma}\left[\frac{1}{\mathrm{~T} _{2}^{3}}-\frac{1}{\mathrm{~T} _{1}^{3}}\right]$

(2) $\frac{\operatorname{rpc}}{3 \varepsilon \sigma}\left[\frac{1}{\mathrm{~T} _{2}^{3}}-\frac{1}{\mathrm{~T} _{1}^{3}}\right]$

(3) $\quad \frac{\operatorname{rpc}}{9 \varepsilon \sigma}\left[\frac{1}{\mathrm{~T} _{2}^{2}}-\frac{1}{\mathrm{~T} _{1}^{2}}\right]$

(4) $\frac{\operatorname{r\rho c}}{3 \varepsilon \sigma}\left[\frac{1}{\mathrm{~T} _{2}}-\frac{1}{\mathrm{~T} _{1}}\right]$

Show Answer

Correct answer: (1)

Solution:

Let $\mathrm{T}$ be the instantaneous temperature of sphere on kelvin scale. $\mathrm{T} _{0} \mathrm{~K}=$ Temperature of surroundings. $\frac{\mathrm{dQ}}{\mathrm{dt}}=$ The rate of radiant energy given by sphere to surroundings

$$ \begin{equation*} =\varepsilon \sigma \mathrm{AT}^{4} \tag{1} \end{equation*} $$

$A=$ surface area of sphere. Also

$$ \begin{equation*} \mathrm{dQ}=\mathrm{mc}(\mathrm{dT}) \tag{2} \end{equation*} $$

where $m$ is mass of sphere. From Eqns. (1) and (2) we have

$$ \begin{equation*} \frac{\mathrm{dT}}{\mathrm{dt}}=\frac{\varepsilon \sigma \mathrm{A}}{\mathrm{mc}} \mathrm{T}^{4} \tag{2} \end{equation*} $$

Also $\frac{\mathrm{A}}{\mathrm{m}}=\frac{4 \pi \mathrm{r}^{2}}{\frac{4 \pi}{3} \mathrm{r}^{3} \rho}=\frac{3}{\mathrm{r} \rho}$.

$\therefore \mathrm{dt}=\frac{\mathrm{r} \rho \mathrm{c}}{3 \varepsilon \sigma}\left(\frac{\mathrm{dT}}{\mathrm{T}^{4}}\right)$

$\therefore \quad \int _{0}^{\mathrm{t}} \mathrm{dt}=\frac{\mathrm{r} \rho \mathrm{c}}{3 \varepsilon \sigma} \int _{\mathrm{T} _{1}}^{\mathrm{T} _{2}} \frac{\mathrm{dT}}{\mathrm{T}^{4}}=\frac{\mathrm{r} \rho \mathrm{c}}{9 \varepsilon \sigma}\left[\frac{1}{\mathrm{~T} _{2}^{3}}-\frac{1}{\mathrm{~T} _{1}^{3}}\right]$

68. Equal volume of aniline (R.D $=1.02)$ and water are allowed to cool from $55^{\circ} \mathrm{C}$ to $50^{\circ} \mathrm{C}$ in same surroundings. The time taken are 4 minute and 7.5 minute respecitvely. Specific heat of aniline is (nearly)

(1) $0.4 \mathrm{cal} \mathrm{g}^{-1}\left({ }^{0} \mathrm{C}\right)^{-1}$

(2) $0.4 \mathrm{~J} \mathrm{~g}^{-1}\left({ }^{0} \mathrm{C}\right)^{-1}$

(3) $0.52 \mathrm{cal} \mathrm{g}^{-1}\left({ }^{0} \mathrm{C}\right)^{-1}$

(4) $0.52 \mathrm{~J} \mathrm{~kg}^{-1}(\mathrm{~K})^{-1}$

Show Answer

Correct answer: (3)

Solution:

Let $m _{1}$ and $m _{2}$ be mass of aniline and water respectively. Then

$$ \frac{\mathrm{m} _{1}}{\mathrm{~m} _{2}}=\frac{\rho _{1}}{\rho _{2}}=1.02 $$

$\rho _{1}=$ density of aniline and $\rho _{2}=$ density of water. Let $\mathrm{Q}$ be heat lost by aniline of specific heat $\mathrm{c} _{1}$ in cooling from $55^{\circ} \mathrm{C}$ to $50^{\circ} \mathrm{C}$ in time $\mathrm{t} _{1}$. Let $\theta^{\circ} \mathrm{C}$ be constant temperature of surrounding. Then from Newton’s law of cooling.

$$ \begin{equation*} \mathrm{m} _{1} \mathrm{c} _{1}[55-50]=\mathrm{k} \times\left[52.5-\theta _{0}\right] \times \mathrm{t} _{1} \tag{1} \end{equation*} $$

Similarly for water

$$ \begin{equation*} \mathrm{m} _{2} \mathrm{c} _{2}[55-50]=\mathrm{k}\left[52.5-\theta _{0}\right] \times \mathrm{t} _{2} \tag{2} \end{equation*} $$

From Eqns. (1) and (2) we have

$$ \frac{\mathrm{m} _{1} \mathrm{c} _{1}}{\mathrm{~m} _{2} \mathrm{c} _{2}}=\frac{\mathrm{t} _{1}}{\mathrm{t} _{2}} \quad \text { or } \quad 1.02 \times \frac{\mathrm{c} _{1}}{\mathrm{c} _{2}}=\frac{4}{7.5} $$

$\therefore \frac{\mathrm{c} _{1}}{\mathrm{c} _{2}}=0.52$

Taking $\mathrm{c} _{2}=1 \mathrm{cal} \quad \mathrm{g}^{-1}{ }^{0} \mathrm{C}^{-1} ; \mathrm{c} _{1}=0.52 \mathrm{cal} \quad \mathrm{g}^{-10} \mathrm{C}^{-1}$;

69. A cubical vassel of side $50 \mathrm{~mm}$ of negligible heat capacity is filled with water. It is placed in room whose walls are maintained at a constant temperature of $26.0^{\circ} \mathrm{C}$. According to Newton’s law of cooling; the rate of heat lost, $\frac{\mathrm{dQ}}{\mathrm{dt}}$ is

$$ \frac{\mathbf{d Q}}{\mathbf{d t}}=\mathbf{k A}\left(\theta-\theta _{0}\right) $$

where $A$ is area of cross-section of body losing heat $\theta-\theta _{0}=$ excess temperature of body over surroundings $\mathrm{k}=5.00 \times 10^{1} \mathrm{Cal} \mathrm{s}^{-1} \mathrm{~m}^{-2}\left({ }^{0} \mathrm{C}\right)^{-1}$. The time taken by water in vassel to cool from $30^{\circ} \mathrm{C}$ to $28^{\circ} \mathrm{C}$ is

(1) $10^{3} \mathrm{~s}$

(2) $1111 \mathrm{~s}$

(3) $911 \mathrm{~s}$

(4) $1200 \mathrm{~s}$

Show Answer

Correct answer: (2)

Solution:

$M=$ Mass of water in cubical vassel

$$ =\left(5 \times 10^{-2}\right)^{3} \times 10^{3} \mathrm{~kg}=125 \times 10^{-3} \mathrm{~kg} $$

$\mathrm{H}=$ The heat lost by water in vassel

$$ =125 \times 10^{-3} \times 1 \times 2 \mathrm{k} \mathrm{cal}=250 \times 10^{-3} \mathrm{k} \mathrm{cal} $$

Let $t$ be the time taken. The average rate of cooling

$$ \begin{equation*} \mathrm{R}=\frac{\mathrm{H}}{\mathrm{t}}=\frac{250 \times 10^{-1}}{\mathrm{t}} \mathrm{kcals}^{-1}=\frac{250}{\mathrm{t}} \mathrm{cals}^{-1} \tag{1} \end{equation*} $$

The surface area of cubical vassel $=6 \times\left[5 \times 10^{-2}\right]^{2} \mathrm{~m}^{2}$

$$ =150 \times 10^{-4} \mathrm{~m}^{2} $$

The average excess temperature of water in vassel over surroundings $=\left(\frac{30+28}{2}\right)-26.0=3^{\circ} \mathrm{C}$. From Newton’s law

$$ \begin{align*} \mathrm{R}= & 5.00 \times 10^{1} \times 150 \times 10^{-4} \times 3 \mathrm{cal} \quad \mathrm{s}^{-1} \\ & =225 \times 10^{-3} \mathrm{cal} \quad \mathrm{s}^{-1} \tag{2} \end{align*} $$

From Eqns. (1) and (2) we have

$$ \frac{250}{\mathrm{t}}=225 \times 10^{-3} \quad \text { or } \quad \mathrm{t}=\frac{250 \times 10^{3}}{225} \simeq 1111 \mathrm{~s} $$

70. A body cools from $72^{\circ} \mathrm{C}$ to $68^{\circ} \mathrm{C}$ in 1 minute and from $62^{\circ} \mathrm{C}$ to $58^{\circ} \mathrm{C}$ in 1.25 minute and from $\theta^{\circ} \mathrm{C}$ to $38^{\circ} \mathrm{C}$ in 2.5 minute. The surroundings is at a constant temperature of $\theta _{0} \mathrm{C}$. Then

(1) $\theta _{0}=\mathbf{2 0} \quad \boldsymbol{\theta}=\mathbf{4 2}$

(2) $\boldsymbol{\theta} _{0}=\mathbf{2 0} \quad \boldsymbol{\theta}=\mathbf{4 0}$

(3) $\theta _{0}=18 \quad \theta=44$

(4) $\boldsymbol{\theta} _{0}=\mathbf{2 0} \quad \boldsymbol{\theta}=\mathbf{4 3}$

Show Answer

Correct answer: (1)

Solution:

Let $m$ and $c$ be mass and specific heat of body. Then

$$ \begin{align*} & \mathrm{m} \times \mathrm{c} \times[72-68]=\mathrm{k} \times\left[\left(\frac{72+68}{2}\right)-\theta _{0}\right] \times 1 \times 60 \\ & 4 \mathrm{mc}=\mathrm{k}\left[70-\theta _{0}\right] \times 60 \tag{1} \end{align*} $$

where $k$ is a constant of proportionality. Similarly

$$ \begin{align*} & 4 \mathrm{mc}=\mathrm{k}\left[\left(\frac{62+58}{2}\right)-\theta _{0}\right] \times 75 \\ & =\mathrm{k}\left[60-\theta _{0}\right] \times 75 \tag{2} \end{align*} $$

From Eqns. (1) and (2) we have

$$ \begin{aligned} & \left(70-\theta _{0}\right) \times 60=\left(60-\theta _{0}\right) \times 75 \\ & 4\left(70-\theta _{0}\right)=5\left(60-\theta _{0}\right) \end{aligned} $$

$\therefore \quad \theta _{0}=20^{\circ} \mathrm{C}$

When body cools from $\theta^{\circ}$ to $38^{\circ} \mathrm{C}$ in 2.5 minute;

$$ \begin{equation*} \mathrm{m} \times \mathrm{c}[\theta-38]=\frac{\left[\left(\frac{\theta+38}{2}\right)-20\right] \times 150}{50 \times 60} \tag{3} \end{equation*} $$

From Eqns. (1) and (3) we have

$$ \frac{\theta-38}{4}=\frac{\left[\left(\frac{\theta+38}{2}\right)-20\right] \times 150}{50 \times 60} $$

$\therefore \theta=42^{\circ} \mathrm{C}$

71. A composite rod is made by joining end to end two rods $P$ and $Q$ of same cross-section. At $25^{\circ} \mathrm{C}$ the length of composite rod is $1 \mathrm{~m}$ of which $0.3 \mathrm{~m}$ is of $P$. The composite rod is heated to $125^{\circ} \mathrm{C}$. Its length increases by $1.91 \mathrm{~mm}$. Coefficient of linear expansion of $P=1.7 \times 10^{-5}\left({ }^{0} \mathrm{C}\right)^{-1}$. The coefficient of linear expansion of $Q$ is

(1) $2 \times 10^{-4}\left({ }^{0} \mathrm{C}\right)^{-1}$

(2) $1.5 \times 10^{-5}\left({ }^{0} \mathrm{C}\right)^{-1}$

(3) $2 \times 10^{-5}\left({ }^{0} \mathrm{C}\right)^{-1}$

(4) $2.5 \times 10^{-4}\left({ }^{0} \mathrm{C}\right)^{-1}$

Show Answer

Correct answer: (3)

Solution:

Let $\ell _{\mathrm{P}}$ and $\ell _{\mathrm{Q}}$ be length of $\operatorname{rod} \mathrm{P}$ and $\mathrm{Q}$ at $25^{\circ} \mathrm{C}$. Given

$$ \ell _{\mathrm{P}}=0.3 \mathrm{~m} ; \quad \ell _{\mathrm{P}}+\ell _{\mathrm{Q}}=1 \mathrm{~m} ; \quad \therefore \ell _{\mathrm{Q}}=0.7 \mathrm{~m} $$

Let $(\Delta \ell) _{\mathrm{P}}$ and $(\Delta \ell) _{\mathrm{Q}}$ be increase in length of $\mathrm{P}$ and $\mathrm{Q}$ when temperature is raised to $125^{\circ} \mathrm{C}$. Then

$$ \begin{aligned} & (\Delta \ell) _{\mathrm{P}}=0.3 \times 1.7 \times 10^{-5} \times 100 \\ & (\Delta \ell) _{\mathrm{Q}}=0.7 \times \alpha \times 100 \end{aligned} $$

Given $\Delta \ell=(\Delta \ell) _{\mathrm{P}}+(\Delta \ell) _{\mathrm{Q}}=1.91 \times 10^{-3} \mathrm{~m}$

$\therefore 1.91 \times 10^{-3}=5.1 \times 10^{-4}+70 \alpha$

or $\quad \alpha=\frac{(1.91-0.51) \times 10^{-3}}{70}=2 \times 10^{-5}\left({ }^{0} \mathrm{C}\right)^{-1}$

72. Two rods one of aluminium and the other of steel; having initial lengths $\ell _{1}$ and $\ell _{2}$ at $0^{\circ} \mathrm{C}$ are connected together to form a single rod of length $\left(\ell _{1}+\ell _{2}\right)$. If the length of each rod increases by the same amount on increasing temperature by $\theta^{\circ} \mathbf{C}$; the ratio $\frac{\ell _{1}}{\left(\ell _{1}+\ell _{2}\right)}$ in terms of coefficents of linear expansions $\alpha _{1}$ and $\alpha _{2}$ is

(1) $\frac{\alpha _{1}}{\alpha _{2}}$

(2) $\frac{\alpha _{2}}{\alpha _{1}}$

(3) $\frac{\alpha _{1}}{\alpha _{1}+\alpha _{2}}$

(4) $\frac{\alpha _{2}}{\alpha _{1}+\alpha _{2}}$

Show Answer

Correct answer: (4)

Solution:

The increase in length of the two rods on raising temperation by $\theta^{\circ} \mathrm{C}$ is same. Therefore

$\ell _{1} \alpha _{1} \theta=\ell _{2} \alpha _{2} \theta \quad$ or $\quad \frac{\ell _{2}}{\ell _{1}}=\frac{\alpha _{1}}{\alpha _{2}}$ $\therefore \frac{\ell _{2}}{\ell _{1}}+1=\frac{\alpha _{1}}{\alpha _{2}}+1$

or $\frac{\ell _{1}+\ell _{2}}{\ell _{1}}=\frac{\alpha _{1}+\alpha _{2}}{\alpha _{2}}$

$\therefore \frac{\ell _{1}}{\ell _{1}+\ell _{2}}=\frac{\alpha _{2}}{\alpha _{1}+\alpha _{2}}$

73. A vertical glass tube closed at bottom contains mercury up to a height of $500 \mathrm{~mm}$ at a temperature of $10^{\circ} \mathrm{C}$. The height of mercury column at $30^{\circ} \mathrm{C}$ changes by

$$ \left(\gamma _{\mathrm{Hg}}=18 \times 10^{-5}\left({ }^{0} \mathrm{C}\right)^{-1} ; \quad \alpha _{\text {glass }}=0.8 \times 10^{-5} \mathrm{C}^{-1}\right) $$

(1) $-0.2 \mathrm{~mm}$

(2) $+1.6 \mathrm{~mm}$

(3) $-1.6 \mathrm{~mm}$

(4) $+0.2 \mathrm{~mm}$

Show Answer

Correct answer: (2)

Solution:

Let $\mathrm{a} _{1}, \ell _{1}, \rho _{1}$ and $\mathrm{v} _{1}$ denote area of cross-section length of mercury column; density of mercury and volume of mercury in glass tube at $10^{\circ} \mathrm{C}$. The corresponding quantites at $30^{\circ} \mathrm{C}$ are $\mathrm{a} _{2}, \ell _{2}, \rho _{2}$ and $\mathrm{v} _{2}$ respectively. The mass of mercury in tube remains same, therefore

$$ \begin{equation*} a _{1}, \ell _{1}, \rho _{1}=a _{2}, \ell _{2}, \rho _{2} \tag{1} \end{equation*} $$

Also,

$$ a _{2}=a _{1}\left[1+2 \alpha _{g} \times 20\right] $$

or $\quad \frac{\mathrm{a} _{1}}{\mathrm{a} _{2}}=\frac{1}{\left[1+40 \times 0.8 \times 10^{-5}\right]}=\left[1+32 \times 10^{-5}\right]^{-1}$

$$ \begin{equation*} \simeq 1-32 \times 10^{-5} \tag{2} \end{equation*} $$

Also,

$$ \rho _{1}=\rho _{2}\left[1+\gamma _{\mathrm{Hg}} \times 20\right]=\rho _{2}\left[1+18 \times 10^{-5} \times 20\right] $$

or $\frac{\rho _{1}}{\rho _{2}}=1.0036$

From Eqns. (1), (2) and (3) we have

$$ \begin{aligned} \ell _{2}= & \ell _{1}\left(\frac{a _{1}}{a _{2}}\right)\left(\frac{\rho _{1}}{\rho _{2}}\right) \\ & =500\left[1-32 \times 10^{-5}\right][1.0036] \simeq 501.6 \mathrm{~mm} \end{aligned} $$

The change in height of mercury in tube $=501.6-500=1.6 \mathrm{~mm}$

74. A block of ice at $-10^{\circ} \mathrm{C}$ is slowly heated and converted to steam at $100^{\circ} \mathrm{C}$ which of the following curves represent the phenomenon qualitatively?

Show Answer

Correct answer: (1)

Solution:

First heat is supplied to raise temperature of ice from $-10^{\circ} \mathrm{C}$ to $0^{\circ} \mathrm{C}$. Now heat supplied is latent heat of fusion of ice. During this stage temperature remains constant at $0^{\circ} \mathrm{C}$. Now heat supplied raises temperature of water formed from $0^{\circ} \mathrm{C}$ to $100^{\circ} \mathrm{C}$. Then heat supplied is latent heat of vaporisation. There is no change in temperature due to heat given. These features are correctly represented by curve (1).

75. $60 \mathrm{~g}$ of steam at $373 \mathrm{~K}$ is mixed with $450 \mathrm{~g}$ of ice at $253 \mathrm{~K}$. In the final state the mass of water in the system is

[Given: Latent heat of vaporisation of steam $=540 \mathrm{Cal} \quad \mathrm{g}^{-1}$

Latent heat of fusion of ice $=80 \mathrm{Cal} \quad \mathrm{g}^{-1}$

Specific heat of ice $=0.5 \mathrm{Cal} \quad \mathrm{g}^{-1}\left({ }^{0} \mathrm{C}\right)^{-1}$; specific heat of water $\left.=1 \mathrm{Cal} \mathrm{g}^{-1}\left({ }^{0} \mathrm{C}\right)^{-1}\right]$

(1) $\quad 475.5 \mathrm{~g}$

(2) $\quad 483.15 \mathrm{~g}$

(3) $\quad \mathbf{5 0 0 . 0 0} \mathrm{g}$

(4) $\quad 510.00 \mathrm{~g}$

[IIT 2006]

Show Answer

Correct answer: (2)

Solution:

$\mathrm{H} _{1}=$ Heat required to melt ice completely

$=450 \times 0.5 \times[0-(-20)]+450 \times 80$

$=40,500 \mathrm{cal}$.

$\mathrm{H} _{2}^{\prime}=$ Heat released when entire mass of steam gets converted into water at $100^{\circ} \mathrm{C}$

$$ =60 \times 540=32,400 \mathrm{cal} $$

$\mathrm{H} _{2}^{\prime \prime}=$ Heat released if water at $100^{\circ} \mathrm{C}$ cools to $0^{\circ} \mathrm{C}$

$$ =60 \times 1 \times 100=6000 \mathrm{cal} $$

Total heat that can be released by steam and subsequent cooling of water to $0^{\circ} \mathrm{C}=\mathrm{H} _{2}^{\prime}+\mathrm{H} _{2}^{\prime \prime}$

$$ =32,400+6,000=38,400 \mathrm{cal} $$

Since $\mathrm{H} _{1}>\mathrm{H} _{2}$; sufficient heat is not available to melt entire mass of ice. The mass of ice melted, $\mathrm{m} _{1}$; is

$$ \mathrm{m} _{1}=\frac{38,400}{80}=26.25 \mathrm{~g} $$

Total mass of water; in equilibrium; at $0^{\circ} \mathrm{C}$

$$ \begin{aligned} & =60+(450-26.25) \\ & =483.75 \mathrm{~g} \end{aligned} $$

76. A geyser heats water flowing in it at the rate of $50 \mathrm{cc} \quad \mathrm{s}^{-1}$ from $27^{\circ} \mathrm{C}$ to $77^{\circ} \mathrm{C}$. The geyser operates on a gas burner. It consumes $0.6 \mathrm{~kg}$ of gas per hour. The heat of combustion of gas is

(1) $6.3 \times 10^{4} \mathrm{~kJ}(\mathrm{~kg})^{-1}$

(2) $6.3 \times 10^{4} \mathrm{~J}(\mathrm{~kg})^{-1}$

(3) $6.3 \times 10^{3} \mathrm{~kJ}(\mathrm{~kg})^{-1}$

(4) $6.3 \times 10^{2} \mathrm{~kJ}(\mathrm{~kg})^{-1}$

Show Answer

Correct answer: (1)

Solution:

Heat absorbed by water flowing in $1 \mathrm{~s}$

$$ \begin{aligned} & =50 \times 1 \times 1 \times(77-27) \mathrm{Cal} \\ & =2500 \mathrm{Cal} .=2500 \times 4.2 \mathrm{~J}=1.05 \times 10^{4} \mathrm{~J} \end{aligned} $$

Total heat absorbed in one hour $=1.05 \times 10^{4} \times 3600$

$$ \begin{equation*} =37.8 \times 10^{6} \mathrm{~J} \tag{1} \end{equation*} $$

Let $\alpha$ be the heat of combustion of fuel in joule per $\mathrm{kg}$.

Heat liberated by fuel in joule in one hour $=0.6 \times \alpha \hspace{40mm}. . . . . . . (2)$

From Eqns (1) and (2) we have

$37.8 \times 10^{6}=0.6 \alpha$

$$ \begin{aligned} \therefore \quad \alpha & =\frac{37.8}{0.6} \times 10^{6} \mathrm{~J} \mathrm{~kg}^{-1} \\ & =6.3 \times 10^{7} \mathrm{~J} \mathrm{~kg}^{-1}=6.3 \times 10^{4} \mathrm{~kJ} \mathrm{~kg}^{-1} \end{aligned} $$

77. A copper calorimeter of mass $0.1 \mathrm{~kg}$ contains $\mathrm{m} \quad \mathrm{kg}$ of iec at $4^{\circ} \mathrm{C}$. The temperature of calorimeter and content rises from $-4^{\circ} \mathrm{C}$ to $-2^{\circ} \mathrm{C}$ when $0.52 \mathrm{kcal}$ of heat is given. To raise temperature of calorimeter and content by $4^{\circ} \mathrm{C}$ an additional amount of $41.54 \mathrm{kcal}$ has to be added. $C$ is specific heat of copper. Then $m$ and $C$ are

(Latent heat of fusion of ice $=80 \mathrm{k} \quad \mathrm{cal} \quad \mathrm{kg}^{-1}$ specific heat of ice $=0.5 \mathrm{kcal}^{-1}{ }^{0} \quad \mathrm{C}^{-1}$ )

(1) $\mathrm{m}=0.5 \mathrm{~kg} ; \mathrm{C}=0.1 \mathrm{kcal} \quad {kg^{-1}} \quad { }^{0} \mathrm{C}^{-1}$

(2) $\mathrm{m}=0.5 \mathrm{~kg} ; \mathrm{C}=0.15 \mathrm{kcal} \quad \mathrm{kg}^{-1} \quad { }^{0} \mathrm{C}^{-1}$

(3) $\mathrm{m}=0.4 \mathrm{~kg} ; \mathrm{C}=0.1 \mathrm{kcal} \quad {kg^{-1}} \quad { }^{0} \mathrm{C}^{-1}$

(4) $\mathrm{m}=0.4 \mathrm{~kg} ; \mathrm{C}=0.2 \mathrm{kcal} \quad \mathrm{kg}^{-1} \quad { }^{0} \mathrm{C}^{-1}$

Show Answer

Correct answer: (1)

Solution:

Given

$0.1 \times \mathrm{C} \times[(-2)-(-4)]+\mathrm{m} \times 0.5[-2-(-4)]=0.52$

$0.2 \mathrm{C}+\mathrm{m}=0.52 \hspace{40mm}. . . . . . . . (1)$

When temperature of calorimeter and contents rises by $4^{\circ} \mathrm{C}$ from $-2^{\circ} \mathrm{C}$; the final temperature attained is $+2^{\circ} \mathrm{C}$. In this process calorimeter + ice will absorb heat $\mathrm{Q} _{1}$ to raise temperature from $-2^{\circ} \mathrm{C}$ to $0^{\circ} \mathrm{C}$. Now heat $\mathrm{Q} _{2}$ is absorbed to melt ice. $\mathrm{Q} _{3}$ is heat required to raise temperature of calorimeter and water obtained due to melting of ice from $0^{\circ} \mathrm{C}$ to $2^{\circ} \mathrm{C}$. Given

$$ \mathrm{Q} _{1}+\mathrm{Q} _{2}+\mathrm{Q} _{3}=41.54 \mathrm{kcal} $$

$\mathrm{Q} _{1}=0.1 \times \mathrm{C} \times 2+\mathrm{m} \times 0.5 \times 2=0.2 \mathrm{C}+\mathrm{m} \quad \mathrm{kcal}$

$\mathrm{Q} _{2}=\mathrm{m} \times 80 \mathrm{kcal}, \mathrm{Q} _{3}=0.1 \times \mathrm{C} \times 2+\mathrm{m} \times 1 \times 2 \mathrm{kcal}$

$\therefore 0.2 \mathrm{C}+\mathrm{m}+80 \mathrm{~m}+0.2 \mathrm{C}+2 \mathrm{~m}=41.54$

or $\quad 82 \mathrm{~m}+0.4 \mathrm{C}=41.54 \hspace{40mm}. . . . . . . . (2)$

Solving Eqns. (1) and (2) we have

$\mathrm{m}=0.5 \mathrm{~kg} ; \mathrm{C}=0.1 \mathrm{kcal} \quad \mathrm{kg}^{-1}{ }^{0} \quad \mathrm{C}^{-1}$

78. A copper bar $M N$ of length $50 \mathrm{~cm}$ has a water layer of $100^{\circ} \mathrm{C}$ thickness $0.5 \mathrm{~mm}$ at end $m$ as shown in Fig. 50. The temperatures maintained at ends are as shown in Fig. $\theta$ is nearly.

Given:

Thermal conductivity of copper $=45 \times 10^{-2} \mathrm{Wm}^{-1}(\mathrm{~K})^{-1}$

Thermal conductivity of water $\left.=60 \times 10^{-4} \mathrm{Wm}^{-1}(\mathrm{~K})^{-1}\right)$

(1) $98^{\circ} \mathrm{C}$

(2) $96^{\circ} \mathrm{C}$

(3) $93^{\circ} \mathrm{C}$

(4) $90^{\circ} \mathrm{C}$

Show Answer

Correct answer: (3)

Solution:

The rate of flow of heat in water layer at end $\mathrm{M}$ and copper bar $\mathrm{MN}$ is same. Therefore

$$ \frac{60 \times 10^{-4}[100-\theta]}{5 \times 10^{-4}}=\frac{45 \times 10^{-2} \cdot \mathrm{A}[\theta-0]}{0.5} $$

or $\quad 4[100-\theta]=0.3 \theta$

or $\quad \theta=\frac{400}{4.3} \simeq 93^{\circ} \mathrm{C}$

79. Two identical conducting rods are first connected simultaneously to two vassels one containing water at $100^{\circ} \mathrm{C}$ and the other containing ice at $0^{\circ} \mathrm{C}$. In second case the two rods are joined end to end and connected to the same two vessels. Let $q _{1}$ and $q _{2}$ rate of melting of ice in the two cases respectively. The ratio $\frac{q _{1}}{q _{2}}$ is

(1) $\frac{1}{2}$

(2) $\frac{2}{1}$

(3) $\frac{4}{1}$

(4) $\frac{1}{4}$

Show Answer

Correct answer: (3)

Solution:

Case I

Fig. 51

Fig. 51 (a) shows the two rods A and B. Let a and $\ell$ denote area of cross-section and of length of each rod. $\mathrm{K}$ is thermal conductivity of material of rods.

$\mathrm{Q} _{1}=$ Rate of flow of heat $=2\left[\mathrm{Ka} \frac{(100-0)}{\ell}\right]$

$$ \begin{equation*} =\frac{200 \mathrm{Ka}}{\ell} \tag{1} \end{equation*} $$

$\mathrm{q} _{1}=$ The rate of melting of ice $=\frac{\mathrm{Q} _{1}}{\mathrm{~L}}=\frac{200 \mathrm{Ka}}{\ell \mathrm{L}}$

where $L$ is latent heat of fusion of ice.

Case II

The arrangment of rods is an shown in Fig. 51 (b)

$\mathrm{Q} _{2}=$ Rate of flow of heat $=\left[\mathrm{Ka} \frac{(100-0)}{2 \ell}\right]=\frac{50 \mathrm{Ka}}{\ell}$

$\mathrm{q} _{2}=$ The rate of melting of ice $=\frac{\mathrm{Q} _{2}}{\mathrm{~L}}=\frac{50 \mathrm{Ka}}{\ell \mathrm{L}}$

$\therefore \frac{\mathrm{q} _{1}}{\mathrm{q} _{2}}=4$

80. Two metal blocks $P$ and $Q$ have thermal capacities $C _{1}$ and $\mathrm{C} _{2}$ respectively. The blocks are connected to one another by a rod of cross-sectional area $A$; length $L$ of negligible heat capacity. The arrangment is thermally insulated from surroundings. $T _{1}-T _{2}=T$ is the instantaneous difference ot temperature between $P$ and $Q \cdot \frac{d \theta}{d t}$ is

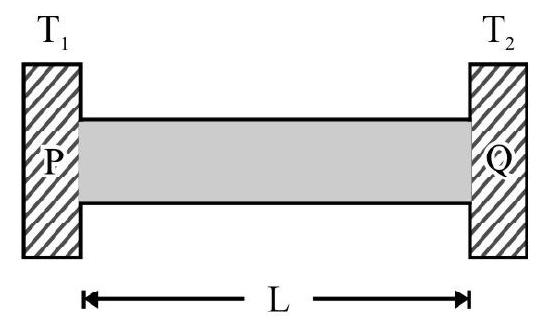
Fig. 52

(1) $\frac{\mathrm{KA}}{\mathrm{LC} _{1}}$

(2) $\frac{\mathrm{KA}}{\mathrm{LC} _{2}}$

(3) $\frac{\mathrm{KA}}{\mathrm{L}}\left[\frac{1}{\mathrm{C} _{1}}-\frac{1}{\mathrm{C} _{2}}\right]$

(4) $-\frac{\mathrm{KA}}{\mathrm{L}}\left[\frac{1}{\mathrm{C} _{1}}+\frac{1}{\mathrm{C} _{2}}\right]$

Show Answer

Correct answer: (4)

Solution:

The rate of flow of heat from $\mathrm{P}$ toQ

$$ =\frac{\mathrm{KA} \theta}{\mathrm{L}} $$

The rate of loss of temperature of $\mathrm{P}=-\left[\frac{\mathrm{KA} \theta}{\mathrm{LC} _{1}}\right]$

The rate of rise of temperature of $\mathrm{Q}=-\frac{\mathrm{KA} \theta}{\mathrm{LC} _{2}}$

The instantaneous rate of change of $\theta=\frac{\mathrm{d} \theta}{\mathrm{dt}}$

$$ =-\frac{\mathrm{KA} \theta}{\mathrm{L}}\left[\frac{1}{\mathrm{C} _{1}}+\frac{1}{\mathrm{C} _{2}}\right] $$

81. Three rods of identical cross-section made of the same material form the three sides of the of an issoceles triangle $\mathrm{ABC}$; right angled at $\mathrm{B}$. The points $A$ and $B$ are maintained at temperature $T$ and $\sqrt{2} T$ respectively. In steady state temperature of point $C$ is $T _{C}$. Assuming that only conduction takes $\frac{T _{C}}{T}$ is

(1) $\frac{1}{2(\sqrt{2}-1)}$

(2) $\frac{3}{(\sqrt{2}+1)}$

(3) $\frac{3}{\sqrt{3}(\sqrt{2}-1)}$

(4) $\frac{1}{(\sqrt{2}+1)}$

Show Answer

Correct answer: (2)

Solution:

Given $T _{A}=T ; T _{B}=\sqrt{2} T>T _{A}$.

In $\operatorname{rod} \mathrm{AB}$ heat flow from $\mathrm{B}$ to $\mathrm{A}$ to maintain temperature at end $\mathrm{B}$ heat must flow from $\mathrm{C}$ to $\mathrm{B}$. Therefore in rod $\mathrm{AC}$ heat flows from $\mathrm{A}$ to $\mathrm{C}$. The rate of flow of heat in $\mathrm{AC}$ and $\mathrm{BC}$ must be same. Therefore

$$ \begin{aligned} & \quad \frac{\mathrm{Ka}}{\sqrt{2} \ell}\left[\mathrm{T}-\mathrm{T} _{\mathrm{C}}\right]=\frac{\mathrm{Ka}}{\ell}\left[\mathrm{T} _{\mathrm{C}}-\frac{\sqrt{2}}{\ell}\right] \\ & \text { or } \quad \frac{\mathrm{T}-\mathrm{T} _{\mathrm{C}}}{\sqrt{2}}=\mathrm{T} _{\mathrm{C}}-\sqrt{2} \mathrm{~T} \\ & \text { or } \quad \mathrm{T}-\mathrm{T} _{\mathrm{C}}=\sqrt{2} \mathrm{~T} _{\mathrm{C}}-2 \mathrm{~T} \\ & \therefore \quad 3 \mathrm{~T}=(1+\sqrt{2}) \mathrm{T} _{\mathrm{C}} \\ & \text { or } \quad \frac{\mathrm{T} _{\mathrm{C}}}{\mathrm{T}}=\frac{3}{(\sqrt{2}+1)} \end{aligned} $$

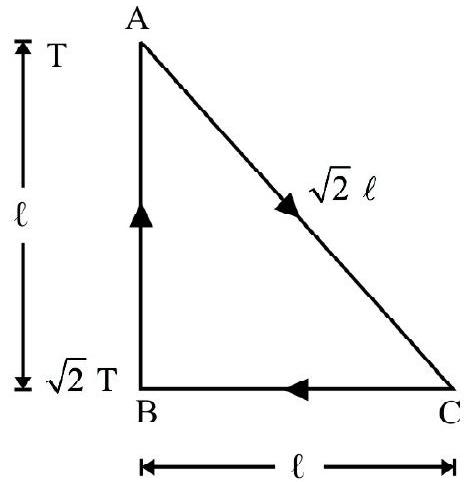Fig. 53

82. Three rods $A, B$ and $C$ of same length $\ell$ and cross-sectional area a are joined together as shown in Fig. $K _{A}=K _{B}=K$ and $K _{C}=\frac{K}{2}$. The temperature of common end $O$ in steady state,is

(1) $50^{\circ} \mathrm{C}$

(2) $54^{\circ} \mathrm{C}$

(3) $55^{\circ} \mathrm{C}$

(4) $60^{\circ} \mathrm{C}$

Show Answer

Correct answer: (2)

Solution:

Let $\theta$ be temperature of common end $\mathrm{O}$. Let $\mathrm{Q} _{\mathrm{A}} ; \mathrm{Q} _{\mathrm{B}}$ and $\mathrm{Q} _{\mathrm{C}}$ be rate of flow of heat in $\operatorname{rod} \mathrm{A}<\mathrm{B}$ and $\mathrm{C}$ respectively. Obviously

$$ \begin{equation*} \mathrm{Q} _{\mathrm{A}}=\mathrm{Q} _{\mathrm{B}}+\mathrm{Q} _{\mathrm{C}} \tag{1} \end{equation*} $$

Also, $\mathrm{Q} _{\mathrm{A}}=\frac{\mathrm{Ka}(\theta-0)}{\ell}$ and $\mathrm{Q} _{\mathrm{C}}=\left(\frac{\mathrm{K}}{2}\right) \mathrm{a} \frac{(90-\theta)}{\ell}$

$\therefore \quad \frac{\mathrm{Ka} \theta}{\ell}=\frac{\mathrm{Ka}}{\ell}(90-\theta)+\frac{\mathrm{Ka}}{\ell}\left(\frac{90-\theta}{2}\right)$

or $\quad \theta=\frac{3(90-\theta)}{2}$

$\therefore \quad \theta=\frac{270}{5}=54$