Unit 06 Gravitation
Introduction
The force between material objects is called gravitational force. It is caused by the mass of the objects. Gravitational force (or gravity) is one of four fundamental forces is nature which makes the universe exist as we know now.
Newton’s Law of Gravitation
The law of gravitation was discovered by Sir Issac Newton, a british mathematician, in the year 1665. Newton’s law states that every body in this universe attracts every other body with a force which is directly proportional to the product of the masses of the two bodies and inversely proportional to the square of the distance between their centres.
According to this law, if $\mathrm{m} _{1}$ and $\mathrm{m} _{2}$ are two point masses separated by a distance of $\mathrm{r}$, then the gravitational force between them will have magnitude ’ $\mathrm{F}$ ’ given as:
$$ \begin{aligned} \mathrm{F} & \propto \frac{\mathrm{m} _{1} \mathrm{~m} _{2}}{\mathrm{r}^{2}} \\ \text { or } \quad \mathrm{F} & =\frac{\mathrm{Gm} _{1} \mathrm{~m} _{2}}{\mathrm{r}^{2}} \end{aligned} $$
Here, the proportionality constant ’ $G$ ’ is called the universal gravitational constant. The value of $G$ is determined by the British scientist Henry Cavendish in 1798 and it is equal to $6.67 \times 10^{-11} \mathrm{~N}-\mathrm{m}^{2} \mathrm{Kg}^{-2}$. The dimensions of $\mathrm{G}$ are $\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-3}\right]$.
The value of $\mathrm{G}$ is a universal constant which has same value every where irrespective of time, space and physical or chemical conditions. $G$ is a scalar quantity. Because $G$ is a universal constant, Newton’s law of gravitation is also called universal law of gravitation.
Charecterstics of Gravitational Force
1. It obeys Newton’s third law of motion.
2. Gravitational force is always attractive.
3. Gravitational force between two bodies does not depend on the presence of a third body.
4. It is a central force (This means that the line of action of the gravitational force pass through the centres of centre of gravity of the two bodies).
5. Being central force, gravitational force does not produce any torque. Hence the angular momentum (L) of the two attracting bodies will remain as a constant. Therefore gravitational forces do not cause any change in angular momentum (L).
6. It is conservative in nature. That is the work done by or against gravitational force does not depend on the path followed.
7. It is the weakest force in nature. Gravitational force is approximately $10^{38}$ times weaker than strong nuclear force and $10^{36}$ times weaker than electrostatic force.
8. Gravitational force does not depend on the intervening medium, where as electric and magnetic forces depend on the medium.
9. Gravitational force cannot be shielded.
10. It obeys inverse square law.
11. It obeys principles of superposition.
12. It is a long range force, which extend, theoretically, up to infinity.
Newton’s Law of Gravitation in Vector Form
$\mathbf{F} _{21}=$ Gravitational on man $\mathrm{m} _{2}$ due to $\mathrm{m} _{1}$. Let $\mathbf{r} _{1}$ and $\mathbf{r} _{2}$ be position vector of mass $m _{1}$ and $m _{2}$ respectively as shown in Fig. $\mathbf{r} _{21}$ is position vector of mass $\mathrm{m} _{2}$ w.r.t. mass $\mathrm{m} _{2}$.
Then, $\mathbf{F} _{21}=-\left[\frac{G \mathrm{~m} _{1} \mathrm{~m} _{2}}{\mathrm{r}^{2}}\right] \mathbf{r} _{21}$
Similarly, $\mathbf{F} _{12}=$ Gravitational force on mass $\mathrm{m} _{1}$ due to mass $\mathrm{m} _{2}$
$$ =-\left[\frac{G \mathrm{~m} _{1} \mathrm{~m} _{2}}{\mathrm{r}^{2}}\right] \mathbf{r} _{12} $$
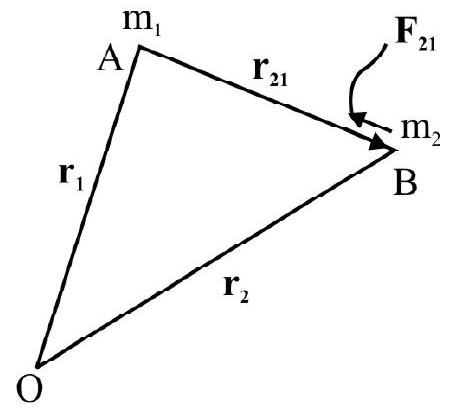
Obviously $\mathbf{r} _{12}=-\mathbf{r} _{21}$; therefore $\mathbf{F} _{12}=-\mathbf{F} _{21}$
Superposition Principle for Gravitational Attraction
Since gravitational force is always attractive, it is comparatively easier to find the resultant force on one body due to several other bodies. Suppose there are several bodies of masses $\mathrm{m} _{1}, \mathrm{~m} _{2}, \mathrm{~m} _{3}$ etc. situated at specific locations defined by position vector $\mathbf{r} _{1}, \mathbf{r} _{2}, \mathbf{r} _{3}$ etc.
The resultant force on $\mathrm{m} _{1}$ due to all other masses can then be obtained as:
$$ \mathbf{F} _{1}=\mathbf{F} _{12}+\mathbf{F} _{13}+\ldots \ldots \ldots $$
where $\mathbf{F} _{1}$ is resultant force on $\mathrm{m} _{1}$
$\mathbf{F} _{12}$ is gravitational attraction on $\mathrm{m} _{1}$ by $\mathrm{m} _{2}$
$\mathbf{F} _{13}$ is gravitational attraction on $\mathrm{m} _{1}$ by $\mathrm{m} _{3}$ and so an.
Also, $\mathbf{F} _{1}=\frac{\mathrm{Gm} _{1} \mathrm{~m} _{2}}{\mathrm{r} _{12}^{2}} \mathbf{r} _{12}+\frac{\mathrm{Gm} _{1} \mathrm{~m} _{3}}{\mathrm{r} _{13}^{2}} \mathbf{r} _{13}+\ldots$.
$$ =-G m _{1} \sum _{j=2}^{N}\left(\frac{m _{j}}{r _{1 j}^{2}}\right) $$
Example-1:
Two heavy bodies of $200 \mathrm{~kg}$ and $500 \mathrm{~kg}$ are separated by a distance of $10 \mathrm{~m}$. What is gravitational force between then?
Show Answer
Solution:
Given: $\mathrm{m} _{1}=200 \mathrm{Kg}$
$$ \begin{aligned} & \mathrm{m} _{2}=500 \mathrm{Kg} \\ & \mathrm{r}=10 \mathrm{~m} \\ & \mathrm{G}=6.67 \times 10^{-11} \mathrm{~N}-\mathrm{m}^{2} \mathrm{Kg}^{-2} \\ & \therefore \quad \mathrm{F}=\frac{\mathrm{Gm} _{1} \mathrm{~m} _{2}}{\mathrm{r}^{2}}=\frac{6.67 \times 10^{-11} \times 200 \times 500}{(10)^{2}}=6.67 \times 10^{-8} \mathrm{~N} \end{aligned} $$
(Please note that this force is negligible in magnitude, even though the masses are heavy. Our feeling that they are heavy is because of their weight which is none other than the gravitational attraction on then by earth).
Example-2:
Earth, considered spherical in shape, has a radius of $6400 \mathrm{Km}$. Its mass is $6.0 \times 10^{24} \mathrm{Kg}$. A body of mass $50 \mathrm{Kg}$ is situated on the surface of earth. What is the gravitational force on the body due to earth?
Show Answer
Solution:
The figure represents the situation given in the question. The distance between the centres of earth and the body $=\mathrm{R}$.
$\therefore \mathrm{r}=\mathrm{R}=6400 \times 10^{3} \mathrm{~m}$
$\mathrm{m} _{1}=\mathrm{m}=50 \mathrm{Kg}$
$\mathrm{m} _{2}=\mathrm{M}=6 \times 10^{24} \mathrm{Kg}$
Now, $F=\frac{G m _{1} m _{2}}{r^{2}}$
$$ \begin{aligned} & =\frac{\mathrm{G} \mathrm{mm}}{\mathrm{R}^{2}} \\ & =\frac{6.67 \times 10^{-11} \times 50 \times 6 \times 10^{24}}{\left(6400 \times 10^{3}\right)^{2}} \\ & =\frac{6.67 \times 3}{64 \times 64} \times 10^{5} \\ & =488.5 \mathrm{~N} \end{aligned} $$

(Note that this attractive force on $50 \mathrm{Kg}$ is practically large and it is directed towards the centre of earth. This is called the weight of the body. We all feel this gravitational attraction or ‘weight’ which enables us to walk and move on the surface of the earth).
Example-3:
Calculate the gravitational force between a proton and electron separated by a distance of 1 femtometer.
Given mass of proton $=1.67 \times 10^{-27} \mathrm{Kg}$
Mass of electron $=9.1 \times 10^{-31} \mathrm{Kg}$
and 1 femtometer $=10^{-15} \mathrm{~m}$
Show Answer
Solution:
$\mathrm{F}=\frac{\mathrm{Gm} _{1} \mathrm{~m} _{2}}{\mathrm{r}^{2}}$
$$ \begin{aligned} & =\frac{6.67 \times 10^{-11} \times 1.67 \times 10^{-27} \times 9.1 \times 10^{-31}}{\left(10^{-15}\right)^{2}} \\ & =101.36399 \times 10^{-39} \mathrm{~N} \\ & =1.01 \times 10^{-37} \mathrm{~N} \end{aligned} $$
(Note that this force is extremely negligible. In comparison, the electrostatic force between the same proton and electron is:
$\mathrm{F} _{\mathrm{e}}=\frac{1}{4 \pi \varepsilon _{0}} \cdot \frac{\mathrm{q} _{1} \mathrm{q} _{2}}{\mathrm{r}^{2}}$ $\left[\frac{1}{4 \pi \varepsilon _{0}}=9 \times 10^{9}\right.$ SI units
$$ \begin{aligned} & =\frac{9 \times 10^{9} \times 1.6 \times 10^{-19} \times 1.6 \times 10^{-19}}{\left(10^{-15}\right)^{2}} \\ & =23.04 \times 10 \\ & =230.4 \mathrm{~N} \quad \text { (Attractive) } \end{aligned} $$
(This is very large compared to the gravitational force between them).
Example-4:
Three identical particles, each of mass ’ $m$ ‘, are placed at the vertices of an equilateral triangle of side ’ $a$ ‘. Find the gravitational force exerted by this system on an identical particle, of mass m placed at (i) the midpoint of one side of the triangle and (ii) the centroid of the triangle.
Show Answer
Solution:
(i) Figure represents the position of the fourth particle at D. It is clear that two forces on $\mathrm{m}$ at $\mathrm{D}$; due to mass at $\mathrm{B}$ and $\mathrm{C}$, are equal and opposite. So they cancel out.
$\therefore$ The third force, directed from $\mathrm{D}$ to $\mathrm{A}$ is the resultant force on $\mathrm{m}$ at D.
$\therefore \quad F _{D}=\frac{G m \times m}{(A D)^{2}}=\frac{G m^{2}}{\left(\frac{3}{4} a^{2}\right)}=\frac{4}{3} \frac{G m^{2}}{a^{2}}$
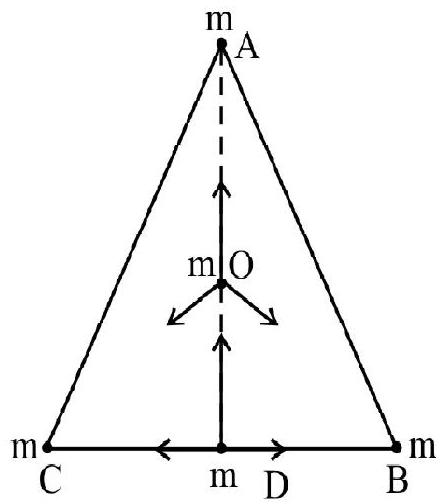
(ii) When the fourth particle is placed at the centroid $\mathrm{O}$, the three forces on the mass $\mathrm{m}$ at $\mathrm{O}$ due to the other three have equal magnitude of $\mathrm{F}$ each. The angle between any two of these forces is $120^{\circ}$. Therefore the third force (i.e. along OA) will become the equilibrant of the other two. Hence the net force would be zero.
Example-5:
Two variable masses $m _{1}$ and $m _{2}$ are placed at a variable distance $r$ from each other. Plot graphs showing the variation of the gravitational force $(\mathrm{F})$ between then with:
(i) product of the masses $\left(\mathrm{m} _{1} \mathrm{~m} _{2}\right)$
(ii) $\mathrm{r}$
Show Answer
Solution:
We have, $F=\frac{G m _{1} m _{2}}{r^{2}}$
or
$\mathrm{F} \propto \mathrm{m} _{1} \mathrm{~m} _{2}$
and
$\mathrm{F} \propto \frac{1}{\mathrm{r}^{2}}$
(i)

(ii)

Gravitational Field at a Point
From Newton’s law of gravitation, $F=\frac{G m _{1} m _{2}}{r^{2}}$, it follows that the magnitude of gravitational force becomes zero, only when $\mathrm{r} \rightarrow \infty$. But, as the distance increases to large value, $\mathrm{F}$ becomes negligible. Hence, practically the force $\mathrm{F}$ is experienced up to a limited distance.
The region around a body in which the gravitational attractive force of it can be experienced by other bodies is called its gravitational field (or field region).
It is a three dimensional space around a body (or source mass). At different points of this field region the strength of the force experienced by another body / mass will be different.
In order to predict how much force would a body or mass experience when placed at a particular point in the field region of a source mass, it would be convenient if we introduce a physical concept called ‘gravitational field intensity’ at a point.
Gravitational field intensity (I) at a point, near a source mass, is the force experienced by a unit ’test’ mass placed at that point.
$$ \text { i.e. } \mathbf{I}=\frac{\mathbf{F}}{\mathrm{m} _{0}} \quad\left[\mathrm{~m} _{0}=\text { test mass, } \mathbf{F}=\text { Force experienced by the test mass }\right] $$
Consider a point $\mathrm{P}$ in the field around a source mass ’ $\mathrm{m}$ ‘. Let $\mathrm{OP}=$ $r$ be the distance of $P$ from the centre of the source mass.
Let us place a test mass $m _{0}$ at $P$. The gravitational force (attraction)

$\mathrm{m} _{0}$ due to $\mathrm{m}$ is:
$$ \mathrm{F}=\frac{\mathrm{Gmm} _{0}}{\mathrm{r}^{2}} $$
By definition, $\mathrm{I}=\frac{\mathrm{F}}{\mathrm{m} _{0}}$
$\therefore \quad \mathrm{I}=\frac{\mathrm{Gm}}{\mathrm{r}^{2}}$
In vector farm, $\mathbf{F}=-\left(\frac{\mathrm{Gmm} _{0}}{\mathrm{r}^{2}}\right) \mathbf{r}$
$\therefore \quad \mathbf{I}=-\left(\frac{\mathrm{Gm}}{\mathrm{r}^{2}}\right) \mathbf{r}$
The negative sign indicates that I is opposite to $r$ measured from $\mathrm{O}$ to $\mathrm{P}$. The unit of is $\mathrm{N} \mathrm{Kg}^{-1}$ or ms ${ }^{-2}$. So I is in fact an acceleration. If $m _{0}$ is allowed to move under the influence of $\mathbf{F}$, it will accelerate towards the source mass $\mathrm{m}$, with $\mathrm{a}=\mathrm{I}=\frac{\mathrm{F}}{\mathrm{m} _{0}}$ acceleration.
The net intensity of gravitational field $\mathbf{I}$ at any point $\mathrm{P}$ due to point masses $\mathrm{m} _{1}, \mathrm{~m} _{2}, \ldots \ldots \mathrm{m} _{\mathrm{J}}, \ldots . \mathrm{m} _{\mathrm{N}}$ located at $\mathbf{r} _{1}$, $\mathbf{r} _{2}, \ldots . . \mathbf{r} _{\mathbf{j}}, \ldots . \mathbf{r} _{\mathrm{N}}$ is vector sum of intensity at $\mathrm{P}$ due to each point mass as if it was present alone. Let $\mathbf{I} _{\mathrm{j}}$ be intensity at $P$ due to mass $\mathrm{m} _{\mathrm{j}}$, then
$$ I=\sum _{j=1}^{N} \mathbf{I} _{j} $$
Gravitational Potential at a Point
Gravitational potential (V) at a point, in the gravitational field of a source mass, is defined as the work done, by an external agent, per unit mass, in bringing a test mass from infinity $($ where $F=0)$ to that point.
If $\mathrm{W}$ is the work done, in bringing a test mass $\mathrm{m} _{0}$ from infinity to the given point, then the potential at that point is:
$$ \mathrm{V}=\frac{\mathrm{W}}{\mathrm{m} _{0}} $$

The S.I unit of $\mathrm{V}$ is $\mathrm{J} \mathrm{kg}^{-1}$
Gravitational potential is a scalar quantity, while force and intensity of gravitational field are vector quantities.
Gravitational potential at a point due to a point mass $m$ is given by the formula:
$$ \mathrm{V}=-\frac{\mathrm{Gm}}{\mathrm{r}} $$
(The negative sign for $\mathrm{V}$ shows that the force involved is attractive).
Gravitational Potential Energy (U)
Suppose we move a body of mass $\mathrm{m} _{0}$ from $\mathrm{r}=\infty$ to a point $\mathrm{P}$ where distance of $\mathrm{P}$, from a source mass of $\mathrm{m}$, is $\mathrm{r}$. The work done for this is:
$$ \mathrm{W}=\int _{x=\infty}^{\mathrm{r}} \frac{\mathrm{Gmm}}{x^{2}} \mathrm{~d} x $$
or $\mathrm{W}=-\frac{\mathrm{Gmm} _{0}}{\mathrm{r}}$
As the mass $\mathrm{m} _{0}$ is stationary at $\mathrm{P}$, this work done gets stored with the mass $\mathrm{m} _{0}$. Thus $\mathrm{W}$ becomes the potential energy of $m _{0}$ at $P$. This potential energy $(U)$ of $m _{0}$ is obviously due to $m$.
Thus, we write:
$$ \mathrm{W}=\mathrm{U}=-\frac{\mathrm{Gmm} _{0}}{\mathrm{r}} $$
But, $=\frac{-\mathrm{Gm}}{\mathrm{r}}=\mathrm{V}$, the gravitational potential
$\therefore \mathrm{U}=\mathrm{Vm} _{0}$
or $\quad$ Potential energy $=$ Potential $\times$ mass
Since gravitational force is only attractive, the potential energy is always negative. The maximum value of gravitational potential energy (and thus potential) is zero (at $\mathrm{r}=\infty$ from the source mass).
When we move $m _{0}$ away from $m$, the potential energy of $m _{0}$ will increase.
Relation between Gravitational Field and Potential
A mass $\mathrm{m} _{0}$ is moved from point $\mathrm{A}$ to a near by point $\mathrm{B}$.
Let $\mathbf{A B}=\Delta x$. Since $\Delta x$ is very small, the force on $\mathrm{m} _{0}$ due to $\mathrm{m}$ is almost a constant, from $\mathrm{A}$ to $\mathrm{B}$.
Therefore, the work done in moving $\mathrm{m} _{0}$ from $\mathrm{A}$ to $\mathrm{B}$ is:

$$ \Delta \mathrm{W}=\mathrm{F} \Delta x $$
Now, the potential difference from A to B is:
$$ \mathrm{V} _{\mathrm{A}}-\mathrm{V} _{\mathrm{B}}=-\Delta \mathrm{V} \quad\left(\mathrm{V} _{\mathrm{A}}<\mathrm{V} _{\mathrm{B}}\right) $$
But $-\Delta \mathrm{V}=\frac{\Delta \mathrm{W}}{\mathrm{m} _{0}}$
$\therefore-\Delta \mathrm{V}=\frac{\mathrm{F}}{\mathrm{m} _{0}} \cdot \Delta x$
or $\quad-\Delta \mathrm{V}=\mathrm{I} . \Delta x$
Hence $\mathrm{I}=-\frac{\Delta \mathrm{V}}{\Delta x}$
We can also write:
$$ \mathrm{I}=\operatorname{Lt} _{\Delta x \rightarrow 0}\left(-\frac{\Delta \mathrm{V}}{\Delta x}\right) $$
or $\quad I=-\frac{d V}{d x}$
i.e. Field intensity $=-$ ve potential gradient
[Note that the formula for $\mathrm{U}$ and $\mathrm{F}$ namely $\mathrm{U}=-\frac{\mathrm{Gmm} _{0}}{\mathrm{r}}$ and $\mathrm{F}=\frac{\mathrm{Gmm} _{0}}{\mathrm{r}^{2}}$ leads us to the conclusion that $\mathrm{U}$ and $\mathrm{F}$ are related as: $\mathrm{F}=-\frac{\mathrm{dU}}{\mathrm{dr}}$.
Gravitational Field and Potential due to a Thin Spherical Shell
Case-I: For a shell of mass M, point inside the shell, the field intensity will be zero as all the forces cancel out. (Don’t be confused with shielding - this is not shielding).
$\therefore \mathrm{I}=0$, inside the shell.
Case-II: For point just on outer surface of the shell, at $r=R$, the field is maximum.
$$ \mathrm{I} _{\max }=\frac{\mathrm{GM}}{\mathrm{R}^{2}} $$
Case-III: Point outside shell; i.e. $\mathrm{r}>\mathrm{R}$, I decreases inversely as square of $\mathrm{r}$, as shown in the graph (I-r graph).
For any point on the shell or inside it, the gravitational potential will remain as constant and it is:
$$ \mathrm{V}=-\frac{\mathrm{GM}}{\mathrm{R}} $$
For points outside the sphere, $r>R, V=-\frac{G M}{r}$
For $\mathrm{r}>\mathrm{R}, \mathrm{V}$ will vary inversely as $\mathrm{r}$, as shown in the $\mathrm{V}-\mathrm{r}$ graph.
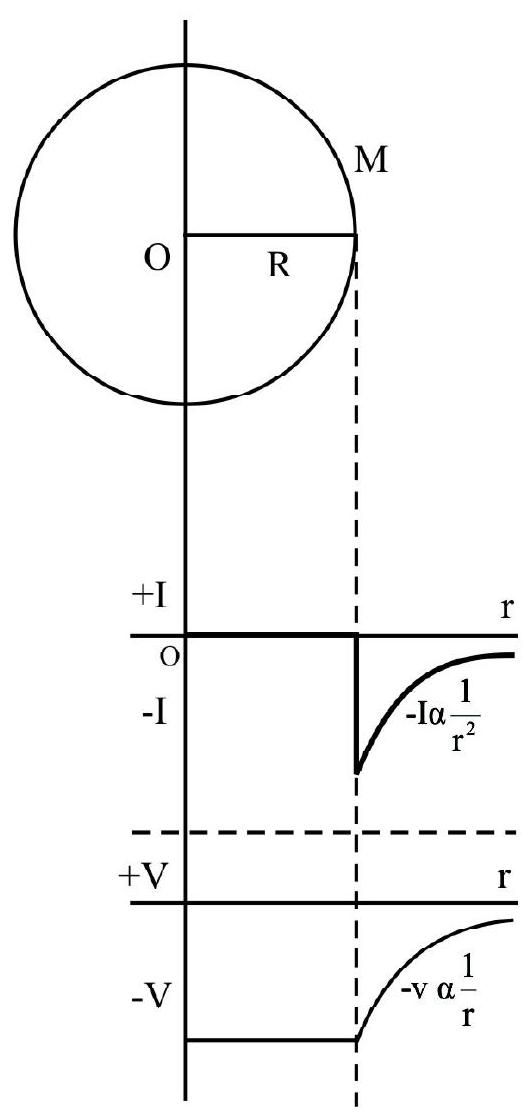
For a point on surface or outside; the entire mass of shell can be considered as concentrated at its center. This is not so for points inside shell.
Gravitational Field and Potential due to a Uniform Solid Sphere
Case-I: Point outside sphere.
At point $A(r>R)$, the gravitational field due to the solid sphere is:
$$ \mathbf{I} _{\mathrm{A}}=\frac{\mathrm{GM}}{\mathrm{r}^{2}}(-\mathbf{r}) $$
or $\mathbf{I} _{\mathrm{A}}=\frac{\mathrm{GM}}{\mathrm{r}^{2}}$, along $\mathbf{A O}$.
The gravitational potential at this point is:
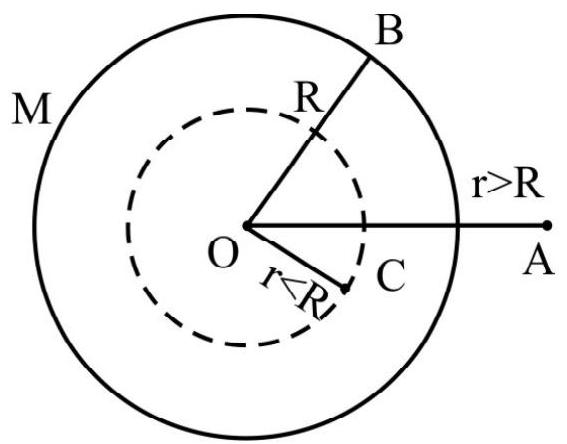
$\mathrm{V} _{\mathrm{A}}=-\frac{\mathrm{GM}}{\mathrm{r}} \quad(\mathrm{r}>\mathrm{R})$
Case-II: Point on the surface of sphere
For point $\mathrm{B}(\mathrm{r}=\mathrm{R})$, just on the surface,
$\mathrm{I} _{\mathrm{B}}=\frac{\mathrm{GM}}{\mathrm{R}^{2}} \quad$ (along BO)
and $\quad \mathrm{V} _{\mathrm{B}}=-\frac{\mathrm{GM}}{\mathrm{R}} \quad(\mathrm{r}=\mathrm{R})$
Case-III: Point Inside Sphere
For any point $\mathrm{C}$ inside the sphere $(\mathrm{r}<\mathrm{R})$
$\mathrm{I} _{\mathrm{C}}=-\frac{\mathrm{GM}}{\mathrm{R}^{2}}\left(\frac{\mathrm{r}}{\mathrm{R}}\right) \quad(\mathrm{I} \propto \mathrm{r}$ for $\mathrm{r}<\mathrm{R})$
and $\quad \mathrm{V} _{\mathrm{C}}=\frac{\mathrm{GM}}{2 \mathrm{R}^{3}}\left(3 \mathrm{R}^{2}-\mathrm{r}^{2}\right)$
At the centre of this solid sphere:
$$ \mathrm{I} _{0}=\mathrm{O} $$
and $\quad \mathrm{V} _{\mathrm{O}}=-\frac{3}{2} \frac{\mathrm{GM}}{\mathrm{R}}$
The graphical variation of $\mathrm{I}$ and $\mathrm{V}$ with $\mathrm{r}$ is shown in figure below.

Gravitational Field and Potential due to a Circular Ring

Gravitational field intensity at a point distance $r$ on the axis of this ring is:
$$ \mathrm{I} _{\rho}=\frac{\mathrm{GMr}}{\left(\mathrm{r}^{2}+\mathrm{R}^{2}\right)^{3 / 2}} \text { along PO } $$
The gravitational potential at point $\mathrm{P}$ is:
$$ \mathrm{V} _{\rho}=-\frac{\mathrm{GM}}{\sqrt{\mathrm{r}^{2}+\mathrm{R}^{2}}} $$
At the centre of the ring, where $r=0$,
$$ \mathrm{I} _{0}=\mathrm{O} $$
and $\quad \mathrm{V} _{0}=-\frac{\mathrm{GM}}{\mathrm{R}}$
The value of I on the axis of the circular ring is maximum at $r=\frac{R}{\sqrt{2}}$ and this maximum value of I is:
$$ \mathrm{I} _{\max }=\frac{\mathrm{GM}}{\sqrt{2}\left(\frac{3}{2}\right)^{3 / 2} \mathrm{R}^{2}} $$
The variation of I with $r$ along the axis of a ring is show below.

Example-6:
Three masses are placed in configuration as shown below. Find the total gravitational potential energy of the configuration. What is the binding energy of this system?
Show Answer
Solution:

Here, $\mathrm{r} _{12}=4 \mathrm{~m}$ and $\mathrm{r} _{31}=\mathrm{r} _{13}=3 \mathrm{~m}$
$$ \mathrm{r} _{23}=\mathrm{r} _{32}=\sqrt{4^{2}+3^{2}}=5 \mathrm{~m} $$
$\mathrm{m} _{1}=1 \mathrm{Kg}, \mathrm{m} _{2}=2 \mathrm{Kg}$ and $\mathrm{m} _{3}=2 \mathrm{Kg}$
The gravitational potential energy of the system is:
$$ \begin{aligned} \mathrm{U}=- & \frac{\mathrm{Gm} _{1} \mathrm{~m} _{2}}{\mathrm{r} _{12}}+-\frac{\mathrm{Gm} _{2} \mathrm{~m} _{3}}{\mathrm{r} _{23}}+-\frac{\mathrm{Gm} _{3} \mathrm{~m} _{1}}{\mathrm{r} _{31}} \\ & =-6.67 \times 10^{-11}\left(\frac{1 \times 2}{4}+\frac{2 \times 2}{5}+\frac{2 \times 1}{3}\right) \\ & =-6.67 \times 10^{-11} \frac{59}{30} \end{aligned} $$
$$ =-1.31 \times 10^{-10} \mathrm{~J} $$
The binding energy of the system is:
B.E $=-(\mathrm{U})$
$$ \begin{aligned} & =-\left(-1.31 \times 10^{-10} \mathrm{~J}\right) \\ & =1.31 \times 10^{-10} \mathrm{~J} \end{aligned} $$
Example-7:
The radius of the earth is $6.37 \times 10^{6} \mathrm{~m}$, its mean density is $5.5 \times 10^{3} \mathrm{Kgm}^{-3}$ and $\mathrm{G}=6.67 \times 10^{-11} \mathrm{Nm}^{2} \mathrm{Kg}^{-2}$. Calculate the gravitational potential at:
(i) the surface of the earth.
(ii) a depth of $\frac{\mathrm{R}}{2}$
(iii) the centre of the earth
Show Answer
Solution:
(i) For the surface,
$$ \begin{aligned} \mathrm{V}= & -\frac{\mathrm{GM}}{\mathrm{R}}=-\frac{\mathrm{G}}{\mathrm{R}} \times \frac{4}{3} \pi \mathrm{R}^{3} \rho \\ & =-\frac{4}{3} \pi \mathrm{GR}^{2} \rho \\ & =-\frac{4}{3} \times 3.14 \times 6.67 \times 10^{-11} \times\left(6.37 \times 10^{6}\right)^{2} \times 5.5 \times 10^{3} \\ & =-6.235 \times 10^{7} \mathrm{~J} \mathrm{Kg}^{-1} \end{aligned} $$
(ii) At a depth of $\frac{\mathrm{R}}{2}$,
$$ \begin{aligned} V= & -\frac{G M}{2 R^{3}}\left(3 R^{2}-r^{2}\right) \\ & =-\frac{G M}{2 \times R^{3}}\left(3 R^{2}-\frac{R^{2}}{4}\right) \end{aligned} $$
$$ \begin{aligned} & =-\frac{\mathrm{GM}}{2 \times \mathrm{R}^{3}} \times \frac{11}{4} \times \mathrm{R}^{2} \\ & =-\frac{11}{8} \frac{\mathrm{GM}}{\mathrm{R}} \\ & =-\frac{11}{8} \times 6.235 \times 10^{7} \\ & =-8.57 \times 10^{7} \mathrm{~J} \mathrm{Kg}^{-1} \end{aligned} $$
(iii) At the centre,
$$ \begin{aligned} \mathrm{V}= & -\frac{3}{2} \frac{\mathrm{GM}}{\mathrm{R}} \\ & =-\frac{3}{2} \times 6.235 \times 10^{7} \\ & =-9.35 \times 10^{7} \mathrm{~J} \mathrm{Kg}^{-1} \end{aligned} $$
Gravity and Acceleration due to Gravity of Earth
Gravity is the property of heavenly bodies by virtue of which they attract other bodies towards their centre. Acceleration due to gravity is the acceleration produced for a body when it falls freely under the gravity alone.
This acceleration is denoted by ’ $\mathrm{g}$ ‘. It is a vector quantity with unit $\mathrm{ms}^{-2}$ and it is directed towards the centre of the earth, in case of earth.
It is common knowledge that the weight $(\mathrm{W})$ of a body of mass $m$, near the earth’s surface, is:
$$ \mathrm{W}=\mathrm{mg} \quad\left(\text { where } \mathrm{g}=9.8 \mathrm{~ms}^{-2}\right) $$
Also we know that weight is the force with which earth attracts a body towards its centre due to gravity.
From Newton’s law of gravitation, this attractive force is:
$$ \mathrm{F}=\mathrm{W}=\frac{\mathrm{GMm}}{\mathrm{R}^{2}} $$
where $\mathrm{M}$ is the mass of the earth and $\mathrm{R}$ in its radius.
Therefore, $\mathrm{mg}=\frac{\mathrm{GMm}}{\mathrm{R}^{2}}$
or $\quad g=\frac{G m}{R^{2}}$
This formula is true when the body is very near to earth’s surface. But this formula is applicable to any celestrial body.
For a body of mass $m$ on the surface of the earth, the mass M of earth can be assumed concentrated at its centre $\mathrm{O}$. Therefore, the gravitation force on $m$ by earth is $F=\frac{G M m}{R^{2}}$.
Now, the gravitational field intensity (I) at the point, where m is situated, is:
$$ \mathrm{I}=\frac{\mathrm{F}}{\mathrm{m}} \quad \text { or } \quad \mathrm{I}=\frac{\mathrm{GM}}{\mathrm{R}^{2}} $$

Therefore, we conclude that the gravitational field intensity (I) is same as the acceleration due to gravity (g) at the same point.
or $\quad \mathrm{I}=\mathrm{g}$
Hence, here onwards we use ‘g’ instead of I.
Acceleration due to gravity of earth can be written in terms of the mean density ( $\rho$ ) of the earth as:
$$ \begin{aligned} & \mathrm{g}=\frac{\mathrm{GM}}{\mathrm{R}^{2}} \\ & =\frac{\mathrm{G}}{\mathrm{R}^{2}}\left(\frac{4}{3} \pi \mathrm{R}^{3} \rho\right) \\ & =\frac{4}{3} \pi \mathrm{R} \rho \mathrm{G} \end{aligned} $$
For a point which is at a distance of h from the surface of the earth, the value of $g$ is given as:
$$ g=\frac{G M}{(R+h)^{2}} $$
Variation of $g$ with Attitude
On the surface of the earth we use the notation g for acceleration due to gravity. For any other position we use $\mathrm{g}^{\prime}$ for it. Consider a point which is at an attitude of h above the surface. A body of mass $m$ is placed here. The force of gravity on $m$, due to earth is:
$$ \mathrm{F}=\frac{\mathrm{GMm}}{\mathrm{r}^{2}} $$
or $\quad \mathrm{W}^{\prime}=\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})^{2}} \quad\left(\mathrm{~W}^{\prime}=\right.$ weight at height $\left.\mathrm{h}\right)$
But $\quad \mathrm{W}^{\prime}=\mathrm{mg}^{\prime} \quad\left(\mathrm{g}^{\prime}=\right.$ acceleration due to gravity at height $\left.\mathrm{h}\right)$
$\therefore \mathrm{g}^{\prime}=\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})^{2}}$

Thus we see that $\mathrm{g}^{\prime}$ decreases as $\mathrm{h}$ increases.
Case-I: When $\mathrm{h}$ is large or comparable with $\mathrm{R}$, we use the formula:
$$ \mathrm{g}^{\prime}=\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})^{2}} $$
Case-II: When $\mathrm{h}$ is small $(\mathrm{h}«\mathrm{R})$, then:
$$ \mathrm{g}^{\prime}=\frac{\mathrm{GM}}{\mathrm{R}^{2}\left(1+\frac{\mathrm{h}}{\mathrm{R}}\right)^{2}} $$
or $\quad g^{\prime}=g\left(1+\frac{h}{R}\right)^{-2}$
$$ \mathrm{g}^{\prime}=\mathrm{g}\left(1-\frac{2 \mathrm{~h}}{\mathrm{R}}\right) $$
(neglecting higher powers)
(This formula is used when $\mathrm{h}$ is very small i.e. only up to few kilometers).
From the formula: $g^{\prime}=g\left(1-\frac{2 h}{R}\right)$
$$ g-g^{\prime}=g \frac{2 h}{R} $$
or $\quad \Delta \mathrm{g}=\mathrm{g}\left(\frac{2 \mathrm{~h}}{\mathrm{R}}\right)$
or $\quad \frac{\Delta \mathrm{g}}{\mathrm{g}}=\frac{2 \mathrm{~h}}{\mathrm{R}}$
(i.e. fractional change in $g=\frac{2 h}{R}$ )
$\therefore \%$ ge change in $\mathrm{g}$ is:
$$ \frac{\Delta \mathrm{g}}{\mathrm{g}} \times 100 \%=\frac{2 \mathrm{~h}}{\mathrm{R}} \times 100 \% $$
Variation of $g$ with Depth
On the surface of the earth,
$$ \mathrm{g}=\frac{\mathrm{GM}}{\mathrm{R}^{2}} $$
or $\quad \mathrm{g}=\frac{4}{3} \pi \mathrm{GR} \rho \hspace{40mm}. . . . . . (1)$
Here $\rho=\frac{M}{\frac{4}{3} \pi R^{3}}$ is the mean density of the earth.
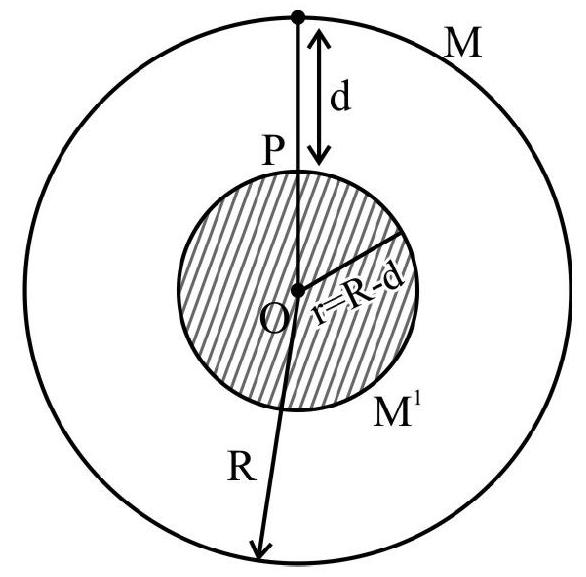
Now, at a depth $\mathrm{d}$ from the surface,
$\mathrm{F}=$ net gravitational force on mass $\mathrm{m}$ at point $\mathrm{P}=\mathrm{F} _{1}+\mathrm{F} _{2}$
$\mathrm{F} _{1}=$ Force on $\mathrm{m}$ due to solid sphere of radius ( $\mathrm{R}-\mathrm{d}$ ) (The mass $\mathrm{m}$ lies on the surface of this part of earth)
$\mathrm{F} _{2}=$ Force on $\mathrm{m}$ due to the remaining part of earth. (mass $\mathrm{m}$ lies inside this shell and so $\mathrm{F} _{2}=\mathrm{O}$ )
$\therefore \quad \mathrm{F}=\mathrm{F} _{1}=\mathrm{W}^{\prime}=\mathrm{mg}^{\prime}=\frac{\mathrm{GM}^{\prime} \mathrm{m}}{(\mathrm{R}-\ell)^{2}}$
$\mathrm{M}^{\prime}=$ Mass of sphere of radius $(\mathrm{R}-\mathrm{d})=\frac{4 \pi}{3}(\mathrm{R}-\mathrm{d})^{3} \rho$
$\therefore \quad \mathrm{g}^{\prime}=\frac{4}{3} \pi \mathrm{G}(\mathrm{R}-\mathrm{d}) \rho \hspace{40mm}. . . . . . (2)$
From(1) and (2):
$$ \mathrm{g}^{\prime}=\mathrm{g}\left(1-\frac{\mathrm{d}}{\mathrm{R}}\right) $$
Here, $\%$ change in $g=\frac{d}{R} \times 100 \%$
(Note that at the centre of the earth, $\mathrm{g}^{\prime}=0$ or $\mathrm{w}^{\prime}=0$. Hence weight of body is zero at the centre of the earth. But mass remains as $m$ )
The graph of $g$ vs $r(r=$ distance from the centre of earth is shown below.)
Variation of $g$ with Latitude
Due to rotation of the earth around

change in latitude angle $(\lambda)$. The variation is given by the formula:
$$ g^{\prime}=g-R \omega^{2} \cos ^{2} \lambda \quad(g=m e a n ~ v a l u e) $$
At equator, $\lambda=0$
$$ \therefore \quad \mathrm{g} _{\text {equator }}=\mathrm{g}-\mathrm{R} \omega^{2} $$
At poles, $\lambda=90^{\circ}$
$$ \therefore \quad g _{\text {pole }}=\mathrm{g} $$
(This shows that $\mathrm{g}$ at equator is slightly less than $\mathrm{g}$ at the poles).
From the formula: $g=\frac{G M}{R^{2}}$, we obtain:
$$ \frac{\Delta \mathrm{g}}{\mathrm{g}}=-\frac{2 \Delta \mathrm{R}}{\mathrm{R}}+\frac{\Delta \mathrm{M}}{\mathrm{M}} $$
Therefore, when $\mathrm{R}$ increases, keeping $\mathrm{M}$ constant, $\mathrm{g}$ decreases and when $\mathrm{M}$ increases, keeping $\mathrm{R}$ constant, $g$ increases.
Gravitational Potential and Potential Energy due to Earth
Assuming earth is solid sphere of radius $\mathrm{R}$ and mean density $\rho ; M=\frac{4}{3} \pi R^{3} \quad \rho=$ Mass of earth.
The gravitational potential $(\mathrm{V})$ at a point due to earth will, therefore, be the same as that due to a solid sphere.
Hence, on its surface, $\mathrm{V}=-\frac{\mathrm{GM}}{\mathrm{R}}$
At a height $h$ above the surface,
$$ \mathrm{V}=-\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}} $$
or $\quad \mathrm{V}=-\frac{\mathrm{GM}}{\mathrm{r}} \quad(\mathrm{r}=\mathrm{R}+\mathrm{h}$ is the distance from the centre of the earth $)$
The potential energy of body of mass $m$, on the surface of the earth is defined as the work done, is bringing this mass $\mathrm{m}$ from $\mathrm{r}=\infty$ to $\mathrm{r}=\mathrm{R}$, without accelerating it.
$\therefore$ Potential energy, $\mathrm{U}=\int _{\infty}^{\mathrm{R}} \mathrm{dW}$
or $\quad \mathrm{U}=\int _{\mathrm{r}=\infty}^{\mathrm{r}=\mathrm{R}} \frac{\mathrm{GMm}}{\mathrm{r}^{2}} \mathrm{dr}$
or
$$ \mathrm{U}=-\frac{\mathrm{GMm}}{\mathrm{R}} $$
U of $m$ at height $h$ above the surface is:
$$ \begin{aligned} & \mathrm{U}=-\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})} \\ & \mathrm{U}=-\frac{\mathrm{GMm}}{\mathrm{r}} \quad(\mathrm{r}=\mathrm{R}+\mathrm{h}) \end{aligned} $$
Change in Potential Energy, when $h$ is Small
Suppose a body be moved from the surface of earth to a height $h$ above the surface $(\mathrm{h}«\mathrm{R})$.
We have to do work against the gravitational attraction, to move the body up. Therefore the potential energy of this body will increase, here.
$$ \begin{array}{ll} \mathrm{U} _{\mathrm{i}}=-\frac{\mathrm{GMm}}{\mathrm{R}} & \text { (on the surface) } \\ \mathrm{U} _{\mathrm{f}}=-\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})} & \text { (at height } \mathrm{h}) \end{array} $$
$\therefore \quad \mathrm{U} _{\mathrm{f}}-\mathrm{U} _{\mathrm{i}}=\mathrm{GMm}\left[\frac{1}{\mathrm{R}}-\frac{1}{\mathrm{R}+\mathrm{h}}\right]$
or
$$ \Delta \mathrm{U}=\mathrm{GMm}\left[\frac{\mathrm{h}}{\mathrm{R}(\mathrm{R}+\mathrm{h})}\right] $$
or
$$ \Delta \mathrm{U}=\frac{\mathrm{GMm}}{\mathrm{R}^{2}}\left(\frac{\mathrm{h}}{1+\frac{\mathrm{h}}{\mathrm{R}}}\right) $$
or
$$ \Delta \mathrm{U}=\operatorname{gmh}\left(1-\frac{\mathrm{h}}{\mathrm{R}}\right) $$
or $\Delta \mathrm{U}=\mathrm{gmh}$
$$ \left(\text { as } \frac{\mathrm{h}}{\mathrm{R}}«1\right) $$
or $\Delta \mathrm{U}=\mathrm{mgh}$
Thus we say that when a body of mass $m$ is moved through a height $h$, its potential energy increases by mgh.
Change in Gravitational Potential Energy, when $h$ is Large
Let $\mathrm{h}=\mathrm{nR}$ (Here $\mathrm{h}$ is large)
On the surface, $U _{i}=-\frac{G M m}{R}=$ Initial gravitational P.E of mass $m$ At $h=n R$,
$\mathrm{U} _{\mathrm{f}}=$ The final gravitational P.E of mass $\mathrm{m}=-\frac{\mathrm{GMm}}{\mathrm{R}+\mathrm{nR}}=-\frac{\mathrm{GMm}}{\mathrm{R}(\mathrm{n}+1)}$
$\therefore \Delta \mathrm{U}=\mathrm{U} _{\mathrm{f}}-\mathrm{U} _{\mathrm{i}}$ The change in gravitational P.E
or $\quad \Delta \mathrm{U}=\frac{\mathrm{GMm}}{\mathrm{R}}\left[1-\frac{1}{\mathrm{n}+1}\right]$
or $\quad \Delta \mathrm{U}=\frac{\mathrm{GMm}}{\mathrm{R}}\left[\frac{\mathrm{n}}{\mathrm{n}+1}\right]$
or $\quad \Delta \mathrm{U}=\operatorname{mgR}\left[\frac{\mathrm{n}}{\mathrm{n}+1}\right]$
(Note that this $\Delta \mathrm{U}$ is equal to the work done by us on the mass $\mathrm{m}$ ).
Example-8:
If the ratio of radii and density of a planet and the earth is $3: 4$ and 2:3 respectively, what would be the weight of a person on the planet, if he weighs $600 \mathrm{~N}$ on earth?
Show Answer
Solution:
We have, $\mathrm{g}=\frac{4}{3} \pi \mathrm{GR} \rho$
$\therefore \frac{\mathrm{g} _{\mathrm{P}}}{\mathrm{g} _{\mathrm{E}}}=\frac{\mathrm{R} _{\mathrm{P}} \rho _{\mathrm{P}}}{\mathrm{R} _{\mathrm{E}} \rho _{\mathrm{E}}}=\left(\frac{\mathrm{R} _{\mathrm{P}}}{\mathrm{R} _{\mathrm{E}}}\right)\left(\frac{\rho _{\mathrm{P}}}{\rho _{\mathrm{E}}}\right)$ $=\frac{3}{4} \times \frac{2}{3}=\frac{1}{2}$
$\therefore \frac{\mathrm{W} _{\mathrm{P}}}{\mathrm{W} _{\mathrm{E}}}=\frac{\mathrm{mg} _{\mathrm{P}}}{\mathrm{mg} _{\mathrm{E}}}=\frac{1}{2}$
or $\quad \mathrm{W} _{\mathrm{P}}=\frac{\mathrm{W} _{\mathrm{E}}}{2}=\frac{600}{2} \mathrm{~N}=300 \mathrm{~N}$
Example-9:
The ratio of density and radius for two planets is 1:3 and 2:3 respectively. What is the ratio of time periods of oscillations of a simple pendulum on these planets?
Show Answer
Solution:
Here, $\mathrm{g}=\frac{4}{3} \pi \mathrm{GR} \rho$
$\therefore \frac{\mathrm{g} _{1}}{\mathrm{~g} _{2}}=\frac{\mathrm{R} _{1}}{\mathrm{R} _{2}} \cdot \frac{\rho _{1}}{\rho _{2}}$ $=2: 9$
Now, $\mathrm{T}=2 \pi \sqrt{\frac{\ell}{\mathrm{g}}} \quad(\ell=$ constant $)$
$\therefore \frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=\frac{\sqrt{\mathrm{g} _{2}}}{\sqrt{\mathrm{g} _{1}}}$
$=\sqrt{9}: \sqrt{2}$
Example-10:
The radius of the earth shrinks by $5 \%$, mass remaining constant. What is the change in the value of acceleration due to gravity?
Show Answer
Solution:
We have $\frac{\Delta \mathrm{g}}{\mathrm{g}}=-\frac{2 \Delta \mathrm{g}}{\mathrm{R}}+\frac{\Delta \mathrm{M}}{\mathrm{M}}$
Here, $\Delta \mathrm{M}=0$
$$ \begin{aligned} & \text { and } \frac{\Delta \mathrm{R}}{\mathrm{R}}=-5 \% \\ & \begin{aligned} \therefore \quad \frac{\Delta \mathrm{g}}{\mathrm{g}} & =-2 \times-5 \% \\ & =10 \% \end{aligned} \end{aligned} $$
$\therefore$ g increases by $10 \%$
Example-11:
At what height above the surface of the earth, the acceleration due to gravity will be $\frac{1}{9}$ th of its value at the surface. Take $\mathrm{R}=6400 \mathrm{~km}$.
Show Answer
Solution:
Note that the decrease in $\mathrm{g}$ is large. Therefore the height $\mathrm{h}$ is large.
So, we don’t use the formula:
$\mathrm{g}^{\prime}=\mathrm{g}\left(1-\frac{2 \mathrm{~h}}{\mathrm{R}}\right)$, which is applicable only for $\mathrm{h}«\mathrm{R}$.
We know, $\mathrm{g}=\frac{\mathrm{GM}}{\mathrm{R}^{2}}$
and $\quad g^{\prime}=\frac{G M}{(R+h)^{2}}$
$\therefore \frac{g^{\prime}}{g}=\frac{R^{2}}{(R+h)^{2}}$
or $\quad \frac{1}{9}=\frac{\mathrm{R}^{2}}{(\mathrm{R}+\mathrm{h})^{2}}$
$\therefore \frac{1}{3}=\frac{\mathrm{R}}{\mathrm{R}+\mathrm{h}}$
or $\mathrm{h}=2 \mathrm{R}$
$=2 \times 6400 \mathrm{~km}$
$=12800 \mathrm{~km}$
Example-12:
What is the percentage decrease in the weight of a body, when it is taken to a depth of $32 \mathrm{~km}$ below the surface of the earth?
Show Answer
Solution:
We have $g^{\prime}=g\left(1-\frac{d}{R}\right)$
$\therefore \frac{\Delta \mathrm{g}}{\mathrm{g}}=\frac{\mathrm{d}}{\mathrm{R}}$
Now, $\frac{\Delta \mathrm{g}}{\mathrm{g}}$ is same $\frac{\Delta \mathrm{W}}{\mathrm{W}}$, the $\%$ ge decrease in weight.
$\therefore \%$ ge decrease in weight $=\frac{\Delta \mathrm{g}}{\mathrm{g}}=\frac{\mathrm{d}}{\mathrm{R}} \times 100 \%$
$$ \begin{aligned} & =\frac{32}{6400} \times 100 \% \\ & =0.5 \% \end{aligned} $$
Example-13:
At what depth below the surface of the earth would the value of ’ $\mathrm{g}$ ’ be same as that at a height of $64 \mathrm{Km}$ above the surface of the earth!
Show Answer
Solution:
At a depth $d, g^{\prime}=g\left(1-\frac{d}{R}\right)$
At a height $\mathrm{h}$, since $\mathrm{h}«\mathrm{R} ; \mathrm{g}^{\prime}=\mathrm{g}\left(1-\frac{2 \mathrm{~h}}{\mathrm{R}}\right)$
Equating, $\mathrm{d}=2 \mathrm{~h}=128 \mathrm{~km}$
Kepler’s Laws
The three laws of planetory motion, formulated by Johannes Kepler (1571-1630) can be stated as follows:
(i) Law of Orbits: All planets move in elliptical orbits, with the sun situated at one of the foci.

$\mathrm{a}=$ semi-major axis
$\mathrm{b}=$ semi-minor axis
(ii) Law of Areas: This law states that the line that joins a planet with the sun sweeps equal areas in equal intervals of time. OR, it states that the areal velocity of a planet is a constant.
Fig. shows planet moving from $P$ to $P$ in some finite time interval. It moves from $Q$ to $Q _{1}$ in same time interval. Then area $\mathrm{OPP} _{1}=$ area $\mathrm{OQQ} _{1}$ or $\operatorname{arc} \mathrm{QQ} _{1}>\operatorname{arc} \mathrm{PP} _{1}$.

Therefore, the planet moves slower when it is farther from sun and vice versa.
(iii) Law of Periods: The law states that the square of time period of revolution of a planet around the sun is proportional to the cube of the semi-major axis of the elliptical orbit of the planet around the sun.
i.e. $\mathrm{T}^{2} \propto \mathrm{r}^{3}$
$\mathrm{r}=$ semi-major axis of the orbit.
(If not mentioned otherwise, we consider the orbit as circular is shape and ’ $r$ ’ as the radius of that circular orbit)
Escape Velocity
It is the minimum velocity imparted to a body which is on the surface of a planet, in order that the body just escapes from the gravitation field region of that planet, and never comes back.
Escape velocity is represented as $\mathrm{v} _{\mathrm{e}}$. An expression for $\mathrm{v} _{\mathrm{e}}$ can be obtained easily from the concept of energy conservation. Suppose a body of mass ’ $m$ ’ be situated on the surface of planet of mass $M$ and radius $\mathrm{R}$. If we project this body with the just required escape velocity $(\mathrm{v_e})$, we find that the total energy of the body just at the moment of projection is:
$$ \mathrm{E} _{\mathrm{i}}=\mathrm{U} _{\mathrm{i}}+\frac{1}{2} \mathrm{mv} _{\mathrm{e}}^{2} $$
or
$$ \mathrm{E} _{\mathrm{i}}=-\frac{\mathrm{GMm}}{\mathrm{R}}+\frac{1}{2} \mathrm{mv} _{\mathrm{e}}^{2} $$
Since the body is capable of just escaping the field of this planet, as $v=v _{e}$, the final anergy $E _{f}$ at the boundary of field is $\mathrm{E} _{\mathrm{f}}=0+-\frac{\mathrm{GMm}}{\propto}=0+0=0$.
(Remember that when we say the body just escapes the field, we consider that the body just comes to rest at the boundary of the field).
Now, $\mathrm{E} _{\mathrm{i}}=\mathrm{E} _{\mathrm{f}}$ (conservation of energy)
$$ \begin{aligned} & \therefore \quad-\frac{\mathrm{GMm}}{\mathrm{R}}+\frac{1}{2} \mathrm{mv} _{\mathrm{e}}^{2}=0 \\ & \therefore \mathrm{v} _{\mathrm{e}}=\sqrt{2 \frac{\mathrm{GM}}{\mathrm{R}}} \\ & \text { or } \quad \mathrm{v} _{\mathrm{e}}=\sqrt{2 \mathrm{gR}} \quad\left(\because \mathrm{g}=\frac{\mathrm{GM}}{\mathrm{R}^{2}}\right) \end{aligned} $$
Escape velocity of a body from the surface of the earth is:
$$ \begin{array}{ll} \mathrm{v} _{\mathrm{e}}=\sqrt{2 \mathrm{gR}} & \left(\mathrm{g}=9.8 \mathrm{~ms}^{-2} \text { and } \mathrm{R}=6400 \mathrm{~km}\right) \\ =11.2 \mathrm{kms}^{-1} & \end{array} $$
Satellite
A satellite is a comparatively lighter body which continuously moves around a heavier body.
Natural satellite is a celestial body revolving around a planet, like moon around the earth.
Artificial satellite is a man-made body which is put into an orbit around a planet. There are a large number of artificial satellites put in to orbits around the earth, including many by India.
In order to put a satellite in to orbit, it is first taken to height beyond the dense atmosphere of earth using a rocket and then launched into the orbit, with certain specific velocity, called the orbital velocity $\left(\mathrm{v} _{0}\right)$, because of which the satellite remain in that orbit, moving around the earth continuously.
Orbital Velocity of a Satellite
It is the specific velocity required for a satellite to remain, continuously moving around the earth, in a particular orbit. It is denoted by $\mathrm{v} _{0}$.
For the satellite to orbit around the earth, in a circular path of radius $r$, the centripetal force required is $\frac{\mathrm{mv} _{0}^{2}}{\mathrm{r}}$. This must be provided by the gravitational force exerted by earth on the satellite.
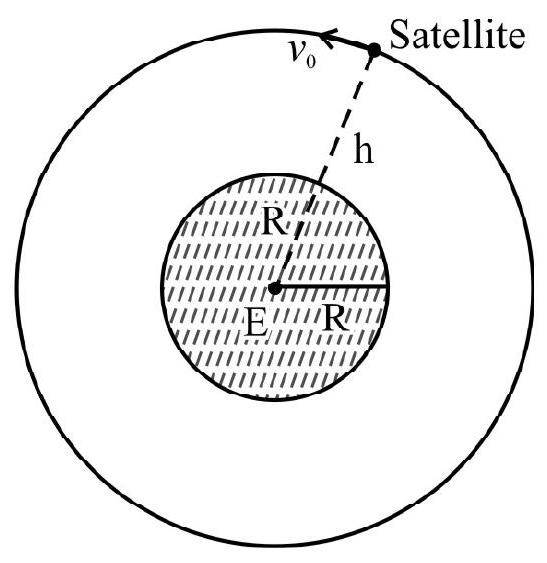
$\therefore \frac{\mathrm{mv} _{0}^{2}}{\mathrm{r}}=\frac{\mathrm{GMm}}{\mathrm{r}^{2}}$
or $\quad \mathrm{v} _{0}=\sqrt{\frac{\mathrm{GM}}{\mathrm{r}}}$
If $h$ is the height of the satellite from the surface of the earth, then:
$$ \begin{array}{r} r=\mathrm{R}+\mathrm{h} \\ \therefore \quad \mathrm{v} _{0} \sqrt{\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}}} \end{array} $$
Note that orbital velocity $\left(\mathrm{v} _{0}\right)$ does not depend on the mass of the satellite.
Also, longer the radius of the orbit smaller will be the value of orbital velocity. If the satellite is very near to the earth surface, $\mathrm{h}«\mathrm{R}$, then:
$$ \mathrm{v} _{0}=\sqrt{\frac{\mathrm{GM}}{\mathrm{R}}} $$
or
$$ \mathrm{v} _{0}=\sqrt{\mathrm{gR}} $$
We have, $\mathrm{v} _{\mathrm{e}}=\sqrt{2 \mathrm{gR}}$
Therefore, $\frac{\mathrm{v} _{\mathrm{e}}}{\mathrm{v} _{0}}=\sqrt{2} \quad$ (When $\left.\mathrm{h}«\mathrm{R}\right)$
This shows that if the orbital velocity, of a satellite nearer to earth’s surface, is increased to $\sqrt{2} \mathrm{v} _{0}$, it will escape in to outer space.
Note that this means we are increasing the velocity of the satellite by $41.4 \%$ of its orbital velocity to make it escape from the gravitational field of earth.
Time Period of Satellite
The time taken by the satellite to complete one revolution around the planet is called its time period. It is denoted by T.
$\therefore \mathrm{T}=\frac{2 \pi \mathrm{r}}{\mathrm{v} _{0}}$
or $\quad \mathrm{T}=\frac{2 \pi \mathrm{r}}{\sqrt{\frac{\mathrm{GM}}{\mathrm{r}}}}$
or $\quad \mathrm{T}^{2}=4 \pi^{2} \mathrm{r}^{2} \times \frac{\mathrm{r}}{\mathrm{GM}}$
or $\quad \mathrm{T}^{2}=\left(\frac{4 \pi^{2}}{\mathrm{GM}}\right) \mathrm{r}^{3}$
or $\quad \mathrm{T}^{2} \propto \mathrm{r}^{3}$
(This is Kepler’s law of period)
Height of Satellite
The time period of satellite in an orbit of radius $r$ is:
$$ \begin{aligned} & \mathrm{T}^{2}=\left(\frac{4 \pi^{2}}{\mathrm{GM}}\right) \mathrm{r}^{3} \\ & \therefore \quad \mathrm{r}^{3}=\left(\frac{\mathrm{GM}}{4 \pi^{2}}\right) \mathrm{T}^{2} \end{aligned} $$
or
$$ \mathrm{r}=\left[\frac{\mathrm{GM}}{4 \pi^{2}} \mathrm{~T}^{2}\right]^{1 / 3} $$
or
$$ \mathrm{R}+\mathrm{h}=\left[\frac{\mathrm{GM}}{4 \pi^{2}} \mathrm{~T}^{2}\right]^{1 / 3} $$
or $\quad \therefore \mathrm{h}=\left[\frac{\mathrm{GM}}{4 \pi^{2}} \mathrm{~T}^{2}\right]^{1 / 3}-\mathrm{R} \quad(\mathrm{h}=$ height of satellite from the surface of earth $)$
Energy of a Satellite in the Orbit
A satellite in the orbit has: (i) K.E due to orbital velocity and (ii) P.E due to gravitational field of earth.
For both these energies mass of the satellite $(\mathrm{m}$ ) is an important factor.
K.E. $=\frac{1}{2} \mathrm{mv} _{0}^{2}$
$$ =\frac{1}{2} \mathrm{~m}\left(\frac{\mathrm{GM}}{\mathrm{r}}\right) $$
$=\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}$
P.E. $=-\frac{\mathrm{GMm}}{\mathrm{r}}$
$\therefore$ P.E $=-2$ K.E
The total energy of the satellite, therefore, is:
$\mathrm{E}=\mathrm{K} . \mathrm{E}+\mathrm{P} . \mathrm{E}$
or
$\mathrm{E}=\mathrm{K} . \mathrm{E}+(-2 \mathrm{~K} . \mathrm{E})$
or $\quad \mathrm{E}=-\mathrm{K} . \mathrm{E}$
or $\quad \mathrm{E}=-\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}$
Note, $\mathrm{K} . \mathrm{E}=\mid$ T.E $\mid$ and $\mathrm{P} . \mathrm{E}=2$ (T.E.)
Geostationary Satellite
A geostationary satellite appears stationary to an observer on the earth. A satellite becomes geostationary if the following two conditions are satisfied.
(i) Its orbit is circular and coplanar with the equatorial plane of the earth.
(ii) Its angular velocity is same as that of earth, in magnitude and direction. (So their period revolution around the earth is 24 hours).
The height of geostationary satellite from the surface of earth is:
or
$$ \begin{aligned} & \mathrm{h}=\left[\frac{\mathrm{GM}}{4 \pi^{2}} \mathrm{~T}^{2}\right]^{1 / 3}-\mathrm{R} \\ & \mathrm{h}=\left[\frac{\mathrm{gR}^{2} \mathrm{~T}^{2}}{4 \pi^{2}}\right]-\mathrm{R} \end{aligned} $$
On substituting the values of $\mathrm{g}=9.8 \mathrm{~ms}^{-2}, \mathrm{R}=6.4 \times 10^{6} \mathrm{~m}$ and $\mathrm{T}=24 \times 60 \times 60$ second, we get:
$$ \mathrm{h}=36000 \mathrm{~km} $$
and
$$ \mathrm{v} _{0}=3.1 \mathrm{kms}^{-1} $$
Weightlessness in an Artificial Satellite
Consider a body of mass $m _{0}$ placed in an artificial satellite. If this body experiences a normal reaction force of $\mathrm{N}$ from the floor of the satellite, we say, their is an apparent weight $\mathrm{W}=\mathrm{N}$ for the body.
Now, consider all the forces acting on this body. They are:
(i) Gravitational force of attraction, towards the earth, equal to $\frac{\mathrm{GMm} _{0}}{\mathrm{r}^{2}}$
(ii) Centrifugal force equal to $\frac{\mathrm{m} _{0} \mathrm{v} _{0}^{2}}{\mathrm{r}}$, directed away from the centre of the earth.
(iii) Normal reaction $\mathrm{N}$ from the floor, directed away from the centre of the earth.
Therefore, the net force on the mass $\mathrm{m} _{0}$ inside the satellite is:
$$ \frac{\mathrm{GMm} _{0}}{\mathrm{r}^{2}}-\mathrm{N}-\frac{\mathrm{m} _{0} \mathrm{v} _{0}^{2}}{\mathrm{r}}=0 $$
or
$$ \frac{\mathrm{GMm} _{0}}{\mathrm{r}^{2}}-\mathrm{N}=\frac{\mathrm{m} _{0} \mathrm{v} _{0}^{2}}{\mathrm{r}} $$
or
$$ \frac{\mathrm{GMm} _{0}}{\mathrm{r}^{2}}-\mathrm{N}=\frac{\mathrm{m} _{0}}{\mathrm{r}} \times \frac{\mathrm{GM}}{\mathrm{r}} $$
or
$$ \frac{\mathrm{GMm} _{0}}{\mathrm{r}^{2}}-\mathrm{N}=\frac{\mathrm{GMm} _{0}}{\mathrm{r}^{2}} $$
$\therefore \mathrm{N}=0$
or $\quad \mathrm{W}=0$
Hence, the body of mass $m _{0}$ will experience weightlessness, inside the satellite.
Example-14:
Two bodies of masses $\mathrm{m} _{1}=10 \mathrm{~kg}$ and $\mathrm{m} _{2}=20 \mathrm{~kg}$ are at rest at a distance $\mathrm{d}=1.0 \mathrm{~m}$ apart. They are then released from this position. Due to mutual attraction they move towards each other. Find their speeds when the distance between them reduces to $0.5 \mathrm{~m}$.
Show Answer
Solution:
Total initial energy of the system is:
$$ \begin{aligned} & \mathrm{E} _{\mathrm{i}}=\mathrm{K} \cdot \mathrm{E} _{\mathrm{i}}+\mathrm{P} \cdot \mathrm{E} _{\mathrm{i}} \\ & =0+\frac{-\mathrm{Gm} _{1} \mathrm{~m} _{2}}{\mathrm{~d}} \end{aligned} $$
When they start moving, their P.E. will decrease and the K.E will increase (from zero)
When $\mathrm{d}$ becomes $\frac{\mathrm{d}}{2}$, the find energy becomes:
$$ \begin{aligned} & \mathrm{E} _{\mathrm{f}}=\mathrm{K} \cdot \mathrm{E} _{\mathrm{f}}+\Delta \cdot \mathrm{E} _{\mathrm{f}} \\ &=\left(\frac{1}{2} \mathrm{~m} _{1} \mathrm{v} _{1}^{2}+\frac{1}{2} \mathrm{~m} _{2} \mathrm{v} _{2}^{2}\right)+\frac{-\mathrm{Gm} _{1} \mathrm{~m} _{2}}{\mathrm{~d} / 2} \\ &=\frac{1}{2} \mathrm{~m} _{1} \mathrm{v} _{1}^{2}+\frac{1}{2} \mathrm{~m} _{2} \mathrm{v} _{2}^{2}-\frac{2 \mathrm{Gm} _{1} \mathrm{~m} _{2}}{\mathrm{~d}} \end{aligned} $$
Now, $\mathrm{E} _{\mathrm{f}}=\mathrm{E} _{\mathrm{i}}$ (Conservation of energy)
$\therefore \quad \frac{1}{2} \mathrm{~m} _{1} \mathrm{v} _{1}^{2}+\frac{1}{2} \mathrm{~m} _{2} \mathrm{v} _{2}^{2}=\frac{\mathrm{Gm} _{1} \mathrm{~m} _{2}}{\mathrm{~d}}$
or
$$ \mathrm{m} _{1} \mathrm{v} _{1}^{2}+\mathrm{m} _{2} \mathrm{v} _{2}^{2}=\frac{2 \mathrm{Gm} _{1} \mathrm{~m} _{2}}{\mathrm{~d}} $$
Now, (from the conservation of linear momentum)
$$ \mathrm{m} _{1} \mathbf{v} _{1}+\mathrm{m} _{2} \mathbf{v} _{2}=0 $$
$\therefore \quad \mathbf{v} _{1}=-\left(\frac{\mathrm{m} _{2}}{\mathrm{~m} _{1}}\right) \mathbf{v} _{2}$
or $\quad \mathrm{v} _{1}=-\frac{\mathrm{m} _{2}}{\mathrm{~m} _{1}} \mathrm{v} _{2}$ (as they move along the same line)
Therefore, $\mathrm{m} _{1}\left(-\frac{\mathrm{m} _{2}}{\mathrm{~m} _{1}} \mathrm{v} _{2}\right)^{2}+\mathrm{m} _{2} \mathrm{v} _{2}^{2}=\frac{2 \mathrm{Gm} _{1} \mathrm{~m} _{2}}{\mathrm{~d}}$ or $\quad\left(\frac{\mathrm{m} _{2}^{2}}{\mathrm{~m} _{1}}+\mathrm{m} _{2}\right) \mathrm{v} _{2}^{2}=\frac{2 \mathrm{Gm} _{1} \mathrm{~m} _{2}}{\mathrm{~d}}$
$\therefore \quad \mathrm{v} _{2}^{2}=\frac{2 \mathrm{G} \mathrm{m} _{1}^{2}}{\left(\mathrm{~m} _{1}+\mathrm{m} _{2}\right) \mathrm{d}}=\frac{2 \times 6.67 \times 10^{-11} \times 10^{2}}{30 \times 1}$
or $\quad \mathrm{v} _{2}^{2}=4.45 \times 10^{-10}$
$$ \mathrm{v} _{2}=2.1 \times 10^{-5} \mathrm{~ms}^{-1} $$
$\mathrm{v} _{1}=-\frac{\mathrm{m} _{2}}{\mathrm{~m} _{1}} \times \mathrm{v} _{2}$
$$ \begin{aligned} & =-2 \times 2.1 \times 10^{-5} \\ & =-4.2 \times 10^{-5} \mathrm{~ms}^{-1} \end{aligned} $$
Example-15:
A saturn year is 29.4 earth year. How far is saturn from the sun, if the earth is $1.5 \times 10^{8} \mathrm{Km}$ from the sun?
Show Answer
Solution:
By Keplers law: $\mathrm{T}^{2} \propto \mathrm{r}^{3}$
$$ \begin{aligned} & \frac{\mathrm{T} _{\mathrm{S}}^{2}}{\mathrm{~T} _{\mathrm{E}}^{2}}=\frac{\mathrm{r} _{\mathrm{S}}^{3}}{\mathrm{r} _{\mathrm{E}}^{3}} \\ \therefore \quad \mathrm{r} _{\mathrm{s}}= & \left(\frac{\mathrm{T} _{\mathrm{S}}}{\mathrm{T} _{\mathrm{E}}}\right)^{2 / 3} \times \mathrm{r} _{\mathrm{E}} \\ & =\left(\frac{29.4 \times \mathrm{T} _{\mathrm{E}}}{\mathrm{T} _{\mathrm{E}}}\right)^{2 / 3} \times 1.5 \times 10^{8} \mathrm{~km} \\ & =1.43 \times 10^{9} \mathrm{~km} \end{aligned} $$
Example-16:
A body is projected from the surface of the earth with a velocity equal to three times the escape velocity ( $v _{e}$ $=11.2 \mathrm{Kms}^{-1}$ ) for the surface of the earth. Ignoring the presence of other celestial objects, find the velocity of this body far away from the earth.
Show Answer
Solution:
Here , $E_i= E_f \quad or \quad K.E_i + P.E_i = K.E_f + P.E_f$
$\therefore \frac{1}{2} \mathrm{mv} _{\mathrm{i}}^{2}+\frac{-\mathrm{GMm}}{\mathrm{R}}=\frac{1}{2} \mathrm{mv} _{\mathrm{f}}^{2}+\frac{-\mathrm{GMm}}{\propto}$
or $\quad\left(3 v _{e}\right)^{2}-v _{e}^{2}=v _{f}^{2}$
$\therefore \quad \mathrm{v} _{\mathrm{f}}=\sqrt{8} \mathrm{v} _{\mathrm{e}}$
$=2.828 \times 11.2 \mathrm{kms}^{-1}$
$=31.67 \mathrm{kms}^{-1}$
Example-17:
Two heavy spheres, each of mass $100 \mathrm{~kg}$ and small radius, are placed $1.0 \mathrm{~m}$ away from each other, on a smooth horizontal table. What is the gravitational field intensity and potential at the midpoint of the line joining the two. Will an object of $10 \mathrm{~g}$ placed at this point remain in equilibrium? If so, is the equilibrium stable or unstable?
Show Answer
Solution:
At point $\mathrm{O}$ the intensities due to masses $\mathrm{m} _{1}$ and $\mathrm{m} _{2}$ are:
$$ \mathrm{I} _{1}=\frac{\mathrm{Gm} _{1}}{\mathrm{r} _{1}^{2}}=\frac{\mathrm{G} \times 100}{(1 / 2)^{2}}=400 \mathrm{G}, \text { towards } \mathrm{m} _{1} $$
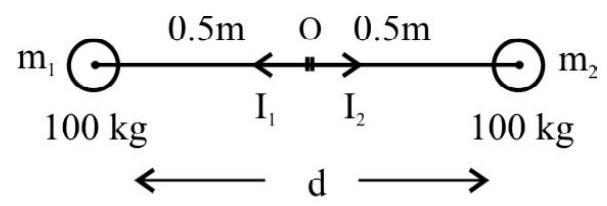
and, $\mathrm{I} _{2}=400 \mathrm{G}$, towards $\mathrm{m} _{2}$
So, $\mathrm{I} _{1}=-\mathrm{I} _{2}$
$\therefore \mathrm{I} _{0}=0$
$$ \begin{aligned} \mathrm{V} _{0}=\mathrm{V} _{1} & +\mathrm{V} _{2}=\frac{-\mathrm{Gm} _{1}}{\left(\frac{1}{2}\right)}+\frac{-\mathrm{Gm} _{2}}{\left(\frac{1}{2}\right)} \\ & =-6.67 \times 10^{-11} \times 400 \\ & =-2.66 \times 10^{-8} \mathrm{~J} \mathrm{~kg}^{-1} \end{aligned} $$
As $\mathrm{I} _{0}=0$, there is no force on the $10 \mathrm{~g}$ body placed at 0 . So it will remain in equilibrium at 0 . However, if we move it aside a little, the attractive force due to $\mathrm{m} _{1}$ or $\mathrm{m} _{2}$ will become greater and therefore, it move towards that mass from which attractive force is greater, and will never come back. Therefore, the equilibrium is unstable.
Example-18:
The gravitational field due to certain mass distribution is represented as: $\mathrm{I}=\mathrm{Ax}$ in the $x$-direction. If $\mathrm{A}$ is a constant, what is the gravitational potential at a distance $x$ ? (Gravitational potential is taken as zero at $x=\propto)$
Show Answer
Solution:
We have $\mathrm{I}=-\frac{\mathrm{dV}}{\mathrm{d} x}$
$\therefore \mathrm{V}=-\int \mathrm{I} \mathrm{d} x$
$$ =-\mathrm{A} \int _{x=\infty}^{x} x^{-4} \mathrm{~d} x $$
$$ \begin{aligned} & =-\mathrm{A}\left[\frac{x^{-4+1}}{-4+1}\right] _{\infty}^{x} \\ & =\frac{\mathrm{A}}{3} x^{-3}=\frac{\mathrm{A}}{3 x^{3}} \end{aligned} $$
Example-19:
Consider two concentric thin spherical shells of masses $m$ and $2 \mathrm{~m}$ with radii $\mathrm{r} _{1}$ and $\mathrm{r} _{2}\left(\mathrm{r} _{1}<\mathrm{r} _{2}\right)$ respectively.
Find the gravitational field and potential at a point distant $\frac{\mathrm{r} _{1}+\mathrm{r} _{2}}{2}$ from their common centre.
Show Answer
Solution:
Let $\mathrm{P}$ be this point, which will be in between the two shells.
There is no field due to the outer shell at $\mathrm{P}$.
$\therefore \mathrm{I} _{\mathrm{p}}=$ field of $\mathrm{m} _{1}$ only
$$ =\frac{G m _{1}}{\left(\frac{r _{1}+r _{2}}{2}\right)^{2}}=\frac{4 G m _{1}}{\left(r _{1}+r _{2}\right)^{2}} $$
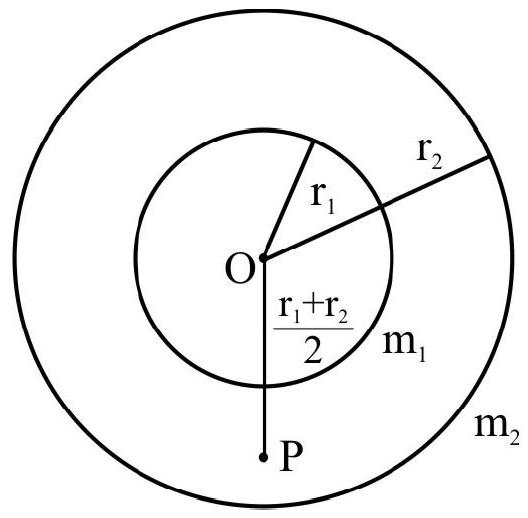
Now, as $\mathrm{P}$ is inside the outer shell, the potential due to $\mathrm{m} _{2}$ is $\mathrm{V} _{2}=\frac{-\mathrm{Gm} _{2}}{\mathrm{r} _{2}}$
(Inside a shell potential due to that shell is constant)
Therefore, the net potential at $\mathrm{P}$ is:
$\mathrm{v} _{\mathrm{p}}=\mathrm{v} _{1}+\mathrm{v} _{2}$
$$ \begin{aligned} & =\frac{-\mathrm{Gm} _{1}}{\left[\left(\mathrm{r} _{1}+\mathrm{r} _{2}\right) / 2\right]}+\frac{-\mathrm{Gm} _{2}}{\mathrm{r}^{2}} \\ & =-\mathrm{G}\left[\frac{2 \mathrm{~m} _{1}}{\mathrm{r} _{1}+\mathrm{r} _{2}}+\frac{\mathrm{m} _{2}}{\mathrm{r} _{2}}\right] \end{aligned} $$
Example-20:
An artificial satellite is moving in an orbit with a speed equal to half the magnitude of escape velocity from the earth. What is the height of this satellite?
Show Answer
Solution:
$\mathrm{v} _{0}=\frac{1}{2} \mathrm{v} _{\mathrm{e}}$
$\mathrm{v} _{0}^{2}=\frac{1}{4} \mathrm{v} _{\mathrm{e}}^{2}$
or $\quad \frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}}=\frac{1}{4} \times \frac{\mathrm{GM}}{\mathrm{R}}$
$\therefore 4 \mathrm{R}=\mathrm{R}+\mathrm{h}$
or $\mathrm{h}=3 \mathrm{R}=3 \times 6400 \mathrm{~km}=19200 \mathrm{~km}$
Example-21:
If gravitational force varies as $\frac{1}{\mathrm{r}^{5}}$, then how will the orbital velocity vary with $\mathrm{r}$ ? How will the time period vary with r?
Show Answer
Solution:
Suppose $\mathrm{F} \propto \frac{1}{\mathrm{r}^{\mathrm{n}}}$ i.e. $\mathrm{F}=\frac{\mathrm{GMm}}{\mathrm{r}^{\mathrm{n}}}$
Then $\frac{\mathrm{GMm}}{\mathrm{r}^{\mathrm{n}}}=\frac{\mathrm{mv}^{2}}{\mathrm{r}} \quad(\mathrm{v}=$ orbital velocity $)$ $\therefore \mathrm{v}=\sqrt{\frac{\mathrm{GM}}{\mathrm{r}^{\mathrm{n}-1}}}$
Here, $\mathrm{n}=5$
$\therefore \quad v=\sqrt{\frac{\mathrm{GM}}{\mathrm{r}^{5-1}}}=\sqrt{\frac{\mathrm{GM}}{\mathrm{r}^{4}}}=\frac{1}{\mathrm{r}^{2}} \sqrt{\mathrm{GM}}$
$\therefore \quad \mathrm{v} \propto \frac{1}{\mathrm{r}^{2}}$
Now, $\mathrm{T}=\frac{2 \pi \mathrm{r}}{\mathrm{v}}=\frac{2 \pi \mathrm{r}}{\sqrt{\frac{\mathrm{GM}}{\mathrm{r}^{\mathrm{n}-1}}}}=\frac{2 \pi}{\sqrt{\mathrm{GM}}} \cdot \sqrt{\mathrm{r}^{\mathrm{n}-1} \times \mathrm{r}^{2}}$
or $\quad \mathrm{T}=\frac{2 \pi}{\sqrt{\mathrm{GM}}} \cdot \sqrt{\mathrm{r}^{\mathrm{n}+1}}$
or $\quad \mathrm{T}=\frac{2 \pi}{\sqrt{\mathrm{GM}}} \cdot \mathrm{r}^{\left(\frac{\mathrm{n}+1}{2}\right)}$
Hence, $\mathrm{n}=5$
$\therefore \mathrm{T}=\frac{2 \pi}{\sqrt{\mathrm{GM}}} \cdot \mathrm{r}^{\frac{5+1}{2}}$
$=\frac{2 \pi}{\mathrm{GM}} \cdot \mathrm{r}^{3}$
or
$$ \mathrm{T} \propto \mathrm{r}^{3} $$
PROBLEMS FOR PRACTICE
1. Find the gravitation force between a proton and a neutron separated by distance of $0.25 \mathrm{~A}^{0}$. (given mass proton $=$ mass of neutron $=1.67 \times 10^{-27} \mathrm{~kg}$ )
Show Answer
Answer.: $2.976 \times 10^{-43} \mathrm{~N}$2. Four masses of $5 \mathrm{~kg}, 10 \mathrm{~kg}, 15 \mathrm{~kg}$ and $20 \mathrm{~kg}$ are placed at the corners A, B, C and D respectively of a square. $A B C D$ of side $50 \mathrm{~cm}$. Find the gravitational field and potential at its centre.
Show Answer
Answer.: $18.89 \times 10^{-10} \mathrm{~ms}^{-2}, 2.125 \times 10^{-8} \mathrm{~N} / \mathrm{kg}$ )3. A body weights $72 \mathrm{~kg}$ on the surface of the earth. How much will it weigh on the surface of mars, whose mass is $\frac{1}{9}$ th and rading is $\frac{1}{2}$ of earth?
Show Answer
Answer.: $32 \mathrm{~kg}$4. Weigh the sun using the following data.
Distance of earth from sun $=1.5 \times 10^{11} \mathrm{~m}$
Time period of revolution of earth $=3.15 \times 10^{7} \mathrm{~s}$
$\mathrm{G}=6.67 \times 10^{-11} \mathrm{~N}-\mathrm{m}^{2} \mathrm{~kg}^{-2}$
Show Answer
Answer.: $\mathrm{M} _{\mathrm{s}}=2.01 \times 10^{30} \mathrm{~kg}$5. What is the percentage decrease in the weight of a $200 \mathrm{~kg}$ body when taken to the bottom of a mine of $64 \mathrm{~km}$ depth. $(\mathrm{R}=6400 \mathrm{~km}$ for earth $)$
Show Answer
Answer.: $1 \%$6. A rocket is fired from the earth towards sun. Find the location of point where gravitational force on the rocket becomes zero. (Neglect the presence of other celestial object).
Given : Mass of sun $=2 \times 10^{30} \mathrm{~kg}$
Mass of earth $=6 \times 10^{24} \mathrm{~kg}$
Orbital radius of the earth $=1.50 \times 10^{11} \mathrm{~m}$
Show Answer
Answer.: $2.58 \times 10^{8} \mathrm{~m}$ from earth7. A geostationary satellite of $2000 \mathrm{~kg}$ orbits around the earth. Using the known data for its height from earth and the radius and mass of earth, find the gravitational potential energy of the satellite.
Show Answer
Answer.: $\mathrm{U}=1.888 \times 10^{10} \mathrm{~J}$8. Suppose that the radius of earth shrinks by $1.5 \%$, mass being constant. What is the percentage change in its acceleration due to gravity?
Show Answer
Answer.: $3 \%$9. What is the time period of a seconds pendulum when taken to a height of $h=R$, from the surface of earth? $(\mathrm{R}=6400 \mathrm{~km})$
Show Answer
Answer.: $4 \mathrm{~s}$10. A body is projected with a speed of $15 \mathrm{kms}^{-1}$ from the surface of the earth. With what velocity will it escape from the gravitational field of earth?
Show Answer
Answer.: $9.78 \mathrm{kms}^{-1}$11. A satellite of mass $1000 \mathrm{~kg}$ is to be put in to an orbit of radius, $r=7000 \mathrm{~km}$ around the earth, of radius $\mathrm{R}=6400 \mathrm{~km}$. Calculate the energy needed to place the satellite in this orbit, neglecting all the energy losses. Take $\mathrm{g}=10 \mathrm{~ms}^{-2}$.
(Hint: $\mathrm{E} _{\mathrm{i}}=\frac{\mathrm{GMm}}{\mathrm{R}}+0, \mathrm{E} _{\mathrm{f}}=-\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}$ )
Show Answer
Answer.: $3.47 \times 10^{10} \mathrm{~J}$12. The largest and the smallest distances of earth from the sun are 4 and 6 units. What is the distance of the earth from the sun when it is on the perpendicular, to the major axis, drawn through the sun?
(Hint: If the required distance is $\mathrm{r}$, then $\left(\frac{1}{\mathrm{r}}+\frac{1}{\mathrm{r}}=\frac{1}{\mathrm{r} _{1}}+\frac{1}{\mathrm{r} _{2}}\right)$ ).
Show Answer
Answer.: 4.8 units13. Assuming that the earth has become a black-hole what would be maximum radius of that black hole?
(Hint: For a black-hole $\mathrm{v} _{\mathrm{e}} \geq \mathrm{c}$, the velocity of light. $\mathrm{M}=6 \times 10^{24} \mathrm{~kg}$ for earth).
Show Answer
Answer.: $9 \mathrm{~mm}$14. Calculate the time period of a simple pendulum of length $5 \mathrm{R}$.
(Hint: $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{R}}{\left(1+\frac{\mathrm{R}}{\ell}\right) \mathrm{g}}}, \ell=$ length )
Show Answer
Answer.: $\mathrm{T}=1.287$ Hrs.)15. Plot the graph between (i) gravitational field intensity and (ii) potential, with distance from the centre for a spherical shell.
16. Plot the graph between (i) gravitation field intensity and (ii) potential with the distance from the centre, of a uniform solid sphere.
17. A cyclic hexagon of side $20 \mathrm{~cm}$ has five equal masses of $5 \mathrm{~kg}$ each placed at its five corners. Calculate the net gravitational field and potential at its centre.
Show Answer
Answer.: $8.3375 \times 10^{-19} \mathrm{~ms}^{-2} ;-8.3375 \times 10^{-9} \mathrm{~J} / \mathrm{kg}$ )18. If $a$ and $b$ are the minimum and maximum distances of a planet from the sun, then what is the angular momentum (L) of the planet with respect to the centre of the sun, in terms of the mass (M) of the sun and mass ( $\mathrm{m})$ of the planet.
(Hint: $\mathrm{r}=\frac{2 \mathrm{ab}}{\mathrm{a}+\mathrm{b}}$ and $\mathrm{v}=\sqrt{\frac{\mathrm{GM}}{\mathrm{r}}}$ )
Show Answer
Answer.: $L=m \sqrt{\frac{2 G M a b}{a+b}}$19. A rocket is fired vertically from the surface of mars with a speed of $2 \mathrm{kms}^{-1}$. If $20 \%$ of its initial energy is lost due to martian atmospheric resistance, how far will the rocket go from the surface of mars, before returning to it?
Given: Mass of mars $=6.4 \times 10^{23} \mathrm{~kg}$
Radius of mars $=3395 \mathrm{~km}$
$\mathrm{G}=6.67 \times 10^{-11} \mathrm{Nm}^{2} \mathrm{~kg}^{-2}$
Show Answer
Answer.: $495 \mathrm{~km}$20. Three particles each of mass ’ $m$ ’ are placed at the corners of an equilateral triangle of side ’ $b$ ‘. What will be the gravitational potential energy of the system? How much work will be required to increase the sides of the triangle to three times $b$ ?
Show Answer
Answer.: $-\frac{3 \mathrm{Gm}^{2}}{\mathrm{~b}}, \frac{2 \mathrm{Gm}^{2}}{\mathrm{~b}}$Question Bank
Key Learning Points
1. According to Newton’s law of gravitation,
$$ \mathrm{F}=\frac{\mathrm{Gm} _{1} \mathrm{~m} _{2}}{\mathrm{r}^{2}} $$
where $\mathrm{m} _{1}$ and $\mathrm{m} _{2}$ are two point masses at distance of $\mathrm{r}$ apart and $\mathrm{G}$ is universal gravitational constant.
2. Value of $\mathrm{G}=6.67 \times 10^{-11} \mathrm{~N}-\mathrm{m}^{2} \mathrm{~kg}^{-2}$
and $[\mathrm{G}]=\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right]$. $\mathrm{G}$ is scalar quantity.
3. As $r$ in Newton’s law is the distance between the two point objects, when we consider extended objects / bodies, $\mathrm{r}$ is to be taken as the distance between the centres of gravity of the bodies.
4. Gravitational force $(\mathrm{F})$ is central force and hence no change in angular momentum is produced because of $\mathrm{F}$, as $\tau=0$ due to this force.
5. Gravitational force (or field) is conservative.
6. In vector form gravitational force is expressed as:
$$ \mathbf{F} _{12}=-\left[\frac{\mathrm{Gm} _{1} \mathrm{~m} _{2}}{\mathrm{r}^{2}}\right] \mathbf{r} _{12} $$
and $\quad \mathbf{F} _{21}=-\left[\frac{\mathrm{Gm} _{1} \mathrm{~m} _{2}}{\mathrm{r}^{2}}\right] \mathbf{r} _{21}$
$\therefore \mathbf{F} _{12}=-\mathbf{F} _{21} \quad$ (in accordance with Newton’s third law of motion)
7. Superposition principle is applicable to gravitational force. According to this principle, force on one mass $\mathrm{m} _{1}$ due to several other masses $\mathrm{m} _{2}, \mathrm{~m} _{3}$ etc. is:
$$ \mathbf{F} _{1}=\mathbf{F} _{12}+\mathbf{F} _{13}+\mathbf{F} _{14}+\ldots \ldots \ldots $$
8. Gravitational field intensity at a given point gives the strength of the field at that point and it is denoted as I. It is vector quantity. I is defined as the force per unit mass placed at the point. Unit of I is $\mathrm{ms}^{-2}$.
$$ \mathrm{I}=\frac{\mathrm{F}}{\mathrm{m} _{0}} $$
or $\quad \mathrm{I}=\frac{\mathrm{GM}}{\mathrm{r}^{2}}$
9. I in vector form is given as:
$$ \mathbf{I}=-\frac{\mathrm{GM}}{\mathrm{r}^{2}} \mathbf{r} $$
10. Since $\mathrm{I}=\frac{\text { Force }}{\text { mass }}$, $\mathrm{i}$ is acceleration. This acceleration is called acceleration due to gravity.
11. Gravitational potential $(\mathrm{V})$ is defined as the work done is moving unit mass from infinity to a point, against force of gravity.
$$ \mathrm{V}=\frac{\mathrm{W}}{\mathrm{m} _{0}} $$
$\mathrm{V}$ is a scalar quantity with unit $\mathrm{J} \mathrm{kg}^{-1}$.
12. V at a point distance $\mathrm{r}$ from a source mass $\mathrm{M}$ is:
$$ \mathrm{V}=-\frac{\mathrm{GM}}{\mathrm{r}} $$
(The-ve sign, here, shows that the force involved is attractive in nature).
13. The maximum value of gravitational potential is zero (at $\mathrm{r}=\propto$ from an object).
14. Gravitational potential energy $(\mathrm{U})$ is the work done (total) is moving a body of mass $m$ from infinity to a given point.
$$ \mathrm{U}=\mathrm{W}=-\frac{\mathrm{GMm}}{\mathrm{r}} $$
$\therefore \mathrm{U}=\mathrm{Vm}$
or Potential energy $=$ Potential $\times$ mass
15. $I=-\frac{d V}{d r}$
or Gravitational field $=-($ potential gradient at the point $)$
16. $\mathrm{F}=-\frac{\mathrm{dU}}{\mathrm{dr}}, \mathrm{U}=$ gravitational potential energy.
17. For a thin spherical shell, of radius $\mathrm{R}$ and mass $\mathrm{M}$, $\mathrm{I}=\mathrm{O}$ for $\mathrm{r}<\mathrm{R} \quad(\mathrm{R}=$ radius of the shell $)$
$$ \begin{array}{ll} \mathrm{I}=\frac{\mathrm{GM}}{\mathrm{R}^{2}} & (\mathrm{r}=\mathrm{R}) \\ \mathrm{I}=\frac{\mathrm{GM}}{\mathrm{r}^{2}} & (\mathrm{r}>\mathrm{R}) \end{array} $$
Also, $V=-\frac{G M}{R} \quad$ (for any point on or inside the spherical shell)
$$ \mathrm{V}=-\frac{\mathrm{GM}}{\mathrm{r}} \quad(\mathrm{r}>\mathrm{R}) $$
18. For uniform solid sphere of radius $\mathrm{R}$ and mass $\mathrm{M}$,
$$ \begin{aligned} & \mathrm{I}=\frac{\mathrm{GM}}{\mathrm{r}^{2}} \quad(\mathrm{r}>\mathrm{R}) \\ & \mathrm{I}=\frac{\mathrm{GM}}{\mathrm{R}^{2}}\left(\frac{\mathrm{r}}{\mathrm{R}}\right) \quad(\text { for } \mathrm{r}<\mathrm{R}) \\ & \mathrm{I}=\mathrm{O} \text { at the centre. } \end{aligned} $$
Also, $V=-\frac{G M}{r} \quad(r>R)$
$$ \begin{aligned} & \mathrm{V}=-\frac{\mathrm{GM}}{\mathrm{R}} \quad(\mathrm{r}=\mathrm{R}) \\ & \mathrm{V}=-\frac{\mathrm{GM}}{2 \mathrm{R}^{3}} \quad\left(3 \mathrm{R}^{2}-\mathrm{r}^{2}\right) \quad(\mathrm{r}<\mathrm{R}) \\ & \mathrm{V}=-\frac{3}{2} \frac{\mathrm{GM}}{\mathrm{R}} \text { at the centre. } \end{aligned} $$
19. For a circular ring of radius $\mathrm{R}$ and mass $\mathrm{m}$, at any point on the axis,
$$ \begin{aligned} & \mathrm{I}=\frac{\mathrm{GMr}}{\left(\mathrm{r}^{2}+\mathrm{R}^{2}\right)^{3 / 2}} \quad(\mathrm{r}=\text { distance along the axis }) \\ & \mathrm{V}=-\frac{\mathrm{GM}}{\sqrt{\mathrm{r}^{2}+\mathrm{R}^{2}}} \end{aligned} $$
20. Acceleration due to gravity of earth is:
$$ g=\frac{G M}{R^{2}} \text { on the surface } $$
$\mathrm{g}^{\prime}=\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})^{2}}$ at a height $\mathrm{h}$ above the surface.
21. For heights $\mathrm{h}$ above and for $\mathrm{h}«\mathrm{R}$,
$$ \mathrm{g}^{\prime}=\mathrm{g}\left(1-\frac{2 \mathrm{~h}}{\mathrm{R}}\right)(\mathrm{R}=\text { radius of earth }) $$
22. For depth ’d’, the value of g’ is:
$$ \mathrm{g}^{\prime}=\mathrm{g}\left(1-\frac{\mathrm{d}}{\mathrm{R}}\right) $$
23. $\mathrm{g}=\frac{4}{3} \pi \mathrm{R} \rho \mathrm{G}(\rho=$ density of earth material $)$
24. $\frac{\Delta \mathrm{g}}{\mathrm{g}}=-\frac{2 \Delta \mathrm{R}}{\mathrm{R}}+\frac{\Delta \mathrm{m}}{\mathrm{M}}(\Delta \mathrm{g}=$ change in $\mathrm{g})$
25. For height $\mathrm{h}«\mathrm{R}$, the increase in potential energy when mass $\mathrm{m}$ is moved from ground to a height $\mathrm{h}$ is:
$$ \begin{aligned} \Delta \mathrm{U} & =\mathrm{U} _{\mathrm{f}}-\mathrm{U} _{\mathrm{f}}=-\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})}-\left(\frac{-\mathrm{GMm}}{\mathrm{R}}\right) \\ & =\mathrm{mgh} \end{aligned} $$
26. When $\mathrm{h}=\mathrm{nR}$,
$$ \Delta \mathrm{U}=\operatorname{mg} R\left(\frac{\mathrm{n}}{\mathrm{n}+1}\right) $$
27. Kepler’s Laws:
(i) Law of orbits: planets move in elliptical orbits with sun at one foci.
(ii) Law of areas: the areal velocity of a planet is always a constant.
(iii) Law of periods: $\mathrm{T}^{2} \propto \mathrm{r}^{3}$
28. Escape velocity $\left(v _{e}\right)$ is the minimum velocity with which a body be projected from a planet in order that it escapes from the gravitational pull of that planet.
$$ \mathrm{v} _{\mathrm{e}}=\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}=\sqrt{2 \mathrm{gR}} $$
$\mathrm{v} _{\mathrm{e}}=11.2 \mathrm{Kms}^{-1}$ for earth.
29. Orbital velocity $\left(\mathrm{v} _{0}\right)$ - the velocity required for a satellite to remain is an orbit.
$$ \begin{aligned} & \mathrm{v} _{0}=\sqrt{\frac{\mathrm{GM}}{\mathrm{r}}}=\sqrt{\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}}} \\ & \mathrm{v} _{0}=\sqrt{\frac{\mathrm{GM}}{\mathrm{R}}} \text { if } \mathrm{h}«\mathrm{R} \end{aligned} $$
30. Time period of a satellite ( $\mathrm{T})$
$$ \mathrm{T}^{2}=\frac{4 \pi^{2}}{\mathrm{GM}} \cdot \mathrm{r}^{3} $$
31. Height of a satellite: $h=\left[\frac{\mathrm{GM}}{4 \pi^{2}} \cdot \mathrm{T}^{2}\right]^{1 / 3}-\mathrm{R}$
32. Energy of a satellite in orbit:
$$ \begin{aligned} & \mathrm{K} . \mathrm{E}=\frac{1}{2} \mathrm{mv} _{0}^{2}=\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}} \\ & \mathrm{P} . \mathrm{E}=-\frac{\mathrm{GMm}}{\mathrm{r}} \\ & \mathrm{P} . \mathrm{E}=-2(\mathrm{~K} . \mathrm{E}) \end{aligned} $$
Total energy $\mathrm{E}=-\mathrm{K} . \mathrm{E}$
or $\mathrm{E}=-\frac{\mathrm{GMm}}{2 \mathrm{r}}$
33. Height of geostationary satellite is $36000 \mathrm{~km}$.
1. The time period of satellite of earth at an altitude, equal to the radius of the earth, is 4 hours. If the separation between the earth’s surface and the satellite is increased by 6 times the radius of the earth, the time period of the satellite would become:
(1) 90 hours
(2) 60 hours
(3) 32 hours
(4) 26 hours
Show Answer
Correct answer: (3)
Solution:
By Kepler’s law, $\mathrm{T}^{2} \propto \mathrm{r}^{3}$
In the first case, $4^{2} \propto(2 \mathrm{R})^{3}$
$$ (\mathrm{r}=\mathrm{R}+\mathrm{h}, \therefore \mathrm{r}=\mathrm{R}+\mathrm{R}) $$
In the second case, $\mathrm{T}^{2} \propto(8 \mathrm{R})^{3} \quad$ ( $\mathrm{h}$ is increased by $6 \mathrm{R}, \therefore \mathrm{h}=\mathrm{R}+6 \mathrm{R}=7 \mathrm{R} \quad \therefore \mathrm{r}=\mathrm{R}+7 \mathrm{R}$ )
$$ \begin{aligned} & \therefore \quad \frac{4^{2}}{\mathrm{~T}^{2}}=\frac{8 \mathrm{R}^{3}}{8^{3} \mathrm{R}^{3}} \\ & \therefore \quad \mathrm{T}^{2}=8^{2} \times 4^{2} \\ & \mathrm{~T}=8 \times 4 \\ & =32 \text { Hours } \end{aligned} $$
2. If ’ $g$ ’ is the acceleration due to gravity on the surface of the earth, the percentage gain in potential energy of an object, when it is raised from sea level to an altitude equal to a fourth of earth’s radius is:
(1) Infinite
(2) 75
(3) 50
(4) 20
Show Answer
Correct answer: (4)
Solution:
$$ \mathrm{h}=\frac{\mathrm{R}}{4} $$
At see level, $\mathrm{u} _{\mathrm{i}}=-\frac{\mathrm{GMm}}{\mathrm{R}}=-\left(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\right) \mathrm{mR}=-(\mathrm{mgR})$
At $\mathrm{h}=\frac{\mathrm{R}}{4}, \mathrm{u} _{\mathrm{f}}=-\frac{\mathrm{GMm}}{\mathrm{R}+\mathrm{h}}=-\frac{\mathrm{GMm}}{\frac{5}{4} \mathrm{R}}=-\left(\frac{4}{5} \mathrm{mgR}\right)$
$\therefore \Delta \mathrm{u}=\mathrm{u} _{\mathrm{f}}-\mathrm{u} _{\mathrm{i}}=\frac{1}{5} \mathrm{MgR}$
Hence, %age increase is $\frac{\Delta \mathrm{u}}{\left|\mathrm{u} _{\mathrm{i}}\right|} \times 100=20 \%$
3. An astronaut in artificial satellite experiences weightlessness because:
(1) The value of ’ $\mathrm{g}$ ’ is zero at the satellite
(2) The gravitational pull on him is balanced by that of the sun
(3) The astronaut and the satellite are in continuous free fall
(4) The body of the satellite shields the astronaut from the gravitational pull of earth
Show Answer
Correct answer: (3)
Solution:
A satellite is ejected into the orbit with a velocity $v _{0}=\sqrt{\frac{G M}{r}}$. This satellite will have two motions-(i) free fall with an acceleration equal to $g$ at distance $r$ and (ii) forward motion due to $v _{0}$. The forward motion is such that the distance from the earth’s surface remains a constant, or in other words, the satellite orbits the earth.
As the satellite and astronaut are in free fall, the apparent weight will be zero, or the astronaut feels weightlessness.
4. Two satellites are moving around the earth in coplanar circular orbits of radii $r _{1}$ and $r _{2}\left(r _{1}<\right.$ $r _{2}$ ) respectively moving in opposite direction with respect to one another. The time internal which separates the periodic approaches of the satellite to each other, in terms of the time period $T _{1}$, of the first satellite, is:
(1) $\left(\frac{\sqrt{\mathrm{r} _{1}}}{\sqrt{\mathrm{r} _{1}}+\sqrt{\mathrm{r} _{2}}}\right) \mathrm{T} _{1}$
(2) $\left(\frac{\sqrt{\mathrm{r} _{2}}}{\sqrt{\mathrm{r} _{1}}+\sqrt{\mathrm{r} _{2}}}\right) \mathrm{T} _{1}$
(3) $\left(\frac{\sqrt{\mathrm{r} _{1} \mathrm{r} _{2}}}{\sqrt{\mathrm{r} _{1}}+\sqrt{\mathrm{r} _{2}}}\right) \mathrm{T} _{1}$
(4) $\left(\frac{\sqrt{\mathrm{r} _{2}}}{\sqrt{\mathrm{r} _{1}}-\sqrt{\mathrm{r} _{2}}}\right) \mathrm{T} _{1}$
Show Answer
Correct answer: (2)
Solution:
Let A and B be the satellites. The relative velocity of $A$ with respect to $\mathrm{B}$, as observed from ground, is:
$$ \mathrm{v}=\mathrm{v} _{1}+\mathrm{v} _{2} $$
The time interval of approach of A to $B$ is:
$\Delta t=\frac{2 \pi r _{1}}{v _{1}+v _{2}}$
$$ =\frac{2 \pi r _{1}}{\sqrt{\frac{\mathrm{GM}}{\mathrm{r} _{1}}}+\sqrt{\frac{\mathrm{GM}}{\mathrm{r} _{2}}}} $$
$$ \left(\because \mathrm{v} _{0}=\sqrt{\frac{\mathrm{GM}}{\mathrm{r}}}\right) $$
or $\quad \Delta t=\frac{2 \pi \mathrm{r} _{1}}{\sqrt{\mathrm{GM}}} \cdot \frac{1}{\left(\frac{1}{\sqrt{\mathrm{r} _{1}}}+\frac{1}{\sqrt{\mathrm{r} _{2}}}\right)}$
or $\quad \Delta t=\frac{\mathrm{T} _{1}}{\sqrt{\mathrm{r} _{1}}} \cdot \frac{\sqrt{\mathrm{r} _{1}} \cdot \sqrt{\mathrm{r} _{2}}}{\sqrt{\mathrm{r} _{1}}+\sqrt{\mathrm{r} _{2}}}$
$$ \left(\because \mathrm{T}=\frac{2 \pi \mathrm{r}}{\sqrt{\mathrm{GM}}} \cdot \sqrt{\mathrm{r}}\right) $$
or $\quad \Delta \mathrm{t}=\mathrm{T} _{1}\left(\frac{\sqrt{\mathrm{r} _{2}}}{\sqrt{\mathrm{r} _{1}}+\sqrt{\mathrm{r} _{2}}}\right)$
5. The acceleration due to gravity of earth, on its surface, is $9.81 \mathrm{~ms}^{-2}$. Moon is at a distance of 59 earth radius away from earth. The centripetal acceleration of moon due to its orbital motion is:
(1) $0.16 \times 10^{-3} \mathrm{~ms}^{-2}$
(2) $2.82 \times 10^{-3} \mathrm{~ms}^{-2}$
(3) $2.72 \times 10^{-3} \mathrm{~ms}^{-2}$
(4) $1.64 \mathrm{~ms}^{-2}$
Show Answer
Correct answer: (3)
Solution:
The centripetal acceleration of the moon is equal to the acceleration due to gravity of earth at the moon.
$\therefore \quad \mathrm{a} _{\mathrm{c}}=\mathrm{g} _{1}=\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})^{2}}$
$$ \begin{array}{ll} =\frac{\mathrm{GM}}{(59+1)^{2} \mathrm{R}^{2}} & {[\because \mathrm{r}=\mathrm{h}+\mathrm{R}=(59+1) \mathrm{R}=60 \mathrm{R}]} \\ =\frac{\mathrm{g}}{(60)^{2}} \\ =\frac{9.81}{60 \times 60} & \\ =2.72 \times 10^{-3} \mathrm{~ms}^{-2} \end{array} $$
6. A particle of mass $M$ is at a distance ’ $r$ ’ from the surface of a thin spherical shell of radius $R$ and mass $M$. The net gravitational potential and field at the centre of the shell are, respectively:
(1) $-\frac{\mathrm{GM}}{\mathrm{r}}$ and $\frac{\mathrm{GM}}{\mathrm{r}^{2}}$, towards the particle
(2) $-\mathrm{GM} \frac{\mathrm{r}+2 \mathrm{R}}{(\mathrm{r}+\mathrm{R}) \mathrm{R}}$ and $\frac{\mathrm{GM}}{(\mathrm{r}+\mathrm{R})^{2}}$, towards the particle
(3) $-\mathrm{GM}\left(\frac{\mathrm{r}+2 \mathrm{R}}{\mathrm{R}^{2}}\right)$ and $\frac{\mathrm{GM}}{(\mathrm{r}+\mathrm{R})^{2}}$, towards the particle
(4) $-\mathrm{GM}\left(\frac{\mathrm{r}+2 \mathrm{R}}{(\mathrm{r}+\mathrm{R}) \mathrm{R}}\right)$ and zero
Show Answer
Correct answer: (2)
Solution:
At $\mathrm{O}$, there are two gravitational potentials:
(i) Due to the particle, $V _{1}=\frac{-G M}{r+R}$
 (ii) Due to the shell, $\mathrm{V} _{2}=-\frac{\mathrm{GM}}{\mathrm{R}}$
(ii) Due to the shell, $\mathrm{V} _{2}=-\frac{\mathrm{GM}}{\mathrm{R}}$
$\therefore$ Net gravitational potential at $\mathrm{O}$ is:
$$ \begin{aligned} & \mathrm{V}= \mathrm{V} _{1}+\mathrm{V} _{2}=-\mathrm{GM}\left(\frac{1}{\mathrm{r}+\mathrm{R}}+\frac{1}{\mathrm{R}}\right) \\ &=-\mathrm{GM}\left(\frac{2 \mathrm{R}+\mathrm{r}}{(\mathrm{r}+\mathrm{R}) \mathrm{R}}\right) \end{aligned} $$
At $\mathrm{O}$, the field intensity due to the shell is zero. So, gravitational field at ’ $\mathrm{O}$ ’ is due to the particle only.
$\therefore \quad \mathrm{I}=\frac{\mathrm{GM}}{(\mathrm{r}+\mathrm{R})^{2}}$, towards the particle.
7. Two thin spherical shell $A$ and $B$ of mass $M$ and $3 M$ and having radii a and 2a, respectively, have common centre at $O$. A particle is moved from a point distant $\frac{3}{2}$ a from $O$ to a point which is at 3a from $O$. The percentage change in the force on this particle due the spheres is equal to:
(1) zero
(2) Infinite
(3) $300 \%$
(4) $50 \%$
Show Answer
Correct answer: (1)
Solution:
Let ’ $m$ ’ be the mass of the particle.
At $\mathrm{C},\left(\mathrm{r}=\frac{3}{2} \mathrm{a}\right)$, the force due to shell $\mathrm{B}$ is zero because $\mathrm{C}$ is inside shell $\mathrm{B}$.
$\therefore \quad \mathrm{F} _{\mathrm{C}}=\frac{\mathrm{GMm}}{\left(\frac{3}{2} \mathrm{a}\right)^{2}}+0=\frac{4}{9} \frac{\mathrm{GMm}}{\mathrm{a}^{2}} \hspace{40mm} . . . . . . .(1)$
At point $\mathrm{D},(\mathrm{r}=3 \mathrm{a})$, the shells $\mathrm{A}$ and $\mathrm{B}$ behave like point masses at $O$ because $D$ lies outside both $A$ and $B$.
$\therefore$ Total mass at $\mathrm{O}$ is $4 \mathrm{M}$
Hence, force of the particle of mass $m$, at $D$ is:
$$ \begin{equation*} \mathrm{F} _{\mathrm{D}}=\frac{\mathrm{G} 4 \mathrm{Mm}}{(3 \mathrm{a})^{2}}=\frac{4}{9} \frac{\mathrm{GMm}}{\mathrm{a}^{2}} \tag{2} \end{equation*} $$

From (1) and (2), we get
$\mathrm{F} _{\mathrm{C}}=\mathrm{F} _{\mathrm{D}}$
$\therefore$ Change in force is zero.
8. A uniform ring of mass ’ $m$ ’ and radius ’ $r$ ’ is placed directly above a uniform sphere of mass ’ $M$ ’ and of equal radius. The centre of the ring is at a distance of $\sqrt{8} \mathrm{r}$ from the centre of the sphere. The gravitational force exerted by the ring on the sphere is:
(1) $\frac{\mathrm{GMm}}{(\sqrt{8}+1)^{2} \mathrm{r}^{2}}$
(2) $\frac{\mathrm{GMm}}{(\sqrt{8}-1)^{2} \mathrm{r}^{2}}$
(3) $\frac{1}{8} \frac{\mathrm{GMm}}{\mathrm{r}^{2}}$
(4) $\frac{\sqrt{8}}{27} \frac{\mathrm{GMm}}{\mathrm{r}^{2}}$
Show Answer
Correct answer: (4)
Solution:
The gravitational field intensity at $\mathrm{O}$, due to the ring is:
$$ \begin{gathered} \mathrm{I}=\frac{\mathrm{Gm} x}{\left(x^{2}+\mathrm{r}^{2}\right)^{3 / 2}}=\frac{\mathrm{Gm} \sqrt{8} \mathrm{r}}{\left(8 \mathrm{r}^{2}+\mathrm{r}^{2}\right)^{3 / 2}} \\ =\frac{\mathrm{Gm} \sqrt{8} \mathrm{r}}{\left(3^{2} \mathrm{r}^{2}\right)^{3 / 2}} \\ =\frac{\sqrt{8}}{27} \frac{\mathrm{Gm}}{\mathrm{r}^{2}} \end{gathered} $$
$\therefore$ Force on the sphere $=$ Force on mass $\mathrm{M}$ at $\mathrm{O}$

$$ =\mathrm{MI} $$
$$ =\frac{\sqrt{8}}{27}\left(\frac{\mathrm{GMm}}{\mathrm{r}^{2}}\right) $$
9. A solid uniform sphere has a mass $M$ and a radius $R$. Point $A$ is at normal distance of $\frac{R}{2}$ from the surface of the sphere and point $B$ is at a normal depth of $\frac{R}{2}$. The ratio of gravitational intensities at $A$ to that at $B$ is:
(1) $2: 9$
(2) $4: 9$
(3) $8: 9$
(4) $1: 1$
Show Answer
Correct answer: (3)
Solution:
$$ \mathrm{I} _{\mathrm{A}}=\frac{\mathrm{GM}}{\mathrm{r}^{2}}=\frac{\mathrm{GM}}{\left(\frac{3}{2} \mathrm{R}\right)^{2}} $$
or $\quad \mathrm{I} _{\mathrm{A}}=\frac{4}{9} \frac{\mathrm{GM}}{\mathrm{R}^{2}}$
$\mathrm{I} _{\mathrm{B}}=\frac{\mathrm{GM}}{\mathrm{R}^{2}}\left(\frac{\mathrm{r}}{\mathrm{R}}\right)$, when $\mathrm{r}<\mathrm{R}$ for solid sphere.
or $\quad \mathrm{I} _{\mathrm{B}}=\frac{\mathrm{GM}}{\mathrm{R}^{2}}\left(\frac{\mathrm{R} / 2}{\mathrm{R}}\right)$
or $\quad \mathrm{I} _{\mathrm{B}}=\frac{1}{2} \frac{\mathrm{GM}}{\mathrm{R}^{2}}$
$\therefore \quad \frac{\mathrm{I} _{\mathrm{A}}}{\mathrm{I} _{\mathrm{B}}}=\frac{4 / 9}{1 / 2}=\frac{8}{9}$
or $\mathrm{I} _{\mathrm{A}}: \mathrm{I} _{\mathrm{B}}=8: 9$

10. A solid uniform sphere of mass $M$ and radius $R$ has its centre $O$ coinciding with the origin of coordinate system, as shown. Three identical smaller spheres $A, B$ and $C$ of diameter $\frac{R}{2}$ are cut and removed from the main sphere. $A, B$ and $C$ are centered at $\frac{\mathbf{R}}{\mathbf{2}}(+\hat{\mathbf{i}}), \frac{\mathbf{R}}{\mathbf{2}}(-\hat{\mathbf{i}})$ and $\frac{\mathbf{R}}{\mathbf{2}}(+\hat{\mathbf{j}})$ respectively.
The net gravitational field intensity at $O$, due to the remaining part of the sphere is:
(1) $\frac{\mathrm{GM}}{16 \mathrm{R}^{2}}(-\mathbf{j})$
(2) zero
(3) $\frac{\mathrm{GM}}{4 \mathrm{R}^{2}}(-\mathbf{j})$
(4) $\frac{\mathrm{GM}}{16 \mathrm{R}^{2}}(+\mathbf{j})$
Show Answer
Correct answer: (1)
Solution:
As the spheres A and B are symmetrically located, their presence or absence will not contribute to the net field at $\mathrm{O}$, as their individual fields cancel out.
Now, as sphere $\mathrm{C}$ is not paired, the removal of sphere $\mathrm{C}$ will create a net field due to a similar sphere located geometrically opposite to $\mathrm{C}$, i.e. at $\mathrm{R}\left(-\frac{\hat{\mathrm{j}}}{2}\right)$. This will produce a net field at $\mathrm{O}$, directed along $(-\mathbf{j})$. All other regions of the sphere together will produce zero net field at $\mathrm{O}$.
So, the field at $\mathrm{O}$ will be the field due to a existing small sphere, of radius $\frac{\mathrm{R}}{4}$, located at $\mathrm{R}\left(-\frac{\mathbf{j}}{2}\right)$.
i.e. $\mathrm{I} _{\mathrm{net}}=\frac{\mathrm{GM}^{\prime}}{(\mathrm{R} / 2)^{2}}$
But $\mathrm{M}^{\prime}=\frac{4}{3} \pi\left(\frac{\mathrm{R}}{4}\right)^{3} \times \rho$
$=\frac{4}{3} \pi \frac{\mathrm{R}^{3}}{64} \cdot \frac{\mathrm{M}}{\frac{4}{3} \pi \mathrm{R}^{3}}$
$=\frac{M}{64}$
$\therefore \quad \mathrm{I} _{\text {net }}=\frac{\mathrm{G}}{\frac{\mathrm{R}^{2}}{4}} \times \frac{\mathrm{M}}{64}$
or $\quad I _{\text {net }}=\frac{1}{16} \frac{\mathrm{GM}}{\mathrm{R}^{2}}$, along $(-\mathbf{j})$
or $\quad I _{n e t}=\frac{G M}{16 R^{2}}(-\mathbf{j})$
11. A body is projected vertically from the surface of earth with speed equal to $\alpha$ times the escape speed for earth $(\alpha<1)$. If $R$ is the radius of the earth, then the distance to which the body would move, from the centre of the earth is:
(1) $\frac{\alpha}{\left(1-R^{2}\right)}$
(2) $\frac{2 R}{\left(1-\alpha^{2}\right)}$
(3) $\frac{\mathrm{R}}{\left(1-\alpha^{2}\right)}$
(4) $\frac{\mathrm{R}}{(1-\alpha)}$
Show Answer
Correct answer: (3)
Solution:
Let $r$ be the maximum distance to which the body moves, from the center of the earth. The increase in potential energy of the body will be:
$$ \Delta \mathrm{U}=\mathrm{U} _{\mathrm{f}}-\mathrm{U} _{\mathrm{f}}=-\frac{\mathrm{GMm}}{\mathrm{r}}+\frac{\mathrm{GMm}}{\mathrm{R}} $$
or $\quad \Delta \mathrm{U}=\mathrm{GMm}\left(\frac{1}{\mathrm{R}}-\frac{1}{\mathrm{r}}\right)$
Now, this increase in potential energy occurs due to the K.E.of projection.
$\therefore \quad \mathrm{K} . \mathrm{E}-\Delta \mathrm{U}$
or $\quad \frac{1}{2} \mathrm{mv}^{2}=\operatorname{GMm}\left(\frac{1}{\mathrm{R}}+\frac{1}{\mathrm{r}}\right)$
or $\quad \frac{1}{2} \mathrm{~m} \alpha^{2} \mathrm{v} _{\mathrm{e}}^{2}=\operatorname{GMm}\left(\frac{1}{\mathrm{R}}-\frac{1}{\mathrm{r}}\right)$
or $\quad \frac{1}{2} \mathrm{~m} \alpha^2 \cdot \frac{2 \mathrm{GM}}{\mathrm{R}}=\mathrm{GMm}\left(\frac{1}{\mathrm{R}}-\frac{1}{\mathrm{r}}\right)$ $$ \because \mathrm{v}_{\mathrm{e}}=\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}} $$ $\therefore \quad \alpha^2=\mathrm{R}\left(\frac{1}{\mathrm{R}}-\frac{1}{\mathrm{r}}\right)$ or $\quad \alpha^2=1-\frac{\mathrm{R}}{\mathrm{r}}$ or $\quad \frac{R}{r}=1-\alpha^2$ $$ \therefore \quad r=\frac{R}{1-\alpha^2} $$
12. Let $M _{1}$ and $M _{2}$ be the masses of earth and moon respectively and ’ $d$ ’ be the distance between their centres. The minimum speed with which a body be projected, from a point midway between the centres of earth and moon, so that the body escapes the gravitational pull of earth and moon is:
(1) $2 \sqrt{\frac{M _{1}-M _{2}}{d}}$
(2) $\sqrt{\frac{2 \mathrm{G}\left(\mathrm{M} _{1}+\mathrm{M} _{2}\right)}{\mathrm{d}}}$
(3) $\sqrt{\frac{2 \mathrm{G}\left(\mathrm{M} _{1}-\mathrm{M} _{2}\right)}{\mathrm{d}}}$
(4) $2 \sqrt{\frac{G\left(M _{1}+M _{2}\right)}{d}}$
Show Answer
Correct answer: (4)
Solution:
Let the mass of body be $\mathrm{m}$. The potential energy of the particle at the middle point $\mathrm{O}$ is:
$$ \begin{aligned} \mathrm{U}= & \frac{-\mathrm{GM} _{1} \mathrm{~m}}{(\mathrm{~d} / 2)}+\frac{-\mathrm{GM} _{2} \mathrm{~m}}{(\mathrm{~d} / 2)} \\ & =\frac{-2 \mathrm{GM}}{\mathrm{d}}\left(\mathrm{M} _{1}+\mathrm{M} _{2}\right) \end{aligned} $$

The K.E $=\frac{1}{2} \mathrm{mv}^{2}$, provided to the body should increase the potential energy to zero, when it reaches infinte distance from both earth and moon.
$\therefore \quad \frac{1}{2} \mathrm{mv}^{2}=\frac{2 \mathrm{GM}}{\mathrm{d}}\left(\mathrm{M} _{1}+\mathrm{M} _{2}\right)$
or $\quad v=2 \sqrt{\frac{\left(M _{1}+M _{2}\right) G}{d}}$
13. If some how on its own the radius of earth were to decrease by $\frac{1}{n}$ of its present value, keeping its mass the same, the percentage increase in its duration of the day will be:
(1) $\left(\frac{\mathrm{n}^{2}}{1-\mathrm{n}^{2}}\right) \times 100 \%$
(2) $\left(\frac{(\mathrm{n}-1)^{2}}{\mathrm{n}^{2}}\right) \times 100 \%$
(3) $\left(\frac{1-2 n}{n^{2}}\right) \times 100 \%$
(4) $\left(\frac{n^{2}}{1-2 n}\right) \times 100 \%$
Show Answer
Correct answer: (3)
Solution:
Since charge occurs on its own, there is no external force and therefore no external torque.
The angular momentum of earth remains conserved, $\mathrm{I} _{1} \omega _{1}=\mathrm{I} _{2} \omega _{2}$
Moment of inertia of earth, being a solid sphere is $\mathrm{I}=\frac{2}{5} \mathrm{MR}^{2}$
$\therefore \quad \mathrm{I} _{1}=\frac{2}{5} \mathrm{MR} _{1}^{2}$ and $\mathrm{I} _{2}=\frac{2}{5} \mathrm{MR} _{2}^{2}$
and $\quad \omega _{1}=\frac{2 \pi}{\mathrm{T} _{1}} \quad$ (where $\mathrm{T} _{1}=24$ hours)
$$ \omega _{2}=\frac{2 \pi}{\mathrm{T} _{2}} \quad \text { (where } \mathrm{T} _{2} \text { is the new time period of changed earth around its own axis) } $$
Here, $\mathrm{I} _{1} \omega _{1}=\mathrm{I} _{2} \omega _{2}$
or $\quad \frac{2}{5} \mathrm{MR} _{1}^{2}\left(\frac{2 \pi}{\mathrm{T} _{1}}\right)=\frac{2}{5} \mathrm{MR} _{2}^{2}\left(\frac{2 \pi}{\mathrm{T} _{2}}\right)$
or $\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=\frac{\mathrm{R} _{1}^{2}}{\mathrm{R} _{2}^{2}}$
or $\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}=\frac{\mathrm{R} _{2}^{2}}{\mathrm{R} _{1}^{2}}$
But $\quad \mathrm{R} _{2}=\mathrm{R} _{1}-\frac{\mathrm{R} _{1}}{\mathrm{n}}=\mathrm{R} _{1}\left(1-\frac{1}{\mathrm{n}}\right)$
$\therefore \frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}=\frac{\mathrm{R} _{1}^{2}\left(1-\frac{1}{\mathrm{n}}\right)^{2}}{\mathrm{R} _{1}^{2}}$
or $\frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}=\left(1-\frac{1}{\mathrm{n}}\right)^{2}$ $\therefore \frac{\mathrm{T} _{2}-\mathrm{T} _{1}}{\mathrm{~T} _{1}}=\left[\left(1-\frac{1}{\mathrm{n}}\right)^{2}-1\right]=\frac{1-2 \mathrm{n}}{\mathrm{n}^{2}}$
Hence, $\%$ ge change in duration of the day $=\frac{1-2 \mathrm{n}}{\mathrm{n}^{2}} \times 100 \%$
14. An infinite number of identical point objects, each of mass ’ $m$ ‘, are placed on the $x$-axis at points $x=1, x=2, x=4, x=8, \ldots \ldots$. , where $\mathrm{x}$ is measured in metres. The net gravitational potential and field at the origin are, respectively.
(1) $-\frac{\mathrm{GM}}{2}$ and $\frac{3}{4} \mathrm{GM}(\hat{\mathrm{i}})$
(2) $-2 \mathrm{GM}$ and $\frac{4}{3} \mathrm{GM}(\hat{\mathrm{i}})$
(3) $-\frac{3}{4} \mathrm{GM}$ and $\frac{3}{4} \mathrm{GM}(\hat{\mathrm{i}})$
(4) $-\frac{2}{5} \mathrm{GM}$ and $\frac{5}{4} \mathrm{GM}(\hat{\mathrm{i}})$
Show Answer
Correct answer: (2)
Solution:
The gravitational potential, $\mathrm{V}=-\frac{\mathrm{GM}}{\mathrm{r}}$. Therefore the net gravitational potential at the origin will be:
$$ \mathrm{V} _{\mathrm{net}}=\mathrm{V} _{1}+\mathrm{V} _{2}+\mathrm{V} _{3}+\ldots \ldots \ldots \ldots \ldots $$
or
$$ \mathrm{V} _{\mathrm{net}}=-\mathrm{GM}\left[\frac{1}{1}+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\ldots\right] $$
or
$$ \mathrm{V} _{\mathrm{net}}=-\mathrm{GM}\left(\frac{1}{1-\frac{1}{2}}\right) $$
or $\mathrm{V} _{\text {net }}=-2 \mathrm{GM}$
Now, $\mathrm{I}=\frac{\mathrm{GM}}{\mathrm{r}^{2}}(\mathrm{i})$ (as the field $\mathrm{I}$ is directed towards the mass)
$\therefore \quad I_{\text {net }} $=$G M[\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{4^2}+\frac{1}{8^2}+\ldots \ldots .]\hat{(i)} $
$ =G M[\frac{1}{1}+\frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\ldots \ldots .]\hat{(i)} $
$ =G M[\frac{1}{1-\frac{1}{4}}]\hat{(i)} $
$ =\frac{4}{3} G M \hat{(i)} $
$ =\frac{4}{3} G M(i)$
15. A pendulum is shifted from the surface of the earth $(R=6400 \mathrm{Km})$ to a position of $400 \mathrm{~m}$ above the surface. The time loss for the pendulum in a day is:
(1) 5.4 second
(2) 10.8 second
(3) 2.7 second
(4) 54 second
Show Answer
Correct answer: (1)
Solution:
At the height $h$, the value of $g$ is:
$$ g=g _{0}\left(1-\frac{2 h}{R}\right), \text { when } \mathrm{h}«\mathrm{R} $$
$\therefore \%$ age decrease in $\mathrm{g}=\frac{2 \mathrm{~h}}{\mathrm{R}} \times 100 \%$
$$ \begin{aligned} & =\frac{2 \times 400}{6400 \times 1000} \times 10 \% \\ & =\frac{1}{80} \% \end{aligned} $$
Now, $\mathrm{T}=2 \pi \sqrt{\frac{\ell}{\mathrm{g}}}$
or $\mathrm{T}^{2}=4 \pi^{2} \frac{\ell}{\mathrm{g}} \quad(\ell=$ constant $)$
$\therefore \frac{\Delta \mathrm{T}}{\mathrm{T}}=-\frac{1}{2} \frac{\Delta \mathrm{g}}{\mathrm{g}}=-\frac{1}{2} \times \frac{-1}{80}=\frac{1}{160} \%$
So, the time period of the pendulum increases by $\frac{1}{160} \%$
$\therefore$ Loss in 1 second $=\frac{1}{16000}$
or $\quad$ Loss in 1 day $=\frac{1}{16000} \times 86400$
$=5.4$ second
16. A particle of mass $M$ is situated at the centre $O$ of a spherical shell of same mass $M$ and radius ’ $a$ ‘. The gravitational potential and gravitational field, at a point situated at a distance $\left(\frac{a}{2}\right)$ from $O$ are, respectively.
(1) $-4 \frac{\mathrm{GM}}{\mathrm{a}}$ and zero
(2) $-3 \frac{\mathrm{GM}}{\mathrm{a}}$ and $4 \frac{\mathrm{GM}}{\mathrm{a}^{2}}$ towards $\mathrm{O}$
(3) $-3 \frac{\mathrm{GM}}{\mathrm{a}}$ and zero
(4) $-4 \frac{\mathrm{GM}}{\mathrm{a}}$ and $4 \frac{\mathrm{GM}}{\mathrm{a}^{2}}$ towards $\mathrm{O}$
Show Answer
Correct answer: (2)
Solution:
The gravitational potential at any point on or inside the spherical shell is
$$ \mathrm{V} _{1}=-\frac{\mathrm{GM}}{\mathrm{a}} $$
The gravitational potential at $\mathrm{P}$ due to mass $\mathrm{M}$ at $\mathrm{O}$ is:
$$ \mathrm{V} _{2}=-\frac{\mathrm{GM}}{\mathrm{a} / 2} $$
or $\quad \mathrm{V} _{2}=-\frac{2 \mathrm{GM}}{\mathrm{a}}$
$\therefore$ Net gravitational potential at $\mathrm{P}$ is:
$$ \begin{aligned} & V _{P}=V _{1}+V _{2} \\ & =-\frac{3 G M}{a} \end{aligned} $$
The gravitational field (I) at any point inside the shell due to itself is zero.
$\therefore \mathrm{I}$ at point $\mathrm{P}$ is due to the mass $\mathrm{M}$ at $\mathrm{O}$ only.
or $\quad I _{P}=\frac{-G M}{(a / 2)^{2}}$
or $\mathrm{I} _{\mathrm{P}}=\frac{-4 \mathrm{GM}}{\mathrm{a}^{2}}=\frac{4 \mathrm{GM}}{\mathrm{a}^{2}}$ towards $\mathrm{O}$
17. The density of a newly discovered planet is twice that of earth. The acceleration due to gravity at the surface of the planet is equal to $25 \%$ of that on the surface of the earth. If the radius of the earth is $\mathrm{R}$, the radius of the planet is:
(1) $\frac{R}{2}$
(2) $\frac{R}{4}$
(3) $\frac{R}{8}$
(4) $\frac{\mathrm{R}}{12}$
Show Answer
Correct answer: (3)
Solution:
On the surface of the earth, $g=\frac{G M}{R^{2}}$
or $\quad \mathrm{g}=\mathrm{G} \cdot \frac{4}{3} \frac{\pi \mathrm{R}^{3} \rho}{\mathrm{R}^{2}}$
or $\quad \mathrm{g}=\mathrm{G} \cdot \frac{4}{3} \pi \mathrm{R} \rho \hspace{40mm}. . . . . . . (1) $
On the surface of the planet, of radius $r$,
$$ \begin{array}{r} \mathrm{g}^{\prime}=\frac{\mathrm{g}}{4}=\frac{\mathrm{GM}^{\prime}}{\mathrm{r}^{2}} \\ \therefore \frac{\mathrm{g}}{4}=\mathrm{G} \cdot \frac{\frac{4}{3} \pi \mathrm{r}^{3}(2 \rho)}{\mathrm{r}^{2}} \end{array} $$
or $\quad \mathrm{g}=\mathrm{G} \cdot \frac{4}{3} \pi \rho \mathrm{r} \times 8 \hspace{40mm}. . . . . . . (2) $
Equating (1) and (2), we get
$$ r=\frac{R}{8} $$
18. A satellite of mass ’ $m$ ’ is orbiting close to the surface of earth $(R=6400 \mathrm{Km})$. The satellite has a kinetic energy of $\mathrm{K}$. An additional kinetic energy of equal amount is given to this satellite. The radius of its orbit will now become equal to:
(1) $2 \mathrm{R}$
(2) $4 \mathrm{R}$
(3) $36000 \mathrm{Km}$
(4) Infinite
Show Answer
Correct answer: (4)
Solution:
Given : Kinetic energy of the satellite $=\mathrm{K}$
We know that the potential energy of a satellite is: $U=-2 K$
Now, if kinetic energy of this satellite is doubled, the total energy of the satellite would become:
$\mathrm{E}=2 \mathrm{~K}+-2 \mathrm{~K}=0$
when $\mathrm{E}=0$, the satellite cannot remain bound to earth (for which $-\mathrm{E} \neq 0$ is must).
Hence the orbital radius of the satellite would become infinite.
19. The mass of a planet is six times that of the earth and its radius is twice that of the earth. A satellite of mass ’ $m$ ’ orbits around the earth at a certain distance from it. Another satellite of same mass orbits around the planet, also at same distance as that of the earth’s satellite. The ratio of the total energy of these satellites is equal to:;
(1) $1: 1$
(2) $1: 3$
(3) $1: 6$
(4) $1: 12$
Show Answer
Correct answer: (3)
Solution:
For satellite around the earth, $v _{0}=\sqrt{\frac{\mathrm{GM} _{\mathrm{e}}}{\mathrm{e}}}$
$\therefore$ Kinetic energy of the satellite around earth is: $\mathrm{K} _{\mathrm{es}}=\frac{1}{2} \mathrm{mv} _{0}^{2}=\frac{1}{2} \mathrm{~m} \frac{\mathrm{GM} _{\mathrm{e}}}{\mathrm{r}}$
or $\quad \mathrm{K} _{\mathrm{es}}=\frac{1}{2} \frac{\mathrm{GM} _{\mathrm{e}} \mathrm{m}}{\mathrm{r}}$
Now, total energy, $\mathrm{E} _{\mathrm{es}}=-\mathrm{K} _{\mathrm{es}}=-\frac{1}{2} \frac{\mathrm{GM} _{\mathrm{e}} \mathrm{m}}{\mathrm{r}}$
For the planet, $M _{P}=6 M _{e}$
$\therefore \quad v _{0}=\sqrt{\frac{\mathrm{G} \times 6 \mathrm{M} _{\mathrm{e}}}{\mathrm{r}}}$, for the satellite of the planet.
$\therefore$ Kinetic energy of the satellite of the planet is:
$$ \mathrm{K} _{\mathrm{PS}}=\frac{1}{2} \mathrm{mv} _{0}^{2}=\frac{1}{2} \times 6 \frac{\mathrm{GM} _{\mathrm{e}} \mathrm{m}}{\mathrm{r}} $$
Now, the total energy of this satellite is : $\mathrm{E} _{\mathrm{PS}}=-\mathrm{K} _{\mathrm{PS}}$
$$ \mathrm{E} _{\mathrm{PS}}=-\frac{1}{2} \times \frac{6 \mathrm{GM} _{\mathrm{e}} \mathrm{m}}{\mathrm{r}} $$
Hence, $\frac{\mathrm{E} _{\mathrm{es}}}{\mathrm{E} _{\mathrm{PS}}}=1: 6$
20. A thin uniform rod of length ’ $L$ ’ has a mass $M$. A point mass ’ $m$ ’ is kept at a distance ’ $r$ ’ from one of its ends, along the line of the rod. The magnitude of the gravitational force on ’ $m$ ’ due to the rod is:
(1) $\frac{\mathrm{GMm}}{\mathrm{r}(\mathrm{r}+\mathrm{L})}$
(2) $\frac{4 \mathrm{GMm}}{(2 \mathrm{r}+\mathrm{L})^{2}}$
(3) $\frac{\mathrm{GMm}}{(\mathrm{r}+\mathrm{L})^{2}}$
(4) $\frac{\mathrm{GMm}}{\left(\mathrm{r}^{2}+\mathrm{L}^{2}\right)}$
Show Answer
Correct answer: (1)
Solution:
The mass of a small element of the rod, of length $d x$ is:
$$ \mathrm{dM}=\frac{\mathrm{M}}{\mathrm{L}} \mathrm{d} x $$
The gravitational field intensity at point $\mathrm{O}$ due to one such element at a distance of $x$ from $\mathrm{O}$ is:
$$ \mathrm{dI}=\frac{\mathrm{GdM}}{x^{2}}=\frac{\mathrm{GM}}{\mathrm{L}} x^{-2} \mathrm{~d} x $$
$\therefore$ The total intensity at $\mathrm{O}$ due to the entire rod is:
$$ \begin{aligned} \mathrm{I}=\int \mathrm{dI} & =\frac{\mathrm{GM}}{\mathrm{L}} \int _{x=\mathrm{r}}^{x=\mathrm{r}+\mathrm{L}} x^{-2} \mathrm{~d} x \\ & =\frac{\mathrm{GM}}{\mathrm{L}}\left(-\frac{1}{x}\right) _{\mathrm{r}}^{\mathrm{r}+\mathrm{L}}=\frac{\mathrm{GM}}{\mathrm{L}}\left(\frac{1}{x}\right) _{\mathrm{r}+\mathrm{L}}^{\mathrm{r}} \end{aligned} $$
$$ =\frac{\mathrm{GM}}{\mathrm{L}}\left[\frac{1}{\mathrm{r}}-\frac{1}{\mathrm{r}+\mathrm{L}}\right]=\frac{\mathrm{GM}}{\mathrm{L}}\left[\frac{\mathrm{L}}{\mathrm{r}(\mathrm{r}+\mathrm{L})}\right] $$
or $\mathrm{I}=\frac{\mathrm{GM}}{\mathrm{r}(\mathrm{r}+\mathrm{L})}$
$\therefore$ Force, $\mathrm{F}=\mathrm{mI}=\frac{\mathrm{GMm}}{\mathrm{r}(\mathrm{r}+\mathrm{L})}$
21. The ratio of the radius of earth to that of another planet is $2: 3$ and the ratio of their mean densities is 4:5. If an astronaut can jump to a maximum height of $1.5 \mathrm{~m}$ on the earth, with the same effort, the maximum height he can jump in the planet is:
(1) $1.25 \mathrm{~m}$
(2) $1.00 \mathrm{~m}$
(3) $0.80 \mathrm{~m}$
(4) $0.50 \mathrm{~m}$
Show Answer
Correct answer: (3)
Solution:
Let $R _{E}=R$ and $\rho _{E}=\rho$
Then $\mathrm{R} _{\mathrm{\rho}}=\frac{3}{2} \mathrm{R}$ and $\rho _{\mathrm{P}}=\frac{5}{4} \rho$
Now, $\mathrm{g} _{\mathrm{E}}=\mathrm{g}=\mathrm{G} \frac{4}{3} \pi \mathrm{R} \rho$
and $\quad \mathrm{g} _{\rho}=\mathrm{G} \frac{4}{3} \pi\left(\frac{3}{2} \mathrm{R}\right)\left(\frac{5}{4} \rho\right)$
or $\quad g _{\rho}=\frac{15}{8} \mathrm{~g}$
Suppose, $\mathrm{W}$ be the effort put in by the astronaut. Then:
$$ \mathrm{W}=\mathrm{mgh} _{\mathrm{E}} $$
and $\mathrm{W}=\mathrm{mg} _{\rho} \mathrm{h} _{\rho}$
$\therefore \mathrm{gh} _{\mathrm{E}}=\mathrm{g} _{\mathrm{\rho}} \mathrm{h} _{\mathrm{\rho}}$
or $\mathrm{g} \times 1.5=\frac{15}{8} \mathrm{~g} \times \mathrm{h} _{\rho}$
or $\quad \mathrm{h} _{\rho}=0.8 \mathrm{~m}$
22. The escape velocity of a body from the surface of the earth is $11 \mathrm{Kms}^{-1}$. Assume that the mass and radius of earth are 81 times and 4 times the mass and radius, respectively, of the moon. The escape velocity from the surface of the moon is:
(1) $2.44 \mathrm{~ms}^{-1}$
(2) $2.49 \mathrm{~ms}^{-1}$
(3) $3.97 \mathrm{~ms}^{-1}$
(4) $6.81 \mathrm{~ms}^{-1}$
Show Answer
Correct answer: (1)
Solution:
Let $v _{m}$ be the escape velocity on the surface of moon. Then:
$$ \mathrm{v} _{\mathrm{m}}=\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}} $$
where $\mathrm{M}=$ mass of moon and $\mathrm{R}=$ radius of moon.
Now, for earth, $M _{E}=81 \mathrm{M}$ and $R _{E}=4 R$
$\therefore \mathrm{v} _{\mathrm{e}}=\sqrt{\frac{2 \mathrm{G} \times 81 \mathrm{M}}{4 \mathrm{R}}}$
or $\quad \mathrm{v} _{\mathrm{e}}=\frac{9}{2} \sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}$ or $\quad \mathrm{v} _{\mathrm{e}}=\frac{9}{2} \mathrm{v} _{\mathrm{m}}$
$\therefore \quad \mathrm{v} _{\mathrm{m}}=\frac{2 \mathrm{v} _{\mathrm{e}}}{9}=\frac{2 \times 11}{9}=2.44 \mathrm{~ms}^{-1}$
23. At what depth, from the surface of the earth would the value of acceleration due to gravity become equal to its value at a height of $9800 \mathrm{~km}$ from the surface of the earth?
(Given: radius of earth $=\mathbf{6 4 0 0} \mathrm{km}$ )
(1) $3200 \mathrm{~km}$
(2) $5376 \mathrm{~km}$
(3) $6144 \mathrm{~km}$
(4) $6286 \mathrm{~km}$
Show Answer
Correct answer: (2)
Solution:
Given: $\mathrm{R}=6400 \mathrm{~km}$
$$ \begin{aligned} & \mathrm{h}=9800 \mathrm{~km} \\ & =\frac{3}{2} \mathrm{R} \end{aligned} $$
Now, $\mathrm{g} _{\mathrm{h}}=\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})^{2}}=\frac{4}{25}\left(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\right)=\frac{4}{25} \mathrm{~g}$
Also, $g _{d}=g\left(1-\frac{d}{R}\right)$
Given $\mathrm{g} _{\mathrm{d}}=\mathrm{g} _{\mathrm{n}}$; therefore
$$ g\left(1-\frac{d}{R}\right)=\frac{4}{25} g $$
or $\frac{\mathrm{d}}{\mathrm{R}}=1-\frac{4}{25}$
or $\quad \mathrm{d}=\frac{21}{25} \mathrm{R}$
$=5376 \mathrm{~km}$
24. If gravitational force were to vary as:
$$ \mathbf{f} \propto \frac{1}{\mathbf{r}^{3}} $$
then the graphs plotted for ‘orbital velocity $\left(v _{0}\right)$ vs (r)’ and ’time period (T) vs(r) for a satellite of earth will be respectively:
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)

Show Answer
Correct answer: (2)
Solution:
Given $\mathrm{f} \propto \frac{1}{\mathrm{r}^{3}}$
$$ \therefore \quad \mathrm{f}=\frac{\mathrm{GMm}}{\mathrm{r}^{3}} $$
Now, for orbital velocity $\mathrm{v} _{0}$ of the satellite, $\mathrm{f}=$ centripetal force
$$ \frac{\mathrm{GMm}}{\mathrm{r}^{3}}=\frac{\mathrm{mv} _{0}^{2}}{\mathrm{r}} $$
$$ \text { or } \mathrm{v} _{0}^{2}=\frac{\mathrm{GM}}{\mathrm{r}^{2}} $$
or $\quad \mathrm{v} _{0}=\frac{\sqrt{\mathrm{GM}}}{\mathrm{r}}$
or $\quad \mathrm{v} _{0} \propto \frac{1}{\mathrm{r}}$
Hence the graph is:

Now, $\mathrm{T}=\frac{2 \pi \mathrm{r}}{\mathrm{v} _{0}}$ or $\quad \mathrm{T}=\frac{2 \pi \mathrm{r} \times \mathrm{r}}{\sqrt{\mathrm{GM}}}$
or $\quad \mathrm{T}=\left(\frac{2 \pi}{\sqrt{\mathrm{GM}}}\right) \mathrm{r}^{2}$
$\therefore \mathrm{T} \alpha \mathrm{r}^{2}$
Hence the graph is porabolic as shown below

25. A satellite is moving in a circular orbit around the earth with an orbital velocity equal to one third of the magnitude of the escape velocity from the surface of the earth. Suppose this satellite by stopped suddenly in the orbit and thereafter allowed to fall freely to the surface of the earth. Neglecting air friction, the speed (in $\mathrm{Kms}^{-1}$ ) with which it will hit the surface is nearly equal to:
(1) 8
(2) 9
(3) 10
(4) 11
Show Answer
Correct answer: (3)
Solution:
We know that: $v _{0}=\sqrt{\frac{G M}{R+h}}=\left(\sqrt{\frac{g}{R+h}}\right) R$
and $\mathrm{v} _{\mathrm{e}}=\sqrt{2 \mathrm{gR}}$
Given: $\mathrm{v} _{0}=\frac{1}{3} \mathrm{v} _{\mathrm{e}}$
$\therefore \mathrm{R} \sqrt{\frac{\mathrm{g}}{\mathrm{R}+\mathrm{h}}}=\frac{1}{3} \sqrt{2 \mathrm{gR}}$
or $\quad \mathrm{R}^{2}\left(\frac{\mathrm{g}}{\mathrm{R}+\mathrm{h}}\right)=\frac{1}{9}(2 \mathrm{gR})$
or $\quad 9 R^{2}=2 R^{2}+2 R h$
or $\quad 7 \mathrm{R}=2 \mathrm{~h}$
$\therefore \mathrm{h}=3.5 \mathrm{R}$
Now, when the satellite is stopped in the orbit, its $\mathrm{K} . \mathrm{E}=0$ and gravitational potential energy $=\frac{-\mathrm{GMm}}{\mathrm{R}+\mathrm{h}}$
This potential energy decreases to $\frac{-\mathrm{GMm}}{\mathrm{R}}$, when the satellite hits the ground. Hence, its kinetic energy will increase from 0 to $\frac{1}{2} \mathrm{mv}^{2}$, such that:
$$ \begin{array}{ll} & \frac{-G M m}{R+h}=\frac{1}{2} m v^{2}+\left(\frac{-G M m}{R}\right) \\ \text { or } \quad & \frac{-G M}{R+h}+\frac{G M}{R}=\frac{1}{2} v^{2} \\ \text { or } \quad & \frac{-g R^{2}}{R+h}+g R=\frac{1}{2} v^{2} \\ \text { or } \quad & \frac{g R h}{R+h}+\frac{1}{2} v^{2} \\ \therefore \quad & v^{2}=\frac{2 g h}{1+\frac{h}{R}} \end{array} $$
Here, $\mathrm{h}=3.5 \mathrm{R}$
$\therefore \quad \mathrm{v}^{2}=\frac{2 \mathrm{~g} \times 3.5 \mathrm{R}}{4.5}=\frac{2 \times .9 .8 \times 3.5 \times 6.4 \times 10^{6}}{45}$
or $ \quad \mathrm{v}^{2}=100 \times 10^{6} \mathrm{~m}^{2} \mathrm{~s}^{-2}$
$\therefore \mathrm{v}^{2}=100 \mathrm{~km}^{2} \mathrm{~s}^{-2}$
or
$$ \mathrm{v}=10 \mathrm{kms}^{-1} $$
26. The gravitational field intensity on the surface of the earth is $9=9.8 \mathrm{~ms}^{-2}$ and on the surface of mars is $4.0 \mathrm{~ms}^{-2}$. Suppose a $60 \mathrm{Kg}$ passenger travels in a spaceship from earth to mars, with a constant velocity. Neglecting the effects of all other objects in the space, which of the following graphical representations most correctly indicates the variation of weight of the passenger as a function of time?

(1) a
(2) b
(3) $\mathrm{c}$
(4) d
Show Answer
Correct answer: (2)
Solution:
The weight of the passenger on earth is $588 \mathrm{~N}$ and on mars is $240 \mathrm{~N}$. At some point, on the way, the net force on the passenger, due to earth’s and mar’s gravity together, should be zero. There the weight of the passenger becomes zero. But weight cannot be less than zero in magnitude. This point, where net weight of the person becomes zero, is obviously closer to mars, as its gravity is lesser. So after this point, where the weight is zero, the time of travel will be lesser (with constant speed). Hence the correct plot is (b).
27. Consider a simple pendulum of large length, equal to half the radius of earth. The time period ( $T$ ) of this pendulum can be given as:
(1) $2 \pi \sqrt{\frac{3 R}{g}}$
(2) $2 \pi \sqrt{\frac{R}{g}}$
(3) $2 \pi \sqrt{\frac{\mathrm{R}}{3 g}}$
(4) $2 \pi \sqrt{\frac{\mathrm{R}}{5 \mathrm{~g}}}$
Show Answer
Correct answer: (3)
Solution:
The diagram represents the extreme position of the pendulum, for small amplitude of oscillation. The restoring force on the bob of the pendulum is:
$$ \mathrm{F}=-\mathrm{mg} \sin (\theta+\phi) $$
or $\quad \mathrm{F}=-\operatorname{mg}(\theta+\phi)$
($\theta \quad and \quad \phi$ are small)
or $\quad \mathrm{F}=-\mathrm{mg}\left(\frac{x}{\ell}+\frac{x}{\mathrm{R}}\right)$
or $\quad \mathrm{F}=\frac{-\mathrm{mg}}{\mathrm{R}}\left(\frac{\mathrm{R}}{\ell}+1\right) x$
$\therefore$ Acceleration, $\mathrm{a}=\frac{-\mathrm{g}}{\mathrm{R}}\left(\frac{\mathrm{R}}{\ell}+1\right) x$
This is of the form, $\mathrm{a}=-\omega^{2} x$ for SHM.
$\therefore \omega=\sqrt{\frac{\mathrm{g}}{\mathrm{R}}\left(\frac{\mathrm{R}}{\ell}+1\right)}$
or $\mathrm{T}=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathrm{R}}{\mathrm{g}\left(\frac{\mathrm{R}}{\ell}+1\right)}}$
Here, $\ell=\frac{\mathrm{R}}{2}$
$\therefore \quad T=2 \pi \sqrt{\frac{R}{g(2+1)}}=2 \pi \sqrt{\frac{R}{3 g}}$
28. Two satellites $A$ and $B$ revolve around the earth at distances $2 R$ and $5 R$ respectively from the surface of earth. $R$ is the radius of the earth. Their periods of revolution will be in the ratio:
(1) $1: 4$
(2) $1: 2.828$
(3) $1: 2$
(4) $2: 5$
Show Answer
Correct answer: (2)
Solution:
Refer to diagram
Here, $\mathrm{r} _{\mathrm{A}}=2 \mathrm{R}+\mathrm{R}=3 \mathrm{R}$
$$ \mathrm{r} _{\mathrm{B}}=5 \mathrm{R}+\mathrm{R}=6 \mathrm{R} $$
We have $\mathrm{T}^{2} \propto \mathrm{r}^{3}$, by Kepler’s law.
$$ \therefore \frac{\mathrm{T} _{\mathrm{A}}^{2}}{\mathrm{~T} _{\mathrm{B}}^{2}}=\frac{\mathrm{r} _{\mathrm{A}}^{3}}{\mathrm{r} _{\mathrm{B}}^{2}} $$
or $\frac{\mathrm{T} _{\mathrm{A}}^{2}}{\mathrm{~T} _{\mathrm{B}}^{2}}=\frac{3^{3}}{6^{3}}$
$$ \begin{aligned} & =\frac{1}{2^{3}} \\ & =\frac{1}{8} \end{aligned} $$
$\therefore \frac{\mathrm{T} _{\mathrm{A}}}{\mathrm{T} _{\mathrm{B}}}=\frac{1}{\sqrt{8}}=\frac{1}{2.828}$
29. Imagine a tunnel made along the diameter of earth and a ball is released at a depth of $d=\frac{R}{2}$. This ball will have a period of oscillatory motion equal to:
(1) $2 \pi \sqrt{\frac{\mathrm{R}}{2 \mathrm{~g}}}$
(2) $\pi \sqrt{\frac{R}{g}}$
(3) $2 \pi \sqrt{\frac{R}{g}}$
(4) $2 \pi \sqrt{\frac{2 \mathrm{R}}{\mathrm{g}}}$
Show Answer
Correct answer: (3)
Solution:
The acceleration due to gravity (a) at the depth $d$ is:
$$ a=-g\left(\frac{R-d}{R}\right) $$
(-ve sign indicating that a is towards $\mathrm{O}$ ).

Let $\mathrm{y}=\mathrm{R}-\mathrm{d}$, be the displacement of ball, from $\mathrm{O}$.
Then $a=-\left[\frac{g}{R} y\right]$
This is of the form:
$$ \begin{aligned} & a=-\omega^{2} y \text { for SHM } \\ \therefore \quad \omega & =\sqrt{\frac{g}{R}} \\ \text { or } \quad T & =\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{R}{g}} \end{aligned} $$
( $\mathrm{T}$ does not depend on the position of releasing of the ball).
30. The ratio of the acceleration due to gravity on two planets $A$ and $B$ is $K _{1}$. The ratio of their respective radii is $K _{2}$. The ratio of their mean densities is $K _{3}$. What is the ratio of their respective escape velocities?
(1) $\mathrm{K} _{2} \sqrt{\mathrm{K} _{3}}$
(2) $\mathrm{K} _{1} \sqrt{\mathrm{K} _{3}}$
(3) $\sqrt{\mathrm{K} _{2} \mathrm{~K} _{3}}$
(4) $\sqrt{\mathrm{K} _{1} \mathrm{~K} _{3}}$
Show Answer
Correct answer: (1)
Solution:
$$ \begin{aligned} & \mathrm{v} _{\mathrm{e}}=\sqrt{2 \mathrm{gR}} \\ & \therefore \frac{\mathrm{v} _{\mathrm{A}}}{\mathrm{v} _{\mathrm{B}}}=\frac{\sqrt{2 \mathrm{~g} _{\mathrm{A}} \mathrm{R} _{\mathrm{A}}}}{\sqrt{2 \mathrm{~g} _{\mathrm{B}} \mathrm{R} _{\mathrm{B}}}}=\sqrt{\frac{\mathrm{g} _{\mathrm{A}}}{\mathrm{g} _{\mathrm{B}}} \cdot \frac{\mathrm{R} _{\mathrm{A}}}{\mathrm{R} _{\mathrm{B}}}}=\sqrt{\mathrm{K} _{1} \mathrm{~K} _{2}} \end{aligned} $$
But this is not given as option
Therefore, we use the formula;
$$ \mathrm{v} _{\mathrm{e}}=\sqrt{2 \mathrm{G} \cdot \frac{4}{3} \pi \mathrm{R}^{2} \rho}=\mathrm{R} \sqrt{\rho}\left(\sqrt{\frac{8}{2} \pi \mathrm{G}}\right) $$
Hence, $\frac{\mathrm{v} _{\mathrm{A}}}{\mathrm{v} _{\mathrm{B}}}=\frac{\mathrm{R} _{\mathrm{A}}}{\mathrm{R} _{\mathrm{B}}} \cdot \sqrt{\frac{\rho _{\mathrm{A}}}{\rho _{\mathrm{B}}}}$
$$ =\mathrm{K} _{2} \sqrt{\mathrm{K} _{3}} $$
31. An object is thrown vertically upwards from the surface of the earth, with a speed of $v _{0}$. Its speed at a height $h(h«R)$ is $v$. The value of $v _{0}^{2}-v^{2}$ is:
(1) $\frac{\mathrm{GMh}}{\mathrm{R}(\mathrm{R}+\mathrm{h})}$
(2) $2 \mathrm{gRh}$
(3) $\operatorname{gh}\left(1-\frac{\mathrm{h}}{\mathrm{R}}\right)$
(4) $2 \operatorname{gh}\left(1-\frac{\mathrm{h}}{\mathrm{R}}\right)$
Show Answer
Correct answer: (4)
Solution:
Total initial energy $=$ Total find energy
$\therefore \frac{1}{2} \mathrm{mv} _{0}^{2}+\frac{-\mathrm{GMm}}{\mathrm{R}}=\frac{1}{2} \mathrm{mv}^{2}+\frac{-\mathrm{GMm}}{\mathrm{R}+\mathrm{h}}$
or $\quad \mathrm{v} _{0}^{2}-\mathrm{v}^{2}=2 \mathrm{GM}\left[\frac{1}{\mathrm{R}}-\frac{1}{\mathrm{R}+\mathrm{h}}\right]$
$$ \begin{aligned} & =2 \mathrm{GM}\left[\frac{\mathrm{h}}{\mathrm{R}(\mathrm{R}+\mathrm{h})}\right] \\ & =2 \mathrm{gR}^{2}\left(\frac{\mathrm{h}}{\mathrm{R}(\mathrm{R}+\mathrm{h})}\right) \quad\left(\mathrm{g}=\frac{\mathrm{GM}}{\mathrm{R}^{2}}\right) \\ & =2 \mathrm{gh}\left(\frac{\mathrm{R}}{\mathrm{R}+\mathrm{h}}\right) \\ & =2 \mathrm{gh}\left(\frac{1}{1+\frac{\mathrm{h}}{\mathrm{R}}}\right) \\ & =2 \mathrm{gh}\left(1+\frac{\mathrm{h}}{\mathrm{R}}\right)^{-1} \\ & =2 \mathrm{gh}\left(1-\frac{\mathrm{h}}{\mathrm{R}}\right) \quad(\because \mathrm{h}«\mathrm{R}) \end{aligned} $$
32 Four small spheres of masses 2 kg, 5 kg, 10 kg and 20 kg are placed respectively at the corners A, B, C and D of a square ABCD of side $6.414 \mathrm{~m}$. The binding energy of the system is:
(1) $4.4 \times 10^{-9} \mathrm{~J}$
(2) $4.0 \times 10^{-9} \mathrm{~J}$
(3) $3.7 \times 10^{-9} \mathrm{~J}$
(4) $3.0 \times 10^{-9} \mathrm{~J}$
Show Answer
Correct answer: (2)
Solution:
Let the side of the square be ’ $a$ ‘.
Binding Energy $=-($ Gravitational Potential Energy $)$
$$ =-U $$
Now,
$$ \begin{aligned} & -U=\frac{G}{a}\left[(2 \times 5)+\left(\frac{2 \times 10}{\sqrt{2}}\right)+(5 \times 10)+(2 \times 20)+\left(\frac{5 \times 20}{\sqrt{2}}\right)+(10 \times 20)\right] \\ & =\frac{G}{a}[10+10 \sqrt{2}+50+40+50 \sqrt{2}+200] \\ & =\frac{G}{a}[300+60 \sqrt{2}] \\ & =\frac{G}{a} \times 60(5+\sqrt{2}) \\ & =\frac{G \times 60}{6.414} \times 6.414=\mathrm{G} \times 60=6.67 \times 10^{-11} \times 60 \\ & \quad=4.0 \times 10^{-9} \mathrm{~J} \end{aligned} $$

33. Imagine that a body is projected from the surface of the earth with a speed equal to $40 \%$ of the escape speed from earth. What is the maximum height attained by the body? $(R=6400$ $\mathrm{km}$ is the radius of the earth).
(1) $1024 \mathrm{Km}$
(2) $5760 \mathrm{Km}$
(3) $12160 \mathrm{Km}$
(4) $12800 \mathrm{Km}$
Show Answer
Correct answer: (3)
Solution:
We have the formula for $h _{\text {max }}$ as:
$$ \mathrm{h} _{\max }=\frac{\mathrm{v} _{0}^{2}}{2 \mathrm{~g}-\left(\frac{\mathrm{v} _{0}^{2}}{\mathrm{R}}\right)} $$
(where $\mathrm{v} _{0}=$ velocity of projection from ground)
Here, $\mathrm{v} _{0}=40 \% \mathrm{v} _{\mathrm{e}}$
$$ \begin{aligned} = & 0.4 \times \sqrt{2 \mathrm{gR}} \\ \therefore \quad \mathrm{h} _{\max } & =\frac{0.16 \times 2 \mathrm{gR}}{2 \mathrm{~g}-0.16 \times 2 \mathrm{~g}} \\ & =\left(\frac{0.32}{2-0.32}\right)^{\mathrm{R}} \\ & =\left(\frac{0.32}{1.68}\right)^{\mathrm{R}} \\ & =1.9 \times 6400 \mathrm{Km} \\ & =12160 \mathrm{Km} \end{aligned} $$
34. Two bodies of masses $m _{1}$ and $m _{2}$ are placed at a distance $r$ apart. At certain point on the line joining $m _{1}$ and $m _{2}$, the gravitational field due to them is zero. The gravitational potential at this point is:
(1) $-\frac{\mathrm{G}}{\mathrm{r}} \sqrt{\mathrm{m} _{1}+\mathrm{m} _{2}+2 \mathrm{~m} _{1} \mathrm{~m} _{2}}$
(2) $-\frac{\mathrm{G}}{\mathrm{r}}\left(\mathrm{m} _{1}+\mathrm{m} _{2}+2 \sqrt{\mathrm{m} _{1} \mathrm{~m} _{2}}\right)$
(3) $-\frac{\mathrm{G}}{\mathrm{r}}\left(\sqrt{\mathrm{m} _{1}}+\sqrt{\mathrm{m} _{2}}+2 \sqrt{\mathrm{m} _{1} \mathrm{~m} _{2}}\right)$
(4) $-\frac{\mathrm{G}}{\mathrm{r}}\left(\mathrm{m} _{1}+\mathrm{m} _{2}+2 \mathrm{~m} _{1} \mathrm{~m} _{2}\right)$
Show Answer
Correct answer: (2)
Solution:
Let $\mathrm{I}=0$ at a distance of $x$ from $\mathrm{m} _{1}$
Here, $\frac{\mathrm{Gm} _{1}}{x^{2}}=\frac{\mathrm{GM} _{2}}{(\mathrm{r}-x)^{2}}$

or $\quad \frac{(\mathrm{r}-x)^{2}}{x^{2}}=\frac{\mathrm{m} _{2}}{\mathrm{~m} _{1}}$
or $\quad \frac{\mathrm{r}-x}{x}=\frac{\sqrt{\mathrm{m} _{2}}}{\sqrt{\mathrm{m} _{1}}}$
or $\quad \frac{\mathrm{r}}{\mathrm{x}}=1+\frac{\sqrt{\mathrm{m} _{2}}}{\sqrt{\mathrm{m} _{1}}} \quad$ or $\quad \frac{\mathrm{r}}{x}=\frac{\sqrt{\mathrm{m} _{1}}+\sqrt{\mathrm{m} _{2}}}{\sqrt{\mathrm{m} _{1}}}$
Hence, $x=\left[\frac{\sqrt{\mathrm{m} _{1}}}{\sqrt{\mathrm{m} _{1}}+\sqrt{\mathrm{m} _{2}}}\right] \mathrm{r} \hspace{40mm}. . . . . . . (1)$
$\therefore \mathrm{r}-x=\frac{\sqrt{\mathrm{m} _{2}} \mathrm{r}}{\sqrt{\mathrm{m} _{1}}+\sqrt{\mathrm{m} _{2}}} \hspace{40mm}. . . . . . . (2)$
The gravitational potential at the point where $\mathrm{I}=0$ is:
$\mathrm{V}=\mathrm{V} _{1}+\mathrm{V} _{2}$
or $\mathrm{V}=\frac{-\mathrm{Gm} _{1}}{x}+\frac{-\mathrm{Gm} _{2}}{\mathrm{r}-x}$
or $\mathrm{V}=-\mathrm{G}\left(\frac{\mathrm{m} _{1}}{x}+\frac{\mathrm{m} _{2}}{\mathrm{r}-x}\right)$
or $V=-G\left[\frac{m _{1}\left(\sqrt{m _{1}}+\sqrt{m _{2}}\right)}{\sqrt{m _{1} r}}+\frac{m _{2}\left(\sqrt{m _{1}}+\sqrt{m _{2}}\right)}{\sqrt{m _{2}} \mathrm{r}}\right]$ ( using equations (1) and (2) )
$$ \begin{aligned} & =\frac{-\mathrm{G}}{\mathrm{r}}\left[\sqrt{\mathrm{m} _{1}}\left(\sqrt{\mathrm{m} _{1}}+\sqrt{\mathrm{m} _{2}}\right)+\sqrt{\mathrm{m} _{2}}\left(\sqrt{\mathrm{m} _{1}}+\sqrt{\mathrm{m} _{2}}\right)\right] \\ & =\frac{-\mathrm{G}}{\mathrm{r}}\left[\mathrm{m} _{1}+\sqrt{\mathrm{m} _{1} \mathrm{~m} _{2}}+\mathrm{m} _{2}+\sqrt{\mathrm{m} _{1} \mathrm{~m} _{2}}\right] \\ & =-\frac{\mathrm{G}}{\mathrm{r}}\left[\mathrm{m} _{1}+\mathrm{m} _{2}+2 \sqrt{\mathrm{m} _{1} \mathrm{~m} _{2}}\right] \end{aligned} $$
35. A geo stationary satellite is orbiting the earth at a distance of $7 \mathrm{R}$ from the centre of the earth. ( $R$ is the radius of the earth). The time period of another satellite orbiting the earth at a height of $2.5 \mathrm{R}$ from the surface of the earth is:
(1) $9.592 \mathrm{Hrs}$
(2) $8.484 \mathrm{Hrs}$
(3) $4.796 \mathrm{Hrs}$
(4) $4.242 \mathrm{Hrs}$
Show Answer
Correct answer: (2)
Solution:
By Kepler’s law, $\mathrm{T}^{2} \propto \mathrm{r}^{3}$
$\therefore \frac{\mathrm{T} _{1}^{2}}{\mathrm{~T} _{2}^{2}}=\frac{\mathrm{r} _{1}^{3}}{\mathrm{r} _{2}^{3}}$
$$ \left(\mathrm{T} _{1}=24 \text { Hrs, } \mathrm{T} _{2}=?\right) $$
$\frac{(24)^{2}}{\mathrm{~T} _{2}^{2}}=\left(\frac{7 \mathrm{R}}{3.5 \mathrm{R}}\right)^{3}$
$$ \left(\mathrm{r} _{1}=7 \mathrm{R}, \mathrm{r} _{2}=2.5 \mathrm{R}+\mathrm{R}=3.5 \mathrm{R}\right) $$
$\therefore \quad \mathrm{T} _{2}^{2}=\frac{24 \times 24}{8}=3^{2} \times 8$
$\therefore \mathrm{T} _{2}=3 \times \sqrt{8}$
$$ =3 \times 2.808 $$
$$ =8.484 \mathrm{Hrs} $$
36. Imagine that the universal gravitational constant $(G)$ becomes time-dependent. For a particle, moving under such a gravitational field, which of the following quantities would be still conserved?
(1) total energy
(2) kinetic energy
(3) angular momentum
(4) linear momentum
Show Answer
Correct answer: (3)
Solution:
Though $G$ has become time dependent the gravitational force is still radial. Hence torque due to gravitational force is zero. The angular momentum would, therefore be still conserved.
37. Let $M _{S}$ and $M _{E}$ be mass of sun and earth. Given $\frac{M _{S}}{M _{E}}=3.2 \times 10^{5}$. Sun in nearly 400 times as far from moon as moon is from earth. The ratio of gravitational force on moon due to sun and earth is
(1) 1
(2) 2
(3) 400
(4) $10^{5}$
Show Answer
Correct answer: (2)
Solution:
$\mathrm{F} _{\mathrm{S}}=$ gravitational force due to sun on moon
$$ =G \frac{M _{S} M _{m}}{\left(r _{S m}\right)^{2}} $$
$\mathrm{F} _{\mathrm{E}}=$ gravitational force due to earth on moon
$=\mathrm{G} \frac{\mathrm{M} _{\mathrm{E}} \mathrm{M} _{\mathrm{m}}}{\left(\mathrm{r} _{\mathrm{Em}}\right)^{2}}$
$=\frac{F_{S}}{F_{E}}=(\frac{M _{S}}{M _{E}})(\frac{r _{E _{m}}}{r _{S m}})^{2}$
Given $\frac{M _{S}}{M _{E}}=3.2 \times 10^{5} ; \frac{r _{S m}}{r _{E m}}=400$
$\therefore \frac{\mathrm{F} _{\mathrm{S}}}{\mathrm{F} _{\mathrm{E}}}=\frac{3.2 \times 10^{5}}{(400)^{2}}=2$
38.

Figure shows a point mass $m$ fixed at origin $O$. A one dimensional rod $A B$ of length $L$ is placed along $x$-axis as shown. The linear mass density $\lambda$ of rod is
$$ \lambda=\lambda _{0} x $$
where $\lambda _{0}$ is a constant. The gravitational force $F$ on mass $m$ due to $\operatorname{rod} A B$ is
(1) $\frac{\mathrm{mG} \lambda _{0} \mathrm{~L}^{2}}{2\left(\mathrm{~L} _{0}+\frac{\mathrm{L}}{2}\right)^{2}}$
(2) $2.303 \mathrm{mG} \lambda _{0} \log \left(1+\frac{\mathrm{L}}{\mathrm{L} _{0}}\right)$
(3) $2.303 \mathrm{mG} \lambda _{0} \log \left(1+\frac{\mathrm{L} _{0}}{\mathrm{~L}}\right)$
(4) $\frac{\mathrm{mG} \lambda _{0} \mathrm{~L}^{2}}{2\left(\mathrm{~L}+\mathrm{L} _{0}\right)^{2}}$
Show Answer
Correct answer: (2)
Solution:

Consider a small element PQ of the rod, of length $\mathrm{d} x$, as shown in Fig. $\mathrm{dm}=$ mass of element $\mathrm{PQ}=\lambda \mathrm{d} x=\lambda x \mathrm{~d} x$
$\mathrm{dF}=$ gravitational force on mass $\mathrm{m}$ at $\mathrm{O}$ due to elements $\mathrm{PQ}$
$$ =\frac{\mathrm{Gmdm}}{x^{2}}=\operatorname{Gm} \lambda _{0} \frac{\mathrm{d} x}{x} $$
$\mathrm{F}=\int _{x=\mathrm{L} _{0}}^{\mathrm{L} _{0}+\mathrm{L}} \mathrm{dF}=\mathrm{Gm} \lambda _{0} \int _{\mathrm{L} _{0}}^{\mathrm{L} _{0}+\mathrm{L}} \frac{\mathrm{d} x}{x}=\mathrm{Gm} \lambda _{0} \ln \left(\frac{\mathrm{L} _{0}+\mathrm{L}}{\mathrm{L} _{0}}\right)$
$=2.303 \mathrm{Gm} \lambda _{0} \log \left(1+\frac{\mathrm{L}}{\mathrm{L} _{0}}\right)$
39. Three particle each of mass $M$ be on $x-y$ plane at three points having co-ordinates $(0,0)$. $(0, a) ;(a, 0)$. The net gravitational force on particle at $(0, a)$ is
(1) $\mathbf{F}=\frac{\mathrm{GM}^{2}}{\mathrm{a}^{2}}[\mathbf{i}+\mathbf{j}]$
(2) $\mathbf{F}=\frac{\mathrm{GM}^{2}}{\mathrm{a}^{2}}\left[\mathbf{i}+\frac{\mathbf{j}}{2}\right]$
(3) $\mathbf{F}=\frac{\mathrm{GM}^{2}}{\mathrm{a}^{2}}\left[\frac{\mathbf{i}}{2 \sqrt{2}}-\left(1+\frac{1}{2 \sqrt{2}}\right) \mathbf{j}\right]$
(4) $\mathbf{F}=\frac{\mathrm{GM}^{2}}{\mathrm{a}^{2}}\left[\frac{\mathbf{i}}{2 \sqrt{2}}+(1+2 \sqrt{2}) \mathbf{j}\right]$
Show Answer
Correct answer: (3)
Solution:
Fig. shows three particles each of mass $\mathrm{M}$ located at $\mathrm{O}, \mathrm{A}$ and $\mathrm{B}$.
We want net gravitational force on mass at $\mathrm{B}$.
$\mathbf{F} _{0}=$ gravitational force on $\mathrm{B}$ due to mass at $\mathrm{O}$.
$$ =\frac{\mathrm{GM}^{2}}{\mathrm{a}^{2}}(-\mathbf{j}) $$
$F _{A}=$ magnitude of gravitational force on $B$ due to mass $A$
$$ =\frac{\mathrm{GM}^{2}}{(\sqrt{2} \mathrm{a})^{2}}=\frac{\mathrm{GM}^{2}}{2 \mathrm{a}^{2}} $$

Resolving $\mathbf{F} _{\mathrm{A}}$ into rectangular components along $\mathrm{x}$ and $\mathrm{y}$-axis; we can write
$$ \begin{aligned} \mathbf{F} _{\mathrm{A}}= & \left(\frac{\mathrm{GM}^{2}}{2 \mathrm{a}^{2}} \cos 45\right) \mathbf{i}+\left(\frac{\mathrm{GM}^{2}}{2 \mathrm{a}^{2}} \sin 45^{0}\right)(-\mathbf{j}) \\ = & \frac{\mathrm{GM}^{2}}{\mathrm{a}^{2}}\left[\frac{\mathbf{i}}{2 \sqrt{2}}-\frac{\mathbf{i}}{2 \mathrm{r} 2}\right] \end{aligned} $$
$\mathbf{F}=$ net gravitational force on mass at point $\mathrm{B}$
$$ =\mathbf{F} _{0}+\mathbf{F} _{\mathrm{A}}=\frac{\mathrm{GM}^{2}}{\mathrm{a}^{2}}\left[\frac{\mathbf{i}}{2 \sqrt{2}}-\left(1+\frac{1}{2 \sqrt{2}}\right) \mathbf{j}\right] $$
40. Two particles $A$ and $B$ each of mass $2 m$ are fixed in their respective positions. $A$ third particle $O$ of mass $m$ is initially at $O$ and is free to move under the gravitational force of $A$ and $B$. The particle at $O$ is let go. The initial acceleration of $O$ is
(1) $\left(\frac{G m}{a^{2}}\right) \mathbf{i}$
(2) $\left(\frac{2 \mathrm{Gm}}{\mathrm{a}^{2}}\right) \mathbf{j}$
(3) $\left(\frac{\sqrt{3} G m}{a^{2}}\right)$ i
(4) $\left(\frac{\sqrt{3} \mathrm{Gm}}{2 \mathrm{a}^{2}}\right) \mathbf{j}$
Show Answer
Correct answer: (4)
Solution:
$\mathrm{OA}=\left[(\mathrm{a})^{2}+(\sqrt{3 \mathrm{a}})^{2}\right]^{1 / 2}=2 \mathrm{a}$
$\left|\mathbf{F} _{\mathrm{A}}\right|=\left|\mathbf{F} _{\mathrm{B}}\right|=\frac{2 \mathrm{Gm}^{2}}{(2 \mathrm{a})^{2}}=\frac{\mathrm{Gm}^{2}}{2 \mathrm{a}^{2}}$
Resolve $\mathbf{F} _{\mathrm{A}}$ and $\mathbf{F} _{\mathrm{B}}$ into rectangular components.
The new unbalanced force
$\mathbf{F}=\left(2 \mathrm{~F} _{\mathrm{A}} \cos \theta\right) \mathbf{j}=\frac{\sqrt{3}}{2}\left(\frac{\mathrm{Gm}^{2}}{\mathrm{a}^{2}}\right) \mathbf{j} \quad\left[\because \theta=30^{\circ}\right]$
The initial acceleration $\mathbf{a} _{0}$ is
$$ \mathbf{a} _{0}=\frac{\mathbf{F}}{\mathrm{m}}=\frac{\sqrt{3} \mathrm{Gm}}{2 \mathrm{a}^{2}} \mathbf{j} $$
41.
Equal masses, each $\mathrm{m}$; are placed at the corners of a square $\mathrm{OABC}$ of side a. The intensity of the net gravitational field, at $O$, is
(1) $\frac{2 \mathrm{Gm}}{\mathrm{a}^{2}} \mathbf{i}$
(2) $\frac{\mathrm{Gm}}{\mathrm{a}^{2}}[\mathbf{i}+\mathbf{j}]$
(3) $\frac{G m}{\sqrt{2} a^{2}}[\mathbf{i}+\mathbf{j}]$
(4) $\left(1+\frac{1}{2 \sqrt{2}}\right) \frac{\mathrm{Gm}}{\mathrm{a}^{2}}[\mathbf{i}+\mathbf{j}]$
Show Answer
Correct answer: (4)
Solution:
$$ \begin{gathered} \mathbf{I} _{\mathrm{A}}=\frac{\mathrm{Gm}}{\mathrm{a}^{2}}(\mathbf{i}) ; \mathbf{I} _{\mathrm{B}}=\frac{\mathrm{Gm}}{2 \mathrm{a}^{2}}\left[\frac{\mathbf{i}+\mathbf{j}}{\sqrt{2}}\right] \\ \mathbf{I} _{\mathrm{C}}=\frac{\mathrm{Gm}}{\mathrm{a}^{2}} \mathbf{j} \\ \mathbf{I}=\mathbf{I} _{\mathrm{A}}+\mathbf{I} _{\mathrm{B}}+\mathbf{I} _{\mathrm{C}} \\ =\frac{\mathrm{Gm}}{\mathrm{a}^{2}}\left[1+\frac{1}{2 \sqrt{2}}\right][\mathbf{i}+\mathbf{j}] \end{gathered} $$
42. Three identical point masses each of mass $m$ are located at the vertices of an equilateral triangle of side a. They revolve in a circular orbit circumscribing the triangle, maintaining their relative positions, under the influence of their gravitational force. The speed of each is
(1) $\sqrt{\frac{\mathrm{Gm}}{\mathrm{a}}}$
(2) $\sqrt{\frac{2 \mathrm{Gm}}{\mathrm{a}}}$
(3) $\sqrt{\frac{3 \mathrm{Gm}}{\mathrm{a}}}$
(4) $\sqrt{\frac{2 \mathrm{Gm}}{3 \mathrm{a}}}$
Show Answer
Correct answer: (1)
Solution:
Let $\mathrm{PQR}$ be the equilateral triangle side a. Let $\mathrm{O}$ be centeroid of the triangle. The circular orbit circumscribing the triangle is a circle of center $\mathrm{O}$ and radius $\mathrm{r}=\mathrm{OP}=\frac{\mathrm{a}}{\sqrt{3}}$.
Let $f=\frac{\mathrm{Gm}^{2}}{\mathrm{a}^{2}}$ be gravitational force on $\mathrm{P}$ due to mass at $\mathrm{Q}$ or $\mathrm{R}$. The net force on mass at
$$ \mathrm{P}=\mathrm{F}=\sqrt{3} \mathrm{f}=\sqrt{3} \frac{\mathrm{Gm}^{2}}{\mathrm{a}^{2}} $$
For circular orbit;
centripetal force $=$ net gravitational force
or $\frac{\mathrm{mv}^{2}}{(\mathrm{a} / \sqrt{3})}=\sqrt{3} \frac{\mathrm{Gm}^{2}}{\mathrm{a}^{2}}$

or $\quad v=\sqrt{\frac{G m}{a}}$
43. $O _{1}$ and $O _{2}$ are centers two identical spheres, each of mass M. $O _{1}$ and $O _{2}$ are a distance $2 d$ apart. A mass $m$ is released from rest at point $A$ as shown in Fig. $m$ moves under gravitational force of $O _{1}$ and $O _{2}$. The initial acceleration of mass $m$ is $a _{0}$. Its speed when it reach point $O$ is $\mathbf{v}$. Then
(1) $\mathrm{a} _{0}=\frac{\mathrm{GM}}{4 \mathrm{~d}^{2}} ; \mathrm{v}=\sqrt{\frac{\mathrm{GM}}{\mathrm{d}}}$
(2) $\mathrm{a} _{0}=\frac{\sqrt{3} \mathrm{GM}}{4 \mathrm{~d}^{2}} ; \mathrm{v}=\sqrt{\frac{2 \mathrm{GM}}{\mathrm{d}}}$
(3) $\mathrm{a} _{0}=\frac{\mathrm{GM}}{2 \sqrt{2} \mathrm{~d}^{2}} ; \mathrm{v}=\sqrt{\frac{\mathrm{GM}}{2 \mathrm{~d}}}$
(4) $\mathrm{a} _{0}=\frac{\sqrt{3} \mathrm{GM}}{2 \mathrm{~d}^{2}} ; \mathrm{v}=\sqrt{\frac{2 \mathrm{GM}}{\mathrm{d}}}$
Show Answer
Correct answer: (2)
Solution:
From Fig. $\mathrm{O} _{1} \mathrm{~A}=\mathrm{O} _{2} \mathrm{~A}=\sqrt{(\mathrm{d})^{2}+(\sqrt{3} \mathrm{~d})^{2}}=2 \mathrm{~d}$
$\mathrm{f}=$ gravitational force on mass $\mathrm{m}$; at a due to $\mathrm{O} _{1}$ or $\mathrm{O} _{2}$
$$ =\frac{\mathrm{GMm}}{(2 \mathrm{~d})^{2}}=\frac{\mathrm{GMm}}{4 \mathrm{~d}^{2}} $$
$F=$ net gravitational force on mass $m$ at $A=2 f \cos \theta=2\left(\frac{G M m}{4 d^{2}}\right) \times \frac{\sqrt{3}}{2}$
$$ =\frac{\sqrt{3} \mathrm{GMm}}{4 \mathrm{~d}^{2}} $$
$\mathrm{a} _{0}=$ initial acceleration of mass $\mathrm{m}$ at $\mathrm{A}=\frac{\mathrm{F}}{\mathrm{m}}$
$$ =\frac{\sqrt{3} \mathrm{GM}}{4 \mathrm{~d}^{2}} $$
$\mathrm{E} _{\mathrm{e}}=$ initial total energy of mass $\mathrm{m}$ at $\mathrm{A}$
$$ =-2\left[\frac{\mathrm{GMm}}{2 \mathrm{~d}}\right] $$
$\mathrm{E} _{\mathrm{f}}=$ Total final energy of mass $\mathrm{m}$ at $\mathrm{O}$
$$ =\frac{1}{2} \mathrm{mv}^{2}+\left(-\frac{2 \mathrm{GMm}}{\mathrm{d}}\right) $$
From law of conservation of energy, $\mathrm{E} _{\mathrm{e}}=\mathrm{E} _{\mathrm{f}}$
$\therefore \quad-\frac{2 \mathrm{GMm}}{2 \mathrm{~d}}=\frac{1}{2} \mathrm{mv}^{2}+\left(-\frac{2 \mathrm{GMm}}{\mathrm{d}}\right)$
or $\quad \frac{2 \mathrm{GM}}{2 \mathrm{~d}}=\frac{1}{2} \mathrm{v}^{2}$
or $\quad v=\sqrt{\frac{2 \mathrm{GM}}{\mathrm{d}}}$
44.
A thin wire of uniform linear density $\lambda$ is bent into a semi-circle of radius $R$. What is the intensity of gravitational field at center $O$ ?
(1) $\frac{2 \mathrm{GM}}{\mathrm{R}^{2}} \mathrm{j}$
(2) $\frac{2 \mathrm{GM}}{\pi \mathrm{R}^{2}} \mathrm{j}$
(3) $\frac{\sqrt{2} \mathrm{GM}}{\mathrm{R}^{2}} \mathrm{j}$
(4) $\frac{3 \mathrm{GM}}{2 \mathrm{R}^{2}} \mathbf{j}$
Show Answer
Correct answer: (2)
Solution:
Consider the semi-circle as made up of large number of point masses (identical). The magnitude of $\mathbf{d I}$ is same but direction is different. The total intensity $\mathbf{I}=\int \mathrm{d} \mathbf{I}$
$$ |\mathrm{d} \mathbf{I}|=\frac{\mathrm{G}(\lambda \mathrm{Rd} \theta)}{\mathrm{R}^{2}}=\left|\mathrm{d} \mathbf{I}^{\prime}\right| $$
Resolve $\mathrm{dI}$ and $\mathrm{d} \mathbf{I}^{\prime}$ into rectangular components along $\mathrm{x}$ and $\mathrm{y}-$ axis. The $\mathrm{x}-$ components cancel and $\mathrm{y}-$ component and up.
There resultant intensity I is along y-axis. Also
$$ \begin{aligned} |\mathbf{I}|= & 2 \int _{0}^{\pi / 2} \mathrm{dI} \cos \theta=\frac{2 \lambda \mathrm{G}}{\mathrm{R}} \int _{0}^{\pi / 2} \cos \theta \mathrm{d} \theta \\ & =\frac{2 \lambda \mathrm{G}}{\mathrm{R}}|\sin \theta| _{0}^{\pi / 2}=\frac{2 \lambda \mathrm{G}}{\mathrm{R}} \\ & =\frac{2(\pi \mathrm{R} \lambda) \mathrm{G}}{\pi \mathrm{R}^{2}}=\frac{2 \mathrm{GM}}{\pi \mathrm{R}^{2}} \\ \therefore \quad \mathbf{I} & =\frac{2 \mathrm{GM}}{\pi \mathrm{R}^{2}} \mathbf{j} \end{aligned} $$
45. Assume earth to be a uniform sphere of radius $6400 \mathrm{Km}$ and density $5.5 \mathrm{~g} / \mathrm{cc}$. A body dropped from a tower travels a distance of $19.6 \mathrm{~m}$ in $2 \mathrm{~s}$. Value of $G$ is
(1) $6.6 \times 10^{-8} \frac{\mathrm{Nm}^{2}}{\mathrm{~kg}^{2}}$
(2) $6.6 \times 10^{-11} \frac{\mathrm{Nm}^{2}}{\mathrm{~kg}^{2}}$
(3) $6.6 \times 10^{-11} \frac{\text { dyne }-\mathrm{cm}^{2}}{\mathrm{~g}^{2}}$
(4) $6.6 \times 10^{-10} \frac{\mathrm{Nm}^{2}}{\mathrm{~kg}^{2}}$
Show Answer
Correct answer: (2)
Solution:
Let ’ $\mathrm{g}$ ’ acceleration due to gravity on earth.
Given $\mathrm{u}=0 ; \mathrm{S}=19.6 \mathrm{~m} ; \mathrm{a}=\mathrm{g} ; \mathrm{t}=2 \mathrm{~s}$. Therefore
$$ \begin{aligned} & 19.6=\frac{1}{2} g \times(2)^{2} \\ & \text { or } \quad g=9.8 \mathrm{~ms}^{-2} \\ & M=\text { mass of earth }=\frac{4}{3} \pi R^{3} \rho \\ & \text { Now, } g=\frac{G M}{R^{2}} \\ & \therefore \quad \mathrm{G}=\frac{g R^{2}}{M}=\frac{g R^{2}}{\frac{4 \pi}{3} R^{3} \rho}=\frac{3 g}{4 \pi R \rho} \end{aligned} $$
Given $\rho=5.5 \mathrm{~g} / \mathrm{cc}=\frac{5.5 \times 10^{-3} \mathrm{Kg}}{\left(10^{-2} \mathrm{~m}\right)^{3}}=5.5 \times 10^{3} \mathrm{~kg} / \mathrm{m}^{3}$
$$ \mathrm{R}=6400 \mathrm{Km}=6.4 \times 10^{6} \mathrm{~m} $$
$$ \begin{aligned} \therefore \quad \mathrm{G} & =\frac{3 \times 9.8}{4 \times 3.14 \times\left(6.4 \times 10^{6}\right) \times 5.5 \times 10^{3}} \text { SI unit } \\ & =6.6 \times 10^{-11} \frac{\mathrm{Nm}^{2}}{\mathrm{~kg}^{2}} \end{aligned} $$
46. Consider earth to be a uniform sphere of radius $6400 \mathrm{~km}$. Given $1 \mathrm{kgf}=9.8 \mathrm{~N}$. Mass of earth is
(G=6.67 $\left.\times 10^{-7} \frac{\mathrm{Ncm}^{2}}{\mathrm{~kg}^{2}}\right)$
(1) $6.02 \times 10^{24} \mathrm{~kg}$
(2) $6.02 \times 10^{20} \mathrm{~kg}$
(3) $6.02 \times 10^{18} \mathrm{~kg}$
(4) $6.02 \times 10^{15} \mathrm{~kg}$
Show Answer
Correct answer: (1)
Solution:
$1 \mathrm{Kgf}=\mathrm{g}$ Newton $=9.8 \mathrm{~N}$
$\therefore \mathrm{g}=9.8 \frac{\mathrm{m}^{2}}{\mathrm{~s}}$
$\mathrm{G}=6.67 \times 10^{-7} \times 10^{-4} \frac{\mathrm{Nm}^{2}}{\mathrm{~kg}^{2}}=6.67 \times 10^{-11} \frac{\mathrm{Nm}^{2}}{\mathrm{~kg}}$
Let $\mathrm{M}$ be mass of earth and $\mathrm{R}=6400 \mathrm{Km}$ its radius.
$$ \begin{aligned} & \mathrm{G}=\frac{\mathrm{GM}}{\mathrm{R}^{2}} \quad \text { or } \quad \mathrm{M}=\frac{8 \mathrm{R}^{2}}{\mathrm{G}} \\ & \therefore \quad \mathrm{M}=\frac{9.8 \times\left(6.4 \times 10^{6}\right)}{6.67 \times 10^{-11}} \mathrm{~kg} \\ & \quad \simeq 6.02 \times 10^{24} \mathrm{~kg} \end{aligned} $$
47. Assume earth to be a uniform sphere of radius $\mathrm{R}$, mass $\mathrm{m}$, desntiy $\rho _{0} . \mathrm{g}$ is acceleration due to gravity on surface of earth. If earth is replaced by a sphere of same radius having a density variation as
$$ \boldsymbol{\rho}=\boldsymbol{\rho} _{0} \quad \mathbf{0} \leq \mathbf{r} \leq \frac{\mathbf{R}}{\mathbf{2}} $$
$$ \boldsymbol{\rho}=\boldsymbol{\rho} _{0} \mathbf{r} \quad \frac{\mathbf{R}}{\mathbf{2}} \leq \mathbf{r} \leq \mathbf{R} $$
The value of acceleration due to gravity on the surface would be
(1) $\mathrm{g}$
(2) $\frac{\mathrm{g}}{8}$
(3) $\sim 0.83 \mathrm{~g}$
(4) $\frac{\mathrm{g}}{8}[1+5.625 \mathrm{R}]$
Show Answer
Correct answer: (4)
Solution:
We know for present earth
$$ \begin{equation*} \mathrm{g}=\frac{\mathrm{GM}}{\mathrm{R}^{2}} \tag{1} \end{equation*} $$
Let $M _{1}$ and $M _{2}$ be mass of part of earth of radius $\frac{R}{2}$ and the part of earth radius varying from $\frac{R}{2}$ to $R$ respectively. Then
$$ \begin{aligned} M _{1}= & \frac{4 \pi}{3}\left(\frac{R}{2}\right)^{3} \rho _{0}=\frac{M}{8} \\ M _{2}= & \int _{R / 2}^{R} 4 \pi r^{2}\left(\rho _{0} r\right) d r=4 \pi \rho _{0} \int _{R / 2}^{R} r^{3} d r \\ & =4 \pi \rho _{0}\left[\frac{15 R^{4}}{64}\right]=\left(\frac{4 \pi}{3} R^{3} \rho _{0}\right)\left(\frac{45}{64} R\right) \\ & =\frac{45}{64} M R \end{aligned} $$
$M^{\prime}=$ The total mass of new earth
$$ =\mathrm{M} _{1}+\mathrm{M} _{2}=\frac{\mathrm{M}}{8}\left[1+\frac{45}{8} \mathrm{R}\right] $$
$$ =\frac{\mathrm{M}}{8}[1+5.625 \mathrm{R}] $$
$\mathrm{g}^{\prime}=$ Acceleration due to gravity on surface of new earth $=\frac{\mathrm{GM}^{\prime}}{\mathrm{R}^{2}}$
$$ \begin{aligned} & =\frac{\mathrm{GM}}{8 \mathrm{R}^{2}}[1+5.625 \mathrm{R}] \\ & =\frac{\mathrm{g}}{8}[1+5.625 \mathrm{R}] \end{aligned} $$
48. A hollow sphere has mass $M$, radius $R$. Choosing center of sphere at origin of co-ordinates and any diameter as $x$-axis, the graph giving variation of (i) intensity (I) of gravitational field & (2) gravitational potential (V) with distance $(x)$ from center of sphere is
(1)
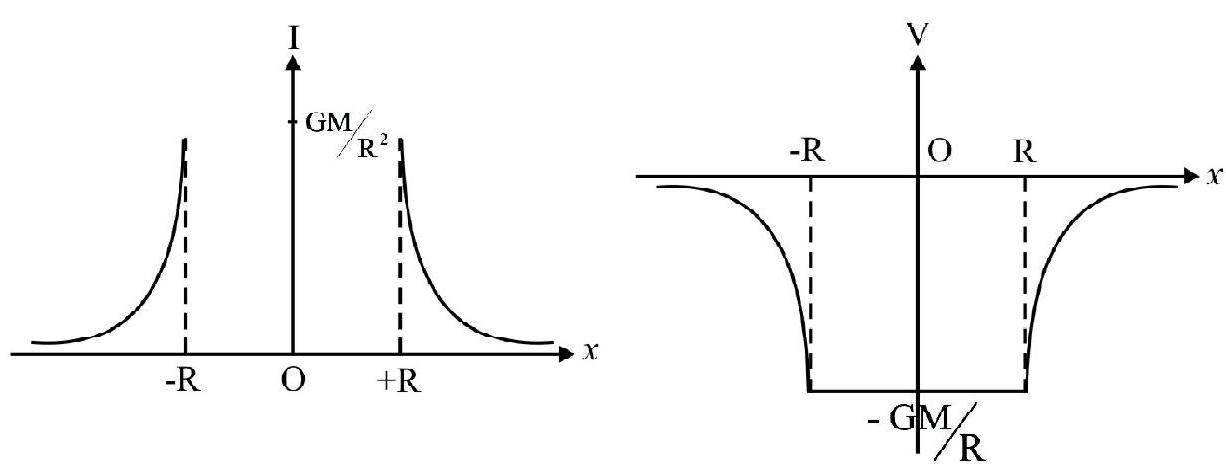
(2)
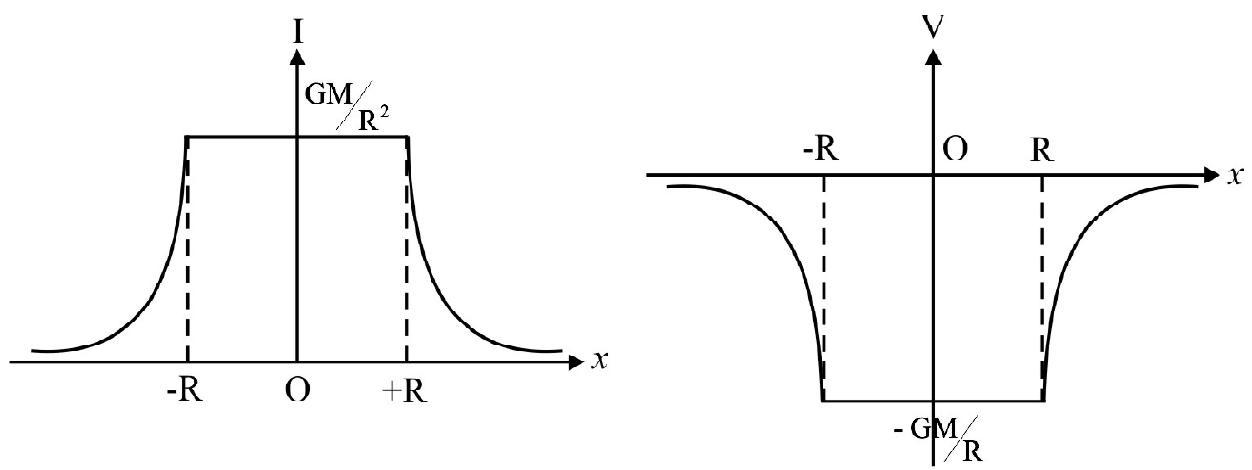
(3)
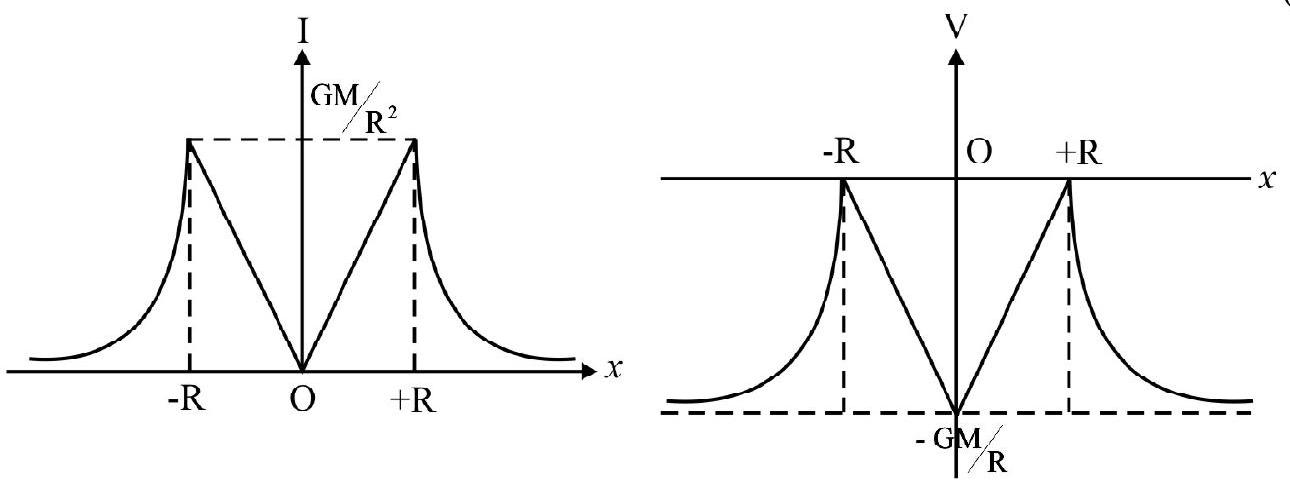
(4)
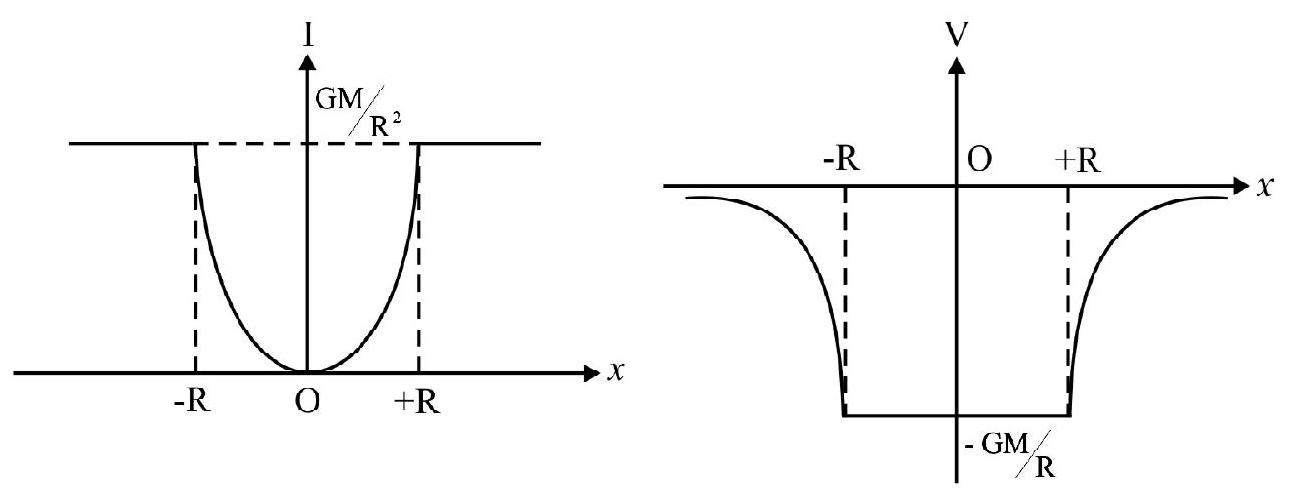
Show Answer
Correct answer: (1)
Solution:
Gravitational field is zero at all points inside hollow sphere. For points on surface and outside, sphere behaves as if entire mass is concentrated at center O. i.e. I $\propto \frac{1}{x^{2}}$
The gravitational potential $(\mathrm{V})$ is constant and equals potential on surface; for all points inside hollow sphere. For points outside $\mathrm{V} \propto \frac{1}{x}$.
49. A uniform solid sphere has mass $M$; radius $R$. Taking center of sphere as origin and any diameter as $x$-axis, the graph showing variation of (a) intensity of gravitational field (I) & (b) gravitational potential (V) with $x$ is:
(1)
Show Answer
Correct answer: (1)
Solution:
The gravitational field I at points inside solid sphere is
$$ \mathrm{I}=-\frac{\mathrm{GM}}{\mathrm{R}^{3}} x \quad \text { or } \quad \mathrm{I} \propto x $$
For points outside sphere
$$ \mathrm{I}=-\frac{\mathrm{GM}}{x^{2}} \quad \text { or } \quad \mathrm{I} \propto \frac{1}{x^{2}} $$
The gravitational potential $\mathrm{V}$ at points inside solid sphere is
$$ V=-G M \frac{\left(3 R^{2}-x^{2}\right)}{2 R^{3}} $$
For points outside solid sphere
$$ \mathrm{V}=\frac{-\mathrm{GM}}{x} $$
50. An object of mass $50 \mathrm{~kg}$ is taken from surface of earth to a height of $200 \mathrm{~km}$ above the surface of earth. Take radius of earth as $6400 \mathrm{~km}$. The mass and weight of object at this height is
( $\mathrm{g}$ on surface of earth $=9.8 \mathrm{~ms}^{-2}$ )
(1) $47.01 \mathrm{~kg}$ and $490 \mathrm{~N}$
(2) $50 \mathrm{~kg}$ and $490 \mathrm{~N}$
(3) $50 \mathrm{~kg}$ and $460.7 \mathrm{~N}$
(4) $50 \mathrm{~kg}$ and $484.8 \mathrm{~N}$
Show Answer
Correct answer: (3)
Solution:
Mass of body is independent of height (h) above surface of earth. Therefore mass of body remains $50 \mathrm{~kg}$. Let $g$ and $g _{h}$ be acceleration due to gravity on surface of earth and a height $h$ above surface of earth. Then
$$ \begin{aligned} & \frac{g _{h}}{g}=\left(\frac{R}{R+h}\right)^{2} \\ \therefore \quad & g _{h}=9.8\left(\frac{64}{66}\right)^{2} \mathrm{~ms}^{-2} \\ & =9.215 \mathrm{~ms}^{-2} \end{aligned} $$
The weight of body at height ’ $\mathrm{h}$ ’ $=\mathrm{mg} _{\mathrm{h}}$
$$ \begin{aligned} & =50 \times 9.215 \mathrm{~N} \\ & =460.7 \mathrm{~N} \end{aligned} $$
51. Two particle of mass $M$ and $4 M$ are placed a distance $3 d$ apart. The gravitational potential $V$ at a point, where the gravitational field due to the two masses is zero; is
(1) $\mathrm{V}=0$
(2) $V=-\frac{5 \mathrm{GM}}{3 \mathrm{~d}}$
(3) $V=-\frac{3 G M}{d}$
(4) $V=-\frac{5 G M}{2 d}$
Show Answer
Correct answer: (3)
Solution:
Fig. (a) show the given point masses. The gravitational field is zero at point $\mathrm{O} \cdot \mathrm{AO}=x=$ distance of point from mass $\mathrm{M}$. Then
$$ \begin{gathered} \frac{\mathrm{GM}}{x^{2}}=\frac{\mathrm{G} 4 \mathrm{M}}{(3 \mathrm{~d}-x)^{2}} \\ \text { or } \quad \frac{3 \mathrm{~d}-x}{x}=2 \text { or } x=\mathrm{d} \end{gathered} $$
Fig. (a)
The net gravitational potential at $\mathrm{O}$ is
$\mathrm{v}=-\frac{\mathrm{GM}}{\mathrm{d}}-\frac{\mathrm{G}(4 \mathrm{~m})}{2 \mathrm{~d}}$
$=-\frac{3 \mathrm{GM}}{\mathrm{d}}$
 Fig. (b)
Fig. (b)
52. Identical particles each of mass $m$ are initially at infinite distance apart. $W _{1}$ is work done in assembling arrangement (a). Now mass at point 1 is moved to the point shown in Fig. (b). $\mathrm{W} _{2}$ is additional work done. The ratio $\frac{\mathrm{W} _{1}}{\mathrm{~W} _{2}}$ is nearly

(1) 3
(2) $3 \sqrt{3}$
(3) 164
(4) $30 \sqrt{\frac{3}{2}}$
Show Answer
Correct answer: (3)
Solution:
$\mathrm{U} _{1}=\mathrm{W} _{1}=$ The gravitational P.E of system in Fig. $(\mathrm{a})=\frac{1}{2} \sum _{\mathrm{i}=1}^{4} \sum _{\mathrm{j}=1}^{4}-\frac{\mathrm{Gm}^{2}}{\mathrm{r} _{\mathrm{ij}}}$
$$ \mathrm{i} \neq \mathrm{j} $$
$$ =\frac{1}{2}\left[\left(\mathrm{U} _{12}+\mathrm{U} _{13}+\mathrm{U} _{14}\right)+\left(\mathrm{U} _{21}+\mathrm{U} _{23}+\mathrm{U} _{24}\right)+\left(\mathrm{U} _{31}+\mathrm{U} _{32}+\mathrm{U} _{34}\right)+\left(\mathrm{U} _{41}+\mathrm{U} _{42}+\mathrm{U} _{43}\right)\right] $$
$\mathrm{r} _{12}=\mathrm{r} _{13}=\mathrm{r} _{14}=\frac{\ell}{\sqrt{3}}$ and $\mathrm{r} _{23}=\mathrm{r} _{34}=\mathrm{r} _{24}=\ell$
$\therefore \quad \mathrm{W} _{1}=\left[\left(\mathrm{U} _{12}+\mathrm{U} _{13}+\mathrm{U} _{14}\right)+\left(\mathrm{U} _{23}+\mathrm{U} _{24}+\mathrm{U} _{34}\right)\right]$
$$ =-\mathrm{Gm}^{2}\left[\left(\frac{1}{\mathrm{r} _{12}}+\frac{1}{\mathrm{r} _{13}}+\frac{1}{\mathrm{r} _{14}}\right)+\left(\frac{1}{\mathrm{r} _{23}}+\frac{1}{\mathrm{r} _{24}}+\frac{1}{\mathrm{r} _{34}}\right)\right] $$
$$ =-\mathrm{Gm}^{2}\left[\frac{3 \sqrt{3}}{\ell}+\frac{3}{\ell}\right] \simeq-8.2 \frac{\mathrm{Gm}^{2}}{\ell} $$
$\mathrm{U} _{1}^{\prime}=\mathrm{W} _{1}^{\prime}=$ work done in forming assembly shown in Fig. (b)
Now, $\mathrm{r} _{12}=\mathrm{r} _{14}=\frac{\ell}{2} ; \mathrm{r} _{13}=\frac{\sqrt{3} \ell}{2} ; \mathrm{r} _{23}=\mathrm{r} _{34}=\mathrm{r} _{24}=\ell$
$\therefore \quad \mathrm{W} _{1}^{\prime}=-\mathrm{Gm}^{2}\left[\left(\frac{2}{\ell}+\frac{2}{\sqrt{3} \ell}+\frac{2}{\ell}\right)+\frac{3}{\ell}\right]=-8.15 \frac{\mathrm{Gm}^{2}}{\ell}$
$\mathrm{W} _{2}=$ additional work done in charging arrangement from Fig. (a) to Fig. (b) $=\mathrm{U} _{1}^{\prime}-\mathrm{U} _{1}=0.05 \frac{\mathrm{Gm}^{2}}{\ell}$
$\therefore \frac{\mathrm{W} _{1}}{\mathrm{~W} _{2}}=\frac{8.2}{0.05} \simeq 164$
53. A uniform sphere has mass $M$ and radius $R$. A part of radius $\frac{R}{2}$ as shown in Fig. is cut-out. A point mass $m$ is placed at a distance $x$ from center of original sphere. The gravitational force $\mathbf{F}$ on mass $m$ due to the remaining sphere is
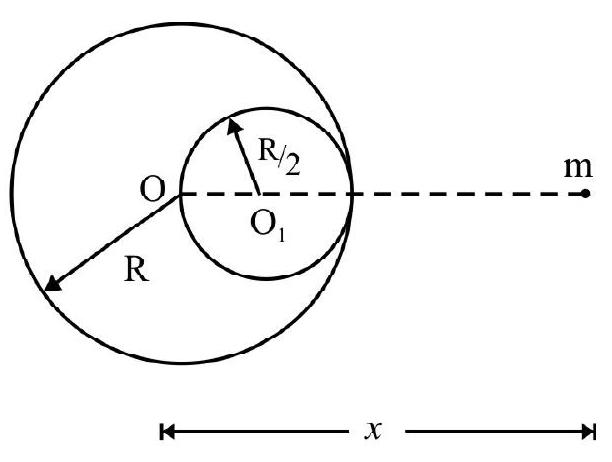
(1) $\mathrm{F}=\frac{3 \mathrm{GMm}}{4 x^{2}}$
(2) $\mathrm{F}=\frac{7 \mathrm{GMm}}{8 x^{2}}$
(3) $\mathrm{F}=\frac{\mathrm{GMm}}{x^{2}}\left[1-\frac{1}{8}\left(1-\frac{\mathrm{R}}{x}\right)^{-2}\right]$
(4) $\mathrm{F}=\frac{\mathrm{GMm}}{x^{2}}\left[1-\frac{1}{8}\left(1-\frac{\mathrm{R}}{2 x}\right)^{-2}\right]$
Show Answer
Correct answer: (4)
Solution:
Let $F _{1}$ be magnitude of gravitational force on $m$ due to complete sphere of radius $R$. Then
$$ \mathrm{F} _{1}=\frac{\mathrm{GMm}}{x^{2}} $$
Let $\mathrm{m}^{\prime}$ be mass of the sphere cut-out $\mathrm{m}^{\prime}=\frac{4 \pi}{3}\left(\frac{\mathrm{R}}{2}\right)^{3} \rho=\frac{\mathrm{M}}{8}$.
The distance of mass $\mathrm{m}$ from center $\mathrm{O} _{1}$ of the cut-out part is $\left(x-\frac{\mathrm{R}}{2}\right)$.
$\mathrm{F} _{2}=$ magnitude of gravitational force on $m$ due to cut-out part $=\frac{\mathrm{G} \frac{\mathrm{M}}{8} \mathrm{~m}}{\left(x-\frac{\mathrm{R}}{2}\right)^{2}}$
$\mathrm{F}=$ magnitude of net gravitational force on $\mathrm{m}$ due to the remaining part of sphere $=\mathrm{F} _{1}-\mathrm{F} _{2}$
$$ \begin{aligned} & =\frac{\mathrm{GMm}}{x^{2}}-\frac{\mathrm{GMm}}{8 x^{2}\left(1-\frac{\mathrm{R}}{2 x}\right)^{2}} \\ & =\frac{\mathrm{GMm}}{x^{2}}\left[1-\frac{1}{8}\left(1-\frac{\mathrm{R}}{2 x}\right)^{-2}\right] \end{aligned} $$
54. Fig. shows two concentric spherical shells having mass $M$ and $2 M$. Their radii are $R$ and 2R. The graph showing variation of gravitational potential $\mathrm{V}$ with $x$ is
(1)
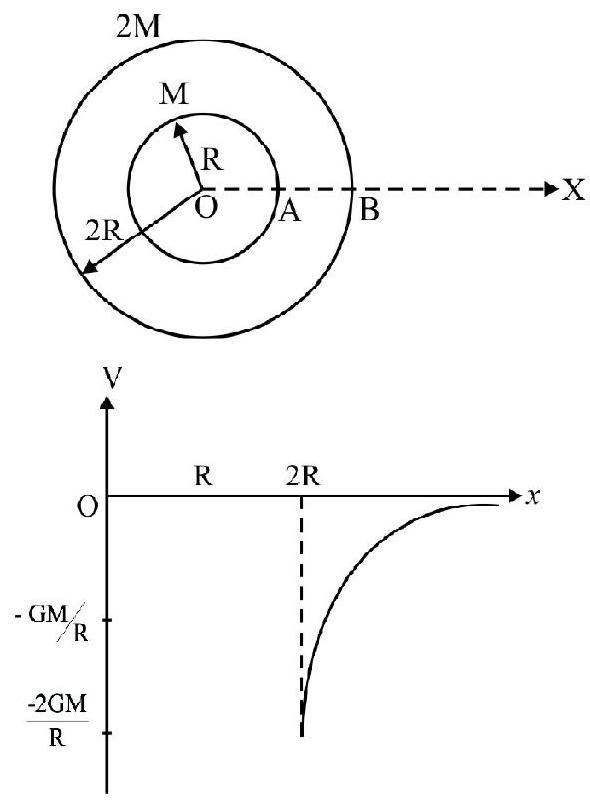 (2)
(2)
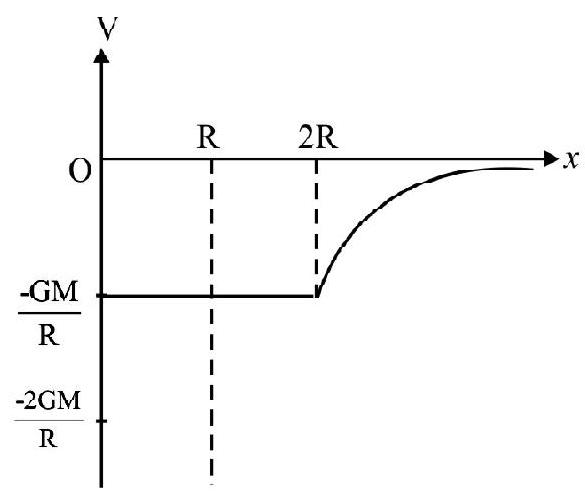 (3)
(3)
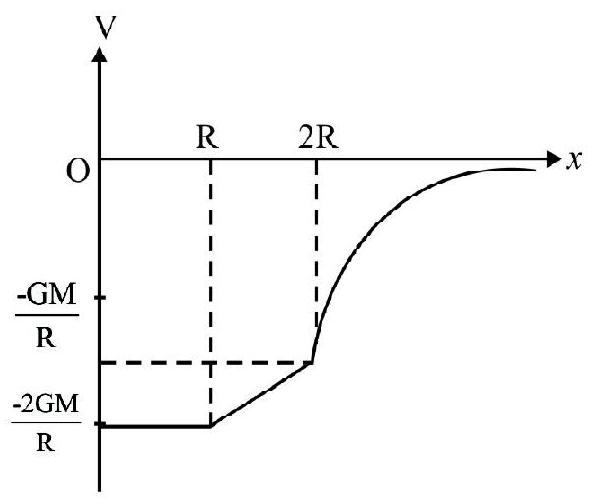 (4)
(4)
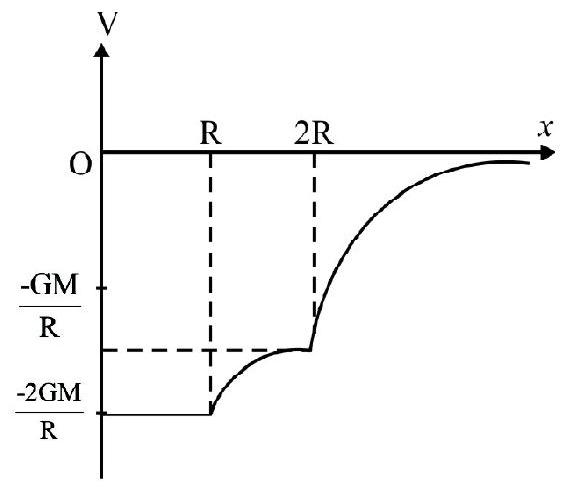
Show Answer
Correct answer: (4)
Solution:
(i) For points $0 \leq x \leq \mathrm{R}$; (internal points for both shells)
$$ \mathrm{V}=\mathrm{V} _{1}+\mathrm{V} _{2} $$
$\mathrm{V} _{1}=$ potential at internal point due to inner shell $=-\frac{\mathrm{GM}}{\mathrm{R}}$
$V _{2}=$ potential at internal point due to outer shell $=-\frac{G(2 M)}{2 R}=-\frac{G M}{R}$
$$ \therefore \mathrm{V}=-\frac{2 \mathrm{GM}}{\mathrm{R}} $$
Therefore, $\mathrm{V}$ is constant $\left(=\frac{-2 \mathrm{GM}}{\mathrm{R}}\right)$ for $0 \leq x \leq \mathrm{R}$
(ii) For points $\mathrm{R} \leq x \leq 2 \mathrm{R}$. (points outside inner shell but inside outer shell), the new potential $\mathrm{V}$ is
$$ \mathrm{V}=-\frac{\mathrm{GM}}{x}-\frac{\mathrm{G}(2 \mathrm{M})}{2 \mathrm{R}} $$
$$ =-\frac{\mathrm{GM}}{x}-\frac{\mathrm{GM}}{\mathrm{R}} $$
For point on surface of outer shell $x=2 \mathrm{R}$
$\therefore \quad \mathrm{V}=-\frac{\mathrm{GM}}{2 \mathrm{R}}-\frac{\mathrm{GM}}{\mathrm{R}}=-\frac{3 \mathrm{GM}}{2 \mathrm{R}}$
Therefore, $\mathrm{V}$ increases non-linearly from
$\mathrm{V}=\frac{-2 \mathrm{GM}}{\mathrm{R}}$, at $x=\mathrm{R}$, to $\mathrm{V}=\frac{-3 \mathrm{GM}}{2 \mathrm{R}}$, at $x=2 \mathrm{R}$
(iii) For $x>2 \mathrm{R}$; the point is external point for both shells; therefore
$$ \mathrm{V}=-\frac{\mathrm{G}(3 \mathrm{M})}{x} $$
55. Two hollow concentric spheres have masses M and 2 M. There radii are $R$ and $2 R$ as shown in Fig. The graph showing variation of intensity of gravitational field with $x$ is
(1)
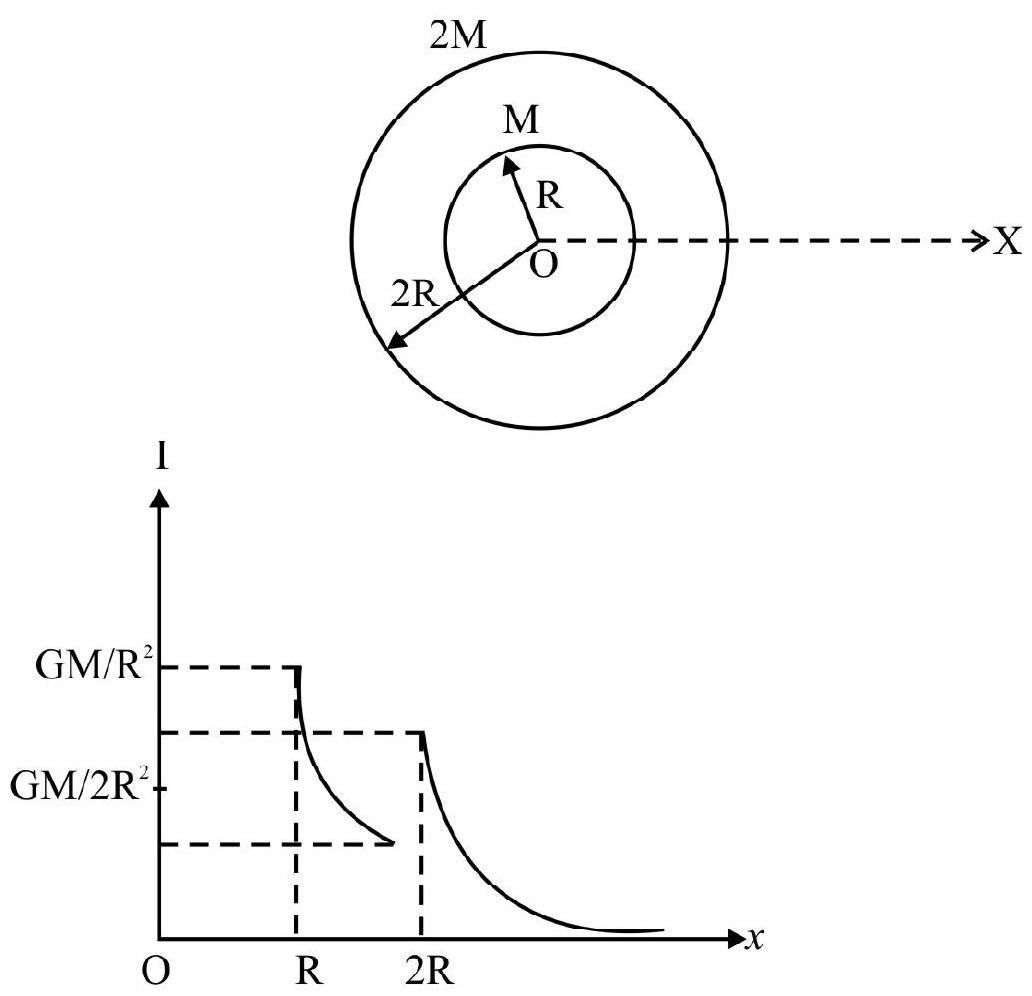
(2)
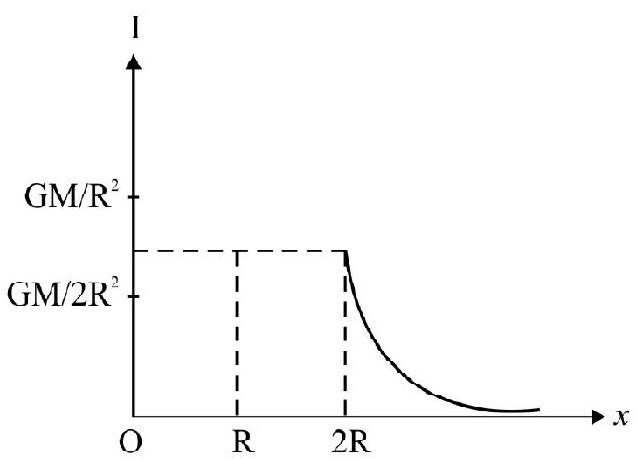
(3)
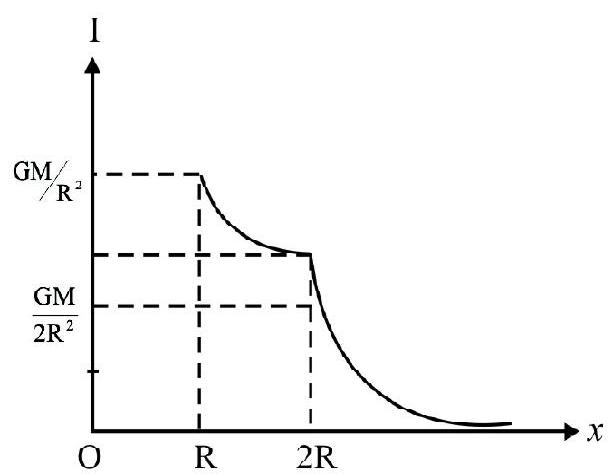
(4)
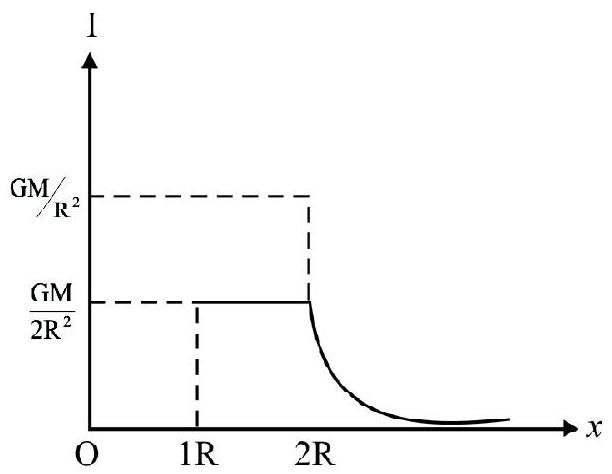
Show Answer
Correct answer: (1)
Solution:
(i) For points $0<x<\mathrm{R}$; the points are inside both hollow spheres, the intensity of gravitational field due to each sphere is zero.
(ii) For points $\mathrm{R}<x<2 \mathrm{R}$, the points are outside inner sphere but inside outer sphere. The intensity $\mathrm{I} _{1}$ due to inner sphere various as $\frac{1}{x^{2}}$. The intensity $I _{2}$ due to outer sphere is zero. At point on the inner surface of outer sphere; the resultant intensity I is
$$ \mathrm{I}=\frac{\mathrm{GM}}{(2 \mathrm{R})^{2}}=\frac{\mathrm{GM}}{4 \mathrm{R}^{2}} $$
However for point on outer surface of outer sphere the intensity I is
$$ \begin{aligned} I= & \frac{G M}{(2 R)^{2}}+\frac{G(2 M)}{(2 R)^{2}} \\ & =\frac{G M}{4 R^{2}}+\frac{G M}{2 R^{2}}=\frac{3}{4} \frac{G M}{R^{2}} \end{aligned} $$
For points $x>2 \mathrm{R}$;
$$ \mathrm{I}=\frac{\mathrm{G}(3 \mathrm{M})}{x^{2}} $$
56. A rocket of mass $10^{3} \mathrm{~kg}$ is fired vertically upwards from surface of earth with an initial speed of $6 \mathrm{~km} / \mathrm{s} . \quad \mathrm{g}=9.8 \mathrm{~ms}^{-2}, \mathrm{R}=$ radius of earth $=6400 \mathrm{~km}$. The maximum vertical height attained by rocket is
(1) $\sim 1840 \mathrm{~km}$
(2) $\sim 2000 \mathrm{~km}$
(3) $\sim 2580 \mathrm{~km}$
(4) $\sim 3580 \mathrm{~km}$
Show Answer
Correct answer: (3)
Solution:
$\mathrm{E} _{\mathrm{i}}=$ Total initial energy of rocket
$$ =\frac{1}{2} \mathrm{mv}^{2}+\left(-\frac{\mathrm{GMm}}{\mathrm{R}}\right) $$
Let $h$ be maximum vertical height attained by rocket. The instantaneous speed of rocket is zero here and its distance from center of earth $=\mathrm{R}+\mathrm{h}$.
Therefore $\mathrm{E} _{\mathrm{f}}=$ Total final energy of rocket.
$$ =0+\left(-\frac{\mathrm{GMm}}{\mathrm{R}+\mathrm{h}}\right) $$
From law of conservation of energy, $\mathrm{E} _{\mathrm{i}}=\mathrm{E} _{\mathrm{f}}$
$\frac{1}{2} \mathrm{mv}^{2}=\frac{\mathrm{GMm}}{\mathrm{R}}=\frac{\mathrm{GMm}}{\mathrm{R}+\mathrm{h}}$
or $\quad \frac{1}{2} \mathrm{mv}^{2}=\mathrm{GMm}\left[\frac{1}{\mathrm{R}}-\frac{1}{\mathrm{R}+\mathrm{h}}\right]$
or $\quad \mathrm{v}^{2}=2 \mathrm{GM}\left[\frac{\mathrm{h}}{\mathrm{R}(\mathrm{R}+\mathrm{h})}\right]$
$=\frac{2 g R^{2} h}{2(R+h)}=\frac{2 g h R}{(R+h)}$
$\therefore\left(6 \times 10^{3}\right)^{2}=\frac{2 \times 9.8 \mathrm{~h} \times 6.4 \times 10^{6}}{\left(6.4 \times 10^{6}+\mathrm{h}\right)}$
$\therefore \mathrm{h} \approx 2.85 \times 10^{6} \mathrm{~m}$
$=2.58 \times 10^{3} \mathrm{~km}$
$\sim 2580 \mathrm{~km}$
57. A meteorite is at rest at a height of $9 R$ above the surface of earth. On its own it starts moving towards earth. The speed (v) with which meteorite would hit earth is
$(R=$ radius of earth $)$
(1) $\frac{2}{3} \sqrt{2 \mathrm{gR}}$
(2) $\sqrt{\frac{\mathrm{gR}}{10}}$
(3) $3 \sqrt{\frac{8 \mathrm{R}}{5}}$
(4) $\sqrt{8 \mathrm{R}}$
Show Answer
Correct answer: (3)
Solution:
Let $\mathrm{m}$ be mass of meteorite and $\mathrm{M}$ be mass of earth. $\mathrm{E} _{\mathrm{i}}=$ The total initial energy of meteorite $=-\frac{\mathrm{GMm}}{10 \mathrm{R}}$. Let $\mathrm{v}$ be the speed with which meteorite hits earth. $\mathrm{E} _{\mathrm{f}}=$ The total final energy of meteorite $=$ $\frac{1}{2} \mathrm{mv}^{2}+\left(-\frac{\mathrm{GMm}}{\mathrm{R}}\right)$
From law of conservation of energy; $\mathrm{E} _{\mathrm{i}}=\mathrm{E} _{\mathrm{f}}$
$$ -\frac{\mathrm{GMm}}{10 \mathrm{R}}=\frac{1}{2} \mathrm{mv}^{2}-\frac{\mathrm{GMm}}{\mathrm{R}} $$
or $\quad \frac{9}{10} \frac{\mathrm{GMm}}{\mathrm{R}}=\frac{1}{2} \mathrm{mv}^{2}$
or $\quad \mathrm{v}=\sqrt{\frac{9}{5} \frac{\mathrm{GM}}{\mathrm{R}}}=3 \sqrt{\frac{\mathrm{gR}^{2}}{5 \mathrm{R}}}$ $\simeq 3 \sqrt{\frac{8 \mathrm{R}}{5}}$
58. A satellite of mass $m$ is moving in a circular orbit at a height $h$ above surface of earth $M$ and $R$ denote mass and radius of earth respectively. Due to friction satellite starts losing energy at a constant rate $k$. The time taken by satellite to fall on earth is
(1) $\frac{\mathrm{gRhm}}{2 \mathrm{k}(\mathrm{R}+\mathrm{h})}$
(2) $\frac{\mathrm{ghm}}{\mathrm{k}(\mathrm{R}+\mathrm{h})}$
(3) $\frac{g R^{2} h m}{\mathrm{k}(\mathrm{R}+\mathrm{h})}$
(4) $\frac{\mathrm{gRhm}}{\mathrm{k}\left(\mathrm{R}^{2}+\mathrm{h}\right)}$
Show Answer
Correct answer: (1)
Solution:
Let $\mathrm{E}$ be the total energy of satellite when $\mathrm{r}$ is the instantaneous radius of its circular path around earth. We know
$$ \mathrm{E}=-\frac{\mathrm{GMm}}{2 \mathrm{r}} \quad\left[\text { off T.E }=\frac{1}{2} \mathrm{P} . \mathrm{E}\right] $$
$\therefore \frac{\mathrm{dE}}{\mathrm{dt}}=\frac{\mathrm{GMm}}{2 \mathrm{r}^{2}}\left(\frac{\mathrm{dr}}{\mathrm{dt}}\right)$
Given $\frac{\mathrm{dE}}{\mathrm{dt}}=-\mathrm{k}$; therefore
$$ \mathrm{dt}=-\left[\frac{\mathrm{GMm}}{2 \mathrm{k}}\left(\frac{\mathrm{dr}}{\mathrm{r}^{2}}\right)\right] $$
Integrating,
$$ \mathrm{t}=\int _{0}^{\mathrm{t}} \mathrm{dt}=-\frac{\mathrm{GMm}}{2 \mathrm{k}} \int _{\mathrm{R}+\mathrm{h}}^{\mathrm{R}} \frac{\mathrm{dr}}{\mathrm{r}^{2}}=\frac{\mathrm{GMmh}}{2 \mathrm{k}(\mathrm{R}+\mathrm{h}) \mathrm{R}}=\frac{\mathrm{gRhm}}{2 \mathrm{k}(\mathrm{R}+\mathrm{h})} \quad\left(\because \mathrm{GM}=\mathrm{gR}^{2}\right) $$
59. Two stars each of mass $3 \times 10^{30} \mathrm{~kg}$ are initially $10^{9} \mathrm{~km}$ apart. Their speeds at this distance apart are negligible. They start moving towards one another under their gravitational force. The speed $(v)$ of each star when they collide is
(Radius of each star $=10^{5} \mathrm{~km}, \mathrm{G}=6.67 \times 10^{-11} \mathrm{Nm}^{2} \mathrm{~kg}^{-2}$ )
(1) $8.96 \times 10^{4} \mathrm{~km} / \mathrm{s}$
(2) $4.48 \times 10^{4} \mathrm{~km} / \mathrm{s}$
(3) $6 \times 10^{5} \mathrm{~km} / \mathrm{s}$
(4) $4.48 \times 10^{6} \mathrm{~km} / \mathrm{s}$
Show Answer
Correct answer: (2)
Solution:
(a)

Fig. (a) shows initial position of stars. $\mathrm{E} _{\mathrm{i}}$, the total initial energy $=\frac{\mathrm{GM}^{2}}{\mathrm{r}} \hspace{40mm}. . . . . . . (1)$
Fig. (b) shows the position when stars just collide with one another. Let $\mathrm{v}$ be speed of each star at this moment. Then $\mathrm{E} _{\mathrm{f}}=$ The total find energy
$$ \begin{equation*} =2\left(\frac{1}{2} \mathrm{Mv}^{2}\right)+\left(-\frac{\mathrm{GM}^{2}}{2 \mathrm{R}}\right) \tag{2} \end{equation*} $$
From law of conservation of energy $\mathrm{E} _{\mathrm{i}}=\mathrm{E} _{\mathrm{f}}$
$\therefore-\frac{\mathrm{GM}^{2}}{\mathrm{r}}=\mathrm{Mv}^{2}-\frac{\mathrm{GM}^{2}}{2 \mathrm{R}}$
or $\quad \mathrm{v}^{2}=\mathrm{GM}\left[\frac{1}{2 \mathrm{R}}-\frac{1}{\mathrm{r}}\right]$
$$ =6.67 \times 10^{-11} \times 3 \times 10^{3}\left[\frac{1}{2 \times 10^{8}}-\frac{1}{10^{12}}\right] $$
or
$$ \begin{aligned} & \mathrm{v} \simeq 4.48 \times 10^{7} \mathrm{~ms}^{-1} \\ & =4.48 \times 10^{4} \mathrm{~km} / \mathrm{s} \end{aligned} $$
60. A space vehicle of mass $m$ approaches a planet of mass $M$ and radius $r$. The space vehicle has a speed (linear) $v$, when it is very-very far off from the planet. If the space vehicle had moved along a straight line path it would have missed the center of planet by a distance $R$. If
space vehicle just misses the surface of planet, then
(1) $\mathrm{R}=\frac{\mathrm{GMv}}{2 \mathrm{r}}$
(2) $\mathrm{R}=\frac{\mathrm{r}}{\mathrm{v}}\left[\mathrm{v}^{2}+\frac{2 \mathrm{GM}}{\mathrm{r}}\right]^{1 / 2}$
(3) $\mathrm{R}=\frac{\mathrm{r}^{2}}{\mathrm{v}}\left[\mathrm{v}^{2}+\frac{2 \mathrm{GM}}{\mathrm{r}}\right]$
(4) $\mathrm{R}=\mathrm{vr}\left[\mathrm{v}^{2}+\frac{2 \mathrm{GM}}{\mathrm{r}}\right]^{1 / 2}$
Show Answer
Correct answer: (2)
Solution:
Let $\mathrm{V}$ be the speed of space vehicle as it just misses the planet. From law of conservation of energy.
Total initial energy $=$ Total final energy
$$ \begin{equation*} \frac{1}{2} \mathrm{mv}^{2}+0=\frac{1}{2} \mathrm{mV}^{2}+\left(-\frac{\mathrm{GMm}}{\mathrm{r}}\right) \tag{1} \end{equation*} $$
The motion of space vehicle is under gravitational force of planet on vehicle. Regarding planet and space vehicle as one system, there is no external force and therefore no external torque. The angular momentum of system is conserved. Therefore
$$ \begin{equation*} \mathrm{mvR}=\mathrm{mVr} \quad \text { or } \quad \mathrm{V}=\mathrm{v}\left(\frac{\mathrm{R}}{\mathrm{r}}\right) \tag{2} \end{equation*} $$
From eqns. (1) and (2) we have
$$ \frac{1}{2} \mathrm{mv}^{2}=\frac{1}{2} \mathrm{mv}^{2}\left(\frac{\mathrm{R}}{\mathrm{r}}\right)^{2}-\frac{\mathrm{GMm}}{\mathrm{r}} $$
or $\quad R^{2}=\frac{r^{2}}{v^{2}}\left[v^{2}+\frac{2 G M}{r}\right]$
$\therefore \quad \mathrm{R}=\frac{\mathrm{r}}{\mathrm{v}}\left[\mathrm{v}^{2}+\frac{2 \mathrm{GM}}{\mathrm{r}}\right]^{1 / 2}$
61. A rocket of mass $m$ is fired vertically upwards from earth with an initial speed $v _{0}$. It looses $\mathbf{2 5 \%}$ of its initial energy in crossing earth’s atmosphere. Neglecting the height of earth’s atmosphere; the maximum height to which rocket rises is
( $g$ = acceleration due to gravity on surface of earth, $R=$ radius of earth)
(1) $\frac{3 v _{0}^{2}}{8 \mathrm{gR}}$
(2) $\frac{\mathrm{R}}{\left(\frac{8 \mathrm{gR}}{3 \mathrm{v} _{0}^{2}}-1\right)}$
(3) $\frac{\mathrm{R}}{\left(\frac{3 \mathrm{v} _{0}^{2}}{8 \mathrm{gR}}-1\right)}$
(4) $\left(\frac{3 \mathrm{v} _{0}^{2}}{8 \mathrm{gR}}-1\right)$
Show Answer
Correct answer: (2)
Solution:
$E=$ initial K.E energy of rocket $=\frac{1}{2} \mathrm{mv} _{0}^{2}$
$\mathrm{E}^{\prime}=\mathrm{K} . \mathrm{E}$ of rocket as it emerges out of the atmosphere around earth $=\mathrm{E}-\frac{\mathrm{E}}{4}=\frac{3}{4} \mathrm{E}$
$\frac{3}{4}\left(\frac{1}{2} \mathrm{mv} _{0}^{2}\right)=$ Work done against gravity of earth, in rising to height $\mathrm{h}$
$$ =\int _{\mathrm{R}}^{\mathrm{R}+\mathrm{h}}-\frac{\mathrm{GMm}}{x^{2}} \mathrm{~d} x=\mathrm{GMm}\left[\frac{1}{\mathrm{R}}-\frac{1}{\mathrm{R}+\mathrm{h}}\right] $$
or $\quad \frac{3}{8} \mathrm{mv} _{0}^{2}=\frac{\mathrm{GMmh}}{\mathrm{R}(\mathrm{R}+\mathrm{h})}=\frac{\mathrm{gR}^{2} \mathrm{mh}}{\mathrm{R}(\mathrm{R}+\mathrm{h})}$
or $\quad \frac{3 \mathrm{v} _{0}^{2}}{8}=\frac{\mathrm{gRh}}{(\mathrm{R}+\mathrm{h})}$
or $\frac{\mathrm{R}+\mathrm{h}}{\mathrm{h}}=\frac{8 \mathrm{gR}}{3 \mathrm{v} _{0}^{2}}$
$$ \frac{\mathrm{R}}{\mathrm{h}}=\left(\frac{8 \mathrm{gR}}{3 \mathrm{v} _{0}^{2}}-1\right) $$
$\therefore \mathrm{h}=\frac{\mathrm{R}}{\left(\frac{8 \mathrm{gR}}{3 \mathrm{v} _{0}^{2}}-1\right)}$
62. A planet is spherical in shape having mass $M$; radius $R$ and uniform density $\rho$. A satellite of mass $m$ is moving around planet in an orbit of radius nearly equal to $R$. The time period of the satellite is:
(1) $\mathrm{T} \propto \mathrm{R}^{3 / 2}$
(2) $\mathrm{T} \propto \mathrm{R}^{1 / 2}$
(3) $\mathrm{T} \propto \mathrm{R}^{0}$
(4) $\mathrm{T} \propto \mathrm{R}^{-1 / 2}$
Show Answer
Correct answer: (3)
Solution:
For a circular orbit of radius $r \simeq R$;
$$ \frac{\mathrm{GMm}}{\mathrm{R}^{2}}=\frac{\mathrm{mv}^{2}}{\mathrm{R}} $$
$\mathrm{v}=$ velocity of satellite in orbit. Let $\mathrm{T}$ be time period of satellite in orbit. Then $\mathrm{T}=\frac{2 \pi \mathrm{R}}{\mathrm{v}}$
$\therefore \frac{\mathrm{GMm}}{\mathrm{R}^{2}}=\frac{\mathrm{m}}{\mathrm{R}}\left(\frac{2 \pi \mathrm{R}}{\mathrm{T}}\right)^{2}$
or $\quad \mathrm{T}=\frac{2 \pi \mathrm{R}^{3 / 2}}{\sqrt{\mathrm{GM}}}$
Also $M=\frac{4 \pi}{3} R^{3} \rho$. Therefore,
$$ \begin{gathered} \mathrm{T}=\frac{2 \pi \mathrm{R}^{3 / 2}}{\sqrt{\mathrm{G} \frac{4 \pi}{3} \mathrm{R}^{3} \rho}} \\ =\sqrt{\frac{3 \pi}{\mathrm{G} \rho}} \end{gathered} $$
$\mathrm{T}$ is independent of $\mathrm{R}$.
63. If law of gravitation changes and gravitational force is given by
$$ \mathbf{F}=\frac{\mathrm{C}}{\mathrm{r}^{\mathrm{n}}} \hat{\mathbf{r}} $$
where $C$ is a constant. Consider a particle of mass $m$ moving in a circular orbit of radius $r$ around another mass $M$. The time period $T$ of $m$ is
(1) $T \propto r^{n / 2}$
(2) $\mathrm{T} \propto \mathrm{r}^{(n+1) / 2}$
(3) $\mathrm{T} \propto \mathrm{r}^{-(n+1) / 2}$
(4) $\mathrm{T} \propto \mathrm{r}^{(n-1) / 2}$
Show Answer
Correct answer: (2)
Solution:
Let $v$ be the speed of mass $m$ when it is moving in a circular orbit of radius $r$. Then
$$ \begin{array}{r} \frac{\mathrm{mv}^{2}}{\mathrm{r}}=\frac{\mathrm{C}}{\mathrm{r}^{\mathrm{n}}} \\ \text { or } \quad \mathrm{v}^{2}=\frac{\mathrm{C}}{\mathrm{mr}^{\mathrm{n}-1}} \tag{1} \end{array} $$
The time period $\mathrm{T}$ of mass $\mathrm{m}$ is
$$ \mathrm{T}=\frac{2 \pi \mathrm{r}}{\mathrm{v}} $$
$$ \begin{align*} & =\frac{2 \pi r}{\sqrt{\frac{C}{m}} r^{-(n-1) / 2}} \\ & =2 \pi \sqrt{\frac{m}{C}} r^{(n+1) / 2} \tag{2} \end{align*} $$
$\therefore \mathrm{T} \propto \mathrm{r}^{(n+1) / 2}$
64. Earth revolves around its own axis with a time-period $T _{1}$. A satellite is in an equatorial orbit around earth at a height $h$ above surface of earth. The satellite is revolving in same direction as rotation of earth around its $0 \mathrm{wn}$ axis $i . e$. west to east. $T _{2}$ is time-period of satellite in orbit. The time interval between two successive times at which the satellite appears vertically overhead to an observer fixed on equator of earth is
(1) $\mathrm{T} _{1} \mathrm{~T} _{2}$
(2) $\frac{T _{1} T _{2}}{T _{1}-T _{2}}$
(3) $\frac{T _{1} T _{2}}{T _{1}+T _{2}}$
(4) $\frac{\mathrm{T} _{1}^{2} \mathrm{~T} _{2}^{2}}{\mathrm{~T} _{1}^{2}-\mathrm{T} _{2}^{2}}$
Show Answer
Correct answer: (2)
Solution:
$\omega _{1}=$ angular speed of earth around its own axis $=\frac{2 \pi}{\mathrm{T} _{1}}$
$\omega _{2}=$ angular speed of satellite in orbit $=\frac{2 \pi}{\mathrm{T} _{2}}$
$\omega _{\mathrm{r}}=$ The relative angular speed of satellite with respect to earth $=\omega _{2}-\omega _{1}$
$$ =2 \pi\left(\frac{1}{\mathrm{~T}^{2}}-\frac{1}{\mathrm{~T} _{1}}\right)=2 \pi \frac{\left(\mathrm{T} _{1}-\mathrm{T} _{2}\right)}{\mathrm{T} _{1} \mathrm{~T} _{2}} $$
The time interval between successive positions when satellite is vertically above observer fixed to equator on earth $=\frac{2 \pi}{\omega _{\mathrm{r}}}=\frac{\mathrm{T} _{1} \mathrm{~T} _{2}}{\mathrm{~T} _{1}-\mathrm{T} _{2}}$
65. A body of mass $m$ is raised to a height above surface of earth. It is projected with a velocity $v$ in a direction perpendicular to the line joining the center of the earth and body. The body moves in a circular orbit around earth with time period T. $\frac{v}{T}$ is
(1) $\frac{g}{2 \pi}\left(\frac{R}{R+h}\right)$
(2) $\frac{\mathrm{g}}{2 \pi}\left(\frac{\mathrm{R}}{\mathrm{R}+\mathrm{h}}\right)^{2}$
(3) $\frac{g}{2 \pi}\left(\frac{R^{2}}{R+h}\right)$
(4) $\frac{2 \pi}{\mathrm{g}}\left(\frac{\mathrm{R}+\mathrm{h}}{\mathrm{R}}\right)^{2}$
Show Answer
Correct answer: (2)
Solution:
For body to move in circular orbit at height $h$;
$$ \frac{\mathrm{mv}^{2}}{\mathrm{R}+\mathrm{h}}=\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})^{2}} $$
or $\quad v=\sqrt{\frac{G M}{R+h}}=\sqrt{\frac{g R^{2}}{R+h}} \hspace{40mm}. . . . . . . (1)$
The time-period, T; of body in orbit is:
$$ \begin{equation*} \mathrm{T}=\frac{2 \pi(\mathrm{R}+\mathrm{h})}{\mathrm{V}}=\frac{2 \pi(\mathrm{R}+\mathrm{h})^{3 / 2}}{\sqrt{\mathrm{gR}^{2}}} \tag{2} \end{equation*} $$
From equations (1) and (2) we have,
$$ \frac{\mathrm{v}}{\mathrm{T}}=\frac{\mathrm{gR}^{2}}{2 \pi(\mathrm{R}+\mathrm{h})^{2}} $$
66. Saturn has a number of rings around it. Assume each ring is due to particles following their own circular orbits around saturn. The radius of the inner most and outer most ring is nearly $7 \times 10^{4} \mathrm{~km}$ and $1.35 \times 10^{5} \mathrm{~km}$ respectively. What is the ratio of the time period of particles in the inner most and outer most ring?
(1) $\sim 0.373$
(2) $\sim 2.68$
(3) $\sim 3.72$
(4) $\sim 0.27$
Show Answer
Correct answer: (1)
Solution:
Let $T _{0}$ and $T _{i}$ be the time period of the particle in the outer most and inner most ring respectively. Let $R _{0}$ and $\mathrm{R} _{\mathrm{i}}$ be the corresponding radii of the orbit. Using Kepler’s third law.
$$ \begin{aligned} & \left(\frac{\mathrm{T} _{\mathrm{i}}}{\mathrm{T} _{0}}\right)^{2}=\left(\frac{\mathrm{R} _{\mathrm{i}}}{\mathrm{R} _{0}}\right)^{3} \\ & \text { or } \quad \frac{\mathrm{T} _{\mathrm{i}}}{\mathrm{T} _{0}}=\left(\frac{\mathrm{R} _{\mathrm{i}}}{\mathrm{R} _{0}}\right)^{3 / 2}=\left(\frac{7 \times 10^{4}}{1.35 \times 10^{5}}\right)^{3 / 2}=\left(\frac{7}{13.5}\right)^{3 / 2} \\ & \simeq 0.373 \end{aligned} $$
67. A satellite of mass $100 \mathrm{~kg}$ is to be put in a circular orbit at a height of $600 \mathrm{~km}$ above surface of earth. The satellite acquires a vertical speed of $4 \mathrm{kms}^{-1}$ when it reaches this height. Radius of earth $=6400 \mathrm{~km} ; \mathrm{g}=10 \mathrm{~ms}^{-2}$. The impulse imported to satellite at this height so that it is put into the desired orbit is
(1) $\sim 7.65 \times 10^{5} \mathrm{kgms}^{-1}$; horizontal
(2) $\sim 4 \times 10^{5} \mathrm{kgms}^{-1}$; vertical
(3) $\sim 8.63 \times 10^{5} \mathrm{kgms}^{-1}$; horizontal
(4) $\sim 8.63 \times 10^{5} \mathrm{kgms}^{-1}$; at angle of $\sim 29.7^{0}$ with horizontal
Show Answer
Correct answer: (4)
Solution:
$\mathrm{v} _{\text {sat }}=$ The satellite velocity required at height of $600 \mathrm{~km}=\sqrt{\frac{\mathrm{GM}}{\mathrm{r}}}=\sqrt{\frac{\mathrm{gR^2}}{\mathrm{r}}}$
where $\mathrm{r}=6400+600=7000 \mathrm{Km}$
$$ \begin{aligned} & \therefore \quad \mathrm{v} _{\mathrm{sat}}=\sqrt{\frac{10 \times\left(6.4 \times 10^{6}\right)^{2}}{7 \times 10^{6}} \mathrm{~ms}^{-1}} \\ & \quad \simeq 7.648 \times 10^{3} \mathrm{~ms}^{-1} \end{aligned} $$
$\mathrm{p} _{1}=$ Linear momentum of satellite at $\mathrm{h}=600 \mathrm{Km}$
$=\mathrm{m} \times \mathrm{v}=10^{2} \times 4 \times 10^{3}=4 \times 10^{5} \mathrm{Kgms}^{-1}$, vertically upwards
$\mathrm{p} _{2}=$ Linear momentum required by satellite to put into circular orbit at $\mathrm{h}=600 \mathrm{Km}$ $\mathrm{mv} _{\text {sat }}=7.648 \times 10^{5} \mathrm{~ms}^{-1} ;$ horizontal
 The impulse required equals change in linear momentum $=\mathbf{p} _{2}-\mathbf{p} _{1}$
The impulse required equals change in linear momentum $=\mathbf{p} _{2}-\mathbf{p} _{1}$
$\therefore$ Magnitude of impulse $=\sqrt{\mathrm{p} _{1}^{2}+\mathrm{p} _{2}^{2}} \simeq 8.63 \times 10^{5} \mathrm{kgms}^{-1}$
$$ \tan \alpha=\frac{\mathrm{p} _{1}}{\mathrm{p} _{2}}=\frac{4}{7.648}=0.57 ; \alpha \simeq 29.7^{0} $$
68. Two satellites $S _{1}$ and $S _{2}$ move in coplaner circular orbits of radius $r _{1}$ and $r _{2}$, around a gravitating mass, in same sense. Their periods of revolution are $1 \mathrm{hr}$ and $2 \sqrt{2}$ hr respectively $r _{1}=10^{4} \mathrm{~km}$. The relative speed of $S _{2}$ w.r.t $S _{2}$ when the two are closest is
(1) $\pi \times 10^{4} \mathrm{kmhr}^{-1}$
(2) $\frac{\pi}{\sqrt{2}} \times 10^{4} \mathrm{kmhr}^{-1}$
(3) $\sqrt{2} \pi \times 10^{4} \mathrm{kmhr}^{-1}$
(4) $\pi(\sqrt{2}-2) \times 10^{4} \mathrm{kmhr}^{-1}$
Show Answer
Correct answer: (4)
Solution:
Let $\omega _{1}$ and $\omega _{2}$ be angular speed of the two satellites in their respective orbits. Then
$$ \mathrm{mr} _{1} \omega _{1}^{2}=\frac{\mathrm{GMm}}{\mathrm{r} _{1}^{2}} ; \mathrm{mr} _{2} \omega _{2}^{2}=\frac{\mathrm{GMm}}{\mathrm{r} _{2}^{2}} $$
or $\mathrm{r} _{1}^{3} \omega _{1}^{2}=\mathrm{r} _{2}^{3} \omega _{2}^{2}$
$\omega _{1}=\frac{2 \pi}{\mathrm{T} _{1}}=\frac{2 \pi}{1} \mathrm{rad} \mathrm{hr}^{-1} ; \quad \omega _{2}=\frac{2 \pi}{\mathrm{T} _{2}}=\frac{2 \pi}{2 \sqrt{2}} \mathrm{radhr}^{-1}$
Also $\mathrm{r} _{1}=10^{4} \mathrm{~km}$; therefore
$$ \begin{aligned} & r _{2}^{3}=\left(10^{4}\right)^{3} \times\left(\frac{\omega _{1}}{\omega^{2}}\right)^{2} \\ & =\left(10^{4}\right)^{3} \times(2 \sqrt{2})^{2} \end{aligned} $$
or $\mathrm{r} _{2}=2 \times 10^{4} \mathrm{Km}$
$\mathrm{v} _{1}=$ linear speed of $\mathrm{S} _{1}=\mathrm{r} _{1} \omega _{1}=2 \pi \times 10^{4} \mathrm{~km} \mathrm{hr}^{-1}$
$\mathrm{v} _{2}=$ linear speed of $\mathrm{S} _{2}=\mathrm{r} _{2} \omega _{2}=2 \times 10^{4} \times \frac{2 \pi}{2 \sqrt{2}}$
$$ =\sqrt{2} \pi \times 10^{4} \mathrm{~km} \mathrm{hr}^{-1} $$
relative speed of $S _{2}$ w.r.t $S _{1}=v _{2}-v _{1}$
$$ =(\sqrt{2}-2) \pi \times 10^{4} \mathrm{~km} \mathrm{hr}^{-1} $$
69. A body of mass $m$ is projected vertically upwards from surface of earth with an initial velocity equal to escape velocity. The time taken ( $t$ ) by body to reach a height equal to radius of earth $(R)$ is
( $\mathrm{g}=$ acceleration due to gravity on surface of earth)
(1) $\mathrm{t}=\frac{1}{3} \sqrt{\frac{2 \mathrm{R}}{\mathrm{g}}}$
(2) $\mathrm{t}=\frac{1}{3} \sqrt{\frac{2}{\mathrm{~g}}} \mathrm{R}^{3 / 2}$
(3) $\mathrm{t}=\frac{1}{3} \sqrt{\frac{2 \mathrm{R}}{\mathrm{g}}}[2 \sqrt{2}-1]$
(4) $\mathrm{t}=\frac{1}{3} \sqrt{\frac{2 \mathrm{R}}{\mathrm{g}}}(2 \sqrt{2})$
Show Answer
Correct answer: (3)
Solution:
Let $\mathrm{v}$ be instantaneous velocity of body when it is at a distance $x$ from centre of earth. Then instantaneous acceleration $=\mathrm{a}=\frac{\mathrm{dv}}{\mathrm{dt}}=-\frac{\mathrm{GM}}{x^{2}}$
or $\quad \frac{\mathrm{dv}}{\mathrm{d} x} \cdot \frac{\mathrm{d} x}{\mathrm{dt}}=-\frac{\mathrm{GM}}{x^{2}} \quad$ or $\quad \mathrm{vdv}=-\frac{\mathrm{GM}}{x^{2}} \mathrm{~d} x$
Integrating,
$$ \begin{aligned} & \quad \frac{\mathrm{v}^{2}}{2}=\frac{\mathrm{GM}}{x} \quad \text { or } \quad \mathrm{v}=\sqrt{\frac{2 \mathrm{GM}}{x}}=\frac{\mathrm{d} x}{\mathrm{dt}} \\ & \therefore \quad \mathrm{dt}=\frac{1}{\sqrt{2 \mathrm{GM}}} x^{1 / 2} \mathrm{~d} x \end{aligned} $$
Integrate,
$$ \begin{aligned} \int _{0}^{\mathrm{t}} \mathrm{dt} & =\frac{1}{\sqrt{2 \mathrm{GM}}} \int _{\mathrm{R}}^{2 \mathrm{R}} x^{1 / 2} \mathrm{~d} x \\ & =\frac{1}{\sqrt{2 \mathrm{gR}^{2}}}\left[\frac{(2 \mathrm{R})^{3 / 2}-\mathrm{R}^{3 / 2}}{3 / 2}\right] \\ & =\frac{2}{3} \sqrt{\frac{\mathrm{R}}{2 \mathrm{~g}}}\left[2^{3 / 2}-1\right] \\ & =\frac{1}{3} \sqrt{\frac{2 \mathrm{R}}{\mathrm{g}}}[2 \sqrt{2}-1] \end{aligned} $$
70. Satellite is to be launched using a two stage rocket. The first stage takes satellite to height of $\frac{R}{10}$, where $R$ is radius of earth. $W _{1}$ is work done by rocket. The second stage gives necessary velocity to put satellite into orbit at this height. $W _{2}$ is work done by the second stage $\frac{\mathbf{W} _{1}}{\mathbf{W} _{2}}$ is
(1) $\frac{1}{5}$
(2) 5
(3) 0.5
(4) 1
Show Answer
Correct answer: (1)
Solution:
$\mathrm{W} _{1}=$ Work done by 1st stage of rocket
$$ =\int _{\mathrm{R}}^{\frac{11 \mathrm{R}}{10}} \frac{\mathrm{GMm}}{\mathrm{x}^{2}} \mathrm{dx}=\mathrm{GMm}\left[\frac{1}{\mathrm{R}}-\frac{10}{11 \mathrm{R}}\right] $$
$$ =\mathrm{gR}^{2} \mathrm{~m} \times \frac{1}{11 \mathrm{R}}=\frac{\mathrm{mgR}}{11} $$
The second stage does work $\mathrm{W} _{2}$ to give necessary speed to the rocket so that it becomes satellite at height $\frac{\mathrm{R}}{10}$. Therefore $\mathrm{W} _{2}=\frac{1}{2} \mathrm{mv} _{\text {sat }}^{2}$,
where $\mathrm{v} _{\text {sat }}$ is satellite velocity at the height and its value is
$$ \mathrm{v} _{\mathrm{sod}}=\sqrt{\frac{\mathrm{GM}}{\frac{11 \mathrm{R}}{10}}} $$
$\therefore \quad \mathrm{W} _{2}=\frac{1}{2} \mathrm{GMm} \times \frac{10}{11 \mathrm{R}}=\frac{5 \mathrm{mgR}^{2}}{11 \mathrm{R}}=\frac{5}{11} \mathrm{mgR}$
Hence $\frac{\mathrm{W} _{1}}{\mathrm{~W} _{2}}=\frac{1}{5}$
71. Two geo-stationary satellites are used to communicate between the diagonally opposite positions on earth. Radius of earth $=6400 \mathrm{~km} ; g=$ acceleration due to gravity on surface of earth $=9.8 \mathrm{~ms}^{-2}, c=$ speed of light $=3 \times 10^{8} \mathrm{~ms}^{-1}$. Time taken $(t)$ by signal to reach from one point to other is (nearly)
(1) zero
(2) $0.32 \mathrm{~s}$
(3) $0.5 \mathrm{~s}$
(4) $1 \mathrm{~s}$
Show Answer
Correct answer: (2)
Solution:
Let $P$ and $Q$ be the two diagonally opposite points on earth. $S _{1}$ and $S _{2}$ are the two geostationary satellites above $\mathrm{P} \quad and \quad \mathrm{Q}$.
$r=$ radius of orbit of geostationary satellite.
$$ \mathrm{mr} \omega^{2}=\frac{\mathrm{GMm}}{\mathrm{r}^{2}} $$
$\mathrm{m}=$ mass of satellite; $\mathrm{M}=$ mass of earth.
$$ \begin{aligned} & \omega=\frac{2 \pi}{\mathrm{T}}=\frac{2 \pi}{24 \times 3600} \mathrm{rad} / \mathrm{s} \\ \therefore & \mathrm{r}^{3}=\frac{\mathrm{GM}}{\omega^{2}}=\frac{\mathrm{gR}^{2}}{\omega^{2}}=9.8 \times\left(6.4 \times 10^{6}\right)^{2} \times(24 \times 3600)^{2} \\ \text { or } \quad \mathrm{r} & \simeq 4.2 \times 10^{7} \mathrm{~m} \end{aligned} $$
From Fig.; $\mathrm{PS} _{\mathrm{i}}=\sqrt{\mathrm{OS} _{\mathrm{i}}^{2}-\mathrm{PO}^{2}}=\sqrt{\mathrm{r}^{2}-\mathrm{R}^{2}}$
 $$
\simeq 4.15 \times 10^{7} \mathrm{~m}
$$
$$
\simeq 4.15 \times 10^{7} \mathrm{~m}
$$
The length of path of signal in going from $\mathrm{P}$ to $\mathrm{Q}$ via satellite $\mathrm{S} 1 \quad and \quad \mathrm{~S} _{2}=2 \mathrm{PS} _{1}+\mathrm{S} _{1} \mathrm{~S} _{2}=2 \mathrm{PS} _{1}+2 \mathrm{R}$
$$ \simeq 9.574 \times 10^{7} \mathrm{~m} $$
$\therefore$ Time taken $\mathrm{t}=\frac{9.574 \times 10^{7}}{3 \times 10^{8}} \mathrm{~s}$
$\simeq 0.32 \mathrm{~s}$
72. $v$ is escape velocity of an object from a planet of mass $M$, radius $R$, when projected from a height $h$ above the surface of the planet. $\frac{1}{v^{2}}$ vs $h$ graph is shown in Fig. The mass and radius of the planet is
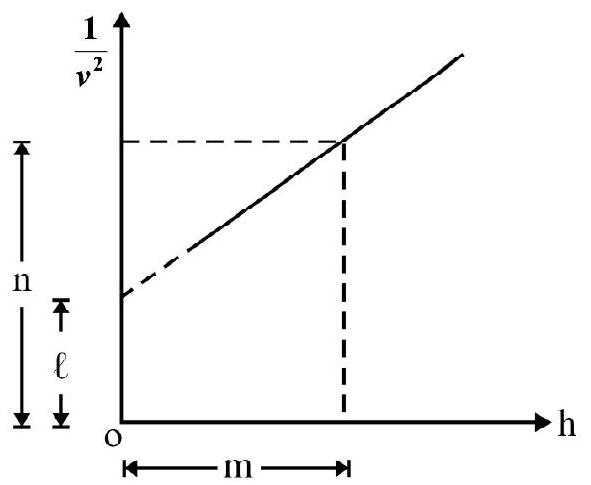
(1) $\mathrm{M}=\frac{\mathrm{m}}{\mathrm{nG}} ; \mathrm{R}=\frac{\mathrm{n} \ell}{\mathrm{G}}$
(2) $\mathrm{M}=\frac{\mathrm{m}}{2 \mathrm{G}(\mathrm{n}-\ell)} ; \mathrm{R}=\frac{\mathrm{m} \ell}{(\mathrm{n}-\ell)}$
(3) $\mathrm{M}=\frac{\mathrm{m} \times \mathrm{n}}{\ell} ; \mathrm{R}=\frac{\ell \mathrm{n}}{\mathrm{G}}$
(4) $\mathrm{M}=\frac{\mathrm{m}}{\mathrm{G}(\mathrm{n}-\ell)} ; \mathrm{R}=\frac{2 \mathrm{~m} \ell}{(\mathrm{n}-\ell)}$
Show Answer
Correct answer: (2)
Solution:
The escape velocity from the planet is
$$ \mathrm{v}=\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}+\mathrm{h}}} $$
or $\mathrm{R}+\mathrm{h}=\frac{2 \mathrm{GM}}{\mathrm{v}^{2}}$
$\therefore \frac{1}{\mathrm{v}^{2}}=\left(\frac{\mathrm{R}}{2 \mathrm{GM}}\right)+\left(\frac{1}{2 \mathrm{GM}}\right) \mathrm{h}$
$\frac{1}{\mathrm{v}^{2}}$ graph is a straight line
Slope of st. line $=\frac{\mathrm{n}-\ell}{\mathrm{m}}=\frac{1}{2 \mathrm{GM}} \hspace{40mm}. . . . . . . (1)$
Intercept on $\frac{1}{\mathrm{v}^{2}}$ axis $=\ell=\frac{\mathrm{R}}{2 \mathrm{GM}} \hspace{40mm}. . . . . . . (2)$
$\therefore \quad M=\frac{m}{2 G(n-\ell)} ; \quad$ and $R=\frac{m \ell}{(n-\ell)}$
73. Assume earth to be a uniform sphere of mass M, radius R.A smooth tunnel is dug along a diameter. A particle of mass $m$ is put inside tunnel at a distance $\frac{R}{2}$ from center of earth. $v$ is speed given to particle at this point so that it just reaches the surface of earth. $g$ is acceleration due to gravity on surface of earth. $v$ is
(1) $\sqrt{\mathrm{gR}}$
(2) $\sqrt{1.25 \mathrm{gR}}$
(3) $\sqrt{1.5 \mathrm{gR}}$
(4) $\sqrt{2 \mathrm{gR}}$
Show Answer
Correct answer: (2)
Solution:
Fig. shows earth with $\mathrm{A} _{1} \mathrm{~A}$ as smooth tunnel. Initially particle of mass $\mathrm{m}$ is at $\mathrm{P}, \mathrm{r}=\frac{\mathrm{R}}{2}=\mathrm{OP}$. Let $\mathrm{V}$ be net gravitational potential at $\mathrm{P}$ due to earth. Then
$$ \begin{equation*} \mathrm{V}=\mathrm{V} _{1}+\mathrm{V} _{2} \tag{1} \end{equation*} $$
$\mathrm{V} _{1}=$ Gravitational potential $\mathrm{P}$ due to a solid sphere of radius $\frac{\mathrm{R}}{2}$
$$ =-\frac{\mathrm{GM} _{1}}{\left(\frac{\mathrm{R}}{2}\right)} $$
Also $\mathrm{M} _{1}=\frac{\mathrm{M}}{4}$. There are
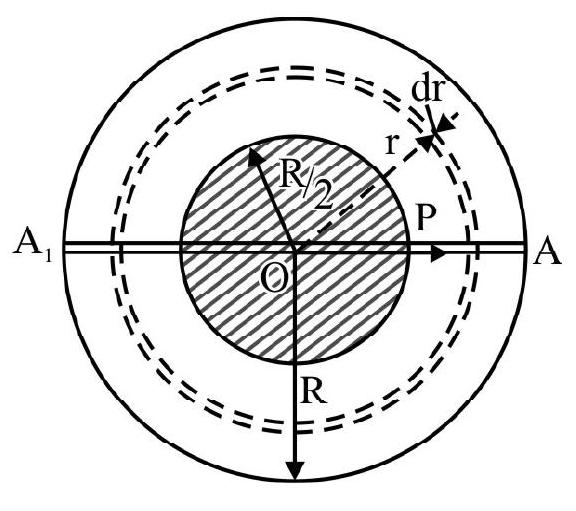
$$ \begin{equation*} \mathrm{V} _{1}=-\frac{\mathrm{GM}}{2 \mathrm{R}} \tag{2} \end{equation*} $$
Let $V _{2}$ be gravitational potential at $\mathrm{P}$ due to remaining part of earth. We consider this part as made of
concentric spherical shells having radius varying from $\frac{R}{2}$ to $R$. Consider an elementary shell of radius $r$, thickness dr as shown in Fig.
$\mathrm{dm}=$ mass of shell considered $=4 \pi \mathrm{r}^{2} \mathrm{dr}$
$\rho=$ density of earth
Since point $\mathrm{P}$ is INSIDE the shell considered, the potential $\mathrm{dV} _{2}$ at $\mathrm{P}$ is same as on surface of shell considered. Therefore
$$ \begin{align*} & \mathrm{dV} _{2}=-\frac{\mathrm{Gdm}}{\mathrm{r}}=-4 \pi \mathrm{G} \rho \mathrm{rdr} \\ \therefore \quad \mathrm{V} _{2} & =\int _{\mathrm{R} / 2}^{\mathrm{R}} \mathrm{dV} _{2}=-4 \pi \mathrm{G} \rho \int _{\mathrm{R} / 2}^{\mathrm{R}} \mathrm{rdr}=-4 \pi \mathrm{G} \rho\left[\frac{3 \mathrm{R}^{2}}{8}\right] \\ & =-\left(\frac{4 \pi}{3} \mathrm{R}^{3} \rho\right) \mathrm{G}\left(\frac{9 \mathrm{R}^{2}}{8 \mathrm{R}^{3}}\right)=-\frac{9}{8}\left(\frac{\mathrm{GM}}{\mathrm{R}}\right) \tag{3} \end{align*} $$
From eqns. (1), (2) and (3)
$$ \begin{equation*} \mathrm{V}=-\frac{\mathrm{GM}}{2 \mathrm{R}}-\frac{9 \mathrm{GM}}{8 \mathrm{R}}=-\frac{13 \mathrm{GM}}{8 \mathrm{R}} \tag{4} \end{equation*} $$
The total energy $E _{1}$ of particle at $P$, when it is given a speed $v$ is:
$$ \begin{equation*} \mathrm{E} _{1}=\frac{1}{2} \mathrm{mv}^{2}+\mathrm{mV}=\frac{1}{2} \mathrm{mv}^{2}-\frac{13 \mathrm{GMm}}{8 \mathrm{R}} \tag{5} \end{equation*} $$
The total energy $\mathrm{E} _{2}$ of particle as it reaches surface of earth is
$$ \mathrm{E} _{2}=0+\left(-\frac{\mathrm{GMm}}{\mathrm{R}}\right) \quad[\mathrm{K} . \mathrm{E} \text { of particle at } \mathrm{A} \text { is zero }] $$
From law of conservation of energy $\mathrm{E} _{1}=\mathrm{E} _{2}$. Therefore
$$ \frac{1}{2} \mathrm{mv}^{2}-\frac{13 \mathrm{GMm}}{8 \mathrm{R}}=-\frac{\mathrm{GMm}}{\mathrm{R}} $$
or $\quad \mathrm{v}^{2}=\frac{5 \mathrm{GM}}{4 \mathrm{R}}=\frac{1.25 \mathrm{gR}^{2}}{\mathrm{R}}$
$\therefore \quad \mathrm{v}=\sqrt{1.25 \mathrm{gR}}$
74. Regard earth as a uniform sphere of mass $m$, radius $R$. A smooth tunnel is dug along a diameter. A particle of mass $m$ is released from rest at a distance $\frac{R}{\sqrt{2}}$ inside tunnel. The speed of particle as it reaches center of earth is
(1) $\sqrt{\frac{3}{2} g R}$
(2) $\left[\left(\frac{3}{2}+\sqrt{2}\right) \mathrm{gR}\right]^{\frac{1}{2}}$
(3) $\left[\left(\frac{3}{2}-\sqrt{2}\right) g R\right]^{1 / 2}$
(4) $[2 \sqrt{2} \mathrm{gR}]^{1 / 2}$
Show Answer
Correct answer: (3)
Solution:
Let $\mathrm{P}$ be point, $\mathrm{OP}=\frac{\mathrm{R}}{\sqrt{2}}$ inside tunnel where particle is released from rest. The gravitational potential energy of particle at $\mathrm{P}$
$$ \begin{aligned} \mathrm{U} _{1}= & -\frac{\mathrm{G}(\mathrm{M} / 2) \mathrm{m}}{\mathrm{R} / \sqrt{2}}-4 \pi \rho \mathrm{G} \int _{\mathrm{R} / \sqrt{2}}^{\mathrm{R}} \mathrm{rdr} \\ & =-\frac{\mathrm{GMm}}{\sqrt{2} \mathrm{R}}-\left(\frac{4 \pi}{3} \mathrm{R}^{3} \rho\right) \mathrm{G}\left(\frac{3 \mathrm{R}^{2}}{4 \mathrm{R}^{3}}\right) \\ & =-\frac{\mathrm{GMm}}{\sqrt{2} \mathrm{R}}-\frac{3 \mathrm{Gm}}{4 \mathrm{R}}=-\left(\frac{1}{\sqrt{2}}+\frac{3}{4}\right) \frac{\mathrm{GMm}}{\mathrm{R}} \end{aligned} $$
The gravitational potential energy $U _{2}$ of mass $m$ at center of earth is
$$ \mathrm{U} _{2}=-\frac{3 \mathrm{GM}}{2 \mathrm{R}} $$
Let $v$ be speed of mass at centre of earth. From law of conservation of energy
$$ \begin{aligned} & 0+\left[-\left(\frac{1}{\sqrt{2}}+\frac{3}{4}\right) \frac{\mathrm{GMm}}{\mathrm{R}}\right]=\frac{1}{2} \mathrm{mv}^{2}+\left[-\frac{3}{2} \frac{\mathrm{GMm}}{\mathrm{R}}\right] \\ & \therefore \quad \mathrm{v}^{2}=\left(\frac{3}{2}-\sqrt{2}\right) \frac{\mathrm{GM}}{\mathrm{R}}=\left(\frac{3}{2}-\sqrt{2}\right) \mathrm{gR} \\ & \text { or } \quad \mathrm{v}=\left[\left(\frac{3}{2}-\sqrt{2}\right) \mathrm{gR}\right]^{1 / 2} \end{aligned} $$
75. A body of mass $m$ is projected from surface of earth with an initial speed equal to twice the escape velocity. Its speed when it just escapes gravitational pull of earth expressed as a percentage of its initial speed is
(1) $50 \%$
(2) $66.67 \%$
(3) $75 \%$
(4) $86.6 \%$
Show Answer
Correct answer: (4)
Solution:
$\mathrm{v} _{\text {esp }}=$ Escape velocity from surface of earth $=\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}$
$\mathrm{M}=$ mass of earth; $\mathrm{R}=$ radius of earth.
$\mathrm{v} _{\mathrm{e}}=$ initial speed of projection of body $=3 \mathrm{v} _{\text {esp }}$
Let $\mathrm{v}$ be its speed when it has just escaped gravitational pull of earth. From law of conservation of energy.
$$ \begin{aligned} & \frac{1}{2} \mathrm{~m}\left(2 \mathrm{v} _{\text {esp }}\right)^{2}-\frac{\mathrm{GMm}}{\mathrm{R}}=\frac{1}{2} \mathrm{mv}^{2}+0 \\ & 2 \mathrm{mv} _{\mathrm{esp}}^{2}-\frac{1}{2} \mathrm{mv} _{\mathrm{esp}}^{2}=\frac{1}{2} \mathrm{mv}^{2} \\ & \therefore \mathrm{v}=\sqrt{3} \mathrm{v} _{\mathrm{esp}} \\ & \therefore \frac{\mathrm{v}}{\mathrm{v} _{\mathrm{i}}} \times 100=\frac{\sqrt{3}}{2} \times 100=86.6 \% \end{aligned} $$
76. A man can throw a ball with a maximum speed of nearly $38 \mathrm{~ms}^{-1}$. The man is on a planet having a uniform density of $2.9 \mathrm{~g} / \mathrm{cc}$. On throwing the ball with maximum speed, the man finds that ball just fails to return to the planet. The radius of planet is nearly; $\left(G=6.67 \times 10^{-11}\right.$ SI Unit)
(1) $2.987 \mathrm{~km}$
(2) $2.987 \mathrm{~km}$
(3) $29.87 \mathrm{~km}$
(4) $29.87 \mathrm{~km}$
Show Answer
Correct answer: (2)
Solution:
Since the ball thrown with a speed of $38 \mathrm{~ms}^{-1}$ just fails to return to the surface of the planet, the escape velocity $\left(v _{\text {esp }}\right)$ from planet is $38 \mathrm{~ms}^{-1}$. Let $\mathrm{M}$ be mass and $\mathrm{R}$ radius of planet. Then
$\mathrm{v} _{\text {esp }}=\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}=\sqrt{\frac{2 \mathrm{G}\left(\frac{4 \pi}{3} \mathrm{R}^{3} \rho\right)}{\mathrm{R}}}$
$=\sqrt{\frac{8 \pi \mathrm{G} \rho}{3}} \cdot \mathrm{R}$
$$ \begin{aligned} \therefore \quad \mathrm{R} & =\mathrm{v} _{\text {esp }} \sqrt{\frac{3}{8 \pi \mathrm{G} \rho}} \\ & =38 \sqrt{\frac{3}{8 \times 3.14 \times 6.67 \times 10^{-11} \times 2.9 \times 10^{3}}} \\ & \simeq 2987 \mathrm{~m} \\ & =2.987 \mathrm{~km} \end{aligned} $$
77. Two spherical gravitating bodies have mass $M _{1}$ and $M _{2}$ and radii $R _{1}$ and $R _{2}$ respectively as shown in Fig. The center of the two are a distance $d$ apart. A mass $m$ is located at $A$ dividing $\mathrm{O} _{1} \mathrm{O} _{2}$ into two parts in the ratio of 1:2. The minimum velocity of mass $m$ so that it
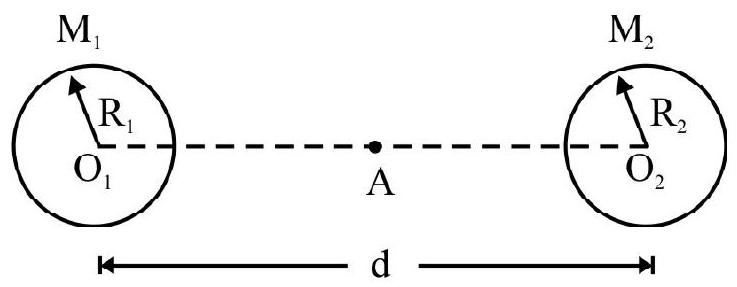 escapes gravitational pull of both bodies is
escapes gravitational pull of both bodies is
(1) $v=\sqrt{\frac{G\left(M _{1}+M _{2}\right)}{d}}$
(2) $\quad v=\sqrt{\frac{3 G\left(2 M _{1}+M _{2}\right)}{d}}$
(3) $\quad v=\sqrt{\frac{3 G\left(M _{1}+2 M _{2}\right)}{d}}$
(4) $\mathrm{v}=\sqrt{\frac{2 \mathrm{G}\left(\mathrm{M} _{1}+\mathrm{M} _{2}\right)}{\mathrm{d}}}$
Show Answer
Correct answer: (2)
Solution:
Let $\mathrm{r} _{1}$ and $\mathrm{r} _{2}$ be distance of mass at $\mathrm{A}$ from $\mathrm{O} _{1}$ and $\mathrm{O} _{2}$. Then $\mathrm{r} _{1}=\frac{\mathrm{d}}{3}$ and $\mathrm{r} _{2}=\frac{2 \mathrm{~d}}{3}$. Let $\mathrm{v}$ be minimum speed of mass (m) at A ,so that it just escapes gravitational pull of $M _{1}$ and $M _{2}$. From law of conservation of energy.
$$ \begin{aligned} & \frac{1}{2} \mathrm{mv}^{2}+\left(-\frac{\mathrm{GMm}}{\mathrm{r} _{1}}\right)+\left(-\frac{\mathrm{GM} _{2} \mathrm{~m}}{\mathrm{r} _{2}}\right)=0 \\ & \text { or } \frac{1}{2} \mathrm{v}^{2}=\frac{\mathrm{GM} _{1}}{(\mathrm{~d} / 3)}+\frac{\mathrm{GM}^{2}}{(2 \mathrm{~d} / 3)}=\frac{3 \mathrm{G}}{2 \mathrm{~d}}\left(2 \mathrm{M} _{1}+\mathrm{M} _{2}\right) \\ & \text { or } \mathrm{v}=\sqrt{\frac{3 \mathrm{G}\left(2 \mathrm{M} _{1}+\mathrm{M} _{2}\right)}{\mathrm{d}}} \end{aligned} $$
78. A planet of mass $m$ is moving in an elliptical orbit around sun (S). When it is in position $A$ its velocity $v _{1}$ $=1.1 \mathrm{v} _{0}$ where $\mathrm{v} _{0}$ is velocity for a circular orbit of radius $r _{1}$ around sun. When the planet is in position
$B$ its distance from sun is $r _{2}$. Then $\frac{r _{2}}{r _{1}}$ is
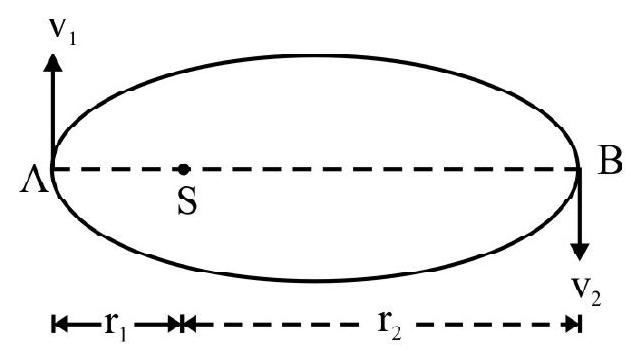
(1) $\quad \sim 1.1$
(2) $\sim 1.21$
(3) $\sim 1.5$
(4) $\sim 1.414$
Show Answer
Correct answer: (3)
Solution:
Since $v _{0}$ is velocity of circular orbit of radius $r _{1}$;
$$ \begin{equation*} \frac{\mathrm{mv} _{0}^{2}}{\mathrm{r} _{1}}=\frac{\mathrm{GMm}}{\mathrm{r} _{1}^{2}} \quad \text { or } \quad \mathrm{v} _{0}^{2}=\frac{\mathrm{GM}}{\mathrm{r} _{1}} \tag{1} \end{equation*} $$
$\mathrm{L} _{\mathrm{A}}=$ angular momentum of planet at $\mathrm{A}=\mathrm{mv} _{1} \mathrm{r} _{1}$
$\mathrm{E} _{\mathrm{A}}=$ Total energy of planet at $\mathrm{A}=\frac{1}{2} \mathrm{~m}\left(1.1 \mathrm{v} _{0}\right)^{2}-\frac{\mathrm{GMm}}{\mathrm{r} _{1}}$
$$ =\frac{121}{200} \frac{\mathrm{GMm}}{\mathrm{r} _{1}}-\frac{\mathrm{GMm}}{\mathrm{r} _{1}}=-\frac{79}{200} \frac{\mathrm{GMm}}{\mathrm{r} _{1}} \hspace{40mm}. . . . . . . (2) $$
Let $\mathrm{v} _{2}$ be speed of planet at $\mathrm{B}$. Then
$\mathrm{L} _{\mathrm{B}}=$ angular momentum of planet at $\mathrm{B}=\mathrm{mv} _{2} \mathrm{r} _{2}$
From law of conservation of angular momentum $\mathrm{L} _{\mathrm{A}}=\mathrm{L} _{\mathrm{B}}$
or $\mathrm{mv} _{1} \mathrm{r} _{1}=\mathrm{mv} _{2} \mathrm{r} _{2}$ or $\mathrm{v} _{2}=\frac{1 . \mathrm{lv} _{0} \mathrm{r} _{1}}{\mathrm{r} _{2}} \hspace{40mm}. . . . . . . (3)$
$E _{B}=$ Total energy of planet at $B$
$$ =\frac{1}{2} \mathrm{mv} _{2}^{2}-\frac{\mathrm{GMm}}{\mathrm{r}^{2}}=\frac{1}{2} \mathrm{~m}\left(\frac{121}{100}\right)\left(\frac{\mathrm{r} _{1}}{\mathrm{r} _{2}}\right)^{2} \frac{\mathrm{GM}}{\mathrm{r} _{1}}-\frac{\mathrm{GMm}}{\mathrm{r} _{2}} $$
Using law of conservation of energy
$$ \frac{121}{200} \mathrm{GMm}\left(\frac{\mathrm{r} _{1}}{\mathrm{r} _{2}^{2}}\right)-\frac{\mathrm{GMm}}{\mathrm{r} _{2}}=-\frac{79}{200} \frac{\mathrm{GMm}}{\mathrm{r} _{1}} $$
or $\quad 121\left(\frac{r _{1}}{r _{2}}\right)^{2}-200\left(\frac{r _{1}}{r _{2}}\right)=-79$
or $\quad \frac{\mathrm{r} _{1}}{\mathrm{r} _{2}}=200 \pm \frac{\sqrt{4000-38236}}{242}$
$\simeq 0.653$
$\therefore \frac{\mathrm{r} _{2}}{\mathrm{r} _{1}} \sim 1.5$
79. A satellite of mass $10^{2} \mathrm{~kg}$ is revolving around earth in a circular orbit at a height of $10^{3} \mathrm{~km}$. The additional velocity needed to make the satellite escape gravitational pull of earth is (radius of earth $=6400 ; \mathrm{g}=10 \mathrm{~ms}^{-2}$ )
(1) $\sim 3.8 \mathrm{~km} / \mathrm{s}$
(2) $\sim 10.5 \mathrm{~km} / \mathrm{s}$
(3) $\sim 3.1 \mathrm{~km} / \mathrm{s}$
(4) $\sim 2.8 \mathrm{~km} / \mathrm{s}$
Show Answer
Correct answer: (3)
Solution:
$\mathrm{v} _{\text {sat }}$ is velocity of satellite at hight $h$. Then
$$ \mathrm{v} _{\mathrm{sat}}=\sqrt{\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}}}=\sqrt{\frac{\mathrm{gR}}{\mathrm{R}+\mathrm{h}}} $$
$$ =\sqrt{\frac{10 \times\left(6.4 \times 10^{6}\right)^{2}}{7.4 \times 10^{6}}} \mathrm{~ms}^{-1} \simeq 7.44 \times 10^{3} \mathrm{~ms}^{-1} $$
Let $\mathrm{v} _{\text {esp }}$ be escape velocity from a height ’ $h$ ’ above surface of earth.
$$ \begin{aligned} \mathrm{v} _{\text {esp }} & =\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}+\mathrm{h}}}=\sqrt{\frac{2 \mathrm{gR}^{2}}{\mathrm{R}+\mathrm{h}}}=\sqrt{2} \mathrm{v} _{\text {sat }} \\ & =1.414 \times 7.44 \times 10^{3} \mathrm{~ms}^{-1} \\ & \simeq 10.52 \times 10^{3} \mathrm{~ms}^{-1} \end{aligned} $$
Therefore additional velocity needed
$$ \begin{aligned} & =(10.52-7.44) \times 10^{3} \mathrm{~ms}^{-1} \\ & \simeq 3.08 \times 10^{3} \mathrm{~ms} \\ & \simeq 3.1 \mathrm{~km} / \mathrm{s} \end{aligned} $$
80. Earth moves around sun in a nearly circular orbit of radius $R$. $T$ is time period of earth around sun. Imagine that the mass of sun increases by $50 \%$ and the radius of earth’s orbit
is $2 R$. If the time-period of earth now is $T^{\prime}$, the ratio $\left(\frac{T^{\prime}}{T}\right)$ is (nearly).
(1) 1
(2) 2.8
(3) 2.34
(4) 3
Show Answer
Correct answer: (3)
Solution:
Let $M _{S}$ and $M _{E}$ denote mass of sun and earth. Let $v$ be speed of earth around sun; in orbit of radius $R$. Then
$$ \frac{\mathrm{GM} _{\mathrm{S}} \mathrm{M} _{\mathrm{E}}}{\mathrm{R}^{2}}=\frac{\mathrm{M} _{\mathrm{E}} \mathrm{v}^{2}}{\mathrm{R}} $$
or $\quad \mathrm{v}^{2}=\frac{\mathrm{GMs}}{\mathrm{R}}$
$\mathrm{T}=$ Time-period of earth around sun $=\frac{2 \pi \mathrm{R}}{\mathrm{V}}$
$$ \begin{equation*} \therefore \quad \mathrm{T}^{2}=\frac{4 \pi^{2} \mathrm{R}^{3}}{\mathrm{GM} _{\mathrm{S}}} \tag{1} \end{equation*} $$
Given $M _{S}^{\prime}=1.5 M _{s} ; R^{\prime}=2 R$. Let $T^{\prime}$ be the time-period of earth, in orbit, now. Then from equation(1)
$$ \begin{aligned} & \quad\left(\frac{\mathrm{T}^{\prime}}{\mathrm{T}}\right)^{2}=\left(\frac{\mathrm{R}^{\prime}}{\mathrm{R}}\right)^{3}\left(\frac{\mathrm{M} _{\mathrm{S}}}{\mathrm{M} _{\mathrm{S}}^{\prime}}\right)=(2)^{3} \frac{2}{3} \\ & \therefore \quad \frac{\mathrm{T}^{\prime}}{\mathrm{T}}=\frac{4}{\sqrt{3}}=\frac{4}{1.73} \simeq 2.34 \end{aligned} $$










