Unit 05 Rotational Motion
Rigid body
The particles constituting the body are so arranged that there is no change either in shape or size when external forces are applied.
Motion of a Rigid Body
1. Translational motion: There is a change in position of body in space.
2. Rotational motion: There is no change in position of body in space but the body turns or rotates around an axis in space. This motion is purely rotational in nature.
3. Simultaneous motion of rotation and translation. Examples: (a) Car moving on road; wheels have rotational motion and the position of car, as a whole, changes in space. (b) A sphere rolling down an inclined plane without slipping. (c) Mass attached to a string passing over a fixed pulley. As the mass descends; mass has translational motion and pulley rotational motion.
Translational Motion
Use is made of Newton’s laws of motion. Newton’s $2^{\text {nd }}$ law stated as
$$ \mathbf{F}=\mathrm{ma} $$
is strictly valid for a ‘point mass’. For a finite sized rigid body; we consider rigid body as made up of a large number of point masses. There are external forces as well as internal forces on any point mass considered. We can write down equation of motion of every point mass constituting the body. Equation of motion of $j^{\text {th }}$ mass is
$$ \mathrm{m} _{\mathrm{j}} \frac{\mathrm{d}^{2} \mathbf{r} _{\mathrm{j}}}{\mathrm{dt}^{2}}=\mathbf{F} _{\mathrm{j}}^{\mathrm{ext}}+\sum _{\substack{i \neq j \ \mathrm{i}=\mathrm{1} \mathrm{\quad to \quad N}}} \mathbf{f} _{\mathrm{ij}} $$
We have a very large number of “differential equations”. Simultaneous solution of all equations is almost impossible. There is a need to simplify the problem. The ‘overall’ motion is studied easily using the concept of the center of mass of the system. We consider:
(1) The entire mass of the body to be concentrated at the center of mass.
(2) All external forces are imagined to act simultaneously at the center of mass.
(3) The equation of motion, describing translation motion is
$$ \mathrm{M} \frac{\mathrm{d}^{2} \mathbf{R}}{\mathrm{dt}^{2}}=\mathbf{F} _{\text {ext }}^{\text {Total }} $$
$\mathbf{R}$ is the instantaneous position of the center of mass of the system.
(4) The total linear momentum $\mathbf{P}$ of the system
$$ \mathbf{P}=\sum \mathbf{p} _{\mathrm{j}}=\sum \mathrm{m} _{\mathrm{j}} \mathbf{v} _{\mathrm{j}}=\mathrm{MV} $$
V is the instantaneous velocity of C.M of the system.
Using concept of C.M, the translational motion of rigid body is reduced to the problem of a single point mass. The problem can be solved using the methods used in solving problems of a single point mass. However first important step is to find the position vector $\mathbf{R}$ of the center of mass. It can be shown that for a collection of $n$ discrete point masses $\mathrm{m} _{1}, \mathrm{~m} _{2}$, .. $\mathrm{m} _{\mathrm{j}}$ .. $\mathrm{m} _{\mathrm{n}}$
$$ \begin{equation*} \mathbf{R}=\frac{\sum _{j=1}^{n} m _{j} \mathbf{r} _{j}}{\sum _{j=1}^{n} m _{j}} \tag{1} \end{equation*} $$
$\mathbf{r} _{\mathrm{j}}$ is the instantaneous position vector of the $\mathrm{j}^{\text {th }}$ mass.

For a continuous distribution of mass; summation in Eqn. (1) is replaced by integration.
$$ \begin{equation*} \mathbf{R}=\frac{\int \mathbf{r}(\rho \mathrm{dV})}{\int(\rho \mathrm{dV})} \tag{2} \end{equation*} $$
Main draw back of C.M. concept is:
1. No information regarding detail of motion of individual particles making system can be obtained.
2. No information regarding relative motion of the particle of the system can be obtained.
Example-1 :
Show that center of mass of two particles $A$ and $B$ of mass $m _{1}$ and $m _{2}$ a distance $r$ apart divides the line $A B$ into two parts in the inverse ratio of masses.
Show Answer
Solution :
Fig. 2 shows masses $m _{1}$ and $m _{2}$ distance $A B=r$, apart. Choose line $A B$ as $x$-axis and $A$ as origin of coordinates. Co-ordinates of $A$ and $B$ are $(0)$ and $(r)$ respectively. Let $C$ be the center of mass of the two particle system. Then
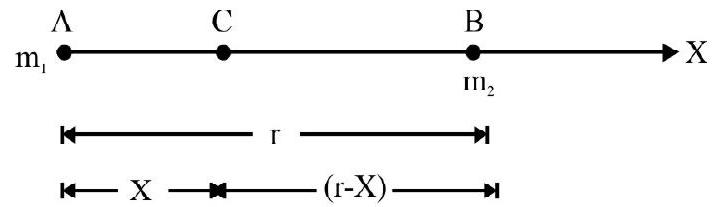
Fig. 2
$\mathrm{AC}=\mathrm{X}=\frac{\mathrm{m} _{1} 0+\mathrm{m} _{2} \mathrm{r}}{\mathrm{m} _{1}+\mathrm{m} _{2}}=\frac{\mathrm{m} _{2} \mathrm{r}}{\mathrm{m} _{1}+\mathrm{m} _{2}}$
$\mathrm{BC}=\mathrm{r}-\mathrm{X}=\frac{\mathrm{m} _{1} \mathrm{r}}{\mathrm{m} _{1}+\mathrm{m} _{2}}$
$\therefore \quad \frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{m} _{2}}{\mathrm{~m} _{1}} \quad$ or $\quad \mathrm{AC}: \mathrm{BC}:: \frac{1}{\mathrm{~m} _{1}}: \frac{1}{\mathrm{~m} _{2}}$
Example-2 :
A particle $A$ of mass $m$ is located in space at $\mathbf{r} _{A}=3 \hat{i}-2 \hat{j}+\hat{k}$. A second particle $B$ of mass $2 m$ is placed at point $B$. The position vector, $R$, of $C$.M. of system is
$$ \mathbf{R}=\hat{i}+\hat{j}-2 \hat{k} $$
What is $\mathrm{r} _{\mathrm{B}}$ ?
Show Answer
Solution :
We know,
$\mathbf{R}=\frac{m \mathbf{r} _{\mathrm{A}}+2 \mathrm{~m} \mathbf{r} _{\mathrm{B}}}{\mathrm{m}+2 \mathrm{~m}}$
or
$$ \hat{i}+\hat{j}-2 \hat{k}=\frac{1}{3}\left[(3 \hat{i}-2 \hat{j}+\hat{k})+2 \mathbf{r} _{B}\right] $$
$\therefore \quad 2 \mathbf{r} _{\mathrm{B}}=(3 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}-6 \hat{\mathrm{k}})-(3 \hat{\mathrm{i}}-2 \hat{\mathrm{j}}+\hat{\mathrm{k}})$
or $\quad \mathbf{r} _{B}=\frac{5 \hat{j}-7 \hat{k}}{2}$
Example-3 :
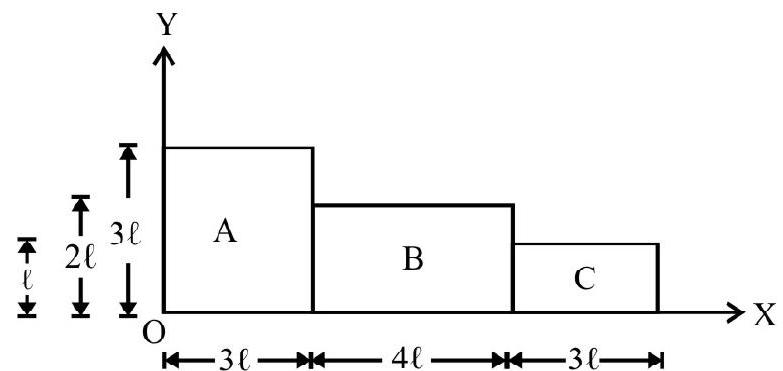
Fig. 3
Fig. 3 shows three blocks A, B and C of same material of surface mass density $\sigma$. Locate C.M. of the arrangement.
Show Answer
Solution :
Let $\mathrm{m} _{1}, \mathrm{~m} _{2}$ and $\mathrm{m} _{3}$ be masses of $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ respectively. Obviously.
$$ \mathrm{m} _{1}=(3 \ell)^{2} \sigma=9 \ell^{2} \sigma ; \mathrm{m} _{2}=(2 \ell \times 4 \ell) \sigma=8 \ell^{2} \sigma ; \mathrm{m} _{3}=(\ell \times 3 \ell) \sigma=3 \ell^{2} \sigma $$
Let $\mathrm{O} _{1}$ and $\mathrm{O} _{2}$ and $\mathrm{O} _{3}$ be the mid point of $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$. These points are C.M. of each block. The system shown is equivalent to point masses $\mathrm{m} _{1}, \mathrm{~m} _{2}, \mathrm{~m} _{3}$ placed at $\mathrm{O} _{1}, \mathrm{O} _{2}$ and $\mathrm{O} _{3}$ as shown in Fig. 4. Co-ordinates of $\mathrm{O} _{1}, \mathrm{O} _{2}$ and $\mathrm{O} _{3}$ are
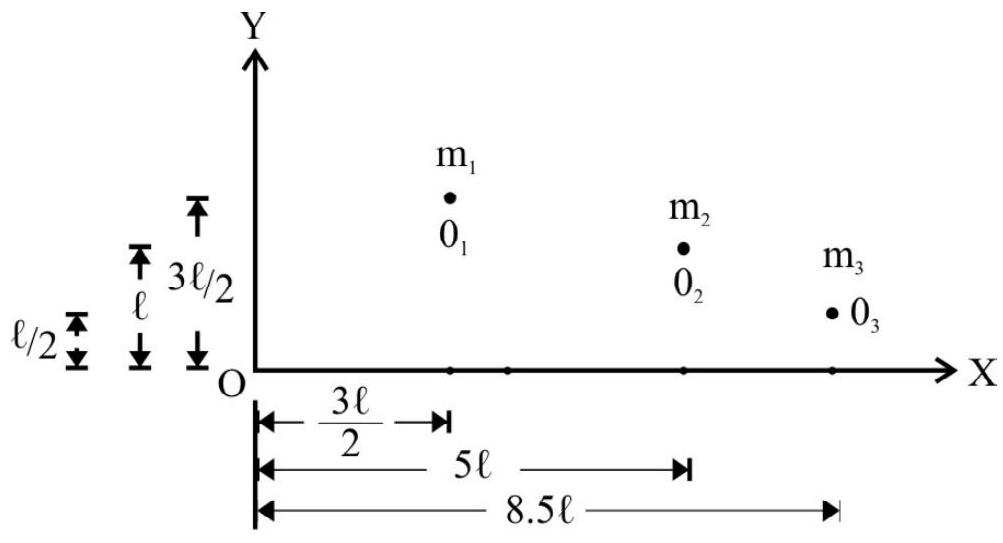
Fig. 4
$\mathrm{O} _{1}\left(\frac{3 \ell}{2} ; \frac{3 \ell}{2}\right), \mathrm{O} _{2}(5 \ell ; \ell), \mathrm{O} _{3}\left(8.5 \ell ; \frac{\ell}{2}\right)$
Let $(\mathrm{X}, \mathrm{Y})$ be the co-ordinates of C.M. of system
$$ \begin{aligned} & X=\frac{\left(9 \ell^{2} \sigma\right)\left(\frac{3 \ell}{2}\right)+\left(8 \ell^{2} \sigma\right)(5 \ell)+3 \ell^{2} \sigma(8.5 \ell)}{20 \ell^{2} \sigma}=\left(\frac{79}{20}\right) \ell \\ & Y=\frac{\left(9 \ell^{2} \sigma\right)\left(\frac{3 \ell}{2}\right)+\left(8 \ell^{2} \sigma\right)+\left(3 \ell^{2} \sigma\right) \frac{\ell}{2}}{20 \ell^{2} \sigma}=\left(\frac{23}{20}\right) \ell \end{aligned} $$
Example-4 :
A uniform circular disc of radius $R$; has a circular part of radius $r$ center $O _{1}$ cut-out and a square of side a center $\mathrm{O} _{2}$ placed on it as shown in Fig. 5 (a). Mass per unit area of circular disc and square is $\sigma _{1}$ and $\sigma _{2}$ respectively. What is location of C.M. of the arrangement?
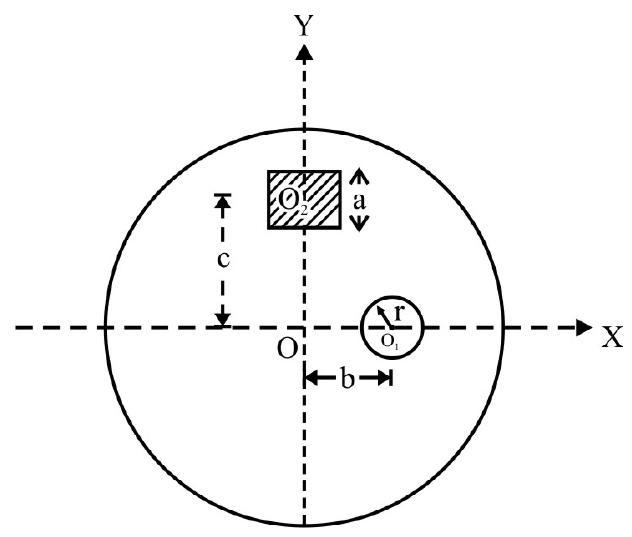
Fig. 5 (a)
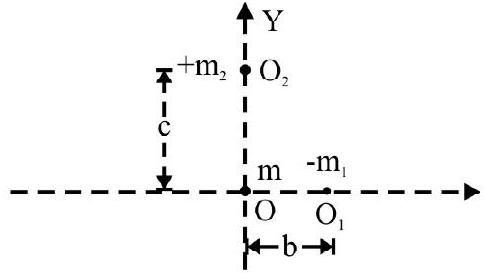
Fig. 5 (b)
Show Answer
Solution :
$\mathrm{m}=$ mass of circular (complete) disc of radius $\mathrm{R}=\pi \mathrm{R}^{2} \sigma _{1}$
$\mathrm{m} _{1}=$ mass of circular disc cut-out $=\pi \mathrm{r}^{2} \sigma _{1}$
$\mathrm{m} _{2}=$ mass of square $=\mathrm{a}^{2} \sigma _{2}$
The arrangement is equivalent to mass $\mathrm{m},-\mathrm{m} _{1}$ and $+\mathrm{m} _{2}$ placed at $\mathrm{O}, \mathrm{O} _{1}$ and $\mathrm{O} _{2}$ respectively. $(\mathrm{X}, \mathrm{Y})$ are co-ordinates of C.M.
$$ \begin{aligned} & X=\frac{m \times 0+\left(-m _{1}\right) b+m _{2}(0)}{m+\left(-m _{1}\right)+m _{2}}=-\frac{r^{2} b}{\left[\left(R^{2}-r^{2}\right)+\left(\frac{\sigma _{2}}{\pi \sigma _{1}}\right) a^{2}\right]} \\ & Y=\frac{m \times 0+\left(-m _{1}\right) x _{0}+m _{2} \times c}{m+\left(-m _{1}\right)+m _{2}}=-\frac{a^{2} c}{\left[\frac{\pi \sigma _{1}}{\sigma _{2}}\left(R^{2}-r^{2}\right)+a^{2}\right]} \end{aligned} $$
Example-5 :
A bomb of mass $M$ at rest; some how on its own explodes into three fragments having masses in ratio of 1:2:3 flying off in direction making an angle of $25^{\circ}, 40^{\circ}$ and $55^{\circ}$ with horizontal. Locate the position of C.M of fragments?
Show Answer
Solution :
Initially C.M. of bomb is at rest at its center. The bomb explodes on its own i.e. there is no external force. The equation of motion of C.M. of fragments is
$$ \left(\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{2}\right) \frac{\mathrm{d}^{2} \mathbf{R}}{\mathrm{dt}^{2}}=0 $$
or
$$ \mathrm{MA}=0 $$
Since $\mathrm{M} \neq 0 ; \mathbf{A}=\frac{\mathrm{d} \mathbf{v}}{\mathrm{dt}}=0$. Since $\frac{\mathrm{d} \mathbf{v}}{\mathrm{dt}}=0 ; \mathbf{v}=\mathbf{v} _{0}=$ Initial speed of center of mass $=0$
The center of mass remains at the center of the bomb, i.e. in its original position.
Example-6 :
A ball of mass $M$ is at rest at a height $H$ above ground in a vertical plane in gravity of earth. After dropping through a height $\mathrm{H} / 4$; it on its own, breaks up into n fragments moving in different directions in the plane of motion. What is path of C.M. of fragments?
Show Answer
Solution :
Let vertical downward direction be the direction of $\mathrm{z}$-axis and initial position of ball as origin of co-ordinates. Let $\mathrm{z}$ be the instantaneous position co-ordinate of C.M of ball, before explosion. The equation of motion of C.M is
$$ \begin{equation*} \mathrm{M} \frac{\mathrm{d}^{2} \mathrm{z}}{\mathrm{dt}}=\mathrm{Mg} \quad \text { or } \quad \frac{\mathrm{d}^{2} \mathrm{z}}{\mathrm{dt}^{2}}=\mathrm{g} \tag{1} \end{equation*} $$
The center of mass moves along $\mathrm{z}$-axis with uniform acceleration $\mathrm{g}$.
When ball breaks up, on its own; there is no other external force. The equation of motion of C.M. of fragments is
$$ \left[\sum _{j=1}^{n} m _{j}\right] \frac{d^{2} z}{d t^{2}}=\sum _{n=1}^{m} m _{j} g \quad \text { or } \quad \frac{d^{2} z}{d t^{2}}=g $$
This is same as Eqn. (1). Hence C.M of fragment continues moving along $z$-axis with uniform acceleration $=\mathrm{g}$
Rotational Motion of a Rigid Body about a Fixed Axis
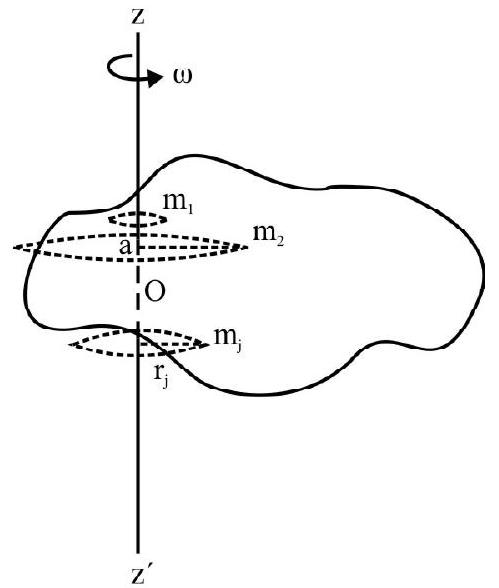
Fig. 6
Fig. 6 shows a rigid body rotating about a fixed axis zoz’ with a constant angular speed $\omega$. Consider rigid body as made up of point masses $\mathrm{m} _{1}, \mathrm{~m} _{2} \ldots \ldots . \mathrm{m} _{\mathrm{j}} \ldots \ldots . \mathrm{m} _{\mathrm{n}}$ as shown in Fig. 6. As rigid body rotates each point moves along a circle. The radius of circle equals the perpendicular distance $r _{j}$ of the $j^{\text {th }}$ mass from axis $z o z$. The value of $\mathrm{r} _{\mathrm{j}}$ changes as $\mathrm{j}$ takes values $1,2 \ldots . . \mathrm{n}$. However every point mass completes one circle in same time $\mathrm{T}$. $\mathrm{T}$ equals time taken by the rigid body to complete one full circle (or one revolution). Therefore angular speed of each point mass making the body is same. However the linear speed of each point mass in rigid body is different. $v _{j}=$ The linear speed of $j^{\text {th }}$ mass $=r _{j} \omega$.
We want to develop rotational dynamics in a manner similar to translational motion. Corresponding to every concept in Newtonian mechanics, there is a similar concept in rotational dynamics. The development of basics involves circular motion of each of the individual point masses. We will, therefore, describe basic concepts, using a single point mass and then generalize the concept for the rigid body.
Angular Speed and Angular Velocity

For a particle moving in a circle of radius $\mathrm{r}$; the instantaneous position $\mathrm{P}$, of the particle is given by its angular position $\theta \cdot\lfloor\mathrm{XOP}=\theta$ is the angle between the line $\mathrm{OP}$ and a conveniently chosen reference line say $X O X^{\prime}$. The instantaneous angular speed.
$$ \begin{equation*} \omega=\operatorname{Lt} _{\Delta t \rightarrow 0} \frac{\Delta \theta}{\Delta \mathrm{t}}=\frac{\mathrm{d} \theta}{\mathrm{dt}} \tag{1} \end{equation*} $$
The linear speed, $\mathrm{v}$ of particle $\mathrm{P}$ is
$$ \begin{gather*} \mathrm{v}=\operatorname{Lt} _{\Delta t \rightarrow 0}\left(\frac{\operatorname{arc} \mathrm{PQ}}{\Delta \mathrm{t}}\right)=\underset{\Delta t \rightarrow 0}{\operatorname{Lt}}\left(\frac{\mathrm{r} \Delta \theta}{\Delta \mathrm{t}}\right) \\ =\mathrm{r} \underset{\Delta t \rightarrow 0}{ }\left(\frac{\Delta \theta}{\Delta \mathrm{t}}\right)=\mathrm{r} \omega \tag{2} \end{gather*} $$
The angular velocity $\omega$ has to be assigned a direction in addition to its magnitude as defined by Eqn. (1). The direction of $\omega$ is always (i) perpendicular to the plane in which particle moves (ii) sense of $\omega$ is given by the right hand screw rule i.e. place a right handed screw perpendicular to the plane of circle. Rotate screw in direction of motion of particle. The direction in which screw advances is direction of $\boldsymbol{\omega }$. Therefore
$$ \boldsymbol{\omega}=\left(\frac{\mathrm{d} \theta}{\mathrm{dt}}\right) \hat{\mathrm{n}}=\omega \hat{ n } $$
$\hat{\mathrm{n}}$ is a unit vector in the direction of outward normal to the plane of motion. The relation between linear velocity $\mathbf{v}$ and angular velocity $\omega$ is shown in Fig. 7 (c). $\mathbf{v}$ is in the direction of tangent to circle at the instantaneous position $\mathrm{P}$ of the particle. Obviously
$$ \mathbf{v}=\boldsymbol{\omega} \times \mathbf{r} $$
Note: If $\omega$ is constant; the angular speed is also constant and the motion takes place is a fixed plane. $\omega$ changes if either magnitude of $\omega$ changes but plane of motion remains same or if magnitude of $\omega$ remains same but plane of motion changes as shown in Fig. 7 (d).
$\mathbf{v}$ is an axial vector i.e. there is no lateral inversion in $\mathbf{v}$ when mirror image of system is considered with mirror placed at position of axis of relation.
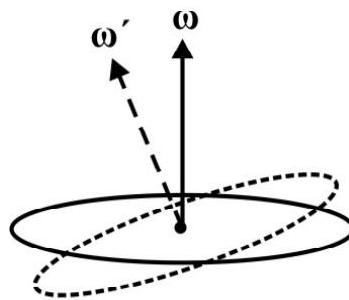
Fig. 7 (d)
Angular Momentum
In linear motion (translational motion) the quantity of motion is measured in terms of the linear momentum of a particle. The linear momentum $\mathbf{p}=\mathrm{mv}$. The quantity of rotational motion of a particle is measured in terms of angular momentum or moment of momentum $\ell$.
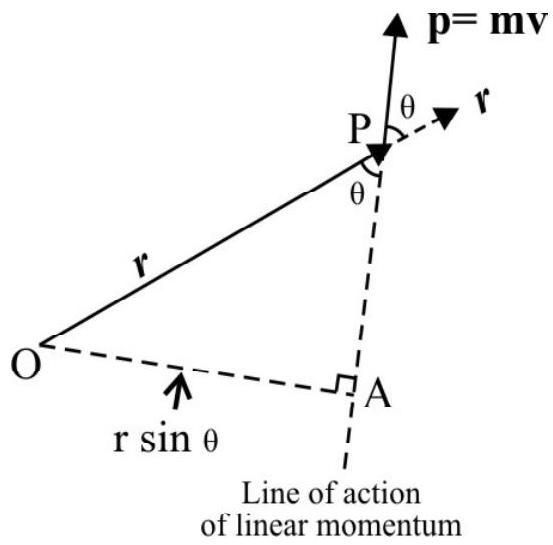
Fig. 8
For a particle of mass $\mathrm{m}$ at a position $\mathrm{P}$ given by $\mathbf{O P}=\mathbf{r}$; having instantaneous linear momentum $\mathbf{p}=\mathrm{m} \mathbf{v}$; the magnitude of instantaneous angular momentum $\ell$ about point $\mathrm{O}$ is defined as
$|\ell|=$ Linear momentum $\times$ distance of line of action of $\mathbf{p}$ from point 0
$$ =p \times O A=p \times r \sin \theta $$
$\theta=$ angle between $\mathbf{r}$ and $\mathbf{p}$. The direction of $\ell$ is always perpendicular to the plane containing $\mathbf{p}$ and $\mathbf{r}$. Its sense of given y the right-hand screw rule. In terms of vectors
$$ \ell=\mathbf{r} \times \mathbf{p} $$
For a rigid body the angular momentum $\mathbf{L}$ about any point $\mathrm{O}$ is the vector sum of the angular momentum of various point masses constituting the body. Let $\mathbf{r} _{\mathrm{j}}$ be the position vector of the $j^{\text {th }}$ point mass $m _{j} . \omega$ is the angular speed of the body. The linear velocity $\mathbf{v} _{\mathrm{j}}$ of $\mathrm{j}^{\text {th }}$ mass is $\mathbf{v} _{\mathrm{j}}=\boldsymbol{\omega} \times \mathbf{r} _{\mathrm{j}}$. Therefore
$$ \mathbf{L}=\sum \mathbf{r} _{\mathrm{j}} \times \mathbf{p} _{\mathrm{j}}=\sum \mathbf{m} _{\mathrm{j}} \mathbf{r} _{\mathrm{j}} \times\left(\boldsymbol{\omega} \times \mathbf{r} _{\mathrm{j}}\right) $$
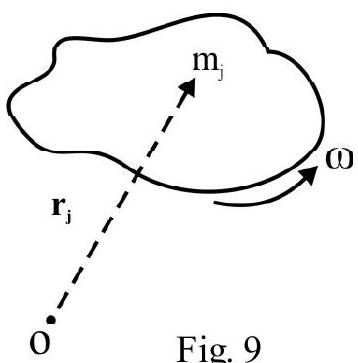
Fig. 9
It can be shown that for a rigid body rotating about a fixed axis; the angular momentum can be written as
$$ \mathrm{L}=\mathrm{I} \omega $$
where $\mathrm{I}$ is the moment of inertia of the rigid body about the axis of rotation. Note expression for $\mathrm{L}$ is exactly similar to $\mathrm{p}=\mathrm{mv}$ for linear motion.
Torque or Moment of a Force
Torque measures the rotational effect of an applied force. It plays same role in rotational motion as is the role of a force in translational motion. It is obvious that rotational effect of a force depends not only on the magnitude of the applied force but also on the position of point of application of the force.
1. For opening a ‘door’ hinged at one end we apply external force on the handle. The handle is positioned at a large, convenient distance from the hinge. If handel is nearer the hinges a larger force is required to open the door.
2. The steering wheel of a car or truck is a circular ring of conveniently large radius. A small applied external force can easily turn the car i.e. turning effect of force is large.
3. The jack used to lift a car is used having a rod of fairly large length. A small external applied force, can easily “lift up” the car via the jack.
The torque $\tau$ or moment of a force is defined as
$|\tau|=$ applied force $\times \perp$ distance of line of action of force from say point $\mathrm{O}$, about which torque of force is to be calculated $=\mathrm{F} \times \mathrm{OA}=\mathrm{Fr} \sin \theta$
For $\mathrm{F} \neq 0 ; \mathrm{r} \neq 0$ the torque is zero if
$\sin \theta=0$ or $\theta=0$ or $\pi$
The torque of force is zero if line of action of force is parallel
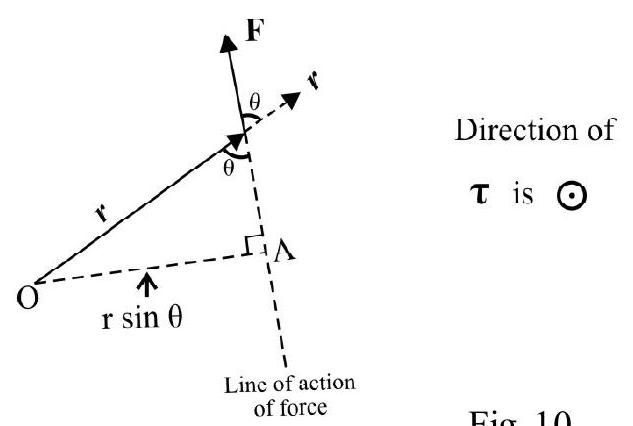
Fig. 10
or antiparallel to $\mathbf{r}$. We can also conclude that $\tau=0$, if line of action of force passes through point $\mathrm{O}$, about which torque of force is to be calculate.
Torque is a vector quantity. Its direction is always
(1) Perpendicular to the plane containing $\mathbf{r}$ and $\mathbf{F}$
(2) The sense of $\tau$ is given by the right-hand screw rule i.e. ‘place’ a rigid-handed screw perpendicular to the plane containing $\mathbf{r}$ and $\mathbf{F}$. Rotate screw so that $\mathbf{r}$ goes and coincides with $\mathbf{F}$. The direction in which screw advances is direction of $\tau$. In Fig. $10 \tau$ is perpendicular to plane of page and has an “anticlockwise direction”. It is represented as $\odot$. In terms of vectors.
$$ \tau=\mathbf{r} \times \mathbf{F} $$
Just as an unbalanced force is the cause of translational motion; an unbalanced torque is the cause of rotational motion. For a large number of forces $\mathbf{F} _{j} ; j=1,2, \ldots \mathrm{n}$; acting at points having position vectors $\mathbf{r} _{j}$; the net torque about origin of co-ordinates is
$$ \tau=\sum _{\mathrm{j}=1}^{\mathrm{n}}\left(\mathbf{r} _{\mathrm{j}} \times \mathbf{F} _{\mathrm{j}}\right) $$
There can be a torque on a system with zero net force (Fig. 11a). There can be a zero torque with a net force (Fig. 11b). In a system shown in (Fig. 11c) neither F nor $\tau$ is zero.

Law of Conservation of Angular Momentum
We know,
$$ \mathbf{L}=\mathbf{r} \times \mathbf{p} \quad \text { and } \quad \tau=\mathbf{r} \times \mathbf{F} $$
$\therefore \quad \frac{\mathrm{d} \mathbf{L}}{\mathrm{dt}}=\frac{\mathrm{d} \mathbf{r}}{\mathrm{dt}} \times \mathbf{p}+\mathbf{r} \times \frac{\mathrm{d} \mathbf{p}}{\mathrm{dt}}$
$$ =(\mathbf{v} \times \mathrm{m} \mathbf{v})+(\mathbf{r} \times \mathbf{F}) \quad\left[\because \frac{\mathrm{d} \mathbf{p}}{\mathrm{dt}}=\mathbf{F} . \text { Newton’s 2nd law of motion }\right] $$
Since $\mathbf{v} \times \mathbf{v} \equiv 0$; we have
$$ \tau=\frac{\mathrm{d} \mathbf{L}}{\mathrm{dt}} $$
If there is no external torque i.e. $\tau=0$;
$$ \frac{\mathrm{d} \mathbf{L}}{\mathrm{dt}}=0 \quad \text { or } \quad \mathbf{L}=\text { constant } $$
This is the law of conservation of angular momentum. i.e. if there is no net external torque on a system, the total angular momentum of system is a constant. The law of conservation of angular momentum is a very convenient tool for solving problems in rotational dynamics.
Example-7 :
A particle of mass $m$ is initially at point having position vector $\mathbf{r} _{0}$. The particle moves with a uniform velocity $\mathbf{v} _{0}$. What is the instantaneous angular momentum of particle about origin of coordinates?
Show Answer
Solution :
The instantaneous position vector $\mathbf{r}$ is
$$ \mathbf{r}=\mathbf{r} _{0}+\mathbf{v} _{0} \mathbf{t} $$
The instantaneous linear momentum, $\mathbf{p}$; is
$$ \mathbf{p}=\mathbf{m} \mathbf{v} _{0} $$
The instantaneous angular momentum $\mathbf{L}$ about origin of co-ordinates is
$$ \begin{aligned} & \mathbf{L}=\mathbf{r} \times \mathbf{p} \\ & =\left(\mathbf{r} _{0}+\mathbf{v} _{0} \mathrm{t}\right) \times \mathbf{m} \mathbf{v} _{0} \\ & =\mathbf{r} _{0} \times \mathrm{m} \mathbf{v} _{0} \quad\left[\because \mathbf{v} _{0} \times \mathbf{v} _{0} \equiv 0\right] \end{aligned} $$
Example-8 :
A particle of mass $100 \mathrm{~g}$ is moving along a straight line in $\mathrm{X}-\mathrm{Y}$ plane with a constant speed of $2 \mathrm{~ms}^{-1}$. The equation of straight line is
$$ y=\frac{x}{\sqrt{3}}+3 $$
$x$ and $y$ are in meter. What is angular momentum of particle about origin of co-ordinates?
Show Answer
Solution :
Fig. 12 shows straight line along which particle moves. The line makes an angle of $30^{\circ}$ with $x$-axis.
$$ \begin{aligned} & \mathrm{p}=\text { linear momentum of particle } \\ & =\mathrm{mv}=0.1 \times 2=0.2 \mathrm{kgms}^{-1} \\ & \ell _{0}=\text { magnitude of angular momentum of } \mathrm{P} \\ & \quad \quad \text { about } \mathrm{O} \\ & =\mathrm{p} \times \mathrm{OA}=\mathrm{p} \times \mathrm{OC} \sin 30^{0} \\ & =0.2 \times 3 \times 0.5=0.3 \mathrm{kgm}^{2} \mathrm{~s}^{-1} \end{aligned} $$
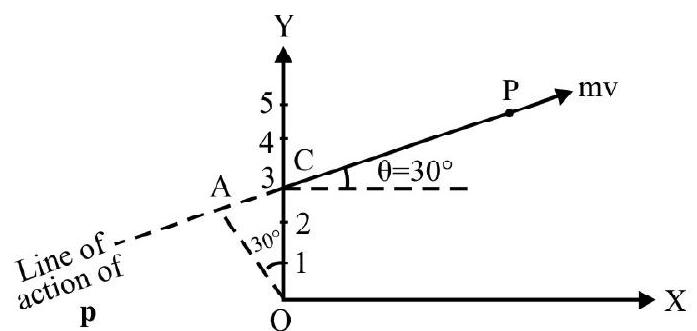
Fig. 12
Example-9 :
A conical pendulum of length $\ell$ has a bob of mass $m$; moving in a horizontal circle with uniform angular speed $\omega$. What is angular momentum of bob about the center of its circular path?
Show Answer
Solution :
Fig. 13 shows the conical pendulum. $\mathrm{O} _{1}$ is point of suspension and $\mathrm{O} _{1} \mathrm{P}=\ell=$ length of pendulum.
$\mathrm{OP}=\mathrm{r}=\ell \sin \theta=$ radius of circular path of bob
$\mathrm{v}=$ linear speed of bob $=\mathrm{r} \omega$
$\mathrm{L} _{0}=$ magnitude of angular momentum of bob about 0.
$$ \begin{aligned} & =\mathrm{mvr}=\mathrm{mr}^{2} \omega \\ & =\mathrm{m} \ell^{2} \omega \sin ^{2} \theta \end{aligned} $$
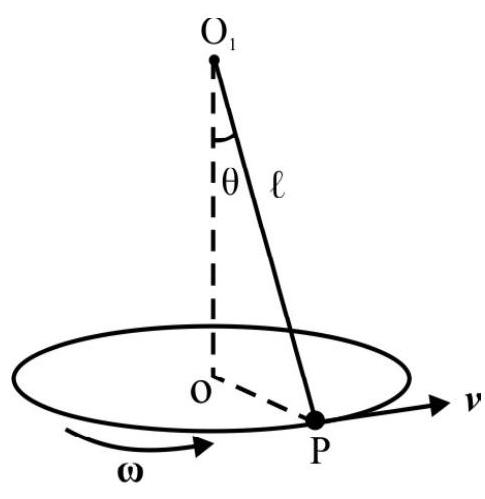
Fig. 13
Example-10 :
Fig. 14 shows two particles $P$ and $Q$ moving as shown. The net angular momentum of $P$ and $Q$ about point $O$ is 4 mva. What is $y$ ?
Show Answer
Solution :
$\mathrm{L} _{\mathrm{P}}=$ Angular momentum of $\mathrm{P}$ about 0
$=2 \mathrm{mv} _{0} \cdot$; clockwise
$\mathrm{L} _{\mathrm{Q}}=$ Angular momentum of $\mathrm{Q}$ about 0
$=8 \mathrm{mv} _{0} . \mathrm{y}$; anticlockwise
$\mathrm{L}=$ The net angular momentum $=\mathrm{L} _{\mathrm{Q}}-\mathrm{L} _{\mathrm{P}}$
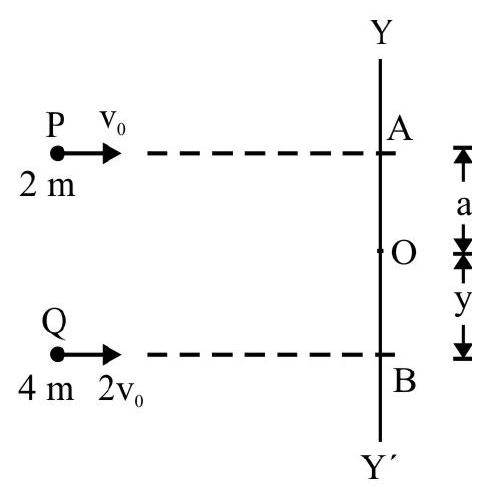
Fig. 14
$=2 \mathrm{mv} _{0}[4 \mathrm{y}-\mathrm{a}]$; anticlockwise
$=4 \mathrm{mv} _{0} \mathrm{a} \quad$ (Given)
$$ \therefore \quad 4 y-a=2 a \quad \text { or } \quad y=\frac{3 a}{4} $$
Example-11 :
A sphere of mass $M$, radius $R$ is placed on a rough inclined plane of inclination $\theta$ as shown in Fig. 15. A string is attached to sphere as shown. The sphere is kept in equilibrium by pulling string with a constant force $F$. What is tension in string?
Show Answer
Solution :
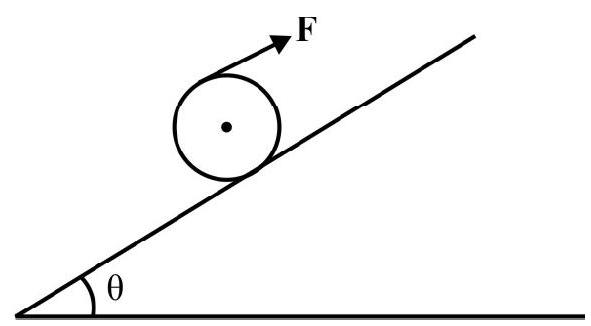
Fig. 15
Fig. 16 shows free-body diagram of sphere. Since sphere is in equilibrium there is neither a motion of translation nor rotation. For translation equilibrium
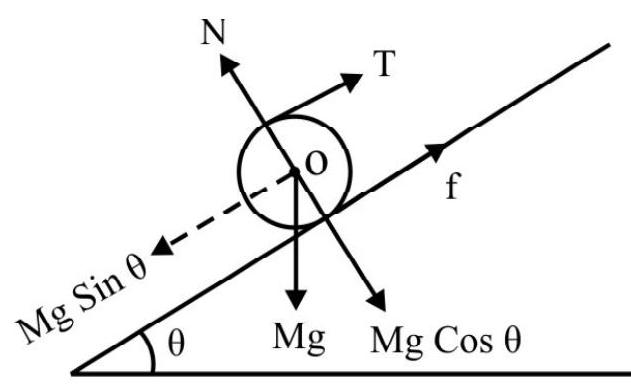
Fig. 16
$$ \begin{equation*} M g \sin \theta=f+T \tag{i} \end{equation*} $$
For rotational equilibrium; the net torque about $\mathrm{O}$ is zero. Therefore
$$ \begin{align*} & \mathrm{TR}=\mathrm{f} . \mathrm{R} \\ & \text { or } \quad \mathrm{T}=\mathrm{f} \tag{ii} \end{align*} $$
From Eqns. (i) and (ii) we have
$$ \mathrm{T}=\frac{\mathrm{Mg} \sin \theta}{2} $$
Rotational Inertia - Moment of Inertia
A rotating body possesses “rotational inertia” i.e. a body at rest does not start rotating on its own and a body rotating does not stop rotating on its own. This property is similar to the linear inertia. The linear inertia is determined by the mass of a body $(\mathrm{m})$. The rotational inertia however depends not only on the mass but the axis of rotation also. Fig. 17 shows a rigid body rotating about zoz’ as axis with a constant angular speed $\omega . \mathrm{m} _{\mathrm{j}}$ is the $j^{\text {th }}$ mass (point) of the rigid body at a perpendicular distance $r _{i}$ from axis of rotation. As rigid body rotates $m _{j}$ moves in a circle of radius $r _{j}$. The K.E. of $j^{\text {th }}$ mass
$$ \mathrm{k} _{\mathrm{j}}=\frac{1}{2} \mathrm{~m} _{\mathrm{j}} \mathrm{v} _{\mathrm{j}}^{2}=\frac{1}{2} \mathrm{~m} _{\mathrm{j}}\left(\mathrm{r} _{\mathrm{j}} \omega\right)^{2} $$
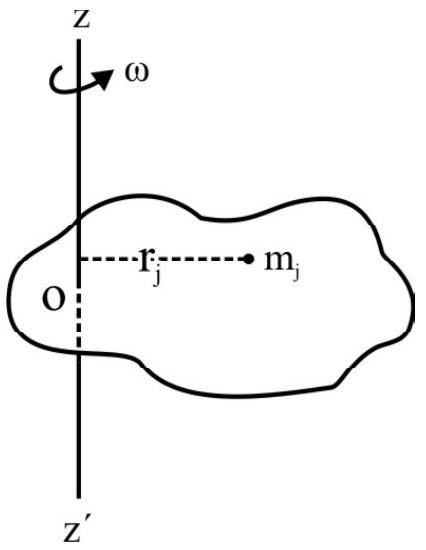
Fig. 17
$K=$ The total rotational K.E. of the body $=\sum k _{j}$
$$ \begin{aligned} & =\frac{1}{2}\left(\sum \mathrm{m} _{\mathrm{j}} \mathrm{r} _{\mathrm{j}}^{2}\right) \cdot \omega^{2} \equiv \frac{1}{2} \mathrm{I} \omega^{2} \\ & \therefore \quad \mathrm{I}=\sum \mathrm{m} _{\mathrm{j}} \mathrm{r} _{\mathrm{j}}^{2} \end{aligned} $$
For a body having continuous distribution of mass
$$ \mathrm{I}=\int(\rho \mathrm{dv}) \mathrm{r}^{2} $$
where $\mathrm{dv}$ is an infitesimally small volume element at a perpendicular distance $r$ from the axis of rotation. Though M.I and mass are similar quantities; M.I depends on (i) axis of rotation and (ii) distribution of mass whereas linear inertia or mass does not depend on the direction of motion. Mass is a scalar quantity, whereas in general M.I is much more complex quantity known as a TENSOR. However for a fixed axis of rotation M.I behaves like a scalar quantity. We will restrict ourselves only to rotational motion about a fixed axis.
The theorem of (1) parallel and (2) perpendicular axes are very convient tools to calculate M.I about different axes.
M.I is also defined numerically in a manner exactly similar to definition of mass in linear motion. We know, for linear motion
$$ \mathrm{m}=\frac{\mathrm{F}}{\mathrm{a}} $$
Similarly for rotational motion;
$$ \mathrm{I}=\frac{\tau}{\alpha} $$
Theorem of Parallel Axes
Fig. 18 shows a rigid body of mass M. Point G is the C.G. of rigid body. ZOZ’ is the axis about which body rotates. The M.I of body about ZOZ’ $^{\prime}$ axis is $I$. Let $Z _{1} \mathrm{GZ} _{1}{ }^{\prime}$ be an axes parallel to $Z O Z^{\prime}$ passing through C.G . The M.I. of body about $Z _{1} \mathrm{GZ} _{1}^{\prime}$ as axes is Ig.
$\mathrm{h}=$ perpendicular distance between the two parallel axes.
According to theorem of parallel axes
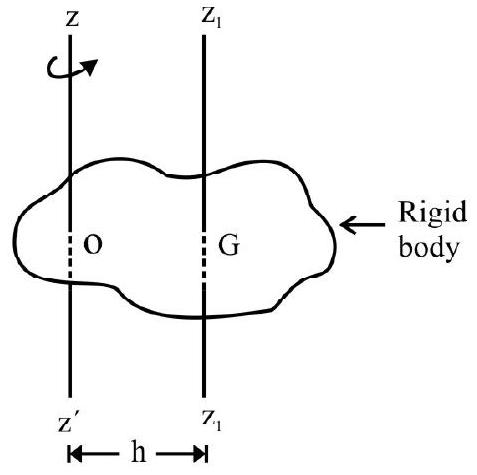
$$ \mathrm{I}=\mathrm{I} _{\mathrm{g}}+\mathrm{Mh}^{2} $$
Consider a number of parallel axes $1,2,3$ etc. through a rigid body. The M.I about these axes is $\mathrm{I} _{1} , \mathrm{I} _{2}, \mathrm{I} _{3}$ etc. Let $I _{g}$ be M.I about a parallel axis through C.G. Then
$$ I _{\min }=I _{g} $$
Theorem of Perpendicular Axes
(1) A Laminar Body : A laminar body is a two dimensional body. Fig. 19(a) shows a laminar body in $x-y$ plane. $x$, $y$ and $z$ are three mutually perpendicular axis through same point O. $x$ and $\mathrm{y}$ are mutually perpendicular in plane of lamina. $\mathrm{z}-\mathrm{axis}$ is perpendicular to plane of lamina. Let $\mathrm{I} _{x}, \mathrm{I} _{\mathrm{y}}$ and $\mathrm{I} _{\mathrm{z}}$ be M.I of body about $x$-, y and $z$-axis respectively. According to theorem of perpendicular axis
$$ \mathrm{I} _{\mathrm{z}}=\mathrm{I} _{x}+\mathrm{I} _{\mathrm{y}} $$
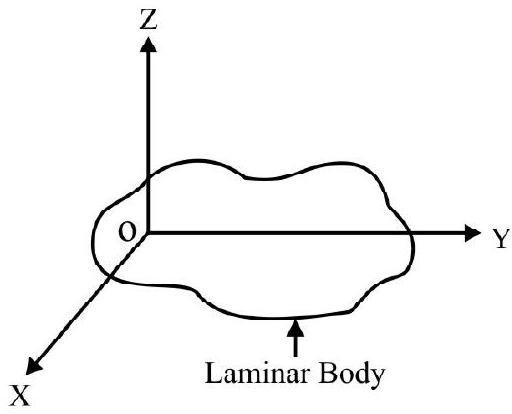
Fig. 19(a)
In words; M.I of laminar body about an axis perpendicular to plane of lamina equals the sum of moments of inertia of body about two mutually perpendicular axes in the plane of lamina. All three axes must pass through same point $\mathrm{O}$ on the body.
(2) Three Dimensional Body
Fig. 19(b) shows a three dimensional rigid body. $x, \mathrm{y}, \mathrm{z}$ are axis making a Cartesian co-ordinate system. $\mathrm{I} _{x}, \mathrm{I} _{\mathrm{y}}, \mathrm{I} _{\mathrm{z}}$ is M.I of rigid body $\mathrm{x}-, \mathrm{y}-$ and $\mathrm{z}$ axis.
Consider an elementary mass $(\delta \mathrm{m})$ at point $\mathrm{P}$, distant $\mathrm{r} _{0}=\mathrm{OP}$ from origin. According to theorem of perpendicular axis.
$$ \mathrm{I} _{x}+\mathrm{I} _{\mathrm{y}}+\mathrm{I} _{\mathrm{z}}=2\left[\sum(\delta \mathrm{m}) \mathrm{r} _{0}^{2}\right] $$
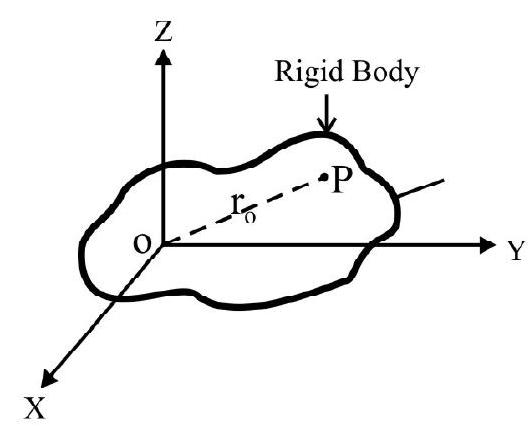
Fig. 19(b)
Moment of Inertia vs. Mass
The mass of a body is a constant. It does not depend on direction of motion. M.I of a rigid body is not a constant it depends on
(i) axis of rotation
(ii) distribution of mass
Radius of Gyration
Radius of gyration $\mathrm{k}$ about an axis is perpendicular distance from the axis where the entire mass of body is imagined to be concentrated so that M.I of this point mass is same as the actual M.I of the rigid body. Expressed mathematically
$$ \begin{aligned} & \mathrm{I}=\mathrm{Mk}^{2}=\sum _{\mathrm{j}=1}^{\mathrm{n}} \mathrm{m} _{\mathrm{j}} \mathrm{r} _{\mathrm{j}}^{2} \\ & k=\sqrt{\frac{I}{M}}=\sqrt{\frac{\sum _{j=1}^{n} m _{j} r _{j}^{2}}{\sum _{j=1}^{n} m _{j}}} \end{aligned} $$
Radius of gyration depends on axis of rotation.
Expressions of Moment of Inertia
| S.No. | Shape of Body | Dimensions | Axis of Rotation | Moment of Inertia |
|---|---|---|---|---|
| 1. | Circular Ring | $\mathrm{M}=$ mass $\mathrm{R}=$ radius |
i) Through center $O$ and $\perp$ to plane of ring ii) Any diameter iii) Any tangent in its own plane |
$\mathrm{MR}^2$ $\frac{1}{2} \mathrm{MR}^2$ $\frac{3}{2} \mathrm{MR}^2$ |
| 2 | Uniform Circular Disc |
$\mathrm{M}=$ mass $\mathrm{R}=$ radius |
i) Through center $\mathrm{O}$ and $\perp$ to plane of disc ii) Any diameter iii) Any tangent in plane of disc |
$\frac{\mathrm{MR}^2}{2}$ $\frac{\mathrm{MR}^2}{4}$ $\frac{5 \mathrm{MR}^2}{4}$ |
| 3. | Hollow sphere OR (spherical shell) | $\mathrm{M}=$ mass $\mathrm{R}=$ radius |
i)Any diameter ii) Any tangent |
$\frac{2}{3} \mathrm{MR}^2$ $\frac{5}{3} \mathrm{MR}^2$ |
| 4. | Solid sphere | $\mathrm{M}=$ mass $\mathrm{R}=$ radius |
i)Any diameter ii) Any tangent |
$\frac{2}{5} \mathrm{MR}^2$ $\frac{7}{5} \mathrm{MR}^2$ |
| 5. | Solid Cylinder | $\mathrm{M}=$ mass $\mathrm{R}=$ radius $\mathrm{L}=$ length |
i)Own axis ii)Through midpoint $\mathrm{O}$ and perpendicular to length of cylinder |
$\frac{\mathrm{MR}^2}{2}$ $\mathrm{M}\left(\frac{\mathrm{R}^2}{4}+\frac{\mathrm{L}^2}{12}\right)$ |
| 6. | Thin Rod (One-dimensional) |
$\mathrm{M}=$ mass $\mathrm{L}=$ length |
i)Midpoint $\mathrm{O}$ and perpen- dicular to length of rod ii)One end and $\perp$ to length iii) Midpoint $\mathrm{O}$ making an angle $\theta$ with length |
$\frac{\mathrm{ML}^2}{12}$ $\frac{\mathrm{ML}^2}{3}$ $\frac{\mathrm{ML}^2}{12} \sin ^2 \theta$ |
| 7. | Rectangular Lamina |
$\mathrm{M}=$ mass $\mathrm{L}=$ length $\mathrm{B}=$ breadth |
i)Midpoint $\mathrm{O}$ and parallel to length ii) Midpoint $\mathrm{O}$ and parallel to breadth iii) Midpoint $\mathrm{O}$ and perpen- dicular to plane of lamina |
$\frac{\mathrm{MB}^2}{12}$ $\frac{\mathrm{ML}^2}{12}$ $\mathrm{~m}\left(\frac{\mathrm{L}^2+\mathrm{B}^2}{12}\right)$ |
| 8. | Parallel lopeid | $\mathrm{M}=$ mass $\mathrm{L}=$ length $\mathrm{B}=$ breadth H = Height |
i)Midpoint $\mathrm{O}$ and parallel to height ii) Midpoint $\mathrm{O}$ and parallel to length iii) Midpoint O and parallel to breadth |
$\frac {M(L^2+B^2}{12})$ $\frac {M(B^2+H^2}{12})$ $\frac {M(L^2+H^2}{12})$ |
Example-12 :
Eight identical point mass each of mass, $m$; are placed at the corners of a mass-less cube of side a as shown in Fig. 20. $I _{1}$ and $I _{2}$ denote M.I of system about axis 1 and axis 2 as shown
in Fig. 20. What is $\frac{I _{1}}{I _{2}}$ ?
Show Answer
Solution :
For axis-1
$\mathrm{I} _{\mathrm{A}}=\mathrm{I} _{\mathrm{B}}=0$
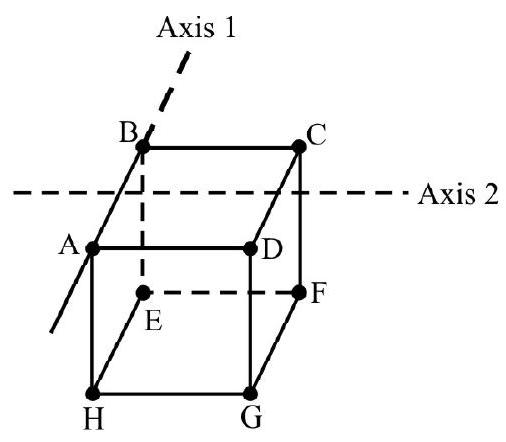
Fig. 20
$I _{C}=I _{D}=I _{E}=I _{H}=m a^{2}$
$I _{G}=I _{F}=m(\sqrt{2 a})^{2}$
$\therefore \quad \mathrm{I} _{1}=4 \mathrm{ma}^{2}+2 \mathrm{~m}(\sqrt{2} \mathrm{a})^{2}=8 \mathrm{ma}^{2} \hspace{40mm} . . . . . . . (i)$
For axis-2
Through midpoint of side $\mathrm{AB}$ and $\mathrm{CD}$
$\mathrm{I} _{\mathrm{A}}=\mathrm{I} _{\mathrm{B}}=\mathrm{I} _{\mathrm{C}}=\mathrm{I} _{\mathrm{D}}=\mathrm{m}\left(\frac{\mathrm{a}}{2}\right)^{2}$
The perpendicular distance of points E, F, G and $\mathrm{H}$ from axis $=\sqrt{(\mathrm{a})^{2}+\left(\frac{\mathrm{a}}{2}\right)^{2}}=\frac{\sqrt{5}}{2} \mathrm{a}$
Hence,
$$ \begin{gather*} \mathrm{I} _{2}=4\left[\mathrm{~m}(\mathrm{a} / 2)^{2}\right]+4\left[\mathrm{~m}\left(\sqrt{\frac{5}{2} \mathrm{a}}\right)^{2}\right] \\ =6 \mathrm{ma}^{2} \tag{ii} \end{gather*} $$
$\therefore \quad \frac{\mathrm{I} _{1}}{\mathrm{I} _{2}}=\frac{4}{3}$
Example-13 :
A uniform ring of mass $M$, radius $R$ has a moment of inertia $I$ about axis through its center and perpendicular to its plane. A uniform disc of same mass as ring has M.I of $\frac{\mathrm{I}}{2}$ about a tangent in its own plane as axis. The radius of disc is
(a) $\frac{\mathrm{R}}{2}$
(b) $\quad \frac{2}{5} \mathrm{R}$
(c) $\sqrt{\frac{2}{5}} \mathrm{R}$
(d) $\sqrt{\frac{3}{2}} \mathrm{R}$
Show Answer
Solution :
$\mathrm{I}=$ M.I of ring about given axis $=\mathrm{MR}^{2}$
Let $\mathrm{r}$ be radius of disc. The M.I, of disc, $\mathrm{I} _{1}$, about a tangent in its own plane is
$$ \mathrm{I} _{1}=\frac{\mathrm{Mr}^{2}}{4}+\mathrm{Mr}^{2}=\frac{5 \mathrm{Mr}^{2}}{4} $$
[Theorem of parallel axis]
Given $\frac{I}{2}=I _{1}$. Therefore
$$ \frac{\mathrm{MR}^{2}}{2}=\frac{5}{4} \mathrm{Mr}^{2} $$
or $\quad r=\sqrt{\frac{2}{5}} \mathrm{R}$
Example-14 :

A thin $\operatorname{rod} \mathrm{AB}=2 \mathrm{~L}$ has a mass of $2 \mathrm{M}$. It lies along $\mathrm{X}$-axis. Its moment of inertia about $\mathrm{YOY}^{\prime}$ as axis [refer to Fig. 21(a)] is $I _{1}$. The rod is bent at its midpoint $O$ as shown in Fig. 21(b). The M.I about same axis $\mathrm{I} _{2}$. What is $\frac{\mathrm{I} _{1}}{\mathrm{I} _{2}}$ ?
Show Answer
Solution :
$\mathrm{I} _{1}=\frac{1}{12}(2 \mathrm{M})(2 \mathrm{~L})^{2}=\frac{2}{3} \mathrm{ML}^{2} \hspace{40mm} . . . . . . .(i)$
In Fig. 21(b); the axis $\mathrm{YY}$ ’ is perpendicular to part $\mathrm{OB}$ and passes through its end $\mathrm{O}$
$\therefore \quad \mathrm{I}^{\prime}=\frac{1}{3}(\mathrm{M})(\mathrm{L})^{2}=\frac{\mathrm{ML}^{2}}{3}$
The part OA; makes an angle $\theta=60^{\circ}$ with axis YOY’ passing through end O. Its M.I,
$\mathrm{I}^{\prime \prime}=\frac{1}{3} \mathrm{ML}^{2} \sin ^{2} 60=\frac{\mathrm{ML}^{2}}{4}$
$\mathrm{I} _{2}=$ M.I of arrangement of both rods about given axis.
$=\mathrm{I}^{\prime}+\mathrm{I}^{\prime \prime}=\frac{\mathrm{ML}^{2}}{3}+\frac{\mathrm{ML}^{2}}{4}=\frac{7}{12} \mathrm{ML}^{2} \hspace{40mm}. . . . . . . (ii)$
$\therefore \frac{\mathrm{I} _{1}}{\mathrm{I} _{2}}=\frac{\frac{2}{3} \mathrm{ML}^{2}}{\frac{7}{4} \mathrm{ML}^{2}}=\frac{8}{21}$
Example-15 :
Three thin rods $\mathrm{OA}, \mathrm{OB}$ and $\mathrm{OC}$ has same length $\mathrm{L}$. The linear density of the three rods is $\lambda _{1}, \lambda _{2}$ and $\lambda _{3}$ respectively. $\mathbf{I} _{x}, \mathbf{I} _{\mathbf{y}}, \mathbf{I} _{\mathbf{z}}$ M.I of the system about $x, y$ and $z$-axis. What is $I _{x}: I _{y}: I _{z}$ ?

Show Answer
Solution :
$\mathrm{I} _{x}=$ M.I of system about $x$-axis
$$ \begin{aligned} & =\mathrm{I} _{\mathrm{OA}}+\mathrm{I} _{\mathrm{OB}}+\mathrm{I} _{\mathrm{OC}} \\ & =0+\frac{1}{3}\left(\lambda _{2} \mathrm{~L}\right) \mathrm{L}^{2}+\frac{1}{3}\left(\lambda _{3} \mathrm{~L}\right) \mathrm{L}^{2} \\ & =\frac{\left(\lambda _{2}+\lambda _{3}\right)}{3} \mathrm{~L}^{3} \end{aligned} $$
Similarly,
$$ \begin{aligned} & \mathrm{I} _{\mathrm{y}}=\left(\frac{\lambda _{3}+\lambda _{1}}{3}\right) \mathrm{L}^{3} \text { and } \mathrm{I} _{\mathrm{z}}=\left(\frac{\lambda _{1}+\lambda _{2}}{3}\right) \mathrm{L}^{3} \\ & \therefore \quad \mathrm{I} _{x}: \mathrm{I} _{\mathrm{y}}: \mathrm{I} _{\mathrm{z}}::\left(\lambda _{2}+\lambda _{3}\right):\left(\lambda _{3}+\lambda _{1}\right):\left(\lambda _{1}+\lambda _{2}\right) \end{aligned} $$
Example-16:
Three identical thin rods $\mathrm{AB} ; \mathrm{AC}$ and $\mathrm{BC}$ each of mass $M$ length $L$ are joined together to form an equilateral triangle. $I _{1}$ is M.I of system about side $A B$ as axis. $I _{2}$ M.I of system about axis through end $A$ and perpendicular to plane of triangle. $\frac{I _{1}}{I _{2}}$ is
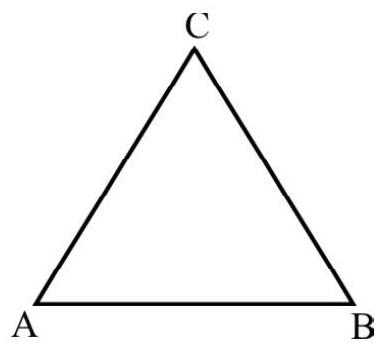
Fig. 23(a)
(1) 1
(2) $\frac{1}{3}$
(3) $\frac{2}{3}$
(4) $\frac{3}{2}$
Show Answer
Solution :
$\mathrm{I} _{1}=\mathrm{I} _{\mathrm{AB}}+\mathrm{I} _{\mathrm{AC}}+\mathrm{I} _{\mathrm{BC}}$
$\mathrm{I} _{\mathrm{AB}}=0 ; \mathrm{I} _{\mathrm{AC}}=\mathrm{I} _{\mathrm{BC}}=\frac{1}{3} \mathrm{ML}^{2} \sin ^{2} 60=\frac{\mathrm{ML}^{2}}{4}$
$\therefore \quad \mathrm{I} _{1}=\frac{\mathrm{ML}^{2}}{2} \hspace{40mm}. . . . . . . . .(1)$
Similarly,
$\mathrm{I} _{2}=\frac{1}{3} \mathrm{ML}^{2}+\frac{1}{3} \mathrm{ML}^{2}+\mathrm{I} _{\mathrm{BC}}$

From right angled $\triangle \mathrm{ABD}$ in fig. 23(b); we have
$$ \begin{align*} & \frac{\mathrm{AD}}{\mathrm{AB}}=\cos 30 \quad \therefore \mathrm{AD}=\frac{\sqrt{3}}{2} \mathrm{~L} \\ & \therefore \quad \mathrm{I} _{\mathrm{BC}}=\frac{1}{12} \mathrm{ML}^{2}+\mathrm{M}\left(\frac{\sqrt{3}}{2} \mathrm{~L}\right)^{2} \quad \text { [Clf theorem of } | \text { axis] } \\ & \quad=\frac{5}{6} \mathrm{ML}^{2} \tag{ii} \\ & \mathrm{I} _{2}=\frac{2}{3} \mathrm{ML}^{2}+\frac{5}{6} \mathrm{ML}^{2}=\frac{3}{2} \mathrm{ML}^{2} \\ & \therefore \quad \frac{\mathrm{I} _{1}}{\mathrm{I} _{2}}=\frac{1}{3} \end{align*} $$
Example-17 :
Five identical spheres each of mass $M$, radius $R$ are rigidly joined to one another as shown in Fig. 24. The M.I of system about $\mathrm{zz}^{\prime}$ as axis; (shown in Fig. 24) is
(1) $25 \mathrm{MR}^{2}$
(2) $35 \mathrm{MR}^{2}$
(3) $45 \mathrm{MR}^{2}$
(4) $55 \mathrm{MR}^{2}$
Show Answer
Solution :
$I _{A}, I _{B}, I _{C}, I _{D}, I _{E}$ denote M.I of, spheres A, B, C, D and E respectively about $\mathrm{zz}^{\prime}$ as axis. $\mathrm{zz}^{\prime}$ as tangent to sphere $\mathrm{B}$ and $\mathrm{D}$. Therefore,
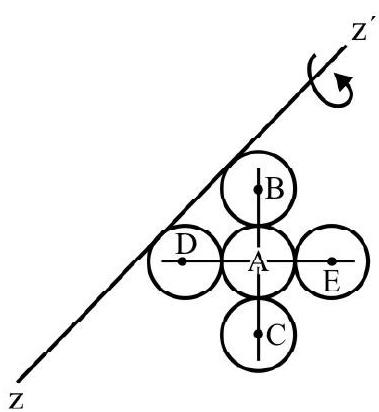
$$ \mathrm{I} _{\mathrm{B}}=\mathrm{I} _{\mathrm{D}}=\frac{2}{5} \mathrm{MR}^{2}+\mathrm{MR}^{2} $$
Using theorem of parallel axis
$$ \mathrm{I} _{\mathrm{A}}=\frac{2}{5} \mathrm{MR}^{2}+\mathrm{M}(3 \mathrm{R})^{2} $$
and $\quad \mathrm{I} _{\mathrm{C}}=\mathrm{I} _{\mathrm{E}}=\frac{2}{5} \mathrm{MR}^{2}+\mathrm{M}(4 \mathrm{R})^{2}$
$$ \begin{aligned} \therefore \quad \mathrm{I} & =\left(\frac{2}{5} \mathrm{MR}^{2}+9 \mathrm{MR}^{2}\right)+2\left(\frac{2}{5} \mathrm{MR}^{2}+\mathrm{MR}^{2}\right)+2\left(\frac{2}{5} \mathrm{MR}^{2}+16 \mathrm{MR}^{2}\right) \\ & =45 \mathrm{MR}^{2} \end{aligned} $$
Equations of Pure Rotational Motion of a Rigid Body
Consider a body rotating about a fixed axis. The equation of motion (rotational motion) is
$$ \text { I } \alpha=\tau $$
or $\quad \mathrm{I} \frac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}=\tau$
$\mathrm{I}=$ M.I of body about axis of rotation.
$\tau=$ Net torque of forces about axis of rotation.
$\alpha=$ Angular acceleration.
For a body having “uniformly accelerated” rotational motion the kinematical equations describing motion are:
$$ \begin{aligned} & \omega(\mathrm{t})=\omega(0)+\alpha \mathrm{t} \\ & \theta=[\omega(0)] \mathrm{t}+\frac{1}{2} \alpha \mathrm{t}^{2} \\ & {[\omega(\mathrm{t})]^{2}-[\omega(0)]^{2}=2 \alpha \theta} \end{aligned} $$
where $\omega(0)$ and $\omega(t)$ denote initial (i.e. $t=0$ ) and instantaneous (i.e. $t=t$ ) angular speed of body. $\alpha$ is the uniform angular acceleration and $\theta$ is angle described in time $t=t$.
Simultaneous Motion of Rotation and Translation
A rotating body can have simultaneously motion of rotation and translation. For example:
1. A car moving on a road. As a whole car has a translational motion and wheels of car have a rotational motion.
2. A mass attached to a pulley via a massless, inextensible string. When let go mass has translational motion and pulley rotational motion.
3. A sphere or cylinder rolling down a rough inclined plane.
The motion can be analyzed in terms of
1. Translational motion of center of mass of rigid body. The equation of translational motion is
$$ \mathrm{M} \frac{\mathrm{d}^{2} \mathbf{R}}{\mathrm{dt}^{2}} \equiv \mathrm{MA}=\mathbf{F} $$
F is the resultant of all forces as if they are acting on C.M.
2. The rotational part of motion is considered as rotation about axis through C.M. Equation of rotational motion is
$$ \mathrm{I} \alpha \equiv \mathrm{I} \frac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}=\tau $$
where $\tau$ is net torque of forces about axis of rotation.
3. For a body rolling down without slipping;
$\mathrm{A}=$ Linear acceleration of C.M. $=\mathrm{R} \alpha$
$\mathrm{V}=$ Linear velocity of C.M. $=\mathrm{R} \omega$
It an be shown that for a body of circular cross-section, rolling down a rough inclined plane of inclination $\theta$; without slipping.
$\mathrm{A}=$ Linear acceleration of C.M. $=\frac{\mathrm{g} \sin \theta}{\left(1+\frac{\mathrm{I}}{\mathrm{MR}^{2}}\right)}$
$\mathrm{V}=$ Linear speed of C.M., at bottom of inclined plane of vertical height $\mathrm{H}$; starting from rest at the top of inclined plane $=\sqrt{\frac{2 \mathrm{gH}}{\left(1+\frac{\mathrm{I}}{\mathrm{MR}^{2}}\right)}}$
The problem can also be analysed using law of conservation of energy. For a body of circular mass section rolling down, a rough inclined plane, without slipping.
Loss is gravitational potential energy $=$ Gain in translation and rotational kinetic energy.
Example-18 :
A block of square cross-section of side a has height $h$. It is placed on a rough inclined plane of inclination $\theta \cdot \mu$ is coefficient of friction between block and inclined plane. Show that
1. Block will topple over without slipping if $\mu>\frac{\mathrm{a}}{\mathrm{h}}$.
2. Block will slide before it topples over if $\mu<\frac{a}{h}$.
Show Answer
Solution :
In Fig. $25 \mathrm{ABCD}$ is block. $\mathrm{AB}=\mathrm{a} ; \mathrm{AD}=\mathrm{h}$. The free body diagram is as shown. Obviously
$$ \mathrm{f} _{\mu}=\mu \mathrm{N}=\mu \mathrm{mg} \cos \theta $$
If $\mathrm{mg} \sin \theta \leq \mathrm{f} _{\ell t} ;$ block does not slide down the inclined plane. It will topic over if torque due to weight about end $\mathrm{A}$ is more than torque due to force of friction. i.e.
$$ (\mathrm{mg} \sin \theta) \frac{\mathrm{h}}{2}>(\mathrm{mg} \cos \theta)\left(\frac{\mathrm{a}}{2}\right) $$
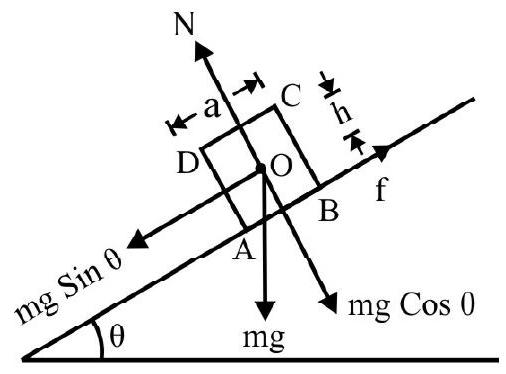
Fig. 25
i.e. $\quad \tan \theta>\frac{\mathrm{a}}{\mathrm{h}}$
Therefore block does not slide before toppling if
$$ \begin{align*} & \tan \theta>\frac{\mathrm{a}}{\mathrm{h}}<\mu \\ & \therefore \mu>\frac{\mathrm{a}}{\mathrm{h}} \tag{1} \end{align*} $$
The block will slide down before toppling if
$\mathrm{mg} \sin \theta>f _{t \mathrm{t}}$
$\mathrm{mg} \sin \theta>\mu \mathrm{mg} \cos \theta$
or $\quad \tan \theta>\mu$
In other words block slides before toppling if
$$ \mu<\frac{\mathrm{a}}{\mathrm{h}} $$
Example-19:
A uniform circular disc of mass $M$, radius $R$ is free to rotate about its own axis. It experiences a torque $\tau$; given by
$$ \tau=\alpha \theta+\beta $$
where $\alpha$ and $\beta$ are constants. $\theta$ is angular displacement of disc. Obtain an expression for angular speed, $\omega$; in terms of $\theta$.
Show Answer
Solution :
The M.I of disc about its own axis
$$ \mathrm{I}=\frac{\mathrm{MR}^{2}}{2} $$
The instantaneous angular acceleration; $\alpha$, is
$$ \begin{align*} & \alpha=\frac{\tau}{\mathrm{I}}=\frac{2(\alpha \theta+\beta)}{\mathrm{MR}^{2}} \tag{i} \\ & \alpha=\frac{\mathrm{d} \omega}{\mathrm{dt}}=\frac{\mathrm{d} \omega}{\mathrm{d} \theta} \times \frac{\mathrm{d} \theta}{\mathrm{dt}}=\omega \frac{\mathrm{d} \omega}{\mathrm{d} \theta} \tag{ii} \end{align*} $$
From Eqns. (i) and (ii); we have
$$ \omega \mathrm{d} \omega=\frac{2}{\mathrm{MR}^{2}}(\alpha \theta+\beta) \mathrm{d} \theta $$
Integrate,
$$ \int _{0}^{\omega} \omega \mathrm{d} \omega=\frac{2}{\mathrm{MR}^{2}} \int _{0}^{\theta}(\alpha \theta+\beta) \mathrm{d} \theta $$
or $\quad \frac{\omega^{2}}{2}=\frac{2}{\mathrm{MR}^{2}}\left[\frac{\alpha \theta^{2}}{2}+\beta \theta\right]$
$\therefore \quad \omega=\left[\frac{2}{\mathrm{MR}^{2}}\left(\alpha \theta^{2}+2 \beta \theta\right)\right]^{1 / 2}$
Example-20 :
A cylinder of mass $M$, radius $R$, length $L$ is suspended in a vertical plane from a rigid support by two strings $A B$ and $C D$ of fixed length as shown in Fig. 26. There is another string wound uniformly. The free and $E$ of this string is pulled vertically down with a constant force $F$. The cylinder is free to rotate about its own axis. What is length of string unwound in time t?
Show Answer
Solution :
Since strings $A B$ and $C D$ are of a fixed length; the cylinder can only rotate about its own axis i.e. it has pure rotational motion. The torque, $\tau$; of external applied force.
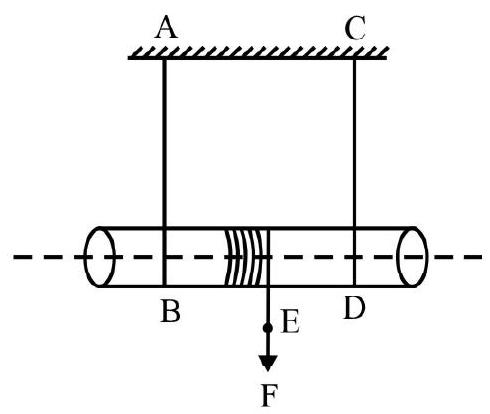
Fig. 26
$$ \tau=\mathrm{FR} $$
The angular acceleration; $\alpha$, is
$$ \alpha=\frac{\tau}{\mathrm{I}}=\frac{\mathrm{FR}}{\left(\frac{\mathrm{MR}^{2}}{2}\right)}=\frac{2 \mathrm{~F}}{\mathrm{MR}} $$
The motion of cylinder is uniformly accelerated. Let $\theta$ be angle described in time t. Obviously
$$ \begin{gathered} \theta=\frac{1}{2} \alpha \mathrm{t}^{2}=\frac{\mathrm{Ft}^{2}}{\mathrm{MR}} \\ \ell=\text { The length of string unwound }=\mathrm{R} \theta=\left(\frac{\mathrm{F}}{\mathrm{M}}\right) \mathrm{t}^{2} \end{gathered} $$
Example-21 :
A cylinder of mass M, radius $R$; length $L$ is rotating about its own axis with an angular speed $\omega _{1}$. It gathers dust, at rest; uniformly from all sides at a constant rate till its radius is doubled. The mass of dust collected is $\frac{\mathrm{M}}{4}$. What is final angular speed of the arrangement?
Show Answer
Solution :
Regarding cylinder and dust as a system; there is no external force and therefore no external torque, the angular momentum is conserved.
$\mathrm{L} _{1}=$ The initial angular momentum
$$ \begin{equation*} =\left(\frac{1}{2} \mathrm{MR}^{2}\right) \omega _{1} \tag{i} \end{equation*} $$
Let $\mathrm{I} _{2}$ be the M.I of cylinder + dust collected about axis of rotation. Then
$$ \mathrm{I} _{2}=\frac{\mathrm{MR}^{2}}{2}+\frac{1}{2}\left(\frac{\mathrm{M}}{4}\right)\left[(2 \mathrm{R})^{2}+\mathrm{R}^{2}\right]^{*}=\frac{9}{8} \mathrm{MR}^{2} $$
Let $\omega _{2}$ be the final angular speed of system. Then
$\mathrm{L} _{2}=$ The final angular momentum
$$ \begin{equation*} =\mathrm{I} _{2} \omega _{2}=\left(\frac{9}{8} \mathrm{MR}^{2}\right) \omega _{2} \tag{ii} \end{equation*} $$
From law of conservation of angular momentum
$$ \begin{aligned} & \mathrm{L} _{1}=\mathrm{L} _{2} \quad \text { or } \quad \frac{\mathrm{MR}^{2} \omega _{1}}{2}=\frac{9 \mathrm{MR}^{2} \omega _{2}}{8} \\ \therefore \quad \omega _{2} & =\frac{4}{9} \omega _{1} \end{aligned} $$
Example-22 :
A thin rod $O A$ of mass $M$; length $L$ is pivoted at end $O$ in a vertical position. The rod is free to rotate about a horizontal axis through end $O$. At $t=0$; the end $A$ is given an initial speed $v _{0}$ as shown in Fig. 27 and let go. What is angular speed of rod when it has turned through an angle of $60^{\circ}$ ?
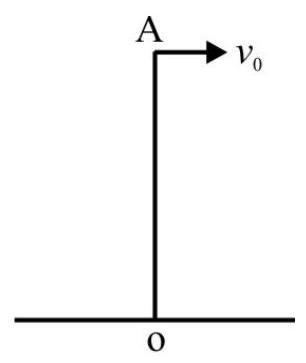
Fig. 27
Show Answer
Solution :
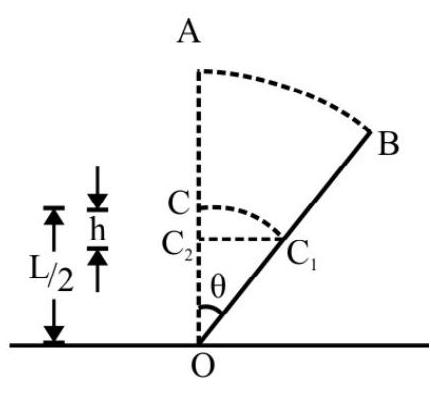
In Fig. 28; OB is instantaneous position of rod when it has rotated through angle $\theta$. The rod is moving in a vertical plane in gravity of earth, there is a loss in gravitational potential energy. C is C.G of rod initially. $C _{1}$ is instantaneous position of C.G as shown in Fig. 28.
$\mathrm{h}=$ The vertical distance by which $\mathrm{C} . \mathrm{G}$ goes down $=\mathrm{CC} _{2}=\mathrm{OC}-\mathrm{OC} _{2}$
$$ =\frac{\mathrm{L}}{2}(1-\cos \theta) $$
Fig. 28
The loss in gravitational P.E $=\operatorname{Mgh}=\frac{\mathrm{MgL}}{2}(1-\cos \theta) \hspace{20mm}. . . . . . . . .(i)$
Let $\omega$ be the instantaneous angular speed of rod.
The gain in rotational $K . E=\frac{I}{2}\left[\omega^{2}-\omega _{0}^{2}\right]$
$$ \begin{equation*} =\frac{1}{2}\left(\frac{\mathrm{ML}^{2}}{3}\right)\left[\omega^{2}-\left(\frac{\mathrm{v} _{0}}{\mathrm{~L}}\right)^{2}\right] \tag{ii} \end{equation*} $$
From law of conservation of energy
$$ \begin{align*} & \frac{\mathrm{MgL}}{2}(1-\cos \theta)=\frac{\mathrm{ML}^{2}}{6}\left[\omega^{2}-\frac{\mathrm{v} _{0}^{2}}{\mathrm{~L}^{2}}\right] \\ & \therefore \quad \omega^{2}=\frac{3 \mathrm{~g}}{\mathrm{~L}}(1-\cos \theta)+\frac{\mathrm{v} _{0}^{2}}{\mathrm{~L}^{2}} \tag{iii} \end{align*} $$
Given $\theta=60^{\circ}$. Therefore
$$ \omega^{2}=\frac{3 g}{2 \mathrm{~L}}+\frac{\mathrm{v} _{0}^{2}}{\mathrm{~L}^{2}}=\left(\frac{2 \mathrm{v} _{0}^{2}+3 \mathrm{gL}}{2 \mathrm{~L}^{2}}\right) $$
or $\quad \omega=\frac{1}{\mathrm{~L}}\left[\frac{2 \mathrm{v} _{0}^{2}+3 \mathrm{gL}}{2}\right]^{1 / 2}$
Example-23 :
Fig. 29 shows a pulley P; fixed on top of an inclined plane. A massless, inextensible string is wrapped around the pulley. The free end of string is attached to a block of mass $200 \mathrm{~g}$ as shown. $\mu=0.1$ is coefficient of friction between inclined plane and block. M.I of pulley about its own axis is $0.8 \mathbf{~ k g m}^{2}$ and its radius is 40 $\mathrm{cm}$. The system is let go from rest. The mass $m$ descends a distance of $1 \mathrm{~m}$ along the inclined plane. What is linear speed of $\mathrm{m}$ ? There is no slipping of string on pulley. $\mathrm{g}=10 \mathrm{~ms}^{-2}$.
Show Answer
Solution :
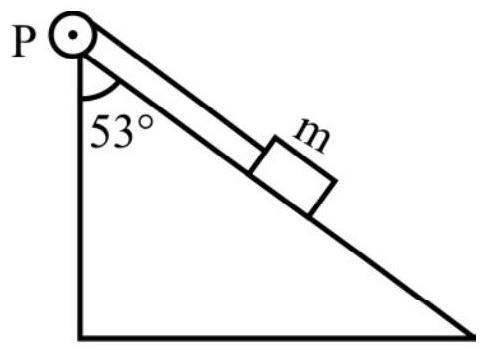
Fig. 29
When $\mathrm{m}$ descends down by a distance of $1 \mathrm{~m}$ along the plane; the vertical distance, $\mathrm{h}$, is
$$ \mathrm{h}=1 \times \cos 53^{\circ}=0.6 \mathrm{~m} $$
The loss in gravitational P.E of $\mathrm{m}=\mathrm{mgh}$
$$ \begin{equation*} =0.2 \times 10 \times 0.6=1.2 \mathrm{~J} \tag{i} \end{equation*} $$
The work done against force of friction between block and inclined plane $=\left(\mu \mathrm{mg} \cos 37^{\circ}\right) \times 1$
$$ \begin{equation*} =0.1 \times 0.2 \times 10 \times 0.8 \times 1 \simeq 0.16 \mathrm{~J} \tag{ii} \end{equation*} $$
The gain in $\mathrm{K} . \mathrm{E}=\frac{1}{2} \times 0.2 \times \mathrm{v}^{2}+\frac{1}{2}(0.8) \omega^{2}$
$\mathrm{v}=$ linear speed of mass M; $\omega=$ angular speed of pulley. Since there is no slipping $\mathrm{v}=\mathrm{R} \omega$. Therefore
The gain in K.E $=0.1 \mathrm{v}^{2}+0.4\left(\frac{\mathrm{v}}{0.4}\right)^{2}=2.6 \mathrm{v}^{2}$
From law conservation of energy
$$ \begin{aligned} 1.2-0.16 & =2.6 \mathrm{v}^{2} \\ \therefore \quad \mathrm{v} & =\sqrt{\frac{1.04}{2.6}} \simeq 0.63 \mathrm{~ms}^{-1} \end{aligned} $$
PROBLEMS FOR PRACTICE
1. $\mathrm{PQRS}$ is a square plate of side a. Surface mass density $\sigma$. Locate its center of mass. What is change in position of C.M if
(a) square 1 and 3 are cut out
(b) all four squares are cut out
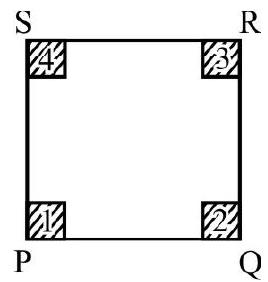
Fig. 30
Show Answer
Answer: (a) & (b) No change2. A uniform circular disc of radius $\mathrm{R}$ has a circular part of radius $\frac{\mathrm{R}}{6}$ having its center at a distance $\frac{\mathrm{R}}{2}$ from that of disc; cut out. Locate C.M of remaining part of disc.
Show Answer
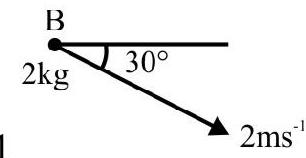
Answer: $\frac{\mathrm{R}}{70}$3. Fig. 31 shows two balls $A$ and $B$ of mass $1 \mathrm{~kg}$ and $2 \mathrm{~kg}$ respectively moving with same speed of $2 \mathrm{~ms}^{-1}$ as shown in fig. 31 . What is velocity of C.M of A and B?
Show Answer
Answer: $\left.\left[\left(\frac{2}{3}+\frac{2}{\sqrt{3}}\right) \hat{\mathrm{i}}-\frac{2}{3} \hat{\mathrm{j}}\right]\right]$
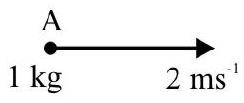
Fig. 31
4. Two particles $\mathrm{A}$ and $\mathrm{B}$ have masses in ratio of 1:3. The particle $\mathrm{A}$ is pushed towards C.M of $\mathrm{A}$ and $B$ by a distance of $5 \mathrm{~cm}$. By what distance $B$ be moved so that C.M does not change?
Show Answer
Answer: $17 \mathrm{~cm}$5. $\mathrm{OAB}$ is an equilateral triangle of side $\ell$. Mass $\mathrm{m}, 2 \mathrm{~m}$ and 3 mare placed at the three corners as shown in Fig. 32. Taking $\mathrm{O}$ as origin; $\mathrm{OB}$ as $\mathrm{x}-$ axis and $\mathrm{y}$-axis through $\mathrm{O}$ perpendicular to $\mathrm{OB}$ locate co-ordinates of C.M of the arrangement.
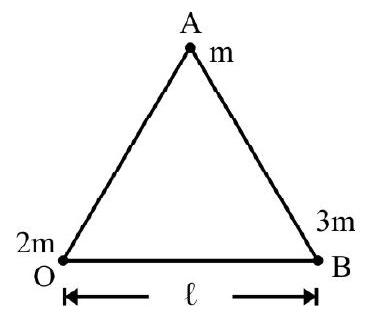
Fig. 32
Show Answer
Answer: $\left[x=\frac{2 \ell}{3} ; \mathrm{y}=\frac{\ell}{4 \sqrt{3}}\right]$6. A uniform wooden log has mass M; length L. It is at rest on a smooth horizontal surface. A ball of mass $\left(\frac{M}{n}\right)$ is at rest at one end of log. Some how on its own the ball starts moving towards the opposite end with a constant speed v. What is distance moved by wooden log when ball reaches the other end?
Show Answer
Answer: $\frac{\mathrm{L}}{(\mathrm{n}+1)}$7. Two particles of mass $0.5 \mathrm{~kg}$ and $1 \mathrm{~kg}$ are located at origin and a point having co-ordinate $+4 \mathrm{~m}$ on $x$-axis. The two masses move towards one another under their mutual force of attraction where the two masses collide one another.
Show Answer
Answer: $2.67 \mathrm{~m}$ from initial position of $0.5 \mathrm{~kg}$ mass8. A particle of mass $200 \mathrm{~g}$ is projected in a vertical plane in gravity of earth with an initial speed of $2 \mathrm{~ms}^{-1}$, in a direction so as to have maximum horizontal range. What is its angular momentum about point of projection when it is at the highest point on its parabolic path?
Show Answer
Answer: $2.83 \times 10^{-2} \mathrm{kgm}^{2} \mathrm{~s}^{-1}$9. A particle of mass $1 \mathrm{~kg}$ moves along a straight line $x=\mathrm{y}-2$ with a speed of $2 \mathrm{~ms}^{-1}$. Calculate its angular momentum about origin of co-ordinates.
Show Answer
Answer: $2 \sqrt{2} \mathrm{kgm}^{2} \mathrm{~s}^{-1}$10. Regard earth as a sphere of radius $\mathrm{R}=6400 \mathrm{~km}$ and mass $=\mathrm{M}=6 \times 10^{24} \mathrm{~kg}$. What is angular momentum of earth around its own axis?
Show Answer
Answer: $7.12 \times 10^{33} \mathrm{kgm}^{2} \mathrm{~s}^{-1}$11. A particle of mass $m$ moves into a circular orbit of radius $\mathrm{R}$ around a fixed mass $\mathrm{M}$ under their gravitational force. Calculate angular momentum of $m$ around center of its circular path.
Show Answer
Answer: $.\left[\mathrm{GM}^{2} \mathrm{mR}\right]^{1 / 2}$12. An electron moves in a circular orbit of principle quantum number $\mathrm{n}$ in a hydrogen atom. What is torque of electrostatic force on electron due to proton about the center of its orbit?
Show Answer
Answer: zero13. A pulley of mass $\mathrm{M}$, radius $\mathrm{R}$ is suspended from a rigid support as shown in Fig. 33. It is free to rotate about a horizontal axis through its center O. A massless string passes around the pulley. The two ends of string are pulled with force $F _{1}$ and $\mathrm{F} _{2}\left(\mathrm{~F} _{1}>\mathrm{F} _{2}\right)$ as shown. What is (i) the torque and (ii) angular acceleration; of the pulley?
Show Answer
Answer: (i) $\left(\mathrm{F} _{1}-\mathrm{F} _{2}\right) \mathrm{R}$, anticlockwise (ii) $\frac{2\left(\mathrm{~F} _{1}-\mathrm{F} _{2}\right)}{\mathrm{MR}}$ ]
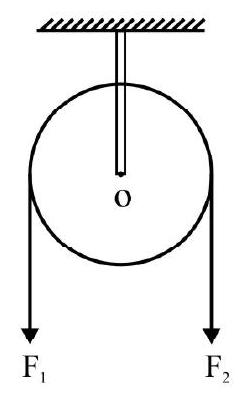
Fig. 33
14. A fly wheel of M.I $0.4 \mathrm{kgm}^{2}$ is rotating about its own axis with a speed of $600 \mathrm{rpm}$. It is brought to rest by applying a constant torque in 10s. What is torque applied? What is change in angular momentum at $\mathrm{t}=5 \mathrm{~s}$ ?
Show Answer
Answer: (i) $0.8 \pi \mathrm{N}-\mathrm{m}$ (ii) $4 \pi \mathrm{kgm}^{2} \mathrm{~s}^{-1}$; decrease15. The engine of an aeroplane has power of 2000 H.P. What is torque developed by the engine. When rotor has acquired an angular speed of $40 \mathrm{rps}$ ?
Show Answer
Answer: $5973 \mathrm{~N}-\mathrm{m}$16. A rotor has a radius of $4 \mathrm{~m}$. It can with stand a maximum acceleration 10 times $\mathrm{g}(=$ acceleration due to gravity of earth). What is maximum number of revolutions per second the rotor can make without breaking?
Show Answer
Answer: $\frac{5}{2 \pi}$17. A door of length $2.5 \mathrm{~m}$, breadth $1.25 \mathrm{~m}$ has a mass of $10 \mathrm{~kg}$. It is free to rotate about its length as axis in a vertical plane. A bullet of mass $50 \mathrm{~g}$ moving horizontally with a speed of $200 \mathrm{~ms}^{-1}$ hits the door at its midpoint and get embedded in the door. Calculate the loss of kinetic energy.
Show Answer
Answer: $996.3 \mathrm{~J}$18. A thin rod of mass $400 \mathrm{~g}$ is $1 \mathrm{~m}$ long. It is held in a vertical position at rest; with one end pivoted to ground. It is given a fluck so that it starts moving a vertical plane. What is linear speed of free end of rod as it just hits ground? $\mathrm{g}=10 \mathrm{~ms}^{-2}$
Show Answer
Answer: $5.48 \mathrm{~ms}^{-1}$19. A uniform circular disc of radius $\mathrm{R}$ has a part of radius $\frac{\mathrm{R}}{2}$ cut out. The mass of remaining annular disc is M. Calculate M.I about an axis through center of mass and perpendicular to plane of disc.
Show Answer
Answer: $\frac{37 \mathrm{Ma}^{2}}{72}$20. A cylinder of mass $5 \mathrm{~kg}$ diameter $60 \mathrm{~cm}$ is at rest and free to rotate about its own axis. It is given angular impluses, each of magnitude $3 \mathrm{~kg} \mathrm{~m}^{2} \mathrm{~s}^{-1}$ at a regular interval of $4 \mathrm{~s}$. What is angular speed of cylinder 30s after first impulse?
Show Answer
Answer: $106.6 \mathrm{rad} \mathrm{s}^{-1}$21. A cylinder of mass $\mathrm{M}$, radius $\mathrm{R}$ is held at rest in a horizontal position by suspending the cylinder from a rigid support by two massless, inextensible strings wrapped around it. The system is let go at $\mathrm{t}=0$.
(i) What is the instantaneous angular speed of cylinder?
(ii) What is tension in each string?
Show Answer
Answer: $\left(\frac{2 \mathrm{~g}}{3 \mathrm{R}}\right) \mathrm{t} ; \frac{1}{6} \mathrm{Mg}$22. A body of mass $\mathrm{M}$, has radius of gyration $\mathrm{k}$ about its own axis. It rolls down a rough inclined plane of inclination $\theta$ from rest without slipping. What is force of friction acting on body?
Show Answer
Answer: $\frac{\mathrm{Mg} \sin \theta}{\left(1+\frac{\mathrm{R}^{2}}{\mathrm{k}^{2}}\right)}$23. A disc; hollow sphere and solid sphere have same mass and radius. The three are released together from top of inclined plane. $\mu _{\mathrm{k}}$ is coefficient of friction between inclined plane and each body. The disc and hollow sphere slip down the inclined plane. The solid sphere rolls down without slipping. $t _{1}$, $\mathrm{t} _{2}$ and $\mathrm{t} _{3}$ is time taken by the three to reach the bottom of inclined plane. Given $\mu _{\mathrm{k}}=0.5, \theta=\frac{\pi}{4}$. What is $\mathrm{t} _{1}, \mathrm{t} _{2}$ and $\mathrm{t} _{3}$ ?
Show Answer
Answer: $\mathrm{t} _{1}=\mathrm{t} _{2}=\left(\frac{4 \sqrt{2} \ell}{\mathrm{g}}\right)^{1 / 2}, \mathrm{t} _{3}=\left(\frac{14 \sqrt{2} \ell}{\mathrm{g}}\right)^{1 / 2}$24. A uniform cylinder of mass $\mathrm{M}$, radius $\mathrm{R}$ is released from rest from top of a rough inclined plane of inclination $\theta$. It rolls down the inclined without slipping. What is K.E of cylinder at bottom of inclined plane?
Show Answer
Answer: $.\frac{11}{12} \mathrm{Mg} \ell \sin \theta$25.
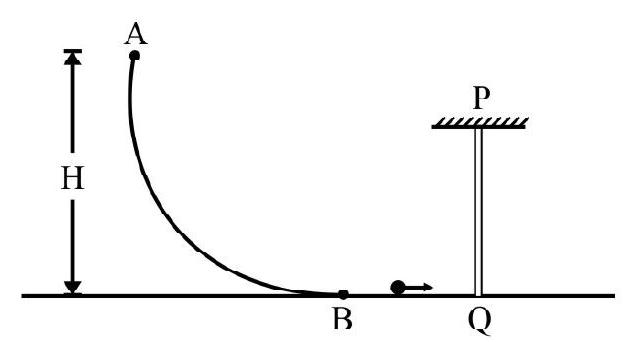
Fig. 34
Show Answer
In Fig. $34 \mathrm{AB}$ is a smooth curved track in a vertical plane. A particle of mass $m$ is released from rest at A. It gets off track at B and moves on a smooth horizontal surface. B then hits a thin vertical rod at rest at its end $\mathrm{Q}$ and sticks to rod. The rod is free to rotate about a horizontal axis through end $\mathrm{P}$. What is maximum angular deflection of rod? Mass of $\mathrm{rod}=2 \mathrm{~m}$.Answer: $.\cos ^{-1}\left(1-\frac{3 \mathrm{~m}}{10 \mathrm{~L}}\right)$
Question Bank
Key Learning Points
1. A rigid body does not change its shape or size when external force (s) act on it.
2. It can have
(a) translational motion
(b) rotational motion about a fixed axis
(c) both translational and rotational motion simultaneously.
3. To describe only translational motion in space; we use the concept of center of mass. The center of mass is a point where the entire mass of the body is imagined to be concentrated.
For a collection of point masses $\mathrm{m} _{1}, \mathrm{~m} _{2}, \ldots \ldots . \mathrm{m} _{\mathrm{j}} \ldots \ldots . . \mathrm{m} _{\mathrm{n}}$ having position vectors $; \mathbf{r} _{1}, \mathbf{r} _{2}, \ldots . \mathbf{r} _{\mathrm{j}}, \ldots \ldots \mathbf{r} _{\mathrm{n}}$; the position vector, $\mathbf{R}$, of C.M is
$$ \mathbf{R}=\frac{\sum _{j=1}^{n} m _{j} \mathbf{r} _{j}}{\sum _{j=1}^{n} m _{j}} $$
For a body having a continuous distribution of mass,
$$ \mathbf{R}=\frac{\int(\rho \mathrm{dv}) \mathbf{r}}{\int \rho \mathrm{dv}} $$
where $\mathrm{dm}=\rho \mathrm{dv}$ is an elementary mass on body around a point having position $\mathbf{r}$.
4. The equation of translational motion of C.M is
$$ \mathrm{M} \frac{\mathrm{d}^{2} \mathbf{R}}{\mathrm{dt}^{2}}=\mathrm{MA}=\mathbf{F} _{\mathrm{ext}}^{\text {Total }} $$
$\mathbf{F} _{\text {ext }}^{\text {Total }}$ is resultant of all external forces on body if there were acting at center of mass.
5. For a rigid body having a pure rotational motion about a fixed axis; every point mass making body moves in circular path. The radius $\mathrm{r} _{\mathrm{j}}$ of circular path of $\mathrm{j}^{\text {th }}$ particle is its perpendicular distance from axis of rotation. $r _{j}$ is different for different point masses making body. The angular speed, $\omega _{j}$, of every point is same. The linear speed, $\mathrm{v} _{\mathrm{j}}$, of $\mathrm{j}^{\text {th }}$ masses is
$$ v _{j}=r _{j} \omega $$
6. The quantity of rotational motion of a particle of mass $m$, having velocity $\mathbf{v}$ when its instantaneous position vector $\mathbf{r}$, is known as its angular momentum or moment of momentum $\ell$. By definition
$$ \ell=\mathbf{r} \times \mathbf{p} $$
$|\ell|=$ magnitude of $\mathbf{p} \times \perp$ distance of line of action of $\mathbf{p}$ from point $\mathrm{O}$ about which angular momentum is calculated.
7. For a large collection of point masses;
$\mathbf{L}=$ Total angular momentum of system.
$$ =\sum _{j=1}^{n} \ell _{j}=\sum _{j=1}^{n}\left(\mathbf{r} _{j} \times \mathbf{p} _{j}\right) $$
For a rigid body rotating about a fixed axis, it can be shown, that
$$ \mathrm{L}=\mathrm{I} \omega $$
I = Moment of inertia of rigid body about axis of rotation.
$\omega=$ angular speed of rigid body.
8. The torque; $\boldsymbol{\tau}$; of a force about a point $\mathrm{O}$ is $\tau=\mathbf{r} \times \mathbf{F}$. $\mathbf{r}$ is the position vector of point, $\mathrm{P}$ where force acts w.r.t point $\mathrm{O}$.
9. Torque is also known as moment of force. It is cause of rotational motion.
10. The equation of rotational motion is
$$ \frac{\mathrm{d} \mathbf{L}}{\mathrm{dt}}=\tau $$
For a body rotating about a fixed axis it reduces to
$$ \mathrm{I} \alpha=\tau $$
$\alpha=$ angular acceleration of rigid body.
$\mathrm{I}=$ M.I of rigid body about axis of rotation.
11. The law of conservation of angular momentum states that if there is no net external torque, the angular momentum is a constant.
12. The rotational inertia of a body is known as moment of inertia (I). For a point mass, $m$, moving in a circle of radius $\mathrm{r}$, the moment of inertia $\mathrm{I}=\mathrm{rm}^{2}$. For a discrete collection of point masses;
$$ I=\sum _{j=1}^{n} m _{j} r _{j}^{2} $$
$r _{j}$ is perpendicular distance of $j^{\text {th }}$ mass from axis of rotation.
For a body, having a continuous distribution of mass;
$$ \mathrm{I}=\int(\mathrm{dm}) \mathrm{r}^{2}=\int(\rho \mathrm{dv}) \mathrm{r}^{2} $$
where $\mathrm{dm}=\rho \mathrm{dv}$ is an elementary mass at a perpendicular distance $\mathrm{r}$ from axis of rotation.
13. The moment of inertia, $\mathrm{I}$; of a rigid body is also defined using Newton’s second law of rotational motion, i.e.
$$ \tau=\mathrm{I} \alpha $$
M.I (I) is numerically equal to torque required to produce unit angular acceleration about a given axis.
14. M.I of a rigid body is not a constant. It depends on:
(a) axis of rotation and
(b) distribution of mass
15. The radius of gyration, $\mathrm{k}$, of a rigid body about a given axis is
$\mathrm{I}=\mathrm{Mk}^{2}$
where $\mathrm{k}$ is perpendicular distance of a point, where the entire mass of rigid body is imagined to be concentrated; from axis of rotation.
16. For calculation of M.I, two theorems are very useful. These are:
(a) Theorem of parallel axis: The M.I, (I) of a rigid body of mass M; about a given axis equals its M.I about a parallel axis through C.G (i.e. Ig) plus product of mass (M) and square of perpendicular distance (h) between the two parallel axis. Expressed mathematically
$$ \mathrm{I}=\mathrm{Ig}+\mathrm{Mh}^{2} $$
(b) Theorem of perpendicular axis: For a laminar body lying in $x$-y plane; the M.I about $\mathrm{z}$-axis (i.e. axis perpendicular to plane of body) is sum of M.I of body about two mutually perpendicular axis, (say $\mathrm{x}$-and $\mathrm{y}$-axis) in its own plane. All three axis pass through same point O. Expressed mathematically
$$ \mathrm{I} _{\mathrm{z}}=\mathrm{I} _{x}+\mathrm{I} _{\mathrm{y}} $$
17. The kinematical equations describing uniformly accelerated rotational motion about a fixed axis are:
$$ \begin{aligned} & \omega(\mathrm{t})=\omega(0)+\alpha \mathrm{t} \\ & \theta=[\omega(0)] \mathrm{t}+\frac{1}{2} \alpha \mathrm{t}^{2} \\ & {[\omega(\mathrm{t})]^{2}-[\omega(0)]^{2}=2 \alpha \theta} \end{aligned} $$
18. For a body having simultaneous rotational and translational motion; the motion is described in terms of
(a) The translational motion of C.M of body. The equation of translational motion is
$$ \mathrm{MA}=\mathbf{F} $$
$\mathbf{A}=$ Linear acceleration of C.M, $\mathbf{F}=$ Resultant of all forces as it they were acting on C.M.
(b) The rotational motion is described in terms of rotation about an axis through C.M. The equation of rotational motions is
$$ \mathrm{I} \alpha=\tau $$
$\alpha=$ angular acceleration of rigid body. I = M.I of rigid body about axis through C.M. $\tau$ is net external torque.
(c) For body rolling down without slipping;
$$ \mathrm{v}=\mathrm{R} \omega \quad \text { and } \mathrm{A}=\mathrm{R} \alpha $$
19. For a body rolling without slipping kinetic energy has two parts:
(a) Translation K.E. $\left(\mathrm{K} _{\mathrm{T}}\right)$ of C.M. It is
$$ \mathrm{K} _{\mathrm{T}}=\frac{1}{2} \mathrm{MV}^{2} $$
$\mathrm{V}=$ velocity of C.M of body.
(b) Rotational K.E $\left(\mathrm{K} _{\mathrm{R}}\right)=\frac{1}{2} \mathrm{I} \omega^{2}$
For body rolling down with slipping $\mathrm{V}=\mathrm{R} \omega$
20. For a body of circular cross-section rolling down a rough inclined plane of inclination $\theta$, without slipping; the linear acceleration, a ofC.M is
$$ \mathrm{a}=\frac{\mathrm{g} \sin \theta}{\left(1+\frac{\mathrm{I}}{\mathrm{MR}^{2}}\right)} $$
21. The law of conservation of energy is a convenient tool to describe motion of a body rolling down without slipping.
1. Particle $A$ of mass $2 \mathrm{~m}$ and $B$ of mass $4 \mathrm{~m}$ are placed at $x=-a$ and $x=+2 \mathrm{a}$ respectively on $x$-axis. What % of mass of $B$ be transferred to $A$ so that the centre of mass of the system shifts to origin of co-ordinates?
(1) $25 \%$
(2) $50 \%$
(3) $75 \%$
(4) $100 \%$
Show Answer
Correct answer: (2)
Solution:

Let $\mathrm{m} _{1}$ be mass moved from B to A as shown in Fig. 1(b). The co-ordinates of C.M is at origin of co-ordinates i.e. $\mathrm{X}=0$
$\therefore 0=\frac{\left(2 \mathrm{~m}+\mathrm{m} _{1}\right)(-\mathrm{a})+\left(4 \mathrm{~m}-\mathrm{m} _{1}\right) \times 2 \mathrm{a}}{6 \mathrm{~m}}$
or $\left(2 m+m _{1}\right)=2\left(4 m-m _{1}\right)$
$\therefore \mathrm{m} _{1}=2 \mathrm{~m}$
$\frac{\mathrm{m} _{1}}{4 \mathrm{~m}} \times 100=$ Percentage of mass of B transferred $=50 \%$
2. Masses $\mathbf{m} ; \mathbf{m}$ and $2 \mathbf{m}$ are placed at points having position vectors.
$$ \mathbf{r} _{1}=\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-\hat{\mathrm{k}} ; \mathbf{r} _{2}=4 \hat{\mathrm{i}}-\hat{\mathrm{j}}+2 \hat{\mathrm{k}} ; \mathbf{r} _{3}=? $$
in such a manner that center of mass of system is at $\mathbf{R}=\hat{\dot{i}}+\hat{j} \cdot \mathbf{r} _{3}$ is
(1) $(-\hat{i}+3 \hat{j}-\hat{k}) / 2$
(2) $(\hat{i}+3 \hat{j}-\hat{k}) / 2$
(3) $(\hat{\mathrm{i}}-3 \hat{\mathrm{j}}-\hat{\mathrm{k}}) / 2$
(4) $(-\hat{i}-3 \hat{j}+\hat{k}) / 2$
Show Answer
Correct answer: (1)
Solution:
Let $\mathbf{r} _{3}=x \hat{\dot{i}}+y \hat{j}+z \hat{k}$. Then $\mathbf{R}=\frac{m \mathbf{r} _{1}+m \mathbf{r} _{2}+2 m \mathbf{r} _{3}}{m+m+2 m}$
or $\quad \hat{i}+\hat{j}=(\hat{i}+2 \hat{j}-\hat{k})+(4 \hat{i}-\hat{j}+2 \hat{k})+2(x \hat{i}+y \hat{j}+z \hat{k}) / 4$
or $\quad 4(\hat{\mathrm{i}}+\hat{\mathrm{j}})=(5+2 x) \hat{\mathrm{i}}+(1+2 \mathrm{y}) \hat{\mathrm{j}}+(1+2 \mathrm{z}) \hat{\mathrm{k}}$
Equating coefficient of $\hat{i}, \hat{j}$ and $\hat{k}$ we have
$4=5+2 x \hspace{40mm}. . . . . . . . .(i)$
$4=1+2 \mathrm{y} \hspace{40mm}. . . . . . . . .(ii)$
$0=1+2 \mathrm{z} \hspace{40mm}. . . . . . . . .(iii)$
Therefore $x=-\frac{1}{2} ; \mathrm{y}=\frac{3}{2} ; \mathrm{z}=-\frac{1}{2}$. Obviously
$\mathbf{r} _{3}=(-\hat{\mathbf{i}}+3 \hat{\mathbf{j}}-\hat{\mathrm{k}}) / 2$
3. $A B C$ is an equilateral triangle of side $\ell$. $O$ is centroid of triangle. Mass $m$ each are placed at $A, B$ and $C$. A mass of $2 \mathrm{~m}$ is placed at $O$ choosing $O$ as origin of co-ordinates and $x, y-$ axis as shown in Fig. 2; the co-ordinates of C.M of the arrangement are:
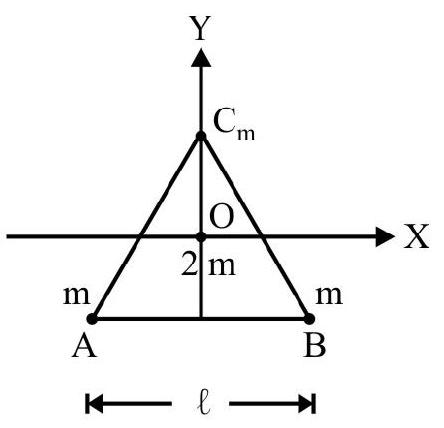
Fig. 2
(1) $\left(0 ; \frac{\sqrt{3}}{2} \ell\right)$
(2) $\left(\frac{\ell}{2} ; \frac{\sqrt{3}}{2} \ell\right)$
(3) $\left(\frac{\ell}{2} ; 0\right)$
(4) $\left(0 ; \frac{\ell}{5 \sqrt{3}}\right)$
Show Answer
Correct answer: (4)
Solution:
For the system shown co-ordinates of $\mathrm{A}\left(-\frac{\ell}{2} ;-\frac{\ell}{2 \sqrt{3}}\right) ; \mathrm{B}\left(\frac{\ell}{2} ;-\frac{\ell}{2 \sqrt{3}}\right) \mathrm{C}\left(0 ; \frac{\ell}{\sqrt{3}}\right)$ and $0(0,0)$. Let $\mathrm{X}$ and $\mathrm{Y}$ be the co-ordinates of C.M. Then
$$ \begin{aligned} & \mathrm{X}=\frac{\mathrm{m}\left(-\frac{\ell}{2}\right)+\mathrm{m}\left(\frac{\ell}{2}\right)+\mathrm{m}(0) ;+2 \mathrm{~m}(0)}{5 \mathrm{~m}}=0 \\ & \mathrm{Y}=\frac{\mathrm{m}\left(-\frac{\ell}{2 \sqrt{3}}\right)+\mathrm{m}\left(-\frac{\ell}{2 \sqrt{3}}\right)+2 \mathrm{~m}\left(\frac{\ell}{\sqrt{3}}\right)}{5 \mathrm{~m}}=\frac{\ell}{5 \sqrt{3}} \end{aligned} $$
4. $\mathrm{OAB}$ is an equilateral triangle of side $\ell, \mathrm{C}, \mathrm{D}$ and $\mathrm{E}$ are midpoints of the three sides. Points mass are placed on these points as shown in Fig. 3. The co-ordinates of C.M of system are
(1) $\left(\frac{\ell}{2}, \frac{\ell}{2}\right)$
(2) $\left(\frac{\ell}{2}, \frac{\sqrt{3} \ell}{2}\right)$
(3) $\left(\frac{\ell}{2}, \frac{\ell}{2 \sqrt{3}}\right)$
(4) $\left(\frac{\sqrt{3} \ell}{2}, \frac{\ell}{2}\right)$
Show Answer
Correct answer: (3)
Solution:
Choose $x-y$ axis as shown in Fig. 3. Co-ordinates of different points are:
$0(0,0) ; \mathrm{A}(\ell, 0) \cdot \mathrm{B}\left(\frac{\ell}{2}, \frac{\sqrt{3}}{2} \ell\right)$
$\mathrm{C}\left(\frac{\ell}{2} ; 0\right) ; \mathrm{D}\left(\frac{\ell}{4}, \frac{\sqrt{3}}{4} \ell\right) ; \mathrm{E}\left(\frac{3 \ell}{4}, \frac{\sqrt{3}}{4} \ell\right)$
(X, Y) are co-ordinates of C.M.
$X=\frac{m \times 0+m(\ell)+m\left(\frac{\ell}{2}\right)+2 m\left(\frac{\ell}{2}\right)+2 m\left(\frac{\ell}{4}\right)+2 m\left(\frac{3 \ell}{4}\right)}{m+m+m+3(2 m)}$
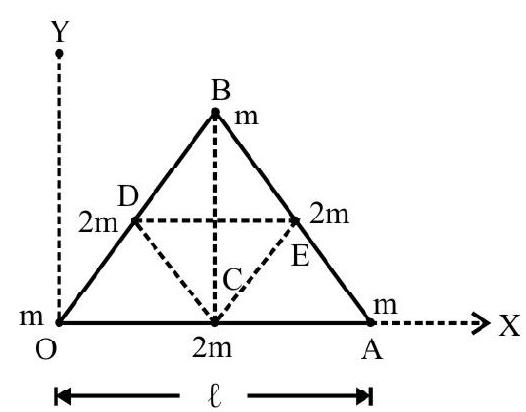
Fig. 3
$$ =\frac{9 \mathrm{~m} \ell}{2 \times 9 \mathrm{~m}}=\frac{\ell}{2} $$
$$ \begin{aligned} Y= & \frac{\mathrm{m} \times 0+\mathrm{m} \times 0+\mathrm{m}\left(\frac{\sqrt{3}}{2} \ell\right)+2 \mathrm{~m} \times 0+2 \mathrm{~m}\left(\frac{\sqrt{3}}{4} \ell\right)+2 \mathrm{~m}\left(\frac{\sqrt{3}}{4} \ell\right)}{9 \mathrm{~m}} \\ & =\frac{3 \sqrt{3} \mathrm{~m} \ell}{2 \times 9 \mathrm{~m}}=\frac{\ell}{2 \sqrt{3}} \end{aligned} $$
5. A uniform semi-circular disc of radius $R$ has a mass $M$. The distance of the centre of mass from $O$ of the disc on its radius $O C$ dividing the disc symmetrically is
(1) $\frac{R}{3}$
(2) $\frac{R}{2}$
(3) $\frac{2 R}{3}$
(4) $\frac{3 R}{8}$
Show Answer
Correct answer: (3)
Solution:
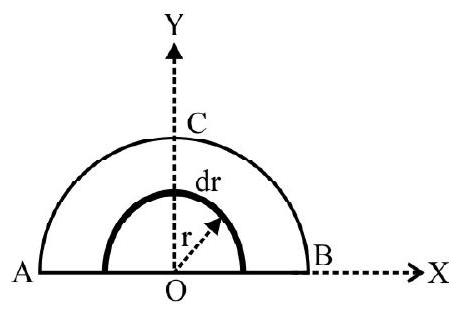
Fig. 4
Fig. 4 shows a uniform circular disc of radius R. Consider the disc as made up of concentric semi-circular rings. The radius of rings varies from 0 to $R$. By symmetry the center of mass lies on y-axis. Consider an elementary ring of radius $r$ thickness dr as shown in Fig. 4.
$\mathrm{dm}=$ Mass of elementary ring considered $=\pi(\mathrm{rdr}) \sigma ; \quad \sigma=$ mass $/$ area $=$ constant
$Y=$ Coordinate of $C . M=\frac{\int _{0}^{R} r d m}{\int _{0}^{R} d m}$
$=\frac{\int _{0}^{\mathrm{R}} \pi \sigma r^{2} d r}{\int _{0}^{\mathrm{R}} \pi \sigma r d r}=\frac{\frac{\mathrm{R}^{3}}{3}}{\frac{\mathrm{R}^{2}}{2}}=\frac{2 \mathrm{R}}{3}$
6. From a uniform circular disc of radius $R$ a part of radius $\frac{R}{4}$ is cut-out with center at $0 _{1}$ as shown in Fig. 5. The center of mass of the remaining part of disc is at:
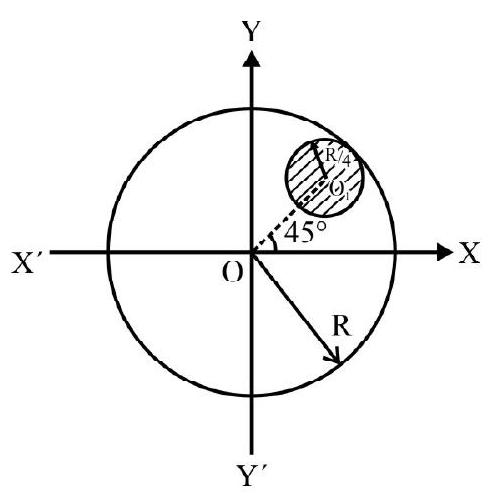
(1) $\mathrm{X}=-\frac{\mathrm{R}}{20} ; \mathrm{Y}=-\frac{\mathrm{R}}{20}$
(2) $\mathrm{X}=-\frac{\mathrm{R}}{20 \sqrt{2}} ; \mathrm{Y}=+\frac{\mathrm{R}}{20 \sqrt{2}}$
(3) $\mathrm{X}=-\frac{\mathrm{R}}{20 \sqrt{2}} ; \mathrm{Y}=-\frac{\mathrm{R}}{20 \sqrt{2}}$
(4) $\mathrm{X}=+\frac{\mathrm{R}}{20 \sqrt{2}} ; \mathrm{Y}=+\frac{\mathrm{R}}{20 \sqrt{2}}$
Show Answer
Correct answer: (3)
Solution:
Let $\mathrm{m}$ be mass of complete disc of radius R.The mass $\mathrm{m} _{1}$ of the part removed is $\frac{\mathrm{m}}{16}$. To obtain C.M of remaining disc we consider mass $\mathrm{m}$ to be placed at $\mathrm{O}$ and $-\left(\frac{\mathrm{m}}{16}\right)$ at $\mathrm{O} _{1}$ as shown in Fig. 6. Distance $\mathrm{OO} _{1}=\frac{3 \mathrm{R}}{4}$. The co-ordinates of $\mathrm{O} _{1}$ are $\left(\frac{3 \mathrm{R}}{4} \times \frac{1}{\sqrt{2}} ; \frac{3 \mathrm{R}}{4} \times \frac{1}{\sqrt{2}}\right)$
The co-ordinates (X, Y) of C.M are:
$X=\frac{m \times 0+\left(-\frac{m}{16}\right) \frac{3 R}{4 \sqrt{2}}}{m+\left(-\frac{m}{16}\right)}=-\left(\frac{R}{20 \sqrt{2}}\right)$
Similarly $\mathrm{Y}=-\left(\frac{\mathrm{R}}{20 \sqrt{2}}\right)$
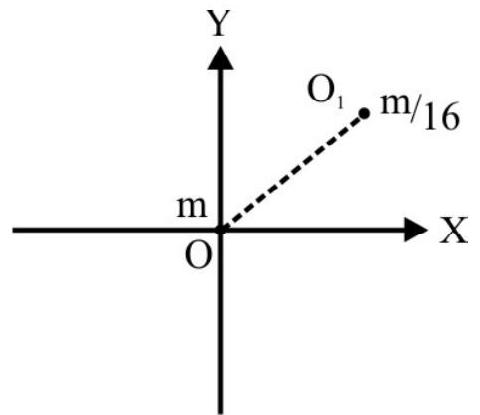
Fig. 6
7. Fig. 7 shows a uniform disc of center $O$, radius $R$ of a material of mass per unit area $\sigma$. $A$ part of center $O _{1}$ and radius $r$ is removed. Another disc of center $O _{2}$ radius $r$, of material of mass per unit area $2 \sigma$ is placed on the larger disc. The center of mass of the arrangement is at
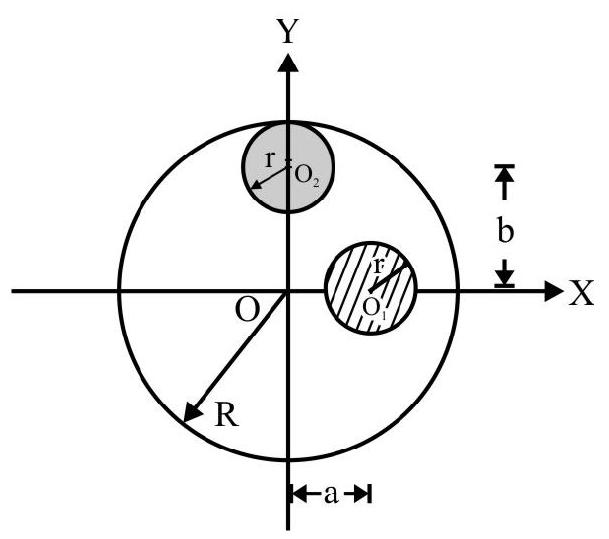
Fig. 7
(1) $x=\frac{\mathrm{r}^{2} \mathrm{a}}{\left(\mathrm{R}^{2}-\mathrm{r}^{2}\right)} ; y=\frac{\mathrm{r}^{2} \mathrm{~b}}{\left(\mathrm{R}^{2}-\mathrm{r}^{2}\right)}$
(2) $x=-\left[\frac{\mathrm{r}^{2} \mathrm{a}}{\left(\mathrm{R}^{2}+\mathrm{r}^{2}\right)}\right] ; y=\frac{2 \mathrm{r}^{2} \mathrm{~b}}{\left(\mathrm{R}^{2}+\mathrm{r}^{2}\right)}$
(3) $x=-\left[\frac{\mathrm{r}^{2} \mathrm{a}}{\left(\mathrm{R}^{2}+\mathrm{r}^{2}\right)}\right] ; y=-\left[\frac{2 \mathrm{r}^{2} \mathrm{~b}}{\left(\mathrm{R}^{2}+\mathrm{r}^{2}\right)}\right]$
(4) $x=-\left[\frac{\mathrm{r}^{2} \mathrm{a}}{\left(\mathrm{R}^{2}+\mathrm{r}^{2}\right)}\right] ; y=-\left[\frac{\mathrm{r}^{2} \mathrm{~b}}{\left(\mathrm{R}^{2}+\mathrm{r}^{2}\right)}\right]$
Show Answer
Correct answer:(2)
Solution:
Let $\mathrm{m} _{1}=$ Mass of complete disc of radius $\mathrm{R}=\pi \mathrm{R}^{2} \sigma$
$\mathrm{m} _{2}=$ Mass of disc of radius $\mathrm{r}$, removed $=\pi \mathrm{R}^{2} \sigma$
$m _{3}=$ Mass of disc of radius $r$, placed with center at
$\mathrm{O} _{2}=\pi \mathrm{r}^{2}(2 \sigma)=2 \pi \mathrm{r}^{2} \sigma$
The given arrangement is equivalent to what is shown in Fig. 8. Note mass at $\mathrm{O} _{1}$ has negative sign because it has been removed. Co-ordinates of $\mathrm{O}(0$, $0) ; \mathrm{O} _{1}(\mathrm{a}, 0)$ and $\mathrm{O} _{2}(0, \mathrm{~b})$
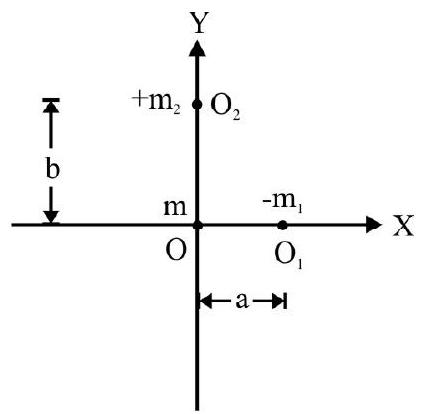
Fig. 8
Let $(\mathrm{X}, \mathrm{Y})$ be the co-ordinates of $\mathrm{C} . \mathrm{M}$ of the arrangement. Then
$$ \begin{aligned} X= & \frac{m(0)+\left(-m _{1}\right) a+m _{2}(0)}{m+\left(-m _{1}\right)+m _{2}} \\ & =-\left[\frac{m _{1} a}{\left(m-m _{1}+m _{2}\right)}\right]=-\left[\frac{\pi r^{2} \sigma a}{\pi\left[R^{2}-r^{2}+2 r^{2}\right] \sigma}\right] \\ & =-\left(\frac{r^{2} a}{R^{2}+r^{2}}\right) \end{aligned} $$
Similarly,
$$ \begin{aligned} & \mathrm{Y}= \frac{\mathrm{m}(0)+\left(-\mathrm{m} _{1}\right)(0)+\mathrm{m} _{2} \times \mathrm{b}}{\mathrm{m}+\left(-\mathrm{m} _{1}\right)+\mathrm{m} _{2}} \\ &=\frac{2 \pi \mathrm{r}^{2} \sigma \cdot \mathrm{b}}{\pi\left[\mathrm{R}^{2}-\mathrm{r}^{2}+2 \mathrm{r}^{2}\right] \sigma}=\frac{2 \mathrm{r}^{2} \mathrm{~b}}{\left(\mathrm{R}^{2}+\mathrm{r}^{2}\right)} \end{aligned} $$
8. A particle $A$ of mass $M$ is falling freely, from rest, under gravity of earth. At a height $h$, above ground it somehow on its own breaks up into two fragments $B$ and $C\left(m _{B}>m _{C}\right)$. The change in the path of C.M of $A$ and C.M of $B$ and $C$ is
(1) no change
(2) moves towards path of B
(3) moves towards path of $\mathrm{C}$
(4) change depends on height, h; where A breaks into fragments
Show Answer
Correct answer: (1)
Solution:
Particle A is moving freely under gravity; the C.M of A moves downwards along the vertical line path of A. Since A breaks up to two fragments on its own i.e. their is no external force; the equation of motion of C.M of $B$ and $C$ is same as of particle $A$. This means there is no change in path of C.M of fragments A and B.
9. A thin uniform rod of mass $M$ length $L$ is placed along $x$-axis as shown in Fig. 9. The rod is replaced by a non-uniform rod of same dimensions. The linear mass density $\lambda$ at a distance $x$ from origin is
$$ \lambda=\lambda _{0}(\mathrm{~L}-x) $$
where $\lambda _{0}$ is a constant. The distance by which center of mass of original rod shifts is:
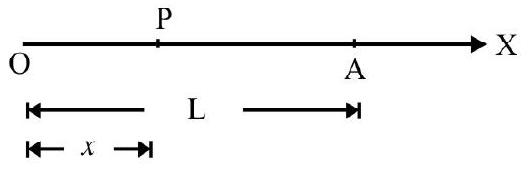
Fig. 9
(1) zero
(2) $\frac{\mathrm{L}}{3}$
(3) $\frac{L}{4}$
(4) $\frac{L}{6}$
Show Answer
Correct answer: (4)
Solution:
For uniform rod OA, the center of mass $X _{0}=\frac{L}{2}$. For non-uniform rod, the position X, of C.M is
$$ \begin{array}{r} \mathrm{X}=\frac{\int _{0}^{\mathrm{L}}(x \lambda \mathrm{d} x)}{\int _{0}^{\mathrm{L}} \lambda \mathrm{d} x}=\frac{\lambda _{0} \int _{0}^{\mathrm{L}}(\mathrm{L}-x) x \mathrm{~d} x}{\lambda _{0} \int _{0}^{\mathrm{L}}(\mathrm{L}-x) \mathrm{d} x} \\ =\frac{\left(\frac{\mathrm{L}^{3}}{2}-\frac{\mathrm{L}^{3}}{3}\right)}{\left(\mathrm{L}^{2}-\frac{\mathrm{L}^{2}}{2}\right)}=\frac{\mathrm{L}^{3}}{6} \times \frac{2}{\mathrm{~L}^{2}}=\frac{\mathrm{L}}{3} \end{array} $$
The change in position of $C \cdot M=\frac{L}{2}-\frac{L}{3}=\frac{L}{6}$
10. Two particles $A$ and $B$ of mass $m$ and $2 \mathrm{~m}$ are placed at $x _{A}=0$ and $x _{B}=3 a$. At $t=0 ; B$ starts moving towards $A$ with a constant speed $v _{0}$. The center of mass of system is at $X=a$; at time $\mathbf{t} _{1}$. Then $\mathbf{t} _{1}$ is
(1) $\frac{\mathrm{a}}{\mathrm{v} _{0}}$
(2) $\frac{2 \mathrm{a}}{\mathrm{v} _{0}}$
(3) $\frac{a}{2 v _{0}}$
(4) $\frac{3 \mathrm{a}}{2 \mathrm{v} _{0}}$
Show Answer
Correct answer: (4)
Solution:
The initial position $\mathrm{X} _{0}$ of the C.M. of system (i. e. $t=0$ ) is
$\mathrm{X} _{0}=\frac{\mathrm{m}(0)+2 \mathrm{~m}(3 \mathrm{a})}{\mathrm{m}+2 \mathrm{~m}}=2 \mathrm{a}$
$\mathrm{v} _{0}=$ The initial speed of. $\mathrm{C.M}$ of system
$$ =\frac{\mathrm{m} \times 0-2 \mathrm{mv} _{0}}{\mathrm{~m}+2 \mathrm{~m}}=-\left(\frac{2 \mathrm{v} _{0}}{3}\right) $$
When B starts moving towards A; there is no external force. The speed of center of mass remains same at all times. The instantaneous position, X of C.M is
$$ X=X _{0}+v _{0} t=2 a-\left(\frac{2 v _{0}}{3}\right) \mathrm{t} $$
Let $\mathrm{X}=\mathrm{a}$ at $\mathrm{t}=\mathrm{t} _{1}$. Then $\mathrm{a}=2 \mathrm{a}-\left(\frac{2 \mathrm{v} _{0}}{3}\right) \mathrm{t} _{1}$
$\therefore \mathrm{t} _{1}=\frac{3 \mathrm{a}}{2 \mathrm{v} _{0}}$
11. Two point masses $m _{1}$ and $m _{2}$ lie a distance $D$ apart as shown in Fig. 10. At $t=0$; an external force $F$ is applied on $m _{2}$ and system is let go. $S$ and $S _{1}$ denote distance traveled by C.M and the instantaneous separation between the two masses; then
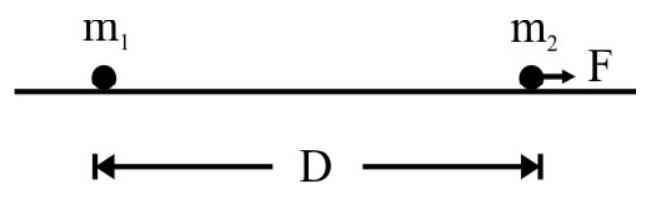
Fig. 10
(1) $S=\frac{1}{2}\left(\frac{F}{m _{1}}\right) t^{2} ; S _{1}=\frac{1}{2}\left(\frac{F}{m _{2}}\right) t^{2}$
(2) $\mathrm{S}=\frac{1}{2}\left(\frac{\mathrm{F}}{\mathrm{m} _{1}+\mathrm{m} _{2}}\right) \mathrm{t}^{2} ; \mathrm{S} _{1}=\frac{1}{2}\left(\frac{\mathrm{F}}{\mathrm{m} _{1}}\right) \mathrm{t}^{2}$
(3) $\mathrm{S}=\frac{1}{2}\left(\frac{\mathrm{Ft}^{2}}{\mathrm{~m} _{1}+\mathrm{m} _{2}}\right) ; \mathrm{S} _{1}=\mathrm{D}+\frac{1}{2}\left(\frac{\mathrm{F}}{\mathrm{m} _{2}}\right) \mathrm{t}^{2}$
(4) $\mathrm{S}=\frac{1}{2} \frac{\mathrm{Ft}^{2}}{\mathrm{~m} _{2}} ; \mathrm{S} _{1}=\mathrm{D}+\frac{1}{2}\left(\frac{\mathrm{F}}{\mathrm{m} _{2}}\right) \mathrm{t}^{2}$
Show Answer
Correct answer: (3)
Solution:
Let $a _{1}$ and $a _{2}$ be the acceleration of mass $m _{1}$ and $m _{2}$ respectively. Then $a _{1}=0$ (There is no external force applied on $m _{1}$ ), and
$$ \mathrm{a} _{2}=\frac{\mathrm{F}}{\mathrm{m} _{2}} $$
Let $a _{c}$ be acceleration of C.M. Then
$$ \mathrm{a} _{\mathrm{c}}=\frac{\mathrm{m} _{1} \mathrm{a} _{1}+\mathrm{m} _{2} \mathrm{a} _{2}}{\mathrm{~m} _{1}+\mathrm{m} _{2}}=\frac{\mathrm{F}}{\left(\mathrm{m} _{1}+\mathrm{m} _{2}\right)}=\mathrm{constant} $$
$\mathrm{S}=$ Distance traveled by C.M in time $\mathrm{t}$
$$ =\frac{1}{2} \mathrm{a} _{\mathrm{c}} \mathrm{t}^{2}=\frac{1}{2}\left(\frac{\mathrm{Ft}^{2}}{\mathrm{~m} _{1}+\mathrm{m} _{2}}\right) $$
$\mathrm{S} _{1}=$ Instantaneous distance between $\mathrm{m} _{1}$ and $\mathrm{m} _{2}$ $=\mathrm{D}+$ distance traveled by $\mathrm{m} _{2}$ in time $\mathrm{t}$
$=\mathrm{D}+\frac{1}{2} \mathrm{a} _{2} \mathrm{t}^{2}=\mathrm{D}+\frac{1}{2}\left(\frac{\mathrm{Ft}^{2}}{\mathrm{~m} _{2}}\right)$
12. $O A$ is a thin rod of mass $4 \mathrm{~m}$, length $2 \mathrm{~L}$ placed along $x$-axis as shown in Fig. 11. A particle $P$, of mass $m$ starts moving along rod with a constant speed $v _{0}$. The variation of position co-ordinate $X$ of C.M. of system with time (t); till $P$ reaches end $A$ is

Show Answer
Correct answer: (4)
Solution:
The entire mass $4 \mathrm{~m}$ of rod can be considered as concentrated at its center i.e. $x _{1}=\mathrm{L}$. The instantaneous position of $\mathrm{P}=x _{2}=\mathrm{v} _{0} \mathrm{t}$. The instantaneous position of C.M X is
$$ \mathrm{X}=\frac{4 \mathrm{~m} \times \mathrm{L}+\mathrm{mv} _{0} \mathrm{t}}{4 \mathrm{~m}+\mathrm{m}}=0.8 \mathrm{~L}+0.2 \mathrm{v} _{0} \mathrm{t} $$
$\mathrm{X}$ vs $\mathrm{t}$ graph is a straight line. Also $\mathrm{X}(\mathrm{t}=0)=0.8 \mathrm{~L}$
Let $P$ reach end A of rod at $t=t _{1}=\frac{2 L}{v _{0}}$. Then
$$ \mathrm{X}\left(\mathrm{t}=\mathrm{t} _{1}\right)=0.8 \mathrm{~L}+0.4 \mathrm{~L}=1.2 \mathrm{~L} $$
13. A rod $O A$ of mass $M$; length $L$ lies along $x$-axis with one end at origin of co-ordinates. $A$ particle of mass $m$ is initially at rest at the other end $A$. At $t=0$; particle starts moving towards end $O$ with a uniform acceleration a. For $0 \leq \mathrm{t} \leq \tau$; where $\tau$ is time taken by particle to reach end $O$ the instantaneous position of $C . M$ of system, $X$ is:
(1) $\frac{\mathrm{L}}{2}-\frac{1}{2} \mathrm{at}^{2}$
(2) $\left[\frac{(M+2 m) L}{2(M+m)}\right]-\frac{1}{2}\left(\frac{m a}{M+m}\right) \mathrm{t}^{2}$
(3) $\left[\frac{L}{2}\right]-\left[\frac{M a}{2(M+m)}\right] \mathrm{t}^{2}$
(4) $\left[\frac{M L}{M+m}\right]-\left[\frac{m a}{2(M+m)}\right] t^{2}$
Show Answer
Correct answer: (2)
Solution:
The mass $\mathrm{M}$ of rod is considered as concentrated at its midpoint $\mathrm{O} _{1} ; x _{1}=\frac{\mathrm{L}}{2}$. Let $\mathrm{P}$ be the instantaneous position of particle on rod. The instantaneous position co-ordinate of $\mathrm{P}$
$$ x _{2}=\left(\mathrm{L}-\frac{1}{2} \mathrm{at}{ }^{2}\right) $$
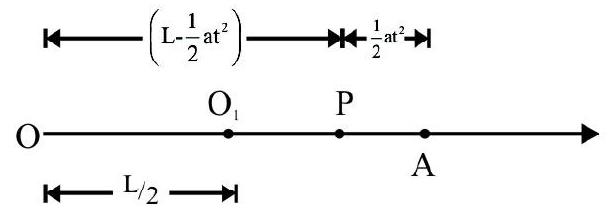
$\mathrm{X}=$ The instantaneous position co-ordinate of C.M
$$ \begin{aligned} & =\frac{\mathrm{m}\left(x _{1}\right)+\mathrm{m}\left(x _{2}\right)}{\mathrm{M}+\mathrm{m}}=\frac{\mathrm{M}\left(\frac{\mathrm{L}}{2}\right)}{(\mathrm{M}+\mathrm{m})}+\left(\frac{\mathrm{m}}{\mathrm{M}+\mathrm{m}}\right)\left(\mathrm{L}-\frac{1}{2} a \mathrm{t}^{2}\right) \\ & =\left[\frac{\mathrm{M}+2 \mathrm{~m}}{2(\mathrm{M}+\mathrm{m})}\right] \mathrm{L}-\left[\frac{\mathrm{ma}}{2(\mathrm{M}+\mathrm{m})}\right] \mathrm{t}^{2} \end{aligned} $$
14. A long planck of mass $10 \mathrm{~kg}$ lies on an absolutely smooth horizontal surface. A ball of mass $0.5 \mathrm{~kg}$ is initially at rest on one end of planck. At $t=0$, the ball start moving with a constant speed $v _{0}$. As it moves from one end to the other end; the planck acquires a speed of $0.2 \mathrm{~ms}^{-1}$. Then $\mathrm{v} _{0}$ is
(1) $0.2 \mathrm{~ms}^{-1}$
(2) $2 \mathrm{~ms}^{-1}$
(3) $4.2 \mathrm{~ms}^{-1}$
(4) $4.0 \mathrm{~ms}^{-1}$
Show Answer
Correct answer: (3)
Solution:
As the ball moves on planck there is no external force. The center of mass of ‘planck-ball’ system is initially at rest, it remains at rest as ball moves on planck. Let ball travel a distance L (= the length of planck) is time t. Then $\mathrm{v} _{0}=\frac{\mathrm{L}}{\mathrm{t}}$. In this time the planck moves by a distance
$$ \ell=\frac{\mathrm{mL}}{(\mathrm{M}+\mathrm{m})} $$
$\mathrm{v}=$ The speed acquired by planck $=\frac{\ell}{\mathrm{t}}=\frac{\mathrm{m}\left(\frac{\mathrm{L}}{\mathrm{t}}\right)}{\mathrm{M}+\mathrm{m}}$
$$ =\frac{\mathrm{mv} _{0}}{(\mathrm{M}+\mathrm{m})} $$
Given $\mathrm{M}=10 \mathrm{~kg} ; \mathrm{m}=0.5 \mathrm{~kg} ; \mathrm{v}=0.2 \mathrm{~ms}^{-1}$, therefore
$$ \begin{aligned} \mathrm{v} _{0}= & \frac{0.2(10+0.5)}{0.5} \mathrm{~ms}^{-1} \\ & =4.2 \mathrm{~ms}^{-1} \end{aligned} $$
15. Two particles $A$ and $B$ of mass $m _{1}$ and $m _{2}$ are moving with velocity $u _{1}$ and $u _{2}$ in “Lab-frame of reference”. In a frame of reference attached to the center of mass of $A$ and $B$; the total linear momentum of $A$ and $B$ is
(1) zero
(2) $\mathrm{m} _{1} \mathbf{u} _{1}+\mathrm{m} _{2} \mathbf{u} _{2}$
(3) $\left(\mathrm{m} _{1}+\mathrm{m} _{2}\right) \mathbf{v}$; where $\mathbf{v}$ is velocity of C.M of A and B
(4) Less than $\left(\mathrm{m} _{1} \mathbf{u} _{1}+\mathrm{m} _{2} \mathbf{u} _{2}\right)$
Show Answer
Correct answer: (1)
Solution:
The initial velocity $\mathbf{V} _{0}$ of center of mass A and B is
$$ \begin{equation*} \mathbf{V} _{0}=\frac{\mathrm{m} _{1} \mathbf{u} _{1}+\mathrm{m} _{2} \mathbf{u} _{2}}{\mathrm{~m} _{1}+\mathrm{m} _{2}}=\mathrm{constant} \tag{i} \end{equation*} $$
Let $\mathbf{v} _{1 c}$ and $\mathbf{v} _{2 c}$ be velocity of A and B in C.M frame of reference. Then
$$ \mathbf{v} _{1 \mathrm{c}}=\mathbf{u} _{1}-\mathbf{V} _{0} ; \mathbf{v} _{2 \mathrm{c}}=\mathbf{u} _{2}-\mathbf{V} _{0} $$
$\mathbf{P} _{\mathrm{c}}=$ The total linear momentum of A and B in C.M frame of reference.
$$ \begin{align*} & =\mathbf{m} _{1} \mathbf{v} _{1 \mathrm{c}}+\mathbf{m} _{2} \mathbf{v} _{2 \mathrm{c}}=\mathrm{m} _{1}\left(\mathbf{u} _{1}-\mathbf{V} _{0}\right)+\mathrm{m} _{2}\left(\mathbf{u} _{2}-\mathbf{V} _{0}\right) \\ & =\left(\mathrm{m} _{1} \mathbf{u} _{1}+\mathrm{m} _{2} \mathbf{u} _{1}\right)-\left(\mathrm{m} _{1}+\mathrm{m} _{2}\right) \mathbf{V} _{0} \tag{ii} \end{align*} $$
From Eqns. (i) and (ii) we have,
$$ \mathbf{P} _{\mathrm{c}}=\text { zero } $$
16. Two point masses $m _{1}$ and $m _{2}$ are at rest a distance 2D apart. At $t=0$; the two start moving towards one another, under their mutual force of interaction. What is distance traveled by the center of mass when separation between particle is reduced to $D$ ?
(1) zero
(2) $\mathrm{D} / 2$
(3) Less than $\mathrm{D} / 2$
(4) More than $\mathrm{D} / 2$ but less than $\mathrm{D}$
Show Answer
Correct answer: (1)
Solution:
Fig. 12 shows position of masses $\mathrm{m} _{1}$ and $\mathrm{m} _{2}$ at $\mathrm{t}=0$.
$\mathrm{X} _{0}=$ Initial co-ordinate of C.M
$$ =\frac{\mathrm{m} _{1} \times 0+\mathrm{m} _{2}(2 \mathrm{D})}{\mathrm{m} _{1}+\mathrm{m} _{2}}=\frac{2 \mathrm{~m} _{2} \mathrm{D}}{\left(\mathrm{m} _{1}+\mathrm{m} _{2}\right)} $$

Fig. 12
$\mathrm{V} _{0}=$ The initial velocity of $\mathrm{C} . \mathrm{M}$
$$ =\frac{\mathrm{m} _{1} \times 0+\mathrm{m} _{2} \times 0}{\mathrm{~m} _{1}+\mathrm{m} _{2}}=0 $$
The equation of motion of C.M of system is
$$ \left(\mathrm{m} _{1}+\mathrm{m} _{2}\right) \frac{\mathrm{d}^{2} \mathrm{X}}{\mathrm{dt}}=0 $$
Note there is no external force. Masses move towards one another due to their mutual force of interaction, which is an internal force. Therefore
$$ \frac{\mathrm{d}^{2} \mathrm{X}}{\mathrm{dt}^{2}}=\frac{\mathrm{dV}}{\mathrm{dt}}=0 $$
$\therefore \mathrm{V}=\mathrm{V} _{0}=0$
The center of mass is initially at rest and it remains at rest throughout. Therefore distance traveled by center of mass is zero.
17. A particle of mass $m$, moves with a velocity $\mathbf{v}=\mathrm{v} _{0} \hat{\mathrm{j}}, \mathrm{v} _{0}$ is constant along a straight line parallel to $\mathbf{Y}$-axis as shown in Fig. 13. $P$ is the instantaneous position of particle. $r$ and $\theta$ are as shown in Fig. 13. The instantaneous angular momentum $L _{0}$ of $P$ about origin $\mathrm{O}$; is
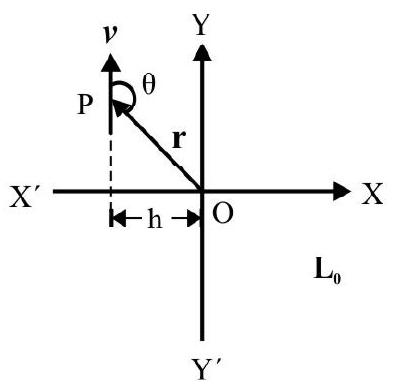
Fig. 13
(1) directly proportional to r only
(2) independent of $r$ and $\theta$
(3) directly proportional to $\cos \theta$ only
(4) directly proportional to $r$ and $\theta$ only
Show Answer
Correct answer: (2)
Solution:
Let $\mathrm{h}$ be the perpendicular distance of line along which particle moves from $\mathrm{O}$. The angular momentum $\mathrm{L} _{0}$ is
$$ \mathrm{L} _{0}=\mathrm{mv} _{0} \mathrm{~h} $$
$\mathrm{L} _{0}$ does not depend on $\mathrm{r}$ or $\theta$ ( $\mathrm{r}$ and $\theta$ both change in such a manner that $\mathrm{h}=\mathrm{r} \sin \theta=$ constant.)
Alternative Solution :
Since there is no external force i.e. $\mathbf{F} _{\text {ext }}=0$; there is no external torque, therefore $\mathbf{L}$ is constant.
18. A particle of mass $m$ moves along a curved path in $x-y$ plane about origin of co-ordinates as axis in such a manner that instantaneous acceleration is always perpendicular to instantaneous velocity. The magnitude of linear velocity and acceleration is $\alpha$ and $\beta$ respectively. The angular momentum of particle about origin $(0)$ of co-ordinates is
(1) $\mathrm{m} \alpha \beta$
(2) $\frac{m \alpha^{2}}{\beta}$
(3) $\frac{m \alpha^{3}}{\beta}$
(4) $\mathrm{m}\left(\frac{\alpha}{\beta}\right)^{2}$
Show Answer
Correct answer: (3)
Solution:
Since instantaneous velocity is always perpendicular to instantaneous acceleration, the particle moves in a circle with center $\mathrm{O}$. Let $\mathrm{R}$ be radius of circular path. The magnitude of acceleration is
$$ \beta=\frac{\alpha^{2}}{R} \quad \text { or } \quad R=\frac{\alpha^{2}}{\beta} $$
The magnitude of linear momentum of particle $=\mathrm{m} \alpha$. The magnitude of angular momentum; $\ell$; about $\mathrm{O}$ is
$$ \ell=p \times R=(m \alpha) \frac{\alpha^{2}}{\beta}=\frac{m \alpha^{3}}{\beta} $$
19.
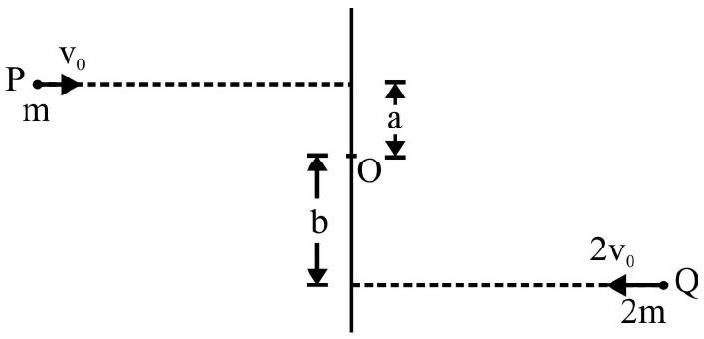
Fig. 14
Two particle $P$ and $Q$ of mass $m$ and $2 m$ are moving in the plane of page as shown in Fig. 14 The angular momentum of the two particle system about point $O$ is
(1) $\mathrm{mv} _{0} \mathrm{a}$; clockwise
(2) $4 \mathrm{mv} _{0} \mathrm{~b}$; anticlockwise
(3) $\mathrm{mv} _{0}(\mathrm{a}+2 \mathrm{~b})$; clockwise
(4) $\mathrm{mv} _{0}[4 \mathrm{~b}-\mathrm{a}]$ anticlockwise
Show Answer
Correct answer: (4)
Solution:
$\mathbf{L}=$ Total angular momentum of the two particle system about point $\mathrm{O}=\mathbf{L} _{\mathrm{P}}+\mathbf{L} _{\mathrm{Q}}$
$\mathbf{L} _{\mathrm{P}}=$ Angular momentum of $\mathrm{P}$ about $\mathrm{O}=\mathrm{mv} _{0}a$; clockwise
$\mathbf{L} _{\mathrm{Q}}=$ Angular momentum of $\mathrm{Q}$ about $\mathrm{O}=4 \mathrm{mv} _{0}$; anticlockwise
$$ \begin{aligned} \therefore \quad|\mathbf{L}| & =\left|\mathbf{L} _{\mathrm{Q}}\right|-\left|\mathbf{L} _{\mathrm{P}}\right| \\ & =\mathrm{mv} _{0}[4 \mathrm{~b}-\mathrm{a}] \end{aligned} $$
The direction of $\mathbf{L}$ is anticlockwise
20. A uniform disc of mass $2 \mathrm{~m}$ radius $\mathrm{R}$ is pivoted at its center $\mathrm{O}$ on a smooth horizontal surface. The disc in free to rotate about a vertical axis $\mathrm{ZOZ}^{\prime}$ through its center $O$. The disc is initially at rest. A particle of mass $m$ is moving on the horizontal surface with an initial speed $v$ as shown in Fig. 15. The particle hits disc at its edge $A$ and sticks to the disc. What is angular speed of “discuss system” when $m$ just sticks to it at $A$ ? Somehow on its own the mass $m$ starts moving towards center of disc. What is angular speed of the system when $m$ reaches $O$ ?
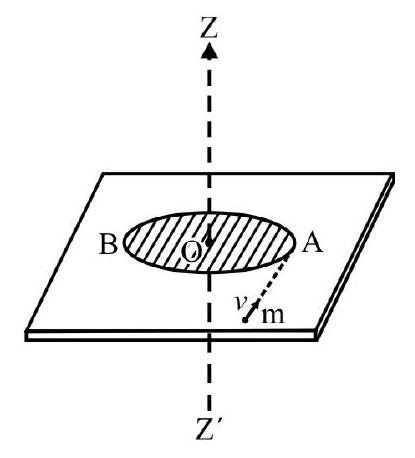
Fig. 15
(1) $\frac{\mathrm{V}}{2 \mathrm{R}} ; \frac{\mathrm{v}}{\mathrm{R}}$
(2) $\frac{\mathrm{v}}{\mathrm{R}} ; \frac{\mathrm{v}}{\mathrm{R}}$
(3) $\frac{2 \mathrm{v}}{\mathrm{R}} ; \frac{\mathrm{v}}{\mathrm{R}}$
(4) $\frac{2 \mathrm{v}}{\mathrm{R}} ; \frac{\mathrm{v}}{2 \mathrm{R}}$
Show Answer
Correct answer: (1)
Solution:
For “disc-mass system”; there is no external force, therefore no external torque. The angular momentum of system is conserved.
$\mathrm{L} _{\mathrm{i}}=\mathrm{L} _{\text {DISC }}+\mathrm{L} _{\text {mass }}=0+\mathrm{mvR}$
$\mathrm{L} _{\mathrm{f}}=\mathrm{I} \omega _{0}$
$\mathrm{I}=\mathrm{I} _{\text {DISC }}+\mathrm{I} _{\text {mass }}=\frac{1}{2}(2 \mathrm{~m}) \mathrm{R}^{2}+\mathrm{mR}^{2}=2 \mathrm{mR}^{2}$
$\therefore \quad \mathrm{mvR}=2 \mathrm{mR}^{2} \omega _{0} \quad$ or $\quad \omega _{0}=\frac{\mathrm{v}}{2 \mathrm{R}}$
The mass m moves on disc, somehow on its own.e. there is no external force. Angular momentum is again conserved.
$$ \begin{aligned} & \mathrm{I} \omega _{0}=\mathrm{I}^{\prime} \omega^{\prime} ; \quad \omega^{\prime}=\text { angular speed of system as mass } \mathrm{m} \text { reach } \mathrm{O} . \\ & \mathrm{I}^{\prime}=\mathrm{I} _{\mathrm{DISC}}=\mathrm{mR}^{2} \\ & \therefore \quad \omega^{\prime}=\left(\frac{2 \mathrm{mR}^{2}}{\mathrm{mR}^{2}}\right) \omega _{0}=2 \omega _{0}=\frac{\mathrm{v}}{\mathrm{R}} \end{aligned} $$
21. A particle of mass $m$ is moving in a vertical plane. It is projected with a speed $v _{0}$ at an angle $\theta$ with the horizontal, from the origin of co-ordinates. The angular momentum of particle, about origin of co-ordinates, when it is at same horizontal level as point of projection is
(1) zero
(2) $\frac{\mathrm{mv} _{0}^{2} \sin ^{2} \theta}{\mathrm{g}}$
(3) $\frac{2 m v _{0}^{3} \sin \theta \cos ^{2} \theta}{g}$
(4) $\frac{2 \mathrm{mv} _{0}^{3} \sin ^{2} \theta \cos \theta}{\mathrm{g}}$
Show Answer
Correct answer: (4)
Solution:
Fig. 16 show the parabolic path of particle when it is in position $P$. The velocity of particle is $\mathrm{v} _{0}$ as shown in Fig. 16. OQ is perpendicular from origin $\mathrm{O}$ on the line of action of linear momentum of particle at $\mathrm{P}$.
$\ell=$ angular momentum of particle at $\mathrm{P}$ about $\mathrm{O}=\mathrm{mv} _{0} \times \mathrm{OQ}$
$=\mathrm{mv} _{0} \mathrm{R} \sin \theta$
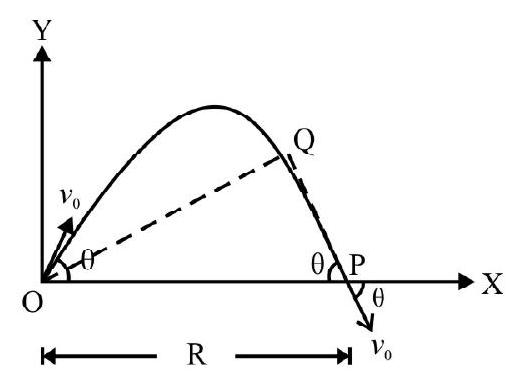
Fig. 16
$\text { where } \mathrm{OP}=\mathrm{R}=\frac{\mathrm{v}_0^2 \sin 2 \theta}{\mathrm{g}}=\text { horizontal range of } \mathrm{P} \text {. }$
$$ \therefore \quad \ell=\frac{\mathrm{mv} _{0}^{3} \sin 2 \theta \sin \theta}{\mathrm{g}} $$
$$ =\frac{2 \mathrm{mv} _{0}^{3} \sin ^{2} \theta \cos \theta}{\mathrm{g}} $$
22. A sphere $P$ of mass $M$, radius $R$ is moving on a smooth horizontal surface with an angular speed $\omega$. The speed of center of mass is $v$. P undergoes a perfectly clastic head-on collision with an identical sphere $B$ at rest. The angular speeds of $P$ and $Q$ after collision are $\omega _{1}$ and $\omega _{2}$. Then
(1) $\omega _{1}<\omega _{2}$
(2) $\omega _{1}=\omega _{2} \neq \omega$
(3) $\omega _{1}=0$
(4) $\omega _{1}=\omega$
Show Answer
Correct answer: (4)
Solution:
There is no friction between $\mathrm{P}$ and surface in contact. When $\mathrm{P}$ and $\mathrm{Q}$ collide there is no transfer of angular momentum from P to Q. Sphere P only transfers its linear momentum to Q. Hence after collision P has same angular speed as before collision. Therefore $\omega _{1}=\omega$.
23. Two point masses $m _{1}$ and $m _{2}$ are fixed at the ends of a massless rod of length $\ell$. The system revolves around an axis through C.M and perpendicular to the length of rod. It is completing $n$ revolutions per second. The angular momentum of the system about axis of rotation is
(1) $\left(\frac{m _{1} m _{2}}{m _{1}+m _{2}}\right) \ell^{2} \cdot n^{2}$
(2) $2 \pi\left(\frac{m _{1} m _{2}}{m _{1}+m _{2}}\right) \ell^{2} \cdot n$
(3) $\left(\frac{m _{1} m _{2}}{m _{1}+m _{2}}\right) \ell^{2} \cdot\left(\frac{n^{2}}{2 \pi^{2}}\right)$
(4) $4 \pi^{2}\left(m _{1}+m _{2}\right) \ell^{2} n^{2}$
Show Answer
Correct answer: (2)
Solution:
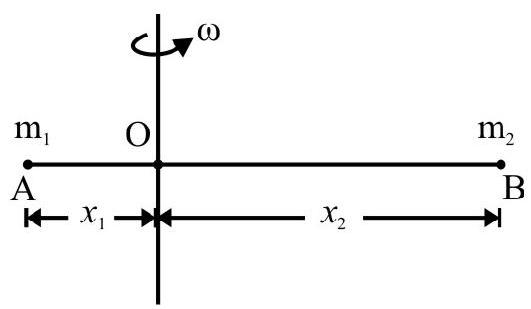
Fig. 17
The moment of inertia $(J)$ of the system about axis through C.M $(\mathrm{O})$ and perpendicular to $A B$ is
$$ \begin{aligned} & \mathrm{I}=\mathrm{m} _{1} x _{1}^{2}+\mathrm{m} _{1} x _{2}^{2} \\ & x _{1}=\frac{\mathrm{m} _{2} \ell}{\mathrm{m} _{1}+\mathrm{m} _{2}} ; x _{2}=\frac{\mathrm{m} _{1} \ell}{\mathrm{m} _{1}+\mathrm{m} _{2}} \\ & \therefore \quad \mathrm{I}=\mathrm{m} _{1}\left(\frac{\mathrm{m} _{2} \ell}{\mathrm{m} _{1}+\mathrm{m} _{2}}\right)^{2}+\mathrm{m} _{2}\left(\frac{\mathrm{m} \ell}{\mathrm{m} _{1}+\mathrm{m} _{2}}\right)^{2} \\ & =\frac{\mathrm{m} _{1} \mathrm{~m} _{2} \ell^{2}}{\left(\mathrm{~m} _{1}+\mathrm{m} _{2}\right)} \end{aligned} $$
The angular speed $(\omega)$ of the system is $\omega=2 \pi \mathrm{n}$
The angular momentum L; of the system about axis of rotation;
$$ \begin{aligned} & \mathrm{L}=\mathrm{I} \omega \\ & =2 \pi\left(\frac{\mathrm{m} _{1} \mathrm{~m} _{2}}{\mathrm{~m} _{1}+\mathrm{m} _{2}}\right) \ell^{2} \mathrm{n} \end{aligned} $$
24. A particle of mass $m$, tied to one end of a string is whirled into a horizontal circle. The length of string is gradually reduced in such a manner that the angular momentum of particle about center of circle remains same. $T$ is tension in string when instantaneous radius of circle is $r$; then
(1) $\mathrm{T} \propto \mathrm{r}^{-1}$
(2) $\mathrm{T} \propto \mathrm{r}^{-2}$
(3) $\mathrm{T} \propto \mathrm{r}^{-3}$
(4) $\mathrm{T} \propto \mathrm{r}$
Show Answer
Correct answer: (3)
Solution:
Let $\omega$ be the instantaneous angular speed of stone when instantaneous radius of circle is $r$. The angular momentum $\ell$, of stone about center of circle.
$$ \begin{equation*} \ell=\mathrm{mr}^{2} \omega=\text { constant } \tag{i} \end{equation*} $$
The instantaneous tension $\mathrm{T}$ in string provides necessary centripetal force. Therefore,
$$ \begin{aligned} & \mathrm{T}=\mathrm{mr} \omega^{2} \\ & =\mathrm{mr}\left(\frac{\ell}{\mathrm{mr}^{2}}\right)^{2} \quad[\mathrm{Clf}=\mathrm{n}(\mathrm{i})] \\ & =\frac{\ell^{2}}{\mathrm{mr}^{3}} \quad \text { Since } \ell \text { and m are constant, therefore } \\ & \mathrm{T} \propto \mathrm{r}^{-3} \end{aligned} $$
25.
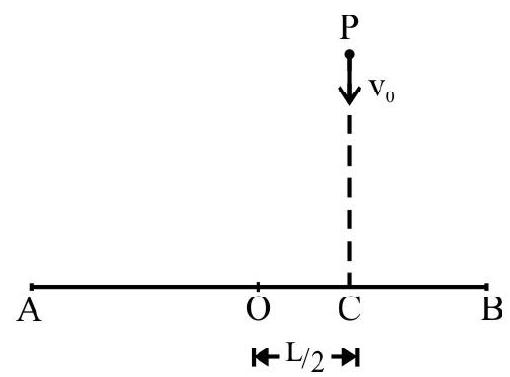
Fig. 18
A thin uniform rod $A B$ of mass $2 m$ has length $2 \mathrm{~L}$. The rod is pivoted at midpoint $O$ on a smooth horizontal surface. A particle $P$ of mass $m$ moving with speed $v _{0}$ as shown in Fig. 18; hits rod at point $C$ and sticks to it. The rod-mass system rotates with an angular speed $\omega$. Then
(1) $\mathrm{v} _{0}=\frac{2}{3} \sqrt{\omega} \mathrm{L}$
(2) $\mathrm{v} _{0}=\frac{11}{6} \sqrt{\omega} \mathrm{L}$
(3) $\mathrm{v} _{0}=\frac{7}{12} \sqrt{\omega} \mathrm{L}$
(4) $\mathrm{v} _{0}=\frac{5}{12} \sqrt{\omega} \mathrm{L}$
Show Answer
Correct answer: (2)
Solution:
Consider “rod-particle system”. Since there is no external force angular momentum of system is conserved.
$\mathrm{L} _{\mathrm{i}}=$ Initial angular momentum of system about $\mathrm{O}=\mathrm{mv} _{0}(\mathrm{~L} / 2)$
$\mathrm{L} _{\mathrm{f}}=$ Final angular momentum of system about $\mathrm{O}=\mathrm{I} \omega$.
$\mathrm{I}=$ M.I of rod particle system about axis through midpoint $\mathrm{O}$ and perpendicular to length of rod
$$ \begin{aligned} & =\frac{1}{12}(2 \mathrm{~m})(2 \ell)^{2}+\mathrm{m}\left(\frac{\ell}{2}\right)^{2} \\ & =\frac{2}{3} \mathrm{~m} \ell^{2}+\frac{\mathrm{m} \ell^{2}}{4}=\frac{11}{12} \mathrm{~m} \ell^{2} \end{aligned} $$
From law of conservation of angular momentum
$$ \begin{aligned} & \mathrm{L} _{\mathrm{i}}=\mathrm{L} _{\mathrm{f}} \quad \text { or } \quad \frac{\mathrm{mv} _{0} \mathrm{~L}}{2}=\frac{11}{12} \mathrm{~m} \ell^{2} \omega \\ & \therefore \quad \mathrm{v} _{0}=\frac{11}{6} \ell \omega \end{aligned} $$
26. A uniform disc of mass $2 m$, radius $R$ is at rest in a vertical position. It is free to rotate about a horizontal axis through center $O$. A particle of $m$ moving with speed $v$ is aimed towards the edge of the disc as shown in Fig. 19. The particle hits disc and gets embedded in it. The angular speed; $\omega$, of the arrangement when particle gets embedded is (neglect gravity)
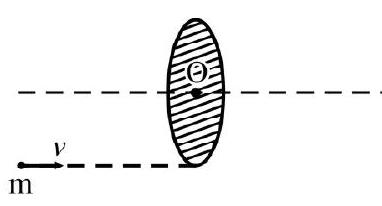
Fig. 19
(1) $\frac{\mathrm{V}}{\mathrm{R}}$
(2) $\frac{v}{2 R}$
(3) $\frac{2 \mathrm{v}}{\mathrm{R}}$
(4) $\frac{3}{2} \frac{\mathrm{v}}{\mathrm{R}}$
Show Answer
Correct answer: (2)
Solution:
Consider disc-particle system; there is no external force and therefore no external torque. The angular momentum of systemabout $\mathrm{O}$ is conserved.
$\mathrm{L} _{\mathrm{i}}=$ The total initial angular momentum $=\mathrm{mvR}$
$\mathrm{L} _{\mathrm{f}}=$ The total final angular momentum $=\left(\mathrm{I} _{\text {disc }}+\mathrm{I} _{\text {particle }}\right) \omega$
$$ =\left[\frac{1}{2}(2 m) R^{2}+m R^{2}\right] \omega=2 m R^{2} \omega $$
Now, $\mathrm{L} _{\mathrm{i}}=\mathrm{L} _{\mathrm{f}}$; therefore
$$ \begin{aligned} & \mathrm{mvR}=2 \mathrm{mR}^{2} \omega \\ & \omega=\frac{\mathrm{v}}{2 \mathrm{R}} \end{aligned} $$
27. A disc of mass $\mathrm{M}$; radius $\mathrm{R}$ is rotating about $\mathrm{ZOZ}^{\prime}$ as axis. $\mathrm{PQ}$ is a chord on the disc. A bead of mass $m$ is held at $P$. The arrangement is given an initial angular speed $\omega _{0}$. At the same time bead starts moving along chord from $P$ to $Q$. The angular speed $\omega$ vs time $(t)$ graph of the arrangement is
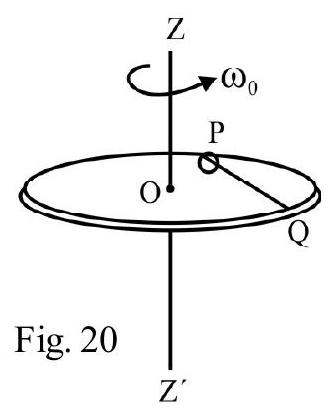

Show Answer
Correct answer: (4)
Solution:
As bead slides along chord PQ there is no external force and therefore no external torque. The angular momentum of system remains constant. However the M.I (I) of the system varies as bead moves. The M.I decreases becomes minimum when bead is at middle of chord PQ and then increases. M.I with bead at end $\mathrm{P}$ and $\mathrm{Q}$ is same. Therefore $\omega$ first increases acquires a maximum value when $\mathrm{I}$ is minimum and then starts decreasing. Final value of $\omega=\omega _{0}$ when bead reaches end Q. The variation of I is non-linear as shown in(4).
28. A wire of mass $m$ is bent into an equilateral triangle of side $\ell$. Two beads (identical) each of mass $m _{0}$ can slide freely along sides $P Q$ and $Q R$ of triangle. The triangle is set into rotation about axis $\mathrm{ZZ}^{\prime}$ and simultaneously beads are let go from point $P$. As system rotates beads slide down. For the system, what is conserved?
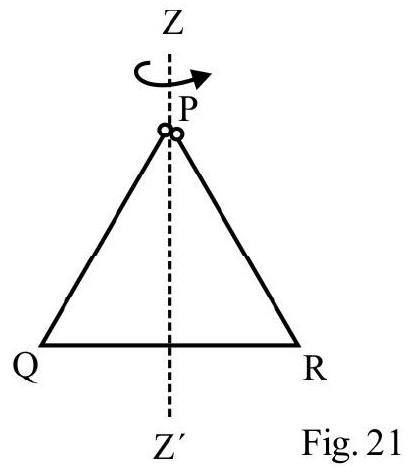
(1) Angular speed and total energy
(2) Angular momentum and moment of inertia
(3) Total energy (i.e. sum of kinetic and potential energy) and total angular momentum
(4) Kinetic energy and angular momentum
Show Answer
Correct answer: (3)
Solution:
As beads slide down sides PQ and PR there is no external force (sides of $\triangle \mathrm{PQR}$ are smooth) and therefore no external torque. The total angular momentum of system is, therefore, conserved.
As beads slide down the beads lose gravitational potential, but their is a gain in K.E. The total energy is, therefore, conserved.
29. A charged particle having charge $q ;$ mass $m$ is under the action of an electric field $\mathbf{E}=\mathrm{E} _{0} \hat{\mathrm{i}}$. At some instant of time its position co-ordinates are $(a, b)$. What is the magnitude of torque of force on particle due to electric field about origin of co-ordinates at this moment of time?
(1) zero
(2) $\mathrm{qE} _{0} \cdot \mathrm{a}$
(3) $\mathrm{qE} _{0} \mathrm{~b}$
(4) $\mathrm{qE} _{0} \mathrm{a} \cdot \mathrm{b}$
Show Answer
Correct answer: (3)
Solution:
The instantaneous force $\mathbf{F}$ on particle is $\mathbf{F}=\mathrm{q}=\mathrm{qE} _{0} \hat{\mathrm{i}}$. The instantaneous position vector $\mathbf{r}$ of particle is
$$ \mathbf{r}=a \hat{i}+b \hat{j} $$
The instantaneous torque $\tau=\mathbf{r} \times \mathbf{F}$
$$ \begin{aligned} & =(a \hat{i}+b \hat{j}) \times q E _{0} \hat{i} \\ & =-q E _{0} b(\hat{k}) \end{aligned} $$
30. In a hypothetical region of space gravitational force is
$$ \mathbf{F}=\frac{(-\mathrm{k})}{\mathrm{r}^{5 / 2}} \hat{\mathrm{r}} $$
where $k$ is a constant. In this region a planet of mass $m$ moves around another body of mass $M$. The torque of gravitational force on $m$ due to $M$; about position of $M$ is ( $r$ is position vector of $m$ with respect to $M$ )
(1) zero
(2) $\frac{\mathrm{k}}{\mathrm{r}^{3 / 2}}$
(3) $\mathrm{kr}$
(4) $\frac{\mathrm{k}}{\mathrm{r}}$
Show Answer
Correct answer: (1)
Solution:
Since the gravitational force is still a radial force i.e. is directed along the line joining $\mathrm{m}$ and $\mathrm{M}$; torque of gravitational force on $\mathrm{m}$ due to $\mathrm{M}$, about position of $\mathrm{M}$, is zero. The perpendicular distance of line of action of $\mathbf{F}$ from position of $M$ is zero.
31. A particle is moving in $x-y$ plane. The instantaneous position co-ordinates of particle are (a, b). There are two forces $F _{1}=2 F _{0} \hat{i} ; F _{2}=F _{0} \hat{j}$ acting on the particle. The torque of forces on particle about origin of co-ordinates is
(1) $\left(2 \mathrm{~F} _{0} \mathrm{a}\right) \hat{\mathrm{i}}$
(2) $\left(\mathrm{F} _{0} \mathrm{~b}\right) \hat{\mathrm{j}}$
(3) $\left[\mathrm{F} _{0}(\mathrm{a}-2 \mathrm{~b})\right] \hat{\mathrm{k}}$
(4) $\left[\mathrm{F} _{0}(2 \mathrm{a}+\mathrm{b})\right] \hat{\mathrm{k}}$
Show Answer
Correct answer: (3)
Solution:
$\mathbf{r}=$ The instantaneous position vector of particle $=a \hat{i}+b \hat{j}$
The instantaneous torque of forces on particle about origin of co-ordinates is
$$ \begin{aligned} \tau=\mathbf{r} & \times\left(\mathbf{F} _{1}+\mathbf{F} _{2}\right) \\ & =(\mathrm{a} \hat{\mathrm{i}}+\mathrm{b} \hat{\mathrm{j}}) \times\left[2 \mathrm{~F} _{0} \hat{\mathrm{i}}+\mathrm{F} _{0} \hat{\mathrm{j}}\right] \\ & =2 \mathrm{~F} _{0} \mathrm{~b}(\hat{\mathrm{j}} \times \hat{\mathrm{i}})+\mathrm{F} _{0} \mathrm{a}(\hat{\mathrm{i}} \times \hat{\mathrm{j}}) \\ & =\left[\mathrm{F} _{0}(\mathrm{a}-2 \mathrm{~b})\right] \hat{\mathrm{k}} \end{aligned} $$
32. A force $\mathbf{F} _{1}=0.5 \hat{j}$ newton acts at a point having position co-ordinate $\mathbf{r} _{1}=3 \hat{i}$ meter. Another force $\mathbf{F} _{2}=-0.6 \hat{i}$ acts at a point having position vector $\mathbf{r} _{2}=4 \hat{j}$ meter. The net torque of the two forces about origin of co-ordinates is
(1) zero
(2) $0.9 \mathrm{Nm} ; \hat{\mathrm{k}}$
(3) $3.9 \mathrm{Nm}, \hat{k}$
(4) $-3.9 \mathrm{Nm} ; \hat{\mathrm{k}}$
Show Answer
Correct answer: (3)
Solution:
$\tau _{1}=$ Torque of force $\mathbf{F} _{1}=\mathbf{r} _{1} \times \mathbf{F} _{1}=3 \hat{\mathrm{i}} \times 0.5 \hat{\mathrm{j}}=1.5 \hat{\mathrm{k}}=1.5 \hat{\mathrm{k}} ; \mathrm{N}-\mathrm{m}$
$\tau _{2}=$ Torque of force $\mathbf{F} _{2}=\mathbf{r} _{2} \times \mathbf{F} _{2}=4 \hat{\mathrm{j}} \times(-0.6 \hat{\mathrm{i}})$
$$ =-2.4 \hat{\mathrm{j}} \times \hat{\mathrm{i}}=2.4 \hat{\mathrm{k}} ; \mathrm{N}-\mathrm{m} $$
Then net torque $\tau$ is
$\tau=\tau _{1}+\tau _{2}=3.9 \mathrm{~N}-\mathrm{m} ; \hat{\mathrm{k}}$
33. A thin rod $O A$ of length $L$ has a linear mass density that increases on moving from $O$ towards $A$. The rod is free to rotate about on axis perpendicular to $O A$ passing through either end $O$ or $A$. A constant force $F$ is applied at the free end of rod perpendicular to its length. Which of the following quantities does not depend on whether rod rotates about axis through end $O$ or $A$ is
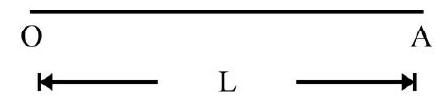
(1) external applied torque
(2) angular acceleration
(3) moment of inertia
(4) angular momentum at the end of $1 \mathrm{~s}$.
Show Answer
Correct answer:(1)
Solution:
The magnitude of the external applied torque $=\mathrm{F} \times \mathrm{L}$
whether rod is rotating about axis through end $\mathrm{O}$ or $\mathrm{A}$.
The M.I of rod about axis through end $\mathrm{O}$ and $\mathrm{A}$ is not same. $\mathrm{I} _{\mathrm{O}}>\mathrm{I} _{\mathrm{A}}$. This is due to variation of $\mathrm{I}$ with distribution of mass. Therefore angular speed or angular acceleration will be different when axis passes through end $\mathrm{O}$ or $\mathrm{A}$
34. A uniform rod $P Q$ has mass $M$; length $L$. In Fig. $23 \mathrm{X}-\mathrm{Y}$ plane is vertical. The rod is pivoted at point $O$. The rod is at rest in a vertical position. It is given a flick and let go. The torque due to weight of rod about point $O$ is
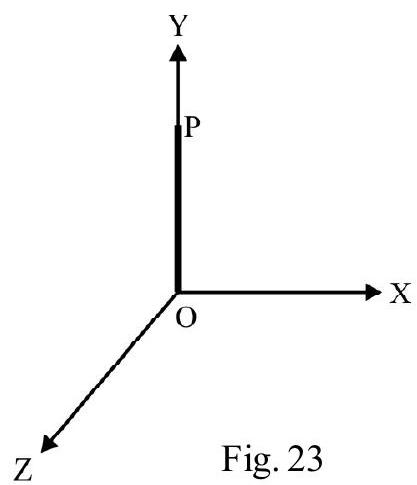
(1) zero
(2) a uniform torque
(3) a non-uniform torque of constant magnitude
(4) a non-uniform torque of constant direction
Show Answer
Correct answer: (4)
Solution:
Due to flick imparted to rod the rod rotates in a vertical plane (X-Y plane) about axis through end O. Let $\theta$ be the instantaneous angle rod makes with vertical as shown in Fig. 24. Then
$\mathbf{w}=$ The weight of rod $=-(\mathrm{mg}) \hat{\mathrm{j}}$
$\mathbf{r}=$ The instantaneous position vector of C.G.
$$ =\left(\frac{L}{2} \sin \theta\right) \hat{\mathrm{i}}+\left(\frac{\mathrm{L}}{2} \cos \theta\right) \hat{\mathrm{j}} $$
The instantaneous torque about $\mathrm{O}$ due to weight of rod is
$$ \begin{aligned} & \tau=\mathbf{r} \times \mathbf{F} \\ & =\left[\left(\frac{L}{2} \sin \theta\right) \hat{i}+\left(\frac{L}{2} \cos \theta\right) \hat{j}\right] \times(-m g) \hat{j} \\ & =-\left(\frac{m g L}{2} \sin \theta\right) \hat{k} \end{aligned} $$
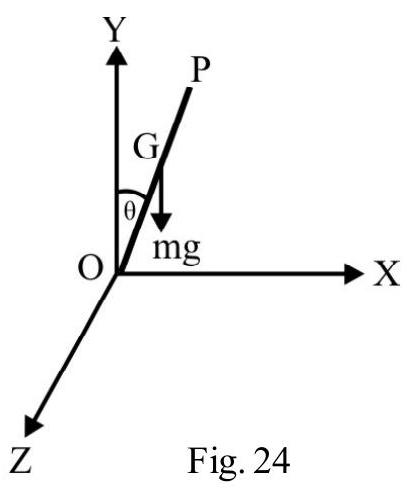
Fig. 24
The magnitude of torque changes with time $t$ because $\theta$ varies with time. However direction of $\tau$ is same at all times.
35. A cylinder of mass $M$ is placed on a smooth inclined plane of inclination $\theta$ as shown in Fig. 25. A massless rope is passing around cylinder. One end of rope is fixed as shown. The other end of rope is pulled upwards with a force $F$ with rope kept vertical. The cylinder is in equilibrium if
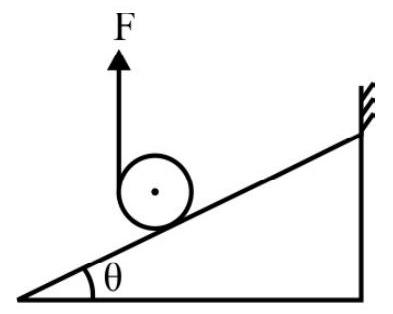
Fig. 25
(1) $\mathrm{F}=\mathrm{Mg} \sin \theta$
(2) $\mathrm{F}=\mathrm{Mg} \cos \theta$
(3) $\mathrm{F}=\frac{\mathrm{Mg} \sin \theta}{(1+\sin \theta)}$
(4) $\mathrm{F}=\frac{\mathrm{Mg} \cos \theta}{(1+\sin \theta)}$
Show Answer
Correct answer: (3)
Solution:
The forces acting on cylinder are shown in Fig. 26. Taking moment of forces about point A at equilibrium.
$\operatorname{Mg}(\mathrm{AB})=\mathrm{F} . \mathrm{CD}$
$$ =\mathrm{F}(\mathrm{CO}+\mathrm{OD}) $$
or $\quad \operatorname{Mgr} \sin \theta=\mathrm{F}(\mathrm{r}+\mathrm{r} \sin \theta)$
where $\mathrm{OA}=\mathbf{r}=$ The radius of cylinder. Therefore
$$ F=\frac{M g \sin \theta}{(1+\sin \theta)} $$
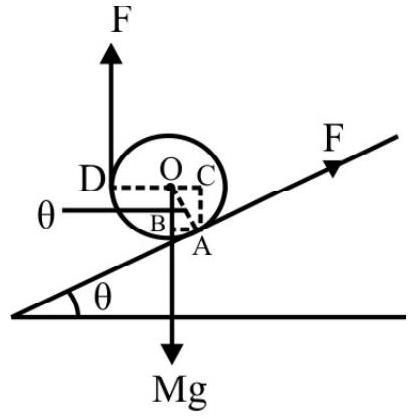
Fig. 26
36. A uniform ring of mass $M$ radius $R$ has two identical beads $P$ and $Q$ each of mass $m$; free to move along it. Initially beads are in position $P$ and $Q$. The M.I of “ring-bead” system about axis through center $O$ and perpendicular to plane of ring is $I$. The beads are moved to position $P^{\prime}$ and $Q$ ’ as shown in Fig. 27. The M.I of system is now I’. Then
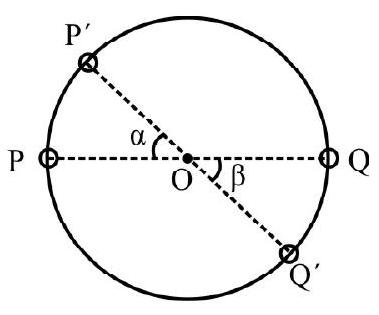
(1) $\mathrm{I}=\mathrm{MR}^{2} ; \mathrm{I}=\mathrm{I}^{\prime}$
(2) $I=(M+m) R^{2} ; I \neq I^{\prime}$
(3) $I=(M+2 m) R^{2} ; I \neq I^{\prime}$
(4) $I=(M+2 m) R^{2} ; I=I^{\prime}$
Show Answer
Correct answer: (4)
Solution:
$I=$ M.I of “ring bead system” about given axis $=I _{\text {ring }}+I _{P}+I _{Q}$
$$ \begin{aligned} & =\mathrm{MR}^{2}+\mathrm{mR}^{2}+\mathrm{mR}^{2} \\ & =(\mathrm{M}+2 \mathrm{~m}) \mathrm{R}^{2} \end{aligned} $$
When beads move to position $\mathrm{P}^{\prime}$ and $\mathrm{Q}^{\prime}$ their perpendicular distance from axis of rotation remain same. Hence I’ $=$ I
37. Fig. 28 shows a uniform ring of mass $2 \mathrm{~m}$; radius $R$. $P$ and $Q$ are two identical beads each of mass $\mathrm{m}$. The ring-bead system is rotating about $X^{\prime} X^{\prime}$ as axis. The beads are moved to position $P^{\prime}$ and $Q^{\prime}$ as shown in Fig. 28. The change in moment of inertia of the system is
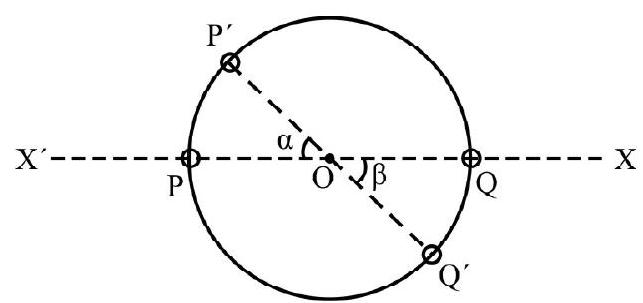
Fig. 28
(1) zero
(2) $\mathrm{mR}^{2}\left[\sin ^{2} \alpha+\sin ^{2} \beta\right]$
(3) $\mathrm{mR}^{2}\left[\cos ^{2} \alpha+\cos ^{2} \beta\right]$
(4) $\mathrm{mR}^{2}\left[\sin ^{2} \alpha+\cos ^{2} \beta\right]$
Show Answer
Correct answer: (2)
Solution:
$\mathrm{I}=$ The initial M.I of ring-bead system
$$ =\mathrm{I} _{\mathrm{ring}}+\mathrm{I} _{\mathrm{P}}+\mathrm{I} _{\mathrm{Q}}=\frac{1}{2}(2 \mathrm{~m}) \mathrm{R}^{2}=\mathrm{mR}^{2} $$
$I _{P}$ and $I _{Q}$ is zero because beads are lying on the axis of rotation. Their perpendicular distance from axis of rotation is zero.
$I^{\prime}=$ The final M.I of ring bead system
$$ \begin{aligned} & =\frac{1}{2}(2 m) R^{2}+m(R \sin \alpha)^{2}+m(R \sin \beta)^{2} \\ & =m R^{2}+m R^{2}\left(\sin ^{2} \alpha+\sin ^{2} \beta\right) \end{aligned} $$
$\therefore \Delta \mathrm{I}=$ The change in M.I of the system
$$ =I^{\prime}-I=m R^{2}\left(\sin ^{2} \alpha+\sin ^{2} \beta\right) $$
38. A uniform wire of length $2 \mathrm{~L}$, mass per unit length $\lambda$ is bent into a circular loop of 2 turns.
The M.I of the loop about any tangent in its own plane is
(1) $\frac{3 \lambda L^{3}}{4 \pi^{2}}$
(2) $\frac{\lambda L^{3}}{\pi^{2}}$
(3) $\frac{2 \lambda L^{3}}{\pi^{2}}$
(4) $\frac{\lambda L^{2}}{2 \pi^{2}}$
Show Answer
Correct answer: (1)
Solution:
$\mathrm{M}=$ Total mass of circular loop $=$ Mass of wire $=2 \lambda \mathrm{L}$
Let $r$ be radius of each turn of circular loop formed. Then
$$ 2(2 \pi r)=2 L \quad \text { or } \quad r=\frac{L}{2 \pi} $$
The M.I of one turn about any tangent in its own plane.
$$ \begin{aligned} & =\frac{1}{2}\left(\frac{\mathrm{M}}{2}\right) \mathrm{r}^{2}+\left(\frac{\mathrm{M}}{2}\right) \mathrm{r}^{2} \\ & =\frac{3 \mathrm{Mr}^{2}}{4}=\frac{3 \mathrm{M}}{4}\left(\frac{\mathrm{L}}{2 \pi}\right)^{2}=\frac{3 \mathrm{ML}^{2}}{16 \pi^{2}} \end{aligned} $$
$I=$ The total M.I of the two turn loop
$$ =2\left[\frac{3 \mathrm{ML}^{2}}{16 \pi^{2}}\right]=\frac{3(2 \mathrm{~L} \lambda) \mathrm{L}^{2}}{8 \pi^{2}}=\frac{3 \lambda \mathrm{L}^{3}}{4 \pi^{2}} $$
39. Three thin rods each of mass $m$; length $\ell$ are joined to form a hollow equilateral triangle ABC. The M.I of the system about an axis through centroid $O$ of triangle and perpendicular to its plane is same as M.I of ring of mass $M$ radius $\ell$ about axis through its center and perpendicular to the plane of ring. Then
(1) $M=3 \mathrm{~m}$
(2) $\mathrm{M}=\frac{3}{2} \mathrm{~m}$
(3) $\mathrm{M}=\mathrm{m}$
(4) $\mathrm{M}=\frac{\mathrm{m}}{2}$
Show Answer
Correct answer: (4)
Solution:
In Fig. $29 \mathrm{AB}, \mathrm{BC}$ and $\mathrm{AC}$ are the three rods. $\mathrm{O}$ is centroid of the triangle.
$x=\mathrm{OD}=\mathrm{OE}=\mathrm{OF}$
$=$ Perpendicular distance of each rod from axis of rotation.
From right angled triangle OAD
$\frac{x}{(\ell / 2)}=\tan 30^{\circ} \quad \therefore \quad x=\frac{\ell}{2 \sqrt{3}}$
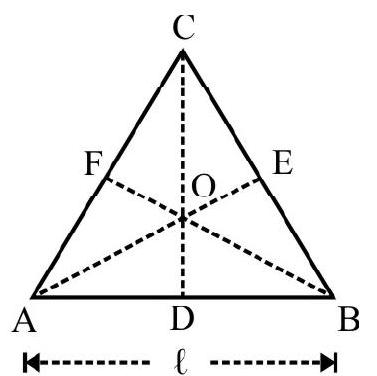
Fig. 29
Let $\mathrm{I} _{1}$ be M.I of any rod about axis through $\mathrm{O}$ and perpendicular to plane of triangle. Using theorem of parallel axis.
$\mathrm{I} _{1}=\frac{\mathrm{m} \ell^{2}}{12}+\mathrm{m}(x)^{2}=\frac{\mathrm{m} \ell^{2}}{12}+\mathrm{m}\left(\frac{\ell}{2 \sqrt{3}}\right)^{2}=\frac{\mathrm{m} \ell^{2}}{6}$
$\therefore \mathrm{I}=$ The total M.I of the system $=3 \mathrm{I} _{1}=\frac{\mathrm{m} \ell^{2}}{2}$
Given $\mathrm{I}=\mathrm{M} \ell^{2}$. Therefore,
$$ \mathrm{M}=\frac{\mathrm{m}}{2} $$
40. A thin non-uniform rod $O A$ of length $L$ is placed along $X$-axis with one end $O$ at origin of coordinates. The linear mass density $\lambda$ at a point distance $x$ from $O$ is
$$ \lambda=\lambda _{0} x $$
$\lambda _{0}$ is a constant. The M.I of rod about an axis through its center of mass and perpendicular to it length is:
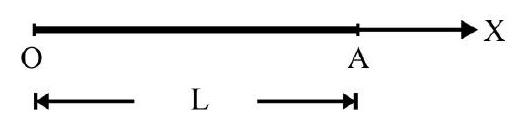
Fig. 30
(1) $\frac{\mathrm{ML}^{2}}{9}$
(2) $\frac{2 \mathrm{ML}^{2}}{9}$
(3) $\frac{4 \mathrm{ML}^{2}}{9}$
(4) $\frac{\mathrm{ML}^{2}}{18}$
Show Answer
Correct answer: (4)
Solution:
Let $\mathrm{M}$ be the total mass of rod. Then
$$ \begin{equation*} \mathrm{M}=\int _{0}^{\mathrm{L}} \lambda \mathrm{d} x=\lambda _{0} \int _{0}^{\mathrm{L}} x \mathrm{~d} x=\frac{\lambda _{0} \mathrm{~L}^{2}}{2} \tag{i} \end{equation*} $$
Let $x$ be the position co-ordinate of C.M, C of rod. Then
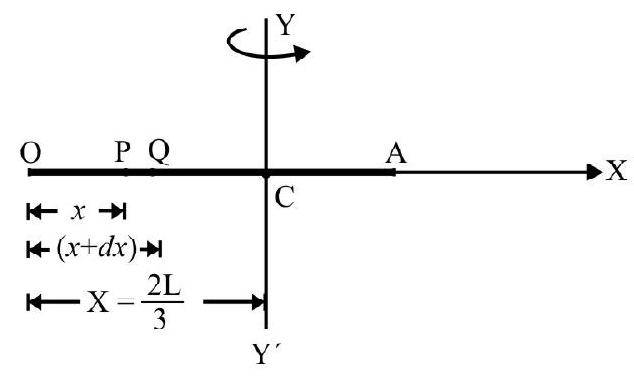
$\mathrm{X}=\frac{\int _{0}^{\mathrm{L}} x \mathrm{dm}}{\int _{0}^{\mathrm{L}} \mathrm{dm}}=\frac{\lambda _{0} \int _{0}^{\mathrm{L}} x^{2} \mathrm{~d} x}{\lambda _{0} \int _{0}^{\mathrm{L}} x \mathrm{~d} x}=\frac{2}{3} \mathrm{~L}$
YOY’ is axis through C.M perpendicular to length of rod. PQ is an elementary mass, dm, as shown in Fig. 31 $\mathrm{dI}=(\mathrm{dm})[\mathrm{X}-x]^{2}=\lambda _{0}\left[\frac{2 \mathrm{~L}}{3}-x\right]^{2} x \mathrm{~d} x$
$\therefore \quad \mathrm{I}=\lambda _{0} \int _{0}^{\mathrm{L}}\left(\frac{2 \mathrm{~L}}{3}-x\right)^{2} x \mathrm{~d} x=\frac{\lambda _{0} \mathrm{~L}^{4}}{36}=\frac{\mathrm{ML}^{2}}{18}$
41. A uniform thin rod has mass $M$ length L. $I$ is M.I of rod about an axis through its midpoint making angle $\theta$ with the rod. I vs $\theta$ graph is

Show Answer
Correct answer: (3)
Solution:
$I=$ M.I of rod about given axis is
$$ =\frac{\mathrm{ML}^{2}}{12} \sin ^{2} \theta $$
I is $\theta$ graph is as shown in (3)
42. PQRS is a square lamina of side a. The M.I of lamina about $\mathrm{XOX}^{\prime}$ as axis is I. The M.I about line $C D$ as axis is
(1) I
(2) $I \cos \theta$
(3) I $\sin \theta$
(4) I $\sin \theta \cos \theta$
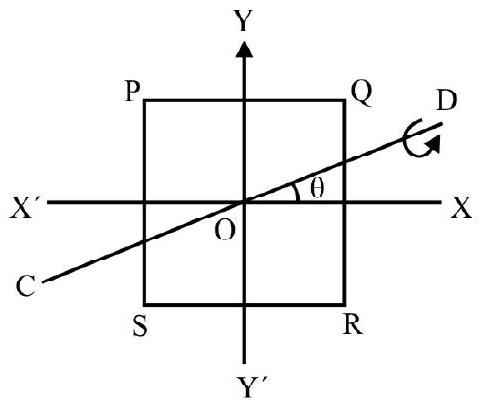
Fig. 32
Show Answer
Correct answer: (1)
Solution:
Choose $\mathrm{X}^{\prime}$ and $\mathrm{Y}^{\prime}$ as shown in Fig. 33. Consider an elementary mass $\delta \mathrm{m}$ at $\mathrm{pt} \mathrm{P}$. Let co-ordinates of $\mathrm{P}$ be $(x, \mathrm{y})$ in $\mathrm{X}-\mathrm{Y}$ axis and be $\left(x^{\prime}, \mathrm{y}^{\prime}\right)$ in $\mathrm{X}^{\prime}-\mathrm{Y}^{\prime}$ axis. Obviously $\mathrm{OA}=x, \mathrm{OB}=\mathrm{y}, \mathrm{OA}^{\prime}=x^{\prime} ; \mathrm{OB}^{\prime}=\mathrm{y}^{\prime}$.
From Fig. 33 we have
$\mathrm{OA}=\mathrm{OA} _{1}-\mathrm{A} _{2} \mathrm{~A}^{\prime}$ $=\mathrm{OA}^{\prime} \cos \theta-\mathrm{PA}^{\prime} \sin \theta$
or $\quad x=x^{\prime} \cos \theta-y^{\prime} \sin \theta$
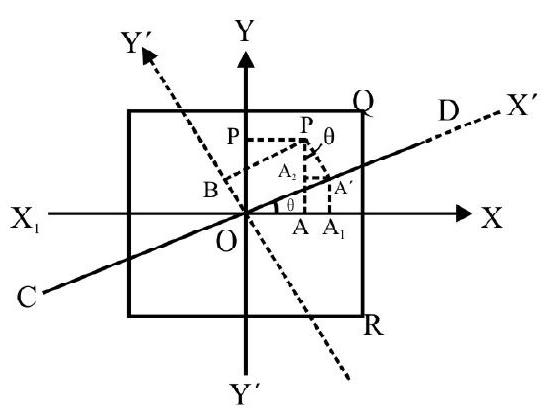
Fig. 33
Similarly $\mathrm{y}=x^{\prime} \sin \theta+\mathrm{y}^{\prime} \cos \theta$
By definition,
$\mathrm{I}=$ M.I about $\mathrm{COX}^{\prime}$ as axis $=\sum(\delta \mathrm{m}) \mathrm{y}^{2}$
$$ \begin{align*} & =\sum \delta \mathrm{m}\left(x^{\prime} \sin \theta+y^{\prime} \cos \theta\right)^{2} \\ & =\sum\left(\delta m x^{\prime 2}\right) \sin ^{2} \theta+\sum\left(\delta m y^{\prime 2}\right) \cos ^{2} \theta+2 \sum \delta m x^{\prime} \cdot y^{\prime} \sin \theta \cos \theta \tag{i} \end{align*} $$
By definition,
$$ \mathrm{I}^{\prime}=\sum \delta \mathrm{m}\left(x^{\prime}\right)^{2} ; \mathrm{I}^{\prime \prime}=\sum \delta \mathrm{m}\left(\mathrm{y}^{\prime}\right)^{2} $$
and I’ equals II" as the square is completely symmetrical about any two mutually perpendicular lines through center $\mathrm{O}$.
Also $\sum \delta \mathrm{m}\left(x^{\prime} \cdot \mathrm{y}^{\prime}\right)=0$. The body balances about its center of gravity $\mathrm{O}$. Therefore
$$ \sum(\delta m) g \cdot y^{\prime}=0 $$
We can rewrite Eqn. (i) as
$$ \mathrm{I}=\mathrm{I}^{\prime}\left(\sin ^{2} \theta+\cos ^{2} \theta\right)=\mathrm{I}^{\prime} $$
43. A uniform sphere of mass $M$; radius $R$ has a moment of inertia, $I$; about its symmetry axis. The sphere is reshaped into a uniform circular disc. The M.I of disc about a tangent perpendicular to plane of disc is $\frac{3}{5} \mathrm{I}$. The radius of disc is
(1) $\frac{R}{2}$
(2) $\frac{3 R}{5}$
(3) $\frac{2 R}{3}$
(4) $\frac{3 R}{2}$
Show Answer
Correct answer: (3)
Solution:
The symmetry axis of sphere is any diameter of sphere. Therefore
$$ \begin{equation*} \mathrm{I}=\frac{2}{5} \mathrm{MR}^{2} \tag{i} \end{equation*} $$
Let $\mathrm{r}$ be radius of disc into which sphere is reshaped. Mass of disc is same as that of sphere i.e. M. The M.I, I; of disc about given axis is
$$ \begin{equation*} \mathrm{I}^{\prime}=\frac{\mathrm{Mr}^{2}}{2}+\mathrm{Mr}^{2}=\frac{3}{2} \mathrm{Mr}^{2} \tag{ii} \end{equation*} $$
Given I’ $=\frac{3}{5}$ I. Therefore
$$ \frac{3}{5}\left(\frac{3}{2} \mathrm{Mr}^{2}\right)=\frac{2}{5} \mathrm{MR}^{2} $$
or
$$ \mathrm{r}=\frac{2}{3} \mathrm{R} $$
44. A uniform wooden cylinder has mass $M$; radius $R$, length $L=\sqrt{3} R$. I is M.I of cylinder about an axis through its midpoint and perpendicular to its length. The cylinder is shaved reducing its radius till its mass becomes $50 \%$ of its earlier value. $I^{\prime}$ is moment of inertia of cylinder now about same axis as before. The fractional change in M.I of cylinder is
(1) -1
(2) -0.5
(3) $-5 / 8$
(4) $-5 / 16$
Show Answer
Correct answer: (3)
Solution:
$I=$ M.I of calender about an axis through its midpoint and perpendicular to the length of cylinder.
$$ =\mathrm{M}\left(\frac{\mathrm{R}^{2}}{4}+\frac{\mathrm{L}^{2}}{12}\right)^{*}=\mathrm{M}\left[\frac{\mathrm{R}^{2}}{4}+\frac{(\sqrt{3} \mathrm{R})^{2}}{12}\right]=\frac{\mathrm{MR}^{2}}{2} $$
Let $\mathrm{r}$ be radius of shaved cylinder. Then
mass of shaved cylinder $=\frac{1}{2}$ mass of given cylinder
$\pi \mathrm{r}^{2} \mathrm{~L} \rho=\frac{1}{2}\left[\pi \mathrm{R}^{2} \mathrm{~L} \rho\right] \quad \therefore \mathrm{r}^{2}=\frac{\mathrm{R}^{2}}{2}$
I’ $=$ M.I of “shaved” cylinder about given axis.
$$ =\frac{\mathrm{M}}{2}\left[\frac{\mathrm{r}^{2}}{4}+\frac{\mathrm{L}^{2}}{12}\right]=\frac{\mathrm{M}}{2}\left[\frac{\mathrm{R}^{2}}{8}+\frac{(\sqrt{3} \mathrm{R})^{2}}{12}\right]=\frac{3}{16} \mathrm{MR}^{2} $$
$\Delta \mathrm{I}=$ Change in $\mathrm{M} . \mathrm{I}=\mathrm{I}^{\prime}-\mathrm{I}=-\left(\frac{5}{16}\right) \mathrm{MR}^{2}$
$\frac{\Delta \mathrm{I}}{\mathrm{I}}=$ Fractional change in M.I $=-\left(\frac{5}{8}\right)$
45. A uniform lamina of surface mass density $\sigma$ is cut into shape shown in Fig. 34. The M.I of the lamina about an axis through center $O$ and perpendicular to plane of lamina is
(1) $\frac{3 \pi \mathrm{R}^{4} \sigma}{8}$
(2) $\frac{5 \pi \mathrm{R}^{4} \sigma}{4}$
(3) $\frac{19 \pi \mathrm{R}^{4} \sigma}{8}$
(4) $\frac{19 \pi \mathrm{R}^{4} \sigma}{16}$
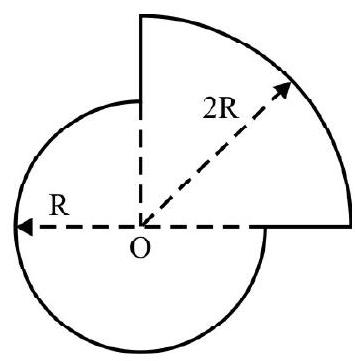
Fig. 34
Show Answer
Correct answer: (3)
Solution:
Let $I _{1}$ be moment of inertia, of the part of radius $R$ about given axis;. Then
$$ \mathrm{I} _{1}=\frac{3}{4}\left(\pi \mathrm{R}^{2} \sigma\right)\left(\frac{\mathrm{R}^{2}}{2}\right)=\frac{3 \pi \mathrm{R}^{4} \sigma}{8} $$
Let $\mathrm{I} _{2}$ be the moment of inertia of the part of radius $2 \mathrm{R}$ about given axis. Then
$$ \mathrm{I} _{2}=\frac{1}{4}\left[\pi(2 \mathrm{R})^{2} \sigma\right]\left(\frac{2 \mathrm{R}^{2}}{2}\right)=2 \pi \mathrm{R}^{4} \sigma $$
$\mathrm{I}=$ M.I of the given lamina; about given axis
$$ =\mathrm{I} _{1}+\mathrm{I} _{2}=\left(\frac{3}{8}+2\right) \pi \mathrm{R}^{4} \sigma=\frac{19 \pi \mathrm{R}^{4} \sigma}{8} $$
46. A uniform wire of mass per unit length $\lambda$ is used to make a wheel consisting of a rim of radius $R$ and 12 spokes joined together. The M.I of wheel about its symmetry axis is I.The same straight wire of length $L$ has M.I; about an axis through its mid-point and perpendicular to its length; as I. Then $\frac{\mathrm{L}}{\mathrm{R}}$ is
(1) $(\pi+2)^{1 / 3}$
(2) $(2 \pi+4)^{1 / 3}$
(3) $2(3 \pi+2)^{1 / 3}$
(4) $\frac{(3 \pi+2)^{1 / 3}}{2}$
Show Answer
Correct answer: (3)
Solution:
Fig. 35 shows the wheel. The mass of rim $=\mathrm{M} _{1}=2 \pi \mathrm{R} \lambda$. Mass of each spoke $=\mathrm{M} _{2}=\mathrm{R} \lambda$. The symmetry axis is axis through center $\mathrm{O}$ and perpendicular to plane of wheel. The M.I., about symmetry axis.
$$ \begin{align*} I= & M _{1} R^{2}+12\left(\frac{1}{3} M _{2} R^{2}\right) \\ = & \lambda R^{3}\left[2 \pi+\frac{4}{3}\right] \tag{i} \end{align*} $$
The M.I of the rod of length L; about given axis.
$$ \begin{equation*} \mathrm{I}=\frac{1}{12}(\lambda \mathrm{L}) \mathrm{L}^{2}=\frac{\lambda \mathrm{L}^{3}}{12} \tag{ii} \end{equation*} $$
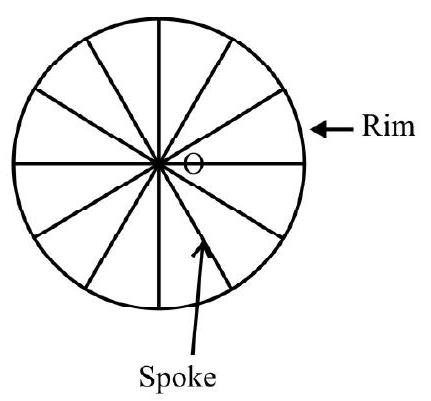
Fig. 35
From Eqn. (i) and (ii) we have
$\lambda \mathrm{R}^{3}\left(\frac{6 \pi+4}{3}\right)=\frac{\lambda \mathrm{L}^{3}}{12}$
$\therefore \frac{\mathrm{L}}{\mathrm{R}}=[4(6 \pi+4)]^{1 / 3}=2[3 \pi+2]^{1 / 3}$
47. A uniform disc of mass $\mathrm{M}$ radius $\mathrm{R}$ has moment of inertia $\mathrm{I}$ about diameter $\mathrm{XOX}^{\prime}$ as axis. 1,2 and 3 are chords passing through same point $P$ on the disc. $I _{1}, I _{2}, I _{3}$ is M.I of disc about 1,2 and 3 as axis. Then
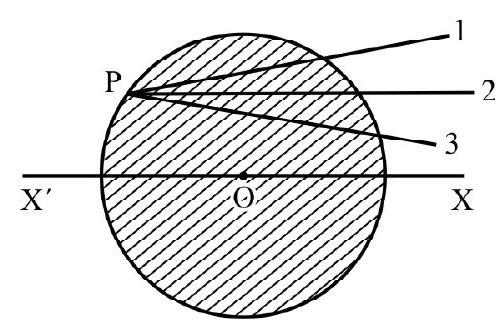
Fig. 36
(1) $I_1=I_2=I_3$
(2) $I_1 \neq I_2 \neq I_3$
(3) I $_1<$ I $_2>$ I $_2$
(4) I $ _{3}<$ I $ _{2}>$ I $ _{1}$
Show Answer
Correct answer: (4)
Solution:
Let $\mathrm{h}$ be perpendicular distance of point $\mathrm{P}$ from $\mathrm{XOX}^{\prime}$. Consider diameter $\mathrm{X} _{1} \mathrm{OX} _{1}^{\prime}$ parallel to chord $\mathrm{P} 1$. The perpendicular distance of $\mathrm{P} 1$ from $\mathrm{X} _{1} \mathrm{OX} _{1}^{\prime}$ is $\mathrm{h}^{\prime}$. Therefore
$$ \mathrm{I} _{1}=\frac{1}{2} \mathrm{MR}^{2}+\mathrm{M}\left(\mathrm{h}^{\prime}\right)^{2} $$
Similarly,
$$ \mathrm{I} _{2}=\frac{\mathrm{MR}^{2}}{2}+\mathrm{Mh}^{2} $$
and $I _{3}=\frac{\mathrm{MR}^{2}}{2}+\mathrm{M}\left(\mathrm{h}^{\prime \prime}\right)^{2}$
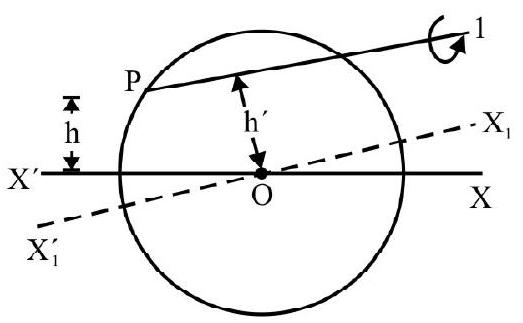
Fig. 37
Since $\mathrm{h}^{\prime}>\mathrm{h}>\mathrm{h} “$, therefore $\mathrm{I} _{1}>\mathrm{I} _{2}>\mathrm{I} _{3}$.
48. In Fig. $38 \quad \mathrm{AOB}$ and $\mathrm{COD}$ are two sectors of circles of radius $R _{1}$ and $R _{2}$ joined at $O$. The surface mass density of the two parts is $\sigma _{1}$ and $\sigma _{2}$ respectively. The M.I of the two parts about an axis through $O$ and perpendicular to their plane are equal. Then
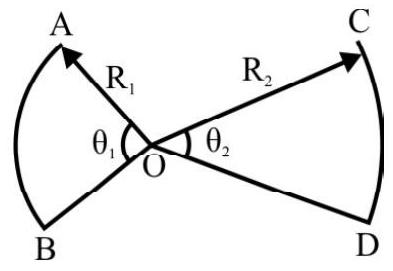
Fig. 38
(1) $\frac{\sigma _{1}}{\sigma _{2}}=\left(\frac{R _{2}}{R _{1}}\right)^{4}$
(2) $\frac{\sigma _{1}}{\sigma _{2}}=\left(\frac{\theta _{2}}{\theta _{1}}\right)\left(\frac{\mathrm{R} _{2}}{\mathrm{R} _{1}}\right)^{4}$
(3) $\frac{\sigma _{1}}{\sigma _{2}}=\left(\frac{\theta _{1}}{\theta _{2}}\right)\left(\frac{\mathrm{R} _{1}}{\mathrm{R} _{2}}\right)^{4}$
(4) $\frac{\sigma _{1}}{\sigma _{2}}=\left(\frac{R _{2} \theta _{2}}{R _{1} \theta _{1}}\right)^{2}$
Show Answer
Correct answer: (2)
Solution:
The M.I; of sector $\mathrm{OAB} ; \mathrm{I} _{1}$, is
$\mathrm{I} _{1}=\left(\frac{\theta _{1}}{2 \pi}\right)\left[\frac{\pi \mathrm{R} _{1}^{2} \sigma _{1}}{2} \mathrm{R} _{1}^{2}\right]=\left(\frac{\theta _{1}}{2 \pi}\right)\left[\frac{\pi \sigma _{1} \mathrm{R} _{1}^{4}}{2}\right]$
Similarly; the M.I of sector OCD; $\mathrm{I} _{2}$; is
$\mathrm{I} _{2}=\left(\frac{\theta _{2}}{2 \pi}\right)\left[\frac{\pi \sigma _{1} \mathrm{R} _{2}^{4}}{2}\right]$
Given $I _{1}=I _{2}$. Therefore
$$ \begin{aligned} & \left(\frac{\theta _{1}}{2 \pi}\right)\left(\frac{\pi \mathrm{R} _{1}^{4} \sigma _{1}}{2}\right)=\left(\frac{\theta _{2}}{2 \pi}\right)\left(\frac{\pi \mathrm{R} _{2}^{4} \sigma _{2}}{2}\right) \\ & \therefore \quad \frac{\sigma _{1}}{\sigma _{2}}=\left(\frac{\theta _{2}}{\theta _{1}}\right)\left(\frac{\mathrm{R} _{2}}{\mathrm{R} _{1}}\right)^{4} \end{aligned} $$
49. A uniform circular disc has radius R. A part of radius $\frac{R}{2}$ has been cutout as shown in Fig. 39. M is mass of annular disc. The M.I about an axis through $\mathrm{O} _{1}$ and perpendicular to plane of disc is
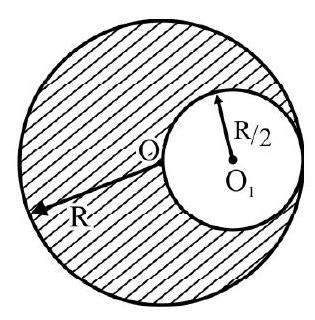
Fig. 39
(1) $\frac{23}{24} \mathrm{MR}^{2}$
(2) $\frac{7}{24} \mathrm{MR}^{2}$
(3) $\frac{23}{32} \mathrm{MR}^{2}$
(4) $\frac{23}{30} \mathrm{MR}^{2}$
Show Answer
Correct answer: (1)
Solution:
Let $\mathrm{M} _{1}$ be mass of complete disc of radius R. Its M.I; $\mathrm{I} _{1}$, about axis considered is (using theorem of parallel axis).
$I _{1}=\frac{M _{1} R^{2}}{2}+M _{1}\left(\frac{R}{2}\right)^{2}=\frac{3 M _{1} R^{2}}{4} \hspace{40mm} . . . . . .(i)$
Let $M _{2}$ be mass of part of disc cut-out. Obviously $M _{2}=\frac{M _{1}}{4}$. The M.I, $I _{2}$, of this part about given axis is
$\mathrm{I} _{2}=\frac{\mathrm{M} _{2}}{2}\left(\frac{\mathrm{R}}{2}\right)^{2}=\frac{\mathrm{M} _{1} \mathrm{R}^{2}}{32} \hspace{40mm} . . . . . .(ii)$
The M.I, I; of the annular disc;
$\mathrm{I}=\mathrm{I} _{1}-\mathrm{I} _{2}=\frac{23}{32} \mathrm{M} _{1} \mathrm{R}^{2} \hspace{40mm} . . . . . .(iii)$
The mass, $M$, of annular disc is $\left(M _{1}-\frac{M _{1}}{4}\right)=3 \frac{M _{1}}{4} \quad$ or $\quad M _{1}=\frac{4}{3} M$
Therefore,
$$ I=\frac{23}{32}\left(\frac{4}{3} M\right) R^{2}=\frac{23}{24} M R^{2} $$
50. A hemisphere of mass $M$; radius $R$ is rotating about a chord parallel to its diameter at a perpendicular distance of $\frac{3 R}{4}$ as axis. The radius of gyration about the axis of rotation is (Given center of mass of hemisphere is at a height of $\frac{3 R}{8}$ from the base).
(1) $\frac{R}{\sqrt{5}}$
(2) $\sqrt{\frac{2}{5}} \mathrm{R}$
(3) $\frac{5 R}{4}$
(4) $\frac{\mathrm{R}}{\sqrt{10}}$
Show Answer
Correct answer: (1)
Solution:
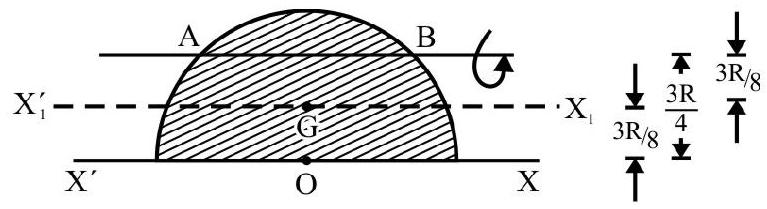
Fig. 40
Fig. 40 shows hemisphere $\mathrm{X} _{1} \mathrm{OX}^{\prime}{ } _{1}$ is a diameter. The M.I, $\mathrm{I} _{1}$ about XOX’ as axis $\frac{2}{5} \mathrm{MR}^{2}$. In Fig. 40, $\mathrm{G}$ is position of C.G. of hemisphere $\mathrm{X} _{1} \mathrm{GX}^{\prime}{ } _{1}$ is axis through C.G. parallel to diameter XOX’. Let $\mathrm{I} _{\mathrm{g}}$ be M.I about $\mathrm{X} _{1} \mathrm{GX}^{\prime}{ } _{1}$ as axis. From theorem of parallel axis.
$$ \begin{align*} \mathrm{I} _{1} & =\mathrm{I} _{\mathrm{g}}+\mathrm{M}\left(\frac{3 \mathrm{R}}{8}\right)^{2} \\ \text { or } \quad \mathrm{I} _{\mathrm{g}} & =\left(\frac{2}{5}-\frac{9}{64}\right) \mathrm{MR}^{2}=\frac{83}{320} \mathrm{MR}^{2} \tag{i} \end{align*} $$
In Fig. $40 \mathrm{AB}$ is the desired axis about which radius of gyration, $\mathrm{k}$ is to be calculated. Let $\mathrm{I} _{2}$ be M.I about $\mathrm{AB}$ as axis. From Theorem of parallel axes
$$ \begin{aligned} I _{2}= & I g+M\left(\frac{3 R}{4}-\frac{3 R}{8}\right)^{2} \\ & =\left(\frac{83}{320}+\frac{9}{64}\right) MR^{2}=\frac{2}{5} M R^{2} \end{aligned} $$
Also $\mathrm{I} _{2}=\mathrm{Mk}^{2}$. Therefore,
$$ \mathrm{k}=\sqrt{\frac{2}{5}} \mathrm{R} $$
51. A uniform cylinder lies on a horizontal surface and is free to rotate about its own axis. It is imparted an impulse by applying a force $\mathrm{F}$ as shown in Fig. 41. The cylinder begins to roll without slipping after the impulse has been imparted. $M, R$, and $L$ denote mass, radius and length of cylinder. Then
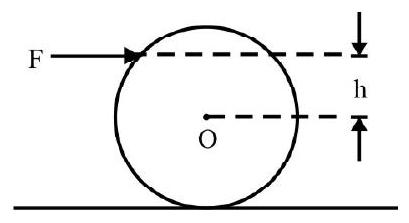
Fig. 41
(1) $\mathrm{h}=\frac{\mathrm{R}}{2}$
(2) $\mathrm{h}=\mathrm{R}$
(3) $\mathrm{h}=\frac{\mathrm{L}}{\mathrm{R}}$
(4) $\mathrm{h}=\frac{\mathrm{R}}{4}$
Show Answer
Correct answer: (1)
Solution:
Let $\mathrm{I} _{\mathrm{m}}$ and $\mathrm{J}$ denote the linear and angular impulse imparted to cylinder. By definition.
$$ \begin{equation*} I _{m}=\int F \cdot d t \tag{i} \end{equation*} $$
$$ \begin{equation*} \mathrm{J}=\int \tau . \mathrm{dt}=\int(\mathrm{F} \cdot \mathrm{h}) \mathrm{dt} \tag{ii} \end{equation*} $$
From Eqns (i) and (ii) we have,
$$ \begin{equation*} \mathrm{J}=\left(\mathrm{I} _{\mathrm{m}}\right) \times \mathrm{h} \tag{iii} \end{equation*} $$
Let $v$ be the velocity of center of mass and $\omega$ the angular speed of cylinder, just after impulse has been imparted. Obviously
$\mathrm{I} _{\mathrm{m}}=$ Change in linear momentum
$$ \begin{equation*} =(\mathrm{MV}-0)=\mathrm{MV} \tag{iv} \end{equation*} $$
$\mathrm{J}=$ Change in angular momentum $=\mathrm{I} \omega-0$
$$ \begin{equation*} =\frac{1}{2} \mathrm{MR}^{2} \omega \tag{v} \end{equation*} $$
From Eqn. (iii), (iv) and (v); we have
$$ \frac{1}{2} \mathrm{MR}^{2} \omega=\mathrm{MVh} $$
Also $\mathrm{V}=\mathrm{R} \omega$; there is no slipping. Therefore
$$ \mathrm{h}=\frac{\mathrm{R}}{2} $$
52. A uniform disc of mass $M$, radius $R$ is rotating in a horizontal plane about its own axis with a constant angular speed $\omega _{0}$. A ring of mass $\frac{M}{2}$; radius $\frac{R}{2}$ is initially at rest. The ring is gently placed concentrically on rotating platform. The system starts rotating with constant angular speed $\omega$. The loss in rotational K.E. is
(1) zero
(2) $\frac{\mathrm{MR}^{2} \omega _{0}^{2}}{20}$
(3) $\frac{\mathrm{MR}^{2} \omega _{0}^{2}}{5}$
(4) $\frac{\mathrm{MR}^{2} \omega _{0}^{2}}{4}$
Show Answer
Correct answer: (2)
Solution:
Let $\mathrm{I} _{1} ; \mathrm{J} _{1}$ and $\mathrm{K} _{1}$ denote the moment of inertia; angular momentum and rotational K.E. of rotating disc. Then
$$ \mathrm{I} _{1}=\frac{1}{2} \mathrm{MR}^{2} ; \quad \mathrm{J} _{1}=\mathrm{I} _{1} \omega _{1}=\frac{\mathrm{MR}^{2} \omega _{0}}{2} \text { and } \mathrm{K} _{1}=\frac{\mathrm{J} _{1}^{2}}{2 \mathrm{I} _{1}} $$
The ring has been placed on rotating disc and the system has acquire a steady state angular speed $\omega$. Let $\mathrm{I} _{2} ; \mathrm{J} _{2}$ and $\mathrm{K} _{2}$ be the corresponding quantities for the system. Then
$\mathrm{I} _{2}=\frac{1}{2} \mathrm{MR}^{2}+\left(\frac{\mathrm{M}}{2}\right)\left(\frac{\mathrm{R}}{2}\right)^{2}=\frac{5 \mathrm{MR}^{2}}{8}$
$$ \mathrm{J} _{2}=\mathrm{I} _{2} \omega=\mathrm{J} _{1} \quad \text { (Law of conservation of angular momentum) } $$
and $\quad \mathrm{K} _{2}=\frac{\mathrm{J} _{2}^{2}}{2 \mathrm{I} _{2}}=\frac{\mathrm{J} _{1}^{2}}{2 \mathrm{I} _{2}} \quad\left[\because \mathrm{J} _{1}=\mathrm{J} _{2}\right]$
$\Delta \mathrm{K}=$ Change in rotational K.E. $=\mathrm{K} _{1}-\mathrm{K} _{2}=\frac{\mathrm{J} _{1}^{2}}{2}\left(\frac{1}{\mathrm{I} _{1}}-\frac{1}{\mathrm{I} _{2}}\right)$
$$ \begin{aligned} & =\frac{\mathrm{J} _{1}^{2}}{2}\left[\frac{2}{\mathrm{MR}^{2}}-\frac{8}{5 \mathrm{MR}^{2}}\right]=\frac{\mathrm{J} _{1}^{2}}{5 \mathrm{MR}^{2}} \\ & =\frac{\mathrm{MR}^{2} \omega _{0}^{2}}{20} \end{aligned} $$
53. A uniform sphere of mass $M$; radius $R$ has M.I, $I$ about any diameter as axis. The sphere is recast into a cube. The M.I of cube about an axis through its mid-point parallel to any side of cube is
(1) $\frac{1}{8}$
(2) $(\pi)^{3 / 2} \mathrm{I}$
(3) $\frac{5}{3}\left(\frac{\pi}{6}\right)^{2 / 3} \mathrm{I}$
(4) I
Show Answer
Correct answer: (3)
Solution:
The moment of inertia, I, of sphere about diameter as axis is
$$ \mathrm{I}=\frac{2}{5} \mathrm{MR}^{2} $$
Let $\mathrm{L}$ be the side of the cube formed when sphere is recast. Then
$$ M=\frac{4 \pi}{3} R^{3} \rho=L^{3} \rho $$
or $\quad \mathrm{L}=\left(\frac{4 \pi}{3}\right)^{1 / 3} \mathrm{R}$
$I _{1}=$ M.I. of cube about given axis
$$ =M\left[\frac{\mathrm{L}^{2}+\mathrm{L}^{2}}{12}\right]=\frac{\mathrm{ML}^{2}}{6}=\frac{\mathrm{M}}{6}\left(\frac{4 \pi}{3}\right)^{2 / 3} \mathrm{R}^{2} $$
$$ \begin{aligned} & =\frac{1}{6}\left(\frac{4 \pi}{3}\right)^{2 / 3} \times \frac{5}{2} \mathrm{I}=\frac{5}{3}\left[\frac{4 \pi}{3(4) \frac{3}{2}}\right]^{2 / 3} \mathrm{I} \\ & =\frac{5}{3}\left[\frac{\pi}{6}\right]^{2 / 3} \mathrm{I} \end{aligned} $$
54. The radius of gyration of a solid sphere of mass $M$, radius $R$ about some axis is $\sqrt{2} R$. By what distance the axis of rotation be shifted so that radius of gyration becomes $2 R$ ?
(1) $\sqrt{1.6} \mathrm{R}$
(2) $\sqrt{3.6} \mathrm{R}$
(3) $(\sqrt{3.6}-\sqrt{1.6}) \mathrm{R}$
(4) $(\sqrt{3.6}+\sqrt{1.6}) \mathrm{R}$
Show Answer
Correct answer: (3)
Solution:
Let $\mathrm{I} _{1}$ be M.I of sphere about axis having $\mathrm{k} _{1}=\sqrt{2} \mathrm{R}$. Let $\mathrm{h} _{1}$ be distance of the axis from a parallel axis through C.G. From theorem of parallel axis.
$$ \begin{gather*} \mathrm{M}(\sqrt{2} \mathrm{R})^{2}=\mathrm{Ig}+\mathrm{Mh} _{1}^{2} \\ 2 \mathrm{MR}^{2}=\frac{2}{5} \mathrm{MR}^{2}+\mathrm{Mh} _{1}^{2} \\ \text { or } \mathrm{h} _{1}=\sqrt{\frac{8}{5}} \mathrm{R}=\sqrt{1.6} \mathrm{R} \tag{i} \end{gather*} $$
Let $h _{2}$ be distance of second axis from a parallel axis through C.G., so that $I _{2}=\mathrm{Mk} _{2}^{2}$ and $k _{2}=2 R$. Obviously
$\mathrm{M}(2 \mathrm{R})^{2}=\frac{2}{5} \mathrm{MR}^{2}+\mathrm{Mh} _{2}^{2}$
$\therefore \mathrm{h} _{2}=\sqrt{\frac{18}{5}} \cdot \mathrm{R}=\sqrt{3.6} \mathrm{R}\hspace{40mm} . . . . . .(ii)$
Change in position of axis of rotation.
$$ =\mathrm{h} _{2}-\mathrm{h} _{1}=[\sqrt{3.6}-\sqrt{1.6}] \mathrm{R} $$
55. A thin rod $A B$ of length $2 L$ is made up of two equal parts $A O$ and $O B$ of different materials. $\lambda _{1}$ and $\lambda _{2}$ is mass per unit length of the two parts of rod. What is moment of inertia of rod about an axis through one end $A$ and perpendicular to length of rod?
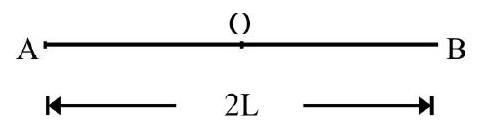
Fig. 42
(1) $\left(\lambda _{1}+5 \lambda _{2}\right) \frac{\mathrm{L}^{2}}{3}$
(2) $\left(\lambda _{1}+7 \lambda _{2}\right) \frac{L^{2}}{3}$
(3) $\left(\lambda _{1}+4 \lambda _{2}\right) \frac{L^{3}}{3}$
(4) $\left(\lambda _{1}+7 \lambda _{2}\right) \frac{L^{3}}{3}$
Show Answer
Correct answer: (4)
Solution:
Let $\mathrm{I} _{1}$ be M.I of part AO about given axis. Axis passes through one end A of rod; therefore
$$ \mathrm{I} _{1}=\mathrm{m} _{1} \frac{\mathrm{L}^{2}}{3}=\frac{\lambda _{1} \mathrm{~L}^{3}}{3} \quad\left[\because \mathrm{m} _{1}=\lambda _{1} \mathrm{~L}\right] $$
Let $\mathrm{I} _{2}$ be moment of inertia of part $\mathrm{OB}$ of rod. Let $\mathrm{I} _{\mathrm{g}}$ be M.I of part $\mathrm{OB}$ about exist through its midpoint $\mathrm{O} _{1}$ and perpendicular to $\mathrm{OB}$. Then
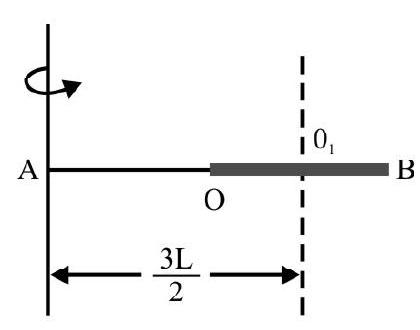
Fig. 43
$$ \mathrm{I} _{\mathrm{g}}=\mathrm{m} _{2} \frac{\mathrm{L}^{2}}{12}=\frac{\lambda _{2} \mathrm{~L}^{3}}{12} $$
From theorem of parallel axis
$$ \mathrm{I} _{2}=\mathrm{I} _{\mathrm{g}}+\mathrm{m} _{2}\left(\frac{3 \mathrm{~L}}{2}\right)^{2}=\mathrm{m} _{2} \frac{\mathrm{L}^{2}}{12}+\frac{9}{4} \mathrm{~m} _{2} \mathrm{~L}^{2} $$
$$ =\frac{7}{3} \mathrm{~m} _{2} \mathrm{~L}^{2}=\frac{7}{3} \lambda _{2} \mathrm{~L}^{3} $$
$I=$ M.I of complete rod about given axis.
$$ =\mathrm{I} _{1}+\mathrm{I} _{2}=\left(\lambda _{1}+7 \lambda _{2}\right) \frac{\mathrm{L}^{3}}{3} $$
56. Two identical solid spheres each of mass $M$, radius $R$ are connected to one another by a thin rod of length $2 \sqrt{3} \mathrm{R}$ as shown in Fig. 44. Mass of rod is 0.28 M. The M.I of the arrangement about an axis through midpoint of rod and perpendicular to its length is
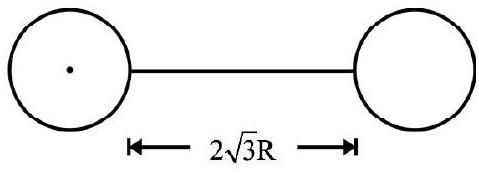
Fig. 44
(1) $1.8 \mathrm{MR}^{2}$
(2) $7.08 \mathrm{MR}^{2}$
(3) $7.85 \mathrm{MR}^{2}$
(4) $16 \mathrm{MR}^{2}$
Show Answer
Correct answer: (4)
Solution:
$I _{1}=$ M.I of rod about given axis.
$$ =0.28 \mathrm{M}\left[\frac{(2 \sqrt{3} \mathrm{R})^{2}}{12}\right]=0.28 \mathrm{MR}^{2} $$
$I _{2}=$ M.I of each sphere about given axis.
$$ \begin{aligned} & =\frac{2}{5} \mathrm{MR}^{2}+\mathrm{M}[(1+\sqrt{3}) \mathrm{R}]^{2} \\ & =0.4 \mathrm{MR}^{2}+7.46 \mathrm{MR}^{2}=7.86 \mathrm{MR}^{2} \end{aligned} $$
$I=$ M.I of the arrangement about gives axis.
$$ \begin{aligned} & =\mathrm{I} _{1}+2 \mathrm{~J} _{2}=0.28 \mathrm{MR}^{2}+2 \times 7.86 \mathrm{MR}^{2} \\ & =(0.28+15.72) \mathrm{MR}^{2} \\ & =16 \mathrm{MR}^{2} \end{aligned} $$
57. A uniform cylinder is rotating about it’s own axis with a constant angular speed $\omega$. Very gently it is placed on a rough horizontal surface at $t _{1}$. At $t=t _{2}$ it starts rolling without slipping. The rotational kinetic energy of cylinder at $t _{1}, t _{2}$ and $t _{3}\left(>t _{2}\right)$ is $K _{1}, K _{2}$ and $K _{3}$ respectively. Then
(1) $\mathrm{K} _{1}=\mathrm{K} _{2}=\mathrm{K} _{3}$
(2) $\mathrm{K} _{1}=\mathrm{K} _{2} ; \mathrm{K} _{2}=\mathrm{K} _{3}$
(3) $\mathrm{K} _{1}>\mathrm{K} _{2}>\mathrm{K} _{3}$
(4) $\mathrm{K} _{1}<\mathrm{K} _{2} ; \mathrm{K} _{2} \neq \mathrm{K} _{3}$
Show Answer
Correct answer:(2)
Solution:
When rotating cylinder is gently placed on rough horizontal surface at $t=t _{1}$; it initially slips. But at $t=t _{2}$, slipping stops. There is loss of energy due to friction between horizontal surface and cylinder i.e $\mathrm{K} _{2}<\mathrm{K} _{1}$. At $t>t _{2}$; the cylinder moves with speed it has acquired and its energy remains same as at $t=t _{2}$ i.e $\mathrm{K} _{2}=\mathrm{K} _{3}$.
58. A wheel is free to rotate about its own axis. It starts from rest and has an angular acceleration.
$$ \alpha=\mathrm{a}-\mathrm{bt} $$
$a$ and $b$ are constants. The number of revolutions it makes before it momentarily comes to rest and begins to rotate in a direction opposite to the earlier is
(1) $\frac{a}{b}$
(2) $\frac{2 \mathrm{a}}{\mathrm{b}^{2}}$
(3) $\frac{2 a^{3}}{3 b^{2}}$
(4) $\frac{\mathrm{a}^{3}}{3 \pi \mathrm{b}^{2}}$
Show Answer
Correct answer: (4)
Solution:
The wheel has a non-uniformly acceleration motion. Given
$$ \begin{gather*} \alpha=\frac{\mathrm{d} \omega}{\mathrm{dt}}=\mathrm{a}-\mathrm{bt} \\ \therefore \quad \omega=\int _{0}^{\omega} \mathrm{d} \omega=\int _{0}^{\omega}(\mathrm{a}-\mathrm{bt}) \mathrm{dt} \\ \omega=\mathrm{at}-\frac{\mathrm{bt}^{2}}{2} \tag{i} \end{gather*} $$
$\omega=0$ at $\mathrm{t}=\mathrm{t} _{1}$, when wheel is momentarily at rest. Obviously $\mathrm{t} _{1}=\frac{2 \mathrm{a}}{\mathrm{b}}$. Let $\theta$ be the angular displacement of wheel. We have
$$ \omega=\frac{\mathrm{d} \theta}{\mathrm{dt}}=\mathrm{at}-\frac{\mathrm{bt}^{2}}{2} $$
$\therefore \int _{0}^{\theta} \mathrm{d} \theta=\int _{0}^{\mathrm{t}}\left(\mathrm{at}-\frac{\mathrm{bt}^{2}}{2}\right) \mathrm{dt} \quad$ or $\quad \theta=\frac{\mathrm{at}^{2}}{2}-\frac{\mathrm{bt}^{3}}{6}$
$\therefore \theta\left(a t \quad \mathrm{t}=\mathrm{t} _{1}\right)=\frac{\mathrm{at} _{1}^{2}}{2}-\frac{\mathrm{b}}{6} \mathrm{t} _{1}^{3}=\frac{\mathrm{a}}{2}\left(\frac{2 \mathrm{a}}{\mathrm{b}}\right)^{2}-\frac{\mathrm{b}}{6}\left(\frac{2 \mathrm{a}}{\mathrm{b}}\right)^{3}=\frac{2 \mathrm{a}^{3}}{3 \mathrm{~b}^{2}}$
The number of revolutions $=\frac{\theta}{2 \pi}=\frac{\mathrm{a}^{3}}{3 \pi \mathrm{b}^{2}}$
59. A motor of power $0.5 \mathrm{KW}$ operates at a speed of $1500 \mathrm{r}$.p.m. under a given load. The motor drives a pulley of radius $50 \mathrm{~mm}$ using a belt. The difference in tension between the two parts of belt, in newton, is
(1) $\frac{200}{\pi}$
(2) $\frac{100}{\pi}$
(3) $100 \pi$
(4) $200 \pi$
Show Answer
Correct answer: (1)
Solution:
Let $\tau$ be the torque produces by the motor when rotating at $\omega=1500$ r.p.m. $=\frac{1500 \times 2 \pi}{60} \mathrm{rod} / \mathrm{s}$.
We know
$$ \begin{gathered} \tau \omega=\mathrm{P} \quad \text { or } \quad \tau=\frac{\mathrm{P}}{\omega} \\ \therefore \quad \tau=\frac{0.5 \times 10^{3}}{\left(\frac{1500}{60} \times 2 \pi\right)} \mathrm{N}-\mathrm{m} \\ \quad=\frac{10}{\pi} \mathrm{N}-\mathrm{m} \end{gathered} $$
Let $\Delta \mathrm{T}=\mathrm{T} _{1}-\mathrm{T} _{2}$ be the difference in the tension in the two parts of belt. $\mathrm{R}=$ radius of pulley. Clearly $\tau=\left(\mathrm{T} _{1}-\mathrm{T} _{2}\right) \cdot \mathrm{R}=(\Delta \mathrm{T}) \cdot \mathrm{R}$
$\therefore \frac{10}{\pi}=(\Delta \mathrm{T}) \times 5 \times 10^{-2}$
or $\Delta \mathrm{T}=\frac{200}{\pi}$ newton
60. A thin rod $O A$ of mass $M$, length $L$ has a point mass $m$ attached to its end $A$. The rod is in a vertical plane in gravity of earth. The end $O$ of rod is pivoted. The rod is free to rotate about a horizontal axis through $O$. The system is let go from rest in the position shown in Fig. 45. The initial angular acceleration of the arrangement is
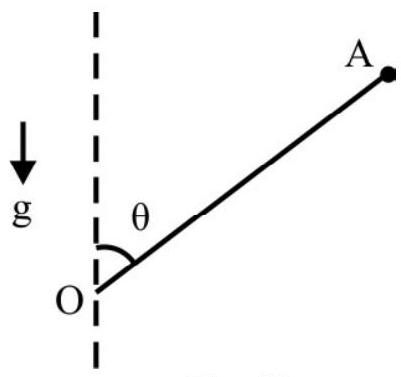
Fig. 45
(1) $\left(\frac{3}{2} \frac{\mathrm{g}}{\mathrm{L}}\right) \sin \theta$
(2) $\left(\frac{3 m}{M}\right) \frac{g \sin \theta}{L}$
(3) $\left[\frac{3(M+m)}{M}\right] \frac{g \sin \theta}{L}$
(4) $\left[\frac{3(M+2 m)}{2(M+3 m)}\right] \frac{g \sin \theta}{L}$
Show Answer
Correct answer: (4)
Solution:
The torque, $\tau$, on the system is due to weight $\mathrm{Mg}$ of rod and $\mathrm{mg}$ of point mass at A. From Fig. 46
$$ \begin{gathered} \tau=\text { Total torque }=\mathrm{Mg} \times \mathrm{CC} _{1}+\mathrm{Mg} \times \mathrm{AA} _{1} \\ =\frac{\mathrm{MgL}}{2} \sin \theta+\mathrm{mgL} \sin \theta \end{gathered} $$
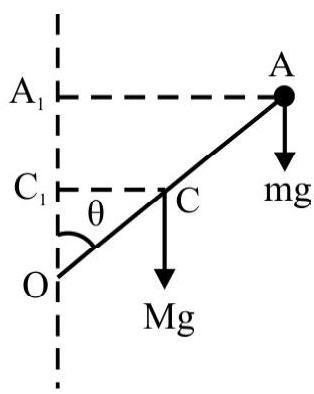
Fig. 46
$$ =\left(\frac{M}{2}+m\right) g L \sin \theta=\left(\frac{M+2 m}{2}\right) g L \sin \theta $$
$\mathrm{I}=$ The M.I of system about horizontal axis through end O.
$$ =\frac{1}{3} \mathrm{ML}^{2}+\mathrm{mL}^{2}=\left(\frac{\mathrm{M}+3 \mathrm{~m}}{3}\right) \mathrm{L}^{2} $$
The initial acceleration $=\alpha=\frac{\tau}{I}=\left[\frac{3(M+2 m)}{2(M+3 m)}\right]\left[\frac{g \sin \theta}{L}\right]$
61. A uniform cylinder rolls down an rough inclined plane without slipping. Which of the following statements is incorrect?
(1) Force of friction coming into play equals limiting value of friction.
(2) Force of friction does not act as a dissipative force.
(3) Rotational motion is because of force of friction.
(4) Total energy of the system is conserved.
Show Answer
Correct answer:(1)
Solution:
Force of friction coming into play is not necessarily equal to the limiting friction.It is $\mathrm{f} ; 0<\mathrm{f} \leq \mathrm{f} _{\mathrm{tt}}$.
Friction does not act as a dissipative force. The loss in translation K.E., due to friction, is exactly equal to gain in rotational K.E., which is due to force of friction.
62. $A B$ is a rod of length $2 \mathrm{~m}$. It is placed against a vertical wall with its end $A$ is in contact with wall. The end B of rod (in contact with horizontal floor) is pulled along the floor with a constant speed of $0.5 \mathrm{~ms}^{-1}$. The speed of the end $A$ of the rod when it makes angle of $37^{0}$ with floor is
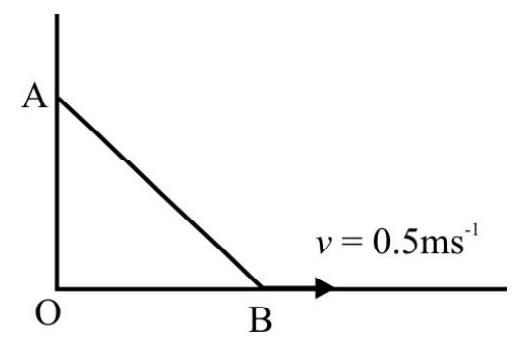
Fig. 47
(1) $0.4 \mathrm{~ms}^{-1}$
(2) $0.3 \mathrm{~ms}^{-1}$
(3) $0.5 \mathrm{~ms}^{-1}$
(4) $0.67 \mathrm{~ms}^{-1}$
Show Answer
Correct answer: (2)
Solution:
Fig. 48 shows ladder when $\theta=37^{\circ}$.
Let $(x, 0)$ and $(0, \mathrm{y})$ be the instantaneous co-ordinates of end $\mathrm{B}$ and $\mathrm{A}$ respectively. The length $\mathrm{AB}=\ell$ of rod is $\ell^{2}=x^{2}+y^{2}$
Differentiate w.r.t time $(\mathrm{t})$
$$ 0=2\left[x \frac{\mathrm{d} x}{\mathrm{dt}}+\mathrm{y} \frac{\mathrm{dy}}{\mathrm{dt}}\right] $$
or $\frac{\mathrm{dy}}{\mathrm{dt}}=-\left(\frac{x}{\mathrm{y}}\right) \frac{\mathrm{d} x}{\mathrm{dt}} \hspace{40mm} . . . . . .(i)$
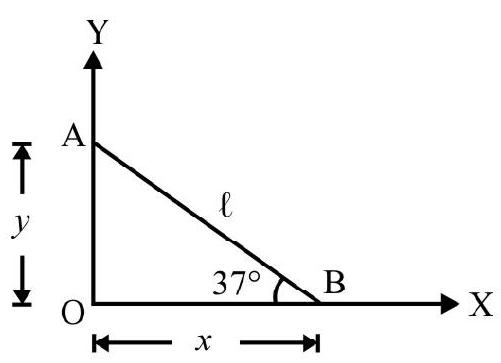
Fig. 48
Obviously $\frac{\mathrm{d} x}{\mathrm{dt}}=\mathrm{v} _{\mathrm{B}}=0.5 \mathrm{~ms}^{-1}$ (Given). Also $\frac{x}{\mathrm{y}}=\cot 37=\frac{0.8}{0.6}=\frac{4}{3}$
Therefore, velocity of end $A ;{ v} _{A}$ is
$$ \mathrm{v} _{\mathrm{A}}=\frac{\mathrm{dy}}{\mathrm{dt}}=-\frac{4}{3} \times \mathrm{v} _{\mathrm{B}}=-\frac{4}{3} \times 0.5=-0.67 \mathrm{~ms}^{-1} $$
Negative sign indicates that end A moves vertically downwards.
63. A thin rod $\mathrm{OA}$ of mass $\mathrm{M}$; length $L$ is free to rotate about an axis through end $O$ perpendicular to length of rod. A constant force $F$ is applied at the end $A$ of rod such that $F$ is always perpendicular to the original position of rod. The angular momentum of rod when it has rotated through an angle of $30^{\circ}$ is
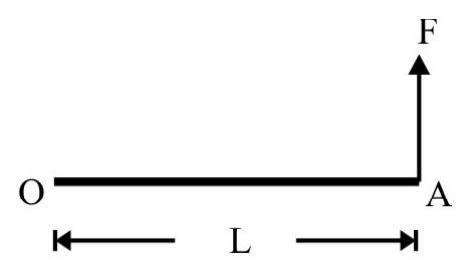
Fig. 49
(1) $\left[\frac{\mathrm{MFL}}{\sqrt{3}}\right]^{1 / 2}$
(2) $\left[\frac{\mathrm{MFL}^{3}}{3}\right]^{1 / 2}$
(3) $\left[\frac{2 \mathrm{MFL}^{3}}{\sqrt{3}}\right]^{1 / 2}$
(4) $\left[\frac{2 \mathrm{MFL}^{3}}{3}\right]^{1 / 2}$
Show Answer
Correct answer: (2)
Solution:
Fig. 50 shows instantaneous position $\mathrm{OB}$ of rod when it has turned through an angle $\theta$. The work done, $w$, on the rod by the applied force.
$$ \begin{align*} \mathrm{w}= & \int _{0}^{\theta}(\mathrm{F} \ell \cos \theta) \mathrm{d} \theta \quad[\because \tau=\mathrm{F} \ell \cos \theta] \\ & =\mathrm{F} \ell \sin \theta \tag{i} \end{align*} $$
Let $\omega$ be the angular speed acquired by rod. From work energy theorem
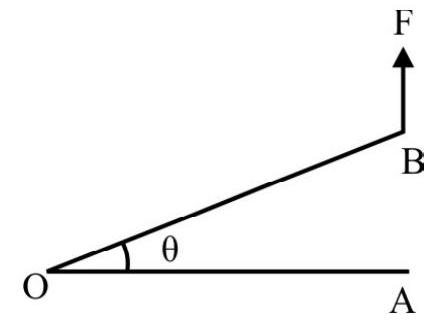
Fig. 50
$\mathrm{K}=$ Rotation K.E. of $\mathrm{rod}=\mathrm{w}=\mathrm{F} \ell \sin \theta$
The instantaneous angular momentum of rod
$$ =\mathrm{J}=\sqrt{2 \mathrm{~J}} \mathrm{~K}=\sqrt{\frac{2 \mathrm{FMl}^{3} \sin \theta}{3}} $$
Given $\theta=30^{\circ}$; therefore
$$ \mathrm{J}=\sqrt{\frac{\mathrm{FML}^{3}}{3}} $$
64. A cylinder rolls up an inclined plane without slipping starting from the bottom of the inclined plane. It reaches up to some height on the plane and starts rolling down without slipping. The direction of force of friction acting on the calender is:
(1) up the inclined while ascending and down the inclined while descending.
(2) up the inclined both during ascent and descent.
(3) down the inclined both during ascent and decent.
(4) down the inclined while ascending and up the incline while descending.
Show Answer
Correct answer: (2)
Solution:
The linear acceleration or retardation of C.M during ascent and descent have same magnitude. This is only possible if direction of force of friction; f; coming into play is directed up the plane; both during ascent and descent.
65. A thin uniform rod $A B$ of mass $M$; length $L$ is placed on a smooth horizontal table. Forces $F _{1}$ and $F _{2}$ are applied on rod as shown in Fig. 51. There is no rotational motion of rod. The linear acceleration of rod is Equation of Rotational Motion
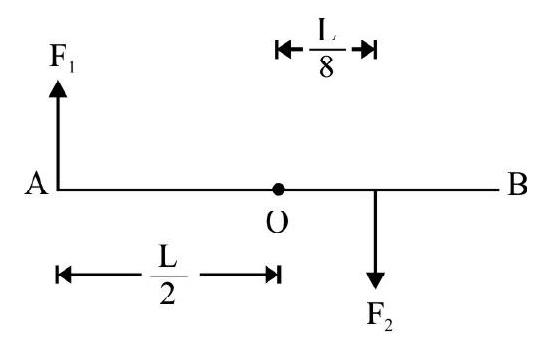
Fig. 51
(1) $\frac{F _{1} \sim F _{2}}{M}$
(2) $\frac{2 \mathrm{~F} _{1}}{\mathrm{M}}$
(3) $\frac{3 \mathrm{~F} _{1}}{\mathrm{M}}$
(4) $\frac{3 \mathrm{~F} _{2}}{\mathrm{M}}$
Show Answer
Correct answer: (3)
Solution:
Since there is no rotational motion of rod; the net torque on rod about its center O; due to applied forces must be zero. Therefore,
$$ \begin{equation*} \mathrm{F} _{1} \times \frac{\mathrm{L}}{2}=\mathrm{F} _{2} \times \frac{\mathrm{L}}{8} \end{equation*} $$
or $\mathrm{F} _{2}=4 \mathrm{~F} _{1} \hspace{40mm} . . . . . .(i)$
The net force on $\operatorname{rod}=\mathrm{F}=\mathrm{F} _{2}-\mathrm{F} _{1}=3 \mathrm{~F} _{1}$
The linear acceleration, a, of rod is
$$ \begin{equation*} \mathrm{a}=\frac{3 \mathrm{~F} _{1}}{\mathrm{M}} \tag{ii} \end{equation*} $$
66. In Fig 52 pulley has mass M, radius R. A massless, inextensible string is wrapped around the pulley. $m=\frac{M}{2}$ is attached to free end of string. The system is let go from rest. The linear acceleration of $m$ is (there is no slipping between the string and the pulley).
Fig. 52
(1) $\mathrm{g}$
(2) $0.5 \mathrm{~g}$
(3) $0.67 \mathrm{~g}$
(4) $0.33 \mathrm{~g}$
Show Answer
Correct answer: (2)
Solution:
Fig. 53(a) and (b) show free body diagram of mass $m$ and pulley respectively. $\mathrm{T}$ is tension in string. Let a be linear acceleration of $\mathrm{m}$. Its equation of motion is
$$ \begin{equation*} \mathrm{ma}=\mathrm{mg}-\mathrm{T} \tag{i} \end{equation*} $$
or $\quad \frac{M a}{2}=\frac{M}{2} g-T$

Fig. 53
$\mathrm{I} \alpha=\tau \quad \text { or } \quad\left(\frac{1}{2} \mathrm{MR}^2\right) \alpha=\mathrm{TR} \hspace{40mm} . . . . . .(ii)$
Let $\alpha$ be the angular acceleration of pulley. Equation of rotational motion of pulley is
Since there is no slipping between pulley and string;
$$ \begin{equation*} \mathrm{a}=\mathrm{R} \alpha \tag{iii} \end{equation*} $$
From Eq ns (i), (ii) and (iii) we have
$$ a=\frac{g}{2} $$
67. Fig. 54 shows a cylinder of mass $M=4 \mathrm{~m}$ placed on a rough horizontal surface attached to mass $\mathrm{m}$; and a massless, inextensible string passing over a massless pulley. The system is let go from rest. There is no slipping; the acceleration (linear) of mass $m$ is
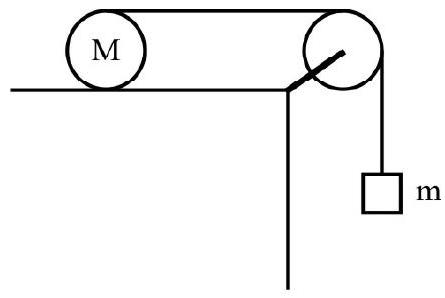
Fig. 54
(1) $\frac{g}{4}$
(2) $\frac{\mathrm{g}}{5}$
(3) $\frac{4 \mathrm{~g}}{5}$
(4) $\frac{3 \mathrm{~g}}{5}$
Show Answer
Correct answer: (3)
Solution:
Let a be linear acceleration of mass $\mathrm{m}$ and $\mathrm{T}$ the tension in string. $\mathrm{f}$ is force of friction coming into play between table top and cylinder. Let $\alpha$ be the angular acceleration of cylinder. The linear acceleration of C.M of cylinder also is a. Fig. 55 (a) and (b) show free-body diagram of mass $m$ and cylinder.The equations of motion are:
$$ \begin{align*} & \mathrm{mg}-\mathrm{T}=\mathrm{ma} \tag{i} \\ & \mathrm{T}-\mathrm{f}=4 \mathrm{ma} \tag{ii} \\ & (\mathrm{T}+\mathrm{f}) \mathrm{R}=\mathrm{I} \alpha \tag{iii} \end{align*} $$

Fig. 55
Since there is no slipping;
$$ \begin{equation*} \mathrm{a}=\mathrm{R} \alpha \tag{iv} \end{equation*} $$
From above equations;
$$ \mathrm{a}=\left(\frac{4}{5}\right) \mathrm{g} $$
68. A body of circular cross-section starts from rest from top of a rough inclined plane of inclination $30^{0}$, vertical height $0.875 \mathrm{~m} ; \mu _{\mathrm{k}}=0.3$. It rolls down without slipping; reaching the bottom of inclined in $1 \mathrm{~s}$. The shape of body is $\left(\mathrm{g}=9.8 \mathrm{~ms}^{-2}\right)$
(1) Ring
(2) Disc
(3) Hollow sphere
(4) Solid sphere
Show Answer
Correct answer:(4)
Solution:
The slant side, $\ell$; of inclined plane is
$$ \frac{\mathrm{h}}{\ell}=\sin 30 \quad \text { or } \quad \ell=\frac{\mathrm{h}}{\sin 30}=2 \times 0.875 \mathrm{~m}=1.75 \mathrm{~m} $$
Let a be the linear acceleration of center of mass of body. Given
$\mathrm{u}=0 ; \mathrm{S}=\ell=1.75 \mathrm{~m} ; \mathrm{t}=1 \mathrm{~s} ; \mathrm{a}=$ ?
$\therefore 1.75=\frac{1}{2} \times \mathrm{a} \times(1)^{2}$
or $\quad \mathrm{a}=3.5 \mathrm{~ms}^{-2} \hspace{40mm} . . . . . .(i)$
Let I be the M.I of the body about axis through its center of mass. We know
$$ \mathrm{a}=\frac{\mathrm{g} \sin \theta}{\left(1+\frac{\mathrm{I}}{\mathrm{mR}^{2}}\right)} $$
3.$5=\frac{9.8 \times 0.5}{1+\frac{\mathrm{I}}{\mathrm{mR}^{2}}}$
or $\quad \mathrm{I}=\mathrm{mR}^{2}\left[\frac{4.9}{3.5}-1\right]$
$=\frac{2}{5} \mathrm{mR}^{2}$
The body is a solid sphere.
69. A body slides down a smooth inclined plane of inclination $30^{\circ}$, vertical height, $h$. It starts from rest from the top and acquires a speed $v _{1}$ on reaching the bottom of inclined plane. The body is recast in the shape of a uniform disc. The disc starts from rest from top of an identical rough inclined plane $(\mu=0.2)$ as before. It rolls down without slipping. It acquires a linear speed $v _{2}$ as it reaches the bottom of the inclined plane $\frac{v _{2}}{v _{1}}$ is
(1) 1
(2) $\sqrt{\frac{2}{3}}$
(3) $\sqrt{\frac{2}{5}}$
(4) $\sqrt{\frac{2}{7}}$
Show Answer
Correct answer: (2)
Solution:
The acceleration of body down smooth inclined plane is $g \sin \theta$. The speed $v _{1}$ is
$$ \begin{equation*} \mathrm{v} _{1}=\sqrt{2 \mathrm{gh}} \tag{i} \end{equation*} $$
Let a be the linear acceleration of C.M of circular disc as it rolls down the inclined plane. Then
$$ \mathrm{a}=\frac{\mathrm{g} \sin \theta}{1+\left(\frac{\frac{1}{2} \mathrm{mR}^{2}}{\mathrm{mR}^{2}}\right)}=\frac{2}{3} \mathrm{~g} \sin \theta $$
The speed, $\mathrm{v} _{2}$ as it reaches the bottom of inclined plane is
$$ \mathrm{v} _{2}^{2}=2\left(\frac{2}{3} \mathrm{~g} \sin \theta\right) \ell $$
$$ \begin{aligned} & =\frac{4}{3} \mathrm{gh} \quad[\because \mathrm{h}=\ell \sin \theta] \\ & \therefore \quad \frac{\mathrm{v} _{2}^{2}}{\mathrm{v} _{1}^{2}}=\frac{4}{3 \times 2}=\frac{2}{3} \quad \text { or } \quad \frac{\mathrm{v} _{2}}{\mathrm{v} _{1}}=\sqrt{\frac{2}{3}} \end{aligned} $$
70. A massless, inextensible string is wrapped around a solid cylinder of mass $M$; radius $\mathbf{R}$. The string is pulled up vertically to prevent the center of mass from falling down as the string unwinds itself. The work done by the applied force when cylinder acquires angular speed $\omega _{1}$ is
(1) $\mathrm{MR}^{2} \omega _{1}^{2}$
(2) $\frac{\mathrm{MR}^{2} \omega _{1}^{2}}{2}$
(3) $\frac{\mathrm{MR}^{2} \omega _{1}^{2}}{4}$
(4) $\frac{2 \mathrm{MR}^{2} \omega _{1}^{2}}{3}$
Show Answer
Correct answer: (3)
Solution:
Fig. 56 shows cylinder with vertical string pulled up by a force F. As C.M of cylinder is at rest; $\mathrm{F}=\mathrm{Mg}$. The torque; $\tau$; due to applied force about $\mathrm{O}$ is
$$ \tau=\mathrm{F} . \mathrm{R}=\mathrm{MgR} $$
The M.I of cylinder about its symmetry axis $=\mathrm{I}=\frac{\mathrm{MR}^{2}}{2}$
$\alpha=$ The angular acceleration of cylinder $=\frac{\tau}{\mathrm{I}}=\frac{2 \mathrm{~g}}{\mathrm{R}}$
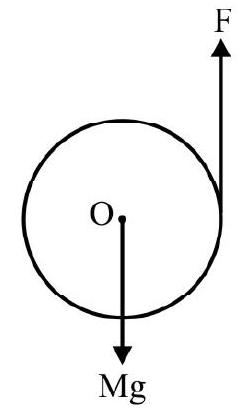
Fig. 56
Let $\theta$ be the total angle describe by cylinder as it accquires angular speed $\omega _{1}$. Then
$\omega _{1}^{2}-(0)^{2}=2\left(\frac{2 \mathrm{~g}}{\mathrm{R}}\right) \theta$
$\therefore \theta=\frac{\mathrm{R} \omega _{1}^{2}}{4 \mathrm{~g}}$
The work done $=\tau . \theta$
$$ =\frac{\mathrm{MR}^{2} \omega _{1}^{2}}{4} $$
Alternately,
$\mathrm{w}=$ Change in rotational $\mathrm{KE}=\frac{1}{2} \cdot\left(\frac{1}{2} \mathrm{MR}^{2}\right) \omega _{1}^{2}=\frac{1}{4} \mathrm{MR}^{2} \omega _{1}^{2}$
71. A uniform disc of mass $1.2 \mathrm{~kg}$ radius $200 \mathrm{~mm}$ is rotating about its own axis with an angular speed of $\frac{600}{\pi}$ r.p.m. It is gently placed on a rough horizontal surface $(\mu=0.15)$. The disc comes to rest in
(1) $1 \mathrm{~s}$
(2) $1.5 \mathrm{~s}$
(3) $2 \mathrm{~s}$
(4) $3 \mathrm{~s}$
Show Answer
Correct answer: (3)
Solution:
There is an external torque $\tau$, on disc due to friction between horizontal surface and disc. To calculated $\tau$ consider an elementary ring of radius $x$ thickness $\mathrm{d} x$. The mass, $\mathrm{dm}$; of ring considered.
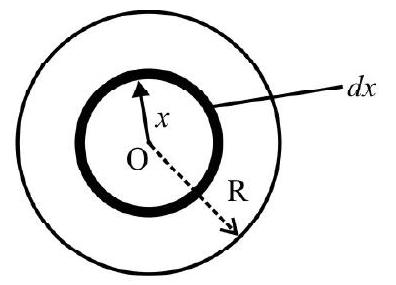
Fig. 57
$$ \begin{aligned} \mathrm{dm}= & (2 \pi x \quad \mathrm{~d} x)\left(\frac{\mathrm{M}}{\pi \mathrm{R}^{2}}\right) \\ & =\left(\frac{2 \mathrm{M}}{\mathrm{R}^{2}}\right) x \mathrm{~d} x \end{aligned} $$
$\mathrm{d} \tau=$ Torque on elementary ring about center $\mathrm{O}$
$$ =\mu(\mathrm{dm}) \mathrm{g} \cdot x=\left(\frac{2 \mu \mathrm{Mg}}{\mathrm{R}^{2}}\right) x^{2} \mathrm{~d} x $$
$\therefore \quad \tau=$ The total torque on disc $=\int _{0}^{R} \mathrm{~d} \tau$
$$ =\frac{2 \mu \mathrm{MgR}}{3} $$
Let $\alpha$ be angular retardation of disc
$\alpha=\frac{\tau}{\mathrm{I}}=\frac{2 \mu \mathrm{Mg} \frac{\mathrm{R}}{3}}{\frac{\mathrm{MR}^{2}}{2}}=\frac{4 \mu \mathrm{g}}{3 \mathrm{R}}$
Let $\omega _{0}$ be initial angular speed of disc. Then
$$ \omega=0 ; \quad \alpha=-\frac{4 \mu \mathrm{g}}{3 \mathrm{R}} ; \quad \mathrm{t}=? $$
$\therefore 0=\omega _{0}-\omega \mathrm{t} \quad$ or $\quad \mathrm{t}=\frac{\omega _{0}}{\alpha}=\frac{3 \omega _{0} \mathrm{R}}{4 \mu \mathrm{g}}$
Given $\omega _{0}=\frac{600}{\pi} \mathrm{rpm}=\frac{600 \times 2 \pi}{\pi \times 60} \mathrm{rad} \quad \mathrm{s}^{-1}=20 \mathrm{rad} \quad \mathrm{s}^{-1}$
$R=200 \mathrm{~mm}=0.2 \mathrm{~m} ; \mu=0.15 ; \mathrm{g}=10 \mathrm{~ms}^{-2}$
$\therefore \mathrm{t}=\frac{3 \times 20 \times 0.2}{4 \times 0.15 \times 10} \mathrm{~s}$
$=2 \mathrm{~s}$
72. A hollow sphere of mass $M=6 \mathrm{~m}$; radius $R$ is filled with water of mass $\mathrm{m}$. It is rolling without slipping on a rough horizontal surface. The linear velocity of the system is $v$. The energy of the arrangement is
(1) $4 \mathrm{mv}^{2}$
(2) $4.5 \mathrm{mv}^{2}$
(3) $5.0 \mathrm{mv}^{2}$
(4) $5.5 \mathrm{mv}^{2}$
Show Answer
Correct answer: (4)
Solution:
The sphere has energy $\mathrm{K} _{1}$ due to both rotational and translation motion. Obviously
$$ \mathrm{K} _{1}=\frac{1}{2}\left[\frac{2}{3} \times 6 \mathrm{mR}^{2}\right] \cdot \omega^{2}+\frac{1}{2}(6 \mathrm{~m}) \mathrm{v}^{2} $$
Since sphere rolls without slipping.
$$ \begin{aligned} \mathrm{v} & =\mathrm{R} \omega \\ \therefore \quad \mathrm{K} _{1} & =\frac{1}{2}\left[\frac{2}{3} \times 6 \mathrm{mv}^{2}\right]+3 \mathrm{mv}^{2}=5 \mathrm{mv}^{2} \end{aligned} $$
The water inside sphere has only translational motion. Its energy $\mathrm{K} _{2}$ is
$\mathrm{K} _{2}=\frac{1}{2} \mathrm{mv}^{2}=0.5 \mathrm{mv}^{2}$
$\mathrm{K}=$ The total energy of the system.
$$ =\mathrm{K} _{1}+\mathrm{K} _{2}=5.5 \mathrm{mv}^{2} $$
73. A uniform disc is revolving around its own axis. Due to friction at the axis; it experiences an angular retardation directly proportional to its instantaneous angular speed. It makes $z$ revolutions when its angular speed becomes $50 \%$ of its initial value. How many more revolutions it will make in coming to rest?
(1) $\mathrm{z}$
(2) $2 \mathrm{z}$
(3) $\frac{\mathrm{z}}{2}$
(4) $\frac{3 z}{2}$
Show Answer
Correct answer: (1)
Solution:
Let $\alpha$ and $\omega$ denote the instantaneous acceleration and angular speed of disc. Given
$$ \alpha=\frac{\mathrm{d} \omega}{\mathrm{dt}}=-\mathrm{k} \omega $$
where $\mathrm{k}$ is a constant. Therefore
$\int_{-w_0}^{w} \frac{d \omega}{\omega}=-k \int_0^t d t$
$\therefore \omega=\omega _{0} \mathrm{e}^{-k t} \hspace{40mm} . . . . . .(i)$
We know $\omega=\frac{\mathrm{d} \theta}{\mathrm{dt}}$. Therefore
$$ \mathrm{d} \theta=\omega _{0} \mathrm{e}^{-\mathrm{kt}} \mathrm{dt} $$
or $\quad \int _{0}^{\theta} d \theta=\omega _{0} \int _{0}^{t} e^{-k t} d t$
$\therefore \quad \theta=\frac{\omega _{0}}{\mathrm{R}}\left[1-\mathrm{e}^{-\mathrm{kt}}\right]$
$n=$ Number of revolution completed in time $t$.
$$ \begin{equation*} =\frac{\theta}{2 \pi}=\frac{\omega _{0}}{2 \pi \mathrm{k}}\left[1-\mathrm{e}^{-\mathrm{kt}}\right] \tag{ii} \end{equation*} $$
Let $\omega=\frac{\omega _{0}}{2}$ at $\mathrm{t}=\mathrm{t} _{1}$
From Eqn(i) we have
$$ \frac{\omega _{0}}{2}=\omega _{0} \mathrm{e}^{-\mathrm{k} t _{1}} \quad \text { or } \quad \mathrm{e}^{-k t _{1}}=\frac{1}{2} $$
From Eqn (ii) we have
$$ \mathrm{n}=\mathrm{z}=\frac{\omega _{0}}{2 \pi \mathrm{k}}\left[1-\mathrm{e}^{-\mathrm{kt _{1 }}}\right]=\frac{\omega _{0}}{4 \pi \mathrm{k}} $$
Let $\mathrm{N}$ be total number of revolutions made by wheel in coming to rest, i.e. $\mathrm{t} \rightarrow \infty$. From Eqn (i)
$$ \mathrm{N}=\frac{\omega _{0}}{2 \pi \mathrm{k}}=2 \mathrm{z} $$
The additional number of revolution mode $=\mathrm{N}-\mathrm{n}$
$$ =2 \mathrm{z}-\mathrm{z}=\mathrm{z} $$
74. A small sized ball A of mass $m$ moves on a smooth horizontal table $P$ with a speed $v _{1} . O$ is a fixed sphere of mass $M$ and radius $R$ capable of rotating about a diameter as axis. The ball A jumps from $P$, comes in contact with sphere and rolls over it without slipping and then jumps to table $Q$. The linear speed of ball on table $Q$ is $\mathbf{v} _{2}$. Then $\frac{\mathrm{v} _{2}}{\mathrm{v} _{1}}$ is
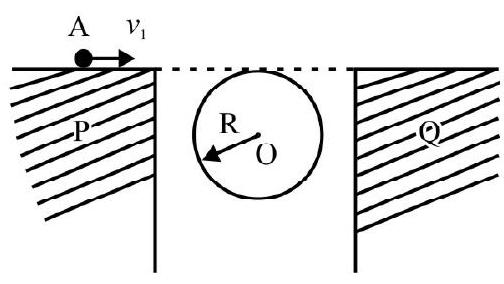
Fig. 58
(1) $\frac{m}{M+m}$
(2) $\frac{m}{m+2 M}$
(3) $\frac{2 m}{M+3 m}$
(4) $\frac{5 m}{5 m+2 m}$
Show Answer
Correct answer: (4)
Solution:
Regarding ball and sphere as a system; there is no external force and therefore no external torque. The angular momentum of system is conserved. Let $\mathrm{v} _{2}$ be linear speed of ball as it jumps off to table $\mathrm{Q}$ from sphere. Let $\omega$ be angular speed acquired by sphere. Since there is no slipping between $A$ and sphere, $\mathrm{v} _{2}=\mathrm{R} \omega$. Using law of conservation of angular momentum (Take angular momentum about point $\mathrm{O}$ ).
$$ \begin{aligned} & \mathrm{mv} _{1} \mathrm{R}=\frac{2}{5} \mathrm{MR}^{2} \omega+\mathrm{mv} _{2} \mathrm{R} \\ & \mathrm{mv} _{1} \mathrm{R}=\frac{2}{5} \mathrm{MR}^{2}\left(\frac{\mathrm{v} _{2}}{\mathrm{R}}\right)+\mathrm{mv} _{2} \mathrm{R} \\ & \mathrm{mv} _{1}=\left(\frac{2 \mathrm{M}}{5}+\mathrm{m}\right) \mathrm{v} _{2} \\ & \therefore \frac{\mathrm{v} _{2}}{\mathrm{v} _{1}}=\frac{5 \mathrm{~m}}{5 \mathrm{~m}+2 \mathrm{M}} \end{aligned} $$
75. A thin rod $A$ of mass $M$, length $L$ fits into a hollow tube (thin) B of mass $\frac{M}{3}$ and length $L$ as shown in Fig. 59. The arrangement rotates with an angular speed $\omega _{0}$ about $\mathrm{YY}^{\prime}$ as axis. Due to rotation A start slipping through B. The angular speed of the arrangement when $A$ is just about to come out of $B$ is
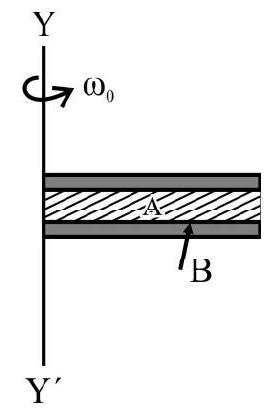
Fig. 59
(1) $\frac{\omega _{0}}{11}$
(2) $\frac{2 \omega _{0}}{11}$
(3) $\frac{4 \omega _{0}}{13}$
(4) $\frac{2 \omega _{0}}{13}$
Show Answer
Correct answer: (2)
Solution:
There is no external force and therefore no external torque. The angular momentum of system is conserved.
$\mathrm{L} _{1}=$ The initial angular momentum $=\mathrm{I} _{1} \omega _{0}$
$\mathrm{I} _{1}=\mathrm{I} _{\mathrm{A}}+\mathrm{I} _{\mathrm{B}}=\frac{1}{3}\left(\frac{\mathrm{M}}{3}\right) \mathrm{L}^{2}+\frac{1}{3} \mathrm{ML}^{2}=\frac{4 \mathrm{ML}^{2}}{9}$
$\therefore \quad \mathrm{L} _{1}=\frac{4 \mathrm{ML}^{2} \omega _{0}}{9} \hspace{40mm} . . . . . .(i)$
Fig. 60 shows the system when rod A is about to emerge out of B. Let $\mathrm{I} _{2}$ be M.I of, arrangement about $\mathrm{YY}^{\prime}$ as axis.
$$ \begin{aligned} \mathrm{I} _{2}= & \frac{1}{3}\left(\frac{\mathrm{M}}{3}\right) \mathrm{L}^{2}+\left[\frac{1}{12} \mathrm{ML}^{2}+\mathrm{M}\left(\frac{3 \mathrm{~L}}{2}\right)^{2}\right] \\ & =\frac{22}{9} \mathrm{ML}^{2} \end{aligned} $$
$\mathrm{L} _{2}=$ The final angular momentum of the system
$$ \begin{equation*} =\mathrm{I} _{2} \omega=\frac{22}{9} \mathrm{ML}^{2} \omega \tag{ii} \end{equation*} $$
From law of conservation of angular momentum $\mathrm{L} _{1}=\mathrm{L} _{2}$. Therefore
$$ \frac{4 \mathrm{ML}^{2} \omega _{0}}{9}=\frac{22}{9} \mathrm{ML}^{2} \omega \quad \text { or } \quad \omega=\frac{2}{11} \omega _{0} $$
76. A cylinder of mass $M$; radius $R$ is set into motion on a rough horizontal surface with a linear speed $v _{0}$ in forward direction and an angular speed of $\frac{V _{0}}{3 R}$ in anticlockwise direction. $\mu$ is coefficient of friction between cylinder and horizontal surface. The linear speed of cylinder when it starts rolling is:
(1) $\frac{\mathrm{v} _{0}}{2}$
(2) $\frac{4 \mathrm{v} _{0}}{5}$
(3) $\frac{5 \mathrm{v} _{0}}{7}$
(4) $\frac{7 \mathrm{v} _{0}}{9}$
Show Answer
Correct answer: (4)
Solution:
Given $\omega _{0}=\frac{\mathrm{v} _{0}}{3 \mathrm{R}}$. Since $\mathrm{v} _{0} \neq \mathrm{R} \omega$; the cylinder slips an horizontal surface. Consider motion about an axis fixed to ground and passing through the instantaneous point of contact of cylinder with ground. There is no net torque about this axis; therefore angular momentum is conserved. Let $\mathrm{v}$ and $\omega$ denote the linear and angular speed when cylinder stops slipping i.e. it starts rolling. Then
$$ \begin{aligned} & \left(\frac{1}{2} \mathrm{MR}^{2}\right) \omega _{0}+\mathrm{Mv} _{0} \mathrm{R}=\left(\frac{1}{2} \mathrm{MR}^{2}\right) \omega+\mathrm{MvR} \\ & \frac{1}{2} \mathrm{MR}^{2}\left(\frac{\mathrm{v} _{0}}{3 \mathrm{R}}\right)+\mathrm{Mv} _{0} \mathrm{R}=\frac{1}{2} \mathrm{MR}^{2}\left(\frac{\mathrm{v}}{\mathrm{R}}\right)+\mathrm{MvR} \end{aligned} $$
$$ \begin{aligned} & \frac{7 \mathrm{Mv} _{0} \mathrm{R}}{6}=\frac{3 \mathrm{MvR}}{2} \\ & \therefore \quad \mathrm{v}=\frac{7}{9} \mathrm{v} _{0} \end{aligned} $$
77. A uniform “Catherine Wheel” consists of many thin circular turns of a combustible material. The wheel is free to rotate about a vertical axis through its center in a horizontal plane. The combustive material burns at a constant rate $\alpha$ producing a constant thrust $F$ acting in the tangential direction. The speed, $\omega$, acquired by wheel, starting from rest, when its radius is half of the initial value $R$ is ( $M _{0}=$ Initial mass of Catherine wheel)
(1) $\frac{4 \pi \mathrm{F} \sigma \mathrm{R}}{\mathrm{M} _{0} \alpha}$
(2) $\frac{2 \pi \mathrm{FR}}{\mathrm{M} _{0} \alpha}$
(3) $\frac{2 \pi \mathrm{F} \sigma \mathrm{R}^{2}}{\mathrm{M} _{0} \alpha}$
(4) $\frac{4 \pi \mathrm{F} \sigma}{\mathrm{M} _{0} \alpha}$
Show Answer
Correct answer: (1)
Solution:
Let $\mathrm{M}$ be the instantaneous mass of wheel when its instantaneous radius is $\mathrm{r}$. Then
$$ \begin{equation*} \frac{\mathrm{M}}{\mathrm{M} _{0}}=\left(\frac{\mathrm{r}}{\mathrm{R}}\right)^{2} \quad \text { or } \quad \mathrm{M}=\mathrm{M} _{0}\left(\frac{\mathrm{r}}{\mathrm{R}}\right)^{2} \tag{i} \end{equation*} $$
The instantaneous M.I, of wheel about axis of rotation.
$$ =\mathrm{I}=\frac{1}{2} \mathrm{Mr}^{2}=\frac{\mathrm{M} _{0} \mathrm{r}^{4}}{2 \mathrm{R}^{2}} $$
The instantaneous torque $=\tau=$ F.r
The instantaneous acceleration is
$$ \begin{equation*} \alpha=\frac{\mathrm{d} \omega}{\mathrm{dt}}=\frac{\tau}{\mathrm{I}}=\frac{2 \mathrm{FR}^{2}}{\mathrm{M} _{0} \mathrm{r}^{3}} \tag{ii} \end{equation*} $$
We have $\mathrm{M}=\mathrm{M} _{0}-\alpha \mathrm{t} \quad$ or $\quad \pi \mathrm{r}^{2} \sigma=\pi \mathrm{R}^{2} \sigma-\alpha \mathrm{t}$
$$ \mathrm{r}^{2}=\mathrm{R}^{2}-\left(\frac{\alpha}{\pi \sigma}\right) \mathrm{t} $$
where $\sigma=$ mass per unit area of wheel.
Differentiate w.r.t time $(\mathrm{t})$
$$ 2 \mathrm{r} \frac{\mathrm{dr}}{\mathrm{dt}}=-\left(\frac{\alpha}{\pi \sigma}\right) $$
or $\frac{\mathrm{dr}}{\mathrm{dt}}=-\frac{\alpha}{2 \pi \mathrm{r} \sigma}$
From Eqns (ii) and (iii) we have
$$ \begin{aligned} & \frac{\mathrm{d} \omega}{\mathrm{dt}}=\frac{\mathrm{d} \omega}{\mathrm{dr}} \cdot \frac{\mathrm{dr}}{\mathrm{dt}}=-\left(\frac{\alpha}{2 \pi \sigma r}\right) \frac{\mathrm{d} \omega}{\mathrm{dr}} \\ & \therefore \quad \mathrm{d} \omega=-\frac{4 \pi \mathrm{F} \sigma \mathrm{R}^{2}}{\mathrm{M} _{0} \alpha \mathrm{r}^{2}} \mathrm{dr} \end{aligned} $$
Integrating we have
$$ \int _{0}^{\omega} \mathrm{d} \omega=-\frac{4 \pi \mathrm{F} \sigma \mathrm{R}^{2}}{\mathrm{M} _{0} \alpha} \int _{\mathrm{R}}^{\mathrm{R} / 2} \mathrm{r}^{-2} \mathrm{dr} $$
$$ \therefore \quad \omega=\frac{4 \pi \mathrm{F} \sigma \mathrm{R}}{\mathrm{M} _{0} \alpha} $$
78. Fig. 61 shows a parabolic track $y=k x^{2}$; The part $A O$ is frictional and part $O B$ is smooth. A cylinder of radius $R$; mass $M$, is let go from rest from point $P$. It rolls down $A O$ without slipping. It ascends on the other side of track up to point $Q$. There is no loss of energy when cylinder moves from part $A O$ to $O B$ at point $O$. Then
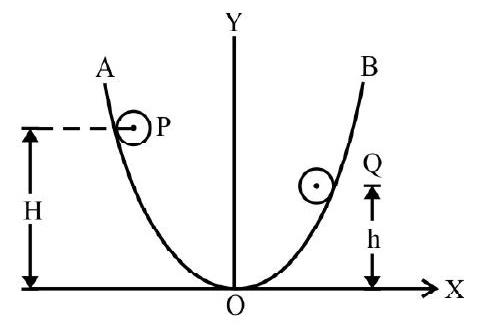
Fig. 61
(1) $\mathrm{h}=\frac{2 \mathrm{H}+\mathrm{R}}{3}$
(2) $\mathrm{h}=\frac{\mathrm{H}+\mathrm{R}}{3}$
(3) $\mathrm{h}=\frac{2(\mathrm{H}+\mathrm{R})}{3}$
(4) $\mathrm{h}=\frac{\mathrm{H}}{3}+\frac{\mathrm{R}}{2}$
Show Answer
Correct answer: (1)
Solution:
Let $v$ and $\omega$ be linear speed of C.M and angular speed of cylinder at O. From law of conservation of energy.
Loss in gravitational P.E. $=$ Gain in K.E.
$$ \operatorname{Mg}(\mathrm{H}-\mathrm{R})=\frac{1}{2} \mathrm{Mv}^{2}+\frac{1}{2}\left(\frac{1}{2} \mathrm{MR}^{2}\right) \omega^{2} $$
Since there is no slipping $\mathrm{v}=\mathrm{R} \omega$. Therefore
$$ \begin{align*} & \mathrm{Mg}(\mathrm{H}-\mathrm{R})=\frac{1}{2} \mathrm{Mv}^{2}+\frac{1}{4} \mathrm{MR}^{2}\left(\frac{\mathrm{V}}{\mathrm{R}}\right)^{2} \\ & \text { or } \quad \mathrm{v}^{2}=\frac{4 \mathrm{~g}(\mathrm{H}-\mathrm{R})}{3} \tag{i} \end{align*} $$
Since the part OB of track is smooth; as cylinder climbs up it losses translational part of its kinetic energy.
The loss in translation K.E equals gain in gravitational P.E. Therefore
$$ \begin{equation*} \frac{1}{2} \mathrm{Mv}^{2}=\mathrm{Mg}(\mathrm{h}-\mathrm{R}) \end{equation*} $$
or $\quad \mathrm{v}^{2}=2 \mathrm{~g}(\mathrm{~h}-\mathrm{R}) \hspace{40mm} . . . . . .(ii)$
From Eqns (i) and (ii) we have
$\frac{4 \mathrm{~g}(\mathrm{H}-\mathrm{R})}{3}=2 \mathrm{~g}(\mathrm{~h}-\mathrm{R})$
or $\mathrm{h}=\frac{(2 \mathrm{H}+\mathrm{R})}{3}$
79. A uniform cylinder of mass $M$, radius $R$ is rotating about its own axis with a speed of $n$ r.p.s. It is gently placed against a corner as shown in Fig. 62. Coefficient of friction between walls and cylinder is $\mu$. The number of revolutions completed by cylinder before coming to rest is
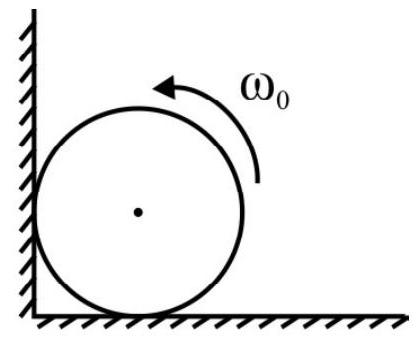
Fig. 62
(1) $\frac{\mathrm{n}^{2} \mathrm{R}\left(\mu^{2}+1\right)}{16 \pi \mu \mathrm{g}(\mu+1)}$
(2) $\frac{n^{2} R\left(\mu^{2}+1\right)}{32 \pi^{2} \mu g(\mu+1)}$
(3) $\frac{\mathrm{n}^{2} \mathrm{R}(\mu+1)}{2 \pi \mu \mathrm{g}\left(\mu^{2}+1\right)}$
(4) $\frac{n^{2} R^{2}\left(\mu^{2}+1\right)}{32 \pi^{2} \mu g(\mu+1)}$
Show Answer
Correct answer:(2)
Solution:
The forces acting are shown in Fig. 63. There is no translational motion therefore.
$$ \begin{equation*} \mathrm{N} _{1}+\mathrm{f} _{2}=\mathrm{Mg} \tag{i} \end{equation*} $$
and $\mathrm{N} _{2}=\mu \mathrm{N} _{1} \hspace{40mm} . . . . . .(ii)$
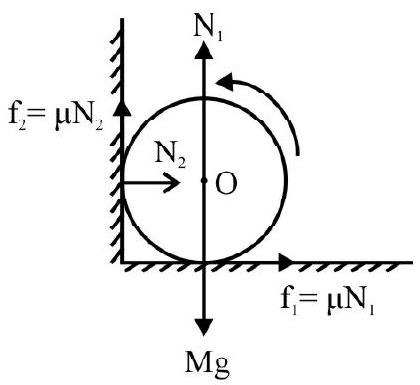
Fig. 63
From Eqns (i) and (ii) we have
$\mathrm{N} _{1}=\frac{\mathrm{Mg}}{\mu^{2}+1}$ and $\mathrm{N} _{2}=\frac{\mu \mathrm{Mg}}{\mu^{2}+1}$
Taking torque of forces about $\mathrm{O}$.
$\tau=\left(\mathrm{f} _{1}+\mathrm{f} _{2}\right) \mathrm{R}=\frac{\mu(\mu+1)}{\left(\mu^{2}+1\right)} \operatorname{MgR}$
$\tau$ is in clockwise direction.
Let $\alpha$ be the angular retardation. Then
$$ \begin{align*} & \left(\frac{1}{2} \mathrm{MR}^{2}\right) \alpha=\tau \\ \therefore \quad & \alpha=\frac{2 \mu \mathrm{g}(\mu+1)}{\left(\mu^{2}+1\right) \mathrm{R}} \tag{iv} \end{align*} $$
Given $\omega _{0}=2 \pi \mathrm{n} ; \omega=0 ; \alpha=-\frac{2 \mu \mathrm{g}(\mu+1)}{\left(\mu^{2}+1\right) \mathrm{R}} ; \theta=$ ?
$\therefore \quad \theta=\frac{\mathrm{n}^{2} \mathrm{R}\left(\mu^{2}+1\right)}{16 \mu \mathrm{g}(\mu+1)}$
The number of revolution $==\frac{\theta}{\pi}=\frac{n^{2}\left(\mu^{2}+1\right) R}{32 \pi^{2} \mu g(\mu+1)}$
80. A thin uniform rod $O A$ of length $L$, mass $M$ is pivoted to ground at end $O$ in a vertical plane. The rod is free to rotate about a horizontal axis through $O$. It is released from rest in position $O A$. When it is in position $O B$, the angular speed of rod is
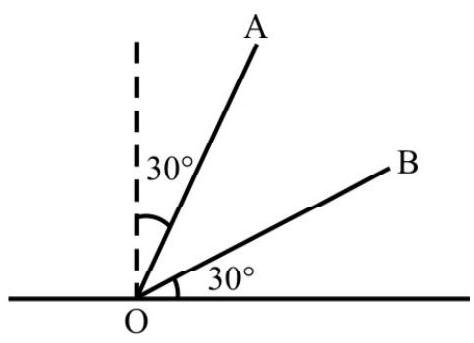
Fig. 64
(1) $\left[\frac{(3 \sqrt{3}-1) \mathrm{g}}{2 \mathrm{~L}}\right]^{1 / 2}$
(2) $\left[\frac{(3 \sqrt{3}-1) g}{L}\right]^{1 / 2}$
(3) $\left[\frac{(\sqrt{3}-1) g}{2 L}\right]^{1 / 2}$
(4) $\left[\frac{(\sqrt{3}-\sqrt{2}) \mathrm{g}}{\mathrm{L}}\right]^{1 / 2}$
Show Answer
Correct answer: (1)
Solution:
The loss is gravitational P.E in moving from position OA to position OB.
$$ =\operatorname{Mg} \frac{\mathrm{L}}{2}[\cos 30-\cos 60]=\frac{\mathrm{MgL}}{4}[\sqrt{3}-1] $$
This energy is converted into rotational K.E. of rod. Let $\omega$ be angular speed of rod in position OB.
Gain in rotational $\mathrm{K} . \mathrm{E}=\frac{1}{2} \mathrm{I} \omega^{2}=\frac{1}{2}\left(\frac{1}{3} \mathrm{ML}^{2}\right) \omega^{2}$
From law of conservation of energy
$\frac{\operatorname{MgL}}{4}[\sqrt{3}-1]=\frac{\mathrm{M}}{6} \mathrm{~L}^{2} \omega^{2}$
or $\quad \omega^{2}=\left[\frac{3(\sqrt{3}-1)}{2}\right]\left(\frac{g}{L}\right)$
$\therefore \omega=\left[\frac{(3 \sqrt{3}-1) \mathrm{g}}{2 \mathrm{~L}}\right]^{1 / 2}$










