Introduction

In study of kinematics we do not discuss about cause of motion. The study of Newtonian mechanics analysis in detail the cause of motion. This part of Physics is also known as dynamics. Newton’s laws of motion, three in number, give logic to the study of motion of bodies.

1. Force: It is as external agency which charges or tries to charge the state of rest or motion of a body or the direction of motion of the body. It is a vector quantity. It SI unit is newton (N). Dimensionally $\mathrm{F}=\left[\mathrm{MLT}^{-2}\right]$.

Some important forces in nature are:

(a) Gravitational force

(b) Electrostatic force

(c) Electromagnetic force

(d) Interatomic or intermolecular forces

(5) Nuclear force

2. Inertia : It is the property of a body by which it continues to be in state of rest or uniform motion along a straight path unless an external unbalanced force acts on the body. Inertia is of three types:

(a) Inertia of rest

(b) Inertia of motion

(c) Inertia of direction

Inertia to linear motion is measured by the mass of the body. Larger the mass; greater is the inertia of the body i.e. it is more difficult to change the state of rest or uniform motion of the body.

In absence of friction between a passenger and the bus, the passenger will not move with the bus when it starts. As a result, he will hit the back of the bus (Inertia of rest).

Likewise when the brakes are applied to the moving bus in above situation, the passenger will hit the front of the bus (Inertia of motion).

If the bus takes a turn to left, the passenger will the thrown towards right (Inertia of direction). This is because the directional inertia of the body of the passenger.

Linear Momentum : It is the quantity of motion present in a body. Mathematically, it is measured as product of mass and velocity $\mathbf{v}$ of the body.

Momentum $\mathbf{p}=\mathrm{m} \mathbf{v}$

It is a vector in the direction of velocity. Its SI unit is $\mathrm{kg} \mathrm{ms}^{-1}$ or Ns. Dimensionally momentum is $\mathrm{MLT}^{-1}$.

Laws of Motion

1. Newton’s First Law of Motion

It states that every body continues to be in a state of rest or uniform motion along a straight line unless an external unbalanced force is applied to change its state. The law gives qualitative definition of force.

Here the significance of the words external and unbalanced must be clearly understood. Internal forces are forces exerted on one another by the bodies making the system. The external forces are forces exerted on the system by everything else, except the system, known as surroundings. There is no overall motion of a system due to internal forces. For example, it is not possible to move a car by pushing it when we are sitting inside the car. The force is this case is internal force.

Similarly, an individual may not be able to move a loaded truck by pushing or pulling if. The force applied in this case is balanced by an equal and opposite force (or friction) which is apparently not visible.

2. Newton’s Second Law of Motion

According to second law the rate of change of linear momentum of a body is directly proportional to the net external applied force. The change in momentum takes place in the direction of the force.

The law gives a relation between force and momentum. It also gives a quantitative definition or measure of the force.

Mathematically,

$$ \begin{aligned} \mathbf{F}=\frac{\mathrm{d} \mathbf{p}}{\mathrm{dt}} & =\frac{\mathrm{d}}{\mathrm{dt}}(\mathrm{m} \mathbf{v})=\mathrm{m} \frac{\mathrm{d} \mathbf{v}}{\mathrm{dt}} \text { (for a system with constant mass) } \\ & =\mathrm{ma} \end{aligned} $$

$\mathbf{a}=\frac{\mathrm{d} \mathbf{v}}{\mathrm{dt}}=$ Instantaneous acceleration of body.

Remember

1. For a constant mass and changing velocity.

$$ \mathbf{F}=\mathrm{m} \frac{\mathrm{d} \mathbf{v}}{\mathrm{dt}} $$

2. For constant velocity and changing mass.

$$ \mathbf{F}=\mathbf{v} \frac{\mathrm{dm}}{\mathrm{dt}} $$

3. In terms of rectangular components of the force and momentum

$$ \mathrm{F} _{x}=\frac{\mathrm{dp} _{x}}{\mathrm{dt}} ; \mathrm{F} _{\mathrm{y}}=\frac{\mathrm{dp} _{\mathrm{y}}}{\mathrm{dt}} \text { and } \mathrm{F} _{\mathrm{z}}=\frac{\mathrm{dp} _{\mathrm{z}}}{\mathrm{dt}} $$

4. A force applied along $\mathrm{X}$-direction does not affect the momenta of the body along $\mathrm{Y}$ and $\mathrm{Z}$ directions and $\mathbf{F} _{y}$ does not affect $\mathbf{p} _{x}$ and $\mathbf{p} _{z}$. Similarly $\mathbf{F} _{z}$ does not produce any change in $\mathbf{p} _{x}$ and $\mathbf{p} _{y}$.

3. Newton’s Third Law of Motion

It states: To very action, there is an equal and opposite reaction.

Mathematically, $\mathbf{F} _{\mathrm{BA}}=-\mathbf{F} _{\mathrm{AB}}$

Where $\mathbf{F} _{\mathrm{BA}}$ is force on $\mathrm{B}$ due to $\mathrm{A}$ and $\mathbf{F} _{\mathrm{AB}}$ is force on $\mathrm{A}$ due to B. Therefore,

$$ \mathbf{F} _{\mathrm{AB}}+\mathbf{F} _{\mathrm{BA}}=0 $$

Remember

1. The forces of action and reaction do not cancel each other because they act on different bodies.

Units of Force : Absolute unit of force in SI system is newton. IN $=1 \mathrm{~kg} . \mathrm{m} / \mathrm{s}^{2}$

The gravitational unit of force in $\mathrm{kg}$ wt or $\mathrm{kg} \mathrm{f}$.

$1 \mathrm{~kg} \mathrm{wt}=1 \mathrm{~kg} \mathrm{f}=9.8 \mathrm{~kg} \mathrm{~m} / \mathrm{s}^{2}=9.8 \mathrm{~N}$

Impulse of a Force : A large force acting for a small time interval is said to impart an impulse to the object.

The impulse of a force is numerically equal to the product of the force $(\mathbf{F})$ applied and the time $(\Delta t)$ for which it acts, i.e. Impulse $=\mathbf{F} \times \Delta t$

The impulse of a force in equal to the change in momentum of the body.

$\therefore$ Impulse $=$ Force $\times$ Time

$=$ Change in momentum

The change in momentum of a body is large if a larger force in applied or if the force is applied for a larger duration of time.

Impulse in a vector quantity in the direction of force.

Impulse $\mathbf{J}=\mathbf{F}$.t ; if force is constant

$=\int \mathbf{F} . \mathrm{dt}$; if the force in variable

$$ =\mathbf{p} _{2}-\mathbf{p} _{1}=\mathrm{m}(\mathbf{v}-\mathbf{u}) $$

Impulse of a force can also be measured as the area under the force time graph.

A large force acting for a short duration is called impulsive force (See figure). The shaded area gives the impulse of the force applied.

The SI Unit of impulse is $\mathrm{N}-\mathrm{s}$ or $\mathrm{kg} \mathrm{ms}^{-1}$.

Dimensionally impulse is $\mathrm{MLT}^{-1}$.

Note that impulse and momentum have same dimensional formula and same units.

Sometimes it is simpler to use the impulse momentum relation in terms

of their components as under:

$$ \begin{aligned} & \mathbf{J} _{x}=\int \mathbf{F} _{x} \mathrm{dt}=\Delta \mathbf{p} _{x}=\mathrm{m}\left(\mathbf{v} _{x}-\mathbf{u} _{x}\right) \\ & \mathbf{J} _{y}=\int \mathbf{F} _{y} \mathrm{dt}=\Delta \mathbf{p} _{y}=\mathrm{m}\left(\mathbf{v} _{y}-\mathbf{u} _{y}\right) \\ & \mathbf{J} _{z}=\int \mathbf{F} _{z} \mathrm{dt}=\Delta \mathbf{p} _{z}=\mathrm{m}\left(\mathbf{v} _{z}-\mathbf{u} _{z}\right) \end{aligned} $$

Apparent Weight of a Body in a Lift

(i) In a lift at rest or in uniform motion (upwards or downwards) i.e. when $\mathbf{a}=0$; the weight of a body is its true weight.

We have $\mathbf{R}=\mathrm{mg}$

(ii) When a lift moves upwards with uniform acceleration ’ $Q$ ‘, apparent weight of a body in the lift increase.

We have $\mathbf{R}-\mathrm{mg}=\mathrm{ma}$

$$ \therefore \mathbf{R}=\mathrm{m}(\mathbf{g}+\mathbf{a})>\mathrm{m} \mathbf{g} $$

(iii) When a lift moves downwards with a uniform acceleration ’ $\mathbf{a}$ ‘; apparent weight of a body is less than its actual weight.

From the figure:

$$ \begin{aligned} & \mathbf{F}+\mathbf{F} _{\mathrm{fic}}=\mathrm{m} \mathbf{a} \\ & \mathrm{m} \mathbf{g}-\mathbf{R}=\mathrm{m} \mathbf{a} \end{aligned} $$

$$ \therefore \mathbf{R}=\mathrm{m}(\mathbf{g}-\mathbf{a})<\mathrm{m} \mathbf{g} $$

(iv) In a lift falling freely, we have $\mathbf{a}=\mathbf{g}$

$$ \therefore \quad \mathbf{R}=\mathrm{m}(\mathbf{g}-\mathbf{g})=0 $$

The body experience weightlessness.

Important : When a person of mass $m$ climbs up a rope suspended from a rigid support with acceleration ’ $\mathbf{a}$ ‘; the tension in the rope in $\mathbf{T}=\mathrm{m}(\mathbf{g}+\mathbf{a})$

When the person climbs down the rope with acceleration ’ $\mathbf{a}$ ‘; the tension in the rope is $\mathbf{T}=\mathrm{m}(\mathbf{g}-\mathbf{a})$.

If the rope supports the weight of the man (with man neither climbing up nor down); the tension in the rope equals his weight i.e. $\mathrm{T}=\mathrm{mg}$

To solve problem, in a non-initial frame, using newton’s second law, we have,

$$ \mathbf{F}+\mathbf{F} _{\mathrm{fic}}=\mathrm{m} \mathbf{a} $$

Note that when lift accelerates upwards or downwards, the mass inside the lift experiences a force ma; in addition to its weight. The direction of this force is always opposite to the direction of acceleration of the lift. In other words, ma acts vertically downwards when lift accelerates upwards. The force ma is vertically upwards if the lift accelerates downwards. This extra force is known as an inertial force or a fictitious force. This force is purely due to acceleration of the frame of reference, i.e. the left.

Inertial and Non-inertial Frames of Reference

A frame of reference either at rest or having a uniform motion is an INERTIAL frame of reference. The external forces acting on a body in this frame are real or physical forces $\mathbf{F}$. We use Newton’s second law in the form $\mathbf{F}=$ ma; to solve problems.

Any frame having an accelerated motion is a non-inertial frame. In such a frame, the body experiences:

(i) Physical force (F) and

(ii) Pseudo or Fictitious force, $\mathbf{F} _{\mathrm{fic}}=\mathrm{m}\left(-\mathbf{a}^{*}\right)$

where $\mathbf{a}^{*}$ is acceleration of frame of reference. To solve problem, in a non-inertial frame; using Newton’s second law, we have,

$$ \mathbf{F}+\mathbf{F} _{\mathrm{fic}}=\mathrm{ma} $$

Example-1 :

A heavy block is supported by a chord C from a rigid support and another chord D is attached on the other side of the block as shown. If the free end of the chord $D$ is given a sudden pull; the chord $\mathrm{D}$ breaks. If the chord $\mathrm{D}$ is pulled steadily; chord $\mathrm{C}$ breaks. Why?

Show Answer

Solution :

The difference can be explained by law of inertia. When the free end of $\mathrm{D}$ is given a sudden jerk; the block was at rest and continues to remain at rest. So the chord D breaks.

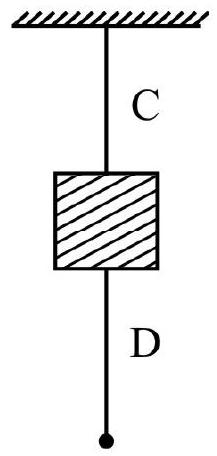
If $\mathrm{D}$ is pulled steadily; the block comes in motion and due to inertia continues to be in motion. Hence chord C breaks.

Example-2 :

An object in thrown vertically upwards with a certain velocity. At the instant, the object attains the maximum height, the gravity is turned off. What will be the motion of the object thereafter?

Show Answer

Solution :

At the highest point, the object comes to rest. Normally it starts its downwards journey under gravity. In this case, since there is no force acting on the object it will continue to be at rest.

Example-3 :

A $5000 \mathrm{~kg}$ rocket is set for vertical firing. The exhaust gases move at $800 \mathrm{~ms}^{-1}$ and give the rocket an upward acceleration of $20 \mathrm{~ms}^{-2}$. The mass of gases rejected per second is

(1) $187.5 \mathrm{~kg}$

(2) $185.5 \mathrm{~kg}$

(3) $137.5 \mathrm{~kg}$

(4) $127.5 \mathrm{~kg}$

Show Answer

Solution :

We have $\mathbf{F}=\mathbf{u} _{\text {ext }} \frac{\mathrm{dm}}{\mathrm{dt}}$

In this case;

$\mathrm{F}-\mathrm{mg}=\mathrm{ma}$

$$ \begin{aligned} & F=M(g+a) \\ & =(5000)(10+20) \\ & =30 \times 5000 \mathrm{~N} \end{aligned} $$

Also, $30 \times 5000=800 \times x \quad\left(x=\frac{\mathrm{dm}}{\mathrm{dt}}\right)$

$\therefore x=\frac{1500}{8}=187.5 \mathrm{~kg}$

Option (1) is correct.

Example-4 :

A $200 \mathrm{gm}$ ball moving normal towards a wall at $20 \mathrm{~m} / \mathrm{s}$ rebounds at $10 \mathrm{~m} / \mathrm{s}$. The change in momentum of the ball during impact is

(1) $2000 \mathrm{~kg} \mathrm{~m} / \mathrm{s}$ towards the wall

(2) $6000 \mathrm{~kg} \mathrm{~m} / \mathrm{s}$ towards the wall

(3) $6 \mathrm{~kg} \mathrm{~m} / \mathrm{s}$ towards the wall

(4) $6 \mathrm{~kg} \mathrm{~m} / \mathrm{s}$ away from the wall

Show Answer

Solution :

We have $\mathrm{m}=200 \mathrm{gm}=\frac{1}{5} \mathrm{~kg}$

$$ \begin{aligned} & \mathrm{u}=20 \mathrm{~m} / \mathrm{s} \text { towards wall } \\ & \mathrm{v}=10 \mathrm{~m} / \mathrm{s} \text { away from the wall } \end{aligned} $$

$\therefore$ Change in momentum $=\mathrm{m}(\mathrm{v}-\mathrm{u})$

$$ \begin{aligned} & =\frac{1}{5}[10-(-20)] \\ & =6 \mathrm{~kg} \mathrm{~m} / \mathrm{s} \text { away from the wall. } \end{aligned} $$

Example-5 :

A body of mass $2 \mathrm{~kg}$ in uniform circular motion at $10 \mathrm{~m} / \mathrm{s}$ moves from a point A to a diametrically opposite point $B$ in its path. The magnitude of change in momentum is

(1) zero

(2) $40 \mathrm{~kg} \mathrm{~m} / \mathrm{s}$

(3) $20 \sqrt{2} \mathrm{~kg} \mathrm{~m} / \mathrm{s}$

(4) $20 \mathrm{~kg} \mathrm{~m} / \mathrm{s}$

Show Answer

Solution :

Given $\mathrm{m}=2 \mathrm{~kg}$

$\mathrm{u} _{\mathrm{A}}=+10 \mathrm{~m} / \mathrm{s}$

$\mathrm{v} _{\mathrm{B}}=-10 \mathrm{~m} / \mathrm{s}$ [The direction of velocity is reversed.]

$\therefore$ Change in momentum $=\mathrm{mv}-\mathrm{mu}$

$$ =-10-10=-20 \mathrm{~kg} \mathrm{~m} / \mathrm{s} $$

$\therefore$ Magnitude of change in momentum $=|-20|$

$$ =20 \mathrm{~kg} \mathrm{~m} / \mathrm{s} $$

Important : Here we may note that the change in magnitude of momentum is zero.

$$ \left|\mathbf{p} _{\mathrm{A}}\right|=\left|\mathbf{p} _{\mathrm{B}}\right| \quad \therefore\left|\Delta \mathbf{p} _{\mathrm{A}}\right|-\left|\Delta \mathbf{p} _{\mathrm{B}}\right|=0 $$

But magnitude of change in momentum.

$$ =|\Delta \mathbf{p}|=\left|\mathbf{p} _{\mathrm{B}}-\mathbf{p} _{\mathrm{A}}\right| \neq 0 $$

Example-6 :

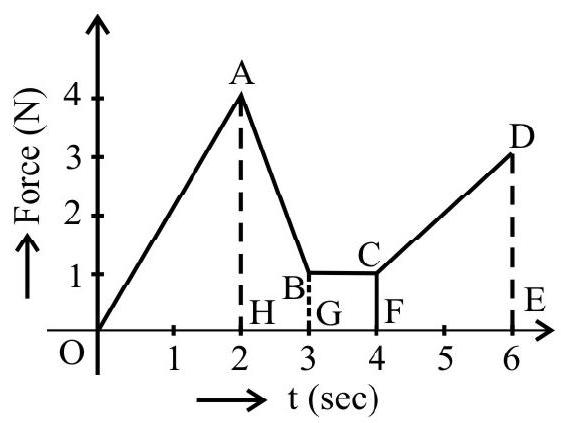
A body of mass $5 \mathrm{~kg}$ initially at rest is subjected to force varying with time as shown in $\mathrm{F} \quad v/ \mathrm{s} \quad \mathrm{t} \quad \mathrm{graph}$. Calculate the velocity of the body after 4 second.

Show Answer

Solution :

Given $\mathrm{m}=5 \mathrm{~kg}$

$$ \begin{aligned} & \mathrm{u}=0 \\ & \mathrm{v}=? \end{aligned} $$

We have impulse $=$ Change in momentum

$$ =\mathrm{m}(\mathrm{v}-\mathrm{u})=\mathrm{mv} $$

Also impulse $=$ Area under force - time graph

$$ =\mathrm{Ar} \mathrm{OABCF} $$

$$ \begin{aligned} & =\operatorname{Ar}(\mathrm{OAH})+\operatorname{Ar}(\mathrm{BCFG})+\operatorname{Ar}(\mathrm{ABGH}) \\ & =\frac{1}{2} \times 2 \times 4+(1 \times 1)+\frac{1}{2}(4+1) \times 1 \\ & =4+1+\frac{5}{2}=7.5 \mathrm{~N}-\mathrm{s} \end{aligned} $$

$\therefore \mathrm{mv}=7.5 \Rightarrow \mathrm{v}=\frac{7.5}{5}=1.5 \mathrm{~ms}^{-1}$

Example-7 :

A body of mass $2 \mathrm{~kg}$ initially moving at $10 \mathrm{~m} / \mathrm{s}$ is subjected to a time dependent force $F(t)=(2 t+3) \mathrm{N}$ where $t$ is in seconds. Calculate the velocity of the body at the end of five seconds.

Show Answer

Solution :

Given $\mathrm{m}=2 \mathrm{~kg}$

$$ \begin{aligned} & \mathrm{u}=10 \mathrm{~m} / \mathrm{s} \\ & \mathrm{v}=? \\ & \mathrm{t}=5 \mathrm{~s} \end{aligned} $$

We have change in momentum $=$ impulse

$$ \begin{aligned} & \mathrm{m}(\mathrm{v}-\mathrm{u})=\int _{\mathrm{t}=0}^{5 \mathrm{~s}} \mathrm{~F}(\mathrm{t}) \mathrm{dt} \\ & =\int _{\mathrm{t}=0}^{5 \mathrm{~s}}(2 \mathrm{t}+3) \mathrm{dt} \\ & =\left|2 \cdot \frac{\mathrm{t}^{2}}{2}+3 \mathrm{t}\right| _{0}^{5} \\ & =\left|\mathrm{t}^{2}+3 \mathrm{t}\right| _{0}^{5}=40 \mathrm{Ns} \\ & \therefore \mathrm{v}-\mathrm{u}=\frac{40}{\mathrm{~m}}=20 \mathrm{~m} / \mathrm{s} \\ & \mathrm{v}=(20+\mathrm{u})=(20+10) \mathrm{m} / \mathrm{s} \\ & =30 \mathrm{~m} / \mathrm{s} \end{aligned} $$

Example-8 :

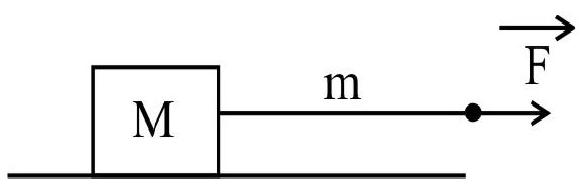
A body of mass $M$ in being pulled by a string of mass $m$. A force $\mathbf{F}$ is applied at the free end of the string to pull the mass. Calculate the force exerted by the string on the body.

Show Answer

Solution :

For the system; total mass $=\mathrm{m}+\mathrm{M}$

Force $=\mathrm{F}$

Acceleration $\mathrm{a}=\frac{\mathrm{F}}{\text { Total mass }}=\frac{\mathrm{F}}{\mathrm{m}+\mathrm{M}}$

For the body; $\mathrm{T}=\mathrm{Ma}$

$$ =M\left(\frac{F}{m+M}\right) $$

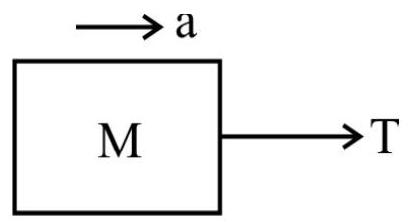
$\therefore$ Force on the block $=\frac{F M}{F+m}$

Example-9 :

Two blocks of mass $12 \mathrm{~kg}$ and $2 \mathrm{~kg}$ are tied to the ends of a string. If the table and the pulley are smooth and the string in light; calculate the acceleration of $2 \mathrm{~kg}$ block and the tension in the string.

Show Answer

Solution :

For $12 \mathrm{~kg}$ object

$\mathrm{T}=12$. $\mathrm{a} \hspace{40mm} . . . . . .(1)$

For $2 \mathrm{~kg}$ object $\mathrm{T}-2 \times 9.8=2 . \mathrm{a} \hspace{40mm} . . . . . .(2)$

$\therefore 12 \mathrm{a}-2 \mathrm{a}=2 \times 9.8$

$10 a=19.6$

$\mathrm{a}=1.96 \mathrm{~m} / \mathrm{s}^{2}$

$\mathrm{T}=12 \mathrm{a}=12 \times 1.96 \simeq 23.5 \mathrm{~N}$

Example-10 :

Three blocks A, B and C wth mass $1.5 \mathrm{~kg}, 2 \mathrm{~kg}$ and $1 \mathrm{~kg}$ respectively are placed on a rough surface with coefficient of friction 0.2 with the blocks. Calculate the force $\mathrm{F}$ required to produce an acceleration of $3 \mathrm{~m} / \mathrm{s}^{2}$ in the system. What is the force exerted by (i) A on B (ii) B on C?

Show Answer

Solution :

Let ’ $a$ ’ be the acceleration o the system towards the direction o the applied force. The frictional force $\mu\left(\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}\right) \mathbf{g}$ acts towards left opposite to $\mathbf{F}$.

$\therefore \mathbf{F}-\mu\left(\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}\right) \mathbf{g}=\left(\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}\right) \mathbf{a}$

or $\quad \mathbf{F}=\left(\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}\right)(\mathbf{a}+\mu \mathbf{g})$

$$ \begin{aligned} & =(1.5+2+1)(3+0.2 \times 9.8) \\ & =4.5 \times 4.96=22.3 \mathrm{~N} \end{aligned} $$

The blocks $\mathrm{B}$ and $\mathrm{C}$ move due to force of $\mathrm{A}$ on $\mathrm{B}$.

$\therefore$ Force on $B=\left(\mathrm{m} _{\mathrm{B}}+\mathrm{m} _{\mathrm{C}}\right) \mathbf{a}+\left(\mathrm{m} _{\mathrm{B}}+\mathrm{m} _{\mathrm{C}}\right) \mu \mathbf{g}$

$$ \begin{aligned} & =(3)(3+1.96) \\ & =3 \times 4.96=14.88 \mathrm{~N} \end{aligned} $$

Force on $\mathrm{C}=\mathrm{m} _{\mathrm{C}}(\mathrm{a}+\mu \mathrm{g})$

$$ =1(3+1.96)=4.96 \mathrm{~N} $$

Example-11 :

Two bodies of mass $6 \mathrm{~kg}$ and $9 \mathrm{~kg}$ are connected with a light inextensible string passing over a smooth pulley with one of the bodies on a smooth inclined plane $\left(\theta=30^{\circ}\right)$ and the other hanging freely from the other end. Show that the time taken by $9 \mathrm{~kg}$ to pull $6 \mathrm{~kg}$ up the entire length is half the time taken by $6 \mathrm{~kg}$ to pull $9 \mathrm{~kg}$ over the same plane.

Show Answer

Solution :

The two situation are shown in Fig. (a) and Fig. (b).

Case (1) Fig. (a) Let $\mathrm{a} _{1}$, be the acceleration of $6 \mathrm{~kg}$ object

Then $6 \mathrm{~g}-\mathrm{T}=6 \mathrm{a} _{1} \hspace{40mm} . . . . . .(1)$

$T-9 g \sin 30=9 a _{1} \hspace{40mm} . . . . . .(2)$

$(1)+(2)$ given $6 g-9 g \sin 30=15 a _{1}$

$$ 1.5 \mathrm{~g}=15 \mathrm{a} _{1} \text { or } \mathrm{a} _{1}=\frac{\mathrm{g}}{10} $$

To cover a distance ’ $\ell$ ‘; time ’ $t _{1}$ ’ is given by

$$ \begin{align*} & \frac{1}{2} \mathrm{a} _{1} \mathrm{t} _{1}^{2}=\ell \quad \text { or } \quad \mathrm{t} _{1}^{2}=\frac{2 \ell}{\mathrm{a}}-\frac{2 \ell}{\mathrm{g} / 10}=\frac{20 \ell}{\mathrm{g}} \\ & \text { or } \mathrm{t} _{1}=\sqrt{\frac{20 \ell}{\mathrm{g}}} \tag{3} \end{align*} $$

Case (2) Fig. (b) $9 g-T=9 a _{2} \hspace{40mm} . . . . . .(4)$

$$ \begin{equation*} T-6 g \sin 30-6 a _{2} \tag{5} \end{equation*} $$

(4) $+(5)$ give,

$6 \mathrm{~g}=15 \mathrm{a} _{2}$

$\therefore$ Time $ _{2}$ for motion up the entire length ’ $\ell$ ’ of the in incline in given by

$$ \begin{align*} & \frac{1}{2} \mathrm{a} _{2} \mathrm{t} _{2}^{2}=\ell \\ & \mathrm{t} _{2}=\sqrt{\frac{2 \ell}{\mathrm{a} _{2}}}=\sqrt{\frac{2 \ell}{2 / 5 \mathrm{~g}}}=\sqrt{\frac{5 \ell}{\mathrm{g}}} \tag{6} \\ & \therefore \frac{\mathrm{t} _{2}}{\mathrm{t} _{1}}=\frac{\sqrt{5 \ell / g}}{\sqrt{\frac{20}{\mathrm{~g}}}}=\frac{1}{2} \end{align*} $$

Example-12 :

Two masses $\mathrm{m} _{1}$ and $\mathrm{m} _{2}$ are attached to a spring balance $\mathrm{S}$ as shown. Assuming the pulleys to be light and frictionless, calculate the reading in the spring balance. (Take $\mathrm{m} _{1}>\mathrm{m} _{2}$ ).

Show Answer

Solution :

The spring balance will read tension.

We have $\mathrm{m} _{1} \mathrm{~g}-\mathrm{T}=\mathrm{m} _{1} \mathrm{a} \quad \quad \quad \quad \quad \quad (1) $

$\mathrm{T}-\mathrm{m_2} \mathrm{~g} $= $ \mathrm{m_2} \mathrm{a} \hspace{40mm} . . . . . .(2)$

$\therefore(1)+(2)$ gives $\left(\mathrm{m} _{1}-\mathrm{m} _{2}\right) \mathrm{g}=\left(\mathrm{m} _{1}+\mathrm{m} _{2}\right) \mathrm{a}$

$\Rightarrow \mathrm{a}=\left(\frac{\mathrm{m} _{1}-\mathrm{m} _{2}}{\mathrm{~m} _{1}+\mathrm{m} _{2}}\right) \mathrm{g}$

Using in (1) $T=m _{1} g-m _{1}\left(\frac{m _{1}-m _{2}}{m _{1}+m _{2}}\right) g$

$$ \begin{aligned} & =\mathrm{m} _{1} \mathrm{~g}\left[1-\frac{\mathrm{m} _{1}-\mathrm{m} _{2}}{\mathrm{~m} _{1}+\mathrm{m} _{2}}\right] \\ & =2 \frac{\mathrm{m} _{1} \mathrm{~m} _{2}}{\mathrm{~m} _{1}+\mathrm{m} _{2}} \mathrm{~g} \end{aligned} $$

is the reading in the balance.

Example-13 :

An elevator with a total mass of $4000 \mathrm{~kg}$ has an upward acceleration due to a $48000 \mathrm{~N}$ tension in the supporting cable. Calculate the acceleration and the time it takes to cover $9.0 \mathrm{~m}$. What will the reading in a weighing machine in the elevator with a $60 \mathrm{~kg}$ man standing on the machine. $\left[\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right.$ ]

Show Answer

Solution :

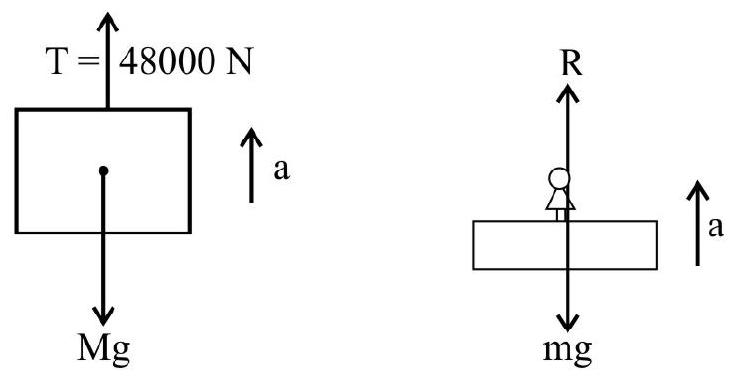
We have $\mathrm{T}-\mathrm{mg}=\mathrm{ma}$

$$ \begin{aligned} & 48000-4000 \times 10=\mathrm{ma} \\ & \mathrm{a}=\frac{8000}{4000}=2 \mathrm{~m} / \mathrm{s}^{2} \end{aligned} $$

Again $\mathrm{S}=\frac{1}{2} \mathrm{at}^{2} \Rightarrow \mathrm{t}=\sqrt{\frac{2 \mathrm{~s}}{\mathrm{a}}}=\sqrt{\frac{2 \times 9}{2}}=3$ second .

For the man on weighing machine

$\mathrm{R}-\mathrm{mg}=\mathrm{ma}$

$\therefore \mathrm{R}=\mathrm{m}(\mathrm{g}+\mathrm{a})=60(10+2)$

$=60 \times 12 \mathrm{~N}$

$=6 \times 12 \mathrm{~kg} \mathrm{wt}=72 \mathrm{~kg} \mathrm{wt}$

Law of Conservation of Linear Momentum

According to this Law:

The total linear momentum, of a given system, remains conserved if the net external force acting on this system is zero.

$\therefore$ If $\mathbf{F} _{\text {ext }}=0$, We have,

$\mathbf{p} _{1}+\mathbf{p} _{2}+\ldots . .+\mathbf{p} _{\mathrm{n}}=$ a constant

or $\mathrm{m} _{1} \mathbf{v} _{1}+\mathrm{m} _{2} \mathbf{v} _{2}+\ldots .+\mathrm{m} _{\mathrm{n}} \mathbf{v} _{\mathrm{n}}=$ a constant

For a system of two bodies, undergoing a collision, we have,

$\mathrm{m} _{1} \mathbf{v} _{1}+\mathrm{m} _{2} \mathbf{v} _{2}=\mathrm{m} _{1} \mathbf{u} _{1}+\mathrm{m} _{2} \mathbf{u} _{2}$

Let us apply this law to a bullet and the gun system. Here the system is at rest to start with.

Hence, when a bullet is fired from a gun we have,

Initial momentum $=$ zero

$\therefore$ Final momentum of the bullet and gun system must again be zero.

$\therefore \mathrm{mv}+\mathrm{MV}=0$

$\therefore$ Recoil velocity of the gun.

$$ \mathbf{V}=-\frac{\mathrm{m} \mathbf{v}}{\mathrm{M}} $$

Rocket Propulsion / Body with Variable Mass

For a rocket moving in force free space; when a rocket is fired; the backward momentum of the ejected gases imports an equal forward momentum to the rocket. As the fuel is burnt; the mass of the rocket decreases and the acceleration keeps on increasing.

Consider a rocket of total mass (sum of mass of body of rocket and fuel gases inside) $\mathrm{m} _{0}$ starting from rest in a force free space. Let $\alpha=\frac{\mathrm{dm}}{\mathrm{dt}}=$ the constant rate of burning of fuel.

$\mathrm{u}=$ The exhaust speed of ejected out gases with respect to rocket, $\mathrm{u}$ is constant.

The thrust, F, on rocket due to fuel ejected is $u \alpha=u \frac{\mathrm{dm}}{\mathrm{dt}}$. By applying law of conservation of linear momentum, it can be shown that the instantaneous speed, $\mathrm{v}$, acquired by rocket is given by

$$ \mathrm{v}=2.303 \mathrm{u} \log \left(\frac{\mathrm{m} _{0}}{\mathrm{~m}}\right) $$

where $\mathrm{m}=\mathrm{m} _{0}-\alpha \mathrm{t}=$ The instantaneous mass of the rocket.

Concurrent Forces

The forces acting at the same point of a body are called concurrent forces.

Equilibrium of Concurrent Forces: For a number of concurrent forces acting on a body in equilibrium, the forces can be represented by a closed polygon taken in order or the resultant force is zero.

$$ \mathbf{F} _{1}+\mathbf{F} _{2}+\mathbf{F} _{3}+\ldots \ldots+\mathbf{F} _{\mathrm{n}}=0 $$

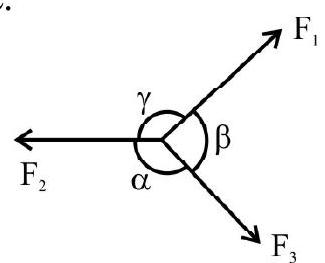
Lami’s Theorem: For three forces acting on a particle to keep it in equilibrium, we have,

$$ \frac{F _{1}}{\sin \alpha}=\frac{F _{2}}{\sin \beta}=\frac{F _{3}}{\sin \gamma} $$

The theorem is very useful in solving problems related to three concurrent forces in equilibrium.

We may also write

$$ \begin{align*} & \mathbf{F} _{1 x}+\mathbf{F} _{2 x}+\mathbf{F} _{3 x}=0 \tag{1} \\ & \mathbf{F} _{1 y}+\mathbf{F} _{2 y}+\mathbf{F} _{3 y}=0 \tag{2} \end{align*} $$

$$ \begin{equation*} \mathbf{F} _{1 z}+\mathbf{F} _{2 z}+\mathbf{F} _{3 z}=0 \tag{3} \end{equation*} $$

The above three equation in terms of the components have to be simultaneously satisfied for the system to be in equilibrium.

Example-14 :

A neutron having a mass of $1.67 \times 10^{-27} \mathrm{~kg}$ moving at $10^{8} \mathrm{~ms}^{-1}$ collides with a deuteron at rest and sticks to it. If the mass of the deuteron is $3.34 \times 10^{-27} \mathrm{~kg}$, find the speed of the combination.

Show Answer

Solution :

We have, $\mathrm{m} _{\mathrm{n}}=1.67 \times 10^{-27} \mathrm{~kg}$

$$ \begin{aligned} & \mathrm{u} _{\mathrm{n}}=10^{8} \mathrm{~m} / \mathrm{s} \\ & \mathrm{m} _{\mathrm{d}}=3.34 \times 10^{-27} \mathrm{~kg} \\ & \mathrm{u} _{\mathrm{d}}=0 \end{aligned} $$

Mass of the combination after collision.

$$ \begin{gathered} =\mathrm{m} _{\mathrm{n}}+\mathrm{m} _{\mathrm{d}}=\left(1.67 \times 10^{-27}+3.34 \times 10^{-27}\right) \mathrm{kg} \\ =5.01 \times 10^{-27} \mathrm{~kg} \end{gathered} $$

By principle of momentum conservation.

Momentum after collision $=$ momentum before collision .

$5.01 \times 10^{-27} \mathrm{~V}=1.67 \times 10^{-27} \times 10^{8}$

$\therefore \mathrm{V}=\frac{1}{3} \times 10^{8} \mathrm{~m} / \mathrm{s}$

Example-15:

A disc of mass $50 \mathrm{~g}$ is kept floating horizontally by throwing 10 marbles per second against if from its bottom. If mass of each marble is $20 \mathrm{gm}$, calculate the velocity with which each marble hits the disc to keep it afloat. Assume the marbles hit the disc normally and rebound with equal speed.

Show Answer

Solution :

Mass of the disc $=50 \mathrm{gm}=5 \times 10^{-2} \mathrm{~kg}$

Mass of each marble $=20 \mathrm{gm}=20 \times 10^{-3} \mathrm{~kg}$

Number of marbles per $\mathrm{sec}=10$

Let velocity each marble the $\mathrm{V} \mathrm{m} / \mathrm{s}$.

Then change in momentum of each marble.

$$ =\mathrm{mV}-(-\mathrm{mV})=2 \mathrm{mV} $$

$2 \times 20 \times 10^{-3} \times \mathrm{V} \mathrm{kg} \quad \mathrm{m} / \mathrm{s}$

Total change in momentum of the mables per sec.

$$ \begin{aligned} & =10 \times 2 \times 20 \times 10^{-3} \mathrm{~V} \\ & =0.4 \mathrm{~V} \\ & =\text { Force (by II law) } \end{aligned} $$

To keep the disc afloat;

Force due to marbles $=$ weight of the disc

or $$ \begin{aligned} 0.4 \mathrm{~V} & =\mathrm{m} _{\text {disc }} \mathrm{g} \\ & =5 \times 10^{-2} \times 10 \end{aligned} $$

$\therefore \mathrm{V}=\frac{50 \times 10^{-2}}{.4}=1.25 \mathrm{~m} / \mathrm{s}$

Example-16:

A bomb of mass $11 \mathrm{~kg}$ at rest at $\mathrm{O}$ explodes splitting into there pieces. Two of the pieces fly as shown. Calculate the speed of third piece. In which direction does it fly?

Show Answer

Solution :

Here initial momentum $=$ zero

$\therefore$ Total final momentum $=$ zero

Total momentum of the two pieces shown can be calculated by using law of vector addition.

We have $\mathbf{p} _{1}=10 \mathrm{~kg} \mathrm{~m} / \mathrm{s}, \mathbf{p} _{2}=10 \mathrm{~kg} \mathrm{~m} / \mathrm{s} ; \theta=120^{\circ}$

$\therefore \mathrm{p} _{\text {net }}=\sqrt{\mathrm{p} _{1}^{2}+\mathrm{p} _{2}^{2}+2 \mathrm{p} _{1} \mathrm{p} _{2} \cos 120}=\mathrm{p} _{1}=10 \mathrm{~kg} \mathrm{~m} / \mathrm{s}$

By symmetry $\mathbf{p} _{\text {net }}$ acts in a direction bisecting the angle between $\mathbf{p} _{1}$ and $\mathbf{p} _{2}$.

Total final momentum $=0$

$\therefore$ Momentum of the third piece $=\mathbf{p} _{3}=-\mathbf{p}$ along OA

$$ =10 \mathrm{kgm} / \text { along } \mathbf{O B} $$

Mass of third piece $=(11-2-5)$ by $=4 \mathrm{~kg}$

$\therefore 4 \mathbf{v}=10$ along $\mathbf{O B}$

or $\mathbf{v}=2.5 \mathrm{~m} / \mathrm{s}$ at $120^{\circ}$ with $\mathbf{p} _{1}$ or $\mathbf{p} _{2}$ as shown.

Example-17:

A ball of mass $2 \mathrm{~kg}$ hangs in equilibrium from two strings $\mathrm{OP}$ and $\mathrm{OQ}$ as shown. Calculate the tension in $\mathrm{OP}$ and OQ.

Show Answer

Solution :

Various forces acting at point ’ $\mathrm{O}$ ’ are as shown in the figure.

As $20 \mathrm{~N} ; \mathrm{T} _{1}$ and $\mathrm{T} _{2}$ are in equilibrium; we have

$$ \frac{\mathrm{T} _{1}}{\sin 150}=\frac{\mathrm{T} _{2}}{\sin 120}=\frac{20}{\sin 90} \quad \text { (Lami’s theorem) } $$

or $\frac{\mathrm{T} _{1}}{\sin 30}=\frac{\mathrm{T} _{2}}{\sin 60}=20 \mathrm{~N}$

$\therefore \mathrm{T} _{1}=20 \sin 30=10 \mathrm{~N}$

$\mathrm{T} _{2}=20 \sin 60^{\circ}=10 \sqrt{3} \mathrm{~N}$

Example-18 :

A body of mass ’ $\mathrm{m}$ ’ is suspended by means of strings OA and OB. Assuming the strings to be light and inextensible, calculate $\mathrm{T} _{1}$ and $\mathrm{T} _{2}$.

Show Answer

Solution :

From the free body diagram shown, we have

$$ \mathrm{T} _{1} \cos \alpha=\mathrm{T} _{2} \cos \beta $$

or $\quad \mathrm{T} _{2}=\mathrm{T} _{1} \frac{\cos \alpha}{\cos \beta}$

$$ \begin{gathered} \mathrm{T} _{1} \sin \alpha+\mathrm{T} _{2} \sin \beta=\mathrm{mg} \\ \text { or } \quad \mathrm{T} _{1} \sin \alpha+\mathrm{T} _{1} \frac{\cos \alpha}{\cos \beta} \sin \beta=m g \end{gathered} $$

$\mathrm{T} _{1} \frac{[\sin \alpha \cos \beta+\cos \alpha \sin \beta]}{\cos \beta}=\mathrm{mg}$

$\therefore \mathrm{T} _{1}=\frac{\mathrm{mg} \cos \beta}{\sin (\alpha+\beta)}$

Similarly, $\mathrm{T} _{2}=\frac{\mathrm{mg} \cos \alpha}{\sin (\alpha+\beta)}$

The Free Body Diagrams

A diagram for each body in a system indicating all the forces exerted on the body by the remaining parts of the system and the external agents is called free-body diagram.

In mechanics, we usually come across systems consisting of a number of bodies / particles under the action of a number of forces due to their mutual interaction; gravitational forces, frictional force, force due to strings, springs (called tension); supports etc.

Solution of such problems can be simplified by using the following steps:

1. Draw a diagram showing various parts of the system with links, supports etc.

2. Select any convenient part of the system.

3. Draw a separate diagram for the part selected above showing all the forces on it by the remaining parts of the system and also by external agents. This diagram is called the free body diagram.

4. Remember to include the information about the magnitude and direction of forces which are given and which you are sure of. The remaining forces are treated as unknown. Use Newton’s second law of motion to get an equation of motion for the chosen part i.e. equate the net force acting in a particular direction to the product of mass and acceleration of the body in that particular direction.

5. Follow the same procedure for any other part of the system to get more equations. You need as many independent equations to solve the problem as the number of unknowns.

6. Solve the equations obtained for different parts of the system to obtain the values of the desired unknowns or to get a desired equation.

Following points must be kept in mind while drawing the free body diagram (FBD)

• The reaction force (called normal reaction) always acts normal to the surface in contact or on which the body is placed. (See diagram below)
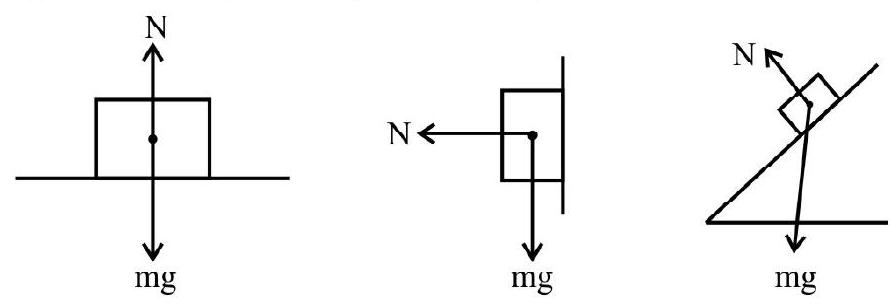
• Tension in a string arises due to the restoring forces caused by intermolecular forces of interaction. It is the force exerted by one part of the string on the other part. The tension in each branch of the string must form action - reaction pair. It always acts towards the support (Hand / pulley).

In the above system, tension on $\mathrm{m} _{1}$ is towards $\mathrm{m} _{2}$ and that on $\mathrm{m} _{2}$ is towards $\mathrm{m} _{1}$.

• A pulley is used to change the direction of force to a more convenient direction. For a light (massless); frictionless pulley with on inextensible string passing over it without any kinks, the tension on either side of the string is the same.
• In a FBD; take into account all the forces acting on the body.

Inter Connected Bodies

(i) Bodies in Contact

When three masses $\mathrm{m} _{1} ; \mathrm{m} _{2}$ and $\mathrm{m} _{3}$ are placed in contact on a smooth horizontal surface and pushed with a force $\mathrm{F}$ applied on $\mathrm{m} _{1}$ as shown, we have acceleration.

$$ \mathrm{a}=\frac{\mathrm{F}}{\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}} $$

Force on $\mathrm{m} _{1}=\mathrm{F} _{1}=\mathrm{F}$.

We have acceleration $a=\frac{F}{m _{1}+m _{2}+m _{3}}$

The weights are balanced by the normal reaction on the bodies.

Force on $\mathrm{m} _{1}=\mathrm{F} _{1}=\left(\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}\right) \mathrm{a}=\mathrm{F}$

Force on $\mathrm{m} _{2}=\mathrm{F} _{2}=\left(\mathrm{m} _{2}+\mathrm{m} _{3}\right)$ a

$$ =\frac{\left(\mathrm{m} _{1}+\mathrm{m} _{2}\right) \mathrm{F}}{\left(\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}\right)} $$

Force on $\mathrm{m} _{3}=\mathrm{F} _{3}=\mathrm{m} _{3} \mathrm{a}$

$$ =\frac{\mathrm{m} _{3} \mathrm{~F}}{\mathrm{~m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}} $$

(ii) Inter Connected Bodies suspended from a Rigid support

When two masses $m _{1}$ and $m _{2}$ are suspended vertically from a rigid, non-yielding support using strings as shown and a pulling force $\mathrm{F}$ is applied to pull the mass $\mathrm{m} _{2}$ down, we have $\mathrm{T} _{2}=\mathrm{F}+\mathrm{m} _{2} \mathrm{~g}$

and $\mathrm{T} _{1}=\mathrm{F}+\left(\mathrm{m} _{1}+\mathrm{m} _{2}\right) \mathrm{g}$

(iii) For two interconnected bodies with a rope passing over a smooth support or smooth light pulley;

$$ \begin{aligned} & \mathrm{a}=\frac{\left(\mathrm{m} _{2}-\mathrm{m} _{1}\right) \mathrm{g}}{\left(\mathrm{m} _{1}+\mathrm{m} _{2}\right)} \\ & \mathrm{T}=\frac{2 \mathrm{~m} _{1} \mathrm{~m} _{2} \mathrm{~g}}{\mathrm{~m} _{1}+\mathrm{m} _{2}} \end{aligned} $$

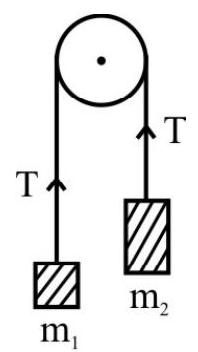
Note that $\mathrm{a}<\mathrm{g}$ for the system.

(iv) For two masses $m _{1}$ and $m _{2}$ attached to the ends of a string passing over a smooth pulley with mass $\mathrm{m} _{2}$ on a smooth horizontal surface, we have.

$a=\frac{m _{1} g}{m _{1}+m _{2}} \quad(<g)$

$\mathrm{T}=\frac{\mathrm{m} _{1} \mathrm{~m} _{2}}{\mathrm{~m} _{1}+\mathrm{m} _{2}} \mathrm{~g}$

Equation of motion of $\mathrm{m} _{1}$ in $\mathrm{m} _{2} \mathrm{~g}-\mathrm{T}=\mathrm{m} _{1} \mathrm{a}$

Equation of motion of $\mathrm{m} _{2}$ is $\mathrm{T}=\mathrm{m} _{2} \mathrm{a}$

(v) For a body on a smooth inclined plane, acceleration down the plane is given by

$$ \mathrm{a}=\mathrm{g} \sin \theta $$

For a system of three masses connected as shown; we have (surface and pulleys are assumed frictionless).

$\mathrm{m} _{1} \mathrm{~g}-\mathrm{T} _{1}=\mathrm{m} _{1} \mathrm{a} \hspace{40mm} . . . . . .(1)$

$\mathrm{T} _{1}-\mathrm{T} _{2}=\mathrm{m} _{2} \mathrm{a} \hspace{40mm} . . . . . .(2)$

$\mathrm{T} _{2}-\mathrm{m} _{3} \mathrm{~g}=\mathrm{m} _{3} \mathrm{a} \hspace{40mm} . . . . . .(3)$

Adding (1), (2) and (3), we get

$a\left(m _{1}+m _{2}+m _{3}\right)=\left(m _{1}-m _{3}\right) g$

$\therefore \mathrm{a}=\left(\frac{\mathrm{m} _{1}-\mathrm{m} _{3}}{\mathrm{~m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}}\right) \mathrm{g}$

$\therefore$ From (1)

$\mathrm{T} _{1}=\left[\mathrm{m} _{1}-\frac{\mathrm{m} _{1}\left(\mathrm{~m} _{1}-\mathrm{m} _{3}\right)}{\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}}\right] \mathrm{g}$

$=\frac{\mathrm{m} _{1}\left(2 \mathrm{~m} _{3}+\mathrm{m} _{2}\right)}{\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}} \mathrm{~g}$

$\mathrm{T} _{2}=\frac{\mathrm{m} _{3}\left(2 \mathrm{~m} _{1}+\mathrm{m} _{2}\right)}{\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}} \mathrm{~g}$

(vii) In the interconnected bodies shown; if $\mathrm{m} _{2}$ slides down and $\mathrm{m} _{1}$ slides up the double smooth inclined plane; the acceleration ’ $a$ ’ and the tension $T$ in the string is given by

$a=\frac{\left(m _{2} \sin \beta-m _{1} \sin \alpha\right) g}{m _{1}+m _{2}}$

$\mathrm{T}=\frac{\mathrm{m} _{1} \mathrm{~m} _{2} \mathrm{~g}(\sin \alpha+\sin \beta)}{\mathrm{m} _{1}+\mathrm{m} _{2}}$

Net tension at $\mathrm{O}=$ Reaction at $\mathrm{O}$

$$ \begin{aligned} & =\sqrt{\mathrm{T}^{2}+\mathrm{T}^{2}+2 \mathrm{~T}^{2} \sin \gamma} \\ & =\mathrm{T} \sqrt{2(1+\sin \gamma)} \\ & =\sqrt{2} \mathrm{~T} \sqrt{1+\sin (180-\alpha-\beta)} \\ & =\sqrt{2} \mathrm{~T} \sqrt{1-\sin (\alpha+\beta)} \end{aligned} $$

and $\mathrm{m} _{1} \sin \alpha=\mathrm{m} _{2} \sin \beta \quad$ [For equilibrium or for $\mathrm{a}=0$ ]

Friction

Whenever a body moves or tends to move over the surface of another body, a force comes into play to opposes their relative motion. This force is known as force of friction. It opposes motion and acts parallel to the surface of contact of bodies.

Frictional force may sometimes act in the direction of motion of the body. The following examples illustrate the situations where the force of friction ‘acts’ in the direction of motion of the object.

• For a man walking due north, the frictional force also acts due north.
• In a bicycle; the driving forces are connected to the rear wheel. The direction of frictional force on the rear wheel at point of contact with the ground is in the direction of motion whereas that on the front wheel is opposite to the direction of motion.

Static Friction

The force of friction which comes into play between two bodies before one object actually begins to move over the other is called static friction ( $f _{s}$. Static friction is a self adjusting force (both in magnitude as well as direction). It is always equal and opposite to the applied force as long as there is no relative motion.

Limiting Friction

The maximum force of static friction which comes into play when a body just starts moving over the surface of another body is called limiting friction or the maximum force of static friction $\left(f _{s}^{\max }\right)$. The force of friction never exceeds $\mathrm{f} _{\mathrm{s}}^{\max }$.

Kinetic Friction

The force of friction which comes into play when a body is in motion over the surface of another body is called kinetic or dynamic friction. It is denoted by $\mathrm{f} _{\mathrm{k}}$ and is less than limiting friction.

Laws of Limiting Friction

(1) The force of limiting friction depends on the nature of the two surfaces in contact and their state of roughness.

(2) The force of limiting friction acts tangential to the surfaces in contact and in a direction opposite to that of the applied force.

(3) The force of limiting friction between any two surfaces is independent of the shape and the area of contact so long as the normal reaction remains unchanged.

(4) The force of limiting friction between two given surfaces is directly proportional to the normal reaction between the surfaces.

$\mathrm{f} \alpha \mathrm{N}$ or $\mathrm{f}=\mu _{\mathrm{s}} \mathrm{N}$ where $\mu _{\mathrm{s}}$ is coefficient of limiting friction.

So, $\mu _{\mathrm{s}}=\frac{\mathrm{f} _{\mathrm{s}}^{\max }}{\mathrm{N}}=\frac{\text { Limiting Friction }}{\text { Normal Reaction }}$

and coefficient of kinetic friction $\mu _{\mathrm{k}}=\frac{\mathrm{f} _{\mathrm{k}}}{\mathrm{N}}$

We have $\mu _{\mathrm{k}}<\mu _{\mathrm{s}}$ because $\mathrm{f} _{\mathrm{k}}$ is always less than $\mathrm{f} _{\mathrm{s}}^{\max }$.

Let $\mathrm{F}$ be the external force applied on a body and $\mathrm{f} _{\mathrm{s}}^{\max }$; the limiting value of static friction. Then

(i) $\mathrm{F} \leq \mathrm{f} _{\mathrm{s}}^{\max }$, body does not move.

(ii) $\mathrm{F} \geq \mathrm{f} _{\mathrm{s}}^{\max }$, body starts moving.

If $\mathrm{F} \leq \mathrm{f} _{\mathrm{s}}^{\max }$, the force of friction which comes into play equals $\mathrm{F}$.

Angle of Friction

It is the angle which the resultant of the force of limiting friction and the normal reaction makes with the normal reaction.

We have $\tan \theta=\frac{\mathrm{f} _{\mathrm{s}}^{\max }}{\mathrm{N}}$

$=\mu _{\mathrm{s}}$

Angle of Repose

It is the minimum angle that an inclined plane makes with the horizontal when a body placed on it just begins to slide down the plane. Fig. shows forces acting on a body of mass $m$ about to slide down the inclined plane.

We have, $\mathrm{f} _{\mathrm{ms}}=\mathrm{mg} \sin \phi$

$$ \begin{aligned} \mathrm{N} & =\mathrm{mg} \cos \phi \\ \therefore \frac{\mathrm{f} _{\mathrm{ms}}}{\mathrm{N}}=\mu _{\mathrm{s}} & =\tan \phi \end{aligned} $$

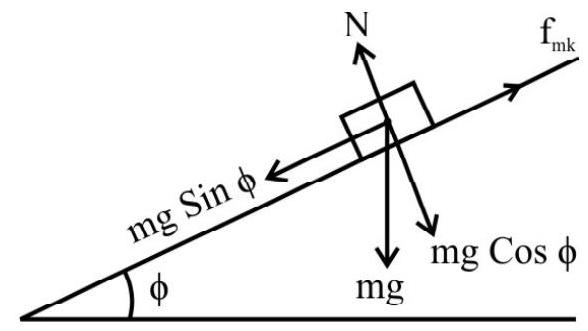
Motion of a Body on a Rough Inclined

(1) Motion - Down the Plane

Let $m$ be the mass of the body moving down rough inclined plane of inclination $\theta$.

$\mu _{\mathrm{k}}:$ Coefficient of kinetic friction.

The forces acting on the body are shown in Fig.

Normal reaction $\mathrm{N}=\mathrm{mg} \cos \theta$

Frictional force $f _{k}=\mu _{k} N=\mu _{k} m g \cos \theta$ up the plane.

Net force down the plane $=m g \sin \theta-f _{k}$

$$ \begin{aligned} & =m g \sin \theta-\mu _{\mathrm{k}} \mathrm{mg} \cos \theta \\ & =\mathrm{mg}\left(\sin \theta-\mu _{\mathrm{k}} \mathrm{mg} \cos \theta\right) \end{aligned} $$

Acceleration down the plane $=\mathrm{a}=\mathrm{g}\left(\sin \theta-\mu _{\mathrm{k}} \cos \theta\right)$

Note that the acceleration down the plane is independent of mass of the body.

Minimum force applied up the plane to prevent slipping $=m g\left(\sin \theta-\mu _{\mathrm{k}} \cos \theta\right)$

If $u=0$ and the body is let go from top of the incline.

Velocity at the bottom of the plane $=\mathbf{v}=\sqrt{2 \mathrm{~g} \ell\left(\sin \theta-\mu _{\mathrm{k}} \cos \theta\right)}$

Time taken to slide down the plane $=t=\sqrt{\frac{2 \ell}{g\left(\sin \theta-\mu _{\mathrm{k}} \cos \theta\right)}}$

Work done against the force of friction $=\mu _{\mathrm{k}} \mathrm{mg} \ell \cos \theta$

From work-energy theorem;

The net work done on the body $=$ increase in $\mathrm{KE}$

$$ =m g \ell\left(\sin \theta-\mu _{\mathrm{k}} \cos \theta\right) $$

(2) Motion of a Body up an Inclined Plane

Fig. shows forces acting on a body; accelerating up the plane with constant acceleration ’ $\mathbf{a}$ ‘. F is external applied force up the plane.

When $\mathrm{a}=0$, i.e. when the body is just pulled up the inclined plane, the force required equals

$\operatorname{mg}\left[(\sin \theta)+\left(\mu _{\mathrm{k}} \cos \theta\right)\right]$

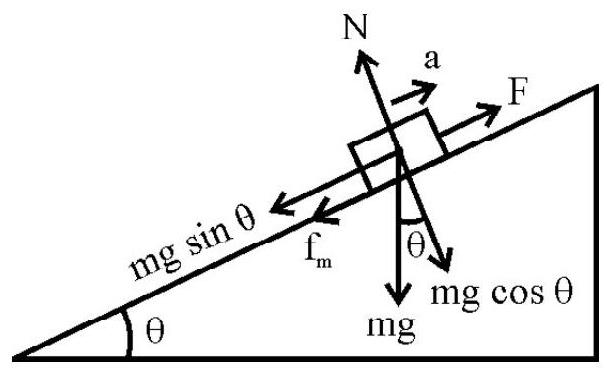
When a body is pushed upwards along an inclined plane with initial speed $\mathrm{v} _{0}$ so that it just reaches the top of the plane; they is not ext applied force F.

The acceleration of body is $\mathrm{a}=-\mathrm{g}\left(\sin \theta+\mu _{\mathrm{k}} \cos \theta\right)$

The time, $t$, taken to reach from bottom to top, is given by

$0=\mathrm{v} _{0}+(-\mathrm{a}) \mathrm{t}$

$\therefore \mathrm{t}=\frac{\mathrm{v} _{0}}{\mathrm{a}}=\frac{\mathrm{v} _{0}}{\mathrm{~g}\left(\sin \theta+\mu _{\mathrm{k}} \cos \theta\right)}$

The force $\mathrm{F}$ required to move a body up an inclined with an acceleration ’ $\mathbf{a}$ ‘, is given by

$\mathrm{F}-\left\{\mathrm{mg}\left(\sin \theta+\mu _{\mathrm{k}} \cos \theta\right)\right\}=\mathrm{ma}$

Motion of Two Bodies, One Resting on the other

Case-I : Force applied on A-Three possibilities arise.

(a) No frictional force between surfaces in contact.

In this case $\mathrm{a} _{\mathrm{A}}=\frac{\mathrm{F}}{\mathrm{m}}$

$\mathrm{a} _{\mathrm{B}}=0$

(b) There is friction between A and B only. The body A will begin to slide on B only

$$ \text { when } \mathrm{F}>\mathrm{f} _{\mathrm{s}}^{\max } \quad \text { or } \quad \mathrm{F}>\mu _{\mathrm{s}}(\mathrm{mg}) $$

Both $A$ and $B$ will move together with a common acceleration;

$$ \mathrm{a} _{\mathrm{A}}=\mathrm{a} _{\mathrm{B}}=\frac{\mathrm{F}}{\mathrm{m}+\mathrm{M}} $$

if there is no slipping between A and B.

(c) When $\mathrm{F}>\mathrm{f} _{\mathrm{s}}^{\max }$; the two bodies will move in the direction of the applied force. The acceleration produced in the two will be different.

The FBD of A and B are shown in Fig. (a) & Fig. (b) respectively.

We have, $\mathrm{f} _{\mathrm{k}}=\mu _{\mathrm{k}} \mathrm{mg}$

B moves due to $\mathrm{f} _{\mathrm{k}}$

$\therefore \mathrm{a} _{\mathrm{B}}=\frac{\mathrm{f} _{\mathrm{k}}}{\mathrm{M}}=\frac{\mu _{\mathrm{k}} \mathrm{mg}}{\mathrm{M}}$

Fig. (a)

For motion of A; we have,

$\mathrm{F}-\mathrm{f} _{\mathrm{k}}=\mathrm{ma} _{\mathrm{A}}$

$\mathrm{a} _{\mathrm{A}}=\frac{\mathrm{F}-\mathrm{f} _{\mathrm{k}}}{\mathrm{m}}$

Fig. (b)

Case-II : Force $\mathrm{F} _{\text {applied }}$ on the Lower Object B; Three subcases arise:

(a) When there in no friction; $a _{B}=\frac{F}{M}$

$\mathrm{a} _{\mathrm{A}}=0$

( $\therefore$ There is no pulling force)

A will have a relative backward motion and will fall off.

(b) When friction acts between A and B; the two bodies will move together i.e. there is no slipping between $\mathrm{A}$ and $\mathrm{B}$. The common acceleration is

$a=\left(\frac{F}{m+M}\right)$

Force on $A=F^{\prime}=m a=m\left(\frac{F}{m+M}\right)$

The bodies A & B move together till

$\mathrm{F}^{\prime} \leq \mathrm{f} _{\mathrm{s}}^{\max } \quad$ or $\quad \mathrm{F}^{\prime} \leq \mu _{\mathrm{s}} \mathrm{mg}$

(c) If $\mathrm{F}>\mu _{\mathrm{s}}(\mathrm{m}+\mathrm{M}) \mathrm{g}$; the acceleration in $\mathrm{A}$ and $\mathrm{B}$ will be different.

$$ \mathrm{ma} _{\mathrm{A}}=\mathrm{f} _{\mathrm{k}}=\mu _{\mathrm{k}} \mathrm{mg} $$

$\mathrm{a} _{\mathrm{A}}=\mu _{\mathrm{k}} \mathrm{g}$

For B; $F-f _{k}=\mathrm{Ma} _{\mathrm{B}}$ or $\mathrm{a} _{\mathrm{B}}=\frac{F-f _{k}}{M}$

or $\mathrm{a} _{\mathrm{B}}=\frac{\mathrm{F}-\mu _{\mathrm{k}} \mathrm{mg}}{\mathrm{M}}$

Example-19:

A block A of mass $8 \mathrm{~kg}$ is placed on another block B of mass $10 \mathrm{~kg}$ with $B$ resting on a smooth horizontal surface. To slide $A$ on $B$, a horizontal force of $24 \mathrm{~N}$ is required. Calculate the maximum horizontal force that can be applied on B so that both A and B move together. Calculate the acceleration produced by this force.

Show Answer

Solution :

Here $\mathrm{m}=8 \mathrm{~kg}, \mathrm{M}=10 \mathrm{~kg}$

Force applied on $\mathrm{A}=24 \mathrm{~N}$

This force has to be equal to kinetic friction.

$\therefore \mathrm{f} _{\mathrm{k}}=\mu _{\mathrm{k}} \mathrm{mg} \quad$ or $24=\mu _{\mathrm{k}} \times 8 \times \mathrm{g}$

$\therefore \mu _{\mathrm{k}}=\frac{24}{80}=\frac{3}{\mathrm{~g}}$

Let $F$ be external applied force on $B$. The acceleration a of the system (Block A and B move together) is

$\mathrm{a}=\frac{\mathrm{F}}{(\mathrm{M}+\mathrm{m})}\hspace{40mm} . . . . . .(1)$

The FBD of block A is as shown in Fig. If $\mathrm{F} _{\mathrm{fic}} \leq \mathrm{f} _{\mathrm{A}, \max }$; block A does not move B.

However if $\mathrm{F} _{\mathrm{fic}}>\mathrm{f} _{\mathrm{A}, \max }$ block A starts slipping on $\mathrm{B}$.

For blocks to move together, $\mathrm{a} _{\max }$ is given by $\mathrm{F} _{\text {fic }}=\mathrm{f} _{\text {A max }}$;

or $\mathrm{ma} _{\max }=\mu \mathrm{mg}$ or $\mathrm{a} _{\max }=\mu \mathrm{g} \hspace{40mm} . . . . . .(2)$

From(1) and (2)

$\mathrm{F} _{\max }=(\mathrm{M}+\mathrm{m}) \mathrm{a} _{\max }=\mu(\mathrm{M}+\mathrm{m}) \mathrm{g}$

$\therefore \mathrm{F}=\frac{3}{\mathrm{~g}} \times(18) \times(\mathrm{g})=54 \mathrm{~N}$

$\therefore \mathrm{a} _{\max }=\frac{\mathrm{F} _{\max }}{(\mathrm{m}+\mathrm{M})}=\frac{54}{8+10}=3 \mathrm{~ms}^{-2}$

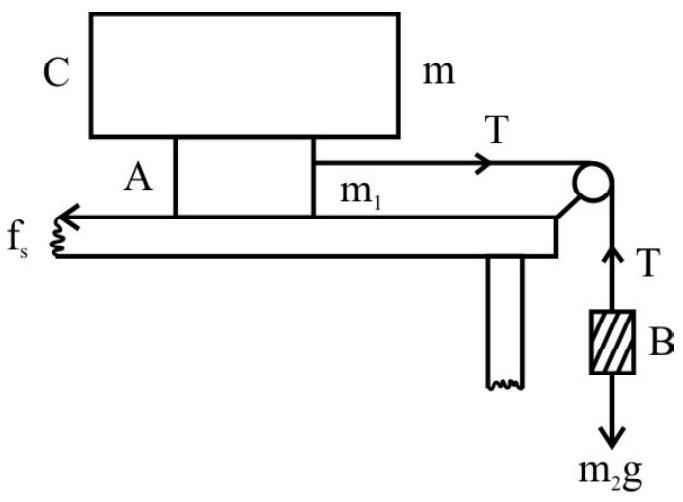
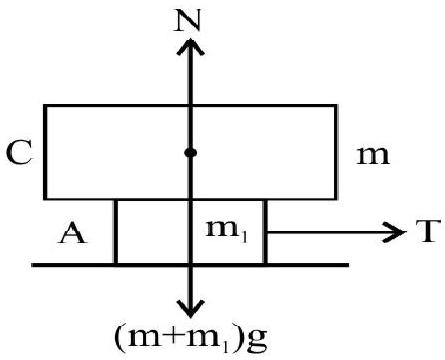
Example-20 :

Two block $\mathrm{A}$ and $\mathrm{B}$ have masses $10 \mathrm{~kg}$ and $5 \mathrm{~kg}$ respectively. What should be the minimum mass of a block $\mathrm{C}$ that should be placed on $\mathrm{A}$ so as the prevent $\mathrm{A}$ from slipping. Coefficient of static friction between the table and the block $\mathrm{A}$ is 0.3

Show Answer

Solution :

To prevent the system from slipping; all three blocks have to be in equilibrium.

i.e. $F _{A}=F _{B}=F _{C}=$ zero

[Net forces]

For $\mathrm{A} ; \mathrm{N}=\left(\mathrm{m}+\mathrm{m} _{1}\right) \mathrm{g}=(10+\mathrm{m}) \mathrm{g}$

and $\mathrm{T}=\mathrm{f} _{\mathrm{s}}=\mu \mathrm{N}=0.3(10+\mathrm{m}) \mathrm{g} \hspace{40mm} . . . . . .(1)$

For $\mathrm{B}, \mathrm{T}=\mathrm{m} _{2} \mathrm{~g}=5 \mathrm{~g}$

$\therefore 0.3(10+\mathrm{m}) \mathrm{g}=5 \mathrm{~g}$

[Using (1)]

$$ \mathrm{m}=6.7 \mathrm{~kg} $$

$\therefore 10+\mathrm{m}=\frac{5}{0.3}=\frac{50}{3}=16.7$

Example-21 :

A metal block of mass $1 \mathrm{~kg}$ when placed over an inclined plane of an angle of $30^{\circ}$ slides down without acceleration. If the inclination is increased by $15^{\circ}$, what would be the acceleration of the block?

Show Answer

Solution :

In Fig (a); the block slides down without acceleration. So angle of repose is $30^{\circ}$

$$ \mu=\tan 30^{\circ}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3} $$

In Fig. (b); $\theta=30^{\circ}+15^{\circ}=45^{\circ}$

If ’ $a$ ’ is the acceleration down the plane, we have,

$\mathrm{F} _{\text {net }}=\mathrm{mg} \sin \theta-\mathrm{f}$ [Down the plane]

or

$$ \mathrm{ma}=\mathrm{mg} \sin \theta-\mu \mathrm{mg} \cos \theta $$

or

$$ \begin{aligned} & a=g(\sin \theta-\mu \cos \theta) \\ & =g[\sin 45-\mu \cos 45] \\ & =10\left[\frac{1}{\sqrt{2}}-\frac{\sqrt{3}}{3} \frac{1}{\sqrt{2}}\right] \\ & =\frac{10}{\sqrt{2}}\left[\frac{\sqrt{3}-1}{\sqrt{3}}\right]=\frac{10 \times 0.732}{\sqrt{6}} \\ & =\frac{7.32}{\sqrt{6}}=3 \mathrm{~m} / \mathrm{s}^{2} \end{aligned} $$

The acceleration does not change with mass.

Example-22 :

A truck tows a trailer of mass $3000 \mathrm{~kg}$ at $20 \mathrm{~m} / \mathrm{s}$ on a level road. The tension in the coupling in $2500 \mathrm{~N}$. (i) What is the power expended on the trailer? (ii) What will be tension in the coupling if the truck hauls the trailer up an incline rising 1 in 6 ? Assume the frictional forces on the incline to be the same as that on the level road.

Show Answer

Solution :

On the level road; the motion being uniform; $\mathrm{a}=0$

$\therefore \mathrm{F} _{\text {applied }}=\mathrm{f} _{\text {friction }}=2500 \mathrm{~N}$

Speed $v=20 \mathrm{~m} / \mathrm{s}$

$\therefore$ Power $\mathrm{P}=\mathrm{Fv}=2500 \times 20=50 \mathrm{~kW}$

Up an incline: The truck has to overcome friction f and also the component

of the weight down the plane.

$\therefore$ Tension in the coupling

$\mathrm{T}=\mathrm{mg} \sin \theta+\mathrm{f}$

$$ \begin{aligned} & =3000 \times 10\left(\frac{1}{6}\right)+2500 \\ & =7500 \mathrm{~N} \end{aligned} $$

Circular Motion

Abody is circular motion is always accelerated due to change in direction of velocity. The magnitude may or may not very. The acceleration which changes the direction of motion so as to enable the body move along a circular path is called centripetal acceleration. The force producing this acceleration is called centripetal force.

We have, $F=\frac{mv^{2}}{r}=m r \omega^{2}=m r\left(\frac{2 \pi}{T}\right)^{2}$

$$ =\frac{4 \pi^{2} \mathrm{mr}}{\mathrm{T}^{2}} $$

Body on Level Circular Road

The friction between the tyres and the road provides the centripetal force.

We have, $\frac{\mathrm{mv}^{2}}{\mathrm{r}}=\mu \mathrm{mg}$

or $\quad \mathrm{v}=\sqrt{\mu \mathrm{rg}}$

which gives maximum safe speed of a vehicle on road for negotiating a curve of radius ’ $r$ ‘. (Without skidding).

Banking of Roads (Tracks)

Curved roads and tracks are banked to reduce the role of friction for providing centripetal force on curves. For a track / road of radius ’ $r$ ’ banked at an angle $\theta$; the maximum safe speed at which a vehicle can negotiate a curve is given by

$$ \mathrm{v}=\sqrt{\mathrm{gr} \tan \theta} $$

The above max safe speed does not take into account the friction between the tyres and the road.

If the force of friction is also taken into account; we have,

$$ \mathrm{v}=\sqrt{\operatorname{rg}\left(\frac{\mu+\tan \theta}{1-\mu \tan \theta}\right)} $$

Bending of a Cyclist

In order to negotiate a circular turn of radius ’ $r$ ’ at a speed $v$; a cyclist must bend at an angle $\theta$ with the vertical such that

$$ \tan \theta=\frac{\mathrm{v}^{2}}{\mathrm{rg}} $$

Motion in a Vertical Circle

Consider a body of mass ’ $m$ ’ moving along a circle of radius ’ $r$ ’ in a vertical plane tied at one end of a string.

Let $\mathrm{v} _{\mathrm{A}}$ be speed of particle at the lowest point $\mathrm{A}$ on the vertical circle. As particle moves along vertical circle; speed and velocity both very. The motion is neither with uniform speed not uniform velocity. $P$ is the instantaneous position of particle on vertical circle; string OP makes an instantaneous angle $\theta$ with vertical. Let $\mathrm{v}$ be instantaneous speed at $\mathrm{P}$. From law of conservation of energy.

$$ \frac{1}{2} \mathrm{mv} _{\mathrm{A}}^{2}=\frac{1}{2} \mathrm{mv}^{2}+\mathrm{mgh} $$

Also from Fig;

$$ \begin{align*} & \mathrm{AQ}=\mathrm{h}=\mathrm{OA}-\mathrm{OQ}=\mathrm{r}-\mathrm{r} \cos \theta=\mathrm{r}(1-\cos \theta) \\ & \therefore \mathrm{v}^{2}=\mathrm{v} _{\mathrm{A}}^{2}-2 \operatorname{gr}(1-\cos \theta) \tag{1} \end{align*} $$

Fig. shows forces on mass $m$ at point $\mathrm{P}$. The instantaneous tension $\mathrm{T}$ is string is

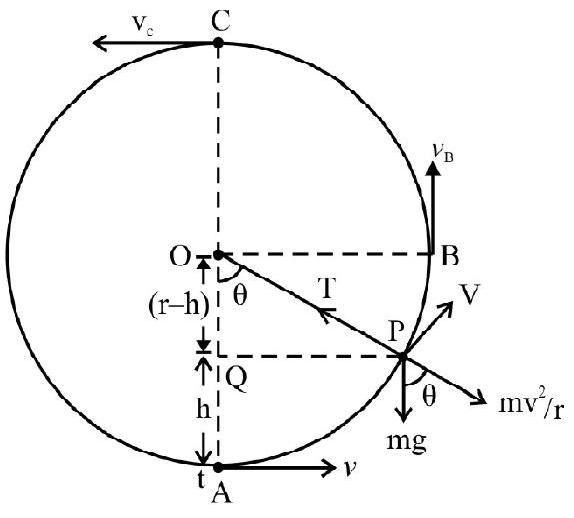
$\mathrm{T}=\mathrm{mg} \cos \theta+\frac{\mathrm{mv}^{2}}{\mathrm{r}}$

$$ \begin{align*} & =m g \cos \theta+\frac{m v _{\mathrm{A}}^{2}}{\mathrm{r}}-2 \mathrm{mg}(1-\cos \theta) \\ & =\frac{\mathrm{mv} _{\mathrm{A}}^{2}}{\mathrm{r}}-2 \mathrm{mg}+3 \mathrm{mg} \cos \theta \tag{2} \end{align*} $$

(1) Particle at lowest point an vertical circle i.e. $\theta=0$; From equation (2)

$$ \begin{equation*} \mathrm{T} _{\mathrm{A}}=\frac{\mathrm{mv} _{\mathrm{A}}^{2}}{\mathrm{r}}+\mathrm{mg} \tag{3} \end{equation*} $$

(2) Particle in position B i.e. string is horizontal obviously $\theta=\frac{\pi}{2}$. From equations n (1) and (2)

$$ \begin{equation*} \mathrm{v} _{\mathrm{B}}^{2}=\mathrm{v} _{\mathrm{A}}^{2}=2 \mathrm{gr} ; \mathrm{T} _{\mathrm{B}}=\frac{\mathrm{mv} _{\mathrm{A}}^{2}}{\mathrm{r}}-2 \mathrm{mg} \tag{4} \end{equation*} $$

(3) Particle at highest point on vertical circle i.e. at C. Obviously $\theta=\pi$ from equations (1) and (2); we have,

$\mathrm{v} _{\mathrm{C}}^{2}=\mathrm{v} _{\mathrm{A}}^{2}-4 \mathrm{gr} ; \mathrm{T} _{\mathrm{C}}=\frac{\mathrm{mv} _{\mathrm{A}}^{2}}{\mathrm{r}}-5 \mathrm{mg} \hspace{40mm} . . . . . .(5)$

From equation (5) $T _{C}$ is negative if $\frac{\mathrm{mv} _{\mathrm{A}}^{2}}{\mathrm{r}}<5 \mathrm{mg}$.

This means string slackens and particle cannot complete motion along vertical circle,

$$ \begin{gather*} \left(\mathrm{T} _{\mathrm{C}}\right) _{\mathrm{mm}}=0 \\ \therefore\left(\mathrm{v} _{\mathrm{A}}\right) _{\mathrm{mm}}=\sqrt{5 \mathrm{gr}} \tag{6} \end{gather*} $$

For $\mathrm{v} _{\mathrm{A}}=\left(\mathrm{v} _{\mathrm{A}}\right) _{\mathrm{mm}}, \mathrm{v} _{\mathrm{C}}$ is given by

$\mathrm{v} _{\mathrm{C}}^{2}=5 \mathrm{gr}-4 \mathrm{gr}$

$\mathrm{v} _{\mathrm{C}}=\sqrt{\mathrm{gr}}$

Example-23 :

A pendulum suspended from the roof of a car by a string shifts through an angle $\theta[\tan \theta=0.36]$ when the car negotiates a curve of radius $200 \mathrm{~m}$. Find the speed of the car.

Show Answer

Solution :

The forces acting on the pendulum bob are:

(i) Weight $\mathrm{mg}$ vertically downwards.

(ii) Tension T up the string.

(iii) Centripetal force.

Resolving the forces and applying equilibrium conditions along and perpendicular to the string, we get

$m g \sin \theta=\frac{m v^{2}}{r} \cos \theta$

$v^{2}=r g \tan \theta$

$\mathrm{v}=\sqrt{\mathrm{rg} \tan \theta}$

$$ \begin{aligned} & =\sqrt{200 \times 9.8 \times 0.36} \\ & \simeq 26.6 \mathrm{~m} / \mathrm{s} \end{aligned} $$

Example-24 :

A train has to negotiate a curve of $400 \mathrm{~m}$ radius. If the distance between the rails is $1 \mathrm{~m}$, by how much should the outer rail the raised w.r.t. the inner rail for a safe speed of $48 \mathrm{~km} / \mathrm{hr}$.

Show Answer

Solution :

We have $\mathrm{v}=48 \mathrm{~km} / \mathrm{h}=\frac{40}{3} \mathrm{~m} / \mathrm{s}$

$\mathrm{r}=400 \mathrm{~m} ; \ell=1 \mathrm{~m}$

Let ’ $h$ ’ be the required height of the outer rail.

We have $\sin \theta=\frac{\mathrm{h}}{\ell}=\mathrm{h}$

For small value of $\theta ; \sin \theta \simeq \tan \theta=h$

$\therefore \frac{\mathrm{v}^{2}}{\mathrm{rg}}=\tan \theta=\mathrm{h}$

$\mathrm{h}=\frac{\mathrm{v}^{2}}{\mathrm{rg}}=\frac{40 / 3 \times 40 / 3}{400 \times 10}$

$\mathrm{h}=\frac{40}{3} \times \frac{40}{3} \times \frac{1}{4000} \mathrm{~m}$

$=0.444 \mathrm{~m}$

Example-25 :

A circular race track of radius $300 \mathrm{~m}$ is banked at $15^{\circ}$. If $\mu=0.2$; what is the optimum speed of a race car to avoid wear and tear of the tyres. Also calculate the maximum permissible speed to prevent slipping.

Show Answer

Solution :

Optimum speed of the car $=v=\sqrt{\operatorname{rg} \tan 15}=\sqrt{300 \times 9.8 \times \tan 15^{0}}$

$$ =28.1 \mathrm{~m} / \mathrm{s} $$

Maximum permissible speed of the race car using frictional force as well is

$\mathrm{v} _{\text {max }}=\sqrt{\operatorname{rg}\left(\frac{\mu _{5}+\tan \theta}{1-\mu _{5}+\tan \theta}\right)}=38.1 \mathrm{~ms}^{-1}$

Example-26:

An aeroplane is flying at $360 \mathrm{~km} \mathrm{~h}^{-1}$ in a vertical circle of radius $200 \mathrm{~m}$. Calculate the force with which a 75 $\mathrm{kg}$ pilot presses his seat at the

(a) highest point

(b) lowest point

in the circle. [Use $g=10 \mathrm{~m} / \mathrm{s}^{2}$ ]

Show Answer

Solution :

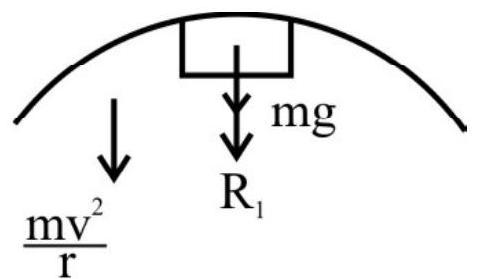
(a) At the highest point.

$\mathrm{R} _{\mathrm{i}}+\mathrm{mg}$ provide centripetal force.

$\therefore \mathrm{R} _{1}+\mathrm{mg}=\frac{\mathrm{mv}^{2}}{\mathrm{r}}$

$\mathrm{R} _{1}=\frac{\mathrm{mv}^{2}}{\mathrm{r}}-\mathrm{mg}$

$=\mathrm{m}\left[\frac{\mathrm{v}^{2}}{\mathrm{r}}-\mathrm{g}\right]$

We have $\mathrm{m}=75 \mathrm{~kg} ; \mathrm{v}=360 \mathrm{~km} / \mathrm{h}=100 \mathrm{~m} / \mathrm{s}, \mathrm{r}=20 \mathrm{~m}$ and $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}$

$\therefore \mathrm{R} _{1}=75\left[\frac{100 \times 100}{200}-10\right]=75 \times 40 \mathrm{~N}$

$=\frac{75 \times 40}{10} \mathrm{~kg} \mathrm{wt}=300 \mathrm{~kg} \mathrm{wt}$

(b) At the lowest point

$\mathrm{R} _{2}-\mathrm{mg}=\frac{\mathrm{mv}^{2}}{\mathrm{r}}$

$$ \begin{aligned} & \mathrm{R} _{2}=\mathrm{m}\left[\frac{\mathrm{v}^{2}}{\mathrm{r}}+\mathrm{g}\right] \\ & =75\left[\frac{100 \times 100}{200}+10\right]=75 \times 60 \mathrm{~N} \\ & =75 \times 6 \mathrm{~kg} \mathrm{wt} \\ & =450 \mathrm{~kg} \mathrm{wt} \end{aligned} $$

Constrained Motion

It is a motion of a body subjected to certain restriction to its free motion. The constraints arise due to contact between bodies or when the bodies are interconnected.

We can consider following examples of constained motion.

(a) Body on a floor is constrained to move along $x$-direction along.

We have $\mathrm{y}=0$

$\mathrm{v} _{\mathrm{y}}=0, \mathrm{a} _{\mathrm{y}}=0$

(b)

In all the cases shown in the diagram, if the string / rod connecting the bodies in inextensible; we use a contrain that the length of the string is fixed.

Distance $x _{\mathrm{A}}=x _{\mathrm{B}}$

Speed $\left|\overrightarrow{\mathrm{v}} _{\mathrm{A}}\right|=\left|\overrightarrow{\mathrm{v}} _{\mathrm{B}}\right|$

Acceleration $\left|\overrightarrow{\mathrm{a}} _{\mathrm{A}}\right|=\left|\overrightarrow{\mathrm{a}} _{\mathrm{B}}\right|$

It is important to note that the velocities and accelerations may be in different directions.

(c) In case of a moveable pulley shown

We have, $\mathrm{F}=2 \mathrm{~T}$ and $\mathrm{T}=\mathrm{Ma} _{\text {block }}$

If the block moves a distance $x$; the pulley moves a distance $\frac{x}{2}$

as the length of string remains constant.

We have, $\mathrm{v} _{\text {pulley }}=\frac{1}{2} \mathrm{v} _{\text {block }}$

$\mathrm{a} _{\text {pulley }}=\frac{\mathrm{a} _{\text {block }}}{2}$

$=\frac{\mathrm{T}}{2 \mathrm{~m}}=\frac{\mathrm{F} / 2}{2 \mathrm{~m}}=\frac{\mathrm{F}}{4 \mathrm{~m}}$

(d) Ring on a smooth rod

For a ring of mass $m$ connected through a string of length ‘L’ with a block of mass M;

We have, $\mathrm{L}=\sqrt{\mathrm{d}^{2}+\mathrm{y}^{2}}+x$ (Constant)

We have, $\frac{\mathrm{dL}}{\mathrm{dt}}=0=\frac{1}{2} \frac{2 \mathrm{y}}{\sqrt{\mathrm{d}^{2}+\mathrm{y}^{2}}} \cdot \frac{\mathrm{dy}}{\mathrm{dt}}+\frac{\mathrm{d} x}{\mathrm{dt}}$

As $\frac{\mathrm{dy}}{\mathrm{dt}}=\mathrm{v} _{\mathrm{m}}$ and $\frac{\mathrm{d} x}{\mathrm{dt}}=\mathrm{v} _{\mathrm{M}}$

and $\cos \theta=\frac{\mathrm{y}}{\sqrt{\mathrm{d}^{2}+\mathrm{y}^{2}}}$

$\left|\mathbf{v} _{\mathrm{M}}\right|=\left|\mathbf{v} _{\mathrm{m}} \cos \theta\right| \hspace{40mm} . . . . . . .(1)$

Acceleration can be obtained by differentiating (1) w.r.t. time. Note that $\theta$ also changes with time.

(e) For two blocks connected as shown; we have

Length of the string $=\mathrm{L}=\mathrm{OA}+\mathrm{AB}+x$

$=20 \mathrm{~A}+x$

$=2 \sqrt{\mathrm{d}^{2}+\mathrm{y}^{2}}+x=$ constant

$\therefore \frac{\mathrm{dL}}{\mathrm{dt}}=0=\frac{2 \times 2 \mathrm{y}}{2 \sqrt{\left(\mathrm{d}^{2}+\mathrm{y}^{2}\right)}} \frac{\mathrm{dy}}{\mathrm{dt}}+\frac{\mathrm{d} x}{\mathrm{dt}}$

or

$2 \mathrm{v} _{\mathrm{m}} \cos \theta+\mathrm{v} _{\mathrm{M}}=0$

$\mathrm{v} _{\mathrm{M}}=-2 \mathrm{v} _{\mathrm{m}} \cos \theta$

(f) Block sliding on a wedge

Consider a block sliding on a moving wedge. As the block slides from $\mathrm{O}$ to $\mathrm{D}$ (through a distance $x _{1}$ ) on the wedge; the wedge moves through a distance $\mathrm{OE}$.

We have $\mathrm{y} _{1}=\mathrm{DE}=\mathrm{OE} \sin \theta$

$$ =x \sin \theta $$

$\therefore\left|\overrightarrow{\mathrm{v}} _{\text {block }}\right|=\left|\overrightarrow{\mathrm{v}} _{\text {wedge }} \sin \theta\right|$

$\left|\overrightarrow{\mathbf{a}} _{\text {block }}\right|=\left|\overrightarrow{\mathbf{a}} _{\text {wedge }} \sin \theta\right|$

ADDITIONAL EXAMPLES

1. A point particle of mass $m$, moves along the uniformly rough track $P Q R$ as shown in the figure. The coefficient of friction, between the particle and the rough track equals $\mu$. The particle is released, from rest, from the point $\mathrm{P}$ and it comes to rest at a point $\mathrm{R}$. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from $\mathrm{PQ}$ to $\mathrm{QR}$. The values of the coefficient of friction $\mu$ and the distance $x(=\mathrm{QR})$, are, respectively close to:

(a) 0.2 and $3.5 \mathrm{~m}$

(b) 0.29 and $3.5 \mathrm{~m}$

(c) 0.29 and $6.5 \mathrm{~m}$

(d) 0.2 and $6.5 \mathrm{~m}$

Show Answer

Correct option is (2)

(IIT 2016)

Solution:

Work done, over the paths. PQ and QR, are, respectively,

$\mathrm{W} _{1}=\mu \mathrm{mg} \cos \theta \frac{2}{\sin \theta}=(2 \mathrm{mg} \sqrt{3} \mu)$

and $\mathrm{W} _{2}=\mu \mathrm{mg} \quad x$

Since $\mathrm{W} _{1}=\mathrm{W} _{2}$, we get

$x=2 \sqrt{3} \mathrm{~m} \simeq 3.5 \mathrm{~m}$

or loss in P.E. $=(\mathrm{mg}) \times 2$

$\therefore 2 \mathrm{mg}=\mathrm{W} _{1}+\mathrm{W} _{2}=4 \mathrm{mg} \sqrt{3} \mu$

This given $\mu=\frac{2}{2 \sqrt{3}}=0.29$

2. A mass ’ $m$ ’ is supported by a massless string wound around a uniform hollow cylinder of mass $m$ and radius $R$. If the string does not slip on the cylinder, with what acceleration will the mass fall on release?

(a) $\frac{5 \mathrm{~g}}{6}$

(b) $\mathrm{g}$

(c) $\frac{2 \mathrm{~g}}{3}$

(d) $\frac{\mathrm{g}}{2}$

Show Answer

Correct option is (1)

(IIT 2014)

Solution:

The equation of motion of mass $m$ is

$$ \mathrm{mg}-\mathrm{T}=\mathrm{ma} $$

For the cylinder, we have

$$ \mathrm{T} . \mathrm{R}=\mathrm{I} \alpha $$

But $\alpha=\frac{\mathrm{a}}{\mathrm{R}}$, (as the string does not slip)

and $\mathrm{I}=\mathrm{mR}^{2}$

$\therefore \mathrm{T}=\mathrm{ma}$

We this get

$a=\frac{g}{2}$

PROBLEMS FOR PRACTICE

1. A stone thrown on a window pane smashes it but a bullet fired from a gun makes a clean hole in it. Explain.

2. An athlete has to run through a certain distance after crossing the finishing line. Explain.

3. The students in a Physics class make the following statements.

(a) Linear momentum is the quantity of motion contained in the body.

(b) Impulse and acceleration make an angle of $180^{\circ}$ with change in momentum.

(c) Change in momentum is a measure of impulse.

(d) The linear momentum of a body remains constant when it is in circular motion with a constant speed.

Which of the following is correct:

(1) All the above statements are correct.

(2) Only (a) and (c) are correct.

(3) Only (a) and (b) are correct.

(4) (b), (c) and (d) are correct.

4. Which of the following statements is correct?

The internal forces can change:

(1) Linear momentum but not kinetic energy.

(2) Kinetic energy but not linear momentum.

(3) Both kinetic energy and linear momentum.

(4) Neither kinetic energy nor linear momentum.

5. A truck starts from rest and moves down a hill with constant acceleration covering $400 \mathrm{~m}$ in $20 \mathrm{~s}$. Calculate the acceleration and the force on it, if its mass in 5 metric tonnes.

Show Answer

Answer: $2 \mathrm{~m} / \mathrm{s}^{2} ; 10000 \mathrm{~N}$

6. In an X-ray machine, an electron $\left(\mathrm{m} \simeq 9 \times 10^{-31} \mathrm{~kg}\right)$ is subjected to a force of $10^{-23} \mathrm{~N}$. Calculate the time in which it covers $10 \mathrm{~cm}$.

Show Answer

Answer: $1.33 \times 10^{-4} \mathrm{~s}$

7. A balloon has $5 \mathrm{~kg}$ air in it. The air escape at a uniform rate with a velocity of $5 \mathrm{~m} / \mathrm{s}$. If the entire air escapes in $2 \mathrm{~s}$, find the average force on the balloon.

Show Answer

Answer: $12.5 \mathrm{~N}$

8. A machine gun fires a bullet of mass $40 \mathrm{gm}$ at $1200 \mathrm{~ms}^{-1}$. The person holding the machine gun can support a maximum force of $144 \mathrm{~N}$. Calculate the number of bullets that can be fired from the gun in one second.

Show Answer

Answer: 3 bullets / sec.

9.

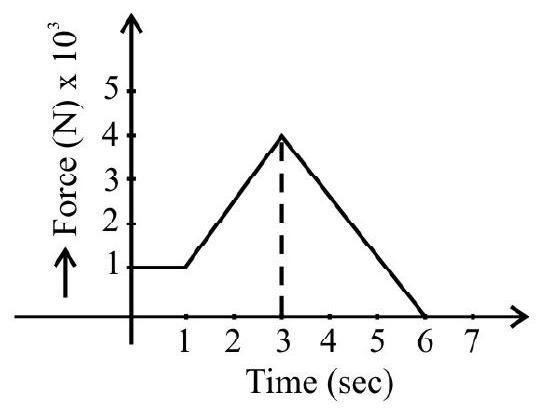
The above graph shows the force exerted on a ball struck by a bat. Using the graph determine.

(i) the impulse delivered to the ball.

(ii) the average force the ball.

(iii) the maximum force applied.

Show Answer

Answer:

(i) $1.2 \times 10^{4} \mathrm{~kg} \mathrm{~m} / \mathrm{s}$

(ii) $2000 \mathrm{~N}$

(iii) $4000 \mathrm{~N}$

10. A man weighing $x \mathrm{~kg}$ can descend by means of a parachute with a minimum acceleration of $\frac{\mathrm{g}}{4}$. Calculate $x$ if the strings of the parachute can bear a maximum tension of $72 \mathrm{~kg}$ weight.

[Hint: $\left.\mathrm{T} _{\max }=\mathrm{m}\left(\mathrm{g}-\mathrm{a} _{\min }\right)\right]$

Show Answer

Answer: $96 \mathrm{~kg} \mathrm{wt}$

11. A ball of mass $200 \mathrm{gm}$ moving at $5 \mathrm{~m} / \mathrm{s}$ collides with another ball of half its mass moving at $4 \mathrm{~m} / \mathrm{s}$ in opposite direction. The balls stick together and move with a common velocity v. Calculate v.

Show Answer

Answer: $2 \mathrm{~m} / \mathrm{s}$

12. A $60 \mathrm{~kg}$ boy running at $5 \mathrm{~m} / \mathrm{s}$ jumps on a stationary trolley of mass $100 \mathrm{~kg}$. Calculate the velocity with which the trolley begins to move.

Show Answer

Answer: $\frac{15}{8} \mathrm{~m} / \mathrm{s}$

13. A balloon of mass $m$ is rising up with an acceleration ’ $a$ ‘. Show that the fraction of weight which must be removed from it so as to double its acceleration is $\left(\frac{\mathrm{ma}}{2 \mathrm{a}+\mathrm{g}}\right)$ assuming the upward force to remain the same.

14.

Four identical blocks are connected by light inextensible strings and pulled by a force $\mathrm{F}$ on a smooth horizontal surface. Show that $\mathrm{T} _{3}: \mathrm{T} _{2}: \mathrm{T} _{1}$ is $6: 2: 1$.

15.

For the system of masses shown above, calculate the tension in the string between $\mathrm{m} _{2}$ and $\mathrm{m} _{3}$.

Show Answer

Answer: $\frac{2 \mathrm{~m} _{1} \mathrm{~m} _{3} \mathrm{~g}}{\mathrm{~m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}}$

16. A bullet of mass $20 \mathrm{gm}$ is fired on an $8 \mathrm{~kg}$ wooden block at rest on a horizontal surface. The bullet gets embedded in the block and the combinations moves $20 \mathrm{~m}$ before coming to rest. With what speed did the bullet hit the block? Given $\mu _{\mathrm{k}}=0.25$

Show Answer

Answer: $4010 \mathrm{~m} / \mathrm{s}$

17. A suitcase is gently dropped on a conveyor belt moving at $6 \mathrm{~ms}^{-1}$. If the coefficient of friction between the belt and the suitcase is 0.5 , how for will the suitcase move on the belt before coming to rest?

Show Answer

Answer: $3.68 \mathrm{~m}$

18. Two blocks of mass $2 \mathrm{~kg}$ and $5 \mathrm{~kg}$ connected by an ideal string passing over a smooth, light pulley as shown. Calculate the acceleration of the system and the tension in the string. [Use $g=9.8 \mathrm{~m} / \mathrm{s}^{2}$ ]

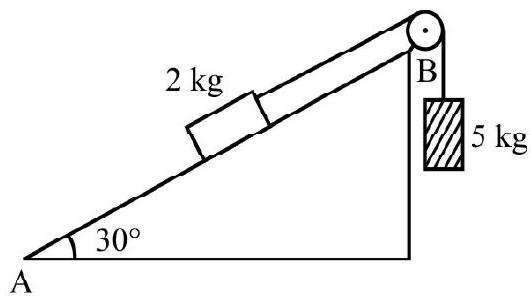
Show Answer

Answer: $4.87 \mathrm{~m} / \mathrm{s}^{2} ; 24.65 \mathrm{~N}$

19. A $100 \mathrm{gm}$ ball in suspended by a $30 \mathrm{~cm}$ long light string. Keeping the string always taut, the ball describes a horizontal circle of radius $15 \mathrm{~m}$. Calculate angular speed.

Show Answer

Answer: $6.14 \mathrm{rad} / \mathrm{s}$

20. A motor cyclist drives at $144 \mathrm{~km} \mathrm{~h}^{-1}$ on a $320 \mathrm{~m}$ radius circular track. Calculate the angle through which he should lean with the vertical to keep his balance. $\left(g=10 \mathrm{~ms}^{-2}\right)$

Show Answer

Answer: $\frac{\pi}{4}$

21. The railway bridge over a canal is in the form of an arc of a circle of radius $20 \mathrm{~m}$. What is the minimum speed with which a car can cross the bridge without leaving contact with the ground at the highest point.

[Use $\mathrm{g}=9.8 \mathrm{~m} / \mathrm{s}^{2}$ ]

Show Answer

Answer: $14 \mathrm{~ms}^{-1}$

Key Learning Points

1. Force is an external agent which changes or tries to change the state of rest or uniform motion of a body along a straight path.

2. Inertia is the property of a body by virtue of which it opposes a change in its state of rest or uniform motion along a straight path. Mass is a measure of inertia of the body.

3. The quantity of motion contained in a body is called momentum. It is measured as product of mass and velocity of the body. Its SI unit is $\mathrm{kg} \mathrm{ms}^{-1}$. Dimensionally momentum is $\mathrm{MLT}^{-1}$.

4. The three laws of motion are:

(a) Every object in the universe continuous in its state of rest or uniform motion along a straight path unless an external unbalanced force changes its state. This law is also known as the law of inertia.

(b) The rate of change of momentum of a body is directly proportional to the net external force and the change in momentum takes place in the direction of the force.

Mathematically $\mathbf{F}=\frac{\mathrm{d} \mathbf{p}}{\mathrm{dt}}=\mathrm{m} \frac{\mathrm{d} \mathbf{v}}{\mathrm{dt}}=\mathrm{ma}$

(c) To every action, there is an equal and opposite reaction. Action and reaction act on different bodies and hence never cancel each other.

5. SI unit of force is newton $\mathrm{N}=1 \mathrm{~kg} \mathrm{~ms}^{-2}$

6. The gravitational unit of force is $\mathrm{kg}$ wt or $\mathrm{kg} \quad \mathrm{f}$.

$1 \mathrm{~kg} \mathrm{wt}=1 \mathrm{~kg} \mathrm{f}=9.8 \mathrm{~N}=9.8 \mathrm{~kg} \mathrm{~ms}^{-2}$

7. Impulse of a force is the product of force and the time for which it acts.

Mathematically, Impulse $=\mathbf{J}=\mathbf{F}$.t (for constant force)

$$ =\int \mathbf{F} \cdot \mathrm{dt} \quad \text { (for variable force) } $$

8. Impulse is related to change in momentum as $\mathbf{J}=$ Change in momentum

$$ =\Delta \mathbf{p}=\mathbf{p} _{\mathbf{f}}-\mathbf{p} _{\mathbf{i}}=\mathrm{m}(\mathbf{v}-\mathbf{u}) $$

9. The total momentum of a system remains conserved if there is no net external force acting on the system.

10. A rocket is a system of varying mass. The instantaneous speed ’ $\mathrm{v}$ ’ acquired by a rocket in given by $\mathrm{v}=2.303 \mu \log \left(\frac{\mathrm{m} _{0}}{\mathrm{~m}}\right)$ where $\mathrm{m}=\mathrm{m} _{0}-\alpha \mathrm{t}=$ The instantaneous mass of rocket.

11. For a body in equilibrium under the action of three concurrent forces, we have.

$$ \frac{F _{1}}{\sin \alpha}=\frac{F _{2}}{\sin \beta}=\frac{F _{3}}{\sin \gamma} $$

This is known as Lami’s theorem.

12. The free body diagram in a system indicates all the forces exerted on the body by the remaining parts of the system and the external agents.

13. A frame of reference at rest or in uniform motion is an inertial frame. The laws of motion $(\mathrm{F}=\mathrm{ma})$ are valid in such frame.

14. An accelerated frame of reference is a non-inertial frame. Fictitious forces have to the included before applying the laws of motion.

1. Two projectiles are simultaneously fired from a point ’ $O$ ’ with velocities $u _{1}$ and $u _{2}$ at angles $\alpha _{1}$ and $\alpha _{2}$ with the horizontal. The trajectory of the second projectile as observed from the first will be:

(1) an irregular curve

(2) a parabola

(3) a straight line with slope $\frac{u _{2} \sin \alpha _{2}-u _{1} \sin \alpha _{1}}{u _{2} \cos \alpha _{2}-u _{1} \cos \alpha _{1}}$

(4) a straight line with slope $\frac{u _{2} \cos \alpha _{2}-u _{1} \cos \alpha _{1}}{u _{2} \sin \alpha _{2}-u _{1} \sin \alpha _{1}}$

Show Answer

Correct answer: (3)

Solution:

Choose co-ordinates $\mathrm{X}-\mathrm{Y}$ as shown in Fig. Consider motion of each projectile in terms of components along $\mathrm{X}$ and $\mathrm{Y}$-axes.

For projectile 1

$x _{1}=\left(\mathrm{u} _{1} \cos \alpha _{1}\right) \mathrm{t} \quad \mathrm{y} _{1}=\left(\mathrm{u} _{1} \sin \alpha _{1}\right) \mathrm{t}-\frac{1}{2} \mathrm{gt}^{2}$

For projectile 2

$x _{2}=\left(\mathrm{u} _{2} \cos \alpha _{2}\right) \mathrm{t} \quad \mathrm{y} _{2}=\left(\mathrm{u} _{2} \sin \alpha _{2}\right) \mathrm{t}-\frac{1}{2} \mathrm{gt}^{2}$

$\therefore \mathrm{y} _{2}-\mathrm{y} _{1}=\left[\mathrm{u} _{2} \sin \alpha _{2}-\mathrm{u} _{2} \sin \alpha _{1}\right] \mathrm{t}$

$x _{2}-x _{1}=\left[\mathrm{u} _{2} \cos \alpha _{2}-\mathrm{u} _{1} \cos \alpha _{1}\right] \mathrm{t}$

$\Rightarrow \frac{\mathrm{y} _{2}-\mathrm{y} _{1}}{x _{2}-x _{1}}=\frac{\mathrm{u} _{2} \sin \alpha _{2}-\mathrm{u} _{1} \sin \alpha _{1}}{\mathrm{u} _{2} \cos \alpha _{2}-\mathrm{u} _{1} \cos \alpha _{1}}$

$\left(\mathrm{y} _{2}-\mathrm{y} _{1}\right)=\left(x _{2}-x _{1}\right)\left(\frac{\mathrm{u} _{2} \sin \alpha _{2}-\mathrm{u} _{1} \sin \alpha _{1}}{\mathrm{u} _{2} \cos \alpha _{2}-\mathrm{u} _{1} \cos \alpha _{1}}\right)$

The above is equation of a st. line with slope $\frac{u _{2} \sin \alpha _{2}-u _{1} \sin \alpha _{1}}{u _{2} \cos \alpha _{2}-u _{1} \cos \alpha _{1}}$

2. A partile is in uniform circular motion. If $\mathbf{a} _{t} ; \mathbf{a} _{\mathrm{c}}$ and a respectively denote the average values of the tangential, centripetal and net acceleration respectively, which of the following statements is correct?

(1) $\mathbf{a}=\mathbf{a} _{\mathbf{c}} \neq \mathbf{a} _{\mathbf{t}}$

(2) $\mathbf{a} _{\mathbf{c}}=\mathbf{a} _{\mathbf{t}} \neq \mathbf{a}$

(3) $\mathbf{a}>\mathbf{a} _{\mathbf{c}}>\mathbf{a} _{\mathbf{t}}$

(4) $\mathbf{a}<\mathbf{a} _{\mathbf{c}}<\mathbf{a} _{\mathbf{t}}$

Show Answer

Correct answer: (1)

Solution:

For uniform circular motion $\mathrm{a} _{\mathrm{t}}=0$ and $\mathrm{a}=\sqrt{\mathrm{a} _{\mathrm{c}}^{2}+\mathrm{a} _{\mathrm{t}}^{2}}$

$\therefore$ Option(1) is correct.

3. A train of mass $5500 \mathrm{~kg}$ is traveling on a level track with uniform velocity. The last carriage of mass $500 \mathrm{~kg}$ gets detached from the train. The driver of the car notices the same after traveling $1 \mathrm{~km}$ and switches off the engine. Assuming the resistance to motion as uniform and proportional to mass and the engine to exert a constant hauling force, the distance between the train and the carriage after both come to rest is

(1) $\frac{11}{10} \mathrm{~km}$

(2) $\frac{12}{11} \mathrm{~km}$

(3) $\frac{13}{12} \mathrm{~km}$

(4) $\frac{14}{10} \mathrm{~km}$

Show Answer

Correct answer: (1)

Solution:

Let $\mathrm{M}$ be the total initial mass.

Initial force of resistance $=\mathrm{k} \mathrm{M} ; \mathrm{K}$ is a constant.

Since train moves with uniform velocity; net force on it is zero, therefore,

The hauling force of engine $=\mathrm{kM}$

After the carriage is detached from the train; hauling force remains unchanged $(\mathrm{kM})$ and the resistance reduces to $\mathrm{k}(\mathrm{M}-\mathrm{m})$.

$\therefore$ Energy acquired by train in traveling a distance $\ell=[\mathrm{kM}-\mathrm{k}(\mathrm{M}-\mathrm{m})] \ell=\mathrm{km} \ell$

One switching off engine, the only force acting is resistive force of track. Let the additional distance covered by train in coming to rest be $\ell^{\prime}$. The energy acquired by train is spent in doing work against resistive force.

We have, $\mathrm{k}(\mathrm{M}-\mathrm{m}) \ell^{\prime}=\mathrm{km} \ell$

$$ \ell^{\prime}=\left(\frac{\mathrm{m}}{\mathrm{M}-\mathrm{m}}\right) \ell=\frac{500}{5000} \ell=\frac{1}{10} \mathrm{~km} $$

$\therefore$ Total distance $\left(1+\frac{1}{10}\right) \mathrm{km}=\frac{11}{10} \mathrm{~km}$

4. Two masses $m$ and $n m$ are placed on surfaces $A B$ and $A C$ symmetrically inclined at $A$ as shown. The coefficients of friction for the surfaces are $\mu$ and $2 \mu$ respectively.

For the system to just slide down along $\mathrm{AC}$; $\mathrm{n}$ should be

(1) $\frac{1+\mu}{1-2 \mu}$

(2) $\frac{\mu-1}{2 \mu-1}$

(3) $\frac{1-2 \mu}{1+\mu}$

(4) $\frac{2 \mu-1}{\mu-1}$

Show Answer

Correct answer: (1)

Solution:

Fig. (a) & (b) show free body diagram of mass $m$ and $n m$ respectively.

(i) For mass $m$ to be in equilibrium

$\mathrm{T}=\mathrm{mg} \sin 45+\mu \mathrm{mg} \cos 45^{\circ}$

(ii) For mass $\mathrm{nm}$

$\mathrm{nmg} \sin 45=\mathrm{T}+2 \mu \mathrm{nmg} \cos 45^{\circ}$ or $\mathrm{T}=\mathrm{nmg} \sin 45^{\circ}-2 \mu \mathrm{nmg} \cos 45^{\circ}$

$\therefore \mathrm{nmg}\left[\sin 45-2 \mu \cos 45^{\circ}\right]=\mathrm{mg} \sin 45+\mu \mathrm{mg} \cos 45$

$\therefore \mathrm{n}=\frac{1+\mu}{1-2 \mu}$

5. A body of mass $6 \mathrm{~m}$ is projected with a velocity $\mathrm{v}$ at $30^{\circ}$ with the vertical. At the highest point in the trajectory; the body splits up into three parts; $A$ (mass $m$ ) moves vertically up with velocity $v _{1}$; B (mass $2 m$ ) moves vertically down with velocity $v _{2}$ and the third part (mass $3 \mathrm{~m})$ moves with a velocity $\mathrm{v} _{3}$. Then after explosion, we have

(1) $\mathrm{v} _{2}=2 \mathrm{v} _{1} ; \mathrm{v} _{3}=2 \mathrm{v}$

(2) $\mathrm{v} _{1}=2 \mathrm{v} _{2} ; \mathrm{v} _{3}=\frac{\mathrm{v}}{2}$

(3) $\mathrm{v} _{2}=\frac{\mathrm{v} _{1}}{2} ; \mathrm{v} _{3}=\mathrm{v}$

(4) $\mathrm{v} _{2}=\mathrm{v} _{1}=\frac{\mathrm{v} _{3}}{2}$

Show Answer

Correct answer: (3)

Solution:

At the highest point of trajectory; the body has only horizontal momentum.

$\therefore \mathrm{p} _{\mathrm{i}}=6 \mathrm{~m}(\mathrm{v} \sin 30)=3 \mathrm{mv}($ horizontal $)$

Applying law of conservation of linear momentum along horizontal direction.

$\therefore$ Final horizontal component of momentum $=3 \mathrm{mv}=\mathrm{m} _{\mathrm{c}} \mathrm{v} _{\mathrm{f}} \Rightarrow \mathrm{v} _{\mathrm{f}}=\frac{3 \mathrm{mv}}{3 \mathrm{~m}}=\mathrm{v}$

Applying law of conservation of linear momentum in vertical direction.

$\mathrm{p} _{\text {vertical }}=0 \Rightarrow \mathrm{m} _{\mathrm{B}} \mathrm{v} _{2}-\mathrm{m} _{\mathrm{A}} \mathrm{v} _{1} \Rightarrow 2 \mathrm{mv} _{2}=\mathrm{mv} _{1}$

or $\quad \mathrm{v} _{2}=\frac{\mathrm{v} _{1}}{\mathrm{v}}$

$\therefore$ Option (3) is correct

6. A block of mass $M$ lying on a smooth inclined plane is being pulled up by applying a force $F$ to the free end of a string passing over a pulley as show. The other end of the string in fixed to a rigid support on top of the incline. The minimum force $F$ required to move the block up the plane is

(1) $\frac{\operatorname{Mg}(1+\cos \theta)}{\sin \theta}$

(2) $\frac{M g(1-\sin \theta)}{\cos \theta}$

(3) $\frac{\mathrm{Mg}}{2 \mathrm{~F}} \tan \theta$

(4) $\frac{\operatorname{Mg}(1-\cos \theta)}{\sin \theta}$

Show Answer

Correct answer: (4)

Solution:

Fig. shows F.B.D. of system. Resolve F into rectangular components as shown.

The body is on brink of moving up, if

$\mathrm{F}+\mathrm{F} \cos \theta=\mathrm{Mg} \sin \theta$

$\therefore \mathrm{F}=\mathrm{Mg} \frac{\sin \theta}{1+\cos \theta}$

$$ =\operatorname{Mg} \frac{\sin \theta(1-\cos \theta)}{1-\cos ^{2} \theta}=\operatorname{Mg} \frac{(1-\cos \theta)}{\sin \theta} $$

$\therefore$ Option (4) is correct.

7. A body at rest explodes into three pieces. Two of the pieces carry momentum $p _{1}$ and $p _{2}$ equal in magnitude along different directions, an angle $\frac{2 \pi}{3}$ apart. If $p _{3}$ is the momentum of the third piece, we have,

(1) $\left|\overrightarrow{\mathbf{p}} _{3}\right|=\left|\overrightarrow{\mathbf{p}} _{1}\right|$

(2) $\left|\overrightarrow{\mathbf{p}} _{\mathrm{B}}\right|>\left|\overrightarrow{\mathbf{p}} _{1}\right|$

(3) $\left|\overrightarrow{\mathbf{p}} _{\mathrm{B}}\right|<\left|\overrightarrow{\mathbf{p}} _{1}\right|$

(4) $\left|\overrightarrow{\mathbf{p}} _{\mathrm{B}}\right|=2\left|\overrightarrow{\mathbf{p}} _{1}\right|$

Show Answer

Correct answer: (1)

Solution:

Total initial momentum = zero

$\therefore$ Total final momentum $=$ zero.

i.e. $\overrightarrow{\mathrm{p}} _{1}+\overrightarrow{\mathrm{p}} _{2}+\overrightarrow{\mathrm{p}} _{3}=0$ or $\overrightarrow{\mathrm{p}} _{3}=-\left(\overrightarrow{\mathrm{p}} _{1}+\overrightarrow{\mathrm{p}} _{2}\right)$

Also $\left|\overrightarrow{\mathrm{p}} _{1}\right|=\left|\overrightarrow{\mathrm{p}} _{2}\right|$ and $\theta=\frac{2 \pi}{3}=120^{\circ}$

$\therefore$ Resultant of $\overrightarrow{\mathrm{p}} _{1}$ and $\overrightarrow{\mathrm{p}} _{2}$ is given by

$\left|\overrightarrow{\mathrm{p}} _{3}\right|=\sqrt{\mathrm{p} _{1}^{2}+\mathrm{p} _{2}^{2}+2 \mathrm{p} _{1} \mathrm{p} _{2} \cos 120^{0}}$

$$ =\sqrt{\mathrm{p} _{1}^{2}+\mathrm{p} _{1}^{2}+2 \mathrm{p} _{1}^{2}\left(-\frac{1}{2}\right)}=\left|\overrightarrow{\mathrm{p}} _{1}\right| $$

$\therefore$ Option (1) is correct.

8. A glass container of the shape shown is filled with water and mounted on a turn table. On relating; the water level

(1) Moves down in $\mathrm{A}$ and $\mathrm{B}$ and rises in $\mathrm{C}$

(2) Moves up in $\mathrm{A}$ and down in $\mathrm{B}$

(3) Moves up in $\mathrm{A}$ and $\mathrm{B}$ and moves down in $\mathrm{C}$

(4) Remains unchanged in all the three tubes

Show Answer

Correct answer: (3)

Solution:

The rotation of the turn table results in an outward force away from the centre (C). So the water level in C moves down and that in A and B moves up. Hence option(3) is correct.

9. A light inextensible; rope is fixed at one end to a clamp C fixed in ground. The other end of the rope passes over a pole $\mathrm{AB}$ assumed to be frictionless as shown in Fig. (a). The clamp can be uprooted with a minimum $400 \mathrm{~N}$ force. In order the pull the clamp a $50 \mathrm{~kg}$ boy hangs on the free end of the rope. In order to just pull the clamp; the boy must have a minimum acceleration

of (Take $g=10 \mathrm{~m} / \mathrm{s}^{2}$ )

(1) $8 \mathrm{~m} / \mathrm{s}^{2}$ upwards

(2) $8 \mathrm{~m} / \mathrm{s}^{2}$ downwards

(3) $6 \mathrm{~m} / \mathrm{s}^{2}$ upwards

(4) $6 \mathrm{~m} / \mathrm{s}^{2}$ downwards

Show Answer

Correct answer: (3)

Solution:

Let $\mathrm{T}$ be the tension in the rope. Then at $\mathrm{C}$; the components of $\mathrm{T}$ are:

$\mathrm{T} \cos 30$ horizontal

$\mathrm{T} \sin 30$ vertical

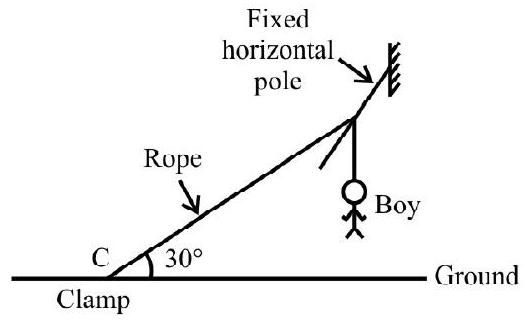
Fig. (a)

To just pull the clamp out

$\mathrm{T} \sin 30=400$ or $\mathrm{T}=800 \mathrm{~N}$

From F.B.D. of boy; as shown in Fig. (c)

$\mathrm{T}-\mathrm{mg}=\mathrm{ma}$

(As $\mathrm{T}$ acts upwards)

$800-50 \times 10=50 \mathrm{a}$

or $\mathrm{a}=\frac{300}{50}=6 \mathrm{~m} / \mathrm{s}^{2}$ upwards

$\therefore$ Option (3) is correct.

10. The $S-t$ graph for a body is as shown. The net force acting on the body in zero in the parts.

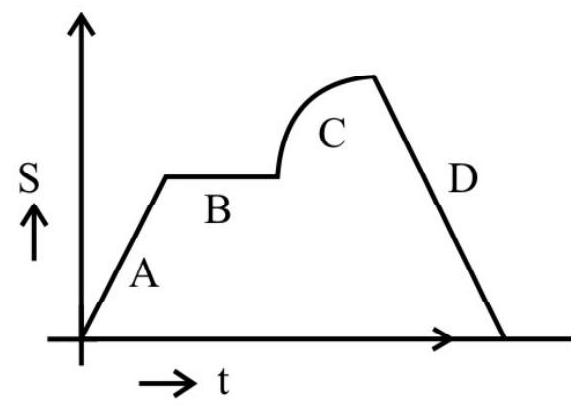
(1) C only

(2) A;B and D

(3) A and $\mathrm{D}$ but not in $\mathrm{C}$ and $\mathrm{D}$

(4) B only

Show Answer

Correct answer: (2)

Solution:

The parts A; B and D of the $\mathrm{S}-\mathrm{t}$ graph are linear and hence represent uniform motion. So acceleration $\mathrm{a}=0$ and hence no force acts on the body.

$\therefore$ Option (2) is correct.

11. Two balls with linear momentum $p _{1}=p i$ and $p _{2}=-p i$ and are subjected to a force $F=x \mathbf{j}+\mathbf{y k}$ for a short duration changing the momentum of the balls to $p _{1}^{\prime}$ and $p _{2}^{\prime}$.

If all the coefficients $p, x, y, a _{1}, b _{1}, c _{1}, a _{2}, b _{2}$ and $c _{2}$ are non-zero; which of the following combinations is possible.

(1) $\mathbf{p} _{2}^{\prime}=a _{1} \mathbf{i}+a _{1} \mathbf{j}+a _{1} \mathbf{k} $

$ \quad \mathbf{p} _{2}^{\prime}=\mathrm{b} _{2} \mathbf{j}+\mathrm{c} _{1} \mathbf{k}$

(2) $\mathbf{p} _{1}^{\prime}=\mathrm{a} _{1} \mathbf{i}+\mathrm{c} _{1} \mathbf{k}$

$\quad \mathbf{p} _{2}^{\prime}=\mathrm{a} _{2} \mathbf{i}+\mathrm{c} _{2} \mathbf{k}$

(3) $\mathbf{p} _{1}^{\prime}=b _{1} \mathbf{j}+c _{1} \mathbf{k}$

$\quad \mathbf{p} _{2}^{\prime}=\mathrm{b} _{2} \mathbf{j}+\mathrm{c} _{2} \mathbf{k}$

(4) $\mathbf{p} _{1}^{\prime}=b _{1} \mathbf{j}+\mathrm{c} _{2} \mathbf{k}$

$\quad \mathbf{p} _{2}^{\prime}=\mathrm{a} _{2} \mathbf{i}+\mathrm{b} _{2} \mathbf{j}$

Show Answer

Correct answer: (3)

Solution:

Initially; the total momentum in X-direction is zero. So final momentum in $x$ should also be zero.

The force $\mathbf{F}$ applied on the system has no component along $\mathrm{X}$-direction but has only $\mathrm{Y}$ and $\mathrm{Z}$ components.

So the system will have a net momentum in $\mathrm{Y}$ and $\mathrm{Z}$ direction but not in $\mathrm{X}$-direction.

In option (1) and (4), the system has X-component of momentum. So these options are ruled out. In option (2); the system does not have Y component. So the option is incorrect. Option (3) is correct as $\mathrm{X}$-component is zero and, we have momentum in $\mathrm{Y}$ and $\mathrm{Z}$ direction.

Option (3) is correct.

12. A $\frac{15}{4} \mathrm{~m}$ long plane with inclination $30^{\circ}$ is placed in a lift. The motor of the lift produces an upward acceleration of $5 \mathrm{~m} / \mathrm{s}^{2}$. A body is released from the top of the incline (assumed frictionless). The time taken by the body to slide down the plane is

(1) $\frac{1}{2} \mathrm{~s}$

(2) $1 \mathrm{~s}$

(3) $\frac{1}{2 \sqrt{2}} \mathrm{~s}$

(4) $\sqrt{\frac{3}{2}} \mathrm{~s}$

Show Answer

Correct answer: (2)

Solution:

For the lift accelerated upward; effective weight of objects in the lift $=m(g+a)$

$\therefore$ Acceleration of the block down the plane $=(g+a) \sin \theta$

$$ \begin{aligned} & =15 \sin 30^{\circ} \\ & =7.5 \mathrm{~m} / \mathrm{s}^{2} \\ \therefore \mathrm{S}=\text { ut }+ & \frac{1}{2} \mathrm{at}^{2} \Rightarrow \frac{15}{4}=0+\frac{1}{2} \times \frac{15}{2} \times \mathrm{t}^{2} \\ \text { or } \mathrm{t} & =\mathrm{ts} \end{aligned} $$

Hence option (2) is correct.

13. A body of mass $\mathbf{m}$ is placed on a horizontal surface. $\mathbf{A}$ force $\mathbf{F}$ has to be applied to move the block in any direction. If $\mu$ is coefficient of friction between the block and the surface; the minimum force required to move the block is

(1) $\mu \mathrm{mg}$

(2) $\frac{\mu \mathrm{mg}}{\sqrt{1+\mu^{2}}}$

(3) $\frac{\sqrt{1+\mu^{2}}}{\mu} \mathrm{mg}$

(4) $\frac{\mu \mathrm{mg}}{\sqrt{1-\mu^{2}}}$

Show Answer

Correct answer: (2)

Solution:

Let the force $\mathrm{F}$ be applied at an angle $\theta$ with the horizontal.

From the F.B.D. diagram $F \sin \theta+\mathrm{N}=\mathrm{mg} \Rightarrow \mathrm{N}=\mathrm{mg}-\mathrm{F} \sin \theta$ For the body to just slide; we have,

Force $F \cos \theta=\mu(m g-F \sin \theta)$

or $F(\cos \theta+\mu \sin \theta)=\mu \mathrm{mg}$

or $F=\frac{\mu \mathrm{mg}}{(\cos \theta+\mu \sin \theta)}$

For minimum F; $(\cos \theta+\mu \sin \theta)$ should be maximum.

or $\frac{d(\cos \theta+\mu \sin \theta)}{d \theta}=0 \Rightarrow-\sin \theta+\mu \cos \theta=0$

or $\mu=\tan \theta$ $\therefore \mathrm{F}=\frac{\mu \mathrm{mg}}{\frac{1}{\sqrt{1+\mu^{2}}}+\mu \frac{\mu}{\sqrt{1+\mu^{2}}}}=\mu\left(\frac{\sqrt{1+\mu^{2}}}{1+\mu^{2}}\right) \mathrm{mg}=\frac{\mu \mathrm{mg}}{\sqrt{1+\mu^{2}}}$

Option (2) is correct.

14. A block is moving on an inclined plane making an angle $45^{\circ}$ with the horizontal. The coefficient of friction is $\mu$. The force required to just push the block up is three times the force required to just prevent it from sliding down. If $\mathbf{N}=10 \mu$; then $\mathbf{N}$ is

(1) 10

(2) $\frac{1}{10}$

(3) 5

(4) $\frac{1}{5}$

Show Answer

Correct option: (3)

Solution:

Fig. (a) & (b) give the F.B.D. of block as it is on brink of moving up or down the inclined plane.

In Fig. (a)

$F _{1}=m g \sin 45+f _{f r}=m g \sin 45+\mu m g \cos 45^{\circ}$

In Fig. (b)

$\mathrm{F} _{2}=\mathrm{mg} \sin 45-\mu \mathrm{mg} \cos 45^{\circ}$

As $\mathrm{F} _{1}=3 \mathrm{~F} _{2}$; we have,

$\sin 45+\mu \cos 45=3\left(\sin 45-\mu \cos 45^{\circ}\right)$

Fig (a)

Fig (b)

$$ \begin{aligned} & 1+\mu=3-3 \mu \quad \text { or } 4 \mu=2 \text { or } \mu=\frac{1}{2} \\ & \therefore N=10 \mu=5 \end{aligned} $$

15. A system of two masses $5 \mathrm{~kg}$ and $20 \mathrm{~kg}$ is in equilibrium of rest. The spring is elastic and has a force constant $k$.

The string between the masses is now cut. The acceleration of the masses 20 $\mathbf{k g}$ and $5 \mathrm{~kg}$ after the mass $5 \mathrm{~kg}$ is just let go are [Take $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}$ ]

(1) $\frac{5}{2} \mathrm{~m} / \mathrm{s}^{2}$ upwards; $10 \mathrm{~m} / \mathrm{s}^{2}$ downwards

(2) $2.5 \mathrm{~m} / \mathrm{s}^{2}$ upwards, $5 \mathrm{~m} / \mathrm{s}^{2}$ downwards

(3) $10 \mathrm{~m} / \mathrm{s}^{2}$ upwards, $40 \mathrm{~m} / \mathrm{s}^{2}$ downwards

(4) $20 \mathrm{~m} / \mathrm{s}^{2}$ upwards, $10 \mathrm{~m} / \mathrm{s}^{2}$ downwards

Show Answer

Correct answer: (1)

Solution:

After the string is cut to just let go $5 \mathrm{~kg}$ mass, we have

$\mathrm{ma}=\mathrm{mg}$ (for $5 \mathrm{~kg}$ mass)

$\therefore \mathrm{a}=\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}$

From the equilibrium forces acting on $\mathrm{M}$ now downward force of $50 \mathrm{~N}$ is no longer there. There is a net upward force of $50 \mathrm{~N}$ on $\mathrm{M}$.

$=\mathrm{Ma}=5 \times 10 \mathrm{~N}$

or $20 \mathrm{a}=50$

$\Rightarrow \mathrm{a}=\frac{50}{20}=\frac{5}{2} \mathrm{~m} / \mathrm{s}^{2}$ upwards

Correct option is (1)

16. A particle moving in $\mathrm{XOY}$ plane is subjected to a force $\mathrm{F}$ and has a linear momentum.

$$ p(t)=[25 \cos 200 \pi t \hat{i}-25 \sin 200 \pi t \hat{j}] \mathrm{kg} \mathrm{m} / \mathrm{s} $$

The angle between the force and the momentum is

(1) $0^{0}$

(2) $30^{0}$

(3) $60^{\circ}$

(4) $90^{\circ}$

Show Answer

Correct answer: (4)

Solution:

Given $\mathbf{p}(\mathrm{t})=25 \cos 200 \pi \mathrm{t} \hat{\mathrm{i}}-25 \sin 200 \pi \mathrm{t} \hat{\mathrm{j}}$

$\therefore$ Force $\mathbf{F}=\frac{\mathrm{d} \mathbf{p}}{\mathrm{dt}}=[-\{25(200 \pi) \hat{\mathrm{i}} \sin (200 \pi \mathrm{t}) \hat{\mathrm{i}}\}-\{25(200 \pi) \hat{\mathrm{j}} \cos (200 \pi \mathrm{t}) \hat{\mathrm{j}}\}]$

$\therefore \mathbf{F} \cdot \mathbf{p}=25[(\cos 200 \pi t) \hat{\mathrm{i}}-(\sin 200 \pi t) \hat{\mathrm{j}}] \cdot 25(200 \pi)[(-\sin 200 \pi \mathrm{t}) \hat{\mathrm{i}}(-\cos 200 \pi \mathrm{t}) \hat{\mathrm{j}}]$

or Fp $\cos \theta=625(200 \pi)[-\cos (200 \pi t) \cdot \sin (200 \pi t)+\operatorname{si}(n 200 \pi t) \cdot \cos 200 \pi t]$

$$ =0 $$

$\therefore \cos \theta=0$ or $\theta=90^{\circ}$

Option (4) is correct.

17. Two fixed frictionless pulleys are suspended from a rigid support AB. A massless inextensible string passing over the pulleys supports a body of mass ’ $m$ ‘. The angle $\theta$ is a function of time as the mass is pulled up by means of the strings. If the free ends $P$ and $Q$ are pulled with a uniform speed $u$; the instantaneous upward speed of the mass $M$ is

(1) $\mathrm{u} \cos \theta$

(2) $2 \mathrm{u} \cos \theta$

(3) $\frac{2 \mathrm{u}}{\cos \theta}$

(4) $\frac{\mathrm{u}}{\cos \theta}$

Show Answer

Correct answer: (4)

Solution:

From the diagram; ’ $a$ ’ is constant irrespective of position of M. The speed along DA and DB is equal to ’ $u$ ‘, the speed with which the free ends are being pulled.

We have, $\mathrm{a}^{2}+\mathrm{y}^{2}=\ell^{2}$

$\therefore \mathrm{y}^{2}=\ell^{2}-\mathrm{a}^{2}$

Differentiating w.r.t. time t; we get

$2 \mathrm{y} \frac{\mathrm{dy}}{\mathrm{dt}}=2 \ell \frac{\mathrm{d} \ell}{\mathrm{dt}}-0$

$\frac{\mathrm{dy}}{\mathrm{dt}}=\frac{\ell}{\mathrm{y}}\left(\frac{\mathrm{d} \ell}{\mathrm{dt}}\right)=\frac{1}{\mathrm{y} / \ell} \frac{\mathrm{d} \ell}{\mathrm{dt}}=\left(\frac{1}{\cos \theta}\right) \mathrm{u}$

$\therefore$ Upward speed of the mass $=\frac{\mathrm{dy}}{\mathrm{dt}}=\frac{\mathrm{u}}{\cos \theta}$

Option (4) is correct.

18. A string of negligible mass passing over a smooth clamped $2 \mathrm{~kg}$ pulley supports a $5 \mathrm{~kg}$ mass as shown. The force on the pulley by the clamp is [Take $g=10 \mathrm{~m} / \mathrm{s}^{2}$ ]

(1) $50 \sqrt{2} \mathrm{~N}$

(2) $10 \sqrt{74} \mathrm{~N}$

(3) $20 \sqrt{2} \mathrm{~N}$

(4) $\sqrt{290} \mathrm{~N}$

Show Answer

Correct answer: (2)

Solution:

Let $\mathrm{T}$ be the tension in the string.

For $5 \mathrm{~kg}$ block to be in equilibrium, $\mathrm{T}-5 \times \mathrm{g}=0$

$$ \mathrm{T}=50 \mathrm{~N} $$

For free body diagram of the pulley, the forces are

(i) $70 \mathrm{~N}$ vertically down

(ii) $\mathrm{T}=50 \mathrm{~N}$ horizontal

F.B.D of pulley

$\therefore \mathrm{N}=\mathrm{Net}$ force on the clamp $=\sqrt{70^{2}+50^{2}}$

$$ \begin{aligned} & =\sqrt{4900+2500} \\ & =10 \sqrt{74} \mathrm{~N} \end{aligned} $$

Hence the clamp exerts a force of equal magnitude on the pulley.

Option (2) is correct.

19. A train is moving on a level straight track with a constant acceleration ’ $a$ ‘. An observer in the train throws a ball forward with a speed of $10 \mathrm{~m} / \mathrm{s}$ at an angle of $60^{\circ}$ with the horizontal. The observer has to move $1.15 \mathrm{~m}$ forward to catch the ball back at the initial height. The acceleration of the train is

(1) $10 \mathrm{~m} / \mathrm{s}^{2}$

(2) $5 \mathrm{~m} / \mathrm{s}^{2}$

(3) $\frac{10}{\sqrt{3}} \mathrm{~m} / \mathrm{s}^{2}$

(4) $5 \sqrt{3} \mathrm{~m} / \mathrm{s}^{2}$

Show Answer

Correct answer: (2)

Solution:

The train accelerates horizontally, there is no fictitious force in vertical direction but there is a fictitious force horizontally in backward direction.

Time of flight of the ball $=\mathrm{T}=\frac{24 \sin \theta}{\mathrm{g}}$

$$ =\frac{2 \times 10 \times \sin 60}{10}=\sqrt{3} \mathrm{~s} $$

The forward acceleration of the train gives a pseudo force on the boy i.e. produces a negative acceleration.

$\therefore \mathrm{S}=\mathrm{u} _{x} \mathrm{t}+\frac{1}{2} \mathrm{a} _{x} \mathrm{t}^{2}$

$1.15=5 \times \mathrm{t}-\frac{1}{2} \mathrm{at}^{2}$

$$ \begin{aligned} & =5 \sqrt{3}-\frac{1}{2} \mathrm{a}(\sqrt{3})^{2} \\ & =5 \sqrt{3}-\frac{3}{2} \mathrm{a} \end{aligned} $$

$$ \frac{3}{2} \mathrm{a}=5 \times 1.73-1.15=7.5 \text { or } \mathrm{a}=\frac{15}{3}=5 \mathrm{~m} / \mathrm{s}^{2} $$

Option (2) is correct.

20. A block is released from rest at the top of a $45^{\circ}$ smooth incline. It slides down a distance ’ $d$ ‘. If the time taken to slide down a rough incline through an equal distance in $\mathbf{n}$ times the time taken on the smooth incline, the coefficient of friction between the block and the plane is

(1) $\mathrm{n}^{2}-1$

(2) $1-\frac{1}{\mathrm{n}^{2}}$

(3) $\left(\frac{1}{\mathrm{n}^{2}}-1\right)$

(4) $\left(1-\frac{1}{n}\right)$

Show Answer

Correct answer: (2)

Solution:

(1) Motion on smooth plane

The free body diagram of the block is as shown in Fig. (a)

As there is no friction; acceleration down the plane $=\mathrm{a}=\frac{\mathrm{mg} \sin 45^{\circ}}{\mathrm{m}}$

$$ =\mathrm{g} \sin 45^{\circ} $$

Time taken to slide through a distance ’ $\mathrm{d}$ ’ in given by

$$ \begin{equation*} \mathrm{d}=\frac{1}{2} a \mathrm{t}^{2}=\frac{1}{2}(\mathrm{~g} \sin 45) \mathrm{t}^{2} \tag{1} \end{equation*} $$

(2) On a rough incline

The F.B.D is as shown in Fig. (b)

(a) $\therefore$ Acceleration $\mathrm{a}^{\prime}=\mathrm{g}(\sin 45-\mu \cos 45)$

$\mathrm{d}=\frac{1}{2} \mathrm{at}^{\prime 2}=\frac{1}{2} \mathrm{~g}(\sin 45-\mu \cos 45) \mathrm{t}^{\prime 2} \hspace{40mm}. . . . . (2) $

Equating the distances

$\frac{1}{2} \mathrm{~g}(\sin 45-\mu \cos 45) \mathrm{t}^{\prime 2}=\frac{1}{2}(\mathrm{~g} \sin 45) \mathrm{t}^{2}$

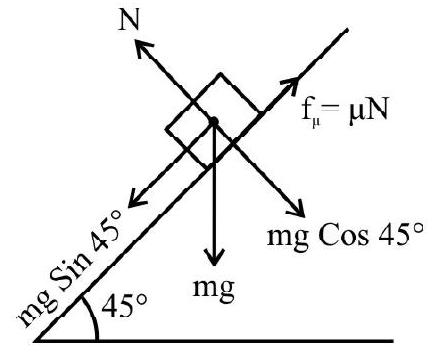
(b)

$\therefore \frac{\mathrm{t}^{\prime 2}}{\mathrm{t}^{2}}=\frac{\sin 45}{\sin 45-\mu \cos 45}=\mathrm{n}^{2}$

$$ \frac{1}{1-\mu}=n^{2} $$

or $\quad 1-\mu=\frac{1}{\mathrm{n}^{2}}$

or $\quad \mu=1-\frac{1}{\mathrm{n}^{2}}$

Option (2) is correct.

21. In the adjoining figure, blocks $A$ and $B$ with masses $M _{1}$ and $M _{2}$ are connected by a light string passing over a smooth pulley. A block $C$ is placed on $A$ to prevent it from sliding over the surface. If $\mu _{\mathrm{s}}$ is coefficient of static friction between $A$ and the surface in contact, the minimum value of ’ $m$ ’ is

(1) $\frac{\mathrm{M} _{2}}{\mu _{\mathrm{s}}}-\mathrm{M} _{1}$

(2) $\mu _{s} \mathrm{M} _{1}-\mathrm{M} _{2}$

(3) $\mu _{\mathrm{s}}^{2}\left(\mathrm{M} _{1}+\mathrm{m}\right)-\mathrm{M} _{2}$

(4) $\mathrm{M} _{2}-\mu _{\mathrm{s}}\left(\mathrm{M} _{1}+\mathrm{m}\right)$

Show Answer

Correct answer: (1)

Solution:

If the block ’ $A$ ’ does not slide; $B$ is also in equilibrium.

$\therefore \mathrm{T}=\mathrm{M} _{2} \mathrm{~g}$

Considering free body diagram of A; we get

$\mathrm{T}=\mathrm{f} _{\mathrm{S}}=\mu _{\mathrm{s}}\left(\mathrm{M} _{1}+\mathrm{m}\right) \mathrm{g}$

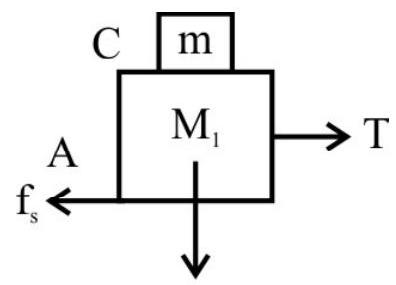
$\left(\mathrm{M} _{1}+\mathrm{m}\right) \mathrm{g}$

or $\quad \mathrm{M} _{2} \mathrm{~g}=\mu _{\mathrm{s}}\left(\mathrm{M} _{1}+\mathrm{m}\right) \mathrm{g}$

$\Rightarrow \mathrm{m}=\frac{\mathrm{M} _{2}}{\mu _{\mathrm{s}}}-\mathrm{M} _{1}$

Option (1) is correct.

22. A block of mass $5 \mathrm{~kg}$ on a frictionless horizontal table is connected to a block of mass $3 \mathrm{~kg}$ by means of a system of light pulleys $P _{1}$ and $P _{2}$ and massless, inextensible strings as shown. If $a _{1}$ and $a _{2}$ are the acceleration in the to masses and $T _{1} ; T _{2}$ the tension as shown; we have

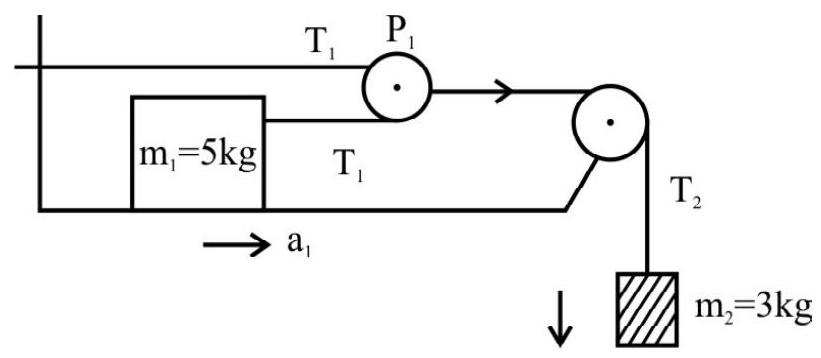
(1) $\frac{\mathrm{a} _{1}}{\mathrm{a} _{2}}=2 ; \frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=2$

(2) $\frac{\mathrm{a} _{1}}{\mathrm{a} _{2}}=2 ; \frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}=2$

(3) $\frac{\mathrm{a} _{2}}{\mathrm{a} _{1}}=2 ; \frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=2$

(4) $\frac{\mathrm{a} _{2}}{\mathrm{a} _{1}}=2 ; \frac{\mathrm{T} _{2}}{\mathrm{~T} _{1}}=2$

Show Answer

Correct answer: (2)

Solution:

As $3 \mathrm{~kg}$ mass and the moveable light pulley $\mathrm{P} _{1}$ are connected; they must have same acceleration $\mathrm{a} _{2}$ so as to move together. If $\mathrm{P} _{1}$ moves a distance $x, \mathrm{~m} _{1}$ must move a distance $2 x$ ( $x$ each for upper and lower parts) in a time ’ $t$ ‘. So acceleration of $m _{1}$ must be twice that of $m _{2}$.

$\therefore \mathrm{a} _{1}=2 \mathrm{a} _{2}$

This rules out option (3) and (4)

Again $\mathrm{T} _{2}-2 \mathrm{~T} _{1}=$ Mass of $\mathrm{P} _{1} \times \mathrm{a}=(0) \times \mathrm{a}=0$

As the pulley $\mathrm{P} _{1}$ is massless

$\therefore \mathrm{T} _{2}=2 \mathrm{~T} _{1}$

Hence option (2) is correct.

23. A block of mass $10 \mathrm{~kg}$ is pushed against a wall by a force $\mathrm{F}$ making a angle of $45^{\circ}$ with the horizontal. Given $\mu=0.3$ and $g=10 \mathbf{m} / \mathbf{s}^{2}$. The minimum and maximum values of force $F$ that allow the block to remain stationary are

Fig. (a)

(1) $109 \mathrm{~N} ; 202 \mathrm{~N}$

(2) $70 \mathrm{~N} ; 130 \mathrm{~N}$

(3) $130 \mathrm{~N} ; 160 \mathrm{~N}$

(4) $100 \mathrm{~N} ; 130 \mathrm{~N}$

Show Answer

Correct answer: (1)

Solution:

(i) When the block is on brink of sliding down, $\mathrm{F}$ is minimum.

The free body diagram is as shown.

We have $\mathrm{N}=\mathrm{F} \cos 45=\frac{\mathrm{F}}{\sqrt{2}}$

$\mathrm{F} \sin 45+\mu \mathrm{N}=\mathrm{mg}$

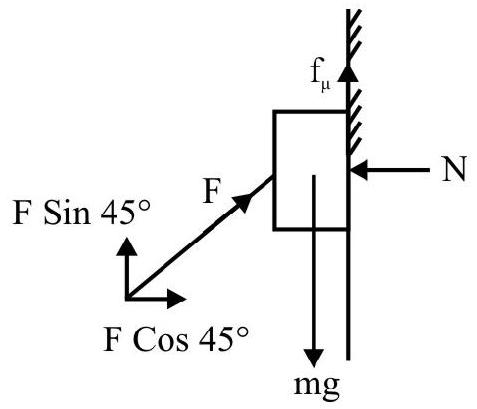
Fig. (b)

$\mathrm{F} \sin 45+\mu \mathrm{F} \cos 45=10 \times 10=100$

$\mathrm{F}\left[\frac{1}{\sqrt{2}}+\frac{0.3}{\sqrt{2}}\right]=100 \Rightarrow \mathrm{F}=\frac{100 \sqrt{2}}{1.3}=\frac{1414}{13}=109 \mathrm{~N}$

$$ \mathrm{F}=109 \mathrm{~N} $$

(ii) $\mathrm{F}$ is maximum if block is on brink of moving upwards; the force of friction must act downwards. The free body diagram in this case is as shown in Fig. (c)

Along horizontal $\mathrm{N}=\mathrm{F} \cos 45^{\circ}$

Along vertical $\mathrm{F} \sin 45=\mathrm{mg}+\mathrm{f} _{\mu}$ $=\mathrm{Mg}+\mu \mathrm{F} \cos 45$

$\mathrm{F}(\sin 45-\mu \cos 45)=\mathrm{mg}=100$

$\mathrm{F}\left[\frac{1}{\sqrt{2}}-\frac{0.3}{\sqrt{2}}\right]=100$

$\mathrm{F}=\frac{100 \sqrt{2}}{0.7}=\frac{100 \times 1.414}{.7}=\frac{1414}{7}$

$=202 \mathrm{~N}$

Option (1) is correct. $\mathrm{F} \operatorname{Sin} 45^{\circ}$

Fig. (c)

24. In the diagram shown; $A C$ in a smooth inclined plane with mass $m$ and $2 m$ on it connected by a massless string. Another mass $M$ hangs vertically by means of another light string passing over a frictionless light pulley.

If $M$ is twice the mass required to keep the system in equilibrium; the tension $T _{2}$ is

(1) $2 \mathrm{mg}$

(2) $\frac{3}{2} \mathrm{mg}$

(3) $\mathrm{mg}$

(4) $\frac{1}{2} \mathrm{mg}$

Show Answer

Correct answer: (2)

Solution:

The F.B.D. of different masses are shown in Fig. (2)

Fig. 2

For system to be in equilibrium;

From Fig. 2(a), we have

$$ \begin{equation*} \mathrm{T} _{1}-\mathrm{Mg}=0 \text { or } \mathrm{T} _{1}=\mathrm{Mg} \tag{1} \end{equation*} $$

From Fig. 2(b), we have

$$ \begin{equation*} \mathrm{T} _{1}=\mathrm{T} _{2}+\mathrm{mg} \sin 30 \tag{2} \end{equation*} $$

From Fig. 2(c), we have

$$ \begin{equation*} \mathrm{T} _{2}=2 \mathrm{mg} \sin 30 \tag{3} \end{equation*} $$

From equations (2) and (3), we get

$\Rightarrow \mathrm{T} _{1}=3 \mathrm{mg} \sin 30=\frac{3}{2} \mathrm{mg}$

$\therefore \mathrm{Mg}=\frac{3}{2} \mathrm{mg} \quad$ or $\quad \mathrm{M}=\frac{3}{2} \mathrm{mg}$

If the mass is doubled; we have

$$ \mathrm{M}=2 \times \frac{3}{2} \mathrm{~m}=3 \mathrm{~m} $$

The free body diagrams are as shown in Fig. (3)

Let ’ $a$ ’ be the acceleration of the system

From Fig. 3(a), we have

$$ \begin{equation*} 3 \mathrm{mg}-\mathrm{T} _{1}=3 \mathrm{ma} \tag{4} \end{equation*} $$

From Fig. 3(b), we have

$$ \begin{equation*} \mathrm{T} _{1}-\mathrm{T} _{2}-\mathrm{mg} \sin 30=\mathrm{ma} \tag{5} \end{equation*} $$

From Fig. 3(c), we have

$$ \begin{equation*} \mathrm{T} _{2}-2 \mathrm{mg} \sin 30=(2 \mathrm{~m}) \mathrm{a} \tag{6} \end{equation*} $$

Adding equation $=\mathrm{n}(4),(5)$ and (5), we get

$3 \mathrm{mg}-\frac{3}{2} \mathrm{mg}=6 \mathrm{ma}$

$$ 6 \mathrm{ma}=\frac{3}{2} \mathrm{mg} $$

or $\quad \mathrm{a}=\frac{\mathrm{g}}{4}$

From equation (3) $\mathrm{T} _{2}=2 \mathrm{ma}+2 \mathrm{mg} \sin 30$

$$ =2 \mathrm{~m}\left(\frac{\mathrm{g}}{4}\right)+\mathrm{mg}=\frac{3}{2} \mathrm{mg} $$

Option (2) is correct.

25. Two blocks of mass $M _{1}$ and $M _{2}$ are suspended from a rigid support at point ’ $O$ ’ by two inextensible wires of $1 \mathrm{~m}$ each. The upper wire has negligible mass and the lower one has a mass $x \mathrm{~kg} / \mathrm{m}$. The whole system has an upward acceleration ’ $a$ ’ including the support. The tension $T _{1}($ at $A)$ and $T _{2}$(at B) ; A & B are midpoints of respective strings are given by

(1) $\mathrm{T} _{1}=\mathrm{M} _{2}(\mathrm{~g}+\mathrm{a}) ; \mathrm{T} _{2}=\left(\mathrm{M} _{1}+\mathrm{M} _{2}+x\right)(\mathrm{g}+\mathrm{a})$

(2) $\mathrm{T} _{1}=\left(\mathrm{M} _{2}+\frac{x}{2}\right)(\mathrm{g}+\mathrm{a}) ; \mathrm{T} _{2}=\left(\mathrm{M} _{1}+\mathrm{M} _{2}\right)(\mathrm{g}+\mathrm{a})$

(3) $\mathrm{T} _{1}=\left(\mathrm{M} _{2}+\frac{x}{2}\right)(\mathrm{g}+\mathrm{a}) ; \mathrm{T} _{2}=\left(\mathrm{M} _{1}+\mathrm{M} _{2}+x\right)(\mathrm{g}+\mathrm{a})$

(4) $\mathrm{T} _{1}=\left(\mathrm{M} _{2}+\frac{x}{2}\right) \mathrm{g} ; \mathrm{T} _{2}=\left(\mathrm{M} _{1}+\mathrm{M} _{2}+x\right) \mathrm{g}$

Show Answer

Correct answer: (3)

Solution:

The F.B.D. of point A is shown in Fig. (a) $\therefore \mathrm{T} _{1}-\left(\mathrm{M} _{2}+\frac{x}{2}\right) \mathrm{g}=\left(\mathrm{M} _{2}+\frac{x}{2}\right) \mathrm{a}$

$\therefore \mathrm{T} _{1}=\left(\mathrm{M} _{2}+\frac{x}{2}\right)(\mathrm{g}+\mathrm{a})$

F.B.D. of point B is shown in Fig. (b)

$\mathrm{T} _{2}-\left(\mathrm{M} _{1}+\mathrm{M} _{2}+x\right) \mathrm{g}=\left(\mathrm{M} _{1}+\mathrm{M} _{2}+x\right) \mathrm{a}$

$\therefore \mathrm{T} _{2}=\left(\mathrm{M} _{1}+\mathrm{M} _{2}+x\right)(\mathrm{g}+\mathrm{a})$

Option (3) is correct.

26. A block of mass $10 \mathrm{~kg}$ rests on a rough inclined plane making an angle of $30^{\circ}$ with the horizontal. The coefficient of static friction between the block and the plane is 0.7 . The frictional force on the block is $\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right.$ )

(1) $50 \mathrm{~N}$

(2) $0.7 \times 50 \times \sqrt{3}$

(3) $50 \sqrt{3} \mathrm{~N}$

(4) $70 \mathrm{~N}$

Show Answer

Correct answer: (1)

Solution:

The F.B.D. of block is shown in Fig. obviously $\mathrm{N}=\mathrm{mg} \cos 30^{\circ}$

As $\mu _{\mathrm{s}}=0.7$

So maximum force of static friction.

$$ \begin{gathered} \mathrm{f} _{\ell \mathrm{t}}=\mu _{\mathrm{s}} \mathrm{N}=0.7(100) \frac{\sqrt{3}}{2}=(50)(.7) \sqrt{3} \\ \simeq 60.6 \mathrm{~N} \end{gathered} $$

Force down the plane on mass $m=100 \sin 30$

$$ =50 \mathrm{~N} $$

Since the force trying to move block is less than $\mathrm{f} _{\mathrm{ft}}$; the block does not move. The friction coming into play equals the force trying to move the block i.e. force of friction $=50 \mathrm{~N}$.

Option (1) is correct.

27. A simple pendulum of length $L$ and bob of mass $M$ is oscillating in a vertical plane about a vertical line within angular limits $-\theta _{0}$ to $+\theta _{0}$. For an angular displacement $\theta\left(|\theta|<\theta _{0}\right)$; the tension in the string is $T$ and the velocity of bob is $v$. Which of the following statements is incorrect?

(1) $\mathrm{T}=\mathrm{Mg} \cos \theta+\frac{\mathrm{Mv}^{2}}{\mathrm{~L}}$

(2) $\mathrm{a} _{\text {tangential }}=\mathrm{g} \sin \theta$

(3) $\mathrm{T}=\mathrm{Mg} \cos \theta _{0}$, at $\theta=\theta _{0}$

(4) $\mathrm{a} _{\text {net }}=\mathrm{g}$

Show Answer

Correct answer: (4)

Solution:

The motion of a pendulum bob in circular motion with radius ’ $\mathrm{L}$ ‘. The forces are resolved along the string (radius) and $\perp$ radius. Net force along radius should be $\frac{\mathrm{Mv}^{2}}{\mathrm{R}}$.

We have, $\mathrm{T}-\mathrm{Mg} \cos \theta=\frac{\mathrm{Mv}^{2}}{\mathrm{~L}}$ or $\mathrm{T}=\mathrm{Mg} \cos \theta+\frac{\mathrm{Mv}^{2}}{\mathrm{~L}} \hspace{40mm}. . . . . . . .(1)$

$M a _{T}=M g \sin \theta \Rightarrow \mathrm{a} _{\mathrm{T}}=\mathrm{g} \sin \theta$

$\mathrm{a} _{\text {net }} \neq{ }^{\prime} \mathrm{g} ’ \quad(\because$ the tension also acts in addition to weight $)$

28. A smooth pulley of mass $M$ is lying on a smooth table. A light string passes round the pulley and has masses $m$ and $m$ ’ attached to its ends with the masses hanging vertically as shown. The acceleration of the pulley is

(1) $\frac{4 m^{\prime} g}{4 m+\left(M+m^{\prime}\right)}$

(2) $\frac{2\left(m-m^{\prime}\right) g}{\left(M+m+m^{\prime}\right)}$

(3) $\frac{\left[\left(m+m^{\prime}\right)-M\right] g}{m+m^{\prime}+M}$

(4) $\frac{4 mm^{\prime} g}{4 mm^{\prime}+M\left(m+m^{\prime}\right)}$

Fig. 1

Show Answer

Correct answer: (4)

Solution:

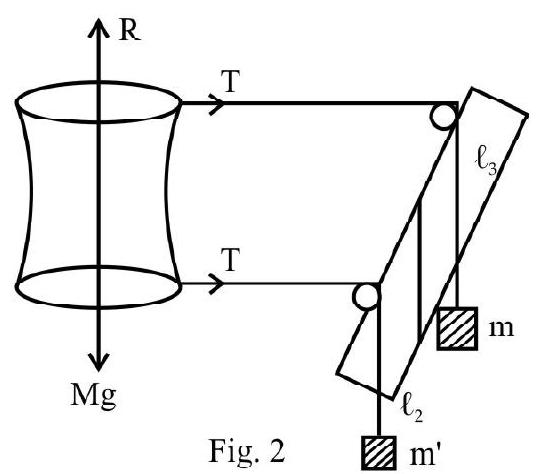
Let $\ell _{1}, \ell _{2}$ and $\ell _{3}$ denote the lengths of portion of the string as shown. If the pulley moves towards right through $x$ on the table m’ down by y and m moves up by z; then

$$ \ell _{1}^{\prime}=\ell _{1}-x ; \ell _{2}^{\prime}=\ell _{2}+\mathrm{y} \quad and \quad \ell _{3}^{\prime}=\ell _{3}-\mathrm{z} $$

As the length of the string is constant, we have

$$ 2 \ell _{1}+\ell _{2}+\ell _{3}=2\left(\ell _{1}-x\right)+\ell _{2}+\mathrm{y}+\ell _{3}-\mathrm{z} $$

or $\quad 2 x=\mathrm{y}-\mathrm{z}$

Differentiating twice with respect to time; we get

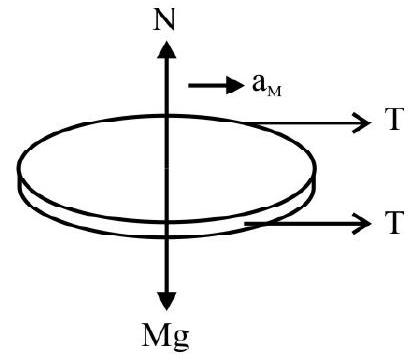
Fig. 3(a)

$$ 2 \frac{\mathrm{d}^{2} x}{\mathrm{dt}^{2}}=\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dt}^{2}}-\frac{\mathrm{d}^{2} \mathrm{z}}{\mathrm{dt}^{2}} $$

or $\quad 2 \mathrm{a} _{\mathrm{M}}=\mathrm{a} _{\mathrm{m}}^{1}-\mathrm{a} _{\mathrm{m}} \hspace{40mm} . . . . . . (1) $

Using free body diagram shown in Fig., we get

$$ \begin{align*} & 2 \mathrm{~T}=\mathrm{Ma} _{\mathrm{M}} \tag{2} \\ & \mathrm{m}^{\prime} \mathrm{g}-\mathrm{T}=\mathrm{m}^{\prime} \mathrm{a} _{\mathrm{m}}^{\prime} \tag{3} \end{align*} $$

and $\quad \mathrm{T}-\mathrm{mg}=\mathrm{ma} _{\mathrm{m}}$

Substituting for $\mathrm{a} _{\mathrm{M}}, \mathrm{a} _{\mathrm{m}}$ and $\mathrm{a} _{\mathrm{m}}^{\prime}$ from (2), (3) and (4) in(1), we get

$$ \begin{aligned} 2 \cdot \frac{2 T}{\mathrm{M}} & =\left(\mathrm{g}-\frac{\mathrm{T}}{\mathrm{m}^{\prime}}\right)-\left(\frac{\mathrm{T}}{\mathrm{m}}-\mathrm{g}\right) \\ & =2 \mathrm{~g}-\mathrm{T} \frac{\mathrm{m}+\mathrm{m}^{\prime}}{\mathrm{mm}^{\prime}} \end{aligned} $$

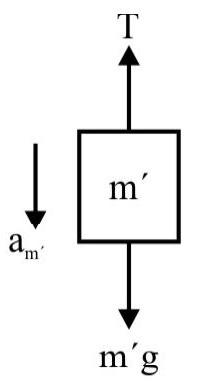
Fig. 3(b)

Fig. 3(c)

or $\quad T\left(\frac{m+m^{\prime}}{m^{\prime}}+\frac{4}{M}\right)=2 g$

$\therefore \mathrm{T}=\frac{2 \mathrm{Mm} \mathrm{m}^{\prime} \mathrm{g}}{4 \mathrm{~mm}^{\prime}+\mathrm{M}\left(\mathrm{m}+\mathrm{m}^{\prime}\right)}$

and $\quad a _{M}=\frac{2}{M} T=\frac{4 m m^{\prime} g}{4 m m^{\prime}+M\left(m+m^{\prime}\right)}$

Option (4) is correct.

29. A ladder of mass $m$ leaning against a smooth wall is in static equilibrium making an angle $\theta$ with the horizontal floor. The coefficient of friction between the ladder and the floor is $\mu$, then $\mu$ and $\theta$ are related as

(1) $\mu=\frac{1}{2 \tan \theta}$

(2) $\mu=\frac{2}{\tan \theta}$

(3) $\mu=\frac{1}{2} \tan \theta$

(4) $\mu=\frac{2 \sin ^{2} \theta}{\cos \theta}$

Show Answer

Correct answer: (1)

Solution:

As the ladder is in equilibrium;

$\mathbf{F} _{\text {net }}=0$

$\tau _{\mathbf{B}}=0$

The F.B.D. diagram is as shown in Fig.

or $\mathrm{N} _{1}=\mu \mathrm{N} _{2} \quad($ Horizontal force $=0)$

$\mathrm{N} _{2}=\mathrm{mg} \quad($ Vertical force $=0)$

Taking torque of forces about point B; we have

$\mathrm{mg} \frac{\mathrm{L}}{2} \cos \theta=\mathrm{N} _{1} \mathrm{~L} \sin \theta \quad\left(\tau _{\mathrm{B}}=0\right)$

or $\mathrm{N} _{1}=\frac{\mathrm{mg}}{2} \cot \theta$

$\therefore \mathrm{N} _{2}=\frac{\mathrm{N} _{1}}{\mu}=\frac{\mathrm{mg}}{2 \mu} \cot \theta=\mathrm{mg}$

or $\mu=\frac{\cot \theta}{3}=\frac{1}{2 \tan \theta}$

Option (1) is correct.

30. During paddeling of a bicyble, the force of friction exerted by the ground on the two wheels is such that it acts

(1) in the backward direction on both the front and the rear wheels

(2) in the forward direction on both the front and the rear wheels

(3) in the backward direction on the front wheel and in the forward direction of the rear wheel

(4) in the forward direction on the front wheel and in the backward direction in the rear wheel

Show Answer

Correct answer: (3)

Solution:

We apply a force of a action on ground in background direction when the cycle is paddled. The reaction force on backward wheel is due to friction between ground and wheel. It acts is forward direction. There is no force of action on front wheel. It moves forward. The force of friction opposes this motion & therefore acts in backward direction.

Option (3) is correct.

31. A long horizontal rod has a bead which can slide along its length and is initially placed at a distance $L$ from one end $A$ of the rod $A B$. The rod is set in angular motion about $A$ with a constant angular acceleration $\alpha$. The coefficient of friction between the lead and the rod is $\mu$. Neglecting gravity, the time at which the lead starts slipping is

(1) Infinitesimally small

(2) $\sqrt{\frac{\mu}{\alpha}}$

(3) $\frac{\mu}{\sqrt{\alpha}}$

(4) $\frac{1}{\sqrt{\mu \alpha}}$

Show Answer

Correct answer: (2)

Solution:

The reaction of the rod on the bead provides tangential force $\mathrm{F} _{\mathrm{t}}$ and the centripetal force $\left(\mathrm{F} _{\mathrm{C}}\right)$ is provided by friction $\mathrm{f} _{\mathrm{r}}$. The bead slides when $\mathrm{f} _{\mathrm{r}}$ equals limiting friction.

We have, $\mathrm{F} _{\mathrm{t}}=\mathrm{ma}=\mathrm{m} \alpha \mathrm{L}=\mathrm{N} \hspace{40mm} . . . . . . (1)$

$\left(\mathrm{f} _{\mathrm{r}}\right) _{\max }=\mu \mathrm{N}=\mu \mathrm{m} \alpha \mathrm{L} \hspace{40mm} . . . . . . (2)$

Also $\omega=\omega _{0}+\alpha \mathrm{t}=\alpha \mathrm{t} $

At time ’ $\mathrm{t}$ ‘, $\mathrm{F} _{\mathrm{C}}=\mathrm{mL} \omega^{2}=\mathrm{mL} \alpha^{2} \mathrm{t}^{2} \hspace{40mm} . . . . . . (3)$

From (2) and (3),

$$ m L \alpha^{2} t^{2}=\mu m \alpha L \Rightarrow t=\sqrt{\frac{\mu}{\alpha}} $$

Option (2) is correct.

32. In the given system, when the hall of mass $m$ is released, from point $A$, it will swing along the dotted arc. A nail is located at $N$; a distance $0.6 _{\ell}$ below $O$, the point of suspension. The tension in the string just before touching $\mathrm{N}$ and after touching $\mathrm{N}$ are

(1) $\mathrm{mg}$ and $\mathrm{mg}$

(2) $\mathrm{mg}$ and $\frac{2}{5} \mathrm{mg}$

(3) $3 \mathrm{mg}$ and $6 \mathrm{mg}$

(4) $3 \mathrm{mg}$ and $3 \mathrm{mg}$

Show Answer

Correct answer: (3)

Solution:

Just before touching the nail; the ball is moving along a circle of radius $\ell$.

$\therefore \mathrm{T}=\mathrm{mg}+\frac{\mathrm{mv}^{2}}{\ell}$

Also $\mathrm{v}^{2}=2 \mathrm{~g} \ell$

[Using $\mathrm{mg} \mathrm{L}=\frac{1}{2} \mathrm{mv}^{2}$ ]

$\therefore \mathrm{T}=\mathrm{mg}+\frac{\mathrm{m}}{\ell} 2 \mathrm{~g} \ell=3 \mathrm{mg}$

After touching nail, the ball moves along a circle of radius $[\ell-0.6 \ell(=0.4 \ell)]$

$\therefore \mathrm{T}^{\prime}=\mathrm{mg}+\frac{\mathrm{mv}^{2}}{0.4 \ell}=\mathrm{mg}+\frac{\mathrm{m} 2 \mathrm{~g} \ell}{0.4 \ell}$

$=\mathrm{mg}+5 \mathrm{mg}=6 \mathrm{mg}$

Optino (3) is correct.

33. A $1 \mathrm{~kg}$ particle initially moving with a velocity of $5 \mathrm{i} \quad \mathrm{m} / \mathrm{s}$ is subjected to forces $F _{1}$ and $F _{2}$ whose magnitude vary with time as shown in the graph. The velocity of the particle at $t=2 \mathrm{~s}$ (neglecting gravity) is

(1) $10 \mathbf{i}-5 \mathbf{j}$

(2) $11 \mathbf{i}-5 \mathbf{j}$

(3) $-\mathbf{i}-5 \mathbf{j}$

(4) $5 \mathbf{i}+5 \mathbf{j}$

Show Answer

Correct answer: (3)

Solution:

In 2 second; impulse of $F _{1}=$ Area under $F _{1}$ vs t graph.

$$ =-6 \mathrm{Ns}=-6 \mathrm{~kg} \mathrm{~m} / \mathrm{s} $$

-ve because the force $\mathbf{F} _{1}$ is in $-\mathrm{X}$ direction

$\therefore \mathrm{m}\left(\mathrm{v} _{x}-\mathrm{u} _{x}\right)=-6$ or $\mathrm{mv} _{x}=-6+5=-1$

$\therefore \mathrm{v} _{x}=-1 \quad($ As $\mathrm{m}=1 \mathrm{~kg})$

$\therefore \mathrm{v} _{x}=-\mathbf{i} ; \mathrm{ms}^{-1}$

Again impulse of $\mathrm{kg} \quad F_{2}=$ Area under $\mathrm{F} _{2}$ vst graph.

$=-\frac{1}{2}(2)(5)=-5 \mathrm{~kg} \mathrm{~m} / \mathrm{sec}$

As the force $\mathrm{F} _{2}$ is in $-\mathrm{y}$ direction. $\therefore \mathrm{m}\left(\mathrm{v} _{\mathrm{y}}-\mathrm{u} _{\mathrm{y}}\right)=-5 \Rightarrow \mathrm{v} _{\mathrm{y}}=-5 \mathbf{j}$

$\therefore \mathbf{v}=-\mathbf{i}-5 \mathbf{j}$

Option (3) is correct.

34. A ball of mass $5 \mathrm{~kg}$ is moving on a smooth XOY plane at $0.6 \mathrm{~m} / \mathrm{s}$ along $+X$ direction. It is subject to a constant force of $2 \mathrm{~N}$ in $\mathrm{Y}$ direction. After ’ $t$ ‘second the speed of the ball becomes $1 \mathrm{~m} / \mathrm{s}$. The value of ’ $t$ ’ (in second) is

(1) $1 \mathrm{~s}$

(2) $2 \mathrm{~s}$

(3) $3 \mathrm{~s}$

(4) $4 \mathrm{~s}$

Show Answer

Correct answer: (2)

Solution:

Initial momentum along $\mathrm{X}$-axis $=\mathbf{p} _{x}=5 \times 0.6=3 \mathrm{~kg} \mathrm{~m} / \mathrm{s}$

Suppose momentum imparted by the applied force $=\mathbf{p} _{\mathrm{y}}(\because$ Force is in y-direction $)$.

Given $\left|\mathbf{p} _{\mathrm{f}}\right|$ magnitude of final linear momentum $=\mathrm{mv}=5 \times 1=5 \mathrm{~kg} \mathrm{~m} / \mathrm{s}$

Also $\mathrm{p} _{\mathrm{f}}^{2}=\mathrm{p} _{x}^{2}+\mathrm{p} _{\mathrm{y}}^{2} \Rightarrow \mathrm{p} _{\mathrm{y}}^{2}=25-9=16$

or $\mathrm{p} _{\mathrm{y}}=4 \mathrm{~kg} \mathrm{~m} / \mathrm{s}$

Momentum imported in $\mathrm{Y}$ direction $=\mathrm{F} _{\mathrm{y}} \cdot \mathrm{t}$

$$ 4=2(t) $$

or $\mathrm{t}=2 \mathrm{~s}$

Option (2) is correct.

35. A block of mass $m$ is on a rough inclined plane of angle $\theta$ with $\tan \theta$ exceeding $\mu$, the coefficient of friction. The block is held stationary by applying a force $P$ parallel to the plane. The force $P$ up the plane is taken to be positive.

As $P$ in varied from $P _{1}=m g(\sin \theta-\mu \cos \theta)$ to $P _{2}=m g(\sin \theta-\mu \cos \theta)$;

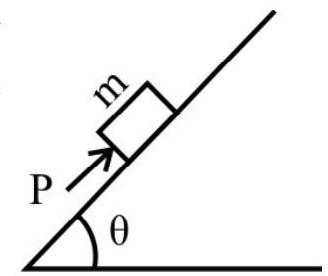the variation of the frictional force of with $P$ can be represented as

Show Answer

Correct answer: (2)

Solution:

For $\mathrm{P}<\mathrm{mg} \sin \theta$, the block tends to slide down the inclined plane. Force of friction $\mathrm{f}$ coming into play, acts upwards.

For equilibrium $\mathrm{P}+\mathrm{f}=\mathrm{mg} \sin \theta$

$\mathrm{f}=\mathrm{mg} \sin \theta-\mathrm{P}$ is positive (for $\mathrm{P}=\mathrm{P} _{1}$ ) acting upwards

For $\mathrm{P}=\mathrm{mg} \sin \theta$

$\mathrm{P}+\mathrm{f}=\mathrm{mg} \sin \theta$

or $\mathrm{f}=0$

For $\mathrm{P}>\mathrm{mg} \sin \theta$, the block tends to slide up the plane. Force of friction $\mathrm{f}$ coming into play acts down the plane.

Therefore for equilibrium; $\mathrm{f}+\mathrm{mg} \sin \theta=\mathrm{P}$

or $\mathrm{f}=\mathrm{P}-\mathrm{mg} \sin \theta$ is negative. (for $\mathrm{P}=\mathrm{P} _{2}$ ) (acting down the plane)

This variation in ’ $\mathrm{f}$ ’ is represented in option (2).

36. A $10 \mathrm{gm}$ bullet moving horizontally hits the centre of a $200 \mathrm{gm}$ ball placed on top of a $5 \mathrm{~m}$ high pole. (See figure) The two move independently thereafter. The ball hits the ground 20 $\mathrm{m}$ away from the pole and the bullets hit $100 \mathrm{~m}$ away as shown. The initial velocity of the bullet is $\left(\right.$ Take $\left.g=10 \mathrm{~m} / \mathrm{s}^{2}\right)$

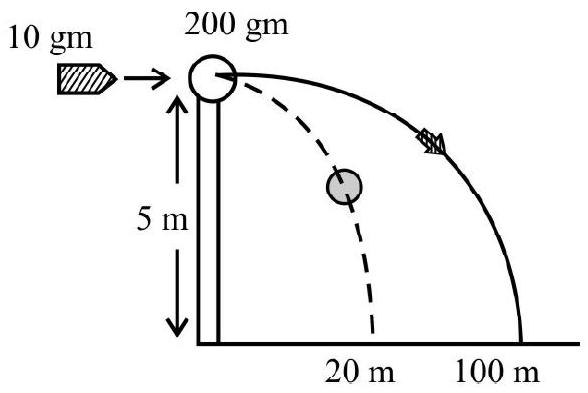
(1) $250 \mathrm{~m} / \mathrm{s}$

(2) $400 \mathrm{~m} / \mathrm{s}$

(3) $500 \mathrm{~m} / \mathrm{s}$

(4) $1000 \mathrm{~m} / \mathrm{s}$

Show Answer

Correct answer: (3)

Solution:

Consider vertical motion of bullet after collision.

Time taken by the ball to fall to the ground = ’ $t$ ’ is

$\mathrm{h}=\frac{1}{2} \mathrm{gt}^{2}$

or $\mathrm{t}=\sqrt{\frac{2 \times 5}{1}}=1 \mathrm{~s}$

Horizontal distance covered by the ball $=20 \mathrm{~m}$

$\mathrm{v} _{1}=$ Horizontal velocity of bullet after collision $=20 \mathrm{~m} / \mathrm{s}$

Similarly, final horizontal velocity of the bullet after collision $=100 \mathrm{~m} / \mathrm{s}$

Let u be horizontal speed of bullet before collision. Using principle of momentum conservation along horizontal, we get.

$\mathrm{mu}=\mathrm{mv} _{1}+\mathrm{mv} _{2}$

$\left(\frac{10}{1000}\right) \mathrm{u}=\left(\frac{10}{1000}\right)(100)+\left(\frac{200}{1000}\right)(20)$

$10 \mathrm{u}=50000$ or $\mathrm{u}=500 \mathrm{~m} / \mathrm{s}$

Option (3) is correct.

37. A $0.20 \mathrm{~kg}$ projectile is fired from a point on a level ground at $50 \mathrm{~m} / \mathrm{s}$ at an angle $\theta\left(=\tan ^{-1} \frac{4}{3}\right)$. At the highest point of the trajectory, the projectile is hit at its centre by a bullet moving horizontally at $500 \mathrm{~m} / \mathrm{s}$. The projectile and the bullet move independently thereafter. If the projectile and the bullet cover a further horizontal distance of $160 \mathrm{~m}$ and $400 \mathrm{~m}$ respectively; the mass of the bullet is

(1) $40 \mathrm{gm}$

(2) $20 \mathrm{gm}$

(3) $10 \mathrm{gm}$

(4) $5 \mathrm{gm}$

Show Answer

Correct answer: (4)

Solution:

We have $\tan \theta=\frac{4}{3}$

$\therefore \sin \theta=\frac{4}{5} ; \cos \theta=\frac{3}{5}$

$$ \begin{aligned} & \mathrm{u} _{x}=50 \cos \theta=30 \mathrm{~m} / \mathrm{s} \quad \mathrm{u} _{\mathrm{y}}=50 \sin \theta=40 \mathrm{~m} / \mathrm{s} \\ & \mathrm{H} _{\max }=\frac{\mathrm{u}^{2} \sin ^{2} \theta}{2 \mathrm{~g}}=50 \times 50 \times \frac{4}{5} \times \frac{4}{5} \times \frac{1}{2 \times 10}=80 \mathrm{~m} \end{aligned} $$

Time taken by projectile to fall through a vertical distance of $80 \mathrm{~m}$ is given by

$$ \frac{1}{2} \mathrm{gt}^{2}=\mathrm{h} \quad \text { or } \quad \mathrm{t}=\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}=\sqrt{\frac{2 \times 80}{10}}=4 \mathrm{~s} $$

Horizontal distance covered by projectile $=160 \mathrm{~m}$

$\therefore$ Horizontal speed after being hit $=\frac{160}{4}$

$$ =40 \mathrm{~m} / \mathrm{s} $$

Final horizontal velocity of the bullet $=\frac{400}{4}$

$$ =100 \mathrm{~m} / \mathrm{s} $$

Applying principle of momentum conservation to horizontal motion, we get

$$ \begin{aligned} & \mathrm{mu}+\mathrm{MU}=\mathrm{mv}+\mathrm{MV} \quad(\mathrm{m}=\text { Bullet, } \mathrm{M}=\text { Ball }) \\ & \mathrm{m}(500)+(0.2)(30)=\mathrm{m}(100)+(0.2)(40) \\ & 400 \mathrm{~m}=8-6=2 \\ & \mathrm{~m}=\frac{2}{400}=\frac{1}{200} \mathrm{~kg}=5 \mathrm{gm} \end{aligned} $$

Option (4) is correct.

38. Two blocks with masses $M _{1}$ and $M _{2}$ are connected with a light spring of stiffness $\mathrm{K} \mathrm{Nm}^{-1}$. The blocks are placed on a smooth horizontal surface and pulled by forces $F _{1}$ and $F _{2}$ as shown. When the blocks attain constant and equal acceleration; the extension in the spring is

(1) $\frac{M _{1} F _{1}+M _{2} F _{2}}{\left(M _{1}+M _{2}\right) K}$

(2) $\frac{\mathrm{M} _{1} \mathrm{~F} _{2}+\mathrm{M} _{2} \mathrm{~F} _{1}}{\left(\mathrm{M} _{1}+\mathrm{M} _{2}\right) \mathrm{K}}$

(3) $\frac{\mathrm{F} _{1}-\mathrm{F} _{2}}{\mathrm{~K}}$

(4) $\frac{F _{1}+F _{2}}{K}$

Show Answer

Correct answer: (1)

Solution:

Let $\mathrm{T}$ be the tension in the spring. The equations of motion of $\mathrm{M} _{2}$ and $\mathrm{M} _{1}$ are:

$\mathrm{F} _{1}-\mathrm{T}=\mathrm{M} _{2} \mathrm{a} \hspace{40mm} . . . . . . (1)$

$\mathrm{T}-\mathrm{F} _{2}=\mathrm{M} _{1} \mathrm{a} \hspace{40mm} . . . . . . (2)$

Adding (1) and (2), we get

$\therefore \mathrm{F} _{1}-\mathrm{F} _{2}=\left(\mathrm{M} _{1}+\mathrm{M} _{2}\right) \mathrm{a} \Rightarrow \mathrm{a}=\frac{\mathrm{F} _{1}-\mathrm{F} _{2}}{\mathrm{M} _{1}+\mathrm{M} _{2}}$

$\therefore \mathrm{T}=\mathrm{F} _{2}+\mathrm{M} _{1}\left(\frac{\mathrm{F} _{1}-\mathrm{F} _{2}}{\mathrm{M} _{1}+\mathrm{M} _{2}}\right)$

[Using (2)]

$=\frac{\mathrm{M} _{1} \mathrm{~F} _{2}+\mathrm{M} _{2} \mathrm{~F} _{2}+\mathrm{M} _{1} \mathrm{~F} _{1}-\mathrm{M} _{1} \mathrm{~F} _{2}}{\mathrm{M} _{1}+\mathrm{M} _{2}}$

$$ =\frac{\mathrm{M} _{1} \mathrm{~F} _{1}+\mathrm{M} _{2} \mathrm{~F} _{2}}{\mathrm{M} _{1}+\mathrm{M} _{2}} $$

Extension in the spring $=x=\frac{T}{K}=\frac{M _{1} F _{1}+M _{2} F _{2}}{\left(M _{1}+M _{2}\right) K}$

Option (1) is correct.

39. The velocity of a $2 \mathrm{~kg}$ object initially moving at $(-2 \mathbf{i}+3 \mathbf{j}-5 \mathbf{k}) \mathrm{m} / \mathrm{s}$ changes to $(\mathbf{i}+3 \mathbf{j}+4 \mathbf{k})$ $\mathrm{m} / \mathrm{s}$ after $3 \mathrm{~s}$. The magnitude of force acting on the body is

(1) $2 \sqrt{3} \mathrm{~N}$

(2) $2 \sqrt{10} \mathrm{~N}$

(3) $6 \sqrt{3} \mathrm{~N}$

(4) $12 \sqrt{3} \mathrm{~N}$

Show Answer

Correct answer: (2)

Solution:

Change in velocity of the body $=\mathbf{v}-\mathbf{u}$

$$ =+3 \mathbf{i}+9 \mathbf{k} $$

Change in momentum $=\mathrm{m}(\mathrm{v}-\mathrm{u})$

$$ =6 \mathbf{i}+18 \mathbf{k} $$

Force $=$ Rate of change of momentum

$$ =\frac{1}{3}(6 \mathbf{i}+18 \mathbf{k})=2 \mathbf{i}+6 \mathbf{k} $$

$|\mathbf{F}|=\sqrt{2^{2}+6^{2}}=\sqrt{40}=2 \sqrt{10} \mathrm{~N}$

Option (2) is correct.

40. A clock with $7 \mathrm{~cm}$ long light seconds hand carries a $100 \mathrm{gm}$ mass at its free tip. The change in momentum of the mass in $10 \mathrm{~s}$ is

(1) $\frac{11}{15} \times 10^{-3} \mathrm{Ns}$

(2) $\frac{22}{15} \times 10^{-3} \mathrm{Ns}$

(3) $\frac{11}{9} \times 10^{-5} \mathrm{Ns}$

(4) $\frac{15}{11} \times 10^{-3} \mathrm{Ns}$

Show Answer

Correct answer: (1)

Solution:

We have mass $\mathrm{m}=10 \mathrm{gm}=\frac{1}{100} \mathrm{~kg}$

$$ \begin{aligned} & \left|\mathbf{v} _{1}\right|=\mathrm{v} \\ & \left|\mathbf{v} _{2}\right|=\mathrm{v} \end{aligned} $$

Angle swept in $10 \mathrm{~s}=\frac{360}{60} \times 10=60^{\circ}$

$$ \begin{aligned} & \theta=60^{\circ} \\ \Delta \mathrm{v}= & \sqrt{\mathrm{v}^{2}+\mathrm{v}^{2}-2 \mathrm{v} \cdot \mathrm{v} \cos 60} \\ & =\sqrt{2 \mathrm{v}^{2}(1-\cos 60)}=\sqrt{2 \mathrm{v}^{2} 2 \sin ^{2} 30} \\ & =2 \mathrm{v} \sin 30=\mathrm{v}=\frac{2 \pi \mathrm{r}}{\mathrm{T}}=2 \times \frac{22}{7} \times \frac{7}{100 \times 60} \end{aligned} $$

$$ =\frac{11}{1500} \mathrm{~m} / \mathrm{s} $$

$\Delta \mathrm{p}=\mathrm{m}(\Delta \mathbf{v})=\frac{100}{1000} \times \frac{11}{1500}=\frac{11}{15000} \mathrm{Ns}$

Option (1) is correct.

41. A ball of mass $m$ is projected vertically upwards from ground at $40 \mathrm{~m} / \mathrm{s}$ and at the same time another identical ball is thrown downwards at $10 \mathrm{~m} / \mathrm{s}$ along the same vertical line from a height of $100 \mathrm{~m}$. The two balls collide and move together thereafter to finally fall on the ground. The total time of flight of the balls is

(1) $8 \mathrm{sec}$

(2) $6 \mathrm{sec}$

(3) $5 \mathrm{sec}$

(4) $4 \mathrm{sec}$

Show Answer

Correct answer: (3)

Solution:

For the ball moving up,

Distance $\mathrm{S} _{1}=40 \mathrm{t}-\frac{1}{2} \mathrm{gt}^{2} \quad$ [Retarded motion $]$

For the ball moving downwards

$\mathrm{S} _{2}=10 \mathrm{t}+\frac{1}{2} \mathrm{gt}^{2} \quad[\text { Accelerated motion }]$

For the balls to collide at time ’ $t$ ‘, we have

$\mathrm{S} _{1}+\mathrm{S} _{2}=100 \mathrm{~m}$

or $50 \mathrm{t}=100 \mathrm{~m} \Rightarrow \mathrm{t}=2 \mathrm{~s}$

Upward velocity of first ball at $t=2 \mathrm{~s}=\mathrm{v} _{1}=\mathrm{u}-\mathrm{gt}$

$=40-10(2)$

$=20 \mathrm{~m} / \mathrm{s}$

Downward velocity of second ball at $\mathrm{t}=2 \mathrm{~s}=\mathrm{v} _{2}=10+10(2)$

$$ =30 \mathrm{~m} / \mathrm{s} $$

For velocity of the combination after collision

$20 \mathrm{~m}$ (upwards) $-30 \mathrm{~m}$ (downwards) $=2 \mathrm{mv}$

$\therefore \mathrm{v}=5 \mathrm{~m} / \mathrm{s}$ downwards

Height at which bodies collide

$=$ Distance covered by the first ball in $2 \mathrm{~s}$

$$ =u t-\frac{1}{2} \mathrm{gt}^{2}=40(2)-\frac{1}{2}(10)(4)=60 \mathrm{~m} $$

For motion of the balls after collision

$$ \begin{aligned} & \mathrm{u}=5 \mathrm{~m} / \mathrm{s} \\ & \mathrm{S}=60 \mathrm{~m} \\ & \mathrm{a}=+10 \mathrm{~m} / \mathrm{s}^{2} \end{aligned} $$

We have $\mathrm{S}=\mathrm{ut}+\frac{1}{2} \mathrm{at}^{2}$

$$ 60=5 \mathrm{t}+\frac{1}{2}(10) \mathrm{t}^{2} $$

$5 \mathrm{t}^{2}+5 \mathrm{t}-60=0$

$\mathrm{t}^{2}+\mathrm{t}-12=0$

$(\mathrm{t}+4)(\mathrm{t}-3)=0 \Rightarrow \mathrm{t}=-4 \mathrm{~s} ; \mathrm{t}=3 \mathrm{~s}$

Neglect $\mathrm{t}=-4 \mathrm{~s}$ (extraneous)

We get $\mathrm{t}=3 \mathrm{sec}$.

$\therefore$ Total time of flight $=2 \mathrm{~s}$ (Before collision)

$$ \begin{aligned} & +3 \mathrm{~s}(\text { After collision }) \\ & =5 \mathrm{~s} \end{aligned} $$

Option (3) is correct.

42. The driver of a truck, driving at a certain speed, notices a wall ahead at a distance ’ $d$ ‘. To prevent a collision; he may turn the truck to safety by applying a turning force $\mathrm{F} _{\mathrm{T}}$. He may also prevent collision by a braking force $F _{B}$. The forces are related as

(1) $\mathrm{F} _{\mathrm{T}}=2 \mathrm{~F} _{\mathrm{B}}$

(2) $\mathrm{F} _{\mathrm{B}}=2 \mathrm{~F} _{\mathrm{T}}$

(3) $\mathrm{F} _{\mathrm{T}}=\pi \mathrm{F} _{\mathrm{B}}$

(4) $\mathrm{F} _{\mathrm{B}}=\pi \mathrm{F} _{\mathrm{T}}$

Show Answer

Correct answer: (1)

Solution:

If $v$ is the initial speed of the truck; to stop it over a distance ’ $d$ ‘; the braking force $F _{B}$ must produce an acceleration ’ $a$ ’ given by

$$ \begin{aligned} & 2 \mathrm{ad}=(0)^{2}-\mathrm{v}^{2} \\ & \mathrm{a}=-\frac{\mathrm{v}^{2}}{2 \mathrm{~d}} \end{aligned} $$

Breaking force $\left|F _{B}\right|=m|a|=\frac{m^{2}}{2 d}$

To turn the truck to safely, he must take the truck along a circular path of radius ’ $\mathrm{d}$ ‘.

So turning force $=\mathrm{F} _{\mathrm{T}}=$ Centripetal force

$$ =\frac{\mathrm{mv}^{2}}{\mathrm{~d}} $$

$$ \therefore \mathrm{F} _{\mathrm{T}}=2 \mathrm{~F} _{\mathrm{B}} $$

Option (1) is correct.

43. A man standing on a weighing machine in a lift records his weight in the machine as under:

(i) $\mathrm{w} _{1}$ when the lift acceleration upwards at $5 \mathrm{~m} / \mathrm{s}^{2}$

(ii) $\mathbf{w} _{2}$ when the lift acceleration downwards at $5 \mathrm{~m} / \mathrm{s}^{2}$

(iii) $\mathbf{w} _{3}$ when the lift moves up at $5 \mathrm{~m} / \mathrm{s}$

(iv) $w _{4}$ when the lift moves down at $5 \mathrm{~m} / \mathrm{s}$

Which of the following gives a correct relation between their relative values.

(1) $\mathrm{w} _{1}>\mathrm{w} _{2}>\mathrm{w} _{3}>\mathrm{w} _{4}$

(2) $\mathrm{w} _{1}=\mathrm{w} _{2}>\mathrm{w} _{3}>\mathrm{w} _{4}$

(3) $\mathrm{w} _{1}<\mathrm{w} _{2}<\mathrm{w} _{3}<\mathrm{w} _{4}$

(4) $\mathrm{w} _{1}>\mathrm{w} _{3}=\mathrm{w} _{4}<\mathrm{w} _{1}$

Show Answer

Correct answer: (4)

Solution:

When lift acceleration upwards fictitious force acts downwards and vice-versa. Therefore

$$ \mathrm{w} _{1}>\mathrm{w} _{2} $$

When left moves up or down with a constant speed, the weight of man equals his true weight. Therefore

$$ \mathrm{w} _{3}=\mathrm{w} _{4} $$

Option (4) is correct.

44. The given figure represents the position time graph for a body with a certain mass $m$. Which of the following graphs correctly represents the impulse received by the body. Take impulse along motion as positive and against the motion as negative.

Show Answer

Correct answer: (1)

Solution:

At $t=2 \mathrm{~s}$; the velocity changes from $u$ to $-\mathrm{u}$. The impulse imparted equals change in linear momentum and is opposite to the motion and hence negative. So the impulse is $-2 \mathrm{mu}$ or $2 \mathrm{mu}$ in downward direction.

Similarly at $\mathrm{t}=4 \mathrm{~s}$, velocity changes from $-\mathrm{u}$ to $\mathrm{u}$. The impulse imparted is $+2 \mathrm{mu}$. This process repeats itself. These changes are shown in graph (A).

Option (1) is correct.

45. A stone of mass $m$ tied to a string of length ’ $L$ ’ is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time, the stone is at its lowest position and has a speed ’ $u$ ‘. The magnitude of change in its linear momentum as it reaches a position where the string in horizontal, is

(1) $\sqrt{m^{2} u^{2}-2 m g L}$

(2) $\sqrt{2 m^{2}-g L}$

(3) $m^{2} \sqrt{u^{2}-g L}$

(4) $\mathrm{m} \sqrt{2\left(\mathrm{u}^{2}-\mathrm{gL}\right)}$

Show Answer

Correct answer: (4)

Solution:

As the body moves from intial position I to final position $\mathrm{F}$, we have change in velocity

$\Delta \mathbf{v}=\mathbf{v}-\mathbf{u}$

$$ =\mathrm{v} \mathbf{j}-\mathrm{u} \mathbf{i} $$

$|\Delta \mathbf{v}|=\sqrt{\mathbf{v}^{2}+\mathbf{u}^{2}}\hspace{40mm} . . . . . . (1)$

Also $\frac{1}{2} \mathrm{mu}^{2}-\frac{1}{2} \mathrm{mv}^{2}=2 \mathrm{gL}$

$$ \begin{equation*} \mathrm{u}^{2}-\mathrm{v}^{2}=2 \mathrm{gL} \tag{2} \end{equation*} $$

$\therefore|\Delta \mathbf{v}|=\sqrt{u^{2}-2 g L+u^{2}}=\sqrt{2\left(u^{2}-g L\right)}$

Change in momentum $|\Delta \overrightarrow{\mathrm{v}}|=\mathrm{m} \sqrt{2\left(\mathrm{u}^{2}-\mathrm{gL}\right)}$

Option (4) is correct.

46. A block of mass $m$ is placed on a surface with a vertical cross-section given by $y=\frac{x^{3}}{6}$. If the coefficient of friction is 0.5 ; the maximum height above ground at which the block can be placed without slipping is

(1) $\frac{1}{2} \mathrm{~m}$

(2) $\frac{1}{3} \mathrm{~m}$

(3) $\frac{1}{6} \mathrm{~m}$

(4) $\frac{2}{3} \mathrm{~m}$

Show Answer

Correct answer: (3)

Solution:

We have $\mathrm{y}=\left(\frac{x^{3}}{6}\right)$

With the block at height y as shown, we have

Slope $\tan \theta=\frac{\mathrm{dy}}{\mathrm{d} x}=\frac{\mathrm{d}}{\mathrm{d} x}\left(\frac{x^{3}}{6}\right)$

$$ =\frac{1}{6}\left(3 x^{2}\right)=\frac{x^{2}}{2} $$

At maximum height, the friction is maximum.

We have $\mu=\tan \theta \quad$ or $\quad \frac{x^{2}}{2}=0.5 \Rightarrow x^{2}=1$

or

$$ x= \pm 1 $$

$\therefore$ From $\mathrm{y}=\frac{x^{3}}{6}$; we get $\mathrm{y}=+\frac{1}{6} \mathrm{~m} \quad$ or $\quad \mathrm{y}=-\frac{1}{6} \mathrm{~m}$

Hence the maximum possible height above the ground where we can place the block without slipping in $\frac{1}{6} \mathrm{~m}$.

Option (3) is correct.

47. A uniform rope of mass $M$ and length $L$ lying on a smooth horizontal surface is pulled from one end by a constant force $F$. The tension in the rope at a distance ’ $\ell$ ’ from the end where the force is applied is

(1) $\mathrm{F} \frac{\ell}{\mathrm{L}}$

(2) $\mathrm{F}\left(\frac{\mathrm{L}-\ell}{\mathrm{L}}\right)$

(3) $F\left(\frac{L}{L-\ell}\right)$

(4) $\mathrm{F} \frac{\ell^{2}}{\mathrm{~L}^{2}}$

Show Answer

Correct answer: (2)

Solution:

The rope can be considered as made of two parts of length $\ell$ and $(\mathrm{L}-\ell)$ as shown.

Acceleration in the rope $=\mathrm{a}=\frac{\mathrm{F}}{\mathrm{M}} \hspace{40mm} . . . . . . (1)$

Let $\mathrm{T}$ be the tension at $\mathrm{C}$.

Then equation of motion of length $\ell$ is $\mathrm{F}-\mathrm{T}=\mathrm{m} _{\mathrm{AC}} \mathrm{a}=\frac{\mathrm{M}}{\mathrm{L}}(\ell) \mathrm{a}\hspace{40mm} . . . . . . (2)$

and for part $C B ; T=m _{B C} a=\frac{M}{L}(L-\ell) a \hspace{40mm} . . . . . . (3)$

$$ =\frac{\mathrm{M}}{\mathrm{L}}(\mathrm{L}-\ell) \frac{\mathrm{F}}{\mathrm{M}}=\mathrm{F}\left(\frac{\mathrm{L}-\ell}{\mathrm{L}}\right) $$

Option (2) is correct.

48. The barrel of a gun of mass $M$ makes an angle $\alpha$ with the horizontal. It fires a shell of mass $m$. The gun is mounted on a frictionless track. If the muzzle velocity of the shell relative to the gun in ’ $v$ ‘; the absolute muzzle speed in given by

(1) $v \sqrt{1-\frac{m(m+2 M)}{(m+M)^{2}} \cos ^{2} \alpha}$

(2) $v \sqrt{1-\frac{m(m+2 M)}{(m+M)^{2}} \sin ^{2} \alpha}$

(3) $v \sqrt{\frac{(m+M)^{2}}{2 M} \cos \alpha}$

(4) $v \sqrt{\frac{m+M}{2 M} \tan \alpha}$

Show Answer

Correct answer: (1)

Solution:

As the recoil is frictionless, there is no horizontal force.

$\therefore$ Momentum along horizontal is conserved. If the shell is fired with a relative velocity $\mathrm{v}$, then relative horizontal velocity $=\mathrm{v} \cos \alpha$

$\therefore \mathrm{v} \cos \alpha=\mathrm{v} _{\mathrm{abs}}-(-\mathrm{V})$

$\Rightarrow \mathrm{v} _{\mathrm{abs}}=\mathrm{v} \cos \alpha-\mathrm{V} \hspace{40mm} . . . . . . (1)$

By conservation of linear momentum along horizontal, we get

$$ \mathrm{m}(\mathrm{v} \cos \alpha-\mathrm{V})-\mathrm{MV}=0 $$

or $\quad \mathrm{V}=\frac{\mathrm{mv} \cos \alpha}{\mathrm{m}+\mathrm{M}} \hspace{40mm} . . . . . . (2)$

$V$ being the recoil velocity of the gun.

Vertical component of absolute velocity of the gun $=v \sin \alpha$

$\therefore \mathrm{v} _{\mathrm{abs}}=\sqrt{(\mathrm{v} \cos \alpha-\mathrm{V})^{2}+(\mathrm{v} \sin \alpha)^{2}}$

$=\sqrt{\mathrm{v}^{2}+\mathrm{V}^{2}-2 \mathrm{vV} \cos \alpha}$

$=\sqrt{v^{2}+\frac{m^{2} v^{2} \cos ^{2} \alpha}{(m+M)^{2}}-2 v\left(\frac{m v \cos \alpha}{m+M}\right) \cos \alpha}$

$=v \sqrt{1+\frac{m^{2} \cos ^{2} \alpha}{(m+M)^{2}}-\frac{2 m \cos ^{2} \alpha}{m+M}}$

$=v \sqrt{1+\frac{m^{2}-2 m(m+M)}{(m+M)^{2}} \cos ^{2} \alpha}$

$=v \sqrt{1+\frac{-m^{2}-2 m M}{(m+M)^{2}} \cos ^{2} \alpha}$

$=v \sqrt{1-\frac{m(m+2 M)}{(m+M)^{2}} \cos ^{2} \alpha}$

$\therefore$ Option (1) is correct.

49. A uniform flexible chain of length ’ $\ell$ ’ with mass $\lambda \mathrm{kgm}^{-1}$ passes over a small, light and smooth pulley. It is released from rest with a length $x$ on one side. Assuming that the chain accelerates downwards from this side; the acceleration of the chain as a function of ’ $x$ ’ is

(1) $\left(1-\frac{2 x}{\ell}\right) \lambda \mathrm{g}$

(2) $\left(\frac{2 x}{\ell}-1\right) \mathrm{g}$

(3) $\left(\frac{2 x}{\ell}-1\right) \lambda \mathrm{g}$

(4) $\left(1-\frac{2 x}{\ell}\right) \mathrm{g}$

Show Answer

Correct answer: (2)

Solution:

From the diagram,

Mass of chain on side $x=x \lambda \mathrm{kg}$

Downward force $=($ mass $) \mathrm{g}=x \lambda \mathrm{g}$

Mass on side $(\ell-x)=(\ell-x) \lambda \mathrm{kg}$

Weight $=(\ell-x) \lambda \mathrm{g} \mathrm{kg}$

Net unbalanced force $=x \lambda \mathrm{g}-[(\ell-x) \lambda] \mathrm{g}$

$$ =(2 x-\ell) \lambda \mathrm{g} $$

$\therefore$ Acceleration of the chain $=\frac{\text { Force }}{\text { mass }}=\frac{2 x-\ell}{\ell \lambda} \lambda \mathrm{g}$

$$ =\left(\frac{2 x}{\ell}-1\right) \mathrm{g} $$

Option (2) is correct.

50. A and $B$ are two blocks placed on frictionless inclined planes making angles of $30^{\circ}$ and $60^{\circ}$ respectively with the vertical. The relative vertical acceleration of ’ $A$ ’ with respect to $B$ is

(1) $4.9 \mathrm{~m} / \mathrm{s}^{2}$ upwards

(2) $4.9 \mathrm{~m} / \mathrm{s}^{2}$

(3) zero

(4) $9.8 \mathrm{~m} / \mathrm{s}^{2}$ downwards

Show Answer

Correct answer: (2)

Solution:

Taking free body diagram of A; the acceleration down the plane in

$$ \mathrm{a} _{1}=\frac{\mathrm{mg} \cos 30}{\mathrm{~m}}=\mathrm{g} \cos 30^{\circ} $$

Components of the acceleration $a _{1}$ along horizontal and vertical are

$\mathrm{a} _{1} \cos 30$ vertical $=(\mathrm{g} \cos 30) \cos 30$

$=\mathrm{g} \cos ^{2} 30$ vertically downwards and $\mathrm{a} _{1} \sin 30^{\circ}$ along horizontal.

Similarly component of acceleration of $\mathrm{a} _{2}$ (for block B) is $\mathrm{g} \cos ^{2} 60^{\circ}$ vertically downwards.

$\therefore$ Acceleration of A w.r.t. B along vertical

$$ \begin{aligned} & =\mathrm{g} \cos ^{2} 30-\mathrm{g} \cos ^{2} 60 \\ & =\mathrm{g}\left[\left(\frac{\sqrt{3}}{2}\right)^{2}-\left(\frac{1}{2}\right)^{2}\right]=\frac{\mathrm{g}}{2}=4.9 \mathrm{~m} / \mathrm{s}^{2} \text { downwards } \end{aligned} $$

Option (2) is correct.

51. A pendulum is suspended from the ceiling of a lift. The time period of the pendulum in the lift moving upwards with an acceleration ’ $a$ ’ is measured to be half the period when it has an equal downwards acceleration. The value of ’ $a$ ’ is $\left(\right.$ Take $=g 10 \mathrm{~m} / \mathrm{s}^{2}$ )

(1) $10 \mathrm{~m} / \mathrm{s}^{2}$

(2) $3 \mathrm{~m} / \mathrm{s}^{2}$

(3) $4.5 \mathrm{~m} / \mathrm{s}^{2}$

(4) $6 \mathrm{~m} / \mathrm{s}^{2}$

Show Answer

Correct answer: (4)

Solution:

In lift accelerating downwards

$$ \mathrm{T}=2 \pi \sqrt{\frac{\ell}{\mathrm{g}-\mathrm{a}}} $$

…..(1) $\quad($ Net acceleration $=g-a)$

In lift accelerating upwards

$$ \mathrm{T}^{\prime}=2 \pi \sqrt{\frac{\ell}{\mathrm{g}+\mathrm{a}}}=\frac{\mathrm{T}}{2} $$

…..(2) $\quad($ Net acceleration $=g+a)$

$(1) \div(2)$ gives

$$ 2=\sqrt{\frac{g+a}{g-a}} $$

or

$$ g+a=4 g-4 a $$

$5 \mathrm{a}=3 \mathrm{~g}$ or $\mathrm{a}=\frac{30}{5}=6 \mathrm{~m} / \mathrm{s}^{2}$

Option (4) is correct.

52. A block of mass $2.5 \mathrm{~kg}$ is placed on a rough horizontal surface. The block requires a minimum force of $15 \mathrm{~N}$ along horizontal to slide. It is further observed that the block slides through the first $10 \mathrm{~m}$ after being gently pushed and set in motion with $15 \mathrm{~N}$ force.

Take $g=10 \mathrm{~m} / \mathrm{s}^{2}$. The values of coefficient of static and kinetic friction are respectively.

(1) $0.6 ; 0.6$

(2) $0.6 ; 0.52$

(3) $0.52 ; 0.6$

(4) $0.6 ; 0.26$

Show Answer

Correct answer: (2)

Solution:

Given $\mathrm{m}=2.5 \mathrm{~kg}, \quad \mathrm{~F} _{\text {limiting }}=15 \mathrm{~N}$

As $\mathrm{F}=\mu _{\mathrm{s}} \mathrm{R}=\mu _{\mathrm{s}} \mathrm{mg}$; we get $\mu _{\mathrm{s}}=\frac{\mathrm{F}}{\mathrm{mg}}=\frac{15}{2.5 \times 10}=\frac{15}{25}=0.6$

Using $S=u t+\frac{1}{2} a t^{2}$.

We get $\mathrm{a}=\frac{2 \mathrm{~S}}{\mathrm{t}^{2}}=\frac{2 \times 10}{5 \times 5}=0.8 \mathrm{~ms}^{-2} \quad(\mathrm{As} \quad \mathrm{u}=0)$

Friction in motion is $\mu _{\mathrm{k}} \mathrm{R}=\mu _{\mathrm{k}} \mathrm{mg}$

$\therefore \mathrm{F} _{\text {applied }}-\mathrm{f} _{\mathrm{fr}}($ kinetic $)=\mathrm{ma}$

$15-\mu _{\mathrm{k}}(2.5)(10)=(2.5)(0.8)$

$$ \mu _{\mathrm{k}}=\frac{13}{25}=\frac{52}{100}=0.52 $$

Option (2) is correct.

53. A constant force of $20 \mathrm{~N}$ is applied on a block of mass $M(=2 \mathrm{~kg})$ connected to two blocks of masses $m _{1}$ and $m _{2}$ as shown. The pulleys are light and frictionless. If $m _{1}=1 \mathrm{~kg}$ and $m _{2}=$ $2 \mathrm{~kg}$, then the magnitudes of acceleration $a _{1}$ of $m _{1} ; a _{2}$ of $m _{2}$ and $A$ of $M$ are related as

[Take $\left.\mathrm{g}=\mathbf{1 0} \mathrm{m} / \mathrm{s}^{2}\right]$

(1) $a=a _{2}=10 \mathrm{~m} / \mathrm{s}^{2}, a _{1}=5 \mathrm{~m} / \mathrm{s}^{2}$

(2) $a=a _{1}=a _{2}=6 \mathrm{~m} / \mathrm{s}^{2}$

(3) $a=2 \mathrm{~m} / \mathrm{s}^{2} \mathrm{a} _{1}=\mathrm{a} _{2}=4 \mathrm{~m} / \mathrm{s}^{2}$

(4) $\mathrm{a}=\mathrm{a} _{1}=\mathrm{a} _{2}=2 \mathrm{~m} / \mathrm{s}^{2}$

Show Answer

Correct answer: (2)

Solution:

From free body diagrams (a), (b) and (c)

$\mathrm{F}-\mathrm{T}=\mathrm{Ma}$ or $20-\mathrm{T}=2 \mathrm{a} \hspace{40mm} . . . . . . (1)$

$2 \mathrm{~T}-\mathrm{m} _{1} \mathrm{~g}=$ or $2 \mathrm{~T}-10=\mathrm{a} _{1} \hspace{40mm} . . . . . . (2)$

$\mathrm{M} _{2} \mathrm{~g}-\mathrm{T}=\mathrm{m} _{2} \mathrm{a} _{2}$ or $20-\mathrm{T}=2 \mathrm{a} _{2} \hspace{40mm} . . . . . . (3) $

Again if $\mathrm{M}$ moves a distance $x$ towards left and $\mathrm{m} _{2}$ moves down through $x$; then $\mathrm{m} _{2}$ moves upwards through $2 x$

$\therefore \mathrm{a}+\mathrm{a} _{2}=2 \mathrm{a} _{1} \hspace{40mm} . . . . . . (4)$

(1) $+(2)+(3)$ gives $20-10+20=2\left(a+a _{2}\right)+a _{1}$

or $30=2\left(2 a _{1}\right)+a _{1}=5 a _{1}$

$$ \therefore \mathrm{a} _{1}=6 \mathrm{~m} / \mathrm{s}^{2} $$

$\therefore$ From (2);

$$ (2 \mathrm{~T}=16 \text { or } \mathrm{T}=8 \mathrm{~N}) $$

Using $\mathrm{T}$ in (1) & (3), we get

$\mathrm{a}=\mathrm{a} _{1}=\mathrm{a} _{2}=6 \mathrm{~m} / \mathrm{s}^{2}$

Option (2) is correct.

54. A balloon of mass $M$ is descending with an acceleration a $(<\mathrm{g})$. A mass $m$ is removed from the balloon and it begin to rise wth an acceleration $\frac{a^{\prime}}{2}$. The mass removed is

(1) $\frac{\mathrm{Ma}}{\mathrm{g}+\mathrm{a}}$

(2) $\frac{\mathrm{Ma}}{\mathrm{g}-\mathrm{a}}$

(3) $\frac{3 \mathrm{Ma}}{(\mathrm{g}+\mathrm{a})}$

(4) $\frac{3 \mathrm{Ma}}{(2 \mathrm{~g}+\mathrm{a})}$

Show Answer

Correct answer: (4)

Solution:

Fig. (a) shows force acting on balloon descending down with acceleration $\mathrm{a}$. $\mathrm{F}$ is buoyant force of balloon.

Equation of motion is

$\mathrm{Mg}-\mathrm{F}=\mathrm{Ma} \hspace{40mm} . . . . . . (1)$

Fig. (b) shows forces acting when ballon ascends upwards with acceleration $\frac{\mathrm{a}}{2}$.

The equation of motion is

$\mathrm{F}-(\mathrm{M}-\mathrm{m}) \mathrm{g}=(\mathrm{M}-\mathrm{m}) \frac{\mathrm{a}}{2} \hspace{40mm} . . . . . . (2)$

Adding (1) & (2);

$$ M g-(M-m) g=(3 M-m) \frac{a}{2} $$

or $\quad \mathrm{mg}=(3 \mathrm{M}-\mathrm{m}) \frac{\mathrm{a}}{2}$

or $\quad \mathrm{m}\left(\mathrm{g}+\frac{\mathrm{a}}{2}\right)=\frac{3 \mathrm{Ma}}{2}$

or $\quad \mathrm{m}=\frac{3 \mathrm{Ma}}{2 \mathrm{~g}+\mathrm{a}}$

Option (4) is correct.

55. A chord connects two bodies of mass $m _{1}$ and $m _{2}$ placed on an inclined plane. The coefficient of friction between the inclined plane and $m _{1}$ is $\mu _{1}$ and that with $m _{2}$ is $\mu _{2}$. When the motion of blocks is about to take place downwards; the inclination $\alpha$ will be

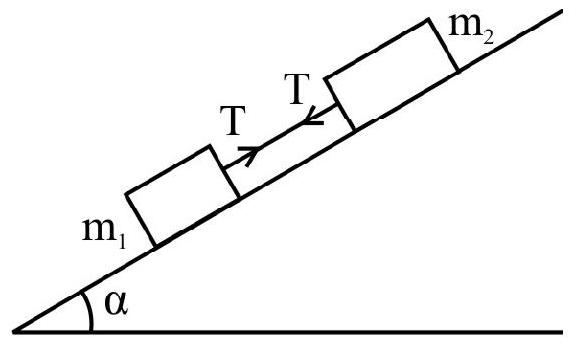
(1) $\tan ^{-1}\left(\frac{\mu _{1} m _{1}+\mu _{2} m _{2}}{m _{1}+m _{2}}\right)$

(2) $\tan ^{-1}\left(\frac{\mu _{1} m _{2}+\mu _{2} m _{1}}{m _{1}+m _{2}}\right)$

(3) $\tan ^{-1}\left(\frac{\mu _{1} \mu _{2} \mathrm{~m} _{1} \mathrm{~m} _{2}}{\mu _{1} \mathrm{~m} _{1}+\mu _{2} \mathrm{~m} _{2}}\right)$

(4) $\tan ^{-1}\left(\frac{m _{1}-m _{2}}{m _{1}+m _{2}}\right)\left(\frac{\mu _{1} \mu _{2}}{\mu _{1}+\mu _{2}}\right)$

Show Answer

Correct answer: (1)

Solution:

Fig. shows the forces acting on the system. The system is in equilibrium, therefore

for $\mathrm{m} _{1}$; we have

$$ \begin{equation*} \mathrm{m} _{1} g \sin \alpha=T+\mu _{1} \mathrm{~m} _{1} g \cos \alpha \tag{1} \end{equation*} $$

For $\mathrm{m} _{2}$; we have

$$ \begin{equation*} \mathrm{m} _{2} \mathrm{~g} \sin \alpha+\mathrm{T}=\mu _{2} \mathrm{~m} _{2} \mathrm{~g} \cos \alpha \tag{2} \end{equation*} $$

Equating $\mathrm{T}$ from (1) and (2) we get

$m _{1} g \sin \alpha-\mu _{1} m _{1} g \cos \alpha=\mu _{2} m _{2} g \cos \alpha-m _{2} g \sin \alpha$

$$ g \sin \alpha\left(m _{1}+m _{2}\right)=g \cos \alpha\left(\mu _{1} m _{1}+\mu _{2} m _{2}\right) $$

$\tan \alpha=\left(\frac{\mu _{1} \mathrm{~m} _{1}+\mu _{2} \mathrm{~m} _{2}}{\mathrm{~m} _{1}+\mathrm{m} _{2}}\right)$

Option (1) is correct.

56. A smooth inclined plane has two parallel and similar tracks provided on it. A particle $P$, released from rest, from the top of the plane, of length $L$ (on one of the tracks), slides down the plane and reaches its bottom in $2 \mathrm{n}$ seconds.

A second particle, $Q$, projected (simultaneously) from the bottom of the plane (on the other track), with a speed $\mathrm{v}$, goes up the plane a distance $\ell$, comes to rest there, and when it reaches the bottom of the plane again, the total time of its complete journey is also $2 \mathrm{n}$ seconds. The ratio $\left(\frac{\ell}{\mathbf{L}}\right)$ equals

(1) $\left(\frac{1}{4}\right)$

(2) $\left(\frac{1}{2}\right)$

(3) $\left(\frac{2}{3}\right)$

(4) $\left(\frac{3}{4}\right)$

Show Answer

Correct answer: (1)

Solution:

For the particle $P$, the acceleration down the plane is $g \sin \theta$ ( $\theta=$ angle of inclination of the plane).

Hence, $\mathrm{L}=0+\frac{1}{2}(\mathrm{~g} \sin \theta)(2 \mathrm{n})^{2}$

$\therefore \mathrm{L}=(2 \mathrm{~g} \sin \theta) \mathrm{n}^{2}$

The time, for the upward and downwards journeys of the particle $Q$, would be $\frac{2 n}{2}(=n)$ seconds. Also it would again experience an acceleration $(\mathrm{g} \sin \theta)$ down the plane. We, therefore, have (Consider the upward journey of particle Q)

$$ \begin{aligned} & \mathrm{O}=\mathrm{v}-(\mathrm{g} \sin \theta) \mathrm{n} \\ & \therefore \mathrm{v}=(\mathrm{g} \sin \theta) \mathrm{n} \end{aligned} $$

The distance, $\ell$, moved by the particle $\mathrm{Q}$, up the plane, is related to $\mathrm{v}$ through the relation.

$\mathrm{O}^{2}-\mathrm{v}^{2}=2(-\mathrm{g} \sin \theta) \ell$ $\therefore \ell=\frac{\mathrm{v}^{2}}{2 \mathrm{~g} \sin \theta}=\frac{(\mathrm{g} \sin \theta) \mathrm{n}^{2}}{2}$

$\therefore \frac{\ell}{\mathrm{L}}=\frac{(\mathrm{g} \sin \theta) \mathrm{n}^{2}}{2} \times \frac{1}{(2 \mathrm{~g} \sin \theta) \mathrm{n}^{2}}=\frac{1}{4}$

Option (1) is correct.

57. The position time graph of a particle ( $\operatorname{mass}=5 \mathrm{~kg}$ ) is as shown. The impulse, on this particle, around $t=5 \mathrm{~s}$ and $t=10 \mathrm{~s}$, would be

(1) $20 \mathrm{~kg} \mathrm{~ms}^{-1}$ and $-20 \mathrm{~kg} \mathrm{~ms}^{-2}$, respectively

(2) $-20 \mathrm{~kg} \mathrm{~ms}^{-1}$ and $20 \mathrm{~kg} \mathrm{~ms}^{-2}$, respectively

(3) $-5 \mathrm{~kg} \mathrm{~ms}^{-1}$ and $20 \mathrm{~kg} \mathrm{~ms}^{-2}$, respectively

(4) $-20 \mathrm{~kg} \mathrm{~ms}^{-1}$ and $25 \mathrm{~kg} \mathrm{~ms}^{-2}$, respectively

Show Answer

Correct answer: (2)

Solution:

As seen from the graph, the particle is

(i) at rest from $t=0$ to $t=5 \mathrm{~s}$

(ii) moving with a constant velocity of $\left(\frac{5-15}{7.5-5}\right) \mathrm{m} / \mathrm{s}$, i.e. $-4 \mathrm{~ms}^{-1}$

(iii) at rest again from $t=7.5 \mathrm{~s}$ to $\mathrm{t}=10 \mathrm{~s}$

(iv) moving with a constant velocity of $\left(\frac{25-5}{15-10}\right) \mathrm{m} / \mathrm{s}$ i.e. $4 \mathrm{~ms}^{-1}$

$\therefore$ Change in momentum (= impulse), around $\mathrm{t}=5 \mathrm{~s}$, is $[(5 \times-4)-0] \mathrm{kg} \mathrm{ms}^{-1}=-20 \mathrm{~kg} \mathrm{~ms}^{-1}$ and change in momentum (= impulse), around $\mathrm{t}=10 \mathrm{~s}$, is $[5 \times 4-0] \mathrm{kg} \mathrm{ms}^{-1}=-20 \mathrm{~kg} \mathrm{~ms}^{-1}$

Option (2) is correct.

58. A stream of glass balls, moving vertically upwards with a speed u, strike a horizontal plate (of mass M) and rebound, therefrom, with the same speed. The disc can be kept floating horizontally, if the number of glass balls (each of mass $m$ ), striking it per second, equals.

(1) $\left(\frac{2 \mathrm{mU}}{\mathrm{Mg}}\right)$

(2) $\left(\frac{M g}{2 m U}\right)$

(3) $\left(\frac{\mathrm{Mg}}{\mathrm{mU}}\right)$

(4) $\left(\frac{\mathrm{mU}}{\mathrm{Mg}}\right)$

Show Answer

Correct answer: (2)

Solution:

Let $\mathrm{N}$ be the required number of balls striking the plate per second. The change in momentum of each ball, upon striking the plate is

$$ \mathrm{mU}-(-\mathrm{mU})=2 \mathrm{mU} $$

$\therefore$ Total change in momentum, per second, when $\mathrm{N}$ balls strike the ball in one second, is

$$ (2 \mathrm{mU}) \times \mathrm{N}=2 \mathrm{mUN} $$

This rate of change of momentum equals the force exerted on the plate by the glass balls, striking it from

below. It is this force that balances the weight of the horizontally floating plate. Hence,

$$ \begin{aligned} & 2 \mathrm{mUN}=\mathrm{Mg} \\ & \therefore \quad \mathrm{N}=\left(\frac{\mathrm{Mg}}{2 \mathrm{mU}}\right) \end{aligned} $$

Option (2) is correct.

59. A particle, of mass $200 \mathrm{~g}$, is initially moving with a speed of $15 \mathrm{~ms}^{-1}$, along the $X$-axis. It is acted upon by a force that remains directed along the $\mathbf{X}$-axis but whose magnitude varies with time in the manner shown. The final speed of the particle, at $t=20 \mathrm{~s}$, would be

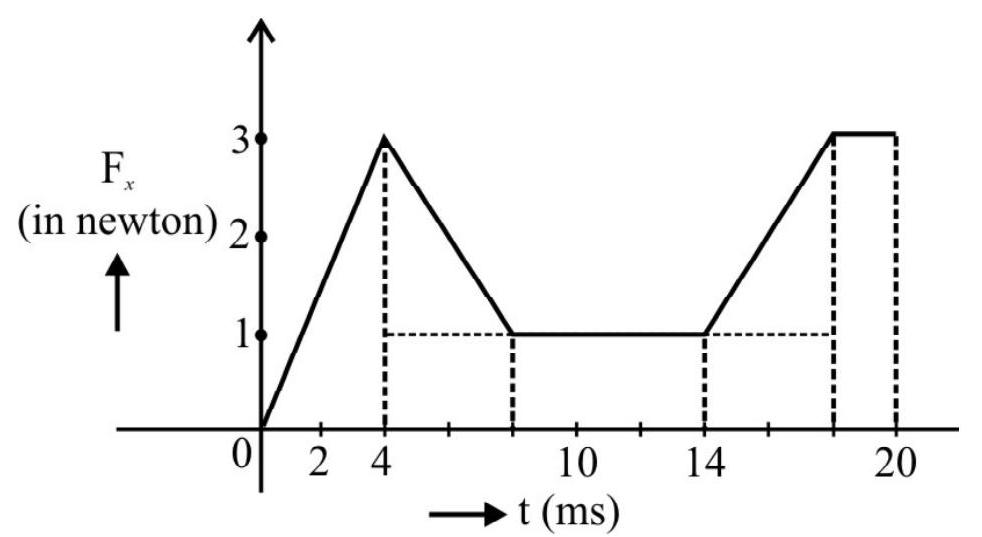
(1) $160 \mathrm{~ms}^{-1}$

(2) $165 \mathrm{~ms}^{-1}$

(3) $180 \mathrm{~ms}^{-1}$

(4) $185 \mathrm{~ms}^{-1}$

Show Answer

Correct answer: (4)

Solution:

We known that $F=\frac{d p}{d t}$

$\therefore$ Fdt $=\mathrm{dp}$

$\therefore \int F d t=\int d p=p _{f}-p _{i}$

The integral, on the left, representing impulse, equals the area under the $\mathrm{F} \quad v \mathrm{~s} \quad \mathrm{t}$ graph.

From the given figure, this area is

$$ \begin{aligned} & =\left[\frac{1}{2} \times 4 \times 3+\left(\frac{1}{2} \times 4 \times 2+4 \times 1\right)+(6 \times 1)+\left(\frac{1}{2} \times 4 \times 2+4 \times 1\right)+(2 \times 3)\right] \mathrm{N}-\mathrm{s} \\ & =34 \mathrm{~N}-\mathrm{s} \end{aligned} $$

$\therefore$ Change in momentum $=34 \mathrm{~N}-\mathrm{s}$

$\therefore$ Final momentum, after $20 \mathrm{~s}=\left(\frac{200}{1000} \times 15+34\right) \mathrm{N}-\mathrm{s}$

$$ =37(\mathrm{~N}-\mathrm{s}) $$

$\therefore$ Final speed of the ball $=\left(\frac{37}{200 / 1000}\right) \mathrm{ms}^{-1}$

$$ =185 \mathrm{~ms}^{-1} $$

Option (4) is correct.

60. An object, of mass $5 \mathrm{~m}$ (initially at rest), breaks up into three fragments whose masses are in the ratio 1:1:3. The two equal mass pieces fly off with equal speeds, along mutually perpendicular directions. If the speed of the heavier fragment is $v$, the speed of each of the other two fragments, is

(1) $3 \sqrt{2} \mathrm{v}$

(2) $\left(\frac{\sqrt{2}}{3}\right) \mathrm{v}$

(3) $1.5 \sqrt{2} \mathrm{v}$

(4) $\left(\frac{\sqrt{2}}{1.5}\right) \mathrm{v}$

Show Answer

Correct answer: (3)

Solution:

Let u be the common speed of either of the two ’equal mass’ fragments. The total momentum, of these two fragments, has a magnitude

$$ |\mathrm{p}|=\left[(\mathrm{mu})^{2}+(\mathrm{mu})^{2}\right]^{1 / 2} $$

$\therefore \mathrm{p}=\sqrt{2} \mathrm{mu}$

This is directed midway between the two mutually perpendicular directions. Since the total momentum, after the ‘break up’, has to again equal zero, we must have,

$(3 \mathrm{~m}) \mathrm{v}=\sqrt{2}(\mathrm{mu})$

$\therefore \mathrm{u}=\left(\frac{3}{\sqrt{2}}\right) \mathrm{v}=(1.5 \sqrt{2}) \mathrm{v}$

Option (3) is correct.

61. A system of two masses $M _{1}$ and $M _{2}$, a smooth inclined plane, a light inextensible string and a smooth pulley is set up as shown. The time taken by the mass $M _{1}$, to get hauled up the plane, when the mass $M _{2}$ is ’let-go’, is $t _{1}$. On interchanging the two masses, the corresponding time is $t _{2}$.

The ratio $\left(\frac{t _{1}}{t _{2}}\right)$ equals

(1) $\left(\frac{M _{1}-M _{2} \sin \theta}{M _{2}-M _{1} \sin \theta}\right)^{1 / 2}$

(2) $\left(\frac{M _{2}-M _{1} \sin \theta}{M _{1}-M _{2} \sin \theta}\right)^{1 / 2}$

(3) $\left(\frac{M _{2}-M _{1} \sin \theta}{M _{1}-M _{2} \sin \theta}\right)$

(4) $\left(\frac{M _{1}-M _{2} \sin \theta}{M _{2}-M _{1} \sin \theta}\right)$

Show Answer

Correct answer: (1)

Solution:

Let $\mathrm{a} _{1}$ be the common acceleration of the two masses in the case shown. Using the free body diagrams for the two masses, we get

$T-M _{1} g \sin \theta=M _{1} a _{1}$

$\mathrm{M} _{2} \mathrm{~g}-\mathrm{T}=\mathrm{M} _{2} \mathrm{a} _{1}$

Adding, we get

$\mathrm{g}\left(\mathrm{M} _{2}-\mathrm{M} _{1} \sin \theta\right)=\left(\mathrm{M} _{1}+\mathrm{M} _{2}\right) \mathrm{a} _{1}$

$\therefore \mathrm{a} _{1}=\frac{\left(\mathrm{M} _{2}-\mathrm{M} _{1} \sin \theta\right)}{\left(\mathrm{M} _{1}+\mathrm{M} _{2}\right)} \mathrm{g}$

We have,

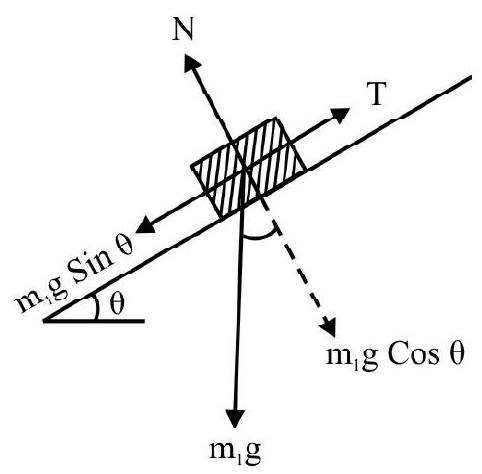
$$ \begin{aligned} \mathrm{L} & =0+\frac{1}{2} \mathrm{a} _{1} \mathrm{t} _{1}^{2} \\ \text { or } \quad \mathrm{t} _{1}^{2} & =\frac{2 \mathrm{~L}}{\mathrm{a} _{1}}=\frac{2 \mathrm{~L}\left(\mathrm{M} _{1}+\mathrm{M} _{2}\right)}{\left(\mathrm{M} _{2}-\mathrm{M} _{1} \sin \theta\right) \mathrm{g}} \end{aligned} $$

On interchanging $M _{1}$ and $M _{2}$, we would have

$$ \mathrm{t} _{2}^{2}=\frac{2 \mathrm{~L}}{\mathrm{a} _{2}}=\frac{2 \mathrm{~L}\left(\mathrm{M} _{2}+\mathrm{M} _{1}\right)}{\left(\mathrm{M} _{1}-\mathrm{M} _{2} \sin \theta\right) \mathrm{g}} $$

$\therefore \frac{\mathrm{t} _{1}^{2}}{\mathrm{t} _{2}^{2}}=\frac{\left(\mathrm{M} _{1}-\mathrm{M} _{2} \sin \theta\right)}{\left(\mathrm{M} _{2}-\mathrm{M} _{1} \sin \theta\right)}$

$\therefore \frac{\mathrm{t} _{1}}{\mathrm{t} _{2}}=\left(\frac{\mathrm{M} _{1}-\mathrm{M} _{2} \sin \theta}{\mathrm{M} _{2}-\mathrm{M} _{1} \sin \theta}\right)^{1 / 2}$

Option (1) is correct.

62. A box, of mass $M$, is (i) pulled (ii) pushed, on a horizontal floor, by applying a force $F$ (is a direction inclined at an angle $\theta$ to the horizontal), in each case. The coefficient of friction, between the base of the box and the floor is $\mu$.

If the time taken, to move the box through a distance $L$, in the two cases is $t _{1}$ and $t _{2}$, respectively, the ratio $\left(\frac{t _{1}}{t _{2}}\right)$ is

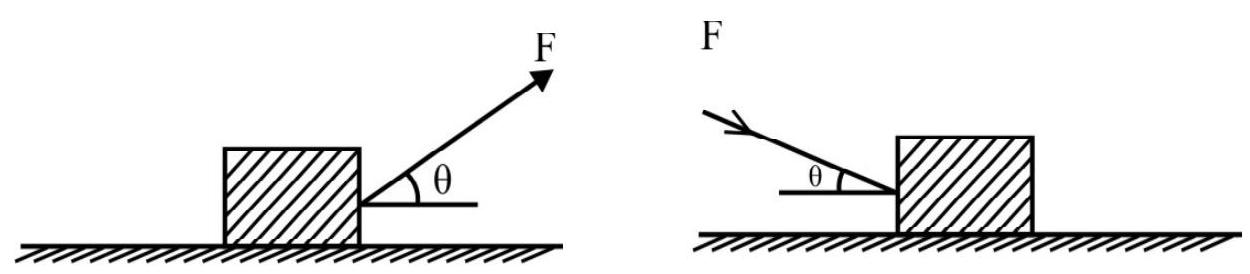
(1) $\left[\frac{\mathrm{F}(\cos \theta-\mu \sin \theta)+\mu \mathrm{Mg}}{\mathrm{F}(\cos \theta+\mu \sin \theta)+\mu \mathrm{Mg}}\right]^{1 / 2}$

(2) $\left[\frac{\mathrm{F}(\cos \theta+\mu \sin \theta)+\mu \mathrm{Mg}}{\mathrm{F}(\cos \theta-\mu \sin \theta)+\mu \mathrm{Mg}}\right]^{1 / 2}$

(3) $\left[\frac{\mathrm{F}(\cos \theta-\mu \sin \theta)-\mu \mathrm{Mg}}{\mathrm{F}(\cos \theta+\mu \sin \theta)-\mu \mathrm{Mg}}\right]^{1 / 2}$

(4) $\left[\frac{\mathrm{F}(\cos \theta+\mu \sin \theta)-\mu M g}{\mathrm{~F}(\cos \theta-\mu \sin \theta)-\mu M g}\right]^{1 / 2}$

Show Answer

Correct answer: (3)

Solution:

The free body diagrams, for the two cases, are as shown. For case (i) we have

$$ \begin{gathered} \mathrm{N}+\mathrm{F} \sin \theta=\mathrm{Mg} \\ \text { or } \quad \mathrm{N}=(\mathrm{Mg}-\mathrm{F} \sin \theta) \end{gathered} $$

and $\mathrm{F} \cos \theta-\mu \mathrm{N}=\mathrm{Ma} _{1}$

$\therefore \mathrm{a} _{1}=\frac{\mathrm{F} \cos \theta-\mu(\mathrm{Mg}-\mathrm{F} \sin \theta)}{\mathrm{M}}$

$$ =\frac{F(\cos \theta+\mu \sin \theta)-\mu M g}{M} $$

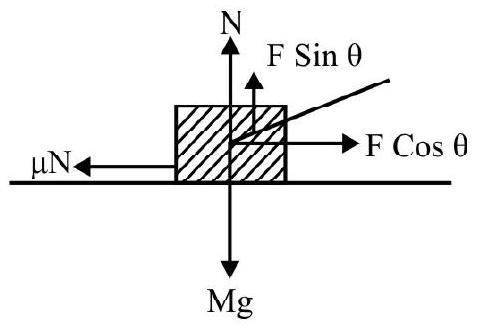
(i)

$\therefore \mathrm{t} _{1}^{2}=\frac{2 \mathrm{~L}}{\mathrm{a} _{1}}=\frac{2 \mathrm{ML}}{\mathrm{F}(\cos \theta+\mu \sin \theta)-\mu \mathrm{Mg}}$

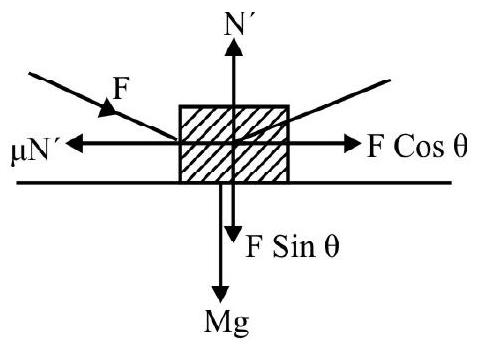
(ii)

For case(ii) , we have

$N^{’}(Mg + F Sin \theta)$

and $\quad \mathrm{F} \cos \theta-\mu \mathrm{N}^{\prime}=\mathrm{Ma} _{2}$

or $\quad \mathrm{a} _{2}=\frac{\mathrm{F}(\cos \theta-\mu \sin \theta)-\mu \mathrm{Mg}}{\mathrm{M}}$

$\therefore \quad \mathrm{t} _{2}^{2}=\frac{2 \mathrm{~L}}{\mathrm{a} _{2}}=\frac{2 \mathrm{ML}}{\mathrm{F}(\cos \theta-\mu \sin \theta)-\mu \mathrm{Mg}}$

$\therefore \frac{\mathrm{t} _{1}}{\mathrm{t} _{2}}=\left[\frac{\mathrm{F}(\cos \theta-\mu \sin \theta)-\mu \mathrm{Mg}}{\mathrm{F}(\cos \theta+\mu \sin \theta)-\mu \mathrm{Mg}}\right]^{1 / 2}$

63. Three identical blocks, of mass $M$ each, are connected to each other by inextensible strings and are kept on a smooth horizontal floor. On applying a force $F$, as shown, the system moves with an acceleration a. If the tensions in the two strings are $T _{1}$ and $T _{2}$, respectively, the ratios $\left(\frac{F}{T _{2}}\right)$ and $\left(\frac{F}{T _{1}}\right)$ equal respectively to

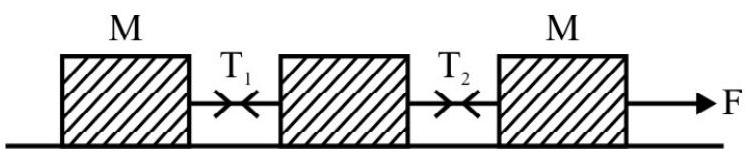
(1) 3 and 1.5

(2) 1.5 and 3

(3) 2 and 1

(4) 1 and 2

Show Answer

Correct answer: (2)

Solution:

For the first mass, on the right, we have

$$ \mathrm{F}-\mathrm{T} _{2}=\mathrm{Ma} $$

For the second mass, we have

$$ \mathrm{T} _{2}-\mathrm{T} _{1}=\mathrm{Ma} $$

For the third mass, we have

$$ \mathrm{T} _{1}=\mathrm{Ma} $$

Adding the three equations, we get

$$ \mathrm{F}=3 \mathrm{Ma} \quad \text { or } \quad \mathrm{a}=\frac{\mathrm{F}}{3 \mathrm{M}} $$

$\therefore \quad \mathrm{F}-\mathrm{T} _{2}=\frac{\mathrm{M} . \mathrm{F}}{3 \mathrm{M}}=\frac{\mathrm{F}}{3}$

$\therefore \mathrm{T} _{2}=\frac{2 \mathrm{~F}}{3}$

Also, $T _{1}=M a=\frac{M . F}{3 M}=\frac{F}{3}$

$\therefore \frac{\mathrm{F}}{\mathrm{T} _{2}}=\frac{3}{2}=1.5$

and $\frac{\mathrm{F}}{\mathrm{T} _{1}}=3$

Option (2) is correct.

64. An elevator, in a building, starts from rest; accelerates uniformly upwards. It takes a time $t _{1}$ to go up to second floor, situated at a height $H$, above the ground. The corresponding time, for its downward journey, is $t _{2}$.

If a person were to hold a mass $M$ with the help of a massless string, the ratio of the respective tensions in the string, in the two cases, would be

(1) $\frac{\left(\mathrm{gt} _{1}^{2}+2 \mathrm{H}\right)}{\left(\mathrm{gt} _{2}^{2}-2 \mathrm{H}\right)}\left(\frac{\mathrm{t} _{2}^{2}}{\mathrm{t} _{1}^{2}}\right)$

(2) $\frac{\left(\mathrm{gt} _{1}^{2}-2 \mathrm{H}\right)}{\left(\mathrm{gt} _{2}^{2}+2 \mathrm{H}\right)}\left(\frac{\mathrm{t} _{1}^{2}}{\mathrm{t} _{2}^{2}}\right)$

(3) $\frac{\left(2 \mathrm{gt} _{1}^{2}+\mathrm{H}\right)}{\left(2 \mathrm{gt} _{2}^{2}-\mathrm{H}\right)}\left(\frac{\mathrm{t} _{2}^{2}}{\mathrm{t} _{1}^{2}}\right)$

(4) $\frac{\left(2 \mathrm{gt} _{1}^{2}-\mathrm{H}\right)}{\left(2 \mathrm{gt} _{2}^{2}+\mathrm{H}\right)}\left(\frac{\mathrm{t} _{1}^{2}}{\mathrm{t} _{2}^{2}}\right) $

Show Answer

Correct answer: (1)

Solution:

For the upward journey; if $\mathrm{a} _{1}$ is the (uniform) acceleration of the elevator, we have $\mathrm{H}=\frac{1}{2} \mathrm{a} _{1} \mathrm{t} _{1}^{2}$

$\therefore \mathrm{a} _{1}=\left(\frac{2 \mathrm{H}}{\mathrm{t} _{1}^{2}}\right)$

The apparent weight, of the mass $\mathrm{M}$, during the upward journey, would be

$\mathrm{W} _{1}=\mathrm{M}\left(\mathrm{g}+\mathrm{a} _{1}\right)=\mathrm{M}\left(\mathrm{g}+\frac{2 \mathrm{H}}{\mathrm{t} _{1}^{2}}\right)$

For the downward journey, if $\mathrm{a} _{2}$ is the (uniform) acceleration, of the elevator, we have

$\mathrm{H}=\frac{1}{2} \mathrm{a} _{2} \mathrm{t} _{2}^{2}$

$\therefore \mathrm{a} _{2}=\left(\frac{2 \mathrm{H}}{\mathrm{t} _{2}^{2}}\right)$

The apparent weight, of the mass M, during the downward journey, would be

$\mathrm{W} _{2}=\mathrm{M}\left(\mathrm{g}-\mathrm{a} _{2}\right)=\mathrm{M}\left(\mathrm{g}-\frac{2 \mathrm{H}}{\mathrm{t} _{2}^{2}}\right)$

The tensions, in the string, in the two cases, equal these apparent weights. Hence, the ratio of the tensions, in the two cases, is

$\frac{\mathrm{T} _{1}}{\mathrm{~T} _{2}}=\frac{\mathrm{W} _{1}}{\mathrm{~W} _{2}}=\left(\frac{\mathrm{gt} _{1}^{2}+2 \mathrm{H}}{\mathrm{gt} _{2}^{2}-2 \mathrm{H}}\right)\left(\frac{\mathrm{t} _{2}^{2}}{\mathrm{t} _{1}^{2}}\right)$

Option (1) is correct.

65. A system of two masses, a light inextensible string and a smooth pulley, is set up as shown. The masses are ’let-go’ at $t=0 \mathrm{~s}$ and are allowed to move for $n$ seconds. At $t=n$, the string is suddenly cut-off. The ratio of the displacements of the masses $m$ and $M$, in the next $N$ seconds, would equal.

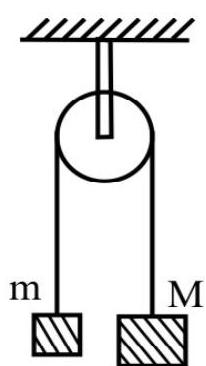
(1) $\left[\frac{N(M+m)+2(M-m) n}{N(M+m)-2(M-m) n}\right]$

(2) $\left[\frac{n(M+m)+2(M-m) N}{n(M+m)-2(M-m) N}\right]$

(3) $\left[\frac{n(M+m)-2(M-m) N}{n(M+m)+2(M-m) N}\right]$

(4) $\left[\frac{N(M+m)-2(M-m) n}{N(M+m)+2(M-m) n}\right]$

Show Answer

Correct answer: (4)

Solution:

The equations of motion of the two masses, for $0<\mathrm{t}<\mathrm{n}$, are

$\mathrm{T}-\mathrm{mg}=\mathrm{ma}$ and $\mathrm{Mg}-\mathrm{T}=\mathrm{Ma}$

These give $a=\left(\frac{M-m}{M+m}\right) g$

Hence the speeds of the two masses at the end of $n$ seconds are

for mass $m \Rightarrow\left(\frac{M-m}{M+m}\right)$ gn (upwards)

for mass $M \Rightarrow\left(\frac{M-m}{M+m}\right)$ gn (downwards)

The displacements of two masses, is $\mathrm{N}$ seconds, after the string is cut, now, are those of two freely falling masses having these respective initial velocities.

Hence,

$S _{1}=$ Displacement of mass $m$ (in the next $N$ seconds $)=\left[\left(\frac{M-m}{M+m}\right) g n\right] N+\frac{1}{2}(-g) N^{2}$

$$ \begin{aligned} & =\left[\left(\frac{M-m}{M+m}\right) n-\frac{N}{2}\right] g N=\frac{g N}{2(M+m)}[2(M-m) n-N(M+m)] \\ & =\left(\frac{-g N}{2(M+m)}\right)[N(M+m)-2(M-m) n] \end{aligned} $$

and $S _{2}=$ Displacement of mass $M$, in the next $N$ seconds $=-\left[\left(\frac{M-m}{M+m}\right) g n . N+\frac{1}{2} \mathrm{gN}^{2}\right]$

$$ =-[2(M-m) n+N(M+m)] \frac{g N}{2(M+m)} $$

$\therefore \frac{S _{1}}{S _{2}}=\left[\frac{N(M+m)-2(M-m) n}{N(M+m)+2(M-m) n}\right]$

Option (4) is correct.

66. A particle, of mass $100 \mathrm{~g}$, initially at rest at the origin, is acted upon by two forces $F _{1}$ and $F _{2}$, (in the $X-Y$ plane), directed as shown, for $10 \mathrm{~s}$. The coordinates of the particle, at $t=10 \mathrm{~s}$, in m would be (nearly)

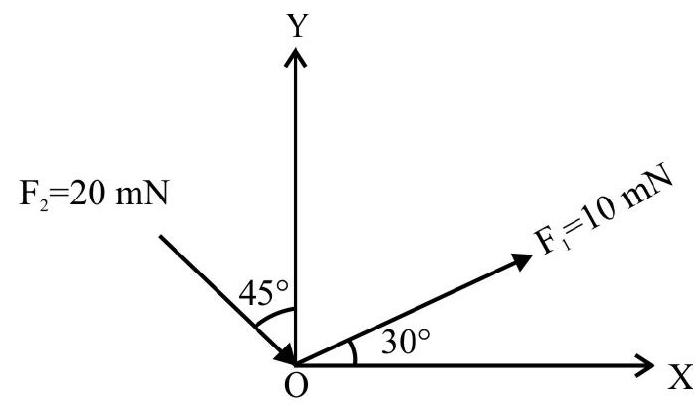
(1) $(22.8),(-9.14)$

(2) (11.4), (-4.57)

(3) $(11.4),(-4.57)$

(4) $(2.64),(-4.57)$

Show Answer

Correct answer: (2)

Solution:

We have,

$\mathbf{F} _{1}=\left[\hat{\mathbf{i}}\left(10 \cos 30^{0}\right)+\left(10 \sin 30^{0}\right) \hat{\mathbf{j}}\right] \times 10^{-3}$

$$ =[(5 \sqrt{3}) \hat{\mathbf{i}}+(5) \hat{\mathbf{j}}] \times 10^{-3} \mathrm{~N} $$

and $\quad \mathbf{F} _{2}=\left[20 \cos \left(-45^{0}\right) \hat{\mathbf{i}}+20 \sin \left(40^{0}\right) \hat{\mathbf{j}}\right] \times 10^{-3} \mathrm{~N}$

$$ =[(10 \sqrt{2}) \hat{\mathbf{i}}-(10 \sqrt{2}) \hat{\mathbf{j}}] \times 10^{-3} \mathrm{~N} $$

$\therefore$ Net force on the particle $=\left(\mathbf{F} _{1}+\mathbf{F} _{2}\right)$

$$ \begin{aligned} & =\mathbf{F}=[(5 \sqrt{3}+10 \sqrt{2}) \hat{\mathbf{i}}+(5-10 \sqrt{2}) \hat{\mathbf{j}}] \times 10^{-3} \mathrm{~N} \\ & \cong[(22.80) \hat{\mathbf{i}}-(9.14) \hat{\mathbf{j}}] \times 10^{-3} \mathrm{~N} \end{aligned} $$

$\therefore$ Net acceleration of the particle $=\frac{F}{M}$

$$ \begin{aligned} & =\mathrm{a}=\left[\frac{22.80 \hat{\mathbf{i}}-9.14 \hat{\mathbf{j}}}{0.1}\right] \times 10^{-3} \\ & =0.228 \mathbf{i}-.0914 \mathbf{j} \end{aligned} $$

$\therefore$ Displacement, along $\mathrm{X}$-axis, in $10 \mathrm{~s}$

$$ \begin{aligned} & =0+\frac{1}{2} \mathrm{a} _{x} \times 10^{2} \\ & =50 \mathrm{a} _{x}=50 \times(.228) \mathrm{m}=11.4 \mathrm{~m} \end{aligned} $$

Displacement, along $\mathrm{Y}$-axis, in $10 \mathrm{~s}$

$$ \begin{aligned} & =0+\frac{1}{2} \mathrm{a} _{\mathrm{y}} \times 10^{2}=50 \mathrm{a} _{\mathrm{y}} \\ & =50 \times(.0914) \mathrm{m}=-=4.57 \mathrm{~m} \end{aligned} $$

$\therefore$ The coordinates of the particle, at $\mathrm{t}=10 \mathrm{~s}$, $\operatorname{are}[(11.4 \mathrm{~m}),(-4.57) \mathrm{m}]$

Option (2) is correct.

67. Two identical particles, each of mass, $m$ initially located at the points $(-a, 0)$ and $(a, 0)$, are joined to each other by a massless string of length 2a. If a force $F(=-F \mathbf{j})$, acts continuously on the midpoint of this string, the relative (horizontal) acceleration of the two masses, when the (horizontal) distance between then becomes $\frac{4 a}{3}$, is

(1) $\frac{0.4 \sqrt{5} \mathrm{~F}}{\mathrm{~m}}$

(2) $\frac{0.2 \sqrt{5} \mathrm{~F}}{\mathrm{~m}}$

(3) $\frac{0.25 \sqrt{8} \mathrm{~F}}{\mathrm{~m}}$

(4) $\frac{0.5 \sqrt{8} \mathrm{~F}}{\mathrm{~m}}$

Show Answer

Correct answer: (1)

Solution:

The ‘set-up’ would be of the form shown here when the horizontal distance between the particles becomes $\left(\frac{4 \mathrm{a}}{3}\right)$.

If $\mathrm{T}$ is the tension in each string at this instant, we would have

$$ \mathrm{T} \cos \theta+\mathrm{T} \cos \theta=\mathrm{F} $$

or $\mathrm{T}=\frac{\mathrm{F}}{2 \cos \theta}$

The horizontal force on each particle in $T \sin \theta$. Hence the horizontal acceleration, of each particle, is $\frac{T \sin \theta}{\mathrm{m}}$.

The particles are approaching each other (The particle, on the left of the origin, experiences a horizontal force, directed towards right due to the tension in the ‘right side’ part of the string and vice-versa). Hence their relative (horizontal) acceleration is $\frac{2 \mathrm{~T} \sin \theta}{\mathrm{m}}$.

$\therefore$ Relative (horizontal) acceleration of the two masses when the distance between them becomes $\frac{2 a}{3}$, is

$$ \begin{gathered} \frac{2 \mathrm{~T} \sin \theta}{\mathrm{m}}=\frac{2}{\mathrm{~m}} \cdot \frac{\mathrm{F}}{2 \cos \theta} \sin \theta=\frac{\mathrm{F}}{\mathrm{m}}(\tan \theta) \\ =\frac{\mathrm{F}}{\mathrm{m}} \cdot \frac{(2 \mathrm{a} / 3)}{\left[\mathrm{a}^{2}-\left(\frac{2 \mathrm{a}}{3}\right)^{2}\right]^{1 / 2}} \\ =\left(\frac{0.4 \sqrt{5} \mathrm{~F}}{\mathrm{~m}}\right) \end{gathered} $$

Option (1) is correct.

68. The ‘set-up’ shown here, is used to raise a mass $M$ through a height $h$ above the ground. The vertically upward force, $F(z)$ applied by an external agency, varies with the height, $\mathrm{z}$, above the ground as $\mathbf{F}(\mathbf{z})=\mathbf{F}(\mathbf{0})-\mathbf{k z}$.

The instantaneous speed, acquired by the mass $M$, when it has been raised through a height $h$, is given by

(1) $\left[\frac{2 \mathrm{~h}(\mathrm{~F}(0)+\mathrm{Mg})+\mathrm{kh}^{2}}{\mathrm{M}}\right]^{1 / 2}$

(2) $\left[\frac{2 \mathrm{~h}(\mathrm{~F}(0))-\mathrm{kh}^{2}}{\mathrm{M}}\right]^{1 / 2}$

(3) $\left[\frac{2 \mathrm{~h}(\mathrm{~F}(0)-\mathrm{Mg})-\mathrm{kh}^{2}}{\mathrm{M}}\right]^{1 / 2}$

(4) $\left[\frac{\mathrm{h}(\mathrm{F}(0)-\mathrm{Mg})+\mathrm{kh}^{2}}{\mathrm{M}}\right]^{1 / 2}$

Show Answer

Correct answer: (3)

Solution:

The net upward force, acting on the mass $\mathrm{M}$, when it is at a height $\mathrm{z}$ above the ground, is

$\mathrm{F}($ net $)=\mathrm{F}(\mathrm{z})-\mathrm{Mg}$

$$ =[\mathrm{F}(0)-\mathrm{kz}-\mathrm{Mg}] $$

Let a be the instantaneous acceleration at the height. We have

$\mathrm{Ma}=\mathrm{F}$ (net)

$\therefore \mathrm{M} \frac{\mathrm{dv}}{\mathrm{dt}}=\mathrm{F}(0)-\mathrm{kz}-\mathrm{Mg}$

( $\mathrm{v}=$ instantaneous velocity)

But $\frac{\mathrm{dv}}{\mathrm{dt}}=\frac{\mathrm{dv}}{\mathrm{dz}} \cdot \frac{\mathrm{dz}}{\mathrm{dt}}=\mathrm{v} \frac{\mathrm{dv}}{\mathrm{dz}}$

$\therefore \mathrm{v} \frac{\mathrm{dv}}{\mathrm{dz}}=\frac{\mathrm{F}(0)-\mathrm{kz}-\mathrm{Mg}}{\mathrm{M}}$

or $\quad v d v=\frac{(F(0)-k z-M g)}{M} d z$

$\therefore$ If $\mathbf{v}$ is the instantaneous speed of the mass $\mathrm{M}$ when it is at a height $\mathrm{h}$ above the ground, we have

$$ \int _{0}^{v} v d v=\int _{0}^{h} \frac{F(0)-k z-M g}{M} d z $$

$\therefore \mathrm{v}^{2}=\frac{2}{\mathrm{M}}\left[\mathrm{h}(\mathrm{F}(0)-\mathrm{Mg})-\frac{\mathrm{kh}^{2}}{2}\right]$

or $\quad v=\left\{\frac{1}{M}\left[2 h(F(0)-M) g-kh^{2}\right]\right\}^{1 / 2}$

Option (3) is correct.

69. Two massess $M$ and $2 M$, are arranged to be at the same initial height $H$, above the ground, by using a massless inextensible string and a smooth pulley. The masses are ’let-go’, at $t=0$, and the string is suddenly cut when the mass $M$ has risen through a height $\left(\frac{H}{2}\right)$. The velocity, with which the mass $2 \mathrm{M}$ would hit the ground, is given by

(1) $\sqrt{\frac{4 \mathrm{gH}}{5}}$

(2) $\sqrt{\frac{3 \mathrm{gH}}{4}}$

(3) $\sqrt{\frac{4 \mathrm{gH}}{3}}$

(4) $\sqrt{\frac{g H}{2}}$

Show Answer

Correct answer: (3)

Solution:

The equations of motion of the two masses are $\mathrm{T}-\mathrm{Mg}=\mathrm{Ma}$

and $2 \mathrm{Mg}-\mathrm{T}=2 \mathrm{Ma}$

$\therefore \mathrm{a}=\frac{\mathrm{Mg}}{3 \mathrm{M}}=\frac{\mathrm{g}}{3}$

When the mass M rises through a height $\frac{H}{2}$, the mass $2 M$ falls down through a distance $\frac{H}{2}$.

The downward velocity of mass $2 M$, when it has moved downward through a distance $\frac{H}{2}$, is, given by $\mathrm{v}^{2}-\mathrm{o}^{2}=2\left(\frac{\mathrm{g}}{3}\right)\left(\frac{\mathrm{H}}{2}\right)=\frac{\mathrm{gH}}{3}$

$\therefore \mathrm{v}=\sqrt{\frac{\mathrm{gH}}{3}}$

At this instant the string is cut. The mass, $2 \mathrm{~m}$, therefore, falls subsequently as a freely falling mass with an acceleration g. It is, at this instant, at a height $\frac{\mathrm{H}}{2}$ above the ground. Hence the velocity, V, with which it would hit the ground, is given by

$$ \mathrm{V}^{2}-\mathrm{v}^{2}=2(\mathrm{~g})\left(\frac{\mathrm{H}}{2}\right) $$

or $\quad \mathrm{V}^{2}-\left(\frac{\mathrm{gH}}{3}\right)=\mathrm{gH}$

or $\quad \mathrm{V}=\sqrt{\frac{4 \mathrm{gH}}{3}}$

Option (3) is correct.

70. A trolley, having an open rear end, has a small box at mass $m$, put on it at a distance $\ell$ from that open rear end. The coefficient of friction between the box and the trolley is $\mu$. If the trolley (initially at rest on a horizontal floor), were to be given a constant acceleration a, the distance, it would travel before the box falls off it, would equal

(1) $\ell \frac{(a+\mu g)}{a}$

(2) $\ell \frac{a}{(a+\mu g)}$

(3) $\ell \frac{a}{(a-\mu g)}$

(4) $\ell \frac{(\mathrm{a}-\mu \mathrm{g})}{\mathrm{a}}$

Show Answer

Correct answer: (3)

Solution:

When trolley accelerates from left to right, with an acceleration a, the box has a force (= ma), acting on it from right to left. The free body diagram, showing the forces acting on the box, is as shown. The net force, on the box, directed from right to left, is $(m a-\mu N)=(m a-\mu \mathrm{mg})=m(a-\mu g)$.

Hence the net acceleration of the box, directed from right to left, is $\frac{\mathrm{m}(\mathrm{a}-\mu \mathrm{g})}{\mathrm{m}}$ i.e. $(\mathrm{a}-\mu \mathrm{g})$.

The box needs to move a distance $\ell$ (from right to left) before it falls off. If it takes a time $t$, for this purpose, we would have

$\ell=0+\frac{1}{2}(\mathrm{a}-\mu \mathrm{g}) \mathrm{t}^{2}$

$\therefore \mathrm{t}=\left[\frac{2 \ell}{(\mathrm{a}-\mu \mathrm{g})}\right]^{1 / 2}$

The distance, $\mathrm{s}$, moved by the trolley, in this time, is

$$ \begin{aligned} & \mathrm{s}=0+\frac{1}{2} \mathrm{at}{ }^{2}=\frac{1}{2} \mathrm{a} \frac{2 \ell}{(\mathrm{a}-\mu \mathrm{g})} \\ &=\ell\left(\frac{\mathrm{a}}{\mathrm{a}-\mu \mathrm{g}}\right) \end{aligned} $$

Option (3) is correct.

71. A system of three masses $m _{1}, m _{2}, m _{3}\left[m _{3}>\left(m _{1}+m _{2}\right)\right]$, a smooth inclined plane, two smooth light pulleys and inextensible massless strings, is set up as shown. The acceleration, of the mass $m _{3}$, if the masses were ’let-go’, would equal

(1) $\frac{\left(m _{3}-m _{2}-m _{1}\right)}{\left(m _{1}+m _{2}+m _{3}\right)} g$

(2) $\frac{\left(\mathrm{m} _{3}-\mathrm{m} _{2} \sin \theta-\mathrm{m} _{1}\right)}{\left(\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}\right)} \mathrm{g}$

(3) $\frac{\left(m _{3}-m _{2} \cos \theta-m _{1}\right)}{\left(m _{1}+m _{2}+m _{3}\right)}$ g

(4) $\frac{\left(\mathrm{m} _{3}+\mathrm{m} _{2} \sin \theta-\mathrm{m} _{1}\right)}{\left(\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}\right)} \mathrm{g}$

Show Answer

Correct answer: (2)

Solution:

Let (i) $T _{1}$ be the tension in the string between masses $m _{1}$ and $m _{2}$ and (ii) $T _{2}$ the tension in the string between masses $\mathrm{m} _{2}$ and $\mathrm{m} _{3}$.

The free body diagrams of the three masses (which would all have an acceleration, say a, of the same magnitude) are as shown.

Their corresponding equations of motion are

$\mathrm{T} _{1}-\mathrm{m} _{1} \mathrm{~g}=\mathrm{m} _{1} \mathrm{a}$

$\mathrm{T} _{2}-\mathrm{T} _{1}-\mathrm{m} _{2} \mathrm{~g} \sin \theta=\mathrm{m} _{2} \mathrm{a}$

and $\mathrm{m} _{3} \mathrm{~g}-\mathrm{T} _{2}=\mathrm{m} _{3} \mathrm{a}$

Adding, we get

$$ \begin{aligned} & \left(m _{3}-m _{2} \sin \theta-m _{1}\right) g=\left(m _{1}+m _{2}+m _{3}\right) a \\ \therefore \quad & a=\frac{\left(m _{3}-m _{2} \sin \theta-m _{1}\right)}{\left(m _{1}+m _{2}+m _{3}\right)} g \end{aligned} $$

Option (2) is correct.

72. A smooth inclined plane, of mass $m _{1}$, has a mass $m _{2}$ kept on it, as shown. The inclined plane is kept on a smooth horizontal surface. A light inextensible string and a light smooth pulley are used to connect it to a mass $M$ hanging vertically. It is observed that when the mass $M$ is ’let-go’, the mass $m _{2}$ does not slip over the inclined plane. The relation between $M, m _{1}$

and $m _{2}$, is, then

(1) $\mathrm{M}=\frac{\mathrm{m} _{1}+\mathrm{m} _{2}}{(\cot \theta-1)}$

(2) $M=\frac{m _{1}+m _{2}}{(\tan \theta-1)}$

(3) $M=\frac{m _{1}+m _{2} \sin \theta}{(\cot \theta-1)} $

(4) $M=\frac{m _{1}+m _{2} \sin \theta}{(\tan \theta-1)}$

Show Answer

Correct answer: (1)

Solution:

Let ’ $a$ ’ be the common acceleration of the mass $M$ and the (staying intact) ‘combination’ of the inclined plane and the mass $\mathrm{m} _{2}$. The mass $\mathrm{m} _{2}$, by itself, can slide down the inclined plane with an acceleration $g \sin \theta$. It would not slip over the inclined plane if the component of the horizontal acceleration, $s$, of the ‘combination’, equals $\mathrm{g} \sin \theta$. We thus need to have

$\mathrm{a} \cos \theta=\mathrm{g} \sin \theta \hspace{40mm} . . . . . . (1)$

To find ’ $a$ ’ we look at the free body diagrams of (i) mass $M$ and (ii) the ‘combination’ of masses $m _{1}$ and $m _{2}$. We then have,

$$ \mathrm{Mg}-\mathrm{T}=\mathrm{Ma} $$

and $\mathrm{T}=\left(\mathrm{m} _{1}+\mathrm{m} _{2}\right) \mathrm{a}$

$\therefore \mathrm{Mg}=\left(\mathrm{M}+\mathrm{m} _{1}+\mathrm{m} _{2}\right) \mathrm{a}$

$\therefore a=\frac{M}{\left(\mathrm{M}+\mathrm{m} _{1}+\mathrm{m} _{2}\right)} \mathrm{g}$

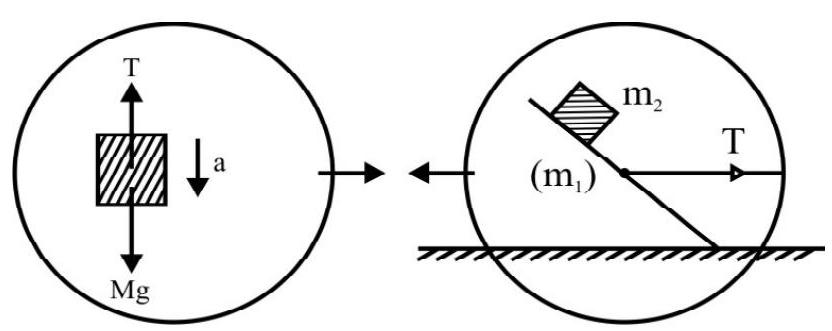
Putting this value of ’ $\mathbf{a}$ ‘, in the above equation (1), we get

$\left(\frac{M}{M+m _{1}+m _{2}} g\right) \cos \theta=g \sin \theta$

$\therefore \mathrm{M} \cot \theta=\mathrm{M}+\mathrm{m} _{1}+\mathrm{m} _{2}$

$\therefore \mathrm{M}=\frac{\left(\mathrm{m} _{1}+\mathrm{m} _{2}\right)}{(\cot \theta-1)}$

Option (1) is correct.

73. A system of two blocks, of masses $m _{1}$ and $m _{2}$, a smooth inclined plane, a light pulley and an inextensible light string, arranged as shown, is observed to be in equilibrium. If the normal reaction, due to the inclined plane, on the mass $m _{1}$ equals that due to a mass $M$, on a horizontal surface, we would have

(1) $\mathrm{M}=\sqrt{\mathrm{m} _{1}^{2}+\mathrm{m} _{2}^{2}}$

(2) $\mathrm{M}=\sqrt{\mathrm{m} _{1}^{2}-\mathrm{m} _{2}^{2}}$

(3) $\quad M=\left(m _{1} \sin \alpha+m _{2}\right)$

(4) $\quad M=\left(m _{1} \cos \alpha+m _{2}\right)$

Show Answer

Correct answer: (2)

Solution:

The free body diagrams, for the masses $\mathrm{m} _{1}$ and $\mathrm{m} _{2}$, are as shown. Since the system is in equilibrium (i.e. has zero acceleration), we have

$$ \begin{equation*} \mathrm{m} _{2} \mathrm{~g}-\mathrm{T}=0 \tag{1} \end{equation*} $$

and $\mathrm{N}=\mathrm{m} _{1} \mathrm{~g} \cos \alpha \hspace{40mm} . . . . . . (2)$

and $\quad \mathrm{T}-\mathrm{m} _{1} \mathrm{~g} \sin \alpha=0 \hspace{40mm} . . . . . . (3)$

Adding (1) & (3)

$\left(\mathrm{m} _{2} \mathrm{~g}-\mathrm{m} _{1} \mathrm{~g} \sin \alpha\right)=0$

$\therefore \sin \alpha=\frac{\mathrm{m} _{2}}{\mathrm{~m} _{1}}$

$\therefore \mathrm{N}=\mathrm{m} _{1} \mathrm{~g} \cos \theta=\mathrm{m} _{1} \mathrm{~g} \sqrt{1-\sin ^{2} \alpha}$

$$ \begin{aligned} & =m _{1} g \sqrt{1-\frac{m _{2}^{2}}{m _{1}^{2}}} \\ & =m _{1} g \sqrt{\frac{\left(m _{1}^{2}-m _{2}^{2}\right)}{m _{1}}}=g \sqrt{\left(m _{1}^{2}-m _{2}^{2}\right)} \end{aligned} $$

For the mass $\mathrm{m} _{1}$ on the horizontal surface, we have

$$ \mathrm{N}=\mathrm{Mg} $$

$\therefore \mathrm{Mg}=\sqrt{\mathrm{m} _{1}^{2}-\mathrm{m} _{2}^{2}}$

or $\mathrm{M}=\sqrt{\left(\mathrm{m} _{1}^{2}-\mathrm{m} _{2}^{2}\right)}$

Option (2) is correct.

74. A given box gets crushed when a mass of $M \mathrm{~kg}$ is kept on its top. If this box were to be kept in an elevator, with a mass $m$ on its top $(m<M)$, the box would get crushed if the elevator were to start

(1) ascending with an acceleration $\left(\frac{M}{m}\right) g$

(2) descending with an acceleration $\left(\frac{m}{M}\right) g$

(3) ascending with an acceleration $\left(\frac{M}{m}-1\right) g$

(4) descending with an acceleration $\left(1-\frac{m}{M}\right) g$

Show Answer

Correct answer: (3)

Solution:

For the box to get crushed, the apparent weight, of the mass $\mathrm{m}$, should be come equal to the normal weight of mass $\mathrm{M}(=\mathrm{Mg})$.

The apparent weight needs to increase. Hence the elevator must start ascending with an acceleration ’ $a$ ‘, such that

$\mathrm{m}(\mathrm{a}+\mathrm{g})=\mathrm{Mg}$

$\therefore \mathrm{a}=\frac{(\mathrm{M}-\mathrm{m}) \mathrm{g}}{\mathrm{m}}$

$$ =\left(\frac{\mathrm{M}}{\mathrm{m}}-1\right) \mathrm{g} $$

Option (3) is correct.

75. A simple pendulum, having a bob of mass $m$, is suspended from the roof of a car. It is observed that when the car starts moving with an acceleration a, the string, of the pendulum, gets inclined at an angle $\alpha$ to the vertical. The acceleration, $a$, of the car, and the tension, $T$, in the string of the pendulum are, then, given by

(1) $\mathrm{a}=\mathrm{g} \sec \alpha ; \mathrm{T}=\mathrm{mg} \tan \alpha$

(2) $\mathrm{a}=\mathrm{g} \tan \alpha ; \mathrm{T}=\mathrm{mg \operatorname {sec } \alpha}$

(3) $\mathrm{a}=\mathrm{g} \tan \alpha ; \mathrm{T}=\mathrm{mg} \tan \alpha$

(4) $\mathrm{a}=\mathrm{g} \sec \alpha ; \mathrm{T}=\mathrm{mg} \sec \alpha$

Show Answer

Correct answer: (2)

Solution:

The three forces, keeping the bob, in equilibrium, in the accelerated car are, as shown. We then have, by Lami’s theorem.

$$ \frac{\mathrm{ma}}{\sin (\pi-\alpha)}=\frac{\mathrm{mg}}{\sin \left(\frac{\pi}{2}+\alpha\right)}=\frac{\mathrm{T}}{\sin \frac{\pi}{2}} $$

$\therefore a=\frac{g \sin \alpha}{\cos \alpha}=g \tan \alpha$

and $\quad \mathrm{T}=\mathrm{mg} \frac{1}{\cos \alpha}=\mathrm{mg} \sec \alpha$

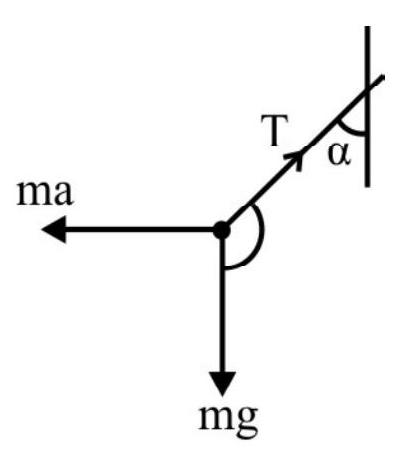
Option (2) is correct.

76. A train starts moving with a uniform velocity $u$, along a straight horizontal track, at $t=0$. Brakes are applied to it, at $t=100 \mathrm{~s}$, and these produce a uniform retardation ’ $a$ ‘, on the train, for the next $10 \mathrm{~s}$.

The displacement (relative to the train, of a small object, kept on a smooth long (horizontal top table), as a function of time, would be represented by the graph, labelled as graph

(1) A

(2) $\mathrm{B}$

(3) $\mathrm{C}$

(4) D

Show Answer

Correct answer: (1)

Solution:

There is no force acting on the object as long as the train is moving with a uniform velocity. The object, in this inertial frame of reference, does not move, relative to the train, from $(t=0)$ to $(t=100 \mathrm{~s})$.

When the brakes are applied, the train experiences a backward force that produces a uniform retardation. The object would, therefore, experience a forward force that would give it a forward acceleration $(=\mathrm{a})$. The displacement, of the object, relative to the train, from $(t=100 \mathrm{~s})$ to $(t=110 \mathrm{~s})$ would then be represented by

$$ \mathrm{s}=\mathrm{ut}+\frac{1}{2} \mathrm{at}^{2} $$

(Where $t$ would now take the values from 0 to 10 ).

The graph, showing the displacement of the object, relative to the train, from $(t=0 \mathrm{~s})$ to $(t=110 \mathrm{~s})$, would, therefore, have the form shown in graph $\mathrm{A}$.

Option (1) is correct.

77. A system of two light smooth pulleys and light inextensible strings, has two masses $M _{1}$ and $M _{2}$, attached as shown. The pulley $P _{2}$ is movable and pulley $P _{1}$ is a fixed pulley. If the mass $M _{2}$ moves up and the mass $M _{1}$ moves down, the accelerations of the masses $M _{1}$ and $M _{2}$, are, respectively

(1) $\left(\frac{4 M _{1}-2 M _{2}}{4 M _{1}+M _{2}}\right)$ g and $\left(\frac{2 M _{1}-M _{2}}{4 M _{1}+M _{2}}\right) g$

(2) $\left(\frac{2 M _{1}-M _{2}}{4 M _{1}+M _{2}}\right)$ g and $\left(\frac{4 M _{1}-2 M _{2}}{4 M _{1}+M _{2}}\right) g$

(3) $\left(\frac{M _{1}-2 M _{2}}{4 M _{1}+M _{2}}\right)$ g and $\left(\frac{2 M _{1}-4 M _{2}}{4 M _{1}+M _{2}}\right) g$

(4) $\left(\frac{4 M _{1}-2 M _{2}}{4 M _{1}+2 M _{2}}\right)$ g and $\left(\frac{2 M _{1}-M _{2}}{4 M _{1}+2 M _{2}}\right) g$

Show Answer

Correct answer: (1)

Solution:

Let $T _{1}$ and $T _{2}$ be the tensions in the strings, as shown. We see that

$$ \mathrm{T} _{1}=2 \mathrm{~T} _{2} $$

Pulley $P _{2}$ is massless. If there is a net force on it, acceleration will approach infinity. For the mass $M _{2}$, moving upward, the acceleration will be half that of the mass $\mathrm{M} _{1}$, moving downwards. [This is because a downward displacement, $\Delta x$, of mass $\mathrm{M} _{1}$, will result in an upward displacement of $\left(\frac{\Delta x}{2}\right)$ of mass $\mathrm{M} _{2}$ ]. Hence the equations of motion of the two masses are

$$ \begin{equation*} \mathrm{T} _{1}-\mathrm{M} _{2} \mathrm{~g}=\mathrm{M} _{2} \frac{\mathrm{a}}{2} \tag{1} \end{equation*} $$

and $\mathrm{M} _{1} \mathrm{~g}-\mathrm{T} _{2}=\mathrm{M} _{1} \mathrm{a} \hspace{40mm} . . . . . . (2)$

Also $2 \mathrm{~T} _{2}-\mathrm{M} _{2} \mathrm{~g}=\mathrm{M} _{2} \frac{\mathrm{a}}{2} \hspace{40mm} . . . . . . (3)$

Again $2 \mathrm{M} _{1} \mathrm{~g}-2 \mathrm{~T} _{2}=2 \mathrm{M} _{1} \mathrm{a} \hspace{40mm} . . . . . . (4)$

Adding (3) and (4), we get

$\left(2 M _{1}-M _{2}\right) g=\frac{a}{2}\left(M _{2}+4 M _{1}\right)$

$\therefore a=\frac{2\left(2 M _{1}-M _{2}\right)}{\left(4 M _{1}+M _{2}\right)} g=\left(\frac{4 M _{1}-2 M _{2}}{4 M _{1}+M _{2}}\right) g$

The acceleration of mass $\mathrm{M} _{1}$ is, therefore,

$\left(\frac{4 M _{1}-2 M _{2}}{4 M _{1}+M _{2}}\right) g$ and that of mass $M _{2}$ is

$=\frac{\left(2 M _{1}-M _{2}\right)}{\left(4 M _{1}+M _{2}\right)} g$

Option (1) is correct.

78. A block, of mass $M$, is kept on a smooth inclined plane, of incline ’ 1 in $\ell$ ‘. When the inclined plane is given a horizontal acceleration a, it is observed that the block says stationary relative to the ‘incline’. The acceleration, a, equals

(1) $\frac{g}{\sqrt{\ell^{2}+1}}$

(2) $\frac{g}{\sqrt{\ell^{2}-1}}$

(3) $\mathrm{g}\left(\frac{1}{\ell}\right)$

(4) $\mathrm{g} \frac{\left(\sqrt{\ell^{2}-1}\right)}{\ell}$

Show Answer

Correct answer: (2)

Solution:

For the given incline, we have

$\sin \theta=\frac{1}{\ell}$

$\cos \theta=\left(\frac{\sqrt{\ell^{2}-1}}{\ell}\right)$

The acceleration, of the block, down the inclined plane is $g \sin \theta$.

The component of the horizontal acceleration, a, of the ‘incline’, along the inclined plane, is a $\cos \theta$.

The block will remain stationary, relative to the incline, if

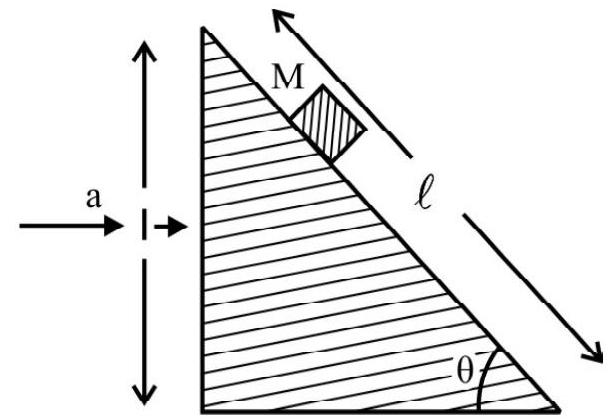
$$ \mathrm{a} \cos \theta=\mathrm{g} \sin \theta $$

or $\mathrm{a}=\mathrm{g} \tan \theta$

$=\mathrm{g} \frac{1}{\sqrt{\ell^{2}-1}}$

Option (2) is correct.

79. An insect, of mass $7 \mathrm{~m}$, is at the bottom of a hemispherical bowl of radius $R$. The coefficient of friction, between the legs of the insect, and the surface of the bowl, is $\mu$. The insect starts crawling up the hemisphere, but slides down after climbing up a height $h$ above its starting point. The equation, connecting $h$ and $R$, is

(1) $\mathrm{h}^{2}-(2 \mathrm{R}+\mu) \mathrm{h}+\mu \mathrm{R}=0$

(2) $h^{2}+(2 R+\mu) h-\mu R=0$

(3) $\mu \mathrm{h}^{2}+2 \mathrm{Rh}-\mu \mathrm{R}=0$

(4) $\mu \mathrm{h}^{2}+(2 \mathrm{R}+\mu) \mathrm{h}+\mu \mathrm{R}=0$

Show Answer

Correct answer: (1)

Solution:

The insect can keep on crawling up till the component of its weight, down the bowl, equals the force of limiting friction between the insect and the bowl.

At the height, $h$, we then have

$$ \mathrm{N}=\mathrm{mg} \cos \alpha $$

and $\mathrm{F}=$ force of limiting friction

$$ =\mu \mathrm{N}=\mathrm{mg} \sin \alpha $$

$\therefore \mu=\tan \alpha$

In $\triangle \mathrm{OAB}, \angle \mathrm{OAB}=\pi-\left[\left(\frac{\pi}{2}\right)+\alpha\right]$

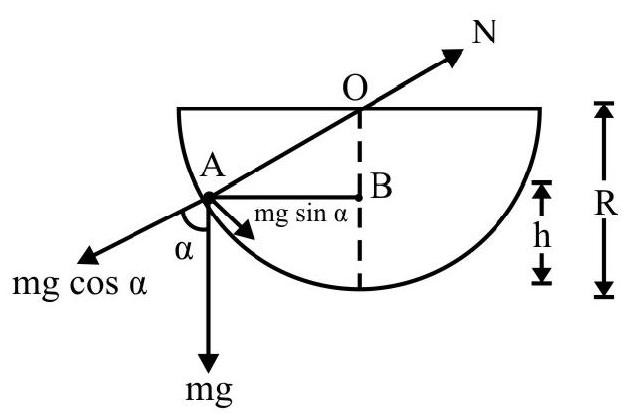
$(\frac{\pi}{2}-\alpha)$

$\therefore \tan \left(\frac{\pi}{2}-\alpha\right)=\frac{\mathrm{OB}}{\mathrm{AB}}=\frac{(\mathrm{R}-\mathrm{h})}{\sqrt{\mathrm{R}^{2}-(\mathrm{R}-\mathrm{h})^{2}}}$

or $\quad \cot \alpha=\frac{(\mathrm{R}-\mathrm{h})}{\left(2 \mathrm{hR}-\mathrm{h}^{2}\right)}$

$\therefore$ We have $\frac{2 \mathrm{hR}-\mathrm{h}^{2}}{\mathrm{R}-\mathrm{h}}=\mu$

$\therefore 2 \mathrm{hR}-\mathrm{h}^{2}=\mu(\mathrm{R}-\mathrm{h})$

or $\quad(2 R+\mu) h-h^{2}-\mu R=0$

or $\quad h^{2}-(2 R+\mu) h+\mu R=0$

Option (1) is correct.

80. A force, $F$, acts, in the direction shown, on a block of mass M. The coefficient of friction, between the block, and the horizontal surface is $\mu$. If the block is initially at rest, the speed acquired by it when it has moved a distance, $s$, on the horizontal surface, is

(1) $\left\{\frac{2 \mathrm{~s}}{\mathrm{M}}[\mathrm{F}(\sin \theta+\mu \cos \theta)+\mu \mathrm{Mg}]\right\}^{1 / 2}$

(2) $\left\{\frac{2 s}{M}[F(\sin \theta-\mu \cos \theta)-\mu M g]\right\}^{1 / 2}$

(3) $\left\{\frac{2 s}{M}[F(\cos \theta-\mu \sin \theta)-\mu M g]\right\}^{1 / 2}$

(4) $\left\{\frac{2 \mathrm{~s}}{\mathrm{M}}[\mathrm{F}(\cos \theta+\mu \sin \theta)+\mu \mathrm{Mg}]\right\}^{1 / 2} $

Show Answer

Correct answer: (3)

Solution:

The free body diagram, for the forces acting on the block, is as shown.

We then have $\mathrm{N}=\mathrm{Mg}+\mathrm{F} \sin \theta$

and $f=$ force of friction

$$ =\mu \mathrm{N}=\mu[\mathrm{Mg}+\mathrm{F} \sin \theta] $$

The net force, accelerating the block, along the horizontal surface, is

$$ \begin{aligned} \mathrm{F} _{\mathrm{Net}} & =\mathrm{F} \cos \theta-f \\ & =\mathrm{F} \cos \theta-\mu[\mathrm{Mg}+\mathrm{F} \sin \theta] \\ & =\mathrm{F}(\cos \theta-\mu \sin \theta)-\mu \mathrm{Mg} \end{aligned} $$

Acceleration, along the horizontal, $\left(=\frac{F}{m}\right)$, is given by

$$ \mathrm{a}=\left[\frac{\mathrm{F}(\cos \theta-\mu \sin \theta)}{\mathrm{M}}-\mu \mathrm{g}\right] $$

If $v$ is the speed of the block, after moving a distance $s$, we have

$$ \begin{gathered} v^{2}-o^{2}=2 a s \\ \therefore \quad v^{2}=\frac{2 s}{M}[F(\cos \theta-\mu \sin \theta)-\mu M g] \\ \therefore \quad v=\left\{\frac{2 s}{M}[F(\cos \theta-\mu \sin \theta)-\mu M g]\right\}^{1 / 2} \end{gathered} $$

Option (3) is correct.