Unit 02 Kinematics
KINEMATICS
Mechanics in one of oldest of physical sciences. It is the study of objects in motion. Kinematics is a branch of mechanics in which we study motion without inquiring about the cause of motion. A particle is an infinitesimally small part of matter. It has a negligible size but a definite position. A body is a finite amount of matter having a finite size, shape occupying definite space.
Basic Definitions
1. Frame of reference
A frame of reference is a conveniently chosen co-ordinate system. The position of particle is described in the frame of reference chosen.
2. Rest and motion
A body is at rest in a chosen frame of reference if its position does not change with time. On the other hand, if position of particle or body changes with time the particle or body is in motion. Rest and motion are relative. A body at rest in one frame, can be in motion in another frame of reference. There is nothing like absolute rest.
3. Position Vector
It describes the instantaneous position of a particle in a frame of reference. It is a vector joining the origin of co-ordinates to the instantaneous position of particle. For a particle at rest; position vector is same at all times. For a particle in motion, the position vector changes with time.
4. Distance and Displacement
The actual path along which a particle moves is known as the trajectory. The distance traveled by a particle equals the actual length of the path described. It is a scalar quantity. It is a positive number which does not decreases with time and can never be zero for a particle in motion.
The displacement is a vector joining the initial and the final position of the particle. In Fig. 1 a particle moves along curved path, from a point A to B . A B is a straight line joining initial portion $A$ and final position B. A B = S Displacement. The magnitude of the displacement is less than or equal to the distance traveled. if a particle comes back to its initial position the displacement is zero but distance traveled finite.
Example-1 :
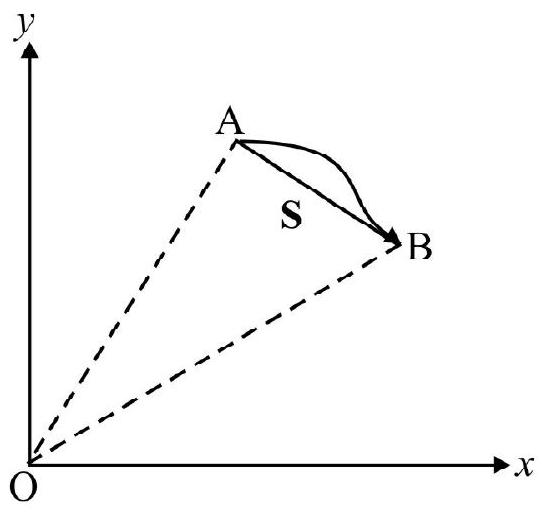
Fig. 1
A particle moves along a circle of radius $r$. What is distance traveled and displacement, when particle describes.
(a) One quadrant
(b) $\frac{3}{4}$ th of circle.
Show Answer
Solution :
(a) From Fig. 2(a); we have
distance traveled $=\frac{2 \pi \mathrm{r}}{4}=\frac{\pi \mathrm{r}}{2}$
Magnitude of displacement
$=$ Length of chord $\mathrm{AB}=\sqrt{2} \mathrm{r}$
(b) From Fig. 2(b), we have
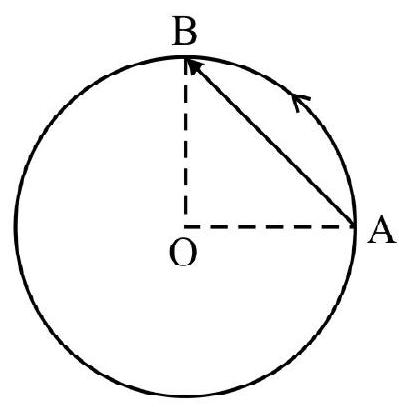
(a)
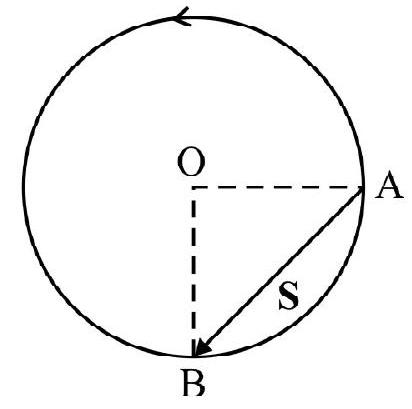
(b)
Fig. 2
Distance traveled $=\frac{3}{4}(2 \pi \mathrm{r})=\frac{3 \pi \mathrm{r}}{2}$
Magnitude of displacement $=$ Length of chord $A B=\sqrt{2} r$
Motion in One, Two and Three Dimensions
(a) One dimensional motion of a particle :
is that motion in which only ONE of the three co-ordinates is used to describe its position changes. In one dimensional motion the object moves along a straight line path. This is also known as linear or rectilinear motion.
(b) Two dimensional motion :
is that motion in which two out of three co-ordinates specifying the position of the particle change. The object moves in one plane. For example:
(1) an insect crawling on a floor.
(2) a billiard ball moving on billiard table.
(c) Three dimensional motion :
is that motion in which all the three co-ordinates describing the position change with time. The object moves in space. A kite flying on a windy day; a leaf falling off a tree branch are examples of motion in three dimensions.
Speed
The speed of a particle relates the distance traveled by the body and the time taken. The average speed, $V _{a v}$, is the ratio of the total distance traveled to the total time taken. It is the distance traveled per unit time. Speed is a scalar quantity.
$$ \text { Average speed }=\frac{\text { Total distance traveled }}{\text { Total time taken }}=\frac{\mathrm{S}}{\mathrm{T}} $$
Its SI unit is $\mathrm{ms}^{-1}$, and its dimensions are $\mathrm{LT}^{-1}$.
The instantaneous speed, $v$, is defined as
$$ v=\operatorname{Lt} _{\Delta \mathrm{t} \rightarrow 0}\left[\frac{\Delta \mathrm{s}}{\Delta \mathrm{t}}\right]=\frac{\mathrm{ds}}{\mathrm{dt}} $$
where $\Delta \mathrm{s}$ is a small distance traveled by the body in the interval $\mathrm{t}$ and $\mathrm{t}+\Delta \mathrm{t}$
For a particle having a one dimensional motion, say along $x$-axis; the instantaneous speed is slope of tangent of $x$ vs t graph at the moment of time considered.
Velocity
The speed of a moving body does not give us any information regarding the direction of motion. The velocity of a particle at a given time is a quantity giving the speed and direction of motion at that time.
The average velocity $\mathbf{v} _{\mathrm{av}}$, is in the direction of the displacement vector $\mathbf{s}$. Its magnitude is ratio of the magnitude of displacement and the total time taken, i.e.
$$ \mathbf{v} _{\mathrm{av}}=\text { Average velocity }=\frac{\text { Displacement }}{\text { Time taken }}=\frac{\mathbf{s}}{\mathrm{t}} $$
The instantaneous velocity, $\boldsymbol{v}$, is defined as
$$ \mathbf{v}=\mathrm{Lt} _{\Delta \mathrm{t}-0}\left[\frac{\Delta \mathbf{s}}{\overrightarrow{\Delta \mathrm{t}}}\right]=\frac{\mathbf{d s}}{\mathrm{dt}} $$
where $\Delta \mathbf{s}$ is infinitesimally small displacement in time interval $\mathrm{t}$ and $\mathrm{t}+\Delta \mathrm{t}$.
Example-2 :
A particle moves along a right angled isosceles triangle $\mathrm{ABC}$. It moves from vertex $\mathrm{A}$ to $\mathrm{C}$ along path $\mathrm{A} \rightarrow \mathrm{B} \rightarrow \mathrm{C}$ in time $\mathrm{t}$ as shown in Fig. 3. What is the
(a) Average speed.
(b) Magnitude of the average velocity of the particle.
Show Answer
Solution :
(a) The total distance traveled $=\mathrm{s}$. Obviously
$$ \begin{align*} & \mathrm{s}=\mathrm{AB}+\mathrm{BC}=2 \mathrm{a} \\ & \text { Average speed }=v _{\mathrm{av}}=\frac{\mathrm{s}}{\mathrm{t}}=\frac{2 \mathrm{a}}{\mathrm{t}} \tag{1} \end{align*} $$
(b) The net displacement $=\mathbf{S}=\mathbf{A B}$
Magnitude of net displacement $=|\mathbf{s}|=\mathrm{AC}=\sqrt{2} \mathrm{a}$
The magnitude of the average velocity $=\left|\mathbf{v} _{\mathrm{av}}\right|=\frac{\sqrt{2} \mathrm{a}}{\mathrm{t}}$
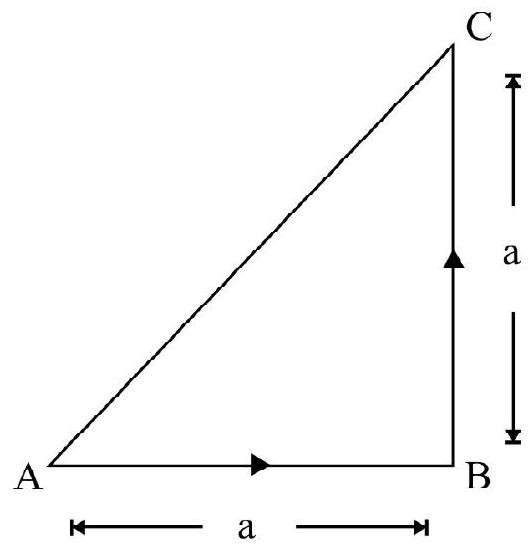
Fig. 3
Example-3 :
A particle moves along $x$-axis. It travels distances $\mathrm{S} _{1}, \mathrm{~S} _{2}, \ldots .$. with constant speed $\mathrm{V} _{1}, \mathrm{~V} _{2}, \ldots$. , respectively. What is the average speed?
Show Answer
Solution :
The total distance travelled $=\mathrm{S}=\mathrm{S} _{1}+\mathrm{S} _{2}+\ldots \ldots . .=\sum _{\mathrm{i}=1}^{\mathrm{n}} \mathrm{S} _{\mathrm{i}}$
The total time taken $=\mathrm{T}=\mathrm{t} _{1}+\mathrm{t} _{2}+\ldots \ldots . .=\sum _{\mathrm{i}=1}^{\mathrm{n}} \mathrm{t} _{\mathrm{i}}$
$$ \text { or } \mathrm{T}=\frac{\mathrm{S} _{1}}{\mathrm{~V} _{1}}+\frac{\mathrm{S} _{2}}{\mathrm{~V} _{2}}+\frac{\mathrm{S} _{3}}{\mathrm{~V} _{3}} \ldots \ldots . .=\sum _{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{\mathrm{S} _{\mathrm{i}}}{\mathrm{V} _{\mathrm{i}}}\right) $$
The averages speed, $v _{\mathrm{av}}$ is
$$ \mathrm{V} _{\mathrm{av}}=\frac{\mathrm{S}}{\mathrm{T}}=\frac{\sum _{\mathrm{i}=1}^{\mathrm{n}} \mathrm{S} _{\mathrm{i}}}{\sum _{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{\mathrm{S} _{\mathrm{t}}}{\mathrm{V} _{\mathrm{i}}}\right)} $$
Let $\mathrm{S} _{1}=\mathrm{S} _{2}=\mathrm{S}$. The body covers two equal distances with different speeds $\mathrm{V} _{1}$ and $\mathrm{V} _{2}$. Then
$$ \mathrm{V} _{\mathrm{av}}=\frac{2 \mathrm{~S}}{\left(\frac{\mathrm{S}}{\mathrm{V} _{1}}+\frac{\mathrm{S}}{\mathrm{V} _{2}}\right)}=\frac{2 \mathrm{~V} _{1} \mathrm{~V} _{2}}{\mathrm{~V} _{1}+\mathrm{V} _{2}} $$
The average speed equal the harmonic mean of individual speeds.
Example-4 :
A particle travels for $n$ equal time intervals, each equal to $t$, with speed $V _{1}, V _{2}, \ldots . . V _{N}$. Show that the average speed equals the arithmetic mean of individual speeds.
Show Answer
Solution :
Let $\mathrm{S} _{1}, \mathrm{~S} _{2}, \ldots \ldots \mathrm{S} _{\mathrm{n}}$ be distances traveled in $1^{\text {st }}, 2^{\text {nd }} \ldots . . . \mathrm{n}^{\text {th }}$ time interval, each equal to $t$. Obviously
$$ S _{1}=V _{1} t ; S _{2}=V _{2} t, \ldots \ldots S _{n}=V _{n} t $$
The total distance traveled $\mathrm{S}=\mathrm{S} _{1}+\mathrm{S} _{2}+\ldots \ldots+\mathrm{S} _{\mathrm{n}}$
$$ =\left(\mathrm{V} _{1}+\mathrm{V} _{2}+\ldots . . \mathrm{V} _{\mathrm{n}}\right) \mathrm{t} $$
The total time taken $=\mathrm{T}=\mathrm{nt}$
$\therefore$ Average speed $=\frac{\mathrm{S}}{\mathrm{T}}=\frac{\mathrm{V} _{1}+\mathrm{V} _{2}+\ldots . \mathrm{V} _{\mathrm{N}}}{\mathrm{n}}$
$=$ Arithmetic mean of the individual speeds.
Uniform Motion in a Straight Line
A body has a uniform motion if its velocity is same at all moments of time. For a particle having uniform, one dimensional motion, say along $x$-axis; the particle has equal displacement in equal time intervals howsoever small the interval be.
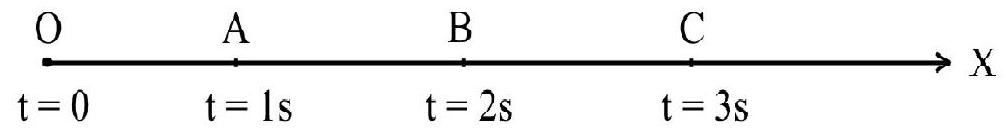
Fig. 4
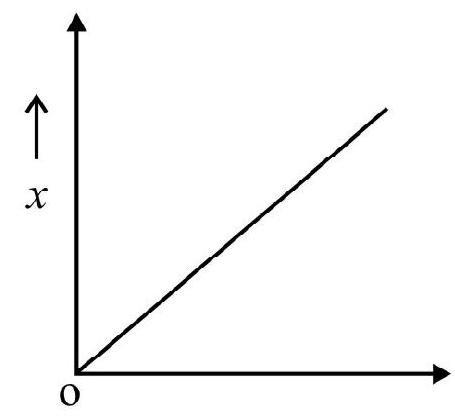
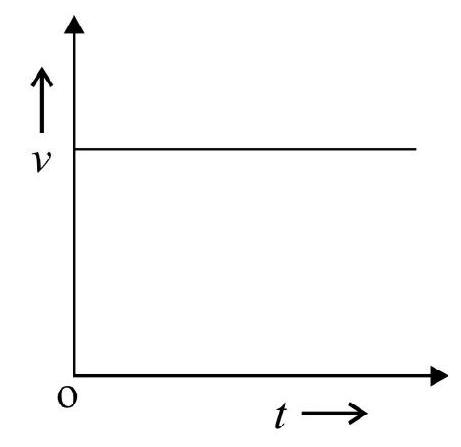
In Fig. 4, particle starts moving from origin $\mathrm{O}$ at $\mathrm{t}=0$ along the $x$-axis with uniform velocity. $\mathrm{A}, \mathrm{B}, \mathrm{C}$ denotes its position at $\mathrm{t}=1 \mathrm{~s}, 2 \mathrm{~s}$ and $3 \mathrm{~s}$ respectively. Then $\mathrm{OA}=\mathrm{AB}=\mathrm{BC}$. The position $(x)$ vs time $(\mathrm{t})$ graph of uniform motion along +ve $x$-axis is shown in Fig 5(a). Fig 5(b) shows velocity $(v)$ vs time (t). The slope of $x$ vs t graph equals the velocity of the particle.
(a)
(b)
Fig. 5
Non-Uniform Motion
An object undergoing unequal displacement in equal time intervals, has a non-uniform motion. In non uniform motion velocity varies with time. The motion is also referred to as accelerated motion. The average acceleration over a finite time interval is ratio of change in velocity and time taken. Expressed mathematically
$$ \mathbf{a} _{\mathrm{av}}=\frac{\mathbf{v} _{2}-\mathbf{v} _{\mathbf{1}}}{\mathrm{t} _{2}-\mathrm{t} _{1}}=\frac{\Delta \mathbf{v}}{\Delta \mathrm{t}} $$
where $\mathbf{v} _{1}$ and $\mathbf{v} _{2}$ denote instantaneous velocity at $t=t _{1}$ and $t=t _{2}$ respectively.
The instantaneous acceleration a is
$$ \mathbf{a}=\operatorname{Lt} _{\Delta \mathrm{t} \rightarrow 0}\left[\frac{\Delta \mathbf{v}}{\Delta \mathrm{t}}\right]=\frac{\mathbf{d v}}{\mathrm{dt}} $$
The instantaneous acceleration is slope of tangent to velocity vs time graph at the moment of time considered. Acceleration of a body can be either a positive or a negative member. It velocity of body increases as time increases, acceleration is a positive number. If velocity of body decreases as time increases;acceleration is a negative number. Negative acceleration is also known as retardation.
For a body having same acceleration at all times; we say motion is uniformly accelerated. However if acceleration is not same at all times, we have non-uniformly accelerated motion.
Graphical Interpretation of Velocity and Acceleration
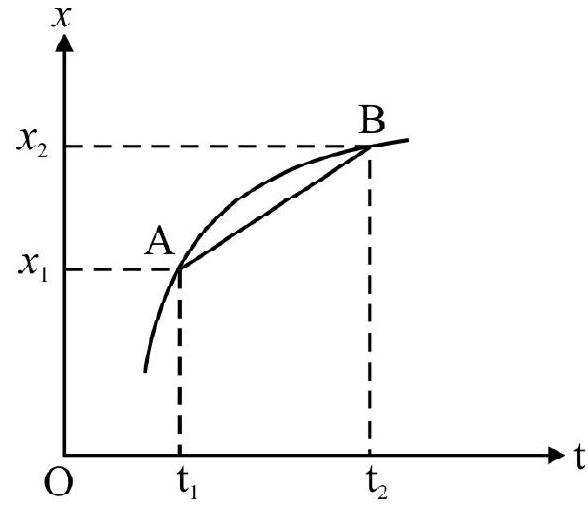
The average velocity in time interval between $t=t _{1}$ and $t=t _{2}$ equals the slope of the chord joining the two points considered on displacement vs time graph.
(a)
(b)
Fig. 6
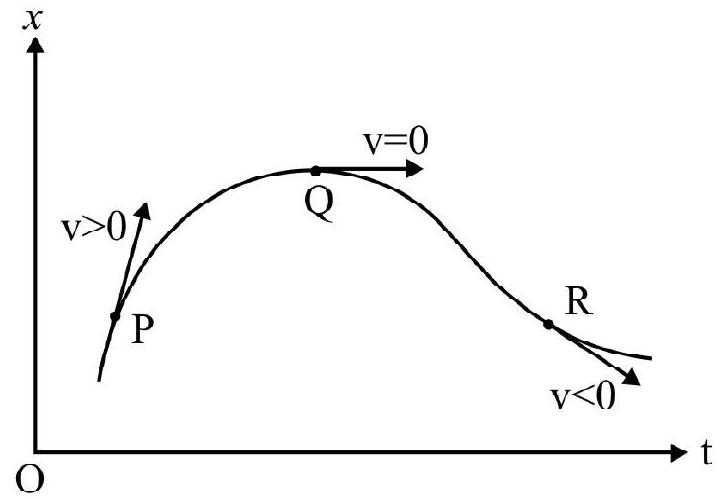
Fig. 6 (c)
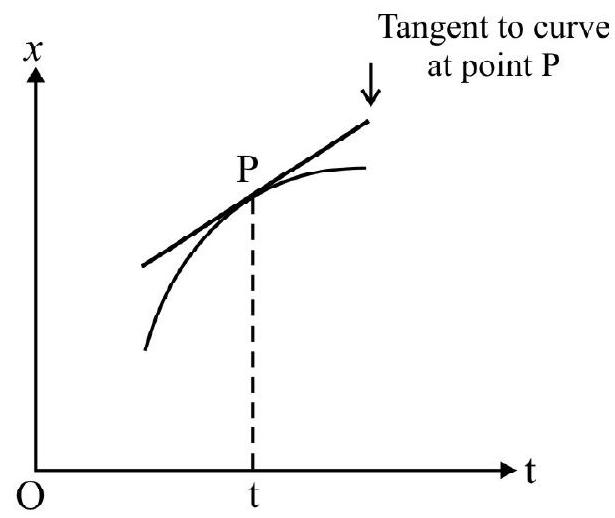
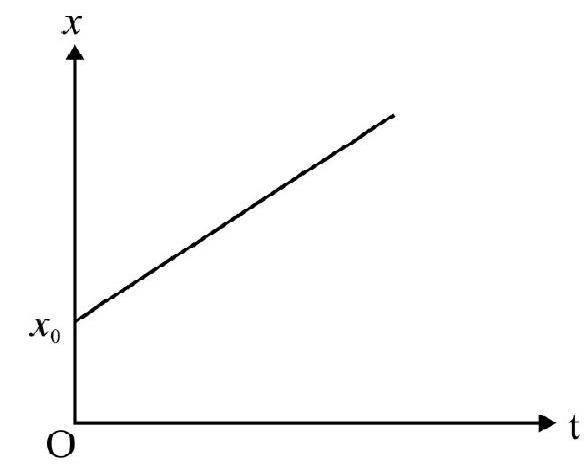
In Fig. 6(a) the slope of chord $A B$ is the average velocity in time interval $\Delta t=t _{2}-t _{1}$. The instantaneous velocity at time $t$, is the slope of tangent to $x$ vs t graph at the point $\mathrm{P}$ considered. This is shown in Fig. 6(b). The instantaneous velocity can be positive, zero or negative as shown in Fig. 6(c) Fig. 7(a) and 7(b) given below shows $x$ vs $t$ and $v$ vs $t$ graph of a body having uniform motion.
(a)
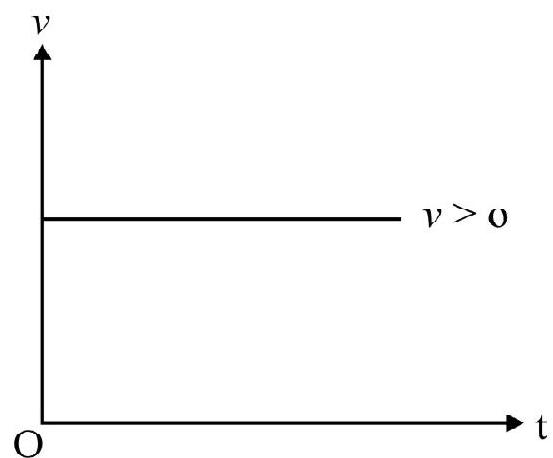
(b)
Fig. 7
Uniform Motion
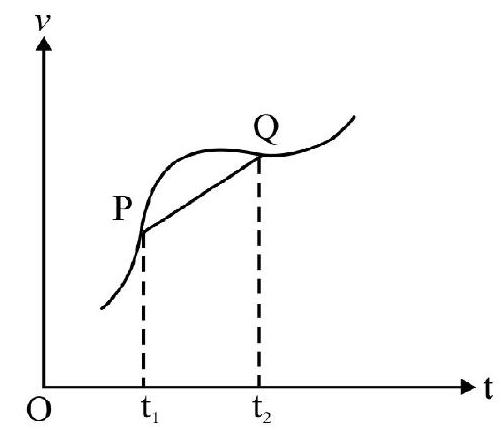
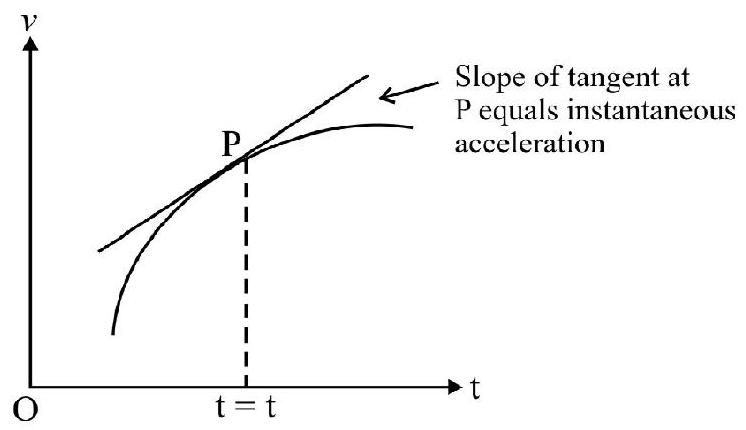
The acceleration of a body in motion in obtained from velocity $(v)$ vs time $(t)$ graph. The average acceleration is the slope of chord joining the two points considered on $v$ vs t graph. In Fig. 8(a) slope of chord PQ is the average acceleration in time interval $\left(\mathrm{t} _{2}-\mathrm{t} _{1}\right)$. The instantaneous acceleration is slope of tangent to $v \mathrm{vs} \mathrm{t}$ graph at the point considered as shown in Fig. 8(b) Fig. 8(c) shows positive, zero and negative acceleration.
(a)
(b)
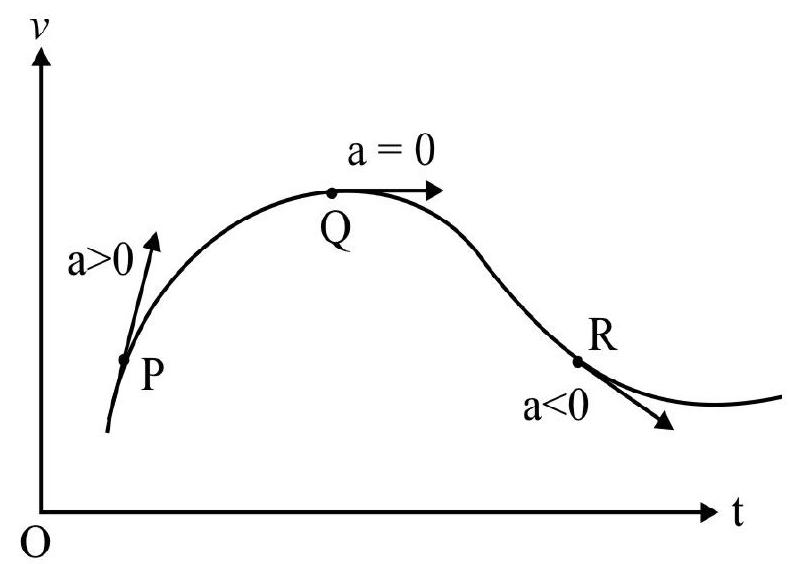
Fig. 8 (c)
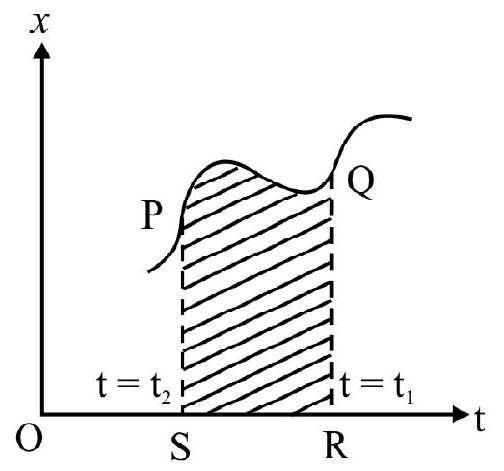
Fig. 9
Distance and Displacement from Velocity vs Time Graph
The total area; without assigning negative sign to any part of area; under velocity vs time graph equals total distance traveled.
The algebraic sum of areas under velocity vs time graph gives the magnitude of the displacement. In Fig. 9; area PQRS equals total distance travelled in the interval $\left(t _{2}-t _{1}\right)$. The area can be calculated graphically or using integration.
Example-5 :
A particle moves along $x$-axis. The position $(x)$ vs time (t) graph is as shown in Fig. 10.
(a) What is the instantaneous speed at (i) $\mathrm{t}=2 \mathrm{~s}$, (ii) $\mathrm{t}=5 \mathrm{~s}$, (iii) $\mathrm{t}=10 \mathrm{~s}$ ?
(b) What is average speed over time interval $0-12 \mathrm{~s}$ ?
(c) Plot velocity $(v)$ vs time (t) graph.
Show Answer
Solution :
(a) (i) $\quad v=$ slope of $x$ vs t graph at $\mathrm{t}=2 \mathrm{~s}$
$$ =\frac{8-2}{4-0}=1.5 \mathrm{~ms}^{-1} $$
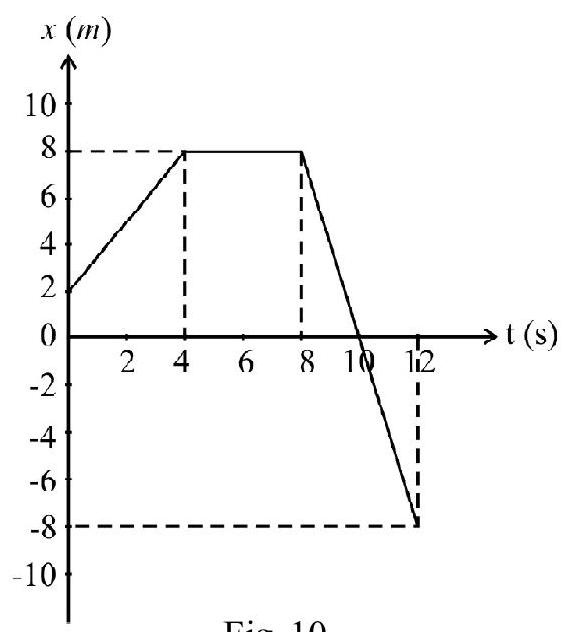
Fig. 10
(ii) $v(\mathrm{at} \quad \mathrm{t}=5 \mathrm{~s})=$ Zero
(iii) $\quad \mathrm{v}(\mathrm{at}=10 \mathrm{~s})=\frac{-8-8}{12-8}=-4 \mathrm{~ms}^{-1}$
(b) The total distance traveled in time interval $0-12 \mathrm{~s}$
$$ =6+8+8=22 \mathrm{~m} $$
$\mathrm{V} _{\mathrm{av}}=\frac{\text { Total distance traveled }}{\text { Total time taken }}=\frac{22}{12} \simeq 1.83 \mathrm{~ms}^{-1}$
(c) For time interval
(i) $0 \leq \mathrm{t} \leq 4 \mathrm{~s} ; \quad \mathrm{v}=1.5 \mathrm{~ms}^{-1}$
(ii) $4 \leq \mathrm{t} \leq 8 \mathrm{~s} ; \quad \mathrm{v}=0$
(ii) $8 \leq \mathrm{t} \leq 12 \mathrm{~s} ; \quad \mathrm{v}=-4 \mathrm{~ms}^{-1}$
$v$ vs $t$ graph for motion is shown in Fig. 11
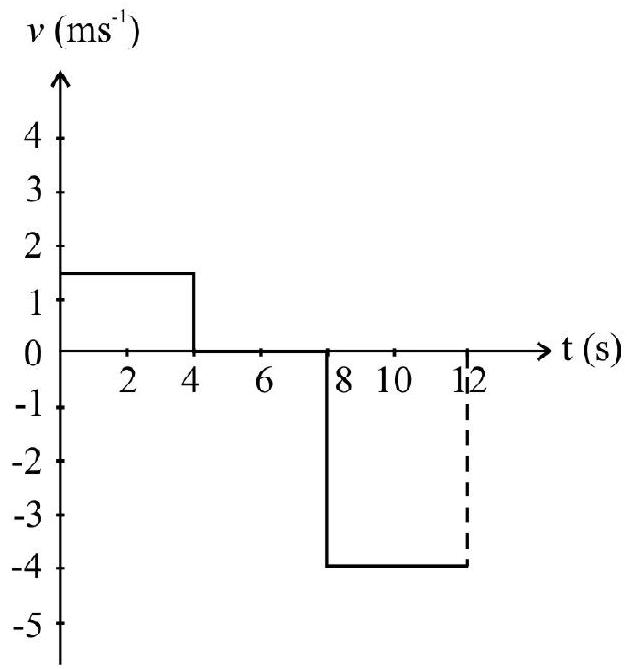
Fig. 11
Example-6 :
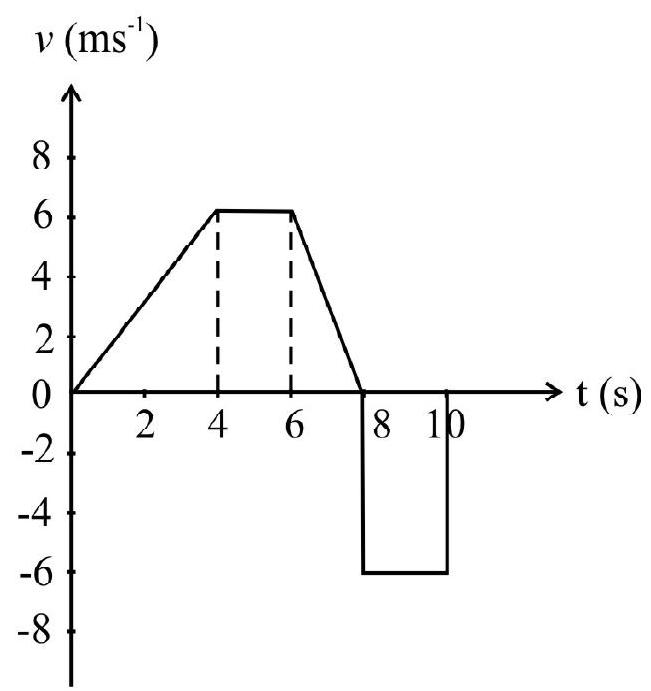
Fig. 12
$v$ vs t graph of a particle moving along $\mathrm{z}$-axis is shown in Fig. 12. What is
(a) average speed, (b) average velocity from 0 to $10 \mathrm{~s}$ ?
Show Answer
Solution:
(a) $\mathrm{S}=$ the total distance traveled in $10 \mathrm{~s}$
$$ \begin{aligned} & =\left(\frac{1}{2} \times 4 \times 6\right)+(2 \times 6)+\left(\frac{1}{2} \times 2 \times 6\right)+(6 \times 2) \\ & =12+12+6+12=42 \mathrm{~m} \end{aligned} $$
$\mathrm{T}=$ Total time taken $=10 \mathrm{~s}$
$\therefore$ Average speed $=\mathrm{V} _{\mathrm{av}}=\frac{\mathrm{S}}{\mathrm{T}}=\frac{42}{10}=4.2 \mathrm{~ms}^{-1}$
[Note: In calculating S we have NOT assigned negative sign to area in time interval 8 to 10s.]
(b) The magnitude of total displacement $=|\mathbf{s}|$
$=12+12+6+(-12)=18 \mathrm{~m}$
[Note: Negative sign assigned to area under v vs t graph in time interval 8 to 10s.]
The magnitude of average velocity $=\frac{18}{10}=1.8 \mathrm{~ms}^{-1}$
Example-7 :
For a particle moving along $x$-axis; the instantaneous position $x$ is given by
$$ x=4 \mathrm{t}-2 \mathrm{t}^{2}+\mathrm{t}^{3} $$
where $x$ is in meter and $\mathrm{t}$ in second. What is instantaneous (i) velocity and (ii) acceleration at $\mathrm{t}=1 \mathrm{~s}$ ? Is motion uniformly accelerated?
Show Answer
Solution :
By define the instantaneous velocity $v$ is
$$ \begin{equation*} v=\frac{\mathrm{d} x}{\mathrm{dt}}=4-4 \mathrm{t}+3 \mathrm{t}^{2} \tag{i} \end{equation*} $$
and instantaneous acceleration, $a$, is
$$ \begin{equation*} a=\frac{\mathrm{d} v}{\mathrm{dt}}=-4+6 \mathrm{t} \tag{ii} \end{equation*} $$
At $t=1 s ;$
$$ \begin{aligned} & v(\mathrm{t}=1 \mathrm{~s})=4-4+3=3 \mathrm{~ms}^{-1} \\ & \mathrm{a}(\mathrm{t}=1 \mathrm{~s})=-4+6=2 \mathrm{~ms}^{-2} \end{aligned} $$
Since acceleration varies with time, motion is NOT uniformly accelerated.
Example-8 :
The instantaneous velocity $v$ of a particle moving along a straight line is
$$ v=\left(\mathrm{t}^{2}-4\right) \mathrm{ms}^{-1} $$
What is:
(a) instantaneous acceleration at $\mathrm{t}=2 \mathrm{~s}$.
(b) displacement in time interval $0-4 \mathrm{~s}$
(c) distance traveled in time interval $0-4 \mathrm{~s}$ ?
Show Answer
Solution :
(a) Given $v=\mathrm{t}^{2}-4$
$\therefore \mathrm{a}=\frac{\mathrm{d} v}{\mathrm{dt}}=2 \mathrm{t}$
$\mathrm{a}(\mathrm{t}=2 \mathrm{~s})=4 \mathrm{~ms}^{-2}$
(b) Let particle move along $x$-axis. Then
$$ v=\frac{\mathrm{d} x}{\mathrm{dt}}=\mathrm{t}^{2}-4 $$
Displacement $=\int \mathrm{d} x=\int _{0}^{4}\left(\mathrm{t}^{2}-4\right) \mathrm{dt}$
$=\left|\frac{\mathrm{t}^{3}}{3}\right| _{0}^{4}-4|\mathrm{t}| _{0}^{4}$
$=\frac{64}{3}-16=\frac{16}{3} \mathrm{~m}$
(c) Note $v$ is negative in time interval $0 \leq \mathrm{t} \leq 2 \mathrm{~s}$ and positive in time interval $2 \leq \mathrm{t} \leq 4 \mathrm{~s}$. Distance traveled $\mathrm{S}$ is
$$ \begin{aligned} & \mathrm{S}=\left|\int _{0}^{2}\left(\mathrm{t}^{2}-4\right) \mathrm{dt}\right|+\int _{2}^{4}\left|\mathrm{t}^{2}-4\right| \mathrm{dt} \\ & =\frac{16}{3}+\frac{16}{3}=\frac{32}{3} \mathrm{~m} \end{aligned} $$
Equations of Uniformly Accelerated Motion
Consider one dimensional motion of a particle having uniform acceleration. Let
$$ \mathrm{v} _{0}=\text { initial speed of particle, at } \mathrm{t}=0 $$
$\mathrm{v}=$ instantaneous speed of particle at $\mathrm{t}=\mathrm{t}$
$\mathrm{a}=$ uniform acceleration
$\mathrm{S}=$ total distance traveled by the particle in time $\mathrm{t}$
$\mathrm{s} _{\mathrm{n}}=$ distance traveled in $\mathrm{n}^{\text {th }}$ second of motion.
The equations of motion are:
$$ \begin{align*} & v=v _{0}+\mathrm{at} \tag{1} \\ & \mathrm{S}=\mathrm{v} _{0} \mathrm{t}+\frac{1}{2} \mathrm{at}^{2} \tag{2} \\ & v^{2}-v _{0}^{2}=2 \mathrm{as} \tag{3} \\ & \mathrm{s} _{\mathrm{n}}=v _{0}+\frac{\mathrm{a}}{2}[2 \mathrm{n}-1] \tag{4} \end{align*} $$
Eqn (1) and (2) are represented by graphs shown in Fig. 13(a) and 13(b) respectively.

Example-9 :
A car has an initial speed of $108 \mathrm{kmhr}^{-1}$. Brakes are applied producing uniform retardation. The speed of car is reduced to $36 \mathrm{kmhr}^{-1}$ in traveling a distance of $200 \mathrm{~m}$. What is
(a) retardation,
(b) time taken?
Show Answer
Solution :
Given,
(a) $\quad v _{0}=108 \mathrm{kmhr}^{-1}=108 \times \frac{5}{18} \mathrm{~ms}^{-1}=30 \mathrm{~ms}^{-1}$ $v=36 \mathrm{kmhr}^{-1}=36 \times \frac{5}{18} \mathrm{~ms}^{-1}=10 \mathrm{~ms}^{-2}$
$\mathrm{S}=200 \mathrm{~m} ; \mathrm{a}=?$
From, $v^{2}-v _{0}^{2}=2 \mathrm{aS}$, we have
$(10)^{2}-(30)^{2}=2 \mathrm{a} \times 200$
$\therefore \mathrm{a}=-2 \mathrm{~ms}^{-2}$
Negative sign of a indicates retardation
(b) Let t be the time taken. Using $\mathrm{v}=\mathrm{v} _{0}+$ at, we have
$$ 10=30+(-2) \mathrm{t}, \text { or } \mathrm{t}=10 \mathrm{~s} $$
Example-10 :
A particle starts from rest and has a uniform acceleration of $2 \mathrm{~ms}^{-2}$ for $5 \mathrm{~s}$. The subsequent motion is retarded and particle comes to rest in next $2 \mathrm{~s}$. What is the
(1) retardation,
(2) total distance traveled?
Show Answer
Solution :
Given,
(1) $v _{0}=0 ; \mathrm{a}=+2 \mathrm{~ms}^{-2} ; \mathrm{t} _{1}=5 \mathrm{~s}$
$\therefore v _{1}=0+2 \times 5=10 \mathrm{~ms}^{-1}$
$\mathrm{S} _{1}=0+\frac{1}{2} \times 2 \times(5)^{2}=25 \mathrm{~m}$
The particle is brought to rest in $2 \mathrm{~s}$ having an initial speed of $10 \mathrm{~ms}^{-1}$. The retardation $\mathrm{a} _{2}$ is $0=10+\mathrm{a} _{2} \times 2 \quad, \quad \therefore \mathrm{a} _{2}=-5 \mathrm{~ms}^{-2}$
$\mathrm{S} _{2}=$ distance traveled in time interval $\mathrm{t}=5 \mathrm{~s}$ to $\mathrm{t}=7 \mathrm{~s}$
$=10 \times 2+\frac{1}{2}(-5)(2)^{2}=10 \mathrm{~m}$
$\mathrm{S}=$ The total distance traveled $=\mathrm{S} _{1}+\mathrm{S} _{2}=25+10=35 \mathrm{~m}$
(2) For time interval $0 \leq \mathrm{t} \leq 5 \mathrm{~s}$; the instantaneous speed is
$$ v=0+2 \times t=2 t $$
For time interval $5 \leq \mathrm{t} \leq 7 \mathrm{~s}$; the instantaneous speed is
$v=10+(-5) \mathrm{t}=10-5 \mathrm{t}$
Taking these factors into account $v$ vs $t$ graph is as shown in Fig. 14.
Let $x$ be the instantaneous position co-ordinate of particle starting from origin at $t=0$. For time interval $0 \leq \mathrm{t} \leq 5$ s.
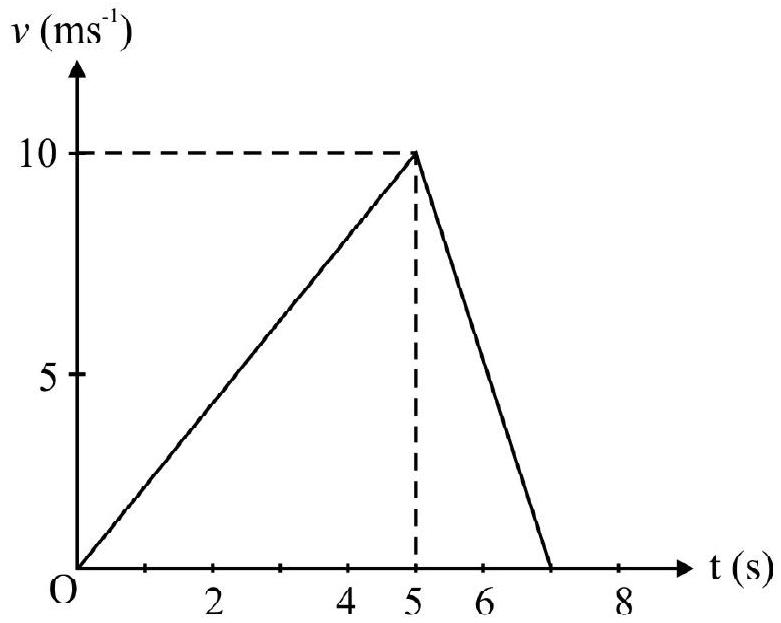
Fig. 14
$x($ at $\mathrm{t}=5 \mathrm{~s})=25 \mathrm{~m}$. For time interval $5 \leq \mathrm{t} \leq 7 \mathrm{~s}$; the instantaneous position coordinate is
$$ \begin{align*} & x=25+10(\mathrm{t}-5)+\frac{1}{2}(-5)(\mathrm{t}-5)^{2} \\ & =25+10(\mathrm{t}-5)-2.5(\mathrm{t}-5)^{2} \tag{2} \\ & x(\mathrm{t}=7 \mathrm{~s})=25+10(7-5)-2.5(7-5)^{2} \\ & =25+20-10=35 \mathrm{~m} \end{align*} $$
These characteristics are shown in $x$ vs $\mathrm{t}$ graph in Fig. 15.
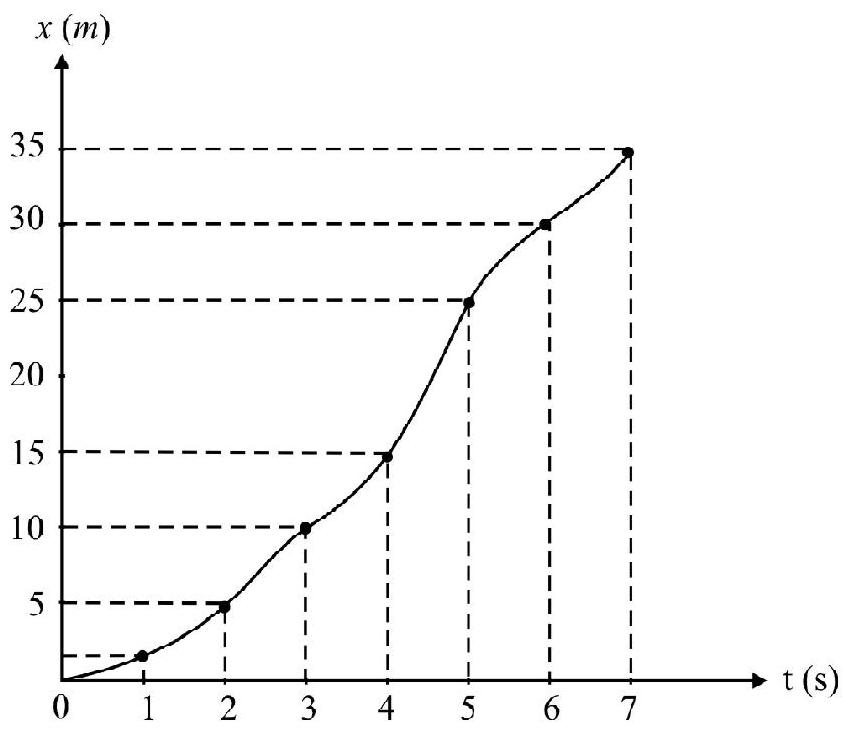
Fig. 15
Example-11 :
A car is moving with an initial speed $v _{0}$. It is uniformly accelerated. The distance traveled by car in $7^{\text {th }}$ and $9^{\text {th }}$ second of motion is $17 \mathrm{~m}$ and $21 \mathrm{~m}$ respectively. What is $\mathrm{v} _{0}$ and $\mathrm{a}$ ?
(b) What is speed of car and total distance traveled in 10s?
Show Answer
Solution :
We know, the distance $\mathrm{s} _{\mathrm{n}}$; traveled in $\mathrm{n}^{\text {th }}$ second is
$$ \mathrm{s} _{\mathrm{n}}=v _{0}+\frac{\mathrm{a}}{2}[2 \mathrm{n}-1] $$
Given $\mathrm{s} _{7}=17 \mathrm{~m}$ and $\mathrm{s} _{9}=21 \mathrm{~m}$. Therefore
$$ \begin{equation*} 17=v _{0}+\frac{\mathrm{a}}{2}[2 \times 7-1]=v _{0}+\frac{13}{2} \mathrm{a} \tag{1} \end{equation*} $$
and $\quad 21=v _{0}+\frac{\mathrm{a}}{2}[2 \times 9-1]=v _{0}+\frac{17}{2} \mathrm{a}$
From equations (1) and (2)
$$ \mathrm{a}=2 \mathrm{~ms}^{-1} \text { and } \mathrm{v} _{0}=4 \mathrm{~ms}^{-1} $$
Let $v _{10}$ be the speed acquired by car at $\mathrm{t}=10 \mathrm{~s}$
$$ \begin{aligned} & v _{0}=v _{0}+\mathrm{a} \times 10 \\ & =4+2 \times 10=24 \mathrm{~ms}^{-1} \end{aligned} $$
Let $\mathrm{S}$ be the total distance traveled in $\mathrm{t}=10 \mathrm{~s}$. We have
$$ \mathrm{S}=4 \times 10+\frac{1}{2} \times 2 \times(10)^{2}=140 \mathrm{~m} $$
Example-12 :
A particle starts moving from origin along $x$-axis in the positive direction of $x$-axis. $x$ is instantaneous position co-ordinate and $v$ the instantaneous velocity. Given $v=\mathrm{k} \sqrt{x}$, where $\mathrm{k}$ is a constant. Prove that $v$ is directly proportional to $t$.
Show Answer
Solution :
Given,
$$ v=\frac{\mathrm{d} x}{\mathrm{dt}}=\mathrm{k} x^{1 / 2} \text { or } \frac{\mathrm{d} x}{x^{1 / 2}}=\mathrm{kdt} $$
Integrate
$$ \int _{0}^{x} x^{-1 / 2} \mathrm{~d} x=\mathrm{k} \int _{0}^{\mathrm{t}} \mathrm{dt} \quad \text { or } \quad 2 x^{1 / 2}=\mathrm{kt} \quad \text { or } \quad x=\left(\frac{\mathrm{k}^{2}}{4}\right) \mathrm{t}^{2} $$
The instantaneous velocity, $v$, is
$$ v=\frac{\mathrm{d} x}{\mathrm{dt}}=2\left(\frac{\mathrm{k}^{2}}{4}\right) \mathrm{t}=\frac{\mathrm{k}^{2}}{2} \mathrm{t} $$
Obviously $v$ is directly proportional to t.
Motion Under Gravity - Free Fall
A particle is released from a point at a height $h$ above ground. $\mathrm{R}=6400 \mathrm{~km}$ is radius of earth. If $\mathrm{h}«\mathrm{R}$. and air resistance is negligible; the particle falls towards earth with a constant acceleration, $g=9.8 \mathrm{~ms}^{-2}$. This is called free fall of body (undergravity). Equations of uniformly accelerated motion are used to described this motion.
A very convenient way of describing motion is choosing an appropriate; convenient coordinate system and describe (i) position (ii)

(a) velocity and (iii) acceleration of the body in motion using appropriate positive and negative signs. To understand $+v e$ and $-v$ e sign consider a particle projected vertically upwards from $\mathrm{O}$ with initial velocity $v _{0}$. Choosing $\mathrm{O}$ as origin of co-ordinates and vertically upward direction as direction of positive Z-axis; during the upward motion; if the particle is at point $\mathrm{P}$ position co-ordinate $\mathrm{z}$ is $+\mathrm{ve}$; instantaneous velocity $v$ is $+\mathrm{ve}$ and acceleration due to gravity is negative. This is shown in Fig. 16(a). Particle acquires maximum height at A and starts moving down. For downward motion; $\mathrm{P}^{\prime}$ is instantaneous position of particle as shown in Fig. 16(b). Now position coordinate $\mathrm{z}$ is a +ve number; instantaneous velocity $v$ is negative and acceleration due to gravity is negative. The equation giving instantaneous, velocity, $v$, and instantaneous position $z$ are:
$$ \begin{gathered} v=\mathrm{v} _{0}+(-\mathrm{g}) \mathrm{t} \\ \mathrm{z}=\mathrm{v} _{0} \mathrm{t}+\frac{1}{2}(-\mathrm{g}) \mathrm{t}^{2} \end{gathered} $$
From these two equations every information regarding motion of particle can be easily obtained. The +ve or $-v e$ sign of $v, z$, etc. are to be interpreted properly. This is illustrated in examples discussed.
Example-12 :
A ball is projected vertically upwards from ground with an initial speed of $20 \mathrm{~ms}^{-1}$.
(a) What is maximum height of the ball from ground? How long after projection the ball is at maximum height from ground?
(b) What is instantaneous velocity and position of particle at (i) $t=1.5 \mathrm{~s}$ and (ii) $t=3 \mathrm{~s}$ ? $\mathrm{g}=10 \mathrm{~ms}^{-2}$
Show Answer
Solution :

Choose point of projection $\mathrm{O}$ as origin and vertically upward direction as positive $\mathrm{z}$-axis. as shown in Fig. 17. Given
$$ v _{0}=20 \mathrm{~ms}^{-1}, \mathrm{a}=-10 \mathrm{~ms}^{-2}, \mathrm{z} _{0}=0 $$
Note carefully + and $-\mathrm{ve}$ sign of $v _{0}$ and a. Let $\mathrm{v}$ and $\mathrm{z}$ be the instantaneous velocity and position coordinate of ball. Then
$$ \begin{align*} & \mathrm{v}=\mathrm{v} _{0}+\mathrm{at}=20-10 \mathrm{t} \tag{i} \\ & \mathrm{z}=\mathrm{v} _{0}+\frac{1}{2} a \mathrm{t}^{2}=20 \mathrm{t}-5 \mathrm{t}^{2} \tag{ii} \end{align*} $$
(a) Let particle attain maximum height from ground at $t=t _{1}$. This is shown as point $\mathrm{A}$ in Fig. 17(a). At maximum height instantaneous velocity is zero. For point $A ; v _{A}=0 ; t=t _{1}$. FromEqn. (i)
$0=20-10 \mathrm{t} _{1} \quad \therefore \mathrm{t} _{1}=2 \mathrm{~s}$
The position co-ordinate $\mathrm{z} _{\mathrm{A}}$ of point A gives maximum height of ball. From Eqn. (ii) $\mathrm{H}=20 \times 2-5(2)^{2}=20 \mathrm{~m}$
(b) (i) $\mathrm{At} \quad t=1.5 \mathrm{~s}$; from Eqn. (i) and (ii) we have
$$ \begin{aligned} & \mathrm{v}(\mathrm{t}=1.5 \mathrm{~s})=20-15=5 \mathrm{~ms}^{-1} \\ & \mathrm{z}(\mathrm{t}=1.5 \mathrm{~s})=20 \times 1.5-5 \times(1.5)^{2}=18.75 \mathrm{~m} \end{aligned} $$
The +ve sign of $v$ shows that ball is moving vertically upwards. The $+v e$ sign of $z$ means ball at this moment is above ground at a height of $18.75 \mathrm{~m}$. This is shown in Fig. 17(b).
(ii) $\mathrm{At} \quad t=3 \mathrm{~s}$; from Eqn. (i) and (ii) we have
$$ \begin{aligned} & \mathrm{v}(\mathrm{t}=3 \mathrm{~s})=20-30=-10 \mathrm{~ms}^{-1} \\ & \mathrm{z}(\mathrm{t}=3 \mathrm{~s})=20 \times 3-5(3)^{2}=15 \mathrm{~m} \end{aligned} $$
The negative sign of $v$ indicates the ball is moving vertically downwards. The +ve sign of z indicates ball in above ground at a height of $15 \mathrm{~m}$. This is shown in Fig. 17(c).
Example-13 :
A vertical tower is $100 \mathrm{~m}$ high. From the top of tower, a ball A is dropped. Simultaneously a second ball B is projected vertically upwards from ground with a speed of $40 \mathrm{~ms}^{-1}$. Where and when the two balls cross one another? What is instantaneous velocity of the each ball at this moment of time? $g=10 \mathrm{~ms}^{-2}$

Show Answer
Solution :
In Fig. 18(a) $\mathrm{O}$ is point an ground and $\mathrm{O} _{1}$ is the top of tower. Choose $\mathrm{O}$ as origin and vertically upward direction as positive $\mathrm{z}$-axis.
For ball A;
$\mathrm{v} _{\mathrm{AO}} 1=0 ; \mathrm{a} _{\mathrm{A}}=-10 \mathrm{~ms}^{-2} ; \mathrm{z} _{\mathrm{AO}}=+100 \mathrm{~m}$
$$ \therefore \mathrm{v} _{\mathrm{A}}=-10 \mathrm{t} $$
$$ \begin{equation*} \mathrm{z} _{\mathrm{A}}=100+\left(-5 \mathrm{t}^{2}\right) \tag{i} \end{equation*} $$
For ball B,
$$ \begin{align*} & \mathrm{v} _{\mathrm{B}}=+40 \mathrm{~ms}^{-1}, \mathrm{a} _{\mathrm{B}}=-10 \mathrm{~ms}^{-2}, \mathrm{z} _{\mathrm{BO}}=0 \\ & \therefore \mathrm{v} _{\mathrm{B}}=40-10 \mathrm{t} \\ & \mathrm{z} _{\mathrm{B}}=40 \mathrm{t}-\mathrm{st}^{2} \tag{ii} \end{align*} $$
When the two balls cross one another, their instantaneous position co-ordinate is same, i.e. $z _{A}=z _{B}$. From Eqns. (i) and (ii)
$$ \begin{aligned} & 100-5 t^{2}=40 t-5 t^{2} \\ & \text { or } t=2.5 \mathrm{~s} \end{aligned} $$
The two balls cross one another $2.5 \mathrm{~s}$ after projection. The instantaneous position co-ordinate of a from Eqn. (i) is
$$ \mathrm{z} _{\mathrm{A}}=100-5(2.5)^{2}=68.75 \mathrm{~m} $$
The two balls cross one another at a point $68.75 \mathrm{~m}$ above ground. Let $\mathrm{v} _{\mathrm{A}}$ and $\mathrm{v} _{\mathrm{B}}$ be their instantaneous velocity. Obviously
$$ \begin{aligned} & \mathrm{v} _{\mathrm{A}}=-10 \times 2.5=-25 \mathrm{~ms}^{-1} \\ & \mathrm{v} _{\mathrm{B}}=40-20 \times 2.5=+15 \mathrm{~ms}^{-1} \end{aligned} $$
Negative sign of $\mathrm{v} _{\mathrm{A}}$ indicates that ball $\mathrm{A}$ is moving vertically downwards. The positive sign of $\mathrm{v} _{\mathrm{B}}$ indicates that ball B is moving vertically upwards. This is shown in Fig. 18(b).
Example-14 :
A helicopter is ascending vertically upwards with a constant speed of $1080 \mathrm{kmhr}^{-1}$. When the helicopter is $2 \mathrm{~km}$ above ground a small packet is dropped from it.
(a) What is maximum height of packet above ground?
(b) How long after being dropped, the packet hits ground? What is its velocity just before hitting ground? $\left(\mathrm{g}=10 \mathrm{~ms}^{-2}\right)$
Show Answer
Solution:

In Fig. 19(a). $\mathrm{O}$ is point on ground and $\mathrm{A}$ is the position of helicopter at $\mathrm{t}=0$ when packet is dropped. Choose $\mathrm{O}$ is origin and vertically upward direction as $+\mathrm{z}-\mathrm{axis}$.
$$ \begin{aligned} & \mathrm{v} _{0}=\text { The initial velocity of packet }=\text { Velocity of helicopter at this moment of time } \\ & =1080 \times \frac{8}{18} \mathrm{~ms}^{-1}=300 \mathrm{~ms}^{-1} \\ & \mathrm{a}=\text { acceleration of packet }=-10 \mathrm{~ms}^{-2} ; \mathrm{z} _{0}=2000 \mathrm{~m} \end{aligned} $$
Let $\mathrm{v}$ and $\mathrm{z}$ denote the instantaneous velocity and position co-ordinate of packet. We have
$$ \begin{align*} & v=300-10 t \tag{1} \\ & z=2000+\left(300 t-5 t^{2}\right) \tag{2} \end{align*} $$
Let packet attain maximum height from ground at $\mathrm{t}=\mathrm{t} _{1}$. In Fig. 19(b); $\mathrm{P}$ is instantaneous position of packet. The instantaneous velocity of packet at $\mathrm{P}$ is zero. From Eqn. (1)
$$ 0=300-10 \mathrm{t} _{1} \quad \therefore \mathrm{t} _{1}=30 \mathrm{~s} $$
$\mathrm{z}\left(\right.$ at $\left. _{1}=30 \mathrm{~s}\right)=\mathrm{H}=$ maximum height of packet above ground. From Eqn. (2)
$$ \mathrm{H}=2000+300 \times 30-5 \times(30)^{2}=6500 \mathrm{~m}=6.5 \mathrm{~km} $$
(b) Let the packet hit ground at $\mathrm{t}=\mathrm{t} _{2}$ and after being dropped. The instantaneous $\mathrm{z} - \mathrm{co}-$ordinate of packet is zero. From Eqn. (2) we have
$$ \begin{aligned} & 0=2000+300 \mathrm{t} _{2}-5 \mathrm{t} _{2}^{2} \\ & \text { or } \mathrm{t} _{2}^{2}-60 \mathrm{t} _{2}-400=0 \\ & \therefore \mathrm{t} _{2}=\frac{60 \pm \sqrt{3600+1600}}{2} \\ & \quad=\frac{60 \pm 72.1}{2}=66.5 \mathrm{~s} \quad \text { [Negative value to } \mathrm{t} _{2} \text { is not possible.] } \end{aligned} $$
The packet hits ground $66.5 \mathrm{~s}$ after being dropped. The instantaneous velocity of packet is
$$ \mathrm{v}=300-660.5=-360.5 \mathrm{~ms}^{-1} $$
Negative sign of $v$ indicates packet is moving vertically downwards.
VECTORS
Scalars and Vectors
Many physical quantities that we study can be broadly divided into two categories, known as (i) scalars and (ii) vectors.
(i) Scalars are those physical quantities which have only a magnitude. They add according to law of ordinary algebra. Mass, volume,work are some example of scalar quantities.
(ii) Vectors are physical quantities having both a magnitude and a direction. Vectors add according to triangle law of vectors and satisfy commutative property of vector addition. Velocity, acceleration, force, linear momentum are some examples of vectors.

Fig. 20
In print; a vector represented by a bold face letter $\mathbf{A}$ is vector. A vector is represented by a straight line with a arrow head on it an shown in Fig. 20 is the tail and $\mathrm{P}$ is the head of A shown in Fig. 20. The magnitude of vector is known as the modulus of vector. In Fig. 20 length OP, on the chosen scale; is the magnitude of $\mathbf{A}$.
Two equal vectors have same magnitude and direction. The negative of a vector $\mathbf{A}$, written as $-\mathbf{A}$, has same magnitude as $\mathbf{A}$ but $-\mathbf{A}$ has a direction opposite to that of $\mathbf{A}$ as shown in Fig. 21(b).

Vectors having equal or unequal magnitudes but acting along same or parallel lines are colinear vectors. Vectors acting in same plane are known as coplanar vectors.
The angle $\theta$ between $\mathbf{A}$ and $\mathbf{B}$ is the angle between the two arrowed lines representing the vectors when their tails coincide as shown in Fig. 22(a)



$\theta=\pi / 2$
Zero or Null Vector
It is a vector having zero magnitude in arbitrary direction. When the magnitude of a vector is added to itself we get zero vector. For example.
(1) The velocity vector of a particle at rest is a zero vector.
(2) The position vector of origin of co-ordinates is a zero vector.
The multiplication of any vector with zero produces a zero vector.
Addition of Vectors
(1) Triangle Law of Vectors
The two sides LM and MN of triangle LMN, taken in order; represents $\mathbf{A}$ and $\mathbf{B}$ (i.e. the two vectors to be added) in magnitude and direction. The third side $L N$ taken in opposite order is resultant $\mathbf{R}$ of $\mathbf{A}$ and $\mathbf{B}$.

$$ \begin{gathered} \mathbf{R}=\mathbf{A}+\mathbf{B} \\ \mathrm{R}=\sqrt{\mathrm{A}^{2}+\mathrm{B}^{2}+2 \mathrm{AB} \cos \theta} \end{gathered} $$
Let the resultant $\mathbf{R}$ make an angle $\alpha$ with $\mathbf{A}$. Then
$$ \tan \alpha=\frac{\mathrm{B} \sin \theta}{\mathrm{A}+\mathrm{B} \cos \theta} $$
(2) Parallelogram Law of Vectors
Let the two adjacent sides of a parallelogram represent in magnitude and direction the two vectors $\mathbf{A}$ and $\mathbf{B}$ to be added. The resultant $\mathbf{R}$ is represented in magnitude and direction by the diagonal of parallelogram such that tail of $\mathbf{A}, \mathbf{B}$ and $\mathbf{R}$ is at same point. This is shown in Fig. 24. It is obvious from Fig. 24 that
$$ \mathbf{A}+\mathbf{B}=\mathbf{B}+\mathbf{A} $$
This is known as commutative property of vector addition.
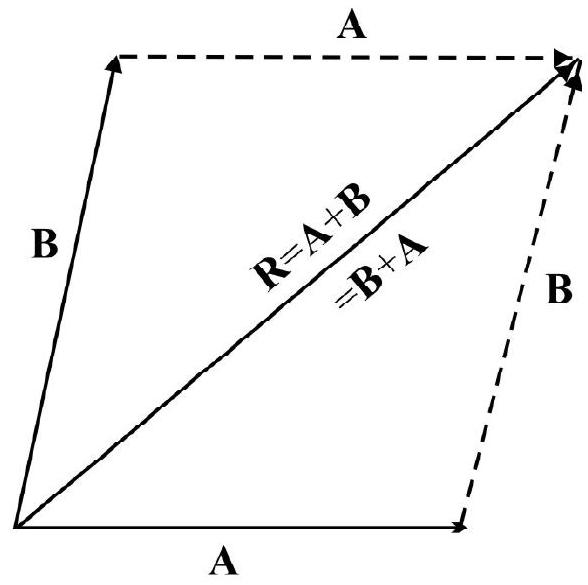
Fig. 24
(3) Polygon Law of Vectors
Polygon law of vectors is useful in adding more than two vectors, graphically. Let $\mathbf{A}, \mathbf{B}, \mathbf{C}, \mathbf{D}$ and $\mathbf{E}$ be the vectors to be added.
$$ \mathbf{R}=\mathbf{A}+\mathbf{B}+\mathbf{C}+\mathbf{D}+\mathbf{E} $$
Draw a polygon with consecutive sides taken in cyclic order, representing in magnitude and direction the vectors to be added. The resultant $\mathrm{R}$, is represented by the closing side of the polygon taken in opposite order. This is shown in Fig. 25.
When vectors to be added form a closed polygon; the resultant is zero.
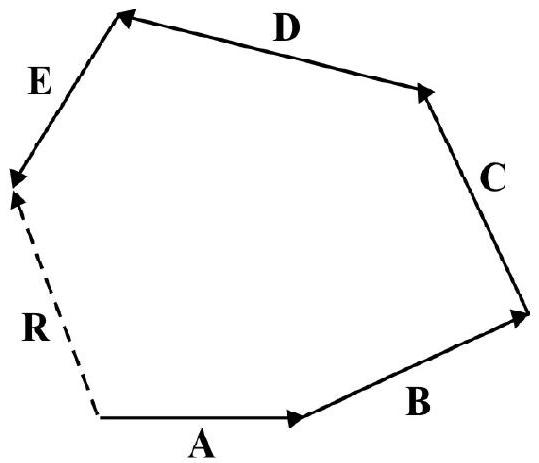
Fig. 25
Note the important properties of vector addition.
(1) Vector addition is commutative, i.e.
$$ \mathbf{A}+\mathbf{B}=\mathbf{B}+\mathbf{A} $$
(2) Vector addition is associative, i.e.
$$ \mathbf{A}+(\mathbf{B}+\mathbf{C})=\mathbf{B}+(\mathbf{C}+\mathbf{A})=\mathbf{C}+(\mathbf{A}+\mathbf{B}) $$
(3) Vector addition in distributive, i.e.
$$ \mathrm{m}(\mathbf{A}+\mathbf{B})=\mathrm{mA}+\mathrm{m} \mathbf{B} $$
Components of a Vector
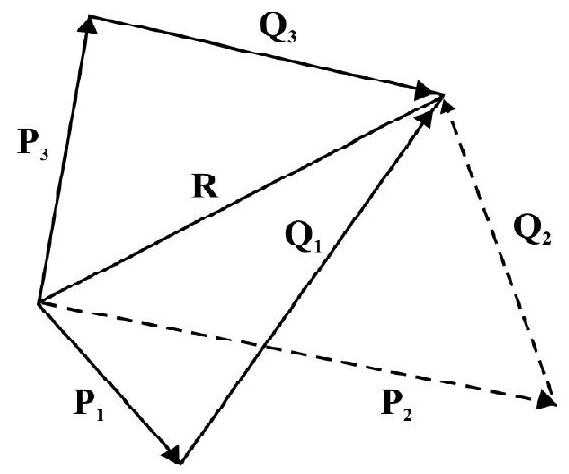
Any two vectors say $\mathbf{P}$ and $\mathbf{Q}$ whose resultant equals $\mathbf{R}$ are known as components of vector $\mathbf{R}$. This is shown in Fig. 26(a). There are any infinite number of ways in which given vector $\mathbf{R}$ can be resolved into components. Fig. 26(b) shown a few different sets of components of $\mathbf{R}$.
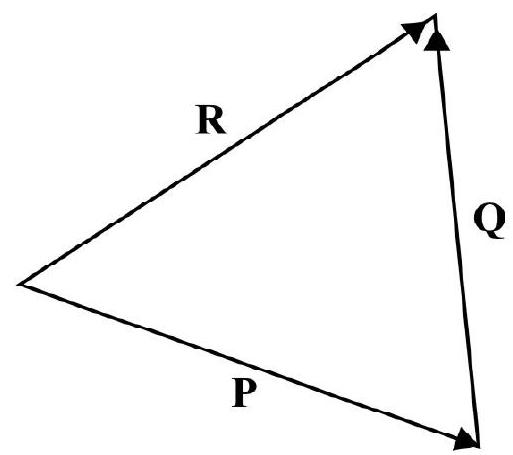
(a)
(b)
Fig. 26
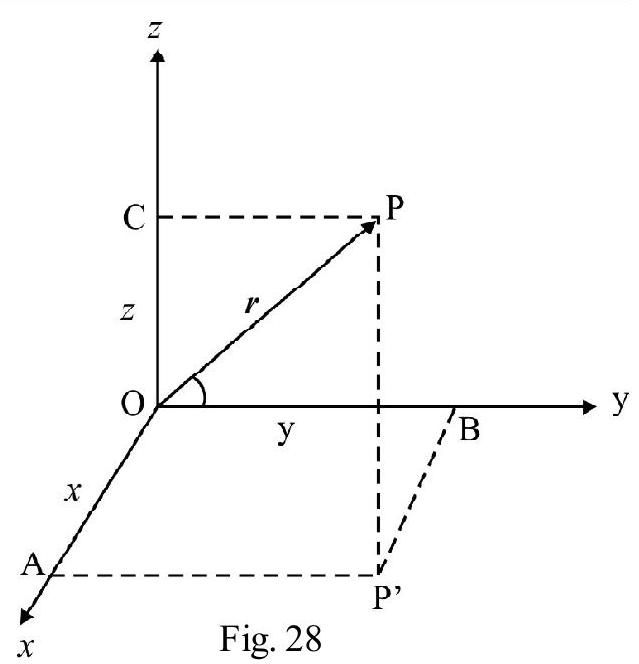
The components of a vector in two mutually perpendicular directions are the rectangular components of vector. In Fig. 27. $\mathrm{OA}$ and $\mathrm{OB}$ are rectangular components of $\mathrm{OC}=\mathrm{R}$. Let $\mathbf{R}$ make an angle $\theta$ with $x$-axis.
$\mathrm{OA}=\mathrm{R} _{x}=\mathrm{X}$ - Components of $\mathbf{R}=\mathrm{R} \cos \theta$
$\mathrm{OB}=\mathrm{R} _{y}=\mathrm{Y}-$ Components of $\mathbf{R}=\mathrm{R} \cos \theta$
Unit Vector
Consider a vector $\mathrm{A}$, the unit vector $\mathrm{A}$ is a vector having a magnitude of unity and same direction as given vector i.e. A. We can write
$$ \widehat{\mathrm{A}}=\frac{\mathbf{A}}{\mathrm{A}} \quad \text { or } \quad \mathbf{A}=|\mathbf{A}| \widehat{\mathrm{A}} $$
For a Cartesian co-ordinate system shown in Fig. $27 \hat{i}, \hat{j}$ and $\hat{k}$ are unit vector along $x, y$ and $z$-axis. $P$ is a point having co-ordinates $(x, y, z) . \mathbf{O P}=\mathbf{r}=$ position vector of $\mathrm{P}$ in terms of $\hat{\mathrm{i}}, \hat{\mathrm{j}}$ and $\hat{\mathrm{k}}$;
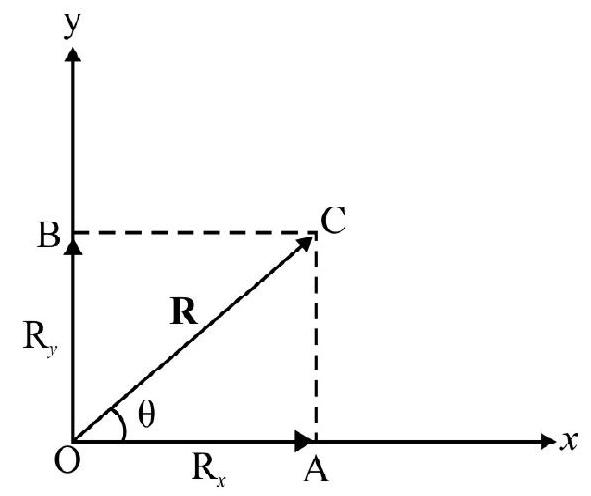
Fig. 27
$$ \mathbf{r}=x \hat{i}+y \hat{j}+z \hat{k} $$
$|\mathbf{r}|=\mathbf{r}=$ Magnitude of position vector $=\sqrt{x^{2}+\mathrm{y}^{2}+\mathrm{z}^{2}}$
Let $\alpha, \beta$ and $\gamma$ be angle OP makes with $x$, $y$ and $z$-axis respectively. Then
$$ \begin{aligned} & \cos \alpha=\frac{x}{\mathrm{r}} ; \quad \cos \beta=\frac{\mathrm{y}}{\mathrm{r}} \quad \text { and } \quad \cos \gamma=\frac{\mathrm{z}}{\mathrm{r}} \\ & \cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma=1 \end{aligned} $$
$\cos \alpha, \cos \beta$ and $\cos \gamma$ are known as direction cosines of $\mathbf{r}$.
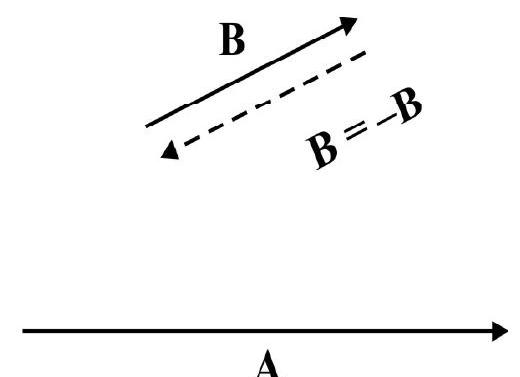
Substraction of Vectors
Let $\mathbf{A}$ and $\mathbf{B}$ be two given vector. Let us subtract $\mathbf{B}$ from $\mathbf{A}$ and write this as
$$ \begin{aligned} & \mathbf{C}=\mathbf{A}-\mathbf{B} \\ & =\mathbf{A}+\mathbf{B}^{\prime} \end{aligned} $$
where $\mathbf{B}^{\prime}=-\mathbf{B}$. To subtract $\mathbf{B}$ from $\mathbf{A}$; we add $\mathbf{B}^{\prime}$ which is negative of $\mathbf{B}$; to $\mathbf{A}$ using triangle law this is shown in Fig. 29.
A
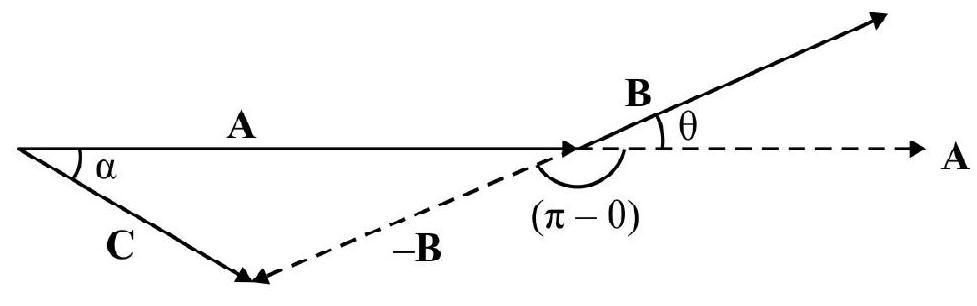
Fig. 29
Obviously from Fig. 29(b)
$$ C=\sqrt{A^{2}+B^{2}+2 A B \cos (\pi-\theta)} $$
and $\quad \tan \alpha=\frac{\mathrm{B} \sin (\pi-\theta)}{\mathrm{A}+\mathrm{B} \cos (\pi-\theta)}$
Note; vector subtraction is NOT communicative, i.e. $\mathbf{A}-\mathbf{B} \neq \mathbf{B}-\mathbf{A}$
Vector subtraction is also not associative, i.e. $\mathbf{A}-(\mathbf{B}-\mathbf{C}) \neq \mathbf{C}-(\mathbf{A}-\mathbf{C})$
Relative Position or Relative Velocity Vector
(a)
(b)
Fig. 30
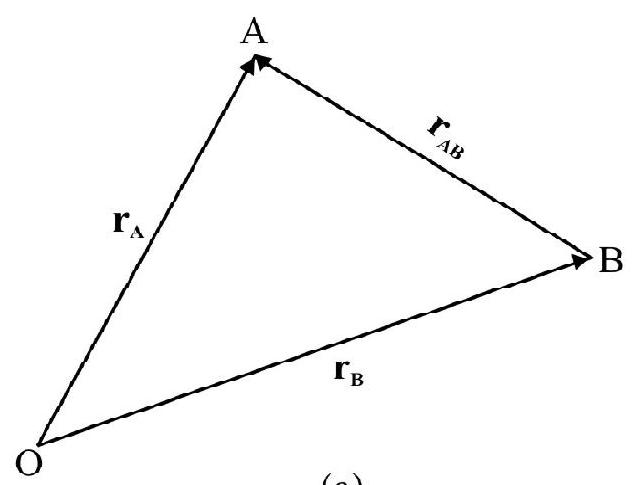
Fig. 30(a) shows two points A and B having position vector $\mathbf{r} _{A}$ and $\mathbf{r} _{B}$ respectively.
$\mathbf{r} _{\mathbf{A B}}=\mathbf{B A}=$ Position vector of A relative to $\mathrm{B}$.
From triangle law of vectors.
$$ \begin{aligned} & \mathbf{r} _{\mathbf{A}}=\mathbf{r} _{\mathrm{B}}+\mathbf{r} _{\mathrm{AB}} \\ & \text { or } \mathbf{r} _{\mathrm{AB}}=\mathbf{r} _{\mathrm{A}}-\mathbf{r} _{\mathrm{B}} \end{aligned} $$
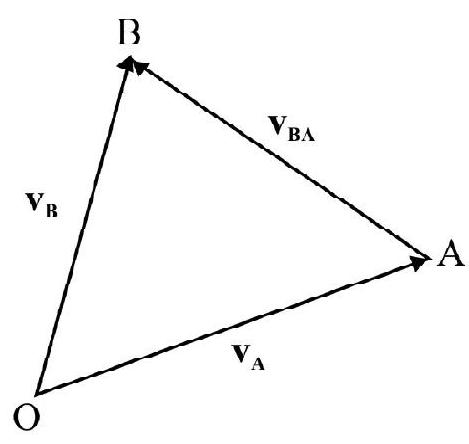
In Fig. 30(b), $\mathbf{v} _{\mathbf{A}}$ and $\mathbf{v} _{\mathbf{B}}$ are two velocity vectors.
$\mathbf{v} _{\text {BA }}=$ Relative velocity of B w.r.t A. Obviously
$$ \mathbf{v} _{B A}=\mathbf{v} _{B}-\mathbf{v} _{A} $$
Example-15 :
The maximum and minimum resultant of two vectors is 14 and 6 respectively. What is angle between the two vectors if their resultant is 12.5 ?
Show Answer
Solution :
Let $A$ and $B$ be the magnitude of the two given vectors $(A>B)$. $C$ is the magnitude of their resultant. Given $\mathrm{C} _{\max }=\mathrm{A}+\mathrm{B}=14 \quad$ and $\mathrm{C} _{\text {min }}=\mathrm{A}-\mathrm{B}=6$
$$ \therefore A=10 \text { and } B=4 $$
Let $\theta$ be angle between $\mathbf{A}$ and $\mathbf{B}$, so that the magnitude of their resultant, $\mathbf{C}$, is 12.5. From triangle law
$$ \begin{aligned} & (12.5)^{2}=(10)^{2}+(4)^{2}+2 \times 4 \times 10 \cos \theta \\ & \text { or } \cos \theta \simeq 0.867 \quad \therefore \theta=60^{\circ} \end{aligned} $$
Example-16:
A man can swim at a speed of $4 \mathrm{kmhr}^{-1}$ in a still river. The river is flowing at a speed of $2 \mathrm{kmhr}^{-1}$.
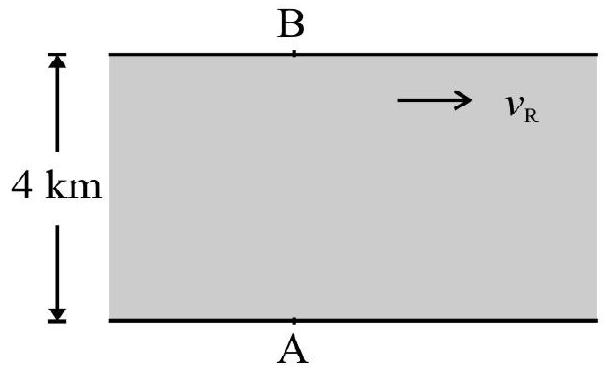
(a) In which direction a man must swim to reach a point on the other side of river directly opposite his starting point? If width of river is $4 \mathrm{~km}$; what is time taken?
(b) What is the direction in which man swims if he wants to cross the river in minimum time? What is $\operatorname{t_{min}}$ ?
Show Answer
Solution :
(a)
(b)
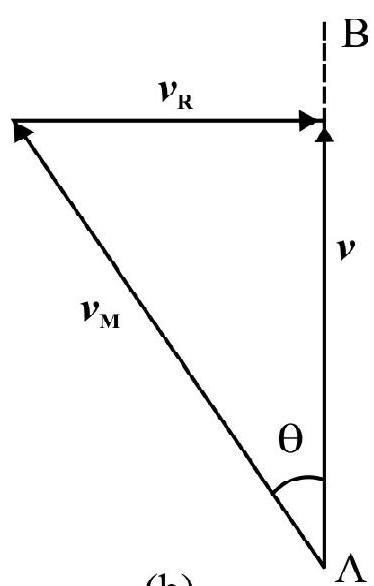
Fig. 31(a) shows river flowing at velocity $\mathbf{v} _{\mathbf{R}}$. The man is at point $A$ and wants to swim to point B. If man aims towards point $B$ the flow of river will make him reach opposite end at a point to right of $B$. Let man swim in a direction making an angle $\theta$ with line $\mathrm{AB}$ in such a manner that his resultant velocity is directed along $\mathrm{AB}$. This is shown in Fig. 31(b). Obviously.
$$ \sin \theta=\frac{\mathrm{v} _{\mathrm{R}}}{\mathrm{v} _{\mathrm{M}}}=\frac{2}{4}=0.5 \quad \therefore \theta=30^{\circ} $$
The magnitude, $\mathrm{v}$, of the resultant velocity is
$$ \mathrm{v}=\sqrt{\mathrm{v} _{\mathrm{M}}^{2}-\mathrm{v} _{\mathrm{R}}^{2}}=\sqrt{(4)^{2}-(2)^{2}}=2 \sqrt{3} \mathrm{kmhr}^{-1} $$
$t=$ The time taken by man to move from A to B
$$ =\frac{4 \mathrm{~km}}{2 \sqrt{3} \mathrm{kmhr}^{-1}}=\frac{2}{\sqrt{3}} \mathrm{hr} $$
(b) When man swims in a direction making an angle $\theta$ with the direction of flow of river, his resultant velocity v, has a magnitude;
$$ v=\sqrt{v _{\mathrm{M}}^{2}+v _{\mathrm{R}}^{2}+2 v _{\mathrm{m}} v _{\mathrm{R}} \cos \theta} $$
The man swims across river in minium time if $v$ is maximum. Obviously $v$ is maximum if $\theta=0^{0}$. Therefore The direction of $\mathrm{v} _{\max }$ is shown in Fig. 31. Let $\mathrm{t}$ be the time taken. Obviously
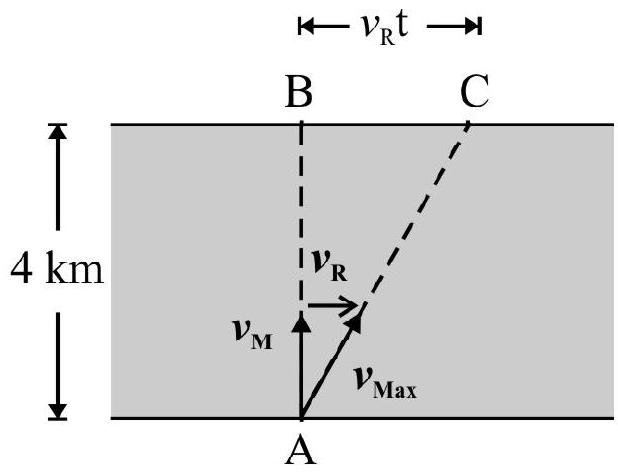
$$ 4=\mathrm{v} _{\mathrm{m}} \mathrm{t} \text { or } \mathrm{t}=\frac{4}{4}=1 \text { hour } $$
Fig. 32
The man will reach opposite end at point $C$, such that
$$ \mathrm{BC}=\mathrm{v} _{\mathrm{R}} \mathrm{t}=2 \times 1=2 \mathrm{~km} $$
Example-17 :
A river is flowing at a constant speed of $3 \mathrm{kmhr}^{-1}$. Two men A and B can swim at same speed of $5 \mathrm{kmhr}^{-1}$. Man A moves down stream a distance of $4 \mathrm{~km}$ and comes back to starting point swimming up the stream. Man $B$ also moves between two points $4 \mathrm{~km}$ apart in a direction perpendicular to direction of flow of river. Man B aims himself during forward and backward journey in such a manner that he moves in a direction perpendicular to stream. What is ratio of time taken by $\mathrm{A}$ and $\mathrm{B}$ in their respective journey?
Show Answer
Solution :

Fig. 33(a) and (b) show the velocity $\mathbf{v} _{\mathbf{M}}$ of man and river $\mathbf{v} _{\mathbf{R}}$ during forward and backward journey. The resultant $v _{1}$ and $v _{2}^{\prime}$ in the two cases have magnitude of
$$ \begin{aligned} & \mathrm{v} _{1}=\mathrm{v} _{\mathrm{M}}+\mathrm{v} _{\mathrm{R}}=5+3=8 \mathrm{kmhr}^{-1} \\ & \mathrm{v} _{\mathrm{i}}^{\prime}=\mathrm{v} _{\mathrm{M}}-\mathrm{v} _{\mathrm{R}}=2 \mathrm{kmhr}^{-1} \end{aligned} $$
$\mathrm{T} _{\mathrm{A}}=$ The total time taken by $\operatorname{man} \mathrm{A}=\frac{4}{8}+\frac{4}{2}=2.5 \mathrm{hr}$
(2) For Man B

Fig. 34(a) and 34(b) show $\mathbf{v} _{\mathbf{M}}$ and $\mathbf{v} _{\mathbf{R}}$ during forward and backward journey. The resultant velocity $\mathbf{v} _{2}$ and $\mathbf{v} _{2}^{\prime}$ have same magnitude and it is:
$$ \mathrm{v} _{2}=\sqrt{(5)^{2}-(3)^{2}}=4 \mathrm{kmhr}^{-1} $$
$\mathrm{T} _{\mathrm{B}}=$ Total time taken by man $\mathrm{B}=2\left[\frac{4}{4}\right]=2 \mathrm{~h}$
$\therefore \quad \frac{\mathrm{T} _{\mathrm{A}}}{\mathrm{T} _{\mathrm{B}}}=\frac{2.5}{2}=1.25$
Example-18 :
Two cars A and B are $10 \mathrm{~km}$ apart at $t=0$ as shown in Fig. 35. Both cars start moving simultaneously. Car A moves with a speed of $20 \mathrm{kmhr}^{-1}$ from east to west. Car B moves with same speed as A from south to north. What is their distance of closest approach and what is time taken to attain the position of closest approach?
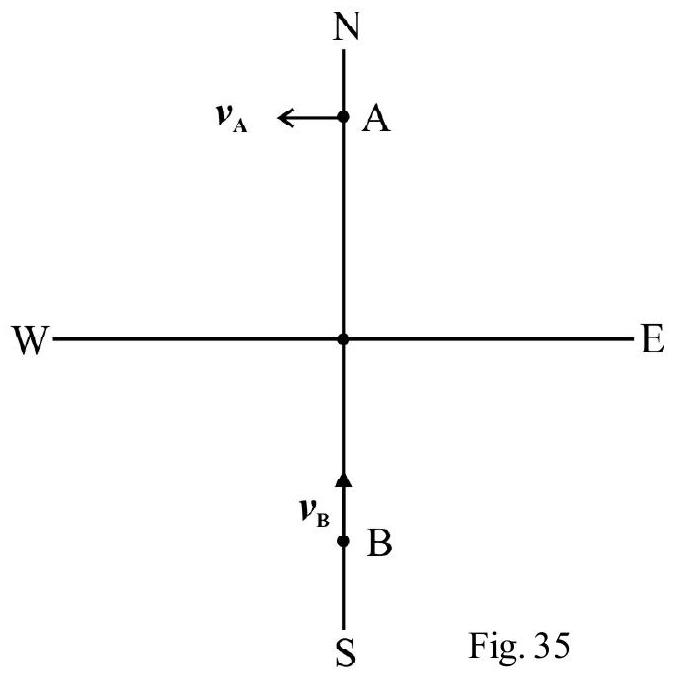
Show Answer
Solution :

Choosing $x-\mathrm{y}$ axis as show in Fig. 36(a); A and B represent position of two cars at $\mathrm{t}=0$. Given $\mathrm{AB}=10 \mathrm{~km}$.
Also, $\mathbf{v} _{\text {BA }}=-20 \hat{\mathrm{i}} ; \quad \mathbf{v} _{\mathbf{B}}=20 \hat{\mathrm{j}}$
The relative velocity of $\mathrm{B}$ with respect to $\mathrm{A}$.
$$ \mathbf{v} _{\mathbf{B A}}=\mathbf{v} _{\mathbf{B}}-\mathbf{v} _{\mathbf{A}}=20(\hat{\mathrm{i}}+\hat{\mathrm{j}}) ; \mathrm{kmhr}^{-1} $$
$\mathbf{v} _{\text {BA }}$ is shown in Fig. 36(b). To driver of car A, car B appears to move along $\mathbf{v} _{\text {BA }}$. The minimum distance between to cars is AC; as shown in Fig. 36(c). Obviously
$$ \mathrm{AC}=\mathrm{AB} \sin 45^{\circ}=\frac{10}{\sqrt{2}} \mathrm{~km} \simeq 7.07 \mathrm{~km} $$
$\mathrm{T}=$ Time taken to acquire minimum distance
$$ =\frac{\mathrm{BC}}{\mathrm{v} _{\mathrm{BA}}}=\frac{\frac{10}{\sqrt{2}}}{20 \sqrt{2}}=\frac{1}{4} \mathrm{hr}=15 \text { mintue } $$
Example-19:
A man walks from to west to east at a speed of $5 \mathrm{~ms}^{-1}$. To the man wind appears to be blowing from north to westwards. The man doubles his speed and wind appears to be blowing in north-east direction. What is actual velocity of wind?
Show Answer
Solution :

Choose a Cartesian co-ordinate system as shown in Fig. 37(a). Let the velocity of wind be
$$ \mathbf{v} _{\mathbf{w}}=\mathrm{v} _{x} \hat{\mathrm{i}}+\mathrm{v} _{\mathrm{y}} \hat{\mathrm{j}} ; \mathrm{ms}^{-1} $$
$\mathrm{v} _{x}$ and $\mathrm{v} _{\mathrm{y}}$ are the $\mathrm{x}-$ and $\mathrm{y}$ - components of velocity of wind.
Case I: Given
$$ \begin{equation*} \mathbf{v} _{\mathbf{M}}=5 \hat{\mathrm{i}} ; \mathrm{ms}^{-1}, \mathbf{v} _{\mathbf{W M}}=\mathrm{v} _{\mathrm{RM}}(-\hat{\mathrm{j}}) \tag{i} \end{equation*} $$
We know,
$$ \begin{equation*} \mathbf{v} _{\mathbf{w M}}=\mathbf{v} _{\mathbf{w}}-\mathbf{v} _{\mathbf{m}}=\left(\mathrm{v} _{x}-5\right) \hat{\mathrm{i}}+\mathrm{v} _{y} \hat{\mathrm{j}} \tag{ii} \end{equation*} $$
From Eqns. (i) and (ii)
$$ \begin{equation*} \mathrm{v} _{x}-5=0 \quad \text { or } \quad \mathrm{v} _{x}=5 \mathrm{~ms}^{-1} \tag{iv} \end{equation*} $$
Case II:
$$ \begin{equation*} \mathbf{v} _{\mathrm{M}}^{\prime}=10 \hat{\mathrm{i}}, \mathbf{v} _{\mathrm{wM}}^{\prime}=\mathbf{v} _{\mathrm{wM}}\left[\frac{1}{\sqrt{2}}(-\hat{\mathrm{i}})+\frac{1}{\sqrt{2}} \hat{\mathrm{j}}\right] \tag{v} \end{equation*} $$
Also, $\mathbf{v} _{\mathbf{M}}{ }^{\prime}=(5-10) \hat{\mathrm{i}}+\mathrm{v} _{\mathrm{y}} \hat{\mathrm{j}} \mathrm{\hspace{70mm}}(vi)$
From Eqns (v) and (vi); we have
$$ \mathrm{v} _{\mathrm{y}}=5-10 \text { or } \mathrm{v} _{\mathrm{y}}=-5 \mathrm{~ms}^{-1} $$
The velocity of wind, $\mathrm{v} _{\mathrm{w}}$; is
$$ \mathbf{v} _{\mathbf{w}}=(5 \hat{\mathrm{i}}-5 \hat{\mathrm{j}}) \mathrm{ms}^{-1} $$
The speed of wind is $5 \sqrt{2} \mathrm{~ms}^{-1}$; and it is blowing in south-east direction.
Scalar or Dot Product of Vectors
Consider two vectors $\mathbf{A}$ and $\mathbf{B}$ making an angle $\theta$ with one another. The dot product $\mathbf{A} \cdot \mathbf{B}$ by definition is $\mathbf{A} \cdot \mathbf{B}=\mathrm{ab} \cos \theta$
It is a scalar quantity. In words, dot product of $\mathbf{A}$ and $\mathbf{B}$ is product of magnitude of $\mathbf{A}$ and component of $\mathbf{B}$ in the direction of $\mathbf{A}$ or vice-versa. The dot product of two non zero vectors, i.e. $A \neq 0, B \neq 0$ can be a positive or -ve number depending on $\theta$ whether is an acute or obtuse angle. If $\mathrm{A} \neq 0, \mathrm{~B} \neq 0$, but $\mathbf{A} \cdot \mathbf{B}=0 ; \cos \theta=0$ or $\theta=\frac{\pi}{2}$. Dot product of perpendicular vectors is zero. Dot product is commutative, i.e. $\mathbf{A} \cdot \mathbf{B}=\mathbf{B} \cdot \mathbf{A}$. Dot product is also distributive i.e.
$$ \mathbf{A}(\mathbf{B}+\mathbf{C})=\mathbf{A} \cdot \mathbf{B}+\mathbf{A} \cdot \mathbf{C} $$
Scalar product of a vector with itself equals square of magnitude of vector. i.e. $\mathbf{A} \cdot \mathbf{A}=A^{2}$
$\text { Let } \hat{\mathrm{i}}, \hat{\mathrm{j}} \text { and } \hat{\mathrm{k}} \text { be unit vectors along } x-, \mathrm{y} \text {-and } \mathrm{z} \text {-axis of a Cartesian co-ordinate system. Then }$
$\hat{i} \cdot \hat{j}=\hat{j} \cdot \hat{k}=\hat{k} \cdot \hat{i}=0 ; \hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k} \cdot \hat{k}=1$
In a Cartesian co-ordinate system; let
$$ \mathbf{A}=\mathrm{A} _{x} \hat{\mathrm{i}}+\mathrm{A} _{\mathrm{y}} \hat{\mathrm{j}}+\mathrm{A} _{z} \hat{\mathrm{k}} \quad \text { and } \quad \mathbf{B}=\mathrm{B} _{x} \hat{\mathrm{i}}+\mathrm{B} _{y} \hat{\mathrm{j}}+\mathrm{B} _{z} \hat{\mathrm{k}} $$
Then, $\mathbf{A} \cdot \mathbf{B}=\mathrm{A} _{x} \mathrm{~B} _{x}+\mathrm{A} _{\mathrm{y}} \mathrm{B} _{\mathrm{y}}+\mathrm{A} _{\mathrm{z}} \mathrm{B} _{\mathrm{z}}$
Example-20 :
$$ \begin{aligned} & \mathbf{A}=2 \hat{i}+4 \hat{j}-\hat{k} \\ & \mathbf{B}=-3 \hat{i}+\hat{j}+\hat{k} \end{aligned} $$
What is angle between $\mathbf{A}$ and $\mathbf{B}$ ?
Show Answer
Solution :
$\mathbf{A}=|\mathbf{A}|=\sqrt{(2)^{2}+(4)^{2}+(-1)^{2}}=\sqrt{21}, \mathrm{~B}=|\mathbf{B}|=\sqrt{(-3)^{2}+(1)^{2}+(1)^{2}}=\sqrt{11}$
$\mathbf{A} \cdot \mathbf{B}=2 \times(-3)+4 \times 1+(-1) \times 1=-3$
Also, $\mathbf{A} \cdot \mathbf{B}=\mathrm{AB} \cos \theta$, therefore
$$ -3=\sqrt{21} \times \sqrt{11} \cos \theta $$
or $\cos \theta=-\left[\frac{3}{\sqrt{231}}\right] \simeq-\left[\frac{3}{15.1}\right] \simeq 0.2 \quad \theta=\cos ^{-1}(-0.2) \simeq 101.5^{0}$
Example-21 :
$$ \mathbf{A}=3 \hat{i}+2 \hat{j} $$
What is component of $\mathbf{A}$ in the direction of $\hat{i}+\hat{j}$ ?
Show Answer
Solution :
Let $\mathbf{B}=\hat{i}+\hat{j}$
$$ |\mathbf{A}|=\mathrm{A}=\sqrt{(3)^{2}+(2)^{2}}=\sqrt{13},|\mathbf{B}|=\mathrm{B}=\sqrt{(1)^{2}+(1)^{2}}=\sqrt{2} $$
$\mathbf{A} \cdot \mathbf{B}=3 \times 1+2 \times 1=5$
$=($ Components of $\mathbf{A}$ along $\mathbf{B}) \times B$
$\therefore$ Magnitude of component of $\mathbf{A}$ along $(\hat{i}+\hat{j})=\frac{5}{\sqrt{2}}$. Also, $\hat{B}=\frac{\mathbf{B}}{|\mathbf{B}|}=\frac{\hat{i}+\hat{j}}{\sqrt{2}}$
In terms of $\hat{i}$ and $\hat{j}$; component of $\mathbf{A}$ along $(\hat{i}+\hat{j})$ is
$$ \frac{5}{\sqrt{2}} \hat{\mathrm{B}}=\frac{5}{2}(\hat{\mathrm{i}}+\hat{\mathrm{j}}) $$
Vector or Cross Product of Vectors
Let $\mathbf{C}=\mathbf{A} \times \mathbf{B}, \mathbf{C}$ is the cross or vector product of $\mathbf{A}$ and $\mathbf{B}$. By definition
$$ \mathrm{C}=(\mathrm{AB} \sin \theta) \hat{\mathrm{n}} $$
where $\hat{\mathrm{n}}$ is a unit vector whose direction is given by the Right-hand-screw rule. According to right-handscrew rule; place a right handed screw perpendicular to plane containing $\mathbf{A}$ and $\mathbf{B}$. Rotate screw so that $\mathbf{A}$ goes and coincides with $\mathbf{B}$. The direction in which screw advances is direction of $\hat{n}$. This is shown in Fig. 38(a).

$\mathbf{C}$ is perpendicular to both $\mathbf{A}$ and $\mathbf{B}$. Vector or cross product is NOT commutative, i.e.
$\mathbf{A} \times \mathbf{B} \neq \mathbf{B} \times \mathbf{A}$
Vector product is distributive, i.e.
$$ \mathbf{A} \times(\mathbf{B}+\mathbf{C})=\mathbf{A} \times \mathbf{B}+\mathbf{A} \times \mathbf{C} $$
Vector product of two parallel vectors i.e. $\theta=0^{0}$, is zero. Vector product has maximum magnitude if vectors are perpendicular to one another. i.e. $\theta=\frac{\pi}{2}$. For a Cartesian co-ordinate system:
$\hat{i} \times \hat{i}=\hat{j} \times \hat{j}=\hat{k} \times \hat{k}=0 ;$ and $\hat{i} \times \hat{j}=\hat{k} ; \hat{j} \times \hat{k}=\hat{i} ; \hat{k} \times \hat{i}=\hat{j}$
In Cartesian co-ordinates; for two vector
$$ \mathbf{A}=\mathrm{A} _{x} \hat{\mathrm{i}}+\mathrm{A} _{y} \hat{\mathrm{j}}+\mathrm{A} _{\mathrm{z}} \hat{\mathrm{k}} $$
and
$$ \mathbf{B}=\mathrm{B} _{x} \hat{\mathrm{i}}+\mathrm{B} _{\mathrm{y}} \hat{\mathrm{j}}+\mathrm{B} _{z} \hat{\mathrm{k}} $$
$$ \begin{aligned} & \mathbf{C}=\mathbf{A} \times \mathbf{B}=\left|\begin{array}{ccc} \hat{\mathrm{i}} & \hat{\mathrm{j}} & \hat{\mathrm{k}} \\ \mathrm{A} _{x} & \mathrm{~A} _{\mathrm{y}} & \mathrm{A} _{\mathrm{z}} \\ \mathrm{B} _{x} & \mathrm{~B} _{\mathrm{y}} & \mathrm{B} _{\mathrm{z}} \end{array}\right| \\ & =\left(\mathrm{A} _{\mathrm{y}} \mathrm{B} _{\mathrm{z}}-\mathrm{A} _{\mathrm{z}} \mathrm{B} _{\mathrm{y}}\right) \hat{\mathrm{i}}-\left(\mathrm{A} _{x} \mathrm{~B} _{\mathrm{z}}-\mathrm{A} _{\mathrm{z}} \mathrm{B} _{x}\right) \hat{\mathrm{j}}+\left(\mathrm{A} _{x} \mathrm{~B} _{\mathrm{z}}-\mathrm{A} _{\mathrm{z}} \mathrm{B} _{x}\right) \hat{\mathrm{k}} \end{aligned} $$
Example-22 :
$$ \mathbf{A}=2 \hat{\mathrm{i}}-3 \hat{\mathrm{j}}-\hat{\mathrm{k}} ; \quad \mathbf{B}=-6 \hat{\mathrm{i}}+9 \hat{\mathrm{j}}+3 \hat{\mathrm{k}} $$
Show $\mathbf{A}$ and $\mathbf{B}$ are parallel vectors.
Show Answer
Solution :
We know vector product of two parallel vector is zero. Now
$$ \begin{aligned} & \mathbf{A} \times \mathbf{B}=\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ 2 & -3 & -1 \\ -6 & 9 & 3 \end{array}\right| \\ & =\hat{i}(-9+9)+\hat{j}(6-6)+\hat{k}(18-18)=\text { zero } \end{aligned} $$
Hence $\mathbf{A}$ and $\mathbf{B}$ are parallel vectors.
Example-23 :
$$ \mathbf{A}=2 \hat{i}+\hat{j}+\hat{k}, \quad \mathbf{B}=\hat{i}-\hat{j}+2 \hat{k} $$
Obtain a unit vector perpendicular to both $\mathbf{A}$ and $\mathbf{B}$.
Show Answer
Solution:
Let $\mathbf{C}=\mathbf{A} \times \mathbf{B}$. We know $\mathbf{C}$ is perpendicular to both $\mathbf{A}$ and $\mathbf{B}$. Therefore $\hat{\mathrm{c}}$ is a unit vector perpendicular to both $\mathbf{A}$ and $\mathbf{B}$. Now
$$ \begin{aligned} & \mathbf{C}=\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ 2 & 1 & 1 \\ 1 & -1 & 2 \end{array}\right| \\ & =\hat{i}(2+1)+\hat{j}(1-4)+\hat{k}(-2-1)=3 \hat{i}-3 \hat{j}-3 \hat{k} \end{aligned} $$
Also, $|\mathbf{C}|=\sqrt{(3)^{2}+(-3)^{2}+(-3)^{2}}=3 \sqrt{3}$
$$ \therefore \hat{\mathrm{c}}=\frac{\mathbf{C}}{|\mathbf{C}|}=\frac{1}{\sqrt{3}}[\hat{\mathrm{i}}-\hat{\mathrm{j}}-\hat{\mathrm{k}}] $$
PROJECTILE MOTION
What is a Projectile?
Consider a particle moving in uniform gravitational field of earth in a vertical plane. Let the particle be projected with an initial speed $\mathrm{v} _{0}$ at an angle $\theta$ with the horizontal direction. The particle projected is known as a projectile. In general it moves along a curved path known as its trajectory.
Basic Results of Motion of a Projectile
(K)
Fig. 39
Fig. 39 shows a projectile projected in vertical $\mathrm{X}-\mathrm{Y}$ plane from origin $\mathrm{O}$ with initial speed $\mathrm{v} _{0}$ at an angle $\theta$ with horizontal. The initial position vector $\mathbf{r} _{\mathbf{0}}=0$ and initial velocity $\mathbf{v} _{0}$ is:
$$ \begin{equation*} \mathbf{v} _{0}=\left(\mathrm{v} _{0} \cos \theta\right) \hat{\mathrm{i}}+\left(\mathrm{v} _{0} \sin \theta\right) \hat{\mathrm{j}} \tag{i} \end{equation*} $$
$\mathrm{v} _{x 0}=\mathrm{v} _{0} \cos \theta=\mathrm{x}-$ component of initial velocity, $\mathrm{v} _{y 0}=\mathrm{v} _{0} \sin \theta=\mathrm{y}$ - component of initial velocity.
The acceleration due to gravity acts in vertically downward direction. There is no acceleration along the horizontal direction i.e. $x$-axis. Expressed mathematically.
$$ \begin{equation*} \mathrm{a} _{x}=0, \quad \mathrm{a} _{\mathrm{y}}=-\mathrm{g} \tag{ii} \end{equation*} $$
The motion of projectile is easily analyzed by describing motion in two parts i.e. along $x$-axis and along $\mathrm{y}$-axis. $\mathrm{P}(x, \mathrm{y})$ is the instantaneous position of projectile. The instantaneous position vector $\mathbf{r}$ is:
$$ \mathbf{r}=x \hat{\mathrm{i}}+\mathrm{y} \hat{\mathrm{j}} $$
and the instantaneous velocity is
$$ \mathbf{v}=\mathrm{v} _{x} \hat{\mathrm{i}}+\mathrm{v} _{\mathrm{y}} \hat{\mathrm{j}} $$
Motion along $x$-axis:
Since $\mathrm{a} _{x}=0$; motion along $x$-axis is uniform motion. Also,
$$ \begin{align*} & \mathrm{v} _{x}=\mathrm{v} _{x 0}=\mathrm{v} _{0} \cos \theta \tag{iii} \\ & x=\left(\mathrm{v} _{x 0}\right) \mathrm{t}+\frac{1}{2} \mathrm{a} _{x} \mathrm{t}^{2}=\left(\mathrm{v} _{0} \cos \theta\right) \mathrm{t} \tag{iv} \end{align*} $$
Motion along $y$-axis:
We have $\mathrm{a} _{\mathrm{y}}=-\mathrm{g}$. The motion along $\mathrm{y}-\mathrm{axis}$ is uniformly accelerated. Also
$$ \begin{align*} & \mathrm{v} _{\mathrm{y}}=\mathrm{v} _{0 \mathrm{y}}+\mathrm{a} _{\mathrm{y}} \mathrm{t}=\mathrm{v} _{0} \sin \theta-\mathrm{gt} \tag{v} \\ & \mathrm{y}=\left(\mathrm{v} _{\mathrm{yo}}\right) \mathrm{t}+\frac{1}{2} \mathrm{a} _{\mathrm{y}} \mathrm{t}^{2}=\left(\mathrm{v} _{0} \sin \theta\right) \mathrm{t}-\frac{1}{2} \mathrm{gt}^{2} \tag{vi} \end{align*} $$
Eqns (iii), (iv), (v) and (vi) give complete information regarding motion of projectile. Some important results are discussed in what follows.
1. Equation of Trajectory
The equation of trajectory is relation between $x$ and $y$. Eliminating $t$ from Eqns (iv) and (vi) we easily get
$$ \begin{equation*} \mathrm{y}=(\tan \theta) x=\frac{\mathrm{g} x^{2}}{2 \mathrm{v} _{0}^{2} \cos ^{2} \theta} \tag{vii} \end{equation*} $$
This is equation of a parabola. In other words; in general, the trajectory of a projectile is a parabolic curve.
2. Time of Fight (T)
The time taken by the projectile to move from O to B (refer to Fig. 39) is known as time of flight. For point $B ; y _{B}=0$ at $t=$ T. From Eqn. (vi); we have
$$ \begin{aligned} & 0=\left(\mathrm{v} _{0} \sin \theta\right) \mathrm{T}-\frac{1}{2} \mathrm{gT}^{2} \\ & =\mathrm{T}\left[\left(\mathrm{v} _{0} \sin \theta\right)-\frac{1}{2} \mathrm{gT}\right] \end{aligned} $$
Since $\mathrm{T} \neq 0 ; \mathrm{v} _{0} \sin \theta-\frac{1}{2} \mathrm{gT}=0$
or $\mathrm{T}=\frac{2 \mathrm{v} _{0} \sin \theta}{\mathrm{g}} \hspace{50mm} . . . . . .(viii)$
3. Maximum Vertical Height $(\mathbf{H}) $
In Fig. 39, A is position of projectile when it has acquired maximum vertical height $H$. At point $A$; the instantaneous vertical
component of velocity is zero, i.e. $\left(\mathrm{v} _{\mathrm{y}}\right) _{\mathrm{A}}=0 ; \mathrm{t}=\mathrm{t} _{\mathrm{A}}$. From
Eqn. (v), we have
$$ \mathrm{t} _{\mathrm{A}}=\frac{\mathrm{v} _{0} \sin \theta}{\mathrm{g}}=\frac{\mathrm{T}}{2} $$
The maximum vertical height $\mathrm{H}$, equals $\mathrm{y}$-co-ordinate of point
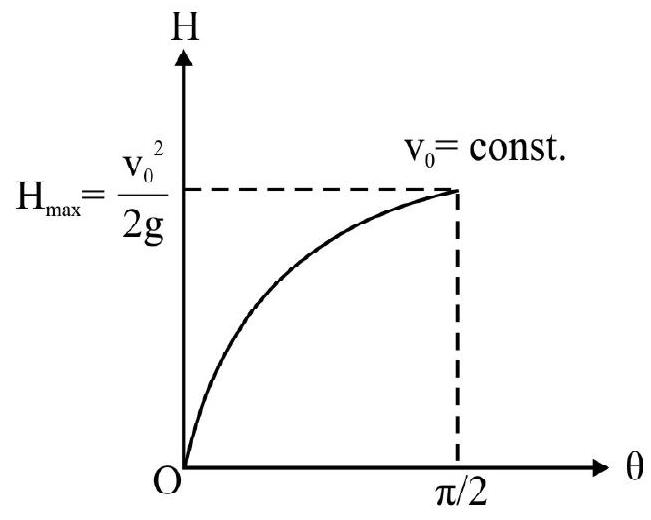
Fig. 40
$A$; i.e. $y _{A}=H \quad $ at $ \quad t=t _{A}$. From Eqn. (vi), we get
$$ \begin{equation*} \mathrm{H}=\frac{\mathrm{v} _{0}^{2} \sin ^{2} \theta}{2 \mathrm{~g}} \tag{ix} \end{equation*} $$
For same value of $\mathrm{v} _{0}$; Fig. 40 shows $\mathrm{H}$ vs $\theta$ graph. Note $\mathrm{H}$ is $\max ^{\mathrm{m}}$ when $\theta=\frac{\pi}{2}$ and $\mathrm{H} _{\max }=\frac{\mathrm{v} _{0}^{2}}{2 \mathrm{~g}}$.
4. Horizontal Range (R)
In Fig. 39, $\mathrm{OB}=\mathrm{R}=$ Horizontal range of projectile. Obviously $x _{\mathrm{B}}=\mathrm{R} ;$ at $\mathrm{t}=\mathrm{T}$
From Eqn (iv), we have
$$ \begin{equation*} \mathrm{R}=\frac{\left(\mathrm{v} _{0} \cos \theta\right)\left(2 \mathrm{v} _{0} \sin \theta\right)}{\mathrm{g}}=\frac{\mathrm{v} _{0}^{2} \sin 2 \theta}{\mathrm{g}} \tag{x} \end{equation*} $$
For a particular value of $\mathrm{v} _{0}$; $\mathrm{R}$ is maximum if $\sin 2 \theta=1$ or $2 \theta=\frac{\pi}{2}, \therefore \theta=\frac{\pi}{4}$. For a particular speed of projection $\mathrm{v} _{0}$ the horizontal range is maximum if $\theta=45^{\circ}$.
For same value of $\mathrm{R}$; there are two directions of projection $\theta _{1}$ and $\theta _{2}$. Obviously.
$$ \begin{align*} & \mathrm{R}=\frac{\mathrm{v} _{0}^{2} \sin ^{2} \theta _{1}}{\mathrm{~g}}=\frac{\mathrm{v} _{0}^{2} \sin ^{2} \theta _{2}}{\mathrm{~g}} \\ & \text { or } \sin 2 \theta _{1}=\sin 2 \theta _{2} \quad \text { or } \quad 2 \theta _{2}=\pi-2 \theta _{1} \\ & \therefore \theta _{1}+\theta _{2}=\frac{\pi}{2} \tag{xi} \end{align*} $$
Let $T _{1}$ and $T _{2}$ be time of flight for $\theta=\theta _{1}$ and $\theta=\theta _{2}$ having same horizontal range; It can be shown that
$$ \mathrm{T} _{1} \mathrm{~T} _{2}=\frac{2 \mathrm{R}}{\mathrm{g}} \text { and } \mathrm{H} _{1} \mathrm{H} _{2}=\frac{\mathrm{R}^{2}}{16} $$
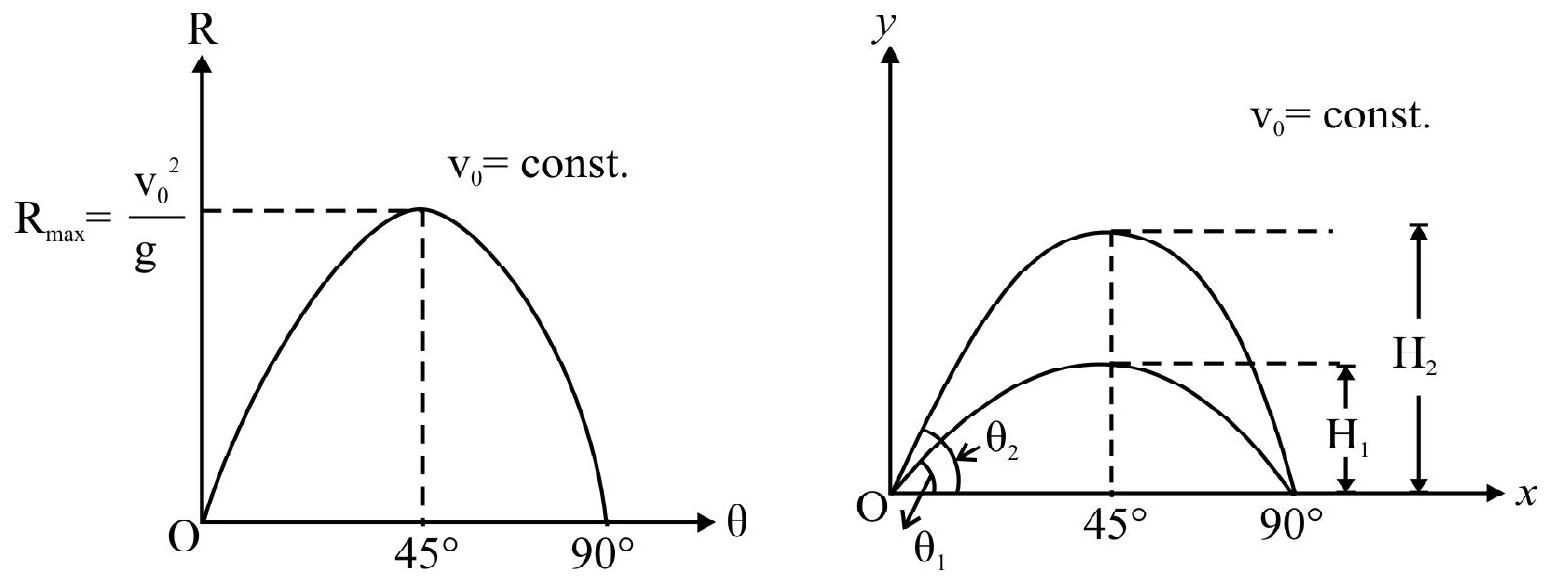
Fig. 41
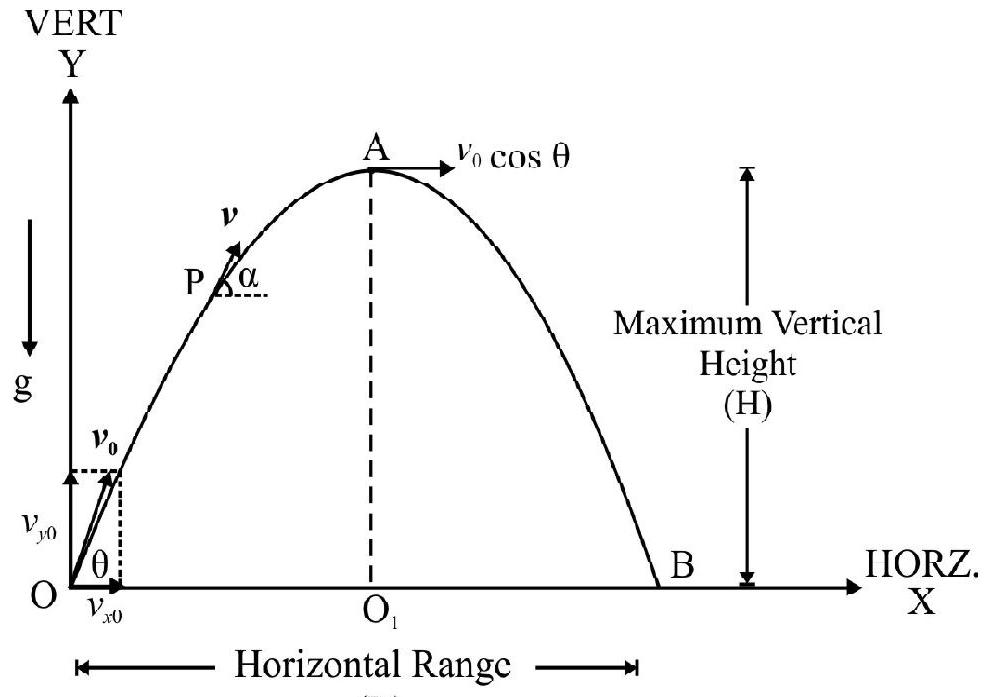
5. Instantaneous Velocity
The instantaneous velocity $\mathbf{v}$; of the projectile is
$$ \mathbf{v}=\left(\mathrm{v} _{0} \cos \theta\right) \hat{\mathrm{i}}+\left(\mathrm{v} _{0} \sin \theta-\mathrm{gt}\right) \hat{\mathrm{j}} $$
The instantaneous speed $v$ is
$$ \mathrm{v}=\sqrt{\mathrm{v} _{x}^{2}+\mathrm{v} _{\mathrm{y}}^{2}}=\sqrt{\left(\mathrm{v} _{0} \cos \theta\right)^{2}+\left(\mathrm{v} _{0} \sin \theta-\mathrm{gt}\right)^{2}} $$
Let $\alpha$ be the angle the instantaneous velocity makes with $x$-axis i.e. horizontal direction, then
$$ \tan \alpha=\frac{\mathrm{v} _{\mathrm{y}}}{\mathrm{v} _{x}}=\frac{\mathrm{v} _{0} \sin \theta-\mathrm{gt}}{\mathrm{v} _{0} \cos \theta} $$
When projectile is at position of maximum vertical height i.e. at point $\mathrm{A} ; \mathrm{v} _{\mathrm{y}}=0$. The speed of particle is miniumum but not zero. Also $\alpha=0$. The instantaneous velocity is horizontal at position of maximum vertical height. Note $x$-component of $\mathbf{v}$ remains same at all times during motion. These characteristics all shown in Fig. 42.

Projectile Motion on an inclined plane
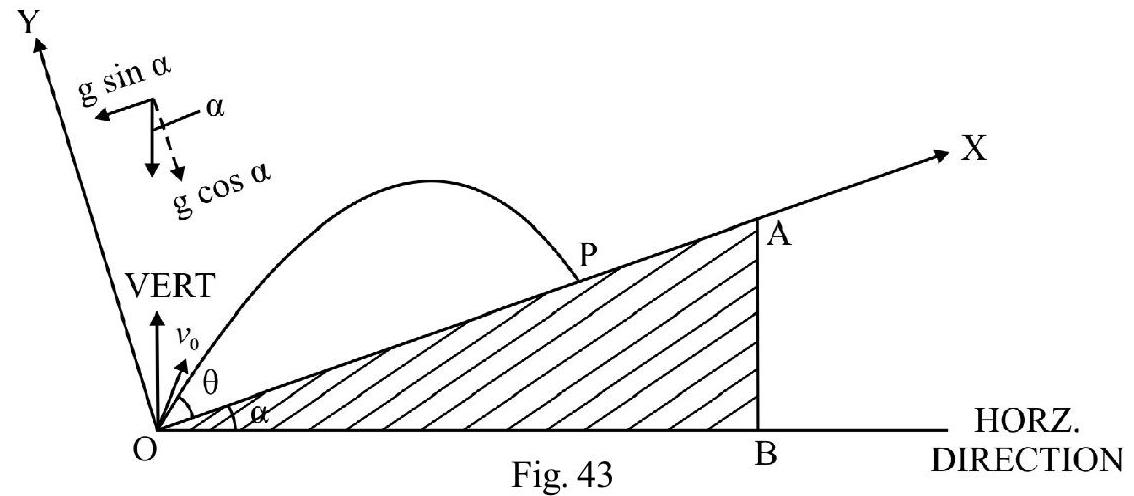
Fig. 42
In Fig. 43, OAB is a fixed inclined plane of inclination $\alpha$. From the foot $\mathrm{O}$ of the inclined plane, a projectile is projected with a speed $v _{0}$ at an angle $\theta(\theta>\alpha)$ with the horizontal. A very convenient way of describing motion is choosing $x$ and $y$-axis as shown in Fig. 43. Resolving initial velocity $\mathbf{v} _{0}$ and acceleration g into component along $x$ and $\mathrm{y}$-axis we have.
$$ \begin{aligned} & \mathrm{v} _{x 0}=\mathrm{v} _{0} \cos (\theta-\alpha) ; \quad \mathrm{v} _{\mathrm{yo}}=\mathrm{v} _{0} \sin (\theta-\alpha) \\ & \mathrm{a} _{x}=-\mathrm{g} \sin \alpha \quad \mathrm{a} _{\mathrm{y}}=-\mathrm{g} \cos \alpha \end{aligned} $$
The instantaneous position co-ordinate $(x, y)$ and the instantaneous $x$ - and $\mathrm{y}$-components of velocity are given by
$$ \begin{align*} & \mathrm{v} _{x}=\mathrm{v} _{x 0}+\mathrm{a} _{x} \mathrm{t}=\mathrm{v} _{0} \cos (\theta-\alpha)-(\mathrm{g} \sin \alpha) \mathrm{t} \tag{i} \\ & x=\left[\mathrm{v} _{0} \cos (\theta-\alpha)\right] \mathrm{t}-\frac{1}{2}(\mathrm{~g} \sin \alpha) \mathrm{t}^{2} \tag{ii} \end{align*} $$
and
$$ \begin{align*} & v _{y}=v _{y 0}+a _{y} t=v _{0} \sin (\theta-\alpha)-(g \cos \alpha) t \tag{iii} \\ & y=\left[v _{0} \sin (\theta-\alpha)\right] t-\frac{1}{2}(g \cos \alpha) t^{2} \tag{iv} \end{align*} $$
Eqns (i), (ii), (iii) and (iv) Five complete information regarding motion of projectile. In Fig. 43 projectile hits inclined plane at point $\mathrm{P}$. Time taken to move from $\mathrm{O}$ to $\mathrm{P}$ is time of flight $\mathrm{T}$. Obviously for point $\mathrm{P}$ $ \quad \mathrm{y} _{\mathrm{P}}=0 ; \mathrm{t}=\mathrm{T}$. From Eqn (iv)
$$ \begin{equation*} \mathrm{T}=\frac{2 \mathrm{v} _{0} \sin (\theta-\alpha)}{\mathrm{g} \cos \alpha} \tag{v} \end{equation*} $$
The distance $\mathrm{OP}=\mathrm{R}=$ Range of projectile along the inclined plane. Obviously for point $\mathrm{P}$;
$$ x=\mathrm{R} \text {, at } \mathrm{t}=\mathrm{T} $$
Using Eqn (ii); we get
$$ \begin{equation*} \mathrm{T}=\frac{2 \mathrm{v} _{0} \sin (2 \theta-\alpha) \cos \theta}{\mathrm{g} \cos ^{2} \alpha} \tag{vi} \end{equation*} $$
$\mathrm{R}$ is maximum, for a fixed value of $\mathrm{v} _{0}$ and $\alpha$; if
$$ \sin (2 \theta-\alpha)=1 $$
$$ \text { or } \theta=\frac{\pi}{4}+\frac{\alpha}{2} $$
and $\quad \mathrm{R} _{\text {max }}=\frac{\mathrm{v} _{0}^{2}(1-\sin \alpha)}{\mathrm{g} \cos ^{2} \alpha}$
Example-24 :
A particle is projected in a vertical plane with a speed of $100 \mathrm{~ms}^{-1}$ at an angle of $30^{\circ}$ with horizontal. What is:
(a) time of flight
(b) horizontal range and
(c) instantaneous velocity $2 \mathrm{~s}$ after projection? $\mathrm{g}=10 \mathrm{~ms}^{-2}$
Show Answer
Solution :
Given $\mathrm{v} _{0}=100 \mathrm{~ms}^{-1}, \theta=30^{0}, \mathrm{~g}=10 \mathrm{~ms}^{-2}$
(a) The time of flight, $T$, is
$$ \mathrm{T}=\frac{2 \mathrm{v} _{0} \sin \theta}{\mathrm{g}}=\frac{2 \times 100 \times \sin 30}{10}=10 \mathrm{~s} $$
(b) The horizontal range, $\mathrm{R}$, is
$$ \mathrm{R}=\frac{\mathrm{v} _{0}^{2} \sin 2 \theta}{\mathrm{g}}=\frac{(100)^{2} \times \sin 60}{10} \mathrm{~m} \simeq 867 \mathrm{~m} $$
(c) Let $\mathrm{v} _{x}$ and $\mathrm{v} _{\mathrm{y}}$ be the instantaneous $x$ - and $\mathrm{y}$-component of velocity at $\mathrm{t}=2 \mathrm{~s}$. Obviously
$$ \mathrm{v} _{x}=\mathrm{v} _{x 0}=100 \cos 30=86.7 \mathrm{~ms}^{-1} $$
$\mathrm{v} _{\mathrm{y}}=\mathrm{v} _{\mathrm{yo}}-\mathrm{gt}=\left(100 \sin 30^{\circ}\right)-10 \times 2$
$=50-20=30 \mathrm{~ms}^{-1}$
$\mathrm{v}=$ The instantaneous speed of projectile.
$=\sqrt{\mathrm{v} _{\mathrm{x}}^{2}+\mathrm{y} _{\mathrm{y}}^{2}}=\sqrt{(86.7)^{2}+(30)^{2}} \simeq 91.6 \mathrm{~ms}^{-1}$
Let $\alpha$ be the angle the instantaneous velocity $\mathbf{v}$ makes with horizontal direction. We know
$$ \tan \alpha=\frac{\mathrm{v} _{\mathrm{y}}}{\mathrm{v} _{\mathrm{x}}}=\frac{30}{86.7} \simeq 0.346 ; \quad \text { or } \quad \alpha=\tan ^{-1}(0.346) \simeq 10.9^{0} $$
Example-25 :
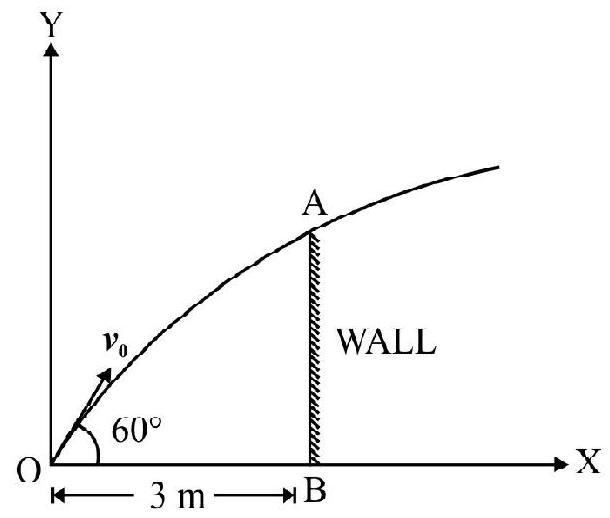
A ball is projected with an initial speed $\mathrm{v} _{0}$ at an angle $60^{\circ}$ with horizontal. The ball just grazes past the edge of a vertical wall at a horizontal distance of $3 \mathrm{~m}$ from point of projection $0.2 \mathrm{~s}$ after projection. What is $\mathrm{v} _{0}$ ? What is height of wall? What is maximum vertical height attained by the ball? $\mathrm{g}=10 \mathrm{~ms}^{-2}$
Show Answer
Solution :
In Fig. 44, $O$ is point of projection of ball and $A B$ is the vertical wall. Choose $x$ - and $y$-axis at shown in Fig. 44. Obviously
$\mathrm{v} _{x 0}=\mathrm{v} _{0} \cos 60=\frac{\mathrm{v} _{0}}{2}$ and $\mathrm{v} _{\mathrm{y} 0}=\mathrm{v} _{0} \sin 60 \simeq 0.867 \mathrm{v} _{0}$
The co-ordinates of point $\mathrm{A}$ of wall are:
$$ x _{\mathrm{A}}=3 \mathrm{~m} ; \quad \mathrm{y} _{\mathrm{A}}=3 \tan 60^{\circ}=4.96 \mathrm{~m} $$
Let the ball graze past point $A$ at $t=0.2 \mathrm{~s}$. Obviously
$$ x _{\mathrm{A}}=3 \mathrm{~m}=\frac{\mathrm{v} _{0}}{2} \times 0.2, \quad \text { or } \quad \mathrm{v} _{0}=30 \mathrm{~ms}^{-1} $$
The vertical height, $h$, of wall equals y co-ordinate of projectile at $5=0.2 \mathrm{~s}$. Therefore,
$$ \begin{aligned} & \mathrm{h}=\left(\mathrm{v} _{0} \sin 60\right) \times 0.2-5(0.2)^{2} \\ & =30 \times 0.867 \times 0.2-0.2 \\ & =5.2-0.2 \simeq 5 \mathrm{~m} \end{aligned} $$
The maximum vertical height attained by the ball, $\mathrm{H}$, is
$$ \mathrm{H}=\frac{\mathrm{v} _{0}^{2} \sin ^{2} \theta}{2 \mathrm{~g}}=\frac{(30)^{2} \times(0.857)^{2}}{2 \times 10} \mathrm{~m} \simeq 33.8 \mathrm{~m} $$
Example-26 :
A stone is projected vertically upwards with a speed of $40 \mathrm{~ms}^{-1}$ at an angle of $30^{\circ}$ with horizontal. How long after projection is it at a height of $15 \mathrm{~m}$ ? What is horizontal distance of stone from the point of projection at this moment of time? $\mathrm{g}=10 \mathrm{~ms}^{-2}$.
Show Answer
Solution :
$\mathrm{v} _{x 0}=40 \cos 30^{\circ}=34.7 \mathrm{~ms}^{-1}$ and $\mathrm{v} _{\mathrm{yo}}=40 \sin 30^{\circ}=20 \mathrm{~ms}^{-1}$
The instantaneous y co-ordinate of stone, $y$, is
$$ \mathrm{y}=\left(\mathrm{v} _{0} \sin \theta\right) \mathrm{t}-\frac{1}{2} \mathrm{gt}^{2}=20 \mathrm{t}-5 \mathrm{t}^{2} $$
Given $\mathrm{y}=15 \mathrm{~m}$. Therefore,
$$ \begin{aligned} & 15=20 \mathrm{t}-5 \mathrm{t}^{2} \text { or } \mathrm{t}^{2}-4 \mathrm{t}+3=0 \\ & \therefore \mathrm{t}=\frac{4 \pm \sqrt{16-12}}{2}=\frac{4+2}{2}=18 \text { or } 3 \mathrm{~s} \end{aligned} $$
The particle attains given vertical height at $t=1 \mathrm{~s}$, while going up towards position of maximum vertical height and at $\mathrm{t}=3 \mathrm{~s}$ while moving downwards. Let $x _{1}$ and $x _{2}$ be the horizontal co-ordinates of particle at $\mathrm{t}=1 \mathrm{~s}$ and $\mathrm{t}=3 \mathrm{~s}$ respectively. Obviously.
$x _{1}=\mathrm{v} _{x 0} \times 1=34.7 \mathrm{~m}$ and $x _{2}=34.7 \times 3=104.1 \mathrm{~m}$
Example-27 :
A table has a vertical height of $2.5 \mathrm{~m}$. From the edge of the table a ball is pushed horizontally with an initial speed of $10 \mathrm{~ms}^{-1}$.
(1) Write equation of trajectory of ball.
(2) How long after projection, the ball hits ground? What is horizontal distance of the point where ball hits ground from the foot of the table?
(3) What is the velocity of ball as it hits ground? $\mathrm{g}=10 \mathrm{~ms}^{-2}$
Show Answer
Solution :
In Fig. 45, O is the position of particle on edge of table. Choose a co-ordinate system as shown in Fig. 45. For the ball
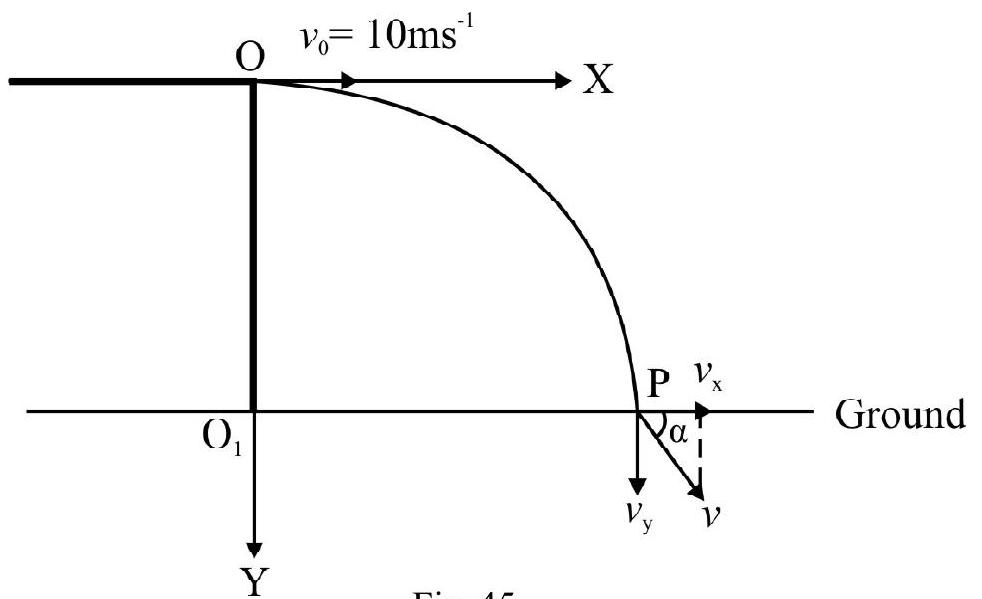
Fig. 45
$$ \begin{align*} & \mathrm{v} _{x 0}=\mathrm{v} _{0}= 10 \mathrm{~ms}^{-1}, \mathrm{v} _{\mathrm{yo}}=0 ; \text { and } \mathrm{a} _{\mathrm{y}}=+10 \mathrm{~ms}^{-1} \text { Therefore; } \\ & \mathrm{v} _{x}=\mathrm{v} _{x 0}=10 \mathrm{~ms}^{-1} \text { at all times } \\ & \mathrm{v} _{\mathrm{y}}=\mathrm{gt}=10 \mathrm{t \quad ms}^{-1} \tag{i} \\ & x=\mathrm{v} _{x 0} \times \mathrm{t}=10 \mathrm{t}, \text { and } \mathrm{y}=\frac{1}{2} \times 10 \mathrm{t}^{2}=5 \mathrm{t}^{2} \tag{ii} \end{align*} $$
From Eqns (ii) we have
$$ \begin{equation*} \mathrm{y}=5\left(\frac{x}{10}\right)^{2}=0.05 x^{2} \tag{iii} \end{equation*} $$
This is equation of trajectory of ball. Let ball hit ground at point $P$, at $t=t$. For point $P ; y=+2.5 \mathrm{~m}$
$$ \therefore 2.5=5 \mathrm{t}^{2} \quad \text { or } \quad \mathrm{t}=\frac{1}{\sqrt{2}} \simeq 0.7 \mathrm{~s} $$
$\mathrm{O} _{1} \mathrm{P}=$ Horizontal distance of $\mathrm{P}$ from the foot $\mathrm{O} _{1}$ of table.
$$ =\mathrm{v} _{x 0} \times \mathrm{t}=10 \times 0.7 \simeq 7 \mathrm{~m} $$
Let $\mathrm{v} _{x}$ and $\mathrm{v} _{\mathrm{y}}$ be the $x$ - and $\mathrm{y}$-components of velocity of ball as it hits ground. Obviously
$$ \begin{aligned} & \mathrm{v} _{x}=\mathrm{v} _{x 0}=10 \mathrm{~ms}^{-1} ; \quad \mathrm{v} _{\mathrm{y}}=10 \mathrm{x} 0.7 \mathrm{~ms}^{-1}=7 \mathrm{~ms}^{-1} \\ & \therefore \mathrm{v}=\sqrt{\mathrm{v} _{x}^{2}+\mathrm{v} _{\mathrm{y}}^{2}}=\sqrt{149} \mathrm{~ms}^{-1} \simeq 12.21 \mathrm{~ms}^{-1} \end{aligned} $$
Let $\alpha$ be the angle the instantaneous velocity makes with horizontal direction. Then:
$$ \tan \alpha=\frac{\mathrm{v} _{\mathrm{y}}}{\mathrm{v} _{x}}=0.7 \quad \text { or } \quad \alpha=\tan ^{-1}(0.7) \simeq 35^{\circ} $$
Example-28 :
A batsman hits a ball at a height of $1.22 \mathrm{~m}$ above ground. The ball leaves bat in a direction at $45^{\circ} \mathrm{with}$ the horizontal. There is a wall of height $7.3 \mathrm{~m}$ at a horizontal distance of $97.5 \mathrm{~m}$ from the position of batsman and has a height of $7.31 \mathrm{~m}$. Had there been no wall the ball would be at a distance of $106.7 \mathrm{~m}$ when it is again at a vertical height of $1.22 \mathrm{~m}$. Will the ball able to clear the wall? $\mathrm{g}=10 \mathrm{~ms}^{-2}$
Show Answer
Solution :
In Fig. 46, A is position of point where the ball hits bat. Choose co-ordinate axis as shown in Fig. 46. Given,
$\mathrm{AB}=\mathrm{R}=106.7=\frac{\mathrm{v} _{0}^{2} \sin 90^{\circ}}{\mathrm{g}}$
$\therefore \mathrm{v} _{0}=\sqrt{1067} \mathrm{~ms}^{-1}=32 \mathrm{~ms}^{-1}$
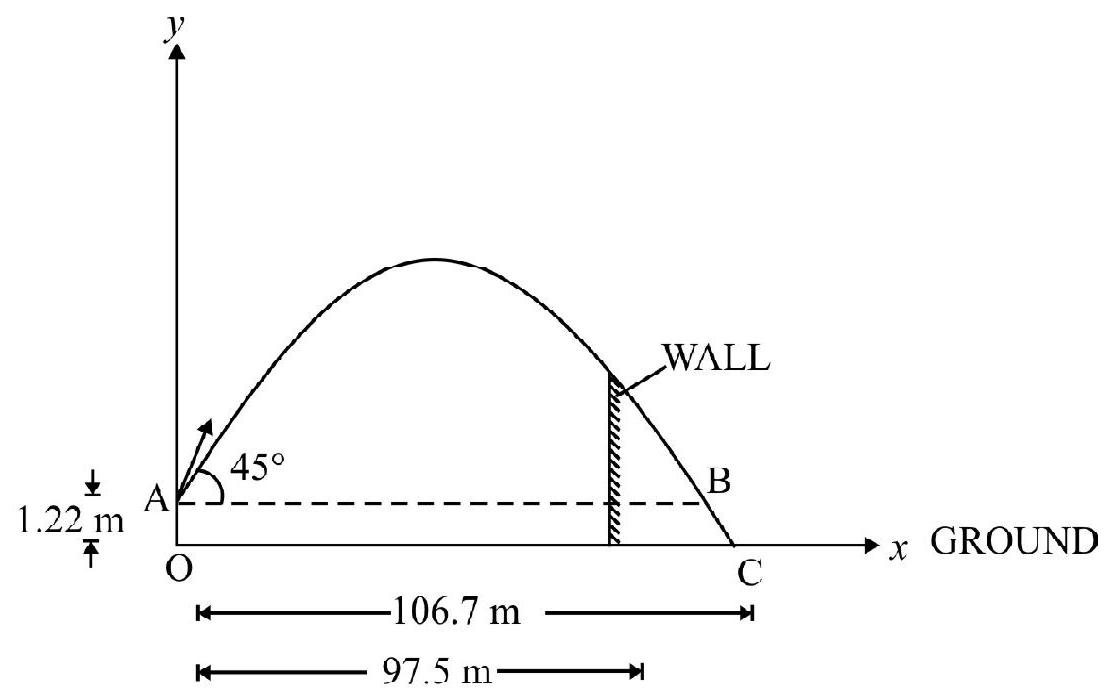
Fig. 46
The question of trajectory of ball is
$$ \begin{align*} & \mathrm{y}=1.22+(\tan 45) x-\frac{10 x^{2}}{2\left(\mathrm{v} _{0} \cos 45\right)^{2}} \\ & =1.22+x-\left[\frac{10 x^{2}}{2 \times\left(\frac{1067}{2}\right)}\right] \\ & =1.22+x-\left[\frac{10 x^{2}}{1067}\right] \tag{i} \end{align*} $$
When ball is at $x=97.5 \mathrm{~m}$; its $\mathrm{y}$-co-ordinate is
$$ y=1.22+97.5-\frac{10(97.5)^{2}}{106.7}=9.58 \mathrm{~m} $$
The height of wall at $x=97.5 \mathrm{~m}$ is $7.3 \mathrm{~m}$. Since $\mathrm{y}>7.3 \mathrm{~m}$; the ball will clear the wall.
Motion Along a Circle
A circular motion is an example of motion in two dimensions. In a circular motion the particle moves along a circle. For example:
(1) motion of hands of a clock.
(2) motion of earth around its own axis.
(3) motion of earth around Sun is approximately along a circular path.
(4) motion of electron around proton in a hydrogen atom.
Consider a particle moving in a circle of radius R. Choosing centre of circle as origin $\mathrm{O}$ and plane of motion as $x-\mathrm{y}-$ plane; the equation of the trajectory is $x^{2}+y^{2}=R$.
The $\mathrm{z}$-axis i.e. line through center and perpendicular to plane of motion is known as axis around which motion takes place. In Fig. 47, z-axis is the axis of motion. The particle can move in a circle either in clockwise or anticlockwise direction.
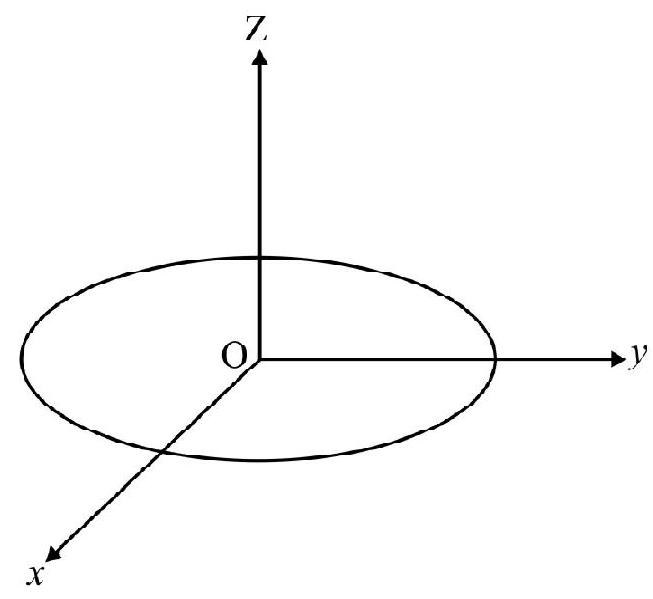
Fig. 47
(1) Terminology used in Circular Motion
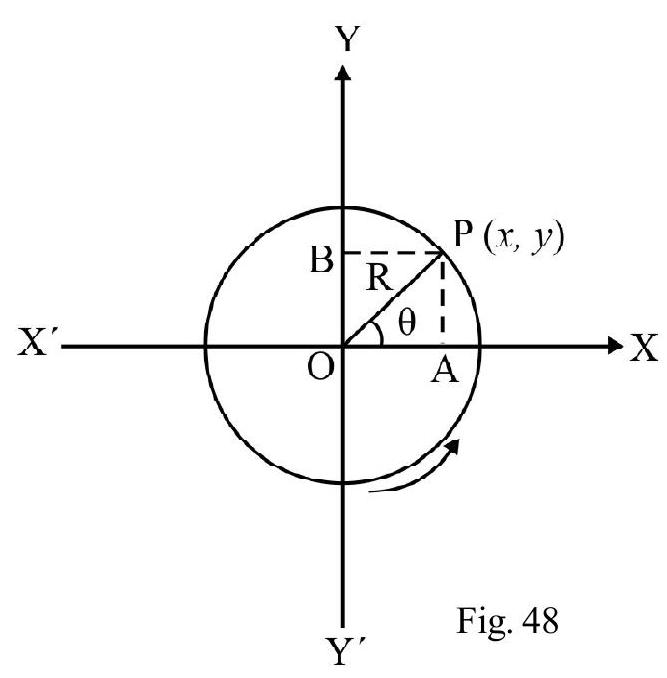
Fig. 48 shows a particle moving in a circle of radius $\mathrm{R}$ in $x-\mathrm{y}$ plane in anti clockwise direction. $P$ is instantaneous position of particle on the circle. Let $x$, y be the instantaneous co-ordinate of P. Obviously $x=\mathrm{OA}=\mathrm{R} \cos \theta$ and $\mathrm{y}=\mathrm{OB}=\mathrm{R} \sin \theta$. Another very convenient way of describing $\mathrm{P}$ is using polar co-ordinates ( $r, \theta$ ). In Fig. 48.
$\mathrm{r}=\mathrm{R}$ and $\mid \mathrm{XOP}=\theta$
For a particle moving in a circle of constant radius, the instantaneous position is described by one co-ordinate i.e. $\theta$ only.
Let $\theta _{1}$ and $\theta _{2}$ be the instantaneous angular position of particle at $\mathrm{t}=\mathrm{t} _{1}$, and $\mathrm{t}=\mathrm{t} _{2}$. Then $\Delta \theta=\theta _{2}-\theta _{1}$ is angular displacement in the interval $\Delta \mathrm{t}=\mathrm{t} _{2}-\mathrm{t} _{1}$
(2) Average and Instantaneous Angular Speed
The average angular speed $\omega _{\mathrm{av}}$ is the ratio of angular displacement $\Delta \theta$ and time taken $\Delta \mathrm{t}$; i.e.
$$ \omega _{\mathrm{av}}=\frac{\Delta \theta}{\Delta \mathrm{t}} $$
SI unit of angular speed is radian per second.
The instantaneous angular speed, $\omega$, is
$$ \omega=\operatorname{Lt} _{\Delta t \rightarrow 0}\left[\frac{\Delta \theta}{\Delta \mathrm{t}}\right]=\frac{\mathrm{d} \theta}{\mathrm{dt}} $$
The angular speed, $\omega$, is also expressed in terms of revolutions per second i.e. r.p.s. For a particle making $v$ r.p.s., angular speed $\omega=2 \pi v$.
The angular velocity $\omega$ of a particle is $\boldsymbol{\omega}={\omega}$$\hat{n}$. The direction $\hat{n}$ of angular velocity is always perpendicular to plane of motion. The sense of $\hat{n}$ is given by the right-hand-screw rule.
(3) Linear Speed and Linear Velocity of Particle

Fig. 49(a) shows a particle moving in a circle of constant radius R. P and Q are the instantaneous position of particle at $t=t _{1}$ and $t=t _{2}$. The linear distance $\Delta s$ traveled by the particle in the interval $\Delta t$ is length of $\operatorname{arc} P Q=$ R. $\Delta \theta$
where $\Delta \theta=\theta _{2}-\theta _{1}$. The average linear speed, $\mathrm{v} _{\mathrm{av}}$, is
$$ \begin{equation*} \mathrm{v} _{\mathrm{av}}=\frac{\Delta \mathrm{s}}{\Delta \mathrm{t}}=\mathrm{R}\left(\frac{\Delta \theta}{\Delta \mathrm{t}}\right)=\mathrm{R} \omega _{\mathrm{av}} \tag{i} \end{equation*} $$
The average velocity is
$$ \mathbf{v} _{\mathrm{av}}=\frac{\Delta \mathbf{s}}{\Delta \mathrm{t}} $$
where $\Delta \mathbf{s}=\mathbf{P Q}$. Magnitude of $\Delta \mathbf{s}$ equals chord PQ. The direction of $\mathbf{v} _{\mathrm{av}}$ is same as direction of chord $\mathbf{P Q}$.
The instantaneous speed, $v$ is :
$$ v=\underset{\Delta t \rightarrow 0}{\operatorname{Lt}}\left[\frac{\Delta \mathrm{s}}{\Delta \mathrm{t}}\right]=\underset{\Delta \mathrm{t} \rightarrow 0}{\mathrm{Lt}}\left[\frac{\mathrm{R} \Delta \theta}{\Delta \mathrm{t}}\right]=\mathrm{R} \underset{\Delta \mathrm{t} \rightarrow 0}{\mathrm{Lt}}\left[\frac{\Delta \theta}{\Delta \mathrm{t}}\right]=\mathrm{R} \omega $$
The magnitude of instantaneous velocity equals instantaneous speed. The direction of $\mathbf{v}$ is in the direction of tangent to circle at the point $\mathrm{P}$ considered. This is shown in Fig. 49(b).
(4) Angular and Linear Acceleration
For a particle moving in a circle of constant radius $\mathrm{R}$ its angular speed changes with time we have angular acceleration $\alpha$. Let $\Delta \omega=\omega _{2}-\omega _{1}$ be change in angular speed in time interval $\Delta t=t _{2}-t _{1}$.
The average angular acceleration; $\alpha _{\mathrm{av}}$; is
$$ \alpha _{\mathrm{av}}=\frac{\text { Change in angular speed }}{\text { Time taken }}=\frac{\Delta \omega}{\Delta \mathrm{t}} $$
The instantaneous angular acceleration; $\alpha$; is
$$ \alpha=\operatorname{Lt} _{\Delta t \rightarrow 0}\left[\frac{\Delta \omega}{\Delta \mathrm{t}}\right]=\frac{\mathrm{d} \omega}{\mathrm{dt}} $$
Let $a$ be the magnitude of instantaneous linear acceleration. Then
$$ \mathrm{a}=\frac{\mathrm{d}}{\mathrm{dt}}(v)=\frac{\mathrm{d}}{\mathrm{dt}}(\mathrm{R} \omega)=\mathrm{R}\left(\frac{\mathrm{d} \omega}{\mathrm{dt}}\right)=\mathrm{R} \alpha $$
(5) Equations of Uniformly Accelerated Circular Motion
Let the angular acceleration $\alpha$ be a constant; i.e. angular speed changes by equal amounts in equal time intervals. This is known as uniformly accelerated circular motion. Let
$\omega _{0}=$ Initial angular speed i.e. at $\mathrm{t}=0$
$\alpha=$ Uniform angular acceleration
$\omega=$ Instantaneous angular speed i.e. $\mathrm{t}=\mathrm{t}$
$\theta=$ Total angle described in time $t=t$
The equations of uniformly accelerated circular motion are
$$ \omega=\omega _{0}+\alpha t $$
$$ \begin{align*} & \theta=\omega _{0} t+\frac{1}{2} \alpha \mathrm{t}^{2} \tag{i} \\ & \omega^{2}-\omega _{0}^{2}=2 \alpha \theta \end{align*} $$
Example-29:
A particle starts from rest and moves in a circle of radius $20 \mathrm{~cm}$. It acquires a speed of $120 \quad \mathrm{rpm}$ in $\pi$ second. The motion is uniformly accelerated.
(1) What is angular and linear acceleration?
(2) What is angular displacement and the number of circles completed? What is linear distance traveled?
Show Answer
Solution:
(1) Given $\omega _{0}=0 ; \quad \omega=120 \mathrm{rpm}=\frac{120}{60} \mathrm{rps}=2 \times 2 \pi \mathrm{rad} \quad \mathrm{s}^{-1} \quad \mathrm{t}=\pi, \mathrm{s} ; \quad \alpha=$ ?
Using equation $\omega _{0}=\omega _{0}+\alpha$ t, we have
$4 \pi=\alpha . \pi \quad$ or $\quad \alpha=4 \quad \mathrm{rad \quad s}^{-2}$
$\mathrm{a}=$ The magnitude of linear acceleration
$=\mathrm{R} \alpha=0.2 \times 4 \mathrm{~ms}^{-2}=0.8 \mathrm{~ms}^{-2}$
(2) The total angle described $\theta$, is
$\theta=\omega _{0} \mathrm{t}+\frac{1}{2} \alpha \mathrm{t}^{2}=0+\frac{1}{2} \times 4 \times(\pi)^{2}=2 \pi^{2}$ radian
Number of revolution completed $=\frac{\theta}{2 \pi}=\frac{2 \pi^{2}}{2 \pi}=\pi$
The linear distance traveled, $\mathrm{S}$; is
$$ \mathrm{S}=\mathrm{R} \theta=0.2 \times 2 \pi^{2} \simeq 4 \mathrm{~m} \quad\left[\because \pi^{2} \simeq 10\right] $$
Uniform Circular Motion
Consider a particle moving in a circle of constant radius $\mathrm{R}$ with uniform angular speed $\omega$. The linear speed, $v=R \omega$ is also a constant. However linear velocity $v$ is not constant. Though magnitude of $\mathbf{v}$ is constant, the direction of $\mathbf{v}$ changes as particle moves. Fig. 50 shows instantaneous direction of $\mathbf{v}$ at three points $P$, $\mathbf{Q}$ and R. Note $\mathbf{v} _{\mathbf{P}} \neq \mathbf{v} _{\mathbf{Q}} \neq \mathbf{v} _{\mathbf{R}} ;$ but $\left|\mathbf{v} _{\mathbf{P}}\right|=\left|\mathbf{v} _{\mathbf{Q}}\right|=\left|\mathbf{v} _{\mathbf{R}}\right|=\mathrm{v}$.
The motion is with uniform speed but variable velocity.
Since $\mathbf{v}$ is not constant; we have linear acceleration $\mathbf{a}$. By definition.
$\mathbf{a}=\underset{\Delta t \rightarrow 0}{\operatorname{Lt}}\left[\frac{\Delta \mathbf{v}}{\Delta \mathrm{t}}\right]=\frac{\mathbf{d v}}{\mathrm{dt}}$

Fig. 50(b) shows position $P$ and $Q$ of particle at $t=t$ and $t=t+\Delta t$. The change in velocity $\Delta v$ is
$$ \Delta \mathbf{v}=\mathbf{v} _{\mathbf{Q}}-\mathbf{v} _{\mathbf{P}}=\mathbf{M N} $$
It can be shown that
$$ \begin{aligned} & \mathrm{a}=|\mathbf{a}|=\text { The magnitude of linear acceleration } \\ & =\frac{\mathrm{v}^{2}}{\mathrm{R}}=\mathrm{R} \omega \end{aligned} $$
The instantaneous direction of $\mathbf{a}$ is along the instantaneous radius directed towards centre of circle. This is known as centripetal acceleration. Note for motion in a circle of constant radius:
(1) The instantaneous velocity is purely tangential and
(2) The instantaneous acceleration is purely radial.
This is shown in Fig. 52. Since $\mathbf{v}$ and $\mathbf{a}$ are always perpendicular;
$$ \mathbf{v} \cdot \mathbf{a}=0 $$

Non-Uniform Circular Motion
For a particle having non-uniform circular motion; the speed also changes as particle moves along its circular path. The acceleration a has: (1) radial component, $a _{r}$; and (2) tangential component, $a _{n}$. The radial component of linear acceleration
$$ =\mathrm{a} _{\mathrm{r}}=\frac{\mathrm{v}^{2}}{\mathrm{R}}=\mathrm{R} \omega^{2} $$
$\mathrm{v}$ is instantaneous linear speed and $\omega$ is instantaneous angular speed. The tangential component of acceleration
$$ =\mathrm{a} _{\mathrm{t}} \equiv \mathrm{a} _{\mathrm{n}}=\frac{\mathrm{v}^{2}}{\mathrm{R}} $$
The magnitude of net linear acceleration, $\mathrm{a}$, is
$$ \mathrm{a}=\sqrt{\mathrm{a} _{\mathrm{r}}^{2}+\mathrm{a} _{\mathrm{t}}^{2}} $$
Example-30 :
The second’s hand of a clock is $20 \mathrm{~cm}$ long. The second hand of clock moves for $t$ second from position A to position B. The magnitude of change in linear velocity of the tip of second’s hand is $0.67 \pi \mathrm{cms}^{-1}$. What is $\mathrm{t}$ ?
Show Answer
Solution :
$\omega$ =Angular speed of second’s hand of clock
$$ =\frac{2 \pi}{60} \mathrm{rad} \mathrm{s}^{-1}=\frac{\pi}{30} \mathrm{rad} \mathrm{s}^{-1} $$
$v=$ The linear speed of tip of second’s hand of clock
$$ =\ell \omega ;=0.2 \times \frac{\pi}{30} \mathrm{~ms}^{-1} \quad[\text { Given, } \ell=20 \mathrm{~cm}=0.2 \mathrm{~m}] $$
Let the seconds hand of clock rotate through an angle $\theta$ in time t. We have $\theta=\omega t$. In Fig. 52(a) A and B denote initial and final position of tip of second’s hand. $\mathbf{v} _{\mathbf{A}}$ and $\mathbf{v} _{\mathbf{B}}$ is the linear velocity of tip of hand in position A and B.
$\Delta \mathbf{v}=$ The change in linear velocity $=\mathbf{v} _{\mathbf{B}}-\mathbf{v} _{\mathbf{A}}$

From Fig. 52(b); $|\Delta \mathbf{v}|=M N=2 \mathrm{v} \sin \left(\frac{\theta}{2}\right)$. Therefore
$$ \begin{aligned} & 0.67 \pi \times 10^{-2}=0.2 \times \frac{\pi}{30} \sin \left(\frac{\theta}{2}\right), \text { or } \sin \left(\frac{\theta}{2}\right)=\frac{1}{2} \\ & \therefore \theta=60^{\circ}=\frac{\pi}{3} \text { radian } \end{aligned} $$
Now, $\mathrm{t}=\frac{\theta}{\omega}=\frac{\pi \times 30}{3 \times \pi}=10 \mathrm{~s}$
Example-31 :
A particle of mass $500 \mathrm{~g}$ is tied to one end of a string of length $1.5 \mathrm{~m}$. The particle is whirled into a horizontal circle by holding the other end of string in hand. The breaking strength of string is $1.2 \mathrm{kgf}$. What is maximum number of revolutions per minute so that string does not break? $\mathrm{g}=10 \mathrm{~ms}^{-2}$
Show Answer
Solution :
Let $\mathrm{v} _{\max }$ be the maximum linear speed of particle so that string does not break. The tension in string equals to breaking strength of string. The tension in string provides necessary centripetal force on particle. Therefore
$$ \mathrm{T} _{\max }=\frac{\mathrm{mv} _{\max }^{2}}{\ell} $$
Given, $\mathrm{T} _{\text {max }}=1.2 \mathrm{kgf}=12 \mathrm{~N} ; \quad \ell=1.5 \mathrm{~m} ; \quad \mathrm{m}=0.5 \mathrm{~kg}$
$\therefore \mathrm{v} _{\text {max }}=\sqrt{\frac{\mathrm{T} _{\text {max }} \ell}{\mathrm{m}}}=\sqrt{\frac{12 \times 1.5}{0.5}}=6 \mathrm{~ms}^{-1}$
$\omega _{\max }=$ The maximum angular speed of particle $=\frac{\mathrm{v} _{\max }}{\ell}=\frac{6}{1.5}=4 \mathrm{rad} / \mathrm{s}$
$\therefore \mathrm{n} _{\max }=$ The maximum number of revolutions $=\frac{\omega _{\max }}{2 \pi}=\frac{4}{2 \pi} \mathrm{rps}=\frac{4 \times 60}{2 \pi} \mathrm{rpm}$
$$ =\frac{120}{\pi} \mathrm{rpm} $$
Example-32 :
A particle moves in a circle of radius $\mathrm{R}$. The instantaneous angular position, $\theta$ of particle is $\theta=\mathrm{kt}^{2}$ where $\mathrm{k}$ is a constant. What is instantaneous linear acceleration of particle?
Show Answer
Solution :
$\omega=$ The instantaneous angular speed of particle
$$ \begin{equation*} =\frac{\mathrm{d} \theta}{\mathrm{dt}}=2 \mathrm{kt} \tag{1} \end{equation*} $$
As $\omega$ varies with time; the particle has a non-uniform circular motion. The instantaneous linear acceleration, $\mathrm{a}$; has a radial component, $\mathrm{a} _{\mathrm{r}}$; and tangential component $\mathrm{a} _{\mathrm{t}}$. We know
$$ \mathrm{a} _{\mathrm{r}}=\mathrm{R} \omega^{2}=4 \mathrm{k}^{2} \mathrm{Rt}^{2}, \quad \text { and } \quad \mathrm{a} _{\mathrm{t}}=\mathrm{R} \alpha=\mathrm{R}\left(\frac{\mathrm{d} \omega}{\mathrm{dt}}\right)=2 \mathrm{kR} $$
The magnitude of instantaneous linear acceleration, $a$, is
$$ \begin{aligned} & \mathrm{a}=\sqrt{\mathrm{a} _{\mathrm{r}}^{2}+\mathrm{a} _{\mathrm{t}}^{2}}=\sqrt{\left(4 \mathrm{k}^{2} \mathrm{Rt}^{2}\right)^{2}+(2 \mathrm{kR})^{2}} \\ & =2 \mathrm{kR} \sqrt{1+4 \mathrm{k}^{2} \mathrm{t}^{2}} \end{aligned} $$
PROBLEMS FOR PRACTICE
1. A particle moves along $x$-axis. It covers a distance $x _{1}$ with constant speed $\mathrm{v} _{1}$ and a distance $x _{2}$ with a constant speed $\mathrm{v} _{2}$. What is the average speed of the particle?
$\left[\right.$ Ans. $\left.\frac{\left(x _{1}+x _{2}\right) \mathrm{v} _{1} \mathrm{v} _{2}}{x _{1} \mathrm{v} _{2}+x _{2} \mathrm{v} _{1}}\right]$
2. A car covers half of the total distance of its journey with a constant speed $v _{1}$. The other half of the distance is covered as described. For half of the remaining time of journey car moves with a constant speed $\mathrm{v} _{2}$ and the other half time with a constant speed $\mathrm{v} _{3}$. What is the average speed of car?
$\left[\right.$ Ans. $\left.\frac{2 \mathrm{v} _{1}\left(\mathrm{v} _{2}+\mathrm{v} _{3}\right)}{\left(2 \mathrm{v} _{1}+\mathrm{v} _{2}+\mathrm{v} _{3}\right)}\right]$
3. A particle has a one dimensional motion along $\mathrm{z}$-axis. The instantaneous position $\mathrm{z}$ of particle is given by $\mathrm{t}=\sqrt{\mathrm{z}}+3$
$\mathrm{z}$ is the meter and $\mathrm{t}$ in second. Show that the displacement of particle is zero when its instantaneous velocity is zero.
4. A particle having uniformly accelerated motion travels a distance of $2 \mathrm{~m}$ in first $2 \mathrm{~s}$. In next $4 \mathrm{~s}$; the particle travels a distance of $2.2 \mathrm{~m}$. What is (1) initial velocity and (2) acceleration of particle?
[Ans: Initial velocity $=1.15 \mathrm{~ms}^{-1}$, acceleration $=-0.15 \mathrm{~ms}^{-2}$ ]
5. A ball starts from rest and accelerates uniformly for $\mathrm{t} _{1}$ at $0.1 \mathrm{~ms}^{-2}$. It covers some distance with the speed it has acquired at end of $\mathrm{t} _{1}$ second. Then car then retards uniformly at $0.2 \mathrm{~ms}^{-2}$ and comes to rest. The maximum speed acquired by car is $72 \mathrm{kmh}^{-1}$ and the total distance covered is $5 \mathrm{~km}$. What is least time in which car can complete the journey?
[Ans: $400 \mathrm{~s}$ ]
6. A train starts from rest and is again at rest at a station $3 \mathrm{~km}$ away. The train accelerates uniformly for $\frac{2}{3} \mathrm{rd}$ of the journey and retards uniformly for the remaining journey. The total time taken is 3 minute. What is:
(i) acceleration, (ii) retardation, (iii) maximum speed acquired?
[Ans. (i) $\frac{5}{18} \mathrm{~ms}^{-2}$, (ii) $\frac{5}{9} \mathrm{~ms}^{-2}$, (iii) $\left.\frac{100}{3} \mathrm{~ms}^{-1}\right]$
7. $\quad$ Fig. 53 shows $v$ is $t$ graph of particle. What is

(i) total distance traveled, (ii) total displacement and (iii), the average velocity for time interval $=0$ to $\mathrm{t}=40 \mathrm{~s}$ ?
[Ans: (i) 100, (ii) zero, (iii) zero]
8. A particle having one dimensional motion has an instantaneous acceleration, a; given by
$$ \mathrm{a}=-2 \mathrm{t}+\mathrm{r \quad ms}^{-2} $$
The particle is initially at origin of co-ordinates (say $x$-axis) and has an initial speed of $-3 \mathrm{~ms}^{-1}$. Draw (i) v vst and, (ii) $x$ vs t graph for the motion of particle.
[Ans: (i) $v\left(\mathrm{~ms}^{-1}\right)$

9. A ball is projected vertically upwards from top of a tower. Take vertically upward direction as direction of positive $\mathrm{z}$-axis and top of tower as origin of co-ordinates. When the position co-ordinate of ball is $+z _{1}$ its speed is half of what its speed is when its position is $-z _{1}$. Show that maximum height attained by the ball from the top of tower is $\frac{5 z _{1}}{3}$.
10. A particle A, thrown vertically upwards just reaches the top of a tower $100 \mathrm{~m}$ high. When $\mathrm{A}$ is thrown upwards from ground a second particle B is dropped from the top of the tower. Where and when $\mathrm{A}$ and $\mathrm{B}$ cross one another?
[Ans: $75 \mathrm{~m}$ above ground; 2.268 after projection.]
11. A particle undergoes three consecutive displacements. The net displacement is zero. The first displacement is $8 \mathrm{~m}$ westward and the second is $13 \mathrm{~m}$ northwards. What is the third displacement?
[Ans: $15.25 \mathrm{~m} ; 58.5^{\circ}$ South of East]
12. The resultant of two forces $\mathrm{F} _{1}$ and $\mathrm{F} _{2}$ making an angle of $60^{\circ}$ with one other is $20 \mathrm{~N} . \mathrm{F} _{1}: \mathrm{F} _{2}:: 3: 5$. What is $\mathrm{F} _{1}$ and $\mathrm{F} _{2}$ ?
[Ans: $\mathrm{F} _{1}=12 \mathrm{~N} ; \mathrm{F} _{2}=20 \mathrm{~N}$ ]
13. A boy standing at rest on ground hold umbrella at $60^{\circ}$ with vertical so that he does not become wet. The boy throws away umbrella and starts running on road from west to east at $20 \mathrm{~ms}^{-1}$. The rain appears to strike vertically the head of boy. What is:
(i) actual velocity of rain, (ii) velocity of rain wrt to boy?
[Ans: (i) $~ 23 \mathrm{kmh}^{-1}$, (ii) $~ 11.55 \mathrm{kmh}^{-1}$ ]
14. A stream is moving with a speed of $3 \mathrm{~ms}^{-1}$. A motor-boat moves with a speed of $7 \mathrm{~ms}^{-1}$ in still water. The motor-boat starts moving up the stream and drops a packet in stream. The boat travels $4.2 \mathrm{~km}$ up-stream; turns back and picks up to packet dropped. What is total time taken in picking up the packet?
[Ans: 35 minute]
15. Two boats $\mathrm{A}$ and $\mathrm{B}$ start from same point $\mathrm{O}$ in the middle of a river. A moves along the stream and $\mathrm{B}$ across the stream. They cover equal distances and turn back returning to point $\mathrm{O}$. What is ratio of the total time taken by A and B? Given speed of each boat is twice the speed of the river.
[Ans: 1.155]
16. A ball is projected vertically upwards with initial speed $\mathrm{v} _{0}$ at an angle $\theta$ with horizontal. When ball is at a vertical height of $10 \mathrm{~m}$; its instantaneous velocity is
$$ \mathbf{v}=8 \hat{\mathrm{i}}+5 \hat{\mathrm{j}} ; \mathrm{ms}^{-1} $$
(i) What is $\mathrm{v} _{0}$ and $\theta$ ?, (ii) What is maximum vertical height attained by the ball?
[Ans: $\mathrm{v} _{0}=17 \mathrm{~ms}^{-1} ; \theta=61.9^{0}, \mathrm{H}=11.2 \mathrm{~m}$ ]
17. A “basket” in basket-ball game is at a vertical height of $3.5 \mathrm{~m}$ above ground. A boy at a horizontal distance of $10 \mathrm{~m}$ jumps up to a height of $2.5 \mathrm{~m}$ above ground and throws ball with a speed $\mathrm{v} _{0}$ at an angle of $60^{\circ}$ with the vertical in such a manner that the ball enters the basket. What is $\mathrm{v} _{0}$ ? $\left(\mathrm{g}=9.8 \mathrm{~ms}^{-1}\right)$
[Ans: $11.7 \mathrm{~ms}^{-1}$ ]
18. A tower is $100 \mathrm{~m}$ high. From the top of tower a ball is projected upwards with a speed of $40 \mathrm{~ms}^{-1}$ at an angle of $45^{\circ}$ with the vertical.
(a) At what distance from the foot of the tower the ball hits ground? What is its velocity at this moment?
(b) What is the time of flight of ball? $\left(\mathrm{g}=10 \mathrm{~ms}^{-2}\right)$
[Ans: (a) $229.65 \mathrm{~m} ; 59.9 \mathrm{~ms}^{-1}$ at $64.3^{0}$ with the horizontal, (b) $8.12 \mathrm{~s}$ ]
19. A gun fires two cannons each with a speed of $250 \mathrm{~ms}^{-1}$. The first cannon is fired at an angle of $60^{\circ}$ and the second at an angle of $45^{\circ}$ with the horizontal. How long after firing the two cannons hit one
another $\mathrm{g}=9.8 \mathrm{~ms}^{-2}$.
[Ans: $11 \mathrm{~s}$ ]
20. An aeroplane dives towards ground along a straight line path at $37^{\circ}$ with the horizontal. When it is at a height of $720 \mathrm{~m}$ above ground and is moving at a speed of $540 \mathrm{kmhr}^{-1}$; it drops a packet. $\mathrm{X}$ is a point on ground along the line of sight of aeroplane. What is distance of packet from $\mathrm{X}$ as it hits ground? $\left(\mathrm{g}=10 \mathrm{~ms}^{-2}\right)$
[Ans: $240 \mathrm{~m}$ ]
21. An aircraft executes a horizontal loop of radius $1 \mathrm{~km}$ moving with a speed of $900 \mathrm{kmhr}^{-1}$. Express centripetal acceleration as a fraction of acceleration due to gravity. $\mathrm{g}=9.8 \mathrm{~ms}^{-2}$
[Ans: 0.064]
22. An open umbrella of radius $0.5 \mathrm{~m}$ and height $1.4 \mathrm{~m}$ is held in a vertical position on ground. It revolves about it handel as axis at a speed of $20 \mathrm{rpm}$. A water drop on rim of umbrella spins off the umbrella and hits ground. What is distance of the point where water drop hits ground from the foot of the handel of umbrella? $\left(g=10 \mathrm{~ms}^{-2}\right)$
[Ans: $2.054 \mathrm{~m}$ ]
23. A cyclist is moving with a speed of $27 \mathrm{kmhr}^{-1}$. The cyclist moves along a circular road of radius $80 \mathrm{~m}$. He applies brakes and reduces his speed at a constant rate of $0.5 \mathrm{~ms}^{-1}$. What is magnitude and direction of the net acceleration of cyclist?
[Ans $0.86 \mathrm{~ms}-2,35.4^{0}$ with the inward radius]
24. A particle moves in a circle of radius $b$ in such a manner that instantaneous radial and tangential acceleration are equal in magnitude. The initial (i.e. $t=0$ ) linear and angular speed of particle is $\mathrm{v}$ and $\omega$.
(i) Show that instantaneous angular speed is $\left(\frac{\omega}{1-\omega t}\right)$.
(ii) Time taken to complete first revolutions $\frac{\mathrm{b}}{\mathrm{v}}\left[1-\mathrm{e}^{-2 \pi}\right]$
ADDITIONAL EXAMPLES
1. From a tower of height $\mathrm{H}$, a particle is thrown vertically upwards with a speed $u$. The time taken by the particle, to hit the ground, is $n$ times that taken by it to reach the highest point of its path. The relation between $\mathrm{H}$, $\mathrm{u}$ and $\mathrm{n}$ is:
(a) $2 \mathrm{gH}=\mathrm{nu}^{2}(\mathrm{n}-2)$
(b) $\mathrm{gH}=(\mathrm{n}-2) \mathrm{u}^{2}$
(c) $2 \mathrm{gH}=\mathrm{n}^{2} \mathrm{u}^{2}$
(d) $\mathrm{gH}=(\mathrm{n}-2)^{2} \mathrm{u}^{2}$
Show Answer
Correct option is (1)
(IIT 2014)
Solution:
We know that the particle will take a time $\mathrm{t} _{1}\left(=\frac{\mathrm{u}}{\mathrm{g}}\right)$ to reach the highest point $($ for which $\mathrm{v}=0$ ). Let $\mathrm{t} _{2}$ be the time taken by the particle to hit the ground. Then
$$ -\mathrm{H}=\mathrm{ut} _{2}+\frac{1}{2}(-\mathrm{g}) \mathrm{t} _{2}^{2} $$
We are given that $\mathrm{t} _{2}=\mathrm{nt} _{1}$. This gives
$$ 2 \mathrm{gH}=\mathrm{nu}^{2}(\mathrm{n}-2) $$
2. A projectile is given an initial velocity of $(\hat{i}+2 \hat{j}) \mathrm{m} / \mathrm{s}$, where $\hat{i}$ is along the ground and $\hat{j}$ is along the vertical. If $g=10 \mathrm{~m} / \mathrm{s}^{2}$, the equation of its trajectory is:
(a) $y=2 x-5 x^{2}$
(b) $4 y=2 x-5 x^{2}$
(c) $4 y=2 x-25 x^{2}$
(d) $\mathrm{y}=x-5 x^{2}$
Show Answer
Correct option is (1)
(IIT 2016)
Solution:
There is no acceleration along the horizontal direction. Therefore
$$ x=\mathrm{v} _{o x} \mathrm{t}=1 \times \mathrm{t}=\mathrm{t} $$
Also, $y=v _{\text {oy }} \mathrm{t}+\frac{1}{2}(-\mathrm{g}) \mathrm{t}^{2}=2 \mathrm{t}-5 \mathrm{t}^{2}$
Eliminating $\mathrm{t}$ we get
$$ y=2 x-5 x^{2} $$
This is the equation of the trajectory.
3. Two stones are thrown up simultaneously from the edge of a cliff $240 \mathrm{~m} \quad \mathrm{high}$ with initial speed of $10 \mathrm{~m} / \mathrm{s}$ and $40 \mathrm{~m} / \mathrm{s}$ respectively. Which of the following graph best represents the time variation of relative position of the second stone with respect of the first?
(Assume stones do not rebound after hitting the ground and neglect air resistance. (Take g $=10 \mathrm{~m} / \mathrm{s}^{2}$ )
(The figure are schematic and not drawn to scale)

Show Answer
Correct option is (1)
(IIT 2015)
Solution:
For the first object, we have
$\mathrm{y} _{1}=10 \mathrm{t}+\frac{1}{2}(-10) \mathrm{t}^{2}$
If it takes a time $t _{1}$ to reach the ground, we have
$-240=10 \mathrm{t} _{1}=5 \mathrm{t} _{1}^{2} \quad$ or $\quad \mathrm{t} _{1}=8 \mathrm{~s}$
For the second object,
$\mathrm{y} _{2}=40 \mathrm{t}-5 \mathrm{t}^{2}$
Time $t _{2}$, taken by it to reach the ground, comes out to be 12 s. The relative displacement of the second object, with respect to the first, is
$$ \mathrm{y} _{21}=\mathrm{y} _{2}-\mathrm{y} _{1}=30 \mathrm{t} \text { for }(0<\mathrm{t}<8) $$
This is equation of a straight line.
For $8<\mathrm{t}<12$, we would have
$\mathrm{y} _{21}=40 \mathrm{t}-5 \mathrm{t}^{2}$
This is equation of a parabola. The graph would have the shape shown in (1).
Question bank
Key Learning Points
1. A body is in motion when its position changes with time in a conveniently chosen frame of reference (a conveniently chosen co-ordinate system).
2. In kinematics we study motion without bothering about cause of motion.
3. Rest and motion are relative. A object may be at rest in one frame of reference and in motion in another frame of reference. There is no absolute rest.
4. For a body in motion the actual length of path described is distance traveled. It is a scalar quantity. The line joining the initial position and the final position having an arrow head at the final position is known as displacement. It is a vector quantity.
5. The average speed $\left(\mathrm{v} _{\mathrm{av}}\right)$ is ratio of total distance traveled and the total time taken.
The average velocity $\left(\overrightarrow{\mathrm{V}} _{\mathrm{av}}\right)$ is the ratio of the displacement and the time taken.
6. The instantaneous speed, $\mathrm{v}$, is
$$ \mathrm{v}=\mathrm{Lt} _{\Delta \mathrm{t} \rightarrow 0} \frac{\Delta \mathrm{s}}{\Delta \mathrm{t}} \equiv \frac{\mathrm{ds}}{\mathrm{dt}} $$
where $\Delta \mathrm{s}$ is infitesimally small distance traveled in time interval $t, t+\Delta t$. It equals slope of tangent to distance traveled (s) vs time ( $\mathrm{t}$ ) graph at the point considered.
7. For one dimensional motion say along $x$-axis; we have uniform motion; if speed is same at all time. i.e. $\mathrm{v}=$ instantaneous speed $=$ constant.
8. For a body having different velocity at different times, we have non-uniform motion. If $v$ increases with time motion is accelerated. If, however, $v$ decreases as time increases motion is retarded.
The average and instantaneous acceleration are:
$a_{a v}=\frac{u_2-v_1}{t_2-t_1}=\frac{\Delta v}{\Delta t}, a=Lt\underset{\Delta t \rightarrow 0}{ } \frac{\Delta v}{\Delta t} \equiv \frac{d v}{d t}$
9. The instantaneous acceleration is numerically equal to slope of tangent to $v \quad \mathrm{vs} \mathrm{t}$ graph at the moment of time considered.
10. For a body having non-uniform motion the total distance traveled equals area under v vs $t$ graph.
11. A body having same acceleration at all times; motion is uniformly accelerated. Consider uniformly accelerated motion; accelerations $=a$; of a body having initial (i.e. $t=0$ ), speed $v _{0}$; the instantaneous (i.e. $\mathrm{t}=\mathrm{t}$ ); velocity, $\mathrm{v}$, is
$$ \mathrm{v}=\mathrm{v} _{0}+\mathrm{at} $$
The total distance s; traveled in time t; is
$$ \mathrm{s}=\mathrm{v} _{0} \mathrm{t}+\frac{1}{2} \mathrm{at}^{2} ; \text { Also, } \mathrm{v}^{2}-\mathrm{v} _{0}^{2}=2 \mathrm{as} $$
The distance traveled in the $\mathrm{n}^{\text {th }}$ second of motion; $\mathrm{s} _{\mathrm{n}}$; is
$$ \mathrm{s} _{\mathrm{n}}=\mathrm{v} _{0}+\frac{\mathrm{a}}{2}[2 \mathrm{n}-1] $$
These are equations of uniformly accelerated motion. Graphical representation are shown below.

12. A body moving freely under gravity of earth has a uniform acceleration $=\mathrm{g}=9.8 \mathrm{~ms}^{-2}$, if distances involved are very small as compared to radius of earth $(=6400 \mathrm{Km})$
13. Vector are physical quantities having a magnitude and direction. They add up according to triangle law of vector addition. Vector addition is commutative.
14. Fig. 54 shows two vectors $\mathbf{P}$ and $\mathbf{Q}$. $\theta$ is angle between them. Draw two vectors so that their tails coincide. The angle they make with one another is $\theta$.

Let $\mathbf{R}=\mathbf{P}+\mathbf{Q}, \mathbf{R}$ is known as resultant of $\mathbf{P}$ and $\mathbf{Q}$. Fig. 54(b) shows triangle law of vetors. Also,
$\mathrm{R}^{2}=\mathrm{P}^{2}+\mathrm{Q}^{2}+\mathrm{ZPQ} \cos \theta$, and $\tan \alpha=\frac{\mathrm{Q} \sin \theta}{\mathrm{P}+\mathrm{Q} \cos \theta}$
15. For adding more than two vectors the polygon law of vectors is used. According to this law; draw a polygon whose different sides taken in order represent the vector to be added. The resultant is the side that completes the polygon; taken in opposite order. For vectors forming a closed polygon; the resultant is zero.
16. The rectangular component of a vector $\mathrm{P}$, are two mutually perpendicular vectors whose resultant equals $P$.
17. The unit vector $\widehat{\mathrm{A}}$ is a vector having same direction as $\mathrm{A}$, but a magnitude of unity $\widehat{\mathrm{A}}=\frac{\mathbf{A}}{|\mathbf{A}|}$
18. $\quad \hat{\mathrm{i}}, \hat{\mathrm{j}}$ and $\hat{\mathrm{k}}$ are unit vectors along $x-\mathrm{y}-$ and $\mathrm{z}$-axis of a Cartesian co-ordinate system. $\mathbf{r}=$ Position vector of point having co-ordinates $(x, y, z)$ is
$$ \mathbf{r}=x \hat{\mathrm{i}}+\mathrm{y} \hat{\mathrm{j}}+\mathrm{z} \hat{\mathrm{k}} ; \quad \text { and } \quad \mathrm{r}=|\mathbf{r}|=\left(x^{2}+\mathrm{y}^{2}+\mathrm{z}^{2}\right)^{1 / 2} $$
19. Any vector $\mathbf{P}$, can be represented in terms of its $x$, $y$ and $z$ components as
$\mathbf{P}=\mathrm{P} _{x} \hat{\mathrm{i}}+\mathrm{P} _{\mathrm{y}} \hat{\mathrm{j}}+\mathrm{P} _{z} \hat{\mathrm{k}}$
$\mathrm{P} _{x}, \mathrm{P} _{\mathrm{y}}$ and $\mathrm{P} _{\mathrm{z}}$ are $x$, $\mathrm{y}$ and $\mathrm{z}$-components of $\mathbf{P}$.
20. Let $\mathbf{R}=\mathbf{P}-\mathbf{Q}$; i.e. we subtract $\mathbf{Q}$ from $\mathbf{P}$. We obtain $\mathbf{R}$ by, using triangle law of vectors, by adding $\mathbf{Q}$ to $\mathbf{P}$ where $\mathbf{Q}^{\prime}=-\mathbf{Q}$. Vector subtraction is not commutative, i.e.
$$ \mathbf{P}-\mathbf{Q} \neq \mathbf{Q}-\mathbf{P} $$
21. Let $\mathbf{r} _{A}$ and $\mathbf{r} _{B}$ be the position vector of two points $A$ and $B \cdot \mathbf{r} _{A B}=\mathbf{r} _{A}-\mathbf{r} _{B}$ is the relative position vector of Aw.r.t. B. Similarly for two particles A and B having velocity $\mathbf{v} _{\mathbf{A}}$ and $\mathbf{v} _{\mathbf{B}}$; respectively,
$\mathbf{v} _{\mathbf{A B}}=$ Relative velocity of Aw.r.t $\mathrm{B}=\mathbf{v} _{\mathbf{A}}-\mathbf{v} _{\mathbf{B}}$
$\therefore \mathrm{v} _{\mathrm{AB}}=\left[\mathrm{v} _{\mathrm{A}}^{2}+\mathrm{v} _{\mathrm{B}}^{2}+2 \mathrm{v} _{\mathrm{A}} \mathrm{v} _{\mathrm{B}} \cos (\pi-\theta)\right]^{1 / 2}=\left[\mathrm{v} _{\mathrm{A}}^{2}+\mathrm{v} _{\mathrm{B}}^{2}-2 \mathrm{v} _{\mathrm{A}} \mathrm{v} _{\mathrm{B}} \cos \theta\right]^{1 / 2}$
22. The scalar or dot products of two vectors $\mathbf{A}$ and $\mathbf{B}$; by definition, is
$$ \mathbf{A} \cdot \mathbf{B}=\mathrm{AB} \cos \theta $$
where $\theta$ is angle between $\mathbf{A}$ and $\mathbf{B}$. It is equal to magnitude of one vector (say $\mathbf{A}$ ) and the component of the other vector (i.e. B) in the direction of $\mathbf{A} \cdot \mathbf{A} \cdot \mathbf{B}=\mathbf{B} \cdot \mathbf{A}$. For parallel vectors; $\mathbf{A} \cdot \mathbf{B}$ is maximum. The dot product of perpendicular vectors is zero; i.e.
$$ \mathrm{A} \neq 0, \mathrm{~B} \neq 0 ; \mathbf{A} \cdot \mathbf{B}=0 \text { if } \cos \theta=0 \text { or } \theta=\frac{\pi}{2} $$
23. For unit vectors $\hat{i}, \hat{j} \quad and \quad \hat{k}$ in a Cartesian co-ordinate;
$$ \hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k} \cdot \hat{k}=1, \quad \text { and } \quad \hat{i} \cdot \hat{j}=\hat{j} \cdot \hat{k}=\hat{k} \cdot \hat{i}=1 $$
24. Expressing $\mathbf{A}$ and $\mathbf{B}$ in terms of their Cartesian components as:
$$ \begin{aligned} & \mathbf{A}=\mathrm{A} _{x} \hat{\mathrm{i}}+\mathrm{A} _{y} \hat{\mathrm{j}}+\mathrm{A} _{\mathrm{z}} \hat{\mathrm{k}} \\ & \mathbf{B}=\mathrm{B} _{x} \hat{\mathrm{i}}+\mathrm{B} _{\mathrm{y}} \hat{\mathrm{j}}+\mathrm{B} _{\mathrm{z}} \hat{\mathrm{k}} \end{aligned} $$
We have,
$$ \mathbf{A} \cdot \mathbf{B}=\mathrm{A} _{x} \mathrm{~B} _{x}+\mathrm{A} _{y} \mathrm{~B} _{\mathrm{y}}+\mathrm{A} _{\mathrm{z}} \mathrm{B} _{\mathrm{z}} $$
25. The cross or vector product $\mathbf{C}$; of two vector $\mathbf{A}$ and $\mathbf{B}$ is defined as
$$ |\mathbf{C}|=|\mathbf{A} \times \mathbf{B}|=\mathrm{AB} \sin \theta $$
The direction, $\hat{n}$; of $\mathbf{C}$ is given by “Right-hand Screw” rule. Place a right handed screw perpendicular to the plane containing $\mathbf{A}$ and $\mathbf{B}$. Rotate screw so that $\mathbf{A}$ goes and coincides with $\mathbf{B}$. The direction in which screw advances is direction of $\mathbf{C}$ or $\hat{n}$.

The cross-product of parallel vectors or antiparallel vector is zero.
26. In terms of $\hat{i}, \hat{j}$ and $\hat{k}$; in a Cartesian co-ordinate system.
$$ \hat{i} \times \hat{i}=\hat{j} \times \hat{j}=\hat{k} \times \hat{k}=0, \hat{i} \times \hat{j}=\hat{k} ; \quad \hat{j} \times \hat{k}=\hat{i} ; \quad \hat{k} \times \hat{i}=\hat{j} $$
27. For $\mathbf{A}=\mathrm{A} _{x} \hat{\mathrm{i}}+\mathrm{A} _{\mathrm{y}} \hat{\mathrm{j}}+\mathrm{A} _{z} \hat{k} ; \quad \mathbf{B}=\mathrm{B} _{x} \hat{\mathrm{i}}+\mathrm{B} _{y} \hat{\mathrm{j}}+\mathrm{B} _{z} \hat{\mathrm{k}}$
$$ \begin{aligned} & \mathbf{C}=\mathbf{A} \times \mathbf{B}=\left|\begin{array}{ccc} \hat{\mathrm{i}} & \hat{\mathrm{j}} & \hat{\mathrm{k}} \\ \mathrm{A} _{x} & \mathrm{~A} _{\mathrm{y}} & \mathrm{A} _{\mathrm{z}} \\ \mathrm{B} _{x} & \mathrm{~B} _{\mathrm{y}} & \mathrm{B} _{\mathrm{z}} \end{array}\right| \\ & =\hat{\mathrm{i}}\left[\mathrm{A} _{\mathrm{y}} \mathrm{B} _{\mathrm{z}}-\mathrm{A} _{\mathrm{z}} \mathrm{B} _{\mathrm{y}}\right]+\hat{\mathrm{j}}\left[\mathrm{A} _{\mathrm{z}} \mathrm{B} _{x}-\mathrm{A} _{\mathrm{x}} \mathrm{B} _{\mathrm{z}}\right]+\hat{\mathrm{k}}\left[\mathrm{A} _{x} \mathrm{~B} _{\mathrm{y}}-\mathrm{A} _{\mathrm{y}} \mathrm{B} _{x}\right] \end{aligned} $$
28. A body, moving in a vertical plane, in the gravity of earth, having some initial speed $\mathrm{v} _{0}$ at an angle $\theta$ with the horizontal direction; is known as a projectile.
29. To analyse motion of projectile we resolve the motion in two rectangular components. Choosing horizontal direction as $x$-axis and vertically upward direction as direction of positive $y$-axis; and the initial position as origin of co-ordinates we have,
a) Motion along $x$-axis
$\mathrm{v} _{\mathrm{x} 0}=$ Initial velocity along $x$-axis $=\mathrm{v} _{0} \cos \theta ; \mathrm{a} _{x}=0$. These is uniform motion in the horizontal direction. Let $\mathrm{v} _{x}$ be the $x$-component of instantaneous velocity and $x$ be the instantaneous $x$ co-ordinate of projectile. Then
$$ \begin{align*} & \mathrm{v} _{x}=\mathrm{v} _{x 0}=\mathrm{v} _{0} \cos \theta \tag{i} \\ & x=\mathrm{v} _{x 0} \times \mathrm{t}=\left(\mathrm{v} _{0} \cos \theta\right) \mathrm{t} \tag{ii} \end{align*} $$
b) Motion along $y$-axis
$\mathrm{v} _{\mathrm{yo}}=$ Initial velocity along $\mathrm{y}-$ axis, $\mathrm{a} _{\mathrm{y}}=-\mathrm{g}$. We have uniformly accelerated motion along $\mathrm{y}-$ axis. Obviously.
$\mathrm{v} _{\mathrm{y}}=$ The instantaneous $\mathrm{y}$-component of velocity
$=\mathrm{v} _{0} \sin \theta+(-\mathrm{g}) \mathrm{t} \hspace{50mm} . . . . (iii)$
$y=$ The instantaneous $y$-co-ordinate of projectile
$=\left(\mathrm{v} _{0} \sin \theta\right) \mathrm{t}+\frac{1}{2}(-\mathrm{g}) \mathrm{t}^{2} \hspace{50mm} . . . . (iv)$
30. From above four equations every information regarding projectile can be worked.
Some important results of projectile motion are summarized below.
a) Equations of trajectory.
$$ \mathrm{y}=(\tan \theta) x-\frac{g x^{2}}{2 \mathrm{v} _{0}^{2} \cos ^{2} \theta} $$
This is equation of a parabola.
b) Time of flight $(\mathrm{T})$
$$ \mathrm{T}=\frac{2 \mathrm{v} _{0} \sin \theta}{\mathrm{g}} $$
c) Maximum vertical height $(\mathrm{H})$
$$ \mathrm{H}=\frac{\mathrm{v} _{0}^{2} \sin ^{2} \theta}{2 \mathrm{~g}} $$
d) Horizontal range ( $\mathrm{R}$ )
$$ \mathrm{R}=\frac{\mathrm{v} _{0}^{2} \sin ^{2} \theta}{\mathrm{g}} $$
For a given value of $\mathrm{v} _{0}$ range is maximum for $\theta=45^{\circ} . \mathrm{R} _{\max }=\frac{\mathrm{v} _{0}^{2}}{\mathrm{~g}}$. For a constant value of $\mathrm{v} _{0}$ there are two direction of projection, $\theta _{1}$ and $\theta _{2}$ for same horizontal range. $\theta _{1}+\theta _{2}=90^{\circ}$.
e) The instantaneous velocity $\mathbf{v}$ of projectile is
$$ \begin{aligned} & \mathbf{v}=\left(\mathrm{v} _{0} \cos \theta\right) \hat{\mathrm{i}}+\left(\mathrm{v} _{0} \sin \theta-\mathrm{gt}\right) \hat{\mathrm{j}} \\ & \mathrm{v}=|\mathbf{v}|=\left[\left(\mathrm{v} _{0} \cos \theta\right)^{2}+\left(\mathrm{v} _{0} \cos \theta-\mathrm{gt}\right)^{2}\right]^{1 / 2}, \tan \alpha=\frac{\mathrm{v} _{0} \cos \theta-\mathrm{gt}}{\mathrm{v} _{0} \cos \theta} \end{aligned} $$
where $\alpha$ is angle $\mathbf{v}$ makes with horizontal direction.
f) At maximum vertical height.
$\mathbf{v}=\left(\mathrm{v} _{0} \cos \theta\right) \hat{\mathrm{i}}$
and $\mathbf{a} \cdot \mathbf{v}=0$, where $\mathbf{a}$ is acceleration vector.
31. A particle moving in a circle of radius $\mathrm{R}$ has circular motion. A line through center of circle and perpendicular to plane of circle is known as axis of rotation.
32. The instantaneous angular position, $\theta$, is angle instantaneous radius joining the position $\mathrm{P}$ of particle with centre of circle 0 , makes with a conveniently chosen reference line.
33 In circular motion
$\omega _{\mathrm{av}}=$ The average angular speed $=\frac{\text { Total angle described }}{\text { Total time taken }}$
$$ =\frac{\theta _{2}-\theta _{1}}{\mathrm{t} _{2}-\mathrm{t} _{1}}=\frac{\Delta \theta}{\Delta \mathrm{t}} $$
$\omega=$ The instantaneous angular speed
$$ =\operatorname{Lt} _{\Delta t \rightarrow 0}\left(\frac{\Delta \theta}{\Delta \mathrm{t}}\right)=\frac{\mathrm{d} \theta}{\mathrm{dt}} $$
$\mathrm{a} _{\mathrm{av}}=$ The average angular acceleration
$$ =\frac{\text { Total change in angular speed }}{\text { Total time taken }}=\frac{\omega _{2}-\omega _{1}}{\mathrm{t} _{2}=\mathrm{t} _{1}}=\frac{\Delta \omega}{\Delta \mathrm{t}} $$
$\alpha=$ The instantaneous angular acceleration
$$ =\operatorname{Lt} _{\Delta t \rightarrow 0}\left(\frac{\Delta \omega}{\Delta \mathrm{t}}\right)=\frac{\mathrm{d} \omega}{\mathrm{dt}} $$
34. The linear speed, $\mathrm{v}$, is $\mathrm{v}=\mathrm{R} \omega$
$\mathrm{R}=$ radius of circular path. Also, $\mathrm{a}=$ The linear acceleration $=\mathrm{R} \alpha$
35. For a particle moving in a horizontal circle of constant radius R; with a uniform speed (i.e. $\omega=$ const. or $\mathbf{v}=$ const.) the linear velocity $\mathbf{v}$ is not a constant. The direction of $\mathbf{v}$ changes continuously. The instantaneous linear velocity $\mathbf{v}$ is in the direction of tangent to the circle at the point $\mathrm{P}$ considered.
36. For a particle making in a horizontal circle of constant radius $\mathrm{R}$ with uniform speed $\mathrm{v}$; there is linear acceleration, $\mathbf{a}$; due to charge in direction of $\mathbf{v}$.
$\mathrm{a}=$ The magnitude of linear acceleration $=\frac{\mathrm{v}^{2}}{\mathrm{R}}$.
The acceleration is along the direction of the instantaneous radius vector directed towards the centre of circle. It is known as centripetal acceleration. The instantaneous linear velocity, $\mathbf{v}$, the instantaneous acceleration, $\mathbf{a}$; are always mutually perpendicular. Therefore $\mathbf{v} \cdot \mathbf{a}=0$.
37. For circular motion with a variable speed; we have
i) $a _{c}=$ The centripetal component of acceleration $=\frac{v^{2}}{R}=v \omega$.
ii) $\mathrm{a} _{\mathrm{t}}=$ The tangential component of acceleration $=\frac{\mathrm{dv}}{\mathrm{dt}}$.
$$ \mathbf{a}=\left(-a _{c}\right) \hat{r}+a _{t}(\hat{t}) $$
$\hat{r}$ and $\hat{t}$ are unit vector in radially outward and tangential directions.
$\therefore|\mathbf{a}|=\sqrt{\mathrm{a} _{\mathrm{c}}^{2}+\mathrm{a} _{\mathrm{t}}^{2}}$
1. Fig. shows v vs t graph of a particle moving along $x$-axis. For the time interval $\left(t _{2}-t _{1}\right)$
$$ \begin{align*} & \mathrm{v} _{\mathrm{av}}=\frac{x\left(\mathrm{t} _{2}\right)-x\left(\mathrm{t} _{1}\right)}{\mathrm{t} _{2}-\mathrm{t} _{1}} \tag{i} \\ & \mathrm{a} _{\mathrm{av}}=\frac{v\left(\mathrm{t} _{2}\right)-v\left(\mathrm{t} _{1}\right)}{\mathrm{t} _{2}-\mathrm{t} _{1}} \tag{ii} \\ & x\left(\mathrm{t} _{2}\right)=x\left(\mathrm{t} _{1}\right)+\mathrm{v} _{\mathrm{av}}\left(\mathrm{t} _{2}-\mathrm{t} _{1}\right)+\frac{1}{2} \mathrm{a} _{\mathrm{av}}\left(\mathrm{t} _{2}-\mathrm{t} _{1}\right)^{2} \tag{iii} \\ & \text { and } x\left(\mathrm{t} _{2}\right)-x\left(\mathrm{t} _{1}\right)=\text { area ABCD } \tag{iv} \end{align*} $$
Which of the above relation/(s) is/are incorrect?

(1) (i) and (ii)
(2) (iii)
(3) (iii) and (iv)
(4) (i), (ii) and (iii)
Show Answer
Correct answer: (2)
Solution:
In the time interval considered acceleration is not uniform. Eqn (iii) is equation of a uniformly accelerated motion.
2. A car covers $40 \%$ of the total distance of its journey with a constant speed $v$. It moves for half of the total time of journey with a constant speed $2 \mathrm{v}$. For the remaining time of journey it moves with a constant speed $3 \mathrm{v}$. The average speed of the car for the complete journey is:
(1) $2 \mathrm{v}$
(2) $1.8 \mathrm{v}$
(3) $\left(\frac{25}{18}\right) \mathrm{v}$
(4) $\left(\frac{5}{4}\right) \mathrm{v}$
Show Answer
Correct answer: (3)
Solution:
Let $\mathrm{S}$ and $\mathrm{T}$ denote the total distance and the total time of journey. $\mathrm{S} _{1}=0.4 \mathrm{~S}=\frac{25}{5}$ is the distance travelled with constant speed $v$. The time taken, $t _{1}$, is
$$ \begin{equation*} \mathrm{t} _{1}=\frac{2}{5}\left(\frac{\mathrm{S}}{\mathrm{v}}\right) \tag{i} \end{equation*} $$
During the second part of the journey, the time taken $=\mathrm{t} _{2}=\frac{\mathrm{T}}{2}$
The distance travelled $\mathrm{S} _{2}$ is
$$ \begin{equation*} \mathrm{S} _{2}=2 \mathrm{vt} _{2}=\mathrm{vT} \tag{ii} \end{equation*} $$
Let $\mathrm{S} _{3}$ be the distance traveled during the remaining journey and $\mathrm{t} _{3}$ be time taken. Obviously
$$ S _{3}=S-\left[\frac{2 S}{5}+v T\right]=\frac{3 S}{5}-v T $$
and $\quad \mathrm{t} _{3}=\frac{\mathrm{S} _{3}}{3 \mathrm{v}}=\frac{\mathrm{S}}{5 \mathrm{v}}-\frac{\mathrm{T}}{3}$
Now, $\mathrm{T}=\mathrm{t} _{1}+\frac{\mathrm{T}}{2}+\mathrm{t} _{3}$
or $\frac{\mathrm{T}}{2}=\mathrm{t} _{1}+\mathrm{t} _{3}=\frac{2 \mathrm{~S}}{5 \mathrm{v}}+\left(\frac{\mathrm{S}}{5 \mathrm{v}}-\frac{\mathrm{T}}{3}\right)$
or $\frac{5 \mathrm{~T}}{6}=\frac{3 \mathrm{~S}}{5 \mathrm{v}}$
The average speed of the complete journey is
$$ \overline{\mathrm{v}}=\frac{\mathrm{S}}{\mathrm{T}}=\left(\frac{25}{15}\right) \mathrm{v} $$
3. A motorboat moving at a constant speed meets a “raft” at some point $P$. The motor boat
moves for 30 minute and then it turns back. It now meets the same raft at a point $Q . P Q=$ $4 \mathrm{~km}$. The speed of flow of river is:
(1) $4 \quad \mathrm{kmhr}^{-1}$
(2) $2 \quad \mathrm{kmhr}^{-1}$
(3) $1.6 \quad \mathrm{kmhr}^{-1}$
(4) $1.8 \quad \mathrm{kmhr}^{-1}$
Show Answer
Correct answer: (1)
Solution:
Let $\mathrm{V}$ and $\mathrm{V} _{\mathrm{R}}$ denote speed of motor boat and river respectively. When motor boat moves down the stream its resultant velocity is $\left(\mathrm{V}+\mathrm{V} _{\mathrm{R}}\right)$ and when it moves up the stream resultant velocity is $\left(\mathrm{V}-\mathrm{V} _{\mathrm{R}}\right)$. Let $\mathrm{t}$ be time taken by motor boat, after it turns back to meet raft at $\mathrm{Q}$. The total distance $\mathrm{S}$ traveled by boat is:
$$ \begin{equation*} \mathrm{S}=\left(\mathrm{V}+\mathrm{V} _{\mathrm{R}}\right) \frac{1}{2}+\left(\mathrm{V}-\mathrm{V} _{\mathrm{R}}\right) \mathrm{t} \tag{i} \end{equation*} $$
where $\mathrm{V}$ and $\mathrm{V} _{\mathrm{R}}$ are expressed in $\mathrm{kmhr}^{-1}$. Also
$$ \begin{align*} & \mathrm{S}=\text { average speed of boat } \times \text { total time taken } \\ & =\left[\frac{\left(\mathrm{V}+\mathrm{V} _{\mathrm{R}}\right)+\left(\mathrm{V}-\mathrm{V} _{\mathrm{R}}\right)}{2}\right]\left[\frac{1}{2}+\mathrm{t}\right] \\ & =\mathrm{V}\left(\frac{1}{2}+\mathrm{t}\right) \tag{ii} \end{align*} $$
From Eqns (i) and (ii) we have
$$ \begin{aligned} & \left(V+V _{R}\right) \frac{1}{2}+\left(V-V _{R}\right) t=V\left(\frac{1}{2}+t\right) \\ & \text { or } V _{R}+2\left(V-V _{R}\right) t=2 V t \\ & \text { or } V _{R}(1-2 t)=0 \end{aligned} $$
A program to give wings to girl students $\therefore \mathrm{t}=\frac{1}{2} \mathrm{hr}$ $\left[\because \mathrm{V} _{\mathrm{R}} \neq 0\right]$
The total time taken by motor boat $=\frac{1}{2}+\frac{1}{2}=1 \mathrm{hr}$. In this time - raft has traveled a distance $=\mathrm{PQ}$ $=4 \mathrm{~km}$. The raft moves with same speed as river. Hence
$$ \begin{aligned} & V _{R}=\text { Speed of river }=\frac{\text { Total distance travelled }}{\text { Total time taken }} \\ & =4 \mathrm{kmhr}^{-1} \end{aligned} $$
4. A particle start from rest and has a uniformly accelerated motion.s is distance travelled in time interval $t=4 \mathrm{~s}$ to $t=5 \mathrm{~s} . \mathrm{s} _{1}$ is distance travelled in time interval $t=n$ and $t=n+1$. $\frac{\mathrm{s} _{1}}{\mathrm{~s}}=\frac{15}{9} \cdot \mathbf{n}$ is
(1) 7
(2) 8
(3) 5
(4) 9
Show Answer
Correct answer: (1)
Solution:
$\mathrm{s} _{\mathrm{n}}=$ distance travelled in $\mathrm{n}^{\text {th }}$ second by a particle starting from rest having uniform acceleration a
$$ =\frac{\mathrm{a}}{2}[2 \mathrm{n}-1] $$
Time interval $t=4 \mathrm{~s}$ to $\mathrm{t}=5 \mathrm{~s}$ is $5^{\text {th }}$ second of motion. Therefore
$$ s=\frac{a}{2}[2 \times 5-1]=\frac{9 \mathrm{a}}{2} $$
Similarly time interval $\mathrm{t}=\mathrm{n}$ and $\mathrm{t}=\mathrm{n}+1$ is $(\mathrm{n}+1)^{\mathrm{th}}$ second of motion. Therefore
$$ \mathrm{s} _{1}=\frac{\mathrm{a}}{2}[2(\mathrm{n}+1)-1]=\frac{\mathrm{a}}{2}[2 \mathrm{n}+1] $$
Given, $\frac{\mathrm{s} _{1}}{\mathrm{~s}}=\frac{15}{9}=\frac{2 \mathrm{n}+1}{9}$
$\therefore 15=2 \mathrm{n}+1 \quad$ or $\quad \mathrm{n}=7$
5. A ball projected vertically upwards from ground with an initial speed $U$ returns to ground after time T. The maximum height attained by the ball is $H$. The speed of projection of ball is increased by $n$ time its earlier value. The ratio of percentage change in $H$ and $T$ is:
(1) $\mathrm{n}$
(2) $2 \mathrm{n}-1$
(3) $1+\mathrm{n}$
(4) $1+2 \mathrm{n}$
Show Answer
Correct answer : (4)
Solution:
Let ’ $\mathrm{g}$ ’ denote acceleration due to gravity. We know,
$$ \mathrm{T}=\frac{2 \mathrm{U}}{\mathrm{g}} \text { and } \mathrm{H}=\frac{\mathrm{U}^{2}}{2 \mathrm{~g}} $$
The new speed of projection $U^{\prime}$ is
$$ \mathrm{U}^{\prime}=(1+\mathrm{n}) \mathrm{U} $$
Therefore, $\mathrm{T}^{\prime}=\frac{2 \mathrm{U}^{\prime}}{\mathrm{g}}=(1+\mathrm{n}) \mathrm{T} \quad$ and $\quad \mathrm{H}^{\prime}=\frac{\left(\mathrm{U}^{\prime}\right)^{2}}{2 \mathrm{~g}}=(1+\mathrm{n})^{2} \mathrm{H}$
The percentage change in $\mathrm{H}=\alpha=\left(\frac{\mathrm{H}^{\prime}-\mathrm{H}}{\mathrm{H}}\right) \times 100=\left[(1+n)^{2}-1\right] \times 100=\left[\mathrm{n}^{2}+2 \mathrm{n}\right] \times 100$
The percentage change in $\mathrm{T}=\beta=\frac{\mathrm{T}^{\prime}-\mathrm{T}}{\mathrm{T}} \times 100=\mathrm{n} \times 100$
Obviously $\frac{\alpha}{\beta}=\frac{n(1+2 n)}{n}=1+2 n$
6. A particle moves along positive $z$-axis starting from origin of co-ordinates at $t=0$. The instantaneous velocity of particle is
$$ \mathrm{v}=\mathrm{k} \sqrt{\mathrm{z}} $$
where $k$ is a constant. The ratio of the instantaneous velocity when particle has covered distance $z$, and the average velocity for this time of journey, is
(1) 1
(2) $\mathrm{k}$
(3) $1 / \mathrm{k}$
(4) 2
Show Answer
Correct answer: (4)
Solution:
Given,
$$ \begin{equation*} \mathrm{v}=\frac{\mathrm{dz}}{\mathrm{dt}}=\mathrm{kz}^{1 / 2} \tag{i} \end{equation*} $$
or $\mathrm{z}^{-1 / 2} \mathrm{dz}=\mathrm{kdt}$
Integrate,
$$ \begin{aligned} & \int _{0}^{z} z^{-1 / 2} d z=k \int _{0}^{t} d t \\ & 2 z^{1 / 2}=k t \end{aligned} $$
or $\mathrm{z}=\frac{\mathrm{k}^{2} \mathrm{t}^{2}}{4} \hspace{50mm} . .. . . . .(ii)$
$t=$ The time taken to move from $z=0$ to $z=z$
$=\frac{2}{\mathrm{k}} \sqrt{\mathrm{z}}$
$\mathrm{v} _{\mathrm{av}}=$ The average velocity $=\frac{\mathrm{z}}{\mathrm{t}}$
$$ \begin{equation*} =\frac{1}{2} \mathrm{k} \sqrt{\mathrm{z}} \tag{iii} \end{equation*} $$
$\mathrm{v}=$ The instantaneous velocity at $\mathrm{z}=\mathrm{z}$ is given by Eqn (i). Therefore,
$$ \frac{\mathrm{v}}{\mathrm{v} _{\mathrm{av}}}=\frac{\mathrm{k} \sqrt{\mathrm{z}}}{\frac{1}{2} \mathrm{k} \sqrt{\mathrm{z}}}=2 $$
7. A particle moves along $x$-axis. $\mathbf{v} _{\mathbf{0}}$ and $\mathbf{v}$ denote its initial and instantaneous velocity. Fig. shows $\ell \mathrm{n} v$ vs time (t) graph for the motion of particle. The instantaneous velocity at $\mathbf{t}=\frac{1}{\sqrt{3}} \mathbf{s}$ is
(1) $\frac{\mathrm{v}}{\sqrt{3}}$
(2) $\sqrt{3} \ell^{}n v _{0}$
(3) $\frac{\mathrm{v} _{0}}{\mathrm{e}}$
(4) $\mathrm{ev} _{0}$

Show Answer
Correct answer: (3)
Solution:
The equation of given straight line is
$$ \ln (v)=\ln \left(v _{0}\right)+\left(\tan 120^{\circ}\right) \mathrm{t} $$
$$ =\ln \left(v _{0}\right)-\sqrt{3} t $$
or $\quad \ln \left(\frac{\mathrm{v}}{\mathrm{v} _{0}}\right)=-\sqrt{3} \mathrm{t}$
$$ \begin{equation*} \therefore \mathrm{v}=\mathrm{v} _{0} \mathrm{e}^{-\sqrt{3} \mathrm{t}} \tag{i} \end{equation*} $$
At $\quad \mathrm{t}=\frac{1}{\sqrt{3}} \mathrm{~s} ; \quad \mathrm{v}=\mathrm{v} _{0} \mathrm{e}^{-1}=\frac{\mathrm{v} _{0}}{\mathrm{e}}$
8. Particle 1 is at rest at origin of co-ordinates along $x$-axis. At $t=0$ it has a uniform acceleration of $2 \mathrm{~ms}^{-2}$. A second particle 2 is at $+2 \mathrm{~m}$ from particle 1 and has a uniform motion with a constant speed of $1 \mathrm{~ms}^{-1} \cdot x=x _{1}-x _{2}$ is relative position of particle 1 with respect to particle 2 . Which of the followings correctly describe variation of $x$ with time (t)?

Show Answer
Solution:
The instantaneous position co-ordiante $x _{1}$ and $x _{2}$ of the two particles are
$$ \begin{align*} & x _{1}=\frac{1}{2} \times 2\left(\mathrm{t}^{2}\right)=\mathrm{t}^{2} \tag{i} \\ & x _{2}=2+1 \times \mathrm{t}=2+\mathrm{t} \tag{ii} \end{align*} $$
Obviously,
$$ \begin{equation*} x=x _{1}-x _{2}=\mathrm{t}^{2}-2-\mathrm{t} \tag{iii} \end{equation*} $$
$x$ vs $\mathrm{t}$ graph is parabolic in nature. $x$ is a negative number at $\mathrm{t}=0 . x$ is maximum when
$$ \begin{aligned} & \frac{\mathrm{d} x}{\mathrm{dt}}=0=2 \mathrm{t}-1 \\ & \text { or } \mathrm{t}=0.5 \mathrm{~s} \\ & x _{\max }=0.25-2-0.5=-2.25 \mathrm{~m} \end{aligned} $$
Also, $x=0$ if
$\mathrm{t}^{2}-\mathrm{t}-2=0$
or $\quad \mathrm{t}=\frac{1 \pm \sqrt{1+8}}{2}=\frac{1+3}{2}=2 \mathrm{~s}$
For $\mathrm{t}>2 \mathrm{~s} ; x$ is $\mathrm{a}+\mathrm{ve}$ number and varies as a parabolic function of t. These characteristics are shown in (4).
9. A ball A is thrown vertically upwards with an initial speed v. A second ball B is thrown vertically upwards from same point at same speed $n$ second later. The two meet one another before returning back to the point of projection. The maximum value of $n$ is
(1) $\frac{\mathrm{V}}{\mathrm{g}}$
(2) $\frac{2 \mathrm{v}}{\mathrm{g}}$
(3) $\frac{\mathrm{V}}{2 \mathrm{~g}}$
(4) $\frac{3 \mathrm{v}}{2 \mathrm{~g}}$
Show Answer
Correct answer: (2)
Solution:
Choosing the point of projection of balls as origin of co-ordinates and vertically upward direction as direction of $+\mathrm{z}-$ axis the instantaneous position co-ordinates $\mathrm{z} _{1}$ and $\mathrm{z} _{2}$ of the two balls is
$$ \begin{aligned} & \mathrm{z} _{1}=\mathrm{vt}-\frac{1}{2} g \mathrm{t}^{2} \\ & \mathrm{z} _{2}=\mathrm{v}(\mathrm{t}-\mathrm{n})-\frac{1}{2} \mathrm{~g}(\mathrm{t}-\mathrm{n})^{2} \end{aligned} $$
When the two balls meet one another $\mathrm{z} _{1}=\mathrm{z} _{2}$
$$ \begin{aligned} & \therefore \mathrm{vt}-\frac{1}{2} \mathrm{gt}^{2}=\mathrm{v}(\mathrm{t}-\mathrm{n})-\frac{1}{2} \mathrm{~g}(\mathrm{t}-\mathrm{n})^{2} \\ & 0=-\mathrm{nv}-\frac{1}{2} \mathrm{~g}\left(\mathrm{n}^{2}-2 \mathrm{nt}\right) \end{aligned} $$
or $\mathrm{t}=\frac{\mathrm{n}}{2}+\frac{\mathrm{v}}{\mathrm{g}}$
The first ball will hit ground at $t=\frac{2 v}{g}$. The maximum value of $t$ is $\frac{2 v}{g}$. Hence
$$ \begin{aligned} & \frac{2 \mathrm{v}}{\mathrm{g}}=\frac{\mathrm{n} _{\max }}{2}+\frac{\mathrm{v}}{\mathrm{g}} \\ & \therefore \mathrm{n} _{\max }=\frac{2 \mathrm{v}}{\mathrm{g}} \end{aligned} $$
10. A particle is dropped from a point $O$ at a vertical height $H$ above ground. It falls freely under gravity. The particle hits a rigidly fixed planck in its path at a point $P$ as shown is Fig. After hitting the planck the velocity of particle becomes horizontal. It hits ground $t$ second after it was dropped. Assuming that time taken

in impact of $P$ is negligible, $t$ is maximum if $\frac{\mathrm{h}}{\mathrm{H}}$ is
(1) 1
(2) 0.5
(3) 0.25
(4) 2
Show Answer
Correct answer: (2)
Solution:
Let $t _{1}$ be time taken by the ball to move freely under gravity from $\mathrm{O}$ to $\mathrm{P}$. Obviously
$$ \begin{align*} & \mathrm{H}-\mathrm{h}=\frac{1}{2} \mathrm{gt} _{1}^{2} \\ & \therefore \mathrm{t} _{1}=\sqrt{\frac{2(\mathrm{H}-\mathrm{h})}{\mathrm{g}}} \tag{i} \end{align*} $$
After impact at $\mathrm{P}$, velocity of particle becomes horizontal, i.e. its vertical component is zero. Let it take a time $\mathrm{t} _{2}$ to hit ground. Obviously
$$ \begin{align*} & \mathrm{h}=\frac{1}{2} \mathrm{gt} _{2}{ }^{2} \\ & \therefore \mathrm{t} _{1}=\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}} \tag{ii} \end{align*} $$
Now, $\mathrm{t}=\mathrm{t} _{1}+\mathrm{t} _{2}=\sqrt{\frac{2(\mathrm{H}-\mathrm{h})}{\mathrm{g}}}+\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}$
$\mathrm{t}$ is maximum if $\frac{\mathrm{dt}}{\mathrm{dh}}=0$. This gives
$$ \frac{\mathrm{h}}{\mathrm{H}}=\frac{1}{2}=0.5 $$
11. A body starting from rest accelerates uniformly at a rate of $\alpha \mathrm{ms}^{-2}$ for a time of $\tau$ second. The distance travelled by the body is $\mathrm{S}$. The body travels with constant speed it has acquired for $t$ second and then comes to rest at a retardation of $2 \alpha$. The total distance of journey is $3 S$. Then $\frac{t}{\tau}$ is
(1) $\frac{1}{4}$
(2) $\frac{1}{2}$
(3) $\frac{3}{4}$
(4) 1
Show Answer
Correct answer: (3)
Solution:
Since body has uniformly accelerated motion; starting from rest.
$$ \begin{equation*} S=\frac{1}{2} \alpha \tau^{2} \tag{i} \end{equation*} $$
Let $\mathrm{t}^{\prime}$ be time taken by body to come to rest due to retardation $2 \alpha$. Obviously $\mathrm{t}^{\prime}=\frac{\tau}{2}$. The distance travelled $\mathrm{S}^{\prime}$, during this time is
$$ \begin{align*} & S^{\prime}=(\alpha \tau) \frac{\tau}{2}+\frac{1}{2}(-2 \alpha)\left(\frac{\tau}{2}\right)^{2} \\ & =\frac{\alpha \tau^{2}}{2}-\frac{\alpha \tau^{2}}{4}=\frac{\alpha \tau^{2}}{4}=\frac{S}{2} \tag{ii} \end{align*} $$
Let $S _{1}$, be the distance travelled with constant speed $v=\alpha \tau$. Then $S _{1}=(\alpha \tau) t$. Given,
$$ \begin{aligned} & 3 \mathrm{~S}=\mathrm{S}+\mathrm{S} _{1}+\mathrm{S}^{\prime}=\mathrm{S}+\mathrm{S} _{1}+\frac{\mathrm{S}}{2} \\ & \therefore \mathrm{S} _{1}=\frac{3}{2} \mathrm{~S} \\ & \therefore \mathrm{t}=\frac{\mathrm{S} _{1}}{\alpha \tau}=\frac{3}{2}\left(\frac{\mathrm{S}}{\alpha \tau}\right)=\frac{3}{4} \tau \end{aligned} $$
or $\frac{\mathrm{t}}{\tau}=\frac{3}{4}$
12. A particle at the origin of co-ordinates at $t=0$, moves along positive $x$-axis. The instantaneous velocity ( $v$ ) vs time ( $t$ ) graph of the particle is as shown in Fig.

The graph of instantaneous positive $(x)$ vs time (t) is

Show Answer
Correct answer: (2)
Solution:
1. For time interval $0 \leq \mathrm{t} \leq 1 \mathrm{~s}$; the motion is uniformly accelerated with an acceleration $\mathrm{a} _{1}=2 \mathrm{~ms}^{-2}$. The instantaneous positive co-ordinate $x$ is
$$ \begin{equation*} x=\frac{2}{2} \times 2 \times \mathrm{t}^{2}=\mathrm{t}^{2} \tag{1} \end{equation*} $$
Eqn (1) is equation of parabola. At $\mathrm{t} _{1}=1 \mathrm{~s} ; x=1 \mathrm{~m}$.
2. For time interval $1 \leq \mathrm{t} \leq 2 \mathrm{~s}$; the particle has uniform motion with speed $\mathrm{v}=\mathrm{v} _{1}=2 \mathrm{~ms}^{-1}$. The instantaneous position co-ordinate $x$; in this time interval is given by:
$$ \begin{align*} & x=x _{1}+v _{1}(\mathrm{t}-1) \\ & =1+2(\mathrm{t}-1) \tag{2} \end{align*} $$
Eqn (2) is equation of a straight line. At $\mathrm{t} _{2}=2 \mathrm{~s}, x _{2}=1+2(2-1)=3 \mathrm{~m}$.
3. For time interval $2 \leq \mathrm{t} \leq 4 \mathrm{~s}$; the motion is uniformly retarded with retardation $\mathrm{a} _{2}=2 \mathrm{~ms}^{-2}$. The instantaneous position co-ordinate of particle in this time interval is given by
$$ \begin{align*} & x=x _{2}+\left[2(\mathrm{t}-2)+\frac{1}{2}(-2)(\mathrm{t}-2)^{2}\right] \\ & =3+2(\mathrm{t}-2)-(\mathrm{t}-2)^{2} \tag{3} \end{align*} $$
Eqn (3) is equation of parable. At $\mathrm{t} _{3}=3 \mathrm{~s}, \mathrm{v} _{3}=0$ and
$$ x _{3}=3+2(3-2)-(3-2)^{2}=4 $$
At $\mathrm{t} _{4}=4 \mathrm{~s} ; \mathrm{v} _{4}=-2 \mathrm{~ms}^{-1}$. The position co-ordinate $x _{4}$ is
$x _{4}=3+2(4-2)-(4-2)^{2}=3+4-4=3 \mathrm{~m}$
The characteristics are correctly shown in (2).
13. The instantaneous velocity (v) vs instantaneous position ( $x$ ) of a particle is shown in Fig.

The instantaneous acceleration (a) vs $x$ graph is

Show Answer
Correct answer: (2)
Solution:
The equation representing given $\mathrm{v}$ vs $x$ graph is
$$ \begin{align*} & \mathrm{v}=\mathrm{v} _{0}-\left(\frac{\mathrm{v} _{0}}{\alpha}\right) x \\ & =\mathrm{v} _{0}\left[1-\frac{x}{\alpha}\right] \tag{1} \end{align*} $$
The instantaneous acceleration; $a$, is
$$ \begin{align*} & \mathrm{a}=\frac{\mathrm{dv}}{\mathrm{dt}}=\left(\frac{\mathrm{dv}}{\mathrm{d} x}\right)\left(\frac{\mathrm{d} x}{\mathrm{dt}}\right)=\mathrm{v}\left(\frac{\mathrm{dv}}{\mathrm{d} x}\right) \\ & =\mathrm{v} _{0}\left[1-\frac{x}{\alpha}\right]\left[-\frac{\mathrm{v} _{0}}{\alpha}\right] \\ & =\left(\frac{\mathrm{v} _{0}^{2}}{\alpha}\right)+\left(\frac{\mathrm{v} _{0}^{2}}{\alpha^{2}}\right) x \tag{2} \end{align*} $$
Eqn (2) is equation of a straight line with positive slope equal to $\frac{v _{0}^{2}}{\alpha^{2}}$ and a negative intercept on acceleration axis. Also at $x=\alpha ; \mathrm{a}=0$ and at $x=2 \alpha ; \mathrm{a}=\frac{\mathrm{v} _{0}^{2}}{\alpha}$. These characteristics are shown in (2).
14. Choose a co-ordinate system as shown in Fig. A particle is projected vertically upwards from $O$ with a speed of $30 \mathrm{~ms}^{-1} . P$ is a point $25 \mathrm{~m}$ above ground. $Q$ and $R$ are two equidistant point from $P$ as shown in Fig. with $P Q=P R=15$ m. $t _{1}$ is time taken by particle to move from $P$ to $Q$ during its upwards journey. $t _{2}$ is time taken by the particle to move from $\mathrm{P}$ to $\mathrm{R}$ during its downwards journey. $\frac{t _{1}}{t _{2}}$ is nearly $\left(g=10 \mathrm{~ms}^{-2}\right)$

(1) 1
(2) $\frac{2}{3}$
(3) $\frac{3}{2}$
(4) $\frac{1}{2}$
Show Answer
Correct answer:
Solution:
For the co-ordinate system shown, let $\mathrm{z}$ be the instantaneous position co-ordinate of particle. Obviously.
$$ \begin{equation*} \mathrm{z}=30 \mathrm{t}-5 \mathrm{t}^{2} \tag{1} \end{equation*} $$
Let the particle be at point $\mathrm{P}$ at $\mathrm{t}=\mathrm{t} _{\mathrm{P}}$. At this point $\mathrm{z}=\mathrm{z} _{\mathrm{P}}=+25 \mathrm{~m}$
$$ \begin{aligned} & \therefore 25=30 \mathrm{t} _{\mathrm{p}}-5 \mathrm{t} _{\mathrm{p}}^{2} \\ & \text { or } \mathrm{t} _{\mathrm{p}}^{2}-6 \mathrm{t} _{\mathrm{p}}+5=0 \\ & \therefore \mathrm{t} _{\mathrm{p}}=\frac{6 \pm \sqrt{36-20}}{2}=\frac{6 \pm 4}{2}=1 \text { or } 5 \mathrm{~s} \end{aligned} $$
Let particle be at point $\mathrm{Q}$ at $\mathrm{t}=\mathrm{t} _{\mathrm{Q}}$. Then $\mathrm{z}=\mathrm{z} _{\mathrm{Q}}=40 \mathrm{~m}$.
$$ \therefore 40=30 \mathrm{t} _{\mathrm{Q}}-5 \mathrm{t} _{\mathrm{Q}}^{2} \text { or } \mathrm{t} _{\mathrm{Q}}^{2}-6 \mathrm{t} _{\mathrm{Q}}+8=0 $$
or $\quad \mathrm{t} _{\mathrm{Q}}=\frac{6 \pm \sqrt{36-32}}{2}=\frac{6 \pm 2}{2}=2$ or $5 \mathrm{~s}$
Similarly for point $\mathrm{R} ; \mathrm{t}=\mathrm{t} _{\mathrm{R}}$ and $\mathrm{z}=\mathrm{z} _{\mathrm{R}}=+10 \mathrm{~m}$. Therefore
$$ \begin{aligned} & 10=30 \mathrm{t} _{\mathrm{R}}-5 \mathrm{t} _{\mathrm{R}}^{2} \text { or } \mathrm{t} _{\mathrm{R}}^{2}-6 \mathrm{t} _{\mathrm{R}}+2=0 \\ & \therefore \mathrm{t} _{\mathrm{R}}=\frac{6 \pm \sqrt{36-8}}{2} \approx \frac{6 \pm 5.3}{2}=0.35 \text { or } 5.665 \mathrm{~s} \end{aligned} $$
Obviously during upward journey
$$ \mathrm{t} _{1}=\mathrm{t} _{\mathrm{Q}}-\mathrm{t} _{\mathrm{p}}=2-1=1 \mathrm{~s} $$
and during downward journey
$$ \begin{aligned} & \mathrm{t} _{2}=\mathrm{t} _{\mathrm{R}}-\mathrm{t} _{\mathrm{p}} \\ & =5.675-5=0.665 \mathrm{~s} \\ & \therefore \frac{\mathrm{t} _{1}}{\mathrm{t} _{2}}=\frac{1}{0.665} \simeq \frac{3}{2} \end{aligned} $$
15. A particle is at the origin of $x$-axis at $t=0$ having an initial speed $v$ along positive $x$-axis. The instantaneous acceleration (a) of particle is
$$ \mathrm{a}=\mathrm{a} _{0}-\left(\frac{2 \mathrm{a} _{0}^{2}}{\mathrm{v} _{0}}\right) \mathrm{t} \quad \mathrm{ms}^{-2} $$
The position co-ordinate of particle when it is momentarily at rest is:
(1) $\frac{5 v _{0}^{2}}{6 a _{0}}$
(2) $\frac{13 v _{0}^{2}}{6 a _{0}}$
(3) $\frac{v _{0}^{2}}{2 a _{0}}$
(4) $\frac{6 \mathrm{a} _{0}}{\mathrm{v} _{0}^{2}}$
Show Answer
Correct answer: (1)
Solution:
The instantaneous velocity $v$ of particle is
$$ \begin{equation*} \mathrm{v}=\mathrm{v} _{0}+\mathrm{at}=\mathrm{v} _{0}+\left(\mathrm{a} _{0}-\frac{2 \mathrm{a} _{0}^{2}}{\mathrm{v} _{0}}\right) \mathrm{t} \tag{1} \end{equation*} $$
The instantaneous velocity v is zero when particle is momentarily at rest. From Eqn. (1) we get
$$ 0=\mathrm{v} _{0}+\mathrm{a} _{0} \mathrm{t}-\frac{2 \mathrm{a} _{0}^{2}}{\mathrm{v} _{0}} \mathrm{t}^{2} $$
or $\quad\left(\frac{2 \mathrm{a} _{0}^{2}}{\mathrm{v} _{0}}\right) \mathrm{t}^{2}-\mathrm{a} _{0} \mathrm{t}-\mathrm{v} _{0}=0$
$$ \therefore \quad \mathrm{t}=\frac{\mathrm{a} _{0} \pm \sqrt{\mathrm{a} _{0}^{2}+4\left(\frac{2 \mathrm{a} _{0}^{2}}{\mathrm{v} _{0}}\right) \mathrm{v} _{0}}}{\frac{4 \mathrm{a} _{0}^{2}}{\mathrm{v} _{0}}}=\frac{\mathrm{a} _{0} \pm 3 \mathrm{a} _{0}}{\left(\frac{4 \mathrm{a} _{0}^{2}}{\mathrm{v} _{0}}\right)} $$
or $\quad \mathrm{t}=\frac{4 \mathrm{a} _{0}}{\left(\frac{4 \mathrm{a} _{0}^{2}}{\mathrm{v} _{0}}\right)}=\frac{\mathrm{v} _{0}}{\mathrm{a} _{0}}$
To obtain the instantaneous position co-ordinate $x$ of particle we have,
$$ \begin{align*} & \mathrm{v}=\frac{\mathrm{d} x}{\mathrm{dt}}=\mathrm{v} _{0}+\mathrm{a} _{0} \mathrm{t}-\left(\frac{2 \mathrm{a} _{0}^{2}}{\mathrm{v} _{0}}\right) \mathrm{t}^{2} \\ & \text { or } \int _{0}^{x} \mathrm{~d} x=\int _{0}^{\mathrm{t}}\left[\mathrm{v} _{0}+\mathrm{a} _{0} \mathrm{t}-\left(\frac{2 \mathrm{a} _{0}^{2}}{\mathrm{v} _{0}}\right) \mathrm{t}^{2}\right] \mathrm{dt} \\ & \text { or } \quad x=\mathrm{v} _{0} \mathrm{t}+\mathrm{a} _{0} \frac{\mathrm{t}^{2}}{2}-\frac{2 \mathrm{a} _{0}^{2}}{3 \mathrm{v} _{0}} \mathrm{t}^{3} \tag{3} \end{align*} $$
At $t=\frac{\mathrm{v} _{0}}{\mathrm{a} _{0}} ;$ the instantaneous position co-ordinate is
$$ \begin{aligned} & x=\mathrm{v} _{0}\left(\frac{\mathrm{v} _{0}}{\mathrm{a} _{0}}\right)+\frac{\mathrm{a} _{0}}{2}\left(\frac{\mathrm{v} _{0}}{\mathrm{a} _{0}}\right)^{2}-\frac{2 \mathrm{a} _{0}^{2}}{3 \mathrm{v} _{0}}\left(\frac{\mathrm{v} _{0}}{\mathrm{a} _{0}}\right)^{3} \\ & =\frac{\mathrm{v} _{0}^{2}}{\mathrm{a} _{0}}+\frac{\mathrm{v} _{0}^{2}}{2 \mathrm{a} _{0}}-\frac{2 \mathrm{v} _{0}^{2}}{3 \mathrm{a} _{0}}=\frac{5 \mathrm{v} _{0}^{2}}{6 \mathrm{a} _{0}} \end{aligned} $$
16. Two balls $A$ and $B$ are projected vertically upwards with speed $10 \mathrm{~ms}^{-1}$ and $20 \mathrm{~ms}^{-1}$ respectively from ground and top of a tower $60 \mathrm{~m}$ high. $U=U _{B}-U _{A}$ is relative velocity of $B$ with respect to $A$. Graph of $U$ vs $t$ is:

Show Answer
Correct answer: (3)
Solution:

Taking ground as origin of co-ordinates and vertically upward direction as direction of $+z-$ axis Fig. (a) shows position of two particles at $t=0$.
$$ \begin{gathered} \mathrm{U} _{\mathrm{A} 0}=+10 \mathrm{~ms}^{-1} ; \quad \mathrm{U} _{\mathrm{B} \sigma}+20 \mathrm{~ms}^{-1} ; \mathrm{a} _{\mathrm{A}}=\mathrm{a} _{\mathrm{B}}=-10 \mathrm{~ms}^{-2} \\ \mathrm{U} _{0}=\mathrm{U} _{\mathrm{B} 0}-\mathrm{U} _{\mathrm{A} 0}=10 \mathrm{~ms}^{-1} \end{gathered} $$
The instantaneous velocity $U _{A}$ and $U _{B}$ of $A$ and $B$, is given by
$$ \begin{aligned} & \mathrm{U} _{\mathrm{A}}=10-10 \mathrm{t} \text { and } \mathrm{U} _{\mathrm{B}}=20-10 \mathrm{t} \\ & \therefore \mathrm{U}=\mathrm{U} _{\mathrm{B}}-\mathrm{U} _{\mathrm{A}}=10 \mathrm{~ms}^{-1} \end{aligned} $$
The above result is valid for time interval $0 \leq \mathrm{t} \leq 2 \mathrm{~s}$. At $\mathrm{t}=2 \mathrm{~s}$; particle A comes back to ground and subsequently is at rest. At $\mathrm{t}=2 \mathrm{~s}$; particle $\mathrm{B}$ is at its highest position $\mathrm{B} _{1}$ above $\mathrm{B}$ and its instantaneous veloicty is zero. Also $\mathrm{BB} _{1}=\frac{(20)^{2}}{2 \times 10}=20 \mathrm{~m}$. Now B starts falling freely under gravity and it hits ground at $\mathrm{t}=\mathrm{t} _{1}$. Now $\mathrm{z} _{\mathrm{B} 0}=+60 \mathrm{~m}$ and $\mathrm{z} _{\mathrm{B}}=0$ at $\mathrm{t}=\mathrm{t} _{1}$. Therefore
$$ 0=60=20 \mathrm{t} _{1}-5 \mathrm{t} _{1}^{2} $$
or $\quad \mathrm{t} _{1}^{2}-4 \mathrm{t} _{1}-12=0$
$$ \therefore \mathrm{t} _{1}=\frac{4 \pm \sqrt{16+48}}{2}=\frac{4 \pm 8}{2}=6 \mathrm{~s} $$
In time interval $2 \leq \mathrm{t} \leq 6 \mathrm{~s}$; the instantaneous speed of $\mathrm{B}$ is
$$ \mathrm{U} _{\mathrm{B}}=20-10 \mathrm{t} $$
Since $U _{A}=0 ; U=U _{B}-U _{A}=20-10 t$. In time interval $2 \leq t \leq 6 \mathrm{~s} \quad U$ is a negative number. U vs t graph is a straight line. At $t=6 \mathrm{~s} ; \mathrm{U}=20-10 \times 6=-40 \mathrm{~ms}^{-1}$. For $\mathrm{t}>6 \mathrm{~s}$; both $A$ and $\mathrm{B}$ at rest, hence $\mathrm{U}=0$. These characteristics are correctly shown in (3).
17. Two particles $A$ and $B$; initially $75 \mathrm{~m}$ apart are projected vertically upwards with initial speed of $30 \mathrm{~ms}^{-1}$ and $10 \mathrm{~ms}^{-1}$ as shown in Fig. Take ground as origin of co-ordinates and vertically upward direction as direction of +ve $z$-axis. $z _{A}$ and $z _{B}$ denote instantaneous position of $A$ and $B$. Take $z=z _{B}-z _{A}$ as the relative distance between $B$ and $A$. As long as $A$ and $B$ are in motion, $z$ vs $t$ graph is: $\left(g=10 \mathrm{~ms}^{-2}\right)$


Show Answer
Correct answer: (1)
Solution:
Let $\mathrm{z} _{\mathrm{A}}$ and $\mathrm{z} _{\mathrm{B}}$ be the instantaneous position co-ordinate of $\mathrm{A}$ and $\mathrm{B}$. Obvisouly
$$ \begin{equation*} \mathrm{z} _{\mathrm{A}}=30 \mathrm{t}-5 \mathrm{t}^{2} \tag{i} \end{equation*} $$
and $\mathrm{z} _{\mathrm{B}}=75+\left(10 \mathrm{t}-5 \mathrm{t}^{2}\right) \hspace{50mm} . . . . . . . . (ii) $
$\therefore \mathrm{z}=\mathrm{z} _{\mathrm{B}}-\mathrm{z} _{\mathrm{A}}=75-20 \mathrm{t}$
Let $A$ and $B$ hit ground at $t _{A}$ and $t _{B}$ after projection. Then for particle $A, z _{A}=0, t=t _{A}$
$$ \therefore 0=30 \mathrm{t} _{\mathrm{A}}-5 \mathrm{t} _{\mathrm{A}}^{2}=5 \mathrm{t} _{\mathrm{A}}\left(6-\mathrm{t} _{\mathrm{A}}\right) \quad \text { or } \quad \mathrm{t} _{\mathrm{A}}=6 \mathrm{~s} $$
For particle $\mathrm{B} ; \mathrm{z} _{\mathrm{B}}=0$; $\mathrm{at} \mathrm{t}=\mathrm{t} _{\mathrm{B}}$. FromEqn. (ii) we have
$$ \begin{aligned} & 0=75+10 t _{B}-5 t _{B}^{2} \\ & \text { or } t _{B}^{2}-2 t _{B}-15=0 \\ & \text { or } t _{B}=\frac{2 \pm \sqrt{4+60}}{2}=\frac{2+8}{2}=5 \mathrm{~s} \end{aligned} $$
For time interval $0 \leq \mathrm{t} \leq 5 \mathrm{~s}$; both $\mathrm{A}$ and $\mathrm{B}$ are in motion $\mathrm{z}$ is given by Eqn. (iii). $\mathrm{z}$ varies linearly with time $\mathrm{t}$. At $\mathrm{t}=5 \mathrm{~s}$.
$$ \mathrm{z} _{\mathrm{A}}=75-20 \times 5=-25 \mathrm{~m} $$
Since $\mathrm{z}=\mathrm{z} _{\mathrm{B}}-\mathrm{z} _{\mathrm{A}}$ and $\mathrm{z} _{\mathrm{B}}=0 ; \mathrm{z} _{\mathrm{A}}=25 \mathrm{~m}$. At this time A is $25 \mathrm{~m}$ above ground. However $\mathrm{z}$ is a negative number. For time interval $5 \leq \mathrm{t} \leq 6 \mathrm{~s} ; \mathrm{z}=-\mathrm{z} _{\mathrm{A}}\left[\because \mathrm{z} _{\mathrm{B}}=0\right]$. Therefore
$$ z=30 t-5 t^{2} $$
In this time interval $z$ is a parabolic function of $t$. These characteristics all shown correctly in (1).
18. Two particles $A$ and $B$ are at rest at $t=0$ in $x-y$ plane at points having co-ordinates $(\alpha, 0)$ and $(0, \beta)$. They start moving simultaneously towards origin along straight line joining their initial position with origin $O . a _{1}$ and $a _{2}$ denote acceleration (uniform) of $A$ and $B$. The distance between $A$ and $B$ is minimum at
(1) $t=\frac{a _{1} \alpha+a _{2} \beta}{a _{1}+a _{2}}$
(2) $t=\frac{a _{1} \beta+a _{2} \alpha}{a _{1}^{2}+a _{2}^{2}}$
(3) $t=\sqrt{\frac{2\left(\mathrm{a} _{1} \alpha+\mathrm{a} _{2} \beta\right)}{\alpha^{2}+\beta^{2}}}$
(4) $\mathrm{t}=\sqrt{\frac{2\left(\mathrm{a} _{1} \alpha+\mathrm{a} _{2} \beta\right)}{\left(\mathrm{a} _{1}^{2}+\mathrm{a} _{2}^{2}\right)}}$
Show Answer
Solution:
Particle A moves along $x$-axis and $\mathrm{B}$ along $\mathrm{y}$-axis. The instantaneous position co-ordinates of $\mathrm{A}$ and $\mathrm{B}$ are $(x, 0)$ and $(0, y)$. Obviously
$$ x=\alpha-\frac{1}{2} \mathrm{a} _{1} \mathrm{t}^{2} \quad \text { and } \quad \mathrm{y}=\beta-\frac{1}{2} \mathrm{a} _{2} \mathrm{t}^{2} $$
The instantaneous distance and between the two particle is $\mathrm{s}=\sqrt{x^{2}+\mathrm{y}^{2}}$ For $\mathrm{s}$ to be minimum
$$ \frac{\mathrm{ds}}{\mathrm{dt}}=0 \text { i.e. } \frac{1}{2}\left(x^{2}+\mathrm{y}^{2}\right)^{-1 / 2}\left[2 x \frac{\mathrm{d} x}{\mathrm{dt}}+2 \mathrm{y} \frac{\mathrm{dy}}{\mathrm{dt}}\right]=0 $$
This condition is satisfied if
$$ x \frac{\mathrm{d} x}{\mathrm{dt}}+\mathrm{y} \frac{\mathrm{dy}}{\mathrm{dt}}=0 $$
or $\quad\left(\alpha-\frac{1}{2} a _{1} t^{2}\right) a _{1} t+\left(\beta-\frac{1}{2} a _{2} t^{2}\right) a _{2} t=0$ or
$\mathrm{a} _{1} \alpha+\mathrm{a} _{2} \beta=\frac{1}{2}\left(\mathrm{a} _{1}^{2}+\mathrm{a} _{2}^{2}\right) \mathrm{t}^{2}$
$\therefore \mathrm{t}=\sqrt{\frac{2\left(\mathrm{a} _{1} \alpha+\mathrm{a} _{2} \beta\right)}{\mathrm{a} _{1}^{2}+\mathrm{a} _{2}^{2}}}$
19. Given,
$$ \mathbf{P}+\mathbf{Q}+\mathbf{R}+\mathbf{S}=\mathbf{0} $$
The magnitudes of vectors are denoted by $p, q, r$ and s respectively. Which of the followings is correct?
(1) $\mathrm{p}=\mathrm{q}+\mathrm{r}+\mathrm{s}$
(2) p $<$ q $+\mathrm{r}+\mathrm{s}$
(3) $\mathrm{p}>\mathrm{q}+\mathrm{r}+\mathrm{s}$
(4) $\mathrm{p}=\mathrm{q}+2 \mathrm{r}-\mathrm{s}$
Show Answer
Correct answer:
Solution:
Since the resultant of given vectors is zero, they form a closed polygon $A B C D A$ as shown in Fig. We know the sum of the two sides of a triangle is always less than the third side. In triangle $B C D$.
$$ \mathrm{BD}<\mathrm{q}+\mathrm{r} $$
Similarly from triangle $\mathrm{ABD}$
$$ \begin{array}{ll} & \mathrm{AB}=\mathrm{p}<\mathrm{BD}+\mathrm{DA} \\ \text { or } \quad \mathrm{p}<\mathrm{q}+\mathrm{r}+\mathrm{s} \end{array} $$

20. Two forces $F _{1}$ and $F _{2}$ have a maximum and minimum resultant of 11 and $S N$ respectively each force is increased by $2 N$. These two forces $F _{1}^{\prime}$ and $F _{2}^{\prime}$ act at right angles to one another; The resultant force is:
(1) $5 \sqrt{5 \mathrm{~N}}$ at an angle of $\tan ^{-1}(0.5)$ with $\mathbf{F} _{1}^{\prime}$
(2) $5 \sqrt{5 \mathrm{~N}}$ at an angle of $\tan ^{-1}(0.5)$ with $\mathbf{F} _{2}^{\prime}$
(3) $15 \mathrm{~N}$ at $45^{\circ}$ with $\mathbf{F} _{1}^{\prime}$
(4) $5 \mathrm{~N}$ along direction $\mathbf{F} _{1}^{\prime}$
Show Answer
Correct answer: (1)
Solution:
Let $F _{1}$ and $F _{2}$ be the magnitude of the two forces. Given,
$$ \begin{aligned} & \mathrm{F} _{\max }=\mathrm{F} _{1}+\mathrm{F} _{2}=11 \text { and } \mathrm{F} _{\min }=\mathrm{F} _{1}-\mathrm{F} _{2}=5 \\ & \therefore \mathrm{F} _{1}=8 \mathrm{~N} \text { and } \mathrm{F} _{2}=3 \mathrm{~N} \end{aligned} $$
When the forces are increased by $2 \mathrm{~N}$ each; the magnitude $F _{1}^{\prime}$ and $F _{2}^{\prime}$ of the two forces is
$$ \mathrm{F} _{1}^{\prime}=10 \mathrm{~N} \text { and } \mathrm{F} _{2}^{\prime}=5 \mathrm{~N} $$

Now $F _{1}^{\prime}$ and $F _{2}^{\prime}$ act at right angles to one another as shown in Fig. Their resultant
$$ \mathrm{F}^{\prime}=\sqrt{(10)^{2}+(5)^{2}}=\sqrt{125}=5 \sqrt{5} \mathrm{~N} $$
$\tan \alpha=\frac{\mathrm{F} _{2}^{\prime}}{\mathrm{F} _{1}^{\prime}}=0.5 \quad$ or $\quad \alpha=\tan ^{-1}(0.5)$
21. $\mathbf{n + 2}$ vectors each of magnitude $F$ are so oriented that angle between any two consecutive vectors is $\frac{2 \pi}{n}$. The sum of vectors is
(1) $2 \mathrm{~F} \sin \left(\frac{\pi}{\mathrm{n}}\right)$; along the direction of $1^{\text {st }}$ vector
(2) $2 \mathrm{~F} \sin \left(\frac{2 \pi}{\mathrm{n}}\right)$; at angle of $\frac{\pi}{\mathrm{n}}$ with the $1^{\mathrm{st}}$ vector
(3) $2 \mathrm{~F} \cos \left(\frac{\pi}{\mathrm{n}}\right)$; at an angle of $\frac{\pi}{\mathrm{n}}$ with the $1^{\text {st }}$ vector
(4) $2 \mathrm{~F} \cos \left(\frac{2 \pi}{\mathrm{n}}\right)$; at an angle of $\frac{2 \pi}{\mathrm{n}}$ with the $1^{\text {st }}$ vector
Show Answer
Correct answer:
Solution:
Number of given vectors form a closed polygon because total angle between them is $2 \pi$. Their resultant is zero. Therefore sum of all $(n+2)$ vectors is sum of two vectors of same magnitude $\mathrm{F}$ making an angle $\frac{2 \pi}{\mathrm{n}}$ with one other. The resultant $\mathrm{R}$ is shown in Fig. Obviously
$$ \mathrm{R}=2 \mathrm{~F} \cos \alpha ; \text { and } 2 \alpha=\theta=\frac{2 \pi}{\mathrm{n}} \quad \therefore \alpha=\frac{\pi}{\mathrm{n}} $$

or $R=2 F \cos \left(\frac{\pi}{n}\right)$
R makes an angle $\alpha=\frac{\pi}{\mathrm{n}}$ with the first vector.
22. A vector, $P$, makes an angle $\theta$ in anticlockwise direction with positive $x$-axis in $x-y$ plane. The $x$-component of vector is $\mathrm{P} _{x}$. The vector is, rotated by $30^{0}$ in clockwise direction. $\mathrm{P} _{x}^{\prime}$ is $\boldsymbol{x}$-component of vector now. $\frac{\mathrm{P} _{x}^{\prime}}{\mathrm{P} _{x}}=\sqrt{3}$. Another vector $\mathrm{Q}$; having same magnitude as $\mathrm{P}$ is directed along +ve $y$-axis. $Q$ is added to $P$. The ratio of the resultant magnitude of $P$ is
(1) $\sqrt{2+(\sqrt{3})}$
(2) $\sqrt{2}$
(3) $\sqrt{1+\sqrt{3}}$
(4) $(2+\sqrt{3})^{-1 / 2}$
Show Answer
Correct answer: (1)
Solution:
Obviously,
$$ \frac{P _{x}}{P _{x}^{\prime}}=\frac{p \cos \theta}{p \cos (\theta-30)}=\frac{1}{\sqrt{3}} $$
or $\quad \sqrt{3} \cos \theta=\cos (\theta-30)$ $\therefore \theta=60^{\circ}$
Now $\mathbf{P}$ and $\mathbf{Q}$ have same magnitude and angle between them is also $30^{\circ}$. The magnitude of the resultant $\mathbf{R}$ is
$$ \begin{aligned} & \mathrm{R}=\sqrt{\mathrm{p}^{2}+\mathrm{p}^{2}+2 \mathrm{p}^{2} \cos 30^{0}}=\mathrm{p} \sqrt{(2+\sqrt{3})} \\ & \therefore \frac{\mathrm{R}}{\mathrm{P}}=(2+\sqrt{3})^{1 / 2} \end{aligned} $$
23. An insect moves on a horizontal floor. It covers a distance of $5 \mathrm{~m}$ from west to east, $2 \mathrm{~m}$ from north to south and $2 \sqrt{2} \mathrm{~m}$ in west-south direction. The displacement of insect from starting point is (nearly).
(1) $9.8 \mathrm{~km}$ in west-south direction
(2) $5 \mathrm{~m}$ in north-west direction
(3) $5 \mathrm{~m}$ at angle of $\left[\frac{\pi}{2}-\tan ^{-1}\left(\frac{4}{3}\right)\right]$ east of south
(4) $5 \mathrm{~m}$ at angle of $\tan ^{-1}\left(\frac{4}{3}\right)$ north of east
Show Answer
Correct answer:
Solution:

Choose a co-ordinate system on the floor with intial position of insect as origin of co-ordinates. The three displacement vectors $\mathbf{s} _{1}, \mathbf{s} _{2}$ and $\mathbf{s} _{3}$ are as shown in Fig. (a). Expressing the vectors in terms of their rectangular components we have
$$ \begin{aligned} & \mathbf{s} _{1}=5 \hat{i} ; \quad \mathbf{s} _{2}=2 \hat{j} \\ & \mathbf{s} _{3}=(2 \sqrt{2} \cos 45) \hat{i}+\left(2 \sqrt{2} \sin 45^{0}\right)(-\hat{j})=-2 \hat{i}-2 \hat{j} \end{aligned} $$
The resultant displacement $\mathrm{s}$ is
$$ \mathbf{s}=\mathbf{s} _{1}+\mathbf{s} _{2}+\mathbf{s} _{3}=3 \hat{\mathrm{i}}-4 \hat{\mathrm{j}} $$
This is shown in Fig. (b). Magnitude of $\mathbf{s}$ is
$$ \mathrm{s}=\sqrt{(3)^{2}+(-4)^{2}}=5 \mathrm{~m} ; \quad \text { and } \tan \alpha=\frac{4}{3} \quad \therefore \alpha=\tan ^{-1}\left(\frac{4}{3}\right) $$
24. A car A moves with a uniform speed of $30 \mathrm{kmhr}^{-1}$ in a direction $30^{0}$ east of north. The relative velocity of $A$ as observed by the driver of another moving car $B$ is $41 \mathrm{kmhr}^{-1}$ along south-north direction. The velocity of car B s:
(1) $15 \mathrm{kmhr}^{-1}$, in north-east direction
(2) $15 \sqrt{2} \mathrm{kmhr}^{-1}$, in north-east direction
(3) $15 \sqrt{2} \mathrm{kmhr}^{-1}$, in south-east direction
(4) $15 \mathrm{kmhr}^{-1}$, along north-south direction
Show Answer
Correct answer :(2)
Solution:
Choose a co-ordinate system as shown in Fig. Given,
$$ \begin{aligned} & \mathbf{v} _{\mathbf{A}}=(30 \cos 60) \hat{\mathrm{i}}+(30 \sin 60) \hat{\mathrm{j}}=15 \hat{\mathrm{i}}+26 \hat{\mathrm{j}} \\ & \mathbf{v} _{\mathbf{A B}}=41 \hat{\mathrm{j}} \end{aligned} $$
Let velocity of car $B$ be
$$ \mathbf{v} _{\mathbf{B}}=x \hat{\mathrm{i}}+\mathrm{y} \hat{\mathrm{j}} $$
We know,
$$ \begin{aligned} & \mathbf{v} _{\mathbf{A B}}=\mathbf{v} _{\mathbf{A}}-\mathbf{v} _{\mathbf{B}} \\ & =(15-x) \hat{\mathrm{i}}+(26-\mathrm{y}) \hat{\mathrm{j}}=41 \hat{\mathrm{j}} \end{aligned} $$

$\therefore x=15$ and $\mathrm{y}=15$
We have,
$$ \mathbf{v} _{\mathbf{B}}=(15 \hat{\mathrm{i}}+15 \hat{\mathrm{j}}) \mathrm{kmhr}^{-1} $$
Obviously $\mathrm{v} _{\mathrm{B}}=15 \sqrt{2} \mathrm{kmhr}^{-1}$ in north-east direction.
25. Three cars $A, B$ and $C$ are moving on a level road. Car C moves with a velocity of $60 \mathrm{kmhr}^{-1}$ in a direction $60^{0}$ north-east. The relative velocity of $C$ wrt $A$ is $15 \sqrt{3} \mathrm{kmhr}^{-1}$ along south-north direction. The relative velocity of $C$ wrt B is $20 \mathrm{kmhr}^{-1}$ from west to east. Taking a co-ordinate system with west-east direction as positive $x$-axis, we have
(1)
$\mathbf{v} _{\mathbf{A}}=30 \hat{\mathrm{i}}+15 \sqrt{3} \hat{\mathrm{j}} $
$\mathbf{v} _{\mathbf{B}}=10 \hat{\mathrm{i}}+30 \sqrt{3} \hat{\mathrm{j}}$
(2)
$\mathbf{v} _{\mathbf{A}}=-30 \hat{\mathrm{i}}+15 \sqrt{3} \hat{\mathrm{j}}$
$\mathbf{v} _{\mathbf{B}}=10 \hat{\mathrm{i}}-30 \sqrt{3} \hat{\mathrm{j}}$
(3)
$\mathbf{v} _{\mathrm{A}}=30 \hat{\mathrm{i}}-15 \sqrt{3} \hat{\mathrm{j}}$
$\mathbf{v} _{\mathbf{B}}=-10 \hat{\mathrm{i}}-30 \sqrt{3} \hat{\mathrm{j}}$
(4)
$\mathbf{v} _{\mathbf{A}}=30 \hat{\mathrm{i}}+15 \sqrt{3} \hat{\mathrm{j}}$
$\mathbf{v} _{\mathbf{B}}=-10 \hat{\mathrm{i}}+15 \sqrt{3} \hat{\mathrm{j}}$
Show Answer
Correct answer: (1)
Solution:
Choosing the co-ordinate systemas shown in Fig. let $\mathbf{v} _{\mathbf{A}}=x _{1} \hat{\mathrm{i}}+\mathrm{y} _{1} \hat{\mathrm{j}}$; kmhr ${ }^{-1}$ and $\mathbf{v} _{\mathbf{B}}=x _{2} \hat{\mathrm{i}}+\mathrm{y} _{2} \hat{\mathrm{j}} ; \mathrm{kmhr}^{-1}$
Given, $\mathbf{v} _{\mathbf{C}}=30 \hat{\mathrm{i}}+30 \sqrt{3} \hat{\mathrm{j}}$. Also, $\mathbf{v} _{\mathbf{C A}}=30 \sqrt{3} \hat{\mathrm{j}}$
Therefore,
$$ \mathbf{v} _{\mathbf{C A}}=\mathbf{v} _{\mathbf{C}}-\mathbf{v} _{\mathbf{A}} \text { or } 15 \sqrt{3} \hat{\mathrm{j}}=\left(30-x _{1}\right) \hat{\mathrm{i}}+\left(30 \sqrt{3}-\mathrm{y} _{1}\right) \hat{\mathrm{j}} $$
Comparing coefficents of $\hat{i}$ and $\hat{j}$, we get
$$ \begin{aligned} & 30-x _{1}=0 \quad \text { or } x _{1}=30 \text { and } 15 \sqrt{3}=30 \sqrt{3}-\mathrm{y} _{1} \quad \text { or } \mathrm{y} _{1}=15 \sqrt{3} \\ & \therefore \mathrm{v} _{\mathrm{A}}=30 \hat{\mathrm{i}}+15 \sqrt{3} \hat{\mathrm{j}} ; \mathrm{kmhr}^{-1} \end{aligned} $$
Similarly,
$$ \begin{gathered} \mathbf{v} _{\mathbf{C B}}=20 \hat{\mathrm{i}}=\mathbf{v} _{\mathbf{C}}-\mathbf{v} _{\mathbf{B}} \\ \text { or } \quad 20 \hat{\mathrm{i}}=\left(30-x _{2}\right) \hat{\mathrm{i}}-\left(30 \sqrt{3}-\mathrm{y} _{2}\right) \hat{\mathrm{j}} \end{gathered} $$
Comparing coefficients of $\hat{i}$ and $\hat{j}$
$$ \begin{aligned} & 20=30-x _{2} \quad \text { or } \quad x _{2}=10 ; \text { and } \\ & 30 \sqrt{3}-\mathrm{y} _{2}=0 \text { or } \mathrm{y} _{2}=30 \sqrt{3} \\ & \therefore \quad \mathbf{v} _{\mathbf{B}}=10 \hat{\mathrm{i}}+30 \sqrt{3} \hat{\mathrm{j}} \end{aligned} $$

These are expression for $\mathbf{v} _{\mathbf{A}}$ and $\mathbf{v} _{\mathbf{B}}$ in (1)
26. Fig. shows a stream flowing with a constant speed of $4 \mathrm{kmhr}^{-1}$ from left to right. Points $P$ and $Q$ are directly opposite one another on the river banks. Two swimmers are at point $P$ each swimming with same speed of $5 \mathrm{kmhr}^{-1}$. Both start together from point $P$. Swimmer 1 swims in such a direction as to reach end $Q$. Swimmer 2 swims in a direction at right angles to direction of flow of river and then walks back from $R$ to $Q$ with a speed $v$ in such a manner that both swimmers reach point $Q$ simultaneously. $v$ is

(1) $4.5 \mathrm{kmhr}^{-1}$
(2) $3 \mathrm{kmhr}^{-1}$
(3) $\sqrt{41} \mathrm{kmhr}^{-1}$
(4) $6 \mathrm{kmhr}^{-1}$
Show Answer
Correct answer: (4)
Solution:
Let swimmer 1 swim in a direction to left of point $\mathrm{Q}$ in such a manner that his resultant velocity is along PQ. This is shown in Fig. (a). The resultant speed $v _{1}$ of swimmer 1 is
$\mathrm{v} _{1}=\sqrt{\mathrm{v} _{\mathrm{S}}^{2}-\mathrm{v} _{\mathrm{R}}^{2}}=\sqrt{(5)^{2}-(4)^{2}}=3 \mathrm{kmhr}^{-1}$

Let $\omega$ be width of stream in kilometer.
$\mathrm{t} _{1}=$ Time taken by swimmer 1 to move from $P$ to $Q$
$$ \begin{equation*} =\frac{\omega}{\mathrm{v} _{1}}=\frac{\omega}{3} \mathrm{hr} \tag{1} \end{equation*} $$
For swimmer 2; the velocity vectors are as shown in Fig. (b). Let $\mathrm{t} _{2}$ be the total time taken by swimmer 2 to reach Q. Obviously
$$ \begin{aligned} & \mathrm{t} _{2}=\mathrm{t} _{2}^{\prime}+\mathrm{t} _{2}^{\prime} \\ & \mathrm{t} _{2}^{\prime}=\frac{\mathrm{PQ}}{\mathrm{V} _{\mathrm{S}}}=\frac{\omega}{\mathrm{V} _{\mathrm{S}}}=\frac{\omega}{5} ; \text { and } \mathrm{t} _{2}^{\prime}=\frac{\mathrm{QR}}{\mathrm{V}}=\frac{\mathrm{V} _{\mathrm{R}} \mathrm{t} _{2}^{\prime}}{\mathrm{V}} \end{aligned} $$
$$ \text { or } \mathrm{t} _{2}=\frac{\omega}{5}+\frac{4}{\mathrm{~V}} \times\left(\frac{\omega}{5}\right) $$
Given, $\mathrm{t} _{1}=\mathrm{t} _{2}$; therefore
$$ \begin{aligned} & \frac{\omega}{3}=\frac{\omega}{5}+\frac{4}{5} \frac{\omega}{\mathrm{V}} \quad \text { or } \quad \frac{1}{3}-\frac{1}{5}=\frac{4}{5 \mathrm{~V}} \\ & \therefore \mathrm{V}=6 \mathrm{kmhr}^{-1} \end{aligned} $$
27. Given, $\mathbf{A}=a \hat{i}+b \hat{j}$ and $\mathbf{B}=c \hat{i}+2 b \hat{j}$. Also $a^{2}=c^{2}+n b^{2} .(\mathbf{A}+\mathbf{B})$ is perpendicular to $(\mathbf{A}-\mathbf{B}) ; \mathbf{n}$ is
(1) 2
(2) 3
(3) -3
(4) 1
Show Answer
Correct answer: (2)
Solution:
$\mathbf{A}+\mathbf{B}=(a+c) \hat{i}+3 b \hat{j} ; \mathbf{A}-\mathbf{B}=(a-c) \hat{i}-b \hat{j}$
The vectors $(\mathbf{A}+\mathbf{B})$ and $(\mathbf{A}-\mathbf{B})$ are perpendicular to one another; therefore
$$ \begin{aligned} & (\mathbf{A}+\mathbf{B}) \cdot(\mathbf{A}-\mathbf{B})=0 \\ & \left(\mathrm{a}^{2}-\mathrm{c}^{2}\right)-3 \mathrm{~b}^{2}=0 \quad \text { or } \quad\left(\mathrm{c}^{2}+n b^{2}\right)-\mathrm{c}^{2}-3 \mathrm{~b}^{2}=0 \\ & \therefore \mathrm{n}=3 \end{aligned} $$
28. $\mathbf{A}=10 \hat{\mathrm{i}}-2.5 \hat{\mathrm{j}} ; \quad \mathbf{B}=3 \hat{\mathrm{i}}+4 \hat{\mathrm{j}}$. The component of $\mathbf{A}$ in the direction of $\mathbf{B}$ is
(1) $2.4 \hat{i}+3.2 \hat{j}$
(2) $2 \hat{i}+0.5 \hat{j}$
(3) $2.4 \hat{i}-3.2 \hat{j}$
(4) $-2.4 \hat{i}+3.2 \hat{j}$
Show Answer
Correct answer: (1)
Solution:
$\mathrm{A} _{11}=$ Component of $\mathbf{A}$ along $\mathbf{B}$ has a magnitude of $\frac{\mathbf{A} \cdot \mathbf{B}}{|\mathbf{B}|}$.
Now $\mathbf{A} \cdot \mathbf{B}=10 \times 3-2.5 \times 4=20$
and $|\mathbf{B}|=\sqrt{(3)^{2}+(4)^{2}}=5$ $\therefore \mathrm{A} _{11}=\frac{20}{5}=4$
In terms of vectors
$$ \begin{aligned} & \mathbf{A} _{11}=4 \hat{B}=4 \frac{[3 \hat{i}+4 \hat{j}]}{5} \\ & =2.4 \hat{i}+3.2 \hat{j} \end{aligned} $$
29. A particle having charge $\mathbf{q}$ is moving with a velocity. $\mathbf{v}=v _{1} \hat{i}+v _{2} \hat{j}$ in a space having a uniform magnetic field $\mathbf{B}=B \hat{k}$. The charge experiences a force $\mathbf{F}$ given by $\mathbf{F}=\mathrm{q}(\mathbf{V} \times \mathbf{B})$ $P$ is a vector perpendicular to instantaneous force $F$ on charged particle. Writing $\mathbf{P}=x \hat{\mathrm{i}}+\mathrm{y} \hat{\mathrm{j}}+\mathrm{z} \hat{\mathrm{k}}$, we have
(1) $\frac{x}{y}=\frac{v _{1}}{v _{2}} ; \quad z$ can have any value
(2) $\frac{x}{\mathrm{y}}=\frac{\mathrm{v} _{2}}{\mathrm{v} _{1}} ; \quad \mathrm{z}=\mathrm{v} _{1} \mathrm{v} _{2}$
(3) $\frac{x}{\mathrm{y}}=-\frac{\mathrm{v} _{1}}{\mathrm{v} _{2}} ; \quad \mathrm{z}=\mathrm{v} _{1}^{2} \mathrm{v} _{2}$
(4) $\frac{x}{\mathrm{y}}=\mathrm{v} _{1} \mathrm{v} _{2} ; \mathrm{z}=\frac{\mathrm{v} _{1}}{\mathrm{v} _{2}}$
Show Answer
Correct answer: (1)
Solution:
F the instantaneous force on charged particle is
$$ \mathbf{F}=q(\mathbf{v} \times \mathbf{B})=q\left[\left(v _{1} \hat{i}+v _{2} \hat{j}\right) \times B \hat{k}\right] $$
$$ =\operatorname{Bqv} _{1}(-\hat{\mathrm{j}})+\operatorname{Bqv} _{2}(\hat{\mathrm{i}}) $$
Let $\mathbf{P}=x \hat{i}+y \hat{j}+z \hat{k}$. Since $\mathbf{P}$ is perpendicular to $\mathbf{F}, \mathbf{P} \cdot \mathbf{F}=0$
$\therefore \quad(x \hat{i}+y \hat{j}+z \hat{k}) \cdot B q\left(v _{2} \hat{i}-v _{1} \hat{j}\right)=0$
or $\operatorname{Bqv} _{2} x-\operatorname{Bqv} _{1} \mathrm{y}=0 \quad$ or $\quad \frac{x}{\mathrm{y}}=\frac{\mathrm{v} _{1}}{\mathrm{v} _{2}} \hspace{40mm} . . . . . . . . .(i)$
P.F is zero if $x$ and y satisfy Eqn (i); irrespective of value of $z$.
30. The position vector $r _{A}$ and $r _{B}$ of two points $A$ and $B$ are:
$$ \mathbf{r} _{\mathbf{A}}=2 \hat{i}+3 \hat{j}-\hat{k}, \mathbf{r} _{\mathbf{B}}=5 \hat{i}+2 \hat{j}+3 \hat{k} $$
The linear momentum, $P$; of a particle at point $B$ is
$$ \mathbf{P}=3 \hat{i}+2 \hat{j}+4 \hat{k} $$
The angular momentum of particle at $B$ about $A$ is
(1) $5 \hat{\mathrm{i}}-9 \hat{\mathrm{j}}-5 \hat{\mathrm{k}}$
(2) $4 \hat{i}-11 \hat{j}-4 \hat{k}$
(3) $-12 \hat{\mathrm{i}}-9 \hat{\mathrm{j}}$
(4) $-12 \hat{\mathrm{i}}+9 \hat{\mathrm{j}}$
Show Answer
Correct answer: (4)
Solution:
The position vector of particle at $B$ with respect to point $A$ is
$$ \begin{aligned} \mathbf{r} _{B A}= & \mathbf{r} _{B}-\mathbf{r} _{A}=(5 \hat{i}+2 \hat{j}+3 \hat{k})-(2 \hat{i}+3 \hat{j}-\hat{k}) \\ = & 3 \hat{i}-\hat{j}+4 \hat{k} \end{aligned} $$
$\ell _{\mathrm{BA}}$; the angular momentum of particle at $\mathrm{B}$ about point $\mathrm{A}$ is
$$ \begin{aligned} \ell _{\mathbf{B A}} & =\mathbf{r} _{\mathbf{B A}} \times \mathbf{P} \\ & =\left|\begin{array}{ccc} \hat{\mathrm{i}} & \hat{\mathrm{j}} & \hat{\mathrm{k}} \\ 3 & -1 & 4 \\ 3 & 2 & 4 \end{array}\right|=\hat{\mathrm{i}}[-4-8]+\hat{\mathrm{j}}[12-12]+\hat{\mathrm{k}}[6+3] \\ & =-12 \hat{\mathrm{i}}+9 \hat{\mathrm{k}} \end{aligned} $$
31. A particle moves in $x-y$ plane in a circular path of radius $\mathrm{R}$ with a constant angular velocity $\omega$. At $t=t$, the radius vector joining particle with centre of circle makes an angle $\theta$ with $x$-axis. The instantaneous linear velocity $\mathrm{v}$ is
(1) $(R \omega) \hat{i}-(R \omega) \hat{j}$
(2) $(-R \omega \sin \theta) \hat{\mathrm{i}}+(R \omega \cos \theta) \hat{\mathrm{j}}$
(3) $(R \omega \sin \theta) \hat{i}-(R \omega \cos \theta) \hat{j}$
(4) $(-R \omega \cos \theta) \hat{i}+(R \omega \sin \theta) \hat{j}$
Show Answer
Correct answer: (2)
Solution:
Let $(x, y)$ be the Cartesian co-ordinates of instantaneous position $\mathrm{P}$ of particle. The instantaneous position vector is:
$$ \mathbf{r}=(R \cos \theta) \hat{i}+(R \sin \theta) \hat{j} $$
The angular velocity $\omega$ is
$$ \boldsymbol{\omega}=\omega \hat{\mathrm{k}} $$
The instantaneous linear velocity $\mathrm{v}$ is
$$ \mathbf{v}=\boldsymbol{\omega} \times \mathbf{r} $$

$$ \begin{aligned} & =(\omega \hat{k}) \times[(R \cos \theta) \hat{i}+(R \sin \theta) \hat{j}] \\ & =(+R \omega \cos \theta) \hat{j}+(-R \omega \sin \theta) \hat{i} \end{aligned} $$
32. A particle is projected vertically upwards from the foot $O$ of an inclined plane $O A B$ of inclination $30^{\circ}$. The particle hits the inclined plane at $P$ in a direction perpendicular to slant side of the inclined plane. $\theta$ is

(1) $30^{0}+\tan ^{-1}\left(\frac{\sqrt{3}}{2}\right)$
(2) $30^{\circ}+\tan ^{-1}\left(\frac{2}{\sqrt{3}}\right)$
(3) $30^{0}+\cot ^{-1}\left(\frac{\sqrt{3}}{2}\right)$
(4) $30^{0}-\cot ^{-1}\left(\frac{2}{\sqrt{3}}\right)$
Show Answer
Correct answer: (1)
Solution:
Choosing $x^{\prime}$ and $y^{\prime}$ axis as shown in Fig.
$$ \begin{aligned} & \mathrm{v} _{0 \mathrm{x}}^{\prime}=\mathrm{u} \cos (\theta-30) \\ & \mathrm{v} _{0 y}^{\prime}=\mathrm{u} \sin (\theta-30) \end{aligned} $$
Resolving acceleration due to gravity into its components along $x^{\prime}$ and $y^{\prime}$ axis,
$$ \begin{array}{r} \mathrm{a} _{x}^{\prime}=-\mathrm{g} \sin 30=-\left(\frac{\mathrm{g}}{2}\right) \\ \mathrm{a} _{y}^{\prime}=-\mathrm{g} \cos 30=-\left(\frac{\sqrt{3}}{2} \mathrm{~g}\right) \end{array} $$

Let $\mathrm{v} _{x}^{\prime}$ and $\mathrm{v} _{y}^{\prime}$ be the $x^{\prime}$ and $\mathrm{y}^{\prime}$ component of instantaneous velocity of particle at $\mathrm{P}$.
$$ \begin{aligned} & \mathrm{v} _{x}^{\prime}=\mathrm{v} _{\mathrm{o} x}^{\prime}+\mathrm{a} _{x}^{\prime} \mathrm{t}=\mathrm{u} \cos (\theta-30)-\frac{\mathrm{g}}{2} \mathrm{t} \\ & \mathrm{v} _{y}^{\prime}=\mathrm{v} _{\mathrm{o} y}^{\prime}+\mathrm{a} _{y}^{\prime} \mathrm{t}=\mathrm{u} \sin (\theta-30)-\frac{\sqrt{3}}{2} \mathrm{gt} \end{aligned} $$
As $\mathrm{v} _{x}^{\prime}=0$; when particle hits $x^{\prime}-$ axis (i.e. the inclined plane)
$$ \begin{equation*} \therefore \quad \mathrm{t}=\frac{2 \mathrm{u} \cos (\theta-30)}{\mathrm{g}} \tag{1} \end{equation*} $$
Also for piont $\mathrm{P}, \mathrm{y}^{\prime}=0$. Therefore
$$ \begin{align*} & 0=\mathrm{u} \sin (\theta-30) \mathrm{t}-\frac{\sqrt{3}}{4} \mathrm{gt}^{2} \\ & \text { or } \mathrm{t}=\frac{4 \mathrm{u} \sin (\theta-30)}{\sqrt{3} \mathrm{~g}} \tag{2} \end{align*} $$
From Eqns (1) and (2) we have
$$ \frac{2 \mathrm{u} \cos (\theta-30)}{\mathrm{g}}=\frac{4 \mathrm{u} \sin (\theta-30)}{\sqrt{3} \mathrm{~g}} \text { or } \tan \left(\theta-30^{\circ}\right)=\frac{\sqrt{3}}{2} $$
$\therefore \theta=30^{0}+\tan ^{-1}\left(\frac{\sqrt{3}}{2}\right)$
33. Two particles $A$ and $B$ are projected from point $O$ with same speed $\mathbf{u}$ at angle $\theta _{1}$ and $\theta _{2}$ with horizontal. Both particles pass through a point $P$ at a distance $r$ from $O$. Line $O P$ makes an angle $\alpha$ with the horizontal. $t _{A}$ and $t _{B}$ is time taken by $A$ and $B$; then $t _{A} t _{B}$ is proportional to:
(1) $\frac{1}{\mathrm{r}}$
(2) $\frac{1}{\mathrm{r}^{2}}$
(3) $\mathrm{r}$
(4) $\mathrm{r}^{2}$
Show Answer
Correct answer:(3)
Solution:
Fig. shows a particle projected at an angle $\theta$ with horizontal. The particle passes through point $\mathrm{P}, \mathrm{t}$ second after projection. Co-ordinates of $\mathrm{P}$ are
$$ x=r \cos \alpha, y=r \sin \alpha $$
Therefore,
$$ \begin{align*} & x=(u \cos \theta) t=r \cos \alpha \\ & \text { or } t=\frac{r \cos \alpha}{u \cos \theta} \tag{1} \\ & y=(u \sin \theta) t-\frac{1}{2} g^{2} \end{align*} $$

or $\quad r \sin \alpha=u \sin \theta\left(\frac{r \cos \alpha}{u \cos \theta}\right)-\frac{1}{2} g t^{2}$
or $\quad \frac{1}{2} \mathrm{gt}^{2}=\mathrm{r}\left[\frac{\sin \theta \cos \alpha}{\cos \theta}-\sin \alpha\right]$
$$ \begin{align*} & =\mathrm{r}\left[\frac{\sin \theta \cos \alpha-\cos \theta \sin \alpha}{\cos \theta}\right] \\ & \therefore \quad \mathrm{t}^{2}=\frac{2 \mathrm{r} \sin (\theta-\alpha)}{\mathrm{g} \cos \theta} \tag{2} \end{align*} $$
From Enq (2) $t$ is directly proportional to $\sqrt{\mathrm{r}}$, therefore
$\mathrm{t} _{\mathrm{A}} \mathrm{t} _{\mathrm{B}}$ is directly proportional to $(\sqrt{\mathrm{r}} \cdot \sqrt{\mathrm{r}})=\mathrm{r}$
34. The equation of trajectory of projectile is $\mathrm{y}=2 x-\frac{x^{2}}{5}, x$ and $y$ are in meter. Which of the following statements is incorrect? $\left(g=10 \mathrm{~ms}^{-2}\right)$
(1) Speed of projection $=\frac{5 \sqrt{5}}{2} \mathrm{~ms}^{-1}$
(2) Angle of projection, $\theta=\sin ^{-1}\left(\frac{2}{5}\right)$
(3) Maximum vertical height $=\mathrm{H}=5 \mathrm{~m}$.
(4) Time of flight $=\mathrm{T}=1 \mathrm{~s}$
Show Answer
Correct answer:(4)
Solution:
The equation of trajectory of a projectile is:
$$ \begin{equation*} y=(\tan \theta) x-\frac{g x^{2}}{2 v _{0}^{2} \sin ^{2} \theta} \tag{1} \end{equation*} $$
Comaparing given equation of trajectory with Eqn. (1) we have, $\tan \theta=2$.
$\therefore \sin \theta=\frac{\tan \theta}{\sqrt{1+\tan ^{2} \theta}}=\frac{2}{\sqrt{5}} \quad$ or $\quad \theta=\sin ^{-1} \frac{2}{\sqrt{5}}$
Also,
$$ \begin{gathered} \frac{\mathrm{g}}{2 \mathrm{v} _{0}^{2} \sin ^{2} \theta}=\frac{1}{5} \text { or } \mathrm{v} _{0}^{2} \sin ^{2} \theta=\frac{10 \times 5}{2}=25 \\ \therefore \mathrm{v} _{0} \sin \theta=5 \quad \text { or } \quad \mathrm{v} _{0}=\frac{5 \sqrt{5}}{2} \mathrm{~ms}^{-1} \\ \mathrm{H}=\text { The maximum vertical height }=\frac{2 \mathrm{v} _{0}^{2} \sin 2 \theta}{\mathrm{g}}=\frac{2 \times(5)^{2}}{10}=5 \mathrm{~m} \\ \mathrm{~T}=\text { The time of flight }=\frac{2 \mathrm{v} _{0} \sin \theta}{\mathrm{g}}=\frac{2 \times 5}{10}=1 \mathrm{~s} \end{gathered} $$
35. From the top of a tower of vertical height ’ $h$ ‘, a ball $A$ is projected vertically upwards with speed $v _{0}$ at an angle of $60^{0}$ with the horizontal. $n$ second later a second ball $B$ is projected horizontally with same speed $\mathrm{v} _{0}$. The two balls collide with one another. $\mathrm{n}$ is
(1) $\frac{\mathrm{v} _{0}}{\mathrm{~g}}$
(2) $\frac{2 v _{0}}{\sqrt{3} g}$
(3) $\frac{2 \mathrm{v} _{0}}{\mathrm{~g}}$
(4) $\frac{v _{0}}{\sqrt{3} g}$
Show Answer
Correct answer:(2)
Solution:
In Fig. $\mathrm{O}$ is top of tower. Choosing co-ordinate axis as shown in Fig. and $\mathrm{t}=0$ when ball $\mathrm{A}$ is projected; the instantaneous co-ordinates $\left(x _{1}, y _{1}\right)$ of ball A are:
$$ \begin{align*} & x _{1}=\left(\mathrm{v} _{0} \cos 60\right) \mathrm{t}=\frac{\mathrm{v} _{0}}{2} \mathrm{t} \tag{1} \\ & y _{1}=\left(\mathrm{v} _{0} \sin 60\right) \mathrm{t}-\frac{1}{2} \mathrm{gt}^{2} \\ & =\frac{\sqrt{3} \mathrm{v} _{0}}{2} \mathrm{t}-\frac{1}{2} \mathrm{gt}^{2} \tag{2} \end{align*} $$
The instantaneous co-ordinates $\left(x _{2}, \mathrm{y} _{2}\right)$ at $\mathrm{t}=\mathrm{t}$ $(t>n)$ of ball $B$ are
$$ \begin{align*} & x _{2}=\mathrm{v} _{0}(\mathrm{t}-\mathrm{n}) \tag{3} \\ & \mathrm{y} _{2}=-\frac{1}{2} \mathrm{~g}(\mathrm{t}-\mathrm{n})^{2} \tag{4} \end{align*} $$

Let $\mathrm{P}$ be the point where the two balls collide with one another. Co-ordinates of ball $\mathrm{A}$ and $\mathrm{B}$ are same at this moment of time. From Eqns. (1) and (3).
$$ \begin{align*} & \frac{\mathrm{v} _{0}}{2} \mathrm{t}=\mathrm{v} _{0}(\mathrm{t}-\mathrm{n}) \\ & \therefore \mathrm{n}=\frac{\mathrm{t}}{2} \tag{5} \end{align*} $$
From Eqns (2) and (4); we have,
$$ \begin{align*} & \frac{\sqrt{3}}{2} \mathrm{v} _{0} \mathrm{t}-\frac{1}{2} \mathrm{gt}^{2}=-\frac{1}{2} \mathrm{~g}(\mathrm{t}-\mathrm{n})^{2} \\ & \text { or } \sqrt{3} \mathrm{v} _{0} \mathrm{t}-\mathrm{gt}^{2}=-\frac{\mathrm{gt}^{2}}{4} \\ & \text { or } \mathrm{t}=\frac{4 \mathrm{v} _{0}}{\sqrt{3} \mathrm{~g}} \tag{6} \end{align*} $$
Obvisouly, from Eqns. (5) and (6) we have
$$ \mathrm{n}=\frac{\mathrm{t}}{2}=\frac{2 \mathrm{v} _{0}}{\sqrt{3} \mathrm{~g}} $$
36.

$\mathrm{OAB}$ is a right angled wedge fixed to ground as shown in Fig. A ball is projected with a speed $v _{0}$ at an angle of $60^{\circ}$ with horizontal from $O$. The ball hits wedge at point $P$. Then $O P$ is
(1) $\frac{\mathrm{v} _{0}^{2}}{2 \mathrm{~g}}$
(2) $\frac{2 v _{0}^{2}}{g}$
(3) $\frac{2 v _{0}^{2}}{3 g}$
(4) $\frac{2 v _{0}^{2}}{ \sqrt{3} g}$
Show Answer
Correct answer:(2)
Solution:
Choosing $x$ and $y$-axis as shown in Fig., the instantaneous $x$ and y co-ordinates of ball projected from $\mathrm{O}$ are
$$ \begin{align*} & x=\left(\mathrm{v} _{0} \cos 60\right) \mathrm{t}=\left(\frac{\mathrm{v} _{0}}{2}\right) \mathrm{t} \tag{i} \\ & \mathrm{y}=\left(\mathrm{v} _{0} \cos 60\right) \mathrm{t}-\frac{1}{2} \mathrm{gt}^{2}=\frac{\sqrt{3}}{2} \mathrm{v} _{0} \mathrm{t}-\frac{1}{2} \mathrm{gt}^{2} \tag{ii} \end{align*} $$
The equation of straight line $\mathrm{OB}$, giving slant side of wedge is
$$ \begin{equation*} y=-(\tan 30) x=-\frac{x}{\sqrt{3}} \tag{iii} \end{equation*} $$
Let ball hit wedge at $\mathrm{P}, \mathrm{t}$ second after projection. Point $\mathrm{P}$ satisfies Eqns (i) and (ii) as well as Eqn (iii). Therefore,
$$ \begin{align*} & -\left(\frac{1}{\sqrt{3}}\right)\left(\frac{\mathrm{v} _{0}}{2} \mathrm{t}\right)=\frac{\sqrt{3}}{2} \mathrm{v} _{0} \mathrm{t}-\frac{1}{2} \mathrm{gt}^{2} \\ & \therefore \mathrm{t}=\frac{2 \mathrm{v} _{0}}{\sqrt{3} \mathrm{~g}} \tag{iv} \end{align*} $$
Obvisouly $\mathrm{QP}=x$-co-ordinate of ball at $\quad t=\frac{2 x _{0}}{\sqrt{3} g}$. Therefore
$$ \mathrm{QP}=\left(\frac{\mathrm{v} _{0}}{2}\right) \frac{2 \mathrm{v} _{0}}{\sqrt{3} \mathrm{~g}}=\frac{\mathrm{v} _{0}^{2}}{\sqrt{3} \mathrm{~g}} $$
From right angled $\triangle \mathrm{OPQ} \frac{\mathrm{QP}}{\mathrm{OP}}=\cos 30$, therefore
$\mathrm{OP}=\frac{\mathrm{QP}}{\cos 30}=\frac{2}{\sqrt{3}} \times \frac{\mathrm{v} _{0}^{2}}{\sqrt{3} \mathrm{~g}}=\frac{2 \mathrm{v} _{0}^{2}}{3 \mathrm{~g}}$
37. A bird sits on top of a pole of vertical height $h$ at a horizontal distance $\ell$ from a point $O$.A projectile fired from $O$ is so poised as to hit the bird and attain a maximum vertical height $2 \mathrm{~h}$. The moment the projectile is fired the bird starts flying horizontally with a constant speed $v$ in such a manner that the projectile still hits the bird. The ratio of $v$ and horizontal component of initial velocity of the projectile is
(1) $\frac{1}{\sqrt{2}+1}$
(2) $\frac{1}{1+\left(\frac{1}{\sqrt{2}}\right)}$
(3) $\frac{\sqrt{2}}{1+\left(\frac{1}{\sqrt{2}}\right)}$
(4) $\frac{\sqrt{2}}{1+\sqrt{2}}$
Show Answer
Correct answer: (3)
Solution:

In Fig. $A B$ is pole of vertical height $h$. Given $B$ is the position of bird. Given $O C=2 h$ is the maximum vertical height attained by projectile fired from $O$ with speed $v _{0}$ at an angle $\theta$ with the horizontal. Obviously
$$ 2 \mathrm{~h}=\frac{\mathrm{v} _{0}^{2} \sin ^{2} \theta}{2 \mathrm{~g}} $$
$\therefore \mathrm{v} _{0} \sin \theta=2 \sqrt{\mathrm{gh}} \hspace{40mm} . . . . . .(1) $
Let the projectile attain vertical height $h$ at time $t$ after projection. Then
$$ \mathrm{h}=\left(\mathrm{v} _{0} \sin \theta\right) \mathrm{t}-\frac{1}{2} \mathrm{gt}^{2} $$
or $\mathrm{gt}^{2}-\left(2 \mathrm{v} _{0} \sin \theta\right) \mathrm{t}+2 \mathrm{~h}=0$
$\therefore \mathrm{t}=\frac{2 \mathrm{v} _{0} \sin \theta \pm \sqrt{\left(2 \mathrm{v} _{0} \sin \theta\right)^{2}-8 \mathrm{gh}}}{2 \mathrm{~g}}$
$$ =\frac{4 \sqrt{\mathrm{gh}} \pm \sqrt{16 \mathrm{gh}-8 \mathrm{gh}}}{2 \mathrm{~g}}=\frac{(2 \pm \sqrt{2})}{\mathrm{g}} \sqrt{\mathrm{gh}} $$
$$ =(2 \pm \sqrt{2}) \sqrt{\frac{\mathrm{h}}{\mathrm{g}}} $$
Let $t _{1}=(2-\sqrt{2}) \sqrt{\frac{h}{g}}$ and $t _{2}=(2+\sqrt{2}) \sqrt{\frac{h}{g}}$.
The bird gets hit at point $B _{1}$ i.e. at $t=t _{2}$ after projection. Therefore
$$ \mathrm{BB} _{1}=\mathrm{vt} _{2}=\mathrm{v}(2+\sqrt{2}) \sqrt{\frac{\mathrm{h}}{\mathrm{g}}} $$
Also,
$$ \mathrm{BB} _{1}=\left(\mathrm{v} _{0} \cos \theta\right)\left(\mathrm{t} _{2}-\mathrm{t} _{1}\right)=\left(\mathrm{v} _{0} \cos \theta\right) 2 \sqrt{2} \sqrt{\frac{\mathrm{h}}{\mathrm{g}}} $$
Clearly,
$$ \frac{\mathrm{v}}{\mathrm{v} _{0} \cos \theta}=\frac{2 \sqrt{2}}{2+\sqrt{2}}=\frac{\sqrt{2}}{\left(1+\frac{1}{\sqrt{2}}\right)} $$
38. A staircase has identical steps each of width $\omega$ and height $h$. A ball $A$ is pushed horizontally from the topmost step with a speed $u _{1}$. At the same time a second ball B lying on edge of $\mathbf{n}^{\text {th }}$ step below is also pushed horizontally with speed $u _{2}$. Both balls just hit the edge of the $N^{\text {th }}$ step from top simultaneously. The ratio $\frac{\mathrm{u} _{1}}{\mathrm{u} _{2}}$ is
(1) $\sqrt{\frac{\mathrm{N}}{\mathrm{n}}}$
(2) $\sqrt{\frac{N-n}{N}}$
(3) $\sqrt{\frac{N}{N-n}}$
(4) $\sqrt{\frac{N+n}{N-n}}$
Show Answer
Correct answer: (3)
Solution:
For ball A
In hitting $\mathrm{N}^{\text {th }}$ step from top; the ball travels a horizontal distance of $\mathrm{N} \omega$ and vertical distance $\mathrm{Nh}$. Let the ball hit $\mathrm{N}^{\text {th }}$ step $t$ second after projection. Obviously
$$ \begin{align*} & \mathrm{N} \omega=\mathrm{u} _{1} \mathrm{t} \text { and } \mathrm{Nh}=\frac{1}{2} \mathrm{gt}^{2} \\ & \quad \therefore \mathrm{Nh}=\frac{1}{2} \mathrm{~g}\left(\frac{\mathrm{N} \omega}{\mathrm{u} _{1}}\right)^{2} \quad \text { or } \quad \mathrm{u} _{1}^{2}=\frac{\mathrm{gN} \omega^{2}}{2 \mathrm{~h}} \tag{1} \end{align*} $$
For ball B
Ball $\mathrm{B}$ is $\mathrm{n}$ steps below the top most step. In hits step $(\mathrm{N}-\mathrm{n})^{\text {th }}$ below its point of projection. Therefore
$$ \begin{equation*} \mathrm{u} _{2}^{2}=\frac{\mathrm{g}(\mathrm{N}-\mathrm{n}) \omega^{2}}{2 \mathrm{~h}} \tag{2} \end{equation*} $$
From Eqns. (1) and (2), we have
$$ \begin{aligned} & \left(\frac{\mathrm{u} _{1}}{\mathrm{u} _{2}}\right)^{2}=\frac{\mathrm{N}}{\mathrm{N}-\mathrm{n}} \\ & \therefore \frac{\mathrm{u} _{1}}{\mathrm{u} _{2}}=\sqrt{\frac{\mathrm{N}}{\mathrm{N}-\mathrm{n}}} \end{aligned} $$
39. A ball is projected from ground with a speed of $20 \mathrm{~ms}^{-1}$ at an angle of $30^{0}$ with horizontal. It just grazes past the edge of a vertical wall of height $1.8 \mathrm{~m}$. The ratio of the distance of point of projection of ball from wall and the distance of point where it hits ground from the wall is $\left(\mathrm{g}=\mathbf{1 0} \mathrm{ms}^{-2}\right)$
(1) $\frac{1}{9}$
(2) $\frac{1}{10}$
(3) $\frac{9}{10}$
(4) $\frac{8}{9}$
Show Answer
Correct answer: (1)
Solution:
Let $x$ be the horizontal distance of wall from point of projection. Let the ball just grazes past top of wall $\mathrm{t}$ second after projection. $\mathrm{At} \quad \mathrm{t}=\mathrm{t} ; \mathrm{y}=\mathrm{h}=1.8 \mathrm{~m}$. Therefore
$1.8=(20 \sin 30) \mathrm{t}-\frac{1}{2} \times 10 \mathrm{t}^{2}=10 \mathrm{t}-5 \mathrm{t}^{2}$
or $5 \mathrm{t}^{2}-10 \mathrm{t}+1.8=0$
$\therefore \mathrm{t}=\frac{10 \pm \sqrt{100-36}}{10}=\frac{10 \pm 8}{10}=2 \mathrm{~s}$ or $1.8 \mathrm{~s}$
Obvisouly,
$$ \begin{aligned} & x=\left(\mathrm{v} _{0} \cos \theta\right) \mathrm{t}=(10 \sqrt{3}) \times 0.2 \text { or }(10 \sqrt{3}) 1.8 \\ & =2 \sqrt{3} \mathrm{~m} \text { or } 18 \sqrt{3} \mathrm{~m} \end{aligned} $$
The distance of the point where ball hits ground from point of projection equals the horizontal range. Therefore,
$$ \mathrm{R}=\frac{\mathrm{v} _{0}^{2} \sin \theta}{\mathrm{g}}=\frac{400 \times \frac{\sqrt{3}}{2}}{10}=20 \sqrt{3} $$
The required ratio is $\frac{x}{\mathrm{R}-x}$. It is
$\frac{2 \sqrt{3}}{18 \sqrt{3}}=\frac{1}{9} \quad$ or $\quad \frac{18 \sqrt{3}}{2 \sqrt{3}}=9$.
The correct choice is (1)
40. On a horizontal road a car is at a distance $\frac{\mathrm{R}}{4}$ ahead of point $O$ where a gun is placed. The barrel of gun is oriented at an angle $\theta$ with horizontal. $A$ bullet is fired from gun with a speed $v _{0}$. At the same moment of time the car starts moving with a constant speed $V$. The bullet hits the car. The maximum vertical height attained by the bullet is:
(1) $\mathrm{v}^{2} \tan ^{2} \theta$
(2) $\frac{9}{8 \mathrm{~g}} \mathrm{v}^{2} \cot ^{2} \theta$
(3) $\frac{8}{9 \mathrm{~g}} \operatorname{van} \theta$
(4) $\frac{8}{9 \mathrm{~g}} \mathrm{v}^{2} \tan ^{2} \theta$
Show Answer
Correct answer: (4)
Solution:
In Fig. $\mathrm{O}$ and $\mathrm{C}$ are position of gun and car at $\mathrm{t}=0$. The bullet hits ground at point $\mathrm{P} . \mathrm{OP}=$ $\mathrm{R}=$ range of bullet. Let bullet hit ground at point $P$. Let $T$ be time of flight of bullet. The car and bullet reach point $\mathrm{P}$ at same time.
Therefore $\mathrm{OP}=\mathrm{R}=\left(\mathrm{v} _{0} \cos \theta\right) \mathrm{T}$.
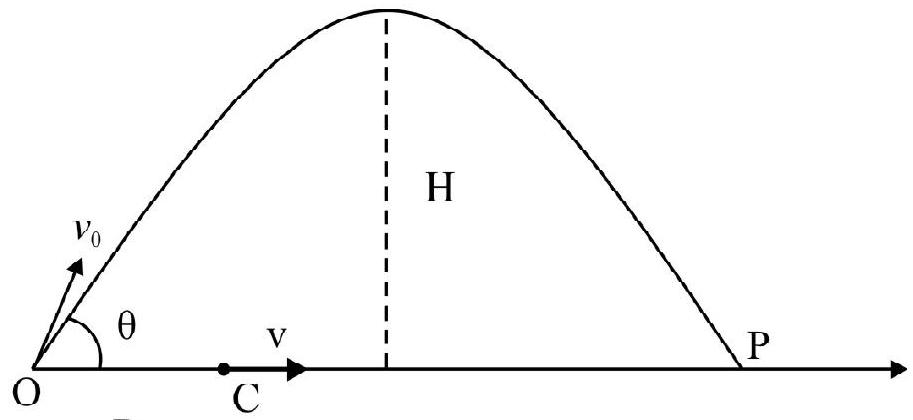 $\mathrm{CP}=\frac{3 \mathrm{R}}{4}=\mathrm{VT}$
$\mathrm{CP}=\frac{3 \mathrm{R}}{4}=\mathrm{VT}$
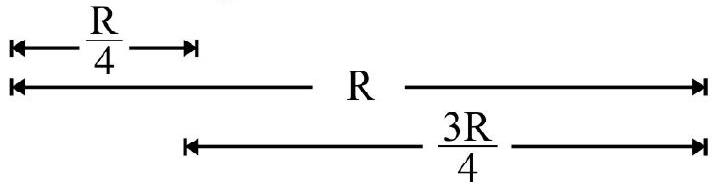 $\therefore \frac{4}{3}=\frac{\mathrm{v} _{0} \cos \theta}{\mathrm{V}} \quad$ or $\quad \mathrm{V}=\frac{3 \mathrm{v} _{0} \cos \theta}{4} \hspace{40mm} . . . . . .(1) $
$\therefore \frac{4}{3}=\frac{\mathrm{v} _{0} \cos \theta}{\mathrm{V}} \quad$ or $\quad \mathrm{V}=\frac{3 \mathrm{v} _{0} \cos \theta}{4} \hspace{40mm} . . . . . .(1) $
The maximum vertical height $\mathrm{H}$; attained by bullet is
$\mathrm{H}=\frac{\mathrm{v} _{0}^{2} \sin ^{2} \theta}{2 \mathrm{~g}}$
$=\frac{\left(\frac{4 \mathrm{~V}}{3 \cos \theta}\right)^{2} \sin ^{2} \theta}{2 \mathrm{~g}}=\frac{8}{9 \mathrm{~g}} \mathrm{~V}^{2} \tan ^{2} \theta$
41. A projectile is fired with a speed of $20 \mathrm{~ms}^{-1}$ at an angle of $60^{0}$ with vertical. It is at a vertical height of $1.8 \mathrm{~m}$ from the point of projection. Take point of projection as origin, the horizontal and vertically upward direction as positive $x$ and $y$-axis respectively; the instantaneous position vector of the projectile is $\left(\mathrm{g}=10 \mathrm{~ms}^{-2}\right)$
(1) $2 \sqrt{3} \hat{i}+1.8 \hat{j}$
(2) $18 \sqrt{3} \hat{i}+1.8 \hat{j}$
(3) $25 \sqrt{3} \hat{i}+1.8 \hat{j}$ or $18 \sqrt{3} \hat{i}+1.8 \hat{j}$
(4) $5 \sqrt{3} \hat{i}+1.8 \hat{j}$ or $18 \sqrt{3} \hat{i}+1.8 \hat{j}$
Show Answer
Correct answer: (3)
Solution:
Let $\mathrm{v} _{0 x}$ and $\mathrm{v} _{\text {oy }}$ denote the initial value of $x$ and $\mathrm{y}$-component of velocity of projectile. Given
$$ \mathrm{v} _{0 x}=20 \cos 30^{\circ}=10 \sqrt{3} \mathrm{~ms}^{-1} ; \text { and } \mathrm{v} _{\mathrm{oy}}=20 \sin 30^{\circ}=10 \mathrm{~ms}^{-1} $$
The instantaneous $x$ and y co-ordinates of projectile are
$$ x=\mathrm{v} _{0 x} \mathrm{t}=10 \sqrt{3} \mathrm{t} \text { and } \mathrm{y}=10 \mathrm{t}-\frac{1}{2}(10) \mathrm{t}^{2}=10 \mathrm{t}-5 \mathrm{t}^{2} $$
The projectile is at a vertical height of $1.8 \mathrm{~m}$, (i.e. $\mathrm{y}=1.8 \mathrm{~m}$ ) at $\mathrm{t}=\mathrm{t}$.
$$ \begin{aligned} & \therefore 1.8=10 \mathrm{t}-5 \mathrm{t}^{2} \text { or } 5 \mathrm{t}^{2}-10 \mathrm{t}+1.8=0 \\ & \mathrm{t}=\frac{10 \pm \sqrt{100-36}}{10}=\frac{10 \pm 8}{10}=0.28 \text { or } 1.8 \mathrm{~s} \end{aligned} $$
The projectile attains $\mathrm{y}=1.8 \mathrm{~m}$ at two times $\mathrm{t} _{1}=0.2 \mathrm{~s}$ or $1.8 \mathrm{~s}$. The corresponding $x$-coordinates are
$$ x=10 \sqrt{3} \times 0.2=2 \sqrt{3} \mathrm{~m} \text { or } x=10 \sqrt{3} \times 1.8=18 \sqrt{3} \mathrm{~m} $$
The position vector of projectile is
$$ \mathbf{r}=2 \sqrt{3} \hat{i}+1.8 \hat{j} \text { or } \mathbf{r}=18 \sqrt{3} \hat{i}+1.8 \hat{j} $$
42. Choose point of projection as origin of co-ordinates; the horizontal and vertically upward direction as direction of positive $x$ and $y$-axis respectively. The initial velocity $v _{0}$ of a projectile is:
$$ \mathbf{v} _{\mathbf{0}}=(10 \sqrt{3}) \hat{\mathrm{i}}+30 \hat{\mathrm{j}} \mathrm{ms}^{-1} $$
The ratio of change in linear momentum of projectile in the 1st and 2nd second of motion is (mass of particle $=100 \mathrm{~g} ; \mathbf{g}=\mathbf{1 0} \mathrm{ms}^{-2}$ )
(1) 0.5
(2) 1
(3) 1.5
(4) 2
Show Answer
Correct answer: (2)
Solution:
Let $\mathbf{v}$ be the instantaneous velocity vector of projectile. Obviously
$$ \mathbf{v}=(10 \sqrt{3}) \hat{\mathrm{i}}+(30-10 \mathrm{t}) \hat{\mathrm{j}} \quad \mathrm{ms}^{-1} $$
$(\Delta \mathbf{p}) _{1}=$ Change in linear momentum in $1^{\text {st }}$ second of motion i.e. time interval $t=0$ to $t=1 \mathrm{~s}$.
$$ \begin{aligned} & =0.1[\{(10 \sqrt{3}) \hat{\mathrm{i}}+20 \hat{\mathrm{j}}\}-\{(10 \sqrt{3}) \hat{\mathrm{i}}+30 \hat{\mathrm{j}}\}] \\ & =-1 \hat{\mathrm{j}} ; \mathrm{kgms}^{-1} \end{aligned} $$
Similarly,
$(\Delta \mathbf{p}) _{2}=$ Change in linear momentum in $2^{\text {nd }}$ second of motion i.e. time interval $t=1 \mathrm{~s}$ to $\mathrm{t}=2 \mathrm{~s}$.
$$ \begin{aligned} & =0.1[\{(10 \sqrt{3}) \hat{i}+10 \hat{j}\}-\{(10 \sqrt{3}) \hat{i}+20 \hat{j}\}]=-1 \hat{j} k g m s^{-1} \\ & \therefore \frac{(\Delta \mathbf{p}) _{1}}{(\Delta \mathbf{p}) _{2}}=1 \end{aligned} $$
43. A bullet is fired in a vertical plane in the gravity of earth with a speed of $20 \sqrt{2} \mathrm{~ms}^{-1}$ in a direction so that its horizontal range is maximum. $t$ second after firing the instantaneous velocity vector of projectile makes an angle of $120^{\circ}$ with instantaneous acceleration of particle; $t$ is $\left(g=10 \mathbf{m s}^{-2}\right)$
(1) $2 \mathrm{~s}$
(2) $2 \sqrt{3} \mathrm{~s}$
(3) $2(\sqrt{3}-1) \mathrm{s}$
(4) $2(\sqrt{3}+1) \mathrm{s}$
Show Answer
Correct answer: (3)
Solution:
The initial direction of firing of bullet is at an angle of $45^{\circ}$ with horizontal. The acceleration vector is always in a vertically downward direction. Since angle between $\mathbf{v}$ and $\mathbf{a}$ is $120^{\circ}, \mathbf{v}$ makes an angle of $30^{\circ}$ with the horizontal. Obviously
$$ \tan 30=\frac{\mathrm{v} _{\mathrm{y}}}{\mathrm{v} _{x}} $$
where $\mathrm{v} _{x}$ and $\mathrm{v} _{\mathrm{y}}$ denote the instantaneous $x$ - and $\mathrm{y}$-component of instantaneous velocity vector i.e. $\mathbf{v}$. We know $\mathrm{v} _{x}=\mathrm{v} _{0 x}=20 \mathrm{~ms}^{-1}$ and $\mathrm{v} _{\mathrm{y}}=\mathrm{v} _{0 \mathrm{y}}-\mathrm{gt}=20-10 \mathrm{t}$.
$$ \therefore \frac{1}{\sqrt{3}}=\frac{20-10 \mathrm{t}}{20} \quad \text { or } \quad \mathrm{t}=2(\sqrt{3}-1) $$
44. A projectile has a mass $m$; horizontal range $R$ and time of flight $T$. At the highest point of its path; the projectile somehow on its own, breaks into two fragments having masses in the ratio of $1: 2$. The behavior fragment hits ground $t _{1}$ second later at a point midway between point of projection and where the original projectile would have hit the ground. The lighter fragment hits ground $t _{2}$ second later. The distance of the point where this fragment hits ground from point of projection and $\frac{t _{2}}{t _{1}}$ is
(1) $\frac{3 \mathrm{R}}{2} ; 2$
(2) $\mathrm{R} ; 1$
(3) $2 \mathrm{R} ; 1$
(4) $\frac{3 \mathrm{R}}{2} ; 1$
Show Answer
Correct answer: (3)
Solution:

Fig. (a) shows the path of the projectile projected from point $\mathrm{O}$. A is the highest point on its parabolic path and $\mathrm{OP}=\mathrm{R}=$ horizontal range of the projectile. The instantaneous speed of projectile at $\mathrm{A} _{\mathrm{v}} \cos \theta$. At A the projectile breaks up into two fragments having mass $\mathrm{m} _{1}=\frac{\mathrm{m}}{3}$ and $\mathrm{m} _{2}=\frac{2 \mathrm{~m}}{3}$ ( $\mathrm{m}$ is original mass of projectile). The breakup of projectile occurs on its own, i.e. there is no external force, therefore, the linear momentum is conserved. Given that fragment of mass $m _{2}$ hits ground at point B. This fragment moves vertically downward. The horizontal component of its velocity is zero. Let $\mathrm{v} _{1}$ be horizontal component of velocity of fragment of mass $m _{1}$. From law of conversation of linear momentum.
$$ \mathrm{mv} _{0} \cos \theta=\frac{\mathrm{m} _{1}}{3} \mathrm{v} _{1}, \quad \mathrm{v} _{1}=3 \mathrm{v} _{0} \cos \theta $$
There is no vertical component of velocity of both fragments. In hitting ground they travel same vertical distance $\mathrm{H}$.
$\therefore \mathrm{t} _{1}=\mathrm{t} _{2}=\frac{\mathrm{T}}{2}$ or $\frac{\mathrm{t} _{1}}{\mathrm{t} _{2}}=1$
Also for the fragment of mass $m _{1}$
$$ \mathrm{BR}=\left(3 \mathrm{v} _{0} \cos \theta\right) \frac{\mathrm{T}}{2}=\frac{3 \mathrm{R}}{2} $$
Obviously,
$$ \mathrm{OR}=\mathrm{OB}+\mathrm{BR}=\frac{\mathrm{R}}{2}+\frac{3 \mathrm{R}}{2}=2 \mathrm{R} $$
45. A particle of $10 \mathrm{~g}$ is attached to one end of a rubber string of length $50 \mathrm{~cm}$. It is whirled into a horizontal circle about the other end of string with a uniform angular speed of 300 r.p.m. The rubber string has a force constant of $0.05 \mathrm{kgfm}^{-1}, \mathrm{~g}=10 \mathrm{~ms}^{-2}$. The tension in string is
(1) $5 \mathrm{~N}$
(2) $6.25 \mathrm{~N}$
(3) $9 \mathrm{~N}$
(4) $12.5 \mathrm{~N}$
Show Answer
Correct answer:
Solution:
$\mathrm{k}=$ Force constant of rubber string $=0.05 \mathrm{kgf} \mathrm{cm}^{-1}=\frac{0.05 \times 10}{10^{-2}} \mathrm{Nm}^{-1}=50 \mathrm{Nm}^{-1}$
$$ \omega=300 \mathrm{r} . \text { p.m. }=5 \mathrm{r} . \mathrm{p} . \mathrm{s} .=10 \pi \mathrm{rad} \quad \mathrm{s}^{-1} $$
Let $x$ be increase in length of rubber string when particle attached to it moves in a horizontal circle. The radius of circle $=\mathrm{r}=(0.5+x) \mathrm{m}$. The tension in string $=\mathrm{T}=\mathrm{mr} \omega^{2}=\mathrm{k} x$
$\therefore 10^{-2}(0.5+x) \times(10 \pi)^{2}=50 x$
or $10^{-2} \times 10^{3}(0.5+x)=50 x \quad\left[\pi^{2} \simeq 10\right]$
$5+10 x=50 x$
$\therefore x=\frac{5}{40} \mathrm{~m}=0.125 \mathrm{~m}$
$\mathrm{T}=\mathrm{k} x=50 \times 0.125=6.25 \mathrm{~N}$
46. A particle moves in a horizontal circle of radius $r$. The angular velocity of particle veries at a constant rate $\alpha$. The acceleration of the particle is
(1) $\frac{\mathrm{v}^{2}}{\mathrm{r}}$
(2) $\mathrm{r} \alpha$
(3) $\frac{v^{2}}{r}+r \alpha$
(4) $\left[\left(\frac{\mathrm{v}^{2}}{\mathrm{r}}\right)^{2}+(\mathrm{r} \alpha)^{2}\right]^{1 / 9}$
Show Answer
Correct answer: (4)
Solution:
The acceleration has two components.
(a) The radial component of acceleration is due to change direction of the velocity and equals $\frac{\mathrm{v}^{2}}{\mathrm{r}}$.
(b) The tangential component is due to change in magnitude of $v$ and equals $r \alpha$.
The two component of acceleration are mutually perpendicular. The net acceleration is $\mathrm{a}=\left[\left(\frac{\mathrm{v}^{2}}{\mathrm{r}}\right)^{2}+(\mathrm{r} \alpha)^{2}\right]^{1 / 2}$
47. A stone of mass $m$, tied to one end of string, is moving in a horizontal circle. The length of string is gradually reduced in such a manner that the instantaneous tension $T$ in string is $\mathrm{T}=\frac{\mathrm{k}}{\mathrm{r}^{3}}$ where $\mathrm{k}$ is a constant. For the motion, the quantity that remains constant is:
(1) Kinetic energy
(2) Linear momentum
(3) Angular momentum
(4) Speed
Show Answer
Correct answer: (3)
Solution:
The instantaneous tension, $\mathrm{T}$, in string is
$$ \mathrm{T}=\frac{\mathrm{mv}^{2}}{\mathrm{r}}=\frac{\mathrm{k}}{\mathrm{r}^{3}} $$
$$ \text { or } \quad \mathrm{v} \alpha \frac{1}{\mathrm{r}} \text { or } \mathrm{vr}=\mathrm{const} $$
The instantaneous angular momentum of particle is mvr. Obviously this is a constant.
- A particle moving in a plane is acted upon by a force of constant magnitude. $F$ and $v$ denote instantaneous force and velocity of particle. F.v is zero at every moment of time. The path of particle is
(1) Straight line
(2) Circle
(3) Hyperbola
(4) Ellipse
Show Answer
Correct answer: (2)
Solution:
Since $\mathbf{F} \cdot \mathbf{v}=0$; the instantaneous velocity is always perpendicular to the instantaneous direction of force. This condition is satisfied for a particle moving in a horizontal circle with uniform speed. The force acting on particle provides the necessary centeripetal force.
49. A particle of mass $100 \mathrm{~g}$ attached to a string moves in a horizontal circle of radius $20 \mathrm{~cm}$. The maximum speed of particle so that string does not break is $200 \mathrm{~cm} / \mathrm{s}$. Another string has a breaking strength $75 \%$ more and its length is double that of the earlier string. What is change in mass of particle attached to this string if breaking speed remains same?
(1) $0.35 \mathrm{~kg}$
(2) $0.25 \mathrm{~kg}$
(3) $0.5 \mathrm{~kg}$
(4) $0.4 \mathrm{~kg}$
Show Answer
Correct answer: (2)
Solution:
Let $\mathrm{m}, \mathrm{v}$, and $\mathrm{r}$ denote mass of particle; speed of particle and length of string. The breaking strength, $\mathrm{T}$; of string is
$\mathrm{T}=\frac{\mathrm{mv}^{2}}{\mathrm{r}}=\frac{0.1 \times(2)^{2}}{0.2}=2 \mathrm{~N}$
$\mathrm{T}^{\prime}=$ Breaking strength of second string $=(1.75) \mathrm{T}=3.5 \mathrm{~N}$
$\mathrm{r}^{\prime}=$ Length of second string $=2 \mathrm{r}=0.4 \mathrm{~m}$
Let $\mathrm{m}$ ’ be mass of particle attached to string. Given,
$$ \begin{gathered} \mathrm{T}^{\prime}=3.5=\frac{\mathrm{m}^{\prime} \mathrm{v}^{2}}{\left(\mathrm{r}^{\prime}\right)} \\ \text { or } \quad \mathrm{m}^{\prime}=\frac{3.5 \times 0.4}{4} \mathrm{~kg}=0.35 \mathrm{~kg} \end{gathered} $$
Change in mass of particle $=\mathrm{m}^{\prime}-\mathrm{m}=0.25 \mathrm{~kg}$
50. A particle moves in a horizontal circle of radius $r$ with a uniform speed $\omega$ in $x-y$ plane as shown in Fig. $\theta$ is the instantaneous angle, the position vector of particle makes with $x$-axis. The instantaneous velocity, $\mathrm{v}$; and the instantaneous acceleration a are:

(1) $\mathbf{v}=\mathrm{r} \omega[(\cos \theta) \hat{\mathrm{i}}+(\sin \theta) \hat{\mathrm{j}}]$
$\mathbf{a}=\mathrm{r} \omega^{2}[(\cos \theta) \hat{\mathrm{i}}-(\sin \theta) \hat{\mathrm{j}}]$
(2) $\quad \mathbf{v}=\mathrm{r} \omega[(-\cos \theta) \hat{\mathrm{i}}+(\sin \theta) \hat{\mathrm{j}}]$
(3) $\mathbf{v}=\operatorname{r\omega }[(-\cos \theta) \hat{\mathrm{i}}+(\sin \theta) \hat{\mathrm{j}}]$
$\mathbf{a}=\mathrm{r} \omega^{2}[(\cos \theta) \hat{\mathrm{i}}+(\sin \theta) \hat{\mathrm{j}}]$
(4) $\mathbf{v}=\mathrm{r} \omega[(\cos \theta) \hat{\mathrm{i}}-(\sin \theta) \hat{\mathrm{j}}]$
$\mathbf{a}=\mathrm{r} \omega^{2}[-(\cos \theta) \hat{\mathrm{i}}+(\sin \theta) \hat{\mathrm{j}}]$
Show Answer
Correct answer: (2)
Solution:
In Fig. $\hat{r}$ and $\hat{t}$ are instantaneous unit vector along radially outward and tangential direction. We know,
$\mathbf{v}=(\mathrm{r} \omega) \hat{\mathrm{t}}$ and $\mathbf{a}=\left(-\mathrm{r} \omega^{2}\right) \hat{\mathrm{r}}$. Resolve $\hat{\mathrm{r}}$ and $\hat{\mathrm{t}}$ into their components along $x$ and $y$-axis. Obviously
$$ \hat{\mathrm{r}}=(\cos \theta) \hat{\mathrm{i}}+(\sin \theta) \hat{\mathrm{j}} $$
and $\hat{\mathrm{t}}=(-\cos \theta) \hat{\mathrm{i}}+(\sin \theta) \hat{\mathrm{j}}$

Obviously (2) in the correct choice.
51. The minutes hand of a clock is $30 \mathrm{~cm}$ long. The magnitude of change in velocity of the tip of minutes hand of clock is $\frac{\pi}{6} \mathrm{mms}^{-1}$. The time interval is
(1) $10 \mathrm{~s}$
(2) 5 minute
(3) 2 minute 30 second
(4) 10 minute
Show Answer
Correct answer: (4)
Solution:
The angular speed, $\omega$, of minutes hand of clock is
$$ \omega=\frac{2 \pi}{60 \times 60} \mathrm{rad} / \mathrm{s} $$
The linear speed $v$ of the tip of the minute’s hands
$$ =\ell \times \omega=\frac{0.3 \times 2 \pi}{60 \times 60} \mathrm{~ms}^{-1}=\frac{\pi}{6} \mathrm{mms}^{-1} $$
Let $\theta$ be the angle through which the minute’s hand of clock has turned in time initial t. The magnitude of change in velocity of the tip of minute’s hand $=2 \mathrm{v} \sin \left(\frac{\theta}{2}\right)$. Therefore
$$ \frac{\pi}{6}=2\left(\frac{\pi}{6}\right) \sin \left(\frac{\theta}{2}\right) \quad \text { or } \quad \sin \left(\frac{\theta}{2}\right)=\frac{\pi}{6} $$
$\therefore \theta=\frac{\pi}{3}=60^{\circ}$
The time interval $=\frac{60}{360} \mathrm{hr}=\frac{1}{6} \mathrm{hr}=10$ minute
52. In space, far off from any gravitating matter; two particles $A$ and $B$ move in horizontal and vertical circles of radii in ratio of 1:2. The speed of the two particles are in ratio of 3:2. Which of the following statement is correct?
(1) For both A and B motion is with uniform speed only
(2) For both $\mathrm{A}$ and $\mathrm{B}$ motion is with uniform velocity
(3) For A motion is with uniform velocity only and for B motion is with non-uniform speed and velocity
(4) For B motion is with uniform velocity only and for A, motion is with non-uniform speed and velocity.
Show Answer
Correct answer: (1)
Solution:
Since there is no gravitating matter nearby; whether particle moves is a horizontal or vertical circle; situation is same. In both cases speed can be constant but velocity is not constant. The direction of velocity changes.
53. A particle $A$ is moving in a horizontal circle of radius $r$. Another particle $B$ moves in a vertical circle, in gravity earth, of same radius $r$. For the motion in the two cases.
(p) Speed only is uniform
(q) Velocity only is uniform
(r) Both speed and velocity are uniform
(s) Neither speed nor velocity is uniform.
The correct statement of motion of $A$ and $B$ is:
(1) For both A and B (p)
(2) For both A and B (r)
(3) For A; (p); For B; (s)
(4) For A; (r); For B (s)
Show Answer
Correct answer: (3)
Solution:
For motion in horizontal circle speed is constant but velocity is not. The direction of velocity changes.
For motion in vertical circle neither speed nor velocity is constant. Speed decreases as particle moves from lowest point of circular path to highest point and increases during the other half part of motion along vertical circle.
54. A bird is sitting on a tree. A shooter at a horizontal distance $D$ fires a shot with speed $v$ aimed at the bird. The shooter misses hitting bird by a vertical distance y. Now shooter again aims at bird but the moment bullet leaves gun bird starts moving vertically downwards with constant speed $v _{1}$ or $v _{2}\left(v _{1}>v _{2}\right)$. In both cases shooter again misses hitting bird by equal distance. The speed, $v$, of bullet is
(1) $\frac{g D}{\left(v _{1}+v _{2}\right)}$
(2) $\frac{\mathrm{gD}}{\left(\mathrm{v} _{1}-\mathrm{v} _{2}\right)}$
(3) $\frac{g D}{2\left(v _{1}+v _{2}\right)}$
(4) $\frac{\mathrm{gD}}{2\left(\mathrm{v} _{1}-\mathrm{v} _{2}\right)}$
Show Answer
Correct answer: (1)
Solution:
Let $t$ be time taken by bullet to travel horizontal distance $D$. Obviously $t=\frac{D}{v} \cdot y=$ The vertical distance by which bullet misses hitting bird $=\frac{1}{2} \mathrm{gt}^{2}$
Let bird fly with vertical speed $\mathrm{v}^{\prime}$ when bullet leaves gun. The distance by which bullet misses hitting bird is $\left(v _{1} t-y\right)$. Similarly the bullet misses hitting bird in $2^{\text {nd }}$ case by distance $\left(y-v _{2} t\right)$. Given,
$$ \mathrm{v} _{1} \mathrm{t}-\mathrm{y}=\mathrm{y}-\mathrm{v} _{2} \mathrm{t} $$
or $\mathrm{t}=\frac{2 \mathrm{y}}{\mathrm{v} _{1}+\mathrm{v} _{2}}=\frac{1}{\left(\mathrm{v} _{1}+\mathrm{v} _{2}\right)} \mathrm{gt}^{2}$
$\therefore \mathrm{t}=\frac{\mathrm{v} _{1}+\mathrm{v} _{2}}{\mathrm{~g}} \quad$ or $\frac{\mathrm{D}}{\mathrm{v}}=\frac{\mathrm{v} _{1}+\mathrm{v} _{2}}{\mathrm{~g}}$
or $\quad v=\frac{\mathrm{gD}}{\left(\mathrm{v} _{1}+\mathrm{v} _{2}\right)}$
55. From a point two balls $A$ and $B$ are projected in opposite directions horizontally with speed $v _{1}$ and $2 v _{1}$ simultaneously. At time $t=t$; the instantaneous velocity vectors of the two are mutually perpendicular. $t$ is
(1) $\frac{\mathrm{v} _{1}}{\mathrm{~g}}$
(2) $\sqrt{2}\left(\frac{\mathrm{v} _{1}}{\mathrm{~g}}\right)$
(3) $\frac{v _{1}}{\sqrt{2} g}$
(4) $\frac{2 \mathrm{v} _{1}}{\mathrm{~g}}$
Show Answer
Correct answer: (2)
Solution:
Fig. shows particles $A$ and $B$ projected from point $O$ horizontally. Given $v _{A}=v _{1}, v _{B}=2 v _{1}$. Let $A _{1}$ and $B _{1}$ be the position of two particles at $t=t$ when their velocities are mutually perpendicular i.e. $\mathrm{A} _{1} \mathrm{O} _{1} \mathrm{~B} _{1}=\frac{\pi}{2}$. Let $\theta _{1}$ and $\theta _{2}$ be the angle the instantaneous velocity vector of $A$ and $B$ make with horizontal. Obviously
$\tan \theta _{1}=\frac{\mathrm{v} _{1}}{\mathrm{gt}} ; \quad \tan \theta _{2}=\frac{2 \mathrm{v} _{1}}{\mathrm{gt}}$
From $\Delta A_1 O B_1 ; \theta_1+\theta_2=\frac{\pi}{2}$ $$ \therefore \tan \theta_2=\tan \left(\frac{\pi}{2}-\theta_1\right)=\cot \theta_1 $$ or $\quad \tan \theta_1 \cdot \tan \theta_2=1$ $$ \therefore \frac{2 \mathrm{v}_1^2}{\mathrm{~g}^2 \mathrm{t}^2}=1 $$ or $\quad t=\sqrt{2}\left(\frac{v_1}{g}\right)$

56. If $|\mathbf{A} \times \mathbf{B}|=\sqrt{3}(\mathbf{A} \cdot \mathbf{B})$, the value of $\frac{1}{2}\left\{|\mathbf{A}+\mathbf{B}|^{2}-|\mathbf{A}-\mathbf{B}|^{2}\right\}$ is:
(1) $2 \mathrm{AB}$
(2) $2\left(\mathrm{~A}^{2}+\mathrm{B}^{2}\right)$
(3) $\mathrm{A}^{2}+\mathrm{B}^{2}$
(4) $\mathrm{AB}$
Show Answer
Correct answer: (4)
Solution:
Given $|\mathbf{A} \times \mathbf{B}|=\sqrt{3}(\mathbf{A} \cdot \mathbf{B})$
$\therefore A B \sin \theta=\sqrt{3} A B \cos \theta \quad$ or $\tan \theta=\sqrt{3}$
$\therefore \theta=60^{\circ}$
Now, $|\mathbf{A}+\mathbf{B}|^{2}=\mathrm{A}^{2}+\mathrm{B}^{2}+2 \mathrm{AB} \times \frac{1}{2}$ $\left[\because \cos 60^{\circ}=\frac{1}{2}\right]$
and $|\mathbf{A}-\mathbf{B}|^{2}=\mathrm{A}^{2}+\mathrm{B}^{2}-2 \mathrm{AB} \times \frac{1}{2}$
$\therefore|\mathbf{A}+\mathbf{B}|^{2}-|\mathbf{A}-\mathbf{B}|^{2}=2 \mathrm{AB}$
or $\frac{1}{2}\left\{|\mathbf{A}+\mathbf{B}|^{2}-|\mathbf{A}-\mathbf{B}|^{2}\right\}=\mathrm{AB}$
Correct answer (4)
57. A particle is released from rest from the top of a tower of height $3 \mathrm{~h}$. The ratio of the intervals of time to travel three equal falls of $h$ each, from the top, is:
(1) $1: \sqrt{2}: \sqrt{3}$
(2) $1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2})$
(3) $1:(\sqrt{2}-1):(\sqrt{3}-2)$
(4) $1:(\sqrt{2}-1):(3-\sqrt{2})$
Show Answer
Correct answer: (2)
Solution:
(i) $\mathrm{h}=0+\frac{1}{2} \mathrm{gt} _{1}^{2}$
$\therefore \mathrm{t} _{1}=\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}$
(ii) $\quad 2 \mathrm{~h}=0+\frac{1}{2} \mathrm{~g}\left(\mathrm{t} _{1}+\mathrm{t} _{2}\right)^{2}$
$\therefore \mathrm{t} _{1}+\mathrm{t} _{2}=\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}} \times \sqrt{2}$
(iii) $3 \mathrm{~h}=0+\frac{1}{2} \mathrm{~g}\left(\mathrm{t} _{1}+\mathrm{t} _{2}+\mathrm{t} _{3}\right)^{2} \therefore \mathrm{t} _{1}+\mathrm{t} _{2}+\mathrm{t} _{3}=\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}} \times \sqrt{3}$

From Eqns. (i), (ii) and (iii), we have
$$ \begin{aligned} & \mathrm{t} _{1}= \sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}} \\ & \mathrm{t} _{2}=\left(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}} \times \sqrt{2}\right)-\mathrm{t} _{1}=\left(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}} \times \sqrt{2}\right)-\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}} \\ &= \sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}[\sqrt{2}-1] \\ & \mathrm{t} _{3}=\left(\mathrm{t} _{1}+\mathrm{t} _{2}+\mathrm{t} _{3}\right)-\left(\mathrm{t} _{1}+\mathrm{t} _{2}\right) \\ &= \sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}} \times \sqrt{3}-\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}} \times \sqrt{2}=\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}[\sqrt{3}-\sqrt{2}] \\ & \therefore \mathrm{t} _{1}: \mathrm{t} _{2}: \mathrm{t} _{3}=1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2}) \end{aligned} $$
Correct answer (2)
58. A man of $50 \mathrm{~kg}$ mass is standing in a gravity free space at a height of $10 \mathrm{~m}$ above the floor. He throws a stone of mass $0.5 \mathrm{~kg}$ downwards with a speed of $2 \mathrm{~ms}^{-1}$. When the stone hits the floor the distance of the man above the floor will be:
(1) $20 \mathrm{~m}$
(2) $9.9 \mathrm{~m}$
(3) $10.1 \mathrm{~m}$
(4) $10 \mathrm{~m}$
Show Answer
Correct answer(3)
Solution:
When the man throws the ball down, he will get a velocity v upwards, such that:
$$ \mathrm{mv}=\mathrm{MV} \quad(\text { Law of conservation of linear momentum) } $$
or $\quad 0.2 \times 2=50 \times \mathrm{V} \quad$ or $\quad \mathrm{V}=\frac{1}{50} \mathrm{~ms}^{-1}$
Time taken by the ball to reach floor is
$\mathrm{t}=\frac{10}{2}=5 \mathrm{~s} \quad$ (The ball will not accelerate in the absence of gravity)
$\therefore$ Distance moved up by the man in this $\mathrm{t}=5 \mathrm{~s}$ is
$$ \mathrm{d}=\mathrm{V} \times \mathrm{t}=\frac{1}{50} \times 5=0.1 \mathrm{~m} ; \text { upwards } $$
Hence the distance of the man from the floor, when the stone hits the floor is
$$ \mathrm{H}=\mathrm{h}+\mathrm{d}=10+0.1=10.1 \mathrm{~m} $$
59. Two fixed frictionless inclined planes, making angles $30^{\circ}$ and $60^{\circ}$ with the vertical, are shown in the figure. Two blocks $A$ and $B$ are placed on these planes. The relative vertical acceleration of $A$ with respect to $B$ is:

(1) $9.8 \mathrm{~ms}^{-2}$
(2) $4.9 \mathrm{~ms}^{-2}$
(3) $2.45 \mathrm{~ms}^{-2}$
(4) zero
Show Answer
Correct answer(2)
Solution:
Acceleration of A down the plane is $\mathrm{g} \sin 60 \mathrm{~g} \cos 30^{\circ}$ as shown in Fig. Resolve acceleration into horizontal and vertical components as shown in Fig. Obvisouly
The vertical acceleration of $\mathrm{A}=\left(\mathrm{g} \cos 30^{\circ}\right) \cos 30^{\circ}=\mathrm{g} \times \frac{3}{4}$

Similarly the vertical acceleration of $\mathrm{B}=\left(\mathrm{g} \cos 60^{\circ}\right) \cos 60^{\circ}=\mathrm{g} \times \frac{1}{4}$
$\therefore$ Relative vertical acceleration of $A$ with respect to $\mathrm{B}=\mathrm{g} \times \frac{3}{4}-\mathrm{g} \times \frac{1}{4}$
$$ =\mathrm{g} \times \frac{2}{4}=\frac{\mathrm{g}}{2}=4.9 \mathrm{~ms}^{-2} $$
60. A point $P$ moves in counter clockwise sense, on a circular path, as shown in the figure. The movement of the point is such that it sweeps out a length, $s=t^{3}+5$, where $s$ is in metre and $t$ is in seconds. The radius of the path is $20 \mathrm{~m}$. The acceleration of $P$ at $t=2 \mathrm{~s}$ is nearly:

(1) $14.5 \mathrm{~ms}^{-2}$
(2) $13.5 \mathrm{~ms}^{-2}$
(3) $12 \mathrm{~ms}^{-2}$
(4) $7.2 \mathrm{~ms}^{-2}$
Show Answer
Correct answer: (1)
Solution:
Given $s=t^{3}+5$. Therefore the instantaneous velocity
$$ \mathrm{v}=\frac{\mathrm{ds}}{\mathrm{dt}}=3 \mathrm{t}^{2} $$
Since this velocity is not constant in magnitude, the point $\mathrm{P}$ will have a tangential acceleration, $\mathrm{a} _{1}=\frac{\mathrm{dv}}{\mathrm{dt}}=3 \times 2 \mathrm{t}=6 \mathrm{t}$
At $\mathrm{t}=2 \mathrm{~s}, \mathrm{a} _{1}=6 \times 2=12 \mathrm{~ms}^{-2}$.
Now, $\mathrm{P}$ is moving in circular path therefore $\mathrm{P}$ will have centripetal acceleration.
$$ \mathrm{a} _{2}=\frac{\mathrm{v}^{2}}{\mathrm{R}}=\frac{\left(3 \mathrm{t}^{2}\right)^{2}}{\mathrm{R}}=\frac{9 \mathrm{t}^{4}}{20} $$
At $\mathrm{t}=2 \mathrm{~s}, \mathrm{a} _{2} \frac{9 \times 2 \times 2 \times 2 \times 2}{20}=7.2 \mathrm{~ms}^{-2}$
$\therefore \quad \mathrm{a}=\sqrt{\mathrm{a} _{1}^{2}+\mathrm{a} _{2}^{2}}=\sqrt{12^{2}+(7.2)^{2}} \approx 14.5 \mathrm{~ms}^{-2}$
61. A bullet, on entering a target, losses $\frac{1}{3}$ rd of its initial velocity, after penetrating through 20m. How far deep will it enter the target?
(1) $60 \mathrm{~m}$
(2) $40 \mathrm{~m}$
(3) $36 \mathrm{~m}$
(4) $16 \mathrm{~m}$
Show Answer
Correct answer: (3)
Solution:
Suppose the bullet loses $\frac{\mathrm{u}}{\mathrm{n}}$ of its initial velocity, after penetrating through distance s. So, final velocity, after traveling distance $\mathrm{s}$ in target, is:
$$ \mathrm{v}=\mathrm{u}-\frac{\mathrm{u}}{\mathrm{n}}=\frac{\mathrm{u}}{\mathrm{n}}(\mathrm{n}-1) $$
If a is the deceleration, then :
$$ \begin{gathered} v^{2}=u^{2}-2 a s \\ \text { or } \quad\left[\frac{u}{n}(n-1)\right]^{2}=u^{2}-2 \text { as } \\ \therefore \quad a=\frac{1}{2 s}\left[u^{2}-\frac{u^{2}}{n^{2}}\left(n^{2}-2 n+1\right)\right] \\ \quad=\frac{1}{2 s}\left[u^{2}-u^{2}+\frac{u^{2}}{n^{2}} \times 2 n-\frac{u^{2}}{n^{2}}\right] \\ \quad=\frac{1}{2 s}\left[\frac{u^{2}}{n^{2}}(2 n-1)\right] \end{gathered} $$
If the bullet goes a further distance $x$, before coming to rest, then
$$ \begin{aligned} & \mathrm{v} _{\mathrm{f}}^{2}=\mathrm{v}^{2}-2 \mathrm{a} x \\ & \text { or } \quad 0=\frac{\mathrm{u}^{2}}{\mathrm{n}^{2}}(\mathrm{n}-1)^{2}-2 \times\left[\frac{1}{2 \mathrm{~s}} \times \frac{\mathrm{u}^{2}}{\mathrm{n}^{2}}(2 \mathrm{n}-1)\right] x \\ & \therefore \quad x=\frac{(\mathrm{n}-1)^{2}}{(2 \mathrm{n}-1)} \mathrm{s} \end{aligned} $$
Given, $s=3 \mathrm{~m}$, therefore
$$ x=\frac{(3-1)^{2}}{(2 \times 3-1)} \times 20=\frac{4}{5} \times 20=16 \mathrm{~m} $$
Therefore, total penetration is
$$ \mathrm{s}+x=20+16=36 $$
Alternatively:
$\mathrm{v}^{2}=\mathrm{u}^{2}+2 \mathrm{as} \hspace{40mm} . . . . . .(1) $
Here, $v=u=\frac{1}{3} u=\frac{2}{3} u$ and $s=20 m$
Since a is -ve, Eqn. (1) can be written as:
$$ \frac{4}{9} u^{2}=u^{2}-29 \times 20 $$
$\therefore 2 \mathrm{a} \times 20=\frac{5}{9} \mathrm{u}^{2}$
or $2 \mathrm{a}=\left(\frac{5}{9}\right) \frac{\mathrm{u}^{2}}{20} \hspace{40mm} . . . . . .(2)$
Now, if ’ $\mathrm{d}$ ’ is the total penetration, then
$$ \mathrm{v} _{\mathrm{f}}^{2}=\mathrm{u}^{2}-2 \mathrm{a} \times \mathrm{d} \quad(\mathrm{a}=\text { deceleration }) $$
$$ \mathrm{O}^{2}=\mathrm{u}^{2}-\left(\frac{5}{9}\right) \frac{\mathrm{u}^{2}}{20} \times \mathrm{d} $$
or $\quad u^{2}=\frac{5}{9} \times \frac{u^{2} \times d}{20}$
$$ \mathrm{d}=\frac{180}{5}=36 \mathrm{~m} $$
62. A particle moving along $y$-axis is at $y=5 \mathrm{~cm}$ at $t=0$ (where $t$ is in second). This particle is observed to trace the following velocity time graph.
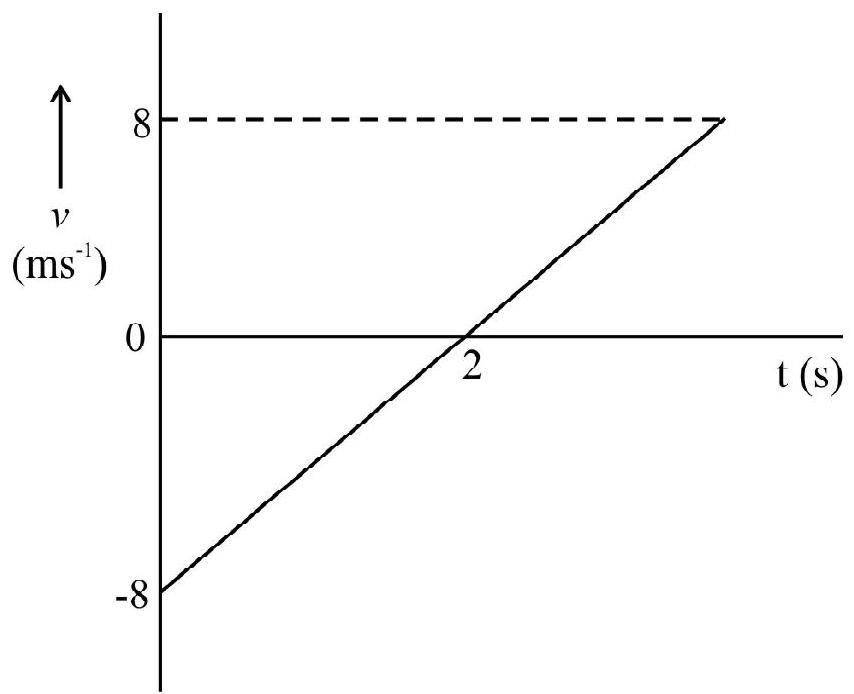
The displacement $y$ of this particle in terms of $t$ can be written as:
(1) $y=5-2 t+8 t^{2}$
(2) $t=2 t^{2}-8 t+5$
(3) $y=8 t^{2}-2 t-5$
(4) $y=5-4 t+2 t^{2}$
Show Answer
Correct answer(2)
Solution:
Given, $\mathrm{y} _{(0)}=+5 \mathrm{~m}$. From the graph,
Velocity $=-8 \mathrm{~ms}^{-1}$ at $\mathrm{t}=0$
$$ \therefore \mathrm{v} _{(0)}=-8 \mathrm{~ms}^{-1} $$
Now, $\mathrm{v}-\mathrm{t}$ graph is a straight line. Therefore acceleration is a constant $\mathrm{a}=$ slope of $\mathrm{v} \quad vs \quad \mathrm{t}$ graph.
$$ =+\frac{8}{2}=+4 \mathrm{~ms}^{-2} $$
The final position at $t=t$ can be written as: $y _{(t)}=y _{(0)}+v _{(0)} t+\frac{1}{2} a t^{2}$
or $\quad y=5-8 t+\frac{1}{2} \times 4 t^{2}$
or $y=2 t^{2}-8 t+5$
63. A stationery body of mass $3 \mathrm{~kg}$ explodes in to three equal pieces. One of the pieces flies off with a velocity of $3 \hat{i} \mathrm{~ms}^{-1}$ and a second one goes with velocity of $4 \hat{j} \mathrm{~ms}^{-1}$. If the time of explosion is $10^{-4} \mathrm{~s}$, the magnitude of the average force experienced by the third piece is:
(1) 70 kilo newton
(2) 50 kilo newton
(3) 40 kilo newton
(4) 30 kilo newton
Show Answer
Correct answer(2)
Solution:
The momentum imparted to the two pieces together is:
$\Delta \mathbf{p}=1 \times(3 \hat{\mathrm{i}}+4 \hat{\mathrm{j}}) \mathrm{N}-\mathrm{s} \quad(\mathrm{m}=1 \mathrm{~kg})$
As the body of $3 \mathrm{~kg}$ is initially at rest the change in momentum for the third piece should be equal and opposite that for the first two taken together.
$\therefore \Delta \mathbf{p}$ for $3^{\text {rd }}$ piece $=-(3 \hat{\mathrm{i}}+4 \hat{\mathrm{j}}) \mathrm{N}-\mathrm{s}$
Time taken for this change, $\Delta \mathrm{t}=10^{-4} \mathrm{~s}$
$\therefore$ Force on the third piece is
$$ \mathbf{F} _{3}=\frac{\Delta \mathrm{p}}{\Delta \mathrm{t}}=-\frac{3 \hat{\mathrm{i}}+4 \hat{\mathrm{j}}}{10^{-4}} \mathrm{~N} $$
$$ \begin{gathered} \mathbf{F} _{3}=-(3 \hat{\mathrm{i}}+4 \hat{\mathrm{j}}) \times 10^{4} \mathrm{~N} \\ \therefore\left|\mathbf{F} _{3}\right|=\mathrm{F} _{3}=\sqrt{3^{2}+4^{2}} \times 10^{4} \mathrm{~N}=5 \times 10^{4} \mathrm{~N} \\ =50 \times 10^{3} \mathrm{~N}=50 \text { Kilo newton } \end{gathered} $$
64. The position ’ $x$ ’ of a particle varies with time ’ $t$ ’ as : $x=\mathbf{m t}^{2}-\mathbf{n t}^{3}$. The acceleration time graph of this particle is:

Show Answer
Correct answer: (1)
Solution:
Given : $x=\mathrm{mt}^{2}-\mathrm{nt}^{3}$. $\therefore \mathrm{v}=\frac{\mathrm{d} x}{\mathrm{dt}}=2 \mathrm{mt}-3 \mathrm{nt}^{2} \hspace{60mm} . . . . . .(i)$
Hence, $\mathrm{a}=\frac{\mathrm{d} v}{\mathrm{dt}}=2 \mathrm{~m}-6 \mathrm{nt} \hspace{40mm} . . . . . .(ii)$
or $\quad a=(-6 n) t+2 m$
Eqn. (ii) is of the form $\mathrm{y}=\mathrm{m} x+\mathrm{c}$ for the equation of a straight line, where $\mathrm{m}$ is slope and $\mathrm{c}$ is $\mathrm{y}$ intercept.
Hence $a-t$ graph is a straight line with
(i) slope of $-6 \mathrm{~m}$.
(ii) of-intercept $=+2 \mathrm{~m}$ and
(iii) a $=0$ at $\mathrm{t}=\frac{2 \mathrm{~m}}{6 \mathrm{n}}=\frac{\mathrm{m}}{3 \mathrm{n}}$
(i), (ii) and (iii) are true only for (1)
65. Two particles $P$ and $Q$ get $6 \mathrm{~m}$ closer each second, while traveling is opposite directions. They get $2.4 \mathrm{~m}$ closer every second while traveling in the same direction. The speeds of $P$ and $Q$ are:
(1) $4.2 \mathrm{~ms}^{-1}$ and $2.4 \mathrm{~ms}^{-1}$
(2) $8.4 \mathrm{~ms}^{-1}$ and $3.6 \mathrm{~ms}^{-1}$
(3) $4.2 \mathrm{~ms}^{-1}$ and $1.8 \mathrm{~ms}^{-1}$
(4) $4.2 \mathrm{~ms}^{-1}$ and $3.6 \mathrm{~ms}^{-1}$
Show Answer
Correct answer: (3)
Solution:
Here, $\mathrm{v} _{1}+\mathrm{v} _{2}=6 \mathrm{~ms}^{-1}$, and $\mathrm{v} _{1}-\mathrm{v} _{2}=2.4 \mathrm{~ms}^{-1}$
$\therefore 2 \mathrm{v} _{1}=8.4 \mathrm{~ms}^{-1}$
or $\mathrm{v} _{1}=4.2 \mathrm{~ms}^{-1}$, and $\mathrm{v} _{2}=1.8 \mathrm{~ms}^{-1}$
66 Figure gives the velocity-time graph of a moving particle. Total displacement of the particle during its non-uniform motion is:
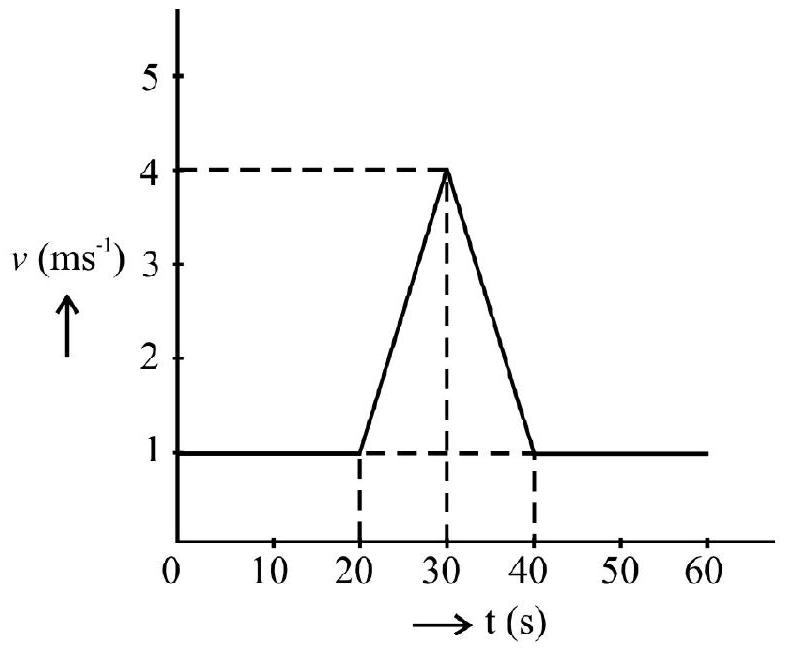
(1) $60 \mathrm{~m}$
(2) $50 \mathrm{~m}$
(3) $30 \mathrm{~m}$
(4) $40 \mathrm{~m}$
Show Answer
Correct answer: (2)
Solution:
The particle is in non-uniform motion from $t=20 \mathrm{~s}$ to $\mathrm{t}=40 \mathrm{~s}$. Total displacement in this interval is equal to the area under the graph in this interval.
$\therefore \mathrm{S}=2 \times\left[\frac{1}{2}(1+4) \times 10\right]=50 \mathrm{~m}$
67. A man of height $h$ walks in a straight path towards a lamp post of height $H$, with a uniform velocity $u$. The velocity of the edge of his shadow on the ground will be
(1) $\left(\frac{H}{H+h}\right) u$
(2) $\left(\frac{H}{H-h}\right) u$
(3) $\left(\frac{H+h}{H}\right) u$
(4) $\left(\frac{H+h}{-h}\right) u$
Show Answer
Correct answer: (2)
Solution:
Suppose $x$ is the length of the shadow. When the man is at $\mathrm{d}$ distance from the pole, as shown in Fig. If he takes $t$ seconds to reach the pole, the edge of his shadow will also reach the pole in the same time $\mathrm{t} \frac{\mathrm{h}}{\mathrm{x}}=\frac{\mathrm{H}}{\mathrm{x}+\mathrm{d}}$ and $\mathrm{d}=$ ut
$\therefore x \mathrm{H}=\mathrm{h} x+\mathrm{hd}$
or $\quad x(\mathrm{H}-\mathrm{h})=\mathrm{hut}$
$\therefore x=\frac{\mathrm{hut}}{\mathrm{H}-\mathrm{h}}$

The distance travelled by the edge of the shadow, in t seconds, is equal to $x+\mathrm{d}$. The velocity of the edge, $v$ is
$$ \begin{aligned} & \mathrm{v}=\frac{x+\mathrm{d}}{\mathrm{t}}=\frac{\left[\frac{\mathrm{hut}}{\mathrm{H}-\mathrm{h}}+\mathrm{ut}\right]}{\mathrm{t}} \\ & =\frac{\mathrm{hu}}{\mathrm{H}-\mathrm{h}}+\mathrm{u}=\left(\frac{\mathrm{h}+\mathrm{H}-\mathrm{h}}{\mathrm{H}-\mathrm{h}}\right) \mathrm{u} \\ & \quad=\left(\frac{\mathrm{H}}{\mathrm{H}-\mathrm{h}}\right) \mathrm{u} \end{aligned} $$$ \qquad $
68. Two bodies of masses in the ratio $5: 4$ are dropped from heights of $16 \mathrm{~m}$ and $25 \mathrm{~m}$ respectively. The ratio of the time taken by them to reach the ground and the ratio of their velocities at the time of hitting the ground are, respectively
(1) $1: 1$ and $4: 5$
(2) $5: 4$ and $1: 1$
(3) $4: 5$ and $4: 5$
(4) $1: 4$ and $1: 4$
Show Answer
Correct answer: (3)
Solution:
Mass does not influence the time and speed. Now, for a body dropped, $\mathrm{u}=0$
$\therefore \mathrm{S}=\mathrm{ut}+\frac{1}{2} \mathrm{at}^{2}$ reduces to
$\mathrm{S}=0+\frac{1}{2} \mathrm{gt}^{2}$
$\therefore \mathrm{S} _{1}=\frac{1}{2} \mathrm{gt} _{1}^{2}$ and $\mathrm{S} _{2}=\frac{1}{2} \mathrm{gt} _{2}^{2}$
So, $\mathrm{t} _{1}: \mathrm{t} _{2}=\sqrt{\mathrm{S} _{1}}: \sqrt{\mathrm{S} _{2}}=4: 5$
Now, $\mathrm{v}=\mathrm{u}+\mathrm{at}=0+\mathrm{gt}$
$\therefore \mathrm{v} _{1}=\mathrm{gt} _{1}$ and $\mathrm{v} _{2}=\mathrm{gt} _{2}$
$\therefore \mathrm{v} _{1}: \mathrm{v} _{2}=\mathrm{t} _{1}: \mathrm{t} _{2}=4: 5$
69. The upper and of a bar $P Q$ of length ’ $\ell$ ’ leans against a smooth vertical wall. The other end of the bar is touching the smooth floor. The end $Q$ beings to move uniformly downwards with speed $v _{y}$ the speed $v _{x}$ with which end $P$ moves along the floor is

(1) $\mathrm{v} _{\mathrm{x}}=-\mathrm{v} _{\mathrm{y}}\left(\frac{\mathrm{y}}{\sqrt{\ell^{2}-\mathrm{y}^{2}}}\right)$
(2) $\mathrm{v} _{x}=-\mathrm{v} _{\mathrm{y}}\left(\frac{\sqrt{\ell^{2}-\mathrm{y}^{2}}}{\mathrm{y}}\right)$
(3) $\mathrm{v} _{x}=-\mathrm{v} _{\mathrm{y}}\left(\frac{\mathrm{y}^{2}}{\ell^{2}-\mathrm{y}^{2}}\right)$
(4) $\mathrm{v} _{x}=-\mathrm{v} _{\mathrm{y}}\left(\frac{\ell^{2}-\mathrm{y}^{2}}{\mathrm{y}^{2}}\right)$
Show Answer
Correct answer: (1)
Solution:
According to the diagram given:
$$ x^{2}+y^{2}=\ell^{2}=\text { constant } $$
Differentiating with respect to time,
$$ 2 x \frac{\mathrm{d} x}{\mathrm{dt}}+2 \mathrm{y} \frac{\mathrm{dy}}{\mathrm{dt}}=0 $$
$\therefore x \mathrm{v} _{x}=-\mathrm{yv} _{\mathrm{y}}$

or $\quad \mathrm{v} _{\mathrm{x}}=-\mathrm{v} _{\mathrm{y}}\left(\frac{\mathrm{y}}{x}\right)$
$\mathrm{v} _{x}=-\mathrm{v} _{y}\left(\frac{\mathrm{y}}{\sqrt{\ell _{2}-\mathrm{y} _{2}}}\right)$
Correct answer: (1)
70. A body moving along $x$-axis is at $x=-5 \mathrm{~m}$ at $\mathrm{t}=0$. It covers $10 \mathrm{~m}$ is the third second and $28 \mathrm{~m}$ in the sixth second. The position of this body at $t=8 \mathrm{~s}$ is
(1) $192 \mathrm{~m}$
(2) $152 \mathrm{~m}$
(3) 147
(4) $40 \mathrm{~m}$
Show Answer
Correct answer : (3)
Solution:
Given,
$x _{0}=-5 \mathrm{~m}$. The distance $\mathrm{s} _{3}$ travelled in third second is
$\mathrm{s} _{3}=\mathrm{u}+\frac{\mathrm{a}}{2}(2 \times 3-1)$
or $\quad 10=\mathrm{u}+\frac{5}{2} \mathrm{a} \hspace{40mm} . . . . . .(1)$
Similarly the distance travelled in $6^{\text {th }}$ second; $\mathrm{s} _{6}$, is
$\mathrm{s} _{6}=\mathrm{u}+\frac{\mathrm{a}}{2}(2 \times 6-1)$
or $\quad 28=u+\frac{11}{2} \mathrm{a} \hspace{40mm} . . . . . .(2)$
From Eqns. (1) and (2) we have $18=3 \mathrm{a}$ or $\mathrm{a}=6 \mathrm{~ms}^{-2}$
From Eqn(1), we get
$10=\mathrm{u}+\frac{5}{2} \times 6 \quad$ or $\mathrm{u}=-5 \mathrm{~ms}^{-1}$
At $\mathrm{t}=8 \mathrm{~s}$, the position $x _{8}$ of particle is
$x _{8}=x _{0}+\left(\mathrm{ut}+\frac{1}{2} \mathrm{at}^{2}\right)$
$=-5+(-5) \times 8+\frac{1}{2} \times 6 \times 8^{2}=-45+192=147 \mathrm{~m}$
71. At time $t=0$, a ball is dropped from a height is $180 \mathrm{~m}$, towards a floor. On each collision, the ball losses a tenth of its speed. The figure below gives the speed-time graph of the ball, taking $\mathbf{g}=10 \mathrm{~ms}^{-1}$

Then corresponding to the point $D$ on the plot, $t$, is:
(1) $10.8 \mathrm{~s}$
(2) $11.4 \mathrm{~s}$
(3) $16.8 \mathrm{~s}$
(4) $18.0 \mathrm{~s}$
Show Answer
Correct answer:(3)
Solution:
Let $\mathrm{t} _{\mathrm{A}}$ be the time taken to fall through height $\mathrm{h}=180 \mathrm{~m}$, after the ball is dropped.
$$ \therefore \mathrm{t} _{0 \mathrm{~A}}=\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}=\sqrt{\frac{2 \times 180}{10}}=6 \mathrm{~s} $$
Now, $\mathrm{v} _{\mathrm{A}}=\mathrm{u}+\mathrm{at}=0+\mathrm{gt}$
$$ =10 \times 6=60 \mathrm{~ms}^{-1} $$
$\mathrm{v} _{\mathrm{B}}=\mathrm{v} _{\mathrm{A}}-10 \% \mathrm{v} _{\mathrm{A}}=60-\left(\frac{1}{10} \times 60\right)$
$$ =60-6=54 \mathrm{~ms}^{-1} $$
Let $t _{B D}$ be the time taken to bounce up from the floor, reach the maximum height and then come down to hit the floor again.
$\therefore \mathrm{t} _{\mathrm{BD}}=\frac{2 \mathrm{u}}{\mathrm{g}}=\frac{2 \times 54}{10}=10.8 \mathrm{~s}$
Hence the total time taken is
$\mathrm{t} _{\mathrm{OD}}=\mathrm{t} _{\mathrm{OA}}+\mathrm{t} _{\mathrm{BD}}=16.8 \mathrm{~s}$
72. Between two stations, a train starts and accelerates uniformly at first, then moves with constant speed and finally retards uniformly, to reach and stop, at the other station. If the ratio of the time taken for these three parts of the motion is $1: 8: 1$, and the greatest speed is $60 \mathrm{kmh}^{-1}$, the average speed of the train is
(1) $30 \mathrm{kmh}^{-1}$
(2) $48 \mathrm{kmh}^{-1}$
(3) $54 \mathrm{kmh}^{-1}$
(4) $60 \mathrm{kmh}^{-1}$
Show Answer
Correct answer: (3)
Solution:
The speed-time graph for the motion of the train is shown in the figure. The total distance covered is:
$S=\left(\frac{1}{2} \times t \times 60\right)+(60 \times 8 t)+\left(\frac{1}{2} t \times 60\right)=540 t$
Total time taken $=t+8 t+t=10 t$
$\therefore$ Average speed $=\frac{540 \mathrm{t}}{10 \mathrm{t}}=54 \mathrm{kmh}^{-1}$

73. In a car race, car $A$ takes a time $t$ less than car $B$ at the finish and passes the finishing point with speed $v$ more than that of car $B$. Assuming that both the cars start from rest and travel with constant acceleration $a _{1}$ and $a _{2}$ repectively, the value of $v$ in terms of $a _{1}, a _{2}$ and $t$ is
(1) $\left(\frac{a _{1} a _{2}}{a _{1}+a _{2}}\right) t$
(2) $\left(a _{1}+a _{2}\right) t$
(3) $\left(\frac{\mathrm{a} _{1}+\mathrm{a} _{2}}{2}\right) \mathrm{t}$
(4) $\left(\sqrt{\mathrm{a} _{1} \mathrm{a} _{2}}\right) \mathrm{t}$
Show Answer
Correct answer: (4)
Solution:
Let $A$ take $t _{1}$ seconds to finish the race. Then, according to the data given, $B$ will take $\left(t _{1}+t\right)$ seconds to finish the race. Also, let $\mathrm{v} _{1}$ be the velocity of $B$ at the finishing point. Then the velocity of $A$ at the finishing point will be $\left(\mathrm{v} _{1}+\mathrm{v}\right)$. Therefore, for $\mathrm{A}$,
$$ \begin{equation*} \mathrm{v} _{1}+\mathrm{v}=0+\mathrm{a} _{1} \mathrm{t} _{1} \tag{1} \end{equation*} $$
and for $\mathrm{B}, \mathrm{v} _{1}=0+\mathrm{a} _{2}\left(\mathrm{t} _{1}+\mathrm{t}\right) \hspace{40mm} . . . . . .(2)$
$\therefore \mathrm{v}=\left(\mathrm{a} _{1}-\mathrm{a} _{2}\right) \mathrm{t} _{1}-\mathrm{a} _{2} \mathrm{t} \hspace{40mm} . . . . . .(3) $
Now, total distance travelled by both $A$ and $B$ is same. i.e. $S _{A}=S _{B}$. Using the formula, $S=u t+\frac{1}{2} a t^{2}$, we get;
$S _{A}=0+\frac{1}{2} a _{1} t _{1}^{2} \quad$ and $\quad S _{B}=0+\frac{1}{2} a _{2}\left(t _{1}+t\right)^{2}$
or $\sqrt{\mathrm{a} _{1}^{\prime}} \mathrm{t} _{1}=\sqrt{\mathrm{a} _{2}^{\prime}}\left(\mathrm{t} _{1}+\mathrm{t}\right)$
$\therefore \mathrm{t} _{1}\left(\sqrt{\mathrm{a} _{1}}-\sqrt{\mathrm{a} _{2}}\right)=\sqrt{\mathrm{a} _{2}} \mathrm{t}$
or $\quad \mathrm{t} _{1}=\frac{\left(\sqrt{\mathrm{a} _{2}}\right) \mathrm{t}}{\left(\sqrt{\mathrm{a} _{1}}-\sqrt{\mathrm{a} _{2}}\right)} \hspace{40mm} . . . . . .(4)$
Subsituting value of $t _{1}$ from Eqn (4) in Enq (3) we have
$$ \begin{aligned} v= & \left(a _{1}-a _{2}\right) \cdot \frac{\sqrt{a _{2}} t}{\left(\sqrt{a _{1}}-\sqrt{a _{2}}\right)}-a _{2} t \\ & =\frac{\left[\sqrt{a _{1}} \sqrt{a _{2}}-a _{2} \sqrt{a _{2}}-a _{2} \sqrt{a _{1}}+a _{2} \sqrt{a _{2}}\right]}{\sqrt{a _{1}}-\sqrt{a _{2}}} t \\ & =\frac{\left(a _{1} \sqrt{a 2}-a _{2} \sqrt{a _{1}}\right)}{\sqrt{a _{1}}-\sqrt{a _{2}}} t \\ & =\sqrt{a _{1} a _{2}} \frac{\left(\sqrt{a _{1}}-\sqrt{a _{2}}\right)}{\left(\sqrt{a _{1}}-\sqrt{a _{2}}\right)} t \\ & =\left(a _{1} a _{2}\right) t \end{aligned} $$
74. A particle is dropped from the top of a tower of height $h$ and at the same moment of time a second particle is projected upwards from the bottom of the tower. The two particles meet when the first one has descended a distance of $h / n$. The velocities of these particles, when they meet, are in the ratio
(1) $\mathrm{v} _{1}: \mathrm{v} _{2}=2:(\mathrm{n}-2)$
(2) $\mathrm{v} _{1}: \mathrm{v} _{2}=(\mathrm{n}-2): \mathrm{n}$
(3) $\mathrm{v} _{1}: \mathrm{v} _{2}=\sqrt{2}:(\mathrm{n}-2)$
(4) $\mathrm{v} _{1}: \mathrm{v} _{2}=1:(\mathrm{n}-1)$
Show Answer
Correct answer: (1)
Solution:
When the two particles meet we have for the first particle,
$$ \begin{equation*} \frac{\mathrm{h}}{\mathrm{n}}=\frac{1}{2} \mathrm{gt}^{2} \tag{1} \end{equation*} $$
and for the second particle
$$ \begin{equation*} \mathrm{h}-\frac{\mathrm{h}}{\mathrm{n}}=\mathrm{u} _{2} \mathrm{t}-\frac{1}{2} \mathrm{gt}^{2} \tag{2} \end{equation*} $$
Adding Eqn, (1) and (2), we have
$$ \begin{equation*} \mathrm{h}=\mathrm{u} _{2} \mathrm{t} \text { or } \mathrm{t}=\frac{\mathrm{h}}{\mathrm{u} _{2}} \tag{3} \end{equation*} $$
Substituting value of t given by Eqn. (3) in Eqn. (1), we get
$$ \begin{align*} & \frac{\mathrm{h}}{\mathrm{n}}=\frac{1}{2} \mathrm{~g} \frac{\mathrm{h}^{2}}{\mathrm{u} _{2}^{2}} \\ & \therefore \mathrm{u} _{2}^{2}=\frac{1}{2} \mathrm{ngh} \tag{4} \end{align*} $$
At time $t$, when the two particle meet for the first particle
$$ \begin{align*} & \mathrm{v} _{1}^{2}=\mathrm{u} _{1}^{2}+2 \mathrm{~g}\left(\frac{\mathrm{h}}{\mathrm{n}}\right) \\ & \therefore \mathrm{v} _{1}^{2}=\mathrm{gh} \frac{2}{\mathrm{~h}} \quad\left(\because \mathrm{u} _{1}=0\right) \tag{5} \end{align*} $$
For the second particle, we have,
$$ \begin{align*} v _{2}^{2}= & u _{2}^{2}-2 g\left(h-\frac{h}{n}\right) \\ & =\frac{1}{2} n g h-g h\left(2-\frac{2}{n}\right) \\ & =\operatorname{gh}\left(\frac{n}{2}-2+\frac{2}{n}\right) \\ & =g h\left[\frac{n^{2}-4 n+4}{2 n}\right] \\ & =g h \frac{(n-2)^{2}}{2 n} \tag{6} \end{align*} $$
From Eqn s. (5) and (6), we have
$$ \frac{v _{1}^{2}}{v _{2}^{2}}=\frac{\operatorname{gh}\left(\frac{2}{n}\right)}{\operatorname{gh} \frac{(n-2)^{2}}{2 n}}=\frac{4}{(n-2)^{2}} $$
$\therefore \frac{\mathrm{v} _{1}}{\mathrm{v} _{2}}=\frac{2}{(\mathrm{n}-2)}$
or $\quad \mathrm{v} _{1}: \mathrm{v} _{2}=2:(\mathrm{n}-2)$
75. A particle is projected vertically upwards from a point $x$ on the ground. It takes a time $t _{1}$ to reach a point $A$, at a height ’ $h$ ’ above the ground. The particle continues to move and takes a time $t _{2}$ to reach the ground. The value of $h$ in terms of $t _{1}$ and $t _{2}$ is
(1) $\left(\frac{\mathrm{t} _{1}+\mathrm{t} _{2}}{2}\right) \mathrm{gt} _{1}$
(2) $\mathrm{gt} _{1} \mathrm{t} _{2}$
(3) $2 \mathrm{gt} _{1} \mathrm{t} _{2}$
(4) $\frac{1}{2} \mathrm{gt} _{1} \mathrm{t} _{2}$
Show Answer
Correct answer: (4)
Solution:
Let ’ $u$ ’ be the velocity of projection of the particle at 0 . The total time taken to reach the ground back is $\mathrm{t} _{1}+\mathrm{t} _{2}$.
From $\mathrm{S}=\mathrm{ut}+\frac{1}{2} \mathrm{at}^{2}$, we have,
$0=\mathrm{u}\left(\mathrm{t} _{1}+\mathrm{t} _{2}\right)+\frac{1}{2}(-\mathrm{g})\left(\mathrm{t} _{1}+\mathrm{t} _{2}\right)^{2}$
$\therefore \mathrm{u}=\frac{\mathrm{g}}{2}\left(\mathrm{t} _{1}+\mathrm{t} _{2}\right) \hspace{40mm} . . . . . .(1)$
Now, for the first $t$, second of motion, we have,
$$ \begin{aligned} \mathrm{h}=\mathrm{ut} _{1} & -\frac{1}{2} \mathrm{gt} _{1}^{2}=\frac{\mathrm{g}}{2}\left(\mathrm{t} _{1}+\mathrm{t} _{2}\right) \mathrm{t} _{1}-\frac{\mathrm{g}}{2} \mathrm{t} _{1}^{2} \\ & =\frac{\mathrm{g}}{2}\left[\mathrm{t} _{1}^{2}+\mathrm{t} _{1} \mathrm{t} _{2}-\mathrm{t} _{1}^{2}\right]=\frac{1}{2} \mathrm{gt} _{1} \mathrm{t} _{2} \end{aligned} $$

76. The two ends of a train, moving with a constant acceleration, pass a pole with velocities $u$ and $v$. The velocity with which the middle point of the train pass the pole is:
(1) $\frac{\mathrm{u}+\mathrm{v}}{2}$
(2) $\frac{u^{2}+v^{2}}{u+v}$
(3) $\sqrt{u^{2}+v^{2}}$
(4) $\sqrt{\frac{u^{2}+v^{2}}{2}}$
Show Answer
Correct answer: (4)
Solution:
Let the total length of the train be $2 x$. Let the velocity of the middle point of the train passing the pole be $v _{m}$. Then, for the first half of the journey of train,
$$ \begin{equation*} \mathrm{v} _{\mathrm{m}}^{2}=\mathrm{u}^{2}+2 \mathrm{a} x \tag{1} \end{equation*} $$
For the second half part of the journey, we have;
$$ \mathrm{v}^{2}=\mathrm{v} _{\mathrm{m}}^{2}+2 \mathrm{a} x $$
or $\mathrm{v} _{\mathrm{m}}^{2}=\mathrm{v}^{2}-2 \mathrm{a} x \hspace{40mm} . . . . . .(2)$
Adding Eqns. (1) and (2) we have
$$ \begin{aligned} & 2 \mathrm{v} _{\mathrm{m}}^{2}=\mathrm{u}^{2}+\mathrm{v}^{2} \\ & \therefore \mathrm{v} _{\mathrm{m}}=\sqrt{\frac{\mathrm{u}^{2}+\mathrm{v}^{2}}{2}} \end{aligned} $$
77. A balloon rises from rest on the ground with a constant acceleration of $\frac{\mathrm{g}}{8}$. A stone is dropped, from the balloon when it has risen to a height of $\mathrm{H}$. The time taken by the stone to reach the ground is
(1) $\sqrt{\frac{\mathrm{H}}{\mathrm{g}}}$
(2) $2 \sqrt{\frac{\mathrm{H}}{\mathrm{g}}}$
(3) $\sqrt{\frac{2 \mathrm{H}}{\mathrm{g}}}$
(4) $\sqrt{\frac{\mathrm{H}}{2 \mathrm{~g}}}$
Show Answer
Correct answer: (4)
Solution:
Let $\mathrm{v}$ be the velocity of the balloon, when it has risen to the height $\mathrm{H}$. Then,
$$ \mathrm{v}^{2}=0^{2}+2\left(\frac{\mathrm{g}}{8}\right) \mathrm{H} $$
$$ \begin{equation*} \text { or } \quad v=\frac{\sqrt{g H}}{2} \tag{1} \end{equation*} $$
This $\mathrm{v}$ will be the initial velocity of the stone when dropped from the balloon. If it is the time taken by the stone to reach the ground, then:
$-\mathrm{H}=\mathrm{v} \times \mathrm{t}-\frac{1}{2} \mathrm{gt}^{2}$
or $\quad-\mathrm{H}=\frac{\sqrt{\mathrm{gH}}}{2} \times \mathrm{t}-\frac{1}{2} \mathrm{gt}^{2}$ or $\quad \mathrm{gt}^{2}-(\sqrt{\mathrm{gH}}) \mathrm{t}-2 \mathrm{H}=0 \hspace{20mm} . . . . . .(2)$
$\therefore \quad \mathrm{t}=\frac{\sqrt{\mathrm{gH}} \pm \sqrt{\mathrm{gH}+8 \mathrm{gH}}}{2 \mathrm{~g}}$
$=\frac{\sqrt{\mathrm{gH}}+3 \sqrt{\mathrm{gH}}}{2 \mathrm{~g}}=2 \sqrt{\frac{\mathrm{H}}{\mathrm{g}}}$
78. To a man walking at the rate of $3 \mathrm{kmh}^{-1}$, rain drop appear to fall vertically. When he doubles his speed, rain drops appear to strike him, from the front, at an angle of $45^{\circ}$ with the downward vertical. The actual speed and the direction of rain drops are
(1) $5 \mathrm{kmh}^{-1}$,at $45^{0}$, with the vertical, to the direction of his motion
(2) $3 \sqrt{2} \mathrm{kmh}^{-1}$ at $45^{0}$, against the direction of his motion
(3) $3 \mathrm{kmh}^{-1}$, at $45^{0}$, against the direction of his motion
(4) $3 \sqrt{2} \mathrm{kmh}^{-1}$, at $45^{\circ}$, with the vertical, and to the direction of his motion
Show Answer
Correct answer: (4)
Solution:
Let $x$-axis be taken along the horizontal and $\mathrm{y}$-axis along the vertical as show in Fig.
The actual velocity of the rain drops, is
$$ \begin{equation*} \mathbf{v} _{\mathbf{r}}=\mathrm{v} _{x} \hat{\mathrm{i}}+\mathrm{v} _{\mathrm{y}} \hat{\mathrm{j}} \tag{1} \end{equation*} $$
For the man, $\mathbf{v} _{\mathbf{m}}=3 \hat{i} \hspace{40mm} . . . . . .(2)$
The relative velocity of the rain drop with respect to the man is:
$$ \mathbf{v} _{\mathbf{m}}=\mathbf{v} _{\mathbf{r}}+\left(-\mathbf{v} _{\mathbf{m}}\right) $$
$$ =\mathrm{v} _{x} \hat{\mathrm{i}}+\mathrm{v} _{y} \hat{\mathrm{j}}+(-3 \hat{\mathrm{i}}) $$

$$ \begin{equation*} =\left(\mathrm{v} _{x}-3\right) \hat{\mathrm{i}}+\mathrm{v} _{\mathrm{y}} \hat{\mathrm{j}} \tag{3} \end{equation*} $$
The relative velocity $\left(\mathbf{v} _{\mathbf{r m}}\right)$ makes an angle $\theta$ with the velocity of the man. Therefore
$$ \begin{equation*} \tan \theta=\frac{\mathrm{v} _{\mathrm{y}}}{\mathrm{v} _{x}-3} \tag{4} \end{equation*} $$
In the first case, drops appear to fall vertically.
$\therefore \tan \theta=270^{\circ}=\propto=\frac{1}{0}$
or $\frac{1}{0}=\frac{\mathrm{v} _{\mathrm{y}}}{\mathrm{v} _{x}-3}$
$\therefore \mathrm{v} _{x}=3 \mathrm{kmh}^{-1} \hspace{40mm} . . . . . .(5)$
FromEqn. (1), $\mathbf{v} _{\mathbf{r}}=3 \hat{\mathrm{i}}+\mathrm{v} _{\mathrm{y}} \hat{\mathrm{j}} \hspace{40mm} . . . . . .(6)$
In the second case,
$$ \mathbf{v} _{m}=6 \hat{\dot{i}} $$
Here, $\mathbf{v} _{\mathbf{r m}}=\mathbf{v} _{\mathbf{r}}+\left(-\mathbf{v} _{\mathbf{m}}\right)$
$$ \begin{align*} & =\left(3 \hat{i}+v _{y} \hat{j}\right)+(-6 \hat{i}) \\ & =-3 \hat{i}+v _{y} \hat{j} \tag{7} \end{align*} $$
Since the rain drops now strike man at $45^{\circ}$ from the front, here $\theta=225^{\circ}$.
$\therefore \tan 225^{\circ}=\frac{\mathrm{v} _{\mathrm{y}}}{-3}$,
or $\quad 1=\frac{\mathrm{v} _{\mathrm{y}}}{-3} \quad \therefore \mathrm{v} _{\mathrm{y}}=-3 \mathrm{kmh}^{-1}$
Therefore, $\mathrm{v} _{\mathrm{r}}=3 \hat{\mathrm{i}}-3 \hat{\mathrm{j}} \mathrm{kmh}^{-1}\hspace{40mm} . . . . . .(8)$
or $\quad \mathrm{v} _{\mathrm{r}}=3 \sqrt{2} \mathrm{kmh}^{-1}$
Here, $\tan \theta=\frac{-3}{3}=-1$
or $\theta=270^{\circ}+45^{\circ}=315^{\circ}$, with $\hat{i}$
Hence, the speed of rain drops is $3 \sqrt{2} \mathrm{kmh}^{-1}$ and the direction is $45^{0}$ with the vertical and in the direction of man motion.
79. A juggler throws balls is to air and catch them. He throws one all whenever the previous ball is at its highest point. How high do the balls rise, if he throws $\mathbf{n}$ balls every second? (Acceleration due to gravity is g).
(1) $\frac{\mathrm{g}}{\mathrm{n}^{2}}$
(2) $\frac{g}{2 n^{2}}$
(3) $\frac{2 \mathrm{~g}}{\mathrm{n}^{2}}$
(4) $\frac{2 \mathrm{~g}}{\mathrm{n}}$
Show Answer
Correct answer: (2)
Solution:
Number of balls thrown is $1 \mathrm{~s}=\mathrm{n}$, Time interval between two balls $=\frac{1}{\mathrm{n}}$
Now, he throws one when the previous one thrown reaches the maximum height.
$\therefore$ Time taken by one ball to reach the maximum height is
$$ \begin{equation*} \mathrm{t}=\frac{1}{\mathrm{n}} \tag{1} \end{equation*} $$
Let $u$ be the velocity with which the ball is thrown. Then the velocity at the highest point is zero, and so,
$$ 0=\mathrm{u}-\mathrm{gt} $$
or $\quad \mathrm{u}=\frac{\mathrm{g}}{\mathrm{n}} \hspace{40mm} . . . . . .(2)$
Now, $\mathrm{v}^{2}=\mathrm{u}^{2}+2$ as
or $\quad 0=\mathrm{u}^{2}-2 \mathrm{gh}$
or $\quad 2 \mathrm{gh}=\frac{\mathrm{g}^{2}}{\mathrm{n}^{2}}$
$\therefore \mathrm{h}=\frac{\mathrm{g}}{2 \mathrm{n}^{2}}$
80. A particle moves in $x-y$ plane such that $x=k _{1}t ; y=k _{1} t\left(1-k _{2} t\right)$ where $k _{1}$ and $k _{2}$ are constant. The magnitude of instantaneous velocity $v$ and instantaneous acceleration, $a$; is
(1) $\mathrm{v}=\mathrm{k} _{1} \sqrt{1+\left(1-2 \mathrm{k} _{2} \mathrm{t}\right)^{2}} \quad \mathrm{a}=2 \mathrm{k} _{1} \mathrm{k} _{2} $
(2) $\mathrm{v}=\mathrm{k} _{1} \sqrt{1+4 \mathrm{k} _{2}^{2}} \quad \mathrm{a}=\frac{2 \mathrm{k} _{1}}{\mathrm{k} _{2}}$
(3) $\mathrm{v}=\mathrm{k} _{1}+\mathrm{k} _{2} \mathrm{t} \quad \mathrm{a}=\frac{\mathrm{k} _{1}}{\mathrm{k} _{2}} $
(4) $\mathrm{v}=\mathrm{k} _{1}+\mathrm{k} _{2} \mathrm{t} \quad \mathrm{a}=\mathrm{k} _{1} \mathrm{k} _{2}$
Show Answer
Correct answer: (1)
Solution:
Let $\mathrm{v} _{x}$ and $\mathrm{v} _{\mathrm{y}}$ be the instantaneous $x$ and $\mathrm{y}$-component of velocity. Then
$\mathrm{v} _{x}=\frac{\mathrm{d} x}{\mathrm{dt}}=\mathrm{k} _{1} ; \quad \mathrm{v} _{\mathrm{y}}=\frac{\mathrm{dy}}{\mathrm{dt}}=\mathrm{k} _{1}\left(1-\mathrm{k} _{2} \mathrm{t}\right)+\mathrm{k} _{1} \mathrm{t}\left(-\mathrm{k} _{2}\right)=\mathrm{k} _{1}\left(1-2 \mathrm{k} _{2} \mathrm{t}\right)$ $\therefore \quad \mathrm{v}=\sqrt{\mathrm{v} _{x}^{2}+\mathrm{v} _{\mathrm{y}}^{2}}=\left[\mathrm{k} _{2}^{2}+\mathrm{k} _{1}^{2}\left(1-2 \mathrm{k} _{2} \mathrm{t}\right)^{2}\right]^{1 / 2}=\mathrm{k} _{1}\left[1+\left(1-2 \mathrm{k}^{2} \mathrm{t}\right)^{2}\right]^{1 / 2}$
The instantaneous $x$ and $y$ component of acceleration are
$$ \begin{aligned} & \mathrm{a} _{x}=\frac{\mathrm{dv} _{x}}{\mathrm{dt}}=0 ; \quad \mathrm{a} _{\mathrm{y}}=\frac{\mathrm{dv} _{\mathrm{y}}}{\mathrm{dt}}=-2 \mathrm{k} _{1} \mathrm{k} _{2} \\ & \therefore \quad \mathrm{a}=\sqrt{\mathrm{a} _{x}^{2}+\mathrm{a} _{\mathrm{y}}^{2}}=2 \mathrm{k} _{1} \mathrm{k} _{2} \end{aligned} $$










