SATHEE: Unit 01 Physics And Measurements

Unit 01 Physics And Measurements

The ‘Need’ for Measurements

Measurements, as we all know, have played a very significant role in the development of all physical sciences. It is ‘observations’, coupled with (progressively precise and accurate) ‘measurements’, that have helped scientist to develop, and improve, their basic theories of nature and natural phenomena.

The ‘Measurement Process’

Measurement is basically a process of comparison. The ‘measure’, of a given physical quantity is obtained by comparing it with a standard, or reference, measure of that quantity and finding how many times (say $n$ times), that standard measure is contained in the given physical quantity. The ‘measure’, of the given physical quantity, is then expressed as (n) units), $\mathrm{n}$ is known as the numerical value.

Unit

The standard, or reference, ‘measure’ of a given physical quantity (chosen after due deliberations, followed by international agreement, as far as possible), is known as the unit of that physical quantity.

Standard

It is often (but not always) possible to have physical embodiments, of the units of different physical quantities. Such a ‘physical embodiment’, of the UNIT of a physical quantity, is known as the standard measure, or just the STANDARD, of that physical quantity.

Fundamental Units

It turns out that one need not define out a ‘unit’ for all the (vast number of) physical quantities. A suitable choice, of an appropriate number of (selected) physical quantities, enables us to define the units of ‘all other physical quantities’, in terms of the units of these (few, carefully selected) physical quantities. The unit, of these few (selected) physical quantities, are known as the fundamental units.

Derived Units

The units of other physical quantities can be defined in terms of the units of these (selected few) units. We call the units of all the other physical quantities, as ‘derived units’.

Derived units may thus be viewed as units that are defined through the (selected, few) fundamental units.

Number of the Fundamental Units

In the initial stages, it was thought that one could define the units of all the other physical quantities by assigning, and defining, the unit of length, mass and time. These three physical quantities - length, mass and time - were, therefore, regarded as the fundamental quantities. The number of fundamental units, in the initial stages, was, therefore, three.

Later on, it was realized that there was a need for taking an additional number of physical quantities as ‘fundamental, or base, quantities.’ The number, presently being used is seven. We now take the seven

quantities. “Length, mass, time, electric current, thermodynamic temperature, luminous intensity and amount of substance” as the (seven) base or fundamental quantities.

Systems of Units

We have had several systems of units, in use, at different places and at different times. The three more prominent systems of units, that have been used earlier, are

(1) The FPS (Foot - found - second) system

(2) The CGS (Centimeter - gram - second) system

(3) The MKS (Meter - kilogram - second) system

In the year 1971, the general conference on weights and measures (CGPM - the conference general des poids et. Measures - having its central office at Sevres, near Paris, in France) developed and recommended a system of units, now known by the abbreviation SI units. It is the system that is now being used internationally for scientific, industrial, technical and commercial works.

The SI Units

The SI or the international system of units (Systeme International d’ units), has seven base (or fundamental) units, two supplementary units (for the angle and the solid angle) and a large number of derived or secondary units.

Two important features, of the SI, namely:

1. It being a coherent system (i.e., a system in which the derived units are obtained from the basic units, by multiplication, or division, without introducing any additional numerical factor).

2. The use of the decimal system in it (which makes conversions, within the system, as simple and convenient).

make this system logically superior to all the earlier system of units.

The definitions, of the seven base units, of the SI, are given below:

metre (m) (Physical quantity : Length)- The metre is defined as the length of the path, moved by light, in vacuum, during a time interval of 1/299 792458 of a second. (Note that the effect of this definition is to fix the speed of light in a vacuum at exactly $299792458 \mathrm{~ms}^{-1}$ ).

kilogram (kg) (Physical quantity : Mass) - The kilogram is the mass of a cylinder of platinum-iridium alloy kept at the international Bureau of Weights and Measures in Paris.

second (s) (Physical quantity : Time) : The second is the duration of 9192631770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom.

ampere (A) (Physical quantity : Electric Current) - This is defined as the constant current which, if maintained in each of two infinitely long, straight, parallel wires, of negligible cross-section, placed $1 \mathrm{~m}$ apart, in vacuum, produces between the wires a force of $2 \times 10^{-7}$ newton per meter of their length.

kelvin (K) (Physical quantity : Thermodynamic Temperature)- In SI units, temperatures are measured on the thermodynamic scale with absolute zero as ‘zero’, and the triple point of water (i.e., the temperature at which ice, water and water vapour are in equilibrium) as the upper fixed point. The interval is divided into 273.15 divisions and each division is taken as the unit of temperature. This units is called the kelvin.

candela (Cd) (Pysical quantity : Luminous Intensity)- The candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency $540 \times 10^{12}$ hertz and that has a radiant intensity, in that direction, $\left(\frac{1}{683}\right)$ of watt per steradian.

mole (mol) (Physical quantity : Amount of Substance) - The moe is the amount of any substance which contains as many elementary entities as there are atoms is $0.012 \mathrm{~kg}$ of the Isotope, ${ } _{6}^{12} \mathrm{C}$, of carbon.

The two supplementary units, for the angle and the solid angle, may be defined as follows:

Radian (rad) (The unit of angle): One radian equals the plane angle, subtended at the centre of a circle, by an arc of that circle that has a length equal to the radius of the circle.

Steradian (sr) (The unit of solid angle) : One steradian equals the solid angle, subtended at the centre of a sphere, by an area (A) on the surface of the sphere where that area (A) equals the area of a square of side equal to the radius of the sphere.

Multiples and Sub-multiples in SI

The SI units, as we have noted, use the decimal system. A number of multiples, and submultiple, corresponding to different powers of ten, are, therefore, an integral part of the SI units.

We list the names of the multiples, and the sub-multiples, associated with the different powers of ten, in the table given below.

	Multiples			Submultiple
Power of’ten’	Name of multiple	Symbol	Power of ’ten’	Name of submultiple	Symbol
$10^{18}$	exa	$\mathrm{e}$	$10^{-18}$	atto	$\mathrm{a}$
$10^{15}$	peta	$\mathrm{P}$	$10^{-15}$	femto	$\mathrm{f}$
$10^{12}$	tera	$\mathrm{T}$	$10^{-12}$	pico	$\mathrm{p}$
$10^{9}$	giga	$\mathrm{G}$	$10^{-9}$	nano	$\mathrm{n}$
$10^{6}$	mega	$\mathrm{M}$	$10^{-6}$	micro	$\mu$
$10^{3}$	kilo	$\mathrm{k}$	$10^{-3}$	milli	$\mathrm{m}$
$10^{2}$	hecto	$\mathrm{h}$	$10^{-2}$	centi	$\mathrm{c}$
$10^{1}$	deka	$\mathrm{da}$	$10^{-1}$	deci	$\mathrm{d}$

Derived SI Units of Some Important Physical Quantities

The table, given below, gives the names of some important derived units. Here it is important to remember that some derived units have been given names of their own. This has been done for the twin purpose of (i) practical convenience and (ii) honouring distinguished scientists, for their contribution in the field relevant to the concerned physical quantity.

For example:

(a) The derived unit of force $\left[=\right.$ kilogram - meter $\left./\left(\operatorname{second} d^{2}\right)\right]$, has been given the name ’newton $(\mathrm{N})$ ‘.

(b) The derived unit of pressure $\left[=\right.$ newton / $\left.(\text { meter })^{2}\right]$, has been given the name ‘pascal’ $(\mathrm{Pa})$.

(c) The derived unit of ‘potential difference’ $[=$ joule / (ampere-second) $]$ has been given the name ‘volt’ $(=\mathrm{V})$.

and, so on.

Physical Quantity	Name of the SI Unit	Symbol
Velocity	meter per second	$\mathrm{ms}^{-1}$
Acceleration	meter per second squared	$\mathrm{ms}^{-2}$
Momentum	kilogram - meter per second	$\mathrm{kg} \mathrm{ms}^{-1}$
Force	newton	$\mathrm{N}$
Pressure	pascal / (newton per meter squared)	$\mathrm{Pa} / \mathrm{Nm}^{-2}$
Work	joule	$\mathrm{J}$
Energy	joule	$\mathrm{J}$
Power	watt	W
Frequency	hertz	$\mathrm{Hz}$
Quantity of heat / heat energy	joule	$\mathrm{J}$
Moment of inertia	kilogram meter squared	$\mathrm{kg} \mathrm{m}^{2}$
Elastic module	newton per meter squared	$\mathrm{Nm}^{-2}$
Stress	newton per meter squared	$\mathrm{Nm}^{-2}$
Sound intensity	watt per meter squared	$\mathrm{Wm}^{-2}$
Illumination	lux	$\mathrm{lx}$
Luminous flux	lumen	$\operatorname{lm}$
Surface tension	newton per metre	$\mathrm{Nm}^{-1}$
Coefficient of viscosity	$\mathrm{pas/(N-s/m^2)}$	$\mathrm{(N-s/m^2)}$
Electric charge	$\mathrm{pas/(N-s/m^2)}$	$\mathrm{(N-s/m^2)}$
Capacitance	fara	F
Inductance	henry	H
Resistance	ohm	$ \Omega $
Potential / emf	vol	V
Absolute permittivity	farad per metre	$\mathrm{Fm^{-1}}$
Electric dipole moment	coulomb metre	C m
Electric field	newton per coulomb or volt per metre	$\mathrm{NC^{-1} or Vm^{-1}}$
Electric polarization	coulomb per metre squared	C m
Electro chemical equivalent	kilogram per coulomb	$\mathrm{kg C^{-1}}$
Specific heat capacity	joule per (kilogram kelvin)	$\mathrm{J kg^{-1}K^{-1}}$
Specific latent heat capacity	joule per kilogram	$\mathrm{J kg{-1}}$
Coefficient of thermal conductivity	watt per (metre-kelvin)	$\mathrm{W m{-1}K{-1}}$
Coefficient of linear / area /volume expansion	per kelvin	$\mathrm{J K{-1}}$
Magnetic flux	weber	Wb
Magnetic field intensity	tesla	T
The vector H	ampere per metre	$\mathrm{Am^{-1}}$
Intensity of magnetization	ampere per metre	$\mathrm{Am^{-1}}$
Absolute permeability	henry per metre	$\mathrm{Hm^{-1}}$

Names of Some Units in General Use

We list below the names, and symbols, of some units (of different physical quantities), that are not a part of the SI units, but are still used, quite often, in actual practice.

Name of Physical Quantity	Its Unit, Still	in General Use	Relation with the Relevant SI Unit
	Name	Symbol
mass	carat	$\mathrm{C}$	$1 \mathrm{C}=2 \times 10^{-4} \mathrm{~kg}$
mass	quintal	$\mathrm{q}$	$1 \mathrm{q}=100 \mathrm{~kg}$
mass	tonne	$\mathrm{t}$	$1 \mathrm{t}=10^{3} \mathrm{~kg}$
time	minute	min	$1 \mathrm{~min}=60 \mathrm{~s}$
time	hour	$\mathrm{h}$	$1 \mathrm{~h}=3600 \mathrm{~s}$
time	day	$\mathrm{d}$	$1 \mathrm{~d}=86400 \mathrm{~s}$
time	year	$\mathrm{y}$	$1 \mathrm{y}=3.156 \times 10^{7} \mathrm{~s}$
length	micron	$\mu \mathrm{m}$	$1 \mu \mathrm{m}=10^{-6} \mathrm{~m}$
length	angstrom	$\mathrm{A}^{\circ}$	$1 \mathrm{~A}^{\circ}=10^{-10} \mathrm{~m}$
area	barn	$\mathrm{b}$	$1 \mathrm{~b}=10^{-28} \mathrm{~m}^{2}$
area	are	$\mathrm{a}$	$1 \mathrm{a}=10^{2} \mathrm{~m}^{2}$
area	hectare	ha	$1 \mathrm{ha}=10^{4} \mathrm{~m}^{2}$
volume	litre	$\mathrm{L}$	$1 \mathrm{~L}=10^{-3} \mathrm{~m}^{3}$
pressure	bar	bar	$1 \mathrm{bar}=10^{5} \mathrm{~Pa}$
pressure	standard	atm	$1 \mathrm{~atm}=1.013 \times 10^{5} \mathrm{~Pa}$
pressure	torr	$\mathrm{Tr}$	$1 \mathrm{Tr}=1 \mathrm{~mm}$ of Hg $\simeq 9.8 \mathrm{~N} / \mathrm{m}^{2}$
angle	degree	0	$1^{0}=\left(\frac{\pi}{180}\right) \mathrm{rad}$

Dimensions

The dimensions, of a physical quantity, are the powers, to which the fundamental (or base) quantities, must be raised to represent it.

The number of fundamental (or base) quantities, needed to represent a given physical quantity, depends on the nature of that quantity. While dealing with mechanical phenomena, we generally need only three fundamental quantities (mass, length and time) to represent the different mechanical quantities. However, while dealing with

(1) thermal phenomenon, we also need another fundamental quantity, which has been taken as the (thermodynamic) temperature.

(2) electric and magnetic phenomenon, we also need an additional fundamental quantity which has been taken as the electric current.

(3) Optical phenomenon, we use the additional fundamental quantity, the luminous intensity.

The seventh fundamental quantity, the amount of substance, is generally not needed in defining the dimensions of different physical quantities.

Example:

1. The dimensions, of the physical quantity, area / volume, are zero each in mass and time but are $2 / 3$ in length. This is because an area/ volume is obtained by multiplying a length with another length / two other lengths. Hence the power to which length, needs to be raised, to represent an area / volume, is $2 / 3$. Thus the dimensions of area / volume are zero in mass, $2 / 3$ in length and zero in time.

2. The specific heat capacity of a substance equals the heat (energy) needed to raise the temperature, of a unit mass of the substance, through one kelvin.

Now energy / work, equals force $\times$ length, which, comes out to be mass multiplied by the square of length divided by square of time. Hence,

Specific heat capacity would correspond to

$$ \frac{\text { mass } \times(\text { length })^{2} \times(\text { time })^{-2}}{\text { mass } \times(\text { temperature })} $$

This equals (length) $)^{2} \times(\text { time })^{-2} \times(\text { temperature })^{-1}$

We may thus say that the dimensions of specific heat capacity are zero in mass; 2 in length; $(-2)$ in time and ( -1 ) in temperature.

3. Electric potential equals ‘work per unit charge’. Now electric charge equals (electric current $\times$ time). Hence the dimensions of electric potential would correspond to

$$ \frac{(\text { mass }) \times(\text { length })^{2} \times(\text { time })^{-2}}{(\text { electric current }) \times(\text { time })} $$

This equals (mass) $\times(\text { length })^{2} \times(\text { time })^{-3} \times(\text { electric current })^{-1}$.

Thus the dimensions of electric potential are 1 in mass, 2 in length, (-3) in time and (-1) in electric current.

We may thus obtain the dimensions, of a given physical quantity, through a use of its basic definition.

Dimensional Formula

The dimensional formula, of a given physical quantity, is a compact way, of expressing its dimensions. For writing the dimensions formula, of different physical quantities, we generally use the symbols $\mathrm{M}, \mathrm{L}, \mathrm{T}$, (I/ A), $\mathrm{K},(\mathrm{C} / \mathrm{cd})$ and (mol), for representing the seven fundamental quantities. The dimensional formula, of a given physical quantity, is thus an expression, in terms of these symbols, that tells us how the given physical quantity is co-related to the seven fundamental quantities. However, a general ‘convention’, that is followed here, is to write out only those fundamental quantities that need to be raised to a fixed (non-zero) power to represent the given physical quantity. This ’ convention’ helps in writing the dimensional formula in a compact form and avoids unnecessary confusion.

For the examples, discussed above, we could then say that the dimensional formula of:

(i) area, is $\mathrm{L}^{2}$

(ii) volume, is $\mathrm{L}^{3}$

(iii) specific heat capacity, is $\left[\mathrm{L}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right]$

(iv) electric potential, is $\left[\mathrm{ML}^{2} \mathrm{~T}^{-3} \mathrm{I}^{-1}\right]$

and so.

The table, given below, gives a list of the dimensional formula of a number of physical quantities. The examples, given above, indicate that we can get the dimension formulae, of other physical quantities also, once we know their definition.

The following table gives the dimensional formulae of some physical quantities:

S. No.	Derived Physical Quantity	Defining Formula	Dimensional Formula
1.	Area	$1 \times \mathrm{b}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}^{0}\right]$
2.	Volume	$1 \times \mathrm{b} \times \mathrm{h}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}^{0}\right]$
3.	Density	$\frac{\mathrm{M}}{\mathrm{V}}$	$\left[\mathrm{M}^{1} \mathrm{~L}^{-3} \mathrm{~T}^{0}\right]$
4.	Specific Gravity	$\frac{\text { Density of Substance }}{\text { Density of Water }}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0}\right]$
5.	Frequency	$\frac{\text { No. of Vibrations }}{\text { Time }}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{-1}\right]$
6.	Angle	$\frac{\text { Arc }}{\text { Radius }}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0}\right]$
7.	Velocity	$\frac{\text { Displacement }}{\text { Time }}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{1} \mathrm{~T}^{-1}\right]$
8.	Speed	$\frac{\text { Distance }}{\text { Time }}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{1} \mathrm{~T}^{-1}\right]$
9.	Areal velocity	$\frac{\text { Area }}{\text { Time }}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}^{-1}\right]$
10.	Acceleration	$\frac{\text { Change in Velocity }}{\text { Time }}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{1} \mathrm{~T}^{-2}\right]$
11.	Linear momentum	$\mathrm{M} \times \mathrm{V}$	$\left[\mathrm{M}^{1} \mathrm{~L}^{1} \mathrm{~T}^{-1}\right]$
12 .	Force	mass $\times$ acceleration	$\left[\mathrm{M}^{1} \mathrm{~L}^{1} \mathrm{~T}^{-2}\right]$
13.	Weight (= a force)	$\mathrm{W}=\mathrm{mg}$	$\left[\mathrm{M}^{1} \mathrm{~L}^{1} \mathrm{~T}^{-2}\right]$
14 .	Moment of force/Torque/Couple	Force $\times$ distance	$\left[\mathrm{M}^{1} \mathrm{~L}^{2} \mathrm{~T}^{-2}\right]$
15.	Impulse	Force $\times$ Time	$\left[\mathrm{M}^{1} \mathrm{~L}^{1} \mathrm{~T}^{-1}\right]$
16 .	Pressure	$\frac{\text { Force }}{\text { Area }}$	$\left[\mathrm{M}^{1} \mathrm{~L}^{-1} \mathrm{~T}^{-2}\right]$
17.	Work	Force $\times$ Distance	$\left[\mathrm{M}^{1} \mathrm{~L}^{2} \mathrm{~T}^{-2}\right]$
18.	Kinetic Energy	$\frac{1}{2} \mathrm{mv}^{2}$	$\left[\mathrm{M}^{1} \mathrm{~L}^{2} \mathrm{~T}^{-2}\right]$
19 .	Potential Energy	mgh	$\left[\mathrm{M}^{1} \mathrm{~L}^{2} \mathrm{~T}^{-2}\right]$
20.	Gravitational constant	$\frac{\text { Force } \times(\text { Length })^{2}}{(\text { mass })^{2}}$	$\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right]$
21.	Gravitational field strength	$\frac{\text { Force }}{\text { mass }}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{1} \mathrm{~T}^{-2}\right]$
22 .	Gravitational Potential	$\frac{\text { Work }}{\text { mass }}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}^{-2}\right]$
23.	Force constant (k), (of a spring)	$\frac{\mathrm{F}}{\mathrm{L}}$	$\left[\mathrm{M}^{1} \mathrm{~L}^{0} \mathrm{~T}^{-2}\right]$
24.	Power	$\frac{\text { Work }}{\text { Time }}$	$\left[\mathrm{M}^{1} \mathrm{~L}^{2} \mathrm{~T}^{-3}\right]$
25 .	Moment of Inertia ( I )	Mass $\times$ Distance $^{2}$	$\left[\mathrm{M}^{1} \mathrm{~L}^{2} \mathrm{~T}^{0}\right]$
26.	Stress	$\frac{\text { Force }}{\text { Area }}$	$\left[\mathrm{M}^{1} \mathrm{~L}^{-1} \mathrm{~T}^{-2}\right]$
27.	Strain	$\frac{\text { Change in length }}{\text { Original length }}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0}\right]$
28.	Modulus of Elasticity	$\frac{\text { Stress }}{\text { Strain }}$	$\left[\mathrm{M}^{1} \mathrm{~L}^{-1} \mathrm{~T}^{-2}\right]$
29.	Poisson’s Ratio	$\frac{\text { Lateral Strain }}{\text { Longitudinal Strain }}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0}\right]$
30.	Velocity gradient	$\frac{\text { Change in velocity }}{\text { Distance }}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{-1}\right]$
31.	Coefficient of dynamic viscosity	$\frac{\text { Tangential stress }}{\text { Velocity gradient }}$	$\left[\mathrm{M}^{1} \mathrm{~L}^{-1} \mathrm{~T}^{-1}\right]$
32.	Surface Tension	$\frac{\text { Force }}{\text { Length }}$	$\left[\mathrm{M}^{1} \mathrm{~L}^{0} \mathrm{~T}^{-2}\right]$
33.	Angular displacement $(\theta)$	$\frac{\text { Arc }}{\text { Radius }}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0}\right]$
34.	Angular velocity $(\omega)$	$\frac{\text { Angular displacement }}{\text { Time }}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{-1}\right]$
35.	Angular acceleration $(\alpha)$	$\frac{\text { Change in angular velocity }}{\text { Time }}$	$\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{-2}\right]$
36.	Angular momentum	L	$\left[\mathrm{ML}^{2} \mathrm{~T}^{-1}\right]$
37.	Angular Impulse	$\Delta \mathrm{L}$	$\left[\mathrm{ML}^{2} \mathrm{~T}^{-1}\right]$
38.	Temperature		$[\mathrm{K}]$
39.	Coefficient of linear expansion $\left({ }^{*}\right)$	$\frac{\left(\ell _{2}-\ell _{1}\right)}{\ell _{1} \times\left(\text { Temp. }\left(\mathrm{t} _{2}-\mathrm{t} _{1}\right)\right)}$	$\left[\mathrm{K}^{-1}\right]$
40.	Specific heat capacity	$\frac{(\text { Heat }) \text { Energy }}{\text { Mass } \times \text { Temp }}$	$\left[\mathrm{L}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right]$
41.	Specific latent heat capacity	$\frac{\text { Energy }}{\text { Mass }}$	$\left[\mathrm{L}^{2} \mathrm{~T}^{-2}\right]$
42.	Entropy	$\frac{\mathrm{Q}}{\theta}$	$\left[\mathrm{M}^{1} \mathrm{~L}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right]$
43.	Thermal capacity	$\frac{\mathrm{H}}{\theta}$	$\left[\mathrm{M}^{1} \mathrm{~L}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right]$
44.	Gas constant	$\frac{\mathrm{PV}}{\mathrm{nT}}$	$\left[\mathrm{ML}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right]$
45.	Coefficient of thermal conductivity	$\frac{\mathrm{Qd}}{\mathrm{A}\left(\theta _{1}-\theta _{2}\right) \mathrm{t}}$	$\left[\mathrm{M}^{1} \mathrm{~L}^{1} \mathrm{~T}^{-3} \mathrm{~K}^{-1}\right]$
46.	Pole strength	ampere $\times$ meter	$\left[\mathrm{M}^0 \mathrm{~L}^1 \mathrm{~T}^0 \mathrm{I}\right]$
47.	Magnetic Moment		$\left[\mathrm{M}^0 \mathrm{~L}^2 \mathrm{~T}^0 \mathrm{I}^1\right]$
48.	Magnetic flux $\phi$		$\left[\mathrm{ML}^2 \mathrm{~T}^{-2} \mathrm{I}^{-1}\right]$
49.	Magnetic field, magnetic flux density (B)		$\left[\mathrm{MT}^{-2} \mathrm{I}^{-1}\right]$
50.	Permeability of free space	$\frac{\mu}{\mu_r}$	$\left[\mathrm{MLT}^{-2} \mathrm{I}^{-2}\right]$
51.	Magnetic susceptibility	$\chi_{\mathrm{m}}=\mu_{\mathrm{r}}-1$	$\left[\mathrm{M}^0 \mathrm{~L}^0 \mathrm{~T}^0\right]$
52.	Electric Charge	$\mathrm{I} \times \mathrm{T}$	$\left[\mathrm{M}^0 \mathrm{~L}^0 \mathrm{~T}^1 \mathrm{I}^1\right]$
53.	Electric potential	$\frac{\text { Work }}{\text { Charge }}$	$\left[\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-3} \mathrm{I}^{-1}\right]$
54.	E.M.F	$\frac{\text { Work }}{\text { Charge }}$	$\left[\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-3} \mathrm{I}^{-1}\right]$
55.	Capacity (Electric)	$\frac{\mathrm{q}}{\mathrm{V}}$	$\left[\mathrm{M}^{-1} \mathrm{~L}^{-2} \mathrm{~T}^4 \mathrm{I}^2\right]$
56.	Resistance (Electric)	$\frac{\mathrm{V}}{\mathrm{i}}$	$\left[\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-3} \mathrm{I}^{-2}\right]$
57.	Resistivity $\rho$	$\frac{\mathrm{RA}}{\mathrm{L}}$	$\left[\mathrm{M}^1 \mathrm{~L}^3 \mathrm{~T}^{-3} \mathrm{I}^{-2}\right]$
58.	Conductivity $\sigma$	$\frac{1}{\rho}$	$\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^3 \mathrm{I}^2\right]$
59.	Permittivity $\varepsilon$	$\varepsilon=\varepsilon_r \varepsilon_0=(1+x) \varepsilon_0$	$\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^4 \mathrm{I}^2\right]$
60.	Electric conductance	$\frac{1}{R}$	$\left[\mathrm{M}^{-1} \mathrm{~L}^{-2} \mathrm{~T}^3 \mathrm{I}^2\right]$
61.	Electric power	$\mathrm{V} \times \mathrm{I}$	$\left[\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-3}\right]$
62.	Electrical Impedance (Z)	$\frac{\mathrm{V}}{i}$	$\left[\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-3} \mathrm{I}^{-2}\right]$
63.	Electrical admittance	$1 / \mathrm{Z}=($ Reciprocal of electric impedance)	$\left[\mathrm{M}^{-1} \mathrm{~L}^{-2} \mathrm{~T}^3 \mathrm{I}^2\right]$
64.	Self Inductance (L)	$\|\mathrm{V}\|=\mathrm{L} \frac{d i}{d t}$	$\left[\mathrm{ML}^2 \mathrm{~T}^{-2} \mathrm{I}^{-2}\right]$
65.	Boltzmann’s constant	$\frac{\text { Energy }}{\text { Temp }}$	$\left[\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right]$
66.	Stefan’s constant	$\frac{\mathrm{E}}{\mathrm{TA} \theta^4}$	$\left[\mathrm{M}^1 \mathrm{~L}^0 \mathrm{~T}^{-3} \mathrm{~K}^{-4}\right]$
67.	Co-efficient of friction	$\mu=\frac{\mathrm{F}}{\mathrm{N}}, \mathrm{N}=$ Normal reaction	$\left[\mathrm{M}^0 \mathrm{~L}^0 \mathrm{~T}^0\right]$
68.	Dielectric constant	It is also called relative permittivity	$\left[\mathrm{M}^0 \mathrm{~L}^0 \mathrm{~T}^0\right]$
69.	Planck’s constant	$\mathrm{E}=h v$	$\left[\mathrm{ML}^2 \mathrm{~T}^{-1}\right]$
70.	Refractive index	$\mu$	$\left[\mathrm{M}^0 \mathrm{~L}^0 \mathrm{~T}^0\right]$

Dimensional Analysis

The concept of dimensions has led to the development of ‘dimensional analysis’. Dimensional analysis has very many uses and applications; its simple uses include.

(a) Checking the correctness, or otherwise, of a given formula or result.

(b) Conversion, from one system of units, to another.

(c) Obtaining relations showing the nature of dependance of a given physical quantity $(\mathrm{X})$ on other (related to it) quantities.

The last of these uses, however, has two built in limitations:

(i) We cannot obtain the exact values of the numerical ‘constants’, or the nature of dependence of $x$, on any (related) dimensionless quantity.

(ii) The form, of the relation (fof $x$ ), can be obtained only for that many number of physical quantities as is the number of fundamental, or ‘base’, quantities, being used.

For example, in mechanics, where we generally use, and need, only three fundamental quantities (mass, length and time), we can obtain the form of relation for $x$ only in terms of (up to) three other (related) physical quantities.

Principle of Dimensional Homogenity

The above listed uses, and application, of dimensional analysis, are based on the “principle of dimensional homogeneity”; According to this principle:

“A relation, between different physical quantities, can be an acceptable (or correct) relation, only if the dimensions, of all the (different) terms, on both sides of the relation, are identical”.

In simple terms, this principle implies that we can equate say, a force only to those terms whose “net dimensions” are identical to those of force. Thus a force cannot be equated to ‘momentum’ but can be equated to ‘rate of change of momentum’.

We now give below some examples, illustrating the above listed uses of ‘dimensional analysis’.

Example:

Check the correctness, or otherwise, of the following dimensional formulae:

(i) Dimensional formula, for specific latent heat capacity, is $\left[\mathrm{ML}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right]$

(ii) The dimensional formula for Planck’s constant (h) (as per the Planck / Einstein suggestion : $\mathrm{h} \times$ frequency of radiation $=$ energy of a ‘photon’ of the radiation) is $\left[\mathrm{ML}^{2} \mathrm{~T}^{-1}\right]$.

Show Answer

Solution:

(i) We know that specific latent heat capacity equals the heat (energy) needed per unit mass, for change of state, at the melting point of the solid / boiling point of the liquid. Hence specific latent heat capacity $=\frac{\text { Energy }}{\text { Mass }}$

$\therefore$ Its dimensional formula is $\left[\frac{\mathrm{MLT}^{-2} \times \mathrm{L}}{\mathrm{M}}\right]$

$$ \text { i.e. }\left[\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}^{-2}\right] $$

The given dimensional formula $\left(=\mathrm{ML}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right)$ is, therefore, incorrect.

(ii) We have $\mathrm{h} \times$ frequency $=$ energy

$$ \begin{gathered} \therefore[\mathrm{h}]=\frac{\text { Energy }}{\text { Frequency }}=\left[\frac{\mathrm{MLT}^{-2} \times \mathrm{L}}{\mathrm{T}^{-1}}\right] \\ =\left[\mathrm{ML}^{2} \mathrm{~T}^{-1}\right] \end{gathered} $$

The given dimensional formula, for Planck’s constant, is, therefore, correct.

Example:

Check the correctness, or otherwise, of the following relations:

(i) $\mathrm{E} _{\mathrm{p}}=$ kmgh

( $\mathrm{E} _{\mathrm{p}}=$ gravitational $/$ potential energy, $\mathrm{k}=$ a numerical constant, $\mathrm{m}=$ mass, $\mathrm{g}=$ acceleration due to gravity, $\mathrm{h}=$ height ( of mass $\mathrm{m}$ )

(ii) $\mathrm{t}=\mathrm{k} \rho^{1 / 2} r^{3 / 2} \mathrm{~s}^{1 / 2}$

(where $\mathrm{t}=$ time period of oscillation of a drop inside a liquid, $\mathrm{k}=$ a numerical constant, $\rho=$ density of liquid; $\mathrm{r}=$ radius of drop; $\mathrm{s}=$ surface tension of liquid).

Show Answer

Solution:

(i) In the relation

$$ \mathrm{E} _{\mathrm{p}}=\mathrm{kmgh} $$

The dimensions, of the term, on the left, are

$$ \mathrm{E} _{\mathrm{P}}=(\text { Energy })=\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right] $$

On the right hand side, the dimensions, of the product of the three terms, on the right, are

$$ \left(\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0}\right) \times(\mathrm{M}) \times\left(\mathrm{LT}^{-2}\right) \times(\mathrm{L})=\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right] $$

The dimensions, on the two sides of the relation are thus seen to be the same. Hence the given relation is (dimensionally) correct.

(ii) In the relation

$$ \mathrm{t}=\mathrm{k} \rho^{1 / 2} r^{3 / 2} \mathrm{~s}^{1 / 2} $$

We have,

Dimensions, of the term, on the left $=\left[\mathrm{M}^{\circ} \mathrm{L}\right.$ T $]$

and dimensions, of the product of the terms, on the right

$$ \begin{aligned} & =\left(\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}\right) \times\left(\mathrm{ML}^{-3}\right)^{1 / 2}(\mathrm{~L})^{3 / 2}\left(\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}}\right)^{1 / 2} \quad(\therefore \text { surface tension }=\text { force/length }) \\ & \quad=\left(\mathrm{MT}^{-1}\right) \end{aligned} $$

The dimensions, on the two sides of the relation, are thus seen to be different. The given relation is, therefore, (dimensionally) incorrect.

Example:

Given that the relations between the fundamental units of mass, length, time, in the FPS (feet, pound, second) system, and the MKS (metre, kilogram, second) system, are

$$ \begin{aligned} & 1 \text { pound }=0.4536 \mathrm{~kg} \\ & 1 \text { feet }=0.5045 \text { metre } \\ & 1 \text { second }=1 \text { second, } \end{aligned} $$

find the relation, between the units of energy (foot poundal in FPS system, and joule in the MKS system).

Show Answer

Solution:

We have,

$$ [\text { Energy }]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right] $$

$\therefore$ The units of energy, in the FPS, system,

$$ \text { Foot poundal }=(\text { pound })(\text { foot })^{2}(\text { second })^{-2} $$

Similarly, the unit of energy, in the MKS system,

$$ \begin{gathered} \text { joule }=(\text { kilogram })(\text { metre })^{2}(\text { second })^{-2} \\ \therefore \frac{1 \text { foot poundal }}{\text { 1joule }}=\left(\frac{\text { pound }}{\text { kilogram }}\right)\left(\frac{\text { foot }}{\text { metre }}\right)^{2}\left(\frac{\text { second }}{\text { second }}\right)^{-2} \\ =\left(\frac{0.4536 \mathrm{~kg}}{1 \mathrm{~kg}}\right)\left(\frac{0.5048 \mathrm{~m}}{1 \mathrm{~m}}\right)^{2}(1)^{-2} \\ =(0.4536)(0.5048)^{2} \times 1 \simeq 0.1255 \end{gathered} $$

Thus 1 foot poundal $\simeq 0.1255$ joule

Example:

The period, of rotation ( $t$ ), of a planet, round the sun, depends on the (i) universal gravitational constant (G), (ii) mass of the sun (M) and (iii) radius (R), of the planetary orbit.

Use the method of dimensional analysis to obtain a formula for $t$, in terms of G, $M$ and $r$.

Show Answer

Solution:

We assume that,

$$ \mathrm{t}=\mathrm{k}[\mathrm{G}]^{\mathrm{a}}[\mathrm{M}]^{\mathrm{b}}[\mathrm{R}]^{\mathrm{C}} \quad(\mathrm{k}=\text { a numerical constant }) $$

Taking dimensions, of the all terms, on the two sides, we get

$$ \left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{1}\right]=\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right]^{\mathrm{a}}[\mathrm{M}]^{\mathrm{b}}[\mathrm{L}]^{\mathrm{c}} $$

$$ =\mathrm{M}^{(-\mathrm{a}+\mathrm{b})} \mathrm{L}^{(3 \mathrm{a}+\mathrm{c})} \mathrm{T}^{(-2 \mathrm{a})} $$

The dimensions, on the two sides, have to be equal. Hence, we get

$(-\mathrm{a}+\mathrm{b})=0 ;(3 \mathrm{a}+\mathrm{c})=0$ and $(-2 \mathrm{a})=1$

$\therefore$ We get $\mathrm{a}=-1 / 2, \mathrm{~b}=-1 / 2$ and $\mathrm{c}=3 / 2$

$\therefore$ The required relation is

$$ \begin{aligned} & \mathrm{t}=\mathrm{k}(\mathrm{G})^{-1 / 2}(\mathrm{M})^{-1 / 2}(\mathrm{R})^{3 / 2} \\ & =\mathrm{k}\left(\frac{\mathrm{R}^{3}}{\mathrm{GM}}\right)^{1 / 2} \\ & \text { or } \mathrm{t}^{2}=\mathrm{k}^{2}\left(\frac{\mathrm{R}^{3}}{\mathrm{GM}}\right) \end{aligned} $$

We thus get the result:

The square, of the time period of a planet, is proportional to the cube of the radius of the planetary orbit. [This result, first obtained by Kepler, is known as Kepler’s third law of planetary motion].

Example:

The dimensional formula, for the universal gravitational constant $(\mathrm{G})$, would equal that of the term:

(1) $\frac{momentum \times area}{density}$

(2) $\frac{\text { velocity } \times \text { volume }}{(\text { mass })^{2}}$

(3) $\frac{acceleration \times area}{mass}$

(4) $\frac{energy \times distance}{mass}$

Show Answer

Correct answer: (3)

Solution:

From Newton’s law, namely

$$ \mathrm{F}=\mathrm{G} \frac{\mathrm{M} _{1} \mathrm{M} _{2}}{\mathrm{r}^{2}} $$

We get,

$$ [\mathrm{G}]=\left[\frac{\mathrm{MLT}^{-2} \times \mathrm{L}^{2}}{\mathrm{M}^{2}}\right]=\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right] $$

Also the term,

$$ \frac{\text { acceleration } \times \text { area }}{\text { mass }}=\left[\frac{\mathrm{LT}^{-2} \times \mathrm{L}^{2}}{\mathrm{M}}\right]=\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right] $$

Hence the dimensional formula, of this term, is identical to that of [G].

[It can be checked that this equality does not hold for the other terms.]

Example:

Out of the following, the only formula that is dimensionally acceptable, is

(1) $\quad v _{c}=(k \eta / r d)$

(2) $v _{c}=\frac{k r d}{\eta}$

(3) $v _{c}=\frac{k r^{2} d}{\eta}$

(4) $v _{c}=\frac{k \eta}{r^{2} d}$

where $v _{c}$ is critical velocity, of a liquid of viscosity $\eta$, flowing in a tube of radius $\mathrm{r}$. ( $\mathrm{d}$ is the density of the liquid).

Show Answer

Correct answer: (1)

Solution:

From Newton’s law, for viscosity, namely

$$ \begin{aligned} & \mathrm{F}=-\eta \mathrm{A} \frac{d v}{d z}, \text { we get } \\ & {[\eta]=\left[\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}^{2} \cdot \mathrm{LT}^{-1}} \mathrm{~L}\right]=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-1}\right]} \end{aligned} $$

Now,

$$ \text { L.H.S. }=\text { velocity }=\left[\mathrm{LT}^{-1}\right] $$

A program to give wings to girl students

and $\quad$ R.H.S. (for option $(1)=\left[\frac{\mathrm{ML}^{-1} \mathrm{~T}^{-1}}{\mathrm{LML}^{-3}}\right]$

$$ =\left[\mathrm{LT}^{-1}\right] $$

Hence, for this option, the dimensions of the two sides are the same. Hence this option is dimensionally acceptable.

[It can be easily seen that the other three options are not dimensionally acceptable options].

Example:

A dimensionally acceptable formula, for the frequency ( $n$ ) of a tuning fork, is

( $\mathrm{k}=$ numerical constant, $\ell=$ length of prongs; $\mathrm{Y}$ and $\mathrm{d}$ denote Young’s modulus and density of the material of fork):

(1) $n=k \ell \sqrt{\frac{y}{d}}$

(2) $n=k \ell \sqrt{\frac{d}{y}}$

(3) $n=\frac{k}{\ell} \sqrt{\frac{y}{d}}$

(4) $n=\frac{k}{\ell} \sqrt{\frac{d}{y}}$

Show Answer

Correct answer: (3)

Solution:

We have L.H.S $=$ frequency $=\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{-1}$

and R.H.S. (for option (3) $=\left[\frac{1}{\mathrm{~L}} \sqrt{\frac{\mathrm{ML}^{-1} \mathrm{~T}^{-2}}{\mathrm{ML}^{-3}}}\right]=\left[\frac{1}{\mathrm{~L}} \sqrt{\mathrm{L}^{2} \mathrm{~T}^{-2}}\right]=\left[\frac{\mathrm{LT}^{-1}}{\mathrm{~L}}\right]$ $=\left[\mathrm{T}^{-1}\right]$

Hence this option gives us a dimensionally acceptable formula. [It can be easily seen that the other three options do not correspond to dimensionally acceptable formulae].

Least Count

The concept of ’least count’ is a concept that is associated with every measuring instrument or device. It equals the smallest magnitude of the physical quantity, that a given instrument, apparatus or device (designed for measuring that physical quantity), can measure on its ‘measuring scale’.

We need to remember that it is not just the vernier calipers, or the screw gage, that have a ’least count’ associated with them. All measuring instruments, (be it the meter scale, the spring balance, the thermometer, the ammeter, the voltmeter, and so on); have an appropriate least count associated with them.

It is interesting to note here that a lower value of the “least count”, is regarded as a “better least count’. Thus a vernier calipers, having a least count of $0.1 \mathrm{~mm}$, has a “better least count’ than a meter scale whose “least count” is (usually) $1 \mathrm{~mm}$ only. This means that a vernier caliper can measure a length more precisely than a meter scale.

Precision in Measurements

The precision, associated with a measurements, depends on the “least count” of the instrument used for making that measurement. An instrument, with a “better least count” gives a more precise measurement. Thus a temperature measurement, done with a thermometer of ’least count’ $0.1^{\circ} \mathrm{C}$, would be more precise than that done with a thermometer whose least count is $0.5^{\circ} \mathrm{C}$. Similarly, an unknown emf, measured with a potentiometer having a potential gradient of $10 \mathrm{mV} / \mathrm{cm}$, would be more precise than that measured with a potentiometer having a potential gradient of $100 \mathrm{mV} / \mathrm{cm}$. And so on.

Very often, an unknown quantity is ‘calculated’, by using a “formula” for it; after measuring the different physical quantities, present in that formula. The precision, of such an indirect measurement, can be calculated through a knowledge of the “least counts” of the different instruments used (for measuring the different quantities present in the formula) and the form of the “formula”.

Accuracy of a Measurement

It many appear logical to think that an increase in the precision of a measurement, would result in a more accurate measurement. This is generally true but we can have situations in which the result of measurements, done with more precise (having “better” least count) instruments, may be less accurate than the result obtained by using less precise measuring instruments. ‘Accuracy’ and ‘Precision’ thus do not, necessarily, go “hand-in-hand”.

Why is this so? This is because of the way “accuracy” (of a measurement) is defined. A measurement of a physical quantity (having a known standard value), is regarded as more accurate if the measured value is closer to its known standard value. Thus, if some physical quantity, having a standard value of say, 10 units, is measured using.

(i) less precise instruments and the result obtained is 9.8 units.

(ii) more precise instruments, and the result obtained is 9.75 units, the first measurement would be regarded as ‘more accurate’, even though it is ’less precise’.

Errors in Measurement

The measurement, of any physical quantity, has a ‘built-in’ limitation, due to the least count/s of the measuring instrument/s, used for its measurement. However, based on the results of different experiments, done with (as high as possible) precision instruments, we generally have standard or accepted values, for different physical quantities.

The result of a particular experiment, done for measuring a given physical quantity, may not match with the accepted, or standard, value of that quantity. The difference, between the result of the experiment, and the standard value, then gives a measure of the error in that experiment.

We can also speak of ’error’ in another context. Suppose one takes a large number of observations during a particular experiment. The mean, or average value of all these measurements, then represent the (best) result of that experiment. The results obtained, from the different individual measurements, generally do not quite match this (best) results of the experiment. The difference, between the result of a particular individual measurement, and the ‘mean value (or best) result’, may than be regarded as a measure of the error in that individual measurement.

It is important to note that the term ’error’ and ‘mistake’ are not quite the same. A mistake may be due to carelessness on the part of the experimentalist, or use of faulty apparatus or devices, or to some other such cause, which can be avoided, or corrected for. Errors, on the other hand, are there in spite of the best inputs of the experimentalist as well as the use of the (best possible) precise instruments. Errors may be viewed as an integral, or essential, ‘unavoidable’ part of the ’experiments’.

Systematic and Random Errors

Errors, in measurements, are generally classified into two broad categories: (i) Systematic errors and (ii) Random errors.

Systematic errors may be regarded as errors that are due to causes that tend to follow the same pattern, or rule, during different observations. They may be thought of as errors that tend to be governed by some definite rule.

For example, some built-in error / defect in the measuring instrument used; some definite imperfection or error in the technique / procedure of the experiment, some definite ‘personal error’ in the observer, are some of the causes that would lead to a ‘systematic error’ in the measurements.

It is easy to realize that once the cause of any such systematic error is located / recognized, one can correct for, or avoid, that systematic error.

Random Errors, on the other hand, are errors that do not have a definite, or well / specified cause. They, therefore, lead to random, or irregular, error in measurements. Physicists have developed a ’theory’ of such errors; this ’theory’ helps us to obtain the ‘best value’ of the result of (careful and precise) measurements of different quantities. It also helps us to estimate the ’net error’ in a result, obtained through different algebraic operations, on the different measurements, of two or more physical quantities.

The following definitions, and rules, are a part of the ’theory’ of ‘random errors’.

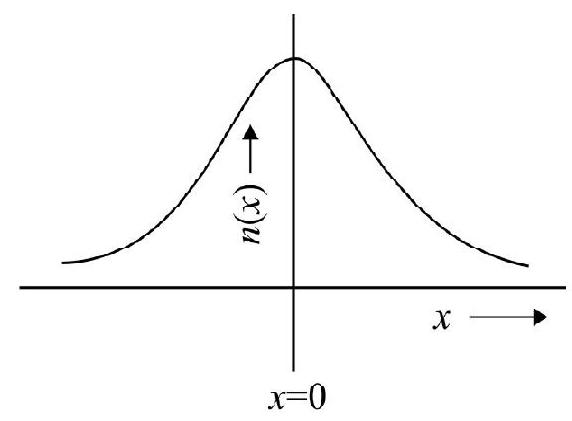
Normal, or Gaussian, Law

Random errors, generally, tend to follow the normal, or Gaussian law. This law, expressed through the graph shown here, implies that the probability of small errors is high while that of large errors decreases (exponentially) with an increase in the magnitude of these errors.

In the graph shown

$x=$ value of the random error.

$\mathrm{n}(x)=$ number of times the error $x$ occurs.

Absolute Error

Let the result of $n$ measurements, of a given physical quantity,

be $x _{1}, x _{2}, x _{3} \ldots \ldots x _{\mathrm{n}}$. The mean value of these $\mathrm{n}$ results, would be $\bar{x}=\frac{1}{n} \sum _{i=1}^{n} x _{i}$

The difference

$$ \Delta x _{i}=\left(x _{i}-\bar{x}\right) $$

i.e., the difference between the result of the $i^{\text {th }}$ measurement and the mean (or ‘best’) value of all the $n$ measurements, is known as the absolute error in the ith $i^{\text {measurement. }}$

For the case where the result (say $x$ ) of the measurements of a physical quantity, is compared with the standard, or accepted value (say X) of physical quantity, the difference.

$$ (x-\mathrm{X}) $$

is known as the absolute error in the result of the measurements done.

Relative Error

The mean, of the magnitudes of the absolute errors of the different (n) measurements, would give us the mean absolute error $(\Delta \bar{x})$ of all the measurement.

The ratio, $\frac{(\Delta \bar{x})}{(\bar{x})}$ is, said to represent the (mean) relative error, in the measurements, done for the physical quantity $(x)$.

Incidently, the ratio $\frac{\left(\Delta \bar{x} _{i}\right)}{(\bar{x})}$ would give the ‘relative error’ in the $i^{\text {th }}$ measurement.

Percentage Error

The relative error, expressed as a percentage, is known as the ‘percentage error’ in the measurements (of $x)$. Thus (mean) percentage error $=\frac{(\Delta \bar{x})}{(\bar{x})} \times 100 \%$

and percentage error in the $\mathrm{i}^{\text {th }}$ measurement $=\frac{\left(\Delta \bar{x} _{i}\right)}{(\bar{x})} \times 100 \%$

Combination of Errors

The values, of different physical quantities, are generally obtained by carrying out different algebraic operations, (multiplication/ division, addition/subtraction, raising to a power etc.) on the measurements of two or more physical quantities. We, therefore, need a ‘set of rules’, for finding the ’net-error’, in the ‘result’, obtained through such algebraic operations. We state below the ‘rules’ that are generally followed, for combining ‘different individual errors’, to get the ’net-error’ in the result.

Rule for Addition / Subtraction

The absolute error, in the sum / difference, of two different physical quantities, must always be taken as the sum of the absolute errors in each of these two different physical quantities. Expressed mathematically, for $x=(\mathrm{a} \pm \mathrm{b}), \Delta x= \pm[\Delta \mathrm{a}+\Delta \mathrm{b}]$.

Rule for Multiple / Division

Let $x=\mathrm{ab}$, or $x=\frac{\mathrm{a}}{\mathrm{b}}$. Then it can be shown that $\frac{\Delta x}{x}= \pm\left[\frac{\Delta a}{a}+\frac{\Delta b}{b}\right]$

The relative error, in the product / quotient, of two different physical quantities, must always be taken as the SUM of the relative errors, in each of these two different physical quantities.

Rule for ’error’, due to taking a power (say $n$ ), of a measured physical quantity:

Let $x=a^{n}$. It can be shown that $\frac{\Delta x}{x}= \pm\left[n \frac{\Delta a}{a}\right]$

The relative error, in the $\mathrm{n}^{\text {th }}$ power, of a measured physical quantity, is $\mathrm{n}$ times the relative error in that physical quantity.

We often need to combine these rules to calculate the relative error / percentage error in a given measurement.

Let a physical quantity, $\mathrm{P}$, be defined as

$$ P=\frac{a^{\ell} b^{m}}{c^{n}} $$

Combining the above described rules, we can then write

$\frac{\Delta P}{P} \pm\left[\ell\left(\frac{\Delta a}{a}\right)+m\left(\frac{\Delta b}{b}\right)+n\left(\frac{\Delta c}{c}\right)\right]$

Example:

Two masses, $\mathrm{M} _{1}$ and $\mathrm{M} _{2}$, are measures with accuracies of $\pm 5 \mathrm{~g}$ and $\pm 2 \mathrm{~g}$, respectively. The error, in their sum, and their difference, would then be, respectively,

(1) $7 \mathrm{~g}$ and $3 \mathrm{~g}$

(2) $3 \mathrm{~g}$ and $7 \mathrm{~g}$

(3) $3 \mathrm{~g}$ and $3 \mathrm{~g}$

(4) $7 \mathrm{~g}$ and $7 \mathrm{~g}$

Show Answer

Correct answer: (4)

Solution:

The (absolute) error, in the sum, or difference, of two quantities, is always taken as the sum of the (absolute) errors in them. Hence the error, in both cases is $(5+2)$ g, i.e. 7 g.

Example:

The length ( $\mathrm{L}$ ), of a table, is measured (in $\mathrm{m}$ ) to an accuracy of $0.01 \mathrm{~m}$ while its breadth (B) is measured (in $\mathrm{m}$ ) to an accuracy of $0.02 \mathrm{~m}$. The errors, in the area (A) of the table, and the ratio, $x$, of its length to breadth, would then be, respectively,

(1) $(0.01 \mathrm{~B}+0.02 \mathrm{~L})$ and $\left(\frac{0.01 \mathrm{~L}+0.02 \mathrm{~B}}{\mathrm{~L}^{2}}\right)$

(2) $(0.01 \mathrm{~L}+0.02 \mathrm{~B})$ and $\left(\frac{0.01 \mathrm{~L}+0.02 \mathrm{~B}}{\mathrm{~L}^{2}}\right)$

(3) $(0.01 \mathrm{~B}+0.02 \mathrm{~L})$ and $\left(\frac{0.01 \mathrm{~B}+0.02 \mathrm{~L}}{\mathrm{~B}^{2}}\right)$

(4) $(0.01 \mathrm{~L}+0.02 \mathrm{~B})$ and $\left(\frac{0.01 \mathrm{~B}+0.02 \mathrm{~L}}{\mathrm{~B}^{2}}\right)$

Show Answer

Correct answer: (3)

Solution:

We have,

$$ \begin{aligned} & \mathrm{A}=\mathrm{LB} \\ & \therefore \frac{\Delta \mathrm{A}}{\mathrm{A}}=\frac{\Delta \mathrm{L}}{\mathrm{L}}+\frac{\Delta \mathrm{B}}{\mathrm{B}}=\frac{0.01}{\mathrm{~L}}+\frac{0.02}{\mathrm{~B}} \\ & \therefore \Delta \mathrm{A}=\left(\frac{0.01}{\mathrm{~L}}+\frac{0.02}{\mathrm{~B}}\right) \times \mathrm{LB}=(0.01 \mathrm{~B}+0.02 \mathrm{~L}) \end{aligned} $$

Also, $\quad x=\frac{\mathrm{L}}{\mathrm{B}}$

$$ \begin{aligned} & \therefore \frac{\Delta x}{x}=\frac{\Delta \mathrm{L}}{\mathrm{L}}+\frac{\Delta \mathrm{B}}{\mathrm{B}}=\frac{0.01}{\mathrm{~L}}+\frac{0.02}{\mathrm{~B}} \\ & \therefore \Delta x=\left(\frac{0.01}{\mathrm{~L}}+\frac{0.02}{\mathrm{~B}}\right) \times\left(\frac{\mathrm{L}}{\mathrm{B}}\right) \\ & =\frac{0.01}{\mathrm{~B}}+\frac{0.02 \mathrm{~L}}{\mathrm{~B}^{2}}=\left[\frac{0.01 \mathrm{~B}+0.02 \mathrm{~L}}{\mathrm{~B}^{2}}\right] \end{aligned} $$

Example:

The formulae, for resistivity ( $\rho$ ) and Young’s modules $(\mathrm{Y})$ are, respectively,

$$ \rho=\frac{\pi \mathrm{r}^{2} \mathrm{R}}{\ell} \text { and } \mathrm{Y}=\frac{\mathrm{FL}}{\pi \mathrm{r}^{2} \ell} $$

The relative errors, in $\rho$ and $Y$, would then be, given, by the respective expressions.

(1) $\left(\frac{\Delta \rho}{\rho}=\frac{2 \Delta \mathrm{r}}{\mathrm{r}}+\frac{\Delta \mathrm{R}}{\mathrm{R}}+\frac{\Delta \ell}{\ell}\right)$ and $\left(\frac{\Delta \mathrm{Y}}{\mathrm{Y}}=\frac{\mathrm{dF}}{\mathrm{F}}+\frac{\Delta \mathrm{L}}{\mathrm{L}}+\frac{2 \Delta \mathrm{r}}{\mathrm{r}}+\frac{\Delta \ell}{\ell}\right)$

(2) $\left(\frac{\Delta \rho}{\rho}=\frac{2 \Delta \mathrm{r}}{\mathrm{r}}+\frac{\Delta \mathrm{R}}{\mathrm{R}}-\frac{\Delta \ell}{\ell}\right)$ and $\left(\frac{\Delta \mathrm{Y}}{\mathrm{Y}}=\frac{\mathrm{dF}}{\mathrm{F}}+\frac{\Delta \mathrm{L}}{\mathrm{L}}-\frac{2 \Delta \mathrm{r}}{\mathrm{r}}+\frac{\Delta \ell}{\ell}\right)$

(3) $\left(\frac{\Delta \rho}{\rho}=\frac{2 \Delta \mathrm{r}}{\mathrm{r}^{2}}+\frac{\Delta \mathrm{R}}{\mathrm{R}}-\frac{\Delta \ell}{\ell}\right)$ and $\left(\frac{\Delta \mathrm{Y}}{\mathrm{Y}}=\frac{\Delta \mathrm{F}}{\mathrm{F}}+\frac{\Delta \mathrm{L}}{\mathrm{L}}-\frac{2 \Delta \mathrm{r}}{\mathrm{r}^{2}}+\frac{\Delta \ell}{\ell}\right)$

(4) $\left(\frac{\Delta \rho}{\rho}=\frac{2 \Delta \mathrm{r}}{\mathrm{r}^{2}}+\frac{\Delta \mathrm{R}}{\mathrm{R}}-\frac{\Delta \ell}{\ell}\right)$ and $\left(\frac{\Delta \mathrm{Y}}{\mathrm{Y}}=\frac{\Delta \mathrm{F}}{\mathrm{F}}+\frac{\Delta \mathrm{L}}{\mathrm{L}}-\frac{2 \Delta \mathrm{r}}{\mathrm{r}^{2}}-\frac{\Delta \ell}{\ell}\right)$

Show Answer

Correct answer: (1)

Solution:

The relative errors, in all the products as well as the quotients, have to be all added to get the relative error in the given quantity.

Note the relative error in $\mathrm{r}^{2}$ is $2\left(\frac{\Delta r}{r}\right)$ and NOT $2\left(\frac{\Delta r}{r^{2}}\right)$. Hence, the two expressions, given only in option (1), correspond to these rules.

Example:

The height (h), and the base radius ( $\mathrm{r}$ ) of a cone, are measured to have values of $9.3 \mathrm{~cm}$ (using a meter scale of least count $0.1 \mathrm{~cm}$ ) and $2.45 \mathrm{~cm}$ (using a vernier calipers of least count $0.01 \mathrm{~cm}$ ). Find the volume,

$\mathrm{V},\left(=\frac{1}{3} \pi r^{2} h\right)$ of the cone, along with the error in it.

Show Answer

Solution:

We have,

$$ \begin{aligned} & \mathrm{V}==\frac{1}{3} \pi r^{2} h \\ & =\frac{1}{3} \pi(2.45)^{2} \times 9.3 \mathrm{~cm}^{3} \cong 58.466 \mathrm{~cm}^{3} \end{aligned} $$

As $\quad \mathrm{V}=\frac{1}{3} \pi r^{2} h$,

We have,

$$ \begin{aligned} & \frac{\Delta \mathrm{V}}{\mathrm{V}}= \pm\left[2 \frac{\Delta r}{r}+\frac{\Delta h}{h}\right] \\ & = \pm\left[2 \times \frac{0.01}{2.45}+\frac{0.1}{9.3}\right] \end{aligned} $$

$$ \begin{aligned} & \simeq \pm[0.0082+0.011]= \pm[0.0192] \\ & \therefore \Delta \mathrm{V}= \pm 0.0192 \times 58.466 \mathrm{~cm}^{3} \simeq \pm 1.12 \mathrm{~cm}^{3} \end{aligned} $$

The error, in V, is, therefore, of the order of $1.1 \mathrm{~cm}^{3}$. We would therefore, approximate the value of V and write it as

$\mathrm{V} \simeq(58.5 \pm 1.1) cm^{3}$

Example:

The length, $\ell$, of the sides of a cube, equals $(4.0 \pm 0.1) \mathrm{cm}$. The mass of the cube is measured to be $(64.8 \pm 0.2) \mathrm{g}$. Obtain the value, of the density of the material of the cube, on the basis of these measurements.

Solution:

We have, density $=\frac{\text { mass }}{\text { volume }}$

$$ \begin{aligned} & \therefore d=\frac{m}{v}=\frac{m}{\ell^{3}} \\ & \therefore \frac{\Delta d}{d}= \pm\left[\frac{\Delta m}{m}+3 \frac{\Delta \ell}{\ell}\right] \\ & = \pm\left(\frac{0.2}{64.8}+3 \times \frac{0.1}{4.0}\right) \\ & = \pm[0.0031+0.075] \simeq \pm 0.078 \end{aligned} $$

But $\quad \mathrm{d}=\frac{64.8}{(4.0)^{3}}\left(\mathrm{~g} / \mathrm{cm}^{3}\right)=1.0125\left(\mathrm{~g} / \mathrm{cm}^{3}\right)$

$$ \begin{aligned} & \therefore \Delta d=1.0125 \times 0.078\left(\mathrm{~g} / \mathrm{cm}^{3}\right) \equiv 0.079\left(\mathrm{~g} / \mathrm{cm}^{3}\right) \\ & \approx 0.08\left(\mathrm{~g} / \mathrm{cm}^{3}\right) \end{aligned} $$

We would, therefore, write (after rounding off to the second place of decimal) the value of d as

$$ d \simeq(1.01 \pm 0.08)\left(\mathrm{g} / \mathrm{cm}^{3}\right) $$

Additional Notes

A. Significant Figures

We know that the limit of precision of any measurement is dependent on the ’least counts’ of instruments used for that measurement. We, therefore, need to express ‘our experimental results’ only up to that number of digits that are ‘permitted’ by the limitations of the measuring instruments. The concept of ‘significant figures’ has been introduced to keep this point in mind.

The ‘significant digits’, in a result, are normally those digits that are known reliably, plus one additional digit that is uncertain. Here it is important to note that (i) a ‘change of units’ (ii) the location of the ‘decimal point’, do not affect the number of significant digits in a number.

We generally follow the following rules / conventions in (i) deciding / counting the number of significant digits in a number and (ii) in fixing the number of significant digits in a result obtained through addition / subtraction; multiplication / division of two or more numbers having their own (respective) number of significant digits.

(1) The number of digits, in a number, counted from the first non-zero digit, on the left, gives the number of significant digits in it.

(2) The last significant digit, in a number, is the (first) digit in it that is (not reliable) / (is uncertain).

(3) The ‘zeroes’, present in a number, are

(i) not counted as significant when they are present immediately after the decimal point.

(ii) not counted as significant when they are present towards the end of a number that has no decimal point in it.

(iii) counted as significant when they are present on the right of a decimal point.

(4) The sum, or difference, of two numbers, is regarded as having only as many significant digits as is the (lowest) number of significant digits, in the numbers being added / subtracted. We, however (increase the previous digit by one) / (do not change the previous digit), if the first digit, being rejected, in the sum / difference, is (5, or more than 5) / (less than 5).

(5) The product / quotient, of two numbers, can have no more significant digits than are present in the less precise, of the two numbers, that are used for calculating it.

It is usual, however, to initially retain ‘one more’ digit, in the product / quotient and then do the ‘rounding off’, following the rule of (more than / less than) 5 , quoted above in point (4).

(6) When the (first) insignificant / uncertain digit in a number is 5 itself, we (i) increase the previous digit by 1 , if it is an even digit (ii) do not change the previous digit, if it is an odd digit.

In addition to all these rules / conventions, we may have to rely on ‘common sense’ to decide the number of significant digits in a ‘result’ obtained through a combination of different algebraic operations.

We also often define / use the following terms in the context of ‘ERRORS’.

Average / Mean Error:

The average, of the mod (magnitudes) of errors, is called the average mean error.

$$ \bar{\delta}=\frac{\left|\bar{\delta} _{1}\right|+\left|\bar{\delta} _{2}\right|+\left|\bar{\delta} _{3}\right|+\ldots . .++\left|\bar{\delta} _{n}\right|}{n} $$

Mean Sqaure Error:

The mean, of the squares of errors, is called the mean sqaure error.

$$ \bar{\delta}^{2}=\frac{\delta _{1}^{2}+\delta _{2}^{2}+\ldots . .+\delta _{n}^{2}}{n} $$

Root Mean Square Error:

The square root, of the mean square error, is called the root mean square (rms) error.

$$ \delta _{m \mathrm{~s}}=\sqrt{\overline{\delta^{2}}}=\sqrt{\frac{\delta _{1}^{2}+\delta _{2}^{2}+\ldots+\delta _{n}^{2}}{n}} $$

Standard Deviation

Let $\bar{x}$ be the mean value of a (large) number of observation, say $x _{1}, x _{2}, x _{3} \ldots \ldots, x _{\mathrm{n}}$. The deviation, $\delta _{i}$, of the $i^{\text {th }}$ observation, from the mean value, is then

$$ \delta _{i}=\left(x _{i}-\bar{x}\right) $$

The mean value, of the squares of all the deviations, is then given by

$$ \bar{\delta}^{2}=\frac{\sum _{i=1}^{n} \delta _{i}^{2}}{n} $$

The square root, of this mean square value, is taken as an indicator of the standard deviation $(\sigma)$, for the given set of observations / data.

$$ \therefore \sigma=\sqrt{\bar{\delta}^{2}}=\left(\frac{\sum _{i=1}^{n} \delta _{i}^{2}}{n}\right)^{1 / 2}=\left[\frac{\sum\left(x _{i}-\bar{x}\right)^{2}}{n}\right]^{1 / 2} $$

The standard deviation, in the sum / difference, product / quotient of two numbers, is calculated through their own standard deviations, by using the following rules:

(i) If $\mathrm{A}=\mathrm{B} \pm \mathrm{C}$; we have $6 _{\mathrm{A}}^{2}=6 _{\mathrm{B}}^{2}+6 _{\mathrm{C}}^{2}$

(ii) If $A=B \times C$; we have $\left(\frac{6 _{A}}{A}\right)^{2}=\left(\frac{6 _{B}}{B}\right)^{2}+\left(\frac{6 _{C}}{C}\right)^{2}$

(iii) If $\mathrm{A}=\frac{\mathrm{B}}{\mathrm{C}}$; we again have $\left(\frac{6 _{\mathrm{A}}}{\mathrm{A}}\right)^{2}=\left(\frac{6 _{\mathrm{B}}}{\mathrm{B}}\right)^{2}+\left(\frac{6 _{\mathrm{C}}}{\mathrm{C}}\right)^{2}$

ADDITIONAL EXAMPLES

1. Let $\left[\varepsilon _{0}\right]$ denote the dimensional formula of the permittivity of vacuum. If $\mathrm{M}=$ mass, $\mathrm{L}=$ length, $\mathrm{T}=$ Time and $\mathrm{A}=$ electric current, then:

(a) $\quad\left[\varepsilon _{0}\right]=\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{~A}^{2}\right]$

(b) $\quad\left[\varepsilon _{0}\right]=\left[\mathrm{M}^{-1} \mathrm{~L}^{2} \mathrm{~T}^{-1} \mathrm{~A}^{-2}\right]$

(d) $\quad\left[\varepsilon _{0}\right]=\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{2} \mathrm{~A}\right]$

Show Answer

Correct option is (1)

(IIT 2013)

Solution:

According to Coulomb’s law

$$ \begin{aligned} & \mathrm{F}=\frac{1}{4 \pi \varepsilon _{0}} \frac{\mathrm{q} _{1} \mathrm{q} _{2}}{\mathrm{r}^{2}} \\ & \therefore \varepsilon _{0}=\frac{\left[\mathrm{A}^{2} \mathrm{~T}^{2}\right]}{\left[\mathrm{MLT}^{-2} \mathrm{~L}^{2}\right]}=\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~A}^{2} \mathrm{~T}^{4}\right] \end{aligned} $$

2. A train is moving on a straight track with speed $v=20 \mathrm{~ms}^{-1}$. It is blowing its whistle at the frequency of $1000 \mathrm{~Hz}$. The percentage change in the frequency, heard by a person (standing near the track), as the train passes him is $\left(v=\right.$ speed of sound $\left.=320 \mathrm{~ms}^{-1}\right)$ close to

(a) $18 \%$

(b) $24 \%$

(d) $12 \%$

Show Answer

Correct option is (4)

(IIT 2015))

Solution:

We know that $v^{\prime}=\left(\frac{v}{V \pm v}\right) v$

$$ \therefore \frac{\Delta v}{v}= \pm 2\left(\frac{v}{V}\right) $$

This gives a percentage change of $12 \%$

PROBLEMS FOR PRACTICE (SET-I)

1. Find the dimensions of (i) universal constant of gravitation (ii) permeability of free space.

Show Answer

Answer: (a)

2. In the formula, for acceleration (f), given below, $\mathrm{a}, \mathrm{b}$ and $\mathrm{c}$ are constants and $\mathrm{t}$ represent time.

$$ f=a t+b t^{2}+c t^{3} $$

The dimensions, of $\mathrm{b}$ and $\mathrm{c}$, should then be, respectively,

(a) $\mathrm{LT}^{-4}$ and $\mathrm{LT}^{-5}$

(b) MLT $^{-2}$ and $\mathrm{MLT}^{-3}$

(d) MLT $^{-4}$ and MLT $^{-5}$

Show Answer

Answer: (a)

3. The dimensional formula, for specific latent heat capacity is

(a) $\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}^{-2}$

(b) $\mathrm{MLT}^{-2}$

(d) $\mathrm{ML}^{2} \mathrm{~T}^{-2}$

Show Answer

Answer: (a)

4. The dimensional formula, for Planck’s constant (h), is

(a) $\mathrm{ML}^{-2} \mathrm{~T}^{-3}$

(b) $\mathrm{ML}^{2} \mathrm{~T}^{-2}$

(d) $\mathrm{ML}^{-2} \mathrm{~T}^{-2}$

Show Answer

Answer: (c)

5. The number of particles, crossing per unit area, perpendicular to $\mathrm{X}$-axis, in unit time is given by:

$$ \mathrm{N}=-\mathrm{D}\left(\frac{n _{2}-n _{1}}{x _{2}-x _{1}}\right) $$

Here, $\mathrm{n} _{1}$ and $\mathrm{n} _{2}$ are, respectively, the number of particles per unit volume, for the values $x _{1}$ and $x _{2}$ of $x$. The dimensions, of the diffusion constant $\mathrm{D}$, are:

(a) $\mathrm{M}^{0} \mathrm{LT}^{2}$

(b) $\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}^{4}$

(d) $\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}^{-1}$

Show Answer

Answer: (d)

6. The relation between the SI unit (watt) and the CGS unit ( $\mathrm{erg} \mathrm{s}^{-1}$ ), of power, is

(a) $1 \mathrm{~W}=10^{5} \mathrm{erg} \quad \mathrm{s}^{-1}$

(b) $1 \mathrm{~W}=10^{6} \mathrm{erg} \quad \mathrm{s}^{-1}$

(d) $1 \mathrm{~W}=10^{8} \mathrm{erg} \quad \mathrm{s}^{-1}$

Show Answer

Answer: (c)

7. If p and $v$ stand for pressure and volume, respectively. The dimensions, of the constant, $a$, in the term $\left(p+\frac{a}{V^{2}}\right)$, should be:

(a) $\mathrm{ML}^{6} \mathrm{~T}^{-2}$

(b) $\mathrm{M}^{2} \mathrm{~L}^{2} \mathrm{~T}^{-2}$

(d) $\mathrm{ML}^{5} \mathrm{~T}^{-2}$

Show Answer

Answer: (d)

8. The dimensional formulae, for specific heat capacity and thermal conductivity, are, respectively

(a) $\mathrm{MLT}^{-3} \mathrm{~K}^{-1}$ and $\mathrm{ML}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}$

(b) $\mathrm{MLT}^{-3} \mathrm{~K}^{-1}$ and $\mathrm{L}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}$

(d) $\mathrm{L}^{2} \mathrm{~T}^{-3} \mathrm{~K}^{-1}$ and $\mathrm{ML}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}$

Show Answer

Answer: (b)

9. The dimensions, of the constant $\varepsilon _{0}$, in Coulomb’s formula, (for the force (F), between two charges $\left(\mathrm{Q} _{1}, \mathrm{Q} _{2}\right)$, separated by a distance (r), $\mathrm{F}=\frac{1}{4 \pi \varepsilon _{0}}\left(\frac{\mathrm{Q} _{1} \mathrm{Q} _{2}}{\mathrm{r}^{2}}\right)$, would be

(a) $\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{I}^{-2}$

(b) $\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{I}^{2}$

(d) $\mathrm{M}^{-1} \mathrm{~L}^{2} \mathrm{~T}^{2} \mathrm{I}^{2}$

Show Answer

Answer: (d)

PROBLEMS FOR PRACTICES (SET-II)

1. Find the ’least count’ of (i) a ‘vernier’ that has 50 divisions on its vernier scale coinciding with 45 divisions on the main scale; the main scale is graduated in $(1 / 2)$ millimeters, (ii) a ‘screw gauge’, that has 100 divisions on its circular scale and a pitch of $0.5 \mathrm{~mm}$.

Show Answer

Answer: (i) $1 / 20 \mathrm{~mm}$, (ii) $0.005 \mathrm{~mm}$

2. Find (with error limits) the surface area of a sphere, whose radius is measured to be $(4.1 \pm 0.1) \mathrm{cm}$.

Show Answer

Answer: $(5.0 \pm 0.2) \mathrm{ms}^{-1}$

3. A particle covers a distance of $(20.5 \pm 0.5) \mathrm{m}$ in a time interval of $(4.1 \pm 0.1) \mathrm{s}$. Find its average speed along with the ‘percentage error’ in the same.

Show Answer

Answer: (a) 4, (b) 2 , (c) 5 , (d) 4 , (e) 3

4. In an experiment on verification of Ohm’s law, the current in the circuit is measured to be 1.3A(using an ammeter of least count $0.1 \mathrm{~A}$ ) and the voltage, across the resistor, is measured to be $5.2 \mathrm{~V}$ (using a voltmeter of least count $0.2 \mathrm{~V}$ ). Find the resistance of the resister used, along with the ’error’, in the result.

Show Answer

Answer: (b)

5. If the errors, in ten observations, of a physical quantity, are $-0.55,+0.43,+0.05,-0.36,0.08,0.05$, $0.00,-0.03,-0.05$ and +0.06 , find the ratio of the (i) average mean error and the (ii) root mean square error, of these observations.

Show Answer

Answer: (a)

6. Give the number of significant digits in the following numbers:

(a) 235.4

(b) 8300

(d) 625.0

(e) $3.46 \times 10^{3}$

Show Answer

Answer: $(211 \pm 10) \mathrm{cm}^{2}$

7. State the result, up to the appropriate number of significant digits, in the following:

(a) $(66.23+3.5)$

(b) $(8.305-3.27235)$

(d) $(7400 \div 21.25)$

Show Answer

Answer: $(4.0 \pm 0.5) \Omega$

8. In the relation

$$ \mathrm{Y}=\frac{\mathrm{WL}}{\pi \mathrm{r}^{2} \ell} $$

The percentage errors in $\mathrm{W}, \ell, \mathrm{r}$, and $\mathrm{L}$ are $1.0 \%, 0.5 \%, 1 \%$ and $2 \%$ respectively. The percentage error in $Y$ would be

(a) $4.5 \%$

(b) $5 \%$

(d) $1 \%$

Show Answer

Answer: (a) 69.7 , (b) 5.033 , (c) 243.85 , (d) 350

9. In the formula $\mathrm{V}=\frac{\pi p r^{4}}{8 \eta \ell}$,

the fractional relative errors in $\mathrm{V}, \mathrm{p}, \eta$ and $\ell$ are known to be $0.06 ; 0.01,0.01$ and 0.02 , respectively. The fractional relative error in, $\mathrm{r}$, would be

(a) 0.02

(b) 0.01

(d) 0.0025

Show Answer

Answer: (c)

10. The diameter (d), and length $(\ell$ ), of a cylindrical wire, are measured by instruments having least counts of $0.0005 \mathrm{~cm}$ and $0.01 \mathrm{~cm}$, respectively. The fractional relative error, in the curved surface area, and volume, of the wire, calculated from these observations, would be

(a) $\left(\frac{0.0005}{\mathrm{~d}}+\frac{0.01}{\ell}\right)$ and,$\left(\frac{0.001}{\mathrm{~d}}+\frac{0.01}{\ell}\right)$, respectively

(b) $\left(\frac{0.001}{\mathrm{~d}}+\frac{0.01}{\ell}\right)$ and, $\left(\frac{0.002}{\mathrm{~d}}+\frac{0.01}{\ell}\right)$, respectively

(c) $\left(\frac{0.001}{\mathrm{~d}}+\frac{0.01}{\ell}\right)$ and, $\left(\frac{0.001}{\mathrm{~d}}+\frac{0.01}{\ell}\right)$, respectively

(d) $\left(\frac{0.0005}{\mathrm{~d}}+\frac{0.01}{\ell}\right)$ and, $\left(\frac{0.0005}{\mathrm{~d}}+\frac{0.01}{\ell}\right)$, respectively

Show Answer

Answer: $(5.0 \pm 0.2) \mathrm{ms}^{-1}$

Question Bank

Key Learning Points

1. The process of measurement has played a very significant role in the development of all physical sciences.

2. Measurement is basically a process of comparison.

3. ‘Fundamental quantities’ are a few selected physical quantities that can be used to define other physical quantities.

4. All physical quantities, that are defined in terms of the ‘fundamental quantities’, are known as ‘derived quantities’.

5. In the initial stages, only three physical quantities - mass, length, time - were taken as ‘fundamental units’.

6. The number of ‘fundamental quantities’ has now been increased to seven. The seven fundamental quantities are:

Mass, length, time, electric current, thermodynamic temperature, amount of substance, luminous intensity.

7. In addition to these seven fundamental quantities, two supplementary quantities - the angle and the solid angle - are also used in defining other quantities.

8. A number of system of units - like the FPS units, the CGS unit and the MKS units - have been used over different times, and in different countries.

9. In the year 1971, a system of units - now known by the abbreviation ‘SI units’, - was developed and recommended, (for use by all countries), by the general conference on weight and measures. The SI units are now being used (almost) all over the world.

10. The seven fundamental, or ‘base’ units, in SI, are are the metre (m), kilogram ( $\mathrm{kg})$, second (s), ampere (A), kelvin (k), mole (mol) and candela (cd), for length, mass, time, electric current (thermodynamic) temperature, amount of substance and luminous intensity.

11. The SI units, for the two supplementary quantities - angle and solid angle, are the radian (rad) and steradian (sr), respectively.

12. All the units, in SI, have been given very precise, and well defined, meaning and definitions.

13. We also use a number of multiples (corresponding to different positive powers of ten) and submultiple (corresponding to different negative powers of ten) in SI. These have all been given definite names and symbols.

14. A number of units, of the ‘derived quantities’, have also been given names of their own.

15. We can co-relate different ‘derived quantities’, with the ‘fundamental quantities’, (in a ‘compact way’) by introducing the concept of ‘dimensions’.

16. The ‘dimensions’, of a given physical quantity, are the ‘powers’, to which the fundamental quantities, must be raised, to represent it.

17. The ‘dimensional formula’, of a physical quantity, is the representation of that quantity, in terms of the (i) symbols of the fundamental quantities and (ii) its own ‘dimensions’.

18. The dimensional formulae, of force and momentum, for example, are $\left[\mathrm{MLT}^{-2}\right]$ and $\left[\mathrm{MLT}^{-1}\right]$, respectively.

19. We have a very useful principle - the principle of dimensional homogeneity. According to the principle: ‘The ‘dimensions’ of all the terms, on both sides of a physically acceptable (or valid) relation, must be identical.”

20. We use ‘dimensional analysis’ (based on the concept of ‘dimensions’ and ‘principle of dimensional homogeneity’) for a number of useful practical applications.

21. The applications of ‘dimensional analysis’ include:

(i) Checking a given formula, or relation.

(ii) Conversion, from one system of units to another.

(iii) Obtaining ‘dimensionally valid’ relations, between different physical quantities.

22. The concept of ’least count’, of a given measuring device / instrument, helps us to know the precision of our measurement.

23. The terms “precision” and ‘accuracy”, in the context of “experimental measurement and their results”, have different meanings.

24. The terms ‘mistake’ and ’error’ have different meanings for experimental measurements.

25. Errors can be “systematic” (which can be reduced, or even eliminated) and “random” (which cannot be eliminated all together).

26. Random errors, generally, tend to follow the normal or ‘Gaussian law’. The probability, of an error $x$, decreases (exponentially) with an increase in the value of $x$.

27. We define the absolute error, in a measurement ( $\operatorname{say} x _{\mathrm{i}}$ ), as the difference between that measurement, and the standard (or mean value $\bar{x}$ of a large number of observations) value, of the relevant physical quantity.

Absolute error $=\left(x _{i}-\bar{x}\right)$

28. The relative error, of a measurement, equals the ratio of the (i) mean of the absolute errors of all the quantities and (ii) mean value of the measured quantity.

29. The relative error, expressed as a percentage, gives the ‘percentage error’.

30. The values, of different physical quantities, are generally calculated by using a relation or ‘formula’, that expresses that physical quantity in terms of ‘other physical quantities’.

31. We, therefore, need to have a set of ‘rules’ that enable us to calculate the absolute / relative error, in the ‘value’ of a given physical quantity, that has been obtained by using a ‘formula’ or a ‘relation’. Each of the different physical quantities, present in that relation, and measured, has an error of its own.

32. The following rules are generally followed for calculating the ’net error’, due to a number of ‘individual errors’.

(i) The absolute error, in a sum or difference, is always taken as the SUM of the absolute errors in the quantities being added / subtracted.

(ii) The relative error, in a product / quotient, always equals the SUM of the relative errors in the terms being multiplied / divided.

(iii) The relative error, in the $\mathrm{n}^{\text {th }}$ power of a physical quantity, is $\mathrm{n}$ time the relative error in that quantity.

33. We often need to combine these rules to calculate the ‘relative error’ in a given situation.

34. We also follow a set of rules, coupled with ’logical reasoning’, to decide the number of ‘significant figures’, that need to be used, while stating the ‘final result’, that is based on a number of algebraic calculations.

1. The SI Unit, of surface tension, equals:

(1) newton/ metre $^{2}$ as well as $\frac{\text { joule }-\mathrm{s}}{\mathrm{m}^{3}}$

(2) newton/ metre as well as $\frac{\text { watt }-\mathrm{s}}{\mathrm{m}^{2}} $

(3) newton/ metre as well as $\frac{\text { joule }-\mathrm{s}}{\mathrm{m}^{2}} $

(4) newton/ metre as well as $\frac{\text { watt }-\mathrm{s}}{\mathrm{m}^{3}} $

Show Answer

Correct answer: (2)

Solution:

Surface tension, by definition, equals

(1) force per unit length as well as,

(2) (mechanical) surface energy per unit area.

The SI units of force and energy are the newton and joule (= watt $-\mathrm{s})$. Hence the SI units of surface tension are (newton/metre) as well as $\frac{\text { watt }-\mathrm{s}}{\mathrm{m}^{2}}$.

2. The SI unit, of the coefficient of viscosity, can be equated to

(1) $\left(\right.$ joule $\times \mathrm{s}$ ) as well as the unit of pressure $\times(\text { length } \times \text { acc })^{1 / 2} $

(2) (joule $\times$ hertz) as weel as the unit of $\frac{\text { torque } \times \text { time period }}{\text { volume }} $

(3) pascal (hertz) $)^{-1}$ as well as the unit of modulus of elasticity $\times(\text { length } / \text { acc. })^{1 / 2} $

(4) $\operatorname{pascal}(\mathrm{s})$ as well as the unit of stress $\times(\text { length } \times \text { acc. })^{1 / 2} $

Show Answer

Correct answer: (3)

Solution:

We have, by Newton’s law,

$$ \mathrm{F}=-\eta \mathrm{A} \frac{d v}{d x} $$

Hence, $\eta$, has units of $\frac{\text { newton } \times \mathrm{m}}{\mathrm{m}^{2} \times \mathrm{ms}^{-1}}$, i.e.,

(newton $\left.\mathrm{m}^{-2} \mathrm{~s}\right)$. This equals $\left(\frac{\text { pascal }}{\text { hertz }}\right)\left(\because\right.$ pascal $=\frac{\text { newton }}{\mathrm{m}^{2}}$ and hertz $\left.=\mathrm{s}^{-1}\right)$. It also equals the unit of modulus of elasticity $\times\left[\text { length } \times(\text { acceleration })^{-1}\right]^{1 / 2}$. This is because the unit of modulus of elasticity is (newton $/ \mathrm{m}^{2}$ ) and that of $\left[\right.$ length $\times\left(\text { acceleration }{ }^{-1}\right]^{1 / 2}$ is $\left[\mathrm{m} \times\left(\mathrm{ms}^{-2}\right)^{-1}\right]^{1 / 2}$, i.e., s.

3. The SI unit of moment of inertia can be equated to the SI units of

(1) $[$ density $\times$ volume $\times$ area $]$ and $\left[\frac{\text { force } \times \text { area }}{\text { acceleration }}\right]$

(2) $[$ density $\times$ volume $/$ area $]$ and $\left[\frac{\text { energy } \times \text { area }}{\text { acceleration }}\right]$

(3) $[$ density $\times$ area $/$ volume $]$ and $\left[\frac{\text { energy } \times \text { area }}{(\text { velocity })^{2}}\right]$

(4) $[$ relative density $\times$ mass $\times$ area $]$ and $\left[\frac{\text { force } \times \text { area }}{(\text { velocity })^{2}}\right]$

Show Answer

Correct answer: (1)

Solution:

The SI unit of moment of inertia is $\left(\mathrm{kg}-\mathrm{m}^{2}\right)$

The SI unit of density $\times$ volume $\times$ area $=\frac{\mathrm{kg}}{\mathrm{m}^{3}} \times \mathrm{m}^{3} \times \mathrm{m}^{2}=\left(\mathrm{kg}-\mathrm{m}^{2}\right)$

and the SI unit of

$$ \frac{\text { force } \times \text { area }}{\text { acceleration }}=\frac{\mathrm{kg} \mathrm{ms}^{-2} \times\left(\mathrm{m}^{2}\right)}{\left(\mathrm{ms}^{-2}\right)}\left(\mathrm{kg}-\mathrm{m}^{2}\right) $$

4. The ‘pair’, having identical SI units, is

(1) Work and torque

(2) Surface tension and pressure

(3) Pressure and Poisson’s ratio

(4) coefficient of viscosity and thrust

Show Answer

Correct answer: (1)

Solution:

We have,

Work $=$ force $\times$ distance

and torque $=$ force $\times($ perpendicular arm’s length $)$

The SI units, of both these terms, is therefore, the same; equal to (N-m).

5. The unit of capacitance, (the fared), expressed in terms of the fundamental units, inSI, is equal to

(1) $\mathrm{kg}^{-1} \mathrm{~m}^{-4} \mathrm{~s}^{2} \mathrm{~A}^{2}$

(2) $\mathrm{kg}^{2} \mathrm{~m}^{-2} \mathrm{~s}^{2} \mathrm{~A}^{4}$

(3) $\mathrm{kgm}^{-2} \mathrm{~s}^{2} \mathrm{~A}^{2}$

(4) $\mathrm{kg}^{-1} \mathrm{~m}^{-2} \mathrm{~s}^{4} \mathrm{~A}^{2}$

Show Answer

Correct answer: (4)

Solution:

We have farad $=\frac{\text { coulomb }}{\text { volt }}$

$$ \begin{aligned} & =\frac{\text { coulomb }}{(\text { joule } / \text { coulomb })}=\frac{(\text { coulomb })^{2}}{\text { joule }} \\ & =\frac{(\text { ampere }-\mathrm{s})^{2}}{\mathrm{~kg} \mathrm{~m}^{2} \mathrm{~s}^{-2}} \\ & =\mathrm{kg}^{-1} \mathrm{~m}^{-2} \mathrm{~s}^{4} \mathrm{~A}^{2} \end{aligned} $$

6. The unit of pressure, in SI units, is related to its unit in CGS units as

(1) 1 pascal $=10^{5}$ dyne $/ \mathrm{cm}^{2} $

(2) 1 pascal $=10^{3}$ dyne $/ \mathrm{cm}^{2} $

(3) 1 pascal $=10$ dyne $/ \mathrm{cm}^{2} $

(4) 1 pascal $=10^{-2}$ dyne $/ \mathrm{cm}^{2} $

Show Answer

Correct answer: (3)

Solution:

We have pressure $=\frac{\text { force }}{\text { area }}$

$$ \begin{aligned} & =\left[\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}^{2}}\right]=\mathrm{ML}^{-1} \mathrm{~T}^{-2} \\ & \therefore \frac{\text { Unit of pressure in SI unit }}{\text { Unit of pressure in CGS units }}=\left(\frac{\mathrm{kg}}{\mathrm{g}}\right)\left(\frac{\mathrm{m}}{\mathrm{cm}}\right)^{-1}\left(\frac{\mathrm{s}}{\mathrm{s}}\right)^{-2} \\ & =10^{3} \times\left(10^{2}\right)^{-1} \times 1=10 \\ & \therefore 1 \text { pascal }=10 \text { dyne } / \mathrm{cm}^{2} \end{aligned} $$

7. The ratio of the SI units, to the FPS unit, of pressure, is equal to the ratio of the corresponding units of

(1) ‘Energy per unit volume’ as well as Poisson’s ratio

(2) ‘Bulk modulus’ as well as ’energy per unit volume’

(3) ‘Poisson’s ratio’ as well as ‘modulus of rigidity’

(4) ‘Coefficient of viscosity’ as well as Young’s modulus $=\frac{\text { Stress }}{\text { Strain }}=\frac{\text { Force } / \text { area }}{(\text { dimensionless })}=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]$

Show Answer

Correct answer: (2)

Solution:

We have,

$$ \text { Pressure }=\frac{\text { force }}{\text { area }}=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right] $$

Also,

Bulk modulus $=\frac{\text { Stress }}{\text { Strain }}=\frac{\text { Force } / \text { area }}{(\text { dimensionless })}=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]$

and, energy per unit volume $=\frac{\text { force } \times \text { distance }}{\text { volume }}$

$$ =\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{~L}^{3}}\right]=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right] $$

$\therefore$ The ratio, of the SI and FPS units, will have the same value for these three quantities.

8. The SI unit of specific heat capacity (say ’ $s_1$ ‘) would be related to its CGS unit (say ’ $s_2$ ’ as }

(1) $1 s _{1}=\left(\frac{10^{4}}{274}\right) s _{2}$

(2) $1 s _{1}=(273) 10^{4} s _{2}$

(3) $1 s _{1}=\left(\frac{10^{4}}{273}\right) s _{2}$

(4) $1 s _{1}=10^{4} s _{2}$

Show Answer

Correct answer: (4)

Solution:

We have specific heat capacity

$$ \begin{aligned} & =\frac{\text { heat (energy) }}{\text { mass } \times \text { change in temperature }} \\ & =\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{M} \times(\mathrm{K})} \\ & =\mathrm{L}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1} \\ & \therefore \frac{s^{1}}{s^{2}}=\left(\frac{m}{c m}\right)^{2}\left(\frac{s}{s}\right)^{2} \frac{K^{-1}}{\left({ }^{\circ} \mathrm{C}\right)^{-1}} \\ & =(100)^{2} \times 1 \times 1 \end{aligned} $$

( $\because$ A change in temperature of $1^{\circ} \mathrm{C}$ also equals a change of one kelvin on the thermodynamic, or kelvin, scale.)

$\therefore \frac{S _{1}}{S _{2}}=10^{4}$

or $\mathrm{s} _{1}=10^{4} \mathrm{~s} _{2}$

9. The horse power (H.P.), a popular unit of power in the FPS units, is related to the SI Unit of power (the watt), as

1 H.P. $=746 \mathrm{~W}$

[The FPS unit of force is the poundal;

Given that $1 \mathrm{~kg}=2.205$ pound and

$1 \mathrm{~m}=3.28$ feet] the relation between the FPS unit of power ( $=\mathrm{ft}-$ poundal $/ \mathrm{s}$ ) and the HP is,

(1) $1 \mathrm{HP}=17.7 \times 10^{3} \mathrm{ft}-$ poundal $/ \mathrm{s}$

(2) $1 \mathrm{HP}=550 \mathrm{ft}-$ poundal $/ \mathrm{s}$

(3) $1 \mathrm{HP}=31.5 \mathrm{ft}-$ poundal $/ \mathrm{s}$

(4) $1 \mathrm{HP}=41.03 \times 10^{4} \mathrm{ft}$-poundal $/ \mathrm{s}$

Show Answer

Correct answer: (1)

Solution:

We have power $=\frac{\text { work }}{\text { time }}=\left[\frac{\mathrm{MLT}^{-2} \mathrm{~L}}{\mathrm{~T}}\right]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-3}\right]$

$\therefore \frac{\text { SI unit of Power }}{\text { FPS unit of power }}=\left(\frac{\mathrm{kg}}{\text { pound }}\right)\left(\frac{\mathrm{m}}{\text { foot }}\right)^{2}\left(\frac{\mathrm{s}}{\mathrm{s}}\right)^{-3}$

or $\frac{\text { watt }}{(\mathrm{ft} \text { - poundal } / \mathrm{s})}=2.205 \times(3.28)^{2} \times(1)^{-3}$

$\simeq 23.72$

$\therefore 1$ watt $\simeq 23.72 \mathrm{ft}-$ poundal $/ \mathrm{s}$

$\therefore 1 \mathrm{HP}=746 \mathrm{~W}=746 \times 746 \times 23.72 \mathrm{ft}-$ poundal $/ \mathrm{s}$

$\cong 17695 \mathrm{ft}-$ poundal/s

$\simeq 17.7 \times 10^{3} \mathrm{ft}-$ poundal $/ \mathrm{s}$

10. The SI value, of $R$, (the universal gas constant) occurring in the equation of state ( $p v=n R T)$ for a perfect gas, would be related to its CGS value as

(1) SI value of $\mathrm{R}=\mathrm{CGS}$ value of $\mathrm{R}$

(2) SI value of $\mathrm{R}=10^{7} \mathrm{CGS}$ value of $\mathrm{R}$

(3) SI value of $\mathrm{R}=273 \times 10^{7} \mathrm{CGS}$ value of $\mathrm{R}$

(4) SI value of $\mathrm{R}=274 \times 10^{7} \mathrm{CGS}$ value of $\mathrm{R}$

Show Answer

Correct answer: (2)

Solution:

We have $\quad \mathrm{R}=\frac{\mathrm{pV}}{\mathrm{nT}}=\left[\frac{\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}^{2}} \times \mathrm{L}^{3}}{\mathrm{~K}}\right]$

$=\left[\mathrm{ML}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right]$

$\therefore \frac{\text { SI value of } \mathrm{R}}{\text { CGS value of } \mathrm{R}}=\left(\frac{\mathrm{kg}}{g}\right)\left(\frac{\mathrm{n}}{\mathrm{cm}}\right)^{2}\left(\frac{1 s}{1 s}\right)^{-2}\left(\left(\frac{\mathrm{k}}{{ }^{\mathrm{\degree c}}}\right)^{-1}\right)$

$=10^{3}\left(10^{2}\right)^{2}(1)(1)^{-1}=10^{7}$

( $\because$ per kelvin equals per ${ }^{0} \mathrm{C}$; the size of the degree, on the kelvin scale, equals that on the celsius (or ${ }^{0} \mathrm{C}$ ) scale)

$\therefore$ SI value of $\mathrm{R}=10^{7} \mathrm{CGS}$ value of $\mathrm{R}$

11. If force (F), velocity (V) and surface tension (S) were taken as the ‘fundamental units’, the dimensional formula, for momentum (p), would be

(1) $\left[\mathrm{VSF}^{-2}\right]$

(2) $\left[\mathrm{F}^{2} \mathrm{~V}^{-1} \mathrm{~S}^{-1}\right]$

(3) $\left[\frac{\mathrm{F}^{2}}{\mathrm{~V}^{2} \mathrm{~S}}\right]\left[\mathrm{F}^{2} \mathrm{~V}^{-2} \mathrm{~S}^{-1}\right]$

(4) $\left[\mathrm{V}^{2} \mathrm{SF}^{-2}\right]$

Show Answer

Correct answer: (2)

Solution:

We have, $[\mathrm{F}]=\left[\mathrm{MLT}^{-2}\right]$

$$ [\mathrm{V}]=\left[\mathrm{LT}^{-1}\right] $$

and $[\mathrm{S}]=($ force $/$ length $)=\left[\mathrm{MT}^{-2}\right]$

$\therefore$ We get

$$ [L]=\frac{F}{S} $$

Also $\left[\frac{\mathrm{F}}{\mathrm{V}}\right]=\left[\mathrm{MT}^{-1}\right]$

$$ \begin{aligned} & \therefore\left[\left(\frac{\mathrm{F}}{\mathrm{V}}\right) \div \mathrm{S}\right]=\mathrm{T} \\ & \therefore[\mathrm{T}]=\left[\left(\frac{\mathrm{F}}{\mathrm{VS}}\right)\right] \\ & \therefore[\mathrm{M}]=\left[\mathrm{ST}^{2}\right]=\frac{\mathrm{S} \cdot \mathrm{F}^{2}}{\mathrm{~V}^{2} \mathrm{~S}^{2}}=\left(\frac{\mathrm{F}^{2}}{\mathrm{VS}}\right) \end{aligned} $$

Now momentum $[\mathrm{p}]=$ mass $\times$ velocity $=\left[\mathrm{MLT}^{-1}\right]$

$$ \begin{aligned} & \therefore[\mathrm{p}]=\left[\frac{\mathrm{F}^{2}}{\mathrm{VS}} \cdot \frac{\mathrm{F}}{\mathrm{S}} \cdot \frac{\mathrm{VS}}{\mathrm{F}}\right]=\left[\frac{\mathrm{F}^{2}}{\mathrm{~V} \cdot \mathrm{S}}\right] \\ & =\mathrm{F}^{2} \mathrm{~V}^{-1} \mathrm{~S}^{-1} \end{aligned} $$

12. If momentum (P), acceleration (A), the specific heat capacity (S) and time (T), were taken as the fundamental units, the dimensional formula, for the coefficient of thermal conductivity $(\sigma)$, would be

(1) $[\sigma]=\left[\mathrm{PA}^{-2} \mathrm{~S}^{+1} \mathrm{~T}^{-4}\right]$

(2) $\sigma=\left[\mathrm{P}^{-1} \mathrm{~A}^{2} \mathrm{~S}^{-1} \mathrm{~T}^{4}\right]$

(3) $\sigma=\left[\mathrm{PA}^{2} \mathrm{~S}^{-1} \mathrm{~T}^{-4}\right]$

(4) $\sigma=\left[\mathrm{P}^{-1} \mathrm{~A}^{-2} \mathrm{~S}^{+1} \mathrm{~T}^{4}\right]$

Show Answer

Correct answer: (1)

Solution:

We have $[\mathrm{P}]=\left[\mathrm{MLT}^{-1}\right]$,

$$ \begin{gathered} {[\mathrm{A}]=\left[\mathrm{LT}^{-2}\right]} \\ {[\mathrm{S}]=\left(\frac{(\text { Heat energy }}{\text { mass } \times \text { temperature }}\right)=\left[\mathrm{L}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right]} \\ \therefore[\mathrm{L}]=\left[\mathrm{AT}^{2}\right][\mathrm{M}]=\left(\frac{\mathrm{P}}{\mathrm{L}} \mathrm{T}\right) \\ \therefore[\mathrm{M}]=\left[\frac{\mathrm{P}}{\mathrm{AT}^{2}} \cdot \mathrm{T}\right]=\left[\mathrm{PA}^{-1} \mathrm{~T}^{-1}\right] \\ \text { Also, }[\mathrm{K}]=\frac{\mathrm{L}^{2} \mathrm{~T}^{-2}}{\mathrm{~S}}=\left[\frac{\mathrm{A}^{2} \mathrm{~T}^{4} \mathrm{~T}^{-2}}{\mathrm{~S}}\right] \\ \quad=\left[\mathrm{S}^{-1} \mathrm{~A}^{2} \mathrm{~T}^{2}\right] \end{gathered} $$

Now rate of heat flow $=\frac{\sigma(\text { area })(\text { temp.difference })}{(\text { distance })}$

$\therefore\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{~T}}\right]=\frac{\sigma\left[\mathrm{L}^{2}\right][\mathrm{K}]}{[\mathrm{L}]}$

$\therefore[\sigma]=\frac{\mathrm{ML}^{2} \mathrm{~T}^{-3}}{\mathrm{LK}}=\left[\mathrm{MLT}^{-3} \mathrm{~K}^{-1}\right]$

Substituting values, we get

$$ \begin{aligned} & {[\sigma]=\left[\mathrm{PA}^{-1} \mathrm{~T}^{-1}\right]\left[\mathrm{AT}^{2}\right]\left[\mathrm{T}^{-3}\right] \times\left[\mathrm{S}^{+1} \mathrm{~A}^{-2} \mathrm{~T}^{-2}\right]} \\ & =\left[\mathrm{PA}^{-2} \mathrm{~S}^{+1} \mathrm{~T}^{-4}\right] \end{aligned} $$

13. If Planck’s constant (h), velocity of light (C) and the universal gravitational constant (G), were to be taken as the fundamental units, the dimensional formula, for surface tension (S), would be

(1) $\left[\mathrm{h}^{-3 / 2} \mathrm{G}^{-1 / 2} \mathrm{C}^{-11 / 2}\right]$

(2) $\left[\mathrm{h}^{3 / 2} \mathrm{G}^{1 / 2} \mathrm{C}^{-11 / 2}\right]$

(3) $\left[\mathrm{h}^{1 / 2} \mathrm{G}^{3 / 2} \mathrm{C}^{-11 / 2}\right]$

(4) $\left[\mathrm{h}^{-1 / 2} \mathrm{G}^{-3 / 2} \mathrm{C}^{11 / 2}\right]$

Show Answer

Correct answer: (4)

Solution:

We have $\mathrm{h} \times$ frequency $=$ energy

$$ \therefore[\mathrm{h}]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-1}\right] $$

Also, $[\mathrm{C}]=\left[\mathrm{LT}^{-1}\right]$

and $[\mathrm{G}]=\left(\frac{\text { Force } \times(\text { distance })^{2}}{\text { mass } \times \text { mass }}\right)=\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}$

$\therefore[\mathrm{hG}]=\mathrm{L}^{5} \mathrm{~T}^{-3}$

and $\mathrm{C}^{5}=\mathrm{L}^{5} \mathrm{~T}^{-5}$

$\therefore\left(\frac{\mathrm{hG}}{\mathrm{C}^{5}}\right)=\mathrm{T}^{2}$ or $[\mathrm{T}]=\mathrm{h}^{1 / 2} \mathrm{G}^{1 / 2} \mathrm{C}^{-5 / 2}$

Also, $[\mathrm{L}]=[\mathrm{CT}]=\left[\mathrm{h}^{1 / 2} \mathrm{G}^{1 / 2} \mathrm{C}^{-3 / 2}\right]$

$\therefore[\mathrm{M}]=\left(\mathrm{h} \cdot \mathrm{L}^{-2} \mathrm{~T}\right)=\left(\frac{\mathrm{h} \cdot \mathrm{h}^{1 / 2} \mathrm{G}^{1 / 2} \mathrm{C}^{-5 / 2}}{\mathrm{hGC}^{-3}}\right)$

$$ =\left[h^{1 / 2} G^{-1 / 2} C^{1 / 2}\right] $$

Now surface tension $S=\frac{\text { force }}{\text { length }}$ $=\left[\mathrm{MT}^{-2}\right]$

$\therefore[\mathrm{S}]=\left(\mathrm{h}^{1 / 2} \mathrm{G}^{-1 / 2} \mathrm{C}^{1 / 2}\right) \times\left(\frac{1}{\mathrm{hGC}^{-5}}\right)$

$=\left[\mathrm{h}^{-1 / 2} \mathrm{G}^{-3 / 2} \mathrm{C}^{1 / 2}\right]$

Changing over to new (assumed) fundamental units

14. If moment of inertia (I), torque $(\tau)$ and frequency $(v)$, were to be taken as the fundamental units, the dimensional formula, for Reynold’s number $\left(\mathbf{N} _{\mathrm{R}}\right)$ could be

(1) $\left[\mathrm{I}^{-1} \tau^{-1} v^{2}\right]$

(2) $\left[\mathrm{I}^{-1} \tau^{-1} v^{-2}\right]$

(3) $\left[\mathrm{I}^{-1} \tau v^{-2}\right]$

(4) $\left[\mathrm{I}^{-1} \tau v^{2}\right]$

Show Answer

Correct answer: (2)

Solution:

Reynold’s number $\left(\mathrm{N} _{\mathrm{R}}\right)$ is defined as a ‘combination’, of terms, that is dimensionless in mass, length, and time. We, therefore, need a ‘combination’, of I, $\tau$ and $v$, that is dimensionless in M, L and T. Now,

$$ \begin{aligned} & {[\mathrm{I}]=\mathrm{ML}^{2}} \\ & {[\tau]=(\text { force } \times \text { distance })=\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right]} \\ & \text { and }[v]=1 / \mathrm{T} \end{aligned} $$

It is easy to see that the combination $\left[\frac{\tau}{\mathrm{I}} \times \frac{1}{v^{2}}\right]$ has zero dimensions in M, L and T.

Hence a dimensional formula, for $\mathrm{N} _{\mathrm{R}}$, in terms of $\mathrm{I}, \tau$ and $v$, could be $\left[\mathrm{N} _{\mathrm{R}}\right]=\left[\mathrm{I}^{-1} \tau v^{-2}\right]$

15. A ‘hypothetical system’ uses the acceleration due to gravity (g), the areal velocity $\left(v _{\mathrm{A}}\right)$ and the momentum (p) as its ‘base’ units. The dimensional formula, for the force (F), in this system, would be

(1) $\left[\mathrm{pg}^{2 / 3} v _{\mathrm{A}}^{-1 / 2}\right]$

(2) $\left[\operatorname{pg}^{-2 / 3} v _{\mathrm{A}}^{1 / 2}\right]$

(3) $\left[\mathrm{p}^{-1} \mathrm{~g}^{-2 / 3} v _{\mathrm{A}}^{-1 / 3}\right]$

(4) $\left[\mathrm{p}^{-1} \mathrm{~g}^{+2 / 3} v _{\mathrm{A}}^{1 / 3}\right]$

Show Answer

Correct answer: (1)

Solution:

We have $\quad[\mathrm{g}]=\left[\mathrm{LT}^{-2}\right],\left[v _{\mathrm{A}}\right]=\left[\mathrm{L}^{2} \mathrm{~T}^{-1}\right]$

and $[\mathrm{p}]=\left[\mathrm{MLT}^{-1}\right]$

$\therefore$ We get,

$[\mathrm{T}]=\left[v _{\mathrm{A}}^{1 / 3 /} \mathrm{g}^{-2 / 3}\right]$

$[\mathrm{L}]=\left[\mathrm{g}^{-1 / 3} v _{\mathrm{A}}^{1 / 3}\right]$

and $[\mathrm{M}]=\left[\mathrm{pg}^{-1 / 3} v _{\mathrm{A}}^{-1 / 3}\right]$

Now force $=\left[\mathrm{MLT}^{-2}\right]$

$$ \begin{aligned} & \therefore[\mathrm{F}]=\left(\mathrm{pg}^{-1 / 2} v _{\mathrm{A}}^{-1 / 3}\right)\left(\mathrm{g}^{-1 / 3} v _{\mathrm{A}}^{2 / 3}\right) \\ & \left(\mathrm{pg}^{-1 / 2} v _{\mathrm{A}}^{-1 / 3}\right)\left(\mathrm{g}^{-1 / 3} v _{\mathrm{A}}^{2 / 3}\right)\left(v _{\mathrm{A}}^{-2 / 3} \mathrm{~g}^{4 / 3}\right) \\ & =\left[\mathrm{pg}^{2 / 3} v _{\mathrm{A}}^{-1 / 3}\right] \end{aligned} $$

16. The ‘dimensions’, of the constant a, in the Van-der-wall equation of state

$$ \left(\mathrm{p}+\frac{\mathrm{a}}{\mathrm{V}^{2}}\right)(\mathrm{V}-b)=\mathrm{nRT} $$

can be obtained by multiplying the dimensions, of the universal gas constant, $\mathrm{G}$, by

(1) $\left[\mathrm{M}^{2} \mathrm{LT}^{2}\right]$

(2) $\left[\mathrm{M}^{2} \mathrm{~L}^{2} \mathrm{~T}^{0}\right]$

(3) $\left[\mathrm{M}^{-2} \mathrm{~L}^{2} \mathrm{~T}^{0}\right]$

(4) $\left[\mathrm{M}^{2} \mathrm{~L}^{2} \mathrm{~T}\right]$

Show Answer

Correct answer: (2)

Solution:

The ‘dimensions’ of $\left(\frac{a}{\mathrm{~V}^{2}}\right)$, must be the same as that of ’ $\mathrm{p}$ ‘.

Hence dimensions of ’ $a$ ’ would correspond to

$$ \frac{\text { Force }}{\text { area }} \times(\text { volume })^{2}=\text { force } \times(\text { length })^{4} $$

The dimensions of ’ $G$ ‘, would correspond to

$$ \begin{aligned} & \frac{\text { force } \times(\text { length })^{2}}{(\text { mass })^{2}} \\ & \therefore \frac{\text { dimensions of } a}{\text { dimension of G }}=(\text { mass })^{2} \times(\text { length })^{2} \end{aligned} $$

$\therefore$ The ‘required multiplication’ needs to be done by the term $\left[\mathrm{M}^{2} \mathrm{~L}^{2}\right]$

17. The dimensions, of the constant $\eta$, obtained from Stokes’ law

$$ \mathrm{F}=6 \pi \eta r v $$

( $\mathrm{F}=$ force, $\mathrm{r}=$ radius, $v=$ velocity)

when used in the Poiseuelli equation

$$ \begin{array}{r} \mathrm{V}=\frac{\pi \mathrm{pr}^{4}}{(8 \eta \ell)} \\ (\mathrm{p}=\text { pressure, } \ell=\text { length }) \end{array} $$

would give the dimensions of $\mathrm{V}$ as

(1) $\left[\mathrm{M}^{0} \mathrm{~L}^{3} \mathrm{~T}^{0}\right]$

(2) $\left[\mathrm{ML}^{-3} \mathrm{~T}\right]$

(3) $\left[\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}^{-1}\right]$

(4) $\left[\mathrm{M}^{0} \mathrm{~L}^{3} \mathrm{~T}^{-1}\right]$

Show Answer

Correct answer: (4)

Solution:

From Stoke’s law equation, we get

$$ [\eta]=\frac{\text { force }}{\text { length } \times \text { velocity }}=\left[\frac{\mathrm{MLT}^{-2}}{\mathrm{~L} \times \mathrm{LT}^{-1}}\right]=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-1}\right] $$

Using this, in Poiseuelli’s equation, we get

$$ \begin{aligned} & {[\mathrm{V}]=\frac{\text { pressure } \times(\text { length })^{3}}{[\eta]}} \\ & =\frac{\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}^{2}} \times \mathrm{L}^{3}}{\left[\mathrm{ML}^{-1} \mathrm{~T}^{-1}\right]}=\left[\mathrm{L}^{3} \mathrm{~T}^{-1}\right] \end{aligned} $$

18. The dimensions, of the inductance $(\mathrm{L}),\left(\right.$ induced $\mathrm{emf}=-\mathrm{L} \frac{d i}{d t}(\boldsymbol{i}=$ current, $\mathrm{t}=$ time $)$ ) and the capacitance $(\mathrm{C})\left(\right.$ angular frequency $\left.=\frac{1}{\sqrt{\mathrm{LC}}}\right)$ are, respectively,

(1) $\left[\mathrm{ML}^{2} \mathrm{~T}^{-2} \mathrm{I}^{-2}\right]$ and $\left[\mathrm{M}^{-1} \mathrm{~L}^{-2} \mathrm{~T}^{4} \mathrm{I}^{2}\right] $

(2) $\left[\mathrm{M}^{-1} \mathrm{~L}^{-2} \mathrm{~T}^{4} \mathrm{I}^{+2}\right]$ and $\left[\mathrm{ML}^{2} \mathrm{~T}^{-2} \mathrm{I}^{-2}\right] $

(3) $\left[\mathrm{M}^{-1} \mathrm{~L}^{-2} \mathrm{~T}^{-2} \mathrm{I}^{-2}\right]$ and $\left[\mathrm{ML}^{2} \mathrm{~T}^{4} \mathrm{I}^{2}\right] $

(4) $\left[\mathrm{ML}^{2} \mathrm{~T}^{4} \mathrm{I}^{2}\right]$ and $\left[\mathrm{M}^{-1} \mathrm{~L}^{-2} \mathrm{~T}^{-2} \mathrm{I}^{-2}\right] $

Show Answer

Correct answer: (1)

Solution:

From induced emf $=-\mathrm{L} \frac{d i}{d t}$,

We get $[L]=\operatorname{emf} \times \frac{\text { time }}{\text { current }}$

$$ \begin{aligned} & =\left(\frac{\text { work }}{\text { charge }} \times \frac{\text { time }}{\text { current }}\right)=\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2} \times \mathrm{T}}{\mathrm{I} \times \mathrm{T} \times \mathrm{T}}\right] \\ & =\left[\mathrm{ML}^{2} \mathrm{~T}^{-2} \mathrm{I}^{-2}\right] \end{aligned} $$

Now angular frequency, $\omega=\frac{1}{\sqrt{\mathrm{LC}}}$ $\therefore[\mathrm{C}]=\frac{1}{[\mathrm{~L}]\left[\omega^{2}\right]}$

$=\mathrm{M}^{-1} \mathrm{~L}^{-2} \mathrm{~T}^{2} \mathrm{I}^{2} \cdot \mathrm{T}^{2}$

$=\left[\mathrm{M}^{-1} \mathrm{~L}^{-2} \mathrm{~T}^{4} \mathrm{I}^{2}\right]$=

19. Magnetic field strength (B) is known to equal force on a unit charge moving with a uniform velocity. We also have

$$ \mathrm{B}=\frac{\mu _{0}}{4 \pi} \sum\left(\frac{\mathrm{Id} \ell \sin \theta}{r^{2}}\right) \quad(\mathrm{d} \ell / r \Rightarrow \text { length }) $$

The dimensions, of B and $\mu _{0}$, are, therefore

(1) $\left[\mathrm{MT}^{-2} \mathrm{I}^{-1}\right]$ and $\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2} \mathrm{I}^{-2}\right]$, respectively

(2) $\left[\mathrm{MLT}^{-1} \mathrm{I}^{-1}\right]$ and $\left[\mathrm{MLT}^{-2} \mathrm{I}^{-1}\right]$, respectively

(3) $\left[\mathrm{MT}^{-2} \mathrm{I}^{-1}\right]$ and $\left[\mathrm{MLT}^{-2} \mathrm{I}^{-2}\right]$, respectively

(4) $\left[\mathrm{MLT}^{-2} \mathrm{I}^{-2}\right]$ and $\left[\mathrm{MT}^{-2} \mathrm{I}^{-1}\right]$, respectively

Show Answer

Correct answer: (3)

Solution:

We have,

$$ \begin{aligned} & {[\mathrm{B}]=\frac{[\text { force }]}{[\text { charge }][\text { velocity }]}=\frac{\left[\mathrm{MLT}^{-2}\right]}{[\mathrm{IT}]\left[\mathrm{LT}^{-1}\right]}} \\ & =\left[\mathrm{MT}^{-2} \mathrm{I}^{-1}\right] \end{aligned} $$

Also,

$\mu_0=\frac{[\mathrm{B}]\left[\text { length }{ }^2\right]}{[\text { current }][\text { length }]}=\frac{\left[\mathrm{MT}^{-2} \mathrm{I}^{-1}\right]\left[\mathrm{L}^2\right]}{[\mathrm{I}][\mathrm{L}]}$

$=\left[\mathrm{MLT}^{-2} \mathrm{I}^{-2}\right]$

20. Electric field strength (E) equals force on a unit charge. Also,

$$ \mathrm{E}=\frac{1}{4 \pi \varepsilon _{0}}\left(\frac{q}{r^{2}}\right) \quad(\mathbf{q}=\text { charge }, \mathbf{r}=\text { distance }) $$

The dimensions of $\mathbf{E}$ and $\varepsilon _{0}$ are, therefore,

(1) $\left[\mathrm{MLT}^{-1} \mathrm{I}^{-1}\right]$ and $\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{2} \mathrm{I}^{2}\right]$, respectively

(2) $\left[\mathrm{MLT}^{-3} \mathrm{I}^{-1}\right]$ and $\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{I}^{2}\right]$, respectively

(3) $\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{I}^{2}\right]$ and $\left[\mathrm{MLT}^{-3} \mathrm{I}^{-1}\right]$, respectively

(4) $\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{2} \mathrm{I}^{2}\right]$ and $\left[\mathrm{MLT}^{-1} \mathrm{I}^{-1}\right]$, respectively

Show Answer

Correct answer: (2)

Solution:

We have,

$$ \begin{aligned} & {[\mathrm{E}]=\frac{\text { force }}{\text { charge }}=\frac{\left[\mathrm{MLT}^{-2}\right]}{[\mathrm{IT}]}} \\ & \therefore[\mathrm{E}]=\left[\mathrm{MLT}^{-3} \mathrm{I}^{-1}\right] \end{aligned} $$

Also,

$$ \begin{aligned} & \mathrm{E}=\frac{1}{4 \pi \varepsilon _{0}}\left(\frac{q}{r^{2}}\right) \end{aligned} $$

$\therefore\left[\varepsilon_0\right]=\frac{\text { Charge }}{[\mathrm{E}]\left[\text { length }{ }^2\right]}=\frac{[\mathrm{IT}]}{\left[\mathrm{MLT}^{-3} \mathrm{I}^{-1}\right]\left[\mathrm{L}^2\right]}$

$$ \begin{aligned} & =\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{I}^{2}\right] \end{aligned} $$

21. The dimensions

$\left[\mathbf{M L}^{2} \mathbf{T}^{-1}\right]$

can correspond to

(1) rate of change of force

(2) impulse

(3) rate of change of momentum

(4) angular momentum

Show Answer

Correct answer: (4)

Solution:

We have angular momentum $=\mathrm{m} v \mathrm{r}$

$\therefore$ [Angular momentum]

$=\left[\mathrm{MLT}^{-1} \times \mathrm{L}\right]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-1}\right]$

[It is easy to verify that the given dimensions do not correspond to the other listed quantities.]

22. The dimensions

$\left[\mathbf{M L}^{2} \mathbf{T}^{-3} \mathbf{I}^{-2}\right]$

can correspond to

(1) Electrical resistance

(2) Self inductance

(3) Capacitance

(4) Rate of change of electric field

Show Answer

Correct answer: (1)

Solution:

We have $\mathrm{R}=\frac{\mathrm{V}}{\mathrm{I}}$

and $\mathrm{V}=\frac{\text { Work }}{\text { Charge }}$

$\therefore[\mathrm{V}]=\left[\frac{\mathrm{MLT}^{-2} \times \mathrm{L}}{\mathrm{IT}}\right]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-3} \mathrm{I}^{-1}\right]$

$\therefore[\mathrm{R}]=\left[\frac{\mathrm{V}}{\mathrm{I}}\right]=\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-3} \mathrm{I}^{-1}}{\mathrm{I}}\right]$

$=\left[\mathrm{ML}^{2} \mathrm{~T}^{-3} \mathrm{I}^{-2}\right]$

[It is easy to see that the given dimensions do not correspond to the other listed quantities.]

23. The dimensions $\left[\mathbf{M L}^{3} \mathbf{T}^{-3} \mathbf{I}^{-1}\right]$ can correspond to

(1) Rate of change of electric field

(2) Rate of change of the capacitance of a parallel plate capacitor with distance between its two plates

(3) Flux of electric field through a surface

(4) Rate of change of potential difference between two points

Show Answer

Correct answer: (3)

Solution:

We have electric field $=\frac{\text { Force }}{\text { Charge }}$

$$ =\left[\frac{\mathrm{MLT}^{-2}}{\mathrm{IT}}\right]=\left[\mathrm{MLT}^{-3} \mathrm{I}^{-1}\right] $$

$\therefore$ Flux of electric field through a surface

$=(\mathrm{ES} \cos \theta)=\left[\mathrm{MLT}^{-3} \mathrm{I}^{-1}\right] \times\left[\mathrm{L}^{2}\right]$

$=\left[\mathrm{ML}^{3} \mathrm{~T}^{-3} \mathrm{I}^{-1}\right]$

[It is easy to see that the given dimensions do not correspond to the other listed quantities.]

24. The dimensions

$\left[\mathbf{M L}^{2} \mathbf{T}^{-2} \mathbf{I}^{-1}\right]$

can correspond to

(1) Flux of electric field through a surface

(2) Magnetic moment of a magnet

(3) Flux of magnetic field through a surface

(4) Rate of change of magnetic field

Show Answer

Correct answer: (3)

Solution:

We have,

$[$ Magnetic field $]=\left(\frac{\text { Force }}{\text { Charge } \times \text { Velocity }}\right)$

$=\left[\frac{\mathrm{MLT}^{-2}}{\mathrm{IT} \times \mathrm{LT}^{-1}}\right]=\left[\mathrm{MT}^{-2} \mathrm{I}^{-1}\right]$

$\therefore$ Flux of magnetic field through a surface

(= magnetic field $\times($ normal) area)

$=\left[\mathrm{MT}^{-2} \mathrm{I}^{-1} \times \mathrm{L}^{2}\right]$

$=\left[\mathrm{ML}^{2} \mathrm{~T}^{-2} \mathrm{I}^{-1}\right]$

[It is easy to see that the given dimensions do not correspond to the other listed quantities.]

25. The dimensions

$\left[\mathbf{M}^{0} \mathbf{L}^{2} \mathbf{T}^{0} \mathbf{I}\right]$ can correspond to

(1) Magnetic dipole moment

(2) Rate of change of magnetic field

(3) Flux of magnetic field through a surface

(4) Magnetic permeability of a medium

Show Answer

Correct answer: (1)

Solution:

We know that,

Torque $=($ Magnetic dipole moment $\times$ magnetic field $)$

$\therefore$ [Magnetic dipole moment]

$=\left(\frac{\text { Torque }}{\text { Magnetic Field }}\right)=\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{MT}^{-2} \mathrm{I}^{-1}}\right]$

$=\left[\mathrm{IL}^{2}\right]$

$=\left[\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}^{0} \mathrm{I}\right]$

[It is easy to see that the given dimensions do not correspond to the other listed quantities.]

26. The following are four pairs of physical quantities:

(A) (Planck’s constant; rate of change of momentum)

(B) (Bulk modulus; pressure)

(D) (Impulse; momentum)

From this, the one pair, that is dimensionally incompatible, is the pair labelled as:

(1) $\mathrm{A}$

(2) $\mathrm{B}$

(3) $\mathrm{C}$

(4) $\mathrm{D}$

Show Answer

Correct answer: (1)

Solution:

We have [Planck’s constant $]=\frac{\text { Energy }}{\text { Frequency }}$

$$ =\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{~T}^{-1}}\right]=\mathrm{ML}^{2} \mathrm{~T}^{-1} $$

and [rate of change of momentum] $=\left(\frac{\text { Change in momentum }}{\text { Time }}\right)$

$$ =\left[\frac{\mathrm{MLT}^{-1}}{\mathrm{~T}}\right]=\left[\mathrm{MLT}^{-2}\right] $$

Thus, the two quantities, in this pair, are dimensionally incompatible.

[It can be verified that the two quantities, in each of the other three pairs, are dimensionally compatible with each other].

27. The dimensions, of the product $\left(\mu _{0} \varepsilon _{0}\right)\left(\frac{\mathrm{L}}{\mathrm{R}}\right)$

( $\mu _{0}=$ magnetic permeability; $\varepsilon _{0}=$ electric permittivity, $L=$ Inductance; $\mathrm{R}=$ resistance)

are,

(1) $\left[\mathrm{MLT}^{-2} \mathrm{I}^{-2}\right] $

(2) $\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{I}^{2}\right] $

(3) $\left[\mathrm{ML}^{2} \mathrm{~T}^{-3} \mathrm{I}^{-2}\right] $

(4) $\left[\mathrm{M}^{0} \mathrm{~L}^{-2} \mathrm{~T}^{-3} \mathrm{I}^{0}\right] $

Show Answer

Correct answer: (4)

Solution:

The dimensions, of the different terms, are

$$ \begin{aligned} & {\left[\mu _{0}\right]=\left[\mathrm{MLT}^{-2} \mathrm{I}^{-2}\right]} \\ & {\left[\varepsilon _{0}\right]=\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{I}^{2}\right]} \\ & {[\mathrm{L}]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-2} \mathrm{I}^{-2}\right]} \\ & {[\mathrm{R}]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-3} \mathrm{I}^{-2}\right]} \\ & \therefore\left(\mu _{0} \varepsilon _{0}\right)\left(\frac{\mathrm{L}}{\mathrm{R}}\right)=\left(\mathrm{L}^{-2} \mathrm{~T}^{2}\right) \cdot \mathrm{T}=\left[\mathrm{L}^{-2} \mathrm{~T}^{3}\right] \end{aligned} $$

Alternatively, We know that

$$ \begin{aligned} & \frac{1}{\sqrt{\mu _{0} \varepsilon _{0}}}=\mathrm{C}=\text { Velocity } \\ & \therefore \mu _{0} \varepsilon _{0}=\left(\frac{1}{\mathrm{C}^{2}}\right)=\left[\frac{1}{\mathrm{~L}^{2} \mathrm{~T}^{-2}}\right] \end{aligned} $$

and $\frac{\mathrm{L}}{\mathrm{R}}=$ time constant $=$ time $=[\mathrm{T}]$

$$ \therefore\left(\mu _{0} \varepsilon _{0}\right)\left(\frac{\mathrm{L}}{\mathrm{R}}\right)=\left[\frac{1}{\mathrm{~L}^{2} \mathrm{~T}^{-2}} \cdot \mathrm{T}\right]=\left[\mathrm{L}^{-2} \mathrm{~T}^{3}\right] $$

28. In the dimensional formula

$$ [\mathbf{X}]=\left[\mathbf{M L}^{-1} \mathbf{T}^{-2}\right] $$

the quantity, $X$, can be

(1) Surface tension of a liquid

(2) Coefficient of viscosity of a liquid

(3) Universal gas constant

(4) Atmospheric pressure

Show Answer

Correct answer: (4)

Solution:

We have,

$$ \begin{aligned} & {[\text { Atmospheric pressure }]=[\text { Pressure }]=\left[\frac{\text { Force }}{\text { Area }}\right]} \\ & =\left[\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}^{2}}\right]=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right] \end{aligned} $$

29. In the dimensional formula

$$ [\mathbf{Y}]=\left[\mathbf{M L T}^{-3} \mathbf{K}^{-1}\right] $$

the quantity $Y$ can correspond to

(1) Specific latent heat

(2) Specific heat capacity

(3) Coefficient of thermal conductivity

(4) Heat energy per unit rise in temperature

Show Answer

Correct answer: (3)

Solution:

The coefficient of thermal conduction (say $\sigma$ ), is defined through the equation

$$ \begin{aligned} & \frac{\Delta \mathrm{H}}{\Delta \mathrm{t}}=\sigma \mathrm{A}\left(\frac{\Delta \theta}{\Delta x}\right) \\ & \begin{aligned} \therefore[\sigma] & =\frac{[\Delta \mathrm{H}] \cdot[\Delta x]}{[\Delta \mathrm{t}][\mathrm{A}][\Delta \theta]} \\ & =\frac{\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right] \cdot[\mathrm{L}]}{[\mathrm{T}]\left[\mathrm{L}^{2}\right][\mathrm{K}]} \\ & =\left[\mathrm{MLT}^{-3} \mathrm{~K}^{-1}\right] \end{aligned} \end{aligned} $$

30. In the dimensional formula

$$ \left.[\mathbf{Z}]=\mathbf{M}^{0} \mathbf{L}^{0} \mathbf{T}^{0} \mathbf{K}^{-1}\right] $$

the quantity $[Z]$ can correspond to the

(1) (ratio of specific heat capacity to specific latent heat) as well as (coefficient of linear expansion)

(2) (ratio of specific latent heat to specific heat capacity) as well as (coefficient of thermal conductivity)

(3) (coefficient of thermal conductivity) as well as (coefficient of volume expansion)

(4) (coefficient of volume expansion) as well as (thermal capacity)

Show Answer

Correct answer: (1)

Solution:

We have,

Specific heat capacity $=\left(\frac{\text { Heat }(\text { energy })}{\text { mass } \times(\text { rise in temperature })}\right)=\frac{\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right]}{[\mathrm{M}][\mathrm{K}]}$

$$ =\left[\mathrm{L}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right] $$

Specific latent heat $=\left(\frac{\text { Heat }(\text { energy })}{\text { Mass }}\right)=\frac{\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right]}{[\mathrm{M}]}$

$=\left[\mathrm{L}^{2} \mathrm{~T}^{-2}\right]$

$\therefore[$ Ratio of the two $]=\left[\mathrm{K}^{-1}\right]=\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0} \mathrm{~K}^{-1}\right]$

Also,

$[$ Coefficient of linear expansion $]=\frac{(\text { Change in length })}{(\text { Original length }) \times(\text { Rise in temperature })}$

$$ \begin{aligned} & =\frac{[\mathrm{L}]}{[\mathrm{L}][\mathrm{K}]}=\left[\mathrm{K}^{-1}\right] \\ & =\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0} \mathrm{~K}^{-1}\right] \end{aligned} $$

31. ‘A given ‘dimensional formula’, cannot give a unique unambiguous identification, of the relevant physical quantity."

The above statement is illustrated through the fact that the ‘dimensional formula’, of ‘specific latent heat’, is identical with the ‘dimensional formula’ of

(1) gravitational P.E. per unit mass

(2) angular momentum per unit mass

(3) linear momentum per unit mass

(4) power per unit mass

Show Answer

Correct answer: (1)

Solution:

We have,

Specific latent heat $=\left(\frac{\text { Heat energy }}{\text { Mass }}\right)=\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{M}}\right]$

$$ =\left[\mathrm{L}^{2} \mathrm{~T}^{-2}\right] $$

Also,

$$ \text { Gravitational P.E. per unit mass }=\left[\frac{\mathrm{mgh}}{\mathrm{m}}\right]=[\mathrm{gh}] $$

$$ =\left[\mathrm{LT}^{-2} \cdot \mathrm{L}\right]=\left[\mathrm{L}^{2} \mathrm{~T}^{-2}\right] $$

The ‘dimensional formula’ of ‘specific latent heat’, is thus sen to be identical with the ‘dimensional formula’ of gravitational P.E. per unit mass.

32. The ratio, of the dimensional formulae, for ’thermal capacity’ and ‘coefficient of volume expansion’, can correspond to the dimensional formula of the

(1) universal gas constant $\mathrm{R}$.

(2) universal gravitational constant, G.

(3) product $\mathrm{p} \Delta \mathrm{v}(\mathrm{p}=$ pressure, $\Delta \mathrm{v}=$ change in volume)

(4) angular momentum

Show Answer

Correct answer: (3)

Solution:

We have $[$ Thermal capacity $]=\left(\frac{\text { Heat energy }}{\text { Rise in temperature }}\right)$

$$ =\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{~K}}\right]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right] $$

and [coefficient of volume expansion $]=\left(\frac{\text { Change in volume }}{\text { Original volume } \times \text { Rise in temperature }}\right)$

$=\left[\frac{\mathrm{L}^{3}}{\mathrm{~L}^{3} \mathrm{~K}}\right]=\left[\mathrm{K}^{-1}\right]$

$\therefore[$ Ratio of the two $]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right]$

Also,

$[$ Pressure $]=\left(\frac{\text { Force }}{\text { Area }}\right)=\left[\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}^{2}}\right]=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]$

and $[$ Change in volume $]=\left[\mathrm{L}^{3}\right]$

$\therefore$ [Product of the two $]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right]$

Thus the dimensional formula, of the (specified), ratio, equals that of the (specified) product.

33. The relation, for the rate of flow $(\mathrm{V})$ of a liquid, through a capillary tube of radius $(r)$ and length $\ell$, in terms of the coefficient of viscosity ( $\eta$ ) of the liquid, and the pressure difference (p), across the ends of the capillary tube, could have the form:

(1) $\mathrm{V}=\mathrm{k}\left(\mathrm{pr}^{2} / \eta \ell\right)$

(2) $\mathrm{V}=\mathrm{k}\left(\mathrm{pr}^{4} / \eta \ell\right)$

(3) $\mathrm{V}=\mathrm{k}\left(\mathrm{p}^{2} \mathrm{r}^{2} / \eta^{2} \ell\right)$

(4) $\mathrm{V}=\mathrm{k}\left(\mathrm{pr}^{2} / \eta^{2} \ell\right)$

Show Answer

Correct answer: (2)

Solution:

We have V $(=$ rate of flow $)=\left(\frac{\text { Volume flowing }}{\text { Time taken }}\right)=\mathrm{L}^{3} \mathrm{~T}^{-1}$

Also, $\mathrm{p}=$ Pressure difference $=\left[\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}^{2}}\right]=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]$

$$ \begin{aligned} & \mathrm{r}=\text { radius }=[\mathrm{L}] \\ & \ell=\text { length }=[\mathrm{L}] \\ & \eta=\text { coefficient of viscosity }=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-1}\right] \end{aligned} $$

$\therefore\left[\frac{\mathrm{pr}^{4}}{\eta \ell}\right]=\left[\frac{\mathrm{ML}^{-1} \mathrm{~T}^{-2} \times \mathrm{L}^{4}}{\mathrm{ML}^{-1} \mathrm{~T}^{-1} \times \mathrm{L}}\right]=\left[\mathrm{L}^{3} \mathrm{~T}^{-1}\right]$

$\therefore \mathrm{V}=\mathrm{k} .\left(\frac{\mathrm{pr}^{4}}{\eta \ell}\right)$ is a dimensionally compatible relation. It is, therefore, a ‘possible’ relation. (The same is NOT true for the other relations).

34. The term

$$ \frac{\left(\mu _{0} \varepsilon _{0}\right) \mathrm{C}^{2} \mathrm{Gm} _{\rho}}{\mathrm{r}^{3} v^{2}} $$

( $\mu _{0}=$ permeability, $\varepsilon _{0}=$ permittivity, $\mathbf{C}=$ velocity, $\mathbf{G}=$ gravitational constant, $\mathrm{m} _{\rho}=$ mass, $r=$ radius, $v=$ frequency) is dimensionally compatible with the term

(1) $\left(\frac{\mathrm{I} \omega}{\tau}\right)(\mathrm{I}=$ moment of inertia, $\omega=$ angular velocity, $\tau=$ torque $)$

(2) $\left(\frac{\mathrm{Gh}}{\varepsilon _{0} \mathrm{C}}\right)\left(\mathrm{G}=\right.$ gravitational constant, $\mathrm{h}=$ Planck’s constant, $\varepsilon _{0}=$ permittivity, $\mathrm{C}=$ velocity $)$

(3) $\left(\frac{\mu _{0} \varepsilon _{0}}{C}\right)\left(\mu=\right.$ permeability; $\varepsilon _{0}=$ permittivity; $C=$ velocity $)$

(4) $\left(\frac{\rho r v}{\eta}\right)(\rho=$ density, $r=$ radius, $v=$ speed, $\eta=$ coefficient of viscosity $)$

Show Answer

Correct answer: (4)

Solution:

We have dimensions of

$$ \begin{aligned} & \frac{\left(\mu _{0} \varepsilon _{0}\right) \mathrm{C}^{2} \cdot \mathrm{G}^{2} \mathrm{~m} _{\rho}}{\mathrm{r}^{3} v^{2}}=\frac{\left(\frac{1}{\mathrm{C}^{2}}\right)\left(\mathrm{C}^{2}\right)\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right][\mathrm{M}]}{\left[\mathrm{L}^{3}\right]\left[\mathrm{T}^{-1}\right]^{2}} \\ & =\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0}\right] \end{aligned} $$

Thus the given term is a dimensionless term.

We also find that the term

$$ \left[\frac{\rho \mathrm{r} v}{\eta}\right]=\left[\frac{\mathrm{ML}^{-3} \cdot \mathrm{L} \cdot \mathrm{LT}^{-1}}{\mathrm{ML}^{-1} \mathrm{~T}^{-1}}\right]=\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0}\right] $$

Thus this term is dimensionally compatible with the given term(Other terms are not so).

35. The term $\left(\frac{\eta \mathrm{s}}{\tau}\right)(\eta=$ coefficient of viscosity, $s=$ surface tension, $\tau=$ torque $)$, would become dimensionally compatible with a term obtained by multiplying, $G$, (the universal gravitational constant) with another quantity, having the dimensions of

(1) (Velocity) $\times$ (pressure)

(2) Time $\times(\text { density })^{2}$

(3) Frequency $\times$ (force)

(4) Momentum/(acceleration $)^{2}$

Show Answer

Correct answer: (2)

Solution:

We have, $\quad[\eta]=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-1}\right]$

$$ \begin{aligned} & {[\mathrm{s}]=\left[\mathrm{MT}^{-2}\right]} \\ & {[\tau]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right]} \end{aligned} $$

$$ \begin{gathered} \therefore\left[\frac{\eta \mathrm{s}}{\tau}\right]=\left[\frac{\mathrm{ML}^{-1} \mathrm{~T}^{-1} \times \mathrm{MT}^{-2}}{\mathrm{ML}^{2} \mathrm{~T}^{-2}}\right] \\ =\left[\mathrm{M}^{+1} \mathrm{~L}^{-3} \mathrm{~T}^{-1}\right] \end{gathered} $$

Also, $[\mathrm{G}]=\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right]$

$\therefore$ The required multiplier is $\left[\mathrm{M}^{2} \mathrm{~L}^{-6} \mathrm{~T}\right]$

This equals time $\times(\text { density })^{2}$ because the dimensional of this term are $(\mathrm{T}) \times\left(\mathrm{ML}^{-3}\right)^{2}$

$$ =\left[\mathrm{M}^{2} \mathrm{~L}^{-6} \mathrm{~T}\right] $$

which are the required dimensions.

36. The length of a wire is measured to be $(10.25 \pm 0.01) \mathrm{cm}$. The radius is measured to be $(0.840 \pm x) \mathrm{cm}$. If the relative error, in the volume of the wire, is calculated to be 0.0158 , the least count of the instrument, used for measuring the radius, is

(1) $0.004 \mathrm{~cm} $

(2) $0.002 \mathrm{~cm} $

(3) $0.001 \mathrm{~cm} $

(4) $0.0005 \mathrm{~cm} $

Show Answer

Correct answer: (2)

Solution:

We have, $\mathrm{V}=\pi \mathrm{r}^{2} \ell$

$$ \therefore \frac{\Delta \mathrm{V}}{\mathrm{V}}=\frac{2 \Delta \mathrm{r}}{\mathrm{r}}+\frac{\Delta \ell}{\ell} $$

Here, $\frac{\Delta \mathrm{V}}{\mathrm{V}}=0.0158$

and $\frac{\Delta \ell}{\ell}=\frac{0.01}{10.25}=0.011$

$$ \begin{aligned} & \therefore \frac{2 \Delta r}{\mathrm{r}}=0.0158-0.011=0.0048 \\ & \therefore \Delta \mathrm{r}=0.0048 \times \frac{0.840}{2} \\ & \quad=0.002 \end{aligned} $$

Thus the least count of the instrument, used for measuring $\mathrm{r}$, is $0.002 \mathrm{~cm}$.

37. The formula $\mathrm{V}=\frac{\pi \mathrm{pr}^{4}}{8 \eta \ell}$

( $V=$ rate of flow, $p=$ pressure difference, $\ell=$ radius, $l=$ length, $\eta=$ Coefficient of viscosity) is used to find $\eta$ for water. The percentage error, in $\eta$, is found to be $9 \%$. If the percentage errors, in the determination of $\mathrm{p}, \mathrm{V}$ and $\ell$ were $2 \%, 3 \%$ and $2 \%$, respectively, the percentage error, in the determination of $r$, is

(1) $12 \%$

(2) $3 \%$

(3) $2 \%$

(4) $0.5 \%$

Show Answer

Correct answer: (4)

Solution:

From the formula $V=\frac{\pi \mathrm{pr}^{4}}{8 \eta \ell}$, we get

$$ \begin{aligned} & \eta=\frac{\pi \mathrm{pr}^{4}}{8 \mathrm{~V} \ell} \\ & \therefore \frac{\Delta \eta}{\eta}=\frac{\Delta \mathrm{p}}{\mathrm{p}}+4 \frac{\Delta \mathrm{r}}{\mathrm{r}}+\frac{\Delta \mathrm{v}}{\mathrm{v}}+\frac{\Delta \ell}{\ell} \end{aligned} $$

$$ \begin{aligned} & \therefore 9 \%=2 \%+4 \frac{\Delta r}{r}+3 \%+2 \% \\ & \therefore \frac{\Delta r}{r}=\frac{2 \%}{4}=0.5 \% \end{aligned} $$

38. In an experiment on determination of resistivity $(\rho)$ of the material of a wire, the following measurements were made:

Resistance of wire $=(40 \pm 1) \Omega$

Length of wire $=(120 \pm 0.1) \mathrm{cm}$

Radius of wire $=(0.26 \pm 0.02) \mathrm{cm}$

Given that $\rho=\frac{\pi \mathrm{r}^{2} \mathrm{R}}{\ell}$, the value of $\rho$ would be quoted as

(1) $(7.08 \pm 1.3) \times 10^{-4} \Omega-\mathrm{m} $

(2) $(7 \pm 1) \times 10^{-4} \Omega-\mathrm{m}$

(3) $(7.079 \pm 1.27) \times 10^{-4} \Omega-\mathrm{m}$

(4) $(7 . \pm 1.3) \times 10^{-4} \Omega-\mathrm{m}$

Show Answer

Correct answer: (2)

Solution:

$\rho=\frac{\pi \mathrm{r}^{2} \mathrm{R}}{\ell}$

$\therefore \frac{\Delta \rho}{\rho}=2 \frac{\Delta \mathrm{r}}{\mathrm{r}}+\frac{\Delta \mathrm{R}}{\mathrm{R}}+\frac{\Delta \ell}{\ell}$

$$ \begin{aligned} & =2 \times \frac{0.02}{26}+\frac{1}{40}+\frac{0.1}{120} \\ & =0.154+0.025+0.0008 \simeq 0.18 \end{aligned} $$

Also, $\rho=\frac{\pi(0.26)^{2} \times 40 \times 10^{-4}}{120 \times 10^{-2}}(\Omega-\mathrm{m})$

$=0.0708 \times 10^{-2} \Omega-\mathrm{m}$

$=7.08 \times 10^{-4} \Omega-\mathrm{m}$

$\therefore \Delta \rho \simeq 1.3 \times 10^{-4} \Omega-\mathrm{m}$

$\therefore \rho \simeq(7 \pm 1) \times 10^{-4} \Omega-\mathrm{m}$

39. The relation $Y=p^{2} q^{3 / 2} r^{5} s^{1 / 2}$ is used to calculate $Y$, on the basis of measurements of $p, q, r$ and $s$. The relative errors, in the measurement of $p, q, r$ and $s$ are $0.005,0.04,0.004$ and $\mathbf{0 . 0 2}$, respectively. If the calculated value, of $Y$, comes out to be 3.528 units, the result should be quoted as:

(1) $(3.528 \pm 0.3528)$ units

(2) $(3.53 \pm 0.35)$ units

(3) $(3.5 \pm 0.4)$ units

(4) $(4 \pm 0.4)$ units

Show Answer

Correct answer: (3)

Solution:

We have $Y=p^{2} q^{3 / 2} r^{5} s^{1 / 2}$

$$ \therefore \frac{\Delta \mathrm{Y}}{\mathrm{Y}}=2 \frac{\Delta \mathrm{p}}{\mathrm{p}}+\frac{3}{2} \frac{\Delta \mathrm{q}}{\mathrm{q}}+5 \frac{\Delta \mathrm{r}}{\mathrm{r}}+\frac{1}{2} \frac{\Delta \mathrm{s}}{\mathrm{s}} $$

$$ \begin{aligned} & =\left(2 \times 0.005+\frac{3}{2} \times 0.04+5 \times 0.04+\frac{1}{2} \times 0.02\right) \\ & =(0.010+0.06+0.02+0.01) \\ & =0.1 \\ & \therefore \Delta Y=0.1 \times 3.528=0.3528 \simeq 0.35 \simeq 0.4 \end{aligned} $$

We should, therefore, quote $\mathrm{Y}$ as

$\mathrm{Y}=(3.5 \pm 0.4)$ units

40. The volume, $\mathrm{V}$, of a cube, is calculated to be

$$ \mathrm{V}=(1000 \pm 6) \mathrm{m}^{3} $$

The side of the cube is

(1) $(10 \pm 2) \mathrm{m} $

(2) $\quad(10.0 \pm 0.2) \mathrm{m} $

(3) $\quad(10.0 \pm .2) \mathrm{m} $

(4) $(10.00 \pm 0.02) \mathrm{m} $

Show Answer

Correct answer: (4)

Solution:

We have $\mathrm{V}=\ell^{3}$

$$ \therefore \ell=\mathrm{V}^{1 / 3}=(1000)^{1 / 3}=10 \mathrm{~m} $$

Also, $\frac{\Delta \mathrm{V}}{\mathrm{V}}=3 \frac{\Delta \ell}{\ell}$

$$ \begin{aligned} & \therefore \frac{6}{1000}=3 \frac{\Delta \ell}{10} \\ & \therefore \Delta \ell=\frac{6}{1000} \times \frac{10}{3}=\frac{2}{100}=0.02 \end{aligned} $$

We, therefore, have

$$ \ell=(10.00+0.02) \mathrm{m} $$

41. The dimensional formula, for the product $X=\frac{C G}{e}(C=$ velocity of light, $\mathbf{G}=$ Universal gravitational constant, $e=$ electronic charge), would be

(1) $\left[\mathrm{ML}^{4} \mathrm{~T}^{-3} \mathrm{I}^{-2}\right] $

(2) $\left[\mathrm{M}^{-1} \mathrm{~L}^{4} \mathrm{~T}^{-4} \mathrm{I}^{-1}\right] $

(3) $\left[\mathrm{ML}^{3} \mathrm{~T}^{-3} \mathrm{I}^{-1}\right] $

(4) $\left[\mathrm{M}^{-1} \mathrm{LT}^{-2} \mathrm{I}^{-2}\right] $

Show Answer

Correct answer: (2)

Solution:

We have $[\mathrm{C}]=\left[\mathrm{LT}^{-1}\right]$

$$ \begin{aligned} {[\mathrm{G}] } & =\left(\frac{\mathrm{F} \cdot \mathrm{r}^{2}}{\mathrm{~m}^{2}}\right)=\left[\frac{\mathrm{MLT}^{-2} \mathrm{~L}^{2}}{\mathrm{M}^{2}}\right] \\ & =\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right] \\ & {[\mathrm{e}]=[\mathrm{IT}] } \end{aligned} $$

$$ \begin{aligned} & \therefore[\mathrm{X}]\left(=\frac{\mathrm{CG}}{\mathrm{E}}\right)=\left[\frac{\mathrm{LT}^{-1} \mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}}{[\mathrm{IT}]}\right] \\ & =\left[\mathrm{M}^{-1} \mathrm{~L}^{4} \mathrm{~T}^{-4} \mathrm{I}^{-1}\right] \end{aligned} $$

42. The dimensional formula, for the ratio $\frac{\left(\frac{L}{R}\right)}{\left(\mu _{0} \varepsilon _{0}\right)}$ ( $\mathbf{L}=$ inductance, $\mathbf{R}=$ resistance, $\mu _{0}=$ permeability, $\varepsilon _{0}=$ permittivity) equals:

(1) $\left[\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}\right]$

(2) $\left[\mathrm{M}^{0} \mathrm{LT}\right] $

(3) $\left[\mathrm{M}^{0} \mathrm{~L}^{-2} \mathrm{~T}\right]$

(4) $\left[\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}^{-1}\right] $

Show Answer

Correct answer: (4)

Solution:

We can do this problem quickly if we remember that:

$\left(\frac{L}{R}\right)=$ time constant

and $\frac{1}{\sqrt{\mu _{0} \varepsilon _{0}}}=C=$ velocity of light

$$ \therefore\left[\frac{\mathrm{L}}{\mathrm{R}}\right]=[\mathrm{T}] $$

and $\left[\mu _{0} \varepsilon _{0}\right]=\left(\frac{1}{\mathrm{C}^{2}}\right)=\left[\mathrm{L}^{-2} \mathrm{~T}^{2}\right]$

$$ \begin{aligned} & \therefore\left[\frac{\left(\frac{\mathrm{L}}{\mathrm{R}}\right)}{\left(\mu_0 \varepsilon_0\right)}\right]=\frac{\mathrm{T}}{\mathrm{L}^2 \mathrm{~T}^2}=\frac{\mathrm{L}^2}{\mathrm{~T}} \ & =\left[\mathrm{M}^0 \mathrm{~L}^2 \mathrm{~T}^{-1}\right] \end{aligned} $$

43. The dimensional formula, of the term $Y$, where $Y=\left[\frac{L _{V} s}{K _{0}}\right]\left(L _{v}=\right.$ specific latent heat, $s=$ specific heat capacity, $\mathrm{K} _{0}=$ thermal conductivity), equals:

(1) $\left[\mathrm{M}^{-1} \mathrm{LT}^{-2} \mathrm{~K}^{-1}\right] $

(2) $\left[\mathrm{M}^{-1} \mathrm{~L}^{2} \mathrm{~T}^{-2} \mathrm{~K}\right] $

(3) $\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right] $

(4) $\left[\mathrm{M}^{-1} \mathrm{~L}^{4} \mathrm{~T}^{-1}\right] $

Show Answer

Correct answer: (3)

Solution:

We have $\mathrm{L} _{\mathrm{v}}=\left(\frac{\text { Heat(energy) }}{\text { Mass }}\right)$

$$ \therefore\left[\mathrm{L} _{\mathrm{V}}\right]=\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{M}}\right]=\left[\mathrm{L}^{2} \mathrm{~T}^{-2}\right] $$

$$ \begin{gathered} \mathrm{s}=\left(\frac{\text { Heat }(\text { energy })}{\text { Mass } \times \text { change in temperature }}\right)=\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{MK}}\right] \\ =\left[\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right] \end{gathered} $$

Also, $\mathrm{Q}=\mathrm{K} _{0} \mathrm{~A} \frac{\mathrm{d} \theta}{\mathrm{d} \ell}$

$\mathrm{[K_0 ]= \frac{Heat energy \times length}{Area \times Change in temperature}}$

= $\mathrm {\frac{ML_3T^{-2}}{L^2 \times K = [MLT^{-2}K^{-1}]}}$

$$ \therefore\left[\frac{\mathrm{L}_{\mathrm{V}} \mathrm{S}}{\mathrm{K}}\right]=\left[\frac{\mathrm{L}^2 \mathrm{~T}^{-2} \times \mathrm{L}^2 \mathrm{~T}^{-2} \mathrm{~K}^{-1}}{\mathrm{MLT}^{-2} \mathrm{~K}^{-1}}\right]=\left[\mathrm{M}^{-1} \mathrm{~L}^3 \mathrm{~T}^{-2}\right] $$

44. The physical quantity, whose dimensional formula matches that of the quantity

$$ Z=\left[\frac{L _{f} \mathrm{~s} \rho \mathrm{T}}{\mathrm{K} _{0}}\right] $$

( $L _{f}=$ specific latent heat of fusion, $s=$ specific heat capacity, $\rho=$ density, $T=$ time of heat flow, $\mathbf{K} _{0}=$ thermal conductivity), is:

(1) frequency

(2) time period

(3) velocity

(4) momentum

Show Answer

Correct answer: (1)

Solution:

We have $\left[\mathrm{L} _{\mathrm{f}}\right]=\left(\frac{\text { Heat energy }}{\text { Mass }}\right)=\left[\mathrm{L}^{2} \mathrm{~T}^{-2}\right]$

$$ \begin{aligned} & {[\mathrm{s}]=\left(\frac{\text { Heat energy }}{\text { Mass } \times \text { change in temperature }}\right)=\left[\mathrm{L}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right]} \\ & {[\rho]=\left[\mathrm{ML}^{-3}\right],[\mathrm{T}]=[\mathrm{T}]} \\ & {\left[\mathrm{K} _{0}\right]=\left[\mathrm{MLT}^{-2} \mathrm{~K}^{-1}\right]} \\ & \therefore[\mathrm{Z}]=\frac{\left[\mathrm{L}^{2} \mathrm{~T}^{-2}\right] \times\left[\mathrm{L}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right] \times\left[\mathrm{ML}^{-3}\right] \times[\mathrm{T}]}{\left[\mathrm{MLT}^{-2} \mathrm{~K}^{-1}\right]} \\ & \quad=\left[\mathrm{T}^{-1}\right] \end{aligned} $$

$\therefore$ This matches the dimensional formula of frequency.

45. The ‘dimensional formula’, of the term

$\mathrm{Z}=\left(\frac{\mathrm{e}^{2} \mathrm{C}}{\varepsilon _{0} \mathrm{R}}\right)$

( $\mathrm{e}=$ change, $\mathrm{C}=$ capacitance, $\varepsilon _{0}=$ permittivity, $\mathrm{R}=$ resistance), equals:

(1) $\left[\mathrm{M}^{0} \mathrm{~L}^{-2} \mathrm{~T}^{0} \mathrm{I}^{-2}\right]$

(2) $\left[\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}^{0} \mathrm{I}^{2}\right]$

(3) $\left[\mathrm{M}^{2} \mathrm{~L}^{-2} \mathrm{TI}\right]$

(4) $\left[\mathrm{M}^{-2} \mathrm{~L}^{2} \mathrm{~T}^{-1} \mathrm{I}\right]$

Show Answer

Correct answer: (2)

Solution:

We have $\left[\mathrm{e}^{2}\right]=[\mathrm{IT}]^{2}=\left[\mathrm{I}^{2} \mathrm{~T}^{2}\right]$

$$ \begin{aligned} & {[\mathrm{C}]=\left[\mathrm{LT}^{-1}\right]} \\ & {\left[\varepsilon _{0}\right]=\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{I}^{2}\right]} \\ & {[\mathrm{R}]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-3} \mathrm{I}^{-2}\right]} \\ & \therefore[\mathrm{Z}]=\frac{\left[\mathrm{I}^{2} \mathrm{~T}^{2}\right]\left[\mathrm{LT}^{-1}\right]}{\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{I}^{2}\right]\left[\mathrm{ML}^{2} \mathrm{~T}^{-3} \mathrm{I}^{-2}\right]} \\ & {\left[\mathrm{L}^{2} \mathrm{I}^{2}\right]} \end{aligned} $$

46. The term $\varepsilon _{0} \mathrm{E}^{2}$ ( $\varepsilon _{0}=$ permittivity, $\mathrm{E}=$ electric field) is dimensionally incompatible with the term

(1) $\mathrm{p}(\mathrm{p}=$ pressure $)$

(2) $\frac{\mathrm{k}}{x}(\mathrm{k}=$ spring constant, $x=$ displacement $)$

(3) $\mathrm{CV}^{2}(\mathrm{C}=$ capacitance, $\mathrm{V}=$ potential difference $)$

(4) $\left(\frac{\mathrm{mgh}}{\mathrm{V}}\right)(\mathrm{m}=$ mass, $\mathrm{h}=$ height, $\mathrm{V}=$ volume, $\mathrm{g}=$ acceleration due to gravity $)$

Show Answer

Correct answer: (3)

Solution:

The term $\varepsilon _{0} \mathrm{E}^{2}$ has the dimensions of energy density, i.e. energy per unit volume. [We know that the energy density, of the electric field, is $\frac{1}{2} \varepsilon _{0} \mathrm{E}^{2}$. (The dimensions of the term can also be obtained through a substitution of the dimensions of $\varepsilon _{0}$ and E)].

$$ \therefore\left[\varepsilon _{0} \mathrm{E}^{2}\right]=\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{~L}^{3}}\right]=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right] $$

Now $\mathrm{p}=\left[\frac{\text { Force / length }}{\text { length }}\right]=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]$

$$ \left[\frac{\mathrm{mgh}}{\mathrm{V}}\right]=\left[\frac{(\mathrm{M})\left(\mathrm{LT}^{-2}\right)(\mathrm{L})}{\left(\mathrm{L}^{3}\right)}\right]=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right] $$

These terms are thus dimensionally compatible with the term $\varepsilon _{0} \mathrm{E}^{2}$.

However, $\left[\mathrm{CV}^{2}\right]=\left(\frac{\text { Ch arge }}{\text { potential }} \times(\text { potential })^{2}\right)$

$$ =\text { Charge } \times \frac{\text { work }}{\text { charge }}=(\text { work })=\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right] $$

This term is, therefore, dimensionally incompatible with $\varepsilon _{0} \mathrm{E}^{2}$.

47. The term $\left(\frac{B^{2}}{\mu _{0}}\right)\left(\mathbf{B}=\right.$ magnetic field, $\mu _{0}=$ permeability $)$ is dimensionally incompatible with the term

(1) $\left(\frac{\mathrm{p}^{2}}{\mathrm{mV}}\right)(\mathrm{p}=$ momentum, $\mathrm{m}=$ mass, $\mathrm{V}=$ volume $)$

(2) $\mathrm{LI}(\mathrm{L}=$ self inductance, $\mathrm{I}=$ current $)$

(3) $\left(\frac{I^{2} R t}{V}\right)(I=$ current, $R=$ resistance, $t=$ time, $V=$ volume $)$

(4) $\left(\frac{\mathrm{S}}{x}\right)(\mathrm{S}=$ surface tension, $x=$ distance $)$

Show Answer

Correct answer: (2)

Solution:

The term $\left(\frac{\mathrm{B}^{2}}{\mu _{0}}\right)$ has the dimensions of energy density, i.e. energy per unit volume. [We know that the energy density of the magnetic field is $\frac{\mathrm{B}^{2}}{2 \mu _{0}}$; (This may also be worked out through a direct use of the dimensions of $\mathrm{B}$ and $\left.\mu _{0}\right)$. Hence the dimensions of $\left(\frac{\mathrm{B}^{2}}{\mu _{0}}\right)$ are $\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{~L}^{3}}\right]$ i.e. $\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]$

Now $\left[\frac{\mathrm{p}^{2}}{\mathrm{mV}}\right]=\left[\frac{\mathrm{M}^{2} \mathrm{~L}^{2} \mathrm{~T}^{-2}}{\mathrm{M} \cdot \mathrm{L}^{3}}\right]=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]$

$$ \begin{aligned} & {\left[\frac{\mathrm{I}^{2} \mathrm{Rt}}{\mathrm{V}}\right]=\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{~L}^{3}}\right]=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-1}\right] \quad\left(\because \mathrm{I}^{2} \mathrm{Rt}=\text { Heat produced }\right)} \\ & \frac{\mathrm{S}}{x}=\left(\frac{\text { Force } / \text { length }}{\text { length }}\right)=\left(\mathrm{ML}^{-1} \mathrm{~T}^{-1}\right) \end{aligned} $$

All these terms are, therefore, dimensinoally compatible with the term $\left(\frac{\mathrm{B}^{2}}{\mu _{0}}\right)$.

However, in the term $(\mathrm{LI})$, we have $[\mathrm{L}]=($ Self inductance $)=\left(\frac{\text { emf } \times \text { time }}{\text { current }}\right)$

$$ \begin{aligned} & \therefore[\mathrm{LI}]=\mathrm{emf} \times \text { time } \\ & =\frac{\text { Work }}{\text { ch arg e }} \times \text { time } \\ & =\left(\mathrm{ML}^{2} \mathrm{~T}^{-2} \mathrm{I}^{-1}\right) \end{aligned} $$

This term is, therefore, dimensionally incompatible with the term $\left(\frac{\mathrm{B}^{2}}{\mu _{0}}\right)$.

48. The term $Z=\frac{s}{u}(s=$ distance, $u=$ speed $)$ is dimensionally incompatible with the term

(1) $\mathrm{LC}(\mathrm{L}=$ self inductance, $\mathrm{C}=$ capacitance $)$

(2) $\frac{\mathrm{L}}{\mathrm{R}}(\mathrm{L}=$ self inductance, $\mathrm{R}=$ resistance $)$

(3) $\mathrm{RC}(\mathrm{R}=$ resistance, $\mathrm{C}=$ capacitance $)$

(4) $\sqrt{\frac{\ell}{g}}(\ell=$ length, $g=$ acceleration $)$

Show Answer

Correct answer: (1)

Solution:

The term $Z\left(=\frac{s}{u}\right)$ has the dimensions of time.

Using the dimensions of $\mathrm{L}\left[[\mathrm{L}]=\mathrm{ML}^{2} \mathrm{~T}^{-2} \mathrm{I}^{-2}\right]$

$\mathrm{R}\left[[\mathrm{R}]=\mathrm{ML}^{2} \mathrm{~T}^{-3} \mathrm{I}^{-2}\right]$ and $\mathrm{C}\left[[\mathrm{C}]=\mathrm{M}^{-1} \mathrm{~L}^{-2} \mathrm{~T}^{4} \mathrm{I}^{2}\right]$

We find that the terms $\left(\frac{\mathrm{L}}{\mathrm{R}}\right)$ and $(\mathrm{RC})$ both have the dimensions of time.

Also, $\left[\sqrt{\frac{\ell}{\mathrm{g}}}\right]=\left[\frac{\mathrm{L}}{\mathrm{LT}^{-2}}\right]^{1 / 2}=[\mathrm{T}]$

$\therefore$ This term also has the dimensions of time.

However, the term $[\mathrm{LC}]=\left[\mathrm{T}^{2}\right]$

It, therefore, is dimensionally incompatible with the given term, i.e. Z.

49. From the following relations, the one, that does not meet the requirement of dimensional compatibility, is the relation:

(1) $\mathrm{V}=\frac{\pi \mathrm{pr}^{4}}{8 \eta \ell}$ (V $=$ rate of flow, $\mathrm{p}=$ pressure, $\mathrm{r}=$ radius, $\ell=$ length, $\eta=$ coefficient of viscosity)

(2) $\mathrm{F}=6 \pi \eta \mathrm{r}^{2} v(\mathrm{~F}=$ force ( viscous), $\mathrm{r}=$ radius, $v=$ velocity (terminal), $\eta=$ coefficient of viscosity)

(3) $\mathrm{S}=\frac{\mathrm{rh} \rho \mathrm{g}}{2 \cos \theta}(\mathrm{S}=$ surface tension, $\mathrm{r}=$ radius, $\mathrm{h}=$ height, $\rho=$ density, $\mathrm{g}=$ acceleration, $\theta=$ angle of contact

(4) $\mathrm{W}=\mathrm{pV}(\mathrm{W}=$ work, $\mathrm{p}=$ pressure, $\mathrm{V}=$ volume $)$

Show Answer

Correct answer: (2)

Solution:

On substituting the dimensions of different terms, we find that the dimensions of the LHS and the RHS, are equal in relations (1), (3) and (4). Hence these relations meet the requirement of dimensional compatibility.

However, in relation (2), dimensions ofLHS and RHS are different. Hence this relation is ‘dimensionally incompatible."

50. The dimensions formula $\left[M^{-1} L^{3} T^{-2}\right]$ can correspond to the dimensional formula of

(1) $\mathrm{G}$ as well as $\left(\frac{\mathrm{I} \alpha}{\mathrm{M}^{2}}\right)(\mathrm{G}=$ universal gravitational constant, $\mathrm{I}=$ moment of inertia, $\alpha=$ acceleration, $M=$ mass)

(2) $\mathrm{G}$ as well as $\left(\frac{\mathrm{A}}{\mathrm{Mt}^{2}}\right)(\mathrm{G}=$ universal gravitational constant, $\mathrm{A}=$ area, $\mathrm{M}=$ mass, $\mathrm{t}=$ time $)$

(3) $\left(\frac{\mathrm{h}}{\mathrm{M}^{2}}\right)$ as well as $\left(\frac{\mathrm{V}}{\mathrm{Mt}^{2}}\right)(\mathrm{h}=$ Planck’s constant, $\mathrm{V}=$ volume, $\mathrm{t}=$ time $)$

(4) $\left(\frac{\mathrm{h} v}{\mathrm{M}^{2}}\right)$ as well as $\left(\frac{\mathrm{S}}{\mathrm{MV}}\right)$ ( $\mathrm{h}=$ Planck’s constant, $v=$ frequency, $\mathrm{M}=$ mass, $\mathrm{S}=$ surface tension, $\mathrm{V}=$ volume)

Show Answer

Correct answer: (1)

Solution:

We find that $[\mathrm{G}]=\frac{\text { Force } \times(\text { distance })^{2}}{(\text { mass })^{2}}=\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right]$

Also, $\left(\frac{\mathrm{I} \alpha}{\mathrm{M}^{2}}\right)=\left[\frac{\left(\mathrm{ML}^{2}\right)\left(\mathrm{LT}^{-2}\right)}{\left(\mathrm{M}^{2}\right)}\right]=\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right]$

Both the terms, in option (1), thus match the given dimensions.

However, one, or both the terms, in the other three option, are NOT dimensionally compatible with the ‘given dimensions’.

51. If force (F), acceleration (a) and surface, tension (S), are taken as the ‘fundamental units’, the dimensional formula, for $G$, the universal gravitational constant would be:

(1) $\left[\mathrm{F} \mathrm{a} \mathrm{s}^{-1}\right]$

(2) $\left[\mathrm{F}^{2} \mathrm{a}^{2} \mathrm{~s}^{-2}\right]$

(3) $\left[\mathrm{F}^{2} \mathrm{a} \mathrm{s}^{-1}\right]$

(4) $\left[\mathrm{F} \mathrm{a}^{2} \mathrm{~s}^{-2}\right]$

Show Answer

Correct answer: (4)

Solution:

We have, $[\mathrm{F}]=\left[\mathrm{MLT}^{-2}\right] ;[\mathrm{a}]=\left[\mathrm{LT}^{-2}\right]$ and $[\mathrm{S}]=\left[\mathrm{MT}^{-2}\right]$

$$ \therefore[\mathrm{M}]=\left[\mathrm{Fa}^{-1}\right] $$

Also, $[\mathrm{T}]=\left[\mathrm{S}^{-1 / 2} \mathrm{~F}^{1 / 2} \mathrm{a}^{-1 / 2}\right] \quad\left(\because \mathrm{T}=\left(\frac{\mathrm{S}}{\mathrm{M}}\right)^{-1 / 2}\right)$

and $[\mathrm{L}]=\left[\mathrm{F} \mathrm{S}^{-1}\right]$

$$ =\left[\mathrm{F} \cdot \frac{\mathrm{F}^{2} \mathrm{~S}^{-2}}{\mathrm{~F}^{2} \mathrm{a}^{-2}}\right]=\left[\mathrm{Fa}^{2} \mathrm{~S}^{-2}\right] $$

[Note: This result may be converted into dimensions in terms of $\mathrm{M}, \mathrm{L}$ and $\mathrm{T}$ and compared with the known dimensions of [G] in terms of $\mathrm{M}, \mathrm{L}$ and $\mathrm{T}$. This ‘checking’ can help in all such questions.]

52. If mass, time, $\varepsilon _{0}$ (permittivity) and $\mu _{0}$ (permeability) are taken as the ‘base’ units, the dimensional formula, for electrical resistance, $R$ would be:

(1) $[\mathrm{R}]=\left[\mathrm{M} \varepsilon _{0}^{1 / 2} \mu _{0}^{1 / 2} \mathrm{~T}\right]$

(2) $[\mathrm{R}]=\left[\mathrm{M}^{0} \varepsilon _{0}^{-1 / 2} \mu _{0}^{1 / 2} \mathrm{~T}^{0}\right]$

(3) $[\mathrm{R}]=\left[\mathrm{M}^{0} \varepsilon _{0}^{1 / 2} \mu _{0}^{-1 / 2} \mathrm{~T}^{0}\right]$

(4) $[\mathrm{R}]=\left[\mathrm{M}^{-1} \varepsilon _{0}^{-1 / 2} \mu _{0}^{1 / 2} \mathrm{~T}^{-1}\right]$

Show Answer

Correct answer: (2)

Solution:

We have, $\left[\varepsilon _{0}\right]=\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{I}^{2}\right]$

and $\left[\mu _{0}\right]=\left[\mathrm{MLT}^{-2} \mathrm{I}^{-2}\right]$

From these, we get

$$ [\mathrm{L}]=\left[\left(\varepsilon _{0} \mu _{0}\right)^{-1 / 2} \cdot \mathrm{T}\right] $$

and $\quad[\mathrm{I}]=\left[\varepsilon _{0}^{1 / 2} \mu _{0}^{3 / 2} \mathrm{M}^{-1} \mathrm{~T}^{+1}\right]^{-\frac{1}{2}}$

Now $[\mathrm{R}]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-3} \mathrm{I}^{-2}\right]$

$$ \begin{aligned} & =\left[\mathrm{MT}^{-3} \frac{\mathrm{T}^{2}}{\left(\varepsilon _{0} \mu _{0}\right)} \cdot\left(\varepsilon _{0}^{1 / 2} \mu _{0}^{3 / 2} \mathrm{M}^{-1} \mathrm{~T}\right)\right] \\ & =\left[\frac{\varepsilon _{0}}{\mu _{0}}\right]^{\frac{1}{2}}=\left[\mathrm{M}^{0} \varepsilon _{0}^{-1 / 2} \mu _{0}^{1 / 2} \mathrm{~T}^{0}\right] \end{aligned} $$

53. It Planck’s constant (h), linear momentum (p) and angular velocity ( $\omega$ ), were taken as the fundamental units, the dimensional formula, for surface tension (S) would be:

(1) $[\mathrm{S}]=\left[\mathrm{h}^{2} \mathrm{p}^{-1} \omega\right]$

(2) $[\mathrm{S}]=\left[\mathrm{h}^{-2} \mathrm{p} \omega\right]$

(3) $[\mathrm{S}]=\left[\mathrm{h}^{-1} \mathrm{p}^{2} \omega\right]$

(4) $[\mathrm{S}]=\left[\mathrm{hp}^{-2} \omega^{-1}\right]$

Show Answer

Correct answer: (3)

Solution:

We have $[\mathrm{h}](=$ energy $\times$ time $)=\left[\mathrm{ML}^{2} \mathrm{~T}^{-1}\right]$

$$ [\mathrm{p}]=\left[\mathrm{MLT}^{-1}\right] $$

and $(\omega)=\left(\mathrm{T}^{-1}\right)$

These give $[\mathrm{T}]=\left[\omega^{-1}\right]$

$$ [\mathrm{L}]=\left[\mathrm{hp}^{-1}\right] $$

and $[\mathrm{M}]=\mathrm{p} \cdot \mathrm{L}^{-1} \mathrm{~T}=\left[\mathrm{ph}^{-1} \mathrm{p}^{+1} \omega^{-1}\right]$

Now,

$$ \begin{aligned} & {[\mathrm{S}]=\frac{\text { Force }}{\text { length }}=\left[\mathrm{MT}^{-2}\right]} \\ & =\left[\mathrm{h}^{-1} \mathrm{p}^{2} \omega^{-1} \omega^{2}\right]=\left[\mathrm{h}^{-1} \mathrm{p}^{2} \omega\right] \end{aligned} $$

54. If $G$ (universal gravitational constant), $h$ (Planck’s constant) and $C$ (Velocity of light) were taken as the fundamental units, the dimensional formula, for pressure (p), would be

(1) $[\mathrm{p}]=\left[\mathrm{h}^{-2} \mathrm{G}^{-1} \mathrm{C}^{7}\right]$

(2) $[\mathrm{p}]=\left[\mathrm{h}^{2} \mathrm{GC}^{-7}\right]$

(3) $[\mathrm{p}]=\left[\mathrm{hG}^{2} \mathrm{C}^{-7}\right]$

(4) $[\mathrm{p}]=\left[\mathrm{h}^{-1} \mathrm{G}^{-2} \mathrm{C}^{7}\right]$

Show Answer

Correct answer: (4)

Solution:

We have $[\mathrm{G}]=\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right]$

$$ \begin{aligned} & {[\mathrm{h}]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-1}\right]} \\ & {[\mathrm{C}]=\left[\mathrm{LT}^{-1}\right]} \end{aligned} $$

From these, we get

$$ [\mathrm{Gh}]=\mathrm{L}^{5} \mathrm{~T}^{-3} $$

Also, $\left[\mathrm{C}^{5}\right]=\mathrm{L}^{5} \mathrm{~T}^{-5}$

$$ \therefore\left[\frac{\mathrm{Gh}}{\mathrm{C}^{5}}\right]=\mathrm{T}^{2} \text { or }[\mathrm{T}]=\mathrm{G}^{1 / 2} \mathrm{H}^{1 / 2} \mathrm{C}^{-5 / 2} $$

$$ \therefore[\mathrm{L}]=[\mathrm{CT}]=\left[\mathrm{G}^{1 / 2} \mathrm{H}^{1 / 2} \mathrm{C}^{-3 / 2}\right] $$

and $[\mathrm{M}]=\left[\mathrm{hL}^{-2} \mathrm{~T}^{+1}\right]=\left[\mathrm{h}\left(\mathrm{G}^{-1} \mathrm{~h}^{-1} \mathrm{C}^{3}\right)\left(\mathrm{G}^{1 / 2} \mathrm{H}^{1 / 2} \mathrm{C}^{-5 / 2}\right)\right]$

$$ =\left[\mathrm{h}^{1 / 2} \mathrm{G}^{-1 / 2} \mathrm{C}^{1 / 2}\right] $$

Now pressure, $\mathrm{p}=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]$

$\therefore[\mathrm{p}]=\left[\mathrm{h}^{-1} \mathrm{G}^{-2} \mathrm{C}^{7}\right]$

55. If specific heat capacity $(S)$, specific latent heat $\left(L _{0}\right)$, mass $(M)$ and time $(T)$, were taken as the ‘base’ units, the dimensional formula for coefficient of thermal conductivity $(\sigma)$, would be:

(1) $[\sigma]=\left[\mathrm{MSL} _{0}^{-1 / 2} \mathrm{~T}^{-1}\right]$

(2) $[\sigma]=\left[\mathrm{M}^{-1} \mathrm{~S}^{-1 / 2} \mathrm{~L} _{0}^{-1 / 2} \mathrm{~T}^{2}\right]$

(3) $[\sigma]=\left[\mathrm{MS}^{-1} \mathrm{~L} _{0}^{1 / 2} \mathrm{~T}^{-2}\right]$

(4) $[\sigma]=\left[\mathrm{M}^{-1} \mathrm{~S}^{1 / 2} \mathrm{~L} _{0}^{-1 / 2} \mathrm{~T}^{-1}\right]$

Show Answer

Correct answer: (1)

Solution:

We have $[\mathrm{S}]=\left[\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right]$

$$ \left[\mathrm{L} _{0}\right]=\left[\mathrm{M}^{0} \mathrm{~L}^{2} \mathrm{~T}^{-2}\right] $$

These give $[\mathrm{K}]=\left[\mathrm{L} _{0} / \mathrm{S}\right]$

and

$$ [\mathrm{L}]=\left[\mathrm{ST}^{2} \mathrm{~K}\right]^{1 / 2} $$

$$ =\left[\mathrm{ST}^{2} \frac{\mathrm{L} _{0}}{\mathrm{~S}}\right]=\left[\mathrm{L} _{0} \mathrm{~T}^{2}\right]^{\frac{1}{2}} $$

Now, $[\sigma]=\left[\mathrm{MLT}^{-2} \mathrm{~K}^{-1}\right]$

$$ \begin{aligned} & \therefore[\sigma]=\left[\mathrm{M}\left(\mathrm{L} _{0} \mathrm{~T}^{2}\right)^{1 / 2}\left(\mathrm{~T}^{-2}\right)\left(\frac{\mathrm{S}}{\mathrm{L} _{0}}\right)\right] \\ & =\left[\mathrm{MSL} _{0}^{-1 / 2} \mathrm{~T}^{-1}\right] \end{aligned} $$

56. It is known, that the units of mass, length and time, in the SI units and FPS system, are related as

$1 \mathrm{~kg} \simeq \mathbf{2 . 2 0 5}$ pound; $1 \mathrm{~m} \simeq 3.28$ feet, $1 \mathrm{~s}=1 \mathrm{~s}$

The value of the surface tension of water is $7.3 \times 10^{-2} \mathrm{~N} / \mathrm{m}$. Its value, in the FPS units, would be

(1) 0.066 FPS units

(2) 0.033 FPS units

(3) 0.16 FPS units

(4) 0.32 FPS units

Show Answer

Correct answer: (3)

Solution:

We have,

$[$ Surface tension $]=\left(\frac{\text { Force }}{\text { length }}\right)=\left[\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}}\right]$

$$ =\left[\mathrm{MT}^{-2}\right] $$

$\therefore \frac{\text { Unit of surface tension in SI units }}{\text { Unit of surface tension in FPS system }}$

$$ \begin{aligned} & =\left(\frac{\mathrm{kg}}{\text { pound }}\right)\left(\frac{\mathrm{s}}{\mathrm{s}}\right)^{-2}=\frac{2.205 \text { pound }}{1 \text { point }}(1)^{-2} \\ & =2.205 \end{aligned} $$

$\therefore 7.3 \times 10^{-2}$ Units in SI Units $=2.205 \times 7.3 \times 10^{-2}$ Units

$\simeq 16.1 \times 10^{-2}$ FPS units

$\simeq 0.16$ FPS Units

57. The specific latent heat of fusion of water is known to be $80 \mathrm{cal} / \mathrm{g}$. Given that $1 \mathrm{cal}=4.2 \mathrm{~J}$, $\mathbf{1 ~ k g}=\mathbf{2 . 2 0 5}$ pound, $\mathbf{1 ~} \mathrm{m}=\mathbf{3 . 2 8}$ feet, the value of this specific latent heat, in FPS units, is

(1) $1102 \times 10^{3}$ FPS units

(2) $3615 \times 10^{3}$ FPS units

(3) $102 \times 10^{3}$ FPS units

(4) $31.2 \times 10^{3}$ FPS units

Show Answer

Correct answer: (2)

Solution:

We have,

$[$ Specific latent heat $]=\left(\frac{\text { Heat energy }}{\text { mass }}\right)=\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{M}}\right]=\left[\mathrm{L}^{2} \mathrm{~T}^{-2}\right]$

$$ \therefore \frac{\text { Unit of surface tension in SI units }}{\text { Unit of surface tension in FPS system }}=\left(\frac{\mathrm{m}}{\mathrm{ft}}\right)^{2}\left(\frac{1 \mathrm{~s}}{1 \mathrm{~s}}\right)^{-2} $$

$=\left(\frac{3.28 \text { feet }}{1 \text { feet }}\right)^{2}(1) \simeq 10.76$

$\therefore$ Specific latent heat of water $=\frac{80 \mathrm{cal}}{\mathrm{g}}=\frac{80 \times 4.2 \mathrm{~J}}{\left(10^{-3} \mathrm{~kg}\right)}$

$=336 \times 10^{3} \mathrm{~J} / \mathrm{kg}=336 \times 10^{3}\left(\mathrm{~m}^{2} \mathrm{~s}^{-2}\right)$

$=\left(336 \times 10^{3} \times 10.76\right)$ FPS Units

$\cong 3615 \times 10^{3}$ FPS Units

58. The Young’s modules of copper is known to have a value $1.3 \times 10^{10}$ in CGS units. Given that 1 pound $=453.5 \mathrm{~g}, 1 \mathrm{foot} \cong \mathbf{3 0 . 5} \mathrm{cm}$, the value of Young’s modulus of copper, in FPS units, is:

(1) $\left(8.7 \times 10^{8}\right)$ FPS units

(2) $\left(8.7 \times 10^{10}\right)$ FPS units

(3) $\left(7.24 \times 10^{5}\right)$ FPS units

(4) $\left(7.24 \times 10^{6}\right)$ FPS units

Show Answer

Correct answer: (1)

Solution:

We have, $[\mathrm{Y}]=\left(\frac{\text { Stress }}{\text { Strain }}\right)=\left[\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}^{2}}\right]=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]$

$$ \begin{align*} & \therefore \frac{\text { Unit of Y in CGS units }}{\text { Unit of Y in FPS units }}=\left(\frac{\mathrm{g}}{\text { pound }}\right)\left(\frac{\mathrm{cm}}{\mathrm{ft}}\right)^{-1}\left(\frac{1 \mathrm{~s}}{1 \mathrm{~s}}\right)^{-2} \\ & =\left(\frac{\mathrm{g}}{453.5 \mathrm{~g}}\right)\left(\frac{\mathrm{cm}}{30.5 \mathrm{~cm}}\right)^{-1}(1) \tag{1}\ & =\frac{30.5}{453.5} \cong 0.067 \\ & \therefore 1.3 \times 10^{10} \mathrm{CGS} \text { units }=1.3 \times 00.67 \times 10^{10} \mathrm{FPS} \text { units } \\ & \simeq 0.087 \times 10^{10} \mathrm{FPS} \text { units } \\ & =8.7 \times 10^{8} \mathrm{FPS} \text { Units } \end{align*} $$

59. The specific heat capacity of water is known to be $1 \mathrm{cal} /\left(\mathrm{g}^{0} \mathrm{C}\right)$.

A system of units uses a unit of mass that equals $500 \mathrm{~g}$, a unit of length that equal $50 \mathrm{~cm}$ and a unit of time that equal 100s. It also uses to Fahrenheit scale of temperature in which there are 180 divisons between the temperature of melting ice $\left(0^{\circ} \mathrm{C}\right)$ and that of (normal) boiling point of water $\left(=100^{\circ} \mathrm{C}\right)$.

The value of the specific heat capacity of water, in this hypothetical system, would be:

(1) $9.3 \times 10^{7}$ units of the hypothetical system

(2) $1.9 \times 10^{7}$ units of the hypothetical system

(3) $1.9 \times 10^{-1}$ units of the hypothetical system

(4) $9.3 \times 10^{-1}$ units of the hypothetical system

Show Answer

Correct answer: (1)

Solution:

We have,

$[$ Specific heat capacity $]=\frac{\text { Heat energy }}{\text { Mass } \times \text { change in temperature }}$

$$ \begin{aligned} & =\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{MK}}\right]=\left[\mathrm{L}^{2} \mathrm{~T}^{-2} \mathrm{~K}^{-1}\right] \\ & \therefore \frac{\text { Unit of specific heat capacity in SI units }}{\text { Unit of specific heat capacity in the hypothetical system }} \end{aligned} $$

$$ =\left(\frac{\mathrm{m}}{50 \mathrm{~cm}}\right)^{2}\left(\frac{\mathrm{s}}{100 \mathrm{~s}}\right)^{-2}\left(\frac{\text { kelvin degree }}{\text { Fahrenheit degree }}\right)^{-1} $$

Now 100 divisions on the celsius scale

(= 100 divisions on the kelvin scale)

$=180$ divisions on the Fahrenheit scale

$\therefore 1$ division on the kelvin scale

$=1.8$ divisions on the Fahrenheit scale

$\therefore$ Above ratio $=\left(\frac{100 \mathrm{~cm}}{50 \mathrm{~cm}}\right)^{2}\left(\frac{1}{100}\right)^{-2}\left(\frac{1.8^{0} \mathrm{~F}}{1^{0} \mathrm{~F}}\right)^{-1}$

$$ \begin{aligned} & =4 \times 10^{4} \times \frac{1}{1.8} \\ & =2.22 \times 10^{4} \end{aligned} $$

Now specific heat capacity of water $=\frac{1 \mathrm{cal}}{\left(\mathrm{g}^{\mathrm{\degree}} \mathrm{C}\right)}$

$$ \begin{aligned} & =\frac{4.25}{10^{-3} \mathrm{~kg}(\mathrm{~K})}=\frac{4.2 \times 10^{3} \mathrm{~J}}{\operatorname{kg}(\mathrm{K})}=4.2 \times 10^{3} \text { SI Units } \\ & =4.2 \times 10^{3} \times\left(2.22 \times 10^{4}\right) \text { units in the hypothetical system } \\ & =9.324 \times 10^{7} \text { units in the hypothetical system } \\ & \simeq 9.3 \times 10^{7} \text { units } \end{aligned} $$

60. The gas constant, $R$, has a vlue of $8.32 \mathrm{~J} \mathrm{~mole}^{-1} \mathrm{~K}^{-1}$ in SI units.

A hypothetical system uses a unit of mass that equals $2 \mathrm{~kg}$, a unit of length that equals $5 \mathrm{~m}$ and a unit of time that equals $1 \mathrm{~ms}$. The system also uses the fahrenheit scale of temperature in which there are 180 divisions between the temperature of melting ice and that of the (normal) boiling point of water $\left(=100^{\circ} \mathrm{C}\right)$.

The value of the gas constant, $R$, in this system would be (nearly):

(1) $30 \times 10^{-8}$ (new energy unit) $\left(\mathrm{mole}^{-1}\right)\left({ }^{0} \mathrm{~F}\right)^{-1}$

(2) $9.2 \times 10^{-8}$ (new energy unit) $\left(\mathrm{mole}^{-1}\right)\left({ }^{0} \mathrm{~F}\right)^{-1}$

(3) $15 \times 10^{-8}$ (new energy unit) $\left(\mathrm{mole}^{-1}\right)\left({ }^{0} \mathrm{~F}\right)^{-1}$

(4) $4.6 \times 10^{-8}$ (new energy unit) $\left(\mathrm{mole}^{-1}\right)\left({ }^{0} \mathrm{~F}\right)^{-1}$

Show Answer

Correct answer: (2)

Solution:

We first note that the 1 mole would still contain the same number of ’entities'.

Also $1 \mathrm{~J}=1 \mathrm{~kg}(1 \mathrm{~m})^{2}(1 \mathrm{~s})^{-2}$ $=\left(\frac{1 \mathrm{~kg}}{2 \mathrm{~kg}}\right)\left(\frac{1 \mathrm{~m}}{5 \mathrm{~m}}\right)^{2}\left(\frac{1 \mathrm{~s}}{1 \mathrm{~ms}}\right)^{-2}$ new energy units

$=2 \times 10^{-8}$ new energy units

Also 100 divisions on the celsius scale $=100$ divisions on the kelvin scale $=180$ divisions on the Fahrenheit scale.

$$ \begin{aligned} & \therefore 1 \mathrm{~K}=1.8{ }^{0} \mathrm{~F} \\ & (1 \mathrm{~K})^{-1}=(1.8)^{-1}\left({ }^{0} \mathrm{~F}\right)^{-1} \\ & \therefore \mathrm{R}=8.32 \mathrm{~J}\left(\mathrm{~mole}^{-1}\right)(\mathrm{K})^{-1} \\ & =8.32\left(2 \times 10^{-8} \text { new energy units) }\left(\mathrm{mole}^{-1}\right)\left[(1.8)^{-1}\left({ }^{0} \mathrm{~F}\right)^{-1}\right]\right. \\ & =\frac{16.64}{1.8} \times 10^{-8} \text { (new energy unit) }(\text { mole })^{-1}\left({ }^{0} \mathrm{~F}\right)^{-1} \\ & =9.23 \times 10^{-8}\left(\text { new energy unit) }(\text { mole })^{-1}\left({ }^{0} \mathrm{~F}\right)^{-1}\right. \\ & \simeq\left(9.2 \times 10^{-8}\right)(\text { new energy unit })(\text { mole })^{-1}\left({ }^{0} \mathrm{~F}\right)^{-1} \end{aligned} $$

61. A beam, made from a material of Young’s modulus $\mathbf{Y}$, has a length $\ell$, a width $\mathbf{b}$ and $\mathbf{a}$ thickness $d$. When it is placed symmetrically on two knife edges, at its ends, and loaded in the middle by a mass $M$, it gets depressed by an amount $\delta$ where

$$ \delta=\left(\frac{M g \ell^{3}}{4 \mathrm{bd}^{3} \mathrm{Y}}\right) $$

The relative errors, in the determinations of $\ell$ and $d$, have identical values of $1 \%$ each. The error, in the determination of $M$ is $0.5 \%$, that in the determination of $b$ is $0.2 \%$ and that in the determinations of $\delta$ is $0.1 \%$. The value of ’ $g$ ’ is used from standard tables.

The relative error, in the determination of $Y$, on the basis of these measurements, would be:

(1) $0.2 \%$

(2) $0.8 \%$

(3) $2.8 \%$

(4) $6.8 \%$

Show Answer

Correct answer: (4)

Solution:

We have,

$$ \begin{aligned} & \mathrm{Y}=\frac{\mathrm{Mg} \ell^{3}}{4 \mathrm{bd}^{3} \delta} \\ & \therefore \frac{\Delta \mathrm{Y}}{\mathrm{Y}}=\frac{\Delta \mathrm{M}}{\mathrm{M}}+\frac{\Delta \mathrm{g}}{\mathrm{g}}+3 \frac{\Delta \ell}{\ell}+\frac{\Delta \mathrm{b}}{\mathrm{b}}+3 \frac{\Delta \mathrm{d}}{\mathrm{d}}+\frac{\Delta \delta}{\delta} \\ & =0.5 \%+0+3 \times 1 \%+0.2 \%+3 \times 1 \%+0.1 \% \\ & =6.8 \% \end{aligned} $$

The relative error, in the determination of $Y$ is, therefore, $6.8 \%$

62. In the relation $\mathrm{t}=\mathrm{k} \sqrt{\frac{\mathrm{\rho r}^{3}}{\sigma}}$,

The quantities $t, \rho, r$ and $\sigma$ refer to the time of oscillation, density, radius and surface tension, respectively. The relative error, in the determination of $\sigma$, is calculated on the basis of the relative errors, of $0.5 \%, 0.1 \%$ and $0.2 \%$ in the measurement of $\rho, r$ and $t$, respectively. This relative error would equal:

(1) $1.2 \%$

(2) $0.8 \%$

(3) $0.6 \%$

(4) $0.4 \%$

Show Answer

Correct answer: (1)

Solution:

We have,

$$ \mathrm{t}=\mathrm{k} \sqrt{\frac{\rho^{3}}{\sigma}} $$

$\therefore \sigma=\mathrm{k}^{2} \frac{\mathrm{pr}^{3}}{\mathrm{t}^{2}}$

$\therefore \frac{\Delta \sigma}{\sigma}=\frac{\Delta \rho}{\rho}+3 \frac{\Delta \mathrm{r}}{\mathrm{r}}+2 \frac{\Delta \mathrm{t}}{\mathrm{t}}$

$=0.5 \%+3(0.1 \%)+2(0.2 \%)$

$=1.2 \%$

63. The modules, of rigidity, $\eta$, the material of a wire, is calculated from the relation

$$ \tau=\mathrm{k} \cdot \frac{\eta \mathrm{r}^{4}}{2 \ell} $$

where $\tau=$ torsional constant (torque per unit twist), $r=$ radius and $\ell=$ length.

The relative error, in the determination of $\eta$, is calculated to be $0.9 \%$. The relative errors, in the determination of $\tau$ and $\ell$ are found to be $0.5 \%$ and $0.2 \%$, respectively. The ratio of the least count of the instrument, used to measure $r$, to the measured (average) value of $r$, would then equal:

(1) 0.001

(2) 0.0005

(3) 0.002

(4) 0.0001

Show Answer

Correct answer: (2)

Solution:

We have,

$$ \begin{aligned} & \tau=\mathrm{k} \cdot \frac{\eta \mathrm{r}^{4}}{2 \ell} \\ & \therefore \eta=\frac{2}{\mathrm{k}} \frac{\ell \tau}{\mathrm{r}^{4}} \end{aligned} $$

$$ \begin{aligned} & \therefore \frac{\Delta \eta}{\eta}=\frac{\Delta \ell}{\ell}+\frac{\Delta \tau}{\tau}+4 \frac{\Delta \mathrm{r}}{\mathrm{r}} \\ & \therefore 0.9 \%=0.2 \%+0.5 \%+4(x) \quad\left(x=\frac{\Delta \mathrm{r}}{\mathrm{r}}\right) \end{aligned} $$

This given $x\left(=\frac{\Delta \mathrm{r}}{\mathrm{r}}\right)=0.05 \%=0.0005$

64. The frequency (n), of a tuning fork, depends upon the length $(\ell)$ of its prongs and the density (d) and Young’s modules (Y) of its material, through the relation

$$ \mathrm{n}=\frac{\mathrm{k}}{\ell} \sqrt{\frac{\mathrm{Y}}{\mathrm{d}}} $$

If the relative percentage errors, in the determination of $\mathrm{n}, \ell$ and $\mathrm{d}$ are $0.1 \%, 0.5 \%$ and $1 \%$, respectively, the relative percentage error, in the determination of $Y$, would be:

(1) $2.2 \%$

(2) $1.6 \%$

(3) $1.1 \%$

(4) $0.95 \%$

Show Answer

Correct answer: (1)

Solution:

We have,

$$ \begin{aligned} & \mathrm{n}=\frac{\mathrm{k}}{\ell} \sqrt{\frac{\mathrm{Y}}{\mathrm{d}}} \\ & \therefore \mathrm{Y}=\frac{\mathrm{n}^{2} \ell^{2} \mathrm{~d}}{\mathrm{k}^{2}} \\ & \therefore \frac{\Delta \mathrm{Y}}{\mathrm{Y}}=2 \frac{\Delta \mathrm{n}}{\mathrm{n}}+2 \frac{\Delta \ell}{\ell}+\frac{\Delta \mathrm{d}}{\mathrm{d}} \end{aligned} $$

$=2(0.1 \%)+2(0.5 \%)+(1 \%)$

$=2.2 \%$

65. The mass $m$, of a stone, that can be moved by flowing stream of water, depends on the velocity $(v)$, of the flowing water, the density ( $\rho$ ) of water and the acceleration due to gravity (g). The relation, between the different quantities, is expressed as

$$ \mathrm{m}=\mathrm{k} v^{\mathrm{n}} \rho \mathrm{g}^{-3} $$

The relative percentage errors, in the determination of $v, \rho$ and $g$ are $1 \%, 0.7 \%$ and $0.1 \%$, respectively. The value of $n$, in the above relation, and the relative percentage error, in the determination of $\mathrm{m}$, are equal, respectively, to:

(1) $5 ; 6 \%$

(2) $6 ; 5 \%$

(3) $7 ; 6 \%$

(4) $6 ; 7 \%$

Show Answer

Correct answer: (4)

Solution:

Using the principle of dimensional homogeneity, in the relation,

$\mathrm{m}=\mathrm{k} v^{\mathrm{n}} \rho \mathrm{g}^{-3}$, we get

$[\mathrm{M}]=\left[\mathrm{LT}^{-1}\right]^{\mathrm{n}}\left[\mathrm{ML}^{-3}\right]\left[\mathrm{LT}^{-2}\right]^{-3}$

We get $-\mathrm{n}+6=0$ or $\mathrm{n}=6$

This value is also consistent with $\mathrm{n}+(-3)+(-3)=0$

$$ \begin{aligned} & \therefore \mathrm{m}=\mathrm{k} v^{6} \rho \mathrm{g}^{-3} \\ & \therefore \frac{\Delta \mathrm{m}}{\mathrm{m}}=6 \frac{\Delta \mathrm{v}}{\mathrm{v}}+\frac{\Delta \rho}{\rho}+3 \frac{\Delta \mathrm{g}}{\mathrm{g}} \\ & =6(1 \%)+(0.7 \%)+3(0.1 \%) \\ & =7 \% \end{aligned} $$

66. It is given that the time period (T) of oscillation, of a gas bubble, formed under water, depends upon pressure $(P)$, density (d) and energy (E), as

$$ \mathrm{T}=\mathrm{k} \rho^{\mathrm{a}} \mathrm{d}^{\mathrm{b}} \mathrm{E}^{\mathrm{c}} $$

The value of $a, b$ and $c$, are:

(1) $(-5 / 6),(1 / 2)$ and $(1 / 3)$

(2) $(-5 / 6),(1 / 3)$ and $(1 / 2)$

(3) $(5 / 6),(1 / 3)$ and $(1 / 2)$

(4) $(5 / 6),(1 / 2)$ and $(1 / 3)$

Show Answer

Correct answer: (1)

Solution:

Putting dimensions, of all the terms, in the relation.

$$ \begin{aligned} & T=k \rho^{a} d^{b} E^{c}, \quad \text { we get } \\ & {[T]=\left[M L^{-1} T^{-2}\right]^{a}[M L-3]^{b}\left[M L^{2} T^{-2}\right]^{c}} \\ & \therefore a+b+c=0 \\ & -a-3 b+2 c=0 \\ & -2 a-2 c=1 \end{aligned} $$

These equations give,

$$ a=-5 / 6, b=1 / 2, c=1 / 3 $$

67. In the relation $\mathrm{T}=\mathrm{kh}^{1 / 2} \mathrm{G}^{1 / 2} \mathrm{C}^{\mathrm{n}}$

( $T=$ Time period; $h=$ Planck’s constant, $G=$ Universal gravitational constant, $C=$ velocity of light), the value of $n$ should be

(1) $\mathrm{n}=\left(+\frac{3}{2}\right)$

(2) $\mathrm{n}=\left(-\frac{5}{2}\right)$

(3) $\mathrm{n}=\left(\frac{1}{2}\right)$

(4) $\mathrm{n}=\left(-\frac{3}{2}\right)$

Show Answer

Correct answer: (2)

Solution:

We have,

$$ \mathrm{T}=\mathrm{kh}^{1 / 2} \mathrm{G}^{1 / 2} \mathrm{C}^{\mathrm{n}} $$

$\therefore$ Putting dimensions, we get

$$ \begin{aligned} & {[\mathrm{T}]=\left(\mathrm{ML}^{2} \mathrm{~T}^{-1}\right)^{1 / 2}\left(\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right)^{1 / 2}\left(\mathrm{LT}^{-1}\right)^{\mathrm{n}}} \\ & \therefore 1+\frac{3}{2}+\mathrm{n}=0 \\ & \text { and }-\frac{1}{2}-1-\mathrm{n}=1 \end{aligned} $$

From either of these, we get $n=-\frac{5}{2}$

68. The dimensions, of the term, $\mathrm{Z}=\mathrm{h}^{\mathrm{a}} \mathrm{CG}^{-1}$

( $\mathrm{h}=$ Planck’s constant, $\mathrm{C}=$ velocity of light, $\mathrm{G}=$ universal gravitational constant) equal $\mathrm{M}^{2}$. The value of $a$, in this term, equals

(1) (4)

(2) (3)

(3) (2)

(4) (1)

Show Answer

Correct answer: (4)

Solution:

We have,

$$ \begin{aligned} & {[\mathrm{h}](=\text { energy } \times \text { time })=\left[\mathrm{ML}^{2} \mathrm{~T}^{-1}\right]} \\ & {[\mathrm{G}]=\left(\frac{\text { Force } \times \text { distance }^{2}}{\mathrm{mass}^{2}}\right)=\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right]} \\ & {[\mathrm{C}]=(\text { Velocity })=\left[\mathrm{LT}^{-1}\right]} \end{aligned} $$

$\therefore$ From the given relation, we get

$$ \left[\mathrm{M}^{2}\right]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-1}\right]^{\mathrm{a}}\left[\mathrm{LT}^{-1}\right]\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right]^{-1} $$

These give,

$$ \mathrm{a}+1=2 ; 2 \mathrm{a}+1-3=0 ;-\mathrm{a}-1+2=0 $$

The value of, $a$, consistent with all these relations, is $a=+1$

69. The length ( $\ell$ ) and breadth (b), of a rectangle, are measured to be

$$ \ell=(10.0 \pm 0.1) \mathrm{cm}, \mathbf{b}=(5.10 \pm 0.05) \mathrm{cm} $$

The perimeter ( $\mathrm{p}$ ), and the area (A), of this rectangle, should be expressed as:

(1) $\mathrm{p}=(30.2 \pm 0.15) \mathrm{cm}, \mathrm{A}=(51 \pm 1) \mathrm{cm}^{2}$

(2) $\mathrm{p}=(30.2 \pm 0.15) \mathrm{cm}, \mathrm{A}=(51.0 \pm 0.5) \mathrm{cm}^{2}$

(3) $\mathrm{p}=(30.20 \pm 0.05) \mathrm{cm}, \mathrm{A}=(51.0 \pm 0.5) \mathrm{cm}^{2}$

(4) $\mathrm{p}=(30.20 \pm 0.05) \mathrm{cm}, \mathrm{A}=(51 \pm 1) \mathrm{cm}^{2}$

Show Answer

Correct answer: (2)

Solution:

We have $\mathrm{p}=2(\ell+\mathrm{b})=2(10.0+5.10)=30.20 \mathrm{~cm}$

The error, in the sum of $\ell$ and $\mathrm{b}$, would be the sum of their individual errors. Thus

$$ \begin{aligned} & \Delta \mathrm{p}=\Delta \ell+\Delta \mathrm{b}=(0.1+0.05) \mathrm{cm} \\ & =0.15 \mathrm{~cm} \end{aligned} $$

We would, therefore, write the perimeter, $\mathrm{p}$, as

$$ \mathrm{p}=(30.2 \pm 0.15) \mathrm{m} $$

Also, area $\mathrm{A}=\ell \mathrm{b}=10.0 \times 5.1=51.0 \mathrm{~cm}^{2}$

Now, $\frac{\Delta \mathrm{A}}{\mathrm{A}}=\frac{\Delta \ell}{\ell}+\frac{\Delta \mathrm{b}}{\mathrm{b}}=\frac{0.1}{10.0}+\frac{0.05}{5.1}$

$$ \begin{aligned} & =0.01+0.0098=0.0198 \\ & \therefore \Delta \mathrm{A}=(0.0198 \times 51.0)^{2}=0.52 \mathrm{~cm}^{2} \end{aligned} $$

We would, therefore, write the area, $\mathrm{A}$, as

$$ \mathrm{A}=(51.0 \pm 0.5) \mathrm{cm}^{2} $$

70. The side, a, of a cube, has been measured as $a=(2.5 \pm 0.1) \mathrm{cm}$

The total surface area (S), and the volume (V), of the cube, would be expressed as:

(1) $\mathrm{S}=(38 \pm 3) \mathrm{cm}^{2} \quad \mathrm{~V}=(15.625 \pm 1.875) \mathrm{cm}^{3}$

(2) $\mathrm{S}=(37.5 \pm 3) \mathrm{cm}^{2} \mathrm{~V}=(15.63 \pm 1.88) \mathrm{cm}^{3}$

(3) $\mathrm{S}=(37.5 \pm 3) \mathrm{cm}^{2} \mathrm{~V}=(15.6 \pm 1.9) \mathrm{cm}^{3}$

(4) $\mathrm{S}=(38 \pm 3) \mathrm{cm}^{2} \quad \mathrm{~V}=(16 \pm 2) \mathrm{cm}^{3}$

Show Answer

Correct answer: (4)

Solution:

We have,

Total surface area, $\mathrm{S}=6\left(\mathrm{a}^{2}\right)$

$$ =6(2.5)^{2} \mathrm{~cm}^{2}=37.5 \mathrm{~cm}^{2} $$

Also, $\frac{\Delta \mathrm{S}}{\mathrm{S}}=2 \frac{\Delta \mathrm{a}}{\mathrm{a}}=\frac{2 \times 0.1}{2.5}=0.08$

$$ \therefore \Delta \mathrm{S}=(0.08 \times 37.5) \mathrm{cm}^{2}=3 \mathrm{~cm}^{2} $$

We should, therefore, express $\mathrm{S}$ as,

$$ \mathrm{S} \simeq(38 \pm 3) \mathrm{cm}^{2} $$

Also volume $\mathrm{V}=\mathrm{a}^{3}=(2.5)^{3} \mathrm{~cm}^{3}=15.625 \mathrm{~cm}^{3}$

$$ \begin{aligned} & \therefore \frac{\Delta \mathrm{V}}{\mathrm{V}}=3 \frac{\Delta \mathrm{a}}{\mathrm{a}}=\frac{3(0.1)}{2.5}=0.12 \\ & \therefore \Delta \mathrm{V}=0.12 \times 15.625 \mathrm{~cm}^{3}=1.875 \mathrm{~cm}^{3} \approx 2 \mathrm{~cm}^{3} \end{aligned} $$

We, should, therefore, express $\mathrm{V}$ as

$$ \mathrm{V} \simeq(16 \pm 2) \mathrm{cm}^{3} $$

71. The voltage $(V)$, across a wire, and the current (I), through it, have been measured as

$$ V=(3.4 \pm 0.2) \text { volt }, I=(0.085 \pm 0.005) \text { ampere } $$

The resistance, $R$, of the wire, as per these measurements, is:

(1) $\mathrm{R}=(40 \pm 5) \Omega$

(2) $\mathrm{R}=(40.0 \pm 4.7) \Omega$

(3) $\mathrm{R}=(40.00 \pm 4.72) \Omega$

(4) $\mathrm{R}=(40 \pm 0) \Omega$

Show Answer

Correct answer: (1)

Solution:

We have, as per Ohm’s law,

$$ \mathrm{R}=\frac{\mathrm{V}}{\mathrm{I}}=\frac{3.4}{0.085} \Omega=40 \Omega $$

Also, $\frac{\Delta \mathrm{R}}{\mathrm{R}}=\frac{\Delta \mathrm{V}}{\mathrm{V}}+\frac{\Delta \mathrm{I}}{\mathrm{I}}$

$$ \begin{aligned} & =\frac{0.2}{3.4}+\frac{0.005}{0.085} \\ & =0.059 \pm 0.059=0.118 \\ & \therefore \Delta \mathrm{R}=(0.118 \times 40) \Omega=4.72 \Omega \\ & \quad \approx 5 \Omega \\ & \therefore \mathrm{R} \cong(40 \pm 5) \Omega \end{aligned} $$

72. The resistance, $R$, of a wire has been measured as $(40.0 \pm 0.02) \Omega$. Its length, and radius, have been measured as

$$ \ell=(120.0 \pm 0.1) \mathrm{cm} \text { and } \mathrm{r}=(2.00 \pm 0.01) \mathrm{mm} $$

The relative percentage error in the resistivity, $\rho\left(\rho=\frac{\mathrm{R} \ell}{\pi \mathrm{r}^{2}}\right)$, of the material of this wire, would be:

(1) $6.08 \%$

(2) $1.6 \%$

(3) $1.08 \%$

(4) $0.6 \%$

Show Answer

Correct answer: (2)

Solution:

We have, $\rho=\frac{\mathrm{R} \ell}{\pi \mathrm{r}^{2}}$

$$ \begin{aligned} & \therefore \frac{\Delta \rho}{\rho}=\frac{\Delta \mathrm{R}}{\mathrm{R}}+\frac{\Delta \ell}{\ell}+2 \frac{\Delta \mathrm{r}}{\mathrm{r}} \\ & =\frac{0.2}{40.0}+\frac{0.1}{120.0}+2 \times \frac{0.01}{2.00} \\ & =0.005+0.008+0.01 \\ & =0.0158 \end{aligned} $$

$\therefore$ Relative percentage error

$$ \simeq 1.6 \% $$

73. If mass (M), permittivity $\left(\varepsilon _{0}\right)$, permeability $\left(\mu _{0}\right)$ and Planck’s constant $(\mathbf{h})$, are taken as the fundamental units, the dimensions of length $(L)$, would be:

(1) $[\mathrm{L}]=\left[\mathrm{M}^{-1} \mathrm{~h} \varepsilon _{0}^{1 / 2} \mu _{0}^{1 / 2}\right]$

(2) $[\mathrm{L}]=\left[\mathrm{Mh}^{-1} \varepsilon _{0}^{1 / 2} \mu _{0}^{1 / 2}\right]$

(3) $[\mathrm{L}]=\left[\mathrm{Mh} \varepsilon _{0}^{-1 / 2} \mu _{0}^{-1 / 2}\right]$

(4) $[\mathrm{L}]=\left[\mathrm{M}^{-1} \mathrm{~h}^{-1} \varepsilon _{0}^{1 / 2} \mu _{0}^{-1 / 2}\right]$

Show Answer

Correct answer: (1)

Solution:

We have

$$ \left[\varepsilon _{0}\right]=\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{I}^{2}\right] $$

$$ \begin{aligned} & {\left[\mu _{0}\right]=\left[\mathrm{MLT}^{-2} \mathrm{I}^{-2}\right]} \\ & {[\mathrm{h}]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-1}\right]} \\ & \therefore\left[\varepsilon _{0} \mu _{0}\right]=\left[\mathrm{L}^{-2} \mathrm{~T}^{2}\right] \end{aligned} $$

Also, $[\mathrm{h}]=\left[\mathrm{ML}^{2} \mathrm{~T}^{-1}\right]$

$$ \begin{aligned} & \therefore \mathrm{h}^{2}=\mathrm{M}^{2} \mathrm{~L}^{4} \mathrm{~T}^{-2} \\ & \therefore\left(\varepsilon _{0} \mu _{0}\right) \mathrm{h}^{2}=\mathrm{M}^{2} \mathrm{~L}^{2} \\ & \therefore[\mathrm{L}]=\left(\frac{\varepsilon _{0} \mu _{0} \mathrm{~h}^{2}}{\mathrm{M}^{2}}\right)^{1 / 2} \\ & \quad=\left[\varepsilon _{0}^{1 / 2} \mu _{0}^{1 / 2} \mathrm{hM}^{-1}\right] \end{aligned} $$

74. The rate of flow of heat $(\mathrm{Q})$, through a conductor, depends on the coefficient of thermal conductivity ( $\sigma$ ), area of cross section (A), temperature difference across the two ends of the rod $(\Delta \theta)$, and the length $(\Delta \ell)$ of the conductor. The relevant formula

$$ \mathrm{Q}=\sigma \mathrm{A} \frac{\Delta \theta}{\Delta \ell} $$

is used to determine $\sigma$ experimentally. The relative percentage errors, in the measurement of different quantities, are as follow:

Flowing heat energy $=2 \%$

Time for which heat flows $=\mathbf{0 . 2} \%$

Temperature difference $=\mathbf{2 \%}$

Length of the rod $=\mathbf{0 . 5 \%}$

Area of cross section of the $\mathrm{rod}=\mathbf{0 . 5 \%}$

The relative percentage error, in the determination of $\sigma$, would be

(1) $0.2 \%$

(2) $5.2 \%$

(3) $0.4 \%$

(4) $2.6 \%$

Show Answer

Correct answer: (2)

Solution:

The relation

$$ \mathrm{Q}=\sigma \mathrm{A} \frac{\Delta \theta}{\Delta \ell} $$

can be rewritten as

$$ \begin{aligned} & \sigma=\left(\frac{\Delta \mathrm{H}}{\Delta \ell}\right) \cdot \frac{\Delta \ell}{\mathrm{A}(\Delta \theta)} \quad\left(\because \mathrm{Q}=\frac{\Delta \mathrm{H}}{\Delta \mathrm{t}}\right) \\ & \therefore \frac{\Delta \sigma}{\sigma}=\frac{\Delta \mathrm{H}}{\mathrm{H}}+\frac{\Delta \mathrm{t}}{\mathrm{t}}+\frac{\Delta(\Delta \ell)}{(\Delta \ell)}+\frac{\Delta(\Delta \theta)}{(\Delta \theta)}+\frac{\Delta \mathrm{A}}{\mathrm{A}} \\ & =2 \%+0.2 \%+0.5 \%+2 \%+0.5 \% \\ & =5.2 \% \end{aligned} $$

75. A dimensionless number $\left(\mathrm{N} _{\mathrm{R}}\right)$, called Reynold’s number, can be made from a suitable combination of $r$ (radius of the tube), $\rho$ (density of the liquid), $v$ (velocity of the fluid) and $\eta$ (the coefficient of viscosity of the liquid). The relative percentage errors, in the measurement of $r, \rho, v$ and $\eta$ are found to be $0.4 \%, 1.5 \%, 2 \%$ and $2.5 \%$ respectively.

The formula, for $\mathrm{N} _{\mathrm{R}}$, and the relative percentage error in its calculated value, are equal, respectively, to:

(1) $\mathrm{N} _{\mathrm{R}}=\frac{\mathrm{r} \rho v}{\eta} ; \quad \frac{\Delta \mathrm{N} _{\mathrm{R}}}{\mathrm{N} _{\mathrm{R}}}=6.4 \%$

(2) $\mathrm{N} _{\mathrm{R}}=\mathrm{r} \rho v \eta ; \quad \frac{\Delta \mathrm{N} _{\mathrm{R}}}{\mathrm{N} _{\mathrm{R}}}=1.4 \%$

(3) $\mathrm{N} _{\mathrm{R}}=\frac{\mathrm{r} \rho v}{\eta} ; \quad \frac{\Delta \mathrm{N} _{\mathrm{R}}}{\mathrm{N} _{\mathrm{R}}}=1.4 \%$

(4) $\mathrm{N} _{\mathrm{R}}=\operatorname{r\rho p\eta } ; \quad \frac{\Delta \mathrm{N} _{\mathrm{R}}}{\mathrm{N} _{\mathrm{R}}}=6.4 \%$

Show Answer

Correct answer: (1)

Solution:

We know that $[\mathrm{r}]=[\mathrm{L}] ;[\rho]=\left[\mathrm{ML}^{-3}\right]$

$$ [v]=\left[\mathrm{LT}^{-1}\right] ; \eta=\left[\mathrm{ML}^{-1} \mathrm{~T}^{-1}\right] $$

These give $\left[\frac{\mathrm{r} \rho v}{\eta}\right]$ as a dimensionless combination.

Thus $\mathrm{N} _{\mathrm{R}}=\frac{\mathrm{r} \rho v}{\eta}$

$$ \begin{aligned} & \therefore \frac{\Delta \mathrm{N} _{\mathrm{R}}}{\mathrm{N} _{\mathrm{R}}}=\frac{\Delta \mathrm{r}}{\mathrm{r}}+\frac{\Delta \rho}{\rho}+\frac{\Delta v}{v}+\frac{\Delta \eta}{\eta} \\ & =0.4 \%+1.5 \%+2 \%+2.5 \%=6.4 \% \end{aligned} $$

76. Stefan’s law, $E=\sigma T^{4}(E=$ energy radiated per unit area per unit time; $T=$ temperature of black body), and Wien’s displacement law $\lambda _{\mathrm{m}} \mathrm{T}=\mathrm{b}\left(\lambda _{\mathrm{m}}=\right.$ wavelength of maximum emission, $T=$ temperature) are used to define the Stefan’s constant,$\sigma$, and the Wien’s constant, $b$. If $\sigma, b$, along with mass and time, are taken as the ‘base units’ the dimensions of the ’thermal capacity’ $\left(\mathrm{C} _{\mathrm{m}}\right)$ of a body, would be:

(1) $\left[\mathrm{b}^{1 / 2} \mathrm{MT}^{-3} \sigma^{-5}\right]$

(2) $\left[b^{1 / 2} \sigma^{1 / 2} M^{-1} T^{-2}\right]$

(3) $\left[\mathrm{M}^{3 / 2} \mathrm{~b} \sigma^{-1 / 2} \mathrm{~T}^{-7 / 2}\right]$

(4) $\left[\mathrm{M}^{3 / 2} \mathrm{~b}^{-1 / 2} \sigma \mathrm{T}^{-5 / 2}\right]$

Show Answer

Correct answer: (3)

Solution:

We have

$$ \begin{aligned} & {[\sigma]=\frac{[\mathrm{E}]}{\left[\mathrm{T}^{4}\right]}=\left[\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{~L}^{2} \mathrm{~T}}\right] \mathrm{K}^{-4}\right]} \\ & =\left[\mathrm{MT}^{-3} \mathrm{~K}^{-4}\right] \quad \therefore \mathrm{K}=\left[\sigma \mathrm{M}^{-1} \mathrm{~T}^{3}\right]^{-1 / 4} \end{aligned} $$

and

$$ \begin{aligned} & {[\mathrm{b}]=\left[\lambda _{\mathrm{m}}^{\mathrm{T}}\right]=[\mathrm{LK}]} \\ & \therefore[\mathrm{L}]=\left[\mathrm{bK}^{-1}\right] \end{aligned} $$

Now thermal capacity $=\left[\mathrm{C} _{\mathrm{m}}\right]=\left[\frac{\text { Heat energy }}{\text { Change in Temperature }}\right]$

$$ \begin{aligned} & =\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{~K}}\right]=\mathrm{M}\left[\mathrm{bK}^{-1}\right]^{2} \mathrm{~T}^{-2}\left(\mathrm{~K}^{-1}\right) \\ & =\mathrm{MbT}^{-2}\left(\sigma \mathrm{M}^{-1} \mathrm{~T}^{3}\right)^{-1 / 2} \\ & =\left[\mathrm{M}^{1 / 2} \mathrm{~b} \sigma^{-1 / 2} \mathrm{~T}^{-7 / 2}\right] \end{aligned} $$

77. If the velocity of light $(C)$, the charge of the electron (e), time ( $T$ ), and the universal gravitational constant (G) were taken as the ‘base ‘units’, the dimensions of ‘moment of inertia’ and electrical potential $(\mathrm{V})$ would be:

(1) $\left[\mathrm{GC}^{-5} \mathrm{~T}^{3}\right]$ and $\left[\mathrm{G}^{-1} \mathrm{C}^{-5} \mathrm{Te}\right]$, respectively

(2) $\left[\mathrm{G}^{-1} \mathrm{C}^{5} \mathrm{~T}^{3}\right]$ and $\left[\mathrm{G}^{-1} \mathrm{C}^{5} \mathrm{Te}^{-1}\right]$, respectively

(3) $\left[\mathrm{GC}^{-5} \mathrm{~T}^{-3}\right]$ and $\left[\mathrm{GC}^{-5} \mathrm{Te}\right]$, respectively

(4) $\left[\mathrm{G}^{-1} \mathrm{C}^{-5} \mathrm{~T}^{3}\right]$ and $\left[\mathrm{GC}^{5} \mathrm{~T}^{-1} \mathrm{e}\right]$, respectively

Show Answer

Correct answer: (2)

Solution:

We have,

$$ \begin{aligned} & {[\mathrm{C}]=\left[\mathrm{LT}^{-1}\right]} \\ & {[\mathrm{e}]=[\mathrm{IT}]} \\ & {[\mathrm{G}]=\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right]} \\ & \therefore[\mathrm{T}]=\left[\mathrm{eT}^{-1}\right] \\ & {[\mathrm{L}]=[\mathrm{CT}]} \end{aligned} $$

and $[\mathrm{M}]=\left[\mathrm{G}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right]$

$\therefore[$ Moment of inertia $]=\left[\mathrm{ML}^{2}\right]$

$$ \begin{aligned} & =\left[\mathrm{G}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2} \mathrm{~L}^{2}\right]=\left[\mathrm{G}^{-1} \mathrm{~L}^{5} \mathrm{~T}^{-2}\right] \\ & =\left[\mathrm{G}^{-1} \mathrm{C}^{5} \mathrm{~T}^{5} \mathrm{~T}^{-2}\right]=\left[\mathrm{G}^{-1} \mathrm{C}^{5} \mathrm{~T}^{3}\right] \end{aligned} $$

and $[$ Electrical potential $]=[\mathrm{V}]=\left(\frac{\text { Work }}{\text { Charge }}\right)$

$$ \begin{aligned} & =\left[\frac{\mathrm{ML}^{2} \mathrm{~T}^{-2}}{\mathrm{IT}}\right]=\left[\frac{\left(\mathrm{G}^{-1} \mathrm{C}^{3} \mathrm{~T}^{3} \mathrm{~T}^{-2}\right)\left(\mathrm{C}^{2} \mathrm{~T}^{2}\right) \mathrm{T}^{-2}}{\mathrm{e}}\right] \\ & {\left[\mathrm{G}^{-1} \mathrm{C}^{5} \mathrm{Te}^{-1}\right]} \end{aligned} $$

78. To find the density of a given material, a solid cuboid of the material was taken and its dimensions as well as its mass were measured. The result of the measurement were:

$$ \begin{aligned} & \ell=(5.10 \pm 0.05) \mathrm{cm} \\ & b=(3.25 \pm 0.05) \mathrm{cm} \\ & h=(1.40 \pm 0.01) \mathrm{cm} \\ & \mathrm{m}=(185.450 \pm 0.002) \mathrm{g} \end{aligned} $$

The volume (V), of the cuboid, and the density $\rho$, of the material equal, respectively.

(1) $(32.2 \pm 0.74) \mathrm{cm}^{3}$ and $(7.99 \pm 0.24) \mathrm{g} / \mathrm{cm}^{3}$

(2) $(23.21 \pm 0.74) \mathrm{cm}^{3}$ and $(8.0 \pm 0.2) \mathrm{g} / \mathrm{cm}^{3}$

(3) $(23.21 \pm 0.74) \mathrm{cm}^{3}$ and $(7.99 \pm 0.24) \mathrm{g} / \mathrm{cm}^{3}$

(4) $(23.2 \pm 0.7) \mathrm{cm}^{3}$ and $(8.0 \pm 0.2) \mathrm{g} / \mathrm{cm}^{3}$

Show Answer

Correct answer: (4)

Solution:

We have, $\mathrm{V}=\ell \mathrm{bh}$

$$ =(5.10 \times 3.25 \times 1.40) \mathrm{cm}^{3}=23.205 \mathrm{~cm}^{3} $$

Also, $\frac{\Delta \mathrm{V}}{\mathrm{V}}=\frac{\Delta \ell}{\ell}+\frac{\Delta \mathrm{b}}{\mathrm{b}}+\frac{\Delta \mathrm{h}}{\mathrm{h}}$

$$ \begin{aligned} & =\frac{0.05}{5.10}+\frac{0.05}{3.25}+\frac{0.01}{1.40} \\ & =0.0098+0.0154+0.0071 \simeq 0.032 \end{aligned} $$

$$ \therefore \Delta \mathrm{V}=0.302 \times 23.205 \mathrm{~cm}^{3} \simeq 0.74 \mathrm{~cm}^{3} $$

We, therefore, write

$$ \mathrm{V}=(23.2 \pm 0.7) \mathrm{cm}^{3} $$

Now density,

$$ \begin{aligned} & \mathrm{d}=\frac{\text { mass }}{\text { volume }}=\frac{185.45}{23.2} \mathrm{~g} / \mathrm{cm}^{3} \\ & =7.99 \mathrm{~g} / \mathrm{cm}^{3} \end{aligned} $$

Also, $\frac{\Delta(\mathrm{d})}{\mathrm{d}}=\frac{\Delta \mathrm{m}}{\mathrm{m}}+\frac{\Delta \mathrm{V}}{\mathrm{V}}$

$$ \begin{aligned} & =\frac{0.002}{185.450}+\frac{0.7}{23.2} \\ & =0.00001+0.03 \simeq 0.03 \\ & \therefore \Delta \mathrm{d}=0.03 \times 7.99 \mathrm{~g} / \mathrm{cm}^{3} \simeq 0.24 \mathrm{~g} / \mathrm{cm}^{3} \end{aligned} $$

We, therefore, write

$$ \mathrm{d}=(8.0 \pm 0.2) \mathrm{g} / \mathrm{cm}^{3} $$

79. The moment of inertia $\mathrm{I}\left(=\right.$ mass $\left.\times(\text { radius) })^{2}\right)$ of a hollow spherical ball of mass $\mathrm{M}(=(500 \pm 1) \mathrm{g})$, has been calculated out to be $\left((8000 \pm 56) \mathrm{g}-\mathrm{cm}^{2}\right)$. The reported value of $I$, and the least count of the instrument used for measuring the radius $(r)$, should then be:

(1) $(8000 \pm 56) \mathrm{g}-\mathrm{cm}^{2}$ and $0.01 \mathrm{~cm}$, respectively

(2) $(8000 \pm 56) \mathrm{g}-\mathrm{cm}^{2}$ and $0.02 \mathrm{~cm}$, respectively

(3) $(8000 \pm 60) \mathrm{g}-\mathrm{cm}^{2}$ and $0.02 \mathrm{~cm}$, respectively

(4) $(8000 \pm 50) \mathrm{g}-\mathrm{cm}^{2}$ and $0.01 \mathrm{~cm}$, respectively

Show Answer

Correct answer: (1)

Solution:

We have, $\mathrm{I}=\mathrm{M} \mathrm{r}^{2}$

$$ \therefore \mathrm{r}^{2}=\frac{8000}{500} \mathrm{~cm}^{2}=16 \mathrm{~cm}^{2} \quad \therefore \mathrm{r}=4 \mathrm{~cm} $$

Also, $\frac{\Delta \mathrm{I}}{\mathrm{I}}=\frac{\Delta \mathrm{M}}{\mathrm{M}}+2 \frac{\Delta \mathrm{r}}{\mathrm{r}}$

$$ \therefore\left(\frac{56}{8000}\right)=\left(\frac{1}{500}+2 \frac{\Delta \mathrm{r}}{\mathrm{r}}\right) $$

This gives $\frac{\Delta \mathrm{r}}{\mathrm{r}}=\frac{1}{2}[0.007-0.002]=\frac{1}{2} \times 0.005$

$$ \therefore \Delta \mathrm{r}=\left[\frac{1}{2} \times .005\right] \times 4=0.01 \mathrm{~cm} $$

The least count of the instrument, used for measuring the radius, is, therefore, $0.01 \mathrm{~cm}$.

80. The dimensional formula, of the term

$$ \mathrm{Z}=\left(\frac{\mathrm{e}^{4} v}{\varepsilon _{0}^{2} \mathrm{~m} _{\mathrm{p}} \mathrm{m} _{\mathrm{e}}^{2} \mathrm{c}^{3} \mathrm{G}}\right) $$

(where $\mathbf{e}=$ charge of electron, $v=$ frequency, $\varepsilon _{0}=$ permittivity, $\mathrm{m} _{\mathrm{p}}=$ mass of proton, $m _{e}=$ mass of electron, $C=$ velocity of light, $G=$ universal gravitational constant) and the ratio, of its values, is the SI and CGS units, are:

(1) $[\mathrm{Z}]=\left[\mathrm{M}^{-2} \mathrm{LT}^{0} \mathrm{I}^{0}\right]$ and $10^{1 / 2}$, respectively

(2) $[\mathrm{Z}]=\left[\mathrm{M}^{-1} \mathrm{~L}^{2} \mathrm{TI}^{0}\right]$ and 10 , respectively

(3) $[\mathrm{Z}]=\left[\mathrm{M}^{-1} \mathrm{LT}^{3} \mathrm{I}^{0}\right]$ and $10^{-1}$, respectively

(4) $\quad[Z]=\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0} \mathrm{I}^{0}\right]$ and $10^{\circ}$, respectively

Show Answer

Correct answer: (4)

Solution:

We have,

$$ \begin{aligned} & {[\mathrm{e}]=[\mathrm{IT}] ;[\mathrm{v}]=\left[\mathrm{T}^{-1}\right]} \\ & {\left[\varepsilon _{0}\right]=\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{I}^{2}\right] ;\left[\mathrm{m} _{\mathrm{p}}\right]=[\mathrm{M}] ;\left[\mathrm{m} _{\mathrm{e}}\right]=[\mathrm{M}]} \\ & {[\mathrm{C}]=\left[\mathrm{LT}^{-1}\right] ;[\mathrm{G}]=\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right]} \\ & \therefore[\mathrm{Z}]=\frac{\left[\mathrm{I}^{4} \mathrm{~T}^{4}\right]\left[\mathrm{T}^{-1}\right]}{\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{I}^{2}\right]^{2}\left[\mathrm{M}^{3}\right]\left[\mathrm{L}^{3} \mathrm{~T}^{-3}\right]\left[\mathrm{M}^{-1} \mathrm{~L}^{3} \mathrm{~T}^{-2}\right]} \\ & \quad=\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0} \mathrm{I}^{0}\right] \end{aligned} $$

This $\mathrm{Z}$ is a dimensionless term.

$\therefore$ The ratio of its values, in the SI and CGS units, is 1 or $10^{\circ}$.

Unit 01 Physics And Measurements

The ‘Need’ for Measurements

The ‘Measurement Process’

Unit

Standard

Fundamental Units

Derived Units

Number of the Fundamental Units

Systems of Units

The SI Units

Multiples and Sub-multiples in SI

Derived SI Units of Some Important Physical Quantities

For example:

Names of Some Units in General Use

Dimensions

Dimensional Formula

Dimensional Analysis

The last of these uses, however, has two built in limitations:

Principle of Dimensional Homogenity

Least Count

Precision in Measurements

Accuracy of a Measurement

Errors in Measurement

Systematic and Random Errors

Normal, or Gaussian, Law

Absolute Error

Relative Error

Percentage Error

Combination of Errors

Rule for Addition / Subtraction

Rule for Multiple / Division

Additional Notes

A. Significant Figures

Average / Mean Error:

Mean Sqaure Error:

Root Mean Square Error:

Standard Deviation

ADDITIONAL EXAMPLES

PROBLEMS FOR PRACTICE (SET-I)

PROBLEMS FOR PRACTICES (SET-II)

Question Bank

Key Learning Points

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Mentorship

NCERT Exercise Video Solution

Menu