Three Dimensional Geometry
Position Vector
The position vector of the point $P(x, y, z)$ from $O(0,0,0)$ is written as $\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$ and $\mathrm{OP}=|\overrightarrow{\mathrm{r}}|=\sqrt{\mathrm{x}^{2}+\mathrm{y}^{2}+\mathrm{z}^{2}}$
Direction cosine and direction ratios of a line
Direction cosine of a line has same meaning as d. $\mathrm{c}^{\prime} \mathrm{s}$ of a vector. If $\ell, \mathrm{m}, \mathrm{n}$ are the d. $\mathrm{c}^{\prime} \mathrm{s}$ of $\overrightarrow{\mathrm{r}}$ along OX, OY \& OZ then $\mathrm{x}=\ell \mathrm{r}, \mathrm{y}=\mathrm{mr}$ and $\mathrm{z}=\mathrm{nr}$ and $\ell^{2}+\mathrm{m}^{2}+\mathrm{n}^{2}=1$
Any three numbers $\mathrm{a}, \mathrm{b}, \mathrm{c}$ proportional to $\mathrm{d} . \mathrm{c}^{\prime} \mathrm{s}$ are direction ratios
i.e. $\dfrac{\ell}{\mathrm{a}}=\dfrac{\mathrm{m}}{\mathrm{b}}=\dfrac{\mathrm{n}}{\mathrm{c}}= \pm \dfrac{1}{\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}+\mathrm{c}^{2}}}$, same sign (either $+\mathrm{ve}$ or $-\mathrm{ve}$ ) should be taken throughout. Direction ratios of a line joining $\left(\mathrm{x} _{1}, \mathrm{y} _{1}, \mathrm{z} _{1}\right) \&\left(\mathrm{x} _{2}, \mathrm{y} _{2}, \mathrm{z} _{2}\right)$ are proportional to $\mathrm{x} _{2}-\mathrm{x} _{1}, \mathrm{y} _{2}-\mathrm{y} _{1}, \mathrm{z} _{2}-\mathrm{z} _{1}$. If $a _{1}, b _{1}, c _{1} \& a _{2}, b _{2}, c _{2}$ be the d. $c^{\prime} s$ of two lines, then the acute angle $\theta$ between them is given by $\cos \theta=\dfrac{\left|\mathrm{a} _{1} \mathrm{a} _{2}+\mathrm{b} _{1} \mathrm{~b} _{2}+\mathrm{c} _{1} \mathrm{c} _{2}\right|}{\sqrt{\mathrm{a} _{1}{ }^{2}+\mathrm{b} _{1}{ }^{2}+\mathrm{c} _{1}{ }^{2}} \sqrt{\mathrm{a} _{2}{ }^{2}+\mathrm{b} _{2}{ }^{2}+\mathrm{c} _{2}{ }^{2}}}$
Straight line in space
Equation of straight line is space is given by
| Given | Vector Equation | Cartesian equation |
|---|---|---|
| Point on the line $\vec{a}$ i.e. $\left(x _{t}, y _{1}, z _{1}\right)$ & $\|^{e l}$ vector $\vec{b}$ i.e.d. $r^{\prime} s$ of $\|^{\text {el line } a, b, c}$ | $\overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{a}}+\lambda \overrightarrow{\mathrm{b}}$ | $\dfrac{x-x _{1}}{a}=\dfrac{y-y _{1}}{b}=\dfrac{z-z _{1}}{c}$ |
| Two points $\vec{a}$ & $\vec{b}$ i.e. $\left(x _{1}, y _{1}, z _{1}\right)$ & $\quad\left(x _{2}, y _{2}, z _{2}\right)$ | $\overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{a}}+\lambda(\overrightarrow{\mathrm{b}}-\overrightarrow{\mathrm{a}})$ | $\dfrac{\mathrm{x}-\mathrm{x} _{1}}{\mathrm{x} _{2}-\mathrm{x} _{1}}=\dfrac{\mathrm{y}-\mathrm{y} _{1}}{\mathrm{y} _{2}-\mathrm{y} _{1}}=\dfrac{\mathrm{z}-\mathrm{z} _{1}}{\mathrm{z} _{2}-\mathrm{z} _{1}}$ |
PLANE
Equation of plane is given by
| Given | Vector equation | Cartesian equation |
|---|---|---|
| Point on the plane $\vec{a}$ i.e. $\left(x _{t}, y _{1}, z _{1}\right)$ Normal $\vec{n}=a \hat{i}+b \hat{j}+c \hat{k}$ | $\overrightarrow{\mathrm{r}} \cdot \overrightarrow{\mathrm{n}}=\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{n}}$ | $\mathrm{a}\left(\mathrm{x}-\mathrm{x} _{1}\right)+\mathrm{b}\left(\mathrm{y}-\mathrm{y} _{1}\right)+\mathrm{c}\left(\mathrm{z}-\mathrm{z} _{1}\right)=0$ |
| $\mathrm{d}, \perp \mathrm{r}$ distance from $(0,0,0)$ $\hat{\mathrm{n}}=\ell \hat{\mathrm{i}}+\mathrm{m} \hat{\mathrm{j}}+\mathrm{n} \hat{\mathrm{k}}$ unit normal to the plane | $\overrightarrow{\mathrm{r}} \cdot \hat{\mathrm{n}}=\mathrm{d}$ | $\ell \mathrm{x}+\mathrm{my}+\mathrm{nz}=\mathrm{d}$ |
| Three points $\vec{a}, \vec{b}, \vec{c}$ | $\overrightarrow{\mathrm{r}}=(1-\lambda-\mu) \overrightarrow{\mathrm{a}}$ | $\left|\begin{array}{ccc}\mathrm{x}-\mathrm{x} _{1} & \mathrm{y}-\mathrm{y} _{1} & \mathrm{z}-\mathrm{z} _{1} \\ \mathrm{x} _{2}-\mathrm{x} _{1} & \mathrm{y} _{2}-\mathrm{y} _{1} & \mathrm{z} _{2}-\mathrm{z} _{1} \\ \mathrm{x} _{3}-\mathrm{x} _{1} & \mathrm{y} _{3}-\mathrm{y} _{1} & \mathrm{z} _{3}-\mathrm{z} _{1}\end{array}\right|=\mathbf{0}$ |
| $\left(\mathrm{x} _{1}, \mathrm{y} _{1}, \mathrm{z} _{1}\right),\left(\mathrm{x} _{2}, \mathrm{y} _{2}, \mathrm{z} _{2}\right)$ & $\left(\mathrm{x} _{3}, \mathrm{y} _{3}, \mathrm{z} _{3}\right)$ | $+\lambda \vec{b}+\mu \vec{c}$ | |
| Point $\overrightarrow{\mathrm{a}}$ & $||^{\text {el }}$ to $\vec{b}$ & $\vec{c}$ | $\overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{a}}+\lambda \overrightarrow{\mathrm{b}}+\mu \overrightarrow{\mathrm{c}}$ i.e. $(\overrightarrow{\mathrm{r}}-\overrightarrow{\mathrm{a}}) \cdot \overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{c}}=0$ | (parametric form) $\lambda, \mu$ are scalars (non parametric farm) |
| Intercepts a, b, & c | $\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1$ |
Equation of the plane passing through the line of intersection of $\mathrm{a} _{1} \mathrm{x}+\mathrm{b} _{1} \mathrm{y}+\mathrm{c} _{1} \mathrm{z}+\mathrm{d} _{1}=0$ and $\mathrm{a} _{2} \mathrm{x}+\mathrm{b} _{2} \mathrm{y}+\mathrm{c} _{2} \mathrm{z}+\mathrm{d} _{2}=0$ is $\left(\mathrm{a} _{1} \mathrm{x}+\mathrm{b} _{1} \mathrm{y}+\mathrm{c} _{1} \mathrm{z}+\mathrm{d} _{1}\right)+\lambda\left(\mathrm{a} _{2} \mathrm{x}+\mathrm{b} _{2} \mathrm{y}+\mathrm{c} _{2} \mathrm{z}+\mathrm{d} _{2}\right)=0$
Plane parallel to $\mathrm{ax}+\mathrm{by}+\mathrm{cz}+\mathrm{d}=0$ is $\mathrm{ax}+\mathrm{by}+\mathrm{cz}+\lambda=0$
Angle of intersection
Angle between
(i) two lines $\dfrac{x-x _{1}}{a _{1}}=\dfrac{y-y _{1}}{b _{1}}=\dfrac{z-z _{1}}{c _{1}}$ & $\dfrac{x-x _{2}}{a _{2}}=\dfrac{y-y _{2}}{b _{2}}=\dfrac{z-z _{2}}{c _{2}}$ is given by $\cos \theta=\dfrac{a _{1} a _{2}+b _{1} b _{2}+c _{1} c _{2}}{\sqrt{a _{1}{ }^{2}+b _{1}{ }^{2}+c _{1}{ }^{2}} \sqrt{a _{2}{ }^{2}+b _{2}{ }^{2}+c _{2}{ }^{2}}}$
(ii) two planes $\mathrm{a} _{1} \mathrm{x}+\mathrm{b} _{1} \mathrm{y}+\mathrm{c} _{1} \mathrm{z}+\mathrm{d} _{1}=0$ & $\mathrm{a} _{2} \mathrm{x}+\mathrm{b} _{2} \mathrm{y}+\mathrm{c} _{2} \mathrm{z}+\mathrm{d} _{2}=0$ given by $\cos \theta=\dfrac{a _{1} a _{2}+b _{1} b _{2}+c _{1} c _{2}}{\sqrt{a _{1}{ }^{2}+b _{1}{ }^{2}+c _{1}{ }^{2}} \sqrt{a _{2}{ }^{2}+b _{2}{ }^{2}+c _{2}{ }^{2}}}$
(iii) line $\dfrac{x-x _{1}}{a _{1}}=\dfrac{y-y _{1}}{b _{1}}=\dfrac{z-z _{1}}{z _{1}}$ & plane $a _{2} x+b _{2} y+c _{2} z+d _{2}=0$ is
given by $\sin \theta=\dfrac{a _{1} a _{2}+b _{1} b _{2}+c _{1} c _{2}}{\sqrt{a _{1}{ }^{2}+b _{1}{ }^{2}+c _{1}{ }^{2}} \sqrt{a _{2}{ }^{2}+b _{2}{ }^{2}+c _{2}{ }^{2}}}$
Distance of a point $\left(\mathrm{x} _{1}, \mathrm{y} _{1}, \mathrm{z} _{1}\right)$ from
$\mathrm{ax}+\mathrm{by}+\mathrm{cz}+\mathrm{d}=0 \text { is }\left|\dfrac{\mathrm{ax} _{1}+\mathrm{by} _{1}+\mathrm{cz} \mathrm{z} _{1}+\mathrm{d}}{\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}+\mathrm{c}^{2}}}\right|$
Distance of a point $P\left(x _{2}, y _{2}, z _{2}\right)$ from $\dfrac{x-x _{1}}{a}=\dfrac{y-y _{1}}{b}=\dfrac{z-z _{1}}{c}$ is given by
$d=\dfrac{|\overrightarrow{P A} \times \vec{b}|}{|\vec{b}|} \text { where } A \text { is }\left(x _{1}, y _{1}, z _{1}\right)$ & $\vec{b}=a \hat{i}+b \hat{j}+c \hat{k}$
- Distance between parallel planes
$ax + by +c z+d _{1}=0$ & $ ax + by +c z+d _{2}=0 $ is given by $\dfrac{\left|d _{1}-d _{2}\right|}{\sqrt{a^{2}+b^{2}+c^{2}}}$
- Shortest distance between two skew lines $\vec{r}=\vec{a} _{1}+\lambda \vec{b} _{1}, \vec{r}=\vec{a} _{2}+\mu \vec{b} _{2}$, is given by
S.D $=\left|\dfrac{\left(\overrightarrow{\mathrm{a}} _{2}-\overrightarrow{\mathrm{a}} _{1}\right) \overrightarrow{\mathrm{b}} _{1} \times \overrightarrow{\mathrm{b}} _{2}}{\left|\overrightarrow{\mathrm{b}} _{1} \times \overrightarrow{\mathrm{b}} _{2}\right|}\right|$
- Distance between two parallel lines $\vec{r}=\vec{a} _{1}+\lambda \vec{b}$ & $\vec{r}=\vec{a} _{2}+\mu \vec{b}$ is given by
$\overrightarrow{\mathrm{r}}=\dfrac{\left|\left(\overrightarrow{\mathrm{a}} _{2}-\overrightarrow{\mathrm{a}} _{1}\right) \times \overrightarrow{\mathrm{b}}\right|}{|\overrightarrow{\mathrm{b}}|}$
- Image $(\alpha, \beta, \gamma)$ of $\left(x _{2}, y _{2}, z _{2}\right)$ in a straight line $\dfrac{x-x _{1}}{a}=\dfrac{y-y _{1}}{b}=\dfrac{z-z _{1}}{c}$ is given by,
$\begin{aligned} & \alpha=2\left(\mathrm{a} \lambda+\mathrm{x} _{1}\right)-\mathrm{x} _{2}, \beta=2\left(\mathrm{~b} \lambda+\mathrm{y} _{1}\right)-\mathrm{y} _{2} ; \gamma=2\left(\mathrm{c} \lambda+\mathrm{z} _{1}\right)-\mathrm{z} _{2} \text { where } \\ & \lambda=\dfrac{\mathrm{a}\left(\mathrm{x} _{2}-\mathrm{x} _{1}\right)+\mathrm{b}\left(\mathrm{y} _{2}-\mathrm{y} _{1}\right)+\mathrm{c}\left(\mathrm{z} _{2}-\mathrm{z} _{1}\right)}{\mathrm{a}^{2}+\mathrm{b}^{2}+\mathrm{c}^{2}} \end{aligned}$
- Image of $\left(\mathrm{x} _{1} \mathrm{y} _{1} \mathrm{z} _{1}\right)$ in the plane $\mathrm{ax}+\mathrm{by}+\mathrm{cz}+\mathrm{d}=0$ is $(\mathrm{x}, \mathrm{y}, \mathrm{z})$ where
$\dfrac{\mathrm{x}-\mathrm{x} _{1}}{\mathrm{a}}=\dfrac{\mathrm{y}-\mathrm{y} _{1}}{\mathrm{~b}}=\dfrac{\mathrm{z}-\mathrm{z} _{1}}{\mathrm{c}}=\dfrac{-2\left|\mathrm{ax} _{1}+\mathrm{by} _{1}+\mathrm{cz} _{1}+\mathrm{d}\right|}{\mathrm{a}^{2}+\mathrm{b}^{2}+\mathrm{c}^{2}}$
Bisecting planes
Equation of the planes bisecting the angle between the planes $a _{1} x+b _{1} y+c _{1} z+d _{1}=0$ and $a _{2} x+b _{2} y+c _{2} z+d _{2}=0$ is $\dfrac{a _{1} x+b _{1} y+c _{1} z+d _{1}}{\sqrt{a _{1}{ }^{2}+b _{1}{ }^{2}+c _{1}{ }^{2}}}= \pm \dfrac{a _{2} x+b _{2} y+c _{2} z+d _{2}}{\sqrt{a _{2}{ }^{2}+b _{2}{ }^{2}+c _{2}{ }^{2}}}$
A program to give wings to girl students
Bisector of acute and obtuse angles between two planes
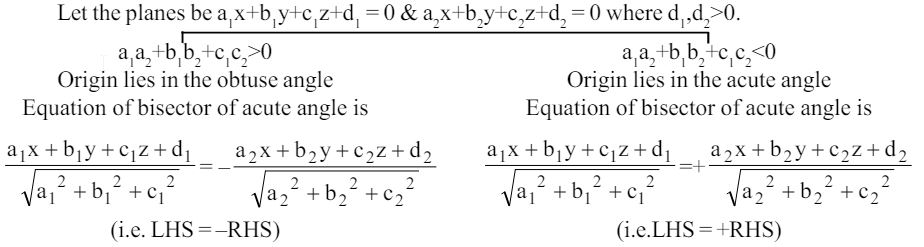
Line of Greatest slope
$\mathrm{AB}$ is the line of intersection of plane $\pi _{1}$ & $\pi _{2}$. Line of greatest slope on a given plane, drawn through $\mathrm{P}$ and perpendicular to the line of intersection of the given plane with any horizontal plane.
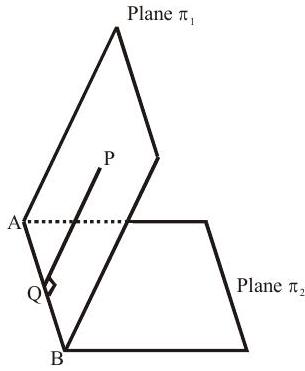
System of planes (Relationship between planes)
In $3 \mathrm{D}, 3$ planes are given by
$\pi _{1} \equiv \mathrm{a} _{1} \mathrm{x}+\mathrm{b} _{1} \mathrm{y}+\mathrm{c} _{1} \mathrm{z}+\mathrm{d} _{1}=0$
$\pi _{2} \equiv \mathrm{a} _{2} \mathrm{x}+\mathrm{b} _{2} \mathrm{y}+\mathrm{c} _{2} \mathrm{z}+\mathrm{d} _{2}=0$
$\pi _{2} \equiv \mathrm{a} _{3} \mathrm{x}+\mathrm{b} _{3} \mathrm{y}+\mathrm{c} _{3} \mathrm{z}+\mathrm{d} _{3}=0$
Let $\mathrm{r}$ & $\mathrm{~s}$ be the rank of coefficient matrix and augmented matrix
Case I
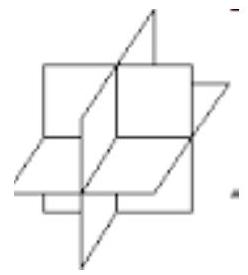
Planes intersect at a point if $r=3 \& s=3$
Case II
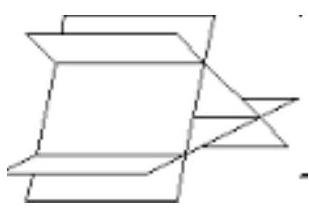
Each plane cut the other two in a line if $\mathrm{r}=2$ $\& s=3$. Planes form a prismatic surface
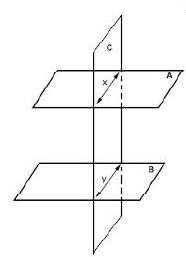
2. parallel planes and the other cuts each in aline.
Two rows of the coefficient matrix are proportional
$\dfrac{\mathrm{a}}{\mathrm{a}^{\ast}}=\dfrac{\mathrm{b}}{\mathrm{b}^{\ast}}=\dfrac{\mathrm{c}}{\mathrm{c}^{\ast}} \neq \dfrac{\mathrm{d}}{\mathrm{d}^{\ast}}$
Case III
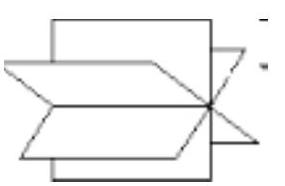
3planes interesting in a line if $\mathrm{r}=2 \& \mathrm{~s}=2$
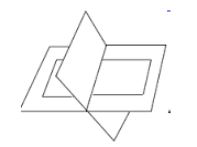
2 coincident planes \& the other intersecting them in a line if $\mathrm{r}=2 & \mathrm{~s}=2$ 2 rows of the augmented matrix are
proportional $\dfrac{\mathrm{a}}{\mathrm{a}^{\ast}}=\dfrac{\mathrm{b}}{\mathrm{b}^{\ast}}=\dfrac{\mathrm{c}}{\mathrm{c}^{\ast}}=\dfrac{\mathrm{d}}{\mathrm{d}^{\ast}}$
Case IV
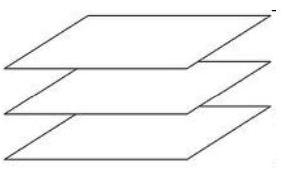
Three parallel planes if $\mathrm{r}=1 \mathrm{~s}=2$
Two coincident planes \& the other parallel if $\mathrm{r}=1, \mathrm{~s}=2$ Two rows of the argument matrix are proportional
$\dfrac{\mathrm{a}}{\mathrm{a}^{\ast}}=\dfrac{\mathrm{b}}{\mathrm{b}^{\ast}}=\dfrac{\mathrm{c}}{\mathrm{c}^{\ast}}=\dfrac{\mathrm{d}}{\mathrm{d}^{\ast}}$
Case V
3 coincident planes $\mathrm{r}=1 \& \mathrm{~s}=1$
SOLVED EXAMPLES
1. Find the image of $(1,3,4)$ in the plane $x+2 y-z+3=0$ is
(a) $(1,1,-6)$
(b) $(-1,-1,6)$
(c) $(-1,1-6)$
(d) None of these
Show Answer
Solution
Image of $\left(\mathrm{x} _{1}, \mathrm{y} _{1}, \mathrm{z} _{1}\right)$ in ax $+\mathrm{by}+\mathrm{cz}+\mathrm{d}=0$ is given by
$$ \begin{aligned} & \dfrac{x-x _{1}}{a}=\dfrac{y-y _{1}}{d}=\dfrac{z-z _{1}}{c}=\dfrac{\left.-2 \mid a _{1}+b _{1}+c _{1}+d\right) \mid}{a^{2}+b^{2}+c^{2}} \\ & \dfrac{x-1}{1}=\dfrac{y-3}{2}=\dfrac{z-4}{-1}=\dfrac{-2|1+6-4+3|}{1+4+1} \\ & \dfrac{x-1}{1}=\dfrac{y-3}{2}=\dfrac{z-4}{-1}=-2 \Rightarrow x=-1, y=-1, z=6 \end{aligned} $$
$\therefore$ image is $(-1,-1,6)$
Answer (b)
2. The distance of $\mathrm{P}(0,2,3)$ to the line $\overrightarrow{\mathrm{r}}=(3 \hat{\mathrm{i}}+\hat{\mathrm{j}}-1 \hat{\mathrm{k}})+\lambda(2 \hat{\mathrm{i}}+\hat{\mathrm{j}}+2 \hat{\mathrm{k}})$
$\mathrm{A}(3,1,-1), \mathrm{P}(0,2,3)$
Show Answer
$$ \begin{aligned} & \overrightarrow{\mathrm{b}}=2 \hat{\mathrm{i}}+\hat{\mathrm{j}}+2 \hat{\mathrm{k}} \\ & \overrightarrow{\mathrm{PA}} \times \overrightarrow{\mathrm{b}}=\left|\begin{array}{ccc} \hat{\mathrm{i}} & \hat{\mathrm{j}} & \hat{\mathrm{k}} \\ 3 & -1 & -4 \\ 2 & 1 & 2 \end{array}\right|=2 \hat{\mathrm{i}}-14 \hat{\mathrm{j}}+5 \hat{\mathrm{k}} \\ & \mathrm{d}=\dfrac{|\overrightarrow{\mathrm{PA}} \times \overrightarrow{\mathrm{b}}|}{|\overrightarrow{\mathrm{b}}|}=\dfrac{\sqrt{4+196+25}}{\sqrt{4+1+4}}=\dfrac{15}{3}=5 \text { units } \end{aligned} $$
Answer (a)
3. $\mathrm{ABCD}$ is a square of unit side. It is folded along the diagonal $\mathrm{AC}$ so that the plane $\mathrm{ABC}$ is perpendicular to the plane ACD. The shortest distance between the lines AB \& CD is
(a) $\sqrt{\dfrac{3}{2}}$
(b) $\dfrac{3}{2}$
(c) $\dfrac{2}{3}$
(d) $\sqrt{\dfrac{2}{3}}$
Show Answer
Solution
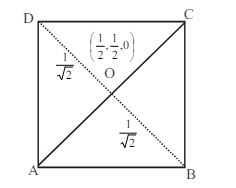
Let $\mathrm{A}(1,0,0) \mathrm{B}(1,1,0), \mathrm{C}(0,1,0), \mathrm{D}(0,0,0)$
Equation of $\mathrm{CD}$ is
$$ \begin{equation*} \overrightarrow{\mathrm{r}}=\overrightarrow{0}+\lambda \hat{\mathrm{j}} \tag{1} \end{equation*} $$
New position of $\mathrm{B}$ is $\left(\dfrac{1}{2}, \dfrac{1}{2}, \dfrac{1}{\sqrt{2}}\right)$
Equation of $\mathrm{AB}$ is
$\overrightarrow{\mathrm{r}}=\hat{\mathrm{i}}+\mu\left(-\dfrac{1}{2} \hat{\mathrm{i}}+\dfrac{1}{2} \hat{\mathrm{j}}+\dfrac{1}{\sqrt{2}} \hat{\mathrm{k}}\right) \quad \overrightarrow{\mathrm{a}} _{2}-\overrightarrow{\mathrm{a}} _{1}=\hat{\mathrm{i}}$
$\overrightarrow{\mathrm{b}} _{1} \times \overrightarrow{\mathrm{b}} _{2}=\hat{\mathrm{j}} \times\left(-\dfrac{1}{2} \hat{\mathrm{i}}+\dfrac{1}{2} \hat{\mathrm{j}}+\dfrac{1}{\sqrt{2}} \hat{\mathrm{k}}\right)=\dfrac{1}{2} \hat{\mathrm{k}}+\dfrac{1}{2} \hat{\mathrm{i}}$
S.D. b|w AB & CD is $\left|\dfrac{\left(\vec{a} _{2}-\vec{a} _{2}\right) \cdot \vec{b} _{1} \times \vec{b} _{2}}{\left|\vec{b} _{1} \times \vec{b} _{2}\right|}\right|$
$=\dfrac{\hat{i} \cdot\left(\dfrac{1}{2} \hat{k}+\dfrac{1}{\sqrt{2}} \hat{\mathrm{i}}\right)}{\left|\dfrac{1}{2} \hat{\mathrm{k}}+\dfrac{1}{\sqrt{2}} \hat{\mathrm{i}}\right|}=\dfrac{\dfrac{1}{\sqrt{2}}}{\sqrt{\dfrac{1}{4}+\dfrac{1}{2}}}=\dfrac{1}{\sqrt{2}} \cdot \dfrac{2}{\sqrt{3}}=\sqrt{\dfrac{2}{3}}$
Answer (d)
4. For what value of $\lambda$ do the planes $x-y+z+1=0, \lambda x+3 y+2 z-3=0,3 x+\lambda y+z-2=0$ form a triangular prism?
(a) 4
(b) -3
(c) 2
(d) $\dfrac{16}{3}$
Show Answer
Solution
$\begin{aligned} & |A|=\left|\begin{array}{ccc} 1 & -1 & 1 \\ \lambda & 3 & 2 \\ 3 & \lambda & 1 \end{array}\right|=(\lambda-4)(\lambda+3)[\mathrm{A}: \mathrm{B}]=\left[\begin{array}{cccc} 1 & -1 & 1 & +1 \\ \lambda & 3 & 2 & -3 \\ 3 & \lambda & 1 & -2 \end{array}\right] \\ & \Delta _{1}=\left|\begin{array}{ccc} -1 & 1 & +1 \\ 3 & 2 & -3 \\ \lambda & 1 & -2 \end{array}\right|=-5(\lambda-2) \end{aligned}$
$\begin{aligned} \Delta_2 & =\left|\begin{array}{ccc} 1 & 1 & 1 \\ \lambda & 2 & -3 \\ 3 & 1 & -2 \end{array}\right|=3 \lambda-16 \ldots \ldots \ldots \ldots \ldots \ldots (3)\\ \Delta_3 & =\left|\begin{array}{ccc} 1 & -1 & 1 \\ \lambda & 2 & -3 \\ 3 & 1 & -2 \end{array}\right|=(\lambda+3)(\lambda-2) …………..(4). \end{aligned}$
Given planes form a prism if $\mathrm{r}=2 \& \mathrm{~s}=3$
i.e. $|\mathrm{A}|=0$ \& none of $\Delta _{1}, \Delta _{2}, \Delta _{3}$ is zero.
From (1), (2), (3) \& (4) we find if $\lambda=4,|A|=0 \&$ none of $\Delta _{1}, \Delta _{2}, \Delta _{3}$ zero.
$\therefore$ For $\lambda=4$ the given planes form a triangular prism.
Answer (a)
5. The plane $\ell \mathrm{x}+\mathrm{my}=0$ is rotated about its line of intersection with the XOY plane through an angle $\alpha$, then the equation of the plane is $\ell \mathrm{x}+\mathrm{my}+\mathrm{nz}=0$ where $\mathrm{n}$ is
(a) $\pm \sqrt{\left(\ell^{2}+m^{2}\right)} \cos \alpha$
(b) $\pm \sqrt{\left(\ell^{2}-m^{2}\right)} \sin \alpha$
(c) $\pm \sqrt{\left(\ell^{2}+m^{2}\right)} \tan \alpha$
(d) $\pm \sqrt{\left(\ell^{2}-m^{2}\right)} \sec \alpha$
Show Answer
Solution
Given planes are $\ell \mathrm{x}+\mathrm{my}=0$ ……………(1) $\& z=0$. …………..(2)
$\therefore$ Equation of the plane passing through the line of intersection of planes (1) \& (2) is $\ell \mathrm{x}+\mathrm{my}+\lambda \mathrm{z}=0$ …………….(3)
(d) $\mathrm{r}^{\prime} \mathrm{s}$ of normal to (3) are $\ell, \mathrm{m}, \lambda$
(d) r’s of normal to (1) are $\ell, \mathrm{m}, 0$
$$ \begin{aligned} & \cos \alpha=\dfrac{\ell . \ell+\mathrm{m} \cdot \mathrm{m}+0}{\sqrt{\ell^{2}+\mathrm{m}^{2}+\lambda^{2}} \sqrt{\ell^{2}+\mathrm{m}^{2}}}=\dfrac{\sqrt{\ell^{2}+\mathrm{m}^{2}}}{\sqrt{\ell^{2}+\mathrm{m}^{2}+\lambda^{2}}} \\ & \sec ^{2} \alpha=\dfrac{\ell^{2}+\mathrm{m}^{2}+\lambda^{2}}{\ell^{2}+\mathrm{m}^{2}}=1+\dfrac{\lambda^{2}}{\ell^{2}+\mathrm{m}^{2}} \\ & \tan ^{2} \alpha=\dfrac{\lambda^{2}}{\ell^{2}+\mathrm{m}^{2}} \Rightarrow \lambda= \pm \sqrt{\left(\ell^{2}+\mathrm{m}^{2}\right)} \tan \alpha \\ & \mathrm{n}=\lambda= \pm \sqrt{\left(\ell^{2}+\mathrm{m}^{2}\right) \tan \alpha} \end{aligned} $$
Answer (c)
6. State the relationship between the planes
$\pi _{1} \equiv 2 \mathrm{x}-3 \mathrm{y}+4 \mathrm{z}-1=0$
$\pi _{2} \equiv \mathrm{x}-\mathrm{y}-\mathrm{z}+1=0$
$\pi _{3} \equiv-\mathrm{x}+2 \mathrm{y}-\mathrm{z}+2=0$
Show Answer
Solution
Given planes are $2 x-3 y+4 z=1$
$\hspace {2 cm}\begin{aligned} & x-y-z=-1 \\ & -x+2 y-z=-2 \end{aligned}$
Coefficient matrix
$A=\left[\begin{array}{ccc} 2 & -3 & 4 \\ 1 & -1 & -1 \\ -1 & 2 & -1 \end{array}\right] ;|A|=\left|\begin{array}{ccc} 2 & -3 & 4 \\ 1 & -1 & -1 \\ -1 & 2 & -1 \end{array}\right| \neq 0 \therefore r=3$
Augmented matrix $[A: B]=\left[\begin{array}{cccc}2 & -3 & 4 & 1 \\ 1 & -1 & -1 & -1 \\ -1 & 2 & -1 & -2\end{array}\right]$
Here $\Delta _{1}=\left|\begin{array}{ccc}-3 & 4 & 1 \\ -1 & -1 & -1 \\ 2 & -1 & -2\end{array}\right| \neq 0 \quad \Delta _{2}=\left|\begin{array}{ccc}2 & 4 & 1 \\ 1 & -1 & -1 \\ -1 & -1 & -2\end{array}\right| \neq 0$
$\Delta _{3}=\left|\begin{array}{ccc}2 & -3 & 1 \\ 1 & -1 & -1 \\ -1 & 2 & -2\end{array}\right| \neq 0$
$\therefore \mathrm{s}=3$
$\therefore$ planes intersect at a paint
Exercise
1. If $z$-axis be vertical, then the equation of the line of greatest slope through the point $(2,-1,0)$ on the plane $2 x+3 y-4 z=1$ is
(a) $\dfrac{x-2}{2}=\dfrac{y+1}{-1}=\dfrac{z}{0}$
(b) $\dfrac{x-2}{3}=\dfrac{y+1}{4}=\dfrac{z}{5}$
(c) $\dfrac{\mathrm{z}-6}{-6}=\dfrac{\mathrm{y}+1}{4}=\dfrac{\mathrm{z}}{12}$
(d) $\dfrac{x-2}{8}=\dfrac{y+1}{12}=\dfrac{z}{13}$
Show Answer
Answer: d2. Through a point $\mathrm{P}(\mathrm{f}, \mathrm{g}, \mathrm{h})$ a plane is drawn at right angles to $\mathrm{OP}$, to meet the axes in $\mathrm{A}, \mathrm{B}, \mathrm{C}$. If $\mathrm{O}$ is $(0,0,0)$ the centroid of $\triangle \mathrm{ABC}$ is
(a) $\left(\dfrac{\mathrm{f}}{3 \mathrm{r}}, \dfrac{\mathrm{g}}{3 \mathrm{r}}, \dfrac{\mathrm{h}}{3 \mathrm{r}}\right)$
(b) $\left(\dfrac{\mathrm{r}^{2}}{3 \mathrm{f}^{2}}, \dfrac{\mathrm{r}^{2}}{3 \mathrm{~g}^{2}}, \dfrac{\mathrm{r}^{2}}{3 \mathrm{~h}^{2}}\right)$
(c) $\left(\dfrac{\mathrm{r}^{2}}{3 \mathrm{f}}, \dfrac{\mathrm{r}^{2}}{3 \mathrm{~g}}, \dfrac{\mathrm{r}^{2}}{3 \mathrm{~h}}\right)$
(d) $\left(\dfrac{\mathrm{r}^{2}}{3 \mathrm{r}^{2}}, \dfrac{\mathrm{g}^{2}}{3 \mathrm{r}^{2}}, \dfrac{\mathrm{h}^{2}}{3 \mathrm{r}^{2}}\right)$
Show Answer
Answer: c3. If a line with d. $\mathrm{r}^{\prime} \mathrm{s} 2: 2: 1$ intersects the line $\dfrac{\mathrm{x}-7}{3}=\dfrac{\mathrm{y}-5}{2}=\dfrac{\mathrm{z}-3}{1}$ and $\dfrac{\mathrm{x}-1}{2}=\dfrac{\mathrm{y}+1}{4}=$ $\dfrac{\mathrm{z}+1}{3}$ at $\mathrm{A} \& \mathrm{~B}$, then $\mathrm{AB}=$
(a) $\sqrt{2}$
(b) 2
(c) $\sqrt{3}$
(d) 3
Show Answer
Answer: d4. A mirror and a source of light are situated at the origin and a point on OX respectively. A ray of light from the source strikes the mirror and is reflected. If the d. $\mathrm{r}^{\prime} \mathrm{s}$ of the normal to the plane of mirror are $1,-1,1$ then the dc’s for the reflectd ray are
(a) $\dfrac{1}{3}, \dfrac{2}{3}, \dfrac{2}{3}$
(b) $\dfrac{1}{3}, \dfrac{-2}{3}, \dfrac{-2}{3}$
(c) $\dfrac{-1}{3}, \dfrac{-2}{3}, \dfrac{-2}{3}$
(d) $\dfrac{-1}{3}, \dfrac{-2}{3}, \dfrac{2}{3}$
Show Answer
Answer: d5. Let $\mathrm{A}(\vec{a})$ and $\mathrm{B}(\vec{b})$ be points on two skew lines $\overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{a}}+\lambda \overrightarrow{\mathrm{p}}$ and $\overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{b}}+\mu \overrightarrow{\mathrm{q}}$ and the shortest distance between the skew lines is 1 , where $\vec{p}$ and $\vec{q}$ are unit vectors forming adjacent sides of a parallelogram enclosing an area of $\dfrac{1}{2}$ sq.units. If an angle between $\mathrm{AB}$ and the line of shortest distance is $60^{\circ}$, then $\mathrm{AB}=$
(a) $1 / 2$
(b) 2
(c) 1
(d) None of these
Show Answer
Answer: b6.* $\mathrm{A}(-1,2,-3), \mathrm{B}(5,0,-6)$ and $\mathrm{c}(0,4,-1)$ are the vertices of the $\triangle \mathrm{ABC}$ then
(a) The d. $\mathrm{r}^{\prime} \mathrm{s}$ of the internal bisector of $\angle \mathrm{BAC}$ are $(25,8,5)$
(b) The d.r’s of the internal bisector of $\angle \mathrm{ABC}$ are $6 \sqrt{66}-35,-2 \sqrt{66}+28,35-3 \sqrt{66}$
(c) The d.r’s of the internal bisector of $\angle \mathrm{BCA}$ are $\sqrt{66}-15,2 \sqrt{66}+12,2 \sqrt{66}+15$
(d) The d. r’ $s$ of the internal bisector of $\angle \mathrm{BCA}$ are 24,6,3
Show Answer
Answer: a, b, c7.* Consider the line $\mathrm{x}=\mathrm{y}=\mathrm{z}$ and the line $2 \mathrm{x}+\mathrm{y}+\mathrm{z}-1=0=3 \mathrm{x}+\mathrm{y}+2 \mathrm{z}-2$ then
(a) The shortest distance between the two lines is $\dfrac{1}{\sqrt{2}}$
(b) The shortest distance between the two lines is $\sqrt{2}$
(c) plane containing $2^{\text {nd }}$ line parallel to $1^{\text {st }}$ line is $y-z+1=0$
(d) The shortest between the two lines is $\dfrac{\sqrt{3}}{2}$
Show Answer
Answer: a, c8. Read the passage and answer the questions that follow.
Given that $\vec{a}=6 \hat{i}+7 \hat{j}+7 \hat{k}, \vec{b}=3 \hat{i}+2 \hat{j}-7 \hat{k} . P(1,2,3)$
(i) The position vector of $L$, the foot of the $\perp r$ from $P$ on the line $\vec{r}=\vec{a}+\lambda \vec{b}$ is
(a) $6 \hat{\mathrm{i}}+7 \hat{\mathrm{j}}+7 \hat{\mathrm{k}}$
(b) $3 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}-2 \hat{\mathrm{k}}$
(c) $3 \hat{\mathrm{i}}+5 \hat{\mathrm{j}}+9 \hat{\mathrm{k}}$
(d) $9 \hat{i}+9 \hat{j}+5 \hat{k}$
(ii) The image of the point $P$ in the line $\vec{r}=\vec{a}+\lambda \vec{b}$ is
(a) $(11,12,11)$
(b) $(5,2,-7)$
(c) $(5,8,15)$
(d) $(17,16,16,7)$
(iii) If A is the point with position vector $\vec{a}$ then area of the triangle $\triangle \mathrm{PLA}$ in sq.units is equal to
(a) $3 \sqrt{6}$
(b) $\dfrac{7 \sqrt{17}}{2}$
(c) $\sqrt{17}$
(d) $\dfrac{7}{2}$
Show Answer
Answer: (i) c (ii) c (iii) b9. The position vector of the point on the line $\vec{r}=\hat{i}+\lambda(\hat{i}+\hat{j}+\hat{k})$ whose distance from $\vec{r}-(\hat{i}+\hat{j})$. $(\hat{\mathbf{i}}-\hat{\mathbf{j}}-\hat{\mathrm{k}})=1$ is $\dfrac{1}{\sqrt{3}}$ units is
(a) $-\hat{\mathrm{i}}-\hat{\mathrm{j}}-2 \hat{\mathrm{k}}$
(b) $\hat{j}$
(c) $2 \hat{\mathrm{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}}$
(d) $3 \hat{i}+2 \hat{j}+2 \hat{k}$
Show Answer
Answer: c10. Match the following
| Column I | Column II | ||
|---|---|---|---|
| (a) | The distance between the line $\overrightarrow{\mathrm{r}}=(2 \hat{\mathrm{i}}-2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})$ $+\lambda(\hat{i}-\hat{j}+4 \hat{k})$ and plane $\vec{r}=(\hat{i}+5 \hat{j}+\hat{k})=5$ | (p) | $\dfrac{25}{3 \sqrt{14}}$ |
| (b) | Distance between parallel planes $\overrightarrow{\mathrm{r}} \cdot(2 \hat{\mathrm{i}}-\hat{\mathrm{j}}+3 \hat{\mathrm{k}})=4$ and $\vec{r} .(6 \hat{i}-3 \hat{j}+9 \hat{k})+13=0$ is | (q) | $\dfrac{13}{7}$ |
| (c) | The distance of a point $(2,5,-3)$ from the plane $\overrightarrow{\mathrm{r}} \cdot(6 \hat{\mathrm{i}}-3 \hat{\mathrm{j}}+2 \hat{\mathrm{k}})=4 \text { is }$ | (r) | $\dfrac{10}{3 \sqrt{3}}$ |
| (d) | The distance of the point $(1,0,-3)$ form the plane $x-y-z-9=0$ measured parallel to the line $\dfrac{x-2}{2}=\dfrac{y+2}{3}=\dfrac{z-6}{-6}$ is | (s) | 7 |










