Sequences and Series (Lecture-02)
Some important Logarithmic and Exponential formulae
1. If $\mathrm{a}^{\mathrm{x}}=\mathrm{y}$, then $\mathrm{x}=\log _{\mathrm{a}} \mathrm{y}$
2. $\log _{\mathrm{a}} \mathrm{a}=1$ & $\log _{\mathrm{a}} 1=0$
3. $\mathrm{a}^{\log _{a} \mathrm{n}}=\mathrm{n}$
4. $\log _{\mathrm{a}} \mathrm{mn}=\log _{\mathrm{a}} \mathrm{m}+\log _{\mathrm{a}} \mathrm{n}$
5. $\log _{a}\left(\dfrac{m}{n}\right)=\log _{a} m-\log _{a} n$
6. $\log _{\mathrm{a}} \mathrm{m}^{\mathrm{n}}=\mathrm{n} \log _{\mathrm{a}} \mathrm{m}$
7. $\log _{\mathrm{b}} \mathrm{a}=\dfrac{\log _{\mathrm{c}} \mathrm{a}}{\log _{\mathrm{c}} \mathrm{b}}$
8. $\log _{a^{n}} a^{m}=\dfrac{m}{n}$
9. $\log _{\mathrm{b}} \mathrm{a}=\dfrac{1}{\log _{\mathrm{a}} \mathrm{b}}$
10. $\log _{e}(1+x)=x-\dfrac{x^{2}}{2}+\dfrac{x^{3}}{3}-\dfrac{x^{4}}{4}+\ldots \ldots \ldots .$
11. $\log _{e}(1-x)=-x-\dfrac{x^{2}}{2}-\dfrac{x^{3}}{3}-\dfrac{x^{4}}{4}\ldots \ldots \ldots .$
12. $\log _{e}(1+x)(1-x)=\log _{e}\left(1-x^{2}\right)=-2\left(\dfrac{x^{2}}{2}+\dfrac{x^{4}}{4}+\dfrac{x^{6}}{6}+\ldots \ldots \ldots \ldots . ..\right)$
13. $\log _{e}\left(\dfrac{1+x}{1-x}\right)=2\left(x+\dfrac{x^{3}}{3}+\dfrac{x^{5}}{5}+\ldots \ldots \ldots \ldots \ldots \ldots . . . .\right)$
14. $\log _{\mathrm{e}} 2=1-\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\ldots \ldots \ldots \ldots .$
15. $\mathrm{e}^{\mathrm{x}}=1+\dfrac{\mathrm{x}}{1 !}+\dfrac{\mathrm{x}^{2}}{2 !}+\dfrac{\mathrm{x}^{3}}{3 !}+\ldots \ldots \ldots \ldots .$
16. $e^{x}+e^{-x}=2\left(1+\dfrac{x^{2}}{2 !}+\dfrac{x^{4}}{4 !}+\ldots \ldots \ldots \ldots .\right)$
17. $e^{x}-e^{-x}=2\left(\dfrac{x}{1 !}+\dfrac{x^{3}}{3 !}+\dfrac{x^{5}}{5 !} \ldots \ldots \ldots \ldots ..\right)$
18. $\mathrm{e}=1+\dfrac{1}{1 !}+\dfrac{1}{2 !}+\dfrac{1}{3 !}+\ldots \ldots \ldots \ldots .$
$\quad \mathrm{e}$ is an irrational number & it lies between $2 & 3 . \mathrm{e} \cong 2.7183$
19. $a^y=e^{y \log _c a}=1+y\left(\log _c a\right)+\dfrac{y^2}{2 !}\left(\log _e a\right)^2+\dfrac{y^3}{3 !}\left(\log _c a\right)^3+\ldots \ldots \ldots \ldots \ldots.$
20. $\log _{2} \log _{2} \sqrt{\sqrt{\sqrt{\sqrt{\ldots \ldots \ldots \ldots \ldots . . \sqrt{2}}}}}=-\mathrm{n}$ when $\mathrm{n}$ is the number of square roots
21. $a^{\sqrt{\log _{a} b}}=b^{\sqrt{\log _{b} a}}$
Vn-Method
(i) To find the sum of series of the form
$\dfrac{1}{a _{1} a _{2} \ldots \ldots \ldots . a _{r}}+\dfrac{1}{a _{2} a _{3} \ldots \ldots \ldots \ldots a _{r+1}}+\ldots \ldots \ldots \ldots \ldots \ldots+\dfrac{1}{a _{n} a _{n+1} \ldots \ldots \ldots \ldots a _{n+r-1}}$ where $a _{1}, a _{2}$,
$\left(\text { Here } T_n=\dfrac{1}{a_n a_{n+1} \ldots \ldots \ldots \ldots a_{n+r-1}}\right)$
………are in A.P. Let $\mathrm{V} _{\mathrm{n}}=\dfrac{1}{\mathrm{a} _{\mathrm{n}+1} \mathrm{a} _{\mathrm{n}+2} \ldots \ldots \ldots \ldots \mathrm{a} _{\mathrm{n}+\mathrm{r}-1}}\left(\right.$ avoiding first term for $\mathrm{V} _{\mathrm{n}}$ ie $\mathrm{a} _{\mathrm{n}}$ in $T _{\mathrm{n}}$ )
$\mathrm{T} _{\mathrm{n}}=\dfrac{-1}{\mathrm{~d}(\mathrm{r}-1)}\left(\mathrm{V} _{\mathrm{n}}-\mathrm{V} _{\mathrm{n}-1}\right)=\dfrac{1}{\mathrm{~d}(\mathrm{r}-1)}\left(\mathrm{V} _{\mathrm{n}-1}-\mathrm{V} _{\mathrm{n}}\right)$
put $\mathrm{n}=1,2,3 \ldots \ldots \ldots \ldots . . \mathrm{n}$ and add to get $\mathrm{S} _{\mathrm{n}}$.
$\mathrm{S} _{\mathrm{n}}=\mathrm{T} _{1}+\mathrm{T} _{2}+\ldots \ldots . \mathrm{T} _{\mathrm{n}}=\dfrac{1}{\mathrm{~d}(\mathrm{r}-1)}\left(\mathrm{V} _{0}-\mathrm{V} _{\mathrm{n}}\right)$
$$ =\dfrac{1}{d(r-1)}\left(\dfrac{1}{a _{1} a _{2} \cdots \ldots . a _{r-1}}-\dfrac{1}{a _{n+1} a _{n+2} \cdots \ldots . a _{n+r-1}}\right) $$
Eg:
(a) $\dfrac{1}{1.2 .3}+\dfrac{1}{2.3 .4}+\ldots \ldots \ldots \ldots . .+\dfrac{1}{\mathrm{n}(\mathrm{n}+1)(\mathrm{n}+2)}=\dfrac{1}{1 .(3-1)}\left(\dfrac{1}{1.2}-\dfrac{1}{(\mathrm{n}+1)(\mathrm{n}+2)}\right)$
$\quad=\dfrac{1}{4}-\dfrac{1}{2(\mathrm{n}+1)(\mathrm{n}+2)}$
(b) $\dfrac{1}{1.2 .3 .4}+\dfrac{1}{2 \cdot 3 \cdot 4.5}+\ldots \ldots \ldots . . \dfrac{1}{n(n+1)(n+2)(n+3)}$
$\quad=\dfrac{1}{1 .(4-1)}\left(\dfrac{1}{1.2 \cdot 3}-\dfrac{1}{(\mathrm{n}+1)(\mathrm{n}+2)(\mathrm{n}+3)}\right)$
(ii) Summation of series of the form $\mathrm{a} _{1} \mathrm{a} _{2} \ldots \ldots \mathrm{a} _{\mathrm{r}}+\mathrm{a} _{2} \mathrm{a} _{3} \ldots \ldots \ldots \mathrm{a} _{\mathrm{r}+1}+$. $\mathrm{a} _{1}, \mathrm{a} _{2} \ldots \ldots$. are in A.P
Here $T _{n}=a _{n} a _{n+1} \cdots \cdots \ldots a _{n+r-1}$
Let $V _{n}{ } _{n}=a _{n} a _{n+1} \cdots \cdots \cdots \ldots \ldots . . . a _{n-r+1} a _{n-r}\left(\right.$ Take one term extra in $T _{n}$ for $\left.V _{n}\right)$
$\mathrm{T} _{\mathrm{n}}=\dfrac{1}{(\mathrm{r}+1) \mathrm{d}}\left(\mathrm{V} _{\mathrm{n}}-\mathrm{V} _{\mathrm{n}-1}\right)$.
Put $\mathrm{n}=1,2,3 \ldots \ldots .$. and add to get $\mathrm{S} _{\mathrm{n}}$
$\mathrm{S} _{\mathrm{n}}=\mathrm{T} _{1}+\mathrm{T} _{2}+\ldots \ldots \ldots \ldots+\mathrm{T} _{\mathrm{n}}=\dfrac{1}{\mathrm{~d}(\mathrm{r}+1)}\left(\mathrm{V} _{\mathrm{n}}-\mathrm{V} _{0}\right)=\dfrac{1}{\mathrm{~d}(\mathrm{r}+1)}\left(\mathrm{a} _{\mathrm{n}} \mathrm{a} _{\mathrm{n}+1} \ldots \ldots \ldots . \mathrm{a} _{\mathrm{n}+\mathrm{r}}-\mathrm{a} _{0} \mathrm{a} _{1} \mathrm{a} _{2} \ldots \ldots \ldots \ldots \mathrm{a} _{\mathrm{r}}\right)$
where $\mathrm{a} _{0}=\mathrm{a} _{1}-\mathrm{d}$
Eg
(a) $1.2+2.3+\ldots \ldots \ldots \ldots \ldots \ldots \ldots+n(\mathrm{n}+1)=\dfrac{1}{1 .(2+1)}((\mathrm{n}+1)(\mathrm{n}+2)-0.1 .2)=\dfrac{\mathrm{n}(\mathrm{n}+1)(\mathrm{n}+2)}{3}$
(b) $1.2 .3 .4+2.3 .4 .5+$ $+\mathrm{n}(\mathrm{n}+1)(\mathrm{n}+2)(\mathrm{n}+3)$
$\quad\begin{aligned} & =\dfrac{1}{1 .(4+1)}(\mathrm{n}(\mathrm{n}+1)(\mathrm{n}+2)(\mathrm{n}+3)(\mathrm{n}+4)-0.1 \cdot 2 \cdot 3 \cdot 4) \\ \\ & =\dfrac{1}{5} \mathrm{n}(\mathrm{n}+1)(\mathrm{n}+2)(\mathrm{n}+3)(\mathrm{n}+4) \end{aligned}$
SOLVED EXAMPLES
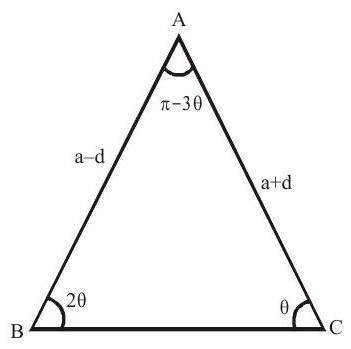
1. If the sides of a triangle are in A.P and the greatest angle of the triangle is double the smallest, then the ratio of sides of the triangle is
(a) $3: 4: 5$
(b) $4: 5: 6$
(c) $5: 6: 7$
(d) None of these
Show Answer
Solution :
Applying sine rule, we have
$\dfrac{\mathrm{a}-\mathrm{d}}{\sin \theta}=\dfrac{\mathrm{a}}{\sin (\pi-3 \theta)}=\dfrac{\mathrm{a}+\mathrm{d}}{\sin 2 \theta}$
$\Rightarrow \dfrac{\mathrm{a}-\mathrm{d}}{\sin \theta}=\dfrac{\mathrm{a}}{3 \sin \theta-4 \sin ^{3} \theta}=\dfrac{\mathrm{a}+\mathrm{d}}{2 \sin \theta \cos \theta}$
$\Rightarrow \dfrac{\mathrm{a}-\mathrm{d}}{1}=\dfrac{\mathrm{a}}{3-4 \sin ^{2} \theta}=\dfrac{\mathrm{a}+\mathrm{d}}{2 \cos \theta}$ gives $\cos \theta=\dfrac{\mathrm{a}+\mathrm{d}}{2(\mathrm{a}-\mathrm{d})}$
Also, $3-4 \sin ^{2} \theta=\dfrac{\mathrm{a}}{\mathrm{a}-\mathrm{d}}$
$\Rightarrow 3-4\left(1-\cos ^{2} \theta\right)=\dfrac{a}{a-d}$ gives $-1+\left(\dfrac{a+d}{a-d}\right)^{2}=\dfrac{a}{a-d}$
$\Rightarrow \dfrac{4 \mathrm{ad}}{\mathrm{a}-\mathrm{d}}=\mathrm{a} \Rightarrow 4 \mathrm{ad}=\mathrm{a}^{2}-\mathrm{ad}$ gives $\mathrm{a}=5 \mathrm{~d}$
$\therefore$ sides $\mathrm{a}-\mathrm{d}: \mathrm{a}: \mathrm{a}+\mathrm{d}$
$\quad \quad \quad 5\mathrm{~d}-\mathrm{d}: 5 \mathrm{~d}: 5 \mathrm{~d}+\mathrm{d}=4: 5: 6$
Answer: (b)
2. The sum of
$\dfrac{3}{1.2} \cdot \dfrac{1}{2}+\dfrac{4}{2.3}\left(\dfrac{1}{2}\right)^{2}+\dfrac{5}{3.4} \cdot\left(\dfrac{1}{2}\right)^{3}+$……………$\mathrm{n}$ terms is
(a) $1-\dfrac{1}{(\mathrm{n}+1) 2^{\mathrm{n}}}$
(b) $1-\dfrac{1}{\mathrm{n} \cdot 2^{\mathrm{n}-1}}$
(c) $1+\dfrac{1}{(\mathrm{n}+1) 2^{\mathrm{n}}}$
(d) None of these
Show Answer
Solution :
$\mathrm{T} _{\mathrm{n}}=\dfrac{\mathrm{n}+2}{\mathrm{n} \cdot(\mathrm{n}+1)} \cdot \dfrac{1}{2^{\mathrm{n}}}=\left(\dfrac{2}{\mathrm{n}}-\dfrac{1}{\mathrm{n}+1}\right) \cdot \dfrac{1}{2^{\mathrm{n}}}$
$\Rightarrow \mathrm{T} _{\mathrm{n}}=\dfrac{1}{\mathrm{n} \cdot 2^{\mathrm{n}-1}}-\dfrac{1}{(\mathrm{n}+1) \cdot 2^{\mathrm{n}}}$
Putting $\mathrm{n}=1,2,3$,……………..,n
$\therefore \mathrm{T} _{1}=\dfrac{1}{1.2^{0}}-\dfrac{1}{2.2^{1}}$
$\mathrm{T} _{2}=\dfrac{1}{2.2^{1}}-\dfrac{1}{3.2^{2}}$
$\mathrm{T} _{3}=\dfrac{1}{3.2^{2}}-\dfrac{1}{4.3^{2}}$
$\mathrm{T} _{\mathrm{n}}=\dfrac{1}{\mathrm{n} \cdot 2^{\mathrm{n}-1}}-\dfrac{1}{(\mathrm{n}+1) 2^{\mathrm{n}}}$
Adding , $\mathrm{T} _{1}+\mathrm{T} _{2}+\mathrm{T} _{3}+\ldots \ldots \ldots+\mathrm{T} _{\mathrm{n}}=\mathrm{S} _{\mathrm{n}}$
$\mathrm{S} _{\mathrm{n}}=1-\dfrac{1}{(\mathrm{n}+1) 2^{\mathrm{n}}}$
Answer: (a)
3. Coefficient of $x^{49}$ in the expansion of $(x-1)(x-3)(x-5)…………….(x-99)$ is
(a) $-99^{2}$
(b) 1
(c) -2500
(d) None of these
Show Answer
Solution :
$({x}-1)({x}-3)({x}-5)………………({x}-99)$
$={x}^{50}-{S} _{1} {x}^{49}+{S} _{2} {x}^{48}$………………..
$\therefore$ Coefficient of ${x}^{49}$ is $-{S} _{1}$
$=-(1+3+5+\ldots \ldots+99) \quad=\quad-50^{2} \quad=\quad-2500$
Answer: (c)
4. The coefficients of $x^{15}$ in the product
$(1-\mathrm{x})(1-2 \mathrm{x})\left(1-2^{2} \mathrm{x}\right) \ldots \ldots \ldots \ldots . .\left(1-2^{15} \mathrm{x}\right)$ is
(a) $2^{105}-2^{121}$
(b) $2^{121}-2^{105}$
(c) $2^{120}-2^{104}$
(d) None of these
Show Answer
Solution :
$\begin{aligned} &(1-\mathrm{x})(1-2 \mathrm{x})\left(1-2^{2} \mathrm{x}\right) \ldots \ldots \ldots \ldots .\left(1-2^{15} \mathrm{x}\right) \\ & \quad=(-1)^{16}(\mathrm{x}-1)(2 \mathrm{x}-1)\left(2^{2} \mathrm{x}-1\right) \ldots \ldots \ldots \ldots \ldots . .\left(2^{15} \mathrm{x}-1\right) \\ & \quad=2^{1} .2^{2} \cdot 2^{3} \ldots \ldots \ldots \ldots \ldots \ldots .^{15}(\mathrm{x}-1)\left(\mathrm{x}-\dfrac{1}{2}\right)\left(\mathrm{x}-\dfrac{1}{2^{2}}\right) \ldots \ldots \ldots . .\left(\mathrm{x}-\dfrac{1}{2^{15}}\right) \\ & \quad=2^{120} \cdot(\mathrm{x}-1)\left(\mathrm{x}-\dfrac{1}{2}\right)\left(\mathrm{x}-\dfrac{1}{2^{2}}\right) \ldots \ldots \ldots .\left(\mathrm{x}-\dfrac{1}{2^{15}}\right) \end{aligned}$
$\therefore \text { coeff of } x^{15} \text { is }-2^{120}\left\{1+\dfrac{1}{2}+\frac{1}{2^2}+\ldots .+\dfrac{1}{2^{15}}\right\}$
$=-2^{120} \cdot 1 \dfrac{\left\{1-\dfrac{1}{2^{16}}\right\}}{1-\frac{1}{2}}=-2^{121}\left(1-\dfrac{1}{2^{16}}\right)=2^{105}-2^{121}$
Answer: (a)
5. The sum to $2 \mathrm{n}$ terms of the series
$\dfrac{3}{4}+\dfrac{7}{4}+\dfrac{15}{16}+\dfrac{31}{16}+\dfrac{63}{64}+\dfrac{127}{64}+$………………is
(a) $3 \mathrm{n}-\dfrac{2}{3}\left(1-\dfrac{1}{4^{\mathrm{n}}}\right)$
(b) $3 \mathrm{n}-\dfrac{10}{21}\left(1-\dfrac{1}{4^{n}}\right)$
(c) $3 n-\dfrac{13}{21} \dfrac{1}{4^{n}}$
(d) None of these
Show Answer
Solution :
Given expression
$\begin{aligned} & =\left(1-\dfrac{1}{4}\right)+\left(2-\dfrac{1}{4}\right)+\left(1-\dfrac{1}{16}\right)+\left(2-\dfrac{1}{16}\right)+\ldots \ldots \ldots \ldots \ldots \ldots \ldots . . . .2 \mathrm{n} \text { terms } \\ & =3 n-2\left(\dfrac{1}{4}+\dfrac{1}{16}+\ldots \ldots \ldots . . n \text { terms }\right) \\ & =3 n-2 \dfrac{1}{4} \dfrac{\left(1-\dfrac{1}{4^{n}}\right)}{1-\dfrac{1}{4}} \\ & =3 n-\dfrac{2}{3}\left(1-\dfrac{1}{4^{n}}\right) \end{aligned}$
Answer: (a)
6. The sum to $n$ terms of the series
$\dfrac{1}{1-\dfrac{1}{4}}+\dfrac{1}{(1+3)-\dfrac{1}{4}}+\dfrac{1}{(1+3+5)-\dfrac{1}{4}}+\ldots \ldots \ldots \infty$
(a) $\dfrac{2 \mathrm{n}}{2 \mathrm{n}+1}$
(b) $\dfrac{4 \mathrm{n}}{2 \mathrm{n}+1}$
(c) $\dfrac{2}{2 n+1}$
(d) None
Show Answer
Solution :
$\mathrm{T} _{\mathrm{n}}=\dfrac{1}{(1+3+5+\ldots \ldots \ldots \ldots+\mathrm{n} \text { terms })}=\dfrac{1}{\mathrm{n}^{2}-\dfrac{1}{4}}$
$=\dfrac{1}{\left(n+\dfrac{1}{2}\right)\left(n-\dfrac{1}{2}\right)}=\dfrac{\left(n+\dfrac{1}{2}\right)-\left(n-\dfrac{1}{2}\right)}{\left(n-\dfrac{1}{2}\right)\left(n+\dfrac{1}{2}\right)}$
$\mathrm{T} _{\mathrm{n}}=2\left\{\dfrac{1}{2 \mathrm{n}-1}-\dfrac{1}{2 \mathrm{n}+1}\right\}$
$\therefore \mathrm{T} _{1}=2\left(\dfrac{1}{1}-\dfrac{1}{3}\right)$
$\mathrm{T} _{2}=2\left(\dfrac{1}{3}-\dfrac{1}{5}\right)$
$\mathrm{T} _{\mathrm{n}}=2\left(\dfrac{1}{2 \mathrm{n}-1}-\dfrac{1}{2 \mathrm{n}+1}\right)$
Adding, $\mathrm{S} _{\mathrm{n}}=\mathrm{T} _{1}+\mathrm{T} _{2}+\ldots \ldots \ldots \ldots+\mathrm{T} _{\mathrm{n}}=2\left(1-\dfrac{1}{2 \mathrm{n}+1}\right)=\dfrac{4 \mathrm{n}}{2 \mathrm{n}+1}$
Answer: (b)
7. $\quad$ The sum of the series
$\dfrac{1}{1.3}+\dfrac{2}{1.3 .5}+\dfrac{3}{1.3 .5 .7}+$……………….$\infty$ is
(a) 1
(b) $\dfrac{1}{2}$
(c) $\dfrac{3}{2}$
(d) None
Show Answer
Solution :
$T _{n}=\dfrac{n}{1.3 .5 \ldots \ldots \ldots \ldots . .(2 n-1)(2 n+1)}$
$\begin{aligned} = & \dfrac{1}{2}\left\{\dfrac{2 \mathrm{n}+1-1}{1.3 .5 \ldots \ldots \ldots \ldots .(2 \mathrm{n}-1)(2 \mathrm{n}+1)}\right\} \\ = & \dfrac{1}{2}\left\{\dfrac{1}{1.3 .5 \ldots \ldots \ldots .(2 \mathrm{n}-1)}-\dfrac{1}{1.3 .5 \ldots \ldots \ldots .(2 \mathrm{n}+1)}\right\} \\ \therefore \mathrm{T} _{1}= & \dfrac{1}{2}\left(\dfrac{1}{1}-\dfrac{1}{1.3}\right) \\ \mathrm{T} _{2}= & \dfrac{1}{2}\left(\dfrac{1}{1.3}-\dfrac{1}{1.3 .5}\right) \\ & \cdot \\ & \cdot \\ \mathrm{T} _{\mathrm{n}}= & \dfrac{1}{2}\left(\dfrac{1}{1.3 .5 \ldots . .(2 \mathrm{n}-1)}-\dfrac{1}{1.3 .5 \ldots . .(2 \mathrm{n}+1)}\right) \\ \mathrm{S} _{\mathrm{n}}= & \dfrac{1}{2}\left(1-\dfrac{1}{1.3 .5 \ldots . .(2 \mathrm{n}-1)(2 \mathrm{n}+1)}\right) \\ \therefore & \mathrm{S} _{\infty}=\dfrac{1}{2}(1-0)=\dfrac{1}{2} \end{aligned}$
Answer: (b)
Exercise
1.* Let $S _{1}, S _{2}, \ldots \ldots \ldots \ldots \ldots . .$. . be squares such that for each $n \geq 1$ the length of a side of $S _{n}$ equals the length of a diagonal of $\mathrm{S} _{\mathrm{n}+1}$. If the length of a side of $\mathrm{S} _{1}$ is $10 \mathrm{~cm}$, then for which of the following values of $\mathrm{n}$ is the area of $\mathrm{S} _{\mathrm{n}}$ less than $1 \mathrm{sq} . \mathrm{cm}$.
(a) 7
(b) 8
(c) 9
(d) 10
Show Answer
Answer: b, c, d2. If $\mathrm{a}, \mathrm{b}, \mathrm{c}$ are is $\mathrm{A} . \mathrm{P}$ and $\mathrm{a}^{2}, \mathrm{~b}^{2}, \mathrm{c}^{2}$ are in H.P, then $\mathrm{b}^{2}=$
(a) $\dfrac{\mathrm{ca}}{2}$
(b) $2 \mathrm{ca}$
(c) $\dfrac{-\mathrm{ca}}{2}$
(d) $-2 \mathrm{ca}$.
Show Answer
Answer: c3. Let the $\mathrm{HM}$ & $\mathrm{GM}$ of two positive numbers $\mathrm{a}$ & $\mathrm{~b}$ be in the ratio $4: 5$ then $\mathrm{a}: \mathrm{b}$ is
(a) $1: 2$
(b) $2: 3$
(c) $3: 4$
(d) $1: 4$
Show Answer
Answer: d4. If $\cos (x-y), \cos x, \cos (x+y)$ are in H.P., then the value of $\cos x \sec \ddfrac{y}{2}$ is
(a) $\pm 1$
(b) $\pm \dfrac{1}{\sqrt{2}}$
(c) $\pm \sqrt{2}$
(d) $\pm \sqrt{3}$
Show Answer
Answer: c5. If $x$ & $y$ are positive real numbers and $m, n$ are positive integers, then the minimum value of $\dfrac{x^{m} y^{n}}{\left(1+x^{2 m}\right)\left(1+y^{2 n}\right)}$ is
(a) 2
(b) $\dfrac{1}{4}$
(c) $\dfrac{1}{2}$
(d) 1
Show Answer
Answer: b6. There are two numbers $a \& b$ whose product is 192 and the quotient of A.M. by H.M. of their greatest common divisor and least common multiple is $\dfrac{169}{48}$. The smaller of $a$ & $b$ is
(a) 2
(b) 4
(c) 6
(d) 12
Show Answer
Answer: b, d7. Consider the sequence 1, 2, 2, 3, 3, 3, where n occurs $n$ times. The number that occurs as $2007^{\text {th }}$ term is
(a) 61
(b) 62
(c) 63
(d) 64
Show Answer
Answer: c8. Read the following paragraph and answer the questions.
Let $A _{1}, G _{1}, H _{1}$ denote the A.M., G.M., H.M of two distinct positive numbers. For $n \geq 2$, let $A _{n-1}$ and $H _{n-1}$ have A.M., G.M., H.M as $A _{n}, G _{n}, H _{n}$ respectively.
(i) Which of the following statements is correct?
(a) $\mathrm{G} _{1}>\mathrm{G} _{2}>\mathrm{G} _{3}>$…………….
(b) $\mathrm{G} _{1}<\mathrm{G} _{2}<\mathrm{G} _{3}<$…………….
(c) $\mathrm{G} _{1}=\mathrm{G} _{2}=\mathrm{G} _{3}=$…………….
(d) $\mathrm{G} _{1}<\mathrm{G} _{3}<\mathrm{G} _{5}$………………and $\mathrm{G} _{2}>\mathrm{G} _{4}>\mathrm{G} _{6}>\ldots$.
(ii) Which are of the following statement is correct?.
(a) $\mathrm{A} _{1}>\mathrm{A} _{2}>\mathrm{A} _{3}>$……………….
(b) $\mathrm{A} _{1}<\mathrm{A} _{2}<\mathrm{A} _{3}<$………………
(c) $\mathrm{A} _{1}>\mathrm{A} _{3}>\mathrm{A} _{5}>$………………and $\mathrm{A} _{2}<\mathrm{A} _{4}<\mathrm{A} _{6}<$………………
(d) $\mathrm{A} _{1}<\mathrm{A} _{3}<\mathrm{A} _{5}<$………………and $\mathrm{A} _{2}>\mathrm{A} _{4}>\mathrm{A} _{6}>$………………
(iii) Which are of the following statement is correct?
(a) $\mathrm{H} _{1}>\mathrm{H} _{2}>\mathrm{H} _{3}>$………………
(b) $\mathrm{H} _{1}<\mathrm{H} _{2}<\mathrm{H} _{3}<$………………
(c) $\mathrm{H} _{1}>\mathrm{H} _{3}>\mathrm{H} _{5}>$………………and $\mathrm{H} _{2}<\mathrm{H} _{4}<\mathrm{H} _{6}<$………………
(d) $\mathrm{H} _{1}<\mathrm{H} _{3}<\mathrm{H} _{5}<$………………and $\mathrm{H} _{2}>\mathrm{H} _{4}>\mathrm{H} _{6}>$………………
Show Answer
Answer: (i) c (ii) a (iii) b9. If $x, y, z>0$ and $x+y+z=1$, the $\dfrac{x y z}{(1-x)(1-y)(1-z)}$ is necessarily
(a) $\geq 8$
(b) $\leq \dfrac{1}{8}$
(c) $<\dfrac{1}{8}$
(d) None of these
Show Answer
Answer: b10.* Match the following:
| Column I | Column II | ||
|---|---|---|---|
| (a) | 3 numbers a,b, c between $2 \& 18$ such that | (p) | $\mathrm{G}-\mathrm{L}=4$ |
| (i) | $a+b+c=25$ | (q) | $\left[\dfrac{\mathrm{G}}{\mathrm{L}}\right]=4$ |
| (ii) | 2, a, b are consecutive terms of an A.P. | (r) | $\mathrm{G}-\mathrm{L}=7$ |
| (iii) | b, c, 18 are consecutive terms of a G.P. | (s) | $\left\lceil\dfrac{\mathrm{G}}{\mathrm{L}}\right\rceil=3$ |
| $\text { If } \mathrm{G}=\max \{\mathrm{a}, \mathrm{b}, \mathrm{c}\}$ & $\mathrm{~L}=\min {\mathrm{a}, \mathrm{b}, \mathrm{c}} \text { then }$ | (t) | $\left[\dfrac{\mathrm{G}}{\mathrm{L}}\right]+\left\lceil\dfrac{\mathrm{G}}{\mathrm{L}}\right\rceil=3$ | |
| (b) | 3 numbers $a, b, c$ are in G.P. Such that | ||
| (i) | $a+b+c=70$ | ||
| (ii) | $4 \mathrm{a}, 5 \mathrm{~b}, 4 \mathrm{c}$ are is A.P. | ||
| If $\mathrm{G}=\operatorname{Max}\{\mathrm{a}, \mathrm{b}, \mathrm{c}\}$ and $\mathrm{L} =\operatorname{Min}\{\mathrm{a}, \mathrm{b}, \mathrm{c}\}$, then |
Show Answer
Answer: $a \rightarrow r, s, b \rightarrow q$11. The coefficient of $\mathrm{x}^{203}$ is the expansion of $(\mathrm{x}-1)\left(\mathrm{x}^{2}-2\right)\left(\mathrm{x}^{2}-3\right)$……………..$\left(\mathrm{x}^{20}-20\right)$ is
(a) -35
(b) 21
(c) 13
(d) 25
Show Answer
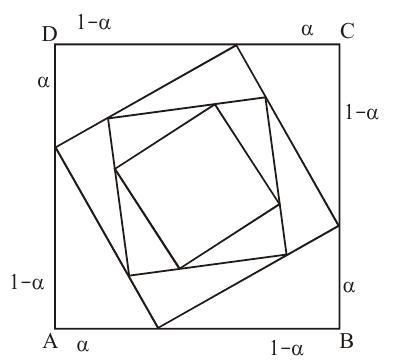
Answer: c12. Read the following passage and answer the questions :Let $\mathrm{ABCD}$ is a unit square and $0<\alpha<1$. Each side of the square is divided in the ratio $\alpha: 1-\alpha$, as shown in the figure. These points are connected to obtain another square. The sides of new square are divided in the ratio $\alpha: 1-\alpha$ and points are joined to obtain another square. The process is continued indefinitely.
Let $a _{n}$ denote the length of side and $A _{n}$ the area of the $n$th square
(i) The value of $\alpha$ for which $\sum \limits _{n=1}^{\infty} A _{n}=\dfrac{8}{3}$ is
(a) $1 / 3,2 / 3$
(b) $1 / 4,3 / 4$
(c) $1 / 5,4 / 5$
(d) $1 / 2$
(ii) The value of $\alpha$ for which side of $\mathrm{n}^{\text {th }}$ square equals the diagonals of $(\mathrm{n}+1)$ th square is
(a) $1 / 3$
(b) $1 / 4$
(c) $1 / 2$
(d) $1 / \sqrt{2}$
(iii) If $a=1 / 4$ and $P _{n}$ denotes the perimeter of the $n^{\text {th }}$ square then $\sum\limits _{n=1}^{\infty} P _{n}$ equals
(a) $8 / 3$
(b) $32 / 3$
(c) $16 / 3$
(d) $\dfrac{8}{3}(4+\sqrt{10})$










