Probability (Lecture-01)
Recap of facts of formulae
1. Sample space
The set of all possible out comes of a random experiment is called the sample space for the event. It is usually denoted by $\mathrm{S}$.
2. Event
A subset of the sample space is one event.
3. Simple (Elementary Event)
An event consisting of a single point is called a simple event.
4. Compound (Mixed / composite) event
The disjoint union of single element subsets of the sample sapce.
5. Equally likely events
Events are said to be equally likely if they have no reason to believe that one is more likely to occur than the other.
6. Exhaustive Events
Events are said to be exhaustive if the occurence of any one of them is a certainity (i.e. their union=S)
7. Mutually exclusive events
Events A and B are said to be mutally exclusive when both cannot happen simultaneously. i.e $\mathrm{A} \cap \mathrm{B}=\phi$.
8. Properties
(i) For every subset $\mathrm{A}$ of $\mathrm{S}, 0 \leq \mathrm{P}(\mathrm{A}) \leq 1$
(ii) $\mathrm{P}(\phi)=0$ and $\mathrm{P}(\mathrm{S})=1$
(iii) If $\mathrm{A}$ and $\mathrm{B}$ are two events, then $\mathrm{P}(\mathrm{A} \cup \mathrm{B})=\mathrm{P}(\mathrm{A})+\mathrm{P}(\mathrm{B})-\mathrm{P}(\mathrm{A} \cap \mathrm{B})$ (Addition Theorem) Here if $A$ and $B$ are mutually exclusive, then $\mathrm{P}(\mathrm{A} \cup \mathrm{B})=\mathrm{P}(\mathrm{A})+\mathrm{P}(\mathrm{B})$
Also $\mathrm{P}(\mathrm{A} \cup \mathrm{B} \cup \mathrm{C})=\mathrm{P}(\mathrm{A})+\mathrm{P}(\mathrm{B})+\mathrm{P}(\mathrm{C})-\mathrm{P}(\mathrm{A} \cap \mathrm{B})-\mathrm{P}(\mathrm{B} \cap \mathrm{C})-\mathrm{P}(\mathrm{C} \cap \mathrm{A})+\mathrm{P}(\mathrm{A} \cap \mathrm{B} \cap \mathrm{C})$
Here if $A, B, C$ are mutually exclusive then $P(A \cup B \cup C)=P(A)+P(B)+P(C)$
The odds in favour of occurence of the event $\mathrm{A}$ are defined by $\mathrm{P}(\mathrm{A}): \mathrm{P}(\overline{\mathrm{A}})$ and the odds against the occurence of $A$ are defined by $\mathrm{P}(\overline{\mathrm{A}}): \mathrm{P}(\mathrm{A})$
$\mathrm{P}$ (exactly one of $\mathrm{A}, \mathrm{B}, \mathrm{C}$ occurs)
$=\mathrm{P}(\mathrm{A})+\mathrm{P}(\mathrm{B})+\mathrm{P}(\mathrm{C})-2 \mathrm{P}(\mathrm{A} \cap \mathrm{B})-2 \mathrm{P}(\mathrm{B} \cap \mathrm{C})-2 \mathrm{P}(\mathrm{C} \cap \mathrm{A})+3 \mathrm{P}(\mathrm{A} \cap \mathrm{B} \cap \mathrm{C})$
$P$ (exactly two of $A, B, C$ occur)
$=\mathrm{P}(\mathrm{A} \cap \mathrm{B})+\mathrm{P}(\mathrm{B} \cap \mathrm{C})+\mathrm{P}(\mathrm{C} \cap \mathrm{A})-3 \mathrm{P}(\mathrm{A} \cap \mathrm{B} \cap \mathrm{C})$
$\mathrm{P}($ at least two occur $)=\mathrm{P}(\mathrm{A} \cap \mathrm{B})+\mathrm{P}(\mathrm{B} \cap \mathrm{C})+\mathrm{P}(\mathrm{C} \cap \mathrm{A})-2 \mathrm{P}(\mathrm{A} \cap \mathrm{B} \cap \mathrm{C})$
(iv) $\mathrm{P}(\overline{\mathrm{A}})=1-\mathrm{P}(\mathrm{A})$
(v) $P(A \cap \bar{B})=P(A)-P(A \cap B)$
$\mathrm{P}(\overline{\mathrm{A}} \cap \overline{\mathrm{B}})=\mathrm{P}(\overline{\mathrm{A} \cup \mathrm{B}})=1-\mathrm{P}(\mathrm{A} \cup \mathrm{B})$
$\mathrm{P}(\overline{\mathrm{A}} \cup \overline{\mathrm{B}})=\mathrm{P}(\overline{\mathrm{A} \cap \mathrm{B}})=1-\mathrm{P}(\mathrm{A} \cap \mathrm{B})$
(vi) If $\mathrm{A} \& \mathrm{~B}$ are two events such that $\mathrm{A} \subseteq \mathrm{B}$, then $\mathrm{P}(\mathrm{A}) \leq \mathrm{P}$ (B)
Also $\mathrm{P}(\mathrm{A} \cap \mathrm{B}) \leq \mathrm{P}(\mathrm{A}) \leq \mathrm{P}(\mathrm{A} \cup \mathrm{B}) \leq \mathrm{P}(\mathrm{A})+\mathrm{P}(\mathrm{B})$
9. Conditional Probability
For two events A & B of S, the probability of A under the condition that event B has already happened is called conditional probability of $A$
$\mathrm{P}(\mathrm{A} / \mathrm{B})=\dfrac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{B})} ; \mathrm{P}(\mathrm{B}) \neq 0$
$=\dfrac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{B})}$
10. Independent Events.
Events $\mathrm{A}$ and $\mathrm{B}$ are said to be independent if $\mathrm{P}(\mathrm{A} / \mathrm{B})=\mathrm{P}(\mathrm{A})$ and $\mathrm{P}(\mathrm{B})(\mathrm{A})=\mathrm{P}(\mathrm{B})$
i.e. $P(A \cap B)=P(A) P(B)$
Also $\mathrm{P}(\mathrm{A} \cap \mathrm{B})=\mathrm{P}(\mathrm{A}) \mathrm{P}(\mathrm{B} / \mathrm{A})=\mathrm{P}(\mathrm{B}) \mathrm{P}(\mathrm{A} / \mathrm{B})$ ( Multiplication theorem)
If $A \& B$ are independint then
- $\mathrm{A} \& \overline{\mathrm{B}}$ are independent
- $\bar{A} \& B$ are independent
- $\bar{A} \& \bar{B}$ are independent
11. Pair wise and mutual independent events.
the events A, B, C are said to be pair wise independent if
- $\quad \mathrm{P}(\mathrm{A} \cap \mathrm{B})=\mathrm{P}(\mathrm{A}) . \mathrm{P}(\mathrm{B})$ (i.e. $\mathrm{A} \& \mathrm{~B}$ are independent)
- $\quad \mathrm{P}(\mathrm{B} \cap \mathrm{C})=\mathrm{P}(\mathrm{B}) . \mathrm{P}(\mathrm{C})$ (i.e. $\mathrm{B} \& \mathrm{C}$ are independent)
- $\quad \mathrm{P}(\mathrm{C} \cap \mathrm{A})=\mathrm{P}(\mathrm{C}) . \mathrm{P}(\mathrm{A})$ (i.e. $\mathrm{C} \& \mathrm{~A}$ are independent)
Along with the above three conclusions if $\mathrm{P}(\mathrm{A} \cap \mathrm{B} \cap \mathrm{C})=\mathrm{P}(\mathrm{A}) . \mathrm{P}(\mathrm{B}) . \mathrm{P}(\mathrm{C})$ then we say $\mathrm{A}, \mathrm{B}, \mathrm{C}$ are mutually independent
If $\mathrm{A} _{1}, \mathrm{~A} _{2}, \ldots \ldots \ldots . \mathrm{A} _{\mathrm{n}}$ are pair wise independent events, then the total number of conditions for their pair wise independence is ${ }^{n} \mathrm{C} _{2}$ where as for their mutual independence there must be ${ }^{n} \mathrm{C} _{2}+{ }^{n} \mathrm{C} _{3}+\ldots \ldots . .+{ }^{\mathrm{n}} \mathrm{C} _{\mathrm{n}}=2{ }^{\mathrm{n}}-\mathrm{n}-1$ conditions.
Mutually independent events are always pairwise independent, but the converse need not be true. Note: In case of only two events associated with the experiment, their is no distinction between pair wise independence and mutual independence.
Law of Total Probalility and Bayes theorem
Let $\mathrm{S}$ be the sample space and let $\mathrm{E} _{1}, \mathrm{E} _{2}, \ldots \ldots ., \mathrm{E} _{\mathrm{n}}$ be $\mathrm{n}$ mutually exclusive and exhaustive events associated with a random experiment.
Then for any event $\mathrm{A}($ where $\mathrm{P}(\mathrm{A}) \neq 0$ ) and for $1 \leq \mathrm{i} \leq \mathrm{n}$,
$\begin{aligned} P(A) & =P\left(E _{1}\right) \cdot P\left(A \mid E _{1}\right)+P\left(E _{2}\right) p\left(A \mid E _{2}\right)+\ldots . .+P\left(E _{n}\right) P\left(A \mid E _{n}\right) \\ & =\sum\limits _{i=1}^{n} P\left(E _{i}\right) P\left(A \mid E _{i}\right) \quad \text { (Law of total probability) } \\ P\left(E _{i} \mid A\right) & =\dfrac{P\left(E _{i}\right) P\left(A \mid E _{i}\right)}{\sum\limits _{i=1}^{n} P\left(E _{i}\right) P\left(A \mid E _{i}\right)} ; i=1,2, \ldots ., n \quad \text { (Bayes theorem) } \end{aligned}$
Random Variable and its Probability distribution
Let $\mathrm{S}$ be the sample space associated with a random experiment. Then a real valued function $\mathrm{X}$
which assigns to each events $\mathrm{W} \in \mathrm{S}$ to to a unique real number $\mathrm{X}(\mathrm{w})$ is a called a random variable. Discrete Random Variable: - If a random variable takes at most a countable number of values, it is called discrete random variable.
Probability Mass Function (p.m.f.)
Let a random variable (discrete) $X$ assumes values $\mathrm{x} _{1}, \mathrm{x} _{2}, \ldots . \mathrm{x} _{\mathrm{n}}$ with probalilities $\mathrm{p} _{1}, \mathrm{p} _{2}, \ldots . \mathrm{p} _{\mathrm{n}}$. i.e. $p _{i}=P\left(X=x _{i}\right)$ where $p _{i}$ satisfy the following conditions
(a) $\mathrm{p} _{\mathrm{i}} \geq 0 \forall \mathrm{i}$ and
(b) $\sum\limits _{\mathrm{i}=1}^{\infty} \mathrm{p} _{\mathrm{i}}=1$
This function $P$ is called the probalility mass function of $X$ and $\left{p _{i}\right}$ is called the probability distribution (p.d) of the random variable (r.v) of X.
Mean (Average) $=\bar{x}($ or $\mu)$
$=\mathrm{E}(\mathrm{x})=\mu(0)\left(1^{\text {st }}\right.$ moment about origin $)=\sum \mathrm{x} _{\mathrm{i}} \mathrm{p} _{\mathrm{i}}$
$2^{\text {nd }}$ moment about origin $\mu^{1}{ } _{2}(0)=\mathrm{E}\left(\mathrm{x}^{2}\right)=\sum \mathrm{x} _{\mathrm{i}}{ }^{2} \mathrm{p} _{\mathrm{i}}$
Variance $\left(=2^{\text {nd }}\right.$ moment about mean or 2 nd central moment)
$=\sigma^{2}=\mu _{2}=\mathrm{E}(\mathrm{x}-\mathrm{E}(\mathrm{x}))^{2}$
$=\mu _{2}^{\prime}(0)-\mu _{1}^{\prime}(0)$
$=\sum \mathrm{x} _{\mathrm{i}}{ }^{2} \mathrm{p} _{\mathrm{i}}-\left(\sum \mathrm{x} _{\mathrm{i}} \mathrm{p} _{\mathrm{i}}\right)^{2}$
Binomial distribution (B.D.)
The probalility of $r$ successes in $n$ independent bernoullian trials is given by $P(x=r)={ }^{n} C _{r} p^{r} q^{n-r} ; r=0,1,2 \ldots \ldots \ldots n$ where $p=P(S), q=P(F)$ such that $p+q=1$ Here $n \& p$ are the parameters of B.D.
i.e. Discrete random variable $\mathrm{X}$ is said to follow B.D. with parameters $\mathrm{n}$, $\mathrm{p}$, if its probability mass function is given by $\mathrm{P}(\mathrm{x}=\mathrm{r})={ }^{\mathrm{n}} \mathrm{C} _{\mathrm{r}} \mathrm{p}^{\mathrm{r}} \mathrm{q}^{\mathrm{n}-\mathrm{r}}$
$\mathrm{r}=0,1, \ldots . \mathrm{n} ; \mathrm{p}+\mathrm{q}=1$
$\mathrm{P}(\mathrm{X}=\mathrm{r})$ is maximum where $\mathrm{r}=[\mathrm{np}]$
Mean $=\overline{\mathrm{x}}=\mu=\mathrm{np}$.
Variance $=\sigma^{2}=$ npq. Also $0 \leq \sigma<\sqrt{\mu}$
In a B.D. mean>variance.
In a B.D., if $p=\dfrac{1}{2}=q$, then the distribution is a symmetrical binomial distribution.
Mode of a distribution is the value of the variable with maximum probalility. In the case of B.D, mode depends on the value of $n p+p$.
$\begin{array}{ll} \mathrm{np}+\mathrm{p}=\mathrm{K} \in \mathrm{Z} & \mathrm{np}+\mathrm{p}=\mathrm{k}+\mathrm{f} \\ 2 \text { modes } & (\mathrm{K} \in \mathrm{Z} \& \text { f is a proper fraction) } \\ \text { i.e. } \mathrm{k} \& \mathrm{k}-2 & \text { One mode i.e.k } \\ \text { (Bimodal binomial } & \text { (the integral part of } \mathrm{np}+\mathrm{p} \text { ) } \\ \text { distribution) } & \text { (unimodal binomial distribution) } \end{array}$
Not : In n independent bernoullian trials are repeated N times, then the expected frequency of r successes is given by
$\begin{aligned} \mathrm{f}(\mathrm{X}=\mathrm{r}) & =\mathrm{N} \mathrm{P}(\mathrm{X}=\mathrm{r}) \\ & =\mathrm{N}^{\mathrm{n}} \mathrm{C} _{\mathrm{r}} \mathrm{p}^{\mathrm{r}} \mathrm{q}^{\mathrm{n}-\mathrm{r}} \quad \mathrm{r}=0,1 ………{n.} \end{aligned}$
$f(X=1)$ is called the Binomial frequency distribution.
Note: The recurrence formula $\dfrac{P(r+1)}{P(r)}=\dfrac{n-r}{r+1} \cdot \dfrac{p}{q}$ is very helpful for quickly computing $P(1)$, $\mathrm{P}(2), \mathrm{P}(3)$ etc. if $\mathrm{P}(0)$ is known.
Poisson Distribution (P.D)
It is the limiting case of Binomial distribution when $\mathrm{p} \rightarrow 0$ and $\mathrm{n} \rightarrow \infty$ such that $\mathrm{np}=\lambda=\mathrm{m}$, $\mathrm{a}$ constant always. Poisson distribution is defined as $\mathrm{P}(\mathrm{X}=\mathrm{r})=\dfrac{\mathrm{e}^{-\lambda} \lambda^{\mathrm{r}}}{\mathrm{r} !} \mathrm{r}=0,1,2,3 \ldots \ldots \infty$ Here $\lambda$ is the parameter of P.D.
Mean $=\overline{\mathrm{x}}=\lambda=\mathrm{np}$
Variance $=\mu _{2}=\sigma^{2}=\lambda$
(In Poisson distribution mean $=$ variance i.e. $\overline{\mathrm{x}}=\sigma^{2}=\lambda$ )
$\mu _{3}=\lambda ; \mu _{4}=3 \lambda^{2}+n ; \beta _{1}=m^{-1}, \beta _{2}=3+m^{-1}$
Note: If $\mathrm{X} _{1} \& \mathrm{X} _{2}$ are two poisson variates with mean $\lambda _{1} \& \lambda _{2}$, then $\mathrm{x} _{1}+\mathrm{x} _{2}$ is also a Poisson variate with mean $\lambda _{1}+\lambda _{2}$,
Note : If the experiment is repeated $\mathrm{N}$ times, then the expected frequency of success of P.D is given by $\mathrm{f}(\mathrm{X}=\mathrm{r})=\mathrm{NP}(\mathrm{X}=\mathrm{r})$
$$ =\mathrm{N} \dfrac{\mathrm{e}^{-\lambda} \lambda^{\mathrm{r}}}{\mathrm{r} !}, \mathrm{r}=0,1,2,3 \ldots \ldots \infty $$
This is called as Poisson frequency distribution.
Continuous Random Variable
If the random variable takes all the values within a certain interval, it is called a continous random variable.
Results for continous Probalility Distribution
Let $f(x)$ be the probalility density function of a random variable $X$, where $X$ in defined from a to b, then
(i) Arithmetic mean $=\int _{a}^{b} x f(x) d x$
(ii) Geometric mean $=\mathrm{e}^{\mathrm{e}^{\mathrm{b}} \log \mathrm{x}(\mathrm{x}) \mathrm{dx}}$
(iii) Harmonic mean $=\dfrac{1}{\int _{\mathrm{a}}^{\mathrm{b}} \dfrac{1}{\mathrm{x}} \mathrm{f}(\mathrm{x}) \mathrm{dx}}$
(iv) The median M is given by $\int _{a}^{M} x f(x) d x=\dfrac{1}{2}$ or $\int _{M}^{b} x f(x) d x=\dfrac{1}{2}$
Normal Distribution
It is a special case of Binomial Distribution when $\mathrm{p}=\mathrm{q}$ and $\mathrm{n} \rightarrow \infty(\mathrm{p} \& \mathrm{q}$ are not very small.)It is a continuous distribution. The standard form of normal curve is $\mathrm{y}=\dfrac{1}{\sigma \sqrt{2 \pi}} \mathrm{e}^{-\mathrm{x}^{2} /\left(2 \sigma^{2}\right)}$
The area under this normal curve is 1 .
Geometrical Probalility
Definition of probability of occurrence of an event fails, if the total number of outcomes of a trial in a random experiment is infinite
In such cases, the general expression for the probalility p of occurrence of an event is given by
$\mathrm{p}=\dfrac{\text { measure of the specified part of the region }}{\text { measure of the whole region }}$
(Here measure means length, area or volume of the region according as we are dealing with one, two or three dimensional space)
Solved Examples
1. Three natural numbers are selected at random from 1 to 100, the probability that their AM is 25 is
(a) $\dfrac{{ }^{77} \mathrm{C} _{2}}{{ }^{100} \mathrm{C} _{3}}$
(b) $\dfrac{{ }^{25} \mathrm{C} _{2}}{{ }^{100} \mathrm{C} _{3}}$
(c) $\dfrac{{ }^{74} \mathrm{C} _{2}}{{ }^{100} \mathrm{C} _{3}}$
(d) None of these
Show Answer
Solution
$\dfrac{\mathrm{x}+\mathrm{y}+\mathrm{z}}{3} \Rightarrow \mathrm{x}+\mathrm{y}+\mathrm{z}=75$
$\therefore \dfrac{{ }^{72+3-1} \mathrm{C} _{3-1}}{{ }^{100} \mathrm{C} _{3}}$ (Applying ${ }^{\mathrm{n+r}-1} \mathrm{C} _{\mathrm{r}-1}$ in the numerator, using the result of distribution of alike objects)
$=\dfrac{{ }^{74} \mathrm{C} _{2}}{{ }^{100} \mathrm{C} _{3}}$
Answer (c)
2. 15 persons among whom are $\mathrm{A}$ and $\mathrm{B}$, sit down at random at round table. The probability that there are exactly four persons between $A$ and $B$ is
(a) $\dfrac{9 !}{14 !}$
(b) $\dfrac{10 !}{14 !}$
(c) $\dfrac{2.9 !}{14 !}$
(d) None of these
Show Answer
Solution
15 persons can be seated round a table in 14 ! ways. If 4 persons are to be included between $A$ and $B$, they can be arranged in ${ }^{13} \mathrm{C} _{4} \times 4$ ! ways, now total number of arrangements is
${ }^{13} \mathrm{C} _{4} \times 4 ! \times 9 ! \times 2 !=2.13$ !
Hence the probaility is $\dfrac{2.13 !}{14 !}=\dfrac{2}{14}=\dfrac{1}{7}$
Answer (d)
3. $2 \mathrm{n}$ boys are divided into two sub-groups containing $\mathrm{n}$ boys each. The probability that the two tallest boys are in different groups is
(a) $\dfrac{\mathrm{n}}{2 \mathrm{n}-1}$
(b) $\dfrac{\mathrm{n}-1}{2 \mathrm{n}-1}$
(c) $\dfrac{2 n-1}{4 n^{2}}$
(d) None of these
Show Answer
Solution
Total number of ways of dividing $2 \mathrm{n}$ boys in two equal groups is ${ }^{2 n} \mathrm{C} _{\mathrm{n}} \cdot{ }^{n} \mathrm{C} _{\mathrm{n}}$.
If we leave the two tallest boys, $2 \mathrm{n}-2$ boys can be divided into two equal groups in ${ }^{2 \mathrm{n}-2} \mathrm{C} \mathrm{n}-1$. ${ }^{n-1} C _{n-1}$ ways and the two tallest boys can be arranged in different groups in 2 ! ways.
$\therefore$ The required probability is
$=\dfrac{{ }^{2 n-2} C _{n-1} \cdot{ }^{n-1} C _{n-1} \cdot 2}{{ }^{2 n} C _{n} \cdot{ }^{n} C _{n}}=\dfrac{n}{2 n-1}$
Answer (a)
4. $\mathrm{~A}$ and $\mathrm{B}$ throw a dice. The probability that $\mathrm{A}^{\prime} \mathrm{s}$ throw is not greater than $\mathrm{B}^{\prime} \mathrm{s}$ is
(a) $\dfrac{5}{12}$
(b) $\dfrac{7}{12}$
(c) $\dfrac{1}{6}$
(d) None of these
Show Answer
Solution
| B’s throw | A’s throw |
|---|---|
| 6 | $1,2,3,4,5,6$ |
| 5 | $1,2,3,4,5$ |
| 4 | $1,2,3,4$ |
| 3 | $1,2,3$ |
| 2 | 1,2 |
| 1 | 1 |
Favourable ways is 21 .
$\therefore$ required probability is $\dfrac{21}{36}=\dfrac{7}{12}$
Answer (b)
5. The probability that the sum of squares of two non-negative integers is divisible by 5 is
(a) $\dfrac{7}{25}$
(b) $\dfrac{8}{25}$
(c) $\dfrac{9}{25}$
(d) $\dfrac{2}{25}$
Show Answer
Solution
Let two non-negative integers be $x \& y$ such that $x=5 a+\alpha$ and $y=5 b+\beta$ where $0 \leq \alpha, \beta \leq 4$
New, $\mathrm{x}^{2}+\mathrm{y}^{2}=25\left(\mathrm{a}^{2}+\mathrm{b}^{2}\right)+10(\mathrm{a} \alpha+\mathrm{b} \beta)+\alpha^{2}+\beta^{2}$
$\Rightarrow \alpha^{2}+\beta^{2}$ should be divisible by 5
$\therefore(\alpha, \beta)$ can have ordered pairs as
${(0,0),(1,2),(2,1),(1,3),(3,1),(2,4),(4,2),(3,4),(4,3)}=9$ ways
$\therefore$ required probability is $\dfrac{9}{25}$
Answer (c)
6. The probability that the length of a randomly selected chord of a circle lies between $\dfrac{2}{3}$ and $\dfrac{5}{6}$ of its diameter is
(a) $\dfrac{5}{16}$
(b) $\dfrac{1}{16}$
(c) $\dfrac{1}{4}$
(d) $\dfrac{2}{3}$
Show Answer
Solution
length of chord is 2 asin $\theta$
$\therefore \dfrac{2}{3}(2 \mathrm{a})<2 \operatorname{asin} \theta<\dfrac{5}{6}(2 \mathrm{a})$
$\Rightarrow \dfrac{2}{3}<\sin \theta<\dfrac{5}{6}$
$\Rightarrow \dfrac{\sqrt{11}}{6}<\cos \theta<\dfrac{\sqrt{5}}{3}$
$\Rightarrow \dfrac{\sqrt{11}}{6} \mathrm{a}<\mathrm{r}<\dfrac{\sqrt{5}}{3} \mathrm{a}$
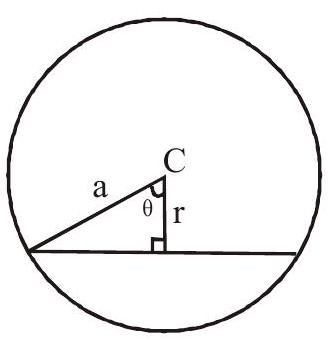
$\therefore$ required probability is $=\dfrac{\pi\left(\dfrac{\sqrt{5}}{3} \mathrm{a}\right)^{2}-\pi\left(\dfrac{\sqrt{11}}{6} \mathrm{a}\right)^{2}}{\pi \mathrm{a}^{2}}=\dfrac{1}{4}$
7. If $p$ is selected from the interval $[0,5]$, then the probability that the equation $4 x^{2}+4 p x+(p+2)=0$ has real roots
(a) $\dfrac{1}{2}$
(b) $\dfrac{1}{4}$
(c) $\dfrac{3}{5}$
(d) $\dfrac{2}{5}$
Show Answer
Solution
For real roots, $\mathrm{D} \geq 0$
$\Rightarrow \mathrm{p}^{2}-\mathrm{p}-2 \geq 0$
$\Rightarrow \mathrm{p} \leq-1 \quad \mathrm{p} \geq 2$
$\therefore \mathrm{p} \in[2,5]$ but $\mathrm{p} \in[0,5]$
$\therefore$ required probability $=\dfrac{5-2}{5-0}=\dfrac{3}{5}$ (length of interval)
8. A dice is thrown three times. The probalility of getting a number large than previous one every time is
Show Answer
| 1 st throw | 2nd throw(fixed) | 3rd throw | |
|---|---|---|---|
| 1 | 2 | $2,3,4,5,6$ | 4 cases |
| 1,2 | 3 | $4,5,6$ | 6 cases |
| $1,2,3$ | 4 | 5,6 | 6cases |
| $1,2,3,4$ | 5 | 6 | 4 cases |
Total no of favourable cases $=20$
Total number of cases $=6 \times 6 \times 6$
Requred probability $=\dfrac{20}{216}=\dfrac{5}{54}$
Exercise
1. Eight players $\mathrm{P} _{1}, \mathrm{P}$ … $\mathrm{P} _{8}$ play a knock-out tournament. It is known that whenever players $\mathrm{P}$ and $\mathrm{P} _{\mathrm{j}}$ play, the player $\mathrm{P} _{i}$ will win if $\mathrm{i}<\mathrm{j}$. Assuming that the players are paired at random in each round, the probability that the player $\mathrm{P} _{4}$ reaches the final is
(a) $\dfrac{1}{8}$
(b) $\dfrac{12}{35}$
(c) $\dfrac{1}{3}$
(d) $\dfrac{4}{35}$
Show Answer
Answer: d2. A is a set containing $n$ elements $A$ subset $P$ of $A$ is chosen at random. The set $A$ is reconstructed by replacing the elements of $\mathrm{P}$. A subset $\mathrm{Q}$ of $\mathrm{A}$ is again chosen at random. The probalility that $\mathrm{P}$ and $\mathrm{Q}$ have no common elements is
(a) $\left(\dfrac{3}{4}\right)^{\mathrm{n}}$
(b) $\left(\dfrac{1}{2}\right)^{\mathrm{n}}$
(c) $\dfrac{{ }^{n} C _{2}}{2^{n}}$
(d) None of these
Show Answer
Answer: a3. A box contains 2 fifty paise coins, 5 twenty five paise coins and a certain fixed number $\mathrm{n}(\geq 2)$ of ten and 5 paise coins. Five coins are taken out of the box at random. The probalility that the total value of these 5 coins is less than one rupee and fifty paise is
(a) $\dfrac{10(\mathrm{n}+2)}{{ }^{\mathrm{n}+7} \mathrm{C} _{5}}$
(b) $1-\dfrac{10(\mathrm{n}+2)}{{ }^{\mathrm{n}+7} \mathrm{C} _{5}}$
(c) $\dfrac{10(\mathrm{n}+2)}{5^{5}}$
(d) None of these
Show Answer
Answer: b4. Read the following passage and answer the question.
0There are $n$ urns each containing $(\mathrm{n}+1)$ balls such that the $\mathrm{i}^{\text {th }}$ urn contains ’ $\mathrm{i}$ ’ white balls and $(\mathrm{n}+1-$ i) red balls. Let $u _{i}$ be the event of selecting $i^{\text {th }}$ urn, $i=1,2,3, \ldots \ldots . . n$ and $W$ denotes the event of getting a white ball.
(i) If $\mathrm{P}\left(\mathrm{u} _{\mathrm{i}}\right) \propto \mathrm{i}$, where $\mathrm{i}=1,2, \ldots \ldots . . \mathrm{n}$, then $\lim _{\mathrm{n} \rightarrow \infty} \mathrm{P}(\mathrm{W})$ is
(a) 1
(b) $\dfrac{2}{3}$
(c) $\dfrac{1}{4}$
(d) $\dfrac{3}{4}$
(ii) If $\mathrm{P}\left(\mathrm{u} _{i}\right)=\mathrm{c}$, where $c$ is a constant, then $\mathrm{P}\left(\mathrm{u} _{n} \mid \mathrm{W}\right)$ is
(a) $\dfrac{2}{n+1}$
(b) $\dfrac{1}{n+1}$
(c) $\dfrac{\mathrm{n}}{\mathrm{n}+1}$
(d) $\dfrac{1}{2}$
(iii) If $\mathrm{n}$ is even and $\mathrm{E}$ denotes the event of choosing even numbered $\operatorname{urn}\left(\mathrm{p}\left(\mathrm{u} _{\mathrm{i}}\right)=\dfrac{1}{\mathrm{n}}\right)$, then the value of $\mathrm{P}(\mathrm{W} \mid \mathrm{E})$ is
(a) $\dfrac{\mathrm{n}+2}{2 \mathrm{n}+1}$
(b) $\dfrac{\mathrm{n}+2}{2(\mathrm{n}+1)}$
(c) $\dfrac{\mathrm{n}}{\mathrm{n}+1}$
(d) $\dfrac{1}{\mathrm{n}+1}$
Show Answer
Answer: (i) b (ii) a (iii) b5. A signal which can be green or red with probalility $\dfrac{4}{5}$ and $\dfrac{1}{5}$ respectively, is received by station A
and then transmitted to station B. The probalility of each station receiving the signal correctly is $\dfrac{3}{4}$. If the signal received at station $B$ is green, then the probalility that the original signal is green is
(a) $\dfrac{3}{5}$
(b) $\dfrac{5}{7}$
(c) $\dfrac{20}{23}$
(d) $\dfrac{9}{20}$
Show Answer
Answer: c6. Let $\omega$ be a complex cube root of unity (i.e. $\omega \neq 1$ ). A fair die is thrown three times. If $r _{1}, r _{2}, \& r _{3}$ are the numbers obtained on the die, then the probalility that $\omega^{\mathrm{r} _{1}}+\omega^{\mathrm{r} _{2}}+\omega^{\mathrm{r} _{3}}=0$ is
(a) $\dfrac{1}{18}$
(b) $\dfrac{1}{9}$
(c) $\dfrac{2}{9}$
(d) $\dfrac{1}{36}$
Show Answer
Answer: c7. An experiment has 10 equally likely outcomes. Let $A \& B$ be two non-empty events of the experiment. If A consists of 4 out comes, the number of outcomes that $B$ must have so that $A \& B$ are independent, is
(a) 2,4 or 8
(b) 3,6 or 9
(c) 4 or 8
(d) 5 or 10
Show Answer
Answer: d8. If $a \in[-6,12]$, the probalility that graph of $y=-x^{2}+2(a+4) x-(3 a+40)$ is strictly below $x-a x i s$ is
(a) $\dfrac{2}{3}$
(b) $\dfrac{1}{3}$
(c) $\dfrac{1}{2}$
(d) $\dfrac{1}{4}$
Show Answer
Answer: c9. Match the following.
If the squares of a $8 \times 8$ chessboard are painted either red or black at random then
| Column I | Column II | ||
|---|---|---|---|
| (a) | $\mathrm{P}$ (not all the squares is any column are alternating in colour) $=$ | (p) | $\dfrac{1}{2^{63}}$ |
| (b) | $\mathrm{P}$ (chessboard contains equal number of red and black square) = | (q) | $\dfrac{\left(2^{8}-2\right)^{8}}{2^{64}}$ |
| (c) | P (all the squares in any column are of same colour and that of a row are of alternating colour is) $=$ | (r) | $\dfrac{{ }^{64} \mathrm{C} _{32}}{2^{64}}$ |
Show Answer
Answer: $\mathrm{a} \rightarrow \mathrm{q} ; \mathrm{b} \rightarrow \mathrm{r} ; \mathrm{c} \rightarrow \mathrm{a}$10.* A square is inscribed in a circle. If $\mathrm{P} _{1}$ is the probalility that a randomly chosen point of the circle lies with in the square and $\mathrm{P} _{2}$ is the probalility that the point lies outside the square, then
(a) $\mathrm{P} _{1}<\mathrm{P} _{2}$
(b) $\mathrm{P} _{1}=\mathrm{P} _{2}$
(c) $\mathrm{P} _{1}>\mathrm{P} _{2}$
(d) $\mathrm{P} _{1}{ }^{2}-\mathrm{P} _{2}{ }^{2}<3$










