Parabola (Lecture-02)
Equation of Normal
| Parabola | Point form | Pt.of contact | Parametric form | Point of contact | slope Form | Pt.of contact |
|---|---|---|---|---|---|---|
| $y^2=4 a x$ | $y-y_1=\frac{-y_1}{2 a}\left(x-x_1\right)$ | $\left(x_1, y_1\right)$ | $y=-t x+2 a t+a t^3$ | $\left(a t^2, 2 a t\right)$ | $y=m x-2 a m-a m^3$ | $\left(a m^2,-2 a m\right)$ |
| $y^2=-4 a x$ | $y-y_1=\frac{y_1}{2 a}\left(x-x_1\right)$ | $\left(x_1, y_1\right)$ | $y=-t x+2 a t+a t^3$ | $\left(-a t^2, 2 a t\right)$ | $y=m x+2 a m+a m^3$ | $\left(-a m^2, 2 a m\right)$ |
| $x^2=4 a y$ | $x-x_1=\frac{x_1}{2 a}\left(y-y_1\right)$ | $\left(x_1, y_1\right)$ | $x=-t y+2 a t+a t^3$ | $\left(2 a t, a t^2\right)$ | $y=m x+2 a+\frac{a}{m^2}$ | $\left(-\frac{2 a}{m}, \frac{a}{m^2}\right)$ |
| $x^2=-4 a y$ | $x-x_1=\frac{x_1}{2 a}\left(y-y_1\right)$ | $\left(x_1, y_1\right)$ | $x=t y+2 a t+a t^3$ | $\left(2 a t,-a t^2\right)$ | $y=m x-2 a-\frac{a}{m^2}$ | $\left(\frac{2 a}{m},-\frac{a}{m^2}\right)$ |
Equation of normal to the parabola $(y-k)^{2}=4(x-h)$ is
$y-k=m(x-h)-2 a m-a^{3}$
Properties of Normal
1. If the normal at the point $\mathrm{P}\left(\mathrm{at} _{1}{ }^{2}, 2 \mathrm{at} _{1}\right)$ meets the parabola at
$\mathrm{Q}\left(\mathrm{at} _{2}{ }^{2}, 2 \mathrm{at} _{2}\right)$, then $\mathrm{t} _{2}=-\mathrm{t} _{1}-\dfrac{2}{\mathrm{t} _{1}}$
2. If the normal at the points $\left(a t _{1}{ }^{2}, 2 \mathrm{at} _{1}\right)$ and $\left(\mathrm{at} _{2}{ }^{2}, 2 \mathrm{at} _{2}\right)$ meet on the parabola $\mathrm{y}^{2}=4 \mathrm{ax}$, then $\mathrm{t} _{1} \mathrm{t} _{2}=2$.
3. No normal other than axis passes through focus.
Important Properties :
- If the tangent and normal at any point ’ $\mathrm{P}$ ’ of the parabola intersect the axis at $\mathrm{T}$ and $\mathrm{N}$ then $\mathrm{ST}$ $=\mathrm{SN}=\mathrm{SP}$ where $\mathrm{S}$ in the focus.
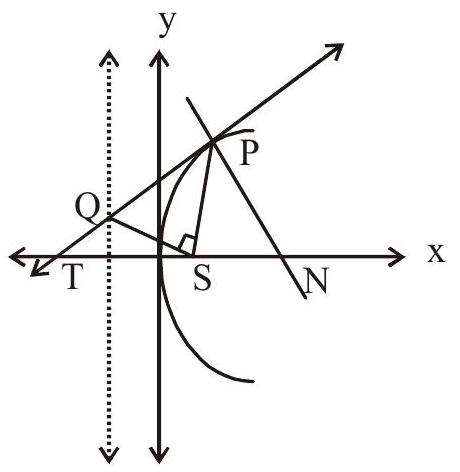
- The portion of a tangent to a parabola cut off between the directrix & the curve subtends a right angle at the focus.
$\angle \mathrm{PSQ}=90^{\circ}$
- Any tangent to a parabola and the perpendicular on it from the focus meet on the tangent at the vertex.
$\angle \mathrm{PQS}=90^{\circ}$
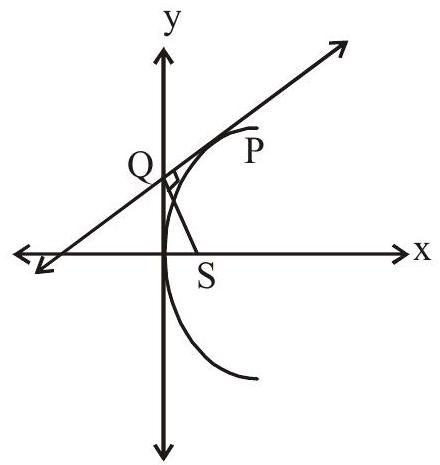
- If the tangents at $\mathrm{A}$ and $\mathrm{B}$ meet in $\mathrm{P}$ then $\mathrm{PA}$ and $\mathrm{PB}$ subtends equal angles at the focus $\mathrm{S}$. $(\mathrm{SP})^{2}=\mathrm{SA} \times \mathrm{SB}$
$\triangle \mathrm{SAP} \sim \triangle \mathrm{SPB}$
$\angle \mathrm{PSA}=\angle \mathrm{PSB}$.
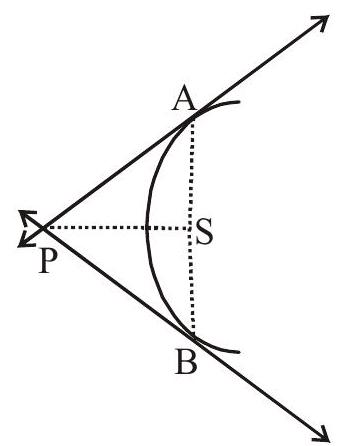
- The area of the triangle formed by three points on a parabola is twice the area of the triangle formed by the tangents at these points.
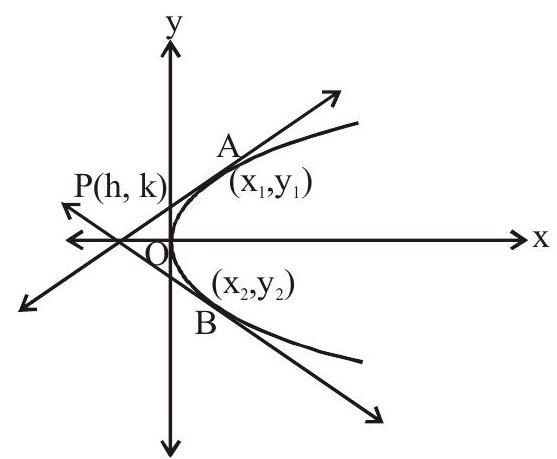
Conormal points:
Let $\mathrm{P}(\mathrm{h}, \mathrm{k})$ be a point and equation of parabola be $\mathrm{y}^{2}=4 \mathrm{ax}$.
Equation of normal is
$y=m x-2 a m-a m^{3}$
If passes through $(\mathrm{h}, \mathrm{k})$ so
$\begin{aligned} & \mathrm{k}=\mathrm{mh}-2 \mathrm{am}-\mathrm{am}^{3} \\ & \mathrm{am}^{3}+2 \mathrm{am}-\mathrm{mh}+\mathrm{k}=0 \end{aligned}$
$\mathrm{am}^{3}+\mathrm{m}(2 \mathrm{a}-\mathrm{h})+\mathrm{k}=0$
Suppose $\mathrm{m} _{1}, \mathrm{~m} _{2}, \mathrm{~m} _{3}$ are the roots of this equation
$\therefore \quad \mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}=0$
$\begin{aligned} & \mathrm{m} _{1} \mathrm{~m} _{2}+\mathrm{m} _{2} \mathrm{~m} _{3}+\mathrm{m} _{3} \mathrm{~m} _{1}=\dfrac{2 \mathrm{a}-\mathrm{h}}{\mathrm{a}} \\ & \mathrm{m} _{1} \cdot \mathrm{m} _{2} \cdot \mathrm{m} _{3}=-\dfrac{\mathrm{k}}{\mathrm{a}} \end{aligned}$
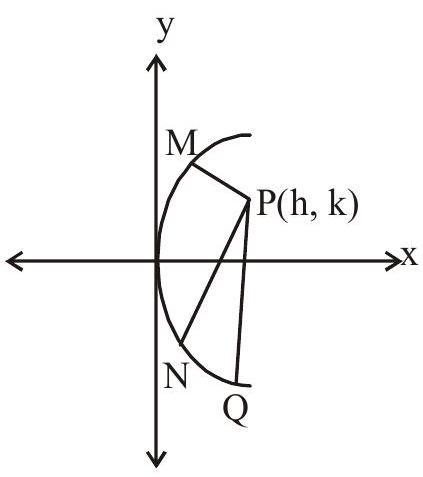
So maximum three normal say PM, PN, PQ drawn through P. Points M, N, Q are called conormal points.
- The algebraic sum of ordinates of the conormal points is zero.
Let the coordinates of conormal points be $\mathrm{M}\left(\mathrm{am} _{1}{ }^{2},-2 \mathrm{am} _{1}\right), \mathrm{N}\left(\mathrm{am} _{2}{ }^{2},-2 \mathrm{am} _{2}\right)$ and
$\mathrm{Q}\left(\mathrm{am} _{3}^{2},-2 \mathrm{am} _{3}\right)$. The ordinates of these points
$\mathrm{y} _{1}+\mathrm{y} _{2}+\mathrm{y} _{3}=-2 \mathrm{am} _{1}-2 \mathrm{am} _{2}-2 \mathrm{am} _{3}$
$=-2 \mathrm{a}\left(\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}\right)$
$=0$
$\Rightarrow \mathrm{y} _{1}+\mathrm{y} _{2}+\mathrm{y} _{3}=0$
- Centroid of the triangle formed by conormal points lies on the axis of parabola.
Let coordinates of conormal points be $\mathrm{M}\left(\mathrm{x} _{2}, \mathrm{y} _{1}\right), \mathrm{N}\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right) \mathrm{Q}\left(\mathrm{x} _{3}, \mathrm{y} _{3}\right)$
Then centroid is $\left(\dfrac{\mathrm{x} _{1}+\mathrm{x} _{2}+\mathrm{x} _{3}}{3}, \dfrac{\mathrm{y} _{1}+\mathrm{y} _{2}+\mathrm{y} _{3}}{3}\right)=\left(\dfrac{\mathrm{x} _{1}+\mathrm{x} _{2}+\mathrm{x} _{3}}{3}, 0\right)$
Since sum of ordinates is zero. Therefore centroid lies on the axis of parabola.
- $\quad$ Normal drown from a point $\mathrm{P}(\mathrm{h}, \mathrm{k})$ to the parabola are real and distinct if $\mathrm{h}>2 \mathrm{a}$.
Chord of Contact
Let $\mathrm{PA}$ and $\mathrm{PB}$ be tangents drawn through the point $\mathrm{P}(\mathrm{h}, \mathrm{k})$.
Equation of tangent at $\mathrm{A}$ is
$\mathrm{yy} _{1}=2 \mathrm{a}\left(\mathrm{x}+\mathrm{x} _{1}\right)$
Equation of chord whose midpoint $\left(x _{1}, y _{1}\right)$ is given :
$\begin{aligned} & \mathrm{S} \equiv \mathrm{y}^{2}-4 \mathrm{ax} \\ & \mathrm{S} _{1} \equiv \mathrm{y} _{1}{ }^{2}-4 \mathrm{ax} \\ & \mathrm{T} \equiv \mathrm{y} _{1}-2 \mathrm{a}\left(\mathrm{x}+\mathrm{x} _{1}\right) \end{aligned}$
Equation of $\mathrm{AB}$ is $\mathrm{T}=\mathrm{S}$
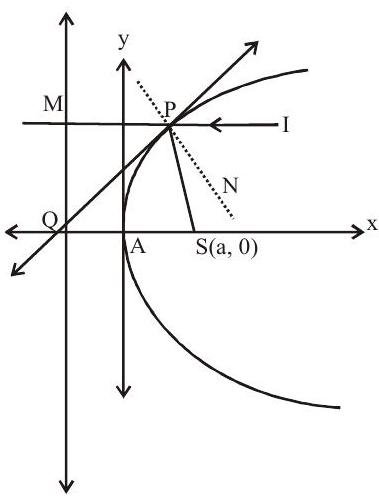
PI is incident ray then PS is reflected ray. So any ray incident parallel to axis of the parabola after reflection it passes through focus.
Example: 17 If the chord of contact of tangent from a point $\mathrm{P}$ to the parabola $\mathrm{y}^{2}=4 \mathrm{ax}$ touches the parabola $\mathrm{x}^{2}=4 \mathrm{by}$. The locus of $\mathrm{P}$ is
(a) Parabola
(b) Hyperbola
(c) ellipse
(d) Circle
Show Answer
Solution: Let the point $\mathrm{P}$ be $(\mathrm{h}, \mathrm{k})$ then equation of chord of contact is $\mathrm{ky}=2 \mathrm{a}(\mathrm{x}+\mathrm{h})$
Now this chord is tangent of parabola $\mathrm{x}^{2}=4 \mathrm{by}$
$\Rightarrow \mathrm{x}^{2}=4 \mathrm{~b} \cdot \dfrac{2 \mathrm{a}}{\mathrm{k}}(\mathrm{x}+\mathrm{h})$
$\Rightarrow \quad x^{2}\left(-\dfrac{8 a b}{k}\right)^{2}-4 x(1)\left(-\dfrac{8 a b h}{k}\right)=0$
$64 \dfrac{\mathrm{a}^{2} \mathrm{~b}^{2}}{\mathrm{k}^{2}}+\dfrac{32 \mathrm{abh}}{\mathrm{k}}=0$
$\Rightarrow \quad \dfrac{2 \mathrm{ab}}{\mathrm{k}}+\mathrm{h}=0$
$\Rightarrow 2 \mathrm{ab}=-\mathrm{hk}$
Locus $o(h, k)$ is $x y=-2 b$. ie. Hyperbola.
Answer: b
Example: 18 Let $P$ and $Q$ be points $(4,-4)$ and $(9,6)$ on the parabola $y^{2}=4 a(x-b)$. $R$ is a point on the parabola so that area $\triangle \mathrm{PRQ}$ is maximum, then
(a) $\angle \mathrm{PRQ}=90^{\circ}$
(b) the point $\mathrm{R}$ is $(4,4)$
(c) the point $\mathrm{R}$ is $\left(\dfrac{1}{4}, 1\right)$
(d) None of these
Show Answer
Solution: $(4,-4)$ lies on $\mathrm{y}^{2}=4 \mathrm{a}(\mathrm{x}-\mathrm{b}) \Rightarrow 16=4 \mathrm{a}(4-\mathrm{b})$
$(9,6)$ lies on $y^{2}=4 a(x-b) \Rightarrow 36=4 a(9-b)$
$\dfrac{9}{4}=\dfrac{9-b}{4-b} \Rightarrow b=0$
$\mathrm{a}=1$
$\therefore \quad \mathrm{y}^{2}=4 \mathrm{x}$
Let $\mathrm{R}$ be $\left(\mathrm{t}^{2}, 2 \mathrm{t}\right)$
area $\triangle \mathrm{PRQ}=\dfrac{1}{2}\left|\begin{array}{ccc}4 & -4 & 1 \\ 9 & 6 & 1 \\ \mathrm{t}^{2} & 2 \mathrm{t} & 1\end{array}\right|=\dfrac{1}{2}\left|\left\{4(6-2 \mathrm{t})+4\left(9-\mathrm{t}^{2}\right)+18 \mathrm{t}-6 \mathrm{t}^{2}\right\}\right|$
$=\dfrac{1}{2}\left(24-8 t+36-4 t^{2}+18 t-6 t^{2}\right)=\dfrac{1}{2}\left(-10 t^{2}+10 t+60\right)$
$=-5\left(t^{2}-t-6\right)=-5\left(t-\dfrac{1}{2}\right)^{2}+30+\dfrac{5}{4}$
Area is maximum when $\mathrm{t}=\dfrac{1}{2}$
Coordinates of $\mathrm{R}\left(\dfrac{1}{4}, 1\right)$
Answer: c
Example: 19 Minimum area of circle which touches the parabola’s $y^{2}=x^{2}+1$ and $y^{2}=x+1$ is
(a) $\dfrac{9 \pi}{32}$ sq.unit
(b) $\dfrac{\pi}{4}$ sq.unit
(c) $\dfrac{7 \pi}{32}$ sq.unit
(d) $\dfrac{9 \pi}{16}$ sq.unit
Show Answer
Solution: $\mathrm{y}=\mathrm{x}^{2}+1$ and $\mathrm{y}^{2}=\mathrm{x}+1$ are symmetrical about $\mathrm{y}=\mathrm{x}$
tangent at point. $\mathrm{A}$ and $\mathrm{B}$ are parallel to the line $\mathrm{y}=\mathrm{x}$
$\mathrm{y}=\mathrm{x}^{2}+1$ $\hspace {3 cm}\mathrm{y}^{2}=\mathrm{x}+1$
$\dfrac{\mathrm{dy}}{\mathrm{dx}}=2 \mathrm{x}=1$ $\hspace {3 cm}\mathrm{y}=\dfrac{1}{2}$
$\mathrm{x}=\dfrac{1}{2}$ $\hspace {4 cm}\mathrm{x}=\dfrac{5}{4}$
$\mathrm{y}=\dfrac{5}{4}$
$\mathrm{A}\left(\dfrac{1}{2}, \dfrac{5}{4}\right) \hspace {3 cm}\mathrm{B}\left(\dfrac{5}{4}, \dfrac{1}{2}\right)$
$\mathrm{AB}=\sqrt{\left(\dfrac{1}{2}-\dfrac{5}{4}\right)^{2}+\left(\dfrac{5}{4}-\dfrac{1}{2}\right)^{2}}=\dfrac{3 \sqrt{2}}{4}$
Area of circle $=\pi \mathrm{r}^{2}=\pi\left(\dfrac{3 \sqrt{2}}{8}\right)^{2}=\dfrac{9 \pi}{32}$ sq.unit
Answer: a
Example: 20 The equation of the common tangents to the parabola $\mathrm{y}=\mathrm{x}^{2}$ and $\mathrm{y}=-(\mathrm{x}-2)^{2}$ is $/$ are
(a) $\mathrm{y}=4(\mathrm{x}-1)$
(b) $y=0$
(c) $y=-4(x-1)$
(d) $y=-30 x-50$
Show Answer
Solution: Let $\mathrm{y}=\mathrm{mx}+\mathrm{c}$ is tangent to $\mathrm{y}=\mathrm{x}^{2}$
$\therefore \quad \mathrm{mx}+\mathrm{c}=\mathrm{x}^{2} \Rightarrow \mathrm{x}^{2}-\mathrm{mx}-\mathrm{c}=0$ has equal roots $\mathrm{m}^{2}+4 \mathrm{c}=0$
$y=m x-\dfrac{m^{2}}{4}$ is tangent to $y=-(x-2)^{2}$ also
$m x-\dfrac{m^{2}}{4}=-x^{2}+4 x-4$
$\mathrm{x}^{2}+(\mathrm{m}-4) \mathrm{x}+4-\dfrac{\mathrm{m}^{2}}{4}=0$ has equal roots
$\therefore \quad(\mathrm{m}-4)^{2}-4\left(4-\dfrac{\mathrm{m}^{2}}{4}\right)=0$
$\mathrm{m}^{2}+16-8 \mathrm{~m}-16+\mathrm{m}^{2}=0$
$\mathrm{m}^{2}-4 \mathrm{~m}=0$
$\mathrm{m}=0,4$
Equation of tangent are $y=0$ and $y=4 x-4$
Answer: a,b
Example 21. $(3,0)$ is the point from which three normals are drawn to the parabola $y^{2}=4 x$ which meet the parabola in the points $\mathrm{P}, \mathrm{Q}$ and $\mathrm{R}$ then
| Column I | Column II | ||
|---|---|---|---|
| i. | Area of $\triangle \mathrm{PQR}$ | (a) | 2 |
| ii. | Radius of circum circle of $\triangle \mathrm{PQR}$ | (b) | $\dfrac{5}{2}$ |
| iii. | Centroid of $\triangle \mathrm{PQR}$ | (c) | $\left(\dfrac{5}{2}, 0\right)$ |
| iv. | Circum centre of $\triangle \mathrm{PQR}$ | (d) | $\left(\dfrac{2}{3}, 0\right)$ |
Show Answer
Solution: Equation of normal is $\mathrm{y}=\mathrm{mx}-2 \mathrm{~m}-\mathrm{m}^{3}$
It passes through $(3,0)$, so
$\begin{aligned} & 3 \mathrm{~m}-2 \mathrm{~m}-\mathrm{m}^{3}=0 \\ & \mathrm{~m}\left(1-\mathrm{m}^{2}\right)=0 \\ & \mathrm{~m}=0,1,-1 \end{aligned}$
Points are given by $\left(\mathrm{m}^{2},-2 \mathrm{~m}\right)$
i.e. $P(0,0), Q(1,-2), R(1,2)$
area of $\triangle \mathrm{PQR}=\dfrac{1}{2}\left|\begin{array}{ccc}0 & 0 & 1 \\ 1 & -2 & 1 \\ 1 & 2 & 1\end{array}\right|=$ 2 sq.units
$\mathrm{R}=\dfrac{\mathrm{abc}}{4 \Delta}=\dfrac{\sqrt{5} \cdot \sqrt{5} \cdot 4}{4 \cdot 2}=\dfrac{5}{2}$
Centroid $\triangle \mathrm{PQR}=\left(\dfrac{2}{3}, 0\right)$
Circum centre $\left(\dfrac{5}{2}, 0\right)$
Comprehension based Questions (Exampels 6 to 8)
Comprehension 1
Consider the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=9$ and the parabola $\mathrm{y}^{2}=8 \mathrm{x}$. They intersect at $\mathrm{P}$ and $\mathrm{Q}$ in the first and the fourth quadrants, respectively. Tangents to the circle at $P$ and $Q$ intersect the $x$-axis at $R$ and tangents to the parabola at $\mathrm{P}$ and $\mathrm{Q}$ intersect the $\mathrm{x}$-axis at $\mathrm{S}$.
Example 22. The ratio of the area of the triangles $\mathrm{PQS}$ and $\mathrm{PQR}$ is
(a) $1: \sqrt{2}$
(b) 1:2
(c) $1: 4$
(d) $1: 8$
Show Answer
Solution: Point of intersection of circle & parabola
$\mathrm{x}^{2}+8 \mathrm{x}-9=0$
$(\mathrm{x}+9)(\mathrm{x}-1)=0$
$\mathrm{X}=1,-9$ (not possible)
$\mathrm{Y}= \pm 2 \sqrt{5}$
$\mathrm{P}(1,2 \sqrt{2}), \quad \mathrm{Q}(1,-2 \sqrt{2})$
Tangent to the parabola at $P$ is $2 \sqrt{2 y}=4(x+1)$
$\mathrm{S}(-1,0)$
Tangent to the circle at $P$ is $\quad x+2 \sqrt{2 y}=9$
$\mathrm{R}(9,0)$
$\dfrac{\operatorname{ar} \triangle \mathrm{PQS}}{\operatorname{ar} \triangle \mathrm{PQR}}=\dfrac{\dfrac{1}{2} \mathrm{xPQxST}}{\dfrac{1}{2} \mathrm{xPQxRT}}=\dfrac{\mathrm{ST}}{\mathrm{RT}}=\dfrac{2}{8}=\dfrac{1}{4}$
Answer: c
Example 23. The radius of the circum circle of the triangle PRS is
(a) 5
(b) $3 \sqrt{3}$
(c) $3 \sqrt{2}$
(d) $2 \sqrt{3}$
Show Answer
Solution: area $\triangle \mathrm{PRS}=\Delta=\dfrac{1}{2} \mathrm{xSRxPT}=\dfrac{1}{2} \times 10 \times 2 \sqrt{2}=10 \sqrt{2}$
$\mathrm{R}=\dfrac{\mathrm{abc}}{4 \Delta}=\dfrac{10 \cdot 6 \sqrt{2} \cdot 2 \sqrt{3}}{4.10 \sqrt{2}}=3 \sqrt{3}$
Answer: b
Example 24. The radius of the in circle of the triangle $\mathrm{PQR}$ is
(a) 4
(b) 3
(c) $\dfrac{8}{3}$
(d) 2
Show Answer
Solution: $\mathrm{r}=\dfrac{\Delta}{\mathrm{S}}=\dfrac{\dfrac{1}{2}=\mathrm{PQxRT}}{\dfrac{\mathrm{PR}+\mathrm{RQ}+\mathrm{QP}}{2}}=\dfrac{\dfrac{1}{2} \cdot 4 \sqrt{2} \cdot 8}{\dfrac{6 \sqrt{2}+6 \sqrt{2}+4 \sqrt{2}}{2}}=\dfrac{16 \sqrt{2}}{8 \sqrt{2}}=2$
Answer: d
COMPREHENSION 2 (EXAMPLES 25 TO 27)
If $y=x$ is tangent to the parabola $y=a x^{2}+c$
25. If $a=2$, then the value of $c$ is
(a) $\dfrac{1}{2}$
(b) $\dfrac{1}{4}$
(c) $\dfrac{1}{8}$
(d) 1
26. If $(1,1)$ is point of contact then ’ $a$ ’ is
(a) 1
(b) $\dfrac{1}{2}$
(c) $\dfrac{1}{3}$
(d) $\dfrac{1}{4}$
27. If $c=2$ then point of contact is
(a) $(4,4)$
(b) $(2,2)$
(c) $(8,8)$
(d) $\left(\dfrac{1}{2}, \dfrac{1}{2}\right)$
Show Answer
Solution: $y=a x^{2}+c$
$\dfrac{\mathrm{dy}}{\mathrm{dx}}=2 \mathrm{ax}=1 \quad$ Point of contact of the tangent is $\left(\dfrac{1}{2 \mathrm{a}}, \dfrac{1}{4 \mathrm{a}}+\mathrm{c}\right)$ since it lies on $\mathrm{y}=\mathrm{x}$
$\therefore \quad c=\dfrac{1}{4 \mathrm{a}}$ thus $\mathrm{c}=\dfrac{1}{8}$ for $\mathrm{a}=2$
Answer: c
If $(1,1)$ is poit of contact then $\mathrm{a}=\dfrac{1}{2}$
Answer: b
If $\mathrm{c}=2$, then point of contact is $\left(\dfrac{1}{2 \mathrm{a}}, \dfrac{1}{4 \mathrm{a}}+2\right)$
Since it lies on the line $y=x$,
$\dfrac{1}{2 a}=\dfrac{1}{4 a}+2 \Rightarrow a=\dfrac{1}{8}$
$\therefore \quad$ point of contact is $(4,4)$
Exercise
1. The point $\mathrm{P}$ on the parabola $\mathrm{y}^{2}=4 \mathrm{ax}$ for which $|\mathrm{PR}-\mathrm{PQ}|$ is maximum, where $\mathrm{R}(-\mathrm{a}, 0), \mathrm{Q}(0, \mathrm{a})$ is
(a) $(4 a,-4 a)$
(b) $(4 a, 4 a)$
(c) $(a, 2 a)$
(d) $(\mathrm{a},-2 \mathrm{a})$
Show Answer
Answer: c2. The shortest distance between the parabola $y^{2}=4 x$ and the circle $x^{2}+y^{2}+6 x-12 y+20=0$ is
(a) $4 \sqrt{2}-5$
(b) $4 \sqrt{2}+5$
(c) $3 \sqrt{2}+5$
(d) $3 \sqrt{2}-5$
Show Answer
Answer: a3. If normals are drawn from a point $p(h, k)$ to the parabola $y^{2}=4 a x$, then the sum of the intercepts which the normals act off from the axis of the parabola is
(a) $4(\mathrm{~h}+0)$
(b) $3(\mathrm{~h}+\mathrm{c})$
(c) $2(\mathrm{~h}+\mathrm{a})$
(d) $(\mathrm{h}+\mathrm{a})$
Show Answer
Answer: c4. If $a \neq 0$ and the line $2 p x+3 q y+4 r=0$ passes through the points of intersection of the parabolas $y^{2}=4 a x$ and $x^{2}=4 a y$, then
(a) $\mathrm{r}^{2}+(3 \mathrm{p}+2 \mathrm{q})^{2}=0$
(b) $r^{2}+(2 p+3 q)^{2}=0$
(c) $\mathrm{r}^{2}+(3 \mathrm{p}-2 \mathrm{q})^{2}=0$
(d) $r^{2}+(2 p-2 q)^{2}=0$
Show Answer
Answer: b5. The equation of the tangent at the vertex of the parabola $x^{2}+4 x+2 y=0$ is
(a) $\mathrm{x}=2$
(b) $x=2$
(c) $y=2$
(d) $y=2$
Show Answer
Answer: d6. The common tangent to the parabolas $y^{2}=4 a x$ and $x^{2}=4 a x$ and $x^{2}=32 a y$ is
(a) $x+2 y-4 a=0$
(b) $x+2 y+4 a=0$
(c) $x-2 y+4 a=0$
(d) $x-2 y-4 a=0$
Show Answer
Answer: b7. The shortest distnae between the parabolas $\mathrm{y}^{2}=4 \mathrm{x}$ and $\mathrm{y}^{2}=2 \mathrm{x}-6$ is
(a) $\sqrt{5}$
(b) 2
(c) 3
(d) none of these
Show Answer
Answer: a8. The largest value of a for which the circle $x^{2}+y^{2}=a^{2}$ falls totally in the interior of the parabola $y^{2}=4(x+4)$ is
(a) 4
(b) $4 \sqrt{3}$
(c) $3 \sqrt{3}$
(d) $2 \sqrt{3}$
Show Answer
Answer: dMultiple choice questions with one or more than one correct answer.
9. Let $P\left(x _{1}, y _{1}\right)$ and $Q\left(x _{2}, y _{2}\right), y _{1}<0, y _{2}, 0$, be the end points of the latus rectum of the ellipse $x^{2}+4 y=4$. The equations of parabolas with latus rectum $\mathrm{PQ}$ are
(a) $x^{2}+2 \sqrt{3} \mathrm{y}=3+\sqrt{3}$
(b) $x^{2}-2 \sqrt{3} y=3+\sqrt{3}$
(c) $x^{2}+2 \sqrt{3} y=3-\sqrt{3}$
(d) $x^{2}-2 \sqrt{3} y=3-\sqrt{3}$
Show Answer
Answer: b, c10. The tangent $\mathrm{PT}$ and the normal $\mathrm{PN}$ to the parabola $\mathrm{y}^{2}=4 \mathrm{ax}$ at a point $\mathrm{P}$ on it meet its axis at point $\mathrm{T}$ and N, respectively. The locus of the centroid of the triangle PTN is a parabola whose
(a) vertex is $\left(\dfrac{2 \mathrm{a}}{3}, 0\right)$
(b) directrix is $x=0$
(c) latus rectum is $\dfrac{2 \mathrm{a}}{3}$
(d) focus is $(a, 0)$
Show Answer
Answer: a, d11. Match the following :
Consider the parabola $\mathrm{y}^{2}=12 \mathrm{x}$
| Column I | Column II | ||
|---|---|---|---|
| (a) | Equation of tangent can be | p. | $2 x+y-6=0$ |
| (b) | Equation of normal can be | q. | $x-2 y-12=0$ |
| (c) | Equation of chord of contact w.r.t. any point on the directrix | r. | $2 x-y=36$ |
| (d) | Equation of chord which subtends right angle at the vertex | s. | $3 x-y+1=0$ |
Show Answer
Answer: $\mathrm{A} \rightarrow \mathrm{s}, \mathrm{B} \rightarrow \mathrm{r}, \mathrm{C} \rightarrow \mathrm{p}, \mathrm{D} \rightarrow \mathrm{q}$Assertion and Reasoning
12. Statement 1 : The curve $y=\dfrac{x^{2}}{2}+x+1$ is symmetric with respect to the line $x=1$.
Statement 2 : A parabola is symmetric about its axis.
(A) Statement 1 is True, Statement 2 is True; Statement 2 is a correct explanations for statement 1 .
(B) Statement 1 is True, statement 2 is true, statement 2 is not a correct explanation for statement 1 .
(C) Statement 1 is true, statement 2 is false.
(D) Statement 1 is false, statement 2 is true.
