Parabola - Conic Section (Lecture-01)
A conic section or conic is the locus of a point $P$ which moves in a plane such that the ratio of its distance from fixed point to the distance form the fixed line always remain same (constant).
$\dfrac{P S}{P M}=e$
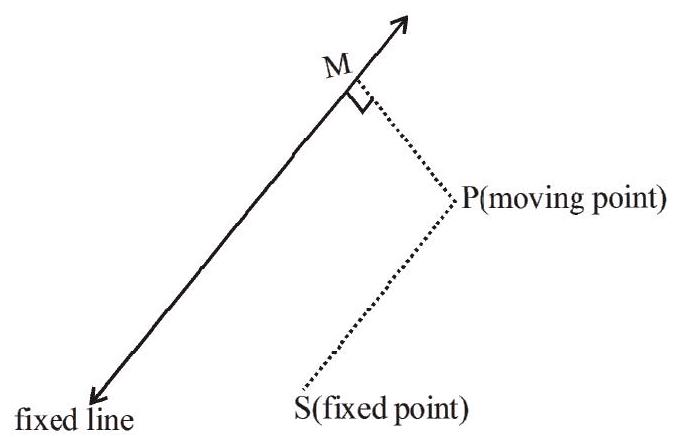
- The fixed point known as Focus.
- The fixed straight line is known as Directrix,
- The constant ratio is called the Eccentricity denoted by e.
- The line passing through the focus and perpendicular to the directrix is known as axis.
- A point of intersection of a conic with its axis is called a vertex.
- The point which bisects every chord of the conic passing through it, is called the centre of the conic.
- The chord passing through the focus and perpendicular to the axis is known as Latus Rectum.
GENERAL EQUATION OF A CONIC SECTION:
Let coordinates of focus be $S(p, q)$, equation of directrix be $a x+b y+c=0$ and e be the eccentricity of a conic. Let $\mathrm{P}(\mathrm{h}, \mathrm{k})$ be a moving point, then by definition.
$\mathrm{SP}=\mathrm{e} \mathrm{PM}$
$\sqrt{(h-p)^{2}+(k-q)^{2}}=e\left|\dfrac{a h+b k+c}{\sqrt{a^{2}+b^{2}}}\right|$
$\Rightarrow(\mathrm{h}-\mathrm{p})^{2}+(\mathrm{k}-\mathrm{q})^{2}=\mathrm{e}\left(\dfrac{\mathrm{ah}+\mathrm{bk}+\mathrm{c}}{\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}}\right)^{2}$
Thus locus of $(\mathrm{h}, \mathrm{k})$ is
$(x-p)^{2}+(y-q)^{2}=e^{2} \dfrac{(a x+b y+c)^{2}}{\left(a^{2}+b^{2}\right)}$
This is equation of conic section which, when simplified, can be written in the form $a x^{2}+2 h x y+b y^{2}+2 g x+2 f y+c=0$ which is general equation of second degree.
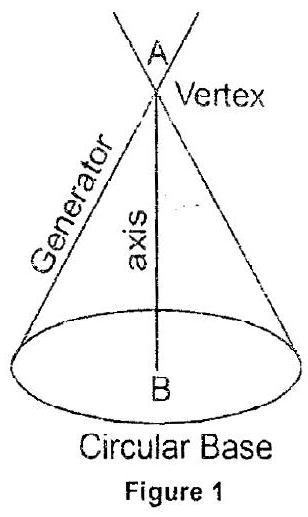
Section of right circular cone by different planes
A right circular cone is as shown in the figure -1
i. Section of a right cone by a plane passing through its vertex is a pair of straight lines passing through the vertex as shown in the figure -2 .
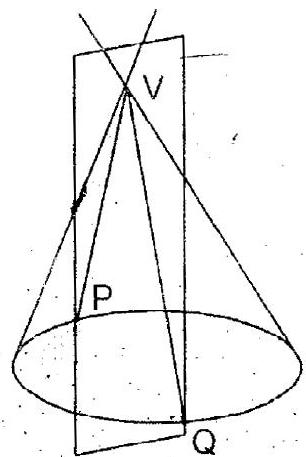
Figure -2
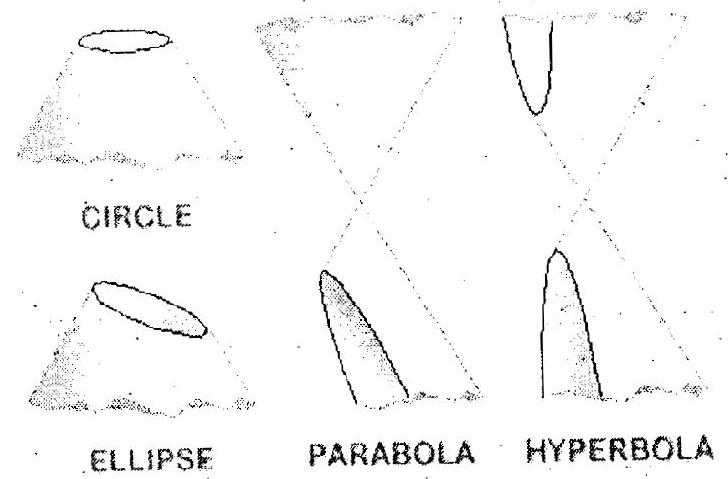
ii. Section of a right circular cone by a plane parallel to its base is a circle as shown in the figure -3 .
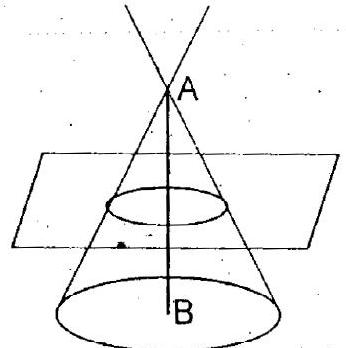
Figure- 3
iii. Section of a right circular cone by a plane parallel to a generator of the cone is parabola as shown in the figure -4 .
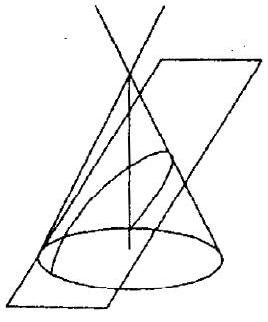
Figure-4
iv. Section of a right circular cone by a plane neither parallel to any generator of the cone nor perpendicular or parallel to the axis of the cone is an ellipse as shown in the figure -5 .
v. Section of a right circular cone by a plane parallel to the axis of the cone is a hyperbola as shown in the figure -6 .
3D View :
Distinguishing various conics:
The nature of the conic section depends upon the position of the focus with respect to the directrix and also upon the value of the eccentricity.
1. If focus lies on the Directrix.
$\Delta \equiv a b c+2 f g h-a f^{2}-b^{2}-c h^{2}=0$
General equation of a conic represents a pair of straight lines, if
- $\mathrm{h}^{2}>\mathrm{ab}$, the lines will be real and distinct
- $\mathrm{h}^{2}=\mathrm{ab}$, the lines will be coincident
- $h^{2}<a b$, the lines will be imaginary (a point)
2. If focus does not lie on Directrix.
i. $\Delta \neq 0, \mathrm{a}=\mathrm{b}, \mathrm{h}=0$, a circle
ii. $\Delta \neq 0, \mathrm{e}=1, \mathrm{~h}^{2}=\mathrm{ab}$, a parabola
iii. $\Delta \neq 0,0<\mathrm{e}<1, \mathrm{~h}^{2}<\mathrm{ab}$, an ellipse
iv. $\Delta \neq 0, \mathrm{e}>1, \mathrm{~h}^{2}>\mathrm{ab}$, a hyperbola
v. $\Delta \neq 0, \mathrm{e}>1, \mathrm{~h}^{2}>\mathrm{ab}, \mathrm{a}+\mathrm{b}=0$, rectangualr hyperbola
$\mathrm{y}^{2}=4 \mathrm{ax}$
Vertex $(0,0)$
Tangent of lotus rectum $\mathrm{x}=0$
Extremities of lotus rectum (a, 2a), (a, $-2 \mathrm{a})$
Length of lotus rectum. 4a
Focal distance (SP) $\quad \mathrm{SP}=\mathrm{PM}=\mathrm{x}+\mathrm{a}$
Parametric form $x=a t 2, y=2 a t, t$ is parameter.
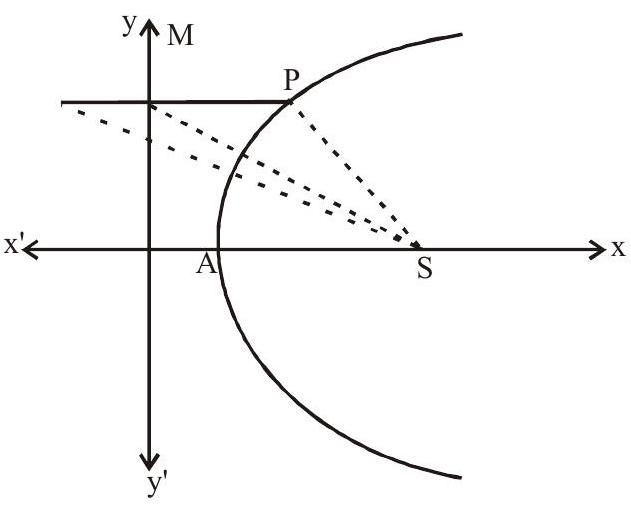
Focal distance - the distance of a point on the parabola from the focus
Focal chord - A chord of the parabola, which passes through the focus.
Double ordinate - A chord of the parabola perpendicular to the axis of the parabola.
Latus Rectum-A double ordinate passing through the focus or a focal chord perpendicular to the axis of parabola.
- Perpendicular distance form focus on directrix = half the latus rectum.
- Vertex is middle point of the focus and the point of intersection of directrix and axis.
- Two parabolas are said to be equal if they have the same lotus rectum.
Other Standard Forms of Parabola:
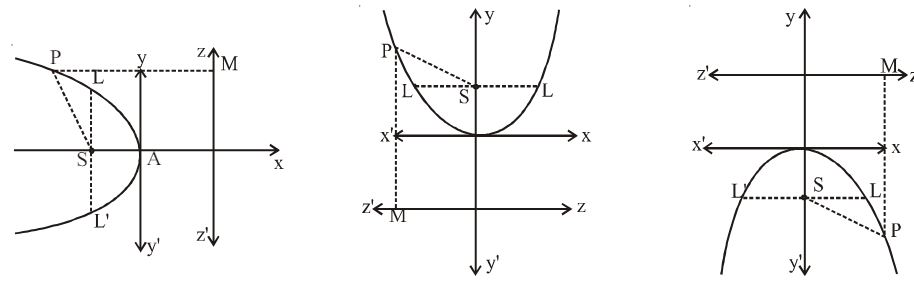
| Equation of curve: | $y^{2}=-4 a x$ | $ x^2=4 a y $ | $ x^2= -4 a y $ |
| Vertex | $(0,0)$ | $ (0,0) $ | $ (0,0) $ |
| Focus | $(-\mathrm{a}, 0)$ | $ (0, a) $ | $ (0, -a) $ |
| Directrix | $\mathrm{x}-\mathrm{a}=0$ | $ y+a=0 $ | $ y-a=0 $ |
| Equation of axis | $\mathrm{y}=0$ | $ x=0 $ | $ x=0 $ |
| Tangent of vertex | $\mathrm{x}=0$ | $ y=0 $ | $ y=0 $ |
| Parametric form | $\left(-a t^{2}, 2 a t\right)$ | $ \left(2 a t, a t^2\right) $ | $ \left(2 a t, -a t^2\right) $ |
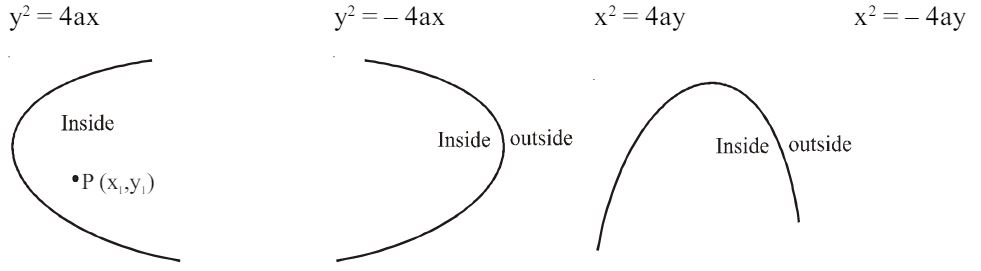
Position of a point with respet ot Parabola
| $\mathrm{S}_1=\mathrm{y}_1{ }^2-4 \mathrm{ax}_1$ | $\mathrm{S}_1=\mathrm{y}_1{ }^2-4 \mathrm{ax}_1$ | $\mathrm{S}_1=\mathrm{x}_1{ }^2-4 \mathrm{ay}_1$ | $\mathrm{S}_1=\mathrm{x}_1^2+4 a y_1$ |
| $\mathrm{S}_1<0 \rightarrow \text { Inside }$ | $\mathrm{S}_1<0 \rightarrow \text { Inside }$ | $\mathrm{~S}_1<0 \rightarrow \text { Inside }$ | $\mathrm{S}_1<0 \leftarrow \text { inside }$ |
| $\mathrm{S}_1>0 \rightarrow \text { Outside }$ | $\mathrm{S}_1>0 \rightarrow \text { Outside }$ | $\mathrm{S}_1>0 \rightarrow \text { Outside }$ | $\mathrm{S}_1>0 \rightarrow \text { Outside }$ |
| $\mathrm{S}_1=0 \rightarrow \text { on the parabola }$ | $\mathrm{S}_1=0 \rightarrow \text { on the parabola }$ | $\mathrm{S}_1=0 \rightarrow \text { on the parabola }$ | $\mathrm{S}_1=0 \rightarrow \text { on the parabola }$ |
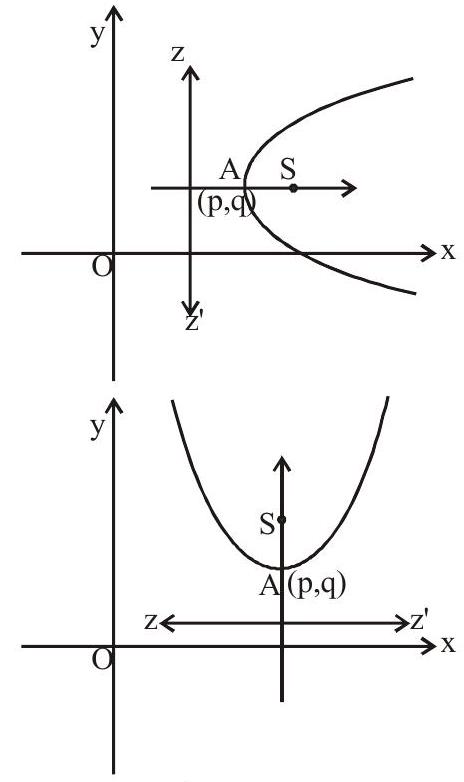
Equation of Parabola when vertex is shifted.
I. Axis is Parallel to $\mathrm{x}$-axis:
Let vertex $A$ be $(p, q)$ then equation of parabola be $(y-q)^{2}=4 a(x-p)$.
II. Axis is parallel to y-axis:
Let vertex $A$ be $(p, q)$ then equation of parabola is $(x-p)^{2}=4 a(y-q)$
Parametric Form:
| $y^{2}=4 a x$ | $y^{2}=-4 a x$ | $x^{2}=4 a y$ | $x^{2}=-4 a y$ | |
|---|---|---|---|---|
| $x=a t^{2}$ | $x=-a t^{2}$ | $x=2 a t$ | $x=2 a t$ | |
| $y=2 a t$ | $y=2 a t$ | $y=a t^{2}$ | $y=-a t^{2}$ | |
| Parametric coordinates | $\left(a t^{2}, 2 a t\right)$ | $\left(-a t^{2}, 2 a t\right)$ | $\left(2 a t, a t^{2}\right)$ | $\left(2 a t,-a t^{2}\right)$ |
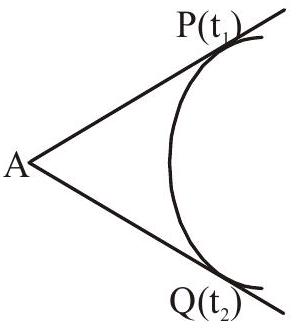
Properties of Focal chord:
1. If the chord joining $\mathrm{P}\left(\mathrm{t} _{1}\right)$ and $\mathrm{Q}\left(\mathrm{t} _{2}\right)$ is the focal chord then $\mathrm{t} _{1} \cdot \mathrm{t} _{2}=-1$.
2. Length of focal chord is $a\left(t+\dfrac{1}{t}\right)^{2}$
3. The length of the focal chord which makes an angle $\theta$ with the positive direction of $x$-axis is $4 \mathrm{a} \operatorname{cosec}^{2} \theta$.
4. Semi latus rectum of a parabola is the harmonic mean between the segments of any focal chord of the parabola.
5. Circle described on the focal length as diameter touches the tangent at vertex.
Equation of tangent:
| Parabola | Point form | Pt. of contact | Parametric form | Pt. of contact | slope form | Pt. of contact |
|---|---|---|---|---|---|---|
| $y^2=4 a x$ | $y y_1=2 a\left(x+x_1\right)$ | $\left(x_1, y_1\right)$ | $t y=x+a t^2$ | $\left(a t^2, 2 a t\right)$ | $y=m x+\frac{a}{m}$ | $\left.\frac{\mathrm{a}}{\mathrm{m}^2}, \frac{2 \mathrm{a}}{\mathrm{m}}\right)$ |
| $y^2=-4 a x$ | $y y_1=-2 a\left(x+x_1\right)$ | $\left(x_1, y_1\right)$ | $t y=-x+a t^2$ | $\left(-a t^2, 2 a t\right)$ | $y=m x-\frac{a}{m}$ | $\left(-\frac{a}{m^2}, \frac{-2 a}{m}\right)$ |
| $x^2=4 a y$ | $x x_1=2 a\left(y+y_1\right)$ | $\left(x_1, y_1\right)$ | $t x=y+a t^2$ | $\left(2 a t, a t^2\right)$ | $x=m y+\frac{a}{m}$ | $\left(\frac{2 a}{m}, \frac{a}{m^2}\right)$ |
| $x^2=-4 a y$ | $x x_1=-2 a\left(y+y_1\right)$ | $\left(x_1, y_1\right)$ | $t x=-y+a t^2$ | $\left(2 \mathrm{at},-\mathrm{at}^2\right)$ | $x=m y-\frac{a}{m}$ | $\left(\frac{-2 a}{m}, \frac{-a}{m^2}\right)$ |
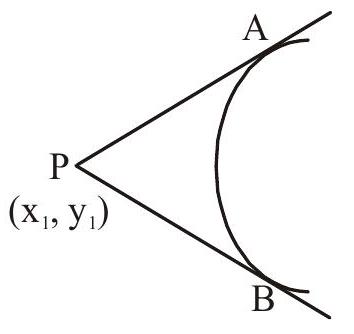
Pair of Tangents from point $\left(x _{1}, y _{1}\right)$
Let eq $q^{n}$ of parabola be $\quad y^{2}=4 a x$
$S \equiv y^{2}-4 a x$
$\mathrm{S} _{1} \equiv \mathrm{y} _{1}^{2}-4 \mathrm{ax}$
$\mathrm{T} \equiv \mathrm{yy} _{1}-2 \mathrm{a}\left(\mathrm{x}+\mathrm{x} _{1}\right)$
Equation of pair of tangents is $\mathrm{SS} _{1}=\mathrm{T}^{2} \quad$ i.e.
$\left(y^{2}-4 a x\right)\left(y _{1}^{2}-4 a _{1}\right)=\left\{y _{1}-2 a\left(x+x _{1}\right)\right\}^{2}$
Properties of Tangents:
1. Point of intersection of two tangents of the parabola:-
Equation of tangent at $P$ is $t _{1} y=x+a t _{1}^{2}$
Equation of tangent at $\mathrm{Q}$ is $\mathrm{t} _{2} \mathrm{y}=\mathrm{x}+\mathrm{at} _{2}^{2}$
Solving these equations, we get
$\mathrm{x}=\mathrm{at} _{1} \mathrm{t} _{2}, \quad \mathrm{y}=\mathrm{at} _{1}+\mathrm{at} _{2}$
$A\left(a t _{1} t _{2}, a\left(t _{1}+t _{2}\right)\right)$
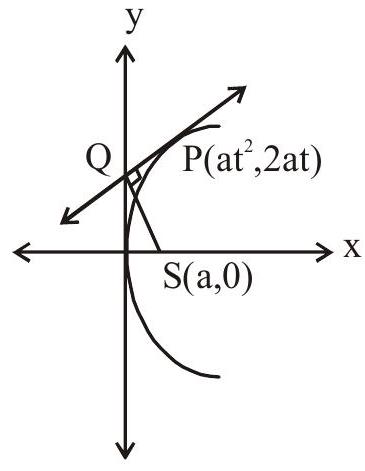
2. Locus of foot of prependicular from focus upon any tangent is tangent at vertex:-
Equation of tengent at $\mathrm{P}$ is $\mathrm{ty}=\mathrm{x}+\mathrm{at}^{2}$
Let the tangent meet $y$-axis at $Q$ then $Q(0$, at $)$
$\begin{aligned} & \therefore \quad \text { slope of } Q S=\dfrac{-\mathrm{at}}{\mathrm{a}}=-\mathrm{t} \\ & \text { slope of tangent }=\dfrac{1}{t} \\ & \dfrac{1}{t} x(-t)=-1 \Rightarrow S Q \perp \text { tangent } \end{aligned}$
3. Length of tangent between the pt. of contact and the point where tangent meets the directrix subtends right angle at focus:-
Equation of tangent at $\mathrm{P}(\mathrm{t})$
$t y=x+a t^{2}$
Point of intersection with directrix $x=-a$ is
$\left(-a, a t-\dfrac{a}{t}\right)$
slope $\mathrm{SP}=\dfrac{2 \mathrm{at}}{\mathrm{at}^{2}-\mathrm{a}}=\dfrac{2 \mathrm{t}}{\mathrm{t}^{2}-1}$
slope $Q S=\dfrac{a t-\dfrac{a}{t}}{-2 a}=\dfrac{t^{2}-1}{-2 t}$
$m _{1} m _{2}=-1$
$\mathrm{PS} \perp \mathrm{QS}$.
4. Tangent at extremities of focal chord are perpendicular adn intersect on directrix
(Locus of intersection point of tangents at extremities of focal chord is directrix)
Let $P\left(a t^{2}, 2 a t\right)$ and $Q\left(\dfrac{a}{t^{2}}, \dfrac{-2 a}{t}\right)$
Equation of tangent at $P \quad t y=x+a t^{2}\quad \quad \quad ……(1)$
Equation of tangent at $Q \quad-\dfrac{1}{t} y=x+\dfrac{a}{t^{2}}$
$\hspace {4 cm}\begin{aligned} y=-t x-\dfrac{a}{t} \end{aligned}\quad \quad \quad ……(2)$
Point of intersection of both tangents, we get after sloving (1) & (2) i.e.
$x+a=0$
A point lies on the directrix.
Example: 1 The focal chord to $\mathrm{y}^{2}=16 \mathrm{x}$ is tangent to $(\mathrm{x}-6)^{2}+\mathrm{y}^{2}=2$, then the possible value of the slope of this chord, are
(a) $\{-1,1\}$
(b) $\{-2,2\}$
(c) $\left\{-2, \dfrac{1}{2}\right\}$
(d) $\left\{2,-\dfrac{1}{2}\right\}$
Show Answer
Solution: The focus of parabola is $(4,0)$. Let slope of focal chord be $m$. Equaiton of focal chord is $y=m(x-4)$. It is tangent to the circle then
$\begin{aligned} & \left|\dfrac{6 m-4 m}{\sqrt{m^{2}+1}}\right|=\sqrt{2} \\ & 4 m^{2}=2\left(m^{2}+1\right) \\ & 2 m^{2}=2 \end{aligned}$
$\mathrm{m}= \pm 1$
Answer: a
Example: 2 The curve represented by $\sqrt{\mathrm{ax}}+\sqrt{\mathrm{by}}=1$, where $\mathrm{a}, \mathrm{b}>0$ is
(a) a circle
(b) a parabola
(c) an ellipse
(d) a hyperbola
$\sqrt{\mathrm{ax}}=1-\sqrt{\mathrm{by}}$
Show Answer
Solution: $\mathrm{ax}=1+\mathrm{by}-2 \sqrt{\mathrm{by}}$
$(\mathrm{ax}-\mathrm{by}-1)^{2}=(-2 \sqrt{\mathrm{by}})^{2}$
$a^{2} x^{2}+b^{2} y^{2}+1-2 a b x y-2 a x+2 b y=4 b y$
$a^{2} x^{2}-2 a b x y+b^{2} y^{2}-2 a x-2 b y+1=0$
$\Delta=\left|\begin{array}{lrr}a^{2} & -a b & -a \\ -a b & b^{2} & -b \\ -a & -b & 1\end{array} \right|=a^{2}\left(b^{2}-b^{2}\right)+a b(-a b-a b)-a\left(a b^{2}+a b^{2}\right)$
$=0-2 a^{2} b^{2}-2 a^{2} b^{2}$
$=-4 a^{2} b^{2} \neq 0$
$\mathrm{h}^{2}-\mathrm{ab}=(-\mathrm{ab})^{2}-\left(\mathrm{a}^{2}\right)\left(\mathrm{b}^{2}\right)=0$
$\therefore$ It is a parabola
Answer: b
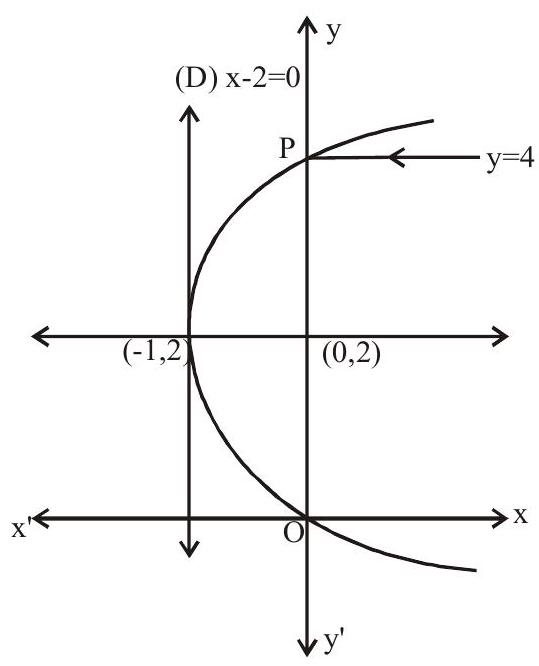
Example: 3 The equation of the directrix of the parabola $y^{2}+4 x+4 y+2=0$ is
(a) $\mathrm{x}=-1$
(b) $\mathrm{x}=1$
(c) $\mathrm{x}=\dfrac{-3}{2}$
(d) $\mathrm{x}=\dfrac{3}{2}$
Show Answer
Solution: $\mathrm{y}^{2}+4 \mathrm{y}=-4 \mathrm{x}-2$
$(y+2)^{2}=-4\left(x-\dfrac{1}{2}\right)$
$\mathrm{y}^{2}=-4 \mathrm{AX}$
Equation of directrix is $\mathrm{X}=$ Ai.e. $\mathrm{x}-\dfrac{1}{2}=1$
$2 \mathrm{x}-3=0$ or $\mathrm{x}=\dfrac{3}{2}$
Answer: d
Example: 4 The locus of the midpoint of the segment joining the focus to a moving point on the parabola $\mathrm{y}^{2}=4 \mathrm{ax}$ is another parabola with directrix
(a) $y=0$
(b) $\mathrm{x}=-\mathrm{a}$
(c) $\mathrm{x}=0$
(d) none of these
Show Answer
Solution: Let $\mathrm{P}\left(\mathrm{at}^{2}, 2 \mathrm{at}\right)$ lies on the parabola
$\mathrm{y}^{2}=4 \mathrm{ax}$
Mid point of PS is Q.
$\mathrm{h}=\dfrac{\mathrm{at}^{2}+\mathrm{a}}{2}, \mathrm{k}=\dfrac{0+2 \mathrm{at}}{2}$
$\dfrac{2 \mathrm{~h}-\mathrm{a}}{\mathrm{a}}=\mathrm{t}^{2}, \dfrac{\mathrm{k}}{\mathrm{a}}=\mathrm{t}$
$\dfrac{2 \mathrm{~h}-\mathrm{a}}{\mathrm{a}}=\left(\dfrac{\mathrm{k}}{\mathrm{a}}\right)^{2}$
$\mathrm{a}(2 \mathrm{~h}-\mathrm{a})=\mathrm{k}^{2}$
Locus of $(h, k)$ is $\quad y^{2}=2 a\left(x-\dfrac{a}{2}\right)$
Equaiton of directrix is $x-\dfrac{a}{2}=-\dfrac{a}{2}$
$\hspace {3 cm}\mathrm{x}=0$
Answer: c
Example: 5 The angle between the tangents drawn from the point $(1,4)$ to the parabola $y^{2}=4 x$ is
(a) $\dfrac{\pi}{6}$
(b) $\dfrac{\pi}{4}$
(c) $\dfrac{\pi}{3}$
(d) $\dfrac{\pi}{2}$
Show Answer
Solution: Equation of tangent of the parabola $\mathrm{y}^{2}=4 \mathrm{x}$ is
$\mathrm{y}=\mathrm{mx}+\dfrac{1}{\mathrm{~m}}$
This equation passes through $(1,4)$ i.e.
$4=\mathrm{m}+\dfrac{1}{\mathrm{~m}}$
$\Rightarrow \mathrm{m}^{2}-4 \mathrm{~m}+1=0$
$\mathrm{m} _{1} \cdot \mathrm{m} _{2}=1$ and $\mathrm{m} _{1}+\mathrm{m} _{2}=4$
Angle between the two tangents is $\tan \theta=\left|\dfrac{\mathrm{m} _{1}-\mathrm{m} _{2}}{1+\mathrm{m} _{1} \mathrm{~m} _{2}}\right|$
$\tan \theta=\left|\dfrac{\sqrt{(4)^{2}-4}}{1+1}\right|=\dfrac{\sqrt{12}}{2}=\sqrt{3}$
$\therefore \theta=\dfrac{\pi}{3}$
Answer: c
Exercise: 6 Tangent to the curve $y=x^{2}+6$ at a point $(1,7)$ touches the circle $x^{2}+y^{2}+16 x+12 y+c$ $=0$ at a point $\mathrm{Q}$ then coordinates of $\mathrm{Q}$ are
(a) $(-6,-11)$
(b) $(-9,-13)$
(c) $(-10,-15)$
(d) $(-6,-7)$
Show Answer
Solution: Equation of tangent at $(1,7)$ to the curve $y=x^{2}+6$ is
$\dfrac{\mathrm{y}+7}{2}=\mathrm{x}+6$
$2 \mathrm{x}-\mathrm{y}+5=0\quad \quad \quad ……(1)$
This line also touches the circle i.e.
Equation of normal of circle passing through
centre $(-8,-6)$.
$\mathrm{x}+2 \mathrm{y}+\lambda=0$
$-8-12+\lambda=0$
$\lambda=20$
$\therefore \mathrm{x}+2 \mathrm{y}+20=0\quad \quad \quad ……(2)$
$\mathrm{Q}$ is intersection point of (1) and (2)
$x=-6, \quad y=-7$
$\mathrm{Q}(-6,-7)$
Answer: d
Exercise: 7 Consider the two curves $c _{1}: y^{2}=4 x, c _{2}: x^{2}+y^{2}-6 x+1=0$. Then
(a) $\mathrm{c} _{1}$ and $\mathrm{c} _{2}$ touch each other only at one point.
(b) $c _{1}$ and $c _{2}$ touch each other only at two points.
(c) $\mathrm{c} _{1}$ and $\mathrm{c} _{2}$ intersect (but do not touch) at exactly two points.
(d) $c _{1}$ and $c _{2}$ neither intersect nor touch each other.
Show Answer
Solution: Let eq ${ }^{\mathrm{n}}$ of tangent of parabola be
$\mathrm{y}=\mathrm{mx}+\dfrac{1}{\mathrm{~m}}$ is also a tangent to the circle then
$\left|\dfrac{3 m+\dfrac{1}{m}}{\sqrt{1+m^{2}}}\right|=2 \sqrt{2}$
$\dfrac{\left(3 m^{2}+1\right)^{2}}{m^{2}}=8\left(1+m^{2}\right)$
$\mathrm{m}^{4}-2 \mathrm{~m}+1=0$
$\mathrm{m}^{2}=1 \Rightarrow \mathrm{m}= \pm 1 \Rightarrow$ Two common tangents are possible.
Exercise: 8 If b, $\mathrm{c}$ are intercepts of a focal chord of the parabola $\mathrm{y}^{2}=4 \mathrm{ax}$ then $\mathrm{c}$ is equal to
(a) $\dfrac{\mathrm{b}}{\mathrm{b}-\mathrm{a}}$
(b) $\dfrac{\mathrm{a}}{\mathrm{b}-\mathrm{a}}$
(c) $\dfrac{a b}{a-b}$
(d) $\dfrac{\mathrm{ab}}{\mathrm{b}-\mathrm{a}}$
Show Answer
Solution: We know that $2 \mathrm{a}=\dfrac{2 \mathrm{xSAxSB}}{\mathrm{SA}+\mathrm{SB}}$
$2 \mathrm{a}=\dfrac{2 \mathrm{bc}}{\mathrm{b}+\mathrm{c}}$
$a b+a c=b c$
$\dfrac{a b}{a-b}=c$
Answer: d
Exercise: 9 The circle $x^{2}+y^{2}-2 x-6 y+2=0$ intersects the parabola $y^{2}=8 x$ orthogonally at the point $P$. The equation of the tangent to the parabola at $P$ can be
(a) $2 x-y+1=0$
(b) $2 x+y-2=0$
(c) $x+y-4=0$
(d) $x-y-4=0$
Show Answer
Solution: Let $y=m x+\dfrac{2}{m}$ be tangent to $y^{2}=8 x$. Since circle intersects the parabola orthogonally. So this tangent is the normal for the circle. Every normal of the circle passes through its centre. So centre $(1,3)$.
$3=\mathrm{m}+\dfrac{2}{\mathrm{~m}} \Rightarrow \mathrm{m}^{2}-3 \mathrm{~m}+2=0$
$(\mathrm{m}-2)(\mathrm{m}-1)=0$
$\mathrm{m}=1,2$.
$\mathrm{y}=\mathrm{x}+2$ or $\mathrm{y}=2 \mathrm{x}+1$
Answer: a
Exercise: 10 A tangent PT is drawn at the point $\mathrm{P}(16,16)$ to the parabola $\mathrm{y}^{2}=16 \mathrm{x}$. PT tangent intersect the $\mathrm{x}$-axis at $\mathrm{T}$. If $\mathrm{S}$ be the focus of the parabola, then $\angle \mathrm{TPS}$ is equal to
(a) $\tan ^{-1} \dfrac{1}{2}$
(b) $\dfrac{\pi}{4}$
(c) $\dfrac{1}{2} \tan ^{-1} \dfrac{1}{2}$
(d) $\tan ^{-1} \dfrac{3}{4}$
Show Answer
Solution: $\mathrm{ST}=4+\mathrm{AT}=16+4=20$
$\mathrm{PS}=4+16=20$
$\triangle$ TPS is isosceles triangle
$\tan 2 \theta=\dfrac{16-0}{16-4}=\dfrac{4}{3}=\dfrac{2 \tan \theta}{1-\tan ^{2} \theta}$
$2 \tan ^{2} \theta+3 \tan \theta-2=0$
$(2 \tan \theta-1)(\tan \theta+2)=0$
$\tan \theta=\dfrac{1}{2}, \quad \tan \theta=-2 \quad$ (Not possible)
$\theta=\tan ^{-1} \dfrac{1}{2} \quad(\theta$ is acute angle $)$
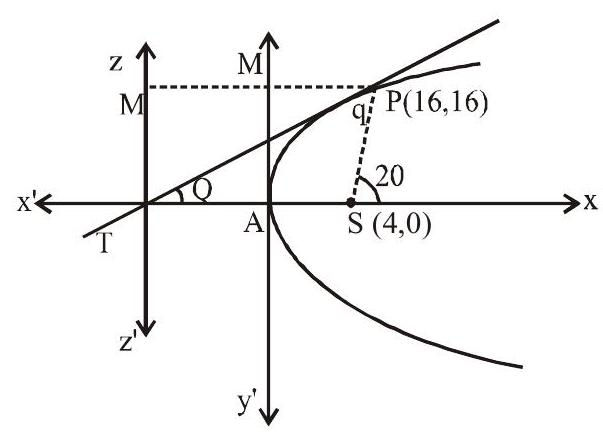
Answer: a
Exercise: 11 If $a, b, c$ are distinct positive real numbers such that the parabolas $y^{2}=4 a x$ and $y^{2}$ $=4 \mathrm{c}(\mathrm{x}-\mathrm{b})$ will have a common normal, then
(a) $0<\dfrac{\mathrm{b}}{\mathrm{a}-\mathrm{c}}<1$
(b) $\dfrac{b}{a-c}<0$
(c) $1<\dfrac{\mathrm{b}}{\mathrm{a}-\mathrm{c}}<2$
(d) $\dfrac{b}{a-c}>2$
Show Answer
Solution: Equation of normals are
$\begin{aligned} & y=m x-2 a m-a m^{3} \quad \quad \quad …….(1)\\ & y=m(x-b)-2 c m-c m^{3} \quad \quad \quad …….(2) \end{aligned}$
Equation 1 and 2 are identical then
$-2 \mathrm{am}-\mathrm{am}^{3}=-\mathrm{bm}-2 \mathrm{~cm}-\mathrm{cm}^{3} \div \mathrm{m}$
$2 \mathrm{a}+\mathrm{am}^{2}=\mathrm{b}+2 \mathrm{c}+\mathrm{cm}^{2}$
$(\mathrm{a}-\mathrm{c}) \mathrm{m}^{2}=\mathrm{b}+2(\mathrm{c}-\mathrm{a})$
$\mathrm{m}^{2}=\dfrac{\mathrm{b}}{\mathrm{a}-\mathrm{c}}-2$
$m= \pm \sqrt{\dfrac{b}{a-c}-2}$
For $m$ be real $\dfrac{b}{a-c}>2$
Answer: d
Exercise: 12 If $\mathrm{AB}$ be a chord of the parabola $\mathrm{y}^{2}=4 \mathrm{ax}$ with vertex at $\mathrm{A} . \mathrm{BC}$ is perpendicular to $\mathrm{AB}$ such that it meets the axis at $\mathrm{C}$. The projection of the $\mathrm{BC}$ on the axis of parabola is
(a) $2 \mathrm{a}$
(b) $4 \mathrm{a}$
(c) $8 \mathrm{a}$
(d) $16 \mathrm{a}$
Show Answer
Solution: Let coordinates of $\mathrm{B}$ be $(\mathrm{x}, \mathrm{y})$
In $\triangle \mathrm{ABD}, \tan \theta=\dfrac{\mathrm{BD}}{\mathrm{AD}}=\dfrac{\mathrm{y}}{\mathrm{x}}$
In $\triangle \mathrm{BCD}, \tan (90-\theta)=\dfrac{\mathrm{BD}}{\mathrm{DC}}$
$\therefore \mathrm{DC}=\mathrm{y} \cdot \dfrac{\mathrm{y}}{\mathrm{x}}=\dfrac{4 \mathrm{ax}}{\mathrm{x}}=4 \mathrm{a}$
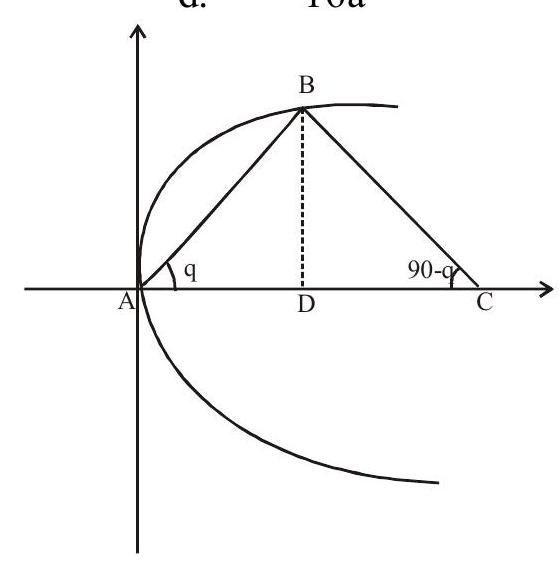
Answer: b
Exercise: 13 A circle is descirbed whose centre is the vertex and whose diameter is three-quarters of the latus rectum of the parabola $\mathrm{y}^{2}=4 \mathrm{ax}$. If $\mathrm{PQ}$ is the common-chord of the circle and the parabola and $\mathrm{L} _{1} \mathrm{~L} _{2}$ is the latus rectum, then the area of the trapezium $\mathrm{PL} _{1} \mathrm{~L} _{2} \mathrm{Q}$ is
(a) $\left(\dfrac{2+\sqrt{2}}{2}\right) \mathrm{a}^{2}$
(b) $4 a^{2}$
(c) $2 \sqrt{2} \mathrm{a}^{2}$
(d) $3 \sqrt{2} \mathrm{a}^{2}$
Show Answer
Solution: Centre of circle $(0,0)$
diameter $=\dfrac{3}{4} \cdot 4 \mathrm{a}=3 \mathrm{a}$
Eq of circle $x^{2}+y^{2}=\dfrac{9 a^{2}}{4}\quad \quad \quad …….(1)$
$\mathrm{Eq}^{\mathrm{n}}$ of parabola $\mathrm{y}^{2}=4 \mathrm{ax}\quad \quad \quad …….(2)$
coordinates of $\mathrm{P}$ and $\mathrm{Q}$, we get after solving (1) and (2).
$\mathrm{x}^{2}+4 \mathrm{ax}=\dfrac{9 \mathrm{a}^{2}}{4}$
$(x+2 a)^{2}=\left(\dfrac{5 a}{2}\right)^{2} \Rightarrow x=-2 a \pm \dfrac{5 a}{2}$
$\mathrm{x}=\dfrac{\mathrm{a}}{2}, \dfrac{-9 \mathrm{a}}{2}(\text { not possible })$
$P\left(\dfrac{a}{2}, \sqrt{2} a\right), Q\left(\dfrac{a}{2},-\sqrt{2} a\right) \quad y= \pm \sqrt{2} a$
$\mathrm{PQ}=2 \sqrt{2} \mathrm{a}, \quad \mathrm{L} _{1} \mathrm{~L} _{2}=4 \mathrm{a}$
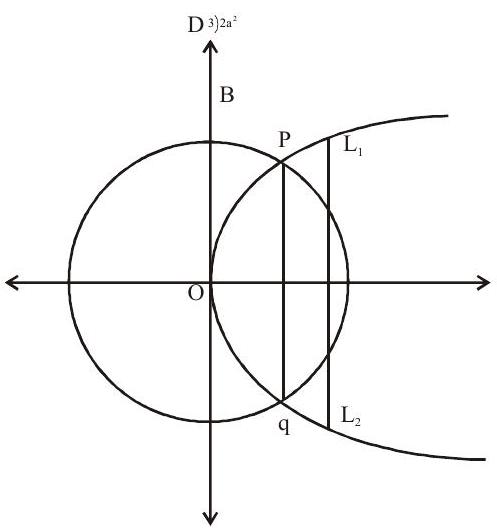
Area of trapezium $\quad=\dfrac{1}{2}\left(\mathrm{PQ}+\mathrm{L} _{1} \mathrm{~L} _{2}\right) \mathrm{x}$ distance between them.
$\begin{aligned} & =\dfrac{1}{2}(2 \sqrt{2} a+4 a) \times\left(a-\dfrac{a}{2}\right) \\ & =\dfrac{(\sqrt{2}+2)}{2} a^{2} \end{aligned}$
Answer: a
Exercise: 14 From the point $(15,12)$ three normals ae drawn to the parabola $y^{2}=4 x$, then centroid of triangle formed by three co-normal points is
(a) $(5,0)$
(b) $(5,4)$
(c) $(9,0)$
(d) $\left(\dfrac{26}{3}, 0\right)$
Show Answer
Solution: Let equation of normal be $\mathrm{y}=-\mathrm{tx}+2 \mathrm{t}+\mathrm{t}^{3}$
It passes through $(15,12)$. So $12=-15 t+2 t+t^{3}$
$\begin{aligned} & \mathrm{t}^{3}-13 \mathrm{t}-12=0 \\ & (\mathrm{t}+1)(\mathrm{t}+3)(\mathrm{t}-4)=0 \\ & \mathrm{t}=-1,-3,4 \end{aligned}$
Points are $\left(\mathrm{at}^{2}, 2\right.$ at) i.e. $(1,-2),(9,-6),(16,8)$
Centroid is $\left(\dfrac{1+9+16}{3}, \dfrac{-2-6+8}{3}\right)=\left(\dfrac{26}{3}, 0\right)$
Answer: d
Exercise: 15 A ray of light travels along a line $y=4$ and strikes the surface of a curve $y^{2}=4(x+y)$ then equation of the line along reflected ray travel is
(a) $\mathrm{x}+1=0$
(b) $\mathrm{y}-2=0$
(c) $\mathrm{x}=0$
(d) $\mathrm{x}-2=0$
Show Answer
Solution: $y^{2}-4 y=4 x$
$(\mathrm{y}-2)^{2}=4(\mathrm{x}+1)$
Focus $(0,2)$
Incident ray is parallel to axis of the parabola, so reflected ray passes through focus $(0,2)$ i.e. $x=0$
Exercise: 16 Let $\mathrm{P}$ be a point of the parabola $\mathrm{y}^{2}=3(2 \mathrm{x}-3)$ and $\mathrm{M}$ is the foot of perpendicular drawn from P on the directrix of the parabola, then length of each side of an equilateral triangle SMP, where S is focus of the parabola is
(a) 6
(b) 8
(c) 10
(d) 11
Show Answer
Solution: Equation of parabola is
$\mathrm{y}^{2}=6\left(\mathrm{x}-\dfrac{3}{2}\right)$
focus $\mathrm{S}(3,0)$
equation of directrix $x=0$
$\mathrm{P}\left(\dfrac{3}{2}+\dfrac{3}{2} \mathrm{t}^{2}, 3 \mathrm{t}\right)$
Coordinates of $\mathrm{M}(0,3 \mathrm{t})$
$\mathrm{MS}=\sqrt{9+9 \mathrm{t}^{2}}$
$\mathrm{MP}=\dfrac{3}{2}+\dfrac{3}{2} \mathrm{t}^{2}$, But $\mathrm{MS}=\mathrm{MP}$
$9+9 \mathrm{t}^{2}=\dfrac{9}{4}+\dfrac{9}{4} \mathrm{t}^{2}+\dfrac{9}{4} \mathrm{t}^{2}$
$\Rightarrow \quad \mathrm{t}^{2}=3$
Length of side $=6$
Answer: a
Exercise
1. The point $(2 a, a)$ lies inside the region bounded by the parabola $x^{2}=4 y$ and its latus rectum. Then
(a) $0<\mathrm{a} \leq 1$
(b) $0<\mathrm{a}<1$
(c) $0 \leq \mathrm{a} \leq 1$
(d) $\mathrm{a}<1$
Show Answer
Answer: b2. Two perpendicular tangents to $\mathrm{y}^{2}=4 \mathrm{ax}$ always intersect on the line
(a) $\mathrm{x}+\mathrm{a}=0$
(b) $\mathrm{x}-\mathrm{a}=0$
(c) $x+2 a=0$
(d) $\mathrm{y}+2 \mathrm{a}=0$
Show Answer
Answer: a3. $\mathrm{C} _{1}: \mathrm{y}^{2}=8 \mathrm{x}$ and $\mathrm{C} _{2}: \mathrm{x}^{2}+\mathrm{y}^{2}=2$. Then
(a) $\mathrm{C} _{1}$ and $\mathrm{C} _{2}$ have only two common tangents which are mutually perpendicular
(b) $\mathrm{C} _{1}$ and $\mathrm{C} _{2}$ have two common tangents which are parallel to each other.
(c) does not have any common tangent.
(d) $\mathrm{C} _{1}$ and $\mathrm{C} _{2}$ have four common tangents.
Show Answer
Answer: a4. Two common tangents to the circle $x^{2}+y^{2}=2 a^{2}$ and $y^{2}=8 a x$ are
(a) $y= \pm(x+a)$
(b) $x= \pm(y+2 a)$
(c) $y= \pm(x+2 a)$
(d) $x= \pm(y+a)$
Show Answer
Answer: c5. The number of points with integral coordinates that lie in the interior of the circle $x^{2}+y^{2}=16$ and the parabola $\mathrm{y}^{2}=4 \mathrm{x}$ are
(a) 6
(b) 8
(c) 10
(d) 12
Show Answer
Answer: b6. The vertex of the parabola $x^{2}+y^{2}-2 x y-4 x+4=0$ is at
(a) $\left(-\dfrac{1}{2},-\dfrac{1}{2}\right)$
(b) $(-1,-1)$
(c) $(1,1)$
(d) $\left(+\dfrac{1}{2}, \dfrac{1}{2}\right)$
Show Answer
Answer: d7. The length of the latus rectum of the parabola $2\left{(x-a)^{2}+(y-a)^{2}\right}=(x+y)^{2}$ is
(a) $\sqrt{2} \mathrm{a}$
(b) $ 2 \mathrm{a}$
(c) $2 \sqrt{2} \mathrm{a}$
(d) $3 \sqrt{2} \mathrm{a}$
Show Answer
Answer: c8. The point on $\mathrm{y}^{2}=4 \mathrm{ax}$ nearest to the focus is
(a) $(0,0)$
(b) $(a, 2 a)$
(c) $(a,-2 a)$
(d) $\left(\dfrac{\mathrm{a}}{4}, \mathrm{a}\right)$
Show Answer
Answer: a9. The angle between the tangents drawn from the origin to the parabola $y^{2}=4 a(x-a)$ is
(a) $45^{\circ}$
(b) $60^{\circ}$
(c) $90^{\circ}$
(d) $\tan ^{-1} \dfrac{1}{2}$
Show Answer
Answer: c10. The circle $x^{2}+y^{2}+2 \lambda x=0, \lambda \varepsilon R$, touches the parabola $y^{2}=4 x$ externally. Then
(a) $\lambda>0$
(b) $\lambda<0$
(c) $\lambda>1$
(d) none of these
