The area bounded by the curve $\mathrm{y}=f(\mathrm{x})$, the $\mathrm{x}-$ axis, the ordinates $\mathrm{x}=\mathrm{a}$ & $\mathrm{x}=\mathrm{b}$ is $\mathrm{A}=|{\int }_{\mathrm{a}}^{\mathrm{b}}f(\mathrm{x})\mathrm{dx}|$.

Curve sketching steps:

For sketching the graph of $f(\mathrm{x})$,

i. Determine domain, identifying where $f$ is not defined.

ii. Determine $\mathrm{x}$ intercept & y intercept, if possible.

iii. Determine asymptotes:

(a) For vertical asymptotes, check for rational function zero denominators, or undefined $\log$ function points.

(b) For horizontal asymptotes, consider $\underset{\mathrm{x}\to \pm \mathrm{\infty }}{lim}f(\mathrm{x})$.

iv. Determine critical numbers,

(check where $f^{\prime }(\mathrm{x})=0$ or $f^{\prime }(\mathrm{x})$ does not exist, and finding intervals where $f$ is increasing or decreasing).

v. Determine inflection points.

(check where $f^{\prime \prime }(\mathrm{x})=0$ or $f^{\prime \prime }(\mathrm{x})$ or does not exist)

vi. plot intercepts, critical points, inflection points, asymptotes and other points as needed.

vii. Connect plotted points with smooth curve.

Some useful results

1. Area between $y^2=4ax$ & $x^2=4$ by is ${\displaystyle \frac{16ab}{3}}$ sq. units.

2. Area between ${\mathrm{y}}^2=4\mathrm{ax}$ & its latus rectum is ${\displaystyle \frac{8{\mathrm{a}}^2}{3}}$ sq.units.

3. Area between ${\mathrm{y}}^2=4\mathrm{ax}$ & line $\mathrm{y}=\mathrm{mx}$ is ${\displaystyle \frac{8{\mathrm{a}}^2}{3{\mathrm{m}}^3}}$ sq. units.

4. Area between $\sqrt{x}+\sqrt{y}=\sqrt{a},x=0$ & $y=0$ is ${\displaystyle \frac{a^2}{6}}$ sq. units.

5. Area enclosed by ${\left({\displaystyle \frac{\mathrm{x}}{\mathrm{a}}}\right)}^{2/3}+{\left({\displaystyle \frac{\mathrm{y}}{\mathrm{b}}}\right)}^{2/3}=1$ is ${\displaystyle \frac{3\pi \mathrm{ab}}{8}}$ sq. units.

6. Area of one $\mathrm{arc}$ of $\mathrm{y}=\mathrm{sinax}($ or $\mathrm{y}=\mathrm{cosax})$ and $\mathrm{x}$ axis is $2/a$ sq. units.

7. Area of the region bounded by $y=|ax+b|($ or $x=|ay+b|)$ and $x$ axis (or $y$ axis) is ${\displaystyle \frac{b^2}{a^2}}sq$. units.

8. Area of ${\displaystyle \frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}}+{\displaystyle \frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}}=1$ is $\pi$ab sq. units.

9. Area bounded by $\{(x,y):{\displaystyle \frac{x^2}{a^2}}+{\displaystyle \frac{y^2}{b^2}}\le 1\le {\displaystyle \frac{x}{a}}+{\displaystyle \frac{y}{b}}\}$ is ${\displaystyle \frac{ab}{4}}(\pi -2)$ sq.units.

10. Area of rhombus formed by $ax\pm by\pm c=0$ is ${\displaystyle \frac{2c^2}{|ab|}}$ sq. units.

11. Area of the triangle formed by $y=m_{1}x+c_1,y=m_{2}x+c_2,y=m_{3}x+c_3$ is ${\displaystyle \frac{1}{2}}|\sum {\displaystyle \frac{{(c_1-c_2)}^2}{m_1-m_2}}|$ sq. units.

Solved Examples:

1. The area of triangle formed by the tangent normal at the point $(1,\sqrt{3})$ on the circle ${\mathrm{x}}^2+{\mathrm{y}}^2=4$ and $\mathrm{x}-$ axis is

(a) 3

(b) $2\sqrt{3}$

(c) $3\sqrt{2}$

(d) 4

Show Answer

Solution:

Equation of tangent is $x+\sqrt{3y}=4$.

Point $\mathrm{Q}$ is $(4,0)$

$\therefore$ Area of triangle $={\displaystyle \frac{1}{2}}\cdot 4\cdot \sqrt{3}=2\sqrt{3}$ sq.units

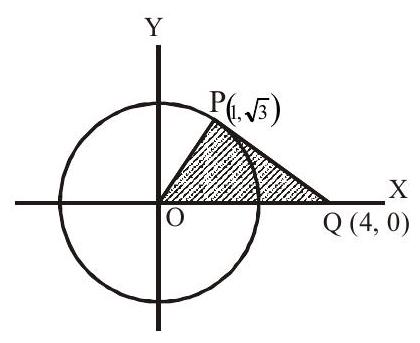
Answer: b

2. The area bounded by the curves $y=\sqrt{5-x^2}$ & $y=|x-1|$ is

(a) ${\displaystyle \frac{5\pi -1}{4}}$

(b) ${\displaystyle \frac{5\pi +1}{4}}$

(c) ${\displaystyle \frac{5\pi -2}{4}}$

(d) ${\displaystyle \frac{5\pi -3}{4}}$

Show Answer

Solution:

The two shaded areas are congruent

$\therefore$ Area $\mathrm{ACEF}={\displaystyle \frac{\text{ Area of circle }}{4}}-$ Area $\mathrm{△}\mathrm{OAD}$

$={\displaystyle \frac{5\pi }{4}}-{\displaystyle \frac{1}{2}}={\displaystyle \frac{5\pi -2}{4}}$ sq.units

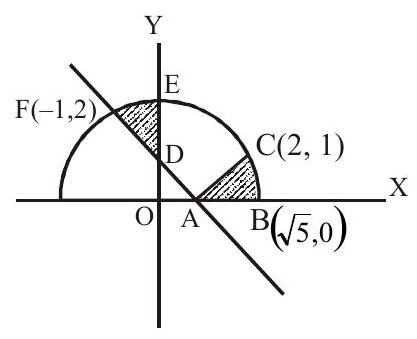
Answer: c

3. If two circles each of unit radius intersect orthogonally, the common area of the circle is

(a) ${\displaystyle \frac{2\pi }{3}}-\sqrt{3}$

(b) ${\displaystyle \frac{2\pi }{3}}+\sqrt{3}$

(c) ${\displaystyle \frac{2\pi }{3}}-{\displaystyle \frac{\sqrt{3}}{2}}$

(d) ${\displaystyle \frac{2\pi }{3}}+{\displaystyle \frac{\sqrt{3}}{2}}$

Show Answer

Solution:

Required area $=2$. Area of sector $\mathrm{ABC}-$ Area of square $\mathrm{ABCD}$

$=({\displaystyle \frac{90}{360}}\cdot \pi )2-1^2={\displaystyle \frac{\pi }{2}}-1$ sq.units.

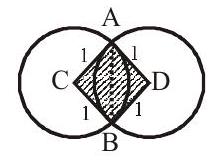
Answer: d

4. The possible values of $m$ for which the area bounded by the curves $y=x-x^2$ and $y=mx$ equal to ${\displaystyle \frac{9}{2}}$ sq. unit is

(a) -4

(b) -2

(c) 2

(d) none of these

Show Answer

Solution: The curves meet at $\mathrm{x}=0$ and $\mathrm{x}=1-\mathrm{m}$

$\begin{array}{rl}& \therefore {\int }_0^{1-m}(x-x^2)-mx\cdot dx=\pm {\displaystyle \frac{9}{2}}\\ \\ & \Rightarrow {\int }_0^{1-m}(1-m)x-x^2\cdot dx=\pm {\displaystyle \frac{9}{2}}\\ \\ & \Rightarrow {((1-m){\displaystyle \frac{x^2}{2}}-{\displaystyle \frac{x^3}{2}})}_0^{1-m}=\pm {\displaystyle \frac{9}{2}}\\ \\ & \Rightarrow (1-m{)}^3({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{3}})={\displaystyle \frac{9}{2}}\\ \\ & \Rightarrow (1-m{)}^3=\pm 27\\ \\ & \Rightarrow 1-m=\pm 3\\ \\ & \Rightarrow m=-2,4\end{array}$

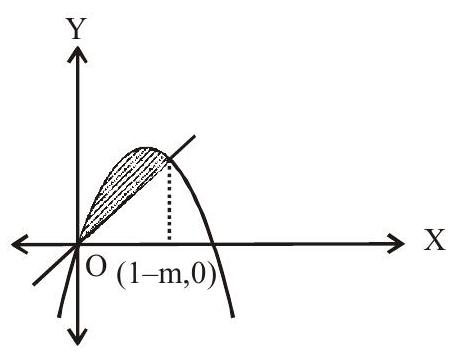
Answer: b

5. The area bounded by the curves $y={\log }_{e}x,y={\log }_e|x|,y=|{\log }_{e}x|$ and $y=\left|{\log }_e\right|x||$ is.

(a) 4

(b) 6

(c) 10

(d) 12

Show Answer

Solution:

$\therefore \mathrm{A}=4{\int }_0^1|{\log }_{\mathrm{e}}\mathrm{x}|\mathrm{dx}=-4{\int }_0^1{\log }_{\mathrm{e}}\mathrm{x}\mathrm{dx}$

$=-4{(x{\log }_{\mathrm{e}}\mathrm{x}-\mathrm{x})}_0^1$

$=-4(-1-0)$

$=4$ sq.units.

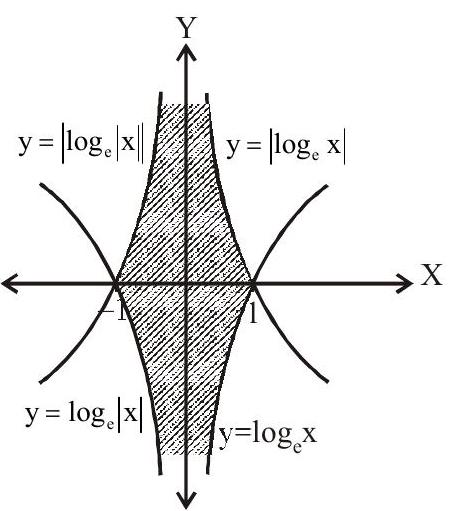
Answer: a

6. The ratio in which the area bounded by the curves $y^2=12x$ & $x^2=12y$ is divided by the line $\mathrm{x}=3$ is

(a) $15:49$

(b) $13:37$

(c) $15:23$

(d) $17:50$

Show Answer

Solution:

Required ratio $={\displaystyle \frac{{\int }_0^3\sqrt{12x}-{\displaystyle \frac{x^2}{12}}\cdot dx}{{\int }_0^3\sqrt{12x}-{\displaystyle \frac{x^2}{12}}\cdot dx}}={\displaystyle \frac{15}{49}}$

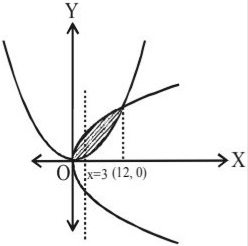
Answer: a

7. The area bounded by the curve $\mathrm{y}=\mathrm{x}+\sin \mathrm{x}$ and its inverse between the ordinates $\mathrm{x}=0$ and $\mathrm{x}=2\pi$ is

(a) $4\pi$

(b) $8\pi$

(c) 4

(d) 8

Show Answer

Solution:

$A=2{\int }_0^{2\pi }(x+\sin x)-xdx=4{\int }_0^{\pi }(x+\sin x)-xdx$

$=2.2(-\cos x{)}_0^{\pi }$

$=4(-\cos \pi +\cos 0)$

$=8$

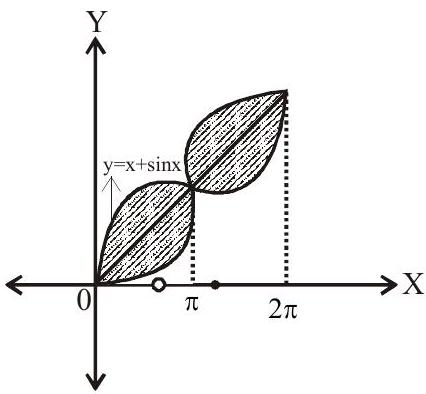
Answer: d

Exercise:

1. The area bounded by $\mathrm{y}=f(\mathrm{x})$, the $\mathrm{x}$-axis and the ordintes $\mathrm{x}=1$ & $\mathrm{x}=\mathrm{b}$ is $(\mathrm{b}-1)\sin (3\mathrm{b}+4)$. Then $f(\mathrm{x})$ is

(a) $(x-1)\cos (3x+4)$

(b) $8\sin (3x+4)$

(c) $\sin (3x+4)+3(x-1)\cos (3x+4)$

(d) none of the above

2. The triangle formed by the tangent to the curve $f(x)=x^2+bx-b$ at the point $(1,1)$ and the coordinate axes, lies in the first quadrant. If its area is 2 , then the value of $b$ is

(a) -1

(b) 3

(c) -3

(d) 1

3. The area bounded by $y=(x-1{)}^2,y=(x+1{)}^2$ & $y={\displaystyle \frac{1}{4}}$

(a) ${\displaystyle \frac{1}{3}}$ sq.unit

(b) ${\displaystyle \frac{2}{3}}$ sq.unit

(c) ${\displaystyle \frac{1}{4}}$ sq.unit

(d) ${\displaystyle \frac{1}{5}}$ sq.unit

4. Let the straight line $\mathrm{x}=\mathrm{b}$ divide the area enclosed by $\mathrm{y}=(1-\mathrm{x}{)}^2,\mathrm{y}=0$ & $\mathrm{x}=0$ into two parts $R_1(0\le x\le b)$ & $R_2(b\le x\le 1)$ such that $R_1-R_2={\displaystyle \frac{1}{4}}$. Then $b$ is

(a) ${\displaystyle \frac{3}{4}}$

(b) ${\displaystyle \frac{1}{2}}$

(c) ${\displaystyle \frac{1}{3}}$

(d) ${\displaystyle \frac{1}{4}}$

5. The area of the quadrilateral formed by the tangents at the end points of latus rectum to the ellipse ${\displaystyle \frac{x^2}{9}}+{\displaystyle \frac{y^2}{5}}=1$ is

(a) ${\displaystyle \frac{27}{4}}$ sq.unit

(b) 9 sq.unit

(c) ${\displaystyle \frac{27}{2}}$ sq.unit

(d) 27 sq.unit

6. The area of the region containing the points ( $x,y$ ) satisfying $4\le x^2+y^2\le 2(|x|+|y|)$ is

(a) 8 sq.units

(b) 2 sq.units

(c) $4\pi$ sq.units

(d) $2\pi$ sq.units

7. The area of the region between the curves $y=\sqrt{{\displaystyle \frac{1+\sin x}{\cos x}}}$ and $y=\sqrt{{\displaystyle \frac{1-\sin x}{\cos x}}}$ bounded by the lines $\mathrm{x}=0$ & $\mathrm{x}={\displaystyle \frac{\pi }{4}}$ is

(a) ${\int }_0^{\sqrt{2}-1}{\displaystyle \frac{\mathrm{tdt}}{(1+{\mathrm{t}}^2)\sqrt{1-{\mathrm{t}}^2}}}$

(b) ${\int }_0^{\sqrt{2}-1}{\displaystyle \frac{4\mathrm{t}}{(1+{\mathrm{t}}^2)\sqrt{1-{\mathrm{t}}^2}}}\mathrm{dt}$

(c) ${\int }_0^{\sqrt{2}+1}{\displaystyle \frac{4\mathrm{t}}{(1+{\mathrm{t}}^2)\sqrt{1-{\mathrm{t}}^2}}}\mathrm{dt}$

(d) ${\int }_0^{\sqrt{2}+1}{\displaystyle \frac{\mathrm{t}}{(1+{\mathrm{t}}^2)\sqrt{1-{\mathrm{t}}^2}}}\mathrm{dt}$

8. Read the passage and answer the following questions:-

If the curve $y=f(x)$ satisfy the equation $y(x+y^3)dx=x(y^3-x)dy$ and $g(x)$

$g(x)={\int }_{1/8}^{{\sin }^{2}x}{\sin }^{-1}\sqrt{t}dt+{\int }_{1/8}^{{\cos }^{2}x}{\cos }^{-1}\sqrt{t}dt$, where $x\in [0,{\displaystyle \frac{\pi }{2}}]$, then

i. Equation of curve $\mathrm{y}=f(\mathrm{x})$ passes through $(4,-2)$ is

(a) $3y=(-54x{)}^{{\displaystyle \frac{1}{3}}}$

(b) $2y=(-16x{)}^{{\displaystyle \frac{1}{3}}}$

(c) $y=(-2x{)}^{{\displaystyle \frac{1}{3}}}$

(d) none of these

ii. Area bounded by curve $\mathrm{y}=f(\mathrm{x}),\mathrm{g}(\mathrm{x})$ and $\mathrm{y}$ axis is

(a) ${\displaystyle \frac{1}{4}}{\left({\displaystyle \frac{3\pi }{16}}\right)}^4$

(b) ${\displaystyle \frac{1}{8}}{\left({\displaystyle \frac{3\pi }{16}}\right)}^4$

(c) ${\displaystyle \frac{1}{8}}{\left({\displaystyle \frac{3\pi }{8}}\right)}^4$

(d) none of these

9. The maximum area of the rectangle whose sides pass through the angular points of a given rectangle of sides $a\mathrm{\&}b$ is

(a) ${\displaystyle \frac{1}{2}}(\mathrm{ab}{)}^2$

(b) ${\displaystyle \frac{1}{2}}(a+b)$

(c) ${\displaystyle \frac{1}{2}}(a+b{)}^2$

(d) none of these

10. Consider a square with vertices at $(1,1),(-1,1),(-1,-1)$ & $(1,-1)$. Let $S$ be the region consisting of all points inside the square which are nearer to the orgin than to any edge. Area of the region is________________________

11. The area bounded by $min(|x|,|y|)=2$ and $max(|x|,|y|)=4$ is

(a) 8 sq.unit

(b) 16 sq.unit

(c) 24 sq.unit

(d) 32 sq.unit

12. The area of the region bounded by

$[x{]}^2=[y{]}^2\text{, if }x\in [1,5]\text{ is }$

(a) 4

(b) 8

(c) 5

(d) 10

13. Match the following:-