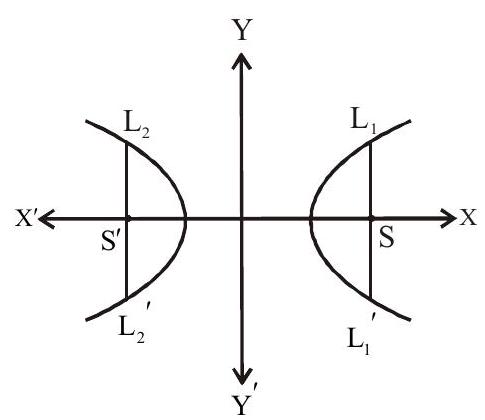
Definition 1 : The locus of a point in a plane, the difference of whose distance from two fixed points in the plane is constant.

According to definition $\left|\mathrm{PF} _{2}-\mathrm{PF} _{1}\right|=$ constant

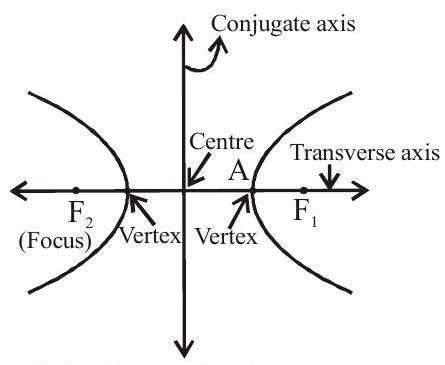
Two fixed points are known as Foci of the hyperbola.

The mid point of the line segment joining the foci is called the centre. The line joining the vertices is known as transverse axis and the line through the centre and perpendicular to transverse axis is known as conjugate axis. The point at which the hyperbola intersect the transverse axis is known as vertices of the hyperbola.

Definition 2 : The locus of a point which moves in a plane such that the ratio of its distance from a fixed point to its perpendicular distance from a fixed straight line (not passing through given fixed point) is always constant and greater than 1 .

$\dfrac{\mathrm{PS}}{\mathrm{PM}}=\mathrm{e}>1$

The equation of hyperbola whose focus is the point $(\mathrm{h}, \mathrm{k})$ and directrix is $a x+b y+c=0$ and whose eccentricity is $e$, is

$(\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{e}^{2} \dfrac{(\mathrm{ax}+\mathrm{by}+\mathrm{c})^{2}}{\mathrm{a}^{2}+\mathrm{b}^{2}}$

Eccentricity :

$\mathrm{e}=\dfrac{\text { Distance between foci }}{\text { Distance between vertices }}=\dfrac{2 \mathrm{c}}{2 \mathrm{a}}=\dfrac{\mathrm{c}}{\mathrm{a}}$

$\mathrm{e}^{2}=\dfrac{\mathrm{c}^{2}}{\mathrm{a}^{2}}=\dfrac{\mathrm{a}^{2}+\mathrm{b}^{2}}{\mathrm{a}^{2}}=1+\dfrac{\mathrm{b}^{2}}{\mathrm{a}^{2}}$

$a^{2} e^{2}=a^{2}+b^{2}$

$\therefore \dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y}^{2}}{\mathrm{a}^{2}\left(\mathrm{e}^{2}-1\right)}=1$

Some terms related to Hyperbola

Equation of hyperbola $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$

1. Centre : All chords passing through a point and bisected at that point is known as centre of hyperbola. $\mathrm{C}(0,0)$

2.Eccentricity : $\mathrm{e}=\dfrac{\text { Distance between foci }}{\text { Distance between vertices }}$

$\mathrm{e}=\sqrt{1+\dfrac{(\text { conjugate axis })^{2}}{(\text { transverse axis })^{2}}}$

$\mathrm{e}=\dfrac{\mathrm{PS}}{\mathrm{PM}}$, where $\mathrm{S}$ is focus, $\mathrm{P}$ is any point on the hyperbola, $\mathrm{PM}$ is distance from directrix.

3.Foci : $\mathrm{S}$ and $\mathrm{S}^{\prime}$ are foci whose coordinates are $\mathrm{S}(\mathrm{ae}, 0)$ and $\mathrm{S}^{\prime}(-\mathrm{ae}, 0)$

4.Directrices : $Z _{1} Z _{1}^{\prime}$ and $Z _{2} Z _{2}^{\prime}$ are the directries whose equation are $x=\dfrac{a}{e}$ and $x=-\dfrac{a}{e}$

5.Vertices : $A$ and $A^{\prime}$ are the vertices of hyperbola . $A(a, 0)$ and $A^{\prime}(-a, 0)$.

6.Axes : The line $\mathrm{A} _{\mathrm{A}^{\prime}}$ is called transverse axis and the line perpendicular to its through the centre of the hyperbola is called conjugate axis. Equations of transverse axis is $y=0$ and equation of conjugate axis is $\mathrm{x}=0$.

Length of transverse axis $=2 \mathrm{a}$

Length of conjugate axis $=2 b$

7.Double Ordinate : A chord of hyperbola which is perpendicular to transverse axis is known as double ordinate $\mathrm{Q} \mathrm{Q}^{\prime}, \mathrm{Q}(\mathrm{h}, \mathrm{k}), \mathrm{Q}^{\prime}(\mathrm{h},-\mathrm{k})$.

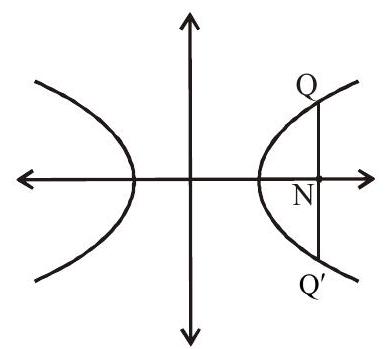
8.Latus rectum : The double ordinates passing through focus is known as latus rectum.

$\mathrm{L} _{1}\left(\mathrm{ae}, \dfrac{\mathrm{b}^{2}}{\mathrm{a}}\right), \mathrm{L} _{1}^{\prime}\left(\mathrm{ae},-\dfrac{\mathrm{b}^{2}}{\mathrm{a}}\right)$

$\mathrm{L} _{2}\left(-\mathrm{ae}, \dfrac{\mathrm{b}^{2}}{\mathrm{a}}\right), \mathrm{L} _{2}^{\prime}\left(-\mathrm{ae},-\dfrac{\mathrm{b}^{2}}{\mathrm{a}}\right)$

9.Focal chard : A chord passing through focus is known as focal chord.

10.Focal Distance :

$P S _{1}=e P M _{1}=e\left(x _{1}-\dfrac{a}{e}\right)$

$=\mathrm{ex} _{1}-\mathrm{a}$

$\mathrm{PS} _{2}=\mathrm{e}\left(\mathrm{x} _{1}+\dfrac{\mathrm{a}}{\mathrm{e}}\right)$

$=\mathrm{ex} _{1}+\mathrm{a}$

$\therefore \mathrm{PS} _{2}-\mathrm{PS} _{1}=2 \mathrm{a}$

Rectangular or Equilateral Hyperbola

If $a=b$, then equation of hyperbola is $\mathrm{x}^{2}-\mathrm{y}^{2}=\mathrm{a}^{2}$ known as rectangular or equilateral hyperbola. The eccentricity of rectangular hyperbola is

$\mathrm{e}^{2}=1+\dfrac{\mathrm{b}^{2}}{\mathrm{a}^{2}}=1+1$

$\mathrm{e}=\sqrt{2}$

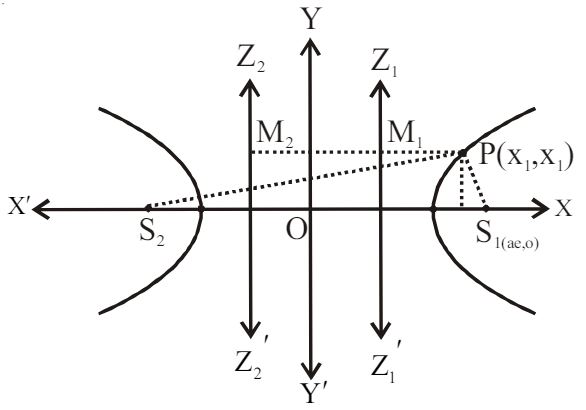
Equation of hyperbola if centre is ( $\mathrm{h}, \mathrm{k}$ ) and axes are parallel to coordinate axes is

$\dfrac{(\mathrm{x}-\mathrm{h})^{2}}{\mathrm{a}^{2}}-\dfrac{(\mathrm{y}-\mathrm{k})^{2}}{\mathrm{~b}^{2}}=1$

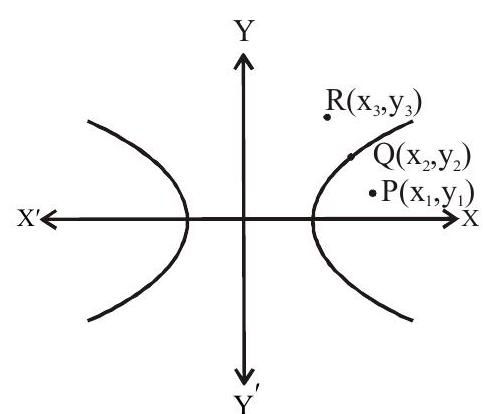
Position of a point :

Let a point $\mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ and equations of hyperbola be $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}-1=0$

$\mathrm{S} _{1}=\dfrac{\mathrm{x} _{1}{ }^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y} _{1}{ }^{2}}{\mathrm{~b}^{2}}-1$

If $S _{1}>0$, point is inside the hyperbola.

If $S _{1}=0$, point is on the hyperbola.

If $\mathrm{S} _{1}<0$, point is outside the hyperbola.

Conjugate Hyperbola :

Corresponding to every hyperbola there exists a hyperbola such that the transverse axis and conjugate axis of one is equal to the conjugate axis and transverse axis of the other. Such hyperbolas are known as conjugate to each other.

Therefore for the hyperbola $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$

Conjugate hyperbola is $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=-1$

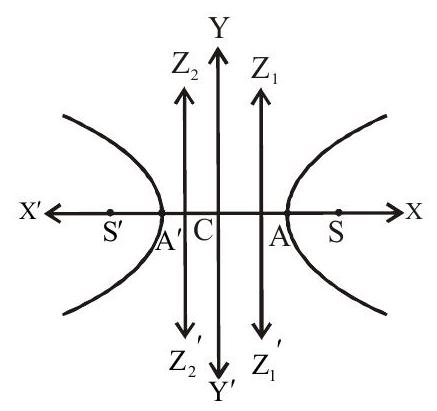
Auxiliary circle and eccentric angle

A circle drawn with centre $\mathrm{O}$ and transverse axis as diameter is known as auxiliary circle. Equation of auxiliary circle is $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{a}^{2}$

A is any point on the circle whose coordinates are $(a \cos \theta$, a $\sin \theta$ ), where $\theta$ is known as eccentric angle.

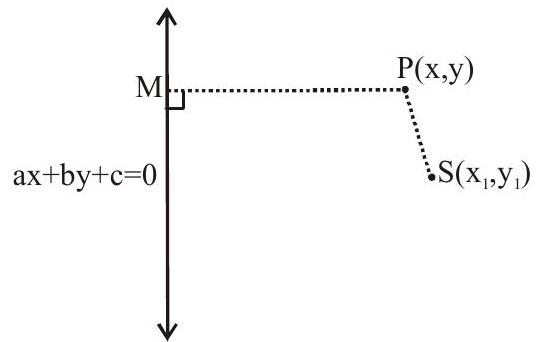
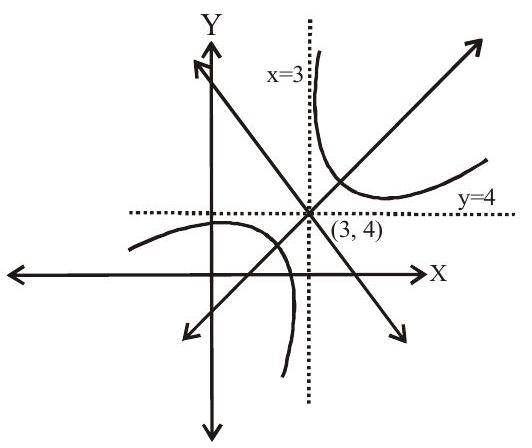
Equation of a Hyperbola referred to two perpendicular lines

Let equation of hyperbola be

$\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$

From diagram $\mathrm{PM}=\mathrm{y}$ and $\mathrm{PN}=\mathrm{x}$

$\dfrac{\mathrm{PN}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{PM}^{2}}{\mathrm{~b}^{2}}=1$

$y= \pm \dfrac{b}{e}$

$\mathrm{e}=\sqrt{1+\dfrac{\mathrm{a}^{2}}{\mathrm{~b}^{2}}}$ or $\mathrm{a}^{2}=\mathrm{b}^{2}\left(\mathrm{e}^{2}-1\right)$

ie. if perpendicular distance of a point $P(x, y)$ from two mutually perpendicular lines say $l _{1}=a _{1} x+b _{1} y+c _{1}=0$ and $\mathrm{l} _{2}=\mathrm{a} _{2} \mathrm{x}+\mathrm{b} _{2} \mathrm{y}+\mathrm{c} _{2}=0$ then

$\dfrac{\left(\dfrac{a _{1} x+b _{1} y+c _{1}}{\sqrt{a _{1}^{2}+b _{1}^{2}}}\right)}{a^{2}}-\dfrac{\left(\dfrac{a _{2} x+b _{2} y+c _{2}}{\sqrt{a _{2}^{2}+b _{2}^{2}}}\right)}{b^{2}}=1$

then the locus of point $\mathrm{P}$ denotes a hyperbola

• centre of the hyperbola, we get after solving $\ell _{1}=0$ and $\ell _{2}=0$

• Transverse axis : $\ell _{2}=0$

• Conjugate axis $: \ell _{1}=0$

• Foci : The foci of the hyperbola is the point of intersection of the lines $\dfrac{a _{1} x+b _{1} y+c _{1}}{\sqrt{a _{1}^{2}+b _{1}^{2}}}= \pm a e$ and $\ell _{2}=0$

• Directrix: $\dfrac{a _{1} x+b _{1} y+c _{1}}{\sqrt{a _{1}^{2}+b _{1}^{2}}}= \pm \dfrac{a}{e}$

• Length of transverse axis $=2 \mathrm{a}$

• Length of conjugate axis $=2 b$

• Length of latus Rectum $=\dfrac{2 b^{2}}{a}$

Equation of tangent

(i) Point Form $\mathrm{T}=\mathbf{0}$

Equation of tangent at point $\mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ to the hyperbola $\dfrac{(\mathrm{x}-\mathrm{h})^{2}}{\mathrm{a}^{2}}-\dfrac{(\mathrm{y}-\mathrm{k})^{2}}{\mathrm{~b}^{2}}=1$ is $\dfrac{(\mathrm{x}-\mathrm{h})\left(\mathrm{x} _{1}-\mathrm{h}\right)}{\mathrm{a}^{2}}-\dfrac{(\mathrm{y}-\mathrm{k})\left(\mathrm{y} _{1}-\mathrm{k}\right)}{\mathrm{b}^{2}}=1$

(ii) Parametric Form :

Parametric equation of hyperbola is $x=a \sec \theta, y=b \tan \theta$

Equation of tangent is

$\dfrac{x}{a} \sec \theta-\dfrac{y}{b} \tan \theta=1$

(iii) Slope Form :

$y=m x \pm \sqrt{a^{2} m^{2}-b^{2}}$

Hyperbola $\left(\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1\right) \quad$ Point of contact.

Point form : $\dfrac{\mathrm{xx} _{1}}{\mathrm{a}^{2}}-\dfrac{\mathrm{yy} _{1}}{\mathrm{~b}^{2}}=1$ $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$

Parametric Form : $\dfrac{\mathrm{x}}{\mathrm{a}} \sec \theta-\dfrac{\mathrm{y}}{\mathrm{b}} \tan \theta=1$ $(\operatorname{asec} \theta, \operatorname{btan} \theta)$

Slope form: $\mathrm{y}=\mathrm{mx} \pm \sqrt{\mathrm{a}^{2} \mathrm{~m}^{2}-\mathrm{b}^{2}}$

$\left( \pm \dfrac{a^{2} m}{\sqrt{a^{2} m^{2}-b^{2}}}, \pm \dfrac{b^{2}}{\sqrt{a^{2} m^{2}-b^{2}}}\right)$

Equation of Pair of Tangents

Let equation of hyperbola be $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ and a point $\mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ then the combined equation of

tangents $\mathrm{PA}$ and $\mathrm{PB}$ is $\mathrm{SS} _{1}=\mathrm{T}^{2}$ where

$\begin{aligned} & \mathrm{S}=\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}-1 \\ & \mathrm{~S} _{1}=\dfrac{\mathrm{x} _{1}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y} _{1}^{2}}{\mathrm{~b}^{2}}-1 \\ & \mathrm{~T}=\dfrac{\mathrm{xx} _{1}}{\mathrm{a}^{2}}-\dfrac{\mathrm{yy} _{1}}{\mathrm{~b}^{2}}=1 \end{aligned}$

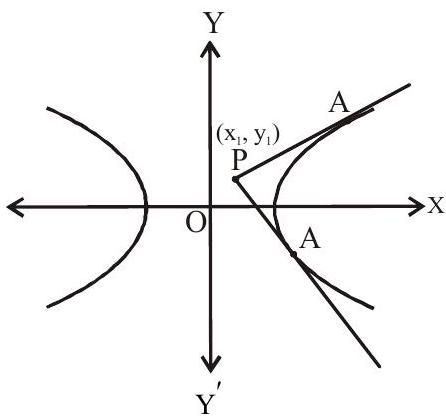
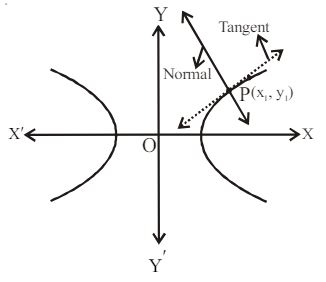
Equation of Normal to the Hyperbola :

i. Point Form

$\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$

Slope to tangent $=+\dfrac{b^{2} x _{1}}{a^{2} y _{1}}$

Slope to normal $=-\dfrac{a^{2} y _{1}}{b^{2} x _{1}}$

Equation of normal $y-y _{1}=-\dfrac{a^{2} y _{1}}{b^{2} x _{1}}\left(x-x _{1}\right)$

$\dfrac{\mathrm{a}^{2} \mathrm{x}}{\mathrm{x} _{1}}+\dfrac{\mathrm{b}^{2} \mathrm{y}}{\mathrm{y} _{1}}=\mathrm{a}^{2}+\mathrm{b}^{2}$

ii. Paramatric Form $\mathrm{P}(\operatorname{asec} \theta, b \tan \theta)$

$\dfrac{\mathrm{ax}}{\sec \theta}+\dfrac{\mathrm{by}}{\tan \theta}=\mathrm{a}^{2}+\mathrm{b}^{2}$

or $a x \cos \theta+b y \cot \theta=a^{2}+b^{2}$

iii. Slope Form

$y=m x \pm \dfrac{m\left(a^{2}+b^{2}\right)}{\sqrt{a^{2}-m^{2} b^{2}}}$

Point of contanct is $\left( \pm \dfrac{a^{2}}{\sqrt{a^{2}-m^{2} b^{2}}}, \mp \dfrac{m b^{2}}{\sqrt{a^{2}-m^{2} b^{2}}}\right)$

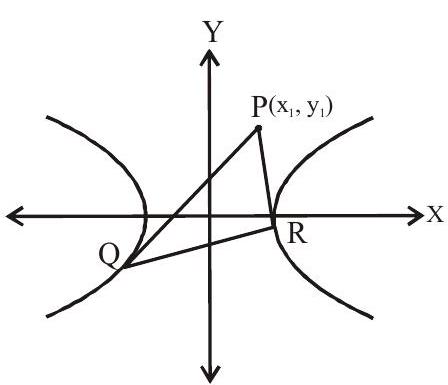
Equation of Chord of Contact

Let equation of hyperbola be $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$,

Equation of Chord of contact is

$\dfrac{\mathrm{xx} _{1}}{\mathrm{a}^{2}}-\dfrac{\mathrm{yy} _{1}}{\mathrm{~b}^{2}}-1=0$

or $\mathrm{T}=0$

where $\mathrm{T}=\dfrac{\mathrm{xx} _{1}}{\mathrm{a}^{2}}-\dfrac{\mathrm{yy} _{1}}{\mathrm{~b}^{2}}-1$

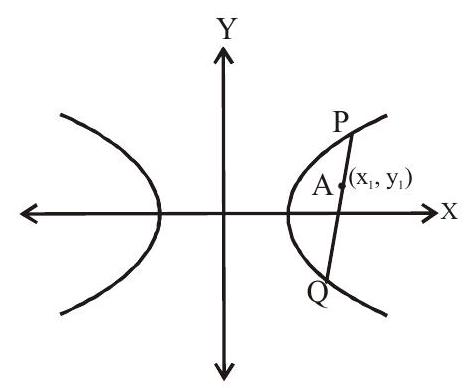
Equation of the chord of the hyperbola whose mid point is given :

$\mathrm{A}$ is the mid point of $\mathrm{PQ}$, then equation of chord is

$\dfrac{\mathrm{xx} _{1}}{\mathrm{a}^{2}}-\dfrac{\mathrm{yy} _{1}}{\mathrm{~b}^{2}}=\dfrac{\mathrm{x} _{1}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y} _{1}^{2}}{\mathrm{~b}^{2}}$

ie. $T=S _{1}$ where

$\mathrm{T}=\dfrac{\mathrm{xx} _{1}}{\mathrm{a}^{2}}-\dfrac{\mathrm{yy} _{1}}{\mathrm{~b}^{2}}-1$

$\mathrm{S} _{1}=\dfrac{\mathrm{x} _{1}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y} _{1}^{2}}{\mathrm{~b}^{2}}-1$

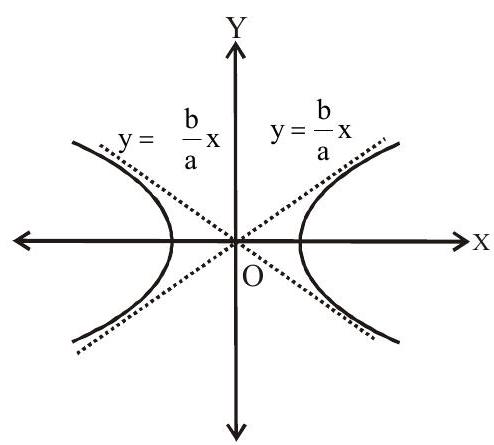
Asymptotes of Hyperbola

An asymptotes of any hyperbola is a straight line which touches in it two points at infinity.

OR

If the length of the perpendicular let fall from a point on a hyperbola to a straight line tends to zero as the point on the hyperbola moves to infinity along the hyperbola, then the straight line is called asymptote of the hyperbola.

The equation of two anymptotes of the hyparbola $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$

are $y= \pm \dfrac{b}{a} x$ or $\dfrac{x}{a} \pm \dfrac{y}{b}=0$

Pair of asymptotoes : $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=0$

1. If $b=a$, then $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$ reduces to $x^{2}-y^{2}=a^{2}$. The asymptotes of rectangular hyperbola $\mathrm{x}^{2}-\mathrm{y}^{2}=\mathrm{a}^{2}$ are $\mathrm{y}= \pm \mathrm{x}$ which are at right angles.

2. A hyperbola and its conjugate hyperbola have the same asyptotes.

3. The angle between the asymptotes of $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$ is $2 \tan ^{-1}\left(\dfrac{b}{a}\right)$

4. The asymptotes pass through the centre of the pyperbola.

5. The bisectors of the angle between the asymptotes are the coordinate axes.

6. Let $\mathrm{H}=\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}-1=0$

$A=\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=0$

and $\mathrm{C}=\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}+1=0$

be the equation of the hyperbola, asymptotes and the conjugate hyperbola respectively, then clearly

$\mathrm{C}+\mathrm{H}=2 \mathrm{~A}$

Rectangular Hyperbola:

A hyperbola whose asymptotes include a right angle is said to be rectangular hyperbola.

OR

If the lengths of transverse and conjugate axes of any hyperbola be equal it is called rectangular or equilateral hyperbola.

Then asymptotes of $x^{2}-y^{2}=a^{2}$ are $x+y=0$ and $x-y=0$. Each of these two asymptotes is inclined at an angle of $45^{\circ}$ with the transverse axis. So, if we rotate the coordinate axes through an angle of $\dfrac{\pi}{4}$ keeping the origin fixed, then the axes coincide with the asymptotes of the hyperbola.

Now equation of asymptotes of new hyperbola is $\mathrm{x}=0$

Then equation of hyperbola is $\mathrm{xy}=\mathrm{k}$ (constant)

The hyperbola passes through the point $\left(\dfrac{\mathrm{a}}{\sqrt{2}}, \dfrac{\mathrm{a}}{\sqrt{2}}\right)$

$\therefore \mathrm{k}=\dfrac{\mathrm{a}^{2}}{2}$

Then equation of hyperbola is $x y=\dfrac{a^{2}}{2}$ or $x y=c^{2}$ where $c^{2}=\dfrac{a^{2}}{2}$

If the asymptotes of a rectangular hyperbola are $x=a, y=b$, then its equation is $(x-a)(y-b)=c^{2}$ $\mathbf{x y}=\mathbf{c}^{2}$

1. Asymptotes : $\mathrm{x}=0, \mathrm{y}=0$

2. Transverse axis: $\mathrm{y}=\mathrm{x}$

Conjugate axis : $\mathrm{y}=-\mathrm{x}$

3. Vertices $\mathrm{A}(\mathrm{c}, \mathrm{c}), \mathrm{A}^{\prime}(-\mathrm{c},-\mathrm{c})$

4. Foci : $\mathrm{S}(\mathrm{c} \sqrt{2}, \mathrm{c} \sqrt{2}), \mathrm{S}^{\prime}(-\mathrm{c} \sqrt{2},-\mathrm{c} \sqrt{2})$

5. Length of transverse axis $=\mathrm{AA}^{\prime}=2 \sqrt{2} \mathrm{c}$

6. Equation of auxiliary circle $\mathrm{x}^{2}+\mathrm{y}^{2}=2 \mathrm{c}^{2}$

7. Equation of director circle $x^{2}+y^{2}=0$

8. $x^{2}-y^{2}=a^{2}$ and $x y=c^{2}$ intersect at right angles

Properties of Rectangular Hyperbola

1. Eccentricity of rectangular hyperbola is $\sqrt{2}$.

2. Since $x=c t, y=\dfrac{c}{t}$ satisfies $x y=c^{2}$

$\therefore(\mathrm{x}, \mathrm{y})=\left(\mathrm{ct}, \dfrac{\mathrm{c}}{\mathrm{t}}\right)(\mathrm{t} \neq 0)$ is called a ’ $\mathrm{t}$ ’ point on the rectangular hyperbola. The $\mathrm{x}=\mathrm{ct}, \mathrm{y}=\dfrac{\mathrm{c}}{\mathrm{t}}$ represents its parametric equation with parameter ’ $\mathrm{t}$ '

3. Equation of chord joining $\mathrm{P}\left(\mathrm{Ct} _{1}, \dfrac{\mathrm{c}}{\mathrm{t} _{1}}\right)$ and $\mathrm{Q}\left(\mathrm{Ct} _{2}, \dfrac{\mathrm{c}}{\mathrm{t} _{2}}\right)$ is

$\begin{aligned} & \mathrm{x}+\mathrm{yt} _{1} \mathrm{t} _{2}-\mathrm{c}\left(\mathrm{t} _{1}+\mathrm{t} _{2}\right)=0 \\ & \text { Slope of chord }=-\dfrac{1}{\mathrm{t} _{1} \mathrm{t} _{2}} \end{aligned}$

4. Equation of tangent at $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ is $\mathrm{xy} _{1}+\mathrm{yx} _{1}=2 \mathrm{c}^{2}$

5. Equation of tangent at is $\dfrac{\mathrm{x}}{\mathrm{t}}+\mathrm{yt}=2 \mathrm{c}$

$\text { Slope of tangent }=-\dfrac{1}{t^{2}}$

6. Equation of normal at $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ is $\mathrm{xx} _{1}-\mathrm{yy} _{1}=\mathrm{x} _{1}{ }^{2}-\mathrm{y} _{1}{ }^{2}$

Equation of normal at is $\mathrm{xt}^{3}-\mathrm{yt}^{2}-\mathrm{ct}^{4}+\mathrm{c}=0$

$\text { Slope of normal }=\mathrm{t}^{2}$

7. Point of intersection of tangents at $t _{1}$ and $t _{2}$ is

$\left(\dfrac{2 c t _{1} t _{2}}{t _{1}+t _{2}}, \dfrac{2 c}{t _{1}+t _{2}}\right)$

8. Point of intersection of normal at $t _{1}$ and $t _{2}$ is

$\left(\dfrac{\mathrm{ct} _{1} \mathrm{t} _{2}\left(\mathrm{t} _{1}{ }^{2}+\mathrm{t} _{1} \mathrm{t} _{2}+\mathrm{t} _{2}{ }^{2}\right)-\mathrm{c}}{\mathrm{t} _{1} \cdot \mathrm{t} _{2}\left(\mathrm{t} _{1}+\mathrm{t} _{2}\right)}, \dfrac{\mathrm{ct} _{1}{ }^{3} \mathrm{t} _{2}{ }^{3}+\mathrm{c}\left(\mathrm{t} _{1}{ }^{2}+\mathrm{t} _{1} \mathrm{t} _{2}+\mathrm{t} _{2}{ }^{2}\right)}{\mathrm{t} _{1} \cdot \mathrm{t} _{2}\left(\mathrm{t} _{1}+\mathrm{t} _{2}\right)}\right)$

Practice Problems

1. Equation of conjugate axis of hyperbola $x y-3 y-4 x+7=0$ is

(a) $x+y=7$

(b) $x+y=3$

(c) $x-y=7$

(d) None of these

Show Answer

Solution:

$\begin{aligned} & x y-3 y-4 x+7=0 \\ & x y-3 y-4 x+12=5 \\ & (x-3)(y-4)=5 \end{aligned}$

Equation of asymptotes are $x-3=0$ and $y-4=0$ Since the hyperbola is rectangular hyperbola, axes are bisectors of asymptotes

Hence their slaps are $\pm 1$

$\therefore$ Equation of conjugate axis is

$y-4=-1(x-3)$

$x+y=7$

Answer (A)

2. If $\mathrm{S} _{1}$ and $\mathrm{S} _{2}$ are the foci of the hyperbola whose transverse axis length is 4 and conjugate axis length is $6, \mathrm{~S} _{3}$ and $\mathrm{S} _{4}$ are the foci of the conjugate hyperbola, then the area of the quadrilateral $\mathrm{S} _{1} \mathrm{~S} _{3} \mathrm{~S} _{2} \mathrm{~S} _{4}$ is

(a) 156

(b) 36

(c) 26

(d) None of these

Show Answer

Solution:

$\mathrm{S} _{1} \mathrm{~S} _{3} \mathrm{~S} _{2} \mathrm{~S} _{4}$ forms a square.

So required area $=4 \times$ area of ${ } _{\Delta} \mathrm{S} _{1} \mathrm{O} \mathrm{S} _{3}=4 \times \dfrac{1}{2}$ ae $\times$ be $ _{1}$

$\hspace{2.5 cm}=2 \mathrm{abee} _{1}=2.2 .3 . \mathrm{e} \mathrm{e} _{1}$

$\hspace{2.5 cm}=12 \mathrm{ee} _{1}$

Now e $=\sqrt{1+\dfrac{9}{4}}=\dfrac{\sqrt{13}}{2}$ & $\mathrm{e} _{1}=\sqrt{1+\dfrac{9}{4}}=\dfrac{\sqrt{13}}{2}$

Hence area $=12 \times \dfrac{\sqrt{13}}{2} \times \dfrac{\sqrt{13}}{3}=26$ sq.units

Answer (C)

3. The ellipse $4 x^{2}+9 y^{2}=36$ and the hyperbola $a^{2} x^{2}-y^{2}=4$ intersect at right angles then the equation of the circle through the points of intersection of two conic is

(a) $x^{2}+y^{2}=25$

(b) $5\left(x^{2}+y^{2}\right)+3 x+4 y=0$

(c) $5\left(x^{2}+y^{2}\right)-3 x-4 y=0$

(d) $\left(\mathrm{x}^{2}+\mathrm{y}^{2}\right)=5$

Show Answer

Solution:

Since ellipse and hyperbola intersect orthogonally, they are confocal.

$\mathrm{e}=\sqrt{1-\dfrac{4}{9}}=\dfrac{\sqrt{5}}{3}$

foci of ellipse $( \pm \sqrt{5}, 0)$

$\begin{aligned} & (a e)^{2}=a^{2}+b^{2} \\ & 5=\dfrac{4}{a^{2}}+4 \Rightarrow a=2 \end{aligned}$

Let point of intersection in the first quadrant be $\mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$. $\mathrm{P}$ lies on both the curves.

$4x _{1}^{2}+9 y _{1}^{2}=36 \quad \text { and } 4 x _{1}^{2}-y _{1}^{2}=4$

Adding these two, we get $8 \mathrm{x} _{1}{ }^{2}+8 \mathrm{y} _{1}{ }^{2}=40$

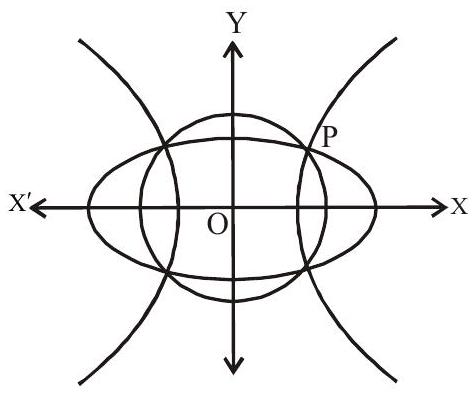
Equation of circle is $x^{2}+y^{2}=5$

$\mathrm{x} _{1}^{2}+\mathrm{y} _{1}^{2}=5$

4. If $\mathrm{is}$ the eccentricity of the hyperbola $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ and $2 \theta$ is angle between the asymptotes then $\cos \theta=$

(a) $\dfrac{1}{\mathrm{e}}$

(b) $\dfrac{1-e}{e}$

(c) $\dfrac{1+\mathrm{e}}{\mathrm{e}}$

(d) None of these

5. From a point $\mathrm{p}(1,2)$ pair of tangents are drawn to a hyperbola in which one tangent to each arm of hyperbola. Equation of asymptotes of hyperbola are $\sqrt{3} x-y+5=0$ and $\sqrt{3} x+y-1=0$ then eccentricity of hyperbola is

(a) $\sqrt{3}$

(b) $\dfrac{2}{\sqrt{3}}$

(c) 2

(d) None of these

Show Answer

Solution:

Equation of asymptotes are

$\sqrt{3} \mathrm{x}-\mathrm{y}+5=0$

$-\sqrt{3} \mathrm{x}-\mathrm{y}+1=0$

$\therefore \mathrm{a} _{1} \mathrm{a} _{2}+\mathrm{b} _{1} \mathrm{~b} _{2}=-3+1<0$

$\therefore$ origin lies in acute angle and $\mathrm{P}(1,2)$ lies in obtuse angle.

$\therefore \mathrm{e}=\sec \theta$ where $2 \theta$ is the angle between asymptotes.

$2 \theta=\dfrac{\pi}{3} \Rightarrow \theta=\dfrac{\pi}{6}$

$\mathrm{e}=\sec \dfrac{\pi}{6}=\dfrac{2}{\sqrt{3}}$

Answer b

6. If a variable line has its intercepts on the coordinate axes $\mathrm{e}, \mathrm{e}^{\prime}$ where $\dfrac{\mathrm{e}}{2}, \dfrac{\mathrm{e}^{\prime}}{2}$ are the eccentricities of a hyperbola and its conjugate hyperbola, then the line always touches the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{r}^{2}$, where $\mathrm{r}=$

(a) 4

(b) 3

(c) 2

(d) Can not be decided

7. If angle between asymptotes of hyperbola $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$ is $120^{\circ}$ and product of perpendiculars drown from foci upon its any tangent is 9 , then locus of point of intersection of perpendicular tangents of the hyperbola can be

(a) $\mathrm{x}^{2}+\mathrm{y}^{2}=18$

(b) $\mathrm{x}^{2}+\mathrm{y}^{2}=6$

(c) $\mathrm{x}^{2}+\mathrm{y}^{2}=9$

(d) $\mathrm{x}^{2}+\mathrm{y}^{2}=3$

8. The equation of the transverse axis of the hyperbola $(x-3)^{2}+(y+1)^{2}=(4 x+3 y)^{2}$ is

(a) $3 x-4 y=0$

(b) $4 x+3 y=0$

(c) $3 x-4 y=13$

(d) $4 x+3 y=9$

Exercise

1. The equation of common tangents to the parabola $y^{2}=8 x$ and hyperbola $3 x^{2}-y^{2}=3$ is

(a) $\mathrm{x} \pm 2 \mathrm{y}-1=0$

(b) $x \pm 2 y+1=0$

(c) $2 \mathrm{x} \pm \mathrm{y}+1=0$

(d) $2 \mathrm{x} \pm \mathrm{y}-1=0$

2. A tangent to the hyperbola $y=\dfrac{x+9}{x+5}$ passing through the origin is

(a) $x-2 y=0$

(b) $5 x-y=0$

(c) $5 \mathrm{x}+\mathrm{y}=0$

(d) $x+225 y=0$

3. The equation of the common tangent to the curves $y^{2}=8 x$ and $x y=-1$ is

(a) $y=x+2$

(b) $y=2 x+1$

(c) $2 \mathrm{y}=\mathrm{x}+8$

(d) $3 y=9 x+2$

4. Let $\mathrm{PQ}$ be a double ordinate of the hyperbola $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$. If $\mathrm{O}$ be the centre of the hyperbola and $\mathrm{OPQ}$ is an equilateral triangle, then eccentricity $\mathrm{e}$ is

(a) $>\sqrt{3}$

(b) $>2$

(c) $>\dfrac{2}{\sqrt{3}}$

(d) None of these

5. The difference between the length 2a of the transverse axis of a hyperbola of eccentricity e and the length of its latus rectum is

(a) $\mathrm{a}\left(2 \mathrm{e}^{2}-1\right)$

(b) $2 \mathrm{a}\left(\mathrm{e}^{2}-1\right)$

(c) $2 \mathrm{a}\left|3-\mathrm{e}^{2}\right|$

(d) $2 \mathrm{a} \mid 2-\mathrm{e}^{2}$

6. The slopes of common tangents to the hyperbolas $\dfrac{x^{2}}{9}-\dfrac{y^{2}}{16}=1$ and $\dfrac{y^{2}}{9}-\dfrac{x^{2}}{16}=1$ are

(a) $\pm 2$

(b) $\pm \sqrt{2}$

(c) $\pm 1$

(d) None of these

7. The two conics $\dfrac{y^{2}}{b^{2}}-\dfrac{x^{2}}{a^{2}}=1$ and $y^{2}=-\dfrac{b}{a} x$ intersect iff

(a) $0<\mathrm{b} \leq \dfrac{1}{2}$

(b) $0<\mathrm{a} \leq \dfrac{1}{2}$

(c) $\mathrm{bPractice Problems}^{2}<\mathrm{a}^{2}$

(d) $b^{2}>a^{2}$

8. The point on the hyperbola $\dfrac{x^{2}}{24}-\dfrac{y^{2}}{18}=1$ which is nearest to the line $3 x+2 y+1=0$ is

(a) $(-6,3)$

(b) $(3,-6)$

(c) $(-6,-3)$

(d) $(6,3)$

9. If $(\operatorname{asec} \theta, b \tan \theta)$ and $(\operatorname{asec} \phi, b \tan \phi)$ be the coordinates of the ends of a focal chord of the hyperbola $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$, then $\tan \dfrac{\theta}{2} \tan \dfrac{\phi}{2}=$

(a) $\dfrac{1+\mathrm{e}}{1-\mathrm{e}}$

(b) $\dfrac{1-\mathrm{e}}{1+\mathrm{e}}$

(c) $\dfrac{\mathrm{e}-1}{\mathrm{e}+1}$

(d) None of these

10. If the latus rectum of a hyperbola through one focus subtends $60^{\circ}$ angle at the other focus, then its eccentricity e is

(a) $\sqrt{2}$

(b) $\sqrt{3}$

(c) $\sqrt{5}$

(d) $\sqrt{6}$