1. The points, where the normal to the ellipse $x^{2}+3 y^{2}=37$ be parallel to the line $6 x-5 y+7=0$ is / are

(a) $(5,2)$

(b) $(2,5)$

(c) $(1,3)$

(d) $(-5,-2)$

Show Answer

Solution:

Let $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ be a point on ellipse then, $\mathrm{x} _{1}{ }^{2}+3 \mathrm{y} _{1}{ }^{2}=37$ ___________________(1)

Equation of normal at $\left(x _{1}, y _{1}\right)$ is $\dfrac{a^{2} x}{x _{1}}-\dfrac{b^{2} y}{y _{1}}=a^{2}-b^{2}$

In ellipse $\dfrac{x^{2}}{37}+\dfrac{y^{2}}{\dfrac{37}{3}}=1$

$ a^{2}=37, b^{2}=\dfrac{37}{3}$

$\therefore \quad \dfrac{37 \mathrm{x}}{\mathrm{x} _{1}}-\dfrac{37 \mathrm{y}}{3 \mathrm{y} _{1}}=37-\dfrac{37}{3}$

$\dfrac{37 \mathrm{x}}{\mathrm{x} _{1}}-\dfrac{37 \mathrm{y}}{3 \mathrm{y} _{1}}=\dfrac{74}{3}$ ___________________(2)

Slope of normal is $\dfrac{\dfrac{37}{x _{1}}}{\dfrac{37}{3 y _{1}}}=\dfrac{3 y _{1}}{x _{1}}$

$\because$ it is parallel to $6 x-5 y+7=0$

$\begin{aligned} & \therefore \dfrac{3 y _{1}}{x _{1}}=\dfrac{6}{5} \\ & y _{1}=\dfrac{2}{5} x _{1} \end{aligned}$

put in(1) we get

$\begin{aligned} & \mathrm{x} _{1}^{2}+\dfrac{12}{25} \mathrm{x} _{1}^{2}=37 \\ & \dfrac{37 \mathrm{x} _{1}^{2}}{25}=37 \\ & \mathrm{x} _{1}^{2}=25 \\ & \mathrm{x} _{1}= \pm 5 \\ & \mathrm{y} _{1}= \pm 2 \end{aligned}$

$\therefore(5,2)$ & $(-5,-2)$

options (a) and (b) are correct

2. If the tangent to the ellipse $x^{2}+4 y^{2}=16$ at the point $P(\theta)$ is a normal to the circle $x^{2}+y^{2}-8 x-4 y=0$ then $\theta$ equals

(a) $\dfrac{\pi}{2}$

(b) $\dfrac{\pi}{4}$

(c) 0

(d) $\dfrac{-\pi}{4}$

Show Answer

Solution:

Given ellipse is $\dfrac{x^{2}}{16}+\dfrac{y^{2}}{4}=1$

Equation of tangent at $P(\theta)$ is $P(a \cos \theta, b \sin \theta)$

i.e. $P(4 \cos \theta, 2 \sin \theta)$ is

$ \dfrac{4 \mathrm{x} \cos \theta}{16}+\dfrac{2 \mathrm{y} \sin \theta}{4}=1 $

$\mathrm{x} \cos \theta+2 \mathrm{y} \sin \theta=4$ _________________(1)

(1) is a normal to the circle $x^{2}+y^{2}-8 x-4 y=0$

$\therefore$ The equation (1) passes through the centre $(4,2)$ of the circle.

$\begin{aligned} & \therefore 4 \cos \theta+4 \sin \theta=4 \\ & \cos \theta+\sin \theta=1 \\ & \text { squaring } \\ & 1+\sin 2 \theta=1 \\ & \sin 2 \theta=0 \\ & 2 \theta=0 \text { or } \pi \end{aligned}$

Hence, $\theta=0$ or $\dfrac{\pi}{2}$

$\therefore$ options are (a) & (c) are correct

3. The slope of a common tangent to the ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{b^{2}}{b^{2}}=1$ and a concentric circle of radius $r$ is

(a) $\tan ^{-1} \sqrt{\dfrac{\mathrm{r}^{2}-\mathrm{b}^{2}}{\mathrm{a}^{2}-\mathrm{r}^{2}}}$

(b) $\sqrt{\dfrac{\mathrm{r}^{2}-\mathrm{b}^{2}}{\mathrm{a}^{2}-\mathrm{r}^{2}}}$

(c) $\left(\dfrac{\mathrm{r}^{2}-\mathrm{b}^{2}}{\mathrm{a}^{2}-\mathrm{r}^{2}}\right)$

(d) $\sqrt{\dfrac{a^{2}-r^{2}}{r^{2}-b^{2}}}$

Show Answer

Solution:

Equation of any tangent to the given ellipse is $y=m x \pm \sqrt{a^{2} m^{2}+b^{2}}$

If it touches the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{r}^{2}$ then

$r=\left|\dfrac{\sqrt{a^{2} m^{2}+b^{2}}}{\sqrt{1+m^{2}}}\right|$

Squaring

$\mathrm{r}^{2}=\dfrac{\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}}{1+\mathrm{m}^{2}}$

$ \mathrm{r}^{3}\left(1+\mathrm{m}^{2}\right)=\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}$

$ \mathrm{~m}^{2}\left(\mathrm{r}^{2}-\mathrm{a}^{2}\right)=\mathrm{b}^{2}-\mathrm{r}^{2}$

$ \mathrm{~m}^{2}=\dfrac{\mathrm{b}^{2}-\mathrm{r}^{2}}{\mathrm{r}^{2}-\mathrm{a}^{2}}$

$ \mathrm{~m}=\sqrt{\dfrac{\mathrm{b}^{2}-\mathrm{r}^{2}}{\mathrm{r}^{2}-\mathrm{a}^{2}}}=\sqrt{\dfrac{\mathrm{r}^{2}-\mathrm{b}^{2}}{\mathrm{a}^{2}-\mathrm{r}^{2}}}$

correct option is (b)

4. $\mathrm{P}$ is a variable point on the ellipse $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ with $\mathrm{AA}^{\prime}$ as the major axis. Then the maximum area of the triangle $\mathrm{AP}{A}^{\prime}$ is

(a) $\mathrm{ab}$

(b) $2 \mathrm{ab}$

(c) $\mathrm{ab} / 2$

(d) None of these

Show Answer

Solution:

Maximum area corresponds to $\mathrm{P}$ when it is at either end of the minor axis and hence area for such a position of $\mathrm{P}$ is $\dfrac{1}{2}(2 \mathrm{a}) .(\mathrm{b})=\mathrm{ab}$.

correct option is (a)

5. An ellipse is described by using an endless string which is passed over two pins. If the axes are $6 \mathrm{~cm}$ and $4 \mathrm{~cm}$, the necessary length of the string and the distance between the pins respectively in cms, are

(a) $6,2 \sqrt{5}$

(b) $6, \sqrt{5}$

(c) $4,2 \sqrt{5}$

(d) None of these

Show Answer

Solution:

Given $2 \mathrm{a}=6 \quad 2 \mathrm{~b}=4$

$\begin{aligned} \text { Therefore e } & =\sqrt{1-\dfrac{\mathrm{b}^{2}}{\mathrm{a}^{2}}} \\ & =\sqrt{1-\dfrac{4}{9}} \\ & =\sqrt{\dfrac{5}{9}} \\ & =\dfrac{\sqrt{5}}{3} \end{aligned}$

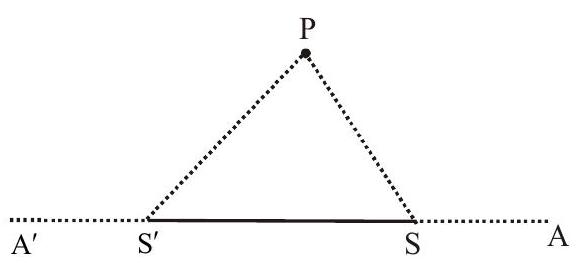
Distance between foci $=2 \mathrm{ae}=6 \dfrac{\sqrt{5}}{3}=2 \sqrt{5}$

length of string $=\mathrm{SP}+\mathrm{S}^{\prime} \mathrm{P}+\mathrm{SS}^{\prime}$

$\begin{aligned} & =2 \mathrm{a}+2 \mathrm{ae} \\ & =6+2 \sqrt{5} \end{aligned}$

Correct option is ’d’

6. If the chords of contact of tangents from two points $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ and $\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right)$ to the ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ are at right angles then $\dfrac{x _{1} x _{2}}{y _{2} y _{2}}$ is equal to

(a) $\dfrac{a^{2}}{b^{2}}$

(b) $\dfrac{-b^{2}}{a^{2}}$

(c) $\dfrac{-\mathrm{a}^{4}}{\mathrm{~b}^{4}}$

(d) $\dfrac{-b^{4}}{a^{4}}$

Show Answer

Solution:

The equations of the chords of contact of tangents drawn from $\left(x _{1}, y _{1}\right)$ and $\left(x _{2}, y _{2}\right)$ to the ellipse $\dfrac{x^{2}}{a^{2}}$ $+\dfrac{\mathrm{b}^{2}}{\mathrm{~b}^{2}}=1$ are

$\dfrac{xx_{1}}{a^2}+\dfrac{y y_1}{b^2}=1$ ___________(1) and $\dfrac{xx_2}{a^2}+\dfrac{y y_2}{b^2}=1$ ______________(2)

It is given that (1) and (2) are at right angles

$\therefore$ product of their slopes is equal to -1 .

$\begin{aligned} & \dfrac{-b^{2} x _{1}}{a^{2} y _{1}} \times \dfrac{-b^{2} x _{2}}{a^{2} y _{2}}=-1 \\ & \dfrac{b^{4}}{a^{4}} \dfrac{x _{1} x _{2}}{y _{1} y _{2}}=-1 \\ & \text { or } \dfrac{x _{1} x _{2}}{y _{1} y _{2}}=\dfrac{-a^{4}}{b^{4}} \end{aligned}$

correct option is c

7. On the ellipse $4 x^{2}+9 y^{2}=1$, the points at which the tangents are parallel to the line $8 x-9 y=0$ are

(a) $\left(\dfrac{2}{5}, \dfrac{1}{5}\right)$

(b) $\left(\dfrac{-2}{5}, \dfrac{1}{5}\right)$

(c) $\left(\dfrac{-2}{5}, \dfrac{-1}{5}\right)$

(d) $\left(\dfrac{2}{5}, \dfrac{-1}{5}\right)$

Show Answer

Solution:

We have equation of ellipse as $4 x^{2}+9 y^{2}=1$

$\dfrac{x^{2}}{\left(\dfrac{1}{4}\right)}+\dfrac{y^{2}}{\left(\dfrac{1}{9}\right)}=1$

$\begin{array}{ll} a^{2}=\dfrac{1}{4} & b^{2}=\dfrac{1}{9} \\ a=\dfrac{1}{2} & b=\dfrac{1}{3} \end{array}$

and tangent line is parallel to $8 x-9 y=0$

$\therefore$ slope of tangent $\mathrm{m}=\dfrac{8}{9}$

The required points are $\left( \pm \dfrac{\mathrm{a}^{2} \mathrm{~m}}{\sqrt{\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}}}, \mp \dfrac{\mathrm{b}^{2}}{\sqrt{\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}}}\right)$

i.e. $\left( \pm \dfrac{\dfrac{1}{4} \times \dfrac{8}{9}}{\sqrt{\dfrac{1}{4} \times \dfrac{64}{81}+\dfrac{1}{9}}}, \mp \dfrac{\dfrac{1}{9}}{\dfrac{5}{9}}\right)=\left( \pm \dfrac{2}{5}, \mp \dfrac{1}{5}\right)$

correct options are (b) & (d)

PRACTICE EXERCISE SECTION - A

1. The equation of the circle drawn with the two foci of $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ as the end points of a diameter is

(a) $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{a}^{2}+\mathrm{b}^{2}$

(b) $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{a}^{2}$

(c) $x^{2}+y^{2}=2 a^{2}$

(d) $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{a}^{2}-\mathrm{b}^{2}$

Show Answer

Answer: d

2. The radius of the circle passing through the foci of the ellips $\dfrac{x^{2}}{16}+\dfrac{y^{2}}{7}=1$ and having its centre $(0,3)$ is

(a) 4

(b) 3

(c) $\sqrt{12}$

(d) $\dfrac{7}{2}$

Show Answer

Answer: a

3. $\dfrac{x^{2}}{r^{2}-r-6}+\dfrac{y^{2}}{r^{2}-6 r+5}=1$ will represents the ellipse, if $r$ lies in the interval

(a) $(-\infty, 2)$

(b) $(3, \infty)$

(c) $(5, \infty)$

(d) $(1, \infty)$

4. The semi latus rectum of an ellipse is

(a) The AM of the segments of its focal chord.

(b) The GM of the segments of its focal chord

(c) The HM of the segments of its focal chord

(d) None of these

5. The following equation represents an ellipse $25\left(x^{2}-6 x+9\right)+16 y^{2}=400$. How should the axes be transformed so that the ellipse is represented by the equation $\dfrac{x^{2}}{16}+\dfrac{y^{2}}{25}=1$ __________

6. Let $\mathrm{P}$ be a variable point on the ellipse $\dfrac{\mathrm{x}^{2}}{16}+\dfrac{\mathrm{y}^{2}}{25}=1$ with foci $\mathrm{S} _{1}$ and $\mathrm{S} _{2}$. It $\mathrm{A}$ be area of the triangle $\mathrm{PS} _{1} \mathrm{~S} _{2}$ then the maximum value of $\mathrm{A}$ is ___________

7. In an ellipse, if the lines joining a focus to the extremities of the minor axis make an equilateral triangle with the minor axis, the eccentricity of the ellipse is

(a) $3 / 4$

(b) $\sqrt{3} / 2$

(c) $1 / 2$

(d) $2 / 3$

8. Column Matching :

For the ellipse $\dfrac{x^{2}}{5}+\dfrac{y^{2}}{4}=1$

	Column I		Column II
1	$\mathrm{x}=0$	a	a directrix
2	$\mathrm{y}=0$	b	a latus rectum
3	$\mathrm{x}=1$	$\mathrm{c}$	minor axis
4	$\mathrm{x}=5$	d	major axis

9. The equation of the ellipse whose focus is ( $1,-1)$, directrix $x-y-3=0$ and eccentricity $1 / 2$ is

(a) $7 x^{2}+2 x y+7 y^{2}-10 x+10 y+7=0$

(b) $7 x^{2}+2 x y+7 y^{2}+7=0$

(c) $7 x^{2}+2 x y+7 y^{2}+10 x-10 y-7=0$

(d) None of these

10. The centre of the ellipse $14 x^{2}-4 x y+11 y^{2}-44 x-58 y+71=0$ is ____________

Show Answer

Answer: 2, 3

PRACTICE EXERCISE SECTION - B

1. The sum of the squares of the reciprocals of two perpendicular diameter of an ellipse is

(a) $\dfrac{1}{4}\left(\dfrac{1}{\mathrm{a}^{2}}+\dfrac{1}{\mathrm{~b}^{2}}\right)$

(b) $\dfrac{1}{2}\left(\dfrac{1}{\mathrm{a}^{2}}+\dfrac{1}{\mathrm{~b}^{2}}\right)$

(c) $\dfrac{1}{\mathrm{a}^{2}}+\dfrac{1}{\mathrm{~b}^{2}}$

(d) None of these

Show Answer

Answer: a

2. Prove that any point on the ellipse whose foci are $(-1,0)$ and $(7,0)$ and eccentcicity $\dfrac{1}{2}$ is $(3+8 \cos \theta, 4 \sqrt{3} \sin \theta), \theta \in R$.

Show Answer

Answer: $\dfrac{(x-3)^2}{64}+\dfrac{y^2}{48}=1$

3. Let $\mathrm{E}$ be the ellipse $\dfrac{\mathrm{x}^{2}}{9}+\dfrac{\mathrm{y}^{2}}{4}=1$ and $\mathrm{C}$ be the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=9$. Let $\mathrm{P}$ and $\mathrm{Q}$ be the points $(1,2)$ and $(2,1)$ respectively. Then

(a) $\mathrm{Q}$ lies inside $\mathrm{C}$ but outside $\mathrm{E}$

(b) $\mathrm{Q}$ lies outside both $\mathrm{C}$ and $\mathrm{E}$

(c) $\mathrm{P}$ lies inside both $\mathrm{C}$ and $\mathrm{E}$

(d) $\mathrm{P}$ lies inside $\mathrm{C}$ but outside $\mathrm{E}$

Show Answer

Answer: d

4. $\mathrm{P}$ is a variable on the ellipse $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ with $\mathrm{AA}^{\prime}$ as the major axis. Then the maximum area of the triangle $\mathrm{APA}^{\prime}$ is

(a) ab

(b) $2 \mathrm{ab}$

(c) $\mathrm{ab} / 2$

(d) None of these

Show Answer

Answer: a

5. A man running round a race course notes that the sum of the distances of two flag-posts from him is always $10 \mathrm{~m}$ and the distance between the flag-posts is $8 \mathrm{~m}$. The area of the path he encloses in square meters is

(a) $15 \pi$

(b) $12 \pi$

(c) $18 \pi$

(d) $8 \pi$

Show Answer

Answer: a

6. If the line $\ell \mathrm{x}+\mathrm{my}+\mathrm{n}=0$ cuts the ellipse $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{25}=1$ in points whose eccentric angles differ by $\dfrac{\pi}{2}$ then $\dfrac{\mathrm{a}^{2} \ell^{2}+\mathrm{b}^{2} \mathrm{~m}^{2}}{\mathrm{n}^{2}}$

(a) 1

(b) 2

(c) 4

(d) $3 / 2$

Show Answer

Answer: b

7. If PSQ is a focal chord if the ellipse $16 x^{2}+25 y^{2}=400$ such that $S P=8$, then $S Q=$

(a) 1

(b) 2

(c) 3

(d) 4

Show Answer

Answer: b

8. If equation of the ellipse is $2 x^{2}+3 y^{2}-8 x+6 y+5=0$ then which of the following are true?

(a) equation of director circle is $x^{2}+y^{2}-4 x+2 y=10$

(b) director circle will pass through $(4,-1)$

(c) equation of auxillary circle is $x^{2}+y^{2}-4 x+2 y+2=0$

(d) None of these

Show Answer

Answer: c

9. The foci of ellipse $\left(\dfrac{\mathrm{x}}{5}\right)^{2}+\left(\dfrac{\mathrm{y}}{3}\right)^{2}=1$ are $\mathrm{S}$ and $\mathrm{S}^{\prime}$. $\mathrm{P}$ is a point on ellipse whose eccentric angle is $\pi / 3$. The incentre of triangle $\mathrm{SPS}^{\prime}$ is

(a) $(2, \sqrt{3})$

(b) $\left(2, \dfrac{2}{\sqrt{3}}\right)$

(c) $\left(2, \dfrac{\sqrt{3}}{2}\right)$

(d) $(\sqrt{3}, 2)$

Show Answer

Answer: b

PRACTICE EXERCISE SECTION - C

1. If $\mathrm{P}(\mathrm{x}, \mathrm{y}), \mathrm{F} _{1}(3,0), \mathrm{F} _{2}(-3,0)$ and $16 \mathrm{x}^{2}+25 \mathrm{y}^{2}=400$, then $\mathrm{PF} _{1}+\mathrm{PF} _{2}$ equals

(a) 8

(b) 6

(c) 10

(d) 12

Show Answer

Answer: c

2. The length of the major axis of the ellipse $(5 x-10)^{2}+(5 y+15)^{2}=\dfrac{(3 x-4 y+7)^{2}}{4}$ is

(a) 10

(b) $\dfrac{20}{3}$

(c) $\dfrac{20}{7}$

(d) 4

Show Answer

Answer: b

3. Angle subtended by common tangents of two ellipses $4(x-4)^{2}+25 y^{2}=100$ and $4(x+1)^{2}+y^{2}=4$ at origin is

(a) $\dfrac{\pi}{3}$

(b) $\dfrac{\pi}{4}$

(c) $\dfrac{\pi}{6}$

(d) $\dfrac{\pi}{2}$

Show Answer

Answer: b

4. The distance of a point on the ellipse $\dfrac{x^{2}}{6}+\dfrac{y^{2}}{2}=1$ from the centre is 2 . Then the eccentric angle of the point is

(a) $\dfrac{\pi}{4}$

(b) $\dfrac{3 \pi}{4}$

(c) $\dfrac{5 \pi}{6}$

(d) $\dfrac{\pi}{6}$

Show Answer

Answer: a, b

5. If the chord through the points whose eccentric angles are $\theta$ and $\phi$ on the ellipse $\dfrac{x^{2}}{25}+\dfrac{y^{2}}{9}=1$ passes through a focus, then the value of $\tan \dfrac{\theta}{2} \tan \dfrac{\phi}{2}$ is

(a) $\dfrac{1}{9}$

(b) -9

(c) $\dfrac{-1}{9}$

(d) 9

Show Answer

Answer: c, d

6. In an ellipse the distance between its foci is 6 and its minor axis is 8, the eccentricity of the ellipse is

(a) $\dfrac{4}{5}$

(b) $\dfrac{3}{5}$

(c) $\dfrac{1}{\sqrt{52}}$

(d) $\dfrac{1}{2}$

Show Answer

Answer: b

7. The number of values of $C$ such that the straight line $y=4 x+c$ touches the curve $\dfrac{x^{2}}{4}+y^{2}=1$, is

(a) 0

(b) 2

(c) 1

(d) $\infty$

Show Answer

Answer: b

8. The line $3 x+5 y=15 \sqrt{2}$ is a tangent to the ellipse $\dfrac{x^{2}}{25}+\dfrac{y^{2}}{9}=1$, at a point whose eccentric angle is

(a) $\dfrac{\pi}{6}$

(b) $\dfrac{\pi}{4}$

(c) $\dfrac{\pi}{3}$

(d) $\dfrac{2 \pi}{3}$

Show Answer

Answer: b

9. Tangents are drawn to the ellipse $3 x^{2}+5 y^{2}=32$ and $25 x^{2}+9 y^{2}=450$ passing through the point $(3,5)$. The number of such tangents are

(a) 2

(b) 3

(c) 4

(d) 0

Show Answer

Answer: b

10. Tangents are drawn to the ellipse $\dfrac{x^{2}}{9}+\dfrac{y^{2}}{5}=1$ at ends of latus rectum. The area of quadrilateral so formed is

(a) 27

(b) $\dfrac{27}{2}$

(c) $\dfrac{27}{4}$

(d) $\dfrac{27}{55}$

Show Answer

Answer: a

11. An ellipse passes through the point ( $4,-1)$ and its axes are along the axes of coordinates. If the line $x+4 y-10=0$ is a tangent to it then its equation is

(a) $\dfrac{\mathrm{x}^{2}}{100}+\dfrac{\mathrm{y}^{2}}{5}=1$

(b) $\dfrac{x^{2}}{8}+\dfrac{y^{2}}{5 / 4}=1$

(c) $\dfrac{x^{2}}{20}+\dfrac{y^{2}}{5}=1$

(d) None of these

Show Answer

Answer: b, c

12. The tangent at the point $\left(4 \cos \phi, \dfrac{16}{\sqrt{11}} \sin \phi\right)$ to the ellipse $16 x^{2}+11 y^{2}=256$ is also a tangent to the circle $x^{2}+y^{2}-2 x=15$, find the value of $\phi$.

Show Answer

Answer: $\pm \dfrac{\pi}{6}$

13. Find the equations of tangents to the ellipse $9 x^{2}+16 y^{2}=144$ which pass through the point $(2,3)$.

Show Answer

Answer: $y=3, x+y=5$

14. Linked Comprehension Type.

For all real $\mathrm{p}$, the line $2 \mathrm{px}+\mathrm{y} \sqrt{1-\mathrm{p}^{2}}=1$ touches a fixed ellipse whose axes are coordinate axes.

(i) The eccentricity of the ellipse is

(a) $\dfrac{2}{3}$

(b) $\dfrac{\sqrt{3}}{2}$

(c) $\dfrac{1}{\sqrt{3}}$

(d) $\dfrac{1}{2}$

(ii) The foci of ellipse are

(a) $(0, \pm \sqrt{3})$

(b) $(0, \pm 2 / 3)$

(c) $( \pm \sqrt{3} / 2,0)$

(d) None of these

(iii) The locus of point of intersection of perpendicular tangents is

(a) $\mathrm{x}^{2}+\mathrm{y}^{2}=5 / 4$

(b) $\mathrm{x}^{2}+\mathrm{y}^{2}=3 / 2$

(c) $\mathrm{x}^{2}+\mathrm{y}^{2}=2$

(d) None of these

Show Answer

Answer: (i) a (ii) d (iii) a

15. $\mathrm{C} _{1}: \mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{r}^{2}$ and $\mathrm{C} _{2}=\dfrac{\mathrm{x}^{2}}{16}+\dfrac{\mathrm{y}^{2}}{9}=1$ intersect at four distinct points $\mathrm{A}, \mathrm{B}, \mathrm{C}$ and $\mathrm{D}$, Their common tangents form a parallelogram $\mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime} \mathrm{D}^{\prime}$.

(i) If $A B C D$ is a square then $r$ is equal to

(a) $\dfrac{12}{5} \sqrt{2}$

(b) $\dfrac{12}{5}$

(c) $\dfrac{12}{5 \sqrt{5}}$

(d) None of these

(ii) If $\mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime} \mathrm{D}^{\prime}$ is a square then $\mathrm{r}$ is equal to

(a) $\sqrt{20}$

(b) $\sqrt{12}$

(c) $\sqrt{15}$

(d) None of these

(iii) If $\mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime} \mathrm{D}^{\prime}$ is a square, then the ratio of area of the circle $\mathrm{C} _{1}$ to the area of the circumcircle of $\triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime}$ is

(a) $\dfrac{9}{16}$

(b) $\dfrac{3}{4}$

(c) $\dfrac{1}{2}$

(d) None of these

Show Answer

Answer: (i) a (ii) d (iii) c

16. The ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ is such that it has the least area but contains the circle $(x-1)^{2}+y^{2}=1$

(i) The eccentricity of the ellipse is

(a) $\dfrac{\sqrt{2}}{3}$

(b) $\dfrac{1}{\sqrt{3}}$

(c) $\dfrac{1}{2}$

(d) None of these

(ii) Equation of auxilliary circle of ellipse is

(a) $\mathrm{x}^{2}+\mathrm{y}^{4}=6.5$

(b) $x^{2}+y^{4}=5$

(c) $\mathrm{x}^{2}+\mathrm{y}^{4}=45$

(d) None of these

(iii) Length of latus rectum of the ellipse is

(a) 2 units

(b) lunit

(c) 3units

(d) 2.5 units

Show Answer

Answer: (i) a (ii) c (iii) b

17. The equation of the straight lines joining the foci of the ellipse $\dfrac{x^{2}}{25}+\dfrac{y^{2}}{16}=1$ to the foci of the ellipse $\dfrac{x^{2}}{24}+\dfrac{y^{2}}{49}=1$ forms a parallelogram. Then the area of the figure formed by the foci of these two ellipse.

(a) 15

(b) 30

(c) 20

(d) 18

Show Answer

Answer: b

PRACTICE EXERCISE SECTION - D

1. In the normal at the end of latus rectum of the ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ with eccentricity e, passes through one end of the minor axis, then :

(a) $\mathrm{e}^{2}\left(1+\mathrm{e}^{2}\right)=0$

(b) $\mathrm{e}^{2}\left(1+\mathrm{e}^{2}\right)=1$

(c) $\mathrm{e}^{2}\left(1+\mathrm{e}^{2}\right)=-1$

(d) $\mathrm{e}^{2}\left(1+\mathrm{e}^{2}\right)=2$

Show Answer

Answer: b

2. If the normals to $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ at the ends of the chords $\ell _{1} x+m _{1} y=1 \quad$ and $\ell _{2} x+m _{2} y=1$ are concurrent, then :

(a) $\mathrm{a}^{2} \ell _{1} \ell _{2}+\mathrm{b}^{2} \mathrm{~m} _{1} \mathrm{~m} _{2}=1$

(b) $\mathrm{a}^{2} \ell _{1} \ell _{2}+\mathrm{b} _{2} \mathrm{~m} _{1} \mathrm{~m} _{2}=-1$

(c) $\mathrm{a}^{2} \ell _{1} \ell _{2}-\mathrm{b}^{2} \mathrm{~m} _{1} \mathrm{~m} _{2}=-1$

(d) None of these

Show Answer

Answer: b

3. If the normal at an end of a latus rectum of an ellipse passes through one extremity of the minor axis, then the eccentricity of the ellipse is given by

(a) $\mathrm{e}^{4}+\mathrm{e}^{2}-1=0$

(b) $\mathrm{e}^{4}+\mathrm{e}^{2}-5=0$

(c) $\mathrm{e}^{3}=\sqrt{5}$

(d) None of these

Show Answer

Answer: a

4. The number of normals that can be drown from a point to a given ellipse is

(a) 2

(b) 3

(c) 4

(d) 1

Show Answer

Answer: c

5. If the normal at any point $P$ on the ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ meets the axes in $G$ and $g$ respectively, then PG:Pg is equal to

(a) $\mathrm{a}: \mathrm{b}$

(b) $\mathrm{a}^{2}: \mathrm{b}^{2}$

(c) $\mathrm{b}^{2}: \mathrm{a}^{2}$

(d) $\mathrm{b}: \mathrm{a}$

Show Answer

Answer: c

6. If normal to ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ at $\left(a e, \dfrac{b^{2}}{a}\right)$ is passing through $(0,-2 b)$, then value of eccentricity is

(a) $\sqrt{2}-1$

(b) $2(\sqrt{2}-1)$

(c) $\sqrt{2(\sqrt{2}-1)}$

(d) None of these

Show Answer

Answer: c

7. If normal at any point $\mathrm{P}$ to the ellipse $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1, \mathrm{a}>\mathrm{b}$ meet the axes at $\mathrm{M}$ and $\mathrm{N}$ so that $\dfrac{\mathrm{PM}}{\mathrm{PN}}$ $=\dfrac{2}{3}$, then value of eccentricity e is

(a) $\dfrac{1}{\sqrt{2}}$

(b) $\sqrt{\dfrac{2}{3}}$

(c) $\dfrac{1}{\sqrt{3}}$

(d) None of these

Show Answer

Answer: c

8. If the tangent drown at point $\left(t^{2}, 2 t\right)$ on the parabola $y^{2}=4 \mathrm{x}$ is same as the normal drawn at point $(\sqrt{5} \cos \theta, 2 \sin \theta)$ on the ellipse $4 x^{2}+5 y^{2}=20$. Then the values of $t$ and $\theta$ are

(a) $\theta=\cos ^{-1}\left(\dfrac{-1}{\sqrt{5}}\right)$ & $\mathrm{t}=\dfrac{-1}{\sqrt{5}}$

(b) $\theta=\cos ^{-1}\left(\dfrac{1}{\sqrt{5}}\right)$ & $\mathrm{t}=\dfrac{1}{\sqrt{5}}$

(c) $\theta=\cos ^{-1}\left(\dfrac{-2}{\sqrt{5}}\right)$ & $\mathrm{t}=\dfrac{-2}{\sqrt{5}}$

(d) None of these

Show Answer

Answer: a

9. The normals at four points on the ellipse $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ meet in the point $(\mathrm{h}, \mathrm{k})$. Then the mean position of the four points is

(a) $\left(\dfrac{\mathrm{a}^{2} \mathrm{~h}}{2\left(\mathrm{a}^{2}+\mathrm{b}^{2}\right)}, \dfrac{\mathrm{b}^{2} \mathrm{k}}{2\left(\mathrm{a}^{2}+\mathrm{b}^{2}\right)}\right)$

(b) $\left(\dfrac{a^{3} h}{2\left(a^{2}+b^{2}\right)}, \dfrac{b^{3} k}{2\left(a^{2}+b^{2}\right)}\right)$

(c) $\left(\dfrac{\mathrm{ah}}{2\left(\mathrm{a}^{2}-\mathrm{b}^{2}\right)}, \dfrac{\mathrm{bk}}{2\left(\mathrm{a}^{2}-\mathrm{b}^{2}\right)}\right)$

(d) $\left(\dfrac{\mathrm{a}^{2} \mathrm{~h}}{2\left(\mathrm{a}^{2}-\mathrm{b}^{2}\right)}, \dfrac{\mathrm{b}^{2} \mathrm{k}}{2\left(\mathrm{a}^{2}-\mathrm{b}^{2}\right)}\right)$

Show Answer

Answer: d

10. The equation of the normal at the point $(2,3)$ on the ellipse $9 x^{2}+16 y^{2}=180$ is

(a) $3 y=8 x-10$

(b) $3 y-8 x+7=0$

(c) $8 y+3 x+7=0$

(d) $3 x+2 y+7=0$

Show Answer

Answer: b

11. Number of distinct normal lines that can be drawn to the ellipse $\dfrac{x^{2}}{169}+\dfrac{y^{2}}{25}=1$ from the point $P$ $(0,6)$ is

(a) one

(b) two

(c) three

(d) four

Show Answer

Answer: c

12. Any ordinate MP of the ellipse $\dfrac{\mathrm{x}^{2}}{25}+\dfrac{\mathrm{y}^{2}}{9}=1$ meets the auxiliary circle at $\mathrm{Q}$, then locus of the point of intersection of normals at $\mathrm{P}$ and $\mathrm{Q}$ to the respective curve is

(a) $\mathrm{x}^{2}+\mathrm{y}^{2}=8$

(b) $x^{2}+y^{2}=34$

(c) $\mathrm{x}^{2}+\mathrm{y}^{2}=64$

(d) $\mathrm{x}^{2}+\mathrm{y}^{2}=15$

Show Answer

Answer: c

13. If the normals at $P(\theta)$ and $Q\left(\dfrac{\pi}{2}+\theta\right)$ to the ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ meet the major axis at $G$ and $g$ respectively, then $\mathrm{PG}^{2}+\mathrm{Qg}^{2}=$

(a) $\mathrm{b}^{2}\left(1-\mathrm{e}^{2}\right)\left(2-\mathrm{e}^{2}\right)$

(b) $\mathrm{a}^{2}\left(\mathrm{e}^{4}-\mathrm{e}^{2}+2\right)$

(c) $\mathrm{a}^{2}\left(1+\mathrm{e}^{2}\right)\left(2+\mathrm{e}^{2}\right)$

(d) $\mathrm{b}^{2}\left(1+\mathrm{e}^{2}\right)\left(2+\mathrm{e}^{2}\right)$

Show Answer

Answer: b