1. Definition of an Ellipse

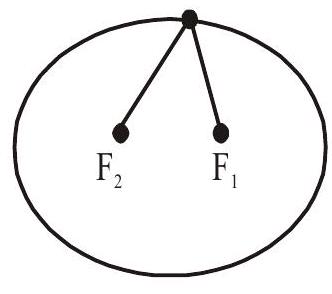
An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant. Fixed points are called focus.

$\mathrm{PF} _{1}+\mathrm{PF} _{2}=$ constant

2. Standard equation of an ellipse.

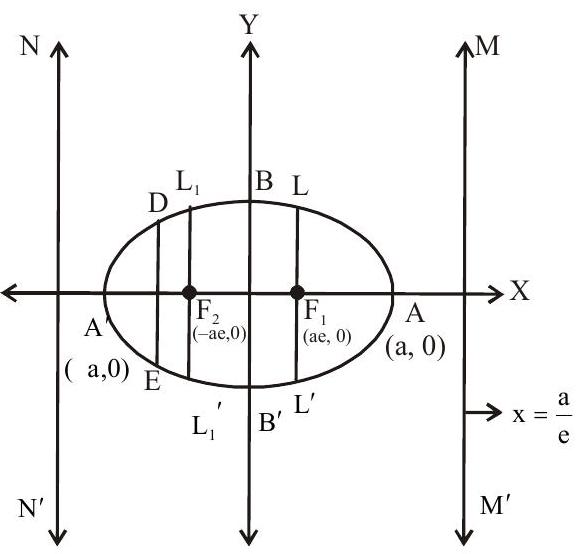
$\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ with $\mathrm{a}>\mathrm{b}$.

Where $\mathrm{b}^{2}=\mathrm{a}^{2}\left(1-\mathrm{e}^{2}\right)$

(i) The line containing the two fixed points (foci) is called focal axis (majoraxis) and points of intersection of the curve with focal axis are called the vertices of the ellipse ie. $A(a, 0)$

$\text { and } \mathrm{A}^{\prime}(-\mathrm{a}, 0)$

The distance between $\mathrm{F} _{1}$ and $\mathrm{F} _{2}$ is called the focal length. $\mathrm{F} _{1} \mathrm{~F} _{2}=2 \mathrm{ae}$.

The distance between the vertices is $\mathrm{A}^{\prime}$ $=2 \mathrm{a}$ is called major axis.

The distance $\mathrm{BB}^{1}=2 \mathrm{~b}$ is called minor axis

(ii) Point of intersection of the major and minor axis is called the centre of the ellipse. Any chord of the ellipse passing through it gets bisected by it and is called diameter.

(iii) Any chord through focus is called a focal chord and any chord perpendicular to the focal axis is called double ordinate $\mathbf{D E}$.

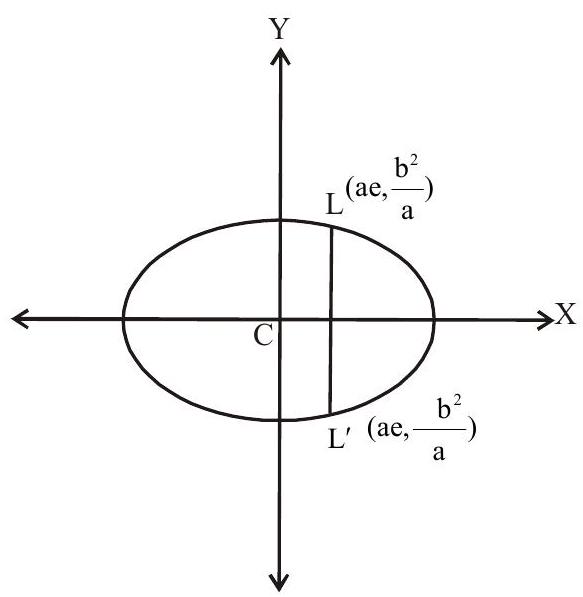
(iv) A particular double ordinate through focus and perpendicular to focal axis is called its latus rectum $\left(L L^{\prime}\right)$. Length of latus rectum $=\dfrac{2 b^{2}}{a}$

(v) $\mathrm{MM}^{\prime}$ and $\mathrm{NN}^{\prime}$ are two directrices of the ellipse and their equations are $\mathrm{x}=\dfrac{\mathrm{a}}{\mathrm{e}}$ and $x=-\dfrac{a}{e}$ respectively

(vi) A chord of the ellipse passing through its focus is called a focal chord.

(vii) An ellipse is the locus of point which moves in a plane such that the ratio of its distance from a fixed point (focus) to the fixed line (directrix). This ratio is called eccentricity and is denoted by e. For an ellipse e $<1$.

(viii) The equation to the ellipse whose focus is (h.k) and directrix is $\ell \mathrm{x}+\mathrm{my}+\mathrm{n}=0$ and whose

centricity $\mathrm{e}<1$, is $(\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{e}^{2}\left(\dfrac{\ell \mathrm{x}+\mathrm{my}+\mathrm{n}}{\sqrt{\ell^{2}+\mathrm{m}^{2}}}\right)^{2}$.

(ix) Special form If the centre of the ellipse is at point ( $\mathrm{k}, \mathrm{k})$ and the directions of the axis are parallel to the co-ordinate axes, then its equation is $\dfrac{(x-h)^{2}}{a^{2}}+\dfrac{(y-k)^{2}}{b^{2}}=1$

If we shift the origin at $(\mathrm{h}, \mathrm{k})$ rotating totaling co-ordinate axes then equation of the ellipse with respect to new origin becomes $\dfrac{\mathrm{X}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{Y}^{2}}{\mathrm{~b}^{2}}=1$

Auxiliary Circle

The circle described on the major axis of an ellipse as diameter is called an auxiliary circle of the ellipse

If $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ is an ellipse then its auxiliary circle is $x^{2}+y^{2}=a^{2}$

Eccentric angle of a point

Let $\mathrm{P}$ be any point on the ellipse $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$

Draw PM perpendicular to major axis from $\mathrm{P}$ and produce MP to meet the auxiliary circle at Q. Join CQ.

$\angle \mathrm{QCA}=\theta$ is called eccentric angle of point $\mathrm{P}$

Note that the angle ACP is not eccentric angle. i.e. eccentric angle of $\mathrm{P}$ on an ellipse is the angle which the radius through the corresponding point on, the auxiliary circle makes with the major axis

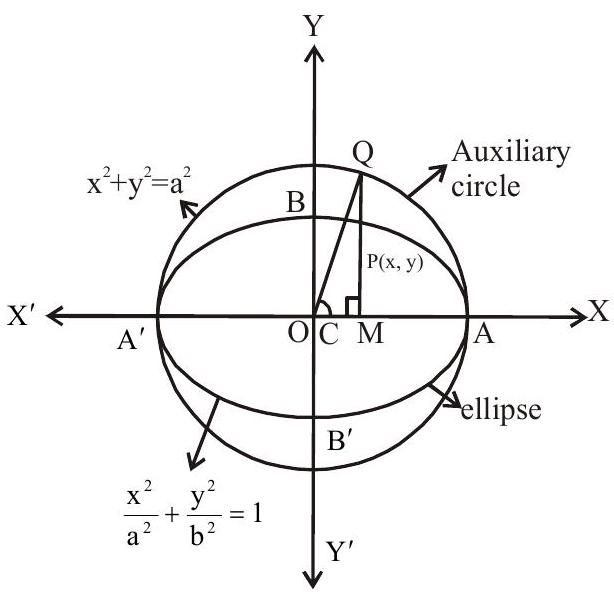
$\therefore \mathrm{Q}(\operatorname{acos} \theta, \operatorname{asin} \theta)$

$\therefore \mathrm{x}$-coordinate of $\mathrm{P}$ is acos $\theta$

$\dfrac{\mathrm{a}^{2} \cos ^{2} \theta}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$

$\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1-\cos ^{2} \theta$

$\mathrm{y}^{2} \quad=\mathrm{b}^{2} \sin ^{2} \theta$

$\mathrm{y} \quad =\mathrm{b} \sin \theta$

$\therefore$ Coordinate of $\mathrm{P}$ is $(\mathrm{a} \cos \theta, \mathrm{b} \sin \theta)$

i.e. $x=\operatorname{acos} \theta$ and $y=b \sin \theta$ is the parameter equations of the ellipse.

$(a \cos \theta, b \sin \theta)$ is also called the point ’ $\theta$ '

Equation of the chord

Let $P(a \cos \theta, b \sin \theta)$ and $Q(a \cos \phi, b \sin \phi)$ be any two points of the ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ then the equation of the chord joining these two points is

$\mathrm{y}-\mathrm{b} \sin \theta=\dfrac{\mathrm{b} \sin \phi-\mathrm{b} \sin \theta}{\mathrm{a} \cos \phi-\mathrm{a} \cos \theta}(\mathrm{x}-\mathrm{a} \cos \theta)$

Simplifying the equation we get

$\dfrac{\mathrm{x}}{\mathrm{a}} \cos \left(\dfrac{\theta+\phi}{2}\right)+\dfrac{\mathrm{y}}{\mathrm{b}} \sin \left(\dfrac{\theta+\phi}{2}\right)=\cos \dfrac{\theta-\phi}{2}$

$\theta$ & $\phi$ are eccentric angle of points $P$ and $Q$ of ellipse

Position of a point $(h, k)$ with respect to an ellipse

Let ellipse be $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$

Now P will lie outside, on or inside the ellipse $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ according as

$\dfrac{\mathrm{h}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{k}^{2}}{\mathrm{~b}^{2}}-1>,=,<0$

Intersection of a line and an ellipse

Line $\mathrm{y}=\mathrm{mn}+\mathrm{c}$______________(1) and ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$________________(2)

Solving equations (1) & (2) we get

$\left(a^{2} m^{2}+b^{2}\right) x^{2}+2 a^{2} \mid c m x+a^{2}\left(c^{2}-b^{2}\right)=0$

If $\mathrm{D}>0$ then $\mathrm{y}=\mathrm{mx}+\mathrm{c}$ is a secant

$\mathrm{D}=0$ then $\mathrm{y}=\mathrm{mx}+\mathrm{c}$ is a tangent

$\mathrm{D}<0 \mathrm{y}=\mathrm{mx}+\mathrm{c}$ does not meet ellipse

Point form

Equation of tangent to the ellipse at point $\left(x _{1}, y _{1}\right)$

Let the equation of ellipse be $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$

Then equation of tangent in point form is $\dfrac{\mathrm{xx} _{1}}{\mathrm{a}^{2}}+\dfrac{\mathrm{yy} _{1}}{\mathrm{~b}^{2}}=1$

Parametric form

Equation of tangent at point $(a \cos \theta, b \sin \theta)$ to the ellipse is $\dfrac{x \cos \theta}{a}+\dfrac{y \sin \theta}{b}=1$

Slope form

$y=m x \pm \sqrt{a^{2} m^{2}+b^{2}}$ is a tangent to an ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ and point of contact is $\left( \pm \dfrac{\mathrm{a}^{2} \mathrm{~m}}{\sqrt{\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}}}, \overline{+} \dfrac{\mathrm{b}^{2}}{\sqrt{\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}}}\right)$

Number of tangents through a given point $P(h, k)$

$y=m x+\sqrt{a^{2} m^{2}+b^{2}}$ is any tangent to the ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$

If it passes through $\mathrm{P}(\mathrm{h}, \mathrm{k})$ then

$\mathrm{k}=\mathrm{mh}+\sqrt{\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}}$

$\mathrm{k}-\mathrm{mh}=\sqrt{\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}}$

$(\mathrm{k}-\mathrm{mh})^{2}=\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}$

$\mathrm{m}^{2}\left(\mathrm{~h}^{2}-\mathrm{a}^{2}\right)-2 \mathrm{hkm}+\left(\mathrm{k}^{2}-\mathrm{b}^{2}\right)=0$

It is a quadratic in $m$ and will give two values of $m$ hence there are two tangents.

Equations of Normals in different forms

(i) Point form

Let equation of ellipse be $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$

Equation of normal is $\dfrac{a^{2} x}{x _{1}}-\dfrac{b^{2} y}{y _{1}}=a^{2}-b^{2}$

(ii) Parametric form

Let equation of ellipse be $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$

Equation of normal is axsec $\phi-\operatorname{bycosec} \phi=\mathrm{a}^{2}-\mathrm{b}^{2}$

$(a \cos \phi, b \sin \phi)$ is parametric coordinates of $\mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right), \mathrm{P}(\operatorname{acos} \phi, \mathrm{bsin} \phi)$

(iii) Slope form

For an ellipse $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$

Equation of normal in terms of slope $(\mathrm{m})$ is

$\mathrm{y}=\mathrm{mx} \pm \dfrac{\mathrm{m}\left(\mathrm{a}^{2}-\mathrm{b}^{2}\right)}{\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2} \mathrm{~m}^{2}}}$

Condition of normality when $y=m x+c$ is the normal of $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ is

$c^{2}=\dfrac{m^{2}\left(a^{2}-b^{2}\right)^{2}}{a^{2}+b^{2} m^{2}}$

1. The eccentric angles of the extremities of latus rectum to the ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ are given by

(a) $\tan ^{-1}$

(b) $\tan ^{-1}\left( \pm \dfrac{\mathrm{be}}{\mathrm{a}}\right)$

(c) $\tan ^{-1}\left( \pm \dfrac{\mathrm{b}}{\mathrm{ae}}\right)$

(d) $\tan ^{-1}\left( \pm \dfrac{\mathrm{a}}{\mathrm{be}}\right)$

Show Answer

Solution:

$\begin{aligned} & \text { Let } L(a \cos \theta, b \sin \theta)=\left( \pm a e, \pm \dfrac{b^{2}}{a}\right) \\ & \operatorname{acos} \theta= \pm a e b \sin \theta= \pm \dfrac{b^{2}}{a} \\ & \tan \theta= \pm \dfrac{b}{a e} \\ & \theta=\tan ^{-1}\left(\dfrac{b}{a e}\right) \end{aligned}$

$\therefore$ correct option is c

2. The foci of the ellipse $25(x+1)^{2}+9(y+2)^{2}=225$, are at

(a) $(-1,2)$ & $(-1,-6)$

(b) $(-2,1)$ and $(-2,6)$

(c) $(-1,-2)$ & $(-2,-1)$

(d) $(-1,-2)$ and $(-1,-6)$

3. If $\dfrac{x^{2}}{f(4 a)}+\dfrac{y^{2}}{f\left(a^{2}-5\right)}=1$ represents an ellipse with major axis as $y-a x i s$ and $f$ is a decreasing function then

(a) $\mathrm{a} \in(-\infty, 1)$

(b) $\mathrm{a} \in(5, \infty)$

(c) $\mathrm{a} \in(1,4)$

(d) $\mathrm{a} \in(-1,5)$

4. The point, at shortest distance from the line $x+y=7$ and lying on an ellipse $x^{2}+2 y^{2}=6$ has coordinates

(a) $(\sqrt{2}, \sqrt{2})$

(b) $(0, \sqrt{3})$

(c) $(2,1)$

(d) $\left(\sqrt{5}, \dfrac{1}{\sqrt{2}}\right)$

Show Answer

Solution:

The tangent at the point of shortest distance from the line $x+y=7$ parallel to the given line $\mathrm{x}+\mathrm{y}=7$.

Any point $\mathrm{P}$ on the ellipse is $(\sqrt{6} \cos \theta, \sqrt{3} \sin \theta)$

Equation of tangent at this point is

$\dfrac{\mathrm{x} \sqrt{6} \cos \theta}{6}+\dfrac{\mathrm{y} \sqrt{3} \sin \theta}{3}=1$

It is parallel to $\mathrm{x}+\mathrm{y}=7$

$\begin{aligned} & \dfrac{-\left(\dfrac{\sin \theta}{\sqrt{3}}\right)}{\dfrac{\cos \theta}{\sqrt{6}}}=-1 \\ & \therefore \dfrac{\cos \theta}{\sqrt{6}}=\dfrac{\sin \theta}{\sqrt{3}}+ \\ & \tan \theta=\dfrac{1}{\sqrt{2}} \\ & \text { Hence } \cos \theta=\dfrac{\sqrt{2}}{\sqrt{3}} \text { and } \sin \theta=\dfrac{1}{\sqrt{3}} \end{aligned}$

$\therefore$ Required coordinate on the ellipse is $\left(\sqrt{6} \times \dfrac{\sqrt{2}}{\sqrt{3}}, \sqrt{3} \times \dfrac{1}{\sqrt{3}}\right)=(2,1)$

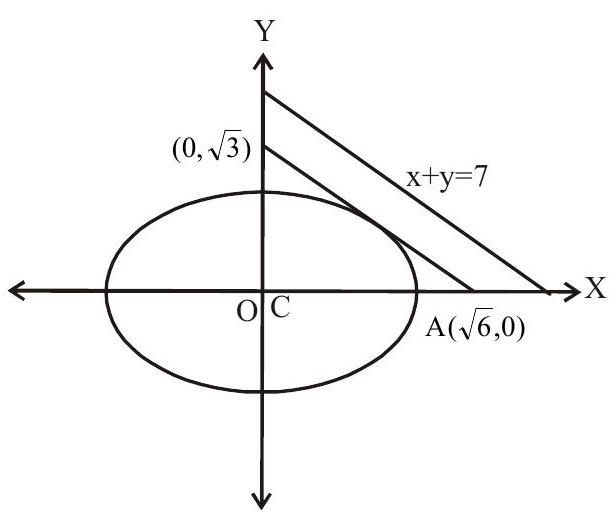
option (c) is correct

5. The length of the common chord of the ellipse $\dfrac{(x-1)^{2}}{9}+\dfrac{(y-2)^{2}}{4}=1$ and the circle $(\mathrm{x}-1)^{2}+(\mathrm{y}-2)^{2}=1$ is

(a) 0

(b) 1

(c) 3

(d) 8

Show Answer

Solution:

Centre of ellipse and circle is $(1,2)$.

Since the ellipse contains the circle and they do not intersect so there is no common chord

$\therefore$ length of common chord is zero

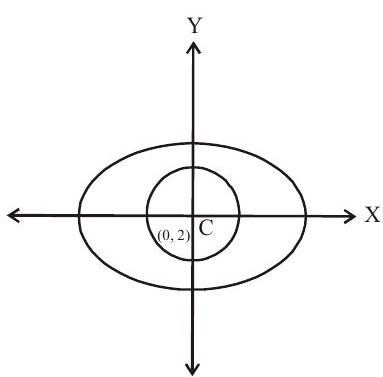
Option ‘a’ is correct

6. If the normal at the end of laturrectum of the ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ passes through $(0,-b)$ then $\mathrm{e}^{4}+\mathrm{e}^{2}$ (where e is eccentricity) equals

(a) 1

(b) $\sqrt{2}$

(c) $\dfrac{\sqrt{5}-1}{2}$

(d) $\dfrac{\sqrt{5}+1}{2}$

7. The area of the parallelogram formed by the tangents at the end of conjugate diameters of an ellipse is

(a) Constant and is equal to the product of the axes

(b) Cannot be constant

(c) Constant and is equal to the two lines of the product of the axes.

(d) None of these

Show Answer

Solution:

Two diameters are said to be conjucgate when each bisects all chords parallel to the other.

Conjugate diameters are diameters passing through centre and product of their slopes is equal to $\dfrac{-b^{2}}{a^{2}}$ Area of parallelogram $=4$ area of parallelogram QDCE

$=4(2 \text { area of } \Delta \mathrm{CDE})$

$=8 \cdot \dfrac{1}{2}\left|\begin{array}{ccc}0 & 0 & 1 \\ \mathrm{a} \cos \alpha & \mathrm{b} \sin \alpha & 1 \\ -\mathrm{a} \sin \alpha & \mathrm{b} \cos \alpha & 1\end{array}\right|$

$=4\left(a b \cos ^{2} \alpha+a b \sin ^{2} \alpha\right)$

$=4 \mathrm{ab}$

$=(2 \mathrm{a}) \times(2 \mathrm{~b})$

$=$ Product of the axes of ellipse

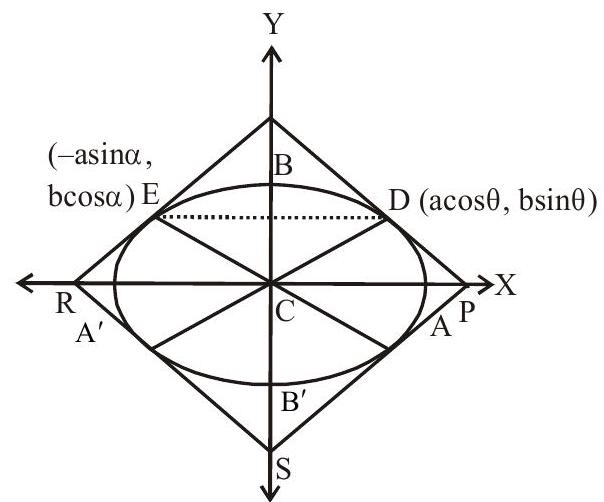
Option (a) is correct

Practice Exercise

1. The eccentricity of the ellipse which meets the straight line $\dfrac{x}{7}+\dfrac{y}{2}=1$ on the axis of $x$ and the straight line $\dfrac{x}{3}-\dfrac{y}{5}=1$ on the axis of $y$ and whose axes lie along the axes of coordinates, is

(a) $\dfrac{3 \sqrt{2}}{7}$

(b) $\dfrac{2 \sqrt{3}}{7}$

(c) $\dfrac{\sqrt{3}}{7}$

(d) None of these

2. The parametric representation of point on the ellipse whose foci are $(-1,0)$ and $(7,0)$ and eccentricity is $\dfrac{1}{2}$, is

(a) $(3+8 \cos \theta, 4 \sqrt{3} \sin \theta)$

(b) $(8 \cos \theta, 4 \sqrt{3} \sin \theta)$

(c) $(3+4 \sqrt{3} \cos \theta, 8 \sin \theta)$

(d) None of these

3. The locus of midpoints of a focal chord of the ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ is

(a) $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=\dfrac{e x}{a}$

(b) $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=\dfrac{\mathrm{ex}}{\mathrm{a}}$

(c) $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{a}^{2}+\mathrm{b}^{2}$

(d) None of these

4. The eccentricity of an ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ whose latus rectum is half of its minor axis is

(a) $\dfrac{1}{\sqrt{2}}$

(b) $\sqrt{\dfrac{2}{3}}$

(c) $\dfrac{\sqrt{3}}{2}$

(d) None of these

5. If $\mathrm{P}(\theta)$ and $\mathrm{Q}\left(\dfrac{\pi}{2}+\theta\right)$ are two points on the ellipse $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$, locus of the mid point of $\mathrm{PQ}$ is

(a) $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=\dfrac{1}{2}$

(b) $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=4$

(c) $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=2$

(d) None of these

6. If $\alpha$ and $\beta$ are eccentric angles of the ends of a focal chord of the ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$, then $\tan \dfrac{\alpha}{2} \tan \dfrac{\beta}{2}$ is equal to

(a) $\dfrac{1-\mathrm{e}}{1+\mathrm{e}}$

(b) $\dfrac{e-1}{e+1}$

(c) $\dfrac{\mathrm{e}+1}{\mathrm{e}-1}$

(d) $\dfrac{e-1}{e+3}$

7. The locus of extremities of the latus-rectum of the family of ellipse $b^{2} x^{2}+y^{2}=a^{2} b^{2}$ is

(a) $x^{2}-a y=a^{2}$

(b) $x^{2}-a y=b^{2}$

(c) $\mathrm{x}^{2}+\mathrm{ay}=\mathrm{a}^{2}$

(d) $x^{2}+a y=b^{2}$

8. The tangents from which of the following points to the ellipse $5 x^{2}+4 y^{2}=20$ are perpendicular

(a) $(1,2 \sqrt{2})$

(b) $(2 \sqrt{2}, 1)$

(c) $(2, \sqrt{5})$

(d) $(\sqrt{5}, 2)$

9. An ellipse passes through the point (4,-1) and its axes are along the axes of coordinate. If the line $x+4 y-10=0$ is a tangent to it then its equation is

(a) $\dfrac{x^{2}}{100}+\dfrac{y^{2}}{5}=1$

(b) $\dfrac{\mathrm{x}^{2}}{80}+\dfrac{\mathrm{y}^{2}}{\dfrac{5}{4}}=1$

(c) $\dfrac{x^{2}}{20}+\dfrac{y^{2}}{5}=1$

(d) None of these

10. Passage

Consider the standard equation of an ellipse whose focus and corresponding foot of directrix are $(\sqrt{7}, 0)$ and $\left(\dfrac{16}{\sqrt{7}}, 0\right)$ and a circle with equation $x^{2}+y^{2}=r^{2}$. If in the first quadrant, the common tangent to a circle of this family and the above ellipse meets the coordinate axes at A and B. On the basis of above information, answer the following questions.

(i) The equation of the ellipse is

(a) $16 x^{2}+9 y^{2}=144$

(b) $9 x^{2}+16 y^{2}=144$

(c) $16 \mathrm{x}^{2}+\mathrm{y}^{2}=144$

(d) $x^{2}+9 y^{2}=144$

(ii) Let $\mathrm{P}$ be a variable point on the ellipse with foci at $\mathrm{S}$ and $\mathrm{S}^{\prime}$. If $\Delta$ be the area of triangle $\mathrm{PSS}^{\prime}$, then the maximum value of $\Delta$ is

(a) $\sqrt{7}$ sq.u.

(b) $2 \sqrt{7}$ sq.u

(c) $3 \sqrt{7}$ sq.u

(d) $4 \sqrt{7}$ sq.u.

(iii) If mid-point of And B is $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ and slope of common tangent be $\mathrm{m}$, then

(a) $2 \mathrm{mx} _{1}+\mathrm{y} _{1}=0$

(b) $2 \mathrm{my} _{1}+\mathrm{x} _{1}=0$

(c) $\mathrm{my} _{1}+\mathrm{x} _{1}=0$

(d) $\mathrm{mx} _{1}+\mathrm{y} _{1}=0$

(iv) The locus of midpoint of $A$ and $B$ is

(a) $y=x \sqrt{\dfrac{r^{2}-9}{16-r^{2}}}$

(b) $y=x \sqrt{\dfrac{16+r^{2}}{9-r^{2}}}$

(c) $y=x \sqrt{\dfrac{16-r^{2}}{r^{2}+9}}$

(d) $y=x \sqrt{\dfrac{r^{2}-9}{r^{2}-16}}$

(v) The domain of value of $\mathrm{r}(\mathrm{r}>0)$ for which the above question is true is

(a) $\mathrm{r} _{\in}(1,2)$

(b) $r \in(3,4)$

(c) $\mathrm{r} _{\in}(4,5)$

(d) $\mathrm{r} _{\in}(5,6)$

11. Assertion and Reason

(A) Both $\mathrm{A}$ and $\mathrm{R}$ are individually true and $\mathrm{R}$ is the correct explanation of $\mathrm{A}$

(B) Both $\mathrm{A}$ and $\mathrm{R}$ are individually true and $\mathrm{R}$ is not the correct explanation of $\mathrm{A}$

(C) $A$ is true but $R$ is false

(D) A is false but $R$ is true

(i) Assertion (A)

Any chord if the ellipse $x^{2}+y^{2}+x y=1$ through $(0,0)$ is bisected at $(0,0)$

Reason (R)

The centre of an ellipse is a point through which every chord is bisected

(a) $\mathrm{A}$

(b) $\mathrm{B}$

(c) $\mathrm{C}$

(d) $\mathrm{D}$

(ii) Assertion A

From the point $(\lambda, 3)$ tangents are drawn to $\dfrac{x^{2}}{9}+\dfrac{y^{2}}{4}=1$ and are perpendicular to each other then $\lambda= \pm 2$

Reason $R$ The locus of point of intersection of perpendicular tangents to $\dfrac{x^{2}}{9}+\dfrac{y^{2}}{4}=1$ is $x^{2}+3 y=13$

(a) $\mathrm{A}$

(b) B

(c) $\mathrm{C}$

(d) $\mathrm{D}$

(iii) Assertion A The equation of the director cirlce to the ellipse $9 x^{2}+16 y^{2}=144$ is $x^{2}+y^{2}=25$

Reason R Director circle is the locus of point of intersection of perpendicular tangents to an ellipse

(a) $\mathrm{A}$

(b) $\mathrm{B}$

(c) $\mathrm{C}$

(d) $\mathrm{D}$

Integer Type

12. If e be the eccentricity of the ellipse $4(x-2 y+1)^{2}+9(2 x+y+2)^{2}=25$, then the value of $2187 e^{2}$ must be

13. If two concentric ellipse be such that the foci of one be on the other and if $3 / 5$ and $4 / 5$ be their eccentricities. If $\theta$ be the angle between their axes, then the volue of $1+\sin \theta+\sin ^{4} \theta$ must be.

14. If the normal at the four points $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right),\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right),\left(\mathrm{x} _{3}, \mathrm{y} _{3}\right)$ and $\left(\mathrm{x} _{4}, \mathrm{y} _{4}\right)$ on the ellipse $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ are concurrent, then the value of $\left(\mathrm{x} _{1}+\mathrm{x} _{2}+\mathrm{x} _{3}+\mathrm{x} _{4}\right)\left(\dfrac{1}{\mathrm{x} _{1}}+\dfrac{1}{\mathrm{x} _{2}}+\dfrac{1}{\mathrm{x} _{3}}+\dfrac{1}{\mathrm{x} _{4}}\right)$ must be

15. Tangents are drawn to the ellipse $\dfrac{x^{2}}{9}+\dfrac{y^{2}}{5}=1$ at ends of latusrectum. If the area of quadrilateral be $\lambda$ sq.u, then the value of $\lambda$ must be