An equation involving independent variable $x$, dependent variable $y$ and derivative of dependent variable with respect to independent variable $\dfrac{\mathrm{dy}}{\mathrm{dx}}$ is called a differential equaitons.

A differentiable equation involving derivatives with respect to single independent variable is called ordinary differentiable equation.

A differentiable equation involving derivatives at least two independent variables and partial derivatives with respect to either of these independents variables is called a partial differentiable equation.

Order of a differential equation is the order of the highest order derivative present in it.

Degree of a differential equaiton is the degree of the highest order derivative present in it after the differential equation has been expressed as a polynomial of derivatives.

Formation of a Differential equaiton

In order to obtain a differential equation whose solution is $\mathrm{f}\left(\mathrm{x}, \mathrm{y}, \mathrm{c}, \mathrm{c} _{1}, \mathrm{c} _{2}, \ldots, \mathrm{c} _{\mathrm{n}}\right)=0$ where $\mathrm{c} _{1}, \mathrm{c} _{2}$, $\mathrm{c} _{3} \ldots . . \mathrm{c} _{\mathrm{n}}$ are $\mathrm{n}$ arbitrary constant different it with respect to $\mathrm{x}, \mathrm{n}$ time $\mathrm{s}$ and then eliminate arbitrary constant $\mathrm{c} _{1}, \mathrm{c} _{2} \ldots \mathrm{c} _{\mathrm{n}}$ from these ( $\mathrm{n}+1$ ) equations.

Solution of a Differential Equation

1. Variable separable form

Consider the equation $\dfrac{d y}{d x}=\dfrac{f(x)}{g(y)}$, which can be written as $g(y) d y=f(x) d x$.

Now integrate both sides we get the solution.

Note: If the equation is of the form $\dfrac{d y}{d x}=f(a x+b y+c)$, put $a x+b y+c=z$, then convert into variable separable form.

General form of variable separation

If we can write the differential equation in the form $f\left(f _{1}(x, y) d\left(f _{1}(x, y)+\phi\left(f _{2}(x, y) d\left(f _{2}\left(x _{1} y\right)+\ldots=0\right.\right.\right.\right.$ then each term can be easily integrated separately (Also refer the table given later)

2. Homogeneous Differential Equation

General form is $\dfrac{d y}{d x}=\dfrac{f(x, y)}{g(x, y)}$ where $\dfrac{f(x, y)}{g(x, y)}$ is a homogeneous functions of degree zero.

Rule :

• Put $y=v x, \dfrac{d y}{d x}=v+x \dfrac{d y}{d x}$
• Reduce to variable separable form and then solve.

Note : Equation of the form $\dfrac{d y}{d x}=\dfrac{d x+b y+c}{A x+B y+c}$ where a, b, c, A, B, C are constants.

Solution is

$A x y+B \dfrac{y^{2}}{2}+C y-a \dfrac{x^{2}}{2}-c x=k$

3. Linear differential equation

4. Bernoullis differential equation

Note: If $n=0$, Bernouilli’s equation reduces to linear differential equaiton. If $n=1$, it reduces to variable separatble for $m$.

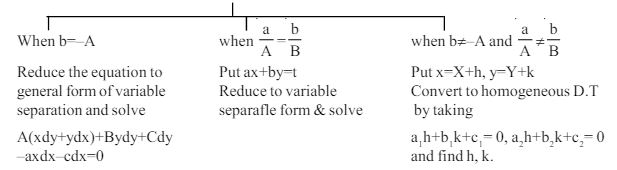
5. Excact differential equation

$M(x, y) d x+N(x, y) d y=0$ is exact differential equation if $\dfrac{\partial M}{\partial y}=\dfrac{\partial N}{\partial x}$. Then there exists a function $u(x, y)$ such that $M=\dfrac{\partial u}{\partial x}, N=\dfrac{\partial u}{d y}$, making the differential equation $\dfrac{\partial u}{\partial x} d x+\dfrac{\partial u}{\partial y} d y=0$ with solution $\mathrm{u}(\mathrm{x}, \mathrm{y})=\mathrm{c}$

i.e. To solve $\mathrm{Mdx}+\mathrm{Ndy}=0$

$\int _{y \text {-constant }} \mathrm{Mdx} _{+}+\int($ terms of $\mathrm{N}$ not containing $\mathrm{x}) \mathrm{dy}=\mathrm{c}$

Note : Sometimes a differential equation of the form $\mathrm{Mdx}+\mathrm{Ndy}=0$ which is not exact can be reduced to an exact form by multiplying by a suitbale function $\mathrm{f}(\mathrm{x}, \mathrm{y})$ which is not identically zero. This function $f(x, y)$ is known as integrating factor. We can find integating factors by inspection (Refer the table given later)

Note : Sometimes transformation to the polar coordinates facilitates separation of variables. Remember the following

If $x=r \cos \theta, y=r \sin \theta$

i. $x d x+y d y=r d r$

ii. $x d y-y d x d \theta$

iii. $d x^{2}+d y^{2}=d r^{2}+r^{2} d \theta^{2}$

Orthogonal Trajectory

Any curve which meet each member of a given family of curves at right angles is called an orthogonal trajectory of the family.

eg. $y=m x$ is an orthogonal trajectory to the family of curves $x^{2}+y^{2}=a^{2}$

Working Rule

i. Let $\mathrm{f}(\mathrm{x}, \mathrm{y}, \mathrm{c})=0$ be the family of curves where $\mathrm{c}$ is an arbitary constant

ii. Differentiate given equaiton w.r.t $\mathrm{x}$ and eliminate $\mathrm{C}$

iii. Put $\dfrac{-d x}{d y}$ for $\dfrac{d y}{d x}$ in the equation obtaiend in step (ii) (This is the differential equation of orthogonal trajectories.

iv. Solve this differential equaiton to obtain the orthogonal trajectory.

Differential equation of first order and higher degree

i. Equation solvable for $\mathrm{P}\left(=\dfrac{-\mathrm{dx}}{\mathrm{dy}}\right)$

If the equation $\mathrm{p}^{\mathrm{n}}+\mathrm{f} _{1}(\mathrm{x}, \mathrm{y}) \mathrm{p}^{\mathrm{n}-1}+\ldots$ $+\mathrm{f} _{\mathrm{n}-1}(\mathrm{x}, \mathrm{y}) \mathrm{p}+\mathrm{f} _{\mathrm{n}}(\mathrm{x}, \mathrm{y})=0$ is solvable for $\mathrm{p}$, then LHS can be written as $\left(\mathrm{p}-\mathrm{g} _{1}(\mathrm{x}, \mathrm{y})\left(\mathrm{p}-\mathrm{g} _{2}(\mathrm{x}, \mathrm{y}) \ldots\left(\mathrm{p}-\mathrm{g} _{\mathrm{n}}(\mathrm{x}, \mathrm{y})\right)=0\right.\right.$

$\Rightarrow \dfrac{d y}{d x}=g _{1}(x, y), \dfrac{d y}{d x}=g _{2}(x, y) \ldots \ldots ., \dfrac{d y}{d x}=g _{n}(x, y)$,

Integrate and find the general solution.

ii. Equations solvable for $\mathrm{y}$

$y=f(x, p) ; p=\dfrac{d y}{d x}$

Differentiating

$\dfrac{d y}{d x}=p=F\left(x, p, \dfrac{d p}{d x}\right)$ which is a differential equation of first order containing $x$ and $p$.Let its solution be $\phi(\mathrm{x}, \mathrm{p}, \mathrm{c})=0$

$\therefore \quad$ The final solution is obtained by elminating $\mathrm{p}$ between $\mathrm{y}=\mathrm{f}(\mathrm{x}, \mathrm{p})$ and $\phi(\mathrm{x}, \mathrm{p}, \mathrm{c})=0$.

Note : If it is difficult to eliminate $p$, then express $x$ and $y$ as a function of $p$.

iii. Equation solvable for $\mathrm{x}$

$\mathrm{x}=\mathrm{f}(\mathrm{y}, \mathrm{p})$

Differentiating w.r.t. y,

$\dfrac{1}{\mathrm{p}}=\dfrac{\mathrm{dx}}{\mathrm{dy}}=\mathrm{g}\left(\mathrm{x}, \mathrm{p}, \dfrac{\mathrm{dp}}{\mathrm{dx}}\right)$ which is a 1st order D.E. cotaining $\mathrm{y}$ and $\mathrm{p}$. Let its solution be $\phi(\mathrm{y}, \mathrm{p}, \mathrm{c})=0$.

Solution is obtained by elimating $\mathrm{p}$ between $\mathrm{x}=\mathrm{f}(\mathrm{y}, \mathrm{p})$ and $\phi(\mathrm{y}, \mathrm{p}, \mathrm{c})=0$

Note : If it is difficult to eliminate $p$, then express $x$ and $y$ as a function of $p$.

iv. Clarauts Equation

If a first order (any degree) differential equation is first degree in $\mathrm{x}, \mathrm{y}$ and is expressible in the form $y=p x+f(p)$ where $p=\dfrac{d y}{d x}$ is called clairauts form.

Its solution is given by $\mathrm{y}=\mathrm{cx}+\mathrm{f}(\mathrm{c})$ which is obtained by replacing $\mathrm{p}$ by $\mathrm{c}$.

Geometrical Applications

i. Equation of tangent at $P(x, y)$ is $Y-y=\dfrac{d y}{d x}(X-x)$

$x$ and $y$ intercepts of tangents are $x-y \dfrac{d x}{d y}$ and $y-x \dfrac{d y}{d x}$.

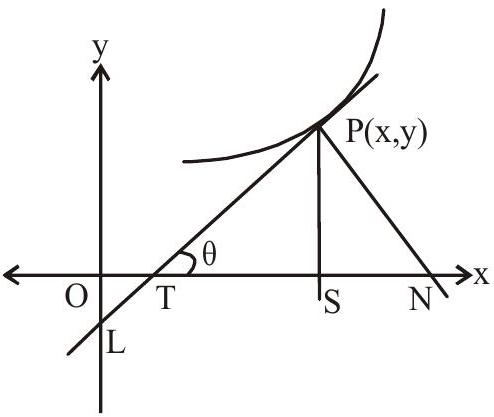
Equation of normal at $P(x, y)$ is $Y-y=-\dfrac{d x}{d y}(X-x)$

$x$ and $y$ intercepts of normal are $x+y \dfrac{d y}{d x}$ and $y+x \dfrac{d x}{d y}$

iii. Length of tangent $\mathrm{PT}=|\mathrm{y} \operatorname{cosec}|=\left|\mathrm{y} \sqrt{1+\cos ^{2} \theta}\right|=\left|\mathrm{y} \sqrt{1+\left(\dfrac{\mathrm{dy}}{\mathrm{dx}}\right)^{2}}\right|$

iv. Length of normal $P N=\left|y \operatorname{cosec} \theta\left(90^{\circ}-\theta\right)\right|=|y \sec \theta|=\left|y \sqrt{1+\tan ^{2}} \theta\right|\left|y \sqrt{1+\left(\dfrac{d y}{d x}\right)^{2}}\right|$

v. Length of subtangent $S T=|y \cot \theta|=\left|y \dfrac{d x}{d y}\right|$

vi. Length of sub normal $\mathrm{SN}=\left|\mathrm{y} \cot \left(90^{\circ}-\theta\right)\right|=|\mathrm{y} \tan \theta|=\left|\mathrm{y} \dfrac{\mathrm{dy}}{\mathrm{dx}}\right|$

Some standard forms to solve differential equaitons (For finding out the integrating factors by inspection).

1. $\mathrm{dx} \pm \mathrm{dy}=\mathrm{d}(\mathrm{x} \pm \mathrm{y})$

2. $\quad y d x+x d y=d(x y)$

3. $\dfrac{y d x-x d y}{y^{2}}=d(x / y)$

4. $\dfrac{x d y-y d x}{x^{2}}=d\left(\dfrac{y}{x}\right)$

5. $\dfrac{\mathrm{xdy}-\mathrm{ydx}}{\mathrm{x}^{2}+\mathrm{y}^{2}}=\mathrm{d}\left(\tan ^{-1}\left(\dfrac{\mathrm{y}}{\mathrm{x}}\right)\right)$

6. $\dfrac{y d x-x d y}{x^{2}+y^{2}}=d\left(\tan ^{-1}\left(\dfrac{x}{y}\right)\right)$

7. $\dfrac{x d y+y d x}{x y}=d(\log (x y))$

8. $\dfrac{x d y-y d x}{x y}=d\left(\log \dfrac{y}{x}\right)$

9. $\dfrac{y d x-x d y}{x y}=d\left(\log \dfrac{x}{y}\right)$

10. $\dfrac{x d x+y d y}{x^{2}+y^{2}}=d\left(\log \sqrt{x^{2}+y^{2}}\right)$

11. $\dfrac{2 y^{2} x d x-2 y x^{2} d y}{y^{4}}=d\left(\dfrac{x^{2}}{y^{2}}\right)$

12. $\dfrac{2 x^{2} y d y-2 x y^{2} d x}{x^{4}}=d\left(\dfrac{y^{2}}{x^{2}}\right)$

13. $\dfrac{-(x d y+y d x)}{x^{2} y^{2}}=d\left(\dfrac{1}{x y}\right)$

14. $2 x d x+2 y d y=d\left(x^{2}+y^{2}\right)$

15. $\dfrac{d x+d y}{x+y}=d\left(\log _{e}(x+y)\right)$

16. $\dfrac{x d x+y d x}{\sqrt{x^{2}+y^{2}}}=d\left(\dfrac{1}{2} \sqrt{x^{2}+y^{2}}\right)$

17. $\dfrac{\mathrm{g}^{1}(\mathrm{x}, \mathrm{y})}{(\mathrm{g}(\mathrm{x}, \mathrm{y}))^{\mathrm{n}}}=\mathrm{d} \dfrac{(\mathrm{g}(\mathrm{x}, \mathrm{y}))^{1-\mathrm{n}}}{1-\mathrm{n}}$

18. $x^{n-1} y^{n-1}(n y d x+n x d y)=d\left(x^{n} y^{n}\right)$

19. $\dfrac{x d y-y d x}{x^{2}-y^{2}}=d\left(\dfrac{1}{2} \log \left(\dfrac{x-y}{x+y}\right)\right)$

20. $\dfrac{1}{\sqrt{x^{2}-y^{2}}}\left(\dfrac{x d y-y d x}{x}\right)=d\left(\operatorname{Sin}^{-1}\left(\dfrac{y}{x}\right)\right)$

Solved Examples

1. Solution of the differential equation $2 y \sin x \cdot \dfrac{d y}{d x}=2 \sin x \cos x-y^{2} \cos x$ satisfying $y\left(\dfrac{\pi}{2}\right)=1$ is

(a) $\mathrm{y}^{2}=\sin \mathrm{x}$

(b) $y=\sin ^{2} x$

(c) $y^{2}=\cos x+1$

(d) None of these

2. The solution of $y\left(2 x^{2} y+e^{x}\right) d x-\left(e^{x}+y^{3}\right) d y=0$, if $y(0)=1$ is

(a) $6 e^{x}+4 x^{3} y-3 y^{3}-3 y=0$

(b) $y^{2} e^{x}-4 x y-3 x^{3}-3=0$

(c) $x^{2} e^{x}-4 x^{3} y-3 x y^{3}-3 x=0$

(d) None of these

3. The solution of $y^{5} x+y-x \dfrac{d y}{d x}=0$ is

(a) $\dfrac{x^{4}}{4}+\dfrac{1}{5} \cdot \dfrac{x^{5}}{y^{5}}=C$

(b) $\dfrac{x^{5}}{5}+\dfrac{1}{4} \dfrac{x^{4}}{y^{4}}=C$

(c) $\dfrac{x^{5}}{y^{5}}+\dfrac{1}{5} \dfrac{x^{4}}{y^{4}}=C$

(d) None of these

4. The solution of $\dfrac{x d y}{x^{2}+y^{2}}=\left(\dfrac{y}{x^{2}+y^{2}}-1\right) d x$ is a) $y=x \cdot \cot (C-x)$

(b) $\cos ^{-1}\left(\dfrac{y}{x}\right)=C-x$

(c) $y=x \tan (C-x)$

(d) $\dfrac{y^{2}}{x^{2}}=x \tan (C-x)$

5. The solution of $\left(y\left(1+x^{-1}\right)+\sin y\right) d x+\left(x+\log _{e} x+x \cos y\right) d y=0$ is

(a) $\left(1+y^{-1} \cdot \sin y\right)+x^{-1} \cdot \log _{e} x=C$

(b) $y+\sin y+x y \log _{e} x=C$

(c) $x y+y \log _{e} x+x \sin y=C$

(d) None of these

6. Solution of the differential equation $\left\{\dfrac{1}{x}-\dfrac{y^{2}}{(x-y)^{2}}\right\} d x+\left\{\dfrac{x^{2}}{(x-y)^{2}}-\dfrac{1}{y}\right\} d y=0$ is

(a) $\log _{\mathrm{e}} \dfrac{\mathrm{x}}{\mathrm{y}}+\dfrac{\mathrm{xy}}{\mathrm{x}-\mathrm{y}}=\mathrm{C}$

(b) $\dfrac{x y}{x-y}=C \cdot e^{x / y}$

(c) $\log _{e} \dfrac{x}{y}=C+\dfrac{x y}{x-y}$

(d) None of these

Exercise

1. A solution of the differential equation $\left(\dfrac{d y}{d x}\right)^{2}-x \dfrac{d y}{d x}+y=0$ is

(a) $\mathrm{y}=2$

(b) $y=2 x$

(c) $y=2 x-4$

(d) $y=2 x^{2}-4$

2. If $x d y=y(d x+y d y), y(1)=1$ and $y(x)>0$. Then $y(-3)$ is equal to

(a) 3

(b) 2

(c) 1

(d) 0

3. Let $\mathrm{f}(\mathrm{x})$ be differentible in the interval $(0, \infty)$ such that $\mathrm{f}(1)=1$, and $\lim _{\mathrm{t} \rightarrow \mathrm{x}} \dfrac{\mathrm{t}^{2} f(\mathrm{x})-\mathrm{x}^{2} f(\mathrm{t})}{\mathrm{t}-\mathrm{x}}=1$ for each $\mathrm{x}>0$. Then $f(\mathrm{x})$ is

(a) $\dfrac{1}{3 \mathrm{x}}+\dfrac{2 \mathrm{x}^{2}}{3}$

(b) $\dfrac{-1}{3 \mathrm{x}}+\dfrac{4 \mathrm{x}^{2}}{3}$

(c) $\dfrac{-1}{\mathrm{x}}+\dfrac{2}{\mathrm{x}^{2}}$

(d) $\dfrac{1}{\mathrm{x}}$

4.* Tangent is drawn at any point $\mathrm{P}$ of a curve which passes through $(1,1)$ cutting $\mathrm{x}$-axis and $\mathrm{y}$-axis at $\mathrm{A}$ and $\mathrm{B}$ respectively. If $\mathrm{BP}: \mathrm{AP}=3: 1$, then

(a) differential equation of the curve is $3 x \dfrac{d y}{d x}+y=0$

(b) differential equation of the curve is $3 x \dfrac{d y}{d x}-y=0$

(c) curve is passing through $\left(\dfrac{1}{8}, 2\right)$

(d) normal at $(1,1)$ is $x+3 y=4$

5.* Let $\mathrm{y}=f(\mathrm{x})$ be a curve passing through $(1,1)$ such that the triangle formed by the coordinate axes and the tangent at any point of the curve lies in the first quadrant has area 2 units. Then the possible curves are

(a) $x+y=2$

(b) $x y=1$

(c) $x-y=2$

(d) $\dfrac{x}{y}=1$

6. A curve passing through the point $(1,1)$ has the property that the perpendicular distance of the origin from the normal at any point $\mathrm{P}$ of the curve is equal to the distance of $\mathrm{P}$ from the $\mathrm{x}$-axis. Equation of the curve is

(a) $x^{2}+y^{2}=-2 x$

(b) $x^{2}+y^{2}=2 x$

(c) $x^{2}-y^{2}=2 x$

(d) none of these

7. Let $f: \mathrm{R} \rightarrow \mathrm{R}$ be a continuous function, which satisfies $f(\mathrm{x})=\int _{0}^{\mathrm{x}} f(\mathrm{t}) \mathrm{dt}$. Then the value of $f\left(\log _{\mathrm{e}} 5\right)$ is

(a) 0

(b) 1

(c) 5

(d) none of these

8. If the function $f(\mathrm{x})=\mathrm{x}^{3}+\mathrm{e}^{\mathrm{x} / 2}$ and $\mathrm{g}(\mathrm{x})=f^{-1}(\mathrm{x})$, then the value of $\mathrm{g}^{1}(1)$

(a) $\dfrac{1}{2}$

(b) 2

(c) 0

(d) none of these

9. Match the following :-

10. Read the following passage and answer the questions that follow :The differential equation $\mathrm{y}=\mathrm{px}+f(\mathrm{p}) \ldots . .$. (1) where $\mathrm{p}=\dfrac{\mathrm{dy}}{\mathrm{dx}}$, is known as Clairout’s equation. To solve equation (1), differentiate it w.r.t. $x$ which gives either $\dfrac{d p}{d x}=0 \Rightarrow p=c$ (2) or $\mathrm{x}+f^{1}(\mathrm{p})=0$

Note : (a) If p is eliminated between polution (1) \& (2) the solution obtained is a general solution of (1)

(b) If $p$ is eliminated between (1) \& (3) then solution obtained does not contain any arbitrary constant and is not particular solution of (1). This solution a called singular solution of (1).

i. Which of the following is about solutions of differential equation $y=x y^{1}+\sqrt{1+\left(y^{1}\right)^{2}}$

(a) The general solution of equation is family of parabolas.

(b) The general solution of equation is family of circles.

(c) The singular solution of equation is circle.

(d) The singular solution of equation is ellipse.

ii. The number of solutions of the equation $f(\mathrm{x})=-1$ and the singular solution of the equation $\mathrm{y}=$ $x \dfrac{d y}{d x}+\left(\dfrac{d y}{d x}\right)^{2}$ is

(a) 1

(b) 2

(c) 4

(d) 0

iii. The singular solution of the differential equation $y=m x+m-m^{3}$ where, $m=\dfrac{d y}{d x}$ passes through the point

(a) $(0,0)$

(b) $(0,1)$

(c) $(1,0)$

(d) $(-1,0)$