Coordinate Geometry-i Straight Line (Lecture-03)
14. Locus of the image of the point
(a)
(b)
(c)
(d) None
Show Answer
Solution:
Let image be
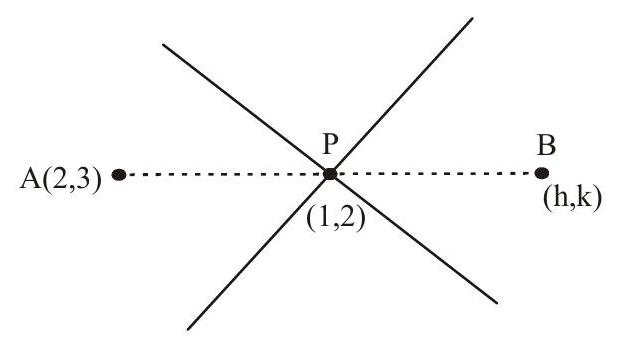
Answer : d
15. If the lines
(a) 0
(b) 1
(c)
(d) None
Show Answer
Solution:
divide by
16. The set of values of ’
(a)
(b)
(c)
(d) None of these
Show Answer
Solution:
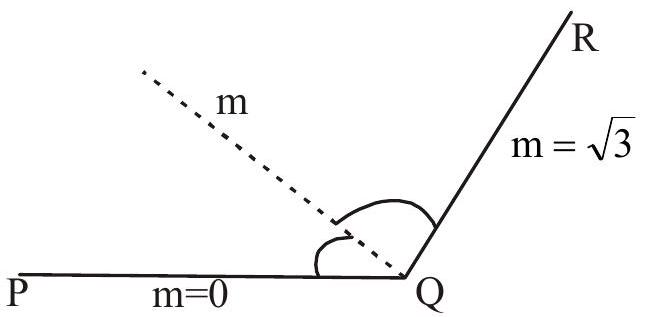
17. Let
(a)
(b)
(c)
(d)
Show Answer
Solution:
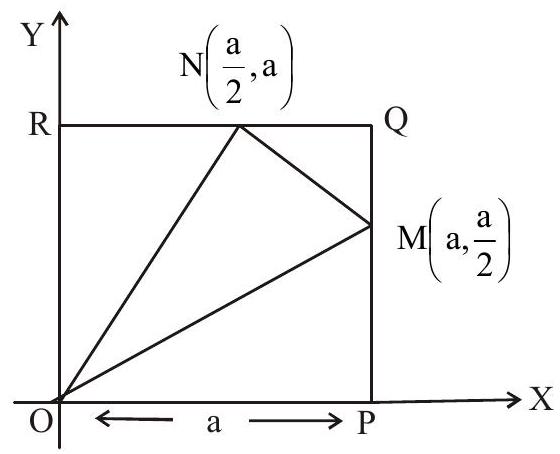
18.
(a) 2
(b) 4
(c) 12
(d) 16
Show Answer
Solution: ar. of square
ar of
Answer : b
19. A pair of perpendicular straight lines drawn through the origin form an isoceles triangle with line
(a)
(b)
(c)
(d)
Show Answer
Solution: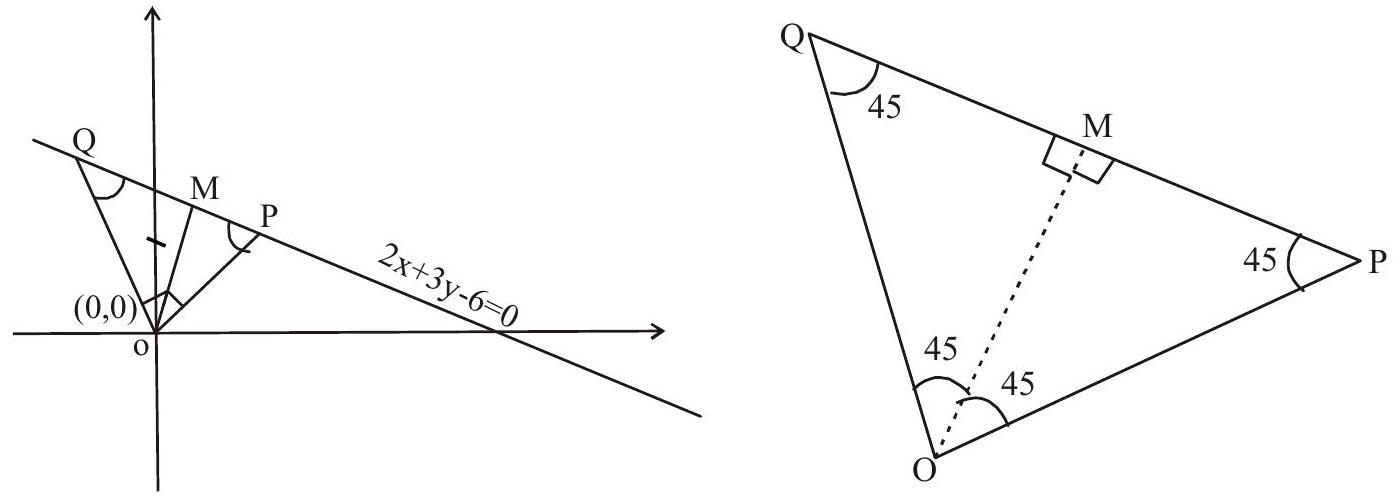
20. Match the column
| Column I | Column II | ||
|---|---|---|---|
| (a) | Two vertices of a triangle are (5,-1) and ( |
(p) | |
| (b) | A point on the line |
(q) | |
| (c) | Orthocentre of the triangle made by the lines |
(r) | |
| (d) | If a,b,c are in A.P., then lines |
(s) |
Show Answer
Solution:
A-p
B-q
C-s
D-s
Exercise
1. If
(a)
(b)
(c)
(d)
Show Answer
Answer: b2. The equation
(a) three real straight lines
(b) three points
(c) combined equationof ast. line & a circle
(d) None of these.
Show Answer
Answer: d3. The three lines whose combined equation is
(a) isosceles
(b) equilateral
(c) right angled
(d) None of these
Show Answer
Answer: dComprehension Type
4. Equation of side
(a)
(b)
(c)
(d)
Show Answer
Answer: b5. Coordinates of vertex
(a)
(b)
(c)
(d)
Show Answer
Answer: c6. Equation of side
(a)
(b)
(c)
(d)
Show Answer
Answer: a7. Assertion and reasoning Type
Lines
Statement 1 : The ratio PR: RQ equals
Statement 2 : In any triangle, bisector of an angle divides the triangle into two similar triangles.
a Statement 1 is true, Statement 2 is True; Statement 2 is a correct explanation for Statement1.
b Statement 1 is True, Statement 2 is True; Statement 2 is NOT a correct explanation for Statement 1 .
c Statement 1 is True, Statement 2 is False.
d Statement 1 is False, Statement 2 is True.
Show Answer
Answer: c8. Matrix-match
This question contains statements given in two columns which have to be matched. Statements a, b, c, d in column I have to be matched with statements p,q, r, s in column II. If the correct match is a
Consider the lines given by
| Column I | Column II | ||
|---|---|---|---|
| (a) | (p) | ||
| (b) | One of |
(q) | |
| (c) | (r) | ||
| (d) | (s) |










