8. Consider the points $\mathrm{A}(0,1)$ and $\mathrm{B}(2,0)$ and $\mathrm{P}$ be a point on the line $4\mathrm{x}+3\mathrm{y}+9=0$. Coordinates of $\mathrm{P}$ such that $|\mathrm{PA}-\mathrm{PB}|$ is maximum are

(a) $({\displaystyle \frac{-12}{5}},{\displaystyle \frac{17}{5}})$

(b) $({\displaystyle \frac{-18}{5}},{\displaystyle \frac{13}{5}})$

(c) $({\displaystyle \frac{31}{7}},{\displaystyle \frac{31}{7}})$

(d) $(0,0)$

Show Answer

Solution: $|\mathrm{PA}-\mathrm{PB}|\le \mathrm{AB}$

Thus |PA-PB| is max. if points A,B,P are collinear. Equation of $AB$ is $y-1={\displaystyle \frac{0-1}{2-1}}(x-0)\Rightarrow x+2y-$ $2=0$

Hence solving $x+2y=2=0$ & $4x+3y+9=0$ we get $(-{\displaystyle \frac{84}{5}},{\displaystyle \frac{13}{5}})$

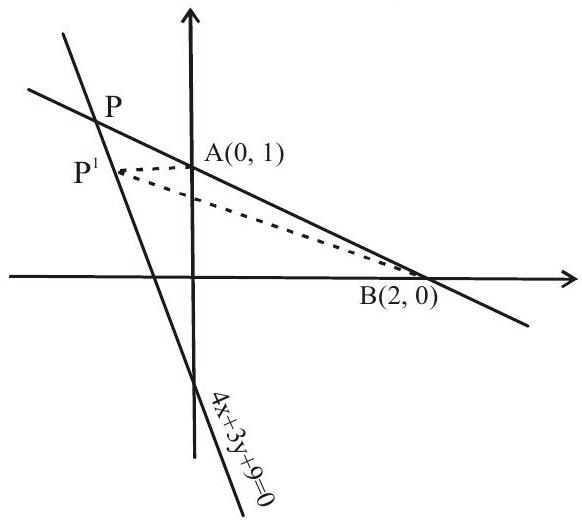
9. A light ray coming along the line $3x+4y=5$ gets reflected from the line $ax+by=1$ and goes along the line $5x-12y=10$. Then

(a) $\mathrm{a}={\displaystyle \frac{64}{115}},\mathrm{b}={\displaystyle \frac{112}{15}}$

(b) $\mathrm{a}={\displaystyle \frac{14}{15}},\mathrm{b}={\displaystyle \frac{-8}{115}}$

(c) $\mathrm{a}={\displaystyle \frac{64}{115}},\mathrm{b}={\displaystyle \frac{-8}{115}}$

(d) $\mathrm{a}={\displaystyle \frac{64}{15}},\mathrm{b}={\displaystyle \frac{14}{15}}$

Show Answer

Solution: $ax+by=1$ will be one of the bisectors of the lines given ${\displaystyle \frac{3\mathrm{x}+4\mathrm{y}-5}{5}}=\pm \left({\displaystyle \frac{5\mathrm{x}-12\mathrm{y}-10}{13}}\right)$

$\Rightarrow 64x-8y=115$ or $14x+112y=15$ On comparing with $ax+by=1$, we get

$\mathrm{a}={\displaystyle \frac{64}{115}},\mathrm{b}={\displaystyle \frac{-8}{115}}$ or $\mathrm{a}={\displaystyle \frac{14}{15}},\mathrm{b}={\displaystyle \frac{112}{15}}$

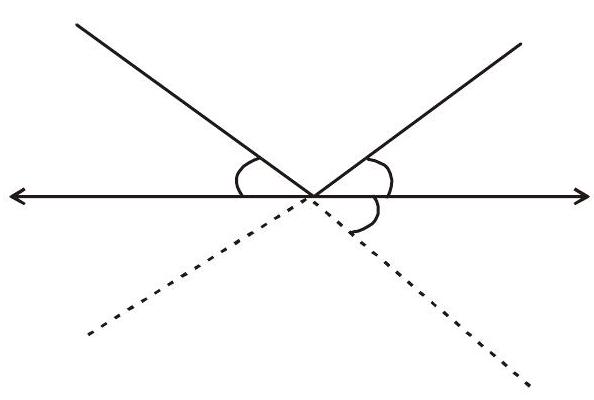
10. If the point $(a,a)$ is placed in between the lines $|x+y|=4$, then a is

(a) $[-2,0]$

(b) $[0,2]$

(c) $(-2,2)$

(d) $[-2,2]$

Show Answer

Solution: $\mathrm{x}+\mathrm{y}=4$

$\mathrm{x}+\mathrm{y}=-4$

& $\mathrm{pt}(2,2)$ & $(-2,-2)$ lies on these lines

Then pt. (a,a) lies between the lines then $\mathrm{a}>-2$ and $\mathrm{a}<2$ ie. $-2<\mathrm{a}<2$.

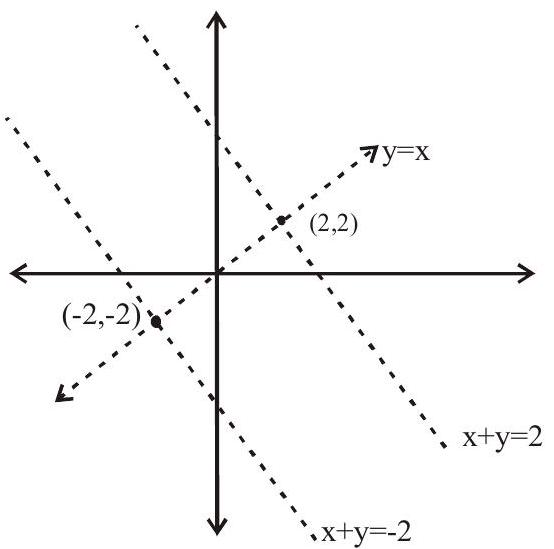
11. Consider the family of lines $5x+3y-2+{\lambda }_1(3x-y-4)=0$ and $x-y+1+{\lambda }_2(2x-y-2)=0$. The equation of a straight line that belongs to both the families is____________________________.

Show Answer

Solution:

$\begin{array}{c}5x+3y=2\\ 3x-y=4\\ x=1\\ y=-1\end{array}$

$\begin{array}{c}x-y=-1\\ 2x-y=2\\ x=3\\ y=4\end{array}$

Equation of a line belongs to both families passes through A and B is

$\begin{array}{rl}& y+1={\displaystyle \frac{4+1}{3-1}}(x-1)\\ & y+1={\displaystyle \frac{5}{2}}(x-1)\\ & 5x-2y-7=0\end{array}$

12. If ${\mathrm{x}}_1,{\mathrm{x}}_2,{\mathrm{x}}_3$ as well as ${\mathrm{y}}_1,{\mathrm{y}}_2,{\mathrm{y}}_3$ are in G.P. with same common ratio then the points $\mathrm{P}({\mathrm{x}}_1$, ${\mathrm{y}}_1),\mathrm{Q}({\mathrm{x}}_2,{\mathrm{y}}_2)$ and $\mathrm{R}({\mathrm{x}}_3,{\mathrm{y}}_3)$

(a) lie on a straight line

(b) lie on an ellipse

(c) lie on a circle

(d) are vertices of a triangle.

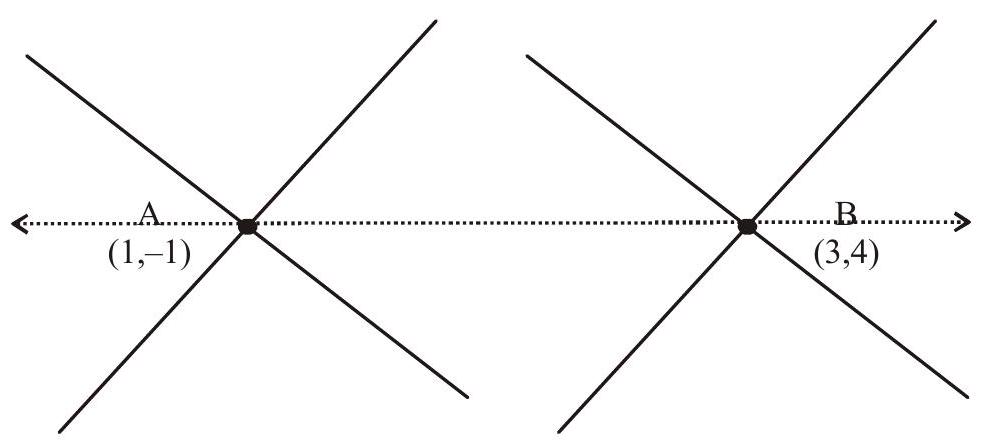
13. A variable straight line is drawn through the point of intersection of the straight lines ${\displaystyle \frac{x}{a}}+{\displaystyle \frac{y}{b}}=1$ and ${\displaystyle \frac{x}{b}}+{\displaystyle \frac{y}{a}}=1$ and meets the coordinate axes at $A$ and $B$, find the locus of the midpoint of $AB$.

Show Answer

Solution: Let mid pt. of $\mathrm{AB}$ be $(\mathrm{h},\mathrm{k})$.

Intersection pt. of given lines is $({\displaystyle \frac{ab}{a+b}},{\displaystyle \frac{ab}{a+b}})$

$P$ is mid pt. of $AB\Rightarrow A(2h,0)$ & $B(0,2k)$.

Now A,B and $Q$ are collinear $\Rightarrow \left|\begin{array}{ccc}2h& 0& 1\\ 0& 2k& 1\\ {\displaystyle \frac{ab}{a+b}}& {\displaystyle \frac{ab}{a+b}}& 1\end{array}\right|=0$

$\Rightarrow 4\mathrm{hk}-{\displaystyle \frac{2\mathrm{hab}}{\mathrm{a}+\mathrm{b}}}-{\displaystyle \frac{2\mathrm{kab}}{\mathrm{a}+\mathrm{b}}}=0$

$\Rightarrow 2\mathrm{xy}(\mathrm{a}+\mathrm{b})=\mathrm{ab}(\mathrm{x}+\mathrm{y})$.

Exercise

1. Orthocenter of triangle with vertices $(0,0),(3,4)$ and $(4,0)$ is

(a) $(3,{\displaystyle \frac{5}{4}})$

(b) $(3,12)$

(c) $(3,{\displaystyle \frac{3}{4}})$

(d) $(3,9)$

2. Area of the triangle formed by the line $x+y=3$ and angle bisectors of the pairs of straight lines $x^2-y^2+2y=1$ is

(a) 2 sq.units

(b) 4 sq.units

(c) 6sq.units

(d) 8 sq.units

3. Let $\mathrm{O}(0,0),\mathrm{P}(3,4),\mathrm{Q}(6,0)$ be the vertices of the triangle OPQ. The point $\mathrm{R}$ inside the ${}_{\mathrm{\Delta }}\mathrm{OPQ}$ is such that the triangle $\mathrm{OPR},\mathrm{PQR},\mathrm{OQR}$ are of equal area. The coordinates of $\mathrm{R}$ are

(a) $({\displaystyle \frac{4}{3}},3)$

(b) $(3,{\displaystyle \frac{2}{3}})$

(c) $(3,{\displaystyle \frac{4}{3}})$

(d) $({\displaystyle \frac{4}{3}},{\displaystyle \frac{2}{3}})$

4. Consider three points $\mathrm{P}(-\sin (\beta -\alpha ),-\cos \beta ),\mathrm{Q}(\cos (\beta -\alpha ),\sin \beta )$ and $\mathrm{R}(\cos (\beta -\alpha +\theta )$, $\sin (\beta -\theta ))$, where $0<\alpha ,\beta ,\theta <{\displaystyle \frac{\pi }{4}}$. Then

(a) $\mathrm{P}$ lies on the line segment $\mathrm{RQ}$.

(b) $\mathrm{Q}$ lies on the line segment PR.

(c) $\mathrm{R}$ lies on the line segment $\mathrm{QP}$.

(d) P, Q, R are non-collinear.

5. The locus of the orthocenter of the triangle formed by the lines $(1+p)x-py+p(1+p)=0$, $(1+q)x-qy+(1+q)q=0$ and $y=0$, where $p\ne q$, is

(a) a hyperbola

(b) a parabola

(c) an ellipse

(d) a straight line.

6. Let points $\mathrm{A}(1,1)$ and $\mathrm{B}(2,3)$. Coordinates of the point $\mathrm{P}$ such that $|\mathrm{PA}-\mathrm{PB}|$ is minimum are

(a) $(2,{\displaystyle \frac{3}{2}})$

(b) $(0,{\displaystyle \frac{11}{4}})$

(c) $(11,3)$

(d) $({\displaystyle \frac{3}{2}},0)$

7. The line $x+7y=14$ is rotated through an angle ${\displaystyle \frac{\pi }{4}}$ in the anticlock wise direction about the point $(0,2)$. The equation of the line in its new position is

(a) $3\mathrm{x}-4\mathrm{y}+8=0$

(b) $3x-4y-8=0$

(c) $4x+3y+8=0$

(d) None of these

8. If one diagonal of a square is the portion of the line ${\displaystyle \frac{x}{a}}+{\displaystyle \frac{y}{b}}=1$ intercepted by the axes, then the extremities of the other diagonal of the square are

(A) $({\displaystyle \frac{a+b}{2}},{\displaystyle \frac{a-b}{2}})$

(b) $({\displaystyle \frac{a-b}{2}},{\displaystyle \frac{a+b}{2}})$

(c) $({\displaystyle \frac{\mathrm{a}-\mathrm{b}}{2}},{\displaystyle \frac{\mathrm{b}-\mathrm{a}}{2}})$

(d) $({\displaystyle \frac{a+b}{2}},{\displaystyle \frac{b-a}{2}})$

9. The image of $\mathrm{P}(\mathrm{a},\mathrm{b})$ in the line $\mathrm{y}=-\mathrm{x}$ is $\mathrm{Q}$ and the image of $\mathrm{Q}$ in the line $\mathrm{y}=\mathrm{x}$ is $\mathrm{R}$, then the midpoint of PR is

(a) $(\mathrm{a}-\mathrm{b},\mathrm{b}+\mathrm{a})$

(b) $({\displaystyle \frac{a+b}{2}},{\displaystyle \frac{b+a}{2}})$

(c) $(\mathrm{a}-\mathrm{b},\mathrm{b}-\mathrm{a})$

(d) $(0,0)$

10. Let $\mathrm{ABC}$ be a triangle. Let $\mathrm{A}$ be the point $(1,2),\mathrm{y}=\mathrm{x}$ is the perpendicular bisector of $\mathrm{AB}$ and $\mathrm{x}-2\mathrm{y}+1=0$ is the angle bisector of $\mathrm{\angle }\mathrm{C}$. If equation of $\mathrm{BC}$ is given by $\mathrm{ax}+\mathrm{by}-5=0$, then $\mathrm{a}+\mathrm{b}$ is

(a) 1

(b) 2

(c) 3

(d) 4