Coordinate Geometry-i - Straight Line (Lecture-01)
Straight Line -
It is a curve such that every point on the line segment joining any two points on it lies on it. Equation of straight line is always of first degree on
General equation of straight line is
Where a,b,c are any real numbers not all zero.
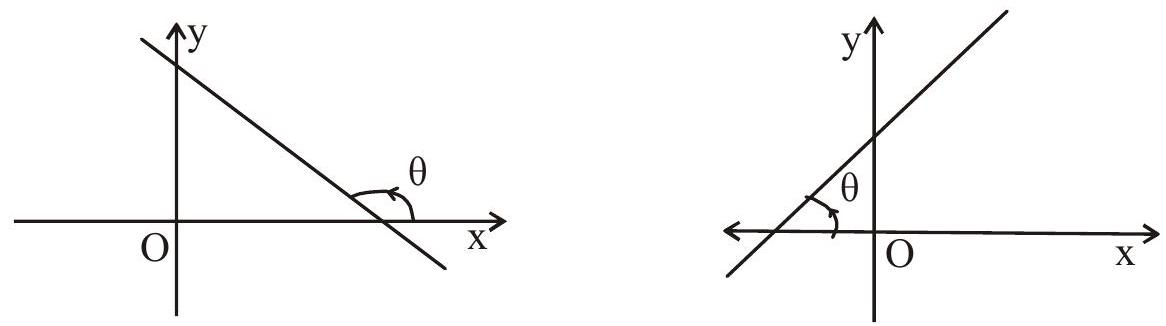
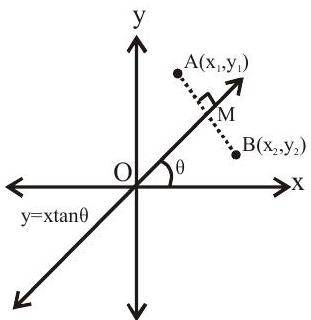
Slope of a line
The trigonometrical tangent of an angle that a line makes with the positive direction of the
Points to remember
(i) Slope of a line parallel to
(ii) If slope is positive then it makes acute angle with positive direction of
(iii) If a line is equally inclined to the axes, that it will make angle of
(iv) It three points
(v) Slope of the line joining two points
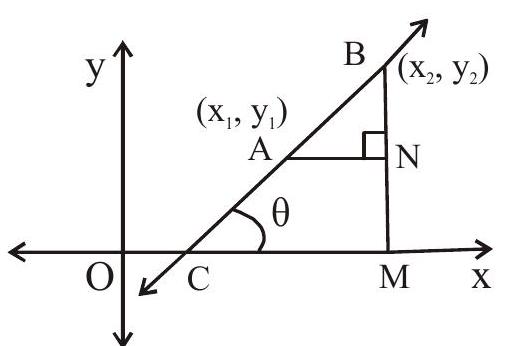
(vi) Equation of
(vii) Equation of
(viii) Equation of line parallel to
(ix) Equation of line parallel to
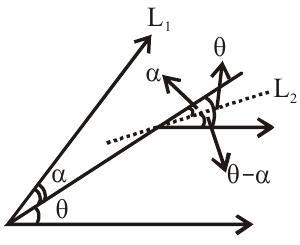
Angle between two lines
The angle
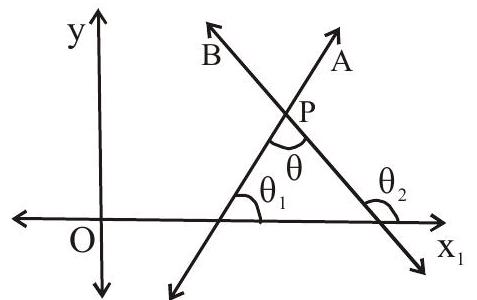
Where
(i) When two lines are parallel then their slopes are equal ie.
(ii) When two lines are perpendicular then the product of their slope is -1
i.e.
A line equally inclined with two lines
Let the two lines with slopes
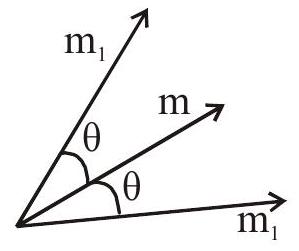
Special form of a line
1. Point slope form
The equation of a line which passes through the point
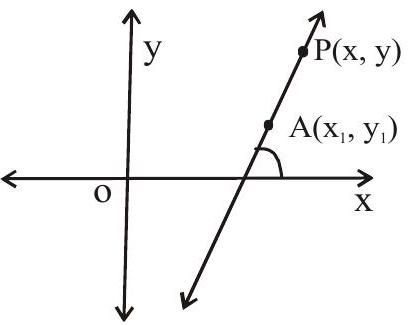
2. Two point form
The equation of a line passing through two points
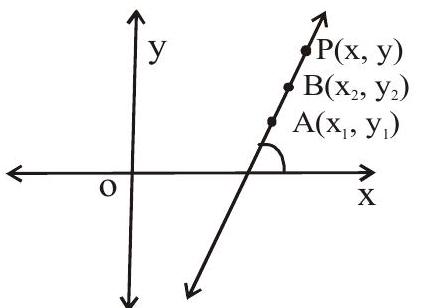
3. Slope and y intercept form [Non Vertical Line]
The equation of a line with slope
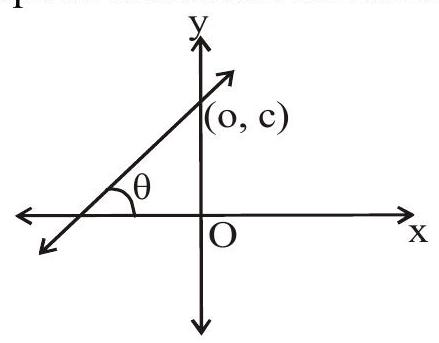
Intercept form
The equation of a straight line which cuts off intercepts 
Normal form (perpendicular form)
The equation of a straight line upon which the length of the perpendicular from the origin is
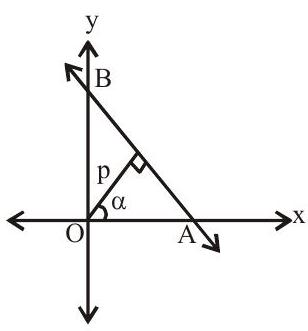
Note Here
Distance form or Symmetric form or Parametric Form
The equation of a straight line passing through the point
Where
Parametric form
From the above equation we get
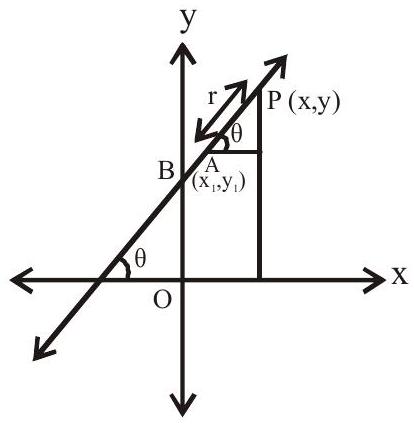
The coordinates
Where the line is inclined at an angle
1. If
2. At a given distance
1. Distance of a line from a point
Length of perpendicular (distance) from the point
Length of perpendicular from the origin to the line
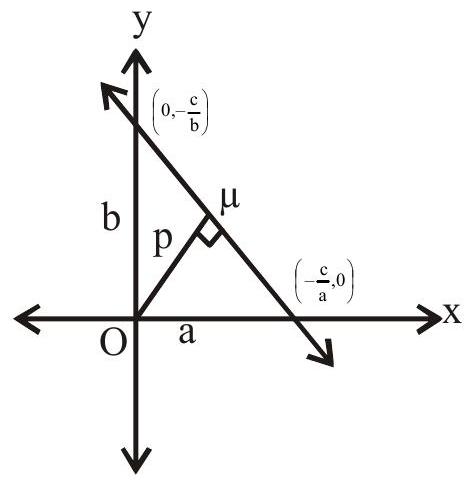
2. Distance between two parallel lines
The distance between two parallel lines
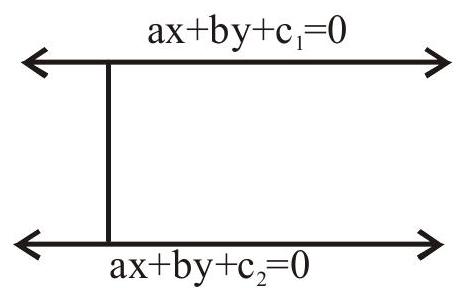
Note that coefficient of
3. Area of a parallelogram
Area of a parallelogram
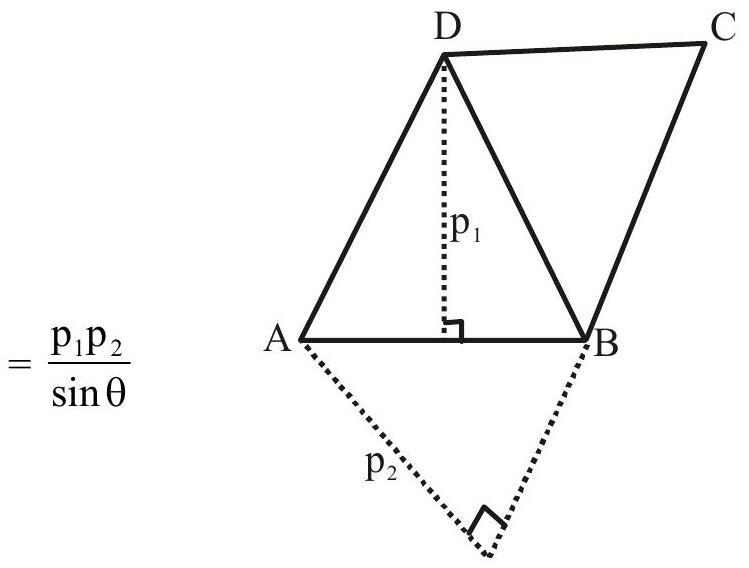
If the sides of a parallelogram be
Area of Rhombus
In case of a rhombus 
Also area of rhombus
Area of a triangle
Area of a triangle whose vertices are
1. If area of a triangle is given then use
2. If three points
3. If
where
Area of polygon
The area of polygon whose vertices are
General Equation of straight line
First degree equation of the form
Reducing general equation to slope intercept form
Given equation is
Rewrite the equation by
divide by
It look like
Reducing to intercept form
Given equation is
Rewrite the equation
It look like
So intercepts are
Reduce to normal form
Given equation be
Re write the equation
Keeping constant term postive
Divide by
It look like
Where
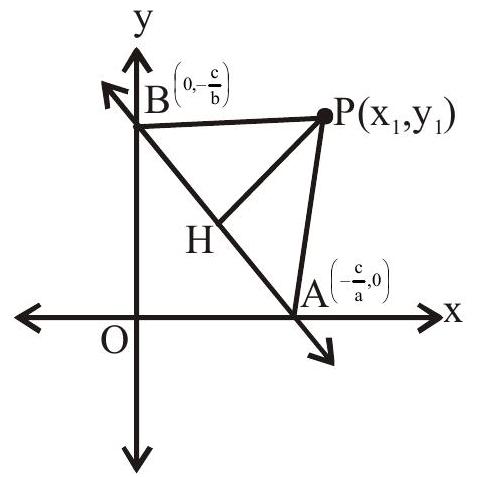
Image of a point in different cases
i. The image of a point with respect to the line mirror
Image of
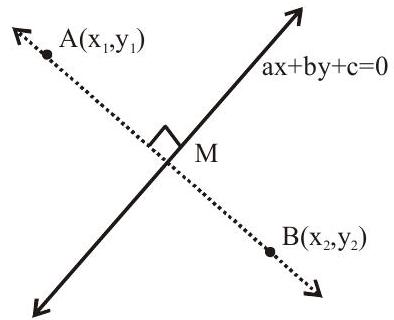
ii. The image of a point with respect to
Let
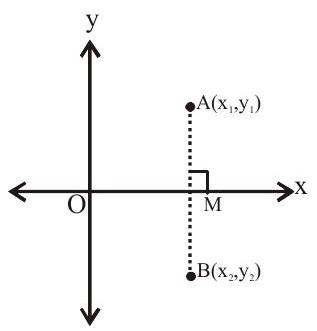
iii. The image of a point with respect to
Let
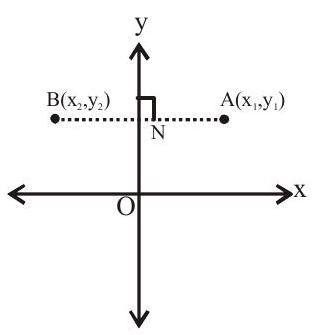
iv. The image of a point with respect to the origin:-
Let
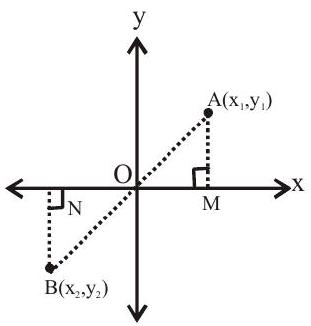
v. The image of a point with respect to the line
Let
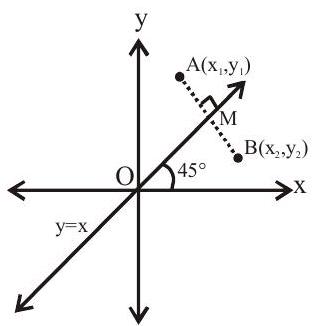
vi The image of a point with respect to the line
Let
Line parallel and perpendicular to given line
Given equation of straight line be
A line parallel to given line is
A line perpendicular to given line is
Here change coordinate of
It the lines
i. Coincident, if
ii. Parallel, if
iii. Intersecting, if
1. Concurrent lines
The three given lines are concurrent if they meet at one point.
i. Find the point of intersection of any two lines by solving them simultaneously. If this point satisfies the third equation also then the given lines are concurrent.
ii. Let three lines be
iii. The three lines
2. Equations of angle bisectors between two lines
The equations of the bisectors of the angles between the lines
are given by
i. Any point on a bisector is equidistant from the given lines.
ii. Locus of points which are equidistant from the two intersecting lines is an angle bisector.
iii. Bisectors are perpendicular to each other.
iv. Equation of the bisector of the acute and of obtuse angle between two lines.
Let
and
is the bisector of the acute or obtuse angle between the lines
again
is the bisector of the acute or obtuse angle between the lines
3. Position of two points relative to a given line
Let the line be
i. If
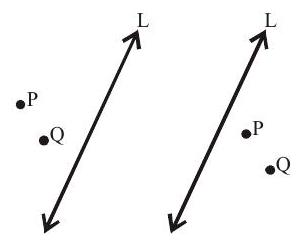
ii. If
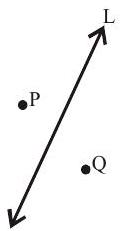
iii. If origin lie on line then the line is known as origin side.
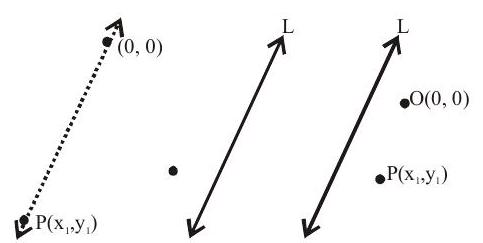
iv. A point
v. A point
Family of straight lines
Let
Then the general equation of any straight line passing through the point of intersection of lines
Equations of straight lines through
Standard points of a triangle
1. Centroid or centre of gravity :-
The centroid of a triangle is the point of intersection of its median’s. the centroid divides the median in the ratio 2:1 (vertex:base).
Coordinates of G are
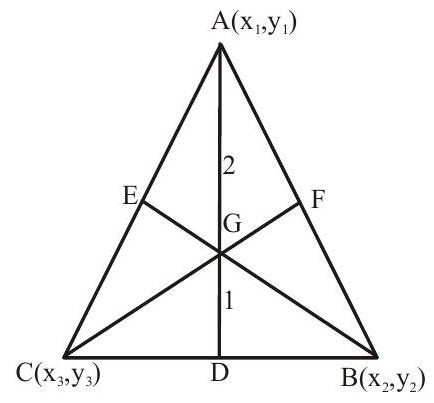
In isosceles triangle median to the equal sides are equal in length and in equilateral triangle all medians are equal in length.
Equations of median can be obtained by using two point form with vertex and the mid point of opposite side.
2. Circumcentre:-
The circumcentre of a triangle is the point of intersection of the perpendicular bisectors of the sides of a triangle.
Coordinates of
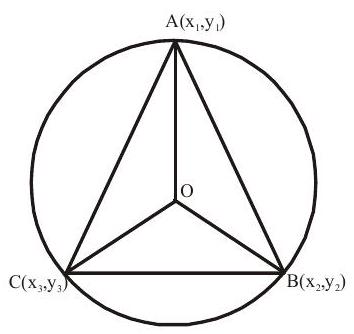
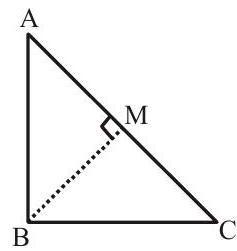
If angles
The circumcentre of a right-angled triangle is the mid-point of its hypotenuse. Therefore the mid-point of hypotenuse is equidstant from its vertices
The circumcentre of the triangle formed by
3. Incentre of a triangle :-
The point of intersection of the internal bisecters of the angles of a
triangle is called the incentre of the triangle.
The coordinates of the incentre of a triangle with vertices
Where
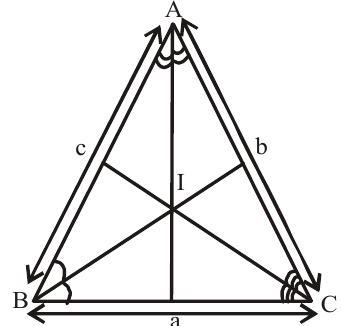
The incentre of the triangle formed by
4. Orthocentre :-
The orthocentre of a triangle is a point intersection of altitudes.
i. Take the equations of any two sides of a triangle. find the eqnations the lines perpendicular to those lines and passing through the opposite vertices. solve these two equations we get orthocentre of the triangle.
ii. If angles
then orthocentre of
iii. If any two lines out of three lines
iv. The orthocentre of the triangle with verties
v. The orthocentre
vi. In an equilateral triangle,orthocentre, centroid, circumcentre and incentre conside.
5. Coordinates of nine point circle :-
If a circle passes through the foot of perpendicular (D,E,F) mid points of sides
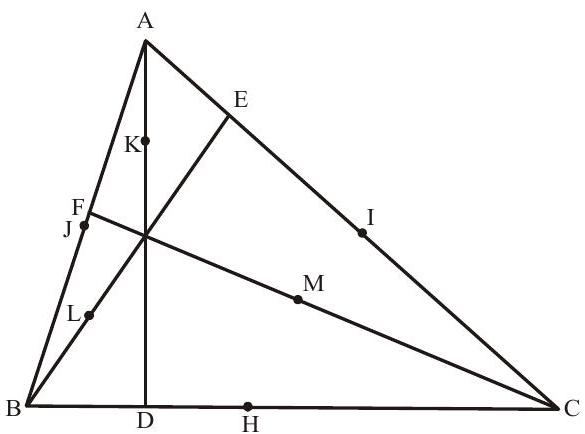
1. The orthocentre (0), nine point centre (N) centroid (G) and circumcentre (C) all lie in the same line i.e. ONGC (oil natural gas corporation)
2. The nine point centre bisects the join of orthocentre (O) and circumcentre (C)
3. The radius of nine point circle is half the radius of circumcircle.
Examples:
1. If the centroid and circumcentre of a triangle are
(a)
(b)
(c)
(d)
Show Answer
Solution: Centroid, circumcentre and orthocenter are collinear such that centroid divides the circumcenter and orthocentre in the ratio 1:2. Ans(-3,5).2. If the algebraic sum of the perpendicular distances from the point
(a)
(b)
(c)
(d)
Show Answer
Solution: Let equation be
A.T.Q.
This shows that
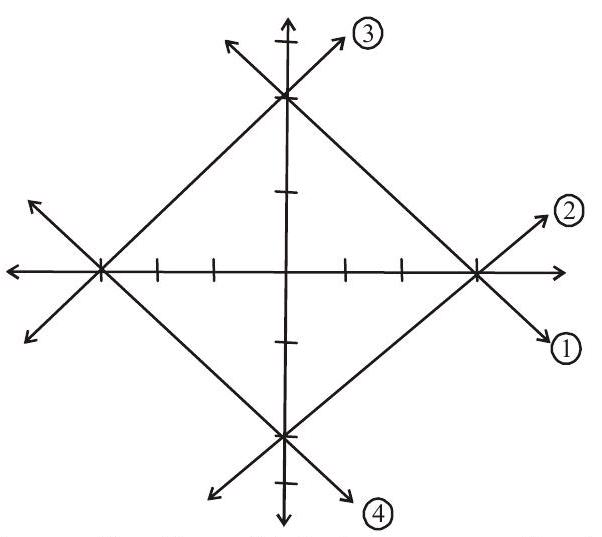
3. The area enclosed by
(a) 3 Sq-units
(b) 12 Sq.units
(c) 9 Sq.units
(d) 24 Sq.units
Show Answer
Solution:
Form a rhombus with diagonals
Area
4. The number of integer values of
(a) 2
(b) 0
(c) 4
(d) 1
Show Answer
Solution: Point of intersection
Hence there are two values of
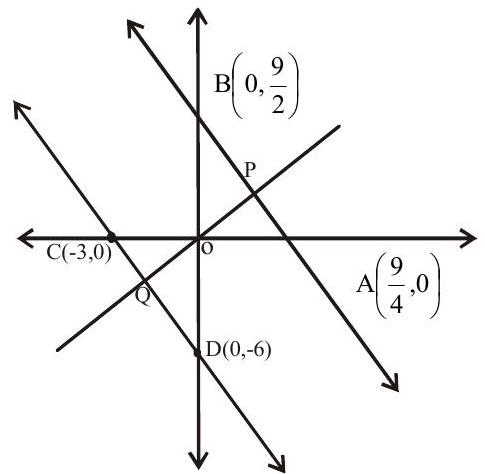
5. A straight line through the origin meets the parallel lines
(a)
(b)
(c)
(d)
Show Answer
Solution: Clearly
6. A family of lines is given by
(a)
(b)
(c)
(d) None of these.
Show Answer
Solution:
The required line is
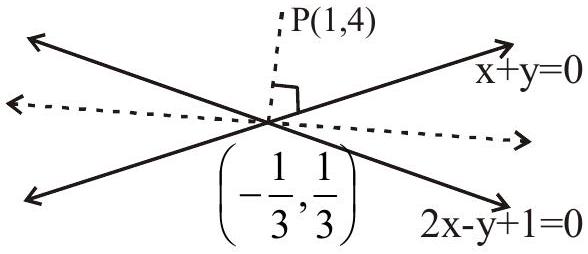
7. The four sides of a quadrilateral are given by the equation
(a)
(b)
(c)
(d)
Show Answer
Solution: ar.of
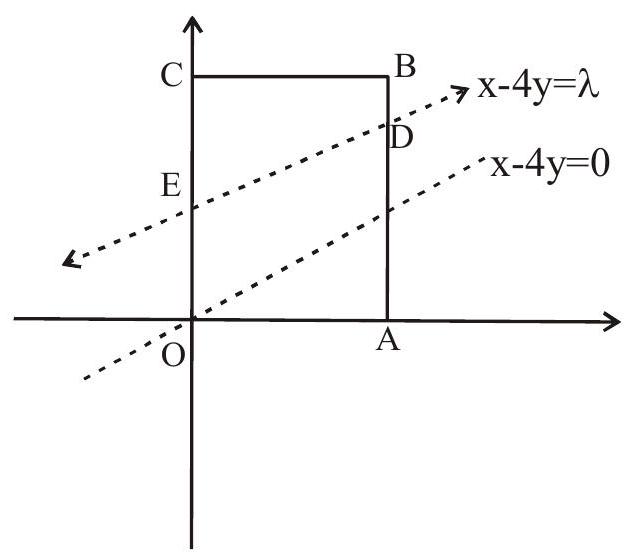
Exercise
1. A triangle
Then the orthocentre of triangle
(a)
(b)
(c)
(d)
Show Answer
Answer: a2. The points
(a)
(b)
(c)
(d)
Show Answer
Answer: c3. Set of values of
(a)
(b)
(c)
(d) None
Show Answer
Answer: a4. Area of the parallelogram formed by the lines
(a)
(b)
(c)
(d)
Show Answer
Answer: d5.
(a) perpendicular to
(b) parallel to
(c) inclined at an angle
(d) None of these.
Show Answer
Answer: b6. The area of the figure formed by
(a)
(b)
(c)
(d) None of these
Show Answer
Answer: b7. The orthocentre, circumcentre, centroid and incentre of the triangle formed by the line
(a)
(b)
(c)
(d)
Show Answer
Answer: b8. Two points
(a) -7
(b) -4
(c) 0
(d) 7










