Complex Numbers And Quadratic Equations - Quadratic Equations (Location of Roots) (Lecture-02)
Let $f(\mathrm{x})=\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}, \mathrm{a}, \mathrm{b}, \mathrm{c} \in \mathrm{R}, \mathrm{a} \neq 0$ and $\alpha, \beta(\alpha<\beta)$ be the roots of $f(\mathrm{x})=0$. Let $\mathrm{k}$ be any real number
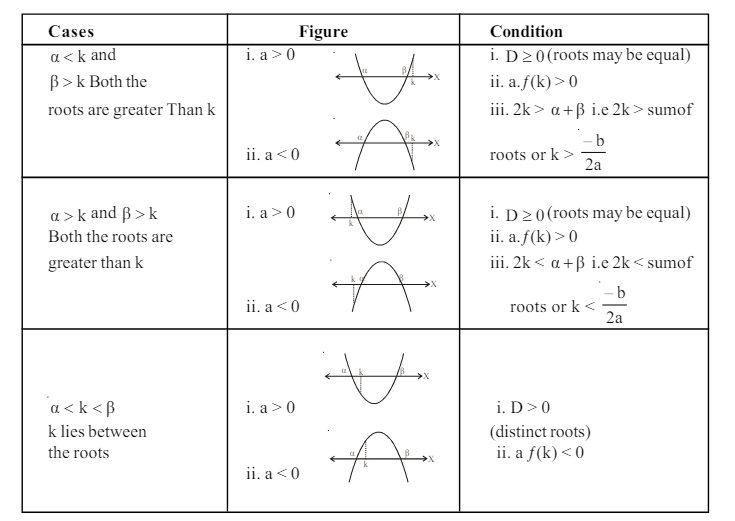
Wavy Curve Method
Let $f(\mathrm{x})=\left(\mathrm{x}-\mathrm{a} _{1}\right)^{\mathrm{k} _{1}}\left(\mathrm{x}-\mathrm{a} _{2}\right)^{\mathrm{k} _{2}} \ldots \ldots\left(\mathrm{x}-\mathrm{a} _{\mathrm{n}}\right)^{\mathrm{k} _{\mathrm{n}}} \quad \quad \quad \quad \quad \quad \quad-(1)$
Where $\mathrm{k} _{\mathrm{i}} \in \mathrm{N} \forall \mathrm{i}$ & $\mathrm{a} _{\mathrm{i}} \in \mathrm{R} \forall \mathrm{i}$ such that $\mathrm{a} _{1}<\mathrm{a} _{2}<\ldots \ldots<\mathrm{a} _{\mathrm{n}}$. Mark $\mathrm{a} _{1}, \mathrm{a} _{2} \ldots \ldots \mathrm{a} _{\mathrm{n}}$ on real axis check the sign of $f(x)$ in each interval. The solution of $f(x)>0$ is the union of all intervals in which we have put plus sign and the solution of $f(\mathrm{x})<0$ is the union of all intervals in which we have put the minus sign.
Exponential Equations
If we have an equation of the form
$\begin{aligned} & a^{x}=b \text { where } a>0, \text { then } \\ & x \in \varphi \text { if } b \leq 0 ; \hspace {1.3 cm} x=\log _{a} b \text { if } b>0, a \neq 1 \\ & x \in \varphi \text { if } a=1, b \neq 1 ; \quad x \in R, \text { if } a=1, b=1 \end{aligned}$
Lagrange’s Identity
If $\mathrm{a} _{1}, \mathrm{a} _{2}, \mathrm{a} _{3}, \mathrm{~b} _{1}, \mathrm{~b} _{2}, \mathrm{~b} _{3} \in \mathrm{R}$ then
$\left(a _{1}^{2}+a _{2}^{2}+a _{3}^{2}\right)\left(b _{1}^{2}+b _{2}^{2}+b _{3}^{2}\right)-\left(a _{1} b _{1}+a _{2} b _{2}+a _{3} b _{3}\right)^{2}$
$=\left(a _{1} b _{2}-a _{2} b _{1}\right)^{2}+\left(a _{2} b _{3}-a _{3} b _{2}\right)^{2}+\left(a _{3} b _{1}-a _{1} b _{3}\right)^{2}$
Note: If $\dfrac{\mathrm{a}}{\mathrm{b}}=\dfrac{\mathrm{c}}{\mathrm{d}}=\dfrac{\mathrm{e}}{\mathrm{f}}$, then each ratio is equal to
i. $\dfrac{\mathrm{a}+\mathrm{c}+\mathrm{e}+\ldots .}{\mathrm{b}+\mathrm{d}+\mathrm{f}+\ldots}$
ii. $\left(\dfrac{\mathrm{pa}^{\mathrm{n}}+\mathrm{qc}^{\mathrm{n}}+\mathrm{re}^{\mathrm{n}}+\ldots .}{\mathrm{pb}^{\mathrm{n}}+\mathrm{qd}^{\mathrm{n}}+\mathrm{rf}^{\mathrm{n}}+\ldots .}\right)^{1 / \mathrm{n}}$ where $\mathrm{p}, \mathrm{q}, \mathrm{r}, \mathrm{n} \in \mathrm{R}$
iii. $\dfrac{\sqrt{\mathrm{ac}}}{\sqrt{\mathrm{bd}}}=\dfrac{\sqrt[n]{\mathrm{ace} \ldots}}{\sqrt[n]{\mathrm{bdf} \ldots}}$
SOLVED EXAMPLES
1. The values of $m$ for which both roots of the equation $x^{2}-m x+1=0$ are less than unity is
(a) $(-\infty,-2)$
(b) $(-\infty,-2]$
(c) $(-2, \infty)$
(d) none of these
Show Answer
Solution:
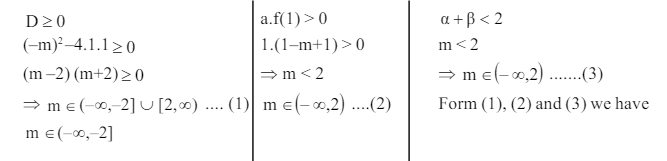
Answer: b
2. The values of $m(m \in R)$, for which both roots of the equation $x^{2}-6 m x+9 m^{2}-2 m+2=0$ exceed 3 is
(a) $(-\infty, 1]$
(b) $(-\infty, 1)$
(c) $[1, \infty)$
(d) none of these
Show Answer
Solution:
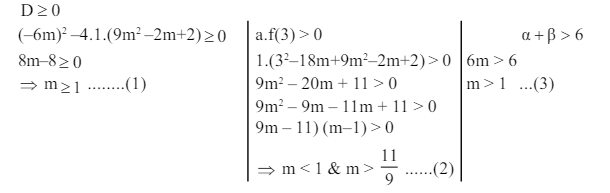
From (1), (2) and (3) $\mathrm{m} \in\left(\dfrac{11}{9}, \infty\right)$
Answer: d
3. The values of $p$ for which 6 lies between the roots of the equation $x^{2}+2(p-3) x+9=0$ is
(a) $\left(-\infty,-\dfrac{3}{4}\right)$
(b) $\left(-\infty,-\dfrac{3}{4}\right]$
(c) $(-\infty, 1]$
(d) none of these
Show Answer
Solution: $\mathrm{D}>0$
$(-2(p-3))^{2}-4.1 .9>0$
$\mathrm{p}^{2}-6 \mathrm{p}>0$
$\mathrm{p}(\mathrm{p}-6)>0$
$\mathrm{p}<0, \mathrm{p}>6$
(a) $f(6)<0$
$1 .(36+12(\mathrm{p}-3)+9))<0$
$\Rightarrow 12 \mathrm{p}+9<0$
$\mathrm{P}<\dfrac{-3}{4}$
From (1) and (2) $p \in\left(-\infty, \dfrac{-3}{4}\right)$
Answer: a
4. If $a, b, c \in R$, and the equation $a x^{2}+b x+c=0$ has no real roots, then
(a) $\quad(\mathrm{a}+\mathrm{b}+\mathrm{c})>0$
(b) $\quad \mathrm{a}(\mathrm{a}+\mathrm{b}+\mathrm{c})>0$
(c) $\quad \mathrm{b}(\mathrm{a}+\mathrm{b}+\mathrm{c})>0$
(d) $\quad \mathrm{c}(\mathrm{a}+\mathrm{b}+\mathrm{c})<0$
Show Answer
Solution:
$\mathrm{a}>0$
$f(0) \Rightarrow \mathrm{c}>0$
$f(2)>0 \Rightarrow \mathrm{a}+\mathrm{b}+\mathrm{c}>0$
$\mathrm{a} f(1)>0$ & $\mathrm{c} f(1)>0$
$\mathrm{a}(\mathrm{a}+\mathrm{b}+\mathrm{c})>0$ and $\mathrm{c}(\mathrm{a}+\mathrm{b}+\mathrm{c})>0$
$\begin{aligned} & \mathrm{a}<0 \\ & f(0)<0 \Rightarrow \mathrm{c}<0 \\ & f(1)<0 \Rightarrow \mathrm{a}+\mathrm{b}+\mathrm{c}<0 \\ & \therefore \mathrm{a} f(1)>0 \& \mathrm{c} \cdot f(1)>0 \\ & \mathrm{a}(\mathrm{a}+\mathrm{b}+\mathrm{c})>0 \text { and } \mathrm{c}(\mathrm{a}+\mathrm{b}+\mathrm{c})>0 \end{aligned}$
Answer: b
Exercise
1. If the roots of equation $x^{2}-2 a x+a^{2}+a-3$ are less than 3 , then
(a) $\mathrm{a}<2$
(b) $\mathrm{a}>4$
(c) $3<\mathrm{a}<4$
(d) $-2<\mathrm{a}<3$
Show Answer
Answer: a2. Read the following passage and answer the questions:-
$f(x)=a x^{2}+b x+c=a(x-\alpha)(x-\beta)$, where $\alpha<\beta$ are the roots of $f(x)=0$. If $\Delta=b^{2}-4 a c$ is negative, then its sign is same as that of $a$, the coefficient of $x^{2}$. If $f(x)=a(x-\alpha)(x-\beta)$, where $\alpha<\beta$, $\mathrm{a}$ is positive, then for any number $\mathrm{p}$ which lies between $\alpha$ & $\beta ; f(\mathrm{p})$ is negative and for any number $\mathrm{q}$ or $\mathrm{r}$ which do not lie between $\alpha$ & $\beta, f(\mathrm{q})$ or $f(\mathrm{r})$ both will be positive. Also if $\mathrm{a}^{2}$ $<\mathrm{x}^{2}<\mathrm{b}^{2}$, then $\mathrm{a}<\mathrm{x}<\mathrm{b}$ or $-\mathrm{b}<\mathrm{x}<-\mathrm{a}$.
i. If $\mathrm{x}^{2}-2(4 \lambda-1) \mathrm{x}+15 \lambda^{2}-2 \lambda-7>0 \forall \mathrm{x} \in \mathrm{R}$, then $\lambda \in$
(a) $(0,2)$
(c) $(2,4)$
(b) $(1,3)$
(d) none of these
ii. Let $f(\mathrm{x})$ be a quadratic expression which is positive for all real $\mathrm{x}$.If $\mathrm{g}(\mathrm{x})=f(\mathrm{x})$ $+f^{\prime}(\mathrm{x})+f^{\prime \prime}(\mathrm{x})$, then for any real $\mathrm{x}$,
(a) $\mathrm{g}(\mathrm{x})>0$
(b) $\mathrm{g}(\mathrm{x}) \geq 0$
(c) $g(x) \leq 0 \mathrm{~d}$.
(d) $\mathrm{g}(\mathrm{x})<0$
iii. The inequality $\dfrac{x^{2}-|x|-2}{2|x|-x^{2}-2}>2$ holds only if
(a) $-1<\mathrm{x}<\dfrac{-2}{3}$ only
(b) only for $\dfrac{2}{3}<x<1$
(c) $-1<\mathrm{x}<1$
(d) $-1<x<\dfrac{2}{3}$ or $\dfrac{2}{3}<x<1$
iv* for real $x$, the function $\dfrac{(x-a)(x-b)}{x-c}$ will assume all real values, provided
(a) $\mathrm{a}<\mathrm{b}<\mathrm{c}$
(b) $\mathrm{a}>\mathrm{b}>\mathrm{c}$
(c) $\mathrm{a}>\mathrm{c}>\mathrm{b}$
(d) $\mathrm{a}<\mathrm{c}<\mathrm{b}$
Show Answer
Answer: (i) c (ii) a (iii) d (iv) c,d3. Values of ’ $a$ ’ for which the roots of the equation $(a+1) x^{2}-3 a x+4 a=0(a \neq-1)$ greater than unity is
(a) $\mathrm{a} \in\left[\dfrac{-16}{7},-1\right]$
(b) $\mathrm{a} \in\left(\dfrac{-16}{7},-1\right)$
(c) $\mathrm{a} \in\left(\dfrac{-16}{7},-1\right]$
(d) none of these
Show Answer
Answer: a4.* If $x \in R$ satisfies $\left(\log _{10}(100 x)\right)^{2}+\left(\log _{10}(10 x)\right)^{2}+\log _{10} x \leq 14$, then the solution set contains the interval
(a) $(1,10]$
(b) $\left\lfloor 10^{-9 / 2}, 1\right]$
(c) $(0, \infty)$
(d) $(-1, \infty)$
Show Answer
Answer: a, b5.* If $a, b$ are the real roots of $x^{2}+p x+1=0$ and $c, d$ are the real roots of $x^{2}+q x+1=0$, then $(a-c)(b-c)(a+d)(b+d)$ is divisible by
(a) $\mathrm{a}-\mathrm{b}-\mathrm{c}-\mathrm{d}$
(b) $\mathrm{a}+\mathrm{b}+\mathrm{c}-\mathrm{d}$
(c) $\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}$
(d) $a+b-c-d$
Show Answer
Answer: c, d6. Match the following:-
| Column I | Column II | ||
|---|---|---|---|
| a. | The value of $x$ for which $\log _{e}(x-3)<1$ is | (p) | $\left(0, \dfrac{\sqrt{5}-1}{2}\right]$ |
| b. | The value of $x$ for which $\log _{1 / 2} x \geq \log _{1 / 3} x$ is | (q) | $(0,1)$ |
| c. | If $\log _{0.3}(x-1)<\log _{0.09}(x-1)$, then $x$ lies in the interval | (r) | $(2,8)$ |
| d. | If $\log _{\cos x} \sin x \geq 2$ and $x \in[0,3 \pi]$ then $\sin x$ lies is the interval | (s) | $(3,3+\mathrm{e})$ |
| (t) | $\left(0, \dfrac{\sqrt{5}+1}{2}\right]$ |
Show Answer
Answer: $\mathrm{a} \rightarrow \mathrm{s} ; \mathrm{b} \rightarrow \mathrm{q} ; \mathrm{c} \rightarrow \mathrm{r} ; \mathrm{d} \rightarrow \mathrm{p}$7. Read the paragraph and answer the questions that follow:
Let $(a+\sqrt{b})^{e(x)}+(a-\sqrt{b})^{e(x)-2 \lambda}=A$, where $\lambda \in N, A \in R$ and $a^{2}-b=1 \therefore(a+\sqrt{b})(a-\sqrt{b})=1$
i.e $\Rightarrow(a \pm \sqrt{b})=(a+\sqrt{b})^{ \pm 1}$ or $(a-\sqrt{b})^{ \pm 1}$
i. If $(4+\sqrt{5})^{[x]}+(4-\sqrt{5})^{[x]}=62$, then
(a) $\quad \mathrm{x} \in[-3,-2) \cup[1,2)$
(b) $\quad x \in[-3,2) \cup[-2,1)$
(c) $\quad \mathrm{x} \in[-2,-1) \cup[2,3)$
(d) $\quad \mathrm{x} \in[-2,3) \cup[-1,2)$
ii. Solution of $(2+\sqrt{3})^{x^{2}-2 x+1}+(2-\sqrt{3})^{x^{2}-2 x-1}=\dfrac{4}{2-\sqrt{3}}$ are
(a) $1 \pm \sqrt{3}, 1$
(b) $1 \pm \sqrt{2}, 1$
(c) $1 \pm \sqrt{3}, 2$
(d) $1 \pm \sqrt{2}, 2$
iii. The number of real solutions of the equation $(15+4 \sqrt{14})^{t}+(15-4 \sqrt{14})^{t}=30$ are where $\mathrm{t}=\mathrm{x}^{2}-2|\mathrm{x}|$
(a) 0
(b) 2
(c) 4
(d) 6
Show Answer
Answer: (i) c (ii) b (iii) c8. The maximum value of $f(x)=\dfrac{3 x^{2}+9 x+17}{3 x^{2}+9 x+7}$ is $5 \mathrm{k}+1$, Then $\mathrm{k}$ is
(a) 41
(b) 40
(c) 8
(d) none of these
Show Answer
Answer: c9. If $\dfrac{x^{2}-y z}{a}=\dfrac{y^{2}-z x}{b}=\dfrac{z^{2}-x y}{c}$, then $(x+y+z)(a+b+c)$ is
(a) $a x+b y+c z$
(b) $\mathrm{a}+\mathrm{b}+\mathrm{c}$
(c) $\dfrac{\mathrm{x}+\mathrm{y}+\mathrm{z}}{3}$
(d) none of these
Show Answer
Answer: a10. The value of $x$ satisfying the equation $|x-1|^{\log _{3} x^{2}-2 \log _{x} 9}=(x-1)^{7}$ is
(a) 3
(b) 9
(c) 27
(d) 81
Show Answer
Answer: d11. If $\left|x^{2}-9 x+20\right|>x^{2}-9 x+20$ then which is true?
(a) $\mathrm{x} \leq 4$ or $\mathrm{x} \geq 5$
(b) $4 \leq \mathrm{x} \leq 5$
(c) $4<x<5$
(d) none of these
Show Answer
Answer: c12. If $x^{2}+p x+1$ is a factor of $a x^{3}+b x+c$, then
(a) $\mathrm{a}^{2}+\mathrm{c}^{2}=-\mathrm{ab}$
(b) $\mathrm{a}^{2}-\mathrm{c}^{2}=-\mathrm{ab}$
(c) $a^{2}-c^{2}=a b$
(d) none of these
Show Answer
Answer: c13. If $\lambda \neq \mu$ and $\lambda^{2}=5 \lambda-3, \mu^{2}=5 \mu-3$, then the equation whose roots one $\dfrac{\lambda}{\mu}$ and $\dfrac{\mu}{\lambda}$ is
(a) $x^{2}-5 x-3=0$
(b) $3 x^{2}+19 x+3=0$
(c) $3 x^{2}-19 x+3=0$
(d) $x^{2}+5 x-3=0$
Show Answer
Answer: c14. If the equation $(\cos p-1) x^{2}+x(\cos p)+\sin p=0$, in the variable $x$, has real roots then ’ $p$ ’ can take any value in the interval.
(a) $(0,2 \pi)$
(b) $(-\pi, 0)$
(c) $\left(\dfrac{-\pi}{2}, \dfrac{\pi}{2}\right)$
(d) $(0, \pi)$
Show Answer
Answer: d15. If $(\cos \alpha+i \sin \alpha)$ is a root of the equation $a^{2}+b x+c=0, a, b, c \in R$, then
(a) $a \cos 2 \alpha+b \sin \alpha+c=0$
(b) $a \cos 2 \alpha+b \cos \alpha+c=0$
(c) $a \sin 2 \alpha+b \sin \alpha+c=0$
(d) none of these










