Quadratic equations

The general form of a quadratic equation over real numbers is $a x^{2}+b x+c=0$ where $a, b, c \in R$ & a $\neq$ 0 . The solution of the quadrati equation $\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}=0$ is given by

$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$. The expression $b^{2}-4 a c$ is called the discriminant of the quadratic equation and is denoted by D.

Nature of roots :

For the quadratic equation $a x^{2}+b x+c=0$, where $a, b, c \in R$ and $a \neq 0$, then

Note 1: If $\alpha$ is a root of $f(\mathrm{x})=0$, then the polynomial $f(\mathrm{x})$ is exactly divisible by $\mathrm{x}-\alpha$ or $(\mathrm{x}-\alpha)$ is a factor of $f(\mathrm{x})$ and vice versa.

Note 2: $ax^{2}+b x+c=0$ cannot have three different roots. If it has, then the equation becomes an identity in $\mathrm{x}$. ie, $\mathrm{a}=\mathrm{b}=\mathrm{c}=0$.

Relation between roots and coefficients

If $\alpha _{1}, \alpha _{2}, \ldots \ldots \ldots \alpha _{n}$ are roots of the equation $f(x)=a _{n} x^{n}+a _{n-1} x^{n-1}+a _{n-2} x^{n-2}+\ldots \ldots \ldots a _{2} x^{2}+a _{1} x+a _{0}=0$, then $f(\mathrm{x})=\mathrm{a} _{\mathrm{n}}\left(\mathrm{x}-\alpha _{1}\right)\left(\mathrm{x}-\alpha _{2}\right)\left(\mathrm{x}-\alpha _{3}\right)$…………………$\left(\mathrm{x}-\alpha _{\mathrm{n}}\right)$

$\therefore \mathrm{a} _{\mathrm{n}} \mathrm{x}^{\mathrm{n}}+\mathrm{a} _{\mathrm{n}-1} \mathrm{x}^{\mathrm{n}-1}+\mathrm{a} _{\mathrm{n}-2} \mathrm{x}^{\mathrm{n}-2}+\ldots \ldots \ldots \ldots+\mathrm{a} _{2} \mathrm{x}^{2}+\mathrm{a} _{1} \mathrm{x}+\mathrm{a} _{0}=\mathrm{a} _{\mathrm{n}}\left(\mathrm{x}-\alpha _{1}\right)\left(\mathrm{x}-\alpha _{2}\right)………..\left(\mathrm{x}-\alpha _{n}\right)$

Comparing the coefficients of like powers of $x$ an both sides, we get,

$\begin{aligned} & S _{1}=\alpha _{1}+\alpha _{2}+\ldots \ldots \ldots \ldots+\alpha _{n}=\sum \alpha _{i}=\dfrac{-a _{n-1}}{a _{n}}=\dfrac{- \text { coeft. of } x^{n-1}}{\text { coeft of } x^{n}} \\ & S _{2}=\alpha _{1} \alpha _{2}+\alpha _{1} \alpha _{3}+\ldots \ldots \ldots \ldots \ldots \sum\limits _{i \neq j} \alpha _{i} \alpha _{j}=(-1)^{2} \dfrac{a _{n-2}}{a _{n}}=(-1)^{2} \dfrac{\text { coeft. of } x^{n-2}}{\text { coeft of } x^{n}} \\ & S _{3}=\alpha _{1} \alpha _{2} \alpha _{3}+\alpha _{2} \alpha _{3} \alpha _{4}+\ldots \ldots \ldots \ldots \ldots \sum\limits _{i \neq j \neq k} \alpha _{i} \alpha _{j} \alpha _{k}=(-1)^{3} \dfrac{a _{n-3}}{a _{n}}=(-1)^{3} \dfrac{\text { coeft. of } x^{n-3}}{\text { coeft of } x^{n}} \end{aligned}$

$\mathrm{S} _{\mathrm{n}}=\alpha_1 \alpha_2 \alpha_3 \ldots \ldots \ldots \ldots \ldots \ldots \alpha _{\mathrm{n}}=(-1)^{\mathrm{n}} \dfrac{\mathrm{a}_0}{\mathrm{a} _{\mathrm{n}}}=(-1)^{\mathrm{n}} \dfrac{\text { constant term }}{\text { coeft of } \mathrm{x}^{\mathrm{n}}}$

Here $\mathrm{S} _{\mathrm{k}}$ denotes the sum of the products of the roots taken ’ $\mathrm{k}$ ’ at a time.

Particular cases :-

Quadratic equation:

If $\alpha$ & $\beta$ are the roots of the quadratic equation $\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}=0$, then $\mathrm{S} _{1}=\alpha+\beta=\dfrac{-\mathrm{b}}{\mathrm{a}},$ & $\mathrm{~S} _{2}=\alpha \beta=\dfrac{\mathrm{c}}{\mathrm{a}}$

Cubic equation:

If $\alpha, \beta, \gamma$ are the roots of the cubic equation $\mathrm{ax}^{3}+\mathrm{bx}^{2}+\mathrm{cx}+\mathrm{d}=0$, then

$\begin{aligned} & \mathrm{S} _{1}=\alpha+\beta+\gamma=\dfrac{-b}{\mathrm{a}} \\ & \mathrm{S} _{2}=\alpha \beta+\beta \alpha+\gamma \alpha=(-1)^{2} \dfrac{\mathrm{c}}{\mathrm{a}}=\dfrac{\mathrm{c}}{\mathrm{a}} \\ & \mathrm{S} _{3}=\alpha \beta \gamma=(-1)^{3} \dfrac{\mathrm{d}}{\mathrm{a}}=\dfrac{-\mathrm{d}}{\mathrm{a}} \end{aligned}$

Biquadratic equation:

If $\alpha, \beta, \gamma, \delta$ are roots of the biquadratic equation $\mathrm{ax}^{4}+\mathrm{bx}^{3}+\mathrm{cx}^{2}+\mathrm{dx}+\mathrm{e}=0$,

then

$\begin{aligned} & \mathrm{S} _{1}=\alpha+\beta+\gamma+\delta=\dfrac{-\mathrm{b}}{\mathrm{a}} \\ & \mathrm{S} _{2}=\alpha \beta+\beta \gamma+\alpha \delta+\beta \gamma+\beta \delta+\gamma \delta=(-1)^{2} \dfrac{\mathrm{c}}{\mathrm{a}} \\ & \text { Or } \mathrm{S} _{2}=(\alpha+\beta)(\gamma+\delta)+\alpha \beta+\gamma \delta=\dfrac{\mathrm{c}}{\mathrm{a}} \\ & \mathrm{S} _{3}=\alpha \beta \gamma+\beta \gamma \delta+\gamma \delta \alpha+\alpha \beta \delta=(-1)^{3} \dfrac{\mathrm{d}}{\mathrm{a}} \\ & \text { Or } \mathrm{S} _{3}=\alpha \beta(\gamma+\delta)+\gamma \delta(\alpha+\beta)=\dfrac{-\mathrm{d}}{\mathrm{a}} \\ & \text { and } \mathrm{S} _{4}=\alpha \beta \gamma \delta=(-1)^{4} \dfrac{\mathrm{e}}{\mathrm{a}}=\dfrac{\mathrm{e}}{\mathrm{a}} \end{aligned}$

Formation of a polynomial equation from given roots

If $\alpha _{1}, \alpha _{2}, \alpha _{3}, \ldots \ldots \ldots \ldots \ldots, \alpha _{\mathrm{n}}$ are the roots of an $\mathrm{n}^{\text {th }}$ degree equation, then the equation is $\mathrm{x}^{\mathrm{n}}-\mathrm{S} _{1} \mathrm{x}^{\mathrm{n}-1}+\mathrm{S} _{2} \mathrm{x}^{\mathrm{n}-2}-\mathrm{S} _{3} \mathrm{x}^{\mathrm{n}-3}+\ldots \ldots \ldots \ldots \ldots+(-1)^{\mathrm{n}} \mathrm{S} _{\mathrm{n}}=0$ where $\mathrm{S} _{\mathrm{k}}$ denotes the sum of the products of roots taken $\mathrm{k}$ at a time.

Particular cases

Quadratic equation :

If $\alpha, \beta$ are the roots of a quadratic equation, then the equation is $x^{2}-S _{1} x+S _{2}=0$ ie, $x^{2}-(\alpha+\beta) x+\alpha \beta=0$.

Cubic equation :

If $\alpha, \beta, \gamma$ are the roots of a cubic equation. Then the equation is, $\mathrm{x}^{3}-\mathrm{S} _{1} \mathrm{x}^{2}+\mathrm{S} _{2} \mathrm{x}-\mathrm{S} _{3}=0$ ie, $\mathrm{x}^{3}-(\alpha+\beta+\gamma) \mathrm{x}^{2}+(\alpha \beta+\beta \gamma+\gamma \alpha) \mathrm{x}-\alpha \beta \gamma=0.$

Biquadratic equation :

If $\alpha, \beta, \gamma, \delta$ are the roots of a biquadratic equation, then the equation is $\mathrm{x}^{4}-\mathrm{S} _{1} \mathrm{x}^{3}+\mathrm{S} _{2} \mathrm{x}^{2}-\mathrm{S} _{3} \mathrm{x}+\mathrm{S} _{4}=0$

i e, $x^{4}-(\alpha+\beta+\gamma+\delta) x^{3}+(\alpha \beta+\beta \gamma+\gamma \delta+\alpha \delta+\beta \delta+\alpha \gamma) x^{2}-$ $(\alpha \gamma \beta+\alpha \beta \delta+\beta \gamma \delta+\alpha \gamma \delta) x+\alpha \beta \gamma \delta=0$.

Quadratic Expression :

An expression of the form $\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}$, where $\mathrm{a}, \mathrm{b}, \mathrm{c} \in \mathrm{R}$ & $\mathrm{a} \neq 0$ is called a quadratic expression in $\mathrm{x}$. So in general quadrati expression is represented as: $f(\mathrm{x})=\mathrm{a} \mathrm{x}^{2}+\mathrm{bx}+\mathrm{c}$ or $\mathrm{y}=$ $a x^{2}+b x+c$.

Graph of a quadratic Expression

Let $\mathrm{y}=\mathrm{a} \mathrm{x}^{2}+\mathrm{bx}+\mathrm{c}$ where $\mathrm{a} \neq 0$.

Then $y=a\left(x^{2}+\dfrac{b}{a} x+\dfrac{c}{a}\right) \Rightarrow y=a\left(x^{2}+\dfrac{b x}{a}+\dfrac{b^{2}}{4 a^{2}}+\dfrac{c}{a}-\dfrac{b^{2}}{4 a^{2}}\right)$

$\Rightarrow y+\dfrac{b^{2}-4 a c}{4 a}=a\left(x+\dfrac{b}{2 a}\right)^{2} \Rightarrow y+\dfrac{D}{4 a}=a\left(x+\dfrac{b}{2 a}\right)^{2}$

Let $y+\dfrac{D}{4 a}=Y$ & $x+\dfrac{b}{2 a}=X$

$\therefore \mathrm{Y}=\mathrm{aX}^{2}$ or $\mathrm{X}^{2}=\dfrac{\mathrm{Y}}{\mathrm{a}}$

Clearly it is the equation of a parabola having its vertex at $\left(\dfrac{-b}{2 a}, \dfrac{-D}{4 a}\right)$.

If $\mathrm{a}>0$, then the parabola open upwards.

If $a<0$, then the parabola open downwards.

Sign of quadratic Expression

(1) The parabola will intersect the $x$-axis in two distinct points if $D>0$.

(i) $\quad \mathrm{a}>0$

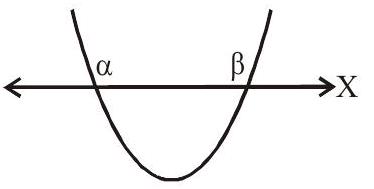
Let $f(x)=0$ have 2 real roots

$\alpha$ & $\beta(\alpha<\beta)$. Then $f(\mathrm{x})>0$

$\forall \mathrm{x} \in(-\infty, \alpha) \cup(\beta \infty)$ and $f(\mathrm{x})<0$

$\forall \mathrm{x} \in(\alpha, \beta)$

(ii) $\quad \mathrm{a}<0$

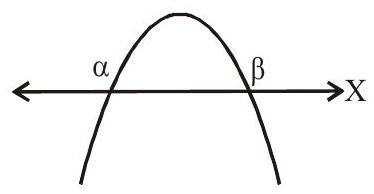
Let $f(\mathrm{x})=0$ have 2 real roots

$\alpha$ & $\beta(\alpha<\beta)$ Then $f(\mathrm{x})<0$

$\forall \mathrm{x} \in(-\infty, \alpha) \cup(\beta \infty)$

& $f(\mathrm{x})>0$ for all $\mathrm{x} \in(\alpha, \beta)$

(2) The parabola will touch the $x$-axis at one point if $D=0$

(i) $\quad \mathrm{a}>0$

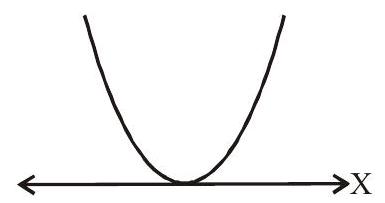
$f(\mathrm{x}) \geq 0 \forall \mathrm{x} \in \mathrm{R}$

(ii) $\mathrm{a}<0$

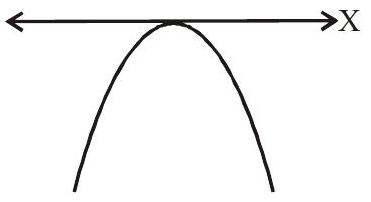
$f(\mathrm{x}) \leq 0 \forall \mathrm{x} \in \mathrm{R}$

(3) The parabola will not intersect $\mathrm{x}$-axis if $\mathrm{D}<0$.

(i) $\mathrm{a}>0$

(ii) $\mathrm{a}<0$

$f(\mathrm{x})>0 \forall \mathrm{x} \in \mathrm{R}$

$f(\mathrm{x})<0 \forall \mathrm{x} \in \mathrm{R}$

NOTE : Condition that a quadratic function $f(\mathrm{x}, \mathrm{y})=\mathrm{ax}^{2}+2 \mathrm{hxy}+\mathrm{by}^{2}+2 \mathrm{gx}+2 f \mathrm{y}+\mathrm{c}$ may be resolved into two linear factions is that

$a b c+2 f g h-a f^{2}-b^{2}-c h^{2}=\left|\begin{array}{lll}\mathrm{a} & \mathrm{h} & \mathrm{g} \\ \mathrm{h} & \mathrm{b} & \mathrm{f} \\ \mathrm{g} & \mathrm{f} & \mathrm{c}\end{array}\right|=0$

NOTE :

(i) For $\mathrm{a}>0, f(\mathrm{x})=\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}$ has least value at $\mathrm{x}=\dfrac{-\mathrm{b}}{2 \mathrm{a}}$. This least value is given by $\dfrac{-\mathrm{D}}{4 \mathrm{a}}$

(ii) For $\mathrm{a}<0, f(\mathrm{x})=\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}$ has greatest value at $\mathrm{x}=\dfrac{-\mathrm{b}}{2 \mathrm{a}}$. This greatest value is given by $\dfrac{-\mathrm{D}}{4 \mathrm{a}}$

Solved Examples

1. If $\alpha, \beta$ are roots of $a x^{2}+b x+c=0 ; \alpha+h$ and $\beta+h$ are roots of $\mathrm{px}^{2}+q x+r=0$ and $D _{1}, D _{2}$ are their discriminants, then $\mathrm{D} _{1}: \mathrm{D} _{2}=$

(a) $\dfrac{\mathrm{a}^{2}}{\mathrm{p}^{2}}$

(b) $\dfrac{b^{2}}{q^{2}}$

(c) $\dfrac{\mathrm{c}^{2}}{\mathrm{r}^{2}}$

(d) None of these

2. If $a \in Z$ and the equation $(x-a)(x-10)+1=0$ has integral roots, then the values of a are

(a) 10,8

(b) 12,10

(c) 12,8

(d) None of these

3. If $\alpha, \beta$ are roots of the equation $(x-a)(x-b)+c=0(c \neq 0)$, then then roots of the equation ( $x-c-$ $\alpha)(\mathrm{x}-\mathrm{c}-\beta)=\mathrm{c}$ are

(a) $a$ and $b+c$

(b) $a+\mathrm{c}$ and $b$

(c) $a+c$ and $b+c$

(d) None of these

4. Let $\Delta^{2}$ be the discriminant and $\alpha, \beta$ be the roots of the equation $\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}=0$. Then $2 \mathrm{a} \alpha+\Delta$ and $2 \mathrm{a} \beta-\Delta$ can be roots of the equation

(a) $\mathrm{x}^{2}+2 \mathrm{bx}+\mathrm{b}^{2}=0$

(b) $\mathrm{x}^{2}-2 \mathrm{bx}+\mathrm{b} 2=0$

(c) $x^{2}+2 b x-3 b^{2}-16 a c=0$

(d) $\mathrm{x}^{2}+2 \mathrm{bx}-3 \mathrm{~b}^{2}+16 \mathrm{ac}=0$

5. The polynomial equation $\left(a x^{2}+b x+c\right)\left(a x^{2}-d x-c\right)=0, a c \neq 0$ has

(a) four real roots

(b) atleast two real roots

(c) atmost two real roots

(d) No real roots

6. If $\alpha, \beta$ are roots of $x^{2}-p(x+1)-q=0$, then the value of $\dfrac{\alpha^{2}+2 \alpha+1}{\alpha^{2}+2 \alpha+q}+\dfrac{\beta^{2}+2 \beta+1}{\beta^{2}+2 \beta+q}$ is

(a) 1

(b) 2

(c) 3

(d) None of these

7. Let $\alpha, \beta, \gamma$ be the roots of the equation $x^{3}+4 x+1=0$, then $(\alpha+\beta)^{-1}+(\beta+\gamma)^{-1}+(\gamma+\alpha)^{-1}$ equals

(a) 2

(b) 3

(c) 4

(d) 5

Exercise

1. The minimum value of $f(x)=x^{2}+2 b x+2 c^{2}$ is greatest than the maximum value of $g(x)=-x^{2}-2 c x+b^{2}$, then ( $x$ being a real )

(a) $|\mathrm{c}|>\dfrac{|\mathrm{b}|}{\sqrt{3}}$

(b) $\dfrac{|\mathrm{c}|}{\sqrt{2}}>|\mathrm{b}|$

(c) $-1<\mathrm{c}<\sqrt{2} \mathrm{~b}$

(d) Non real value of b & c exist

2. If $\mathrm{P}(\mathrm{x})$ is a polynomial of degree less than or equal to 2 and $\mathrm{S}$ is the set of all such polynomials so that $\mathrm{P}(1)=1, \mathrm{P}(0)=0$ and $\mathrm{P}^{1}(\mathrm{x})>0 \forall \mathrm{x} \in[0,1]$, then $\mathrm{S}=$

(a) $\phi$

(b) $\left\{(1-\mathrm{a}) \mathrm{x}^{2}+\mathrm{ax}, 0<\mathrm{a}<2\right\}$

(c) $\left\{(1-\mathrm{a}) \mathrm{x}^{2}+\mathrm{ax}, \mathrm{a}>0\right\}$

(d) $\left\{(1-\mathrm{a}) \mathrm{x}^{2}+\mathrm{ax}, 0<\mathrm{a}<1\right\}$

3. In the quadratic equation $\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}=0$ if $\Delta=\mathrm{b}^{2}-4 \mathrm{ac}$ and $\alpha+\beta, \alpha^{2}+\beta^{2}$ and $\alpha^{3}+\beta^{3}$ are in G.P, where $\alpha, \beta$ are the roots of the equation, then

(a) $\Delta \neq 0$

(b) $\mathrm{b} _{\Delta}=0$

(c) $\mathrm{c} _{\Delta}=0$

(d) $\Delta=0$

4. If $a, b, c$ are the sides of a triangle $A B C$ such that $x^{2}-2(a+b+c) x+3 \lambda(a b+b c+c a)=0$ has real roots, then

(a) $\lambda<\dfrac{4}{3}$

(b) $\lambda>\dfrac{5}{3}$

(c) $\lambda \in\left(\dfrac{4}{3}, \dfrac{5}{3}\right)$

(d) $\lambda \in\left(\dfrac{1}{3}, \dfrac{5}{3}\right)$

5. Let $\alpha$ & $\beta$ be the roots of $x^{2}-6 x-2=0$, with $\alpha>\beta$. If $a _{n}=\alpha^{n}-\beta^{n}$ for $n \geq 1$, then the value of $\dfrac{\mathrm{a} _{10}-2 \mathrm{a} _{8}}{2 \mathrm{a} _{9}}$ is

(a) 1

(b) 2

(c) 3

(d) 4

6. Let $(x, y, z)$ be points with integer coordinates satisfying the system of homogeneous equations, $3 \mathrm{x}-$ $y-z=0,-3 x+z=0,-3 x+2 y+z=0$. Then the number of such points for which $x^{2}+y^{2}+z^{2} \leq 100$ is…….

7. If $x^{2}-10 a x-11 b=0$ have roots $c$ & $d \cdot x^{2}-10 c x-11 d=0$ have roots $a$ & $b$, then $a+b+c+d$ is

(a) 1210

(b) 1120

(c) 1200

(d) None of these

8. If $\mathrm{t} _{\mathrm{n}}$ denotes the $\mathrm{n}^{\text {th }}$ term of an A.P. and $\mathrm{t} _{\mathrm{p}}=\dfrac{1}{\mathrm{q}}$ and $\mathrm{t} _{\mathrm{q}}=\dfrac{1}{\mathrm{p}}$, then which of the following is necessarily a root of the equation $(p+2 q-3 r) x^{2}+(q+2 r-3 p) x+(r+2 p-3 q)=0$ is

(a) $t _{p}$

(b) $t _{\mathrm{q}}$

(c) $\mathrm{t} _{\mathrm{pq}}$

(d) $\mathrm{t} _{\mathrm{p}+\mathrm{q}}$

9. The curve $y=(\lambda+1) x^{2}+2$ intersect the curve $y=\lambda x+3$ in exactly one point, if $\lambda$ equals

(a) $\{-2,2\}$

(b) $\{1\}$

(c) $\{-2\}$

(d) $\{2\}$

10. Read the passage and answer the following questions.

Consider the equation $\mathrm{x}^{4}+(1-2 \mathrm{k}) \mathrm{x}^{2}+\mathrm{k}^{2}-1=0$ where $\mathrm{k}$ is real. If $\mathrm{x}^{2}$ is imaginary, or $\mathrm{x}^{2}<0$, the equation has no real roots. If $\mathrm{x}^{2}>0$, the equation has real roots.

(i)* The equation has no real roots if $\mathrm{k} \in$

(a) $(-\infty-1)$

(b) $(-1,1)$

(c) $\left(1, \dfrac{5}{4}\right)$

(d) $\left(\dfrac{5}{4}, \infty\right)$

(ii) The equation has only two real roots if $\mathrm{k} _{\in}$

(a) $(-\infty-1)$

(b) $(0,1)$

(c) $(1,2)$

(d) $(-1,1)$

(iii) The equation has four real roots if $\mathrm{k} \in$

(a) $(-\infty, 0)$

(b) $(-1,1)$

(c) $\left(1, \dfrac{5}{4}\right)$

(d) $(1, \infty)$

11. If $\alpha, \beta$ are the roots of the equation $a x^{2}+b x+c=0$, then the value of $\left|\begin{array}{ccc}1 & \cos (\beta-\alpha) & \cos \alpha \\ \cos (\alpha-\beta) & 1 & \cos \beta \\ \cos \alpha & \cos \beta & 1\end{array}\right|$ is

(a) $\sin (\alpha+\beta)$

(b) $\sin \alpha \sin \beta$

(c) $1+\cos (\alpha+\beta)$

(d) None of these

12.* If $(1+k) \tan ^{2} x-4 \tan x-1+k=0$ has real roots, then

(a) $\mathrm{k}^{2} \leq 5$

(b) $\tan \left(\mathrm{x} _{1}+\mathrm{x} _{2}\right)=2$

(c) for $\mathrm{k}=2, \mathrm{x} _{1}=\dfrac{\pi}{4}$

(d) for $\mathrm{k}=1, \mathrm{x} _{1}=0$

13. If $p, q \in\{1,2,3,4\}$, the number of equations of the form $\mathrm{px}^{2}+q x+1=0$ having real roots is

(a) 15

(b) 9

(c) 7

(d) 8

14. In ${ } _{\Delta} \mathrm{PQR} \angle \mathrm{R}=\dfrac{\pi}{2}$. If $\tan \dfrac{\mathrm{p}}{2}$ & $\tan \dfrac{\mathrm{Q}}{2}$ are the roots of the equation $\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}=0(\mathrm{a} \neq 0)$ then

(a) $\mathrm{a}+\mathrm{b}=\mathrm{c}$

(b) $\mathrm{b}+\mathrm{c}=0$

(c) $a+\mathrm{c}=\mathrm{b}$

(d) $\mathrm{b}=\mathrm{c}$