Complex Numbers - Rotation Theorem (Lecture-02)
GEOMETRY OF COMPLEX NUMBERS
1.
Distance between two complex numbers $z _{1}$ & $z _{2}$ is $\left|z _{1}-z _{2}\right|$
2. Section formula
Two points $P$ & $Q$ have affixes $z _{1}$ & $z _{2}$ respectively in the argand plane, then the affix of a point $\mathrm{R}$ dividing $\mathrm{PQ}$ is the ratio $\mathrm{m}: \mathrm{n}$
i. internally is $\dfrac{m z _{2}+n z _{1}}{m+n}$
ii. externally is $\dfrac{m z _{2}-n z _{1}}{m-n}$
iii. If $R$ is the mid point $P Q$, then affix of $R$ is $\dfrac{Z _{1}+z _{2}}{2}$
3. Special points of a triangle
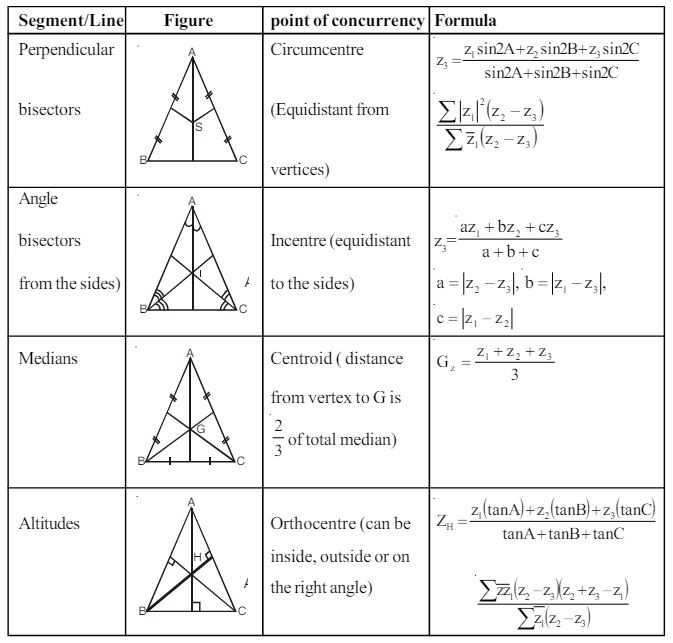
4.
Area of the triangle with vertices $\mathrm{z} _{1}, \mathrm{z} _{2}$ & $\mathrm{z} _{3}$ is $\dfrac{1}{4}\left|\overline{\mathrm{z}} _{1}\left(\mathrm{z} _{2}-\mathrm{z} _{3}\right)\right|$
5. Equilateral triangle
In equilateral $\triangle \mathrm{ABC}$, where the vertices are given by $\mathrm{z} _{1}, \mathrm{z} _{2}, \mathrm{z} _{3}$ and the circumcentre is $\mathrm{z} _{0}$,
i. $\mathrm{z} _{1}^{2}+\mathrm{z} _{2}^{2}+\mathrm{z} _{3}^{2}=3 \mathrm{z} _{0}^{2}$
ii. $\mathrm{z} _{1}^{2}+\mathrm{z} _{2}^{2}+\mathrm{z} _{3}^{2}=\mathrm{z} _{1} \mathrm{z} _{2}+\mathrm{z} _{2} \mathrm{z} _{3}+\mathrm{z} _{3} \mathrm{z} _{1}$
iii. $\dfrac{1}{z _{1}-z _{2}}+\dfrac{1}{z _{2}-z _{3}}+\dfrac{1}{z _{3}-z _{1}}=0$
6.
If $z _{1}, z _{2}, z _{3}, z _{4}$ are vertices of a parallelogram if and only if $z _{1}+z _{3}=z _{2}+z _{4}$.
7.
If $z _{1}, z _{2}, z _{3}, z _{4}$ are vertices of a square in the same order, then
i. $z _{1}+z _{3}=z _{2}+z _{4}$
ii. $\quad\left|z _{1}-z _{2}\right|=\left|z _{2}-z _{3}\right|=\left|z _{3}-z _{4}\right|=\left|z _{4}-z _{1}\right|$
iii. $\left|z _{1}-z _{3}\right|=\left|z _{2}-z _{4}\right|$
iv. $\dfrac{\left|z _{1}-z _{3}\right|}{\left|z _{2}-z _{4}\right|}$ is purely imaginary
8.
Equation of the straight line joining $z _{1} \& z _{2}$ is
i. $\quad \arg \left(\dfrac{z-z _{1}}{z _{2}-z _{1}}\right)=\pi$ or 0 i.e. $\left(\dfrac{z-z _{1}}{z _{2}-z _{1}}\right)$ must be real i.e. $\dfrac{z-z _{1}}{z _{2}-z _{1}}=\dfrac{\bar{z}-\bar{z} _{1}}{\bar{z} _{2}-\bar{z} _{1}}$ or
$\left|\begin{array}{ccc} \mathrm{z} & \overline{\mathrm{z}} & 1 \\ \mathrm{z} _{1} & \overline{\mathrm{z}} _{1} & 1 \\ \mathrm{z} _{2} & \overline{\mathrm{z}} _{2} & 1 \end{array}\right|=0 \text { (non-parametric form) }$
ii. $\quad \mathrm{z}=\lambda \mathrm{z} _{1}+(1-\lambda) \mathrm{z} _{2}$ (parametric form)
iii. General equation of a line is $\bar{a} z+a \bar{z}+b=0$ where $b \in R$.
Note: Condition for 3 points $z _{1}, z _{2}, z _{3}$ to be collinear is that $\arg \dfrac{z _{3}-z _{1}}{z _{3}-z _{2}}=0$ or $\pi$ Two points $z _{1} & z _{2}$ lie on the same side or opposite side of the line $\bar{a} z+a \bar{z}+b=0$ according as $\overline{\mathrm{az}} \mathrm{z} _{1}+\mathrm{a} \overline{\mathrm{z}} _{1}+\mathrm{b}$ and $\overline{\mathrm{a}} \mathrm{z} _{2}+\mathrm{a} \overline{\mathrm{z} _{2}}+\mathrm{b}$ have same sign or opposite sign.
9.
Slope of the line segment joining $z _{1} & z _{2}$ is $\dfrac{z _{1}-z _{2}}{z _{1}-z _{2}}$. Two lines with slopes $\omega _{1} & \omega _{2}$ are
(a) perpendicular if $\omega _{1}+\omega _{2}=0$
(b) parallel if $\omega _{1}=\omega _{2}$
10.
Length of the perpendicular from $z _{1}$ to $\bar{a} \bar{z}+\bar{a} z+b=0$ is $\dfrac{a \overline{z _{1}}+\bar{a} z _{1}+b}{2|a|}$
11.
Equation of the perpendicular bisector of the line segment joining $z _{1} & z _{2}$ is $\mathrm{z}\left(\bar{z} _{1}-\bar{z} _{2}\right)+\bar{z}\left(z _{1}-z _{2}\right)=\left|z _{1}\right|^{2}-\left|z _{2}\right|^{2}$
12. Equation of a circle
i. $\left|\mathrm{z}-\mathrm{z} _{0}\right|=\mathrm{r}$ or $\overline{\mathrm{z}}-\mathrm{z} _{0} \overline{\mathrm{z}}-\overline{\mathrm{z} _{0}} \mathrm{z}+\mathrm{z} _{0} \overline{\mathrm{z} _{0}}-\mathrm{r}^{2}=0$ where $\mathrm{z} _{0}$ the centre $& \mathrm{r}$ is the radius
ii. $\quad\left|z-z _{1}\right|^{2}+\left|z-z _{2}\right|^{2}=\left|z _{1}-z _{2}\right|^{2}$ (circle described on the line joining $z _{1} & z _{2}$ as diameter)
iii. General equation of $a$ circle is $z \bar{z}+a \bar{z}+\bar{a} z+b=0$ where $b \in R$. Centre is $-a$ and radius is $\sqrt{a \bar{a}-b}$
- Four points $z _{1}, z _{2}, z _{3}, z _{4}$ are concyclic if and only if $\dfrac{\left(z _{1}-z _{3}\right)\left(z _{2}-z _{4}\right)}{\left(z _{1}-z _{4}\right)\left(z _{2}-z _{3}\right)}$ is purely real.
13. Loci in complex plane
i. $\left|z-z _{0}\right|=r$ circle with centre $z _{0} &$ radius $r$.
- $\left|\mathrm{z}-\mathrm{z} _{0}\right|<\mathrm{r}$ : interior of this circle
- $\left|z-z _{0}\right|>r$ : exterior of this circle
- $\left|\mathrm{z}-\mathrm{z} _{1}\right|=\left|\mathrm{z}-\mathrm{z} _{2}\right|$
perpendicular bisector of the segment joining $z _{1}$ & $z _{2}$
iii. $\left|z-z _{1}\right|+\left|z-z _{2}\right|=k\left\{\begin{array}{l}\text { is an ellipse if } k>\left|z _{1}-z _{2}\right| \\ \text { is a straight line if } k=\left|z _{1}-z _{2}\right|\end{array}\right.$
iv. $\quad\left|z-z _{1}\right|-\left|z-z _{2}\right|=k\left\{\begin{array}{l}\text { is a hyperbola if } k<\left|z _{1}-z _{2}\right| \\ \text { is a straight line if } k=\left|z _{1}-z _{2}\right|\end{array}\right.$
v. $\quad$ argument $\left(\dfrac{z-z _{1}}{z-z _{2}}\right)=a$, a fixed angle is a circle.
14.
Complex number as a rotation arrow in the argand plane.
Let $\mathrm{z}=\mathrm{re}^{\mathrm{i} \theta}$
$\Rightarrow \quad \mathrm{OP}=\mathrm{r}$ & $\angle \mathrm{XOP}=\theta$
$\mathrm{ze}^{\mathrm{i} \alpha}$ is a complex number whose modulus is $\mathrm{r}$ and argument $\angle \mathrm{XOP}=\theta+\alpha$. To obtain $\mathrm{ze}^{\mathrm{i} \alpha}$, rotate $\mathrm{OP}$ through an angle $\alpha$ in anticlockwise direction.
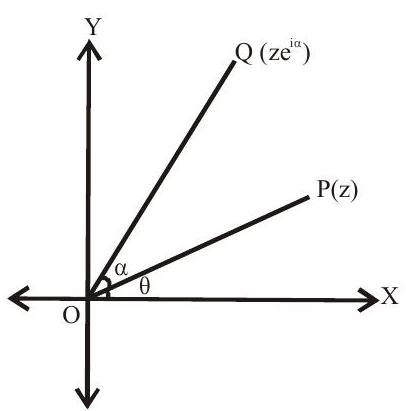
Note: Let $z _{1}$ & $z _{2}$ be two complex represented by P & Q such that $\angle \mathrm{POQ}=\alpha . \mathrm{z} _{1} \mathrm{e}^{\mathrm{i} \omega}$ is a vector of magnitude $\mathrm{OP}=\left|\mathrm{z} _{1}\right|$ along $\overline{\mathrm{OQ}} \cdot \dfrac{\mathrm{z} _{1}}{\left|\mathrm{z} _{1}\right|} \mathrm{e}^{\mathrm{i} \alpha}$ is a unit vector along $\overline{\mathrm{O}} \mathrm{Q}$.
$\therefore \quad$ A vector of magnitude $\left|z _{2}\right|=$ OQ units is given by $\left|z _{2}\right| \dfrac{z _{1}}{\left|z _{1}\right|} e^{i \omega}$
i.e. $\quad z _{2}=\dfrac{\left|z _{2}\right|}{\left|z _{1}\right|} z _{1} \mathrm{e}^{i \omega}$
Note: general formula for rotation
If $A B$ is rotated to $A C$ but $A B \neq A C$, then
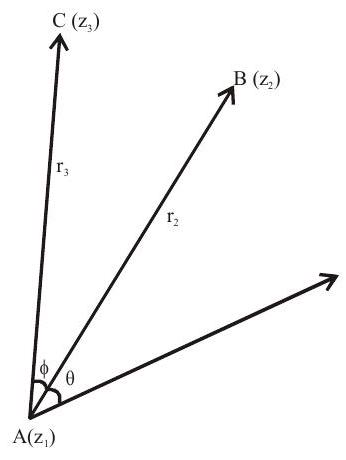
$\dfrac{\mathrm{z} _{3}-\mathrm{z} _{1}}{\mathrm{r} _{3}}=\dfrac{\mathrm{z} _{2}-\mathrm{z} _{1}}{\mathrm{r} _{2}} \mathrm{e}^{\mathrm{i} \varphi}$
1. Multiplication of $\mathrm{z}$ with $\mathrm{i}$ rotates the vector $\mathrm{z}$ through a right angle in anticlockwise direction $\left(\because i=1 \mathrm{e}^{\mathrm{i} \pi / 2}\right)$
1. Multiplication of $z$ by -1 rotates the vector $z$ through an angle of $180^{\circ}$ in anticlockwise direction.
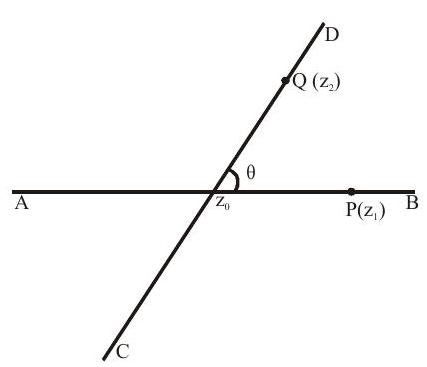
1. Let $\mathrm{AB}$ & $\mathrm{CD}$ intersect at $\mathrm{z} _{0}$. Let $\mathrm{P}\left(\mathrm{z} _{1}\right)$ & $\mathrm{Q}\left(\mathrm{z} _{2}\right)$ be two points on $A B$ & $C D$. Then the angle $\theta$ is given by $\theta=\arg \left(\dfrac{z _{2}-z _{0}}{z _{1}-z _{0}}\right)=\arg \left(z _{2}-z _{0}\right)-\arg \left(z _{1}-z _{0}\right)$
Solved Examples
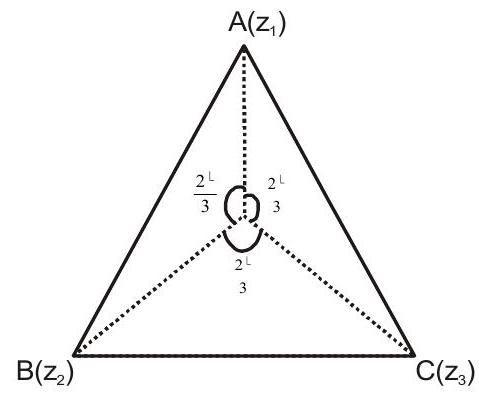
1. If $z _{1}, z _{2}, z _{3}$ are the vertices of an equilateral triangle having its circumcentre at the origin such that $\mathrm{z} _{1}=1+\mathrm{i}$, find $\mathrm{z} _{2}$ and $\mathrm{z} _{3}$.
Show Answer
Solution: Clearly, $\overrightarrow{\mathrm{OB}}$ and $\overrightarrow{\mathrm{OC}}$ are obtained by rotating $\overrightarrow{\mathrm{OA}}$ through $2 \pi / 3$ and $4 \pi / 3$ respectively.
$\therefore \quad \overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OA}} \mathrm{e}^{\mathrm{i} 4 \pi / 3}$ and, $\overrightarrow{\mathrm{OC}}=\overrightarrow{\mathrm{OA}} \mathrm{e}^{\mathrm{i} 4 \pi / 3}$
$\Rightarrow \quad \mathrm{z} _{2}=\mathrm{z} _{1} \mathrm{e}^{\mathrm{i} 2 \pi / 3}$ and, $\mathrm{z} _{3}=\mathrm{z} _{1} \mathrm{e}^{\mathrm{i} 4 \pi / 3}$
$\Rightarrow \quad \mathrm{z} _{2}=(1+\mathrm{i})(\cos 2 \pi / 3+\mathrm{i} \sin 2 \pi / 3)$ and, $\mathrm{z} _{3}=(1+\mathrm{i})(\cos 4 \pi / 3+\mathrm{i} \sin 4 \pi / 3)$
$\Rightarrow \quad \mathrm{z} _{2}=(1+\mathrm{i})(-1 / 2+\mathrm{i} \sqrt{3} / 2)$ and $\mathrm{z} _{3}=(1+\mathrm{i})(-1 / 2-\mathrm{i} \sqrt{3} / 2)$
$\Rightarrow \quad \mathrm{z} _{2}=-\left(\dfrac{\sqrt{3}+1}{2}\right)+\mathrm{i}\left(\dfrac{\sqrt{3}-1}{2}\right)$ and $\mathrm{z} _{3}=-\left(\dfrac{1-\sqrt{3}}{2}\right)-\mathrm{i}\left(\dfrac{1+\sqrt{3}}{2}\right)$
Example: 2 Let $z _{1}$ and $z _{2}$ are roots of the equation $z^{2}+p z+q=0$, where the coefficients $p$ and $q$ may be complex numbers. Let $A$ and $B$ represent $z _{1}$ and $z _{2}$ in the complex plane. If $\angle A O B=\alpha \neq 0$ and $\mathrm{OA}=\mathrm{OB}$, where $\mathrm{O}$ is origin, prove that $\mathrm{p}^{2}=4 \mathrm{q} \cos ^{2} \alpha / 0$.
Show Answer
Solution: Since $\mathrm{z}^{1}$ and $\mathrm{z}^{2}$ are roots of the equation $\mathrm{z}^{2}+\mathrm{pz}+\mathrm{q}=0$
$\therefore \quad \mathrm{z} _{1}+\mathrm{z} _{2}=-\mathrm{p}$ and $\mathrm{z} _{1} \mathrm{z} _{2}=\mathrm{q}$
Since $\mathrm{OA}=\mathrm{OB}$. So, $\overrightarrow{\mathrm{OB}}$ is obtained by rotating $\overrightarrow{\mathrm{OA}}$ in
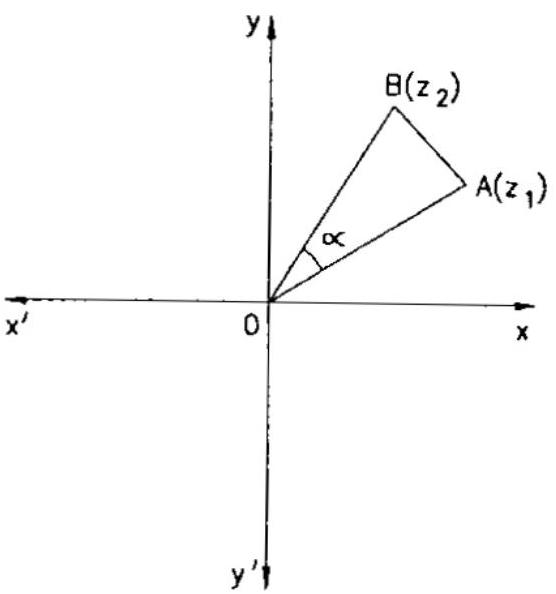
anticlockwise sense through angle $\alpha$.
$\therefore \quad \overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OA}} \mathrm{e}^{\mathrm{i} \omega}$
$\Rightarrow \quad \mathrm{z} _{2}=\mathrm{z} _{1} \mathrm{e}^{\mathrm{i} \alpha}$
$\Rightarrow \quad \dfrac{\mathrm{z} _{2}}{\mathrm{z} _{1}}=\cos \alpha+\sin \alpha$
$\Rightarrow \quad \dfrac{\mathrm{z} _{2}}{\mathrm{z} _{1}}+1=1+\cos \alpha+\mathrm{i} \sin \alpha$
$\begin{aligned} & \Rightarrow \dfrac{z _{2}+z _{1}}{z _{1}}=2 \cos \dfrac{\alpha}{2}\left(\cos \dfrac{\alpha}{2}+i \sin \dfrac{\alpha}{2}\right)=\cos \dfrac{\alpha}{2} e^{i \alpha / 2} \\ & \therefore \\ & \Rightarrow \quad \dfrac{z _{2}+z _{1}}{z _{1}}=2 \cos \dfrac{\alpha}{2} e^{i \alpha / 2} \\ & \Rightarrow \quad\left(\dfrac{z _{2}+z _{1}}{z _{1}}\right)^{2}=4 \cos ^{2} \dfrac{\alpha}{2} e^{i \alpha} \\ & \Rightarrow \quad\left(\dfrac{z _{2}+z _{1}}{z _{1}}\right)^{2}=4 \cos ^{2} \dfrac{\alpha}{2}\left(\dfrac{z _{2}}{z _{1}}\right) \\ & \Rightarrow \quad\left(z _{2}+z _{1}\right)^{2}=4 z _{1} z _{2} \cos ^{2} \dfrac{\alpha}{2} \\ & \Rightarrow \quad(-p)^{2}=4 q \cos ^{2} \dfrac{\alpha}{2} \\ & \Rightarrow \quad p^{2}=4 q \cos ^{2} \dfrac{\alpha}{2} \end{aligned}$
Example: 3 If the points $\mathrm{A}, \mathrm{B}, \mathrm{C}$ represent the complex numbers $\mathrm{z} _{1}, \mathrm{z} _{2}, \mathrm{z} _{3}$ respectively and the angles of the $\triangle \mathrm{ABC}$ at $\mathrm{B}$ and $\mathrm{C}$ are both $\left(\dfrac{\pi-\alpha}{2}\right)$. Prove that $\left(\mathrm{z} _{3}-\mathrm{z} _{2}\right)^{2}=4\left(\mathrm{z} _{3}-\mathrm{z} _{1)}\left(\mathrm{z} _{1}-\mathrm{z} _{2}\right) \sin ^{2}\left(\dfrac{\alpha}{2}\right)\right.$
Show Answer
Solution: We have,
$\begin{aligned} & \angle \mathrm{B}=\angle \mathrm{C}=\dfrac{\pi-\alpha}{2} \\ & \therefore \quad \mathrm{A}=\pi-\left(\dfrac{\pi-\alpha}{2}+\dfrac{\pi-\alpha}{2}\right)=\alpha \end{aligned}$
Since $\overrightarrow{\mathrm{AC}}$ is obtained by rotating $\overrightarrow{\mathrm{AB}}$ through angle $\alpha$.
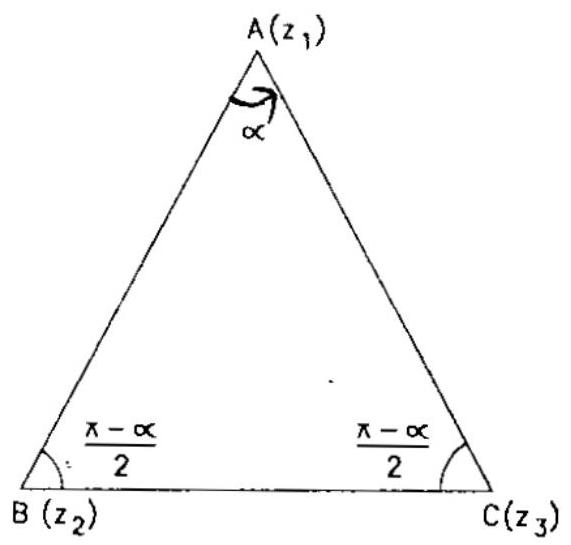 $\therefore \quad \overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{AB}} \mathrm{e}^{\mathrm{i} \alpha}$
$\therefore \quad \overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{AB}} \mathrm{e}^{\mathrm{i} \alpha}$
$\Rightarrow \quad\left(\mathrm{z} _{3}-\mathrm{z} _{1}\right)=\left(\mathrm{z} _{2}-\mathrm{z} _{1}\right) \mathrm{e}^{\mathrm{i} \alpha}$
$\Rightarrow \dfrac{\mathrm{z} _{3}-\mathrm{z} _{1}}{\mathrm{z} _{2}-\mathrm{z} _{1}}=\cos \alpha+\mathrm{i} \sin \alpha$
$\Rightarrow \dfrac{z _{3}-z _{1}}{z _{2}-z _{1}}-1=-1+\cos \alpha+i \sin \alpha$
$\Rightarrow \quad \dfrac{z _{3}-z _{2}}{z _{2}-z _{1}}=-2 \sin ^{2} \dfrac{\alpha}{2}+2 i \sin \dfrac{\alpha}{2} \cos \dfrac{\alpha}{2}$
$\Rightarrow \quad \dfrac{\mathrm{z} _{3}-\mathrm{z} _{2}}{\mathrm{z} _{2}-\mathrm{z} _{1}}=2 \mathrm{i} \sin \dfrac{\alpha}{2}\left(\cos \dfrac{\alpha}{2}+\mathrm{i} \sin \dfrac{\alpha}{2}\right)$
$\Rightarrow \quad \dfrac{\mathrm{z} _{3}-\mathrm{z} _{2}}{\mathrm{z} _{2}-\mathrm{z} _{1}}=2 \mathrm{i} \sin \dfrac{\alpha}{2} \mathrm{e}^{\mathrm{i} / / 2}$
$\Rightarrow\left(\dfrac{\mathrm{z} _{3}-\mathrm{z} _{2}}{\mathrm{z} _{2}-\mathrm{z} _{1}}\right)^{2}=4 \mathrm{i}^{2} \sin ^{2} \dfrac{\alpha}{2}\left(\mathrm{e}^{\mathrm{i} \alpha / 2}\right)^{2}$
$\Rightarrow\left(\dfrac{z _{3}-z _{2}}{z _{2}-z _{1}}\right)^{2}=-4 \sin ^{2} \dfrac{\alpha}{2} \mathrm{e}^{\mathrm{i} \alpha}$
$\Rightarrow\left(\dfrac{z _{3}-z _{2}}{z _{2}-z _{1}}\right)^{2}=-4 \sin ^{2} \dfrac{\alpha}{2}\left(\dfrac{z _{3}-z _{1}}{z _{2}-z _{1}}\right)$
$\Rightarrow \quad\left(z _{3}-z _{2}\right)^{2}=4\left(z _{3}-z _{1}\right)\left(z _{1}-z _{2}\right) \sin ^{2} \dfrac{\alpha}{2}$
Example: 4 Show that the area of the triangle on the Argand plane formed by the complex
numbers $z$, iz and $z+i z$ is $\dfrac{1}{2}|z|^{2}$
Show Answer
Solution: We have, $\mathrm{iz}=\mathrm{ze} \mathrm{e}^{\mathrm{i} \pi / 2}$
This implies that iz is the vector obtained by rotating vector
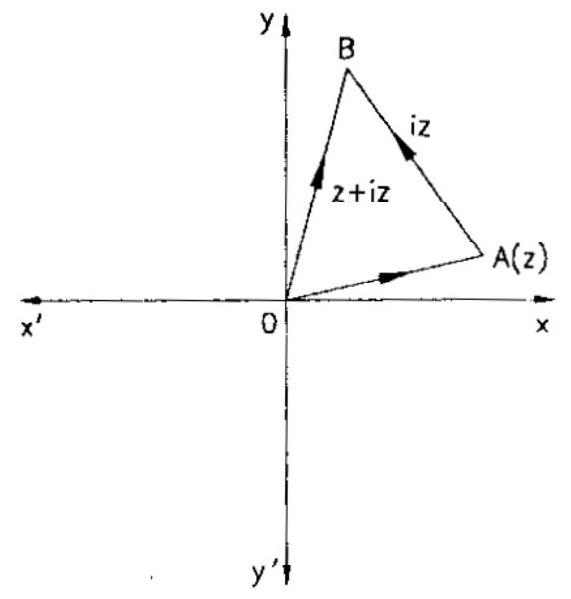
$\mathrm{z}$ in anticlockwise direction through $90^{\circ}$. Therefore, $\mathrm{OA} \perp \mathrm{AB}$. So,
Area of $\triangle \mathrm{OAB}=\dfrac{1}{2} \mathrm{OA} \times \mathrm{OB}$
$=\left.\quad \dfrac{1}{2}|z| i z\left|=\dfrac{1}{2}\right| z\right|^{2}$.
Example: 5 Let $z _{1}, z _{2}, z _{3}$ be the affixes of the vertices $A, B$ and $C$ respectively of a $\triangle A B C$. Prove that the triangle is equilateral if $z _{1}^{2}+z _{2}^{2}+z _{3}^{2}=z _{1} z _{2}+z _{2} z _{3}+z _{3} z _{1}$.
Show Answer
Solution: First, let $z _{1}, z _{2}, z _{3}$ be the affixes of the vertices $A, B, C$ of an equilateral triangle $A B C$.
Then, we have to prove that $z _{1}^{2}+z _{2}^{2}+z _{3}^{2}=z _{1} z _{2}+z _{2} z _{3}+z _{3} z _{1}$.
Since $\triangle \mathrm{ABC}$ is an equilateral triangle.
Therefore,
$\mathrm{AB}=\mathrm{BC}=\mathrm{AC}$ and $\angle \mathrm{A}=\angle \mathrm{B}=\angle \mathrm{C}=\pi / 3$.
Clearly, $\overrightarrow{\mathrm{AC}}$ can be obtained by rotating $\overrightarrow{\mathrm{AB}}$ in anticlockwise sense through $60^{\circ}$.
$\therefore \quad \mathrm{z} _{3}-\mathrm{z} _{1}=\left(\mathrm{z} _{2}-\mathrm{z} _{1}\right) \mathrm{e}^{\mathrm{i} \pi / 3}$ $\quad \quad \quad ……(1)$
Also $\overrightarrow{\mathrm{BC}}$ can be obtained by rotating $\overrightarrow{\mathrm{BA}}$ by $\dfrac{\pi}{3}$ anticlockwise
$\therefore \quad \mathrm{Z} _{2}-\mathrm{Z} _{3}=\left(\mathrm{z} _{1}-\mathrm{Z} _{3}\right) \mathrm{e}^{\mathrm{i} \pi / 3}$ $\quad \quad \quad ……(2)$
From (1) and (2)
$\left(\dfrac{z _{3}-z _{1}}{z _{2}-z _{1}}\right)=\left(\dfrac{z _{2}-z _{3}}{z _{1}-z _{3}}\right)$
Solving we get $z _{1}^{2}+z _{2}^{2}+z _{3}^{2}=z _{1} z _{2}+z _{2} z _{3}+z _{3} z _{1}$.
EXERCISE
1. The complex number $z=x+$ iy which satisfy the equation $\left|\dfrac{z-5 i}{z+5 i}\right|=1$ lie on
(a) the $\mathrm{x}$-axis
(b) the straight line $y=5$
(c) a circle passing through the origin
(d) none of these
Show Answer
Answer: a2. Let $z$ & $w$ be two complex numbers such that $|z| \leq 1,|w| \leq 1$ and $|z+i w|=|z-i w|=2$ then $z=$
(a) 1 or $\mathrm{i}$
(b) i or $-\mathrm{i}$
(c) 1 or -1
(d) $\quad$ i or -1
Show Answer
Answer: c3. Let $z _{1}$ & $z _{2}$ be the nth roots of unity which subtend a right angle at the origin, then $n$ must be of the form (where $k \in z$ )
(a) $4 \mathrm{k}+1$
(b) $4 \mathrm{k}+2$
(c) $4 \mathrm{k}+3$
(d) $4 \mathrm{k}$
Show Answer
Answer: d4. The complex number $z _{1}, z _{2} & z _{3}$ satisfying $\left(\dfrac{z _{1}-z _{3}}{z _{2}-z _{3}}\right)=\dfrac{1-i \sqrt{3}}{2}$ are the vertices of a triangle which is
(a) of area zero
(b) right angled isosceles
(c) equilateral
(d) obtuse-angled isosceles
Show Answer
Answer: c5. For all complex numbers $z _{1}, z _{2}$ satisfying $\left|z _{1}\right|=12$ and $\left|z _{2}-3-4 i\right|=5$, the minimum value of $\left|z _{1}-z _{2}\right|$ is
(a) 0
(b) 2
(c) 7
(d) 17
Show Answer
Answer: b6. The shaded region where $\mathrm{P}=(-1,0), \mathrm{Q}=(-1+\sqrt{2}, \sqrt{2}), \mathrm{R}=(-1+\sqrt{2},-\sqrt{2}), \mathrm{S}=(1,0)$ is represented by
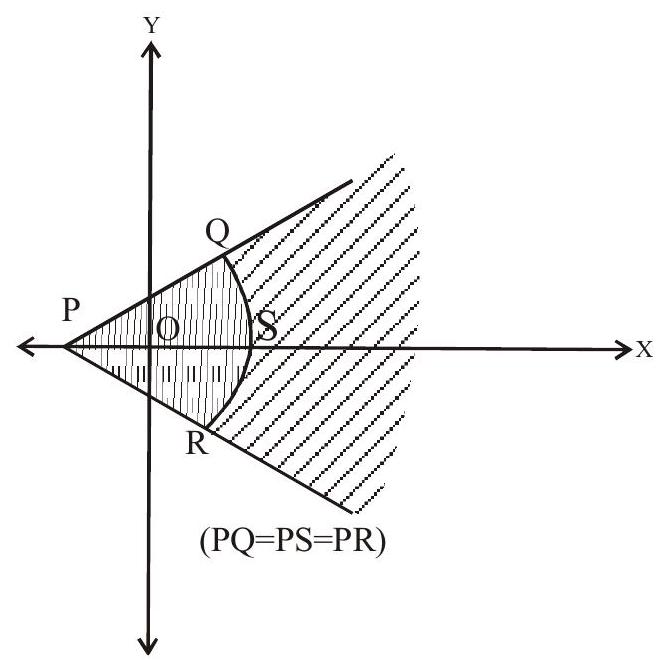
(a) $|z+1|>2,|\arg (z+1)|<\dfrac{\pi}{4}$
(b) $|\mathrm{z}+1|<2,|\arg (\mathrm{z}+1)|<\dfrac{\pi}{2}$
(c) $|z+1|>2,|\arg (z+1)|>\dfrac{\pi}{4}$
(d) $|z-1|<2,|\arg (z+1)|>\dfrac{\pi}{2}$
Show Answer
Answer: a7. A man walks a distance of 3 units from the origin towards the North-East $\left(\mathrm{N} 45^{\circ} \mathrm{E}\right)$ direction. Form there, he walks a distance of 4 units towards the North-West $\left(\mathrm{N} 45^{\circ} \mathrm{W}\right)$ direction to
reach a point $\mathrm{P}$. Then the position of $\mathrm{P}$ is the Argand plane is
(a) $3 \mathrm{e}^{\mathrm{i} \pi / 4}+4 \mathrm{i}$
(b) $(3-4 \mathrm{i}) \mathrm{e}^{\mathrm{i} \pi / 4}$
(c) $(4+3 \mathrm{i}) \mathrm{e}^{\mathrm{i} \pi / 4}$
(d) $(3+4 \mathrm{i}) \mathrm{e}^{\mathrm{i} / 4}$
Show Answer
Answer: d8. A particle $P$ starts from the point $z _{0}=1+2 i$. It moves first horizontally away from origin by 5 units and then vertically away from origin by 3 units to reach a point $z _{1}$. Form $z _{1}$ the particle moves $\sqrt{2}$ units in the direction of the vector $\hat{i}+\hat{j}$ and then it moves through an angle $\dfrac{\pi}{2}$ in anticlockwise direction on a circle with centre at origin to reach a point $z _{2}$. The point $z _{2}$ is given by
(a) $6+7 \mathrm{i}$
(b) $-7+6 \mathrm{i}$
(c) $7+6 \mathrm{i}$
(d) $-6+7 \mathrm{i}$
Show Answer
Answer: d9.* Match the following
| Column I | Column II | ||
|---|---|---|---|
| a. | The set of points $z$ satisfying $|z-i| z||=|z+i| z||$ is contained in or equal to | p. | an ellipse with eccentricity $4 / 5$ |
| b. | The set of points $z$ satisfying $|z+4|+|z-4|=0$ is contained in or equal to | q. | the set of points z $\text { satisfying } \operatorname{Im}(z)=0$ |
| c. | If $|w|=2$, then the set of points $\mathrm{z}=\mathrm{w}-\frac{1}{\mathrm{w}}$ is contained in or equal to | r. | the set of points z $\text { satisfying }|\operatorname{Im}(z)| \leq 1$ |
| d. | If $|w|=1$, then the set of points $\mathrm{z}=\mathrm{w}+\frac{1}{\mathrm{w}}$ is contained in or equal to | s. | the set of points satisfying $|\operatorname{Re}(\mathrm{z})| \leq 2$ |
| t. | the set of points z $\text { satisfying }|z| \leq 3$ |
Show Answer
Answer: $\mathrm{a} \rightarrow \mathrm{q}, \mathrm{r} ; \mathrm{b} \rightarrow \mathrm{p} ; \mathrm{c} \rightarrow \mathrm{p}, \mathrm{s}, \mathrm{t} ; \mathrm{d} \rightarrow \mathrm{q}, \mathrm{s}, \mathrm{r}, \mathrm{t}$10. If $a, b, c$ and $u, v, w$ are complex numbers representing the vertices of two triangles such that $\mathrm{c}=(1-\mathrm{r}) \mathrm{a}+\mathrm{rb}, \mathrm{w}=(1-\mathrm{r}) \mathrm{u}+\mathrm{rv}$, where $\mathrm{r}$ is a complex number, then the two triangles
(a) have the same area
(b) are similar
(c) are congruent
(d) none of these
Show Answer
Answer: b11. The locus of the centre of a circle which touches the circles $\left|z-z _{1}\right|=a$ and $\left|z-z _{2}\right|=b$ externally is
(a) an ellipse
(b) a hyperbola
(c) circle
(d) none of these
Show Answer
Answer: b12.* If one of the vertices of the square circumscribing the circle $|z-1|=\sqrt{2}$ is $2+i \sqrt{3}$, then which of the following can be a vertex of it?
(a) $1-\sqrt{3} \mathrm{i}$
(b) $-\sqrt{3} \mathrm{i}$
(c) $1+\sqrt{3} \mathrm{i}$
(d) none of these
Show Answer
Answer: a, b, c13. Read the passage and answer the following questions:
$\mathrm{A}\left(\mathrm{z} _{1}\right), \mathrm{B}\left(\mathrm{z} _{2}\right), \mathrm{C}\left(\mathrm{z} _{3}\right)$ are the vertices a triangle inscribed in the circle $|\mathrm{z}|=2$. Internal angle bisector of the angle A meets the circum circle again at $\mathrm{D}\left(\mathrm{z} _{4}\right)$.
i. Complex number representing point $\mathrm{D}$ is
(a) $\mathrm{z} _{4}=\dfrac{\mathrm{z} _{1} \mathrm{z} _{2}}{\mathrm{z} _{3}}$
(b) $\mathrm{z} _{4}=\dfrac{\mathrm{z} _{2} \mathrm{Z} _{3}}{\mathrm{z} _{1}}$
(c) $\mathrm{z} _{4}=\dfrac{\mathrm{z} _{1} \mathrm{z} _{2}}{\mathrm{z} _{3}}$
(d) none of these
ii. $\quad$ argument $\left(\mathrm{z} _{4} /\left(\mathrm{z} _{2}-\mathrm{z} _{3}\right)\right.$ is
(a) $\dfrac{\pi}{4}$
(b) $\dfrac{\pi}{3}$
(c) $\dfrac{\pi}{2}$.
(d) $\dfrac{2 \pi}{3}$
iii. For fixed positions of $\mathrm{B}\left(\mathrm{z} _{2}\right)$ and $\mathrm{C}\left(\mathrm{z} _{3}\right)$ all the bisectors(internal) of $\angle \mathrm{A}$ will pass through a fixed point which is
(a) H.M. of $z _{2}$ and $z _{3}$
(b) A.M. of $z _{2}$ and $z _{3}$
(c) G.M. of $\mathrm{z} _{2}$ and $\mathrm{z} _{3}$
(d) none of these










