TRIGONOMETRY - 1 (Trigonometric Functions)
1. (a). Measurement of angles. There are three systems of measurement of angles.
i. Sexagesimal system
Here 1 right angle $=90^{\circ}$ (degrees)
$1^{\circ}=60^{\prime}$ (minutes)
$1^{\prime}=60$ " (seconds)
ii. Centrimal system
Here 1 right angle $=100^{g}$ (grades)
$1^{\mathrm{g}}=100^{\prime}$ (minutes)
$1^{\prime}=100$ " (seconds)
iii. Circular system.
Here an angle is measured in radians. One radian corresponds to the angle subtended by arc of length ’ $r$ ’ at the centre of the circle of radius $r$. It is a constant quantity and does not depend upon the radius of the circle.
(b). Relation between the three systems
$ \pi^{\mathrm{c}}=180^{\circ}=200^{\mathrm{g}}=2 \mathrm{rt} \angle \mathrm{s} $
(c). If $\theta$ is the angle subtended at the centre of a circle of radius ’ $r$ ‘, by an arc of length $\ell$ then $\frac{\ell}{\mathrm{r}}=\theta$.
Note that here $\ell, \mathrm{r}$ are in the same units and $\theta$ is always in radians.
Convention for perpendicular and base in a right triangle
Side opposite to $90^{\circ}$ is called hypotenuse and side opposite to angle $\theta$ considered for Tratios is known as perpendicular and third remaining side is base.
T-Ratios (or Trigonometrical functions)
2. $\sin \theta=\frac{\mathrm{p}}{\mathrm{h}}, \cos \theta=\frac{\mathrm{b}}{\mathrm{h}}, \tan \theta=\frac{\mathrm{p}}{\mathrm{b}}$,
$\operatorname{cosec} \theta=\frac{\mathrm{h}}{\mathrm{p}}$,
$\sec \theta=\frac{h}{b}$ and $\cot \theta=\frac{b}{p}$
‘$\mathrm{p}$ ’ perpendicular; ’ $\mathrm{b}$ ’ base and ’ $\mathrm{h}$ ’ stands for hypotenuse.
3. Domains and ranges of trigonal metrical functions
| Function | Domain | Range |
|---|---|---|
| $\sin x$ | $\mathrm{R}$ | $[-1, 1]$ |
| $\cos x\mathrm{R}$ | $R$ | $[-1, 1]$ |
| $\tan x$ | $\mathrm{R}-\{(2 \mathrm{n}+1) \pi / 2: \mathrm{n} \in \mathrm{Z}\}$ | $R$ |
| $\operatorname{cotx}$ | $\mathrm{R}-\{\mathrm{n} \pi: \mathrm{n} \in \mathrm{Z}\}$ | $\mathrm{R}$ |
| $\sec x$ | $\mathrm{R}-\{(2 \mathrm{n}+1) \pi / 2: \mathrm{n} \in \mathrm{Z}\}$ | $(-\infty,-1] \cup[1, \infty)$ |
| $\operatorname{cosec} x$ | $\mathrm{R}-\{\mathrm{n} \pi: \mathrm{n} \in \mathrm{Z}\}$ | $(-\infty,-1] \cup[1, \infty)$ |
Signs of trigonometrical functions in different quadrants
4. (i). I quadrant: All t-ratios are positive ,
(ii). II quadrant : sin and cosec are positive and all others are negative.
(iii). III quadrant: tan and cot are positive and all others are negative.
(iv). IV quadrant: cos and sec are positive and all others are negative.
5. Values of $t$-ratios of some standard angles:
| $\theta$ | 0 | $\frac{\pi}{6}$ | $\frac{\pi}{4}$ | $\frac{\pi}{3}$ | $\frac{\pi}{2}$ | $\pi$ | $\frac{3 \pi}{2}$ | $2 \pi$ |
| $\sin$ | 0 | $\frac{1}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{\sqrt{3}}{2}$ | $1$ | $0$ | $-1$ | $0$ |
| $\cos$ | 1 | $\frac{\sqrt{3}}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{1}{2}$ | $0$ | $-1$ | $0$ | $1$ |
6. (a). Trigonometric functions of $2 \mathrm{n} \pi+\theta, \mathrm{n} \in \mathrm{Z}$ will be same as of $\theta$
$\quad $i.e., $\sin (2 n \pi+\theta)=\sin \theta, \cos (2 n \pi+\theta)=\cos \theta$, etc.
(b). Trigonometrical functions of $-\theta$, for all values of $\theta$
$\quad $ $\sin (-\theta)=-\sin \theta, \cos (-\theta)=\cos \theta$,
$\quad $ $\tan (-\theta)=-\tan \theta$
$\quad $ $\cot (-\theta)=-\cot \theta, \sec (-\theta)=\sec \theta$,
$\quad $ $\operatorname{\cosec}(-\theta)=-\operatorname{\cosec} \theta$
(c). The values of t-ratios of any angle can be expressed in terms of an angle in first quadrant.
$\quad $ Let $\mathrm{A}=\mathrm{n} \cdot \frac{\pi}{2} \pm \theta$ where $\mathrm{n} \in \mathrm{Z}, 0 \leq \theta<\frac{\pi}{2}$. Then
i. $\quad \sin \left(n \frac{\pi}{2} \pm \theta\right)= \pm \sin \theta$ if $n$ is even $=+\cos \theta$, if $\mathrm{n}$ is odd
ii. $\quad \cos \left(n \frac{\pi}{2} \pm \theta\right)= \pm \cos \theta$ if $n$ is even $=-\sin \theta$, if $\mathrm{n}$ is odd
iii. $\quad \tan \left(\mathrm{n} \frac{\pi}{2} \pm \theta\right)= \pm \tan \theta$ if $n$ is even $= \pm \cot \theta$, if $n$ is odd
iv. $\quad \cot \left(n \frac{\pi}{2} \pm \theta\right)= \pm \cot \theta$ if $n$ is even $= \pm \tan \theta$, if $n$ is odd
v. $\quad \sec \left(n \frac{\pi}{2} \pm \theta\right)= \pm \sec \theta$ if $n$ is even $= \pm \operatorname{cosec} \theta$, if $n$ is odd
vi. $\quad \operatorname{cosec}\left(n \frac{\pi}{2} \pm \theta\right)= \pm \operatorname{cosec} \theta$ if $n$ is even $= \pm \sec \theta$, if $n$ is odd
The sign R.H.S. is decided from the quardrant in which A lies.
Identities
7. $\quad$ 1. $\quad \sin \theta \cdot \operatorname{cosec} \theta=1$ or $\operatorname{cosec} \theta=\frac{1}{\sin \theta}$
$\quad$ 2. $\quad \cos \theta \cdot \sec \theta=1$ or $\sec \theta=\frac{1}{\cos \theta}$
$\quad$ 3. $\quad \tan \theta \cdot \cot \theta=1$ or $\cot \theta=\frac{1}{\tan \theta}$
$\quad$ 4. $\quad \tan \theta=\frac{\sin \theta}{\cos \theta}$
$\quad$ 5. $\quad \cot \theta=\frac{\cos \theta}{\sin \theta}$
$\quad$ 6. $\quad \sin ^{2} \theta+\cos ^{2} \theta=1$ $ \text { or } \sin ^{2} \theta=1-\cos ^{2} \theta$ $\text { or } \cos ^{2} \theta=1-\sin ^{2} \theta$
$\quad$ 7. $\quad \sec ^{2} \theta-\tan ^{2} \theta=1 \quad$ or $\sec ^{2} \theta=1+\tan ^{2} \theta$ or $\tan ^{2} \theta=\sec ^{2} \theta-1$
$\quad$ 8. $\quad \operatorname{cosec}^{2} \theta-\cot ^{2} \theta=1$ or $\operatorname{cosec}^{2} \theta=1+\cot ^{2} \theta$ or $\cot ^{2} \theta=\operatorname{cosec}^{2} \theta-1$
$\quad$ 9. $\quad \sin (A+B)=\sin A \cos \mathrm{B}+\cos \mathrm{A} \sin \mathrm{B}$
$\quad$ 10. $\quad \sin (A-B)=\sin A \cos B-\cos A \sin B$
$\quad$ 11. $\quad \cos (A+B)=\cos A \cos B-\sin A \sin B$
$\quad$ 12. $\quad \cos (\mathrm{A}-\mathrm{B})=\cos \mathrm{A} \cos \mathrm{B}+\sin \mathrm{A} \sin \mathrm{B}$
$\quad$ 13. $\quad \tan (A+B)=\frac{\tan A+\tan B}{1-\tan A \tan B}$
$\quad$ 14. $\quad \cot (\mathrm{A}+\mathrm{B})=\frac{\cot \mathrm{A} \cot \mathrm{B}-1}{\cot \mathrm{A}+\cot \mathrm{B}}$
$\quad$ 15. $\quad \tan (\mathrm{A}-\mathrm{B})=\frac{\tan \mathrm{A}-\tan \mathrm{B}}{1+\tan \mathrm{A} \tan \mathrm{B}}$
$\quad$ 16. $\quad \cot (\mathrm{A}-\mathrm{B})=\frac{\cot \mathrm{A} \cot \mathrm{B}+1}{\cot \mathrm{B}-\cot \mathrm{A}}$
$\quad$ 17. $\quad 2 \sin \mathrm{A} \cos \mathrm{B}=\sin (\mathrm{A}+\mathrm{B})+\sin (\mathrm{A}-\mathrm{B})$
$\quad$ 18. $\quad 2 \cos \mathrm{A} \sin \mathrm{B}=\sin (\mathrm{A}+\mathrm{B})-\sin (\mathrm{A}-\mathrm{B})$
$\quad$ 19. $\quad 2 \cos \mathrm{A} \cos \mathrm{B}=\cos (\mathrm{A}+\mathrm{B})+\cos (\mathrm{A}-\mathrm{B})$
$\quad$ 20. $\quad 2 \sin \mathrm{A} \sin \mathrm{B}=\cos (\mathrm{A}-\mathrm{B})-\cos (\mathrm{A}+\mathrm{B})$
$\quad$ 21. $\quad \sin \mathrm{C}+\sin \mathrm{D}=2 \sin \left(\frac{\mathrm{C}+\mathrm{D}}{2}\right) \cos \left(\frac{\mathrm{C}-\mathrm{D}}{2}\right)$
$\quad$ 22. $\quad\ sin \mathrm{C}-\sin \mathrm{D}=2 \cos \left(\frac{\mathrm{C}+\mathrm{D}}{2}\right) \sin \left(\frac{\mathrm{C}-\mathrm{D}}{2}\right)$
$\quad$ 23. $\quad\cos \mathrm{C}+\cos \mathrm{D}=2 \cos \left(\frac{\mathrm{C}+\mathrm{D}}{2}\right) \cos \left(\frac{\mathrm{C}-\mathrm{D}}{2}\right)$
$\quad$ 24. $\quad\cos \mathrm{C}-\cos \mathrm{D}-2 \sin \left(\frac{\mathrm{C}+\mathrm{D}}{2}\right) \sin \left(\frac{\mathrm{C}-\mathrm{D}}{2}\right)$,
$\quad$ 25. $\quad\sin 2 \theta=2 \sin \theta \cos \theta=\frac{2 \tan \theta}{1+\tan ^{2} \theta}$
$\quad$ 26. $\quad\cos 2 \theta=\cos ^{2} \theta-\sin ^{2} \theta=2 \cos ^{2} \theta-1$
$\quad$$ =1-2 \sin ^{2} \theta=\frac{1-\tan ^{2} \theta}{1+\tan ^{2} \theta} $
$\quad$ 27. $\quad1+\cos 2 \theta=2 \cos ^{2} \theta$ or $\cos \theta=\sqrt{\frac{1+\cos \theta}{2}}$
$\quad$ 28. $\quad1-\cos 2 \theta=2 \sin ^{2} \theta$ or $\sin \theta=\sqrt{\frac{1-\cos 2 \theta}{2}}$
$\quad$ 29. $\quad\tan \theta=\frac{1-\cos 2 \theta}{\sin 2 \theta}=\frac{\sin 2 \theta}{1+\cos 2 \theta}=\sqrt{\frac{1-\cos 2 \theta}{1+\cos 2 \theta}}$
$\quad$ 30. $\quad\tan 2 \theta=\frac{2 \tan \theta}{1-\tan ^{2} \theta}$
$\quad$ 31. $\quad\sin 3 \theta=3 \sin \theta-4 \sin ^{3} \theta$
$\quad$ 32. $\quad\cos 3 \theta=4 \cos ^{3} \theta-3 \cos \theta$
$\quad$ 33. $ \quad \tan 3 \theta=\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}$
$\quad$ 34. $\quad\sin ^{2} \mathrm{~A}-\sin ^{2} \mathrm{~B}=\sin (\mathrm{A}+\mathrm{B}) \cdot \sin (\mathrm{A}-\mathrm{B})$
$\quad$ $=\cos ^{2} \mathrm{~B}-\cos ^{2} \mathrm{~A}$
$\quad$ 35. $\quad\cos ^{2} \mathrm{~A}-\sin ^{2} \mathrm{~B}=\cos (\mathrm{A}+\mathrm{B}) \cdot \cos (\mathrm{A}-\mathrm{B})=\cos ^{2} \mathrm{~B}-\sin ^{2} \mathrm{~A}$
$\quad$ 36. $\quad\sin (A+B+C)=\sin A \cos B \cos C+\sin B \cos A \cos C$
$\quad$ $+\sin C \cos \mathrm{A} \cos \mathrm{B}-\sin \mathrm{A} \sin \mathrm{B} \sin \mathrm{C}$
$\quad$ $=\quad \cos \mathrm{A} \cos \mathrm{B} \cos \mathrm{C}[\tan \mathrm{A}+\tan \mathrm{B}+\tan \mathrm{C}-\tan \mathrm{A} \tan \mathrm{B} \tan \mathrm{C}]$
$\quad$ 37. $\quad\cos (\mathrm{A}+\mathrm{B}+\mathrm{C})=\cos \mathrm{A} \cos \mathrm{B} \cos \mathrm{C}-\sin \mathrm{A} \sin \mathrm{B} \cos \mathrm{C}$
$\quad$ $-\sin A \cos B \sin C-\cos A \sin B \sin C$
$\quad$ $=\quad \cos \mathrm{A} \cos \mathrm{B} \cos \mathrm{C}[1-\tan \mathrm{A} \tan \mathrm{B}-\tan \mathrm{B} \tan \mathrm{C}-\tan \mathrm{C} \tan \mathrm{A}]$
$\quad$ 38. $\quad\tan (\mathrm{A}+\mathrm{B}+\mathrm{C})=\frac{\tan \mathrm{A}+\tan \mathrm{B}+\tan \mathrm{C}-\tan \mathrm{A} \tan \mathrm{B} \tan \mathrm{C}}{1-\tan \mathrm{A} \tan \mathrm{B}-\tan \mathrm{B} \tan \mathrm{C}-\tan \mathrm{C} \tan \mathrm{A}}$
$\quad$ 39. $\quad\sin \alpha+\sin (\alpha+\beta)+\sin (\alpha+2 \beta)+\ldots \ldots . \sin (\alpha+\overline{n-1})$
$\quad$ $ =\frac{\sin \left\{\alpha+\left(\frac{\mathrm{n}-1}{2}\right) \beta\right\} \sin \left(\frac{\mathrm{n} \beta}{2}\right)}{\sin \left(\frac{\beta}{2}\right)} $
$\quad$ 40. $\quad \cos \alpha+\cos (\alpha+\beta)+\cos (\alpha+2 \beta)+$ $\cos (\alpha+\overline{n-1})$
$\quad=\frac{\cos \left\{\alpha+\left(\frac{\mathrm{n}-1}{2}\right) \beta\right\} \sin \left(\frac{\mathrm{n} \beta}{2}\right)}{\sin \left(\frac{\beta}{2}\right)}$
8. Some t-ration of $18^{0}, 72^{0}, 36^{0}, 54^{0}, 15^{0}, 22 \frac{1}{2}^{0}, 67 \frac{1}{2}^{0}, 7 \frac{1}{2}^{0}, 9^{0}, 81^{0}, 27^{0}, 63^{0}$ et(c).
$\quad$ 1. $\sin 18^{\circ}=\frac{\sqrt{5}-1}{4}=\cos 72^{\circ}$
$\quad$ 2. $\cos 36^{\circ}=\frac{\sqrt{5}+1}{4}=\sin 54^{\circ}$
$\quad$ 3. $\cos 18^{\circ}=\frac{\sqrt{10+2 \sqrt{5}}}{4}=\sin 72^{0}$
$\quad$ 4. $\sin 36^{\circ}=\frac{\sqrt{10-2 \sqrt{5}}}{4}=\cos 54^{0}$
$\quad$ 5. $\sin 75^{\circ}=\frac{\sqrt{3}+1}{2 \sqrt{2}}=\cos 15^{0}$
$\quad$ 6. $\tan 75^{\circ}=\frac{\sqrt{3}+1}{\sqrt{3}-1}=\cot 15^{\circ}$
$\quad$ 7. $\sin 15^{\circ}=\frac{\sqrt{3}-1}{2 \sqrt{2}}=\cos 75^{\circ}$
$\quad$ 8. $\tan 15^{\circ}=2-\sqrt{3}=\frac{\sqrt{3}-1}{\sqrt{3}+1}=\cot 75^{\circ}$
$\quad$ 9. $\tan \left(22 \frac{1^{\circ}}{2}\right)=\sqrt{2}-1=\cot \left(67 \frac{1}{2}^{\circ}\right)$
$\quad$ 10. $\tan \left(67 \frac{1}{2}^{\circ}\right)=\sqrt{2}+1=\cot \left(22 \frac{1^{\circ}}{2}\right)$
$\quad$ 11. $\cot \left(7 \frac{1}{2}^{0}\right)=\sqrt{6}+\sqrt{4}+\sqrt{3}+\sqrt{2}=(\sqrt{3}+\sqrt{2})(\sqrt{2}+1)=\tan \left(88 \frac{1^{\circ}}{2}\right)$
$\quad$ 12. $\tan \left(7 \frac{1^{0}}{2}\right)=\sqrt{6}-\sqrt{4}-\sqrt{3}+\sqrt{2}=(\sqrt{3}-\sqrt{2})(\sqrt{2}-1)=\cot \left(82 \frac{1}{2}^{0}\right)$
$\quad$ 13. $\sin 9^{0}=\frac{\sqrt{3+\sqrt{5}}+\sqrt{5-\sqrt{5}}}{4}=\cos 81^{0}$
$\quad$ 14. $\cos 9^{0}=\frac{\sqrt{3+\sqrt{5}}+\sqrt{5-\sqrt{5}}}{4}=\cos 81^{0}$
$\quad$ 15. $\sin 27^{\circ}=\frac{\sqrt{5+\sqrt{5}}-\sqrt{3-\sqrt{5}}}{4}=\cos 63^{\circ}$
$\quad$ 16. $\sin 63^{\circ}=\frac{\sqrt{5+\sqrt{5}}+\sqrt{3-\sqrt{5}}}{4}=\cos 27^{\circ}$
$\quad$ 17. $\alpha \cos \theta+b \sin \theta$ will always lie in the interval $\left\{-\sqrt{a^{2}+b^{2}}, \sqrt{a^{2}+b^{2}}\right\}$, i.e. the maximum and minimum value of $a \cos \theta+b \sin \theta$ is $\sqrt{a^{2}+b^{2}}-\sqrt{a^{2}+b^{2}}$ repectively.
$\quad$ 18. For $0<\theta<\pi$, minimum value of a $\sin \theta+b \operatorname{cosec} \theta$ is $2 \sqrt{a b}$
$\quad$ 19. For $-\pi / 2<\theta<\pi / 2$, minumum value of $a \cos \theta+b \sec \theta$ is $2 \sqrt{a b}$
$\quad$ 20. For $0<\theta<\pi / 2$ or $\pi<\theta<\frac{3 \pi}{2}$, Minimum value of $a \tan \theta+b \cot \theta$ is $2 \sqrt{a b}$
$\quad$ 21. Periods of $\sin x, \cos x, \sec x, \operatorname{cosec} x$, is $2 \pi$ and period of $\tan x$ and $\cot x$ is $\pi$.
$\quad$ 22. If a function is periodic with period $\alpha$, i.e. $\mathrm{f}(\mathrm{x}+\alpha)=\mathrm{f}(\mathrm{x})$, then period of the function
$\quad f\left(\frac{p}{q} x\right) \text { is } \frac{q}{p} \alpha$
$\quad$ 23. If $f(x)$ and $g(x)$ are periodic functions with periods $\alpha$ and $\beta$ repectively, then period of the function $f(x) \pm g(x), f(x) \cdot g(x)$ or $\frac{f(x)}{g(x)}$ is L.C.M of $\alpha \operatorname{and} \beta$
$\quad$ 24. LCM of rational numbers is $\frac{\text { LCM of numerators }}{\text { HCF of denominatiors }}$
$\quad$ 25. Expression of $\sin (\mathrm{A} / 2)$ in terms of $\sin \mathrm{A}$
$\quad \left(\sin \frac{A}{2}+\cos \frac{A}{2}\right)^{2}=1+\sin \mathrm{A}$
$\quad$ and $\left(\sin \frac{A}{2}-\cos \frac{A}{2}\right)^{2}=1-\sin \mathrm{A}$
$\quad$ so that $\sin \frac{\mathrm{A}}{2}+\cos \frac{\mathrm{A}}{2}= \pm \sqrt{1+\sin \mathrm{A}}……..(1)$
$\quad$ and $\sin \frac{A}{2}-\cos \frac{A}{2}= \pm \sqrt{1-\sin A}……..(2)$
$\quad$ By addition and subtraction, we have
$\quad$ $2 \sin \frac{\mathrm{A}}{2}= \pm \sqrt{1+\sin \mathrm{A}} \pm \sqrt{1-\sin \mathrm{A}}……(3)$
$\quad$ and $2 \cos \frac{\mathrm{A}}{2}= \pm \sqrt{1+\sin \mathrm{A}} \mp \sqrt{1-\sin \mathrm{A}}………(4)$
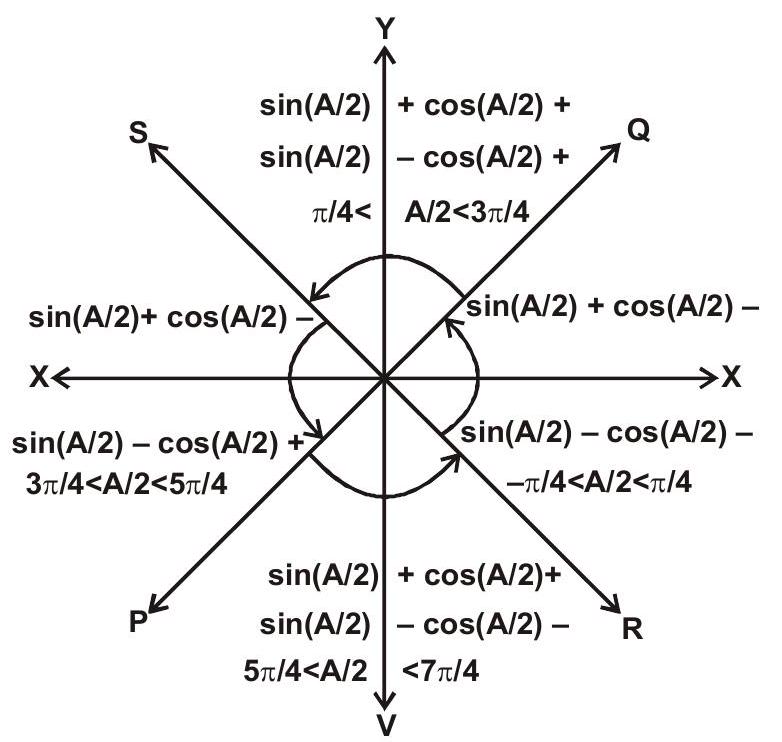
$\quad$ The ambiguities of sign in relation (1) and (2) is determined by the following diagram.
1. i. If $\sin \theta _{1}+\sin \theta _{2}+…….$ $\sin \theta _{\mathrm{n}}=\mathrm{n}$, then
$\quad\sin \theta _{1}=\sin \theta _{2}=……$ $=\sin \theta _{\mathrm{n}}=1$
$\quad$ ii. If $\cos \theta _{1}+\cos \theta _{2}+……$ $\cos \theta _{\mathrm{n}}=\mathrm{n}$, then
$\quad$ $\cos \theta _{1}=\cos \theta _{2}=……..$ $\cos \theta _{\mathrm{n}}=1$
2. i. $\sin \theta+\operatorname{cosec} \theta=2 \Rightarrow \sin \theta=1$
$\quad$ ii. $\cos \theta+\sec \theta=1 \Rightarrow \cos \theta=1$
3. i. $\sin 15^{\circ}+\cos 15^{\circ}=\sin 75^{\circ}+\cos 75^{\circ}=\sqrt{\frac{3}{2}}$
$\quad$ ii. $ \cos 15-\sin 15=\sin 75-\cos 75=\frac{1}{\sqrt{2}}$
4. i. $\quad \tan 15^{\circ}+\cot 15^{\circ}=\tan 75^{\circ}+\cot 75^{\circ}=\frac{1}{\sqrt{2}}$
$\quad$ ii. $\quad \cot 15^{\circ}-\tan 15^{\circ}=\tan 75^{\circ}-\cot 75^{\circ}=2 \sqrt{3}$
5. i. $\cos \theta-\cos \left(60^{\circ}+\theta\right)-\cos \left(60^{\circ}-\theta\right)=0$
$\quad$ ii. $\quad \cos \theta+\cos \left(120^{\circ}+\theta\right)+\cos \left(120^{\circ}-\theta\right)=0$
$\quad$ iii. $\cos \theta+\cos \left(240^{\circ}+\theta\right)+\cos \left(240^{\circ}-\theta\right)=0$
$\quad$ iv. $\sin \theta-\sin \left(60^{\circ}+\theta\right)+\sin \left(60^{\circ}-\theta\right)=0$
$\quad$ v. $\sin \theta+\sin \left(120^{\circ}+\theta\right)-\sin \left(120^{\circ}-\theta\right)=0$
$\quad$ vi. $\sin \theta+\sin \left(240^{\circ}+\theta\right)-\sin \left(240^{\circ}-\theta\right)=0$
6. i. $\tan \left(45^{\circ}+\theta\right) \tan \left(45^{\circ}-\theta\right)=1$
$\quad$ ii. $\quad \cot \left(45^{\circ}+\theta\right) \cot \left(45^{\circ}-\theta\right)=1$
7. i. If $\mathrm{A}+\mathrm{B}=45^{\circ}$ then $(1+\tan \mathrm{A})(1+\tan \mathrm{B})=2$
$\quad$ ii. If $A+B=135^{\circ}$ then $(1-\tan A)(1-\tan B)=2$
$\quad$ iii. If $\mathrm{A}+\mathrm{B}=45^{\circ}$ then $(1-\cot \mathrm{A})(1-\cot \mathrm{B})=2$
$\quad$ iv. If $\mathrm{A}+\mathrm{B}=135^{\circ}$ then $(1+\cot \mathrm{A})(1+\cot \mathrm{B})=2$
8. i. If $\cos x+\cos y=a, \sin x+\sin y=b$, then $\tan \frac{x+y}{2}=\frac{b}{a}$
$\quad$ ii. If $\cos x-\cos y=a, \sin x-\sin y=b$, then $\tan \frac{x+y}{2}=\frac{-a}{b}$
$\quad$ iii. If $\cos x-\cos y=a, \sin x+\sin y=b$, then $\tan \frac{x-y}{2}=\frac{a}{b}$
$\quad$ iv. If $\cos x+\cos y=a, \sin x-\sin y=b$, then $\tan \frac{x-y}{2}=\frac{b}{a}$
9. i. $\sin \theta \sin \left(60^{\circ}+\theta\right) \sin \left(60^{\circ}-\theta\right)=\frac{1}{4} \sin 3 \theta$
$\quad$ ii. $ \sin \theta \sin \left(120^{\circ}+\theta\right) \sin \left(120^{\circ}-\theta\right)=\frac{1}{4} \sin 3 \theta$
10. i. $\cos \theta \cos \left(60^{\circ}+\theta\right) \cos \left(60^{\circ}-\theta\right)=\frac{1}{4} \cos 3 \theta$
$\quad$ ii. $ \cos \theta \cos \left(120^{\circ}+\theta\right) \cos \left(120^{\circ}-\theta\right)=\frac{1}{4} \cos 3 \theta$
11. i. $\tan \theta \tan \left(60^{\circ}+\theta\right) \tan \left(60^{\circ}-\theta\right)=\tan 3 \theta$
$\quad$ ii. $\tan \theta \tan \left(120^{\circ}+\theta\right) \tan \left(120^{\circ}-\theta\right)=\tan 3 \theta$
12. i. $\cot \theta \cot \left(60^{\circ}+\theta\right) \cot \left(60^{\circ}-\theta\right)=\cot 3 \theta$
$\quad$ ii. $\quad \cot \theta \cot \left(120^{\circ}+\theta\right) \cot \left(120^{\circ}-\theta\right)=\cot 3 \theta$
Practice questions
1. If $\cot \alpha+\tan \alpha=m$ and $\frac{1}{\cos \alpha}-\cos \alpha=n$, then
(a) $\mathrm{m}\left(\mathrm{mn}^{2}\right)^{1 / 3}-\mathrm{n}\left(\mathrm{nm}^{2}\right)^{1 / 3}=1$
(b) $\mathrm{m}\left(\mathrm{m}^{2} \mathrm{n}\right)^{1 / 3}-\mathrm{n}\left(\mathrm{mn}^{2}\right)^{1 / 3}=1$
(c) $\mathrm{n}\left(\mathrm{mn}^{2}\right)^{1 / 3}-\mathrm{m}\left(\mathrm{nm}^{2}\right)^{1 / 3}=1$
(d) $n\left(m^{2} n\right)^{1 / 3}-m\left(m n^{2}\right)^{1 / 3}=1$
Show Answer
Solution:
Given that
$ \cot \alpha+\tan \alpha=\mathrm{m} $
$1+\tan ^{2} \alpha=\operatorname{mtan} \alpha$ $\sec ^{2} \alpha=m \tan \alpha$
$ \begin{gathered} \text { also } \frac{1-\cos ^{2} \alpha}{\cos \alpha}=n \\ \frac{\sin ^{2} \alpha}{\cos \alpha}=n \\ \tan ^{2} \alpha=n \sec \alpha \\ \operatorname{squaring}^{\tan ^{4} \alpha}=\mathrm{n}^{2} \sec ^{2} \alpha \\ =\mathrm{n}^{2} \mathrm{~m} \tan \alpha \\ \tan ^{3} \alpha=\mathrm{n}^{2} \mathrm{~m} \\ \tan ^{2}=\left(n^{2} m\right)^{1 / 3} \\ \sec ^{2} \alpha=m\left(n^{2} m\right)^{1 / 3} \\ \sec ^{2} \alpha-\tan ^{2} \alpha=1 \\ m\left(n^{2} m\right)^{1 / 3}-\left(n^{2} m\right)^{2 / 3}=1 \\ m\left(n^{2} m\right)^{1 / 3}-\left(n^{4} m^{2}\right)^{1 / 3}=1 \\ m\left(n^{2} m\right)^{1 / 3}-n\left(n m^{2}\right)^{1 / 3}=1 \end{gathered} $
Correct option is ‘a’
2. If $\cos 2 \alpha=\frac{3 \cos 2 \beta-1}{3-\cos 2 \beta}$, then $\frac{\tan \alpha}{\tan \beta}$ equals
(a) $1$
(b) $-1$
(c) $\sqrt{2}$
(d) $-\sqrt{2}$
Show Answer
Solution:
$\cos 2 \alpha=\frac{3 \cos 2 \beta-1}{3-\cos 2 \beta}$
$\frac{1-\tan ^{2} \alpha}{1+\tan ^{2} \alpha}=\frac{\frac{3\left(1-\tan ^{2} \beta\right)}{1+\tan ^{2} \beta}-1}{3-\frac{1-\tan ^{2} \beta}{1+\tan ^{2} \beta}}$
$=\frac{3-3 \tan ^{2} \beta-\tan ^{2} \beta-1}{3+3 \tan ^{2} \beta-1+\tan ^{2} \beta}$
$=\frac{2-4 \tan ^{2} \beta}{2+4 \tan ^{2} \beta}$
$\frac{1-\tan ^{2} \alpha}{1+\tan ^{2} \alpha}=\frac{1-2 \tan ^{2} \beta}{1+2 \tan ^{2} \beta}$
By componendo and dividendo we get,
$\frac{2}{-2 \tan ^{2} \alpha}=\frac{2}{-4 \tan ^{2} \beta}$
$2=\frac{\tan ^{2} \alpha}{\tan ^{2} \beta}$
$\frac{\tan \alpha}{\tan \beta}= \pm \sqrt{2}$
correct options are ‘c’ & ’d’
3. $\cot 15^{\circ}+\cot 75^{\circ}+\cot 135^{\circ}-\operatorname{cose} 30^{\circ}$ is equal to
(a) $-1$
(b) $0$
(c) $1$
(d) None of these
Show Answer
Solution:
$ \begin{aligned} & \cot 15^{\circ}+\cot 75^{\circ}+\cot 135^{\circ}-\operatorname{cosec} 30^{\circ} \\ & =\cot 15^{\circ}+\tan 15^{\circ}-\tan 45^{\circ}-\operatorname{cosec} 30^{\circ} \\ & =\frac{2}{\sin 30^{\circ}}-1-2 \\ & =4-3 \\ & =1 \\ & \because\left[\cot 15^{\circ}+\tan 15^{\circ}=\frac{\cos 15^{\circ}}{\sin 15^{\circ}}+\frac{\sin 15^{\circ}}{\cos 15^{\circ}}\right. \\ & =\frac{2}{\sin 15^{\circ} \cos 15^{\circ}} \\ & \left.=\frac{2}{\sin 30^{\circ}}\right] \end{aligned} $
Correct option is c
4. If $\sin (y+z-x), \sin (z+x-y)$, and $\sin (x+y-z)$ are in A.P then tan $x$, tany and tanz are in
(a) A.P
(b) GP
(c) HP
(d) None of these
Show Answer
Solution:
$\sin (\mathrm{y}+\mathrm{z}-\mathrm{x}), \sin (\mathrm{z}+\mathrm{x}-\mathrm{y})$ and $\sin (\mathrm{x}+\mathrm{y}-\mathrm{z})$ are in AP
$\therefore \sin (z+x-y)-\sin (y+z-x)=\sin (x+y-z)-\sin (z+x-y)$
$2 \operatorname{coszsin}(x-y)=2 \cos x \sin (y-z)$
$\sin x \cos z \cos y-\cos x \sin y \cos z=\cos x \sin y \cos z-\cos x \cos y \sin z$
Divide by cosx cosy cosz we get
$\tan x-\tan y=\tan y-\tan z$
$\tan x+\tan y=2 \tan y$
$\therefore \tan x, \tan y, \tan z$ are in A.P
Option a is correct
5. If $\alpha+\beta=90$, then the maximum value of $\sin \alpha \sin \beta$ is
(a) $1$
(b) $1 / 2$
(c) $3 / 2$
(d) None of these
Show Answer
Solution:
$ \begin{aligned} & \alpha+\beta=90 \\ & \sin \alpha \sin \beta=\sin \alpha \sin (90-\alpha) \\ & =\sin \alpha \cos \alpha \\ & =\frac{2}{2} \sin \alpha \cos \alpha \\ & =\frac{\sin 2 \alpha}{2} \end{aligned} $
We knew that $-1 \leq \sin 2 \alpha \leq 1$ or $\frac{-1}{2} \leq \frac{\sin 2 \alpha}{2} \leq \frac{1}{2}$
$\therefore$ maximum value of $\sin \alpha \sin \beta=\frac{1}{2}$
Correct option is ‘b’
Exercises
1. The least value of $\sec A+\sec B+\sec C$ in an acute angle triangle is
(a). 3
(b). 6
(c). 2
(d). none of these
Show Answer
Answer: (b)2. The sum of maximum and minimum values of $\cos ^{2} \theta-6 \sin \theta \cos \theta+3 \sin ^{2} \theta+2$ is
(a). $2 \sqrt{10}$
(b). $4$
(c). $8$
(d). none of these
Show Answer
Answer: (c)3. Let $f(\theta)=\sin \theta(\sin \theta+\sin 3 \theta)$. Then $f(\theta)$ is
(a). $ \geq 0$ only when $\theta \geq 0$
(b). $\leq 0$ only real $\theta$
(c). $\geq 0$ for all real $\theta$
(d). $\leq 0$ only when $\theta \leq 0$
Show Answer
Answer: (c)4. Let $\theta \varepsilon\left(0, \frac{\pi}{4}\right)$ and $\mathrm{t} _{1}=(\tan \theta)^{\tan \theta}, \mathrm{t} _{2}=(\tan \theta)^{\cot \theta}, \mathrm{t} _{3}=(\cot \theta)^{\tan \theta}$ and $\mathrm{t} _{4}=(\cot \theta)^{\cot \theta}$, then
(a). $\mathrm{t} _{1}>\mathrm{t} _{2}>\mathrm{t} _{3}>\mathrm{t} _{4}$
(b). $ t _{4}>t _{3}>t _{1}>t _{2}$
(c). $ \mathrm{t} _{3}>\mathrm{t} _{1}>\mathrm{t} _{2}>\mathrm{t} _{4}$
(d). $ \mathrm{t} _{2}>\mathrm{t} _{3}>\mathrm{t} _{1}>\mathrm{t} _{2}$
Show Answer
Answer: (b)5. For a positive integer n, let
$\mathrm{f} _{\mathrm{n}}(\theta)=\tan \left(\frac{\theta}{2}\right)(1+\sec \theta)(1+\sec 2 \theta)(1+\sec 4 \theta) \ldots \ldots .\left(1+\sec 2^{n} \theta\right)$. Then
(a). $\mathrm{f} _{2}\left(\frac{\pi}{16}\right)=1$
(b). $\mathrm{f} _{3}\left(\frac{\pi}{32}\right)=1$
(c). $\mathrm{f} _{4}\left(\frac{\pi}{64}\right)=1$
(d). $\mathrm{f} _{5}\left(\frac{\pi}{128}\right)=1$
Show Answer
Answer: (a, b, c, d)6. The maximum value of $\left(\cos \alpha _{1}\right)\left(\cos \alpha _{2}\right)\left(\cos \alpha _{3}\right) \ldots \ldots . .\left(\cos \alpha _{n}\right)$ under the restrictions $0 \leq \alpha _{1}, \alpha _{2} \ldots \alpha _{n} \leq \frac{\pi}{2}$ and $\left(\cot \alpha _{1}\right),\left(\cot \alpha _{2}\right) \ldots \ldots .\left(\cot \alpha _{n}\right)=1$ is
(a). $\frac{1}{2^{\mathrm{n} / 2}}$
(b). $\frac{1}{2^{n}}$
(c). $\frac{1}{2 n}$
(d). $1$
Show Answer
Answer: (a)7. If $\cos ^{4} \theta+\alpha, \sin ^{4} \theta+\alpha$ are the roots of the equaton $x^{2}+b(2 x+1)=0$ and $\cos ^{2} \theta+\beta, \sin 2 \theta+\beta$ are the roots of the equation $x^{2}+4 x+2=0$, then $b$ is equal to
(a). $1$
(b). $-1$
(c). $2$
(d). $-2$
Show Answer
Answer: (b, c)8. If in $\triangle A B C, \tan A+\tan B+\tan C=6$ and $\tan A \tan B=2$, then $\sin ^{2} A: \sin ^{2} B: \sin ^{2} C$ is
(a). $8: 9: 5$
(b). $8: 5: 9$
(c). $5: 9: 8$
(d). $5: 8: 9$
Show Answer
Answer: (b, d)9. If $\frac{\tan 3 \mathrm{~A}}{\cos \mathrm{A}}=k(k \neq 1)$
(a). $\frac{\cos \mathrm{A}}{\cos 3 \mathrm{~A}}=\frac{\mathrm{k}^{2}-1}{2 \mathrm{k}}$
(b). $\frac{\sin 3 \mathrm{~A}}{\sin \mathrm{A}}=\frac{2 \mathrm{k}}{\mathrm{k}-1}$
(c). $\mathrm{k}<\frac{1}{3}$
(d). $k>3$
Show Answer
Answer: (a, b, c, d)10. If $(\mathrm{x}-\mathrm{a}) \cos \theta+\mathrm{y} \sin \theta=(\mathrm{x}-\mathrm{a}) \cos \phi+\mathrm{y} \sin \phi=\mathrm{a}$ and $\tan \frac{\theta}{2}-\tan \frac{\phi}{2}=2 \mathrm{~b}$, then
(a). $\mathrm{y}^{2}=2 \mathrm{ax}-\left(1-\mathrm{b}^{2}\right) \mathrm{x}^{2}$
(b). $\tan \frac{\theta}{2}=\frac{1}{x}(y+b x)$
(c). $\mathrm{y}^{2}=2 \mathrm{ax}-\left(1-\mathrm{a}^{2}\right) \mathrm{x}^{2}$
(d). $\tan \frac{\phi}{2}=\frac{1}{x}(y-b x)$
Show Answer
Answer: (a, b, d)11. Passage
Increasing product with angles are in GP
$\cos \alpha \cos 2 \alpha \cos 2^{2} \alpha \ldots \ldots \cos 2^{\mathrm{n}} \alpha=\left\{\begin{array}{l}\frac{\sin 2^{\mathrm{n}} \alpha}{2^{\mathrm{n}} \sin \alpha} \text { if } \alpha \neq \mathrm{n} \pi \\ \frac{1}{2^{\mathrm{n}}}, \text { if } \alpha=\frac{\pi}{2^{\mathrm{n}}+1} \mathrm{n} \in \mathrm{I} \\ \frac{-1}{2^{\mathrm{n}}}, \text { if } \alpha=\frac{\pi}{2^{\mathrm{n}}-1}\end{array}\right\}$
On the basis of above infromation, answer the following questions.
i. The value of $\cos \frac{2 \pi}{7} \cos \frac{4 \pi}{7} \cos \frac{6 \pi}{7}$ is
(a). $\frac{-1}{2}$
(b). $\frac{1}{2}$
(c). $\frac{1}{4}$
(d). $\frac{1}{8}$
Show Answer
Answer: (d)ii. If $\alpha=\frac{\pi}{13}$ then the value of $\prod _{\mathrm{r}=1}^{6} \cos \mathrm{r} \alpha$ is
(a). $\frac{1}{64}$
(b). $\frac{-1}{64}$
(c). $\frac{1}{32}$
(d). $-\frac{1}{8}$
Show Answer
Answer: (a)iii. The value of $\sin \frac{\pi}{14} \sin \frac{3 \pi}{14} \sin \frac{5 \pi}{14} \sin \frac{7 \pi}{14} \sin \frac{9 \pi}{14} \sin \frac{16 \pi}{14} \sin \frac{13 \pi}{14}$ is
(a). $1$
(b). $\frac{1}{8}$
(c). $\frac{1}{32}$
(d). $\frac{1}{64}$
Show Answer
Answer: (d)iv. The value of $\sin \frac{\pi}{18} \sin \frac{5 \pi}{18} \sin \frac{7 \pi}{18}$ is
(a). $\frac{1}{16}$
(b). $\frac{1}{8}$
(c). $\frac{1}{8}$
(d). $-1$
Show Answer
Answer: (b)v. The value of $64 \sqrt{3} \sin \frac{\pi}{48} \cos \frac{\pi}{48} \cos \frac{\pi}{24} \cos \frac{\pi}{12} \cos \frac{\pi}{6}$ is
(a). $8$
(b). $6$
(c). $4$
(d). $-1$
Show Answer
Answer: (b)12. Matrix Match Type
| Column I | Column II |
|---|---|
| (a) In triangle $\mathrm{ABC}, 3 \sin \mathrm{A}+4 \cos \mathrm{B}=6$ and $3 \cos A+4 \sin B=1$ then $\angle \mathrm{c}$ can be | (p). $60^{\circ}$ |
| (b) In any triangle if $(\sin \mathrm{A}+\sin \mathrm{B}+\sin \mathrm{C})(\sin \mathrm{A}+\sin \mathrm{B}-\sin \mathrm{C})$ $=3 \sin \mathrm{A} \sin \mathrm{B}$ then the angle $\mathrm{c}$ | (q). $30^{\circ}$ |
| (c) If $8 \sin x \cos ^{5} x-8 \sin ^{5} x \cos x=1$ then $x=$ | (r). $165^{\circ}$ |
| (d) ‘$\mathrm{O}$ ’ is the centre of the inscribed circle in a $30^{\circ}-60^{\circ}-90^{\circ}$ triangle $A B C$ with right angled at $c$. If the circle is tangents to $A B$ at $D$ then the angle $\angle C O D$ is | (s). $75^{\circ}$ |
Show Answer
Answer: $\mathrm{a} \rightarrow \mathrm{q} ; \mathrm{b} \rightarrow \mathrm{p} ; \mathrm{c} \rightarrow \mathrm{s} ; \mathrm{d} \rightarrow \mathrm{r}$13. Assertion and Reason type questions
$\mathrm{A}$ : Both $\mathrm{A}$ and $\mathrm{R}$ individually true and $\mathrm{R}$ is the correct explanation of $\mathrm{A}$
$\mathrm{B}$ : Both $\mathrm{A}$ and $\mathrm{R}$ individually true and $\mathrm{R}$ is not the correct explanation of $\mathrm{A}$
$\mathrm{C}: \mathrm{A}$ is true but $\mathrm{R}$ is false
$\mathrm{D}: \mathrm{A}$ is false but $\mathrm{R}$ is true
If $\mathrm{A}+\mathrm{B}+\mathrm{C}=\pi$, then
(i). Assertion (A): $\cos ^{2} \mathrm{~A}+\cos ^{2} \mathrm{~B}+\cos ^{2} \mathrm{C}$ has its minimum value $3 / 4$
Reason $(\mathrm{R})$ : Maximum value of $\cos \mathrm{A} \cos \mathrm{B} \cos \mathrm{C}$ is $1 / 8$
(a) $\mathrm{A}$
(b) $\mathrm{B}$
(c) $\mathrm{C}$
(d) $\mathrm{D}$
Show Answer
Answer: (a)(ii). Assertion (A): $\sin \pi / 18$ is a roots of $8 x^{3}-6 x+1=0$
Reason (R) : For any $\theta \in R, \sin 3 \theta=3 \sin \theta-4 \sin ^{3} \theta$
(a) $\mathrm{A}$
(b) $\mathrm{B}$
(c) $\mathrm{C}$
(d) $\mathrm{D}$
Show Answer
Answer: (a)(iii). In any $\triangle \mathrm{ABC}$
Assertion (A) : $\ell$ n $\left(\cot \frac{\mathrm{A}}{2}+\cot \frac{\mathrm{B}}{2}+\cot \frac{\mathrm{C}}{2}\right)=\ell \mathrm{n} \cot \frac{\mathrm{A}}{2}+\ell \mathrm{n} \cot \frac{\mathrm{B}}{2}+\ell \mathrm{n} \cot \frac{\mathrm{C}}{2}$
Reason $(\mathrm{R}): \ell \mathrm{n}(1+\sqrt{3}+(2+\sqrt{3}))=\ell \mathrm{n} 1+\ell \mathrm{n} \sqrt{3}+\ell \mathrm{n}(2+\sqrt{3})$










