TRIGONOMETRY TRIANGLES - 2 (Properties of Triangles)
Examples
1. In a $\triangle \mathrm{ABC}$ the inradius and three exradii are $\mathrm{r}, \mathrm{r} _{1}, \mathrm{r} _{2}$ and $\mathrm{r} _{3}$ respectively. In usual notations the value of $\mathrm{r} \cdot \mathrm{r} _{1} \cdot \mathrm{r} _{2} \cdot \mathrm{r} _{3}$ is equal to
(a). $2 \Delta$
(b). $\Delta^{2}$
(c). $\frac{a b c}{4 R}$
(d). None of these
Show Answer
Solution:
$ \begin{aligned} \mathrm{r} \cdot \mathrm{r} _{1} \cdot \mathrm{r} _{2} \mathrm{r} _{3} & =\frac{\Delta}{\mathrm{s}} \cdot \frac{\Delta}{\mathrm{s}-\mathrm{a}} \cdot \frac{\Delta}{\mathrm{s}-\mathrm{b}} \frac{\Delta}{\mathrm{s}-\mathrm{c}} \\ & =\frac{\Delta^{4}}{\Delta^{2}} \\ & =\Delta^{2} \end{aligned} $
Correct option is ‘b’
2. The distance between the circumcentre and the orthocenter of a triangle $\mathrm{ABC}$ is
(a). $\mathrm{R} \sqrt{1-8 \cos \mathrm{A} \cos \mathrm{B} \cos \mathrm{C}}$
(b). $\mathrm{R} \sqrt{1+8 \cos \mathrm{A} \cos B \cos \mathrm{C}}$
(c). $\mathrm{R} \sqrt{1-4 \cos \mathrm{A} \cos \mathrm{B} \cos \mathrm{C}}$
(d). None of these
Show Answer
Solution:
Let $\mathrm{O} \& \mathrm{P}$ be circumcenter and orthocentre respectively of $\triangle \mathrm{ABC}$
$\mathrm{OF} \perp \mathrm{AB}$.
We have $\angle \mathrm{OAF}=90^{\circ}-\mathrm{C}(\because \angle \mathrm{AOF}=\angle \mathrm{C})$
$ =\angle \mathrm{PAE}(\operatorname{In} \triangle \mathrm{ADC}) $
$ \begin{aligned} & \angle \mathrm{OAP}=\angle \mathrm{A}-\angle \mathrm{OAF}-\angle \mathrm{PAE} \\ & =\angle \mathrm{A}-\left(90^{\circ} \angle \mathrm{C}\right)-\left(90^{\circ} \angle \mathrm{C}\right) \\ & =\angle \mathrm{A}+2 \angle \mathrm{C}-180^{\circ} \\ & =\angle \mathrm{A}+2 \angle \mathrm{C}-(\angle \mathrm{A}+\angle \mathrm{B}+\angle \mathrm{C}) \\ & =\angle \mathrm{C}-\angle \mathrm{B} \end{aligned} $
$\mathrm{OA}=\mathrm{R}$ (circum radius) and $\mathrm{PA}=2 \mathrm{R} \cos \mathrm{A}$
In $\triangle$ OAP
$ \mathrm{OP}^{2}=\mathrm{OA}^{2}+\mathrm{PA}^{2}-2(\mathrm{OA})(\mathrm{PA}) \operatorname{COS}(\mathrm{C}-\mathrm{B}) $
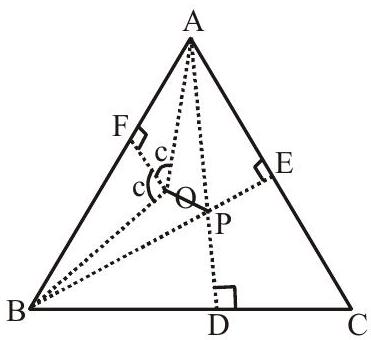
$ =R^{2}+4 R^{2} \cos ^{2} A-4 R^{2} \cos A \cos (C-B) $
$ \begin{aligned} & =R^{2}+4 R^{2} \cos A(\cos A-\cos (C-B) \\ & =R^{2}+4 R^{2} \cos A(-\cos (B+C)-\cos (C-B)) \\ & =R^{2}-4 R^{2} \cos A(\cos (B+C)+\cos (C-B)) \\ & =R^{2}-4 R^{2} \cos A(2 \cos B \cos C) \\ & =R^{2}-8 R^{2} \cos A \cos B \cos C \end{aligned} $
$\mathrm{OP}^{2}=\mathrm{R}^{2}(1-8 \cos \mathrm{A} \cos \mathrm{B} \cos \mathrm{C})$
$\mathrm{OP}=\mathrm{R} \sqrt{1-8 \cos \mathrm{A} \cos \mathrm{B} \cos \mathrm{C}}$
Hence ‘a’ is the correct option
3. The radii $r _{1}, r _{2}, r _{3}$, of escribed circles of the triangle $A B C$ are in HP. If its area is $24 \mathrm{sq} . \mathrm{cm}$ and its perimeter is $24 \mathrm{~cm}$, then the lengths of its sides are
(a). $4, 6, 8$
(b). $3, 9, 11$
(c). $6, 8,1 0$
(d). None of these
Show Answer
Solution:
Given that $r _{1}, r _{2} r _{3}$ are in HP
i.e. $\frac{\mathrm{s}-\mathrm{a}}{\Delta}, \frac{\mathrm{s}-\mathrm{b}}{\Delta}, \frac{\mathrm{s}-\mathrm{c}}{\Delta}$ are in A.P
or $\mathrm{s}-\mathrm{a}, \mathrm{s}-\mathrm{b}, \mathrm{s}-\mathrm{c}$ are in A.P
or a, b, c are in AP
$\mathrm{a}+\mathrm{c}=2 \mathrm{~b}$
$\mathrm{a}+\mathrm{b}+\mathrm{c}=24$
$3 \mathrm{~b}=24$
$\mathrm{b}=8$
$\mathrm{s}=\frac{24}{2}=12$
$\mathrm{a}+\mathrm{c}=16$
$\mathrm{c}=16-\mathrm{a}$
$\Delta^{2}=\mathrm{s}(\mathrm{s}-\mathrm{a})(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})$
$24 \times 24=12(12-\mathrm{a})(12-8)(12-(16-\mathrm{a}))$
$24 \times 24=12 \times 4(12-a)(a-4)$
$12=(12-a)(a-4)$
$a^{2}-16 a+60=0$
$a^{2}-10 a-6 a+60=0$
$(a-10)(a-6)=0$
$\mathrm{a}=10$ or $\mathrm{a}=6$
$\mathrm{a}=10, \mathrm{c}=6, \mathrm{~b}=8$ or $\mathrm{a}=6, \mathrm{~b}=8, \mathrm{c}=10$
Correct option is ‘c’
4. In $\triangle \mathrm{ABC}$ the value of $\frac{\mathrm{r} _{1}+\mathrm{r} _{2}}{1+\cos \mathrm{c}}$ is always equal to
(a). $2 \mathrm{r}$
(b). $2 \mathrm{R}$
(c). $\frac{2 r^{2}}{R}$
(d). $\frac{2 R^{2}}{r}$
Show Answer
Solution:
We know
$ \begin{aligned} & r _{1}+r _{2}=4 R \sin \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}+4 R \sin \frac{B}{2} \cos \frac{C}{2} \cos \frac{A}{2} \\ &=4 R \cos \frac{C}{2}\left(\sin \frac{A}{2} \cos \frac{B}{2}+\cos \frac{A}{2} \sin \frac{B}{2}\right) \\ &=4 R \cos \frac{C}{2}\left(\sin \left(\frac{A+B}{2}\right)\right) \\ &=4 R \cos \frac{C}{2}\left(\cos \frac{C}{2}\right) \\ &=4 R \cos ^{2} \frac{C}{2} \\ &=2 R(1+\cos C) \\ & \quad\left(1+\cos 2 \theta=2 \cos ^{2} \theta\right) \end{aligned} $
$\therefore \frac{\mathrm{r} _{1}+\mathrm{r} _{2}}{1+\cos \mathrm{C}}=2 \mathrm{R}$
5. Let $\mathrm{ABCD}$ be a quadrilateral with area 18 with side $\mathrm{AB}$ parallel to the side $\mathrm{CD}$ and $\mathrm{AB}=2 \mathrm{CD}$. Let $A D$ be perpendicular to $A B$ and $C D$.If a circle is drawn inside the quadrilaterals $A B C D$ touching all the sides, then its radius is
(a). $3$
(b). $2$
(c). $\frac{3}{2}$
(d). $1$
Show Answer
Solution:
Given that $\mathrm{AB}=2 \mathrm{CD}$
Let $\mathrm{CD}=\mathrm{a} \quad \therefore \mathrm{AB}=2 \mathrm{a}$
$\therefore \mathrm{B}(2 \mathrm{a}, 0)$
and $\mathrm{c}(\mathrm{a}, 2 \mathrm{r})$
Let the centre of in circle be $( \mathrm{r}, \mathrm{r})$
Where $r$ is the radius of the circle
Since $A B \| ^\ell$ to $C D$
$\therefore \mathrm{ABCD}$ is a trapezium
$\operatorname{ar}(\mathrm{ABCD})=\frac{1}{2} \mathrm{~h}$ (sum of parallel sides)
$=\frac{1}{2} \times 2 \mathrm{r}(\mathrm{a}+2 \mathrm{a})$
$18=3$ ar
$ar =6$
Now $\mathrm{BC}$ is a tangent to the circle
$ (x-r)^{2}+(y-r)^{2}=r^{2} $
Equation of tangent is $y=-\frac{2 r}{2}(x-2 a)$
$2\mathrm{rx}+\mathrm{ay}-4 \mathrm{ar}=0$
$\therefore \mathrm{r}=\left|\frac{2 \mathrm{r}^{2}+\mathrm{ar}-4 \mathrm{ar}}{\sqrt{4 \mathrm{r}^{2}+\mathrm{a}^{2}}}\right|$
$r=\left|\frac{2 r^{2}-3 a r}{\sqrt{4 r^{2}+a^{2}}}\right|$
squaring
$4 r^{4}+a^{2} r^{2}=4 r^{4}+9 a^{2} r^{2}-12 a r^{3}$
$12 \mathrm{ar}^{3}=8 \mathrm{a}^{2} \mathrm{r}^{2}$
$3 \mathrm{r}=2 \mathrm{a} \quad[\therefore \mathrm{ar}=6]$
$3 \mathrm{r}^{2}=2 \mathrm{ar}$
$3 \mathrm{r}^{2}=12$
$\mathrm{r}^{2}=4$
$\mathrm{r}=2$
6. In a triangle $\mathrm{ABC}, \mathrm{a}: \mathrm{b}: \mathrm{c}=4: 5: 6$. The ratio of the radius of the circumcircle to that of the incircle is
(a). $\frac{15}{4}$
(b). $\frac{11}{5}$
(c). $\frac{16}{7}$
(d). $\frac{16}{3}$
Show Answer
Solution:
$ \begin{aligned} & \mathrm{R}=\frac{\mathrm{abc}}{4 \Delta}, \quad \mathrm{r}=\frac{\Delta}{\mathrm{s}} \\ & \frac{\mathrm{R}}{\mathrm{r}}=\frac{\mathrm{abc}}{4 \Delta} \times \frac{\mathrm{s}}{\Delta} \\ & =\frac{\mathrm{abc} \times \mathrm{s}}{4 \Delta^{2}} \\ & =\frac{\mathrm{abc} \times \mathrm{s}}{4(\mathrm{~s}(\mathrm{~s}-\mathrm{a})(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c}))} \\ & =\frac{2 \mathrm{abc}}{(2 \mathrm{~s}-2 \mathrm{a})(2 \mathrm{~s}-2 \mathrm{~b})(2 \mathrm{~s}-2 \mathrm{c})} \\ & =\frac{2 \mathrm{abc}}{(\mathrm{a}+\mathrm{b}-\mathrm{c})(\mathrm{c}+\mathrm{a}-\mathrm{b})(\mathrm{b}+\mathrm{c}-\mathrm{a})} \\ & =\frac{2.4 .5 .6}{3.5 .7} \\ & =\frac{16}{7} \end{aligned} $
7. The value of $\frac{1}{\mathrm{r} _{1}{ }^{2}}+\frac{1}{\mathrm{r} _{2}{ }^{2}}+\frac{1}{\mathrm{r} _{3}{ }^{2}}+\frac{1}{\mathrm{r}^{2}}$ is
(a). $0$
(b). $\frac{\mathrm{a}^{2}+\mathrm{b}^{2}+\mathrm{c}^{2}}{\Delta^{2}}$
(c). $\frac{\Delta^{2}}{a^{2}+b^{2}+c^{2}}$
(d). $\frac{\mathrm{a}^{2}+\mathrm{b}^{2}+\mathrm{c}^{2}}{\Delta}$
Show Answer
Solution:
$\therefore \frac{1}{\mathrm{r} _{1}{ }^{2}}=\frac{(\mathrm{s}-\mathrm{a})^{2}}{\Delta^{2}} ; \frac{1}{\mathrm{r} _{2}{ }^{2}}=\frac{(\mathrm{s}-\mathrm{b})^{2}}{\Delta^{2}} ; \frac{1}{\mathrm{r} _{3}{ }^{2}}=\frac{(\mathrm{s}-\mathrm{c})^{2}}{\Delta^{2}} ; \frac{1}{\mathrm{r}^{2}}=\frac{\mathrm{s}^{2}}{\Delta^{2}}$
$\therefore \frac{1}{\mathrm{r} _{1}{ }^{2}}+\frac{1}{\mathrm{r} _{2}{ }^{2}}+\frac{1}{\mathrm{r} _{3}{ }^{2}}+\frac{1}{\mathrm{r}^{2}}=\frac{\mathrm{s}^{2}+(\mathrm{s}-\mathrm{a})^{2}+(\mathrm{s}-\mathrm{b})^{2}+(\mathrm{s}-\mathrm{c})^{2}}{\Delta^{2}}$
$=\frac{4 \mathrm{~s}^{2}+\mathrm{a}^{2}+\mathrm{b}^{2}+\mathrm{c}^{2}-2 \mathrm{~s}(\mathrm{a}+\mathrm{b}+\mathrm{c})}{\Delta^{2}}$
$=\frac{4 \mathrm{~s}^{2}+\mathrm{a}^{2}+\mathrm{b}^{2}+\mathrm{c}^{2}-4 \mathrm{~s}^{2}}{\Delta^{2}} \quad(\mathrm{a}+\mathrm{b}+\mathrm{c}=2 \mathrm{~s})$
$=\frac{\mathrm{a}^{2}+\mathrm{b}^{2}+\mathrm{c}^{2}}{\Delta^{2}}$
Practice questions
1. In $\triangle \mathrm{ABC}, \mathrm{a} \geq \mathrm{b} \geq \mathrm{c}$, if $\frac{\mathrm{a}^{3}+\mathrm{b}^{3}+\mathrm{c}^{3}}{\sin ^{3} \mathrm{~A}+\sin ^{2} \mathrm{~B}+\sin ^{3} \mathrm{c}}=8$, then the maximum value of $\mathrm{a}$ is
(a). $\frac{1}{2}$
(b). $2$
(c). $8$
(d). $64$
Show Answer
Answer: (b)2. Sides of triangle $\mathrm{ABC}$ are in $\mathrm{AP}$. If $\mathrm{a}<\min \{\mathrm{b}, \mathrm{c}\}$, then $\cos \mathrm{A}$ may be equal to
(a). $\frac{3 c-4 b}{2 b}$
(b). $\frac{3 \mathrm{c}-4 \mathrm{~b}}{2 \mathrm{c}}$
(c). $\frac{4 \mathrm{c}-3 \mathrm{~b}}{2 \mathrm{~b}}$
(d). $\frac{4 \mathrm{c}-3 \mathrm{~b}}{2 \mathrm{c}}$
Show Answer
Answer: (d)3. In a $\triangle A B C$, angles $A, B, C$ are in $A P$. Then $x \rightarrow c \frac{\sqrt{3-4 \sin A \sin C}}{|A-C|}$ is
(a). 1
(b). 2
(c). 3
(d). 4
Show Answer
Answer: (a)4. In a triangle $\mathrm{ABC}, 2 \mathrm{a}^{2}+4 \mathrm{~b}^{2}+\mathrm{c}^{2}=4 \mathrm{ab}+2 \mathrm{ac}$, then the numerical value of $\cos \mathrm{B}$ is equal to
(a). $0$
(b). $\frac{3}{8}$
(c). $\frac{5}{8}$
(d). $\frac{7}{8}$
Show Answer
Answer: (d)5. If $a, b, c$ be the sides of a $\triangle A B C$ and if roots of the equation $a(b-c) x^{2}+b(c-a) x+c(a-b)=0$ are equal, then $\sin ^{2} \frac{A}{2}, \sin ^{2} \frac{B}{2}, \sin ^{2} \frac{C}{2}$ are in
(a). $\mathrm{AP}$
(b). $\mathrm{GP}$
(c). $\mathrm{HP}$
(d). $\mathrm{AGP}$
Show Answer
Answer: (c)6. In a $\triangle \mathrm{ABC}$ sides $\mathrm{a}, \mathrm{b}, \mathrm{c}$ are in $\mathrm{AP}$ and $\frac{2}{1 ! 9 !}+\frac{2}{3 ! 7 !}+\frac{1}{5 ! 5 !}=\frac{8^{\mathrm{a}}}{(2 \mathrm{~b}) !}$ then the maximum value of $\tan \mathrm{A} \tan \mathrm{B}$ is equal to
(a). $\frac{1}{2}$
(b). $\frac{1}{3}$
(c). $\frac{1}{4}$
(d). $\frac{1}{5}$
Show Answer
Answer: (b)7. If $\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}$ are the angles of quadrilateral, then $\frac{\sum \tan \mathrm{A}}{\sum \cot \mathrm{A}}$ is equal to
(a). $\pi \tan \mathrm{A}$
(b). $\pi \cot \mathrm{A}$
(c). $ \sum \tan ^{2} \mathrm{~A}$
(d). $ \sum \cot ^{2} \mathrm{~A}$
Show Answer
Answer: (a)8. With usual notations, if in a $\triangle \mathrm{ABC}, \frac{\mathrm{b}+\mathrm{c}}{11}=\frac{\mathrm{c}+\mathrm{a}}{12}=\frac{\mathrm{a}+\mathrm{b}}{13}$, then $\cos \mathrm{A}: \cos \mathrm{B}$ : $\cos \mathrm{C}$ is equal to
(a). $7: 19: 25$
(b). $19: 7: 25$
(c). $12: 14: 20$
(d). $19: 25: 20$
Show Answer
Answer: (a)9. In and $\triangle \mathrm{ABC}, \Pi\left(\frac{\sin ^{2} \mathrm{~A}+\sin \mathrm{A}+1}{\sin \mathrm{A}}\right)$ is always greater than
(a). 9
(b). 3
(c). 27
(d). None of these
Show Answer
Answer: (c)10. The radius of the circle passing through the centre of incircle of $\triangle \mathrm{ABC}$, and through the end points of $\mathrm{BC}$ is given
(a). $\left(\frac{\mathrm{a}}{2}\right) \cos \mathrm{A}$
(b). $\left(\frac{a}{2}\right) \sec \left(\frac{A}{2}\right)$
(c). $\left(\frac{a}{2}\right) \sin \mathrm{A}$
(d). $\operatorname{asec}\left(\frac{\mathrm{A}}{2}\right)$
Show Answer
Answer: (b)11. If in a $\triangle \mathrm{ABC}, \mathrm{a}, \mathrm{b}, \mathrm{c}$ are in $\mathrm{AP}$ and $\mathrm{p} _{1}, \mathrm{p} _{2}, \mathrm{p} _{3}$ are the altitude from the vertices $\mathrm{A}, \mathrm{B}, \mathrm{C}$ respectively then
(a). $\mathrm{p} _{1}, \mathrm{p} _{2}, \mathrm{p} _{3}$ are in $\mathrm{AP}$
(b). $\mathrm{p} _{1}, \mathrm{p} _{2}, \mathrm{p} _{3}$ are in $\mathrm{HP}$
(c). $\mathrm{p} _{1}+\mathrm{p} _{2}+\mathrm{p} _{3} \leq \frac{3 \mathrm{R}}{\Delta}$
(d). $\frac{1}{\mathrm{p} _{1}}+\frac{1}{\mathrm{p} _{2}}+\frac{1}{\mathrm{p} _{3}} \leq \frac{3 \mathrm{R}}{\Delta}$
Show Answer
Answer: (b, d)12. If $\tan A, \tan B$ are the roots of the quadratic $a b x^{2}-c^{2} x+a b=0$, where $a, b, c$ are the sides of $a$ triangle, then
(a). $\tan \mathrm{A}=\frac{\mathrm{a}}{\mathrm{b}}$
(b). $\tan \mathrm{B}=\frac{\mathrm{b}}{\mathrm{a}}$
(c). $ \cos \mathrm{C}=0$
(d). $\tan \mathrm{A}+\tan \mathrm{B}=\frac{\mathrm{c}^{2}}{\mathrm{ab}}$
Show Answer
Answer: (a, b, c, d)13. If $\sin \beta$ is the GM between $\sin \alpha$ and $\cos \alpha$, then $\cos 2 \beta$ is equal to
(a). $2 \sin ^{2}\left(\frac{\pi}{4}-\alpha\right)$
(b). $2 \cos ^{2}\left(\frac{\pi}{4}-\alpha\right)$
(c). $2 \cos ^{2}\left(\frac{\pi}{4}+\alpha\right)$
(d). $2 \sin ^{2}\left(\frac{\pi}{4}+\alpha\right)$
Show Answer
Answer: (a, c)14. Passage - I
If $\mathrm{p} _{1}, \mathrm{p} _{2}, \mathrm{p} _{3}$ are altitudes of a triangle $\mathrm{ABC}$ from the vertices $\mathrm{A}, \mathrm{B}, \mathrm{C}$ respectively and $\Delta$ is the area of the triangle and $\mathrm{s}$ is the semipermanent of the triangle. On the basis of above information, answer the following questions :
(i). If $\frac{1}{p _{1}}+\frac{1}{p _{2}}+\frac{1}{p _{3}}=\frac{1}{2}$ then the least value of $p _{1}, p _{2}, p _{3}$ is
(a). 8
(b). 27
(c). 125
(c). 216
Show Answer
Answer: (b)(ii). The value of $\frac{\cos A}{p _{1}}+\frac{\cos B}{p _{2}}+\frac{\cos C}{p _{3}}$ is
(a). $\frac{1}{r}$
(b). $\frac{1}{R}$
(c). $\frac{a^{2}+b^{2}+C^{2}}{2 R}$
(d). $\frac{1}{\Delta}$
Show Answer
Answer: (b)(iii). The minimum value of $\frac{b^{2} p _{1}}{c}+\frac{c^{2} p _{2}}{a}+\frac{a^{2} p _{3}}{b}$ is
(a). $\Delta$
(b). $2 \Delta$
(c). $3 \Delta$
(d). $6 \Delta$
Show Answer
Answer: (d)(iv). The value of $\mathrm{p} _{1}{ }^{-2}+\mathrm{p} _{2}{ }^{-2}+\mathrm{p} _{3}{ }^{-2}$ is
(a). $\frac{\left(\sum \mathrm{a}\right)^{2}}{4 \Delta^{2}}$
(b). $\frac{(\pi \mathrm{a})^{3}}{8 \Delta^{3}}$
(c). $\frac{\sum \mathrm{a}^{2}}{4 \Delta^{2}}$
(d). $\frac{\pi \mathrm{a}^{2}}{8 \Delta^{2}}$
Show Answer
Answer: (c)(v). In the triangle $A B C$, the altitudes are in $A P$, then
(a). a, b, c are in AP
(b). a, b, c are in HP
(c). a, b, c are in GP
(d). angles $\mathrm{A}, \mathrm{B}, \mathrm{C}$ are in $\mathrm{AP}$
Show Answer
Answer: (b)15. Passage II
In a triangle if the sum of two sides is $x$ and this product is $y(x \geq 2 \sqrt{y})$ such that $(\mathrm{x}+\mathrm{z})(\mathrm{x}-\mathrm{z})=\mathrm{y}$ where $\mathrm{z}$ is the third side of the triangle.
On the passes of above information, answer the following questions.
(i). Greatest angle of the triangle is
(a). 105
(b). 120
(c). 135
(d). 150
Show Answer
Answer: (b)(ii). Cerium radius of the triangle is
(a). $\mathrm{x}$
(b). $y$
(c). $\mathrm{z}$
(d). None of these
Show Answer
Answer: (d)(iii). In radius of the triangle is
(a). $\frac{y}{2(z+x)}$
(b). $\frac{z}{2(x+y)}$
(c). $\frac{y \sqrt{3}}{z+x}$
(d). $\frac{z \sqrt{3}}{x+y}$
Show Answer
Answer: (c)(iv). Area of the triangle is
(a). $\frac{\mathrm{y} \sqrt{3}}{4}$
(b). $\frac{x \sqrt{3}}{4}$
(c). $\frac{\mathrm{z} \sqrt{3}}{4}$
(d). None of these
Show Answer
Answer: (a)(v). The sides of the triangle are
(a). $\frac{x \pm \sqrt{x^{2}-4 y}}{2}, z$
(b). $\frac{\mathrm{y} \pm \sqrt{\mathrm{y}^{2}-4 \mathrm{z}}}{2}, \mathrm{z}$
(c). $\frac{z \pm \sqrt{z^{2}-4 x}}{2}, z$
(d). None of these
Show Answer
Answer: (a)Assertion and Reason
16. Assertion (A) : In any $\triangle A B C$, the minimum value of $\frac{r _{1}+r _{2}+r _{3}}{r}$ is
Reason (R) : $\mathrm{AM} \geq \mathrm{GM}$
(a). $\mathrm{A}$
(b). $\mathrm{B}$
(c). $\mathrm{C}$
(d). $\mathrm{D}$
Show Answer
Answer: (b)17. Assertion (A) : If A, B, C D are angle of a cyclic quadrilateral then $\sum \sin A=0$
Reason (R) : If A, B, C, D are angles of cyclic quadrilateral then $\sum \cos A=0$
(a). $\mathrm{A}$
(b). $\mathrm{B}$
(c). $\mathrm{C}$
(d). $\mathrm{D}$
Show Answer
Answer: (d)18. Assertion (A) : In any $\triangle \mathrm{ABC}$, the square of the length of the bisector $\mathrm{AD}$ is $\mathrm{bc}\left(\frac{1-\mathrm{a}^{2}}{(\mathrm{~b}+\mathrm{c})^{2}}\right)$
Reason (R) : In any $\triangle \mathrm{ABC}$, length of bisector $\mathrm{AD}$ is $\frac{2 \mathrm{bc}}{\mathrm{b}+\mathrm{c}} \cos \frac{\mathrm{A}}{2}$
(a). $\mathrm{A}$
(b). $\mathrm{B}$
(c). $\mathrm{C}$
(d). $\mathrm{D}$
Show Answer
Answer: (a)Integer Type Questions
19. If the radius of the circumcircle of a triangle is 12 and that of the incircle is 4 , then the square of the sum of radii of the escribed cirle must be
Show Answer
Answer: 270420. In a $\triangle \mathrm{ABC}$, the maximum value of $1000\left(\frac{\sum \mathrm{a} \cos ^{2} \frac{\mathrm{A}}{2}}{\mathrm{a}+\mathrm{b}+\mathrm{c}}\right)$ must be
Show Answer
Answer: 075021. Matrix Match Type
| Column I | Column II |
|---|---|
| (a). In a $\triangle A B C$, if $2 a^{2}+b^{2}+c^{2}=2 a c+2 a b$, then | (p). $\triangle \mathrm{ABC}$ is equilateral $\Delta$ |
| (b). In a $\triangle A B C$, if $\mathrm{a}^{2}+\mathrm{b}^{2}+\mathrm{c}^{2}=\sqrt{2} \mathrm{~b}(\mathrm{c}+\mathrm{a})$, then | (q). $\triangle \mathrm{ABC}$ is right angled $\Delta$ |
| (c). In a $\triangle \mathrm{ABC}$,if $\mathrm{a}^{2}+\mathrm{b}^{2}+\mathrm{c}^{2}=\mathrm{bc}+\mathrm{ca} \sqrt{3}$, then | (r). $\triangle \mathrm{ABC}$ is scalene $\Delta$ |
| (s). $\triangle \mathrm{ABC}$ is scalene right angled $\Delta$ | |
| (t). Angles $B, C, A$ are in $AP$ |










