TRIGONOMETRY FUNCTIONS - 3 (Inverse Trigonometric Functions - Problem Solving)
A function $f: \mathrm{A} \rightarrow \mathrm{B}$ is invertible if $f$ it is a bijection. The inverse of $f$ is denoted by $f^{-1}$ and is defined as $f^{-1}(\mathrm{y})=\mathrm{x} \Leftrightarrow f(\mathrm{x})=\mathrm{y}$. Trigonometric functions are periodic and hence they are not bijective. But if we restrict their domains and codomains they can be made bijective and we can obtain their inverses.
Domain & range of inverse trigonometric functions
| Function | Domain | Range (Principal value branch) |
|---|---|---|
| $\sin ^{-1} \mathrm{X}$ | $[-1,1]$ | $[-\pi / 2,-\pi / 2]$ |
| $\cos ^{-1} \mathrm{X}$ | $[-1,1]$ | $[0, \pi]$ |
| $\tan ^{-1} \mathrm{X}$ | $(-\infty, \infty)$ | $(-\pi / 2, \pi / 2)$ |
| $\cot ^{-1} \mathrm{X}$ | $(-\infty, \infty)$ | $(0, \pi)$ |
| $\operatorname{cosec}^{-1} \mathrm{x}$ | $(-\infty,-1] \cup[1, \infty)$ | $[-\pi / 2,0) \cup(0, \pi / 2]$ |
| $\sec ^{-1} \mathrm{X}$ | $(-\infty,-1] \cup[1, \infty)$ | $[0, \pi / 2) \cup(\pi / 2, \pi]$ |
Note: If no branch of an inverse trigonometric function is mentioned, then it means the principal value branch of the function.
Properties of inverse trigonometric functions
1. (i). $ \sin ^{-1}(\sin \mathrm{x})=\left\{\begin{array}{l}-2 \mathrm{n} \pi+\mathrm{x}, 2 \mathrm{n} \pi-\frac{\pi}{2} \leq \mathrm{x} \leq 2 \mathrm{n} \pi+\frac{\pi}{2}, \mathrm{n} \in \mathrm{Z} \\ (2 \mathrm{n}+1) \pi-\mathrm{x},(2 \mathrm{n}+1) \pi-\frac{\pi}{2} \leq \mathrm{x} \leq(2 \mathrm{n}+1) \pi+\frac{\pi}{2}, \mathrm{n} \in \mathrm{Z}\end{array}\right.$

Period $=2 \pi \&$ it is an odd function.
(ii). $\cos ^{-1}(\cos x)=\left\{\begin{array}{l}-2 n \pi+x, 2 n \pi \leq x \leq(2 n+1) \pi, n \in Z \\ 2 n \pi-x,(2 n-1) \pi \leq x \leq 2 n \pi, n \in Z\end{array}\right.$

Period $=2 \pi$ and it is an even function
(iii). $\tan ^{-1}(\tan \mathrm{x})=-\mathrm{n} \pi+\mathrm{x}, \mathrm{n} \pi-\frac{\pi}{2}<\mathrm{x}<\mathrm{n} \pi+\frac{\pi}{2}, \mathrm{n} \in \mathrm{Z}$
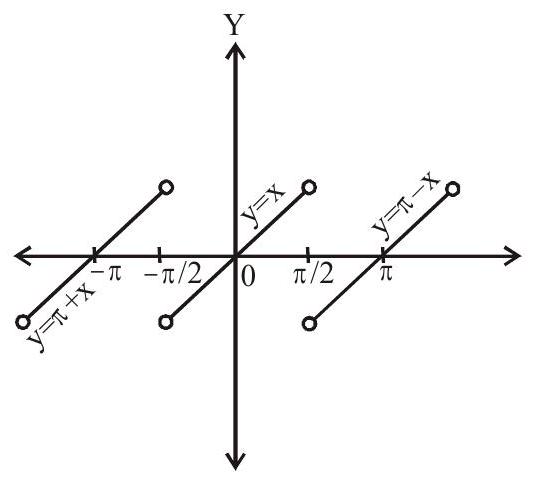
Period $=\pi$
(iv). $\cot ^{-1}(\operatorname{cotx})=-\mathrm{n} \pi+\mathrm{x}, \mathrm{n} \pi<\mathrm{x}<(\mathrm{n}+1) \pi, \mathrm{n} \in \mathrm{Z}$
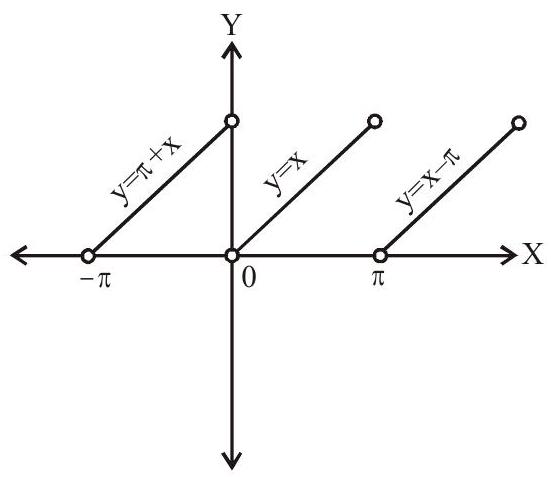
Period $=\pi$
(v). $\sec ^{-1}(\sec x)=\left\{\begin{array}{l}x-2 n \pi, 2 n \pi \leq x \leq(2 n+1) \pi, \quad x \neq 2 \pi+\frac{\pi}{2} \\ -x+2 n \pi,(2 n-1) \pi \leq x \leq 2 n \pi, \quad x \neq\left(2 n \pi-\frac{\pi}{2}, n \in Z\right.\end{array}\right.$
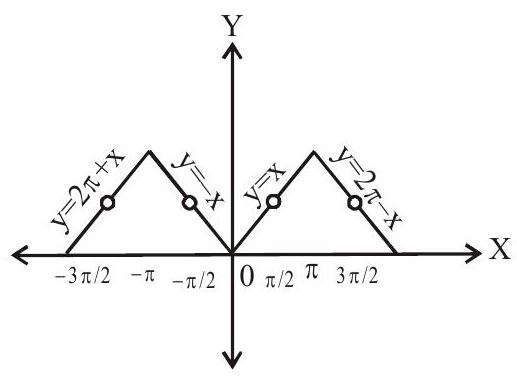
Period $=2 \pi$
(vi). $\operatorname{cosec}^{-1}(\operatorname{cosec} x)=\left\{\begin{array}{l}-2 n \pi+x, 2 n \pi-\frac{\pi}{2} \leq x \leq 2 n \pi+\frac{\pi}{2} \\ (2 n+1) \pi-x,(2 n+1) \pi-\frac{\pi}{2} \leq x \leq(2 n+1) \pi+\frac{\pi}{2}, x \neq n \pi, n \in Z\end{array}\right.$
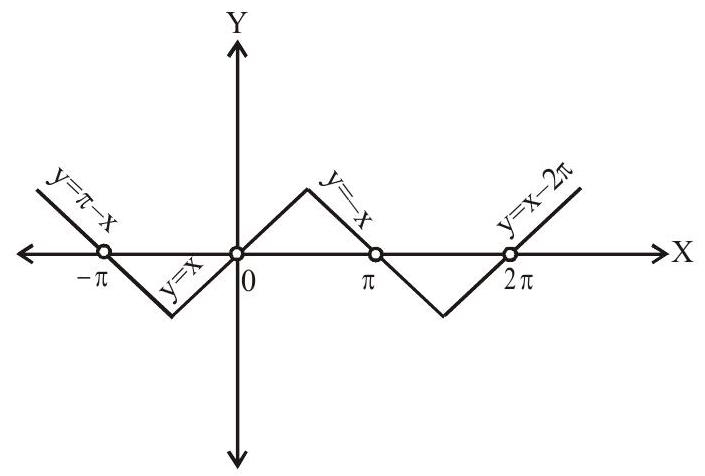
Period $=2 \pi$
2. (i). $\sin \left(\sin ^{-1} x\right)=x,-1 \leq x \leq 1$ $\hspace{1cm}$(ii). $\cos \left(\cos ^{-1} \mathrm{x}\right)=\mathrm{x},-1 \leq \mathrm{x} \leq 1$
(iii). $\tan \left(\tan ^{-1} \mathrm{x}\right)=\mathrm{x}, \mathrm{x} \in \mathrm{R}$ $\hspace{1cm}$(iv). $\cot \left(\cot ^{-1} \mathrm{x}\right)=\mathrm{x}, \mathrm{x} \in \mathrm{R}$
(v). $\sec \left(\sec ^{-1} x\right)=x, x \in R(-\infty,-1] \cup[1, \infty)$
(vi). $\operatorname{\cosec}\left(\operatorname{\cosec}^{-1} \mathrm{x}\right)=\mathrm{x}, \mathrm{x} \in \mathrm{R}(-\infty,-1] \cup[1, \infty)$
3. (i). $\sin ^{-1} x+\cos ^{-1} x=\pi / 2,-1 \leq x \leq 1$
(ii). $\tan ^{-1} \mathrm{x}+\cot ^{-1} \mathrm{x}=\pi / 2, \mathrm{x} \in \mathrm{R}$
(iii). $\sec ^{-1} \mathrm{x}+\operatorname{\cosec}^{-1} \mathrm{x}=\pi / 2, \mathrm{x} \in \mathrm{R}(-\infty,-1] \cup[1, \infty)$
4. (i). $\sin ^{-1} x=\operatorname{\cosec}^{-1} \frac{1}{x},-1 \leq x \leq 1$
(ii). $\cos ^{-1} \mathrm{x}=\sec ^{-1}\left(\frac{1}{\mathrm{x}}\right),-1 \leq \mathrm{x} \leq 1$
(iii). $\tan ^{-1} x=\left\{\begin{array}{l}\cot ^{-1}(1 / x), x>0 \\ -\pi+\cot ^{-1}(1 / x), x<0\end{array}\right.$
5. (i). $\sin ^{-1}(-x)=-\sin ^{-1} x, \quad-1 \leq x \leq 1$
(ii). $\cos ^{-1}(-x)=\pi-\cos ^{-1} x, \quad-1 \leq x \leq 1$
(iii). $\tan ^{-1}(-x)=-\tan ^{-1} x, \quad-\infty<x<\infty$
(iv). $\cot ^{-1}(-x)=\pi-\cot ^{-1} x, \quad-\infty<x<\infty$
(v). $\operatorname{\cosec}^{-1}(-x)=-\operatorname{\cosec}^{-1} x, \quad x \leq-1$ or $x \geq 1$
(vi). $\sec ^{-1}(-x)=\pi-\sec ^{-1} x, \quad x \leq-1$ or $x \geq 1$
6. Conversions of inverse trigonometric functions

$ \begin{aligned} \sin ^{-1} \mathrm{x} & =\cos ^{-1} \sqrt{1-\mathrm{x}^{2}}=\tan ^{-1} \frac{\mathrm{x}}{\sqrt{1-\mathrm{x}^{2}}} \\ & =\cot ^{-1} \frac{\sqrt{1-\mathrm{x}^{2}}}{\mathrm{x}}=\operatorname{cosec}^{-1} \frac{1}{\mathrm{x}}=\sec ^{-1} \frac{1}{\sqrt{1-\mathrm{x}^{2}}} \end{aligned} $

$ \begin{aligned} \cos ^{-1} \mathrm{x} & =\sin ^{-1} \sqrt{1-\mathrm{x}^{2}}=\tan ^{-1} \frac{\sqrt{1-\mathrm{x}^{2}}}{\mathrm{x}} \\ & =\cot ^{-1} \frac{\mathrm{x}}{\sqrt{1-\mathrm{x}^{2}}}=\operatorname{cosec}^{-1} \frac{1}{\sqrt{1-\mathrm{x}^{2}}}=\sec ^{-1} \frac{1}{\mathrm{x}} \end{aligned} $

$\tan ^{-1} \mathrm{x}=$
$ \begin{aligned} & \sin ^{-1} \frac{x}{\sqrt{1+x^{2}}}=\cos ^{-1} \frac{1}{\sqrt{1+x^{2}}}=\cot ^{-1} \frac{1}{x} \\ & \operatorname{cosec}^{-1} \frac{\sqrt{1+x^{2}}}{x}=\sec ^{-1} \sqrt{1+x^{2}} \end{aligned} $
7. (i) $\sin ^{-1} x+\sin ^{-1} y=\left\{\begin{array}{c}\sin ^{-1}\left(x \sqrt{1-y^2}+y \sqrt{1-x^2}\right) \text { if }-1 \leq x, y \leq 1 \& x^2+y^2 \leq 1 \\ \text { or if } x y<0 {\&} x^2+y^2>1 \\ \pi-\sin ^{-1}\left(x \sqrt{1-y^2}+y \sqrt{1-x^2}\right) \text { if } 0<x, y \leq 1 \& x^2+y^2>1 \\ -\pi-\sin ^{-1}\left(x \sqrt{1-y^2}+y \sqrt{1-x^2}\right) \text { if }-1 \leq x, y<0 \& x^2+y^2>1\end{array}\right.$
(ii) $\sin ^{-1} x-\sin ^{-1} y=\left\{\begin{array}{l}\sin ^{-1}\left(x \sqrt{1-y^2}-y \sqrt{1-x^2}\right) \text { if }-1 \leq x, y \leq 1 {\&} x^2+y^2 \leq 1 \\ \text { or if } x y>0 {\&} x^2+y^2>1 \\ \pi-\sin ^{-1}\left(x \sqrt{1-y^2}-y \sqrt{1-x^2}\right) \text { if } 0<x \leq 1,-1<y \leq 0 {\&} x^2+y^2>1 \\ -\pi-\sin ^{-1}\left(x \sqrt{1-y^2}-y \sqrt{1-x^2}\right) \text { if }-1 \leq x<0,0<y \leq 1 {\&} x^2+y^2>1\end{array}\right.$
8. (i) $\cos ^{-1} x+\cos ^{-1} y=\left\{\begin{array}{l}\cos ^{-1}\left(x y-\sqrt{1-x^{2}} \sqrt{1-y^{2}}\right) \text { if }-1 \leq x, y \leq 1 {\&} x+y \geq 0 \\ 2 \pi-\cos ^{-1}\left(x y-\sqrt{1-x^{2}} \sqrt{1-y^{2}}\right) \text { if }-1 \leq x, y \leq 1 {\&} x+y \leq 0\end{array}\right.$
(ii) $ \cos ^{-1} \mathrm{x}-\cos ^{-1} \mathrm{y}=\left\{\begin{array}{l}\cos ^{-1}\left(\mathrm{xy}+\sqrt{1-\mathrm{x}^{2}} \sqrt{1-\mathrm{y}^{2}}\right) \text { if }-1 \leq \mathrm{x}, \mathrm{y} \leq 1 \quad {\&} \mathrm{x} \leq \mathrm{y} \\ -\cos ^{-1}\left(\mathrm{xy}+\sqrt{1-\mathrm{x}^{2}} \sqrt{1-\mathrm{y}^{2}}\right) \text { if }-1 \leq \mathrm{y} \leq 0,0<\mathrm{x} \leq 1 \quad {\&} \mathrm{x} \geq \mathrm{y}\end{array}\right.$
9. (i) $\tan ^{-1} x+\tan ^{-1} y=\left\{\begin{array}{l} \tan ^{-1}\left(\frac{x+y}{1-x y}\right) \text { if } x y<1 \\ \pi+\tan ^{-1}\left(\frac{x+y}{1-x y}\right) \text { if } x>0, y>0 {\&} x y>1 \\ -\pi+\tan ^{-1}\left(\frac{x+y}{1-x y}\right) \text { if } x<0, y<0 {\&} x y>1 \end{array}\right.$
(ii) $\tan ^{-1} x-\tan ^{-1} y=\left\{\begin{array}{l}\tan ^{-1}\left(\frac{x-y}{1+x y}\right) \text { if } x y>-1 \\ \pi+\tan ^{-1}\left(\frac{x-y}{1+x y}\right) \text { if } x>0, y<0 {\&} x y<-1 \\ -\pi+\tan ^{-1}\left(\frac{x-y}{1+x y}\right), \text { if } x<0, y>0 {\&} x y<-1\end{array}\right.$
Remark : If $\mathrm{x} _{1}, \mathrm{x} _{2}, \ldots \ldots \ldots \mathrm{x} _{\mathrm{n}} \in \mathrm{R}$, then $\tan ^{-1} \mathrm{x} _{1}+\tan ^{-1} \mathrm{x} _{2}+\ldots \ldots \ldots+\tan ^{-1} \mathrm{x} _{\mathrm{n}}$ $=\tan ^{-1}\left(\frac{\mathrm{s} _{1}-\mathrm{s} _{3}+\mathrm{s} _{5}-\mathrm{s} _{7} \ldots \ldots \ldots}{1-\mathrm{s} _{2}+\mathrm{s} _{4}-\mathrm{s} _{6}+\ldots \ldots .}\right)$
Where $\mathrm{s} _{\mathrm{k}}$ is the sum of the product of $\mathrm{x} _{1}, \mathrm{x} _{2},……….x_n$ taken $k$ at $a$ time.
ie.
$ \begin{array}{ll} \mathrm{s} _{1}= & \mathrm{x} _{1}+\mathrm{x} _{2}+\ldots \ldots \ldots+\mathrm{x} _{\mathrm{n}}=\sum \mathrm{x} _{\mathrm{i}} \\ \mathrm{s} _{2}= & \mathrm{x} _{1} \mathrm{x} _{2}+\mathrm{x} _{2} \mathrm{x} _{3}+\ldots \ldots .+\mathrm{x} _{\mathrm{n}-1} \mathrm{x} _{\mathrm{n}}=\sum \mathrm{x} _{1} \mathrm{x} _{2} \\ \mathrm{~s} _{3}= & \sum \mathrm{x} _{1} \mathrm{x} _{2} \mathrm{x} _{3} \ldots \ldots \ldots \ldots \ldots \ldots . . \mathrm{etc.} \end{array} $
10. (i). $2 \sin ^{-1} x=\left\{\begin{array}{l}\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right) \text { if } \frac{-1}{\sqrt{2}} \leq x \leq \frac{1}{\sqrt{2}} \\ \pi-\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right), \text { if } \frac{1}{\sqrt{2}} \leq x \leq 1 \\ -\pi-\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right), \text { if }-1 \leq x \leq \frac{-1}{\sqrt{2}}\end{array}\right.$
(ii). $3 \sin ^{-1} x=\left\{\begin{array}{l}\sin ^{-1}\left(3 x-4 x^3\right), \text { if } \frac{-1}{2} \leq x \leq \frac{1}{2} \\ \pi-\sin ^{-1}\left(3 x-4 x^3\right), \text { if } \frac{1}{2}<x \leq 1 \\ -\pi-\sin ^{-1}\left(3 x-4 x^3\right), \text { if }-1 \leq x<\frac{-1}{2}\end{array}\right.$
11. (i). $2 \cos ^{-1} x=\left\{\begin{array}{l}\cos ^{-1}\left(2 x^{2}-1\right), \text { if } 0 \leq x \leq 1 \\ 2 \pi-\cos ^{-1}\left(2 x^{2}-1\right), \text { if }-1 \leq x \leq 0\end{array}\right.$
(ii). $\quad 3 \cos ^{-1} x=\left\{\begin{array}{l}\cos ^{-1}\left(4 x^{3}-3 x\right), \text { if } \frac{1}{2} \leq x \leq 1 \\ 2 \pi-\cos ^{-1}\left(4 x^{3}-3 x\right), \text { if } \frac{-1}{2} \leq x \leq \frac{1}{2} \\ 2 \pi+\cos ^{-1}\left(4 x^{3}-3 x\right) \text {, if }-1 \leq x \leq \frac{-1}{2}\end{array}\right.$
12. (i). $2 \tan ^{-1} x=\left\{\begin{array}{l}\tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right), \text { if }-1<x<1 \\ \pi+\tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right), \text { if } x>1 \\ -\pi+\tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right), \text { if } x<-1\end{array}\right.$
(ii). $3 \tan ^{-1} x=\left\{\begin{array}{l}\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right), \text { if } \frac{-1}{\sqrt{3}}<x<\frac{1}{\sqrt{3}} \\ \pi+\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right), \text { if } x>\frac{1}{\sqrt{3}} \\ -\pi+\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right), \text { if } x<\frac{1}{\sqrt{3}}\end{array}\right.$
Note: If $|x| \leq 1$ then $2 \tan ^{-1} x=\sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right)=\cos ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right)=\tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right)$.
If $|x|>1$, change $x$ to $\frac{1}{x}$ in the above.
Note: In cases of identities in inverse trigonometric functions, principal values are to be taken. As such signs of $x, y$ etc., will determine the quadrant in which the angles will fall. In order to bring the angles of both sides in the same quadrant, adjustment by $\pi$ is to be made.
13. Hyperbolic functions
| (i). $\sin h (-x)$ | $=-\sin h x$ | odd function |
| $\cos h (-\mathrm{x})$ | $=-\cos h \mathrm{x} $ | even function |
| $\tan h (-\mathrm{x})$ | $=\tan h \mathrm{x} $ | odd function |
| (ii). Function | Domain | Range |
| $\sin h ^{-1} \mathrm{x}$ | $\mathrm{R}$ | $ \mathrm{R}$ |
| $\cos h ^{-1} \mathrm{X} $ | $(0, \infty)$ | $ (1, \infty)$ |
| $\tan h ^{-1} \mathrm{x} $ | $\mathrm{R}$ | $ (-1, 1)$ |
| $\operatorname{\cot h}^{-1} \mathrm{x} $ | $ \mathrm{R}-\{0\}$ | $ R-[-1, 1]$ |
| $\operatorname{\sec h}^{-1} \mathrm{X} $ | $(0, \infty)$ | $ (0, 1)$ |
| $\operatorname{\cosec h}^{-1} \mathrm{x} $ | $ \mathrm{R}-\{0\} $ | $ R-\{0\}$ |
| (iii). $\sin h \left(\sin h ^{-1} \mathrm{x}\right)=\mathrm{x}$ | $\sin h ^{-1}(\sin h x)=x$ | |
| $\cos h \left(\cos h ^{-1} \mathrm{x}\right)=\mathrm{x}$ | $\cos h ^{-1}(\cos h x)=x$ | |
| $\tan h \left(\tan h ^{-1} x\right)=x$ | $\tan h ^{-1}(\tan h x)=x$ | |
| $\sin h \left(\sin ^{-1} x\right)=x^{n}$ | $\sin h \left(\sin h ^{-1} x^{n}\right)=x^{n}$ |
(iv). $\sin h ^{-1} \mathrm{x}=\log _{\mathrm{e}}\left(\mathrm{x}+\sqrt{\mathrm{x}^{2}+1}\right)$
$\cos h ^{-1} x=\log _{e}\left(x+\sqrt{x^{2}-1}\right)$
$\tan h ^{-1} x=\frac{1}{2} \log _{e}\left(\frac{x+1}{x-1}\right) x>1, x<-1$
$\operatorname{\cot h}^{-1} x=\frac{1}{2} \log _{e}\left(\frac{x-1}{x+1}\right) x>1, x<-1$
$\operatorname{\sec h}^{-1} x=\log _{e}\left(\frac{1+\sqrt{1-x^{2}}}{x}\right) 0<x \leq 1$
$\operatorname{\cosec h}^{-1} x=\left\{\begin{array}{lll}\log _{e}\left(\frac{1+\sqrt{1+x^{2}}}{x}\right) & \text { if } & x>0 \\ \log _{e}\left(\frac{1-\sqrt{1+x^{2}}}{x}\right) & \text { if } & x<0\end{array}\right.$
(v). $\sin h ^{-1} x=\operatorname{cosech}^{-1}\left(\frac{1}{x}\right)$
$\sin h ^{-1} x=\cos h ^{-1} \sqrt{x^{2}+1}$
$\cos h ^{-1} \mathrm{x}=\sin h ^{-1} \sqrt{\mathrm{x}^{2}-1}$
$\sin h \left(\cos h ^{-1} \mathrm{x}\right)=\sqrt{\mathrm{x}^{2}-1}$
Solved examples
1. The sum to infinite terms of the series
$\tan ^{-1} \frac{1}{3}+\tan ^{-1} \frac{1}{7}+\tan ^{-1} \frac{1}{13}+……………$ is
(a).. $\frac{\pi}{6}$
(b).. $\frac{\pi}{4}$
(c).. $\frac{\pi}{3}$
(d).. None of these
Show Answer
Solution : By method of difference
$ \begin{aligned} & \operatorname{Tn}=\tan ^{-1} \frac{1}{1+\mathrm{n}+\mathrm{n}^{2}} \\ & \operatorname{Tn}=\tan ^{-1} \frac{1}{1+n(n+1)}=\tan ^{-1} \frac{n+1-n}{n(n+1)}=\tan ^{-1}(n+1)-\tan ^{-1} n \\ & \therefore \quad T _{n}=\tan ^{-1}(n+1)-\tan ^{-1} n \\ & \mathrm{~T} _{1}^{\mathrm{n}}=\tan ^{-1} 2-\tan ^{-1} 1 \\ & \mathrm{~T} _{2}=\tan ^{-1} 3-\tan ^{-1} 2 \\ & \mathrm{~T} _{3}=\tan ^{-1} 4-\tan ^{-1} 3 \\ &.\\ &.\\ & T _{n}=\tan ^{-1}(n+1)-\tan ^{-1} n \\ & \text { Adding, } \mathrm{S} _{\mathrm{n}}=\mathrm{T} _{1}+\mathrm{T} _{2}+\ldots \ldots \ldots \ldots+\mathrm{T} _{\mathrm{n}} \\ & =\tan ^{-1}(\mathrm{n}+1)-\tan ^{-1} 1 \\ & \therefore \quad \mathrm{S} _{\infty}=\tan ^{-1} \infty-\tan ^{-1} 1=\frac{\pi}{2}-\frac{\pi}{4}=\frac{\pi}{4} \end{aligned} $
Answer: b
2. The sum to infinite terms of the series $\tan ^{-1} \frac{1}{2.1^{2}}+\tan ^{-1} \frac{1}{2.2^{2}}+\tan ^{-1} \frac{1}{2.3^{2}}+\ldots \ldots \ldots \ldots \ldots \ldots \infty$ is
(a). $\frac{\pi}{4}$
(b). $\frac{\pi}{3}$
(c). $\frac{\pi}{2}$
(d). None
Show Answer
Solution :
$ \begin{aligned} & \operatorname{Tn}=\tan ^{-1} \frac{1}{2 \mathrm{n}^{2}}=\tan ^{-1} \frac{2}{4 \mathrm{n}^{2}}=\tan ^{-1} \frac{(2 \mathrm{n}+1)-(2 \mathrm{n}-1)}{1+(2 \mathrm{n}+1)(2 \mathrm{n}-1)} \\ & \Rightarrow \quad \mathrm{T} _{\mathrm{n}}=\tan ^{-1}(2 \mathrm{n}+1)-\tan ^{-1}(2 \mathrm{n}-1) \\ & \therefore \quad \mathrm{T} _{1}=\tan ^{-1} 3-\tan ^{-1} 1 \\ & \mathrm{~T} _{2}=\tan ^{-1} 5-\tan ^{-1} 3 \\ & \mathrm{~T} _{3}=\tan ^{-1} 7-\tan ^{-1} 3 \end{aligned} $
$.$
$.$
$.$
$ \operatorname{Tn}=\tan ^{-1}(2 n+1)-\tan ^{-1}(2 n-1) $
Adding, $\mathrm{S} _{\mathrm{n}}=\mathrm{T} _{1}+\mathrm{T} _{2}+\ldots \ldots . \mathrm{T} _{\mathrm{n}}=\operatorname{Tan}^{-1}(2 \mathrm{n}+1)-\tan ^{-1} 1$
$ \therefore \quad \mathrm{S} _{\infty}=\tan ^{-1} \infty-\tan ^{-1} 1=\frac{\pi}{2}-\frac{\pi}{4}=\frac{\pi}{4} $
Answer: a
3. The value of
$ \tan ^{-1} \frac{\mathrm{c} _{1} \mathrm{x}-\mathrm{y}}{\mathrm{c} _{1} \mathrm{y}+\mathrm{x}}+\tan ^{-1} \frac{\mathrm{c} _{2}-\mathrm{c} _{1}}{1+\mathrm{c} _{1} \mathrm{c} _{2}}+\tan ^{-1} \frac{\mathrm{c} _{3}-\mathrm{c} _{2}}{1+\mathrm{c} _{2} \mathrm{c} _{3}}+\ldots \ldots \ldots \ldots \ldots \ldots \ldots+\tan ^{-1} \frac{1}{\mathrm{c} _{\mathrm{n}}} \text { is } $
(a). $\tan ^{-1} \frac{x}{y}$
(b). $\tan ^{-1} \frac{y}{x}$
(c). $\tan ^{-1} x-\tan ^{-1} \mathrm{y}$
(d). None
Show Answer
Solution: Write the series as
$ \begin{gathered} \tan ^{-1} \frac{\frac{x}{y}-\frac{1}{c _{1}}}{1+\frac{x}{y} \frac{1}{c _{1}}}+\tan ^{-1} \frac{\frac{1}{c _{1}}-\frac{1}{c _{2}}}{1+\frac{1}{c _{1}} \frac{1}{c _{2}}}+\tan ^{-1} \frac{\frac{1}{c _{2}}-\frac{1}{c _{3}}}{1+\frac{1}{c _{2}} \frac{1}{c _{3}}}+\ldots \ldots . .+\tan ^{-1} \frac{\frac{1}{c _{n-1}}-\frac{1}{c _{n}}}{1+\frac{1}{c _{n-1}} \frac{1}{c _{n}}}+\tan ^{-1} \frac{1}{c _{n}} \\ \Rightarrow\left(\tan ^{-1} \frac{x}{y}-\tan ^{-1} \frac{1}{c _{1}}\right)+\left(\tan ^{-1} \frac{1}{c _{1}}-\tan ^{-1} \frac{1}{c _{2}}\right)+\left(\tan ^{-1} \frac{1}{c _{2}}-\tan ^{-1} \frac{1}{c _{3}}\right)+ \\ \ldots \ldots \ldots \ldots \ldots . .+\left(\tan ^{-1} \frac{1}{c _{n-1}}-\tan ^{-1} \frac{1}{c _{n}}\right)+\tan ^{-1} \frac{1}{c _{n}}=\tan ^{-1} \frac{x}{y} \end{gathered} $
Answer: a
4. The number of positive integral solutions of the equation $\tan ^{-1} x+\cos ^{-1} \frac{y}{\sqrt{1+y^{2}}}$ $=\sin ^{-1} \frac{3}{\sqrt{10}}$ is
(a). 1
(b). 2
(c). 3
(d). None
Show Answer
Solution : $\tan ^{-1} x+\tan ^{-1} \frac{1}{y}=\tan ^{-1} 3$
$\tan ^{-1} \frac{1}{y}=\tan ^{-1} 3-\tan ^{-1} x$
$\Rightarrow \frac{1}{\mathrm{y}}=\frac{3-\mathrm{x}}{1+3 \mathrm{x}}$
$y=\frac{1+3 x}{3-x}$
Put $\mathrm{x}=1$, then $\mathrm{y}=2 \quad$ Put $\mathrm{x}=2$, then $\mathrm{y}=7$
$\therefore(1,2) \&(2,7)$ are two sets.
Answer: b
5. If $\cot ^{-1}\left(\frac{\mathrm{n}}{\pi}\right)>\frac{\pi}{6} ; \mathrm{n} \in \mathrm{N}$, then the maximum value of $\mathrm{n}$ can be
(a). 4
(b). 5
(c). 6
(d). None
Show Answer
Solution : $\frac{\mathrm{n}}{\pi}<\cot \frac{\pi}{6}\left(\because \cot ^{-1} \mathrm{x}\right.$ is a decreasing function $)$
$\Rightarrow \mathrm{n}<\pi \sqrt{3}$
$\mathrm{n}<5.43 \quad \Rightarrow \quad \mathrm{n}=5(\max )$
Answer: b
6. The value of
$ \sin ^{-1}\left\{\cot \left(\sin ^{-1}\left(\sqrt{\frac{2-\sqrt{3}}{4}}\right)+\cos ^{-1} \frac{\sqrt{12}}{4}+\sec ^{-1} \sqrt{2}\right)\right\} $
(a). $0$
(b). $\frac{\pi}{4}$
(c). $\frac{\pi}{2}$
(d). None
Show Answer
Solution : $\because \sin ^{-1} \sqrt{\frac{2-\sqrt{3}}{4}} \quad=\sin ^{-1} \sqrt{\frac{4-2 \sqrt{3}}{8}}$
$ \begin{aligned} & =\sin ^{-1} \sqrt{\frac{3+1-2 \sqrt{3}}{(2 \sqrt{2})^{2}}} \\ & =\sin ^{-1} \sqrt{\left(\frac{\sqrt{3}-1}{2 \sqrt{2}}\right)^{2}} \\ & =\sin ^{-1} \frac{\sqrt{3}-1}{2 \sqrt{2}} \end{aligned} $
$ \begin{aligned} & =\sin ^{-1} \sin \frac{\pi}{12}=\frac{\pi}{12} \\ \therefore \sin ^{-1}\left\{\cot \left(\frac{\pi}{12}+\frac{\pi}{6}+\frac{\pi}{4}\right)\right\} & =\sin ^{-1} \cot \frac{\pi}{2} \\ & =\sin ^{-1} 0=0 \end{aligned} $
Answer: a
7. The greatest value of $\left(\tan ^{-1} x\right)^{2}+\left(\cot ^{-1} x\right)^{2}$ is…………..
Show Answer
Solution :
$\left(\tan ^{-1} x\right)^{2}+\left(\cot ^{-1} x\right)^{2}=\left(\tan ^{-1} x+\cot ^{-1} x\right)^{2}-2 \tan ^{-1} x \cot ^{-1} x$
$=\frac{\pi^{2}}{4}-2 \tan ^{-1} x\left(\frac{\pi}{2}-\tan ^{-1} \mathrm{x}\right)$
Let $\tan ^{-1} \mathrm{x}=\mathrm{y}$, then LHS $=\frac{\pi^{2}}{4}-2 \mathrm{y}\left(\frac{\pi}{2}-\mathrm{y}\right)$
$ \begin{aligned} & =\frac{\pi^{2}}{4}-\pi y+2 y^{2}=2\left(y^{2}-\frac{\pi y}{2}+\frac{\pi^{2}}{16}\right)-\frac{2 \cdot \pi^{2}}{16}+\frac{\pi^{2}}{4} \\ & =2\left(\tan ^{-1} x-\frac{\pi}{4}\right)^{2}+\frac{\pi^{2}}{8} \end{aligned} $
$\therefore$ Minimum value is $\frac{\pi^{2}}{8}$
Answer : $\frac{\pi^{2}}{8}$
Practice questions
1. If $\left(\tan ^{-1} x\right)^{2}+\left(\cot ^{-1} x\right)^{2}=\frac{5 \pi^{2}}{8}$, then $x$ equals
(a). $-1 $
(b). $1$
(c). $0$
(d). None of these
Show Answer
Answer: (a).2. If $\sin ^{-1}\left(x-\frac{x^{2}}{2}+\frac{x^{3}}{4}-\ldots \ldots ..\right)+\cos ^{-1}\left(x^{2}-\frac{x^{4}}{2}+\frac{x^{6}}{4}-\ldots \ldots \ldots.\right)=\frac{\pi}{2}$ for $0<|x|<\sqrt{2}$, then $x$ equals
(a). $\frac{1}{2}$
(b). $1$
(c). $\frac{-1}{2}$
(d). $-1$
Show Answer
Answer: (b).3. Match the conditions / expressions in column I with statement in column II.
Let $(\mathrm{x}, \mathrm{y})$ be such that $\sin ^{-1}(\mathrm{ax})+\cos ^{-1} \mathrm{y}+\cos ^{-1}(\mathrm{bxy})=\frac{\pi}{2}$
| Column I | Column II |
|---|---|
| (a). If $a=1 \& b=0$, then( $x, y)$ | (p). lies on the circle $x^{2}+y^{2}=1$ |
| (b). If $a=1 \& b=1$, then $(x, y)$ | (q). lies on $\left(x^{2}-1\right)\left(y^{2}-1\right)=0$ |
| (c). If $a=1 \& b=2$, then $(x, y)$ | (r). lies on $y=x$ |
| (b). If $a=2 \& b=2$, then( $x, y)$ | (s). lies on $\left(4 x^{2}-1\right)\left(y^{2}-1\right)=0$ |
Show Answer
Answer: a $\rarr$ p, b $\rarr$ q, c $\rarr$ p, d $\rarr$ s4. Sum to $n$ terms of the series
$ \operatorname{cosec}^{-1} \sqrt{10}+\operatorname{cosec}^{-1} \sqrt{50}+\operatorname{cosec}^{-1} \sqrt{170}+\ldots \ldots \ldots+\operatorname{cosec}^{-1} \sqrt{\left(n^{2}+1\right)\left(n^{2}+2 n+2\right)} \text { is } $
(a). $0$
(b). $\infty$
(c). $\tan ^{-1}(\mathrm{n}+1)-\frac{\pi}{4}$
(d). $\ \cot ^{-1}(\mathrm{n}+1)-\frac{\pi}{4}$
Show Answer
Answer: (c).5. Match the following.
Let $t _{1}=\left(\sin ^{-1} x\right)^{\operatorname{\sin}^{-1} x}, t _{2}=\left(\sin ^{-1} x\right)^{\cos ^{-1} x}, t _{3}=\left(\cos ^{-1} x\right)^{\sin ^{-1} x}, t _{4}=\left(\cos ^{-1} x\right)^{\cos ^{-1} x}$
| Column I | Column II |
|---|---|
| (a). $\mathrm{x} \in(0, \cos 1)$ | (p). $\mathrm{t} _{1}>\mathrm{t} _{2}>\mathrm{t} _{4}>\mathrm{t} _{3}$ |
| (b). $\mathrm{x} \in\left(\cos 1, \frac{1}{\sqrt{2}}\right)$ | (q). $\mathrm{t} _{4}>\mathrm{t} _{3}>\mathrm{t} _{1}>\mathrm{t} _{2}$ |
| (c). $\mathrm{x} \in\left(\frac{1}{\sqrt{2}}, \sin 1\right)$ | (r). $\mathrm{t} _{1}>\mathrm{t} _{2}>\mathrm{t} _{4}>\mathrm{t} _{3}$ |
| (c). $\mathrm{x} \in(\sin 1,1)$ | (s). $t _{3}>t _{4}>t _{1}>t _{2}$ |
Show Answer
Answer: a $\rarr$ q, b $\rarr$ s, c $\rarr$ r, d $\rarr$ s6. Read the passage & answer the following questions
If $\tan ^{-1} x: \tan ^{-1} \mathrm{y}=1: 4\left(\right.$ where $|\mathrm{x}|<\tan \frac{\pi}{6}$ ) then
(i). The value of $y$ as an algebraic function of $x$ will be
(a). $\frac{4 x\left(1+x^{2}\right)}{x^{4}-6 x^{2}+1}$
(b). $\frac{4 x\left(1-x^{2}\right)}{x^{4}-6 x^{2}+1}$
(c). $\frac{4 x\left(1+x^{2}\right)}{x^{4}+6 x^{2}+1}$
(d). None of these.
Show Answer
Answer: (b).(ii). The root of the equation $x^{4}-6 x^{2}+1=0$ is
(a). $\tan \frac{\pi}{12}$
(b). $\tan \frac{\pi}{4}$
(c). $\tan \frac{\pi}{8}$
(d). $\tan \frac{\pi}{16}$
Show Answer
Answer: (a).7. If a $\sin ^{-1} \mathrm{x}-\mathrm{b} \cos ^{-1} \mathrm{x}=\mathrm{c}$, then $a \sin ^{-1} \mathrm{x}+\mathrm{b} \cos ^{-1} \mathrm{x}$ is
(a). $0$
(b). $\frac{\pi \mathrm{ab}+\mathrm{c}(\mathrm{b}-\mathrm{a})}{\mathrm{a}+\mathrm{b}}$
(c). $\frac{\pi}{2}$
(d). $\frac{\pi \mathrm{ab}+\mathrm{c}(\mathrm{b}-\mathrm{a})}{\mathrm{a}+\mathrm{b}}$
Show Answer
Answer: (d).8. $\sum _{\mathrm{r}=1}^{\mathrm{n}} \operatorname{Sin}^{-1}\left(\frac{\sqrt{\mathrm{r}}-\sqrt{\mathrm{r}-1}}{\sqrt{\mathrm{r}(\mathrm{r}+1)}}\right)$ is
(a). $\tan ^{-1} \sqrt{\mathrm{n}}-\frac{\pi}{4}$
(b). $\tan ^{-1} \sqrt{\mathrm{n}+1}-\frac{\pi}{4}$
(c). $\tan ^{-1} \sqrt{\mathrm{n}}$
(d). $\tan ^{-1} \sqrt{\mathrm{n}+1}$
Show Answer
Answer: (c).9. If $\left[\cot ^{-1} x\right]+\left[\cos ^{-1} x\right]=0$, then complete set of values of $x$ is
(a). $(\cos 1,1]$
(b). $(\cot 1, \cos 1)$
(c). $(\cot 1, 1)$
(d). None of these
Show Answer
Answer: (c).10. If $\left(\sin ^{-1} x+\sin ^{-1} w\right)\left(\sin ^{-1} y+\sin ^{-1} z\right)=\pi^{2}$, then
$D=\left|\begin{array}{ll}x^{N} 1 & y^{N} 2 \\ z^{N} & w^{N} 4\end{array}\right|$ where $N _{1}, N _{2}, N _{3}, N _{4} \in W$
(a). has a maximum value of $2$
(b). has a minimum value of $0$
(c). 16 different $\mathrm{D}$ are possible
(d). has a minimum value of $-2 .$
Show Answer
Answer: (a, c, d)11. The value of $k(k>0)$ such that the length of the longest interval in which the function $f(x)=\sin ^{-1}|\sin k x|+\cos ^{-1}(\cos k x)$ is constant is $\frac{\pi}{4}$ is $/$ are
(a). 8
(b). 4
(c). 12
(d). 16
Show Answer
Answer: (b).12. Match the following
| Column I | Column II |
|---|---|
| (a). $\left(\sin ^{-1} \mathrm{x}\right)^{2}+\left(\sin ^{-1} \mathrm{y}\right)^{2}=\frac{\pi^{2}}{2\Rightarrow \mathrm{x}^{3}+\mathrm{y}^{3}}=$ | (p). $1$ |
| (b). $\left(\cos ^{-1} \mathrm{x}\right)^{2}+\left(\cos ^{-1} \mathrm{y}\right)^{2}=2 \pi^{2\Rightarrow \mathrm{x}^{5}+\mathrm{y}^{5}}=$ | (q). $-2$ |
| (c). $\left(\sin ^{-1} \mathrm{x}\right)^{2}+\left(\sin ^{-1} \mathrm{y}\right)^{2}=\frac{\pi^{4}}{4}\Rightarrow\mid\mathrm{x}-\mathrm{y}\mid=$ | (r). $0$ |
| (d). $\mid\sin ^{-1} x-\sin ^{-1} y\mid=\pi \Rightarrow \mathrm{x}^{\mathrm{y}}=$ | (s). $2$ |










