TRIGONOMETRY EQUATIONS - 4 (Trigonometric Equations - Problem Solving)
Equations involving trigonometric functions of unknown angles are called trigonometric equations. Numerically least angle is called the principal value (solution).
Since, trigonometric functions are periodic, a solution is generalised by means of periodicity of the function. The solution consisting of all possible solutions of a trigonometric equation is called its general solution .
| Trigonometric Equations | General solutions $\left(\mathbf{n} _{\in} \mathbf{Z}\right)$ |
|---|---|
| $\sin \theta=0$ | $\theta=\mathrm{n} \pi$ |
| $\cos \theta=0$ | $\theta=(2 \mathrm{n}+1) \pi / 2$ |
| $\tan \theta=0$ | $\theta=\mathrm{n} \pi$ |
| $\cot \theta=0$ | $\theta=(2 \mathrm{n}+1) \pi / 2$ |
| $\sin \theta=\sin \alpha$ | $\theta=\mathrm{n} \pi+(-1)^{\mathrm{n}} \alpha$ |
| $\cos \theta=\cos \alpha$ | $\theta=2 \mathrm{n} \pi \pm \alpha$ |
| $\tan \theta=\tan \alpha$ | $\theta=\mathrm{n} \pi+\alpha$ |
| $\sin ^{2} \theta=\sin ^{2} \alpha$ | $\theta=\mathrm{n} \pi \pm \alpha$ |
| $\cos ^{2} \theta=\cos ^{2} \alpha$ | $\theta=\mathrm{n} \pi \pm \alpha$ |
| $\tan ^{2} \theta=\tan ^{2} \alpha$ | $\theta=\mathrm{n} \pi \pm \alpha$ |
Method of an auxiliary angle
Equations of the form $a \cos \theta \pm b \sin \theta=c$ are equivalent to the elementary trigonometric equations
$\cos (\theta \mp \phi)=\frac{\mathrm{c}}{\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}}$ where $\sin \phi=\frac{\mathrm{b}}{\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}}, \cos \phi=\frac{\mathrm{a}}{\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}}$
If $|c|>\sqrt{a^{2}+b^{2}}$, then $a \cos \theta \pm b \sin \theta=c$ has no solution.
If $|c| \leq \sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}$, then put
$\frac{|\mathrm{c}|}{\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}}=\cos \alpha$ so that
$\cos (\theta \mp \phi)=\cos \alpha$
$\Rightarrow \quad \theta \mp \phi=2 \mathrm{n} \pi \pm \alpha$
$\Rightarrow \quad \theta=2 \mathrm{n} \pi \pm \alpha \pm \phi ; \quad \mathrm{n} \in \mathrm{Z}$
Note :
(i). While solving, if you are squaring a trigonometric equation (which should be avoided as for as possible), check the solution for extraneous roots.
(ii). Do not cancel terms containing unknown terms which are in product (it may cause loss of a valid solution)
(iii). Remove all those values (angles) which make any of the terms undefined or infinite.
Solving trigonometric equations graphically
Sketch the graph of each side of the equation. Now look for all the points of intersection within the given interval.
Solved examples
1. The number of distinct solutions of
$ \sin 5 \theta \cos 3 \theta=\sin 9 \theta \cos 7 \theta \text { in }\left[0, \frac{\pi}{2}\right] \text { is } $
(a). 4
(b). 5
(c). 8
(d). 9
Show Answer
Solution :
$2 \sin 5 \theta \cos 3 \theta=2 \sin 9 \theta \cos 7 \theta$
$\Rightarrow \sin 8 \theta+\sin 2 \theta=\sin 16 \theta+\sin 2 \theta$
$\Rightarrow \sin 16 \theta-\sin 8 \theta=0$
$\Rightarrow 2 \cos 12 \theta \cdot \sin 4 \theta=0$
$\sin 4 \theta=0 \quad$ $\hspace{1.5cm}$ or$\hspace{1.5cm}$ $\cos 12 \theta=0$
gives $\theta=\frac{n \pi}{4}$ $\hspace{1.5cm}$ or$\hspace{1.5cm}$ gives $\theta=(2 n+1) \frac{\pi}{24}$
$\therefore \theta=0, \frac{\pi}{4}, \frac{\pi}{2}$ $\hspace{1.5cm}$ or$\hspace{1.5cm}$ $\therefore \theta=\frac{\pi}{24}, \frac{3 \pi}{24}, \frac{5 \pi}{24}, \frac{7 \pi}{24}, \frac{9 \pi}{24}, \frac{11 \pi}{24}$
$\therefore 9$ possible values
Answer: (d)
2. The number of values of $x$ in $[0,5 \pi]$ satisfying $3 \cos 2 x-10 \cos x+7=0$ is
(a). 5
(b). 6
(c). 8
(d). 10
Show Answer
Solution :
$3\left(2 \cos ^{2} x-1\right)-10 \cos x+7=0$
$3 \cos ^{2} \mathrm{x}-5 \cos \mathrm{x}+2=0 \Rightarrow 3 \cos ^{2} \mathrm{x}-3 \cos \mathrm{x}+2=0$
$(3 \operatorname{\cos x}-2) \quad(\operatorname{\cos x}-1)=0$
$\Rightarrow \cos x=\frac{2}{3}, 1$.
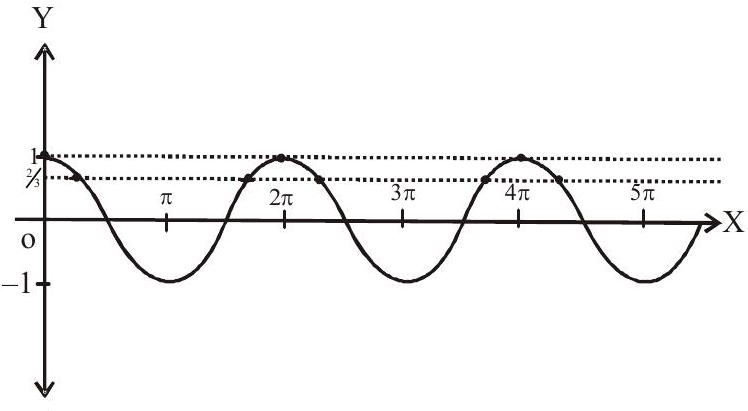
Clearly the lines $\mathrm{y}=\frac{2}{3}, 1$ intersect the graph at 8 points
Hence 8 values
Answer: (c)
3. If $\sin ^{2} \theta-2 \sin \theta-1=0$ is to be satisfied for exactly 4 distinct values of $\theta \in[0, n \pi], \forall n \in N$; then the least value of $n$ is
(a). 2
(b). 6
(c). 4
(d). 8
Show Answer
Solution :
$ \begin{aligned} & \sin ^{2} \theta-2 \sin \theta-1=0 \\ & \sin \theta=1 \pm \sqrt{2} \\ \Rightarrow & \sin \theta=1-\sqrt{2} \text { (as } 1+\sqrt{2} \text { is rejected) } \end{aligned} $
clearly four solutions lie in $[0,4 \pi]$
$\therefore$ least value of $\mathrm{n}$ is 4
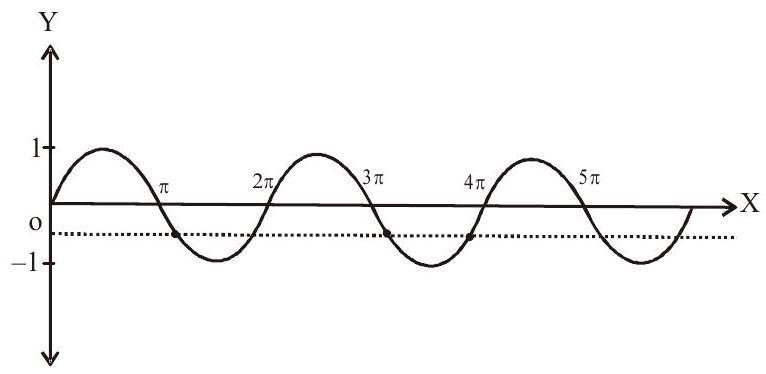
Also $5^{\text {th }}$ solution lies in $[0,5 \pi]$
$\therefore$ greatest value can be 5 .
Answer: (c)
4. The most general solution of sec $x-1=(\sqrt{2}-1) \tan x$ is
(a). $\mathrm{n} \pi+\frac{\pi}{8}$
(b). $2 \mathrm{n} \pi, 2 \mathrm{n} \pi+\frac{\pi}{4}$
(c). $2 \mathrm{n} \pi$
(d). None of these
Show Answer
Solution :
Given equation can be simplified to
$(1-\cos x)=(\sqrt{2}-1) \sin x$
$2 \sin ^{2} \frac{x}{2}-(\sqrt{2}-1) 2 \sin \frac{x}{2} \cos \frac{x}{2}=0$
$2 \sin \frac{x}{2}\left(\sin \frac{x}{2}-(\sqrt{2}-1) \cos \frac{x}{2}\right)=0$
$\Rightarrow \quad \sin \frac{x}{2}=0 \hspace {1cm}$ or $\hspace {1cm} \tan \frac{x}{2}=\sqrt{2}-1$
$\Rightarrow \quad \frac{\mathrm{x}}{2}=\mathrm{n} \pi \hspace {2.4cm} \tan \frac{\mathrm{x}}{2}=\tan \frac{\pi}{8}$
$ \begin{aligned} & \mathrm{x}=2 \mathrm{n} \pi, \mathrm{n} \in \mathrm{Z} \hspace {2.4cm}\frac{\mathrm{x}}{2}=\mathrm{n} \pi+\frac{\pi}{8} \\ & \hspace {3.8cm}\mathrm{x}=2 \mathrm{n} \pi+\frac{\pi}{4}, \mathrm{n} \in \mathrm{Z} \end{aligned} $
Answer: (b)
5. Sum of all the solutions of $\cos x \cdot \cos \left(\frac{\pi}{3}+x\right) \cdot \cos \left(\frac{\pi}{3}-x\right)=\frac{1}{4}, x \in[0,6 \pi]$ is
(a). $15 \pi$
(b). $30 \pi$
(c). $\frac{110 \pi}{3}$
(d). None of these
Show Answer
Solution :
$\frac{1}{4} \cos 3 \mathrm{x}=\frac{1}{4}$
$\cos 3 x=1 \Rightarrow \cos 3 x=\cos 0 \Rightarrow 3 x=2 n \pi \Rightarrow x=\frac{2 n \pi}{3}$
$\therefore \mathrm{x}=0, \frac{2 \pi}{3}, \frac{4 \pi}{3}, \frac{6 \pi}{3}, \frac{8 \pi}{3}, \ldots \ldots \ldots \ldots \ldots, \frac{18 \pi}{3}$
Adding we get the sum as $30 \pi$
Answer: (b)
6. The number of solutions of $\cos x=|1+\sin x|$ for $x \in[0,3 \pi]$, is
(a). 3
(b). 2
(c). 4
(d). None of these
Show Answer
Solution :
It is evident from the figure that, the two graphs intersect at 3 points.
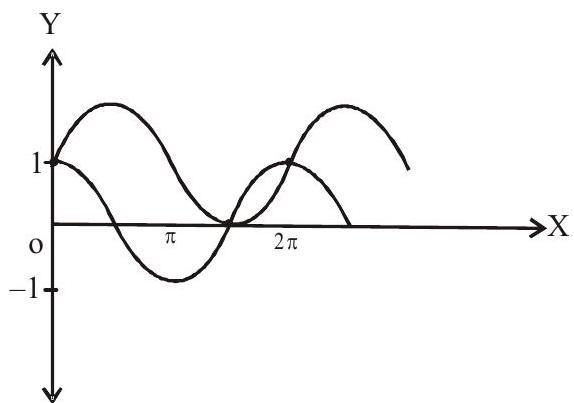
Answer: (a)
7. The number of solutions of $16^{\sin ^{2} x}+16^{\cos ^{2} x}=10$ in $x \in[0,2 \pi]$ is
(a). 8
(b). 6
(c). 4
(d). 2
Show Answer
Solution :
$16^{\sin ^{2} x}+16^{1-\sin ^{2} x}=10$
put $16^{\sin ^{2} x}=y \Rightarrow y+\frac{16}{y}=10$
$\mathrm{y}^{2}-10 \mathrm{y}+16=0 \quad$ gives $\mathrm{y}=8,2$
$\therefore 16^{\sin ^{2} x}=2,8=(16)^{\frac{1}{4}} \&(16)^{\frac{3}{4}}$
$\therefore \sin ^{2} x=\frac{1}{4}, \frac{3}{4}$
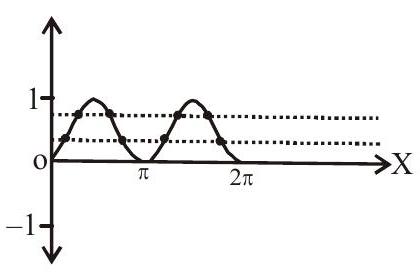
Clearly lines $\mathrm{y}=\frac{1}{4}, \frac{3}{4}$ intersect the graph in 8 points
Hence 8 possible solutions.
Answer: (a)
Practice questions
1. $\begin{aligned} \text { Let } & P=\{\theta: \sin \theta-\cos \theta=\sqrt{2} \cos \theta\} \text { and } \\ & Q=\{\theta: \sin \theta+\cos \theta=\sqrt{2} \sin \theta\} \text { be two sets. Then }\end{aligned}$
(a). $\mathrm{P} \subset \mathrm{Q}$ and $\mathrm{Q}-\mathrm{P} \neq \phi$
(b). $\mathrm{Q} \not \subset \mathrm{P}$
(c). $\mathrm{P} \not \subset \mathrm{Q}$
(d). $\mathrm{P}=\mathrm{Q}$
Show Answer
Answer: (d)2. The number of values of $\theta$ in the interval $\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)$ such that $\theta \neq \frac{n \pi}{5}$ for $n=0, \pm 1, \pm 2$ and $\tan \theta=\cot 5 \theta$ as well as $\sin 2 \theta=\cos 4 \theta$ is
(a). 0
(b). 1
(c). 2
(d). 3
Show Answer
Answer: (d)3. The positive integer value of $n>3$ satisfying the equation
$\frac{1}{\sin \left(\frac{\pi}{n}\right)}=\frac{1}{\sin \left(\frac{2 \pi}{n}\right)}+\frac{1}{\sin \left(\frac{3 \pi}{n}\right)}$ is
(a). 5
(b). 6
(c). 7
(d). 8
Show Answer
Answer: (c)4. All values of $\theta$ in the interval $\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)$ satisfying $(1-\tan \theta)(1+\tan \theta) \sec ^{2} \theta+2^{\tan ^{2} \theta}=0$
(a). $\frac{\pi}{3}$
(b). $\frac{-\pi}{3}$
(c). $0$
(d). None of these.
Show Answer
Answer: (a, b)5. Match the following :-
| Column I | Column II |
|---|---|
| (a). Number of roots of $\cos ^{7} x+\sin ^{4} x=1$ in the interval $[0,2 \pi]$ | (p). 1 |
| (b). Value of ’ $a$ ’ for which $a^{2}-2 a+\sec ^{2} \pi(a+x)=0$ has solution | (q). 0 |
| (c). Number of solutions of $\mid\cos x\mid=2[x]$ | (r). 4 |
Show Answer
Answer: (a $\rarr$ r; b $\rarr$ p; c $\rarr$ q)6. The solution set of $|4 \sin x-1|<\sqrt{5},|x|<\pi$ is
(a). $\left(-\pi,-\frac{4 \pi}{5}\right) \cup\left(-\frac{\pi}{5}, \frac{\pi}{10}\right) \cup\left(\frac{9 \pi}{10}, \pi\right)$
(b). $\left(\frac{-9 \pi}{10}, \frac{-\pi}{10}\right) \cup\left(\frac{3 \pi}{10}, \frac{7 \pi}{10}\right)$
(c). $\left(-\pi, \frac{-9 \pi}{10}\right) \cup\left(\frac{-\pi}{10}, \frac{3 \pi}{10}\right) \cup\left(\frac{7 \pi}{10}, \pi\right)$
(d). $\left(\frac{-7 \pi}{10}, \frac{9 \pi}{10}\right)$
Show Answer
Answer: (c)7. The number of points $(x, y)$ inside the circle $x^{2}+y^{2}=4$ satisfying the equation $\tan ^{4} x+\cot ^{4} x+1=3 \sin ^{2} y$ is
(a). 1
(b). 2
(c). 4
(d). 8
Show Answer
Answer: (c)8. If $\sin x=2 \sin \theta, \cos x=\tan y, \tan x=\cos z$ and $\cos y=\tan z$, then $\theta$ is
(a). $18^{\circ}$
(b). $36^{\circ}$
(c). $54^{\circ}$
(d). $72^{\circ}$
Show Answer
Answer: (a)9. Read the following and then answer the questions.
Consider the system of equations
$\sin x \cos 2 \mathrm{y}=\left(\mathrm{a}^{2}-1\right)^{2}+1, \cos x \sin 2 \mathrm{y}=\mathrm{a}+1$
(i). the number of values of a for which the system has a solution is
(a). 1
(b). 2
(c). 3
(d). infinite.
Show Answer
Answer: (a)(ii). The number of values of $\mathrm{x} \in[0,2 \pi]$ when the system has solution for permissible values of a is
(a). 1
(b). 2
(c). 3
(d). 4
Show Answer
Answer: (b)(iii). The number of values of $y \in[0,2 \pi]$ when the system has solution for permissible values of a
(a). 2
(b). 3
(c). 4
(d). 5
Show Answer
Answer: (d)10. The total number of solutions of $\sin \{x\}=\cos \{x\}$ in $[0,2 \pi]$ is
(a). 5
(b). 6
(c). 8
(d). None of these
Show Answer
Answer: (b)11. If $\sin x+\cos x=\sqrt{\left(y+\frac{1}{y}\right)}, x \in[0, \pi]$ then
(a). $\mathrm{x}=\frac{\pi}{4}, \mathrm{y}=1$
(b). $y=2$
(c). $x=\frac{3 \pi}{4}$
(d). None of these.
Show Answer
Answer: (a)12. If the inequatlity $\sin ^{2} x+a \cos x+a^{2}>1+\cos x$ hods for any $x \in R$ then the largest negative integral value of ’ $a$ ’ is
(a). $-4$
(b). $-3$
(c). $-2$
(d). $-1$
Show Answer
Answer: (b)13. The number of solutions of $x \in[0,2 \pi]$ for which $[\sin x+\cos x]=3+[-\sin x]+[-\cos x]$ is
(a). 0
(b). 4
(c). infinite
(d). 1
Show Answer
Answer: (a)14. The arithmetic mean of the roots of the equation $4 \cos ^{3} x-4 \cos ^{2} x-\cos (315 \pi+x)=1$ in the interval $(0,315)$ is
(a). $50 \pi$
(b). $51 \pi$
(c). $100 \pi$
(d). $315 \pi$
Show Answer
Answer: (b)15. Values of $x$ & y satisfying the equation $\sin ^{7} y=\left|x^{3}-x^{2}-9 x+9\right|+\left|x^{3}-x^{2}-4 x+4\right|+\sec ^{2} 2 y+\cos ^{4} y$ are
(a). $x=1, y=n \pi, n \in Z$
(b). $x=1, y=2 n \pi+\frac{\pi}{2}, n \in Z$
(c). $\mathrm{x}=1, \mathrm{y}=2 \mathrm{n} \pi, \mathrm{n} \in \mathrm{Z}$
(d). None of these










