TRIGONOMETRY EQUATIONS - 3 (Trigonometric Equations)
1. The number of values of $x$ in the internal $[0,3 \pi]$ satisfying the equation $2 \sin ^{2} x+5 \sin x-3=0$ is
(a). $6$
(b). $1$
(c). $2$
(d). $4$
Show Answer
Solution :
We have $2 \sin ^{2} x+5 \sin x-3=0$
$2 \sin ^{2} x+6 \sin x-\sin x-3=0$
$(2 \sin x-1)(\sin x+3)=0$
$\sin \mathrm{x}=\frac{1}{2} \quad(\because \sin \mathrm{x} \neq 3) \quad(\because-1 \leq \sin \mathrm{x} \leq 1)$
$y=\sin x$ and $y=\frac{1}{2}$ intersect in 4 points
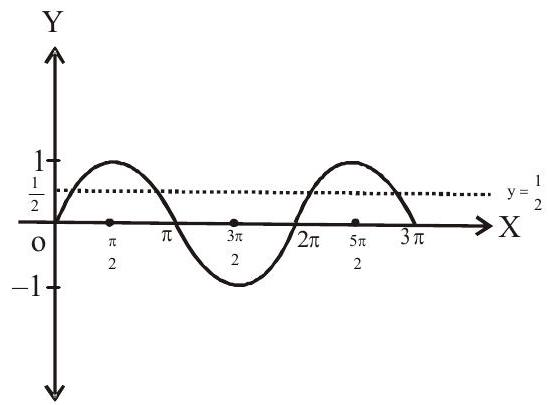
$\therefore$ number of values of $\mathrm{x}$ in the internal $[0,3 \pi]$ is $4.$
2. The number of values of $\theta$ in the internal $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$ such that $\theta \neq \frac{\mathrm{n} \pi}{5}$ for $\mathrm{n}=0, \pm 1, \pm 2$ and $\tan \theta$ $=\cot 5 \theta$ as well as $\sin 2 \theta=\cos 4 \theta$ is
Show Answer
Solution :
Given, $\tan \theta=\cot 5 \theta$
$\tan \theta=\tan \left(\frac{\pi}{2}-5 \theta\right)$
$\frac{\pi}{2}-5 \theta=\mathrm{n} \pi+\theta$
$6 \theta=\frac{\pi}{2}-\mathrm{n} \pi$
$\theta=\frac{\pi}{12}-\frac{\mathrm{n} \pi}{6}$
Also $\cos 4 \theta=\sin 2 \theta$
$\cos 4 \theta=\cos \left(\frac{\pi}{2}-2 \theta\right)$
$4 \theta=2 \mathrm{n} \pi \pm\left(\frac{\pi}{2}-2 \theta\right)$
$\theta=\frac{\mathrm{n} \pi}{2} \pm\left(\frac{\pi}{8}-\frac{\theta}{2}\right)$
| Taking positive | Taking negative |
|---|---|
| $\frac{3 \theta}{2}=\frac{\mathrm{n} \pi}{2}+\frac{\pi}{8} $ | $ \frac{\theta}{2}=\frac{\mathrm{n} \pi}{2}-\frac{\pi}{8}$ |
| $3 \theta=\mathrm{n} \pi+\frac{\pi}{4}$ | $\theta=\mathrm{n} \pi-\frac{\pi}{4}$ |
| $\theta=\frac{4 n \pi+\pi}{12}$ | $\theta=(4 n-1) \frac{\pi}{4}$ |
| $\theta=(4 n+1) \frac{\pi}{12}$ |
These values of $\theta$ gives only 3 common solution lies in the interval $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$.
3. The number of all possible values of $\theta$, where $0<\theta<\pi$, for which the system of equaitons $(\mathrm{y}+\mathrm{z}) \cos 3 \theta=(\mathrm{xyz}) \sin 3 \theta$
$x \sin 3 \theta=\frac{2 \cos 3 \theta}{y}+\frac{2 \sin 3 \theta}{z}$
and $(x y z) \sin 3 \theta=(y+2 z) \cos 3 \theta+y \sin 3 \theta$
have a solution $\left(\mathrm{x} _{0}, \mathrm{y} _{0}, \mathrm{z} _{0}\right)$ with $\mathrm{y} _{0} \mathrm{z} _{0} \neq 0$ is
Show Answer
Solution :
Given equations are $x \sin 3 \theta=\frac{y+z}{y z} \cos 3 \theta$
$x \sin 3 \theta-\frac{\cos 3 \theta}{y}-\frac{\cos 3 \theta}{z}=0…….(1)$
$x \sin 3 \theta-\frac{2 \cos 3 \theta}{y}-\frac{2 \sin 3 \theta}{z}=0…….(2)$
$\mathrm{x} \sin 3 \theta-\frac{1}{\mathrm{z}} \cos 3 \theta-\frac{2}{\mathrm{y}} \cos 3 \theta-\frac{1}{\mathrm{z}} \sin 3 \theta=0…….(3)$
from (2) and (3) we get
$2 \sin 3 \theta=\cos 3 \theta+\sin 3 \theta$
$\sin 3 \theta=\cos 3 \theta$
$\tan 3 \theta=1=\tan \frac{\pi}{4}$
$3 \theta=\frac{\pi}{4}, \frac{5 \pi}{4}, \frac{9 \pi}{4}$ or $\theta=\frac{\pi}{12}, \frac{5 \pi}{12}, \frac{9 \pi}{12}$
4. The solution of the equation $4 \sin ^{4} x+\cos ^{4} x=1$ is
(a). $x=2 n \pi$
(b). $\mathrm{x}=\mathrm{n} \pi+1$
(c). $x=(n+2) \pi$
(d). none of these
Show Answer
Solution :
Given that $4 \sin ^{4} x+\cos ^{4} x=1$
$4 \sin ^{4} x+\left(\cos ^{2} x-1\right)\left(\cos ^{2} x+1\right)=0$
$4 \sin ^{4} x-\sin ^{2} x\left(\cos ^{2} x+1\right)=0$
$\sin ^{2} x\left[4 \sin ^{2} x-\cos ^{2} x-1\right]=0$
$\sin ^{2} x\left[5 \sin ^{2} x-2\right]=0$
$\sin ^{2} x=0$ or $\sin ^{2} x=\frac{2}{5}$
$\sin \mathrm{x}=0$ or $\sin \mathrm{x}= \pm \sqrt{\frac{2}{5}}$
$\mathrm{x}=\mathrm{n} \pi \quad$ or $\quad \mathrm{x}=\mathrm{n} \pi+\alpha \quad$ where $\sin \alpha= \pm \sqrt{\frac{2}{5}}$
$\therefore$ Option d is correct.
5. The solution of the equation $[\sin x+\cos x]^{1+\sin 2 x}=2,-\pi \leq x \leq \pi$ is
(a). $\frac{\pi}{2}$
(b). $\pi$
(c). $\frac{\pi}{4}$
(d). $\frac{3 \pi}{4}$
Show Answer
Solution : $[\sin x+\cos x]^{1+\sin 2 x}$
$ \begin{aligned} & \left(\sqrt{2} \sin \left(\frac{\pi}{4}+x\right)\right)^{1+\sin 2 x} \\ & \text { at } x=\frac{\pi}{4},\left(\sqrt{2} \sin \left(\frac{\pi}{4}+\frac{\pi}{4}\right)\right)^{1+\sin 2 \frac{\pi}{4}}=(\sqrt{2})^{2}=2 \end{aligned} $
$\therefore$ Option c is correct.
6. The most general solutions $2^{\sin x}+2^{\cos x}=2^{1-\frac{1}{\sqrt{2}}}$ are
(a). $\mathrm{n} \pi-\frac{\pi}{4}$
(b). $\mathrm{n} \pi+\frac{\pi}{4}$
(c). $ \mathrm{n} \pi+(-1)^{\mathrm{n}} \frac{\pi}{4}$
(d). $2 \mathrm{n} \pi \pm \frac{\pi}{4}$
Show Answer
Solution : We have $2^{\sin x}+2^{\cos x}=2^{1-\frac{1}{\sqrt{2}}}$
$\mathrm{AM} \geq \mathrm{GM}$
$ \frac{2^{\sin x}+2^{\cos x}}{2} \geq \sqrt{2^{\sin x} 2^{\cos x}} $
$\geq 2 \sqrt{2^{\sin x}+2^{\cos x}}$ (Equality holds when $\sin x=\cos x$ )
$\geq 2 \sqrt{2^{\sin x}+2^{\cos x}}$
But the minimum value of $\sin x+\cos x$ is $-\sqrt{2}$
$\therefore \sin x+\cos x=\sqrt{2} \sin \left(\frac{\pi}{4}+x\right)$
and $-1 \leq \sqrt{2} \sin \left(\frac{\pi}{4}+\mathrm{x}\right) \leq 1$
$-\sqrt{2} \leq \sqrt{2} \sin \left(\frac{\pi}{4}+x\right) \leq \sqrt{2}$
$\therefore \sin x=\cos x$
$\tan x=1=\tan \frac{\pi}{4}$
$\mathrm{x}=\mathrm{n} \pi+\frac{\pi}{4}$
$\therefore$ Option b is correct.
7. The set of values of $\theta$ satisfying the inequation $2 \sin ^{2} \theta-5 \sin \theta+2>0$, where $0<\theta<2 \pi$ is
(a). $\left(0, \frac{\pi}{6}\right) \cup\left(\frac{5 \pi}{6}, 2 \pi\right)$
(b). $\left[0, \frac{\pi}{6}\right] \cap\left[\frac{5 \pi}{6}, 2 \pi\right]$
(c). $\left[0, \frac{\pi}{3}\right] \cup\left[\frac{2 \pi}{3}, 2 \pi\right]$
(d). none of these
Show Answer
Solution : Given inequation $2 \sin ^{2} \theta-5 \sin \theta+2>0$
$2 \sin ^{2} \theta-4 \sin \theta-\sin \theta+2>0$
$2 \sin \theta(\sin \theta-2)-1(\sin \theta-2)>0$
$(2 \sin \theta-1)(\sin \theta-2)>0$
$\Rightarrow \sin \theta<\frac{1}{2}$ or $\sin \theta>2$
but $\sin \theta>2$ not possible
$\therefore \sin \theta<\frac{1}{2}$
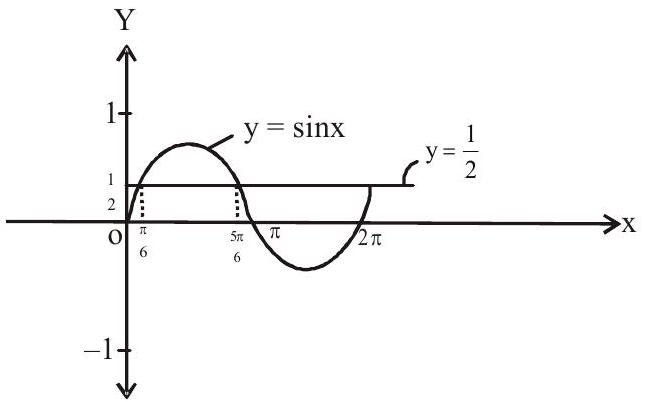
If $\mathrm{x} \varepsilon\left(0, \frac{\pi}{6}\right) \cup\left(\frac{5 \pi}{6}, \pi\right)$ for $\mathrm{x} \in(0,2 \pi)$
$\therefore \sin \theta<\frac{1}{2} \Rightarrow \theta \in\left(0 \frac{\pi}{6}\right) \cup\left(\frac{5 \pi}{6}, \pi\right)$ for $\theta \in(0,2 \pi)$.
Correct option is ’d’
8. Passage
Suppose equation is $f(x)-g(x)=0$ or $f(x)=g(x)=y$ say. Then draw the graphs of $y=f(x)$ and $y=g(x)$. If graphs of $\mathrm{y}=\mathrm{f}(\mathrm{x})$ and $\mathrm{y}=\mathrm{g}(\mathrm{x})$ cuts at one, two, three …., no points, then number of solutions are one, two, three, … zero respectively.
On the basis of above information, answer the following questions.
1. The number of solution of $\sin x=\frac{|x|}{10}$ is
(a). 4
(b). 6
(c). 8
(d). none of these
2. Total number of solutions of the equation $3 x+2 \tan x=\frac{5 \pi}{2}$ in $x \varepsilon[0,2 \pi]$ is equal to
(a). 1
(b). 2
(c). 3
(d). 4
3. Total number of solutions of $\sin \{x\}=\cos \{x\}$, where $\{$.$\}$ denotes the fractional part, in $[0, 2 \pi]$ is
(a). 3
(b). 5
(c). 7
(d). none of these
4. If $1-\sin \mathrm{x}=\frac{\sqrt{3}}{2}\left|\mathrm{x}-\frac{\pi}{2}\right|+\mathrm{a}$ has no solution when $\mathrm{a} \varepsilon \mathrm{R}^{+}$then
(a). $ \mathrm{a} \in \mathrm{R}^{+}$
(b). $ \mathrm{a}>\frac{3}{2}+\frac{\pi}{\sqrt{3}}$
(c). $\mathrm{a} \in\left(0, \frac{3}{2}+\frac{\pi}{\sqrt{3}}\right)$
(d). $ \mathrm{a} \in\left(\frac{3}{2}, \frac{3}{2}+\frac{\pi}{\sqrt{3}}\right)$
Show Answer
Solution :
1. Graphs of $y=\sin x$ and $y=\frac{|x|}{10}$ meet exactly six times. Hence no of solutions $=6$

2. We have $3 x+2 \tan x=\frac{5 \pi}{2}$ in $x \varepsilon[0,2 \pi]$
$\tan \mathrm{x}=\frac{5 \pi}{4}-\frac{3 \mathrm{x}}{2}$
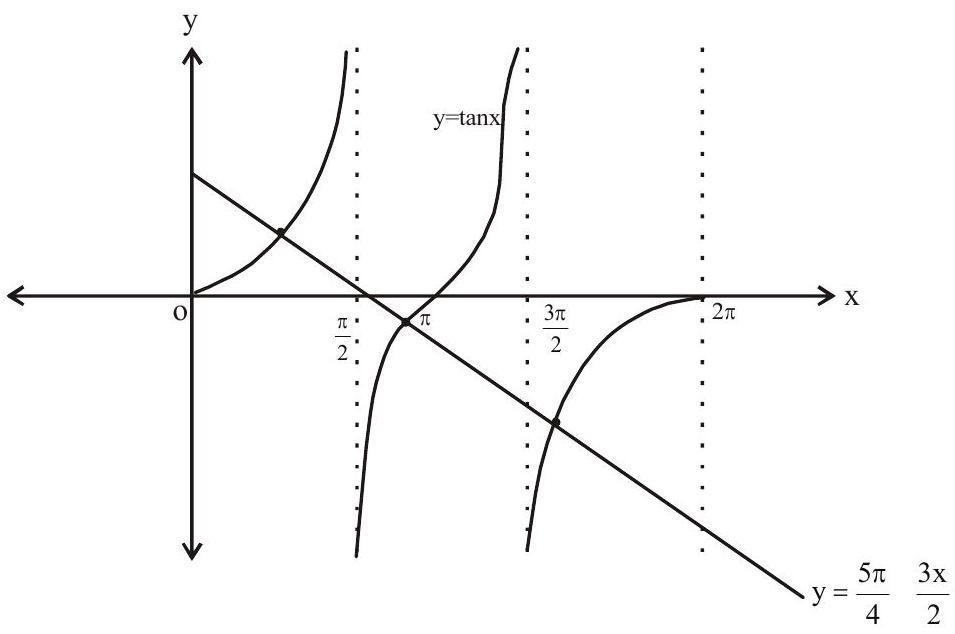
Graphs of $y=\frac{5 \pi}{4}-\frac{3 \pi}{2}$ and $y=\tan x$ meet exactly three times in $[0,2 \pi]$
Thus number of solution $=3$
3. $\sin \{x\}=\cos \{x\}$
Graphs of $y=\sin \{x\}$ and $y=\cos \{x\}$ meet excatly 7 times in $[0,2 \pi]$
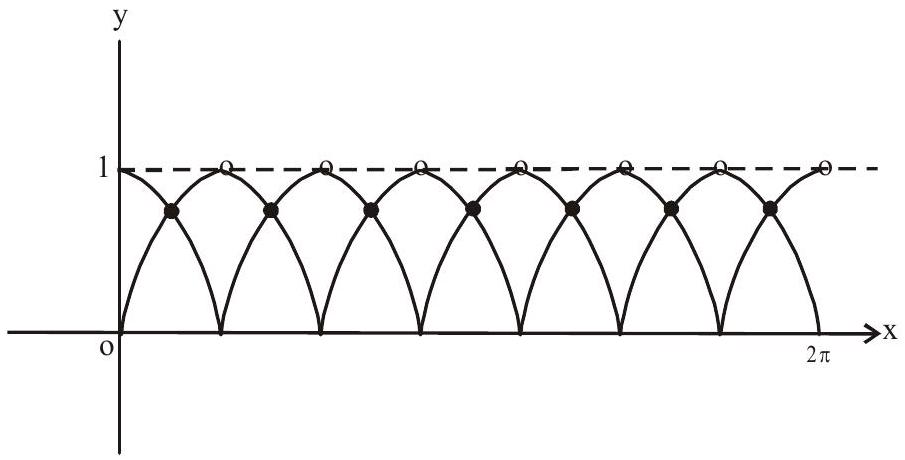
4. slope of $y=1-\sin x$ is $-\cos x$
slope of $\mathrm{y}=\frac{\sqrt{3}}{2}\left|\mathrm{x}-\frac{\pi}{2}\right|+$ a for $\mathrm{x}>\frac{\pi}{2}$ is $\frac{\sqrt{3}}{2}$
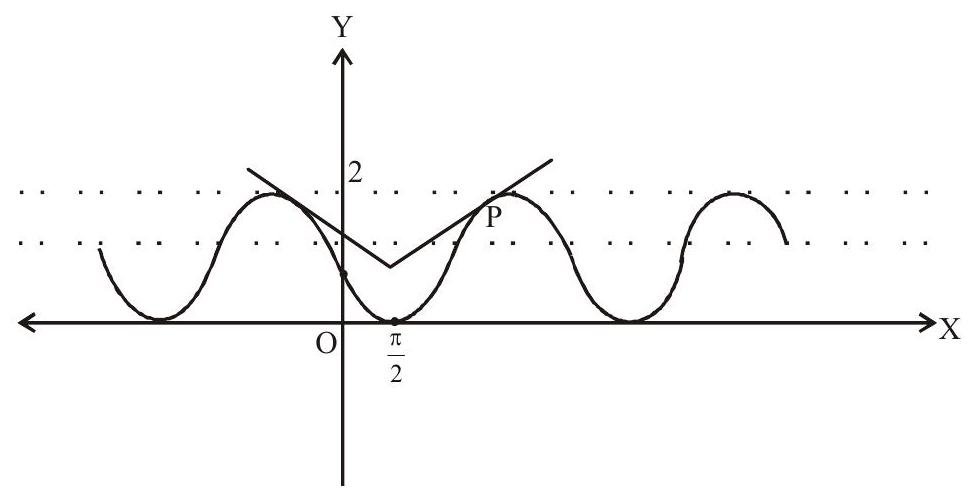
$\cos x=-\frac{\sqrt{3}}{2} \Rightarrow x=\frac{7 \pi}{6} \Rightarrow P=\left(\frac{7 \pi}{6}, \frac{3}{2}\right)$
If $\mathrm{y}=\frac{\sqrt{3}}{2}\left|\mathrm{x}-\frac{\pi}{2}\right|+\mathrm{a}$ passes throgh ’ $\mathrm{P}$ ’ then
$\mathrm{a}=\frac{3}{2}-\frac{\pi}{\sqrt{3}}$
$\Rightarrow \mathrm{a}>\frac{3}{2}-\frac{\pi}{\sqrt{3}}$
Practice questions
1. $\sin \theta+\sqrt{3} \cos \theta=6 x-x^{2}-11,0 \leq \theta \leq 4 \pi, x \in R$, holds for
(a). no values of $x$ and $\theta$
(b). one value of $x$ and two values of $\theta$
(c). two values of $x$ and two values of $\theta$
(d). two points of values of $(x, \theta)$
Show Answer
Answer: (b, d)2. For $0 \leq x \leq 2 \pi$, then $2^{\operatorname{cosec}^{2} x} \sqrt{\frac{1}{2} y^{2}-y}+1 \leq \sqrt{2}$
(a). is satisfied by exactly one value of $y$
(b). is satisfied by exactly two value of $x$
(c). is satisfied by $\mathrm{x}$ for which $\cos \mathrm{x}=0$
(d). is satisfied by $x$ for which $\sin x=0$
Show Answer
Answer: (a, b, c)3. Let $\tan x-\tan ^{2} x>0$ and $|2 \sin x|<1$. Then the intersection of which of the following two sets satisfies both the inequalities?
(a). $ \mathrm{x}>\mathrm{n} \pi, \mathrm{n} \in \mathrm{Z}$
(b). $ \mathrm{x}>\mathrm{n} \pi-\frac{\pi}{6}, \mathrm{n} \in \mathrm{Z}$
(c). $ \mathrm{x}<\mathrm{n} \pi-\frac{\pi}{4}, \mathrm{n} \in \mathrm{Z}$
(d). $ \mathrm{x}<\mathrm{n} \pi+\frac{\pi}{6}, \mathrm{n} \in \mathrm{Z}$
Show Answer
Answer: (a, d)4. The equation $(\operatorname{cosp}-1) \mathrm{x}^{2}+(\cos p) \mathrm{x}+\sin \mathrm{p}=0$ in the varibale $\mathrm{x}$ has real roots. Then $\mathrm{p}$ can take any value in the interval
(a). $(0,2 \pi)$
(b). $(-\pi, 0)$
(c). $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$
(d). $(0, \pi)$
Show Answer
Answer: (d)5. Let $2 \sin ^{2} \mathrm{x}+3 \sin \mathrm{x}-2>0$ and $\mathrm{x}^{2}-\mathrm{x}-2<0$ ( $\mathrm{x}$ is measured in radians). Then $\mathrm{x}$ lies in the interval
(a). $\left(\frac{\pi}{6}, \frac{5 \pi}{6}\right)$
(b). $\left(-1, \frac{5 \pi}{6}\right)$
(c). $(-1,2)$
(d). $\left(\frac{\pi}{6}, 2\right)$
Show Answer
Answer: (d)6. If $\left(\operatorname{cosec}^{2} \theta-4\right) x^{2}+(\cot \theta+\sqrt{3}) x+\cos ^{2} \frac{3 \pi}{2}=0$ holds true for all real $x$, then the most general values of $\theta$ can be given by ( $\varepsilon$ Z )
(a). $2 \mathrm{n} \pi+\frac{11 \pi}{6}$
(b). $2 n \pi+\frac{5 \pi}{6}$
(c). $ 2 n \pi \pm \frac{7 \pi}{6}$
(d). $\mathrm{n} \pi \pm \frac{11 \pi}{6}$
Show Answer
Answer: (a, b)7. If $\sin ^{4} x+\cos ^{4} y+2=4 \sin x \cos y$ and $0 \leq x, y \leq \frac{\pi}{2}$, then $\sin x+\cos y$ is equal to
(a). $-2$
(b). $0$
(c). $2$
(d). $\frac{3}{2}$
Show Answer
Answer: (c)8. The solution of the equation $\sin ^{10} \mathrm{x}+\cos ^{10} \mathrm{x}=\frac{29}{16} \cos ^{4} 2 \mathrm{x}$ is
(a). $\mathrm{x}=\frac{\mathrm{n} \pi}{4}+\frac{\pi}{8}, \mathrm{n} \varepsilon \mathrm{I}$
(b). $\mathrm{x}=\mathrm{n} \pi+\frac{\pi}{4}, \mathrm{n} \varepsilon \mathrm{I}$
(c). $ \mathrm{x}=2 \mathrm{n} \pi+\frac{\pi}{2}, \mathrm{n} \varepsilon \mathrm{I}$
(d). none of these
Show Answer
Answer: (a)9. The most general values of $x$ for which $\sin x+\cos x=\min \left\{1, a^{2}-4 a+6\right\}$, a $R$ are given by
(a). $2 \mathrm{n} \pi, \mathrm{n} \varepsilon \mathrm{N}$
(b). $ 2 \mathrm{n} \pi+\frac{\pi}{2}, \mathrm{n} \varepsilon \mathrm{N}$
(c). $ \mathrm{n} \pi+(-1)^{\mathrm{n}} \frac{\pi}{4}-\frac{\pi}{4}, \mathrm{n} \varepsilon \mathrm{N}$
(d). none of these
Show Answer
Answer: (c)10. Number of solutions of the equations $y=\frac{1}{3}[\sin x+[\sin x]]$ and $[y+[y]]=2 \cos x$ where $[$.$]$ denotes the greatest integer function is
(a). 0
(b). 1
(c). 2
(d). infinite
Show Answer
Answer: (a)11. If $|\cos x|^{\sin ^{2} x-\frac{3}{2} \sin x+\frac{1}{2}}=1$, then possible values of $x$ are
(a). $\mathrm{n} \pi$ or $\mathrm{n} \pi+(-1)^{\mathrm{n}} \frac{\pi}{6}, \mathrm{n} \varepsilon \mathrm{I}$
(b). $n \pi$ or $2 n \pi+\frac{\pi}{2}$ or $n \pi+(-1)^{n} \frac{\pi}{6}$, $n \varepsilon Z$
(c). $\mathrm{n} \pi+(-1)^{\mathrm{n}} \frac{\pi}{6}, \mathrm{n} \varepsilon$ I
(d). $\mathrm{n} \pi, \mathrm{n} \varepsilon \mathrm{I}$
Show Answer
Answer: (b)12. If $\left(\cos ^{2} x+\frac{1}{\cos ^{2} x}\right)\left(1+\tan ^{2} 2 y\right)(3+\sin 3 z)=4$, then
(a). $x$ may be multiple of $\pi$
(b). $x$ cannot be an even multiple of $\pi$
(c). $ \mathrm{z}$ can be a multiple of $\pi$
(d). $y$ can be a multiple of $\frac{\pi}{2}$
Show Answer
Answer: (a, d)13. Matrix match type
| Column I | Column II |
|---|---|
| (a). If $3 \cos ^{2} \theta-2 \sqrt{3} \sin \theta \cos \theta-3 \sin ^{2} \theta=0$ than $\theta=$ | (p). $ \frac{\pi}{6}, \frac{5 \pi}{6}$ |
| (b). If $r \sin \theta=3, r=4(1+\sin \theta)$where $0 \leq \theta \leq 2 \pi$, then $\theta=$ | (q). $2 n \pi+\frac{7 \pi}{6}$ |
| (c). If $\sin \theta=-\frac{1}{2}$ and $\tan \theta=\frac{1}{\sqrt{3}}$, then the general value of $\theta$ which satisfies both the equations is | (r). $\frac{\pi}{6}, \frac{\pi}{3}, \frac{5 \pi}{6}, \frac{2 \pi}{3}$ |
| (d). If $0 \leq x \leq \pi$ and $81^{\sin ^{2} x}+81^{\cos ^{2} x}=30$ then $x$ is | (s). $\frac{n \pi}{2}+\frac{\pi}{6}$ |
Show Answer
Answer: (a $\rarr$ s; b $\rarr$ p; c $\rarr$ q; d $\rarr$ r)14. If $3^{\sin 2 x+2 \cos ^{2} x}+3^{1-\sin 2 x+2 \cos ^{2} x}=28$, then the value of $x$ are given by
(a). $\tan x=1$
(b). $\tan x=-1$
(c). $\cos x=0$
(d). none of these
Show Answer
Answer: (b, c)15. If $e^{\left\{\left(\sin ^{2} x+\sin ^{4} x+\sin ^{6} x+\ldots \infty\right) \log _{c}{ }^{2}\right\}}$ satisfies the equation $x^{2}-9 x+8=0$, then value of $\frac{\cos x}{\cos x+\sin x}$, $0<\mathrm{x}<\frac{\pi}{2}$ is
(a). $\frac{1}{2}(\sqrt{3}+1)$
(b). $\frac{1}{2}(\sqrt{3}-1)$
(c). $\frac{1}{2}$
(d). $0$
Show Answer
Answer: (b)Integer type questions
16. If $\alpha, \beta$ satisfy the equaiton $12 \sin \alpha+5 \cos \alpha=2 \beta^{2}-8 \beta+21$, then $\beta^{2}-2 \beta$, is_______
Show Answer
Answer: 017. The value of $x$ and $y$ satisfy the equaiton $\tan ^{2}(x+y)+\cot ^{2}(x+y)=1-2 x-x^{2}$, then the value of $x^{2}-$ $3 x+2$ is __________
Show Answer
Answer: 618. The integral value of $p$ for which $\sqrt{\mathrm{p}} \cos x-2 \sin x=\sqrt{2}+\sqrt{2-p}$ has a solution, is __________










