PERMUTATION AND COMBINATIONS - 1 (Properties of
Fundametal principle of counting
(i) Addition principle : If an operation can be performed in ’
(ii) Multiplication Principle: If an operation can be performed is ’
Factorial
The continued product of first
value of 0 ! is 1
Exponent of prime
Let
Permutation
Number of permutations of
- Number of ways of filling r places using
Circular Permutation
Number of circular permutations of
Number of circular permutations of
Number of circular permutations of
Note: When position are marked, circular arrangement is assumed to be linear.
Combination
Number of combinations of
Note:
Properties of
i.
ii.
iii.
iv.
v.
vi.
vii.
viii.
Solved examples
1. How many 5-digit numbers divisible by 3 can be formed using digits
Show Answer
Solution:
Sum of digits
so 5 -digit numbrs can be formed using the digits
Answer: 192
2. How many 5 -digit numbers divisible by 4 can be formed using digits
Show Answer
Solution:
Number is divisible by 4 , if the last two digits of the number are a multiple of 4 , so we can have 04 ,
Answer: 228
3. How many 5 -digit numbers divisible by 6 can be formed using digits
Show Answer
Solution:
Sum of digits is
4. The total number of odd natural numbers that can be formed with the digits
(a) 120
(b) 160
(c) 180
(d) none
Show Answer
Solution:
| Odd digits | Even digits |
|---|---|
| 1, 3, 5 | 4 |
| 1 | 4 |
| 1 |
Number of arrangements can be
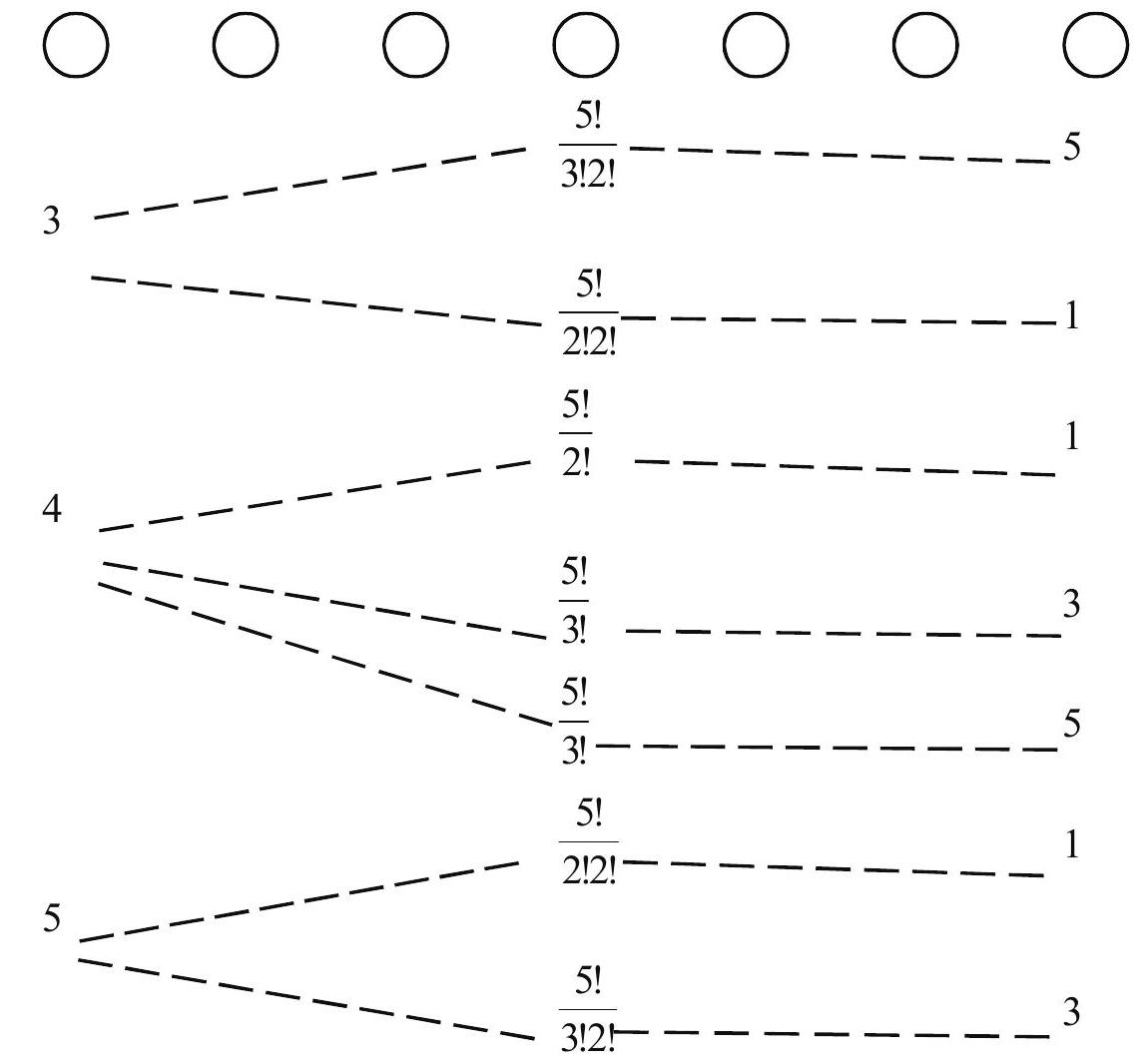
Total no.
Answer: c
5. The total number of 4 digit numbers greater than 4000 , whose sum of digits is odd is
(a).
(b).
(c).
(d). none of these
Show Answer
Solution:
Thousands place can be filled in 6 ways. Hundred’s and Ten’s place can be filled in 10 ways each. First 3 places given the sum either odd or even. In either case last place can be filled in 5 ways.
Answer: b
6. Mohan writes a letter to five of his friends and addresses them. The number of ways in which the letters can be placed in the envelopes so that that three of them are in the wrong envelopes is
(a). 44
(b). 119
(c). 21
(d). 20
Show Answer
Solution:
Answer: d
7. In how many ways the squares of the figure given below be filled up with letters of the word ‘ROHINI’, so that each row contains atleast one letter.

Show Answer
Solution:
as six squares can be slected in such a way that no row is empty is
Answer: 9360
Practice questions
1. Number of polynomials of the form
(a). 30
(b). 1000
(c). 10
(d). none of these
Show Answer
Answer: (c)2. The number of ways in which we can select four numbers from 1 to 30 so as to exclude every selection of four consecutive number is
(a). 27378
(b). 27405
(c). 27399
(d). none of these
Show Answer
Answer: (a)3. The number of ordered pairs of integers
(a). 2
(b). 8
(c). 6
(d). none of these
Show Answer
Answer: (b)4. How many six digit numbers are there in which sum of the digits is divisible by 5
(a).
(b).
(c).
(d). none of these
Show Answer
Answer: (a)5. Ten IIT and 2 DCE students sit in a row. The number of ways in which exactly 3 IIT students sit between 2 DCE students is
(a).
(b).
(c).
(d). none of these
Show Answer
Answer: (a)6. Let there are
(a). 7
(b). 6
(c). 5
(d). none of these
Show Answer
Answer: (c)7. Total number of integers ’
(a). 666
(b). 667
(c). 665
(d). none of these
Show Answer
Answer: (a)8. Match the following:-
| Column I | Column II |
|---|---|
| a. The number of five digit numbers having the product of digits 20 is | p. 77 |
| b. A man took 5 space plays out of an engine to clean them. The number ofways in which he can place atleast two plays in the engine from where they came out is | q. 31 |
| c. The number of integers between 1 and 1000 inclusive in which atleast two consecutive digits are equal is | r. 50 |
| d. Value of |
s. 181 |
Show Answer
Answer: a - r, b - q, c - s, d - p9. The number of ordered triplets
Show Answer
Answer: 7010. Read the paragraph and answer the questions that follow :-
Number of ways of distributing
i. 4 candidates are competing for two managerial posts. In how many ways can the candidates be selected?
(a).
(b).
(c).
(d). none of these
Show Answer
Answer: (b)ii. 8 different balls can be distributed among 3 children so that every child receives at least one ball is
(a).
(b).
(c).
(d). none of these
Show Answer
Answer: (d)iii. 5 letters can be posted into 3 letter boxes in
(a).
(b).
(c).
(d). none of these










