PARABOLA-9
Exercises
1. A tangent PT is drawn at the point
(a).
(b).
(c).
(d).
Show Answer
Solution:
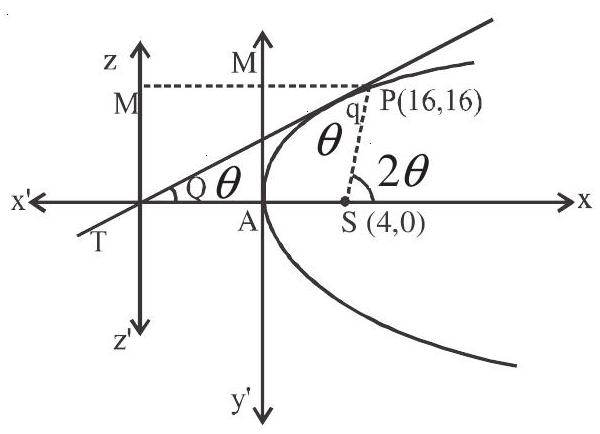
Answer: a
2. If a, b,
(a).
(b).
(c).
(d).
Show Answer
Solution: Equation of normals are
Equation 1 and 2 are identical then
For
Answer: d
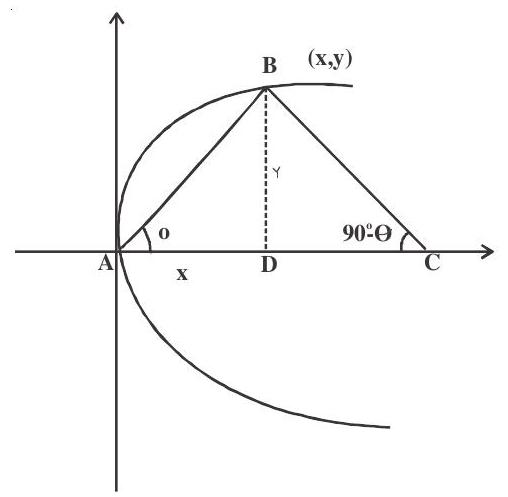
3. If
(a).
(b).
(c).
(d).
Show Answer
Solution: Let coordinates of B be (
In
In
Answer: b
4. A circle is descirbed whose centre is the vertex and whose diameter is three-quarters of the latus rectum of the parabola
(a).
(b).
(c).
(d).
Show Answer
Solution: Centre of circle
diameter
coordinates of
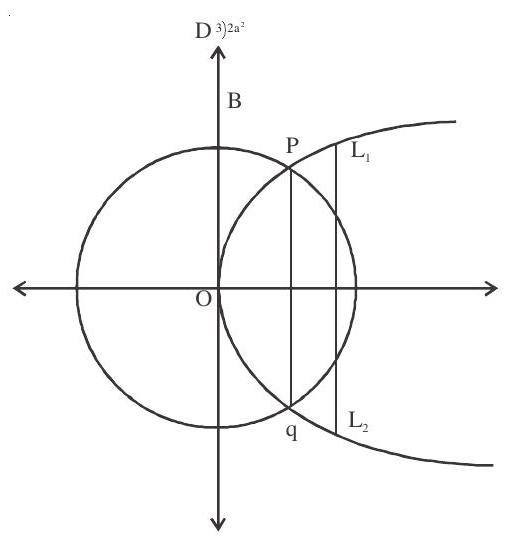
Area of trapezium
Answer: a
5. From the point
(a).
(b).
(c).
(d).
Show Answer
Solution: Let equation of normal be
It passes through
Points are (at
Centroid is
Answer: d
6. Aray of light travels along a line
(a).
(b).
(c).
(d).
Show Answer
Solution:
Focus
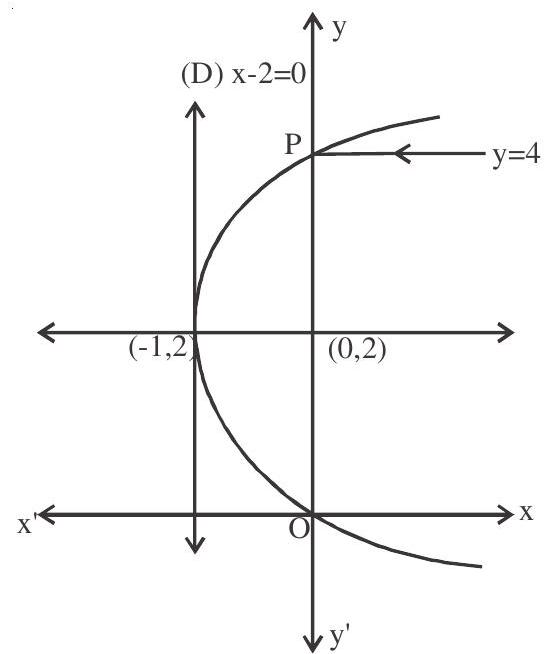
Incident ray is parallel to axis of the parabola, so reflected ray passes through focus
Answer: c
7. Let
Pon the directrix of the parabola, then length of each side of an equilateral triangle SMP, where S is focus of the parabola is
(a). 6
(b). 8
(c). 10
(d). 11
Show Answer
Solution: Equation of parabola is
focus
equation of directrix
P
Coordinates of
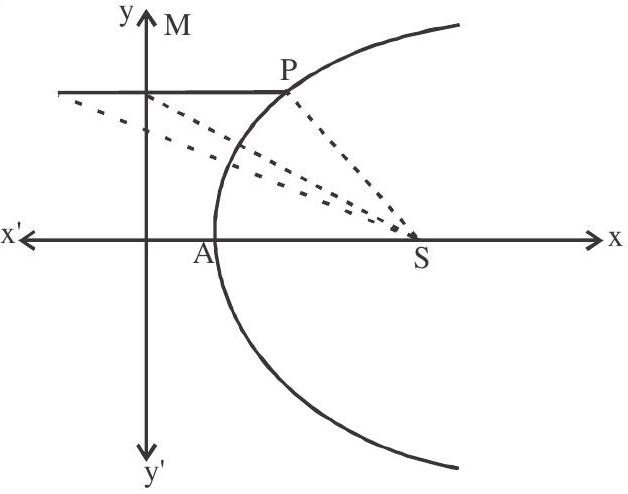
Length of side
Answer: a
Practice questions
1. The point
(a).
(b).
(c).
(d).
Show Answer
Answer: (b)2. Two perpendicular tangents to
(a).
(b).
(c).
(d).
Show Answer
Answer: (a)3.
(a).
(b).
(c). does not have any common tangent.
(d).
Show Answer
Answer: (a)4. Two common tangents to the circle
(a).
(b).
(c).
(d).
Show Answer
Answer: (c)5. The number of points with integral coordinates that lie in the interior of the circle
(a). 6
(b). 8
(c). 10
(d). 12
Show Answer
Answer: (b)6. The vertex of the parabola
(a).
(b).
(c).
(d).
Show Answer
Answer: (d)7. The length of the latus rectum of the parabola
(a).
(b).
(c).
(d).
Show Answer
Answer: (c)8. The point on
(a).
(b).
(c).
(d).
Show Answer
Answer: (a)9. The angle between the tangents drawn from the origin to the parabola
(a).
(b).
(c).
(d).
Show Answer
Answer: (c)10. The circle
(a).
(b).
(c).
(d). none of these










