Conormal points:

Let $\mathrm{P}(\mathrm{h},\mathrm{k})$ be a point and equation of parabola be ${\mathrm{y}}^2=4\mathrm{ax}$.

Equation of normal is

$y=mx-2am-a{m}^3$

If passes through $(\mathrm{h},\mathrm{k})$ so

$\begin{array}{rl}& \mathrm{k}=\mathrm{mh}-2\mathrm{am}-{\mathrm{am}}^3\\ & {\mathrm{am}}^3+2\mathrm{am}-\mathrm{mh}+\mathrm{k}=0\\ & {\mathrm{am}}^3+\mathrm{m}(2\mathrm{a}-\mathrm{h})+\mathrm{k}=0\end{array}$

Suppose ${\mathrm{m}}_1,{\mathrm{m}}_2,{\mathrm{m}}_3$ are the roots of this equation

$\therefore {\mathrm{m}}_1+{\mathrm{m}}_2+{\mathrm{m}}_3=0$

$\begin{array}{rl}& {\mathrm{m}}_1{\mathrm{m}}_2+{\mathrm{m}}_2{\mathrm{m}}_3+{\mathrm{m}}_3{\mathrm{m}}_1=\frac{2\mathrm{a}-\mathrm{h}}{\mathrm{a}}\\ & {\mathrm{m}}_1\cdot {\mathrm{m}}_2\cdot {\mathrm{m}}_3=-\frac{\mathrm{k}}{\mathrm{a}}\end{array}$

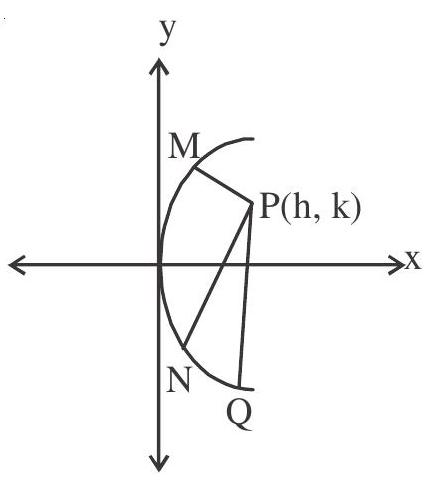
So maximum three normal say PM, PN, PQ drawn through P. Points M, N, Q are called co-normal points.

• The algebraic sum of ordinates of the conormal points is zero. Let the coordinates of conormal points be $\mathrm{M}({\mathrm{am}}_1{}^2,-2{\mathrm{am}}_1),\mathrm{N}({\mathrm{am}}_2{}^2,-2{\mathrm{am}}_2)$ and $\mathrm{Q}({\mathrm{am}}_3^2,-2{\mathrm{am}}_3)$. The ordinates of these points ${\mathrm{y}}_1+{\mathrm{y}}_2+{\mathrm{y}}_3=-2{\mathrm{am}}_1-2{\mathrm{am}}_2-2{\mathrm{am}}_3$ $=-2\mathrm{a}({\mathrm{m}}_1+{\mathrm{m}}_2+{\mathrm{m}}_3)$ $=0$ $\Rightarrow {\mathrm{y}}_1+{\mathrm{y}}_2+{\mathrm{y}}_3=0$

• Centroid of the triangle formed by conormal points lies on the axis of parabola. Let coordinates of conormal points be $\mathrm{M}({\mathrm{x}}_2,{\mathrm{y}}_1),\mathrm{N}({\mathrm{x}}_2,{\mathrm{y}}_2)\mathrm{Q}({\mathrm{x}}_3,{\mathrm{y}}_3)$ Then centroid is $(\frac{{\mathrm{x}}_1+{\mathrm{x}}_2+{\mathrm{x}}_3}{3},\frac{{\mathrm{y}}_1+{\mathrm{y}}_2+{\mathrm{y}}_3}{3})=(\frac{{\mathrm{x}}_1+{\mathrm{x}}_2+{\mathrm{x}}_3}{3},0)$ Since sum of ordinates is zero. Therefore centroid lies on the axis of parabola.

• Normal drawn from a point $\mathrm{P}(\mathrm{h},\mathrm{k})$ to the parabola are real and distinct if $\mathrm{h}>2\mathrm{a}$.

$\begin{array}{rl}& {\mathrm{m}}_1^2+{\mathrm{m}}_2^2+{\mathrm{m}}_3^2>0\\ \Rightarrow & {({\mathrm{m}}_1+{\mathrm{m}}_2+{\mathrm{m}}_3)}^2-2({\mathrm{m}}_1{\mathrm{m}}_2+{\mathrm{m}}_2{\mathrm{m}}_3+{\mathrm{m}}_1{\mathrm{m}}_3)>0\\ \Rightarrow & 0-\frac{2(2\mathrm{a}-\mathrm{h})}{\mathrm{a}}>0\\ \Rightarrow & 2\mathrm{a}-\mathrm{h}<0\\ \Rightarrow & \mathrm{h}>2\mathrm{a}\end{array}$

This shows that position of point

$(h,k)$ should be in shaded region.

• Equation of a circle passing through the conormal points

Let $\mathrm{M}({\mathrm{am}}_1{}^2,-2{\mathrm{am}}_1),\mathrm{N}({\mathrm{am}}_2{}^2,-2{\mathrm{am}}_2)$ and $\mathrm{Q}({\mathrm{am}}_3{}^2,-2{\mathrm{am}}_3)$ be three points on the parabola ${\mathrm{y}}^2=4ax.$

These three normals passes through point $\mathrm{p}(\mathrm{h},\mathrm{k})$

$\therefore {\mathrm{am}}^3+(2\mathrm{a}-\mathrm{h})\mathrm{m}+\mathrm{k}=0\dots \dots (1)$

$\begin{array}{rl}\Rightarrow & m_1+m_2+m_3=0\\ & m_1{m}_2+m_2{m}_3+m_1{m}_3=\frac{2a-h}{a}\\ & m_1{m}_2{m}_3=-\frac{k}{a}\end{array}$

Let equation of circle be $x^2+y^2+2gx+2fy+c=0$

If the point $({\mathrm{am}}^2,-2\mathrm{am})$ lies on the circle then

${\left({\mathrm{am}}^2\right)}^2+(-2\mathrm{am}{)}^2+2\mathrm{g}\left({\mathrm{am}}^2\right)+2\mathrm{f}(-2\mathrm{am})+\mathrm{c}=0$

${\mathrm{a}}^2{\mathrm{m}}^4+4{\mathrm{a}}^2{\mathrm{m}}^2+2{\mathrm{gam}}^2-4\mathrm{afm}+\mathrm{c}=0$

$a^2{m}^4+(4a^2{m}^2+2ga)m^2-4afm+c=0\dots \dots \dots (2)$

This equation has four roots say ${\mathrm{m}}_1,{\mathrm{m}}_2,{\mathrm{m}}_3,{\mathrm{m}}_4$ such

that the circle passes through the points $M(a{m}_1^2,-2{\mathrm{am}}_1)$

$\mathrm{N}({\mathrm{am}}_2{}^2,-2{\mathrm{am}}_2),\mathrm{Q}({\mathrm{am}}_3{}^2,-2{\mathrm{am}}_3)$ and $\mathrm{S}({\mathrm{am}}_4{}^2,-2{\mathrm{am}}_4)$

$\begin{array}{rll}\therefore {\mathrm{m}}_1+{\mathrm{m}}_2+{\mathrm{m}}_3+{\mathrm{m}}_4& =0& \text{ (From equation (2)) }\\ 0+{\mathrm{m}}_4& =0& \text{ (Since }{\mathrm{m}}_1+{\mathrm{m}}_2+{\mathrm{m}}_3=0)\\ \therefore {\mathrm{m}}_4& =0\end{array}$

Therefore circle passes through origin.

$\therefore \mathrm{c}=0$

Now equation (2) is

$\begin{array}{rl}& a^2{m}^4+(4a^2+2ga)m^2-4afm=0(÷am)\\ & a{m}^3+(4a+2g)m-4f=0\end{array}$

Now this equation is identical with equation (1)

$\begin{array}{rl}& \frac{a}{a}=\frac{2a-h}{4a+2g}=\frac{k}{-4f}\\ & \Rightarrow 2g=-(2a+h),2f=-\frac{k}{2}\end{array}$

Equation of circle is

$x^2+y^2-(2a+h)x-\frac{k}{2}y=0$