PARABOLA-6
Equation of Normal
(i) Point form :
$\mathrm{y}^{2}=4 \mathrm{ax}$
Differentiate w.r.t.x
$ \begin{aligned} & 2 y \frac{d y}{d x}=4 a \\ & \frac{d y}{d x}=\frac{2 a}{y} \end{aligned} $
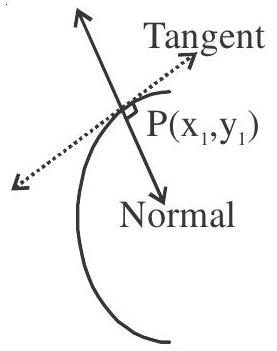
Slope of normal $=-\frac{\mathrm{y} _{1}}{2 \mathrm{a}}$
Equation of normas at $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ is
$ y-y _{1}=-\frac{y _{1}}{2 a}\left(x-x _{1}\right) $
(ii) Parametric form :
$\mathrm{P}\left(\mathrm{at}^{2}, 2 \mathrm{at}\right)$
replace $x _{1}$ by $\mathrm{at}^{2}$ and $\mathrm{y} _{1}$ by 2 at
$ \begin{aligned} & y-2 a t=-\frac{2 a t}{2 a}\left(x-a t^{2}\right) \\ & y=-t x+a t^{3}+2 a t \\ & t x+y-a t^{3}-2 a t=0 \end{aligned} $
(iii) Slope form:
$ \begin{aligned} & \text { Replace } t \text { by }-m \\ & y=m x-2 a m-a^{3} \end{aligned} $
$y=m x+c$ is normal to parabola $y^{2}=4 a x$ if
$\mathrm{c}=-2 \mathrm{am}-\mathrm{am}^{3}$ ie., condition of normal.
Equation of Normal
| Parabola | Point form | Pt.of contact | Parametric form | Point of contact | slope Form | Pt.of contact |
|---|---|---|---|---|---|---|
| $y^2=4 a x$ | $y-y_1=\frac{-y_1}{2 a}\left(x-x_1\right)$ | $\left(x_1, y_1\right)$ | $y=-t x+2 a t+a t^3$ | $\left(a t^2, 2 a t\right)$ | $y=m x-2 a m-a m^3$ | $\left(a m^2,-2 a m\right)$ |
| $y^2=-4 a x$ | $y-y_1=\frac{y_1}{2 a}\left(x-x_1\right)$ | $\left(x_1, y_1\right)$ | $y=-t x+2 a t+a t^3$ | $\left(-a t^2, 2 a t\right)$ | $y=m x+2 a m+a m^3$ | $\left(-a m^2, 2 a m\right)$ |
| $x^2=4 a y$ | $x-x_1=-\frac{x_1}{2 a}\left(y-y_1\right)$ | $\left(x_1, y_1\right)$ | $x=-t y+2 a t+a t^3$ | $\left(2 a t, a t^2\right)$ | $y=m x+2 a+\frac{a}{m^2}$ | $\left(-\frac{2 a}{m}, \frac{a}{m^2}\right)$ |
| $x^2=-4 a y$ | $x-x_1=\frac{x_1}{2 a}\left(y-y_1\right)$ | $\left(x_1, y_1\right)$ | $x=t y+2 a t+a t^3$ | $\left(2 a t,-a t^2\right)$ | $y=m x-2 a-\frac{a}{m^2}$ | $\left(\frac{2 a}{m},-\frac{a}{m^2}\right)$ |
Equation of normal to the parabola $(\mathrm{y}-\mathrm{k})^{2}=4(\mathrm{x}-\mathrm{h})$ is
$ y-k=m(x-h)-2 a m-a m^{3} $
Properties of Normal
1. If the normal at the point $\mathrm{P}\left(\mathrm{at} _{1}{ } _{1}^{2}, 2 \mathrm{at} _{1}\right)$ meets the parabola at
$\mathrm{Q}\left(\mathrm{at} _{2}{ }^{2}, 2 \mathrm{at} _{2}\right)$, then $\mathrm{t} _{2}=-\mathrm{t} _{1}-\frac{2}{\mathrm{t} _{1}}$
Let equation of parabola be $\mathrm{y}^{2}=4 \mathrm{ax}$.
Equation of normal at $\mathrm{P}$ is
$ \mathrm{y}=-\mathrm{t} _{1} \mathrm{x}+2 \mathrm{at} _{1}+\mathrm{at} _{1}^{3} $
Point $\mathrm{Q}$ lies on the normal, so
$ \begin{aligned} & 2 \mathrm{at} _{2}=-\mathrm{at} _{1} \mathrm{t} _{2}{ }^{2}+2 \mathrm{at} _{1}+\mathrm{at} _{1}{ }^{3} \\ & 2 \mathrm{a}\left(\mathrm{t} _{2}-\mathrm{t} _{1}\right)=-\mathrm{at} _{1}\left(\mathrm{t} _{2}{ }^{2}-\mathrm{t} _{1}^{2}\right) \\ & 2=-\mathrm{t} _{1}\left(\mathrm{t} _{2}+\mathrm{t} _{1}\right) \\ & \therefore \mathrm{t} _{2}=-\mathrm{t} _{1}-\frac{2}{\mathrm{t} _{1}} \end{aligned} $
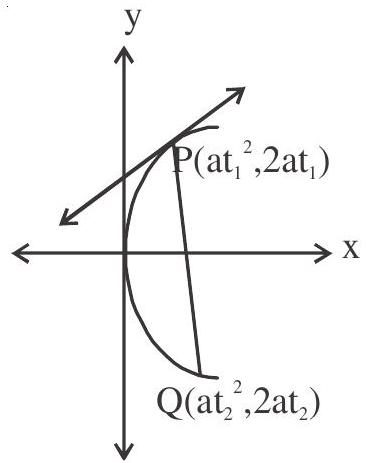
2. If the normal at the points $\left(a t _{1}{ }^{2}, 2 \mathrm{at} _{1}\right)$ and $\left(\mathrm{at} _{2}{ }^{2}, 2 \mathrm{at} _{2}\right)$ meet on the parabola $\mathrm{y}^{2}=4 \mathrm{ax}$, then $\mathrm{t} _{1} \mathrm{t} _{2}=2$.
Let the equation of normal at $\left(\mathrm{at} _{1}{ }^{2}, 2 \mathrm{at} _{1}\right)$ and $\left(\mathrm{at} _{2}{ } _{2}^{2}, 2 \mathrm{at} _{2}\right)$ be
$ \mathrm{y}=-\mathrm{t} _{1} \mathrm{x}+2 \mathrm{at} _{1}+\mathrm{at} _{1}^{3} $
and $y=-\mathrm{t} _{2} \mathrm{x}+2 \mathrm{at} _{2}+\mathrm{at} _{2}{ }^{3}$
meet the parabola $\mathrm{y}^{2}=4 \mathrm{ax}$ at $\left(\mathrm{at} _{3}{ }^{2}, 2 \mathrm{at} _{3}\right)$ then
$ \begin{aligned} & \mathrm{t} _{3}=-\mathrm{t} _{1}-\frac{2}{\mathrm{t} _{1}} \text { and } \mathrm{t} _{3}=-\mathrm{t} _{2}-\frac{2}{\mathrm{t} _{2}} \\ & \therefore-\mathrm{t} _{1}-\frac{2}{\mathrm{t} _{1}}=-\mathrm{t} _{2}-\frac{2}{\mathrm{t} _{2}} \\ & \mathrm{t} _{2}-\mathrm{t} _{1}=2\left(\frac{1}{t _{1}} \frac{1}{t _{2}}\right) \Rightarrow t _{2}-t _{1}=2\left(\frac{t _{2}-t _{1}}{t _{1} t _{2}}\right) \\ & \Rightarrow \mathrm{t} _{1} \mathrm{t} _{2}=2 \end{aligned} $
3. No normal other than axis passes through focus.
Let equation of normal be $y=m x-2 a m-a m^{3}$
passes through $(a, 0)$ ie. focus
$ \begin{aligned} \therefore \quad & 0=m a-2 a m-a^{3} \\ & 0=-a m-a^{3} \\ & 0=-a m\left(\left(1+m^{2}\right) \Rightarrow m=0\right. \text { i.e. axis } \\ & 1+\mathrm{m}^{2}=0 \text { which is not possible. } \end{aligned} $
Example: 1 Three normals to $\mathrm{y}^{2}=4 \mathrm{x}$ pass through the point $(15,12)$. One of the normals is
(a) $x+y=27$
(b) $x+4 y=63$
(c) $3 x-y=33$
(d) $y+3 x=51$
Show Answer
Solution:
Let equation of normal be $y=m x-2 a m-a m^{3}$. $a=1$
$ \therefore \mathrm{y}=\mathrm{mx}-2 \mathrm{~m}-\mathrm{m}^{3} $
passes through $(15,12)$
$ 12=15 \mathrm{~m}-2 \mathrm{~m}-\mathrm{m}^{3} $
$ \begin{gathered} \mathrm{m}^{3}-13 \mathrm{~m}+12=0 \\ (\mathrm{~m}-1)(\mathrm{m}-3)(\mathrm{m}+4)=0 \\ \mathrm{~m}=1,3,-4 \\ \mathrm{~m}=1 \Rightarrow \mathrm{y}=\mathrm{x}-3 \\ \mathrm{~m}=3 \Rightarrow \mathrm{y}=3 \mathrm{x}-33 \\ \mathrm{~m}=-4 \Rightarrow \mathrm{y}+4 \mathrm{x}=72 \end{gathered} $
Answer: (c)
Example: 2 The minimum distance between the curves $x^{2}+y^{2}-12 x+31=0$ and $y^{2}=4 x$ is
(a) $\sqrt{5}$
(b) $2 \sqrt{5}$
(c) $6-\sqrt{5}$
(d) None of these.
Show Answer
Solution:
Centre $(6,0)$ radius $=\sqrt{36+0-31}=\sqrt{5}$
Minimum distance obtained along the common normal.
$ y^{2}=4 x $
Differentiate w.r.t.x
$2 \mathrm{y} \frac{\mathrm{dy}}{\mathrm{dx}}=4$
$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{2}{\mathrm{y}}$
slope of normal at $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ is $-\frac{\mathrm{y} _{1}}{2}$
Also slope of CQ $\quad=\frac{y _{1}-0}{x _{1}-6}=-\frac{y _{1}}{2}$
Points are $(0,0),(4,4),(4,-4)$
$ \Rightarrow y _{1}=0 \text { or } x _{1}=4 $
$\mathrm{OC}=6$
$\mathrm{QC}=2 \sqrt{5}$
$\mathrm{RC}=2 \sqrt{5}$
Minimum distance $\left\{\begin{array}{l}\mathrm{OC}-\mathrm{R}=6-\sqrt{5} \\ \mathrm{QC}-\mathrm{R}=2 \sqrt{5}-\sqrt{5}=\sqrt{5} \\ \mathrm{RC}-\mathrm{R}=2 \sqrt{5}-\sqrt{5}=\sqrt{5}\end{array}\right\}$ is $\sqrt{5}$
Answer: (a)
Important Properties :
- If the tangent and normal at any point ’ $\mathrm{P}$ ’ of the parabola intersect the axis at $\mathrm{T}$ and $\mathrm{N}$ then $\mathrm{ST}$ $=\mathrm{SN}=\mathrm{SP}$ where $\mathrm{S}$ in the focus.
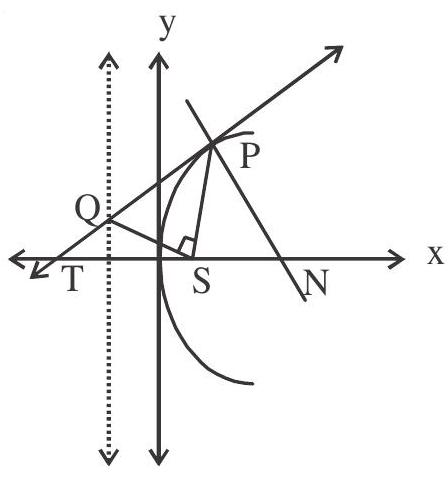
- The portion of a tangent to a parabola cut off between the directrix & the curve subtends a right angle at the focus.
$ \angle \mathrm{PSQ}=90^{\circ} $
- Any tangent to a parabola and the perpendicular on it from the focus meet on the tangent at the vertex.
$\angle \mathrm{PQS}=90^{\circ}$
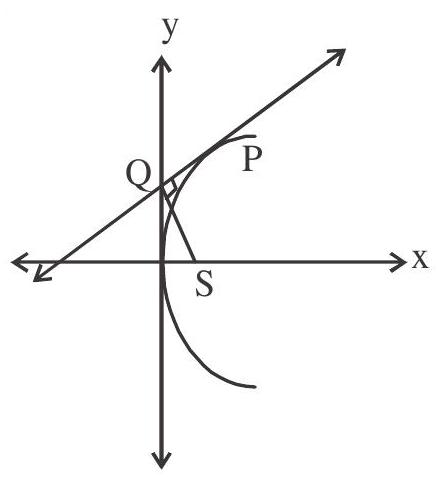
- If the tangents at $\mathrm{A}$ and $\mathrm{B}$ meet in $\mathrm{P}$ then $\mathrm{PA}$ and $\mathrm{PB}$ subtends equal angles at the focus $\mathrm{S}$. $(\mathrm{SP})^{2}=\mathrm{SA} \times \mathrm{SB}$
$\triangle \mathrm{SAP} \sim \triangle \mathrm{SPB}$
$\angle \mathrm{PSA}=\angle \mathrm{PSB}$.
- The area of the triangle formed by three points on a parabola is twice the area of the triangle formed by the tangents at these points.
Practice questions
1. The normal at the point $(2,4)$ of the parabola $y^{2}=8 x$ meets the parabola at the point
(a). $(18,-12)$
(b). $(12,-18)$
(c). $(12,18)$
(d). $(18,12)$
Show Answer
Answer: (a)2. If $y+b=m _{1}(x+a)$ and $y+b=m _{2}(x+a)$ are two tangents to the parabola $y^{2}=4 a x$, then
(a). $\mathrm{m} _{1} \mathrm{~m} _{2}=1$
(b). $\mathrm{m} _{1} \mathrm{~m} _{2}=-1$
(c). $\mathrm{m} _{1}+\mathrm{m} _{2}=0$
(d). $\mathrm{m} _{1}-\mathrm{m} _{2}=0$
Show Answer
Answer: (b)3. If normals at the ends of the double ordinate $x=4$ of parabola $y^{2}=4 x$ meet the curve again in $\mathrm{P}$ and $\mathrm{P}^{\prime}$ respectively, then $\mathrm{P}=$
(a). 10
(b). 6
(c). 12
(d). 18
Show Answer
Answer: (c)4. Radius of the largest circle which passes through the focus of the parabola $y^{2}=4 x$ and contained in it, is
(a). 2
(b). 4
(c). 6
(d). 8
Show Answer
Answer: (b)5. If the normal at $(1,2)$ on the parabola $y^{2}=4 x$ meets the parabola again at the point $\left(t^{2}, 2 t\right)$, then $t$ is
(a). $3$
(b). $1$
(c). $2$
(d). $-3$
Show Answer
Answer: (d)6. If $x=m y+c$ is a normal to the parabola $\frac{x^{2}-\mathrm{a}}{4}+\frac{\mathrm{a}}{\mathrm{a} m \text { Then }} \mathrm{c}=$
(a). $2 a m+a^{3}$
(b).
(c). $-2 \mathrm{am}-\mathrm{am}^{3}$
(d). $-\frac{2 \mathrm{a}}{\mathrm{m}}-\frac{\mathrm{a}}{\mathrm{m}^{3}}$
