Line and Parabola:

Let equation of line be $y=mx+c$ and equation of parabola be $y^2=4ax$.

$(\mathrm{mx}+\mathrm{c}{)}^2=4\mathrm{ax}$

${\mathrm{m}}^2{\mathrm{x}}^2+2\mathrm{x}(\mathrm{mc}-2\mathrm{a})+{\mathrm{c}}^2=0$

$\mathrm{D}=\{2(\mathrm{mc}-2\mathrm{a}){\}}^2-4\cdot {\mathrm{m}}^2\cdot {\mathrm{c}}^2$

$=4(4{\mathrm{a}}^2-4\mathrm{amc})$

If $\mathrm{D}<0$, line do not intersect parabol(a).

i.e. $\mathrm{a}<\mathrm{mc}$

If $\mathrm{D}=0$ i.e. $\mathrm{a}=\mathrm{mc}$, line touches the parabola (condition of tangency)

If $\mathrm{D}>0$ i.e. $\mathrm{a}>\mathrm{mc}$, line intersect the parabola at two points.

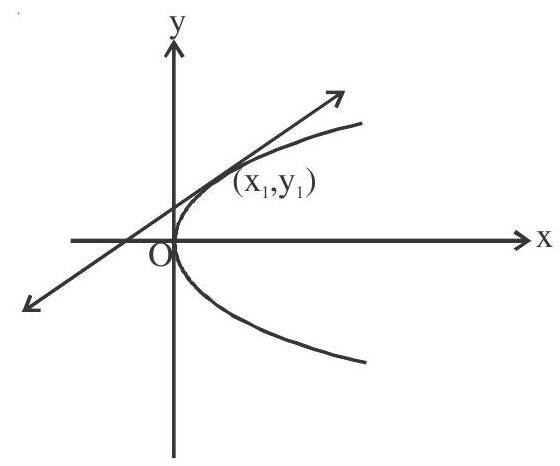
Equation of tangent (Point form)

Equation of parabola ${\mathrm{y}}^2=4\mathrm{ax}$

Differentiate w.r.t.x

$2y\frac{dy}{dx}=4a$

slope of tangent $=\frac{2\mathrm{a}}{{\mathrm{y}}_1}$

Equation of tangent $y-y_1=\frac{2a}{y_1}(x-x_1)$

$\begin{array}{rl}& {\mathrm{y}}_1-{\mathrm{y}}_1^2=2\mathrm{ax}-2{\mathrm{ax}}_1\\ & {\mathrm{y}}_1=2\mathrm{ax}+2{\mathrm{ax}}_1\\ & {\mathrm{y}}_1=2\mathrm{a}(\mathrm{x}+{\mathrm{x}}_1)\end{array}$

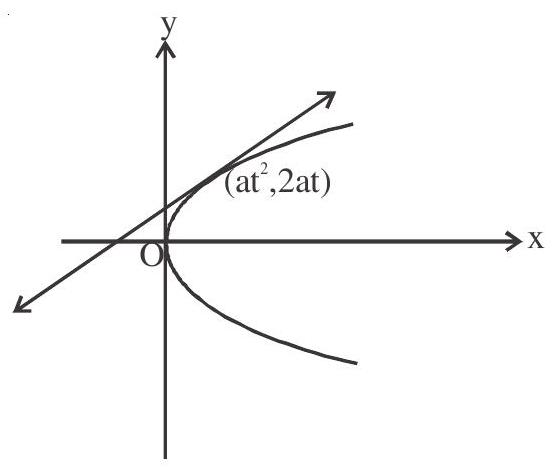
Equation of tangent (Paramatric form)

$\begin{array}{rl}& y\cdot 2at=2a(x+a{t}^2)\\ & ty=x+a{t}^2\end{array}$

Equation of tangent (slope form)

$\mathrm{y}=\mathrm{mx}+\frac{\mathrm{a}}{\mathrm{m}}$

Point of contact $\frac{\mathrm{a}}{{\mathrm{m}}^2},\frac{2\mathrm{a}}{\mathrm{m}}$

• Equation of tangent to the parabola $(\mathrm{y}-\mathrm{k}{)}^2=4\mathrm{a}(\mathrm{x}-\mathrm{h})$ is

$\mathrm{y}-\mathrm{k}=\mathrm{m}(\mathrm{x}-\mathrm{h})+\frac{\mathrm{a}}{\mathrm{m}}$

Equation of tangent:

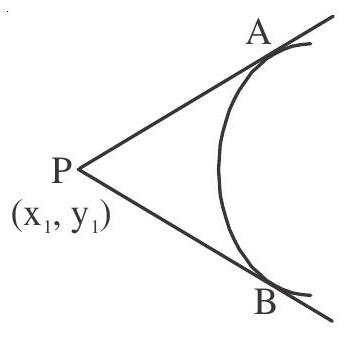
Pair of Tangents from point $(x_1,y_1)$

Let eq of parabola be $y^2=4ax$

$S\equiv {\mathrm{y}}^2-4\mathrm{ax}$

$S_1\equiv y_1^2-4{\mathrm{ax}}_1$

$\mathrm{T}\equiv {\mathrm{yy}}_1-2\mathrm{a}(\mathrm{x}+{\mathrm{x}}_1)$

Equation of pair of tangents is ${\mathrm{SS}}_1={\mathrm{T}}^2$ i.e.

$(y^2-4ax)(y_1^2-4a_1)={\{y_1-2a(x+x_1)\}}^2$

Properties of Tangents:

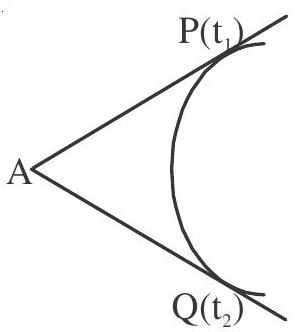
1. Point of intersection of two tangents of the parabola:-

Equation of tangent at $\mathrm{P}$ is ${\mathrm{t}}_1\mathrm{y}=\mathrm{x}+{\mathrm{at}}_1^2$

Equation of tangent at $\mathrm{Q}$ is ${\mathrm{t}}_2\mathrm{y}=\mathrm{x}+{\mathrm{at}}_2^2$

Solving these equations, we get

$\mathrm{x}={\mathrm{at}}_1{\mathrm{t}}_2,\mathrm{y}={\mathrm{at}}_1+{\mathrm{at}}_2$

$\mathrm{A}({\mathrm{at}}_1{\mathrm{t}}_2,\mathrm{a}({\mathrm{t}}_1+{\mathrm{t}}_2))$

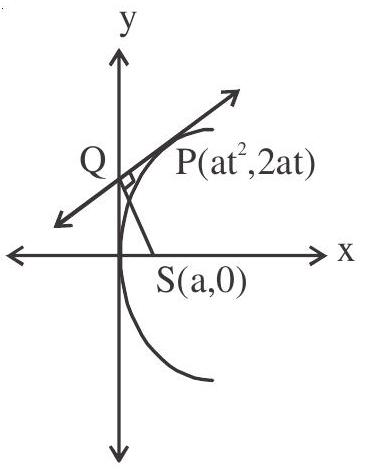
2. Locus of foot of prependicular from focus upon any tangent is tangent at vertex:-

Equation of tangent at $\mathrm{P}$ is ty $=\mathrm{x}+{\mathrm{at}}^2$

Let the tangent meet $\mathrm{y}$-axis at $\mathrm{Q}$ then $\mathrm{Q}(0$, at

$\begin{array}{rl}\therefore & \text{ slope of }QS=\frac{-at}{a}=-t\\ & \text{ slope of tangent }=\frac{1}{t}\\ & \frac{1}{t}\times (-t)=-1SQ\perp \text{ tangent }\end{array}$

3. Length of tangent between the pt. of contact and the point where tangent meets the directrix subtends right angle at focus:-

Eqation of tangent at $P(t)$

$ty=x+a{t}^2$

Point of intersection with directrix $x=-a$ is

$-\mathrm{a},\mathrm{at}-\frac{\mathrm{a}}{\mathrm{t}}$

slope $\mathrm{SP}=\frac{2\mathrm{at}}{{\mathrm{at}}^2-\mathrm{a}}=\frac{2\mathrm{t}}{{\mathrm{t}}^2-1}$

$\begin{array}{rl}\text{ slope }QS=& \frac{at-\frac{a}{t}}{-2a}=\frac{t^2-1}{-2t}\\ & m_1{m}_2=-1\\ & PS\perp QS\end{array}$

4. Tangent at extremities of focal chord are perpendicular and intersect on directrix

(Locus of intersection point of tangents at extremities of focal chord is directrix)

Let $\mathrm{P}(\mathrm{at}{\mathrm{t}}^2$, 2at) and $\mathrm{Q}\frac{\mathrm{a}}{{\mathrm{t}}^2},\frac{-2\mathrm{a}}{\mathrm{t}}$

Equation of tangent at $Pty=x+a{t}^2\dots \dots ..(1)$

Equation of tangent at $Q-\frac{1}{t}y=x+\frac{a}{t^2}$

$y=-tx-\frac{a}{t}\dots \dots .(2)$

Point of intersection of both tangents, we get after sloving (1) & (2) i.e.

$x+a=0$

A point lies on the directrix.

Practice questions

1. If the tangents to the parabola $y^2=4ax$ at the points $(x_1,y_1)$ and $(x_2,y_2)$ meet at the point $(x_3,y_3)$ then

(a). ${\mathrm{y}}_3^2=\sqrt{{\mathrm{y}}_1{\mathrm{y}}_2}$

(b). $2{\mathrm{y}}_3={\mathrm{y}}_1+{\mathrm{y}}_2$

(c).

(d). none of these

2. A right angled triangle $\mathrm{ABC}$ is inscribed in parabola ${\mathrm{y}}^2=4\mathrm{x}$, where $\mathrm{A}$ is vertex of parabola and $\mathrm{\angle }\mathrm{BAC}={90}^{\circ }$. If $\mathrm{AB}=$, then area of $\mathrm{△}\mathrm{ABC}$ is

(a). 40

(b). 10

(c). 20

(d). $4\sqrt{5}$

3. The locus of the point $(\sqrt{3h},\sqrt{3k+2})$ if it lies on the line $x-y-1=0$ is a

(a). circle

(b). parabola

(c). straight line

(d). none of these

4. The length of the chord of the parabola $y^2=x$ which is bisected at the point $(2,1)$ is

(a). 5

(b). 4

(c). $2\sqrt{5}$

(d). $5\sqrt{2}$

5. If $y=mx+c$ touches the parabola $y^2=4a(x+a)$, then

(a). $\mathrm{c}=\frac{\mathrm{a}}{\mathrm{m}}$

(b). $\mathrm{c}=\mathrm{a}+\frac{\mathrm{a}}{\mathrm{m}}$

(c). $\mathrm{c}=\frac{2\mathrm{a}}{\mathrm{m}}$

(d). $\mathrm{c}=\mathrm{am}+\frac{\mathrm{a}}{\mathrm{m}}$

$\frac{\sqrt{25}}{{\mathrm{y}}_3}=\frac{1}{{\mathrm{y}}_1}+\frac{1}{{\mathrm{y}}_2}$