PARABOLA-2 (Parabola)
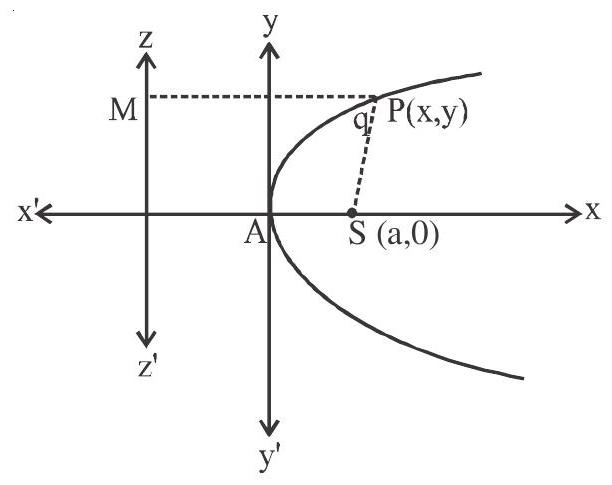
A parabola is the locus of a point, whose distance from a fixed point is equal to the perpendicular distance from a fixed straight line.
Let $\mathrm{S}$ be the focus, $\mathrm{ZZ}^{\prime}$ be the directrix.
Consider $\mathrm{S}(\mathrm{a}, 0)$ and equation of $\mathrm{ZZ}^{\prime}$ is $\mathrm{x}+\mathrm{a}=0$.
Axis of parabola is $\mathrm{x}$-axis.
Now according to definition.
$\mathrm{PS}=\mathrm{PM}$
$ \begin{aligned} & \sqrt{(x-a)^{2}+y^{2}}=\left|\frac{x+a}{\sqrt{1}}\right| \\ & (x-a)^{2}+y^{2}=(x+a)^{2} \\ & y^{2}=4 a x \end{aligned} $
Vertex $(0,0)$
Tangent of latus rectum $\mathrm{x}=0$
Extremities of latus rectum (a, 2a), (a, $-2 \mathrm{a})$
Length of latus rectum. $=4 \mathrm{a}$
Focal distance (SP) $\quad \mathrm{SP}=\mathrm{PM}=\mathrm{x}+\mathrm{a}$
Parametric form $x=a t^{2}, y=2 a t, t$ is parameter.
Focal distance - the distance of a point on the parabola from the focus.
Focal chord - A chord of the parabola, which passes through the focus.
Double ordinate - A chord of the parabola perpendicular to the axis of the parabol(a).
Latus Rectum-A double ordinate passing through the focus or a focal chord perpendicular to the axis of parabol(a).
- Perpendicular distance from focus on directrix = half the latus rectum.
- Vertex is middle point of the focus and the point of intersection of directrix and axis.
- Two parabolas are said to be equal if they have the same latus rectum.
Other Standard Forms of Parabola:
| Equation of curve: | $y^{2}=-4 a x$ | $\mathrm{x}^{2}=4 \mathrm{ay}$ | $\mathrm{x}^{2}=-4 \mathrm{ay}$ |
|---|---|---|---|
| Vertex | $(0,0)$ | $(0,0)$ | $(0,0)$ |
| Focus | $(-a, 0)$ | $(0, a)$ | $(0,-a)$ |
| Directrix | $x-a=0$ | $y+a=0$ | $y-a=0$ |
| Equation of axis | $y=0$ | $x=0$ | $x=0$ |
| Tangent of vertex | $x=0$ | $y=0$ | $y=0$ |
| Parametric form | $\left(-a t^{2}, 2 a t\right)$ | $\left(2 a t, a t^{2}\right)$ | $\left(2 a t,-a t^{2}\right)$ |
Position of a point with respet to Parabola
Equation of Parabola when vertex is shifte(d).
I. Axis is Parallel to $\mathrm{x}$-axis:
Let vertex $A$ be $(p, q)$ then equation of parabola be $(y-q)^{2}=4 a(x-p)$.
II. Axis is parallel to y-axis:
Let vertex $A$ be $(p, q)$ then equation of parabola is $(x-p)^{2}=4 a(y-q)$
Example: 1 The equation of parabola is $y=a x^{2}+b x+c$, find its vertex, focus, directrix,
Show Answer
Solution:
Equation of a is, length of latus rectum.
$ \begin{aligned} & y=a \quad x^{2}+\frac{b}{a} x+\frac{b^{2}}{4 a^{2}}-\frac{b^{2}}{4 a^{2}}+c \\ & y-c=a \quad x+\frac{b}{2 a}^{2}-\frac{b^{2}}{4 a^{2}} \end{aligned} $
$ x+\frac{b}{2 a}^{2}=\frac{1}{a} y+\frac{b^{2}}{4 a}-c $
$X^{2}=4 A Y$ where $X=x+\frac{b}{2 a}, Y=y+\frac{b^{2}-4 a c}{4 a}, 4 A=\frac{1}{a}$
Vertex : $X=0, Y=0$ i.e. $-\frac{b}{2 a},-\frac{b^{2}-4 a c}{4 a}$
Focus: $\mathrm{X}=0, \mathrm{Y}=$ A i.e. $\quad-\frac{\mathrm{b}}{2 \mathrm{a}}, \frac{1+4 \mathrm{ac}-\mathrm{b}^{2}}{4 \mathrm{a}}$
Equation of directrix: $y+\frac{b^{2}-4 a c+1}{4 a}=0$
Equation of axis: $x+\frac{b}{2 a}=0$
Length of latus rectum $=\frac{1}{\mathrm{a}}$
Example: 2 The equation of parabola is $\mathrm{y}^{2}=\mathrm{ax}+\mathrm{ay}$. Find its vertex, focus, directrix, axis and length of latus rectum.
Show Answer
Solution:
$y^{2}-a y=a x$
$y^{2}-a y+\frac{a^{2}}{4}=a x+\frac{a^{2}}{4}$
$y-\frac{a}{2}^{2}=a x+\frac{a}{4}$
$\mathrm{Y}^{2}=4 \mathrm{AX}$
Where: $Y=y-\frac{a}{2}, X=x+\frac{a}{4}, 4 A=a$ ie. $A=\frac{a}{4}$
Vertex $-\frac{\mathrm{a}}{4}, \frac{\mathrm{a}}{2}$
Focus $0, \frac{\mathrm{a}}{2}$
Directrix $x+\frac{a}{2}=0$
Axis $y-\frac{a}{2}=0$
Length of latus rectum $=\mathrm{a}$
Practice questions
1. The equation of parabola whose focus is at $(-1,-2)$ and directrix is $x-2 y+3=0$ is
(a). $4 x^{2}-y^{2}-4 x y+4 x-32 y-16=0$
(b). $x^{2}+4 y^{2}+4 x y+x+6 y+16=0$
(c). $4 x^{2}+y^{2}+4 x y+4 x+32 y+16=0$
(d). $4 x^{2}+y^{2}-4 x y+4 x-32 y-1=0$
Show Answer
Answer: (c)2. The equation of parabola whose vertex is at $(4,-1)$ and focus is $(4,-3)$ is
(a). $y^{2}-8 x+8 y+24=0$
(b). $x^{2}-8 x+8 y+24=0$
(c). $y^{2}-8 x-8 y+24=0$
(d). $x^{2}+8 x-8 y-24=0$
Show Answer
Answer: (b)3. The focal distance of a point on the parabola $y^{2}=8 x$ is 8 , then coordinates of the point (s) is/are
(a). $(4 \sqrt{3}, 6)$
(b). $(6,4 \sqrt{3})$
(c). $(4 \sqrt{3},-6)$
(d). $(6,-4 \sqrt{3})$
Show Answer
Answer: (b, d)4. The equation of the parabola whose focus is $(0,0)$ and tangent at the vertex is $x-y+1=0$ is
(a). $x^{2}+y^{2}+2 x y-4 x+4 y-4=0$
(b). $x^{2}+y^{2}+4 x y+4 x+4 y+4=0$
(c). $x^{2}+y^{2}-4 x y+4 x+4 y-4=0$
(d). $x^{2}+y^{2}-4 x y-4 x-4 y-4=0$
